Prerpints.org logo
Preprint
Article

Coating of Refractory Surfaces with Fine TiO2 Particles via Gas‐Dynamic Cold Spraying

Altmetrics

Downloads

85

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 July 2024

Posted:

30 July 2024

You are already at the latest version

Alerts
Abstract
Refractory materials are used worldwide in process equipment. However, gaseous and liquid process products penetrate the surface layer, and deep into the volume of refractories destructing rather expensive constructions complicated to repair. To address this challenge, there is a need to develop protective coatings for refractory that can limit the penetration of working media and extend their operational lifespan. In this work, the application of gas-dynamic cold spraying (CGDS) to produce a coating on the refractory using fine titanium dioxide (TiO2) particles is explored. These particles are accelerated within a nitrogen flow, passing through a Laval nozzle, and then sprayed onto a fireclay surface. The mechanisms of particle deposition and layer formation on porous surfaces through experiments and numerical simulations were investigated. The geometry of a typical refractory pore was determined, which was then incorporated into Computational Fluid Dynamics (CFD) simulations to model the cold spraying process of porous substrates. As a result, the influence of the particle size on its velocity and angle of penetration into pores was established. Experimental findings demonstrate the effective closure of pores and the formation of a particle layer on the refractory surface. Furthermore, the nanoindentation tests for the refractory samples showcase capabilities for checking coating thickness for porous materials.
Keywords: 
Subject: Engineering  -   Chemical Engineering

1. Introduction

In existing industrial thermal setups, such as coke ovens, blast furnaces, heat boilers, kilns, and others, severe operating conditions prevail [1]. The main elements of these setups are heating partitions, refractory insulation, and lining, designed to transfer heat from the heating elements to the raw materials being processed and protect other structural elements from the adverse effects of high temperatures and aggressive mediums.
In these setups, thermally insulating elements are typically made from fireclay refractories, predominantly composed of SiO2 (47-64%) and Al2O3 (28-45%), and other small inclusions of Fe2O2, TiO2, CaO, MgO, K2O [2].
The technical state of setup elements undergoes significant changes during the production process, leading to a notable reduction in their lifecycle [3,4]. The refractory elements experience the most pronounced degradation and breakdown due to various external factors [5,6,7,8], including:
  • mechanical loads imposed by structural elements;
  • exposure to diverse working environments, such as coke oven gas, combustion products of the gas mixture, raw materials, and ash with low melting temperatures and formation of different corrosion products, such as kaliophilite (K2O-Al2O3-2SiO2), leucite (K(AlSi2O6), and other compounds with volume exceeding the initial volume of refractory;
  • significant temperature fluctuations, ranging from 50 to 500°C, affecting refractory materials, particularly in coke ovens.
The simultaneous operation of these factors compounds the detrimental effects. Consequently, in the most crucial regions of the working surfaces, the lifespan of refractories is substantially shorter compared to other components of the thermal setup, often by a factor of 5-10. For instance, in coke ovens, their lifespan may only extend to 2-3 months after that necessitating costly repairs to restore functionality [9].
Moreover, as thermal setups operate, the properties of refractory elements change due to the infiltration of gaseous and liquid byproducts formed during the processing of raw materials. These byproducts penetrate the surface layer through pores and pass deep into the refractory volume. Preventing such penetration and closing pores on the surface is essential for extending the operational lifespan of the refractory elements.
One effective approach to address this issue is the developing a protective layer on the surface of the refractory material, which reduces the penetration of the medium, and minimises direct contact with gases, liquids, and solid substances during the operation of the equipment.
In current industrial practice, many types of coatings are employed, including ceramic coatings from viscous solutions based on thermally stable inorganic oxides [10], ceramic coatings obtained by "glazing" the outer working surface [11], adhesive insulating coatings (high-temperature adhesives) [12], bilayer alumina/mullite and mullite/alumina coatings deposited by atmospheric plasma spraying [13], coatings obtained by crystallization of melts of high-temperature oxides [14], coatings obtained from colloidal systems [15]. Numerous technologies for applying such coatings on the surface of refractory products are reduced to applying a liquid layer on the surface, which then crystallizes [16]. In the study [17] composite coatings based on titanium oxides were successfully prepared through a detonation spray process of the particles on fine-grained hyper-pressed concrete.
Nevertheless, obtaining hardware support for the application of these coatings poses several challenges. Moreover, highly heat-resistant coatings often exhibit low mechanical strength and high fragility. Consequently, protective coatings obtained through the mentioned methods may not entirely address the challenges related to the durability and tightness of refractories, necessitating further research and development [18].
Targeted alteration of the surface structure by particulate layers is a current subject of intensive research [19,20,21] where, in particular, cold gas-dynamic spraying (CGDS) is an effective coating method [22,23]. Since its invention [22] the cold spray method has undergone continuous optimization for specific applications and is an economically competitive method widely used in the industry today for the modification of metal surfaces. The primary advantage of CGDS lies in its relatively low operating temperatures compared to other thermal spraying methods. This characteristic makes CGDS particularly suitable for mobile setups for repair work, where high temperatures may be impractical. Various studies have demonstrated that CGDS has the potential to enhance the corrosion resistance [23], frictional [24], and wear-resistant properties of metal surfaces [25,26]. Additionally, this method enables the restoration of components to their proper state by selectively applying a protective coating onto the damaged surfaces [27].
For Al surfaces, CGDS was successfully used by Yu et al. [28] in creating resistant coatings of SiCp/Al 5056 composite. Ma et al. [29] performed the coating of Al2O3 ceramic surface with copper particles using vacuum cold spraying and showed that cold spraying provides a self-adaptive repair mechanism when depositing metal films onto rough ceramic substrates.
In this work, CGDS was used for coating of refractory materials. Unlike metal surfaces, refractories have an open pore structure and behave dominantly brittle, which can result in completely different mechanisms of the coating formation (Figure 1).
During the cold spray coating process, fine solid particles are accelerated within a supersonic gas flow generated by a Laval nozzle and collide with the porous substrate. Upon impact, the particle kinetic energy is converted into deformation and heat of the particle and the substrate body. The characteristics of the coating are determined by the complex interplay of transport phenomena in the multiphase flow, including the acceleration of particles within the jet, as well as material deformation and adhesion during particle impact on the surface and on previously deposited particles.
TiO2 powder is readily available within the desired particle size range, significantly smaller than the pore size, and uncritical concerning safety aspects and costs. Furthermore, the thermal expansion coefficients of TiO2 and fireclay closely align in values [2,30].
The objective of this study is to achieve the deposition of TiO2 particles onto the porous surface of the refractory material and to analyze the properties of the resulting initial layer. This experimental investigation is supported by numerical simulations that examine the acceleration behavior of fine particles within a gas flow passing through the Laval nozzle and subsequently sprayed onto the porous surface of the refractory. The efficacy of pore filling on the surface is also thoroughly evaluated.

2. Materials and Methods

2.1. Analysis of Spraying Particle Properties

In this work, TiO2 particles (thermally stable rutile from Sigma-Aldrich) were employed for the coating of the refractory surface. The particle size distribution of TiO2 powders (Figure 2a) was determined using a light scattering method with a laser diffraction spectrometer (HORIBA LA-950V2, Retsch) in the range of 0.2... 1.2 µm with a mean diameter of 0.524 µm and median size of 0.49 µm. The particle size distribution was described by the Weibull function (also known as Rosin-Rammler function simulation used in CFD to generate particles in a Laval nozzle) given as:
Q 3 x p = 1 − exp ⁡ − x p x 0 n
where Q 3   x p is the cumulative volume related distribution function, n is the shape parameter, x 0 is the characteristic particle size, defined as the size at which 63.2% of the particles are smaller.
The fitting curve, displayed in the figure is characterized by the following equation function parameters: x 0 = 0.54 µm (indicated by a red marker in Figure 2a), n   = 3.78.
As depicted in the image (Figure 2b), captured using Scanning Electron Microscopy (SEM) (Hitachi SU8000, FEI Helios Nanolab 650), basically the TiO2 particles have an angular shape.
The thermophysical material properties, sourced from [30], are presented in Table 1.

2.2. Analysis of Properties and Structure of the Substrate

The substrate samples were sourced from raw refractory fireclay bricks brand SHV-42 produced at "Chasiv Yar Refractory Works” (Ukraine). The fireclay composition contents of SiO2 (54.8±0.5%), Al2O3 (42.0±0.5%), Fe2O3 (1.7±0.2%), TiO2 (0.5±0.1%), K2O (0.7±0.15%), Na2O (0.15±0.01%), CaO (0.16±0.02%).
The thermophysical properties of fireclay refractories, as provided in [2], are listed in Table 2.
SEM images of a fireclay surface in its initial state are depicted in Figure 3. The surface reveals cracks, craters, and medium pores (macropores) predominantly located between grains. Additionally, fine pores (micropores) are observed on the grains and along the walls of macropores. Some areas exhibit pore channels formed by groups of pores. Notably, a distinct group of pores comprises cracks formed during the firing process of manufacture.
The bulk density of the fireclay samples was determined gravimetrically. It amounted to 1872 kg/m3. Their true density of 2404 kg/m3 was measured with Quantachrome Ultrapyc 1000 Gas Pycnometer. The obtained values of true and bulk densities were used to estimate the porosity of samples, as described in [31]. The porosity was determined to be 0.22± 0.01.
For the experiments, cuboidal samples measuring 3×4×1.5 mm (as illustrated in Figure 4) were precisely cut and subsequently cleaned using compressed air.
To assess the fundamental geometric parameters of refractory pores the substrate microstructure has been analyzed using computed microtomography (µCT). µCT of samples was performed using an X-ray device TomoScope L (Werth Messtechnik GmbH). Figure 4 displays typical sections of the sample in both horizontal and vertical planes. The YZ plane aligns with the upper face of the sample, which is where the coating was applied.
The analysis of parameters characterizing the pores was conducted by the post-processing self-developed application “MVT µCT Analysis Tool”, which is based on MATLAB Imaging Processing Toolbox, where the function "regionprops" evaluates pores properties according to 2D image (hereinafter - 2D method) and the function "regionprops3" performs it according to 3D volumetric image (hereinafter - 3D method).
Using the 2D method, pore parameters, such as projection area equivalent diameter, minimum and maximum Feret diameter were estimated. Meanwhile, the 3D method was employed to determine the volume equivalent sphere diameter and porosity. Porosity was calculated as the ratio of the total volume of all pores to the volume of the sample. The obtained value of fireclay porosity, which equals 0.21, closely aligns with the previously mentioned value of 0.22±0.01 (as noted in Section 2.1). The slight discrepancy of 4.6% can be attributed to the limitations of the µCT resolution with a voxel size of 2.96 µm, which restricts the accurate detection of smaller pores.
The size parameters of the pores obtained by µCT analysis are summarized in Table 3. These dimensions were subsequently utilized to construct a geometric model of the porous surface for use in the numerical simulation of the cold spraying process, as outlined in Section 2.5.
Figure 5 presents cumulative and differential distributions of pore sizes based on various measurements: minimum and maximum Feret diameters, projection area equivalent diameter, and volume sphere equivalent diameter. Ratio of the average minimum and maximum Feret diameters (Table 3) is 1.75. This shows that mainly the pores in fireclay are not round, but rather elongated shapes.
Besides, it can be seen that the average value of the projection area equivalent diameter is slightly less than the average value of the minimum Feret diameter, which is associated with a large number of pores that are elongated in shape.
Projection area equivalent diameter values are more than two times the corresponding values volume equivalent sphere diameter. This occurs because the 2D method considers only one section, whereas the 3D method averages values over multiple sections. As a result, the 2D method yields a significantly higher equivalent diameter than the volume equivalent sphere diameter calculated by the 3D method.
To construct the geometric model of pores, average values of the minimum and maximum Feret diameters, equal to 61 µm and 107 µm respectively, were employed.

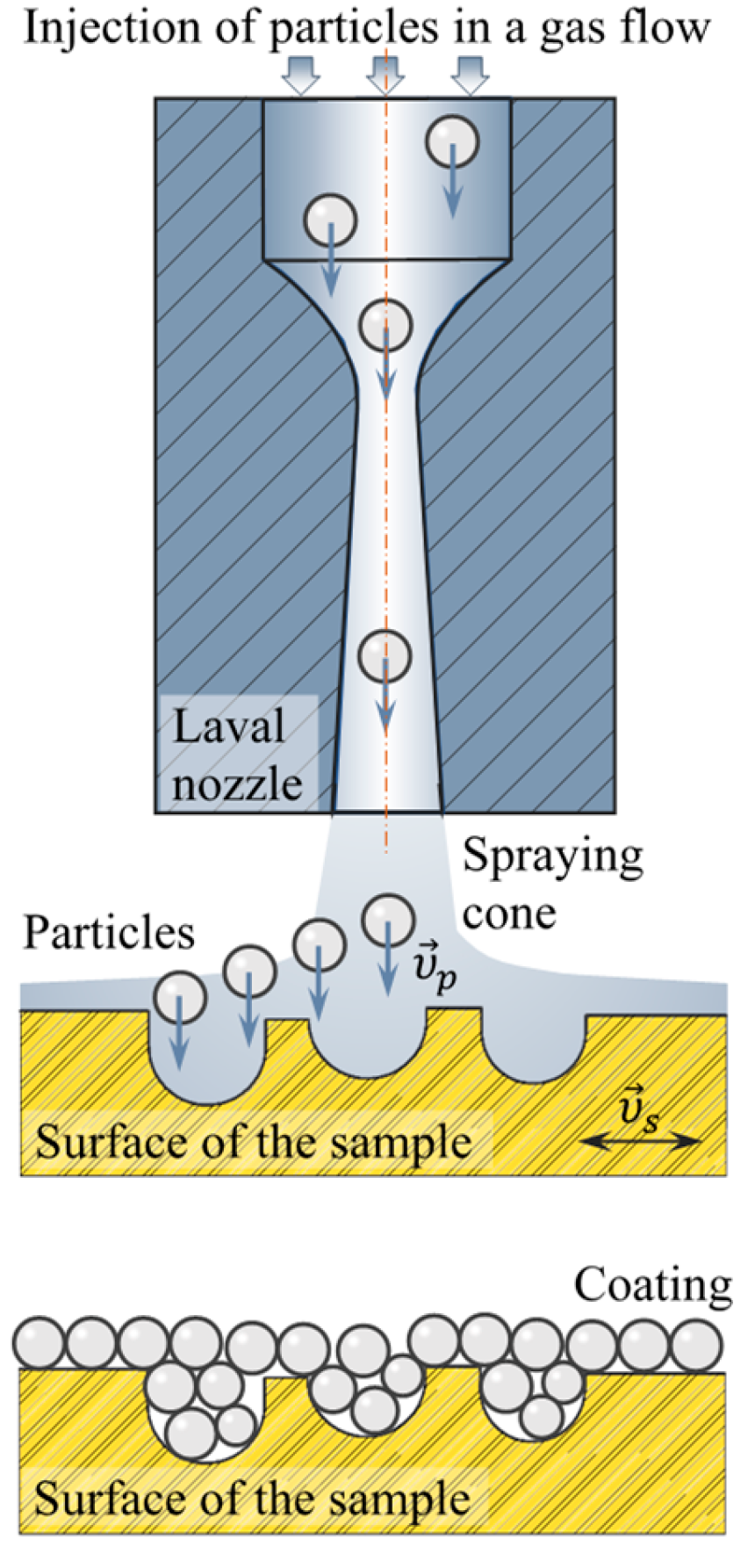
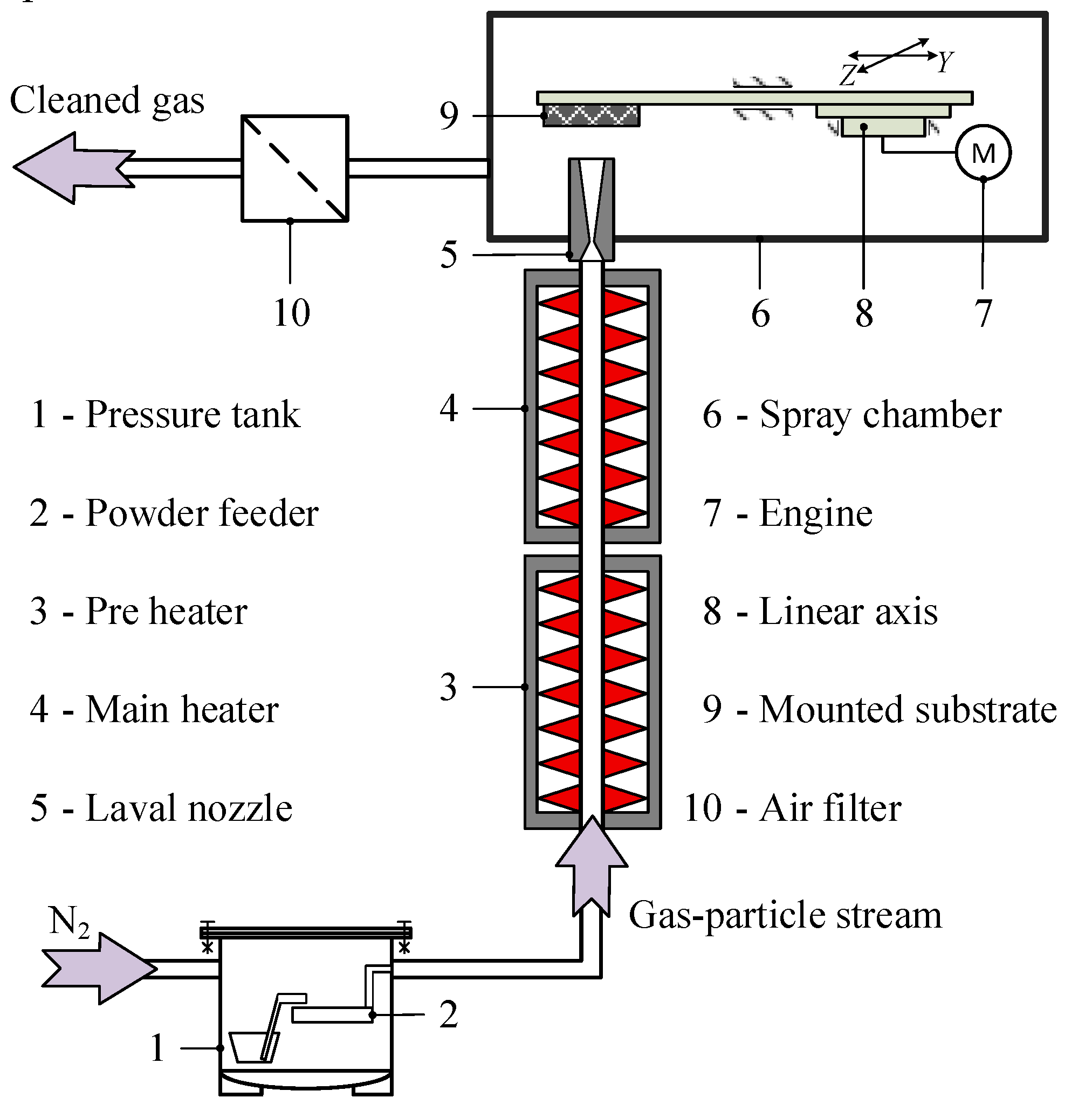
2.3. Setup for the Cold Spray Experiment

The coating of the fireclay substrate surfaces by TiO2 particles was performed with the cold spray setup shown in Figure 6. This setup was developed in our previous works for the coating of metal surfaces with the TiO2 particles [32,33].
The flow of nitrogen used as the carrier gas was compressed to 9 bar and submitted to a pressure tank. The TiO2 powder was fed into the gas stream through a powder disperser (Topas SAG 409) installed in the pressure tank. The gas mass flow was 0.85 g/s, while the mass flow of TiO2 particles was 4 mg/s. Prior to the experiments, the powder underwent drying at 80°C for 48 hours. The gas-solids stream was heated to a temperature of 573 K at the nozzle inlet using a preheater and main heater. Subsequently, the aerosol was accelerated to supersonic velocities through the Laval nozzle and sprayed onto the substrate. The geometry of the Laval nozzle was optimized for efficient acceleration of TiO2 particles in our privious work [33]. It possessed an orifice 0.8 mm (throat) and 1.5 mm (outlet) in diameter and a total length of 30 mm (Fugure 7). The movement of the fireclay substrate was fulfilled relative to the nozzle in the plane perpendicular to the spray direction at a distance of 5 mm using two linear motors with a velocity of 10 mm/s. The time required for one pass of the nozzle along the substrate was 7 seconds, with a step of 0.65 mm between each pass. The sample velocity was adjusted to prevent the formation of a solid covering layer on the surface, enabling the investigation of pore filling mechanisms.

2.4. Analysis of Fireclay Surfaces through Nanoindentation Tests

Nanoindentation tests were conducted on refractory surfaces to examine alterations in their mechanical properties after the spraying of a TiO2 layer. For these tests, a TI Premier nanoindenter (Hysitron) with a Berkovich diamond indenter tip was utilized. For the investigation of the fireclay surface, a high-load indenter (3D OmniProbe) was used. The experiments were conducted with a maximum peak force of 1 N, with a loading time of 20s, a holding time of 10s and an unloading time of 20s, respectively. A low-load indenter (nanoDMA transducer) was employed to examine the thin TiO2 coating. The indentations were conducted with a peak force of 5 mN, a loading time of 10s, a holding time of 5s and an unloading time of 10s.
Prior to conducting the experiments, calibration of the tip area and frame compliance was carried out on fused quartz. A minimum of five tests were conducted in order to ensure meaningful reproducibility. The Oliver and Pharr method [34] was used to determine Young’s modulus E and hardness H from the indentation load-displacement data. This method involves fitting the unloading portion of the load-displacement data to a power-law relationship derived from elastic contact theory [35]:
P = β ( h − h f ) m
where β and m are empirically determined fitting parameters, h is the indenter displacement, hf is the plastic deformation obtained from the curve fit.
The contact stiffness S can be calculated by differentiating the fit of the unloading curve, and evaluating the result at the maximum penetration depth h = hmax as:
S = d P d h h = h m a x = β m ( h m a x − h f ) m − 1
Assuming that deformation is negligible, an elastic model shows that the amount of indentation hs is given by:
h s = ε P m a x S
where P m a x is the maximum applied force, ε is a constant that depends on the geometry of the indenter: ε = 0.75 for Berkovich indenters [36].
The contact depth is determined using the following equation:
h c = h m a x − h s = h m a x − ε P m a x S
In nanoindentation, the hardness of the material is defined as
H = P m a x A c
where A c is the projected contact area of the indenter obtained by measuring the indentation depth h c and inserting it into the calibrated fit [37]:
A c = 3 3 t a n 2 α 2 h c 2 = 24.56 h c 2
where α is the angle of the Berkovich indenter: α = 130.6°.
An intriguing aspect of the nanoindentation technique is its ability to calculate both the hardness and the elastic modulus of the material. The elastic stiffness S of the contact is used to calculate the reduced Young’s modulus E r e d :
E r e d = S 2 π A c
The Young’s modulus of the sample E s is calculated by the following relationship:
1 − ν s 2 E s = 1 E r e d − 1 − ν i 2 E i ,
where ν i and ν s are the Poisson´s ratio of the indenter and the sample (fireclay or TiO2 coating). The mechanical properties of the diamond indenter tip were ν i = 0.07 and E i = 1140   G P a . For the investigated fireclay and TiO2 coating Poisson´s ratio was set to 0.2 and 0.28, respectively.

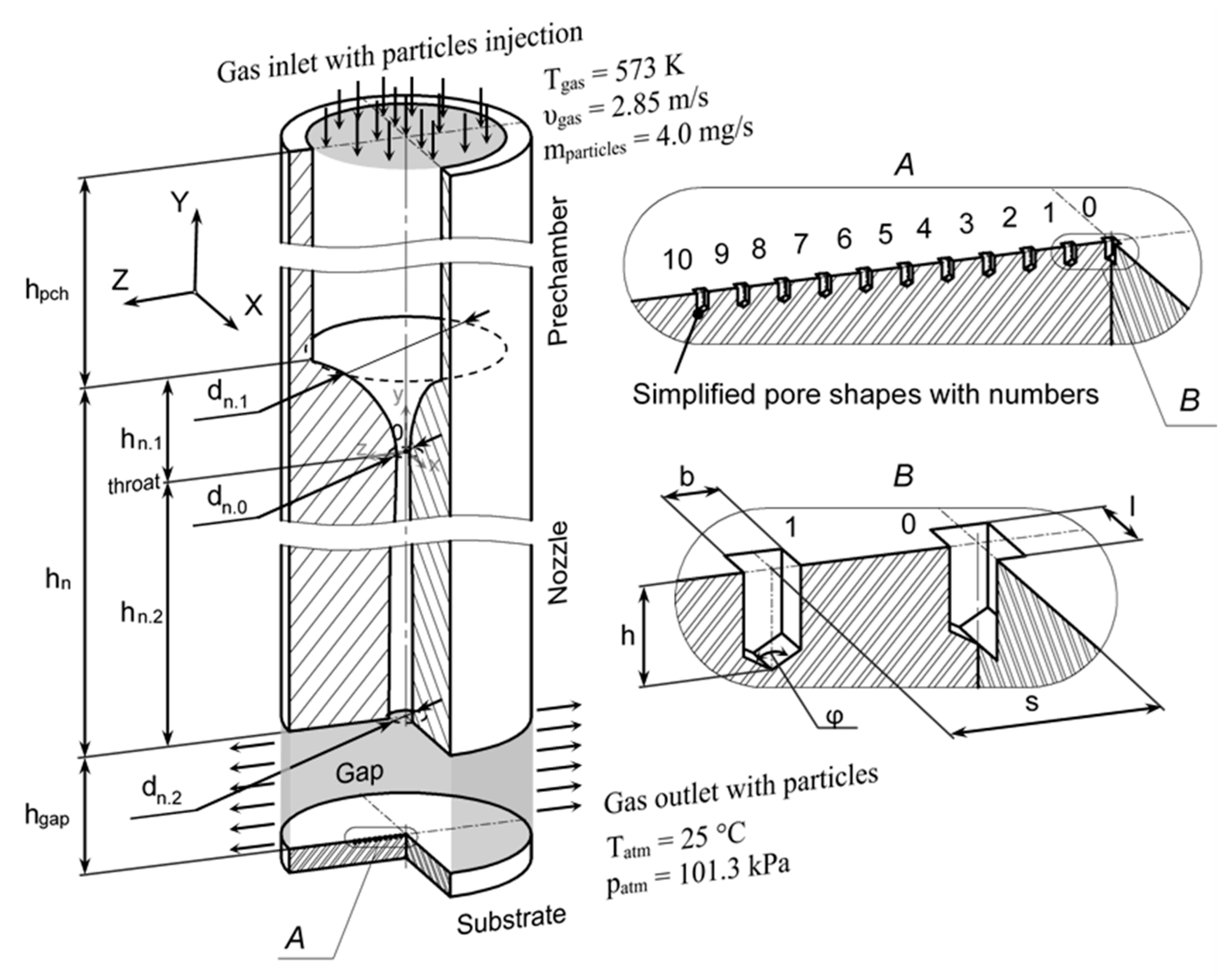
2.5. CFD Setup

To gain a deeper insight into the behavior of TiO2 particles at the inlet of pores on the fireclay surface, simulations of fluid flow and particle motion from the Laval nozzle inlet to the collision point with the substrate’s porous surface were conducted. CFD with Lagrangian particle tracking was used to determine the velocities and penetration angles of particles into pores, as well as the temperatures of both the flow and the particles.
A model consisting of a nitrogen flow with TiO2 particles in a Laval nozzle and a porous fireclay substrate with open pores on the surface (Figure 7) was generated.
During the calculation, the nozzle is assumed not movable. The geometric parameters of the model are presented in Table 4. The dimensions of the Laval nozzle and the sample correspond to the experimental setup. The pore is shaped like a parallelepiped, tapering at the bottom at an angle of 120°. The pore sizes (b×l×h), as determined in Section 2.2., are 61×107×107 µm, respectively. A single row of 11 pores was simulated, arranged radially from the nozzle axis with a step (s) of 220 µm. The distance from the lower edge of the Laval nozzle to the substrate was set at 5 mm.
The influence of the nitrogen fluid on the disperse phase (TiO2 particles) was considered in the simulation. The particles were generated at the inlet of the Laval nozzle. The initial temperature and velocity of the particles match those of the nitrogen flow at the nozzle inlet, which are 573 K and 2.85 m/s, respectively. The mass flow rate of the powder is 4 mg/s. The solid boundaries of the flow field within the Laval nozzle were defined using a constant wall roughness of 0.5 µm [33].
To establish the inlet boundary condition of the fluid flow, a pressure of 9 bar and a temperature of 573 K were specified, consistent with the experimental parameters outlined in Section 2.3. For the outlet boundary condition, an ambient pressure of 1 bar and a temperature of 298 K were employed. The k-ω SST turbulence model [38] was utilized, along with scalable wall functions and 5% turbulence intensity.
Nitrogen was modeled as compressible flow, with its density calculated according to the ideal gas law [39], and the heat capacity was assumed to vary with temperature.
Heat transfer from the flow side and the temperature gradient in the substrate were determined by solving the energy equations:
∂ ∂ t ρ E + ∇ · ( v → ρ E + p ) = ∇ · k e f f ∇ T + τ ̿ · v →
where ρ is density, v → is flow velocity, p is flow pressure, keff is the effective conductivity (k+kt), where k is thermal conductivity, kt is the turbulent thermal conductivity, defined according to the turbulence model being used, T is flow temperature, τ ̿ i s dissipation stress-energy tensor. The right-hand side of Equation (4) represents energy transfer due to conduction and viscous dissipation, respectively.
In Equation (4) E is internal energy, which is defined as:
E = H − p ρ + v → 2 2
where H is enthalpy.
Due to the small concentration of TiO2 particles (2.81⋅10-9 g/mm3) in the flow, their impact on the flow itself can be disregarded. The trajectory of particle motion is determined by integrating the balance of acting forces in:
m p d v → p d t = F → g + F → b + F → d
where m p is the particle mass, v → p is the particle velocity, F → g is the gravitational force, acting on a particle in a flow, F → b is buoyancy force, F → d   is the drag force [40].
The drag force on a particle is calculated by the following equation:
F → d = ρ 2 C d A p ( v → − v → p ) v → − v → p
where C d is the drag coefficient, A p is the cross-section of the particle (the particle is assumed to be spherical).
The drag coefficient is described as a function of the particle Reynolds number R e p which calculated by the following equation:
R e p = ρ v → − v → p d p μ
where μ is the dynamic viscosity of the fluid determined using the Sutherland model [41].
The drag coefficient for the Stokes regime ( R e p ≤ 0.25) is calculated by the following equation:
C d = 24 R e p
The influence of the slip on the motion of fine particles was considered with a Cunningham correction factor in the drag force according to the model described in [42]. It is assumed that the particles are evenly distributed at the entrance to the Laval nozzle.

3. Results and Discussion

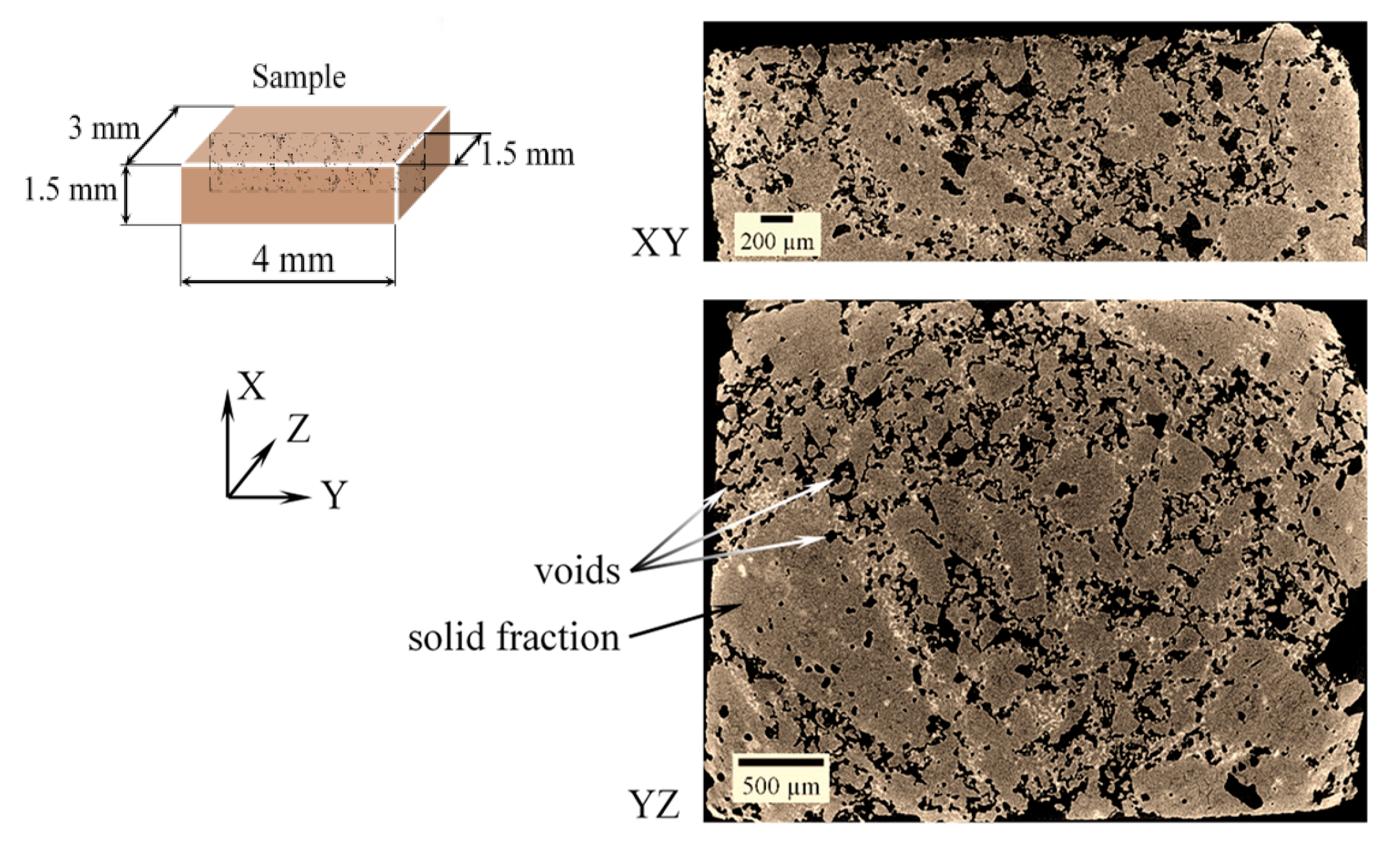
3.1. SEM and µCT Analysis of the Cold Sprayed Refractory Samples

The objective of the experiment was to investigate the mechanism of pore filling. Therefore, particle flow rate, sample velocity, and the number of the nozzle passes were set as to prevent the formation of a coating layer on the surface and complete closure of the pores. Spraying of the sample was carried out in 5 stages. During each stage, 5 passes of the nozzle were made along the entire surface for 35 seconds. Subsequently, the spraying was halted, the sample was removed from the setup, and SEM images of the surface were obtained. This process was repeated for each stage of spraying. Figure 8 shows the image of the sample before the spraying process (Figure 8a) and the images of the different sample areas obtained at each of the five stages of spraying (Figure 8b–f).
In Figure 8a, the characteristic porous structure of the refractory, as described in Section 2.2, is evident. During the first stage of spraying (Figure 8b), TiO2 particles (depicted as white spots) enter micropores and cracks, becoming attached through mechanical interlocking within the cavities. In Figure 8c, the spraying process progresses, with particles continuing to fill the surface of larger pores. Additionally, they begin to bond with deposited particles, forming aggregates. However, no fixed particles are observed on the grains; only individual particles adhere to the inner pore walls. In Figure 8d, a layer of particles is observed on the surface, with particles attached to each other. At this stage, the closing of macropores initiates from the periphery towards the center. The particles not only fill the macropores but also form bridges over them, which are crucial for pore closure and the creation of the first particle layer. Similar mechanisms of pore filling and first layer formation have been observed in surface filtration processes using a porous filter medium, as demonstrated by Hund et al. [43]. On the grains protruding above the surface, only the individual particles are visible.
The central area of macropores larger than about 20 µm in size remains unclosed (Figure 8e). To close these large pores, it is necessary to continue the spraying process.
Upon completion of the cold spraying process, the surface exhibits significant modification (Figure 8f), although the coating is not uniformly deposited. The post-spraying images reveal that particles are deposited both on the surface of the refractory and within the pores. Notably, fine pores (with a width of up to ~5 mean particle diameters) are effectively filled with TiO2 powder. Interestingly, particles within a size range of 0.2...0.5 µm are observed on the surface, while larger particles penetrate deep into the pores due to their higher kinetic energy. The "jamming" of particles within pores occurs as a result of their plastic deformation upon the impact with the substrate, as well as due to high adhesive forces upon collision with each other [44,45] and with the surface of the substrate [46,47].
Figure 9 shows the µCT scan images (voxel size of 0.49 µm) of a fireclay sample following TiO2 cold spraying (the position of the section is shown in Figure 4). In Figure 9a the pink areas represent TiO2 particles. Figure 9b illustrates three distinctive zones where the coating has formed. In the first zone, the pore features gently sloping walls, and the layer of particles entirely fills the pore cavity, resulting in an almost flat surface above it. In this zone, the coating thickness equals the pore depth. On flatter areas (zone 2), the thickness of the coating is uniform. In the third zone, characterized by pores with steep walls, particle deposition occurs, leading to gradual closure of the pore from the periphery to the center. This phenomenon may be attributed to a sharp deceleration of the gas flow in such pores, leading to the formation of a high-pressure zone and, consequently, a deceleration of the particles.

3.2. Results of Nanoindentation Tests

Several indentations were performed on both the initial fireclay sample (Figure 10a) and the coated one (Figure 10b). Crack development at the edges of the Berkovich tip imprint (Fig-ure 10a) confirms the brittle material behaviour of the sample. Figure 10b shows a layer of TiO2 particles after nanoindentation, with no visible cracks. The geometry of the imprint on the coated sample does not correspond to the Berkovich tip shape due to the elastic recovery of the layer during unloading. This indicates that the surface layer formed by the particles is elastically-plastically deformed and adheres well to the surface of the fireclay.
Figure 11 presents force-displacement curves of both coated and uncoated fireclay samples when a nanoindenter tip penetrates a pore and grain. Each curve represents typical results of indentation measurements made at different points of the samples (12 indentation points for the uncoated sample and 8 points for the coated one).
The force curves show the presence of pop-in effects, indicating the entry of the nanoindenter into micropores and microcracks within the sample. In an experiment involving an uncovered pore, these effects are particularly noticeable. They occur when the nanoindenter disrupts the pore wall along its path and enters the next one.
The force curve corresponding to the uncoated grain (depicted in blue) shows a higher slope, suggesting a higher surface stiffness. Conversely, the force curve for the coated grain (depicted in red) exhibits a smaller slope, indicating that the nanoindenter penetrates to a greater depth under the same force. In the initial segment of this curve, the nanoindenter traverses the coating layer with minimal resistance, mainly disrupting bonds between particles rather than the particles themselves. Subsequently, in the following segment, the indenter penetrates the fireclay substrate as evidenced by the slope of this segment being similar to that of the force curve for the uncoated sample. The change in slope angle, marked by the red indicator on the red curve, corresponds to the thickness of the sprayed layer on the fireclay surface. As observed, the thickness of the sprayed layer aligns closely with the mean diameter of TiO2 particles (0.54 μm), consistent with measurements from µCT analysis (Section 3.1).
In comparison to previously described cases, at penetration in an uncoated pore, the nanoindenter achieves greater depth at the same force, evidenced by a smaller slope in the force curve (depicted in green). The indenter traverses the pore cavity and disrupts its partitions, as indicated by observed pop-in effects.
As a result of the tests, the elastic modulus and hardness of the coated and uncoated fireclay samples were determined. The elastic modulus for an uncoated sample (in the grain zone) falls within the range of 12.3-19.6 GPa, while the hardness is in the range of 0.6-1.05 GPa.
To determine the mechanical characteristics of a pore packed with TiO2 particles the indentation was performed for penetration depth up to 1.2 µm.
Figure 12 illustrates positions of nanoindentation (a) and the results of the test (force-displacement curves for the coated pore) (b).
For all three cases of indentation, the area enclosed by the loading and unloading curves is large compared to the area under the unloading curve, indicating a significant plastic component in the deformation of the a pore packed with particles. Based on the test results, the TiO2 layer within the pore has an elastic modulus of 8.26±0.5 GPa and a hardness of 0.152±0.009 GPa.
The behaviour of the sprayed surface of fireclay during nanoindentation, characterized by the absence of pop-in effects on the curves and their smaller slope, demonstrates the effective filling of pores already during the formation of the first layer of deposition.

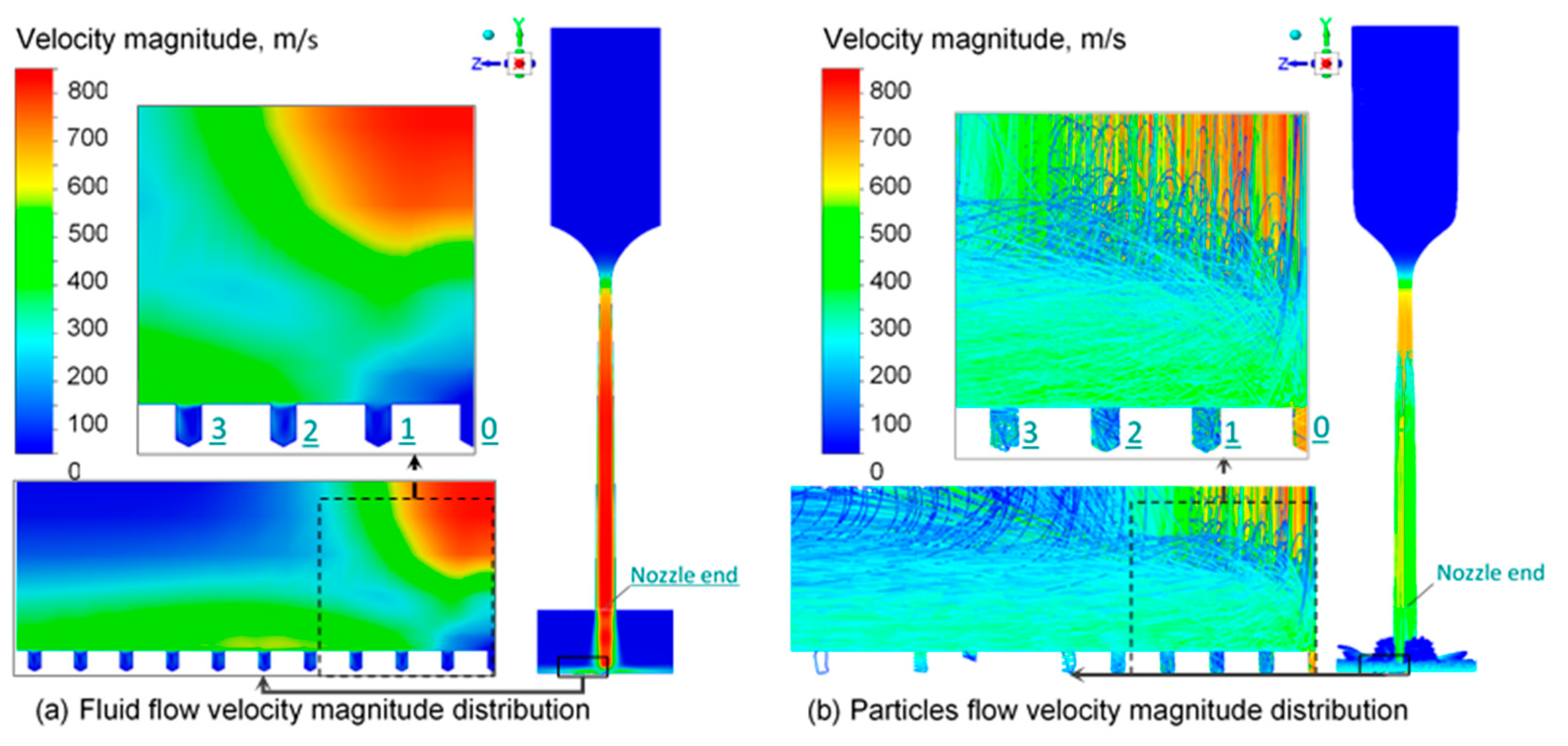
3.3. CFD Simulation Results

The CFD simulations yielded distributions of overpressure and temperature (Figure 12), the Y-component (along the Laval nozzle axis), and the Z-component (tangential to the substrate surface) of gas velocity (Figure 13), along with the magnitude of particle velocity (Figure 14). Notably, the Y-velocity features negative values as per the model’s coordinate system (Figure 7).
The distributions of pressure and temperature of the fluid flow in the expanding part of the nozzle (Figure 13) demonstrate a gradual decrease. This phenomenon occurs because thermal energy is converted into kinetic energy as the fluid expands. The gas flow after exiting the Laval nozzle begins to decelerate. Then, when it comes into contact with the substrate, it is heated to 550 K in the region of central pore #0 and to 525 K in pores #1-3 (Figure 13b). Simultaneously, the pressure in the region of the first two pores (#0, #1) reaches approximately 550 kPa (Figure 13a), decreasing rapidly after pore #3. Although the pressure at the nozzle inlet is 9 bar, the upper limit of the scale in Figure 12a is constrained to 6 bar to provide a more detailed representation of the pressure distribution at the pore inlet.
Of particular interest is the behavior of the fluid flow in the contact zone with the sample surface, in the area of pores.
Over the substrate surface, along the axis of the flow, there is a notable deceleration in the Y-velocity from ~790 m/s to ~50 m/s (Figure 14a). Simultaneously, there’s a significant increase in temperature from ~298 K to ~570 K (Figure 13b), coupled with a rise in pressure from ~ 34 kPa to ~550 kPa (Figure 13a). This can be attributed to converting a portion of the flow’s kinetic energy into thermal energy, subsequently heating both the flow and the substrate due to interaction in the stagnation zone. Such a zone, characterized by a sharp change in flow parameters, is relatively small, approximately 2 mm in diameter and around 0.6 mm high from the substrate surface along the nozzle axis, and encompasses pores #0-#3.
The total velocity magnitude of the fluid flow (Figure 15a) decreases along the flow axis, similar to its Y component (Figure 14a), over a distance of ~0.6 mm above the substrate surface, diminishing from 800 m/s to 100 m/s. Within the pores, this velocity further decreases to ~30 m/s. Upon exiting the stagnation zone, the flow proceeds along the surface of the substrate with a Z velocity greater than a Y velocity. The increase in fluid flow velocity in the Z direction in the boundary layer (above the substrate surface) commences after pore #1, in the region of pore #3, it achieves 460 m/s, and it peaks maximum (540 m/s) in the area around pore #5 (Figure 14b). Additionally, the flow maintains a high speed within the boundary layer, with its height not surpassing the extent of the stagnation zone. Notably, excessively high Z-velocity can result in the separation of particles that have settled on the surface due to significant shear forces.
In the particle velocity diagram (Figure 15b), high velocities of up to 600 m/s are observable in the central pore #0, while velocities of up to 300 m/s are evident in pores #1-3, moreover, all particles have Re< 0.25, as was accepted in Eq. (10). The density of particle trajectories indicates a reduction in the number of particles entering the offset pores.
Due to the greater inertia of the particles, their velocity above the substrate surface differs significantly from the flow velocity. Therefore, for a detailed analysis of particle motion in this zone, the data from ANSYS Fluent were stored in a separate file and analyzed in the software package “Statistica” (see Section 3.2).

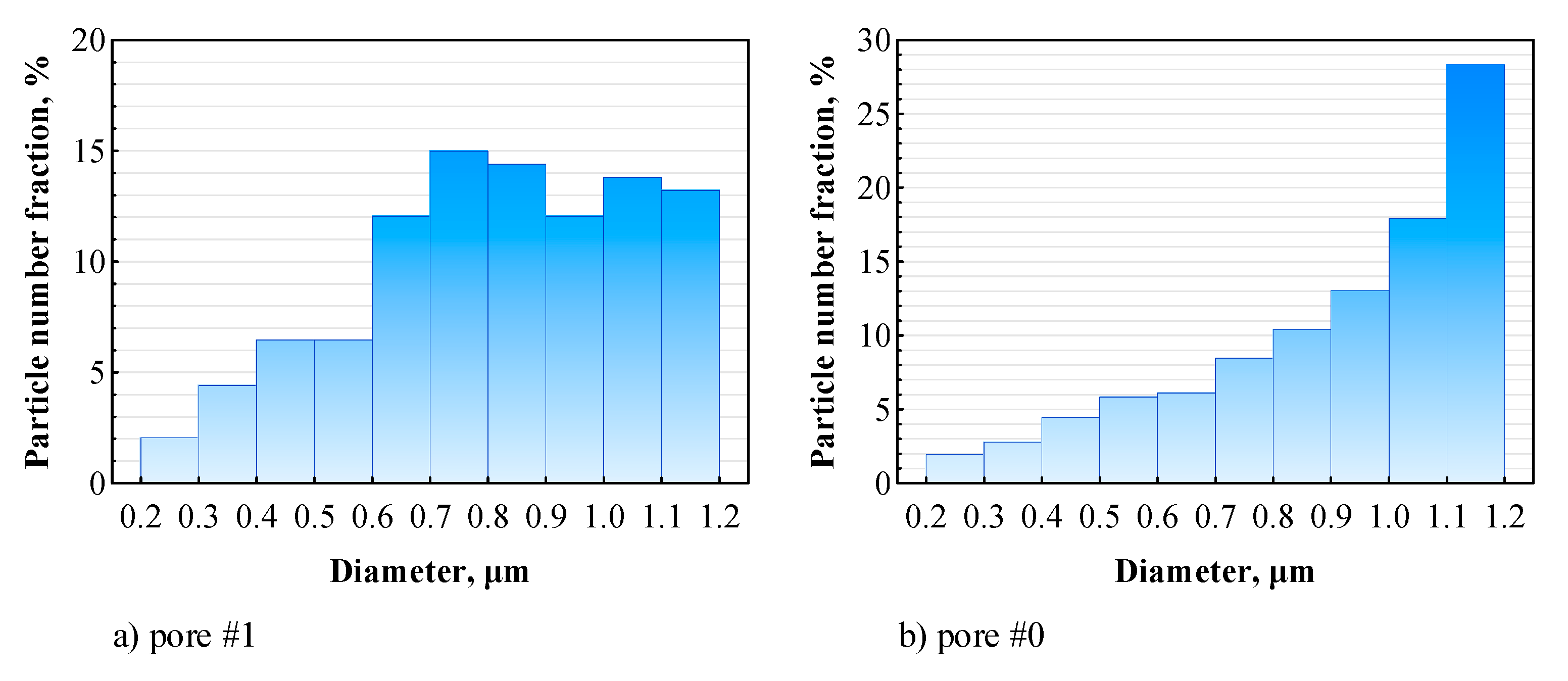
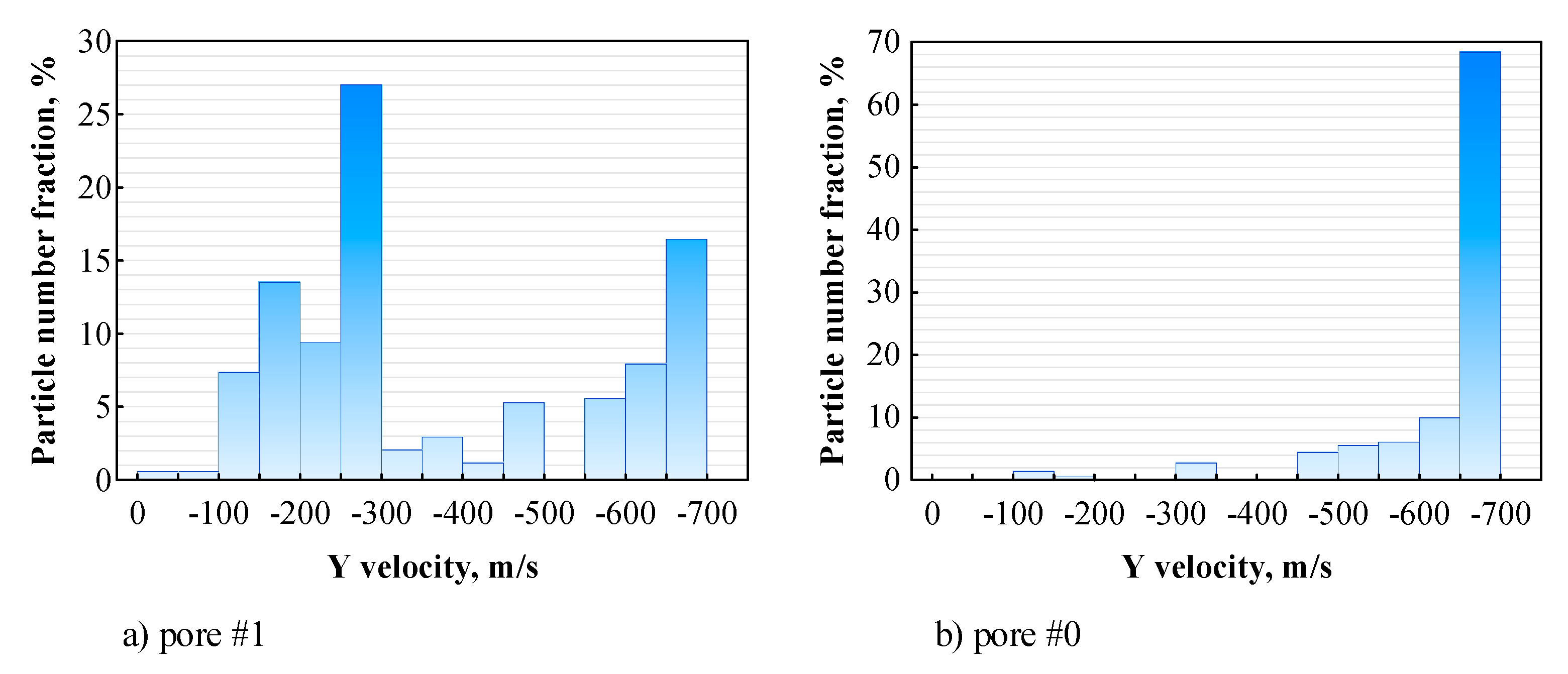
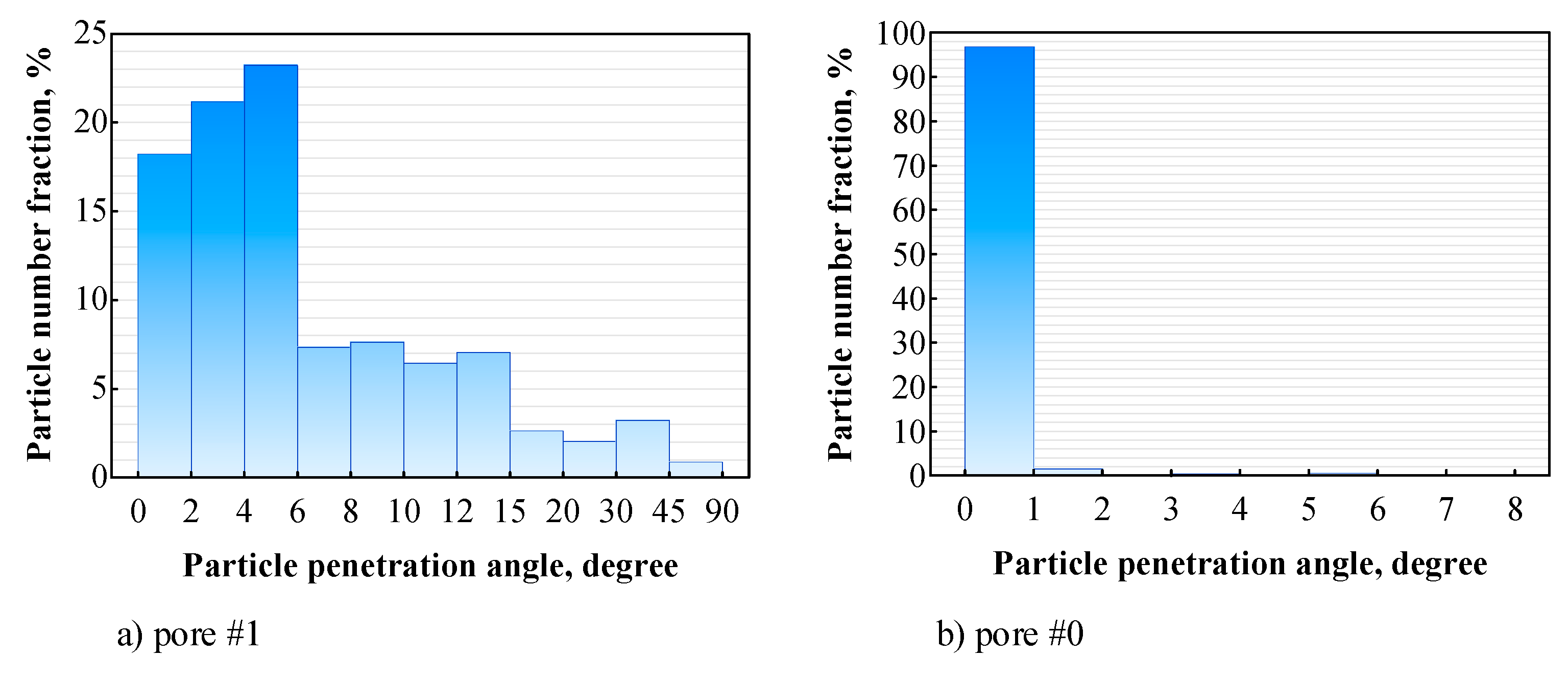
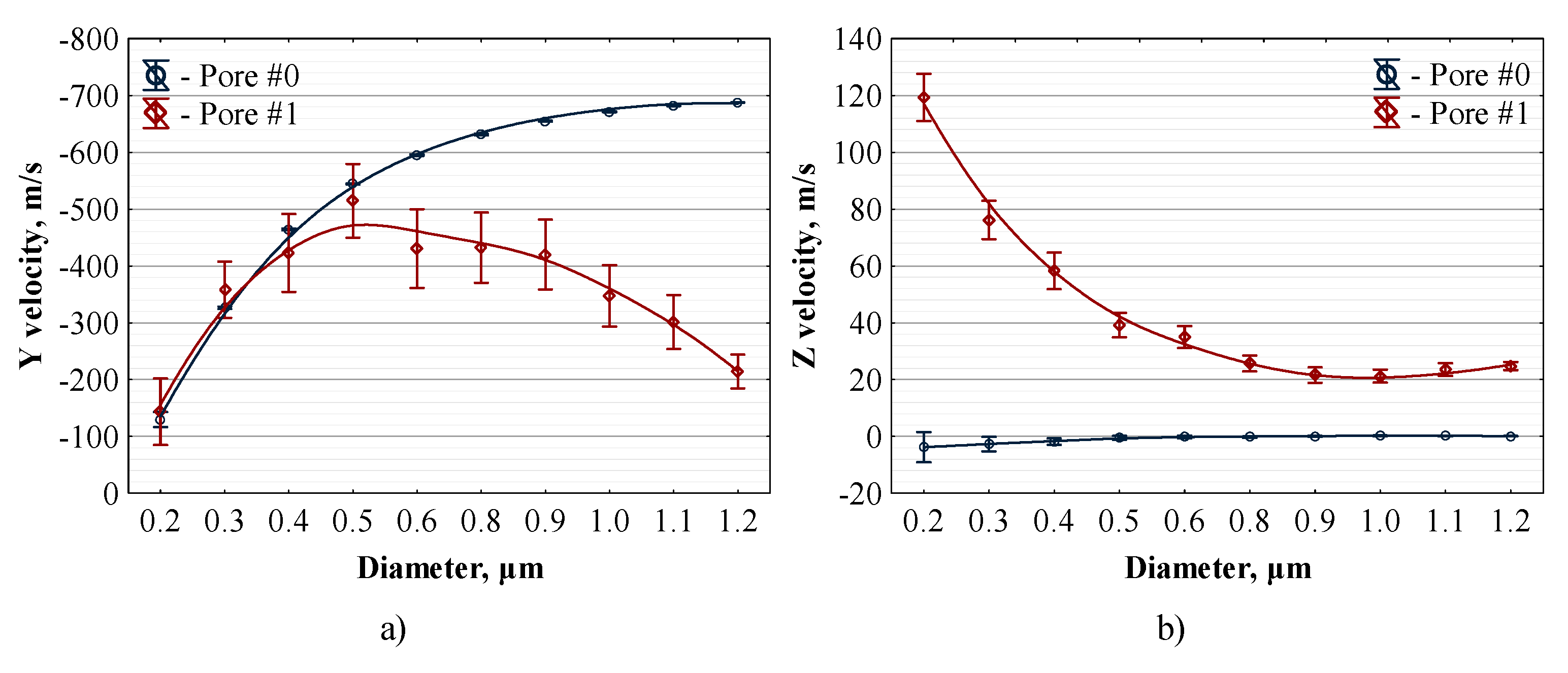
3.4. Distribution of Sprayed Particles across the Pores

Analysis of particle trajectories calculated by the Lagrangian tracking method enabled the acquisition of parameters concerning the movement and temperature of particles penetrating the pores.
Figure 16 shows the quantitative distribution of particles over pores # 0...10, radially located from the central axis of the nozzle. Out of the total 12,530 particles generated at the entrance to the Laval nozzle, 98.7% particles successfully reach the substrate surface. The particles were considered to have penetrated the pores if their center coincided with or was below the surface.
Figure 17 shows characteristics of the motion of particles entering pores, including the central pore #0 and the offset pores #1-4. For each pore, the following parameters are depicted: number fraction (percentage by total particle amount and by particles entering pores), particle diameters and temperature, X-, Y-, Z- velocity components, velocity magnitude, particle penetration angle. The colored bars represent the statistical characteristics: minimum and maximum values, median, mean values, and standard deviation (sd).
The radial distribution of the particle size within pores occurs due to the size-dependent motion of particles in the jet flow, which spreads upon collision with the surface (Figure 14 and Figure 15). The larger particles tend to move vertically and remain in the center of the jet due to their higher inertia. Indeed, the average particle diameter that enters the central pore is about 0.925 μm with a small deviation of ±0.010 μm. Smaller particles, due to their lower inertia, tend to deviate more from vertical movement and are carried by turbulent vortices over longer distances. Consequently, they reach pores that are situated further away from the center of the nozzle. This phenomenon results in an increased fraction of fine particles in pores #1-4 compared to larger particles, which are more likely to concentrate near the center of the jet.
For the central pore, the horizontal X- and Z-components of the particle velocity are minimal, indicating negligible rotation of the flow. However, as the distance from the flow axis increases, the Z-velocity increases while the Y-velocity decreases, suggesting a change in flow direction away from the nozzle axis. By the second offset pore, the average Z-velocity exceeds 140 m/s, which is more than 70% of the Y-velocity. In pores 3 and 4, the horizontal Z-component becomes greater than the vertical Y-component.
As a particle penetration angle in the pores has been considered an angle between the resulting Y-Z particle velocity vector and the vertical axis Y (angle α in Figure 17). This angle influences the contact condition of the particle with surfaces inside the pore and the filling mechanism. A larger angle suggests a higher likelihood of the particle colliding with the side (vertical) wall of the pore. Conversely, a smaller penetration angle indicates deeper penetration of the particle into the pore, leading to collision with its bottom.
As one moves radially away from the centre axis of the nozzle, the angle at which particles penetrate the pores increases significantly. For the particles entering central pore #0, the average angle is close to zero, suggesting a nearly vertical penetration whereas for offset pores it ranges from 7.7 °(pore #1) to 72.6° (pore #4), indicating a much more oblique penetration and predominant collision with the side walls of the pores.
The temperature of particles entering the central pore is notably lower compared to those entering pores #1-3. This distinction can be attributed to the size-dependent behaviour of particles in the flow since particles entering pore #0 are larger and do not have time to heat up passing through the elevated temperature zone near the surface. In contrast, smaller particles are transported over longer distances by turbulent vortices and have more opportunities to interact with the heated flow, leading to their faster heating.
The size distribution of particles entering the pores (Figure 18) reveals the following insights. For central pore #0 (Figure 18b), particles of large diameters predominate, since they are more inertial and can change their trajectory slowly. For pore #1 (Figure 18a), two size fractions can be distinguished: 0.2–0.6 µm (20% of particles entering the pore) and 0.6–1.2 µm (80% of particles entering the pore). The number of particles entering pores #2 and #3 is very small (3.5% and 1.4% of the total number of particles in the first four pores, respectively).
The velocity distributions of penetrated particles presented in Figure 18 and Figure 19 provide further insights into their behavior. In pore #0 (Figure 19b), particles with a Y-velocity ranging from 650 to 700 m/s dominate (69% of the particles entering the pore). Meanwhile, pore #1 (Figure 19a) exhibits a bimodal velocity distribution: particles with velocities below 500 m/s comprise 71% of those entering the pore, while particles with velocities above 550 m/s make up the remaining 29%.
In the central pore (Figure 20b) particles with a Z-velocity in the range of -2...2 m/s (88% of particles entering the pore) are prevailing, i.e. the particles penetrate pore #0 almost vertically (normal to the surface). In pore #1 (Figure 20a) for the majority of particles (86%), the Z-velocity falls within the range of 10...50 m/s. Thus, the Z-velocity distribution of particles entering pore #0 exhibits velocities an order of magnitude lower compared to those in pore #1, as confirmed by the values of penetration angles (Figure 17). The radial distribution of the Z-component of particle velocity is nearly symmetrical due to the symmetric generation of particles at the entrance to the nozzle, generated evenly distributed along the radius.
Figure 21 shows the change in the magnitude velocities of the particles. Given that the Z-component is significantly smaller than the Y-component, the magnitude velocity distributions in the pores closely align with the Y-component.
Figure 22 illustrates the distributions of the particle penetration angle relative to the vertical axis. At the entrance to pore #0, nearly 97% of the particles exhibit an angle less than 1° (Figure 22b). Conversely, for particles entering offset pore #1 (Figure 22a), the angle value increases notably, with approximately 45% of ones having 2...6°, and 28% of the particles falling within the range 6...15°, the angle of the remaining 27% of particles are in the range 15...90°.
Figure 23, Figure 24 and Figure 25 indicate the influence of particle diameter entering pores on their movement parameters and temperature. A confidence interval of 95% was taken for the calculation. For the parameters of particles in the area of pore #1 compared to pore #0, the spread of the obtained values is significantly larger. This disparity arises from the flow decelerating as it moves away from the nozzle axis, causing particles to alter their motion direction, and leading to increased dispersion in particle movement.
As depicted in Figure 23a, the temperature of particles decreases with increasing their diameters. This occurs because large particles, having cooled in the nozzle flow (Figure 13), do not have sufficient time to heat up in the stagnation zone near the surface, where temperatures are high. Conversely, small particles also cool in the flow but have ample time to heat up near the surface before entering the pore. Differences in the temperature trend for particles entering pores #0 and #1 are noticeable for diameters exceeding 0.4 μm, which correlates with disparities in their velocities (Figure 23b).
Figure 23b illustrates averaged velocity magnitude of particles entering pores #0, and #1 as a function of their diameter. For both pores, the velocity magnitude of particles with a diameter of 0.2...0.5 µm uniformly increases to 450 m/s. However, differences in the trend of the curves emerge for particles with a diameter exceeding 0.4 μm. For pore #0, as the diameter increases, the velocity rises and reaches 690 m/s (for particle diameters of 1.2 μm). In contrast, the curve profile of velocity magnitude for particles entering pore #1 peaks 480 m/s (for particle diameters of 0.5 μm). Subsequently, a reverse trend is observed, with the velocity decreasing to 220 m/s (for particle diameters of 1.2 μm). This phenomenon can be explained by the differing behaviors of fine and large particle fractions. Fine particles (0.2...0.5 μm) accelerate quickly, approaching the gas velocity, but slow down rapidly upon reaching the pore due to the significant drop in gas velocity in that region. On the other hand, large particles (0.5...1.2 μm) accelerate less, failing to reach gas velocity, but experience minimal slowing down in the stagnation zone above the pores due to their greater inertia. It is evident that the velocity of particles with a diameter of 0.2...0.5 μm is greatly influenced by the movement characteristics of the gas flow and the velocity of particles with a diameter of 0.5...1.2 μm depends more strongly on their inertial properties.
Figure 24 shows averaged Y- and Z-velocity of particles entering pores #0, and #1 as a function of their diameter.
Comparing the trend of the behavior of Y-velocity in Figure 24а it is noticeable that values of this velocity resemble the values of velocity magnitude (Figure 23b) for both pores. This suggests a substantial contribution of the Y-component to the overall velocity magnitude.
The values of the Z-velocity (Figure 24b) for sprayed particles differ significantly from other components of the velocity magnitude. For the pore #0, Z-velocity of the penetrating particles is very small since they almost do not move along the substrate surface (perpendicular to the axis of the nozzle). The maximum Z-velocity value for particles with a diameter of 0.2…0.5 μm is only - 2 m/s and for particles with a diameter of 0.5…1.2 μm the value of Z-velocity is almost equal to 0. At the entrance to pore #1, the Z- velocity of the particles increases significantly because the flow abruptly changes direction and begins to move along the surface of the substrate. For fine particles (diameter range of 0.2…0.5 μm), the Z-component decreases from 120 to 40 m/s, and for large ones (diameter range of 0.5…1.2 μm), it is in the range of 40…25 m/s.
Figure 25 shows the averaged penetration angle of particles entering pores #0 and #1 as a function of their diameter. A comparison of the penetration angles of the sprayed particles in pores #0 and #1 demonstrates a significant difference in the direction of their movement. For the central pore, this angle is approximately 4° for fine particles (diameter range of 0.2…0.5 μm) and is nearly equal to zero for large ones (diameter range of 0.5…1.2 μm) (Figure 25b). Meanwhile, for the offset pore #1, the penetration angle reaches 40° for small particles and is 10° for large ones (Figure 25a).
The joint analysis of the distributions of Z-velocities (Figure 24b) and particle penetration angles (Figure 25) reveals that for pore #0, both large and small particles move toward the bottom of the pore. However, for pore #1, most of the fine particles tend to move towards the side walls.
Analysis of the behavior of particles entering the pores revealed two distinct groups: the fine particle fraction (diameter range of 0.2…0.5 μm) and the fraction of larger particles (diameter range of 0.5…1.2 μm). The movement and temperature characteristics of the fine particle fraction are jprimarily influenced by the parameters of the gas flow, while the behavior of the large particle fraction is more influenced by their inert properties.
It should also be noted that at a distance between central pore #0 and offset one #1 (220 μm) there are strong changes in the nature of the particle movement. Specifically, the Z-velocity increases by a factor of 30, the penetration angle does by a factor of 10, while the value of the magnitude velocity decreases by a factor of 1.5.

4. Conclusions

In this work, the deposition of TiO2 particles on the porous surface of the refractory (fireclay) has been studied. The particles with a size range of 0.2…1.2 µm were accelerated in a nitrogen flow to a maximum velocity of 690 m/s, passing through the Laval nozzle, and were deposited on the refractory surface.
The filling of sprayed particles into the pores, followed by forming a coating layer on the refractory surface was analysed through SEM and μCT, complemented by nanoindentation measurements. The fixation of particles onto the surface involves their "jamming" into the pores due to their plastic deformation upon the impact. The particles become effectively trapped due to their bonding with the substrate and each other through adhesive forces. This phenomenon facilitates filling fine pores (up to ~ 5 max particle diameters). In essence, such pores become completely "bricked up" with the deposited particles, effectively sealing the surface. Subsequently, a coating layer forms on the surface as particles accumulate and bond together. The closing of larger pores occurs gradually as the coating layer progresses from the periphery towards the centre of the pores.
The post-processing of μCT results has enabled the characterization of the microstructure of the refractory material, including its porosity and the geometry of typical pores. Additionally, the nanoindentation tests for the uncoated and coated refractory samples demonstrated the method’s capabilities for checking coating thickness for porous materials.
To further elucidate the efficiency of filling the pores on refractory surfaces, the unknown velocity, penetration angle, and temperature of the particles entering pores were estimated by CFD simulations of the cold spray process. A distinctive feature of the simulation is the accounting for the influence of the continuous phase with the discrete one. Simulations have investigated the primary factors influencing particle movement parameters as they enter the pores. Firstly, the distance between the pore and the flow axis plays a crucial role. As this distance increases, there is a significant drop in the average particle velocity and the penetration angle of particles into the pore increases. This suggests that particles closer to the flow axis experience higher velocities and more direct trajectories, while those farther away experience slower velocities and more oblique trajectories. Secondly, the diameter of the particles also has a substantial impact on their movement parameters. Larger particles tend to enter the pores at higher velocities. Smaller particles exhibit larger penetration angles, due to their higher susceptibility to changes in flow direction and turbulent effects. Furthermore, the distribution of gas velocity across the flow cross-section and the size of the stagnation zone are important factors affecting particle behaviour.
Given that the majority of particles enter the first two pores (a distance of 0.22 mm from the axis of the nozzle) and at the same time have a high velocity of 270...690 m/s, it is recommended to make a step between the nozzle passes 0.44 mm (2×0.22 mm), that will ensure high-quality closing of pores with sprayed particles. By spacing the passes accordingly, optimal coverage of the refractory surface can be achieved, resulting in improved pore filling and coating uniformity.
Thus, a straightforward yet deliberate alteration of the microstructure of the porous refractory surface is possible through the cold spray process. It can be used to close the pores, thereby impeding the medium penetration deep into the volume of the refractory.
The findings obtained from this study provide initial data that can be leveraged for simulating the bonding mechanism of fine particles to a porous surface within the cold spray process. By understanding the dynamics of particle deposition, including velocity, penetration angle, and temperature, one can develop more accurate models to predict the interaction between particles and the substrate during the coating formation process.
The presented method can be extended to other nonmetallic porous materials. The process can also be combined with post-thermal treatment to increase the adhesion of the deposited particles and sinter them with the base substrate.

Author Contributions

Investigation, simulation, methodology, formal analysis, writing—original draft preparation writing—review and editing, O.A. and M.B.; modelling, data curation, writing—review and editing, P.T. and O.A.; methodology, formal analysis, writing—review and editing, resources, supervision, project administration, A.T. and S.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Philipp Schwartz Initiative der Alexander von Humboldt Foundation.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Gilchrist, J.D. Alumino-Silicate Refractories. In Fuels, Furnaces and Refractories; Elsevier, 1977; pp. 258–272 ISBN 978-0-08-020430-7.
  2. Sarkar, R. Refractory Technology: Fundamentals and Applications; 1st ed.; CRC Press, 2016; ISBN 978-1-315-36805-4.
  3. Smil, V. Modern Ironmaking and Steelmaking. In Still the Iron Age; Elsevier, 2016; pp. 87–114 ISBN 978-0-12-804233-5.
  4. Gilchrist, J.D. Furnace Construction. In Fuels, Furnaces and Refractories; Elsevier, 1977; pp. 193–196 ISBN 978-0-08-020430-7.
  5. Lee, W.E. Refractories. In Comprehensive Composite Materials; Elsevier, 2000; pp. 363–385 ISBN 978-0-08-042993-9.
  6. Mullinger, P.; Jenkins, B. Furnace Construction and Materials. In Industrial and Process Furnaces; Elsevier, 2008; pp. 413–453 ISBN 978-0-7506-8692-1.
  7. Stjernberg, J.; Olivas-Ogaz, M.A.; Antti, M.-L.; Ion, J.C.; Lindblom, B. Laboratory Scale Study of the Degradation of Mullite/Corundum Refractories by Reaction with Alkali-Doped Deposit Materials. Ceramics International 2013, 39, 791–800. [Google Scholar] [CrossRef]
  8. Antonovič, V.; Stonys, R.; Zdanevičius, P.; Mačiulaitis, R.; Boris, R.; Malaiškienė, J. Analysis of the Formed Protective Layer Inhibiting Alkali Corrosion in Aluminosilicate Refractory Castables. Ceramics 2022, 5, 1051–1065. [Google Scholar] [CrossRef]
  9. Tretiakov, P.; Toporov, A.; Aleksieieva, O.; Kostina, O.; Borovlov, V. Revealing the Patterns of Change in the Technical Condition of Refractory Elements in Thermal Units during Operation. EEJET 2020, 6, 81–92. [Google Scholar] [CrossRef]
  10. Yamashita, H.; Inamasu, H.; Horinouchi, S.; Takayama, N. Development of a Ceramic Welding Machine for Coke Oven Carbonization Chamber. In Proceedings of the Int. Congress on the Sci. Technol. Ironmarking, ICSTI, Proc.; 2006; pp. 398–401.
  11. Lv, C.; Ren, J.; Duan, Y.; Wu, Y.; Li, X. Effect of SiO2 Content on the Oxidation Resistance of SiO2–B4C-Glass Coating for Alumina–Carbon Refractories. Ceramics International 2023, 49, 8554–8564. [Google Scholar] [CrossRef]
  12. Bolelli, G.; Cannillo, V.; Lugli, C.; Lusvarghi, L.; Manfredini, T. Plasma-Sprayed Graded Ceramic Coatings on Refractory Materials for Improved Chemical Resistance. Journal of the European Ceramic Society 2006, 26, 2561–2579. [Google Scholar] [CrossRef]
  13. Franco, D.; Vargas, F.; López, E.; Ageorges, H. Tribological Behaviour of Bilayer Alumina and Mullite Plasma-Sprayed Coatings Deposited on a Refractory Substrate at High Temperatures. Ceramics International 2023, 49, 1250–1260. [Google Scholar] [CrossRef]
  14. Ruys, A. Refractory and Other Specialist Industrial Applications of Alumina. In Alumina Ceramics; Elsevier, 2019; pp. 473–499 ISBN 978-0-08-102442-3.
  15. Guo, X.; He, D.; Zhang, J. Properties and Performance Evaluations of Thermal Barrier Coatings. In Thermal Barrier Coatings; Elsevier, 2023; pp. 267–292 ISBN 978-0-12-819027-2.
  16. Chate, G.R.; Rangaswamy, N.; Shettar, M.; Chate, V.R.; Kulkarni, R.M. Ceramic Materials for Coatings: An Introduction and Future Aspects. In Advanced Flexible Ceramics; Elsevier, 2023; pp. 527–540 ISBN 978-0-323-98824-7.
  17. Sirota, V.V.; Vashchilin, V.S.; Ogurtsova, Y.N.; Gubareva, E.N.; Podgornyi, D.S.; Kovaleva, M.G. Structure and Photocatalytic Properties of the Composite Coating Fabricated by Detonation Sprayed Ti Powders. Ceramics International 2024, 50, 739–749. [Google Scholar] [CrossRef]
  18. Refractory Lining Systems. In Fluid Catalytic Cracking Handbook; Elsevier, 2020; pp. 189–213 ISBN 978-0-12-812663-9.
  19. Kotoulas, K.T.; Campbell, J.; Skirtach, A.G.; Volodkin, D.; Vikulina, A. Surface Modification with Particles Coated or Made of Polymer Multilayers. Pharmaceutics 2022, 14, 2483. [Google Scholar] [CrossRef]
  20. Acting Principles of Nano-Scaled Matrix Additives for Composite Structures; Sinapius, M., Ziegmann, G., Eds.; Research Topics in Aerospace; Springer International Publishing: Cham, 2021; ISBN 978-3-030-68522-5.
  21. Barbosa, A.P.M.; Barros, L.M.; Moreira, M.I.R.; Roldão, C.P.; De Souza, T.D.; Kessler, F.; Felipe, C.A.S. Surface Modification of Particles in a Photochemical Fluidized Bed. Chemical Engineering and Processing - Process Intensification 2024, 196, 109658. [Google Scholar] [CrossRef]
  22. Buhl, S.; Schmidt, K.; Sappok, D.; Merz, R.; Godard, C.; Kerscher, E.; Kopnarski, M.; Sauer, B.; Antonyuk, S.; Ripperger, S. Surface Structuring of Case Hardened Chain Pins by Cold-Sprayed Microparticles to Modify Friction and Wear Properties. Particuology 2015, 21, 32–40. [Google Scholar] [CrossRef]
  23. Moridi, A.; Hassani-Gangaraj, S.M.; Guagliano, M.; Dao, M. Cold Spray Coating: Review of Material Systems and Future Perspectives. Surface Engineering 2014, 30, 369–395. [Google Scholar] [CrossRef]
  24. Thielen, S.; Breuninger, P.; Hotz, H.; Burkhart, C.; Schollmayer, T.; Sauer, B.; Antonyuk, S.; Kirsch, B.; Aurich, J.C. Improving the Tribological Properties of Radial Shaft Seal Countersurfaces Using Experimental Micro Peening and Classical Shot Peening Processes. Tribology International 2021, 155, 106764. [Google Scholar] [CrossRef]
  25. Buhl, S.; Schmidt, K.; Sappok, D.; Merz, R.; Godard, C.; Kerscher, E.; Kopnarski, M.; Sauer, B.; Antonyuk, S.; Ripperger, S. Surface Structuring of Case Hardened Chain Pins by Cold-Sprayed Microparticles to Modify Friction and Wear Properties. Particuology 2015, 21, 32–40. [Google Scholar] [CrossRef]
  26. Breuninger, P.; Krull, F.; Huttenlochner, K.; Müller-Reno, C.; Ziegler, C.; Merz, R.; Kopnarski, M.; Antonyuk, S. Microstructuring of Steel Surfaces via Cold Spraying with 316L Particles for Studying the Particle-Wall Collision Behavior. Surface and Coatings Technology 2019, 379, 125054. [Google Scholar] [CrossRef]
  27. Champagne, V.; Helfritch, D. Critical Assessment 11: Structural Repairs by Cold Spray. Materials Science and Technology 2015, 31, 627–634. [Google Scholar] [CrossRef]
  28. Yu, M.; Li, W.-Y.; Suo, X.K.; Liao, H.L. Effects of Gas Temperature and Ceramic Particle Content on Microstructure and Microhardness of Cold Sprayed SiCp/Al 5056 Composite Coatings. Surface and Coatings Technology 2013, 220, 102–106. [Google Scholar] [CrossRef]
  29. Ma, K.; Zhang, Q.-F.; Zhang, H.-Y.; Li, C.-J.; Li, C.-X. Influence of the Gas Preheating Temperature on the Microstructure and Electrical Resistivity of Copper Thin Films Prepared via Vacuum Cold Spraying. Coatings 2023, 13, 1870. [Google Scholar] [CrossRef]
  30. Krzosa, R.; Makowski, Ł.; Orciuch, W.; Özcan-Taşkın, G.; Adamek, R.; Wojasiński, M. Characterization of Structures and Properties of TiO2 Powders. Powder Technology 2023, 421, 118437. [Google Scholar] [CrossRef]
  31. Seville, J.; Wu, C.-Y. Bulk Solid Characterization. In Particle Technology and Engineering; Elsevier, 2016; pp. 17–38 ISBN 978-0-08-098337-0.
  32. Schmidt, K.; Buhl, S.; Davoudi, N.; Godard, C.; Merz, R.; Raid, I.; Kerscher, E.; Kopnarski, M.; Müller-Renno, C.; Ripperger, S.; et al. Ti Surface Modification by Cold Spraying with TiO 2 Microparticles. Surface and Coatings Technology 2017, 309, 749–758. [Google Scholar] [CrossRef]
  33. Buhl, S.; Breuninger, P.; Antonyuk, S. Optimization of a Laval Nozzle for Energy-Efficient Cold Spraying of Microparticles. Materials and Manufacturing Processes 2018, 33, 115–122. [Google Scholar] [CrossRef]
  34. Oliver, W.C.; Pharr, G.M. An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
  35. Broitman, E. Indentation Hardness Measurements at Macro-, Micro-, and Nanoscale: A Critical Overview. Tribol Lett 2017, 65, 23. [Google Scholar] [CrossRef]
  36. Pharr, G.M.; Oliver, W.C.; Brotzen, F.R. On the Generality of the Relationship among Contact Stiffness, Contact Area, and Elastic Modulus during Indentation. J. Mater. Res. 1992, 7, 613–617. [Google Scholar] [CrossRef]
  37. Fischer-Cripps, A.C. Introduction to Contact Mechanics; Mechanical Engineering Series; Springer US: Boston, MA, 2007; ISBN 978-0-387-68187-0. [Google Scholar]
  38. Menter, F. Zonal Two Equation K-w Turbulence Models For Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference; American Institute of Aeronautics and Astronautics: Orlando,FL,U.S.A., July 6 1993.
  39. Raymond, K.W. General, Organic, and Biological Chemistry. Hauptbd.; 4. ed.; Wiley: Hoboken, N.J, 2014; ISBN 978-1-118-35258-8.
  40. Ounis, H.; Ahmadi, G.; McLaughlin, J.B. Brownian Diffusion of Submicrometer Particles in the Viscous Sublayer. Journal of Colloid and Interface Science 1991, 143, 266–277. [Google Scholar] [CrossRef]
  41. Sutherland, W. LII. The Viscosity of Gases and Molecular Force. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1893, 36, 507–531. [CrossRef]
  42. Sorensen, C.M.; Wang, G.M. Note on the Correction for Diffusion and Drag in the Slip Regime. Aerosol Science and Technology 2000, 33, 353–356. [Google Scholar] [CrossRef]
  43. Hund, D.; Lösch, P.; Kerner, M.; Ripperger, S.; Antonyuk, S. CFD-DEM Study of Bridging Mechanisms at the Static Solid-Liquid Surface Filtration. Powder Technology 2020, 361, 600–609. [Google Scholar] [CrossRef]
  44. Aleksieieva, O.; Dereviankina, L.; Breuninger, P.; Bozoglu, M.; Tretiakov, P.; Toporov, A.; Antonyuk, S. Simulation of Particle Interaction with Surface Microdefects during Cold Gas-Dynamic Spraying. Coatings 2022, 12, 1297. [Google Scholar] [CrossRef]
  45. Yao, H.-L.; Yang, G.-J.; Li, C.-J. Molecular Dynamics Simulation and Experimental Verification for Bonding Formation of Solid-State TiO2 Nano-Particles Induced by High Velocity Collision. Ceramics International 2019, 45, 4700–4706. [Google Scholar] [CrossRef]
  46. Seders Dietrich, L.A.; Sahu, M.; Biswas, P.; Fein, J.B. Experimental Study of TiO2 Nanoparticle Adhesion to Silica and Fe(III) Oxide-Coated Silica Surfaces. Chemical Geology 2012, 332–333, 148–156. [Google Scholar] [CrossRef]
  47. Gilson, L.; Kozhar, S.; Antonyuk, S.; Bröckel, U.; Heinrich, S. Contact Models Based on Experimental Characterization of Irregular Shaped, Micrometer-Sized Particles. Granular Matter 2014, 16, 313–326. [Google Scholar] [CrossRef]
Preprints 113658 g001
Figure 1. Scheme of the cold spray coating process of a porous surface of refractory materials.
Figure 1. Scheme of the cold spray coating process of a porous surface of refractory materials.
Preprints 113658 g001
Preprints 113658 g002
Figure 2. Particle size distribution of the TiO2 particles: (a) cumulative curve; (b) SEM image of the bulk particles.
Figure 2. Particle size distribution of the TiO2 particles: (a) cumulative curve; (b) SEM image of the bulk particles.
Preprints 113658 g002
Preprints 113658 g003
Figure 3. SEM images of the fireclay surface.
Figure 3. SEM images of the fireclay surface.
Preprints 113658 g003
Preprints 113658 g004
Figure 4. Fireclay sample µCT scans.
Figure 4. Fireclay sample µCT scans.
Preprints 113658 g004
Preprints 113658 g005
Figure 5. Pore size distributions of the fireclay samples by * 3D and ** 2D analysis of µCT images.
Figure 5. Pore size distributions of the fireclay samples by * 3D and ** 2D analysis of µCT images.
Preprints 113658 g005
Preprints 113658 g006
Figure 6. Scheme of experimental setup for the cold spraying of TiO2 particles.
Figure 6. Scheme of experimental setup for the cold spraying of TiO2 particles.
Preprints 113658 g006
Preprints 113658 g007
Figure 7. Geometrical model of Laval nozzle and substrate with pores on the surface.
Figure 7. Geometrical model of Laval nozzle and substrate with pores on the surface.
Preprints 113658 g007
Preprints 113658 g008
Figure 8. SEM images of the refractory sample by different stages of TiO2 cold spraying.
Figure 8. SEM images of the refractory sample by different stages of TiO2 cold spraying.
Preprints 113658 g008
Preprints 113658 g009
Figure 9. µCT image of the fireclay sample cold sprayed with TiO2 particles, showing a zone on the coated surface (a), and its cross-sections (b).
Figure 9. µCT image of the fireclay sample cold sprayed with TiO2 particles, showing a zone on the coated surface (a), and its cross-sections (b).
Preprints 113658 g009
Preprints 113658 g010
Figure 10. SEM images of an imprint from the Berkovich tip for the uncoated (a) and coated (b) fireclay samples.
Figure 10. SEM images of an imprint from the Berkovich tip for the uncoated (a) and coated (b) fireclay samples.
Preprints 113658 g010
Preprints 113658 g011
Figure 11. Sections of typical force curves by nanoindentation of the coated and uncoated fireclay samples.
Figure 11. Sections of typical force curves by nanoindentation of the coated and uncoated fireclay samples.
Preprints 113658 g011
Preprints 113658 g012
Figure 12. Nanoindentation of the coated pore: (a) positions of conducted indentations of TiO2 layer; (b) measured force displacement curves.
Figure 12. Nanoindentation of the coated pore: (a) positions of conducted indentations of TiO2 layer; (b) measured force displacement curves.
Preprints 113658 g012
Preprints 113658 g013
Figure 13. Fluid flow distributions of pressure and temperature.
Figure 13. Fluid flow distributions of pressure and temperature.
Preprints 113658 g013
Preprints 113658 g014
Figure 14. Y- and Z-velocity distributions of fluid flow.
Figure 14. Y- and Z-velocity distributions of fluid flow.
Preprints 113658 g014
Preprints 113658 g015
Figure 15. Velocity magnitude distributions of fluid flow and particles.
Figure 15. Velocity magnitude distributions of fluid flow and particles.
Preprints 113658 g015
Preprints 113658 g016
Figure 16. Distribution of penetrating particles across the pores.
Figure 16. Distribution of penetrating particles across the pores.
Preprints 113658 g016
Preprints 113658 g017
Figure 17. Property distributions of particles entering pores along the radial distance from the nozzle.
Figure 17. Property distributions of particles entering pores along the radial distance from the nozzle.
Preprints 113658 g017
Preprints 113658 g018
Figure 18. Size distribution of particles at the entrance to pores.
Figure 18. Size distribution of particles at the entrance to pores.
Preprints 113658 g018
Preprints 113658 g019
Figure 19. Y-velocity distribution of the particles at the entrance to pores.
Figure 19. Y-velocity distribution of the particles at the entrance to pores.
Preprints 113658 g019
Preprints 113658 g020
Figure 20. Z-velocity distribution of particles at the entrance to pores.
Figure 20. Z-velocity distribution of particles at the entrance to pores.
Preprints 113658 g020
Preprints 113658 g021
Figure 21. Velocity magnitude distribution of particles at the entrance to pores.
Figure 21. Velocity magnitude distribution of particles at the entrance to pores.
Preprints 113658 g021
Preprints 113658 g022
Figure 22. Particle penetration angle distribution of particles at the entrance to pores.
Figure 22. Particle penetration angle distribution of particles at the entrance to pores.
Preprints 113658 g022
Preprints 113658 g023
Figure 23. Influence of particle size on their average temperature (а) and velocity magnitude (b) upon entering the pores.
Figure 23. Influence of particle size on their average temperature (а) and velocity magnitude (b) upon entering the pores.
Preprints 113658 g023
Preprints 113658 g024
Figure 24. Influence of particle size on their averaged Y- (а) and Z-velocity (b) upon entering the pores.
Figure 24. Influence of particle size on their averaged Y- (а) and Z-velocity (b) upon entering the pores.
Preprints 113658 g024
Preprints 113658 g025
Figure 25. Influence of particle size on their averaged penetration angle upon entering pore #1 (а) and pore #0 (b).
Figure 25. Influence of particle size on their averaged penetration angle upon entering pore #1 (а) and pore #0 (b).
Preprints 113658 g025
Table 1. Properties of TiO2 particles.
Table 1. Properties of TiO2 particles.
Property Units Value
Density kg·m-3 4260
Specific heat capacity (at 25°C) J·kg-1·K-1 683
Thermal conductivity (at 25°C) W·m-1·K-1 4.8
Table 2. Properties of the fireclay.
Table 2. Properties of the fireclay.
Property Units Value Ref. Temp., °C
Specific heat capacity J·kg-1·K-1 833 100
Specific heat capacity J·kg-1·K-1 1251 1500
Thermal conductivity W·m-1·K-1 1.6 25
Thermal conductivity W·m-1·K-1 1.7 200
Thermal conductivity W·m-1·K-1 1.9 600
Thermal conductivity W·m-1·K-1 2.0 800
Table 3. Pore size parameters of fireclay sample obtained from µCT images.
Table 3. Pore size parameters of fireclay sample obtained from µCT images.
Pore Size Volume Equivalent Sphere Diameter 1, µm Projection Area Equivalent Diameter 2, µm Minimum Feret Diameter2, µm Maximum Feret Diameter2, µm
Average 22.6 ± 0.7 58.8 ± 0.2 61.1 ± 0.2 107.0± 0.4
Median 17.5 52.2 45.1 80.0
Percentile 95% 52.5 164.2 198.7 360.2
1 3D analysis; 2 2D analysis.
Table 4. Geometric parameters of the model.
Table 4. Geometric parameters of the model.
Parameter Value, mm Parameter Value, mm
hpch 15.5 hn.1 4.5
hn 30.0 hn.2 25.5
hgap 5.0 l 0.107
dn.1 8.0 b 0.061
dn.0 0.8 h 0.107
dn.2 1.466 s 0.220
φ 120°
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated