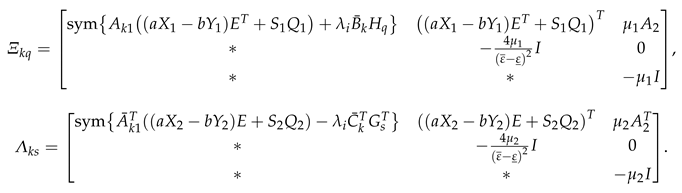Prerpints.org logo
Preprint
Article

Consensus of T-S Fuzzy Fractional Order Singular Perturbation Multi-Agent Systems

Altmetrics

Downloads

64

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 July 2024

Posted:

31 July 2024

You are already at the latest version

Alerts
Abstract
This article focuses on the leader-following consensus of fuzzy fractional order singular perturbation multi-agent systems (FOSPMASs) with order in 0,2. By employing the T-S fuzzy modeling approach, a fuzzy FOSPMAS is constructed. Subsequently, a fuzzy observer-based controller is designed and the error system corresponding to each agent is derived. Through a series of equivalent transformations, the error system is decomposed into fuzzy singular fractional order systems (SFOSs). According to the admissibility of SFOSs, the consensus conditions of the fuzzy FOSPMAS are obtained based on linear matrix inequalities (LMIs) without equality constraint. Finally, the effectiveness of the criteria is verified through an RLC circuit model.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

In recent decades, the control towards multi-agent systems (MASs) has become a leading research subject, stemming from the superior efficiency of multiple agents collaborating to execute tasks compared to an individual agent [1]. MASs hold significant applications spanning various domains, including service robotics [2,3], hazardous environment detection [4], and unmanned aerial vehicle formation flying [5]. Consensus control of MASs is a fundamental and core issue based on tracking control [6,7]. A significant amount of research has emerged on the consensus of MASs [8,9,10,11,12]. Ren [8] constructed MASs with second-order integrator dynamics by analyzing the swarming model and designed a consensus protocol. Tian and Liu [9] attained two decentralized consensus conditions of MASs with diverse input and communication delays. Wen et al. [10] introduced an innovative protocol designed by using synchronous intermittent local feedback for second-order consensus of MASs. Zhang et al. [11] proposed event-trigger output feedback control approaches, enabling that all connected communication graphs reach consensus. Tan et al. [12] derived the consensus criteria for cyber-physical systems under sampled data control, employing suitable Lyapunov function. The above studies predominantly concentrate on achieving consensus of MASs with integer order, which is difficult to describe the actual systems in nature and industry.
Fractional order systems (FOSs) are capable of more accurately modeling and computing genetic and memory effects in various complex processes than integer order systems [13]. Similarly, the consensus of fractional order MASs (FOMASs) has attracted widespread interest [14,15,16,17,18,19]. Su and Ye proposed a control strategy with input delays to achieve the consensus of general linear and nonlinear FOMASs under event-triggered in [14,15], respectively. Yang et al. [16] considered the consensus of nonlinear distributed and input delayed FOMASs, and further explored the performance of FOMASs in terms of leader-following and leaderless global consensus in [17]. Hu et al. [18] developed an adaptive controller that employed an event-triggered scheme without Zeno behavior, aiming to realize the consensus of FOMASs. Bahrampour et al. [19] proposed new Lyapunov-based LMIs conditions to determine the state feedback controller gains on the distributed consensus control of heterogeneous FOMASs with interval uncertainties. However, many practical MASs exhibit multiple time-scale characteristics, which refer to the coupled coexistence of fast dynamics and slow dynamics. The design of controllers for these systems frequently encounters difficulties due to the presence of high dimensionality and pathological values [20,21].
Singular perturbation systems (SPSs) have multiple time-scale and inherently pathological dynamical properties [22,23,24]. SPSs with certain parasitic parameter ε are modeled to describe real systems. In power system modeling, ε is used to represent transient phenomena in machine reactors or voltage regulators [25]. In industrial control systems, it signifies small time constants between control and response [26]. Numerous scholars have intensively studied SPSs [27,28,29,30,31,32]. On one hand, two commonly employed strategies for solving control problems of SPSs are the quasi-steady-state method [27] and the block diagonalization method [28], which decompose the system into slow and fast subsystems. But these methods rely on the assumption that the fast subsystem matrix is nonsingular and are not applicable to non-standard SPSs that cannot be easily decomposed. On the other hand, Yang et al. [29], Gao et al. [30] and Liu et al. [31] proposed the integral sliding mode control method for full-order SPSs with mismatched disturbances, uncertainty and nonlinear input, respectively. Their methods are based on a full-order model, which significantly eliminates the need to decompose the system. Furthermore, techniques such as Lyapunov functions and LMIs are also applied to system analysis. Fridman [32] derived the LMIs criteria for the stability of SPSs for delay proportional to ε and delay independent of ε , respectively. Additionally, for singular perturbation MASs (SPMASs), both Ben Rejeb et al. [33] and Tognetti et al. [34] designed the decentralized controllers, enabling systems to synchronize and ensuring global performance. Xu et al. [35] presented the sliding-mode controller with memory output for addressing consensus of SPMASs in finite time. Zhang et al. [36] achieved global Mittag-Leffler consensus tracking for fractional SPMASs modeled by discontinuous function with nondecreasing property. However, in practical application, the exact value of the parameter ε is often difficult to obtain directly. By analyzing the background information of specific problems in depth, the reasonable change range of ε is effectively estimated. Given ε in known interval , the design of controllers for achieving consensus of nonlinear FOSPMASs remains an open problem in the field of control theory.
T-S fuzzy models possess the capability of approximating nonlinear dynamics, thereby the well-established control methods for linear systems is extended to the analysis and design of nonlinear systems. Therefore, numerous scholars have done extensive research endeavors focusing on T-S fuzzy SPSs [37,38,39,40]. Yang and Zhang [37] proposed a design method of state feedback controller depending on ε for T-S fuzzy SPSs. Chen et al. [38] focused on nonlinear SPSs and presented two novel methods to design static output feedback H ∞ controller based on LMIs. Visavakitcharoen et al. [39] designed an event-triggered controller based on integral feedback for nonlinear SPSs with a fuzzy model. Zhang and Han [40] proposed two diverse feedback controllers aiming to attain the stabilization criteria of fuzzy FOSPSs with order α ∈ 0 , 1 . Nevertheless, the research on the consensus control of fuzzy fractional order singular perturbation MASs (FOSPMASs) is still relatively limited.
Inspired by previous discussions, this paper focuses on filling this research gap. The following is an overview of the main contributions of this research:
  • To provide a more accurate portrayal of complex systems in practice, a T-S fuzzy FOSPMAS with α ∈ 0 , 2 is formulated to reduce the difficulty of directly studying nonlinear systems. Compared to integer order systems, the constructed model exhibits more enhanced accuracy and complexity. A fuzzy FOSPS with error as a variable is derived by designing a fuzzy observer-based controller.
  • The fuzzy FOSPS is analyzed by transforming it into a fuzzy SFOS using the system augmentation method. In comparison to the existing work [41], the proposed approach not only relaxes the assumption that the fast subsystem matrix must be nonsingular, but also avoids the ill-conditioned issue arising from the parameter ε .
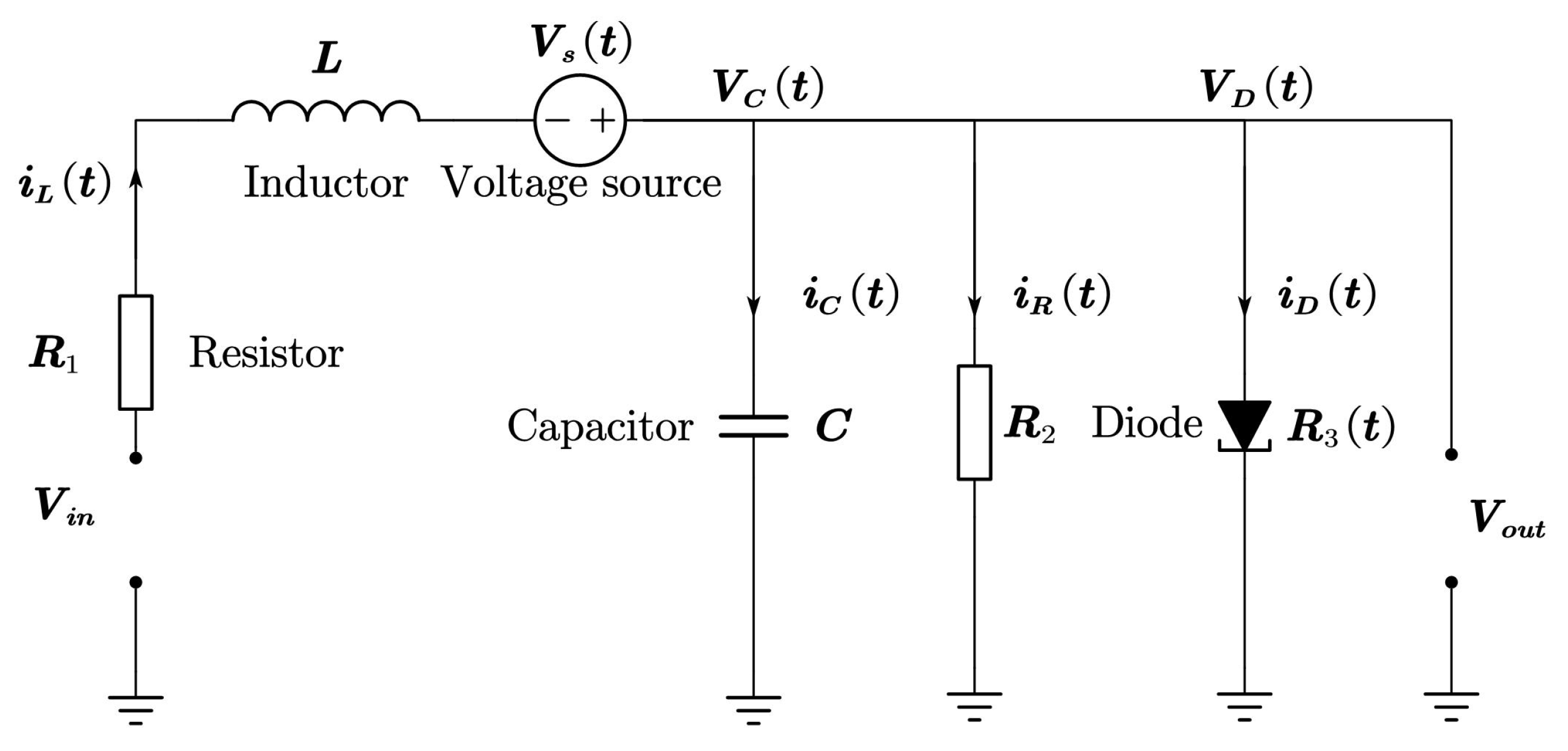
  • The consensus conditions for fuzzy FOSPMASs with α ∈ 0 , 1 and 1 , 2 are formulated in this study for any ε ∈ ε ̲ , ε ¯ , where ε ̲ and ε ¯ are given lower and upper boundaries, respectively. The results are presented based on LMIs without equality constraints, reducing solution difficulties. It is demonstrated through an RLC circuit model that the proposed methods are effective in practice.
The remaining parts are structured in the following manner: Section 2 provides foundational definitions in graph theory and correlative lemmas. The establishment of system model and the primary findings on the consensus of FOSPMASs are detailed in Section 3. Section 4 presents two practical examples. Lastly, Section 5 summarizes the study.
Notations: X > 0 and X ⩾ 0 signify that the matrix X is positive definite and positive semi-definite, respectively. X T stands for transpose of the matrix X, and sym X = X + X T . spec E , A is the spectrum of det s α E − A = 0 . Symbol * is the symmetric element of a matrix. ⊗ denotes the Kronecker product. For α ∈ 0 , 2 , a = sin α π 2 , b = cos α π 2 , Θ denotes a b − b a . diag · represents a diagonal matrix. ⌈ α ⌉ stands for rounding α up to the nearest integer.

2. Preliminaries

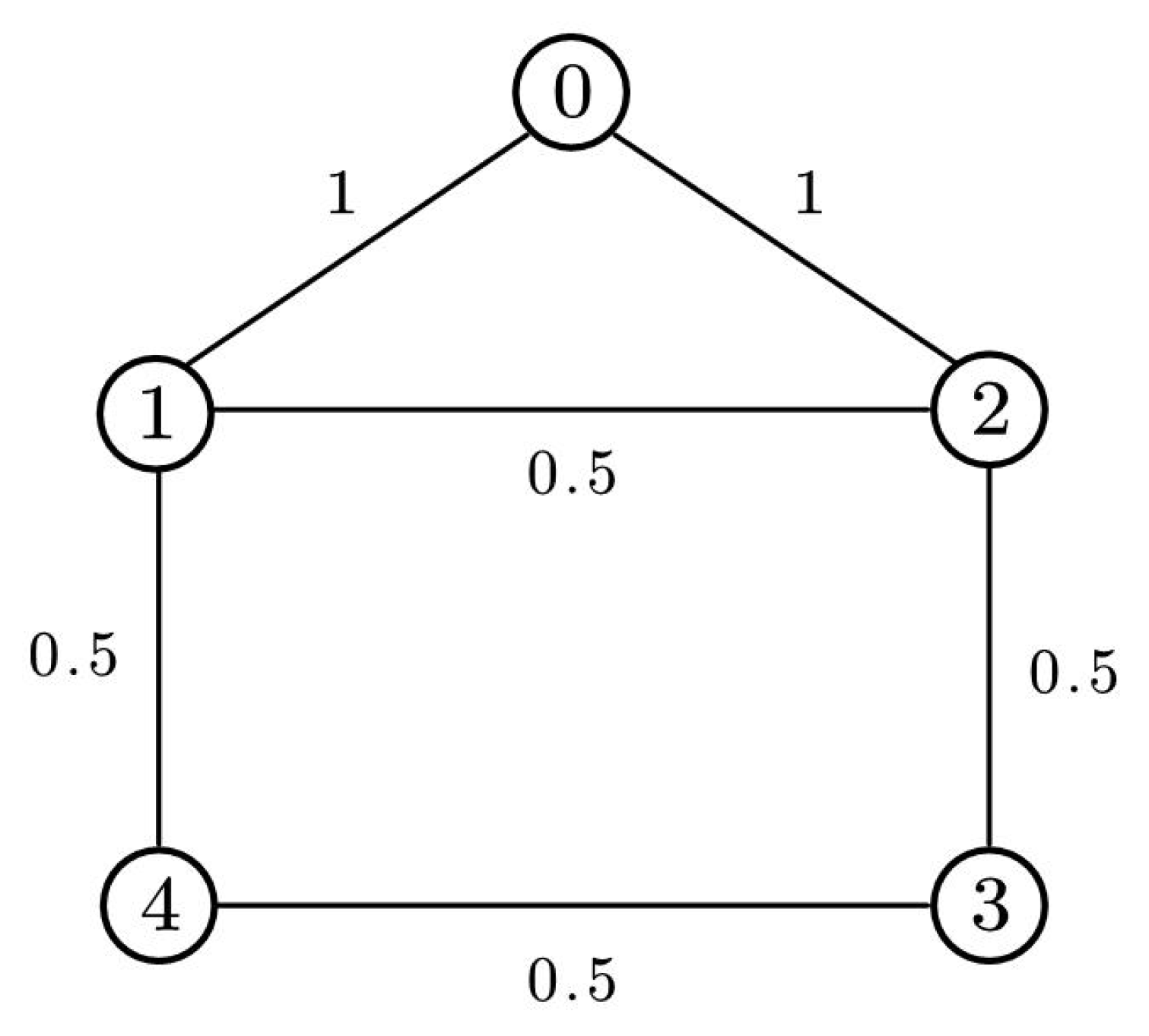
2.1. Graph Theory

Consider the case of an MAS comprising a single leader and N followers. The information exchanged between N agents is presented by an undirected graph G . The Laplace matrix of the graph G is defined as L = l i j ∈ R N × N , where l i j = − a i j , i = j ∑ j = 1 N a i j , i ≠ j and a i j is the element of weighted adjacency matrix A of graph G . a i j > 0 means that follower i communicates with follower j, otherwise a i j = 0 . When G is undirected, A is symmetric. Similarly, h i represents the communication between the leader and follower i, and h i > 0 means follower i receives information from the leader, or else h i = 0 .

2.2. Preliminary Lemmas

Consider a continuous linear singular FOS (SFOS) with α ∈ 0 , 2 described by
E D α x t = A x t ,
where A , E ∈ R n × n are the system matrices, rank E = m < n . x t ∈ R n represents the state. D α denotes the Caputo fractional order derivative, defined as
D α f t = 1 Γ ⌈ α ⌉ − α ∫ 0 t f ⌈ α ⌉ τ t − τ α + 1 − ⌈ α ⌉ d τ ,
where Γ · is the Euler Gamma function. Indicate (1) by the triple E , A , α .
When E = I , system (1) is simplified to a normal FOS
D α x t = A x t .
Lemma 1.
[42] System (2) is stable iff arg spec A > α π 2 .
Lemma 2.
[43] Choose two nonsingular matrices U and V such that
U E V = I m 0 0 0 , U A V = A 1 A 2 A 3 A 4 ,
then system (1) is regular, impulse-free and stable, defined admissible, iff A 4 is nonsingular and
arg spec A 1 − A 2 A 4 − 1 A 3 > α π 2 .
Lemma 3.
[44] System (1) is admissible with α ∈ 1 , 2 iff there exists a matrix P ∈ R n × n satisfying
E P = P T E T ⩾ 0 , sym Θ ⊗ A P < 0 .
Lemma 4.
[43] System (1) is admissible with α ∈ 0 , 1 iff there exist two matrices X , Y ∈ R n × n satisfying
E X E Y − E Y E X = X T E T − Y T E T Y T E T X T E T ⩾ 0 , sym A a X − b Y < 0 .
Lemma 5.
[45] Given a symmetric constant matrix Z and constant matrices U , V , the inequality
Z + U F V + V T F T U T < 0
holds for all F satisfying F T F ⩽ S iff there exist some ρ > 0 such that
Z + ρ − 1 V T ρ U S 0 0 I ρ − 1 V ρ U T < 0 .

3. Main Results

3.1. System Model Description

Consider an MAS consisting of a leader and N followers, and the dynamic of each agent is modeled by a T-S fuzzy FOSPS. This nonlinear system is described by the fuzzy rules as follows:
Rule k: IF ξ 1 t is Π k 1 and ⋯ and ξ p t is Π k p ,
THEN the dynamic description of each agent is written as
E ε D α x i t = A k x i t + B k u i t y i t = C k x i t
E ε D α x 0 t = A k x 0 t y 0 t = C k x 0 t
where
E ε = I n 1 0 0 ε I n 2 , n 1 + n 2 = n , i = 1 , 2 , ⋯ , N .
x i t ∈ R n , u i t ∈ R l and y i t ∈ R v represent the state, control input and output of follower i, respectively. x 0 t ∈ R n and y 0 t ∈ R v represent the state and output of leader. The system matrices A k ∈ R n × n , B k ∈ R n × l , and C k ∈ R v × n are constant. Additionally, Π k j are the fuzzy sets of the premise variables ξ j t , where j = 1 , ⋯ , p and k = 1 , ⋯ , r . Here, r represents the number of rules.
According to procedures of defuzzification, the global model of the T-S fuzzy FOSPMAS (4)-(5) is derived:
E ε D α x i t = ∑ k = 1 r η k ξ A k x i t + B k u i t y i t = ∑ k = 1 r η k ξ C k x i t
E ε D α x 0 t = ∑ k = 1 r η k ξ A k x 0 t y 0 t = ∑ k = 1 r η k ξ C k x 0 t
where η k ξ = ∏ j = 1 p ω k j ξ j t ∑ k = 1 r ∏ j = 1 p ω k j ξ j t is the weighting function, and ω k j ξ j t is the membership function, satisfying η k ξ t ⩾ 0 , ∑ k = 1 r η k ξ t = 1 , ∏ j = 1 p ω k j ξ j t ⩾ 0 and ∑ k = 1 r ∏ j = 1 p ω k j ξ j t > 0 .
Utilizing the complete state information for controller design is often challenging owing to economic constraints and measurement limitations. To address this issue and design a consensus protocol for the fuzzy FOSPMAS (6)-(7), a fuzzy observer is formulated as
E ε D α x ^ i t = ∑ k = 1 r η k ξ A k x ^ i t + ∑ k = 1 r η k ξ B k u i t + z i t z i t = ∑ s = 1 r η s ξ W s ∑ j = 1 N a i j y ˜ i t − y ˜ j t + h i y ˜ i t
where x ^ i t signifies the estimated state of the follower i, and y ˜ i t = y i t − ∑ k = 1 r η k ξ C k x ^ i t represents the error between the actual output y i and the weighted sum of estimated outputs. Furthermore, W s ∈ R n × v denotes the gain matrix.
To achieve the consensus of (6)-(7), a distributed control protocol based on (8) is designed:
u i t = ∑ q = 1 r η q ξ K q ∑ j = 1 N a i j x ^ i t − x ^ j t + h i x ^ i t − x 0 t .
Let x e i t = x i t − x 0 t and x ^ e i t = x i t − x ^ i t . By substituting (9) into (6) and subtracting (6) from (8), the error system is written as
E ε D α x e i t = ∑ k = 1 r η k ξ A k x e i t + ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B k K q · ∑ j = 1 N a i j x e i t − x e j t − x ^ e i t − x ^ e j t + h i x e i t − x ^ e i t ,
E ε D α x ^ e i t = ∑ k = 1 r η k ξ A k x ^ e i t − ∑ s = 1 r ∑ k = 1 r η s ξ η k ξ W s C k · ∑ j = 1 N a i j x ^ e i t − x ^ e j t + h i x ^ e i t .
Let x ¯ e t = x e T t x ^ e T t T , where
x e t = x e 1 T t , ⋯ , x e N T t T , x ^ e t = x ^ e 1 T t , ⋯ , x ^ e N T t T .
The compact form of system (10)-(11) is
I N ⊗ E ε D α x e t = I N ⊗ ∑ k = 1 r η k ξ A k x e t + M ⊗ ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B k K q x e t − x ^ e t ,
I N ⊗ E ε D α x ^ e t = I N ⊗ ∑ k = 1 r η k ξ A k x ^ e t − M ⊗ ∑ s = 1 r ∑ k = 1 r η s ξ η k ξ W s C k x ^ e t .
where M = L + diag h 1 , h 2 , ⋯ , h N .
By combining (12)-(13), the error system is described as
E ¯ ε D α x ¯ e t = A ¯ x ¯ e t ,
where
E ¯ ε = I N ⊗ E ε 0 0 I N ⊗ E ε , A ¯ = A ¯ 1 A ¯ 2 0 A ¯ 4 , A ¯ 1 = I N ⊗ ∑ k = 1 r η k ξ A k + M ⊗ ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B k K q , A ¯ 2 = − M ⊗ ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B k K q , A ¯ 4 = I N ⊗ ∑ k = 1 r η k ξ A k − M ⊗ ∑ s = 1 r ∑ k = 1 r η s ξ η k ξ W s C k .

3.2. Equivalent Transformations

In this section, equivalence conditions of the consensus of fuzzy FOSPMASs are derived by addressing the stability problem of system (14).
Based on graph theory, it is known that matrix M is positive definite. Therefore, an orthogonal matrix V exists such that V T M V = diag λ 1 , λ 2 , ⋯ , λ N and all eigenvalues λ i of the matrix M possess positive real parts, where i = 1 , 2 , ⋯ , N .
Let X ˜ e t = X e t T X ^ e t T T , where X e = V T ⊗ I N x e t , X ^ e = V T ⊗ I N x ^ e t . According to the properties of Kronecker product, system (14) is transformed into the subsequent form:
E ˜ ε D α X ˜ e i t = A ˜ X ˜ e i t ,
where
E ˜ ε = E ε 0 0 E ε , A ˜ = A ˜ 1 A ˜ 2 0 A ˜ 4 , [ 0 ] A ˜ 1 = ∑ k = 1 r η k ξ A k + λ i ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B k K q , A ˜ 2 = − λ i ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B k K q , A ˜ 4 = ∑ k = 1 r η k ξ A k − λ i ∑ s = 1 r ∑ k = 1 r η s ξ η k ξ W s C k .
In order to analyze the stability of system (15), two independent SPSs are constructed as follows:
E ε D α X e i t = A ˜ 1 X e i t ,
E ε D α X ^ e i t = A ˜ 4 X ^ e i t .
Lemma 6.
System (15) is stable iff both systems (16) and (17) are stable.
Proof. 
According to Lemma 1, system (15) is stable iff arg spec E ˜ − 1 ε A ˜ > π 2 α .
Factorize the characteristic determinant of the system (15) as
det s α E ˜ ε − A ˜ = det s α E ε − A ˜ 1 × det s α E ε − A ˜ 4 .
It implies that the stability of system (15) is dependent on the stability of two subsidiary systems (16) and (17). Thus, system (15) is stable iff systems (16) and (17) are simultaneously stable. □
Definition 1.
The consensus of T-S fuzzy FOSPMAS (6)-(7) is achieved via protocol (9) if
lim t → ∞ ∥ x i t − x 0 t ∥ = 0 , i = 1 , 2 , ⋯ , N .
From Definition 1 and Lemma 6, for achieving the consensus of fuzzy FOSPMAS (6)-(7), it is necessary for both systems (16) and (17) to be stable. Therefore, in order to derive the stability conditions of (16) and (17), the following equivalent transformation is presented.
The matrix E ε is decomposed into
E ε = E 1 + ε − β E 2 ,
where the scalar β > 0 , E 1 = I n 1 0 0 β I n 2 , E 2 = 0 0 0 I n 2 .
Let f 1 t = D α X e i t , x z t = X e i T t , f 1 T t T . (16) is derived as
E D α x z t = ∑ k = 1 r η k ξ A k 1 + ε − β A 2 + λ i ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B ¯ k K ¯ q x z t ,
where E = I n 0 0 0 , A k 1 = 0 I n A k − E 1 , A 2 = 0 0 0 − E 2 , B ¯ k = 0 B k , K ¯ q = K q 0 .
Similarly, denote f 2 t = D α X ^ e i t , x ^ z t = X ^ e i T t , f 2 T t T . (17) is reformulated as
E D α x ^ z t = ∑ k = 1 r η k ξ A ¯ k 1 + ε − β A 2 − λ i ∑ s = 1 r ∑ k = 1 r η s ξ η k ξ W ¯ s C ¯ k x ^ z t ,
where A ¯ k 1 = 0 A k I n − E 1 , W ¯ q = W q 0 , C ¯ k = 0 C k .
Lemma 7.
With ε > 0 , system (16) is stable iff system (18) is admissible.
Proof. 
Based on the aforementioned analysis, system (18) is reformulated as
E D α x z t = 0 I n ∑ k = 1 r η k ξ A k + λ i ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B k K q − E ε x z t .
According to Lemma 2, set U = V = I in (3), then system (20) is admissible iff E ε is nonsingular and
arg spec E − 1 ε ∑ k = 1 r η k ξ A k + λ i ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B k K q > π 2 α .
Rewrite system (16) as
D α X e i t = E − 1 ε ∑ k = 1 r η k ξ A k + λ i ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B k K q X e i t .
By Lemma 1, it is obtained from (21) that system (16) is stable iff system (18) is admissible. □
According to Lemma 7, the stability conditions of systems (16) and (17) are interpreted as the admissibility conditions for systems (18) and (19).

3.3. Consensus Conditions of T-S Fuzzy FOSPMAS

In this section, the LMI criteria for consensus of fuzzy FOSPMAS (6)-(7) are proposed by studying the admissibility of systems (18) and (19).
Theorem 1.
Given 0 < ε ̲ < ε ¯ , the consensus of fuzzy FOSPMAS (6)-(7) with α ∈ 1 , 2 and any ε ∈ ε ̲ , ε ¯ is achieved via protocol (9), if there exist matrices P 1 , P 2 , H q , G s , and positive scalars μ 1 , μ 2 such that
E P 1 = P 1 T E T ⩾ 0 ,
Φ k k < 0 , k = 1 , 2 , ⋯ , r ,
Φ k q + Φ q k < 0 , 1 ⩽ k < q ⩽ r ,
E T P 2 = P 2 T E ⩾ 0 ,
Ψ k k < 0 , k = 1 , 2 , ⋯ , r ,
Ψ k s + Ψ s k < 0 , 1 ⩽ k < s ⩽ r ,
where
Φ k q = sym Θ ⊗ A k 1 P 1 + λ i B ¯ k H q I 2 ⊗ P 1 T Θ ⊗ μ 1 A 2 − 4 μ 1 ε ¯ − ε ̲ 2 I 2 0 ∗ ∗ − μ 1 I 2 ,
Ψ k s = sym Θ ⊗ A ¯ k 1 T P 2 − λ i C ¯ k T G s T I 2 ⊗ P 2 T Θ ⊗ μ 2 A 2 T ∗ − 4 μ 2 ε ¯ − ε ̲ 2 I 2 0 ∗ ∗ − μ 2 I 2 .
The gain matrices are derived as
K ¯ q = H q P 1 − 1 , W ¯ s = P 2 − T G s .
Proof. 
Reformulate (18) with β = ε ̲ + ε ¯ 2 as
E D α x z t = ∑ k = 1 r η k ξ A k 1 + ε − ε ̲ + ε ¯ 2 A 2 + λ i ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B ¯ k K ¯ q x z t .
From η k ξ ⩾ 0 , (23) and (24) ensure that the following inequality holds:
Δ 1 I 2 ⊗ P 1 T μ 1 Θ ⊗ A 2 ∗ − 4 μ 1 ε ¯ − ε ̲ 2 I 2 0 ∗ ∗ − μ 1 I 2 < 0 ,
where
Δ 1 = sym Θ ⊗ ∑ k = 1 r η k ξ A k 1 P 1 + λ i ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B ¯ k H q .
By pre- and post-multiplying (29) with diag I , I μ 1 , I μ 1 , it is transformed as follows:
Δ 1 I 2 ⊗ P 1 T μ 1 μ 1 Θ ⊗ A 2 ∗ − 4 ε ¯ − ε ̲ 2 I 2 0 ∗ ∗ − I 2 < 0 .
According to the Schur complement, (30) is equivalent to
Δ 1 + I 2 ⊗ P 1 T μ 1 μ 1 Θ ⊗ A 2 ε ¯ − ε ̲ 2 4 I 0 0 I I 2 ⊗ P 1 μ 1 μ 1 Θ ⊗ A 2 T < 0 .
Considering ε − ε ̲ + ε ¯ 2 ⩽ ε ¯ − ε ̲ 2 in (31) and Lemma 5, it gives
Δ 1 + ε − ε ̲ + ε ¯ 2 sym Θ ⊗ A 2 P 1 < 0 .
Substituting ∑ q = 1 r η q ξ H q = ∑ q = 1 r η q ξ K ¯ q P 1 into (32), it yields the subsequent expression as
sym Θ ⊗ ∑ k = 1 r η k ξ A k 1 + ε − ε ̲ + ε ¯ 2 A 2 + λ i ∑ k = 1 r ∑ q = 1 r η k ξ η q ξ B ¯ k K ¯ q P 1 < 0 .
According to Lemma 3, system (28) with α ∈ 1 , 2 is admissible from (22) and (33).
Similarly, substituting β = ε ̲ + ε ¯ 2 into system (19), it yields
E D α x ^ z t = ∑ k = 1 r η k ξ A ¯ k 1 + ε − ε ̲ + ε ¯ 2 A 2 − λ i ∑ s = 1 r ∑ k = 1 r η s ξ η k ξ W ¯ s C ¯ k x ^ z t .
Based on η k ξ ⩾ 0 , the following inequality is derived from (26) and (27):
Δ 2 I 2 ⊗ P 2 T μ 2 Θ ⊗ A 2 T ∗ − 4 μ 2 ε ¯ − ε ̲ 2 I 2 0 ∗ ∗ − μ 2 I 2 < 0 ,
where
Δ 2 = sym Θ ⊗ ∑ k = 1 r η k ξ A ¯ k 1 T P − λ i ∑ s = 1 r ∑ k = 1 r η s ξ η k ξ C ¯ k T G s T .
By pre- and post-multiplying (35) with diag I , I μ 2 , I μ 2 , it is transformed as
Δ 2 I 2 ⊗ P 2 T μ 2 μ 2 Θ ⊗ A 2 T ∗ − 4 ε ¯ − ε ̲ 2 I 2 0 ∗ ∗ − I 2 < 0 .
In the same way, (36) is equivalent to
Δ 2 + I 2 ⊗ P 2 T μ 2 μ 2 Θ ⊗ A 2 T ε ¯ − ε ̲ 2 4 I 0 0 I I 2 ⊗ P 2 μ 2 μ 2 Θ ⊗ A 2 T T < 0 .
From Lemma 5 and ε − ε ̲ + ε ¯ 2 ⩽ ε ¯ − ε ̲ 2 , it yields
Δ 2 + ε − ε ̲ + ε ¯ 2 sym Θ ⊗ A 2 T P 2 < 0 .
Substituting ∑ s = 1 r η s ξ G s = P 2 T ∑ q = 1 r η q ξ W ¯ s into (38), it gives
sym Θ ⊗ ∑ k = 1 r η k ξ A ¯ k 1 + ε − ε ̲ + ε ¯ 2 A 2 − λ i ∑ s = 1 r ∑ k = 1 r η s ξ η k ξ C ¯ k W ¯ s T P 2 < 0 .
Given the equivalence between the admissibility of E , A , α and that of E T , A T , α , from (25) and (39), it is deduced that system (34) with α ∈ 1 , 2 is admissible according to Lemma 3. To sum up, (6)-(7) achieves leader-following consensus via observer-based protocol (9). □
Remark 1. The conditions in Theorem 1 involve LMIs with equality constraints, rendering them fragile and potentially prone to computational difficulty. Consequently, the subsequent theorem presents strict LMI conditions to address these issues and enhance computational accuracy.
Theorem 2.
Given 0 < ε ̲ < ε ¯ , the consensus of fuzzy FOSPMAS (6)-(7) with α ∈ 1 , 2 and any ε ∈ ε ̲ , ε ¯ is achieved via protocol (9), if there exist matrices X 1 > 0 , X 2 > 0 , Y 1 , Y 2 , H q , G s , and positive scalars μ 1 , μ 2 such that
Γ k k < 0 , k = 1 , 2 , ⋯ , r ,
Γ k q + Γ q k < 0 , 1 ⩽ k < q ⩽ r ,
Υ k k < 0 , k = 1 , 2 , ⋯ , r ,
Υ k s + Υ s k < 0 , 1 ⩽ k < s ⩽ r ,
where
Preprints 113587 i001
S 1 , S 2 ∈ R n × n − m are arbitrary matrices with full column rank satisfying E S 1 = 0 a n d E T S 2 = 0 . The gain matrices are derived as
K ¯ q = H q X 1 E T + S 1 Y 1 − 1 , W ¯ s = X 2 E + S 2 Y 2 − T G s .
Proof. 
Assume that there exist matrices X 1 > 0 , X 2 > 0 , Y 1 , Y 2 , H q , G q , and scalars μ 1 > 0 , μ 2 > 0 such that (40)-(43). Let
P 1 = X 1 E T + S 1 Y 1 , P 2 = X 2 E + S 2 Y 2 .
Then by (40)-(43), it is easy to verify P 1 , P 2 , H q , G q and scalars μ 1 > 0 , μ 2 > 0 satisfying (22)-(27). Therefore, by Theorem 1, (6)-(7) achieves the consensus. □
Theorem 3.
Given 0 < ε ̲ < ε ¯ , the consensus of fuzzy FOSPMAS (6)-(7) with α ∈ 0 , 1 and any ε ∈ ε ̲ , ε ¯ is achieved via protocol (9), if there exist matrices X 1 , X 2 , Y 1 , Y 2 , H q , G s , and positive scalars μ 1 , μ 2 such that
E X 1 E Y 1 − E Y 1 E X 1 = X 1 T E T − Y 1 T E T Y 1 T E T X 1 T E T ⩾ 0 ,
Π k k < 0 , k = 1 , 2 , ⋯ , r ,
Π k q + Π q k < 0 , 1 ⩽ k < q ⩽ r ,
E T X 2 E T Y 2 − E T Y 2 E T X 2 = X 2 T E − Y 2 T E Y 2 T E X 2 T E ⩾ 0 ,
Ω k k < 0 , k = 1 , 2 , ⋯ , r ,
Ω k s + Ω s k < 0 , 1 ⩽ k < s ⩽ r ,
where
Preprints 113587 i001
Choose the gain matrices as
K ¯ q = H q a X 1 − b Y 1 − 1 , W ¯ s = a X 2 − b Y 2 − T G s .
Proof. 
The proof parallels that of Theorem 1 and bases on Lemma 4, which is omitted here for brevity. □
Theorem 4.
Given 0 < ε ̲ < ε ¯ , the consensus of fuzzy FOSPMAS (6)-(7) with α ∈ 0 , 1 and any ε ∈ ε ̲ , ε ¯ is achieved via protocol (9), if there exist matrices X 1 , X 2 , Y 1 , Y 2 , Q 1 , Q 2 , H q , G s , and positive scalars μ 1 , μ 2 such that
X 1 Y 1 − Y 1 X 1 > 0 ,
Ξ k k < 0 , k = 1 , 2 , ⋯ , r ,
Ξ k q + Ξ q k < 0 , 1 ⩽ k < q ⩽ r ,
X 2 Y 2 − Y 2 X 2 > 0 ,
Λ k k < 0 , k = 1 , 2 , ⋯ , r ,
Λ k s + Λ s k < 0 , 1 ⩽ k < s ⩽ r ,
where
Preprints 113587 i003
S 1 , S 2 satisfy conditions in Theorem 2. The gain matrices are chosen as
K ¯ q = H q a X 1 − b Y 1 E T + S 1 Q 1 − 1 , W ¯ s = a X 2 − b Y 2 E + S 2 Q 2 − T G s .
Proof. 
Assume that there exist matrices X 1 , X 2 , Y 1 , Y 2 , Q 1 , Q 2 , H q , G q , and scalars μ 1 > 0 , μ 2 > 0 such that (50)-(55). Let
X ¯ 1 = X 1 E T + a − 1 S 1 Q 1 , Y ¯ 1 = Y 1 E T , X ¯ 2 = X 2 E + a − 1 S 2 Q 2 , Y ¯ 2 = Y 2 E .
By (50)-(55), it is easy to verify X ¯ 1 , X ¯ 2 , Y ¯ 1 , Y ¯ 2 , H q , G q and scalars μ 1 > 0 , μ 2 > 0 satisfying (44)-(49). Therefore, by Theorem 3, the consensus of (6)-(7) is achieved. □

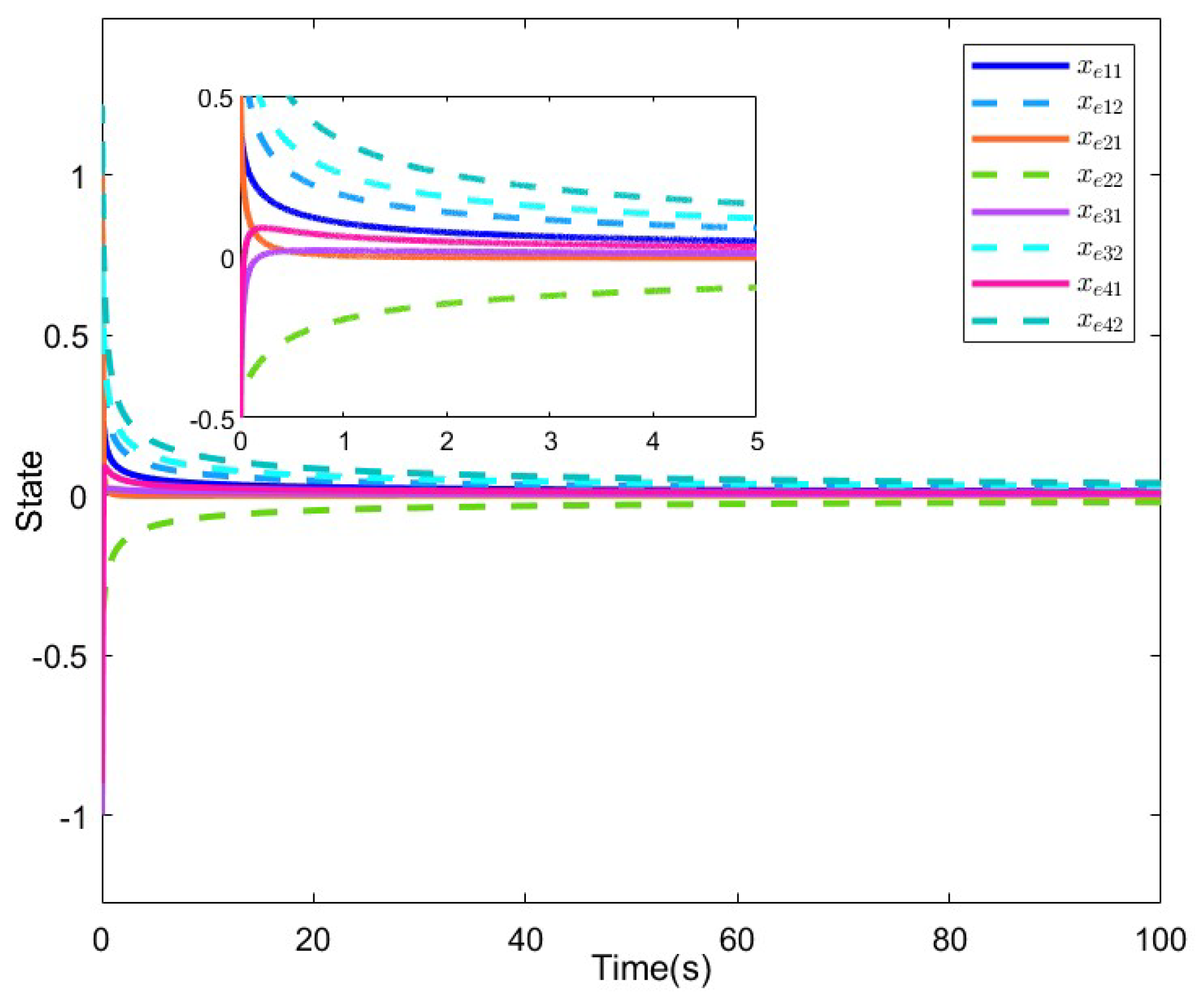
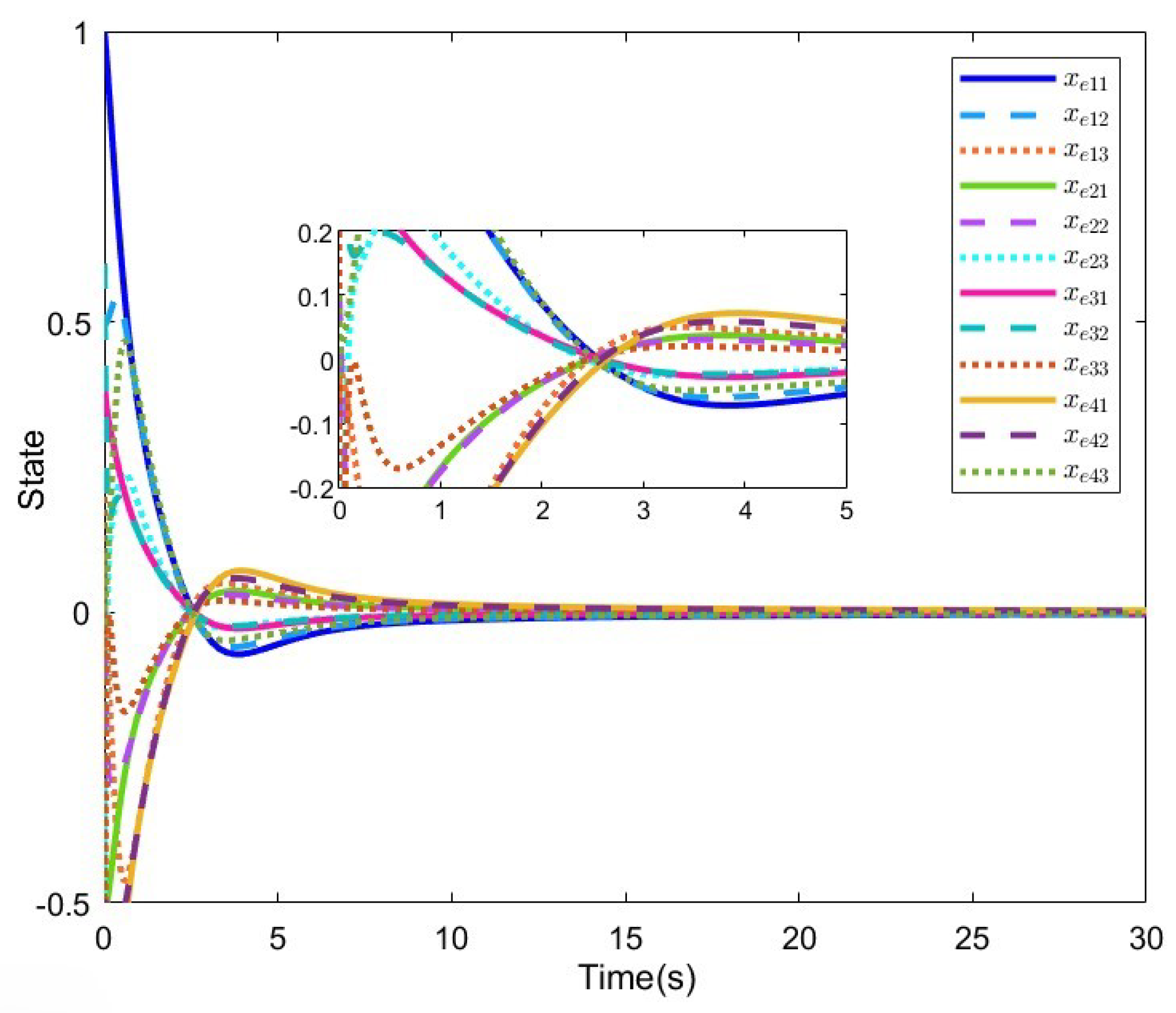
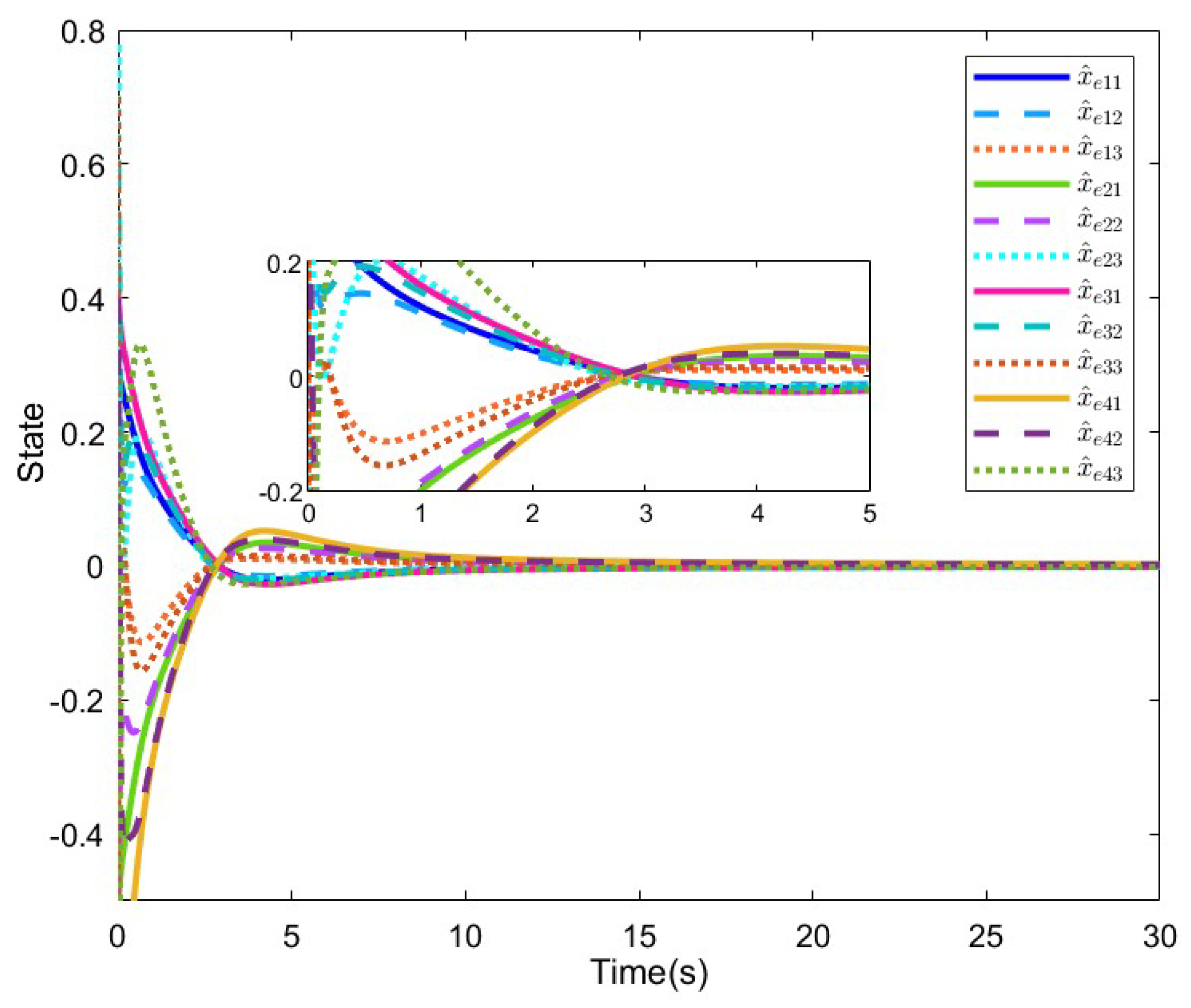
4. Numerical Examples

This section presents two demonstrative instances that highlight the effectiveness of control protocol in achieving the consensus of fuzzy FOSPMASs with order α in 0 , 1 and 1 , 2 , respectively.
Example 1. Consider a T-S fuzzy FOSPMAS composed of one leader and four followers, and the behavior of each agent is described by the fractional order RLC circuit model as shown in Figure 1.
The capacitor and inductor have fractional characteristics with order α . L represents a very small parasitic inductance. R 1 , R 2 denote the resistance of corresponding resistors. R 3 is a diode and its characteristic function is R 3 = 1 / 0 . 4 + 0 . 15 V D 2 t . It is known that the relationships between voltages are V D t = V C t and V S t = − V C t . The dynamic of each agent is subsequently described by
C D α V C t = − V C t R 2 − V C t R 3 + i L t L D α i L t = V S t − V C t + R 1 i L t + u t
Let x i 1 t = V C t , x i 2 t = i L t , ε = L , then the circuit model (56) is reformulated as follows:
D α x i 1 t ε D α x i 2 t = − 1 R 2 C − 1 C 0 . 4 + 0 . 15 x i 1 2 t 1 C − 2 R 1 x i 1 t x i 2 t + 0 1 u i t ,
where i = 1 , 2 , 3 , 4 .
The parameters are chosen as C = 0 . 3 F , ε = 0 . 02 H , R 1 = 0 . 1 Ω , R 2 = 0 . 5 Ω , α = 0 . 5 . It is assumed that x 11 t belongs to − 2 , 2 . Subsequently, the fuzzy rules are set as follows:
Rule 1: If the value of x 11 t is approximately 0, then
E ε D α x i t = A 1 x i t + B 1 u i t y i t = C 1 x i t and E ε D α x 0 t = A 1 x 0 t y 0 t = C 1 x 0 t
Rule 2: If the value of x 11 t is approximately ± 2 , then
E ε D α x i t = A 2 x i t + B 2 u i t y i t = C 2 x i t and E ε D α x 0 t = A 2 x 0 t y 0 t = C 2 x 0 t
where
E ε = 1 0 0 ε , A 1 = − 8 3 − 2 0.1 , A 2 = − 10 3 − 2 0.1 ,
B 1 = B 2 = 0 1 T , C 1 = C 2 = 1 0.5 .
The fuzzy weighting function is selected as η 1 ξ t = 1 − 0 . 25 x e 11 2 t , η 2 ξ t = 1 − η 1 ξ t . The communication network between these agents is depicted in Figure 2.
With ε ̲ = 0 . 001 , ε ¯ = 0 . 04 , by solving LMIs (50)-(55) in Theorem 4, the feasible solutions are obtained as
K ¯ 1 = 0.4367 − 0.0916 0 0 ,
K ¯ 2 = 0.4371 − 0.0916 0 0 ,
W ¯ 1 = 1.4511 0.1933 0 0 T ,
W ¯ 2 = 1.4562 0.1938 0 0 T .
Let ε = 0 . 02 , then the tracking errors and estimation errors are depicted in Figure 3 and Figure 4. The consensus errors to zero means that each follower converges toward the leader, which demonstrates that system achieves the consensus by using the observer-based protocol (9). It indicates the practical applicability and efficacy of the proposed method in α ∈ 1 , 2 .
Example 2. Considering the T-S fuzzy FOSPMAS (6)-(7) within the topology in Figure 2, the fuzzy rules of the system are established in the manner outlined below:
Rule 1: If x e 11 t is Π k 1 , then
E ε D α x i t = A 1 x i t + B 1 u i t y i t = C 1 x i t and E ε D α x 0 t = A 1 x 0 t y 0 t = C 1 x 0 t
Rule 2: If x e 11 t is Π k 2 , then
E ε D α x i t = A 2 x i t + B 2 u i t y i t = C 2 x i t and E ε D α x 0 t = A 2 x 0 t y 0 t = C 2 x 0 t
The remaining parameters are proposed as follows:
α = 1 . 2 , E ε = 1 0 0 0 1 0 0 0 ε , A 1 = − 5 9 5 12 − 5 13 5 − 10 − 5 , A 2 = − 4 5 5 5 − 18 15 5 − 10 − 5 ,
B 1 = 1 1 0.5 T , B 2 = 0.5 0.5 1 T ,
C 1 = 1 0.5 1 , C 2 = 0.5 1 0.5 .
Assuming that the state x e 11 t belongs to − 1 , 1 , the fuzzy weighting function is selected as η 1 ξ t = x e 11 , η 2 ξ t = 1 − η 1 ξ t .
Considering ε ̲ = 0 . 001 , ε ¯ = 0 . 03 , the feasible solutions are presented based on the LMIs (40)-(43) in Theorem 2:
K ¯ 1 = 0 . 1193 − 0 . 2976 − 0 . 1530 0 0 0 ,
K ¯ 2 = − 0.0783 0.1285 0.0181 0 0 0 ,
W ¯ 1 = − 0.0009 − 0.5099 0.0147 0 0 0 T ,
W ¯ 2 = 0.0150 0.4288 0.0108 0 0 0 T .
Figure 5 and Figure 6 present the simulation results of the error system (14) with ε = 0 . 02 . As depicted in Figure 5, the state of follower agents exhibits a successful tracking of the state of leader agent, indicating that the consensus issue of fuzzy FOSPMAS (6)-(7) with α ∈ 1 , 2 is solved by the criteria in Theorem 2.

5. Conclusions

In this paper, the T-S fuzzy FOSPMAS with α ∈ 0 , 2 has been modeled and studied for more accurately describing actual complex systems. The consensus problem of T-S fuzzy FOSPMAS (6)-(7) is transformed into admissibility assessment of fuzzy SFOSs (18) and (19). In distinction to the methodologies in previous literature, the proposed method not only overcomes the pathological problem arising from multiple time-scale, but also is applicable to both standard and non-standard SPMASs. Theorems 1 and 3 provide sufficient conditions for achieving the consensus of (6)-(7) with α ∈ 0 , 1 and 1 , 2 . Furthermore, strict LMI criteria are given in Theorems 2 and 4, which are solved easily with LMI toolbox. Future research is certainly required to overcome the challenges in consensus and H ∞ control of uncertain FOSPMASs.

Author Contributions

Conceptualization, methodology, validation, X.W. and X.Z.; writing—original draft preparation, X.W.; writing—review and editing, X.W. and X.Z.; visualization, X.W. and S.-H.Y.; supervision, W.P. and D.B.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 62103093, the National Key Research and Development Program of China under Grant 2022YFB3305905, fundamental research funds for the central universities N2224005-3 and national key research and development program topic 2020YFB1710003.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Santos, G.; Pinto, T.; Praça, I.; Vale, Z. MASCEM: Optimizing the performance of a multi-agent system. Energy 2016, 111, 513–524. [Google Scholar] [CrossRef]
  2. Jiménez, A.C.; García-Díaz, V.; Bolaños, S. A decentralized framework for multi-agent robotic systems. Sensors 2018, 18, 417. [Google Scholar] [CrossRef] [PubMed]
  3. Iñigo-Blasco, P.; Diaz-del-Rio, F.; Romero-Ternero, M.C.; Cagigas-Muñiz, D.; Vicente-Diaz, S. Robotics software frameworks for multi-agent robotic systems development. Robotics and Autonomous Systems 2012, 60, 803–821. [Google Scholar] [CrossRef]
  4. Florez-Lozano, J.; Caraffini, F.; Parra, C.; Gongora, M. Cooperative and distributed decision-making in a multi-agent perception system for improvised land mines detection. Information Fusion 2020, 64, 32–49. [Google Scholar] [CrossRef]
  5. Yan, Z.W.; Han, L.; Li, X.D.; Dong, X.W.; Li, Q.D.; Ren, Z. Event-triggered formation control for time-delayed discrete-time multi-agent system applied to multi-UAV formation flying. Journal of the Franklin Institute 2023, 360, 3677–3699. [Google Scholar] [CrossRef]
  6. Zhang, J.X.; Xu, K.D.; Wang, Q.G. Prescribed Performance Tracking Control of Time-Delay Nonlinear Systems With Output Constraints. IEEE/CAA Journal of Automatica Sinica 2024, 11, 1557–1565. [Google Scholar] [CrossRef]
  7. Zhang, J.X.; Yang, G.H. Low-Complexity Tracking Control of Strict-Feedback Systems With Unknown Control Directions. IEEE Transactions on Automatic Control 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
  8. Ren, W. On Consensus Algorithms for Double-Integrator Dynamics. IEEE Transactions on Automatic Control 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
  9. Tian, Y.P.; Liu, C.L. Consensus of Multi-Agent Systems With Diverse Input and Communication Delays. IEEE Transactions on Automatic Control 2008, 53, 2122–2128. [Google Scholar] [CrossRef]
  10. Wen, G.H.; Duan, Z.S.; Yu, W.W.; Chen, G.R. Consensus in multi-agent systems with communication constraints. International Journal of Robust and Nonlinear Control 2012, 22, 170–182. [Google Scholar] [CrossRef]
  11. Zhang, H.; Feng, G.; Yan, H.C.; Chen, Q.J. Observer-Based Output Feedback Event-Triggered Control for Consensus of Multi-Agent Systems. IEEE Transactions on Industrial Electronics 2014, 61, 4885–4894. [Google Scholar] [CrossRef]
  12. Tan, M.C.; Song, Z.Q.; Zhang, X.M. Robust leader-following consensus of cyber-physical systems with cyber attack via sampled-data control. ISA Transactions 2021, 109, 61–71. [Google Scholar] [CrossRef]
  13. Hilfer, R. Applications of fractional calculus in physics; World scientific, 2000.
  14. Ye, Y.Y.; Su, H.S. Leader-following consensus of general linear fractional-order multiagent systems with input delay via event-triggered control. International Journal of Robust and Nonlinear Control 2018, 28, 5717–5729. [Google Scholar] [CrossRef]
  15. Ye, Y.Y.; Su, H.S. Leader-following consensus of nonlinear fractional-order multi-agent systems over directed networks. Nonlinear Dynamics 2019, 96, 1391–1403. [Google Scholar] [CrossRef]
  16. Yang, R.; Liu, S.; Tan, Y.Y.; Zhang, Y.J.; Jiang, W. Consensus analysis of fractional-order nonlinear multi-agent systems with distributed and input delays. Neurocomputing 2019, 329, 46–52. [Google Scholar] [CrossRef]
  17. Yang, R.; Liu, S.; Li, X.Y.; Zhao, X.W.; Pan, G. Consensus of fractional-order delayed multi-agent systems in Riemann-Liouville sense. Neurocomputing 2020, 396, 123–129. [Google Scholar] [CrossRef]
  18. Hu, T.T.; He, Z.; Zhang, X.J.; Zhong, S.M. Leader-following consensus of fractional-order multi-agent systems based on event-triggered control. Nonlinear Dynamics 2020, 99, 2219–2232. [Google Scholar] [CrossRef]
  19. Bahrampour, E.; Asemani, M.H.; Dehghani, M.; Tavazoei, M. Consensus control of incommensurate fractional-order multi-agent systems: An LMI approach. Journal of the Franklin Institute 2023, 360, 4031–4055. [Google Scholar] [CrossRef]
  20. Fridman, E. Robust sampled-data H∞ control of linear singularly perturbed systems. IEEE Transactions on Automatic control 2006, 51, 470–475. [Google Scholar] [CrossRef]
  21. Yang, C.Y.; Zhang, L.L.; Sun, J. Anti-windup controller design for singularly perturbed systems subject to actuator saturation. IET Control Theory & Applications 2016, 10, 469–476. [Google Scholar]
  22. Saksena, V. R; O’reilly, J.; Kokotovic, P.V. Singular perturbations and time-scale methods in control theory: survey 1976-1983. Automatica 1984, 20, 273–293. [Google Scholar] [CrossRef]
  23. Naidu, D. Singular perturbations and time scales in control theory and applications: An overview. Dynamics of Continuous Discrete and Impulsive Systems Series B 2002, 9, 233–278. [Google Scholar]
  24. Wang, Y.Y.; Shi, P.; Yan, H.C. Reliable control of fuzzy singularly perturbed systems and its application to electronic circuits. IEEE Transactions on Circuits and Systems I: Regular Papers 2018, 65, 3519–3528. [Google Scholar] [CrossRef]
  25. Munje, R.; Patre, B.; Tiwari, A.; Munje, R.; Patre, B.; Tiwari, A. State feedback control using linear quadratic regulator. Investigation of Spatial Control Strategies with Application to Advanced Heavy Water Reactor 2018, 61–77. [Google Scholar]
  26. Xia, G.Q.; Zhang, Y.; Zhang, W.; Chen, X.M.; Yang, H.Y. Multi-time-scale 3-D coordinated formation control for multi-underactuated AUV with uncertainties: Design and stability analysis using singular perturbation methods. Ocean Engineering 2021, 230, 109053. [Google Scholar] [CrossRef]
  27. Nagarale, R.M.; Patre, B.M. Composite fuzzy sliding mode control of nonlinear singularly perturbed systems. ISA Transactions 2014, 53, 679–689. [Google Scholar] [CrossRef]
  28. Litkouhi, B.; Khalil, H. Multirate and composite control of two-time-scale discrete-time systems. IEEE Transactions on Automatic Control 1985, 30, 645–651. [Google Scholar] [CrossRef]
  29. Yang, C.Y.; Che, Z.Y.; Shen, L.P. Integral sliding mode control for singularly perturbed systems with matched disturbances. 2017 Chinese Automation Congress (CAC), 2017, pp. 2452-2456. [CrossRef]
  30. Gao, Y.B.; Sun, B.H.; Lu, G.P. Passivity-Based Integral Sliding-Mode Control of Uncertain Singularly Perturbed Systems. IEEE Transactions on Circuits and Systems II: Express Briefs 2011, 58, 386–390. [Google Scholar] [CrossRef]
  31. Liu, W.; Wang, Y.Y.; Wang, Z.M. H∞ observer-based sliding mode control for singularly perturbed systems with input nonlinearity. Nonlinear Dynamics 2016, 85, 573–582. [Google Scholar] [CrossRef]
  32. Fridman, E. Effects of small delays on stability of singularly perturbed systems. Automatica 2002, 38, 897–902. [Google Scholar] [CrossRef]
  33. Ben Rejeb, J.; Morărescu, I.-C.; Daafouz, J. Control design with guaranteed cost for synchronization in networks of linear singularly perturbed systems. Automatica 2018, 91, 89–97. [Google Scholar] [CrossRef]
  34. Tognetti, E.S.; Calliero, T. R; Morărescu, I.-C.; Daafouz, J. Synchronization via output feedback for multi-agent singularly perturbed systems with guaranteed cost. Automatica 2021, 128, 109549. [Google Scholar] [CrossRef]
  35. Xu, J.; Niu, Y.G.; Zou, Y.Y. Finite-time consensus for singularity-perturbed multiagent system via memory output sliding-mode control. IEEE Transactions on Cybernetics 2021, 52, 8692–8702. [Google Scholar] [CrossRef] [PubMed]
  36. Zhang, Y.Q.; Wu, H.Q.; Cao, J.D. Global Mittag-Leffler consensus for fractional singularly perturbed multi-agent systems with discontinuous inherent dynamics via event-triggered control strategy. Journal of the Franklin Institute 2021, 358, 2086–2114. [Google Scholar] [CrossRef]
  37. Yang, C.Y.; Zhang, Q.L. Multiobjective Control for T-S Fuzzy Singularly Perturbed Systems. IEEE Transactions on Fuzzy Systems 2009, 17, 104–115. [Google Scholar] [CrossRef]
  38. Chen, J.X.; Sun, Y.G.; Min, H.B.; Sun, F.C.; Zhang, Y.G. New results on static output feedback H∞ control for fuzzy singularly perturbed systems: a linear matrix inequality approach. International Journal of Robust and Nonlinear Control 2013, 23, 681–694. [Google Scholar] [CrossRef]
  39. Visavakitcharoen, A.; Assawinchaichote, W.; Shi, Y.; Angeli, C. Event-triggered fuzzy integral control for a class of nonlinear singularly perturbed systems. ISA Transactions 2023, 139, 71–85. [Google Scholar] [CrossRef]
  40. Zhang, X.F.; Han, Z.R. Output feedback control of fractional order Takagi-Sugeno fuzzy singularly perturbed systems. Journal of Vibration and Control 2022, 28, 3162–3172. [Google Scholar] [CrossRef]
  41. Koskie, S.; Coumarbatch, C.; Gajic, Z. Exact slow-fast decomposition of the singularly perturbed matrix differential Riccati equation. Applied Mathematics and Computation 2010, 216, 1401–1411. [Google Scholar] [CrossRef]
  42. Matignon, D. Stability results for fractional differential equations with applications to control processing. Computational engineering in systems applications. Lille, France, 1996, Vol. 2, pp. 963-968.
  43. Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0<α<1 case. ISA Transactions 2018, 82, 42–50. [Google Scholar]
  44. Marir, S.; Chadli, M.; Bouagada, D. New admissibility conditions for singular linear continuous-time fractional-order systems. Journal of the Franklin Institute 2017, 354, 752–766. [Google Scholar] [CrossRef]
  45. Lee, H.J.; Park, J.B.; Chen, G.R. Robust fuzzy control of nonlinear systems with parametric uncertainties. IEEE Transactions on fuzzy systems 2001, 9, 369–379. [Google Scholar]
Preprints 113587 g001
Figure 1. The RLC circuit with the diode.
Figure 1. The RLC circuit with the diode.
Preprints 113587 g001
Preprints 113587 g002
Figure 2. The weighted undirected graph.
Figure 2. The weighted undirected graph.
Preprints 113587 g002
Preprints 113587 g003
Figure 3. Errors between leader and followers in Example 1.
Figure 3. Errors between leader and followers in Example 1.
Preprints 113587 g003
Preprints 113587 g004
Figure 4. Estimation errors of followers in Example 1.
Figure 4. Estimation errors of followers in Example 1.
Preprints 113587 g004
Preprints 113587 g005
Figure 5. Errors between leader and followers in Example 2.
Figure 5. Errors between leader and followers in Example 2.
Preprints 113587 g005
Preprints 113587 g006
Figure 6. Estimation errors of followers in Example 2.
Figure 6. Estimation errors of followers in Example 2.
Preprints 113587 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated