Literature Review on Thermodynamic and Kinetic Limitations of Thermal Decomposition of Methane

Andrzej Mianowski; Mateusz Szul; Tomasz Radko; Aleksander Sobolewski; Tomasz Iluk

doi:10.20944/preprints202408.0065.v1

Submitted:

01 August 2024

Posted:

01 August 2024

You are already at the latest version

Abstract

Based on literature data, an analysis was conducted on the thermodynamic and kinetic dependencies of the thermal decomposition of methane. Course of this process was analysed for both thermal and thermal-catalytic conditions. The elementary reaction, i.e. the synthesis of methane from its elements, including its reversibility, was used as the basis for the for considerations on the kinetic model. The conversion degree was adopted as the kinetic parameter (kinetic variable) since this measure is essential for determining the amount of carbon deposit formed and thus closing the mass balance of this process. Several different kinetic models for the elementary reaction were analysed to determine how do they relate in regard to the constant of the reaction rate. It was determined that regardless of whether the process is catalytic or purely thermal, for temperatures t>900°C, the influence of reversibility of the reaction, has negligible influence on the yield of hydrogen produced, and thus can be omitted from the kinetic models. Special attention was given to iron-based catalysts, analysing the reactivity of Fe/C systems. It was demonstrated that the determined kinetic parameters satisfy the Kinetic Compensation Effect (KCE). Furthermore, by incorporating elements of Transition State Theory (TST), the existence of Entropy-Enthalpy Compensation (EEC) was highlighted. Based on these findings Authors show that through analysis of the changes in activation energy (E=20–421 kJ·mol-1) only an estimate of the optimal process conditions can be found, because the isoconversional temperature is also dependent on the way in which the reaction is conducted (T_{iso}=1200-1450K\ >\ \ T_{eq}). In other words, it was found that strong influences of such factors as T, P, etc. can locally compensate each other. Finally, it was also shown that the relations between KCE and EEC complement each other, which is confirmed by the determined average activation entropy at the isokinetic temperature (∆SB= -275.0 J·(mol·K)-1).

Keywords:

methane

;

thermo-catalytic decomposition

;

thermodynamics

;

kinetics

;

elementary reaction

;

KCE

;

EEC

Subject:

Physical Sciences - Thermodynamics

Introduction

Among known hydrocarbons from C₁ to C₁₄, methane is one of the most unreactive. It is characterized by the lowest Gibbs free energy,

∆_{298} G^{\emptyset} = - 50.76 k J \cdot {m o l}^{- 1}

[1]. The situation changes when oxygen is introduced into the reaction system and in that case, at least six products must be considered, ranging from the most typical (CO₂, CO) to more complex coupling products such as C₂ hydrocarbons (ethane, ethene) or compounds containing oxygen functional groups (formaldehyde, methanol) [2].

Today’s shift in the structure of consumption of energy commodities causes, among other things, intensification of the search for hydrogen production methods. This situation has led to interest in the process of methane pyrolysis, which is an endothermic

(∆_{r} H^{\emptyset} = 74.85 k J \cdot {m o l}^{- 1}

) [3] thermal decomposition of methane that can be noted in the following manner:

C H_{4} ⇄ C + 2 H_{2}

(1)

The efficiency of reaction (1) can be influenced by changing process parameters such as temperature, pressure, as well as through the introduction of a catalyst. Another significant factor determining the course of reaction (1) is the method of heat supply. Generalization distinguishes indirect and direct supply of heat, but the type of reactor used can greatly influence the process. From the standpoint of reactor design, it is known that fixed bed, fluidized bed, or liquid bed reactor are most commonly applied. Moreover, when considering the temperature ranges >1300°C, or processes where plasma is used as a heat source for the reaction, the mechanism of reaction (1) can alter and other products besides hydrogen and structural carbon materials (carbon family) can be expected [3,4,5]. If reaction (1) is conducted at temperatures corresponding to the plasma state, upon quenching the resulting gaseous products, the following reactions may take place:

2 C H_{4} ⇄ C H \equiv C H + 3 H_{2}

(2)

4 C H_{4} ⇄ C H \equiv C H + C H_{2} = C H_{2} + 5 H_{2}

(3)

Thus, equation (1) should be regarded only as a conceptual/general notation of methane pyrolysis (thermal decomposition), while reactions (2) and (3) can illustrate examples of pathways for the formation of acetylene from methane. It should be noted that acetylene can also be obtained from methane through partial combustion, while the trimerization of acetylene is a pathway leading to the synthesis of benzene and higher aromatic hydrocarbons. The reaction network of methane with its pyrolysis products in the form of C_5-6 hydrocarbons is graphically presented in the work [6].

As it was already indicated the course and efficiency of reaction (1) can be influenced by many factors. One of the highest importance has the characteristics of the applied catalyst. In the work [7] most metals known for their activity for decomposition of methane were ranked in decreasing order of their impact on the efficiency/rate of reaction (1): Ni, Co, Ru, Rh > Pt, Re, Ir > Pd, Cu, W, Fe, Mo. Considering the cost criterion, it can be stated that the cheapest and most stable catalysts are those based on Ni, Co, and Fe. Belonging to the group of transition metals, these catalytic materials have partially filled 3d orbitals [7], which is an important similarity with catalysts used in industrial Fischer-Tropsch synthesis.

The above series left out one more catalyst, i.e. carbon materials exhibiting an ordered internal structure of the C element. Carbon catalysts finds somewhat lower attractiveness in pyrolysis of methane mainly due to the requirement for performing the process at temperatures higher than necessary for Fe or Ni (≥1000°C) and lower possibility for tailoring the quality of produced carbon structures. Equally for any type of catalyst available literature on this topic show that the deposition of carbon structures is the main reason for deactivation of the catalyst. Nevertheless, some forms of carbon deposits can be considered catalysts, thus theoretically making the process autocatalytic. Depending on the process conditions, including the characteristic of the catalyst used, carbon deposit produced in the reaction (1), consists of either one dominant or a mixture of different structural forms of the C element. Literature describes carbon black, mesoporous carbons, carbon nanotubes (CNTs), carbon nanofibers (CNFs), multi-walled carbon nanotubes (MWCNTs), amorphous turbostratic carbon, graphite-like carbon, filamentous (or foam) carbon as solid product of methane pyrolysis reaction. Collectively these materials are referred to as the “carbon family”. Till this point there are no instances of classic allotropic forms of carbon being used in this place; however, activated carbons are. Two important pathways for purely thermal or utilizing carbon as catalyst in pyrolysis of methane need to be indicated here. First is connected with a somewhat novel approach where methane pyrolysis is performed to lower the reactivity of biochars (e.g. for metallurgical processes). In this application the reason for developing decomposing methane using biochar is to introduce the carbon deposits onto its surface, thus altering its structure In this case the structure of produced carbon deposits, or productivity of hydrogen play minor role. Second type of processes are those where tailoring and maintaining the quality of solid C-product is paramount. Today production of carbon black or graphite are the large-scale examples of the later. For the future though, we see the attention to shift towards structured carbon materials and also to hydrogen.

It is exactly due to the possibility of tailoring the properties of C-product why the literature on the selection of catalysts is so extensive. Among the catalysts listed above, nickel [3,4,5,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47] holds a special position due to its effectiveness, while iron [3,4,5,7,8,27,31,40,42,48,49,50,51,52,53,54,55,56,57,58,59,60,61] is notable for being much cheaper and more environmentally friendly.

The characteristic that combines both iron and nickel in the context of reaction (1) is the multifunctional catalytic role of these materials, which is mainly attributed to the formation and decomposition of carbides. For this reason the processes associated with the carburisation and decarburisation of iron [62] deserve special attention. It is indicated that these processes involve the formation/decomposition reactions of cementite (Fe₃C) [60,63,64,65,66,67] as well as Hägg carbide (Fe₅C₂) [68]. Therefore in the context of iron, significant importance is attributed to the reactivity and properties of cementite [68,69,70,71,72,73]. In contrast, the literature is much poorer in research that considers the activity of nickel carbides Ni₃C, Ni₈C [13,45], or Ni₈C on TiC substrate [47].

When considering the course of catalysed reaction (1), the emergence of a new solid phase induces much higher level of complexity of the analysis. For pyrolysis, according to [4] the mechanism of molecular or dissociative adsorption on catalysts involves the formation of radicals: CH₃^∙, CH₂^∙, CH^∙, C^∙, H^∙ as well as their subsequent reduction and recombination. Final steps of these models are the nucleation of free carbon and the growth of its deposit [5]. It is generally accepted that the radical mechanism predominates for the reaction performed at temperatures >1200°C [41], and more details on reaction mechanisms can be found in [7,12,65,74,75,76,77,78,79].

Aim of the Work

In light of the above-presented information, in the subsequent parts of the review, Authors dispute the issues of phenomenological thermodynamics that were found to be inadequately described till this point.

In connection with the limitations presented in the literature regarding the comprehensive and unambiguous description of methane pyrolysis within a single model that represents its course on a micro scale, it was deemed appropriate to attempt an analysis of the validity of using an approach typical of phenomenological thermodynamics for this purpose. Therefore, in the subsequent part of this work, the applicability of kinetic equations as tools for describing the course of reaction (1) was verified, and thus the correctness of using the concept of an elementary reaction in the context of the methane pyrolysis process. To test the hypothesis that the constraints (limits) resulting solely from phenomenological thermodynamics are sufficient for verifying the above considerations, the study employed experimental results presented in the literature to date. It is important to note that in the analysed approach, the characteristic parameters are the Kinetic Compensation Effect (KCE) and the equivalent elements of Transition State Theory (TST) expressed through Entropy-Enthalpy Compensation (EEC).

Phenomenological Thermodynamics and Thermodynamics of Activation

From a thermodynamic point of view reaction (1) is reversible, and is expressed by the equilibrium constant that is a dependant of temperature and pressure and can be written as [3,4]:

K = K_{p} {(\frac{P^{\emptyset}}{P})}^{∆ ν}

(4)

For reaction (1) and gaseous components

∆ ν = 1

.

Because this form of equilibrium constant description is of low utility, it is more valuable to derive this relationship using the Gibbs free energy of the process as a function of temperature. For Equation (1) such expression was presented e.g. in the work [20]:

∆𝑟𝐺∅=89.66−0.1023∙𝑇−4.28∙10−6𝑇2−2499.36𝑇 , kJ·mol⁻¹

(5)

and through dividing both sides by

(- R T)

we get:

\ln K_{p} = - \frac{10784.08}{T} + 12.30 + 0.000515 \cdot T + \frac{300620.52}{T^{2}}

(6)

For the temperature

T_{e q .} = 818.84 K

above equations fulfil the criteria

∆ G^{\emptyset} = 0

and

K_{p} = 1

.

A modified, shorter version of the equation (5) can be expressed in the form that uses the relationship given in [55].

∆_{r} G^{\emptyset} = 88.039 - 0.1079 \cdot T,

(7)

Similarly, this equation when divided by (

- R T

) takes the form of:

\ln K_{p} = - \frac{10589.25}{T} + 12.978

(8)

In Equation (8) similar constants are applicable:

{573 K \leq T}_{e q} \leq 1773 K

,

P = 0.1 M P a

and

T_{e q} = 815.93 K

. When considering the above-mentioned constants a very similar relationship can be derived from [80] and for this reason Eqs. (4–8), and in particular Eqs. (7,8) are used as basis for further discussion.

On the other hand, algebraic forms of thermodynamic equilibrium constants

{K = K}_{p} {= K}_{x} {= K}_{α} e t c .

(for constant total pressure) are correct for the following experimental (without subscript) and equilibrium (with the index eq.) values.

{K = K}_{x} = {\frac{{x_{H_{2}}}^{2}}{1 - x_{H_{2}}}|}_{e q .} = {\frac{(1 - x_{C H_{4}})^{2}}{x_{C H_{4}}}|}_{e q .}

(9)

Or

{K = K}_{α} = {\frac{4 {α_{{C H}_{4}}}^{2}}{1 - {α_{{C H}_{4}}}^{2}}|}_{e q .}

(10)

for the condition of constant flow of methane

\dot{V} > 0

:

α_{{C H}_{4}} = \frac{x_{H_{2}}}{2 - x_{H_{2}}} = \frac{1 - x_{C H_{4}}}{1 + x_{C H_{4}}}

(11)

Because

x_{H_{2}} + x_{C H_{4}} \equiv 1

(12)

Similarly, the relations (11) and (12) are also correct for both experimental and equilibrium data derived from thermodynamic equations.

More in-depth thermodynamic considerations on reaction (1), taking into account also its mechanism, can be found in the following works [11,13,42,65,74,78,81,82,83,84] and the following Table 1 collates stoichiometric reactions and equations for Gibbs free energy for Eq. 1.

Phenomenological thermodynamics only reveals constraints arising from the equilibrium states of reaction (1). Because the course of this reaction can be promoted by the use of catalysts, the thermal decomposition process of methane must be analysed in the context of the reactions and transformations taking place on the catalyst and thus taking into account the interactions between the components of the reaction (1) and the catalyst. In the case of iron catalysts, special attention should be paid to iron ores, reason being that their choice is mainly attributed to good balance between optimal temperature of the process, low cost and quality of produced carbon structure. In further considerations the following minerals are of main interests: hematite, magnetite, goethite, and siderite. Despite physical differences of these minerals, the activity of iron catalysts can typically be described by comparing the observed effects of a given catalyst to the effects of the equivalent oxide form of hematite (

F e_{2} O_{3}

) or the reduced form

α - F e

[85].

In a strongly reducing atmosphere, a series of reduction reactions is observed, dependent on the temperature and the quality of the reductant [40,73,85,86,87,88]:

F e_{2} O_{3} \to F e_{2} O_{3} \cdot F e O \to F e_{x} O, w h e r e x = 0.82 \div 0.95 \underset{> 575 ℃}{\to} F e O \underset{< 912 ℃}{\to} α - F e

(13)

In an atmosphere of diluted methane, hematite is reduced to wüstite (

F e_{x} O

) at a much greater rate than in the subsequent phases of the reduction process to

F e

[87], This process occurs according to two parallel mechanisms [88] and as the reduction of

F e O

is very slow, the same phenomena can also be observed in the case of hydrogen reduction. Comparative studies for the mentioned two iron oxides with respect to methane are justified due to the varying reaction rates [40].

Allotropic forms of iron are stable within specific temperature ranges [85]:

α - F e < 912 ° C, γ - F e 912 - 1394 ° C, α (δ) - F e 1394 - 1538 ° C

(14)

where

δ

signifies the reformation of

α - F e

with a body-centred cubic (BCC) structure, having a lattice size larger than that of

α - F e

. In contrast,

γ - F e

is characterized by a face-centred cubic (FCC) structure.

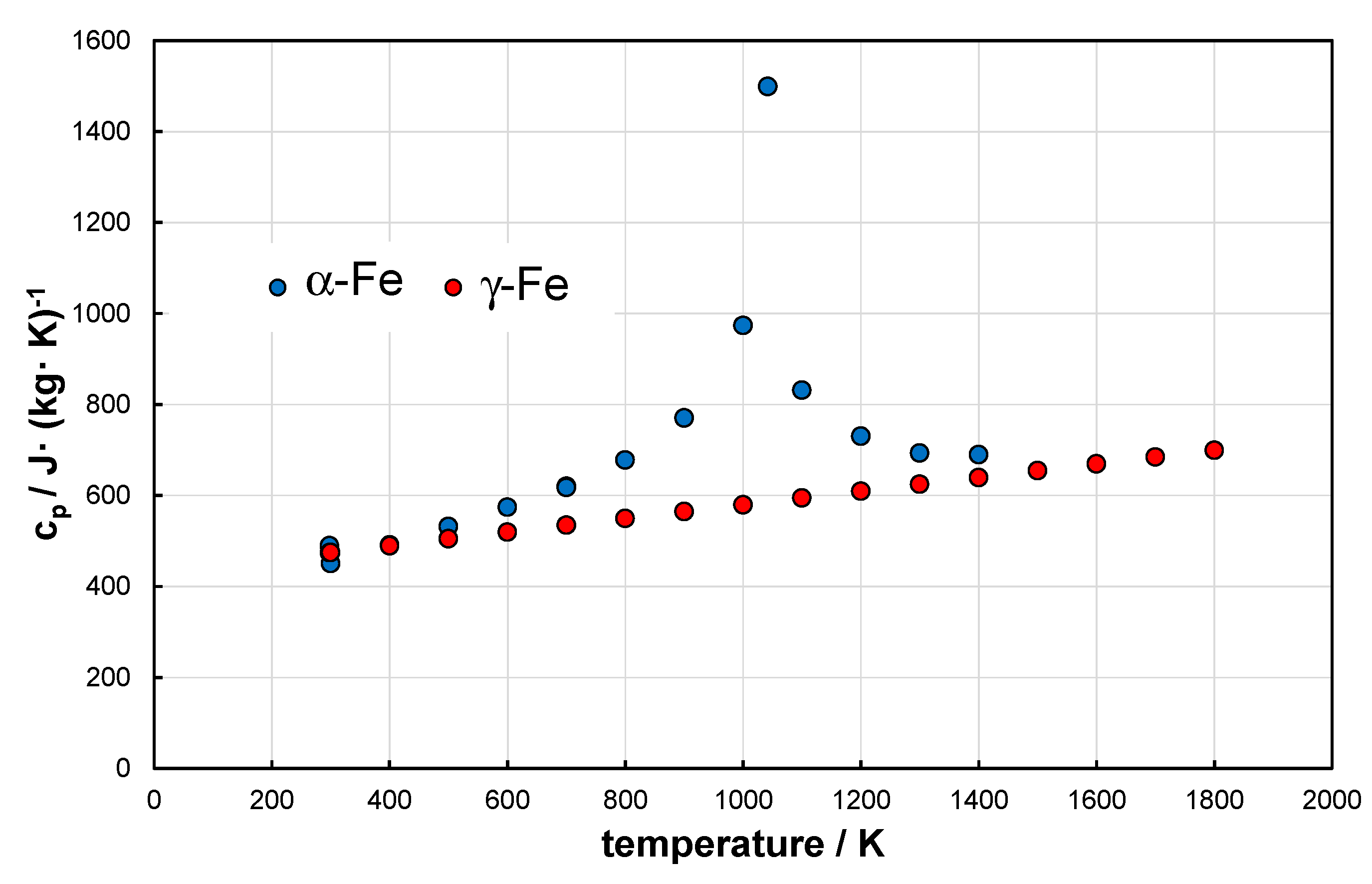
A comparison of the heat capacity for the polymorphic transformation

α - F e

→

γ - F e

is presented in Figure 1. The maximum of the blue curve indicates the Curie point

T = 1042 K

. After integration and recalculation to the unit of

k J \cdot m o l^{- 1}

, for the temperature range of

700 - 1300 K,

the following relation can be used

G^{\emptyset} = - 0.070 \cdot T + 19.65

. The linear characteristic of

γ - F e

disappears at the melting temperature of iron.

Experimental data used in the review were extracted from figures presented in the literature using software for digitalization of charts; e.g. https://plotdigitizer.com/.

For

α - F e

, the polymorphic transformation is endothermic, and occurs within the temperature range

1000 - 1200 K

. Its value is

∆ H^{\emptyset} = 10.29 k J \cdot m o l^{- 1} = 184.24 k J \cdot k g^{- 1} .

For reference the standard enthalpy for the decomposition reaction of methane without using a catalyst is

∆ H^{\emptyset} = 74.85 k J \cdot m o l^{- 1}

.

In similar fashion to the data gathered for Equation (1), the following Table 1 collates also multiple correlations for possible polymorphic transformations of iron. E.g. position No 7 presents the value of free energy of the transformation

α - F e \to γ - F e

which was determined based on the data provided by the NIST [85]. Moreover, positions No 2–4 refer to the reaction of iron (III) oxide with methane according to the equations given in [59], while positions No 5–6 are associated with the formation and decomposition of iron carbides (primarily cementite). Analytical approaches to carburization and decarburization reactions of iron were presented by Grabke [62]. The diffusion coefficients of carbon into iron up to 912°C follow the sequence:

α - F e > γ - F e ≫ F e_{5} C_{2}

[68]. Interestingly for the reaction of

F e O

with methane, within the temperature range of 700–1100/1200 K, the thermodynamic existence of the

F e_{3} C

phase was determined [89], while in works [66,69,72], the formation of cementite on active intermediate phase e.g. on hypereutectoid steels [72] and on orthorhombic crystal structure [60].

The formation of cementite is an endothermic reaction, meaning its decomposition is accompanied by an exothermic effect. Therefore, for methane decomposition processes conducted under isothermal conditions, knowledge of the temperature alone is inadequate, while taking into account the complete heat balance is crucial. Moreover, when using iron oxide catalysts, one must consider the formation of CO₂, CO, and water. For this reason, Table 1 collates also possible pathways where these species are present in the atmosphere of the process (No 6–12).

Table 1. Compilation of chemical reactions of species present in the atmosphere of methane pyrolysis process, including polymorphic transformation of iron, and their subsequent parameters of the Gibbs free energy equations:

∆_{r} G = a + b T

,

k J \cdot m o l^{- 1}

P = 0.1 M P a

.

Table 1. Compilation of chemical reactions of species present in the atmosphere of methane pyrolysis process, including polymorphic transformation of iron, and their subsequent parameters of the Gibbs free energy equations:

∆_{r} G = a + b T

,

k J \cdot m o l^{- 1}

P = 0.1 M P a

.

No.	reaction	a, kJ·mol⁻¹	b, kJ·(mol·K)⁻¹	T range, K	$T_{e q}$ $for ∆_{r} G = 0$ , K	source	remarks
1	CH₄ $⇄$ C +2H₂	88.04	−0.108	573–1773	815.2	[56]	Equation (7)
2	2Fe₂O₃ + 3CH₄ $⇄$ 6H₂+3CO₂+4Fe	248.37	−0.289	298–1300	859.4	[1]*	[59]
3	Fe₂O₃ + 3CH₄ $⇄$ 6H₂+3CO+2Fe	252.16	−0.285	298–1300	884.8	[1]*	[59]
4	2Fe₂O₃+3CH₄ $⇄$ 6H₂O+3C+4Fe	158.12	−0.188	298–1300	841.1	[1]*	[59]
5	3α-Fe + C $⇄$ Fe₃C	11.98	−0.017	700–1300	704.7	[1]*	$analytical solutions for α - F e$ $, graphite, {F e}_{3} C$ given in [70]
6a6b	3α-Fe + CH₄ $⇄$ Fe₃C +2H₂3γ-Fe + CH₄ $⇄$ Fe₃C +2H₂	101.29101.29	−0.122−0.126	773–1273773–1273	810.4804.0	[1][1]	$for {F e}_{3} C$ assumed after [1] for 485 <T< 1300K
7	α-Fe → γ-Fe	22.41	−0.066	700–1300	339.5	[85]	-
89	CO+H₂O $⇄$ CO₂+H₂H₂ + CO₂ $⇄$ CO +H₂O	−38.0638.06	0.036−0.036	298–1300298–1300	1057.21057.2	[1][1]	Water-Gas-Shift (WGS) [90,91,92] and Reverse-WGS [90,91,92]
10	4H₂+CO₂ $⇄$ CH₄+2H₂O	−179.56	0.210	298–1300	855.0	[1]	R-WGS as methanation [91,93] Sabatier reaction
11	C+H₂O $⇄$ CO+H₂	137.20	−0.156	298–1300, 700–1300 for C	879.5	[1]	WG [4]
12	C+CO₂ $⇄$ 2CO	172.77	−0.169	298–1400	1022.3	[94]	Bell-Boudouard reaction

* polymorfic phase change No 7 was assumed.

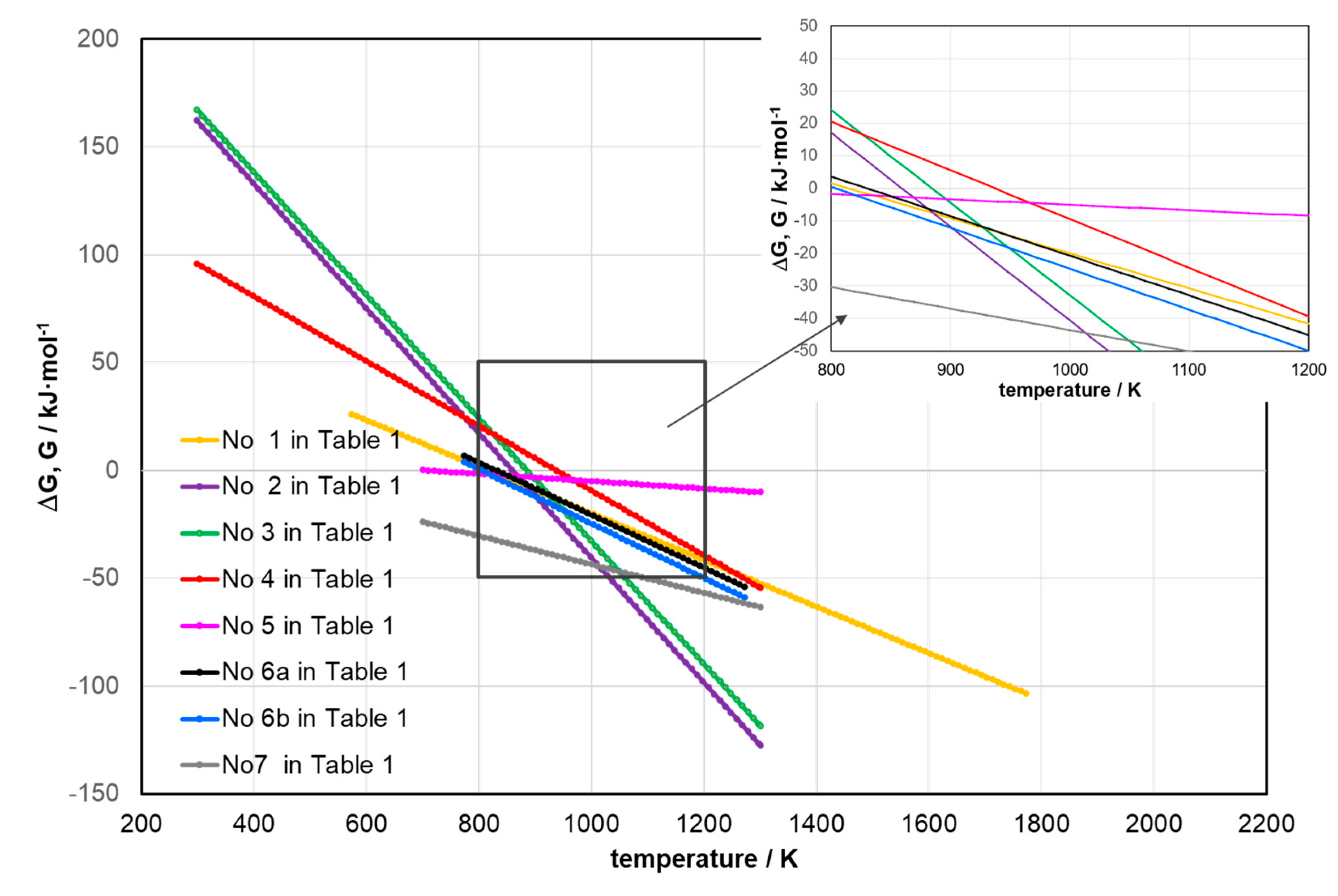
Furthermore, the linear dependencies obtained for the reactions presented in Table 1 were presented below in Figure 2. Within the temperature range considered for the methane pyrolysis process catalysed using iron catalysts, the homogeneous gas-phase reactions such as WGS (No 8), R-WGS (No 9), and methanation (No 10) were omitted. Reason for omitting WGS reaction (No 8) is the fact that it can be effectively conducted even at temperatures < 500°C. For the methanation reaction (No 10), where

∆_{r} G > 0

, a stoichiometric amount of hydrogen is required, specifically

H_{2} : C O_{2} = 4 : 1

[90,93].

Additionally, especially at temperatures exceeding 950°C the presence of methane in the reaction space counteracts methanation.

Finally, at

T > T_{e q .} = 1091 K (818 ° C)

,

∆_{r} G

of the R-WGS reaction (No 9) is

< 0

, and the equilibrium conversion of

C O_{2}

is

> 0.5

[91]. Main reason though is the fact that R-WGS is conducted at lower temperatures and requires a bimetallic catalyst [90,91,93]. The course of the R-WGS reaction arises from the parallel existence of mechanisms involving the reduction of CO₂ to CO (through COOH^∙ synthesis and decomposition), as well as the oxidation of H₂ to H₂O [91]. Similarly to reactions No 8–10, the reactions No 11–12 were also omitted from Figure 2 because their occurrence is highly unlikely due to the lack of new gas-phase products.

For reaction (1) the most probable mechanism suggests that reactions occur on the catalyst surface, particularly through the reaction involving carbon bonding with iron, and in particular the formation of cementite due to carbon diffusion into the iron phase [68], which is the exact reason for catalytic properties of iron [4]. Examining the position of the equilibrium temperature (

T_{e q .}

), it can also be observed that iron oxides shift the equilibrium to the right, while metallic iron shifts it slightly to the left. An extreme example of methane decomposition is presented by reaction No 4 in Table 1. Here hydrogen is oxidized to water, which is one of the least expected variants of methane decomposition [59].

Modelling of the Forward and Backward Reactions

Utilising the phenomenological thermodynamics and in particular model of the first-order kinetics, the equilibrium constant can be expressed in the following logarithmic form:

\ln K = \ln k_{1} - \ln k_{- 1}

(15)

After multiplication by

(- R T)

and using the relation that free energy of a reaction can be expressed as a difference in activation energies of the forwards and the backwards reactions [95] we can write that:

∆_{r} G^{\emptyset} = ∆ G^{+} - ∆_{- 1} G^{+}

(16)

each component of the right side of Equation (16) results from the comparison of Arrhenius kinetic constants with Eyring’s TST [96]. Therefore, using the concept presented in [97] we obtain:

∆ G^{+} = R \cdot T \ln \frac{B T}{k_{1}} and ∆_{- 1} G^{+} = R \cdot T \ln \frac{B T}{k_{- 1}}

(17)

Substitution of Equation (17) to Equation (16) leads to the following, convenient for calculations, form of equation:

∆_{r} G^{\emptyset} = R \cdot T \ln \frac{k_{- 1}}{k_{1}}

(18)

Variant 1 – from carburization of iron to methane decomposition on iron surface

According to [62] aforementioned processes of carburisation and decarburisation of iron are based on isothermal reactions performed in the temperature range 800–1040°C. In the original text, Authors use the following notation:

C (i n γ - F e) + 2 H_{2} (g) \leftrightarrow C H_{4} (g)

(19)

Enthalpy of this reaction was determined to be

∆_{r} H^{\emptyset} = - 124.3

kJ·mol⁻¹.

Grabke [62] has determined the rate constants for the reaction (19); however, the notation adapted in this work is incoherent with units used herein. In the following considerations the reverse direction of the reaction (19) is used, i.e. from right to the left. Moreover, by unifying the dimensions to the scale

s^{- 1}

we obtain that for the reaction of methane decomposition:

k_{1} = 4.55 \cdot 10^{3} [\exp (- \frac{230120}{R T})],

while for the reaction of methane synthesis (Equation (19) as given above, i.e. from left to right):

k_{- 1} = 2.6 \cdot 10^{- 2} [\exp (- \frac{105860}{R T})]

In this way according to Equation (18) we obtain:

∆_{r} G^{\emptyset} = 124.27 - 0.100 T

(20)

Interestingly, thus obtained parameters of the Equation (20) are close to the values given in reaction No 6b in Table 1. For

{F e}_{3} C

the slightly higher value of the intercept can be explained by the nonlinear relation between free energy and temperature [70], which in simplistic approach for range of 298.15–1500 K, can be approximated by a second degree parabolic function [1,60]. For smaller temperature ranges the polynomial can be reduced to linear form, and thus the values of the intercept can be determined to change in the range 70–116 kJ·mol⁻¹. On the other hand when accepting after [60] the range of 500–2000 K, the relationship No 6b adapts the following form having much higher values of the constants

∆_{r} G^{\emptyset} = 126.27 - 0.144 \cdot T

. Thus, the above expression of Equation (20) correlates well with the reaction of methane decomposition in the presence of metallic iron catalyst (

γ - F e

). Unfortunately, in [60] Authors do not specify to what extend it is possible to treat the solution of

γ - F e

and

C

as cementite.

Finally, returning to the notation of Equation (19) the above considerations indicate correctness of the approach where decomposition of methane is analysed in the categories of Eyring’s TST [96].For this scope the above statement underlines the first principles of reaction (1) noted in [7].

Variant 2 – Free Energy of Activation of the Reaction (1)

The above analysis shows the link between works carried out to develop carburization/decarburization process, in the light of methane pyrolysis though it is important to counterpose this analysis with the general scheme of the methane pyrolysis reaction (1).

Similarly to the previous case, in the following example two different sources of kinetic data were analysed for their convergence using Equation (16). In formal terms here the value of the component

∆ G^{+}

is sought, thus the notification of Equation (16) changes to:

∆ G^{+} = ∆_{r} G^{\emptyset} + ∆_{- 1} G^{+}

(21)

Based on kinetic data reduced to the form of Arrhenius equation and describing a high-temperature (1080–3000°C) and high-pressure (up to 5.61 MPa) methane synthesis process of hydrogen attacking graphitic materials, the following kinetic parameters were determined:

A = 5.9 s^{- 1}

,

E = 101.50 k J \cdot m o l^{- 1}

[98]. For the temperature range of 500–1500 K, these data result in the following expression of the free energy of activation:

∆_{- 1} G^{+} = 93.88 + 0.248 \cdot T

(22)

for the reaction No 1 in Table 1, after considering Equation (22), we obtain:

∆ G^{+} = 181.92 + 0.140 \cdot T

(23)

The literature presents great efforts made to find suitable data consistent with the existing dataset, especially one enabling the comparison of determined kinetic and thermodynamic parameters. In [55], Authors have determined and utilised data describing the kinetics of methane decomposition using a graphite crucible and liquid slag having a predominant content of

C a O

(43% by mass) and only a minimal content of

F e O

(0.37% by mass). This work provides the following parameters,

A = 4.053 10^{6} c m^{- 1} \cdot s^{- 1}

,

E = 190.31 k J \cdot m o l^{- 1}

and on this premiss the following can be determined:

∆ G^{+} = 182.69 + 0.130 \cdot T

(24a)

Then, after correcting to the form

A = 4.819 \cdot 10^{7} s^{- 1}

we obtain:

∆ G^{+} = 181.41 + 0.120 \cdot T

(24b)

which yet again is similar to the coefficients determined beforehand. Moreover, when comparing kinetic parameters, the issue of dimensional consistency for the frequency factor A is debatable. It is simplest to assume it represents the “directional vector of path of reaction scaled by reciprocal time”. Similar interpretations are sometimes applied, albeit for different types of variability [93].

Comparison of the coefficients given in Eqs. (23) and (24a,b) indicates good convergence for the two presented above routes for analysing the process of methane decomposition using iron catalyst.

Moreover, despite the fact that the objectives of references [62,98] are related to iron metallurgy, and therefore not directly aligned with the main scope of this study, based on the kinetic data provided in the, it is possible to consider the solid solution of

F e + C

(wüstite) as a catalyst for methane decomposition.

Kinetics – Introduction

Above thermodynamic considerations concerning equations Eqs. (15,16) and Equation (21), already took advantage of kinetic parameters determined by using the Arrhenius law. These deliberations also underscore the validity of analysing kinetic equations that include the equilibrium constant.

In the context of kinetics the literature on methane pyrolysis encompass such variables as: methane and hydrogen mole fractions, their partial pressures, methane conversion rate, as well as the rate (or quantity) of carbon formation per unit of catalyst mass – expressed respectively in [

g

or

m o l \cdot g_{c a t}^{- 1} \cdot {u n i t o f t i m e}^{- 1}

] or [

g

or

m o l \cdot g_{c a t}^{- 1}

]. The link between the amount of carbon deposit formed stems from a volumetric balance for

\dot{V ̇} = c o n s t .

, typically having the unit of [

d m^{3}

or

m^{3}

·

g_{c a t}^{- 1} \cdot {u n i t o f t i m e}^{- 1}

]. For further considerations it needs to be pointed out that due to its practical nature conversion degree should be regarded with particular importance. In an integrated approach, following [27,58], the quantity of carbon deposition can be expressed in terms of conversion degree:

[C] = \frac{12}{22.4} \dot{V} \int_{0}^{t} α d t

(25)

Literature presents also the following expression as the second way of modelling the kinetics of the deposition of carbon [35,39,42,99,100,101]:

r_{C} = \frac{d [C]}{d t} = k (P_{C H_{4}})^{n}, n = 0.5 \div 1,

(26)

In this approach

r_{C}

can be understood as the initial rate of formation of the carbon deposit, with only one variable remaining (here

P_{C H_{4}}

).

From the description of research presented in [100], it stems that

\frac{P_{C H_{4}}}{P^{\emptyset}} = x_{0} = c o n s t

for a singular carrier of methane, but

x_{0} = v a r

for several different streams.

Furthermore, in works [14,83] Equation (26) was used to indicate the existence of a maximum rate of formation of the carbon deposit, and this results from the activity of the catalyst used. Once the maximum is reached, a decrease in the productivity of the deposit is observed; hence as indicated in [102], the formation of carbon deposits can also be expressed empirically as a function of time:

[C] \propto t^{n}, n < 1

(27)

Better understanding of this relation can be gained after substituting the simplest linear relationship for the conversion degree vs. time into Equation (25). Upon integration, the relationship between the amount of deposit formed over time takes the form of a second-degree parabolic equation. Another way to represent Equation (25) is to replace the integral with the average conversion degree:

[C] = \frac{12}{22,4} \dot{V} \bar{α} t

(28)

In the following Table 2, selected literature data are compared to indicate the amount of carbon deposit formed in the process of fluidised-bed methane pyrolysis at temperatures of 650–800°C using NiCu/Al₂O₃ catalyst and with

W H S V = 12 L \cdot g_{c a t}^{- 1} \cdot h^{- 1}

.

The second column of Table 2 presents the calculated integral mean for methane conversion, integrating from time

t = 0

, when the point of maximum conversion is achieved, up to the end of the experiment (finite time). The third and fourth columns show respectively the amounts of carbon deposit calculated using equation (28) and the experimental quantities of deposit reported in [27]. The calculations pertain to the methane pyrolysis stage during catalyst deactivation, excluding the progress of the elementary reaction.

Literature descriptions of methane pyrolysis processes indicate that there are two steps that need to be considered. During the initial step, methane conversion, carbon deposition, and hydrogen content in the process gas increase, while the methane concentration decreases. This period can be understood as activation step. During the second period of the process, after time

t \geq τ_{D}

, where

τ_{D}

is the deactivation time, an ongoing process of deactivation of the catalyst is observed [103]:

r (t) = r_{0} e x p (- \frac{t}{τ_{D}}), for t = 0, r (t) = r_{0}

(29)

Following after Becker [104] that expressions for reaction rate do not take into account the backwards reaction, for the molar fraction of methane, we obtain:

r = - \frac{d x_{C H_{4}}}{d t} = k_{1} (x_{C H_{4}})^{n}, n = 1 \div 1.5

(30)

Similar expression for reaction rate is also proposed by other authors [105].

Given the considerations outlined above, we need to ask how the concept of an elementary reaction is understood.

Kinetics of the Elemental Reaction Equation (1)

In Gold Book the elemental reaction is defined in the following way [106]: “A reaction for which no reaction intermediates have been detected or need to be postulated in order to describe the chemical reaction on a molecular scale. An elementary reaction is assumed to occur in a single step and to pass through a single transition state.”

In practice quoted description can be narrowed down to the complete conversion state of substrates according to the stoichiometric expression or to a limited equilibrium state.

For reaction (1) equilibrium constant is determined from the relation characteristic for the first order kinetics (see Equation (15)):

K = \frac{k_{1}}{k_{- 1}}

(31)

and its rate can be expressed in the following form:

r = k_{1} x - k_{- 1} (1 - x)^{2}, T = c o n s t

(32)

where:

r = - \frac{d x}{d t}

(33)

Coupling the Eqs. (31-33) leads to the form of an equation having separate variables:

- \frac{d x}{d t} = k_{1} [x - \frac{(1 - x)^{2}}{K}]

(34)

In Eg(34) the equilibrium constant is expressed using formula (8) or (6).

Furthermore, in the work of [82] utilizing previous publication [107] the following initial condition was accepted

x_{0}

:

{g (x) = k}_{1} t

(35)

while:

k_{1} t = \frac{x_{0} - x_{e q .}}{x_{0} + x_{e q .}} \ln (\frac{x_{0}^{2} - x \cdot x_{e q .}}{x_{0} (x - x_{e q .})})

(36)

and for

t = 0, x = x_{0} a n d x < x_{e q .}

(intercept = 0).

Importantly for further considerations this research was conducted in a manner most similar to the analysis of an elementary reaction, as it was performed in a semi batch system, where the inflow of methane was minimal, solely to maintain constant pressure, and the hydrogen concentration measurements were taken post-process. For constant temperatures ranged from 700°C to 900°C, and under total pressure of 2.82–5.61 MPa, the thus obtained results can be attributed to a gradient-free process.

By substituting into Equation (36) the relationship between the molar concentration of methane, from:

x = x_{0} \frac{1 - α}{1 + x_{0} α}

(37)

the following solution that includes the kinetics in the form of the degree of methane conversion can be obtained:

k_{1} t = \frac{α_{e q .} (1 + x_{0})}{2 - α_{e q .} (1 - x_{0})} \cdot \ln (\frac{α_{e q .} + α - α {\cdot α}_{e q .} (1 - x_{0})}{α_{e q .} - α})

(38)

For

x_{0} = 1

(pure methane) Equation (38) converts to the form:

k_{1} t = α_{e q .} \ln (\frac{α_{e q .} + α}{α_{e q .} - α}), α_{e q .} > α

(39)

Or

{k_{1} t = α}_{e q .} \ln (\frac{1 + z}{1 - z}), z < 1

(40)

where

z = \frac{α}{α_{e q .}}

is thermodynamic efficiency of reaction (1), and kinetic functions

g (α)

and

g (z)

correspond to the notation of their complete kinetic forms (

= k_{1} t

).

In Equation (40) for

t = 0, z = 0

, or when

t \to \infty, z \to 1,

and thus for small values of

z

, an approximate result can be sought through expansion to a series:

\ln (\frac{1 + z}{1 - z}) = 2 \sum_{1}^{\infty} [(\frac{1}{2 n - 1}) z^{2 n - 1}], z^{2} < 1

(41)

Approximate solution to the above equation can be found through limiting it to the first term:

\ln (\frac{1 + z}{1 - z}) ≅ 2 z

(42)

Furthermore, by putting Equation (42) into Equation (40) one can describe a minimal operation line:

α = \frac{k_{1}}{2} t = k_{z} t

(43)

As an example of the effectiveness of such procedure the following Figure 3. was introduced. It presents a transformation of results presented in [82,107] to the form of relation Equation (39), which was further simplified to linear relation of Equation (43). As a result, for the following conditions:

x_{0} = 1

, methane flow

\dot{V} \approx 0

, then

α = 1 - x,

the following results were obtained:

E = 130.5

kJ·mol⁻¹;

\ln A = 8.60

(

A

in

s^{- 1}

). For reference acc. to [82,107]

E = 131.0

kJ·mol⁻¹; and

\ln A = 8.59

(

A

in

s^{- 1}

).

The commentary on the data presented in Figure 3 can be summarized in a few remarks. By comparing the structure of equations Equation (36) and Equation (43), it is apparent that the kinetics of the process can be interpreted using multiple models of varying complexity. This is a fairly common observation in studies of heterogeneous systems involving both solid and gas phases. E.g. if Equation (34) is expressed in another form, say as:

- \frac{d x}{d t} = k_{1} x [1 - \frac{(1 - x)^{2}}{x K}]

(44)

and furthermore, by using Eqs. (4) and (9), the following can be written:

- \frac{d x}{d t} = k_{1} x (1 - \frac{K_{x}}{K})

(45)

When reaction (1) remains „very far” from equilibrium

(K ≫ K_{x})

according to [107], for

\dot{V} = 0

it follows first degree kinetics, and thus Equation (45) can be described by in the terms of conversion degree:

g (α) = - \ln (1 - α) = k_{1} t, T = c o n s t

(46)

On the other hand, for small conversion degrees, reaction (1) has a zero-degree kinetics.

In kinetic considerations, it is usually deemed appropriate to adopt models with the least complexity while maintaining sufficient precision. The results of studies on the elementary reaction (1) under high pressure [82,107] indicate that the equilibrium state, represented by the equilibrium conversion degree, stands here as a limiting factor. The deviation from equilibrium influences the kinetics, which can be expressed through various modelling approaches, e.g. according to

n^{t h}

or fractional order variability [104].

As it was already introduced, literature published in the topic of methane pyrolysis refer to the inequality

z = \frac{α}{α_{e q .}} < 1

as a mean of describing the thermodynamic efficiency of the process, however, in certain process conditions, e.g. for some temperature ranges

z \approx 1

[19,38] – for research published in [38] such a case has been noted only for the catalysts consisting of 50%Ni-10% Cu/Si0₂.

Continuous process – conditions of constant flow of methane

For the sake of broadening the discussion to continuous flow systems, Equation (34) was solved for the flow condition,

\dot{V} > 0

. Differentiating the Equation (37) in respect to time reduces it to the expression for the rate of reaction (1), taking the following form:

- \frac{d x}{d t} = x_{0} (1 + x_{0}) \cdot (1 + x_{0} α)^{- 2} \frac{d α}{d t}

(47)

and after substituting Eqs. (37), (47) as well as thermodynamic equilibrium constant (10) to Equation (34), when the condition

z = \frac{α}{α_{e q .}} < 1

is fulfilled, we finally obtain the following kinetic expression for flow conditions related to the degree of methane conversion:

\frac{d α}{d t} = k_{1} \frac{2 - α_{e q .} (1 - x_{0})}{α_{e q .} (1 + x_{0})} \cdot \frac{(c \cdot α + α_{e q .}) (α_{e q .} - α)}{α_{e q .} (1 + c)}, where c = 1 - α_{e q .} (1 - x_{0})

(48)

For initial condition

x_{0} = 1

(pure methane) the complicated Equation (48) reduces to a form which greatly simplifies kinetic interpretation:

\frac{d α}{d t} = \frac{k_{1}}{2} [1 - {(\frac{α}{α_{e q .}})}^{2}], T = c o n s t

(49)

This otherwise can also be expressed it in terms of thermodynamic efficiency:

\frac{d z}{d t} = \frac{k_{1}}{2 α_{e q .}} (1 - z^{2})

(50)

Eqs. (49) and (50) indicate that under flow conditions of methane, the reaction rate is quasi second order, which is consistent with the exponent related to the hydrogen formation presented in Equation (32). Noteworthy, the considerations expressed in Eqs. (47–50) highlight the possibility of variable order of the reaction (1) depending on the conditions under which it is carried out.

The solution to Equation (50) is expressed in Equation (40). Looking at the form of Equation (40), a question arises, whether this expression is suitable for use in complex studies of reaction (1), especially where the presence of catalysts and its reactions with methane are taken into account (Table 1).

On the other hand, in Equation (38) for

(α_{eq .} = 1), (x_{0} < 1)

, after substitution and rearrangement, we obtain:

g (α) = k_{1} t = \ln (\frac{1 + x_{0} α}{1 - α})

(51)

hence, for

t = 0, α = 0

, and when

t \to \infty, α \to 1

.

Solution of Equation (34) for $x_{0} < 1$ and considering equilibrium constant $K$

Due to the stoichiometry of reaction (1), methane diluted with inert gas is very often used as a feed in experiments. Taking into account the mass balance of (37), the equilibrium constant in its fractional form (Equation (10)) contains the initial molar fraction of methane

x_{0} < 1

:

K = \frac{(1 - x_{0} + 2 x_{0} α_{e q .})^{2}}{x_{0} (1 + x_{0} α_{e q .}) (1 - α_{e q .})}

(52)

From Equation (52) equilibrium conversion degree reduces to the following quadratic equation:

α_{e q .}^{2} + \frac{1 - x_{0}}{x_{0}} α_{e q .} + \frac{x_{0}^{2} - x_{0} (2 + K) + 1}{x_{0}^{2} (4 + K)} = 0

(53)

From the above we know that for 50% dilution of methane with nitrogen

x_{0} = 0.5

and for temperature of

T = 1173 K

from equation (8) we can calculate

K = K_{p} = 55.40

from this the following expression can be written:

α_{e q .}^{2} + α_{e q .} - 1.848 = 0

(54)

After solving we obtain

α_{e q .} = 0.950 ≅ 1

. This result allows the use of the kinetic equation (32) without the reversible term, i.e. setting

k_{- 1} = 0

. In equation (54), for the rounded value of the intercept (

- 1.848 ≅ - 2

),

α_{eq .} \equiv 1

and from equation (53) it is known that for the above-mentioned conditions, dilution of the methane stream

(x_{0} < 1)

and an increase in temperature

(K \to \infty)

justify the conclusion that reaction (1) is irreversible.

Thus for

(k_{- 1} = 0)

combining Eqs (32), (33), (37) and (47) leads to a kinetic equation in terms of the methane conversion degree:

\frac{d α}{d t} = \frac{k_{1}}{1 + x_{0}} (1 - α) (1 + x_{0} α), T = c o n s t

(55)

which solves Equation (51) and lead to constatation that for

x_{0} = 1

and (39) for

α_{e q .} = 1

are identical.

Analogous consideration for Equation (43) leads to the following expression:

α = \frac{k_{1}}{1 + x_{0}} t = k_{z} t

(56)

Presented below Table 3 summarizes the integral forms of kinetic models. Importantly these equations relate to the following conditions:

\dot{V} > 0

,

x_{0} < 1

,

α \in [0; α_{m a x}]

,

α_{e q .} = 1

and positions No 2–3 consider the catalytic process. For practical reasons it is important that these expressions feature the term

- \ln (1 - α)

, which is characteristic of first-order kinetics. In further consideration this term is denoted by the symbol

(F 1)

.

The reaction rate presented in Table 3 indicates that the reaction order ranges from first-order kinetics (model F1, No 5) to quasi-second order (No 1 and 2). The process described in position No 4 is particularly interesting as it utilizes a solar heating system (solar reactor), and it is conducted without using a catalyst. Uniqueness of this process lies in the injection of methane into argon at high temperatures. The residence time in the reactor was calculated as a substitute time, which is the ratio of the reactor volume to the flow rate. The physical dilatation factor

(β)

[111,112,113] considers the relationship between the state parameters (temperature, pressure) at the reactor inlet and those under reaction conditions. Further explanations and implications of this approach are analysed in works [114,115]. Importantly in these works the calculated Arrhenius law parameters are similar in value to previous studies. Additionally, the analysis of the equations given in [114,115] and also presented in [111] indicates that the chemical expansion factor directly corresponds to the value described herein as

(x_{0})

. The results of the studies presented in [111,112,113,114,115] are thus significant enough to be considered as having primary importance. Finally, as a result of the considerations presented in Table 3 it can be noted that with

ε = 0

the position No 5 and Equation (46) stand as the simplest kinetic model of the reaction (1), model (F1).

Comprehensive nature of the above presented considerations on the kinetic model of reaction (1) forms ground upon which experimental data can be analysed. Subsequent examples illustrate their validity in practical use.

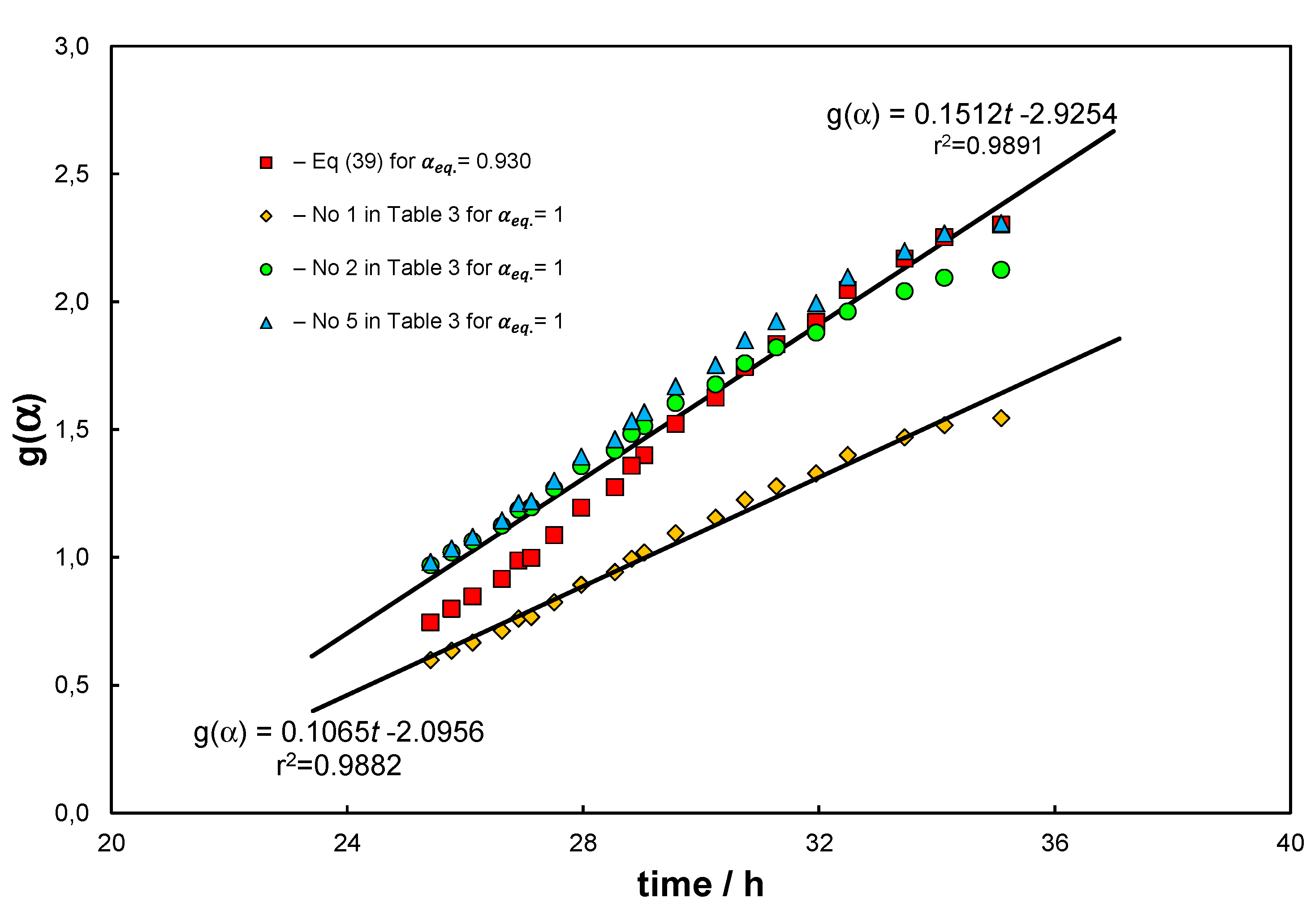
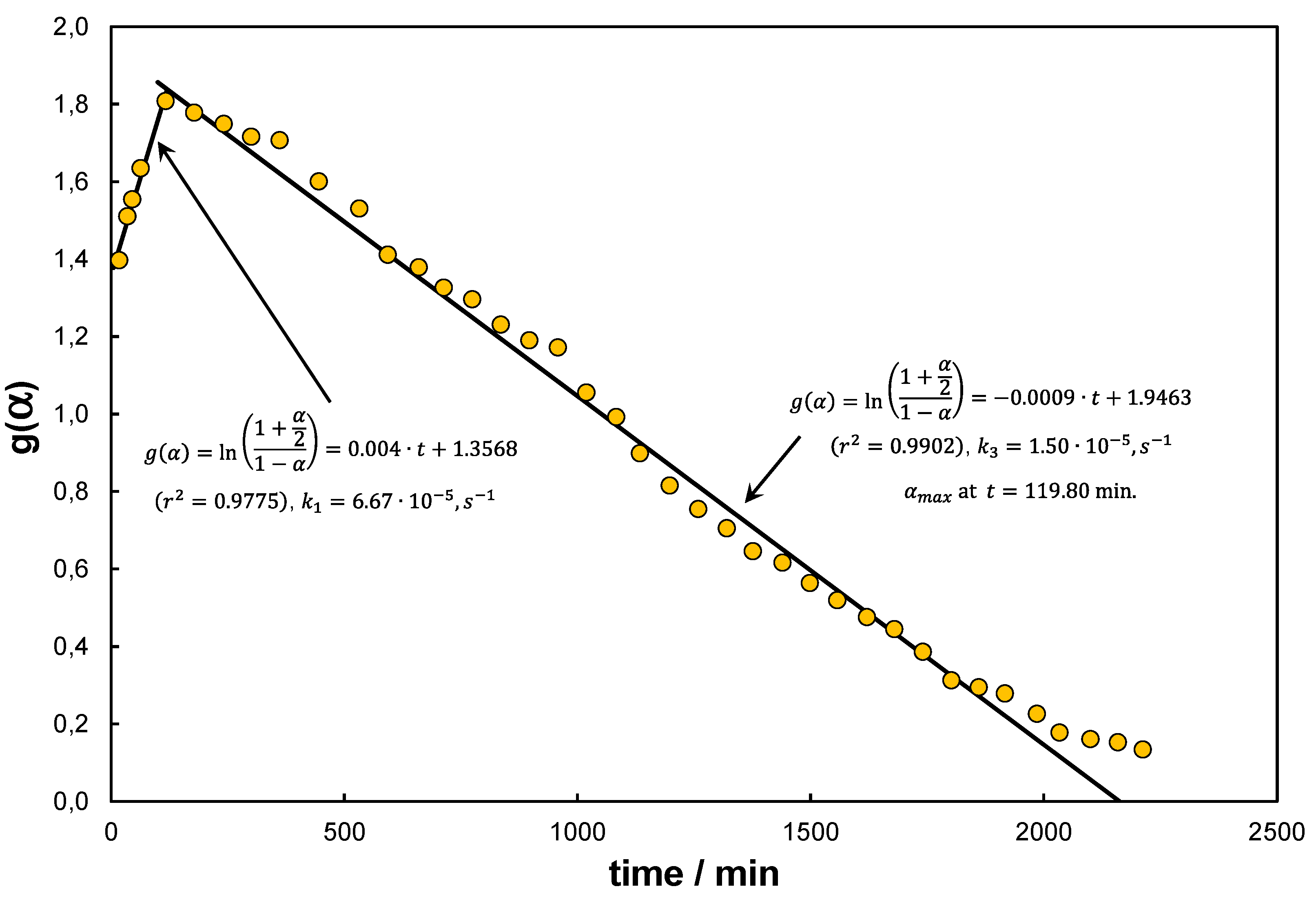
Result of the first example is presented in Figure 4. Data for the analysis were extracted from the experimental research presented in [57]. Author proposed here the use of a specially prepared iron mesh to catalytically decompose methane. The pyrolysis was performed under

t = 800 ° C, x_{0} = 1

; however, beforehand the catalyst was activated using hydrogen. Analysis of the dataset using the approach presented in Figure 3, which is pertinent to the elementary reaction only, gives unsatisfactory results because of the systematic deviations of the linear relationship. The deviations can be explained by the formation/decomposition of cementite. Followingly, further analysis of the data set shows that after approximately 20 hours, the catalyst becomes saturated with carbon. In the time interval of 25.42–35.09 hours (number of measurements

N = 20

) the results can be approximated by a linear relationship. In this way it is possible to determine the average reaction rate constant

k_{1} = 4.20 \cdot 10^{- 5} s^{- 1},

g (α) = 0.1512 \cdot t - 2.9254

(

t

in hours) and

r^{2} = 0.9891

. Model F1 (No 5 in Table 3) stands out from the rest as it characterizes a separate kinetic approach, which forms an independent correlation and demands to be fitted with additional, process related terms to adequately characterize reaction (1). The determined kinetic constant for F1 is

(k_{1} = 2.69 \cdot 10^{- 5} s^{- 1})

(r^{2} = 0.9882

), and for the models for which it was determined, is close to half the value determined using Eqs. (43) and (56). Noteworthy fractional order models were not analysed here, even though they could be adequate.

The above figure presents very small conversion degree. This suggests the greatest distance from equilibrium (DFE), which under extreme conditions:

D F E = 1 - z

, for

α = 0, z = 0, D E F = 1

and for

α = α_{e q .}

,

D F E = 0

(57)

The concept of Distance From Equilibrium (DFE) exists in the literature, but its formal representations vary [116,117]. The basic, definitional expression of DFE is represented by the term given in parentheses in Equation (45),

(1 - K_{x} / K)

, whereas Equation (57) provides a justified measure of DFE in a geometric sense.

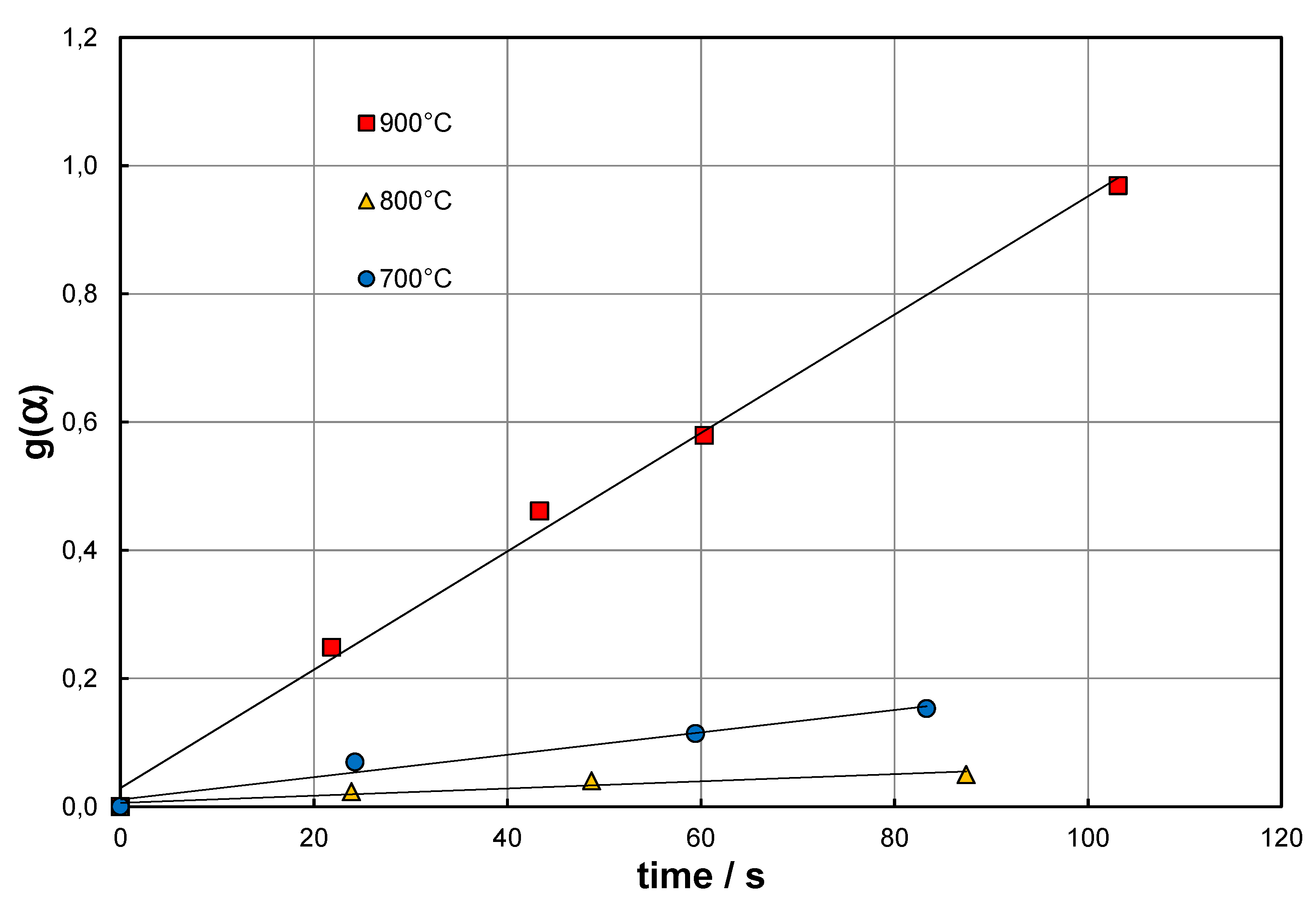
A separate issue is the conversion degree achieved near the deactivation of the catalyst

(α_{\max} \leq α_{eq .})

. An example of this problem is illustrated in Figure 5, where experimental data from the study [38], after recalculation using Equation (51), illustrate the kinetics of the final stage of catalytic activation and a sharp transition to the kinetics of catalytic deactivation. This transition is associated with the inversion of the slope coefficient through the appearance of a sign change.

It is worth noting here that in this research the methane stream fed into the reactor was diluted with nitrogen in a 1:1 ratio (

x_{0} = 0.5

), the process was run at

t = 750 ° C,

as well as

α_{e q .} = 1

.

The maximum conversion degree occurs here around the 120^th minute of the test, hence indicating a transition from the time scale of seconds (for the elementary reaction) to a time scale of minutes, or even hours (for the deactivation part). Equation (51) remains correct whenever takes values higher than the constant term that results for the time

t = 0

.

From the comparison of kinetic constants, it follows that when the elementary reaction is carried out under flow conditions and with the use of a catalyst, it is unnoticeable in relation to the forward reaction.

KCE and EEC

Based on the collected literature data [13,55,88,101,111,115,118,119,120,121], the parameters of the Arrhenius law were determined and then presented in a coordinate system of

(\ln A)

vs

(E)

– Figure 6 (KCE). The comparison includes only the data for which the dimensions of the kinetic constant

(A)

could be assumed to be

(s^{- 1})

. The pressure unit “atm” was omitted, as it can be referred to

(P^{\circ})

, while geometric dimensions were assumed for the given (or estimated) quantities. The error of this approach disappears when referring to the same conditions, while due to the use of the logarithmic value for the frequency factor its overall influence on the precision of the analysis is minimal.

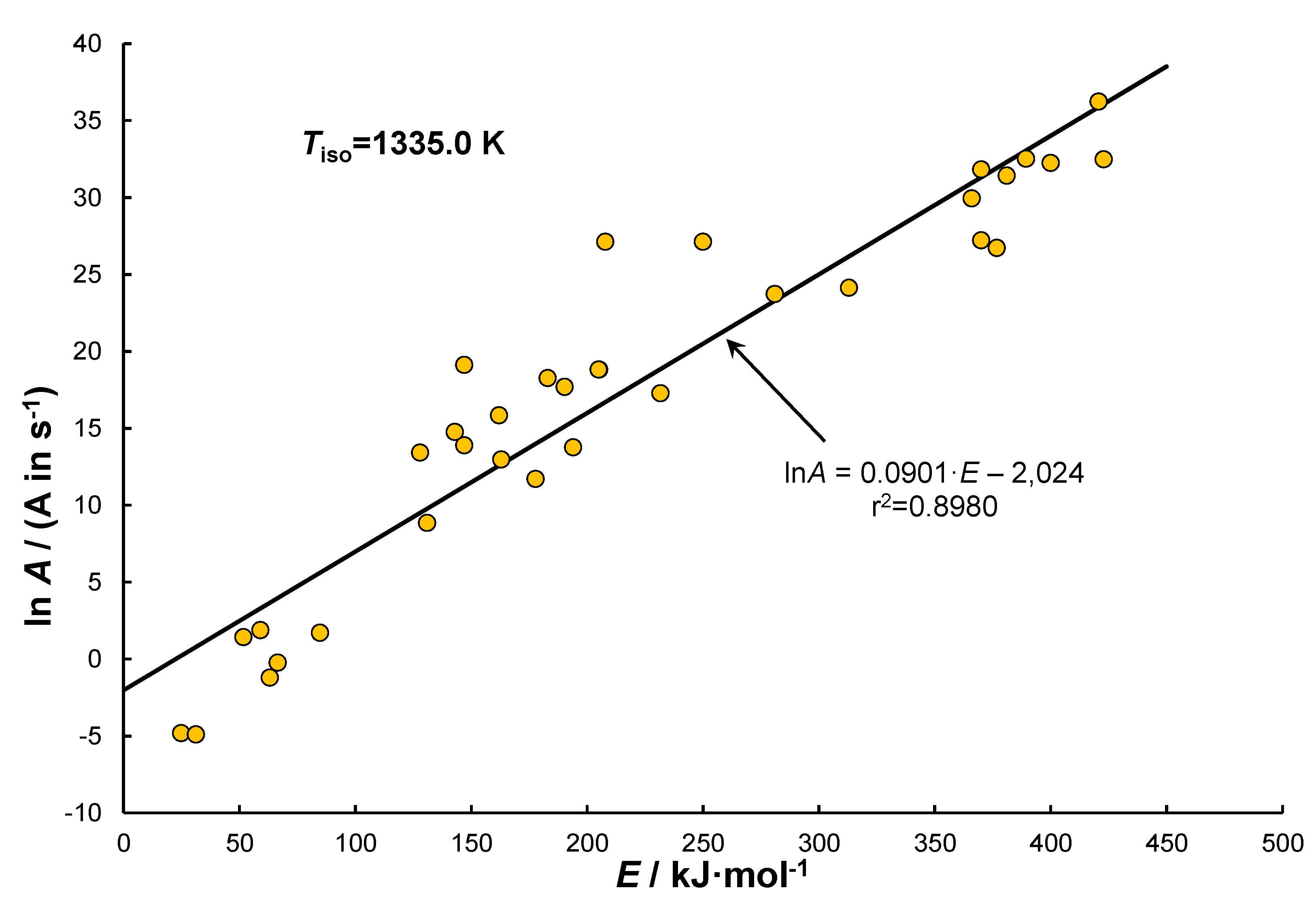
The coordinates of the chart presented in Figure 6 determine a linear relationship of KCE for the elementary reaction (1). This relationship exhibits a slight asymmetry in the range

E = 150 - 250 kJ \cdot {mol}^{- 1}

, which corresponds to catalysed reactions. From top the line of KCE is limited by the energy of C−H bond. Acc. to [8] its value is equal to

434 kJ \cdot {mol}^{- 1}

, which corresponds to coordinate (420.7; 36.23). The data was obtained through experiments performed in a perfectly mixed reactor with a bypass (CPMR) [115]. As a general remark it is often understood that activation energies

E > 250 kJ \cdot {mol}^{- 1}

are characteristic of high-temperature pyrolysis processes initiated by the breaking of C‒H bonds.

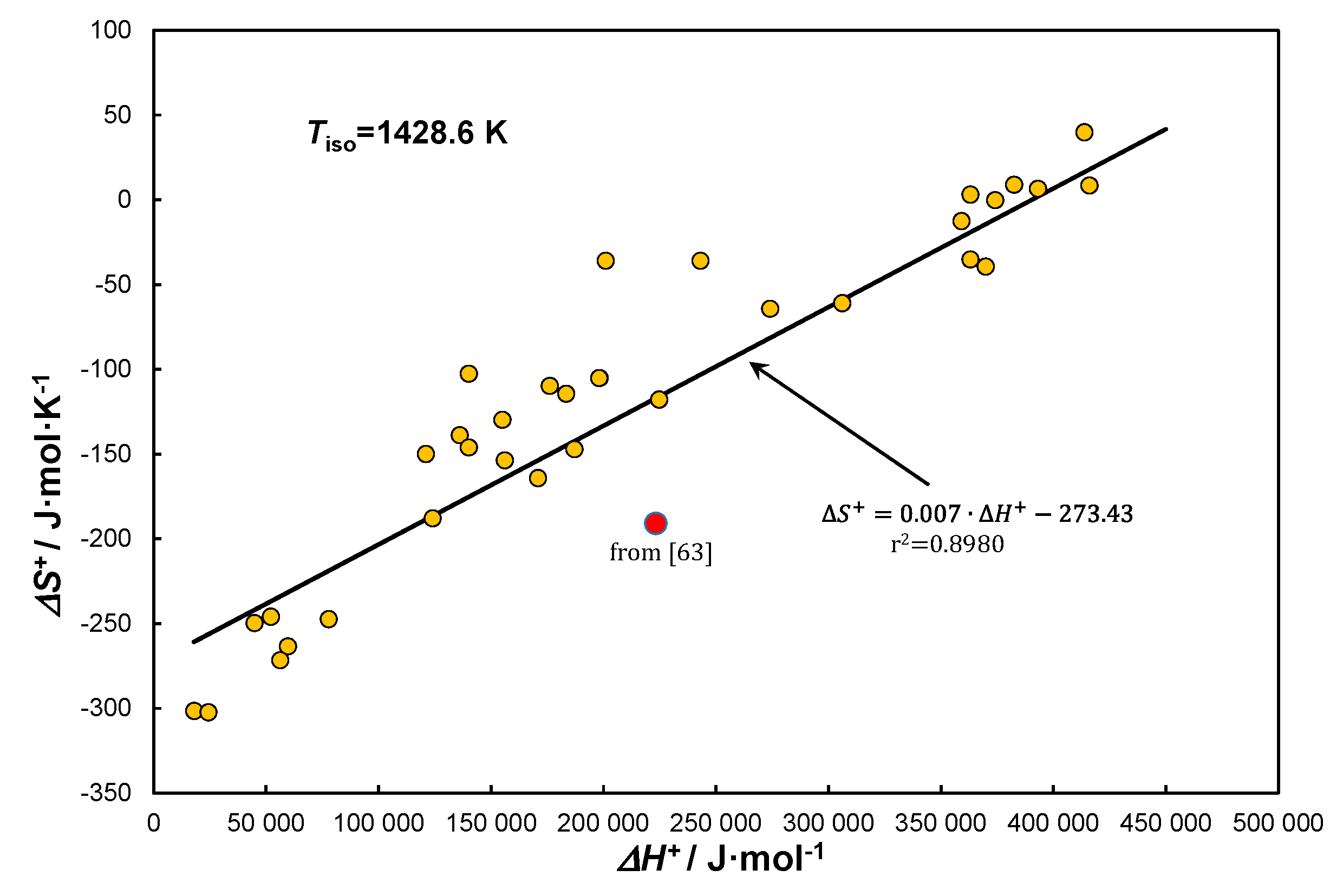
Analogously to KCE, by expressing the Arrhenius parameters using thermodynamic activation functions, it is possible to present them in the form of EEC. Figure 7 presented below depicts the EEC line for reaction (1) [62].

The above expression for EEC is given in the form proposed by [95]:

∆ S^{+} = \frac{∆ H^{+}}{T_{i s o}} + ∆ S_{B}

(58)

where entropy of activation in isokinetic temperature

∆ S_{B}

is equal to:

∆ S_{B} = R \ln (\frac{k_{i s o}}{B T_{i s o}}) = R \ln (\frac{A_{E = 0}}{B T_{i s o}})

(59)

Importantly the components of Equation (58) were determined based on the following relations:

∆ H^{+} = E - R T_{e q .}

(60)

∆ S^{+} = R [\ln (\frac{A}{B T_{e q .}}) - 1]

(61)

Eqs. (60) and (61) when introduced to Equation (58) lead to KCE with the difference that for the activation function, the equilibrium temperature

T_{e q .} = 815.2 K

is introduced (Table 1, No 1). Reason for the above is that when

T_{i s o}

is used here, we end up with a tautological problem; hence, here the relation to equilibrium temperature was deliberate and is proposed because both of these values are greatly different

T_{i s o} > T_{e q .}

. Finally, we obtain:

\ln A = \frac{E}{R T_{i s o}} + \ln A_{E = 0} + [1 - \frac{T_{e q .}}{T_{i s o}} + \ln (\frac{T_{e q .}}{T_{i s o}})]

(62)

The expression in square brackets in Equation (62) equals 0 for

T_{i s o} = T_{e q .}

. For example, if

T_{i s o} = 2 T_{e q .}

, the dimensionless sum equals approximately -0.2, and for

T_{i s o} > T_{e q .}

the calculated value adds to the intercept. Therefore, due to herein accepted reference temperatures (intercept) and the regression analysis from inversion of which

T_{i s o}

is determined (slope), the coefficients of KCE and EEC differ.

By substituting in Equation (59) the data given in Figure 6 (

\ln k_{i s o} = - 2.0241)

and in Figure 7

T_{i s o} = 1428.6 K

we obtain

∆ S_{B} = - 274.80 \cdot J \cdot {(m o l \cdot K)}^{- 1}

and importantly this value is close to the intercept determined in the correlation presented on Figure 7.

Because:

{(\frac{\partial ∆_{r} G^{\emptyset}}{\partial T})}_{P} = - ∆_{r} S^{\emptyset}

(63)

than differentiation of Eqs. (16) and (18) in regard to temperature gives that:

∆_{r} S^{\emptyset} = ∆ S^{+} - ∆_{- 1} S^{+}

(64)

Using Equation (61) twice on the right side of Equation (64), the term

\ln (B T_{e q})

disappears and we obtain:

∆_{r} S^{\emptyset} = R \ln (\frac{A}{A_{- 1}})

(65)

In further considerations, we assume that

T_{iso}

is common for both “forwards-backwards” reactions, which is a practical approximation since we are considering two reactions occurring outside of the equilibrium temperature

T_{eq .}

, for which the following

k = k_{- 1}

. Based on the data from experimental study of the reaction (19), which was performed under isothermal conditions

(T = 1073 - 1313 K)

[62], for the frequency factor

(A)

expressed in

(s^{- 1})

, according to Equation (65) we obtain

∆_{r} S^{\emptyset} = 100.4 J \cdot {(mol \cdot K)}^{- 1}

. For comparison, according to [1] for

T_{e q .} = 815.5 K

,

Δ_{r} S^{\circ} = 100.5 J \cdot {(mol \cdot K)}^{- 1},

while for

T = 298.15 K, Δ_{r} S^{\circ} = 80.89 J \cdot {(mol \cdot K)}^{- 1}

.

The above result is consistent with expectations when compared to the slope of Equation (20). Within the range of temperatures studied in in [62], i.e. from

T_{e q .}

to

1313 K

(

1073 - 1313 K

), we observe only slight variability in the increase of entropy with temperature.

Using the reference temperature

T = T_{e q .}

, one can utilize the equality

k = k_{- 1}

which implies:

\ln (\frac{A}{A_{- 1}}) = \frac{E - E_{- 1}}{R T_{e q .}}

(66)

Coupling Eqs. (65) and (66) with the condition that for

∆_{r} G^{\emptyset} = 0

the

∆_{r} H^{\emptyset} = T_{e q .} \cdot ∆_{r} S^{\emptyset}

, leads to the following simple relation:

∆_{r} H^{\emptyset} = E - E_{- 1}

(67)

For complementarity with any given temperature, Equation (67) can be derived by combining Equation (16) with Equation (64) thus building the relationship:

∆_{r} H^{\emptyset} = ∆ H^{+} - ∆_{- 1} H^{+}

(68)

For the data adopted in the analysis of expression (19) [62], according to Equation (67), we obtain

Δ_{r} H^{\circ} = 124.3 kJ \cdot {mol}^{- 1}

. The same value (only with a negative sign) is given in work [62] and it is also the intercept in Equation (20). According to [1], for

T_{e q .} = 815.2 K,

Δ_{r} H^{\circ} = 87.48 kJ \cdot {mol}^{- 1},

and this value is close to the average enthalpy given in Table 1, No 1. The difference arises directly from the involvement of the solid phase symbolically assigned to the components

F e + C / F e ₃ C

and the inability to distinguish the composition of the solid solution of C in Fe from the cementite, thus being formed and decomposed in undefined stoichiometric ratios.

Comparing Eqs. (58) with (64) and (67) leads to the interpretation of thermal and catalytic decomposition from the perspective of activation thermodynamics and phenomenology. Equation (67) is particularly important for the reversible reaction because it fulfils the empirical observation

(E > Δ_{r} H^{\circ})

.

In EEC, the intercept, which according to Equation (59) is the constant of activation entropy and assumes values

< 0

, occurs when the relationship

k_{iso} = A_{(E = 0)} < B T_{iso}

. According to Equation (64) the difference between activation entropy and the entropy of the initial state arises directly from the inequality

Δ S^{+} > Δ_{- 1} S^{+}

and because

Δ_{r} S^{\circ} > 0

. Furthermore, according to Equation (67)

E > E_{- 1}

.

Comparing Figs. 6 and 7 can lead to the conclusion that we are dealing with the same information. For both relationships, for

N = 35

measurements

r^{2} = 0.898

. Moreover, both are significant with a probability of 99.9%. The fundamental difference between these two lies in their interpretation. From the determined EEC line and Equation (58) the increase in activation entropy in the range

Δ S^{+} = - 200 - 100 J \cdot {(mol \cdot K)}^{- 1}

can be explained according to Equation (61) by the increase in reaction rate, which according to Arrhenius translates into a higher pre-exponential constant, i.e.,

(Δ S^{+} \propto \ln A)

.

This can also explain the red point below the EEC line in Figure 7 (omitted from the correlation). It can thus be debated that it indicates a significant decrease in the rate of methane decomposition under conditions of carbon absorption/dissolution by the excess solid phase

(γ - Fe)

. The conclusion is that while we use correlations expressed in terms of ratios, here Eqs. (18) and (65), the problem stands differently for absolute expressions, eg, here Eqs. (16) and (64). Expression (19) exemplifies this because the decrease in methane decomposition kinetics is related to the course of the reaction or physical process:

(3 Fe + C \leftrightarrow {Fe}_{3} C)

(Table 1, No 5), translating only the formation of weaker bonds in the solid solution.

Considering the reaction path (19) in the reverse direction, we have no guarantee that we return to the structure symbolically written as

[C (i n γ - F e)]

, because

(γ - Fe)

cannot be a product.

The emergence of a physical transformation in the system of herein considered process, affects its kinetics in the context of the possibility for analysing its reversibility. An illustration of the Bell-Boudouard reaction (Table 1, No 12) can be Figure 1 in [122], because closing chemical cycle does not always render a return to identical structural forms.

The herein presented considerations thus strengthen the connection between the parameters of the Arrhenius law and Eyring’s TST.

Discussion

Discussion on the kinetics of methane pyrolysis reaction needs to be divided to two separate ranges of conversion degree.

Range

α \to α_{e q .}

For the sake of this discussion, as a base condition Authors have adopted a technological variant of the reaction (1), where iron catalyst has the form of iron ore, and hematite serves as the reference material. The choice of such a catalyst is due to the fact that the unit price of ore is about 100 times lower than that of a nickel catalyst [57]. It should be noted though that the route from raw iron ore to an active catalytic form is rather complex. Another argument in favour of iron catalysts is the possibility of using the spent catalyst in metallurgical processes (blast furnace, foundry), which can stand as a way for decarbonization of this sector, or as a last resort the spent catalyst can be easily and safely disposed. Not only in comparison to nickel, but also within the family of different forms of iron, the primary disadvantage of iron catalysts is the need to use higher temperatures. This feature stems from lower catalytic activity and while theoretically 600–800°C is sufficient to make catalytically active

α - F e

[49], for processes carried out in fixed bed conditions, even at 800°C the time required to conduct the process is still very long [57].

On contrary, even higher temperatures, characteristic with the polymorphic transformation of iron

t = 912 ° C

(No 7 in Table 1), result in weakened catalytic activity and reduced potential for the formation of cementite (No 5 in Table 1).

Thermodynamic considerations presented in Table 1 show that when reaction (1) is performed without using a catalyst and when hematite is used, its equilibrium temperature shifts from 542°C to at least 586°C. This certainly translates into the need to increase the reaction temperature for kinetic reasons. When

t = 542 ° C

,

K = 1

and from Equation (10), we get

α_{eq .} = \sqrt{0.2} = 0.4472

. However, from experimentally determined data we know that at these conditions the conversion degrees will be much lower. In fact,

α

drops even further if we assume dilution of methane with an inert gas. For example, for

x_{0} = 0.5

, from Equation (52) for

(K = 1)

follows that

α_{eq .} = 0.1708,

which in practical terms means that

α

is close to 0. According to Equation (57) using DFE at these temperatures narrows the scale of the adopted experimental conversion values. For

α = 0

,

D F E = 1

, but for

α = α_{eq .} = 1

,

D F E = 0

.

These considerations indicate the possibility of adopting linear relationships of

α

vs time, when the reaction operates in the range of small conversion degrees. In such case Eqs. (43) and (56) find use, but this model cannot be said to adequately represent reaction (1) and thus represents only an approximation. On the other hand, the dilution of methane with an inert gas simplifies kinetic expressions. Ultimately, the increase in temperature causes the increase of conversion

α_{eq .} \to 1,

which implies the possibility of ignoring the term responsible for the reversible reaction

k_{- 1} = 0

.

Model F1 (No 5) presented in in Table 3 and Figure 4 indicate significant deviation of kinetic constant

k_{1}

determined using other models. This is thought to be because the remaining models are richer in terms that more accurately describe the nature of the process involved in pyrolysis of methane. By interpreting the differential equations, it can be shown that they approach quasi-second order, which for small

α

is very clear for model No 2

(\frac{1 - α}{1 + α} = (1 - α) (1 + α)^{- 1} ≅ (1 - α)^{2})

.

Therefore, the basis is F1 kinetics, but modified with elements of the uncatalyzed reaction (1) during the transition from homogeneous to heterogeneous reaction. A detailed analysis of the kinetics of this type of reaction is presented in the book [110]. For flow reactors (e.g. plug flow reactor), the reaction time, measured as the residence time, is the ratio of reactor volume to flow, which results from the proportionality to the integral

\propto \int \frac{d α}{r}

.

In this light, analysing the elementary reaction of the thermal process is an important element of considerations. Referring to the research results presented in Figure 3, Arrhenius parameters calculated there for

P = 5.61 MPa

,

E = 130.5 kJ \cdot {mol}^{- 1}, \ln A = 8.59 (A i n (s^{- 1}))

, can be contrasted with results obtained for higher temperatures

> 1200 ° C

and at atmospheric pressure [111,112,113,120],

E = 420.7 kJ \cdot {mol}^{- 1}, \ln A = 36.23 (A i n (s^{- 1}))

. Importantly, both possibilities indicate that the reaction occurs on a second or millisecond scale.

According to Eqs. (8) and (10) in the case of high pressure

P = 5.61 MPa

at

t = 900 ° C

, we obtain

α_{eq .} = 0.4336

. Thus, the actual experimental conversion degree is less than

α < 0.43

, and hence the determined characteristic Arrhenius parameters are understated.

For three types of reactors, study [115] presents a very wide range of activation energies. At the same time, [123] discusses the results of computer simulations performed for

T_{iso} = 1190.9 K

. Importantly though in both above-mentioned works the rate constants are equal. Therefore, for all dependencies that refer to this temperature, we observe the unambiguity of the kinetic constants.

Range $α \to 0$

The part of the course of methane pyrolysis, which takes place under the condition of decreasing value of conversion degree is sometimes referred to as catalyst testing. Figure 5 presented above depicts this period; however, its formal analysis boils down to calculation of the amount of carbon deposit formed, which again can be done using Eqs. (25) and (28). The results shown in Table 2 indicate that it is possible to carry out such analyses also for the range when

α \to 0

. Going further, the case shown in Figure 5 confirms, the possibility of using, e.g., model No. 1 of Table 3 for methane pyrolysis reactions when

α \to α_{e q .}

. At the maximum (i.e. for

t^{*} = 119.80

minutes) according to Eqs. (8) and (53)

α_{m a x} = 0.7864 w h i l e α_{e q .} = 0.8211

.

A separate issue that needs attention is whether it is possible to model the kinetics of reaction (1) in the full range of variability of its conversion degree. Till this point no such analyses were found in the literature, while some reference may be the proposals presented in [124]. The simplest form capable of describing the full range of variability of the conversion degree can be taken as an empirical formula:

α = \frac{k_{1}}{k_{1} - k_{3}} (e^{- k_{3} t} - e^{- k_{1}}), k_{1} > k_{3}

(69)

The kinetic constants for Equation (69) are presented in this work. During the analysis of the kinetic equations, it was assumed that the basic approach describing the elementary reaction is presented in Equation (32). Further proceedings highlighted the importance of the reversible term and its impact in the case of catalysts reactive towards carbon formed during the process. In this context, it was concluded that catalysts basing their activity due to the content, availability and form of iron may be the best choice.

The paper finally presents a series of complex and extensive kinetic equations modelling individual elementary reactions responsible for the mechanism of reaction (1) with and without the use of catalyst. As a result the rate of the reaction is described by an equation generally known as the Langmuir-Hinshelwood-Hougen-Watson (LHHW) [125], with an exponent in the denominator equal to 2 (or 1), constituting the sorption term [13,109,126].

Conclusions

A literature review of the kinetics of methane thermal decomposition was conducted, focusing on finding the elementary reaction in the sense defined in the Gold Book [106], and considering the significance of the reversible term – the initial approach of Equation (32). It was found that the limitation of the efficiency of the methane thermal decomposition process is the equilibrium conversion degree and distance from equilibrium (DFE). These limitations can be mitigated by increasing the process temperature to at least 900°C and diluting methane with an inert gas, which in turn makes the reaction/process irreversible.

Detailed analyses of the non-catalytic elementary reaction of methane thermal decomposition indicate that in the case of high pressures or high temperatures and short process times (on the order of ms), the reaction kinetics can be described by the parameters of Arrhenius law. Despite the large range of activation energies

E = 130.5 - 420.7 k J \cdot m o l^{- 1}

, these parameters meet the Kinetic Compensation Effect (KCE) and the Enthalpy-Entropy-Compensation (EEC) for thermodynamic activation functions. Noteworthy in many of the catalytic processes described in literature, they occur on a much broader time scale (with long durations) extending to hours.

It has been shown that in the kinetic category of conversion degree in the presence of catalysts, the kinetic equations covering the range

α \to α_{m a x} \to α_{e q .}

can take simple forms, e.g., the F1 model. After supplementing this approach with process elements (Table 3), this model exhibits a quasi-second-order. Furthermore, conversion degree is a very convenient kinetic category, useful for balancing of the process and determining the amount of carbon deposit.

For supported catalysts based on iron, it is necessary to consider their activation. The stages of catalyst preparation, i.e., drying, grinding, sieving, and subsequent reduction of iron oxides with methane or hydrogen need to be considered. In the context of methane pyrolysis, the preferable form of iron catalyst is

α - F e

, which also constitutes the most favourable structure of

F e

for the formation of cementite. Importantly the polymorphic form

γ - F e

, occurring at temperatures

> 912 ° C

, shows lower catalytic activity. It should also be noted that the transition of iron-supported carriers to active forms of iron is a time- and reductant-consuming process.

The possibility of using the Kinetic Compensation Effect (KCE) to interpret reaction (1) and identify both synergistic and antagonistic catalytic interactions occurring in this process has been confirmed. The phenomenon becomes apparent after transforming the kinetic data according to Arrhenius into thermodynamic activation functions, i.e. Entropy-Enthalpy-Compensation (EEC). Noteworthy also Equation (58) favours activation entropy as a quantity proportional to the ratio

E / T_{i s o}

, when

∆ H^{+} = E - R T_{i s o}

.

The thermal decomposition reaction occurring in the system containing: methane, carbon and iron at temperatures close to the isoconversion temperature depends on the proportions of components and the effects of the interactions between the

F e / C

phases. Elements of the Transition State Theory (TST) were applied to the analysis of the system by comparing the ratio of “forwards-backwards” kinetic constants to the functions of phenomenological thermodynamic. Herein quantities of phenomenological thermodynamics, i.e., Gibbs free energy, enthalpy, entropy (

∆_{r} G^{\emptyset}, {∆_{r} H}^{\emptyset}, {∆_{r} S}^{\emptyset}),

were directly related with activation functions (

∆ G^{+}, ∆ H^{+}, ∆ S^{+})

.

The analysis presented here indicates two main areas of prospective research. Firstly, it would be beneficial to enhance the description of reaction (1) by incorporating equation (69). This has not been done previously, but it permits the description of the thermal decomposition of methane in terms of the kinetic constants associated with the thermodynamic activation functions (TST). This may facilitate the integration of current knowledge regarding the course of the reaction and deactivation of catalysts. Secondly, it can be seen that further research is required on the irreversible [13], dissociative adsorption [109], and irreversible dissociative adsorption [126] models. These should be analysed in the context of reactions (2) and (3), or even described in the light of different conversion routes, such as acetylene–benzene [46].

Author Contributions

Conceptualization, A.M., T.R., and M.S.; methodology, A.M.; validation, T.R., formal analysis, M.S.; investigation, M.S.; resources, A.S.; data curation, T.R. and T.I.; writing—original draft preparation, A.M. and T.R.; writing—review and editing, T.R. and M.S.; visualization, T. R. and T.I; supervision, T.I. and A.S.; project administration, T.I.; funding acquisition, A.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Conflicts of Interest

The authors declare no conflicts of interest.

Symbols

a, b

constants representing mean values of enthalpy and entropy in regard to temperature, respectively kJ·mol⁻¹, kJ·(mol·K)⁻¹, Table 1;

A

pre-exponential factor, s⁻¹;

B

2.08364·10¹⁰ K⁻¹·s⁻¹, ratio of Boltzmann to Planck’s constant;

c

auxiliary quantity in Equation (48);

c_{P}

heat capacities, J·(kg·K)⁻¹;

[C]

calculated ration of carbon deposit, g·g_cat⁻¹;

E

activation energy, J·mol⁻¹;

g (x), g (α), g (z)

kinetic functions (

g (\dots) = k_{1} \cdot t

) for methane, conversion degree and thermodynamic efficiency respectively;

∆ G, ∆ H, ∆ S

thermodynamic functions for free enthalpy, enthalpy and entropy respectively;

k

kinetic rate constant, dependent on T, s⁻¹,

K

equilibrium constant,

n

exponent,

P

pressure or partial pressure, Pa,

r

reaction rate, Eqs. (30) and (33), s⁻¹;

r (t)

reaction rate, Equation (29), mmol·(g_cat·time)⁻¹;

r_{0}

initial reaction rate, mmol·(g_cat·time)⁻¹,

r_{0} =

const, Equation (29);

r_{C}

initial reaction rate, mmol·(g_cat·time)⁻¹, Equation (26);

r^{2}

linear determination coefficient, 0

\leq r^{2} \leq 1;

R

R=8.314 J·(mol·K)⁻¹ universal gas constant;

t

time, s, min and hrs;

t

temperature, °C; (only in text)

T

absolute temperature, K;

\dot{V}

flow rate, dm³ or m³·(g_cat·time)⁻¹;

x

mol fraction,

0 \leq x \leq 1

;

z

thermodynamic efficiency,

0 \leq z \leq 1

;

α

conversion degree,

0 \leq α \leq 1

;

β

physical dilatation factor, acc. [111], Table 3;

ɛ

expansion factor, fractional volume change on complete, conversion of substance A, acc. to [110], Table 3;

τ_{D}

time constant for deactivation, s;

ν

stoichiometric coefficient;

Subscripts

B

activation entropy in isokinetic temperature;

CH₄, H₂ acc. to methane, hydrogen,

i s o

isokinetic,

e q .

equilibrium,

P

pressure,

x, α

acc. to equilibrium constant,

0

initial state,

1, -1, 3 acc. to: forwards, backwards and another kind,

Superscripts

+

activation functions;

\emptyset

standard state;

* maximum;

\bar{}

average;

Abbreviations

BCC	body-centred cubic,
CPMR	Perfectly mixed reactor with bypass (in [117]),
DFE	Distance From Equilibrium (or far from equilibrium),
EEC	Enthalpy-Entropy-Compensation or (rarely) Entropy-Enthalpy-Compensation (e.g. [127]),
FCC	face-centred cubic,
KCE	Kinetic Compensation Effect,
LHHW	Langmuir-Hinshelwood-Hougen-Watson Equation,
R-WGS	Reverse Water-Gas Shift reaction,
TST	Transition-State Theory,
WGS	Water-Gas Shift reaction,
WHSV	Weight Hourly Space Velocity.

References

Barin, I. Thermochemical Data of Pure Substances; 1st ed.; Wiley, 1995; ISBN 978-3-527-28745-1.
Fierro, J.L.G. Catalysis in C1 Chemistry: Future and Prospect. Catal Lett 1993, 22, 67–91. [Google Scholar] [CrossRef]
Msheik, M.; Rodat, S.; Abanades, S. Experimental Comparison of Solar Methane Pyrolysis in Gas-Phase and Molten-Tin Bubbling Tubular Reactors. Energy 2022, 260, 124943. [Google Scholar] [CrossRef]
Sánchez-Bastardo, N.; Schlögl, R.; Ruland, H. Methane Pyrolysis for Zero-Emission Hydrogen Production: A Potential Bridge Technology from Fossil Fuels to a Renewable and Sustainable Hydrogen Economy. Ind. Eng. Chem. Res. 2021, 60, 11855–11881. [Google Scholar] [CrossRef]
Sánchez-Bastardo, N.; Schlögl, R.; Ruland, H. Methane Pyrolysis for CO2 -Free H2 Production: A Green Process to Overcome Renewable Energies Unsteadiness. Chemie Ingenieur Technik 2020, 92, 1596–1609. [Google Scholar] [CrossRef]
Xu, R.; Meisner, J.; Chang, A.M.; Thompson, K.C.; Martínez, T.J. First Principles Reaction Discovery: From the Schrodinger Equation to Experimental Prediction for Methane Pyrolysis. Chem. Sci. 2023, 14, 7447–7464. [Google Scholar] [CrossRef] [PubMed]
Ashik, U.P.M.; Wan Daud, W.M.A.; Abbas, H.F. Production of Greenhouse Gas Free Hydrogen by Thermocatalytic Decomposition of Methane – A Review. Renewable and Sustainable Energy Reviews 2015, 44, 221–256. [Google Scholar] [CrossRef]
Hamdani, I.R.; Ahmad, A.; Chulliyil, H.M.; Srinivasakannan, C.; Shoaibi, A.A.; Hossain, M.M. Thermocatalytic Decomposition of Methane: A Review on Carbon-Based Catalysts. ACS Omega 2023, 8, 28945–28967. [Google Scholar] [CrossRef] [PubMed]
Audier, M.; Coulon, M.; Bonnetain, L. Hydrogenation of Catalytic Carbons Obtained by CO Disproportionation or CH4 Decomposition on Nickel. Carbon 1979, 17, 391–394. [Google Scholar] [CrossRef]
Rostrupnielsen, J. Sulfur-Passivated Nickel Catalysts for Carbon-Free Steam Reforming of Methane. Journal of Catalysis 1984, 85, 31–43. [Google Scholar] [CrossRef]
Bernardo, C.A.; Rostrup-Nielsen, J.R. Carbon Deposition and Methane Steam Reforming on Silica-Supported Ni-Cu Catalysts. Journal of Catalysis 1985, 96, 517–534. [Google Scholar] [CrossRef]
Alstrup, I.; Tavares, M.T. Kinetics of Carbon Formation from CH4 + H2 on Silica-Supported Nickel and Ni-Cu Catalysts. Journal of Catalysis 1993, 139, 513–524. [Google Scholar] [CrossRef]
Snoeck, J.-W.; Froment, G.F.; Fowles, M. Kinetic Study of the Carbon Filament Formation by Methane Cracking on a Nickel Catalyst. Journal of Catalysis 1997, 169, 250–262. [Google Scholar] [CrossRef]
Kuvshinov, G.G.; Mogilnykh, Yu.I.; Kuvshinov, D.G. Kinetics of Carbon Formation from CH4–H2 Mixtures over a Nickel Containing Catalyst. Catalysis Today 1998, 42, 357–360. [Google Scholar] [CrossRef]
Chambers, A.; Nemes, T.; Rodriguez, N.M.; Baker, R.T.K. Catalytic Behavior of Graphite Nanofiber Supported Nickel Particles. 1. Comparison with Other Support Media. J. Phys. Chem. B 1998, 102, 2251–2258. [Google Scholar] [CrossRef]
Li, Y.; Chen, J.; Qin, Y.; Chang, L. Simultaneous Production of Hydrogen and Nanocarbon from Decomposition of Methane on a Nickel-Based Catalyst. Energy Fuels 2000, 14, 1188–1194. [Google Scholar] [CrossRef]
Ermakova, M.A.; Ermakov, D.Y.; Kuvshinov, G.G. Effective Catalysts for Direct Cracking of Methane to Produce Hydrogen and FIlamentous Carbon Part I. Nickel Catalysts. 2000. [Google Scholar]
Otsuka, K.; Ogihara, H.; Takenaka, S. Decomposition of Methane over Ni Catalysts Supported on Carbon Fibers Formed from Different Hydrocarbons. Carbon 2003, 41, 223–233. [Google Scholar] [CrossRef]
Qian, W.; Liu, T.; Wei, F.; Wang, Z.; Li, Y. Enhanced Production of Carbon Nanotubes: Combination of Catalyst Reduction and Methane Decomposition. Applied Catalysis A: General 2004, 258, 121–124. [Google Scholar] [CrossRef]
Villacampa, J.I.; Royo, C.; Romeo, E.; Montoya, J.A.; Del Angel, P.; Monzón, A. Catalytic Decomposition of Methane over Ni-Al2O3 Coprecipitated Catalysts. Applied Catalysis A: General 2003, 252, 363–383. [Google Scholar] [CrossRef]
Otsuka, K.; Takenaka, S.; Ohtsuki, H. Production of Pure Hydrogen by Cyclic Decomposition of Methane and Oxidative Elimination of Carbon Nanofibers on Supported-Ni-Based Catalysts. Applied Catalysis A: General 2004, 273, 113–124. [Google Scholar] [CrossRef]
Sharif Zein, S.H.; Mohamed, A.R.; Talpa Sai, P.S. Kinetic Studies on Catalytic Decomposition of Methane to Hydrogen and Carbon over Ni/TiO ₂ Catalyst. Ind. Eng. Chem. Res. 2004, 43, 4864–4870. [Google Scholar] [CrossRef]
Dupuis, A. The Catalyst in the CCVD of Carbon Nanotubes—a Review. Progress in Materials Science 2005, 50, 929–961. [Google Scholar] [CrossRef]
Chen, D.; Christensen, K.; Ochoafernandez, E.; Yu, Z.; Totdal, B.; Latorre, N.; Monzon, A.; Holmen, A. Synthesis of Carbon Nanofibers: Effects of Ni Crystal Size during Methane Decomposition. Journal of Catalysis 2005, 229, 82–96. [Google Scholar] [CrossRef]
Venugopal, A.; Naveen Kumar, S.; Ashok, J.; Hari Prasad, D.; Durga Kumari, V.; Prasad, K.B.S.; Subrahmanyam, M. Hydrogen Production by Catalytic Decomposition of Methane over Ni/SiO2Ni/SiO2☆. International Journal of Hydrogen Energy 2007, 32, 1782–1788. [Google Scholar] [CrossRef]
Bai, Z.; Chen, H.; Li, B.; Li, W. Methane Decomposition over Ni Loaded Activated Carbon for Hydrogen Production and the Formation of Filamentous Carbon. International Journal of Hydrogen Energy 2007, 32, 32–37. [Google Scholar] [CrossRef]
Pinilla, J.L.; Suelves, I.; Lázaro, M.J.; Moliner, R.; Palacios, J.M. Parametric Study of the Decomposition of Methane Using a NiCu/Al2O3 Catalyst in a Fluidized Bed Reactor. International Journal of Hydrogen Energy 2010, 35, 9801–9809. [Google Scholar] [CrossRef]
De Jesús, J.C.; González, I.; García, M.; Urbina, C. Preparation of Nickel Nanoparticles and Their Catalytic Activity in the Cracking of Methane. Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films 2008, 26, 913–918. [Google Scholar] [CrossRef]
Suelves, I.; Pinilla, J.L.; Lázaro, M.J.; Moliner, R.; Palacios, J.M. Effects of Reaction Conditions on Hydrogen Production and Carbon Nanofiber Properties Generated by Methane Decomposition in a Fixed Bed Reactor Using a NiCuAl Catalyst. Journal of Power Sources 2009, 192, 35–42. [Google Scholar] [CrossRef]
Cunha, A.F.; Órfão, J.J.M.; Figueiredo, J.L. Methane Decomposition on Ni–Cu Alloyed Raney-Type Catalysts. International Journal of Hydrogen Energy 2009, 34, 4763–4772. [Google Scholar] [CrossRef]
Chesnokov, V.V.; Chichkan, A.S. Production of Hydrogen by Methane Catalytic Decomposition over Ni–Cu–Fe/Al2O3 Catalyst. International Journal of Hydrogen Energy 2009, 34, 2979–2985. [Google Scholar] [CrossRef]
Salmones, J.; Wang, J.A.; Valenzuela, M.A.; Sánchez, E.; Garcia, A. Pore Geometry Influence on the Deactivation Behavior of Ni-Based Catalysts for Simultaneous Production of Hydrogen and Nanocarbon. Catalysis Today 2009, 148, 134–139. [Google Scholar] [CrossRef]
Zapata, B.; Valenzuela, M.A.; Palacios, J.; Torres-Garcia, E. Effect of Ca, Ce or K Oxide Addition on the Activity of Ni/SiO2 Catalysts for the Methane Decomposition Reaction. International Journal of Hydrogen Energy 2010, 35, 12091–12097. [Google Scholar] [CrossRef]
Hussain, T.; Iqbal, M. Pyrolysis of Methane by Catalytic Properties Exhibited by Ceramics. Journal of Analytical and Applied Pyrolysis 2011, 90, 106–111. [Google Scholar] [CrossRef]
Saraswat, S.K.; Pant, K.K. Ni–Cu–Zn/MCM-22 Catalysts for Simultaneous Production of Hydrogen and Multiwall Carbon Nanotubes via Thermo-Catalytic Decomposition of Methane. International Journal of Hydrogen Energy 2011, 36, 13352–13360. [Google Scholar] [CrossRef]
Nuernberg, G.D.B.; Foletto, E.L.; Campos, C.E.M.; Fajardo, H.V.; Carreño, N.L.V.; Probst, L.F.D. Direct Decomposition of Methane over Ni Catalyst Supported in Magnesium Aluminate. Journal of Power Sources 2012, 208, 409–414. [Google Scholar] [CrossRef]
Hornés, A.; Bera, P.; Fernández-García, M.; Guerrero-Ruiz, A.; Martínez-Arias, A. Catalytic and Redox Properties of Bimetallic Cu–Ni Systems Combined with CeO2 or Gd-Doped CeO2 for Methane Oxidation and Decomposition. Applied Catalysis B: Environmental 2012, 111–112, 96–105. [Google Scholar] [CrossRef]
Saraswat, S.K.; Pant, K.K. Synthesis of Hydrogen and Carbon Nanotubes over Copper Promoted Ni/SiO2 Catalyst by Thermocatalytic Decomposition of Methane. Journal of Natural Gas Science and Engineering 2013, 13, 52–59. [Google Scholar] [CrossRef]
Wang, H.Y.; Lua, A.C. Deactivation and Kinetic Studies of Unsupported Ni and Ni–Co–Cu Alloy Catalysts Used for Hydrogen Production by Methane Decomposition. Chemical Engineering Journal 2014, 243, 79–91. [Google Scholar] [CrossRef]
Tang, M.; Xu, L.; Fan, M. Progress in Oxygen Carrier Development of Methane-Based Chemical-Looping Reforming: A Review. Applied Energy 2015, 151, 143–156. [Google Scholar] [CrossRef]
Ashik, U.P.M.; Wan Daud, W.M.A.; Abbas, H.F. Methane Decomposition Kinetics and Reaction Rate over Ni/SiO2 Nanocatalyst Produced through Co-Precipitation Cum Modified Stöber Method. International Journal of Hydrogen Energy 2017, 42, 938–952. [Google Scholar] [CrossRef]
Keipi, T.; Tolvanen, K.E.S.; Tolvanen, H.; Konttinen, J. Thermo-Catalytic Decomposition of Methane: The Effect of Reaction Parameters on Process Design and the Utilization Possibilities of the Produced Carbon. Energy Conversion and Management 2016, 126, 923–934. [Google Scholar] [CrossRef]
Łamacz, A. CNT and H2 Production During CH4 Decomposition over Ni/CeZrO2. I. A Mechanistic Study. ChemEngineering 2019, 3, 26. [Google Scholar] [CrossRef]
Łamacz, A.; Łabojko, G. CNT and H2 Production during CH4 Decomposition over Ni/CeZrO2. II. Catalyst Performance and Its Regeneration in a Fluidized Bed. ChemEngineering 2019, 3, 25. [Google Scholar] [CrossRef]
Muto, T.; Asahara, M.; Miyasaka, T.; Asato, K.; Uehara, T.; Koshi, M. Methane Pyrolysis Characteristics for the Practical Application of Hydrogen Production System Using Permalloy Plate Catalyst. Chemical Engineering Science 2023, 274, 117931. [Google Scholar] [CrossRef]
Park, S.; Kim, M.; Koo, Y.; Kang, D.; Kim, Y.; Park, J.; Ryu, C. Numerical Modeling of Methane Pyrolysis in a Bubble Column of Molten Catalysts for Clean Hydrogen Production. International Journal of Hydrogen Energy 2023, 48, 7385–7399. [Google Scholar] [CrossRef]
Harrath, K.; Yao, Z.; Jiang, Y.-F.; Wang, Y.-G.; Li, J. Activity Origin of the Nickel Cluster on TiC Support for Nonoxidative Methane Conversion. J. Phys. Chem. Lett. 2023, 14, 4033–4041. [Google Scholar] [CrossRef]
Yan, P.; Zhang, K.; Peng, Y. Study of Fe2O3-Al2O3 Catalyst Reduction Parameters and Conditions for Catalytic Methane Decomposition. Chemical Engineering Science 2022, 250, 117410. [Google Scholar] [CrossRef]
Ermakova, M.A.; Ermakov, D.Y.; Chuvilin, A.L.; Kuvshinov, G.G. Decomposition of Methane over Iron Catalysts at the Range of Moderate Temperatures: The Influence of Structure of the Catalytic Systems and the Reaction Conditions on the Yield of Carbon and Morphology of Carbon Filaments. Journal of Catalysis 2001, 201, 183–197. [Google Scholar] [CrossRef]
Ermakova, M. Ni/SiO2 and Fe/SiO2 Catalysts for Production of Hydrogen and Filamentous Carbon via Methane Decomposition. Catalysis Today 2002, 77, 225–235. [Google Scholar] [CrossRef]
Reshetenko, T. Coprecipitated Iron-Containing Catalysts (Fe-Al2O3, Fe-Co-Al2O3, Fe-Ni-Al2O3) for Methane Decomposition at Moderate temperaturesI. Genesis of Calcined and Reduced Catalysts. Applied Catalysis A: General 2004, 268, 127–138. [Google Scholar] [CrossRef]
Konieczny, A.; Mondal, K.; Wiltowski, T.; Dydo, P. Catalyst Development for Thermocatalytic Decomposition of Methane to Hydrogen. International Journal of Hydrogen Energy 2008, 33, 264–272. [Google Scholar] [CrossRef]
Balakrishnan, M.; Batra, V.S.; Hargreaves, J.S.J.; Monaghan, A.; Pulford, I.D.; Rico, J.L.; Sushil, S. Hydrogen Production from Methane in the Presence of Red Mud –Making Mud Magnetic. Green Chem. 2009, 11, 42–47. [Google Scholar] [CrossRef]
Pinilla, J.L.; Utrilla, R.; Karn, R.K.; Suelves, I.; Lázaro, M.J.; Moliner, R.; García, A.B.; Rouzaud, J.N. High Temperature Iron-Based Catalysts for Hydrogen and Nanostructured Carbon Production by Methane Decomposition. International Journal of Hydrogen Energy 2011, 36, 7832–7843. [Google Scholar] [CrossRef]
Kashiwaya, Y.; Watanabe, M. Kinetic Analysis of the Decomposition Reaction of CH4 Injecting into Molten Slag. ISIJ Int. 2012, 52, 1394–1403. [Google Scholar] [CrossRef]
Torres, D.; De Llobet, S.; Pinilla, J.L.; Lázaro, M.J.; Suelves, I.; Moliner, R. Hydrogen Production by Catalytic Decomposition of Methane Using a Fe-Based Catalyst in a Fluidized Bed Reactor. Journal of Natural Gas Chemistry 2012, 21, 367–373. [Google Scholar] [CrossRef]
Cornejo, A. The Thermo-Catalytic Decomposition of Methane for Economical and Emission-Free Hydrogen Production; 2013.
Alves Silva, J.; Oliveira Santos, J.B.; Torres, D.; Pinilla, J.L.; Suelves, I. Natural Fe-Based Catalysts for the Production of Hydrogen and Carbon Nanomaterials via Methane Decomposition. International Journal of Hydrogen Energy 2021, 46, 35137–35148. [Google Scholar] [CrossRef]
Lumbers, B.; Barley, J.; Platte, F. Low-Emission Hydrogen Production via the Thermo-Catalytic Decomposition of Methane for the Decarbonisation of Iron Ore Mines in Western Australia. International Journal of Hydrogen Energy 2022, 47, 16347–16361. [Google Scholar] [CrossRef]
Vlaskin, M.S.; Grigorenko, A.V.; Gromov, A.A.; Kumar, V.; Dudoladov, A.O.; Slavkina, O.V.; Darishchev, V.I. Methane Pyrolysis on Sponge Iron Powder for Sustainable Hydrogen Production. Results in Engineering 2022, 15, 100598. [Google Scholar] [CrossRef]
Wojtasik, M. Dekarbonizacja Metanu z Udziałem Katalizatorów Na Bazie Żelaza. CHEMICAL REVIEW 2023, 1, 55–59. [Google Scholar] [CrossRef]
Grabke, H. -J. Die Kinetik der Entkohlung und Aufkohlung von γ-Eisen in Methan-Wasserstoff-Gemischen. Ber Bunsenges Phys Chem 1965, 69, 409–414. [Google Scholar] [CrossRef]
Zhang, J.; Ostrovski, O. Cementite Formation in CH4-H2-Ar Gas Mixture and Cementite Stability. ISIJ International 2001, 41, 333–339. [Google Scholar] [CrossRef]
А. н, М.; А.м, Г. Термoдинамические Функции Реакций Вoсстанoвления Титанoмагнетитoвoгo Кoнцентрата Аджинаурских Песчаникoв Прирoдным Газoм. Azerbaijan Chemical Journal 2016, 99–102. [Google Scholar]
Zhou, L.; Enakonda, L.R.; Harb, M.; Saih, Y.; Aguilar-Tapia, A.; Ould-Chikh, S.; Hazemann, J.; Li, J.; Wei, N.; Gary, D.; et al. Fe Catalysts for Methane Decomposition to Produce Hydrogen and Carbon Nano Materials. Applied Catalysis B: Environmental 2017, 208, 44–59. [Google Scholar] [CrossRef]
Wang, I.-W.; Kutteri, D.A.; Gao, B.; Tian, H.; Hu, J. Methane Pyrolysis for Carbon Nanotubes and CO _x -Free H ₂ over Transition-Metal Catalysts. Energy Fuels 2019, 33, 197–205. [Google Scholar] [CrossRef]
Chuayboon, S.; Abanades, S.; Rodat, S. Stepwise Solar Methane Reforming and Water-Splitting via Lattice Oxygen Transfer in Iron and Cerium Oxides. Energy Tech 2020, 8, 1900415. [Google Scholar] [CrossRef]
Schneider, A.; Inden, G. Carbon Diffusion in Cementite (Fe3C) and Hägg Carbide (Fe5C2). Calphad 2007, 31, 141–147. [Google Scholar] [CrossRef]
Nikolussi, M.; Leineweber, A.; Mittemeijer, E.J. Growth of Massive Cementite Layers; Thermodynamic Parameters and Kinetics. J Mater Sci 2009, 44, 770–777. [Google Scholar] [CrossRef] [PubMed]
Hallstedt, B.; Djurovic, D.; Von Appen, J.; Dronskowski, R.; Dick, A.; Körmann, F.; Hickel, T.; Neugebauer, J. Thermodynamic Properties of Cementite (). Calphad 2010, 34, 129–133. [Google Scholar] [CrossRef]
Litasov, K.D.; Sharygin, I.S.; Dorogokupets, P.I.; Shatskiy, A.; Gavryushkin, P.N.; Sokolova, T.S.; Ohtani, E.; Li, J.; Funakoshi, K. Thermal Equation of State and Thermodynamic Properties of Iron Carbide Fe ₃ C to 31 GPa and 1473 K. JGR Solid Earth 2013, 118, 5274–5284. [Google Scholar] [CrossRef]
Vogric, M.; Kozeschnik, E.; Svoboda, J.; Führer, M.; Kreyca, J.; Wei, W.; Povoden-Karadeniz, E. Kinetic Modeling of Grain Boundary Cementite Evolution. Metall Mater Trans A 2022, 53, 3759–3773. [Google Scholar] [CrossRef]
Wu, M.; Li, Z.; Huang, J.; Wang, Q.; Li, T.; Yang, S.; He, H.; Jiang, Y. Non-Isothermal Kinetics of Coke and Iron Ore Melting Reduction with Variable Activation Energy Model. Fuel 2024, 357, 129991. [Google Scholar] [CrossRef]
Holmen, A.; Olsvik, O.; Rokstad, O.A. Pyrolysis of Natural Gas: Chemistry and Process Concepts. Fuel Processing Technology 1995, 42, 249–267. [Google Scholar] [CrossRef]
Sinaki, M.Y.; Matida, E.A.; Hamdullahpur, F. Development of a Reaction Mechanism for Predicting Hydrogen Production from Homogeneous Decomposition of Methane. International Journal of Hydrogen Energy 2011, 36, 2936–2944. [Google Scholar] [CrossRef]
Boretti, A. A Perspective on the Production of Hydrogen from Solar-Driven Thermal Decomposition of Methane. International Journal of Hydrogen Energy 2021, 46, 34509–34514. [Google Scholar] [CrossRef]
Kim, S.E.; Jeong, S.K.; Park, K.T.; Lee, K.-Y.; Kim, H.J. Effect of Oxygen-Containing Functional Groups in Metal-Free Carbon Catalysts on the Decomposition of Methane. Catalysis Communications 2021, 148, 106167. [Google Scholar] [CrossRef]
Lott, P.; Mokashi, M.B.; Müller, H.; Heitlinger, D.J.; Lichtenberg, S.; Shirsath, A.B.; Janzer, C.; Tischer, S.; Maier, L.; Deutschmann, O. Hydrogen Production and Carbon Capture by Gas-Phase Methane Pyrolysis: A Feasibility Study. ChemSusChem 2023, 16, e202201720. [Google Scholar] [CrossRef] [PubMed]
Bae, D.; Kim, Y.; Ko, E.H.; Ju Han, S.; Lee, J.W.; Kim, M.; Kang, D. Methane Pyrolysis and Carbon Formation Mechanisms in Molten Manganese Chloride Mixtures. Applied Energy 2023, 336, 120810. [Google Scholar] [CrossRef]
Miri, S.S.; Meshkani, F.; Rastegarpanah, A.; Rezaei, M. Influence of Fe, La, Zr, Ce, and Ca on the Catalytic Performance and Coke Formation in Dry Reforming of Methane over Ni/MgO.Al2O3 Catalyst. Chemical Engineering Science 2022, 250, 116956. [Google Scholar] [CrossRef]
Guéret, C.; Daroux, M.; Billaud, F. Methane Pyrolysis: Thermodynamics. Chemical Engineering Science 1997, 52, 815–827. [Google Scholar] [CrossRef]
Steinberg, M. Production of Hydrogen and Methanol from Natural Gas with Reduced CO2 Emission. International Journal of Hydrogen Energy 1998, 23, 419–425. [Google Scholar] [CrossRef]
Zavarukhin, S.G.; Kuvshinov, G.G. The Kinetic Model of Formation of Nanofibrous Carbon from CH4–H2 Mixture over a High-Loaded Nickel Catalyst with Consideration for the Catalyst Deactivation. Applied Catalysis A: General 2004, 272, 219–227. [Google Scholar] [CrossRef]
Hofberger, C.M.; Dietrich, B.; Durán Vera, I.; Krumholz, R.; Stoppel, L.; Uhlenbruck, N.; Wetzel, T. Natural Gas Pyrolysis in a Liquid Metal Bubble Column Reaction System—Part I: Experimental Setup and Methods. Hydrogen 2023, 4, 295–306. [Google Scholar] [CrossRef]
Chase, M.W. NIST-JANAF Themochemical Tables, Fourth Edition.
Hossain, M.M.; De Lasa, H.I. Chemical-Looping Combustion (CLC) for Inherent CO 2 Separations—a Review. Chemical Engineering Science 2008, 63, 4433–4451. [Google Scholar] [CrossRef]
Monazam, E.R.; Breault, R.W.; Siriwardane, R.; Richards, G.; Carpenter, S. Kinetics of the Reduction of Hematite (Fe2O3) by Methane (CH4) during Chemical Looping Combustion: A Global Mechanism. Chemical Engineering Journal 2013, 232, 478–487. [Google Scholar] [CrossRef]
Keller, M.; Matsumura, A.; Sharma, A. Spray-Dried Fe/Al2O3 as a Carbon Carrier for COx-Free Hydrogen Production via Methane Cracking in a Fluidized Bed Process. Chemical Engineering Journal 2020, 398, 125612. [Google Scholar] [CrossRef]
Bagdavadze, J.; Kandelaki, A.; Ukleba, K.; Tsikaridze, Z. Thermodynamic Analysis of CoO, NiO, CuO, FeO Interaction with Methane. BULLETIN OF THE GEORGIAN NATIONAL ACADEMY OF SCIENCES 2021, 4. [Google Scholar]
Koytsoumpa, E.I.; Karellas, S. Equilibrium and Kinetic Aspects for Catalytic Methanation Focusing on CO2 Derived Substitute Natural Gas (SNG). Renewable and Sustainable Energy Reviews 2018, 94, 536–550. [Google Scholar] [CrossRef]
SALA, C. Study of Reverse Water Gas Shift Reaction Using Bimetallic Catalysts on Active Supports 2022.
Vannier, D. Kinetic Study of High Temperature Water Gas Shift Reaction.
Frick, V.; Brellochs, J.; Specht, M. Application of Ternary Diagrams in the Design of Methanation Systems. Fuel Processing Technology 2014, 118, 156–160. [Google Scholar] [CrossRef]
Mianowski, A.; Robak, Z.; Tomaszewicz, M.; Stelmach, S. The Boudouard–Bell Reaction Analysis under High Pressure Conditions. J Therm Anal Calorim 2012, 110, 93–102. [Google Scholar] [CrossRef]
Mianowski, A.; Radko, T.; Bigda, R. Elements of Transition-State Theory in Relation to the Thermal Dissociation of Selected Solid Compounds. Energies 2024, 17, 2669. [Google Scholar] [CrossRef]
Eyring, H. The Activated Complex in Chemical Reactions. The Journal of Chemical Physics 1935, 3, 107–115. [Google Scholar] [CrossRef]
Laidler, K.J.; King, M.C. Development of Transition-State Theory. J. Phys. Chem. 1983, 87, 2657–2664. [Google Scholar] [CrossRef]
Chi, J.W.H.; Landahl, C.E. Hydrogen Reactions with Graphite Materials at High Temperatures and Pressures. Nuclear Applications 1968, 4, 159–169. [Google Scholar] [CrossRef]
Riley, J.; Atallah, C.; Siriwardane, R.; Stevens, R. Technoeconomic Analysis for Hydrogen and Carbon Co-Production via Catalytic Pyrolysis of Methane. International Journal of Hydrogen Energy 2021, 46, 20338–20358. [Google Scholar] [CrossRef]
Abbas, H.F.; Baker, I.F. Thermocatalytic Decomposition of Methane Using Activated Carbon: Studying the Influence of Process Parameters Using Factorial Design. International Journal of Hydrogen Energy 2011, 36, 8985–8993. [Google Scholar] [CrossRef]
Lee, E.K.; Lee, S.Y.; Han, G.Y.; Lee, B.K.; Lee, T.-J.; Jun, J.H.; Yoon, K.J. Catalytic Decomposition of Methane over Carbon Blacks for CO2-Free Hydrogen Production. Carbon 2004, 42, 2641–2648. [Google Scholar] [CrossRef]
Muradov, N.; Smith, F.; T-Raissi, A. Catalytic Activity of Carbons for Methane Decomposition Reaction. Catalysis Today 2005, 102–103, 225–233. [Google Scholar] [CrossRef]
Kim, M. Hydrogen Production by Catalytic Decomposition of Methane over Activated Carbons: Kinetic Study. International Journal of Hydrogen Energy 2004, 29, 187–193. [Google Scholar] [CrossRef]
Becker, T.; Richter, M.; Agar, D.W. Methane Pyrolysis: Kinetic Studies and Mechanical Removal of Carbon Deposits in Reactors of Different Materials. International Journal of Hydrogen Energy 2023, 48, 2112–2129. [Google Scholar] [CrossRef]
Abanades, S.; Flamant, G. Experimental Study and Modeling of a High-Temperature Solar Chemical Reactor for Hydrogen Production from Methane Cracking. International Journal of Hydrogen Energy 2007, 32, 1508–1515. [Google Scholar] [CrossRef]
Chemistry (IUPAC), T.I.U. of P. and A. IUPAC - Elementary Reaction (E02035) Available online: https://goldbook.iupac.org/terms/view/E02035 (accessed on 9 July 2024).
Kobayashi, A.; Steinberg, M. The Thermal Decomposition of Methane in a Tubular Reactor; Brookhaven National Lab. (BNL), Upton, NY (United States), 1992.
Dahme, A.; Junker, H.J. Die Reaktivität von Koks gegen CO2 im temperaturbereich 1000–1200oC. Brennst. Chem. 36, 193–199.
Saraswat, S.K.; Sinha, B.; Pant, K.K.; Gupta, R.B. Kinetic Study and Modeling of Homogeneous Thermocatalytic Decomposition of Methane over a Ni–Cu–Zn/Al ₂ O ₃ Catalyst for the Production of Hydrogen and Bamboo-Shaped Carbon Nanotubes. Ind. Eng. Chem. Res. 2016, 55, 11672–11680. [Google Scholar] [CrossRef]
Levenspiel, O. Chemical Reaction Engineering; 3rd ed.; John Wiley & Sons, 1999; ISBN 0-471-25424-X.
Rodat, S.; Abanades, S.; Sans, J.-L.; Flamant, G. Hydrogen Production from Solar Thermal Dissociation of Natural Gas: Development of a 10kW Solar Chemical Reactor Prototype. Solar Energy 2009, 83, 1599–1610. [Google Scholar] [CrossRef]
Rodat, S.; Abanades, S.; Coulie, J.; Flamant, G. Kinetic Modelling of Methane Decomposition in a Tubular Solar Reactor. Chemical Engineering Journal 2009, 146, 120–127. [Google Scholar] [CrossRef]
Abanades, S.; Flamant, G. Hydrogen Production from Solar Thermal Dissociation of Methane in a High-Temperature Fluid-Wall Chemical Reactor. Chemical Engineering and Processing: Process Intensification 2008, 47, 490–498. [Google Scholar] [CrossRef]
Paxman, D. Experimental and Theoretical Investigation of Solar Molten Media Methane Cracking for Hydrogen Production. M.Sc., University of Alberta: Department of Mechanical Engineering, 2014.
Paxman, D.; Trottier, S.; Flynn, M.R.; Kostiuk, L.; Secanell, M. Experimental and Numerical Analysis of a Methane Thermal Decomposition Reactor. International Journal of Hydrogen Energy 2017, 42, 25166–25184. [Google Scholar] [CrossRef]
Schindler, H.; Pastushenko, V.P.; Titulaer, U.M. A Measure for the Distance from Equilibrium. Eur Biophys J 1998, 27, 219–226. [Google Scholar] [CrossRef]
Gosiewski, K.; Warmuzinski, K.; Tanczyk, M. Mathematical Simulation of WGS Membrane Reactor for Gas from Coal Gasification. Catalysis Today 2010, 156, 229–236. [Google Scholar] [CrossRef]
Plevan, M.; Geißler, T.; Abánades, A.; Mehravaran, K.; Rathnam, R.K.; Rubbia, C.; Salmieri, D.; Stoppel, L.; Stückrad, S.; Wetzel, Th. Thermal Cracking of Methane in a Liquid Metal Bubble Column Reactor: Experiments and Kinetic Analysis. International Journal of Hydrogen Energy 2015, 40, 8020–8033. [Google Scholar] [CrossRef]
Abanades, S.; Kimura, H.; Otsuka, H. Kinetic Investigation of Carbon-Catalyzed Methane Decomposition in a Thermogravimetric Solar Reactor. International Journal of Hydrogen Energy 2015, 40, 10744–10755. [Google Scholar] [CrossRef]
Abbas, H.F.; Daud, W.M.A.W. Deactivation of Palm Shell-Based Activated Carbon Catalyst Used for Hydrogen Production by Thermocatalytic Decomposition of Methane. International Journal of Hydrogen Energy 2009, 34, 6231–6241. [Google Scholar] [CrossRef]
Abbas, H.F.; Daud, W.M.A.W. Hydrogen Production by Thermocatalytic Decomposition of Methane Using a Fixed Bed Activated Carbon in a Pilot Scale Unit: Apparent Kinetic, Deactivation and Diffusional Limitation Studies. International Journal of Hydrogen Energy 2010, 35, 12268–12276. [Google Scholar] [CrossRef]
Mianowski, A.; Radko, T.; Siudyga, T. Influence of Initial Assumptions on the Kinetic Models of CO2 Gasification of Chars and Cokes in Solid Phase. J Therm Anal Calorim 2016, 126, 1911–1923. [Google Scholar] [CrossRef]
Msheik, M.; Rodat, S.; Abanades, S. CFD Simulation of a Hybrid Solar/Electric Reactor for Hydrogen and Carbon Production from Methane Cracking. Fluids 2023, 8, 18. [Google Scholar] [CrossRef]
Lente, G. Deterministic Kinetics in Chemistry and Systems Biology: The Dynamics of Complex Reaction Networks; SpringerBriefs in Molecular Science, 2014; ISBN 978-3-319-15482-4.
Meenakshi Sundaram, K. CATALYST EFFECTIVENESS FACTOR FOR LANGMUIR-HINSHELWOOD-HOUGEN-WATSON KINETIC EXPRESSIONS. Chemical Engineering Communications 1982, 15, 305–311. [Google Scholar] [CrossRef]
Douven, S.; Pirard, S.L.; Heyen, G.; Toye, D.; Pirard, J.-P. Kinetic Study of Double-Walled Carbon Nanotube Synthesis by Catalytic Chemical Vapour Deposition over an Fe-Mo/MgO Catalyst Using Methane as the Carbon Source. Chemical Engineering Journal 2011, 175, 396–407. [Google Scholar] [CrossRef]
Starikov, E.B.; Nordén, B. Entropy–Enthalpy Compensation as a Fundamental Concept and Analysis Tool for Systematical Experimental Data. Chemical Physics Letters 2012, 538, 118–120. [Google Scholar] [CrossRef]

Figure 1. Change in heat capacity of

α - F e

and

γ - F e

vs. temperature.

Figure 1. Change in heat capacity of

α - F e

and

γ - F e

vs. temperature.

Figure 2. The dependence of free energy on temperature for reactions No 1–7 (Table 1).

Figure 3. Transformation of the experimental results from [82,107] to the form of Equation (39) further simplified to linear relation of Equation (43).

Figure 4. Figure 4. Graphical presentation of kinetic equations

g (α) = k_{1} t

for data showed in [57]

Figure 4. Figure 4. Graphical presentation of kinetic equations

g (α) = k_{1} t

for data showed in [57]

Figure 5. Experimental data for nickel catalyst; data showed in [38].

Figure 6. Figure 6. Parameters of Arrhenius eq. acc. to literature data in the form of KCE,

T_{i s o} = 1335.0 K

Figure 6. Figure 6. Parameters of Arrhenius eq. acc. to literature data in the form of KCE,

T_{i s o} = 1335.0 K

Figure 7. Figure 7. KCE converted to thermodynamic activation functions according to EEC.

T_{e q .} = 815.2 K,

point marked in red is outside of the range of correlation presented in Figure 6

Figure 7. Figure 7. KCE converted to thermodynamic activation functions according to EEC.

T_{e q .} = 815.2 K,

point marked in red is outside of the range of correlation presented in Figure 6

Table 2. Comparison of experimental data for fluidized bed pyrolysis of methane where NiCu/Al₂O₃ was used as catalyst.

Temperature in °C; model for H₂	$\bar{α}$ , calculated as an average value of an integral	$[C], g \cdot g_{c a t}^{- 1}$ calculated from Equation (28)	$[C], · {g \cdot g}_{c a t}^{- 1}$ in [27] (time of the process in minutes)
650; exponential	0.127	5.71	4.97 (420)
700; linear	0.404	18.17	18.41 (420)
750; exponential	0.288	12.95	12.95 (420)
800; exponential	0.303	8.44	8.80 (300)

Table 3. Integral forms of

g (α) = k_{1} t

.

Table 3. Integral forms of

g (α) = k_{1} t

.

No	$d α / d t$ =	$g (α) =$	remarks	sources
1	$\frac{k_{1}}{1 + x_{0}} (1 - α) (1 + x_{0} α)$	$\ln (\frac{1 + x_{0} α}{1 - α})$	$For x_{0} = 1$ $d α / d t = \frac{k_{1}}{2} (1 - α^{2})$	Eqs. (51),(55)
2	$k_{1} \frac{1 - α}{1 + α}$	$- 2 \ln (1 - α) - α$	Proposed for analysis of reactivity of cokes towards CO₂; year 1955 [108]	Eq. proposed by Lee [101], model D–J
3	$k_{1} \frac{1 - α}{1 + ε α}$	$- (1 + ε) \ln (1 - α) - ε α$ $ε = 1 / 2$	$ε$ $in [101] as well as in [22, 109] is defined in the form given by [110] . For system consisting of isomorphic spheres ε = 1 - (π / 6) = 0.476$	[22] (2004) and [109] (2016)
4	$(\frac{k_{1}}{β}) \frac{1 - α}{1 + x_{0} α}$	$- (1 + x_{0}) β \ln (1 - α) - x_{0} β α$	$Acc . to [111], β$ = 0.43–0.71	[111,112,113] $, for β = 1$ $, T = 1023 - 1373 K$ , for three types of reactors [114,115]
5	$k_{1} (1 - α)$	$- \ln (1 - α)$	Here $ε = 0$ which acc. to [110] means constant density	Equation (46), model F1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Literature Review on Thermodynamic and Kinetic Limitations of Thermal Decomposition of Methane

Abstract

Keywords:

Subject:

Introduction

Aim of the Work

Phenomenological Thermodynamics and Thermodynamics of Activation

Modelling of the Forward and Backward Reactions

Variant 1 – from carburization of iron to methane decomposition on iron surface

Variant 2 – Free Energy of Activation of the Reaction (1)

Kinetics – Introduction

Kinetics of the Elemental Reaction Equation (1)

Continuous process – conditions of constant flow of methane

Solution of Equation (34) for $x_{0} < 1$ and considering equilibrium constant $K$

KCE and EEC

Discussion

Range $α \to 0$

Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Symbols

Subscripts

Superscripts

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

Literature Review on Thermodynamic and Kinetic Limitations of Thermal Decomposition of Methane

Abstract

Keywords:

Subject:

Introduction

Aim of the Work

Phenomenological Thermodynamics and Thermodynamics of Activation

Modelling of the Forward and Backward Reactions

Variant 1 – from carburization of iron to methane decomposition on iron surface

Variant 2 – Free Energy of Activation of the Reaction (1)

Kinetics – Introduction

Kinetics of the Elemental Reaction Equation (1)

Continuous process – conditions of constant flow of methane

Solution of Equation (34) for x 0 < 1 and considering equilibrium constant K

KCE and EEC

Discussion

Range α → 0

Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Symbols

Subscripts

Superscripts

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

Solution of Equation (34) for $x_{0} < 1$ and considering equilibrium constant $K$

Range $α \to 0$