Prerpints.org logo
Preprint
Article

Eis Behavior of Polyethylene+graphite Composite Considered as an Approximation to an Ensemble of Microelectrodes

Altmetrics

Downloads

45

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

01 August 2024

Posted:

01 August 2024

You are already at the latest version

Alerts
Abstract
The electrical percolation of alternating current through two-phase polyethylene/graphite composite electrodes with different contents of graphite microparticles immersed in aqueous KCl solutions has been studied. Above the graphite content of the first percolation threshold, the electrochemical impedance response of this electrode is associated with an equivalent circuit of resistance Ru in series with a constant phase element CPE. An insulator material+conductive filler model is proposed in which the electroactive surface is considered as the intersection of the percolation cluster through the solid and the cluster associated with the interfacial region. CPE is analyzed assuming a distribution of micro-capacitors of the graphite particles in contact with the dielectric solution and inside the dielectric polymeric phase.
Keywords: 
Subject: Chemistry and Materials Science  -   Ceramics and Composites

1. Introduction

Most organic coatings and plastics are composite materials that contain some kind of inorganic fillers. Their formulations depend on the chemical-physical properties required in their respective specific applications. Often, a common research topic for their design and development is to predict how the filler ratio in the polymer matrix is affected by possible environmental perturbations on these materials. Technological composites based on polymeric materials reinforced with carbon particles or fibers are increasingly investigated at long of time by means electrochemical techniques from a wide different perspectives [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Therefore, they are also increasingly used in the manufacture of electrodes and membranes for conventional electrochemical cells and reactors, as well as in electronic devices for daily use, such as smartphones or personal computers. AC-electrical Percolation is an experimental resource to obtain morphological information about the inner of the material and its surface. This has been very useful in the inhibition of corrosion processes in metals, studies on biomaterials, and in the development of energy storage devices, as well as in the development of sensors or in the manufacture of building materials, paints, enamels and varnishes with specific properties.
Historically, the first composite conducting materials were manufactured by dispersing micrometric conductive particles in insulating polymeric matrices. Today, the number of possible benefits and applications of composites of the polymer+conductive charge type has increased enormously, but it should be noted that the theoretical concepts on the Percolation Theory, developed mainly during the 20th century in electrochemical fields [22,23,24,25,26,27,28,29,30,31,32,33,34,35], are still useful for contributing to the design of supercapacitors, electrochemical reactors or sensors as well as special paints in which these composite materials are used. Today, the surface modification of organic electrodes as graphite with substances having high electronegativity heteroatoms is a topic of great promising technological importance for the development of electrochemical energy storage systems [36].
An apparently simple model of an insulating polymer+conductive composite is the system consisting of the dispersion of graphite particles in a polyethylene matrix. Both materials are of great technological importance on their own. In this work, alternating current is used to characterize the composite material in a three-electrode conventional cell. An attempt is made to obtain information on the effect of the graphite content on the percolation of electric current through it. The electrochemical impedance response of the composite electrode/KCl aqueous solution system is analyzed in order to correlate its surface properties with those of the solid composite and the interfacial regions. This work focuses on the impedance spectroscopy response EIS of the high density graphite+polyethylene (GHDPE) bicomponent system [37,38,39,40,41,42,43,44,45]. An attempt is made to correlate the concepts of the Percolation Theory with its phenomenological electrochemical behavior.
For chronoamperometric processes controlled by diffusion, it is widely accepted [31,46,47,48,49,50] that the current density referred to the geometric area of the electrode Ao obeys to the Cottrell’s law depending on the fractal dimension d F of the electrode surface:
j t = σ F . t − d F − 1 2
where σ F is a constant. Consequently, for example, applying a potential ramp, one could obtain these fractal dimension values from the dependence on the peak intensity of the voltammograms on the scan rate v , because j p would be analogously proportional to v − d F − 1 2 . Then, from the perspective of electrochemical kinetics, the deviation of the ½ value of the exponent of Cottrell’s law of the faradaic process (Equation Error! Reference source not found.) in a composite electrode depends on the fractal dimension of its electrode surface and, therefore, also on the experimental ohmic drop of the cell [40,51,52,53]. In this way, the experimental fractal dimension could be considered as a characteristic magnitude of the morphology of the surface[54,55]. Generally, this fractal dimension is associated with surface roughness [56,57].
Since linear scanning cyclic voltammetry, chronoamperometry, and EIS are widely used in laboratories, the calculated values of d F by means these classical electrochemical techniques could be of immense practical usefulness for the design and quality control of composite materials in electrochemical devices where electrochemical reactions occurs. However, the material transfer processes, passivation and other chemical physical processes as well as secondary chemical reactions coupled with the electron transfer steps can complicate to understand the physical meaning of the calculated d F values.
It is well known that polyethylene is a good model of nonconductive polymer, and the graphite is also a model of conducting filler used in technological uses. The dispersion of conductive graphite particles within the non-conductive polyethylene plastic material above the volume content v C of the percolation threshold produces a multi-micro electrode ensemble on the surface of the electrode composite. The aim of this work is to analyze the electrical percolation through the graphite+polyethylene of high density (GHDPE electrodes) by electrochemical impedance spectroscopy (EIS). The objective is to analyze the fractal dimension of the electrode surfaces of this biphasic composite in the absence of significative faradaic processes, since this electrochemical technique provides direct information on the electrical properties of the material together the electrode/solution interfaces [37,38,39,40,41,58] .
The electrochemical processes on GHDPE electrode should be takes place in the interfacial region formed between the graphite particles on the composite surface and the aqueous solution of the cell. Obviously, the geometric surface area Ao is not equal to the electroactive area A e q of the electrode. In any case, the fractal dimension of the electrochemical surface d F is a function of the content of conductive filler into the solid but depends also on the interfacial region. In this scheme, the electrode surface could be considered as the intersection of two percolative clusters: on the one hand, the cluster defined by the transport of electrons through the composite (composite cluster) with a fractal dimension d C and, on the other hand, the cluster in the interfacial region which could define by means of the lines of force of the charge transfer in absence of convection (interfacial cluster) d S . The voltammetry allows to obtain information quickly about this electrode process and of such important magnitudes as the fractal dimension d F ≅ 1.7 as well as the effect of the ohmic drop [38,39]. Although some approximations are required for its calculations [40], the dependence of the electroactive area A e q with the content in volume of graphite is consistent with the geometric calculation in the case of a composite of this type [37] . However, the kinetic complications themselves and the overlap of the faradaic and capacitive response introduce an uncertainty in the interpretation of the results. A possible advantage could be to perturb the composite electrodes by means of an alternating potential applying the EIS technique in the absence of a depolarizer in the solution in order to simplify the system under study.

2. Materials and Methods

KCl (Aldrich-Sigma; 99%) and K3Fe(CN)6 (Panreac,Castellar del Vallés, Barcelona, Spain) 99%) have been used as electrolytes solutions. The polymer matrix used to produce these composite materials is a high-density polyethylene (HDPE, Alcudia, REPSOL S.A.,Puertollano, Spain) grade. Graphite (Merck 4020, Madrid, Spain) of 16.2±0.2 µm average diameter from the size distribution of the powder particles was used. Experiments using cyclic voltammetry (see in Figure S1 in supplementary materials) and EIS were carried out as in previous works by means of a PAR 273A (EG&G) potentiostat/galvanostat was used [3,37,38,39,40,41] and a AUTOLAB PGSTAB 302 (Metrhom AG, Herisau, Switzerland) in new experiments. In all experiments, Ag/AgCl/KCl(sat.) reference electrode was used (Metrohm). DC resistance measurements of work electrodes were made also with a Fluke Mod 45 DC multimeter (Fortive Corporation, NYSE:DHR, Everett, Washington, EE. UU.). A conventional double-walled three-electrode cell was used at 298±1 K. The steps for performing the electrodes whit different amounts of graphite consist of: 1) Mixing with a roller mill.2) Cold crushing with a blade mill.3) A saucer press was used.4) It was cut using a diamond saw. The electrodes were made in the form of square prisms of 1.0 cm high with square bases of 0.4×0.6 cm, (see Figure S1 in supplementary material) one of the faces by silver paint (Quick Dry Colloidal Silver A 1208, Biorad, Hercules, California, EE. UU.) and the other the electrode surface was polished with 600 sandpaper. The electrodes were mounted embedded in epoxy resin. For corroborating the nominal proportions of graphite, the amount of graphite is experimentally measured by thermogravimetric analysis (TGA) in the Technological Institute of Plastics AIMPLAS (Paterna, Spain). To do this, the GHDPE sample is subjected to 640 ºC in an inert atmosphere (N2), a temperature at which the polymer matrix is decomposed.
The volume content of graphite v [3] has been calculated from its weight content m g and the densities of polyethylene ρ P E and graphite ρ g :
v = m g ρ g m g ρ g + 1 − m g ρ P E
From experimental measures of the dependence of the resistance on graphite content, values v C = 0.14 and t = 3.4 are calculated. Below this critical percolation volume, the composite material shows a resistive behavior (See Figure S2 in supplementary materials).

3. Results

3.1. A Fractal Perspective of the EIS of GHDPE/ KCl Aqueous Solution Composite

The interfacial region is formed when the electrical circuit in the cell is closed and then, the electrochemical potential gradient associated to the charge migration remains commonly normal to the electrode surface. Therefore, the fractal dimension ( d F   ) of the electrode surface must be of the same order as those calculated through this Equation Error! Reference source not found. for diffusion-controlled processes. In the limiting case, for a well-polished inert metallic electrode the fractal dimension of the electrode surface would approximate the Euclidean dimension d F ≈ 2   .
Our hypothesis leads to d F of the electrode/solution surface is associated to the intersection of two transport cluster (Figure 1). One corresponds to the flow of electrons through the internal cluster of the condensed composite material fractal dimension (dC) and, the other, to the ion transport of formation of the interfacial region (double layer). The electrochemical surface is the intersection of the composite percolative cluster with the interfacial cluster formed by the vector gradients of the electrochemical potentials at the interfacial region.
Hence, the fractal dimension dF of the surface electrode is defined as the intersection of a 2D plane embedded into three-dimensional object d E = 3 [59] as is the studied electrode:
d F = d C + 2 − d E = d C + 2 − 3   = d C − 1
The fractal dimension of the polymer+graphite composite material d C depends increasingly on the probability of occupancy of the particles within the material p, i.e., on their volume content v (Figure 2). Therefore, consistent with Equation (3) , the fractal dimension of the fractal dimension of the electrode surface d F should increase with graphite content to a value close to 2.
A modulated ac perturbation on the composite-solution system allows to obtain valuable information on the electrical percolation through the system at each stabilization potential E 0 and applied frequency ω . As is commonly accepted, alternating current flows through the composite material of the working electrode, by three different ways: polarization, tunnel effect and directly by electron-hopping through the clusters formed by the conductive particles in contact.
By perturbing the dissolution-electrode system with an applied potential at a given frequency ( ω = 2 π f ) :
E ω , t = E 0 + ∆ E   s e n ⁡ ( ω t )
the modulated linear electrochemical response is out of phase in time with a phase angle ( φ ) according to the sinusoidal intensity function:
i ( ω , t ) = i 0 + ∆ i cos ⁡ ( ω t + φ )
Immediately, one can conclude that the measure of phase angle points of the nature of the percolation of ac perturbation through the material: φ   decreases from a limit value of π / 2 rad in the absence of graphite to values typical of a resistive behavior when the content of conducting particles is greater than the first percolation threshold [4]. This implies that the impedance transfer function   Z ( ω ) = E ( ω , t ) / i ( ω , t ) provides information on the conductivity of the composite material and the permittivity   ε of the interfacial region. Then, both electrical magnitudes are dependent on the volumetric content of graphite   v . Therefore, the dependences of real and imaginary components of impedance shows an interesting direct information about the system. However, the electrochemical processes that occur in the presence of electroactive substances, including the presence of oxygen in the solution, complicate the interpretation of the electrochemical impedance of the system (Figure S3, results shown as Supplementary Material).
of graphite: 0.185 (black), 0.229 (red), 0.267 (blue), 0.308 (pink), 0.356 (purple). E0 = 0.4V; ΔE = 10 mV; 1M KCl. T = 298K.
The experimental values are fitted to a simple equivalent circuit R-CPE:
Z =   R u + ( j w q ) − n = R u + Q ( j w ) − n =   R u + q − n ( j w ) − n
where j = − 1 , and R u   if the value of the ohmic drop through the cell is negligible compared to that of the composite material while Q and n are fitting coefficients of the real Z’ and imaginary Z” of the impedance:
Z ' = R e Z =   cos ⁡   ( n π 2     ) ( q ω ) n   +   R u
Z       Z = j   s e n   ( n π 2     ) ( q ω ) n
The fractal dimension is related to this exponent but it depends on the geometry of the cell and its elements [55] and the electrode model considered as well as the particular electrode process. In any case, d F must be related to the CPE exponent n which, is due to the existence of a time constants distribution on the electroactive surface, as is generally accepted [60,61,62]. Although this topic is extraordinarily complex, a simple relationship could be postulated as a first approximation to the problem for a planar polished electrode and if it is sufficiently far from the another parallel plane counter electrode:
n = d D L = d F + 2 − d E = d F + 2 − 3   = d F − 1
Then, the postulated Equation (9) is consistent with the insertion of the electrochemical surface of fractal dimension with a virtual plane of the interfacial region or double layer embedded in a 3D space between the surface and a virtual second plane of the interfacial capacitor. In this case the electrode surface was placed horizontally to avoid gravitational convection. A platinum, foil placed parallel to the working electrode was also used as an auxiliary electrode. In this case the fractal dimension of the cluster formed by the lines of force in the interfacial region, being a monodirectional transport by migration, d D L = n   ≤ 1 .
From other perspective, the interfacial region can be modelized of a framework of graphite particles in contact with the solution in a surface 2D of a geometrical d F fractal dimension. Also, this interfacial region can be modelized by means an electrical framework of micro-capacitors of an overall C d l ≃   Q = ( q − n ) because above the percolation threshold v C = 0.14 the values of n are close to unity.
Assuming that the electrode surface consists of squares, whose minimum size is ( δ 0 ) 2 and maximum A 0 , and assuming that the double layer capacities C λ associated with the electrode/dissolution interface are proportional to the number of graphite particles on the surface and their occupied area N λ , the fractality of the electrode surface can be expressed as follows according to the scaling unit λ (an arbitrary value of area):
( q − n ) λ   =   Q = C λ ⋅ N λ =   C λ C m a x C λ d F ∝ C λ ( 1 − d F )
It can be inferred that n = 1 − d F , which is the same as
d F = n + 1
As the capacitance is an extensive magnitude proportional to the surface area it is easy to induce the Equation (11) since in the limit case of an ideal polish electrode surface d F   = 2 and n = 1, corresponding a pure capacitor of de double layer.
Despite GHDPE not shows hygroscopic chemical interaction nor porous, this hypothesis is quite controversial and represents a drastic approach proposed for this particular model under study. In fact, the correlation between the fractal dimension of fractal electrodes with the exponent of the CPE has been rigorously considered for different electrode models in the literature (Table 1).
The Equation (3) supposes that the interfacial region has an apparent percolative structure formed by the resultant vector of the electrochemical potential gradient, which is considered normal to the plane containing the electroactive graphite particles of the composite surface in contact with the solution. Therefore, the values of d F are related to the electroactive area occupied A , which is theoretically lesser than the Euclidean geometric one for a well-polished electrode A O , because the heterogenous electrode surface forme by conducting graphite particles dispersed between non-conductive areas of plastic
Following the same ideal way, it is possible to propose a second hypothesis: If we consider that the associated dimension fractal of the interfacial region depends on the capacitance distribution, analogously in Equation (9) the exponent of the CPE can be considered a fractal dimension of the intersection cluster of the electroactive surface with the cluster of electric charges of the plane-parallel equivalent capacitor, both embedded in a raised 3D space. This assumption considers that capacitance associated to the interfacial region Q is the magnitude of the experimental observation, however more general is considerer into acount the dimensions of the magnitudes. Physical objects [59] considered fractal are defined as fractal geometric objects in a range [ λ m i n ,   λ m a x ]. The number of elements N λ of a range is proportional to λ − d F :
N λ = λ m a x λ d F ,
but the concept can be extended to capacitance quantities. If it is accepted that there are a number of squares on the electrode surface N λ  
N λ = q λ m a x q λ d F
contributing to the experimental capacitance in each range of graphite content in the composite analogously to the equation will be fulfilled:
Q = q − n =   q λ q λ m a x q λ d F ∝ q λ ( 1 − d F )
It follows to the Equation(9).
From this perspective, the fractal dimension of the interfacial region is that of the cluster associated with the electrochemical potential gradients normal to the electrode surface: d S = n   . This means that by adjusting the impedance measurements to an equivalent circuit consisting of a resistance in series with the CPA, it is possible to estimate d F values (Table 2). In the extreme ideal case of a well-polished inert metal electrode, the n exponent would approach unity in accordance with double layer model of an ideally polarizable electrode, so the fractal dimension of the electrode surface it would coincides with the Euclidean fractal dimension of a surface d F ≈ 2. While in the case of the real composite, although the electrode surface is polished, the constant Q of the CPA will depend on the area of the electroactive fraction as well as the on the contribution of the excess concentration of the electrolyte in the interfacial region, which depends also on the ionic strength of the electrolyte in consistence with the proposed model.
In the electrochemical set-up of the experiments carried out, in the absence of convection, and the counter electrode being a platinum foil parallel to the working electrode, the fractal dimension of the percolation cluster through the interfacial region is the intersection of the fractal of the surface with this migration transport cluster immersed in 3D of the solution.

3.2. Relation between the Experimental Imaginary Part of the Impedance and the Fractal Dimensions

Laser diffractometry has been used to measure the size dispersion of graphite particles. (Figure 4).
= 16.2 ± 0.2 μm.
The first percolation threshold v C ≈ 0.14 have been calculated from the dependence of the resistance R u on v measured by dc and EIS (See Figure S2 in supplementary materials). The second percolation threshold corresponds approximately to the volume fraction of graphite that the material loses its consistency v C ' ≅ 0.41 . Then, the theoretical occupational factor of GHDPE is f ≈ (0.14+0.41) = 0.55, and the probability of percolation. This value agrees the theoretical 0.247±0.005 for a percolation of links for a simple cubic structure [59,81,82]. This value is approximately the one obtained by a simulation. (Figure 2, Figure 5) Therefore, the coordination index, z, of a percolation tree is related to the critical threshold by z = 1/pc. Substituting the experimental value pc ≈ 0.254, we find for GHDPE that z = 3.94 ≈ 4. This value is consistent with the calculated occupancy factor in accordance with the anisotropic conductance of the graphite particles.
= 16.2 μm , respectively. Only a limited number of surface graphite particles pertain a conductive cluster (red squares in b). The overall number of squares of the electrode surface is 92226. The overall number of cubes of the electrodes samples are approximately 56444026. Simulated v C = 0.154 (3D) and v C = 0.44 (2D) where calculated.
EIS provides valuable information in the case of the GHDPE system immersed in an electrolyte dissolution. From the real component of the impedance, extrapolating to infinite frequency, the values of R u could be calculated. From the module of the imaginary component, the capacitive character of the electrode is extracted.
From the limit at high frequencies of the real impedance component, the resistance R u is calculated, but in addition, also the CPE parameters, which provide information on the distribution of potentials and time constants on the electrode surface, which is directly related to the fractal dimension d F of the electrode surface. Q increases as the proportion of surface occupied by graphite is greater, in agreement with the predictions of the Percolation Theory and the experimental data obtained by EIS (Figure 6a). The parabolic curve starts from the point corresponding to the percolation threshold v C ≈ 0.14 to the theorical maximum capacitance associated with the double layer of the electrode-solution interface   C D L A 0 ≃ 51.73   μ F
on the volume percentage of graphite. b) Dependence on the ratio of the overall electrical active surface of the graphite particles SCG and their separation   δ G G v . At the same conditions of Table 2.
From the values of the CPE coefficients for the samples with different contents of conductive filler, two qualitatively different ranges are distinguished over the percolation threshold: in a range which the values of Q and n grow on the graphite content, and another, in which both parameters vary little (Table 2 and Figure 6b). Despite the probability of current passage across the bulk over v C = 0.14 is P   = 1 in both ranges, the potential dispersion at the multi-micro electrodes of the graphite particles on the surface of the composite is lesser over v = 0.25, showing that the surface reaches a single behavior in the interfacial region because the calculated n remains practically constant (Table 2). These results are consistent with the initial hypothesis that the electrode surface is the result of the intersection of the cluster of the composite with the cluster associated at the perpendicular plane interfacial region.
It is necessary to consider the CPE to explain the capacitive behavior of composites due to the heterogeneity of the surface. In this way the magnitude R explains the percolation through the bulk of the composite, the CPE gives basic information on the heterogeneity of the surface, and hypothetically on the 2D distribution of time constants of the processes that take place in the interfacial region. The Equation Error! Reference source not found. and Equation Error! Reference source not found. are based on the fractal modeling of the three-dimensional percolative cluster of the solid composite d C (see last column of Table 2 ) and are close to the theoretically [59] calculated for an infinite cluster d C = 2.523.
If the coefficient n has been associated with the fractal dimension of the surface of the electrode, the physical meaning of the constant Q   is clear when the parameter n   tends to unity. For graphite contents, v   ≥ 0.25 the capacity of the double layer can be considered as corresponding to the equivalent associated
capacitors of   C i , formed by the individual graphite particles on the surface in contact with the aqueous KCl solution. Therefore, it can be simplified, assuming that the interfacial region shows a phenomenological capacitance that depends on an apparent dielectric permittivity ε of the dissolution and an apparent thickness δ D L of the double layer, named frequently reciprocal Debye length:
( C d l ) λ = ε   A λ / δ D L
being A λ , the area of a selected electroactive experimental surface of the electrode. Therefore, the value of this parameter can be considered proportional to the fraction of area occupied by the graphite particles located on the surface of the electrode. At low concentration of KCl, his Debye length varies with the square root of the inverse ionic strength if the interfacial region is considered as an equivalent parallel plate capacitor [83,84,85].
In accordance with the assumption of Equation (9), the exponent of the CPA can be considered directly as a fractal dimension of the intersection cluster of the electrochemical surface cluster of   d F of with the electrical charges of the other capacitor plate of   d F ' ≈ 2 , both embedded in a 3D space. That justifies the hypothesis embodied in Equation (7) in the simple model proposed, where the CPE is directly related to the electrical properties of the interfacial region only. However, if the CPE included in the equivalent circuit is directly associated to the solid electrode as well as the case of deposited films [86] or porous and rough electrodes (Table 2), the interpretation of the constant-phase-element is in general more complicated [41,87,88]. In this composite, the real and imaginary components of the impedance depend on both CPE parameters following Equations (9) and (10). This suggest that the proposed model based on the self-definition of the R-CPE circuit is apparently useful for describing the electrochemical behavior of the composite electrode/solution for graphite contents v ≥ v C . But, this hypothesis, based in in the intuitive idea that the imaginary component of the impedance depends only of the interphase electrode/solution requires a further discussion, because the surface morphology of the electrode depends directly on the percolation inside the material and, therefore, in this system, lacking porosity and significant faradaic processes, the CPE associated to the imaginary part must depend on the distribution of graphite particles on the surface and also inside the material. That is, on the particle/solution interfaces at the surface, as well as to a large extent on the graphite particle/polyethylene interface inside the material.

4. Discussion

Assuming that the average particle radius is 16±2µm and the Debye length δ D L ≃ 0.3 nm for a 1 M electrolyte 1:1 solution, and considering that the relative dielectric permeability of the solution ε   K C l   1 M ≃ 74 at room T= 298 K [84], an approximate value of the double layer capacitance of the electrode/solution interfacial region (Table 3) can be estimated according to the equation:
C D L =   ( 74 ) ( 8,854   10 − 12   F . m − 1 )   A   ( 0,3   10 − 9   m )
Assuming that all NG particles of graphite N G  
N G   = v ( 16.2 ) 3   240 10 9
possess this same average size and show 4 conductive faces to give rise to microcapacitors, it is possible to calculate a total area susceptible to act as an array of graphite/polyethylene interface microcapacitors S C G , whose average spacing is near to:
δ G G v = 1 − v v 3   δ 0
decreases as the partial volume of polyethylene decreases.
Where C D L is the double layer capacitance associated with all the graphite particles on the surface belonging to conductive clusters that are in contact with the solution (Figure 5b), taking into account that the fraction of surface area occupied by these particles can calculated as:
θ = Q C D L A 0
where C D L A 0 = 51.73   μ F   is the double-layer capacitance calculated according to Equation (16) for the 0.24 mm2 surface area electrode assuming that the entire geometric surface area of the electrode was occupied by conductive particles.
The ϴ values in Table 3 assume that not all graphite particles in each plane perpendicular to the current direction participate in the percolative cluster. This is consistent if we consider that the polarization conduction of the alternating current is added to the DC current conduction of the direct contact and the tunnel effect. This fact causes an increase of the electroactive area of the composite electrodes. Which is consistent with the fact that the relatively high experimental values of the electroactive area in faradaic processes (Table 3).
This involvement of the graphite/polyethylene interfaces in the electrode/dissolution double layer values would explain the phenomenological behavior of these materials as macroscopic electrodes. Only at ratios close to the percolation threshold (zone A in Figure 6b), when there are few percolating clusters with terminal graphite particles, would the surface microcapacitors be associated in parallel, but as the proportion of graphite increases, the interparticle distance decreases and the total particle area within the material increases dramatically (zone B in Figure 6b). Also, the distance between them δ g g c θ ≃ 1 − θ θ 2 δ 0 decreases and consequently the surface percolation increases (zone C in Figure 6b).
Q reaches previsibly to the limit of the double-layer capacity C D L A 0 . This maximum value is consistent with that the surface microcapacitors are associated in serie covering all the electroactive surface. For a calculated total area of the graphite particles of less than 0.01 m2 (ν less than 0.176), the number of graphite particles on the electrode surface belonging to a conductive cluster is very small. In the intermediate zone B there is a transition from a dispersion of microelectrodes to a content of v greater than 0.22 in the behavior is clearly as macroscopic electrode. One explanation for this transition may be based on the fact that polyethylene has a strong tendency to accumulate charge.
As the number of microparticles increases, the average distance between them decreases and the composite behaves macroscopically as a homogeneous semiconductor. This can be explained on the basis that when the distance between the particles is of the order of their size, the circuit is short-circuited by the interfacial region through the solution.
Looking at the dependence of the characteristic time   τ ≃ R u ∙ Q with the graphite content there is a change in trend for values above v   = 0.22. Also, it is striking that the values of n are close to those corresponding to a pure capacitor, as if it were a macroelectrode, which is consistent with the relative values of the electroactive area calculated for the faradaic process of reduction of the K3 [Fe(CN)6], although in case of electrochemical reaction controlled by mass transfer on pulished electrodes, the value of n should be close to ½, since in the species they can move equiprobably by diffusion in two senses, while there is only one direction sense of movement of the charged particles by migration which is imposed by the instantaneous electric field.
In spite of the practical interest of the Equations (16)-(19), it is necessary to cofirm they accurance for these and others similar composite materials by means complementary experimental techniques [89] in different media.

5. Conclusions

This material does not shows porosity nor water absorption so it is proposed a simple model to discern the effect of the dispersion of conductive particles in an insulating matrix, although the low value of the percolation threshold and the interaction index z ≈ 4 is probably due to the anisotropy of the particles. The response to the alternating current of the electrode/solution has been analyzed and a model is proposed in which the fractal dimension of the electrode surface is correlated with the exponent of the CPE, in which the electroactive surface is the intersection of two clusters: that of the solid and that formed by the perpendicular electric fields to the surface. From this perspective, the value of the CPE constant Q is related to the association of micro-capacitors that form in the interfacial region between the graphite particles dispersed on the surface of the composite and the solution. This approach is consistent with the fact that the real component of the impedance is associated with the electrical d C (3D) percolation through the solid composite and the imaginary component of the impedance to the formation of the interfacial region on a electrode surface of fractal dimension d F (2D), which agrees with the exponent n of the CPE could be considered a fractal dimension d S 1 D of the interfacial region.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Figure S1. The shape of the voltammograms of the electrodes; Figure S2. The resistance measured (DC curve) agrees well with that measured by EIS; Figure S3. Faradaic processes associated with the presence of oxygen in the solution; Figure S4. The total surface area of the particles and their separations depend on the shape and size distribution.

Author Contributions

JNL, JA, JGJ, FV: Conceptualization, methodology, validation, formal analysis, resources, data curation, writing—original draft preparation, writing—review and editing, visualization, project administration, funding acquisition.

Funding

Thanks to the support of the Spanish Network of Excellence Environmental and Energy Applications of Electrochemical Technology. Spanish E3TECH-PLUS Research Network, grant number RED2022-134552-T, MICINN/AEI.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available under demand.

Acknowledgments

Thanks to Dr. José Trijueque (Instituto Tecnológico del Plástico AIMPLAS, Paterna, Spain) for having helped in the manufacture of the composite and in the discussion of results.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Lin, L.; Ning, H.; Song, S.; Xu, C.; Hu, N. Flexible Electrochemical Energy Storage: The Role of Composite Materials. Compos. Sci. Technol. 2020, 192, 108102. [CrossRef]
  2. Islam, J.; Chowdhury, F.; Uddin, J.; Amin, R.; Uddin, J. Review on Carbonaceous Materials and Metal Composites in Deformable Electrodes for Flexible Lithium-Ion Batteries. RSC Adv. 2021, 11, 5958–5992. [CrossRef]
  3. Navarro-Laboulais, J.; Trijueque, J.; García-Jareño, J.J.; Vicente, F. Impedance Analysis of Graphite + Polyethylene and Graphite + Epoxy Composite Electrodes. Journal of Electroanalytical Chemistry 1995, 399, 115–120. [CrossRef]
  4. Agrisuelas, J.; García-Jareño, J.J.; Guillén, E.; Vicente, F. RGB Video Electrochemistry of Copper Electrodeposition/Electrodissolution in Acid Media on a Ternary Graphite:Copper:Polypropylene Composite Electrode. Electrochim. Acta 2019, 305, 72–80. [CrossRef]
  5. Li, G.; Xia, Y.; Tian, Y.; Wu, Y.; Liu, J.; He, Q.; Chen, D. Review—Recent Developments on Graphene-Based Electrochemical Sensors toward Nitrite. J. Electrochem. Soc. 2019, 166, B881. [CrossRef]
  6. Li, G.; Xia, Y.; Tian, Y.; Wu, Y.; Liu, J.; He, Q.; Chen, D. Review—Recent Developments on Graphene-Based Electrochemical Sensors toward Nitrite. J. Electrochem. Soc. 2019, 166, B881–B895. [CrossRef]
  7. Himadri Reddy, P.C.; Amalraj, J.; Ranganatha, S.; Patil, S.S.; Chandrasekaran, S. A Review on Effect of Conducting Polymers on Carbon-Based Electrode Materials for Electrochemical Supercapacitors. Synthetic Metals 2023, 298, 117447. [CrossRef]
  8. Gao, X.; Li, W.; Wang, P.; Lu, Y.; Zhou, J.; Wang, X.Q. Advancing Energy Solutions: Carbon-Based Cementitious Composites in Energy Storage and Harvesting. Journal of Building Engineering 2024, 91, 109720. [CrossRef]
  9. Peinado, F.; Roig, A.; Vicente, F.; Vilaplana, J.; López, J. Electrochemical Characterization of Cement/Graphite and Cement/Aluminium Materials. J Mater Sci Lett 1994, 13, 609–612. [CrossRef]
  10. Das, N.C.; Maiti, S. Electromagnetic Interference Shielding of Carbon Nanotube/Ethylene Vinyl Acetate Composites. J Mater Sci 2008, 43, 1920–1925. [CrossRef]
  11. Miller, E.E.; Hua, Y.; Tezel, F.H. Materials for Energy Storage: Review of Electrode Materials and Methods of Increasing Capacitance for Supercapacitors. Journal of Energy Storage 2018, 20, 30–40. [CrossRef]
  12. Faga, M.; Duraccio, D.; Di Maro, M.; Pedraza, R.; Bartoli, M.; d’Ayala, G.; Torsello, D.; Ghigo, G.; Malucelli, G. Ethylene-Vinyl Acetate (EVA) Containing Waste Hemp-Derived Biochar Fibers: Mechanical, Electrical, Thermal and Tribological Behavior. Polymers 2022, 14, 4171. [CrossRef]
  13. Subiela, J.R.; López, J.; Balart, R.; García-Jareño, J.J.; Vicente, F. Electrical Properties of EVA Filled by Zinc Powder. J Mater Sci 2006, 41, 6396–6402. [CrossRef]
  14. Fang, H.; Yang, D.; Su, Z.; Sun, X.; Ren, J.; Li, L.; Wang, K. Preparation and Application of Graphene and Derived Carbon Materials in Supercapacitors: A Review. Coatings 2022, 12, 1312. [CrossRef]
  15. Wang, P.; Song, T.; Abo-Dief, H.M.; Song, J.; Alanazi, A.K.; Fan, B.; Huang, M.; Lin, Z.; Altalhi, A.A.; Gao, S.; et al. Effect of Carbon Nanotubes on the Interface Evolution and Dielectric Properties of Polylactic Acid/Ethylene–Vinyl Acetate Copolymer Nanocomposites. Adv Compos Hybrid Mater 2022, 5, 1100–1110. [CrossRef]
  16. Agrisuelas, J.; Balart, R.; García-Jareño, J.J.; López-Martínez, J.; Vicente, F. A Macroscopic Interpretation of the Correlation between Electrical Percolation and Mechanical Properties of Poly-(Ethylene Vinyl Acetate)/Zn Composites. Materials 2024, 17, 2527. [CrossRef]
  17. Vovchenko, L.; Perets, Yu.; Ovsienko, I.; Matzui, L.; Oliynyk, V.; Launetz, V. Shielding Coatings Based on Carbon–Polymer Composites. Surface and Coatings Technology 2012, 211, 196–199. [CrossRef]
  18. Peng, Y.; Burtovyy, R.; Bordia, R.; Luzinov, I. Fabrication of Porous Carbon Films and Their Impact on Carbon/Polypropylene Interfacial Bonding. J. Compos. Sci. 2021, 5, 108. [CrossRef]
  19. Kratofil Krehula, L.; Peršić, A.; Popov, N.; Krehula, S. Polymer Composites of Low-Density Polyethylene (LDPE) with Elongated Hematite (α-Fe2O3) Particles of Different Shapes. J. Compos. Sci. 2024, 8, 73. [CrossRef]
  20. Sadeghi, P.; Goli, A.; Fini, E. Carbon Sequestration via Bituminous Composites Containing Recycled High-Density Polyethylene. J. Compos. Sci. 2024, 8, 100. [CrossRef]
  21. Kou, Y.; Cheng, X.; Macosko, C.W. Degradation and Breakdown of Polymer/Graphene Composites under Strong Electric Field. J. Compos. Sci. 2022, 6, 139. [CrossRef]
  22. Kahanda, G.L.M.K.S.; Tomkiewicz, M. Fractality and Impedance of Electrochemically Grown Silver Deposits. J. Electrochem. Soc. 1990, 137, 3423. [CrossRef]
  23. Sunde, S. Calculation of Conductivity and Polarization Resistance of Composite SOFC Electrodes from Random Resistor Networks. J. Electrochem. Soc. 1995, 142, L50. [CrossRef]
  24. De Arcangelis, L.; Redner, S.; Coniglio, A. Anomalous Voltage Distribution of Random Resistor Networks and a New Model for the Backbone at the Percolation-Threshold. Phys. Rev. B 1985, 31, 4725–4727. [CrossRef]
  25. De Arcangelis, L.; Redner, S.; Coniglio, A. Multiscaling Approach in Random Resistor and Random Superconducting Networks. Phys. Rev. B 1986, 34, 4656–4673. [CrossRef]
  26. Angulo, R.; Medina, E. Conductance Distributions in Random Resistor Networks - Self-Averaging and Disorder Lengths. J. Stat. Phys. 1994, 75, 135–151. [CrossRef]
  27. Koch, D.L.; Sangani, A.S. The AC Electrical Impedance of a Fractal Boundary to an Electrolytic Solution. J. Electrochem. Soc. 1991, 138, 475. [CrossRef]
  28. Lust, L.; Kakalios, J. Computer-Simulations of Conductance Noise in a Dynamical Percolation Resistor Network. Phys. Rev. E 1994, 50, 3431–3435. [CrossRef]
  29. Babalievski, F. Algorithm to Extract the Spanning Clusters and Calculate Conductivity in Strip Geometries. Phys. Rev. E 1995, 51, 6230–6234. [CrossRef]
  30. Kolek, A. Voltage Distribution in a Two-Component Random System. Phys. Rev. B 1996, 53, 14185–14195. [CrossRef]
  31. Batrouni, G.G.; Hansen, A.; Larson, B. Current Distribution in the Three-Dimensional Random Resistor Network at the Percolation Threshold. Phys. Rev. E 1996, 53, 2292–2297. [CrossRef]
  32. Barta, S.; Dieska, P. A Computer-Simulation Study of Anomalous Diffusion on Percolating Clusters Near to the Critical-Point. Physica A 1995, 215, 251–260.
  33. Lopez, J.; Rodriguez, M.; Pesquera, L. Analysis of Self-Averaging Properties in the Transport of Particles Through Random-Media. Phys. Rev. E 1995, 51, R1637–R1640. [CrossRef]
  34. Bunde, A.; Havlin, S.; Porto, M. Are Branched Polymers in the Universality Class of Percolation. Phys. Rev. Lett. 1995, 74, 2714–2716. [CrossRef]
  35. Scher, H.; Zallen, R. Critical Density in Percolation Processes. J. Chem. Phys. 1970, 53, 3759-. [CrossRef]
  36. Gupta, R.; Malik, A.; Kumari, K.; Singh, S.K.; Vivier, V.; Mondal, P.C. Metal-Free Platforms for Molecular Thin Films as High-Performance Supercapacitors. Chem. Sci. 2024, 10.1039.D4SC00611A. [CrossRef]
  37. Navarro-Laboulais, J.; Garcı́a-Jareño, J.J.; Vicente, F. Kramers–Kronig Transformation, Dc Behaviour and Steady State Response of the Warburg Impedance for a Disk Electrode Inlaid in an Insulating Surface. Journal of Electroanalytical Chemistry 2002, 536, 11–18. [CrossRef]
  38. Beaunier, L.; Keddam, M.; Garcia-Jareno, J.J.; Vicente, F.; Navarro-Laboulais, J. Surface Structure Determination by SEM Image Processing and Electrochemical Impedance of Graphite plus Polyethylene Composite Electrodes. J. Electroanal. Chem. 2004, 566, 159–167. [CrossRef]
  39. Navarro-Laboulais, J.; Trijueque, J.; García-Jareño, J.J.; Vicente, F. Ohmic Drop Effect on the Voltammetric Behaviour of Graphite + Polyethylene Composite Electrodes. Journal of Electroanalytical Chemistry 1997, 422, 91–97. [CrossRef]
  40. Navarro-Laboulais, J.; Trijueque, J.; Garcı́a-Jareño, J.J.; Benito, D.; Vicente, F. Determination of the Electroactive Area of Graphite+polyethylene Composite Electrodes. Uncompensated Resistance Effects and Convolution Analysis of Chronoamperograms. Journal of Electroanalytical Chemistry 1998, 443, 41–48. [CrossRef]
  41. Navarro-Laboulais, J.; Trijueque, J.; García-Jareño, J.J.; Benito, D.; Vicente, F. Electrochemical Impedance Spectroscopy of Conductor—Insulator Composite Electrodes: Properties in the Blocking and Diffusive Regimes. Journal of Electroanalytical Chemistry 1998, 444, 173–186. [CrossRef]
  42. Bhattacharya, S.; Tandon, R.P.; Sachdev, V.K. Electrical Conduction of Graphite Filled High Density Polyethylene Composites; Experiment and Theory. J Mater Sci 2009, 44, 2430–2433. [CrossRef]
  43. Panwar, V.; Mehra, R. m. Analysis of Electrical, Dielectric, and Electromagnetic Interference Shielding Behavior of Graphite Filled High Density Polyethylene Composites. Polymer Engineering & Science 2008, 48, 2178–2187. [CrossRef]
  44. Luo, W.; Cheng, C.; Zhou, S.; Zou, H.; Liang, M. Thermal, Electrical and Rheological Behavior of High-Density Polyethylene/Graphite Composites. Iran Polym J 2015, 24, 573–581. [CrossRef]
  45. Krupa, I.; Novák, I.; Chodák, I. Electrically and Thermally Conductive Polyethylene/Graphite Composites and Their Mechanical Properties. Synthetic Metals 2004, 145, 245–252. [CrossRef]
  46. Agrisuelas, J.; García-Jareño, J.J.; Gimenez-Romero, D.; Negrete, F.; Vicente, F. The Fractal Dimension as Estimator of the Fractional Content of Metal Matrix Composite Materials. J. Solid State Electrochem. 2009, 13, 1599–1603. [CrossRef]
  47. Ghanbari, K.; Mousavi, M.F.; Shamsipur, M.; Rahmanifar, M.S.; Heli, H. Change in Morphology of Polyaniline/Graphite Composite: A Fractal Dimension Approach. Synth. Met. 2006, 156, 911–916. [CrossRef]
  48. Lee, S.-B.; Pyun, S.-I. Determination of the Morphology of Surface Groups Formed and PVDF-Binder Materials Dispersed on Graphite Composite Electrodes in Terms of Fractal Geometry. Journal of Electroanalytical Chemistry 2003, 556, 75–82. [CrossRef]
  49. Nyikos, L.; Pajkossy, T. Fractal Dimension and Fractional Power Frequency-Dependent Impedance of Blocking Electrodes. Electrochim. Acta 1985, 30, 1533–1540. [CrossRef]
  50. Dassas, Y.; Duby, P. Diffusion toward Fractal, Interfaces Potentiostatic, Galvanostatic, and Linear Sweep Voltammetric Techniques. J. Electrochem. Soc. 1995, 142, 4175–4180. [CrossRef]
  51. Navarro-Laboulais, J.; Vilaplana, J.; López, J.; García-Jareño, J.J.; Benito, D.; Vicente, F. Prussian Blue Films Deposited on Graphite+epoxy Composite Electrodes: Electrochemical Detection of the Second Percolation Threshold. Journal of Electroanalytical Chemistry 2000, 484, 33–40. [CrossRef]
  52. Trijueque, J.; Garcı́a-Jareño, J.J.; Navarro-Laboulais, J.; Sanmatı́as, A.; Vicente, F. Ohmic Drop of Prussian-Blue/Graphite+epoxy Electrodes. Electrochimica Acta 1999, 45, 789–795. [CrossRef]
  53. Garcı́a-Jareño, J.J.; Sanmatı́as, A.; Navarro-Laboulais, J.; Vicente, F. Chronoamperometry of Prussian Blue Films on ITO Electrodes: Ohmic Drop and Film Thickness Effect. Electrochim. Acta 1999, 44, 4753–4762. [CrossRef]
  54. Pajkossy, T.; Nyikos, L. Scaling-Law Analysis to Describe the Impedance Behavior of Fractal Electrodes. Phys. Rev. B 1990, 42, 709–719. [CrossRef]
  55. Sapoval, B.; Gutfraind, R.; Meakin, P.; Keddam, M.; Takenouti, H. Equivalent-Circuit, Scaling, Random-Walk Simulation, and an Experimental-Study of Self-Similar Fractal Electrodes and Interfaces. Phys. Rev. E 1993, 48, 3333–3344. [CrossRef]
  56. Dobrescu, G.; Georgescu-State, R.; Papa, F.; Staden, J. (Koos) F.V.; State, R.N. Fractal Properties of Composite-Modified Carbon Paste Electrodes—A Comparison between SEM and CV Fractal Analysis. Fractal Fract 2024, 8, 205. [CrossRef]
  57. Gimenezromero, D. Correlation between the Fractal Dimension of the Electrode Surface and the EIS of the Zinc Anodic Dissolution for Different Kinds of Galvanized Steel. Electrochemistry Communications 2004, 6, 148–152. [CrossRef]
  58. Aoki, K.J. Frequency-Dependence of Electric Double Layer Capacitance without Faradaic Reactions. Journal of Electroanalytical Chemistry 2016, 779, 117–125. [CrossRef]
  59. Isichenko, M.B. Percolation, Statistical Topography, and Transport in Random Media. Rev. Mod. Phys. 1992, 64, 961–1043. [CrossRef]
  60. Alexander, C.L.; Tribollet, B.; Orazem, M.E. Contribution of Surface Distributions to Constant-Phase-Element (CPE) Behavior: 2. Capacitance. Electrochimica Acta 2016, 188, 566–573. [CrossRef]
  61. Orazem, M.E.; Tribollet, B.; Vivier, V.; Riemer, D.P.; White, E.; Bunge, A. On the Use of the Power-Law Model for Interpreting Constant-Phase-Element Parameters. J. Braz. Chem. Soc. 2014, 25, 532–539. [CrossRef]
  62. Gateman, S.M.; Gharbi, O.; Gomes De Melo, H.; Ngo, K.; Turmine, M.; Vivier, V. On the Use of a Constant Phase Element (CPE) in Electrochemistry. Current Opinion in Electrochemistry 2022, 36, 101133. [CrossRef]
  63. Jaroniec, M. The Fractal Approach to Heterogeneous Chemistry: Surfaces, Colloids, Polymers. Edited by David Avnir, Wiley, New York. 1989, 460 Pp., $75.00. AIChE Journal 1990, 36, 1456–1456. [CrossRef]
  64. Meakin, P.; Sapoval, B. Random-Walk Simulation of the Response of Irregular or Fractal Interfaces and Membranes. Phys. Rev. A 1991, 43, 2993–3004. [CrossRef]
  65. Kaplan, T.; Liu, S.; Gray, L. Inverse-Cantor-Bar Model for the Ac Response of a Rough Interface. Phys. Rev. B 1986, 34, 4870–4873. [CrossRef]
  66. Liu, S.; Kaplan, T.; Gray, L. Ac Response of Fractal Interfaces. Solid State Ion. 1986, 18–9, 65–71. [CrossRef]
  67. Nyikos, L.; Pajkossy, T. Diffusion to Fractal Surfaces. Electrochim. Acta 1986, 31, 1347–1350. [CrossRef]
  68. Pajkossy, T.; Nyikos, L. Impedance of Fractal Blocking Electrodes. J. Electrochem. Soc. 1986, 133, 2061–2064. [CrossRef]
  69. Nyikos, L.; Pajkossy, T.; Martemyanov, S. Diffusion to a Rotating-Disk Electrode with Fractal Surface. Soviet Electrochemistry 1989, 25, 1381–1384.
  70. Nyikos, L.; Pajkossy, T. Electrochemistry at Fractal Electrodes. In Proceedings of the Instationary Processes and Dynamic Experimental Methods in Catalysis, Electrochemistry and Corrosion; Sandstede, G., Kreysa, G., Eds.; V C H Verlagsgesellschaft: Weinheim, 1989; Vol. 120, pp. 361–371.
  71. Pajkossy, T.; Nyikos, L. Diffusion to Fractal Surfaces .2. Verification of Theory. Electrochim. Acta 1989, 34, 171–179. [CrossRef]
  72. Pajkossy, T.; Borosy, A.; Imre, A.; Martemyanov, S.; Nagy, G.; Schiller, R.; Nyikos, L. Diffusion Kinetics at Fractal Electrodes. J. Electroanal. Chem. 1994, 366, 69–73. [CrossRef]
  73. Gouyet, J.; Rosso, M.; Sapoval, B. Fractal Structure of Diffusion and Invasion Fronts in 3-Dimensional Lattices Through the Gradient Percolation Approach. Phys. Rev. B 1988, 37, 1832–1838. [CrossRef]
  74. Rosso, M.; Sapoval, B.; Gouyet, J. Fractal Nature of Diffusion, Invasion and Corrosion Fronts. Solid State Ion. 1988, 26, 172–173. [CrossRef]
  75. Sapoval, B.; Chazalviel, J.; Peyriere, J. Electrical Response of Fractal and Porous Interfaces. Phys. Rev. A 1988, 38, 5867–5887. [CrossRef]
  76. Sapoval, B.; Chazalviel, J.; Peyriere, J. Effective Impedance of a Non-Blocking Fractal Electrode. Solid State Ion. 1988, 28, 1441–1444. [CrossRef]
  77. Maritan, A.; Stella, A.; Toigo, F. Anomalous Warburg Impedance and Universal Surface Magnetic Exponent for Gaussian Models in the Presence of Fractal Boundaries. Phys. Rev. B 1989, 40, 9269–9273. [CrossRef]
  78. Borosy, A.; Nyikos, L.; Pajkossy, T. Diffusion to Fractal Surfaces .5. Quasi-Random Interfaces. Electrochim. Acta 1991, 36, 163–165. [CrossRef]
  79. Arvia, A.; Salvarezza, R. Progress in the Knowledge of Irregular Solid Electrode Surfaces. Electrochim. Acta 1994, 39, 1481–1494. [CrossRef]
  80. Garcia, M.; Gomez, M.; Salvarezza, R.; Arvia, A. Kinetics of Roughness Relaxation at Gold Electrodes. J. Electrochem. Soc. 1994, 141, 2291–2296. [CrossRef]
  81. Galam, S.; Mauger, A. Universal Formulas for Percolation Thresholds. Phys. Rev. E 1996, 53, 2177–2181. [CrossRef]
  82. van der Marck, S.C. sComment on ``Universal Formulas for Percolation Thresholds’’. Phys. Rev. E 1997, 55, 1228–1229. [CrossRef]
  83. Singh, M.B.; Kant, R. Debye–Falkenhagen Dynamics of Electric Double Layer in Presence of Electrode Heterogeneities. Journal of Electroanalytical Chemistry 2013, 704, 197–207. [CrossRef]
  84. Jeanmairet, G.; Rotenberg, B.; Salanne, M. Microscopic Simulations of Electrochemical Double-Layer Capacitors. Chem. Rev. 2022, 122, 10860–10898. [CrossRef]
  85. AL-Bazali, T. Insight into Debye Hückel Length (Κ−1): Smart Gravimetric and Swelling Techniques Reveals Discrepancy of Diffuse Double Layer Theory at High Ionic Concentrations. J Petrol Explor Prod Technol 2022, 12, 461–471. [CrossRef]
  86. Córdoba-Torres, P. Relationship between Constant-Phase Element (CPE) Parameters and Physical Properties of Films with a Distributed Resistivity. Electrochimica Acta 2017, 225, 592–604. [CrossRef]
  87. Orazem, M.E.; Frateur, I.; Tribollet, B.; Vivier, V.; Marcelin, S.; Pébère, N.; Bunge, A.L.; White, E.A.; Riemer, D.P.; Musiani, M. Dielectric Properties of Materials Showing Constant-Phase-Element (CPE) Impedance Response. J. Electrochem. Soc. 2013, 160, C215. [CrossRef]
  88. Gharbi, O.; Dizon, A.; Orazem, M.E.; Tran, M.T.T.; Tribollet, B.; Vivier, V. From Frequency Dispersion to Ohmic Impedance: A New Insight on the High-Frequency Impedance Analysis of Electrochemical Systems. Electrochimica Acta 2019, 320, 134609. [CrossRef]
  89. García-Jareño, J.J.; Agrisuelas, J.; Vicente, F. Overview and Recent Advances in Hyphenated Electrochemical Techniques for the Characterization of Electroactive Materials. Materials 2023, 16, 4226. [CrossRef]
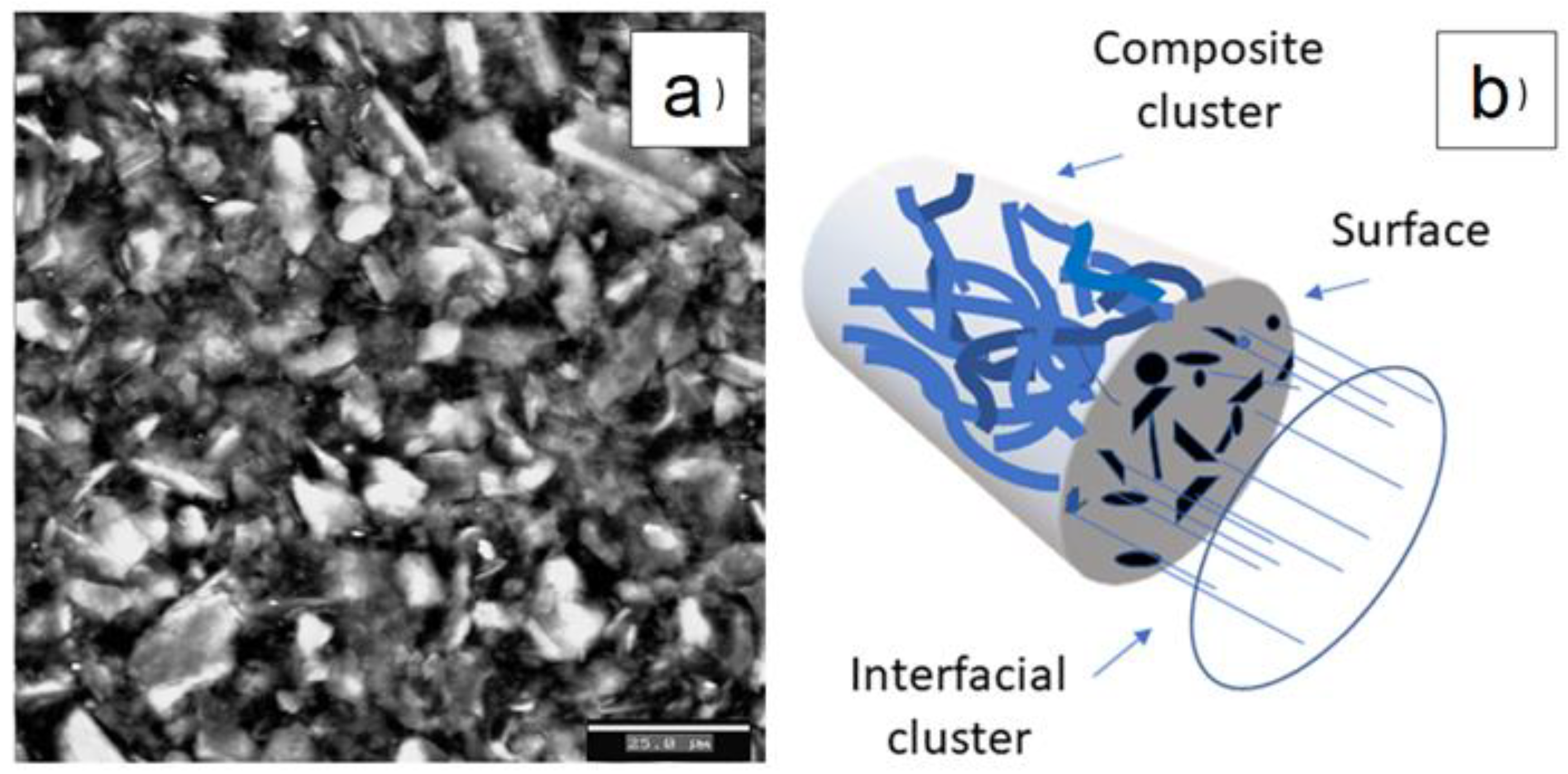
Preprints 114033 g001
Figure 1. Surface of the composite. a) The surface of GHDPE electrode by SEM with 35% graphite by weight. The bar in the lower right margin represents 25 μm. b) Schematic 3D representation of a cylindrical sample of the composite material of GHDPE electrode.
Figure 1. Surface of the composite. a) The surface of GHDPE electrode by SEM with 35% graphite by weight. The bar in the lower right margin represents 25 μm. b) Schematic 3D representation of a cylindrical sample of the composite material of GHDPE electrode.
Preprints 114033 g001
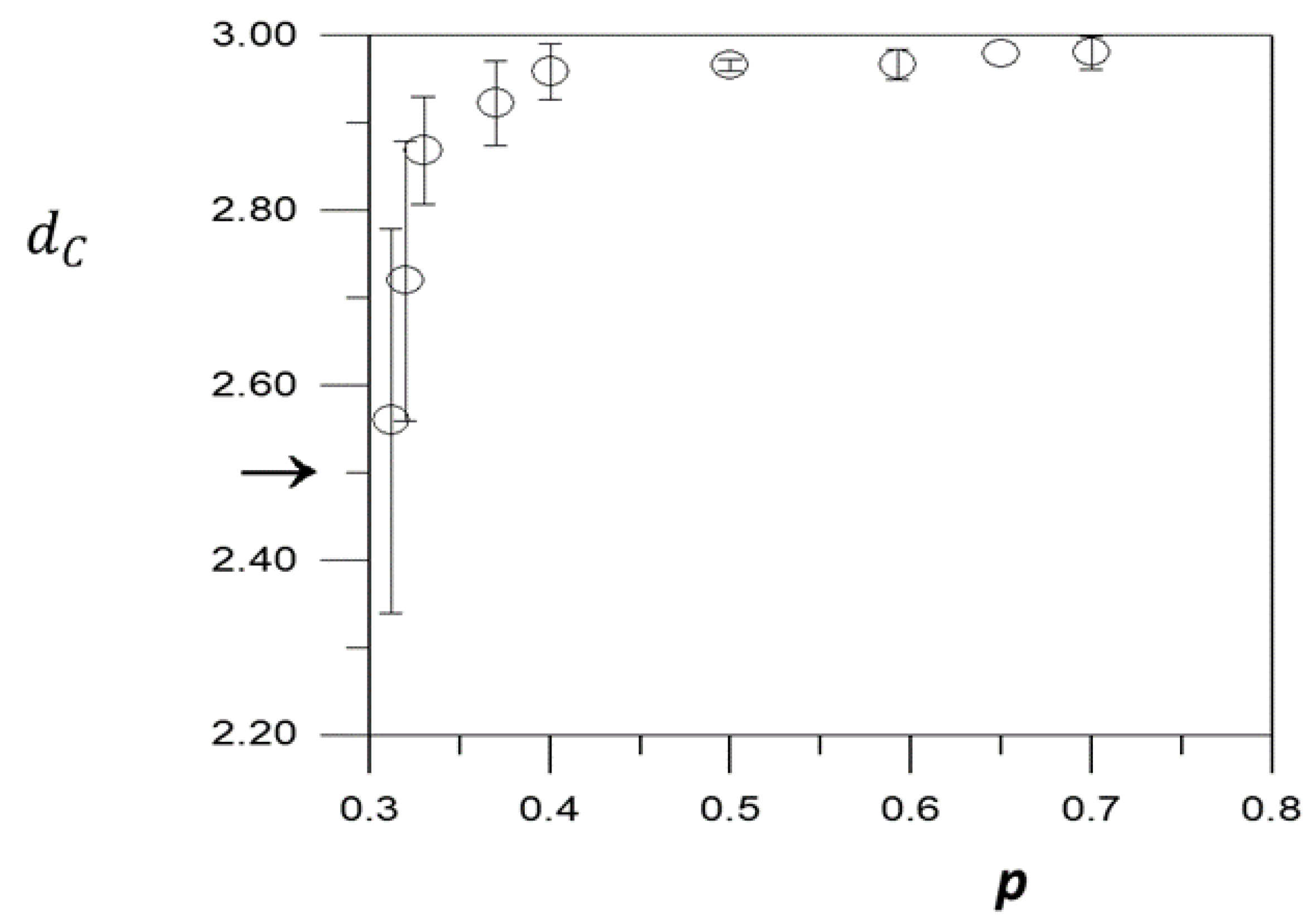
Preprints 114033 g002
Figure 2. Theorical determination of the fractal dimension of percolation aggregates dC as a function of the probability of occupation, p. The fractal dimension has been determined by the box-counting method. The arrow on the graph indicates the theoretical value. The error bars have been calculated as the standard deviation of various realizations. It can be seen that the data dispersion follows a law of similarity.
Figure 2. Theorical determination of the fractal dimension of percolation aggregates dC as a function of the probability of occupation, p. The fractal dimension has been determined by the box-counting method. The arrow on the graph indicates the theoretical value. The error bars have been calculated as the standard deviation of various realizations. It can be seen that the data dispersion follows a law of similarity.
Preprints 114033 g002
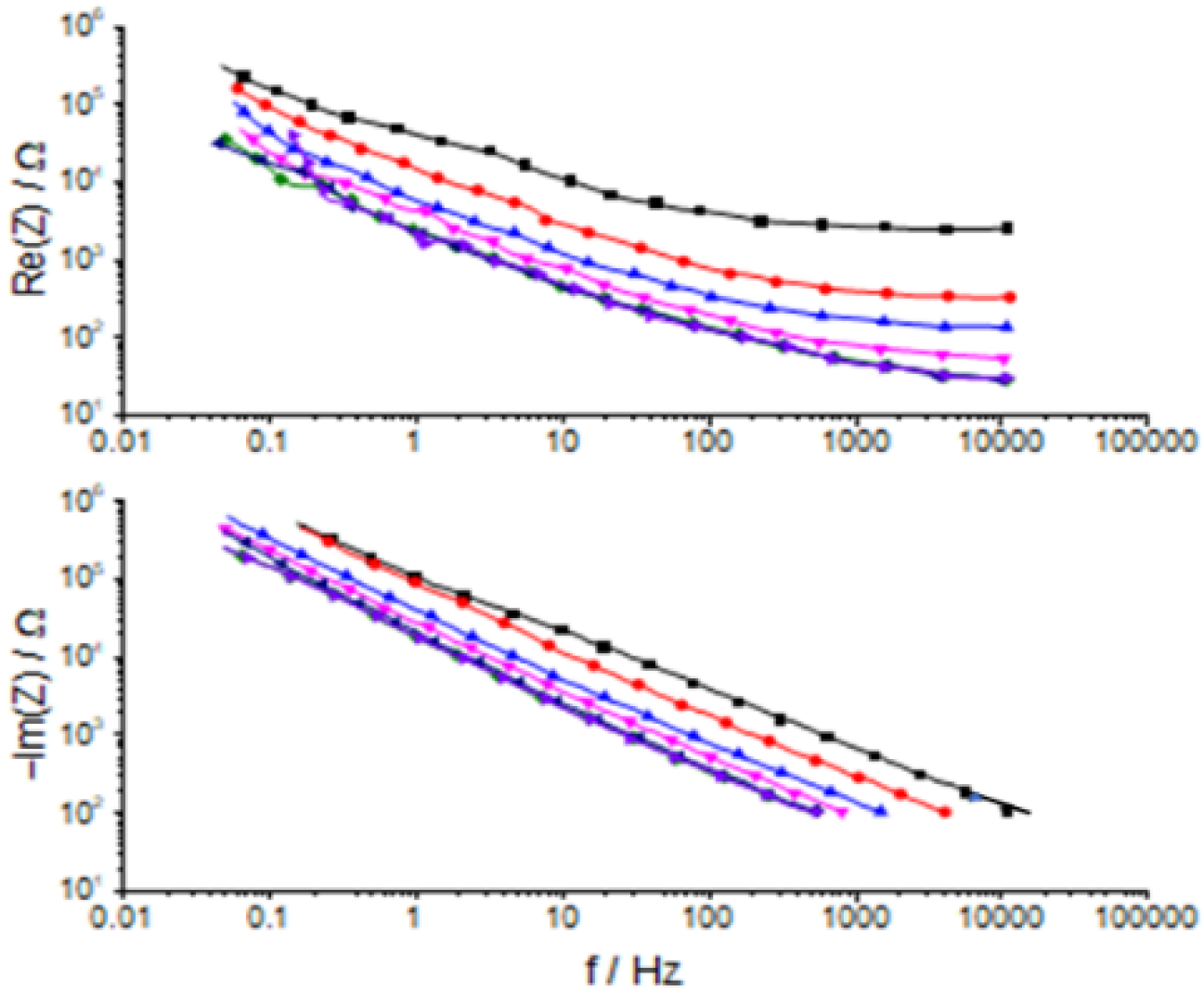
Preprints 114033 g003
Figure 3. Dependence of the real Re(Z) and imaginary Im(Z) components on the frequency of the 1mpedance of the composite electrode samples on the content v
Figure 3. Dependence of the real Re(Z) and imaginary Im(Z) components on the frequency of the 1mpedance of the composite electrode samples on the content v
Preprints 114033 g003
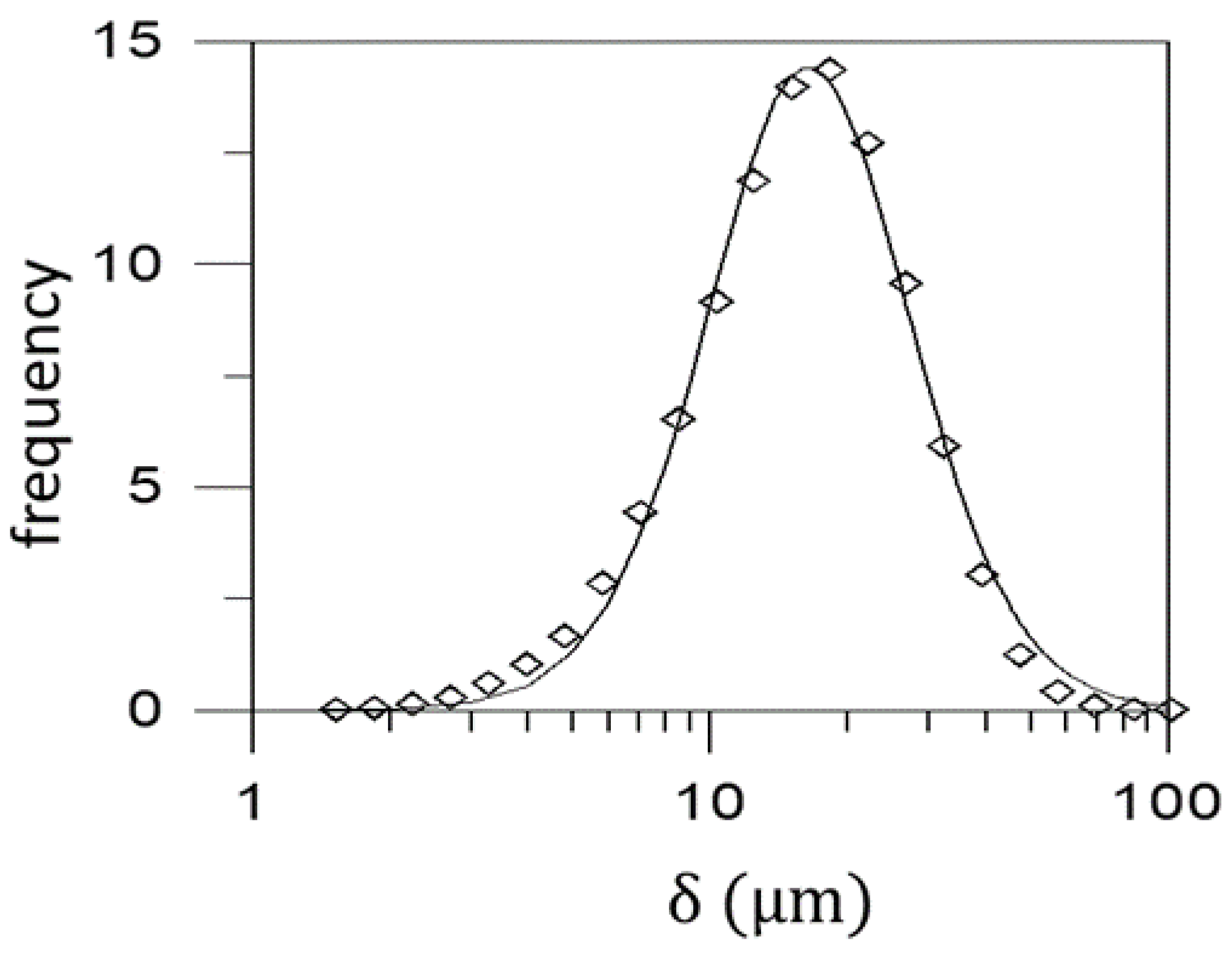
Preprints 114033 g004
Figure 4. Distribution function of the graphite particles used in the preparation of the composite materials. The line corresponds to a combination of functions obtaining as an average value δ 0
Figure 4. Distribution function of the graphite particles used in the preparation of the composite materials. The line corresponds to a combination of functions obtaining as an average value δ 0
Preprints 114033 g004
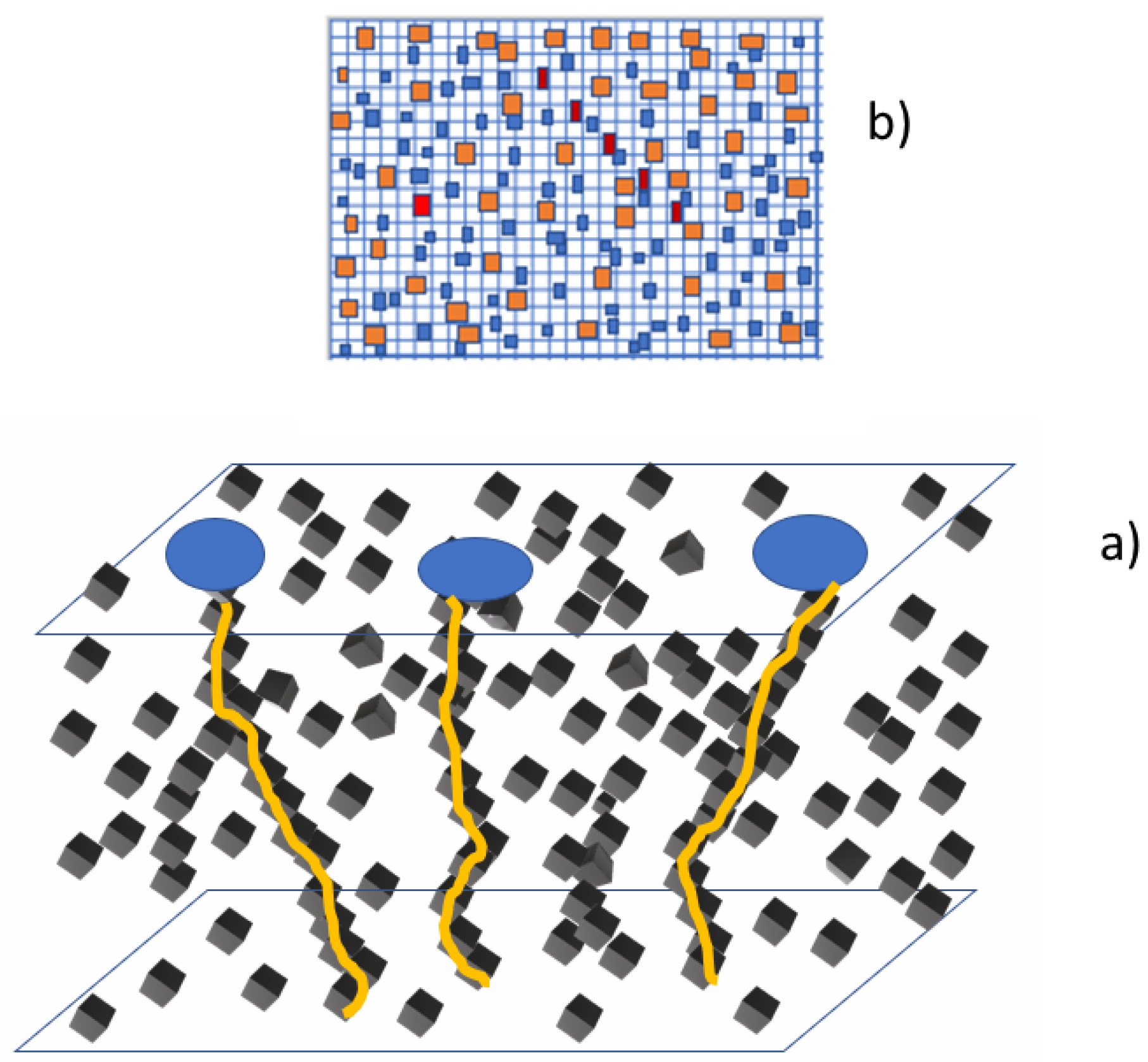
Preprints 114033 g005
Figure 5. Montecarlo simulation of the bulk (a) and surface electrode (b), considering that each graphite particles occupies cubes and squares of sides δ 0
Figure 5. Montecarlo simulation of the bulk (a) and surface electrode (b), considering that each graphite particles occupies cubes and squares of sides δ 0
Preprints 114033 g005
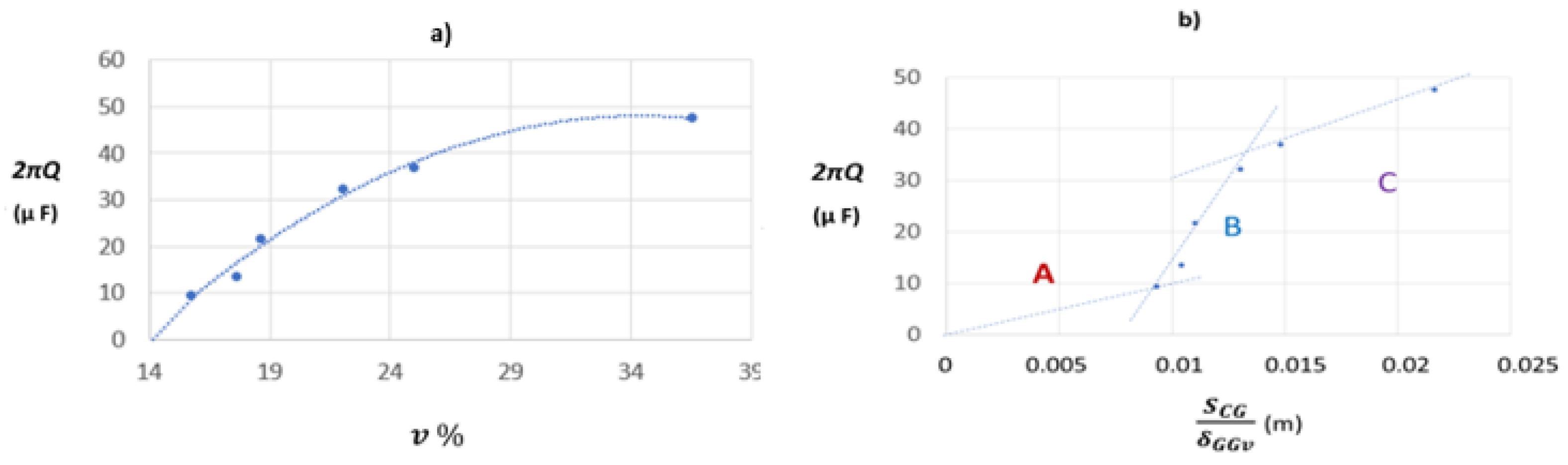
Preprints 114033 g006
Figure 6. a) Dependence of the value of   Q
Figure 6. a) Dependence of the value of   Q
Preprints 114033 g006
Table 1. Some referred dependences of the n C P E on the d F .
Table 1. Some referred dependences of the n C P E on the d F .
Equations Conditions References
n = 1 Capacitor
n = 0.5 Warburg
n = 0 Resistance
n = - 1 Inductor
n = 1 d F − 1 2 < d F < 3
Porous or roughhouse electrodes		 [49]
n = 1 d F Koch curve
porous/dendritic electrodes		 [22,55,63,64]
n = 3 − d F 3D Cantor-bar model [65,66]
n = d F − 1 2 EIS in diffusive control [50,67,68,69,70,71,72,73,74,75,76,77,78,79,80]
n = d F − 1 Plane ensemble of micro electrodes This work
Table 2. Values of the fractal dimensions of the composite material d C and its surface d F   estimated from Equations (11) and (13).
Table 2. Values of the fractal dimensions of the composite material d C and its surface d F   estimated from Equations (11) and (13).
m g v R u
Ω		 Q
µ F		 n d F d C
0.38 0.157 70000 1.50 0.68 1.68 2.68
0.41 0.176 8400 2.10 0.85 1.85 2.85
0.45 0.186 1900 3.46 0.86 1.86 2.86
0.50 0.220 520 5.13 0.87 1.87 2.87
0.52 0.250 180 5.90 0.88 1.88 2.88
0.65 0.365 25 7.58 0.90 1.90 2.90
Table 3. An stimation of the fraction ϴ occupied on surface of the particles that pertains a DC conducting clusters. Approximated distances between the graphite particles considered as cubes of δ 0 = 16.2 nm: δ G G v , which occupes an timated overalls area SCG considering z = 4. The electroactive area A e q was obtained from potentiostatic reduction of 1.0 mM of K3 [Fe(CN)6] in KCl 1 M [41] on composite electrodes of A0 = 0.24 mm2 of Euclidean area. T = 298 K. E = - 0.4 V vs Ag/AgCl/KCl (sat.) 1M KCl.
Table 3. An stimation of the fraction ϴ occupied on surface of the particles that pertains a DC conducting clusters. Approximated distances between the graphite particles considered as cubes of δ 0 = 16.2 nm: δ G G v , which occupes an timated overalls area SCG considering z = 4. The electroactive area A e q was obtained from potentiostatic reduction of 1.0 mM of K3 [Fe(CN)6] in KCl 1 M [41] on composite electrodes of A0 = 0.24 mm2 of Euclidean area. T = 298 K. E = - 0.4 V vs Ag/AgCl/KCl (sat.) 1M KCl.
v
…		 Q
µ F		 SCG
m2 		δ G G v
µ m		 ϴ A e q
mm2 		τ
µ s
0.157 1.50 0.010 27 0.029 0.211 105
0.176 2.10 0.011 26 0.041 0.234 18
0.186 3.46 0.014 24 0.067 0.240 6
0.220 5.13 0.015 23 0.092 0.246 3
0.250 5.90 0.021 20 0.114 0.250 5
0.365 7.58 0.024 18 0.147 0.274 7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated