Prerpints.org logo
Preprint
Article

Performance of a Combined Energy System Consisting of Solar Collector, Biogas Dry Reforming and Solid Oxide Fuel Cell – An Indian Case Study

This version is not peer-reviewed.

Submitted:

01 August 2024

Posted:

02 August 2024

You are already at the latest version

Abstract
An energy production system consisting solar collector, biogas dry reforming reactor and solid oxide fuel cell (SOFC) was assumed to be installed in Kolkata, India. This study aims to understand the impact of climate condition on the performance of solar collectors with different lengths of parabolic trough solar collector (dx) and mass flow rate of heat transfer fluid (m). In addition, this study has evaluated the amount of H2 produced by biogas dry reforming (GH2), the amount of power generated by SOFC (PSOFC) and the maximum possible households (N) whose electricity demand could be met by the energy system proposed, considering the performance of solar collector with the different dx and m. As a result, the optimum dx was found to be 4 m. This study revealed that temperature of heat transfer fluid (Tfb) decreased with the increase in m. Tfb in March, April and May was higher than that in other months, while Tfb from June to December was the lowest. GH2, PSOFC and N in March, April and May were higher than that in other months irrespective of m. The optimum m was 0.030 kg/s.
Keywords: 
Subject: 
Engineering  -   Energy and Fuel Technology

1. Introduction

The energy consumption has been increasing with economy development rapidly. According to the Energy White Paper [1], the energy consumption was 14.4 billion ton based on equivalent of oil in 2022. On the other hand, the renewable energy is paid attention to introduce mode to meet the increase in energy consumption as well as to solve the global warming problem. According to the data base [1], the ratio of renewable energy including hydro to total energy consumption was 14.2 % in 2022 [1]. It is expected that the renewable energy will increase more and more in the world.
Using renewable energy to produce H2 is a promising way to utilize renewable energy. There are several approaches to produce H2, including producing H2 from biogas dry reforming. Biogas which consists of CH4 (ratio: 55–75 vol%) and CO2 (ratio: 25–45 vol%) [2] can be produced by fermentation of the action of anaerobic microorganisms on raw materials such as garbage, livestock and sewage sludge. It is known from the International Energy Agency [3] that the biogas equivalent to 1.46 EJ was produced in 2020. According to the International Energy Agency [3], the amount of produced biogas based on energy value was approximately five times as large as that in 2000. We can expect that the produced biogas will increase more and more. Biogas is usually used as a fuel for gas engine and micro gas turbine [4]. However, the power generation is smaller than using a natural gas due to consisting of CO2 of approximately 40 vol%. In this study, a biogas is proposed to be used as a feedstock to produce H2 via a thermally powered biogas dry reforming process. The produced H2 can be used as a fuel for solid oxide fuel cell (SOFC) [5]. CO which is a by-product of biogas dry reforming can also be used as a fuel for SOFC, resulting a more effective energy production system.
This study proposes a system combining the above described energy production system with a solar collector to supply the heat, which is needed for a biogas dry reforming, because it is an endothermic reaction. There are some studies reporting the combined system with a solar collector to produce H2 using a heat for the chemical reaction [6,7,8,9,10,11,12,13,14]. The numerical investigating the effect of peak heat flux, inlet flow rate and CH4/CO2 feed ratio on reaction temperature, reaction rates, conversion of syngas, syngas yield, carbon deposition, and other thermochemical characteristics of the porous material filled in solar collector under high-flux concentrated irradiation was reported [6]. Energy conversion equation and heat transfer equation, e.g. the equation on radiation heat transfer as well as chemical reactions were solved by CFD. As a result, the peak heat flux of the incident solar radiation performed a linear relation with the reaction temperature. The peak heat flux over 0.734 MW/m2 would decrease CH4 conversion and H2 yield, resulting in the reduction of the syngas yield. The experimental study using solar scheffler collector for biogas dry reforming was conducted [7]. The parabolic solar collector which could increase the temperature of biogas from 383 K to 773 K performed H2 yield of 16 % and CO yield of 10 %. CH4 conversion as well as CO2 conversion increased with the rise in temperature. The solar thermochemical system including a parabolic trough solar collector and a membrane reactor was proposed and investigated experimentally to decrease the reaction temperature of dry reforming to a mid/low temperature range (573 K–773 K) [8]. The conversion rate of CH4 at 673 K and 698 K reached 20.27 % and 30.00 %, respectively. Compared to a traditional system powered by fossil fuel energy, the CO2 emission could reduce 6.26 kg/m3 annually at 773 K with H2 permeate pressure of 10-3 bar. The thermodynamic analysis on solar CH4 steam reforming with H2 permeation membrane reactor at mid/low temperature was carried out numerically [9]. Solar trough collector was assumed to provide the heat for CH4 steam reforming. An optimal conversion rate range of CH4 for efficient solar CH4 membrane reforming was calculated, resulting that the net solar-to-fuel efficiency reached 38.25 % at 673 K which was lower temperature than normal operation temperature due to non-equilibrium state of CH4 steam reforming by means of membrane. A reflux solar CH3OH steam reforming reactor system was proposed and investigated numerically [10]. Parabolic solar collector was adopted to provide the heat for CH3OH steam reforming. When the length of flow channel of the reflux solar CH3OH steam reforming reactor was lengthened, the reaction was carried out thoroughly. Since the temperature in the reactor increased generally due to the recovery of the outlet fluid heat, the radiative heat loss increased slightly. The energy conversion efficiency varied slightly with the inlet mass flow rate. The parabolic trough solar receiver-reactor was proposed and investigated numerically using the CFD software, ANSYS Fluent for continuous and efficient H2 production via CH3OH steam reforming reaction [11]. A larger inlet temperature caused a higher reaction temperature and a consequent higher reaction rate. However, a higher working temperature also provided a relatively larger energy fraction of thermal loss. The parabolic trough solar receiver-reactors of gradually varied porosity catalyst beds were proposed and investigated for cost efficient H2 production [12]. A 3D comprehensive model was developed for the parabolic trough solar receiver-reactors of CH3OH steam reforming reaction in porous Cu/ZnO/Al2O3 catalyst packed beds, by combining the finite volume method with a comprehensive kinetic model. The top part of the reactor had lower temperature with a larger porosity, resulting that a relatively larger fluid flow velocity and heat convection between the bottom part and the top part of the reactor occurred. The average Nu number increased by 24.39 % though the average friction factor decreased by 5.91 %.
According to NEDO Renewable Energy Technology White Paper [13], parabolic trough type, Fresnel type, tower type and dish type are main type of concentration solar collectors installed in the world. The efficiency of parabolic trough type, Fresnel type, tower type and dish type is 15 %, 8 %– 10 %, 20 % – 35 % and 25 % – 30 %, respectively. Additionally, the land utilization efficiency for parabolic trough type, Fresnel type and tower type is 25 % – 40 %, 60 % – 80 % and 20 % – 25 %, respectively. When using the solar thermal power generation for the plant size below 250 MW and over 250 MW, the power generation cost of parabolic trough type is approximately 0.2 USD/kWh – 0.3 USD/kWh and 0.22 USD/kWh – 0.27 USD/kWh, respectively. Although the power generation cost depends on the sun light illumination condition strongly in this study, the parabolic trough solar collector was selected to be studied.
Considering the system proposed by this study, the location where the system is installed is important since the solar intensity influences the performance of solar collector [5]. In addition, the energy consumption and the CO2 emission in Asia, e.g. China, India, Japan and so on increase rapidly [1]. The average global horizontal solar irradiance in India is 5.0 kWh/(m2・day) – 5.5 kWh/(m2・day), which is much larger than that in China and Japan, e.g. 3.0 kWh/(m2・day) – 4.5 kWh/(m2・day) and 3.0 kWh/(m2・day) – 3.5 kWh/(m2・day), respectively [14]. Therefore, this paper conducted a hypothetical case study by assuming to install the proposed system in Kolkata, India.
However, there is no study on assessment of performance of solar collector as well as the energy production system proposed by this study which is assumed to be installed in India. Therefore, the aim of this study is to understand the influence of the climate data in India on the performances of solar collectors with different sizes and heat mass flow rate of transfer fluid, e.g. the simulated biogas as well as the performance of the combination system proposed. The weather data of Kolkata was from METPV-ASIA [15]. This study used the developed heat transfer model of the parabolic trough solar collector in previous studies [16]. The temperature of heat transfer fluid out of the parabolic trough solar collector could range approximately 700 K – 873 K [17,18]. Since the biogas dry reforming could happen in the temperature range from 673 K to 873 K as per the previous experimental studies conducted by authors [19,20], this study thinks that the parabolic trough solar collector is suitable. The authors have also adopted the specific characteristics of a biogas dry reforming reactor developed previously to calculate the amount of produced H2 [19,20] and the power generated by SOFC using H2 obtained from a biogas dry reforming reactor. The heat transfer fluid which consists of CH4 and CO2 flows into the solar collector. After the heat transfer fluid is heated by solar collector, it flows into the biogas dry reforming reactor. H2 will then be produced in the reactor via the biogas dry reforming process. The produced H2 is provided to SOFC as a fuel, resulting that the electricity is generated. In this study, the impact of climate condition of Kolkata in India on the performance of solar collectors with different lengths of parabolic trough solar collector (dx) and mass flow rate of heat transfer fluid (m) has been investigated. In addition, the amount of H2 produced by biogas dry reforming (GH2), the amount of power generated by SOFC (PSOFC) and the maximum possible households (N) whose electricity demand could be met by the energy system proposed have been also evaluated considering the performance of solar collector with the different dx and m.

2. Heat Transfer Model to Assess the Proposed Solar Collector

2.1. Governing Equations

Figure 1 illustrates the schematic drawing for the simplified heat transfer model of the solar collector proposed in this study. A solar radiation is mainly absorbed on the outer surface of the absorber tube in this model [8]. The absorbed heat transports to the heat transfer fluid by conduction through the tube wall and convection from the inner surface of the tube to the fluid (Qh). Other heat transfers as a radiation loss to the inner surface of the glass tube through the vacuum space (Qr) and then by conduction from the inner surface of the glass tube to the outer surface of it (Qc). The heat transferred to ambient from the outlet surface of the glass tube via two mechanisms as follows: (i) the convection to the surrounding air (Qa), (ii) the radiation to the sky (Qs).
Figure 2 exhibits the thermal resistance diagram of the heat transfer process in the model proposed by this study [21]. In this model, R1 means the thermal resistance because of convection from the heat transfer fluid to the absorber [(m・K)/W]. R2 means the thermal resistance because of conduction via the absorber [(m・K)/W]. R3 means the thermal resistance because of radiation via vacuum [(m・K)/W]. R4 means the thermal resistance because of conduction via the glass tube [(m・K)/W]. R5 means the thermal resistance because of convection to the surrounding air [(m・K)/W]. R6 means the thermal resistance because of radiation to the surrounding surfaces (sky) [(m・K)/W].
This study assumes the surrounding surface temperature is equal to the ambient air temperature. The model equation for a single glass tube can be expressed as following [16].
I α τ D π d x = T t o − T f b R 1 + T t o − T s R 5 − 1 + R 6 − 1 − 1
m c d T f b d x = m c T f b , o u t − T f b , i n d x = T t o − T f b R 1
T t o − T g i R 3 = T t o − T s R 3 + R 5 − 1 + R 6 − 1 − 1
where I means the solar intensity [W/m2], α means the absorptivity of absorber tube [-], τ means the transmissivity of glass tube [-], D means the diameter of absorber [m], dx means the length of absorber [m], m means the mass flow rate of heat transfer fluid assumed to be a biogas [kg/s], c means the specific heat of heat transfer fluid [J/(kg・K)], Tfb means the temperature of heat transfer fluid [K], Tfb, out and Tfb, in mean the temperature of heat transfer fluid at outlet [K] and inlet [K], respectively.
Each thermal resistance is defined as following [16]:
R 1 = 1 2 π r t i h
R 2 = 1 2 π k t ln r t o r t i
R 3 = 1 2 π σ r t o 1 ε t + 1 − ε g ε g r t o r g i T t o 2 + T g i 2 T t o + T g i − 1
R 4 = 1 2 π k g ln r g o r g i
R 5 = 1 2 π r g o h o
R 6 = 1 ε g σ 2 π r g o T g o + T s T g o 2 + T s 2
Where rti means the inner radius of absorber [m], rto means the outlet radius of absorber [m], rgi means the inner radius of glass tube [m], rgo means the outlet of glass tube [m], σ means Stefan-Boltzmann constant [W/(m2・K4)], h means the heat transfer coefficient between the heat transfer fluid and the inner surface of absorber [ W/(m2・K)], ho means the heat transfer coefficient from the outer surface of glass tube to the surrounding air [W/(m2・K)], kt means the thermal conductivity of absorber [W/(m・K)], kg means the thermal conductivity of glass tube [W/(m・K), εt means the emissivity of absorber [-], εg means the emissivity of glass tube [-], Tto means the temperature of outer surface of absorber [-], Tgi means the temperature of inner surface of glass tube [K], Tgo means the temperature of outer surface of glass tube [K], Ts means the temperature of sky [K] and Ta means the temperature surrounding air (= 293) [K]. We assume Ts ≒ Ta.

2.2. Calculation Procedure of Heat Transfer Coefficient

The convective heat transfer coefficient of the turbulent flow in a tube was calculated by Dittus-Boelter correlations [22] in this study as following:
N u = 0.023 Re 0.8 Pr 1 3
Additionally, the above equation is summarized in detail which is well known dimensionless number and equation as following:
N u = h D k a
Re = ρ a u a D μ a
Pr = C p , a μ a k a
h o = 0.0191 + 0.006608 u a
where Cp, a means the specific heat of surrounding air [J/(kg・K)], μa means the viscosity [Pa・s], ka means the thermal conductivity of surrounding air [W/(m・K)], ua means the velocity of surrounding air [m/s] and ρa means the density of surrounding air [m/s]. From the reference [16], the temperature of fluid flowing through the absorber was calculated well be means of the ho equation shown by Equation (14). Consequently, the authors think the ho equation shown by Equation (14) can be applied.

2.3. Calculation Procedure of Tfb

According to Equations (1) and (2), the following equation can be drawn:
T f b , o u t = d x m c I α τ D π d x − T t o − T s R 5 + R 6 R 3 R 5 + R 6 + R 5 R 6 + T f b , i n
Moreover, R3 can be decided from Equation (3) as following:
R 3 = T t o − T g i R 5 R 6 R 5 + R 6 − T s + T g i
According to Equations (6) and (16), Tto can be obtained as following:
T t o = R 5 + R 6 − T s + T g 2 π σ t t o R 5 R 6 × r g i + r t o 1 − ε g ε t r g i + T g i 4 1 4
Tfb can be calculated by averaging Tfb, in and Tfb, out as following:
T f b = T f b , i n + T f b , o u t 2
Tfb is calculated with changing dx according to the above equations in this study. D was set to be 1.5 m according to the previous study [5]. The weather data, i.e. I, ua and Ta in Kolkata from METPV-ASIA [15] were used. In this study, the mirror and solar reflection as well as to consider the variable angle and solar radiation were ignored [21]. The heat transfer fluid was a mixture of CH4 and CO2. The molar ratio of CH4 : CO2 was 1.5 : 1. The following assumptions were made in this study [21]:
(i)
The distance between absorber and glass tube is 1/10 D.
(ii)
Tfb, in is 283 K.
(iii)
Ts ≒ Ta.
(iv)
The thickness of absorber and glass tube is 0.005 m and 0.010 m, respectively.
R2 and R4 are ignored since they are very small compared with the other thermal resistances.
(v)
Tti equals to Tto.
(vi)
Tgi equals to Tgo, which is 373 K.
(vii)
The mirror and solar reflection is ignored.
(viii)
The variable angle of solar radiation is ignored.
Table 1 lists the physical properties which were used in this study. Before the calculation of Tfb, we could not predict the exact value of it. If We calculate Tfb considering the change of physical properties with the temperature under an unsteady state condition, the calculation is too complex and huge. The physical properties listed in Table 1 were assumed to be temperature independent, and the values at 283 K were listed and used. Comparting to the other heat transfer models, a few papers reported on the heat transfer analysis using Hottel-Whiller-Bliss model for a solar collector recently [23,24,25]. However, these papers investigated on a flat plate solar collector [23,24,25], while this study investigates a parabolic trough solar collector. Moreover, the Hotel-Whiller-Bliss model considered thermal conduction only in these previous studies [23,24,25], while the model investigated in this study considers the thermal conduction, the thermal convection and the thermal radiation heat transfer, resulting in the assessment of the whole heat transfer mechanism in this study. Consequently, the authors think the model investigated in this study has the merit and the superiority to Hottel-Whiller-Bliss model.

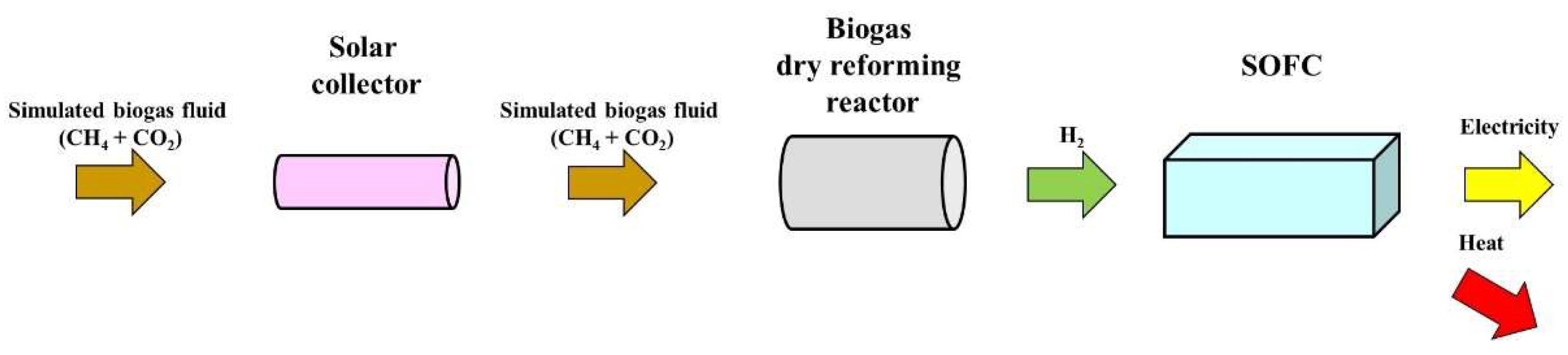
3. Combined Energy Production System Proposed by This Study

Figure 3 illustrates the proposed system consisting of solar collector, biogas dry reforming reactor and SOFC. In the proposed system, the heat transfer fluid which consists of CH4 and CO2 flows into solar collector. After being heated by solar collector, the heat transfer fluid flows into biogas dry reforming reactor. H2 is produced in the reactor via biogas dry reforming process. The produced H2 is supplied for SOFC as a fuel. As a result, the electricity and heat is generated (In this study, only the electricity is considered). The by-product of the process, CO was not considered in this study.
To calculate the amount of H2 produced through the biogas dry reforming reactor, this study follows the reaction scheme of biogas dry reforming as follows:
CH4 + CO2 → 2H2 + 2CO
We set the molar ratio of CH4 and CO2 is 2.51×10-3 mol/s and 1.67×10-3 mol/s, respectively when m = 0.005 kg/s. In this study, m is changed by 0.005, 0.010, 0.015 and 0.030 kg/s. According to Equation (19) and the molar flow rate when m = 0.005 kg/s, the molar flow rate of produced H2 can be estimated to be 3.34×10-3 mol/s. According to the authors’ previous experimental studies investigating the impact of the reaction temperature on the performance of biogas dry reforming corresponding to Tfb in this study from 673 K to 873 K [19,20], the best performance of biogas dry reforming was obtained at 873 K. The conversion ratio of H2 is assumed to be 100 % and 10 % respectively [19,20].
To calculate the power generated by SOFC, the lower heating value of H2 (= 10.79 MJ/m3N) and the power generation efficiency of commercial SOFC of 55 % [26] were used. The power generated by SOFC in the case of the conversion ratio of H2 = 100 % can be estimated as follows:
(3.34×10-3 [mol/s]×22.4 [L/mol])÷(1000 [L/m3]×0.55×(10.79 [MJ/(m3N)] ) = 0.444 [kW]
In addition, this study estimated the number of maximum possible households whose electricity demand could be met by the power generated by SOFC. The monthly data for the electricity demand of a couple households was used in this study [27].

4. Results and Discussion

4.1. Tfb through Year with Different dx and m

The climate data, I, ua and Ta in Kolkata, India according to METPV-ASIA [15] were used for the calculation of Tfb and are shown in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13 and Table 14.
Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 show the changes of Tfb with time in different months. In these figures, dx and m were also changed. The monthly mean values are shown in these figures. According to Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13 and Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15, the change in Tfb followed the change in I mainly. Additionally, it can also be seen from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 that Tfb rises with the increase in dx. This is due to the increase in heat transfer area for receiving the solar heat, which can be understood from Equation (15) [21]. However, some conditions exhibited Tfb over 2000 K in the case of dx = 5 m, indicating that it was not practically possible due to the durability of material of solar collector. For example, the melting point of SUS 405 is 1700 K [28]. In the following discussion, the results were based on dx = 4 m. In addition, it is shown from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 that Tfb decreases with the increase in m. Since the heat capacity is larger with the increase in m as shown in Equation (15), Tfb decreases with the increase in m. It can be found that Tfb is below 1000 K even dx = 5 m for some months. Moreover, it can be seen that Tfb in March, April and May is higher than the other months. In India, March, April and May belongs to a summer season which exhibits longer sunshine duration and higher I, resulting from Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13. On the other hand, it can be seen from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 that Tfb from June to December is lower than the other months. Since June to December is the rainy season in Kolkata, Tfb is lower due to lower I. Therefore, it can be revealed that Tfb is determined by the climate characteristics.

4.2. H2 Produced by Biogas Dry Reforming and Power Generated by SOFC

This study assumed that H2 can be produced by biogas dry reforming when Tfb is over 873 K. Table 14, Table 15, Table 16 and Table 17 list GH2, PSOFC and N per month changing m at dx = 4 m according to the duration when Tfb is over 873 K shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15.
Table 14. Comparison of GH2, PSOFC and N among different months for m = 0.005 kg/s at dx = 4 m.
Table 14. Comparison of GH2, PSOFC and N among different months for m = 0.005 kg/s at dx = 4 m.
GH2 [kg] PSOFC [Wh] N [-]
January 4.48 82639 0.5
February 5.39 99522 0.7
March 5.97 110185 0.7
April 6.50 119959 0.8
May 6.71 123958 0.8
June 5.78 106631 0.7
July 5.97 110185 0.7
August 5.97 110185 0.7
September 5.05 93302 0.6
October 5.22 96412 0.6
November 5.05 93302 0.6
December 5.22 96412 0.6
Total 67.31 1242691 8.04
It can be fromTable 14, Table 15, Table 16 and Table 17 that GH2, PSOFC and N in March, April and May were higher than that in the other months irrespective of m. The durations when Tfb was over 873 K in March, April and May were longer than that in the other months since Is in March, April and May were higher. In addition, GH2, PSOFC and N increased when m was larger. Since the mass of simulated biogas, e.g. heat transfer fluid increased, GH2 was larger, causing larger PSOFC and N. However, GH2, PSOFC and N decreased if m was set over 0.05 kg/s. This was due to the increase in heat capacity with the increase in m as shown in Equation (15). Therefore, this study has concluded that the optimum m should be 0.03 kg/s.
Considering N, it is not sufficient to cover the citizen living in Kolkata. However, this study thinks the following approach is efficient:
(i)
Increase the number of proposed system
(ii)
Increase D and re-optimize the size of solar collector
(iii)
Concentrate the solar light with installing the equipment in order to increase the solar intensity
This study would like to investigate these subjects in the near future.

5. Conclusions

This study simulated the performances of solar collectors with different dx and m and the energy system proposed with the weather condition in Kolkata, India. In addition, this study has also evaluated GH2, PSOFC and N. The following conclusions can be drawn from this study:
The optimum dx was founded to be 4 m considering the melting point of material of solar collector.
(i)
It is revealed that Tfb decreases with the increase in m.
(ii)
Tfb in March, April and May are higher than that in other months since March, April and May are summer in India. On the other hand, Tfb from June to December were lower due to the rainy season.
(iii)
GH2, PSOFC and N in March, April and May were all higher than that in other months irrespective of m.
(iv)
This study reveals that the optimum m is around 0.030 kg/s.

Author Contributions

Conceptualization and writing—original draft preparation, A.N.; methodology, R.S. and R.N.; writing—review and editing, E.H.

Funding

This research was founded by the 19th KRI Grant-in-Aid for Exploratory Research.

Data Availability Statement

The original data presented in this study are openly available in Akira Nishimura who is the corresponding author of this paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Agency for Natural Resources and Energy. Energy White Paper 2024. Available online: https://www.enecho.meti.go.jp/about/whitepaper/2024/pdf/2_2.pdf (accessed on 23 July 2024).
  2. Jelle, B. P. Building integrated photovoltaics: A concise research pathways. Energies 2015, 9. [Google Scholar] [CrossRef]
  3. World Bioenergy Association. Global Bioenergy Statistics. Available online: https://worldenergy.org (accessed on 23 July 2024).
  4. Mao, C.; Chen, S.; Shang, K.; Liang, L.; Ouyang, J. Highly active Ni-Ru bimetallic catalyst integrated with MFI zeolite-loaded cerium zirconium oxide for dry reforming of methane. ACS Applied Materials Interfaces 2022, 14, 47616–47632. [Google Scholar] [CrossRef] [PubMed]
  5. Nishimura, A.; Sato, R.; Hu, E. An energy production system powered by solar heat with biogas dry reforming reactor and solid oxide fuel cell. Smart Grid Renewable Energy 2023, 14, 85–106. [Google Scholar] [CrossRef]
  6. Zhang, H.; Shuai, Y.; Yuan, Y.; Longou, B. G.; Jiang, B.; Wang, F.; Cheng, Z. Thermal-chemical reaction characteristics of Ni/Al2O3 catalytic porous material filled solar reactor for dry reforming of methane process. Applied Thermal Engineering 2020, 180. [Google Scholar] [CrossRef]
  7. Rathod, V. P.; Shete, J.; Bhale, P. V. Experimental investigation on biogas reforming to hydrogen rich syngas production using solar energy. International Journal of Hydrogen Energy 2016, 41, 132–138. [Google Scholar] [CrossRef]
  8. Zhao, Q.; Su, B.; Wang, H.; He, A.; He, B.; Kong, H.; Hu, X. Mid/low-temperature solar hydrogen generation via dry reforming of methane enhanced in a membrane reactor. Energy Conversion and Management 2021, 240. [Google Scholar] [CrossRef]
  9. Wang, H.; Liu, M.; Kong, H.; Hao, Y. Thermodynamic analysis on mid/low temperature solar methane steam reforming with hydrogen permeation membrane reactors. Applied Thermal Engineering 2019, 152, 925–936. [Google Scholar] [CrossRef]
  10. Zhang, T.; Tang, X. Y.; Yang, W. W.; Ma, Xu. Comprehensive performance study on reflux solar methanol steam reforming reactor for hydrogen production. International Journal of Hydrogen Energy 2023, 48, 879–893. [Google Scholar] [CrossRef]
  11. Cheng, Z. D.; Leng, Y. K.; Men, J. J.; He, Y. L. Numerical study on a novel parabolic trough solar receiver-reactor and a new control strategy for continuous and efficient hydrogen production. Applied Energy 2020, 261. [Google Scholar] [CrossRef]
  12. Cheng, Z. D.; Men, J. J.; He, Y. L.; Tao, Y. B.; Ma, Z. Comprehensive study on novel parabolic trough solar receiver-reactors of gradually-varied porosity catalyst beds for hydrogen production. Renewable Energy 2019, 143, 1766–1781. [Google Scholar] [CrossRef]
  13. Jose, R.; Nicolas, V.; Jesus, C. A mathematical model to develop a scheffler-type solar concentrator coupled with a stirling engine. Applied Energy 2013, 101. [Google Scholar] [CrossRef]
  14. NREL Transforming Energy. NSRDB National Solar Radiation Database. Available online: https://nsrdb.nrel.gov/data-viewer (accessed on 23 July 2024).
  15. New Energy and Industrial Technology Development Organization. METPV-ASIA. Available online: https://www.nedo.go.jp/library/ZZFF_100038.html (accessed on 23 July 2024).
  16. Mohamad, A.; Orfi, J.; Alansary, H. Heat loss from parabolic system trough solar collectors. International Journal of Energy Research 2014, 38, 20–28. [Google Scholar] [CrossRef]
  17. Badar, R.; Pedretti, A.; Barbato, M.; Steingeld, A. An air-based corrugated cavity-receiver for solar parabolic trough concentrators. Applied Energy 2015, 138, 337–345. [Google Scholar] [CrossRef]
  18. Valladares, O. G.; Velazquez, N. Numerical simulation of parabolic trough solar collector. Improvement using counter flow concentric circular heat exchangers. International Journal of Heat and Mass Transfer 2009, 52, 597–609. [Google Scholar] [CrossRef]
  19. Nishimura, A.; Ohata, S.; Okukura, K.; Hu, E. The impact of operating conditions on the performance of a CH4 dry reforming membrane reactor for H2 production. Journal of Energy and Power Technology 2020, 2, 1–19. [Google Scholar] [CrossRef]
  20. Nishimura, A.; Takata, T.; Ohata, S.; Kolhe, M. L. Biogas dry reforming for hydrogen through membrane reactor utilizing negative pressure. fuels 2021, 2, 194–209. [Google Scholar] [CrossRef]
  21. Nishimura, A.; Sato, R.; Hu, E. Performance of an energy production system consisting of solar collector, biogas dry reforming reactor and solid oxide fuel cell. fuels 2024, 5, 278–296. [Google Scholar] [CrossRef]
  22. Kreith, F.; Freider, J.K. Preprints of thermodynamics and heat transfer applied to solar energy. In Solar Energy Handbook, 1st ed.; McGraw-Hill: New York, 1981; p. 1. [Google Scholar]
  23. Dhaundiyal, A. Rheological behavior of air in the two-pass solar collector. Frontiers in Energy Research 2022, 16. [Google Scholar] [CrossRef]
  24. Dhaundiyal, A.; Gebremicheal G., H. The stack effect on the thermal-fluid behavior of a solar collector. energies 2022, 15. [Google Scholar] [CrossRef]
  25. Goodfriend, W.; Pieters, E. B.; Tsvetelina, M.; Solomon, A.; Ezema, F.; Rau, U. Development and improvement of a transient temperature model of PV modules: concept of trailing data. Progress in Photovoltaic Research Application. 2024, 1. [Google Scholar] [CrossRef]
  26. NEDO (New Energy and Industry Technology Development Organization), Road Map of 2017 of NEDO Fuel Cell and Hydrogen. Available online: https://www.nedo.go.jp/content/100871873.pdf (accessed on 24 July 2024).
  27. Power Design Com. Daily Power Consumption of General Household. Power Design. Com. Available online: https://standard-profect.net/energy/statistics/energy-consumption-day.html (accessed on 25 July 2024).
  28. The Japan Society of Mechanical Engineers. JSME Heat Transfer Handbook, 1st ed.; Maruzen: Tokyo, Japan, 1993; p. 371. [Google Scholar]
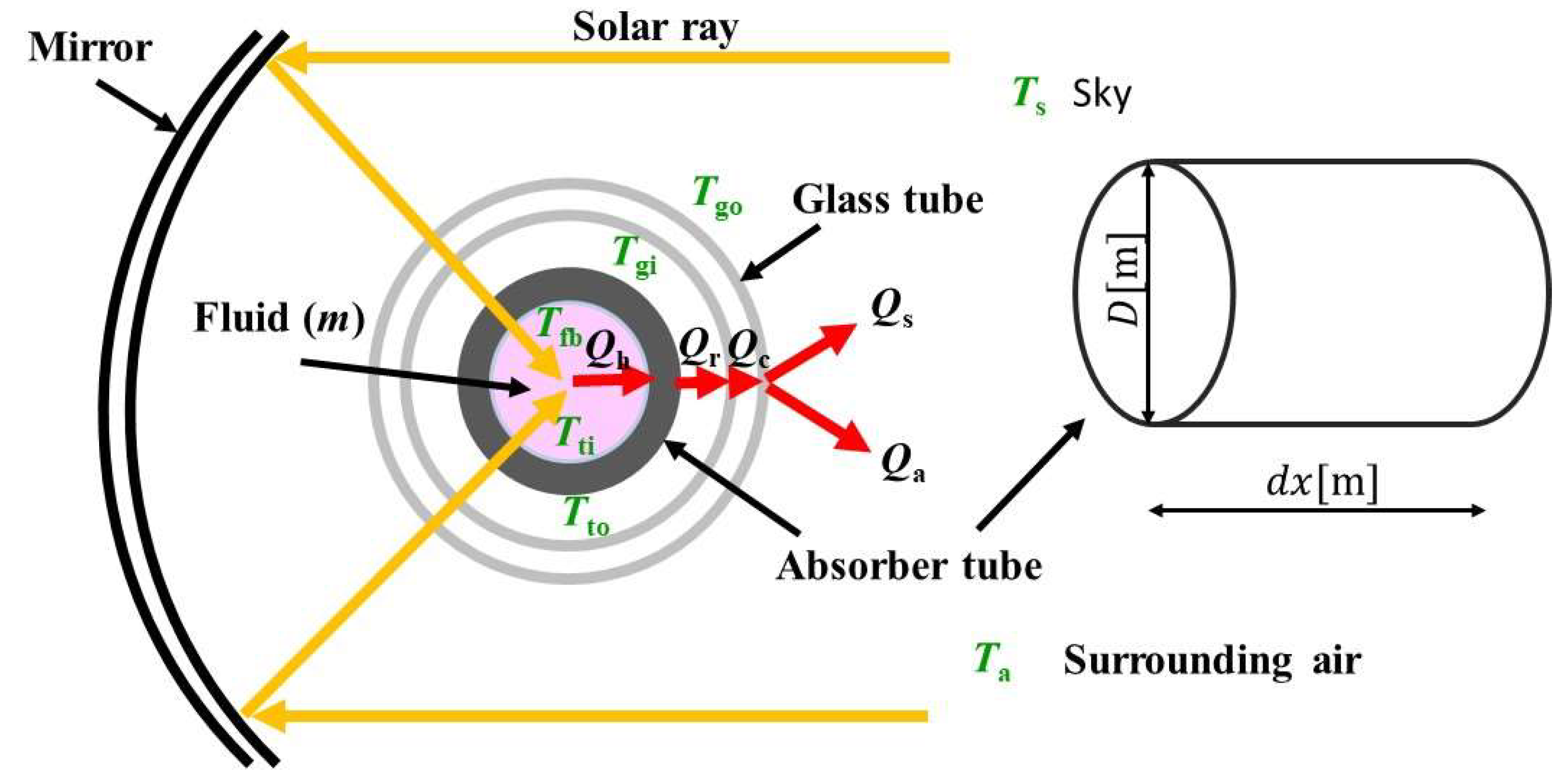
Preprints 114006 g001
Figure 1. Schematic drawing of heat transfer model of solar collector investigated in this study.
Figure 1. Schematic drawing of heat transfer model of solar collector investigated in this study.
Preprints 114006 g001
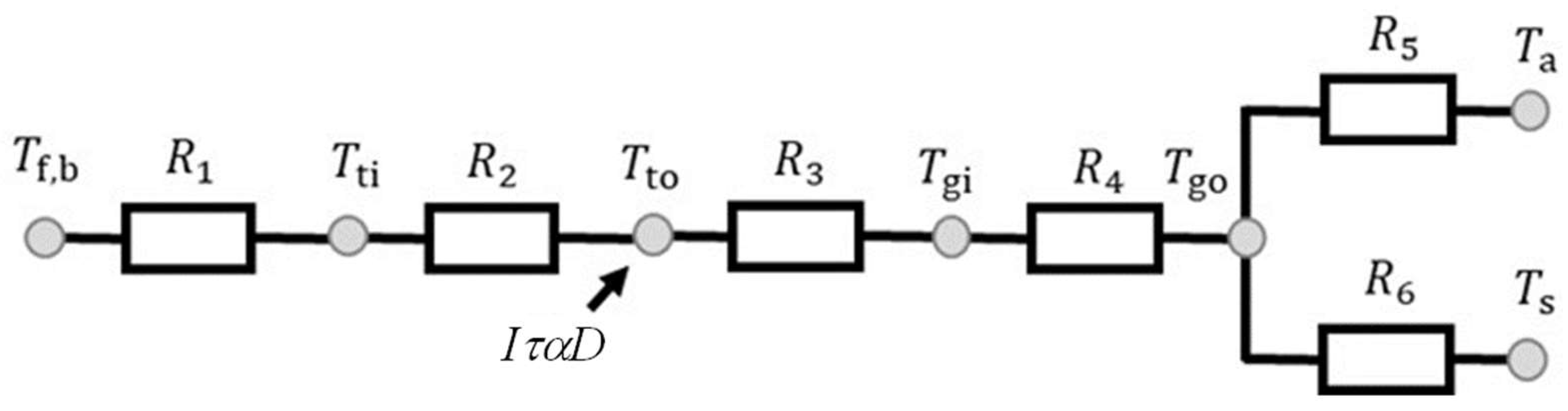
Preprints 114006 g002
Figure 2. Thermal resistance diagram of heat transfer model proposed by this study.
Figure 2. Thermal resistance diagram of heat transfer model proposed by this study.
Preprints 114006 g002
Preprints 114006 g003
Figure 3. Combined energy production system consisting of solar collector, biogas dry reforming reactor and SOFC proposed by this study.
Figure 3. Combined energy production system consisting of solar collector, biogas dry reforming reactor and SOFC proposed by this study.
Preprints 114006 g003
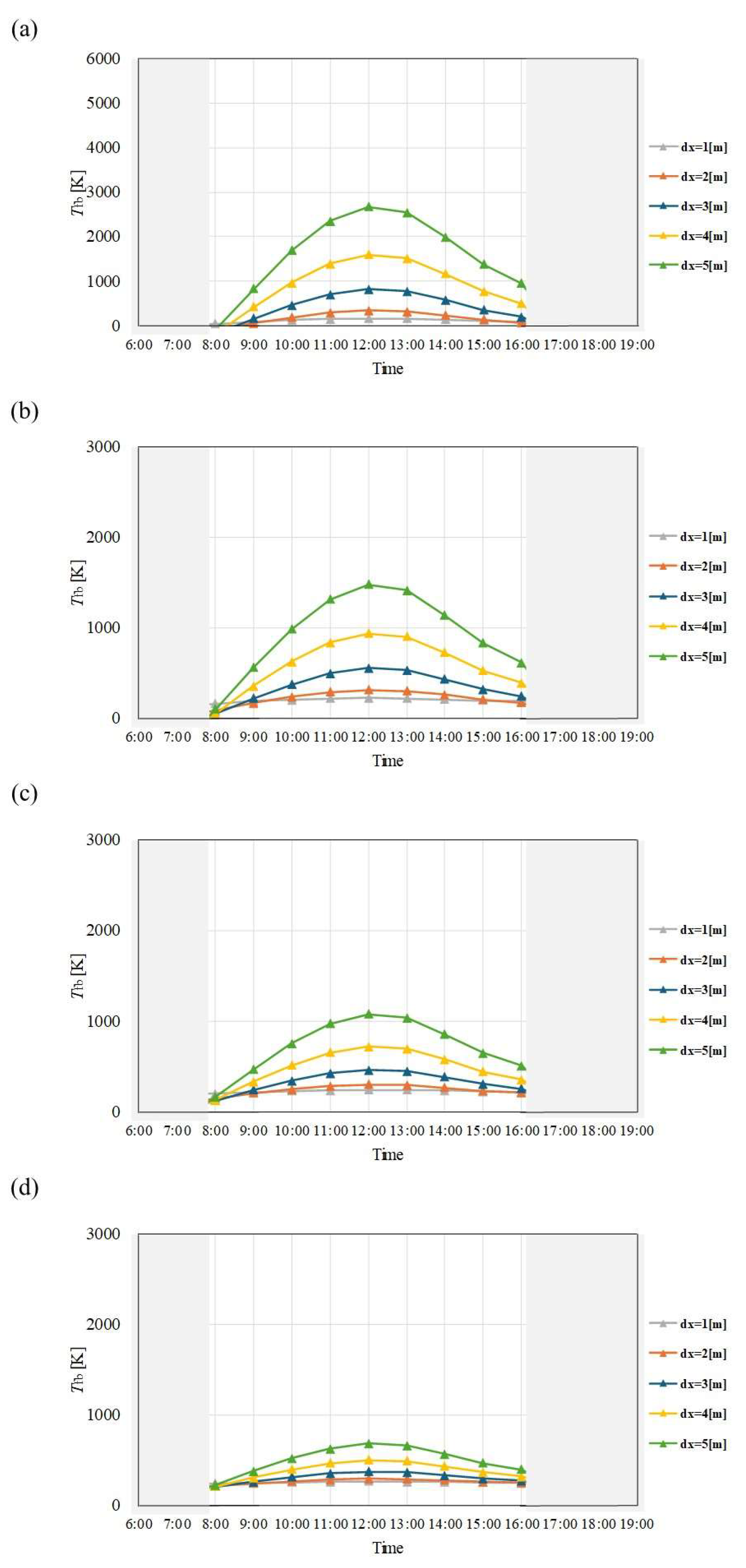
Preprints 114006 g004
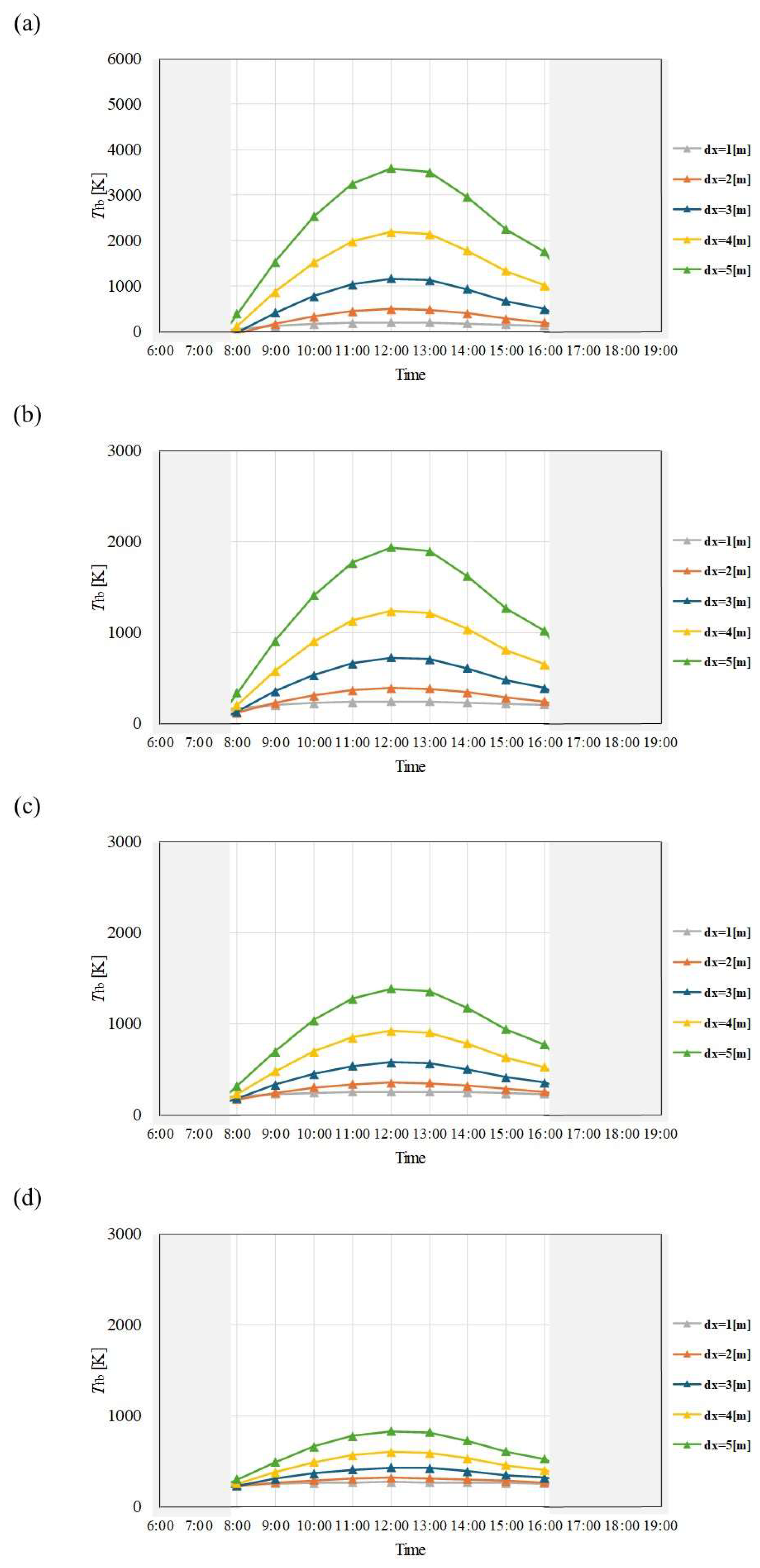
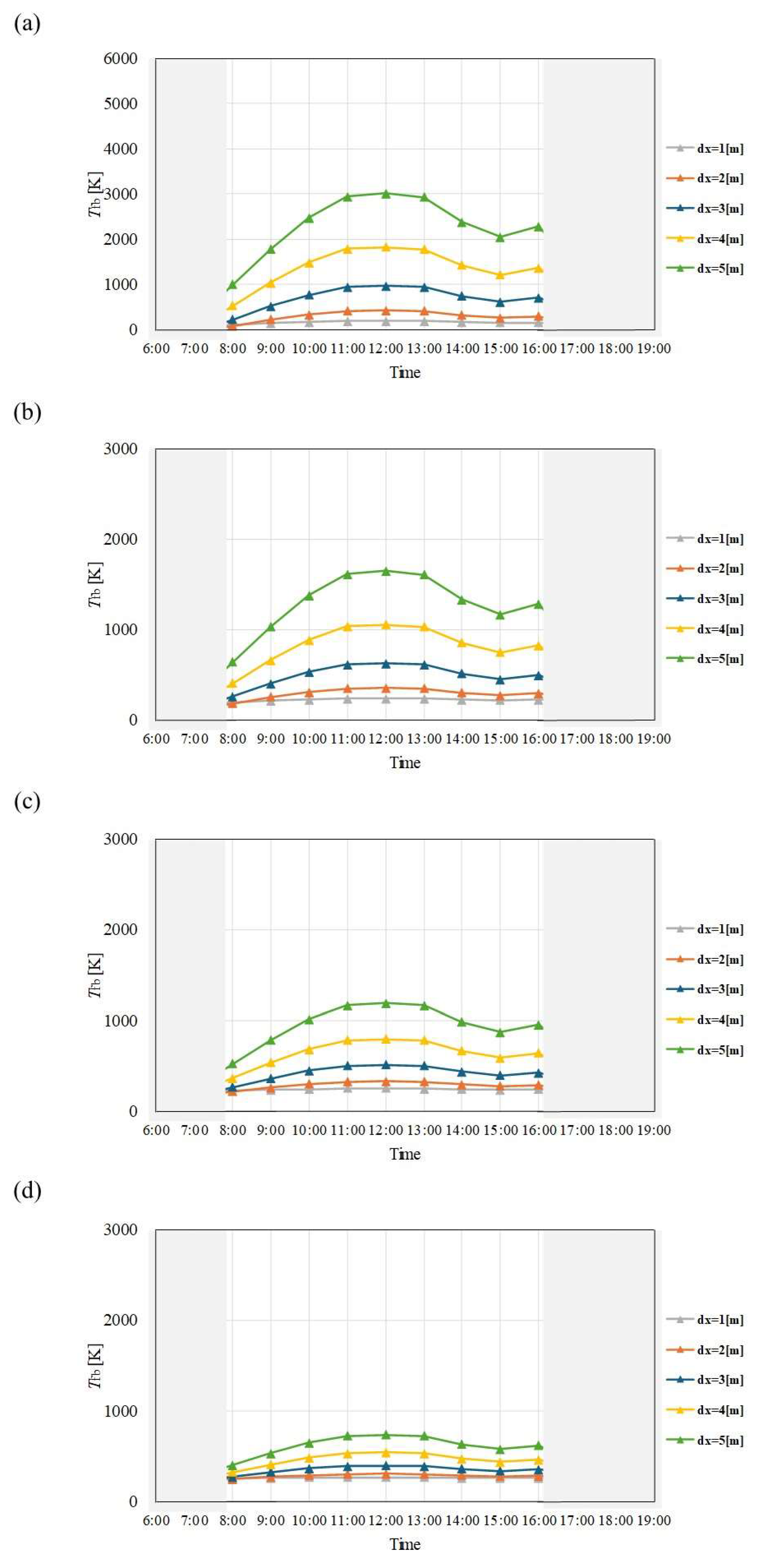
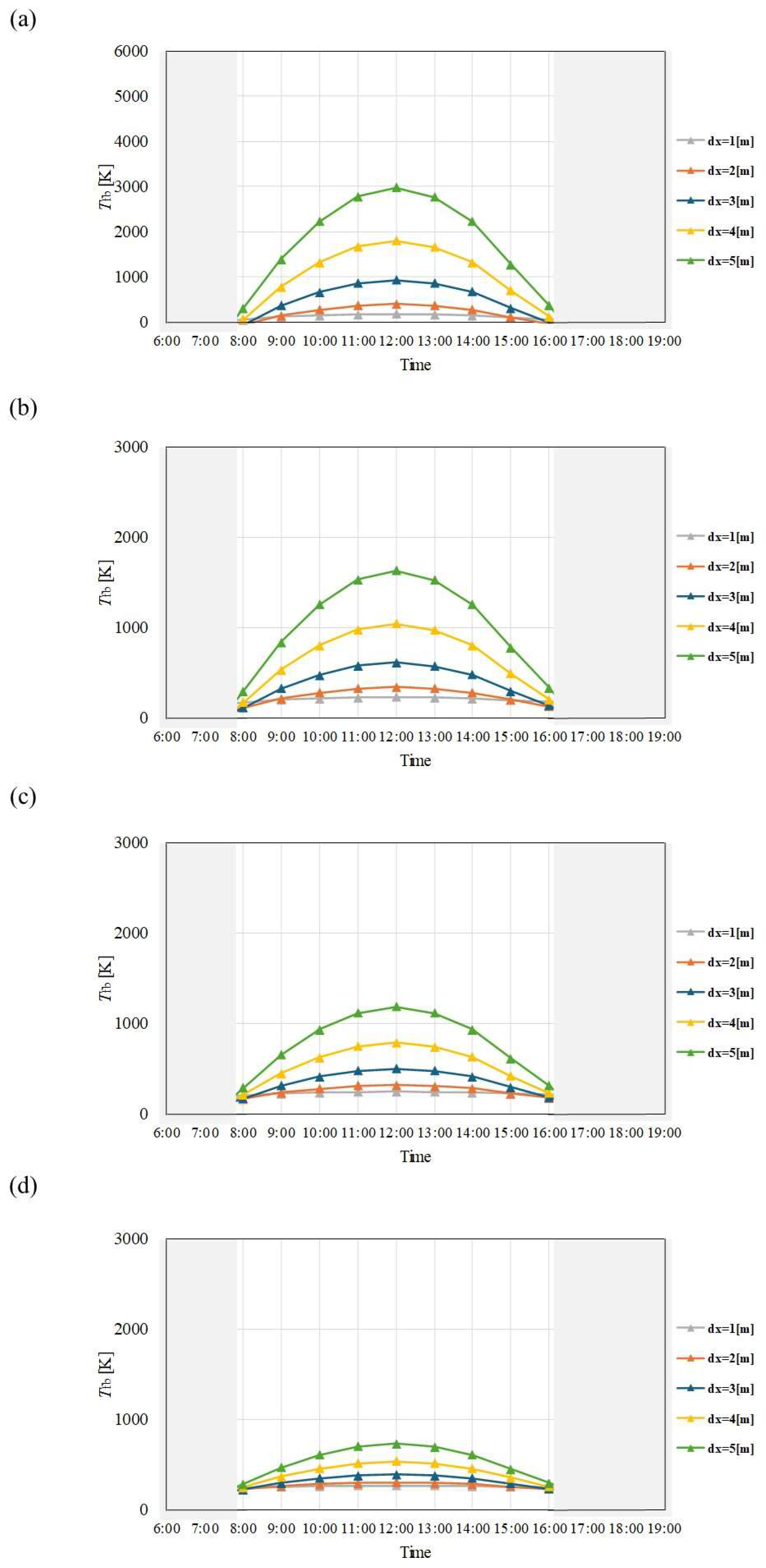
Figure 4. Comparison of change of Tfb with time among different dx and m in January. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 4. Comparison of change of Tfb with time among different dx and m in January. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g004
Preprints 114006 g005
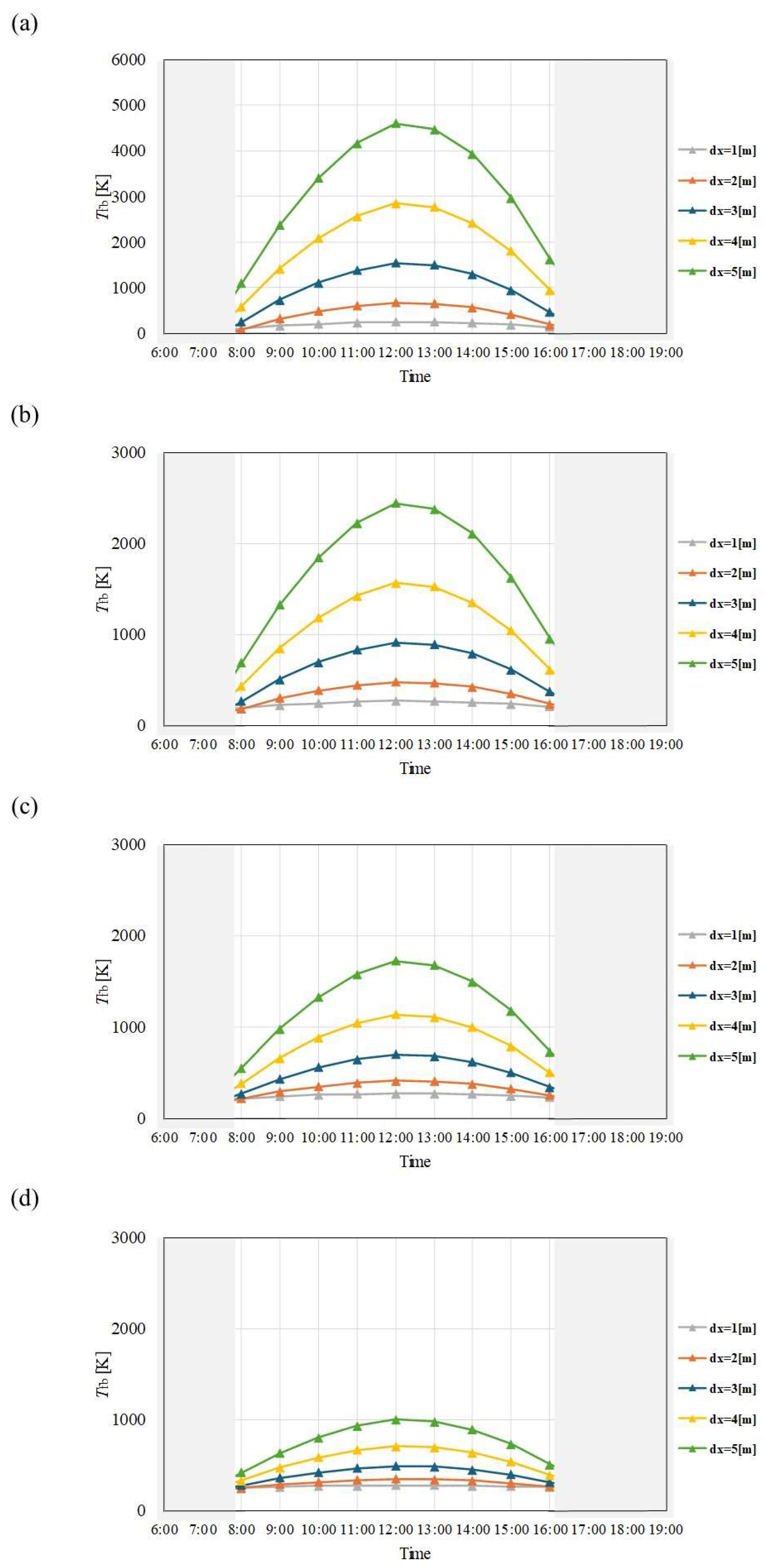
Figure 5. Comparison of change of Tfb with time among different dx and m in February. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 5. Comparison of change of Tfb with time among different dx and m in February. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g005
Preprints 114006 g006
Figure 6. Comparison of change of Tfb with time among different dx and m in March. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 6. Comparison of change of Tfb with time among different dx and m in March. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g006
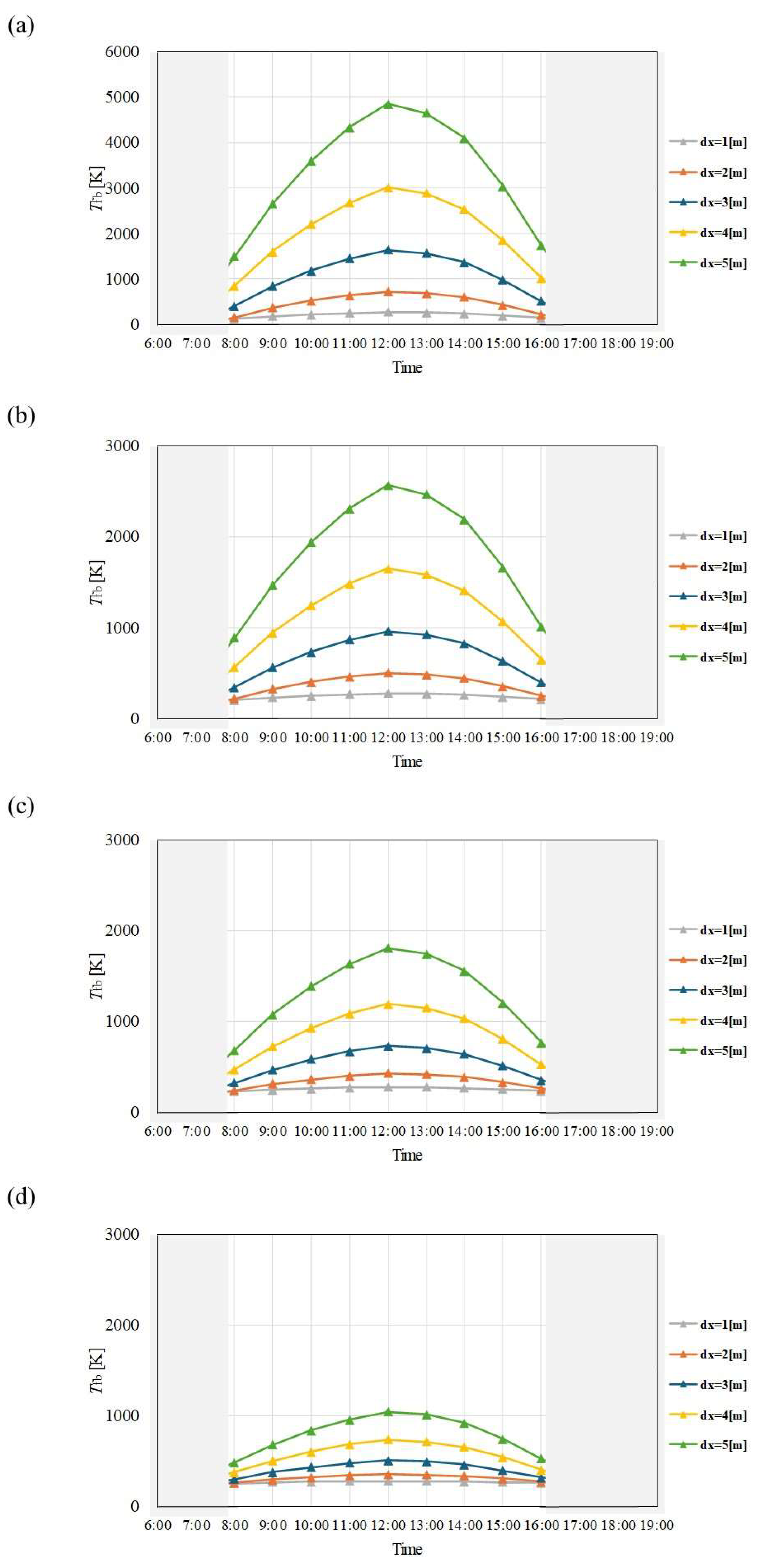
Preprints 114006 g007
Figure 7. Comparison of change of Tfb with time among different dx and m in April. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 7. Comparison of change of Tfb with time among different dx and m in April. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g007
Preprints 114006 g008
Figure 8. Comparison of change of Tfb with time among different dx and m in May. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 8. Comparison of change of Tfb with time among different dx and m in May. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g008
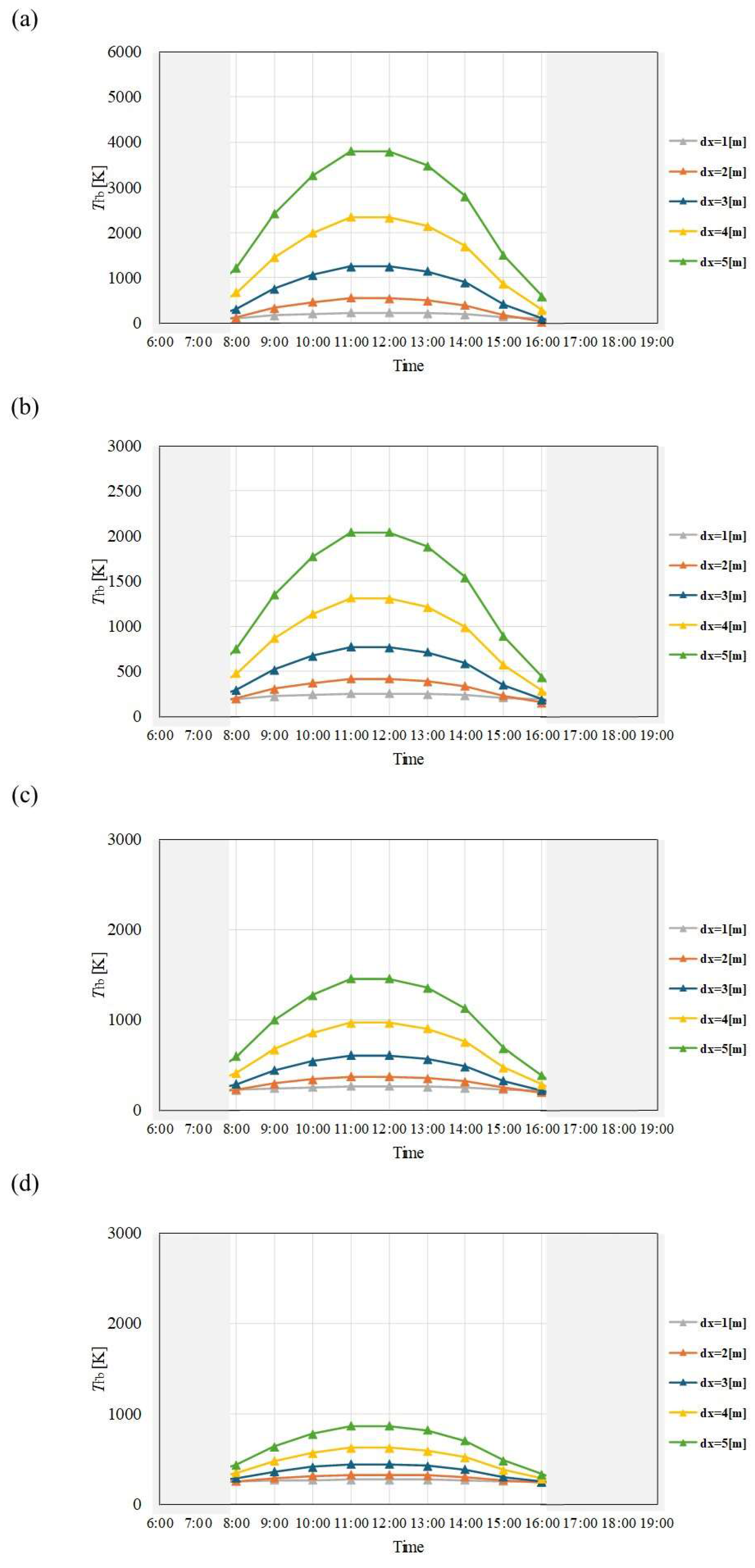
Preprints 114006 g009
Figure 9. Comparison of change of Tfb with time among different dx and m in June. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 9. Comparison of change of Tfb with time among different dx and m in June. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g009
Preprints 114006 g010
Figure 10. Comparison of change of Tfb with time among different dx and m in July. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 10. Comparison of change of Tfb with time among different dx and m in July. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g010
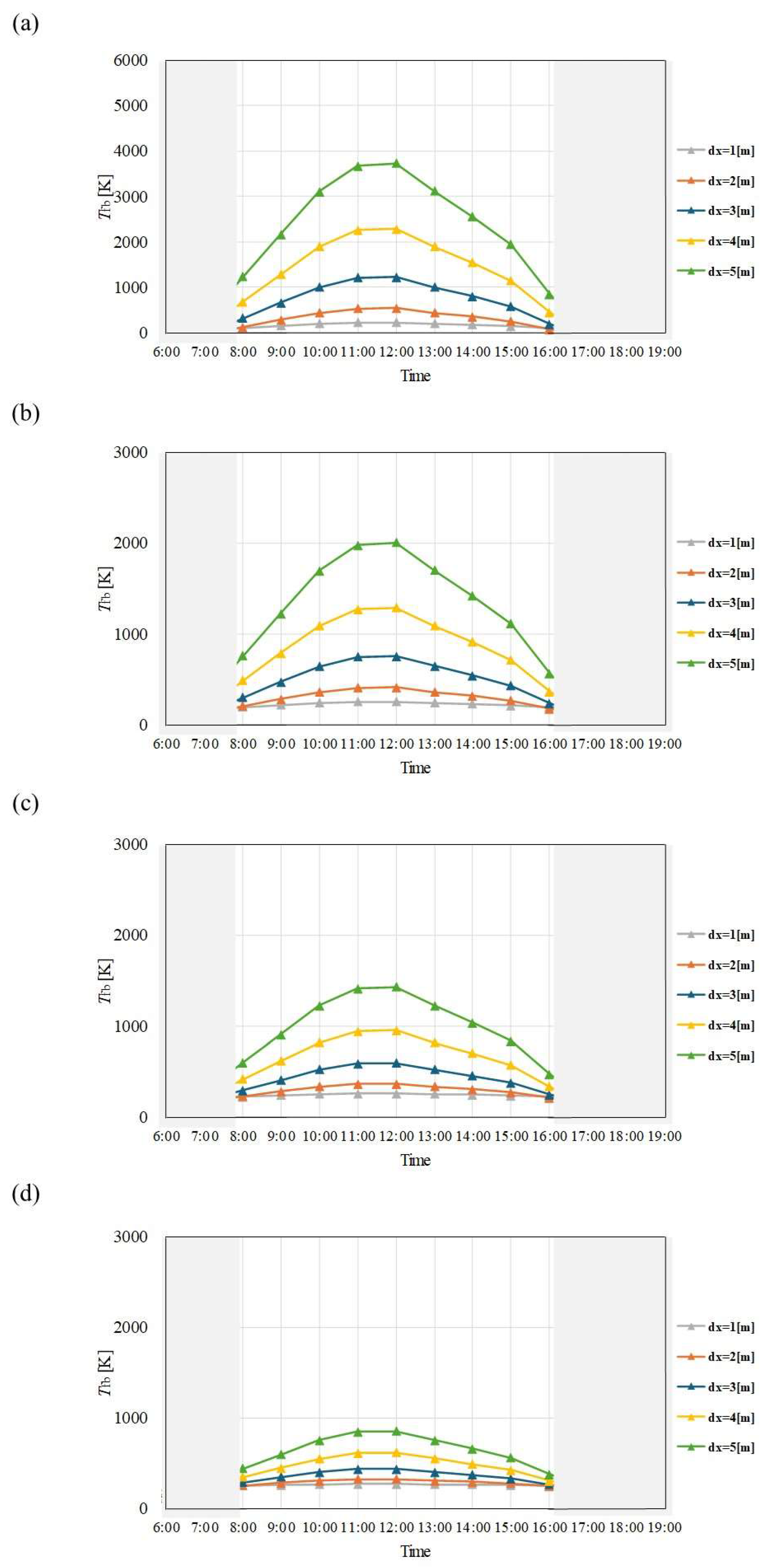
Preprints 114006 g011
Figure 11. Comparison of change of Tfb with time among different dx and m in August. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 11. Comparison of change of Tfb with time among different dx and m in August. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g011
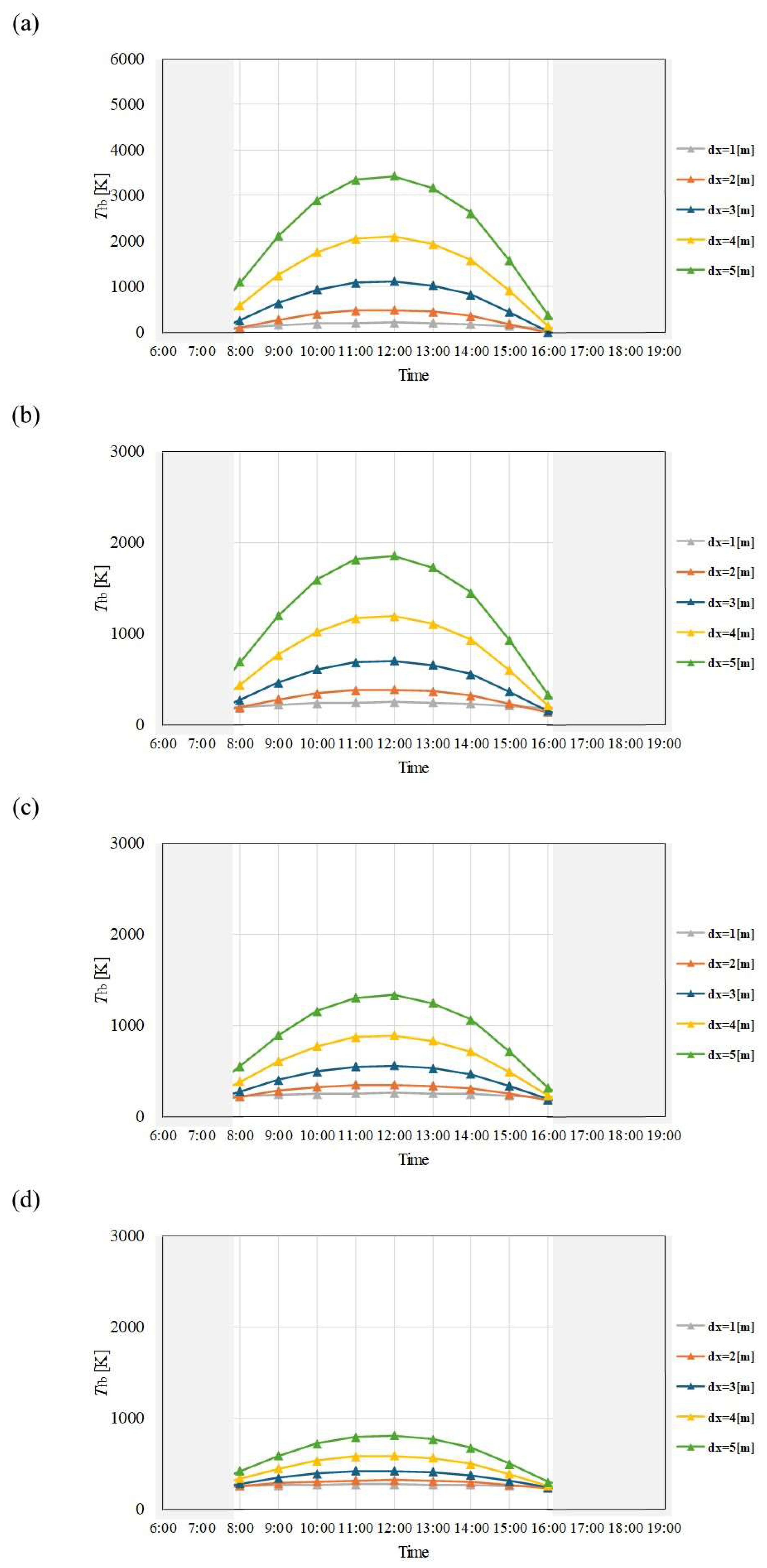
Preprints 114006 g012
Figure 12. Comparison of change of Tfb with time among different dx and m in September. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 12. Comparison of change of Tfb with time among different dx and m in September. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g012
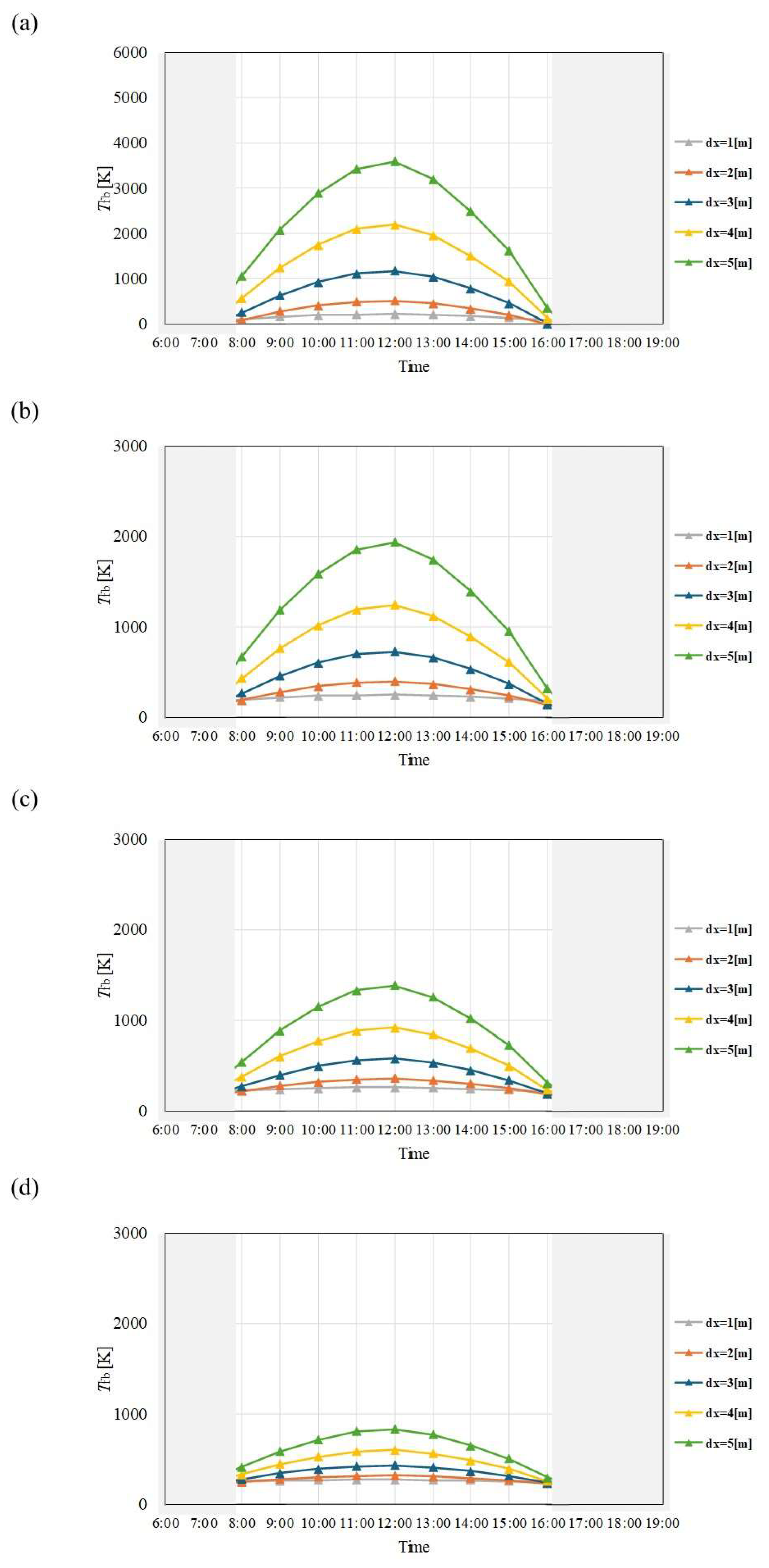
Preprints 114006 g013
Figure 13. Comparison of change of Tfb with time among different dx and m in October. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 13. Comparison of change of Tfb with time among different dx and m in October. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g013
Preprints 114006 g014
Figure 14. Comparison of change of Tfb with time among different dx and m in November. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 14. Comparison of change of Tfb with time among different dx and m in November. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g014
Preprints 114006 g015
Figure 15. Comparison of change of Tfb with time among different dx and m in December. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Figure 15. Comparison of change of Tfb with time among different dx and m in December. ((a): m = 0.005kg/s, (b): m = 0.010 kg/s, (c): m = 0.015 kg/s, (d): m = 0.030 kg/s).
Preprints 114006 g015
Table 1. The physical properties which are adopted in this study [5,16,21].
Table 1. The physical properties which are adopted in this study [5,16,21].
Property Value Information
α [-] 0.94 -
τ [-] 0.94 -
εt [-] 0.9 -
c [J/(kg・K)] 1.335 for CH4:CO2 = 1.5:1
σ [W/(m2・K4)] 5.67×10-8 Stefan-Boltzmann coefficient
εg [-] 0.94 Glass smooth surface
ka [W/(m・K)] 0.0257 Surrounding air
ρa [kg/m3] 1.166 Surrounding air
μa [Pa・s] 1.82×10-5 Surrounding air
Cp,a [J/(kg・K)] 1006 Surrounding air
kt [W/(m・K)] 16 Stainless steel
Kg [W/(m・K)] 1.3 Quartz glass
Table 2. Climate data of I, ua and Ta in Kolkata, India in January.
Table 2. Climate data of I, ua and Ta in Kolkata, India in January.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.087 0.258 287.02
8:00 0.498 0.323 287.02
9:00 0.877 1.000 294.94
10:00 1.271 1.000 294.94
11:00 1.576 1.000 294.94
12:00 1.725 1.000 294.94
13:00 1.666 1.000 294.94
14:00 1.413 0.935 294.94
15:00 1.134 0.194 293.85
16:00 0.935 0.194 293.85
17:00 0.389 0.194 293.85
18:00 0.003 0.194 293.85
Table 3. Climate data of I, ua and Ta in Kolkata, India in February.
Table 3. Climate data of I, ua and Ta in Kolkata, India in February.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.162 0.214 289.65
8:00 0.700 0.214 289.65
9:00 1.173 0.214 299.87
10:00 1.674 0.964 299.87
11:00 1.966 0.964 299.87
12:00 2.124 0.964 299.87
13:00 2.085 0.964 299.87
14:00 1.830 0.964 299.87
15:00 1.508 0.214 298.80
16:00 1.282 0.214 298.80
17:00 0.660 0.214 298.80
18:00 0.090 0.214 298.80
Table 4. Climate data of I, ua and Ta in Kolkata, India in March.
Table 4. Climate data of I, ua and Ta in Kolkata, India in March.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.406 0.548 295.34
8:00 1.000 0.548 295.34
9:00 1.534 1.065 304.23
10:00 2.012 1.065 304.23
11:00 2.364 1.065 304.23
12:00 2.565 1.065 304.23
13:00 2.505 1.065 304.23
14:00 2.255 1.065 304.23
15:00 1816 0.581 303.07
16:00 1.199 0.581 303.07
17:00 0.681 0.581 303.07
18:00 0.108 0.581 303.07
Table 5. Climate data of I, ua and Ta in Kolkata, India in April.
Table 5. Climate data of I, ua and Ta in Kolkata, India in April.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.643 0.867 298.37
8:00 1.163 0.867 298.37
9:00 1.657 1.600 305.65
10:00 2.092 1.600 305.65
11:00 2.433 1.600 305.65
12:00 2.672 1.600 305.65
13:00 2.581 1.600 305.65
14:00 2.323 1.600 305.65
15:00 1.844 1.333 304.17
16:00 1.239 1.333 304.17
17:00 0.744 1.333 304.17
18:00 0.158 1.333 304.17
Table 6. Climate data of I, ua and Ta in Kolkata, India in May.
Table 6. Climate data of I, ua and Ta in Kolkata, India in May.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.744 0.355 299.41
8:00 1.266 0.355 299.41
9:00 1.771 1.290 306.59
10:00 2.223 1.290 306.59
11:00 2.555 1.290 306.59
12:00 2.684 1.290 306.59
13:00 2.555 1.290 306.59
14:00 2.241 1.290 306.59
15:00 1.786 1.613 304.49
16:00 1.150 1.613 304.49
17:00 0.517 1.613 304.49
18:00 0.184 1.613 304.49
Table 7. Climate data of I, ua and Ta in Kolkata, India in June.
Table 7. Climate data of I, ua and Ta in Kolkata, India in June.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.651 1.033 300.15
8:00 1.029 1.033 300.15
9:00 1.552 1.367 305.26
10:00 1.939 1.367 305.26
11:00 2.191 1.367 305.26
12:00 2.187 1.367 305.26
13:00 2.046 1.367 305.26
14:00 1.729 1.367 305.26
15:00 1.138 1.200 302.89
16:00 0.722 1.200 302.89
17:00 0.302 1.200 302.89
18:00 0.133 1.200 302.89
Table 8. Climate data of I, ua and Ta in Kolkata, India in July.
Table 8. Climate data of I, ua and Ta in Kolkata, India in July.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.556 0.484 300.25
8:00 0.926 0.484 300.25
9:00 1.260 1.452 304.60
10:00 1.579 1.452 304.60
11:00 1.796 1.452 304.60
12:00 1.828 1.452 304.60
13:00 1.792 1.452 304.60
14:00 1.538 1.452 304.60
15:00 1.390 1.097 303.29
16:00 1.504 1.097 303.29
17:00 0.997 1.097 303.29
18:00 0.454 1.097 303.29
Table 9. Climate data of I, ua and Ta in Kolkata, India in August.
Table 9. Climate data of I, ua and Ta in Kolkata, India in August.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.586 0.645 300.31
8:00 1.037 2.032 300.31
9:00 1.434 2.032 305.28
10:00 1.871 2.032 305.28
11:00 2.133 2.032 305.28
12:00 2.155 2.032 305.28
13:00 1.874 2.032 305.28
14:00 1.614 2.032 305.28
15:00 1.346 1.323 302.75
16:00 0.844 1.323 302.75
17:00 0.444 1.323 302.75
18:00 0.143 1.323 302.75
Table 10. Climate data of I, ua and Ta in Kolkata, India in September.
Table 10. Climate data of I, ua and Ta in Kolkata, India in September.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.518 0.333 299.56
8:00 0.972 0.333 299.56
9:00 1.409 1.267 304.88
10:00 1.775 1.267 304.88
11:00 1.981 1.267 304.88
12:00 2.019 1.267 304.88
13:00 1.901 1.267 304.88
14:00 1.645 1.267 304.88
15:00 1.178 1.033 302.16
16:00 0.622 1.033 302.16
17:00 0.338 1.033 302.16
18:00 0.040 1.033 302.16
Table 11. Climate data of I, ua and Ta in Kolkata, India in October.
Table 11. Climate data of I, ua and Ta in Kolkata, India in October.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.476 0.290 298.05
8:00 0.968 0.290 298.05
9:00 1.404 1.097 303.70
10:00 1.773 1.097 303.70
11:00 2.025 1.097 303.70
12:00 2.100 1.097 303.70
13:00 1.924 1.097 303.70
14:00 1.594 1.097 307.70
15:00 1.203 0.613 300.89
16:00 0.621 0.613 300.89
17:00 0.221 0.613 300.89
18:00 6.452×10-4 0.613 300.89
Table 12. Climate data of I, ua and Ta in Kolkata, India in November.
Table 12. Climate data of I, ua and Ta in Kolkata, India in November.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.340 0.333 292.90
8:00 0.863 0.367 292.90
9:00 1.345 1.133 301.10
10:00 1.749 1.133 301.10
11:00 2.038 1.133 301.10
12:00 2.075 1.133 301.10
13:00 1.942 1.133 301.10
14:00 1.613 1.100 301.10
15:00 1.119 0.267 297.87
16:00 0.680 0.267 297.87
17:00 0.158 0.267 297.87
18:00 0 3.597 297.87
Table 13. Climate data of I, ua and Ta in Kolkata, India in December.
Table 13. Climate data of I, ua and Ta in Kolkata, India in December.
Time I [MJ/m2] ua [m/s] Ta [K]
7:00 0.170 0.168 287.07
8:00 0.676 0.181 287.07
9:00 1.118 0.945 298.35
10:00 1.502 0.971 298.35
11:00 1.760 1.087 298.35
12:00 1.850 1.023 298.35
13:00 1.755 1.003 298.35
14:00 1.504 0.977 298.35
15:00 1.085 0.094 294.41
16:00 0.668 0.071 294.41
17:00 0.163 0.097 294.41
18:00 0 0.142 294.41
Table 15. Comparison of GH2, PSOFC and N among different months for m = 0.010 kg/s at dx = 4 m.
Table 15. Comparison of GH2, PSOFC and N among different months for m = 0.010 kg/s at dx = 4 m.
GH2 [kg] PSOFC [Wh] N [-]
January 7.46 137731 0.9
February 9.43 174163 1.2
March 11.94 220370 1.4
April 11.55 213261 1.4
May 11.94 220370 1.4
June 8.66 159946 1.0
July 11.94 220370 1.4
August 10.44 192824 1.2
September 8.66 159946 1.0
October 10.44 192824 1.2
November 8.66 159946 1.0
December 7.46 137731 0.9
Total 118.59 2189481 14.2
Table 16. Comparison of GH2, PSOFC and N among different months for m = 0.015 kg/s at dx = 4 m.
Table 16. Comparison of GH2, PSOFC and N among different months for m = 0.015 kg/s at dx = 4 m.
GH2 [kg] PSOFC [Wh] N [-]
January 6.71 123958 0.8
February 12.13 223924 1.6
March 15.67 289235 1.8
April 15.16 279905 1.8
May 15.67 289235 1.8
June 12.99 239919 1.6
July 13.43 247916 1.6
August 13.43 247916 1.6
September 12.99 239919 1.6
October 13.43 247916 1.6
November 10.83 199932 1.3
December 11.19 206597 1.3
Total 153.63 2836374 18.35
Table 17. Comparison of GH2, PSOFC and N among different months for m = 0.030 kg/s at dx = 4 m.
Table 17. Comparison of GH2, PSOFC and N among different months for m = 0.030 kg/s at dx = 4 m.
GH2 [kg] PSOFC [Wh] N [-]
January 0 0 0
February 4.04 74641 0.5
March 17.90 330555 2.1
April 21.66 399865 2.6
May 22.38 413194 2.6
June 8.66 159946 1.0
July 0 0 0
August 8.95 165277 1.0
September 0 0 0
October 4.48 82639 0.5
November 0 0 0
December 0 0 0
Total 88.07 1626116 10.48
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated