Prerpints.org logo
Preprint
Article

Discovery of Truncated M-fractional Exact Solitons, and Qualitative Analysis to the Generalized Bretherton Model

Altmetrics

Downloads

131

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 August 2024

Posted:

06 August 2024

You are already at the latest version

Alerts
Abstract
This paper is concerned about the novel exact solitons to the truncated M-fractional (1+1)-dimensional non-linear generalized Bretherton model with arbitrary constants . This model is used to explain the resonant nonlinear interaction between the waves in different phenomenon, including fluid dynamics, plasma physics, ocean waves, and many others. A series of exact solitons, including bright, dark, periodic, singular, singular-bright, singular-dark, and other solitons are obtained by applying the extended sinh-Gordon equation expansion (EShGEE), and the modified (G′/G2)-expansion tech- niques. A novel definition of Fractional derivative provides the solutions distinct from the present solutions. Mathematica software is used to obtain, and verify the solutions. The solutions are shown through 2-D, 3-D, and density plots. The stability process is performed to verify that the solutions are exact and accurate. The modulation instability is used to determine the steady-state stable results to the corresponding equation.
Keywords: 
Subject: Physical Sciences  -   Mathematical Physics

1. Introduction

Naturally taking place natural phenomena are expressed in the form of nonlinear fractional partial differential equations. Many models have been developed in the form of fractional partial differential equations in the different fields of science, and engineering including fractional Phi-4 model [1], fractional Wazwaz-Benjamin-Bona-Mahony model [2], fractional regularized long wave model [3], fractional complex three coupled Maccari’s system [4], fractional paraxial nonlinear Schrödinger model [5], and many more.
In this paper, authors used two simple and useful schemes: EShGEE method and modified ( G ′ / G 2 ) -expansion technique. The concerned schemes have been used for different models. Instantly; EShGEE technique is used for Biswas-Arshed equation [6], hyperbolic and cubic-quintic nonlinear Schrödinger equations [7], generalized non-linear Schrödinger equation [8], Kundu-Eckhaus equation [9], novel liquid crystals model [10], (2+1)-dimensional nonlinear Schrödinger equation with anti-cubic nonlinearity [11], stochastic Phi-4 equation [12], Klein-Gordon-Zakharov equations [13], Nizhnik–Novikov-Veselov system [14], density dependent diffusion-reaction equation [15], Van der Waals equation [16]. Similarly, modified ( G ′ / G 2 ) -expansion scheme is used for third-order dispersion nonlinear Schrödinger equation [17], Fokas-Lenells equation [18], (1+1)-dimensional classical Boussinesq equation [19], coupled Drinfel’d-Sokolov-Wilson equation [20], Wazwaz Kaur Boussinesq equation [21].
The basic purpose of our work is to discover the new distinct exact solitons to (1+1)-dimensional non-linear generalized Bretherton model along truncated M-fractional derivative. A qualitative analysis of the governing model is also performed.
Motivation of our work is investigate the novel wave solitons to the generalized Bretherton model. The truncated M-fractional derivative fulfills the characteristics of both integer and fractional derivatives. This definition of derivative provides the better solutions than the other definitions. Firstly, both the utilized techniques convert the nonlinear fractional partial differential equations into nonlinear ordinary differential equations (ODEs) then solve the obtained ODEs. The extended sinh-Gordon equation expansion technique provides the dark, bright, dark-bright, singular, singular-bright, and other solitons. The modified ( G ′ / G 2 ) -expansion scheme gives the periodic wave, kink soliton and other types of soliton solutions.
There are different sections in the paper; the corresponding model and its mathematical treatment are shown in Section 2, the EShGEE approach and exact solitons are mentioned in Section 3, modified ( G ′ / G 2 ) -expansion technique and its application are shown in Section 4, graphically explanation is mentioned in Section 5, physically description is shown in Section 6, Stability analysis is performed in Section 7, Modulation instability is performed in Section 8, and we concluded our work in Section 9.

Truncated M-fractional derivative (TMFD)

Definition: Consider v ( x ) : [ 0 , ∞ ) → ℜ , therefore truncated M-fractional derivative of v of order ϵ [22]
D M , x ϵ , ϱ v ( x ) = lim ϵ → 0 v ( x E ϱ ( ϵ x 1 − ϵ ) ) − v ( x ) ϵ , ϵ ∈ ( 0 , 1 ] , ϱ > 0 ,
here E ϱ ( . ) represents a truncated Mittag-Leffler function [23]
E ϱ ( z ) = ∑ j = 0 i z j Γ ( ϱ j + 1 ) , ϱ > 0 and z ∈ C .
Properties: Consider a,b ∈ ℜ , and g , f are ϵ − differentiable at a point x > 0 , according to [22]:
( a ) D M , x ϵ , ϱ ( a g ( x ) + b f ( x ) ) = a D M , x ϵ , ϱ g ( x ) + b D M , x ϵ , ϱ f ( x )
( b ) D M , x ϵ , ϱ ( g ( x ) . f ( x ) ) = g ( x ) D M , x ϵ , ϱ f ( x ) + f ( x ) D M , x ϵ , ϱ g ( x )
( c ) D M , x ϵ , ϱ ( g ( x ) f ( x ) ) = f ( x ) D M , x ϵ , ϱ g ( x ) − g ( x ) D M , x ϵ , ϱ f ( x ) ( f ( x ) ) 2
( d ) D M , x ϵ , ϱ ( B ) = 0 , where B is a constant .
( e ) D M , x ϵ , ϱ g ( x ) = x 1 − ϵ Γ ( ϱ + 1 ) d g ( x ) d x .

2. Model presentation and its mathematical treatment

Bretherton proposed the following partial differential equation [24];
v t t + v x x + v x x x x + v − v 2 = 0 .
This is a model of a dispersive wave system to explain the resonant nonlinear interaction between three linear models.
The modified Bretherton equation is given as;
v t t + v x x + v x x x x + v − v 3 = 0 .
Eq.(2) was used by Kudryashov [25]. Different kinds of solitary wave solutions were gained in [26,27].
Our concerning model is a (1+1)-dimensional non-linear generalized Bretherton equation with arbitrary constants given as [28];
v t t + a v x x + b v x x x x + μ v + c v 3 = 0 .
Here v = v ( x , t ) indicates the wave function, while parameters a,b,c, and μ are arbitrary constants. Eq.(3) is discussed by using different schemes including; improved ( G ′ / G ) -expansion scheme [28], extended tanh-function scheme [29].
The (1+1)-dimensional nonlinear generalized Bretherton model with arbitrary constant in the concept of TMFD is given as;
D M , t 2 ϵ , ϱ v + a D M , x 2 ϵ , ϱ v + b D M , x 4 ϵ , ϱ v + μ v + c v 3 = 0 .
Consider a wave transformation;
v ( x , t ) = V ( ℧ ) , ℧ = Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) .
where λ is a soliton velocity.
Using Eq.(5) into Eq.(4), results into;
a + λ 2 V ′ ′ + b V ( 4 ) + c V 3 + μ V = 0
Natural number m is calculated by applying the Homogeneous Balance technique into Eq.(6), and balancing the terms V ( 4 ) and V 3 , we get m = 2 .

3. Explanation and application of EShGEE method

3.1. Description

Here we will mention some of the stages of the scheme.
Stage 1:
Supposing a non-linear fractional PDE:
F ( g , D M , t ϵ , ϱ g 2 , g 2 g x , g x , . . . ) = 0 .
Where, g = g ( x , t ) is a wave profile.
Considering a wave transformation:
g ( x , t ) = G ( ℧ ) , ℧ = ( 1 + ϱ ) ϵ ( x ϵ + κ t θ ) .
Inserting Eq. (8) in Eq. (7), yields:
H ( G , G 2 G ′ , G ′ ′ , . . . ) = 0 .
Stage 2:
Suppose the roots of Eq. (9) given below:
G ( f ) = α 0 + ∑ j = 1 m ( β j sinh ( f ) + α j cosh ( f ) ) j .
Here α 0 , α j , β j ( j = 1 , 2 , 3 , . . . , m ) are to be found. Suppose a new profile f of ℧ that fulfill:
d f d ℧ = sinh ( f ) .
Natural number m is calculate by applying the Homogeneous Balance scheme. Eq. (11) is achieved from the given equation:
q x t = κ sinh ( v ) .
From [30], we obtain the results for Eq. (12) shown as:
sinh f ( ℧ ) = ± csch ( ℧ ) o r cosh f ( ℧ ) = ± coth ( ℧ ) .
And
sinh f ( ℧ ) = ± ι s e c h ( ℧ ) o r cosh f ( ℧ ) = ± tanh ( ℧ ) .
ι 2 = − 1 .
Stage 3:
Inserting Eq. (10) and Eq. (11) in the Eq. (9), results a system including f ′ k ( ℧ ) sinh l f ( ℧ ) cosh m f ( ℧ ) ( k = 0 , 1 ; l = 0 , 1 ; m = 0 , 1 , 2 , . . . ) . Putting each co-efficient of f ′ k ( ℧ ) sinh l f ( ℧ ) cosh m f ( ℧ ) equal to 0, to achieve a set of consisting α j and β j ( j = 1 , 2 , 3 . . . m ) and others.
Stage 4:
By solving the gained set, yields results for unknowns. From obtained solutions, Eqs. (13) and (14), yields the solutions for Eq. (9) given as:
G ( ℧ ) = α 0 + ∑ j = 1 m ( ± β j csch ( ℧ ) ± α j coth ( ℧ ) ) j .
And
G ( ℧ ) = α 0 + ∑ j = 1 m ( ± ι β j s e c h ( ℧ ) ± α j tanh ( ℧ ) ) j .
From this method, one may gain the sech, csch, tanh and coth consisting results.

3.2. Application to the EShGEE scheme

Eq.(10) changes to the given form for m = 2 :
V ( ℧ ) = α 0 + α 1 cosh ( f ( ℧ ) ) + β 1 sinh ( f ( ℧ ) ) + ( α 2 cosh ( f ( ℧ ) ) + β 2 sinh ( f ( ℧ ) ) ) 2 .
Using Eq.(17) into Eq.(6) along Eq.(11), we gain a system containing α 0 , α 1 , α 2 , β 1 , β 2 , λ , and other parameters. By manumitting, results into the given sets :
Set 1:
{ α 0 = 2 b − − 30 b c , α 1 = 0 , β 1 = 0 , α 2 = ± − 15 4 2 3 / 4 b 4 c 4 , β 2 = 0 , λ = − − a − 2 − 15 b + 10 b , μ = 4 ( 7 b − − 15 b ) } .
v 1 ( x , t ) = 2 b c 1 ± − 15 coth ( 2 Γ ( 1 + ϱ ) ϵ ( x ϵ + − a − 2 − 15 b + 10 b t ϵ ) ) .
v 2 ( x , t ) = 2 b c 1 ± − 15 tanh ( 2 Γ ( 1 + ϱ ) ϵ ( x ϵ + − a − 2 − 15 b + 10 b t ϵ ) ) .
Set 2;
{ α 0 = 2 b − − 30 b c , α 1 = 0 , β 1 = 0 , α 2 = ± − 15 4 2 3 / 4 b 4 c 4 , β 2 = 0 , λ = − a − 2 − 15 b + 10 b , μ = 4 ( 7 b − − 15 b ) } .
v 1 ( x , t ) = 2 b c 1 ± − 15 coth ( 2 Γ ( 1 + ϱ ) ϵ ( x ϵ − − a − 2 − 15 b + 10 b t ϵ ) ) .
v 2 ( x , t ) = 2 b c 1 ± − 15 tanh ( 2 Γ ( 1 + ϱ ) ϵ ( x ϵ − − a − 2 − 15 b + 10 b t ϵ ) ) .
Set 3;
{ α 0 = − − 30 b + 2 b c , α 1 = 0 , β 1 = 0 , α 2 = ± − 15 4 2 3 / 4 b 4 c 4 , β 2 = 0 , λ = − − a + 10 b + 2 − 15 b , μ = 4 ( − 15 b + 7 b ) } .
v 1 ( x , t ) = 2 b c − 1 ± − 15 coth ( 2 Γ ( 1 + ϱ ) ϵ ( x ϵ + − a + 10 b + 2 − 15 b t ϵ ) ) .
v 2 ( x , t ) = 2 b c − 1 ± − 15 tanh ( 2 Γ ( 1 + ϱ ) ϵ ( x ϵ + − a + 10 b + 2 − 15 b t ϵ ) ) .
Set 4;
{ α 0 = − − 30 b + 2 b c , α 1 = 0 , β 1 = 0 , α 2 = ± − 15 4 2 3 / 4 b 4 c 4 , β 2 = 0 , λ = − a + 10 b + 2 − 15 b , μ = 4 ( − 15 b + 7 b ) } .
v 1 ( x , t ) = 2 b c − 1 ± − 15 coth ( 2 Γ ( 1 + ϱ ) ϵ ( x ϵ − − a + 10 b + 2 − 15 b t ϵ ) ) .
v 2 ( x , t ) = 2 b c − 1 ± − 15 tanh ( 2 Γ ( 1 + ϱ ) ϵ ( x ϵ − − a + 10 b + 2 − 15 b t ϵ ) ) .
Set 5;
{ α 0 = − 2 − 30 b c , α 1 = 0 , β 1 = 0 , α 2 = ± − 15 4 2 3 / 4 b 4 c 4 , β 2 = 0 , λ = − − a − 20 b , μ = 64 b } .
v 1 ( x , t ) = 2 − 30 b c csc h 2 ( Γ ( 1 + ϱ ) ϵ ( x ϵ + − a − 20 b t ϵ ) ) .
v 2 ( x , t ) = − 2 − 30 b c sec h 2 ( Γ ( 1 + ϱ ) ϵ ( x ϵ + − a − 20 b t ϵ ) ) .
Set 6;
{ α 0 = − 2 − 30 b c , α 1 = 0 , β 1 = 0 , α 2 = ± − 15 4 2 3 / 4 b 4 c 4 , β 2 = 0 , λ = − a − 20 b , μ = 64 b } .
v 1 ( x , t ) = 2 − 30 b c csc h 2 ( Γ ( 1 + ϱ ) ϵ ( x ϵ − − a − 20 b t ϵ ) ) .
v 2 ( x , t ) = − 2 − 30 b c sec h 2 ( Γ ( 1 + ϱ ) ϵ ( x ϵ − − a − 20 b t ϵ ) ) .

4. Explanation of modified ( G ′ / G 2 ) − expansion scheme

In this section, we will explain the main steps of this scheme [17].
Step 1:
Suppose the Eqns. (7), (8) and (9).
Step 2:
Suppose the result for Eq.(9) given as;
Q ( ℧ ) = ∑ j = 0 m α j ( G ′ G 2 ) j ,
where α j ( j = 0 , 1 , 2 , 3 , . . . , m ) are unknowns while α j ≠ 0 . The function G= G ( ℧ ) fulfills the given ODE,
( G ′ G 2 ) ′ = λ 0 + λ 1 ( G ′ G 2 ) 2 ,
here λ 0 and λ 1 are the constants. One can obtain the following cases to Eq. (37) depends on the conditions of λ 0 :
Case 1: if λ 0 λ 1 < 0 , then
( G ′ G 2 ) = − | λ 0 λ 1 | λ 1 + | λ 0 λ 1 | 2 [ C 1 sinh ( λ 0 λ 1 ℧ ) + C 2 cosh ( λ 0 λ 1 ℧ ) C 1 cosh ( λ 0 λ 1 ℧ ) + C 2 sinh ( λ 0 λ 1 ℧ ) ] ,
Case 2: if λ 0 λ 1 > 0 , then
( G ′ G 2 ) = λ 0 λ 1 [ C 1 cos ( λ 0 λ 1 ℧ ) + C 2 sin ( λ 0 λ 1 ℧ ) C 1 sin ( λ 0 λ 1 ℧ ) − C 2 sin ( λ 0 λ 1 ℧ ) ] ,
Case 3: if λ 0 = 0 and λ 1 ≠ 0 , then
( G ′ G 2 ) = − C 1 λ 1 ( C 1 ℧ + C 2 ) .
Here C 1 and C 2 are constants.
Step 3:
Putting Eq. (36) in the Eq. (9) along Eq. (37), and collecting coefficients of every power of ( G ′ G 2 ) j to 0, then solving that algebraic equations obtained including α j , λ 0 , λ 1 , ν and others.
Step 4:
Eq. (36) of which α j , ν and other parameters that are obtained in the step 3 into the Eq. (9), one can gain the results of Eq. (7).

4.1. Application

For m = 2 , Eq.(36) reduces into:
Q ( ℧ ) = α 0 + α 1 G ′ ( ℧ ) G 2 ( ℧ ) + α 2 ( G ′ ( ℧ ) G 2 ( ℧ ) ) 2
Here α 0 , α 1 and α 2 are unknowns. By putting Eq. (41) with Eq. (37) into the Eq. (6), and by solving by Maple software, results into the given sets:
Set 1:
α 0 = ± 2 λ 0 λ 1 − 30 c b c , α 1 = 0 , α 2 = ± 2 − 30 c b λ 1 2 c , λ = − 20 b λ 0 λ 1 − a , μ = 64 λ 0 2 λ 1 2 b .
If  λ 0 λ 1 < 0 , we have
v ( x , t ) = ± 2 λ 1 − 30 c b c ( λ 0 + λ 1 ( − | λ 0 λ 1 | λ 1 + | λ 0 λ 1 | 2 ( ( C 1 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ + 20 b λ 0 λ 1 − a t ϵ ) ) + C 2 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ + 20 b λ 0 λ 1 − a t ϵ ) ) ) / ( C 1 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ + 20 b λ 0 λ 1 − a t ϵ ) ) + C 2 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ + 20 b λ 0 λ 1 − a t ϵ ) ) ) ) ) 2 ) .
If  λ 0 λ 1 > 0 , we have
v ( x , t ) = ± 2 λ 1 − 30 c b c ( λ 0 + λ 1 ( λ 0 λ 1 ( ( C 1 cos ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ + 20 b λ 0 λ 1 − a t ϵ ) ) + C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ + 20 b λ 0 λ 1 − a t ϵ ) ) ) / ( C 1 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ + 20 b λ 0 λ 1 − a t ϵ ) ) − C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ + 20 b λ 0 λ 1 − a t ϵ ) ) ) ) ) 2 ) .
Set 2:
α 0 = ± 2 λ 0 λ 1 − 30 c b c , α 1 = 0 , α 2 = ± 2 − 30 c b λ 1 2 c , λ = 20 b λ 0 λ 1 − a , μ = 64 λ 0 2 λ 1 2 b .
If  λ 0 λ 1 < 0 , we have
v ( x , t ) = ± 2 λ 1 − 30 c b c ( λ 0 + λ 1 ( − | λ 0 λ 1 | λ 1 + | λ 0 λ 1 | 2 ( ( C 1 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − 20 b λ 0 λ 1 − a t ϵ ) ) + C 2 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − 20 b λ 0 λ 1 − a t ϵ ) ) ) / ( C 1 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − 20 b λ 0 λ 1 − a t ϵ ) ) + C 2 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − 20 b λ 0 λ 1 − a t ϵ ) ) ) ) ) 2 ) .
If  λ 0 λ 1 > 0 , we have
v ( x , t ) = ± 2 λ 1 − 30 c b c ( λ 0 + λ 1 ( λ 0 λ 1 ( ( C 1 cos ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − 20 b λ 0 λ 1 − a t ϵ ) ) + C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − 20 b λ 0 λ 1 − a t ϵ ) ) ) / ( C 1 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − 20 b λ 0 λ 1 − a t ϵ ) ) − C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − 20 b λ 0 λ 1 − a t ϵ ) ) ) ) ) 2 ) .
Set 3:
{ α 0 = ∓ ( − − 30 c b + 2 c b ) λ 1 λ 0 c , α 1 = 0 , α 2 = ± 2 − 30 c b λ 1 2 c , λ = − − − 30 c b ( 30 2 c b λ 0 λ 1 b + 10 λ 0 λ 1 b − 30 c b + a − 30 c b ) − 30 c b , μ = − 4 λ 0 2 λ 1 2 b ( 2 c b + 9 − 30 c b ) 2 2 c b − − 30 c b }
Case 1: if λ 0 λ 1 < 0 , then
v ( x , t ) = ∓ ( − − 30 c b + 2 c b ) λ 1 λ 0 c ± 2 − 30 c b λ 1 2 c ( − | λ 0 λ 1 | λ 1 + | λ 0 λ 1 | 2 ( C 1 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) C 1 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) ) ) 2 .
Case 2: if λ 0 λ 1 > 0 , then
v ( x , t ) = ∓ ( − − 30 c b + 2 c b ) λ 1 λ 0 c ± 2 − 30 c b λ 1 2 c ( λ 0 λ 1 ( C 1 cos ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) C 1 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) − C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) ) ) 2 .
where λ is given in Eq.(48).
Set 4:
{ α 0 = ∓ ( − − 30 c b + 2 c b ) λ 1 λ 0 c , α 1 = 0 , α 2 = ± 2 − 30 c b λ 1 2 c , λ = − − 30 c b ( 30 2 c b λ 0 λ 1 b + 10 λ 0 λ 1 b − 30 c b + a − 30 c b ) − 30 c b , μ = − 4 λ 0 2 λ 1 2 b ( 2 c b + 9 − 30 c b ) 2 2 c b − − 30 c b }
Case 1: if λ 0 λ 1 < 0 , then
v ( x , t ) = ∓ ( − − 30 c b + 2 c b ) λ 1 λ 0 c ± 2 − 30 c b λ 1 2 c ( − | λ 0 λ 1 | λ 1 + | λ 0 λ 1 | 2 ( C 1 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) C 1 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) ) ) 2 .
Case 2: if λ 0 λ 1 > 0 , then
v ( x , t ) = ∓ ( − − 30 c b + 2 c b ) λ 1 λ 0 c ± 2 − 30 c b λ 1 2 c ( λ 0 λ 1 ( C 1 cos ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) C 1 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) − C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) ) ) 2 .
where λ is given in Eq.(51).
Set 5:
{ α 0 = ∓ ( 2 c b + − 30 c b ) λ 1 λ 0 c , α 1 = 0 , α 2 = ∓ 2 − 30 c b λ 1 2 c , λ = − − 30 c b ( 30 2 c b λ 0 λ 1 b − 10 λ 0 λ 1 b − 30 c b − a − 30 c b ) − 30 c b , μ = − 4 λ 0 2 λ 1 2 b ( 2 c b − 9 − 30 c b ) 2 2 c b + − 30 c b } .
Case 1: if λ 0 λ 1 < 0 , then
v ( x , t ) = ∓ ( 2 c b + − 30 c b ) λ 1 λ 0 c ∓ 2 − 30 c b λ 1 2 c ( − | λ 0 λ 1 | λ 1 + | λ 0 λ 1 | 2 ( C 1 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) C 1 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) ) ) 2 .
Case 2: if λ 0 λ 1 > 0 , then
v ( x , t ) = ∓ ( 2 c b + − 30 c b ) λ 1 λ 0 c ∓ 2 − 30 c b λ 1 2 c ( λ 0 λ 1 ( C 1 cos ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) C 1 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) − C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) ) ) 2 .
where λ is given in Eq.(54).
Set 6:
{ α 0 = ∓ ( 2 c b + − 30 c b ) λ 1 λ 0 c , α 1 = 0 , α 2 = ∓ 2 − 30 c b λ 1 2 c , λ = − 30 c b ( 30 2 c b λ 0 λ 1 b − 10 λ 0 λ 1 b − 30 c b − a − 30 c b ) − 30 c b , μ = − 4 λ 0 2 λ 1 2 b ( 2 c b − 9 − 30 c b ) 2 2 c b + − 30 c b } .
Case 1: if λ 0 λ 1 < 0 , then
v ( x , t ) = ∓ ( 2 c b + − 30 c b ) λ 1 λ 0 c ∓ 2 − 30 c b λ 1 2 c ( − | λ 0 λ 1 | λ 1 + | λ 0 λ 1 | 2 ( C 1 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) C 1 cosh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 sinh ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) ) ) 2 .
Case 2: if λ 0 λ 1 > 0 , then
v ( x , t ) = ∓ ( 2 c b + − 30 c b ) λ 1 λ 0 c ∓ 2 − 30 c b λ 1 2 c ( λ 0 λ 1 ( ( C 1 cos ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) + C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) ) / ( C 1 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) − C 2 sin ( λ 0 λ 1 Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) ) ) ) ) 2 .
where λ is given in Eq.(57).

5. Graphically explanation

Here, we shown the gained solutions by 2-D, 3-D and contour graphs. The 2-D plots also drawn for different values of ϵ .

6. Physically Interpretation

Here, we will describe the dynamical behaviour of the solutions of the truncated M-fractional generalized Bretherton model.
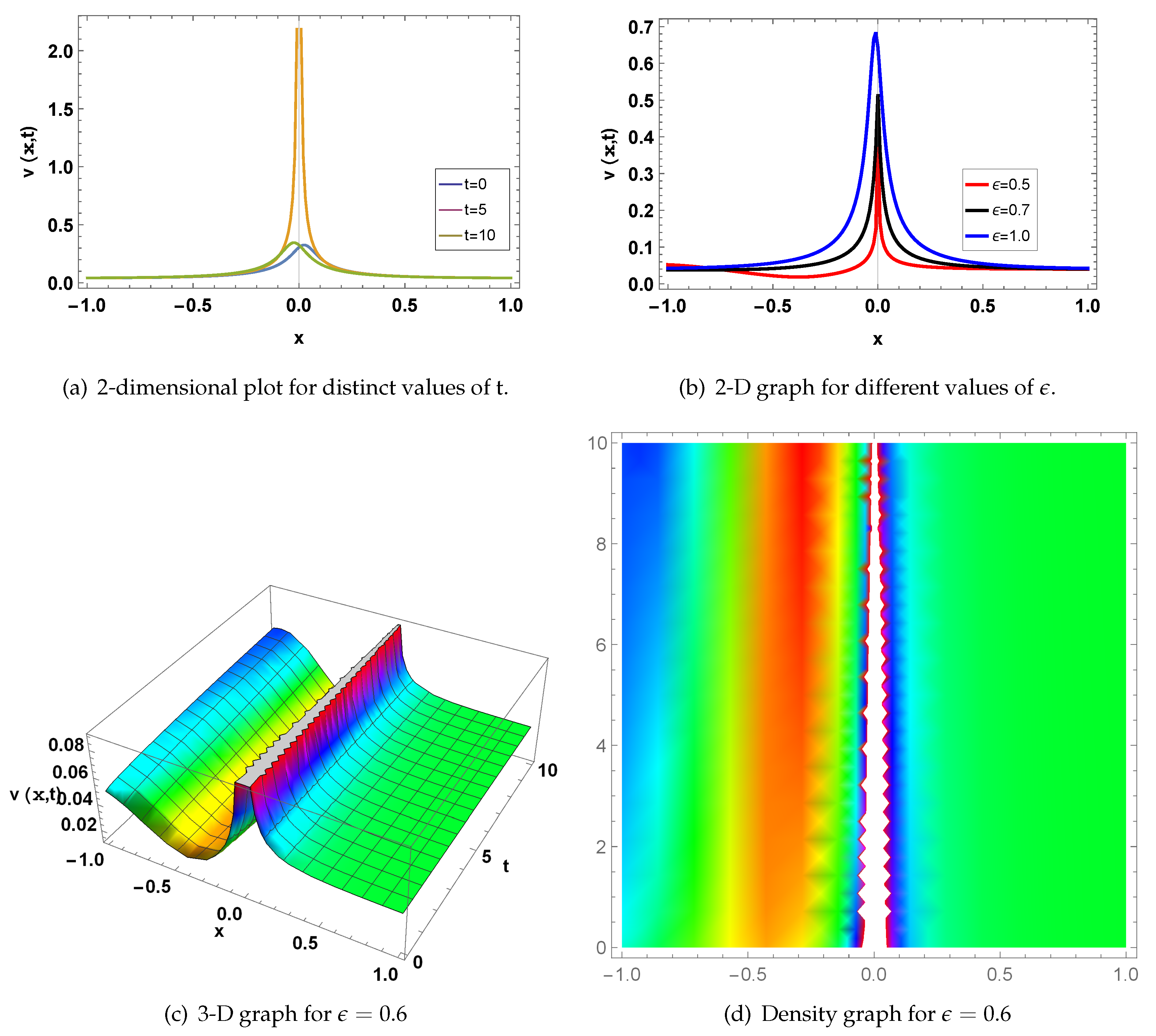
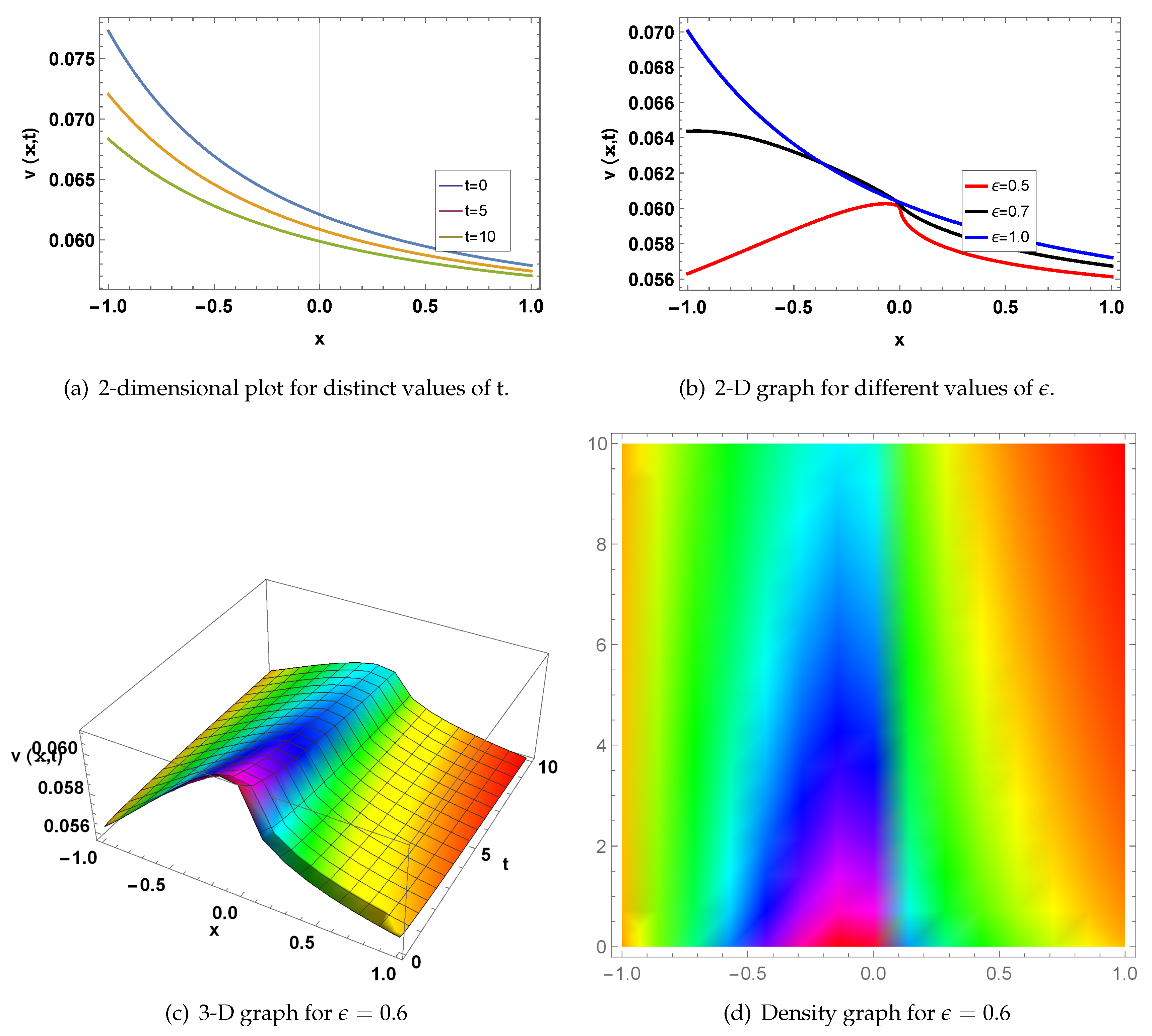
Figure 1: represents a singular soliton at the values of; a = − 0.0001 , b = − 0.0001 , c = − 2 , and ϱ = 0.5 . Fig(a) represents a 2-D graph for − 1 < x < 1 at ϵ = 1 , where the Blue line for t = 0 , Orange line at t = 5 , and Green line at t = 10 . Fig(b) represents a two-dimensional graph for − 1 < x < 1 at t ∈ ( 0 , 10 ) , while Red line at ϵ = 0.5 , Black-line at ϵ = 0.7 , and Blue-line at ϵ = 1.0 . Fig(c) represents a 3-dimensional graph at ϵ = 0.6 for t ∈ ( 0 , 10 ) . Fig(d) shows a density plot for ϵ = 0.6 at t ∈ ( 0 , 10 ) .
Figure 2; represents a dark soliton at the values of; a = 0.005 , b = 0.005 , c = 1 , and ϱ = 0.5 . Fig(a) represents a 2-D graph for − 24 < x < 24 at ϵ = 1 , where the Blue line for t = 0 , Orange line at t = 5 , and Green line at t = 10 . Fig(b) represents a two-dimensional graph for − 24 < x < 24 at t ∈ ( 0 , 10 ) , while Red line at ϵ = 0.5 , Black-line at ϵ = 0.7 , and Blue-line at ϵ = 1.0 . Fig(c) represents a 3-dimensional graph at ϵ = 0.6 for t ∈ ( 0 , 10 ) . Fig(d) shows a density plot for ϵ = 0.6 at t ∈ ( 0 , 10 ) .
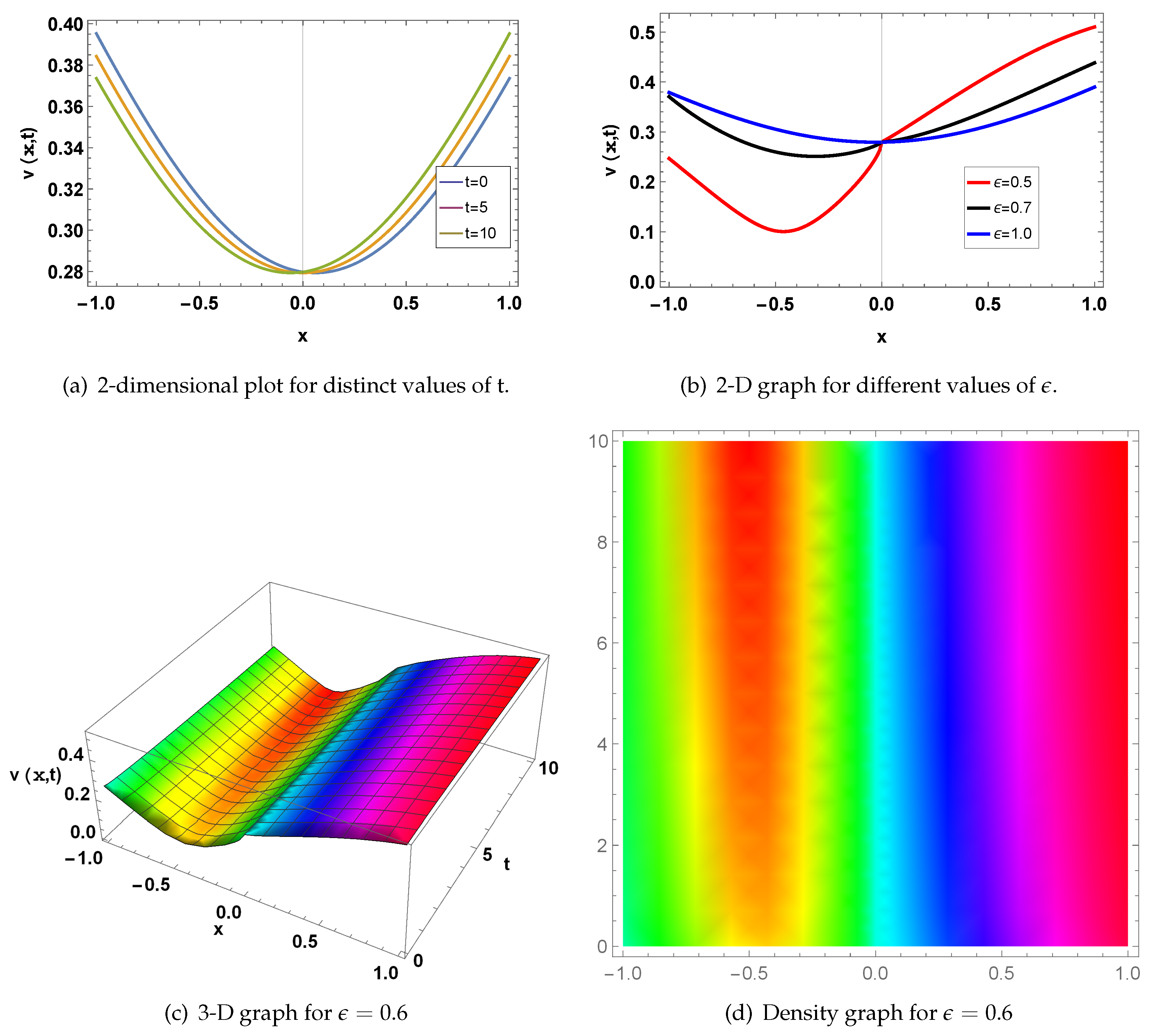
Figure 3; represents a bright soliton at the values of; a = 0.001 , b = − 0.0001 , c = − 0.01 , and ϱ = 0.5 . Fig(a) represents a 2-D graph for − 2 < x < 2 at ϵ = 1 , where the Blue line for t = 0 , Orange line at t = 5 , and Green line at t = 10 . Fig(b) represents a two-dimensional graph for − 2 < x < 2 at t ∈ ( 0 , 10 ) , while Red line at ϵ = 0.5 , Black-line at ϵ = 0.7 , and Blue-line at ϵ = 1.0 . Fig(c) represents a 3-dimensional graph at ϵ = 0.6 for t ∈ ( 0 , 10 ) . Fig(d) shows a density plot for ϵ = 0.6 at t ∈ ( 0 , 10 ) .
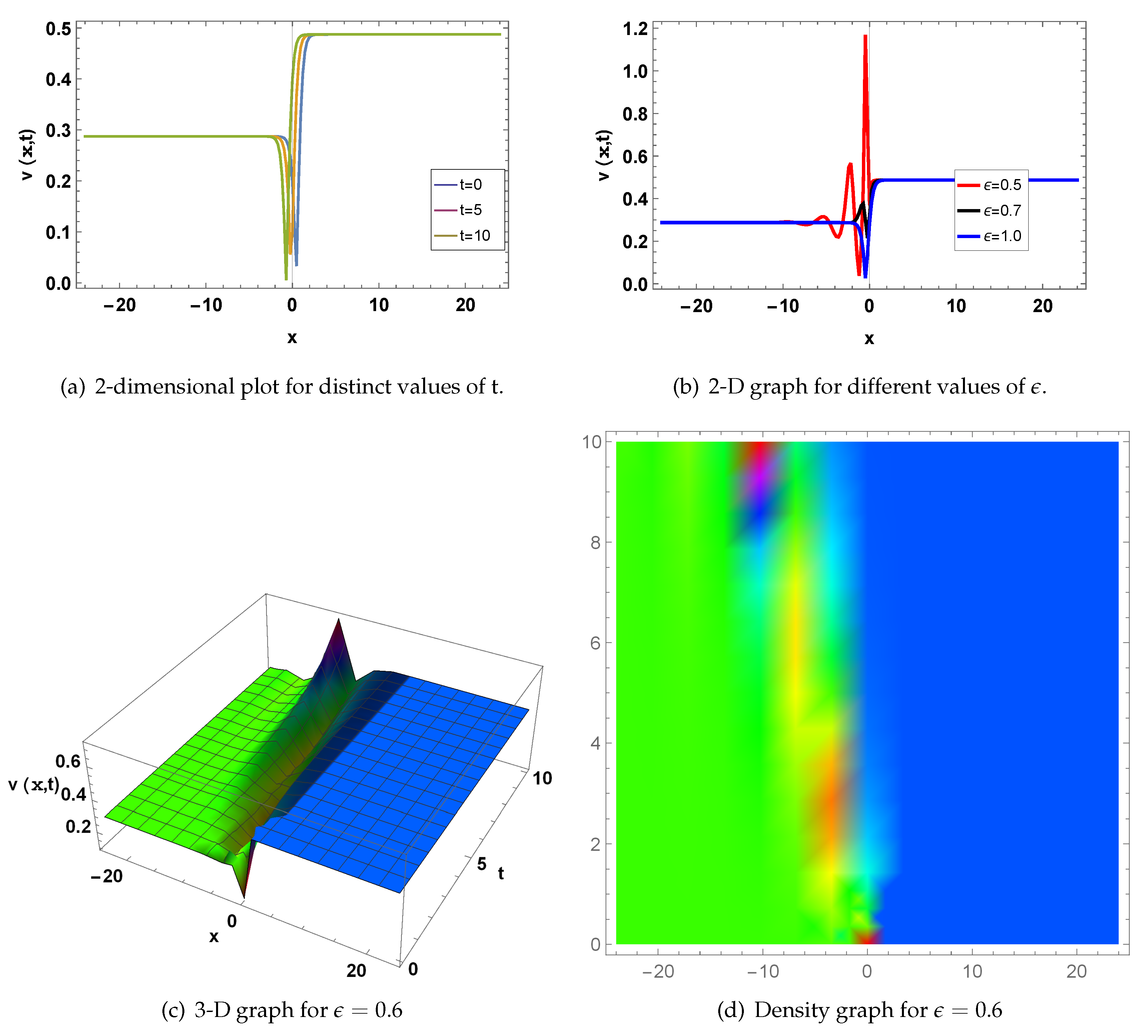
Figure 4; represents a kink soliton at the values of; a = 0.0001 , b = − 0.0001 , c = − 0.01 , λ 0 = − 0.5 , λ 1 = 1 , C 1 = 0.5 , C 2 = 0.3 , and ϱ = 0.5 . Fig(a) represents a 2-D graph for − 1 < x < 1 at ϵ = 1 , where the Blue line for t = 0 , Orange line at t = 5 , and Green line at t = 10 . Fig(b) represents a two-dimensional graph for − 1 < x < 1 at t ∈ ( 0 , 10 ) , while Red line at ϵ = 0.5 , Black-line at ϵ = 0.7 , and Blue-line at ϵ = 1.0 . Fig(c) represents a 3-dimensional graph at ϵ = 0.6 for t ∈ ( 0 , 10 ) . Fig(d) shows a density plot for ϵ = 0.6 at t ∈ ( 0 , 10 ) .
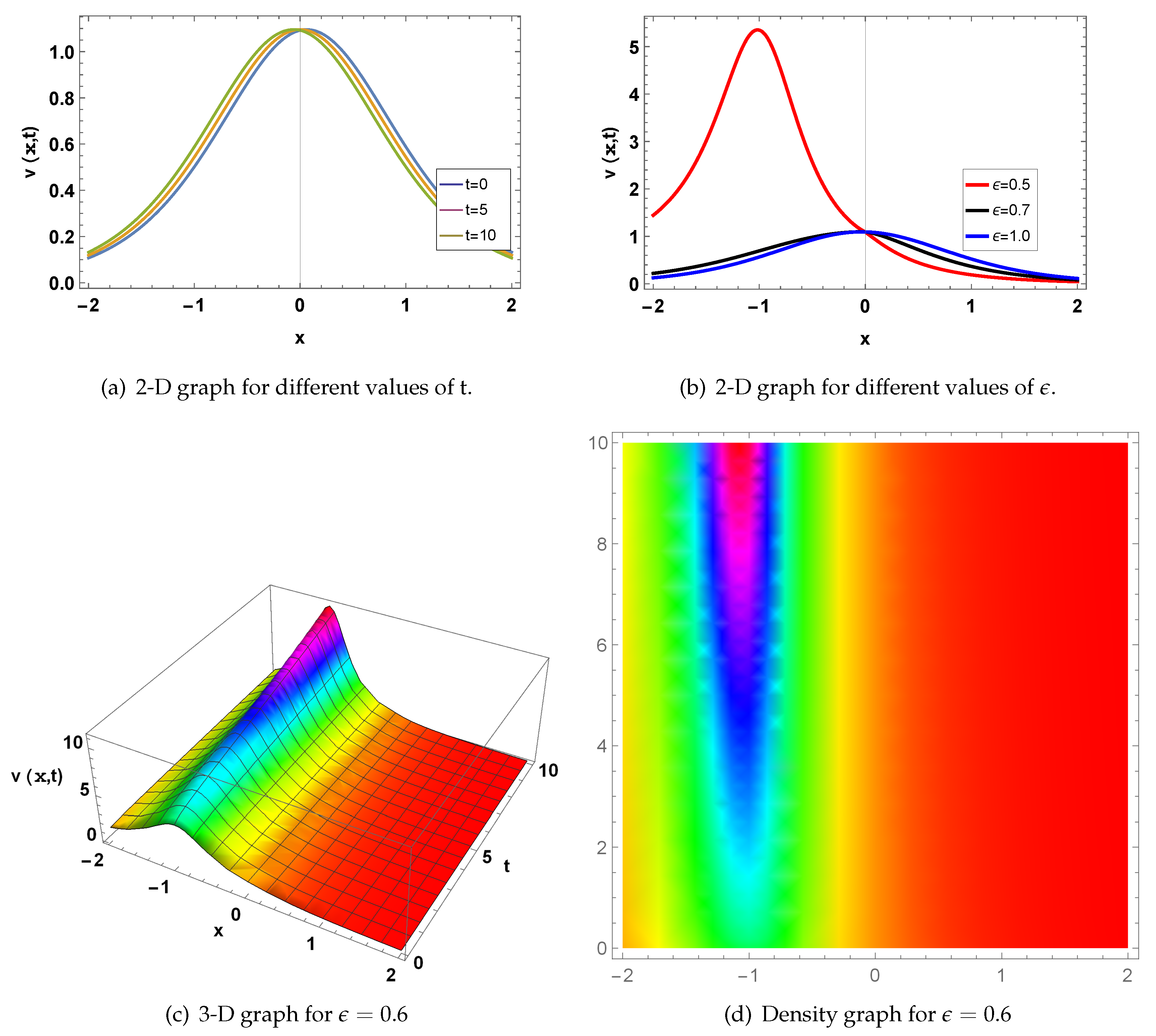
Figure 5; represents a periodic wave solution at the values of; a = − 0.01 , b = 0.0001 , c = − 0.01 , λ 0 = − 0.5 , λ 1 = − 0.1 , C 1 = 0.5 , C 2 = − 0.3 , and ϱ = 0.5 . Fig(a) represents a 2-D graph for − 1 < x < 1 at ϵ = 1 , where the Blue line for t = 0 , Orange line at t = 5 , and Green line at t = 10 . Fig(b) represents a two-dimensional graph for − 1 < x < 1 at t ∈ ( 0 , 10 ) , while Red line at ϵ = 0.5 , Black-line at ϵ = 0.7 , and Blue-line at ϵ = 1.0 . Fig(c) represents a 3-dimensional graph at ϵ = 0.6 for t ∈ ( 0 , 10 ) . Fig(d) shows a density plot for ϵ = 0.6 at t ∈ ( 0 , 10 ) .

7. Stability Analysis

Here, the stability analysis of the concerning model is discussed. The stability analysis is used for many equations likely, [31,32]. For the Eq.(3) stability analysis, one takes the Hamiltonian transformation given as,
S = 1 2 ∫ − ∞ ∞ v 2 d x ,
Here, S denotes a momentum factor, while h ( x , t ) denotes the power of possibility. The necessary condition for the stable solutions is given as;
∂ S ∂ λ > 0 ,
here λ indicates a wave speed, inserting Eq.(32) into Eq.(60) results;
S = 1 2 ∫ − 6 6 ( − ( 2 − 30 b ) c sec h 2 ( ( x + − a − 20 b t ) ) ) 2 d x ,
by using the criterion given in Eq.(61), we get
1920 e 24 ( 1 − e 24 ) b t ( 4 e 12 sinh ( 2 t − a − 20 b ) + ( 1 + e 24 ) sinh ( 4 t − a − 20 b ) ) c ( 2 e 12 cosh ( 2 t − a − 20 b ) + e 24 + 1 ) 4 > 0 .
Hence, Eq.(3) denotes a stable non-linear fractional equation because the condition is satisfied.

8. Modulation instability (MI)

We take the following transformation for the steady-state result of generalized Bretherton model [33]:
v ( x , t ) = V ( x , t ) + τ e ι τ t .
Here τ shows the optical power of normalized. Inserting Eq.(64) into Eq.(3). By linearizing, one gets
a V x x + b V x x x x + μ τ − τ 5 / 2 + 2 ι τ V t + V t t + μ V − τ 2 V = 0 .
Consider the solution of Eq.(65) in the form;
V ( x , t ) = A 1 e ι ( p x − ρ t ) + A 2 e − ι ( p x − ρ t ) .
here ρ and p represent the frequency and normalized wave number of perturbation respectively. Putting the Eq.(66) into Eq.(65). By summing up the co-efficients of e ι ( p x − ρ t ) and e ι ( p x − ρ t ) , one gets the dispersion solution by solving the determinant of the coefficient matrix.
a 2 p 4 − 2 a b p 6 − 2 a μ p 2 + 2 a p 2 ρ 2 + 2 a p 2 τ 2 + b 2 p 8 + 2 b μ p 4 − 2 b p 4 ρ 2 − 2 b p 4 τ 2 + μ 2 − 2 μ ρ 2 − 2 μ τ 2 + ρ 4 − 2 ρ 2 τ 2 + τ 4 = 0 .
Determining the dispersion solution from Eq.(67) for μ , results
μ = ± 2 ρ τ ± a 2 p 4 − 2 a b p 6 + 2 a p 2 ρ 2 + 2 a p 2 τ 2 + b 2 p 8 − 2 b p 4 ρ 2 − 2 b p 4 τ 2 + ρ 4 + 2 ρ 2 τ 2 + τ 4 .
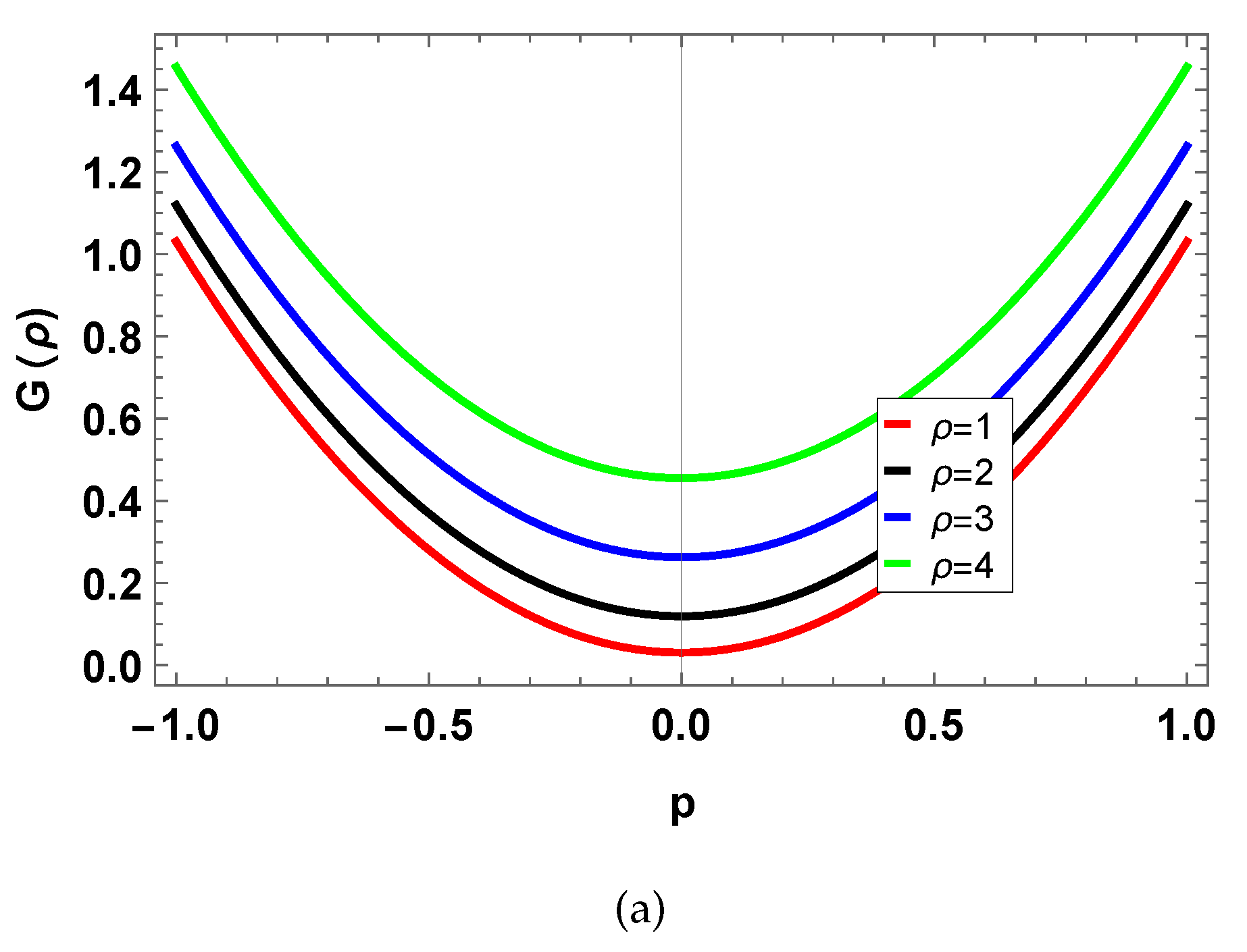
The obtained dispersion form represents the stability of steady state. If a wave number μ is complex then the steady state solution will not be stable because the perturbation grows gradually. If a wave number μ is real then steady state change into the stable against small perturbations. A steady state result is not stable when;
a 2 p 4 − 2 a b p 6 + 2 a p 2 ρ 2 + 2 a p 2 τ 2 + b 2 p 8 − 2 b p 4 ρ 2 − 2 b p 4 τ 2 + ρ 4 + 2 ρ 2 τ 2 + τ 4 < 0 .
MI gain spectrum G ( ρ ) is achieved as;
G ( ρ ) = 2 I m ( μ ) = ± a 2 p 4 − 2 a b p 6 + 2 a p 2 ρ 2 + 2 a p 2 τ 2 + b 2 p 8 − 2 b p 4 ρ 2 − 2 b p 4 τ 2 + ρ 4 + 2 ρ 2 τ 2 + τ 4 .

9. Conclusion

We successfully obtained a new kinds of exact solitons of (1+1)-dimensional non-nonlinear generalized Bretherton model. A series of exact soliton solutions, including bright, dark, periodic, singular, singular-bright, singular-dark, and other solitons are obtained by applying the extended sinh-Gordon equation expansion (EShGEE), and the modified ( G ′ / G 2 ) -expansion techniques. A novel definition of Fractional derivative provides the solutions distinct from the present solutions. Mathematica software is used to obtain, and verify the solutions. The solutions are shown by 2D, 3D, and density graphs. The results are valuable in various areas of applied sciences and engineering. At the end, it is conclude that the used techniques are easy to use and provide the useful results.

Acknowledgments

The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2024/01/921063).

References

  1. Roy, Ripan and Akbar, M Ali and Seadawy, Aly R and Baleanu, Dumitru; Search for adequate closed form wave solutions to space–time fractional nonlinear equations, Partial Differential Equations in Applied Mathematics, 3, 100025, (2021).
  2. Bilal, Muhammad and Ren, Jingli; Dynamics of exact solitary wave solutions to the conformable time-space fractional model with reliable analytical approaches, Optical and Quantum Electronics, 54, 1, 40, (2022).
  3. Behera, Sidheswar and Mohanty, Siddharth and Virdi, Jasvinder Pal Singh; Analytical solutions and mathematical simulation of traveling wave solutions to fractional order nonlinear equations, Partial Differential Equations in Applied Mathematics, 8, 100535, (2023).
  4. Alsharidi, Abdulaziz Khalid and Bekir, Ahmet; Discovery of new exact wave solutions to the M-fractional complex three coupled Maccari’s system by Sardar sub-equation scheme, Symmetry, 15, 8, 1567, (2023).
  5. Razzaq, Waseem and Zafar, Asim and Raheel, M; Searching the new exact wave solutions to the beta-fractional Paraxial nonlinear Schrödinger model via three different approaches, International Journal of Modern Physics B, 38, 09, 2450132, (2024).
  6. Zafar, Asim and Bekir, Ahmet and Raheel, M and Razzaq, Waseem; Optical soliton solutions to Biswas–Arshed model with truncated M-fractional derivative, Optik, 222, 165355, (2020).
  7. Seadawy, Aly R and Kumar, Dipankar and Chakrabarty, Anuz Kumar; Dispersive optical soliton solutions for the hyperbolic and cubic-quintic nonlinear Schrödinger equations via the extended sinh-Gordon equation expansion method, The European Physical Journal Plus, 133, 5, 182, (2018).
  8. Bezgabadi, A Safaei and Bolorizadeh, MA; Analytic combined bright-dark, bright and dark solitons solutions of generalized nonlinear Schrödinger equation using extended sinh-Gordon equation expansion method, Results in Physics, 30, 104852, (2021).
  9. Kumar, Dipankar and Manafian, Jalil and Hawlader, Faisal and Ranjbaran, Arash; New closed form soliton and other solutions of the Kundu–Eckhaus equation via the extended sinh-Gordon equation expansion method, Optik, 160, 159–167, (2018).
  10. Kumar, Dipankar and Joardar, Atish Kumar and Hoque, Ashabul and Paul, Gour Chandra; Investigation of dynamics of nematicons in liquid crystals by extended sinh-Gordon equation expansion method, Optical and Quantum Electronics, 51, 1–36, (2019).
  11. Ilhan, Onur Alp and Manafian, Jalil; Analytical treatment in optical metamaterials with anti-cubic law of nonlinearity by improved exp (-Ω (η))-expansion method and extended sinh-Gordon equation expansion method, Revista mexicana de física, 65, 6, 658–677, (2019).
  12. Batool, Fiza and Rezazadeh, Hadi and Ali, Zeshan and Demirbilek, Ulviye; Exploring soliton solutions of stochastic Phi-4 equation through extended Sinh-Gordon expansion method, Optical and Quantum Electronics, 56, 5, 785, (2024).
  13. Baskonus, HM and Sulaiman, TA and Bulut, H; On the new wave behavior to the Klein–Gordon–Zakharov equations in plasma physics, Indian Journal of Physics, 93, 393–399, (2019).
  14. Cattani, Carlo and Sulaiman, Tukur Abdulkadir and Baskonus, Haci Mehmet and Bulut, Hasan; On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel’d-Sokolov systems, Optical and Quantum Electronics, 50, 1–11, (2018).
  15. Razzaq, Waseem and Alsharidi, Abdulaziz Khalid and Zafar, Asim and Alomair, Mohammed Ahmed; Optical solitons to the beta-fractional density dependent diffusion-reaction model via three different techniques, International Journal of Modern Physics B, 37, 30, 2350268, (2023).
  16. Ali, Nawzad Hasan and Mohammed, Sizar Abid and Manafian, Jalil; New explicit soliton and other solutions of the Van der Waals model through the EShGEEM and the IEEM, J. Modern Tech. Eng, 8, 1, 5–18, (2023).
  17. Yanni Zhang, Liping Zhang, Jing Pang, Application of (G′/G2) Expansion Method for Solving Schrödinger’s Equation with Three-Order Dispersion, Advances in Applied Mathematics, 6, 2, 212-217, (2017).
  18. Nadia Mahak, Ghazala Akram; Exact solitary wave solutions of the (1+1)-dimensional Fokas-Lenells equation, Optik, (2020). [CrossRef]
  19. Aljahdaly, Noufe H; Some applications of the modified (G′/G2)-expansion method in mathematical physics, Results in Physics, 13, 102272, (2019).
  20. Behera, S and Aljahdaly, NH and Virdi, JPS; On the modified (G′/G2)-expansion method for finding some analytical solutions of the traveling waves, Journal of Ocean Engineering and Science, 7, 4, 313–320, (2022).
  21. Saboor, Abdul and Shakeel, Muhammad and Liu, Xinge and Zafar, Asim and Ashraf, Muhammad; A comparative study of two fractional nonlinear optical model via modified (G′/G2)-expansion method, Optical and Quantum Electronics, 56, 2, 259, (2024).
  22. Tukur Abdulkadir Sulaiman, Gulnur Yel and Hasan Bulut; M-fractional solitons and periodic wave solutions to the Hirota-Maccari system, Modern Physics Letters B, 1950052, (2019).
  23. J. Vanterler D A C. Sousa, and E. Capelas D E Oliveira; A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties, International Journal of Analysis and Applications, 16, 1, 83-96, (2018).
  24. F. P. Bretherton, Resonant interactions between waves. The case of discrete oscillations, Journal of FluidMechanics, 20, 457–479, (1964).
  25. N. A. Kudryashov; On types of nonlinear nonintegrable equations with exact solutions, Physics Letters A, 155, 4-5, 269–275, (1991).
  26. N. A. Kudryashov, D. I. Sinelshchikov, and M. V. Demina; Exact solutions of the generalized Bretherton equation, Physics Letters A, 375, 7, 1074–1079, (2011).
  27. N. G. Berloff and L. N. Howard; Nonlinear wave interactions in nonlinear nonintegrable systems, Studies in Applied Mathematics, 100, 3, 195–213, (1998).
  28. M. A. Akbar, H. Norhashidah, A. Mohd, and E. M. E. Zayed; Abundant exact traveling wave solutions of generalized Bretherton equation via improved (G′/G)-expansion method, Communications in Theoretical Physics, 57, 2, 173–178, (2012).
  29. Xiuqing Yu, Fengsheng Xu, and Lihua Zhang; Abundant Exact Solition-Like Solutions to the Generalized Bretherton Equation with Arbitrary Constants, Abstract and Applied Analysis, 7, (2013).
  30. X. L. Yang, J. S. Tang; Travelling wave solutions for Konopelchenko-Dubrovsky equation using an extended sinh-Gordon equation expansion method, Communications in Theoretical Physics,(2008), 50, 10471051.
  31. Tariq, Kalim U and Wazwaz, Abdul-Majid and Javed, Rizwan; Construction of different wave structures, stability analysis and modulation instability of the coupled nonlinear Drinfel’d–Sokolov–Wilson model, Chaos, Solitons & Fractals, 166, 112903, (2023).
  32. Zulfiqar, Hina and Aashiq, Aqsa and Tariq, Kalim U and Ahmad, Hijaz and Almohsen, Bandar and Aslam, Muhammad and Rehman, Hamood Ur; On the solitonic wave structures and stability analysis of the stochastic nonlinear Schrödinger equation with the impact of multiplicative noise, Optik, 289, 171250, (2023).
  33. ur Rehman, Shafqat and Ahmad, Jamshad; Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing, Alexandria Engineering Journal, 60, 1, 1339–1354, (2021).
Preprints 114172 g001
Figure 1. Plot for v ( x , t ) is shown in Eq.(19).
Figure 1. Plot for v ( x , t ) is shown in Eq.(19).
Preprints 114172 g001
Preprints 114172 g002
Figure 2. Plot for v ( x , t ) is shown in Eq.(20).
Figure 2. Plot for v ( x , t ) is shown in Eq.(20).
Preprints 114172 g002
Preprints 114172 g003
Figure 3. Plot for v ( x , t ) is shown in Eq.(32).
Figure 3. Plot for v ( x , t ) is shown in Eq.(32).
Preprints 114172 g003
Preprints 114172 g004
Figure 4. Plot for v ( x , t ) is shown in Eq.(43).
Figure 4. Plot for v ( x , t ) is shown in Eq.(43).
Preprints 114172 g004
Preprints 114172 g005
Figure 5. Plot for v ( x , t ) is shown in Eq.(44).
Figure 5. Plot for v ( x , t ) is shown in Eq.(44).
Preprints 114172 g005
Preprints 114172 g006
Figure 6. Gain spectrum of MI at different values of ρ .
Figure 6. Gain spectrum of MI at different values of ρ .
Preprints 114172 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated