Heat and Mass Transfer on MHD in the Oscillatory Flow of Viscoelastic Fluid between Two Plates with Heat Generation and Chemical Reaction

Preprint

Article

Heat and Mass Transfer on MHD in the Oscillatory Flow of Viscoelastic Fluid between Two Plates with Heat Generation and Chemical Reaction

Altmetrics

Downloads

Views

Comments

Valsamy P,Chiranjeevi B,

Vidyasagar G^*

Valsamy P,Chiranjeevi B,

Vidyasagar G^*

This version is not peer-reviewed

Submitted:

05 August 2024

Posted:

06 August 2024

You are already at the latest version

Alerts

Abstract

In this chapter we study the unstudy effect on MHD preamble porous medium through with thermal absorption and heat generation in the oscillatory flow of visco-elastic fluid between two plates in the presence of Chemical reaction. The expressions for the velocity, temperature and concentration distributions are arthemitiaclly solved by perturbation method.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

Introduction

Phenomenon of heat and mass transfer by MHD (Magneto hydrodynamics) refers to the study of the transfer of heat and mass in the presence of a magnetic field. One specific area of interest in this field is the oscillatory flow of viscoelastic fluid between two plates. This particular phenomenon has gained significant attention due to its spaciousness, making it applicable in various fields of engineering, such as chemistry, the processing industry, food preservation, oil production, rain, electrostatics, polymer technology, and energy engineering. Chen [1] have investigated heat and mass transfer in MHD flow by natural convection from a permeable inclined surface with variable wall temperature and concentration. Kesavaiah et.al [8] is studiedEffects of the chemical reaction and radiation absorption on an unsteady MHD convective heat and mass transfer flow past a semi-infinite vertical permeable moving plate embedded in a medium with heat source and suction. Kumar et. al [11] has analysed MHD flow and heat transfer in a visco-elastic fluid over a flat surface with constant suction. An analytical solution to the problem of radiative heat and mass transfer over an inclined plate at prescribed heat flux with chemical reaction was studied Kumar [12].Nandeppanavaret. al [14] have discussed heat transfer in MHD visco-elastic boundary layer flow over a stretching sheet with thermal radiation and non-uniform heat source/sink.

In the chemistry field, the understanding of heat and mass transfer by MHD in oscillatory flow of viscoelastic fluid between two plates has enabled advancements in chemical reactions and separations. The processing industry has also benefited from this phenomenon, as it allows for efficient heat and mass transfer in various manufacturing processes. In the food preservation sector, knowledge of MHD heat and mass transfer has led to improved methods of preserving food quality and extending shelf life. Daniel and Daniel Y. S [2] is studied Convective flow two immiscible fluids and heat transfer with along an inclined channel with pressure gradient. Hayat et. al. [3] have investigated three-dimensional mixed convection flow of Sisko nano liquid. Ibrahim et.al [5] have analyzed effect of chemical reaction and radiation absorption on the unsteady MHD free convection flow past a semi infinite vertical permeable moving plate with heat source and suction.Jahanet al [7] effects of solar radiation and viscous dissipation on mixed convective Non- Isothermal hybrid Nanofluid over moving thin needle. Khan et al. [9] impact of magnetic field on boundary-layer flow of Sisko liquid comprising nanomaterial’s migration through radially shrinking/stretching surface with zero mass flux.

Furthermore, the oil production industry has capitalized on the phenomenon of heat and mass transfer by MHD. It has been utilized to enhance oil recovery processes, increase production efficiency, and optimize oil reservoir management. The application of MHD in rain and electrostatics has led to better understanding and control of precipitation phenomena, as well as improved methods for electrostatic precipitation.Khan et. al. [10] have investigated MHD boundary layer radiative, heat generating and chemical reacting flow past a wedge moving in a Nanofluid. Hossain et. al. [4] studied free convection radiation interaction from an isothermal plate inclined at a small angle to the horizontal. Iskandaret. al. [6] have analysed hybrid Nanofluid flow past a permeable moving thin needle. Sheikholeslamiet. al. [19] was studied numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation. Sheikholeslamiet. al. [20] Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchange. Makinde and Aziz [13] analysed boundary layer flow of a nano fluid past a stretching sheet with a convective boundary condition.

In the field of polymer technology, MHD heat and mass transfer has found applications in polymer processing, such as extrusion and molding. It has enabled precise control over temperature and mass distribution, resulting in improved product quality and performance. Lastly, in energy engineering, the phenomenon of MHD heat and mass transfer has been harnessed to enhance energy conversion and storage systems, leading to more efficient energy utilization and resource management.Rajuet. al. [15] Soret effects due to natural convection between heat inclined plates with Magnetic field. Sarithaand Satya Narayana [16] thermal diffusion and chemical reaction effects on unsteady MHD free convection flow past a semi infinite vertical permeable moving plate. Seddeek et al [17] Effects of chemical reaction and variable viscosity on hydromagnetic mixed convection heat and mass transfer for Hiemenz flow through media with radiation. Shateyi and Prakash [18] A new numerica approach for MHD laminar boundary layer flow and heat transfer of nanofluids over a moving surface in the presence of thermal radiation.[21] Sivaraj and Kumar [21] Viscoelastic fluid flow over a moving cone and flat plate with variable electric conductivity.Yashkun et al. [22] MHD hybrid nanofluid flow over a permeable stretching/shrinking sheet with thermal radiation effect.

In conclusion, the phenomenon of heat and mass transfer by MHD, particularly in the oscillatory flow of viscoelastic fluid between two plates, has wide-ranging applications in various fields of engineering. Its impact can be seen in chemistry, the processing industry, food preservation, oil production, rain, electrostatics, polymer technology, and energy engineering. The understanding and utilization of this phenomenon have contributed to advancements in technology, efficiency, and sustainability in these industries.

Mathematical Formulation

The unsteady, two – dimentional, oscillatory MHD oscillatory flow of rheological(visco-elastic liquids) and incompressible viscous fluid through a channel and subjected to a transverse magnetic field in the presence of thermal radiation, chemical reaction, radiation absorption and concentration buoyancy effects. Let x-axis be along the lower plate and straight line perpendicular to that as the y – axis. The present visco-elastic fluid model introduces additional terms into the momentum and Energy equations. For free convection flow, the transversely applied magnetic field and magnetic Reynolds number are assumed to be very small so that the induced magnetic field and the Hall effects are negligible. Under the above assumption with usual Boussinesq’s approximation, the conservation equation of momentum, energy and diffusion are governed by the following set of equations.

Momentum equation is:

\frac{\partial u^{*}}{\partial t^{*}} = - \frac{1}{ρ} \frac{\partial p^{*}}{\partial x^{*}} + ν_{1} \frac{\partial^{2} u^{*}}{\partial y^{* 2}} + ν_{2} \frac{\partial^{3} u^{*}}{\partial y^{* 2} \partial t^{*}} - \frac{ϑ_{1}}{k^{*}} u^{*} - \frac{σ_{e} {B_{0}}^{2}}{ρ} u^{*} + g β_{T} (T^{*} - {T_{0}}^{*}) + g β_{C} (C^{*} - {C_{0}}^{*}) \sin φ

(1)

Energy equation is:

ρ C_{p} \frac{\partial T^{*}}{\partial t^{*}} = k \frac{\partial^{2} T^{*}}{\partial {y^{*}}^{2}} - \frac{\partial q}{\partial y^{*}} + \frac{ρ D_{m} K_{r}}{C_{s}} \frac{\partial^{2} C^{*}}{\partial {y^{*}}^{2}} - Q (T^{*} - {T_{0}}^{*}) + Q_{c} (C^{*} - {C_{0}}^{*})

(2)

Species diffusion equation is:

\frac{\partial C^{*}}{\partial t^{*}} = D \frac{\partial^{2} C^{*}}{\partial {y^{*}}^{2}} - K_{r} (C^{*} - {C_{0}}^{*})

(3)

The boundary conditions of the problem are

u^{*} = 0, T^{*} = {T_{w}}^{*}, C^{*} = {C_{w}}^{*} a t y^{*} = 1 u^{*} = 0, T^{*} = {T_{0}}^{*}, C^{*} = {C_{0}}^{*} a t y^{*} = 0

(4)

For an optically thin fluid, we have

\frac{\partial q}{\partial y^{*}} = 4 α^{2} ({T_{0}}^{*} - T^{*})

Here

α^{2} = \int_{0}^{\infty} δ λ \frac{\partial B}{\partial T}

is the absorption coefficient,

λ

is frequency, B is Planck’s function and

δ

is radiation absorption coefficient.

The non-dimensional quantities are

\begin{array}{l} x = \frac{x^{*}}{a}, y = \frac{y^{*}}{a}, u = \frac{u^{*}}{U}, t = \frac{t^{*} U}{a}, R e = \frac{U a}{ϑ_{1}} θ = \frac{(T^{*} - {T_{0}}^{*})}{({T_{w}}^{*} - {T_{0}}^{*})}, \emptyset = \frac{(C^{*} - {C_{0}}^{*})}{(C_{w} - {C_{0}}^{*})}, G c = \frac{g β_{c} ({C_{w}}^{*} - {C_{0}}^{*}) a^{2}}{ϑ_{1} U}, \\ G r = \frac{g β_{T} ({T_{w}}^{*} - {T_{0}}^{*}) a^{2}}{ϑ_{1} U}, P = \frac{a P^{*}}{{ρ ϑ}_{1} U}, D a = \frac{K^{*}}{a^{2}}, K^{2} = \frac{a^{2} σ_{e} B_{0}^{2}}{{ρ ϑ}_{1}}, Q_{1} = \frac{a^{2} Q_{c} (C_{w}^{*} - C_{0}^{*}}{k (T_{w}^{*} - T_{0}^{*})}, P_{e} = \frac{U a ρ c_{p}}{k}, R^{2} = \frac{4 α^{2} a^{2}}{k} \\ S c = \frac{D}{a U}, S^{2} = \frac{1}{D a}, E = \frac{Q a^{2}}{k}, J = \frac{K_{r} a}{U} \end{array}

(5)

With the above substitution in the equations (1) to (3), the system of equations reduced to the dimension less form as

R e \frac{\partial u}{\partial t} = - \frac{\partial p}{\partial x} + \frac{\partial^{2} u}{\partial y^{2}} + γ \frac{\partial^{3} u}{\partial y^{2} \partial t} - (S^{2} + H^{2}) u + {G r}_{1} θ + {G c}_{1} \emptyset

(6)

P_{e} \frac{\partial θ}{\partial t} = \frac{\partial^{2} θ}{\partial y^{2}} + D f \frac{\partial^{2} C}{\partial y^{2}} + (R^{2} - E) θ + Q_{1} \emptyset

(7)

\frac{\partial \emptyset}{\partial t} = S c \frac{\partial^{2} \emptyset}{\partial y^{2}} - J \emptyset

(8)

Here

{G r}_{1} = G r s i n \emptyset a n d {G c}_{1} = G c s i n \emptyset

The boundary conditions on velocity, temperature and concentration in the form of non-dimensional are

u = 0, θ = 1, \emptyset = 1 a t y = 1 u = 0, θ = 0, \emptyset = 0 a t y = 0

(9)

Solution of the problem:

To solve equations (6) to (8) with boundary conditions (9) for purely oscillatory flow, let us assume

- \frac{\partial P}{\partial x} = λ e^{i ω t}, u (y, t) = u_{0} (y) e^{i ω t}, θ (y, t) = θ_{0} (y) e^{i ω t}, ϕ (y, t) = ϕ_{0} (y) e^{i ω t}

(10)

Substituting equation (10) into equations (6) to (8), we get,

(1 + i ω γ) \frac{d^{2} u_{0}}{d y^{2}} - M_{1}^{2} u_{0} = - λ - {G r}_{1} θ_{0} - {G c}_{1} ϕ_{0}

(11)

\frac{d^{2} θ_{0}}{d y^{2}} + M_{2}^{2} θ_{0} = - (Q_{1} + D u M_{3}^{2}) ϕ_{0}

(12)

\frac{d^{2} ϕ_{0}}{d y^{2}} - M_{3}^{2} ϕ_{0} = 0

(13)

The corresponding boundary conditions are

u_{0} = 0, θ_{0} = 1, \emptyset_{0} = 1 a t y = 1 u_{0} = 0, θ_{0} = 0, \emptyset_{0} = 0 a t y = 0

(14)

By solving equations (11) to (13) under the boundary conditions (14), we obtain the solution of Velocity, temperature and concentration distributions as follows

\begin{matrix} u (y, t) = {G r}_{1} & ([\frac{1 + k_{1}}{M_{1}^{2} + L^{2} M_{2}^{2}}] \frac{\sin M_{2} y}{\sin M_{2}} + [\frac{k_{1}}{L^{2} M_{3}^{2} - M_{1}^{2}}] \frac{\sinh M_{3} y}{\sinh M_{3}} \\ - [\frac{1 + k_{1}}{M_{1}^{2} + L^{2} M_{2}^{2}} + \frac{k_{1}}{L^{2} M_{3}^{2} - M_{1}^{2}}] \frac{\sinh \frac{M_{1} y}{L}}{\sinh \frac{M_{1}}{L}}) \\ + \frac{{G c}_{1}}{L^{2} M_{3}^{2} - M_{1}^{2}} [\frac{\sinh \frac{M_{1} y}{L}}{\sinh \frac{M_{1}}{L}} - \frac{\sinh M_{3} y}{\sinh M_{3}}] \\ + \frac{λ}{M_{1}^{2}} (\frac{\sinh \frac{M_{1} y}{L}}{\sinh \frac{M_{1}}{L}} c o s h \frac{M_{1}}{L} - \frac{\sinh \frac{M_{1} y}{L}}{\sinh \frac{M_{1}}{L}} - c o s h \frac{M_{1}}{L} + 1) \end{matrix}

(15)

θ (y, t) = \{(1 + k_{1}) \frac{\sin M_{2} y}{\sin M_{2}} - k_{1} \frac{\sinh M_{3} y}{\sinh M_{3}}\} e^{i ω t}

(16)

\emptyset (y, t) = \frac{\sinh M_{3} y}{\sinh M_{3}} e^{i ω t}

(17)

Result and Discussion

In order to get a physical insight into the problem, a representative set of numerical results is shown graphically in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, to illustrate the influence of physical parameters viz., H=1; Pr=0.71; E=0.5; Gr=4; Gc=4; Re=0.71; J=2; Q1=1.5; S=1.5; R=1.9; Sc=0.6; t=1;

γ

=1; w=1;

λ

=1; w=pi/4; Du=0.5; R=1; a=0.1; p=0.1; n=0.1 on the velocity

f (η)

, temperature

θ (η)

and concentration

φ (η)

The Prandtl number was taken to be Pr = 0.72, which corresponds to air, the values of Schmidt number (Sc) were chosen to be Sc = 0.24, 0.62, 0.78, 2.62, representing diffusing chemical species of most common interest in air like

H_{2}, H_{2} O, N H_{3}

, and Propyl Benzene, respectively. Attention is focused on positive values of the buoyancy parameters, that is, Grashof number Gr > 0 (which corresponds to the cooling problem) and modifiedGrashof number Gc> 0 (which indicates that the chemical species concentration in the free stream region is less than the concentration at the boundary surface).

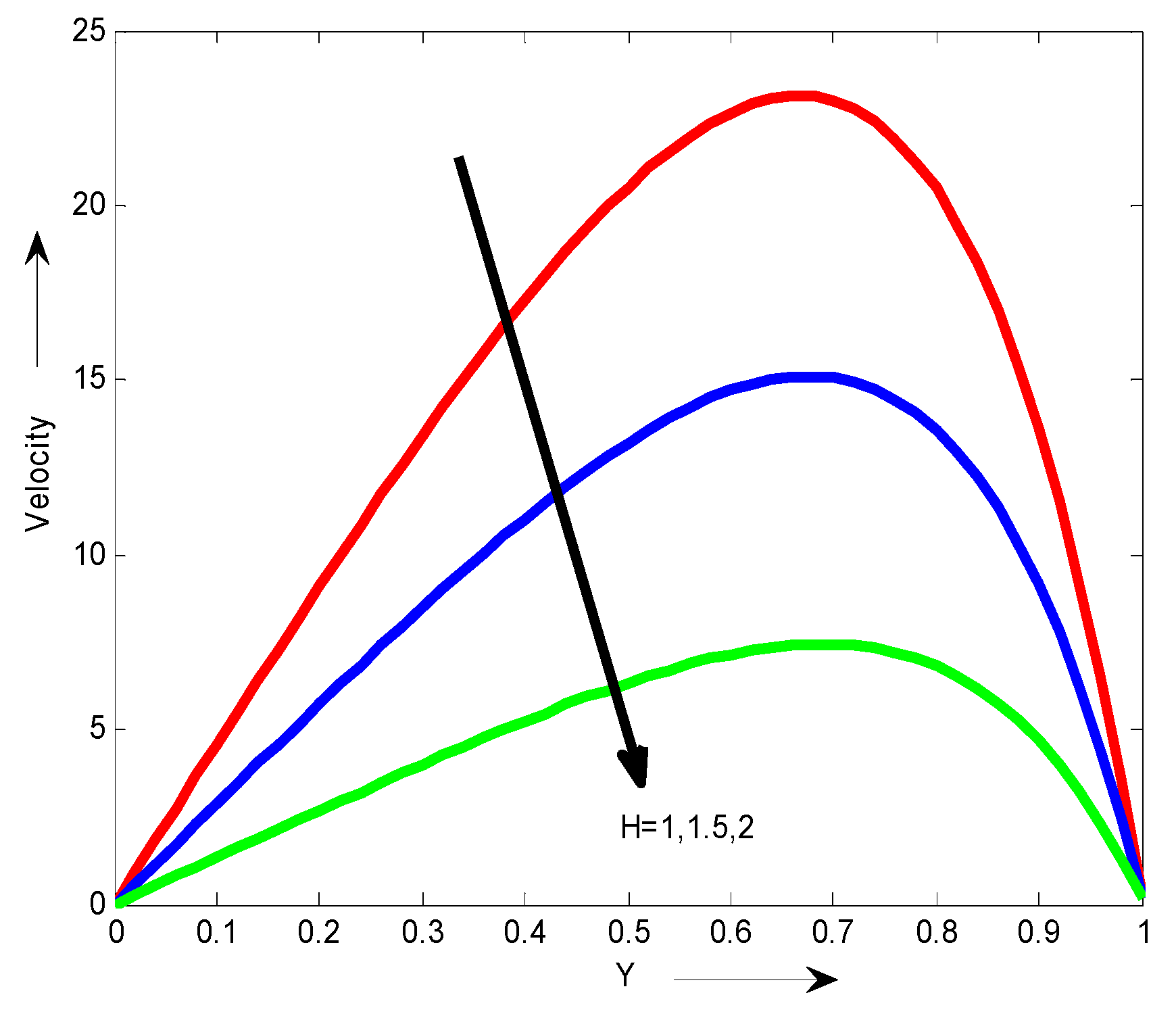
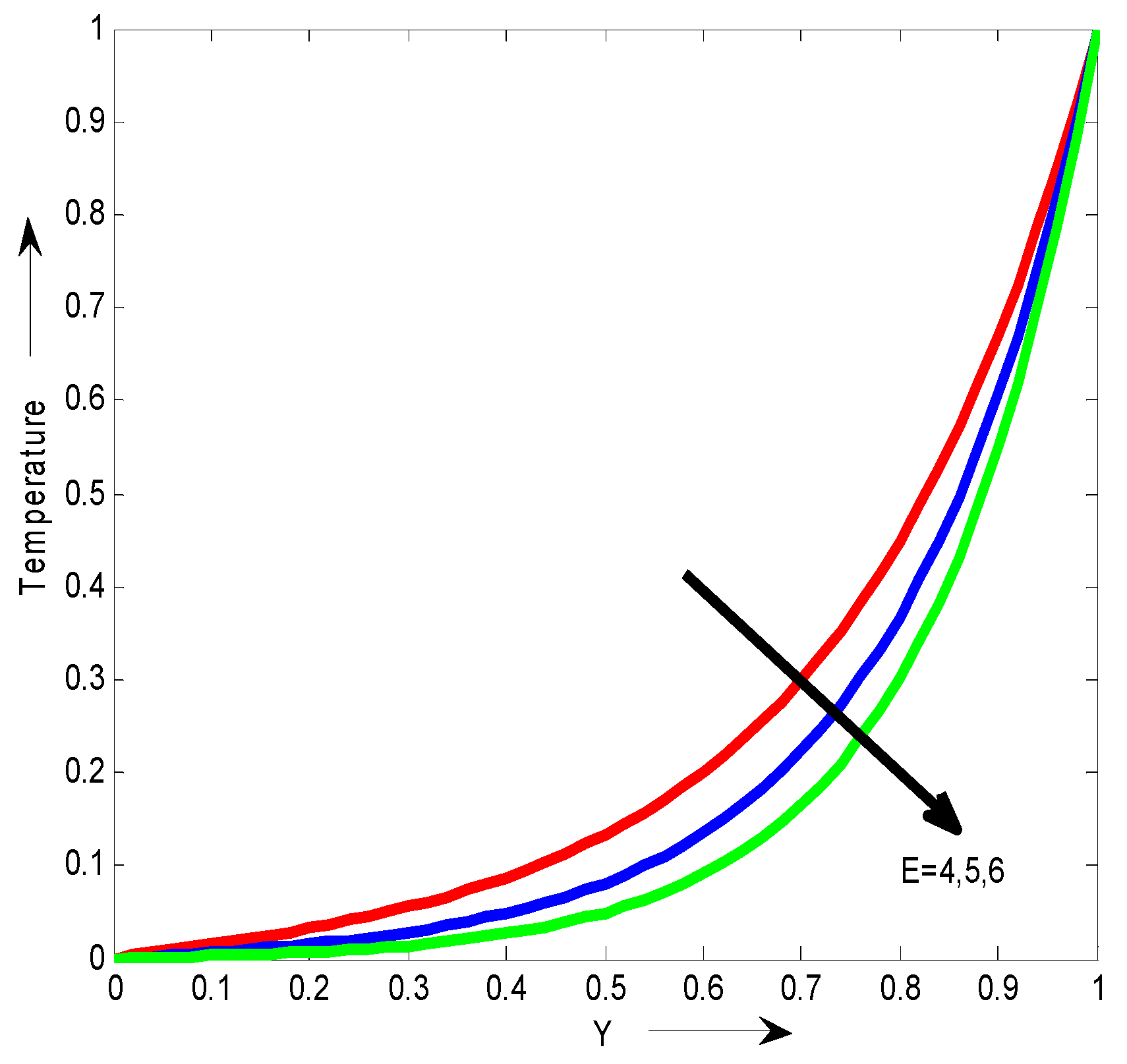
The effects of the Hartman number Hon the velocity are shown in Figure 1. It is observed that an increase in the Hartman number Hresults in a decrease in the velocity. The Echet number on the temperature is shown in Figure 2. It can be seen that the temperature decreases with the increase of Ec.

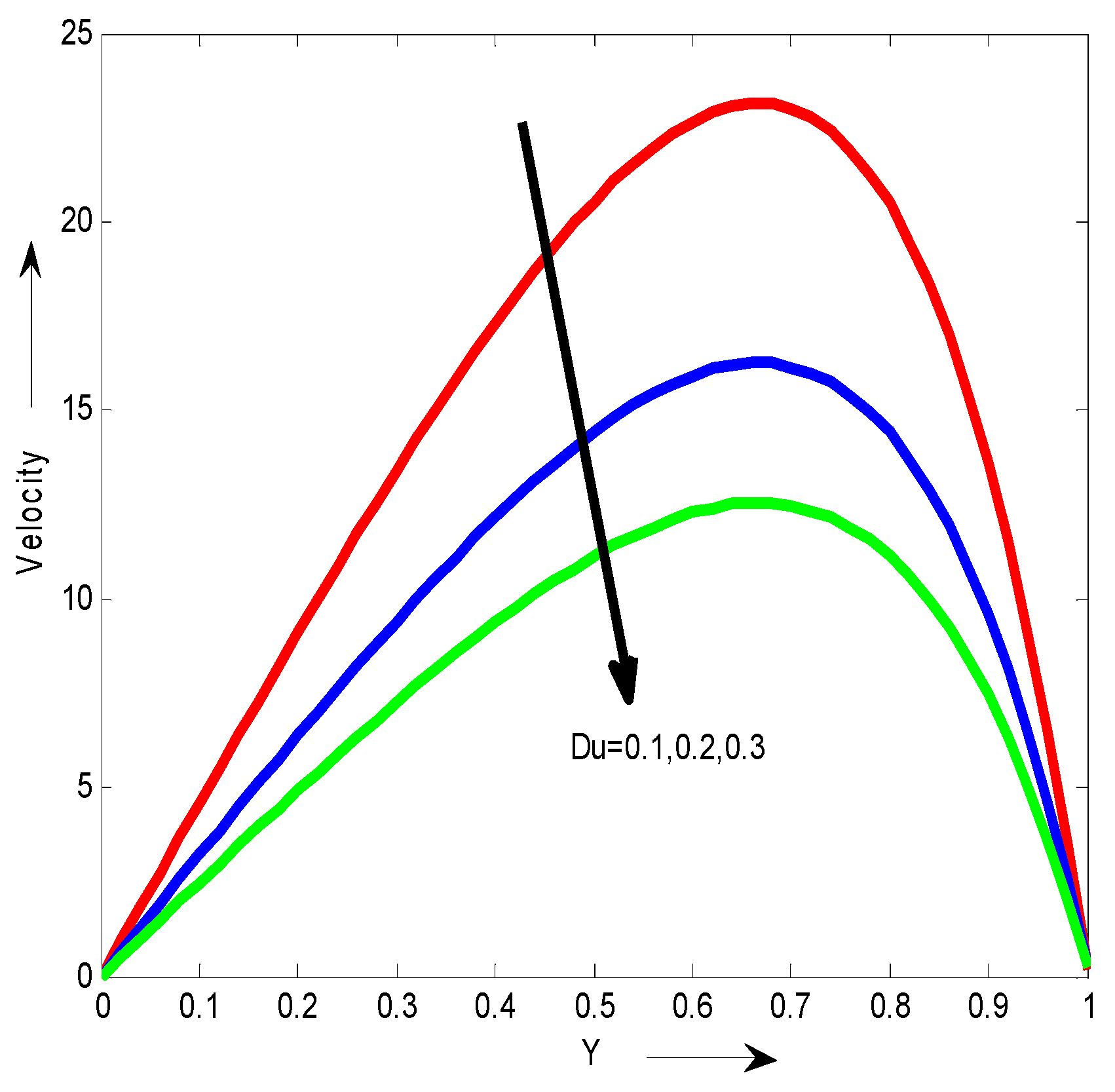
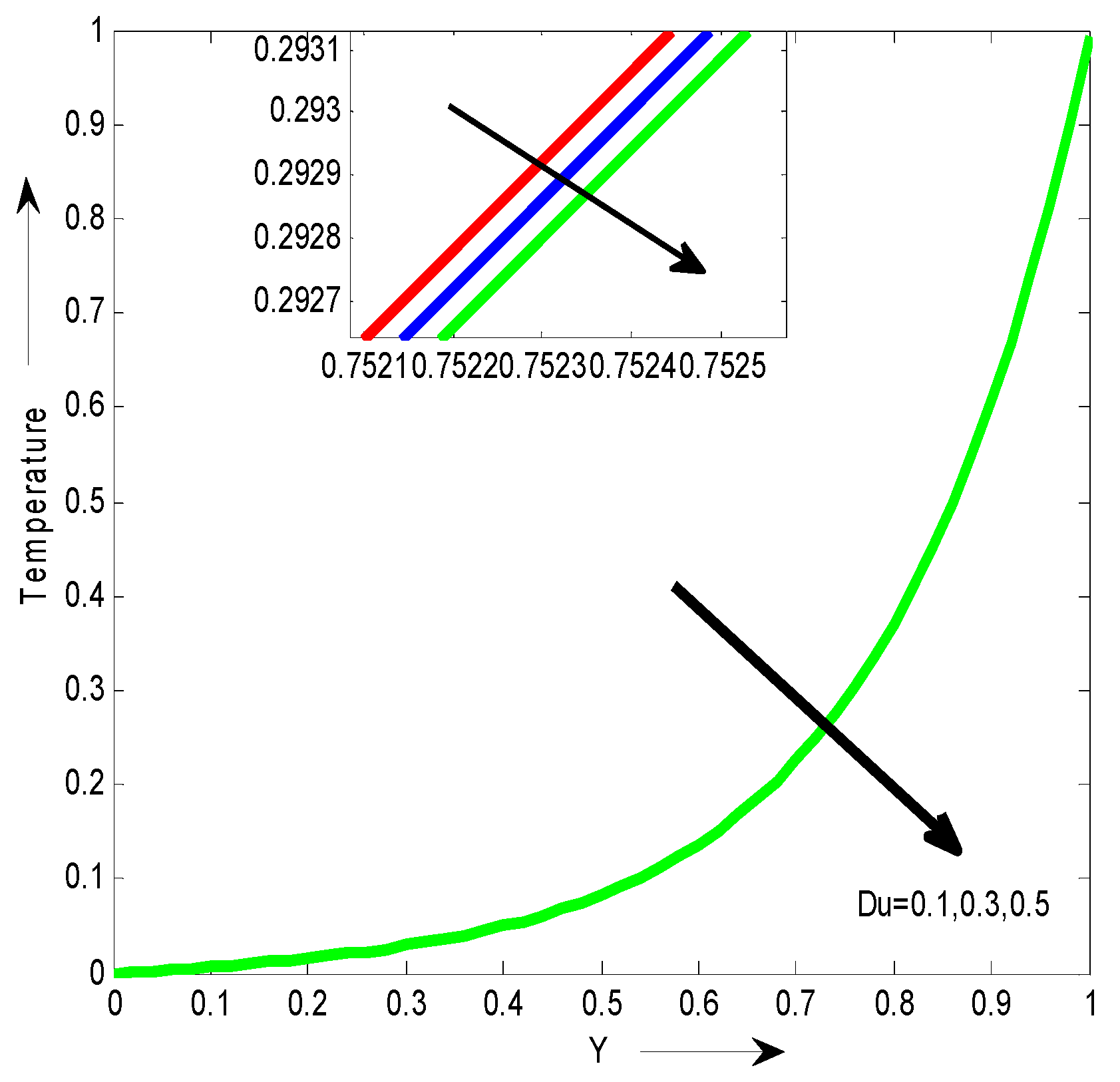
The Dufour effect on the velocity for different values of Dufour effect Du is shown in Figure 3. Weobserved that the velocity decreases with the increase of Du.

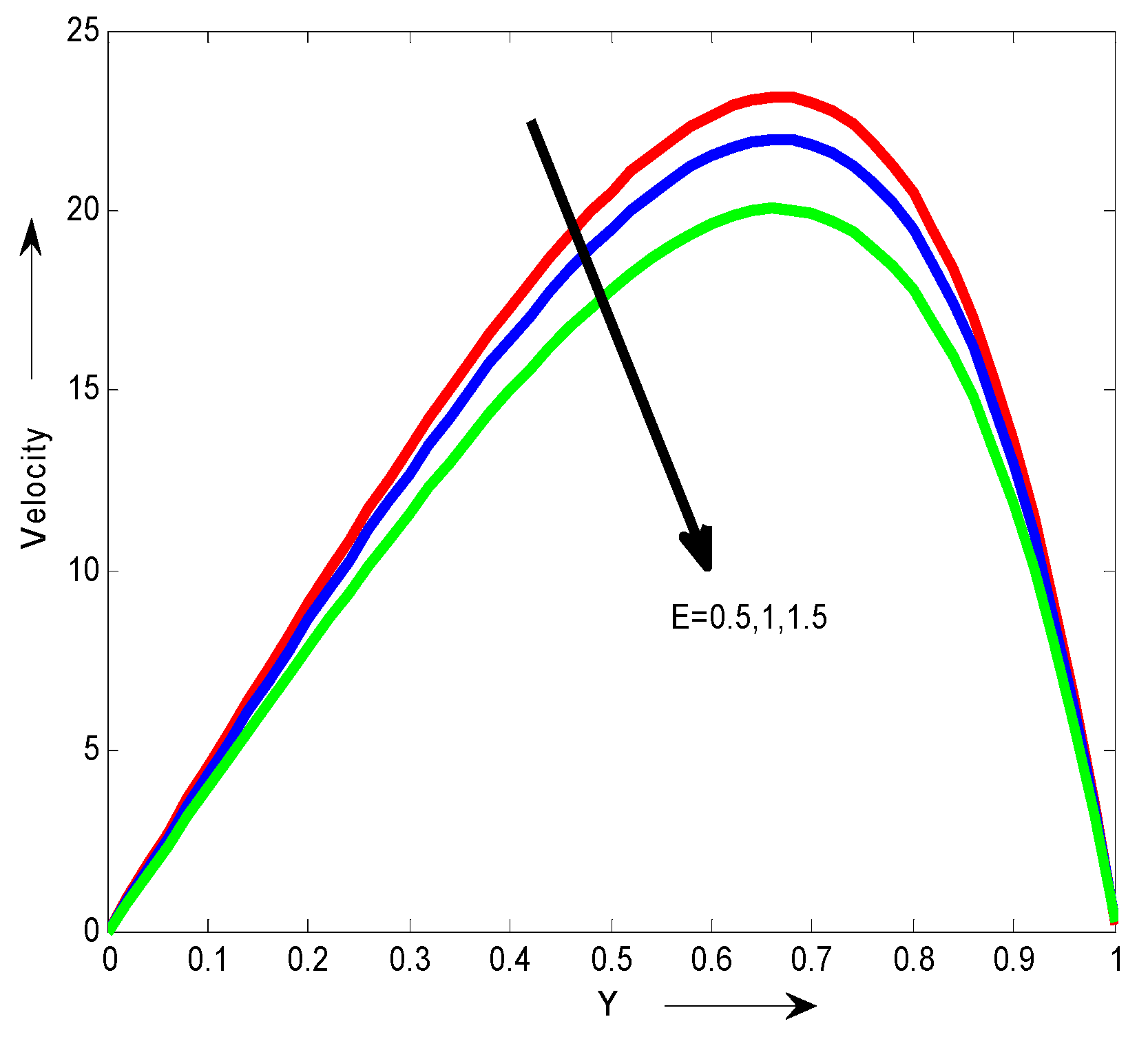
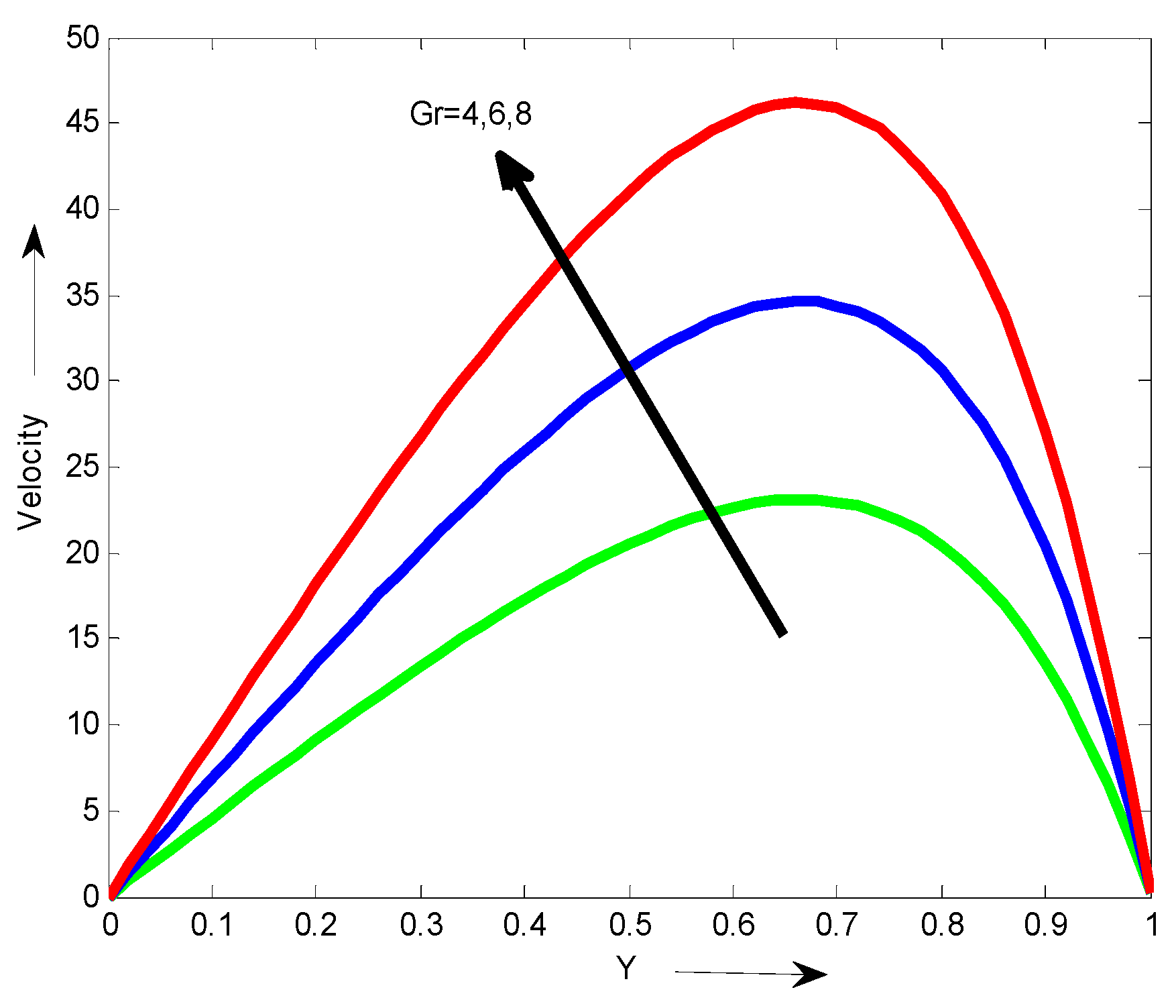
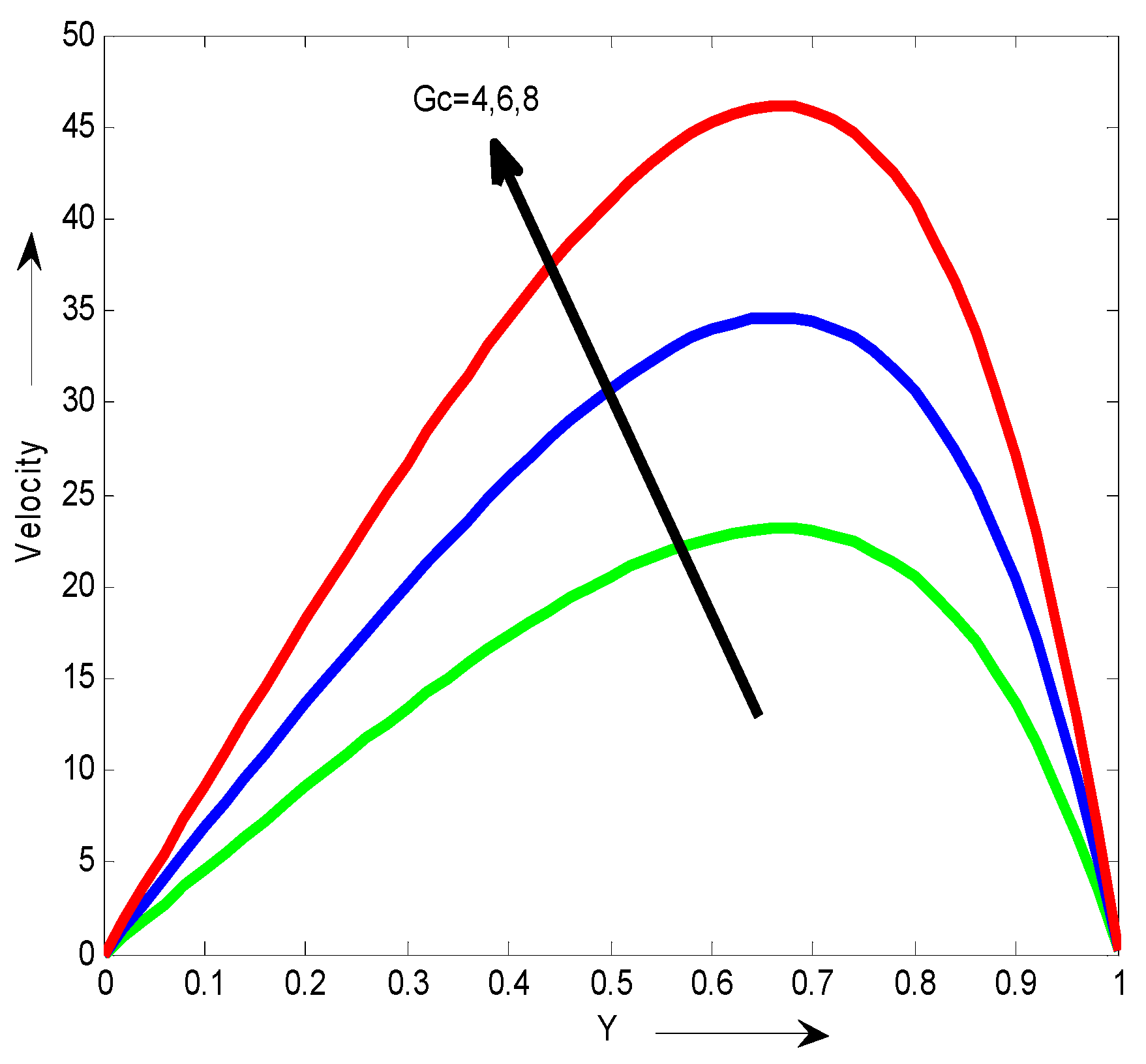
The effects of the Grashof number Gr on the velocity are shown in Figure 4. It is observed that an increases in the Grashof number Grresults in a decrease in the velocity. The influence of the modified Grashof number Gc on the velocity is shown in Figure 5. It is noticed that the velocity profiles increase with the increase of modified Grashof number Gc.

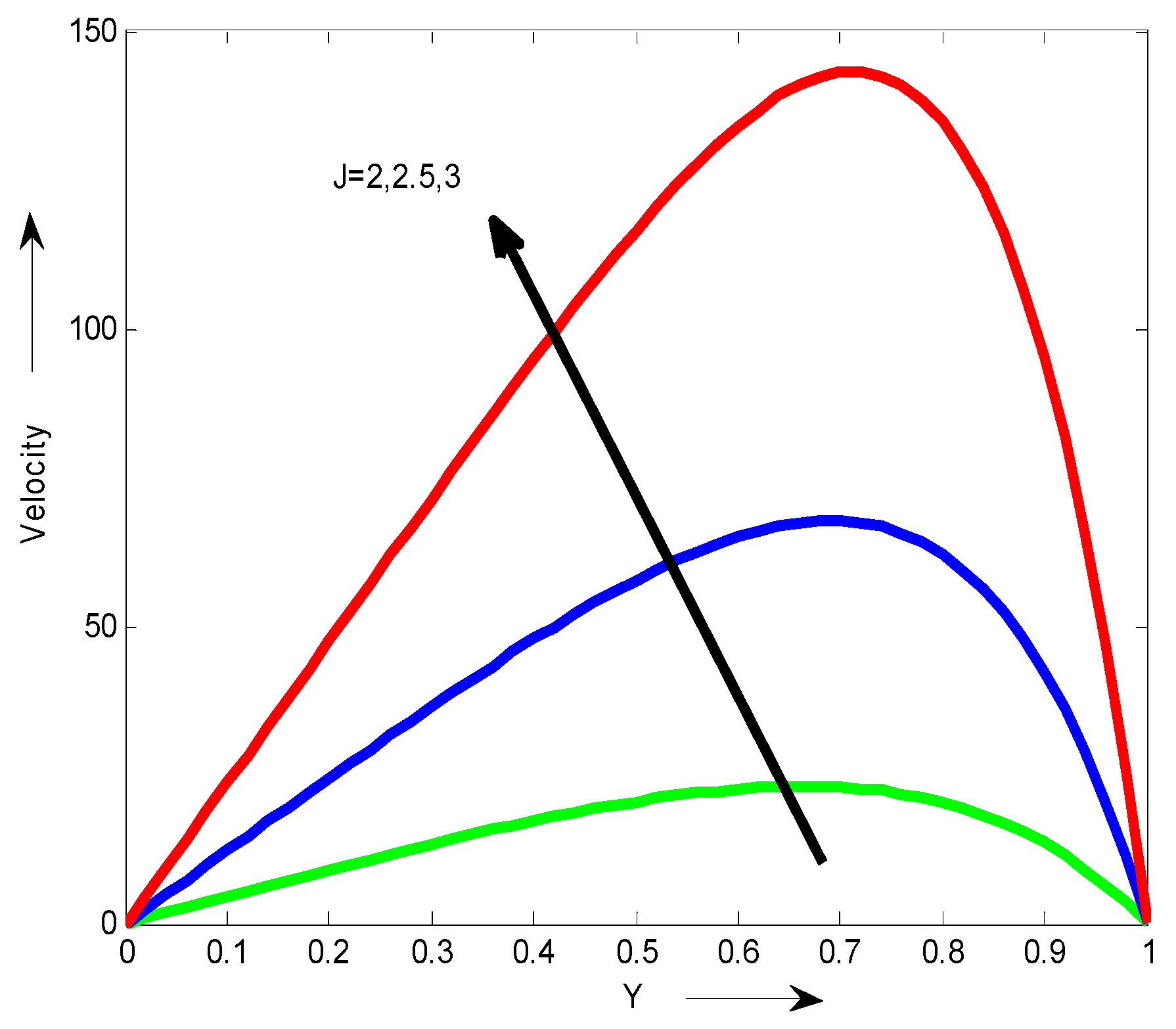
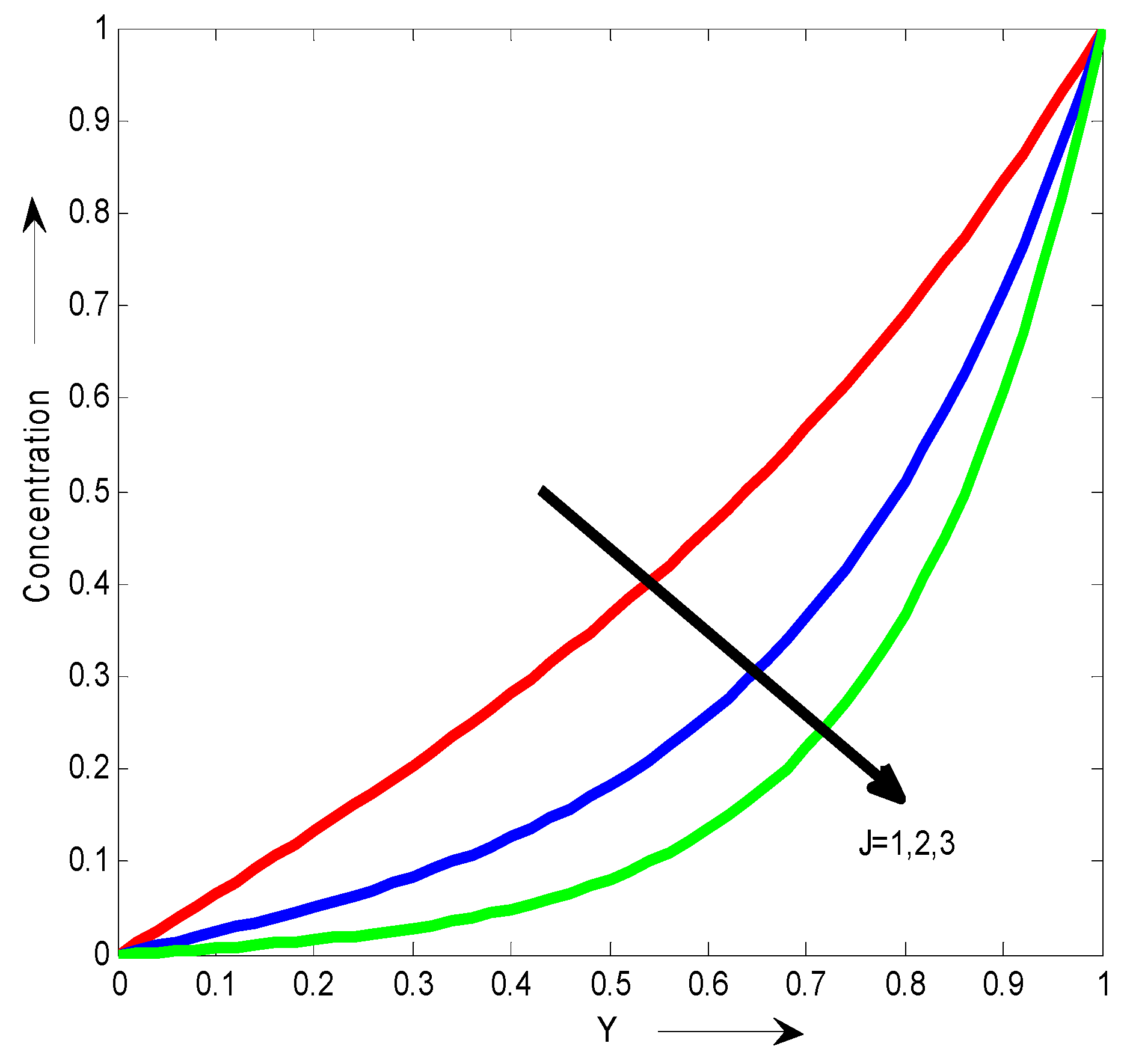
The joule diffusion J on the velocity is shown in Figure 6. We observed that the velocity increases with the increase of joule diffusion J.

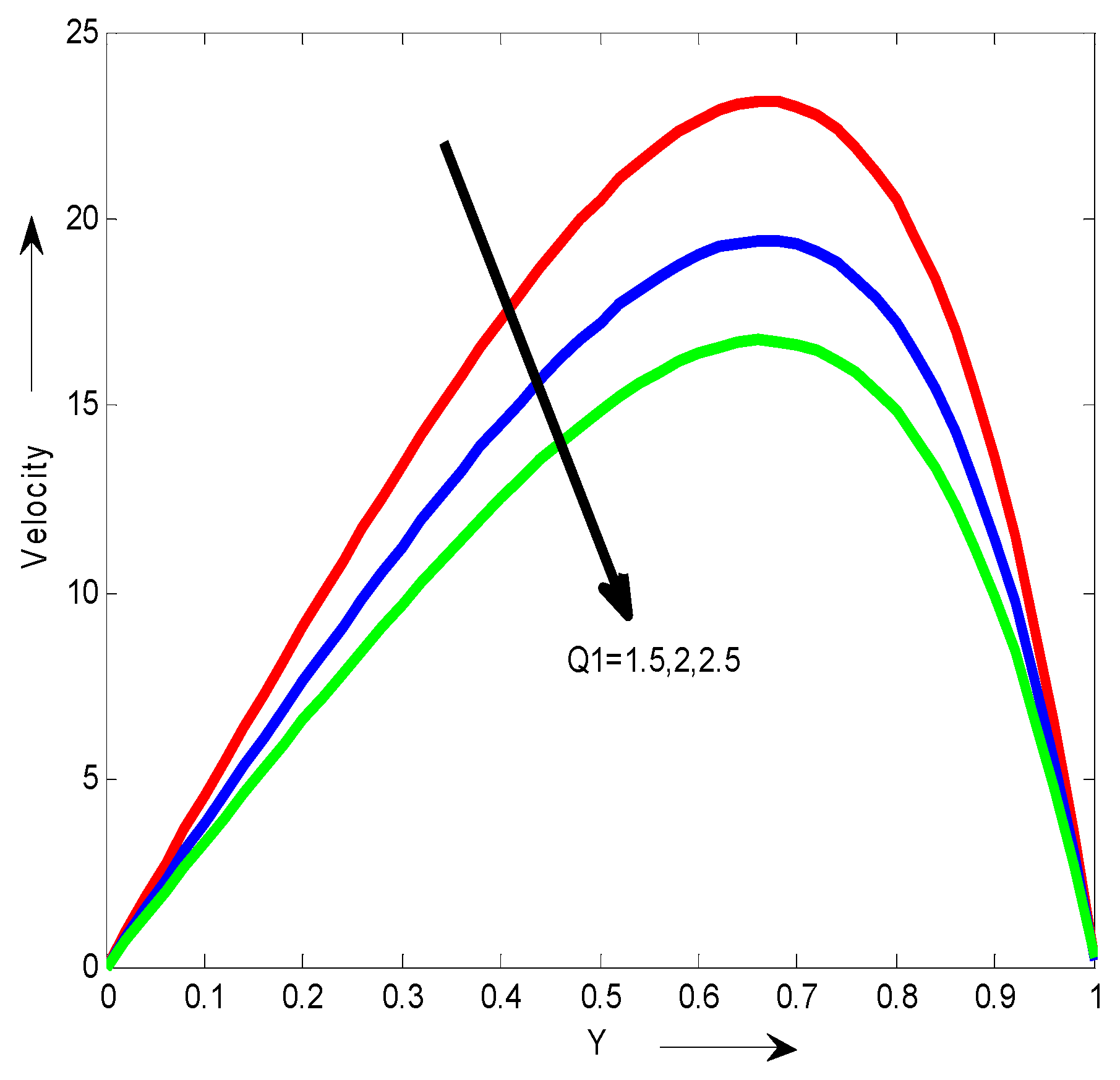
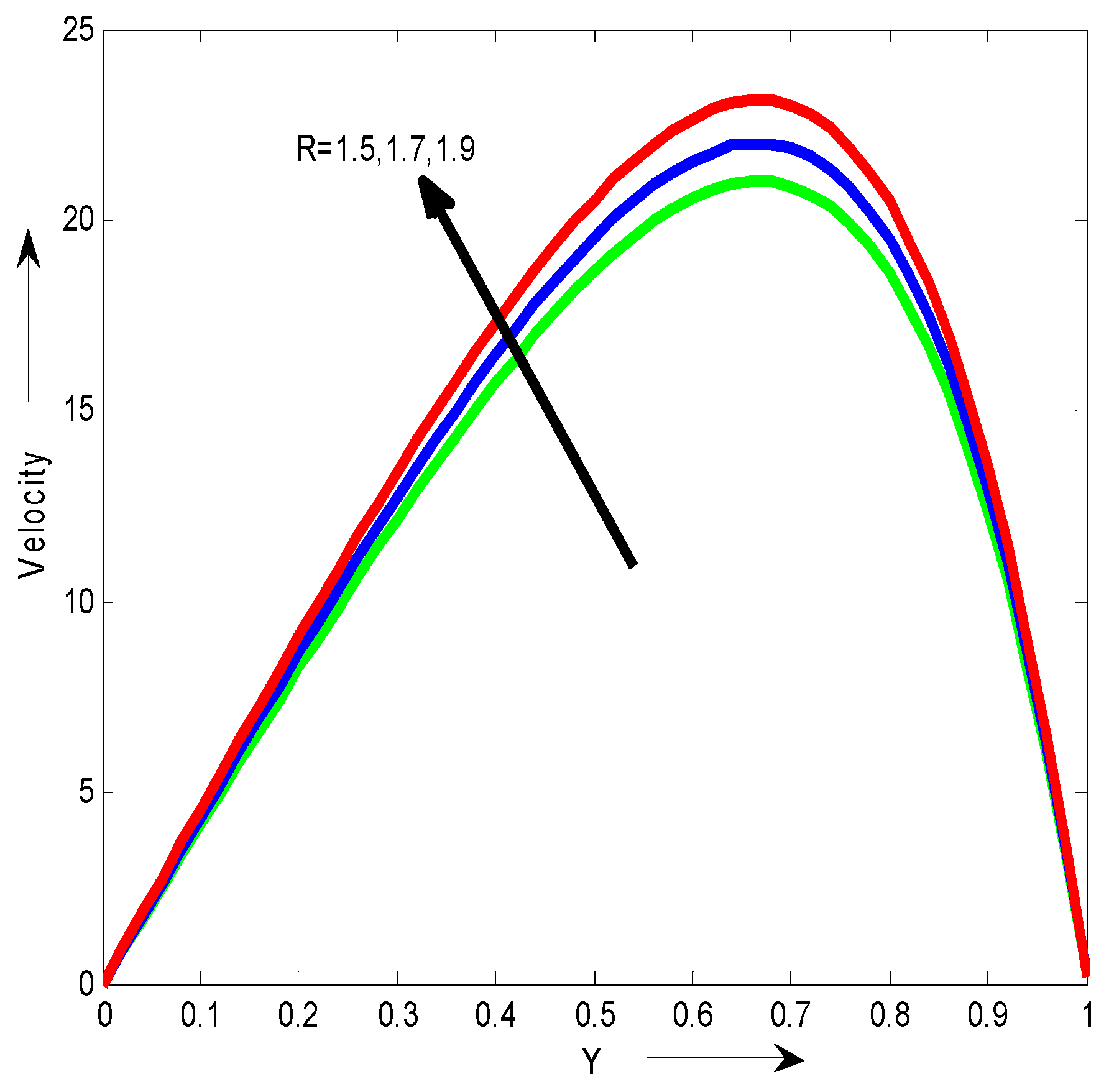
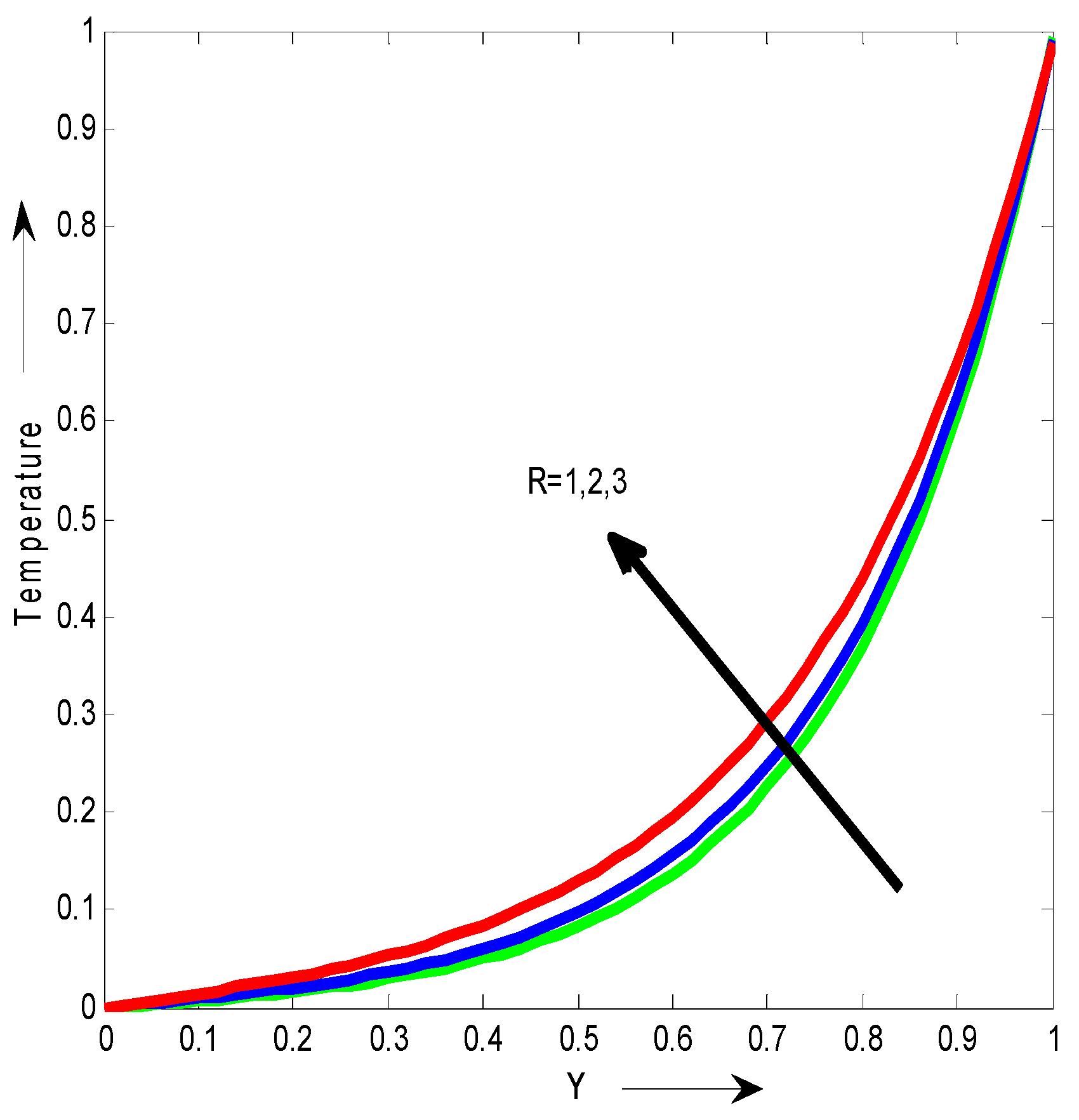
Figure 7 shows the dimensionless velocity for different values of Q1. It can be seen that the velocity decreases with the increase of Q1.From Figure 8 shown that the velocity for different values of radiation parameter R. We observed that the velocity increases with the increase of R.

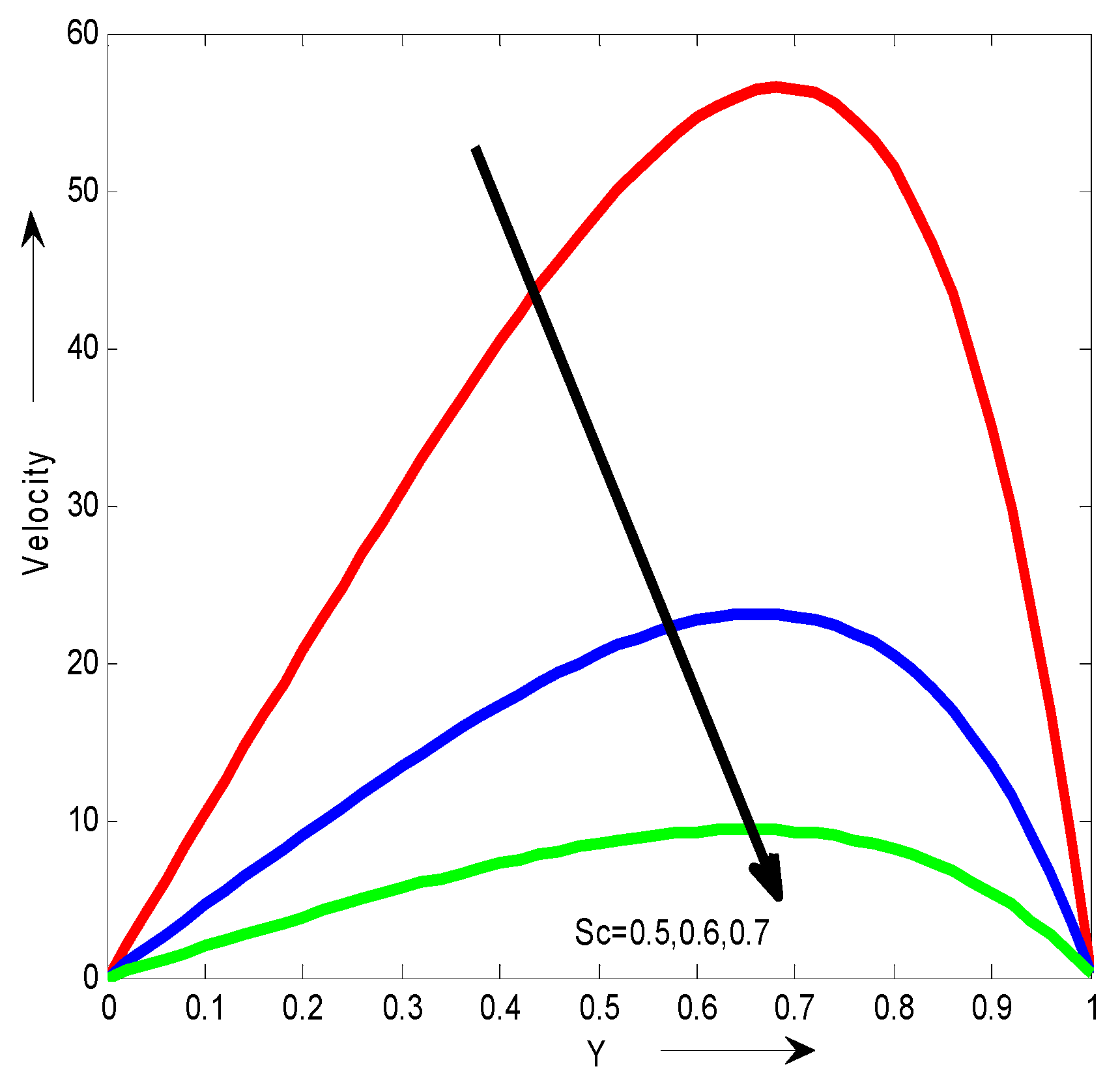
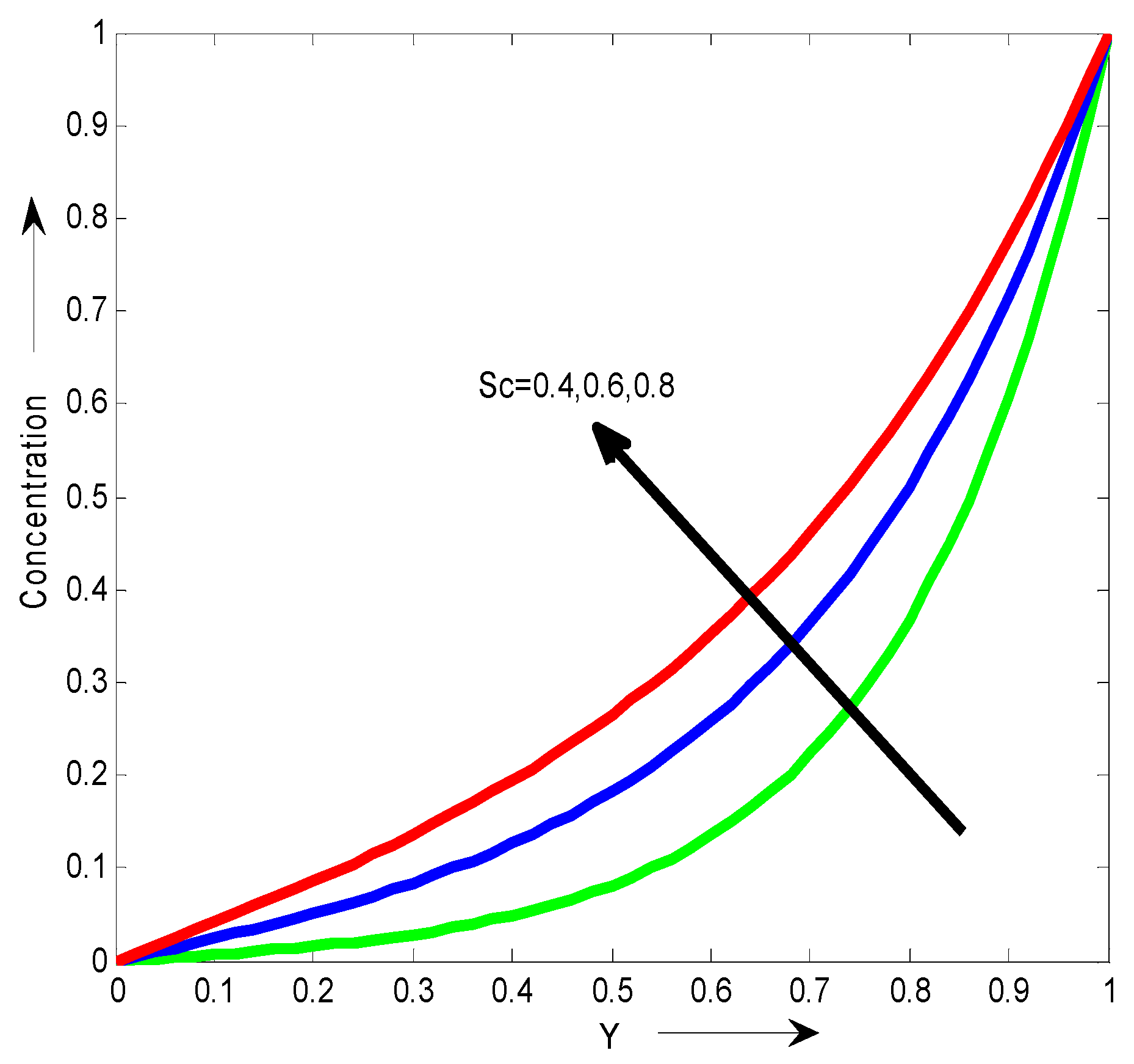
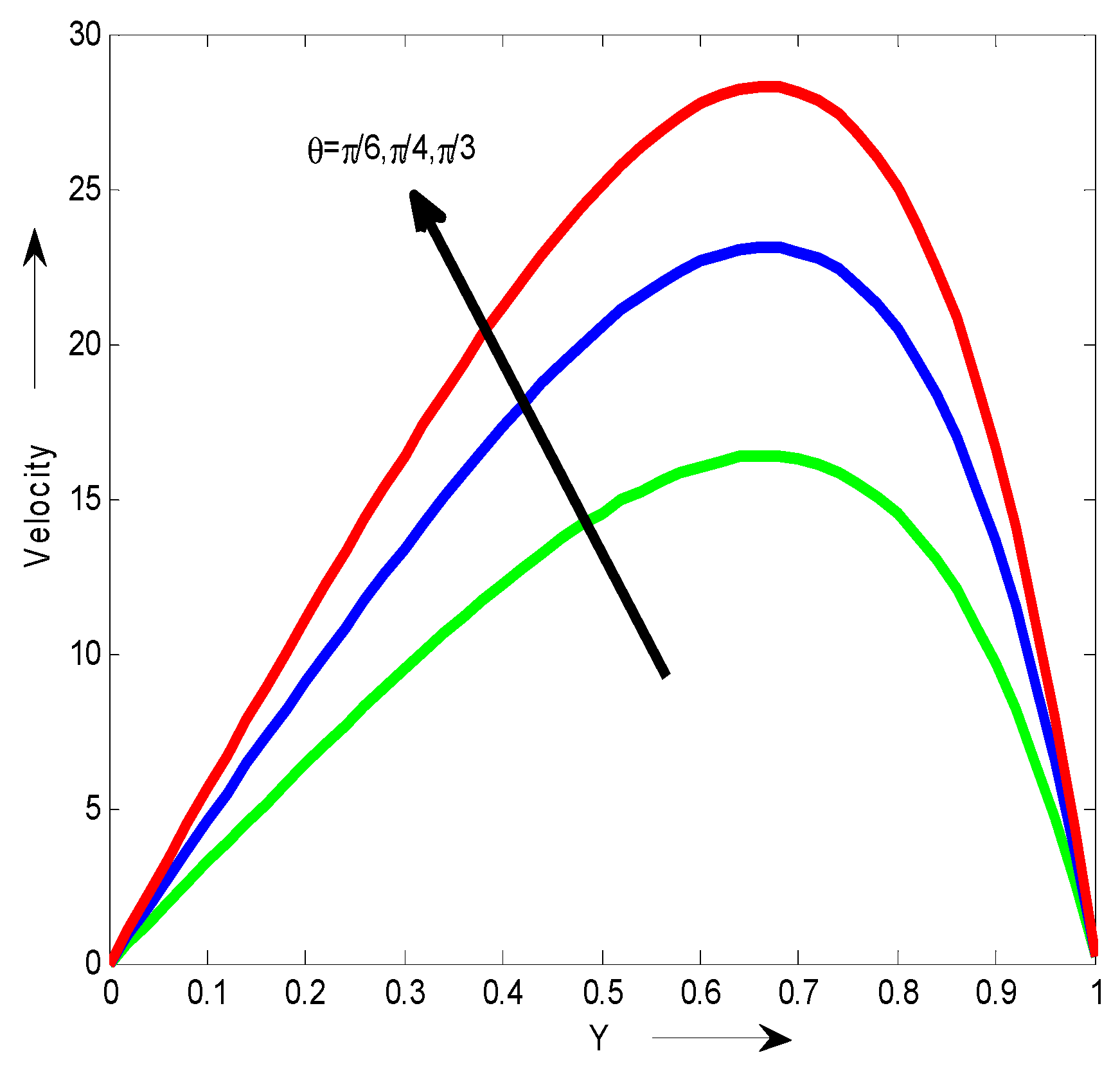
Figure 9 shows the dimensionless velocity for different values of Schmidt number Sc. It can be seen that the velocity decreases with the increase of Schmidt number Sc. Figure 10 shows the dimensionless velocity for different values of

θ

. It can be seen that the velocity increases with the increase of

θ

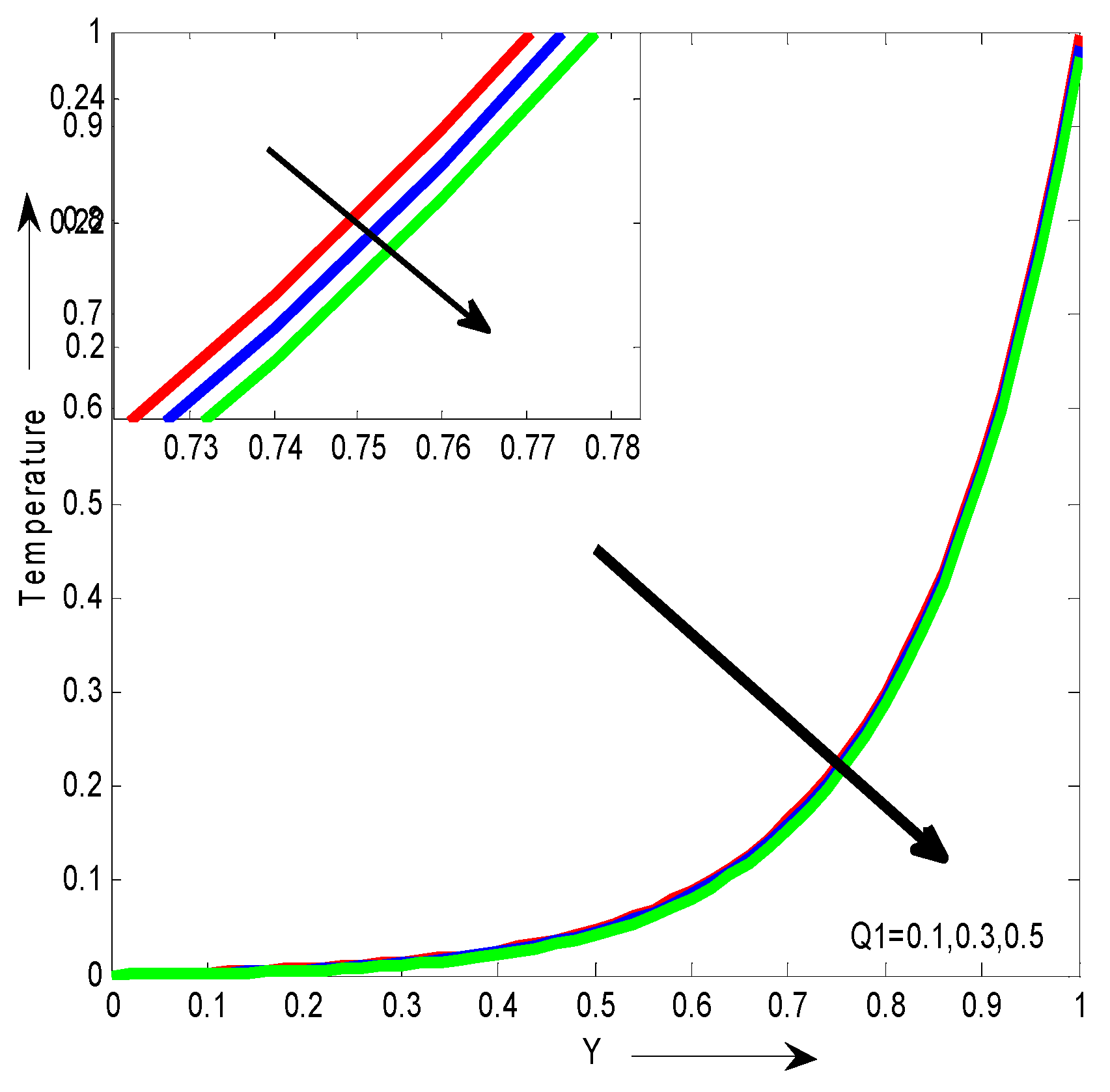
The Echet number on the temperature is shown in Figure 11. It can be seen that the temperature decreases with the increase of Ec. Figure 12 shows the dimensionless temperature for different values of Q1. It can be seen that the temperature decreases with the increase of Q1. From Figure 13 shown that the temperature for different values of radiation parameter R. We observed that the temperature increases with the increase of R.

The Dufour effect on the temperature for different values of Dufour effect Du is shown in Figure 14. We observed that the temperature decreases with the increase of Du.

The joule diffusion J on the Concentration is shown in Figure 15. We observed that the concentration decreases with the increase of joule diffusion J.

Figure 16 shows the dimensionless concentration for different values of Schmidt number Sc. It can be seen that the concentration increases with the increase of Schmidt number Sc.

Conclusion

In this chapter we study the unstudy effect on MHD preamble porous medium through with thermal absortion and heat geerneration in the presence of Chemical reaction. The expressions for the velocity, temperature and concentration distributions are arthemitiacllysolved by pertribution method.

➢: It can be seen that the velocity increases with the increase of $θ$ .
➢: We observed that the velocity decreases with the increase of Du.
➢: It is observed that an increase in the Hartman number Hresults in a decrease in the velocity.
➢: We observed that the velocity increases with the increase of joule diffusion J.
➢: It can be seen that the velocity decreases with the increase of Schmidt number Sc.
➢: We observed that the temperature increases with the increase of R.
➢: We observed that the concentration decreases with the increase of joule diffusion J.

References

Chen. C. H., “Heat and mass transfer in MHD flow by natural convection from a permeable inclined surface with variable wall temperature and concentration”. ActaMechanica 2004, 172, 219–235.
Daniel. S and Daniel. Y. S., “Convective flow two immiscible fluids and heat transfer with along an inclined channel with pressure gradient “. International Journal of Engineering and Science 2013, 2, 12–18.
Hayat T, Ullah I, Alsaedi A, Waqas M and Ahmad B, “ Three-dimensional mixed convection fow of Siskonanoliquid”. International Journal of Mechanical Sciences 2017, 133, 273–282.
HossainM.A et.al., “ Free convection radiation interaction from an isothermal plate inclined at a small angle to the horizontal”. ActaMechanica 1998, 127, 63–73.
Ibrahim.F.Set.al, “ Effect of chemical reaction and radiation absorption on the unsteady MHD free convection flow past a semi infinite vertical permeable moving plate with heat source and suction”. Communication in Nonlinear science and numerical simulation 2008, 13, 1056–1066. [CrossRef]
Iskandar. W, Anuar. I and Loan pop “Hybrid Nanofluid flow past a permeable moving thinneedle”. Mathematics 2020, 8, 612. [CrossRef]
Jahan. S. et al., “Effects of solar radiation and viscous dissipation on mixed convective Non- Isothermal hybrid nanofluid over moving thin needle”. Journal of Advanced Research in Micro and Nano Engineering 2021, 3, 1–11.
Kesavaiah. D. C., Satyanarayana. P. V. and Venkataramana. S., “Effectsof the chemical reaction and radiation absorption on an unsteady MHD convective heat and mass transfer flow past a semi-infinite vertical permeable moving plate embedded in a medium with heat source and suction”. International Journal of Applied Mathematics and Mechanics 2011, 7, 52–69.
KhanU., et al., “Impact of magnetic field on boundary-layer flow of Sisko liquid comprising nanomaterials migration through radially shrinking/stretching surface with zero mass flux”. Journal of Materials research and Technology 2020, 9, 3699–3709. [CrossRef]
KhanM. S., KarimI., IslamM. S, and WahiduzzamanM., “MHD boundary layer radiative, heat generating and chemical reacting flow past a wedge moving in a Nanofluid”. Nanoconvergence 2014, 1, 1–13.
KumarA., RamP. and SinghH., “MHD flow and heat transfer in a visco-elastic fluid over a flat surface with constant suction”. Journal of computer and Mathematical Sciences 2010, 1, 552–565.
KumarH.“An analytical solution to the problem of radiative heat and mass transfer over an inclined plate at prescribed heat flux with chemical reaction”. Journal of the Serbian Chemica Society 2012, 77, 1–14.
Makinde, O.D and Aziz A, “ Boundary layer flow of a nano fluid past a stretching sheet with a convective boundary condition”. International Journal of Thermal Sciences 2011, 50, 1326–1332. [CrossRef]
Nandeppanavar, M. M, Vajravelu K and Abel M.S, “Heat transfer in MHD visco-elastic boundary layer flow over a stretching sheet with thermal radiation and non-uniform heat source/sink”. communication in Nonlinear Science and Numerical Simulation 2011, 16, 3578–90. [CrossRef]
Raju M. C, Varma S.V.K, Reddy P.V and Suman. S, “Soret effects due to natural convection between heat inclined plates with Magnetic field. Journal of Mechanical Engineering 2008, 39, 43–48.
Saritha. S. S. and Satya Narayana P. V, “Thermal diffusion and chemical reaction effects onunsteady MHD free convection flow past a semi infinite vertical permeable movingplate”. Asian journal of Current Engineering and Maths 2012, 1, 131–138.
Seddeek M. A. et al, “Effects of chemical reaction and variable viscosity on hydromagnetic mixed convection heat and mass transfer for Hiemenz flow through media with radiation”. Communication in Nonlinear Science Numerical Simulation 2007, 12, 195–213. [CrossRef]
Shateyi. S and J. Prakash, “A new numerica approach for MHD laminar boundary layer flow and heat transfer of nanofluids over a moving surface in the presence of thermal radiation”. 2014, 2, 1–12.
SheikholeslamiM., AbemanS. and GanjiD. D., “Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation”. International journal of Heat and Mass Transfer 2014, 79, 212–222. [CrossRef]
SheikholeslamiM., HaqR. U., ShafeeA., Li Z and Elaraki Y.G, I. Tlii, “ Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchange. International journal of Heat and mass transfer 2019, 135, 470–478. [CrossRef]
Sivaraj. R and Kumar. B. R, “Viscoelastic fluid flow over a moving cone and flat plate with variable electric conductivity”. International journal of heat and mass transfer 2013, 1, 119–128.
Yashkun. U. et al., “MHD hybrid nanofluid flow over a permeable stretching/shrinking sheetwith thermal radiation effect”. International Journal of Numerical Methods for Heat andFluid Flow 2020, 31, 1014–1031.

Figure 1. Velocity Profile for H.

Figure 2. Velocity Profile for E.

Figure 3. Velocity Profile for Du.

Figure 4. Velocity Profile for Gr.

Figure 5. Velocity Profile for Gc.

Figure 6. Velocity Profile for J.

Figure 7. Velocity Profile for Q1.

Figure 8. Velocity Profile for R.

Figure 9. Velocity Profile for Sc.

Figure 10. Velocity Profile for

θ

Figure 10. Velocity Profile for

θ

Figure 11. Temperature for E.

Figure 12. Temperature for Q1.

Figure 13. Temperature for R.

Figure 14. Temperature for Du.

Figure 15. Concentration for for J.

Figure 16. Concentration for Sc.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Heat and Mass Transfer on MHD in the Oscillatory Flow of Viscoelastic Fluid between Two Plates with Heat Generation and Chemical Reaction

Abstract

Introduction

Mathematical Formulation

Result and Discussion

Conclusion

References

MDPI Initiatives

Important Links

Subscribe