Prerpints.org logo
Preprint
Article

Levitating Control System of Maglev Ruler Based on Active Disturbance Rejection Controller

Altmetrics

Downloads

87

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 August 2024

Posted:

07 August 2024

You are already at the latest version

Alerts
Abstract
The autonomous displacement and displacement measurement functions of the maglev ruler are performed by the mover core. The stability of the four magnetic field in air gaps and the levitation position of the maglev ruler is one of the key factors for the stability of the thrust force on the power core, and it is also one of the key factors for ensuring the precision of the maglev ruler. There is cross-coupling between the two ends of the mover core of the maglev ruler, resulting in a strongly coupled, nonlinear, multi-input and multi-output system for the levitating system of the maglev ruler. This paper establishes a mathematical model for the levitating system of the maglev ruler, and designs a levitating control system for the maglev ruler based on ADRC control algorithm to achieve decoupling and disturbance suppression. Through simulation analysis and experimental testing of the levitating system with starting and disturbance, it is proved that the levitating control system of the maglev ruler has good dynamic characteristics, static characteristics, and robustness.
Keywords: 
Subject: Engineering  -   Chemical Engineering

1. Introduction

The two functions of the maglev ruler(MR), autonomous displacement and displacement measurement, are completed by its mover core (MC) [1]. This MC adopts a step-by-step autonomous displacement [1]. Each step length is the scale of the MR [1]. While performing autonomous displacement, the displacement is converted into a pulse quantity, which is sent to the CPU to complete displacement measurement. Obviously, the stability of the step length improves the precision of the maglev rule [1]. According to Newton's second law of motion, the stability of the thrust force applied to the MC determines the stability of the step length. The stability of the magnetic field in air gaps and the current of the horizontal control coil determine the stability of the thrust force [1,2]. This paper mainly studies how to improve the stability of the magnetic field in air gaps through the levitating control system of the MR.
The maglev ball system can be used as an experimental device to verify the maglev control method [22]. Its working principle is to generate magnetic force through electromagnets to balance the gravity of the ball. Therefore, the ball is stably levitated at the equilibrium point. The coil current of the electromagnet determines the levitating position of the ball [3]. Victor [4] et al. discussed the role of DCDC in magnetic suspension systems and verified the feasibility of a magnetic suspension positioning system included PID algorithm for a maglev ball as the research object. Debdoot Sain [5] proposed a maglev positioning system based on a 2-DOF PID controller, which was used for the positioning of maglev balls [5]. Aysen [6] et al. proposed an opposing artificial electric field algorithm (OBAEFA), which was used in the adjustment of fractional order PID (FOPID) control systems [6]. FOPID was used in the maglev ball positioning system [6]. The OBAEFA is an upgraded version of the AEFA algorithm, using an opposing learning strategy to enhance the search capabilities of the AEFA algorithm [6]. The experimental results verified the superiority of OBAEFA [6]. In the maglev ball positioning system, the OBAEFA was used to debug FOPID, which optimized the transient response of the positioning system by minimized an optimization objective function with a simple structure [7]. T. Deepa [8] compared and analyzed the control performance of PID controller and LQR controller [8]. It proved that the use of LQR controllers improved the performance of maglev systems [8]. S. Pandey [9,10,11] studied how to apply the fractional-order sliding mode controllers in maglev ball positioning systems [9,10,11]. Rahul Sanmugam Gopi et al. [12] proposed an new adaptive control method for ball position controller to improved maglev systems [23]. The method included proportional integral speed plus feed forward in control structure, and used a modified version of the standard tuning rule as the adaptive mechanism [12]. The control method was applied to the maglev ball positioning system [23]. Kim S. K. et al. [13] studied a sensorless nonlinear controller for maglev ball positioning systems [13]. Massive studies have revealed the characteristics of the magnetic field in air gap of the maglev ball and the control method for the levitating position of the maglev ball, providing a reference for the study of the levitating system of the MC of the MR in this paper. Zhou Zhenxiong et al. [14] studied the levitating system of the TU-type maglev platform [14]. The four basic levitation magnetic loops of the TU-type maglev platform are the same as those of the MR [14]. The T-shaped mover of the TU-type maglev platform has three ends [14]. There are two air gaps between each end and the stator yoke, an upper air gap and a lower air gap [14]. The magnetic flux in the upper and lower air gaps determines the force on the ends where they are located, controlling the levitation height of the ends [14]. The magnetic flux in the air gap can also be divided into two parts, one from the permanent magnet and the other from the levitating control coil [14]. The magnetic flux emitted by the levitating control coil is related to the current of the levitating control coil [14]. Therefore, the magnetic flux emitted by the levitating coil can adjust the size of the air gap flux, thus achieving stable levitation of the T-shaped mover [14]. However, the TU-type maglev platform uses one coil to control the upper and lower air gap fluxes at one end, which cannot solve the simultaneous asynchronous interference in the two air gap fluxes [14]. In addition, due to the use of one control coil to adjust the magnetic flux in the upper and lower air gaps, there is a commutation problem in the current of the control coil [14]. The control coil is an inductance and an energy storage element [14]. During current commutation, there is a transition process, causing the current in the control coil to have a turning point at the commutation point [14]. The current in the control coil is not proportional to time at the commutation point. The MR establishes four levitating control magnetic loops [1]. The magnetic flux of each magnetic loop can be independently controlled, eliminating the need for current commutation of the levitating coil, eliminating the inflection point, and allowing independent control of the magnetic flux in each air gap [1]. The working principle of the levitating system of the MR is analyzed and a mathematical model of the levitating system is established in this paper. The levitating system uses an active disturbance rejection control (ADRC) control algorithm to stabilize the levitation position of the MC, while also stabilizing the magnetic field in air gaps.
The structure of this paper is as follows: In the second part, this paper analyzes the characteristics of the maglev system of the MR and establishes a mathematical model. In the third part, this paper designs a maglev control system based on ADRC according to the characteristics of the maglev system of the MR, and conducts simulation analysis on the maglev control system. In every fourth part, this paper conducts experimental testing on the maglev control system.
The organization of this paper is as follows. In Section II, The characteristics of the maglev system of the MR are analyzed, and a mathematical model is established. In Section III, according to the characteristics of the maglev system, a levitating control system based on ADRC was designed, and a simulation analysis of the levitating control system was conducted. In Section IV, an experimental test was conducted on the levitating control system. Finally, conclusions are presented in Section V.

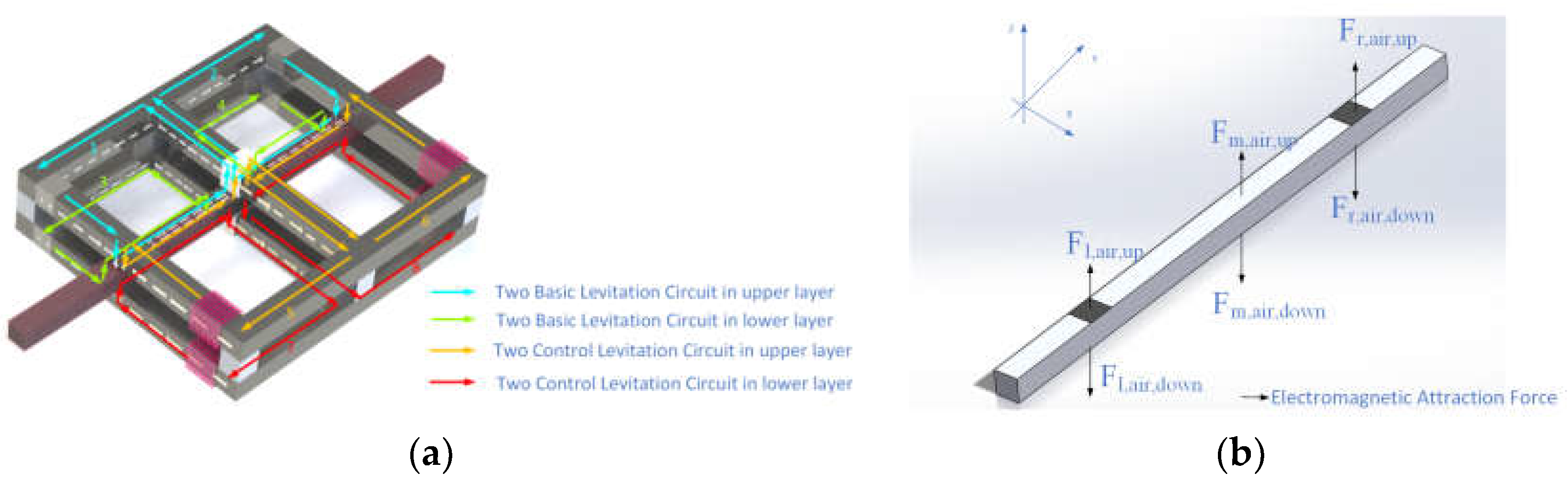
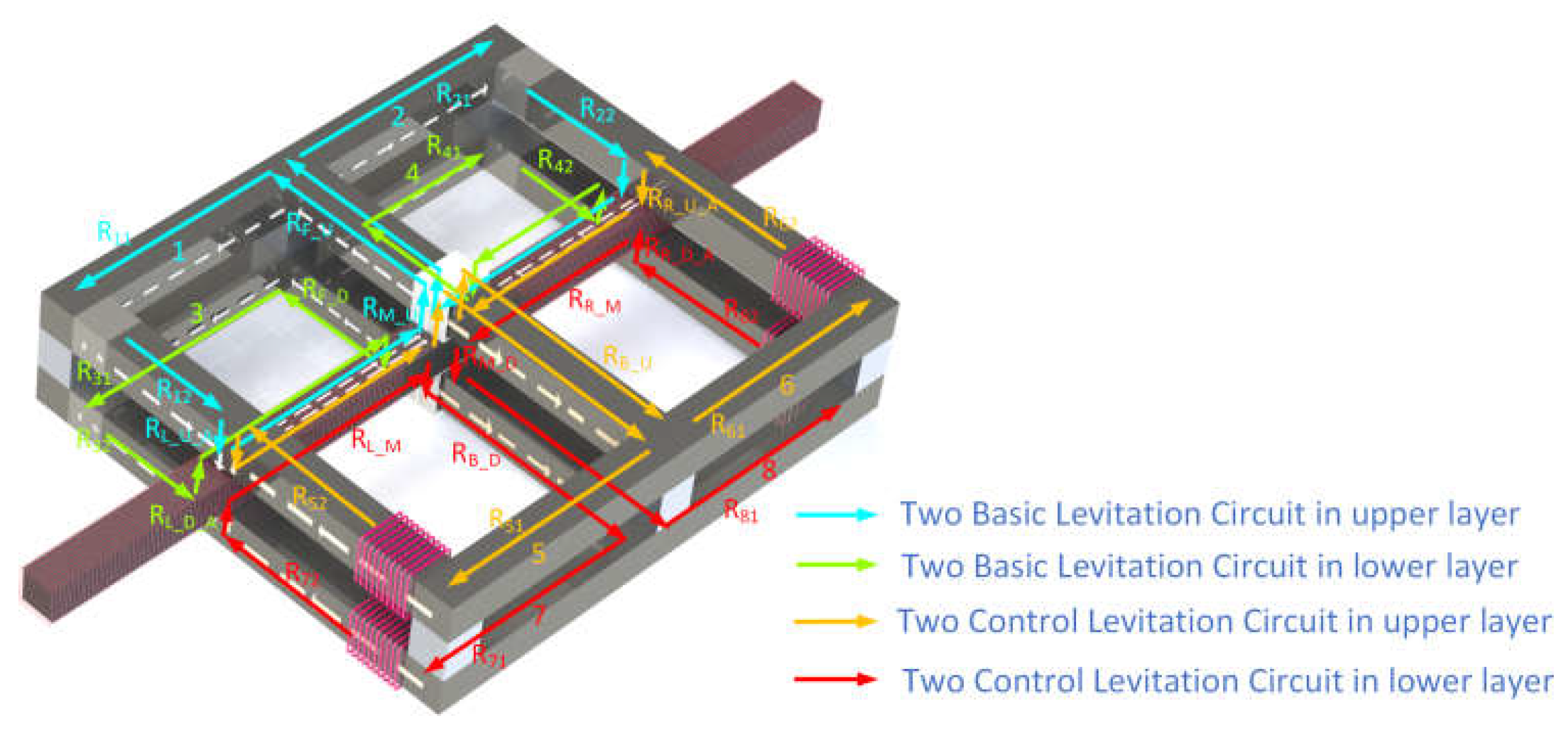
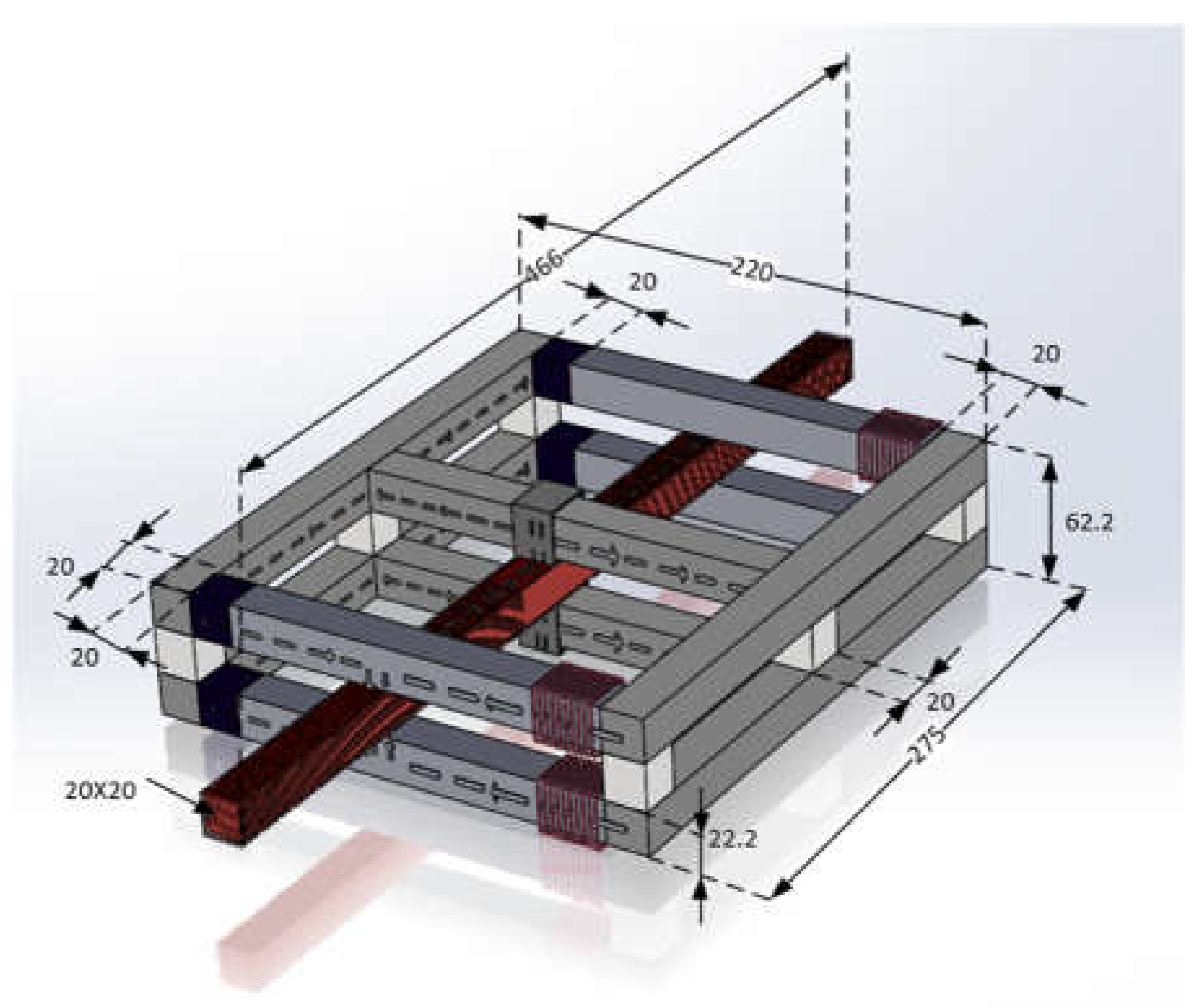
2. Analysis Model of Levitating Force

The MR uses four permanent magnets to provide bias magnetic fields for the six air gaps of the system. The magnetic field strength of the four permanent magnets was analyzed using finite element analysis, and their average values were:
Average magnetic field intensity: HBM=265×103A/m.
The average magnetic potential of permanent magnets: Vm=HBM∙lBM=2650A.
The MR system chooses four permanent magnets of the same size, so the magnetic field strength of the four permanent magnets can also be considered to be the same.
There are two types of magnetic levitating loops: the first is a basic levitating loop based on permanent magnets, which produces bias magnetic fields in the air gap; the second is a control levitating loop based on levitating coils, which produces control magnetic fluxes. During the operation of the MR, its MC is in a magnetic saturation state. Therefore, there must be significant magnetic losses and magnetic leakage in the magnetic loop, and two types of leakage coefficients need to be introduced to compensate for the air gap reluctance model.
The two magnetic leakage coefficients are:
σBM is the leakage factor of the basic levitating loop;
σCM is the leakage factor of the control levitating loop.
The levitating force of the MC comes from three parts: the electromagnetic suction force on the left support, the right support, and the center point. The schematic diagram of the electromagnetic suction force on the magnetic loop and the MC is shown in Figure 1.

2.1. Analysis Model of Buoyancy Force

The MR is divided into three parts, the left, right, and middle, as shown in the right figure of Figure 1. The levitating force in the middle is affected by the levitating forces on the left and right, and these levitating forces are similar. Therefore, this paper first studies the levitating force using the left levitating force as an example.
The second figure in Figure 1 also indicates the electromagnetic suction force acting on the MC. The resultant force of the upper and lower electromagnetic suction forces on the MC is the left levitating force[1]:
F l e f t = F l _ a i r _ u p − F l _ a i r _ d o w n
where Fleft is the levitating force on the left end of MC, Fl_air_up is the upward electromagnetic suction force on the left end of MC, and Fl_air_down is the downward electromagnetic suction force on the left end of MC.
According to the electromagnetic suction force calculation equation [15]:
F R = − 1 2 φ 2 μ 0 ⋅ A
where μ0 is the permeability of the air gap; A is the area of the pole surface, which is vertical intersection of U-shaped conductor and the MC, i.e., the black area on the MC in the right figure of Figure 1. Therefore, the electromagnetic suction force FR is proportional to the square of the magnetic flux φ [1].
There are eight magnetic loops on the MR, which are numbered as shown in the left figure of Figure 1. The magnetic fluxes of the loop 1 to loop 8 magnetic loops are respectively: φ1, φ2, φ3, φ4, φ5, φ6, φ7, and φ8. Among them, φ1, φ2, φ3, and φ4 are the magnetic fluxes of the basic levitating loop; φ5, φ6, φ7, and φ8 are the magnetic fluxes of the control levitating loop [1].
As shown in the upper figure of Figure 1 [1], the magnetic flux in the upper air gap on the left support is the sum of the magnetic flux of the base levitating loop and the control levitating loop, and both directions are downward [1]. Therefore, the calculation equation for the magnetic flux in the upper air gap on the left support is [16]:
φ l _ u p _ a i r = φ 1 + φ 5
Similarly, the magnetic flux in the lower air gap of the left support is also the sum of the magnetic flux of the base levitating loop and the control levitating loop, and both directions are upward [1]. Therefore, the calculation equation for the magnetic flux in the lower air gap of the left support is [16]:
φ l _ d o w n _ a i r = φ 3 + φ 7
The total magnetic flux of the air gap in the upper part of the left support is start from the left upper permanent magnet and the left upper levitating coil. According to Hopkinson’s law [16]:
φ = V R
Where V represents the magnetic potential and R represents the magnetic resistance.
As can be seen from Figure 1, the structures of the eight levitation magnetic loops are similar, consisting of permanent magnets or levitating coils and six magnetic conductors. For ease of calculation, a label is assigned to the magnetic resistance of each magnetic conductor, as shown in Figure 2.
As shown in Figure 2, the MR has 28 magnetic resistors, including R11, R12, R21, R22, R31, R32, R41, R42, R51, R52, R61, R62, R71, R72, R81, R82, RM_U, RM_D, RF_U, RF_D, RB_U, RB_D, RL_M, RR_M, RL_U_A, RL_D_A, RR_U_A, RR_D_A. The air gap length of the MR can also be divided into two parts: the nominal air gap length and the coil air gap length occupied by the coil. In addition, due to the different leakage coefficients of the basic levitating loop and the control levitating loop [1], RM_U, RM_D, RL_U_A, RL_D_A, RR_U_A, RR_D_A can also be decomposed into RM_U_B, RM_U_C, RM_D_B, RM_D_C, RL_U_A_B, RL_U_A_C, RLCU_U, RL_D_A_B, RL_D_A_C, RLCU_D.
The known equation for calculating the magnetoresistance is as follows [17]:
R = 1 μ A
According to the dimensions of the components of the MR shown in Figure 3 [1], combined with the magnetic resistance calculation equation (6) and the finite element analysis results, the following magnetic resistance calculation equations can be obtained:
R 11 = R 21 = R 31 = R 41 = l h μ h _ f A = 0.14 6.93 × 10 − 5 × 0.02 × 0.02 = 5.06 × 10 6 H / m
R 51 = R 61 = R 71 = R 81 = l h μ h _ b A = 0.14 2.1 × 10 − 4 × 0.02 × 0.02 = 1.67 × 10 6 H / m
R L _ M = R R _ M = l h μ h _ m A = 0.14 9.31 × 10 − 5 × 0.02 × 0.02 = 3.76 × 10 6 H / m
R 12 = R 22 = R 32 = R 42 = l s _ y 0 − y μ b _ s A = 0.07 − y 7.39 × 10 × − 4 0.02 × 0.02 = 0.07 − y 2.96 × 10 7 H / m
R 52 = R 62 = R 72 = R 82 = l s _ y 0 + y μ c _ s A = 0.07 + y 5.97 × 10 − 4 × 0.02 × 0.02 = 0.07 + y 2.39 × 10 7 H / m
R F _ D = R F _ U = l m _ y 0 − y μ f _ m A = 0.09 − y 4.54 × 10 − 4 × 0.02 × 0.02 = 0.09 − y 1.82 × 10 7 H / m
R B _ D = R B _ U = l m _ y 0 + y μ b _ m A = 0.09 + y 5.36 × 10 − 4 × 0.02 × 0.02 = 0.09 + y 2.14 × 10 7 H / m
R L _ U _ A _ B = ( l A − z l ) μ a i r A σ B M = ( 6.2 × 10 − 4 − z l ) 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ B M = ( 6.2 × 10 − 4 − z l ) 5.03 × σ B M × 10 10 H / m
R L _ D _ A _ B = ( l A + z l ) μ a i r A σ B M = ( 6.2 × 10 − 4 + z l ) 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ B M = ( 6.2 × 10 − 4 + z l ) 5.03 × σ B M × 10 10 H / m
R R _ U _ A _ B = ( l A − z r ) μ a i r A σ B M = ( 6.2 × 10 − 4 − z r ) 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ B M = ( 6.2 × 10 − 4 − z r ) 5.03 × σ B M × 10 10 H / m
R R _ D _ A _ B = ( l A + z r ) μ a i r A σ B M = ( 6.2 × 10 − 4 + z r ) 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ B M = ( 6.2 × 10 − 4 + z r ) 5.03 × σ B M × 10 10 H / m
R L _ U _ A _ C = ( l A − z l ) μ a i r A σ C M = ( 6.2 × 10 − 4 − z l ) 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ C M = ( 6.2 × 10 − 4 − z l ) 5.03 × σ C M × 10 10 H / m
R L _ D _ A _ C = ( l A + z l ) μ a i r A σ C M = ( 6.2 × 10 − 4 + z l ) 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ C M = ( 6.2 × 10 − 4 + z l ) 5.03 × σ C M × 10 10 H / m
R R _ U _ A _ C = ( l A − z r ) μ a i r A σ C M = ( 6.2 × 10 − 4 − z r ) 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ C M = ( 6.2 × 10 − 4 − z r ) 5.03 × σ C M × 10 10 H / m
R R _ D _ A _ C = ( l A + z r ) μ a i r A σ C M = ( 6.2 × 10 − 4 + z r ) 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ C M = ( 6.2 × 10 − 4 + z r ) 5.03 × σ C M × 10 10 H / m
R M _ U _ B = ( 2 l A − z l − z r ) 2 μ a i r A σ B M = ( 1.24 × 10 − 3 − z l − z r ) 2 × 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ B M = ( 1.24 × 10 − 3 − z l − z r ) 1.01 × σ B M × 10 9 H / m
R M _ U _ C = ( 2 l A − z l − z r ) 2 μ a i r A σ C M = ( 1.24 × 10 − 3 − z l − z r ) 2 × 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 × σ C M = ( 1.24 × 10 − 3 − z l − z r ) 1.01 × σ C M × 10 9 H / m
R M _ D _ B = ( 2 l A + z l + z r ) σ B M 2 μ a i r A = ( 1.24 × 10 − 3 + z l + z r ) ⋅ σ B M 2 × 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 = ( 1.24 × 10 − 3 + z l + z r ) ⋅ σ B M 1.01 × 10 9 H / m
R M _ D _ B = ( 2 l A + z l + z r ) σ B M 2 μ a i r A = ( 1.24 × 10 − 3 + z l + z r ) ⋅ σ B M 2 × 1.00000036 × 0.02 × 0.02 × 4 π × 10 − 7 = ( 1.24 × 10 − 3 + z l + z r ) ⋅ σ B M 1.01 × 10 9 H / m
R L C U _ U _ B = R L C U _ D _ B = R R C U _ U _ B = R R C U _ D _ B = l C U μ C U A σ B M = 4.8 × 10 − 4 0.9999903 × 0.02 × 0.02 × 4 π × 10 − 7 × σ B M = 9 . 55 × 10 5 σ B M H / m
R L C U _ U _ C = R L C U _ D _ C = R R C U _ U _ C = R R C U _ D _ C = l C U μ C U A σ C M = 4.8 × 10 − 4 0.9999903 × 0.02 × 0.02 × 4 π × 10 − 7 × σ C M = 9.55 × 10 5 σ C M H / m
where lh is the length of loops 1, 2, 3, and 4 on the T-shaped conductor arm, and the length of loops 5, 6, 7, and 8 on the bottom of the U-shaped conductor. Ls_y0 is the length of the eight magnetic loops on the U-shaped conductor side arm when the MC is in its center position [1]. Lm_y0 is the length of the eight magnetic loops on the T-shaped conductor vertical arm [1]. LA is the length of each air gap when the MC is in the center position [1]. LCU is the diameter of copper wire [1]. Y is the offset of the MC on the Y axis [1]. Zl is the upward offset of the left end of the MC [1]. Zr is the upward offset of the left support of the MC [1].
After setting the magnetic leakage coefficients σBM=6 and σCM=3, the equation calculates the magnetic flux of eight magnetic loops from equations (8) to (27). This paper takes magnetic loop 1, magnetic loop 5 as examples to analyze the calculation method of the magnetic flux of each magnetic loop [1].
As shown in Figure 2, the magnetic flux of the loop 1 starts from the permanent magnet, travels along the left arm of the U-shaped magnetic conductor, the MC, the vertical arm of the T-shaped magnetic conductor, and then returns to the permanent magnet [1]. According to equation (5), the magnetic flux of the 1 magnetic loop is the ratio of the average magnetic potential of the permanent magnet to the total magnetic resistance of the loop 1. Let the total magnetic resistance of the loop 1 be R1C. The equation for calculating the total magnetic resistance is as follows:
R 1 C = R 11 + R 12 + R L _ U _ A _ B + R L C U _ U _ B + R L _ M + R M _ U _ B + R F _ U
Substituting the average magnetic potential Vm and R1C into equation (5), we can obtain the magnetic flux of the loop 1 φ1:
φ 1 = V m R 1 C = 1 3.81 × 10 3 − 3 . 35 × 10 3 × y − 1 . 8 9 × 10 5 × z l − 6 . 23 × 10 4 × z r
The magnetic flux of the loop 5 starts from the levitating coil, follows the left arm of the U-shaped magnetic conductor, the MC, the vertical arm of the T-shaped magnetic conductor, and then reaches the bottom of the U-shaped magnetic conductor, and finally returns to the levitating coil [1]. According to equation (5), the magnetic flux of the loop 5 is the ratio of the magnetic potential of the levitating coil to the total magnetic resistance of the loop 5. Let the total magnetic resistance of the loop 5 be R5C. The calculation equation for total magnetic resistance is as follows:
R 5 C = R 51 + R 52 + R L _ U _ A _ C + R L C U _ U _ C + R L _ M + R M _ U _ C + R B _ U
Substituting the magnetic potential of the levitating coil and R5C into equation (5), we can obtain the magnetic flux of the loop 5 φ5:
φ 5 = N i 1 R 5 C = i 1 2.26 × 10 4 + 2.78 × 10 4 × y − 3.07 × 10 6 × z l − 1.02 × 10 6 × z r
Where N is the number of windings of the upper left levitating coil, which is 47[1]. Where i1 is the current of the upper left levitating coil [1]. Substituting equations (29) and (31) into equation (3), the magnetic flux in air gap on the upper left side of the MC can be calculated as follows:
φ l _ u p _ a i r = φ 1 + φ 5 = 1 3.81 × 10 3 − 3 . 35 × 10 3 × y − 1 . 8 9 × 10 5 × z l − 6 . 23 × 10 4 × z r + i 1 2.26 × 10 4 + 2.78 × 10 4 × y − 3.07 × 10 6 × z l − 1.02 × 10 6 × z r
It can be seen from equation (32) that the upper left magnetic flux in air gap is controlled by the levitating coil current of the loop 5 [1]. At the same time, the horizontal position and upward offset of the MC also affect the magnetic flux in air gap, which can be seen as external interference.
According to the above calculation method, the magnetic fluxes φ3 and φ7 of the loop 3 and loop 7 can be obtained. Then, according to equation (4), φl_down_air can be calculated. Finally, combining equations (1) and (2), the equation of the left levitating force of the MC can be obtained:
F l e f t = − ( φ 2 l _ a i r _ u p − φ 2 l _ a i r _ d o w n ) 2 μ 0 ⋅ A = − 9.95 × 10 8 [ ( 1 3.81 × 10 3 − 3 . 35 × 10 3 × y − 1 . 8 9 × 10 5 × z l − 6 . 23 × 10 4 × z r + i 1 2.26 × 10 4 + 2.78 × 10 4 × y − 3.07 × 10 6 × z l − 1.02 × 10 6 × z r ) 2 − ( 1 3.81 × 10 3 − 3 . 35 × 10 3 × y + 1 . 8 9 × 10 5 × z l + 6 . 23 × 10 4 × z r + i 3 2.26 × 10 4 + 2.78 × 10 4 × y + 3.07 × 10 6 × z l + 1.02 × 10 6 × z r ) 2 ]
Similarly, the equation of the levitating force of the right side of the MC can be obtained:
F r i g h t = − ( φ 2 r _ a i r _ u p − φ 2 r _ a i r _ d o w n ) 2 μ 0 ⋅ A = − 9.95 × 10 8 [ ( 1 3 . 81 × 10 3 − 3 . 35 × 10 3 × y − 6.23 × 10 4 × z l − 1.89 × 10 5 × z r + i 2 2.26 × 10 4 + 2.78 × 10 4 × y − 1.02 × 10 6 × z l − 3.07 × 10 6 × z r ) 2 − ( 1 3 . 81 × 10 3 − 3 . 35 × 10 3 × y + 6.23 × 10 4 × z l + 1.89 × 10 5 × z r + i 4 2.26 × 10 4 + 2.78 × 10 4 × y + 1.02 × 10 6 × z l + 3.07 × 10 6 × z r ) 2 ]
As can be seen from equations (33) and (34), the levitating forces on both sides of the MC are related to the MC plane position y and the upward offset of the MC [1]. Next, this paper will discuss these characteristics.

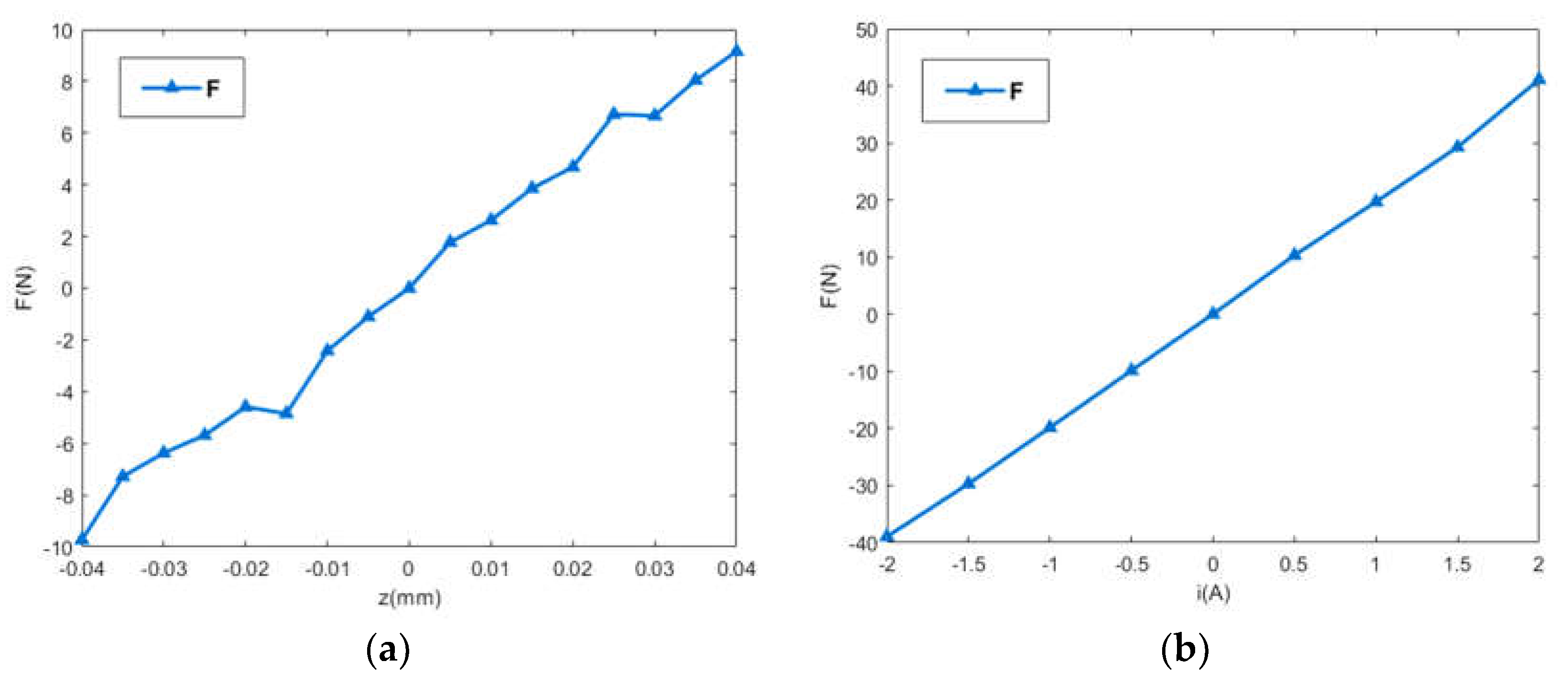
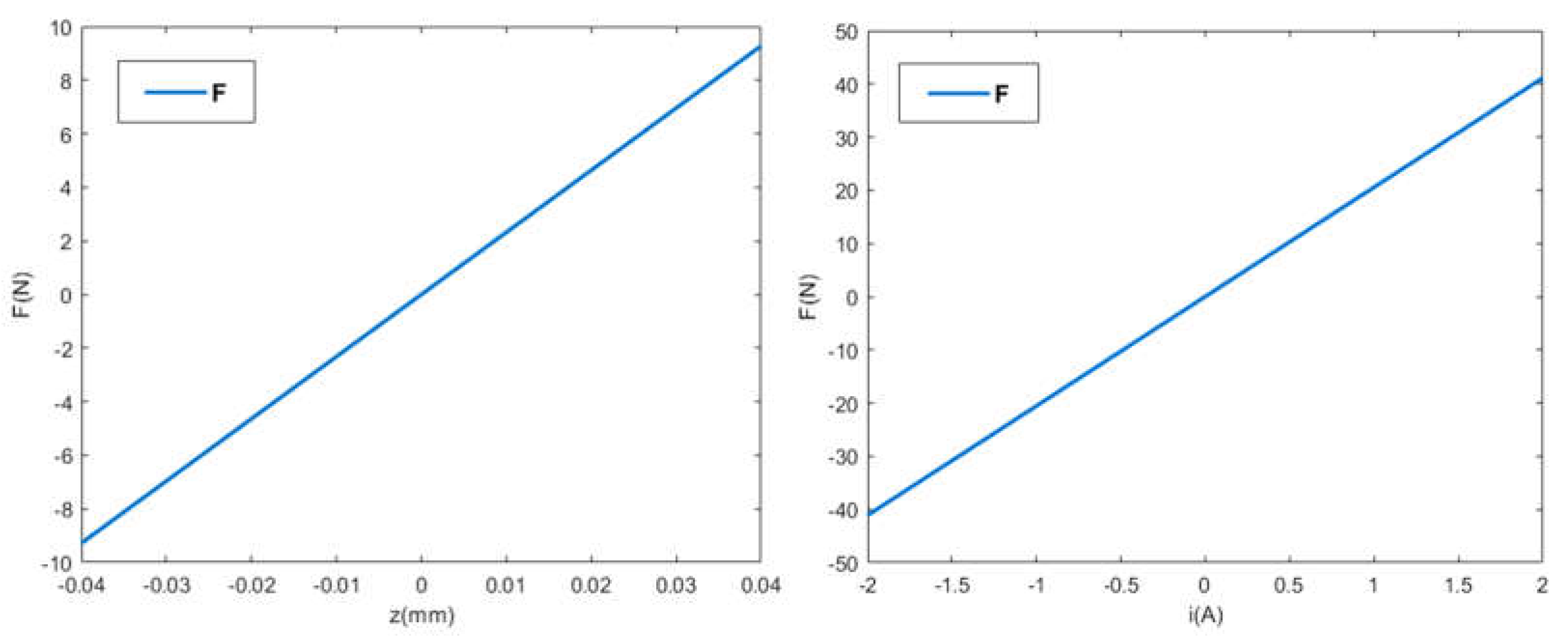
2.2. The Correlation between the Levitating Force and the Levitating Position of the MC

From equations (33) and (34), it can be seen that the levitating force is related to both the upward offset of the MC and the planar position of the MC [1].
Let the current of the levitating coil be zero and the plane position y=0 [1], then equations (33) and (34) can be transformed into:
F l e f t = − ( 1 0.1206 − 5.981 z l − 1.9715 z r ) 2 + ( 1 0.1206 + 5.981 z l + 1.9715 z r ) 2
F r i g h t = − ( 1 0.1206 − 1.9715 z l − 5.981 z r ) 2 + ( 1 0.1206 + 1.9715 z l + 5.981 z r ) 2
From equations (34) and (35), it can be seen that there is a cross-coupling between the levitating force on both sides of the MC and its upward offset.
When the left side of the MC moves upward, its left upward offset zl increases, and the length of the upper left air gap decreases, which also decreases the length of the middle upper air gap, but the decrease is less than that of the left upper air gap. The decrease in two air gaps results in a decrease in two magnetic resistances. Since the magnetic potentials of each magnetic loop remain unchanged, the magnetic fluxes of both loops increase, which is the increase in magnetic flux of loop 1 and loop 2, resulting in an increase in electromagnetic suction force on the upper left side [1]. The decrease in the upper left air gap and the increase in the length of the lower left air gap result in an increase in the magnetic resistance of the lower left air gap, which reduces the magnetic flux of loop 3, resulting in a decrease in electromagnetic suction force on the lower left side. Since the left levitating force Is the sum of the upper electromagnetic suction force and the lower electromagnetic suction force on the left MC, an increase in zl on the left side will result in an increase in levitating force on the left side [1]. At the same time, an increase in magnetic flux of loop 2 results in an increase in electromagnetic suction force on the upper right side, while at this time, the length of the middle lower air gap and the left lower air gap increases, and magnetic flux of loop 3 decreases, resulting in a decrease in electromagnetic suction force on the lower right side. Therefore, the levitating force on the right side also increases upward. Since the upward offset zr of the MC is less than that of the left side, zl has a greater impact on the levitating force on the left side than on the right side. Similarly, zr also has an impact on the levitating force on both sides of the MC. The influence of zr on the right side levitating force is greater than that on the left side. Therefore, it can be seen that there is a strong coupling between the levitating forces on both sides of the MC and their upward offsets.
From equations (32) and (33), it can be seen that the levitating forces on both sides of the MC are affected by the planar position y of the MC. From equations (10), (11), (12), and (13), it can be seen that changes in the planar position y of the MC cause some changes in magnetic resistance, resulting in changes in the magnetic flux of the eight magnetic loops, which ultimately lead to changes in the levitating forces on both sides of the MC.
The Instantaneous upward offset and plane position changes of the MC can cause changes In relative magnetic permeability, but this is not included in the analytical model. To increase the precision of the model, it is necessary to use the actual curve instead of using a linear approximation curve. However, this also increases the complexity of the analytical model and introduces more uncertainties.
The permanent magnet in the MR causes the magnetic loop to be in a magnetic saturation state, so that the magnetization point is only slightly affected by the upward shift and plane position changes of the MC. Therefore, the change in the relative magnetic permeability of the MR is also very small, and can be almost ignored in engineering.

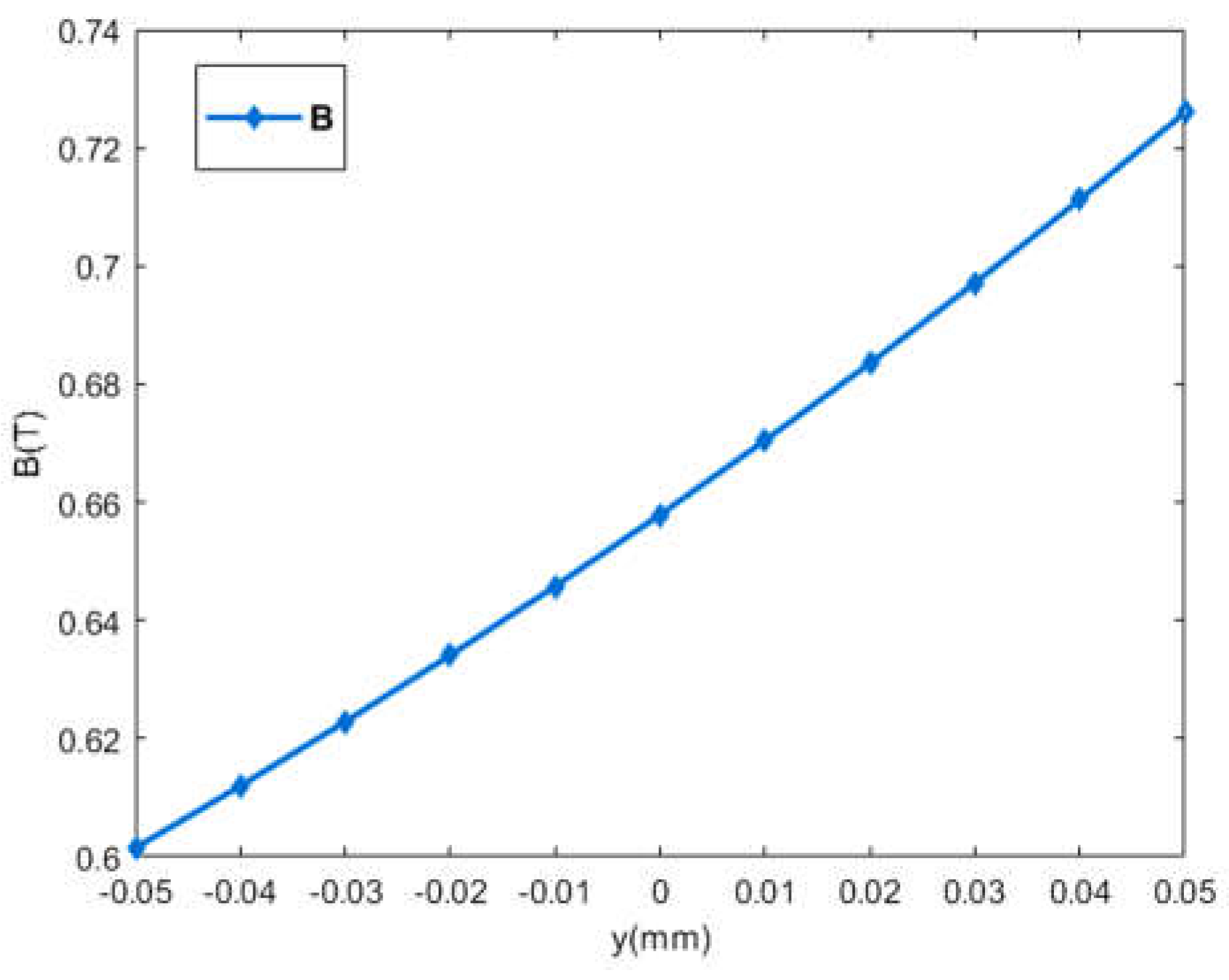
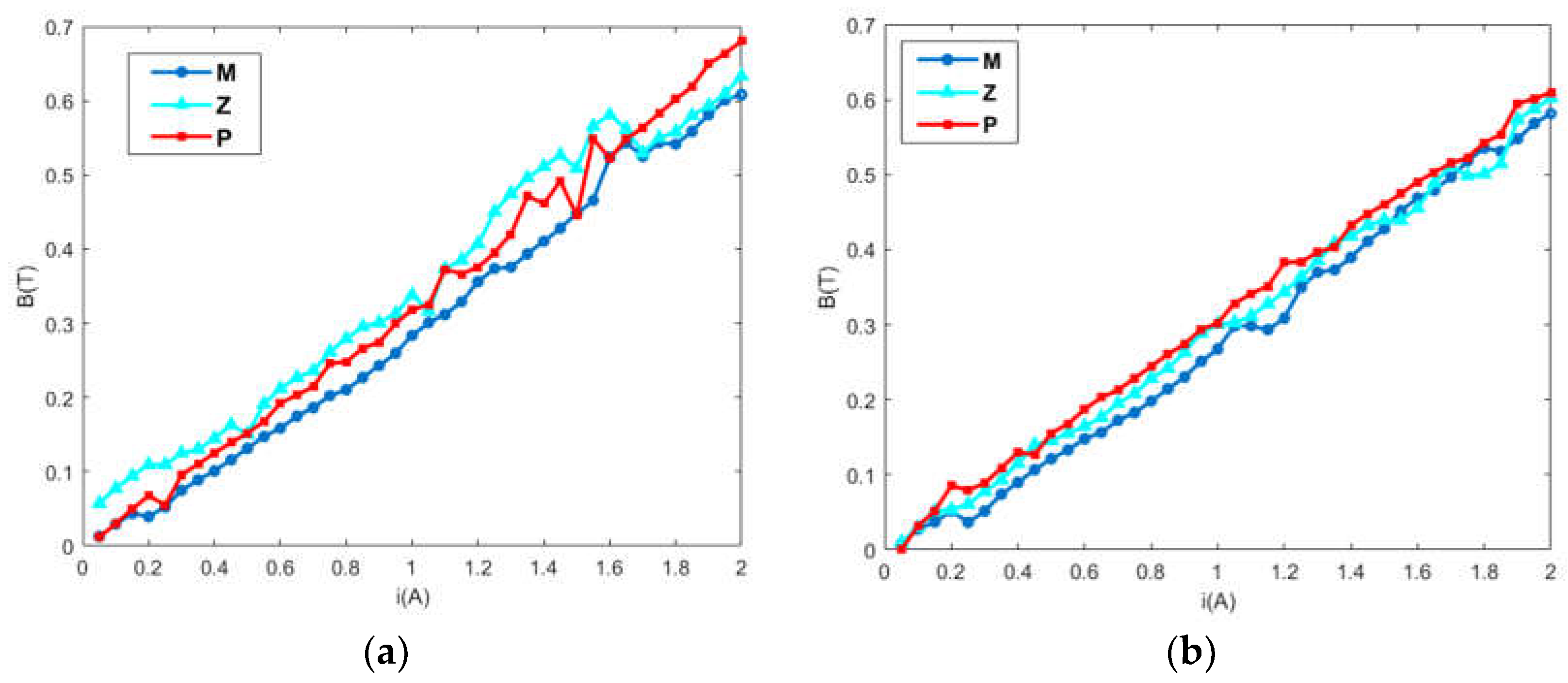
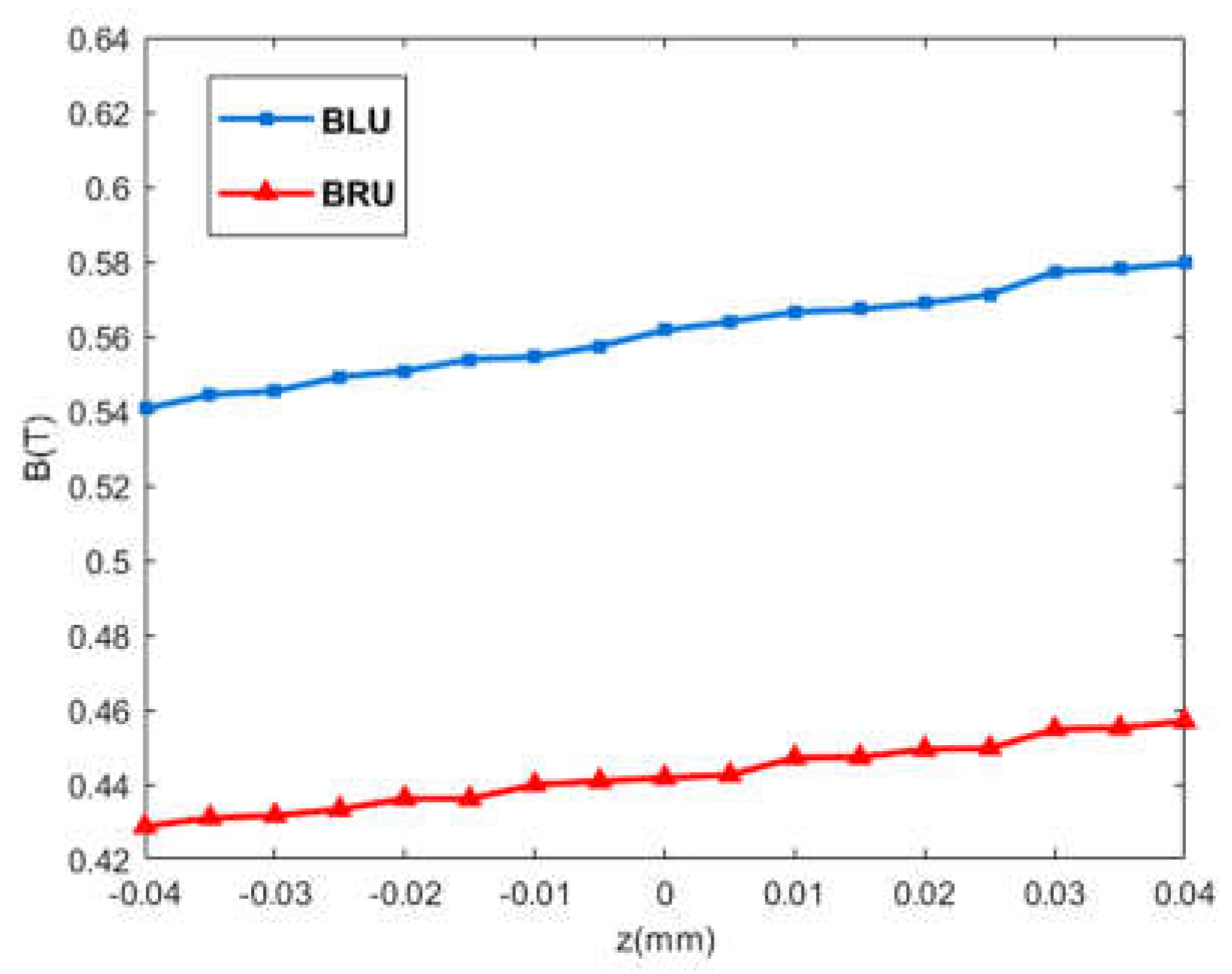
2.3. Verification of the Levitating Force Model and Magnetic Flux Leakage Parameters

It can be seen from the experiment that the change in the planar position of the MC will cause changes in the air gap flux. From equation (32), it can be seen that the air gap flux is the sum of the base levitating loop flux and the control levitating loop flux [1]. In order to study the relationship between the planar position of the MC and the magnetic flux in air gaps, we can set i1=0A, zl=zr=0m, and substitute it into equation (32), which can be calculated as follows:
φ l _ u p _ a i r = 1 1.52 × 10 4 − 2.85 y × 10 4
By testing a corresponding set of air gap flux density values from y=-0.05m to y=0.05m, a relationship curve between the plane position y and the air gap flux density was plotted, as shown in Figure 4.
When passing a current i1=0~2A through the upper left levitating coil, a set of upper left air gap flux density values was measured, and the relationship between the i1 and the magnetic flux in upper left air gap was plotted, as shown in Figure 5a.
When passing a current i3=0~2A through the upper right levitating coil, a set of upper right air gap flux density values were measured, and the relationship between the i3 and the magnetic flux in upper right air gap was plotted, as shown in Figure 5b.
The three colored lines in the figure, M, Z, and P, are data measured at the negative limit position, zero position, and positive limit position of the MC plane position.
The MC is temporarily fixed to the z-direction micro-motion platform, and adjust the height of the MC. The resolution of the z-direction micro-motion platform is 5μm. The relationship between the height change of the MC and the air gap flux density can be detected. The detection conditions are that the current of the horizontal thrust coil i=0A, and zl=zr. The detection results are shown in Figure 6.
The BLU curve in the figure is the relationship between the magnetic flux in upper left air gap and the levitation position of the MC; the BRU curve is the relationship between the magnetic flux in upper right air gap and the levitation position of the MC. From Figure 6, it can be seen that changes in the air gap on the upper part of the MC will lead to changes in air gap flux density.
Static force detection still requires a z-direction micro-motion platform, with the MC temporarily fixed on the platform. A force sensor is added between the MC and the platform to detect the force applied to the MC.
During the detection process, the MC is first placed at the center of the plane, that is, at the plane position y=0, to ensure uniformity of detection. Secondly, the levitating positions of the left and right ends of the MC are ensured to be the same, that is, zl=zr. Under the action of the magnetic field, if the levitation positions of the left and right ends of the MC are not the same, the levitating forces on the left and right ends of the MC will cross-couple and affect each other seriously.
Figure 7 shows the relationship between z and Fleft, as well as ia and Fleft. Ia=i3-i1.
Next, the estimated values of the magnetic flux leakage system and the levitating force model are verified
The equation (33) is obtained after substituting the leakage factor σBM=6 of the basic levitation magnetic loop and controlling the leakage factor σCM=3 of the levitation magnetic loop. The equation before substitution is as follows:
F l e f t = − ( φ 2 l _ a i r _ u p − φ 2 l _ a i r _ d o w n ) 2 μ 0 ⋅ A = − 9.95 × 10 8 [ ( 2650 9.56 × 10 6 + 3.42 × 10 6 σ B M − ( 8.87 × 10 6 × y + 2.98 × 10 9 × z l σ B M + 0.99 × 10 9 × z r σ B M ) + N i 1 6.14 × 10 6 + 3.42 × 10 6 σ C M + 8.94 × 10 6 × y − 2.98 × 10 9 × z l σ C M − 0.99 × 10 9 × z r σ C M ) 2 − ( 2650 9.56 × 10 6 + 3.42 × 10 6 σ B M − 8.87 × 10 6 × y + 2.98 × 10 9 × z l σ B M + 0.99 × 10 9 × z r σ B M + N i 3 6.14 × 10 6 + 3.42 × 10 6 σ C M + 8.94 × 10 6 × y + 2.98 × 10 9 × z l σ C M + 0.99 × 10 9 × z r σ C M ) 2 ]
In equation (38), y=0, i1=i3=0, and zl=zr=z. Then equation (38) can be seen as Fleft=f(z, σBM). Combining with Figure 8(a), the least squares method can be used to estimate σBM =6.1326. In addition, the leakage factor of the base levitation magnetic loop can also be estimated by using Figure 4 and the calculation equation for the magnetic flux φ1 of the No. 1 magnetic loop. The estimated values obtained by the two methods are basically equal.
Then, substitute σBM=6.1326 into equation (38), set y=0, zl=zr=0, and set ia=i3-i1. Equation (38) can be seen as Fleft=f(ia, σBM), and then combined with Figure 7(b), using the least squares method, can be estimated that σCM=2.8765.
Substituting the estimated leakage factor of the base levitating loop and the control levitating loop into equation (38), the relationship between z and Fleft can be obtained, as shown in Figure 8(a), as well as the relationship between ia and Fleft, as shown in Figure 8(b).

2.4 Dynamic Model of Levitating System

According to the analysis of electromagnetic suction force in Figure 1, the MC has two degrees of freedom in the levitating system: 1) vertical motion in the z direction; 2) rotation around the y axis with the center of mass of the MC as the center of rotation, denoted by ψ. This paper uses Newton's second law of motion to describe the vertical motion of the MC; and uses the torque equation to describe the rotational motion of the MC [18].
F = m ⋅ ∂ 2 z a ∂ t 2
M α = J α ⋅ ∂ 2 α ∂ t 2
In equation (39), F is the sum of all forces on the MC in the z direction, m is the mass of the MC, and za is the displacement of the mass center of the MC in the z direction. In equation (40), Mα is the torque of the resultant force of F, Jα is the moment of inertia, and α is the rotation angle. Figure 9 shows the position of the mass center, the force points of the levitating forces on the left and right ends of the MC, and the length of the arm of force.
J α = m h r 2
In equation (41), mh is the mass of the mass center of the MC to the end, and r is the distance from the mass center to the point of action of the levitating force. From this, Jα can be calculated: Jα=1.49×10-2kg∙m2. Ignoring other disturbances, such as base vibration and horizontal thrust, the sum of all forces on the MC in the z direction is:
F = − F g + F l e f t + F r i g h t
In equation (42), Fg=mg=17.93N is the gravity force on the MC. From the dimensions indicated in Figure 9, the moment equation around the y-axis is as follows:
M α = − 0.1275 F l e f t + 0.1275 F r i g h t
According to equation (40), a new equation can be obtained:
− 0.1275 F l e f t + 0.1275 F r i g h t = J α ⋅ ∂ 2 ψ ∂ t 2
From equations (39) and (42), a new equation can be obtained:
F l e f t + F r i g h t − F g = m ⋅ ∂ 2 z a ∂ t 2
Thus, the rigid body dynamics equation of the MC is obtained:
1 1 − 0.1275 0.1275 ⋅ F l e f t F r i g h t + 17.93 0 = 1.83 0 0 0.0273 ∂ 2 z a ∂ t 2 ∂ 2 ψ ∂ t 2
From equations (33) and (34), it can be seen that Fleft and Fright are related to zl and zr, which are in the [zl, zr] coordinate system with the air gap length as the research point. However, equation (45) is in the [za, ψ] coordinate system with the mass center as the research point. A coordinate transformation is needed to convert the air gap length coordinate system to the mass center coordinate system.
As shown in Figure 2, when the MC rotates around the Y-axis, there is a relationship between zl and zr, the displacement of the mass center za, and the rotation angle ψ as follows:
z l = z a − 0.1275 × tan ψ
z r = z a + 0.1275 × tan ψ
Due to the very small length of the air gap, the rotation angle ψ is also very small, so tanψ≈ψ. Therefore, equations (47) and (48) can be written as:
z l z r = 1 − 0.1275 1 0.1275 z a ψ
The above equation can be used to convert the air gap length coordinate system into the centroid coordinate system. Since the left and right side levitating forces are two multivariable, nonlinear functions, the formula is very complex and requires approximate conversion. The conversion method is: 1) Assuming that the MC is at the zero point of the plane; 2) At the zero point of the levitation position, namely [zl, zr]=[0, 0], Taylor expansion is performed and the high-order terms after the first term are truncated, resulting in simplified equations for the left and right end levitating forces of the MC as follows:
F l e f t = 23.11 i a − 13600 z l − 4483 z r
F r i g h t = 23.11 i b − 4483 z l − 13600 z r
In equations (50) and (51), ia=i3-i1, and ib=i4-i2. i1, i2, i3, and i4 are the currents of the four levitating coils, respectively.
3) Perform coordinate system transformation, and the transformation result is as follows:
F l e f t = 23.11 i a − 18083 z a + 1162.42 ψ
F r i g h t = 23.11 i b − 18083 z a − 1162.42 ψ
Substituting equations (52) and (53) into equation (46), the analysis model of the levitating system of the MR is obtained after sorting out:
− 36166 0 0 296 z a ψ + 23.11 23.11 − 2.9465 2.9465 i a i b + 17.93 0 = 1.83 0 0 0.0273 ∂ 2 z a ∂ t 2 ∂ 2 ψ ∂ t 2
From equation (54), it can be seen that the levitating system is a nonlinear system with two inputs and two outputs. Moreover, the system has strong coupling. Conventional linear algorithms cannot achieve effective control of the system. For the levitating system, ADRC is a more suitable controller.

A Levitating Control System Based on Active Disturbance Rejection

3.1. Design of Active Disturbance Rejection Controller for Levitating Control System

Based on an in-depth analysis of the PID control algorithms, Han Jingqing proposed the auto-disturbance rejection control technology [19]. This control technology does not require high precision in the mathematical model, and can estimate and compensate for "internal disturbances" and "external disturbances" in the system in real time, with strong adaptability and good anti-interference performance [19,20].
Due to the susceptibility of the levitating system to working magnetic field, current and load disturbances of the levitating coil, an active disturbance rejection control strategy is an effective solution to restrain the disturbances [19]. Because active disturbance rejection control not only requires lower modeling precision, but also can observe and compensate for coupling disturbances between different degrees of freedom (za and ψ) through an extended state observer, thereby solving the decoupling and disturbance suppression problems in levitating control [19].
The ADRC controller of the levitating system is shown in Figure 10. It mainly consists of a tracking differentiator (TD), an extended state observer (ESO), and a nonlinear state error feedback control law (NLSEF) [24].
Han Jingqing proposed the concept of nonlinear tracking differentiator, whose discrete tracking differentiator has the following form [2]:
1. Tracking differentiator (TD)
When the MR system is started, the given position will undergo a sudden change. However, due to inertia, the position of the MC will not immediately reach the given position, but there will be a relatively slow change process. This leads to the emergence of a transition process. When using classical PID control algorithm for position control, if the za need to track the vz0 as soon as possible, the control quantity should be increased. However, after increasing the control quantity, the za will have an overshoot. The transition process of the za is an objective existence. Therefore, the best way to eliminate the overshoot is to arrange a transition process for the vz0 [2].
The TD in the ADRC can be used to arrange a reasonable transition process for the given position. Equation (55) is a discretized second-order tracking differentiator [2].
v z 1 ( n + 1 ) = v z 1 ( n ) + h v z 2 ( n ) v z 2 ( n + 1 ) = v z 2 ( n ) + h f h a n [ v z 1 ( n ) − v z 0 ( n ) , v z 2 ( n ) , r , h ]
In the equation:
f h a n = − r s i g n ( α ) α > δ − r α δ α ≤ δ   α = v z 2 ( n ) + α 0 − δ 2 s i g n ( y z ( n ) ) y z ( n ) > δ 0 v z 2 ( n ) + h y z ( n ) y z ( n ) ≤ δ 0 α 0 = α 2 + 8 r y z ( n ) δ = r h 0 δ 0 = δ h 0 y z ( n ) = v z 1 ( n ) − v z 0 ( n ) + h 0 v z 2 ( n )
In the equation, vz0(n) is the za initial signal, vz1(n) traces the signal of vz0(n), vz2(n) is the differential signal of vz0(n); h is the integration size of step, tracing speed is determined by r, and h0 control the effect of the noise filtering. r and h0 should be coordinated to get suitable transition process.
2. Extended State Observer (ESO)
According to the active disturbance rejection control law, equation (53) is changed to:
∂ 2 z a ∂ t 2 = b z i a + w z ( t ) ∂ 2 ψ ∂ t 2 = b p i b + w p ( t )
In the equation, wz(t) and wp(t) are the equivalent disturbances of the system, which include coupling and disturbance. ia and ib are control variables. bz and bp in equation (55) are the control parameters of control variables ia and ib. ia=i3-i1, ib=i4-i2. i1, i2, i3, i4 are the currents of the four levitating coils. Let Δia and Δib be the changes of ia and ib respectively, then:
i a + Δ i a = ( i 3 + Δ i a 2 ) − ( i 1 − Δ i a 2 ) i b + Δ i b = ( i 4 + Δ i b 2 ) − ( i 2 − Δ i b 2 )
After compensation, equation (55) can be rewritten as:
∂ 2 z a ∂ t 2 = i a * ∂ 2 ψ ∂ t 2 = i b *
After compensation, za and ψ are decoupled and controllable. Taking za as an example, it can be seen from equation (53) that the system controls za through ia. However, changes in ia also cause changes in ψ, resulting in coupling. In equation (55), after parameter adjustment, ia becomes part of the equivalent disturbance of wp(t), which is then observed and compensated by ESO. Similarly, controlling the other degree of freedom, ib, also causes changes in za. In equation (55), after parameter adjustment, ib becomes part of the equivalent disturbance of wz(t), and then ESO observes and compensates it. The ESO of the levitating system is as follows [2]:
e ( n ) = z 1 ( n ) − y z ( n ) z 1 ( n + 1 ) = z 1 ( n ) + h [ z 2 ( n ) − β e 1 e ( n ) ] z ( n + 1 ) 2 = z 2 ( n ) + h z 3 ( n ) − β e 2 f a l [ e ( n ) , a 1 , δ ] + b 0 u z ( n ) z 3 ( n + 1 ) = z 3 ( n ) − h β e 3 f a l [ e ( n ) , a 2 , δ ]
In the equation:
f a l ( e , a j , δ ) = e a j s i g n ( e ) e > δ e δ 1 − a j e ≤ δ
In the equation: z1(n), z2(n), and z3(n) are the state variables of the ESO, z1(n) and z2(n) are used to trace the state variables of levitating system, and z3(n) is used to trace the state variables of the total disturbance; βe1, βe2, and βe3 are the gains of the ESO. a1 and δ are undetermined parameters. If ai is less than 1, the function has nonlinear characteristics; δ represents the linear range, aiming to avoid oscillation caused by large gain with minimal error.
3. Nonlinear error feedback control law (NLSEF)
In this paper, the levitating control system adopts the following form of NLSEF [2]:
e 1 ( n + 1 ) = w 1 ( n + 1 ) − z 1 ( n + 1 ) e 2 ( n + 1 ) = w 2 ( n + 1 ) − z 2 ( n + 1 ) u 0 ( n + 1 ) = β f 1 f a l [ e 1 ( n + 1 ) , a 3 , δ f 1 ] + β f 2 f a l [ e 2 ( n + 1 ) , a 4 , δ f 1 ]
In the equation, e1(n) and e2(n) are the deviations and derivatives between the expected transition process and the estimated value of the system output; a2, a3, and δf1 are the relevant parameters of fal; u0 is the output of NLSEF; b0 is the compensation coefficient.
4. Interference compensation [2]
Use ESO to track the variable z3(n) expanded from the original system. Use the control variable to compensate for the disturbance. The control variable is:
u ( n + 1 ) = u 0 ( n + 1 ) − z 3 ( n + 1 ) b 0
After a large number of simulation experiments and prototype testing experiments [2], this paper summarizes the parameter tuning method for the levitating control system:
1. Parameter tuning of TD.
There are three parameters in TD that need to be tuned, namely r, h0, and h.
r is the tracking factor. The tracking factor determines the speed at which w1(n) and w2(n) track the za given signal. The larger the tracking factor, the faster the tracing speed and the steeper the tracking curve. The smaller the tracking factor, the slower the tracing speed and the slower the tracking curve. However, it is also necessary to set a suitable tracking factor value based on the inertia of the MC to ensure the tracing effect of w1(n) and w2(n). h0 is the filtering factor. The effect of TD determined by the h0. h0 is related to the execution frequency of the controller [2]. h is the integration step size [2]. The shorter the integration step size, the higher the precision of the integral value, but the stronger the lag. An overly short integration step size can cause system oscillations. However, an overly long integration step size can reduce the precision of the integral value. In this paper, h=h0.
2. Parameter tuning of ESO.
By analyzing the inherent laws of ESO parameters and referring to the bandwidth method, this section proposes an ESO parameter tuning method for the levitation control system.
Suppose:
f a l ( e ,   a j ,   δ ) = f a l ( e ,   a j ,   δ ) e e = ζ i ( e ) e
Where, i=1, 2. Substituting equation (62) into equation (59):
e = z 1 − y z z ˙ 1 = z 1 + h z 2 − β e 1 e z ˙ = 2 z 2 + h z 3 − β e 2 ζ 1 ( e ) e + b 0 u z z ˙ 3 = z 3 − h β e 3 ζ 1 ( e ) e
In order to analyze the characteristics of the function ζi(e) and compare the changes in the output of the function ζi(e) corresponding to different aj values, this article selects aj=0.2, aj=0.4, aj=0.8, and δ=0.1, resulting in the output curve of the function ζi(e) shown in Figure 11.
From Figure 11, it can be seen that as the aj decreases, the nonlinearity of function ζi(e) increases, and the maximum gain increases. It can be seen that too small aj may lead to high-frequency oscillations in the observed values, while a larger aj may make it difficult for ESO to leverage its advantages of fast error attenuation and strong anti-interference capabilities. That is to say, aj can significantly affect the performance of ESO. In addition, if the error e is within the range [-δ, δ], the function ζi(e) is a constant, and ζ i e max = δ a j − 1 . Additionally, an excessively large linear interval δ can cause the nonlinear gain to fail, while a δ that is too small can render the observer unstable. Typically, δ should fall within the range of [0.001, 0.1], with δ=h being suitable in this context; aj must satisfy the condition that a1>a2. According to the empirical values a1=0.5 and a2=0.25.
In ESO, there are three additional parameters that require adjustment, namely βe1, βe2, and βe3. βe3 is the most important of the three parameters. When tuning the parameters, first select the parameter βe3. If βe3 is too small, it will cause insufficient observation precision of z3(n), and z1(n) and z2(n) will lag behind w1(n) and w2(n). If βe3 is too large, it will cause increased system fluctuations and even system oscillations. Therefore, adjust βe3 first to ensure the precision of ESO, and then adjust βe1 and βe2 from small to large to reduce the oscillation of ESO output. Due to the coupling of the levitating system, these two parameter values should be as small as possible while ensuring stable ESO output.
This paper employs the bandwidth method and experimental approach to tune the parameters of ESO. Therefore, based on the optimal parameter settings obtained through simulation in reference [2] and [24], the tuning formulas for βe1, βe2, and βe3 proposed in this paper can be expressed as follows:
β e 1 = 2 ω 0 ， β e 2 = 7 ω 0 2 50 ， β e 3 = ω 0 3 1000
Consequently, the performance of ESO is influenced by ω0. Performing the Laplace transform on equation (63) yields:
e = z 1 − y z s z 1 = z 1 + h z 2 − β e 1 e s z = 2 z 2 + h z 3 − β e 2 ζ 1 ( e ) e + b 0 u z s z 3 = z 3 − h β e 3 ζ 1 ( e ) e
According to equation (65), the transfer function model is obtained as:
z 1 = ( β e 2 h 2 b 0 u z + β e 2 h 2 y z ζ 1 ( e ) ) ( s − 1 ) + β e 3 h 3 y z ζ 2 ( e ) + β e 1 h y z ( s − 1 ) 2 s 3 + ( β e 1 h − 3 ) s 2 + ( β e 2 h 2 ζ 1 ( e ) + 3 − 2 β e 1 h ) s + β e 1 h − 1 + β e 3 ζ 2 ( e ) h 3 − β e 2 ζ 1 ( e ) h 2
z 2 = ( ( b 0 β e 2 h u z + β e 2 h y z ζ 1 ( e ) ) ( s − 1 ) + β e 3 h 2 ζ 2 ( e ) y z ) ( s + β e 1 h − 1 ) s 3 + ( β e 1 h − 3 ) s 2 + ( β e 2 h 2 ζ 1 ( e ) + 3 − 2 β e 1 h ) s + β e 1 h − 1 + β e 3 ζ 2 ( e ) h 3 − β e 2 ζ 1 ( e ) h 2 − β 1 h y z ( β 3 h 2 ζ 2 ( e ) + β 2 h ζ 1 ( e ) ( s − 1 ) ) s 3 + ( β e 1 h − 3 ) s 2 + ( β e 2 h 2 ζ 1 ( e ) + 3 − 2 β e 1 h ) s + β e 1 h − 1 + β e 3 ζ 2 ( e ) h 3 − β e 2 ζ 1 ( e ) h 2
z 3 = ( β e 3 h ζ 2 ( e ) y z ( β e 2 h 2 ζ 1 ( e ) + β e 1 h ( s − 1 ) + ( s − 1 ) 2 ) ) s 3 + ( β e 1 h − 3 ) s 2 + ( β e 2 h 2 ζ 1 ( e ) + 3 − 2 β e 1 h ) s + β e 1 h − 1 + β e 3 ζ 2 ( e ) h 3 − β e 2 ζ 1 ( e ) h 2 − β e 3 h 2 ζ 2 ( e ) ( b 0 β e 2 h u z + β e 2 h ζ 1 ( e ) y z ) s 3 + ( β e 1 h − 3 ) s 2 + ( β e 2 h 2 ζ 1 ( e ) + 3 − 2 β e 1 h ) s + β e 1 h − 1 + β e 3 ζ 2 ( e ) h 3 − β e 2 ζ 1 ( e ) h 2 − β e 1 β e 3 h 2 ζ 2 ( e ) y z ( s − 1 ) s 3 + ( β e 1 h − 3 ) s 2 + ( β e 2 h 2 ζ 1 ( e ) + 3 − 2 β e 1 h ) s + β e 1 h − 1 + β e 3 ζ 2 ( e ) h 3 − β e 2 ζ 1 ( e ) h 2
According to equation (66), ESO exhibits superior suppression of disturbances to uz. However, the effectiveness in suppressing disturbances introduced by yz requires further analysis. Hence, the effects of uz interference and nonlinear factors can be disregarded to simplify the analysis, setting uz=0, ζ1(e)=ζ2(e)=1, and then substituting equation (64) into (66) yields:
z 1 y z = 2 ω 0 s 2 + ( 0.14 × 10 − 3 ω 0 2 − 4 ω 0 ) s + 10 − 6 ω 0 3 − 0.14 × 10 − 3 ω 0 2 + 2 ω 0 1000 s 3 + ( 2 ω 0 − 3 ) s 2 + ( 0.14 × 10 − 3 ω 0 2 − 4 ω 0 + 3 ) s + 10 − 6 ω 0 3 − 0.14 × 10 − 3 ω 0 2 + 2 ω 0 − 1000
With the increase of ω0, the ESO exhibits better dynamic performance, evidenced by more precise disturbance estimation, reduced phase lag in disturbance observation, and accelerated convergence of estimation error. However, the influence of a broad bandwidth on high-frequency noise is significant and cannot be overlooked, potentially resulting in a decline in the suspension control system's performance. Therefore, in practical applications, it is advisable to adjust ω0 gradually until the disturbance observation satisfies the requirements of system.
3. Parameter tuning of NLSEF.
Three parameters of NLSEF needed to be tuned, namely βf1, βf2, and b0. b0 is the coefficient of the control variable u. The adjustment methods for βf1 and βf2 are similar to those for PD parameters.

3.2. Simulation Analysis of the Levitating Control System

In order to facilitate the simulation analysis of the feasibility of the levitating control system, a simulation model of the levitating control system was built using Simulink, as shown in Figure 12.
The parameters of the MC are: Jα=1.49×10-2kg∙m2, r=0.1275m, and mass m=1.83kg. The parameters of ADRC are shown in Table 1.
When t=0s and the Y direction coordinate value of the MC is 0, a given value z*a=0.1mm is suddenly applied with ψ*=0rad/s to detect the response characteristics of the levitating system during system startup.
In addition, when the MC moves along the Y axis, the magnetic field in air gaps will fluctuate, causing changes in the levitating position [1]. Therefore, at t=2.5s, a position disturbance with za=0.008mm is used to replace the fluctuation of the magnetic field in air gaps to simulate the disturbance to the levitating system. The simulation results are shown in Figure 13.
As shown in Figure 13, when the system started, the mover core reached the equilibrium position within 1 second without overshooting. The angle change of the mover core was also very small. The disturbance that occurred at 2.5 seconds had little effect on the levitation position of the mover core. The position change was less than 0.008 mm. The disturbance also had little effect on the angle of the mover core.
Next, the levitating control system was subjected to a system stability test by adding white noise with an amplitude of 0.5 at t=2.5s to simulate external interference. The simulation results are shown in Figure 14.
As can be seen from Figure 14, the white noise that appears at 2.5 seconds is a high-frequency interference signal that had little effect on the levitation position of the mover core and had little effect on the angle of the mover core. The levitation system can overcome the high-frequency interference simulated in the experiment.
Finally, at t=2.5s, the system setting was suddenly changed from 0.1mm to 0.08mm, and then a stability test was conducted. The simulation results are shown in Figure 15.
As shown in Figure 15, there was a sudden change in the set point of system at 2.5 seconds. The mover core stabilized at a new position within 0.5 seconds. Although there was an overshoot during the process, the magnitude of the overshoot was less than 0.005 mm, which met the system requirements.
As can be seen from Figure 13, Figure 14, and Figure 15, the response curve of the levitating control system is relatively smooth, with a relatively small fluctuation amplitude.

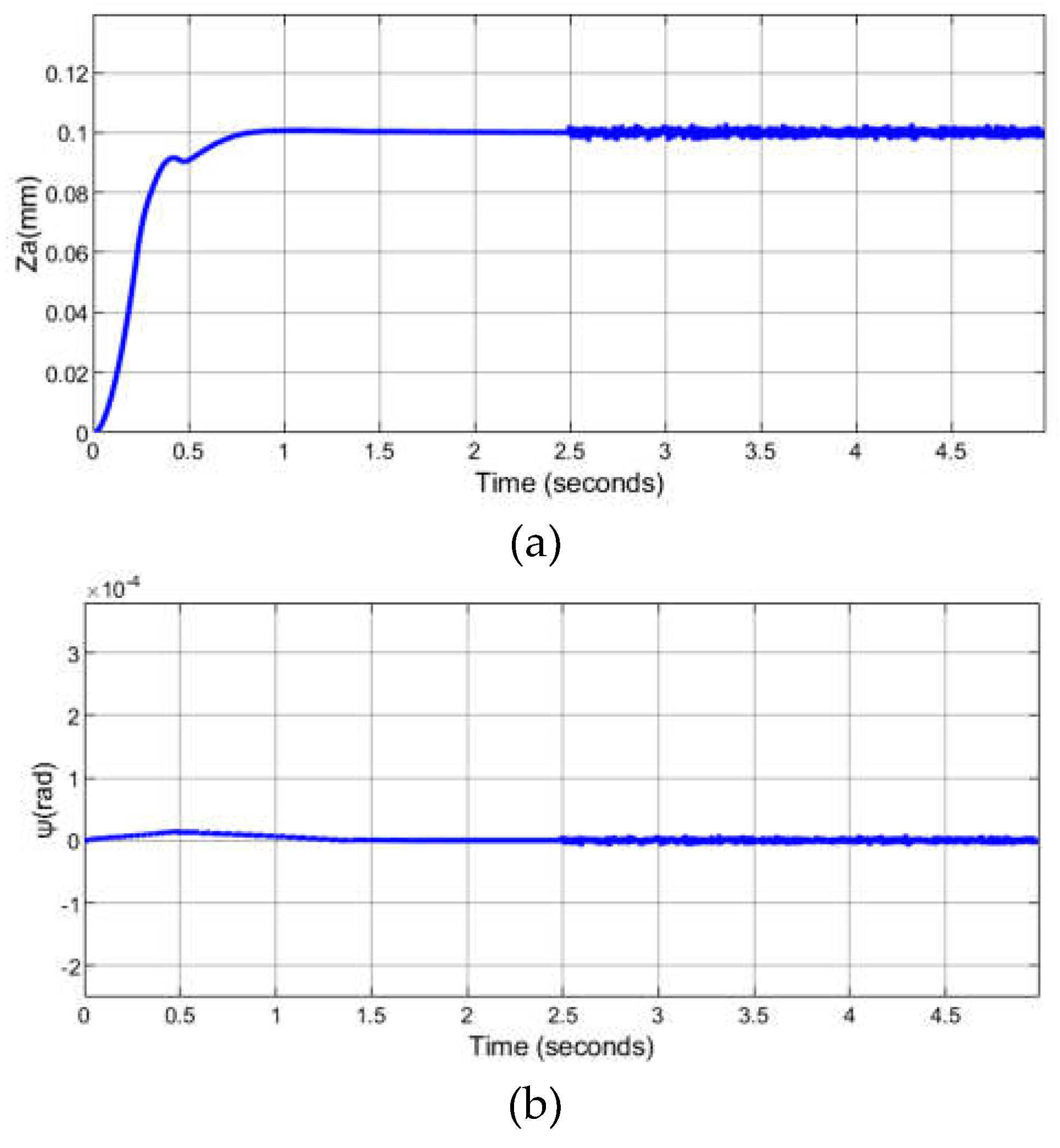
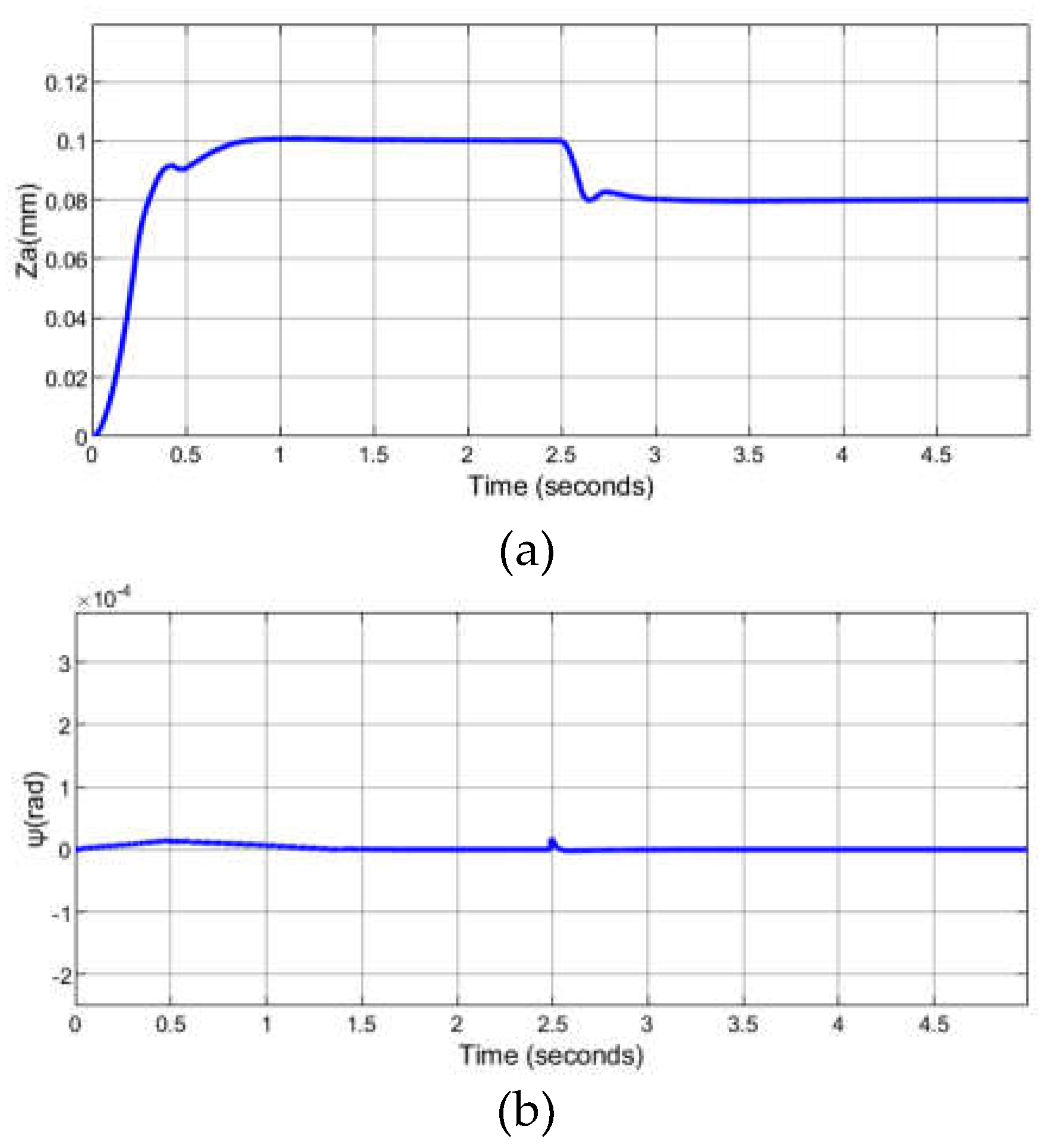
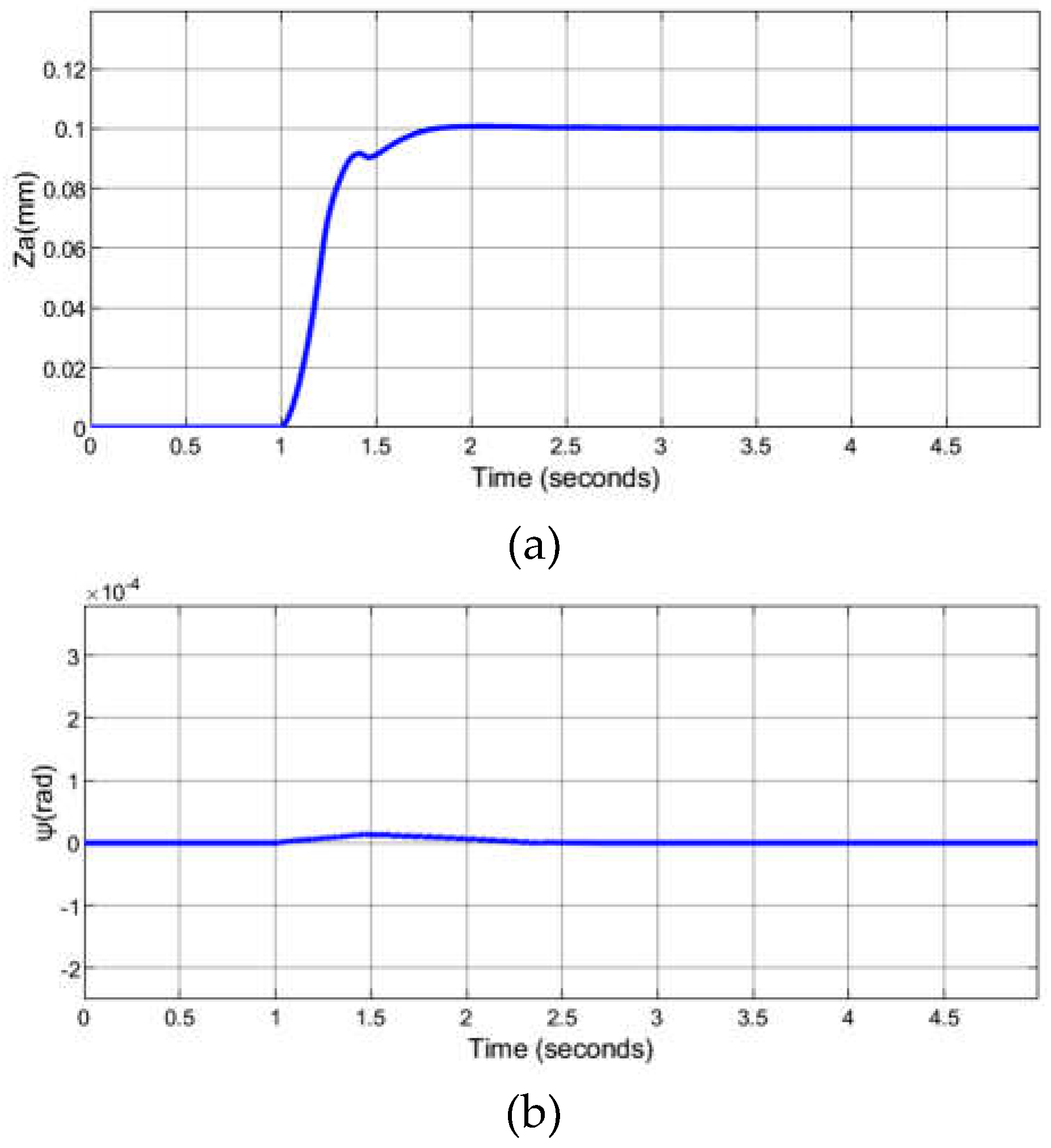
4. Experimental Testing of the Levitating Control System

In order to test the actual test results of the levitating control system, this paper conducted experimental testing of the levitating control of the levitating control system using the hardware platform shown in Figure 16. Figure 17 is the measured start-up response curve of the MC.
As shown in Figure 17, the height and swing angle of the MC are very small after the system is started up and quickly stabilize.

5. Conclusions

This paper proposes a levitating system for MRs, analyzes the levitating system, and establishes a mathematical model. The system establishes eight closed magnetic loops based on four permanent magnets and four levitating coils, achieving magnetic flux independent control for the four air gaps on the MC. In addition, the levitating system is also a nonlinear and strongly coupled system. Classical PID control methods cannot achieve decoupling control. Therefore, a levitating controller base on ADRC is proposed. The TD of ADRC can quickly follow the given value, and the ESO can compensate for internal and external disturbances to achieve decoupling control.
Simulation analysis and experimental testing through system startup, interference addition, white noise addition, and given sudden changes indicate that the levitating control system has good dynamic and static characteristics as well as robustness.

Author Contributions

Conceptualization, J.S., G.T., C.T. and Z.Z.; methodology, J.S., C.T. and Z.Z.; software, G.T. and Z.C.; validation, J.S. and G.T.; formal analysis, J.S. and P.L.; investigation, J.S. and Z.C.; resources, J.S. and Z.C.; data curation, J.S. and G.T.; writing—original draft preparation, J.S.; writing—review and editing, G.T., and P.L.; visualization, Z.C.; supervision, C.T. and Z.Z.; funding acquisition, C.T. and Z.Z. All authors have read and agreed to the published version of the manuscript. C.T and Z.Z. contributed equally to this study.

Funding

This research was funded by General Program of Chongqing Natural Science Foundation, grant number CSTB2022NSCQ-MSX1350, and National Key Research and Development Project, grant number 2019YFB1707505, and Jilin Provincial Science and Technology Department Project, grant number YDZJ202303CGZH001, and Youth Fund of Changchun University of Technology, grant number XQNJJ-2019-02, and Jilin Provincial Science and Technology Development Plan Project, grant number 20200404211YY.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The authors would like to thank the students from the Power Electronics and Electric Drive Innovation Base of the School of Electrical and Information Engineering at Beihua University.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Sun, J.-Y.; Li, P.; Zheng, Y.; Tian, C.-L.; Zhou, Z.-Z. A novel magnetic circuit and structure for magnetic levitation ruler. Measurement and Control 2023, 56, 1545–1561. [Google Scholar] [CrossRef]
  2. Zhou, Z.-Z.; Wang, H.-X.; Liu, B.-S. Levitation position control of a precise 6-DOF Planar magnetic Levitation stage. Machine Tool and Hydraulics 2018, 46, 125–131. [Google Scholar]
  3. Liu, L.-L.; Zhou, J.-H. Parameter Self-adjusting Control Method of Fuzzy PID for Magnetic Levitation Ball System. Control Engineering of China 2021, 28, 354–359. [Google Scholar] [CrossRef]
  4. Hernández-Guzmán, V.M.; Silva-Ortigoza, R.; Marciano-Melchor, M. Position Control of a Maglev System Fed by a DC/DC Buck Power Electronic Converter. Complexity 2020, 2020, 1–16. [Google Scholar] [CrossRef]
  5. Debdoot, S. Real-Time implementation and performance analysis of robust 2-DOF PID controller for Maglev system using pole search technique. Journal of Industrial Information Integration 2019, 15, 183–190. [Google Scholar] [CrossRef]
  6. Aysen, D.; Serdar, E.; Baran, H.; Davut, I. Opposition-based artificial electric field algorithm and its application to FOPID controller design for unstable magnetic ball levitating system. Engineering Science and Technology, an International Journal 2021, 24, 469–479. [Google Scholar] [CrossRef]
  7. Chauhan, D.; Yadav, A. Stability and agent dynamics of artificial electric field algorithm. Journal of Supercomputing 2024, 80, 835–864. [Google Scholar] [CrossRef]
  8. Deepa, T.; Subbulekshmi, D.; Lakshmi, P.; Maheedhar, M.; Kishore, E.; Vinodharanai, M.; Chockalingam, T. Comparative Study of Different Controllers for Levitating Ferromagnetic Material. Advances in Materials Science and Engineering 2022, 2022, 1–8. [Google Scholar] [CrossRef]
  9. Pandey, S.; Dourla, V.; Dwivedi, P.; Junghare, A. Introduction and realization of four fractional-order sliding mode controllers for nonlinear open-loop unstable system: a magnetic levitation study case. Nonlinear Dynamics 2019, 98, 601–621. [Google Scholar] [CrossRef]
  10. Yaseen, H.M.S.; Siffat, S.A.; Ahmad, I.; Malik, A.S. Nonlinear adaptive control of magnetic levitation system using terminal sliding mode and integral backstepping sliding mode controllers. ISA transactions 2022, 126, 121–133. [Google Scholar] [CrossRef]
  11. Acharya, D.S.; Swain, S.K.; Mishra, S.K. Real-Time Implementation of a Stable 2 DOF PID Controller for Unstable Second-Order Magnetic Levitation System with Time Delay. Arabian journal for science and engineering 2020, 45, 6311–6329. [Google Scholar] [CrossRef]
  12. Gopi, R.S.; Srinivasan, S.; Panneerselvam, K.; Teekaraman, Y.; Kuppusamy, R.; Urooj, S. Enhanced Model Reference Adaptive Control Scheme for Tracking Control of Magnetic Levitation System. Energies 2021, 14, 1455. [Google Scholar] [CrossRef]
  13. Kim, S.K.; Ahn, C.K. Sensorless non-linear position-stabilising control for magnetic levitation systems. IET Control Theory and Applications 2020, 14, 2682–2687. [Google Scholar] [CrossRef]
  14. Zhu, H.; Teo, T.J.; Pang, C.K. Magnetically Levitated Parallel Actuated Dual-Stage (Maglev-PAD) System for Six-Axis Precision Positioning. IEEE/ASME Transactions on Mechatronics 2019, 24, 1829–1838. [Google Scholar] [CrossRef]
  15. Trbusic, M.; Jesenik, M.; Trlep, M.; Hamler, A. Energy Based Calculation of the Second-Order Levitation in Magnetic Fluid. Mathematics 2021, 9, 2507. [Google Scholar] [CrossRef]
  16. Li, Y.-Q.; Feng, G.-S.; Wang, X.-F.; Wu, J.-Z.; Ma, J.; Xiao, L.-T.; Jia, S.-T. Reduction of characteristic RL time for fast, efficient magnetic levitation. AIP Advances 2017, 7, 095016. [Google Scholar] [CrossRef]
  17. Wu, C.; Li, S.-S. Modeling, Design and Suspension Force Analysis of a Novel AC Six-Pole Heteropolar Hybrid Magnetic Bearing. Applied Sciences 2023, 13, 1643. [Google Scholar] [CrossRef]
  18. Chen, W.; Tong, J.-Q.; Yang, H.-H.; Liu, F.-L.; Qin, Z.; Ren, Z.-Y. Modeling and Vibration Analysis of a 3-UPU Parallel Vibration Isolation Platform with Linear Motors Based on MS-DT-TMM. Shock and Vibation 2021, 2021, 1–17. [Google Scholar] [CrossRef]
  19. Yu, T.-T.; Zhang, Z.-Z.; Li, Y.; Zhao, W.-L.; Zhang, J.-C. Improved active disturbance rejection controller for rotor system of magnetic levitation turbomachinery. Electronic Research Archive 2023, 31, 1570–1586. [Google Scholar] [CrossRef]
  20. Tan, L.-L.; Chen, Z.-X.; Gao, Q.-H.; Liu, J.-F. Performance recovery of uncertain nonaffine systems by active disturbance rejection control. Measurement and Control 2024, 57, 3–15. [Google Scholar] [CrossRef]
  21. Sun, X.-D.; Jin, Z.-J.; Chen, L.; Yang, Z.-B. Disturbance rejection based on iterative learning control with extended state observer for a four-degree-of-freedom hybrid magnetic bearing system. Mech. Syst. Signal Process 2021, 153, 107465. [Google Scholar] [CrossRef]
  22. Wei, Z.-X.; Huang, Z.-W.; Zhu, J.-M. Position Control of Magnetic Levitation Ball Based on an Improved Adagrad Algorithm and Deep Neural Network Feedforward Compensation Control. Mathematical Problems in Engineering 2020, (2020), 1–13. [Google Scholar] [CrossRef]
  23. Gopi, R.S.; Srinivasan, S.; Panneerselvam, K.; Teekaraman, Y.; Kuppusamy, R.; Urooj, S. Enhanced Model Reference Adaptive Control Scheme for Tracking Control of Magnetic Levitation System. Energies 2021, 14, 1455. [Google Scholar] [CrossRef]
  24. He, H.-C.; Si, T.-T.; Sun, L.; Liu, B.-T.; Li, Z.-B. Linear Active Disturbance Rejection Control for Three-Phase Voltage-Source PWM Rectifier. IEEE Access 2020, 45050–45060. [Google Scholar] [CrossRef]
Preprints 114419 g001
Figure 1. (a) Magnetic loops of MR. (b) The electromagnetic suction force on the MC.
Figure 1. (a) Magnetic loops of MR. (b) The electromagnetic suction force on the MC.
Preprints 114419 g001
Preprints 114419 g002
Figure 2. Eight magnetic loops.
Figure 2. Eight magnetic loops.
Preprints 114419 g002
Preprints 114419 g003
Figure 3. Dimensions of each part of the MR [1].
Figure 3. Dimensions of each part of the MR [1].
Preprints 114419 g003
Preprints 114419 g004
Figure 4. The relationship between y and the air gap flux.
Figure 4. The relationship between y and the air gap flux.
Preprints 114419 g004
Preprints 114419 g005
Figure 5. The relationship between i3 and the air gap flux. (a) in upper left air gap. (b) in upper right air gap.
Figure 5. The relationship between i3 and the air gap flux. (a) in upper left air gap. (b) in upper right air gap.
Preprints 114419 g005
Preprints 114419 g006
Figure 6. The relationship between z and φl_up_air and φR_up_air.
Figure 6. The relationship between z and φl_up_air and φR_up_air.
Preprints 114419 g006
Preprints 114419 g007
Figure 7. (a) The relationship between z and Fleft. (b) The relationship between ia and Fleft.
Figure 7. (a) The relationship between z and Fleft. (b) The relationship between ia and Fleft.
Preprints 114419 g007
Preprints 114419 g008
Figure 8. (a) The relationship between z and Fleft (b) The relationship between ia and Fleft.
Figure 8. (a) The relationship between z and Fleft (b) The relationship between ia and Fleft.
Preprints 114419 g008
Preprints 114419 g009
Figure 9. Force analysis of the MC.
Figure 9. Force analysis of the MC.
Preprints 114419 g009
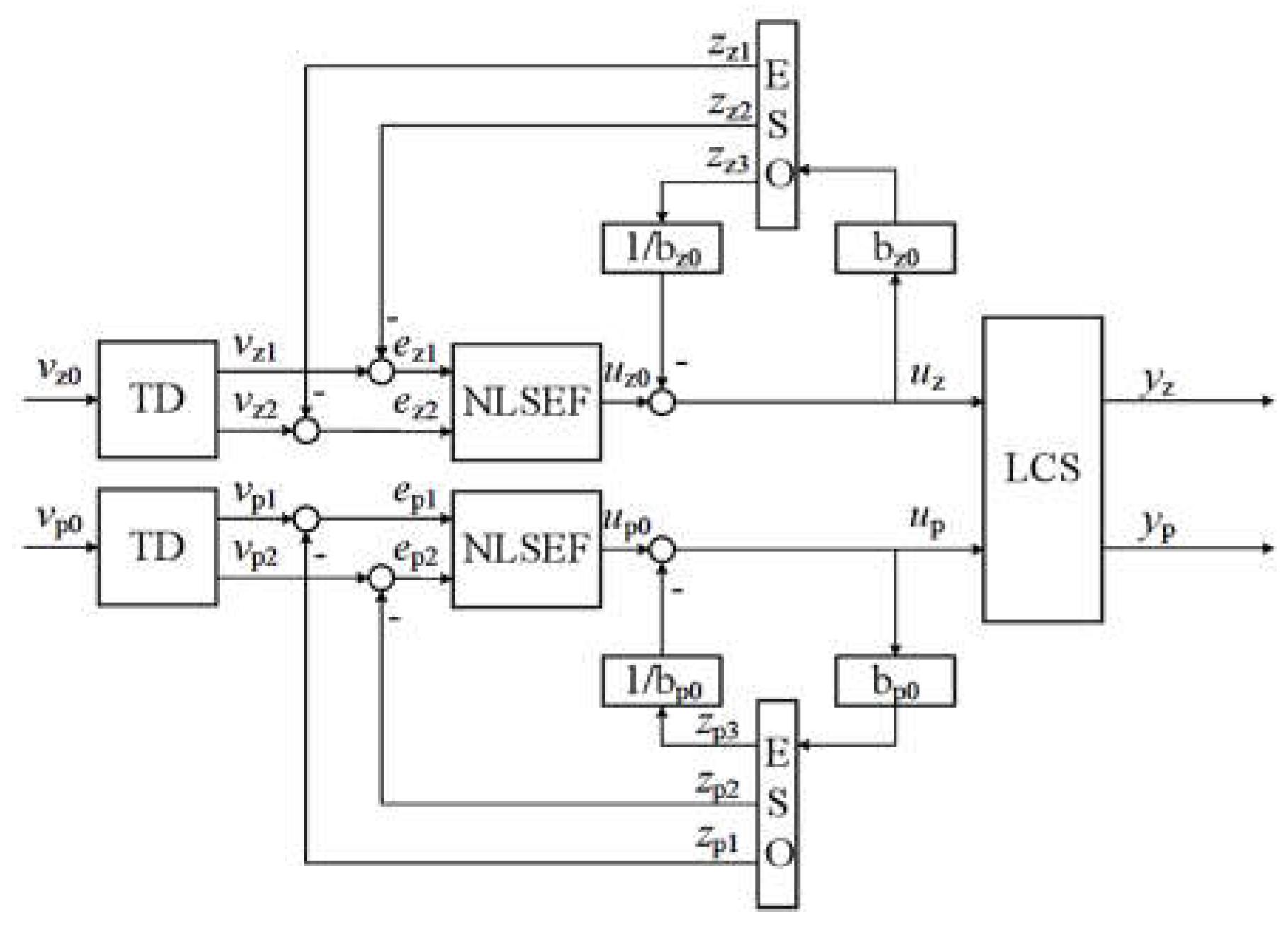
Preprints 114419 g010
Figure 10. Structural diagram of levitating system.
Figure 10. Structural diagram of levitating system.
Preprints 114419 g010
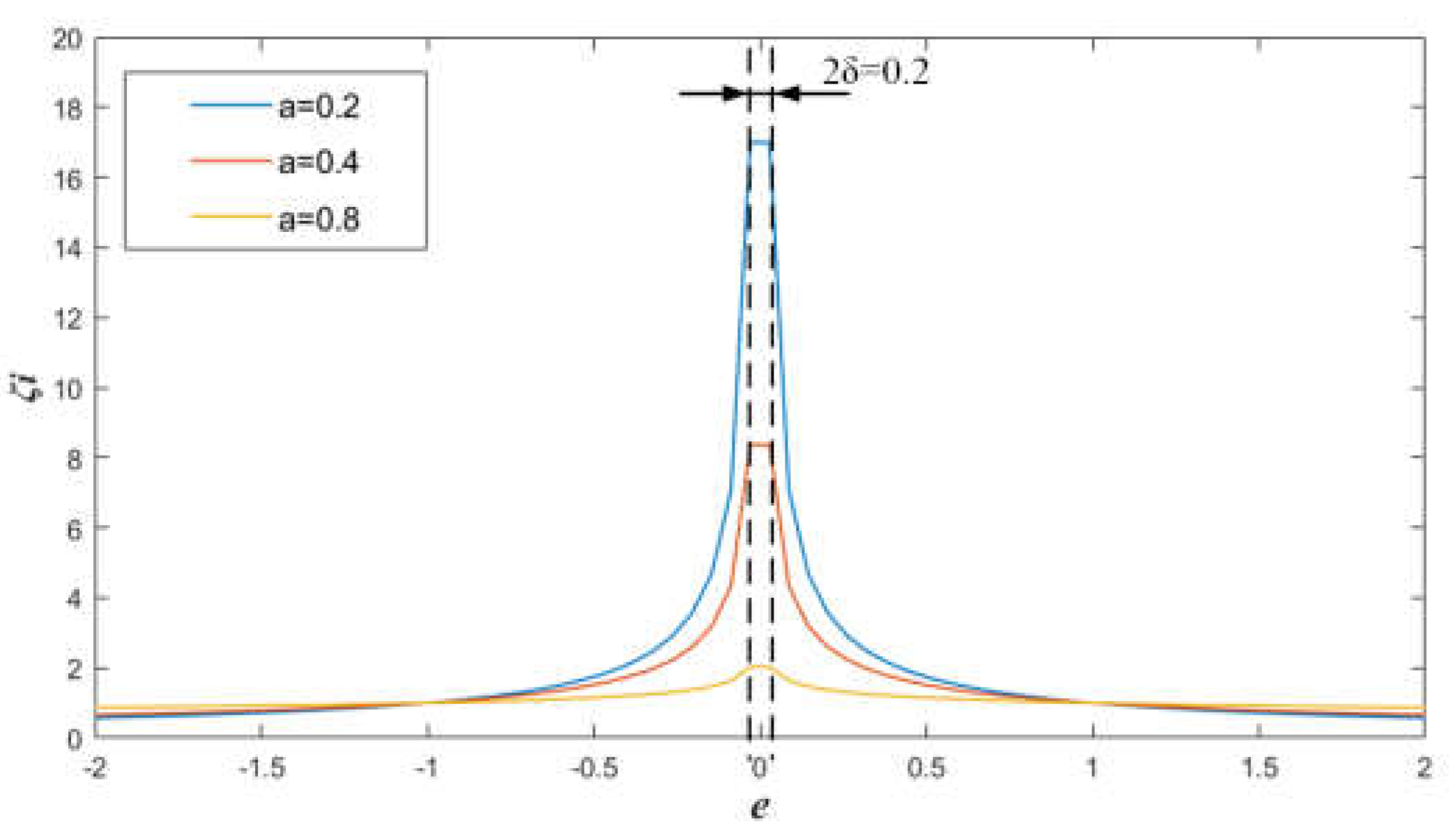
Preprints 114419 g011
Figure 11. Comparison of the output of function ζi(e) corresponding to different aj.
Figure 11. Comparison of the output of function ζi(e) corresponding to different aj.
Preprints 114419 g011
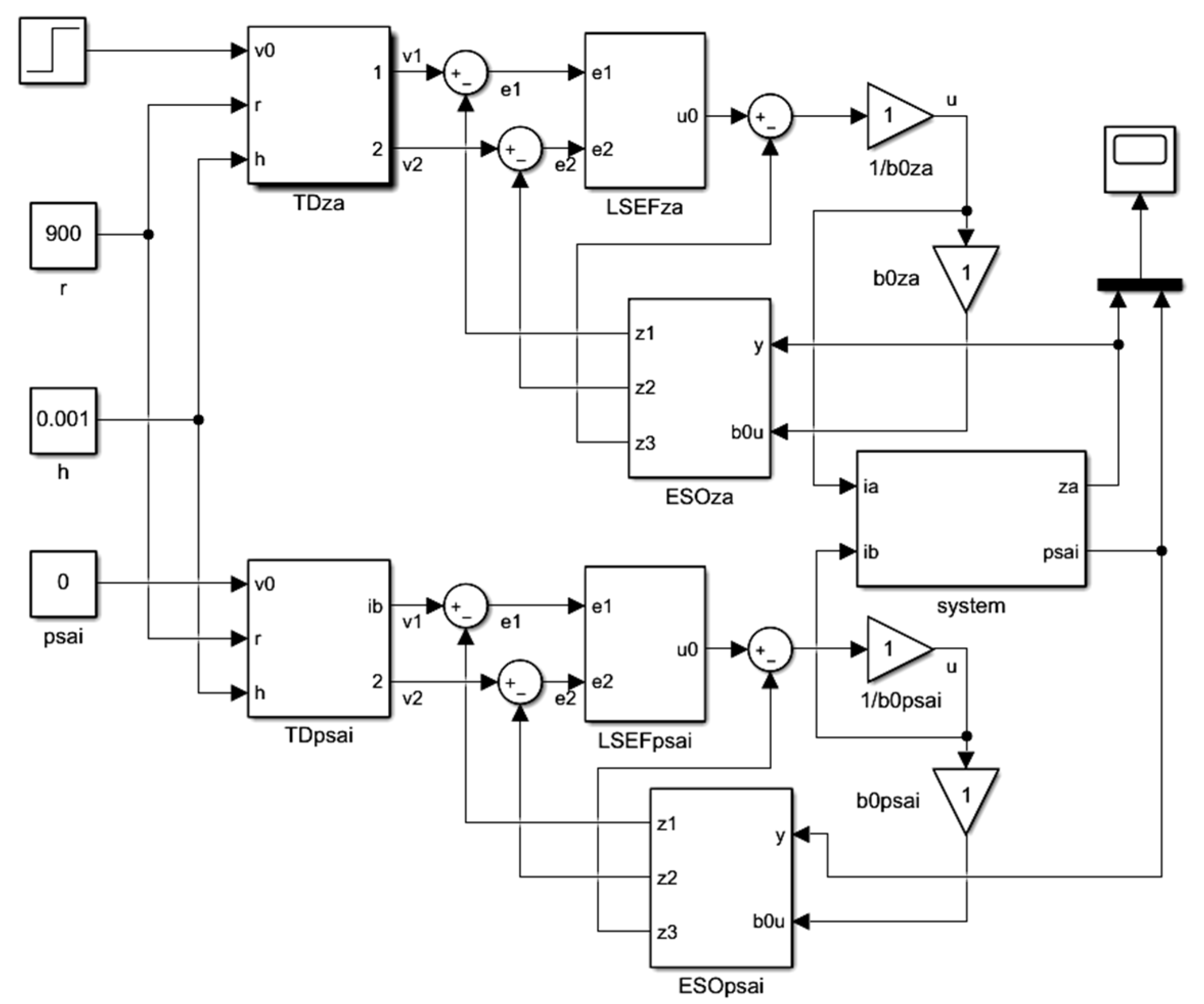
Preprints 114419 g012
Figure 12. Simulation diagram of levitating control system.
Figure 12. Simulation diagram of levitating control system.
Preprints 114419 g012
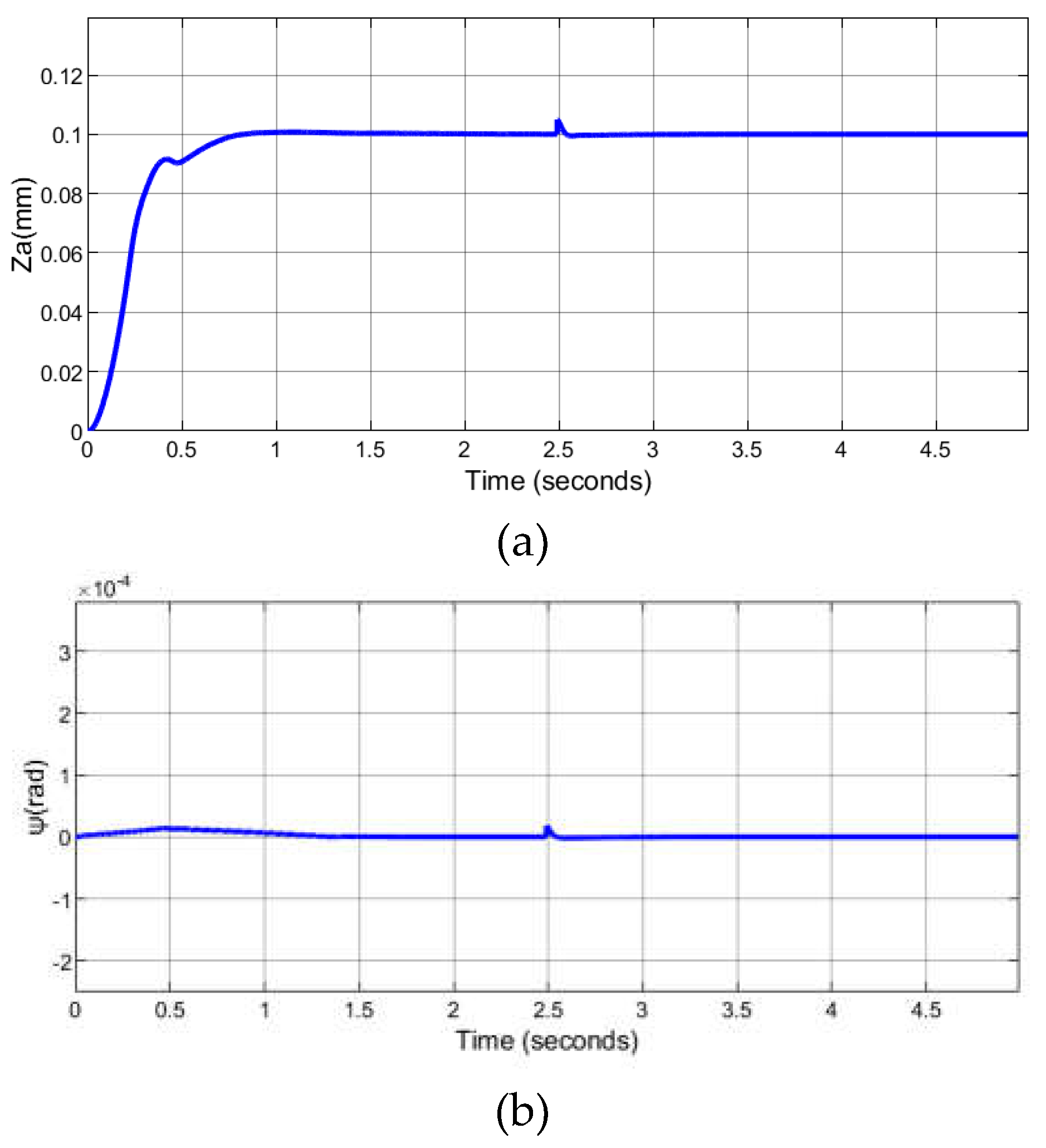
Preprints 114419 g013
Figure 13. Simulation diagram of levitating control system. (a) position variation curve. (b) angle variation curve.
Figure 13. Simulation diagram of levitating control system. (a) position variation curve. (b) angle variation curve.
Preprints 114419 g013
Preprints 114419 g014
Figure 14. Simulation diagram of external interference. (a) position variation curve. (b) angle variation curve.
Figure 14. Simulation diagram of external interference. (a) position variation curve. (b) angle variation curve.
Preprints 114419 g014
Preprints 114419 g015
Figure 15. Simulation diagram of sudden change. (a) position variation curve. (b) angle variation curve.
Figure 15. Simulation diagram of sudden change. (a) position variation curve. (b) angle variation curve.
Preprints 114419 g015
Preprints 114419 g016
Figure 16. The measurement platform of the levitating system.
Figure 16. The measurement platform of the levitating system.
Preprints 114419 g016
Preprints 114419 g017
Figure 17. System response curve during startup. (a) position variation curve. (b) angle variation curve.
Figure 17. System response curve during startup. (a) position variation curve. (b) angle variation curve.
Preprints 114419 g017
Table 1. Main parameters of ADRC.
Table 1. Main parameters of ADRC.
parameter value parameter value parameter value
r 900 βe2 1398 βf2 0.01
h 0.001 βe3 1015 a2 0.25
βe1 200 βf1 30 a3 0.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated