On Proving Ramanujan’s Inequality Using a Sharper Bound for the Prime Counting Function π(x)

Preprint

Article

On Proving Ramanujan’s Inequality Using a Sharper Bound for the Prime Counting Function π(x)

Altmetrics

Downloads

111

Views

Comments

Subham De^*

This version is not peer-reviewed

Submitted:

20 August 2024

Posted:

22 August 2024

You are already at the latest version

Alerts

Abstract

This article provides a proof that the Ramanujan's Inequality given by, \begin{align*} \pi(x)^2 < \frac{e x}{\log x} \pi\left(\frac{x}{e}\right) \end{align*} holds unconditionally for every $x\geq \exp(43.5102146)$. In case for an alternate proof of the result stated above, we shall exploit certain estimates involving the Chebyshev Theta Function, $\vartheta(x)$ in order to derive appropriate bounds for $\pi(x)$, which'll lead us to a much improved condition for the inequality proposed by Ramanujan to satisfy unconditionally.

Keywords:

Subject: Computer Science and Mathematics - Algebra and Number Theory

MSC: Primary 11A41; 11A25; 11N05; 11N37; Secondary 11Y99

1. Introduction

The notion of analyzing the proportion of prime numbers over the real line

R

first came into the limelight thanks to the genius work of one of the greatest and most gifted mathematicians of all time named Srinivasa Ramanujan, as evident from his letters ([12] pp. xxiii-xxx, 349-353) to another one of the most prominent mathematicians of 20^th century, G. H. Hardy during the months of Jan/Feb of 1913, which are testaments to several strong assertions about the Prime Counting Function,

π (x)

[cf. Definition

(2.3)

[15].

In the following years, Hardy himself analyzed some of those results ([13,14] pp. 234-238), and even wholeheartedly acknowledged them in many of his publications, one such notable result is the Prime Number Theorem [cf. Theorem

(2.4)

[15].

Ramanujan provided several inequalities regarding the behavior and the asymptotic nature of

π (x)

. One of such relation can be found in the notebooks written by Ramanujan himself has the following claim.

Theorem 1.1.(Ramanujan’s Inequality [1]) For x sufficiently large, we shall have,

\begin{matrix} {(π (x))}^{2} < \frac{e x}{log x} π (\frac{x}{e}) \end{matrix}

(1)

Worth mentioning that, Ramanujan indeed provided a simple, yet unique solution in support of his claim. Furthermore, it has been well established that, the result is not true for every positive real x. Thus, the most intriguing question that the statement of Theorem (1.1) poses is, is there any

x_{0}

such that, Ramanujan’s Inequality will be unconditionally true for every

x \geq x_{0}

A brilliant effort put up by F. S. Wheeler, J. Keiper, and W. Galway in search for such

x_{0}

using tools such as MATHEMATICA went in vain, although independently Galway successfully computed the largest prime counterexample below

10^{11}

x = 38 358 837 677

. However, (Hassani [3] Theorem 1.2) proposed a more inspiring answer to the question in a way that, ∃ such

x_{0} = 138 766 146 692 471 228

with (1) being satisfied for every

x \geq x_{0}

, but one has to neccesarily assume the Riemann Hypothesis. In a recent paper by A. W. Dudek and D. J. Platt ([2] Theorem 1.2), it has been established that, ramanujan’s Inequality holds true unconditionally for every

x \geq exp (9658)

. Although this can be considered as an exceptional achievement in this area, efforts of further improvements to this bound are already underway. For instance, Mossinghoff and Trudgian [5] made significant progress in this endeavour, when they established a better estimate as,

x \geq exp (9394)

. Later on, Platt and Trudgian ([18] cf. Th. 2) together established that, further improvement is indeed possible, and that

x \geq exp (3915)

. Worth mentioning that, Cully-Hugill and Johnston [19] literally took it to the next level by obtaining an effective bound for (1) to hold unconditionally as,

x \geq exp (3604)

. Unsurprisingly, Johnston and Yang ([20] cf. Th. 1.5) outperformed them in claiming the lower bound for such x satisfying Ramanujan’s Inequality to be

exp (3361)

One recent even better result by Axler [6] suggests that, the lower bound for x, namely

exp (3361)

can in fact be further improved upto

exp (3158.442)

using similar techniques as described in [2], although modifying the error term accordingly adhering to a sharper bound involving

π (x)

and

L i (x)

derived by Fiori, Kadiri, and Swidinsky ([4] cf. Cor. 22).

This paper does indeed adopts a new approach in modifying the existing estimates for

x_{0}

in order for the Ramanujan’s Inequality (cf. Theorem (1.1)) to hold without imposing any further assumptions on it for every

x \geq x_{0}

. By utilizing some effective bounds on the Chebyshev’s ϑ-function, the primary intention is to obtain a suitable bound for

π (x)

, and hence eventually come up with a much better estimate for

x_{0}

by tinkering with the constants while respecting all the stipulated conditions available to us.

2. An Improved Criterion for Ramanujan’s Inequality

Suppose, we define,

\begin{matrix} G (x) : = {(π (x))}^{2} - \frac{e x}{log x} π (\frac{x}{e}) \end{matrix}

(2)

A priori using the Prime Number Theorem ([15] cf. Th.

(2.4)

), we can in fact assert that [2],

\begin{matrix} π (x) = x \sum_{k = 0}^{4} \frac{k!}{{log}^{k + 1} x} + O (\frac{x}{{log}^{6} x}) \end{matrix}

(3)

x \to \infty

. On the other hand, for the Chebyshev’s ϑ-function having the following definition,

\begin{matrix} ϑ (x) : = \sum_{p \leq x} log p, \end{matrix}

(4)

we can indeed summarize certain inequalities (cf. [7,8]) as follows:

Proposition 2.1.

The following holds true for

ϑ (x)

$ϑ (x) < x$ , for $x < 10^{8}$ ,
$| ϑ (x) - x | < 2.05282 \sqrt{x}$ , for $x < 10^{8}$ ,
$|ϑ (x) - x| < 0.0239922 \frac{x}{log x}$ , for $x \geq 758711$ ,
$| ϑ (x) - x | < 0.0077629 \frac{x}{log x}$ , for $x \geq exp (22)$ ,
$| ϑ (x) - x | < 8.072 \frac{x}{{log}^{2} x}$ , for $x > 1$ .

Applying these inequalities, we can compute a suitable bound for

ϑ (x)

as follows:

Lemma 2.2

(cf. [9]). We shall have the following estimate for

ϑ (x)

\begin{matrix} x (1 - \frac{2}{3 {(log x)}^{1.5}}) < ϑ (x) < x (1 + \frac{1}{3 {(log x)}^{1.5}}), f o r x \geq 6400 . \end{matrix}

(5)

Lemma (2.2) does in fact enable us deduce a more effective bound for

π (x)

, which’ll prove to be immensely beneficial for us later on.

Theorem 2.3.

We shall have the following estimate for

π (x)

as follows:

\begin{matrix} \frac{x}{log x - 1 + \frac{1}{\sqrt{log x}}} < π (x) < \frac{x}{log x - 1 - \frac{1}{\sqrt{log x}}}, f o r x \geq 59 . \end{matrix}

(6)

We briefly discuss the proof of the Theorem above following the steps as described in [9] for the convenience of our readers.

Proof.

Applying a well-known inequlity involving

ϑ (x)

and

π (x)

\begin{matrix} π (x) = \frac{ϑ (x)}{log x} + \int_{2}^{x} \frac{ϑ (t)}{t {log}^{2} t} d t \end{matrix}

(7)

and, with the help of (5) in Lemma (2.2), we get,

\begin{matrix} π (x) < \frac{x}{log x} + \frac{x}{3 {(log x)}^{2.5}} + \int_{2}^{x} \frac{d t}{{log}^{2} t} + \frac{1}{3} \int_{2}^{x} \frac{d t}{{(log x)}^{3.5}} \end{matrix}

\begin{matrix} = \frac{x}{log x} (1 + \frac{1}{3 {(log x)}^{1.5}} + \frac{1}{log x}) - \frac{2}{{log}^{2} 2} + 2 \int_{2}^{x} \frac{d t}{{log}^{3} t} + \frac{1}{3} \int_{2}^{x} \frac{d t}{{(log t)}^{3.5}} \end{matrix}

\begin{matrix} < \frac{x}{log x} (1 + \frac{1}{3 {(log x)}^{1.5}} + \frac{1}{log x}) + \frac{7}{3} \int_{2}^{x} \frac{d t}{{log}^{3} t} \end{matrix}

(8)

Moreover, defining the function,

\begin{matrix} h_{1} (x) : = \frac{2}{3} . \frac{x}{{(log x)}^{2.5}} - \frac{7}{3} \int_{2}^{x} \frac{d t}{{log}^{3} t}, f o r x \geq exp (18.25) \end{matrix}

(9)

We can observe that,

h_{1}^{'} (x) > 0

, implying that,

h_{1}

is increasing. Now, for every convex function

u : [a, b] \to R

, where,

a < b, a, b \in R_{> 0}

, we have,

\begin{matrix} \int_{a}^{b} u (x) d x \leq \frac{b - a}{n} (u (a) + u (b) + \sum_{k = 1}^{n - 1} u (a + k \frac{b - a}{n})) . \end{matrix}

(10)

Thus, choosing

u (x) : = \frac{1}{{log}^{3} x}

and

n = 10^{5}

and using (10) on each of the intervals

[2, e]

[e, e^{2}]

, ......,

[e^{17}, e^{18}]

and

[e^{18}, e^{18.25}]

yields,

\begin{matrix} \int_{2}^{exp (18.25)} \frac{d t}{{log}^{3} t} < 16870 . \end{matrix}

Furthermore, one can also verify using MATHEMATICA that,

\begin{matrix} h_{1} (exp (18.25)) > \frac{1}{3} (118507 - 118090) > 0 . \end{matrix}

Therefore, for every

x \geq exp (18.25)

, we must have from (8),

\begin{matrix} π (x) < \frac{x}{log x} (1 + \frac{1}{3 {(log x)}^{1.5}} + \frac{1}{log x}) < \frac{x}{log x - 1 - \frac{1}{\sqrt{log x}}} \end{matrix}

(11)

Again, for

x \leq exp (18.25) < 10^{8}

, we apply

(1)

in Proposition (2.1) to derive,

\begin{matrix} π (x) = \frac{ϑ (x)}{log x} + \int_{2}^{x} \frac{ϑ (x)}{t {log}^{2} t} d t < \frac{x}{log x} + \int_{2}^{x} \frac{d t}{{log}^{2} t} \end{matrix}

\begin{matrix} = \frac{x}{log x} (1 + \frac{1}{log x}) - \frac{2}{{log}^{2} 2} + 2 \int_{2}^{x} \frac{d t}{{log}^{3} t} . \end{matrix}

Furthermore, for

4000 \leq x < 10^{8}

, taking the function,

\begin{matrix} h_{2} (x) : = \frac{x}{{(log x)}^{2.5}} - 2 \int_{2}^{x} \frac{d t}{{log}^{3} t} + \frac{2}{{log}^{2} 2} . \end{matrix}

(12)

We can indeed verify that,

h_{2}^{'} (x) > 0

, implying

h_{2}

is an increasing function. Similarly, with the help of MATHEMATICA, we can compute the sign of

h_{2}

as follows,

\begin{matrix} h_{2} (exp (11)) > 149 - 2 \int_{2}^{exp (11)} \frac{d t}{{log}^{3} t} > 149 - 140 > 0 . \end{matrix}

In summary, thus for

exp (11) \leq x < 10^{8}

\begin{matrix} π (x) < \frac{x}{log x} (1 + \frac{1}{log x} + \frac{1}{{(log x)}^{1.5}}) < \frac{x}{log x - 1 - \frac{1}{\sqrt{log x}}} . \end{matrix}

(13)

In addition to the above, it is important to note that, for

x \geq 6

, the denominator,

log x - 1 - \frac{1}{\sqrt{log x}} > 0

. Which means that, for

6 \leq x \leq exp (11)

, we need to establish,

\begin{matrix} H (x) : = \frac{x}{π (x)} + 1 + {(log x)}^{- 0.5} - log x > 0 . \end{matrix}

(14)

Assuming

p_{n}

to be the

n^{t h}

prime, it can be observed that, H is in fact increasing in

[p_{n}, p_{n + 1})

, thus it only needs to be proven that,

H (p_{n}) > 0

For

p_{n} < exp (11)

, we have the inequality

\frac{1}{\sqrt{log p_{n}}} > 0.3

, which reduces our computation to verifying,

\begin{matrix} \frac{p_{n}}{n} - log p_{n} > - 1.3 \end{matrix}

for every

7 \leq p_{n} \leq exp (11)

, which can be achieved using MATHEMATICA.

In order to establish the lower bound of

π (x)

as claimed in (6), we shall be needing

(1)

in Proposition (2.1) and (5) in Lemma (2.2) under the condition that,

x \geq 6400

. Hence,

\begin{matrix} π (x) - π (6400) = \frac{ϑ (x)}{log x} - \frac{ϑ (6400)}{log (6400)} + \int_{6400}^{x} \frac{ϑ (t)}{t {log}^{2} t} d t . \end{matrix}

(15)

Rigorous computations does yield,

π (6400) = 834

, and,

\frac{ϑ (6400)}{log (6400)} < \frac{6400}{log (6400)} < 731

. Thus, (15) further reduces to,

\begin{matrix} π (x) > 103 + \frac{ϑ (x)}{x} + \int_{6400}^{x} \frac{ϑ (t)}{t {log}^{2} t} d t . \end{matrix}

Using the lower bound of

ϑ (x)

as in (5) of Lemma (2.2) gives,

\begin{matrix} π (x) > 103 + \frac{x}{log x} - \frac{2 x}{3 {log}^{2.5} x} + \frac{x}{{log}^{2} x} - \frac{6400}{{log}^{2} 6400} + 2 \int_{6400}^{x} \frac{d t}{{log}^{3} t} - \frac{2}{3} \int_{6400}^{x} \frac{d t}{{log}^{3.5} t} \end{matrix}

\begin{matrix} > \frac{x}{log x} (1 + \frac{1}{log x} - \frac{2}{3 {log}^{1.5} x}) > \frac{x}{log x - 1 + \frac{1}{\sqrt{log x}}} \end{matrix}

Setting

v = {(log x)}^{- 0.5}

, we can assert that, the above inequality holds true for,

2 v^{3} - 5 v^{2} + 3 v - 1 < 0

, implying,

v (1 - v) (3 - 2 v) \leq \frac{(3 - v)}{4} < 1

. Hence, it can be confirmed that, the statement (6) holds true for

x \geq 6400

Furthermore, for

x < 6400

, we intend on showing that,

\begin{matrix} β (x) : = - \frac{x}{π (x)} + log x - 1 + \frac{1}{\sqrt{log x}} > 0 . \end{matrix}

(16)

Assuming similarly that,

p_{n}

denotes the

n^{t h}

prime, one can observe that, the function

β (x)

is indeed decreasing on

[p_{n}, p_{n + 1})

. Hence, it only suffices to check for the values at

p_{n} - 1

. Now,

p_{n} \leq 6400

implies,

{(log (p_{n} - 1))}^{- 0.5} > 0.337

, and thus, it only is needed to be checked that,

\begin{matrix} \frac{log (p_{n} - 1)}{p_{n} - 1} - \frac{p_{n} - 1}{n - 1} > 0.663 \end{matrix}

(17)

Utilizing proper coding in MATHEMATICA gives us,

n \geq 36

in order for (17) to satisfy. Therefore, we can further verify that, (6) holds for

x \geq 59

, and the proof is complete. □

Significantly, Karanikolov [10] cited one of the applications of (6) which says that for

α \geq e^{1 / 4}

and,

x \geq 364

, we must have,

\begin{matrix} π (α x) < α π (x) . \end{matrix}

(18)

Although, a more effective version of (18) states (cf. Theorem 2 [9]) the following.

Proposition 2.4.(18) holds true for every

α > 1

and,

x > exp (4 {(log α)}^{- 2})

Proof.

We utilize (6) in theorem (2.3) for

α x \geq 6

. Thus,

\begin{matrix} \frac{α x}{log α x - 1 + \frac{1}{\sqrt{log α x}}} < π (α x) < \frac{α x}{log α x - 1 - \frac{1}{\sqrt{log α x}}} \end{matrix}

and,

\begin{matrix} \frac{α x}{log x - 1 + \frac{1}{\sqrt{log x}}} < α π (x) < \frac{α x}{log x - 1 - \frac{1}{\sqrt{log x}}} \end{matrix}

for every

x \geq 59

. Now, assuming

x \geq exp (4 {(log α)}^{- 2})

, we can deduce that,

\begin{matrix} log α > {(log α x)}^{- 0.5} + {(log x)}^{- 0.5} \end{matrix}

which is all that we’re required to show. This completes the proof. □

As for another application of (6), we must mention the work of Udrescu [11], where it was claimed that, if

0 < ϵ \leq 1

, then,

\begin{matrix} π (x + y) < π (x) + π (y), \forall ϵ x \leq y \leq x . \end{matrix}

(19)

Again, further progress have in fact been made in order to improve the result (19). One such notable work in this regard has been done by Panaitopol [9].

Lemma 2.5.(19) is satisfied under additional condition,

x \geq exp (9 ϵ^{- 2})

, where,

ϵ \in (0, 1]

We shall be using all the above derivations in order to obtain a much improved bound for

x_{0}

such that,

G (x) < 0

unconditionally for every

x \geq x_{0}

Choose some

a > 1

such that,

e - a > a > 1

as well. Hence,

\begin{matrix} π (x) = π (e . \frac{x}{e}) = π (a . \frac{x}{e} + (e - a) . \frac{x}{e}) \end{matrix}

(20)

Using (19) by taking,

ϵ = \frac{a}{e - a} < 1

as per our construction yields,

\begin{matrix} π (x) < π (a . \frac{x}{e}) + π ((e - a) . \frac{x}{e}) \end{matrix}

(21)

for every

x \geq \frac{e}{e - a} . exp (9 . {(\frac{a}{e - a})}^{- 2})

. Furthermore, by our selection of a, we can in fact utilize Proposition (2.4) again in order to derive the following estimates,

\begin{matrix} π (a . \frac{x}{e}) < a . π (\frac{x}{e}), \forall x > exp (4 {(log a)}^{- 2} + 1) \end{matrix}

(22)

and,

\begin{matrix} π ((e - a) . \frac{x}{e}) < (e - a) . π (\frac{x}{e}), \forall x > exp (4 {(log (e - a))}^{- 2} + 1) \end{matrix}

(23)

Therefore, combining (20)–(23), we obtain,

\begin{matrix} π (x) < a . π (\frac{x}{e}) + (e - a) . π (\frac{x}{e}) = e . π (\frac{x}{e}) \end{matrix}

(24)

for every such,

\begin{matrix} x \geq max \{\frac{e}{e - a} . exp (9 . {(\frac{a}{e - a})}^{- 2}), exp (4 {(log a)}^{- 2} + 1), exp (4 {(log (e - a))}^{- 2} + 1)\} \end{matrix}

(25)

For our convenience, we consider,

a = 1.359 > 1

Thus, we can verify,

e - a = 1.359281828 > a > 1 a n d, ϵ = 0.999792663 < 1,

as desired. Subsequently, we conclude that, (24) is satisfied for every,

\begin{matrix} x \geq max \{1.999792664 exp (9.003733214), exp (43.5102146), exp (43.45280029)\} \end{matrix}

(26)

In summary, we have,

\begin{matrix} π (x) < e . π (\frac{x}{e}), \forall x \geq exp (43.5102146) . \end{matrix}

(27)

On the other hand, (3) gives us,

\begin{matrix} π (x) > \frac{x}{log x} \end{matrix}

(28)

for sufficiently large values of x. Finally, combining (27) and (28), we get from (2),

\begin{matrix} G (x) = {(π (x))}^{2} + (\frac{x}{log x}) . (- e . π (\frac{x}{e})) < {(π (x))}^{2} + π (x) . (- π (x)) = 0 . \end{matrix}

(29)

and this is valid unconditionally for every

x \geq exp (43.5102146)

. Therefore, we have our

x_{0} = exp (43.5102146)

as desired in order for the Ramanujan’s Inequality to hold without any further assumptions.

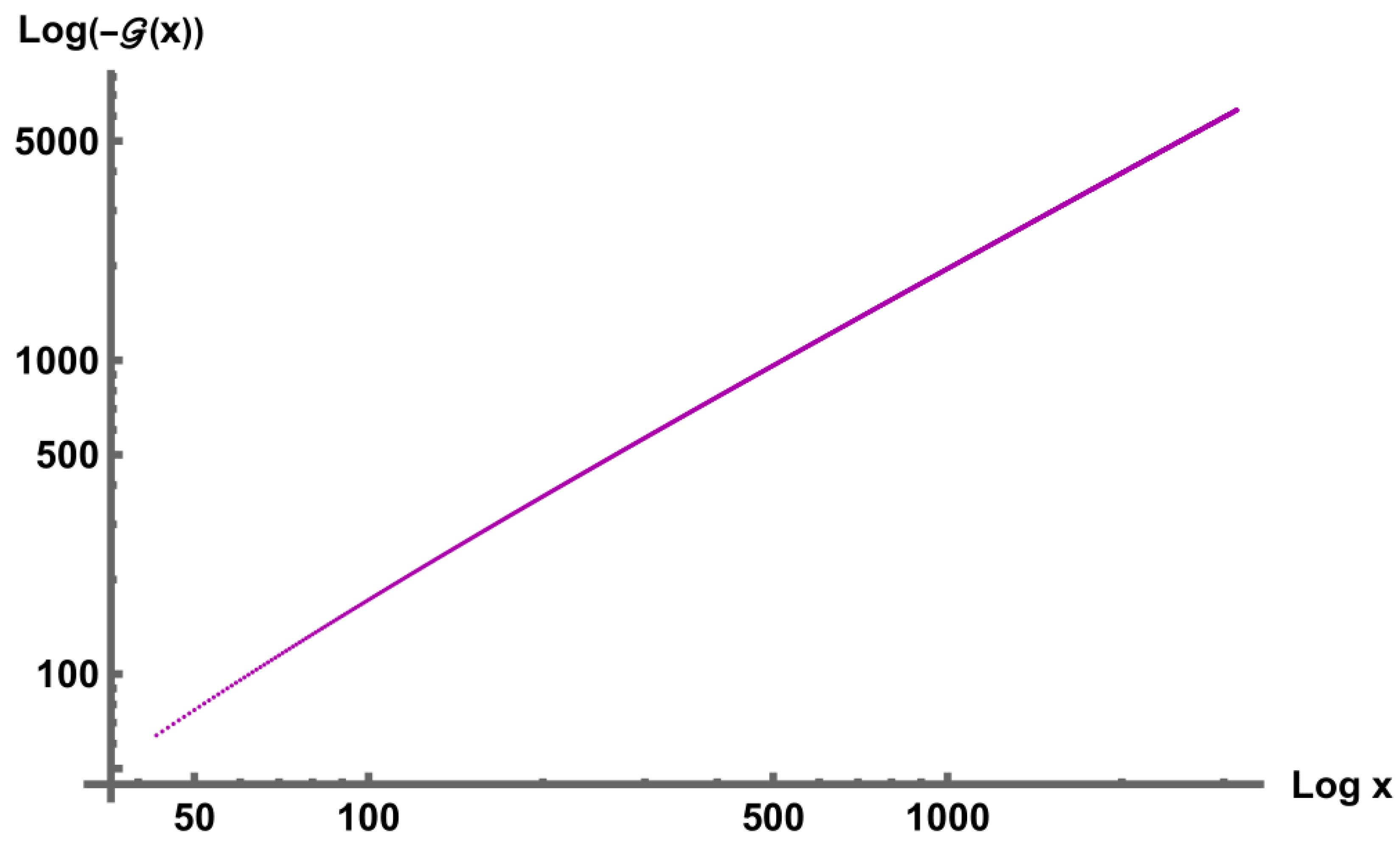
3. Numerical Estimates for $G (x)$

We can indeed verify our claim using programming tools such as MATHEMATICA for example. The numerical data1 from the Table 1 and the plot (Figure 1) representing values of

log (- G (x))

with respect to

log x

for

x \in [exp (43), exp (3159)]

clearly establishes that,

G

is indeed monotone decreasing on the interval

[exp (43.5102146), exp (3159)]

and also is strictly negative. It only suffices to check until

exp (3159)

, as the result has been unconditionally proven for

x \geq exp (3158.442)

by Axler [6].

Table 1. Values of

G (x)

Table 1. Values of

G (x)

x	$G (x)$

$e^{43.5102146}$	$- 1.29848 \times 10^{28}$
$e^{49}$	$- 3.5777143 \times 10^{32}$
$e^{59}$	$- 5.3863026 \times 10^{40}$
$e^{159}$	$- 8.6366147 \times 10^{124}$
$e^{259}$	$- 3.2250049 \times 10^{210}$
$e^{359}$	$- 3.2357043 \times 10^{296}$
$e^{459}$	$- 5.3064365 \times 10^{382}$
$e^{559}$	$- 1.1686993 \times 10^{469}$
$e^{659}$	$- 3.1339236 \times 10^{555}$
$e^{759}$	$- 9.6742945 \times 10^{641}$
$e^{859}$	$- 3.3194561 \times 10^{728}$
$e^{959}$	$- 1.2367077 \times 10^{815}$
$e^{1059}$	$- 4.9214899 \times 10^{901}$
$e^{1159}$	$- 2.0671392 \times 10^{988}$
$e^{1259}$	$- 9.0822473 \times 10^{1074}$
$e^{1359}$	$- 4.1454353 \times 10^{1161}$
$e^{1459}$	$- 1.9549848 \times 10^{1248}$

x	$G (x)$

$e^{1559}$	$- 9.4847597 \times 10^{1334}$
$e^{1659}$	$- 4.7172079 \times 10^{1421}$
$e^{1759}$	$- 2.3980349 \times 10^{1508}$
$e^{1859}$	$- 1.2430367 \times 10^{1595}$
$e^{1959}$	$- 6.5566576 \times 10^{1681}$
$e^{2059}$	$- 3.5131458 \times 10^{1768}$
$e^{2159}$	$- 1.9093149 \times 10^{1855}$
$e^{2259}$	$- 1.0511565 \times 10^{1942}$
$e^{2359}$	$- 5.8557034 \times 10^{2028}$
$e^{2459}$	$- 3.2975152 \times 10^{2115}$
$e^{2559}$	$- 1.8754944 \times 10^{2202}$
$e^{2659}$	$- 1.0765501 \times 10^{2289}$
$e^{2759}$	$- 6.2322859 \times 10^{2375}$
$e^{2859}$	$- 3.6365683 \times 10^{2462}$
$e^{2959}$	$- 2.1376236 \times 10^{2549}$
$e^{3059}$	$- 1.2651826 \times 10^{2636}$
$e^{3159}$	$- 7.5364298 \times 10^{2722}$

4. Future Research Prospects

In summary, we’ve utilized specific order estimates for the Prime Counting Function

π (x)

in addition to several explicit bounds involving Chebyshev’s ϑ-function,

ϑ (x)

, a priori with the help of the Prime Number Theorem in order to conjure up an improved bound for the famous Ramanujan’s Inequality. Although, it’ll surely be interesting to observe whether it’s at all feasible to apply any other techniques for this purpose.

On the other hand, one can surely work on some modifications of Ramanujan’s Inequality For instance, Hassani studied (1) extensively for different cases [3], and eventually claimed that, the inequality does in fact reverses if one can replace e by some

α

satifying,

0 < α < e

, although it retains the same sign for every

α \geq e

In addition to above, it is very much possible to come up with certain generalizations of Theorem (1.1). In this context, we can study Hassani’s stellar effort in this area where, he apparently increased the power of

π (x)

from 2 upto

2^{n}

and provided us with this wonderful inequality stating that for sufficiently large values of x [16],

\begin{matrix} {(π (x))}^{2^{n}} < \frac{e^{n}}{\prod_{k = 1}^{n} {(1 - \frac{k - 1}{log x})}^{2^{n - k}}} {(\frac{x}{log x})}^{2^{n} - 1} π (\frac{x}{e^{n}}) \end{matrix}

Finally, and most importantly, we can choose to broaden our horizon, and proceed towards studying the prime counting function in much more detail in order to establish other results analogous to Theorem (1.1), or even study some specific polynomial functions in

π (x)

and also their powers if possible. One such example which can be found in [17] eventually proves that, for sufficiently large values of x,

\begin{matrix} \frac{3 e x}{log x} {(π (\frac{x}{e}))}^{3^{n} - 1} < {(π (x))}^{3^{n}} + \frac{3 e^{2} x}{{(log x)}^{2}} {(π (\frac{x}{e^{2}}))}^{3^{n} - 2}, n > 1 \end{matrix}

Whereas, significantly the inequality reverses for the specific case when,

n = 1

(Cubic Polynomial Inequality) (cf. Theorem

(3.1)

[17]).

Hopefully, further research in this context might lead the future researchers to resolve some of the unsolved mysteries involving prime numbers, or even solve some of the unsolved problems surrounding the iconic field of Number Theory.

Data Availability Statement

I as the sole author of this article confirm that the data supporting the findings of this study are available within the article.

Acknowledgments

I’ll always be grateful to Prof. Adrian W. Dudek ( Adjunct Associate Professor, Department of Mathematics and Physics, University of Queensland, Australia ) for inspiring me to work on this problem and pursue research in this topic. His leading publications in this area helped me immensely in detailed understanding of the essential concepts.

Conflicts of Interest

I as the author of this article declare no conflicts of interest.

References

Ramanujan Aiyangar, Srinivasa, Berndt, Bruce C., Ramanujan’s Notebooks: Part IV, New York: Springer-Verlag, 1994.
Dudek, Adrian W., Platt, David J., On Solving a Curious Inequality of Ramanujan, Experimental Mathematics, 24:3, 289-294, 2015. [CrossRef]
Hassani, Mehdi, On an Inequality of Ramanujan Concerning the Prime Counting Function, Ramanujan Journal 28 (2012), 435–442. [CrossRef]
Fiori, A. , Kadiri, H., Swidinsky, J., Sharper bounds for the error term in the Prime Number Theorem, Research in Number Theory 9, no. 3 (2023): 63. [CrossRef]
Mossinghoff, M. J. , Trudgian, T. S. Nonnegative Trigonometric Polynomials and a Zero-Free Region for the Riemann Zeta-Function, arXiv:1410.3926, 2014.
Axler, Christian, On Ramanujan’s prime counting inequality, arXiv preprint arXiv:2207.02486 (2022). arXiv:2207.02486.
Rosser, J. B., Schoenfeld, L., Approximate formulas for some functions of prime numbers, Illinois J. Math. 6 (1962), 64–94.
Schoenfeld, L., Sharper bounds for the Chebyshev functions θ(x) and ψ(x), II, Math. Comp. 134 (1976), 337–360. [CrossRef]
Panaitopol, Laurenţiu, "Inequalities concerning the function π(x): applications.", Acta Arithmetica 94, no. 4 (2000): 373-381.
Karanikolov, C. , On some properties of the function π(x), Univ. Beograd Publ. Elektrotehn. Fak. Ser. Mat. 1971, 357–380. [Google Scholar]
Udrescu, V. , Some remarks concerning the conjecture π(x+y) < π(x) + π(y), Roumaine Math. Pures Appl. 20 ( 1975), 1201–1208.
Ramanujan, S, “Collected Papers”, Chelsea, New York, 1962.
Hardy, G. H. , A formula of Ramanujan in the theory of primes, 1. London Math. Soc. 12 ( 1937), 94–98. [CrossRef]
Hardy, G. H. , Collected Papers, vol. II, Clarendon Press, Oxford, 1967.
De, Subham, "On proving an Inequality of Ramanujan using Explicit Order Estimates for the Mertens Function", arXiv preprint arXiv:2407.12052 (2024). [CrossRef]
Hassani, Mehdi, Generalizations of an inequality of Ramanujan concerning prime counting function, Appl. Math. E-Notes 13 (2013) 148-154.
De, Subham, Inequalities involving Higher Degree Polynomial Functions in π(x), arXiv preprint arXiv:2407.18983 (2024). [CrossRef]
Platt, D. J., Trudgian, T. S., The error term in the prime number theorem, Math. Comp. 90 (2021), no. 328, 871-–881.
Cully-Hugill, M. , Johnston, D. R., On the error term in the explicit formula of Riemann–von Mangoldt, preprint, 2021. Available at arxiv.org/abs/2111.10001.
Johnston, D. R. , Yang, A., Some explicit estimates for the error term in the prime number theorem, preprint, 2022. Available at arxiv.org/abs/2204.01980.

1	Codes are available at: https://github.com/subhamde1/Paper-15.git

Figure 1. Plot of

log (- G (x))

with respect to

log x

Figure 1. Plot of

log (- G (x))

with respect to

log x

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On Proving Ramanujan’s Inequality Using a Sharper Bound for the Prime Counting Function π(x)

Abstract

1. Introduction

2. An Improved Criterion for Ramanujan’s Inequality

3. Numerical Estimates for G ( x )

4. Future Research Prospects

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3. Numerical Estimates for $G (x)$