1. Introduction
In recent years, the fruit tree industry has experienced rapid development worldwide. The autonomous navigation technology of unmanned agricultural machinery in orchards has been an important topic of concern in the agricultural field in recent years [
1,
2]. During autonomous operation of agricultural machinery, obstacles such as pedestrians may be encountered, and real-time detection and distance measurement of obstacles are required to provide information for subsequent obstacle avoidance, thereby improving the safety and reliability of autonomous operation of agricultural machinery [
3]. The orchard environment is complex and ever-changing, with high real-time requirements. How to quickly and accurately detect obstacles has become a research focus. Traditional orchard robot navigation technology mainly relies on Global Navigation Satellite System (GNSS) and Inertial Measurement Unit (IMU) [
4]. However, when working between rows of fruit trees, GNSS often cannot provide sufficient positioning accuracy due to factors such as tree obstruction. When using IMU for positioning, accumulated errors will occur over time, and there are also problems of zero bias and temperature drift [
5]. Therefore, visual navigation technology has become an important navigation tool for orchard robots.
In the orchard environment, inter row navigation line extraction refers to using sensors to obtain orchard environment information, and then analyzing and processing it through algorithms to extract navigation lines that can be used for autonomous navigation of agricultural machinery. Common sensors include LiDAR and visual sensors. With the development of computer vision and deep learning technologies, some researchers have begun to explore the use of traditional methods such as K-Means clustering and OTSU threshold segmentation [
6,
7], as well as deep learning methods such as semantic segmentation and object detection, to extract navigation lines. Radcliffe J et al. used the similarity between the shape of the sky in orchard images and the shape of the ground constrained by tree trunks to extract the path plane through the green component and calculate the centroid of the path plane to determine the heading of the navigation path, taking advantage of the large difference between the crown of fruit trees and the sky background [
8]. OPIYO S et al. proposed a machine vision technique based on the intermediate axis to extract orchard navigation lines. This method first converts the RGB image into a grayscale image and extracts texture features. Then, the K-Means clustering method is used to obtain binary images, and finally the middle axis is used as the navigation line [
9].
In terms of research on obstacle detection methods, Bochkovskiy A et al. proposed YOLOv4, a technique for enhancing Mosaic image data [
10]. This method utilizes Path Aggregation Network (PANet) [
11] for multi-scale feature fusion and adopts CIOU loss (Cross Intersection over Union Loss) as the position loss function for prediction boxes [
12], significantly improving detection speed and accuracy. The YOLOv5 proposed by Ultralytics et al. is an improved and optimized single-stage object detection algorithm based on YOLOv3 [
13]. It modularizes the network structure and proposes a new training strategy that can quickly and accurately detect targets. Hsu W Y et al. proposed a pedestrian detection method based on multi-scale adaptive fusion to address the uncertainty and diversity of pedestrians under different scales and occlusion conditions. The method designed a segmentation function to achieve segmentation of non overlapping pedestrian areas in the input image and obtain sub images. Then, a multi-resolution adaptive fusion method was proposed to fuse all sub images with the input image, improving the model’s ability to detect pedestrians of different scales [
14]. Wan et al. proposed an STPH-YOLOv5 algorithm to address the problem of slow detection speed and low detection accuracy caused by pedestrian occlusion and pose changes in dense pedestrian detection. The algorithm uses a layered visual Transformer prediction head (STPH) and coordinate attention mechanism, and uses a weighted bidirectional feature pyramid (BiFPN) in the Neck section to improve sensitivity to targets of different scales and enhance the overall detection capability of the model [
15].Panigrahi S et al. proposed an improved YOLOv5 method, which improves the Darknet19 backbone network and introduces separable convolution and Inception deep convolution modules, aiming to improve model performance with minimal overhead [
16].
In terms of research on visual SLAM localization methods, Wang R et al. used basic matrices to detect feature point inconsistencies and cluster depth images, achieving segmentation of moving objects and removing feature points on moving objects [
17]. Cheng J et al. proposed a Sparse Motion Removal (SMR) model. This model is based on the Bayesian framework and detects dynamic regions based on the similarity between consecutive frames and the difference between the current frame and the reference frame [
18]. Sun Y et al. proposed a visual SLAM algorithm based on RGB-D information for real-time removal of dynamic foreground targets. Due to the use of dense optical flow for tracking, this algorithm is limited and time-consuming in high-speed scenes. As the optical flow method degrades, its segmentation accuracy for dynamic targets also decreases [
19]. Liu G et al. proposed a DMS-SLAM algorithm. This algorithm combines GMS feature matching algorithm and sliding window to construct static initialization map points. Based on the GMS feature matching algorithm and the map point selection method between keyframes, static map points are added to the local map to create a static 3D map that can be used for attitude tracking. However, it is prone to failure when the dynamic target is too large [
20]. G. Li et al. used a small number of feature points to detect moving objects based on epipolar geometric constraints, obtained dynamic feature points, and then obtained dynamic Region of Interest (RoI) regions based on disparity constraints using dynamic feature points. They used an improved SLIC superpixel segmentation algorithm to segment the dynamic RoI regions and obtain dynamic target regions [
21]. Yu C et al. proposed the DS-SLAM algorithm [
22], which utilizes the semantic segmentation network SegNet to segment images and integrates optical flow estimation to distinguish between static and dynamic objects in the environment [
23]. However, it has a high computational cost and poor real-time performance. Bescos B et al. [
24] proposed a DynaSLAM algorithm that combines Mask R-CNN [
25] and multi view geometry to perform pixel segmentation on dynamic objects, obtain dynamic regions, and then remove feature points from the dynamic regions.
By analyzing the current research status of navigation line extraction, obstacle detection, and dynamic visual SLAM positioning methods at home and abroad, this paper aims to use binocular vision and deep learning technology to study the perception and positioning methods of agricultural machinery environment suitable for orchard environment, and to research high-precision and robust algorithms for agricultural machinery orchard environment perception and positioning, providing strong support for the automation and intelligence of orchard operations.
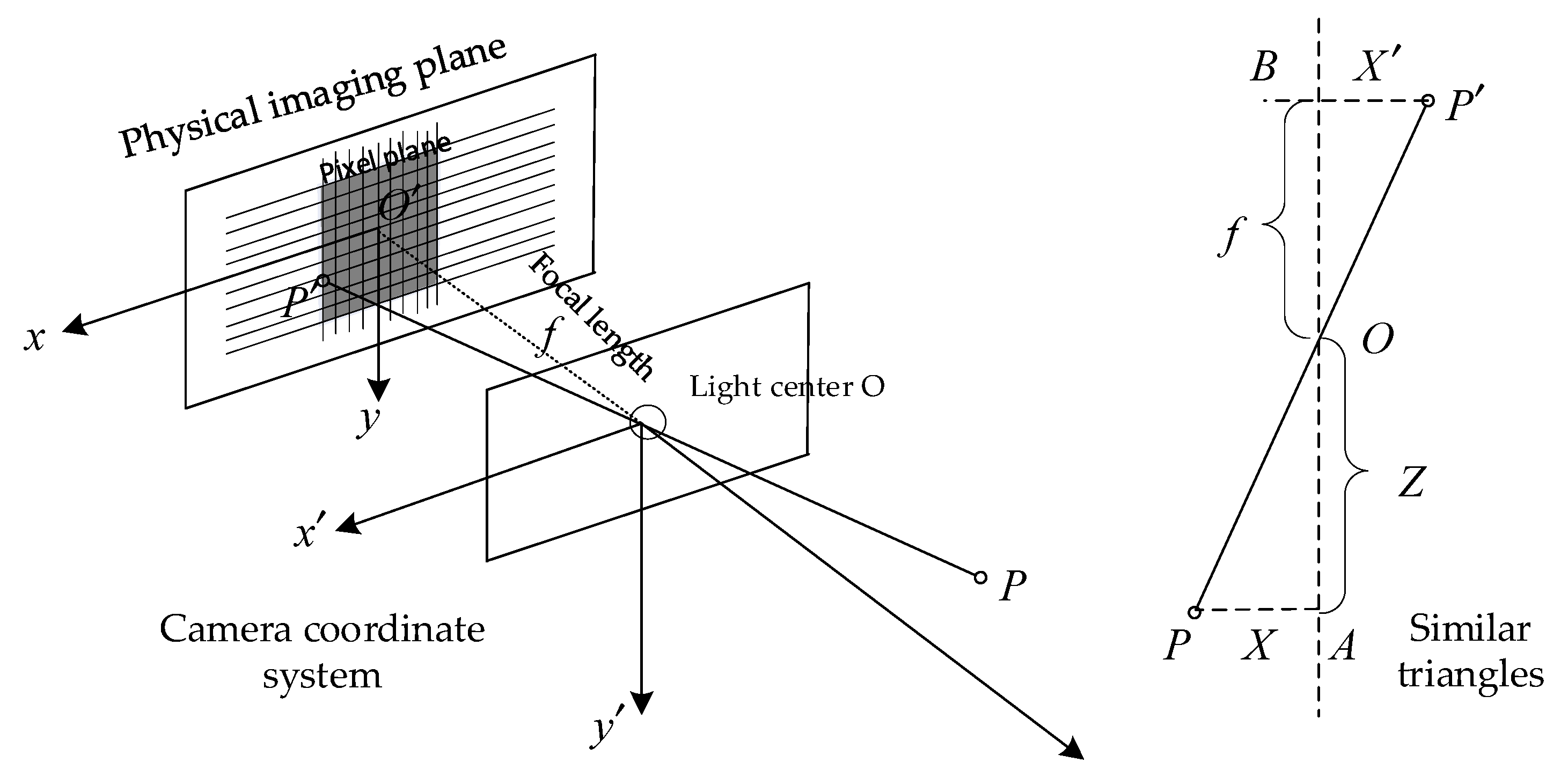
Figure 1.
Pinhole Camera Model.
Figure 1.
Pinhole Camera Model.
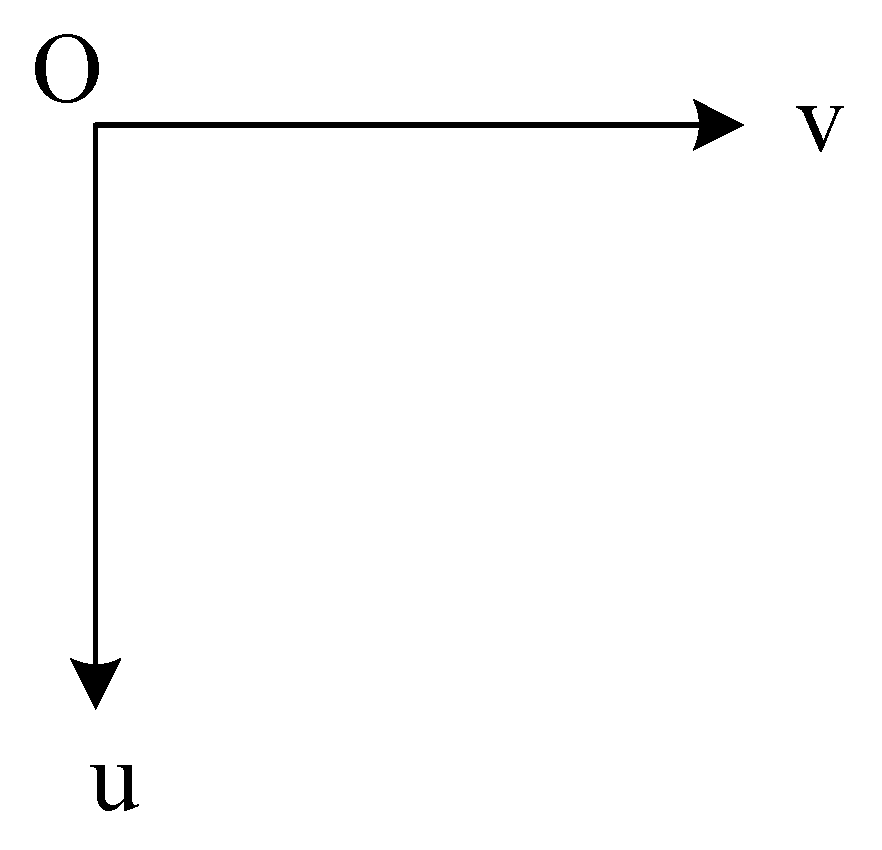
Figure 2.
Pixel Coordinate sSystem.
Figure 2.
Pixel Coordinate sSystem.
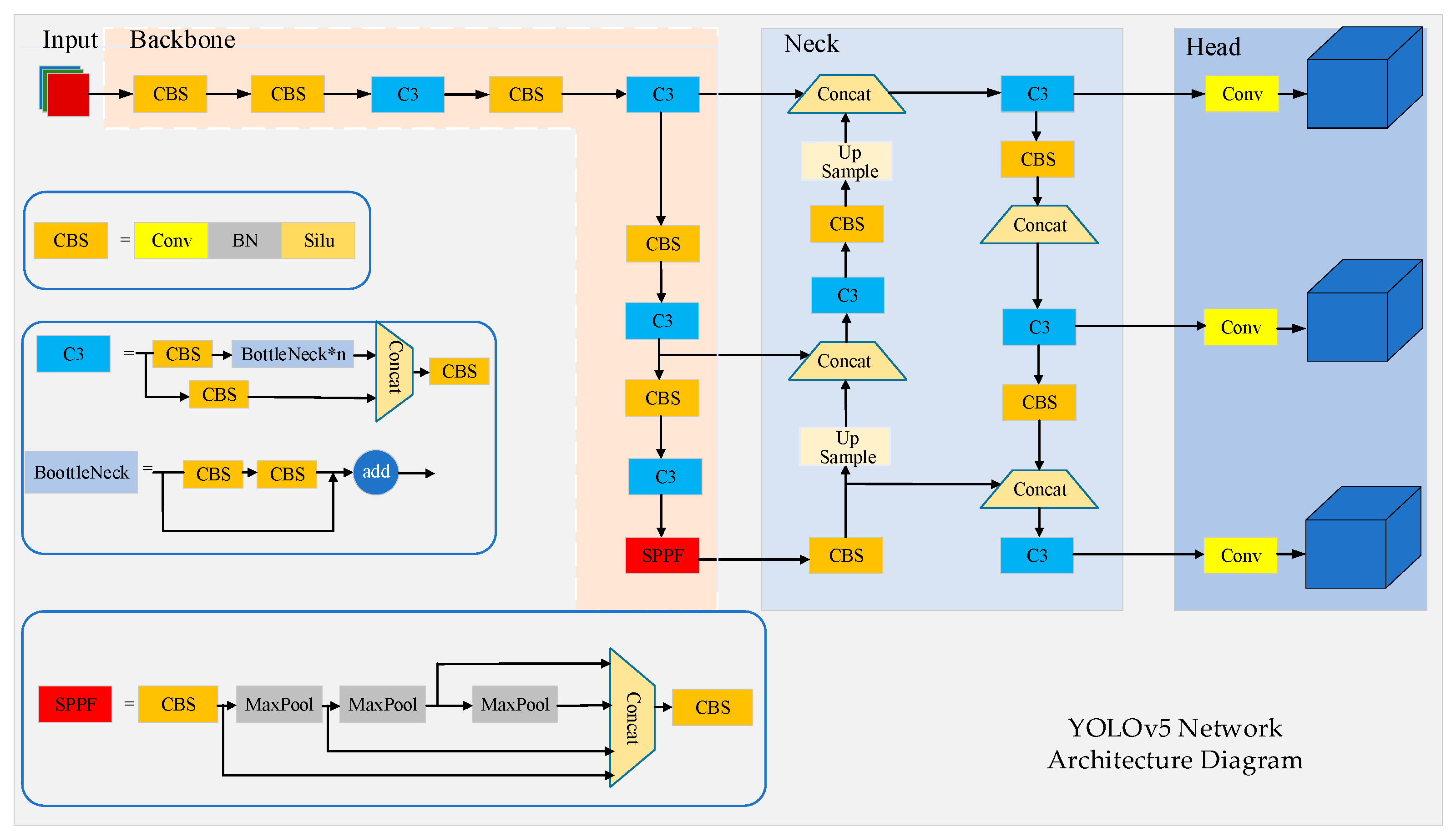
Figure 3.
YOLOv5s algorithm network structure.
Figure 3.
YOLOv5s algorithm network structure.
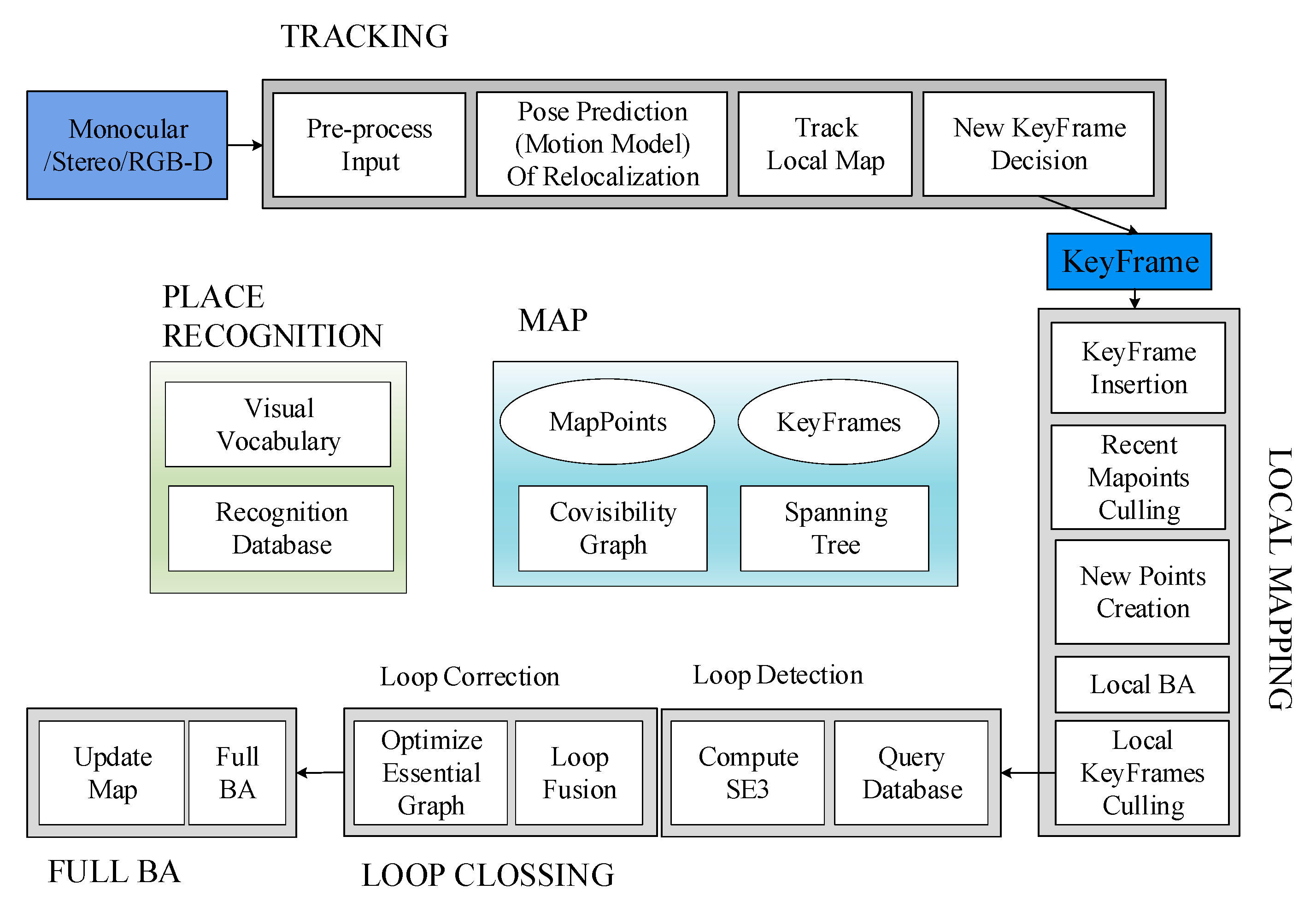
Figure 4.
Overall principle block diagram of ORB-SLAM2.
Figure 4.
Overall principle block diagram of ORB-SLAM2.
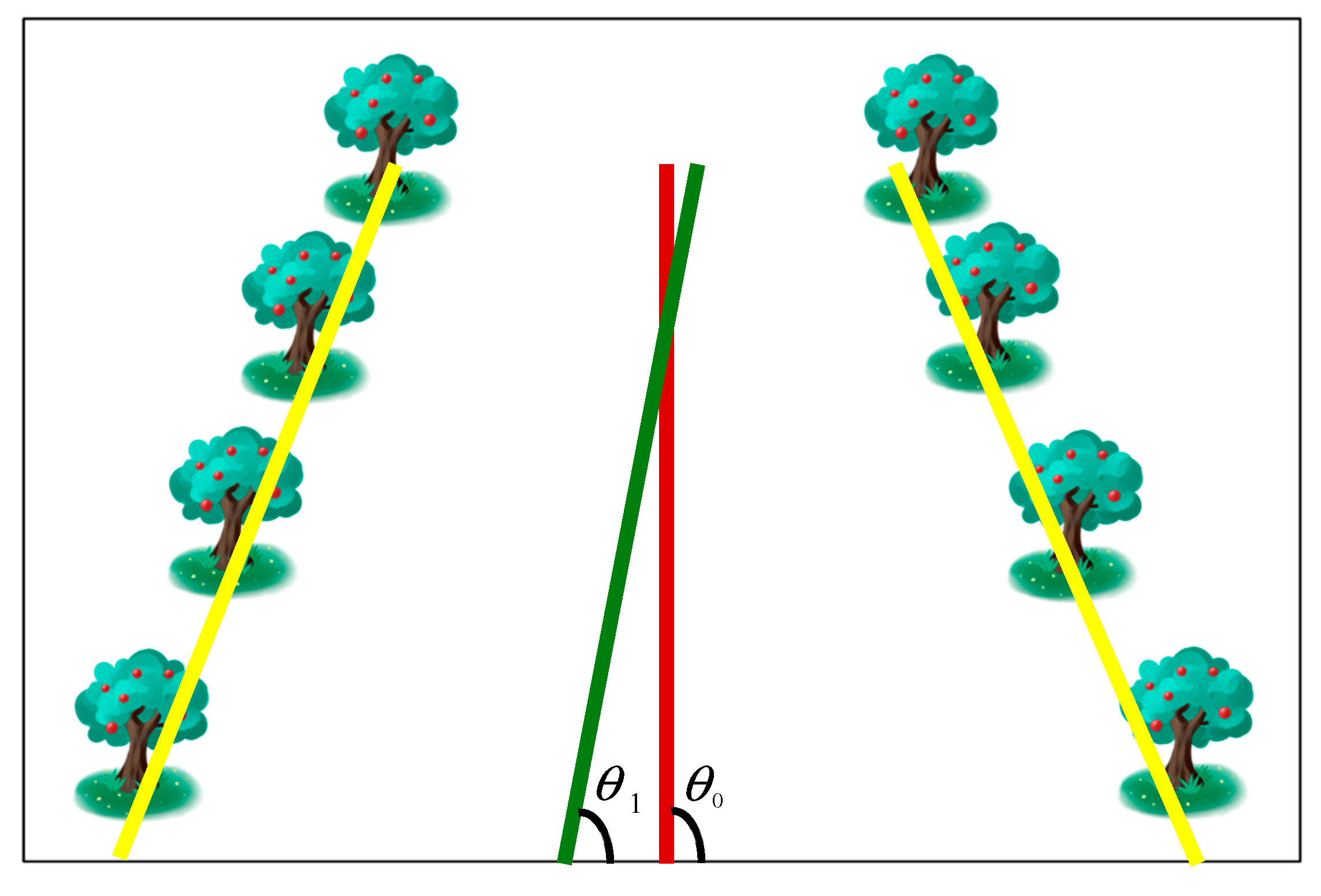
Figure 6.
Problem diagram of extracting navigation lines in Scenario 1.
Figure 6.
Problem diagram of extracting navigation lines in Scenario 1.
Figure 7.
Problem diagram of extracting navigation lines in scenario 2.
Figure 7.
Problem diagram of extracting navigation lines in scenario 2.
Figure 8.
Navigation line extraction diagram.
Figure 8.
Navigation line extraction diagram.
Figure 9.
Navigation line extraction in different orchard scenes.
Figure 9.
Navigation line extraction in different orchard scenes.
Figure 10.
Schematic diagram of evaluation indicators.
Figure 10.
Schematic diagram of evaluation indicators.
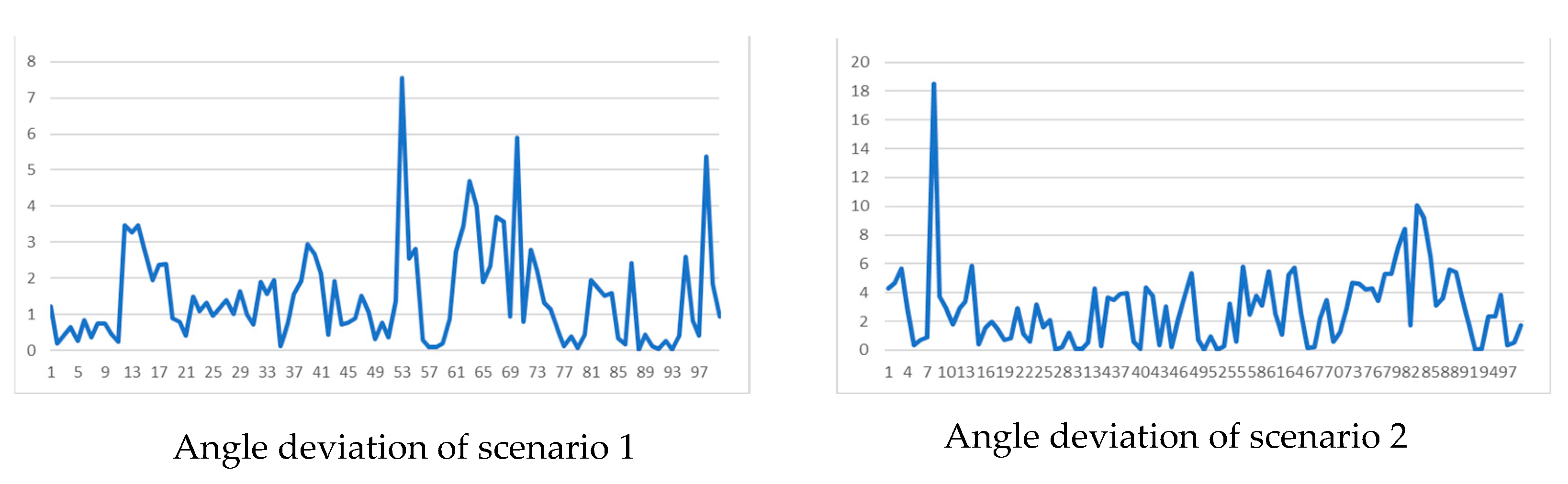
Figure 11.
Angle deviation.
Figure 11.
Angle deviation.
Figure 12.
Schematic diagram of algorithm flow.
Figure 12.
Schematic diagram of algorithm flow.
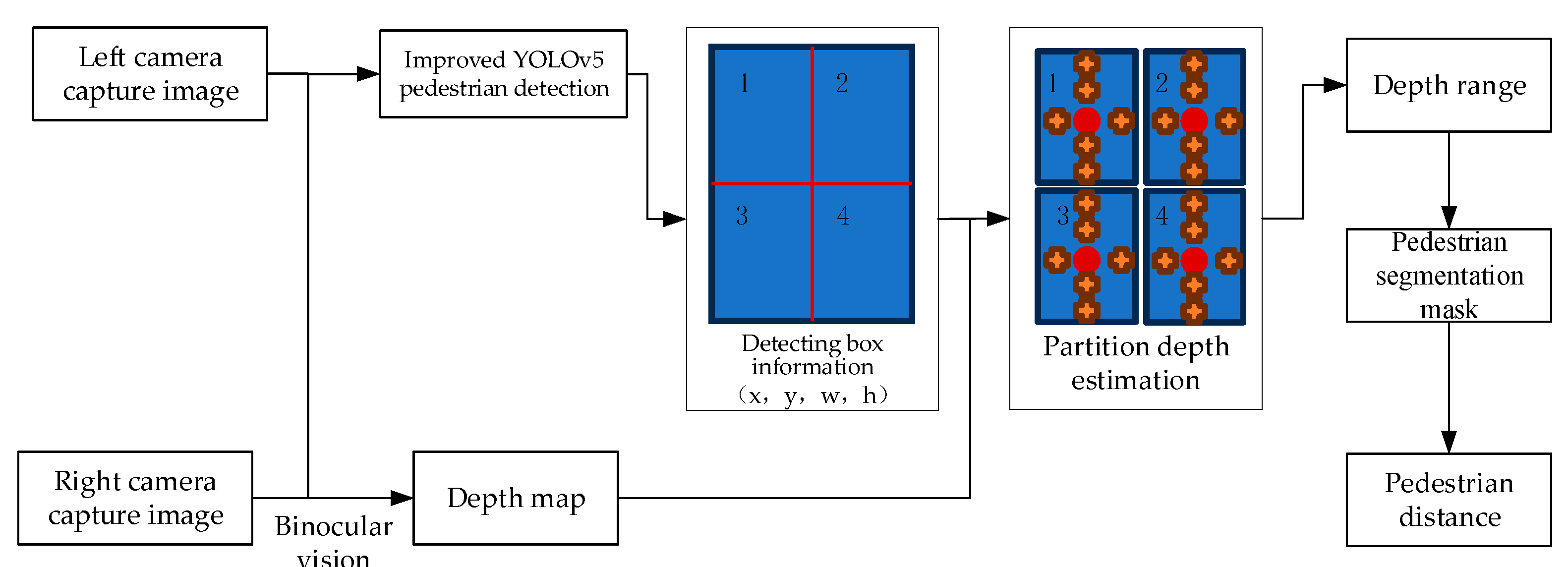
Figure 13.
Pedestrian Distance Measurement Experiment.
Figure 13.
Pedestrian Distance Measurement Experiment.
Figure 14.
Left image and depth map of binocular camera.
Figure 14.
Left image and depth map of binocular camera.
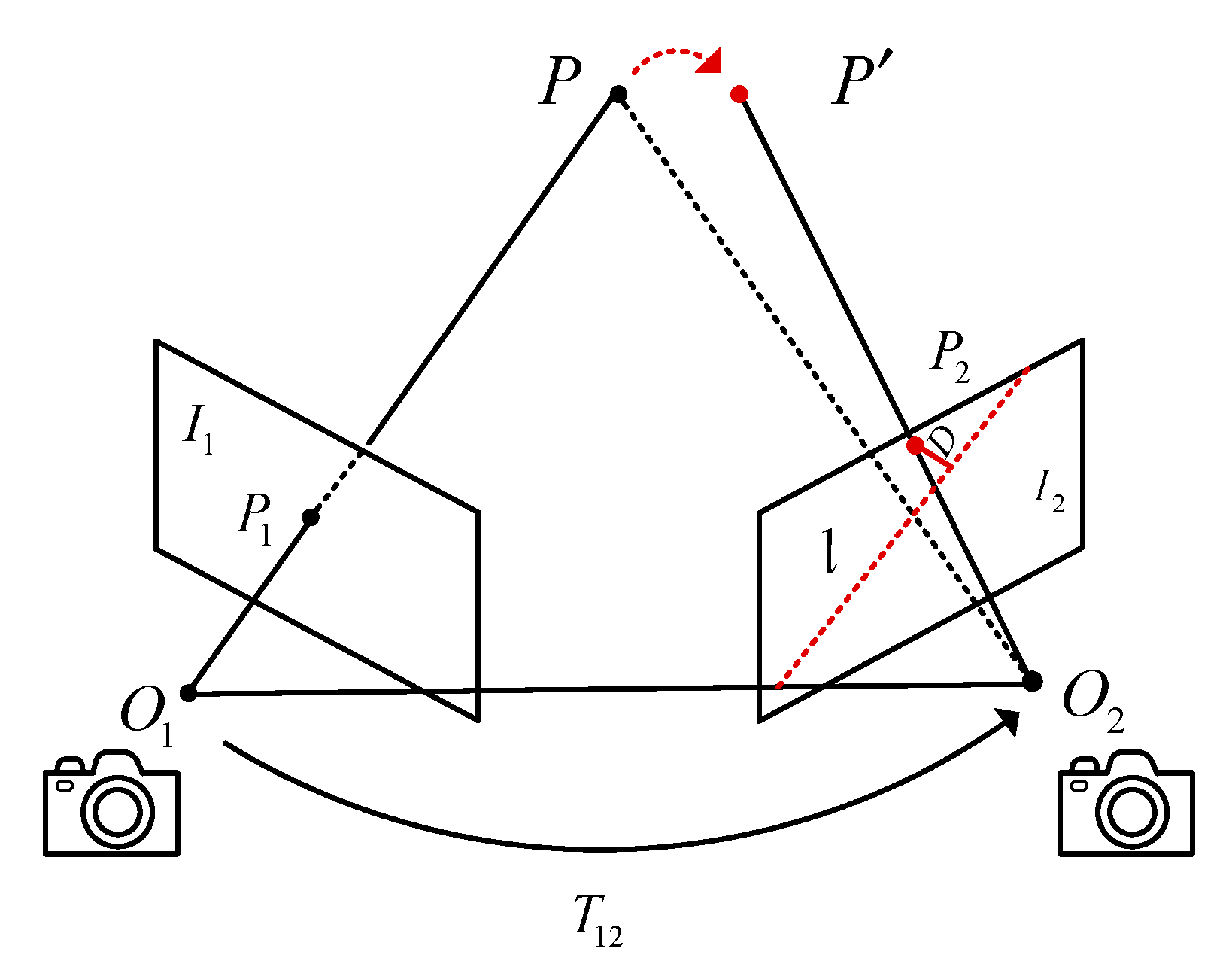
Figure 15.
Geometric Constraints of Polar Lines.
Figure 15.
Geometric Constraints of Polar Lines.
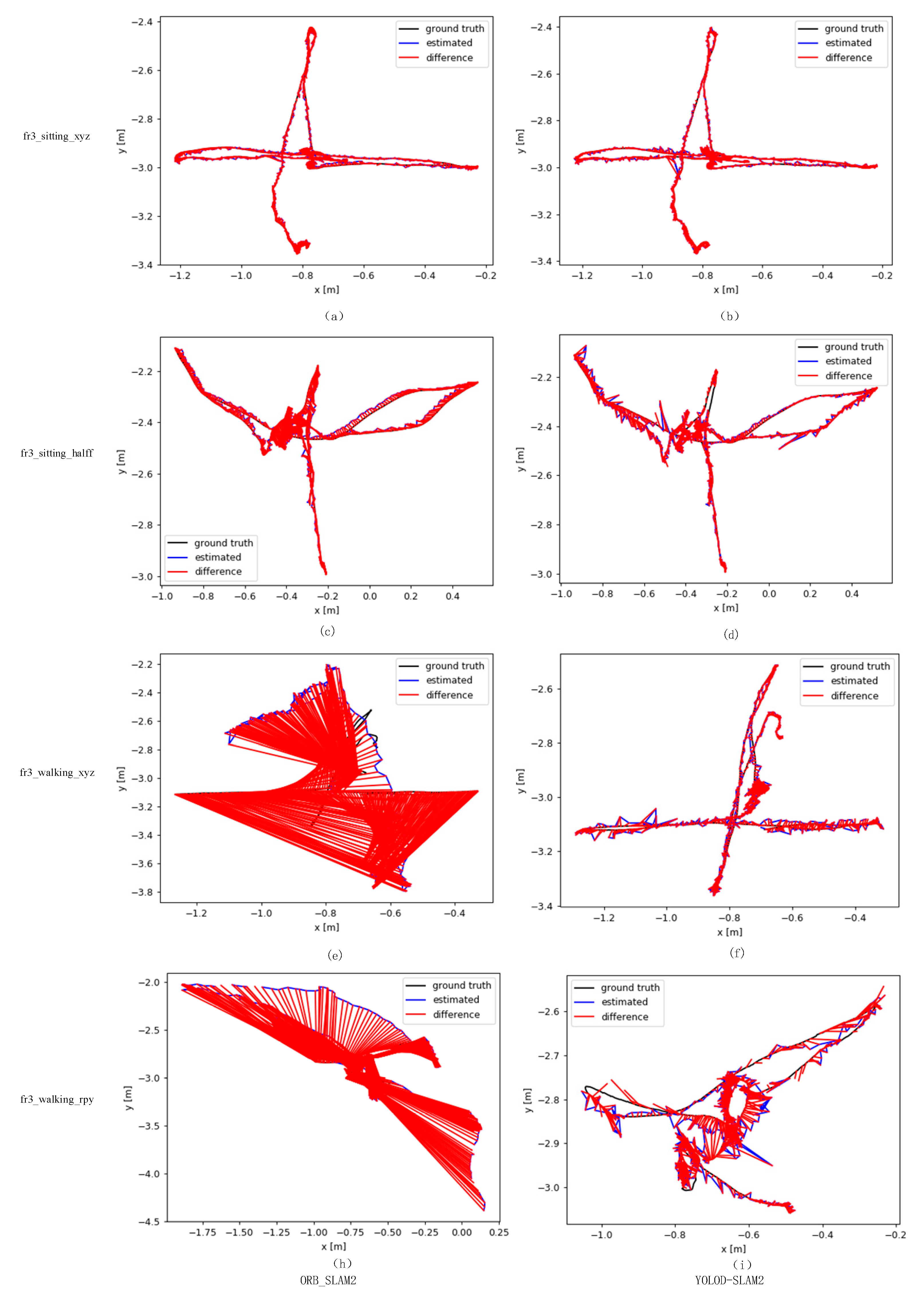
Figure 17.
Comparison of Algorithm Trajectory.
Figure 17.
Comparison of Algorithm Trajectory.
Figure 18.
Actual Orchard Environment Trajectory Map.
Figure 18.
Actual Orchard Environment Trajectory Map.
Table 1.
Analysis of Navigation Line Extraction Error Index in Different Scenarios.
Table 1.
Analysis of Navigation Line Extraction Error Index in Different Scenarios.
| Scenario |
Number of images |
Average angle deviation/(°) |
Standard deviation of angle deviation/(°) |
| Scenario 1 |
100 |
1.4797 |
1.3675 |
| Scenario 2 |
100 |
2.8942 |
2.7102 |
Table 2.
Comparison of Algorithms in Different Scenarios.
Table 2.
Comparison of Algorithms in Different Scenarios.
| Scenario |
Number of images |
Accurate extraction frame rate |
Extraction accuracy |
Average extraction time/ms |
| Scenario 1 |
100 |
97 |
97% |
47.98 |
| Scenario 2 |
100 |
94 |
94% |
56.11 |
Table 5.
Description of TUM RGB-D Dataset.
Table 5.
Description of TUM RGB-D Dataset.
| |
Sequence |
Duration/s |
Length/m |
Content |
| Scenario of people sitting on a chair |
fr3_sitting_xyz |
42.50 |
5.496 |
Maintain the same angle and move the camera along three directions (x, y, z) |
| fr3_sitting_half |
37.15 |
6.503 |
The camera moves on a small hemisphere with a diameter of 1m |
| Scenario of people walking around |
fr3_walking_xyz |
28.83 |
5.791 |
Maintain the same angle and move the camera along three directions (x, y, z) |
| fr3_walking_rpy |
30.61 |
2.698 |
The camera rotates along the main axis (row, pitch, yaw) at the same position. |
Table 6.
ATE Error (m/s).
Table 6.
ATE Error (m/s).
| Sequence |
ORB-SLAM2 |
YOLOD-SLAM2 |
Improvements |
| RMSE |
S.D. |
RMSE |
S.D. |
RMSE |
S.D. |
| fr3_sitting_xyz |
0.0111 |
0.0052 |
0.0108 |
0.0056 |
2.91% |
-7.56% |
| fr3_sitting_half |
0.0287 |
0.0132 |
0.0204 |
0.0124 |
29.03% |
6.27% |
| fr3_walking_xyz |
0.6102 |
0.1677 |
0.018 |
0.0094 |
97.06% |
94.39% |
| fr3_walking_rpy |
0.6994 |
0.3372 |
0.03 |
0.0177 |
95.71% |
94.76% |
Table 7.
Translation T RPE Error (m/s).
Table 7.
Translation T RPE Error (m/s).
| Sequence |
ORB-SLAM2 |
YOLOD-SLAM2 |
Improvements |
| RMSE |
S.D. |
RMSE |
S.D. |
RMSE |
S.D. |
| fr3_sitting_xyz |
0.0117 |
0.0057 |
0.0157 |
0.0076 |
-33.79% |
-33.5% |
| fr3_sitting_half |
0.0413 |
0.0199 |
0.0293 |
0.0163 |
29.00% |
18.02% |
| fr3_walking_xyz |
0.922 |
0.5034 |
0.0256 |
0.0125 |
97.23% |
97.51% |
| fr3_walking_rpy |
1.0223 |
0.5483 |
0.0427 |
0.0229 |
95.83% |
95.82% |
Table 8.
Rotation R RPE Error (°/s).
Table 8.
Rotation R RPE Error (°/s).
| Sequence |
ORB-SLAM2 |
YOLOD-SLAM2 |
Improvements |
| RMSE |
S.D. |
RMSE |
S.D. |
RMSE |
S.D. |
| fr3_sitting_xyz |
0.4798 |
0.2461 |
0.5863 |
0.3007 |
-22.19% |
-22.19% |
| fr3_sitting_half |
0.8586 |
0.356 |
0.7806 |
0.3743 |
9.09% |
-5.13% |
| fr3_walking_xyz |
18.787 |
10.161 |
0.6746 |
0.4035 |
96.41% |
96.03% |
| fr3_walking_rpy |
19.98 |
11.62 |
0.9617 |
0.523 |
95.19% |
95.50% |
Table 9.
Average Time/ms.
Table 9.
Average Time/ms.
| Sequence |
ORB-SLAM2 |
YOLOD-SLAM2 |
| fr3_sitting_xyz |
17.99 |
42.74 |
| fr3_sitting_half |
20.89 |
48.03 |
| fr3_walking_xyz |
20.73 |
42.69 |
| fr3_walking_rpy |
21.65 |
41.73 |