Thermodynamic Factors Controlling Electron Transfer amongst the Terminal Electron Acceptors of Photosystem I: Insight from Kinetic Modelling

Preprint

Article

Thermodynamic Factors Controlling Electron Transfer amongst the Terminal Electron Acceptors of Photosystem I: Insight from Kinetic Modelling

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.zip (555.31KB )

Stefano Santabarbara^*

Anna Paola Casazza

Stefano Santabarbara^*

Anna Paola Casazza

This version is not peer-reviewed

Submitted:

08 August 2024

Posted:

12 August 2024

You are already at the latest version

Alerts

Abstract

Photosystem I is a key component of primary energy conversion in oxygenic photosynthesis. Electron transfer reactions in Photosystem I take place across two, parallel, electron transfer chains that converge after a few electron transfer steps, sharing both the terminal electron acceptors, that are a series of three Iron-Sulphur (Fe-S) clusters known as , and , and the terminal donor, . The two electron transfer chains show kinetic differences which are, due to their close geometrical symmetry, mainly attributable to the tuning of the physical-chemical reactivity of the bound cofactors, exerted by the protein surroundings. The factors controlling the rate of electron transfer between the terminal Fe-S clusters are still not fully understood because of the difficulties of monitoring these events directly. Here we present a discussion concerning the driving forces associated to electron transfer between and as well as and , employing a tunnelling-based description of the reaction rates coupled to the kinetic modelling of forward and recombination reactions. It is concluded that the reorganisation energy for oxidation shall be lower than 1 eV. Moreover, it is suggested that the analysis of mutants with altered redox properties can also provide useful information concerning the upstream, phylloquinone, cofactor energetics.

Keywords:

Subject: Biology and Life Sciences - Biophysics

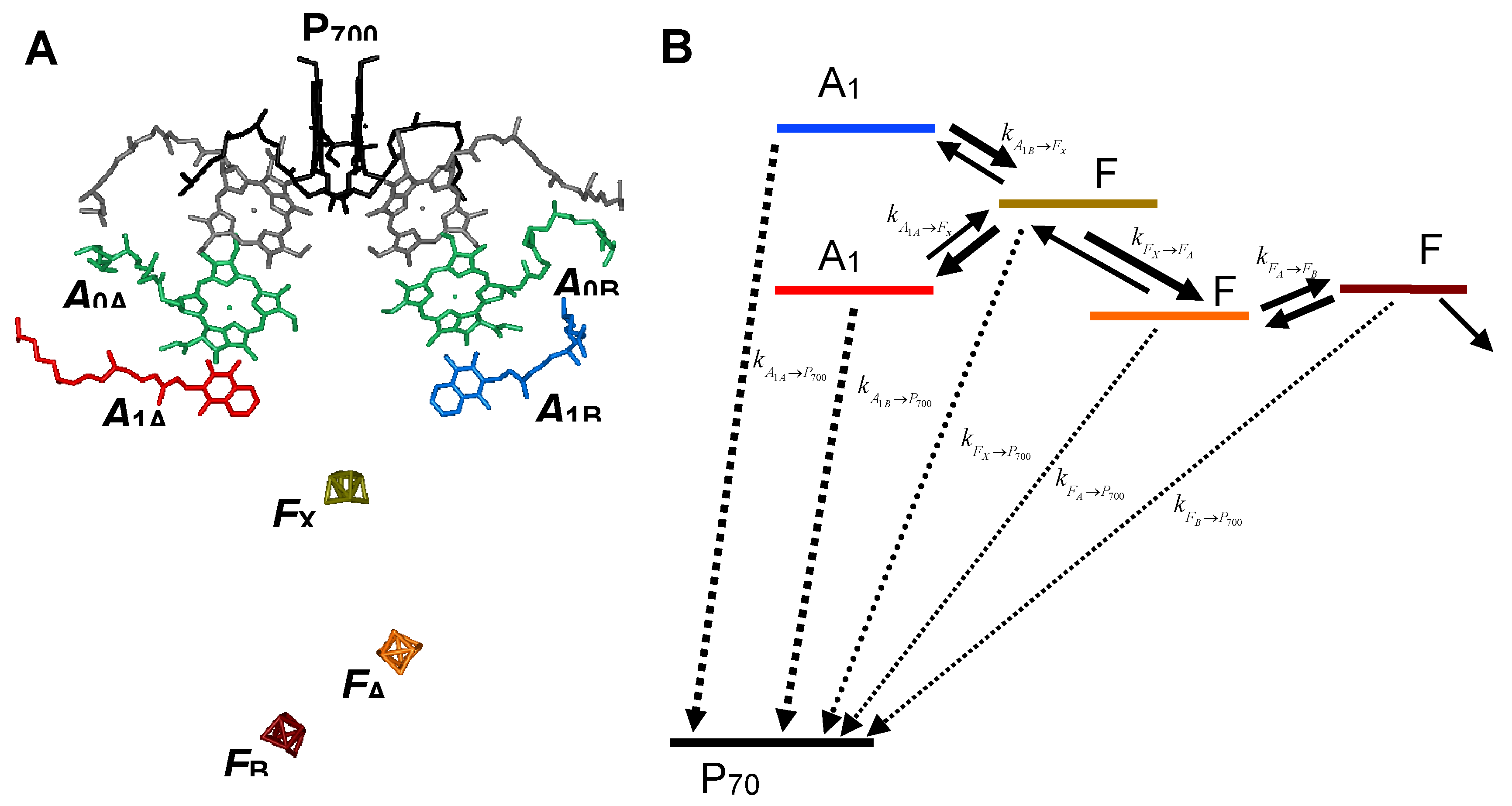
1. Introduction

Photosystem I (PSI) is a fundamental component of the oxygenic photosynthetic electron transport chain. It catalyses the light-dependent oxidation of soluble electron shuttles, most commonly either the cupper-binding protein plastocyanin or the small cytochrome c₆, at its so-called donor side and the reduction of ferredoxin, which is also a soluble protein, at its acceptor side. Photosystem I is a very large membrane-embedded cofactor-protein supercomplex, composed of more than 10 protein subunits (e.g. [1,2]), the exact number of which depends on the species. Under an operational perspective it can be considered as being composed, analogously to the other photosystems, of two functional moieties: i) a core complex which has the role of harvesting sunlight and to perform primary charge separation and successive charge stabilisation through electron transfer (ET) reactions involving a series of redox-active cofactors, and ii) a peripheral antenna, which has light harvesting function only, and which composition in terms of proteins and chromophores, varies largely amongst different organisms.

The characteristics of the subunits composing the core complex of PSI appear instead to be generally well-conserved throughout evolutionary divergent species, particularly considering the two largest subunits PsaA and PsaB which form an heterodimer and coordinate, together with the core-antenna pigments, the majority of the redox-active cofactors. Also well conserved is the PsaC subunit which binds two 4Fe-4S clusters, referred to as

F_{A}

and

F_{B}

, acting as the terminal electron acceptors within the photosystem and being, in turn, responsible for ferredoxin reduction. Structural studies [3,4,5] have shown that, in analogy to all other known photosynthetic reaction centres, the PsaA- and PsaB-coordinated cofactors, identified as participating in ET reactions, are organised in a highly symmetric fashion. The redox-active cofactors display a mirror symmetry arrangement with respect to the reference axis being putatively perpendicular to the membrane plane (Figure 1A). The symmetric organisation of the cofactors results in the presence of two putative ET chains, which are however not completely independent, sharing the (hetero)dimer of Chlorophyll (Chl) a/Chl a’ (the latter being an epimer [3]), assigned to the long-lived, terminal, electron donor,

P_{700}^{(+)}

and the 4Fe-4S cluster

F_{X}

, which is the last PsaA/PsaB-bound acceptor before the PsaC-bound

F_{A}

and

F_{B}

centres. Both

P_{700}^{}

, where the number indicates the maximal absorption bleaching upon oxidation [2,6], and

F_{X}

are coordinated at the interface of PsaA and PsaB.

A general consensus has been reached over the years that in PSI the two parallel cofactor chains are both functional ([2,7,8,9,10,11,12]) and references therein). This represents a major functional difference with respect to Photosystem II, and the purple bacteria Reaction Centre (RC), in which primary photochemistry and ET reactions involve exclusively one cofactor chain, with the exclusion of the terminal electron acceptor, the quinone

Q_{B}

, which is structurally part of the “inactive” chain, but accepts electrons from the “photochemically functional chain” bound quinone,

Q_{A}

, instead. The need to control inter-quinone ET and the full-reduction of

Q_{B}

to quinole, by two consecutive charge separation events, is thought to be one of the main reasons for having an asymmetric, also referred to as mono-directional, ET in Type II photosynthetic RC. In PSI, and generally in Type I RC to whom it belongs, ET reactions involve only one-electron exchange, so that the need to control the accumulation of either oxidative or reducing equivalent at any level of the ET chain is not stringent.

Nonetheless, the probability by which electrons are transferred by each ET chain of PSI remains somewhat debated, with figures ranging from almost equal utilisation [12,13,14,15,16,17,18,19], to very asymmetric proportions in favour of the PsaA-coordinated branch [20,21,22,23,24]. Further functional differences are also apparent at the level of intermediate steps, particularly in the lifetime of oxidation of the reduced phylloquinone,

A_{1}^{}

, by next acceptor in the chain,

F_{X}

. This reaction shows a complex kinetic behaviour, which in its simplest description is accounted by two main phases characterised by lifetimes of 5-20 ns and 200-300 ns [6,7,8,9,10,25,26]. Studies of mutants at the level of the phylloquinone binding site have led to the assignment of the 200-300 ns phase to the oxidation of

A_{1 A}^{-}

[6,7,8,9,10,27,28,29,30,31] (the subscript indicates the subunit which primarily coordinates the cofactor) and the 5-20 ns phase to the oxidation of

A_{1 B}^{-}

[6,7,8,9,10,27,31]. These phases also show significantly different temperature dependences, with the slowest one displaying a larger activation energy (65-130 meV) with respect to the fast one (6-20 meV) [32,33,34]. Since

F_{X}

is a common cofactor to both reactions, and because of the similarity in the co-ordination geometry of the phylloquinones, the one-order-of-magnitude difference in the

A_{1 A}^{-}

and

A_{1 B}^{-}

oxidation kinetics was attributed, in the framework of ET-theory (e.g. [35,36,37] and references therein), to an asymmetry in the driving force for these reactions, with

A_{1 B}^{-}

oxidation being more thermodynamically favourable (e.g.

Δ G_{A_{1 B} \to F_{X}}^{0}

Δ G_{A_{1 A} \to F_{X}}^{0}

) [7,11,38,39]. Even though there is a general consensus concerning this interpretation, different estimates for the free energies have been advanced, also depending on the approach utilised for their evaluation ([12] and reference therein). Because of the very negative value of the phylloquinone potential direct redox titration is, at least, cumbersome [40]. Contradictory results were also obtained for the titration of

F_{X}

, although its potential (

E_{F_{X}}^{0}

) can be safely regarded as less than –680 mV ([41,42,43] and see discussion in [6]). Moreover, even direct titration can suffer of the bias linked to progressive accumulation of charges on the acceptor side (i.e. on

F_{A}

F_{B}

F_{X}

and so on). The direct electrochemically determined midpoint potentials can therefore differ, also significantly, from the “operational” ones, when the nearby cofactors are oxidised instead (see Ptsushenko et al. [44] for further discussion). Thus, most of the estimated

A_{1 A}^{}

and

A_{1 B}^{}

redox potentials were derived either from ET-theory-based modelling of the oxidation kinetic [7,11,38,39] or from structure-based computational methods [44,45,46,47]. None of these approaches is fully water-proof, since both require some specific simplifications and assumptions to address the problem. A detailed description of these issues is beyond the scope of the present paper. Yet, currently only two energetic pictures were proven to account for the oxidation kinetics at room temperature, the temperature dependence of the reactions [48] and the effect of mutations in the phylloquinone binding site, at least, in the latter case, concerning the

A_{1 A}^{-}

F_{X}

reaction [49], for which information are more abundant. These are the so-called “weak driving force” and “large driving force” scenarios. In the former,

A_{1 A}^{-}

oxidation is associated with a free energy difference of ~ – 30 meV <

Δ G_{A_{1 A} \to F_{X}}^{0}

< + 30 meV whereas

A_{1 B}^{-}

oxidation with

Δ G_{A_{1 B} \to F_{X}}^{0}

< – 50 meV (note that the values are broad, and rounded, because they depend on the exact parameters set describing the reaction rate constants) [7,11,12,48,49]. It is worth noticing that in the lower driving force limit

A_{1 A}^{-}

oxidation becomes thermodynamically unfavourable. Within the weak-driving force configuration, experimental observable are semi-quantitatively reproduced considering a total reorganisation energy (

λ_{t o t}

) associated to phylloquinone oxidation, as well as

F_{A}

reduction by

F_{X}

, of about 0.7 eV [7,11,12,48,49]. The “large driving force” scenario invokes that both

Δ G_{A_{1 A} \to F_{X}}^{0}

and

Δ G_{A_{1 B} \to F_{X}}^{0}

< – 50/75 meV and that

Δ G_{A_{1 B} \to F_{X}}^{0}

Δ G_{A_{1 A} \to F_{X}}^{0}

, with the former corresponding to driving forces even larger than ~150 meV [39,44]. This energetic configuration, however, required to consider much larger reorganisation energies, in the order of 1 eV [48,49], to describe the experimental phylloquinone oxidation kinetics. When assuming an homogenous value of

λ_{t o t}

for all the ET reactions, the difference in the values adopted to simulate

A_{1}^{-}

oxidation (i.e. 1 eV with respect to 0.7 eV) resulted in pronounced differences in the simulations of

F_{X}^{}

oxidation for the two energetic configurations described above even when keeping all other relevant simulation parameters, including

Δ G_{F_{X} \to F_{A}}^{0}

which was set at ~ –150 meV [6,7], equal. In this framework, the electron transfer from

F_{X}^{}

to the terminal Fe-S clusters was predicted to be about 5 folds slower for the large

A_{1}^{-}

oxidation driving force than for the weak

A_{1}^{-}

oxidation driving force enegetics ([48] and vide infra for further detail).

The redox potential of the iron-sulphur clusters

F_{A}

F_{B}

is, together with the one of

P_{700}^{+}

, the more accurately determined, even in place of some variability in the estimations [6,50,51,52,53]. Knowledge of these values shall increase the margin of accuracy of kinetic modelling predictions. Nonetheless, the dynamics of ET involving these redox centres are not unambiguously understood yet. This is mainly due to the optical properties of the Fe-S cluster, which possess a broad, relatively unstructured spectrum that abundantly overlaps with those of other PSI-bound chromophores [54,55]. Moreover, ET involving species having close-to-the-same absorption spectra imply a small differential extinction coefficient, making their direct detection by optical methods extremely challenging. Most of the kinetic information relies then on alternative methods, exploiting changes in the electric field through the protein milieu caused by the electron displacement along the ET chain. These include direct methods, such as photovoltage [56,57,58,59,60], and indirect optical probes, like ET-dependent local-stark effect on chlorophylls and carotenoids [25]. From these methods a relatively broad range of values for the

F_{X}

F_{A}

F_{B}

transfer time have been proposed, ranging from less than 25 ns to ~300 ns ([26,61] and references therein). A kinetic phase characterised by lifetimes of 160-180 ns, and attributed to ET between the iron-sulphur clusters, was also resolved in mutants in which the

A_{1 A}^{-}

oxidation phase, to which it is otherwise overlapped, was slowed-down more than 3 times [30,62,63]. A component with similar lifetime is also resolvable in wild-type photosystems in temperature dependence studies, when it appears to have a lower activation, and becomes therefore discernible from the slow phase of

A_{1 (A)}^{-}

oxidation upon cooling [33,34]. Electron transfer between

F_{A}

and

F_{B}

is even less characterised, as the positioning of these cofactors leads to a vectorial ET almost parallel to the membrane plane (perpendicular to the symmetry axis) which is unfavourable for both local-stark and photo-voltage detection. Hence, either only the collective transfer to

F_{A}

F_{B}

is generally detected or, alternatively, transfer to

F_{A}

alone after

F_{B}

is chemically inactivated/destabilised [26,61]. It is commonly assumed that the transfer time across all of the Fe-S shall be faster than 500 ns – 1 μs to account for the rapid reduction of pre-bound ferredoxin, that takes place in about 1 to 3 μs, although even faster sub-microsecond kinetics have been reported [64].

In order to gain further insight into the dynamics of ET reactions involving the Fe-S of PSI, kinetic simulations are here presented in which the effect of the most crucial thermodynamic parameters, i.e. the standard free energy difference and the reorganisation energy, are explored. The ET reactions involving the Fe-S clusters are contextualised within the “weak” and “large” driving force energetic scenarios for

A_{1}^{-}

oxidation. The simulations allow to put forward predictions which could be, in principle, tested experimentally to get a better understanding of these ET events.

2. Results and Discussion

In order to gain some additional information concerning the ET reactions involving the 4Fe-4S centres in PSI, i.e. the reduction of

F_{A}

F_{X}^{-}

(hereafter the sign indicates the reduced state of the FeS centre, not its net charge) and the successive reduction of

F_{B}

F_{A}^{-}

, kinetics simulations were performed starting from the two energetic scenarios which provide a satisfactory, semi-quantitative, description for the wild-type PSI. Successively, perturbations of parameters that control the rate constants of ET between the FeS clusters, mainly the standard free energies (

Δ G_{D A}^{0}

) and the reorganisation energy (

λ_{t o t}

), are introduced.

2.1 Weak Driving Force Scenario for

A_{1}^{-}

Oxidation

Figure 2 shows the simulated population evolutions of the reduced ET cofactors in PSI, after initial population of phylloquinones

A_{1 A}

and

A_{1 B}

, within the so-called “weak-driving” force framework. The parameters used in the calculations are reported in Table 1. In brief, the standard free energy difference for

A_{1 A}^{-}

and

A_{1 B}^{-}

oxidation were taken as

Δ G_{A_{1 A} \to F_{X}}^{0}

= +10 meV and

Δ G_{A_{1 B} \to F_{X}}^{0}

= –50 meV, and those for the 4Fe-4S centres oxidation were

Δ G_{F_{X} \to F_{A}}^{0}

= –150 meV and

Δ G_{F_{A} \to F_{B}}^{0}

= +25 meV. The two latter fall within the range derivable from direct redox titrations of the FeS cofactors [50,51,52,53]. Setting the midpoint potential of

F_{B}

at –555 mV, it then results that

E_{F_{A}}^{0}

= –530 mV,

E_{F_{X}}^{0}

= –680 mV

E_{A_{1 A}}^{0}

= –670 mV and

E_{A_{1 B}}^{0}

= –730 mV. Because of the relative spread of experimentally retrieved

E_{}^{0}

values and considering the effect of piling-up reducing equivalents upon titrations which likely result in a bias in the determined FeS clusters redox potentials, the free energy differences calculated from the experimental titrations and those employed in the simulations might and shall not match exactly. Those used in the simulations rather reflect the so-called “operational” potentials. Even with these approximations, the general consideration that the energy gap between

F_{X}^{}

and

F_{A}

is relatively large, whereas the one between

F_{A}

and

F_{B}

is shallow, with the two PsaC-coordinated centres being almost iso-potential, remains valid. For the parameters described above, and in general for the “weak driving” force model, it is possible to consider a common value of the reorganisation energy for the

A_{1 A}^{-}

A_{1 B}^{-}

and

F_{X}^{-}

oxidation equal to 0.7 eV whereas a larger value of 0.9 eV was considered for

F_{A}^{-}

oxidation. This is justified since the outer shell reconfiguration is expected to be larger for reactions involving metal centres only with respect to organic cofactors.

Figure 2. Panel A: reference energetic scheme for the “weak driving force” scenario for

A_{1}^{-}

oxidation; standard redox potentials (

E^{0}

) are shown relative to

F_{X}

. Panel B: simulated population evolution of the individual redox active cofactors,

A_{1 A}^{-} (t)

: dashed-dot red line,

A_{1 B}^{-} (t)

dashed-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

dot orange line,

F_{B}^{-} (t)

dot burgundy line. Also shown are the total population evolutions of

A_{1, t o t}^{-} (t) = A_{1 A}^{-} (t) + A_{1 B}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t) = F_{X}^{-} (t) + F_{A}^{-} (t) + F_{B}^{-} (t)

(purple line). The inset (C) shows the recombination kinetics simulated in absence of an exit from the system (

k_{o u t}

= 0). Temperature: 290 K.

Figure 2. Panel A: reference energetic scheme for the “weak driving force” scenario for

A_{1}^{-}

oxidation; standard redox potentials (

E^{0}

) are shown relative to

F_{X}

. Panel B: simulated population evolution of the individual redox active cofactors,

A_{1 A}^{-} (t)

: dashed-dot red line,

A_{1 B}^{-} (t)

dashed-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

dot orange line,

F_{B}^{-} (t)

dot burgundy line. Also shown are the total population evolutions of

A_{1, t o t}^{-} (t) = A_{1 A}^{-} (t) + A_{1 B}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t) = F_{X}^{-} (t) + F_{A}^{-} (t) + F_{B}^{-} (t)

(purple line). The inset (C) shows the recombination kinetics simulated in absence of an exit from the system (

k_{o u t}

= 0). Temperature: 290 K.

Specific frequencies of the mean coupled nuclear modes were considered for

A_{1}^{-}

oxidation, corresponding to

ℏ {\bar{ω}}_{A_{1 A} \to F_{X}}

= 22 meV (175 cm^-1) and

ℏ {\bar{ω}}_{A_{1 B} \to F_{X}}

= 46 meV (375 cm^-1). These values were obtained from the analysis of the phylloquinone oxidation kinetics as a function of the temperature [66] and resulted in an improvement of the simulations of the temperature dependence of the kinetics when explicitly considered. A coupling

ℏ {\bar{ω}}_{D A}

= 34 meV (275 cm^-1), which is the mean of the values employed for the quinone oxidation, was used for all other reactions. In the kinetic scheme shown above (Figure 1B) also the recombination reactions between all reduced cofactors and

P_{700}^{+}

were included. In the simulations of the recombination reactions

E_{P_{700}}^{0}

was +450 mV, in accordance with direct estimations from redox titrations [6], and the reorganisation energy was 0.9 eV for all reactions. The recombination reactions have virtually no influence on the simulations of forward ET kinetics because these rates are several order of magnitude slower than productive reactions, due to large distances between the cofactor pairs even in place of large favourable driving forces for all of these processes (see Appendix S1 of the Supplementary Information). However, their inclusion allows to compare the simulated and experimentally determined recombination kinetics, as shown in Figure 2C, simply by suppressing the exit rate from the system (i.e.

F_{B}^{-}

oxidation by external electron acceptors).

For the parameters discussed above it is obtained that, at room temperature (290 K), the system is characterised by five lifetimes (the number corresponding to the states present in the kinetics scheme) of 5.2, 22.5, 136, 243 and 3808 ns, which are common to the description of the population evolution of all cofactors. The 5.2, 22.5 and 243 ns lifetimes are those also retrieved from a three states model that does not explicitly include

F_{A}^{}

and

F_{B}^{}

(e.g. [7,11,12,48,49] and see Appendix S1 Figure S1 and Table S1), so that the remaining lifetimes of 136 and 3808 ns can be related to electron transfer reactions involving the terminal iron-sulphur cluster directly. The longest-lived lifetime describes the exit from the system, when this is considered (

F_{B} \to O u t

). This reaction is not modelled according to ET theory, a phenomenological rate of 1 x 10^-3 ns^-1 is considered instead and it is set to zero, when necessary, to simulate the recombination reactions.

Table 1. Rate-defining Parameters and Simulated ET kinetic for the weak driving force energetic scenario.

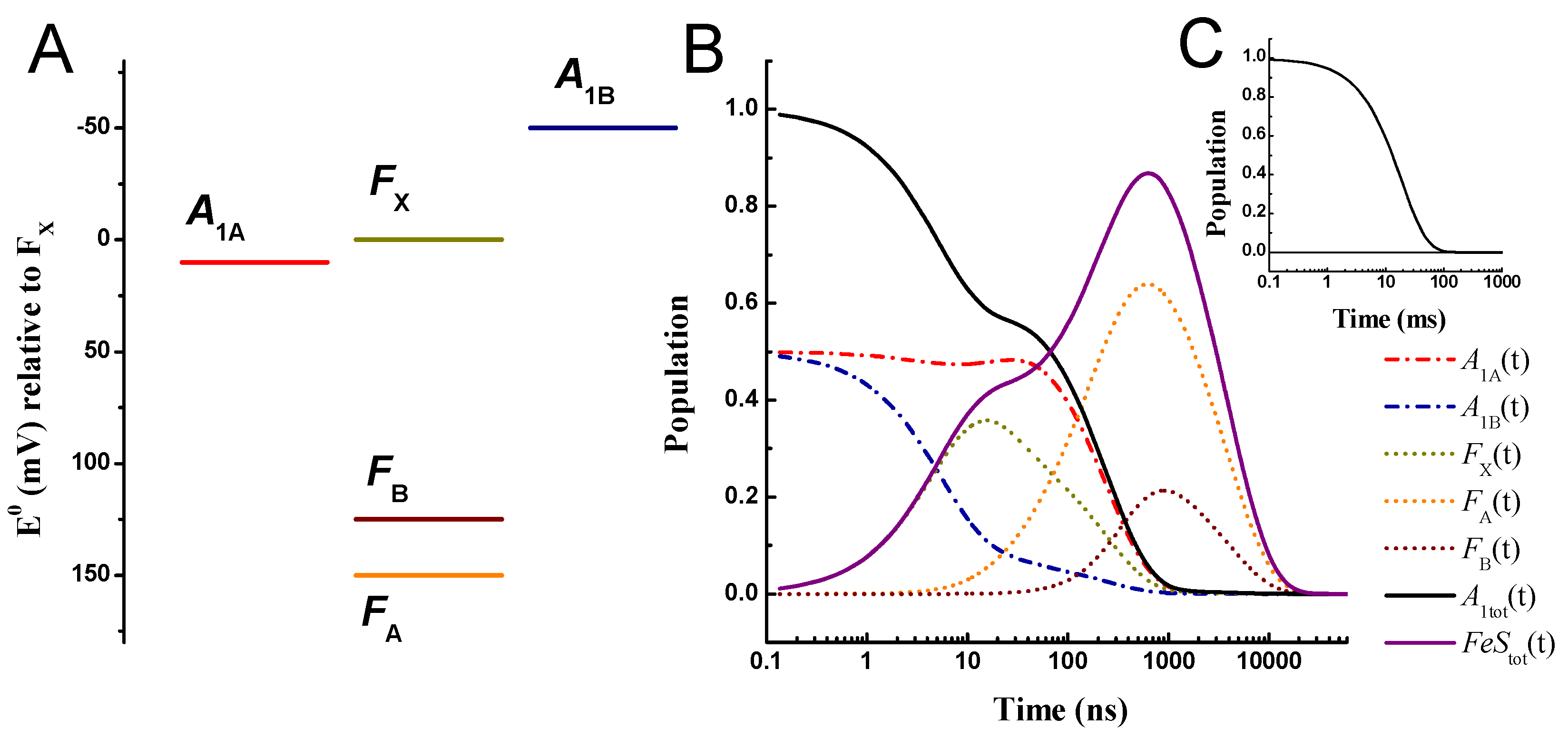
	Rate Determining Parameters						Electron Transfer Simulated Parameters
							Amplitudes
Reaction	$X_{D A}$ (Å)	$Δ G_{D A}^{0}$ (eV)	$λ_{t, D A}$ (eV)	${\bar{ω}}_{D A}$ (eV/cm^-1)	$k_{D \to A}$ (ns^-1)	$τ_{}$ (ns)	$p_{A_{1 A}}$	$p_{A_{1 B}}$	$p_{F_{X}}$	$p_{F_{A}}$	$p_{F_{B}}$	$p_{A_{1 tot}}$	$p_{F e S_{tot}}$
$A_{1 A}^{-} \to F_{X}$	9.1	0.01	0.700	0.022 (175)	0.0181	5.26	0.0754	0.382	-0.489	0.033	0.000	0.457	-0.457
$A_{1 B}^{-} \to F_{X}$	9.0	-0.05	0.700	0.046 (375)	0.145	22.5	-0.173	0.051	0.172	-0.051	0.003	-0.123	0.123
$F_{X}^{-} \to F_{A}$	11.6	-0.15	0.700	0.034 (275)	0.0126	136	0.0035	0.000	0.001	-0.295	0.336	0.004	0.042
$F_{A}^{-} \to F_{B}$	9.5	0.025	0.900	0.034 (275)	0.0019	243	0.587	0.067	0.312	-0.489	-0.628	0.654	-0.806
$F_{B}^{-} \to$	–	–	–	–	0.00100	3808	0.0068	0.001	0.005	0.803	0.290	0.008	1.098

Summary of the parameters utilised for the simulation of forward electron transfer in reference PSI within the weak-driving force scenario for

A_{1}^{-}

oxidation. The rate-defining parameters which are common to all forward electron reactions are the electronic coupling matrix element,

{|H_{0}|}^{2}

=1.3 10^-3 eV², the barrier camping factor

β

=1.34 Å^-1 and the temperature T=290 K, which are defined in Equation 1 of the main text.

The table also lista the lifetimes (

τ_{i}

) and associated amplitudes (

p_{i}

) describing the population evolution of each of the cofactors described in the model. The total amplitude associated with the electron transfer kinetics of phylloquinones (

p_{A_{1 tot}}

) and iron-sulphur centres (

p_{F e S_{tot}}

) are also presented in the table. The initial conditions for the amplitude simulations were

A_{1 A}^{-} (0) = A_{1 B}^{-} (0) = 0.5

and zero on all other cofactors considered.

Within this energetic scheme, the oxidation of

A_{1 B}^{-}

is dominated by the two fastest components (~5 and 22.5 ns), resulting in an average decay lifetime of 46 ns, whereas the oxidation of

A_{1 A}^{-}

is dominated by the 243 ns component, and the resulting average decay is 331 ns. Despite the assumption of equal initial population at time zero of

A_{1 A}^{-}

and

A_{1 B}^{-}

the predicted ratio of fast (5 ns and 22.5 ns) to slow (all remaining ones) oxidation phases is 0.33:0.67, which was interpreted as a transient inter-quinone population transfer [67]. Since the detail of the model predictions concerning the phylloquinone ET reactions has already been discussed previously (e.g. [7,11,12,48,49]), more attention will be here dedicated to the transfer involving the 4Fe-4S clusters. Within the above mentioned kinetic/energetic scheme, the average reduction time of

F_{X}^{}

is predicted to be relatively fast, and described uniquely by the 5.2 ns component, whereas the successive oxidation is multiphasic, dominated by the 22.5 and 243 ns lifetimes, giving rise to an average decay lifetime (

τ_{a v}

) of 199 ns, which is only slightly slower than the value simulated for the total quinone oxidation (

A_{1, t o t}^{-}

A_{1 A}^{-}

A_{1 B}^{-}

) being 160 ns. Similarly close values are obtained when comparing the mean population lifetime (i.e. the first moment of the population temporal evolution,

τ_{m}

), that is estimated as being 900 ns for

F_{X}^{-}

with respect to 805 ns for

A_{1, t o t}^{-}

oxidations. The

τ_{m}

are larger than the

τ_{a v}

values because of the increased weight of the slowest component in the parameter estimation, which is at least one order of magnitude slower than all other lifetimes. When the latter is omitted from the calculations, the mean lifetimes for

F_{X}^{-}

and

A_{1, t o t}^{-}

become 240 and 243 ns, respectively, that are then close to

τ_{a v}

. Yet, irrespectively of the parameters considered, these cofactors relax to their neutral state almost simultaneously. This would explain the difficulties in detecting an electrogenic phase specifically associated with the

F_{X}^{}

oxidation/reduction reactions, since this would broadly overlap kinetically with

A_{1}^{-}

oxidation. The successive redox acceptors

F_{A}^{}

and

F_{B}^{}

are reduced with average lifetimes of 192 and 243 ns, respectively, that is, almost co-ordinately with the relaxation of

A_{1, t o t}^{-}

and

F_{X}^{-}

, and are oxidised with average lifetimes of 3.6 μs and 1.9 μs, respectively, clearly limited by the rate of exit from the system. The simulated mean lifetimes of

F_{A}^{-}

and

F_{B}^{-}

population evolutions are 4.0 μs and 4.2 μs, respectively, again indicating that the terminal acceptors are oxidised almost simultaneously, which is due to the weak, slightly endergonic, driving force associated to

F_{A}^{-}

oxidation, leading to the partitioning of reducing equivalents in favour of this cofactor, with respect to the terminal acceptor

F_{B}^{}

Figure 2 also shows the predicted recombination, in the absence of an exit from the system, where the oxidation of the terminal 4Fe-S cluster is dominated by a lifetime of 19 ms, which replaces the longest-lived ~4μs lifetime predicted from the simulations in the presence of an acceptor. The simulated recombination lifetime falls well within the spread of values reported in the literature, that most commonly are in the range of 10 – 200 ms (see [6,26,68,69,70,71] and reference therein). It is also worth mentioning that the observed lifetime, however, does not reflect the (inverse) direct recombination rate from the terminal 4Fe-4S clusters, that are simulated as 2.1 x 10^-17 ns^-1 and 4.8 x 10^-22 ns^-1 for the reactions involving

F_{A}^{-}

and

F_{B}^{-}

respectively. Rather the recombination rate/lifetime is determined by the energetically up-hill repopulation of the upstream cofactors, chiefly

F_{X}^{-}

. The predicted recombination kinetics are virtually unaffected, in the energetic framework discussed above, by arbitrarily setting to zero the values of all the recombination to

P_{700}^{+}

, excluding the direct recombination from the phylloquinones (Appendix S1 Figure S2).

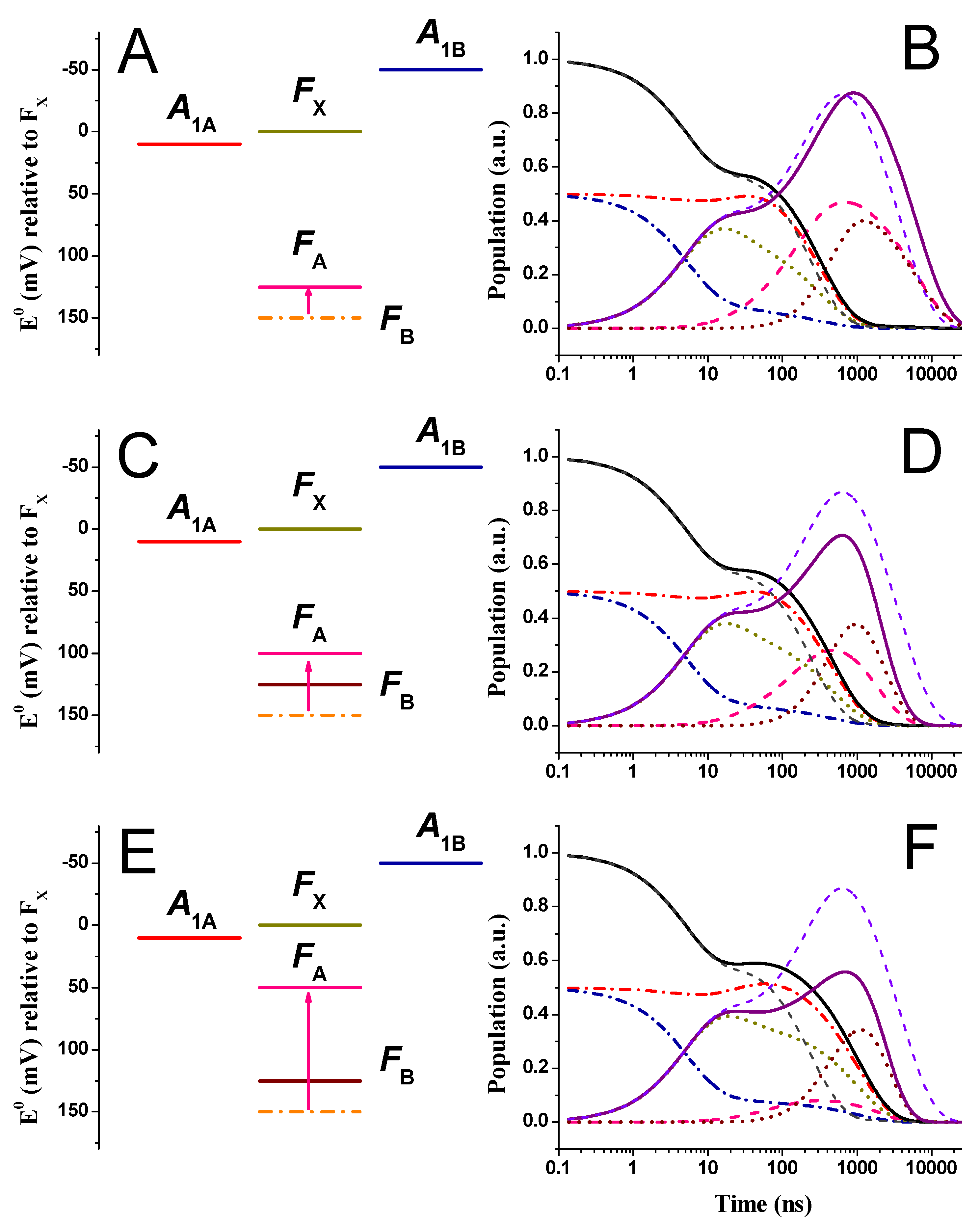
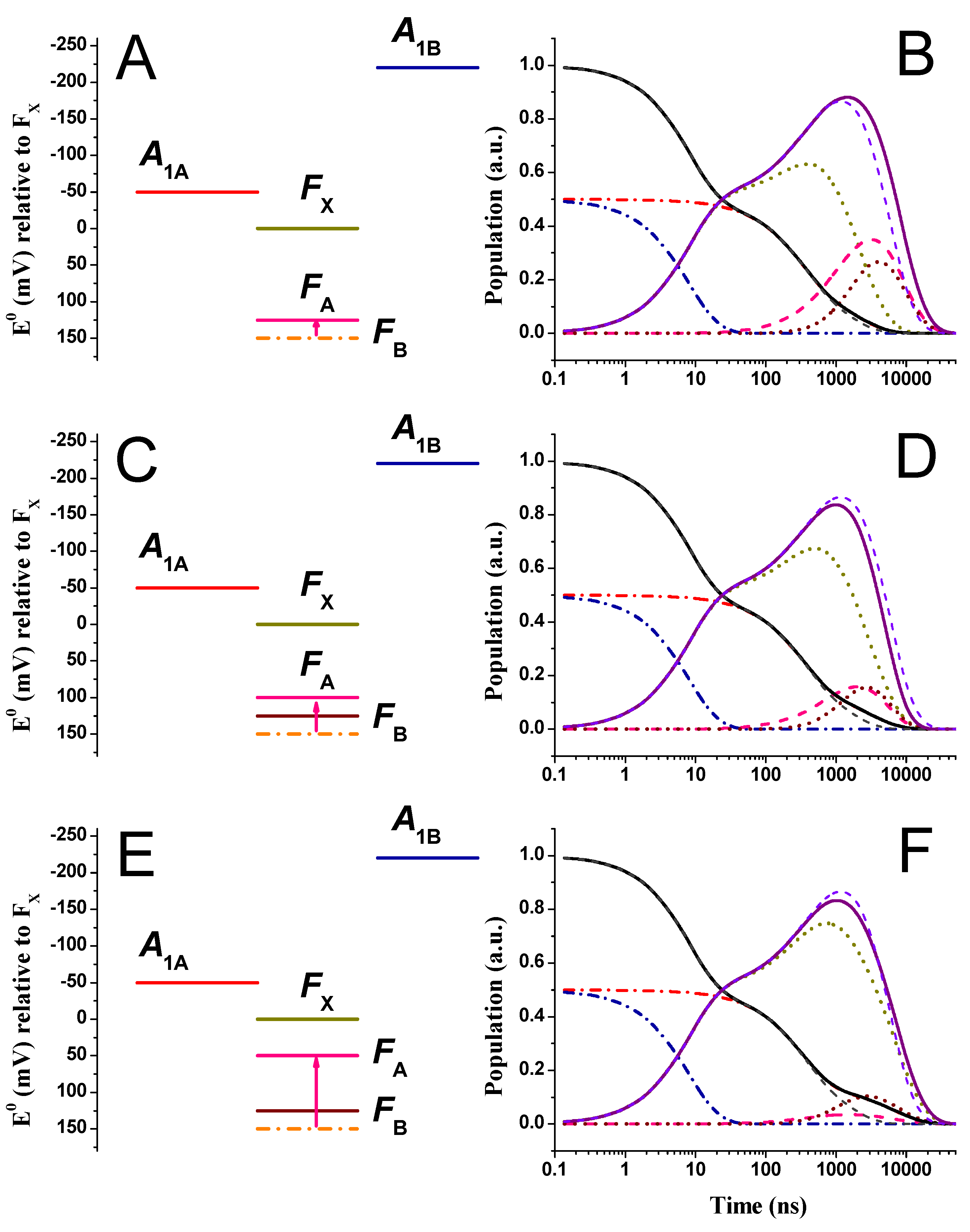
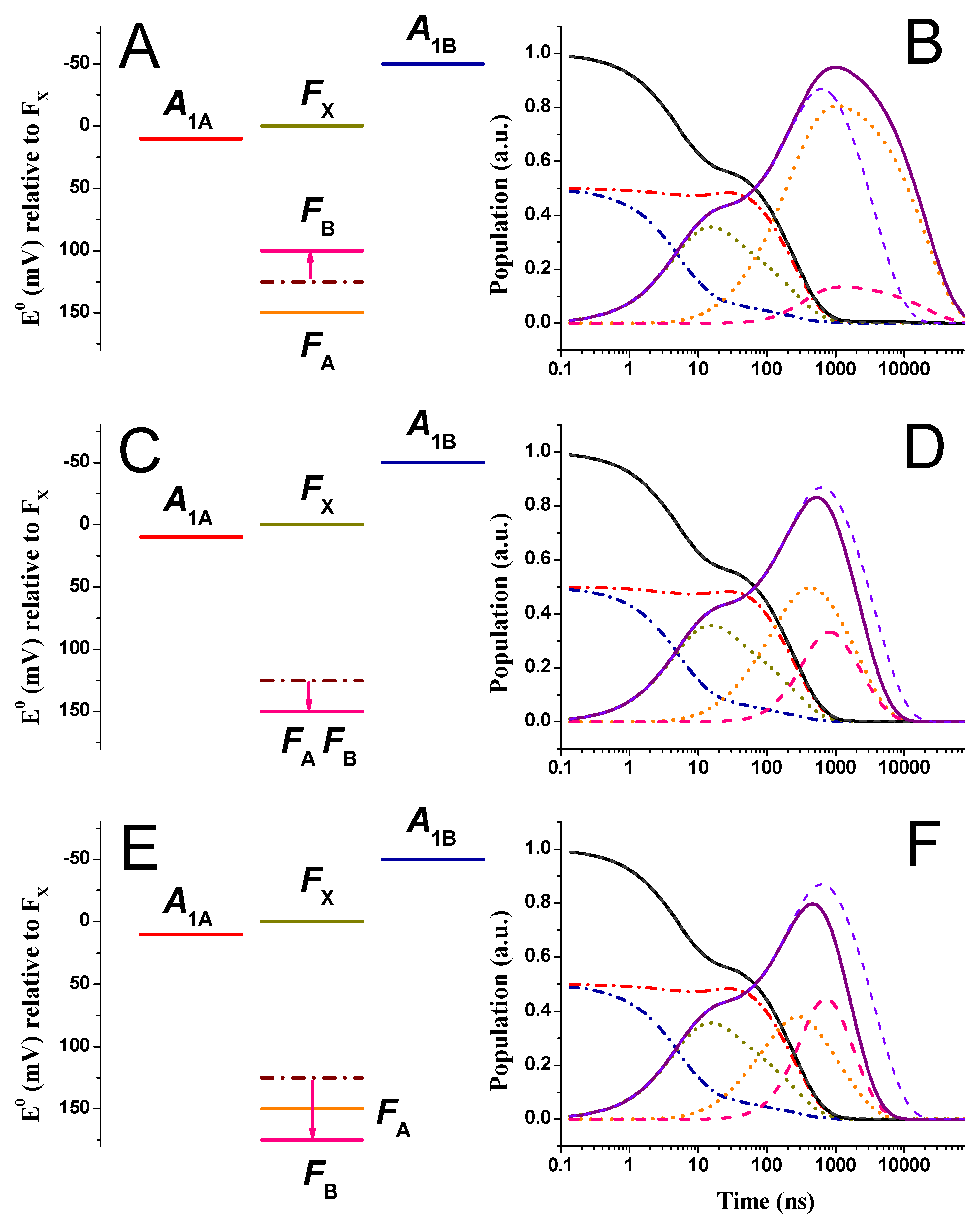
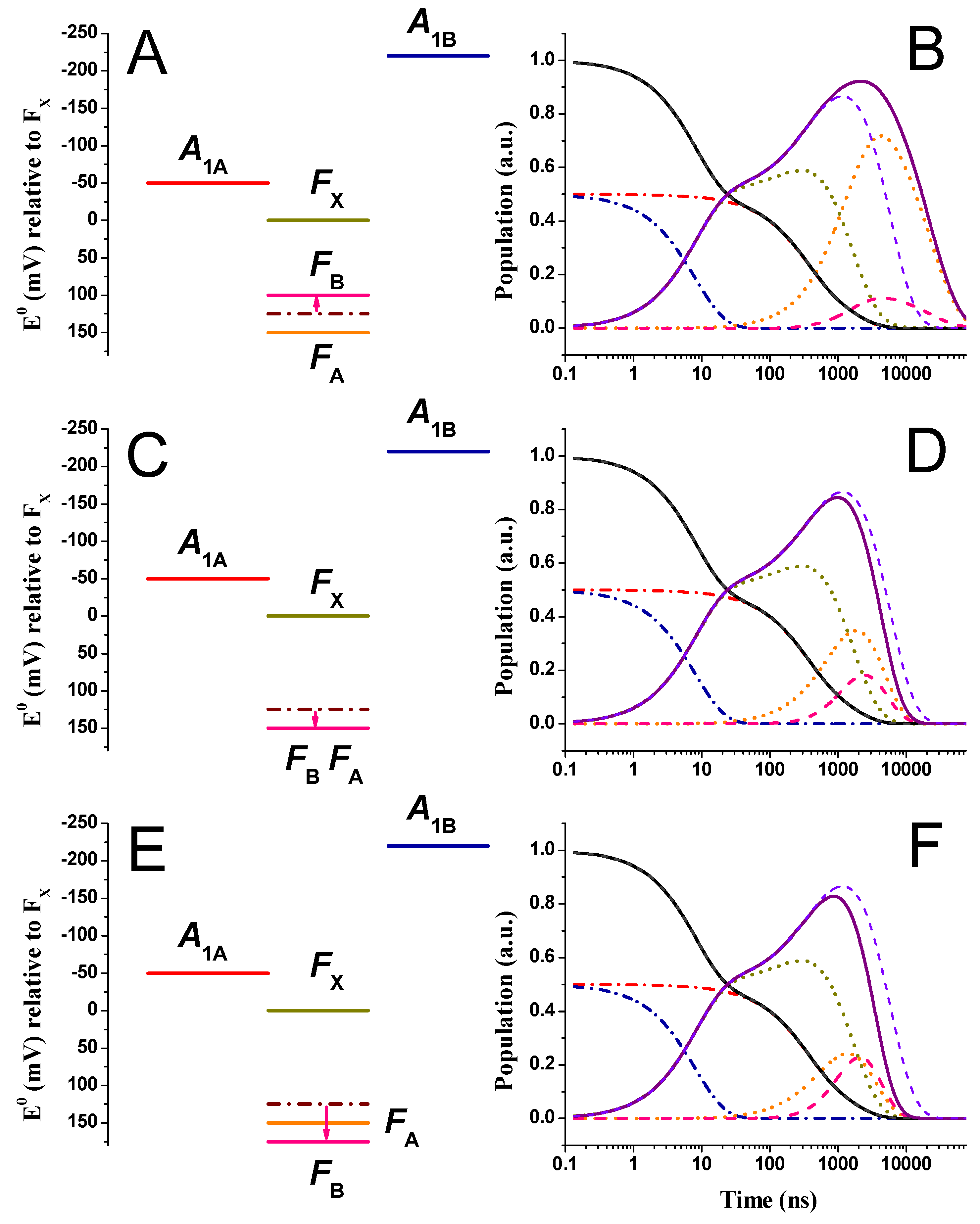
2.2. Large Driving Force Scenario for $A_{1}^{-}$ Oxidation

Figure 3 shows the simulations obtained within the “large driving force” scenario for

A_{1}^{-}

oxidation. In this case, we considered values of

Δ G_{A_{1 A} \to F_{X}}^{0}

= –50 meV and

Δ G_{A_{1 B} \to F_{X}}^{0}

= –220 meV as suggested by Milanovsky et al. [39], whereas the free energies for the other reactions were the same as discussed above,

Δ G_{F_{X} \to F_{A}}^{0}

= –150 meV and

Δ G_{F_{A} \to F_{B}}^{0}

= +25 meV. Setting the midpoint potential of

F_{B}

at –555 mV, it then results that

E_{F_{A}}^{0}

= –530 mV,

E_{F_{X}}^{0}

= –680 mV

E_{A_{1 A}}^{0}

= –730 mV and

E_{A_{1 B}}^{0}

= –900 mV. The parameters set employed in the calculations is listed in Table 2. In order to facilitate the comparison between the two energetic scenarios considered, whenever feasible, the same parameters were adopted in the simulations. The main difference resides in the reorganisation energy value, because within the large driving force scheme, a value of

λ_{t o t}

= 0.7 eV associated to the quinone reactions resulted in simulated lifetimes which are too fast with respect to the measured ones, particularly for the slowest phase of

A_{1}^{-}

oxidation which would be simulated by a lifetime of ~100 ns, that is at least two times faster than the value retrieved from the experiments, i.e. ~250-360 ns (see Appendix S3 of the Supplementary Information Figure S4). It was therefore necessary, as also discussed previously [48], to use a larger value for

λ_{t o t}

of 1 eV for these ET steps, that was extended to the simulation of all other, forward and recombination, reactions. Within this energetic/kinetic scenario, the simulated lifetimes, common to all reactions are: 8.2, 295, 307, 1411 and 4415 ns. The 8.2, 307 and 1411 ns lifetimes are also retrieved for a kinetic scheme that not explicitly considers the terminal iron-sulphur centres (Appendix S1 Figure S1 and Table S1), therefore the remaining 295 and 4415 ns are associated mainly to ET processes directly involving

F_{A}^{}

and

F_{B}^{}

Figure 3. Panel A: reference energetic scheme for the “large driving force” scenario for

A_{1}^{-}

oxidation; standard redox potentials (

E^{0}

) are shown relative to

F_{X}

. Panel B: simulated population evolution of the individual redox active cofactors,

A_{1 A}^{-} (t)

: dashed-dot red line,

A_{1 B}^{-} (t)

dashed-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

dot orange line,

F_{B}^{-} (t)

dot burgundy line. Also shown are the total population evolutions of

A_{1, t o t}^{-} (t) = A_{1 A}^{-} (t) + A_{1 B}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t) = F_{X}^{-} (t) + F_{A}^{-} (t) + F_{B}^{-} (t)

(purple line). The inset (C) shows the recombination kinetics simulated in absence of an exit from the system (

k_{o u t}

= 0). Temperature: 290 K.

Figure 3. Panel A: reference energetic scheme for the “large driving force” scenario for

A_{1}^{-}

oxidation; standard redox potentials (

E^{0}

) are shown relative to

F_{X}

. Panel B: simulated population evolution of the individual redox active cofactors,

A_{1 A}^{-} (t)

: dashed-dot red line,

A_{1 B}^{-} (t)

dashed-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

dot orange line,

F_{B}^{-} (t)

dot burgundy line. Also shown are the total population evolutions of

A_{1, t o t}^{-} (t) = A_{1 A}^{-} (t) + A_{1 B}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t) = F_{X}^{-} (t) + F_{A}^{-} (t) + F_{B}^{-} (t)

(purple line). The inset (C) shows the recombination kinetics simulated in absence of an exit from the system (

k_{o u t}

= 0). Temperature: 290 K.

The oxidation of

A_{1 B}^{-}

is dominated by the 8.2 ns lifetime and that of

A_{1 A}^{-}

by the 307 ns one, with some contribution from the 1,4 μs component. The proportion of fast:slow

A_{1, t o t}^{-}

oxidation phases are simulated as 0.5:0.5, corresponding to the initial populations of these cofactors. Different oxidation phase partitions could be straightforwardly simulated by setting the boundary conditions accordingly. This in turn implies an asymmetric charge separation/stabilisation between the two active ET chains of PSI (e.g. [20,21,22,23,24]). Discussion of this issue is however beyond the scope of this work. For equal initial population of

A_{1 B}^{-}

and

A_{1 A}^{-}

, the resulting average lifetimes are 10.5 and 733 ns, respectively, and 371 ns for

A_{1, t o t}^{-}

. The predicted oxidation of

A_{1 A}^{-}

is somewhat slower, within this energetic scheme and for the conditions described, due to the significant contribution of the 1.4 μs phase, which exact value is in part linked to ET between the Fe-S clusters. Within this model, the reduction of

F_{X}^{}

is multiphasic, with contributions from all the sub-microsecond components, i.e. 8.2, 295, 307 ns (Table 2), giving rise to an average rise lifetime of 143 ns, whereas

F_{X}^{-}

oxidation is largely dominated by the 1.4 μs phase, corresponding closely to the average oxidation (

τ_{a v}

) time and the mean lifetimes of the population evolution (

τ_{m}

), being both 1.6 μs, and hence slower that 1.1 μs estimated for

A_{1, t o t}^{-}

. As apparent form the inspection of the population evolutions (Figure 3B), in this energetic scenario, the oxidation of

F_{X}^{-}

clearly follows that of

A_{1, t o t}^{-}

,whereas the two processes largely overlapped in the simulations performed within the small driving force energetic scheme (Figure 2B). This is associated to the slower rate of

F_{A}^{}

reduction from

F_{X}^{-}

due to the larger reorganisation energy (1 eV rather than 0.7 eV). Although not necessarily impossible, it would be unusual that the reorganisation for an ET event between 4Fe-4S cluster were to be lower than the one associated to ET from phylloquinones to an iron-sulphur centre. For this reason, as well as to minimise the number of variable parameters,

λ_{t o t}

was set to the same value. Simulations for different values of the reorganisation energy are however explored in Appendix S4 of the Supplementary Information where the effect of this parameter can be better appreciated.

Summary of the parameters utilised for the simulations of forward electron transfer in reference PSI within the large-driving-force scenario for

A_{1}^{-}

oxidation. The rate-defining parameters which are common to all forward electron reactions are the electronic coupling matrix element,

{|H_{0}|}^{2}

=1.3 10^-3 eV², the barrier camping factor

β

=1.34 Å^-1 and the temperature T=290 K, which are defined in Equation 1 of the main text.

The tables also list the lifetimes (

τ_{i}

) and associated amplitudes (

p_{i}

) describing the population evolution of each of the cofactors described in the model. The total amplitude associated with the electron transfer kinetics of phylloquinones (

p_{A_{1 tot}}

) and iron-sulphur centres (

p_{F e S_{tot}}

) are also presented in the table. The initial conditions for the amplitude simulations were

A_{1 A}^{-} (0) = A_{1 B}^{-} (0) = 0.5

and zero on all other cofactors considered.

The terminal electron acceptors

F_{A}^{}

and

F_{B}^{}

are reduced with average lifetimes of 1.2 μs and 808 ns, respectively, and oxidised with average lifetimes of 3.4 and 1.8 μs respectively. The terminal acceptors oxidation is, basically, determined by the rate of exit from the system. The slower simulated dynamics of

F_{A}^{-}

oxidation are, as in the “weak driving force” scenario, due to considering a slightly endergonic reduction of

F_{B}^{}

. Nonetheless, the mean lifetimes for

F_{A}^{-}

and

F_{B}^{-}

are 5.8 and 6.2 μs indicating that, as also discussed above, the two centres are predicted to be oxidised almost concertedly by diffusible acceptors.

When the rate of electron donation from

F_{B}^{-}

is suppressed in order to simulate the recombination reactions, these are characterised by a lifetime of ~570 ms, which falls rather outside the spread of values reported in the literature in which the slowest ones are in the order of 100 – 200 ms [6,26,68,69,70,71]. Yet, no specific effort has been made here to reach a good agreement between the measured and simulated recombination rates. An improvement in the match between modelled (between 174 and 89 ms) and experimental values is obtained by increasing

ℏ {\bar{ω}}_{D A}

to 55 meV (450 cm^-1) (Appendix S2, Figure S3), which is the average recommended consensus value from a survey in redox-active proteins [37]. Variation of the values of

λ_{t o t}

(Appendix S3, Figure S6) or application of the parameter sets employed in the “weak driving force” model (Appendix S4, Figure S8), as discussed above, do not appear to improve the description of the recombination kinetics within the “large driving force” energetic scheme. Nonetheless, as in the “weak driving force” case, the recombination rate is limited by the uphill repopulation of

F_{X}^{-}

and, especially,

A_{1 (A, B)}^{-}

. As discussed by Cherepanov and coworkers [72], a more detailed description of the Franck-Condon function, involving multiple nuclear modes and specific electron-phonon coupling terms, as well as explicit consideration of

A_{0 (A, B)}^{-}

(the up-stream electron donor) might be required to describe the recombination reactions in detail, at least within the large driving force energetic picture.

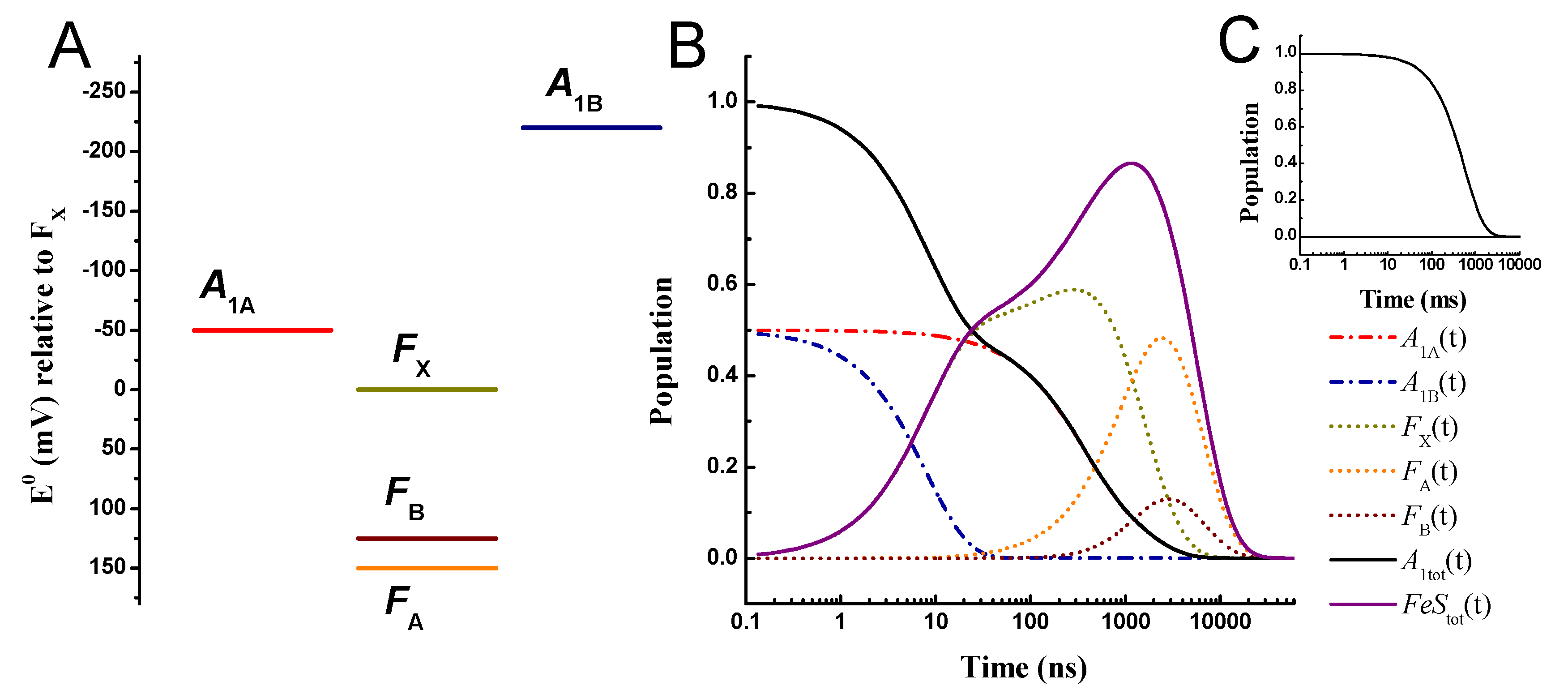
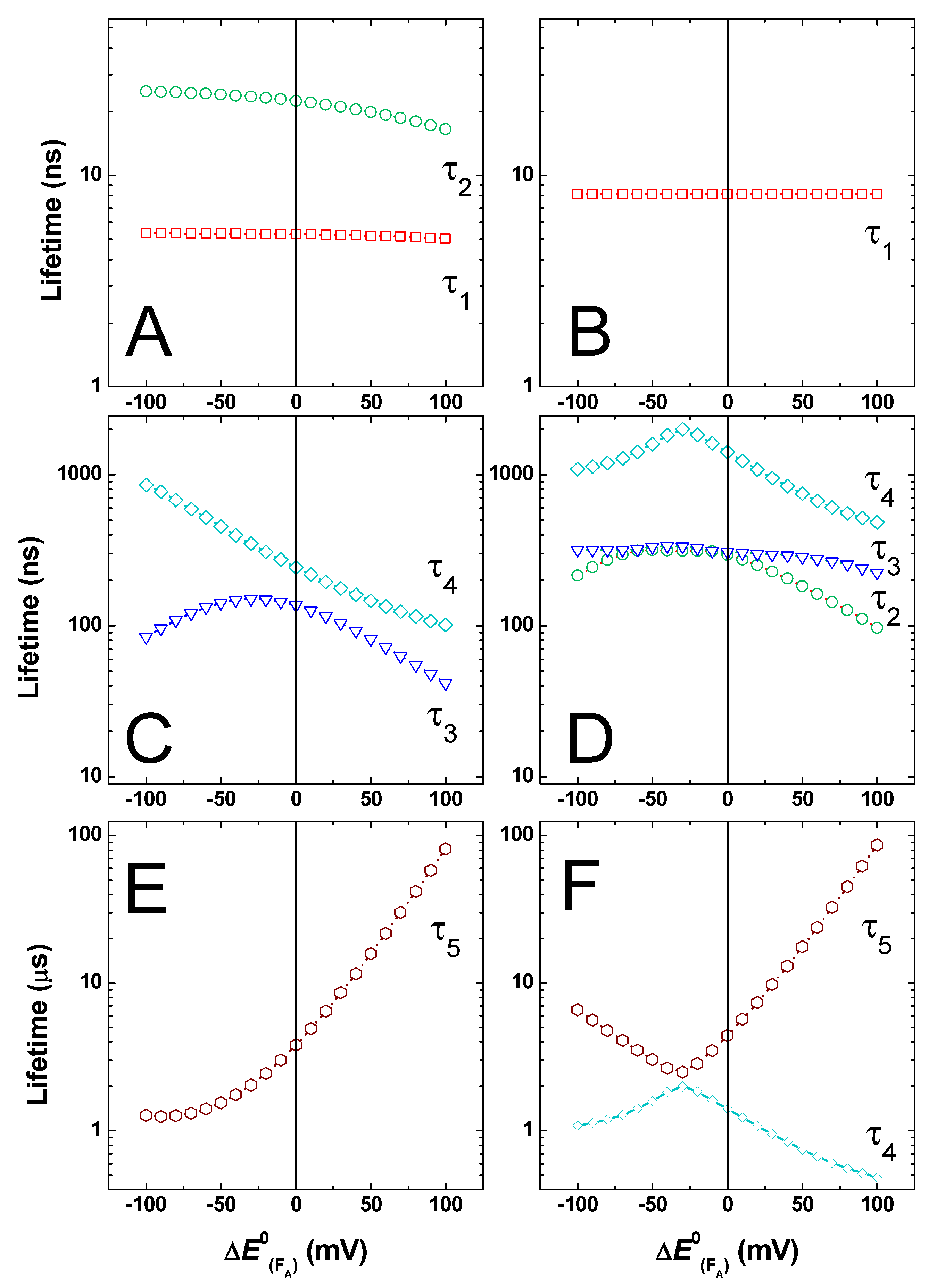
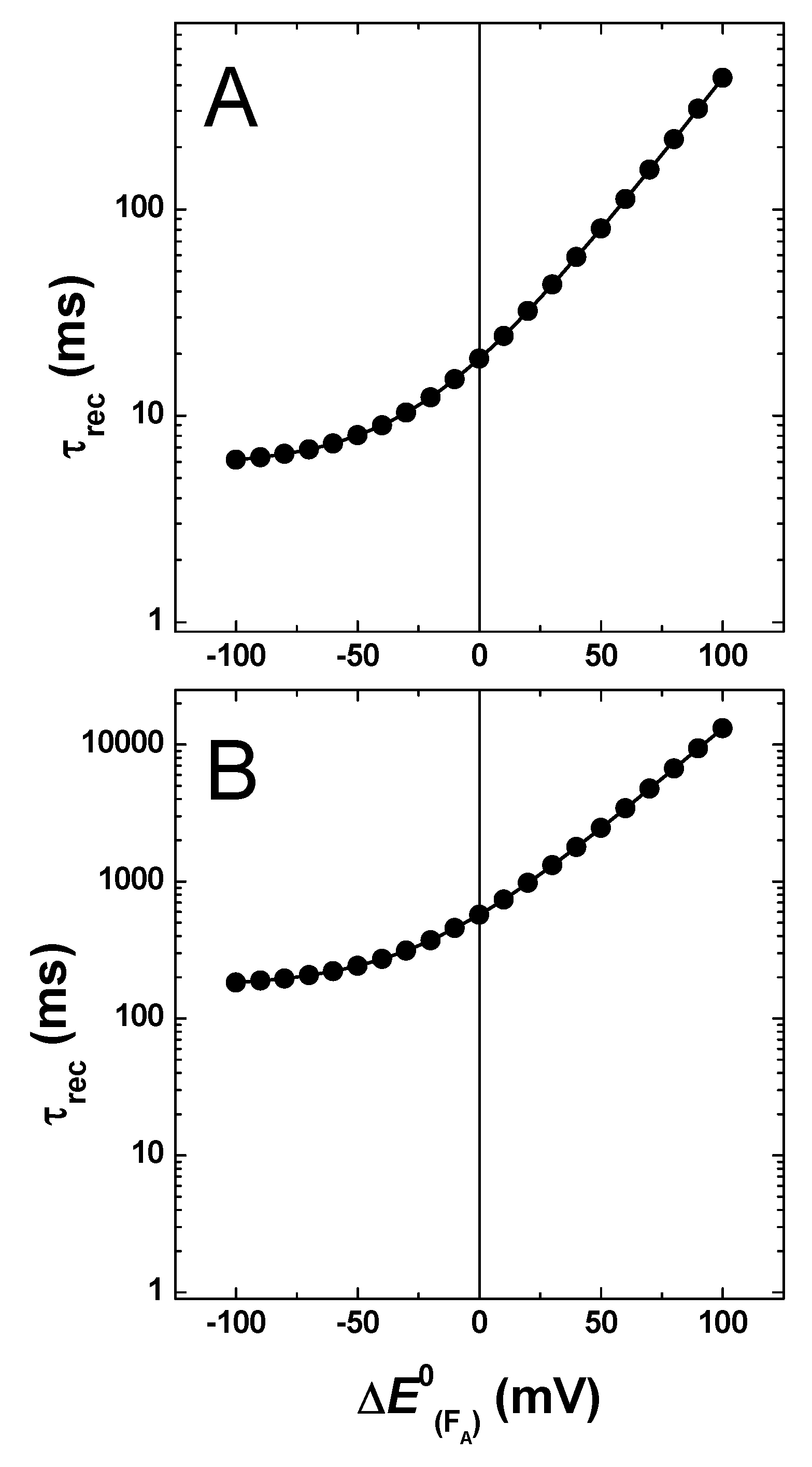
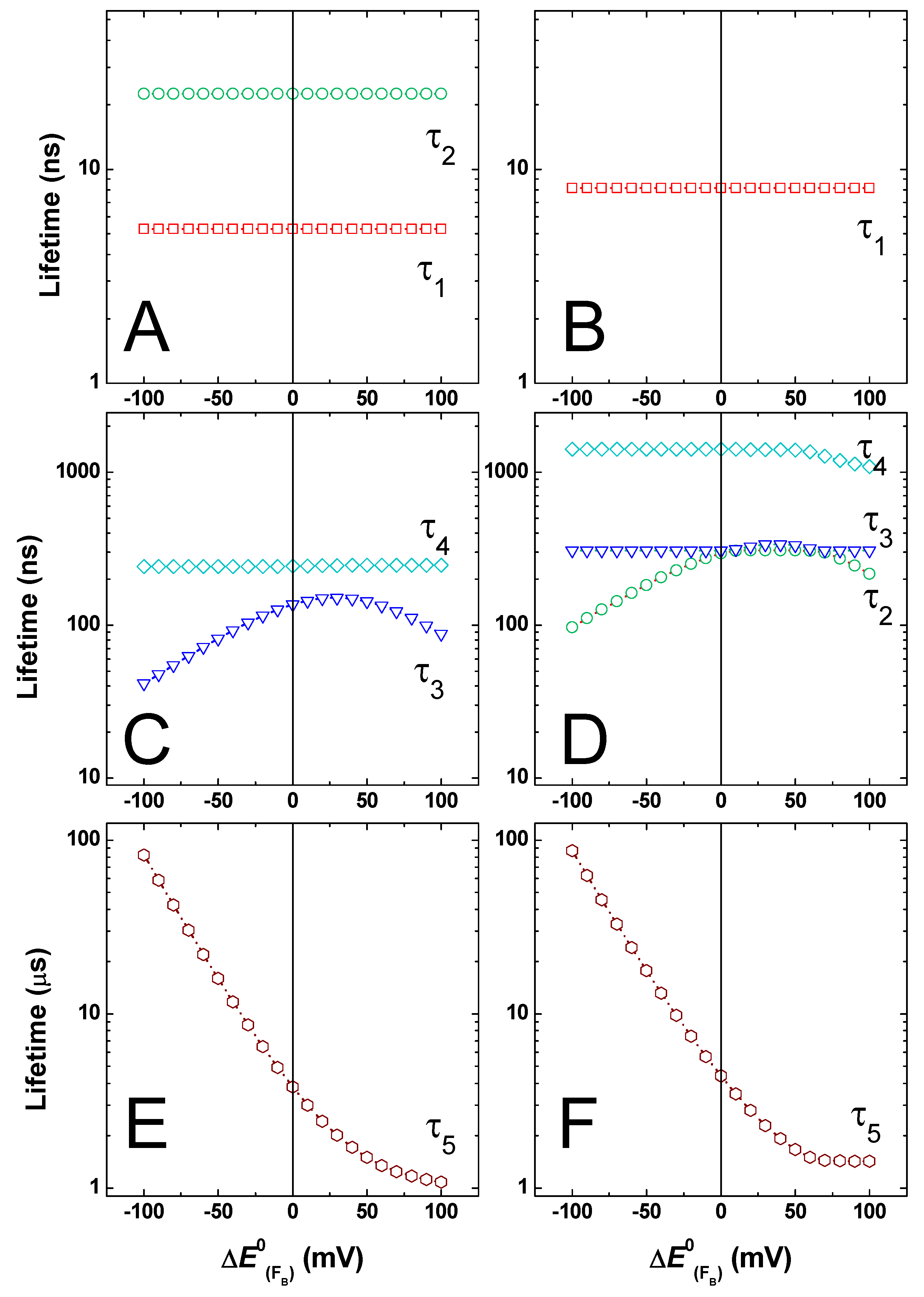
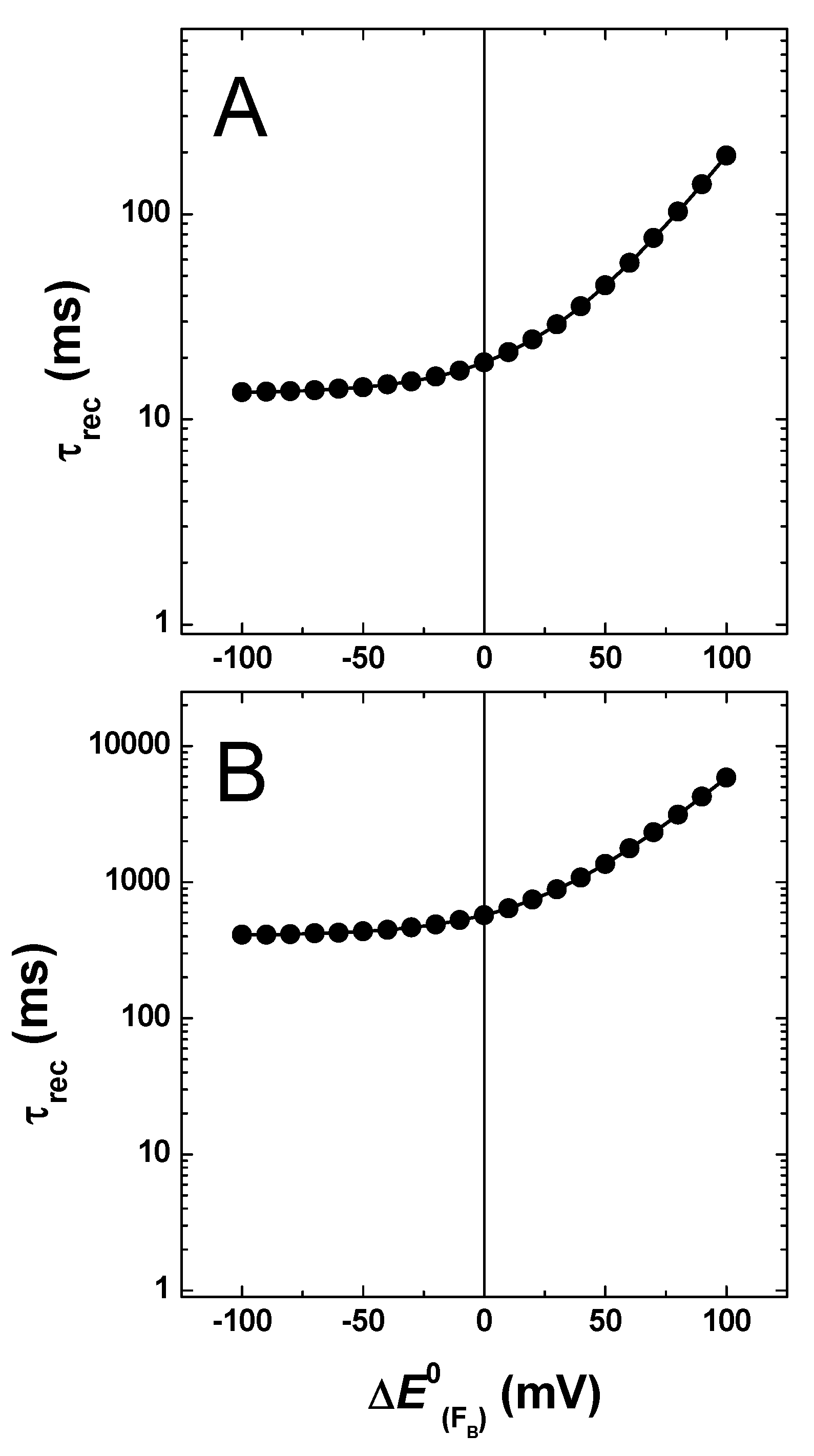
2.3. Effect of Changing the Driving Force of $F_{X}^{-}$ Oxidation ( $Δ G_{F_{X} \to F_{A}}^{0}$ )

The most straightforward change in PSI energetics that affects the ET between the iron-sulphur cluster directly, involves the tuning of the redox potential of the terminal electron acceptors

F_{A}^{}

and

F_{B}^{}

. Mutations in the PsaC subunit that modify the coordination, and hence the redox properties, of

F_{A}^{}

and

F_{B}^{}

have already been reported [73,74,75,76,77,78,79,80,81,82,83,84]. However, the effect of these mutations on the

A_{1 A, B}^{-}

oxidation kinetics has not been investigated in details, since the main target of these studies was to identify the specific nature and coordination site of the terminal acceptor, which has been a matter of controversy before being definitely elucidated by the availability of high resolution structural models. Hence, these studies targeted primarily the residues directly involved in the binding of the FeS clusters [73,74,75,76,77,78,79,80,81,82,83,84], and the kinetic information reported related almost exclusively on the recombination rather than the forward ET reactions [73,74,75,76,77,78,79,80,81,82]. Similarly, mutants affecting either the direct coordination of

F_{X}^{}

[85,86,87,88] and, in some cases, of nearby residues altering the cluster binding niche [89,90,91,92,93,94,95], have also been produced. Actually, these mutants pioneered the application of site-directed mutagenesis to the study of PSI [85,86,87]. The main target of these studies was also the identification of the ligands and the interaction of the

F_{X}^{}

-binding domain with the PSI acceptor side subunits. Most of these mutants resulted however in a loss or very low level of PSI accumulation, in centres lacking or having a heavily modified

F_{X}^{}

centre [85,86,87] as well as in altered binding of PsaC and the neighbouring subunits [86,87,88,89,90,91,92,93,94,95]. This, in turn, restricted the possibility of studying the effect of the specific mutations on forward electron transfer, so that the characterisation of these modified reaction centres was then relatively limited [91,92,93,94,95]. Although mutants leading to the perturbations of the

F_{X}^{}

properties are certainly interesting, these would lead to the simultaneous alteration of factors governing three ET events: the reduction of this cluster by both phylloquinones and its oxidation by

F_{A}^{}

. Here, then, the discussion will be initially focused on changes in the redox potential of

F_{A}^{}

(

E_{F_{A}}^{0}

), since the

F_{X}^{} \to F_{A}

reaction follows immediately the phylloquinones in the ET cascade, but is not expected to modify the uphill reaction rates directly. Yet, any alteration in the

F_{A}^{}

redox potential, leads to changes to both

Δ G_{F_{X} \to F_{A}}^{0}

and

Δ G_{F_{A} \to F_{B}}^{0}

, albeit in the opposite direction, as the driving force for one reaction increase, the other decreases.

Figure 4 shows the simulated kinetics for all redox cofactors described in the energetic/kinetic model in which

E_{F_{A}}^{0}

was shifted by –25 mV (Figure 4A/B), –50 mV (Figure 4C/D) and –100 mV (Figure 4E/F), within the “weak driving force” scenario for phyllosemiquinone oxidation. For the –25 mV shift,

F_{A}^{}

and

F_{B}^{}

are isoenergetic, while for larger potential shifts the driving force for

F_{B}^{}

reduction (by

F_{A}^{}

) increases progressively, whereas that of

F_{A}^{}

reduction by

F_{X}^{-}

decreases accordingly, but always remains favourable from a thermodynamic point of view.

Figure 5 shows simulations for the same alterations of

E_{F_{A}}^{0}

, but within the “large driving force” phyllosemiquinone oxidation scheme.

The simulations of Figure 4 and Figure 5 show some significant differences in the ET kinetics when equal perturbations are applied to the driving forces of reactions which are otherwise described by, basically, the same parameters (Figure 2 and 3).

In the “weak driving force” scheme, together with the modification of the population evolutions of

F_{X, A, B}^{-}

, which are expected since the rate constants associated with these reactions are directly affected by the

F_{A}^{}

redox potential perturbations, also significant alterations of the

A_{1, t o t}^{-}

oxidation kinetics are simulated (

τ_{a v, A_{1}^{-}}

was 258, 360 and 840 ns vs. ~180 ns in the reference energetic scenario). This is particularly clear for the simulated

A_{1 A}^{-}

kinetics, due to the increase in the value of the lifetime that dominates its oxidation, that is simulated as 340 and 530 ns and 1 μs for the

E_{F_{A}}^{0}

perturbations discussed above vs 284 ns in the initial scenario. The kinetics of

A_{1, t o t}^{-}

oxidation became progressively slower as the rate of

F_{X}^{-} \to F_{A}

became slower (7.2 x 10^-3, 5.9 x 10^-3 and 2.1 x 10^-3 ns^-1 vs. 1 x 10^-2 ns^-1 in the starting scenario), because of the decrease in driving force,

Δ G_{F_{X} \to F_{A}}^{0}

. However, irrespectively of the exact shift of the

F_{A}^{}

redox potential,

F_{X}^{-}

reduction remained concerted with that of

A_{1, t o t}^{-}

and, on average, slowed down by the same extent (

τ_{a v, F_{X}^{-}}^{d}

326, ns 413 ns, 1 μs vs 199 ns in the reference system). On the other hand,

F_{A}^{-}

oxidation became progressively faster (as the potential of the cofactor became more reductive), and so did the oxidation of

F_{B}^{-}

, upon shifting from endergonic (Figure 2) to exergonic conditions (Figure 4). The maximal population of these cofactors decreased (

{[F_{(X + A + B)}^{-}]}^{\max}

0.86, 0.70, 0.53 vs. 0.86 in the reference) with increased free energy for the last inter-protein ET step. The effect is clearly more pronounced for the maximal

F_{A}^{-}

reduction level (

{[F_{A}^{-}]}^{\max}

0.45, 0.26 and 0.06 vs. 0.64 in the reference system).

Differently, in the “large driving force” scheme, the modifications of the

F_{A}^{-}

oxidation potential, together with the resulting changes in driving forces associated to the reactions in which this cofactor participates, appear to affect almost exclusively inter-Fe-S electron transfer reactions, whereas the kinetics of

A_{1, t o t}^{-}

oxidation remain almost unaffected (Figure 5). The only significant effect on

A_{1}^{-}

oxidation concerned the amplitude of a minor component displaying a long lifetime (~1.5 μs), which was also simulated for the reference system (Figure 3), but which value increased significantly upon

E_{F_{A}}^{0}

perturbation (

τ

3.7, 5.2 and 14 μs, respectively, vs. 1.4 μs in the reference system). The large value of this lifetime, even when having a small associated amplitude (<10% of total), has a marked impact on the estimation of

τ_{a v, A_{1}^{-}}

(which was 680 ns, 875 ns and 2.2 μs in the

F_{A}^{}

-perturbed vs. ~370 ns in the reference energetic system). It shall be recalled that this slow phase has never been detected experimentally, to the best of our knowledge. It is clearly connected to the explicit consideration of

F_{A}^{-} \to F_{B}

reaction, as it is not simulated otherwise ([48,63,67] and Appendix S1, Table S1). Kinetic coupling in this scenario becomes significant since the rate of

F_{X}^{-} \to F_{A}

transfer (8.8 10^-4 ns^-1) is almost the same as that of

F_{A}^{-} \to F_{B}

(7.7 10^-4 ns^-1) and, especially, of the reverse,

F_{B}^{-} \to F_{A}

, reaction (1.5 10^-4 ns^-1). This is not the case for the “weak driving force” scenario by virtue of the lower reorganisation energy (0.7 vs. 1 eV) required to describe the

A_{1}^{-} \to F_{X}

and

F_{X}^{-} \to F_{A}

reactions. Thus, when the μs-phase(s) is omitted from the calculations of

τ_{a v, A_{1}^{-}}

in the “large driving force” simulations, the values of this parameter was almost unaffected by changes of

E_{F_{A}}^{0}

, varying from 122 ns in the reference system to 139 ns for the largest potential shift of –100 mV considered in the simulations of Figure 5.

Comparing Figure 4 and Figure 5, it can be appreciated that the effect of rendering

F_{A}

potential more reductive, is instead far more pronounced on the ET kinetics involving all iron-sulphur clusters in the case of the large driving force scenario for

A_{1}^{-}

oxidation. The cofactor showing the largest change in ET kinetic is

F_{X}^{-}

, which oxidation/reduction dynamics became progressively slower with average decay lifetimes of 3.8, 5.2 and 13 μs with respect to 2.7 μs in the reference system. When decreasing the driving force for

F_{X}^{-}

oxidation, its depopulation became progressively overlapped with that of

F_{A, B}^{-}

and its maximal population increases from 0.59 in the reference system to 0.69, 0.72 and 0.79 as

F_{A}^{}

becomes more reductive. The maximal cumulative population of the Fe-S clusters did not change significantly, indicating that the increase in transient

F_{X}^{-}

population level is accompanied by a parallel decrease in that of

F_{A + B}^{-}

(Figure 5).

To obtain a more comprehensive picture of the effect resulting from perturbations of the

F_{A}^{}

redox potential, and in turn the

Δ G_{F_{X} \to F_{A}}^{0}

and

Δ G_{F_{A} \to F_{B}}^{0}

free energies, the value of

E_{F_{A}}^{0}

was changed in ±100 mV interval with respect to the reference systems. The effect of tuning the

E_{F_{A}}^{0}

redox potential on the simulated lifetimes is presented in Figure 6 starting from the initial reference being either the “weak” (Figure 6A, C and E) or “large” driving force (Figure 6B, D, F) energetics for

A_{1}^{-}

oxidation. In Figure 6, lifetimes values were separated in classes for ease of presentation and comparison, so that Figure 6A and B show

τ

<~50 ns, Figure 6C and Figure DFigure showFigure ~50Figure ns<

τ

<~1 μs and Figure 6E and F,

τ

>~1 μs. Since the lifetimes change upon

F_{A}^{}

perturbation, this classification is not strict, but refers to the dominant behaviour of a given lifetime component. The values of

τ

<50 are not greatly affected by any perturbation of

E_{F_{A}}^{0}

in the ±100 mV interval considered. These lifetimes,

τ_{1}

and

τ_{2}

in the reference weak-driving force and

τ_{1}

only in the reference large-driving force energetic scheme, reflect principally

A_{1 B}^{-}

oxidation, that is exergonic in both. The simulated kinetics of Figure 4 and 5 show the prediction of little alterations in this kinetic phase when modifying successive ET reactions.

For lifetime values in the 50 ns<

τ

<~1 μs range (Figure 6C and D), starting-model-dependent variations are predicted instead. In the starting weak-driving force case,

A_{1 A}^{-}

oxidation is dominated by the value of

τ_{4}

, which simulated values increase with the increase of

Δ G_{F_{X} \to F_{A}}^{0}

, i.e. with the lowering of the reaction driving force (Figure 6C

τ_{3}

lifetime in this energetic configuration, relates principally to ET reactions amongst the Fe-S clusters and its reference value of ~160 ns is an agreement with experimental estimation [30,33,34]. Its dependence from the variation of

F_{A}^{}

redox potential is not monotonic, consistent with it being determined by the kinetic coupling of reactions influenced by both

Δ G_{F_{X} \to F_{A}}^{0}

and

Δ G_{F_{A} \to F_{B}}^{0}

In the starting large-driving force energetic scheme,

A_{1 A}^{-}

oxidation is dominated by the value of

τ_{3}

instead, which is close to independent from the redox potential of

F_{A}^{}

. As discussed for the simulations of Figure 5, the two main phases of

A_{1}^{-}

oxidation remain largely unaffected by perturbing

E_{F_{A}}^{0}

, even in the large ± 100 mV range, within this reference scenario (Figure 6D), consistently with the phylloquinone oxidation being (mainly) kinetically decoupled from the successive ET steps. For this initial energetic configuration,

τ_{2}

displays a dependence to

E_{F_{A}}^{0}

variation similar to the one simulated for

τ_{3}

in the weak-driving force model, albeit its starting value is somewhat larger (~250 ns, this is because of the slightly larger value of

λ_{t o t}

, i.e. 1 eV vs. 0.9 eV). This component shall then also be taken as reflecting principally transfer between Fe-S clusters. Since it is not simulated when not considering

F_{A}^{}

and

F_{B}^{}

explicitly ([48] and Appendix S1), it most likely reflects ET transfer between the terminal acceptors. This simulated lifetime is in general agreement with the inter 4Fe-4S clusters electron transfer estimated by Nuclear Magnetic Resonance methods in the ferredoxin of Chromatium vinosum (~300 ns) which is structurally analogous to the PsaC subunit [96]. The value of

τ_{4}

is also larger in the reference large driving scheme with respect to the weak-driving force configuration. Its initial value of ~1 μs is the same as the one simulated when

F_{A}^{}

and

F_{B}^{}

are not explicitly taken into account ([48] and Appendix S1) and therefore reflects mainly

F_{X}^{-}

oxidation. This lifetime shows a non monotonic dependence on

E_{F_{A}}^{0}

, with an apparent discontinuity point at –40 mV potential shift (Figure 6D), which is for a decrease of

F_{X}^{-}

oxidation driving force (less exergonic) and an increase in the driving force (more exergonic) for

F_{A}^{-}

oxidation by

F_{B}^{}

Different behaviour with respect to shifts in the

E_{F_{A}}^{0}

value are also simulated for the slowest lifetime (

τ_{5}

). In the reference weak-driving force

A_{1}^{-}

oxidation,

τ_{5}

shows a quasi-monotonic dependence, becoming faster as the driving force for

F_{A}^{-}

oxidation by

F_{B}^{}

increases. For the largest favourable energetic configuration the value of this lifetime approaches the inverse of the out-put from the system

k_{o u t}^{- 1}

~1 μs (Figure 6E). In the large-driving force

A_{1}^{-}

oxidation framework,

τ_{5}

has a more complex dependence, with the lifetime also becoming faster for increased

F_{A}^{-} \to F_{B}

oxidation driving forces. However, similarly to

τ_{4}

, which is also re-plotted in Figure 6F for direct comparison a trend discontinuity point at ~–40 mV potential shift is simulated. Under these energetic conditions, the decrease in driving force for

F_{X}^{-}

oxidation dominates over the increased driving force for the successive ET steps.

In both cases, the slowest values simulated, especially for conditions in which

F_{A}^{-} \to F_{B}

is significantly endergonic, indicates that the equilibration between the terminal electron acceptors can significantly slow down ET to the diffusible acceptors carries (e.g. ferredoxin). A slow

F_{X}^{-} \to F_{A}

ET reaction would have similar consequences, as shown by the

τ_{5}

dependence of Figure 6F as well as the simulations ofFigure 4. The latter effect, to our knowledge has not previously been explicitly considered, whereas it might have important implications for the photosystem functionality.

Figure 7 shows the dependence on the simulated recombination reactions, i.e. when

k_{o u t}^{}

= 0. In both energetic scenarios, the lifetime for charge recombination displays a positive correlation with the increase in driving force for the

F_{X}^{-} \to F_{A}

reaction. For values of

E_{F_{A}}^{0}

that yields

Δ G_{F_{A} \to F_{B}}^{0}

<0 ( i.e. ~< –25 mV shift) the recombination lifetime depends only weakly on the exact value of

Δ G_{F_{X} \to F_{A}}^{0}

. Yet, as the

F_{A}^{-} \to F_{B}

transfer enters the endergonic regime (

Δ G_{F_{A} \to F_{B}}^{0}

>>0), the recombination lifetimes display almost an exponential response with respect to the decrease of

Δ G_{F_{X} \to F_{A}}^{0}

, i.e. an increase in driving force for the forward and a decrease of backward reactions, in agreement with back-population of

F_{X}^{-}

imposing important kinetic limitation to these recombination reactions.

2.4. Effect of Changing the Driving Force of $F_{A}^{-}$ Oxidation ( $Δ G_{F_{A} \to F_{B}}^{0}$ )

The driving force for

F_{A}^{-}

oxidation can be modulated, without directly affecting the energetics of

F_{X}^{-}

, by modifying the redox potential of

F_{B}^{}

(

E_{F_{B}}^{0}

Figure 8 (“weak driving force” energetics) and Figure 9 (“large driving force” energetics) show the simulated kinetics of all redox cofactors considered in the models, upon shifting the

F_{B}^{}

potential by +25 mV (Figure 8/9B), –25 mV (Figure 8/9D) and –50 mV (Figure 8/9F). In this case, for the +25 mV shift,

F_{A}^{-} \to F_{B}^{}

becomes more endergonic (

Δ G_{F_{A} \to F_{B}}^{0}

= +50 meV), for the –25 mV

E_{F_{B}}^{0}

shift

F_{A}^{}

and

F_{B}^{}

are isoenergetic (

Δ G_{F_{A} \to F_{B}}^{0}

= 0 meV), and for the –50 mV shift

F_{A}^{-}

oxidation is exergonic (

Δ G_{F_{A} \to F_{B}}^{0}

= –25 meV). The impact of exploring a ±100 mV variation of

E_{F_{B}}^{0}

on the lifetimes describing ET in PSI is shown in Figure 10.

Comparison of the simulations presented in Figure 8 and Figure 9 indicates that, irrespectively of the reference energetic model utilised to describe

A_{1}^{-}

oxidation, alterations affecting selectively

Δ G_{F_{A} \to F_{B}}^{0}

do not impact on the phyllosemiquinone oxidation kinetics, as they are, in both cases, basically indistinguishable from the respective reference system. The same hold true for wider changes in

E_{F_{B}}^{0}

of ± 100 mV, since the values of

τ_{1}

τ_{2}

, and

τ_{4}

(Figure 10A and C), which dominates

A_{1}^{-}

oxidation in the “weak” driving force scenario, are barely affected by changes in

Δ G_{F_{A} \to F_{B}}^{0}

. The same is observed for

τ_{1}

and

τ_{3}

that dominates

A_{1}^{-}

oxidation in the large-driving force

A_{1}^{-}

oxidation framework (Figure 10B and D). The value of the

τ_{4}

which is also associated with a small-amplitude-μs

A_{1}^{-}

oxidation phase in this energetic configuration, barely depends on

Δ G_{F_{A} \to F_{B}}^{0}

. On the other hand, as expected, changing

Δ G_{F_{A} \to F_{B}}^{0}

affects the kinetics of electron transfer between the Fe-S clusters, especially the temporal evolutions of

F_{A}^{-}

and

F_{B}^{-}

, whereas that of

F_{X}^{-}

is only slightly perturbed. In brief, the overall reduced population of

F_{A}^{}

increased with the decrease in driving force for its oxidation by

F_{B}^{}

, and vice versa, so that with the decrease of

Δ G_{F_{A} \to F_{B}}^{0}

the temporal evolution of the reduced state of this cofactors became less concerted and, basically, sequential for large driving forces.

Interestingly, the values of

τ_{3}

(“weak driving force” reference energetics, Figure 10C

τ_{2}

(“large driving force” reference energetics, Figure 10D) show a non-monotonous dependence on variation of

Δ G_{F_{A} \to F_{B}}^{0}

, with the slowest values simulated, in both cases, upon

F_{A}^{}

and

F_{B}^{}

becoming close to iso-energetic. These behaviours are similar to those simulated for variations in the

E_{F_{A}}^{0}

, which also affected

Δ G_{F_{A} \to F_{B}}^{0}

The lifetime showing the greatest dependence on

E_{F_{B}}^{0}

is the one representing the effective exit from the system (

τ_{5}

). An almost monotonous decrease (decay deceleration) is predicted upon progressive decreasing

Δ G_{F_{A} \to F_{B}}^{0}

, for values of

E_{F_{B}}^{0}

under which the

F_{A}^{-} \to F_{B}

reaction falls in the endergonic regime. A softer dependence is simulated instead for the large exergonic regimes, i.e. for

F_{B}^{}

potential shifts >~60–80 mV (Figure 10 E/F). Under the latter conditions, the value of

τ_{5}

(at least in the weak-driving force scenario) approaches that of

k_{o u t}^{- 1}

(~1 μs).

Figure 11 shows the simulated recombination in the absence of an exit from the system. Irrespectively of the energetics associated to

A_{1}^{-}

oxidation, the kinetics of charge recombination displayed a weak dependence on

Δ G_{F_{A} \to F_{B}}^{0}

, maintaining the value simulated for the reference scenario, for shifts in

E_{F_{B}}^{0}

of less than about ~60 mV. A significant increase is however predicted when

F_{A}^{-} \to F_{B}

enters the large endergonic regime,

Δ G_{F_{A} \to F_{B}}^{0}

> 60 mV. The overall response of charge recombination kinetics is similar, but less pronounced, than the one predicted upon perturbations of

E_{F_{A}}^{0}

, that affects both

Δ G_{F_{A} \to F_{B}}^{0}

and

Δ G_{F_{X} \to F_{A}}^{0}

(Figure 7), albeit in contrasting fashion. This indicates that, although the repopulation of

F_{X}^{-}

imposes the largest kinetic limitations to charge recombination, back-population of

F_{A}^{-}

will also slow this reaction when its oxidation by

F_{B}^{}

becomes largely favourable.

3. Materials and Methods

Kinetic simulations were performed as described previously [12,48,49]. In brief the population evolutions of the redox cofactors considered in the kinetic model (as schematically shown in Figure 1) are obtained from solving a system of ordinary differential equations, which in compact matrix form, is defined by

\dot{P} (t) = K_{i} \cdot P (t)

P (t)

and

\dot{P} (t)

are the vectors describing the temporal evolution of the redox cofactors populations and its first derivative, respectively, and

K_{i}

is a square matrix, frequently referred to as the rate matrix, that has as its elements the rate constants between pairs of electron donors and acceptors. The index i corresponds to the number of cofactors (states) considered in the modelling. The system of linear differential equation has a general solution of the form:

P (t) = \sum_{J = 1}^{i} c_{j} V_{j} e^{ζ {}_{j}t}

, where

ζ_{j}

and

V_{j}

are, the eigenvalues and the eigenvectors, respectively, that diagonalise the matrix

K_{i}

, and

c_{j}

are a set of scalars that need to be determined according to some given initial conditions, that were here considered to be:

A_{1 A}^{-} (0)

A_{1 B}^{-} (0)

= 0.5 and

F_{X} (0)

F_{A} (0)

F_{B} (0)

= 0. The general solution of the system corresponds to the empirical linear combination of weighted exponentials frequently employed to describe the experimental kinetics. Thus, the eigenvalues, that are univocally determined by the eigen-decomposition of

K_{i}

reflect in the experimentally observed lifetimes (

τ_{j, o b s}^{}

) through the relation

τ_{j, o b s}^{} = - ζ_{j}^{- 1}

. The product

c_{j} V_{j}

relates only indirectly to the experimental pre-exponential amplitudes. The modelled amplitudes represent “weighted” molar fractions, and describe only the changes in the relative cofactor concentration over time, whereas the experimental values are also determined by the monitored properties of the cofactors (e.g. the wavelength-dependent extinction coefficient, fluorescence yield/spectra, and so on).

The link with theory is provided by using explicitly a physical description of the rate constants rather than setting their values as free simulation parameters. To this end, here we adopted the description between a pair of donor-acceptor molecules, originally derived by Hopfield [36,65], when considering a single (mean) nuclear mode coupled to the ET event:

\begin{array}{l} k_{D \to A} = \frac{2 π}{ℏ} {|H_{D A}|}^{2} \frac{1}{\sqrt{2 π σ^{2}}} e^{- \frac{{(Δ G_{^{D A}}^{0} + λ_{t o t})}^{2}}{2 σ^{2}}} \\ σ^{2} = λ_{t o t} ℏ \bar{ω} \coth \frac{ℏ \bar{ω}}{2 k_{B} T} \end{array}

(1)

Where

λ_{t o t}

is the total reorganisation energy,

\bar{ω}

is the angular frequency of the mean coupled nuclear mode,

ℏ

is the Dirac constant,

k_{B}

is the Boltzmann constant, T is the temperature and

{|H_{D A}|}^{2}

is the electronic coupling term, which can be to a good level approximated as

{|H_{D A}|}^{2} = {|H_{0}|}^{2} e^{- β (X_{D A} - 3.6)}

where

{|H_{0}|}^{2}

, is the maximal value of the electronic coupling at wavefunctions overlap;

β

, a damping term associated to the probability of tunnelling the potential barrier, X_DA, the edge-to-edge cofactor distance (in Å) and 3.6 represents a correction for the van der Waals radii. When

ℏ \bar{ω}

k_{B} T

σ_{}^{2} = 2 λ k_{B} T

and the expression therefore simplifies, yielding the semi-classical relation derived by Marcus [35].

In the presented simulations values of

{|H_{0}|}^{2}

~1.3 10^-3 eV² (e.g. [48,49]) and

β

=1.38 Å^-1 [37] were considered. Specific values of

Δ G_{D A}^{0}

ℏ \bar{ω}

and

λ_{t o t}

will be discussed below.

It is often convenient to compare the average (

τ_{a v}^{}

) and mean (

τ_{m}^{}

) lifetime obtained from the simulations, rather than comparing the individual pre-exponential amplitudes (

p_{i}^{}

) and lifetimes. These parameters are defined, for each of the level (cofactor) considered, as:

τ_{a v}^{} = \frac{\sum_{i} p_{i} τ_{i}}{\sum_{i} p_{i}}

(2)

Since the sum at the denominator is zero for all cofactors which have no initial population, two other derived parameter associated to it are considered for these cofactors, the average rise (

τ_{a v}^{r}

) and depopulation (

τ_{a v}^{d}

) lifetimes. These are obtained by performing the summations in Eqn. 2 considering only the pre-exponential having negative (

p_{i -}^{}

) or positive (

p_{i +}^{}

) amplitudes, respectively.

The mean lifetimes represent the first moment of the population evolution, that being described by a linear combination of exponential is defined for each cofactors as:

τ_{m}^{} = \frac{\sum_{i} p_{i} τ_{i}^{2}}{\sum_{i} p_{i} τ_{i}}

(3)

which is always defined irrespectively of the initial amplitudes of the cofactors.

4. Conclusions

In this work the effect of altering the redox potential of the terminal acceptors of PSI, the iron-sulphur clusters,

F_{A}^{}

and

F_{B}^{}

, has been explored employing theory-based kinetic model simulations. This approach allows to predict the electron transfer kinetics between the Fe-S clusters, which has proven cumbersome to address experimentally by spectroscopic methods because of the characteristics of these cofactors and because of the spectral crowding occurring in large chromophore-pigment super-complexes, like PSI. The effect of altering

F_{A}^{}

and

F_{B}^{}

redox reactivity was comparatively explored by considering two energetic scenarios for ET reactions involving the upstream redox cofactors, the iron-sulphur cluster

F_{X}^{}

and the phylloquinones

A_{1 A}^{}

and

A_{1 B}^{}

, as the latter are better characterised by time-resolved spectroscopic approaches. From the presented analysis it is possible to infer that:

i) tuning the

F_{A}^{}

redox potential, together with an alteration of the ET kinetics directly involving this redox centre, also affects the phyllosemiquinones oxidation kinetics, particularly of the slow kinetic phase of this process that is dominated by the depopulation of

A_{1 A}^{-}

. Significant kinetic perturbations are predicted within the “weak driving force” scenario for

A_{1}^{-}

oxidation by

F_{X}^{}

. Tuning

E_{F_{A}}^{0}

has instead a limited effect on

A_{1}^{-}

oxidation kinetics when considering the “large driving force” energetic scheme for these cofactors oxidation reactions. Since both energetic schemes describe adequately several measured parameters, they can both be considered realistic. A more in-depth analysis of mutants affecting

F_{A}^{}

coordination in the PsaC subunit, some of which have already been reported (e.g. [73,74,75,76,77,78,79,80,81,82,83,84]) but not studied with sufficient (ns) temporal resolution, is expected to shed further light on the energy gap between

A_{1 (A / B)}^{}

and

F_{X}^{}

, especially since the redox potential of the modified

F_{A}^{}

cofactor shall be accessible by direct electrochemistry and henceforth correlated to the kinetic perturbation. Similar approaches have already been explored and proven feasible (e.g. [75,76,77]) yet, as already discussed, the effect of the mutations on the kinetics of forward ET reactions has not investigated in detail yet.

ii) tuning the

F_{B}^{}

redox potential is predicted to affect almost exclusively ET involving the iron-sulphur clusters instead, especially the oxidation kinetics of

F_{A}^{-}

and

F_{B}^{-}

, without significantly impacting on the

A_{1}^{-}

oxidation kinetics, irrespectively of the energetic scenario employed to describe the latter reaction.

iii) alterations of the

F_{B}^{}

redox potential, which are also been reported for mutants affecting its coordination site in the PsaC subunit (e.g. [73,74,75,76,77,78,79,80,81,82,83,84]), can however help in elucidating the actual energetics of ET between the terminal iron-sulphur clusters, which might be inferred from differences in both the recombination rates and forward ET to ferredoxin, in comparison with similar perturbation of the

F_{A}^{}

redox potential.

iv) the ~180-ns kinetic phase experimentally retrieved in investigations of

A_{1}^{-}

oxidation kinetics [30,33,34,62,63], appears to be associated principally with

F_{A}^{-}

oxidation by

F_{B}^{}

, whereas it was previously assigned to

F_{X}^{-}

oxidation by

F_{A}^{}

[30]. The ~180-ns lifetime appears as a significant contribution also in the

F_{X}^{-}

oxidation kinetics, indicating that

F_{A}^{-}

oxidation by

F_{B}^{}

is not fully kinetically decoupled from upstream reactions. This lifetime is correctly predicted in the “weak driving force”

A_{1}^{-}

oxidation scenario, whereas a slight overestimation (~300 ns) is obtained in the “large driving force” energetic scheme.

v) the need to consider

λ_{t o t}^{}

~ 1 eV in the large driving force

A_{1}^{-}

oxidation scenario led to simulate a relatively slow

F_{X}^{-}

oxidation, which couples to a small-amplitude

A_{1 A}^{-}

oxidation phase in the μs windows. This phase has not been detected experimentally either because not present or not resolvable. Multiple pieces of evidence suggest that

F_{X}^{-}

oxidation shall proceed in the sub-μs scale. This can be taken as an indication that

λ_{t o t}^{}

~ 1 eV represents an upper limit/overestimation of this parameter. The calculated recombination rates, which are limited by the back-population of

F_{X}^{-}

, argues in the same direction, as they are overestimated, in general, by about an order of magnitude within the “large driving” force scenario (see Appendixes S2 and S3 for further discussion and simulations).

vi) uphill ET from

F_{A}^{-}

F_{B}^{}

can significantly slow down donation from the terminal electron acceptor(s) to diffusible carriers, at least when pre-bound complexes are formed, i.e. the speed of electron transfer to ferredoxin (or other acceptors) might not depend solely on the rate of transfer from

F_{B}^{-}

to the redox active centre in the acceptor molecules, particularly if the intrinsic rate constant for this reaction is as-fast-as, or comparable with, the electron transfer kinetics involving the terminal electron acceptors within the photosystem..

Supplementary Materials

The supplementary information are organised in appendixes proving additional information concerning the reference schemes for the “weak driving force” and “large driving force” scenario, which serve as the basis to explore perturbations of the physical-chemical properties of the iron-sulphur cluster

F_{A}^{}

and

F_{B}^{}

. In Appendix S1 is shown a comparison of model simulations for a three-cofactor model, comprising only

A_{1 A}^{}

A_{1 B}^{}

and

F_{X}^{}

with respect to the reference five-cofactor models used in the main text (Figure S1 and Table S1). Also presented in this appendix are simulations performed omitting all recombination reactions to

P_{700}^{+}

or leaving only the recombination between

A_{1 A / B}^{-}

and

P_{700}^{+}

. In the latter case also the recombination kinetics in the absence of an exit from

F_{B}

are simulated (Figure S2). In Appendix S2 is shown a comparison of both forward and recombination kinetics when increasing the frequency of the mean coupled mode to the electron transfer reactions in the two reference energetic/kinetic schemes. Two parameter sets are used, in one case

ℏ {\bar{ω}}_{D A}

= 55 meV (450 cm^-1) is considered for all reactions including

A_{1 A / B}^{-}

oxidation, in the other

ℏ {\bar{ω}}_{D A}

= 55 meV (450 cm^-1) is considered for all reactions but specific values, as in the text and Table 1 and Table 2, are used for

A_{1 A / B}^{-}

oxidation. The simulations are shown in Figure S3. In Appendix S3, simulations are shown for the “large driving force” configuration employing different values of the total reorganisation energy,

λ_{t o t}

, common to all electron transfer reactions considered. The simulations of forward electron transfer kinetics for different values of

λ_{t o t}

are shown in Figures S4 and S5 and the simulated recombination reactions in Figure S6. In Appendix S4 are shown the simulations for specific alterations of the electron transfer parameters within the ”large driving force” energetic scheme. Simulations are performed considering specific values for

λ_{t o t, F_{X} \to F_{A}}

and

λ_{t o t, F_{A} \to F_{B}}

corresponding to those employed for the “weak driving force” scenario as well as for different energetics, being exactly the same as those reported in ref. [24] but with the remaining parameter as in the main text and Table 2. The simulated forward electron transfer reactions are shown in Figure S7 and the recombination in Figure S8.

Author Contributions

“Conceptualization, software, writing—original draft: S.S.; methodology, investigation, preparation, writing—review and editing S.S & A.P.C. All authors have read and agreed to the published version of the manuscript.”

Funding

This study was economically supported by Regione Lombardia through the project “Enhancing Photosynthesis” (DSS 16652 30/11/2021) on behalf of the winners of the “Lombardia è Ricerca – 2020” award and by MUR through the National Recovery and Resilience Plan (NRRP/PNRR), Mission 4, Component C2, Investment 1.1, Call for tender No. 104 of the 02/02/202 2 by the Italian Ministry of University and Research (MUR), funded by the European Union –NextGenerationEU– Project Title "Extending the red limit of oxygenic photosynthesis: basic principles and implications for future applications (20224HJWMH)" – CUPs B53D23015880006 Grant Assignment Decree No. 1017 adopted on 07/07/2023 by MUR.

Data Availability Statement

Dataset available on request from the authors

Conflicts of Interest

The authors declare no conflicts of interest.

References

Caffarri, S.; Tibiletti, T.; Jennings, R.C.; Santabarbara, S. A comparison between plant photosystem I and photosystem II architecture and functioning. Curr Protein Pept Sci 2014, 15, 296–331. [Google Scholar] [CrossRef]
Srinivasan, N.; Golbeck, J.H. Protein-cofactor interactions in bioenergetic complexes: The role of the A_1A and A_1B phylloquinones in Photosystem I. Biochim Biophys Acta 2009, 1787, 1057–1088. [Google Scholar] [CrossRef] [PubMed]
Jordan, P.; Fromme, P.; Witt, H.T.; Klukas, O.; Saenger, W.; Krauss, N. Three-dimensional structure of cyanobacterial photosystem I at 2.5 angstrom resolution. Nature 2001, 411, 909–917. [Google Scholar] [CrossRef] [PubMed]
Mazor, Y., Borovikova, A., Caspy, I., Nelson, N. (2017) Structure of the plant photosystem I supercomplex at 2.6 Å resolution. Nat. Plants 3:17014. [CrossRef]
Qin, X. , Suga, M., Kuang, T., Shen, J.R. (2015) Photosynthesis. Structural basis for energy transfer pathways in the plant PSI-LHCI supercomplex. Science. [CrossRef]
Brettel, K. (1997) Electron transfer and arrangement of the redox cofactors in photosystem I. Biochim. Biophys. Acta 1318, 322–373. [Google Scholar] [CrossRef]
Santabarbara, S., Heathcote, P., Evans, M.C.W. (2005) Modelling of the electron transfer reactions in Photosystem I by electron tunnelling theory. Biochim. Biophys. Acta 1708, 283–310. [CrossRef]
Rappaport, F. , Diner, B.A., Redding, K.E. (2006) “Optical Measurements of Secondary Electron Transfer in Photosystem I,” in Photosystem I: The Light–Driven Plastocyanin:Ferredoxin Oxidoreductase, ed. J.H. Golbeck (Dordrecht, Kluwer Academic Publishers), 223–244. [CrossRef]
Redding, K.E. , van der Est, A. (2006). “The Directionality of Electron Transport in Photosystem I,” in Photosystem I: The Light–Driven Plastocyanin:Ferredoxin Oxidoreductase, ed. J.H. Golbeck (Dordrecht, Kluwer Academic Publishers), 413–437. [CrossRef]
Santabarbara, S., Galuppini, L., Casazza, A.P. (2010). Bidirectional electron transfer in the reaction centre of photosystem I. J. Integr. Plant. Biol. 52, 735–749. [CrossRef]
Makita, H., Hastings, G. (2016) Modeling electron transfer in photosystem I. Biochim. Biophys. Acta 1857, 723–733. [CrossRef]
Santabarbara, S.; Casazza, A.P.; Hastings, G. Modelling electron transfer in photosystem I: limits and perspectives. Physiol. Plant. 2019, 166, 73–87. [Google Scholar] [CrossRef] [PubMed]
Santabarbara, S., Kuprov, I., Fairclough, W.V., Purton, S., Hore, P.J., Heathcote, P., Evans, M.C.W. (2005) Bidirectional electron transfer in photosystem I: determination of two distances between P₇₀₀⁺ and A₁^- in spin-correlated radical pairs. Biochemistry 44, 2119–2128. [CrossRef]
Poluektov, O.G., Paschenko, S.V., Utschig, L.M., Lakshmi, K.V., Thurnauer, M.C. (2005) Bidirectional electron transfer in photosystem I: direct evidence from high-frequency time-resolved EPR spectroscopy. J. Am. Chem. Soc. 127, 11910–11911. [CrossRef]
Santabarbara, S., Kuprov, I., Hore, P.J., Casal, A., Heathcote, P., Evans, M.C.W. (2006) Analysis of the spin-polarized electron spin echo of the [P₇₀₀⁺A₁^-] radical pair of photosystem I indicates that both reaction center subunits are competent in electron transfer in cyanobacteria, green algae, and higher plants. Biochemistry 45, 7389–7403. [CrossRef]
Ramesh, V.M.; Gibasiewicz, K.; Lin, S.; Bingham, S.E.; Webber, A.N.A. Replacement of the methionine axial ligand to the primary electron acceptor A₀ slows the A₀⁻ reoxidation dynamics in Photosystem I. Biochim. Biophys. Acta 2007, 1767, 151–160. [Google Scholar] [CrossRef]
Giera, W.; Gibasiewicz, K.; Ramesh, V.M.; Lin, S.; Webber, A. Electron transfer from A₀^- to A₁ in Photosystem I from Chlamydomonas reinhardtii occurs in both the A and B branch with 25-30-ps lifetime. Phys. Chem. Chem. Phys. 2009, 11, 5186–5191. [Google Scholar] [CrossRef]
Santabarbara, S., Kuprov, I., Poluektov, O.G., Casal, A., Russell, C.A., Purton, S., Evans, M.C.W. (2010) Directionality of electron-transfer reactions in photosystem I of prokaryotes: universality of the bidirectional electron-transfer model. J. Phys. Chem. B 114, 15158–15171. [CrossRef]
Poluektov, O.G.; Utschig, L.M. Directionality of Electron Transfer in Type I Reaction Center Proteins: High-Frequency EPR Study of PS I with Removed Iron−Sulfur Centers. J. Phys. Chem. B 2015, 119, 13771–13776. [Google Scholar] [CrossRef] [PubMed]
Xu, W., Chitnis, P.R., Valeva, A., van der Est, A., Brettel, K., Guergova-Kuras, M. et al. (2003) Electron transfer in cyanobacterial photosystem I: II. Determination of forward electron transfer rates of site-directed mutants in a putative electron transfer pathway from A₀ through A₁ to F_X. J. Biol. Chem. 278, 27876–27887. [CrossRef]
Cohen, R.O., Shen, G., Golbeck, J.H., Xu, W., Chitnis, P.R., Valieva, A.I., van der Est, A., Pushkar, Y., Stehlik, D. (2004) Evidence for asymmetric electron transfer in cyanobacterial photosystem I: analysis of a methionine-to-leucine mutation of the ligand to the primary electron acceptor A₀. Biochemistry 43, 4741–4754. [CrossRef]
Dashdorj, N., Xu, W., Cohen, R.O., Golbeck, J.H., Savikhin, S. (2005) Asymmetric electron transfer in cyanobacterial Photosystem I: charge separation and secondary electron transfer dynamics of mutations near the primary electron acceptor A₀. Biophys. J. 88, 1238–12349. [CrossRef]
Sun, J., Hao, S., Radle, M., Xu, W., Shelaev, I., Nadtochenko, V., Shuvalov, V., Semenov, A.Yu., Gordon, H., van der Est, A., Golbeck, J.H. (2014) Evidence that histidine forms a coordination bond to the A_0A and A_0B chlorophylls and a second H-bond to the A_1A and A_1B phylloquinones in M688H_PsaA and M668H_PsaB variants of Synechocystis sp. PCC 6803. Biochim. Biophys. Acta. 1837, 1362–1375. [CrossRef]
Milanovsky, G.E., Ptushenko, V.V., Golbeck, J.H., Semenov, A.Y., Cherepanov, D.A. (2014) Molecular dynamics study of the primary charge separation reactions in Photosystem I: effect of the replacement of the axial ligands to the electron acceptor A₀. Biochim. Biophys. Acta 1837, 1472–1483. [CrossRef]
Joliot, P., Joliot, A. (1999) In vivo analysis of the electron transfer within photosystem I: are the two phylloquinones involved? Biochemistry 38, 11130–11136. [CrossRef]
Brettel, K.; Leibl, W. Electron transfer in photosystem I. Biochim Biophys Acta 2001, 1507, 100–114. [Google Scholar] [CrossRef] [PubMed]
Guergova-Kuras, M., Boudreaux, B., Joliot, A., Joliot, P., Redding, K.E. (2001) Evidence for two active branches for electron transfer in photosystem I. Proc. Natl. Acad. Sci. U.S.A. 98, 4437–4442. [CrossRef]
Fairclough, W.V.; Forsyth, A.; Evans, M.C.W.; Rigby, S.E.J.; Purton, S.; Heathcote, P. Bidirectional electron transfer in photosystem I: electron transfer on the PsaA side is not essential for phototrophic growth in Chlamydomonas. Biochim Biophys. Acta 2003, 1606, 43–55. [Google Scholar] [CrossRef] [PubMed]
Purton, S. , Stevens, D.R., Muhiuddin, I.P., Evans, M.C., Carter, S., Rigby, S.E., Heathcote, P. (2001). Site-directed mutagenesis of PsaA residue W693 affects phylloquinone binding and function in the photosystem I reaction center of Chlamydomonas reinhardtii. Biochemistry 40, 2167–2175. [CrossRef]
Byrdin, M., Santabarbara, S., Gu, F., Fairclough, V.W., Heathcote, P., Redding, K.E., Rappaport, F. (2006) Assignment of a kinetic component to electron transfer between iron-sulfur clusters F_X and F_A/B of Photosystem I. Biochim. Biophys. Acta 1757, 1529–1538. [CrossRef]
Ali, K., Santabarbara, S., Heathcote, P., Evans, M.C.W., Purton, S. (2006) Bidirectional electron transfer in photosystem I: replacement of the symmetry-breaking tryptophan close to the PsaB-bound phylloquinone A_1B with a glycine residue alters the redox properties of A_1B and blocks forward electron transfer at cryogenic temperatures. Biochim. Biophys. Acta 1757, 1623–1633. [CrossRef]
Ali, K., Santabarbara, S., Heathcote, P., Evans, M.C.W., Purton, S. (2006) Bidirectional electron transfer in photosystem I: replacement of the symmetry-breaking tryptophan close to the PsaB-bound phylloquinone A_1B with a glycine residue alters the redox properties of A_1B and blocks forward electron transfer at cryogenic temperatures. Biochim. Biophys. Acta 1757, 1623–1633. [CrossRef]
Agalarov, R., and Brettel, K. (2003). Temperature dependence of biphasic forward electron transfer from the phylloquinone(s) A₁ in photosystem I: only the slower phase is activated. Biochim. Biophys. Acta 1604, 7–12. [CrossRef]
Santabarbara, S., Redding, K.E., Rappaport, F. (2009). Temperature dependence of the reduction of P₇₀₀⁺ by tightly bound plastocyanin in vivo. Biochemistry 48, 10457–10466. [CrossRef]
Marcus, R.A., and Sutin, N. (1985). Electron transfer in chemistry and biology. Biochim. Biophys. Acta 811, 265–322. [CrossRef]
Devault, D. (1980). Quantum mechanical tunnelling in biological systems. Cambridge University Press.
Moser, C.C., and Dutton, P.L. (1992). Engineering protein structure for electron transfer function in photosynthetic reaction centers. Biochim. Biophys. Acta 1101, 171–176. [CrossRef]
Moser, C.C., and Dutton, P.L. (2006). “Application of Marcus Theory to Photosystem I Electron Transfer,” in Photosystem I: The Light–Driven Plastocyanin:Ferredoxin Oxidoreductase, ed. J.H. Golbeck (Dordrecht, Kluwer Academic Publishers), 583–594.
Milanovsky, G.E., Petrova, A.A., Cherepanov, D.A, Semenov A.Yu. (2017) Kinetic modeling of electron transfer reactions in photosystem I complexes of various structures with substituted quinone acceptors. Photosynth. Res. 133, 185–199. [CrossRef]
Munge, B., Das, S.K., Ilagan, R., Pendon, Z., Yang, J., Frank, H.A., Rusling, J.F. (2003) Electron transfer reactions of redox cofactors in spinach Photosystem I reaction centre proteins in lipid films on electrodes. J. Am. Chem. Soc. 125, 12457–12463. [CrossRef]
Ke, B.; Dolan, E.; Sugahara, K.; Hawkridge, F.M.; Demeter, S.; Shaw, E. Electrochemical and kinetic evidence for a transient electron transfer acceptor in the photochemical charge separation in photosystem I. Plant Cell Physiol. 1977, 3–7, 187–199. [Google Scholar]
Chamorowsky, S.K.; Cammack, R. Direct determination of the midpoint potential of the acceptor X in chloroplast Photosystem I by electrochemical reduction and electron spin resonance. Photochem. Photobiophys. 1982, 4, 195–200. [Google Scholar]
Parrett, K.G., Mehari, T., Warren, P.G., Golbeck, J.H. (1989) Purification and properties of the intact P700- and Fx-containing Photosystem I core protein. Biochim. Biophys. Acta 973, 324–332. [CrossRef]
Ptushenko, V.V., Cherepanov, D.A., Krishtalik, L.I., Semenov, A.Y. (2008). Semi-continuum electrostatic calculations of redox potentials in photosystem I. Photosynth. Res. 97, 55–74. [CrossRef]
Ishikita, H.; Knapp, E.W. Redox potential of quinones in both electron transfer branches of photosystem I. J Biol Chem 2003, 278, 52002–52011. [Google Scholar] [CrossRef] [PubMed]
Karyagina, I.; Pushkar, Y.; Stehlik, D.; van der Est, A.; Ishikita, H.; Knapp, E.W.; Jagannathan, B.; Agalarov, R.; Golbeck, J.H. Contributions of the protein environment to the midpoint potentials of the A₁ phylloquinones and the Fx iron-sulfur cluster in photosystem I. Biochemistry 2007, 46, 10804–10816. [Google Scholar] [CrossRef] [PubMed]
Kawashima, K.; Ishikita, H. Structural Factors That Alter the Redox Potential of Quinones in Cyanobacterial and Plant Photosystem I. Biochemistry 2017, 56, 3019–3028. [Google Scholar] [CrossRef] [PubMed]
Santabarbara, S., Zucchelli, G. (2016) Comparative kinetic and energetic modelling of phyllosemiquinone oxidation in Photosystem I. Phys. Chem. Chem. Phys. 18, 9687–9701. [CrossRef]
Santabarbara, S. Casazza, A.P. (2019) Kinetics and Energetics of Phylloquinone Reduction in Photosystem I: Insight From Modeling of the Site Directed Mutants. Front. Plant Sci. 10, 852. [CrossRef]
Ke, B., Hansen, R.E., Beinert, H. (1973) Oxidation-reduction potentials of bound iron-sulfur proteins of photosystem I. Proc. Natl. Acad. Sci. U.S.A. 70, 2941–2945. [CrossRef]
Evans, M.C.W., Reeves, S.G, Cammack, R. (1974) Determination of the oxidation-reduction potential of the bound iron–sulphur proteins of the primary electron acceptor complex of Photosystem I in spinach chloroplasts. FEBS Lett. 49, 111–114. [CrossRef]
Evans, M.C.W., and Heathcote, P. (1980) Effects of glycerol on the redox properties of the electron acceptor complex in spinach photosystem I particles. Biochim Biophys Acta 590: 89–96. [CrossRef]
Nugent, J.H., Moller, B.L., Evans, M.C.W. (1981) Comparison of the EPR properties of Photosystem I iron–sulphur centres A and B in spinach and barley. Biochim. Biophys. Acta 634, 249–255. [CrossRef]
Hiyama, T.; Ke, B. A further study of P430: a possible primary electron acceptor of photosystem I. Arch. Biochem. Biophys. 1971, 147, 99–108. [Google Scholar] [CrossRef] [PubMed]
Lüneberg, J.; Fromme, P.; Jekow, P.; Schlodder, E. Spectroscopic characterization of PS I core complexes from thermophilic Synechococcus sp. Identical reoxidation kinetics of A₁⁻ before and after removal of the iron–sulfur-clusters F_A and F_B. FEBS Lett. 1994, 338, 197–202. [Google Scholar] [CrossRef] [PubMed]
Leibl, W.; Toupance, B.; Breton, J. Photoelectric characterization of forward electron transfer to iron–sulfur centers in photosystem I. Biochemistry 1995, 34, 10237–10244. [Google Scholar] [CrossRef]
Diaz-Quintana, A.; Leibl, W.; Bottin, H.; Setif, P. Electron transfer in photosystem I reaction centers follows a linear pathway in which iron-sulfur cluster F_B is the immediate electron donor to soluble ferredoxin. Biochemistry 1998, 37, 3429–3439. [Google Scholar] [CrossRef] [PubMed]
Mamedov, M.D.; Gourovskaya, K.N.; Vassiliev, I.R.; Golbeck, J.H.; Semenov, A.Y. Electrogenicity accompanies photoreduction of the iron-sulfur clusters F_A and F_B in photosystem I. FEBS Lett. 1998, 431, 219–223. [Google Scholar]
Mamedova, A.A.; Mamedov, M.D.; Gourovskaya, K.N.; Vassiliev, I.R.; Golbeck, J.H.; Semenov, A.Y. Electrometrical study of electron transfer from the terminal F_A/F_B iron-sulfur clusters to external acceptors in photosystem I. FEBS Lett. 1999, 462, 421–424. [Google Scholar] [CrossRef]
Semenov, A.Y.; Mamedov, M.D.; Chamorovsky, S.K. Photoelectric studies of the transmembrane charge transfer reactions in photosystem I pigment-protein complexes. FEBS Lett. 2003, 553, 223–228. [Google Scholar] [CrossRef] [PubMed]
Semenov, A. Y, Mamedov, M.D., Chamorovsky, S.K. (2006) “Electrogenic Reactions Associated with Electron Transfer in Photosystem I,” in Photosystem I: The Light–Driven Plastocyanin:Ferredoxin Oxidoreductase, ed. J.H. Golbeck (Dordrecht, Kluwer Academic Publishers), 319–338. [CrossRef]
Santabarbara, S., Jasaitis, A., Byrdin, M., Gu, F., Rappaport, F., Redding, K.E. (2008) Additive effect of mutations affecting the rate of phylloquinone reoxidation and directionality of electron transfer within photosystem I. Photochem. Photobiol. 84, 1381–1387. [CrossRef]
Santabarbara, S., Bullock, B., Rappaport, F., Redding, K.E. (2015). Controlling electron transfer between the two cofactor chains of photosystem I by the redox state of one of their components. Biophys. J. 108, 1537–1547. [CrossRef]
Setif, P. (2001) Ferredoxin and flavodoxin reduction by photosystem I. Biochim. Biophys. Acta 1507, 161–179. [Google Scholar] [CrossRef]
Hopfield, J.J. (1974). Electron transfer between biological molecules by thermally activated tunnelling. Proc. Natl. Acad. Sci. U.S.A. 71, 3640–3644. [CrossRef]
Mula, S., McConnell, M.D., Ching, A., Zhao, N., Gordon, H.L., Hastings, G., et al. (2012) Introduction of a hydrogen bond between phylloquinone PhQ_A and a threonine side-chain OH group in photosystem I. J. Phys. Chem. B 116, 14008–14016. [CrossRef]
Santabarbara, S., Reifschneider, K., Jasaitis, A., Gu, F., Agostini, G., Carbonera, D., et al. (2010) Interquinone electron transfer in photosystem I as evidenced by altering the hydrogen bond strength to the phylloquinone(s). J. Phys. Chem. B 114, 9300–9312. [CrossRef]
Shinkarev, V.P.; Zybailov, B.; Vassiliev, I.R.; Golbeck, J.H. Modeling of the P₇₀₀⁺ Charge Recombination Kinetics with Phylloquinone and Plastoquinone-9 in the A₁ Site of Photosystem I. Biophys. J. 2002, 83, 2885–2897. [Google Scholar] [CrossRef]
Makita, H., Hastings, G. (2017) Inverted-region electron transfer as a mechanism for enhancing photosynthetic solar energy conversion efficiency. Proc. Natl. Acad. Sci. U.S.A. 114, 9267–9272. [CrossRef]
Kurashov, V.; Gorka, M.; Milanovsky, G.E.; Johnson, T.W.; Cherepanov, D.A.; Semenov, A.Y.; Golbeck, J.H. Critical evaluation of electron transfer kinetics in P₇₀₀–F_A/F_B, P₇₀₀–F_X, and P₇₀₀–A₁ Photosystem I core complexes in liquid and in trehalose glass. Biochim. Biophys. Acta 2018, 1859, 1288–1301. [Google Scholar] [CrossRef] [PubMed]
Milanovsky, G.; Gopta, O.; Petrova, A.A.; Mamedov, M.D.; Gorka, M.; Cherepanov, D.A.; Golbeck, J.H.; Semenov, A.Y. Multiple pathways of charge recombination revealed by the temperature dependence of electron transfer kinetics in cyanobacterial photosystem I. Biochim. Biophys. Acta 2019, 1860, 601–610. [Google Scholar] [CrossRef] [PubMed]
Cherepanov, D.A., Milanovsky, G.E., Gopta, O.A., Balasubramanian, R., Bryant, D.A., Semenov, A.Yu., Golbeck, J.H. (2018) Electron-Phonon Coupling in Cyanobacterial Photosystem I. J. Phys. Chem. B. 122, 7943–7955. [CrossRef]
Zhao, J., Li N., Warren, P.V., Golbeck, J.H., Bryant, D.A. (1992) Site-directed conversion of a cysteine to aspartate leads to the assembly of a [3Fe-4S] cluster in PsaC of photosystem I. The photoreduction of F_A is independent of F_B. Biochemistry 31, 5093-5099. [CrossRef]
Rodday, S.M., Jun, S.S., Biggins, J. (1993) Interaction of the F_AF_B-containing subunit with the Photosystem 1 core heterodimer. Photosynth. Res. 36, 1-9. [CrossRef]
Yu, L., Zhao, .J, Lu, W., Bryant, D.A., Golbeck, J.H. (1993) Characterization of the [3Fe-4S] and [4Fe-4S] clusters in unbound PsaC mutants C14D and C51D. Midpoint potentials of the single [4Fe-4S] clusters are identical to F_A and F_B in bound PsaC of photosystem I. Biochemistry 32, 8251-8258. [CrossRef]
Yu, L., Bryant, D.A., Golbeck, J.H. (1995) Evidence for a mixed-ligand [4Fe-4S] cluster in the C14D mutant of PsaC. Altered reduction potentials and EPR spectral properties of the F_A and F_B clusters on rebinding to the P700-FX core. Biochemistry 34, 7861-7868. [CrossRef]
Mehari, T. , Qiao, F., Scott, M.P., Nellis, D.F., Zhao, J., Bryant, D.A., Golbeck, J.H. (1995) Modified ligands to FA and FB in photosystem I. I. Structural constraints for the formation of iron-sulfur clusters in free and rebound PsaC. J. Biol. Chem. 270, 28108-28117. [CrossRef]
Rodday, S.M., Do, L.T., Chynwat, V., Frank, H.A., Biggins, J. (1996) Site-directed mutagenesis of the subunit PsaC establishes a surface-exposed domain interacting with the photosystem I core binding site. Biochemistry 35, 11832-11838. [CrossRef]
Jung, Y..S, Vassiliev, I.R., Qiao, F., Yang, F., Bryant, D.A., Golbeck, J.H. (1996) Modified ligands to F_A and F_B in photosystem I. Proposed chemical rescue of a [4Fe-4S] cluster with an external thiolate in alanine, glycine, and serine mutants of PsaC. J. Biol. Chem. 271, 31135-31144. [CrossRef]
Yu, J., Vassiliev, I.R., Jung, Y.S., Golbeck, J.H., McIntosh, L. (1997) Strains of synechocystis sp. PCC 6803 with altered PsaC. I. Mutations incorporated in the cysteine ligands of the two [4Fe-4S] clusters F_A and F_B of photosystem I. J. Biol. Chem. 272, 8032-8039. [CrossRef]
Jung, Y.S., Vassiliev, I.R., Yu, J., McIntosh, L., Golbeck, J.H. (1997) Strains of Synechocystis sp. PCC 6803 with altered PsaC. II. EPR and optical spectroscopic properties of F_A and F_B in aspartate, serine, and alanine replacements of cysteines 14 and 51. J. Biol. Chem. 272, 8040-8049. [CrossRef]
Fischer, N.; Setif, P.; Rochaix, J.-D. Targeted Mutations in the psaC Gene of Chlamydomonas reinhardtii: Preferential reduction of F_B at low temperature is not accompanied by altered electron flow from Photosystem I to Ferredoxin. Biochemistry 1997, 36, 93–102. [Google Scholar] [CrossRef]
Fischer, N.; Setif, P.; Rochaix, J.-D. Site-directed Mutagenesis of the PsaC Subunit of Photosystem I. FB is the cluster interacting with soluble ferredoxin. J. Biol. Chem. 1999, 33, 23333–23340. [Google Scholar] [CrossRef]
Pérez, A.A., Ferlez, B.H., Applegate, A.M., Walters, K., He, Z., Shen, G., Golbeck, J.H., Bryant, D.A. (2018) Presence of a [3Fe-4S] cluster in a PsaC variant as a functional component of the photosystem I electron transfer chain in Synechococcus sp. PCC 7002.. Photosynth Res. 136, 31–48. [CrossRef]
Webber, A.N.; Gibbs, P.B.; Ward, J.B.; Bingham, S.E. Site-directed mutagenesis of the photosystem I reaction center in chloroplasts. The proline-cysteine motif. J. Biol. Chem. 1993, 268, 12990–12995. [Google Scholar] [CrossRef] [PubMed]
Smart, L.B., Warren, P.V., Golbeck, J.H., McIntosh, L. (1993) Mutational analysis of the structure and biogenesis of the photosystem I reaction center in the cyanobacterium Synechocystis sp. PCC 6803. Proc. Natl. Acad. Sci. U.S.A. 90, 1132–1136. [CrossRef]
Warren, P.V., Smart, L.B., McIntosh, L., Golbeck, J.H. (1993) Site-directed conversion of cysteine-565 to serine in PsaB of photosystem I results in the assembly of [3Fe-4S] and [4Fe-4S] clusters in Fx. A mixed-ligand [4Fe-4S] cluster is capable of electron transfer to F_A and F_B. Biochemistry 32, 4411–4419. [CrossRef]
Rodday, S.M., Schulz, R., McLntosh, L., Biggins, J. (1994) Structure-function studies on the interaction of PsaC with the Photosystem 1 heterodimer : The site directed change R561E in PsaB destabilizes the subunit interaction in Synechocystis sp. PCC 6803. Photosynth. Res. 42, 185–190. [CrossRef]
Rodday, S.M., Webber, A.N., Bingham, S.E., Biggins, J. (1995) Evidence that the FX domain in photosystem I interacts with the subunit PsaC: site-directed changes in PsaB destabilize the subunit interaction in Chlamydomonas reinhardtii. Biochemistry 34, 6328–6334. [CrossRef]
Hallahan, B.J., Purton, S., Ivison, A., Wright, D., Evans, M.C.W. (1995) Analysis of the proposed Fe-S_X binding region of Photosystem 1 by site directed mutation of PsaA in Chlamydomonas reinhardtii. Photosynth Res. 46, 257–264. [CrossRef]
Vassiliev, I.R.; Jung, Y.-S.; Smart, L.B.; Schulz, R.; McIntosh, L.; Golbeck, J.H. A Mixed-Ligand Iron-Sulfur Cluster (C556SPSaB or C565SPSaB) in the F_X-Binding Site Leads to a Decreased Quantum Efficiency of Electron Transfer in Photosystem I. Biophys. J. 1995, 69, 1544–1553. [Google Scholar] [CrossRef]
Evans, M.C.W.; Purton SPatel, V.; Wright, D.; Heathcote, P.; Rigby, S.E.J. Modification of electron transfer from the quinone electron carrier, A₁, of Photosystem 1 in a site directed mutant D576->L within the Fe-Sx binding site of PsaA and in second site suppressors of the mutation in Chlamydomonas reinhardtii. Photosynth. Res. 1999, 61, 33–42. [Google Scholar] [CrossRef]
Vassiliev, I.R.; Yu, J.; Jung, Y.-S.; Schulz, R.; Ganago, A.O.; McIntosh, L.; Golbeck, J.H. The Cysteine-proximal Aspartates in the F_X-binding Niche of Photosystem I. J. Biol. Chem. 1999, 274, 9993–10001. [Google Scholar] [CrossRef]
Zeng, M.-T.; Gong, X.-M.; Evans, M.C.W.; Nelson, N.; Carmeli, C. Stabilization of iron–sulfur cluster F_X by intra-subunit interactions unraveled by suppressor and second site-directed mutations in PsaB of Photosystem I. Biochim. Biophys. Acta 2002, 1556, 254–264. [Google Scholar] [CrossRef]
Gong, X-M., Agalarov, R., Brettel, K., Carmeli, C. (2003) Control of Electron Transport in Photosystem I by the Iron-Sulfur Cluster F_X in Response to Intra- and Intersubunit Interactions. J. Biol. Chem. 278, 19141–19150. [CrossRef]
Kümmerle, R.; Gaillard JKyritis, P.; Moulis, J.-M. Intramolecular electron transfer in [4Fe-4S] proteins: estimates of the reoganisation energy and electronic coupling in Chromatium vinosum ferredoxin J. Biol. Inorg. Chem. 2001, 6, 446–451. [Google Scholar] [CrossRef]

Figure 1. Panel A: Arrangement of the redox active cofactors in PS I (from the structural model of Jordan et al. (2001) PDB file # 1JB0). The terminal electron donor (

P_{700}^{(+)}

) is considered as Chl a/Chl a’ hetero-dimer, is shown in black; the so-called accessory Chl a are unlabeled and are shown in grey; the primary Chl a electron acceptors

A_{0 A, B}^{(-)}

are shown in green; the phylloquinone

A_{1 A}^{(-)}

is own in red and

A_{1 B}^{(-)}

in blue. The terminal 4Fe-4S clusters,

F_{X}^{}

F_{A}^{}

and

F_{B}^{}

are shown in gold, orange and burgundy colour, respectively. Panel B: Kinetic scheme utilised in the simulations of electron transfer reactions. Solid arrow indicates forward and backwards rates between pairs of successive redox-active cofactors. Dash and dotted lines represent charge recombination reactions between individual cofactors and

P_{700}^{+}

, involving the phylloquinones and iron-sulphur clusters, respectively. The colour code is the same as in (A) and is maintained throughout the manuscript. Note that the energy gaps are not scaled. Properly scaled

E^{0}

are shown in Figure 2 and Figure 3.

Figure 1. Panel A: Arrangement of the redox active cofactors in PS I (from the structural model of Jordan et al. (2001) PDB file # 1JB0). The terminal electron donor (

P_{700}^{(+)}

) is considered as Chl a/Chl a’ hetero-dimer, is shown in black; the so-called accessory Chl a are unlabeled and are shown in grey; the primary Chl a electron acceptors

A_{0 A, B}^{(-)}

are shown in green; the phylloquinone

A_{1 A}^{(-)}

is own in red and

A_{1 B}^{(-)}

in blue. The terminal 4Fe-4S clusters,

F_{X}^{}

F_{A}^{}

and

F_{B}^{}

P_{700}^{+}

E^{0}

are shown in Figure 2 and Figure 3.

Figure 4. Panels A, C and E: energetic schemes showing the

E_{F_{A}}^{0}

perturbations (altered value, pink line) with respect to the reference model being the “weak driving force” scenario for

A_{1}^{-}

oxidation. The reference

E_{F_{A}}^{0}

potential is indicated by dashed-dotted orange lines. Panel B, D and F: simulated population evolution of the individual redox active cofactors, resulting from

E_{F_{A}}^{0}

perturbations:

A_{1 A}^{-} (t)

: dash-dot red line,

A_{1 B}^{-} (t)

dash-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

thick dash pink line,

F_{B}^{-} (t)

dot burgundy line. The population evolutions of

A_{1, t o t}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t)

(purple line) are also shown and compared with the simulation for the reference scenario (dash grey and violet lines for

A_{1, t o t}^{-} (t)

and

F e S_{t o t}^{-} (t)

, respectively).

Figure 4. Panels A, C and E: energetic schemes showing the

E_{F_{A}}^{0}

perturbations (altered value, pink line) with respect to the reference model being the “weak driving force” scenario for

A_{1}^{-}

oxidation. The reference

E_{F_{A}}^{0}

potential is indicated by dashed-dotted orange lines. Panel B, D and F: simulated population evolution of the individual redox active cofactors, resulting from

E_{F_{A}}^{0}

perturbations:

A_{1 A}^{-} (t)

: dash-dot red line,

A_{1 B}^{-} (t)

dash-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

thick dash pink line,

F_{B}^{-} (t)

dot burgundy line. The population evolutions of

A_{1, t o t}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t)

(purple line) are also shown and compared with the simulation for the reference scenario (dash grey and violet lines for

A_{1, t o t}^{-} (t)

and

F e S_{t o t}^{-} (t)

, respectively).

Figure 5. Panels A, C and E: energetic schemes showing the

E_{F_{A}}^{0}

perturbations (altered value, pink line) with respect to the reference model being the “large driving force” scenario for

A_{1}^{-}

oxidation. The reference

E_{F_{A}}^{0}

potential is indicated by dashed-dotted orange lines. Panel B, D and F: simulated population evolution of the individual redox active cofactors, resulting from

E_{F_{A}}^{0}

perturbations:

A_{1 A}^{-} (t)

: dash-dot red line,

A_{1 B}^{-} (t)

dash-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

thick dash pink line,

F_{B}^{-} (t)

dot burgundy line. The population evolutions of

A_{1, t o t}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t)

(purple line) are also shown and compared with the simulation for the reference scenario (dash grey and violet lines for

A_{1, t o t}^{-} (t)

and

F e S_{t o t}^{-} (t)

, respectively).

Figure 5. Panels A, C and E: energetic schemes showing the

E_{F_{A}}^{0}

perturbations (altered value, pink line) with respect to the reference model being the “large driving force” scenario for

A_{1}^{-}

oxidation. The reference

E_{F_{A}}^{0}

potential is indicated by dashed-dotted orange lines. Panel B, D and F: simulated population evolution of the individual redox active cofactors, resulting from

E_{F_{A}}^{0}

perturbations:

A_{1 A}^{-} (t)

: dash-dot red line,

A_{1 B}^{-} (t)

dash-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

thick dash pink line,

F_{B}^{-} (t)

dot burgundy line. The population evolutions of

A_{1, t o t}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t)

(purple line) are also shown and compared with the simulation for the reference scenario (dash grey and violet lines for

A_{1, t o t}^{-} (t)

and

F e S_{t o t}^{-} (t)

, respectively).

Figure 6. Simulated lifetimes resulting from variation of

E_{F_{A}}^{0}

(±100 meV), starting from the “weak” (A, C, E) and “large” (B, D, F) driving force models for

A_{1}^{-}

oxidation. A, B:

τ

< 50 ns; C, D: 50 ns<

τ

< 1 μs; E, F:

τ

>1 μs.

τ_{1}

: red squares;

τ_{2}

: green circles;

τ_{3}

: blue triangles;

τ_{4}

: cyan diamonds;

τ_{5}

: burgundy hexagon. In panel F,

τ_{4}

(cyan diamonds) is re-plotted to facilitate comparison with

τ_{5}

Figure 6. Simulated lifetimes resulting from variation of

E_{F_{A}}^{0}

(±100 meV), starting from the “weak” (A, C, E) and “large” (B, D, F) driving force models for

A_{1}^{-}

oxidation. A, B:

τ

< 50 ns; C, D: 50 ns<

τ

< 1 μs; E, F:

τ

>1 μs.

τ_{1}

: red squares;

τ_{2}

: green circles;

τ_{3}

: blue triangles;

τ_{4}

: cyan diamonds;

τ_{5}

: burgundy hexagon. In panel F,

τ_{4}

(cyan diamonds) is re-plotted to facilitate comparison with

τ_{5}

Figure 7. Simulated recombination lifetimes resulting from variation of

E_{F_{A}}^{0}

(±100 meV), starting from the “weak” (A) and “large” (B) driving force models for

A_{1}^{-}

oxidation.

Figure 7. Simulated recombination lifetimes resulting from variation of

E_{F_{A}}^{0}

(±100 meV), starting from the “weak” (A) and “large” (B) driving force models for

A_{1}^{-}

oxidation.

Figure 8. Panels A, C and E: energetic schemes showing the

E_{F_{B}}^{0}

perturbations (altered value, pink line) with respect to the reference model being the “weak driving force” scenario for

A_{1}^{-}

oxidation. The reference

E_{F_{B}}^{0}

potential is indicated by dashed-dotted burgundy lines. Panel B, D and F: simulated population evolution of the individual redox active cofactors, resulting from

E_{F_{B}}^{0}

perturbations:

A_{1 A}^{-} (t)

: dash-dot red line,

A_{1 B}^{-} (t)

dash-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

dot orange line,

F_{B}^{-} (t)

thick dash pink line The population evolutions of

A_{1, t o t}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t)

(purple line) are also shown and compared with the simulation for the reference scenario (dash grey and violet lines for

A_{1, t o t}^{-} (t)

and

F e S_{t o t}^{-} (t)

, respectively ).

Figure 8. Panels A, C and E: energetic schemes showing the

E_{F_{B}}^{0}

perturbations (altered value, pink line) with respect to the reference model being the “weak driving force” scenario for

A_{1}^{-}

oxidation. The reference

E_{F_{B}}^{0}

potential is indicated by dashed-dotted burgundy lines. Panel B, D and F: simulated population evolution of the individual redox active cofactors, resulting from

E_{F_{B}}^{0}

perturbations:

A_{1 A}^{-} (t)

: dash-dot red line,

A_{1 B}^{-} (t)

dash-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

dot orange line,

F_{B}^{-} (t)

thick dash pink line The population evolutions of

A_{1, t o t}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t)

(purple line) are also shown and compared with the simulation for the reference scenario (dash grey and violet lines for

A_{1, t o t}^{-} (t)

and

F e S_{t o t}^{-} (t)

, respectively ).

Figure 9. Panels A, C and E: energetic schemes showing the

E_{F_{B}}^{0}

perturbations (altered value, pink line) with respect to the reference model being the “large driving force” scenario for

A_{1}^{-}

oxidation. The reference

E_{F_{B}}^{0}

potential is indicated by dashed-dotted burgundy lines. Panel B, D and F: simulated population evolution of the individual redox active cofactors, resulting from

E_{F_{B}}^{0}

perturbations:

A_{1 A}^{-} (t)

: dashed-dot red line,

A_{1 B}^{-} (t)

dashed-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

dot orange line,

F_{B}^{-} (t)

thick dash pink line The population evolutions of

A_{1, t o t}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t)

(purple line) are also shown and compared with the simulation for the reference scenario (dash grey and violet lines for

A_{1, t o t}^{-} (t)

and

F e S_{t o t}^{-} (t)

, respectively).

Figure 9. Panels A, C and E: energetic schemes showing the

E_{F_{B}}^{0}

perturbations (altered value, pink line) with respect to the reference model being the “large driving force” scenario for

A_{1}^{-}

oxidation. The reference

E_{F_{B}}^{0}

potential is indicated by dashed-dotted burgundy lines. Panel B, D and F: simulated population evolution of the individual redox active cofactors, resulting from

E_{F_{B}}^{0}

perturbations:

A_{1 A}^{-} (t)

: dashed-dot red line,

A_{1 B}^{-} (t)

dashed-dot blue line,

F_{X}^{-} (t)

dot golden line,

F_{A}^{-} (t)

dot orange line,

F_{B}^{-} (t)

thick dash pink line The population evolutions of

A_{1, t o t}^{-} (t)

(black line) and

F e S_{t o t}^{-} (t)

(purple line) are also shown and compared with the simulation for the reference scenario (dash grey and violet lines for

A_{1, t o t}^{-} (t)

and

F e S_{t o t}^{-} (t)

, respectively).

Figure 10. Simulated lifetimes resulting from variation of

E_{F_{B}}^{0}

(±100 meV), starting from the “weak” (A, C, E) and “large” (B, D, F) driving force models for

A_{1}^{-}

oxidation. A, B:

τ

< 50 ns; C, D: 50 ns<

τ

< 1 μs; E, F:

τ

>1 μs.

τ_{1}

: red squares;

τ_{2}

: green circles;

τ_{3}

: blue triangles;

τ_{4}

: cyan diamonds;

τ_{5}

: burgundy hexagon.

Figure 10. Simulated lifetimes resulting from variation of

E_{F_{B}}^{0}

(±100 meV), starting from the “weak” (A, C, E) and “large” (B, D, F) driving force models for

A_{1}^{-}

oxidation. A, B:

τ

< 50 ns; C, D: 50 ns<

τ

< 1 μs; E, F:

τ

>1 μs.

τ_{1}

: red squares;

τ_{2}

: green circles;

τ_{3}

: blue triangles;

τ_{4}

: cyan diamonds;

τ_{5}

: burgundy hexagon.

Figure 11. Simulated recombination lifetimes resulting from variation of

E_{F_{B}}^{0}

(±100 meV), starting from the weak (A) and large (B) driving force models for

A_{1}^{-}

oxidation.

Figure 11. Simulated recombination lifetimes resulting from variation of

E_{F_{B}}^{0}

(±100 meV), starting from the weak (A) and large (B) driving force models for

A_{1}^{-}

oxidation.

Table 2. Rate-defining Parameters and Simulated ET kinetic for the large driving force energetic scenario.

	Rate Determining Parameters						Electron Transfer Simulated Parameters
							Amplitudes
Reaction	$X_{D A}$ (Å)	$Δ G_{D A}^{0}$ (eV)	$λ_{t, D A}$ (eV)	${\bar{ω}}_{D A}$ (eV/cm^-1)	$k_{D \to A}$ (ns^-1)	$τ_{}$ (ns)	$p_{A_{1 A}}$	$p_{A_{1 B}}$	$p_{F_{X}}$	$p_{F_{A}}$	$p_{F_{B}}$	$p_{A_{1 tot}}$	$p_{F e S_{tot}}$
$A_{1 A}^{-} \to F_{X}$	9.1	-0.05	1.0	0.022 (175)	0.00270	8.15	0.002	0.500	-0.504	0.0035	0.0000	0.501	-0.501
$A_{1 B}^{-} \to F_{X}$	9.0	-0.22	1.0	0.046 (375)	0.12249	294.7	0.0020	0.000	-0.003	0.3891	-0.550	0.002	-0.164
$F_{X}^{-} \to F_{A}$	11.6	-0.15	1.0	0.034 (275)	0.00085	307.3	0.307	0.000	-0.414	-0.343	0.650	0.307	-0.107
$F_{A}^{-} \to F_{B}$	9.5	0.025	1.0	0.034 (275)	0.00077	1411	0.187	0.001	0.912	-1.292	-0.468	0.188	-0.847
$F_{B}^{-} \to$	–	–	–	–	0.00100	4415	0.002	0.000	0.001	1.242	0.367	0.002	1.619

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Thermodynamic Factors Controlling Electron Transfer amongst the Terminal Electron Acceptors of Photosystem I: Insight from Kinetic Modelling

Abstract

1. Introduction

2. Results and Discussion

2.2. Large Driving Force Scenario for A 1 − Oxidation

2.3. Effect of Changing the Driving Force of F X − Oxidation ( Δ G F X → F A 0 )

2.4. Effect of Changing the Driving Force of F A − Oxidation ( Δ G F A → F B 0 )

3. Materials and Methods

4. Conclusions

Supplementary Materials

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2.2. Large Driving Force Scenario for $A_{1}^{-}$ Oxidation

2.3. Effect of Changing the Driving Force of $F_{X}^{-}$ Oxidation ( $Δ G_{F_{X} \to F_{A}}^{0}$ )

2.4. Effect of Changing the Driving Force of $F_{A}^{-}$ Oxidation ( $Δ G_{F_{A} \to F_{B}}^{0}$ )