Prerpints.org logo
Preprint
Article

The Need of Chloride-37 Enrichment for Molten Salt Fast Reactors

Altmetrics

Downloads

177

Views

134

Comments

0

This version is not peer-reviewed

Submitted:

07 August 2024

Posted:

12 August 2024

You are already at the latest version

Alerts
Abstract
The use of natural chloride in the salt fuel has been sometimes promoted for the chlorine based molten salt fast reactor using for example NaCl-UCl4- UCl3. Most of the chemistry based R&D has been carried out on natural chloride, while in reactor physics most of the calculations are based on enriched chloride-37. In any case, the use of natural chloride (75.77% 35Cl and 24.23% 37Cl) induces specific ecological and neutron economical issues. An ecological issue is the production of 36Cl by neutron activation of 35Cl. Chlorine-36 is a soluble long live nuclide that makes it a ‘first’ nuclide in the safety assessment of the repository. We explore the build-up of 36Cl with burnup for various 37Cl (activation product) enrichment. The neutron economical aspect is gained by achieving reactor criticality with a lower amount of fissile material achieved through the use of enriched chloride-37. The criticality (k) of a core is much larger for enriched chloride than for the natural one. The reactor with 99% 37Cl would have a k99/knat of 1.04346 which would allow to reduce the required uranium enrichment and thus the fuel cost. This reactivity gain is evaluated for various 37Cl enrichment factors to estimate uranium enrichment gain achievable through 37Cl enrichment. However, from economical point of view it could be of interest to use as some kind of compromise solution natural NaCl, which will be analysed, too. Production/enrichment of 37Cl can be performed by physical separation e.g. gas centrifugation of 1H35/37Cl or by chemical separation using anion partitioning and elution of 23Na35/37Cl on solid adsorbent columns or in liquid – liquid extraction systems. These techniques require however extensive investigations including chemical thermodynamics and hydrodynamics. Comparisons are suggested on the basis of the separation factor α. Recommendations are finally given for utilising 37Cl in the fast molten salt reactor. The enrichment work for 37Cl is smaller than the work needed for 235U enrichment.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

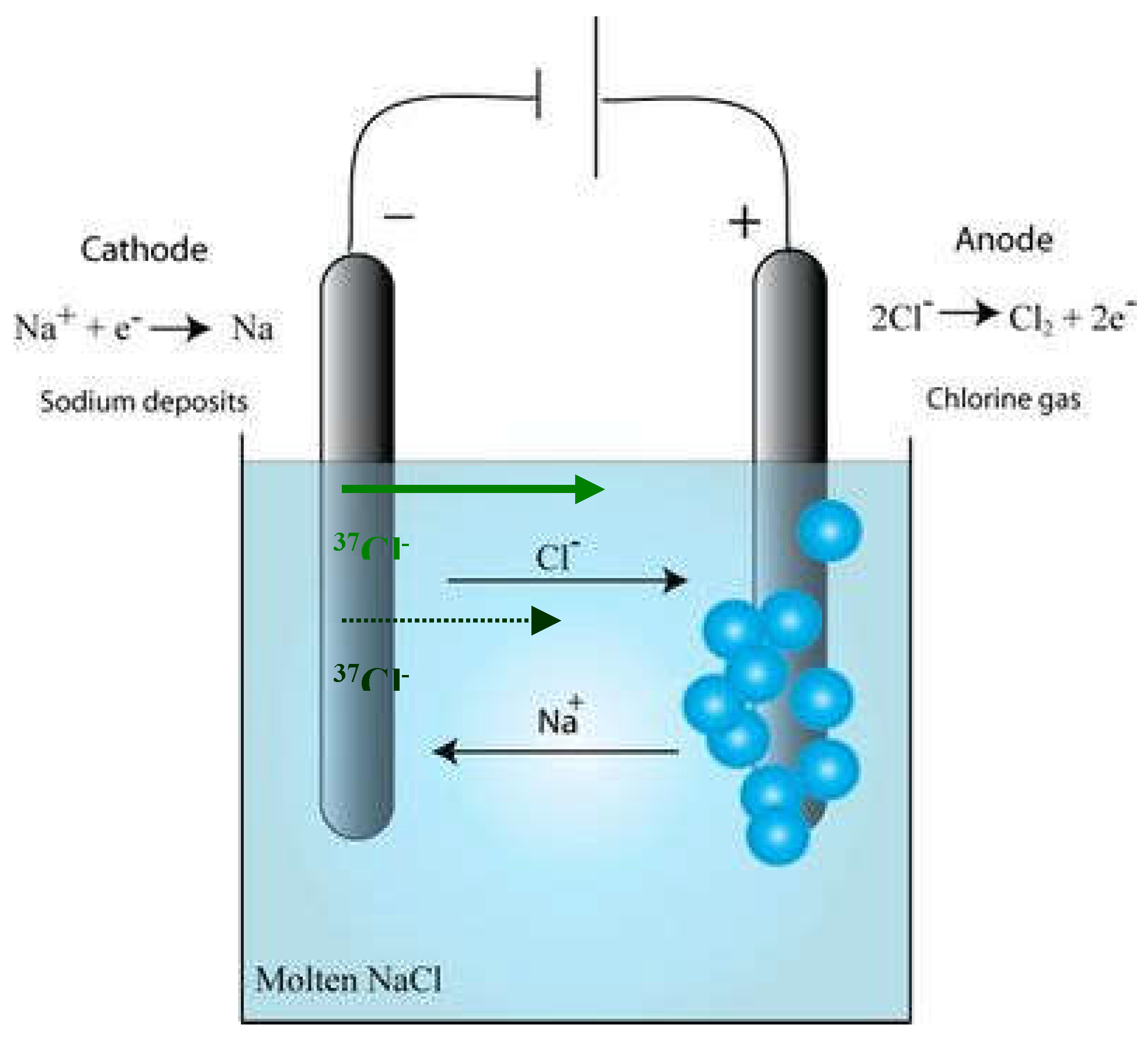
1. Introduction

Molten salt reactors are currently seen as one of the most promising innovative reactor technologies with the potential to create an integrated, closed fuel cycle to assure resource security while producing future sustainable, see Merk et al. (2019) [1], say, potentially renewable, as suggested by Degueldre et al. (2019) [2], energy for future generations on wide scale and for advanced energy applications, see Roper et al. (2022) [3]. In recent years flowing fuel Molten Chloride Fast Reactors (MCFRs) have regained interest e.g. Merk et al. (2019a) [4], Mausolff, et al. (2021) [5], Krepel & Kramer (2021) [6], Serp et al. (2014) [7]. The use of natural chloride as molten salt anion has been originally promoted for these MCFR using for example NaCl-UCl4-UCl3 as carrier salt and fuel salt with stable tetravalent/trivalent uranium chloride species as reported by Martinot (1982) [8] in LiCl-KCl and NaCl-KCl eutectics for example. Most of the R&D has been carried out on natural chloride. However the use of natural chloride (75.77% 35Cl and 24.23% 37Cl) induces specific ecological and neutron economical issues which need to be identified and solved.
Recently, Merk et al. (2019a)[3] for iMAGINE (U MSFR) and He et al. (2020) [9] for the thorium MCFR investigated the effect of 37Cl enrichment. Both molten salt reactors are adapted for breeding, transmutation and fission of transuranic isotopes. The neutron absorption cross section of 35Cl being greater than for 37Cl, affects the MCFR neutron economy of the core. With on-line refuelling and in-line reprocessing/salt clean-up, the influences of 37Cl enrichment on neutron economy, breeding performance, and the production of harmful nuclides were analysed by He et al (2020)[8] in detail. Both groups showed that 37Cl enrichment has a strong impact on the neutron economy of a MCFR in initial criticality as well as in the breeding performance and long term operation. In addition to the absorption effect on reactor criticality, the in the use of natural chlorine, the yields of S isotopes and 36Cl are very high. An enrichment of 37Cl to 97% brings a valuable improvement of the neutronics during Th MCFR operation.
Historically, a centrifuge was the first device to separate the chlorine isotopes. This methodology was first used in 1934 by Jesse Beams from University of Virginia to separate 35Cl from 37Cl. This has been the best method for separating isotopes of elements , however other physical as well as chemical techniques were developed and are currently used today e.g. see Gosling (1999) [10].
The physical isotope separation methodologies considered here are fractionated distillation, mass spectroscopy, gas diffusion and gas centrifugation.
The chemical isotope separation techniques are partitioning on solid or liquid ion exchangers, chromatography, photochemical techniques and to complete, electrochemical based techniques (electro-migration and electrolysis in solution or in molten salt).
Chlorides in the molten salt has been identified as suitable (less scattering) for the molten salt fast reactor (MSFR) using for example NaCl-UCl4-UCl3. Most of the R&D has been carried out on natural chloride. However, the use of natural chloride (75.77% 35Cl and 24.23% 37Cl) induces ecological and economical issues.
A significant ecological issue is the production of 36Cl by neutron activation of 35Cl. The isotope 36Cl is a soluble long live nuclide that makes it a ‘first nuclide’ in the safety assessment of the repository. Separation factor is investigated for gas centrifugation, distillation, chromatography and electrolysis.
This study revisits the neutronics data for a classical U MCFR, give reactivity and 36Cl results as a function of burn-up. It identifies the induced economical and ecological effects. A chlorine isotope separation technique is required for reducing the amount of 36Cl in the MCFR core. It subsequently reviews the isotopic properties and isotope separation methodologies that are physical or chemical. This study guides to identify techniques that could be used for the production of tons of Na37Cl with a 37Cl purity of say 97-99%.

2. Neutronic

During irradiation, the chlorine isotope build-up and decays are described by capture followed by beta (β-) decays.
The chlorine isotope activation reactions are:
35Cl + 1n ⇨ 36Cl # σ: 43.7 b
37Cl + 1n ⇨ 38Cl # σ: 0.42 b
These chlorine isotope productions are followed by beta decay (β-) reactions:
36Cl ⇨ 36Ar + β- # T1/2: 3x105 a
38Cl ⇨ 38Ar + β- # T1/2: 37.2 min
producing in both cases Ar stable isotopes. Now with fast neutron 35Cl reacts producing 35S according to Gooden et al. (2018) [11]:
35Cl + 1n ⇨ 35S + 1H # σ: 4 b
Criticality is consequently modified which affect reactivity and energy conversion yield.

2.1. Code, Model and Methods

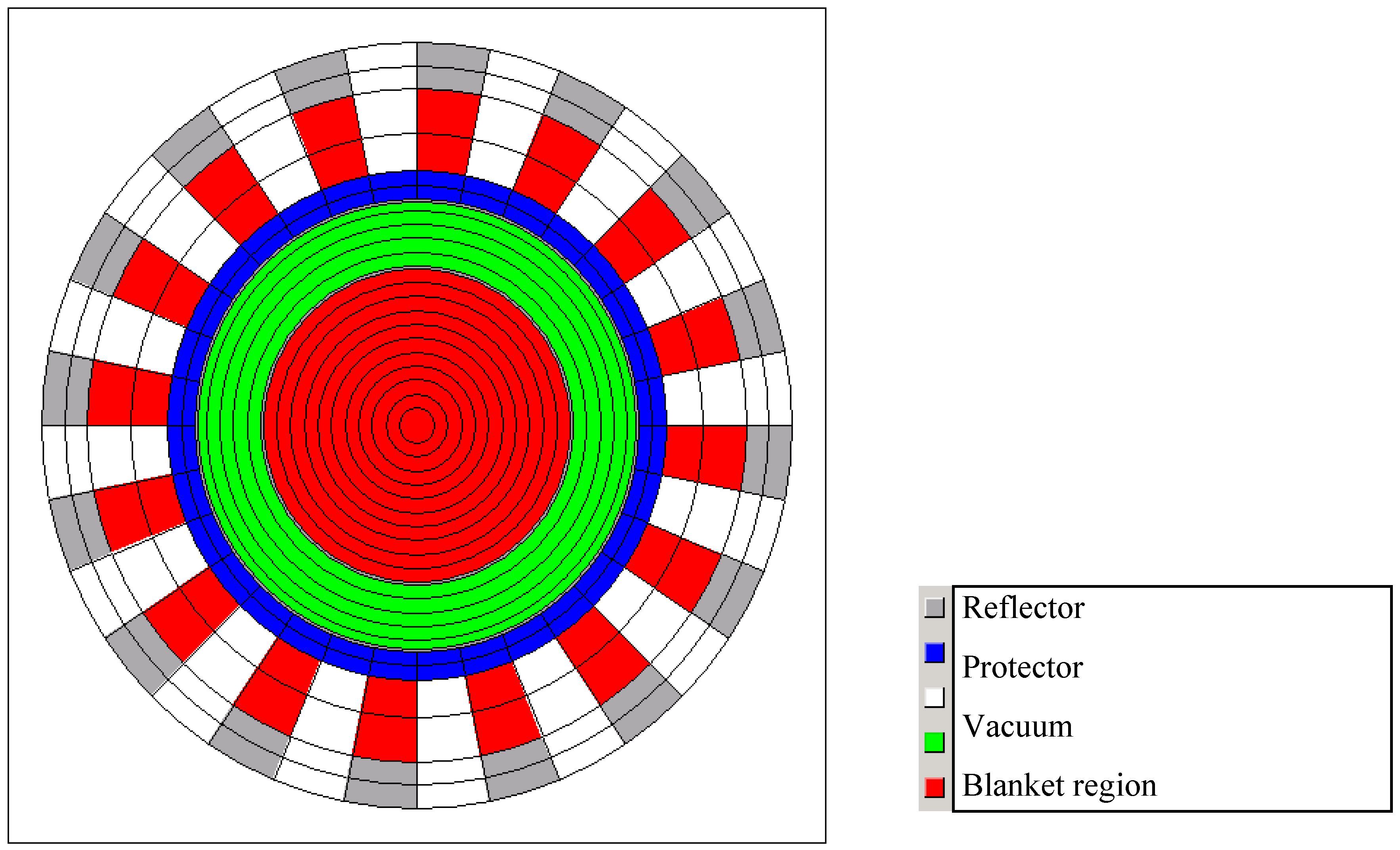
For the simulations, the HELIOS code system versions: HELIOS 2.03 with the internal 173 cross sections group library [12] (based on ENDF/B 7.1). The code is a 2D spectral code with wide unstructured mesh capabilities and a transport solver, based on the collision probability method [13] and a newer extension based on the Method of Characteristics [14]. The general model is based on the EVOL benchmark configuration which is transferred to a volume corrected 2D HELIOS model (see Figure 1). The model has been adopted for an as close as possible reproduction of the 3D structure and the relations between the different materials. Furthermore, the benchmark model has been extended to represent in addition the outer structures, the 16 heat exchanger pipe arrangement for a better representation of the real geometry. The leakage in the third dimension is introduced into the calculation through the insertion of a buckling correction available in HELIOS (BSQ: 0.00002). This value has been fixed by a comparison of 2D and 3D calculations within the EVOL benchmark exercises, see [15]. Using this setting a k of ~1.005 is required for a pseudo 3D keff of 1.0. The leakage in radial direction is directly modelled through vacuum boundary conditions.
The salt system chosen for iMAGINE is based on NaCl-UCl3-UCl4 with the eutectic composition 42.5mol%–17.0mol%–40.5mol%, more detailed discussion of the data of the salt system and the ratio behind the choice is given in Merk et al. (2019) [1]. For the reference case the carrier salt is based on the natural chlorine composition (76% 35Cl and 24% 37Cl), while the chlorine for the uranium salt is 99% enriched. The core size of model has been adopted to a radius of 213 cm and a 235U enrichment of 11.06%. The used data is based on the results of two earlier studies [16,17] based on SCALE/POLARIS [18].
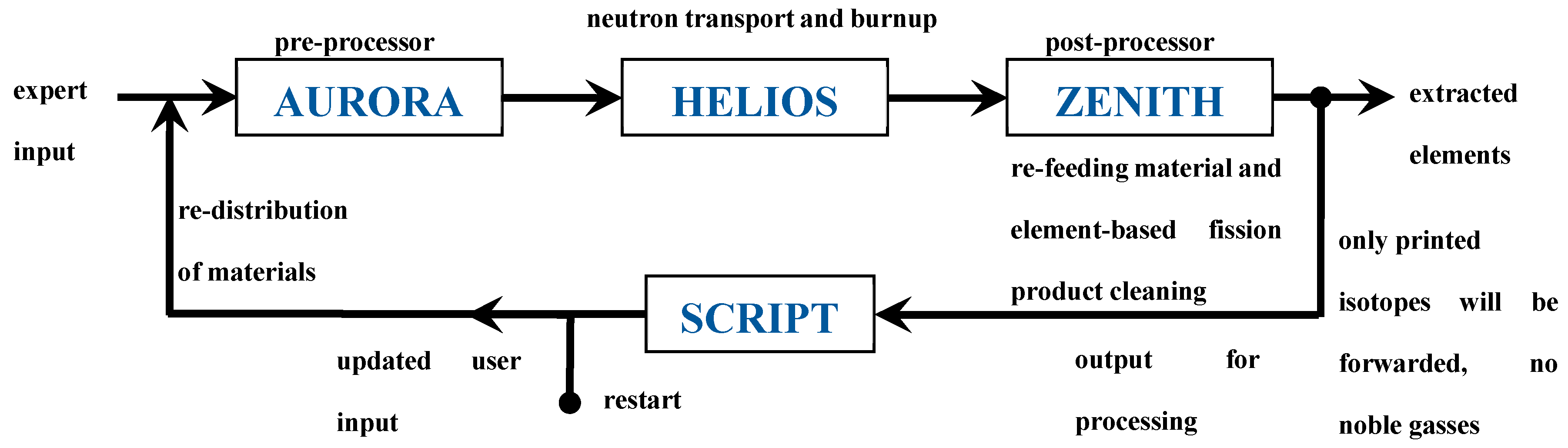
The HELIOS code is an industrial standard software which is designed to perform the neutron transport calculation, the burn up calculation, and if requested the cross section preparation in the whole system or in defined calculation areas under the consideration of the boundary conditions set for the unit cell. Originally, the HELIOS code has been written for the simulation of solid structured fuel assemblies, thus the possibility of online refueling and online reprocessing is not foreseen. To deal with these special features required for the simulation of molten salt reactors a PYTHON script has been developed by Merk et al. (2019) [3], which is based on the special features of the HELIOS package. All input data, which does not change during the whole reactor operation, is stored in a so-called expert input. The changing material configuration is fed into the system through a user input which is re-written in every cycle using a PYTHON script. Within each of the cycles 5 burnup steps are calculated through HELIOS. The expert input and the updated user input are merged in the pre-processor AURORA [13], which creates the updated input for the HELIOS run used for the determination of the neutron flux distribution and the burnup of the materials. The results are finally evaluated at the end of each cycle in the post-processor ZENITH [14]. On the one hand, it is decided here which elements are reduced or increased to which extent, and on the other hand, which isotopes will be fed back into the next, new user input which is created with the help of the PYTHON script (see Figure 2). Theoretically, it would be possible to simulate a molten salt reactor precisely by using small time steps in this calculation loop. In a real MSR two different time scales for the salt cleanup can be observed, based on two different processes, the helium bubbling for gaseous and volatile fission products with a comparably short acting time, and the online salt cleanup for the dissolved fission products with a significantly longer acting time. To improve the modelling of both procedures a new strategy has been developed, based on the use of a reduced burnup per cycle (10 GW d t-1 of HM using five burnup steps in HELIOS), coinciding with a full removal of gaseous and volatile fission products the elements 18 (Ar), 35 (Br), 36 (Kr), 53 (I), 54 (Xe), are not carried forward through ZENITH), while the dissolved fission products can be removed, based on a cleaning efficiency providing the opportunity to set this efficiency elementwise for all considered elements.
The use of the described process has already been validated and used in several peer- reviewed publication Merk et al. (2020) [19] and Jessee et al. (2014) [20]. However, the modelling and simulation quality will be significantly improved due to the new code version and the increased computational power which allow now the use of the 173 energy group cross section set instead of the 47 group set in the earlier publications.
However, due to the characteristics of HELIOS, some approximations still have to be accepted. There is no fuel salt movement, thus an undesired burnup distribution arises during each of the calculation cycles, while the materials are only re-distributed when a new user input is defined. HELIOS is a LWR code and a LWR spectrum is used for the weighting of the master libraries inside each energy group. However, this error will be significantly reduced compared to earlier publications, since the number of energy groups is tripled, thus the width of each energy group has significantly reduced. Comparisons with other codes in the EVOL benchmark, in a fast reactor isotope accumulation test against SERPENT Merk et al. (2015) [21], as well as comparisons with SCALE/POLARIS see Merk et al. (2015) [22] have shown good agreement. This is what is currently available, finally to judge the reliability of the results, a real reactor physics experiment for molten salt reactors would be required as discussed in [1].
The approximations and the use of the HELIOS code package seem to be adequate for the approximation level required for this kind of long term investigation of isotope accumulation to support the development of a clean-up system. The results of the influence of different element on the system criticality has been evaluated against earlier publications Merk & Litskevich (2018) [23] Rachamin et al. (2013) [24]. It is here important to recognize that HELIOS was validated in the EVOL benchmark [23], but this benchmark was for Fluorine based salt.
The accumulation of isotopes is evaluated through a row of calculations of the system using the described dynamic calculation which incorporates the effect of the removal of the gaseous and volatile fission products as given above. All other fission products are left in the system and the accumulation is observed in 10 GW d t-1 of HM steps.

2.2. Neutronic Results

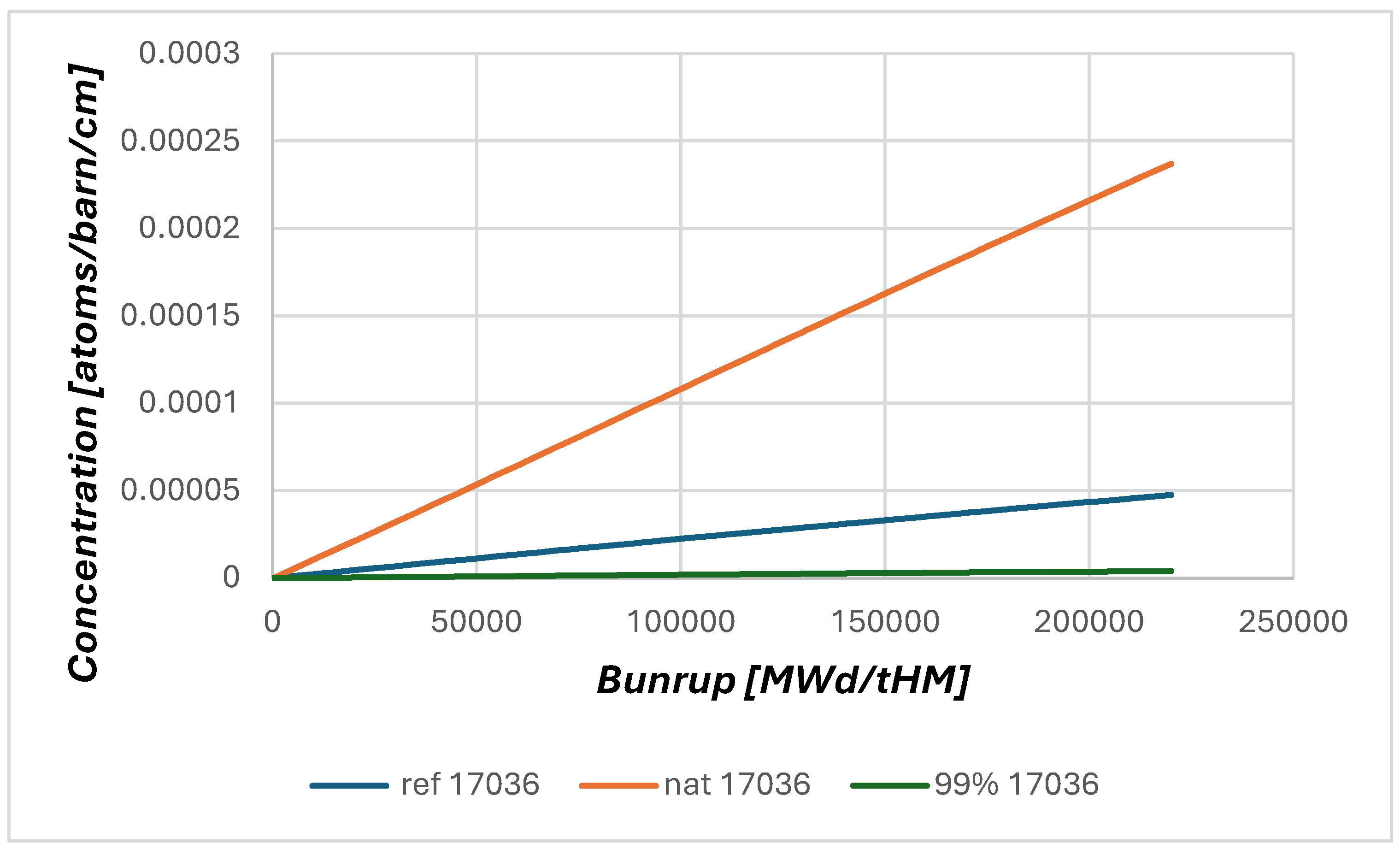
The first investigation of the effect of 37Cl enrichment has identified very strong differences in the criticality effect. In any case the change from natural chlorine (75.77% 35Cl and 24.23% 37Cl) to 99% enriched 37Cl leads to a strong increase in criticality.
The results point to a gain of ~4500 to ~10500 pcm which is an astonishingly large difference between industrially applied codes which are all based on the same cross section library ENDF/B VII.1. However, it should not be forgotten that the calculation of a chlorine based molten salt reactor is clearly outside of the validation based of each of the codes. The differences clearly demonstrate the demand for an experimental investigation of the problem to create a reasonable database for code validation. In addition, it would be of high importance to create a benchmark to investigate the differences in more detail with a wide set of codes.
It has to be recognized here, that the differences appear in the preparation of the master library for the codes or in the codes itself, most probably in the unresolved resonance treatment. Eventual uncertainties in the cross section libraries as already pointed out in literature regarding the issues with Cl-35 cross section and the efforts that have been made to measure (n,p) and (n,γ) cross section in the fast energy range, e.g. [25,26] will come on top or in a lucky incident will lead to error cancellation. Based on this two-fold recognition we would recommend on the on hand differential cross section measurements as already pointed out by in assessment of nuclear data needs for advanced reactor demonstrations, by Palmiotti, et al. (2021) [27], but on the other hand an integral reactor experiment, e.g. by using a pile oscillator, to provide a first reliable validation base for the code developers. These results will be required to improve e.g. the unresolved response treatment in the cross section preparation for the master library of deterministic codes or for determining/improving the p-tables for Monte-Carlo calculation.
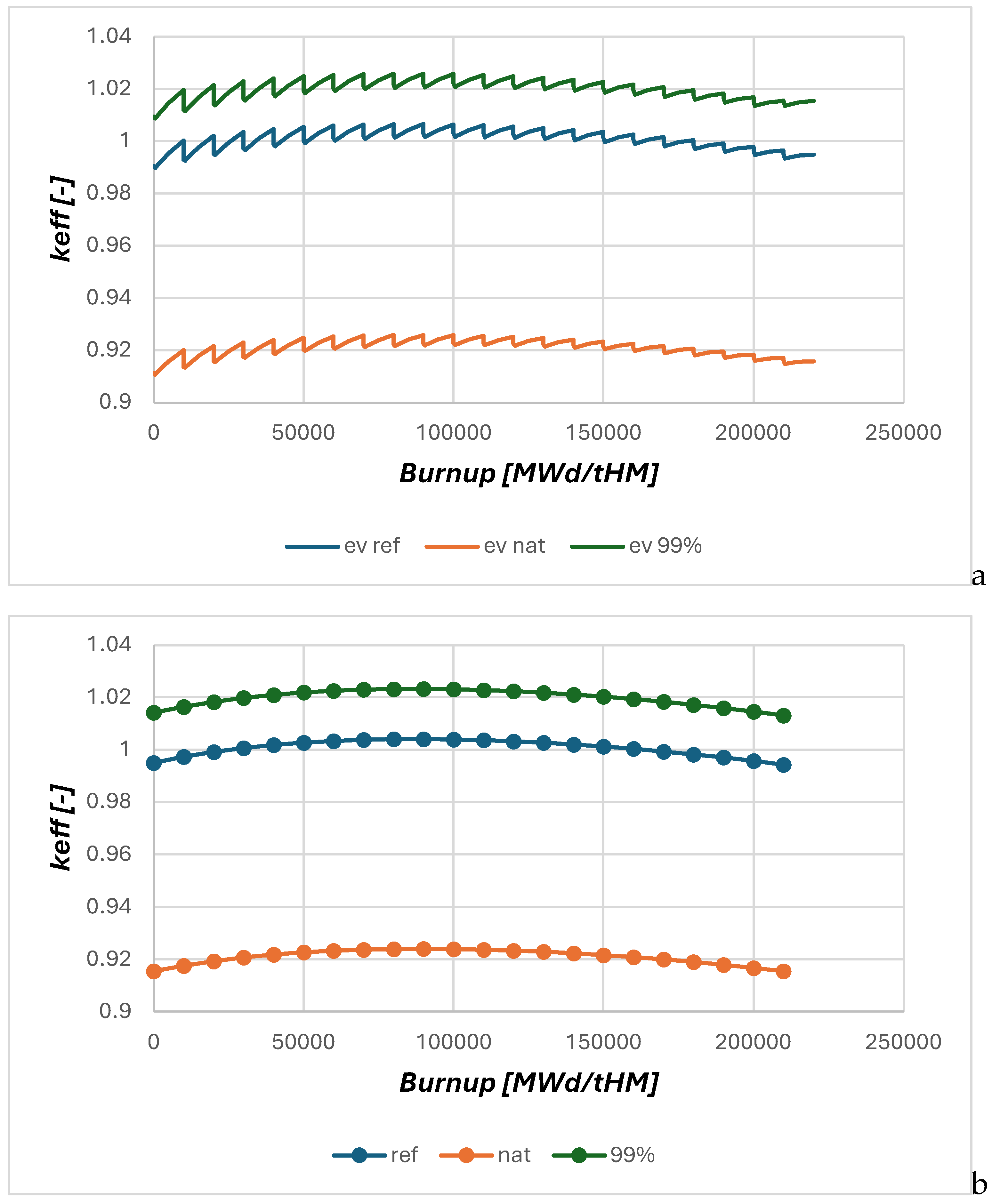
The results of the dynamic calculation using HELIOS (Figure 3) show the effect of changing the 35Cl content form natural chlorine configuration to the reference case (NaCl based on natural Cl, and UClx based on 99% enriched 37Cl), and the case with all chlorine in the reactor enriched to 99%. The steps in the curves indicate the different calculation cycles within the script with a set of classical burnup calculations within HELIOS, each to 10 GWd t-1 of HM, and the change in criticality due to the removal of fission products and the refill of the fertile material, i.e. depleted U (0.3% 235U), with constant U contents (balance) through the script at the end of each 10 GW.d t-1 of HM step. In this configuration the general shape of the reactor behavior over burnup is not significantly changed, but it should be kept in mind that the criticality in the calculation is adopting the neutron source to get keep the calculation critical.
To ease the interpretation of the results all following investigations are based on the evaluation of the averaged criticality per cycle in the script as given in Figure 2.
To overcome the limitation of the criticality normalization of the first calculations, the next step will be to adopt the fissile material enrichment to get all cases to the same starting point which has been used in earlier studies to evaluate long term operation with breeding and the boundary condition that the criticality should be kept between ± 500 pcm around criticality as given in the reference case in Figure 3.
This reference case has an initial enrichment of 11.05% 235U. For the case with natural chlorine an enrichment of 13.29% would be required to crate the same starting criticality, while for the completely 99% enriched 37Cl case only 10.58% 235U enrichment would be required.
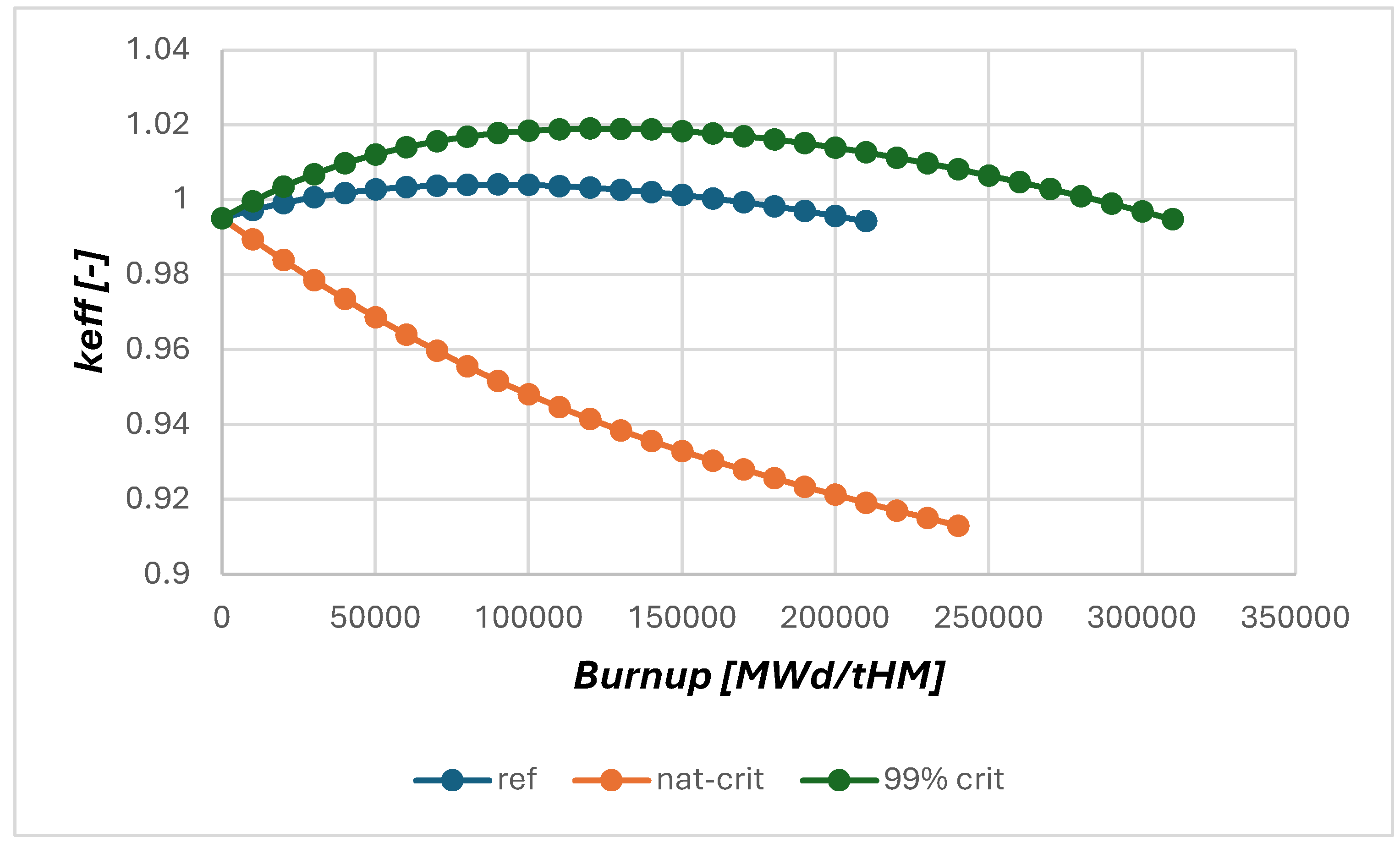
However, obviously not only the initial criticality is heavily influenced by the 37Cl enrichment, but also the breeding behaviour, see Figure 4. The 99% enriched case provides clearly improved breeding and would achieve without further salt clean up about 50% longer reactor operation than the reference case, while the case using natural chlorine is not able to breed at all. There is no increase in criticality which would indicate proper breeding. This can be explained with the significant loss of neutrons in absorption reactions in 35Cl, which clearly reduces the number of neutrons available for breeding.
.a. change in criticality due to the removal of fission products and the refill of the fertile material through the script at the end of each 10 GWd/tHM step.
.b. evaluation of the averaged criticality per cycle in the script as given in with one burnup averaged value per cycle initiated
Conditions: core of 213 cm radius, fuel of NaCl-UCl4- UCl3 composition with a 235U enrichment of 11.06%.
The analysis of the 36Cl formation (Figure 5) indicates exactly the expected effect of neutron absorption in 35Cl leading to 36Cl. This effect is significantly stronger in the case natural chlorine is used. It leads to a 36Cl formation which is by a factor of ~5 higher than for the reference case. A 95% 37Cl enrichment reduces 36Cl content by a factor of 12, a 99% enrichment reduces the 36Cl content by a factor of ~60 and 99.9% 37Cl reduces the content by a factor of ~600. Comparison with 129I build-up, another 1st nuclide for the radioactive waste management may be suggested; however, iodine-129 build-up will be independent of the 37Cl enrichment. In conventional reactor fuel, the problem of 36Cl, which is only an impurity however, the influence in the final disposal studies, e.g. Renn (22013) [28], is almost as big as the effect of 129I which has a considerable fission yield. In our case we speak about much larger amounts of 36Cl which would be produced.
However, the problem is not only the loss of neutrons, it should always be kept in mind that 36Cl- is a very long lived isotope which is currently seen as one of the challenging isotopes in the final disposal scenarios delivering a significant contribution to the release risk for the site. Thus, there are two good reasons for the 37Cl enrichment, the neutron economy as well as the waste management of fuel when it is taken out of the reactor.

3. Isotope Separations

There are basically three types of isotope separation techniques; they are
  • based directly on the atomic weight of the isotope,
  • based on the small differences in chemical reaction rate, and,
  • based on properties such as spectroscopic not directly connected to atomic weight.
The third type of separation is mostly experimental. All practical separation techniques depend in some way on the atomic mass. It is therefore generally easier to separate isotopes with a larger relative mass difference. However, with chlorine and because of its strong reactivity it has the tendency to join with its self or with more or less electronegative elements or molecules, or, with other (lighter or heavier) elements or molecules associated that must be considered in the separation. They are important in isotopic separation, however two isotopes can exchange between two phases according to:
35ClEl + 37Cl ⇔ 37ClEl + 35Cl
with El an element. The molecule ClEl can then be HCl, LiCl, Cl2, ICl, CsCl or CH3Cl as example.
The yield of the separation process is generally quantified using the separation factor α37/35 defined as
α37/35 = 1 + ε37/35 = k37Cl/k35Cl
Where ε37/35 is the separation yield and k35Cl is the retention factor. Isotopic effects allow the separation, which is physical or chemical, e.g. see BigeleiseI (1969) [29].

3.1. Physical Separations Methods

Centrifugation was the first method invented to separate chlorine isotopes by Beams [30]. He separated successfully 35Cl from 37Cl in 1937. The electromagnetic method uses a mass spectrometer, or spectrograph, to send a stream of charged elemental particles through a strong magnetic field and allow the separation of isotope by mass.
In gaseous diffusion molecules of a lighter isotope would pass through a porous barrier, and become isolated from those of a heavier isotope. Separation has also been carried out by fractionated distillation

Separation by Fractionated Distillation…

The separation method is based on the difference between the partial pressure PClE of molecular constituent 35ClEl and 37ClEl. The separation factor α is simply given by the expression:
α37/35 = P37ClEl /P35ClEl
The distillation of chloroform, carbon tetrachloride, methyl alcohol, and benzene were found e.g. Baertschi et al. (1953) [31] to lead to an enrichment of 35Cl in the distillate, whereas the other heavy isotopes such as 37Cl and 18O were enriched in the still pot. A possible general rule is suggested that in isotopic molecules having a central atom, the molecular variety containing the heavier isotope of the central atom will exhibit a somewhat higher vapour pressure than the variety containing the lighter isotope as the central atom. However rules have exceptions…
With PiClEl the partial pressure of iClEl, Liebscher et al. (2006) [32] measured experimentally the chlorine isotope fractionation between vapour and liquid in the system H2O–NaCl. Experiments were performed on the 400°C isotherm between 23 and 28 MPa and on the 450°C isotherm between 38 and 42 MPa. Calculated chlorine isotope fractionation Δ37Clvapor–liquid = δ37Clvapor − δ37Clliquid (1σ = ±0.17‰) between the coexisting vapour and liquid are generally within 0.2‰ of 0, although there is a trend at both 400°C and 450°C in which the Δ37Clvapor–liquid values change with pressure beyond statistical uncertainty.

Separation by Electromagnetic Separation

Mass spectrographic method has been used by Sun et al. (2014) [33] in the determination of chlorine (Cl) isotopes in various substrates. The procedure includes sample treatment, three-step ion chromatographic separation of Cl isotopes, and isotope ratio determination based on Cs2Cl+ ion in positive thermal ionization mass spectrometry. The recovery of the method and the fractionation of Cl isotopes were validated using certified reference standard materials. The pre-treatment strongly eliminated the effects of organic impurities and other anionic interferences, especially soluble nitrates and sulphates.
Inductively coupled plasma mass spectrometry (ICP-MS) may be use for the analysis of cations or anion in solution e.g. Degueldre (2017) [34]. Chlorine isotopes as well as bromide and iodine and metals content can be measured by ICP-MS in drinking water as reported by Quarles Jr. et al. (2020) [35]. These ICPMS isotope separations concern however very small amount of material.

Separation by Diffusion

For two isotopic molecules, diffusion speed (ν) ratio (ρ) is given by …
ρ37/35 = ν37ClEl /ν35ClEl = (μ35ClEl /μ37ClEl)1/2
The lighter is the faster. Effects of mass and of size must be reported.
Kranz & Watson (1953) [36] performed successfully chlorine isotope separation by thermal diffusion. The thermal diffusion constant of HCl has been determined to be +0.010 at Tr = 685 K and -0.009 at Tr = 229 K. Such a rapid change of α37/35 and RT with temperature and an inversion temperature at or above room temperatures seem to be characteristic of strongly polar molecules. The troublesome "memory effects" of HCl in a mass spectrometer can be eliminated by using a pin-hole leak right in the box of the ion source plus a baking out, flushing and repeated-analysis routine. Some details are given of a 6.8-meter hot-wire thermal diffusion column apparatus, having an equilibrium separation factor of 7, and which has provided fairly large samples of HCl enriched to 94% H35Cl and 62% H37Cl for cyclotron beam targets and other experiments.

Separation by Gas Centrifugation

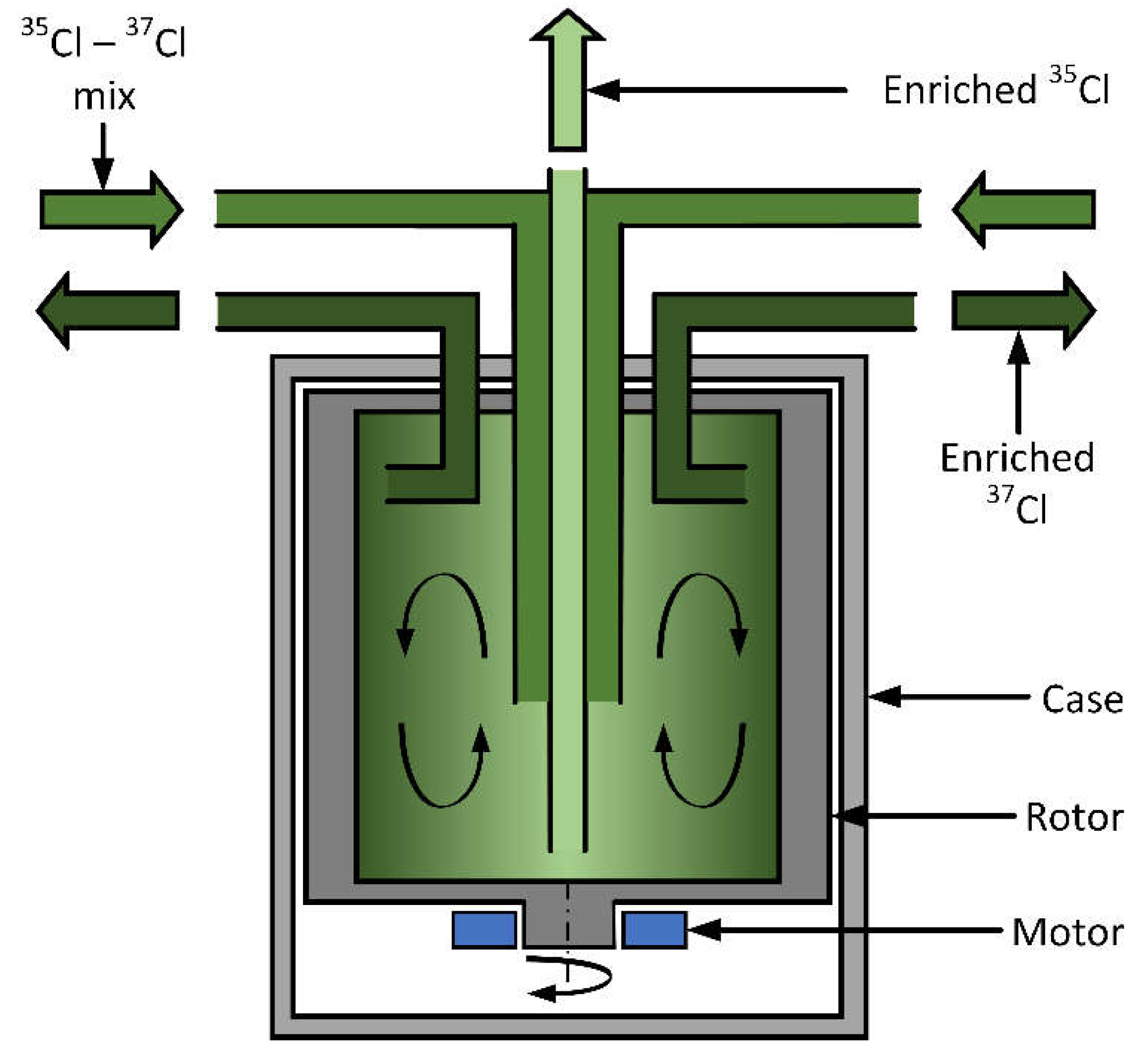
The gas centrifuge works on the principle of partial pressure (p) diffusion, e.g. Kemp (2009) [37]. The centrifuge accelerates gas molecules toward the rotor wall of radius r. A counteracting diffusive force created by the thermal motion (RT) of the molecules seeks to distribute the gas evenly throughout the rotor volume. The two forces balance through a dynamic equilibrium, which gives rise to a pressure distribution in the rotor that is a function of the molecular mass (M) of the gas:
pACl(r) = pACl(0) exp{M(ACl) ω2r2/2R T}
for the isotope A and the partial pressures pACl(r).
Dividing the two equations gives a simple separation factor for the centrifuge, which is a function of the mass difference and the peripheral velocity:
α0,37/35 = {[pA(0)/pB(0)] / [pA(r)/pB(r)]} = exp{[M(37Cl) – M(35Cl)] ω2 r2/2R T}
Equation (4) is valid in the equilibrium conditions where the gas is stationary in the reference frame of the rotor and enough time has passed that the molecules have diffused into their final distribution. However, the performance of a centrifuge can be enhanced by introducing a counter-current flow, in which the gas flows up the centre axis of the rotor and back down along the rotor wall.
Study of isotope separation of some chemical elements in a gas centrifuge was also investigated by Aisen et al. (1996) [38]. Effect of a field on isotope separation is described by the separation factor given by:
α0,37/35 = exp –(ΔM37/35 v2/2RT)
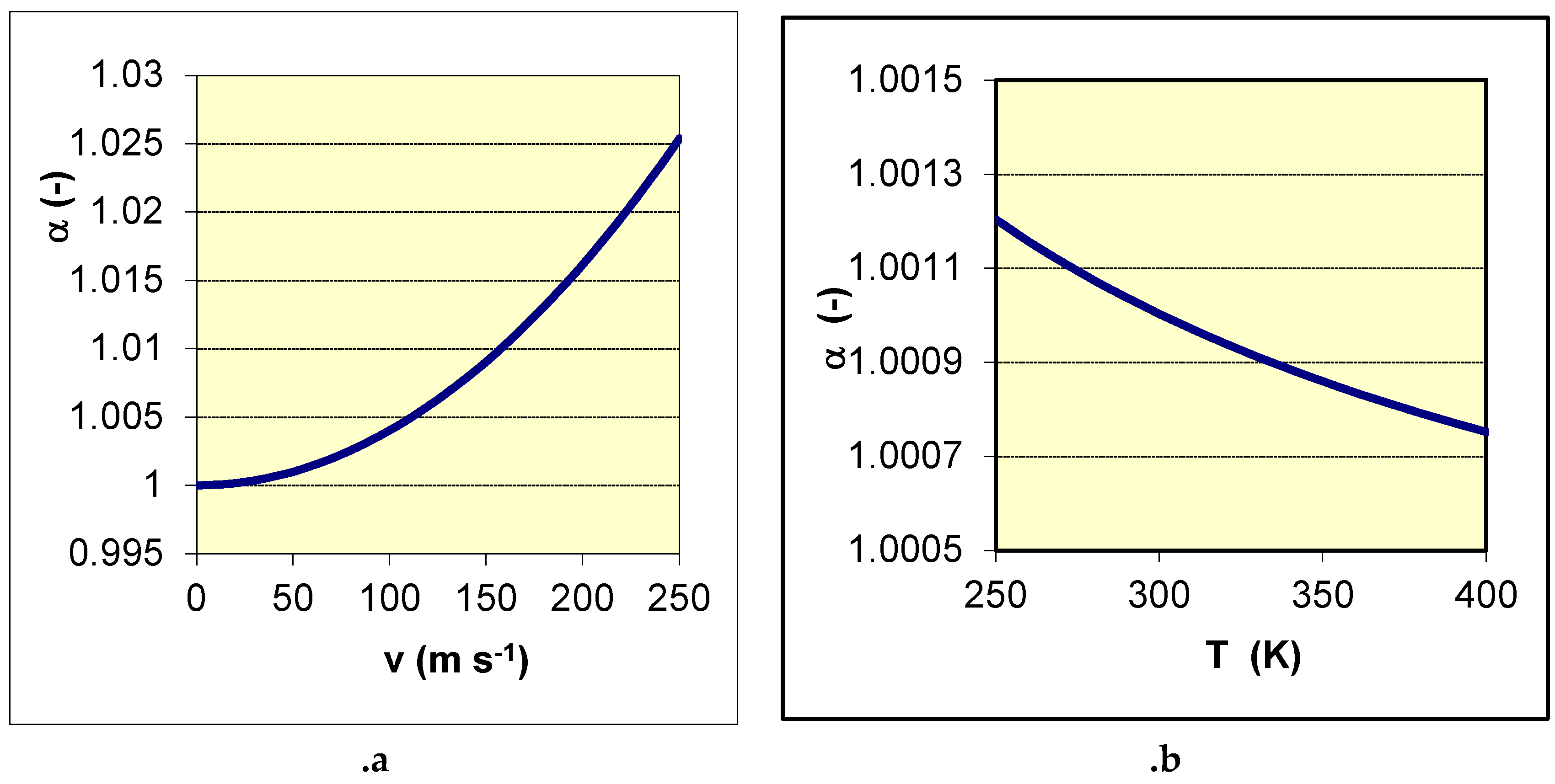
ΔM molar mass difference (kg mol-1) and v the gas linrotor and the heavy in periphery. A schematic ear speed of displacement (m s-1). The light isotope atoms (or molecules) concentrate in centre of of a gas centrifuge is shown in Figure 6.. The separation factor of 37Cl/35Cl is plotted Figure 7 a function of the linear speed v and of the temperature T. The increase of the separation factor α with v is strong and its increase with a decrease of T is observed.
Actually, the simplified linear centrifugation model used in Equations (4)–(6) assumes no gas centrifugal-force-assisted diffusion of species, which leads to a quasi-equilibrium model that assumes that partial pressure of isotopes goes instantaneously to equilibrium. This assumption is not accurately valid as the enrichment of 37Cl over 35Cl is higher, since the effective diffusivity of 37Cl is impeded by the larger 35Cl content. The separation assumptions may then be complemented by a time-dependent diffusion model for centrifugal separation such as presented by Bogovalov (2015) [39].
The separation factor (for molar weight difference), αo, depends on many variables, see Ying et al. (2006) [40], including
construction parameters of the centrifuge unit,
-
length of the gas centrifuge
-
radius of the centrifuge
-
axial location of the feed point
-
parameters of the scoops
operational conditions
-
feed flow rate,
-
pressure at the wall and on physical properties
-
peripheral rotation speed
-
feed rate of the working gas
-
temperature T0 at injection
-
temperature distribution on the wall
-
pressure of the gas at the rotor wall
physical properties of the working gas, such as:
-
molar weight of the isotope reagent
-
viscosity of the gas
-
molar weight of the carrier gas (if any)
-
product density media
-
product diffusion coefficient.

3.2. Chemical Separation Methods

The phase providing retention/separation may be a solid or a liquid. The yield of the separation process is generally quantified using the separation factor a defined as
α37/35 = k35Cl / k37Cl
Where k35Cl is the retention factor of 35Cl in the 35ClEl form onto subtract.

Separation Using Solid Ion Exchangers

Ion exchanger separation is largely used for recovery of metal ions e.g. Musashi et al. (2007) [41]. In the late 70ies Heumann tested the separation of chloride isotopes using strongly basic anion exchangers contacted with aqueous KF, NaBF4 and NaNO3 solutions at 0–60°C, see Heumann & Baier (1980) [42]. These authors found that the separation factor of chlorine isotopes dependents on the nature and concentration of the eluent in these ion chromatography tests. This factor value increases when the eluent salt concentration decreases.
Columns of hydrous zirconium dioxide particles, produced by hydrolysis of zirconyl chloride solution, were also tested by Heumann et al. (1980) [43] for isotope fractionation of chlorine. In separation experiments, using strong basic anion exchange, enrichment of 35Cl- was found in the first fractions, whereas the last fractions showed higher concentrations of 37Cl-. The isotope fractionation decreases when concentration increases. Using a 0.5 M NaNO3 solution the elementary separation effect was calculated ε = 6.1 x 10-4 (α = 1.00061) as reported by Heumann & Baier (1980) [35].
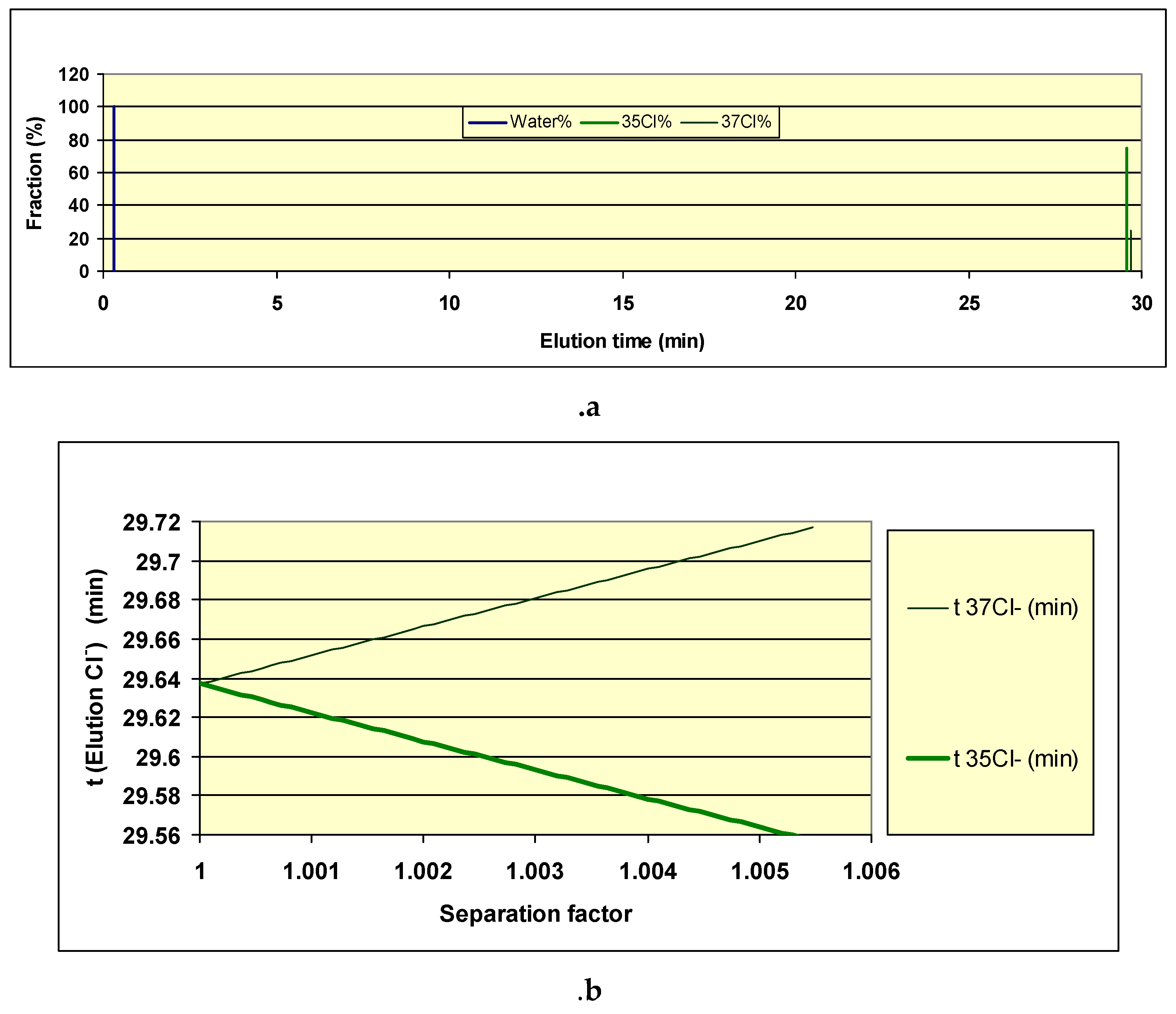
The calculation of the break-through curve maybe easily performed for both Kd35Cl and Kd37Cl the break though curve see Figure 8a.
Chlorine isotope fractionation factors were also determined by strongly basic anion-exchange chromatography with 0.1 M HCl at 25°C by Musashi et al. (2004) [44]. The magnitude of the factor was calculated as a single-stage separation factor of 1.00030 with analytical precision of 0.00006 (1σ). The tests demonstrated that the light isotope was preferentially adsorbed into the resin phase, while the heavy one (37Cl) enriched in the solution. This discrepancy is due isotope effect accompanying hydration rather than an isotope effect due to a phase change Musashi et al. (2007)[34].

Separation Using Liquid - Liquid Extraction

Liquid - liquid extraction has been used successfully for the separation of isotopes. Here, for the partitioning of ClEl between 2 liquids (L1/L2) the separation factor equals:
α37/35 = { [37ClEl]/[35ClEl]}L1/ { [37ClEl]/[35ClEl]}L2
The organic liquid film extraction system has been investigated for the extraction and separation of lithium isotopes using ionic liquid as diluent and Dibenzo-15-crown 5-Ether as the extractant, see Zhang et al. (2020) [45] The authors investigated, the effects of extraction time, the gas flow rate, the temperature, the counter anions of lithium salt, the length of the cationic carbon chain of ionic liquid on extraction, and the separation of lithium isotopes. The maximum separation factor α was 1.037 ± 0.002 and the abundance of 6Li increased from 7.61 to 7.86%.
The values of the single stage separation factor α are 1.0067 ± 0.0035 and 1.025 ± 0.005 and are close to similar values for rectification of boron trifluoride as reported by Khoroshilov & Ivanov (2018) [46].
Chlorine isotope separation by liquid-phase thermal diffusion has been tested successfully by Rabinovich & Ivakhnik, (1978) [47], reporting a factor α of 1.2 ±0.1 for chlorine isotope separation from CCl4; a factor ε37/35 of 0.2 was determined using trichloroethylene and in butyl chloride. While, in gaseous isotopic mixtures this value, as a rule, does not exceed 0.02.

From the Solid - Liquid to the Liquid - Liquid Extraction

The breakthrough by elution through a sorbing/porous column can typically be estimated on the basis of the retardation factor, R, using the relationship:
RCl = 1 + (ρ Kd(Cl-))/ξ
with KdCl the partitioning coefficient of the chloride isotope, ρ the density of this adsorbing material and ξ the porosity of the partitioning phase or Vw/(Vw+Vab), with Vw the volume of water and Vab the volume of absorbent for a given segment of column, when using coating solid or liquid, porosity
The separation factor between the 2 isotopes can be evaluated using:
α37/35 = R37Cl / R35Cl
As anionic extraction/exchanger reagents, e.g. Nesterenko (2019) [48], the amines (e.g. R+ OH-) are well known to easily exchange their OH- by Cl- . The reaction guiding this exchange write:
R+ OH- + Cl- ⇔ R+ Cl- + OH-
.and its equilibrium constant reads:
K(Cl-/OH-) = { [R+ Cl-] [OH-] } / { [R+ OH-] [Cl-] }
Its value for natural Cl- is 22, Ref Bio-Rad (2023) [49]. On the basis of the Kid definition, one can write that
K(Cl-/OH-) = Kd(Cl-)/Kd(OH-)
.with Kd(OH-) postulated to 1 then we obtain Kd(Cl-) = 22. Now for Kd(35Cl-) = 22.1 and Kd(37Cl-) = 21.9 (indicative values) one can calculate the breakthrough and the retardation factor for each isotope, see Figure 8. The breakthrough and separation of 35Cl and 37Cl during their elution in capillary column is also plotted in Figure 8 for their α37/35 values.
a. separation for α = 1.0020,
b. effect of the separation factor from 1.000 to 1.005 on the peak splitting.
Conditions: column length 100 cm, internal radius 1 mm, adsorbent radius 2 mm, porosity 0.25,
eluent water, v: 3 mL min-1, Kd(Cl-): 22 mL g-1.
The basic theory of ion elution into ion exchanger (solid or liquid) column developed by van Deemter et al. (1956) [50]. The authors found that the separation performances may be described by the plate height theory. The van Deemter relationship relates the ‘height equivalent of a theoretical plate’ (HETP) associated to a chromatographic column to flow and kinetic parameters. These parameters cause consequently peak broadening with the Eddy-diffusion, the diffusion coefficient (resulting in dispersion of the eluted species), the mass transfer coefficient and the eluent velocity. For a coated capillary column, the Eddy-diffusion becomes 0 and peak enlargement reduces.

Separation by Photochemistry

Historically, the first photochemistry tests on isotopic separation were carried on chlorine gas. Chlorine isotopes activate specifically. The excitation of 35Cl differs from that of 37Cl as reported by Kuhn & Martin (1932) [51]. One can consequently produce specific isotopic molecular species.
Kuhn et al. (1941 & 1942) [52] observed that on irradiation of ClO2 by ultra violet light (2816.1 Å), the Cl2 liberated a slight excess of 35Cl. The 35Cl/37Cl ratio during the photochemical reaction passes from 3.41 to 3.57, unveiling the potential of this technique.
A similar approach, for chlorine isotope separation, has been used by Liu et al. (1975) [53] and by Zare (1976) [54]. Illumination of iodine mono-chloride at 6053 Å excites selectively I37Cl. The same band of I35Cl is about 15 Å away. The excited I37Cl reacts with added 1,2-dibromoethylene to form the 37Cl enriched ClHC=CHCl. At this wavelength no photo-dissociation of ICl takes place.

Electrolytic Separation

Separation by Ionic Migration

Applying current in a long tube filled by agar-agar gel containing a salt NaCl makes the Cl- zone migrate 3 months over 30 m in the gel. In the case of 35Cl- and 37Cl-, the ½ cells are respectively filled with NaOH (anodic ½ cell) and HCl (cationic ½ cell). Today glass powder is used instead of agar - agar to avoid convection. The light isotope concentrate at the anode and pass from 75.76% to 80.70%.
Separation of chlorine isotopes may be achieved with high resolution for chloride isotopes using capillary zone electrophoresis. The separation conditions are: capillary of 75 μm diameter, 47 cm length, V = 20 kV, T = 25° C, electrolyte chromate/borate and pH 9.2, see Lucy & McDonald (1995) [55].
Similarly, electrolysis separation may be carried out. It includes ionic migration toward the electrode and electro-reaction at the electrode itself.

Separation by Chloride Electrolysis

Electrolysis is known to be powerful for isotope separation. This is the case for 1H vs 2H, e.g. Petek et al. (1980) [56] as well as for 6Li vs 7Li , e.g. Wild et al. (2022) [57].
Klemm (1952) [58] suggested a system including a U tube, filled with 0.13 mm quartz powder the ½ cells are equipped with graphite electrodes. A review of the experimental methods of isotope separation by electrolytic migration. A theoretical explanation of the results in fused salts is developed. NaCl in molten salt form has been investigated at 700°C The published experimental data for enrichment of cations in pure fused LiCl, ZnBr2, ZnCl2, AgI, CdCl2, and TlCl were compared with the theory and found to be in good agreement. Subsequently, Klemm & Lundén (1955) [59] investigated Cl isotope enrichment through electrolytic diffusion of Cl- ions in molten PbCl2 with a solution anode made of molten Pb and with a current density of 5 A cm-1 in 7 days. An enrichment of about 135 with a separation coefficient of 2 was recoded. The diffusion velocities of the Cl- isotopes differ by (0.29 ± 0.02) %. The mass effect for electrolytic diffusion of chlorides is in molten PbCl2 : μ- = -0.052 ± 0.003.
The model geometry and settings are based on a symmetric cell for electrolysis, see Figure 9. Two chlorine electrodes are separated by a liquid electrolyte e.g. NaCl horizontally. The left boundary was set as the cathode (Cl2 production), and the right boundary was set as the anode (Cl2 stripping). The cross-sectional area of the electrodes is 1 cm2. The temperature was 298.15 K, and the total exchange current density at each electrode is 1 mA cm−2. Initially, isotope fractions in the Cl2 electrodes and electrolytes were the natural abundance ratio r0 (= 75%/25% = 3.0). This is equivalent to 0.75 M 35Cl-, 0.25 M 37Cl-, and 1 M cation in the liquid electrolyte. In the fluid phase, the lighter the isotope, the faster it moves.
Methodology may be derived from that developed by Wang et al. (2022) [60].
The electrode reaction {9} is as follows:
2Cl- + 2e- ⇔ Cl2
The electrode equilibrium potentials for 35Cl-/35Cl2 and 37Cl+/37Cl2 are governed by their own Nernst Equations at equilibrium (two separate redox reactions).
The electrolytic separation coefficient α has been determined for the chlorine isotope separation in the electrolysis of sodium chloride solutions at a platinum anode by Johnston & Hutchison (1942) [61]. The separation factor was found rather independent on either temperature (25° to 40°C) or current density on platinum (1.0060±0.0005) and was comparable with the value found on graphite (1.0068±0.0014).

4. Discussion

Isotope separation takes place in fluid phase where the isotopes form a mix in liquid or in gaseous phase. The isotopic separation performance is reduced by antagonism chemical or physical interactions such as isotopic exchanges, kinetic effect or mixing/convection.

Isotopic Exchanges

Isotopic exchanges, which are important antagonist interactions during isotopic separation of two isotopes, involving two molecular species can be written according to:
35ClEl + 37Cl ⇔ 37ClEl + 35Cl
.where El is an element that can be a metal, a non-metal or an organic group.
The equilibrium reaction is characterized by a constant, K :
K = ([37ClEl][ 35Cl])/([ 35ClEl][ 37Cl])
When the exchange includes isotopes at two valence states, the heaviest isotope concentrates in the higher valence state. As an example for chlorine the following equilibrium has been studied e.g. Li & George (2005) [62]:
37ClO3- + 35ClO4- ⇔ 35ClO3- + 37ClO4-
here K = 1.035 and 37Cl concentrates in the ClO4- redox stage.
In the case of Cl2 exchange can also takes place. These reactions can clearly interfere with the separation. As an example for natural Cl the composition is 75.77% 35Cl and 24.23% 37Cl (monoatomic); however for Cl2 after isotopic exchange the following diatomic isotopic compositions of the diatomic gas are found: 63.05% 35Cl2, 31.08% 37Cl35Cl and 5.87% 37Cl2, instead of 57.41% 35Cl2, 36.72% 37Cl35Cl and 5.87% 37Cl2, for the natural composition.

Kinetic Effects…

A study of 35k/37k for the elimination of hydrogen chloride (HCl) from ethyl chloride (CH3CH2Cl) in gas-phase is reported by Christie et al. (1975) [63]. They found at 723 K that K is 1.0015 ± 0.0002. When considering the heavy atom kinetic isotope theory in an attempt to simulate the transition state, a moderate lengthening of the carbon-chlorine bond and a little motion of the chlorine atom gas are found.
More recently, Lewandowicz et al. (2001) [64] have found chlorine isotope kinetic effects during dehalogenation; the reaction is catalysed by an enzyme from Xanthobacter Autothrophicus and the k values reported are 1.0045 ±0.0004 for 1,2 dichloroethane and 1.0066 ±0.0004 for 1 chlorobutane.
The single-stage separation factor for chlorine isotopes (35Cl and 37Cl) was determined by Musashi et al. (2007) [65] to be 1.00034 by anion exchange chromatography. Here the separation is carried out on a 4.5-m column at 25°C. It was noted that the lighter isotope, 35Cl, was faster adsorbing on the resin, while 37Cl the heavier isotope was released into the aqueous solution. It must be noted that theoretical results on Cl- isotope fractionation and the experimental results for Cl isotope separation during NaCl precipitation contradict the 37Cl isotope preferential enrichment into the solid phase. This discrepancy is discussed based on the theory of isotope distribution between two phases. It is suggested that the chromatographic results reflect an isotope effect accompanying hydration and not an isotope effect driven by a phase change.

Convection and Mixing

Convection is single or multiphase fluid flow that may be due to the combined effects of heterogeneities and forces in the bulk of fluid, usually density and gravity. When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow.
Improving the separation performance of the gas centrifuge can be a practical step in reducing enrichment costs e.g. Ghazanfari & Shadman (2022) [66]. For this purpose, it is necessary to accomplish a reliable convection–diffusion equation to predict the separation characteristics of the gas centrifuge. The species continuity equation is derived in the possible complete form and then solved with the finite volume method for a model rotor.
To avoid isotopic mixing, separation must be faster than the remix or turbulence effect.
Specifically the method for laser separation of chlorine isotopes includes irradiating a starting gas in the form of hydrogen chloride HCl with resonance infrared radiation with wavelength 3.782 μm, subsequent exposure to laser radiation in the optical or infrared range, with intensity higher than 1013 W cm-2, and extracting the formed positive ions, wherein the time between the exposure to resonance infrared radiation and laser radiation should not be longer than the decay time of the oscillatory state of hydrogen chloride HCl.
Basically electrolysis produces chlorine bubbles that during their growth move gas phase in the electrolyte solution mixing the isotopes.

From Single Stage to Multi-Stage Separation

Single stage separation unit is affected by the size and geometry of the stage which are intrinsic parameter of the unit. Optimising the flow and the thermodynamic parameters (T,P) affects the separation factor.
When the separation is not efficient enough with a single stage process, multi-stage or cascade approach may be needed. The space-time-concentration relationships of isotopes in an infinitely long separation tube, with end volumes, are calculated theoretically by Klemm (1948) [67].
Johns (2013) [68] showed that chlorine isotopes are separated by the electrolysis of molten zinc chloride over molten zinc electrodes. The chlorine generated at the anode reacts with liquid zinc to reproduce zinc chloride while zinc metal is transported from the anode to the cathode. Since 35Cl has a slightly faster migration rate than 37Cl, the former concentrate at the anode. The migration takes place in a small glass column. To suppress convection currents the column is filled with powdered glass. The column used for separating the chlorine isotopes was about 20 cm long, 5 mm in diameter which use to be common, see Klemm & Lundén (1955). Currents of 0.5 A at 130 V led to a separation factor of about 2, after about a week.

Combined Processes

To complete the discussion it must be noted that combination of processes improve the separation. Some examples are given below.

Evaporation - Precipitation

In nature coupling of evaporation and precipitation occurs. This contributes to local isotopic enrichments. The isotope separation of chlorine during brine evaporation has been reported by Luo, et al. (2012) [69] e.g. for saline lakes. Brine evaporated with complete fractionation and precipitation from brines by continuous precipitation during the evaporation. Samples of precipitate and brine were analysed for their δ 37Cl values. The precipitates enriched with 37Cl relative to the brine samples, and the δ 37Cl of both the precipitate and brine samples decreased gradually during evaporation. The separation factors (α h) between crystallised salt and brine were the highest.

Sorption - Volatilisation

Chlorine isotope separation during preparative capillary gas chromatography was studied by Holmstrand et al. (2006) [70] using 1,1,1-trichloro-2,2-bis(p-chlorophenyl) ethane (DDT) as reference for semi-volatile organochlorine (OCl) compounds. Chlorine analysis by thermal ionization mass spectrometry showed no significant change of the chlorine isotopic fractions. However, isotopic fractionations were found for the front (δ37Cl −5.1‰) and tail (δ37Cl −1.8‰). Isolation of individual OCls by capillary gas chromatography enables accurate off-line analysis of the chlorine isotopes.

Combining Neutronic and Separation

An ecological issue is the production of 36Cl by neutron activation of 35Cl. The isotope 36Cl is a soluble (chloride, non-sorbing tracer) long live nuclide that makes it a first nuclide in the safety assessment of the repository. The build-up of 36Cl with burn-up for various 35Cl (activation product) enrichment what.
The neutron economical aspect is gained by better reactor criticality achieved through the use of enriched 37Cl. The criticality (k) in zero power reactor conditions is much larger for enriched 37Cl than for the natural one. The reactor with 99% 37Cl would have a k of 1.04346 which improve the energy yield or would allow to reduce the required uranium enrichment and thus the fuel cost. This reactivity gain is evaluated for various 37Cl enrichment factors to estimate uranium enrichment gain achievable through 37Cl enrichment.
The reactivity gain (RG) increases with the salt 37Cl fraction, see Table 1. This increases consequently the neutron flux and the output power. An enrichment of 99% would be sufficient at beginning of life (BoL). Comparison of the 129I build up with 36Cl generation (both first nuclides) is very difficult because all iodine isotopes are discarded from the molten fuel by evaporation/boiling (together with the fission gases).
The enrichment of 37Cl is needed and the use of efficient/performant isotopic separation technique is required. Table 2 reports a comparison of the separation factors revisited in this study.
Actually, the α values are dissimilar from one extraction technique to another. They could be limited by isotopic exchange, kinetics and convections. Other issues reducing the separation factor are vibrations, artefacts, thermo-physical, or chemical effects (e.g. 35Cl2, 35Cl37Cl, 37Cl2) during separation. However other factors are to be taken in consideration the electrolytic data of 2 reported by Klemm require 1 week separation.
Production/enrichment of 37Cl can be proposed by gas centrifugation of 1H35/37Cl and chemical separation or by elution of 23Na35/37Cl in anion exchanger resin columns. The later requires however extensive separation studies to reach higher separation factor. Alternatively the molten salt electrolysis is promising..
From an EROEI point of view gas centrifugation separation appears to be better than the chemical one because of a better separation factor. Recommendations need finally to be suggested combining the ecological and economical aspects of utilising 37Cl in the fast molten salt reactor.

5. Conclusion

The need of 37Cl in Molten Salt Fast Reactor for minimizing the ecological issues and for economic reasons is obvious.
The neutronic analysis has pointed out surprisingly large differences between codes which should lead to a two-fold strategy for improvement on the on hand differential cross section measurements as already pointed out by others, but on the other hand an integral reactor experiment, e.g. by using a pile oscillator, to provide a first reliable validation base for the code developers.
The specific ecological issue is the production of 36Cl by neutron activation of 35Cl. The isotope 36Cl is a soluble non-sorbing, in chloride form and long live nuclide that makes it a first nuclide in the safety assessment of the repository. The build-up of 36Cl with burnup has been explored for various fraction of 37Cl justifying the need of enrichment.
The neutron economical aspect is gained by better reactor criticality achieved through the use of enriched chloride in 37Cl. The criticality (k) in zero power reactor conditions is much larger for enriched chloride than for the natural one. The reactor with 99% 37Cl would have a k of 1.04346 which improve the energy yield or would allow to reduce the required uranium enrichment and thus the fuel cost. This reactivity gain is evaluated for various 37Cl enrichment factors to estimate uranium enrichment gain achievable through 37Cl enrichment.
A centrifuge was one of the first device to separate 37Cl from 37Cl, as used by Jesse Beams of the University of Virginia in 1934. In 1940, American physicists thought that the centrifuge was the best possibility for large-scale enrichment. Over the last 80 years numerous techniques have been tested to achieve this separation. The present work revisits physical and chemical method.
Production/enrichment of 37Cl can be proposed by gas centrifugation of 1H35/37Cl and chemical separation or by elution of 23Na35/37Cl in liq – liq extraction or anion exchanger resin columns. The later requires however extensive separation protocol. The among the physical separation methods, gas centrifugation separation appears to be well adapted, from the while liq – liq extraction may promise better separation factor.
The combination of processes should be further explored. They reveal a large potential because the second process may quench the potential of mixing after preliminary separation using the separation scheme.

Acknowledgement

This work is part of the ZPR project which is supported by EPSRC-UK. Dr David Cheneler (LU) is acknowledged for his constructive feedback.

References

  1. B. Merk, D. Litskevich, A. Peakman, M. Bankhead, IMAGINE, A disruptive change to nuclear or how can we make more out of the existing spent nuclear fuel and what has to be done to make it possible in the UK? ATW- internat. Journal for Nuclear Power, 64 (2019) 353-359.
  2. C. Degueldre, R Dawson, V Najdanovic, 'Nuclear fuel cycle, with a liquid ore and fuel: toward renewable energy', Sustainable Energy and Fuels, 3 (2019) 1693-1700. [CrossRef]
  3. R. Roper, M. Harkema, P. Sabharwall, C. Riddle, B. Chisholm, B. Day, P. Marotta, Molten salt for advanced energy applications: A review. Annals of Nuclear Energy 169 (2022) 108924. [CrossRef]
  4. B. Merk, A. Detkina, S. Atkinson, D. Litskevich, G. Cartland-Glover, Evaluation of the breeding performance of a NaCl-UCl-based reactor system. Energy, 12 (2019). [CrossRef]
  5. Z. Mausolff, M. DeHart, S. Goluoglu, Design and assessment of a molten chloride fast reactor , Nuclear Engineering and Design, 379 (2021) 111181. [CrossRef]
  6. J. Krepel, K. J. Kramer, Molten Chloride Fast Reactors (MCFRs), Editor(s): Ehud Greenspan, Encyclopedia of Nuclear Energy, Elsevier, (2021) 625-642. [CrossRef]
  7. J. Serp, M. Allibert, O. Beneš, S. Delpech, O. Feynberg, V. Ghetta, D. Heuer, D. Holcomb, V Ignatiev, J L Kloosterman, Lelio Luzzi, E Merle-Lucotte, J Uhlíř, R Yoshioka, D Zhimin, The molten salt reactor (MSR) in generation IV: Overview and perspectives, Progress in Nuclear Energy, 77(2014) 308-319. [CrossRef]
  8. L. Martinot, Thermodynamic properties of infinitely dilute solutions of UCl3 and UCl4 in the KCl-NaCl-MgCl2 (30:20:50) ternary eutectic, Journal of the Less Common Metals, 86 (1982) 203-210. [CrossRef]
  9. L.Y. He, G.C. Li, S.P. Xia, Jin-Gen Chen, Yang Zou, Gui-Min Liu, Effect of 37Cl enrichment on neutrons in a molten chloride salt fast reactor. Nucl. Sci. Tech., 31 (2020) 27. [CrossRef]
  10. F. G. Gosling, The Manhattan Project: Making the Atomic Bomb (DOE/MA-0001; Washington: History Division, Department of Energy, January 1999), 5-6.
  11. M. E. Gooden, T. A. Bredeweg, J. B. Wilhelmy, M. M. Fowler, R. S. Rundberg, A. J. Silano, A. . P Tonchev, 35Cl(n,p)35S reaction cross-section using monoenergetic neutrons in the intermediate and fast energy regions, 2018-04-1 Los Alamos Technical ReportLA-UR-18-23117. [CrossRef]
  12. HELIOS2 Methods Manual (version 2.03.01), Studsvik, SSP-11/452 Rev 6, January 12, 20214.
  13. E.A. Villarino, R.J.J. Stammler, A. Ferri, J.J. Casal, HELIOS: angularly dependent collision probabilities, Nuclear Science and Engineering 112 (1992) 16-31. [CrossRef]
  14. C.A. Wemple, H-N.M. Gheorghiu , R.J.J. Stamm’ler , E.A. Villarino (2008) Recent Advances in the HELIOS-2 Lattice Physics Code, International Conference on the Physics of Reactors “Nuclear Power: A Sustainable Resource”, Interlaken, Switzerland, September 14-19, 2008.
  15. AURORA USER MANUAL, Studsvik, SSP-11/451 Rev 8, January 12, 2021.
  16. ZENITH USER MANUAL, Studsvik, SSP-11/460 Rev. 5, December 8, 2020.
  17. Evaluation and Viability of Liquid Fuel Fast Reactor System EVOL, DELIVERABLE D2.1, Design parameters definition for most stable salt flux, rev 3 30/04/2012.
  18. M. Brovchenko, J-L Kloosterman, L Luzzi 3, E Merle, D Heuer, A Laureau, O Feynberg, V. Ignatiev, M. Aufiero, A. Cammi, C. Fiorina, F. Alcaro, S. Dulla, P Ravetto, L. Frima, D Lathouwers, B. Merk., Neutronic benchmark of the molten salt fast reactor in the frame of the EVOL and MARS collaborative projects, EPJ Nuclear Sci. Technol. 5, (2019). [CrossRef]
  19. B. Merk, A. Detkina, D, Litskevich, S. Atkinson, G. Cartland-Glover, The Interplay between Breeding and Thermal Feedback in a Molten Chlorine Fast Reactor. Energies, 13 (2020) 1609. [CrossRef]
  20. M. A. Jessee, J. J. Jarrell, W. A. Wieselquist, M. L. Williams, K. S. Kim, T. M. Evans, S. P. Hamilton, C. A. Gentry (2017),“POLARIS - 2D LIGHT WATER REACTOR LATTICE PHYSICS MODULE, in SCALE Code System”, edited by B.T. Rearden, M.A. Jessee, February 2014.
  21. B. Merk, U. Rohde, V. Glivici-Cotruta, D. Litskevich, S. Scholl, On the use of a Molten Salt Fast Reactor to apply an idealized, Transmutation Scenario for the Nuclear Phase Out. PLOS ONE, 9 (2014). [CrossRef]
  22. Merk B, Litskevich D. Transmutation of All German Transuranium under Nuclear Phase Out Conditions - Is This Feasible from Neutronic Point of View? PLoS One., 10 (2015) :e0145652. [CrossRef]
  23. B. Merk, D. Litskevich, A disruptive approach to eliminating weapon-grade plutonium – Pu burning in a molten salt fast reactor. PLoS ONE 13 (2018) e0201757. [CrossRef]
  24. R. Rachamin, C. Wemple, E. Fridman, Neutronic analysis of SFR core with HELIOS-2, Serpent, and DYN3D codes, Annals of Nuclear Energy, 55 (2013). [CrossRef]
  25. Batchelder et al., Phys. Rev. C, vol. 99, no. 4, 2019.
  26. Kuvin et al., Physical Review C, 102, issue 2, 2020, (https://www.oecdnea.org/janisweb/book/neutrons/Cl35/MT103which).
  27. Palmiotti, G., Gehin, J. C., & Cisneros, T. (2021). Assessment of nuclear data needs for advanced reactor demonstrations: application to the molten chloride reactor experiment (MCRE) (No. INL/CON-21-64838-Rev000). Idaho National Lab.(INL), Idaho Falls, ID (United States).
  28. Ortwin Renn (Hrsg.), Partitionierung und Transmutation Forschung – Entwicklung – Gesellschaftliche Implikationen, acatech SUDIE Dezember 2013.
  29. J. Bigeleise, Isotope Separation Practice, in Spindel Ed., Isotope Effects in Chemical Processes Advances in Chemistry; American Chemical Society (1969). [CrossRef]
  30. J. W. Beams, C. Skarstrom, The Concentration of Isotopes by the Evaporative Centrifuge Method, Phys. Rev. 56 (1939) 266 - 272. [CrossRef]
  31. P. Baertschi, W. Kuhn. Vapor pressure differences of isotopic compounds. Infrared as the cause of higher volatility of the heavier species. Helv. Chim. Acta 40 (1957) 1084-1103. [CrossRef]
  32. A Liebscher, J Barnes Z. Sharp, Chlorine isotope vapor–liquid fractionation during experimental fluid-phase separation at 400 °C/23 MPa to 450 °C/42 MPa, Chemical Geology, 2342 (2006) 340-345. [CrossRef]
  33. Sun, Q. Xu, S. Xu, H. Shen, J. Sun, Y. Zhang, Separation and analysis of chlorine isotopes in higher plants, Chemical Geology, 381 (2014) 21-25. [CrossRef]
  34. Degueldre, The analysis of nuclear materials and their environments, Springer – Nature (2017). [CrossRef]
  35. Derrick Quarles Jr. Andrew D.Toms RonaldSmithJr. PatrickSullivan DavidBass JohnLeone. Automated ICP-MS method to measure bromine, chlorine, and iodine species and total metals content in drinking water, Talanta Open, 1 (2020) 100002. [CrossRef]
  36. A. Z. Kranz, W. W. Watson, Chlorine Isotope Separation by Thermal Diffusion, Phys. Rev. 91, (1953) 1469. [CrossRef]
  37. R. Scott Kemp, Gas Centrifuge Theory and Development: A Review of U.S. Programs, The Technical Basis for Arms Control, Disarmament, and Nonproliferation Initiatives, 17 (2009) 1-19. [CrossRef]
  38. E.M Aisen, V.D Borisevich, E.V Levin, G.E Popov, A.V Tikhomirov, S.V Yupatov, Study of isotope separation of some chemical elements in a gas centrifuge. Separation Science and Technology, 374 (1996) 127-131. [CrossRef]
  39. S. V. Bogovalov, Isotope Separation in Concurrent Gas Centrifuges. Physics Procedia, 72 (2015) 297-304. [CrossRef]
  40. Ch. Ying, Sh. Zeng., Y. Nie, X. .Shang, H.G. Wood, Over All Separation Factors for Stable isotopes by Gas Centrifuge, Separation Science and Technology 36 ( 2006) 2006159-175. [CrossRef]
  41. M. Musashi, T. Oi, H. G.M. Eggenkamp, Y. Yato, M. Matsuo, Anion-exchange chromatographic study of the chlorine isotope effect accompanying hydration, Journal of Chromatography A, 1140 (2007) 121-125. [CrossRef]
  42. Kl. G. Heumann, Kl. Baier, Dependence of Chlorine Isotope Separation in Ion Exchange Chromatography on the Nature and Concentration of the Eluent. Z. Naturforsch. 35b (1980) 1538-1540. [CrossRef]
  43. Kl. G. Heumann, Kl. Baier, G. Wibmer, Chlor-Isotopenseparation an einem wasserhaltigen Zirkondioxidaustauscher / Chlorine Isotope Separation Using an Hydrous Zirconium Dioxide Exchanger, Zeitschrift fur Naturforschung B 35 (1980). [CrossRef]
  44. M. Musashi, T. Oi, H. G.M.Eggenkamp, Experimental determination of chlorine isotope separation factor by anion-exchange chromatography, Analytica Chimica Acta, 508 (2004) 37-40. [CrossRef]
  45. Zezheng Zhang, Yongzhong Jia,, Bing Liu, Huaxin Sun, Yan Jing, Quanyou Zhang, Fei Shao, Mixiang Qi, Ying Yao, Extraction and separation of lithium isotopes by using organic liquid film extraction system of crown ether-ionic liquid, Fusion Engineering and Design, 161 (2020) 112015. [CrossRef]
  46. A V Khoroshilov, P I Ivanov, Separation of boron isotopes by chemical exchange in liquid-liquid systems, J. Phys.: Conf. Ser. 1099 (2018) 012006. [CrossRef]
  47. G.D. Rabinovich, V.P. Ivakhnik, Chlorine isotope separation by liquid-phase thermal diffusion. At Energy, 45 (1978) 879–882. [CrossRef]
  48. P.N. Nesterenko, Ion Exchange. Overview., M. Miró, P. Worsfold, C. Poole, A. Townsend (Eds.), Encyclopedia of Analytical Science (third ed.), Academic Press, Oxford (2019), pp. 204-210. [CrossRef]
  49. [ ] Bio-Rad, AG@ 1, AG MP-l and AG 2 Strtng, Anion Exchange Resin Instruction Manual BioRad Laboratories, LIT212 Rev C (2023).
  50. J.J.van Deemter, F.J.Zuiderweg, A.Klinkenberg, Longitudinal diffusion and resistance to mass transfer as causes of nonideality in chromatography Chemical Engineering Science, 5 (1956) 271-289. [CrossRef]
  51. W. Kuhn, H. Martin. Photochemical separation of isotopes, Naturwissenschaften 20, 772(1932). 3. - 27.
  52. W. Kuhn, H. Martin, K. H. Eldau. Enrichment of the chlorine isotopes by irradiation of chlorine dioxide at low pressure (the photochemistry of chlorine dioxide). Z. physik. Chem. 5O (1941) 213-254, Chem. Zentr. I (1942) 579.
  53. D. D. S. Liu, S. Datta, R. N. Zare, Laser separation of chlorine isotopes. Photochemical reaction of electronically excited iodine monochloride with halogenated olefins, J. Am. Chem. Soc., 97, (1975) 2557–2558. [CrossRef]
  54. R. N. Zare, Laser isotope separation by selective excited state photochemistry. Annual progress report, March 31, 1976--February 28, 1977. United States: N. p., 1977. [CrossRef]
  55. CA Lucy, TL McDonald. Separation of chloride isotopes by capillary electrophoresis based on the isotope effect on ion mobility. Anal Chem., 67 (1995) 1074-1078. [CrossRef]
  56. M. Petek, D.W. Ramey, R. D. Taylor, E.H. Kobisk, Tritium isotope separation from light and heavy water by bipolar electrolysis. United States: N. p., 1980. CONF-800427-15.
  57. J. Wild, P. Wang, T. Jin, Y. Yang, Modeling Isotope Separation in Electrochemical Lithium Deposition, Journal of The Electrochemical Society, 169 (2022) 032504. [CrossRef]
  58. Klemm. Separation of isotopes by electrolytic migration of ions, Colloques intern. centr. natl. recherche sci. 39, Electrolyse C18 -C24 (1952).
  59. Klemm. A. Lunden, Isotopenanreicherung beim Chlor durch elektrolytische Überführung in geschmolzenem Bleichlorid, Z. Naturforsch., 10a (1955) 282-284.
  60. C. Wang, H. Ju, X. Zhou, P. Zhang, Z. Xue, L. Mao, F. Shao, Y. Jing, Y. Jia, J. Sun, Separation of lithium isotopes: Electromigration coupling with crystallization (1999), Journal of Molecular Liquids, Volume 355 (2022) 118911. [CrossRef]
  61. H. L. Johnston, D. A. Hutchison, Efficiency of the Electrolytic Separation of Chlorine Isotopes, J. Chem. Phys. 10 (1942) 469. [CrossRef]
  62. Yongtao Li , Ed J George, Analysis of perchlorate in water by reversed-phase LC/ESI-MS/MS using an internal standard technique, Anal Chem. 77 (2005) 4453-8. [CrossRef]
  63. J. R. Christie, W. D. Johnson, A. G. Loudon, Allan MacColl, M. N. Mruzek, Heavy atom kinetic isotope effects. Part 3.—The chlorine kinetic isotope effect in the gas-phase unimolecular decomposition of ethyl chloride. J. Chem. Soc., Faraday Trans. 71, (1975) 1937-1942. [CrossRef]
  64. Lewandowicz, J. Rudziński, L. Tronstad, M. Widersten, P. Ryberg, O. Matsson, P. Paneth. Chlorine Kinetic Isotope Effects on the Haloalkane Dehalogenase Reaction. J. Am. Chem. Soc., 123 (2001) 4550–4555. [CrossRef]
  65. M. Musashi, Takao Oi, Hans G.M.Eggenkamp, YumioYato, Motoyuki Matsuo, Anion-exchange chromatographic study of the chlorine isotope effect accompanying hydration, Journal of Chromatography A, 1140 (2007) 121-125. [CrossRef]
  66. V. Ghazanfari, M. M. Shadman, Numerical solution of a comprehensive form of convection–diffusion equation for binary isotope in the gas centrifuge, Annals of Nuclear Energy, 175, 2022, 109220. [CrossRef]
  67. Klemm. Infinitively long separation tube with end volumes, Z. Naturforsch 3a (1948) 211-216.
  68. T.F. Johns, Isotope separation by multistage methods, in Progress in Nuclear Physics, 6 (2013) 1-25. [CrossRef]
  69. Chong Guang Luo, Ying Kai Xiao, Hai Zhou Ma, Yun Qi Ma, Yan Ling Zhang, Mao Yong He Stable isotope fractionation of chlorine during evaporation of brine from a saline lake, Chinese Science Bulletin , 57 (2012) 1833–1843. [CrossRef]
  70. H. Holmstrand , Manolis Mandalakis , Zdenek Zencak , Örjan Gustafsson , Per Andersson , Chlorine isotope fractionation of a semi-volatile organochlorine compound during preparative megabore-column capillary gas chromatography, Journal of Chromatography A 1103 (2006) 133-138. [CrossRef]
Preprints 114600 g001
Figure 1. Volume corrected 2D HELIOS model of the molten salt reactor. Conditions: core (hot) radius of 213 cm, 235U enrichment of 11.06%, second layer of fuel (cold) returning in core.
Figure 1. Volume corrected 2D HELIOS model of the molten salt reactor. Conditions: core (hot) radius of 213 cm, 235U enrichment of 11.06%, second layer of fuel (cold) returning in core.
Preprints 114600 g001
Preprints 114600 g002
Figure 2. Description of the calculation cycle for MSR based on the HELIOS package.
Figure 2. Description of the calculation cycle for MSR based on the HELIOS package.
Preprints 114600 g002
Preprints 114600 g003
Figure 3. Development of the dynamically calculated criticality over burnup for different contents of 35Cl in the carrier and the fuel salt with explicit documentation of the cycle behaviour showing the steps of the HELIOS calculations as well as the steps of the script cycles.
Figure 3. Development of the dynamically calculated criticality over burnup for different contents of 35Cl in the carrier and the fuel salt with explicit documentation of the cycle behaviour showing the steps of the HELIOS calculations as well as the steps of the script cycles.
Preprints 114600 g003
Preprints 114600 g004
Figure 4. Cycle averaged development of the dynamically calculated criticality over burnup for different isotopic fraction of 37Cl in the carrier and the fuel salt, all cases adopted to the same starting value by changing the initial 37Cl enrichment of the uranium based fuel from natural isotopic composition through the reference case and to 99%.
Figure 4. Cycle averaged development of the dynamically calculated criticality over burnup for different isotopic fraction of 37Cl in the carrier and the fuel salt, all cases adopted to the same starting value by changing the initial 37Cl enrichment of the uranium based fuel from natural isotopic composition through the reference case and to 99%.
Preprints 114600 g004
Preprints 114600 g005
Figure 5. Development of the dynamically calculated 36Cl concentration over burnup for different contents of 35Cl in the carrier and the fuel salt.
Figure 5. Development of the dynamically calculated 36Cl concentration over burnup for different contents of 35Cl in the carrier and the fuel salt.
Preprints 114600 g005
Preprints 114600 g006
Figure 6. A schematic of a gas centrifuge unit during 37Cl separation from 35Cl/37Cl gas mix.
Figure 6. A schematic of a gas centrifuge unit during 37Cl separation from 35Cl/37Cl gas mix.
Preprints 114600 g006
Preprints 114600 g007
Figure 7. Separation factor of 37Cl/35Cl as a function of v and of T. Conditions: ΔM: 2 g mol-1 .a T = 300 K .b v = 50 m s-1 . Note the increase of v enhances strongly the isotope separation, a decrease of T increases slightly α.
Figure 7. Separation factor of 37Cl/35Cl as a function of v and of T. Conditions: ΔM: 2 g mol-1 .a T = 300 K .b v = 50 m s-1 . Note the increase of v enhances strongly the isotope separation, a decrease of T increases slightly α.
Preprints 114600 g007
Preprints 114600 g008
Figure 8. Breakthrough of 35Cl and 37Cl during their elution in capillary column,.
Figure 8. Breakthrough of 35Cl and 37Cl during their elution in capillary column,.
Preprints 114600 g008
Preprints 114600 g009
Figure 9. The schematic diagram for electrochemical 37Cl enrichment in the fluid phase. After applying a constant current density to the cell, solid chloride is electro-generated into the anode electrode (left) with a ratio of [35Cl]/[37Cl] greater than the original natural abundance of 3 as a result of isotope diffusivity.
Figure 9. The schematic diagram for electrochemical 37Cl enrichment in the fluid phase. After applying a constant current density to the cell, solid chloride is electro-generated into the anode electrode (left) with a ratio of [35Cl]/[37Cl] greater than the original natural abundance of 3 as a result of isotope diffusivity.
Preprints 114600 g009
Table 1. Reactivity gain increases with 37Cl fraction in the salt.
Table 1. Reactivity gain increases with 37Cl fraction in the salt.
35Cl (%) 37Cl (%) RG (pcm)
75.8 24.2 0000
05.0 95.0 4118
01.0 99.0 4365
00.1 99.9 4421
Table 2. Comparison of separation factors for some techniques revisited in this study.
Table 2. Comparison of separation factors for some techniques revisited in this study.
Separation Conditions α Ref
Centrifugation T: 300 K 1.0020 This work
Distillation T: 300 K 1.0060 Liebscher et al. (2006)
Chromatography T: 300 K 1.0003 Musashi et al. (2007)
Electrolysis T: 300 K Pt 1.0060 Johnston & Hutchison (1942)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated