Prerpints.org logo
Preprint
Article

A Deep Learning-Based Low-Overhead Beam Tracking Scheme for RIS-Aided MISO Systems with Estimated Channels

Altmetrics

Downloads

124

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

08 August 2024

Posted:

12 August 2024

You are already at the latest version

Alerts
Abstract
The next generation network requires not only ultra high data rate, global coverage and connectivity, but also reducing network deployment costs and energy consumption. The emergence of reconfigurable intelligent surface (RIS) technology provides an effective way to improve efficiency and reduce cost, while the passive elements bring new challenges of channel estimation (CE) and beam tracking. For a RIS-aided multiple-input and single-output (MISO) system, in this paper, to achieve the channel state information (CSI), we propose a principle component analysis (PCA) based staged channel estimation method. Based on the estimated channel, we propose a deep learning (DL) based beam tracking scheme to realize low-complexity RIS reflection coefficient design, which effectively improves the signal-to-noise ratio (SNR) at the user side. Simulation results verify our proposed channel estimation scheme based on PCA and beam tracking scheme based on DNN for the semi-active RIS-aided MISO systems can obtain approximate performances with much lower computational complexity.
Keywords: 
Subject: Computer Science and Mathematics  -   Signal Processing

1. Introduction

1.1. Motivation

Compared with the widely used fifth-generation (5G) network, the beyond 5G and six-generation (6G) network not only require ultra high data rate, global coverage and connectivity, as well as extremely high reliability and low latency, but also focus on reducing network deployment costs and energy consumption, and achieving sustainable development of the green mobile communications [1,2,3]. The emergence of RIS technology provides an effective way to improve efficiency and reduce cost of 6G communications [4]. A RIS is composed of an array of passive intelligent reflection units, which can be used to modify the amplitude and phase of incident signals independently. It is equivalent to improving the characteristics of the wireless channel, which is especially effective in the scenario where the original channel quality is very poor (for example, there are barriers between transceivers). Therefore, RIS can be beneficial for improving the propagation environment and the coverage of wireless systems. However, the implementation of RIS also brings new challenges to the design of wireless communication systems. Firstly, estimating and sharing CSI are challenging tasks with the currently available RIS architectures, which consist of passive elements in most cases. Moreover, designing the reflection coefficients of RIS to generate a well beamforming requires a huge amount of overheads and computational complexity due to the large number of reflecting elements of RIS.

1.2. Related Work

In general, accurate CE is key to the optimization of the reflecting coefficients. There have been various studies on channel estimation in the RIS-aided communication systems [5,6,7,8,9,10,11,12]. For fully passive RIS without RF chains, the CE of the RIS-involved system can only be executed by transmitting pilots from the transmitter (Tx) to the receiver (Rx) via shifting the reflection patterns of the RIS. For instance, in [5,6], the authors recovered the individual channel of Tx-RIS and RIS-Rx based on the aggregated CSI with the compressive sensing (CS) technique. In [7,8,9], the authors proposed CE schemes based on the message passing technique with sparse matrix completion and factorization method. In [10], with the hierarchical search codebook design, the author presented a low-complexity CE scheme. In addition, a least-squares (LS) combined with linear minimum mean-square error (LMMSE) CE scheme is proposed in [11], a pilot training-based multi-round sub-channel estimation method [6] can also be utilized to execute the CE in RIS-aided systems, which requires, however, large training periods. From existing literature, there is a gap regarding the practical channel estimation of communication system with a passive RIS. In contrast, for the RIS that is equipped with active elements like radio frequency (RF) chains [13,14,15,16], the CSI of Tx-RIS and RIS-Rx can be estimated by receiving pilot signals from the base station (BS) and users, where the traditional CE schemes can be applied. For example, in [15], the authors proposed a novel architecture comprising of passive unit elements and a single active RF chain (semi-active RIS), which allows a trade-off between cost and performance.
For the beam tracking of RIS, most of the RIS-aided wireless communication systems generally focus on dynamically changing the reflection coefficient to enhance the strength of the received signal. Therefore, the design of the reflection coefficient is generally aimed at maximizing the signal-to-noise ratio and the achievable rate. To maximize the downlink achievable rate of user terminal (UT), an alternatively optimization algorithm has been proposed in [17], which can obtain a suboptimal solution. Meanwhile, the performance of the MISO system assisted by RIS has been compared with that of the traditional MISO system, and it has been demonstrated that a reasonable design of the reflection coefficient of the RIS can maximize the system capacity. In [18], the beamforming of BS and RIS are jointly optimized by semi-definite relaxation (SDR) to minimize the transmission power of BS, and introduce a discrete phase-shift constraint in [19]. However, these methods still have high computational complexity and the optimization schemes need to be redesigned when considering the heterogeneous RIS systems. Recently, the deep learning (DL) method has attracted wide interest in wireless communication [20,21]. Furthermore, some researches have proved that introducing DL to beamforming design would reduce computing complexity and improve the performance of communication system [22,23]. Meanwhile, the authors in [24] and [25] proposed machine learning based channel estimation techniques for the single-input-single-output (SISO) system, when assuming a nonfully passive RIS, i.e. a RIS having a few active sensing elements to help with the channel estimation.

1.3. Our Contributions

In this paper, we consider both the CE and beam tracking of a semi-active RIS-aided MISO system in a practical manner. As we know, this scenario has not been investigated. The specific contributions of this paper are summarized as follows.
  • Based on the semi-active RIS architecture comprising of passive unit elements and a single active RF chain, we propose a PCA-based CE scheme to estimate the CSI of the RIS-BS, the RIS-UT and the UT-BS. The proposed CE scheme allows a trade-off between cost and performance.
  • Based on the estimated channel, we propose a deep neural network (DNN) to realize low-complexity beam tracking of semi-active RIS-aided system, which effectively improves the SNR at the UT side. Our simulation results verify the accuracy of the proposed schemes on beam tracking for semi-active RIS-aided MISO systems.
The rest of this paper is organized as follows. Section II describes the semi-active RIS-aided MISO system model and formulates the constrained sum-rate maximization problem. The proposed PCA-based CE method is developed in Section III, while the DL-based beam tracking scheme is presented in Section IV. In Section V, we analyze the results of our simulation experiments, while Section VII concludes the paper.
The notations adopted in the paper are described as follows. We use C to denote the complex domain. The small boldface is used to represent vector and the big boldface is used to represent the matrix. Let ( X ) T , ( X ) ∗ , ( X ) H denote the transpose, conjugate, and conjugate transpose of a matrix X , respectively. E { · } represents the expectation, and diag ( · ) denotes diagonalization. Let R e ( · ) and I m ( · ) denote the real and imaginary parts of complex numbers, respectively. v e c ( · ) denotes the vector mapping operation.

2. System Model and Problem Formulation

2.1. System Model

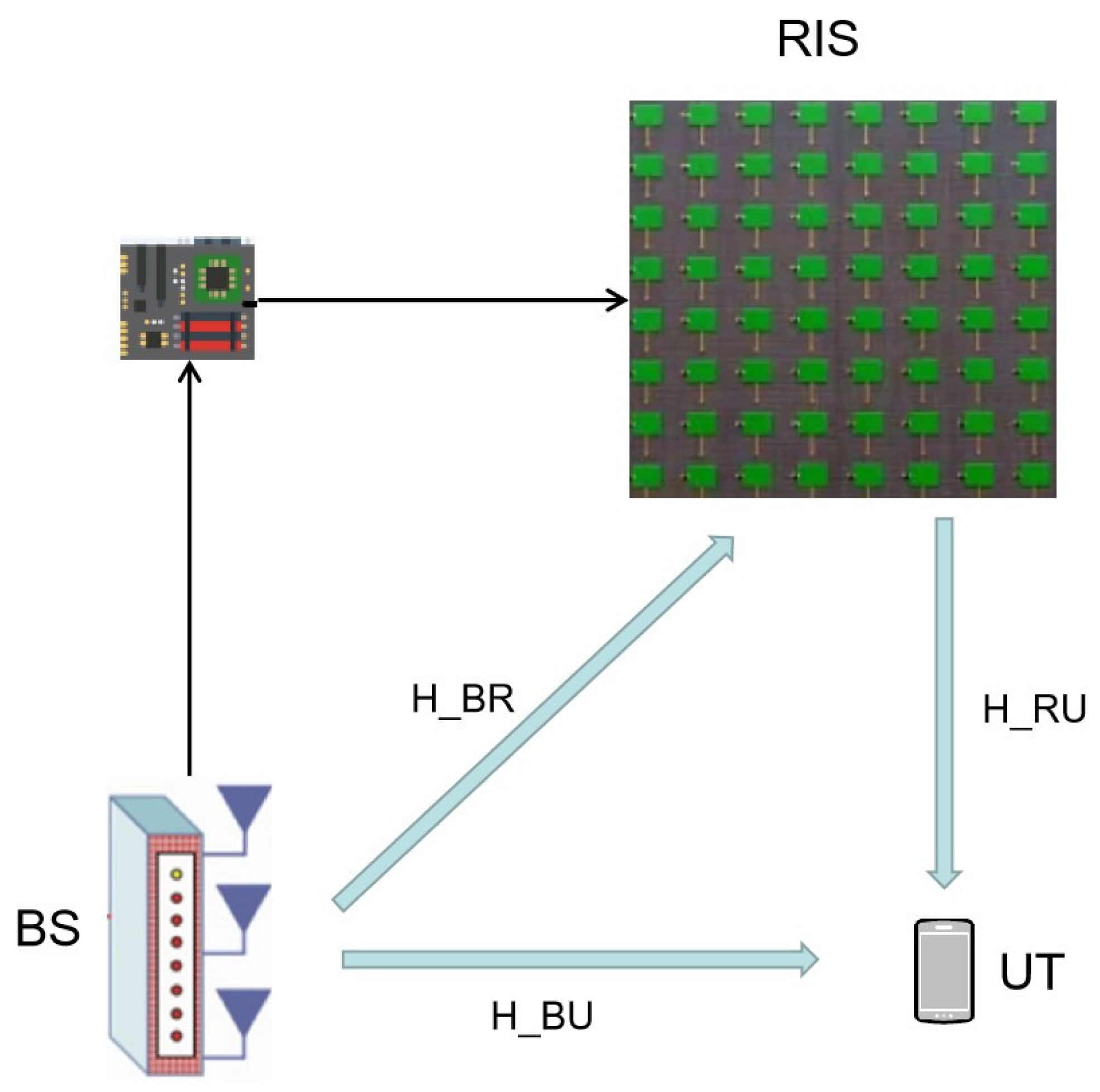
As illustrated in Figure 1, we consider an RIS-aided MISO system. In this system, the BS and the RIS are equipped with M × M antennas and N × N reflecting elements, respectively. The UT is equipped with a single antenna. Meanwhile, the distance between the adjacent antennas of the BS is d B S . The reflecting element spacing of RIS is d R I S .
The received signal y of UT is given by
y = ( H R U ϕ H B R + H B U ) b x + w = H x + w ,
where H B R ∈ C M × N denotes the channel between BS and RIS, H R U ∈ C 1 × M is the channel between RIS and UT, H B U ∈ C 1 × N is the channel between BS and UT, b is the beamforming vector with N × 1 dimension, ϕ denote the reflection coefficient matrix with M × M dimension, x is the complex data symbol intended for UT, w ∼ CN ( 0 , σ 2 ) is the additive white Gaussian noise (AWGN) witch has zero mean and variance σ 2 .
Then, based on the angular domain channel model, H B R can be expressed as
H B R = ∑ p B R = 1 P B R β B R p B R v e c a ( u R I S p B R ) b T ( v R I S p R B ) v e c a ( u B S p B R ) b T ( v B S p B R ) T ,
where p B R denotes the resolvable paths between the BS and RIS, β B R p B R is the path loss between BS and RIS, v e c ( · ) denotes vectorization, a ( u B S p B R ) b T ( v B S p B R ) and a ( u R I S p B R ) b T ( v R I S p B R ) denote the array manifold vector of BS and RIS, respectively. Furthermore, these parameters can be expanded as follows:
a ( u B S p B R ) = [ 1 , exp { j 2 π u B S p B R } , ⋯ , exp { j 2 π ( N − 1 ) u B S p B R } ] T ,
b T ( v B S p B R ) = 1 , exp { j 2 π v B S p B R } , ⋯ , exp { j 2 π ( N − 1 ) v B S p B R } T ,
a ( u R I S p B R ) = [ 1 , exp { j 2 π u B S p B R } , ⋯ , exp { j 2 π ( M − 1 ) u B S p B R } ] T ,
b T ( v R I S p B R ) = 1 , exp { j 2 π v B S p B R } , ⋯ , exp { j 2 π ( M − 1 ) v B S p B R } T ,
where
u B S p B R = d B S λ cos θ B S p B R and v B S p B R = d B S λ sin θ B S p B R cos Φ B S p B R ,
u R I S p B R = d R I S λ cos θ R I S p B R and v R I S p B R = d R I S λ sin θ R I S p B R cos Φ R I S p B R .
Similarly, the channel H R U and H B U can be expressed as
H R U = ∑ p R U = 1 p R U = P R U β R U p R U v e c ( a ( u R U p R U ) b T ( v R U p R U ) ) ,
H B U = ∑ p B U = 1 p B U = P B U β B U p B U v e c ( a ( u B U p B U ) b T ( v B U p B U ) ) .
From (2), (9) and (10), we can observe that the RIS-aided MISO channel is directly related with the DoA angles and path loss. In the following section, we propose a staged channel estimation scheme.

2.2. Problem Formulation

Based on (1), the received signal of UT can be written as
y = ( H R U ϕ H B R + H B U ) b x + w ,
where ϕ is a M × M diagonal matrix, the i-th diagonal element of ϕ is ϕ i = e j 2 π p i , i ∈ [ 0 , M − 1 ] , for any i, p i ∈ [ 0 , 1 ) .
The SNR of the received signal can be expressed as
ε = | ( H R U ϕ H B R + H B U ) b | 2 σ 2 .
According to [26], we realize that for a fixed reflection coefficient matrix ϕ , the beamforming matrix b that maximizes the receive SNR is as follows
b ∗ = P m a x ( H R U ϕ H B R + H B U ) | | ( H R U ϕ H B R + H B U ) | | ,
where P m a x denotes the maximum transmitting power of the base station.
Then, the optimization problem on the reflection coefficient matrix ϕ is given by
max ϕ | | ( H R U ϕ H B R + H B U ) | | 2 s . t . | ϕ i | = 1 , ∀ 0 < = i < M .
The optimization problem 14 is very difficult to solve as it is a typical NP-hard problem and the CSI is hard to estimate. In the following section, we will propose a PCA-based channel estimation scheme to obtain accurate CSI of the RIS-aided system.

3. The Proposed PCA-Based Channel Estimation Algorithm

3.1. Channel Estimation

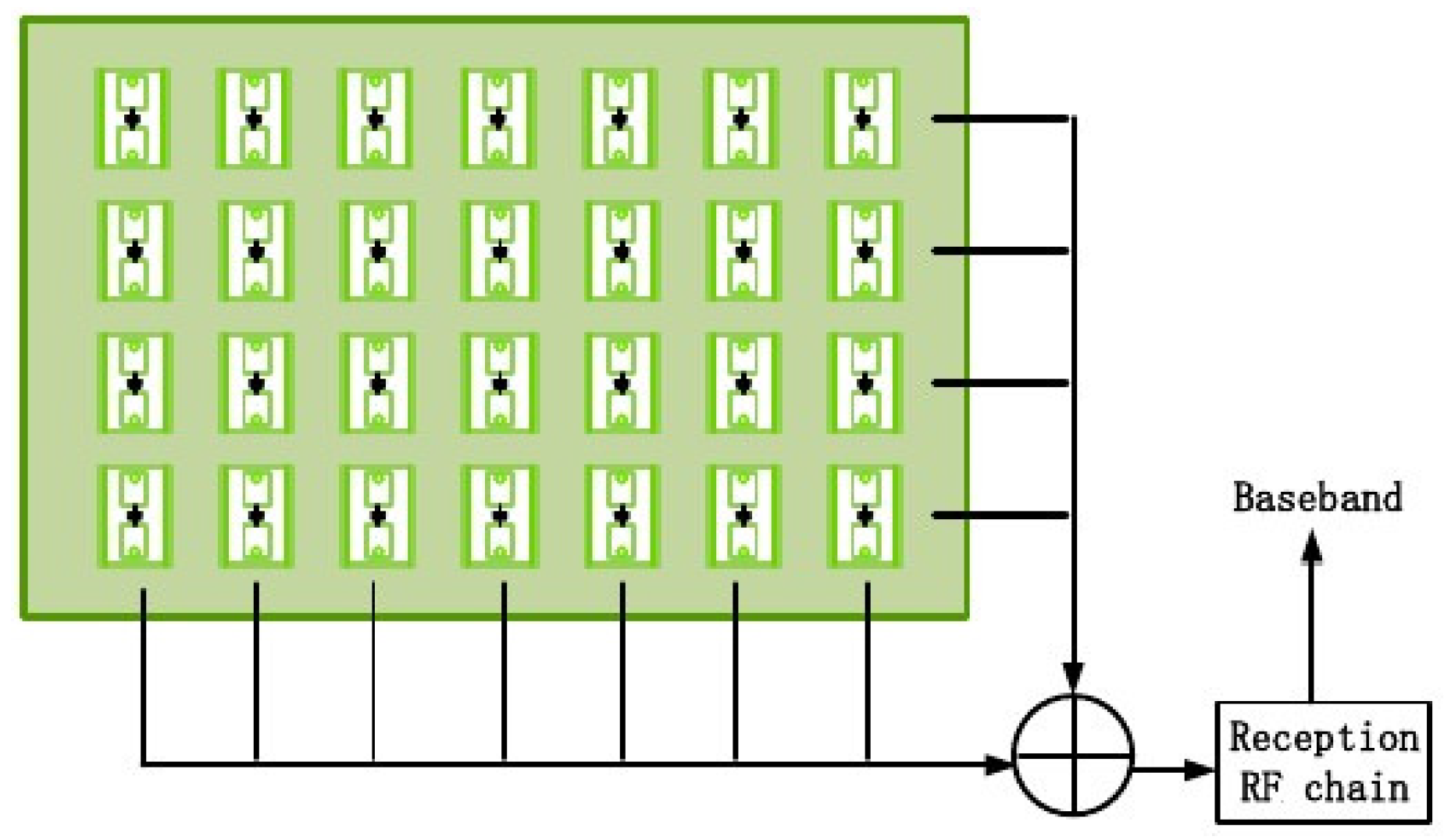
As shown before, we consider a RIS architecture comprising of passive unit elements and a single active RF chain as illustrate in Figure 2. This single RF chain enabling baseband channel estimation via pilot signals consists of a low noise amplifier, a mixer downconverting the signal from RF to baseband, and an analog to digital converter.
We consider that all reflecting elements in RIS are turned off. Therefore, (1) can be rewritten as
y = H B U x + z = H x + w .
According to the formula (15), we can find that the entire system is consistent with conventional massive MISO systems. Then, an adaptive channel estimation algorithm based on PCA is proposed to estimate the channel H B U . Before formally introducing the channel estimation algorithm based on PCA, we first introduce the relevant knowledge of matrix decomposition as the precondition of the research.

3.2. SVD Operation

To obtain the channel matrix from the received signal, the singular value decomposition (SVD) operation can usually be applied to decompose the received signal matrix, which can be expressed as
Y = S Σ D H ,
where S and D are referred to as singular vectors, which are unitary matrix with M × M and N × N dimension, respectively. Σ is called singular value, which is a diagonal matrix with M × N dimension. Besides, we assume that the Σ is sorted in descending order.
According to the array signal processing theory, matrices S and D are related to the DoA angles. However, the computational complexity of SVD operation is very high. Therefore, a low-complexity channel estimation algorithm based on PCA is used to implement the estimation of matrices S and D .

3.3. The PCA-Based Channel Estimation Algorithm

From the analysis in the previous section, the estimation of the DoA angles can be obtained by estimating the matrices S and D . Then, the low complexity estimates of S and D are obtained mainly by estimating covariance matrices. Without loss of generality, we consider recover matrix S first. Then, the correlation covariance matrix is given by
R 1 = E { Y Y H } = ∑ i = 1 P H i ψ i H i H + σ 2 I ,
where R 1 is covariance matrix, ψ i = E { x x ∗ } . Then, introducing EVD operations for analysis, (17) can be rewritten as
R 1 = S P Λ s S P H + S z Λ z 1 S z H ,
where S P is an M × P matrix with eigenvectors corresponding to eigenvalues, λ 1 , ⋯ , λ P , Λ s is a P × P diagonal matrix with entries from λ 1 to λ P , S z is an M × ( M − P ) matrix composed of eigenvectors corresponding to eigenvalues λ P + 1 , ⋯ , λ M and Λ z 1 is a ( M − P ) × ( M − P ) diagonal matrix with entries of eigenvalues from λ P + 1 to λ M .
To estimate matrix S with low computational complexity, an adaptive iterative method based on PCA is proposed in this section. Frist, taking the estimation on S P as an example and assuming that T 1 is the estimation on S P . Then, based on [27], the objective function is given by
min T 1 J ( T 1 ) = t r ( C L ) − 2 t r ( Ω T 1 H C L T 1 ) + t r ( Ω T 1 H C L T 1 T 1 H T 1 ) ,
where C L = E { Y k Y k H } , Ω is a diagonal matrix with the singular values, denoted as w i , i . Based on the analysis in [27], the estimated value of T 1 can be close to S P if the diagonal elements of Ω satisfy w 1 , 1 > w 2 , 2 > · > w P , P > 0 .
Problem (19) can be solved by the gradient descent method, the update rule of T 1 is given by
T 1 , j = T 1 , j − 1 − η ∂ J ( T 1 ) ∂ T 1 | T 1 = T 1 , j − 1 .
The gradient of J ( T 1 ) is as follows
∂ J ( T 1 ) ∂ T 1 = − ( 4 C L T 1 Ω − C L T 1 Ω T 1 H T 1 − T 1 T 1 H C L T 1 Ω − C L T 1 T 1 H T 1 Ω − T 1 Ω T 1 H C L T 1 ) .
Then, (22) can be rewritten as based on (21)
T 1 , j = T 1 , j − 1 + η ( 4 C L T 1 , k − 1 Ω − C L T 1 , j − 1 Ω T 1 H T 1 , j − 1 − T 1 , j − 1 T 1 , j − 1 H C L T 1 , j − 1 Ω − C L T 1 , j − 1 T 1 , j − 1 H T 1 , j − 1 Ω − T 1 , j − 1 Ω T 1 , j − 1 H C L T 1 , j − 1 ) .
[27] proves that T 1 converges to S P when j tends to infinity, therefore, the estimate of S P can be achieved based on (22). However, the covariance matrix C L in (22) is essential for the update of T 1 . Since it is difficult to obtain the C L in the actual process, a sampling covariance matrix proposed in [28] is used for approximate estimation which is given by
C ^ L , j = 1 j ∑ k = 0 j τ j − i Y k Y k H = τ j − 1 j C ^ L , j − 1 + 1 j Y j Y j H ,
where τ ∈ [ 0 , 1 ] denotes the forgetting factor. Then, combined with (23), the update rule of T 1 can be rewritten as
T 1 , k = T 1 , k − 1 + η ( 4 C ^ 1 , k − 1 T 1 , k − 1 Ω − C ^ L , k − 1 T 1 , k − 1 Ω T 1 H T 1 , k − 1 − T 1 , k − 1 T 1 , k − 1 H C ^ 1 , k − 1 T 1 , k − 1 Ω − C ^ 1 , k − 1 T 1 , k − 1 T 1 , k − 1 H T 1 , k − 1 Ω − T 1 , k − 1 Ω T 1 , k − 1 H C ^ 1 , k T 1 , k − 1 ) .
It is worth noting that the step size η is a necessary condition to achieve fast convergence and high accuracy in estimating T 1 . To speed up the convergence, we propose a method for calculating the optimal step size.
To obtain the optimal η , we consider the expression of the optimization function J ( T 1 ) at the ( k + 1 ) t h iteration
J ( T 1 , k + 1 ) = t r ( R 1 , k + 1 ) − 2 t r ( Ω T 1 , k + 1 H R 1 , k + 1 T 1 , k + 1 ) + t r ( Ω T 1 , k + 1 H R 1 , k + 1 T 1 , k + 1 T 1 , k + 1 H T 1 , k + 1 ) .
To simplify subsequent formulas, we use ∇ to replace ∂ J ( T 1 ) ∂ T 1 . Then, combined (22) with (25), (25) can be rewritten as
J ( T 1 , k + 1 , η ) = t r ( C ^ L , k + 1 ) − 2 t r [ Ω ( T 1 , k − η ∇ ) H C ^ L , k + 1 ( T 1 , k − η ∇ ) ] + t r [ Ω ( T 1 , k − η ∇ ) H C ^ L , k + 1 ( T 1 , k − η ∇ ) ( T 1 , k − η ∇ ) H ( T 1 , k − η ∇ ) ] .
Considering that T 1 , k + 1 H T 1 , k + 1 = U H S P H S P U = I , (26) can be rewritten as
J ( T 1 , k + 1 , η ) = t r ( C ^ L , k + 1 ) − t r [ Ω ( T 1 , k − η ∇ ) H C ^ L , k + 1 ( T 1 , k − η ∇ ) ] .
We find that J ( T 1 , k + 1 ) get the global maximum when step size is η o p t . Then, the partial derivative of J ( T 1 , k + 1 ) with respect to ¦Ç can be written as
∂ J ( T 1 , k + 1 , η ) ∂ η = ∂ ∂ η { − 2 t r [ Ω ( T 1 , k − η ∇ ) H C ^ L , k + 1 ( T 1 , k − η ∇ ) ] + t r [ Ω ( T 1 , k − η ∇ ) H C ^ L , k + 1 ( T 1 , k − η ∇ ) ( T 1 , k − η ∇ ) H ( T 1 , k − η ∇ ) ] } = − 2 t r [ Ω ( − ∇ ) H C ^ 1 , k + 1 ( T 1 , k − η ∇ ) ] − 2 t r [ Ω ( T 1 , k − ∇ ) H C ^ L , k + 1 ( − η ∇ ) ] = 2 t r [ Ω ∇ H C ^ L , k + 1 T 1 , k ] − 2 η t r [ Ω ∇ H C ^ L , k + 1 ∇ ] + 2 t r [ Ω T 1 , k H C ^ L , k + 1 ∇ ] − t r [ Ω ∇ H C ^ L , k + 1 ∇ ] .
When ∂ J ( T 1 , k + 1 ) ∂ η = 0 , J ( T 1 , k + 1 ) get the global maximum. Then, η o p t is given by
η o p t = t r [ Ω ∇ H C ^ L , k + 1 T 1 , k ] + t r [ Ω T 1 , k H C ^ L , k + 1 ∇ ] 2 t r [ Ω ∇ H C ^ L , k + 1 ∇ ] .
According to (29), we can achieve the optimal update rule to estimate the target matrix S P . By using the same way, D P can also be recovered.
After implementing the estimation of S P and D P , the MUSIC method is proposed to estimate the u B U and v B U in (10). Then, the pseudospectrum with respect to u B U based on MUSIC method is given by
f ( u ) = 1 ∑ k = P + 1 M | a ( u i ) H s z , k | 2 = 1 p H ( ζ ) S z S z H p ( ζ ) ,
where p ( ζ ) = 1 , ζ , … , ζ ( M − 1 ) T . Furthermore, S z S z H can be obtained by S P , which is given by
S z S z H = I − S P S P H .
Then, inserting (31) into (30), u B U , ∀ 1 ≤ i ≤ P , can be estimated by finding the peaks of the pseuospectrum in (30). Similarly, the same method can be used to estimate v B U from D P .
After estimating u B U and v B U from S P and D P , respectively, it is necessary to match the estimated u B U and v B U . Therefore, we first define projection operation as
P r = < J | K > = t r a c e ( J H K ) ,
where J and K denote two matrices. Then, with the estimated u B U and v B U , the projection of the received data matrix Y on the steering matrix A i ( u i , v j ) can be written as
P r = < A i ( u i , v j ) | Y > = t r a c e ( A i H ( u i , v j ) Y ) = t r a c e ( b ( v j ) ∗ a H ( u i ) Y ) = a H ( u i ) Y b ( v j ) ∗ ,
where i , j = 1 , 2 , 3 … P . Obviously, only when j = i , the value of Pr will reach the maximum since the received signal at the BS are mainly transmitted via the P resolvable paths. In another word, the received signals from P paths have contribute the most on the received energy at the BS. Therefore, by finding the maximum value of Pr in (34), the u B U can be paired with v B U for . After the estimation and paring on u B U and v B U , the corresponding DoA angles can be obtained by the following formula
θ i = arccos ( u i τ ) , ∀ 1 ≤ i ≤ P ,
ϕ i = arccos ( v i τ 1 − ( u i τ ) 2 ) , ∀ 1 ≤ i ≤ P ,
where τ = d λ .

3.4. Staged Channel Estimation Scheme

Based on the PCA algorithm proposed in the previous section, the channel estimation between the UT and the base station in the frist stage can be achieved. In the second stage, we consider turning on the RIS, and the UT side sends a signal to the RIS. Because of the reciprocity of the TDD system channel, the received signal on the RIS side can be expressed as
Y R I S = H R U T x + W = ∑ p R U = 1 p R U = P U R β R U p R U v e c ( a ( u R U p R U ) b T ( v R U p R U ) ) T x + W .
According to (36), it is not difficult to find that the channel estimation between the UT and the RIS at the RIS side is similar to the channel estimation between the UT and the base station at the base station side. Therefore, the PCA-based channel estimation algorithm proposed in previous section can be used to recover the channel H R U by estimating the DoA angles.
In the third stage, we consider that the BS sends a signal to the RIS, the received signal on the RIS can be written as
Y R I S B = H B R x + W = W + ∑ p B R = 1 p B R = P B R β B R p B R v e c ( a ( u B S p B R ) b T ( v B S p B R ) ) v e c ( a ( u R I S p B R ) b T ( v R I S p R B ) ) T .
According to (37) and (3) to (6), it can be known that the recovery of the channel H R B is based on the estimation of the DoA angles. Therefore, considering that the RIS receives signals from three adjacent antennas on the base station, the received signal on the RIS side can be expressed as
Y R I S B a 1 = H B R x + W = ∑ p B R = 1 p B R = P B R β B R − a 1 p B R v e c ( a ( u R I S p B R ) b T ( v R I S p R B ) ) + W ,
where a 1 represents the signal transmitted by the frist antenna on the base station. According to (38), we can obtain the estimate of u R I S and v R I S . Then, selecting the antennas a 2 and a 3 adjacent to the frist antenna in the horizontal and vertical directions, the path gain between BS and RIS has the following relationship
β B R − a 2 = β B R − a 1 exp { j 2 π u B S } ,
β B R − a 3 = β B R − a 1 exp { j 2 π v B S } .
We can achieve the estimate of u B S and v B S based on (39) and (7). Then, the channel H B R can be recovered based on u B S and v B S .

4. The Proposed RIS Beam Tracking Scheme

For the proposed optimization problem, in this section, we will introduce two RIS beam tracking schemes, i.e. the SDR-based algorithm and the DL based scheme. As an RIS usually consists of a large number of elements, the design of reflection coefficients is usually hard and complex. To avoid the problem that the performance of traditional high complexity algorithms cannot be guaranteed during the solution process, a design scheme of reflection coefficient based on DL is proposed in this section.

4.1. The SDR-Based Algorithm

We introduce the auxiliary variables Θ = d i a g ( H R U ) H B R and v = [ v 1 , ⋯ , v i , ⋯ , v M ] H , v n = e j 2 π p i , n ∈ [ 1 , M ] . Then we can find that H R U ϕ H B R = v H Θ . Therefore, the optimization problem (14) can be rewritten as
max v v H Θ Θ H v + v H Θ H B U + H B U H Θ H v , s . t . | v i | = 1 , ∀ 0 < = i < M .
Obviously, (41) is a non-convex quadratic constrained quadratic programming(QCQP) problem, and (41) can be rewritten as a homogeneous QCQP problem. Then, by introducing an auxiliary variable t, problem (41) can be rewritten as
max v ¯ v ¯ H R v ¯ , s . t . | v ¯ i | = 1 , ∀ 0 < = i < = M ,
where
R = Θ Θ H Θ H B U H B U H Θ H 0 , v ¯ = v t .
We define V = v ¯ v ¯ H , which needs to satisfy V ⪰ 0 and r a n k ( V ) = 1 . Since the constraint of rank 1 is non-convex, SDR is used to relax the constraint, so (42) can be rewritten as
max V t r ( R V ) , s . t . V i , i = 1 , ∀ 0 < = i < = M , V ⪰ 0 .
It can be seen that (44) is a standard convex semidefinite problem, and thus can be optimally solved by existing convex optimization solvers like CVX. Finally, we can obtain a suboptimal solution for v:
v ∗ = e j a r g ( [ v ¯ v ¯ M ] ( 0 : M − 1 ) ) ,
where a r g ( · ) denotes the the magnitude of a complex number. [ a ] denotes the first M elements of the vector.

4.2. The Proposed Beam Tracking Scheme Based on DL

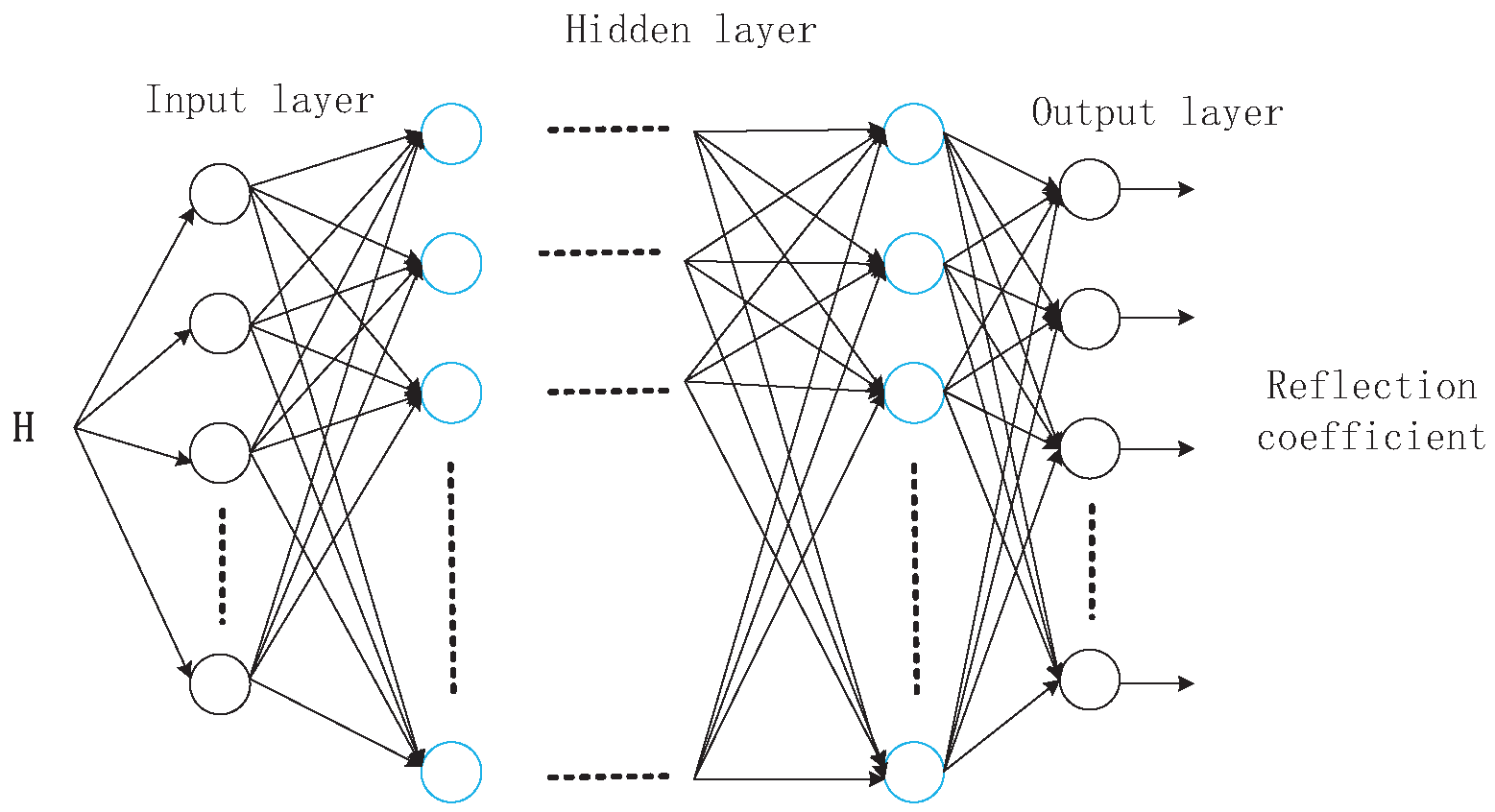
Considering the high computational complexity and unstable performance of SDR-based algorithms, we propose a DL-based framework to achieve a more efficient and stable optimal reflection coefficient of the RIS in this section. Figure 3 is the structure diagram of the DNN designed in this paper, which contains seven hidden layers, one input layer and one output layer.
As shown in Figure 3, H is the input to the network, which consists of channels H B R , H R U and H B U . However, considering that the channel H is a complex matrix, it cannot be directly input to the neural network. Therefore, the virtual and real parts need to be combined as the input, which is given by
H = [ R e ( v e c ( H B R ) ) , I m ( v e c ( H B R ) ) , R e ( H R U ) , I m ( H R U ) , R e ( H B U ) , I m ( H B U ) ] T ,
where R e ( · ) and I m ( · ) denote the real and imaginary parts of complex elements, respectively. Then, the dimension of the input vector H is 1 × ( 2 ∗ M ∗ N + M + N ) . We selects seven hidden layers after repeated experiments. To ensure the scalability of the system, the numbers of neurons in each layer are set to 64 N , 32 N , 16 N , 8 N , 4 N , N , which are proportional to the number of antennas on the base station. In addition, after comparing the network effects under various activation functions, we finally select the linear rectification function (Rectified Linear Unit, ReLu) as the activation function of the hidden layer, and the linear function as the activation function of the output layer. Meanwhile, to prevent the overfitting of the network, we choose to add the BatchNorm layer by comparing the actual effects of the BatchNorm(BN) layer and the Dropout layer.
After setting up the structure of the network, we use negative (14) as the loss function to train the network. Considering that the output value of the network is a real number, and the reflection coefficient of the RIS should be a complex number, the Lambda layer is designed to convert the output value of the real number into complex, which is expressed as
v = c o s ( o ) + j · s i n ( o ) = e j · o ,
where o is the output of the network.
Algorithm 1: 
1: Turn off the RIS and use the PCA-based channel estimation method to estimate the channel between the base station and the UT.
2: The UT sends a pilot sequence to the RIS, the RIS estimate the channel between the UT and the RIS based on the proposed PCA algorithm.
3: According to the channel reciprocity of the TDD system, the channel between the RIS and the UT can be obtained.
4: The base station sends a pilot sequence to the RIS, and estimates the channel between the base station and the RIS according to the correlation between adjacent antennas and the PCA algorithm.
5: Obtain the reflection coefficient by substituting the estimated channel into the trained DNN.
Based on the above analysis and research, the beam tracking scheme for RIS-aided MISO systems can be concluded as Algorithm 1 listed in above.

5. Simulation Results

In order to evaluate the performance of the proposed algorithms, numerical results have been obtained by performing computer simulations. The system configuration is defined by the following choice of parameters: the antenna space and reflecting elements space is set to d s = λ / 2 . In addition, all channels in this paper are modeled using Rayleigh small-scale fading, and the path loss in dB is expressed as 20.4 l o g 10 ( d / d r e f ) , where d and d r e f = 1 m denote distance and reference distance, respectively. Finally, the transmit power is 5 d B m and the noise power is − 70 d B m .

5.1. Convergence Analysis under Different Network Structures

Fristly, we assume that three distinguishable paths between the BS and the UT, the BS and the RIS, and the RIS and the UT. Meanwhile, each path has a corresponding azimuth and elevation angle. To compare the superiority of the network structure proposed in this paper, we replace the BN layer in the designed DNN with the Dropout layer for comparison, both of which are used to avoid overfitting. Then, according to M = 16 , N = 64 , M = 16 , N = 16 and M = 64 , N = 16 three different base station antenna and RIS reflector unit configurations, we randomly generate 100,000 sets of channel data for DNN training. In addition, the initial learning rate of the Adam optimizer is set to 0.001. Also, the epoch and batchsize are set to 50 and 500, respectively.
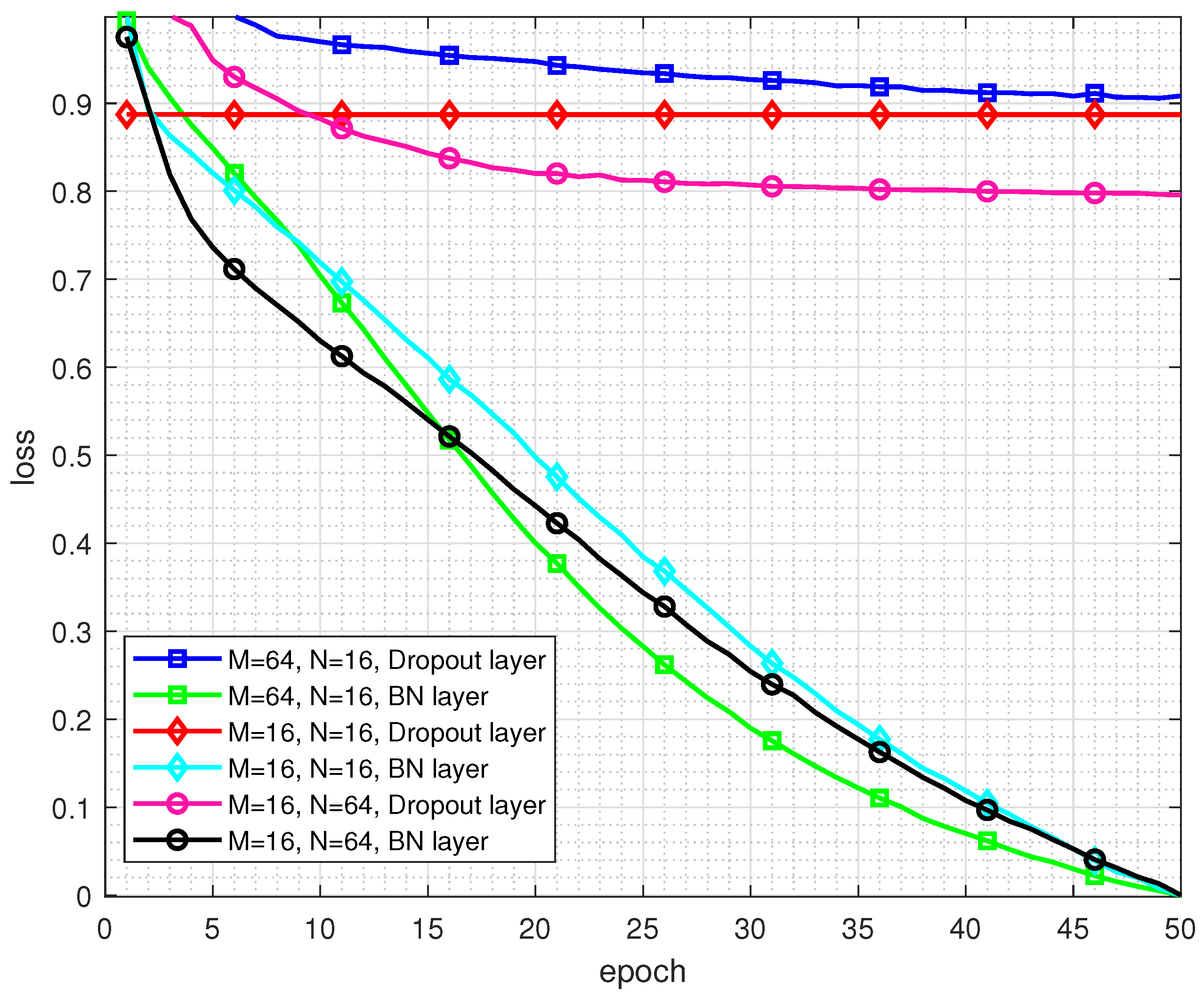
The convergence performance under different network structures is shown in Figure 4. To compare the loss function values under various system configurations intuitively, we normalize and change the value while retaining the original convergence trend. As shown in Figure 4, the networks based on the BN layer can converge very well, while the networks based on the Dropout layer can hardly converge. Therefore, it demonstrates the applicability of the BN layer in this model. Both the BN layer and the Dropout layer are used to avoid overfitting, but for the seven-layer network architecture proposed in this paper, subtle parameter changes will be infinitely amplified. Then, the input distribution will change greatly, which make the network difficult to adapt to changes and fail to converge. Therefore, the normalization of the BN layer can reduce the influence of differences in the distribution of different batches of training data by changing the distribution of the data, and speed up the network convergence and improve the generalization ability of the network.

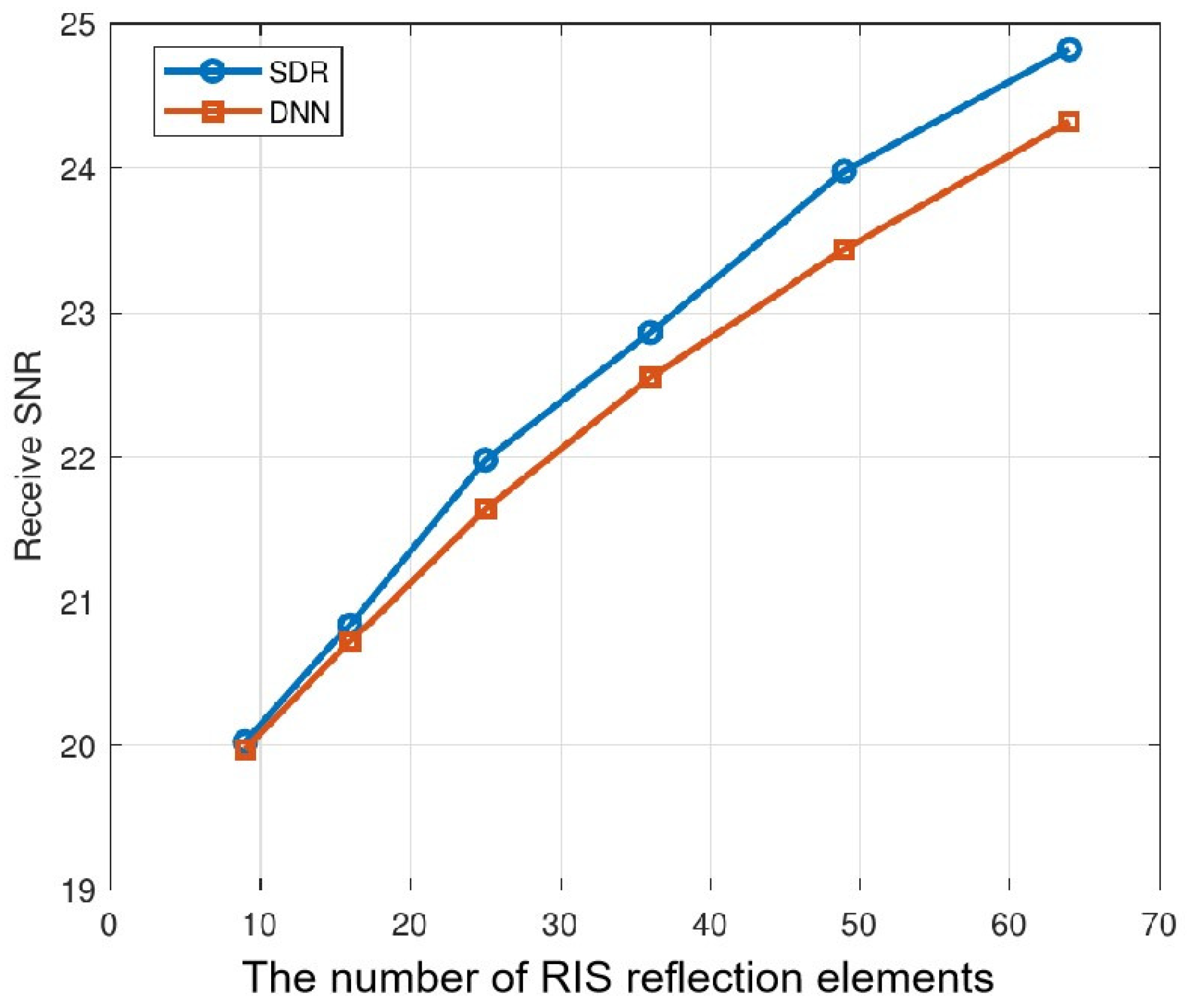
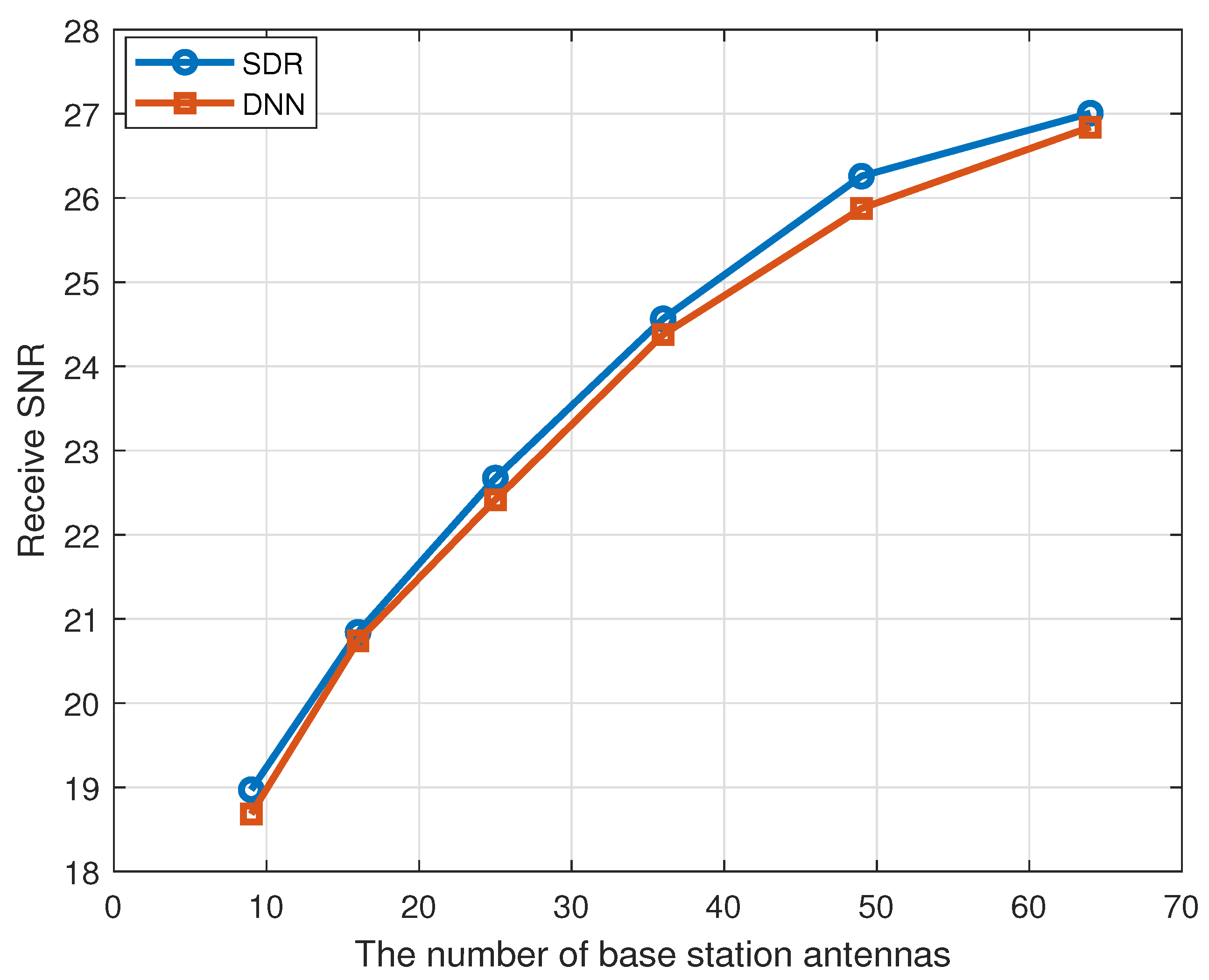
5.2. Performance Analysis under Different Configurations

In this subsection, we generate 1000 sets for prediction based on the network model trained in the previous section. Then, the effects of different configurations of antennas and reflection elements on system performance are analyzed. Among them, the number of base station antennas in Figure 5 is 16, and the number of RIS reflection elements in Figure 6 is 64. From the Figure 5 and Figure 6, we can observe that the received SNR improves as the number of antennas and reflection elements becomes larger. Meanwhile, it is not difficult to find that the performance of the DNN-based reflection coefficient estimation algorithm proposed in this paper is very close to the SDR algorithm.

5.3. Complexity Analysis

Based on [18], the complexity of SDR approach is O ( ( N + 1 ) 6 ) , while the complexity of the proposed DL-based scheme is O ( ( 2788 + 128 M ) N 2 ) . To compare the performance of these two different algorithms, the running times of the two schemes under different RIS configurations are shown in Table 1. Both algorithms run under the configuration of Core i5-9400F and RTX2060s for consistency. Furthermore, both algorithms make predictions on the same 100 sets of data. The SDR-based algorithm spends much more time than the DL-based scheme, which verifies the effectiveness of our proposed DL-based beam tracking algorithm.

6. Conclusions

In this paper, we have proposed a channel estimation and a beam tracking method for RIS-assisted MISO systems. Firstly, we have divided the channel estimation of the system into three stages based on PCA algorithm. Then, we have achieved the channel estimation between the base station and the RIS, and between the RIS and the UT through a specific semi-passive RIS device. Next, we have developed a DNN which is used to estimate the RIS reflection coefficient. Finally, Compared with the traditional SDR algorithm, the simulation results demonstrate the superiority of the proposed scheme in terms of computational complexity.

Author Contributions

Conceptualization: R.G., R.Y.; methodology: R.G., R.Y.; software: J.Y., C.X.; investigation: R.G., G.W., J.Y.; resources: R.G., R.Y.; data curation: J.Y., C.X.; writing—original draft preparation: R.G., J.Y.; writing—review and editing: R.G., R.Y.; visualization: R.G., G.W.; funding acquisition: R.G., R.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by the China Postdoctoral Science Foundation under Grant 2023M743063 and the Zhejiang Provincial Postdoctoral Scholarship under Grant ZJ2022107, in part by the National Natural Science Foundation of China under Grant 61771429, Grant 62302197 and Grant 62271438, Zhejiang Provincial Natural Science Foundation of China under Grant LQ23F020006.

Acknowledgments

The authors would like to thank the China Postdoctoral Science Foundation, the Zhejiang Provincial Postdoctoral Scholarship, National Natural Science Foundation of China (NSFC), Zhejiang Provincial Natural Science Foundation of China (ZPNSFC), Hangzhou City University and Zhejiang University for support this work.

Conflicts of Interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

  1. Liaskos, C.; Nie, S.; Tsioliaridou, A.; Pitsillides, A.; Ioannidis, S.; Akyildiz, I. A new wireless communication paradigm through software-controlled metasurfaces. IEEE Communications Magazine 2018, 56, 162–169. [Google Scholar] [CrossRef]
  2. Liang, Y.C.; Long, R.; Zhang, Q.; Chen, J.; Cheng, H.V.; Guo, H. Large intelligent surface/antennas (LISA): Making reflective radios smart. Journal of Communications and Information Networks 2019, 4, 40–50. [Google Scholar] [CrossRef]
  3. Hu, S.; Rusek, F.; Edfors, O. Beyond massive MIMO: The potential of data transmission with large intelligent surfaces. IEEE Transactions on Signal Processing 2018, 66, 2746–2758. [Google Scholar] [CrossRef]
  4. Cui, T.J.; Qi, M.Q.; Wan, X.; Zhao, J.; Cheng, Q. Coding metamaterials, digital metamaterials and programmable metamaterials. Light: Science & Applications 2014, 3, 218–218. [Google Scholar]
  5. Chen, J.; Liang, Y.C.; Cheng, H.V.; Yu, W. Channel estimation for reconfigurable intelligent surface aided multi-user MIMO systems. arXiv preprint arXiv:1912.03619 2019. arXiv:1912.03619 2019.
  6. Chen, Z.; Tang, J.; Zhang, X.Y.; So, D.K.C.; Jin, S.; Wong, K.K. Hybrid evolutionary-based sparse channel estimation for IRS-assisted mmWave MIMO systems. IEEE Transactions on Wireless Communications 2021, 21, 1586–1601. [Google Scholar] [CrossRef]
  7. He, Z.Q.; Yuan, X. Cascaded channel estimation for large intelligent metasurface assisted massive MIMO. IEEE Wireless Communications Letters 2019, 9, 210–214. [Google Scholar] [CrossRef]
  8. Mirza, J.; Ali, B. Channel estimation method and phase shift design for reconfigurable intelligent surface assisted MIMO networks. IEEE Transactions on Cognitive Communications and Networking 2021, 7, 441–451. [Google Scholar] [CrossRef]
  9. Liu, H.; Yuan, X.; Zhang, Y.J.A. Matrix-calibration-based cascaded channel estimation for reconfigurable intelligent surface assisted multiuser MIMO. IEEE Journal on Selected Areas in Communications 2020, 38, 2621–2636. [Google Scholar] [CrossRef]
  10. Ning, B.; Chen, Z.; Chen, W.; Du, Y. Channel estimation and transmission for intelligent reflecting surface assisted THz communications. In Proceedings of the ICC 2020-2020 IEEE International Conference on Communications (ICC). IEEE; 2020; pp. 1–7. [Google Scholar]
  11. Dai, H.; Zhang, Z.; Gong, S.; Xing, C.; An, J. Training Optimization for Subarray-Based IRS-Assisted MIMO Communications. IEEE Internet of Things Journal 2021, 9, 2890–2905. [Google Scholar] [CrossRef]
  12. Zhou, Z.; Ge, N.; Wang, Z.; Hanzo, L. Joint transmit precoding and reconfigurable intelligent surface phase adjustment: A decomposition-aided channel estimation approach. IEEE transactions on communications 2020, 69, 1228–1243. [Google Scholar] [CrossRef]
  13. Taha, A.; Alrabeiah, M.; Alkhateeb, A. Enabling large intelligent surfaces with compressive sensing and deep learning. IEEE access 2021, 9, 44304–44321. [Google Scholar] [CrossRef]
  14. Liu, S.; Gao, Z.; Zhang, J.; Di Renzo, M.; Alouini, M.S. Deep denoising neural network assisted compressive channel estimation for mmWave intelligent reflecting surfaces. IEEE Transactions on Vehicular Technology 2020, 69, 9223–9228. [Google Scholar] [CrossRef]
  15. Alexandropoulos, G.C.; Vlachos, E. A hardware architecture for reconfigurable intelligent surfaces with minimal active elements for explicit channel estimation. In Proceedings of the ICASSP 2020-2020 IEEE international conference on acoustics, speech and signal processing (ICASSP). IEEE; 2020; pp. 9175–9179. [Google Scholar]
  16. Hu, X.; Zhang, R.; Zhong, C. Semi-passive elements assisted channel estimation for intelligent reflecting surface-aided communications. IEEE Transactions on Wireless Communications 2021, 21, 1132–1142. [Google Scholar] [CrossRef]
  17. Zhang, S.; Zhang, R. Capacity characterization for intelligent reflecting surface aided MIMO communication. IEEE Journal on Selected Areas in Communications 2020, 38, 1823–1838. [Google Scholar] [CrossRef]
  18. Wu, Q.; Zhang, R. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Transactions on Wireless Communications 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
  19. Wu, Q.; Zhang, R. Beamforming optimization for wireless network aided by intelligent reflecting surface with discrete phase shifts. IEEE Transactions on Communications 2019, 68, 1838–1851. [Google Scholar] [CrossRef]
  20. Liang, P.; Fan, J.; Shen, W.; Qin, Z.; Li, G.Y. Deep learning and compressive sensing-based CSI feedback in FDD massive MIMO systems. IEEE Transactions on Vehicular Technology 2020, 69, 9217–9222. [Google Scholar] [CrossRef]
  21. Qin, Z.; Ye, H.; Li, G.Y.; Juang, B.H.F. Deep learning in physical layer communications. IEEE Wireless Communications 2019, 26, 93–99. [Google Scholar] [CrossRef]
  22. Lin, T.; Zhu, Y. Beamforming design for large-scale antenna arrays using deep learning. IEEE Wireless Communications Letters 2019, 9, 103–107. [Google Scholar] [CrossRef]
  23. Elbir, A.M.; Papazafeiropoulos, A.K. Hybrid precoding for multiuser millimeter wave massive MIMO systems: A deep learning approach. IEEE Transactions on Vehicular Technology 2019, 69, 552–563. [Google Scholar] [CrossRef]
  24. Taha, A.; Zhang, Y.; Mismar, F.B.; Alkhateeb, A. Deep reinforcement learning for intelligent reflecting surfaces: Towards standalone operation. In Proceedings of the 2020 IEEE 21st international workshop on signal processing advances in wireless communications (SPAWC). IEEE; 2020; pp. 1–5. [Google Scholar]
  25. Taha, A.; Alrabeiah, M.; Alkhateeb, A. Deep learning for large intelligent surfaces in millimeter wave and massive MIMO systems. In Proceedings of the 2019 IEEE Global communications conference (GLOBECOM). IEEE; 2019; pp. 1–6. [Google Scholar]
  26. Feng, K.; Wang, Q.; Li, X.; Wen, C.K. Deep reinforcement learning based intelligent reflecting surface optimization for MISO communication systems. IEEE Wireless Communications Letters 2020, 9, 745–749. [Google Scholar] [CrossRef]
  27. Xu, L. Least mean square error reconstruction principle for self-organizing neural-nets. Neural networks 1993, 6, 627–648. [Google Scholar] [CrossRef]
  28. Adali, T.; Haykin, S. Adaptive signal processing: next generation solutions; Vol. 55, John Wiley & Sons, 2010.
Preprints 114695 g001
Figure 1. system model.
Figure 1. system model.
Preprints 114695 g001
Preprints 114695 g002
Figure 2. The structure of RIS.
Figure 2. The structure of RIS.
Preprints 114695 g002
Preprints 114695 g003
Figure 3. The DL network structure.
Figure 3. The DL network structure.
Preprints 114695 g003
Preprints 114695 g004
Figure 4. Loss under different configuration.
Figure 4. Loss under different configuration.
Preprints 114695 g004
Preprints 114695 g005
Figure 5. Received SNR versus the number of RIS reflection elements.
Figure 5. Received SNR versus the number of RIS reflection elements.
Preprints 114695 g005
Preprints 114695 g006
Figure 6. Received SNR versus the number of BS antennas.
Figure 6. Received SNR versus the number of BS antennas.
Preprints 114695 g006
Table 1. Running time comparison.
Table 1. Running time comparison.
Configuration Run time
SDR DNN
M = 16 , N = 16 49.8893s 0.1816s
M = 16 , N = 64 107.0052s 0.2233s
M = 64 , N = 16 121.5610s 0.2613s
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated