Effects of Loading and Perforation Parameters on Rock Deformation and Damage Behaviors Induced by Dynamic Loadings Caused by the Fracturing of Tight Oil Reservoirs

Preprint

Article

Effects of Loading and Perforation Parameters on Rock Deformation and Damage Behaviors Induced by Dynamic Loadings Caused by the Fracturing of Tight Oil Reservoirs

Altmetrics

Downloads

Views

Comments

Bo Chen,

Abulimiti Aibaibu,Yuan Liu,Xinwei Guo,Hua Zhou,Xiangyun Zhao,

Bolong Zhu^*

Bo Chen,

Abulimiti Aibaibu,Yuan Liu,Xinwei Guo,Hua Zhou,Xiangyun Zhao,

Bolong Zhu^*

This version is not peer-reviewed

Submitted:

09 August 2024

Posted:

09 August 2024

You are already at the latest version

Alerts

Abstract

This study presents a numerical analysis of rock deformation and damage behaviors induced by dynamic loadings, specifically focusing on the fracturing of tight oil reservoirs. An elastoplastic model based on finite element methods was utilized to simulate the effects of varying loading and perforation parameters. Three distinct scenarios were modeled: a single perforation, boundary loading on three sides, and multiple perforations, each providing unique insights into the mechanical responses of the rock material. The analysis revealed that dynamic effects are highly localized around perforations and loaded boundaries across all scenarios. Acceleration magnitudes are captured with rapid attenuation observed as the distance from the perforation increased. This indicated that the highest stress concentrations and deformation occurred close to the points of loading or perforation. Strain rate analysis in the x direction showed significant fluctuations near the perforations, reflecting intense stress redistributions and compressive deformation, especially prominent in the scenario with multiple perforations. Plastic strain, representing irreversible damage, was found to concentrate near perforation tips and loaded boundaries. However, the pattern of plastic strain accumulation varied: in the small domain scenario with boundary loading, plastic strain did not immediately accumulate next to the loading boundary, whereas in scenarios with single and multiple perforations, damage developed from the loading boundaries. These findings highlight the need for precise control in perforation and dynamic loading processes to manage stress and deformation effectively. It is concluded that optimizing perforation patterns and loading strategies can enhance reservoir stimulation efficiency while minimizing unintended damage to the surrounding formation.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

Hydraulic fracturing has been widely used in the development of tight oil reservoirs. Hydraulic fractures help to establish channels for oil and gas fluid flows in originally low-permeability reservoirs. In some scenarios, pulsated hydraulic fracturing designs are considered as this technique can facilitate loading-induced rock deformation and damage, which helps the formation of main fractures during hydraulic fracturing treatment. Rock deformation and rock failure under complex loading conditions are very relevant in hydraulic fracturing related geomechanics. Accurately quantifying and characterizing these processes is important for optimizing hydraulic fracturing operations and enhancing tight oil recovery.

In order to improve the understanding of these behaviors, recent progresses have focused on experimental methods, numerical simulations, and the integration of multiple approaches to provide comprehensive insights into rock mechanical responses to various types of loadings associated with tight oil development. Relevant experimental techniques are focused on the anisotropic responsive patterns, compression testing techniques, shearing and hydrostatic loadings, and the use of CT imaging for better visualization of deformation and damage. Togashi et al. (2017) introduced an experimental method to characterize anisotropic mechanical responses by measuring deformation magnitudes at different orientations in individual tests. This approach has advanced the understanding of anisotropic behavior in rock mechanics, which is crucial for predicting the response of reservoir rocks under complex loading conditions. Single-stage and multi-stage compression tests were compared to analyze induced damage in rock samples. This comparison quantified the importance of considering the loading history when evaluating rock strength and deformation properties. It also helped the calibration of constitutive models used in numerical simulations (Aghababaei et al. 2019). Kluge et al. (2020) discussed a method to evaluate shear failures in rock samples under hydrostatic loads, emphasizing the effect of hydromechanical interactions in rock deformation. This study improves the understanding of failure mechanisms in reservoir rocks subjected to high-pressure fluid injections. In another study that focuses more on rock mechanical heterogeneities, Chen et al. (2021) conducted numerical and experimental studies on the highly non-uniform mechanical responses in tight rock samples. The matching of experimental data with simulation results improved the reliability of their analyses. In a similar approach, Baumgarten and Konietzky (2013) demonstrated the advantages of combining experimental and numerical methods to characterize post-failure behaviors. In addition to compression tests and numerical simulation, the visualization of deformation and failure is also a helpful strategy. Guo et al. (2021) utilized computed tomography (CT) alongside triaxial compressional tests to better understand heterogeneous mechanical responses and damage accumulations in heterogeneous reservoir rocks. This integration of imaging techniques enhanced the resolution, accuracy, and reliability of rock deformation and damage quantification.

The derivation of governing equations related to rock mechanical responses and its numericalization and also widely used for the improvement of the understanding of rock deformation and damage under complex loadings. An analytical solution in Laplace-Fourier space was derived to capture transient behaviors of the poroelastodynamic field in the near-well reservoir rocks. This analytical approach provides a framework for understanding the dynamic responses of reservoir rocks under various loading conditions, including hydraulic fracturing (Xia et al. 2017). In a series of modeling studies for the rock mechanical behaviors under pulsated fracturing in tight reservoir rocks, Hou et al. (2021, 2022a, 2022b) have characterized the pressure and stress propagations in tight rocks under dynamic loadings induced by pulsating hydraulic fracturing where oscillatory loadings were exerted. The results showed that dynamic loadings help to induce damage accumulation and fracture initiation, with pressure wave propagation closely related to rock mechanical properties and pulse frequencies. Fakhimi et al. (2018) utilized physical and numerical methods to analyze rock strength under impact and dynamic loads using the Split Hopkinson Pressure Bar (SHPB) testing. Kim et al. (2020) then examined the acceleration behaviors caused by the inertia effect of lateral confinement in SHPB testing, providing insights into strain rates caused by dynamic impact loads. These studies have contributed to understanding the behavior of rocks under high strain rates and dynamic loading conditions. In a numerical investigation, Prabhu and Qiu (2021) employed the discrete element method (DEM) to simulate stress-strain relationships for solids under impact loads. This numerical study considered both stress equilibrium and nonequilibrium assumptions, offering a comprehensive perspective on the mechanical response of rocks under dynamic conditions. Based on experimental and numerical understanding of the mechanical responses induced by dynamic loadings, implications for brittleness and fracability quantification are also achieved. Lecampion et al. (2018), Chen et al. (2021), and Guo et al. (2021) promoted the importance of rock mechanical responsive patterns in governing brittleness and fracability. Zhang et al. (2021) proposed an experimental method to quantify the effect of loading rates and lithologies on acoustic emission denoted by Kaiser effects during in-situ stress measurements. The study established loading rate selection criteria, which are crucial for accurate stress measurements in reservoir rocks. Wang et al. (2022) and Wei et al. (2022) discussed strategies for optimizing laboratory determination of formation damage, where permeability evolution was used as an index. Their studies provide references for optimizing perforation designs and modeling fracture initiation processes, essential for enhancing hydraulic fracturing efficiency.

Based on the literature review, it can be noted that recent progresses in the study of rock deformation and failure under various loading conditions have advanced the understanding of geomechanical behaviors in reservoir rocks under dynamic and pulsated loadings. Experimental approaches, numerical simulations, and their integration have provided more accurate and reliable insights into the mechanical responses of rocks, crucial for optimizing hydraulic fracturing operations. In addition to these progresses, it is noted that the numerical investigation of rock mechanical responses to pulsated fracturing can be improved by examining the effect of the hydraulic fracturing perforation parameters.

In this study, an elastoplastic model is used to examine the rock deformation and damage behaviors under dynamic loading caused by hydraulic fracturing in tight reservoir rocks. Both elastic and plastic behaviors are captured in the model with the inertia effect considered. Stress, strain, and acceleration results are discussed in the several scenarios with various perforation configurations and loading parameters. This study helps to provide insights into the optimization of hydraulic fracturing parameters and perforation parameters during the development of tight oil reservoirs.

2. Numerical Model

In this study, a numerical model that considers the dynamics and elastoplastic behaviors is used for quantitative analyses. The dynamic hydraulic fracturing load on the tight oil reservoir rock is treated as a boundary load on the rock solid. The boundary load is also evolving with time. This study is limited to the very early stages of the dynamic loading to reflect the initial rock deformation and failure, which can be used to quantify the easiness of main fracture formation. The plane stress assumption is used in this model. In addition, this model is focused on the solid mechanical field in the reservoir rock.

In the first place, the basic momentum balance equation is shown as:

ρ \frac{\partial^{2} u}{\partial t^{2}} = \nabla \cdot σ + ρ b

(1)

where

u

is the displacement;

σ

is the stress;

ρ

is rock density;

b

is the body force (gravity in this scenario). The time derivative term is used to calculate acceleration and the inertial effect.

The dynamic boundary load introduced by fracturing on the reservoir rock is depicted by:

σ \cdot n = t

(2)

σ \cdot n = 0

(3)

where

t

is used to denote the evolving loading condition. It is prescribed as a boundary condition as a function of time in Eq. (2). Similarly, Eq.(3) indicates a fixed boundary.

After the exertion of loading, in the elastic regime, linear stress and strain relationship is used for calculation. When it enters plasticity, the Drucker-Prager criterion is involved:

F = \sqrt{J_{2}} + α I_{1} - k

(4)

α = \frac{s i n ϕ}{\sqrt{3}}

(5)

k = \frac{2 c \cdot c o s ϕ}{\sqrt{3}}

(6)

Eq. (4) shows the yielding criterion

F

where invariant

I_{1}

and invariant

J_{2}

are involved. In this study, the Drucker-Prager criterion is matched to the Mohr-Coulomb criterion through the two constants

α

and

k

as in Eq. (5) and Eq. (6). As key Mohr-Coulomb constants,

ϕ

is the internal friction angle and

c

is the cohesion.

Since the dissipation problem is involved in solving for the dynamic response in the reservoir rocks, special numerical strategies as shown in Eq. (7) to Eq. (11) are used.

u_{n + 1} = u_{n} + Δ t {\frac{d u}{d t}}_{n} + \frac{Δ t^{2}}{2} ((1 - 2 β) {\frac{d^{2} u}{d t^{2}}}_{n} + 2 β {\frac{d^{2} u}{d t^{2}}}_{n + 1})

(7)

{\frac{d u}{d t}}_{n + 1} = {\frac{d u}{d t}}_{n} + Δ t ((1 - γ) {\frac{d^{2} u}{d t^{2}}}_{n} + γ {\frac{d^{2} u}{d t^{2}}}_{n + 1})

(8)

{\frac{d^{2} u}{d t^{2}}}_{n + 1} = M^{- 1} (f_{n + 1} - K u_{n + 1} - C {\frac{d u}{d t}}_{n + 1})

(9)

u_{n + 1} = u_{n} + Δ t {\frac{d u}{d t}}_{n} + Δ t^{2} ((\frac{1}{2} - β) {\frac{d^{2} u}{d t^{2}}}_{n} + β {\frac{d^{2} u}{d t^{2}}}_{n + 1})

(10)

{\frac{d u}{d t}}_{n + 1} = {\frac{d u}{d t}}_{n} + Δ t ((1 - γ) {\frac{d^{2} u}{d t^{2}}}_{n} + γ {\frac{d^{2} u}{d t^{2}}}_{n + 1})

(11)

where

u

is the displacement; subscripts

n

and

n + 1

are used to denote time steps;

\frac{d^{2} u}{d t^{2}}

is the solid acceleration;

Δ t

is the time step size;

β

and

γ

are numerical parameters denoting damping and stability during the solution;

M

is the mass matrix;

f

is the external force related to

t

;

K

is a stiffness matrix;

C

is a damping matrix.

Eq. (7) is used to update the displacement field. It computes displacement at the next time step based on its current position, velocity, and acceleration. It incorporates the linear motion governed by current velocities and the acceleration effect. Eq. (8) updates the velocity of the system for the next time step. It integrates the acceleration effects into the velocity, accounting for the change due to the forces applied during the time step. Eq. (9) is the acceleration update that is essential for determining the dynamic response of the system to the forces applied. It solves the balance of forces by considering the inertia, the damping effect, and the stiffness of the system, which are used for understanding how the reservoir rocks respond under dynamic loads introduced by fracturing. Eq. (10) and Eq. (11) are used to improve the predictions made by Eq. (7) to Eq. (9) by incorporating additional parameters that control numerical damping and oscillations. They balance the current displacement and velocity with the newly predicted accelerations to provide updated estimates of these quantities

3. Results and Discussion

In the numerical study, several scenarios are investigated. In these cases, different domain sizes and perforation parameters are analyzed. Specifically, three scenarios are considered: the first scenario is a 3 by 15 m domain with loadings exerted on the right boundary; the second scenario is a small near-perforation domain with 5 by 5 cm; the third scenario is 1 by 5 m where multiple perforations in a cluster are modeled.

3.1. Scenario 1

In the first case, a 3 by 15 m domain is used to denote the near-well and near-perforation reservoir. The domain length is 3 m in the x direction and 15 m in the y direction. In the base case, two perforations at (3 m, 5 m) and (3 m, 10 m) are prescribed on the right boundary. The loading on these two locations is 50 MPa/0.01 ms. The Young’s modulus of the reservoir rock is 30 GPa and the Poisson’s ratio is 0.2. Rock density is assumed as 2600 kg/m³. The cohesion is 8 MPa and the internal friction angle is 30°.

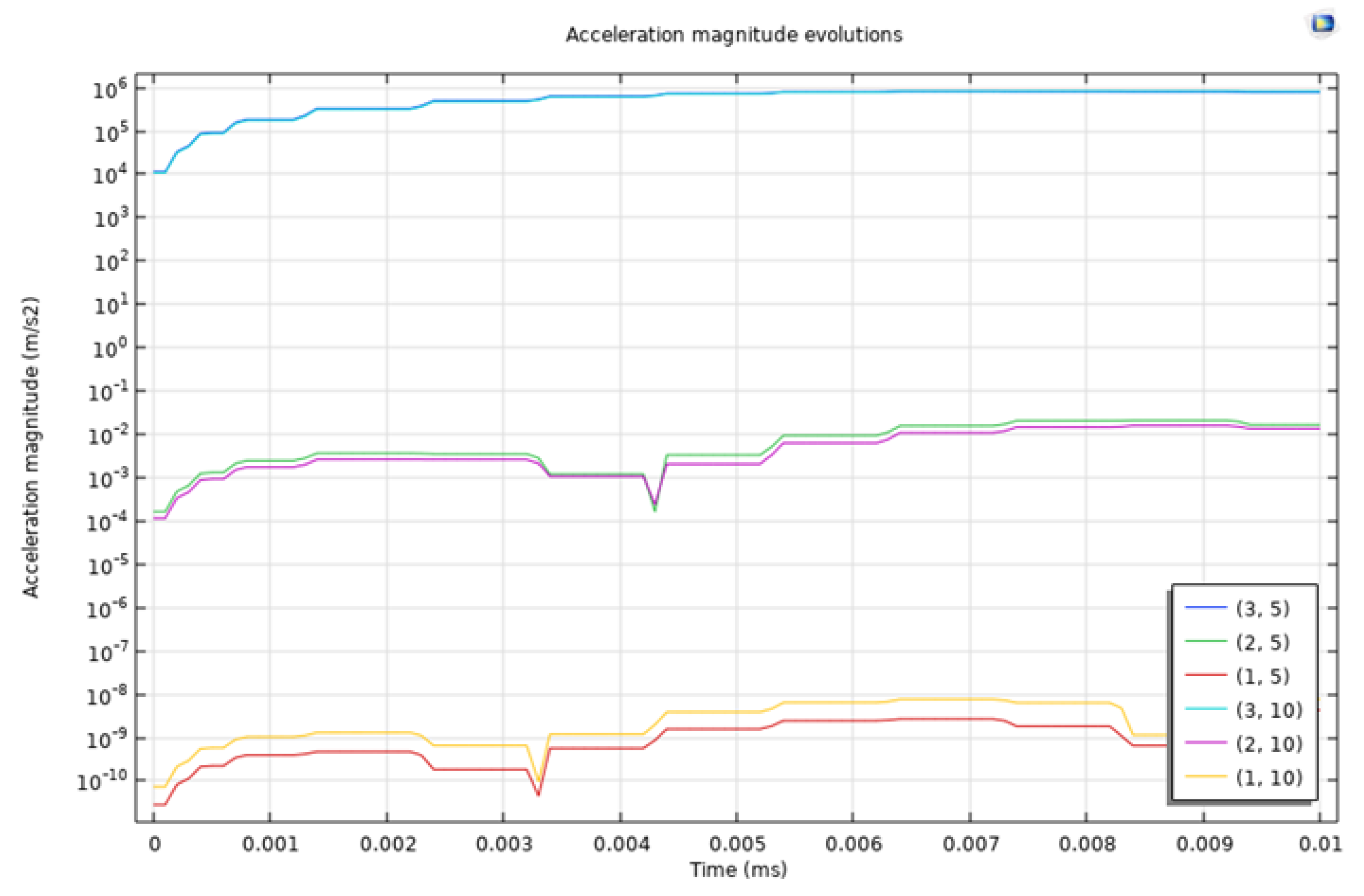
Figure 1 shows the temporal evolution of acceleration at six different monitoring points (1, 5), (2, 5), (3, 5), (1, 10), (2, 10), and (3, 10). Monitoring points (3, 5) and (3, 10) correspond to the two perforations exerting loadings. The graph illustrates the evolution of acceleration magnitudes over a duration of time 0 to 0.01 ms subjected to dynamic loading. The monitoring points (3, 5) and (3, 10) correspond to the highest acceleration magnitudes observed in these points. Specifically, the acceleration magnitude at point (3, 5) reaches values in the range of 10⁶ m/s², which indicates a significant impact due to the dynamic loading caused by fracturing operations. This high acceleration is attributed to the localized stress concentrations and rapid deformation near the perforation, which is driven by the sudden release of energy associated with the hydraulic fracturing process. In contrast, the other monitoring points (1, 5), (2, 5), and (1, 10) show relatively lower acceleration magnitudes, suggesting a more alleviated dynamic response. These points are positioned further away from the perforations. They experience less direct impact from the loadings, resulting in lower accelerations in the range of 10⁻¹⁰ m/s² to 10⁻⁷ m/s². The consistent acceleration curve patterns with small perturbations reflect the relatively consistent propagation of dynamic waves through the material. The observed curve dips at around 0.003 ms indicate interactions of stress waves within the reservoir rock medium, which can be attributed to the effect of domain boundaries.

Figure 1. Acceleration of rock solid in the domain at monitoring points of (1, 5), (2, 5), (3, 5), (1, 10), (2, 10), and (3, 10).

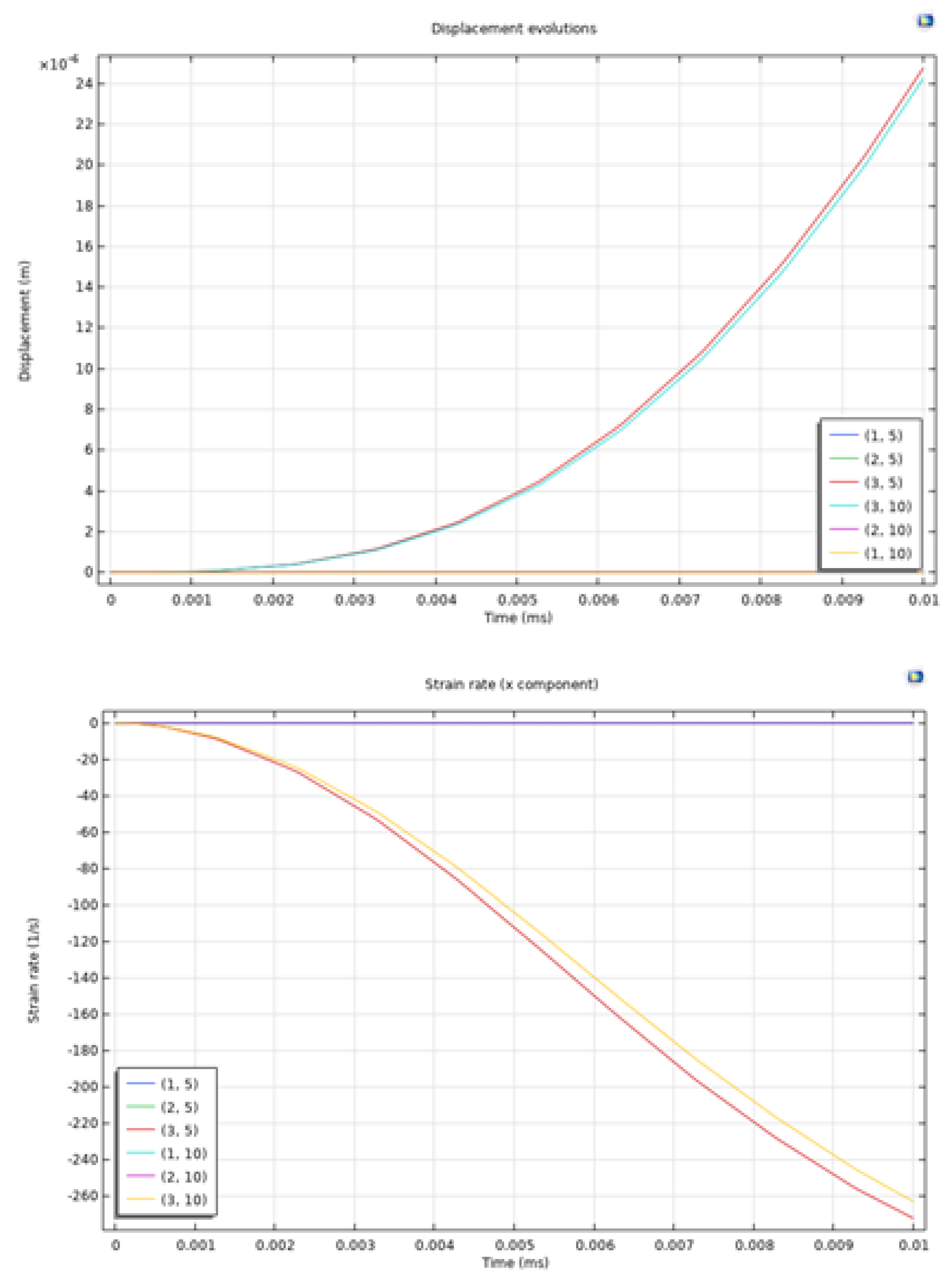
Figure 2 shows the displacement and strain rate in the x direction for these 6 monitoring points. The displacement evolution graph shows a clear trend of increasing displacement over time at various monitoring points, with the highest values observed for points (3, 5) and (3, 10), which are the locations of the perforations. The displacement magnitudes at these points exhibit an exponential growth pattern, reaching approximately 24×10⁻⁴ m at 0.01 ms. This rapid increase in displacement indicates significant deformation near the perforations due to the applied dynamic loadings, indicating the pronounced mechanical response in these regions. Other monitoring points (1, 5), (2, 5), and (1, 10) show similar exponential trends but with lower overall displacements, indicating that while the dynamic effects are existent throughout the medium, they are less intense further from the perforations. The strain rate evolution in the x direction is in accordance with the displacement observations. The graph indicates a decreasing strain rate trend over time, with the most significant changes at points (3, 5) and (3, 10). These points show strain rates decreasing from around -20 1/s to approximately -260 1/s in the same time period. This trend suggests a rapid rate of deformation at the beginning of dynamic loading exertion. The other monitoring points exhibit less rapid changes in strain rates, indicating their lower exposure to the dynamic loadings. All monitoring points experience similar strain rate evolution patterns, suggesting a uniform material response to the applied dynamic loadings. Also, perforation areas experience the most significant strain due to their proximity to the load application.

Figure 2. Displacement and strain rate in the x direction of rock solid in the domain at monitoring points of (1, 5), (2, 5), (3, 5), (1, 10), (2, 10), and (3, 10).

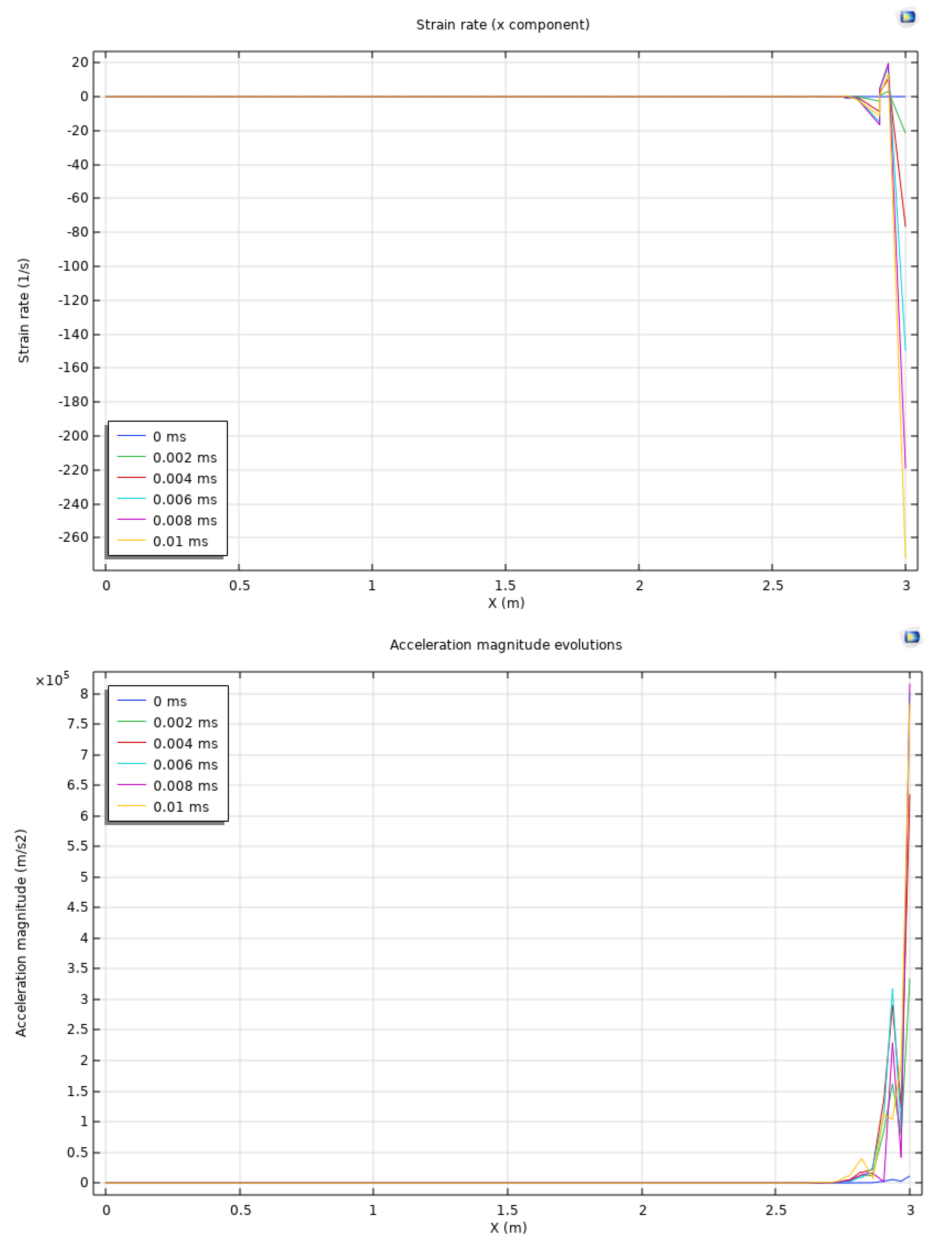
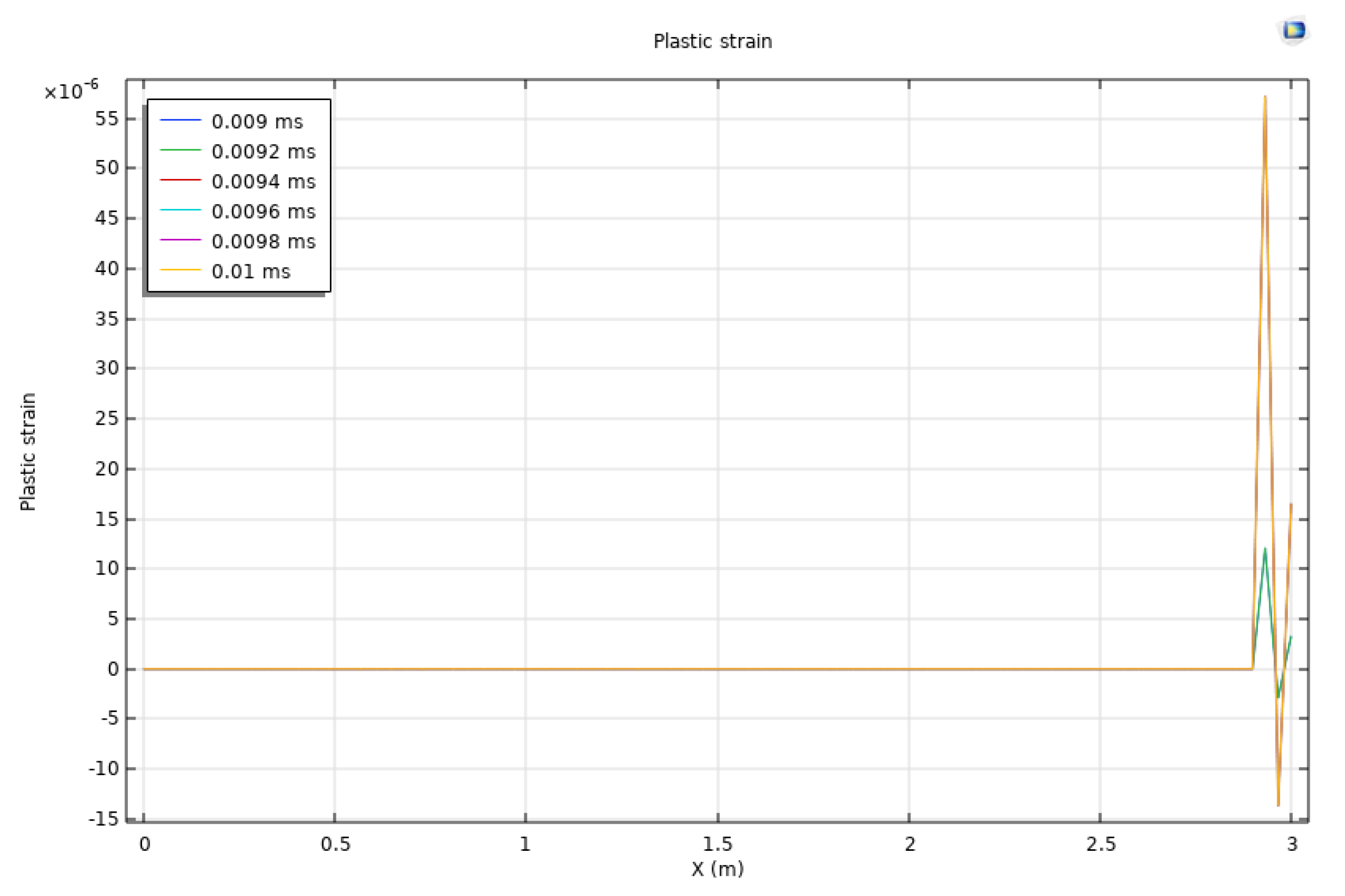
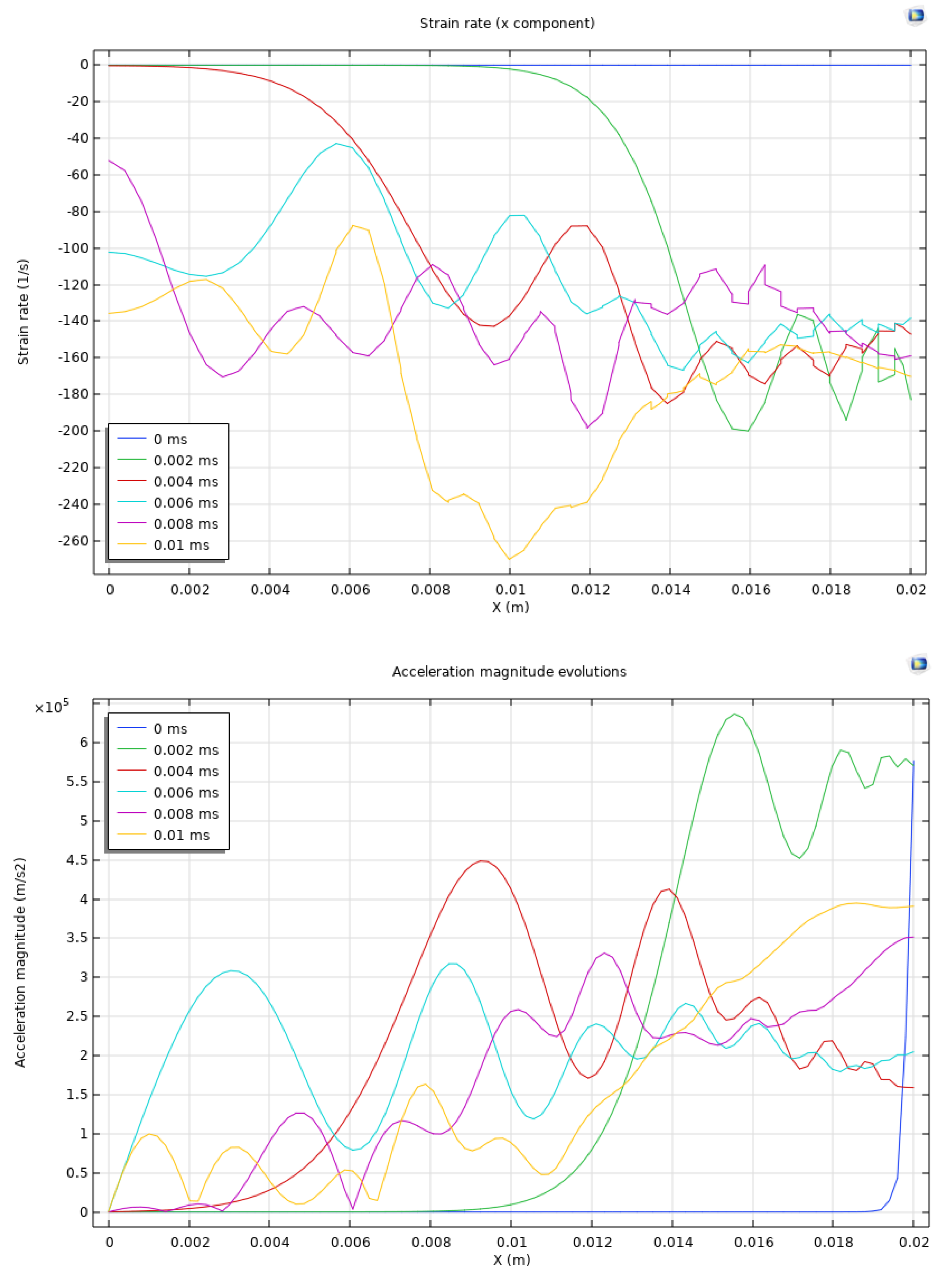
In Figure 3, a monitoring line at y = 6.5 m spanning from x = 0 to x = 3 m is involved. This line is used to examine the scale of the affected area after the exertion of dynamic loadings. Results of strain rate in the x direction, acceleration magnitude, and plastic strain are plotted at 0 ms, 0.002 ms, 0.004 ms, 0.006 ms, 0.008 ms, and 0.01 ms. The strain rate in the x direction shows an initial rapid increase near x=3 due to the location of the perforation. Over time, this strain rate decreases from -20 1/s at 0 ms to approximately -260 1/s by 0.01 ms, indicating that deformation is primarily localized near the perforation region. This sharp gradient in strain rate suggests the high impact of dynamic loading in a confined spatial region, with limited propagation into the reservoir. It also reflects the local stress concentration due to the loading exerted during hydraulic fracturing, while the affected area is limited to a narrow band near the perforations. The acceleration magnitude evolution also indicates the strong dynamic effects near the perforations. Initially, there is a sharp increase in acceleration magnitude, reaching 8×10⁵ m/s² near x = 3 m, and this acceleration is existent over time. In addition, it gradually decreases as the energy dissipates. The acceleration magnitude result shows the immediate and localized nature of the dynamic response, with acceleration rapidly decreasing as it moves away from the two perforations on the right boundary. This trend is in accordance with the patterns from strain rate observations. The limited affected area that is confined to the vicinity of x = 3 m further confirms the localized impact of the dynamic loading. The plastic strain distribution then illustrates the permanent deformation characteristics (or damage) induced by the dynamic loading. Plastic strain is generally negligible throughout the majority of the domain, except near x = 3 m, where it suddenly increases sign to 55×10⁻⁶. This indicates that the reservoir rock has experienced irreversible deformation in the vicinity of the perforations, with the plastic strain accumulating primarily from 0.009 ms to 0.01 ms. The localized nature of plastic strain is substantiated by the substantial and lasting impact of dynamic loadings near the perforation regions. The affected area scale is rather limited, indicating that the structural impact of dynamic loading is restricted to a narrow band around the perforations.

Figure 3. Strain rate in the x direction, acceleration magnitude, and plastic strain are plotted at 0 ms, 0.002 ms, 0.004 ms, 0.006 ms, 0.008 ms, and 0.01 ms. The monitoring line is at y = 6.5 m spanning from x = 0 to x = 3 m.

3.2. Scenario 2

In the second case, a smaller model is investigated to understand the effect of perforation size on the dynamic rock mechanical response in the reservoir rock. In this case, a 5 cm by 5 cm domain is modeled while a perforation with a width of 1 cm and a length of 3 cm is explicitly analyzed. All other modeling inputs are the same as the previous scenario.

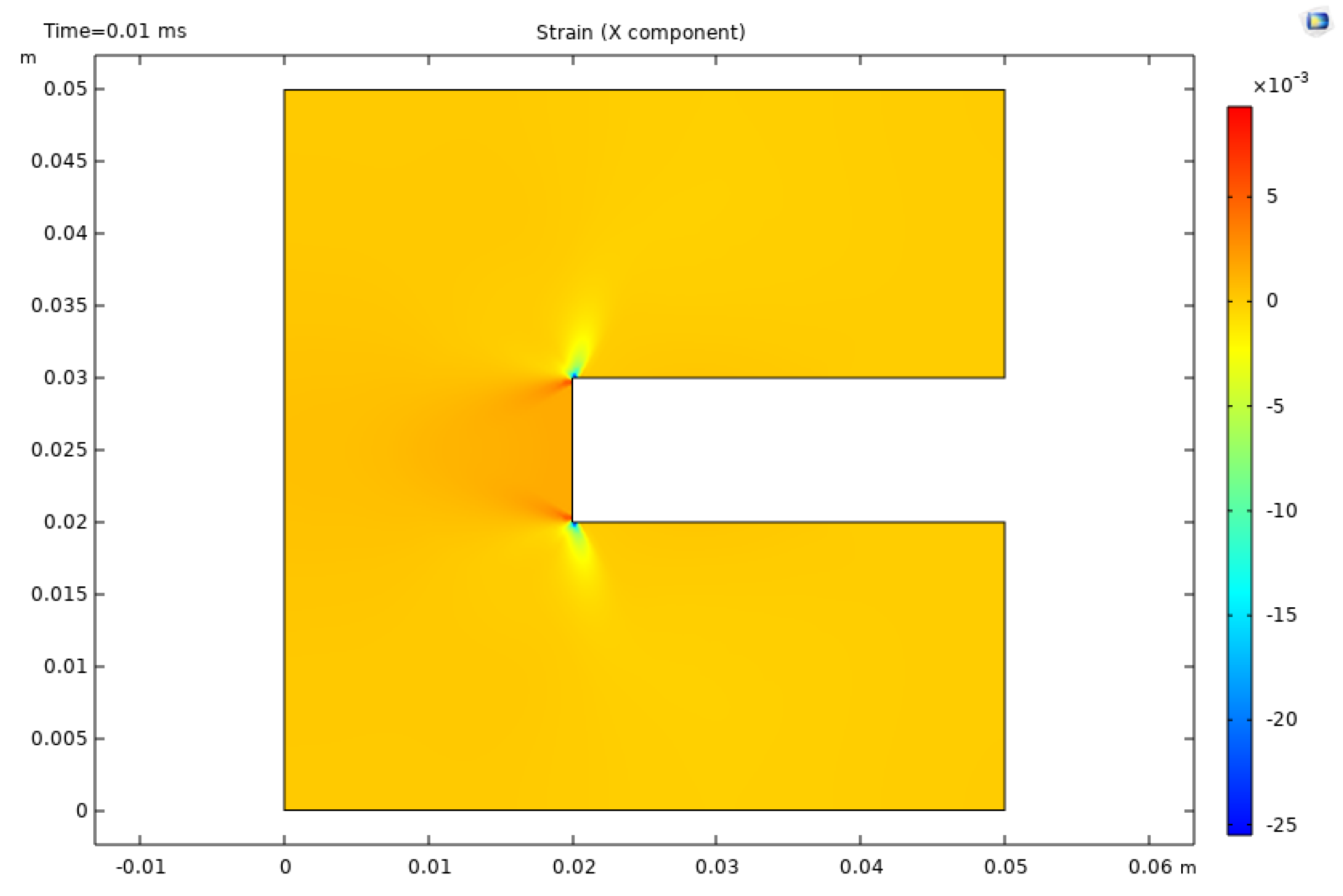
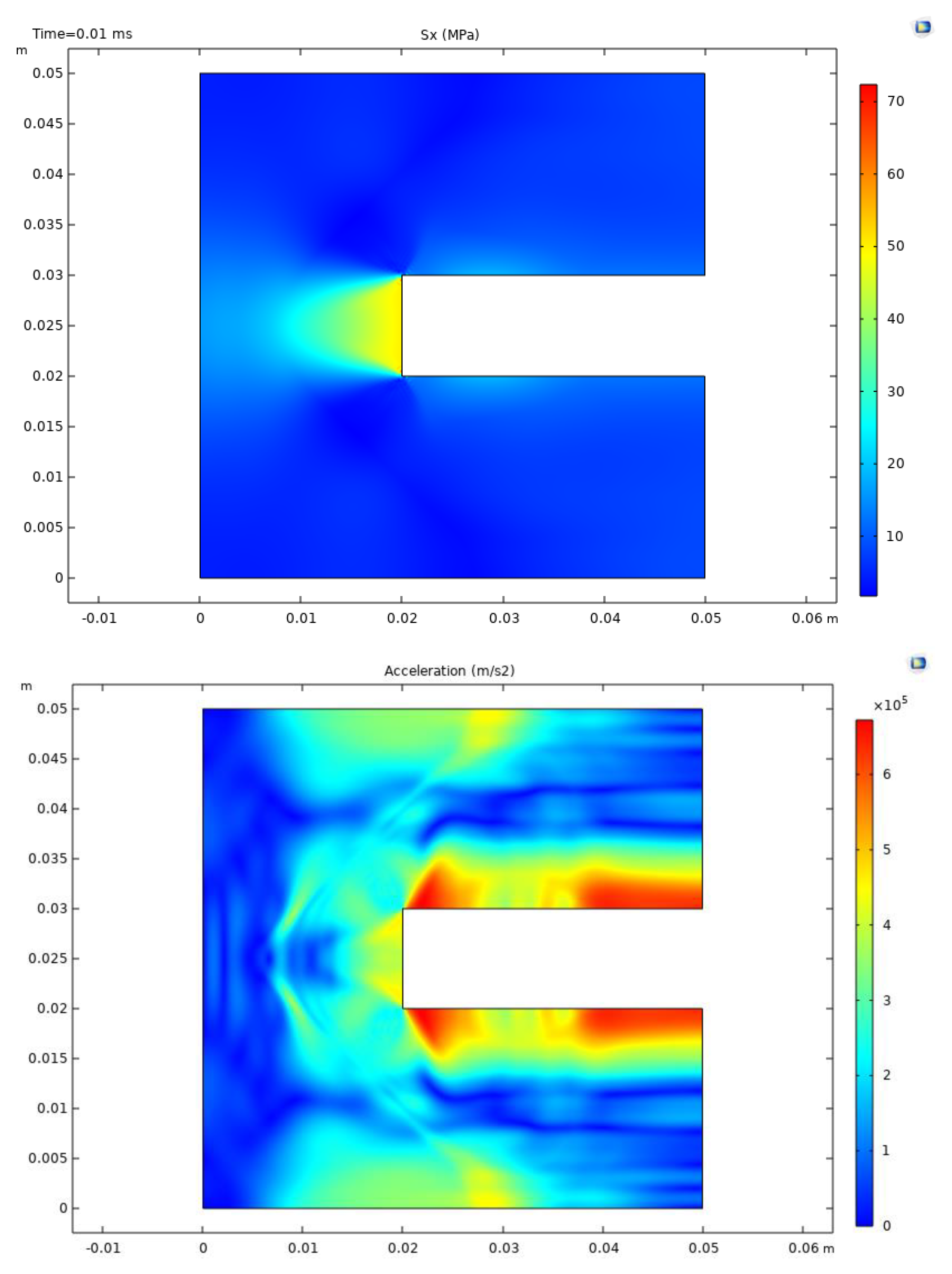
Figure 4 shows the strain in the x direction, stress in the x direction, and acceleration after 0.01 ms of loading. The perforation is explicitly represented by the rectangle. Sharp strain perturbations are observed at the two tips of the perforation with sudden change from positive strains to negative strains. Results of stress in the x direction are largely orientation-dependent, as strong stress increases are observed in the x direction extending from the perforation tip. The acceleration results further indicate the wavy propagation pattern caused by the boundary loading.

Figure 4. Strain, stress, and acceleration results after 0.01 ms of loading in scenario 2.

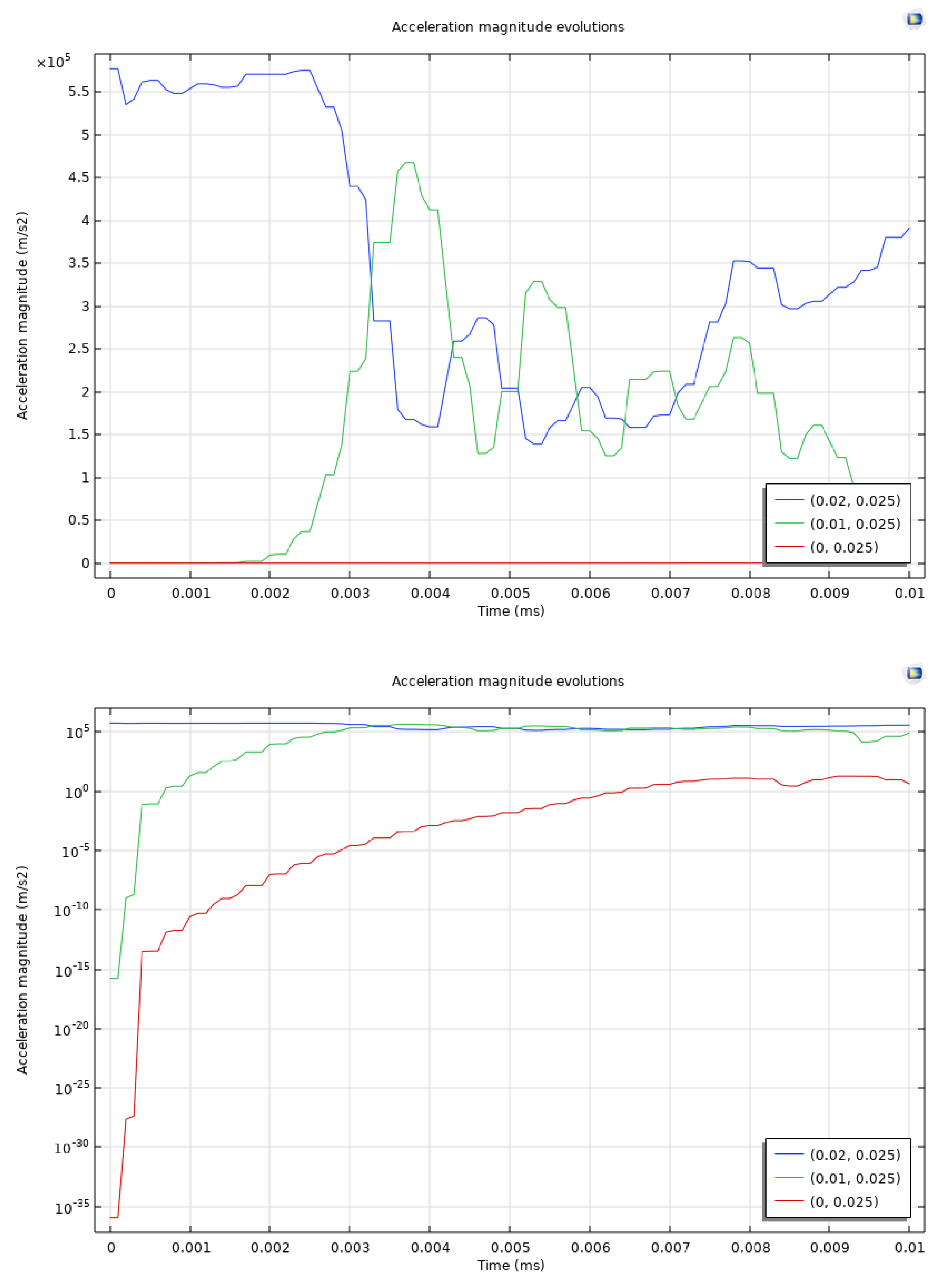
In Figure 5, acceleration of rock solid in the domain at monitoring points of (0.02, 0.025), (0.01, 0.025), and (0, 0.025). In order to better visualize the temporal trends, both Cartesian and semi-log plots are presented. In the Cartesian plot, it is observed that the acceleration magnitude at point (0.02, 0.025) exhibits the highest values, reaching approximately 5.5×10⁵ m/s² within the initial 0.002 ms. This is attributed to the fact that this point at the boundary load experiences the most significant impact due to the dynamic loading, reflecting the high stress and rapid deformation in this region. The acceleration then shows fluctuations, indicating non-uniform interactions and wave propagations within the rock. Similarly, point (0.01, 0.025) experiences great acceleration magnitudes slightly lower than (0.02, 0.025), reaching around 4.5×10⁵ m/s². This indicates that the dynamic effects are still significant but attenuated as the distance from the load increases. In contrast, point (0, 0.025) shows negligible acceleration, remaining nearly constant at a very low value, indicating minimal impact from the dynamic loading at this farthest point. The semi-log plot provides additional visualization of the acceleration evolution trends. It especially quantifies the orders of magnitude differences between the three monitoring points. The initial rapid increase in acceleration for points (0.02, 0.025) and (0.01, 0.025) is also honored, indicating the effect of high dynamic stresses. The acceleration at point (0, 0.025) is orders of magnitude lower, indicating the localized nature of the dynamic loading effects and the limited area affected. These results show the high acceleration values near the perforation, indicating significant local stress and risk for rock failure.

Figure 5. Acceleration of rock solid in the domain at monitoring points of (0.02, 0.025), (0.01, 0.025), and (0, 0.025) plotted in Cartesian and semi-log plots.

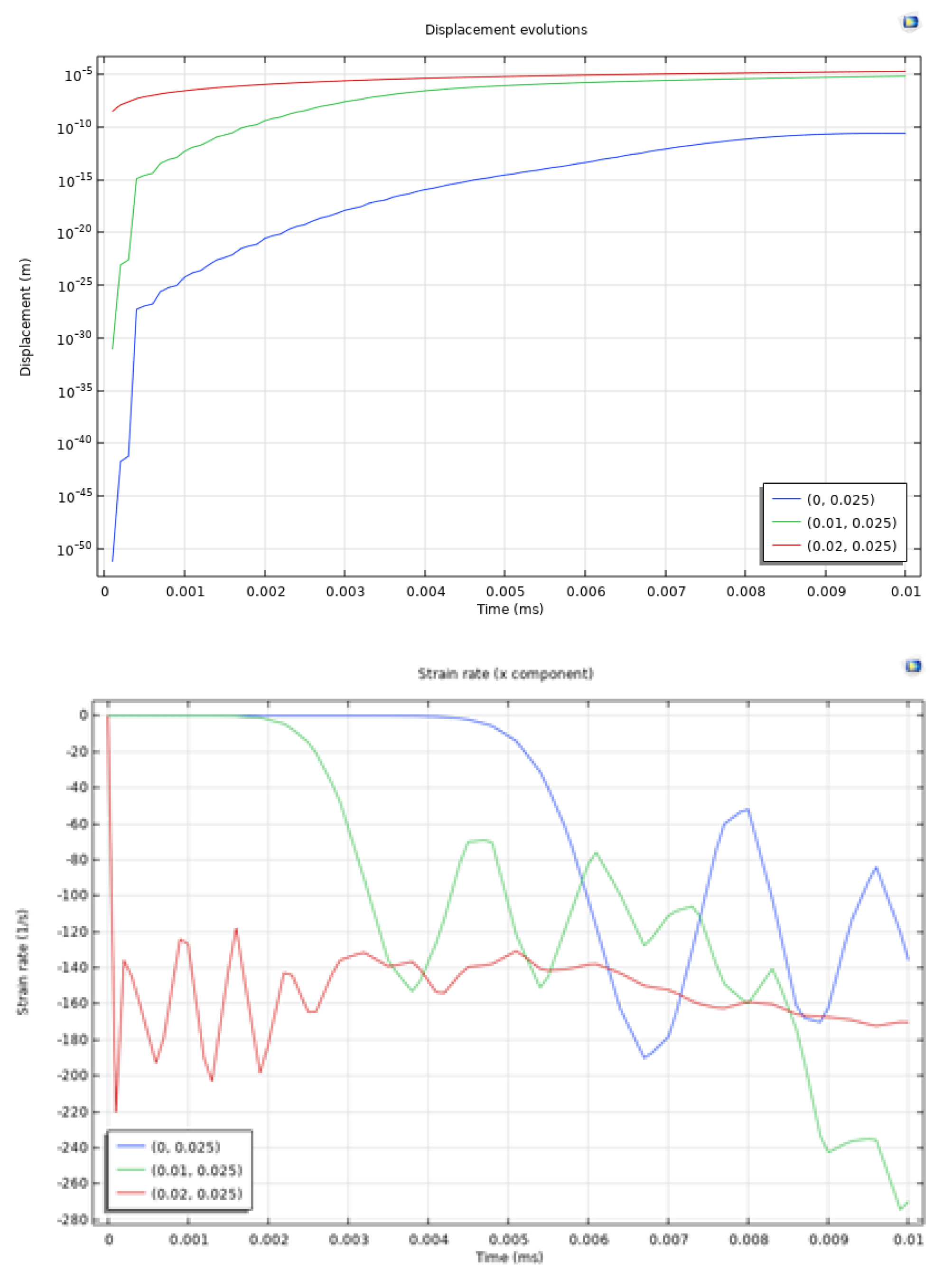
In Figure 6, the displacement and strain rate in the x direction for the rock solid in the domain at the monitoring points (0.02, 0.025), (0.01, 0.025), and (0, 0.025) are presented to understand the rock mechanical response under dynamic loading boundary conditions. The semi-log plot of displacement evolutions demonstrates significant differences in displacement magnitudes at the three monitoring points. Point (0.02, 0.025), located closest to the boundary load, exhibits the highest displacement values, reaching up to 10⁻⁵ m. This rapid increase in displacement indicates significant deformation due to the applied dynamic load. Point (0.01, 0.025) also exhibits significant displacement, indicating an attenuation of the dynamic effects with distance from the loading boundary. In contrast, point (0, 0.025) displays negligible displacement, remaining constant at very values close to zero throughout the time, indicating the limited impact region of the dynamic load. The overall trend suggests that the dynamic loading effects are very localized, with significant deformation confined to areas near the load application. In addition, the strain rate evolution in the x direction helps to further quantify the deformation responses. At point (0.02, 0.025), the strain rate experiences the most significant fluctuation: it initially reaches -100 1/s and then oscillates between -240 1/s and 20 1/s. This indicates the complex wave interaction and stress redistribution near the loading point of the perforation. Point (0.01, 0.025) shows similar patterns while the strain rates are lower, indicating that dynamic effects attenuate as it moves away from the loading boundary. Like previous cases, the strain rate at point (0, 0.025) remains relatively stable, oscillating around -20 1/s, which again substantiates the fact that the dynamic loading boundary can only affect certain localized areas. The displacement and strain rate results indicate that the dynamic responses are highly localized near the perforations. The displacement magnitudes show that the boundary loading regions undergo the most significant deformation, while the strain rate oscillations indicate complex stress redistributions and wave interactions in these areas.

Figure 6. Displacement and strain rate in the x direction of rock solid in the domain at monitoring points of (0.02, 0.025), (0.01, 0.025), and (0, 0.025).

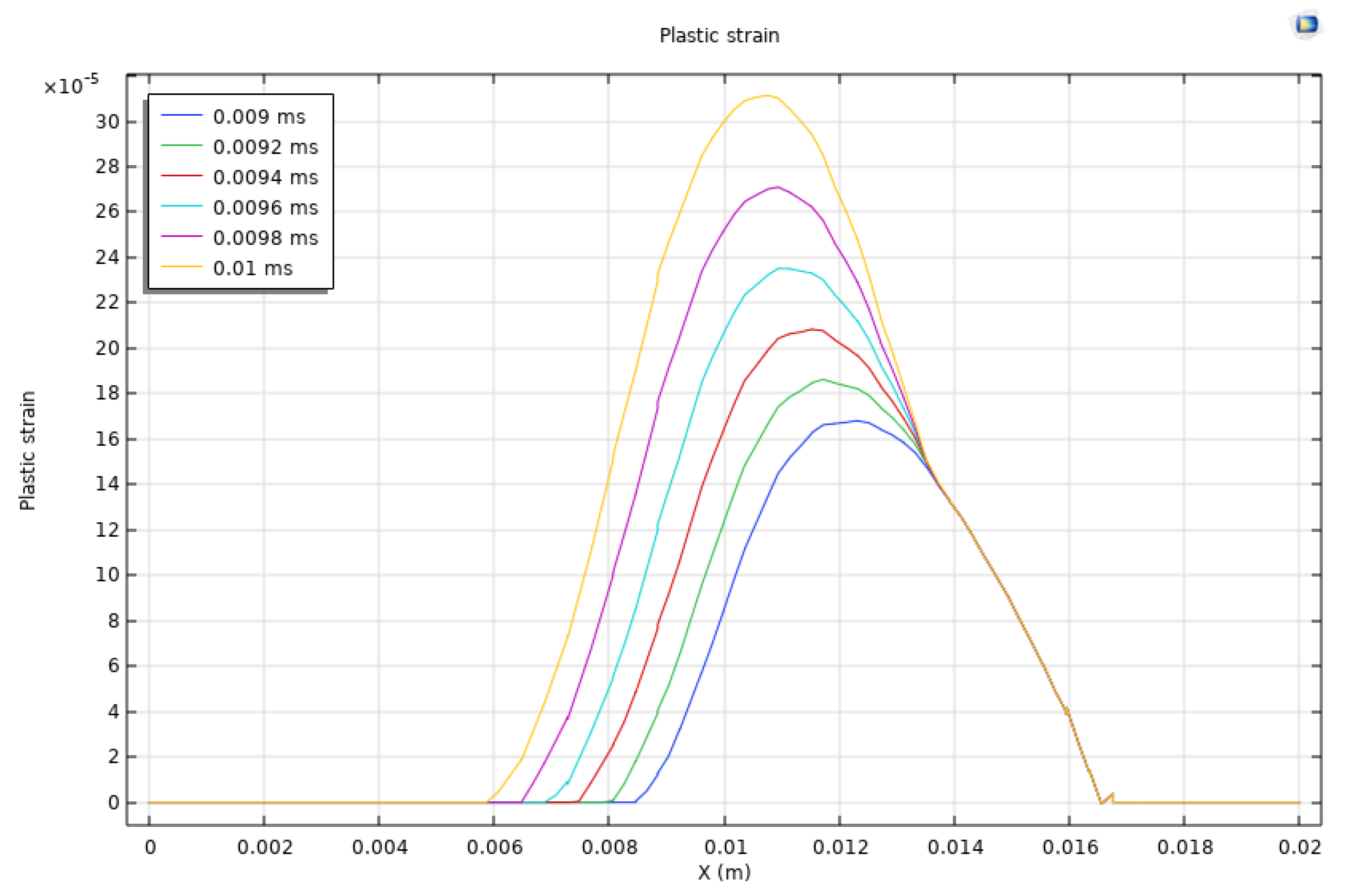
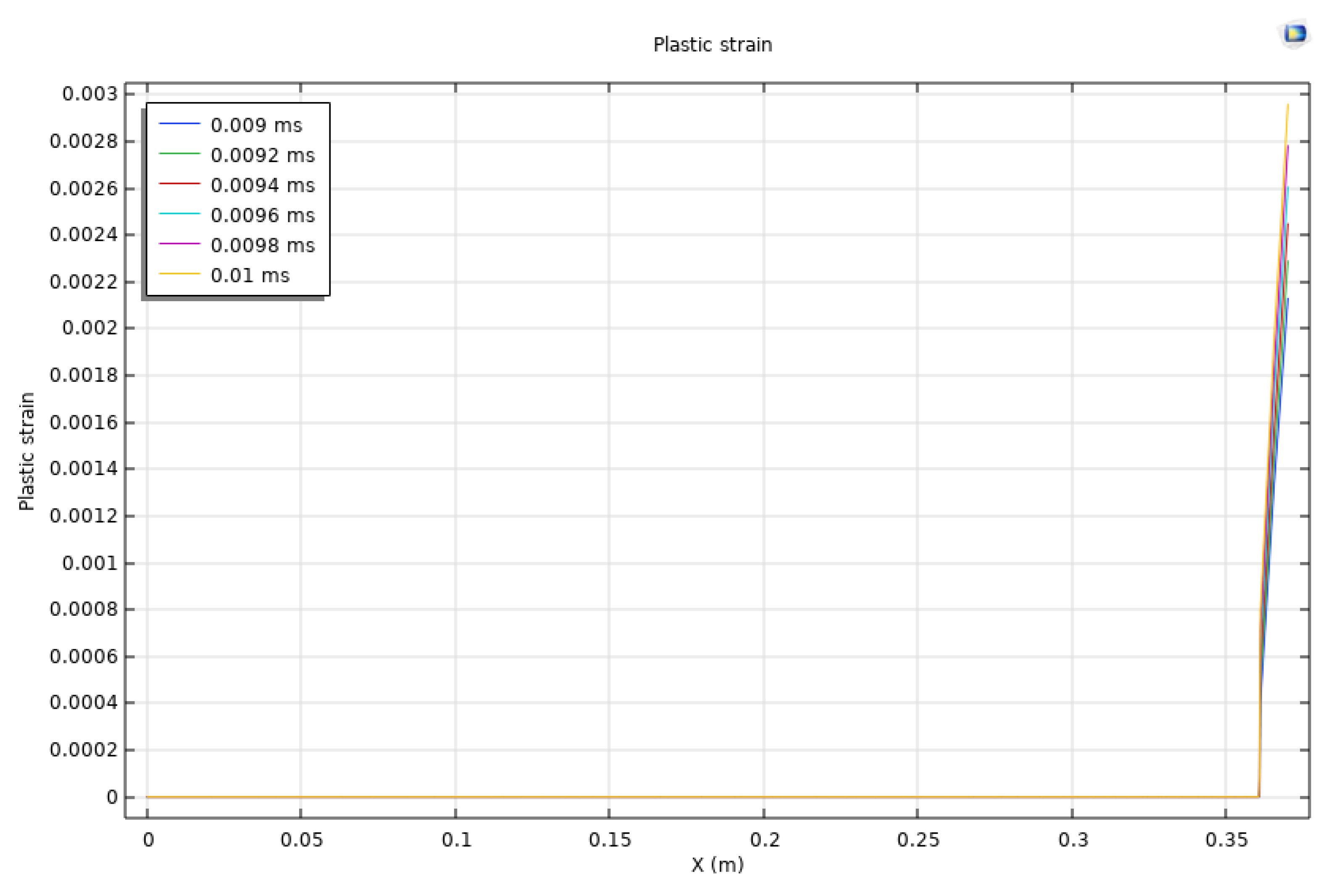
After discussing the temporal evolution patterns at several monitoring points, the spatial distribution patterns at the monitoring line of y = 0.025 m and x spanning from 0 to 0.02 m are investigated in Figure 7. Strain rate in the x direction and acceleration magnitude are plotted at 0 ms, 0.002 ms, 0.004 ms, 0.006 ms, 0.008 ms, and 0.01 ms. The plastic strain is plotted at 0.009 ms, 0.0092 ms, 0.0094 ms, 0.0096 ms, 0.0098 ms, and 0.01 ms. The monitoring line is at y = 0.025 m spanning from x = 0 to x = 0.02 m. Plastic strain results are limited to the later stages due to the fact that plastic strains and irreversible damage are not captured at the beginning.

The strain rate in the x direction displays noticeable variations along the x-axis at different time steps. At early time steps of 0.002 ms and 0.004 ms, the strain rate exhibits strong fluctuations near the boundaries of the perforation. At time steps between 0.006 ms and 0.01 ms, these oscillatory patterns become more pronounced, which reflects the fierce and heterogeneous stress redistribution and wave propagations within the reservoir rock. The acceleration magnitude along the monitoring line shows the dynamic response at various time steps. At 0.002 ms, there is a sudden increase at and around x = 0.01 m reaching 6×10⁵ m/s². It indicates the simultaneous response to the exertion of the applied dynamic load. Over the entire loading time, the acceleration patterns are generally oscillatory. The plastic strain evolution provides quantification of the induced irreversible damage. Note that only results after 0.009 ms are shown as plasticity is only captured at later stages of loading exertion. At time steps of 0.009 ms and 0.0096 ms, the plastic strain gradually increases at and near x = 0.01 m, indicating the onset of permanent deformation and damage. As 0.01 ms, the plastic strain reaches its peak at around 3×10⁻⁵. A nearly normal distribution centered around x = 0.01 m is observed. This pattern indicates that, instead of the boundary loading region, the oscillatory and wavy dynamic responses lead to the most prominent damage within the reservoir rock away from the boundary loading region.

Figure 7. Strain rate in the x direction and acceleration magnitude are plotted at 0 ms, 0.002 ms, 0.004 ms, 0.006 ms, 0.008 ms, and 0.01 ms. The plastic strain is plotted at 0.009 ms, 0.0092 ms, 0.0094 ms, 0.0096 ms, 0.0098 ms, and 0.01 ms. The monitoring line is at y = 0.025 m spanning from x = 0 to x = 0.02 m.

3.3. Scenario 3

In the third case, a more realistic scenario is considered where multiple perforations are modeled. In this case, a cluster with 11 openings is considered where each perforation opening has a length of 0.63 m and a diameter of 0.01 m. The domain size is 1 m by 5 m and the perforations are placed at the right boundary. These parameters are used to represent perforations created by the perforating gun. Other modeling parameters remain the same.

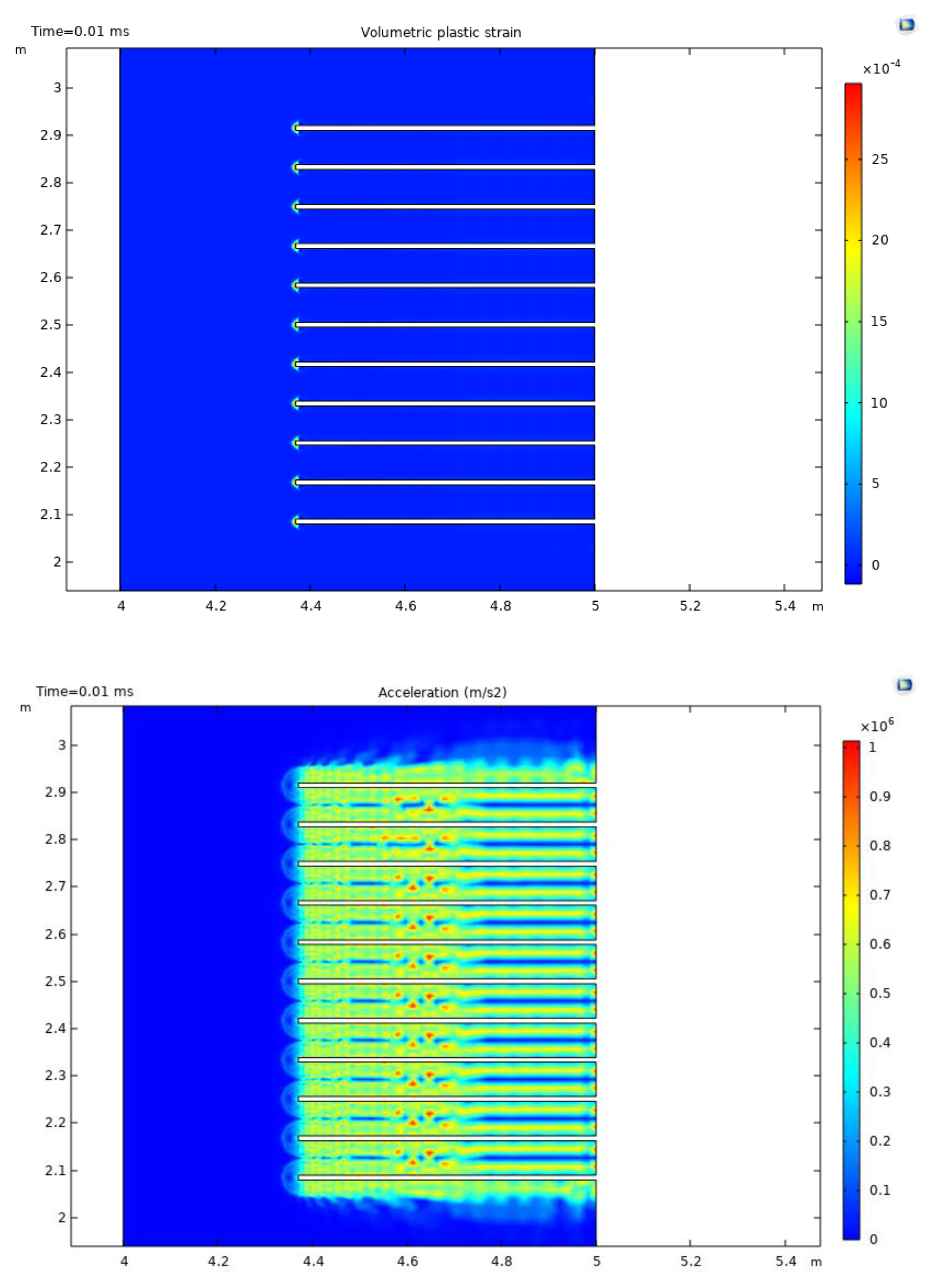
The spatial distribution of volumetric plastic strain and acceleration is plotted in Figure 8. Results show that the irreversible damage is primarily observed at and near tips of perforations, while acceleration magnitudes are relatively significant at and in between perforations. The clustering of perforations does not lead to significant plastic strain overlapping, indicating that irreversible damage is mainly caused individually around each perforation. In contrast, the acceleration contours expand radially around each perforation with strong overlapping effects.

Figure 8. Volumetric plastic strain and acceleration results after 0.01 ms of loading in scenario 3.

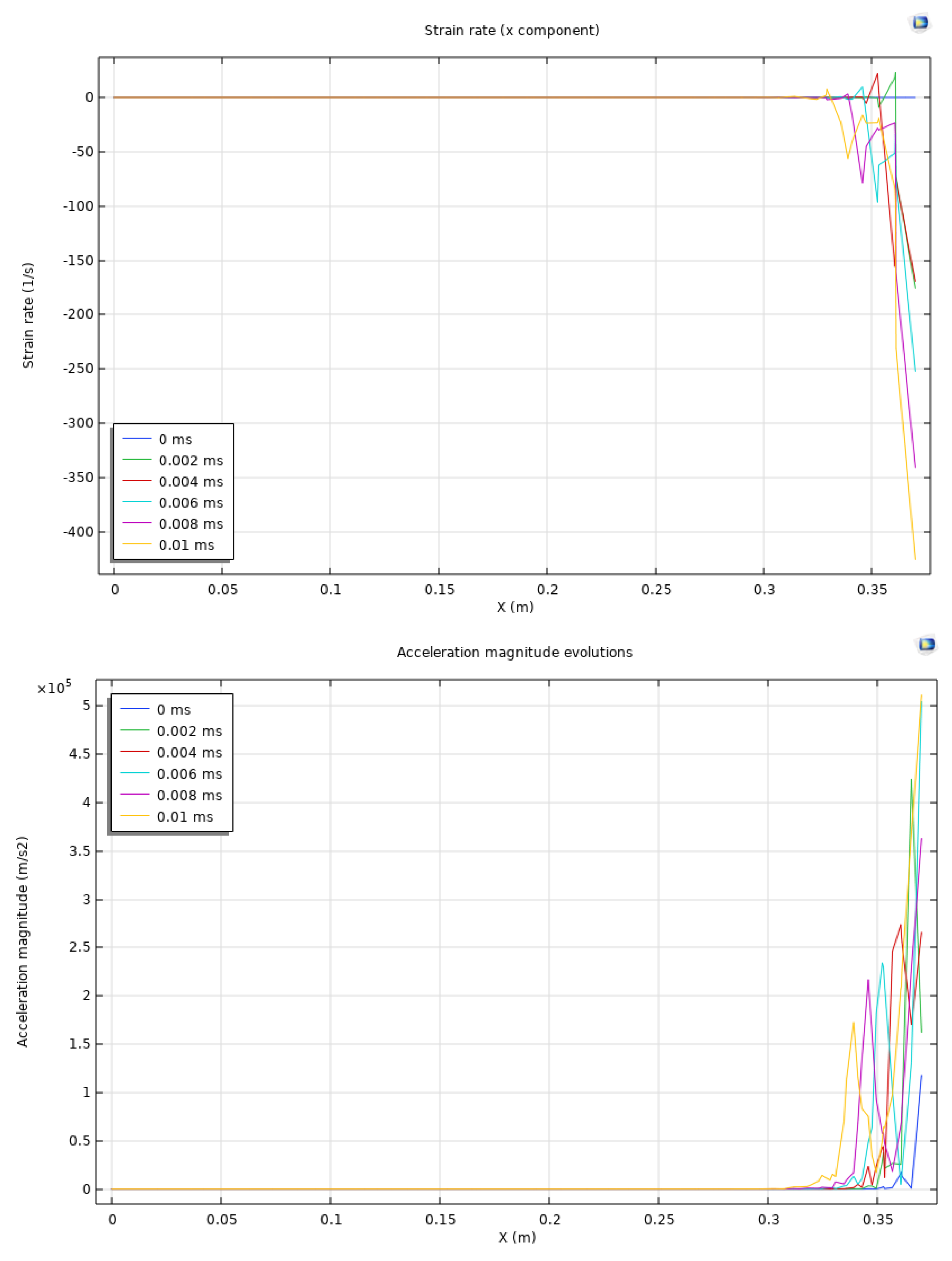
Similarly, the 1D distribution of strain rate in the x direction, acceleration, and plastic strain at 0 ms, 0.002 ms, 0.004 ms, 0.006 ms, 0.008 ms, and 0.01 ms along the monitoring line at y = 2.5 m is plotted in Figure 9. The line at y = 2.5 m is along the center perforation. The strain rate in the x direction shows significant magnitudes near the perforations at and around x=0.35 indicating an obvious compressive state in this region. The strain rate starts near zero at the left boundary at t = 0 ms and rapidly decreases as it approaches the perforations. At 0.01 ms, the strain rate reaches -400 1/s, suggesting intense deformation tendency. The change in strain rate over time indicates the propagation of stress waves and the resultant heterogeneous strain responses in the near-perforation rocks. The acceleration magnitude along the monitoring line exhibits a sharp increase near the perforations, which indicates the fast response of the reservoir rock to the dynamic boundary loading. It is noted that high acceleration magnitudes are concentrated near the perforations. The plastic strain distribution is also plotted along the monitoring line at later time steps. The plastic strain is negligible across most of the domain but shows a steep increase near the perforations. This increase indicates irreversible deformation localized around the perforations. However, the temporal evolution is not very significant in this scenario.

Figure 9. Strain rate in the x direction and acceleration magnitude are plotted at 0 ms, 0.002 ms, 0.004 ms, 0.006 ms, 0.008 ms, and 0.01 ms. The plastic strain is plotted at 0.009 ms, 0.0092 ms, 0.0094 ms, 0.0096 ms, 0.0098 ms, and 0.01 ms. The monitoring line is at y = 2.5 m in scenario 3.

4. Conclusion

This study implements an elastoplastic model based on finite element methods to analyze the effects of loading and perforation parameters on rock deformation and damage behaviors induced by dynamic loadings caused by the fracturing of tight oil reservoirs. Three different scenarios were modeled and discussed. Each scenario provided different insights into the deformation, strain rate, acceleration magnitude, and irreversible damage represented by plastic strain. Conclusions are summarized below.

(1) In all scenarios, the dynamic effects are highly localized around the perforations and loaded boundaries. The acceleration magnitudes can reach 10⁶ m/s² at and near the perforations, with rapid attenuation observed as it moves away. It indicates that the highest stress concentrations and deformation occur close to the points of loading or perforation.

(2) The strain rate in the x direction shows significant fluctuations near the perforations, reflecting intense stress redistributions and compressive deformation. This effect is especially noticeable in the third scenario with the most perforations. The displacement also shows significantly localized deformation.

(3) Plastic strain is concentrated near the perforation tips and loaded boundaries. However, it is observed that damage is not always accumulated starting at the loading boundary: in the second scenario where the domain is small, plastic strain is accumulated not immediately next to the loading boundary; in the first and the third scenarios, plastic strain accumulates and develops from the loading boundaries.

Acknowledgment

The authors acknowledge the support from the CNPC Innovation Fund (2021DQ02-0502).

References

Aghababaei, M., Behnia, M., & Moradian, O. (2019). Experimental investigation on strength and failure behavior of carbonate rocks under multistage triaxial compression. International Journal of Rock Mechanics and Mining Sciences, 123, 104099. [CrossRef]
Baumgarten, L., & Konietzky, H. (2013). Investigations on the fracture behaviour of rocks in a triaxial compression test. In ISRM International Symposium-EUROCK 2013. OnePetro.
Chen, A., Guo, X., Yu, H., Huang, L., Shi, S., & Cheng, N. (2021). A parametric study of hydraulic fracturing interference between fracture clusters and stages based on numerical modeling. Energy Exploration & Exploitation, 39(1), 65-85. [CrossRef]
Chen, B., Ji, J., Lin, J., et al. (2021). Experimental and Numerical Investigation of Characteristics of Highly Heterogeneous Rock Mechanical Responses in Tight Sandy Conglomerate Reservoir Rock Under Tri-axial Compression. Frontiers in Earth Science, 9. [CrossRef]
Fakhimi, A., Azhdari, P., & Kimberley, J. (2018). Physical and numerical evaluation of rock strength in Split Hopkinson Pressure Bar testing. Computers and Geotechnics, 102, 1-11. [CrossRef]
Guo, X., Huang, L., Jin, Y., Lin, B., & Lin, J. (2021). An experimental study of the rock mechanical properties in highly heterogeneous reservoir rocks of tight sandy conglomerates. In ARMA/DGS/SEG International Geomechanics Symposium. OnePetro.
Guo, X., Jin, Y., Zi, J., & Lin, B. (2021). Numerical investigation of the gas production efficiency and induced geomechanical responses in marine methane hydrate-bearing sediments exploited by depressurization through hydraulic fractures. Energy & Fuels, 35(22), 18441-18458. [CrossRef]
Hou, Y., Peng, Y., Chen, Z., Liu, Y., Zhang, G., Ma, Z., & Tian, W. (2021). Investigation on the controlling factors of pressure wave propagation behavior induced by pulsating hydraulic fracturing. SPE Journal, 26(05), 2716-2735. [CrossRef]
Hou, Y., Peng, Y., Chen, Z., Liu, Y., & Tian, Y. (2022a). Investigating heterogeneous distribution of fluid pressure in hydraulic fractures during pulsating hydraulic fracturing. Journal of Petroleum Science and Engineering, 209, 109823. [CrossRef]
Hou, Y., Peng, Y., Liu, Y., Chen, Z., Fan, B., Yin, Z., & Zhang, G. (2022b). Influence of Increasing Mean Stress on Fatigue Properties of Shale during Pulsating Hydraulic Fracturing. Energy & Fuels, 36(23), 14174-14186. [CrossRef]
Kim, D., Sirijaroonchai, K., El-Tawil, S., & Naaman, A. E. (2010). Numerical simulation of the Split Hopkinson Pressure Bar test technique for concrete under compression. International Journal of Impact Engineering, 37(2), 141-149. [CrossRef]
Kluge, C., Blöcher, G., Barnhoorn, A., & Bruhn, D. (2020). Hydraulic-mechanical properties of microfaults in granitic rock using the Punch-Through Shear test. International Journal of Rock Mechanics and Mining Sciences, 134, 104393. [CrossRef]
Lecampion, B., Bunger, A., & Zhang, X. (2018). Numerical methods for hydraulic fracture propagation: A review of recent trends. Journal of Natural Gas Science and Engineering, 49, 66-83. [CrossRef]
Prabhu, S., & Qiu, T. (2022). Simulation of Split Hopkinson Pressure Bar Tests on Sands Using the Discrete-Element Method. International Journal of Geomechanics, 22(2), 06021036. [CrossRef]
Togashi, Y., Kikumoto, M., & Tani, K. (2017). An experimental method to determine the elastic properties of transversely isotropic rocks by a single triaxial test. Rock Mechanics and Rock Engineering, 50, 1-15. [CrossRef]
Wang, Z., Guo, X., Zheng, G., Yu, P., Wang, W., Jin, Y., & Chen, G. (2022). Effects of parent well spacing on the poroelastic behaviors in the infill zone in shale oil reservoirs: A case study in Jimsar Shale Oil, China. Energy Science & Engineering, 10(4), 1043-1054. [CrossRef]
Wei, S., Kuru, E., Jin, Y., & Yang, X. (2022). Numerical investigation of the factors affecting the cement sheath integrity in hydraulically fractured wells. Journal of Petroleum Science and Engineering, 215, 110582. [CrossRef]
Xia, Y., Jin, Y., Chen, M., & Chen, K. (2017). Poroelastodynamic response of a borehole in a non-hydrostatic stress field. International Journal of Rock Mechanics and Mining Sciences, 93, 82-93. [CrossRef]
Zhang, Y., Okere, C. J., & Su, G. (2021). Effect of loading rates on accurate in-situ stress determination in different lithologies via Kaiser effect. Arabian Journal of Geosciences, 14, 1-8. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Effects of Loading and Perforation Parameters on Rock Deformation and Damage Behaviors Induced by Dynamic Loadings Caused by the Fracturing of Tight Oil Reservoirs

Abstract

1. Introduction

2. Numerical Model

3. Results and Discussion

3.1. Scenario 1

3.2. Scenario 2

3.3. Scenario 3

4. Conclusion

Acknowledgment

References

MDPI Initiatives

Important Links

Subscribe