Article
Version 1
This version is not peer-reviewed
Microdosimetric Simulation of Gold-Nanoparticle Enhanced Radiotherapy
Version 1
: Received: 8 August 2024 / Approved: 12 August 2024 / Online: 12 August 2024 (09:41:55 CEST)
How to cite: Azarkin, M.; Kirakosyan, M.; Ryabov, V. Microdosimetric Simulation of Gold-Nanoparticle Enhanced Radiotherapy. Preprints 2024, 2024080778. https://doi.org/10.20944/preprints202408.0778.v1 Azarkin, M.; Kirakosyan, M.; Ryabov, V. Microdosimetric Simulation of Gold-Nanoparticle Enhanced Radiotherapy. Preprints 2024, 2024080778. https://doi.org/10.20944/preprints202408.0778.v1
Abstract
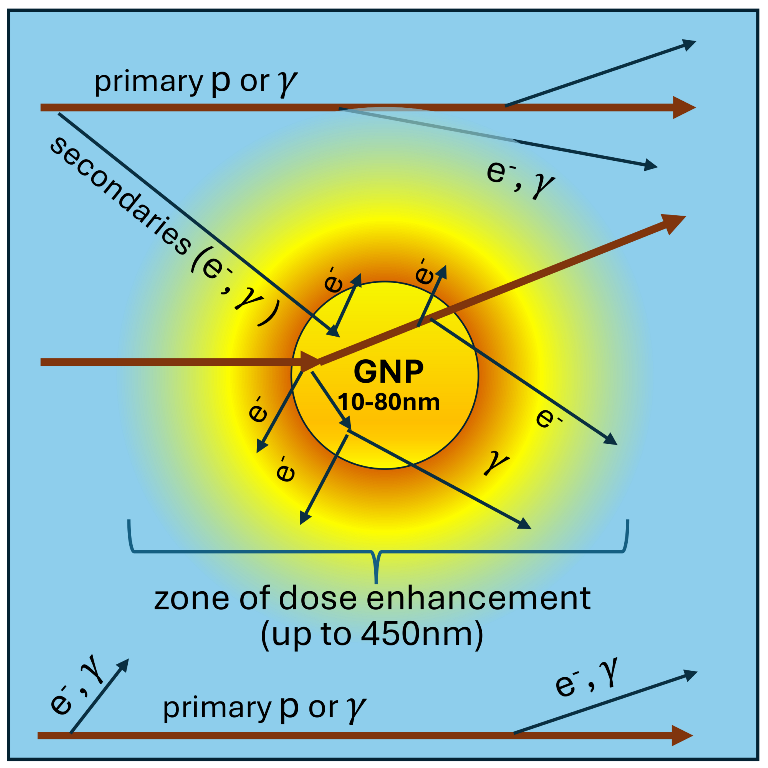
Conventional X-ray therapy (XRT) is commonly applied to suppress cancerous tumors, however it often inflicts collateral damage to nearby healthy tissue. In order to provide a better conformity of the dose distribution in the irradiated tumor, proton therapy (PT) is increasingly being used to treat solid tumors. Furthermore, radiosensitization with gold nanoparticles (GNPs) has been extensively studied to increase the therapeutic ratio. The mechanism of radiosensitization is assumed to be connected with an enhancement of the absorbed dose due to huge photoelectric cross-sections with gold. Nevertheless, numerous theoretical studies mostly based on Monte Carlo (MC) simulations did not provide consistent and thorough picture of dose enhancement and, therefore, radiosensitization effect. Radiosensitization by nanoparticles in PT is even less studied than in XRT. Therefore, we investigate physics picture of GNP-enhanced RT using MC simulation with Geant4 equipped with the most recent physics models, taking into account a wide range of physics processes relevant for realistic PT and XRT. Namely, we measured dose enhancement factors in the vicinity of GNP with diameters ranging from 10 nm to 80 nm. The dose enhancement in the vicinity of GNP reaches high values for XRT, while it is very modest for PT. The macroscopic dose enhancement factors for realistic therapeutic GNP concentrations are rather low for all RT scenarios, therefore other physicochemical and biological mechanisms should be additionally invoked for an explanation of the radiosensitization effect observed in many experiments.
Keywords
gold nanoparticles; MC simulation; microdosimetry; radiosensitization mechanisms
Subject
Biology and Life Sciences, Biophysics
Copyright: This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Comments (0)
We encourage comments and feedback from a broad range of readers. See criteria for comments and our Diversity statement.
Leave a public commentSend a private comment to the author(s)
* All users must log in before leaving a comment