1. Introduction
The global shift towards a clean energy environment has significantly driven the studies of renewable energy sources (RES). These sources are heralded for their environmental friendliness due to their minimal or zero emissions compared to traditional fossil fuels, which are major contributors to carbon dioxide emissions, greenhouse gases, and overall environmental pollution [
1]. As a response to these environmental challenges, there has been a substantial move towards RES like hydroelectric, biomass, wind, solar, wave, tidal, and geothermal energy, which are continually replenished by nature [
2].
Integration of RES within smart grid technology is a crucial development, bridging the gap between energy demand and supply. Smart grids, equipped with advanced metering systems (AMS), energy management systems (EMS), and advanced communication systems, manage the distribution and optimization of renewable energy more effectively than conventional grids. They handle challenges in supply-demand balance, power generation, distribution, and electricity pricing more adeptly [
3,
4].
This paper focuses on the modeling of nano-grids and pico-grids, which are essential components of the smart grid infrastructure. The nano-grid, suitable for individual buildings, and the pico-grid, designed for standalone applications within a building, aim to demonstrate how integration of solar photovoltaic (PV) systems and energy storage can optimize power flow and enhance grid reliability. The smaller power networks, picogrids and nanogrids, should be able to function both in an islanded (stand-alone) and a grid-connected mode and be able to operate steadily in a cluster [
5]. In [
6], a comprehensive review of the recent developments in nano-grid research, including the control topologies and methods that allow for the nano-grid’s intelligent control are covered. Operation of a basic nano-grid with rules-based controller and load behavior in response to fluctuating renewable energy source electricity availability is modelled in [
7]. Open Energy Systems (OESs) concept and architecture for higher-level control of the components of a standalone nanogrid is introduced in [
8]. In [
9], use of optimal energy management system to mitigate the impact of energy uncertainties in an interconnection between microgrid nano-grid were studied. The power management of nano-grid for grid support and deploying power converters to regulate power quality is discussed in [
10]. Recent research and development efforts in nano-grids are also focusing on ability to interconnect nano-grids to trade energy [
11,
12]. A decentralized blockchain mechanisms for demand response program in nano-grids is proposed in [
13]. A predictive optimization-based model for optimal energy sharing plan between a cluster of nano-grids is proposed in [
14].
With the establishment of the Singapore Institute of Technology (SIT) in Punggol Digital District, a Multi-Energy Micro-grid (MEMG) has been implemented and will be fully operational in late 2024, aiming to achieve zero emissions [
15]. Approximately 10,000 m
2 of solar panels will be installed on rooftops to power the campus, significantly reducing reliance on the main utility grid and advancing the institution’s sustainability goals. This development motivates the need for a testbed to model and analyze the operation of both pico-grids and nano-grids in the campus’s west zone.
This paper aims to model and simulate the pico-grid and nano-grid using MATLAB/Simulink to:
- i.
Explore and study the individual subsystems of both the pico-grid and nano-grid.
- i.
Model and integrate relevant components.
- i.
Develop simulation models to analyze power flow.
- i.
Perform tests to assess operations under realistic scenarios.
The primary contributions of this paper include the detailed study, modeling, and simulation of the pico-grid and nano-grid. This work constructs a comprehensive model of these systems using MATLAB/Simulink to facilitate power flow analysis under various operating conditions. In what follows,
Section 2 discusses the proposed architecture for pico-grid and nano-grid and their modeling.
Section 3 presents test conditions and simulation results.
Section 4 concludes the paper and outlines future areas of work.
4. Conclusions
This paper presents the development and analysis of MATLAB/Simulink simulation models for pico-grid and nano-grid systems, specifically designed for the SIT Punggol campus. The study includes a comprehensive examination of the architectures, subsystem modeling, control algorithms, and operational characteristics of both models, with simulations conducted to understand power flow and system functionality.
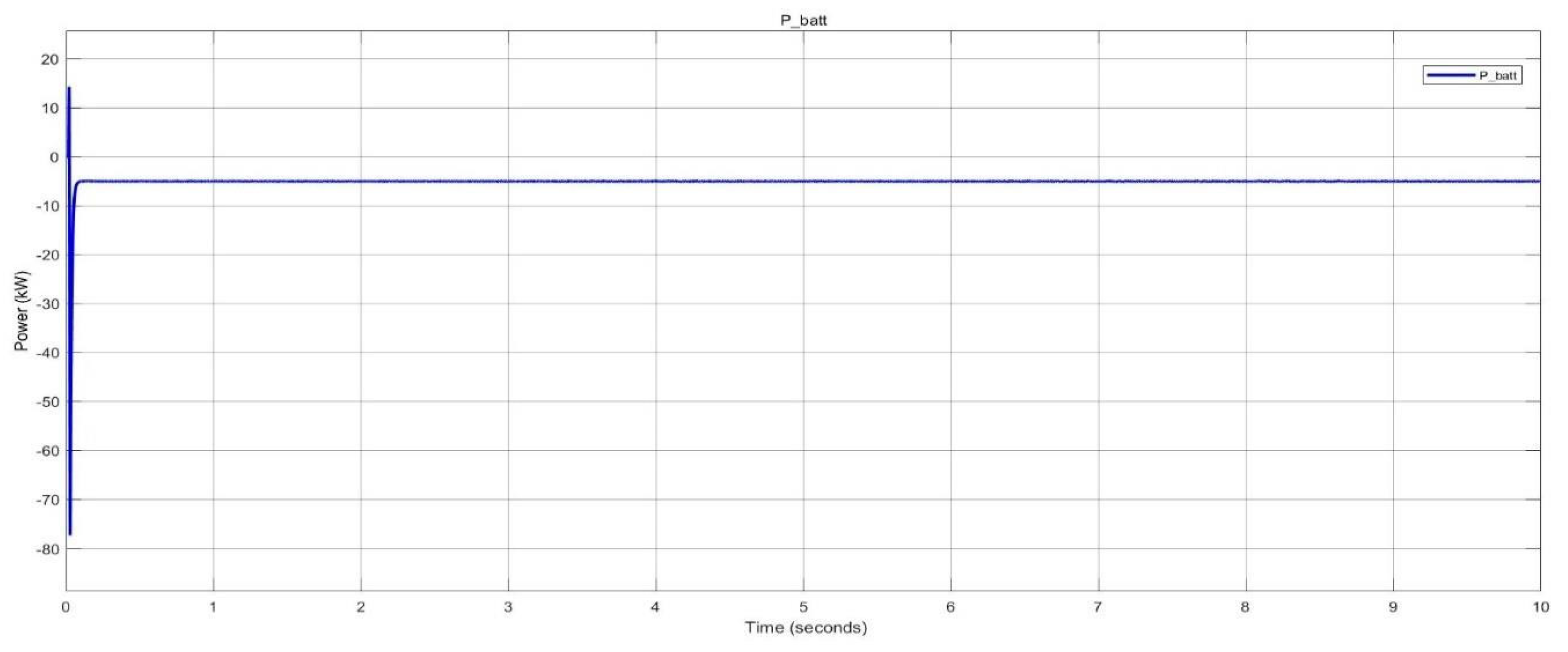
In the pico-grid simulations, various scenarios were explored, including battery discharge to loads, nighttime charging, and the parallel operation of two pico-grids to assess load sharing. The pico-grid system proved effective for applications with lower load demands, relying heavily on battery storage and supplemental grid power. When the battery’s State of Charge (SOC) is low, support from the grid becomes essential. Parallel operation of multiple pico-grids demonstrated the potential for mutual support and reduced reliance on the grid.
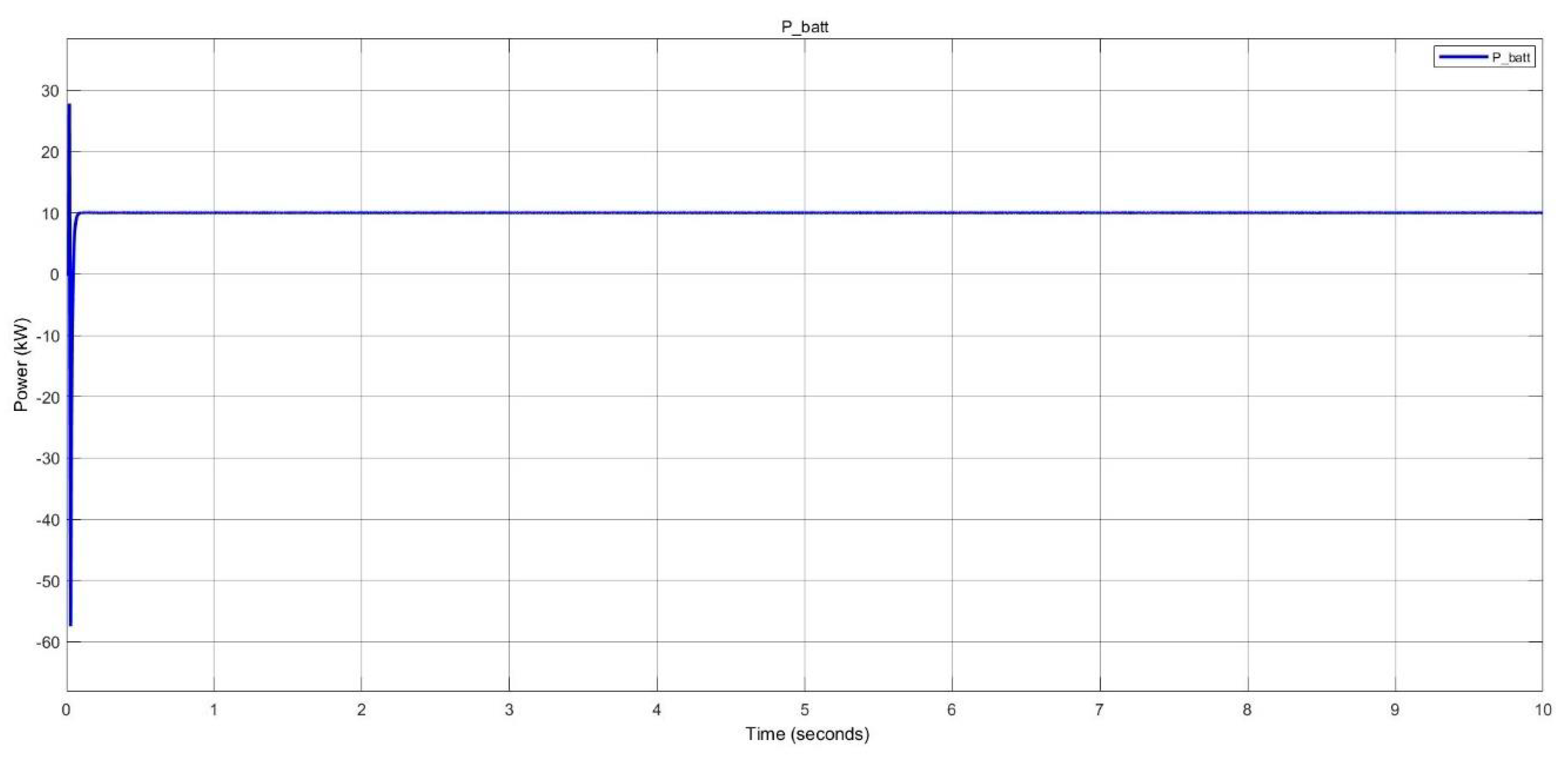
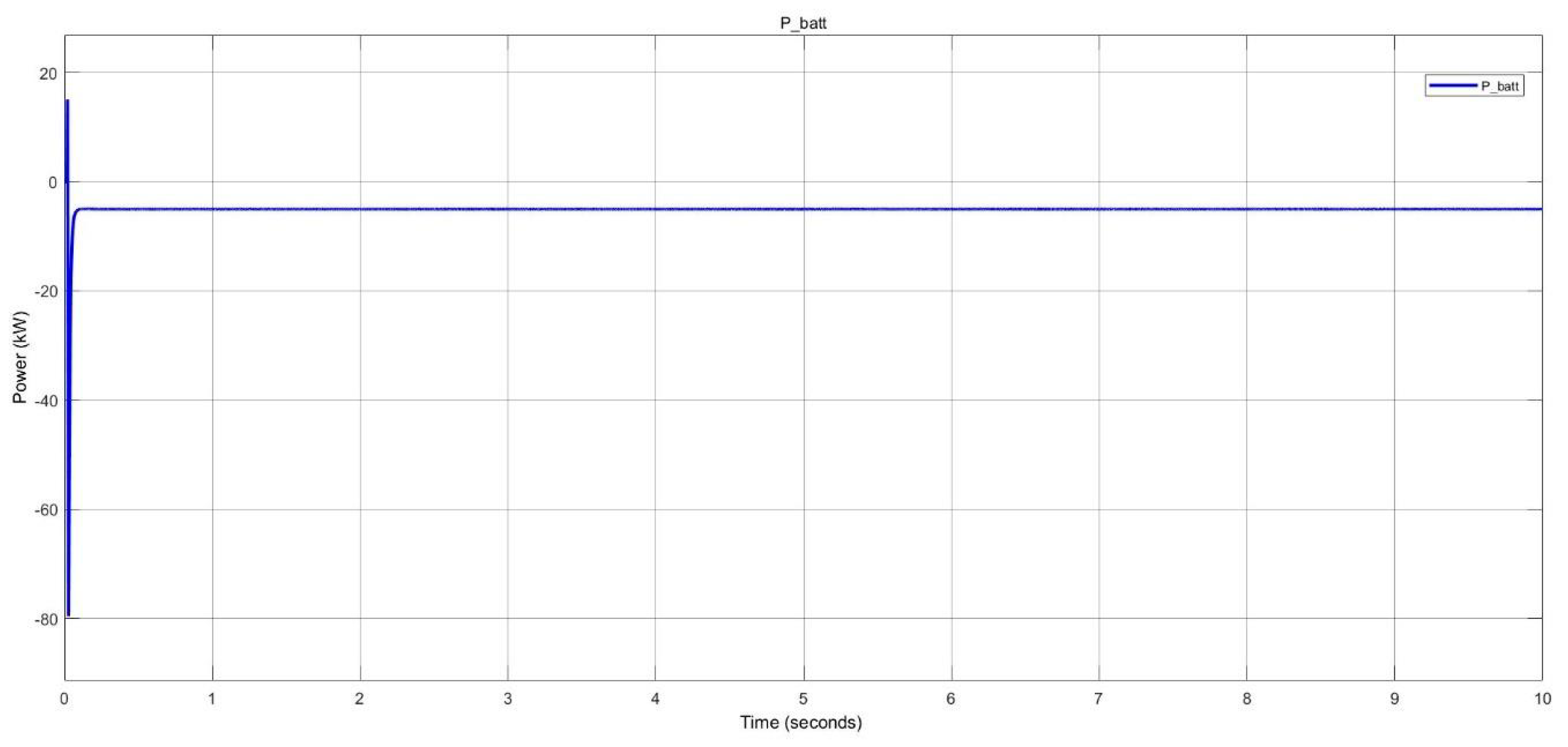
For the nano-grid simulations, scenarios such as solar PV and battery power supply, nighttime battery charging, combined battery and grid power during periods of low solar generation, and the parallel operation of two nano-grids were investigated. The nano-grid system is well-suited for higher load demands due to its integration of solar PV generation and battery storage. However, the variability of solar PV output, which is affected by weather conditions, requires additional support from both the battery and the grid. Connecting multiple nano-grids in parallel enhances system reliability and further reduces grid dependency.
The next phase involves validating the simulation outcomes with a hardware implementation. A small-scale nano-grid system could be set up on a building rooftop using commercially available solar PV panels, battery storage, a DC charge controller, a single-phase inverter, and a load bank. This setup will enable practical power flow analysis, with real-time data collection facilitated by a power quality data logger. Prior to hardware implementation, further research on life cycle costs, manpower management, environmental impact, and battery disposal is recommended. Additionally, investigating ways to minimize losses from circuit components and power semiconductor switching can help improve the overall energy efficiency of the nano-grid system.
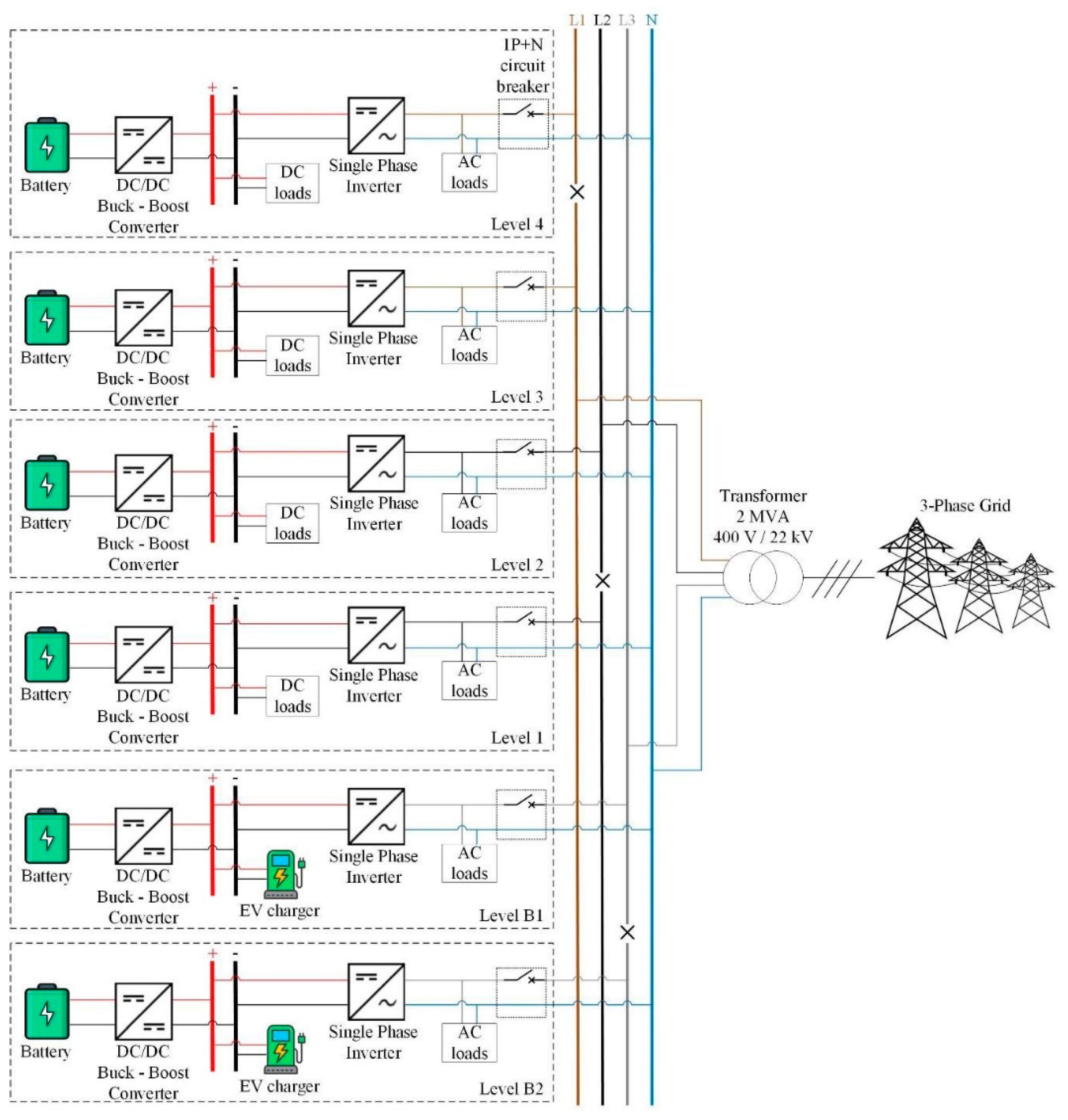
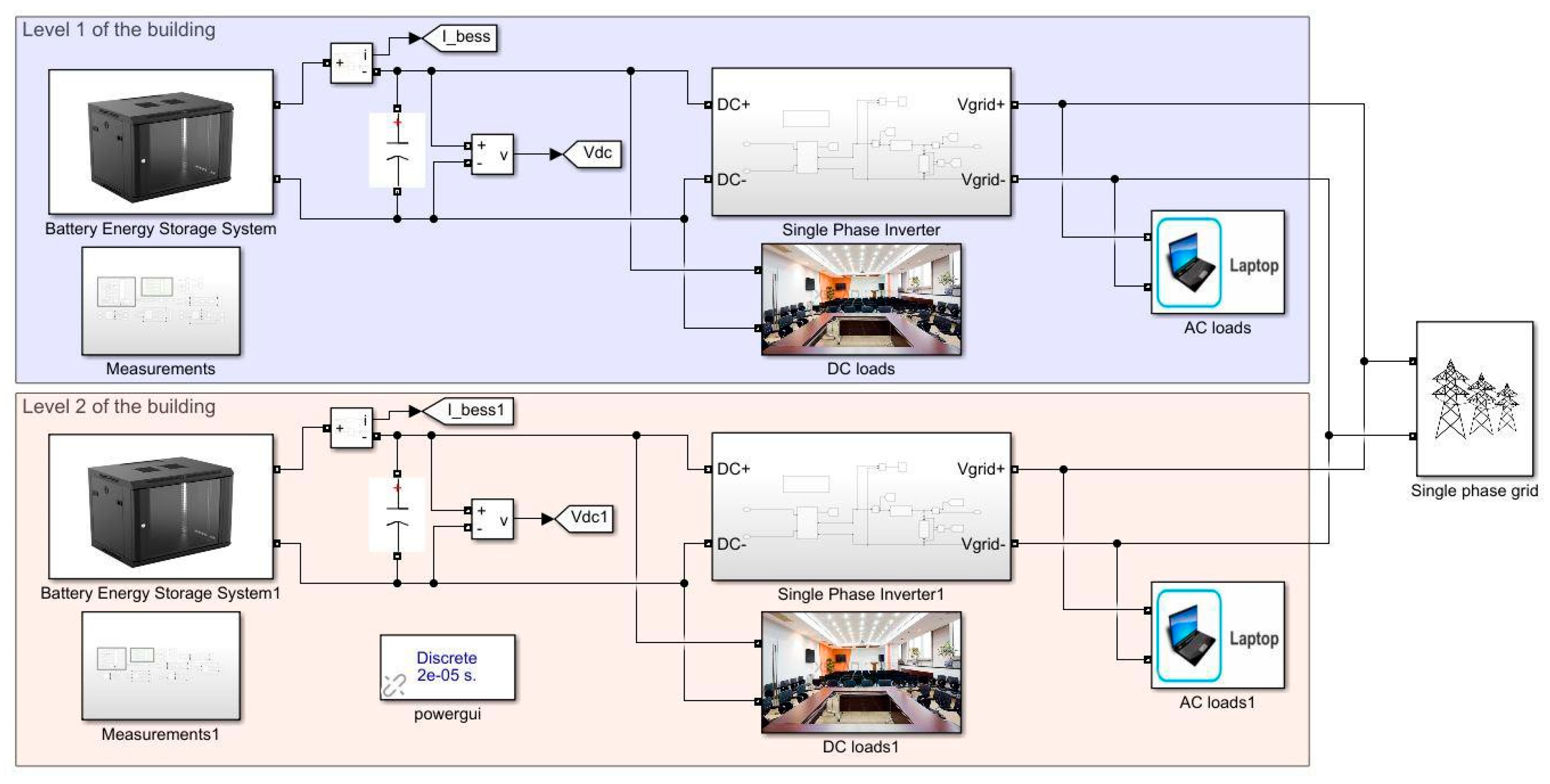
Figure 1.
Overview of a pico-grid in a building at SIT Punggol campus.
Figure 1.
Overview of a pico-grid in a building at SIT Punggol campus.
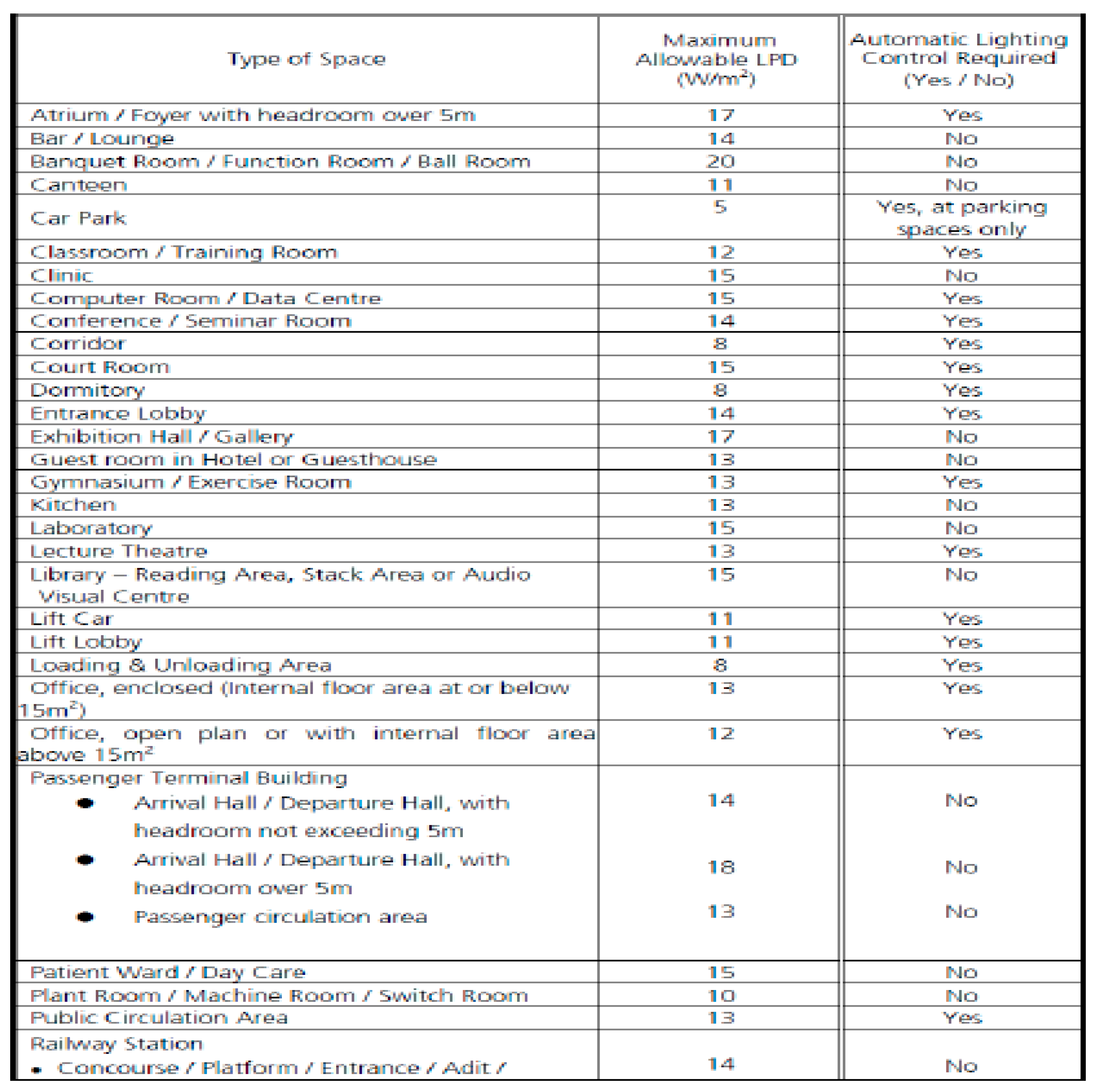
Figure 2.
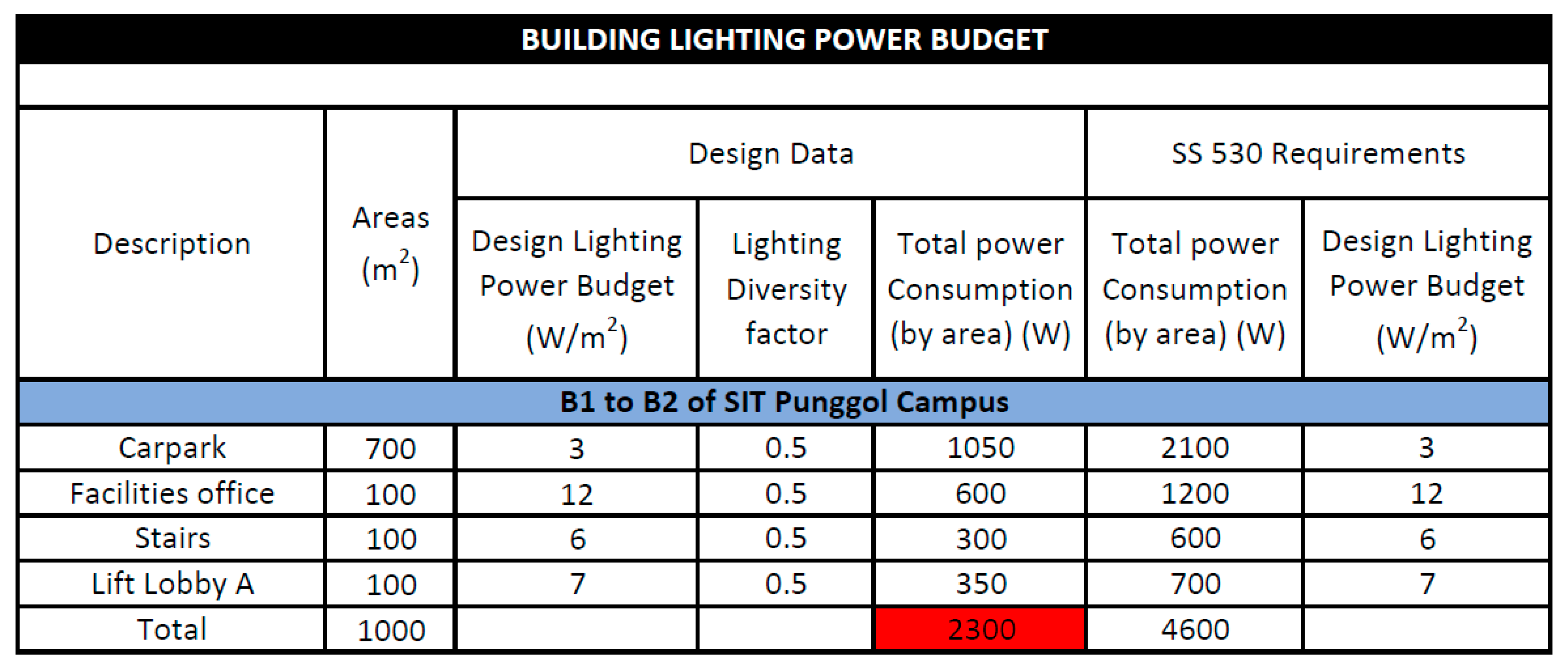
SS530 lighting power density guideline.
Figure 2.
SS530 lighting power density guideline.
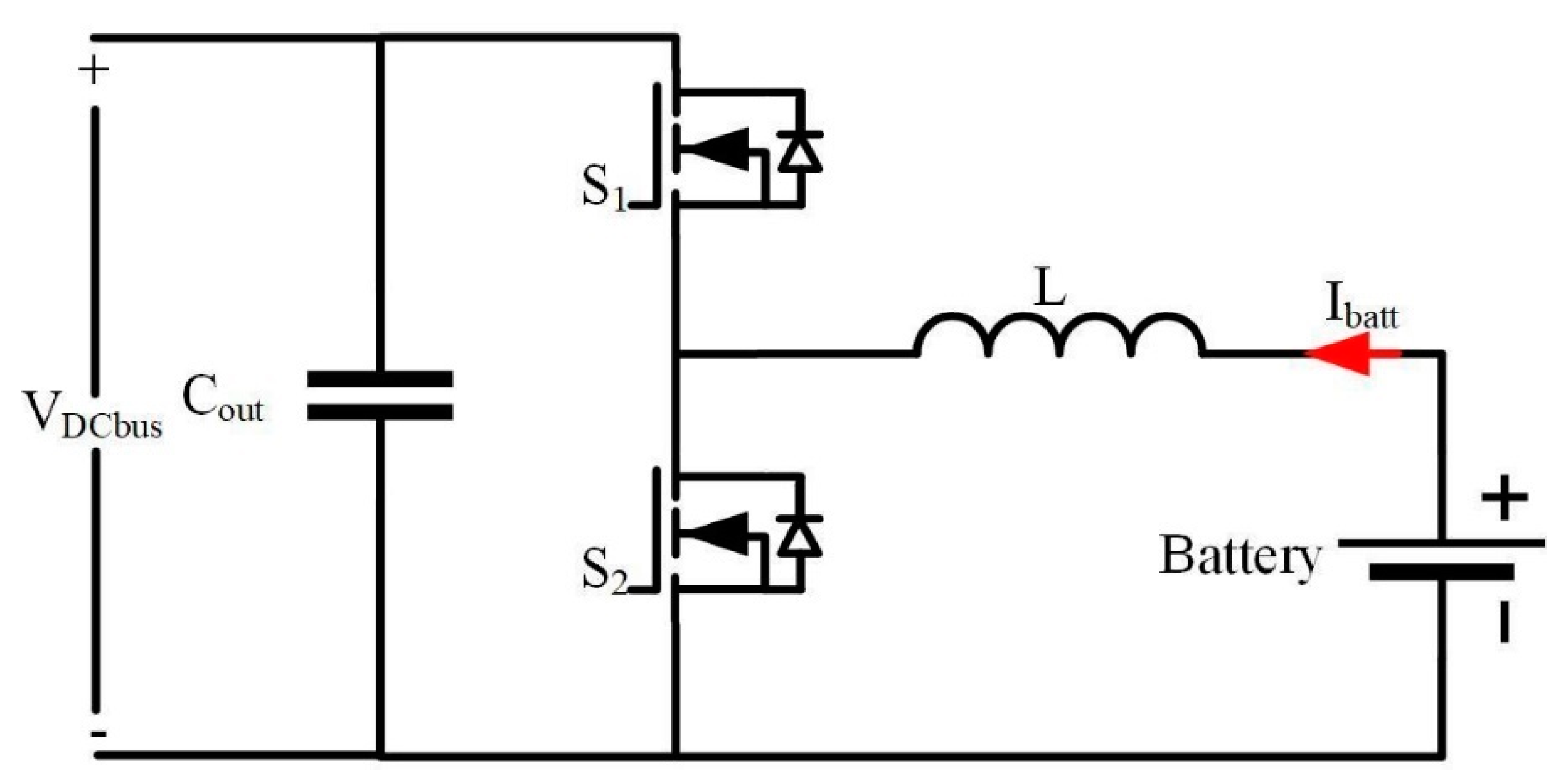
Figure 3.
Proposed topology used in BESS.
Figure 3.
Proposed topology used in BESS.
Figure 4.
Proposed control algorithm used to control BESS.
Figure 4.
Proposed control algorithm used to control BESS.
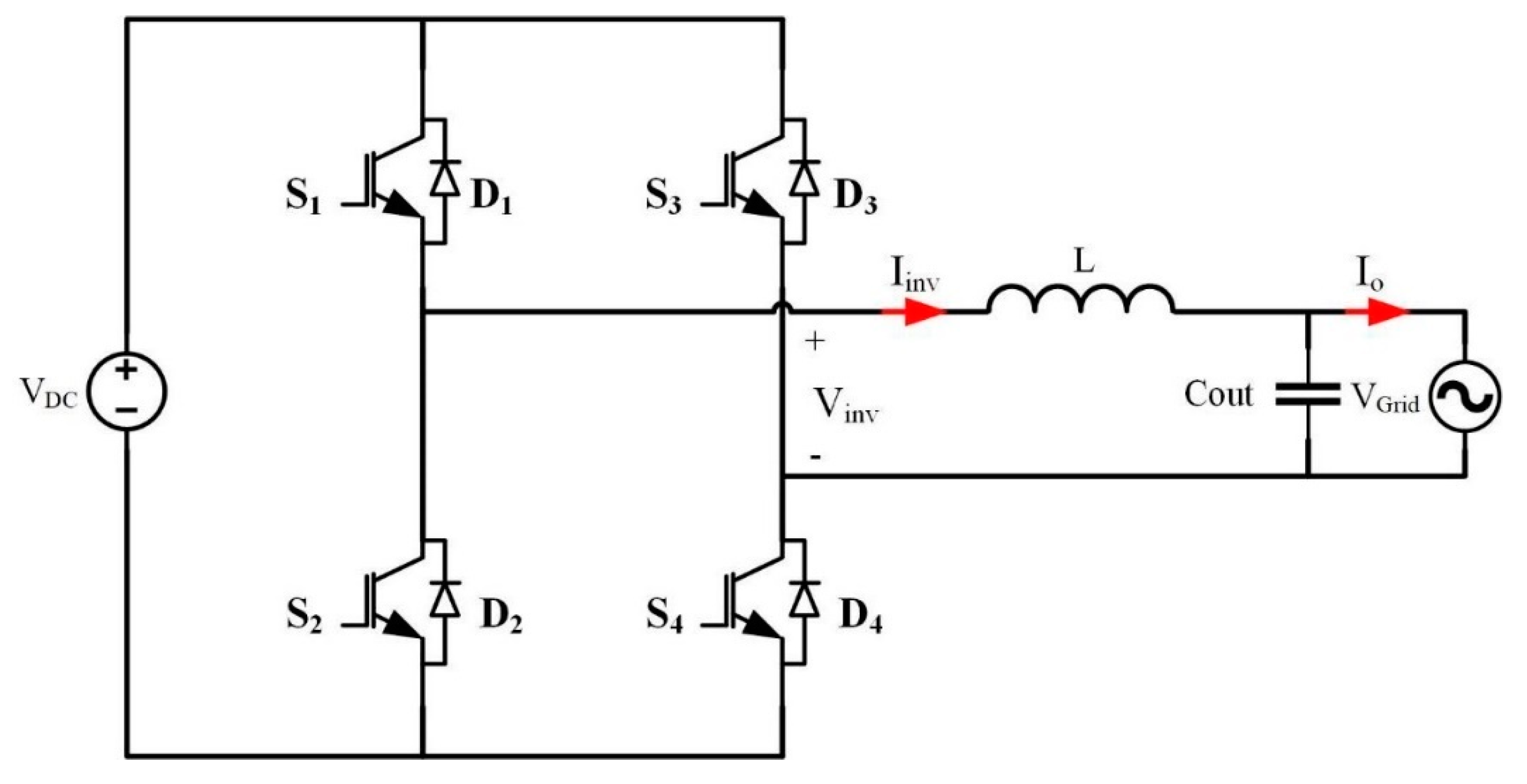
Figure 5.
Proposed topology used in single-phase inverter.
Figure 5.
Proposed topology used in single-phase inverter.
Figure 6.
Proposed topology used in single-phase inverter.
Figure 6.
Proposed topology used in single-phase inverter.
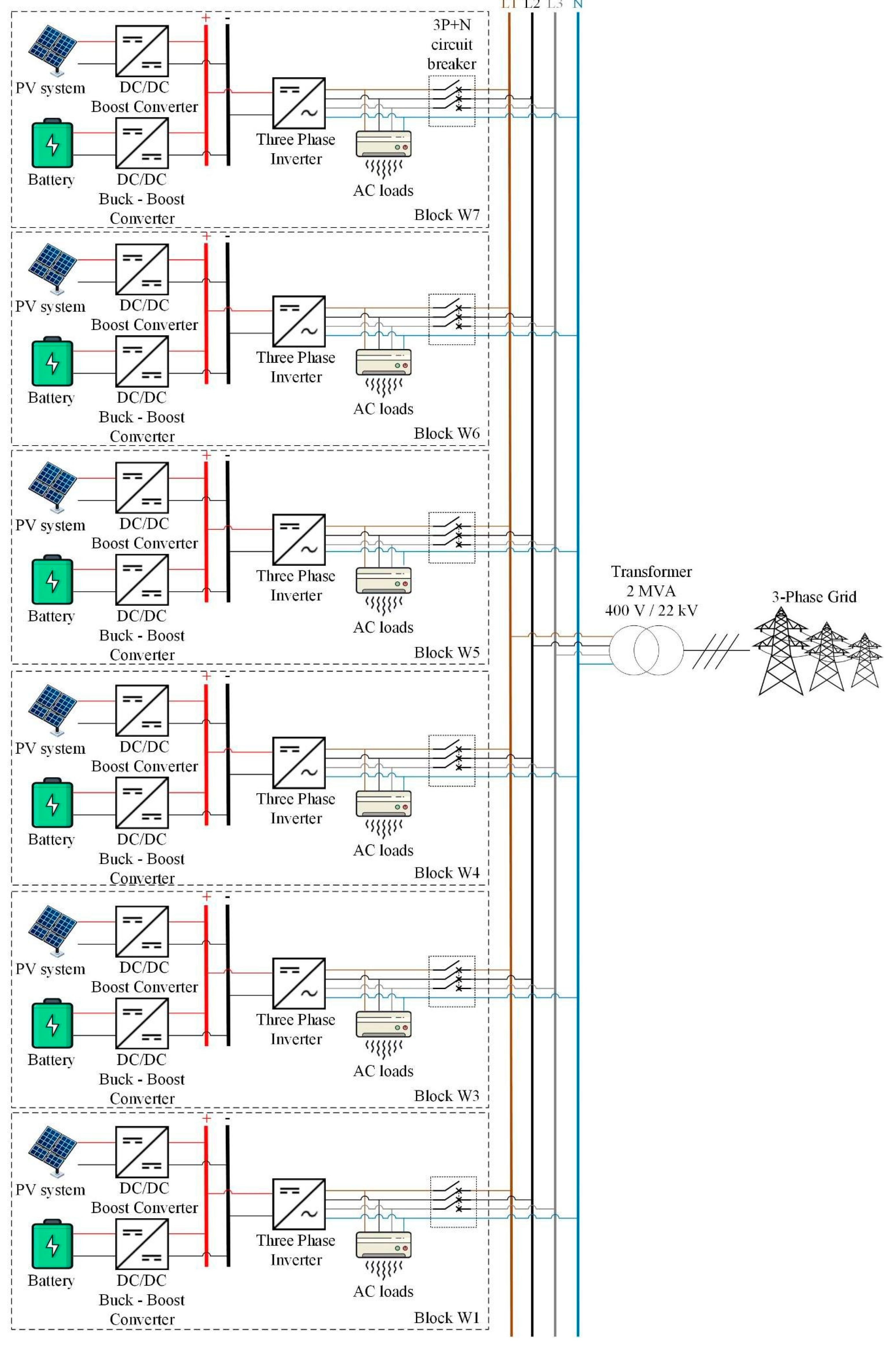
Figure 7.
Overview of nano-grid system a building at SIT Punggol campus.
Figure 7.
Overview of nano-grid system a building at SIT Punggol campus.
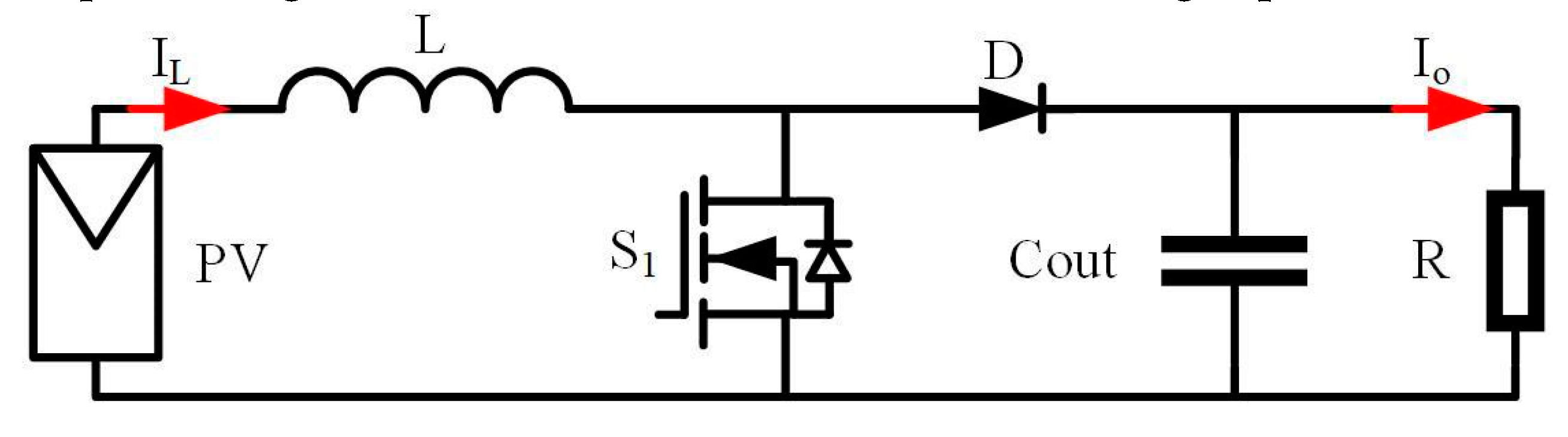
Figure 8.
Proposed topology used in solar PV boost converter.
Figure 8.
Proposed topology used in solar PV boost converter.
Figure 9.
Proposed control algorithm used to control boost converter.
Figure 9.
Proposed control algorithm used to control boost converter.
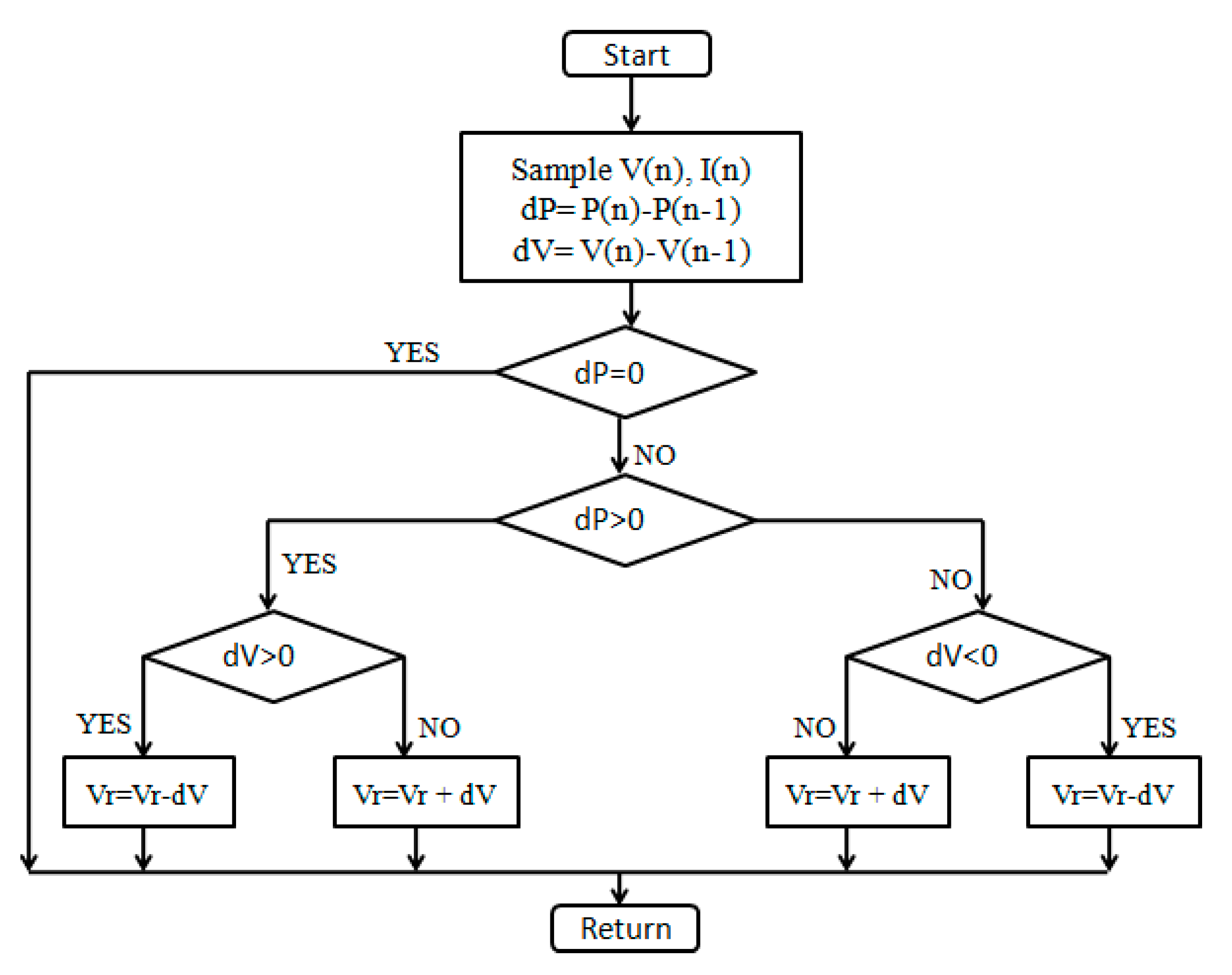
Figure 10.
Proposed P&O algorithm for MPPT operation.
Figure 10.
Proposed P&O algorithm for MPPT operation.
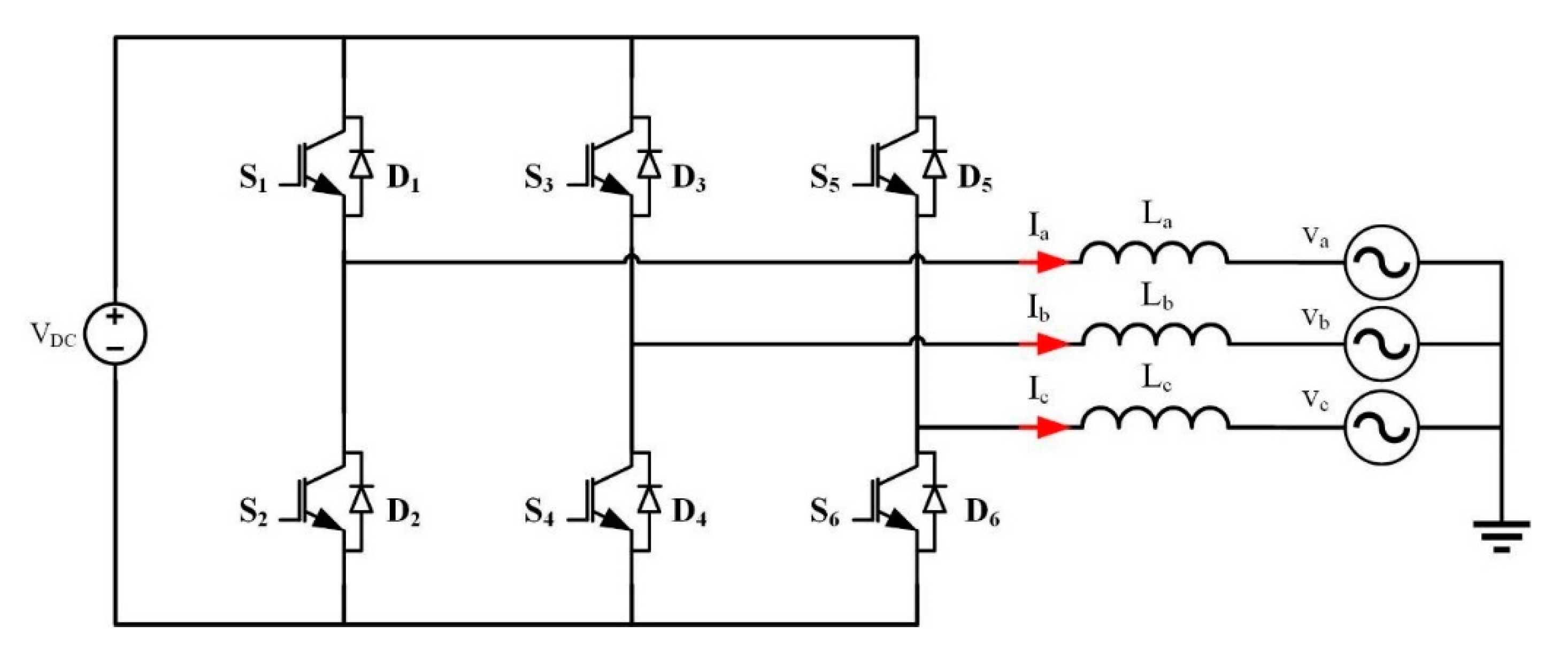
Figure 11.
Proposed topology used in three-phase inverter.
Figure 11.
Proposed topology used in three-phase inverter.
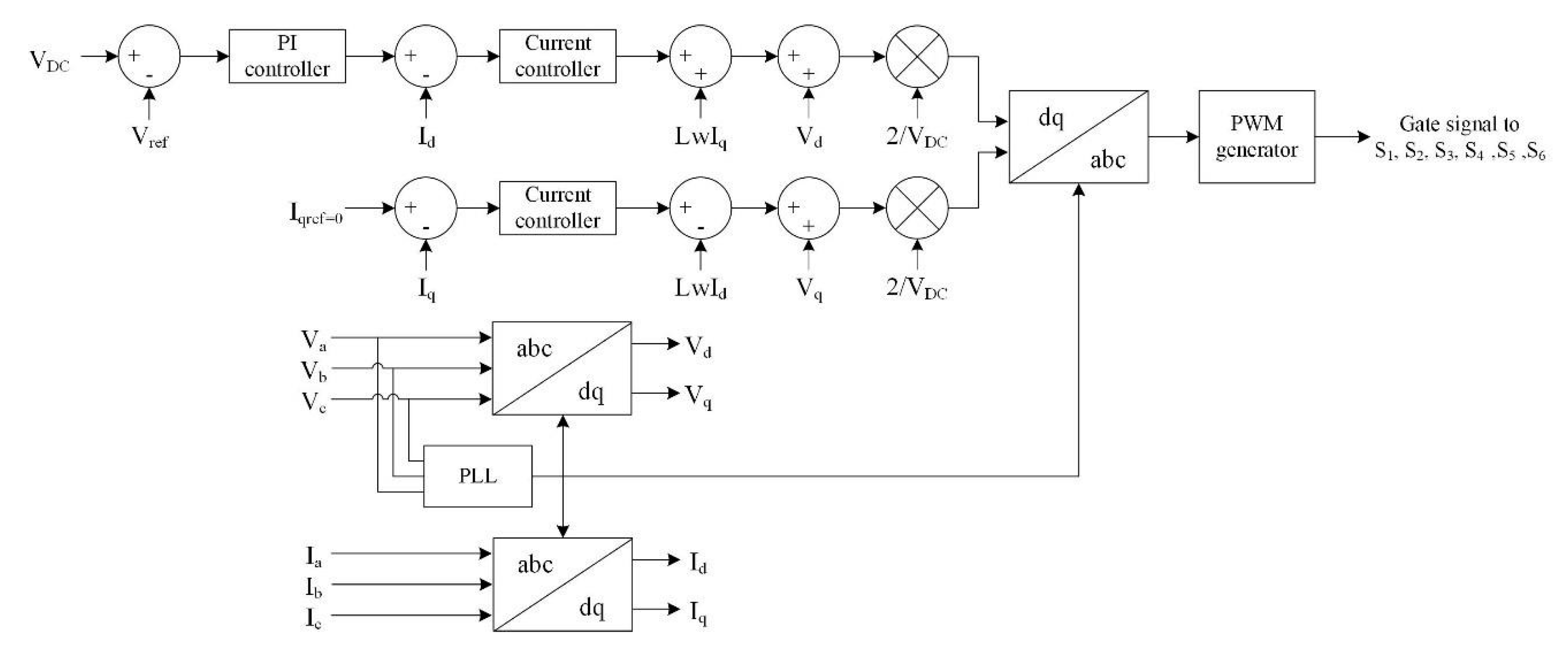
Figure 12.
Proposed control algorithm used to control three-phase inverter.
Figure 12.
Proposed control algorithm used to control three-phase inverter.
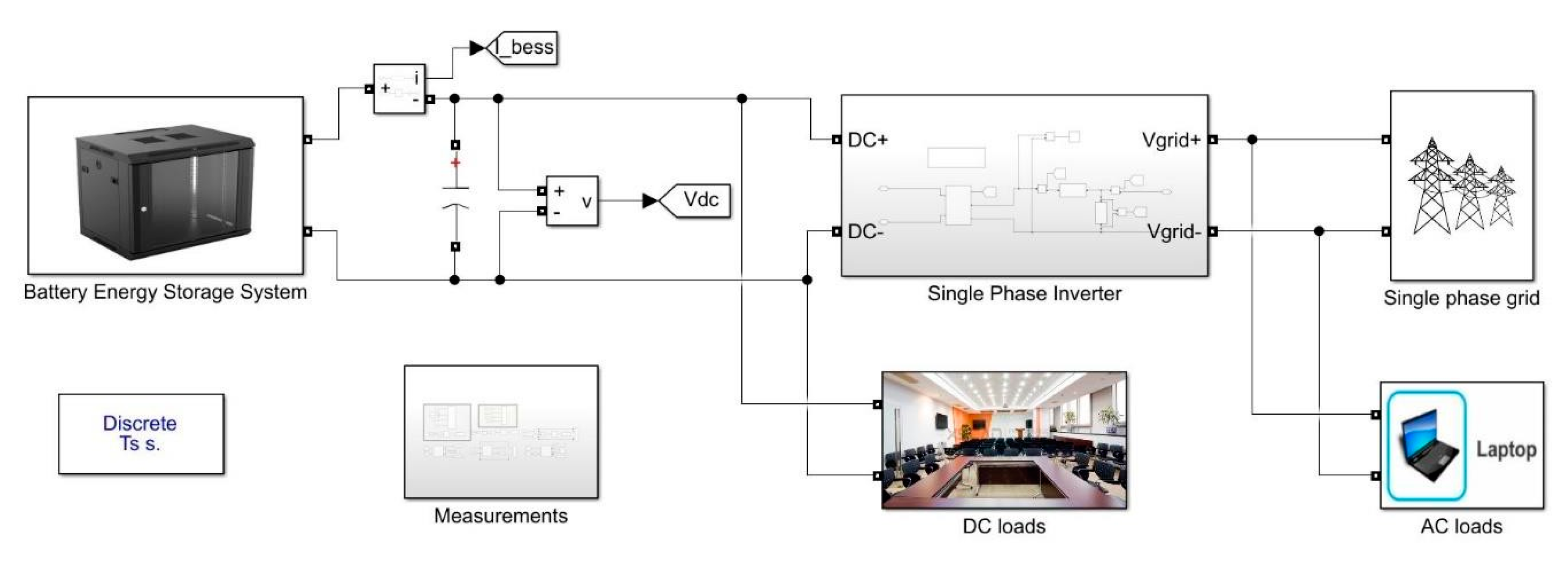
Figure 13.
Simulation model of BESS integration with single-phase inverter.
Figure 13.
Simulation model of BESS integration with single-phase inverter.
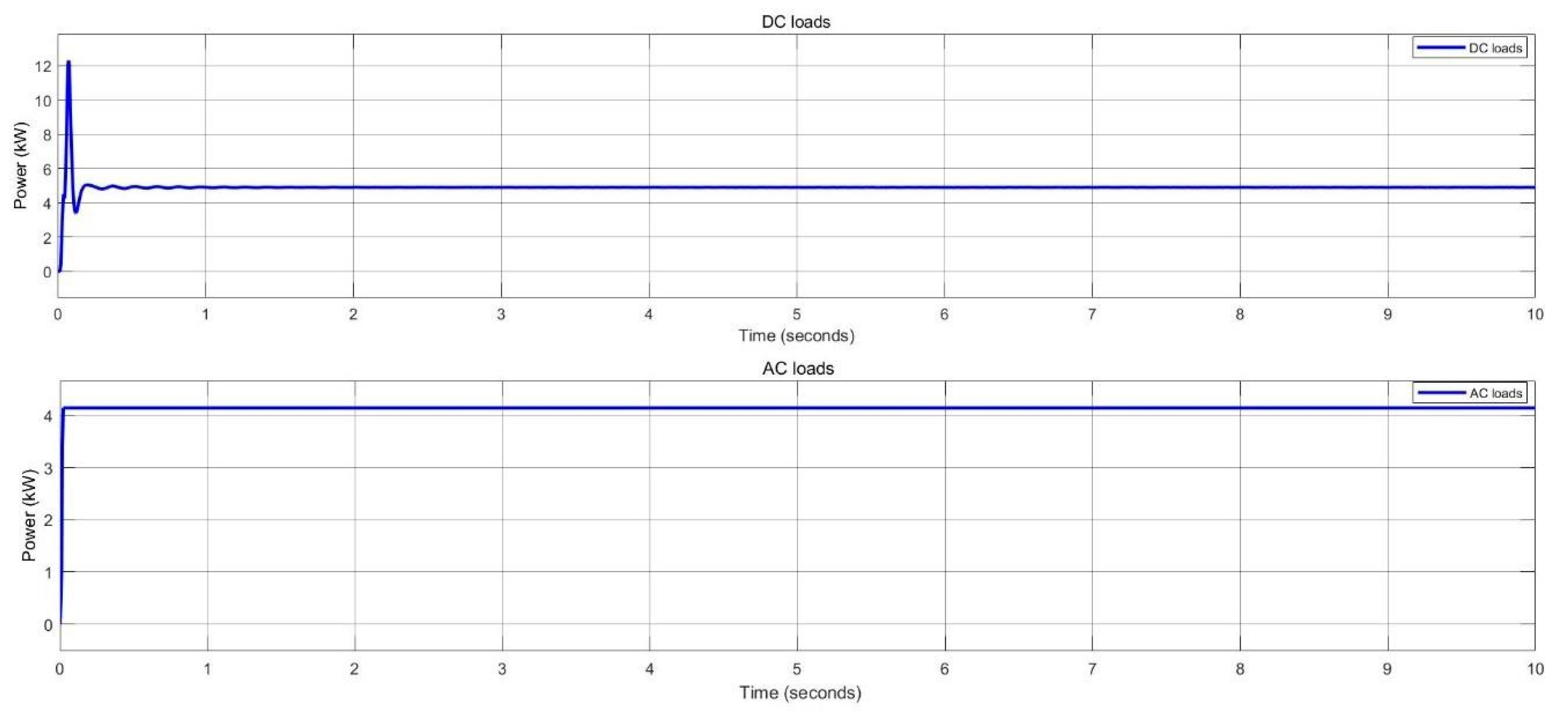
Figure 14.
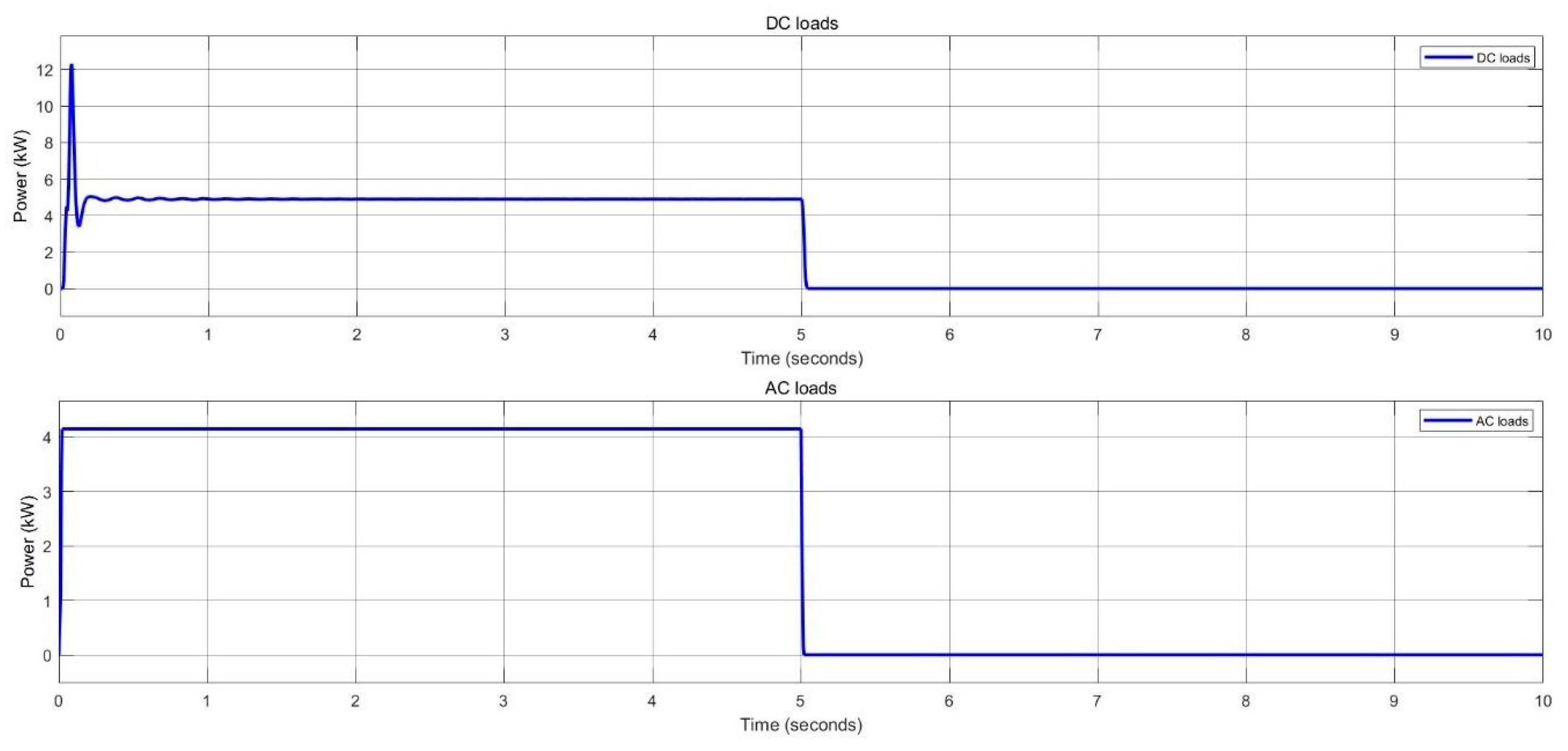
Load demand estimation of DC and AC loads for pico-grid system.
Figure 14.
Load demand estimation of DC and AC loads for pico-grid system.
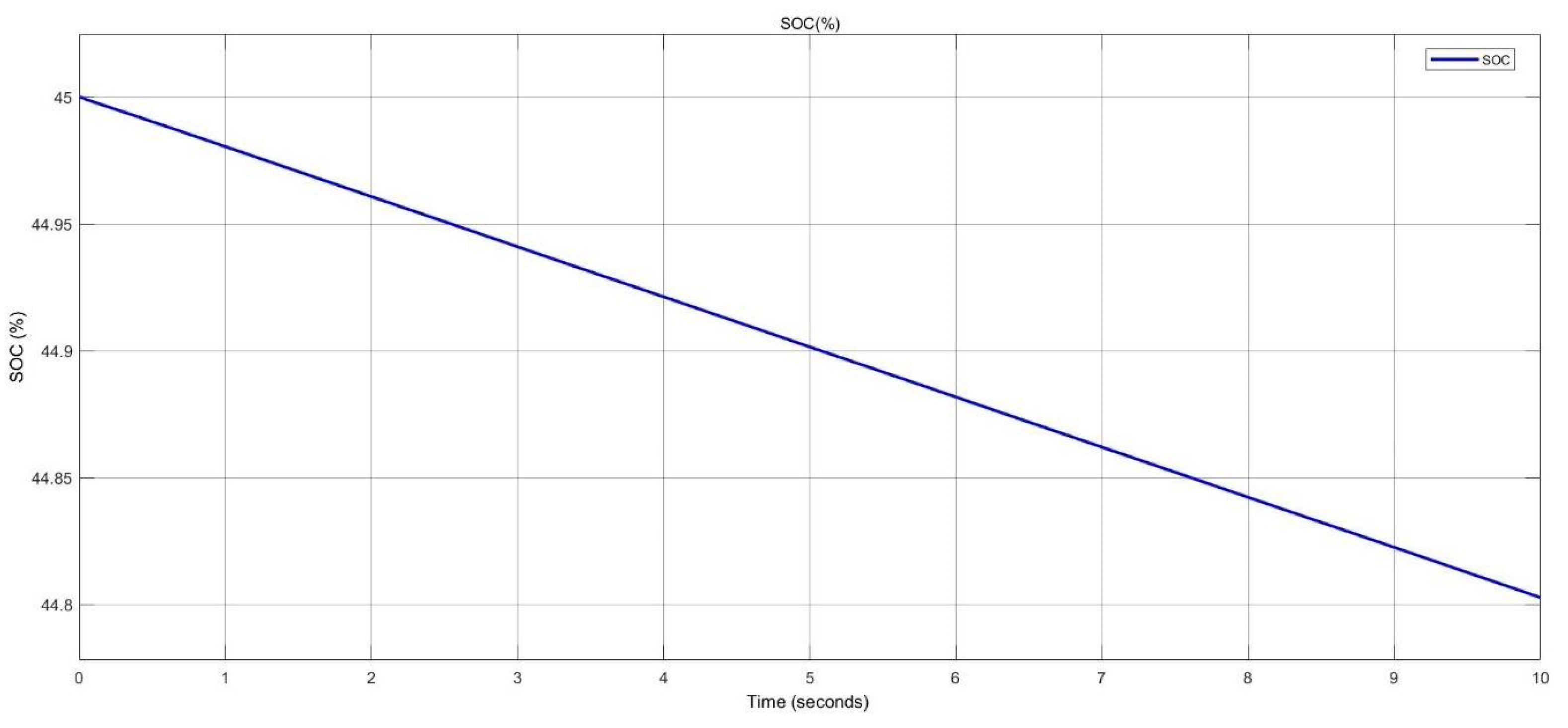
Figure 15.
The SOC level of the BESS during discharging in pico-grid system.
Figure 15.
The SOC level of the BESS during discharging in pico-grid system.
Figure 16.
The battery voltage of the BESS during discharging in pico-grid system.
Figure 16.
The battery voltage of the BESS during discharging in pico-grid system.
Figure 17.
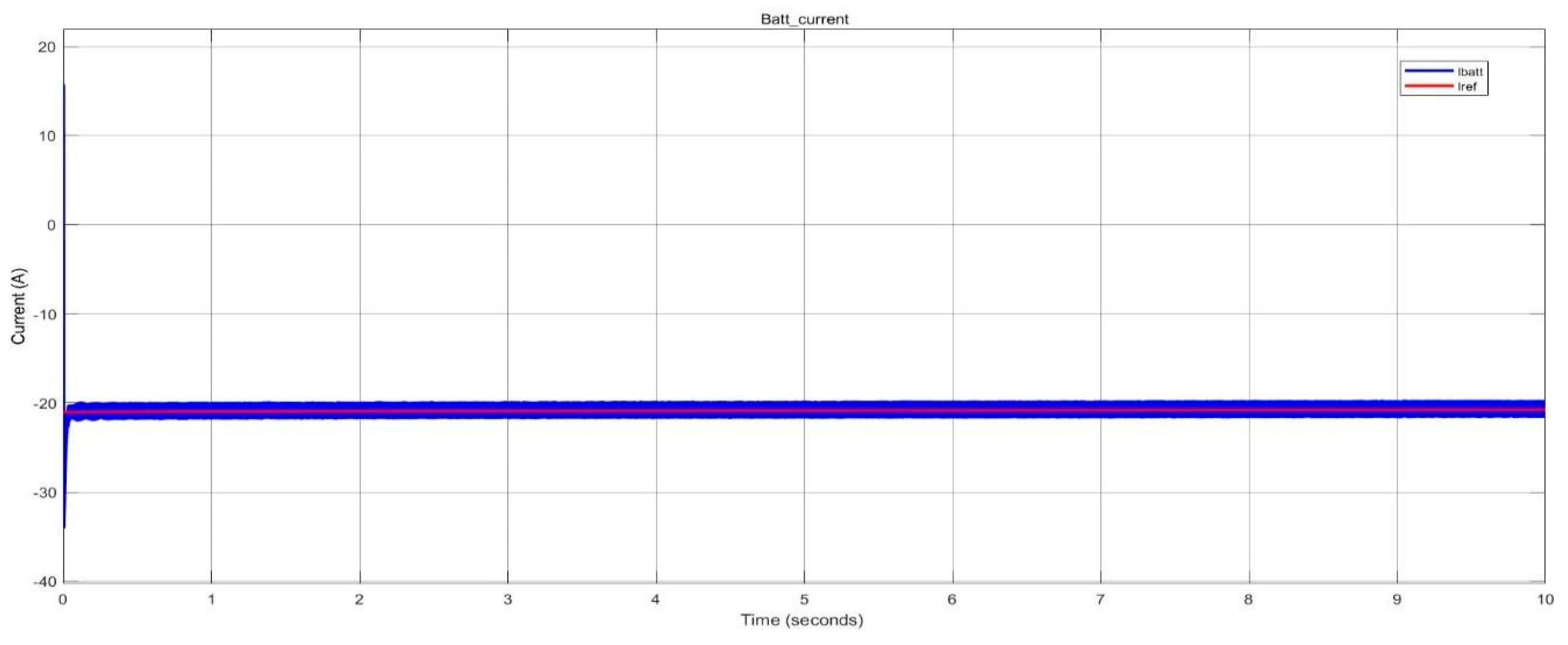
Battery current of BESS during discharging in pico-grid system.
Figure 17.
Battery current of BESS during discharging in pico-grid system.
Figure 18.
Battery capacity of BESS during discharging in pico-grid system.
Figure 18.
Battery capacity of BESS during discharging in pico-grid system.
Figure 19.
Voltage level at DC busbar in pico-grid system.
Figure 19.
Voltage level at DC busbar in pico-grid system.
Figure 20.
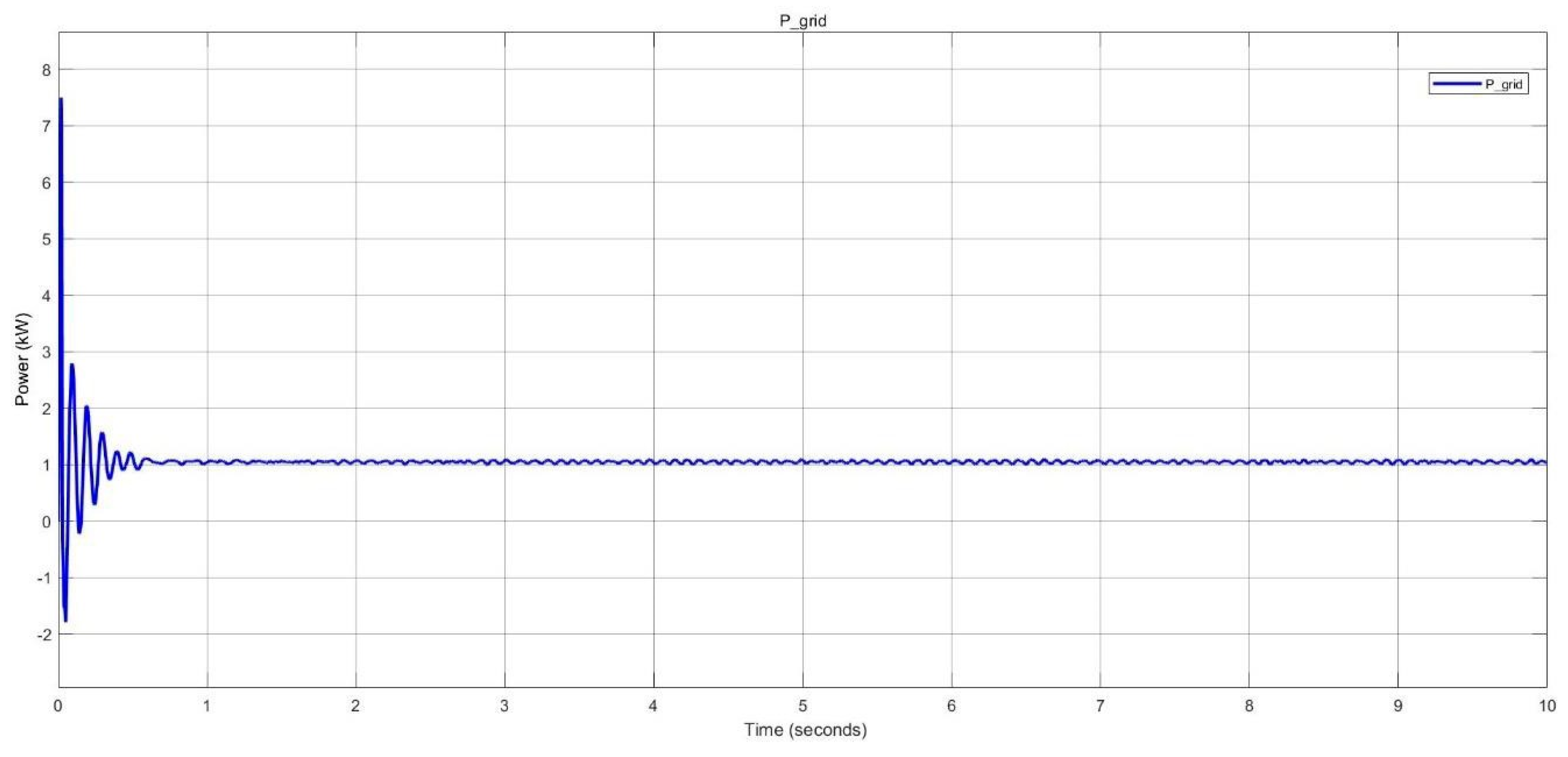
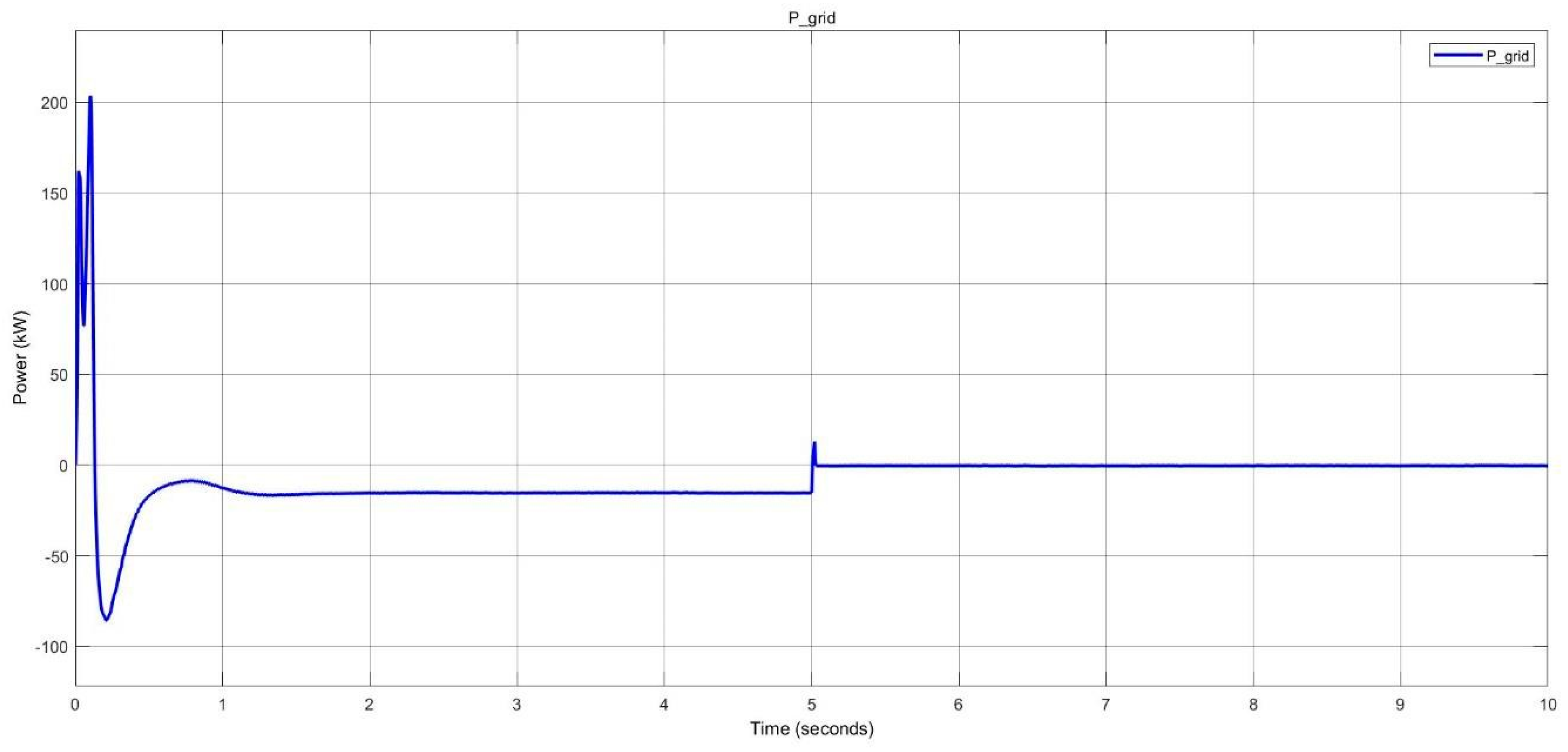
Surplus power delivered to the grid in pico-grid system.
Figure 20.
Surplus power delivered to the grid in pico-grid system.
Figure 21.
SOC level of the BESS during charging in pico-grid system.
Figure 21.
SOC level of the BESS during charging in pico-grid system.
Figure 22.
Battery voltage of the BESS during charging in pico-grid system.
Figure 22.
Battery voltage of the BESS during charging in pico-grid system.
Figure 23.
Battery voltage of the BESS during charging in pico-grid system.
Figure 23.
Battery voltage of the BESS during charging in pico-grid system.
Figure 24.
Battery current of BESS during charging in pico-grid system.
Figure 24.
Battery current of BESS during charging in pico-grid system.
Figure 25.
Battery capacity of BESS during charging in pico-grid system.
Figure 25.
Battery capacity of BESS during charging in pico-grid system.
Figure 26.
Drawing power from the grid to charge the battery in pico-grid system.
Figure 26.
Drawing power from the grid to charge the battery in pico-grid system.
Figure 27.
Two parallel pico-grids connected to the single-phase grid.
Figure 27.
Two parallel pico-grids connected to the single-phase grid.
Figure 28.
DC and AC loads before increase for two pico-grids system.
Figure 28.
DC and AC loads before increase for two pico-grids system.
Figure 29.
DC and AC loads before increase for two pico-grids system.
Figure 29.
DC and AC loads before increase for two pico-grids system.
Figure 30.
Surplus power from the system sent to the grid for two pico-grids system.
Figure 30.
Surplus power from the system sent to the grid for two pico-grids system.
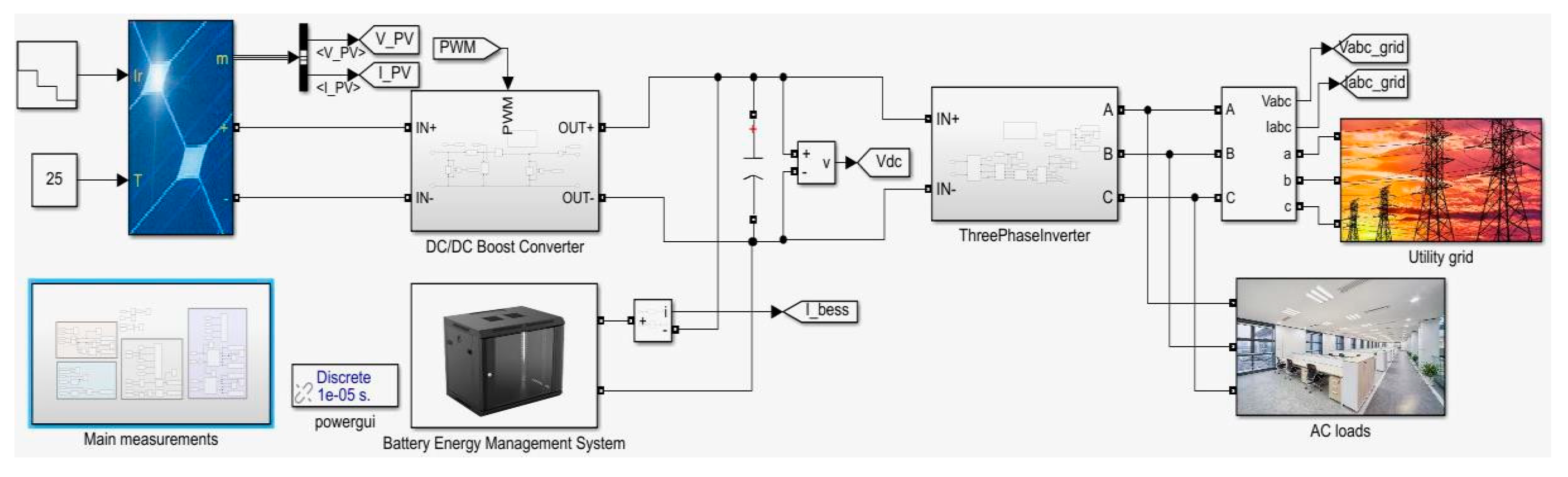
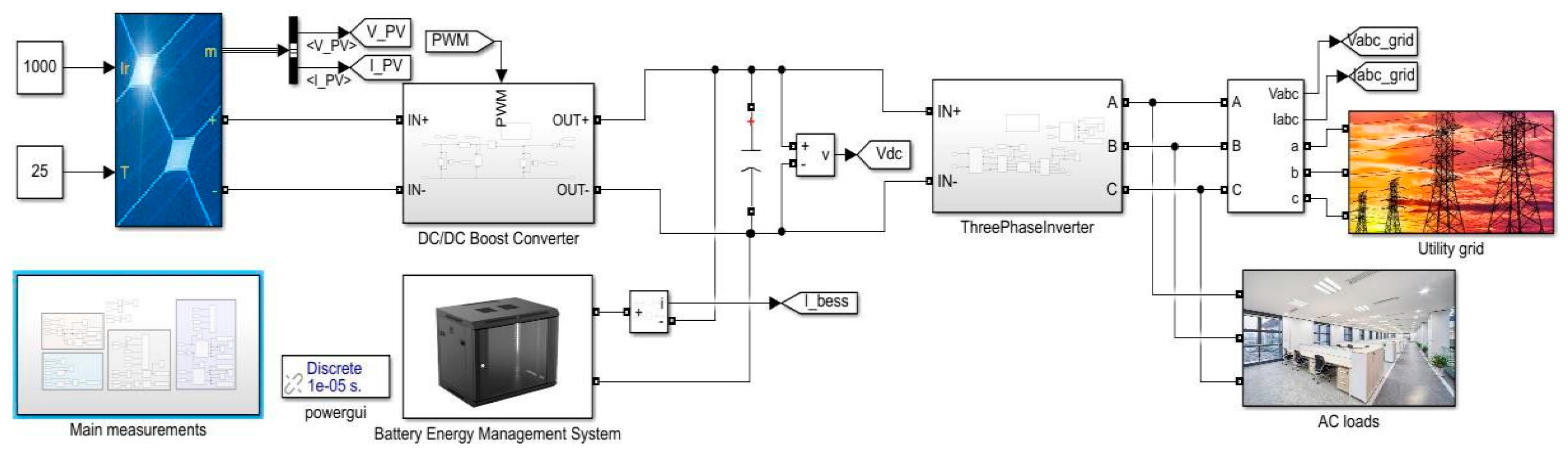
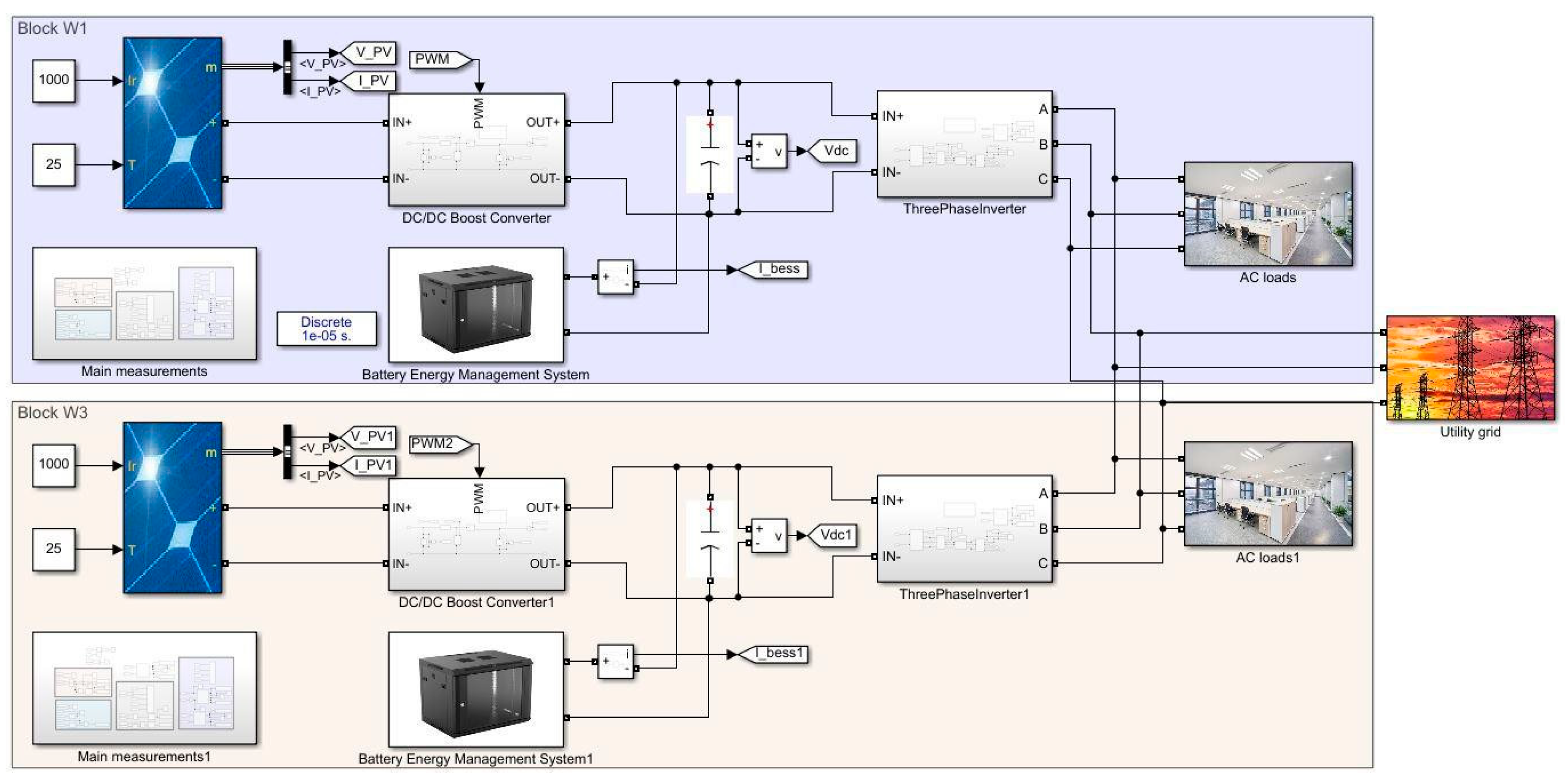
Figure 31.
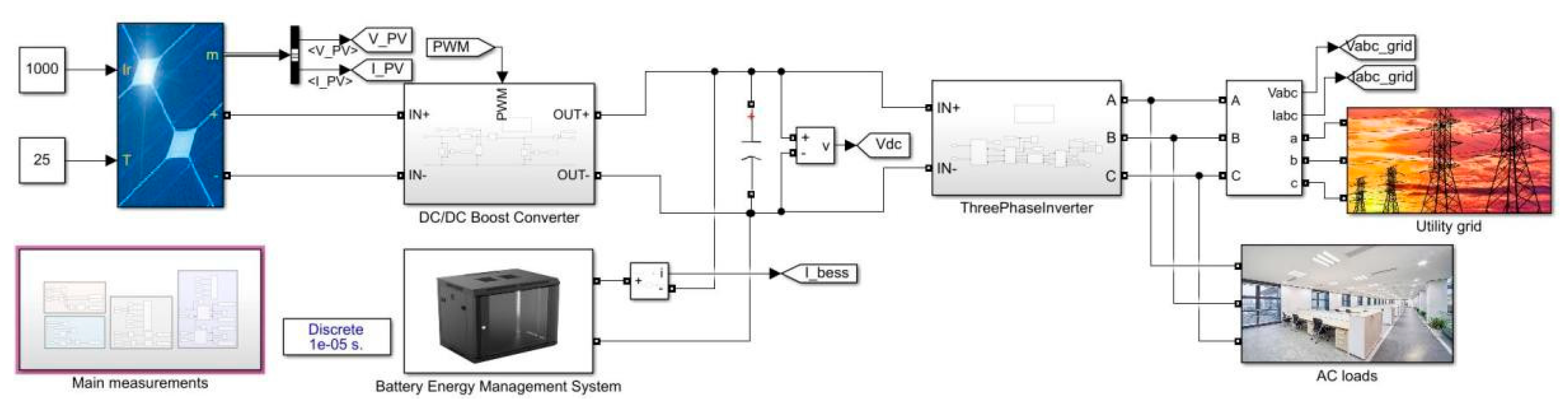
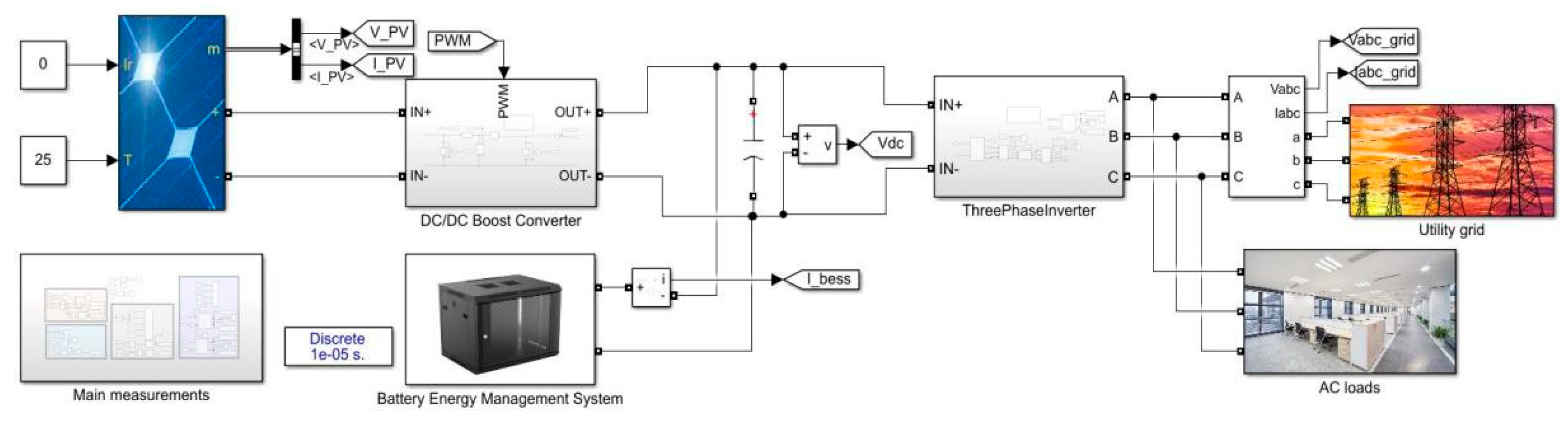
Simulation model of integration of solar PV, BESS with three-phase inverter.
Figure 31.
Simulation model of integration of solar PV, BESS with three-phase inverter.
Figure 32.
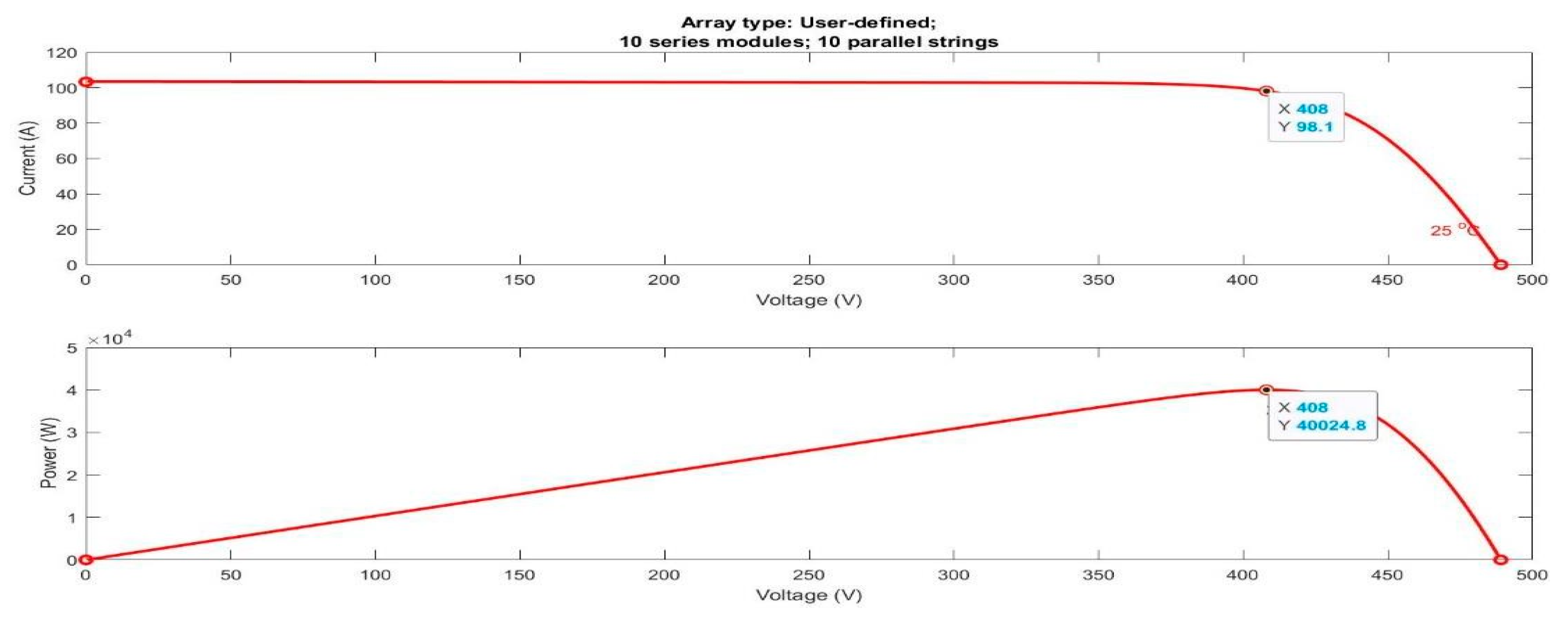
Solar PV array waveform.
Figure 32.
Solar PV array waveform.
Figure 33.
Load demand estimation of AC loads in nano-grid system.
Figure 33.
Load demand estimation of AC loads in nano-grid system.
Figure 34.
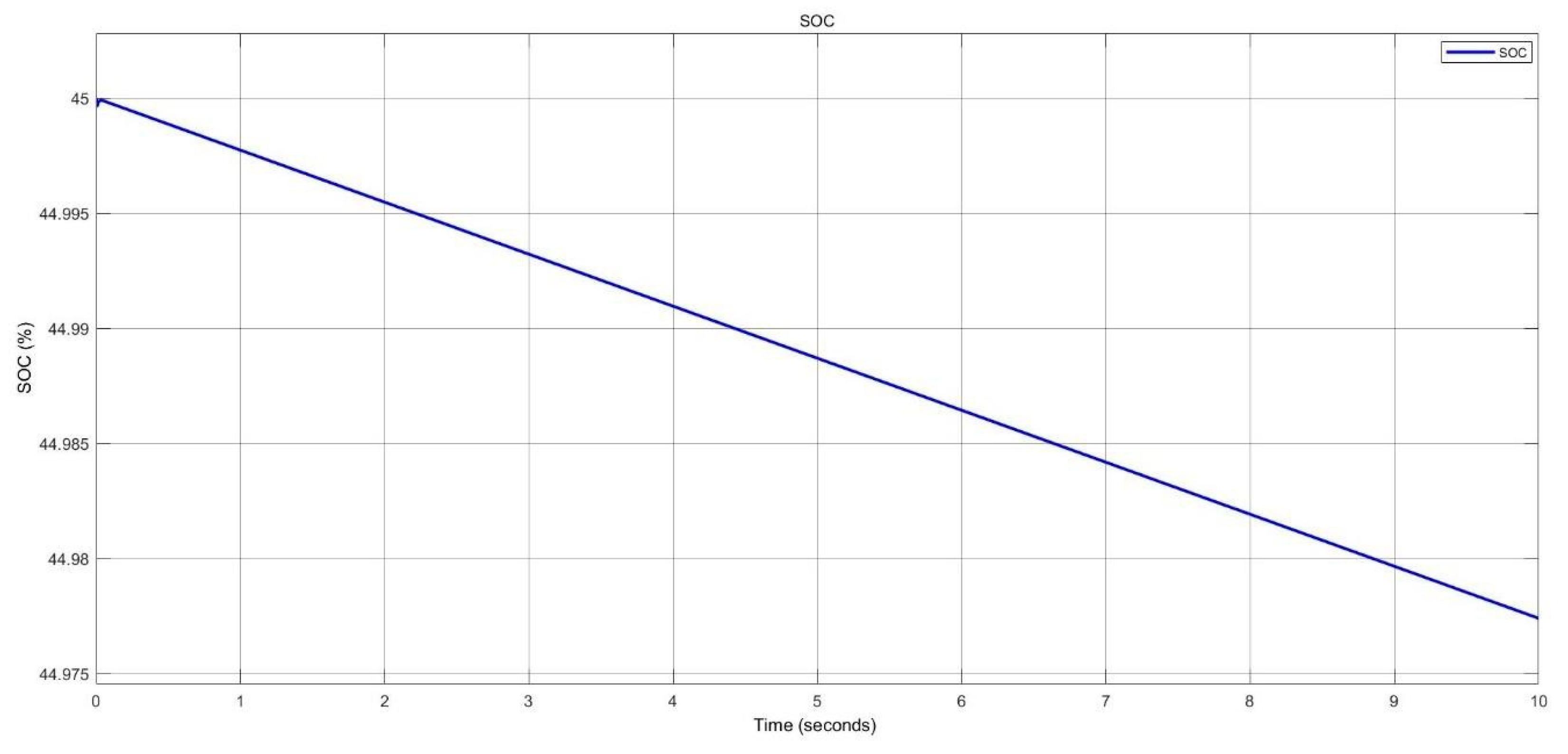
SOC of battery during discharging in nano-grid system.
Figure 34.
SOC of battery during discharging in nano-grid system.
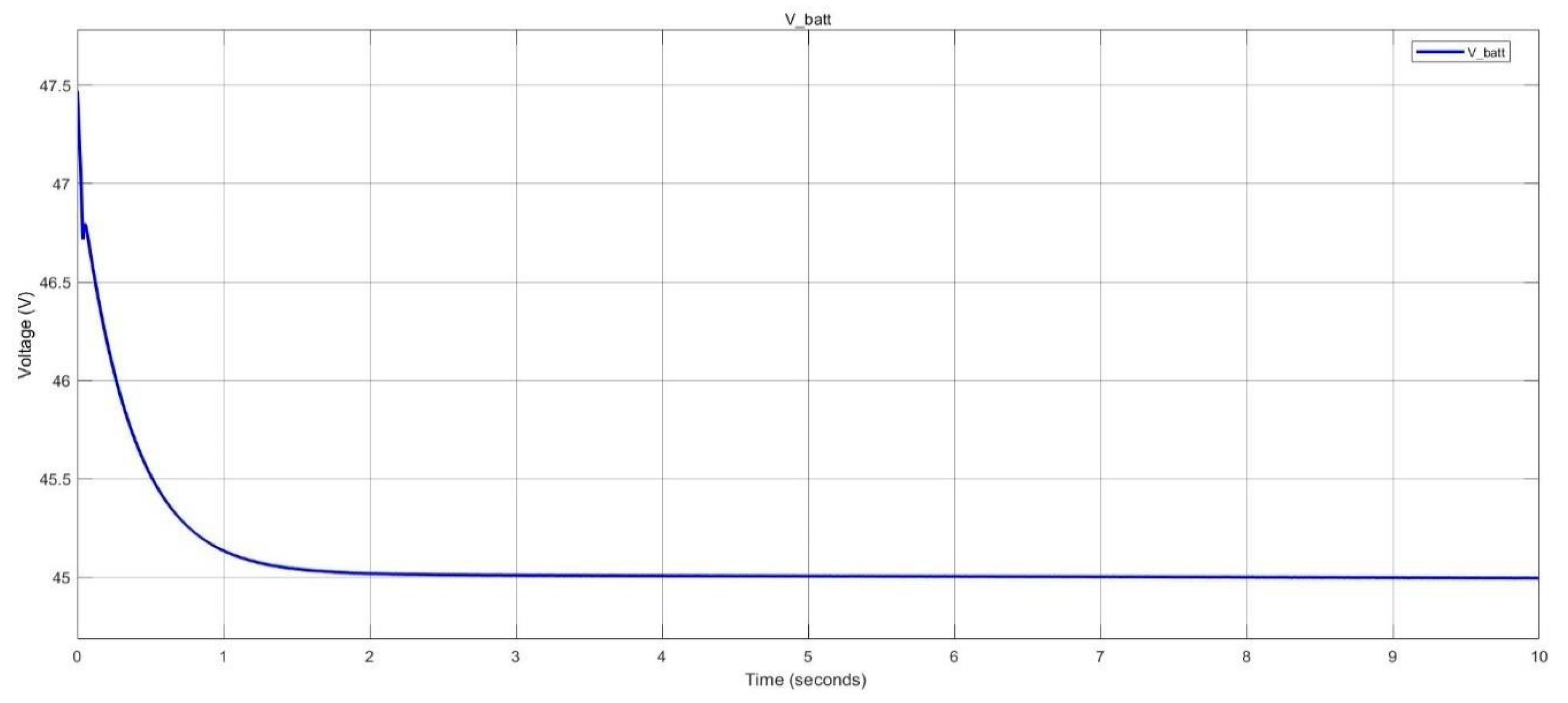
Figure 35.
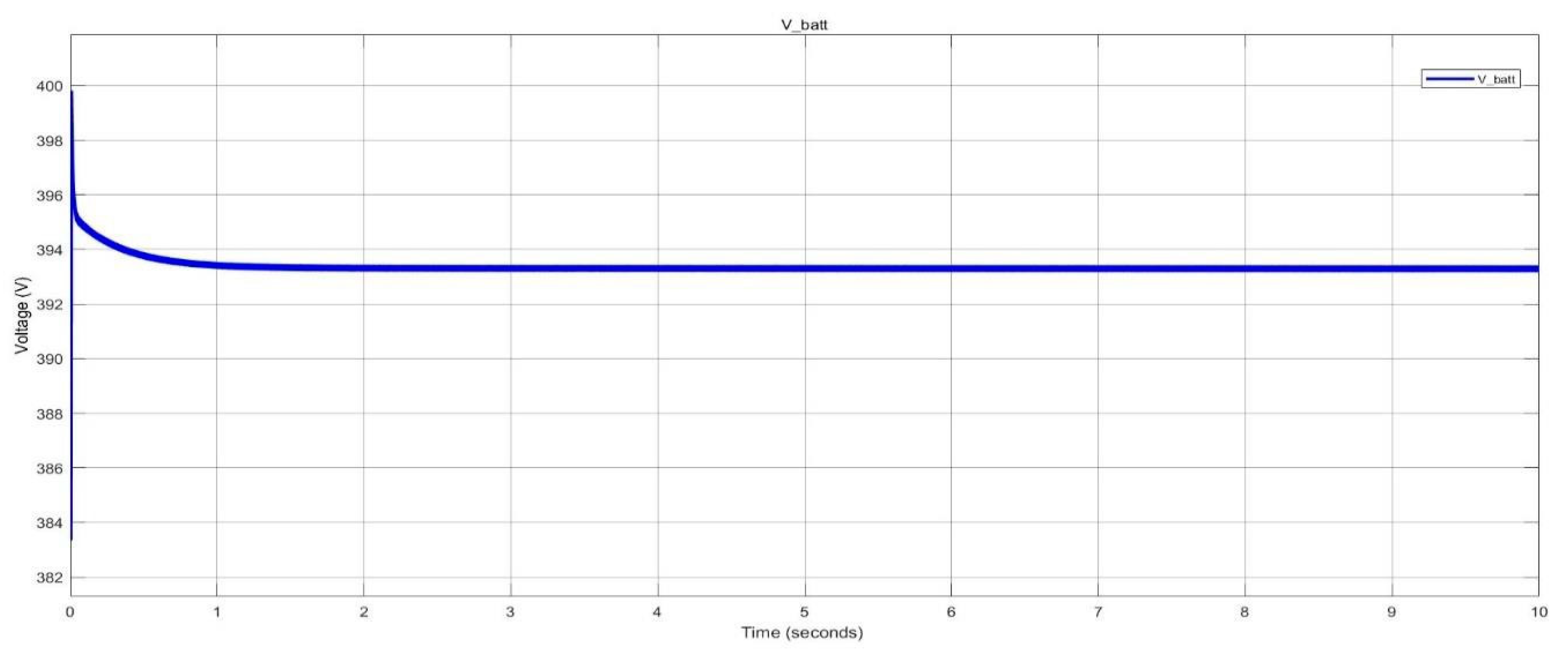
Battery voltage of the BESS during discharging in nano-grid system.
Figure 35.
Battery voltage of the BESS during discharging in nano-grid system.
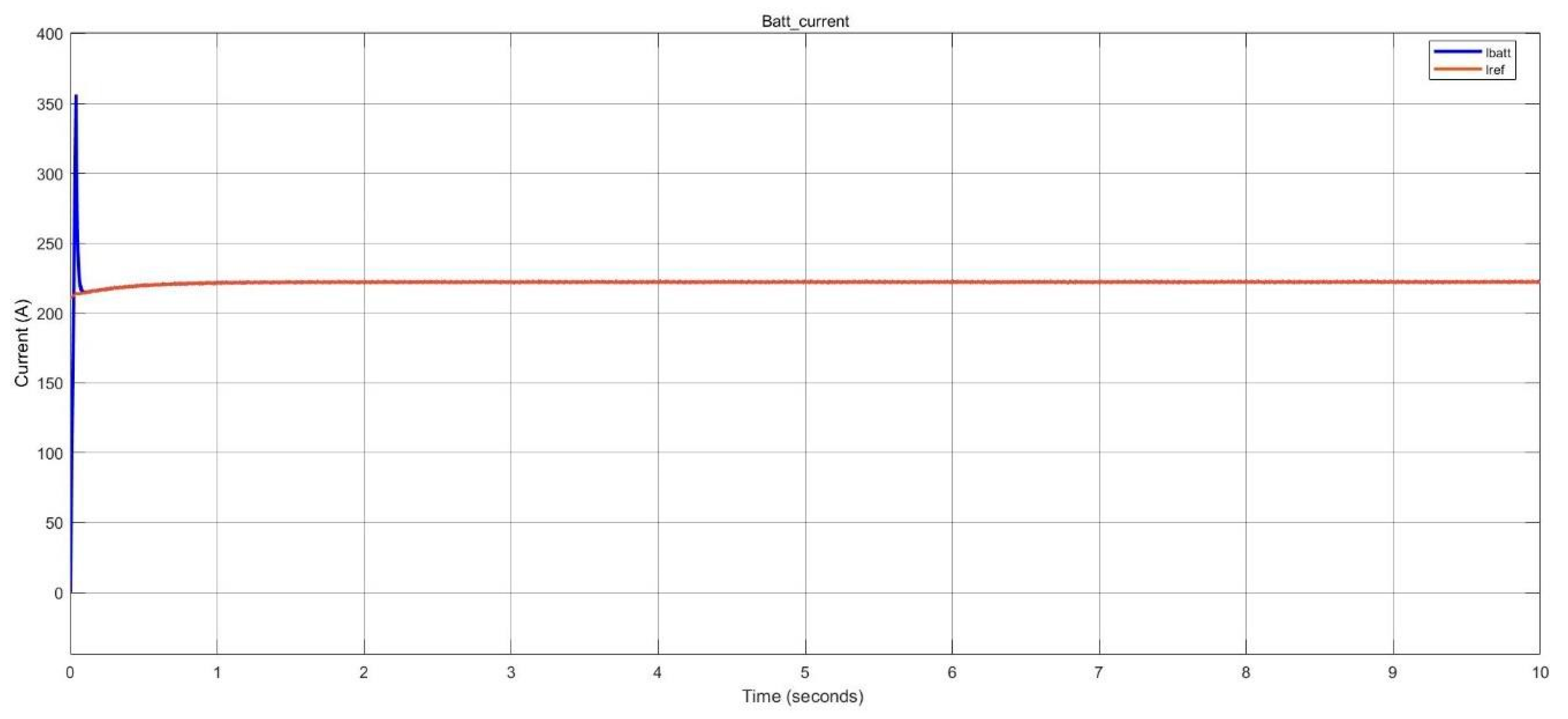
Figure 36.
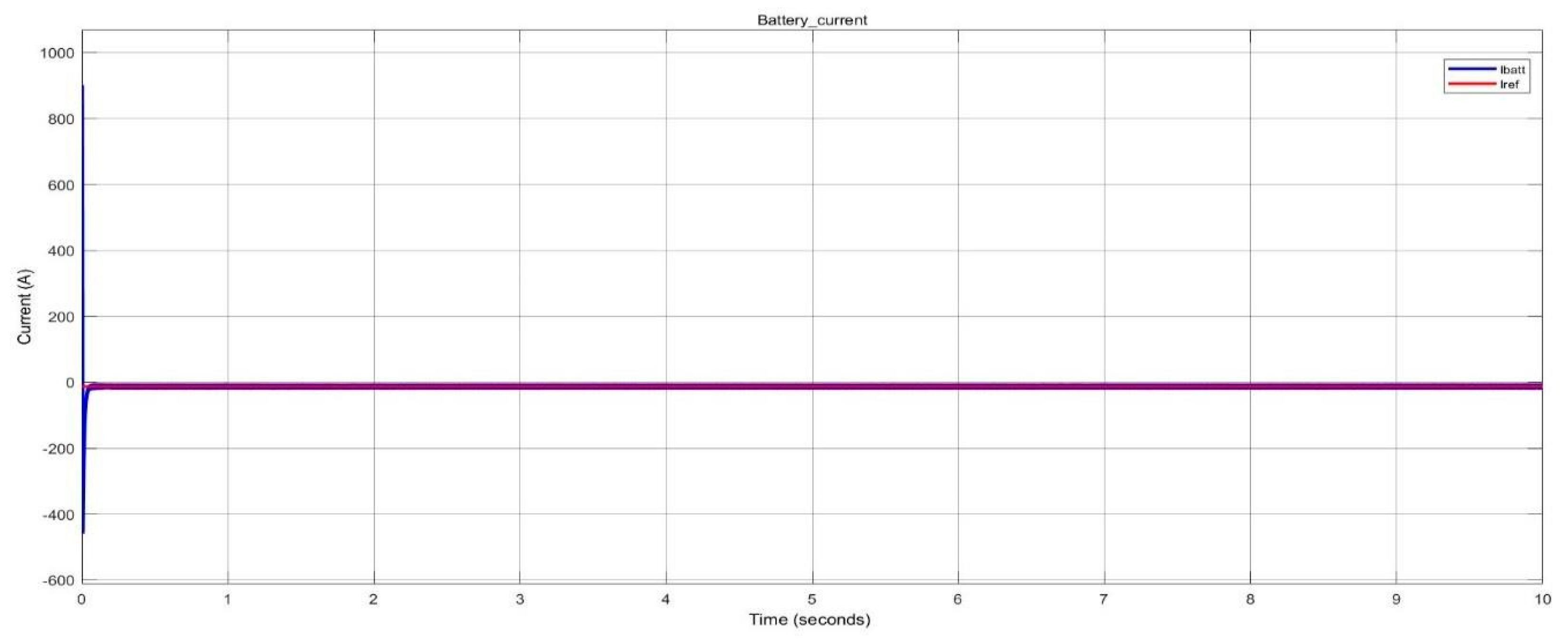
Battery current of BESS during discharging in nano-grid system.
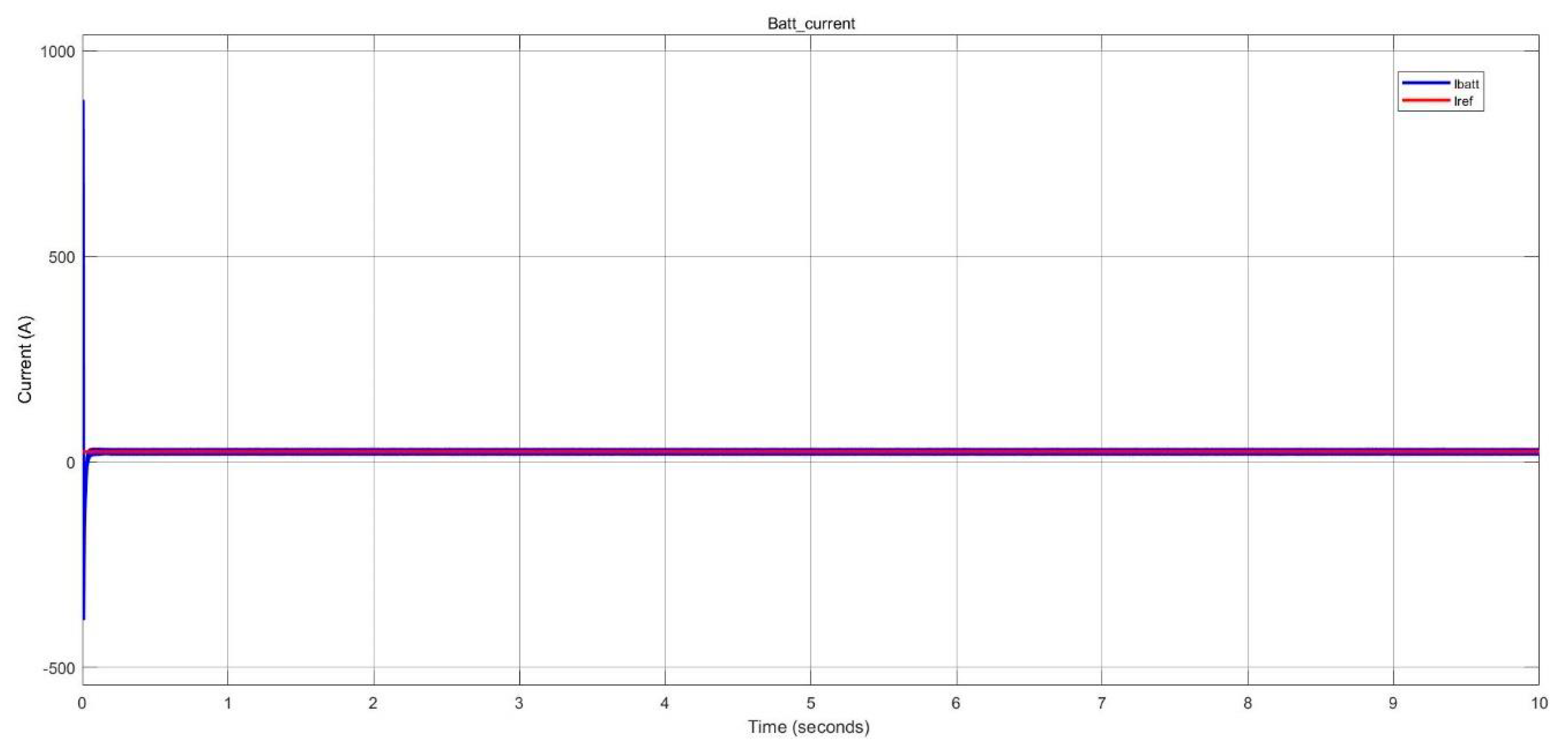
Figure 36.
Battery current of BESS during discharging in nano-grid system.
Figure 37.
Battery capacity of BESS during discharging in nano-grid system.
Figure 37.
Battery capacity of BESS during discharging in nano-grid system.
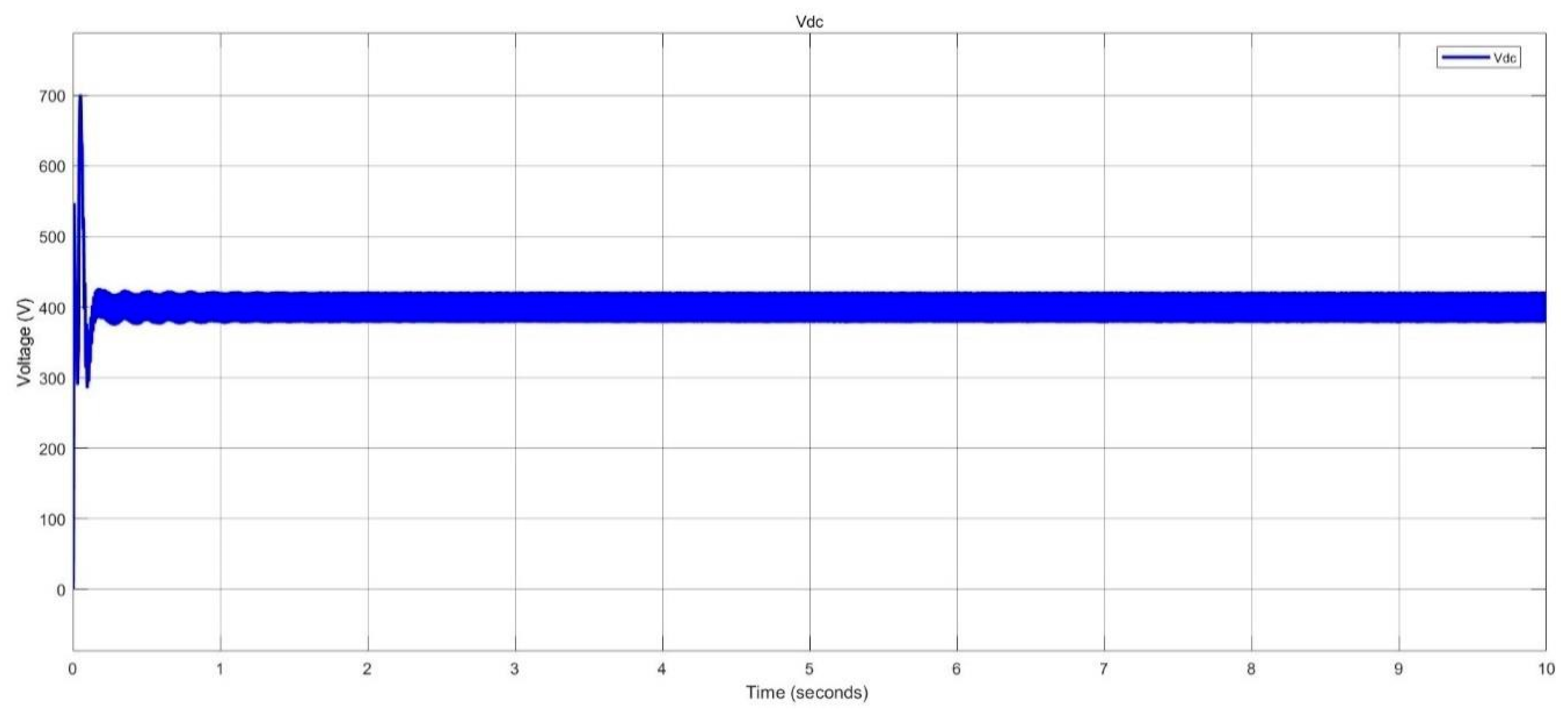
Figure 38.
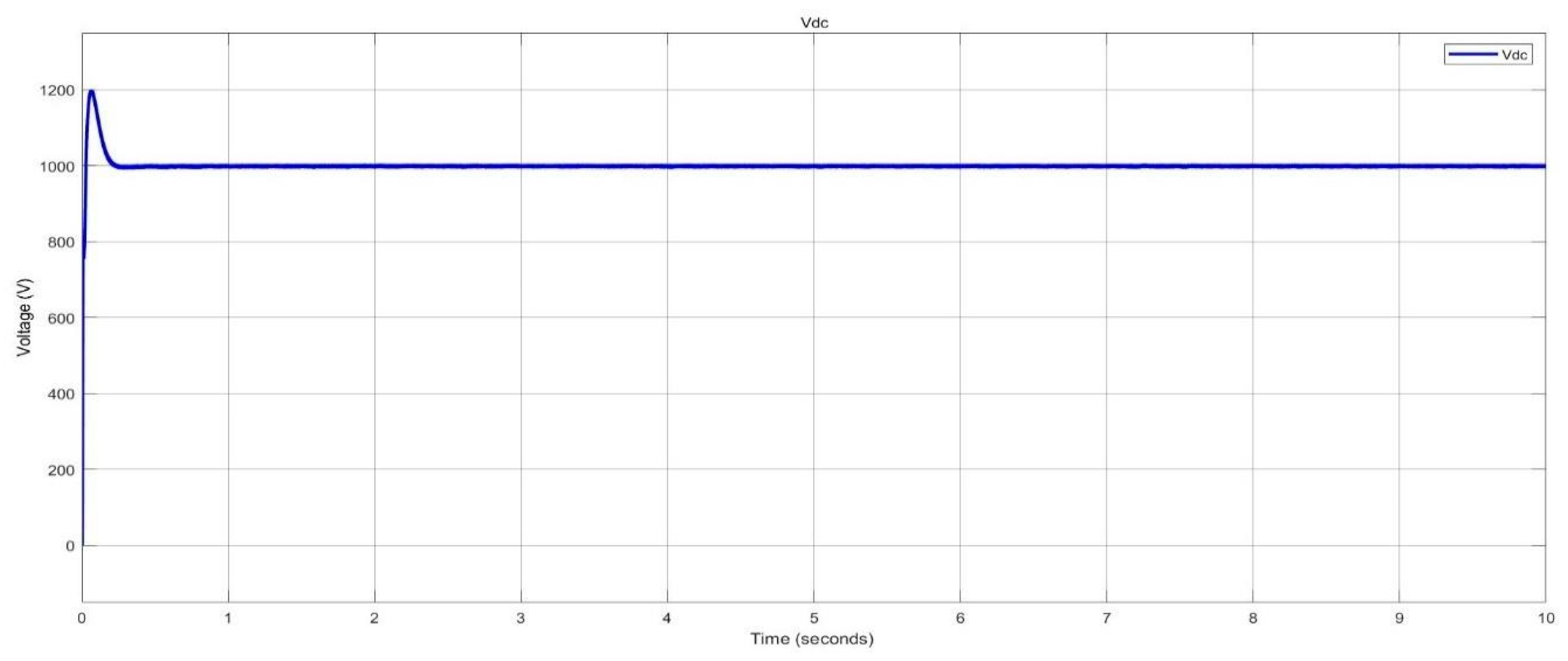
Voltage level at DC busbar in nano-grid system.
Figure 38.
Voltage level at DC busbar in nano-grid system.
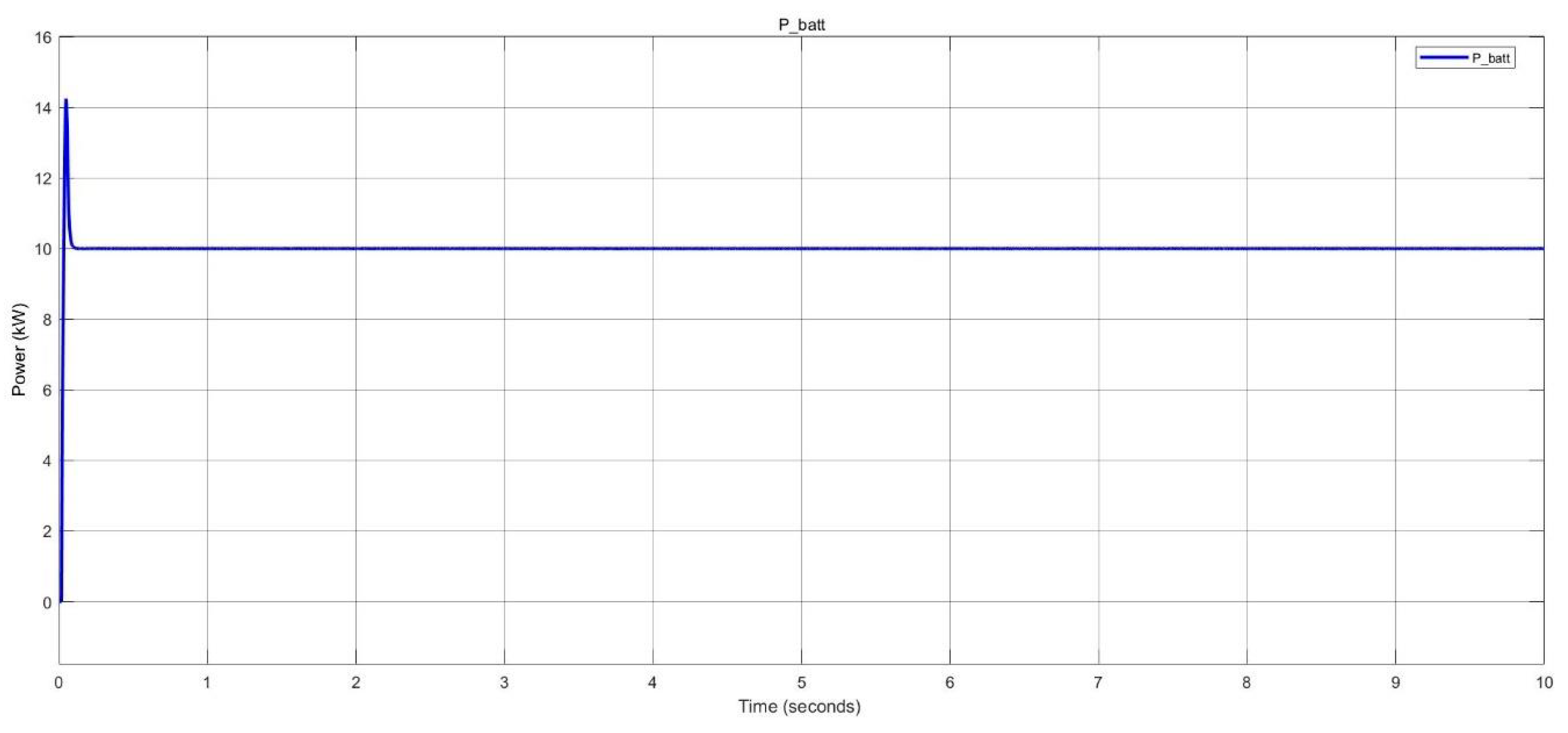
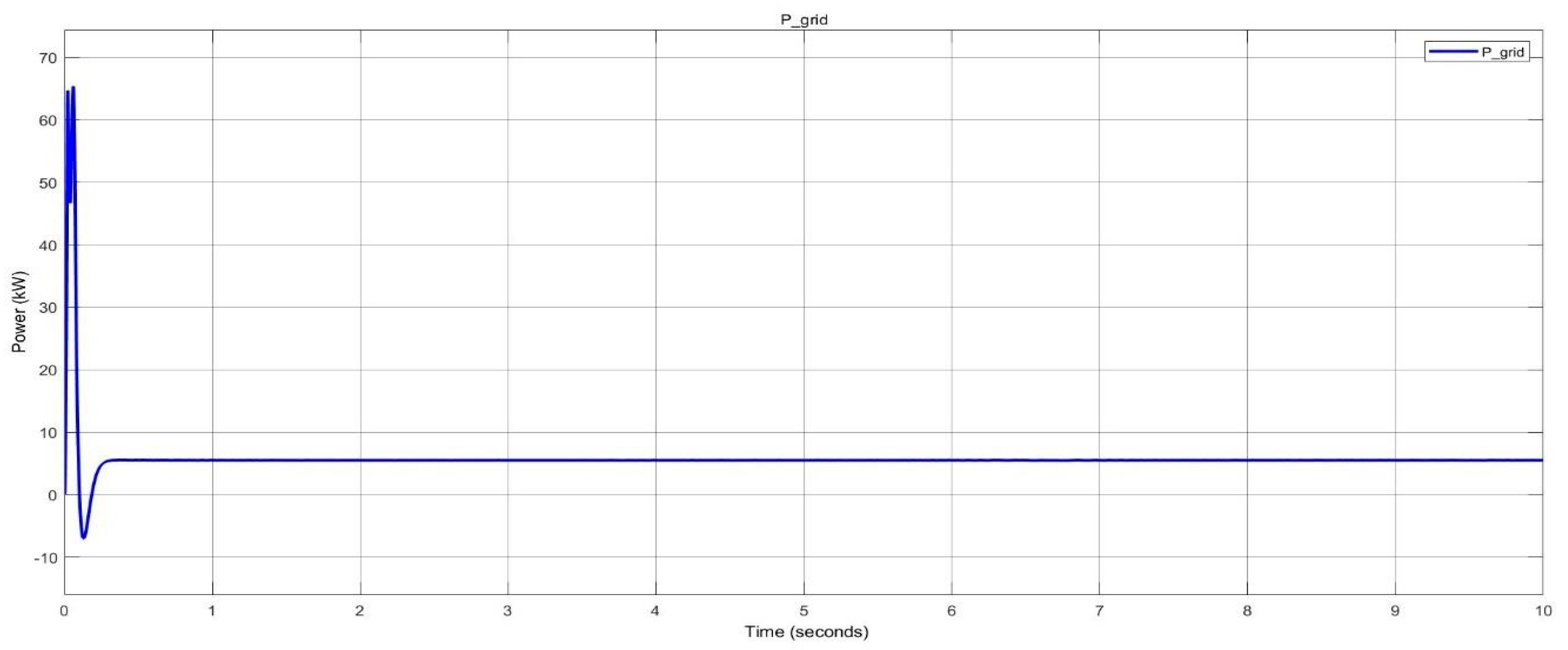
Figure 39.
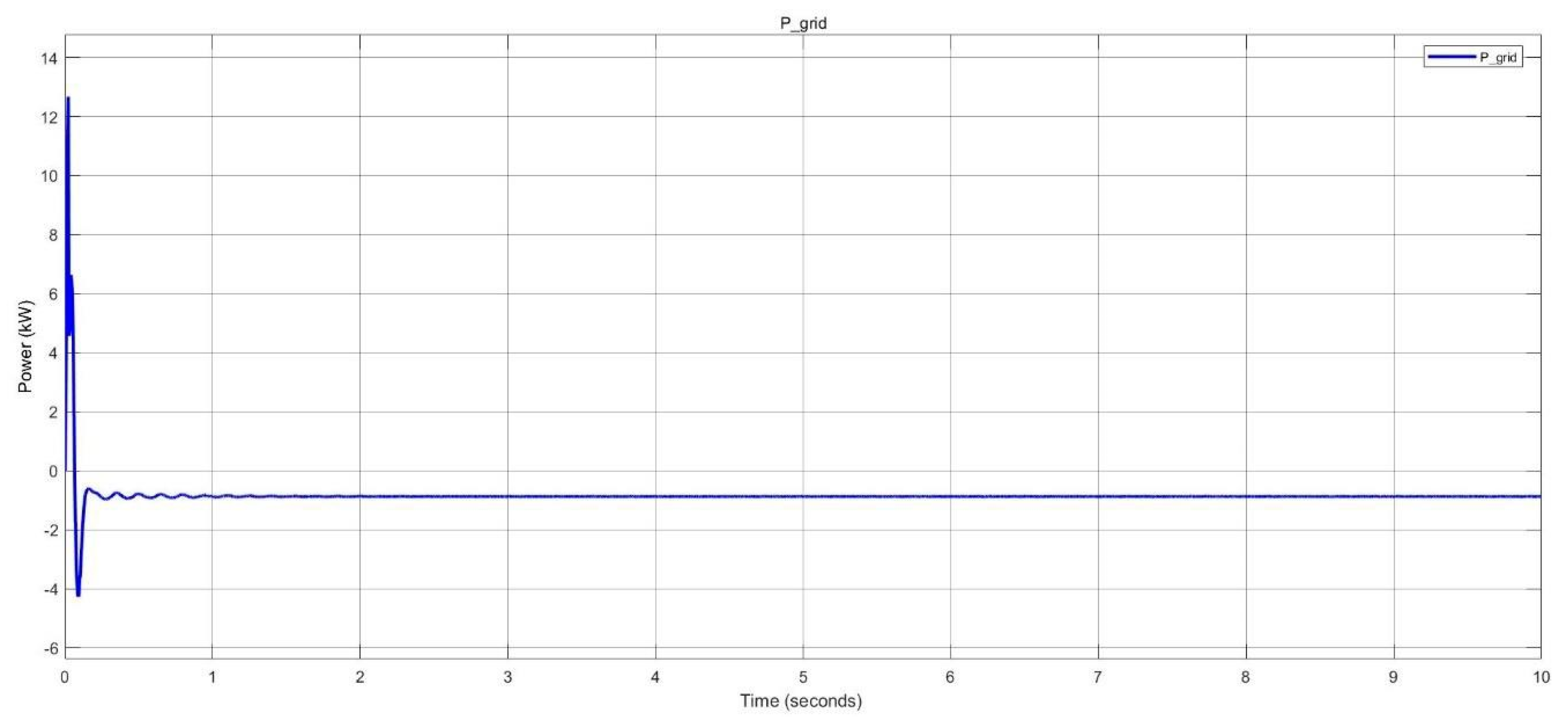
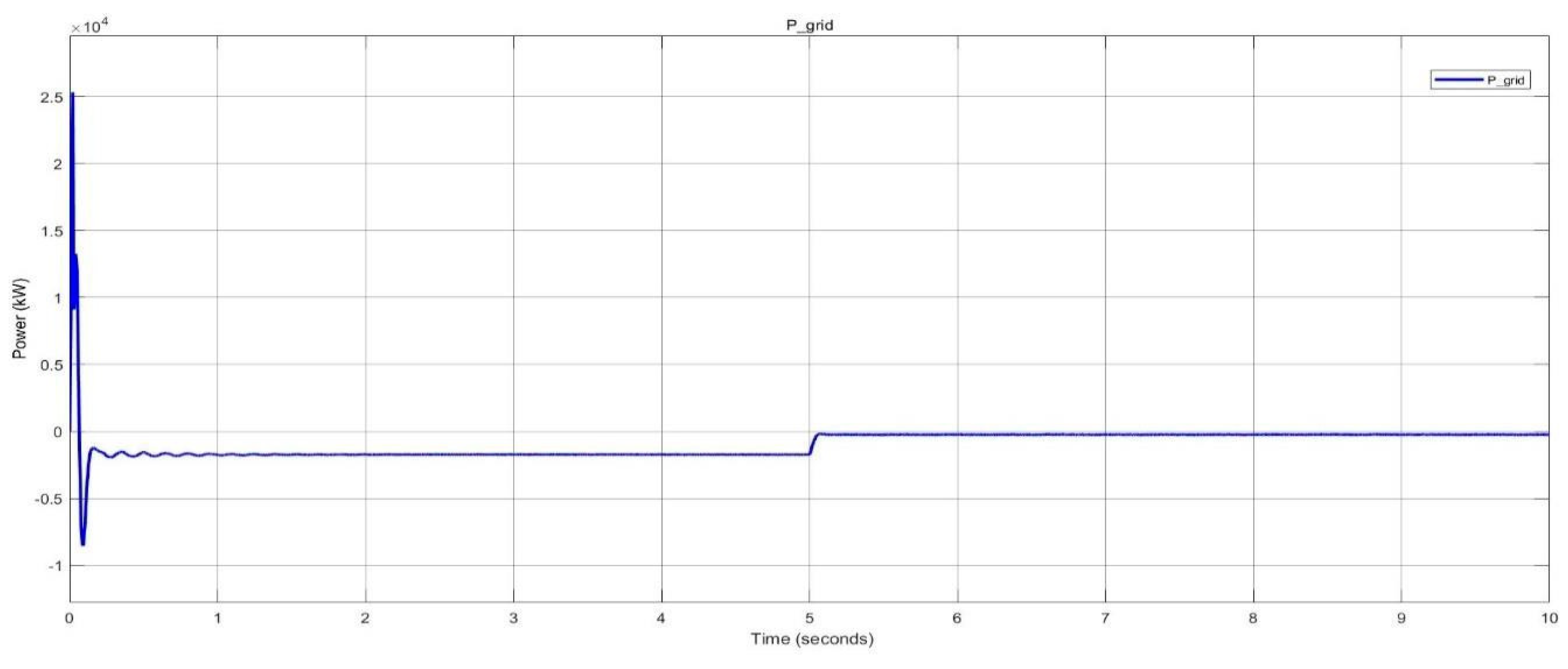
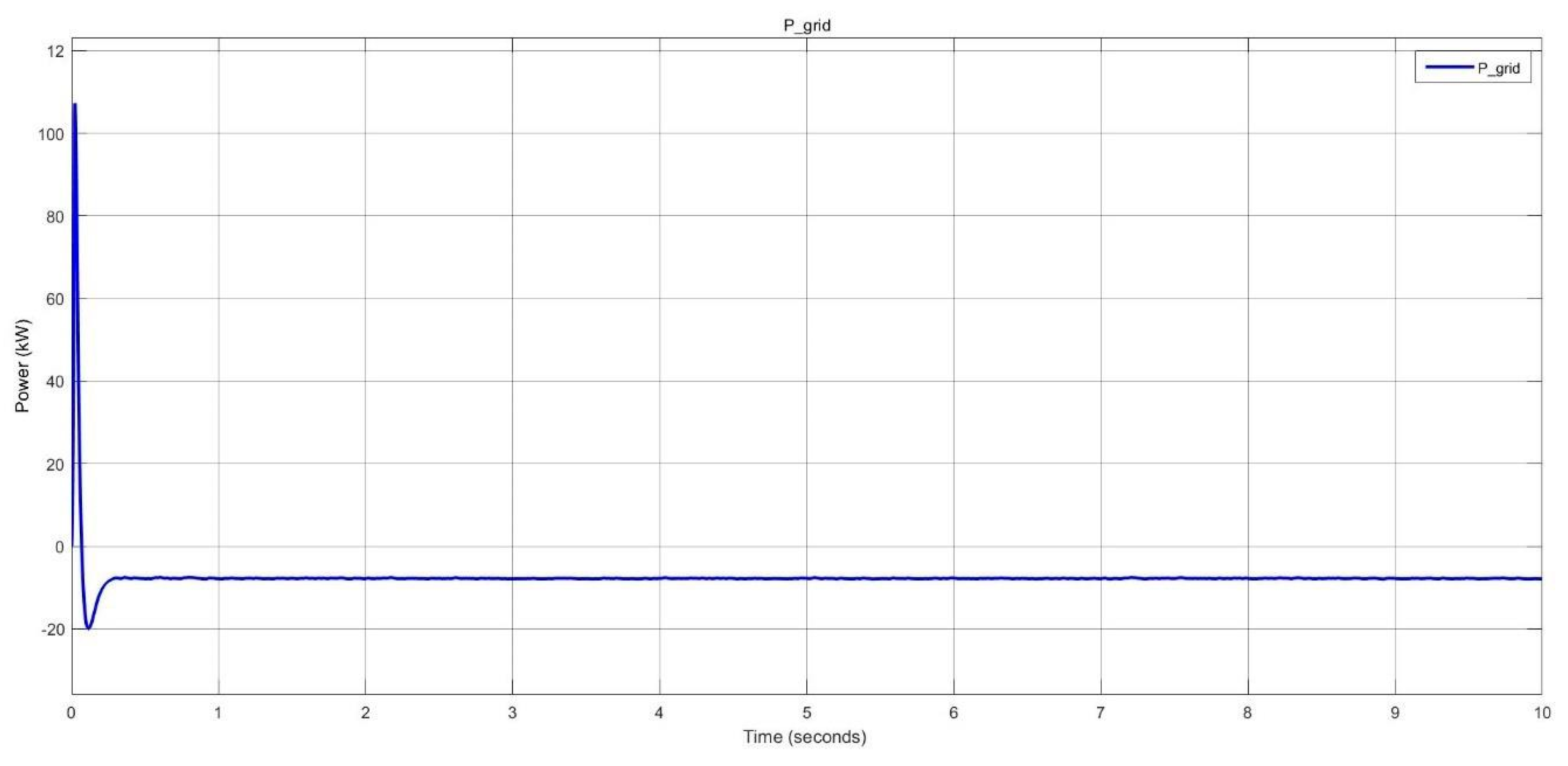
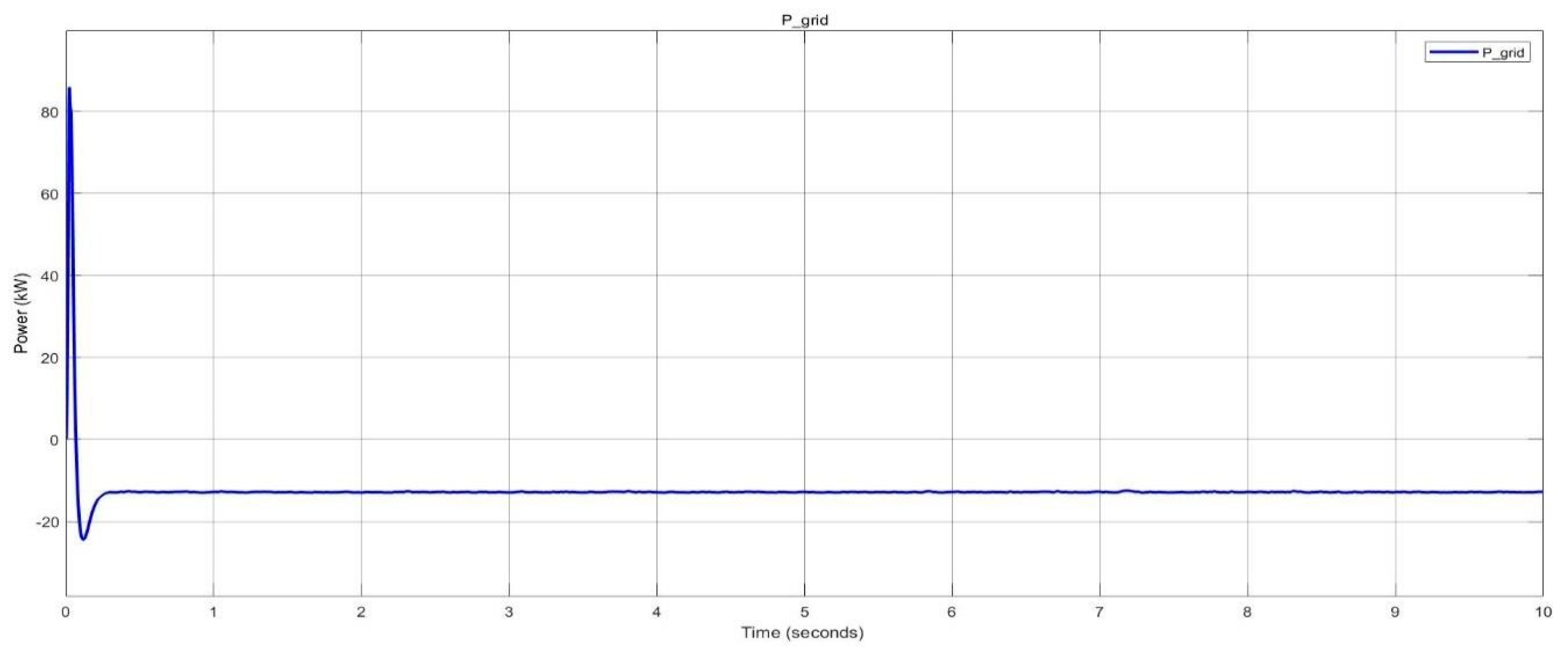
Surplus power delivered to the grid in nano-grid system.
Figure 39.
Surplus power delivered to the grid in nano-grid system.
Figure 40.
Simulation model to demonstrate charging of battery.
Figure 40.
Simulation model to demonstrate charging of battery.
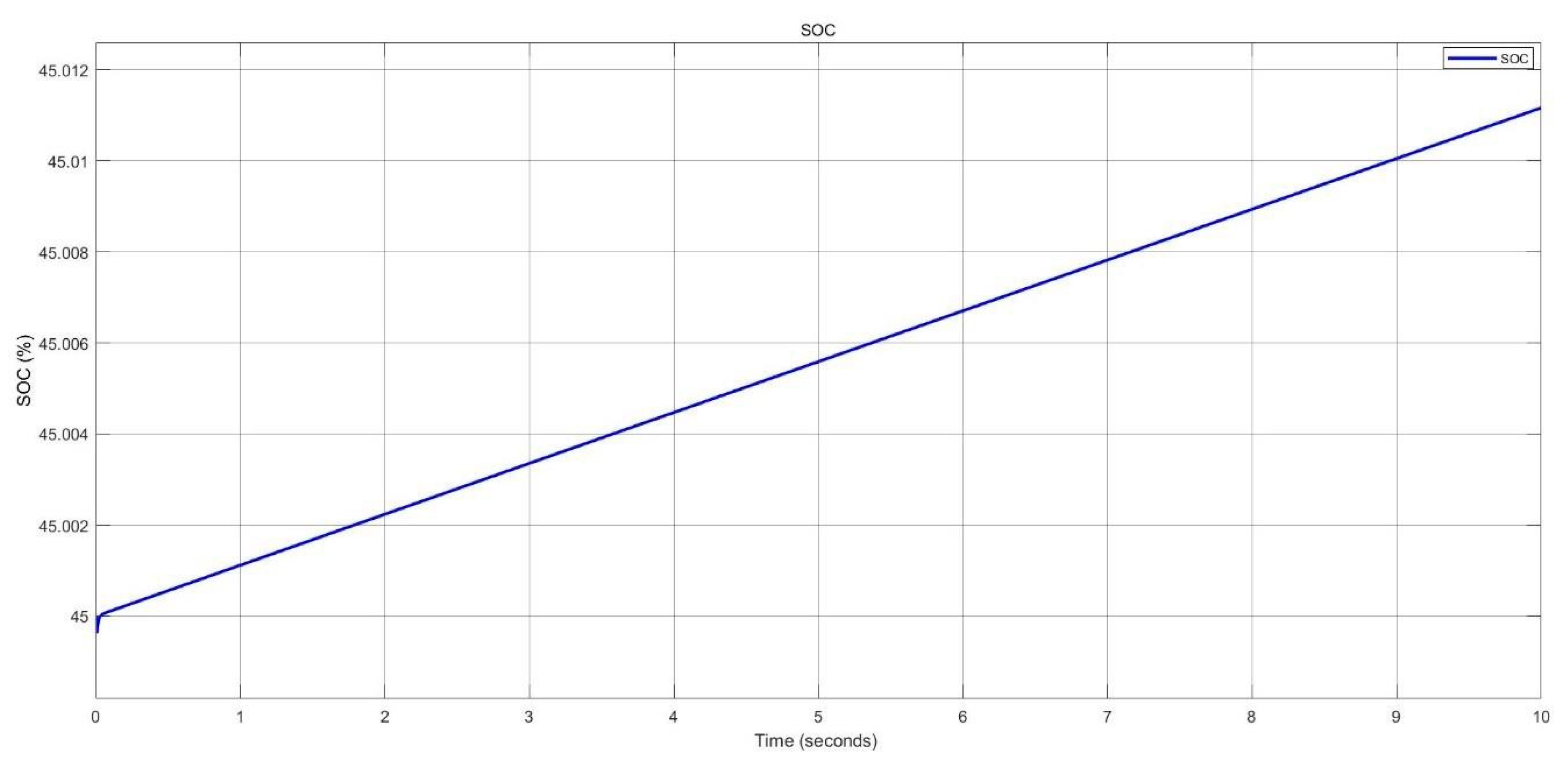
Figure 41.
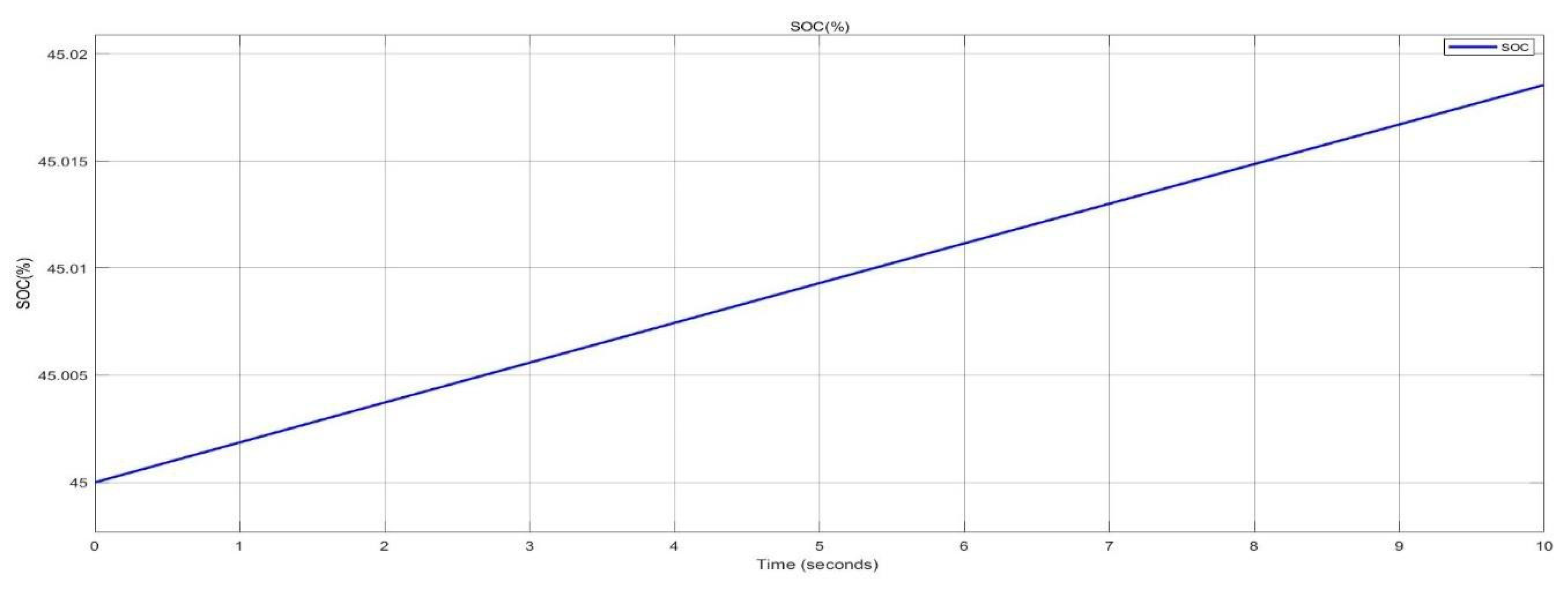
SOC of battery during charging in nano-grid system.
Figure 41.
SOC of battery during charging in nano-grid system.
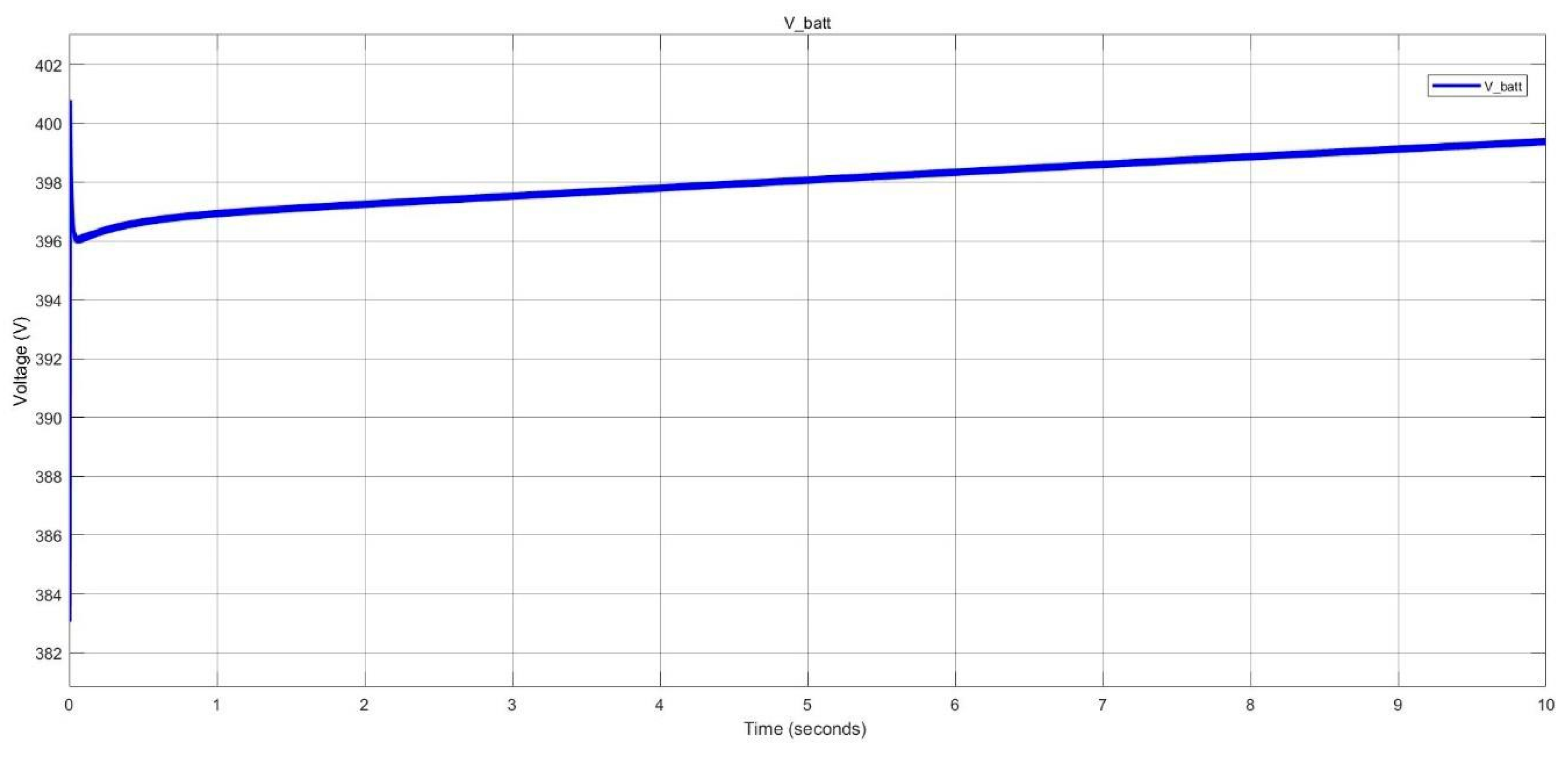
Figure 42.
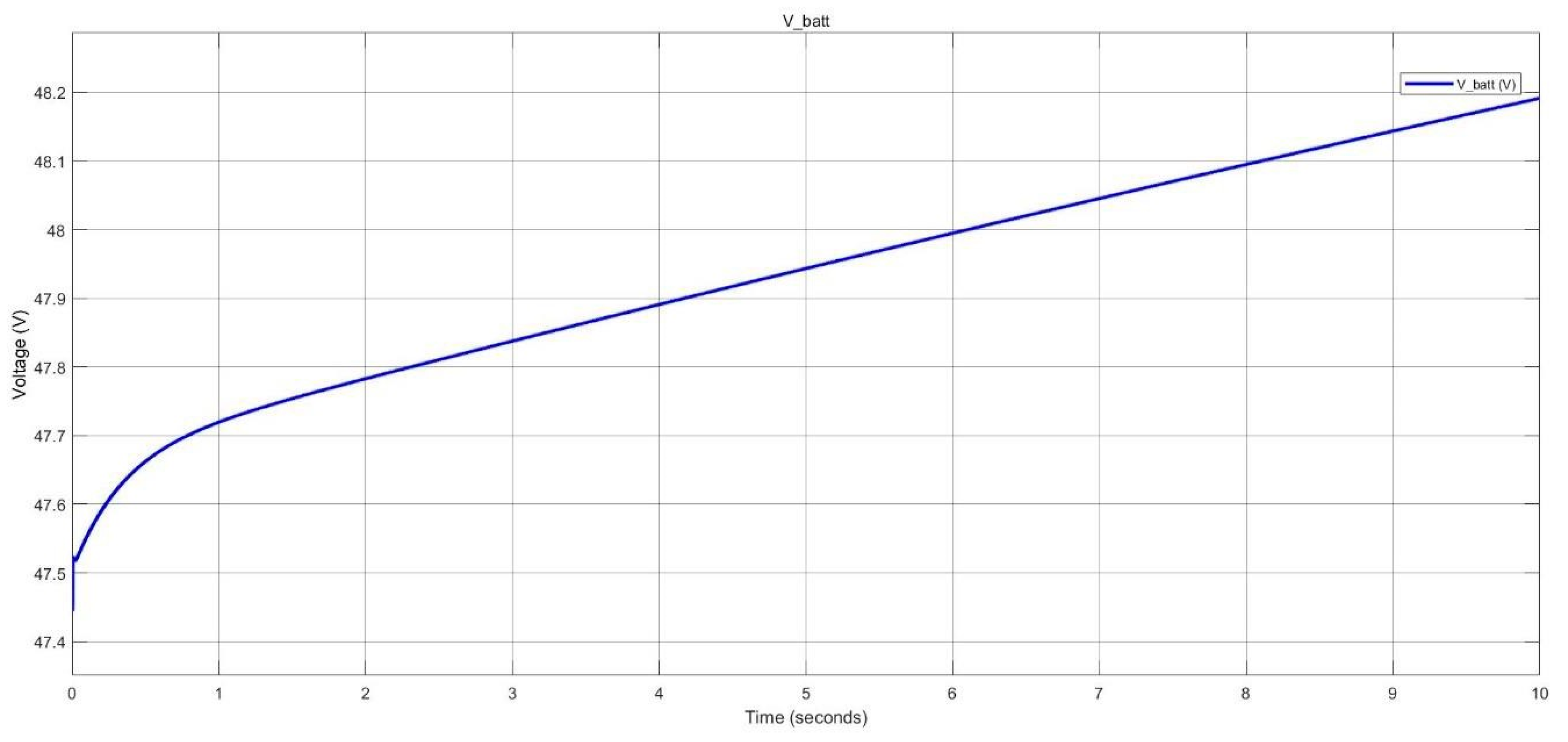
Battery voltage of the BESS during charging in nano-grid system.
Figure 42.
Battery voltage of the BESS during charging in nano-grid system.
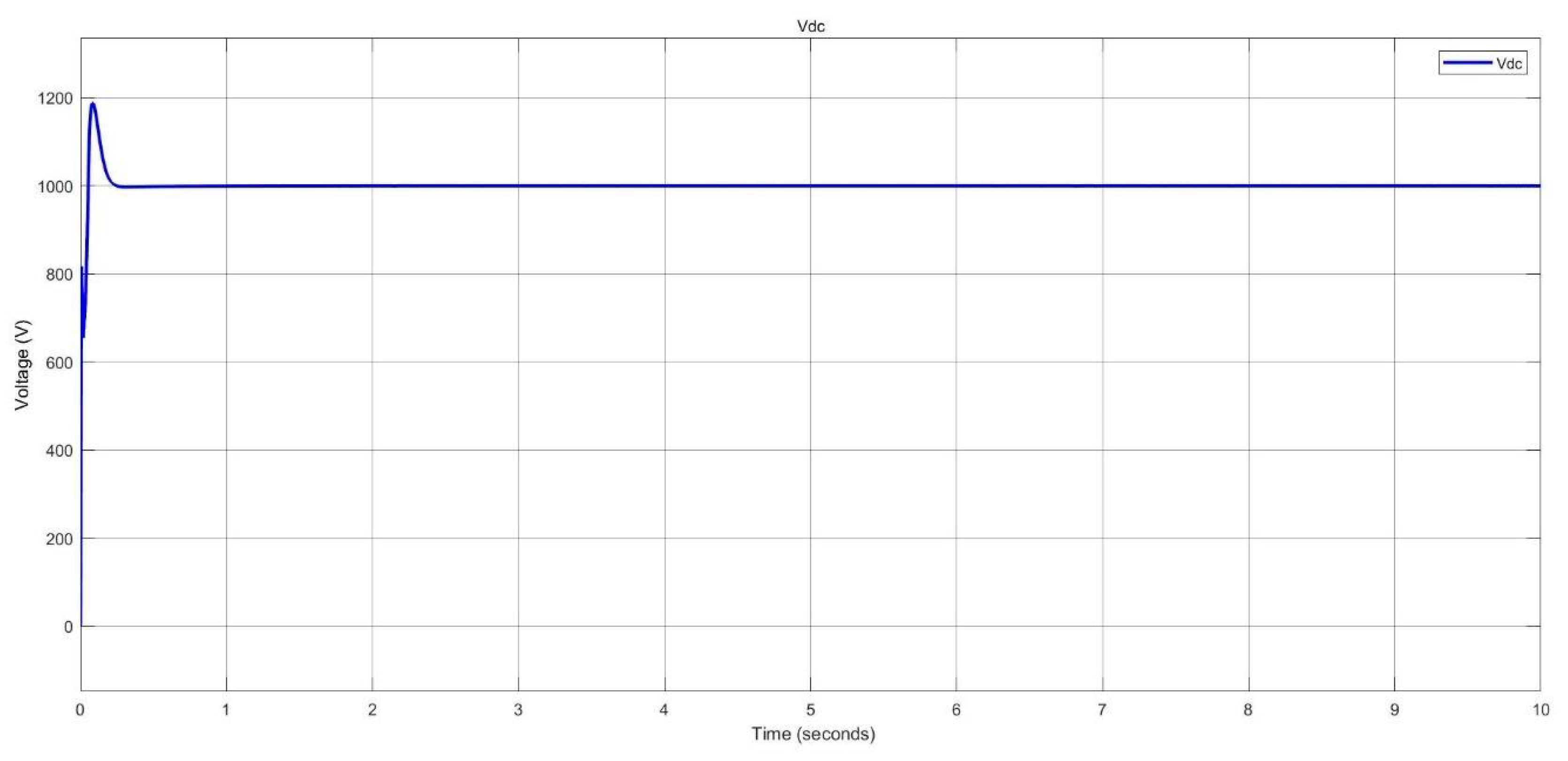
Figure 43.
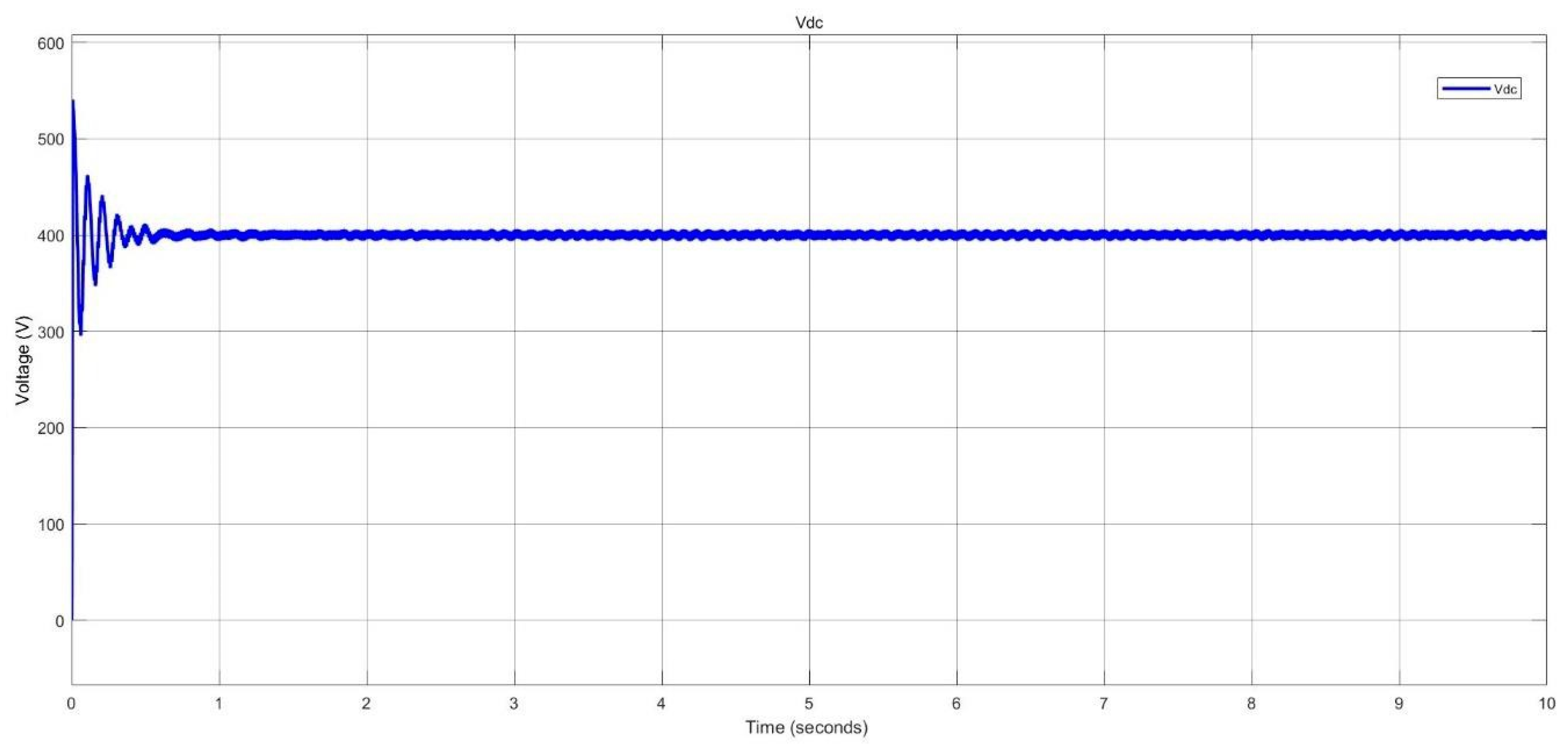
Voltage level at DC busbar in nano-grid system.
Figure 43.
Voltage level at DC busbar in nano-grid system.
Figure 44.
Battery current of BESS during charging in nano-grid system.
Figure 44.
Battery current of BESS during charging in nano-grid system.
Figure 45.
Battery capacity of BESS during charging in nano-grid system.
Figure 45.
Battery capacity of BESS during charging in nano-grid system.
Figure 46.
Drawing power from the grid to charge the battery in nano-grid system.
Figure 46.
Drawing power from the grid to charge the battery in nano-grid system.
Figure 47.
Simulation model to demonstrate a rainy day operation.
Figure 47.
Simulation model to demonstrate a rainy day operation.
Figure 48.
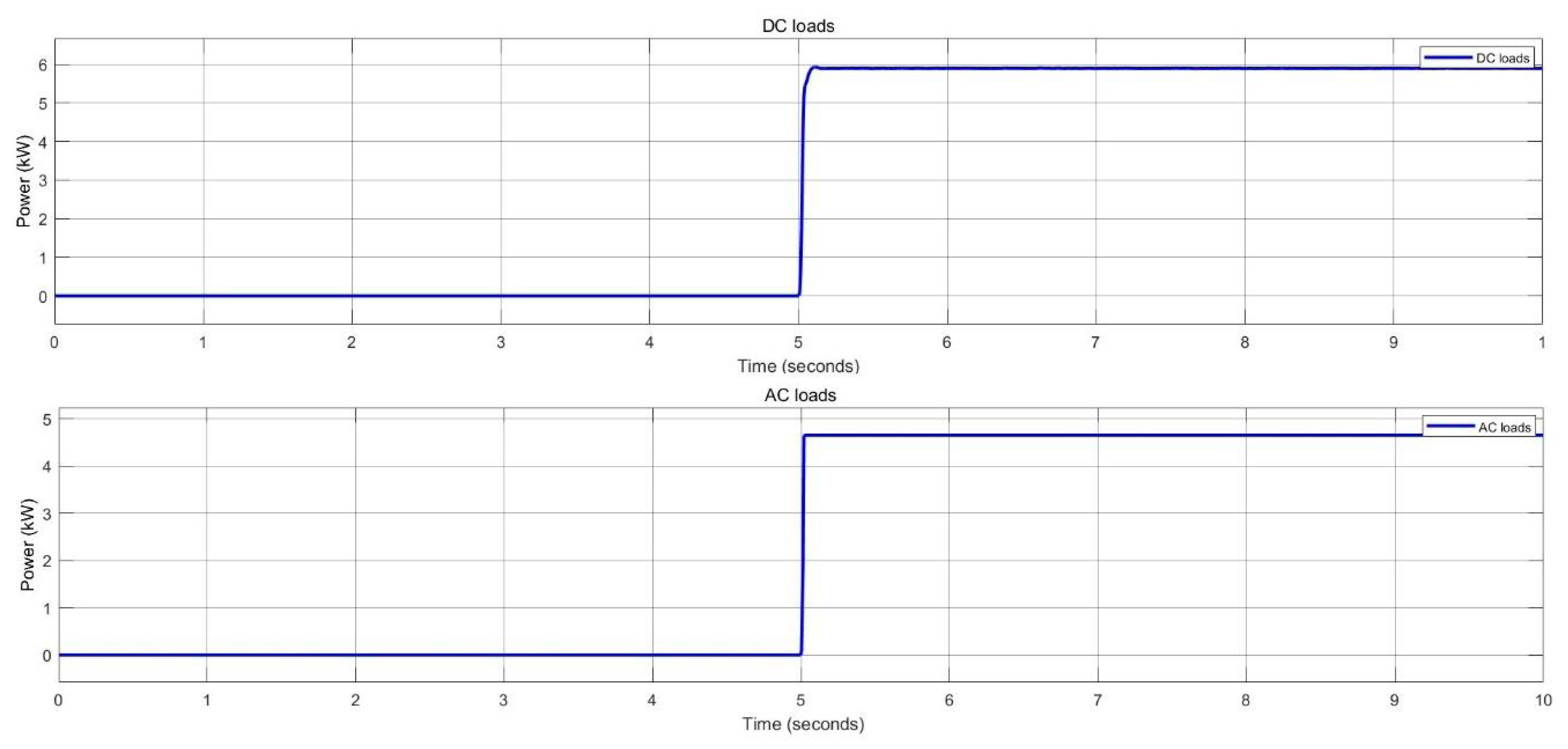
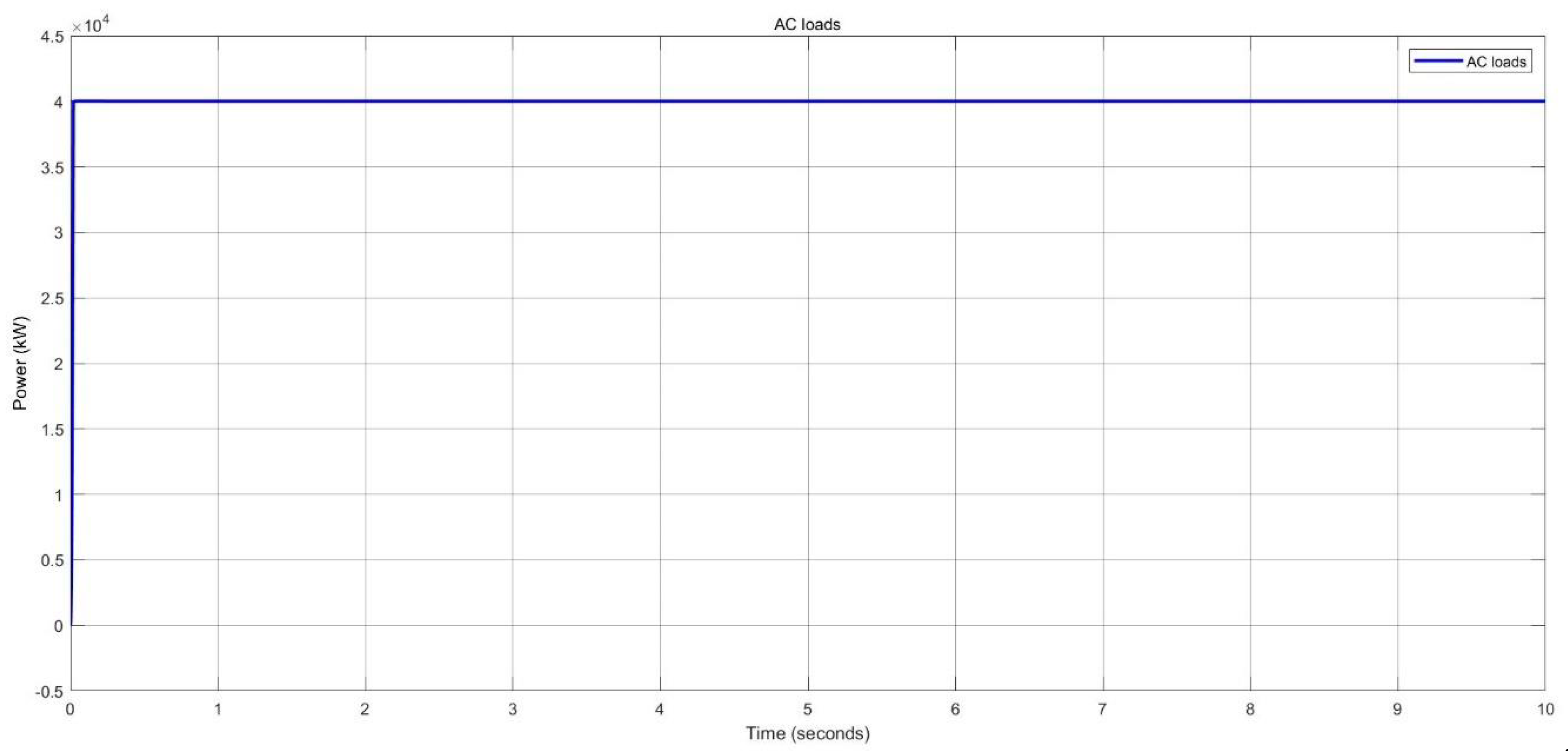
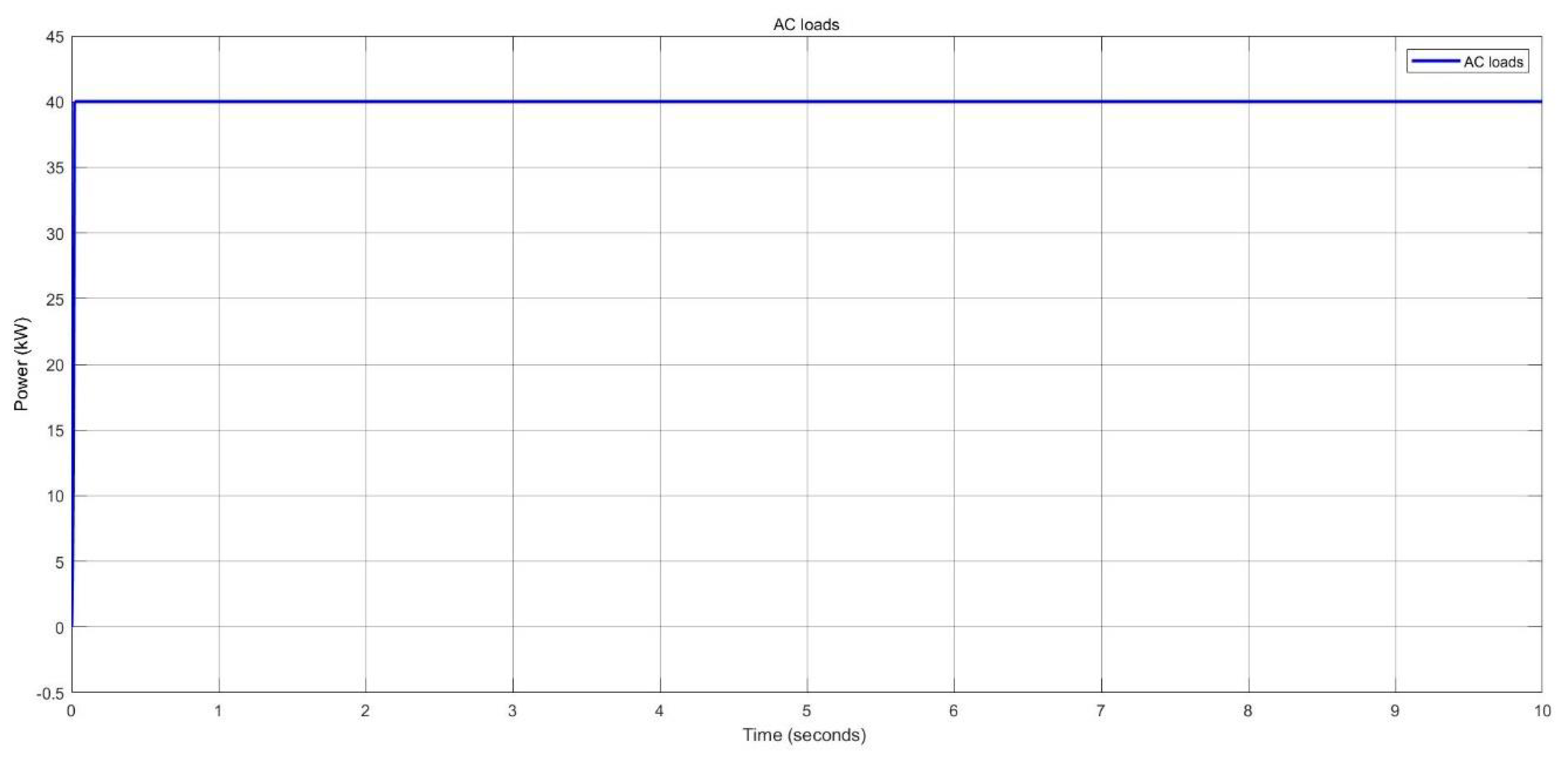
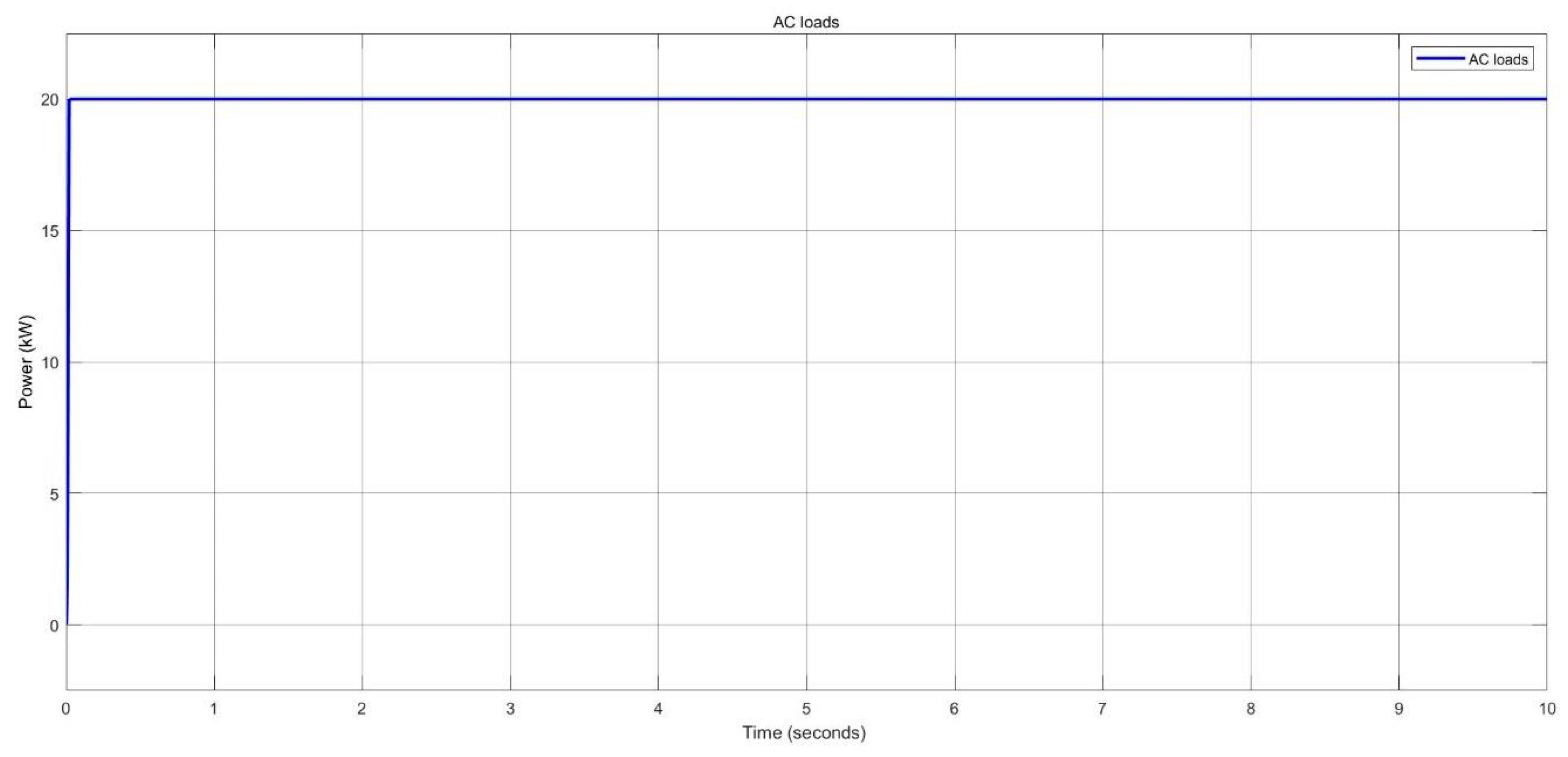
Load demand estimation of AC loads in nano-grid system.
Figure 48.
Load demand estimation of AC loads in nano-grid system.
Figure 49.
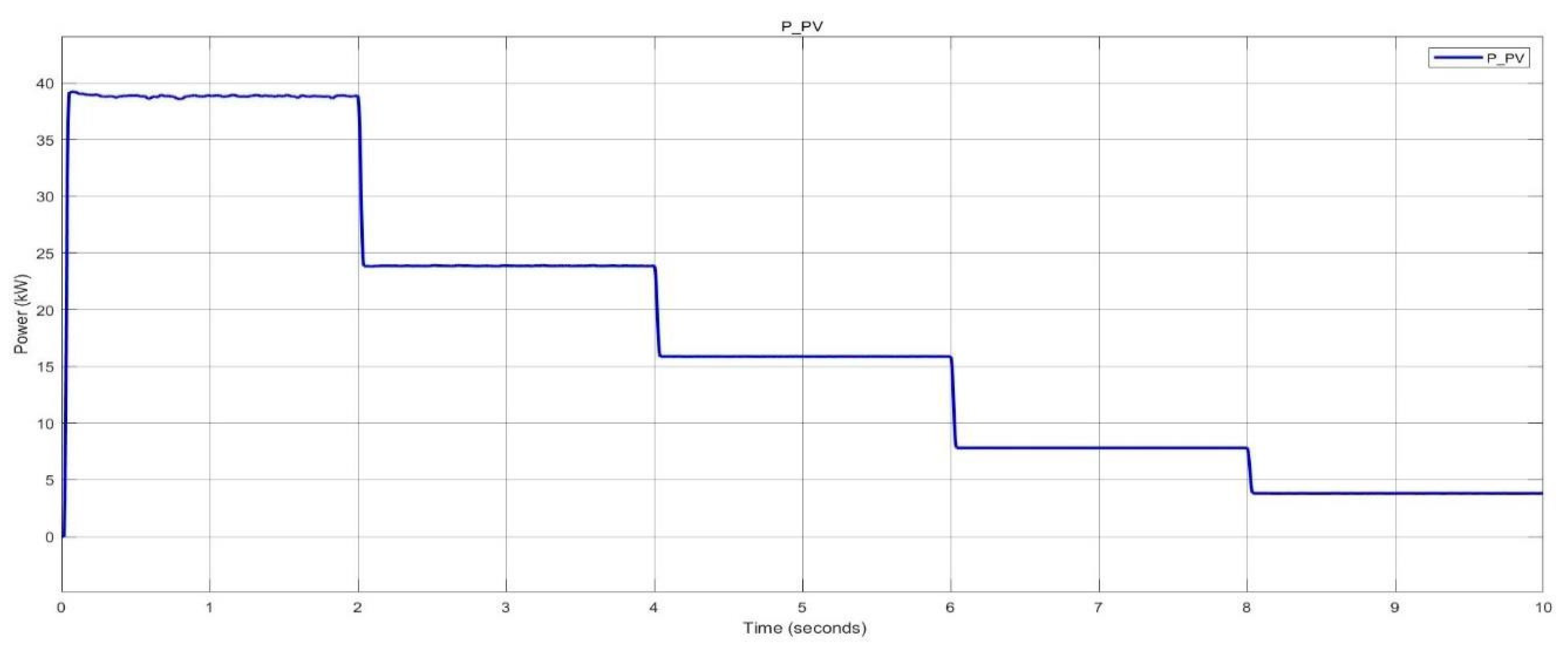
Solar PV power generated using stair generator in nano-grid system.
Figure 49.
Solar PV power generated using stair generator in nano-grid system.
Figure 50.
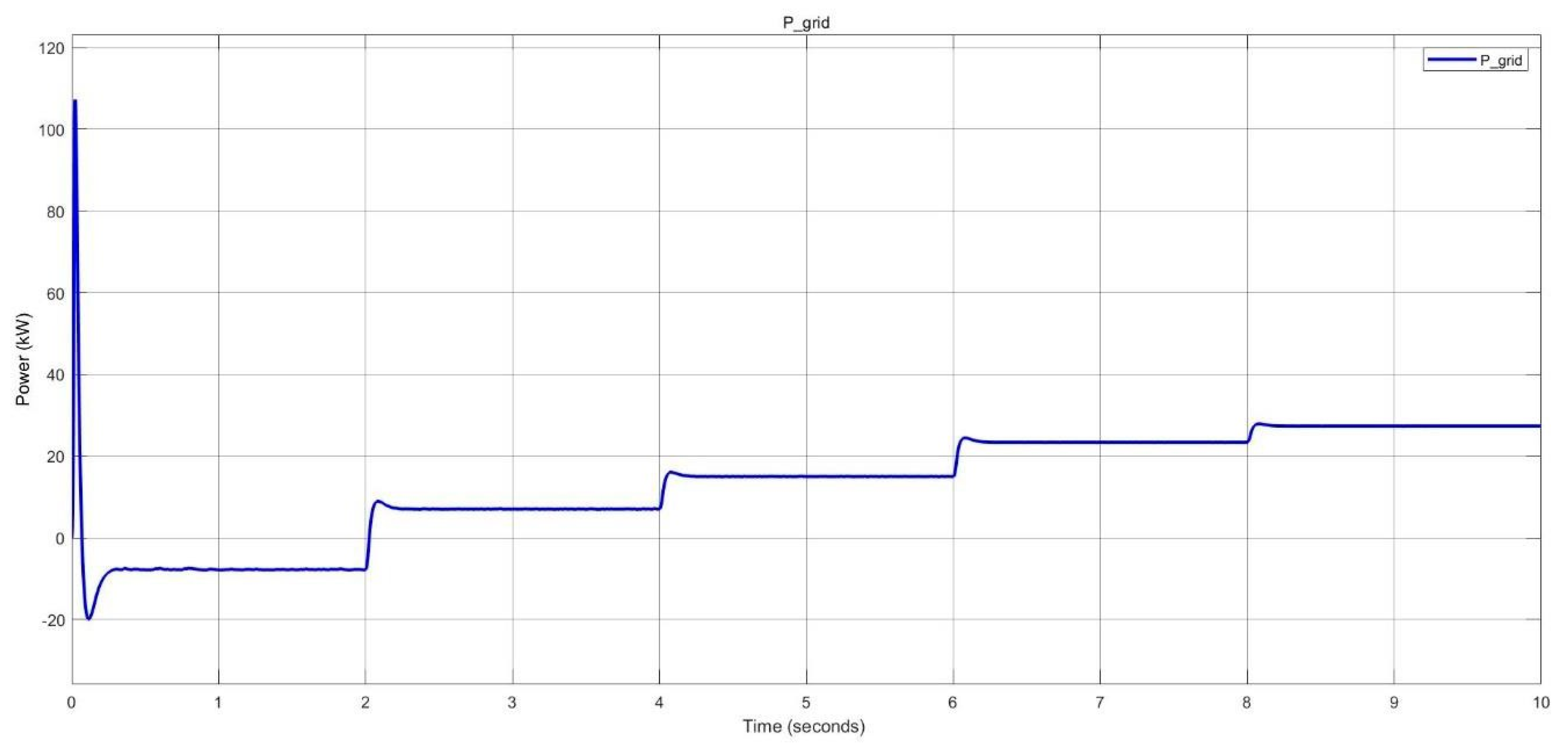
Power supplied by the grid to the load in nano-grid system.
Figure 50.
Power supplied by the grid to the load in nano-grid system.
Figure 51.
Simulation model to demonstrate a sunny day operation.
Figure 51.
Simulation model to demonstrate a sunny day operation.
Figure 52.
Load demand estimation of AC loads in nano-grid system.
Figure 52.
Load demand estimation of AC loads in nano-grid system.
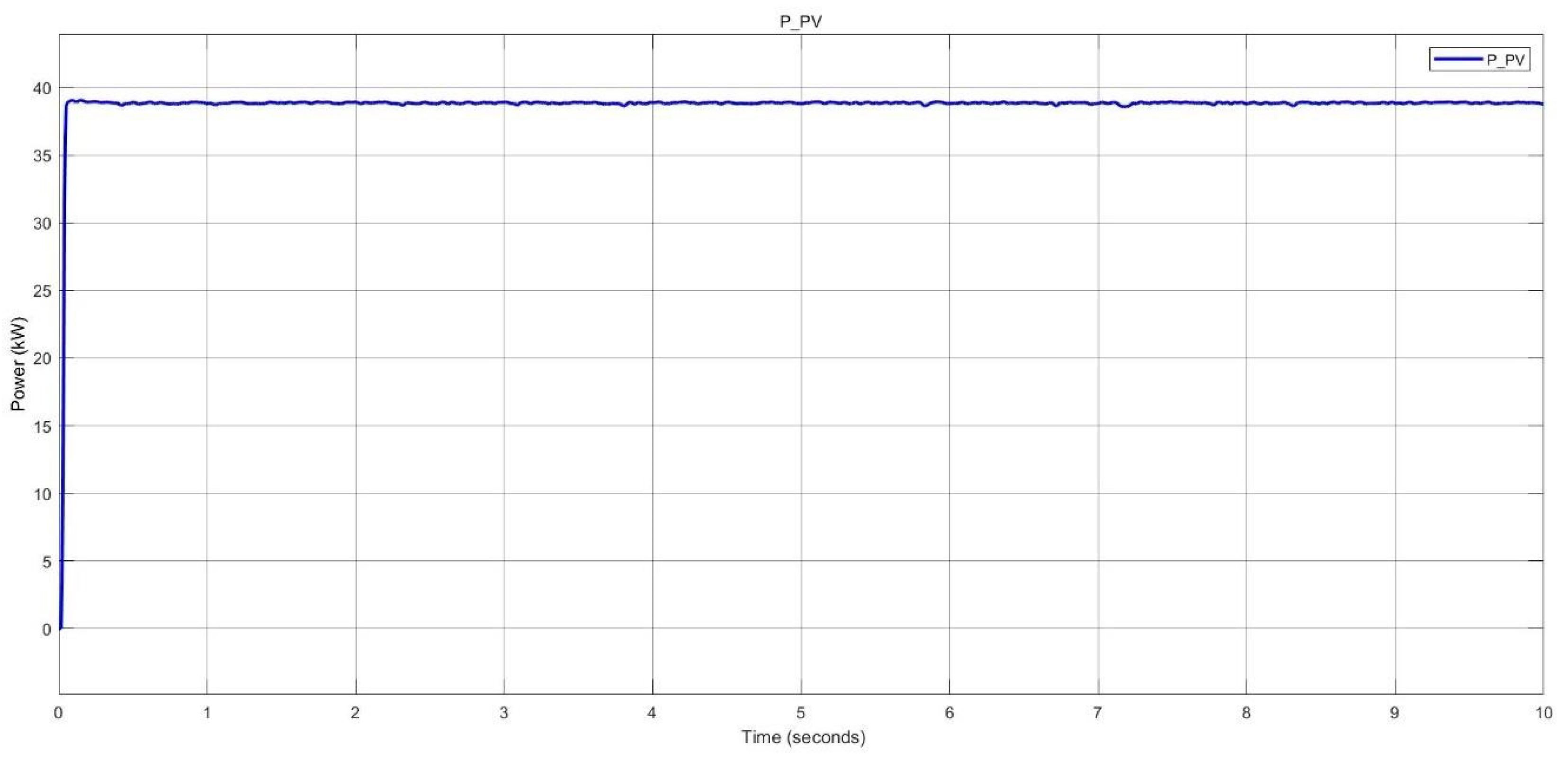
Figure 53.
Solar PV power generated in nano-grid system.
Figure 53.
Solar PV power generated in nano-grid system.
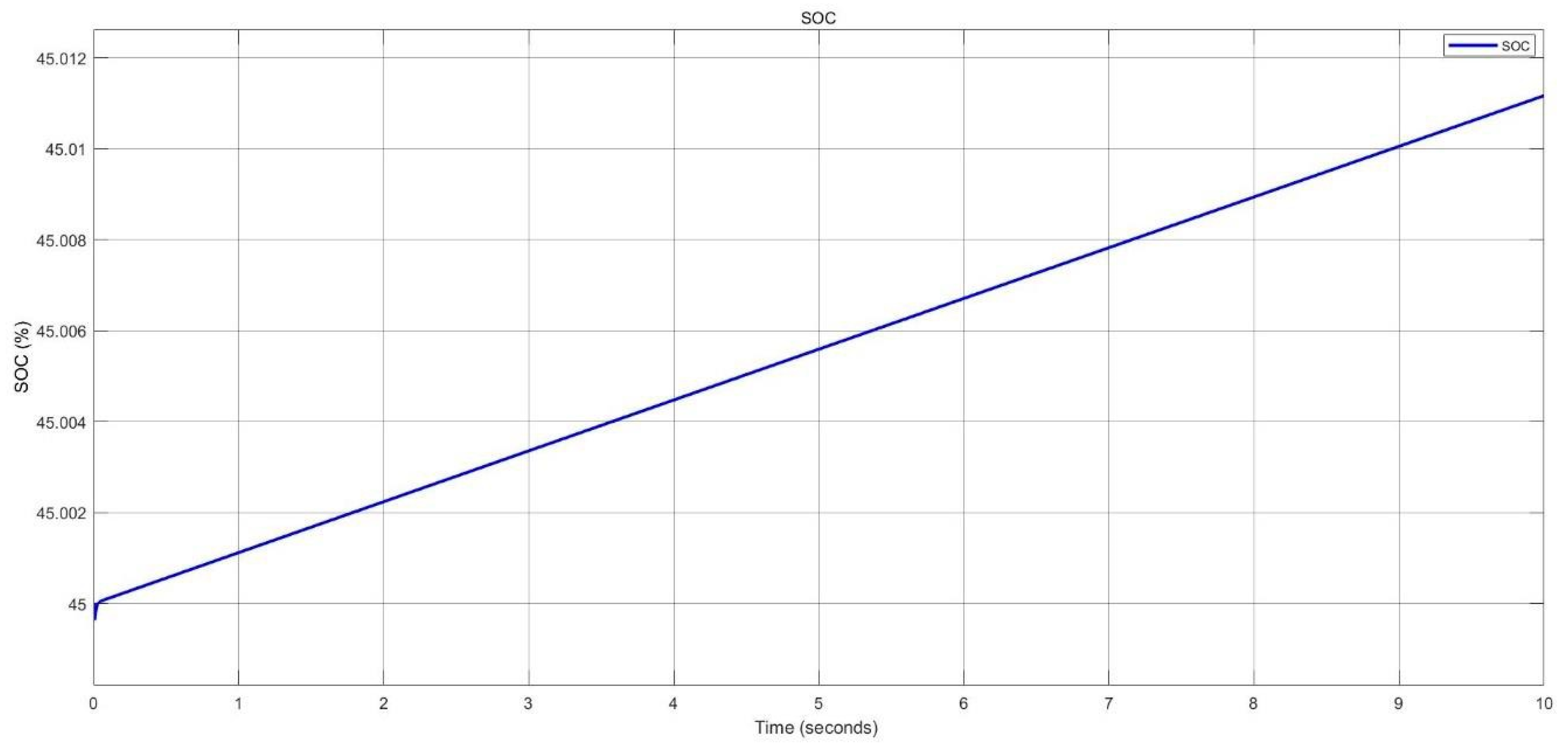
Figure 54.
SOC of battery during charging in nano-grid system.
Figure 54.
SOC of battery during charging in nano-grid system.
Figure 55.
Battery capacity of BESS during charging in nano-grid system.
Figure 55.
Battery capacity of BESS during charging in nano-grid system.
Figure 56.
Surplus power delivered to the grid in nano-grid system.
Figure 56.
Surplus power delivered to the grid in nano-grid system.
Figure 57.
Two parallel nano-grids connected to the three-phase grid.
Figure 57.
Two parallel nano-grids connected to the three-phase grid.
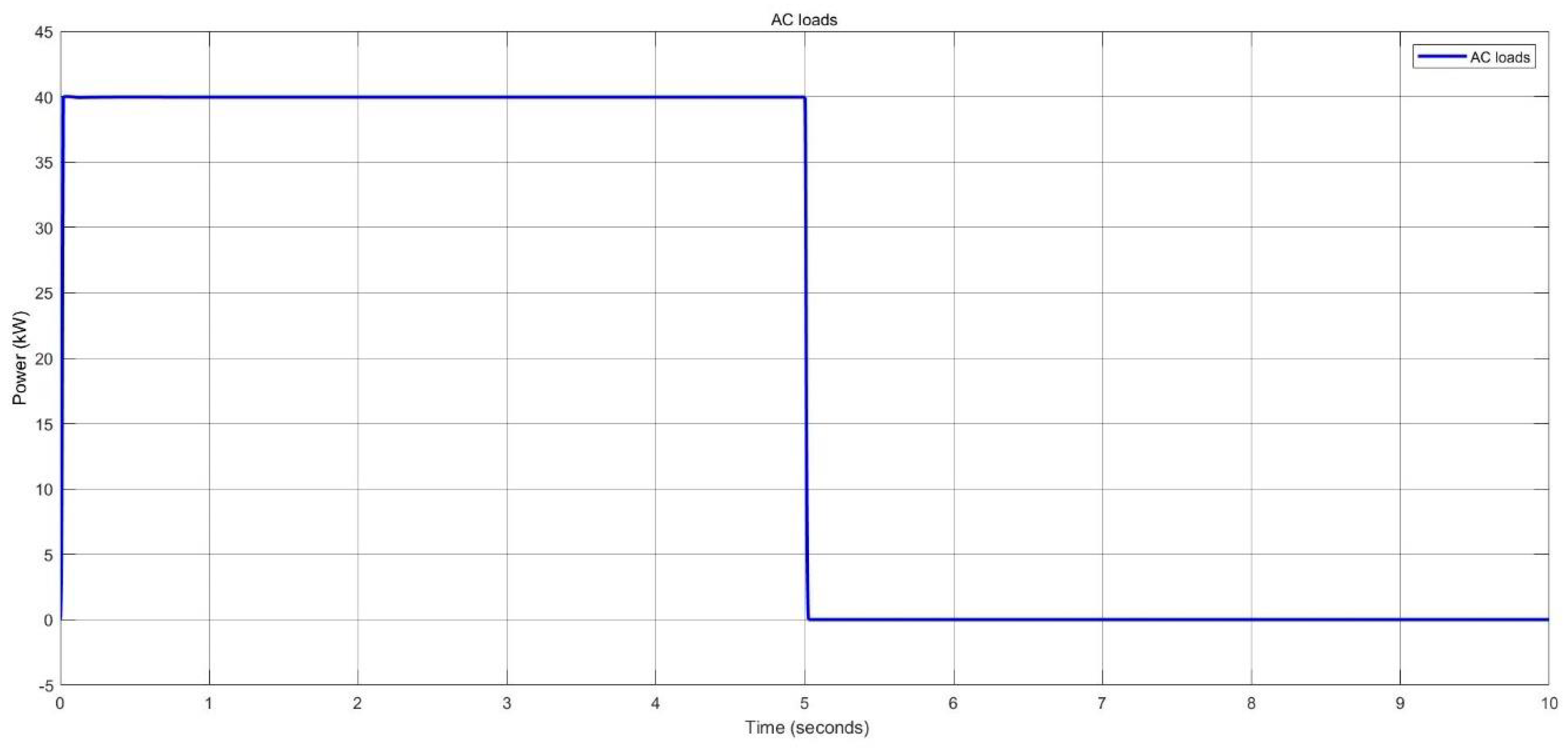
Figure 58.
AC loads before increase for two nano-grids system.
Figure 58.
AC loads before increase for two nano-grids system.
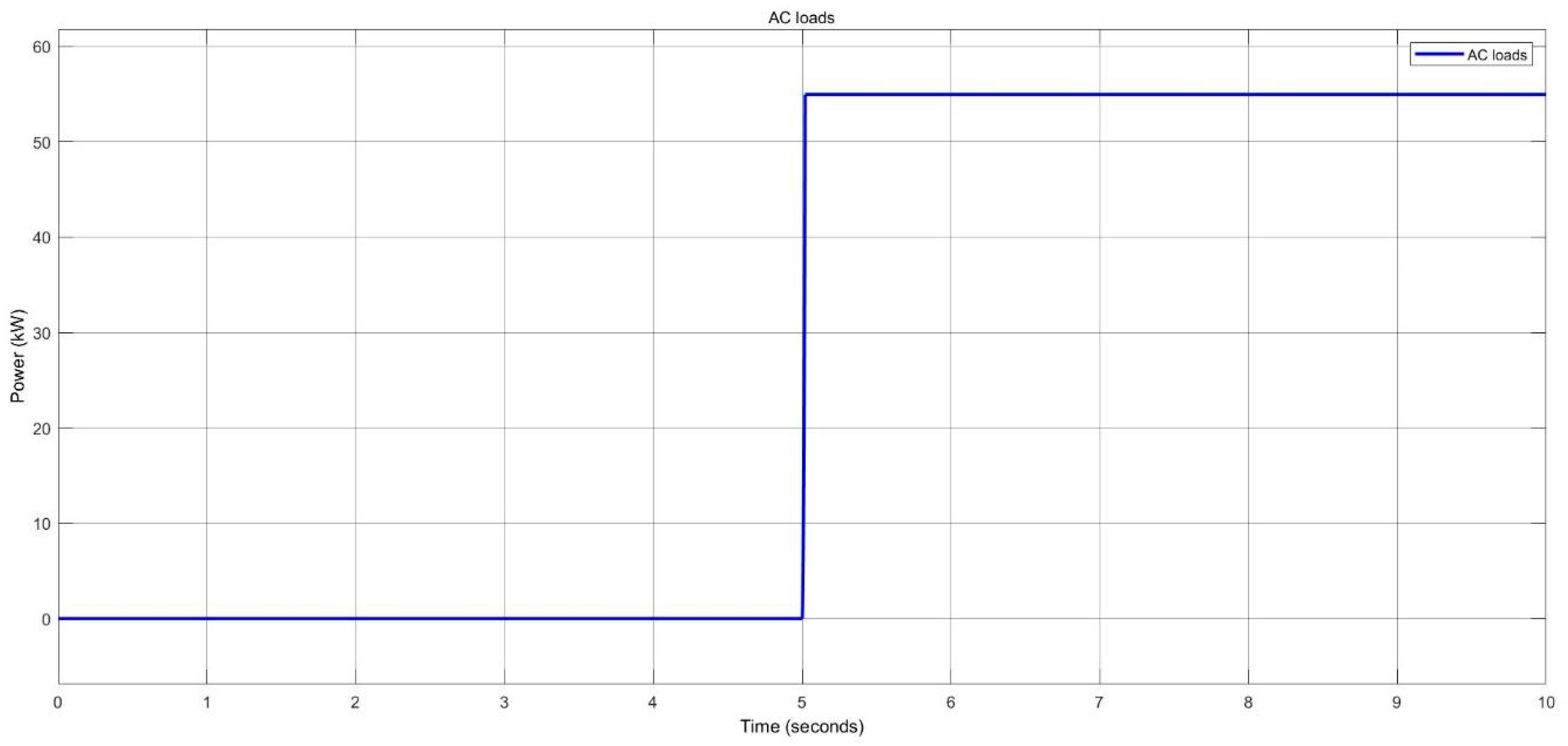
Figure 59.
AC loads after increase for two nano-grids system.
Figure 59.
AC loads after increase for two nano-grids system.
Figure 60.
Surplus power from the system sent to the grid for two nano-grids system.
Figure 60.
Surplus power from the system sent to the grid for two nano-grids system.
Table 1.
Receptacle loads values for different space.
Table 1.
Receptacle loads values for different space.
| Receptacle loads |
Nominal values |
| Computer intensive office |
22 W/m2
|
| General office areas |
16 W/m2
|
| Large conference areas |
11 W/m2
|
| Schools (Tertiary/IHLs) |
8 W/m2
|
| Schools (Primary/Secondary) |
5 W/m2
|
| Server/computer rooms |
540 W/m2
|
Table 2.
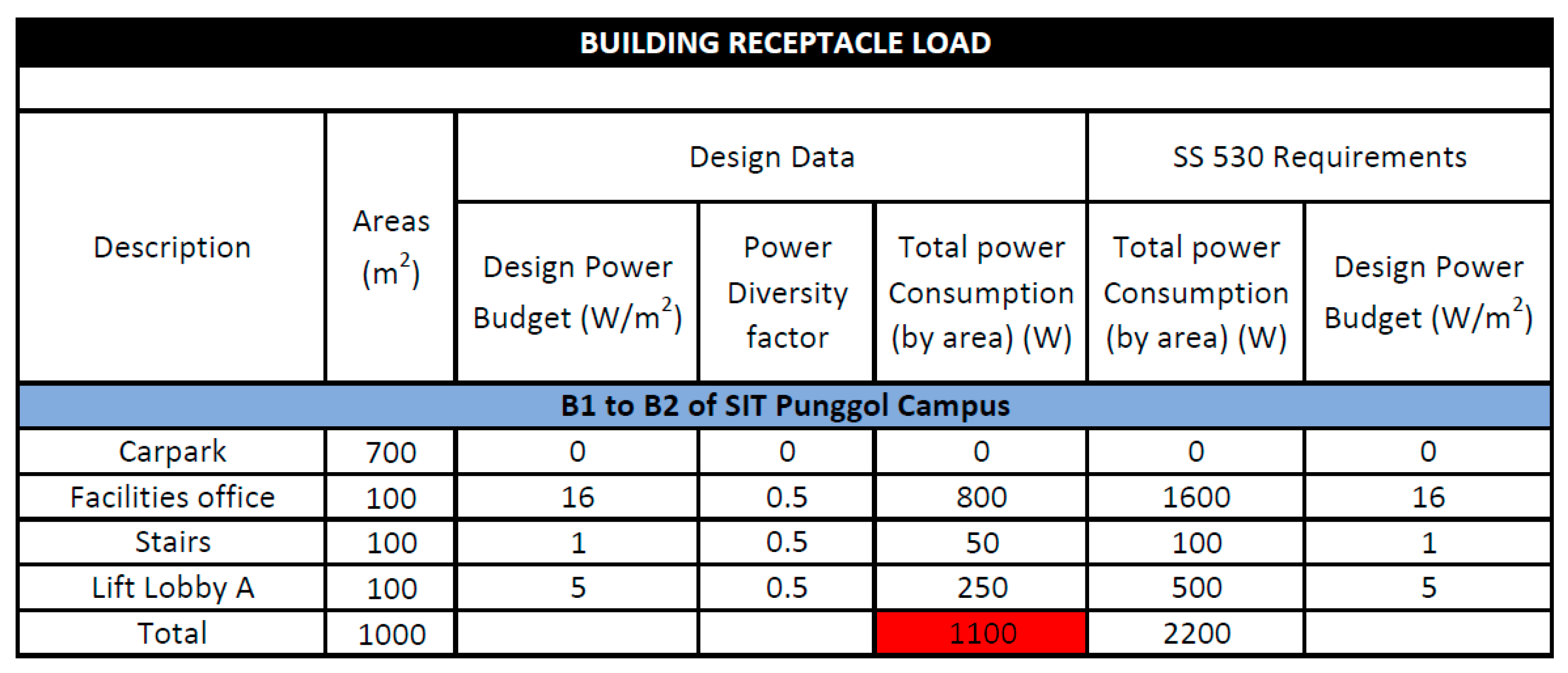
DC loads estimation of Level B1 to B2 of SIT Punggol Campus.
Table 2.
DC loads estimation of Level B1 to B2 of SIT Punggol Campus.
Table 3.
AC loads estimation of Level B1 to B2 of SIT Punggol Campus.
Table 3.
AC loads estimation of Level B1 to B2 of SIT Punggol Campus.
Table 4.
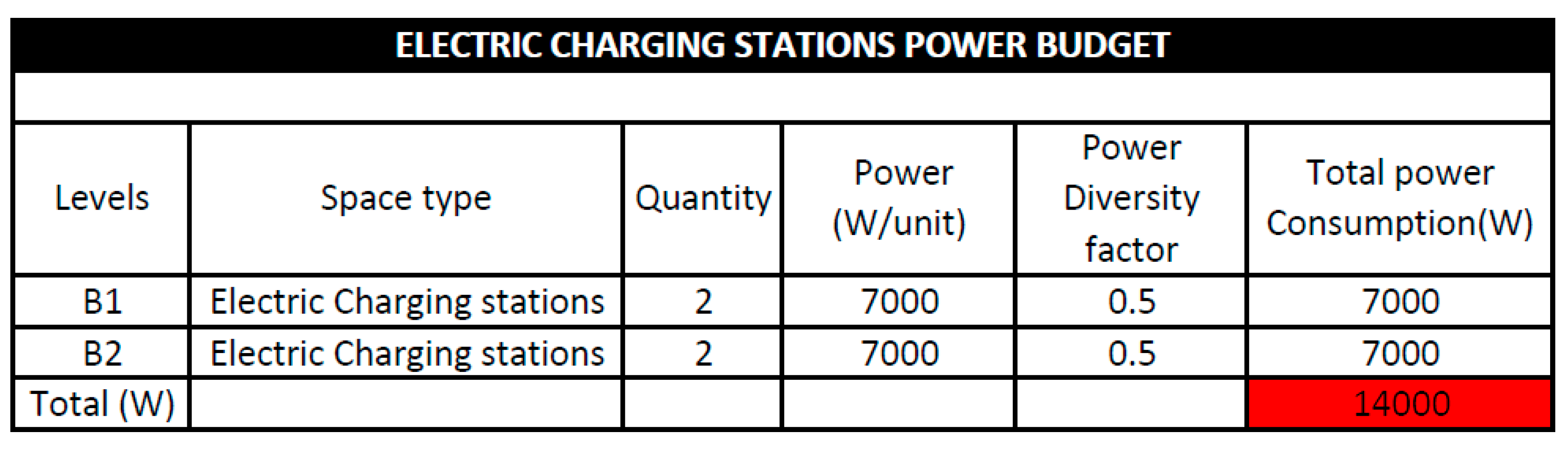
Estimated load demand of Electric Charging Stations for B1 and B2.
Table 4.
Estimated load demand of Electric Charging Stations for B1 and B2.
Table 5.
DC loads estimation of Level L1 to L3 of SIT Punggol Campus.
Table 5.
DC loads estimation of Level L1 to L3 of SIT Punggol Campus.
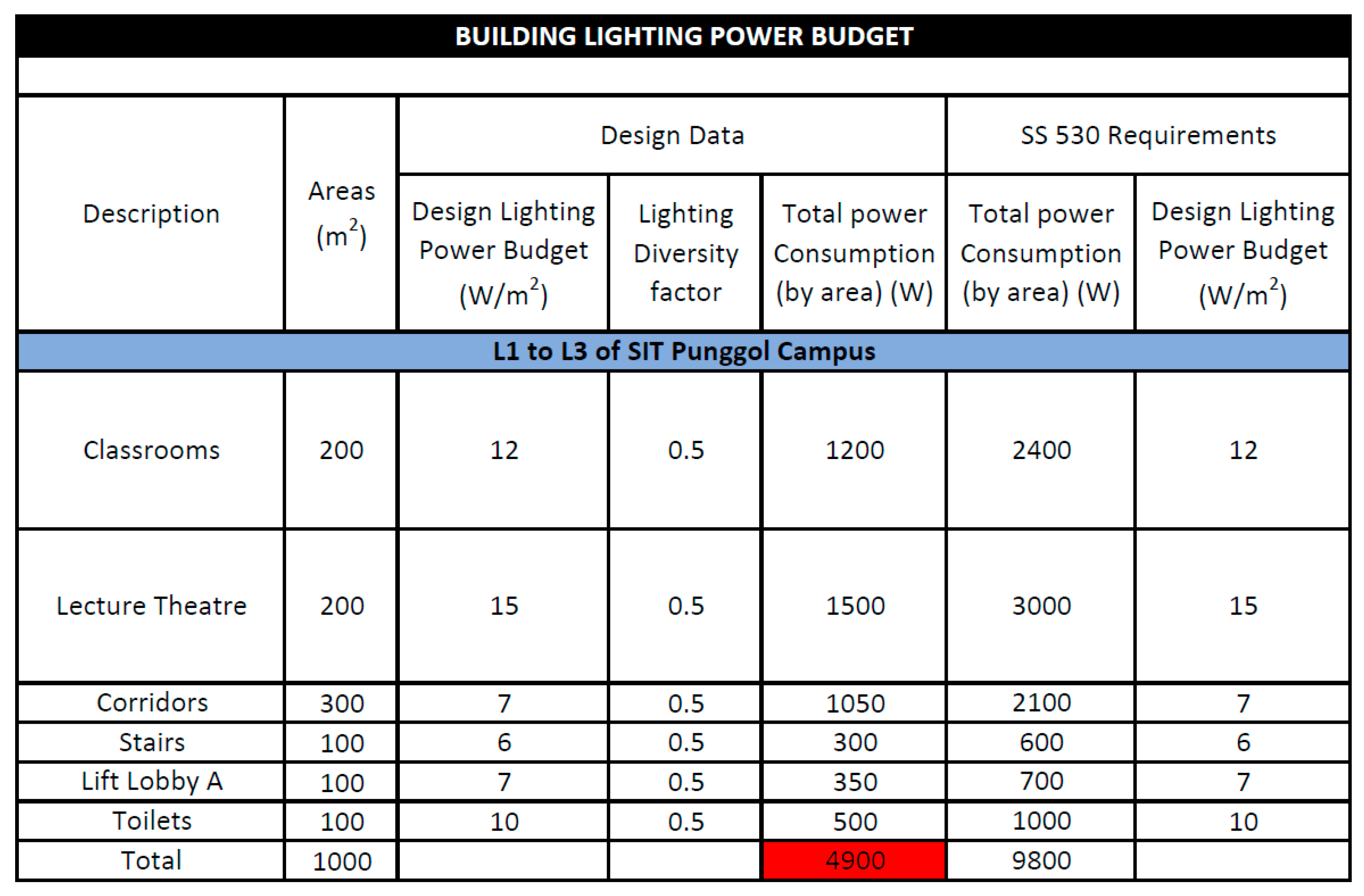
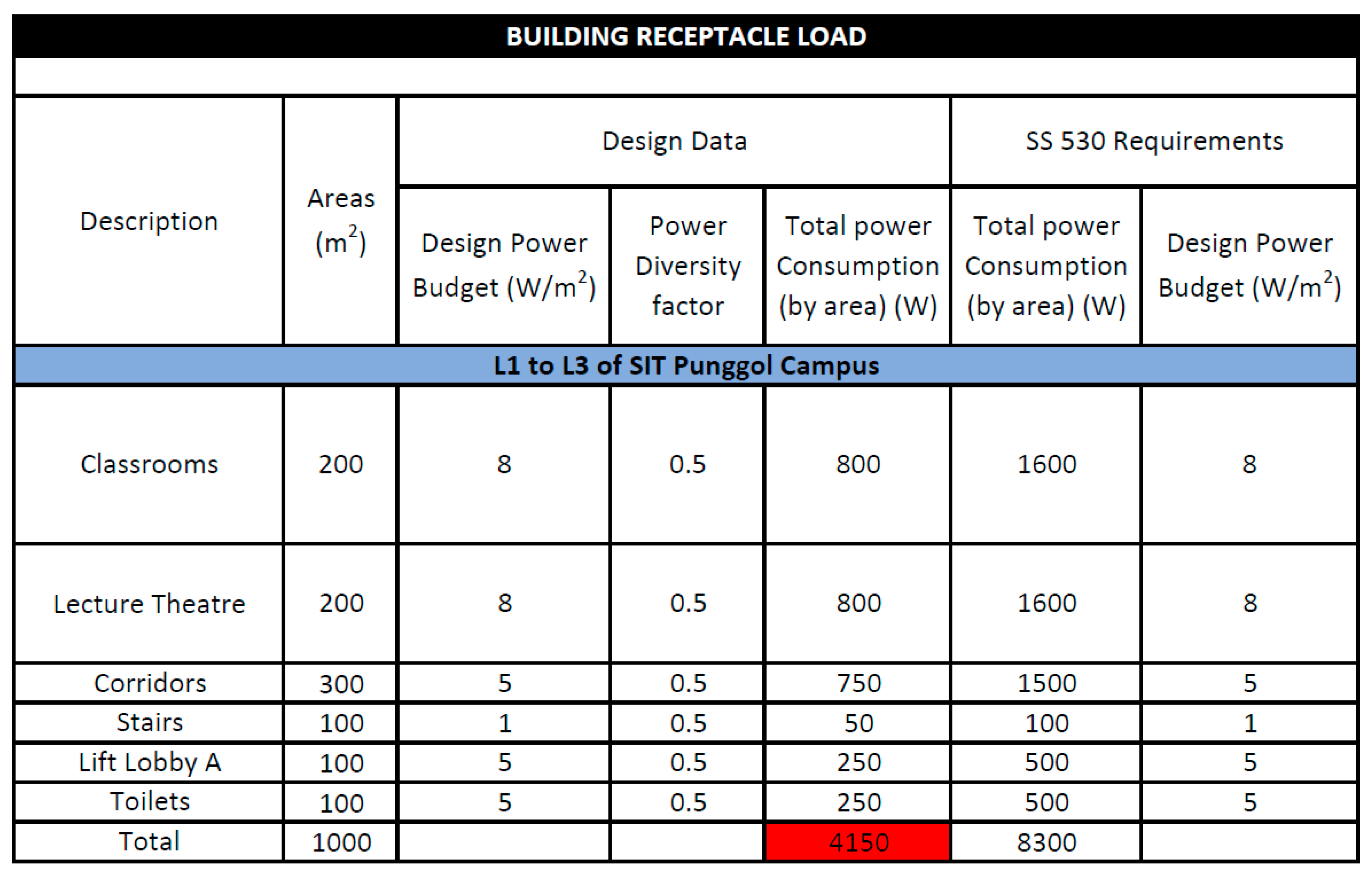
Table 6.
AC loads estimation of Level L1 to L3 of SIT Punggol Campus.
Table 6.
AC loads estimation of Level L1 to L3 of SIT Punggol Campus.
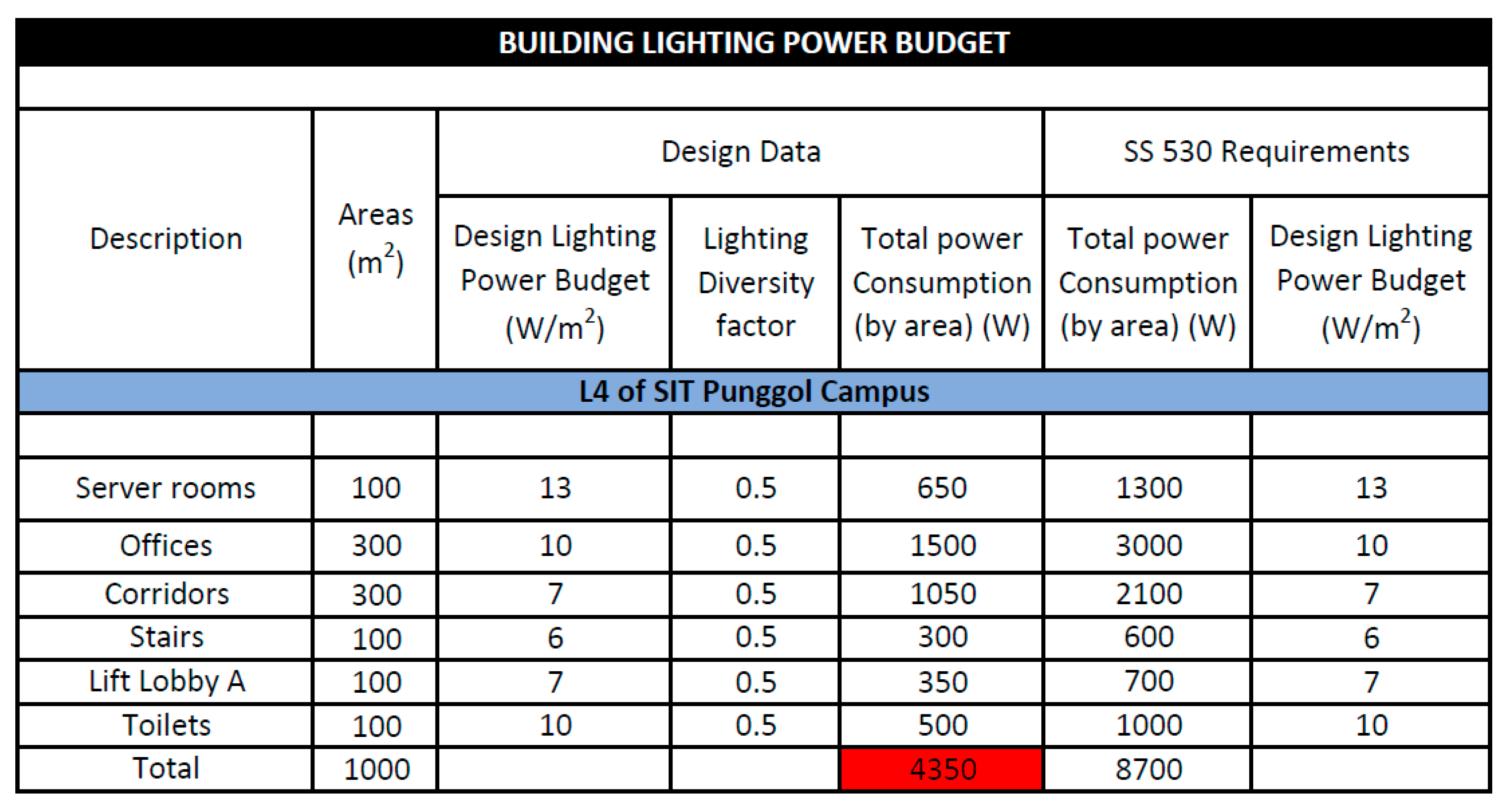
Table 7.
DC loads estimation of Level L4 of SIT Punggol Campus.
Table 7.
DC loads estimation of Level L4 of SIT Punggol Campus.
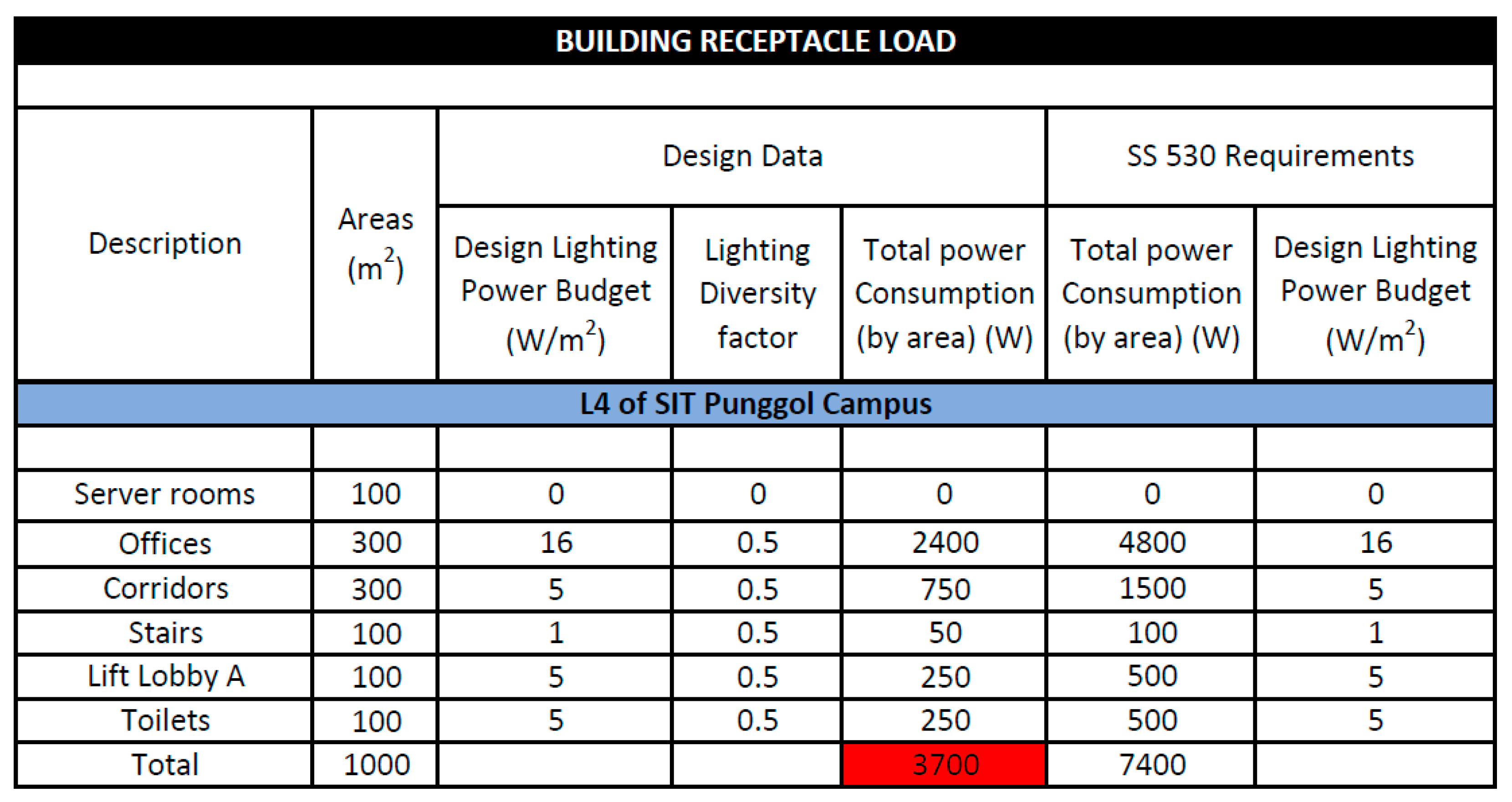
Table 8.
AC loads estimation of Level L4 of SIT Punggol Campus.
Table 8.
AC loads estimation of Level L4 of SIT Punggol Campus.
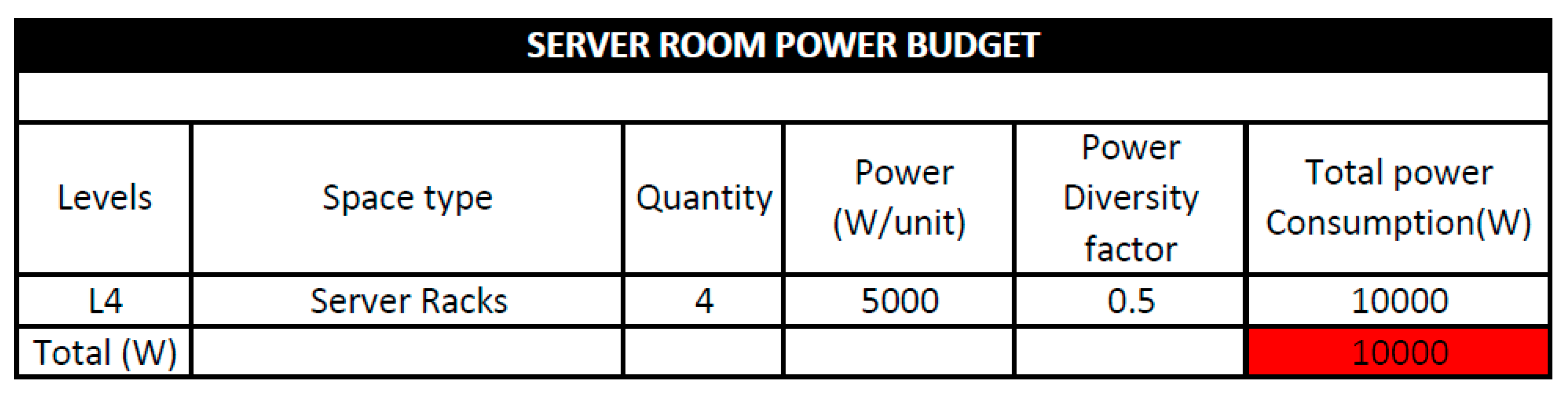
Table 9.
Estimated load demand of server room.
Table 9.
Estimated load demand of server room.
Table 10.
Switching states of the single-phase inverter.
Table 10.
Switching states of the single-phase inverter.
| Cycle |
S1 |
S2 |
S3 |
S4 |
Voltage at Bridge Output |
State |
| Positive half cycle |
ON |
OFF |
OFF |
ON |
VDC |
1 |
| OFF |
ON |
OFF |
ON |
0 |
2 |
| Negative half cycle |
OFF |
ON |
ON |
OFF |
-VDC |
3 |
| ON |
OFF |
ON |
OFF |
0 |
4 |
Table 11.
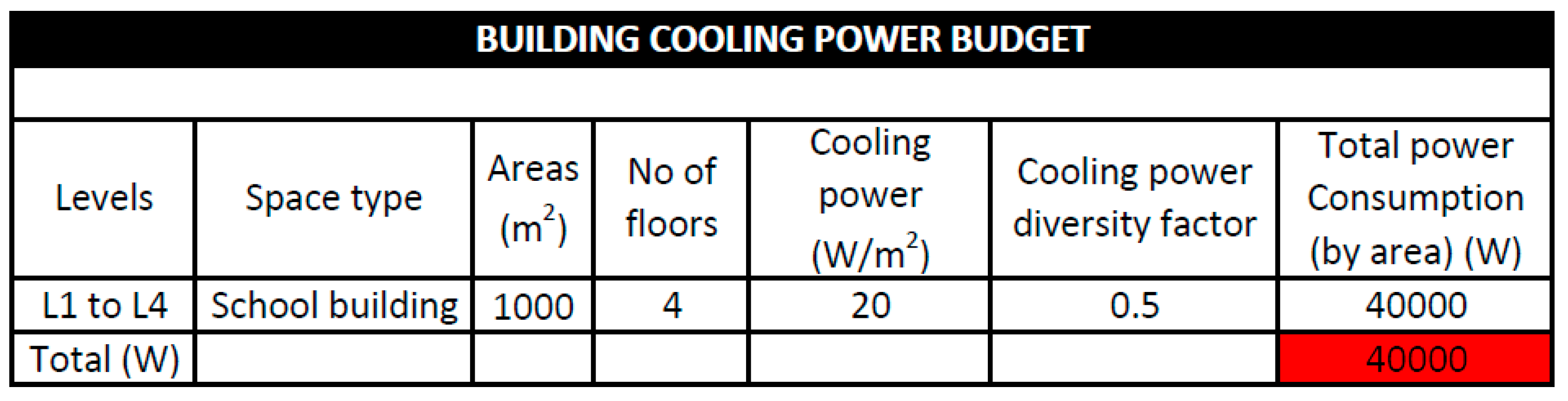
Load demand estimation for centralized cooling.
Table 11.
Load demand estimation for centralized cooling.
Table 12.
Switching states of the three-phase inverter.
Table 12.
Switching states of the three-phase inverter.
| S1
|
S2
|
S3
|
S4
|
S5
|
S6
|
Vab
|
Vbc
|
Vca
|
State No |
| ON |
OFF |
ON |
OFF |
ON |
OFF |
0 |
0 |
0 |
1 |
| OFF |
ON |
ON |
OFF |
ON |
OFF |
-VDC
|
0 |
VDC
|
2 |
| ON |
OFF |
OFF |
ON |
ON |
OFF |
VDC
|
-VDC
|
0 |
3 |
| ON |
OFF |
ON |
OFF |
OFF |
ON |
0 |
VDC
|
-VDC
|
4 |
| ON |
ON |
OFF |
OFF |
ON |
OFF |
0 |
-VDC
|
VDC
|
5 |
| ON |
OFF |
OFF |
ON |
OFF |
ON |
VDC
|
0 |
-VDC
|
6 |
| OFF |
ON |
ON |
OFF |
OFF |
ON |
- VDC
|
VDC
|
0 |
7 |
| OFF |
ON |
OFF |
ON |
OFF |
ON |
0 |
0 |
0 |
8 |
Table 13.
Parameters of BESS.
Table 13.
Parameters of BESS.
| Parameters |
Value |
| Battery nominal voltage |
Vbatt = 48 V |
| Battery rated capacity |
Ibatt = 300 Ah |
| Initial SOC |
SOC = 45% |
| Switching frequency |
Fsw = 20 kHz |
| Inductor value |
L = 5 mH |
Table 14.
Parameters of single-phase inverter.
Table 14.
Parameters of single-phase inverter.
| Parameters |
Value |
| Switching frequency |
Fsw = 5 kHz |
| Filter inductor |
L = 5 mH |
| Filter capacitor |
C = 5 µF |
| DC link voltage |
VDC = 400 V |
| Distribution grid voltage |
Vgrid = 230 V (phase) |
Table 15.
Parameters of solar PV system.
Table 15.
Parameters of solar PV system.
| Parameters |
Value |
| Series connected strings |
10 |
| Parallel connected strings |
10 |
| Vmp
|
Vmp = 40.8 V |
| Imp
|
Imp = 9.81 A |
| Sun irradiance |
Ir = 1000 W/m2
|
| Cell temperature |
T = 25 °C |
Table 16.
Parameters of boost converter.
Table 16.
Parameters of boost converter.
| Parameters |
Value |
| Switching frequency |
Fsw = 5kHz |
| Inductor value |
L = 2.5 mH |
| Input capacitor value |
Cin = 1000 µF |
| Output capacitor value |
Cout = 4000 µF |
Table 17.
Parameters of BESS.
Table 17.
Parameters of BESS.
| Parameters |
Value |
| Battery nominal voltage |
Vbatt = 400 V |
| Battery rated capacity |
Ibatt = 300 Ah |
| Initial SOC |
SOC = 45% |
| Switching frequency |
Fsw = 10 kHz |
| Inductor value |
L = 1 mH |
Table 18.
Parameters of three phase inverter.
Table 18.
Parameters of three phase inverter.
| Parameters |
Value |
| Switching frequency |
Fsw = 10 kHz |
| Inductor value |
L = 10 mH |
| DC link voltage |
VDC = 1000 V |
| Distribution grid voltage |
Vgrid = 400 V (line) |