Prerpints.org logo
Preprint
Article

Research on Finance Risk Management based on Combination Optimization and Reinforcement Learning

Altmetrics

Downloads

99

Views

81

Comments

0

This version is not peer-reviewed

Artificial Intelligence Models, Tools and Applications

Submitted:

11 August 2024

Posted:

14 August 2024

You are already at the latest version

Alerts
Abstract
The impact of financial risks extends beyond the normal operation and survival of industrial and commercial enterprises and financial institutions. They also have the potential to impede the stable development of a country's and even the world's financial economy. This is clearly demonstrated by the severe consequences of the frequent financial crises that have occurred in recent years. It thus follows that the prevention of financial risks has become one of the core tasks of the operation and management of industrial and commercial enterprises and financial institutions. Portfolio optimization techniques are employed in the construction of a variety of asset allocation models, with reinforcement learning algorithms used to dynamically adjust investment strategies with the objective of maximizing returns and minimizing risks. The preliminary construction of an asset allocation model is achieved through the utilization of a genetic algorithm. Genetic algorithms emulate the processes of natural selection and genetic variation to identify the optimal portfolio of assets that will yield the greatest returns at a pre-established level of risk. Subsequently, the Deep Q-Learning algorithm is introduced to facilitate dynamic adjustments and optimization of the asset allocation, based on the initial construction. Deep Q-learning employs deep neural networks to forecast the prospective returns of disparate investment strategies, thereby optimizing the decision-making process through continuous learning and updating. The combination of genetic algorithms and deep Q-learning enables the system to identify the optimal investment strategy under a diverse range of initial conditions and to adapt it in real-time to respond to market fluctuations and uncertainties. The experimental analysis demonstrates that the proposed method exhibits an exemplary capacity for risk control and a robust ability to generate stable income growth across diverse market environments. In simulation experiments, portfolios constructed using this method demonstrate lower volatility and higher average returns than those generated through traditional methods.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning
CCS CONCEPTS: Applied computing ~ Enterprise computing ~ Business process management ~ Business process management systems

1. Introduction

Financial mathematics is a nascent interdisciplinary field that bridges the domains of mathematics and finance. The discipline employs contemporary mathematical theories and methodologies, including stochastic analysis, stochastic optimal control, combinatorial analysis, nonlinear analysis, multivariate statistical analysis, mathematical programming, and modern calculation techniques, to undertake quantitative analysis and research on the theoretical and practical aspects of financial instruments and markets within the financial domain (encompassing investment, creditor rights, funds, futures, options, banking functions, and other financial instruments and markets). The field of financial mathematics has experienced exponential growth, becoming one of the most rapidly expanding branches of applied mathematics [1].
The term 'financial mathematics' was first used in the late 1980s and emerged as a direct result of two significant developments in Wall Street: the advent of portfolio selection theory and option pricing theory. The field's central concerns encompass the theory of optimal investment strategy selection, pricing theory, and market theory in an uncertain environment. The three principal concepts are arbitrage, optimality and equilibrium. It is therefore of particular importance to study the operational rules of financial markets, the selection of asset portfolios, the design and pricing of financial derivatives, the analysis and management of risks, and the analysis of related investment decisions.
The asset portfolio theory provides the foundation for a portfolio decision-making model, which is informed by the mathematical optimization theory and stochastic process processing method. These tools are employed to investigate frontier topics in financial risk management and to develop a portfolio risk decision-making theory. This not only contributes to the enhancement of the financial theory system, but also has significant theoretical implications [2]. The advancement of financial mathematics furnishes a robust theoretical foundation for financial practice, thereby facilitating the innovation and optimization of financial instruments and markets.
Over the past two decades, the global financial market has undergone significant expansion, driven by tremendous factors, including economic globalization, financial integration, the development of modern financial theory, the advent of information technology and the emergence of financial innovation. Nevertheless, the resulting market turbulence has also intensified the risks faced by business enterprises and financial institutions in the financial markets to an unprecedented degree. Despite the profitability of these institutions in the market, they are also facing an increase in financial risk [3]. The potential for financial risks to affect not only the normal operation and survival of enterprises and financial institutions but also the stability of a country's and even the world's financial economy is a significant concern. The severe repercussions of the numerous financial crises that have occurred in recent years serve to exemplify this assertion. Consequently, financial risks have become a focal point of attention for a diverse range of stakeholders, including global industrial and commercial enterprises, financial institutions, policy authorities, and academic circles. The prevention of financial risks has consequently become a pivotal aspect of the operational and managerial strategies of industrial and commercial enterprises and financial institutions [4].
The term "risk" is typically used to describe the potential for uncertain or volatile outcomes in future scenarios. In contemporary business operations, three principal categories of risk may be identified: strategic risks, business risks and financial risks. Among these, financial risk is the most significant and readily quantifiable. Financial risk may be defined as the uncertainty or volatility of a company's future earnings, which is directly related to the volatility of the financial markets themselves. In general, uncertainty regarding future earnings encompasses uncertainty regarding future profits and losses. Financial risk specifically denotes the potential for financial assets or earnings to be impaired due to shifts in financial market variables that negatively impact the enterprise's cash flow, ultimately leading to a decline in its value [5]. To illustrate, fluctuations in interest rates, exchange rates or commodity prices, in addition to the risk of default due to the deterioration of the debtor's debt position, have the potential to negatively impact the value of a company's assets and earnings.
The classification of financial risks is based on their nature and source. There are five principal categories: market risk, credit risk, liquidity risk, operational risk and legal risk. Furthermore, financial risks can be classified according to their internal and external causes, resulting in the distinction between systemic risks and unsystematic risks. Systemic risk can be defined as the risk that arises from changes in macroeconomic factors within the financial environment, including interest rates, exchange rates, global oil prices and inflation. Unsystematic risk is the risk caused by changes in certain factors within the company or organization [6]. These factors may include changes in the company's senior leadership, product quality problems, and some unexpected factors. It is therefore imperative that these financial risks are understood and managed effectively to ensure the continued health and sustainable development of businesses and financial institutions [7]. An efficacious risk management strategy can facilitate not only the avoidance of prospective losses but also the attainment of stable growth in a volatile market environment.

2. Related Work

The fundamental aspects of risk management technology are risk measurement, risk assessment and risk monitoring. Risk measurement provides the foundation for the implementation of other risk management technologies. One of the fundamental principles of risk measurement is the market valuation of each trading position, which is commonly referred to as the "mark-to-market" approach. It is imperative that valuation standards and models be endorsed by the risk management department to guarantee their accuracy and reliability. The second basis is the decomposition of risk, which involves the disaggregation of market risk into its constituent market factor risks [8]. This approach ensures that each risk can be accurately quantified and managed using appropriate measurement methods. The implementation of risk measurement enables companies to anticipate and respond to a range of potential risks by providing a comprehensive and accurate assessment of the potential losses that may be incurred under varying market conditions. In particular, the risk management department is required to implement a comprehensive risk measurement system, comprising both quantitative and qualitative analysis tools. The utilization of quantitative analysis tools including Value at Risk (VaR), Conditional Value at Risk (CVaR), and volatility models, enables companies to gain a comprehensive understanding of their risk exposure. In contrast, qualitative analysis enables companies to identify potential sources of risk and implement corresponding countermeasures. This is achieved through expert assessments, scenario analysis, and stress testing [9].
At the present time, there is a substantial corpus of research on the mean-at-risk (M-VaR) model. In a previous study, G.L. Alexander [10] and colleagues proposed an M-VaR model for comparing the discrepancy between the effective boundaries of the M-V and M-VaR models through analytical methods. The findings indicate that when the confidence level is equal to or greater than a specified threshold, the effective boundary of the M-VaR model is present. As the confidence level approaches 1, the effective boundary of the M-VaR model exhibits a gradual convergence with that of the M-V model. Further discussion reveals that the M-VaR model is a widely utilised tool in the field of financial risk management. The incorporation of VaR, a risk measurement tool, enhances the model's capacity to predict extreme risk events. VaR represents the maximum potential loss that a portfolio may sustain over a specified confidence interval. In comparison to the conventional M-V model, the M-VaR model is more effective in identifying and quantifying the extreme risks inherent in the market. This is of paramount importance in safeguarding investors from substantial losses.
Furthermore, the effective boundary analysis of the M-VaR model offers investors a more comprehensive perspective on the risk-return trade-off. In practice, investors are able to select portfolios that align with their desired level of confidence, thereby optimizing the balance between risk and return. For instance, at elevated levels of confidence, investors may choose to allocate assets in a more conservative manner, thereby ensuring the control of potential losses in the event of an extreme market downturn. In the context of lower confidence levels, investors may elect to pursue more aggressive strategies with the objective of attaining higher expected returns.
Additionally, Wu et al. [11] employed a reinforcement learning model that integrated convolutional neural networks (CNNs) and recurrent neural networks (RNNs) for the purpose of portfolio management. They also proposed a novel reward function based on the Sharpe ratio for the assessment of the developed portfolio management system. In comparison to the conventional trading return reward function, the reward function based on the Sharpe ratio offers a more advantageous means of evaluating the performance of the model. In comparison to the Sharpe ratio, the Sortino ratio imposes a penalty on downward volatility, while demonstrating superior returns during the processes of agent learning and exploration. In particular, the Sharpe ratio reward function assesses the model by quantifying the excess return per unit of risk, thereby emphasizing the equilibrium between benefits and risks.
This approach enables the agent to optimize its investment strategy in accordance with prevailing market conditions, thereby facilitating the attainment of more stable returns. However, the Sharpe ratio incorporates the total volatility both upside and downside into the calculation, which may result in agents being unduly constrained in their pursuit of high returns. In contrast, the Sortino ratio reward function is designed to penalize downside volatility, thereby facilitating the management of downside risk for portfolios. In the context of reinforcement learning, this approach enables the pursuit of higher returns while mitigating the risk of losses. In practical applications, the reward function based on the Sortino ratio allows the agent to demonstrate enhanced adaptability and a superior return level in response to market fluctuations.

3. Methodologies

In this section, we establish a variety of asset allocation models through portfolio optimization techniques and use reinforcement learning algorithms to dynamically adjust investment strategies.

3.2. Combination Optimization

We initially define the initial population, where each individual represents a potential asset allocation vector X . Further, each individual's fitness is assessed using a fitness function, which is typically based on expected benefits and risks. The fitness function is defined as Equation 1.
f x = x T μ − r f √ x T Ε x
Where μ is the expected return vector, r f is the risk-free rate, and Ε is the covariance matrix of the return on assets. Individuals are selected for reproduction according to fitness, and individuals with higher fitness are more likely to be selected. Combining selected individuals to produce offspring, cross-operation is defined as Equation 2.
x c h i l d = α x i + ( 1 − α ) x j
Where x i and x j are the parent individuals, α is the crossover rate. Random variation is introduced through mutation, which is defined as Equation 3, where ϵ is a small random perturbation vector. Finally, the selection, crossover, and mutation process is repeated until a convergence or predetermined number of iterations is reached. This process aims to optimize asset allocation over time by simulating natural evolution to maximize returns at a specific level of risk.
x m u t a t e d = x c h i l d + ϵ
We use the genetic algorithm to construct a preliminary asset allocation model, and find the best asset mix by simulating natural selection and genetic variation to maximize returns at a predetermined risk level. The process involves defining the initial population, assessing individuals using a fitness function based on expected benefits and risks, selecting individuals with higher fitness for reproduction, generating new individuals through crossover and mutation, and iterating until convergence or a predetermined number of iterations is reached. This process improves the overall return and risk management capabilities of the portfolio by gradually optimizing asset allocation.

3.2. Deep Q-Learning

On the basis of the initial construction, we introduce the Deep Q-Learning algorithm to dynamically adjust and optimize asset allocation. Deep Q learning uses deep neural networks to estimate the future returns of different investment strategies and optimize the decision-making process through continuous learning and updating. We define the status of time t st, including relevant market information and current portfolio weights. The status is represented s t = { w t , m t } , where w t is the current asset weight, and m t is the market information vector. The action space defines action at as the redistribution of assets in the portfolio. Actions are expressed as a t = { ∆ w t } , where ∆ w t is the change vector of the asset weight. Use the reward function R t to evaluate the performance of your portfolio. Commonly used reward functions are based on the Sharpe Ratio or other performance metrics. The reward function of the Sharpe ratio is defined as Equation 4.
R t = r p , t − r f σ p , t
Where r p , t is the return of the portfolio at time t , and σ p , t is the standard deviation of the portfolio. To better capture tail risk, a reward function based on CVaR (Conditional Value at Risk) can be used, which is expressed as Equation 5, where C V a R α ( r p ) is the conditional value at risk of the portfolio's return at a confidence level of α .
R t = r p , t − r f C V a R α ( r p )
Use the Bellman equation to update the Q value function. Q-value function Q ( s t , a t ) represents the discounted value of the expected total future return after state s t taking action a t . Bellman's equation is defined as Equation 6, where α is the learning rate, γ is the discount factor, a ' is the next state, and s t + 1 is all possible actions.
Q s t , a t ← Q s t , a t + α R t + γ m a x a ' Q s t + 1 , a ' − Q s t , a t
Deep neural networks use deep neural networks to approximate the Q value function Q. The parameters of the neural network are updated by minimizing the following loss function and express as Equation 7, where θ and θ − are the parameters of the current Q network and the target Q network, respectively. The backpropagation algorithm is used to update the parameters, and the specific process is as θ ← θ − η ∇ θ L ( θ ) .
L θ = E [ ( R t + γ m a x a ' Q s t + 1 , a ' ; θ − − Q s t , a t ; θ ) 2 ]
In order to solve the problem of insufficient consideration of other types of financial risks such as credit risk and liquidity risk, it is possible to comprehensively assess risk exposure by extending the risk model, introducing credit risk and liquidity risk assessment tools, and developing comprehensive measurement tools using indicators such as VaR, CVaR and credit VaR. In addition, expand the portfolio's asset classes to include bonds, options, and derivatives to reduce the impact of a single risk by diversifying your investments. Leverage big data and machine learning techniques to analyze a wider range of financial market data, and establish a real-time risk monitoring system to dynamically adjust risk management strategies.

4. Experiments

4.1. Experimental Setups

To verify the effectiveness of a financial risk management approach based on portfolio optimization and reinforcement learning, we selected specific genetic algorithms and deep Q learning parameters to strike a balance between computational resources and algorithm performance. The genetic algorithm parameters include an initial population size of 100, a crossover rate of 0.8, a variation rate of 0.05, and a number of iterations of 500, with the aim of maintaining population diversity, introducing an appropriate amount of randomness, and ensuring the convergence of the algorithm. The parameters of deep Q learning include a learning rate of 0.001, a discount factor of 0.95, an initial ε of 1.0 and an attenuation rate of 0.995, which aim to stabilize the training process, balance current decision-making and future benefits, and gradually transition from exploration to utilization. These parameter selections are based on common settings for experiments and related literature to optimize the stability and effectiveness of model training. Following Figure 1 shows the distribution of stock prices. We have performed a comprehensive pre-processing of historical financial data from 2019 to 2022. The preprocessing steps include data collection, cleansing, processing missing and outliers, alignment, normalization, and logarithmic transformation, data segmentation, training and test set partitioning, and time series cross-validation, as well as label generation, to calculate daily returns and volatility. These steps ensure the quality and consistency of the input data, which improves the accuracy and reliability of model training and predictions.

4.2. Experimental Analysis

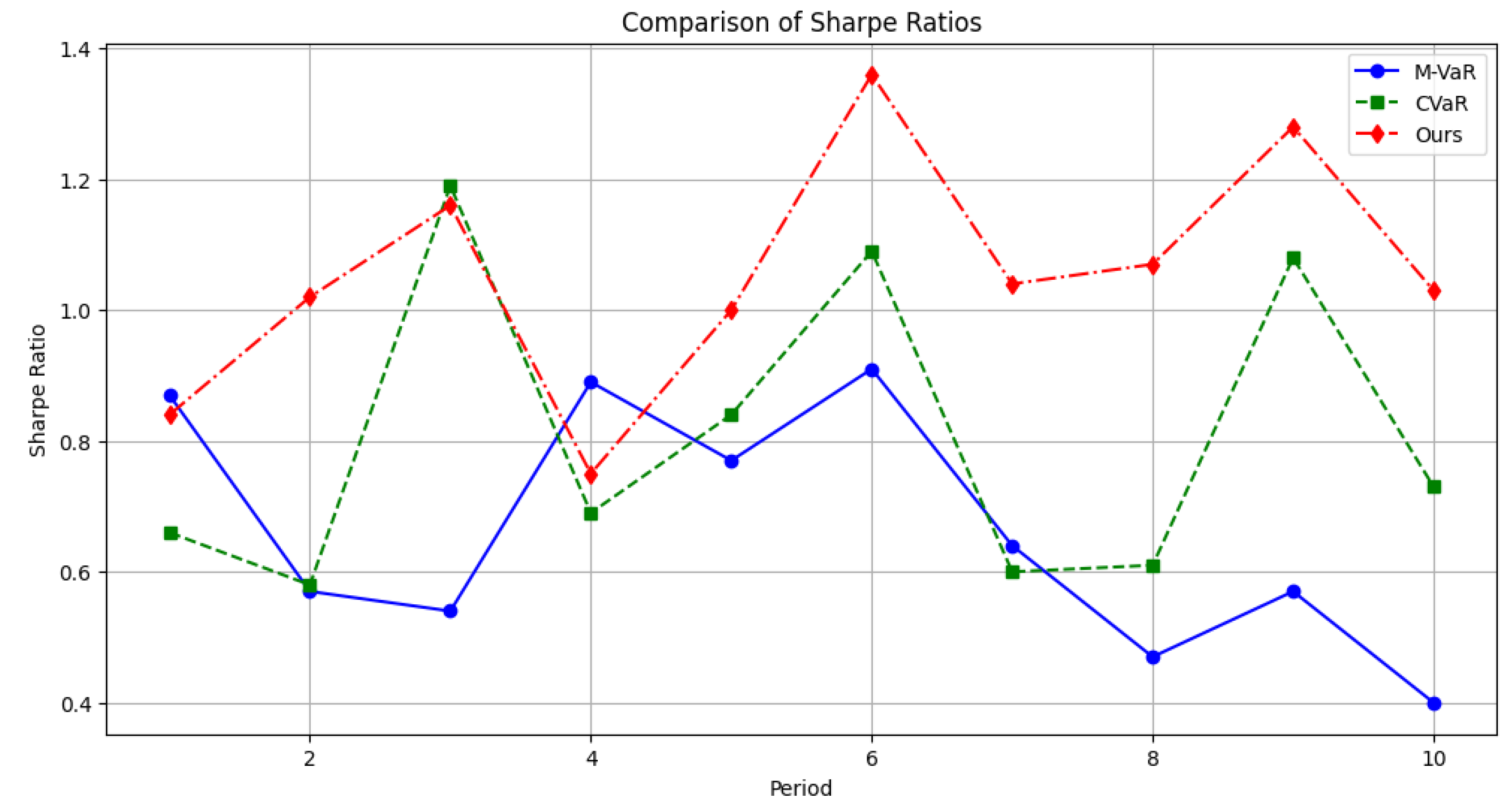
The Sharpe Ratio is a widely used performance measurement metric in the financial sector to measure the excess return per unit of risk. Specifically, the Sharpe ratio evaluates the effectiveness of investment decisions by comparing the difference between a portfolio's returns and the risk-free rate. The core idea is that investors are not only concerned about the absolute value of investment returns, but also about the level of return obtained after taking a certain amount of risk. A higher Sharpe ratio means that the investor receives more returns per unit of risk, indicating a more superior risk-adjusted return for the portfolio.
It is evident in Figure 2 that our approach has higher Sharpe ratios than M-VaR and CVaR over all time periods, indicating a clear advantage in terms of risk-adjusted returns. This result verifies the effectiveness of our combined application of portfolio optimization and reinforcement learning, and demonstrates its potential and advantages in real portfolio management.
Further, VaR measures the maximum loss that a portfolio is likely to incur over a specific period of time given a confidence level. VaR calculations are typically based on historical data or Monte Carlo simulation methods to capture the potential impact of market volatility on a portfolio. In Figure 3, we compare the performance of the three methods (M-VaR, CVaR, and ours) over multiple time periods. The results show that the VaR values of our method are lower than those of M-VaR and CVaR over all time periods, indicating that our method has significant advantages in terms of risk control. Specifically, the VaR values of our method ranged from 0.05 to 0.15, which were significantly lower than the 0.15 to 0.25 of the M-VaR and the 0.1 to 0.2 of the CVaR.

5. Conclusion

In conclusion, the financial risk management method based on portfolio optimization and reinforcement learning shows significant advantages. Through the genetic algorithm for the initial asset allocation optimization, combined with the deep Q learning algorithm to dynamically adjust and optimize the investment strategy, our method has shown excellent risk control ability and return improvement effect in different market environments. Experimental results show that our method is superior to the traditional M-VaR and CVaR methods in terms of Sharpe ratio and value-at-risk, significantly reducing the potential loss and increasing the excess return per unit risk. This study verifies the effectiveness and application potential of portfolio optimization and reinforcement learning in financial risk management, and provides a new way to achieve stable financial growth.

References

  1. Gurtu, Amulya, and Jestin Johny. "Supply chain risk management: Literature review." Risks 9.1 (2021): 16. [CrossRef]
  2. Alabdullah, Tariq Tawfeeq Yousif. "Management accounting insight via a new perspective on risk management-companies' profitability relationship." International Journal of Intelligent Enterprise 9.2 (2022): 244-257. [CrossRef]
  3. Samimi, Amir, Alireza Bozorgian, and Marzieh Samimi. "An Analysis of Risk Management in Financial Markets and Its Effects." (2022): 1-7. [CrossRef]
  4. Alabdullah, Tariq Tawfeeq Yousif, et al. "How Significantly to Emerging Economies Benefit From Board Attributes and Risk Management in Enhancing Firm Profitability." Journal of accounting science 5.2 (2021): 104-113. [CrossRef]
  5. Mensi, Walid, et al. "Dynamic and frequency spillovers between green bonds, oil and G7 stock markets: Implications for risk management." Economic Analysis and Policy 73 (2022): 331-344. [CrossRef]
  6. Settembre-Blundo, Davide, et al. "Flexibility and resilience in corporate decision making: a new sustainability-based risk management system in uncertain times." Global Journal of Flexible Systems Management 22.Suppl 2 (2021): 107-132. [CrossRef]
  7. Chernobai, Anna, Ali Ozdagli, and Jianlin Wang. "Business complexity and risk management: Evidence from operational risk events in US bank holding companies." Journal of Monetary Economics 117 (2021): 418-440. [CrossRef]
  8. Kamiya, Shinichi, et al. "Risk management, firm reputation, and the impact of successful cyberattacks on target firms." Journal of Financial Economics 139.3 (2021): 719-749. [CrossRef]
  9. Niyafard, Sahel, et al. "Exploring the impact of information technology on the relationship between management skills, risk management, and project success in construction industries." International Journal of Business Continuity and Risk Management 14.2 (2024): 97-118. [CrossRef]
  10. Alexander, Gordon J., and Alexandre M. Baptista. "Economic implications of using a mean-VaR model for portfolio selection: A comparison with mean-variance analysis." Journal of Economic Dynamics and Control 26.7-8 (2002): 1159-1193. [CrossRef]
  11. Wu, Mu-En, et al. "Portfolio management system in equity market neutral using reinforcement learning." Applied Intelligence 51.11 (2021): 8119-8131. [CrossRef]
Preprints 114909 g001
Figure 1. Stock Return Evolution in Rate of Change from 2019 to 2022.
Figure 1. Stock Return Evolution in Rate of Change from 2019 to 2022.
Preprints 114909 g001
Preprints 114909 g002
Figure 2. Comparison of Sharpe Ratios.
Figure 2. Comparison of Sharpe Ratios.
Preprints 114909 g002
Preprints 114909 g003
Figure 3. Comparison of Value at Risk (VaR).
Figure 3. Comparison of Value at Risk (VaR).
Preprints 114909 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated