Prerpints.org logo
Preprint
Article

Application of Isokinetic Dynamometry Data in Predicting Gait Deviation Index Using Machine Learning in Stroke Patients

Altmetrics

Downloads

91

Views

44

Comments

0

Submitted:

15 August 2024

Posted:

19 August 2024

You are already at the latest version

Alerts
Abstract
Background: Three-dimensional gait analysis plays a crucial role in the rehabilitation assessment of post-stroke hemiplegic patients. However, the data generated from such analysis is often complex and difficult to interpret in clinical practice, requiring extensive time and complicated procedures. The Gait Deviation Index (GDI) serves as a simplified metric for quantifying the severity of pathological gait. Although isokinetic dynamometry is widely employed in muscle function assessment and rehabilitation, its application in gait analysis remains underexplored. Objective: This study aims to investigate the use of isokinetic muscle strength data obtained from the Biodex system, combined with machine learning techniques, to predict the GDI in hemiplegic patients. Methods: A cohort of 150 post-stroke hemiplegic patients was evaluated. The peak torque, peak torque/body weight, maximum work of repeated actions, coefficient of variation, average power, total work, acceleration time, deceleration time, range of motion, and average peak torque for both flexor and extensor muscles on the affected side were measured at three angular velocities (60°/s, 90°/s, and 120°/s) using the Biodex System 4 Pro. GDI was calculated using data from a Vicon three-dimensional motion capture system. The study employed four machine learning models—Lasso regression, random forest (RF), support vector regression (SVR), and BP neural networks—to model and validate the data. Model performance was evaluated using mean squared error (MSE), the coefficient of determination (R²), and mean absolute error (MAE). SHapley Additive exPlanations (SHAP) analysis was used to enhance model interpretability. Results: The RF model outperformed others in predicting GDI, with an MSE of 16.18, an R² of 0.89, and an MAE of 2.99. In contrast, the Lasso regression model yielded an MSE of 22.29, an R² of 0.85, and an MAE of 3.71. The SVR model had an MSE of 31.58, an R² of 0.82, and an MAE of 7.68, while the BP neural network exhibited the poorest performance with an MSE of 50.38, an R² of 0.79, and an MAE of 9.59. SHAP analysis identified the maximum work of repeated actions of the extensor muscles at 60°/s and 120°/s as the most critical features for predicting GDI, underscoring the importance of muscle strength metrics at varying speeds in rehabilitation assessments. Conclusion: This study highlights the potential of machine learning techniques in analyzing complex clinical data. The developed GDI prediction model, based on isokinetic dynamometry data, offers a novel, streamlined, and effective tool for assessing rehabilitation progress in post-stroke hemiplegic patients, with promising implications for broader clinical application.
Keywords: 
Subject: Medicine and Pharmacology  -   Clinical Medicine

1. Introduction

Stroke remains a leading cause of disability and mortality worldwide, with a rising incidence and recurrence rates [1]. It primarily affects the central nervous system, often resulting in long-term motor dysfunction, particularly in the lower limbs, which frequently manifests as gait abnormalities [2,3]. These gait impairments not only impede patients’ daily activities but are also strongly correlated with increased risks of falls, recurrent strokes, and other complications [4,5,6]. Consequently, these challenges impose significant physical and psychological burdens on patients and present substantial economic strains on families and society. Gait analysis is a critical component of rehabilitation assessment in stroke patients, providing precise kinematic data to inform personalized rehabilitation strategies [7,8]. Accurate gait assessment facilitates not only the monitoring of recovery progress but also the prediction of future fall risks and potential secondary injuries, thereby guiding clinical interventions more effectively [9]. Research indicates that the precision of gait analysis is directly linked to rehabilitation outcomes, underscoring its indispensable role in stroke rehabilitation [10].
Traditional gait assessment methods often rely on clinical visual observations or basic physical measurements, such as gait speed and stride length [11]. While these methods are straightforward and practical, they are prone to subjective biases and fail to capture the complexity of gait patterns [12]. Despite the adoption of modern gait analysis tools, such as three-dimensional motion capture systems and portable gait analysis devices, these systems are often costly, complex to operate, and require specific equipment and environments, limiting their broader clinical application [13,14]. Isokinetic dynamometry, a widely used tool in sports medicine and rehabilitation, accurately measures muscle strength and function, providing vital data on muscle performance during dynamic tests [15]. However, despite the extensive data generated by isokinetic assessments, their potential for gait prediction remains underutilized.
With advances in computational capabilities and the development of big data technologies, machine learning has achieved significant progress in the medical field in recent years. These algorithms are extensively applied in medical imaging analysis, disease prediction, and personalized treatment planning due to their strengths in managing large-scale and complex datasets [16,17,18]. In stroke rehabilitation, machine learning can extract valuable features from multimodal data, enhancing diagnostic and therapeutic accuracy [16]. Integrating isokinetic muscle strength data with machine learning algorithms for gait prediction can effectively address the limitations of traditional methods. Preliminary studies have demonstrated the significant potential of machine learning models in processing biomechanical data, enabling the extraction of key features that influence gait [19]. This approach not only improves prediction accuracy but also facilitates early detection of gait deviations, allowing for more targeted rehabilitation interventions for stroke patients. Previous studies have made significant progress in gait analysis and prediction using machine learning techniques, particularly deep learning approaches that have shown promise in classifying and predicting gait in stroke patients [20,21,22]. However, much of this research has focused on analyzing imaging data or simple gait parameters, with relatively few studies incorporating muscle strength data into gait prediction. Meanwhile, existing models often struggle with generalization when dealing with complex gait features, and the lack of diversity in data samples limits their applicability [23]. In addition, the accuracy of current gait prediction models in identifying gait deviations needs improvement, particularly when dealing with complex movement patterns [24].
This study primarily aims to analyze isokinetic muscle strength data using machine learning algorithms to predict the Gait Deviation Index (GDI) in stroke patients. This work seeks to fill gaps in existing research and provide a novel tool for gait assessment, further optimizing rehabilitation strategies for stroke patients. By developing more accurate gait prediction models, this study aims to make progress in improving the precision and clinical feasibility of gait analysis, thereby enhancing stroke rehabilitation programs and providing valuable references for future research in related fields.

2. Materials and Methods

2.1. Study Design and Participant Selection

This cross-sectional study included 150 post-stroke hemiplegic patients (91 males and 59 females). The inclusion criteria were: (1) age between 18 and 75 years; (2) a confirmed diagnosis of post-stroke hemiplegia with a disease duration of more than 3 months; (3) the ability to walk independently for at least 10 meters; (4) normal cognitive function with a Mini-Mental State Examination (MMSE) score of ≥24 points [25]. Exclusion criteria were: (1) the presence of other neurological diseases affecting gait; (2) severe cardiovascular or other systemic diseases; (3) a history of lower limb surgery within the past 6 months; (4) severe bone or joint diseases. Withdrawal criteria included: (1) occurrence of serious adverse events; (2) failure to complete the assessment as per the established protocol; (3) voluntary withdrawal. The study was approved by the Ethics Committee of Beijing Rehabilitation Hospital, Capital Medical University (Ethics Approval Number: 2022bkky-029). All participants provided written informed consent before participating in the study, which detailed the research process, potential risks, and participants’ rights. The testing procedures were thoroughly explained to the participants, who were allowed to withdraw from the study at any time without consequences.

2.2. Experimental Design and Data Collection

All participants underwent two standard clinical tests to assess their knee joint isokinetic muscle strength and GDI. To ensure consistency in the testing process and data accuracy, all tests were conducted by professional rehabilitation therapists. Initially, muscle strength of the bilateral knee joints was evaluated using the Biodex System 4 Pro device, as shown in Figure 1A. During testing, participants were seated on the Biodex device chair, with their back and thighs secured to minimize interference from other body parts. Each speed test was performed five times, with the average value taken as the final result. Participants were required to warm up adequately before each test to reduce the risk of injury and enhance test accuracy. Peak torque (PT), peak torque/body weight (PT/BW), maximum work of repeated actions, coefficient of variation (CV), average power, total work, acceleration time, deceleration time, range of motion (ROM), and average peak torque were measured for both flexor and extensor muscles at speeds of 60°/s, 90°/s, and 120°/s. Compensation from other body parts, such as the trunk and upper limbs, was not allowed during the test. Subsequently, GDI data were collected and analyzed using the Vicon three-dimensional motion capture system (MX T40-S cameras, Oxford Metrics Limited, UK) in the gait laboratory. The Vicon system was calibrated and validated before testing to ensure data capture accuracy, as shown in Figure 1B. Participants wore tight, non-black, non-reflective clothing to minimize capture errors. The study employed the Plugs-in-gait lower limb model, with 16 reflective markers placed on key anatomical landmarks to establish a lower limb model during walking. Before the test, participants walked back and forth naturally on an 8-meter walkway to acclimate to the experimental environment. During the test, static testing was first conducted to determine the static model, followed by data collection as participants walked back and forth at a comfortable speed on the walkway. GDI for the affected side was automatically calculated after data processing with Vicon Nexus 2.12 software, including filling, smoothing, and filtering, as depicted in Figure 1C.

2.3. Data Preprocessing and Analysis

After data collection, data preprocessing and analysis were conducted using Python 3.11. First, the data were normalized using the Z-score normalization method, where each feature value was adjusted by subtracting the mean and dividing by the standard deviation to ensure that all data were on the same scale. Outliers were identified and handled using the Interquartile Range (IQR) method. For missing data, multiple imputation was applied to maintain data integrity and minimize bias. Next, Recursive Feature Elimination (RFE) with a linear regression model was used to select the 20 most important features as inputs for the models. The selected features were renamed as Feature1, Feature2, …, Feature20, and a feature mapping table was created. Subsequently, various machine learning regression methods, including Lasso Regression, Backpropagation (BP) Neural Networks, Random Forest Regression (RF), and Support Vector Regression (SVR), were used to train models for predicting the GDI in stroke patients. The Lasso regression model, which uses L1 regularization, was effective for feature selection and handling high-dimensional data with multicollinearity [26]. The BP neural network model, known for its strong nonlinear modeling capabilities, was suitable for learning complex data patterns [27]. The RF model offered advantages in handling high-dimensional data and automatic feature selection, along with robustness and resistance to overfitting [28]. The SVR model performed well in scenarios with small samples and high-dimensional data, demonstrating good generalization ability [29].
In the RFE method, based on a linear regression model with L1 regularization, 20 important features were selected, with 10 iterations and a step size of 2 for each iteration. For the Lasso regression model, the regularization strength parameter α was set to 0.01, the maximum number of iterations was 2000, and the random seed was fixed at 21 to ensure reproducibility of the results. The BP neural network model used four hidden layers, each with 12 neurons, the ReLU activation function, Adam optimizer, a learning rate of 0.0005, a batch size of 64, and 300 training epochs. The RF model consisted of 150 decision trees with a maximum depth of 20 and a minimum sample split of 5, with the random seed also set at 21. For the SVR model, the Radial Basis Function kernel was used, with a regularization parameter C set at 0.5, ε set at 0.05, and a maximum of 2000 iterations. The hyperparameters for the models are shown in Table 1.
This study employed data splitting and cross-validation techniques. The dataset was divided into a training set (70%) and a validation set (30%). The training set was used for model learning and tuning, while the validation set was used to evaluate model performance and accuracy. To enhance the robustness of model evaluation, a 10-fold cross-validation method was applied. The training set was evenly divided into 10 subsets, with one subset used as the validation set in each iteration and the remaining 9 subsets used for training the model. This process was repeated 10 times, allowing each subset to serve as the validation set once. The average values across the 10 iterations, including Mean Squared Error (MSE), Mean Absolute Error (MAE), and the coefficient of determination (R2), were calculated.

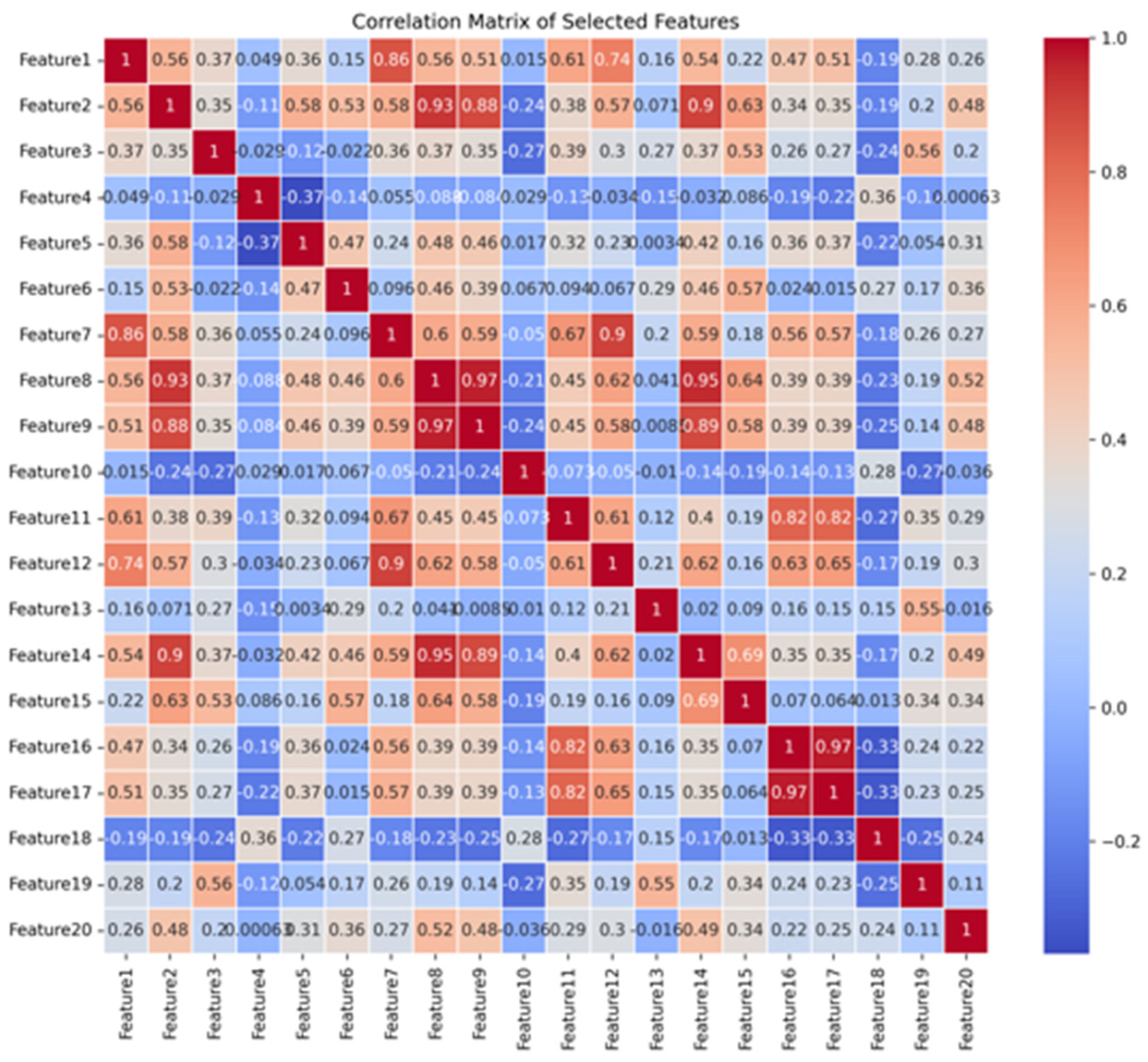
2.4. Interpretability Techniques

To enhance the interpretability of the models, particularly when dealing with black-box models, this study utilized SHAP (SHapley Additive exPlanations) techniques. SHAP is a method for explaining machine learning model predictions, based on the Shapley value from cooperative game theory [30]. It decomposes the influence of each feature into contributions to the prediction, thereby determining the importance of each feature. This approach is valuable for identifying features that have a positive or negative impact on model outputs, which is crucial for further improving diagnostic models.

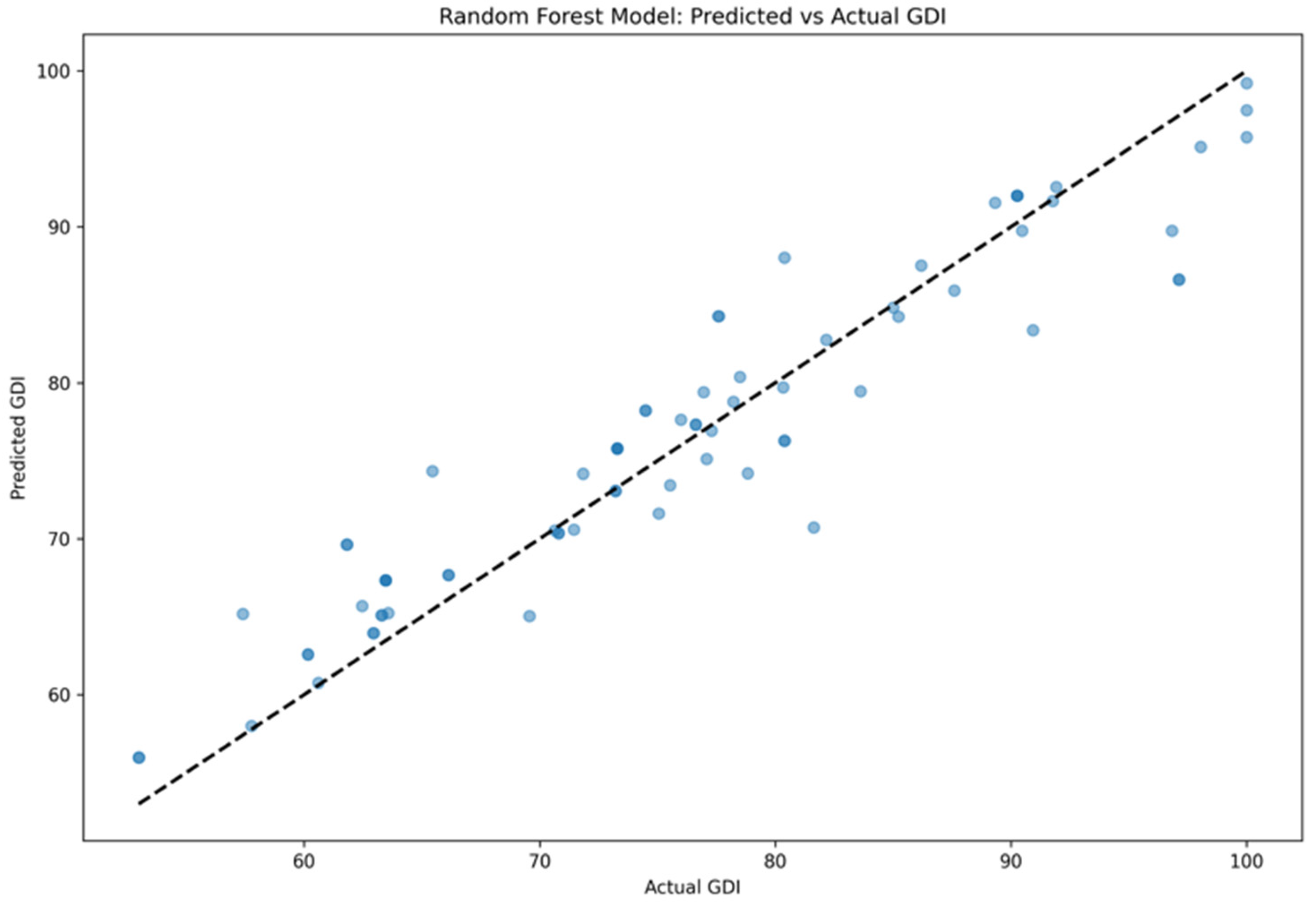
3. Results

In this study, data on knee joint isokinetic muscle strength and GDI were collected and analyzed from a total of 150 post-stroke hemiplegic patients. Table 2 provides a summary of the key parameters measured for the flexor and extensor muscles on both sides at different speeds (60°/s, 90°/s, 120°/s), including the median values and IQR.
Using the RFE method, 20 of the most important features were extracted from the original data on knee joint muscle strength and GDI. For ease of subsequent analysis and presentation, these features were renamed as Feature 1 through Feature 20. The mapping between the original feature names and the new names is detailed in Table 3. The distribution of the extracted features is displayed through histograms, as shown in Figure 2 and Figure 3. The data for Features 1 through 20 are evenly distributed and tend to follow a near-normal distribution. This indicates that the dataset’s attributes and labels are stable, with no significant bias or imbalance.
Table 2. Isokinetic muscle strength test data situation.
Table 2. Isokinetic muscle strength test data situation.
Speed (deg/s) Muscle Group Measurement Side PT (Nm) PT/BW (%) Max Work of Repeated Actions (J) CV (%) Average Power (W) Total Work (J) Acceleration Time (s) Deceleration Time (s) ROM (deg) Average Peak Torque (Nm)
60 Extensor Healthy Side 29.03 (43.15, 72.18) 38.45 (64.12, 102.57) 30.42 (51.38, 81.8) 22.0 (10.9, 32.9) 17.45 (21.85, 39.3) 155.15 (190.62, 345.78) 60.0 (60.0, 120.0) 60.0 (120.0, 180.0) 13.55 (99.03, 112.58) 25.72 (33.12, 58.85)
60 Extensor Affected Side 21.27 (25.43, 46.7) 32.75 (34.56, 67.31) 27.6 (23.6, 51.2) 42.3 (14.3, 56.6) 11.92 (12.28, 24.2) 106.0 (80.9, 186.9) 100.0 (70.0, 170.0) 60.0 (130.0, 190.0) 25.08 (79.38, 104.45) 14.6 (20.36, 34.95)
60 Flexor Healthy Side 17.48 (15.07, 32.55) 24.94 (22.32, 47.26) 26.9 (8.1, 35.0) 45.9 (9.95, 55.85) 9.88 (2.9, 12.78) 99.8 (24.0, 123.8) 100.0 (90.0, 190.0) 170.0 (120.0, 290.0) 17.3 (94.0, 111.3) 16.5 (11.11, 27.6)
60 Flexor Affected Side 8.98 (8.81, 17.79) 15.39 (12.79, 28.18) 13.77 (0.4, 14.17) 49.43 (22.47, 71.9) 4.91 (0.1, 5.01) 40.9 (1.6, 42.5) 80.0 (110.0, 190.0) 110.0 (140.0, 250.0) 25.6 (83.1, 108.7) 7.37 (5.77, 13.14)
90 Extensor Healthy Side 25.12 (37.92, 63.05) 33.42 (58.2, 91.62) 29.83 (46.3, 76.12) 15.02 (7.48, 22.5) 21.27 (30.68, 51.95) 111.2 (206.4, 317.6) 40.0 (80.0, 120.0) 40.0 (120.0, 160.0) 11.25 (101.9, 113.15) 24.73 (31.95, 56.68)
90 Extensor Affected Side 12.84 (12.41, 25.24) 17.16 (19.94, 37.1) 23.45 (4.45, 27.9) 26.65 (12.35, 39.0) 12.35 (2.3, 14.65) 94.5 (11.82, 106.33) 107.5 (112.5, 220.0) 90.0 (130.0, 220.0) 12.12 (100.5, 112.62) 9.54 (10.28, 19.81)
90 Flexor Healthy Side 5.97 (7.9, 13.88) 8.05 (11.73, 19.78) 9.18 (0.33, 9.5) 35.98 (18.42, 54.4) 6.06 (0.1, 6.16) 28.77 (0.93, 29.7) 50.0 (120.0, 170.0) 70.0 (130.0, 200.0) 28.1 (81.6, 109.7) 5.33 (6.37, 11.7)
90 Flexor Affected Side 24.58 (31.9, 56.48) 34.37 (49.52, 83.89) 21.5 (47.4, 68.9) 12.4 (7.1, 19.5) 24.05 (35.12, 59.18) 99.8 (196.8, 296.6) 50.0 (90.0, 140.0) 40.0 (130.0, 170.0) 11.27 (102.2, 113.47) 17.74 (31.21, 48.95)
120 Extensor Healthy Side 12.92 (25.27, 38.2) 18.35 (37.92, 56.27) 23.95 (23.95, 47.9) 15.68 (6.83, 22.5) 21.79 (19.46, 41.26) 115.03 (92.38, 207.4) 70.0 (130.0, 200.0) 60.0 (150.0, 210.0) 26.05 (83.85, 109.9) 9.84 (22.72, 32.55)
120 Extensor Affected Side 10.4 (11.97, 22.38) 14.12 (17.32, 31.45) 19.8 (2.3, 22.1) 24.18 (15.93, 40.1) 14.25 (1.55, 15.8) 80.55 (6.45, 87.0) 67.5 (140.0, 207.5) 77.5 (140.0, 217.5) 11.2 (101.6, 112.8) 9.14 (9.05, 18.19)
120 Flexor Healthy Side 4.59 (9.42, 14.01) 7.04 (13.08, 20.12) 6.83 (0.3, 7.12) 32.3 (24.6, 56.9) 4.7 (0.1, 4.8) 26.83 (1.0, 27.83) 67.5 (142.5, 210.0) 80.0 (140.0, 220.0) 24.5 (85.4, 109.9) 5.2 (6.3, 11.5)
120 Flexor Affected Side 29.03 (43.15, 72.18) 38.45 (64.12, 102.57) 30.42 (51.38, 81.8) 22.0 (10.9, 32.9) 17.45 (21.85, 39.3) 155.15 (190.62, 345.78) 60.0 (60.0, 120.0) 60.0 (120.0, 180.0) 13.55 (99.03, 112.58) 25.72 (33.12, 58.85)
Observing the matrix, we can identify strong positive correlations between certain features. For instance, Features 8 and 9, as well as Features 16 and 17, have correlation coefficients close to 1 (0.97), indicating a very high positive correlation. Similarly, Feature 8 and Feature 14 also exhibit a strong correlation (0.95). These highly positive correlations suggest that these features share similar trends in the dataset and may collectively reflect similar biological or functional information. On the other hand, some features, such as Feature 4 and Feature 5, show a significant negative correlation (-0.37). This indicates that these features have opposite trends in the dataset, potentially representing different or mutually inhibitory physiological mechanisms. Such negative correlations could play a complementary role in model prediction, thereby influencing the overall performance of the model.
Preprints 115361 g004
Figure 4. Correlation matrix of selected features. Note: The colors in the matrix range from blue to red, indicating the direction and strength of the correlations between features. Blue represents negative correlations, while red represents positive correlations, with the intensity of the color reflecting the strength of the correlation.
Figure 4. Correlation matrix of selected features. Note: The colors in the matrix range from blue to red, indicating the direction and strength of the correlations between features. Blue represents negative correlations, while red represents positive correlations, with the intensity of the color reflecting the strength of the correlation.
Preprints 115361 g004
The performance results of the four predictive models are summarized in Table 4. Overall, each model demonstrated varying degrees of effectiveness in predicting the GDI for post-stroke hemiplegic patients, with the Random Forest Regression model showing the best overall performance. Specifically, the Random Forest model had a MSE of 16.18 ± 1.92 and an R2 of 0.89 ± 0.06, indicating higher predictive accuracy and reliability. Additionally, it had the lowest MAE of 2.99 ± 0.69. In comparison, the Lasso Regression model, while effective, performed slightly lower with an MSE of 22.29 ± 3.28 and an R2 of 0.85 ± 0.18. The SVR model and the BP Neural Network model showed moderate to lower performance, with the SVR model yielding an MSE of 31.58 ± 5.48 and an R2 of 0.82 ± 0.13, and the BP Neural Network model having the poorest performance, with an MSE of 50.38 ± 9.12 and an R2 of 0.79 ± 0.21. These results suggest that although all models possess predictive capabilities, the Random Forest Regression model provides the most accurate and consistent results. Figure 5 illustrates a scatter plot comparing the GDI values predicted by the RF model with the actual GDI values. The scatter plot shows that most of the predicted values are close to the dashed line, indicating high predictive accuracy and stability of the model.
Figure 6A to Figure 6D present summary plots of SHAP values for the four different models, which help to interpret the decision-making process by showing each feature’s contribution to the model’s predictions. Figure 6A displays the SHAP values for the Random Forest model, It is evident that Feature 2, Feature 14, and Feature 12 have a substantial positive influence on the model’s predictions. Figure 6B illustrates the distribution of feature importance in the SVR model. In this model, Feature 2, Feature 14, and Feature 9 have a strong impact on the model’s output, while features like Feature 18 and Feature 3 contribute less, and in some cases, may even have a negative effect. This indicates that the importance of features in the SVR model is more dispersed. Figure 6C shows the SHAP value distribution for the BP Neural Network model. Here, Feature 2, Feature 14, and Feature 20 significantly influence the model’s output, highlighting their importance in the neural network. Interestingly, compared to other models, Feature 3 and Feature 1 have more prominent SHAP values, suggesting that the BP Neural Network model relies more heavily on certain key features. Figure 6D presents the SHAP value analysis for the Lasso Regression model. In this model, Feature 2, Feature 14, and Feature 4 have high SHAP values, indicating their crucial role in the model’s predictions. Additionally, Feature 8 and Feature 7 also show considerable influence, suggesting that the Lasso Regression model effectively balances the contributions of multiple features.
Notably, across all four models, Feature 2 and Feature 14 consistently exhibit significant influence, underscoring their importance in predicting GDI. This consistency across models highlights the critical role these features play in the prediction process.
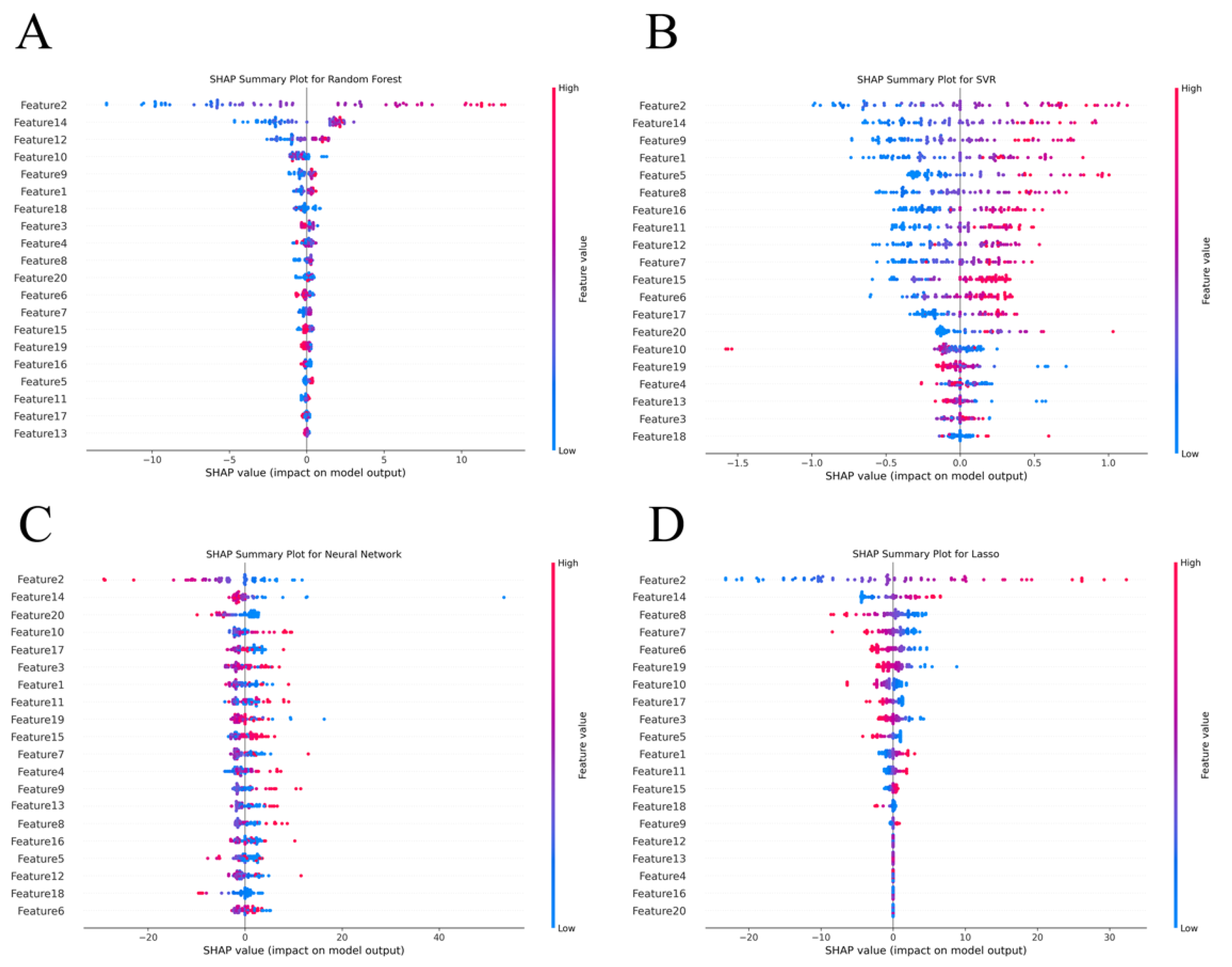
Preprints 115361 g006
Figure 6. SHAP Summary Plot of different models. Note: In these plots, the color gradient from blue (low value) to red (high value) represents the size of the feature values, and the X-axis represents the SHAP values, with larger values indicating a more significant impact of the feature on the model’s output.
Figure 6. SHAP Summary Plot of different models. Note: In these plots, the color gradient from blue (low value) to red (high value) represents the size of the feature values, and the X-axis represents the SHAP values, with larger values indicating a more significant impact of the feature on the model’s output.
Preprints 115361 g006

4. Discussion

This study aimed to predict the GDI in post-stroke hemiplegic patients by integrating knee joint isokinetic strength assessment data with machine learning models. The results indicate that the RF model performed exceptionally well in handling complex biomechanical data, particularly in predicting gait deviations. Its accuracy and stability significantly outperformed traditional models such as SVR and BP Neural Networks. The RF model, by integrating multiple decision trees, effectively reduced the risk of overfitting, demonstrating greater robustness [28]. This finding aligns with existing literature, which confirms the widespread application and superior performance of RF in handling high-dimensional data and complex features. For instance, RF models have shown advantages in predicting survival rates in chronic obstructive pulmonary disease (COPD) patients and assessing cardiovascular disease risks, showcasing their strength in processing multidimensional clinical data [31]. Moreover, the model’s effectiveness in managing nonlinear relationships and noisy data further supports its applicability and reliability in gait analysis [32].
In contrast, while deep learning models excel in processing imaging data, they tend to overfit with smaller sample sizes, leading to insufficient generalization capabilities [33]. The results of this study suggest that in clinical environments with limited resources or smaller datasets, the Random Forest model may be more suitable. This provides clinicians with an efficient and reliable tool for gait prediction, holding significant practical value. Although deep learning models have demonstrated superior predictive accuracy, their “black-box” nature limits their clinical application [34]. This study identified that Feature 2 (maximum work of the affected side’s knee extensors at 60°/s) and Feature 14 (maximum work of the affected side’s knee extensors at 120°/s) were particularly important for predicting GDI. These features reflect the strength performance of knee extensors at different angular velocities, highlighting the critical role of extensor strength in gait stability and coordination. The existing literature widely supports this finding. Research shows that knee extensors play a crucial role during the stance phase of the gait cycle, particularly when patients need to maintain body stability and bear weight [35]. Insufficient extensor strength is often associated with stance phase issues, potentially leading to hyperextension or flexion deformities of the knee, thereby affecting gait stability and symmetry [36]. Additionally, the differences in extensor work across different angular velocities reflect muscle performance under dynamic loading conditions, which is especially important for gait control in post-stroke hemiplegic patients [37,38]. Further research suggests that enhancing knee extensor strength can effectively improve gait performance, reduce the risk of joint injuries, and enhance walking ability and independence [39]. Meanwhile, insufficient extensor strength may increase the risk of gait instability, leading to a higher likelihood of falls and recurrent strokes [40]. This study further validates the importance of knee extensor strength in gait control, particularly in the rehabilitation process of post-stroke hemiplegic patients. Strengthening these key muscle groups can significantly improve gait, reduce fall risk, and accelerate recovery, providing a solid scientific basis for developing personalized rehabilitation plans [35,41].
The use of SHAP technology significantly enhanced the interpretability of complex models by providing consistent and globally interpretable feature contribution values, which is also of great significance in clinical applications. For example, SHAP technology has been successfully applied in cardiovascular risk prediction models, increasing doctors’ confidence in model results [42]. Similarly, SHAP’s application in diabetes management has not only improved model interpretability but also helped in designing more precise personalized treatment plans [43]. By introducing SHAP technology, this study further improved the clinical applicability of machine learning models, making prediction results easier for doctors to understand and apply, thereby optimizing the development of personalized rehabilitation plans [44].
In handling small sample sizes, traditional machine learning models demonstrated significant advantages [45]. BP Neural Networks are prone to overfitting with small samples, resulting in inadequate generalization capabilities. For example, the literature points out that deep learning models often exhibit instability when processing small sample data, requiring regularization or data augmentation techniques for improvement [46]. In contrast, ensemble learning models such as Random Forest are more suitable for handling complex biomechanical data with small sample sizes, as they better manage data noise and avoid overfitting [47]. Moreover, studies have shown that traditional machine learning models often provide more robust predictive results when handling high-dimensional data, especially when the sample size is limited, further supporting the findings of this study [48].
Despite the significant achievements in predicting gait deviations, this study has some limitations. First, the sample size was relatively small, including only 150 post-stroke hemiplegic patients. Although this sample size provided initial validation for model development, its generalizability might be limited when dealing with more complex and diverse patient populations. Future research should expand the sample size and include a more diverse patient population, encompassing different genders, ages, disease courses, and rehabilitation stages. By increasing sample diversity, researchers can develop more generalizable gait prediction models, improving model generalization ability and providing more personalized rehabilitation recommendations for different types of patients. Second, this study primarily relied on knee joint isokinetic strength assessment data. While these data are important for gait prediction, gait deviations result from the interaction of multiple factors, including muscle strength, balance ability, neural control, and external environmental factors. Solely relying on knee joint strength data may not fully capture all the relevant factors of gait deviation. Future research should explore the integration of multimodal data, combining balance ability tests, surface electromyography, gait imaging data, neuroimaging data, and biomarker data, to construct a more comprehensive gait prediction model. Integrating multimodal data will help capture the causes of gait deviations more comprehensively, improving the accuracy of the model’s predictions and providing more precise rehabilitation guidance. Finally, although this study used SHAP technology to enhance model interpretability, machine learning models may still exhibit a “black-box” effect in practical applications. This issue is particularly important in clinical decision-making, as doctors need to understand the specific basis for model predictions to better apply them in patient rehabilitation plans. Future research should continue to explore how to improve the interpretability of machine learning models, developing more intuitive visualization tools and explanatory methods, making it easier for clinicians to understand and apply these models’ predictions. This is crucial for better integrating machine learning models into the clinical decision-making process.

5. Conclusion

In conclusion, this study successfully predicted the GDI in post-stroke hemiplegic patients by integrating knee joint isokinetic strength assessment data with machine learning models. The findings indicate that the Random Forest Regression model performed the best in predicting gait deviations, demonstrating high accuracy and robustness. Additionally, muscle strength metrics at different speeds were found to be crucial for rehabilitation assessment, further validating the importance of knee joint strength in gait control. Future research should focus on addressing the potential biases and unconsidered variables identified in this study to develop even more robust predictive models.

References

  1. Feigin, V.L.; Stark, B.A.; Johnson, C.O.; Roth, G.A.; Bisignano, C.; Abady, G.G.; Abbasifard, M.; Abbasi-Kangevari, M.; Abd-Allah, F.; Abedi, V.; Abualhasan, A. Global, regional, and national burden of stroke and its risk factors, 1990-2019: a systematic analysis for the Global Burden of Disease Study 2019. Lancet Neurol 2021, 20, 795–820. [Google Scholar] [CrossRef] [PubMed]
  2. Li, S.; Francisco, G.E.; Zhou, P. Post-stroke Hemiplegic Gait: New Perspective and Insights. Front Physiol 2018, 9, 1021. [Google Scholar] [CrossRef] [PubMed]
  3. Frenkel-Toledo, S.; Ofir-Geva, S.; Mansano, L.; et al. Stroke Lesion Impact on Lower Limb Function. Front Hum Neurosci 2021, 15, 592975. [Google Scholar] [CrossRef] [PubMed]
  4. Ng, M.M.; Hill, K.D.; Batchelor, F.; et al. Factors Predicting Falls and Mobility Outcomes in Patients With Stroke Returning Home After Rehabilitation Who Are at Risk of Falling. Arch Phys Med Rehabil 2017, 98, 2433–2441. [Google Scholar] [CrossRef] [PubMed]
  5. Bergamini, E.; Iosa, M.; Belluscio, V.; et al. Multi-sensor assessment of dynamic balance during gait in patients with subacute stroke. J Biomech 2017, 61, 208–215. [Google Scholar] [CrossRef] [PubMed]
  6. Nagano, H.; Said, C.M.; James, L.; et al. Biomechanical Correlates of Falls Risk in Gait Impaired Stroke Survivors. Front Physiol 2022, 13, 833417. [Google Scholar] [CrossRef]
  7. Barroso, F.O.; Torricelli, D.; Molina-Rueda, F.; et al. Combining muscle synergies and biomechanical analysis to assess gait in stroke patients. J Biomech 2017, 63, 98–103. [Google Scholar] [CrossRef] [PubMed]
  8. Ferrarello, F.; Bianchi, V.A.; Baccini, M.; et al. Tools for observational gait analysis in patients with stroke: a systematic review. Phys Ther 2013, 93, 1673–1685. [Google Scholar] [CrossRef]
  9. Ishiwatari, M.; Tani, M.; Isayama, R.; et al. Prediction of gait independence using the Trunk Impairment Scale in patients with acute stroke. Ther Adv Neurol Disord 2022, 15, 17562864221140180. [Google Scholar] [CrossRef] [PubMed]
  10. Schwarz, A.; Al-Haj Husain, A.; Einaudi, L.; et al. Reliability and Validity of a Wearable Sensing System and Online Gait Analysis Report in Persons after Stroke. Sensors 2023, 23, 624. [Google Scholar] [CrossRef]
  11. Mohan, D.M.; Khandoker, A.H.; Wasti, S.A.; et al. Assessment Methods of Post-stroke Gait: A Scoping Review of Technology-Driven Approaches to Gait Characterization and Analysis. Front Neurol 2021, 12, 650024. [Google Scholar] [CrossRef] [PubMed]
  12. Visscher, R.M.S.; Sansgiri, S.; Freslier, M.; et al. Towards validation and standardization of automatic gait event identification algorithms for use in paediatric pathological populations. Gait Posture 2021, 86, 64–69. [Google Scholar] [CrossRef] [PubMed]
  13. Homes, R.; Clark, D.; Moridzadeh, S.; et al. Comparison of a Wearable Accelerometer/Gyroscopic, Portable Gait Analysis System (LEGSYS+(TM)) to the Laboratory Standard of Static Motion Capture Camera Analysis. Sensors 2023, 23, 537. [Google Scholar] [CrossRef] [PubMed]
  14. Yeung, L.F.; Yang, Z.; Cheng, K.C.; et al. Effects of camera viewing angles on tracking kinematic gait patterns using Azure Kinect, Kinect v2 and Orbbec Astra Pro v2. Gait Posture 2021, 87, 19–26. [Google Scholar] [CrossRef]
  15. Van Der Woude, D.R.; Ruyten, T.; Bartels, B. Reliability of Muscle Strength and Muscle Power Assessments Using Isokinetic Dynamometry in Neuromuscular Diseases: A Systematic Review. Phys Ther 2022, 102. [Google Scholar] [CrossRef] [PubMed]
  16. Mainali, S.; Darsie, M.E.; Smetana, K.S. Machine Learning in Action: Stroke Diagnosis and Outcome Prediction. Front Neurol 2021, 12, 734345. [Google Scholar] [CrossRef] [PubMed]
  17. Gandolfi, M.; Boscolo Galazzo, I.; Gasparin Pavan, R.; et al. eXplainable AI Allows Predicting Upper Limb Rehabilitation Outcomes in Sub-Acute Stroke Patients. IEEE J Biomed Health Inform 2023, 27, 263–273. [Google Scholar] [CrossRef] [PubMed]
  18. Liu, G.; Wu, J.; Dang, C.; et al. Machine Learning for Predicting Motor Improvement After Acute Subcortical Infarction Using Baseline Whole Brain Volumes. Neurorehabil Neural Repair 2022, 36, 38–48. [Google Scholar] [CrossRef] [PubMed]
  19. Hussain, I.; Park, S.J. Prediction of Myoelectric Biomarkers in Post-Stroke Gait. Sensors 2021, 21, 5334. [Google Scholar] [CrossRef] [PubMed]
  20. Kim, J.K.; Choo, Y.J.; Chang, M.C. Prediction of Motor Function in Stroke Patients Using Machine Learning Algorithm: Development of Practical Models. J Stroke Cerebrovasc Dis 2021, 30, 105856. [Google Scholar] [CrossRef]
  21. Wang, F.C.; Chen, S.F.; Lin, C.H.; et al. Detection and Classification of Stroke Gaits by Deep Neural Networks Employing Inertial Measurement Units. Sensors 2021, 21, 1864. [Google Scholar] [CrossRef]
  22. Morbidoni, C.; Cucchiarelli, A.; Agostini, V.; et al. Machine-Learning-Based Prediction of Gait Events From EMG in Cerebral Palsy Children. IEEE Trans Neural Syst Rehabil Eng 2021, 29, 819–830. [Google Scholar] [CrossRef]
  23. Guo, Y.; Gu, X.; Yang, G.Z. MCDCD: Multi-Source Unsupervised Domain Adaptation for Abnormal Human Gait Detection. IEEE J Biomed Health Inform 2021, 25, 4017–4028. [Google Scholar] [CrossRef]
  24. Veerkamp, K.; Waterval, N.F.J.; Geijtenbeek, T.; et al. Evaluating cost function criteria in predicting healthy gait. J Biomech 2021, 123, 110530. [Google Scholar] [CrossRef]
  25. Folstein, M.F.; Folstein, S.E.; Mchugh, P.R. “Mini-mental state”. A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res 1975, 12, 189–198. [Google Scholar] [CrossRef] [PubMed]
  26. Guo, Y.; Wang, W.; Wang, X. A Robust Linear Regression Feature Selection Method for Data Sets With Unknown Noise. IEEE Transactions on Knowledge and Data Engineering 2023, 35, 31–44. [Google Scholar] [CrossRef]
  27. Fang, X.; Yang, N. A Neural Learning Approach for a Data-Driven Nonlinear Error Correction Model. Comput Intell Neurosci 2023, 2023, 5884314. [Google Scholar] [CrossRef] [PubMed]
  28. Breiman, L. Random Forests. Machine Learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
  29. Yang, W.X.; Wang, F.F.; Pan, Y.Y.; et al. Comparison of ischemic stroke diagnosis models based on machine learning. Front Neurol 2022, 13, 1014346. [Google Scholar] [CrossRef] [PubMed]
  30. Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017) 2017. [Google Scholar]
  31. Nikolaou, V.; Massaro, S.; Garn, W.; et al. The cardiovascular phenotype of Chronic Obstructive Pulmonary Disease (COPD): Applying machine learning to the prediction of cardiovascular comorbidities. Respir Med 2021, 186, 106528. [Google Scholar] [CrossRef] [PubMed]
  32. Pickett, K.L.; Suresh, K.; Campbell, K.R.; et al. Random survival forests for dynamic predictions of a time-to-event outcome using a longitudinal biomarker. BMC Med Res Methodol 2021, 21, 216. [Google Scholar] [CrossRef] [PubMed]
  33. Speiser, J.L. A random forest method with feature selection for developing medical prediction models with clustered and longitudinal data. J Biomed Inform 2021, 117, 103763. [Google Scholar] [CrossRef]
  34. Petch, J.; Di, S.; Nelson, W. Opening the Black Box: The Promise and Limitations of Explainable Machine Learning in Cardiology. Can J Cardiol 2022, 38, 204–213. [Google Scholar] [CrossRef]
  35. Sijobert, B.; Azevedo, C.; Pontier, J.; et al. A Sensor-Based Multichannel FES System to Control Knee Joint and Reduce Stance Phase Asymmetry in Post-Stroke Gait. Sensors 2021, 21, 2134. [Google Scholar] [CrossRef] [PubMed]
  36. Geerars, M.; Minnaar-Van Der Feen, N.; Huisstede, B.M.A. Treatment of knee hyperextension in post-stroke gait. A systematic review. Gait Posture 2022, 91, 137–148. [Google Scholar] [CrossRef]
  37. Sibley, A.R.; Strike, S.; Moudy, S.C.; et al. The associations between asymmetries in quadriceps strength and gait in individuals with unilateral transtibial amputation. Gait Posture 2021, 90, 267–273. [Google Scholar] [CrossRef] [PubMed]
  38. Lyle, M.A.; Jensen, J.C.; Hunnicutt, J.L.; et al. Identification of strength and spatiotemporal gait parameters associated with knee loading during gait in persons after anterior cruciate ligament reconstruction. J Athl Train 2021, 2021. [Google Scholar]
  39. Lyle, M.A.; Jensen, J.C.; Hunnicutt, J.L.; et al. Associations of Strength and Spatiotemporal Gait Variables With Knee Loading During Gait After Anterior Cruciate Ligament Reconstruction. J Athl Train 2022, 57, 158–164. [Google Scholar] [CrossRef]
  40. Tanaka, K.; Anan, M.; Tsubouchi, Y.; et al. Gait analysis of a patient who underwent complete resection of the patella and quadriceps femoris for soft tissue sarcoma. Eur J Phys Rehabil Med 2021, 57, 298–302. [Google Scholar] [CrossRef]
  41. Neuman, R.M.; Shearin, S.M.; Mccain, K.J.; et al. Biomechanical analysis of an unpowered hip flexion orthosis on individuals with and without multiple sclerosis. J Neuroeng Rehabil 2021, 18, 104. [Google Scholar] [CrossRef] [PubMed]
  42. Wang, K.; Tian, J.; Zheng, C.; et al. Interpretable prediction of 3-year all-cause mortality in patients with heart failure caused by coronary heart disease based on machine learning and SHAP. Comput Biol Med 2021, 137, 104813. [Google Scholar] [CrossRef] [PubMed]
  43. Khadem, H.; Nemat, H.; Elliott, J.; et al. Interpretable Machine Learning for Inpatient COVID-19 Mortality Risk Assessments: Diabetes Mellitus Exclusive Interplay. Sensors 2022, 22, 8757. [Google Scholar] [CrossRef] [PubMed]
  44. Smole, T.; Zunkovic, B.; Piculin, M.; et al. A machine learning-based risk stratification model for ventricular tachycardia and heart failure in hypertrophic cardiomyopathy. Comput Biol Med 2021, 135, 104648. [Google Scholar] [CrossRef] [PubMed]
  45. Jiang, Z.; Han, Y.; Xu, L.; et al. The NEAT Equating Via Chaining Random Forests in the Context of Small Sample Sizes: A Machine-Learning Method. Educ Psychol Meas 2023, 83, 984–1006. [Google Scholar] [CrossRef] [PubMed]
  46. Zhang, C.; Bengio, S.; Hardt, M.; et al. Understanding deep learning (still) requires rethinking generalization. Commun ACM 2021, 64, 107–115. [Google Scholar] [CrossRef]
  47. Dudek, G. A Comprehensive Study of Random Forest for Short-Term Load Forecasting. Energies 2022, 15, 7547. [Google Scholar] [CrossRef]
  48. Deng, F.; Huang, J.; Yuan, X.; et al. Performance and efficiency of machine learning algorithms for analyzing rectangular biomedical data. Lab Invest 2021, 101, 430–441. [Google Scholar] [CrossRef]
Preprints 115361 g001
Figure 1. A: Isokinetic Dynamometry procedure; B: Vicon 3D gait analysis static calibration; C: software calculation procedure.
Figure 1. A: Isokinetic Dynamometry procedure; B: Vicon 3D gait analysis static calibration; C: software calculation procedure.
Preprints 115361 g001
Preprints 115361 g002
Figure 2. Distribution of selected features.
Figure 2. Distribution of selected features.
Preprints 115361 g002
Preprints 115361 g003
Figure 3. Histogram of data set distribution.
Figure 3. Histogram of data set distribution.
Preprints 115361 g003
Preprints 115361 g005
Figure 5. RF model prediction scatterplot. Note: In the plot, the dashed line represents the reference line for perfect prediction (i.e., where the predicted values equal the actual values).
Figure 5. RF model prediction scatterplot. Note: In the plot, the dashed line represents the reference line for perfect prediction (i.e., where the predicted values equal the actual values).
Preprints 115361 g005
Table 1. Hyperparameters of Each Algorithm Model.
Table 1. Hyperparameters of Each Algorithm Model.
Method Parameter Setting Value
RFE Model Type Linear Regression (L1 Regularization)
Number of Selected Features 20
Number of Iterations 10
Step Size 2
Lasso Regression α (Regularization Strength) 0.01
Max Iterations 2000
Random State 21
BP Neural Network Hidden Layers 4 layers, 12 neurons each
Activation Function ReLU
Optimizer Adam
Learning Rate 0.0005
Batch Size 64
Training Epochs 300
RF Number of Trees 150
Max Depth 20
Min Samples Split 5
Random State 21
SVR Kernel Function RBF
Regularization Parameter C 0.5
ε 0.05
Max Iterations 2000
Table 3. Feature mapping table.
Table 3. Feature mapping table.
New Feature Name Original Feature Name
Feature1 60deg_ext_healthy_max_work
Feature2 60deg_ext_affected_max_work
Feature3 60deg_flex_healthy_rom
Feature4 60deg_flex_affected_cv
Feature5 60deg_flex_affected_total_work
Feature6 60deg_flex_affected_rom
Feature7 90deg_ext_healthy_max_work
Feature8 90deg_ext_affected_max_work
Feature9 90deg_ext_affected_total_work
Feature10 90deg_ext_affected_dec_time
Feature11 90deg_flex_healthy_max_work
Feature12 120deg_ext_healthy_total_work
Feature13 120deg_ext_healthy_rom
Feature14 120deg_ext_affected_max_work
Feature15 120deg_ext_affected_rom
Feature16 120deg_flex_healthy_max_work
Feature17 120deg_flex_healthy_total_work
Feature18 120deg_flex_healthy_acc_time
Feature19 120deg_flex_healthy_rom
Feature20 120deg_flex_affected_total_work
Table 4. Performance results of different models.
Table 4. Performance results of different models.
Model MSE R2 MAE
Lasso 22.29 ± 3.28 0.85 ± 0.18 3.71 ± 0.96
Random Forest 16.18 ± 1.92 0.89 ± 0.06 2.99 ± 0.69
SVR 31.58 ± 5.48 0.82 ± 0.13 7.68 ± 1.70
BP Neural Network 50.38 ± 9.12 0.79 ± 0.21 9.59 ± 1.99
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated