Prerpints.org logo
Preprint
Article

Reduction of Wind Speed Forecast Error in Costa Rica Tejona Wind Farm with Artificial Intelligence

Altmetrics

Downloads

72

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 August 2024

Posted:

16 August 2024

You are already at the latest version

Alerts
Abstract
The energy sector relies on numerical model output forecasts for operational purposes on a short-term scale, up to 10 days ahead. Reducing model errors is crucial, particularly given that coarse resolution models often fail to account for complex topography, such as that found in Costa Rica. Local circulations affect wind conditions at the level of wind turbines, thereby impacting wind energy production. This work addresses a specific need of the Costa Rican Institute of Electricity (ICE) as a public service provider for the energy sector. The developed and implemented product in this study serves as a proof of concept that could be replicated by WMO Members. It demonstrates a product for wind speed forecasting at wind power plants by employing a novel strategy for input selection based on large-scale indicators to enhance Artificial Intelligence-based forecasting methods. The product is developed and implemented based on the full-value chain framework for weather, water, and climate services for the energy sector introduced by the WMO. The results indicate a reduction of wind forecast RMSE by approximately 55% compared to the GFS grid values. The conclusion is that combining coarse model outputs with regional climatological knowledge through AI-based downscaling models is an effective approach for obtaining reliable local short-term wind forecasts up to 10 days ahead.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Tailored weather and climate services for energy play a pivotal role in supporting the global agenda on energy transition and energy efficiency. The world is committed to triple renewables’ capacities and doubling energy efficiency by the end of 2030, as declared during COP28 in December 2023. Tailored and reliable weather forecasts and climate predictions are crucial in achieving these ambitious goals. These services optimize the operation of renewable energy sources, mitigate risks, and enhance resilience in the face of climate variability and change [1].
Efficient operation of wind power plants requires, among other things, a detailed weather forecast of wind speed. Numerical models such as the Weather Research and Forecasting (WRF) model, the Global Forecast System (GFS), and the European Centre for Medium-Range Weather Forecasts (ECMWF) provide grid point data of wind speed and direction for hours and days ahead. However, in regions with complex terrain, it is necessary to consider the differences between observed wind data and numerical forecasts. One approach to adjust model outputs to observations is by using artificial intelligence (AI) methods.
The adjustment of numerical model output to observed weather variables is a procedure in use since the first operational forecasts were issued [2]. This began with Model Output Statistics (MOS) in the early 1970s [3] and has evolved over decades to include the recent use of Machine Learning methods for refining numerical outputs to better align with observations [4,5]
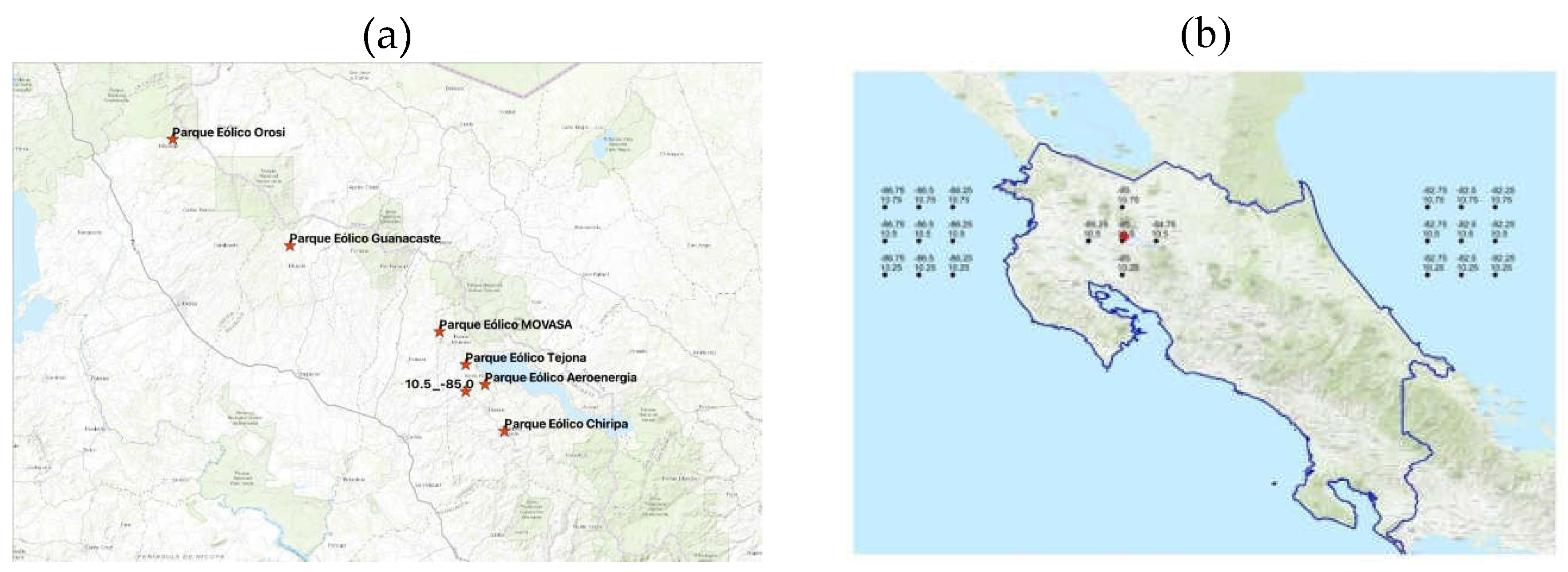
Regions with complex topography present significant challenges for numerical weather prediction and Central America exemplifies this complexity. Costa Rica, for instance, is located in one of the narrowest parts of Central America, with a width ranging from approximately 150 to 250 km. The wind farms in Costa Rica are situated to the west of the rugged mountain ranges that traverse the country from northwest to southeast, specifically the “Cordilleras de Guanacaste and Talamanca”, which are flanked by coastal plains. The location of the wind farms in Costa Rica can be seen in Figure 1a.
The Central American region, where Costa Rica is located, represents a dividing line between the typical climatic regimes of the Western Tropical Atlantic Ocean and the Eastern Tropical Pacific Ocean. Additionally, it is influenced by two large nearby continental masses, North and South America. The Pacific Ocean exhibits the El Niño/La Niña phenomenon as a major influence on the region’s climate. The Tropical Atlantic Ocean, east of Costa Rica, is characterized by the Caribbean Low-Level Jet (CLLJ), a low-level air current that interacts with the North Atlantic Subtropical High, and the monsoon regime of Mexico and Southern United States. This region is also influenced by the rainfall regimes in Northwestern South America.
The CLLJ is present throughout the year [6], peaking in intensity in June and July, with a secondary peak in December and January. Its horizontal and vertical structure shows a maximum over the Caribbean Sea, east of Costa Rica, with more intense values vertically between 975 and 925 hPa. These strong easterly winds reach the central mountain range of Costa Rica (see Figure 1a). This leads to rainfall on the eastern slopes of the mountains and a rain shadow effect to the west. On the western side of the mountain range, downslope winds associated with the topography interact with the mountain’s nocturnal circulation, producing strong winds that blow towards the west.
The occurrence of the El Niño/La Niña phenomenon, which manifests most strongly in the Tropical Pacific Ocean, influences the position of the Intertropical Convergence Zone (ITCZ) and the associated Trade Winds. The Trade Winds interact with the CLLJ, thereby, impacting wind patterns in Costa Rica. During El Niño conditions, easterly winds in Costa Rica tend to be stronger, whereas during La Niña episodes, they generally weaken [6].In the Atlantic Ocean, the North Atlantic Subtropical High (NHSH), particularly its southern branch, directly influences the intensity the CLLJ. According to [6], the CLLJ’s strength correlates with the phase of the North Atlantic Oscillation (NAO). A more intense (weaker) NHSH is associated with a strengthening (weakening) of the CLLJ and corresponds to the positive (negative) phase of the NAO. The Atlantic Multidecadal Oscillation (AMO) may be used as an indicator of the NAO since it is associated with the dominant pattern [8].
In addition to climatic factors, transient meteorological events such as the formation and passage of tropical cyclones, as well as the passage of cold fronts, influence the local wind regime in Costa Rica [7].
The objective of this study is to utilize available numerical model output for Costa Rica and wind power plant data to minimize errors in wind speed at turbine height. The region was chosen as a means of a proof of concept funded and leaded by the World Meteorological Organization (WMO). The developed demonstration and operational model can potentially be applied to other regions and countries facing similar challenges, supporting efforts to enhance energy efficiency and expand renewable energy harvesting. This initiative aligns with commitments made during COP28, which aimed to triple renewable energy capacities and double energy efficiency worldwide.
The novelty of this work may be summarized as follows: (a) the strategic approach to the development of the AI-based prediction model, and (b development and implementation of a tailored product following full value chain approach introduced by the WMO [1] with user interaction at its heart that addresses everything from user needs to the final operational product.
Section 2 provides detailed historical wind data and numerical weather prediction output used and outlines the strategy to develop the model’s features. Section 3 presents the results obtained, and Section 4 focuses on discussion and conclusions.

2. Materials and Methods

As part of this project, wind data from the turbines at the Tejona wind farm located at 10.54N, -85.00W in Tejona, Guanacaste, at an elevation of approximately 700 meters above sea level, were provided by the Instituto Costarricense de Electricidad- ICE. The wind farm has an installed capacity of 19.8 MW, featuring 30 VESTAS V42-660KW self-generating turbines, each with a power output of 660 kW. Wind speed measurements are taken every 10 minutes. These turbines operate within a wind speed range of 4 m.s-1 to of 25 m.s-1.
In a complex topographic scenario, numerical weather forecast models must have high resolution to adequately define local circulation, especially wind speed and direction. These models also require initial conditions that accurately describe meteorological variables such as pressure, temperature, relative humidity, wind speed and direction across the entire model domain. However, even with high resolution, models often exhibit forecast errors due to insufficient initial conditions or highly variable topography. These errors can be minimized when observational data is available.
We aim here to correct forecast errors using AI methods. The correction will certainly be more effective if the underlying model is of the highest quality. Among the operational weather forecast models available for the Costa Rica region, the global GFS and ECMWF were considered, as well as regional simulations with the WRF model run by ICE with 3 km resolution. Ultimately, GFS historical forecast data was used due to limitations with the other datasets, including sufficient archived historical data available at no cost. The GFS reforecasts were downloaded from
https://psl.noaa.gov/forecasts/reforecast2/ .
The wind speed data from the Tejona meteorological station includes measurements at 40 m, 60 m, and 81 m above the surface for the years 2013 to 2023. These three levels were used to consolidate a unique data series representing the location.
The first verification involved determining the number of null values (zero values). The data series does not contain a code for missing values; instead, a recorded value of zero indicates that the instrument was either not operational or not transmitting. Table 1 shows the number of zeros for each measurement height. It is important to note that the number of zeros was calculated based on data in 3-hour intervals, which align with GFS forecast times. Null values constitute approximately 5% of the total measurements.
To create a unified time series of consolidated wind speed for Tejona, the data from the 81 m height level was used. Zero values were replaced by non-zero values from either the 60 m or 40 m levels. Pairwise, correlations between the three height levels consistently exceeded 0.98, indicating strong similarity among the wind speed series. For this reason, a filtering criterion was applied to identify sets of wind speed measurements where the speed at one level differed by more than 1.2 times (20%) compared to the speeds at the other two levels. In such cases, the entire set of measurements was flagged as an outlier and excluded from further analysis, as there might be issues with the stations’ measurement sensors.
On the other hand, correlations were calculated between the wind predicted by the GFS model (e.g., w800_GFS at the 800 hPa level) and the observed wind in Tejona, using the consolidated wind speed at 81 m. The altitude of Tejona is around 700 m ASL while the peaks of the mountain range to the East reach between 1200 and 1900 m ASL This suggested that winds from different GFS levels should be considered. The correlation coefficients and the Root Mean Square Error (RMSE) are presented in Table 2. The RMSE values shown in Table 3 are higher for GFS levels closer to the surface, likely due to the complex topography of the location. Table 4 provides insights into errors for different time horizon periods for the 800 hPa atmospheric level.
The application of AI techniques requires the selection of a defined set of input variables. From a variety of data, machine learning models derive rules that may provide improved pattern recognition and eventually correct random errors [9].
One approach involves utilizing hundreds of output data from the numerical model [10]. We propose an alternative method to correct numerical model forecasts so that local wind data are more closely reproduced. Basically, we assume that wind errors are a function of the larger scale synoptic patterns that is changed by local features such as topography, large lakes, among others. Thus, we look for indicators of the large-scale weather systems as well as selected variables of the numerical model output in the proximity of the focus area.
To produce accurate wind prediction in Tejona region, using AI, the following variables are utilized as predictors: wind speed and direction data from 950 to 800 hPa sourced from the GFS at five specific grid points near Tejona, as shown in Figure 1b. Wind speed and direction data at 950 hPa over the Atlantic Ocean that may represent strong winds potentially impacting the mountainous terrain where wind turbines, like those in Tejona, are located. These winds are typically associated with the Caribbean Low-Level Jet (CLLJ) and modulated by the Atlantic Multidecadal Oscillation (AMO). Frontal activity is captured by the forecast winds near Tejona. To the west, winds over the Pacific Ocean serve as indicators of potential tropical cyclone proximity and are modulated by ENSO. Figure 1b illustrates the locations of the GFS grid points utilized.
The GFS model contains in its data assimilation and prediction all aspects of the region’s climate, such as the CLLJ, the condition of the North Atlantic Subtropical High, the Intertropical Convergence Zone, among others. The objective of emphasizing specific variables in the AI model assembly is to reduce systematic errors by leveraging grid points over the ocean where forecast errors tend to be smaller. In the AI model development, any data that do not contribute significantly to the variability in the historical record are automatically discarded.
In a more inclusive strategy, the following data from the GFS output have been utilized: near Tejona, the zonal and meridional components (u and v) of the wind, temperature and specific humidity at 2 meters, and sea-level pressure. Winds from GFS at different levels close to Tejona were tested as predictors. Additionally, the same variables were derived in quadrants over the sea to the west and east of Costa Rica, as shown in Figure 1b. The winds from GFS at 950, 900, 850 and 800 hPa were used individually for different AI models. The values in the east and west quadrants are the averages of the indicated grid points. Sea Surface Temperature (SST) data at the east and west locations are also included, along with the Niño 3.4 and AMO indicators. Other climatic indicators were not included.
The process of analyzing results on the AI models involved the evaluation and comparison of different machine learning techniques [11]:
  • Multiple Linear Regression (MLR), Ridge, Lasso, and ElasticNet [12];
  • K-Nearest Neighbors (KNN) [13];
  • Classification and Regression Trees (CART) [14];
  • Random Forest (RF) [15];
  • AutoML (Automated Machine Learning) [16].
All these mentioned techniques can be found in the SKlearn library, widely used for data analysis [11]. While these approaches were not specifically designed to model temporally dependent data, such as wind, they are commonly used to solve regression problems like those being addressed. The main goal of this test is to describe wind behavior through several models and compare the preliminary results with the meteorological model that ICE currently uses.
For model development the time series has been divided in three sets, one for development (70%), one for testing (15%) and the other for validation (15%). The data in the complete series is randomly shuffled into these three subsets to ensure better representation of different forecast scenarios, independent of when they originally occurred in the past.

3. Results

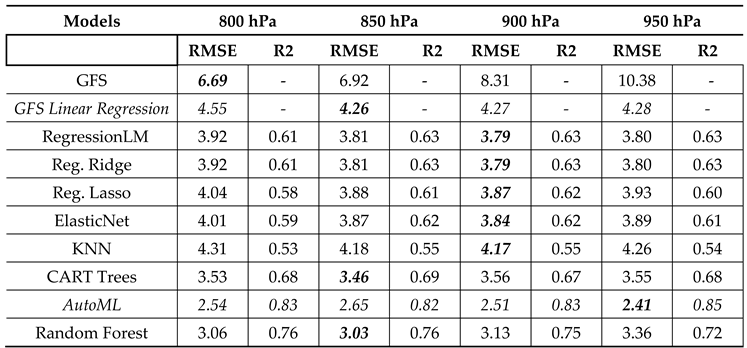
The application of the several AI techniques resulted in new forecasts for the testing set cases that have been compared to the original GFS forecast. Table 5 summarizes the results by technique for the level of the GFS used as input in Tejona. The first two rows correspond to the direct forecast made by the GFS for the region and a version of the GFS adjusted using univariate linear regression with the observed wind in Tejona.
An improvement in the forecast is evident, especially when comparing the best AI model built at the 950 hPa level (see AutoML in Table 5 RMSE = 2.41 m.s-1) with the GFS forecast adjusted using linear regression (RMSE = 4.26 m.s-1 for the 850 hPa level). The RMSE reduction for the AutoML is 43% between these two cases.
The adjusted model using AutoML with GFS 950 hPa winds has been selected and named “Wind Adjustment with AI (WAAI)”. For the Tejona plant the model is called WAAI_Tej. Table 6 shows the RMSE for different forecast times, the first 24 hours, the 24 to 96 hours and the final 6 days. Reduction of RMSE with respect to the original GFS is between 53 and 56%.
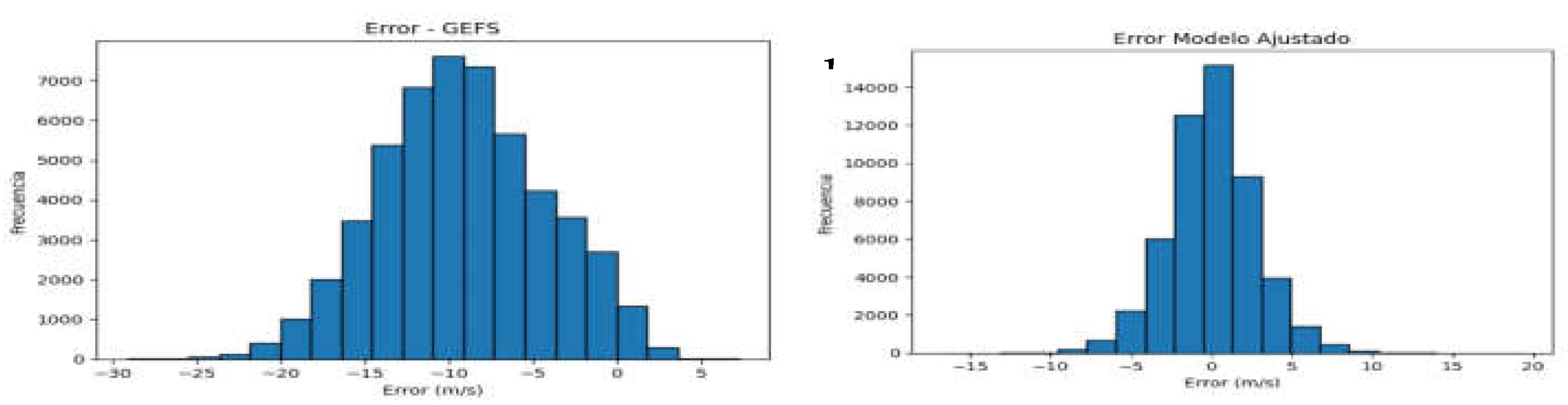
Figure 2 shows the error distribution of the GFS model (linear regression, 800 hPa) and the WAAI_Tej for the independent dataset. The figure highlights the GFS model’s tendency to underestimate wind speed in the region. However, when the model is adjusted, the error distribution more closely aligns with the actual data. This adjustment reduces the GFS model’s error, transforming it from predominantly underestimating wind speed to a more balanced distribution of positive and negative errors in the WAAI_Tej.
  • Final product in operation
The WAAI_Tej has been integrated into the ICE server and is automatically executed once a day. The implementation was carried out in Python 3.8 and coordinated using the Scheduler library (version 1.2.1). This is the Python library that manages the whole process to ensure periodic and automatic execution of the model. The data generated by WAAI_Tej is stored in a local PostgreSQL database, ensuring its availability and easy access for further analysis. Additionally, a visualization dashboard has been developed in a Business Intelligence (BI) tool, which directly consumes the data stored in the database, allowing users to easily access and interpret the forecasts generated by the model. This integration provides a comprehensive and efficient solution for wind forecasting and visualization for Tejona. 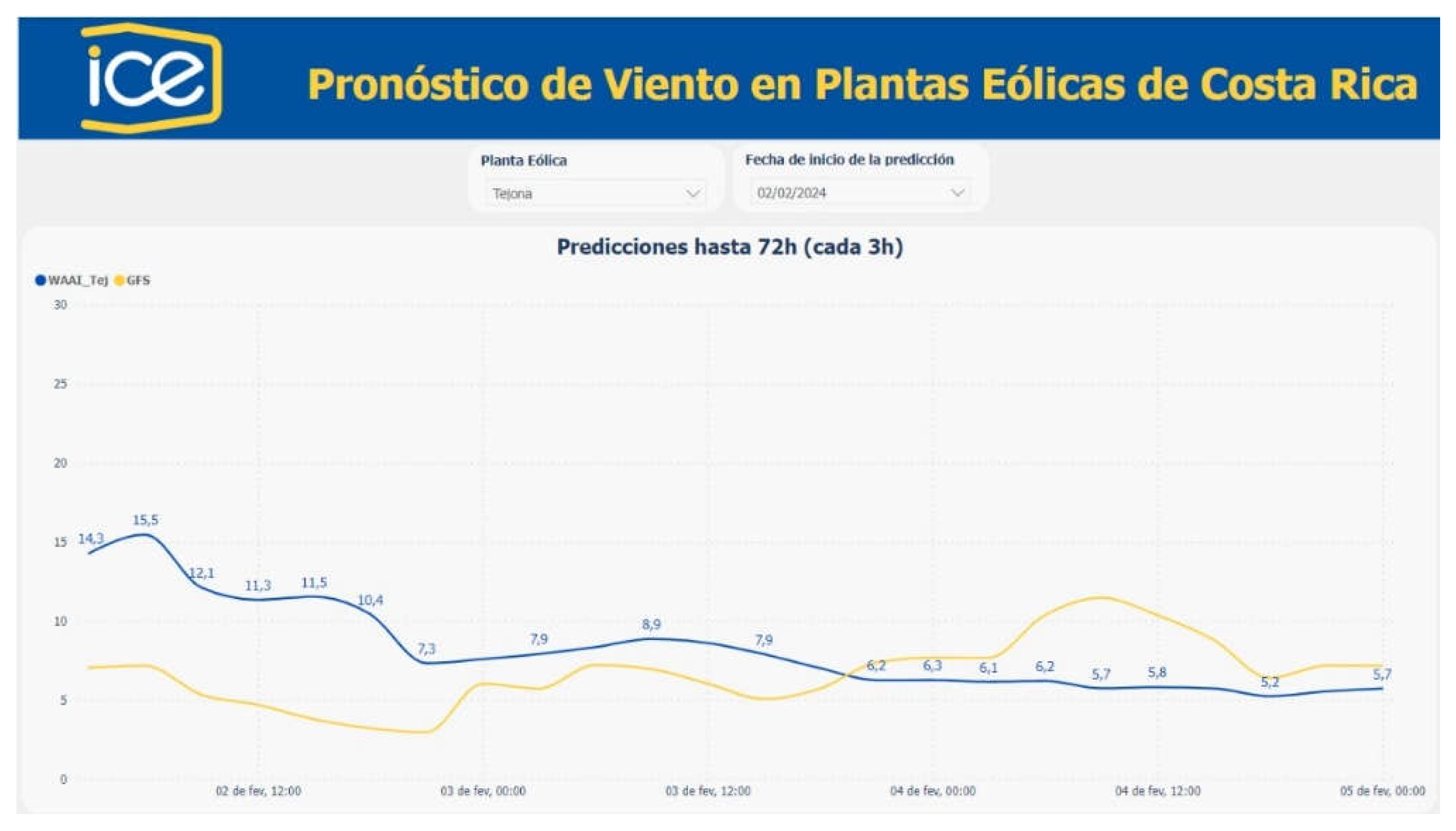Figure 3 shows an example of the output for a forecast generated on February 2, 2024. The GFS and WAAI_Tej forecasts are plotted together for comparison. It may be noted that the result is more than a simple bias correction having variable corrections for different times. This is a result of the AutoML capturing different large-scale atmospheric patterns in the GFS output and producing the optimized correction.

4. Discussion and conclusions

The use of AI for model error correction is seen as a promising venture in many publications (e.g., [17]). Specifically for the GFS forecast an example is seen where the procedure of model correction is included in the data assimilation phase and then applied to the 10-day forecasts [18] with improvements in the wind forecasts of the order of 13 to 20%. In this case, as in many others, the improvement is checked against a grid-point analysis.
The case presented here is different in the sense that the aim is to adjust the wind forecast to a local station data close to turbine height in a wind farm in Costa Rica. The model resolution is not enough to resolve the details of the local complex topography and thus this correction is a necessary step towards the operational use of wind forecast for the wind farm planning purposes.
The novelty of the present work lies in the strategic use of a few selected grid points of the GFS model, located near the wind farm and in key positions in the neighboring oceans to the east and to the west of Costa Rica. This approach aims to capture large-scale features of the regional climatology that may impact the wind speed errors at the Tejona wind farm. With this method the RMSE has been reduced to around 55% compared to that of the numerical model alone making the new forecast a useful tool for planning purposes by ICE.
The main conclusion of this study is that it is possible to reduce the GFS model error in wind speed forecasting in Tejona, Costa Rica, using machine learning methods. However, it is important to note that, in addition to model adjustment, understanding the regional dynamics and deriving variables that highlight these behaviors were also integral parts of the strategy used.
Among the techniques, AutoML and Random Forests stand out, achieving errors of 2.5 and 3 m/s. This improvement is likely due to their “divide and conquer” nature of attempting to create various models that represent different subspaces of data [10]..
The successful operational use of WAAI_Tej in the ICE offices in Costa Rica is a result of this Proof of Concept project that could be scaled up to other locations facing similar challenges in terms of topography and regional climatology.

Author Contributions

Conceptualization, MAFSD, HB,DVN; methodology MAFSD, YMS, BB,DVN.; ICEdata, DAF, DVN, CMA, MPC; software, YMS, ETCMA, DVN, CMA, MPC.; validation; JAZM,DVN, CMA, HB, RB.; formal analysis, MAFSD, YMS, BB .; investigation, MASD, YMS, DVN, CMA.; resources, RB,HB.;. writing—original draft preparation, MAFSD, YMS, ET.; reviewing and editing – all;. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the World Meteorological Organization with ref number 31186-2022/GS/CNS. The opinions, findings, interpretations, and conclusions expressed in this article are those of the authors and do not purport to reflect the opinions of the WMO or its Members.

Data Availability Statement

ICE provided the wind farm data and operational GFS output. The GFS data for development was downloaded from https://psl.noaa.gov/forecasts/reforecast2/. ENSO3.4 index is obtained from https://psl.noaa.gov/gcos_wgsp/ /Nino34/ and AMO index from https://www1.ncdc.noaa.gov/pub/data/cmb/ersst/v5/index/ersst.v5.amo.dat

Acknowledgments

The authors would like to thank the WMO SERCOM Study Group on Integrated Energy Services and the WMO Climate and Energy Team for their overall guidance, as well as the Costa Rican Electricity Institute and the National Meteorological Institute of Costa Rica for facilitating the project.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. WMO, 2023, Integrated Weather and Climate Services in Support of Net Zero Energy Transition (WMO-No.1312). https://library.wmo.int/idurl/4/66273.
  2. Haupt, S.E., W. Chapman, S. V. Adams, C. Kirkwood, J.S. Hoskins, N.H. Robinson, S. Lerch, A. C. Subramanian Towards implementing artificial intelligence post-processing in weather and climate: proposed actions from the Oxford 2019 workshop. Philosophical Transactions of the Royal Society A Mathematical, Physical and Engineering Sciences, 2021, 379 Issue 2194. [CrossRef]
  3. Glahn HR, Lowry DA. The use of model output statistics (MOS) in objective weather forecasting. J. Appl. Meteor. 1972, 11, 1203–1211. [CrossRef]
  4. Zhao X., Q. Sun, W. Tang, S. Yu, B. Wang A comprehensive wind speed forecast correction strategy with an artificial intelligence algorithm. Front. Environ. Sci. 2022, 10. [CrossRef]
  5. Bastani H. 2021, Doctorate thesis big data analysis application in the renewable energy market: wind power. http://hdl.handle.net/10347/27211.
  6. Wang, C. Variability of the Caribbean Low-Level Jet and its relations to climate. Clim Dyn 2007, 29, 411–422. [Google Scholar] [CrossRef]
  7. Vargas Navarro, L.D. , Pronostico Hicrometeorológico en la Cuenca del río Reventazón. Thesis de Maestria en Ciencias de la Atmosfera. Universidad de Costa Rica, 2016.
  8. Alexander, M. A., K. H. Kilbourne, J.A. Nye, Climate variability during warm and cold phases of the Atlantic Multidecadal Oscillation (AMO) 1871 – 2008, Journal of Marine Systems 2014, 133, 14–26. [CrossRef]
  9. Jones, N. How machine learning could help improve climate forecasts. Nature 2017, 548, 379. [Google Scholar] [CrossRef] [PubMed]
  10. Lam, Remi et al. Learning skillful medium-range global weather forecasting. Science, 2023,382, 6677, 1416-1421, 2023. https://www.science.org/doi/full/10.1126/science.adi2336. [CrossRef]
  11. Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., ... & Duchesnay, É. Scikit-learn: Machine learning in Python. The Journal of Machine Learning Research 2011, 12, 2825–2830. https://www.jmlr.org/papers/volume12/pedregosa11a/pedregosa11a.pdf?ref=https:/.
  12. Al Dabal, M. A. A. A comparative study of ridge, LASSO and elastic net estimators (Doctoral dissertation, Carleton University). 2021.
  13. Kramer, O.. K-Nearest Neighbors. In: Dimensionality Reduction with Unsupervised Nearest Neighbors. 2013 Intelligent Systems Reference Library, vol 51. Springer, Berlin, Heidelberg. [CrossRef]
  14. Loh, W.-Y. , Classification and regression trees. WIREs Data Mining Knowl Discov, 2011 1: 14-23. [CrossRef]
  15. Schonlau, M., & Zou, R. Y. The random forest algorithm for statistical learning. The Stata Journal 2020, 20, 3–29. [CrossRef]
  16. Karmaker, S.K.; et al. AutoML to Date and Beyond: Challenges and Opportunities. ACM Computing Surveys 2021, 54. [Google Scholar] [CrossRef]
  17. Bonavita, M.; Laloyaux, P. Machine Learning for Model Error Inference and Correction. Journal of Advances in Modeling Earth Systems 2020, 12. [Google Scholar] [CrossRef]
  18. Chen, T-C, et al. Correcting Systematic and State-Dependent Errors in the NOAA FV3-GFS Using Neural Networks. Journal of Advances in Modeling Earth Systems 2022, 14. [CrossRef]
Preprints 115349 g001
Figure 1. (a) Location of wind farms in Costa Rica over a topographical map; (b) location of grid points of GFS used.
Figure 1. (a) Location of wind farms in Costa Rica over a topographical map; (b) location of grid points of GFS used.
Preprints 115349 g001
Preprints 115349 g002
Figure 2. Error distribution in wind speed prediction of the GFS model (a) and the WAAI_Tej (b).
Figure 2. Error distribution in wind speed prediction of the GFS model (a) and the WAAI_Tej (b).
Preprints 115349 g002
Preprints 115349 g003
Figure 3. (a) Display of results and example of model run for 72 hours after Feb 2, 2024. In yellow for the GFS forecast and in blue for WAAI_Tejona.
Figure 3. (a) Display of results and example of model run for 72 hours after Feb 2, 2024. In yellow for the GFS forecast and in blue for WAAI_Tejona.
Preprints 115349 g003
Table 1. Number of zero values for each measurement height at Tejona station Measurement height (m).
Table 1. Number of zero values for each measurement height at Tejona station Measurement height (m).
Measurement height (m) Number of zeros Total number of 3-hourly data
40 1,436 331,537
60 801 331,537
81 1,004 331,537
Table 2. Correlations between wind speed observed in Tejona and the GFS model wind speed at levels 800, 850, 900 and 950 hPa.
Table 2. Correlations between wind speed observed in Tejona and the GFS model wind speed at levels 800, 850, 900 and 950 hPa.
W800_GFS W850_GFS W900_GFS W950_GFS Observed
W800_GFS 1.00 0.94 0.87 0.80 0.62
W850_GFS 0.94 1.00 0.96 0.90 0.67
W900_GFS 0.87 0.96 1.00 0.96 0.68
W950_GFS 0.80 0.90 0.96 1.00 0.68
Table 3. Root mean squared error of the GFS model wind speed compared to observational data at 81 m at Tejona station.
Table 3. Root mean squared error of the GFS model wind speed compared to observational data at 81 m at Tejona station.
Level (hPa) RMSE (m.s-1)
800 6.69
850 6.92
900 8.31
950 10.28
Table 4. RMSE of the GFS 800 hPa with respect to observed winds for 1-day, 4-day, and 6-day ahead forecast.
Table 4. RMSE of the GFS 800 hPa with respect to observed winds for 1-day, 4-day, and 6-day ahead forecast.
GFS RMSE (m.s-1)
24h (1-day) - 8 measurements) 6.20
96h (4-day) - 32 measurements) 6.93
( 6 days)- 48 measurements 7.25
Table 5. Testing errors of the adjusted model using data excluded from the training and validation process units of RMSE in m.s-1. The smaller value in each row is indicated.
Table 5. Testing errors of the adjusted model using data excluded from the training and validation process units of RMSE in m.s-1. The smaller value in each row is indicated.
Preprints 115349 i001
Table 6. Testing errors of the WAAI_Tej using data not used in training and validation.
Table 6. Testing errors of the WAAI_Tej using data not used in training and validation.
Model Time interval RMSE % reduction of RMSE
GFS 1 – (First 24h – 8 forecast times) 6.20
2 – (24-96h – 32 forecast times) 6.93
3 – (Last 6 days – 48 forecast times) 7.25
WAAI_Tej 1 – (First 24h – 8 forecast times) 2.94 52
2 – (24-96h – 32 forecast times) 3.00 56
3 – (Last 6 days – 48 forecast times) 3.26 55
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated