Results on Cumulative Entropic Properties of Consecutive Systems

Preprint

Article

Results on Cumulative Entropic Properties of Consecutive Systems

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

18 August 2024

Posted:

20 August 2024

You are already at the latest version

Alerts

Abstract

This paper reveals some properties of the cumulative entropy of consecutive k-out-of-n:F system's lifetime. First, we introduce a method for calculating the cumulative entropy of their lifetime and explore its preservation properties using established stochastic orders. Ad- ditionally, we obtain useful bounds that can used in situations where the distribution function of the system's component lifetimes are complicated or systems have large components. To support practical applications, we present two nonparametric estimators for the cumulative entropy of these systems. The efficiency and performance of these estimators are illustrated with simulated datasets and further validated with real data sets.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Over the past three decades, extensive research has focused on k-out-of-n systems with consecutive structure and their different variations. A consecutive k-out-of-n system can be classified by the arrangement of its components as either linear or circular, and by its functioning principle as either a failure or a good system. A linear consecutive k-out-of-n:F system consisting of n components (with independent and identically distributed (i.i.d.) lifetimes) set out linearly fails if, and only if, at least k consecutive components fail. This classic example illustrates a linear consecutive k-out-of-n:F system. Consider an oil pipeline with n equally spaced pump stations, each 100 km apart, capable of transporting oil up to 400 km. Consequently, the failure of four consecutive pump stations results in system failure, characterizing it as a linear consecutive 4-out-of-n:F system. The consecutive n-out-of-n:F system, requiring all n components to fail, corresponds to a classical system with parallel structure. In contrast, the 1-out-of-n:F system, which requires at least one component to fail, represents a series system. Comprehensive reviews of previous research on this area are available in Jung and Kim [1], Shen and Zuo [2], Kuo and Zuo [3], Chang et al. [4], Boland and Samaniego [5], and EryÄ±lmaz [6,7], among others.

The scenario where

2 k \geq n

in linear consecutive k-out-of-n:F systems is particularly significant for researchers in applied probability and reliaiblity due to its mathematical simplicity. In these systems, the lifetime of each component is denoted by

X_{i}, 1 \leq i \leq n .

Each component is assumed to follow a probability density function (pdf)

f (x)

and a cumulative distribution function (cdf)

F (x)

. The overall system’s lifetime is represented by the random variable (rv)

T_{k | n : F}

. A key finding in this area, established by Eryilmaz [8], shows that when

2 k \geq n

, the cdf of the consecutive k-out-of-n:F system can be expressed as:

F_{k | n : F} (x) = (n - k + 1) F^{k} (x) - (n - k) F^{k + 1} (x), x > 0 .

(1)

The Shannon differential entropy is given by

H (X) = - E [log f (X)]

for a nonnegative continuous rv X with pdf

f (x)

, is widely utilized for its versatility. This concept originated from Shannon’s pioneering work [9]. Rao et al. [10] initiated another intuitive measure of information using

S (x) = 1 - F (x)

instead of

f (x)

, as follows:

E (X) = - \int_{0}^{\infty} \bar{F} (x) log \bar{F} (x) d x .

(2)

For a detailed study of preliminary aspects of (2), the associated dynamic form and its various generalizations we refer the reader to Asadi and Zohrevand [11], Navarro et al. [12], and Toomaj et al. [13]. In the spirit of (2), Di Crescenzo and Longobardi [14] initiated cumulative entropy (CE) by replacing

S (x)

with the cumulative distribution function (cdf)

F (x)

, as

\begin{matrix} CE (X) & = & - \int_{0}^{\infty} F (x) log F (x) d x, \end{matrix}

(3)

\begin{matrix} = & \int_{0}^{1} \frac{ξ (u)}{f (F^{- 1} (u))} d u, \end{matrix}

(4)

where

F^{- 1} (u) = inf {x; F (x) \geq u}

and

ξ (u) = - u log (u), 0 \leq u \leq 1 .

A key advantage of the CE measure is its connection to the mean inactivity time (MIT) function, given by

\tilde{m} (x) = E (x - X | X \leq x)

. Di Crescenzo and Longobardi showed that the CE is the expected value of the MIT function, expressed as

E (\tilde{m} (X)) = CE (X)

. This relationship underscores the CE’s utility in reliability theory, given that the MIT function is commonly used to characterize the aging properties of systems or components.

Researchers have explored the information properties of the order statistics. This interest extends to reliability engineering, where many studies have examined information properties. For example, Toomaj et al. [13] utilized system signatures to analyze the criteria entropy of mixed systems. Alomani and Kayid [15] applied system signature to study the fractional cumulative residual entropy of coherent systems. In another study, Shrahili and Kayid [16] investigated the cumulative entropy of the lifetime of an n-component coherent system under the condition that all components fail at time

t .

They presented various properties, including formulations, bounds, and orderings for this measure, along with a method to have a sense of a better system based on the cumulative KullbackâLeibler information quantity which is a discriminating tool. Additionally, Kayid and Shrahili [17] examined Rényi entropy for coherent systems with n components provided that all components fail at time

t .

They presented a number of results which reveal calculative formulas for this entropic measure, obtain some bounds for it, and establish stochastic ordering results. Motivated by the established body of research on information measures in reliability, this paper delves into uncertainty properties of CE specifically within the framework of consecutive k-out-of-n:F systems. By building upon this foundation, we aim to contribute to a deeper understanding of CE properties within this particular system configuration.

This paper is structured as is outlined below:

In Section 2, we derive a representation of the CE for consecutive k-out-of-n:F systems with lifetime

T_{k | n : F}

based on samples from any continuous distribution function F. This representation is related to the CE from samples drawn from a uniform distribution. We also analyze the preservation of stochastic ordering properties for this system. The section further includes useful bounds for the CE of consecutive k-out-of-n:F systems. Section 3 presents several characterization results, while Section 4 offers computational results that validate our derived outcomes. To this aim, we introduce two nonparametric estimators for the CE of consecutive systems, demonstrating their utility with real and simulated data. In Section 5, we conclude our study by summarizing the key findings and the main contributions.

2. CE of Consecutive k-out-of-n:F System

This section is divided into two main parts. First, we derive a mathematical expression for the CE of a consecutive k-out-of-n:F system and analyze the preservation properties of its stochastic ordering. In the second part, we establish a set of useful bounds for studying consecutive k-out-of-n:F systems.

2.1. Expression and Stochastic Orders

Hereafter, we derive an explicit expression for the CE of a consecutive k-out-of-n:F system with lifetime

T_{k | n : F}

, where component lifetimes follow a common continuous distribution function F. We employ the probability integral transformation

U_{k | n : F} = F (T_{k | n : F})

to obtain the useful formula. The transformations of the system’s components,

U_{i} = F (X_{i})

for

i = 1, \dots, n

, are i.i.d. random rvs uniformly distributed on

[0, 1]

. Using (1), when

2 k \geq n

, the cdf of

U_{k | n : F}

is given by

G_{k | n : F} (u) = (n - k + 1) u^{k} - (n - k) u^{k + 1},

(5)

for all

0 < u < 1 .

We are now prepared to present the following theorem based on the previous analysis.

Theorem 1.

For

2 k \geq n,

the CE of

T_{k | n : F},

can be expressed as follows:

CE (T_{k | n : F}) = \int_{0}^{1} \frac{ξ (G_{k | n : F} (u))}{f (F^{- 1} (u))} d u,

(6)

where

ξ (x) = - x log x, 0 < x < 1,

and

G_{k | n : F} (u)

is define in (5).

Proof.

By employing the change of

u = F (x)

and referring to (1) and (3), we can derive the following results:

\begin{matrix} CE (T_{k | n : F}) & = & - \int_{0}^{\infty} F_{k | n : F} (x) log F_{k | n : F} (x) d x \\ = & \int_{0}^{\infty} ξ (F_{k | n : F} (x)) d x \end{matrix}

(7)

\begin{matrix} = & \int_{0}^{\infty} ξ ((n - k + 1) F^{k} (x) - (n - k) F^{k + 1} (x)) d x \\ = & \int_{0}^{1} \frac{ξ ((n - k + 1) u^{k} - (n - k) u^{k + 1})}{f (F^{- 1} (u))} d u \end{matrix}

(8)

\begin{matrix} = & \int_{0}^{1} \frac{ξ (G_{k | n : F} (u))}{f (F^{- 1} (u))} d u, \end{matrix}

and this completes the proof. □

Following the representation in equation (6), we now present an illustrative example.

Example 1.

Consider a linear consecutive k-out-of-6:F for

k = 3, 4, 5, 6,

system with a lifetime

T_{k | 6 : F} = min (X^{1 : k}, X^{2 : k + 1}, \dots, X^{7 - k : 6})

where

X^{[j : m]} = max (X_{j}, \dots, X_{m})

for

1 \leq j < m \leq 6 .

Assume further that the lifetimes of the components are i.i.d. following the common Fréchet distribution, also known as inverse Weibull distribution, with the cdf as

F (x) = e^{- x^{- α}}, x > 0,

(9)

where

α > 0

is a shape parameter. It is worth noting that Fréchet distribution is a special case of the generalized extreme value distribution. The pdf of this distribution is

f (x) = α x^{- (α + 1)} e^{- x^{- α}}, x > 0 .

It is not hard to see that

f (F^{- 1} (u)) = α u {(- log (u))}^{\frac{α + 1}{α}}

for all

0 < u < 1

. So, we can derive the following expression

\begin{matrix} CE (T_{k | 6 : F}) = α \int_{0}^{1} ξ (G_{k | n : F} (u)) u {(- log (u))}^{\frac{α + 1}{α}} d u . \end{matrix}

(10)

Due to the difficulty of obtaining an explicit analytical expression, we use a computational approach to explore the relationship between

CE (T_{k | 6 : F})

and the parameter

α

for values of

k = 3, 4, 5, 6 .

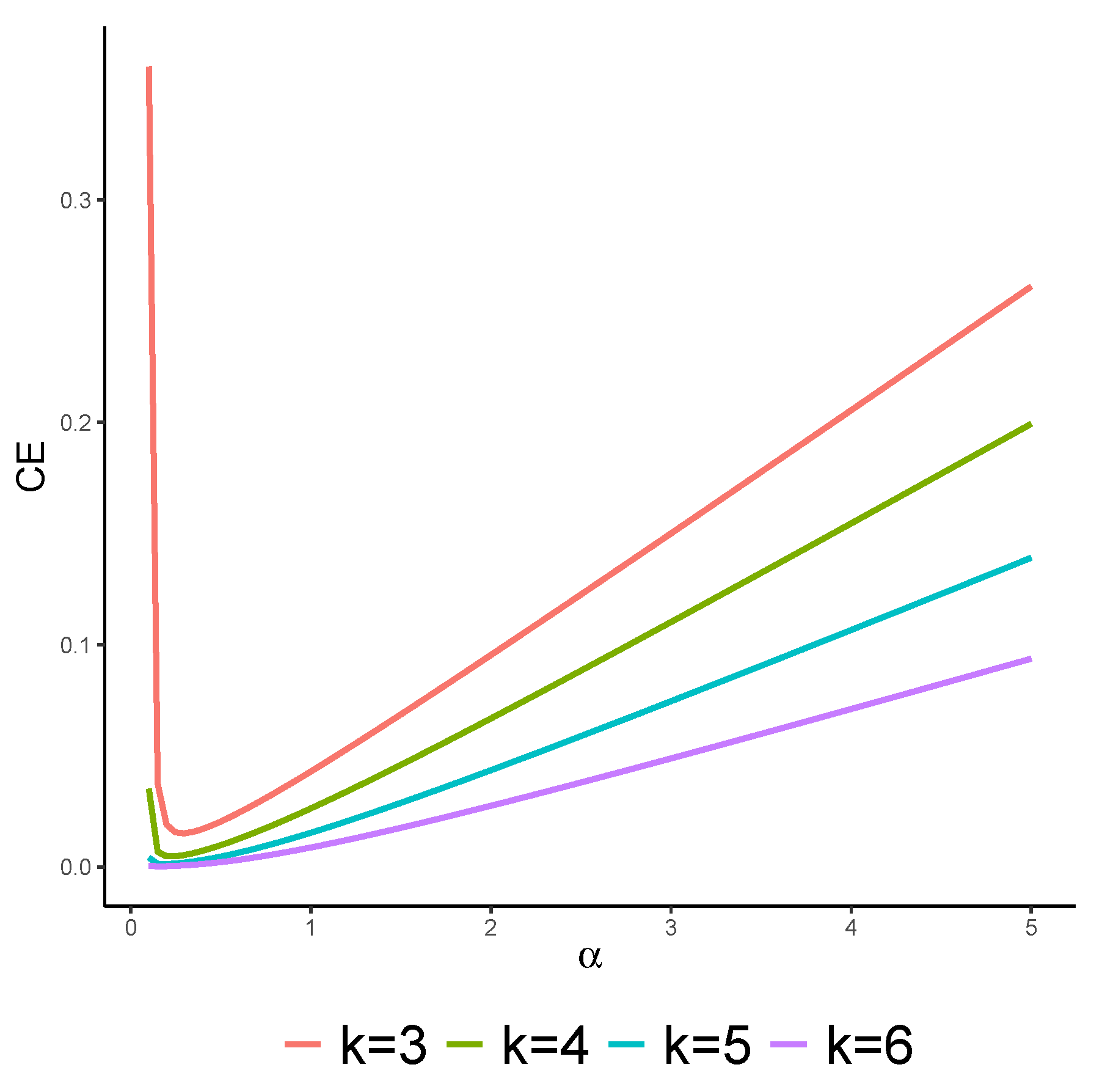
This method sheds light on how the Fréchet distribution parameter affects the CE of the consecutive k-out-of-6:F system. Figure 1 summarizes the numerical analysis, displaying the relationship between

CE (T_{k | 6 : F})

and

α

for

k = 3, 4, 5, 6 .

As the shape parameter

α

increases, the system’s uncertainty regarding the CE initially decreases and then increases. These results reveal the significant influence of the Fréchet distribution parameter

α

on the CE and the uncertainty of the consecutive k-out-of-6:F system.

Next, we prove that the CE of the consecutive k-out-of-n:F system preserves the dispersive order and also location-independent riskier order. First, we give the definitions of these stochastic orders before going into their details. Hereafter,

R_{+} = {X; X \geq 0}

stands as the set of all nonnegative rvs having support

(0, \infty)

which have an absolutely continuous distribution.

Definition 1.

Let

X \in R_{+}

and

Y \in R_{+}

with pdfs

f_{X}

and

f_{Y},

cdfs

F_{X}

and

F_{Y},

survival functions

S_{X}

and

S_{Y}

and hazard rate (hr) functions

λ_{X} (x) = \frac{f_{X} (x)}{S_{X} (x)}

and

λ_{Y} (x) = \frac{f_{Y} (x)}{S_{Y} (x)},

respectively. Then,

X belongs to increasing [resp. decreasing] failure rate (abbreviated by IFR [resp. DFR]) if $λ_{X}$ is an increasing (a decreasing) function;
X is said to be less than or equal with Y in the hazard rate order (written as $X \leq_{h r} Y$ ) whenever $λ_{X} (t) \geq λ_{Y} (t)$ for all $t > 0;$
X is said to be less than or equal with Y in the dispersive order (written as $X \leq_{d} Y$ ) whenever $F_{X}^{- 1} (v) - F_{X}^{- 1} (u) \leq F_{Y}^{- 1} (v) - F_{Y}^{- 1} (u), 0 < u \leq v < 1;$
X is said to be less than or equal with Y in the location-independent riskier order (written as $X \leq_{l i r} Y$ ) whenever $\int_{0}^{F_{X}^{- 1} (p)} F_{X} (x) d x \leq \int_{0}^{F_{Y}^{- 1} (p)} F_{Y} (x) d x, p \in (0, 1);$
X is said to be less than or equal with Y in the CE order (written as $X \leq_{C E} Y$ ) whenever $CE (X) \leq CE (Y) .$

It is worth noting that the order

\leq_{d}

was firstly utilized by Bickel and Lehmann [18] for some nonparametric inferential purposes, while the order

\leq_{l i r}

was initiated by Jewitt [19] to be used in the theory of expected utility and its applications in insurance. From Shaked and Shanthikumar [20],

X \leq_{d} Y

if, and only if,

f_{Y} (F_{Y}^{- 1} (v)) \leq f_{X} (F_{X}^{- 1} (v)), f o r a l l 0 < v < 1 .

(11)

The following implications are known:

\begin{matrix} if X \leq_{h r} Y and either X or Y is DFR & ⟹ & X \leq_{d} Y ⟹ X \leq_{l i r} Y . \end{matrix}

(12)

From relations () and (12) and since

ξ (u) \geq 0

for all

0 \leq u \leq 1,

thus

X \leq_{d} Y

yields

CE (X) \leq CE (Y)

By using (13), the following conclusion is deduced.

Corollary 1.

X \leq_{h r} Y

and X or Y is DFR, then

CE (X) \leq CE (Y) .

We now examine the integrated distribution function of a rv Z with the cdf H, defined as

η_{Z} (x) = \int_{0}^{x} H (z) d z, x > 0 .

Landsberger and Meilijson [21] showed that

X \leq_{l i r} Y ⟺ η_{Y}^{- 1} (x) - η_{X}^{- 1} (x) is increasing in x > 0 .

(13)

In what follows we consider

T_{k | n : F}^{X}

and

T_{k | n : F}^{Y}

as the lifetimes of two consecutive k-out-of-n:F systems with i.i.d. absolutely continuous component lifetimes having the common pdfs

f_{X}

and

f_{Y}

and cdfs

F_{X}

and

F_{Y},

respectively. We present a theorem demonstrating that the CE of a series system with k components is less than that of a consecutive k-out-of-n:F system, assuming both have components with the DFR property.

Theorem 2.

Let

Z_{1 : m}

be the lifetime of a series system consisting of i.i.d. components with common hr function

h .

Let

l i m_{t \to \infty} r (t) = λ

and

1 \leq k \leq n

, where r is the common hr of X and let

T_{k | n : F}

belong to IFR class such that

h (t) \geq λ \frac{[\frac{n}{k}]}{m}

for all

t \geq 0 .

If Z belongs to DFR class, then

CE (Z_{1 : m}) \leq CE (T_{k | n : F}) .

Proof.

Since Z is DFR, then

Z_{1 : m}

is also DFR. Moreover, under the conditions

T_{k | n : F}

is IFR such that

h (t) \geq λ [n / k] / m

for all

t \geq 0,

we have

Z_{1 : m} \leq_{h r} T_{k | n : F}

due to Theorem 3.2 of EryÄ±lmaz and Navarro [22]. Thus, Corollary 1 concludes the proof. □

The next example illustrates the application of Theorem 2.

Example 2.

Consider a Gamma distribution with the cdf given by

F (t) = 1 - λ t e^{- λ t} - e^{- λ t}

. We find that

r (t) = \frac{2 λ t}{1 + λ t} \to λ

t \to \infty

. Letting

n = 4

and

k = 2

, since X is IFR and a linear consecutive 2-out-of-4:F system preserves the IFR property (see Theorem 4.3.13 of Chang et al. [23]), we conclude that

Z_{1 : 4} \leq_{h r} T_{2 | 4 : F}

for

h (t) \geq \frac{λ}{2}

for all

t \geq 0 .

So, Theorem 2 implies that

CE (Z_{1 : m}) \leq CE (T_{k | n : F})

provided that

h (t)

is a decreasing function in

t .

The next theorem establishes the conditions under which the dispersive order is preserved under the formation of consecutive systems.

Theorem 3.

X \leq_{d} Y,

then

CE (T_{k | n : F}^{X}) \leq CE (T_{k | n : F}^{Y}) .

Proof.

The result can be easily derived from Eqs. (6) and (12). □

As an application of Theorem 3, consider the following example.

Example 3.

Let us consider two consecutive 4-out-of-5:F systems with lifetimes

T_{4 | 5 : F}^{X}

and

T_{4 | 5 : F}^{Y}

. System

T_{4 | 5 : F}^{X}

has i.i.d. component lifetimes

X_{1}, X_{2}, X_{3}, X_{4}, X_{5}

, which follow the Makeham distribution with cdf

F (x) = 1 - e^{- 2 x + e^{- x} - 1}

for

x > 0

. Moreover, system

T_{4 | 5 : F}^{Y}

consists of i.i.d. component lifetimes

Y_{1}, Y_{2}, Y_{3}, Y_{4}

that follow an exponential distribution with cdf

F_{Y} (x) = 1 - e^{- x}

for

x > 0

. The hr functions are

λ_{X} (x) = 2 - e^{- x}

and

λ_{Y} (x) = 1

, showing that

λ_{X} (x) > λ_{Y} (x)

for

x > 0

i.e.

X \leq_{h r} Y .

Since Y possesses the DFR property, relation (13) indicates

X \leq_{d} Y

. Consequently, by Theorem 3, we have

CE (T_{4 | 5 : F}^{X}) \leq CE (T_{4 | 5 : F}^{Y})

, meaning the uncertainty associated with

T_{4 | 5 : F}^{X}

is less than or equal to that of

T_{4 | 5 : F}^{Y}

in terms of the CE measure.

The next theorem outlines the conditions for preserving location-independent riskier order in consecutive systems.

Theorem 4.

X \leq_{l i r} Y,

and

\frac{ξ (G_{k | n : F} (t))}{t}, 0 \leq t \leq 1,

(14)

is a decreasing function of

t,

then

CE (T_{k | n : F}^{X}) \leq CE (T_{k | n : F}^{Y}) .

Proof.

First note that Eq. (1) can be rewritten as

F_{k | n : F} (x) = G_{k | n : F} (F (x)) .

Assumption

X \leq_{l i r} Y

and Eq. (14) imply

\frac{d}{d x} (η_{Y}^{- 1} (x) - η_{X}^{- 1} (x)) = \frac{1}{F_{Y} (η_{Y}^{- 1} (x))} - \frac{1}{F_{X} (η_{X}^{- 1} (x))} \geq 0,

which means

F_{X} (x) \geq F_{Y} (η_{Y}^{- 1} (η_{X} (x))),

(15)

for all

x > 0 .

Now, we get

\begin{matrix} - \int_{0}^{\infty} F_{k | n : F}^{X} (x) log F_{k | n : F}^{X} (x) d x & = & - \int_{0}^{\infty} \frac{F_{k | n : F}^{X} (x) log F_{k | n : F}^{X} (x)}{F_{X} (x)} F_{X} (x) d x \\ = & \int_{0}^{\infty} \frac{ξ (F_{k | n : F}^{X} (x))}{F_{X} (x)} F_{X} (x) d x \\ = & \int_{0}^{\infty} \frac{ξ (G_{k | n : F} (F_{X} (x)))}{F_{X} (x)} F_{X} (x) d x \\ \leq & \int_{0}^{\infty} \frac{ξ (G_{k | n : F} (F_{Y} (η_{Y}^{- 1} (η_{X} (x)))))}{F_{Y} (η_{Y}^{- 1} (η_{X} (x)))} F_{X} (x) d x, \end{matrix}

(16)

where the inequality arises from the fact that

ξ (G_{k | n : F} (t)) / t

decreases for

0 \leq t \leq 1

and using (16). Setting

u = η_{Y}^{- 1} (η_{X} (x))

, we have

d x = \frac{F_{Y} (u)}{F_{X} (η_{X}^{- 1} (η_{Y} (u)))} d u .

Upon using this, (17) reduces to

\begin{matrix} \int_{η_{Y}^{- 1} (η_{X} (0))}^{\infty} \frac{ξ (G_{k | n : F} (F_{Y} (u)))}{F_{Y} (u)} \frac{F_{X} (η_{X}^{- 1} (η_{Y} (u))) F_{Y} (u)}{F_{X} (η_{X}^{- 1} (η_{Y} (u)))} d u \\ = & \int_{η_{Y}^{- 1} (η_{X} (0))}^{\infty} ξ (G_{k | n : F} (F_{Y} (u))) d u \\ = & - \int_{0}^{\infty} F_{k | n : F}^{Y} (u) log F_{k | n : F}^{Y} (u) d u . \end{matrix}

The final equality in the above relation is derived by observing that

η_{Y}^{- 1} (η_{X} (0)) = 0,

which implies

CE (T_{k | n : F}^{X}) \leq CE (T_{k | n : F}^{Y}) .

Thus, the proof is finished. □

2.2. Bounds

Given the absence of closed-form expressions for the CE of consecutive systems for various distributions with complicated distribution functions or having numerous components, it is essential to give some bounds in such situations. Recognizing this challenge, we aim to explore the effectiveness of these bounds in characterizing the CE of consecutive systems. For the first result, we find that the system’s CE is bounded by the common CE of its components.

Theorem 5.

For

2 k \geq n,

the CE of

T_{k | n : F}

are bounded as follows:

\begin{matrix} B_{1} CE (X_{1}) \leq CE (T_{k | n : F}) \leq B_{2} CE (X_{1}) \end{matrix}

where

B_{1} = {inf}_{u \in (0, 1)} \frac{ξ (G_{k | n : F} (u))}{ξ (v)}

B_{2} = {sup}_{u \in (0, 1)} \frac{ξ (G_{k | n : F} (u))}{ξ (u)} .

Proof.

The upper bound can be determined from (6) as shown below

\begin{matrix} CE (T_{k | n : F}) & = \int_{0}^{1} \frac{ξ (G_{k | n : F} (u))}{f (F^{- 1} (u))} d u = \int_{0}^{1} \frac{ξ (G_{k | n : F} (u))}{ξ (u)} \frac{ξ (u)}{f (F^{- 1} (u))} d u \\ \leq sup_{u \in (0, 1)} \frac{ξ (G_{k | n : F} (u))}{ξ (u)} \int_{0}^{1} \frac{ξ (u)}{f (F^{- 1} (u))} d u = B_{2} CE (X_{1}) . \end{matrix}

The lower bound can be derived using a similar approach. □

The upcoming theorem offers additional straightforward and useful bounds based on the extremes of the pdf and the function

ξ (u) .

Theorem 6.

Let

T_{k | n : F}

be the lifetime of consecutive k-out-of-n:F system having the common pdf

f_{X} (x)

and cdf

F_{X} (x) .

If S is the support of f,

m = {inf}_{x \in S} f (x)

and

M = {sup}_{x \in S} f (x)

, then

\begin{matrix} \frac{CE (U_{k | n : F})}{M} \leq CE (T_{k | n : F}) \leq \frac{CE (U_{k | n : F})}{m}, \end{matrix}

(17)

where

CE (U_{k | n : F}) = \int_{0}^{1} ξ (G_{k | n : F} (u)) d u

and

ξ (u) = - u log (u)

Proof.

Since

m \leq f (F^{- 1} (u)) \leq M, 0 < u < 1

, from (6), we have

\begin{matrix} CE (T_{k | n : F}) & = \int_{0}^{1} \frac{ξ (G_{k | n : F} (u))}{f (F^{- 1} (u))} d u \geq \frac{1}{M} \int_{0}^{1} ξ (G_{k | n : F} (u)) d u . \end{matrix}

The upper bound can be obtained similarly. □

It should be noted that

CE (U_{k | n : F})

denotes the cumulative entropy of a consecutive k-out-of-n:F system having a common uniform distribution on

(0, 1)

. The bounds in Eq. (18) depend on the extremes of the probability density function f. If the lower bound m is zero, there is no upper bound; if the upper bound M is infinite, there is no lower bound. The following example illustrates the application of the bounds from Theorems 5 and 6 in the context of a consecutive k-out-of-n:F system.

Example 4.

Assume a linear consecutive 6-out-of-12:F system with lifetime

T_{6 | 12 : F} = max (X_{[1 : 6]}, X_{[2 : 7]}, \dots, X_{[6 : 12]}),

where

X_{[j : m]} = min (X_{j}, \dots, X_{m})

for

1 \leq j < m \leq 12 .

It is straightforward to calculate that

CE (U_{6 | 12 : F}) = 0.1386067

and

B_{1} = 0, B_{2} = 1.783154 .

The bounds in Theorems 5 and 6 can be calculated for common component lifetime distributions. To illustrate, we consider the following models as examples.

(a) Assuming a half-normal distribution with pdf

f_{X} (x) = \frac{\sqrt{2}}{σ \sqrt{π}} e^{- \frac{x^{2}}{2 σ^{2}}}, x > 0, σ > 0,

it is easy to see that

m = 0

and

M = \frac{\sqrt{2}}{σ \sqrt{π}} .

Applying the result from Theorem 6, we can obtain the lower bound

CE (T_{6 | 12 : F}) \geq \frac{0.1960195}{σ \sqrt{π}} .

Furthermore, using the bound provided in Theorem 5, we can derive

CE (T_{6 | 12 : F}) \leq 1.783154 CE (X_{1}) .

By combining these two bounds, we can conclude that

\frac{0.1960195}{σ \sqrt{π}} \leq CE (T_{6 | 12 : F}) \leq 1.783154 CE (X_{1}) .

(b) Suppose that X follows a Fréchet distribution with cdf given in (10). Then

m = 0

and

M = α {(\frac{α}{α + 1})}^{- \frac{α + 1}{α}} e^{- (1 + \frac{1}{α})} .

Furthermore, using the bound provided in Theorem 5, we can derive

CE (T_{6 | 12 : F}) \leq 1.783154 CE (X_{1}) .

By combining these two bounds, we can conclude that

0.1386067 α {(\frac{α}{α + 1})}^{- \frac{α + 1}{α}} e^{- (1 + \frac{1}{α})} \leq CE (T_{6 | 12 : F}) \leq 1.783154 CE (X_{1}) .

3. Characterization Results

This section aims to present some characterization results based on the cumulative entropy properties of consecutive k-out-of-n:F systems. We begin with a lemma that follows directly from the StoneâWeierstrass Theorem (see Aliprantis and Burkinshaw, [24]), which will be used in proving the main results of this section.

Lemma 1.

If ζ is a continuous function on

[0, 1]

such that

\int_{0}^{1} x^{n} ζ (x) d x = 0

for all

n \geq 0,

then

ζ (x) = 0

for any

x \in [0, 1] .

This lemma allows us to uniquely characterize the parent distribution of a lifetime rv using the CE of

T_{k | n : F}

Theorem 7.

Let

T_{k | n : F}^{X}

and

T_{k | n : F}^{Y}

be lifetimes of two consecutive k-out-of-n:G systems having the common pdfs

f_{X} (x)

and

f_{Y} (x)

and cdfs

F_{X} (x)

and

F_{Y} (x),

respectively. Then

F_{X}

and

F_{Y}

belong to the same family of distributions if and only if for a fixed

n,

CE (T_{k | n : F}^{X}) = CE (T_{k | n : F}^{Y}),

(18)

for all

2 k \geq n .

Proof.

The necessity is trivial, so we must demonstrate the sufficiency. First, observe that Eq. (6) can be rewritten as follows:

\begin{matrix} CE (T_{k | n : F}^{X}) & = & \int_{0}^{1} u^{2 k - n} \frac{ϕ (u)}{f_{X} (F_{X}^{- 1} (u))} d u, \end{matrix}

(19)

where

ϕ (u) = - u^{n - k} ((n - k + 1) - (n - k) u) log (G_{k | n : F} (u)), 0 < u < 1 .

The same argument applies to

CE (T_{k | n : F}^{Y}) .

From (19), we have

\int_{0}^{1} [\frac{1}{f_{X} (F_{X}^{- 1} (u))} - \frac{1}{f_{Y} (F_{Y}^{- 1} (u))}] u^{2 k - n} ϕ (u) d u = 0 .

According to Lemma 1, we can conclude that

f_{X} (F_{X}^{- 1} (u)) = f_{Y} (F_{Y}^{- 1} (u)), a . e . u \in (0, 1) .

It follows that

F_{X}^{- 1} (u) = F_{Y}^{- 1} (u) + d

, where d is a constant. Since

{lim}_{u \to 0} F_{X}^{- 1} (u) = {lim}_{u \to 0} F_{Y}^{- 1} (u) = 0

for all

u \in (0, 1)

, we conclude that

F_{X}^{- 1} (u) = F_{Y}^{- 1} (u)

. This indicates that

F_{X}

and

F_{Y}

have the same family of distributions. □

A consecutive n-out-of-n:F system is a series system, as previously mentioned, the following corollary outlines its characteristics.

Corollary 2.

Under the conditions of Theorem 7,

F_{X}

and

F_{Y}

belong to the same family of distributions if and only if

CE (T_{n | n : F}^{X}) = CE (T_{n | n : F}^{Y}),

for all

n \geq 1 .

The subsequent theorem provides a further characterization.

Theorem 8.

Under the conditions of Theorem 7,

F_{X}

and

F_{Y}

belong to the same family of distributions, but for a change in scale, if and only if for a fixed

n,

\frac{CE (T_{k | n : F}^{X})}{CE (X)} = \frac{CE (T_{k | n : F}^{Y})}{CE (Y)},

(20)

for all

2 k \geq n .

Proof.

The necessity is trivial and hence it remains to prove the sufficiency. From (20), we can write

\frac{CE (T_{k | n : F}^{X})}{CE (X)} = \int_{0}^{1} u^{2 k - n} \frac{ϕ (u)}{CE (X) f_{X} (F_{X}^{- 1} (u))} d u .

(21)

The same argument applies to

CE (T_{k | n : F}^{Y}) / CE (Y) .

From (21) and (22), we have

\int_{0}^{1} u^{2 k - n} \frac{ϕ (u)}{CE (X) f_{X} (F_{X}^{- 1} (u))} d u = \int_{0}^{1} u^{2 k - n} \frac{ϕ (u)}{CE (Y) f_{Y} (F_{Y}^{- 1} (u))} d u .

(22)

Let us set

c = CE (Y) / CE (X) .

Then, (23) can be expressed as

\int_{0}^{1} [\frac{1}{f_{X} (F_{X}^{- 1} (u))} - \frac{1}{c f_{Y} (F_{Y}^{- 1} (u))}] u^{2 k - n} ϕ (u) d u = 0 .

Applying Lemma 1, we can conclude that

f_{X} (F_{X}^{- 1} (u)) = c f_{Y} (F_{Y}^{- 1} (u)), a . e . z \in (0, 1) .

It follows that

F_{X}^{- 1} (u) = c F_{Y}^{- 1} (u) + d

, where d is a constant. Since

{lim}_{u \to 0} F_{X}^{- 1} (u) = {lim}_{u \to 0} F_{Y}^{- 1} (u) = 0

for all

u \in (0, 1)

, we conclude that

F_{X}^{- 1} (u) = c F_{Y}^{- 1} (u)

. This indicates that

F_{X}

and

F_{Y}

belong to the same family of distributions but for a change of scale. □

Using Theorem 8, we get the following corollary.

Corollary 3.

Suppose the assumptions of Theorem 8 hold. Then,

F_{X}

and

F_{Y}

belong to the same family of distributions, but for a change in scale, if and only if

\frac{CE (T_{n | n : F}^{X})}{CE (X)} = \frac{CE (T_{n | n : F}^{Y})}{CE (Y)},

for all

n \geq 1 .

4. Nonparametric Estimation

This section develops two nonparametric methods to estimate the cumulative entropy of consecutive k-out-of-n:F systems. Let us assume a sequence of i.i.d. continuous, non-negative rvs

X_{1}, X_{2}, \dots, X_{N}

, where

X_{1 : N} \leq X_{2 : N} \leq \dots \leq X_{N : N}

denote their order statistics. Applying Eq. (6), the CE of

T_{k | n : F}

can be reformulated for the case

2 k \geq n

as follows:

\begin{matrix} CE (T_{k | n : F}) & = & \int_{0}^{1} \frac{ξ (G_{k | n : F} (u))}{f (F^{- 1} (u))} d u = \int_{0}^{1} ξ (G_{k | n : F} (u)) [\frac{d F^{- 1} (u)}{d u}] d u \\ = & \int_{0}^{1} ξ ((n - k + 1) u^{k} - (n - k) u^{k + 1}) [\frac{d F^{- 1} (u)}{d u}] d u . \end{matrix}

(23)

Using Eq. (24), we estimate

CE (T_{k | n : F})

by approximating the derivative of the inverse distribution function at sample points. Following Vasicek [25], we estimate this derivative as

\frac{d F^{- 1} (u)}{d u} = \frac{N (X_{i + m : N} - X_{i - m : N})}{2 m},

where

X_{i : N} = X_{1 : N}

for

i < 1

and

X_{i : N} = X_{N : N}

for

i > N,

N is the sample size and m is a positive integer referred to as the window size, satisfying

m \leq N / 2 .

Consequently, an estimator for

CE (T_{k | n : F})

is obtained as follows:

\begin{matrix} {\hat{CE}}_{1} (T_{k | n : F}) & = & \frac{1}{N} \sum_{i = 1}^{N} ξ (G_{k | n : F} (\frac{i}{N + 1})) (\frac{N (X_{i + m : N} - X_{i - m : N})}{2 m}) \\ = & \frac{1}{N} \sum_{i = 1}^{N} ξ ((n - k + 1) {(\frac{i}{N + 1})}^{k} - (n - k) {(\frac{i}{N + 1})}^{k + 1}) \\ \times & (\frac{N (X_{i + m : N} - X_{i - m : N})}{2 m}) . \end{matrix}

(24)

The second estimator is constructed using the empirical cumulative distribution function associated with

F (x)

of the sample, as follows:

F_{N} (x) = \sum_{i = 1}^{N - 1} \frac{i}{N} I_{[x_{i : N}, x_{(i + 1)}]}, x \geq 0,

where

I_{A} (x) = 1

x \in A .

Based on Eq. (7), the empirical CE estimator for the consecutive k-out-of-n:F system is given by

\begin{matrix} {\hat{CE}}_{2} (T_{k | n : F}) & = & \int_{0}^{\infty} ξ ((n - k + 1) F_{N}^{k} (x) - (n - k) F_{N}^{k + 1} (x)) d x \\ = & \sum_{i = 1}^{N - 1} \int_{X_{i : N}}^{X_{(i + 1)}} ξ ((n - k + 1) F_{N}^{k} (x) - (n - k) F_{N}^{k + 1} (x)) d x \\ = & \sum_{i = 1}^{N - 1} ξ ((n - k + 1) {(\frac{i}{N})}^{k} - (n - k) {(\frac{i}{N})}^{k + 1}) D_{i + 1}, \end{matrix}

(25)

where

D_{i + 1} = X_{i + 1 : N} - X_{i : N}

i = 1, 2, \dots, N - 1,

denotes the sample spacings.

A simulation study using standard exponential distribution is performed to assess the performance of the proposed estimators,

{\hat{CE}}_{1} (T_{k | n : F})

and

{\hat{CE}}_{2} (T_{k | n : F}) .

The average bias and root mean squared error (RMSE) are computed for different sample sizes (

N = 20, 30, 40, 50, 100

) and various combinations of parameters k and

n .

The smoothing parameter m is determined using the heuristic formula

m = [\sqrt{N} + 0.5]

, where

[x]

denotes the integer part of x.

The simulation was run 5,000 times, and the results are shown in Table 1 and Table 2. Based on the analysis of these tables, we have reached the following results:

For all k and $n,$ as the sample size N increases, both bias and RMSE of the estimators decrease.
For fixed n and $N,$ as the number of consecutive working components k increases, both bias and RMSE of the estimator increase.

In general, the results show that the efficiency of the estimator is influenced by the number of components n and the number of consecutive working components k.

Real Data Analysis

We apply the estimator to real data to assess how closely the CE estimators from consecutive k-out-of-n:F systems match the theoretical entropy value. The data includes active repair times (in hours) for an airborne communication transceiver reported by [26]. The actual observations are listed below:

Datasets: 0.2, 0.3, 0.5, 0.5, 0.5, 0.5, 0.6, 0.6, 0.7, 0.7, 0.7, 0.8, 0.8, 1.0, 1.0, 1.0, 1.0, 1.1, 1.3, 1.5, 1.5, 1.5, 1.5, 2.0, 2.0, 2.2, 2.5, 2.7, 3.0, 3.0, 3.3, 3.3, 4.0, 4.0, 4.5, 4.7, 5.0, 5.4, 5.4, 7.0, 7.5, 8.8, 9.0, 10.3, 22, 24.5. This data is modeled using the Weibull distribution with the pdf

f (x) = λ β x^{β - 1} e^{- λ x^{β}}, x > 0,

where

λ > 0

and

β > 0

are scale and shape parameters, respectively. As noted in [27], the datasets were fitted using the Weibull distribution via the maximum likelihood method for parameter estimation. The resulting parameters are

\hat{λ} = 3.391

and

\hat{β} = 0.899

. The KolmogorovâSmirnov statistic is

0.120

with a p-value of

0.517

, confirming a good fit between the observed data and the fitted exponential distribution.

Table 3 shows various combinations of k and

n .

The results indicate a correlation between the theoretical entropy value and its estimation when the functioning components are nearly half of the total (n).

5. Conclusions

This study investigated the application of the CE concept to consecutive k-out-of-n:F systems. We established a key finding: a strong relationship exists between the CE of such systems derived from continuous and uniform distributions. This result simplifies CE calculations in many practical scenarios. However, obtaining closed-form CE expressions becomes challenging for systems with large or complex component distributions. To overcome this hurdle, we proposed a set of useful bounds for the CE of consecutive k-out-of-n:F systems. These bounds offer valuable tools for researchers and practitioners to understand and analyze CE behavior. Furthermore, we introduced two nonparametric estimators specifically tailored for consecutive k-out-of-n:F systems. These estimators are designed for real-world applications, as demonstrated by their use in real data sets. The CE estimation provides valuable insights into the uncertainty of the systems, aiding in informed decision-making and meaningful data analysis. In conclusion, this work makes significant contributions to the understanding of CE in consecutive k-out-of-n:F systems. The results of this study can be extended to other information measures including fractional cumulative entropy, cumulative residual Tsallis entropy, and cumulative Tsallis entropy.

Author Contributions

Methodology, MK; Software, MA; Validation, MK; Formal analysis, MK and MA; Investigation, MK and MA; Resources, MA; Writing original draft, MA; Writing review and editing, MK and MA; Visualization, MK; Supervision, MK; Project administration, MK. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by Researchers Supporting Project number (RSP2024R392), King Saud University, Riyadh, Saudi Arabia.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Jung, K.H.; Kim, H. Linear consecutive-k-out-of-n: F system reliability with common-mode forced outages. Reliability Engineering & System Safety 1993, 41, 49–55. [Google Scholar]
Shen, J.; Zuo, M.J. Optimal design of series consecutive-k-out-of-n: G systems. Reliability Engineering & System Safety 1994, 45, 277–283. [Google Scholar]
Kuo, W.; Zuo, M.J. Optimal reliability modeling: principles and applications; John Wiley & Sons, 2003.
In-Hang, C.; Cui, L.; Hwang, F.K. Reliabilities of consecutive-k systems; Vol. 4, Springer Science & Business Media, 2013.
Boland, P.J.; Samaniego, F.J. Stochastic ordering results for consecutive k-out-of-n: F systems. IEEE Transactions on reliability 2004, 53, 7–10. [Google Scholar] [CrossRef]
Eryılmaz, S. Mixture representations for the reliability of consecutive-k systems. Mathematical and Computer Modelling 2010, 51, 405–412. [Google Scholar] [CrossRef]
Eryilmaz, S. Conditional lifetimes of consecutive k-out-of-n systems. IEEE Transactions on Reliability 2010, 59, 178–182. [Google Scholar] [CrossRef]
Eryılmaz, S. Reliability properties of consecutive k-out-of-n systems of arbitrarily dependent components. Reliability Engineering & System Safety 2009, 94, 350–356. [Google Scholar]
Shannon, C.E. A mathematical theory of communication. The Bell system technical journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: a new measure of information. IEEE transactions on Information Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
Asadi, M.; Ebrahimi, N. Residual entropy and its characterizations in terms of hazard function and mean residual life function. Statistics & probability letters 2000, 49, 263–269. [Google Scholar]
Navarro, J.; del Aguila, Y.; Asadi, M. Some new results on the cumulative residual entropy. Journal of Statistical Planning and Inference 2010, 140, 310–322. [Google Scholar] [CrossRef]
Toomaj, A.; Zarei, R. Some new results on information properties of mixture distributions. Filomat 2017, 31, 4225–4230. [Google Scholar] [CrossRef]
Di Crescenzo, A.; Longobardi, M. On cumulative entropies. Journal of Statistical Planning and Inference 2009, 139, 4072–4087. [Google Scholar] [CrossRef]
Alomani, G.; Kayid, M. Fractional Survival Functional Entropy of Engineering Systems. Entropy 2022, 24, 1275. [Google Scholar] [CrossRef] [PubMed]
Shrahili, M.; Kayid, M. Cumulative Entropy of Past Lifetime for Coherent Systems at the System Level. Axioms 2023, 12, 899. [Google Scholar] [CrossRef]
Kayid, M.; Shrahili, M. Rényi Entropy for Past Lifetime Distributions with Application in Inactive Coherent Systems. Symmetry 2023, 15, 1310. [Google Scholar] [CrossRef]
Bickel, P.J.; Lehmann, E.L. Descriptive statistics for nonparametric models. III. Dispersion. In Selected works of EL Lehmann; Springer, 2011; pp. 499–518.
Jewitt, I. Choosing between risky prospects: the characterization of comparative statics results, and location independent risk. Management Science 1989, 35, 60–70. [Google Scholar] [CrossRef]
Shaked, M.; Shanthikumar, J.G. Stochastic orders; Springer Science & Business Media, 2007.
Landsberger, M.; Meilijson, I. The generating process and an extension of Jewitt’s location independent risk concept. Management Science 1994, 40, 662–669. [Google Scholar] [CrossRef]
Eryılmaz, S.; Navarro, J. Failure rates of consecutive k-out-of-n systems. Journal of the Korean Statistical Society 2012, 41, 1–11. [Google Scholar] [CrossRef]
Chang, J.C.; Hwang, F.K. Reliabilities of consecutive-k systems. In Handbook of reliability engineering; Springer, 2003; pp. 37–59.
Aliprantis, C.D.; Burkinshaw, O. Principles of real analysis; Gulf Professional Publishing, 1998.
Vasicek, O. A test for normality based on sample entropy. Journal of the Royal Statistical Society Series B: Statistical Methodology 1976, 38, 54–59. [Google Scholar] [CrossRef]
Balakrishnan, N.; Leiva, V.; Sanhueza, A.; Cabrera, E. Mixture inverse Gaussian distributions and its transformations, moments and applications. Statistics 2009, 43, 91–104. [Google Scholar] [CrossRef]
Hashempour, M.; Mohammadi, M. A new measure of inaccuracy for record statistics based on extropy. Probability in the Engineering and Informational Sciences 2024, 38, 207–225. [Google Scholar] [CrossRef]

Figure 1. The plot of

CE (T_{k | 6 : F})

with respect to

α

as demonstrated in Example 1.

Figure 1. The plot of

CE (T_{k | 6 : F})

with respect to

α

as demonstrated in Example 1.

Table 1. The Bias and RMSE of the first estimator

{\hat{CE}}_{1} (T_{k | n : F})

for different choices of k and

n .

Table 1. The Bias and RMSE of the first estimator

{\hat{CE}}_{1} (T_{k | n : F})

for different choices of k and

n .

		$N = 20$		$N = 30$		$N = 40$		$N = 50$		$N = 100$
n	k	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE
5	3	-0.124138	0.230344	-0.100742	0.191860	-0.095708	0.171305	-0.093843	0.160603	-0.094036	0.131869
	4	-0.038756	0.263316	0.000577	0.231150	0.036344	0.218155	0.051543	0.201405	0.093028	0.173277
	5	-0.091323	0.287947	-0.009914	0.253112	0.038630	0.247169	0.066143	0.237489	0.147523	0.237116
6	3	0.072069	0.167615	0.070267	0.138012	0.066130	0.124728	0.061647	0.109277	0.040760	0.075014
	4	-0.031567	0.239911	0.010755	0.209871	0.022254	0.184367	0.035022	0.174554	0.055193	0.134261
	5	-0.151385	0.310038	-0.079245	0.260249	-0.048472	0.232668	-0.015527	0.219851	0.041610	0.175196
	6	-0.272339	0.380990	-0.184579	0.315350	-0.127539	0.277684	-0.088733	0.253952	0.009005	0.199077
7	4	0.021823	0.208960	0.042960	0.183286	0.054940	0.161538	0.054626	0.150306	0.057243	0.113776
	5	-0.092157	0.269532	-0.034616	0.238141	-0.008311	0.214772	0.008427	0.198731	0.051931	0.159579
	6	-0.213470	0.350137	-0.135670	0.289292	-0.086826	0.260511	-0.055488	0.242480	0.031440	0.186683
	7	-0.331163	0.417481	-0.230386	0.349043	-0.161969	0.305570	-0.130153	0.279632	-0.007831	0.216406
8	4	0.075346	0.191621	0.080118	0.161910	0.074436	0.143996	0.076248	0.134626	0.059875	0.092973
	5	-0.035972	0.244008	0.000687	0.214961	0.023995	0.194971	0.038143	0.183108	0.061133	0.145446
	6	-0.168064	0.312048	-0.088598	0.260961	-0.048191	0.238333	-0.020311	0.224606	0.037779	0.178471
	7	-0.291871	0.384639	-0.185520	0.314696	-0.129251	0.281766	-0.093509	0.254625	0.004763	0.198204
	8	-0.385751	0.455766	-0.276726	0.378007	-0.211355	0.332942	-0.163147	0.300208	-0.034566	0.218227

Table 2. The Bias and RMSE of the second estimator

{\hat{CE}}_{2} (T_{k | n : F})

for different choices of k and

n .

Table 2. The Bias and RMSE of the second estimator

{\hat{CE}}_{2} (T_{k | n : F})

for different choices of k and

n .

		$N = 20$		$N = 30$		$N = 40$		$N = 50$		$N = 100$
n	k	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE	Bias	RMSE
5	3	-0.025125	0.175512	-0.014116	0.141257	-0.015236	0.123774	-0.012079	0.109911	-0.005279	0.078412
	4	-0.072958	0.267537	-0.050056	0.219368	-0.029108	0.190125	-0.032334	0.172732	-0.012504	0.123541
	5	-0.123044	0.332033	-0.084990	0.272151	-0.055920	0.239984	-0.048001	0.219015	-0.023000	0.156351
6	3	-0.001871	0.132976	0.000809	0.109061	0.000794	0.092947	-0.000688	0.082732	-0.000010	0.058974
	4	-0.045391	0.228448	-0.028728	0.182676	-0.024040	0.157982	-0.016516	0.145011	-0.011101	0.102678
	5	-0.100189	0.299852	-0.064542	0.250162	-0.049838	0.217331	-0.038395	0.195598	-0.018189	0.139785
	6	-0.131134	0.357338	-0.099022	0.297588	-0.077961	0.262055	-0.057160	0.238616	-0.028988	0.170018
7	4	-0.026347	0.182529	-0.018355	0.150178	-0.011043	0.133090	-0.010400	0.117107	-0.006821	0.083850
	5	-0.075611	0.266131	-0.041516	0.221699	-0.037394	0.192767	-0.029404	0.171981	-0.014986	0.122495
	6	-0.124722	0.331439	-0.081209	0.278495	-0.064191	0.245961	-0.050115	0.219265	-0.026817	0.155459
	7	-0.169382	0.377862	-0.106689	0.319331	-0.086256	0.286752	-0.068001	0.256148	-0.032641	0.182052
8	4	-0.002768	0.152239	-0.003317	0.119965	0.000883	0.106233	0.001972	0.094212	-0.000304	0.066692
	5	-0.052062	0.233434	-0.032683	0.190547	-0.027234	0.163031	-0.021617	0.147743	-0.008801	0.104927
	6	-0.096677	0.298313	-0.065127	0.255635	-0.048338	0.221591	-0.041602	0.196996	-0.019996	0.140928
	7	-0.141255	0.362541	-0.094531	0.302222	-0.081784	0.265432	-0.062192	0.240006	-0.026913	0.168080
	8	-0.181689	0.401899	-0.131193	0.343492	-0.091136	0.300505	-0.070395	0.267088	-0.035192	0.200356

Table 3. Comparison of theoretical values and estimates of CE of

T_{k | n : F}

based on Weibull distribution for active repair times (in hours) for an airborne communication transceiver.

Table 3. Comparison of theoretical values and estimates of CE of

T_{k | n : F}

based on Weibull distribution for active repair times (in hours) for an airborne communication transceiver.

k	$CE (T_{k \| 5 : G})$	${\hat{CE}}_{1} (T_{k \| 5 : G})$	${\hat{CE}}_{2} (T_{k \| 5 : G})$	$CE (T_{k \| 6 : G})$	${\hat{CE}}_{1} (T_{k \| 6 : G})$	${\hat{CE}}_{2} (T_{k \| 6 : G})$
3	0.188772	3.202371	2.708464	0.139103	2.307699	1.786721
4	0.252975	4.412466	4.098577	0.225504	3.978375	3.511787
5	0.282173	4.786405	4.902895	0.267998	4.650849	4.532230
6				0.289143	4.779245	5.167557
k	$CE (T_{k \| 7 : G})$	${\hat{CE}}_{1} (T_{k \| 7 : G})$	${\hat{CE}}_{2} (T_{k \| 7 : G})$	$CE (T_{k \| 8 : G})$	${\hat{CE}}_{1} (T_{k \| 8 : G})$	${\hat{CE}}_{2} (T_{k \| 8 : G})$
4	0.191428	3.414607	2.827453	0.151613	2.737446	2.057078
5	0.247997	4.397852	4.073618	0.223027	4.043979	3.538539
6	0.278365	4.738680	4.867858	0.263090	4.605239	4.497665
7	0.294482	4.708580	5.384117	0.285978	4.731164	5.137700
8				0.298730	4.597261	5.563095

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Results on Cumulative Entropic Properties of Consecutive Systems

Abstract

1. Introduction

2. CE of Consecutive k-out-of-n:F System

2.1. Expression and Stochastic Orders

2.2. Bounds

3. Characterization Results

4. Nonparametric Estimation

Real Data Analysis

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe