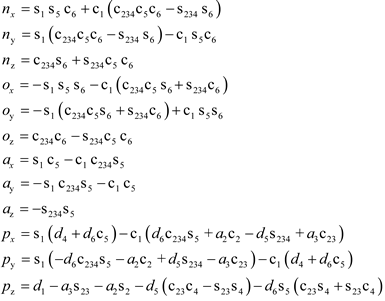Prerpints.org logo
Preprint
Article

Cobot Kinematic Model for Industrial Applications

Altmetrics

Downloads

86

Views

39

Comments

0

supplementary.mov (252.96MB )

Submitted:

21 August 2024

Posted:

23 August 2024

You are already at the latest version

Alerts
Abstract
This paper deals with the formulation of a Cobot kinematic model by developing both the direct and inverse kinematics and choosing the noa transformation matrix for defining the end-effector position and orientation with respect to the base frame. These algorithms have been validated via software in Matlab environment and by means of suitable experimental tests, which have been carried out by using a UR5e Cobot. Moreover, a specific industrial application regarding the robotized assembling of a multi-cylinder IC engine, has been designed in terms of layout and corresponding automatic cycle that is intended as a sequence of the robot elementary actions. In particular, the proposed robotized cell is composed by the UR5e Cobot along with its controller and a suitable electropneumatic circuit that includes a PLC with its user interface, which are both governed by means of a specific electronic board and a switch control box. The IC engine in scale of 1:5 and specific parts of the end-effector, which takes the role of vacuum gripper and torque limiting screwdriver, have been designed and manufactured by using a 3D printer.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

In recent decades, the manufacturing industry has experienced significant evolution due to the introduction of new technologies. Among these, collaborative robots, known as s, represent one of the most promising innovations. Unlike traditional robots, designed to operate in segregated environments and perform repetitive and hazardous tasks without human interaction, Cobots are designed to work closely with human operators. This characteristic makes them particularly suitable for a wide range of industrial applications, enhancing efficiency, safety, and productivity in production processes. In manufacturing, Cobots enable flexible and efficient production systems, allowing safe operation in close proximity to humans, which broadens their applications across various industries. A review of collaborative robots (Cobots) in manufacturing is reported in [1], which highlights their human interaction capabilities without traditional safety barriers. It includes standards, industrial applications, and future trends, emphasizing the need for proper knowledge for optimal use. Similarly, in [2], recent Cobot applications in industrial and service contexts, focusing on stationary COBOTs for flexibility, efficiency, and safety are reviewed, examining AI, machine learning, control interfaces, intention recognition, programming techniques, and virtual reality, with a market analysis of 195 models. The integration of human factors in the Cobot era is critical for the success of modern production systems, and the ergonomic design has an important role together with worker safety, taking into account the contribution of human factors in optimizing Cobot deployment [3]. There is an emphasis on the role of Cobots in optimizing production processes and reducing operational costs in smart manufacturing [4]. Additionally, there is a strategic view on deploying Cobots in Assembly 4.0 systems, highlighting their potential to increase efficiency and reduce downtime [5]. Key challenges in the design and control of hybrid human-robot collaborative manufacturing systems are surveyed in [6], with proposed solutions to enhance effective implementation. Brain-computer interfaces for human-Cobot interaction are explored in [7] for industrial applications, showcasing innovative methods to improve communication and control. A roadmap for future studies on human-robot collaboration highlights the necessity for robust safety standards and the development of user-friendly interfaces [8].
The optimization of robotic manipulators is a focal point in enhancing the performance of Cobots. In the case of serial robots there are many examples of optimization problems, like the one reported in [9]. In [10] the kinematic synthesis of tendon-driven 4R planar robotic arms is explored, providing insights into the design of more flexible and efficient robotic systems. In the case of parallel robots, the experimental validation of the CaPaMan (Cassino Parallel Manipulator) as an earthquake simulator is examined in [11,12], showcasing the application of advanced robotics in simulating complex dynamic environments. Advancements in the precision and control of robotic systems are highlighted through the mechatronic design and control of a 3-RPS parallel manipulator [13].
Cobots are also widely used in the medical and rehabilitative sector, with service robots playing an important role in patient care and medical procedures. A review on the use of service robots in the healthcare sector, highlighting their potential to improve patient outcomes and reduce the workload of healthcare professionals is reported in [14]. The feasibility of using robotics in simulated COVID-19 patient rooms to perform tasks that minimize exposure risk for healthcare workers is well documented in [15]. In [16] a systematic review of collaborative robots for nurses, identifying current applications and areas where further evidence is needed, is provided. The potential of robot skin as an enabler for safe collaboration, immersive teleoperation, and affective interaction in future Cobots is reviewed in [17], which underlines its importance for enhancing human-robot interaction. Homecare robotic systems for Healthcare 4.0, discussed in [18], envision a future where advanced robotics enhance homecare services, providing personalized care and support. In the field of rehabilitation robotics, a deep study of upper limb rehabilitation and mobility assistance using robotic devices, emphasizing the importance of patient-cooperative control strategies in discussed in [19]. In [20] further explore these strategies, highlighting their potential to improve the efficacy of rehabilitation exoskeletons. Another focus is the one related to the manipulability optimization of rehabilitative collaborative robotic systems, proposing design enhancements to improve performance [21].
Safety technologies and standards for robots interacting with humans are reviewed in [22], who emphasizes the need for stringent safety protocols to prevent accidents. The role of collaborative robots in the context of Industrial Revolution 4.0, highlighting their potential to revolutionize industrial processes is deeply discussed in [23]. The expanding role of artificial intelligence in collaborative robots for industrial applications is systematically reviewed in [24], identifying recent advancements and future directions. The role of Cobots over traditional industrial robots in Industry 5.0 is reviewed in [25], which discuss the potential benefits of integrating Cobots into future manufacturing systems [25].
Recent advancements in kinematic modeling have significantly enhanced the precision and flexibility of robotic systems. A validated method for inverse kinematics in 6-DOF industrial robots with offset and spherical joints offers interactive tools for real-time control [26]. Additionally, a kinematic model for a 6-DOF manipulator has been experimentally validated, providing a solid foundation for offline programming and calibration [27]. In collaborative robotics, new kinematic models address both direct and inverse kinematics in shared human-robot tasks, improving system efficiency [28]. For medical applications, an innovative closed-form solution for inverse kinematics in puncture robotics enhances surgical accuracy and optimizes workspace configurations [29]. A versatile kinematic analysis for open architecture 6R robot controllers allows for adaptable models across various robot types, proving accurate in both forward and inverse kinematics [30]. In ecological applications, an improved algorithm for a Tree-Planting Robot significantly enhances trajectory planning and reduces deviation [31]. Furthermore, a comparative study of kinematic analysis methods using the KUKA manipulator shows that particle swarm optimization achieves the highest accuracy, while RoboAnalyzer is the fastest, highlighting the importance of method selection [32].
Thus, although several kinematic models of 6R serial manipulators can be found in literature, instead to merely use commercial and/or available software packages, as RoboDK [28], RoboAnalyzer and Peter Corke Toolbox [32], in this paper, a specific parametric and open-source algorithm for the direct and inverse kinematics of a Cobot UR5e has been completely revised, reformulated and implemented in Matlab, with the aim to analyse the Cobot UR5e kinematic performance for simulation purposes of industrial applications. Moreover, in order to obtain a reliable algorithm, this has been experimentally validated in terms of direct and inverse kinematics, by using a UR5e Cobot and reading the corresponding tool and joint positions by the tech-pendant for several robot poses.
Finally, a specific industrial application regarding the robotized assembling of a multi-cylinder IC engine, has been designed in terms of layout, built and experimentally tested. In particular, the IC engine in scale of 1:5 and specific parts of the end-effector, which takes the role of vacuum gripper and torque limiting screwdriver, have been designed and manufactured by using a 3D printer.

2. Cobot Kinematic Model

The Cobot kinematic model is formulated by using the standard D-H method to define the coordinate system that is attached to each link of the serial chain, along with the four corresponding D-H parameters. Thus, the total homogeneous transformation matrix is obtained between the end-effector moving frame and the fixed base frame.
The direct kinematics (DK) problem is crucial for developing manipulator algorithms, because the joint positions are typically measured by the corresponding sensors, which give the relative position between two consecutive links.
Thus, the DK problem is solved by calculating the homogeneous transformation matrix between the end-effector moving frame and the fixed base frame. On the other hand, the inverse kinematics (IK) can be developed by determining the joint variable as function of a given end-effector configuration.
Figure 1 shows a typical 6R serial kinematic chain of 6 (DOFs), which also corresponds to that of the UR5e robotic arm (Figure 1a), along with D-H reference frames (Figure 1b). In particular, the fixed frame x0y0z0 is attached to the robot base, while the i-th moving frame xiyizi is considered as attached to the i-th link for i = 1, …, 6, where the zi - axis is along the joint axis direction, the xi - axis is perpendicular to both zi and zi−1 axis, and the yi-axis is chosen in agreement with the right-hand rule. The D-H parameters are reported in Table 1, where θi represents the joint angle variable of each UR5e joint, di is the offset of the link, ai denotes the length of the link, αi indicates the joint torsion angle, where i = 1, …, 6 is the joint number.
Thus, the homogeneous transformation matrix between the D-H reference frames that are associated to the joints i−1 and i, takes the form
  i − 1 T i = cos θ i − cos α i sin θ i sin α i sin θ i a i cos θ i sin θ i cos α i cos θ i − sin α i cos θ i a i sin θ i 0 sin α i cos α i d i 0 0 0 1

2.1. Direct Kinematics

The DK problem for a serial kinematic chain consists of finding the position and orientation of the end-effector moving reference frame, when all the joint angles θ i (i = 1, …, 6) are given. Referring to Table 1 and Eq. (1), the D-H homogeneous transformation matrices are obtained as follows
T 0   1 = c 1 0 s 1 0 s 1 0 − c 1 0 0 1 0 d 1 0 0 0 1 T 1   2 = c 2 − s 2 0 − a 2 c 2 s 2 c 2 0 − a 2 s 2 0 0 1 0 0 0 0 1 T 2   3 = c 3 − s 3 0 − a 3 c 3 s 3 c 3 0 − a 3 s 3 0 0 1 0 0 0 0 1 T 3   4 = c 4 0 s 4 0 s 4 0 − c 4 0 0 1 0 d 4 0 0 0 1 T 4   5 = c 5 0 − s 5 0 s 5 0 c 5 0 0 − 1 0 d 5 0 0 0 1 T 5   6 = c 6 − s 6 0 0 s 6 c 6 0 0 0 0 1 d 6 0 0 0 1
where ci and si (i = 1, …, 6) stand for cos θ i and sin θ i , respectively.
Consequently, the direct kinematics solution is obtained by multiplying in sequence and among them, the six homogeneous transform matrices of the Eq. (2), by giving the following T 0   6 resultant matrix
T 0   6 = T 0   1 T 1   2 T 2   3 T 3   4 T 4   5 T 5   6
This can be considered equal to the following 4x4 matrix
T 0   6 = n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1
that includes the noa rotation matrix, whose entries are the Cartesian components of the corresponding unit vectors n, o, and a, respectively, while (px, py, pz) are those of the tool position vector p.
Thus, equating the corresponding entries of the matrices of Eq. (4), one has
Preprints 115885 i001
where s and c stand for sine and cosine, respectively, and one has c 23 = cos ( θ 2 + θ 3 ) , s 23 = sin ( θ 2 + θ 3 ) , c 234 = cos ( θ 2 + θ 3 + θ 4 ) and s 234 = sin ( θ 2 + θ 3 + θ 4 ) .

2.2. Inverse Kinematics

The IK problem for a serial kinematic chain consists of finding the joint angles θ i (i = 1, …6) of the serial kinematic chain, when the position and orientation of the end-effector is given in terms of the noap Cartesian components. The required end-effector pose is given by the Eq. (4) and thus, multiplying each side of it by the inverse matrix T 0   1 − 1 , it obtains the following matrix equation
T 1   6 = T 0   1 − 1 n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1
where T 1   6 is given by T 1   6 = T 1   2 T 2   3 T 3   4 T 4   5 T 5   6 and one has
T 1   6 = c 234 c 5 c 6 − s 234 s 6 − s 234 c 6 − c 234 c 5 s 6 − c 234 s 5 − a 2 c 2 − a 3 c 23 − d 5 s 234 − d 6 c 234 s 5 c 234 s 6 + s 234 c 5 c 6 c 234 c 6 − s 234 c 5 s 6 − s 234 s 5 − a 2 s 2 − a 3 s 23 − d 5 c 234 − d 6 s 234 s 5 s 5 c 6 − s 5 s 6 c 5 d 4 + d 6 c 5 0 0 0 1
Similarly, developing the right side of Eq. (6), one has
T 0   6 = n x c 1 + n y s 1 o x c 1 + o y s 1 a x c 1 + a y s 1 p x c 1 + p y s 1 n z o z a z p z − d 1 n x s 1 − n y c 1 o x s 1 − o y c 1 a x s 1 − a y c 1 p x s 1 − p y c 1 0 0 0 1
The joint angles θ i for i = 1, …, 6 are obtained by equating the right sides of the Eqs. (7) and (8), excluding the fourth row, and thus obtaining a system of twelve non-linear equations, which are coupled two by two, in order to obtain six sub-systems of two equations for each. In particular, developing the first sub-system, which is obtained by equating the two entries of the third row with the columns three and four, θ 1 is given by
θ 1 = atan 2 d 4 , ± a y d 6 − p y 2 + p x − a x d 6 2 − d 4 2 − atan 2 a y d 6 − p y , p x − a x d 6
Likewise, the joint angles θ 5 and θ 6 are obtained by equating the two entries of the third row with the columns one and two. One has
θ 5 = atan 2 ± n x s 1 − n y c 1 2 + o x s 1 − o y c 1 2 , a x s 1 − a y c 1
θ 6 = atan 2 − o x s 1 − o y c 1 s 5 , n x s 1 − n y c 1 s 5
The joint angle θ 234 is obtained by equating the two entries of the first and second rows with the column three and after a suitable development, one has
θ 234 = θ 2 + θ 3 + θ 4 = atan 2 − a z s 5 , − a x c 1 + a y s 1 s 5
Similarly, the joint angles θ 2 and θ 23 are obtained by equating the first and second rows with the fourth column and thus, one has
θ 2 = atan 2 a 3 2 − a 2 2 − A 2 − B 2 2 a 2 A 2 + B 2 , ± 1 − a 3 2 − a 2 2 − A 2 − B 2 2 a 2 A 2 + B 2 2 − atan 2 A , B
θ 23 = atan 2 − B − a 2 s 2 a 3 , − A − a 2 c 2 a 3
where the coefficients A and B are expressed as follows
A = p x c 1 + p y s 1 − d 5 s 234 + d 6 c 234 s 5 B = p z − d 1 + d 5 c 234 + d 6 s 234 s 5
Finally, referring to Eqs. (12), (13) and (14), the joint angles θ 3 and θ 4 are given by
θ 3 = θ 23 − θ 2
θ 4 = θ 234 − θ 23

2.3. Experimental Validation for One Pose

The proposed algorithms for solving the inverse and direct kinematics of the UR5e Cobot have been experimentally validated by referring to an arbitrary Cobot reference pose, which is given by the teach pendant in terms of the tool position vector p and the rotation vector r, along with the joint angles θ i for i = 1, …, 6, respectively. Vectors p and r have Cartesian components with respect to the base frame of (px, py, pz) and (rx, ry, rz), respectively. In particular, the rotation vector r of magnitude θ, define the rotation axis of the tool end-effector, along with the corresponding rotation angle θ, which is not a joint angle, since referred to the axis of unit vector u. In fact, one has
θ = r x 2 + r y 2 + r z 2
u = 1 θ r x r y r z
where rx, ry and rz are the Cartesian components of r with respect to base frame.
Consequently, the homogeneous transformation matrix T 0   6 , which includes the noa rotation matrix that corresponds to a given rotation vector r of angle θ and unit vector u, along with the tool position vector p, can be expressed as follows
T 0   6 = u x 2 1 − c θ + c θ u x u y 1 − c θ − u z s θ u x u z 1 − c θ + u y s θ p x u x u y 1 − c θ + u z s θ u y 2 1 − c θ + c θ u y u z 1 − c θ − u x s θ p y u x u z 1 − c θ − u y s θ u y u z 1 − c θ + u x s θ u z 2 1 − c θ + c θ p z 0 0 0 1
Therefore, referring to Table 2 that contains the experimental Cartesian components of vectors p and r for the assigned UR5e Cobot pose, applying Eqs. (18) and (19) to determine the rotation angler θ = 3.1113 rad and the unit vector u = 0.7071   − 0.7071   0.0064 , and finally substituting in Eq. (20), one has
T 0   6 = − 0.0002 − 0.9999 − 0.0123 135.0 − 0.9995 0.0002 − 0.0305 − 292.1 0.0305 0.0123 − 0.9995 523.8 0 0 0 1
According to the proposed IK algorithm, the assigned experimental Cartesian components of p and r of Table 2, the corresponding joint angles θ i for i = 1, …6 are reported in Table 3, as follows
Likewise, the DK is solved by using as input data, the joint angles θ i for i = 1, …6 of Table 3, which are substituted into the Eq. (2) in order to obtain the whole homogeneous transformation matrix T 0   6 of Eq. (3), as follows
T 0   6 = − 0.0000 − 0.9999 − 0.0119 135.1514 − 0.9996 0.0003 − 0.0280 − 292.2861 0.0280 0.0119 − 0.9995 523.2706 0 0 0 1
However, the teach pendant of the UR5e Cobot gives the tool end-effector pose in terms of p and r components, for which, the following matrix is introduced
T 0   6 = r 13 r 12 r 13 p x r 21 r 22 r 23 p y r 31 r 32 r 33 p z 0 0 0 1
where the first three numbers of the fourth column of Eq. (22) correspond to the Cartesian components of vector p, respectively.
Developing Eq. (23), one has
θ = cos − 1 r 11 + r 22 + r 33 − 1 2
u = 1 2 s θ r 32 − r 23 r 13 − r 31 r 21 − r 12 T
and thus, the rotation vector r is given by
r = θ u x u y u z
which numerical results, along with p, are reported in Table 4, as follows
This experimental validation procedure of the proposed algorithm for the UR5e Cobot direct and inverse kinematics is extensively applied in the next session by referring to the robotized assembling of a multi-cylinder IC engine. Particular attention will be devoted to the first Operation of the whole automatic cycle and then all Cobot poses will be also considered for the validation purposes of the proposed kinematic model.

3. Application: Robotized Assembling of a Multi-Cylinder IC Engine

A specific industrial application regarding the robotized assembling of a multi-cylinder IC engine, has been designed in terms of layout and corresponding automatic cycle that is intended as a sequence of the robot elementary actions. In particular, the proposed robotized cell is composed by the UR5e Cobot along with its controller and a suitable electropneumatic circuit that includes a PLC with its user interface, which are both governed by means of a specific electronic board and a switch control box.
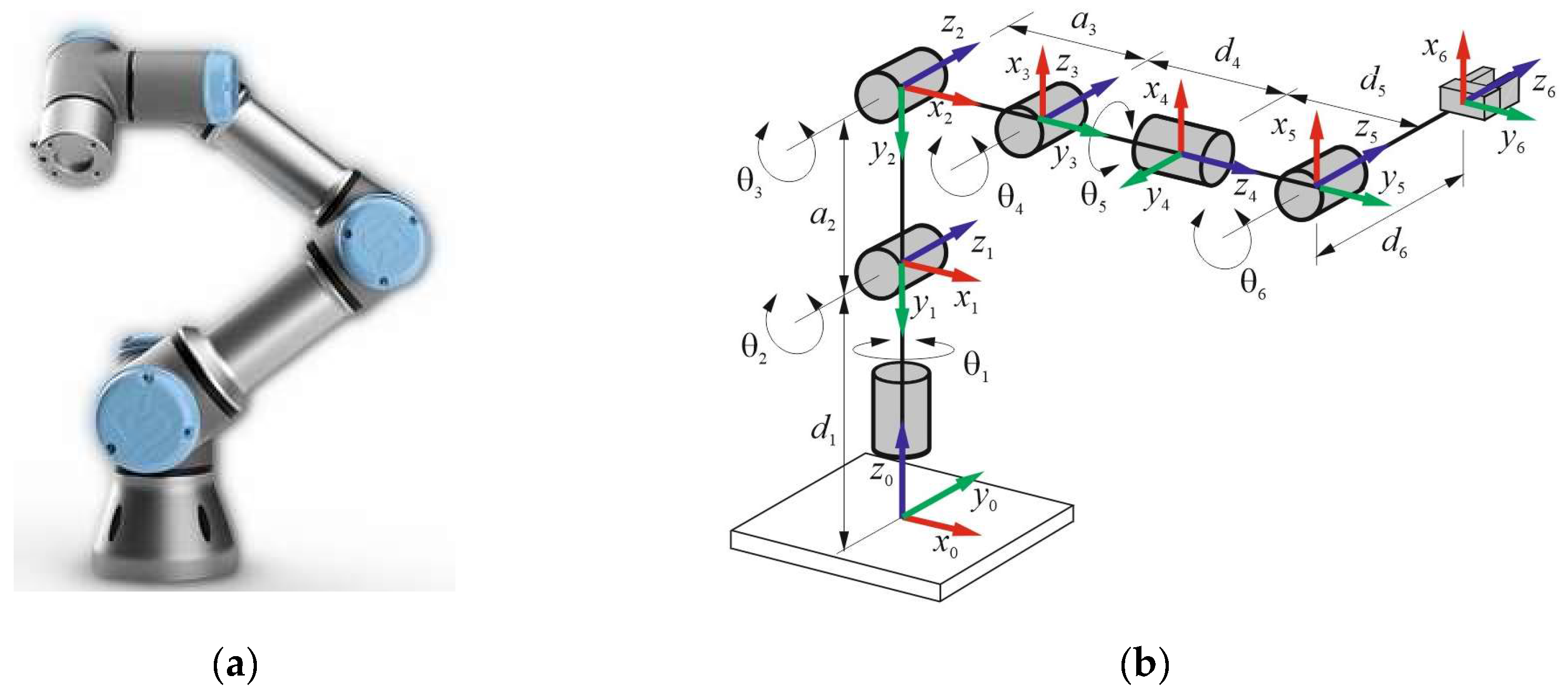
Referring to Figure 2, the robotized assembling of a multi-cylinder IC engine is carried out by means of a suitable automatic cycle and in agreement with the main engine components, which are: 1) engine block; 2) cylinder head; 3) cylinder head cover; 4) head gaskets. Consequently, these components are suitably positioned on a working table and in such a way to be reachable by the Cobot end-effector, as sketched in Figure 3.
The automatic cycle has been conceived of five fundamental operations, where four consist of the assembling of the following components on the engine block that is fixed on the working table: 1) the first head gasket; 2) the cylinder head; 3) the second head gasket; 4) the cylinder head cover. The fifth operation consists of the nut screwing in order to assembly all engine components safely. Moreover, each operation has been distinguished in a suitable number of elementary actions. The proposed Cobot kinematic model has been further validated during a manipulation and not only in a given pose.

3.1. Automatic Cycle: Operation 1

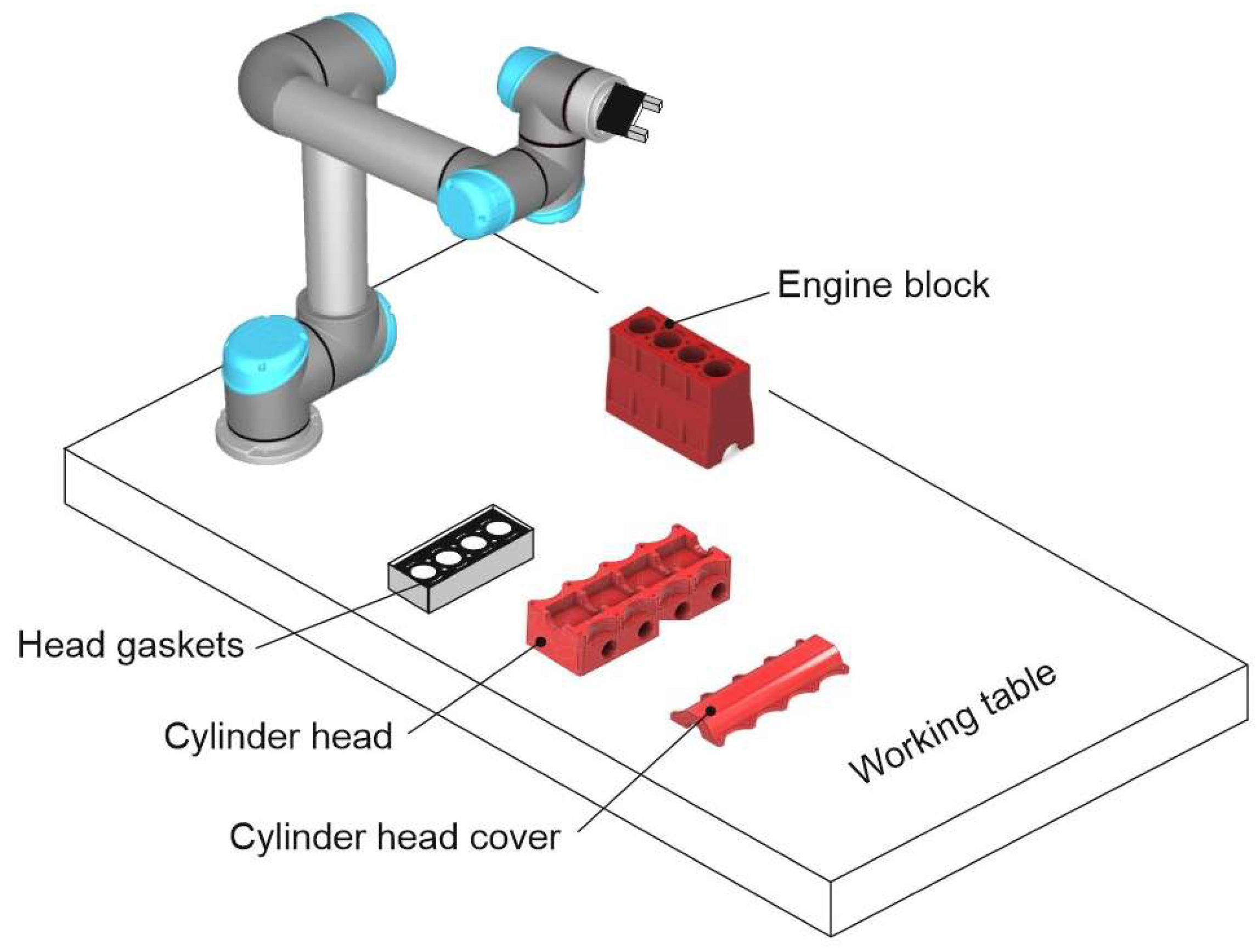
The first operation of the whole automatic cycle is aimed to assemble the first head gasket on the fixed cylinder block, which elementary actions, starting by the home Cobot position (A) and referring to the sketch of Figure 4, are: 1) the end-effector reaches the position B; 2) it grasps the vacuum gripper in C; 3) it moves back to B; 4) it moves to D; 5) it grasps the first head gasket in E; 6) it moves to F; 7) it moves to G; 8) it assembles the first head gasket on the cylinder block in H.
Therefore, referring to Table 5, which contains the Cartesian components of vectors p and r for each Cobot pose, which corresponds to the end-effector position from A to H for the Operation 1, the proposed IK Cobot model has allowed to determine all the corresponding joint angles θ i for i = 1, …, 6.
Moreover, the proposed IK Cobot model has been implemented in Matlab by giving the graphical result of Figure 5 for the Operation 1, along with the corresponding joint angles of Table 6. This has allowed the experimental validation of the proposed Cobot kinematic model during a manipulation and not only in a given pose, as in session 2.3.
In fact, referring to the Operation 1 of Figure 4 and the assigned input data of Table 5, the numerical and experimental six joint angles θ i for i = 1, …, 6 of the UR5e Cobot have been obtained by the proposed IK Cobot model and the tech-pendant screen, respectively. These results can be correspondingly compared among them, by showing a very good approximation between the numerical and the experimental results.
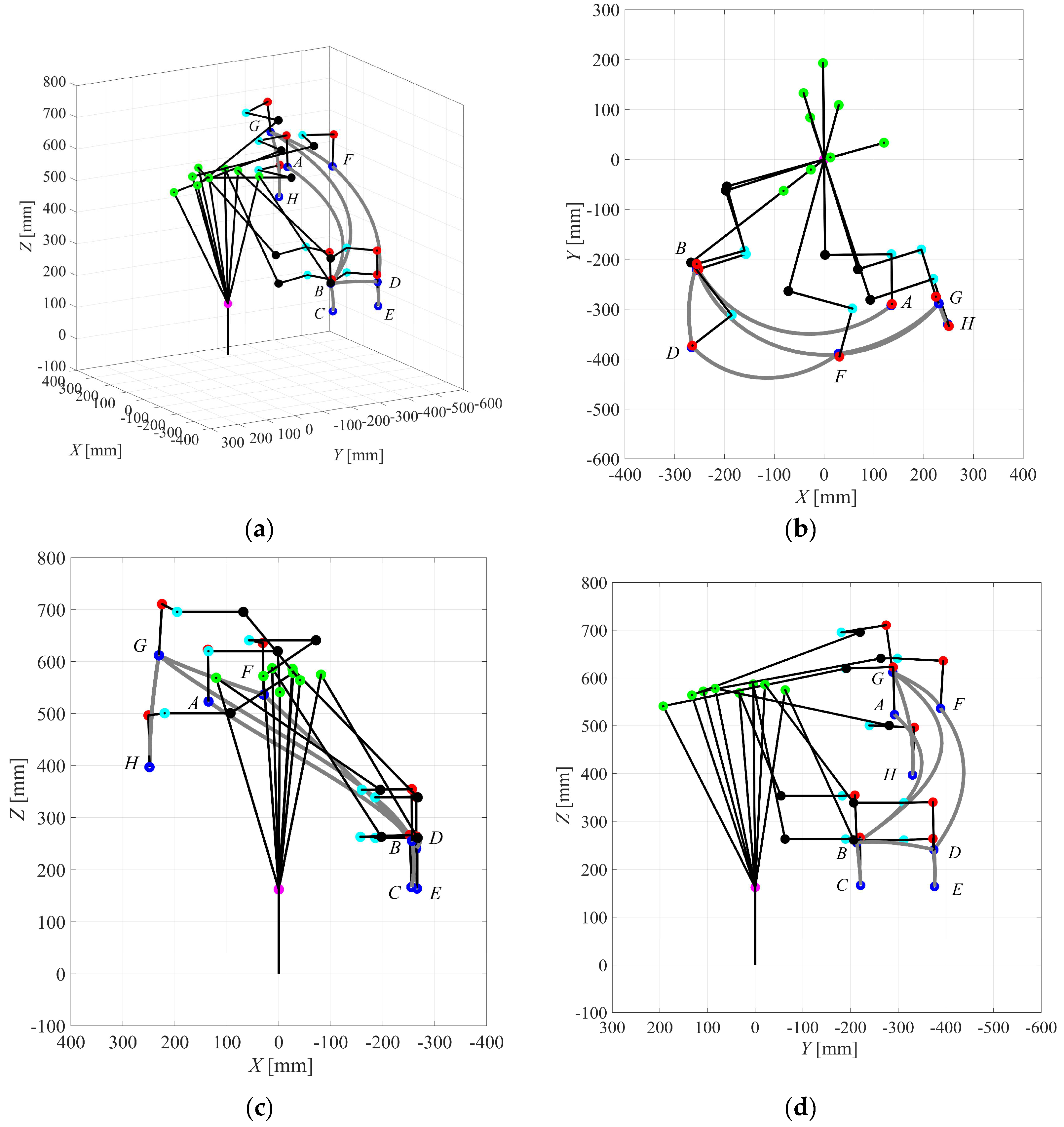
Thus, the proposed parametric and open-source algorithm for the direct and inverse kinematics of the Cobot UR5e has been experimentally validated with a good reliability. Moreover, a further validation has been carried out by calculating both the position and the orientation vectors p and r for each joint and pose of the Cobot UR5e, as reported in Table 7 along with the graphical representation of Figure 5, which shows the Cobot kinematic chain in each pose of the Operation 1. In particular, Figure 5 (a) shows a 3 D view, while Figure 5 (b), Figure 5 (c) and Figure 5 (d) show the XY, XZ and the YZ planar views.
The same approach has been used to analyze and simulate the other four Operations of the whole automatic cycle, as reported in the next section.

3.2. Automatic Cycle: Operations 2 to 5

Using the same approach that has been applied in section 3.1 and referring to the Operations 2 to 5, since the first was considered in the previous section, the numerical and the experimental joint angles have been determined with reference to the input data of Table 8 for the end-effector position and the orientation vectors p and r.
According to the Cobot UR5e inverse kinematics, the numerical results in terms of joint angles are reported on the left side of Table 9, while the corresponding experimental results are shown on the right side. A good approximation is obtained by comparing the corresponding numerical and experimental joint angles.
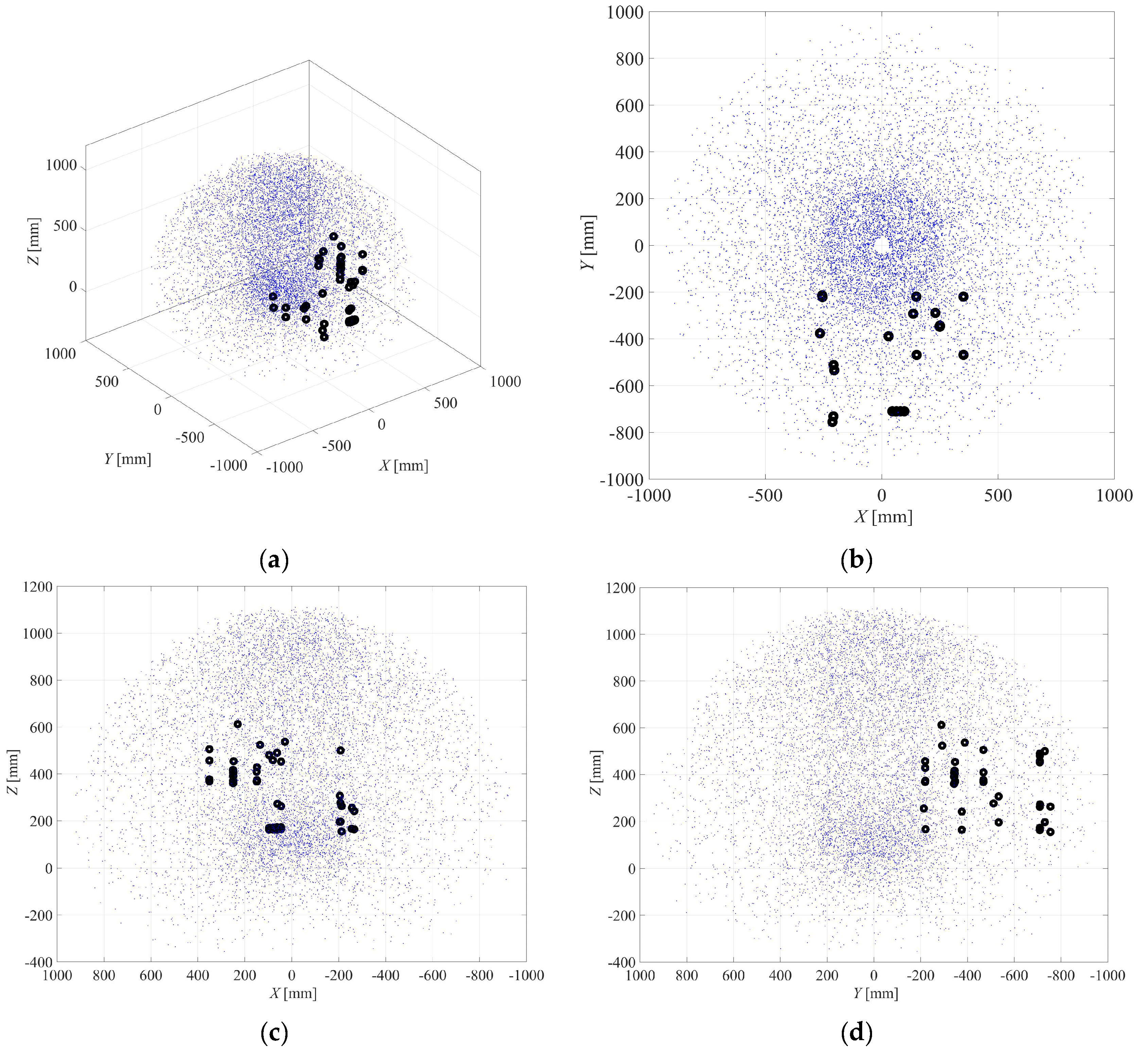
Moreover, the Pj points could for j = 1 to 39, which correspond to the Operations 2 to 5 of the whole automatic cycle of the robotized work cell, are graphically shown in Figure 6, along with the 8 points, from A to H, of the Operation 1, for a total of 47 points, which fall inside the Cobot workspace. In particular, the 3D view is shown in Figure 6 (a), while Figure 6 (b), Figure 6 (c) and Figure 6 (d) show its XY, XZ, and YZ planar projections.

3.3. Experimental Set-Up of the Robotized Work Cell

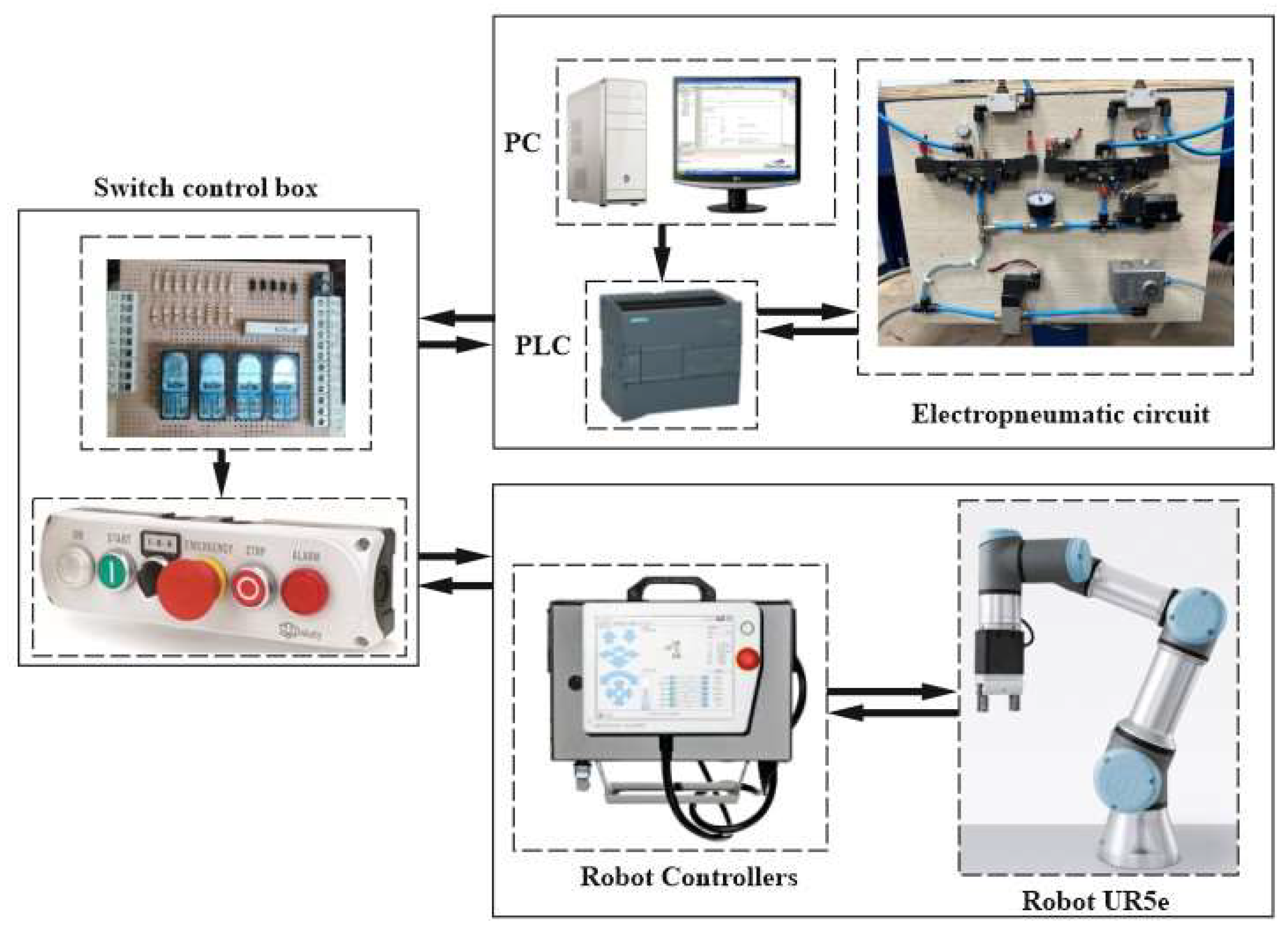
According to the sketch of Figure 3, the whole robotized work cell for assembling a multi-cylinder IC engine has been designed and built at LARM (Laboratory of Robotics and Mechatronics) of DICEM (Department of Civil and Mechanical Engineering) of the University of Cassino and Southern Lazio. This has required the mechatronic design, along with the building and the assembling of other suitable devices and systems, which cooperate among them and with the UR5e Cobot according to a specific automatic cycle.
In particular, the mechatronic scheme of the proposed robotized work cell is shown in Figure 7, where the UR5e Cobot and its controller cooperate with a suitable electropneumatic system that is controlled and programmed through a PLC of Siemens S7-1200 type. Both automatic systems are governed by means of a suitable switch control box, which is installed on the working table.
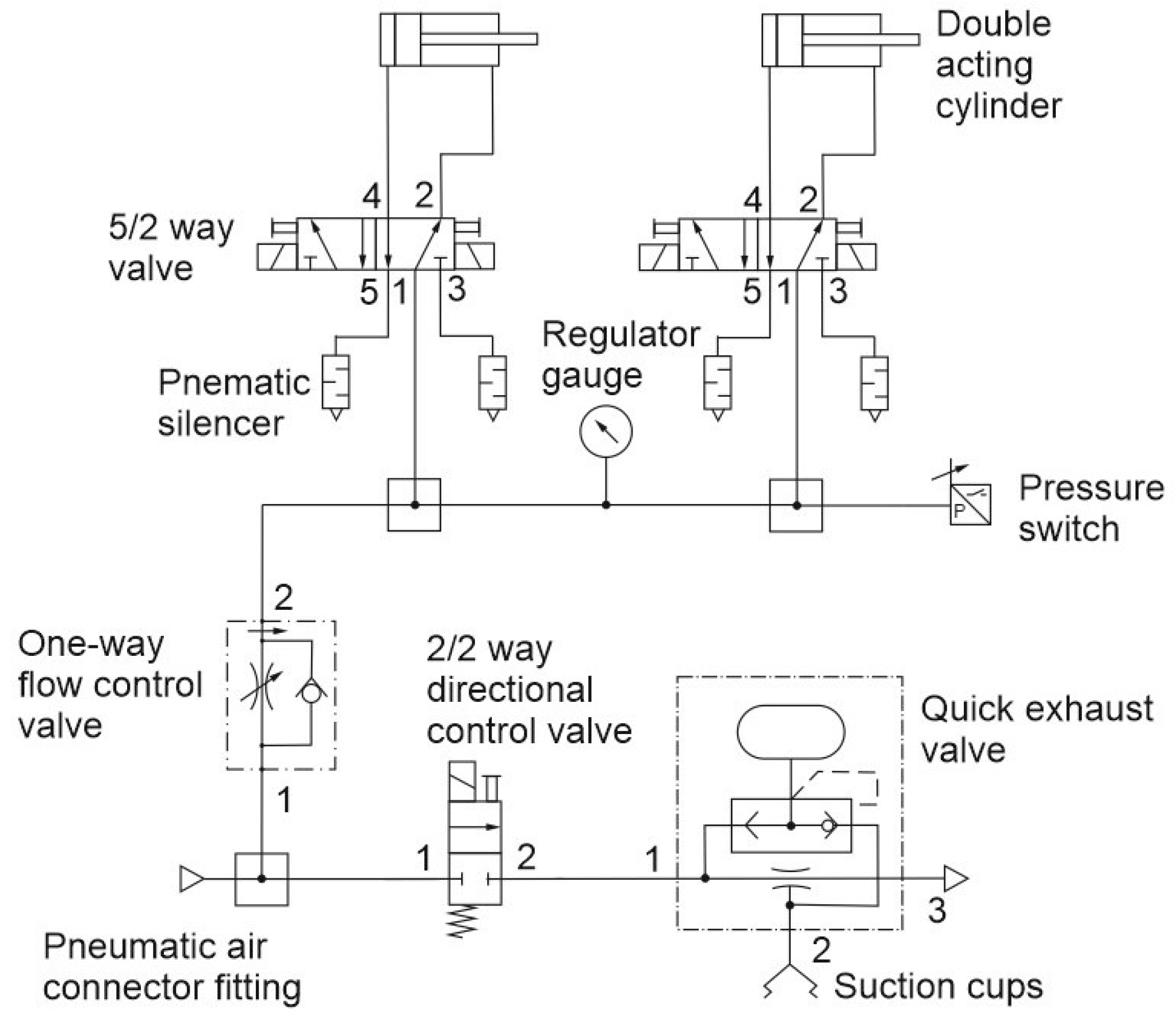
A detail on the electropneumatic circuit is shown in Figure 8, which can be considered as composed by two main parts, where the first part is devoted to perform the vacuum grasp by means of four suction-cups and ejectors (only one is shown in Figure 8), where each of them is provided by a suitable quick exhaust valve, while the second part of the electropneumatic circuit refers to the locking device of the engine block, which is mainly composed by two double-acting pneumatic cylinders, along with their operating electrovalves of 5/2 type.
Therefore, the whole robotized work cell for assembling a multi-cylinder IC engine has been experimentally tested at LARM according to the proposed automatic cycle, which is composed by five main Operations.
Referring to Figure 9, the Cobot end-effector: grasps the vacuum gripper (Figure 9a); grasps the first head gasket (Figure 9b); assembles it on the cylinder block (Figure 9c); releases the vacuum gripper (Figure 9d); grasps the cylinder head (Figure 9e); assembles the cylinder head by using the two-finger gripper (Figure 9f); grasps the vacuum gripper (Figure 9g); assembles the second head gasket (Figure 9h); release the vacuum gripper and grasps the cylinder head cover (Figure 9i); assembles the cylinder cover on the block (Figure 9l); grasps a nut (Figure 9m); screws one nut for time by using the torque limiting screwdriver (Figure 9n).
Moreover, the IC engine in scale of 1:5 and specific parts of the end-effector, have been designed and manufactured by using a 3D printer. Referring to Figure 10, these specific parts consist of the four suction cups of the vacuum gripper (Figure 10a), the two-finger gripper (Figure 10b) and the torque limiting screwdriver (Figure 10c).

Conclusions

A specific parametric and open-source algorithm for the direct and inverse kinematics of a Cobot UR5e has been completely revised, reformulated and implemented in Matlab with the main target to analyze the Cobot UR5e kinematic performance for simulation purposes of industrial applications. Several experimental tests with reference to a specific industrial application for assembling a multi-cylinder IC engine have allowed the validation of the proposed algorithm by giving a good reliability. Specific devices for obtaining the end-effector performance, as vacuum gripper and torque limiting screwdriver, have been designed and manufactured by using a 3D printer. The proposed approach and algorithm can be used to simulate and test different robotized cells which include Cobot and electropneumatic systems to perform several industrial applications.

Acknowledgments

The authors wish to thank the master students Alessia Ampola, Alessandro Capoccia, Domenico Guida and Davide Recchia for their technical support in the development of the proposed industrial application at LARM (Laboratory of Robotics and Mechatronics) of DiCEM, University of Cassino and Southern Lazio.

References

  1. Matheson, E.; Minto, R.; Zampieri, E.G.G.; Faccio, M.; Rosati, G. Human–robot collaboration in manufacturing applications. A review. Robotics 2019, 8, 100. [CrossRef]
  2. Taesi, C.; Aggogeri, F.; Pellegrini, N. COBOT Applications—recent advances and challenges. Robotics 2023, 12, 79. [CrossRef]
  3. Faccio, M.; Granata, I.; Menini, A.; Milanese, M.; Rossato, C.; Bottin, M.; Minto, R.; Pluchino, P.; Gamberini, L.; Boschetti, G.; Rosati, G. Human factors in Cobot era: A review of modern production systems features. Journal of Intelligent Manufacturing 2023, 34, 85–106. [CrossRef]
  4. Othman U.; Yang, E. An Overview of Human-Robot Collaboration in Smart Manufacturing. In 27th International Conference on Automation and Computing (ICAC), Bristol, United Kingdom, (2022), pp. 1–6. [CrossRef]
  5. Cohen, Y.; Shoval, S.; Faccio, M. Strategic View on Cobot Deployment in Assembly 4.0 Systems. IFAC-Papers On Line, 2019, 52, 13, pp. 1519–1524, ISSN 2405-8963. [CrossRef]
  6. Hashemi-Petroodi, S. E.; Thevenin, S.; Kovalev, S.; Dolgui, A.; Operations management issues in design and control of hybrid human-robot collaborative manufacturing systems: a survey. Annual Reviews in Control 2020, 49, 264–276, ISSN 1367-5788. [CrossRef]
  7. Dmytriyev, Y.; Zaki, A. M. A.; Carnevale, M.; Insero, F.; Giberti, H. Brain computer interface for human-Cobot interaction in industrial applications. In 3rd International Congress on Human-Computer Interaction, Optimization and Robotic Applica-tions (HORA), Ankara, Turkey, 2021, pp. 1–6. [CrossRef]
  8. Weiss, A.; Wortmeier, A. -K.; Kubicek, B. Cobots in industry 4.0: a roadmap for future practice studies on human–robot collaboration. IEEE Transactions on Human-Machine Systems 2021, 51 (4), 335–345. [CrossRef]
  9. Ceccarelli, M.; Lanni, C. Multi objective optimum design of general 3R manipulators for prescribed workspace limits. Mechanism and Machine Theory 2004, 39; 119–132, ISSN: 0094-114X.
  10. Lanni, C.; Figliolini, G.; D’Angelo, M. Kinematic Synthesis of a Tendon-Driven 4R Planar Robotic Arm. In CISM International Centre for Mechanical Sciences, Courses and Lectures, 2022, 606, pp. 238–245.
  11. Ceccarelli, M.; Carvalho, J.C.M.; Pugliese, F.; Lanni, C. CaPaMan (Cassino Parallel Manipulator) as Sensored Earthquake Simulator. In International Conference on Robots and Sistems, IROS’99, Kyongiu, 1999, 3, pp. 1501–1506.
  12. Lanni, C.; Pugliese, F.; Ceccarelli, M. Experimental Validation of CaPaMan as Earthquake Simulator. In IEEE/ASME Inter-national Conference on Advanced Intelligent Mechatronics AIM’01, Como, 2001, pp. 153–158.
  13. Figliolini, G.; Lanni, C.; Rea, P.; Gallinelli, T. Mechatronic Design and Control of a 3-RPS Parallel Manipulator. Ferraresi C., Quaglia G. (eds) Advances in Service and Industrial Robotics. In RAAD 2017 Mechanisms and Machine Science, Springer, Cham, 2017, 49, pp. 74–81. doi.org/10.1007/978-3-319-61276-8_9, ISBN 978-3-319-61275-1.
  14. Holland, J.; Kingston, L.; McCarthy, C.; Armstrong, E.; O’Dwyer, P.; Merz, F.; McConnell, M. Service robots in the healthcare sector. Robotics 2021, 10, 47. [CrossRef]
  15. Freeman, W.D.; Sanghavi, D.K.; Sarab, M.S.; Kindred, M.S.; Dieck, E.M.; Brown, S.M.; Szambelan, T.; Doty, J.; Ball, B.; Felix, H.M.; Dove, J.C.; Mallea, J.M.; Soares, C.; Simon, L.V. Robotics in Simulated COVID-19 Patient Room for Health Care Worker Effector Tasks: Preliminary, Feasibility Experiments. Mayo Clin Proc Innov Qual Outcomes. 2021, 5, 1, pp.161–170. [CrossRef]
  16. Babalola, G.T.; Gaston, J.-M.; Trombetta, J.; Tulk Jesso, S.) A systematic review of collaborative robots for nurses: where are we now, and where is the evidence? Front. Robot. AI 2024, 11, 398140. [CrossRef]
  17. Pang, G.; Yang, G.; Pang, Z. Review of robot skin: A potential enabler for safe collaboration, immersive teleoperation, and affective interaction of future collaborative robots. IEEE Transactions on Medical Robotics and Bionics 2021, 3 (3), 681–700. [CrossRef]
  18. Yang, G.; Pang, Z.; Jamal Deen, M.; Dong, M.; Zhang, Y.; Lovell, N.; Rahmani, A. M. Homecare robotic systems for healthcare 4.0: visions and enabling technologies. IEEE Journal of Biomedical and Health Informatics 2020, 24 (9), 2535–2549. [CrossRef]
  19. MajidiRad, A; Yihun, YS. Upper Limb Rehabilitation and Mobility Assistance Using Robotic Devices: A Review. In Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 43rd Mechanisms and Robotics Conference. Anaheim, California, USA. August 18–21, 2019, 5A, V05AT07A039. [CrossRef]
  20. Dalla Gasperina, S.; Roveda, L.; Pedrocchi, A.; Braghin, F.; Gandolla, M. Review on Patient-Cooperative Control Strategies for Upper-Limb Rehabilitation Exoskeletons. Front. Robot. AI 2021, 8, 745018. [CrossRef]
  21. Chiriatti, G.; Bottiglione, A.; Palmieri, G. Manipulability Optimization of a Rehabilitative Collaborative Robotic System. Machines 2022, 10, 452. [CrossRef]
  22. Bogue, R. Robots that interact with humans: a review of safety technologies and standards. Industrial Robot: An International Journal 2017, 44 (4). [CrossRef]
  23. Sherwani, F.; Asad, M. M.; Ibrahim, B. S. K. K. Collaborative Robots and Industrial Revolution 4.0 (IR 4.0). In 2020 Interna-tional Conference on Emerging Trends in Smart Technologies, ICETST, Karachi, Pakistan, 2020, pp. 1–5. [CrossRef]
  24. Borboni, A.; Reddy, K.V.V.; Elamvazuthi, I.; AL-Quraishi, M.S.; Natarajan, E.; Azhar Ali, S.S. The expanding role of artificial intelligence in collaborative robots for industrial applications: a systematic review of recent works. Machines 2023, 11, 111. [CrossRef]
  25. Sahan, A. S. M.; Kathiravan, S.; Lokesh, M.; Raffik, R. Role of Cobots over Industrial Robots in Industry 5.0: A Review. In 2nd International Conference on Advancements in Electrical, Electronics, Communication, Computing and Automation, ICAECA, Coimbatore, India, 2023, pp. 1–5. [CrossRef]
  26. Galin, R.; Meshcheryakov, R.; Samoshina, A. Mathematical Modelling and Simulation of Human-Robot Collaboration. In Proceedings of 2020 International Russian Automation Conference (RusAutoCon), Sochi, Russia, 2020, pp. 1058-1062. [CrossRef]
  27. Dikmenli, S. Forward & Inverse Kinematics Solution of 6-DOF Robots Those Have Offset & Spherical Wrists. Eurasian J. Sci. Eng. Technol. 2022, 3, 14–28.
  28. Li, L.; Huang, Y.; Guo, X.X. Kinematics modelling and experimental analysis of a six-joint manipulator. Journal Européen des Systèmes Automatisés 2019, 52 (5), 527–533. [CrossRef]
  29. Abdelaziz, O.; Minzhou, L.; Guanwu, J.; Saixuan, C. Multiple configurations for puncturing robot positioning. International Journal of Advance Robotics & Expert Systems (JARES) 2019, 1 (4), 1–19.
  30. Wang, C.; Liu, D.; Sun, Q.; Wang, T. Analysis of open architecture 6R robot forward and inverse kinematics adaptive to structural variations. Mathematical Problems in Engineering 2021, 4516109, 11 pages, . [CrossRef]
  31. Wang, X.; Zhang, Z.; Meng, X. Kinematic analysis and trajectory planning for a tree planting robot in forest environment. Journal of Vibroengineering 2023, 25 (3), 630–640. [CrossRef]
  32. Elhadidy, M. S.; Abdalla, W. S.; Abdelrahman, A. A.; Elnaggar, S.; Elhosseini, M. Assessing the accuracy and efficiency of kinematic analysis tools for six-DOF industrial manipulators: The KUKA robot case study. AIMS Mathematics 2024, 9 (6): 13944-13979. [CrossRef]
Preprints 115885 g001
Figure 1. UR5e Cobot: a) a 3D view; b) D-H reference frames.
Figure 1. UR5e Cobot: a) a 3D view; b) D-H reference frames.
Preprints 115885 g001
Preprints 115885 g002
Figure 2. Multi-cylinder IC engine: main components.
Figure 2. Multi-cylinder IC engine: main components.
Preprints 115885 g002
Preprints 115885 g003
Figure 3. Robotized work cell: working table.
Figure 3. Robotized work cell: working table.
Preprints 115885 g003
Preprints 115885 g004
Figure 4. Operation 1 of the automatic cycle: elementary actions.
Figure 4. Operation 1 of the automatic cycle: elementary actions.
Preprints 115885 g004
Preprints 115885 g005
Figure 5. Operation 1: (a) 3D view; (b) XY-plane; (c) XZ-plane; (d) YZ-plane.
Figure 5. Operation 1: (a) 3D view; (b) XY-plane; (c) XZ-plane; (d) YZ-plane.
Preprints 115885 g005
Preprints 115885 g006
Figure 6. Automatic cycle – Operations 1 to 5 (workspace and points cloud): (a) 3D view; (b) XY-plane; (c) XZ-plane; (d) YZ-plane.
Figure 6. Automatic cycle – Operations 1 to 5 (workspace and points cloud): (a) 3D view; (b) XY-plane; (c) XZ-plane; (d) YZ-plane.
Preprints 115885 g006
Preprints 115885 g007
Figure 7. Robotized work cell: mechatronic scheme.
Figure 7. Robotized work cell: mechatronic scheme.
Preprints 115885 g007
Preprints 115885 g008
Figure 8. The electro-pneumatic circuit.
Figure 8. The electro-pneumatic circuit.
Preprints 115885 g008
Preprints 115885 g009
Figure 9. Application: robotized assembling of a multi-cylinder IC engine.
Figure 9. Application: robotized assembling of a multi-cylinder IC engine.
Preprints 115885 g009
Preprints 115885 g010
Figure 10. End-effector devices: a) suction cups of the vacuum gripper; b) two-finger gripper; c) torque limiting screwdriver.
Figure 10. End-effector devices: a) suction cups of the vacuum gripper; b) two-finger gripper; c) torque limiting screwdriver.
Preprints 115885 g010
Table 1. D-H parameters for the UR5e Cobot.
Table 1. D-H parameters for the UR5e Cobot.
Link number i θ i [rad] di [mm] ai [mm] α i [rad]
1 θ1 162.5 0 π / 2
2 θ2 0 − 425 0
3 θ3 0 − 392.2 0
4 θ4 133.3 0 π / 2
5 θ5 99.7 0 − π / 2
6 θ6 99.6 0 0
Table 2. Cartesian components of p and r for the assigned UR5e Cobot pose.
Table 2. Cartesian components of p and r for the assigned UR5e Cobot pose.
px [mm] py [mm] pz [mm] rx [rad] ry [rad] rz [rad]
135.00 − 292.13 523.81 2.22 − 2.19 0.022
Table 3. Joint angles for the assigned UR5e Cobot pose of Table 2.
Table 3. Joint angles for the assigned UR5e Cobot pose of Table 2.
θ1 [°] θ2 [°] θ3 [°] θ4 [°] θ5 [°] θ6 [°]
90.5785 −117.0569 105.3867 279.9306 − 90.7226 − 89.4325
Table 4. Tool end-effector position and orientation.
Table 4. Tool end-effector position and orientation.
px [mm] py [mm] pz [mm] rx [rad] ry [rad] rz [rad]
135.1514 − 292.2861 523.2706 2.2012 − 2.2016 0.0178
Table 5. Operation 1: experimental Cartesian components of vectors p and r for each Cobot pose.
Table 5. Operation 1: experimental Cartesian components of vectors p and r for each Cobot pose.
Point px [mm] py [mm] pz [mm] rx [rad] ry [rad] rz [rad]
Home (A) 135.00 − 292.13 523.81 2.22 − 2.19 0.022
B − 256.31 − 213.52 255.33 2.22 − 2.18 0.040
C − 255.12 − 220.86 166.42 2.22 − 2.22 − 0.021
D − 265.84 − 375.95 241.53 2.22 − 2.21 0.021
E − 265.72 − 375.91 163.90 2.21 − 2.22 0.021
F 29.16 − 388.82 536.41 3.14 − 0.001 − 0.032
G 230.32 − 288.63 612.22 3.01 − 0.011 0.094
H 250.10 − 344.72 417.03 3.14 − 0.031 0.001
Table 6. IK Cobot model: Numerical and experimental joint angles θ i (i = 1, …, 6).
Table 6. IK Cobot model: Numerical and experimental joint angles θ i (i = 1, …, 6).
Numerical Joint Angles Experimental Joint Angles
Point θ1 [°] θ2 [°] θ3 [°] θ4 [°] θ5 [°] θ6 [°] θ1 [°] θ2 [°] θ3 [°] θ4 [°] θ5 [°] θ6 [°]
A 90.5785 −117.0569 105.3867 279.9306 −90.7226 −89.4325 89.92 −1167.49 105.33 283.18 −88.73 −89.39
B 15.5453 −107.0629 140.3619 235.9249 −87.8703 −164.4402 15.35 −107.17 140.69 234.91 −87.93 −163.49
C 17.5589 −91.77808 147.6393 212.2606 −89.8548 −162.4388 17.67 −91.80 147.38 213.06 −90.27 −164.11
D 37.6901 −85.4407 124.6513 229.1634 −89.0490 −142.2964 37.87 −85.27 123.70 232.34 −89.50 −141.09
E 37.6981 −75.9854 129.2307 215.1258 −89.0492 −142.2884 37.85 −76.14 128.36 218.44 −89.51 −141.09
F 74.7950 −105.4460 95.2677 283.1362 −91.9135 −195.0839 75.01 −105.92 95.08 281.11 −91.08 −194.97
G 107.1736 −109.1401 89.5395 280.9065 −89.1269 −162.3781 107.03 −108.80 88.91 282.65 −88.53 −162.51
H 108.3671 −102.3689 113.4437 251.2545 −92.6226 −160.6629 107.57 −101.31 109.98 261.99 −89.49 −161.36
Table 7. Operation 1: Numerical results for the Cartesian components of p and r for each joint in different poses.
Table 7. Operation 1: Numerical results for the Cartesian components of p and r for each joint in different poses.
Point Joint n. px [mm] py [mm] pz [mm] rx [rad] ry [rad] rz [rad]
Home (A) 1 0 0 162.5000 1.2042 1.2169 1.2169
2 − 2.0205 192.9354 541.1778 − 0.3774 1.5366 − 0.3613
3 2.0027 − 191.2330 620.0405 1.0530 1.3050 1.0666
4 135.2954 − 189.8371 620.0405 1.1810 1.1934 − 1.2145
5 136.3390 − 289.4927 622.8243 0.0161 − 3.1292 0.0438
6 135.1514 − 292.2861 523.2706 2.2012 − 2.2016 0.0178
B 1 0 0 162.5000 1.5603 0.2124 0.2124
2 120.4221 33.3960 568.7120 0.8237 1.5046 − 1.2297
3 − 195.4594 − 54.2057 353.3853 1.5909 − 0.2491 0.6652
4 − 159.8366 − 182.6576 353.3853 2.0614 0.2805 − 2.0904
5 − 255.902 − 209.2987 354.77773 1.8885 2.4841 − 0.0520
6 − 256.2650 − 213.1871 255.2539 2.1983 − 2.2016 0.0390
C 1 0 0 162.5000 1.5573 0.2411 0.2411
2 12.7247 4.0365 587.2903 0.9615 1.3580 − 1.0037
3 − 197.4053 − 62.6207 262.9093 1.5704 − 0.5438 0.9932
4 − 157.0994 − 189.6810 262.9093 2.0175 0.3123 − 2.0892
5 − 252.0746 − 219.8089 266.3888 −1.8446 − 2.5205 0.0472
6 − 255.2828 − 221.1913 166.8500 2.1984 − 2.1983 − 0.0202
D 1 0 0 162.500 1.5087 0.5151 0.5151
2 − 26.3834 − 20.3914 586.1899 0.7651 1.4151 − 0.6517
3 − 267.2045 − 206.5191 338.8388 1.6707 − 0.0204 1.0378
4 − 185.6880 − 311.9892 338.8388 1.8299 0.6247 − 1.8524
5 − 264.5671 − 372.9539 340.0569 1.3805 2.8122 − 0.0280
6 − 264.5730 − 374.9358 240.4766 2.2096 − 2.2132 0.0220
E 1 0 0 162.5000 1.5087 0.5151 0.5151
2 − 81.3511 − 62.8753 574.8757 0.8722 1.3354 − 0.5232
3 − 267.2388 − 206.5456 260.8288 1.6974 − 0.2310 1.2208
4 − 185.7222 − 312.0157 260.8288 1.8118 0.6186 − 1.8664
5 − 264.5725 − 372.9581 263.7866 1.3829 2.8175 − 0.0539
6 − 265.8470 − 376.1401 164.2456 2.1993 − 2.1987 0.0211
F 1 0 0 162.5000 1.3231 1.0116 1.0116
2 29.5910 108.9131 572.2405 − 0.0028 1.5862 − 0.4186
3 − 71.6460 − 263.7012 641.0194 1.2109 1.1076 0.8781
4 56.9907 − 298.6510 641.0194 1.4456 1.1053 − 1.3719
5 30.8862 − 394.7313 635.8015 − 0.4106 − 3.0872 − 0.0877
6 29.0655 − 388.8379 536.3927 3.0823 − 0.0014 − 0.0282
G 1 0 0 162.5000 1.0519 1.4268 1.4268
2 −41.1234 132.8483 564.1033 − 0.4893 1.4927 − 0.0260
3 68.1333 − 220.1031 695.6674 0.7623 1.5222 1.1783
4 195.4719 − 180.6852 695.6674 0.8933 1.2117 − 1.0386
5 224.6225 − 274.8556 710.5761 − 0.4647 3.0603 − 0.2265
6 230.5206 − 288.6189 612.1081 3.0017 − 0.0087 0.0900
H 1 0 0 162.5000 1.0408 1.4405 1.4405
2 − 27.7451 83.8936 578.2127 − 0.4107 1.5168 0.0864
3 92.9731 − 281.1248 500.6915 1.2119 1.3673 1.5799
4 219.5315 − 239.2696 500.6915 0.9959 1.3784 − 0.9551
5 250.8091 − 333.8443 496.5165 0.4973 − 3.0859 − 0.0625
6 248.6744 − 330.1575 397.0077 − 3.1044 0.0295 0.0338
Table 8. Automatic cycle: Operations 2 to 5.
Table 8. Automatic cycle: Operations 2 to 5.
Point px [mm] py [mm] pz [mm] rx [rad] ry [rad] rz [rad]
P1 249.70 − 342.81 360.58 3.16 − 0.02 0.004
P2 − 204.10 − 533.41 306.78 2.22 − 2.25 0.013
P3 − 204.10 − 533.41 195.63 2.22 − 2.25 0.013
P4 − 207.12 − 511.45 276.62 2.22 − 2.25 0.013
P5 247.87 − 346.82 454.02 3.16 0.02 0.03
P6 249.59 − 345.17 371.00 3.16 − 0.02 0.03
P7 249.47 − 343.13 404.36 3.16 0.03 0.04
P8 249.88 − 343.05 391.14 3.16 0.04 0.04
P9 − 212.24 − 754.73 262.86 2.22 − 2.23 − 0.004
P10 − 212.26 − 754.73 154.67 2.22 − 2.23 − 0.004
P11 − 208.00 − 730.99 196.68 2.22 − 2.23 − 0.004
P12 − 208.00 − 730.99 500.27 2.22 − 2.23 − 0.004
P13 249.43 − 343.44 407.36 3.16 0.03 − 0.007
P14 249.43 − 343.44 391.06 3.16 0.03 − 0.007
P15 45.39 − 709.32 262.09 3.14 − 0.02 − 0.003
P16 45.38 − 709.34 172.66 3.14 − 0.02 − 0.003
P17 45.43 − 709.33 164.43 3.14 − 0.02 − 0.003
P18 62.98 − 709.34 172.67 3.14 − 0.02 − 0.003
P19 62.97 − 709.34 489.97 3.14 − 0.02 − 0.003
P20 350.91 − 219.13 457.07 2.23 2.21 − 0.003
P21 350.91 − 219.13 369.34 2.23 2.21 − 0.003
P22 80.48 − 709.35 458.41 3.14 − 0.02 − 0.003
P23 62.97 − 709.34 162.52 3.14 − 0.02 − 0.003
P24 80.01 − 709.34 170.84 3.14 − 0.02 − 0.003
P25 79.98 − 709.34 163.14 3.14 − 0.02 − 0.003
P26 148.41 − 219.39 428.21 2.19 − 2.25 − 0.001
P27 148.41 − 219.39 373.21 2.19 − 2.25 − 0.001
P28 148.14 − 218.82 368.50 2.19 − 2.25 − 0.001
P29 96.81 − 709.35 480.33 3.14 − 0.02 − 0.003
P30 96.83 − 709.36 169.82 3.14 − 0.02 − 0.003
P31 96.85 − 709.35 163.01 3.14 − 0.02 − 0.003
P32 351.10 − 468.05 505.43 2.23 2.21 − 0.003
P33 351.10 − 468.07 376.59 2.23 2.21 − 0.003
P34 351.10 − 468.05 368.62 2.23 2.21 − 0.003
P35 45.39 − 709.32 262.09 3.14 − 0.02 − 0.003
P36 45.36 − 709.32 452.23 3.14 − 0.02 − 0.003
P37 149.74 − 468.35 409.49 2.19 − 2.25 − 0.001
P38 149.76 − 468.34 368.40 2.19 − 2.25 − 0.001
P39 61.33 − 710.24 272.55 3.14 − 0.03 − 0.001
Table 9. Operations 2 to 5: Numerical and experimental joint angles θ i (i = 1, …, 6).
Table 9. Operations 2 to 5: Numerical and experimental joint angles θ i (i = 1, …, 6).
Numerical Joint Angles Experimental Joint Angles
Point θ1 [°] θ2 [°] θ3 [°] θ4 [°] θ5 [°] θ6 [°] θ1 [°] θ2 [°] θ3 [°] θ4 [°] θ5 [°] θ6 [°]
P1 107.6365 −99.3506 117.1694 253.1430 −89.5350 −161.6433 107.57 −99.60 116.06 254.39 − 89.56 − 161.88
P2 55.4440 −76.0835 101.2743 245.8053 −89.3297 −123.7928 55.36 −76.52 100.45 246.85 − 89.30 − 123.86
P3 55.3847 −67.5512 108.7537 229.7942 −89.3307 −123.8521 55.35 −68.33 108.27 230.86 − 89.35 − 125.19
P4 53.8547 −76.5769 106.8856 240.7056 −89.3576 −125.3819 53.76 −77.12 106.13 241.79 − 89.33 − 124.87
P5 106.9999 −101.6459 105.1439 267.2125 −88.6524 −163.7341 106.71 −101.65 103.86 268.53 − 88.64 − 163.99
P6 107.2986 −99.6532 115.8993 254.4402 −88.6399 −161.9843 106.94 −99.95 114.79 255.92 − 88.56 − 162.26
P7 107.2833 −101.1141 112.0731 259.6551 −88.3009 −163.8136 106.95 −101.36 110.97 260.96 − 88.43 − 164.28
P8 107.3434 −100.6818 113.7019 257.6038 −88.3004 −164.1163 107.01 −100.98 112.64 258.91 − 88.44 − 164.32
P9 64.5092 −45.9403 61.4529 254.8084 −90.0401 −115.2331 64.51 −46.20 60.45 256.33 − 89.82 − 115.30
P10 64.5079 −40.0146 67.4887 2424.8470 −90.0401 −115.2345 64.50 −40.45 66.91 244.21 − 89.83 − 115.27
P11 64.0138 −45.8566 71.6477 244.5296 −90.0429 −115.7286 64.02 −46.33 70.95 245.96 − 89.84 − 115.76
P12 64.0073 −49.9489 33.2644 287.0053 −90.0429 −115.7351 64.03 −49.06 30.27 289.36 − 89.79 − 115.86
P13 107.6691 −100.9279 111.3508 260.6680 −89.9295 −163.4194 107.74 −101.04 110.22 261.57 − 89.98 − 163.23
P14 107.6691 −100.4465 113.4000 258.1374 −89.9295 −163.4194 107.74 −101.61 112.30 259.06 − 89.98 − 163.23
P15 82.8660 − 56.0413 79.0811 246.8603 −90.0984 −186.4042 82.91 −56.55 78.44 248.18 − 89.98 − 186.47
P16 82.8344 −50.2574 83.8791 236.3032 −89.8807 −186.5817 82.90 −50.97 83.53 237.49 − 90.00 − 186.45
P17 82.8383 −49.6330 84.1870 235.3772 −89.8807 −186.5777 82.90 −50.36 83.85 236.56 − 90.00 − 186.45
P18 84.2996 −50.0972 83.5904 236.4094 −90.1009 −184.9706 84.33 −50.81 83.24 237.63 − 90.00 − 185.02
P19 84.2988 −60.0954 51.5179 2784793 −90.1009 −184.9714 84.35 −59.06 45.24 283.87 − 89.94 − 185.11
P20 129.2453 −103.6014 106.3970 267.0796 −90.0980 −230.2387 129.33 −103.66 105.13 268.50 − 90.05 − 230.04
P21 129.2358 −101.5551 117.9751 253.0543 −90.0607 −229.9885 129.30 −101.86 116.74 255.09 − 90.07 − 230.04
P22 85.7261 −60.3614 56.5674 273.6991 −90.1033 −183.5441 85.78 −60.29 55.10 275.25 − 89.95 − 183.66
P23 84.2988 −49.3263 83.9575 235.2715 −90.1009 −184.9714 84.33 −50.06 83.64 236.48 − 90.00 − 185.02
P24 85.6877 −49.7631 83.2668 236.3714 −90.1032 −183.5825 85.72 −50.48 82.95 237.59 − 89.99 − 183.63
P25 85.6869 −49.1795 83.5740 235.5107 −90.1032 −183.5833 85.71 −49.91 83.25 236.72 − 89.99 − 183.63
P26 93.9046 −128.0236 123.5710 274.4155 −90.1001 −84.5470 93.85 −127.87 122.20 275.78 − 89.99 − 84.92
P27 93.8978 −128.0929 131.6145 266.3776 −90.1001 −84.5538 93.81 −128.16 130.34 267.93 − 89.92 − 84.92
P28 93.8468 −128.1713 132.3510 265.7830 −90.1001 −84.6048 93.75 −128.25 131.06 267.30 − 89.92 − 84.99
P29 87.0558 −59.6669 52.2767 277.2964 −90.1053 −182.3640 87.11 −59.49 50.64 278.91 − 89.94 − 182.34
P30 87.0575 −49.4445 82.8882 236.4625 −90.1053 −182.3587 87.09 −50.16 82.55 237.67 − 89.99 − 182.26
P31 87.0590 −48.9304 83.1335 235.7032 −90.1053 −182.3571 87.09 −49.66 82.81 236.91 − 89.99 − 182.26
P32 113.7164 −79.3580 75.4713 273.7401 −90.0610 −245.7675 113.79 −79.34 74.42 274.87 − 89.97 − 245.61
P33 113.7138 −77.6356 92.6656 254.8234 −90.0610 −245.7701 113.77 −77.99 91.73 256.21 − 90.00 − 245.58
P34 113.7155 −77.3475 93.5163 253.6847 −90.0610 −245.7684 113.77 −77.72 92.59 255.08 − 90.00 − 245.58
P35 82.8660 −56.0415 79.0819 246.8584 −90.0981 −186.5502 82.91 −56.55 78.44 248.18 − 89.99 − 186.47
P36 82.8635 −60.9276 58.3409 272.4855 −90.0981 −186.5526 82.92 −60.88 56.91 274.03 − 89.95 − 186.52
P37 92.0212 −91.4461 102.9689 258.4368 −90.0989 −86.4304 92.02 −91.68 101.84 259.95 − 89.87 − 86.75
P38 92.0237 −89.9950 107.7454 252.2092 −90.0989 −86.4279 92.01 −90.37 106.72 253.76 − 89.88 − 86.75
P39 84.1624 −56.3150 77.8781 248.3497 −90.0285 −184.8159 84.19 −56.90 77.43 249.29 − 89.89 − 184.75
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated