Parameter Identification of Photovoltaic Module based Triple-Diode using Hybrid Optimization Algorithms

Identification the parameters of triple-diode electrical circuit structure of PV-module is a challenging issue and has been emphasized as an important research area. Accordingly, a hybrid evolutionary optimization algorithm is presented in this paper. Differential evolution algorithm (DEA) is hybridized with electromagnetism-like algorithm (EMA) in the mutation stage to enhance the reliability and efficiency of DEA. The presented algorithm is called differential evolution with integrated mutation per iteration (DEIMA). A new formula is presented to adapt the control parameters (mutation factor and crossover rate) of DEA and is based on a sigmoid function in terms of the current and previous fitness function values. Seven different experimental data sets are used to assess the performance of the proposed DEIMA. The results of the proposed PV modeling method are evaluated with other approaches in literature. According to different statistical criteria, DEIMA offered superiority in terms of root mean square error and main bias error by at least 5.4% and 10%, respectively, as compared to other methods. Furthermore, DEIMA needs 27.69 sec. as an average execution time less than other compared methods.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The plant pollution and the fluctuation of fossil fuel prices due to political and economic crises around the world are the main problems that affect the energy field. As well as for the aforementioned drawbacks of conventional energy sources, the fossil fuel is not abundant and sustainable [1]. Furthermore, the energy demand is dramatically increasing with time, due to the luxury live style demands. Therefore, finding a new sustainable energy source is a hot topic of research. Solar energy has been represented as one of the important and promising alternative energy sources [2,3]. The photovoltaic (PV) technology is playing an important role for converting the solar irradiance into direct current electricity. The long-life cycle time of PV and environmentally friendly are presenting the most advantages of this technology [4]. In addition, the price of PV module is also decreasing overtime [4]. The basic drawback of PV module is the low efficiency of converting solar energy into electricity [5]. This issue makes the output of PV module is limited and suffers from weather fluctuations. Therefore, the modeling of PV module has to be more accurate to enable the project administrator to use an appropriate number of PV modules in order to achieve the reliability and cost-effective PV system. Modeling PV module significantly depends on the process of estimating the identification unknown parameters of equivalent electrical circuit of module. These parameters are unknown and sensitive to weather conditions. Generally, estimating PV module parameters is obtained via three approaches; analytical, numerical, and artificial intelligent (AI)-based method [6]. In analytical method, a relationship is presented between the parameters of PV module under the standard test condition (STC) and other weather condition using manufacturer data [7]. The importance of analytical approaches is tended to be fast and simple for calculating the parameters [8]. The main issue of analytical method is the significant deviation between the experimental and simulated performance due to the impact of geographical situation on PV module parameters.

The numerical method is proposed by scholars to overcome the drawbacks of analytical method. In numerical method, all the points of I-V characteristic curve are used based on an iteration method to extract the parameters of PV module [9]. The numerical method offers an accurate estimation for PV modules parameters than analytical method. The drawbacks of numerical method are its requirement for big I-V data curve, and the accuracy of results is affected by the assumed initial conditions of parameters [10]. Furthermore, the numerical method needs for great computational resources. A combination of numerical and analytical methods (compound method) have been presented by [11,12,13] to obtain the benefit of the aforementioned methods. The drawbacks of both analytical and numerical methods are still existed in the compound method.

The third type of PV modeling method that based on AI. Many research works adopted artificial neural network (ANN) for modeling PV module [14]. The ANN-based PV modeling represents as a black box that requires a big data of I-V characteristic points. Moreover, it represents a complex location dependent modeling method.

Due to the reliability and efficiency of metaheuristic algorithms, the last are extensively used for modeling PV module [15]. The I-V characteristic of PV module is nonlinear, so the metaheuristic is an appropriate choice for handling the modeling problem. Big research efforts are devoted for estimating the parameters of single diode model (SDM) and double diodes model (DDM) of PV module using various metaheuristic algorithms since last decade. On the other hand, a humble research works was devoted for determining the parameters of triple diode model (TDM) of PV module. In [16], the authors have utilized an iterative process using the PSO algorithm to estimate PV model parameters and by fitting the measured I-V curves to the calculated I-V curves. The series resistance parameter has been considered to vary linearly with the load current through the device. The proposed TDM in [16] is demonstrated in comparison to the two-diode model, and the findings indicated how the TDM performance is better than DDM. Meanwhile, nine unknown parameters of the TDM PV module have been extracted via a novel implementation of the coyote optimization algorithm (COA) which has been presented in [17]. The obtained ideal design variables of the presented COA-TDM have been studied against the ideal variables achieved through whale optimization algorithm (WOA)-based TDM PV model, genetic algorithm (GA), and simulated annealing (SA), for both modules (KC200GTand MSX-60). The proposed COA-TDM showed an optimal design variable that are really close to that achieved by applying other metaheuristic optimization algorithms regarding both two commercial PV modules. In [18] a compound of analytical and an improved differential evolution algorithm called IDEA is presented to identify the parameters of DDM and TDM of PV module. For both the TDM and DDM, the parameters were partially extracted via analytical process (seven TDM parameters and five DDM parameters) and by using optimization techniques (both TDM and DDM have two variables). In [19] a slime mould algorithm (SMA) is presented according to the slime mould’s natural oscillation. Based on a unique mathematical expression, the SMA is introduced which adapting the weights to collect negative and positive feedback of the slime mould propagation wave. According to the results of [19], the SMA showed better performance as compared to other heuristic methods in TDM, DDM and SDM. A transient search optimization (TSO) is proposed in [20] which is based on a novel competent meta-heuristic optimizer and aims to estimate the TDM PV module’s optimal nine-parameter. Different companies have applied the TSO for given objective function to identify three PV modules. Accordingly, the PV’s I-V characteristics have been validated by the measured data with regards to different solar radiations and temperatures. The TSO algorithm has proved his effectiveness as compared to other models as it has been indicated through the convergence curves. Authors in [21] have customized collected data and mathematical representation of PV model of different diode numbers (SDM/DDM/TDM), where the optimal parameters of the studied approach have been determined according to the fractional chaotic ensemble particle swarm optimizer FC-EPSO variants and other models. The root mean square error (RMSE) is also one of the datasets that has been calculated and assessed and adapted as an objective function by the proposed algorithm. To justify the superiority of the presented approach, it has been justified against other approaches presented in literature. The outcomes in [21] have showed a least deviation between the estimated and measured curves with fastest convergence.

Integrating the computation and harris hawk optimization (HHO) algorithm is another approach that is presented in [22] to determine the parameters of TDM regarding PV module. In this work, the authors utilized the standard test conditions (STC) datasheet values of PV modules with normal operating cell temperature (NOCT) to analytically examine four parameters while finding the remaining five parameters by relying on the HHO model. Seeking to estimate the parameters, two commercial PV panels have been used as monocrystalline CS6K280M and multi-crystal KC200GT. The results in [22] has proved the efficacy of the presented model and by depending on the datasheet values only it can simply implement to find the electrical parameters of any commercial PV panel. In [23] a new optimization method namely interval branch and bound algorithm is introduced and validated for three different parameter estimation models of PV cells (SDM, DDM and TDM). outcomes have been justified against other results in literature of the same data set. The behavior of the presented model is examined with regards to convergence speed and results in variability as comparison to metaheuristics. The estimated performance features of the tested cells for both P-V and I-V shown to be very similar to the experimental data and the obtained findings are really close to other efficient algorithms. In [24], an improved wind driven optimization (IWDO) model is presented and applied to calculate triple-diode parameters of the PV cell model. In order to evaluate the proposed model, IWDO model has been implemented on three various PV model techniques, which are poly-crystalline, mono-crystalline, and thin- film. Accordingly, the obtained results have been compared with other findings collected from other contributions to validate its accuracy. According to results of [24], the presented algorithm showed superiority over other models in terms of accuracy and convergence speed. The authors of [25] have relied on manta ray foraging optimization (MRFO) to find the unknown parameters of PV cells. using MRFO is adapted to extract the optimal PV parameters of the single, double, and three-diode algorithms. Based on comparative results between different metaheuristic algorithms and MRFO, findings proved that MRFO has supported a better balance among experimental and calculated I–V curves. In [26] an enhanced LSHADE optimization model called Chaotic LSHADE (CLSHADE) model which is traced to the Lambert W-function and has been presented to estimate TDM and DDM parameters of the PV equivalent circuits. The outcomes indicated that the accuracy of the CLSHADE model could be enhanced through adapting the presented solar cell current expressions where the RMSE is calculated based on them. For the purpose of investigating a complete photovoltaic algorithm, authors in [27] have proposed an improved spherical evolution technique that is based on a novel dynamic sine-cosine mechanism (DSCSE). The experimental findings have indicated the superiority of DSCSE over other comparative approaches with different models and provided superior outcomes regardless different temperatures and light intensities. Based on the DE (HDE), a novel heterogeneous mechanism is presented in [28] to identify PV model parameters. Parameter fitting for the DDM, SDM, STP6-120/36 MM, TDM, Photowatt-PWP201 MM, and STM6-40/36 MM were determined by HDE. The findings indicated the superiority of the HDE for majority of PV techniques. Moreover, the HDE also takes low execution time to conduct its task. Although the HDE showed necessary features, its behavior regarding few PV models like TDM and DDM can be further improved. In [29], an enhanced model of the slime mould technique and based on Lambert W-function (ImSMA_LW) is proposed for extracting parameters of SDM, DDM, and TDM of PV module. According to [29], ImSMA_LW offered compromised results under various scenarios with different conditions.

A combination of two metaheuristic algorithms is proposed for estimating the nine parameters of TDM in this research. The electromagnetism-like algorithm (EMA) used the attraction-repulsion concept to synergic the mutation strategy of conventional DE algorithm. The proposed metaheuristic is called differential evolution with integrated mutation per iteration algorithm (DEIMA). In DEIMA, both mutation strategies of EMA and DEA are applied in the same iteration. Furthermore, a new adaptive formula has proposed in this paper to realize adaptive mutation factor and crossover rate values of DEA’S mutation strategy. The adaptive technique in this formula is based on evolution of the fitness function. The proposed PV modeling method is validated by experimental I-V data for seven operation conditions. In addition, the results of the proposed DEIMA are evaluated through conducting a comparison with other related contributions in literature.

The manuscript is structured as follows; the introduction part is presented in section one. In section two, the model of triple diode PV module and the formulating of PV module parameter estimation process as optimization problem are discussed. The proposed DEIMA is discussed in section 3. Next, the evaluation criteria that utilized for evaluating results of DEIMA are presented in section 4. The results of the proposed DEIMA-based PV modeling method are presented, discussed, and evaluated in section 5. The conclusion of this contribution and suggestions for future work are drawn in section 6.

2. PV Modeling Method

In this section, the mathematical representation of triple-diode PV module is presented. Furthermore, parameter estimation of the TDM-PV module that considered as an optimization problem is discussed.

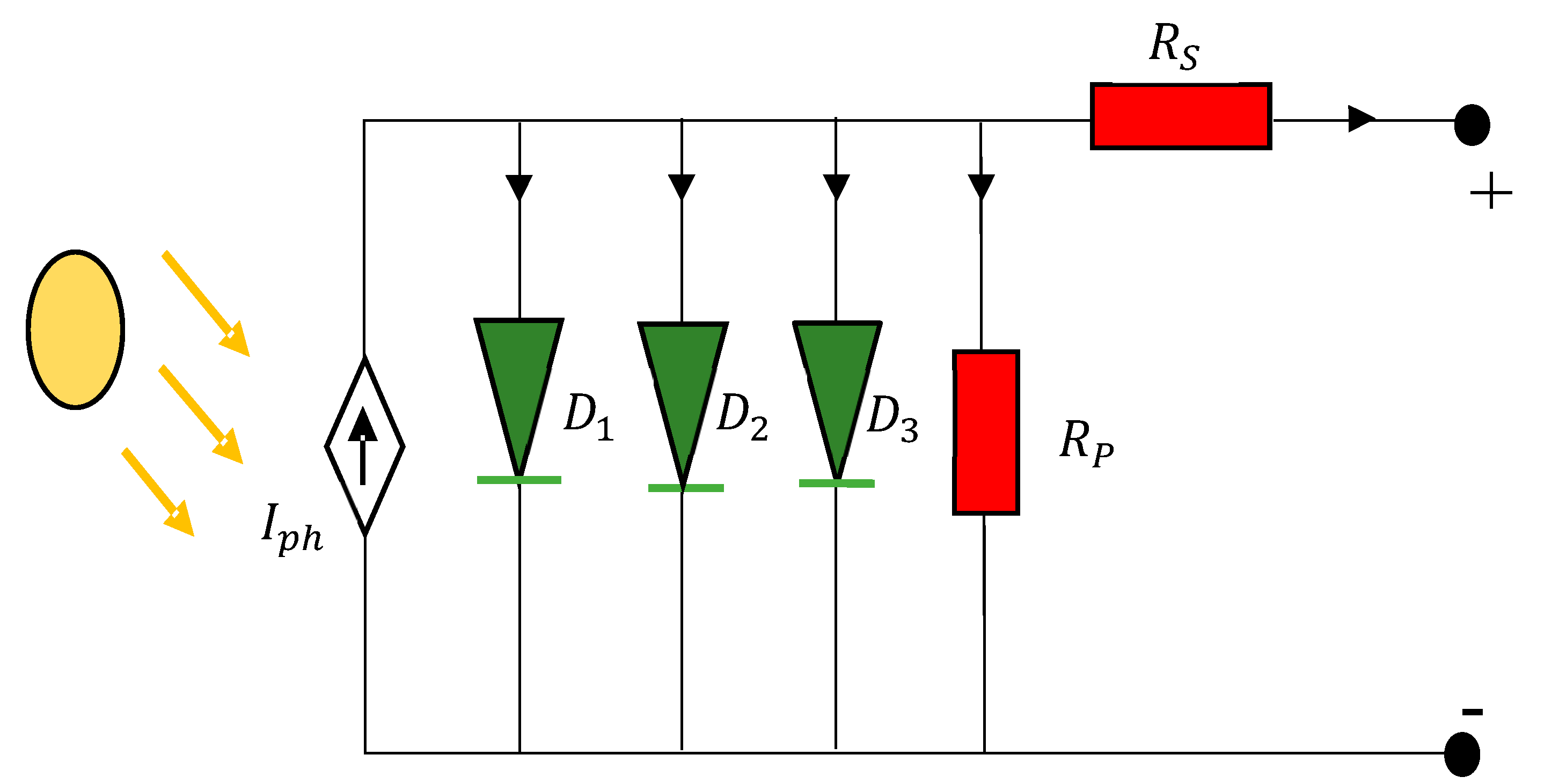
2.1. Triple-Diode PV Module Model

The TDM of PV module comprises three diodes that connected in parallel as shown in Figure 1. The third diode is added into equivalent electrical circuit of PV module to simulate the recombination in grain sites and defect regions. The PV output current can be formulated by [22]:

I {= I}_{p h} - I_{o 1} [e x p (q \frac{V + I R_{S}}{a_{1} B T_{C}}) - 1] - I_{o 2} [e x p (q \frac{V + I R_{S}}{a_{2} B T_{C}}) - 1] - I_{o 3} [e x p (q \frac{V + I R_{S}}{a_{3} B T_{C}}) - 1] - \frac{V + I R_{S}}{R_{P}}

(1)

Where

I

and

I_{p h}

are the PV output current (A) and photogenerated current (A), respectively.

I_{o 1}, I_{o 2}, and I_{o 3}

are respectively the saturation currents (A) that flows in the first, second, and third diodes.

V

is the PV output voltage (V).

a_{1}, a_{2}, and a_{3}

are respectively the ideality factors of the first, second, and third diodes.

q

B

, and

T_{C}

are the electron charge (1.60217646E-19C), Boltzman constant (1.3806503E-23J/K), and cell temperature (K), respectively.

R_{S}

and

R_{P}

are the series and parallel resistors (Ω), respectively.

According to Eq. (1), there are nine indefinite parameters that should be precisely estimated. As it was stated previously, these parameters are related to weather conditions, specifically the ambient temperature and solar irradiance.

2.2. Problem Formulation

The issue of estimating nine indefinite parameters in TDM-PV module can be formulated as an optimization problem with nine decision variables and an objective function as follows;

O F = \sqrt{\frac{1}{n} (\sum_{i = 1}^{n} f {(I_{e}, V, δ)}^{2})}

(2)

where;

f (I_{e}, V, δ) = I_{e} - I

(3)

where

I_{e}

is the experimental output current (A) of PV module. While,

I

refers to the computed current of PV module according to the estimated parameters that described by vector

δ = [I_{p h}, I_{o 1}, I_{o 2}, I_{o 3}, a_{1}, a_{2}, a_{3}, R_{S}, R_{P}]

. Variable

n

represents the total number of points in the experimental I-V characteristic curve.

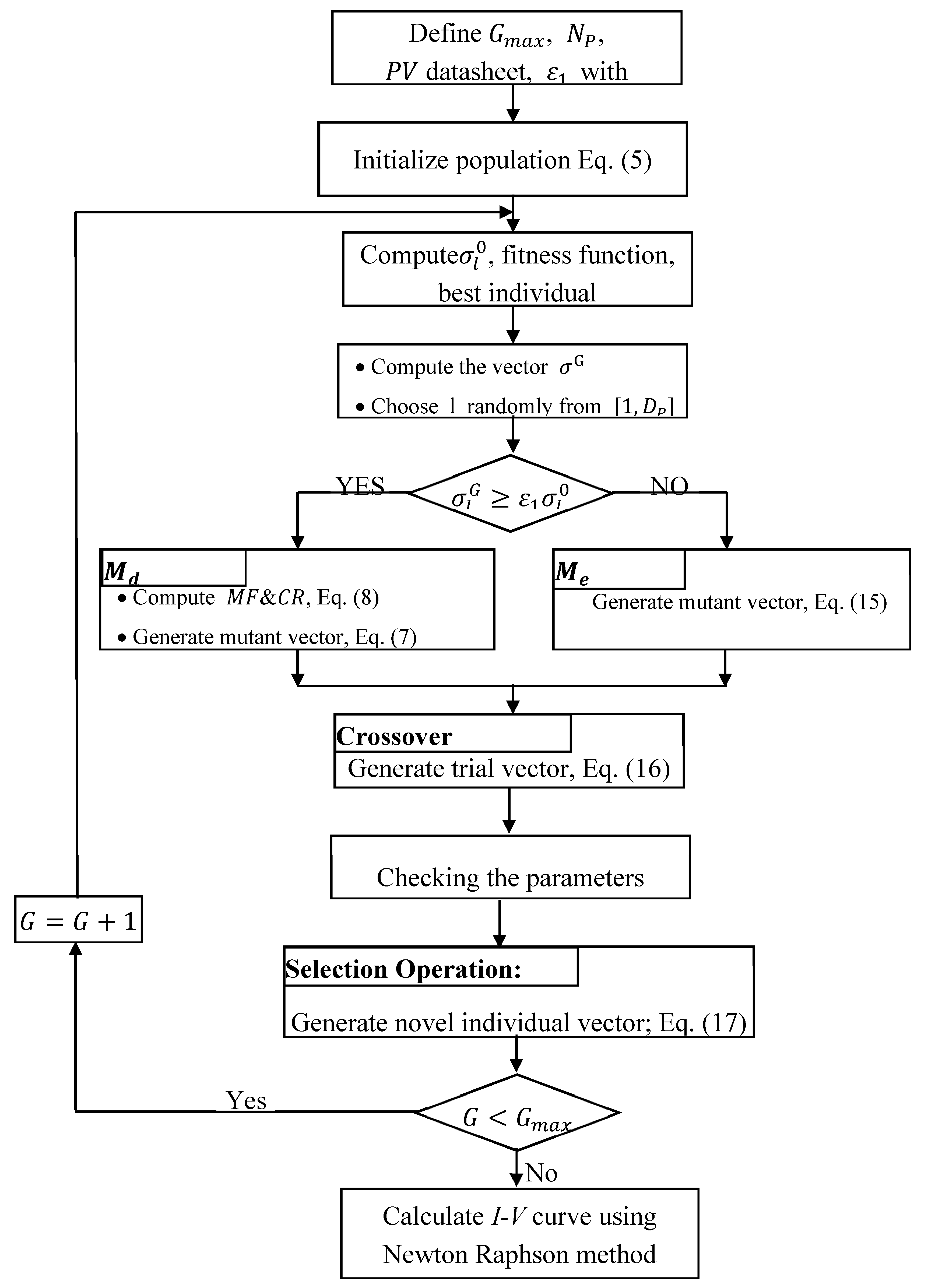
3. DEIMA Optimization Algorithm

The proposed PV-modeling method is based on DEIMA and the strategy of deriving an adaptive formula for the mutation and crossover rate control parameters of DEIMA are presented in the current section. DEIMA is a stochastic metaheuristic optimization algorithm, which is initiated by hybridizing DEA and EMA algorithms. The attraction-repulsion concept of EMA is utilized synergically with the conventional mutation stage of DEA. The four steps of DEIMA will be discussed in details in the following subsections.

3.1. Initialization

The first step of DEIMA is initializing

D_{P} \times N_{P}

population, where

D_{P}

is the number of decision variables and

N_{P}

refers to the number of candidate individual vectors. It is worth mentioning that each individual vector comprises

D_{P}

decision variables. The population (

p o p

) can be described as follows:

p o p = (\begin{matrix} x_{11} & x_{12} & \begin{matrix} \dots & x_{1 N_{P}} \end{matrix} \\ \begin{matrix} x_{21} \\ ⋮ \end{matrix} & \begin{matrix} x_{22} \\ ⋮ \end{matrix} & \begin{matrix} \begin{matrix} \dots \\ ⋱ \end{matrix} & \begin{matrix} x_{2 N_{P}} \\ ⋮ \end{matrix} \end{matrix} \\ x_{D_{P} 1} & x_{D_{P} 2} & \begin{matrix} \dots & x_{D_{P} N_{P}} \end{matrix} \end{matrix})

(4)

The

D_{P}

parameters of

i^{t h}

individual vector is randomly initiated using Eq. (5) and uniformly distributed within the interval of

j^{t h}

decision variable

[{X L}_{j}, {X H}_{j}]

, where

{X L}_{j}

is the lower boundary and

{X H}_{j}

is the upper bounds of search space.

X_{j i}^{0} = {X L}_{j i} + r a n d \times ({X H}_{j i} - {X L}_{j i})

(5)

where

r a n d

is a random number, which is selected randomly within (0, 1).

3.2. Mutation

The proposed DEIMA has utilized two different types of mutation (

M_{e}

and

M_{d}

). Both types are used in each iteration and based on the following criterion.

M u t a t i o n o p e r a t i o n = \{\begin{matrix} M_{e} & i f θ_{l}^{G} < ε_{1} θ_{l}^{0} \\ M_{d} & o t h e r w i s e \end{matrix},

(6)

where

θ_{l}^{0}

and

θ_{l}^{G}

refer to the

l^{t h}

standard deviation vectors of the row vectors of

p o p

population in the initial and

G

generations, respectively.

l

is a random number, which is randomly chosen within

[1, D_{P}]

interval.

ε_{1}

is a constant control parameter with value belongs to [0,1] [30]. The

ε_{1}

controls the switch between

M_{e}

and

M_{d}

mutation operations within the population. The

M_{d}

mutation operation is achieved by computing the mutant vector

{\hat{X}}_{i}^{G}

as follows:

{\hat{X}}_{i}^{G} = {\hat{X}}_{r 1}^{G} + F ({\hat{X}}_{r 2}^{G} - {\hat{X}}_{r 3}^{G})

(7)

Where

{\hat{X}}_{r 1}^{G}, {\hat{X}}_{r 2}^{G}

and

{\hat{X}}_{r 3}^{G}

are three distinct individual vectors randomly selected from population. In other words,

r_{1}

r_{2}

and

r_{3}

are distinct indices and belong to the period

[1, N_{P}]

F

is the mutation control factor having values within [0.5, 1] [31]. It is worth mentioning that the control parameter

F

and crossover control rate (

C R

) in crossover step are adaptive in each iteration and are being set by using a novel formula as follow:

F, C R = d (\frac{L}{1 + e x p (- k (w - w_{0})} + b)

(8)

The above formula based on sigmoid function. Where the maximum value is labeled as

L

of sigmoid function curve,

k

and

w_{0}

are the steepness of the curve and midpoint of x-axis sigmoid function, respectively. In the current research work,

L

k

and

w_{0}

are set 1, 12 and 0 according to many experiments.

b

and

d

are constants; which are chosen to maintain

F

and

C R

within [0.5, 1], where

b

set 1 and

d

equal to 0.5.

w

refers to the random weighted difference between the best objective function value of

w

and is computed by:

w = [O F (X_{b e s t}^{G}) - O F (X_{b e s t}^{G - 1})] * r a n d

(9)

As it was stated previously, the second part of mutation is

M_{e}

mutation operation. The last operation utilized the total force exerted on

X_{r 1}^{G}

X_{r 2}^{G}

and

X_{r 3}^{G}

to compute the mutant vector

X_{i}^{G}

. The force exerted by any individual vector on another one depends on the charge between them, which is calculated as below;

q_{r 1 r 2}^{G} = \frac{O F (X_{r 1}^{G}) - O F (X_{r 2}^{G})}{O F (X_{w o r s t}^{G}) - O F (X_{b e s t}^{G})}

(10)

q_{r 1 r 3}^{G} = \frac{O F (X_{r 1}^{G}) - O F (X_{r 3}^{G})}{O F (X_{w o r s t}^{G}) - O F (X_{b e s t}^{G})}

(11)

where

O F (X^{G}

) refers to the objective function value of individual vector X in the

G^{t h}

iteration.

X_{w o r s t}^{G}

and

X_{b e s t}^{G}

are the worst and best solution in the

G^{t h}

iteration, respectively. Consequently, the exerted forces by

X_{r 2}^{G}

and

X_{r 3}^{G}

on the individual vector

X_{r 1}^{G}

are described by [32],

F_{r 1 r 2}^{G} = {(X}_{r 2}^{G} - X_{r 1}^{G}) * q_{r 1 r 2}^{G}

(12)

F_{r 1 r 3}^{G} = {(X}_{r 3}^{G} - X_{r 1}^{G}) * q_{r 1 r 3}^{G}

(13)

Then, the resultant force exerted by

X_{r 2}^{G}

and

X_{r 3}^{G}

X_{r 1}^{G}

is calculated by,

F_{r 1}^{G} = F_{r 1 r 2}^{G} + X_{r 1 r 3}^{G}

(14)

Next, the

M_{e}

mutation operation produces the

X_{i}^{G}

mutant vector in

G^{t h}

iteration and is corresponding to

X_{i}^{G}

as follows:

{\hat{X}}_{i}^{G} = X_{r 1}^{G} + F_{α}^{G}

(15)

3.3. Crossover

In this step, the trial vector of

G^{t h}

iteration

y_{j, i}^{G}

is initiated by utilizing both the corresponding target

X_{r 1}^{G}

or mutant

{\hat{X}}_{i}^{G}

vector based on the following formula.

Y_{j, i}^{G} = \{\begin{matrix} {\hat{X}}_{j, i}^{G} & i f r a n d \leq C R o r j = I_{i} \\ X_{j, i}^{G} & o t h e r w i s e \end{matrix}

(16)

Where

I_{i}

is an index number, which is randomly selected from the interval

[1, D_{P}]

. As it was stated in the previous subsection,

C R

is a crossover control rate which has an adaptive value computed by Eq. (8). At the end of crossover step, the element of trial vector (decision variables) will be checked to determine if one of them violates the boundaries of corresponding search space. Eq. (5) is used to initiate the element of trail vector when it is unphysical value.

3.4. Selection

The last step of DEIMA is the selection step to select between the trail vector and the corresponding individual vector for

G^{t h}

iteration based on the following formula:

X_{i}^{G + 1} = \{\begin{matrix} Y_{i}^{G} & i f O F (Y_{i}^{G}) < O F (X_{i}^{G}) \\ X_{i}^{G} & o t h e r w i s e \end{matrix}

(17)

At the end of selection step, the individual vector of generation (

G + 1

) is generated to constitutes the new population.

Figure 2 illustrates the proposed DEIMA method for estimating the unknown nine parameter of TDM-PD module.

4. Evaluation Criteria

In the current research work, seven criteria are utilized to assess the performance of the introduced PV-modeling method as compared to other methods. More details about the evaluation criteria will be presented in the next subsection.

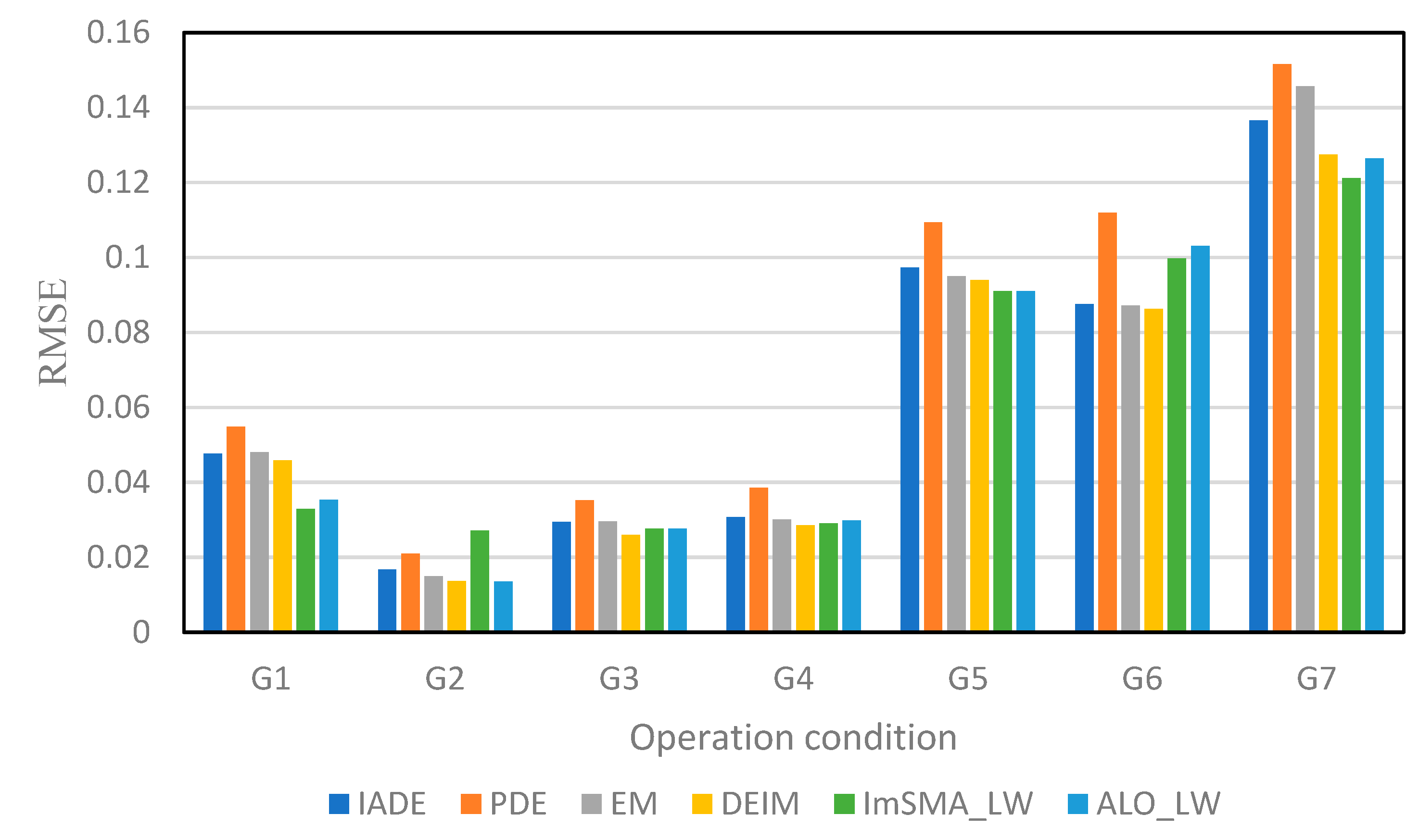
4.1. Root Mean Square Error ( $R M S E$ )

The

R M S E

criterion presents the deviation between the computed and experimented points of the I-V characteristic curve along n-data set as depicted in below.

R M S E = \sqrt{\frac{1}{n}} \sum_{t = 1}^{n} {(I_{e t} - I_{c t})}^{2}

(18)

where

I_{e t}

and

I_{c t}

are the experimental and computed currents at

i^{t h}

point of I-V curve.

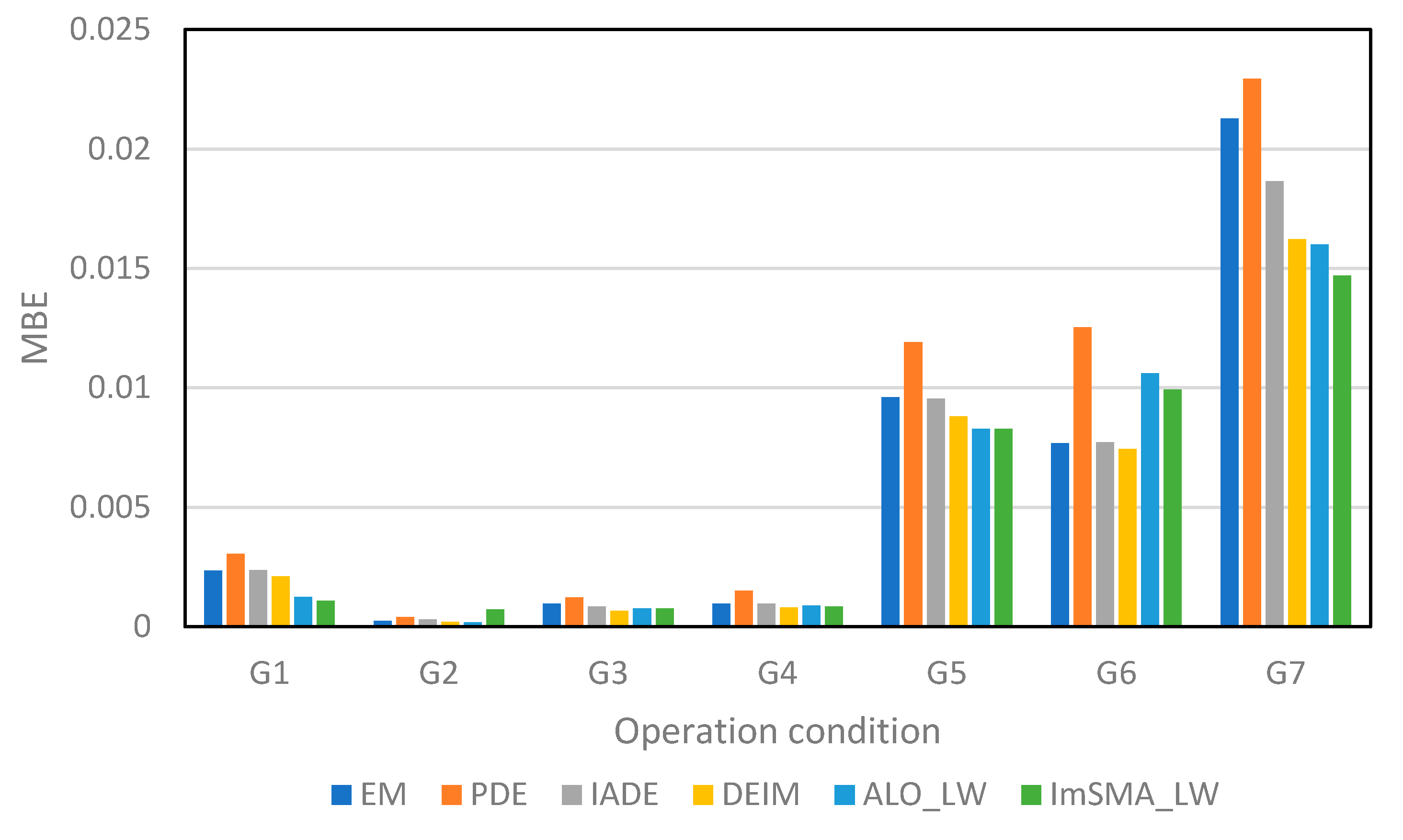
4.2. Mean Bias Error ( $M B E$ )

The overall bias error between the computed and experimented I-V characteristic curve is measured by using

M B E

formula as presented below:

M B E = \frac{1}{n} \sum_{t = 1}^{n} {(I_{e t} - I_{c t})}^{2}

(19)

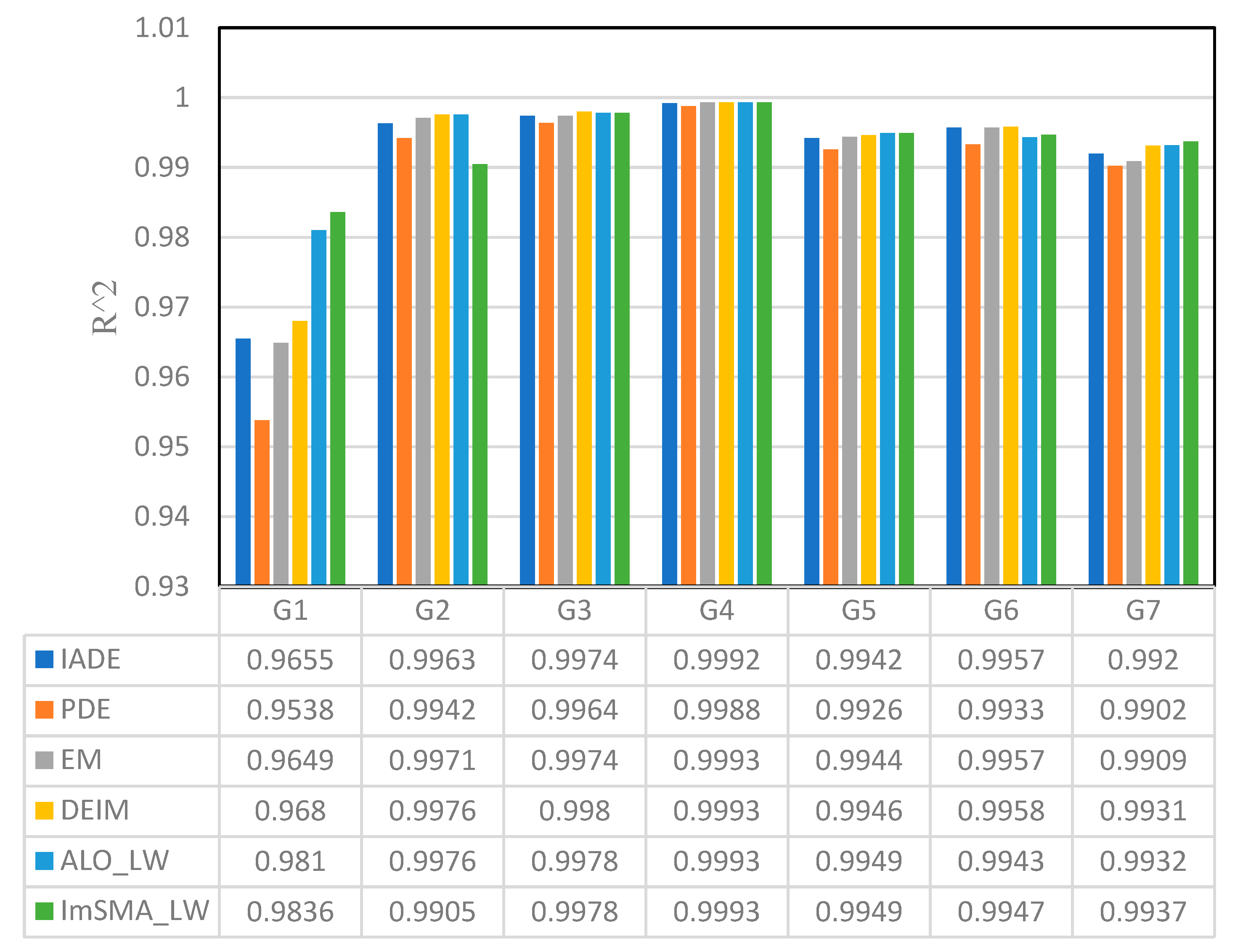
4.3. Coefficient of Determination ( $R^{2}$ )

R^{2}

is another criterion that utilized to assess the accuracy and performance of the proposed PV-modeling method. This coefficient explains the degree of ability that a computed I-V curve follows the experimental one. It is worth mentioning that the better value of

R^{2}

criterion should be close to 1. The

R^{2}

is computed by:

R^{2} = 1 - \frac{\sum_{t = 1}^{n} {(I_{c t} - I_{e t})}^{2}}{\sum_{t = 1}^{n} {(I_{e t} - \bar{I_{e}})}^{2}}

(20)

where,

\bar{I_{e}} = \frac{1}{n} \sum_{t = 1}^{n} I_{e t}

(21)

4.4. Average Absolute Error ( $A A E$ )

Absolute error shows the absolute difference between the experimental and calculated currents. The average value of absolute error is computed by finding the average of absolute error over the whole points of the I-V curve. The

A A E

is calculated by.

A A E = \frac{1}{n} \sum_{t = 1}^{n} |I_{c t} - I_{e t}|

(22)

4.5. Deviation of RMSE ( $d_{m}$ )

The evaluation criterion

d_{m}

refers to the deviation of

R M S E

for each solar irradiance from the mean

R M S E

of the all seven operation conditions as formulated below.

d_{m} = {R M S E}_{m} - \bar{R M S E}

(23)

Where

{R M S E}_{m}

refers to the

R M S E

m^{t h}

solar irradiance (operation condition), and

\bar{R M S E}

is the arithmetic mean of

R M S E

of overall operation conditions (

G_{1} - G_{7}) . \bar{R M S E E}

is computed by:

\bar{R M S E} = \frac{1}{r} \sum_{t = 1}^{r} {R M S E}_{t}

(24)

where r is the total number of operation conditions.

4.6. Standard Test Deviation ( $S T D$ )

Another statistical criterion,

S T D

, is used to evaluate the performance of the proposed PV-modeling method.

S T D

value explains the average deviation of

R M S E

for the seven operation conditions.

S T D

is computed by:

S T D = \sqrt{\frac{1}{(r - 1)} \sum_{m = 1}^{r} {(d_{m})}^{2}}

(25)

4.7. CPU-Execution Time (CET)

The last criterion used to evaluate the results of the proposed PV-modeling method is the required time by CPU for executing the DEIMA.

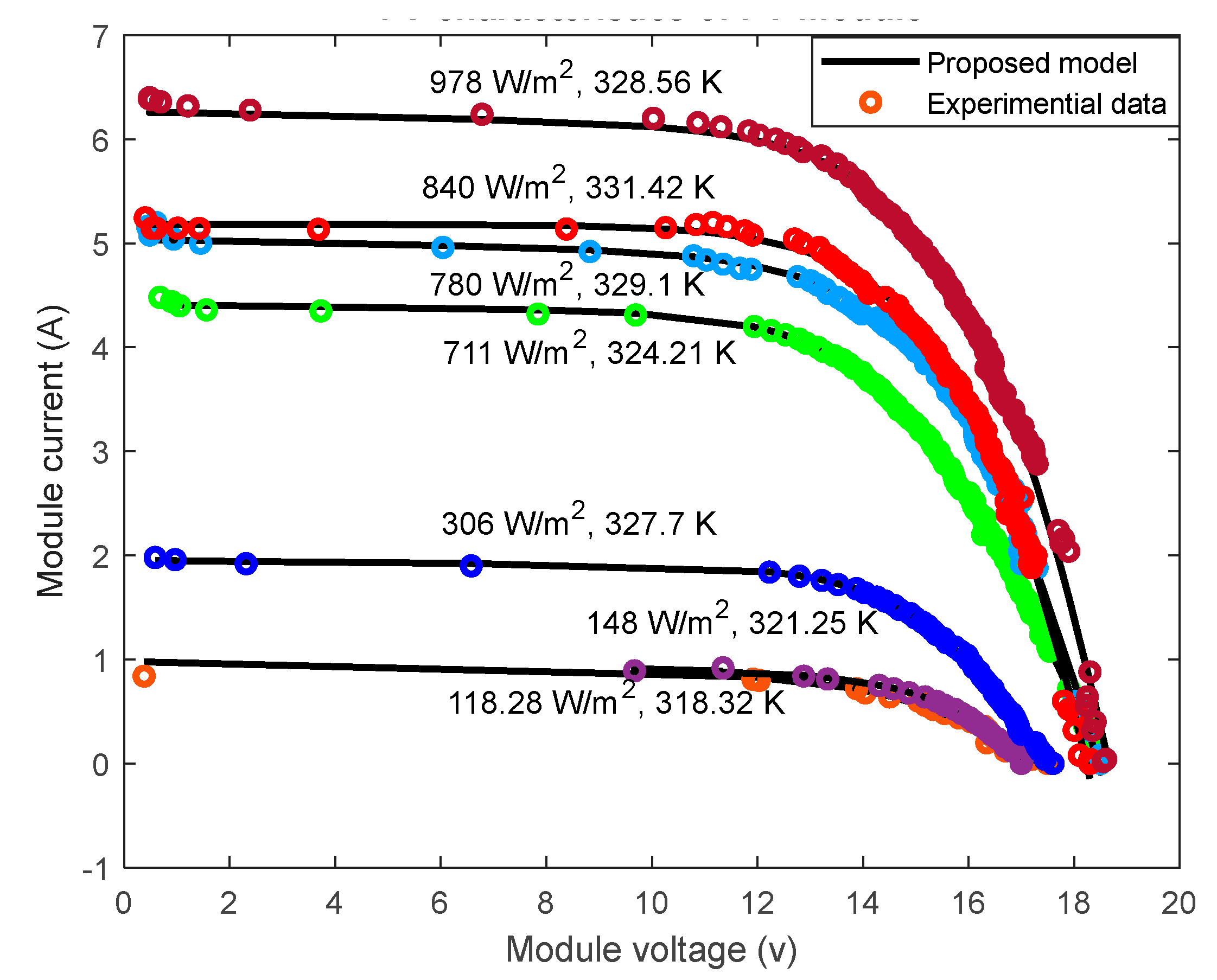
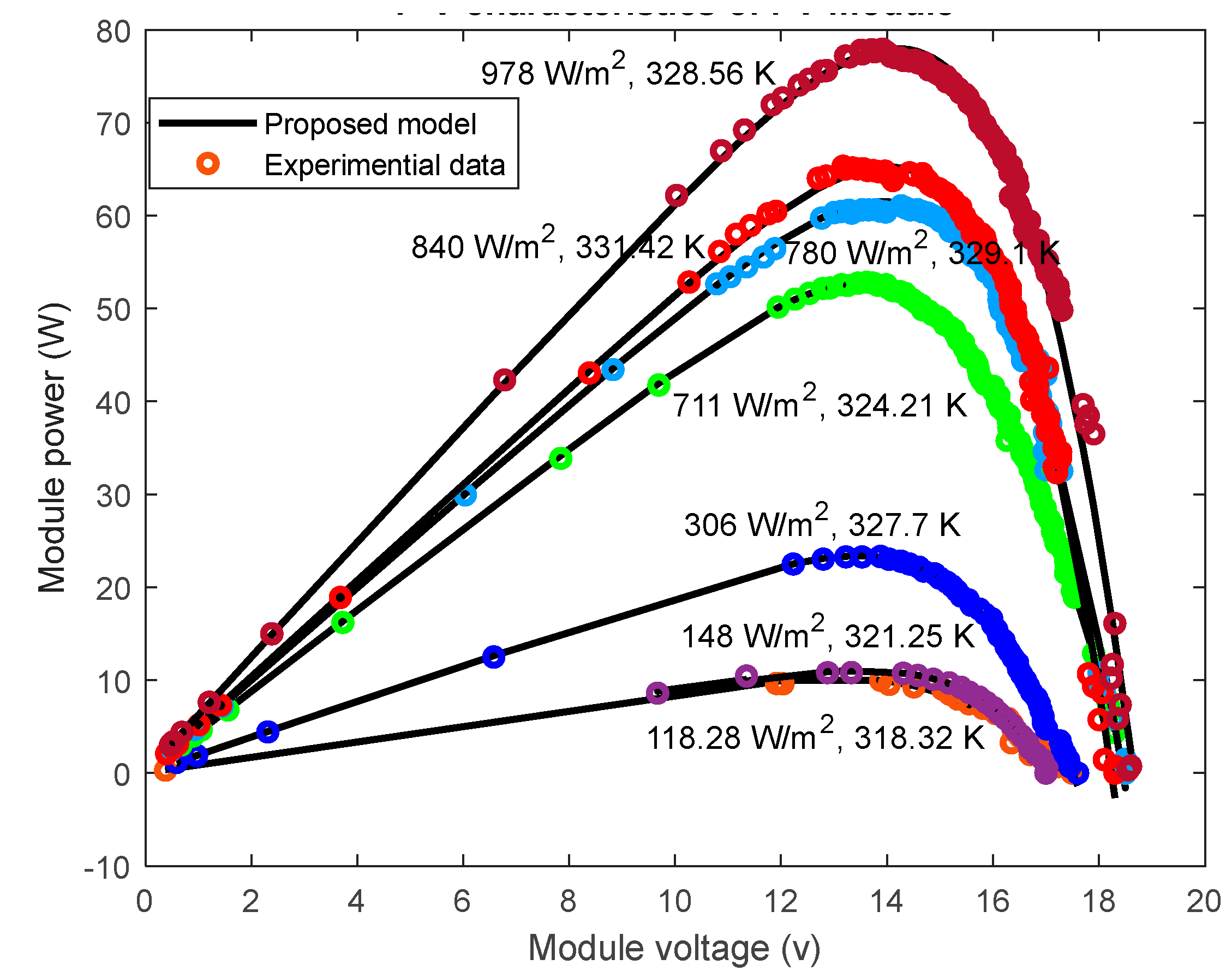
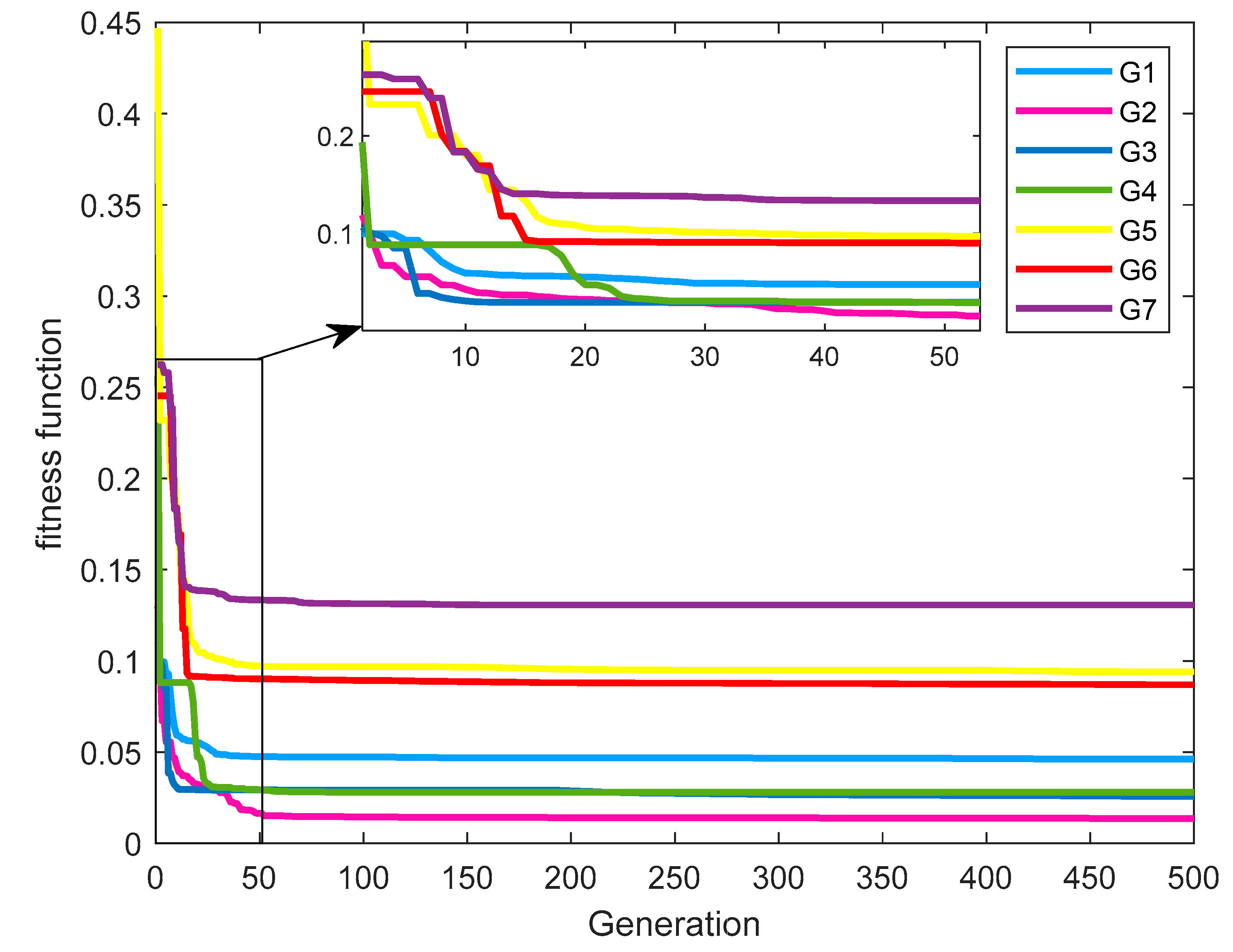
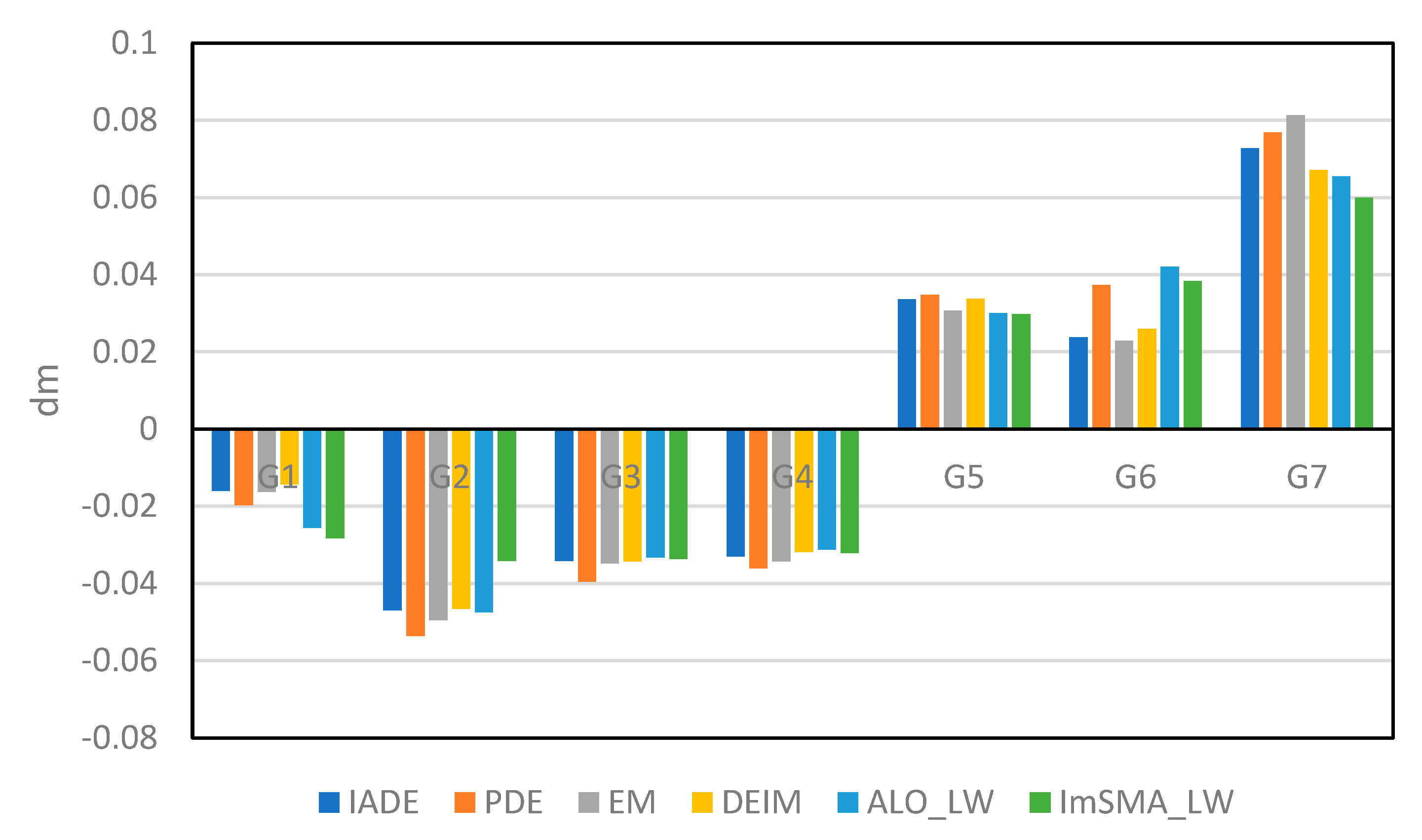
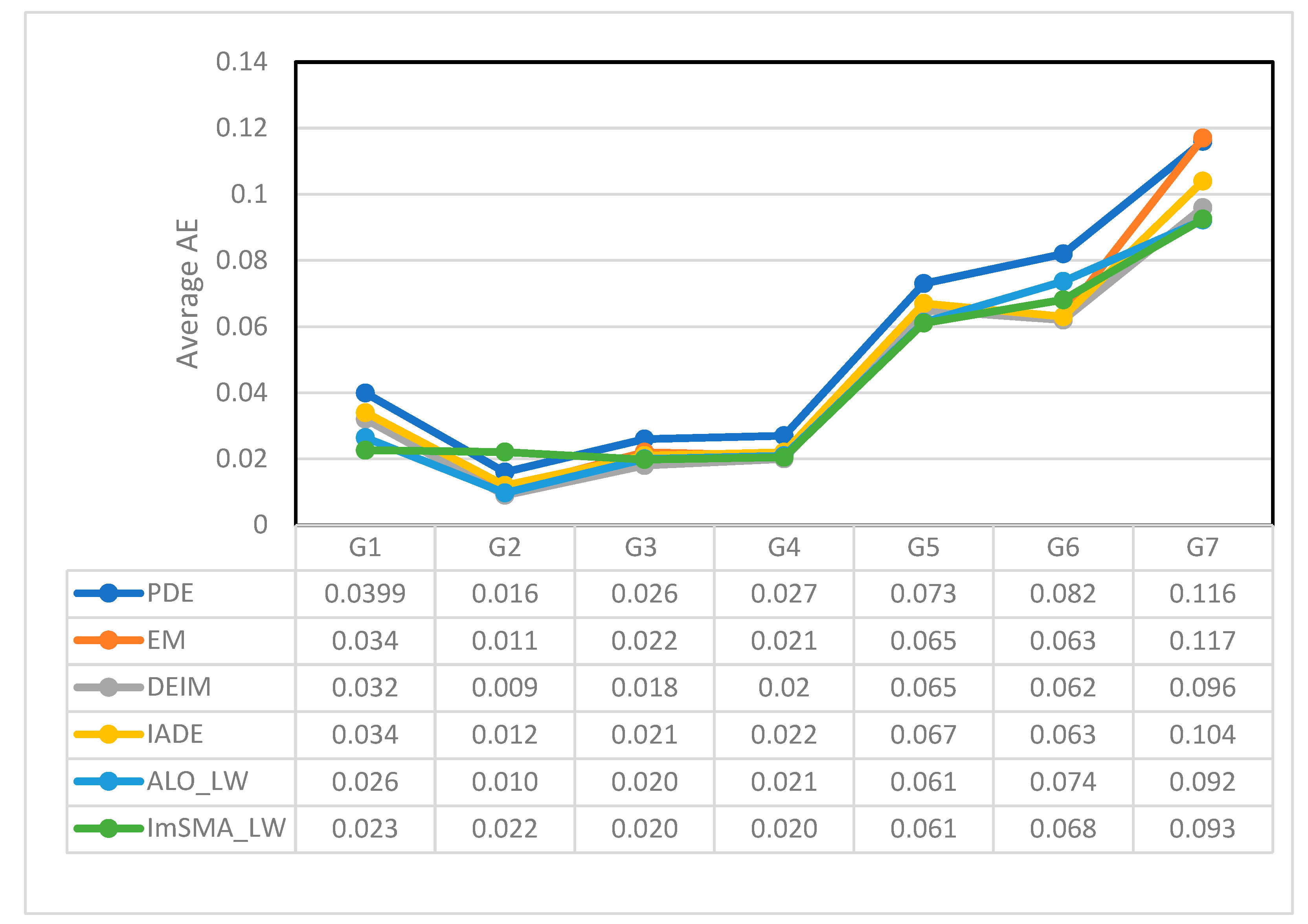
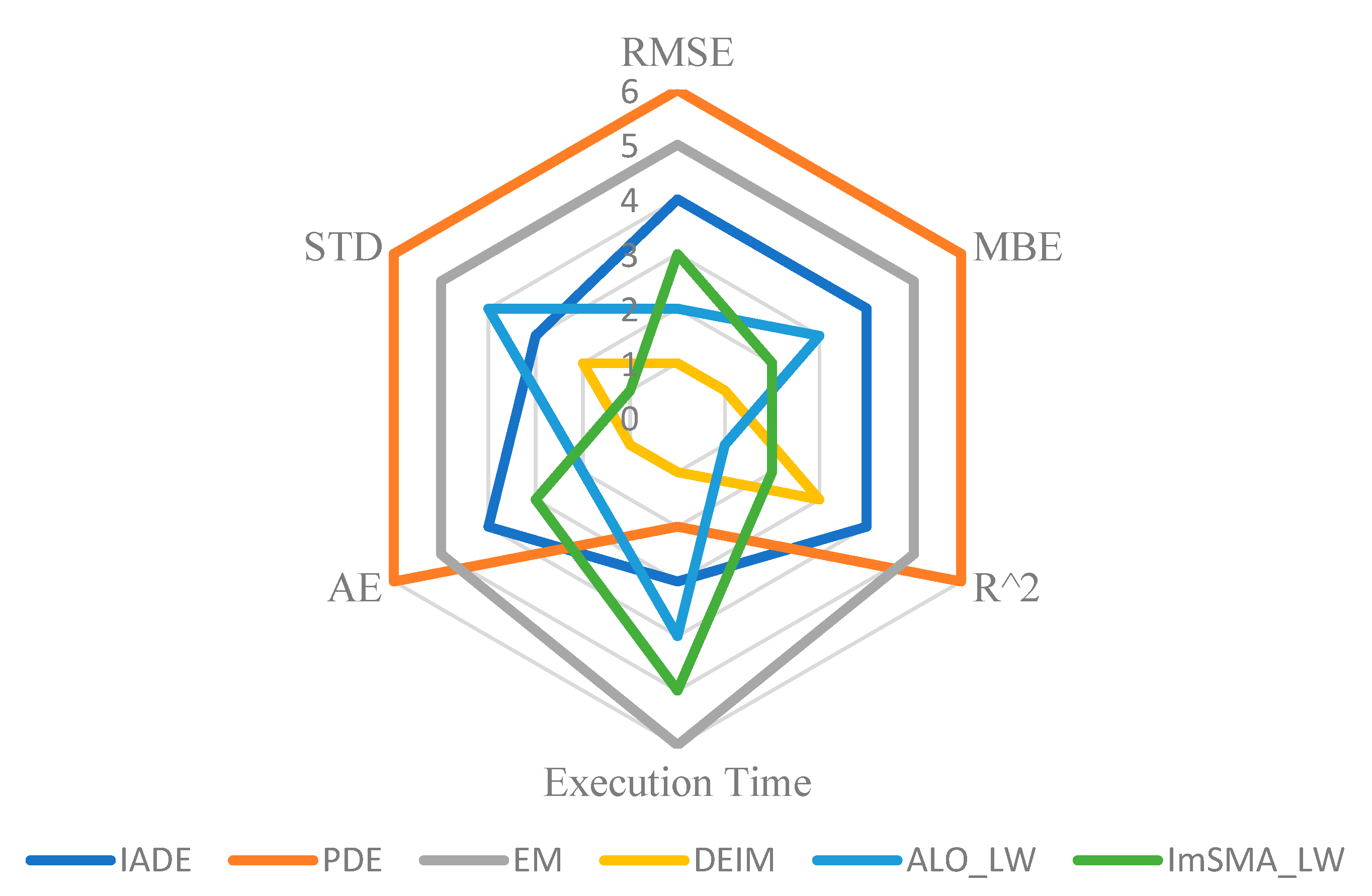
5. Results and Discussion

A multicrystaline Kyocera KC120-1 with 120Wp capacity PV module is used in this paper for testing the proposed modeling method. The specifications of the aforementioned PV module are tabulated in Table 1.

Seven different operation conditions are used as experimental data to extract the parameters of PV module. These operation conditions are denoted by G1 to G7 and they are tabulated in Table 2. The first and second columns of Table 2 comprise the solar irradiance and cell temperature of various operation conditions. It is worth mentioning that each operation condition includes various length of experimental I-V data points that explained in the fourth column of Table 2. It should be noted that the weather conditions and operation conditions terms are interchangeably used through this paper.

A different evolution with integrated mutation per each iteration was adopted to estimate the unknown parameters of TDM. Since the dimension of PV-module optimization problem is 9, then the decision variables (

D_{P}

) are 9, and the number of individual solutions will be

10 D

[33,34]. The maximum number of iteration (

G_{m a x}

) for DEIMA and other methods that adopted for comparison issue is proposed 500 as a typical value that is based on several trial-and-error tests. According to many operations, the switching control parameter (

ε_{1}

) founds 0.28 present as the best performance of DEIMA. In the meanwhile, the mutation factor and crossover rate of DEIMA are adaptive according to the proposed formula that discussed previously.

The search space range of nine parameters regarding TDM is based to literature. The photocurrent,

R_{S}

R_{P}

,, diode saturation currents (

I_{o 1}, I_{o 2}, {and I}_{o 3}

), and diode ideality factors (

a_{1}, a_{2}, a n d a_{3}

) are chosen to be [1,8] A, [0.1, 2] Ω, [100, 5000] Ω, [1E-12, 1E-5] A, and [1,2], respectively [35].

The nine parameters of TDM PV module that estimated based on DEIMA are explained in Table 3. Based on the estimated parameters and Newton-Raphson method, the I-V and P-V curves of TDM PV module under seven different operation conditions can be obtained as illustrated in Figure 3 and Figure 4, respectively. According to Figure 3 and Figure 4, it can be visually concluded that I-V and P-V curves obtained by DEIMA-based PV modeling method are closer to experimental ones. It is worth to mention that experimental I-V and P-V curves of PV module are irregular due to the error in I-V generator that used in the field to collect the experimental data.

Figure 5 shows the evolution of objective function within the whole generation under seven operation conditions for DEIMA to calculate TDM parameters of PV-module. The presented DEIMA shows fast convergence and minimum objective function values for all operation conditions. It should be noted that the proposed modeling method based on DEIMA exhibits a stable objective function value at the first 20 iterations.

In order to prove the superiority of the proposed PV modeling method based on DEIMA, a fair comparison was done with other methods in literature. The penalty differential evolution algorithm (PDEA) [36], the improved adaptive differential evolution algorithm (IADEA) [37], electromagnetism-like algorithm (EMA) [38], ImSMA_LW [29], and ant lion optimizer with Lambert W function (ALO_LW) [39] were used as bench marks for comparison purposes to indicate the effectiveness of DEIMA. The experimental conditions including the size of population, maximum number of generations, and search space of decision variables of the whole aforementioned methods are the same for all methods to ensure fair comparisons. It should be noted that the mutation factor and crossover rate of DEIMA and IADEA are dynamically adaptive according to a formula. Meanwhile, the mutation factor and crossover rate of PDEA are chosen to be 0.5 and 1, respectively [36].

Figure 6 shows the

R M S E

of the proposed DEIMA and other compared algorithms under seven operation conditions. The proposed DEIMA offers the lowest

R M S E

values under the whole operation conditions with average value around 0.06024. The ALO_LW, ImSMA_LW, IADEA, and EMA provided the second, third, fourth, and fifth low

R M S E

values, respectively. While, the PDEA exhibited the worse

R M S E

value as compared to other methods. The DEIMA presents the lowest

M B E

as compared to other methods with average

M B E

of 0.00518 over seven operation conditions as shown in Figure 7. The PDEA is still have the worst

M B E

values over the whole operation conditions. Figure 8 shows the coefficient of determination of various algorithms as bar chart. The proposed DEIMA also offers compromise

R^{2}

values, which are close to one over the seven operation conditions. The average

R^{2}

of DEIMA, ALO_LW, ImSMA_LW, IADEA, EMA, and PDEA are 0.9923, 0.994, 0.9935, 0.9915, 0.9914, and 0.9885, respectively.

The CPU-execution times of various algorithms are tabulated in Table 4 over seven weather conditions. The average execution time of DEIMA is around 27.69 sec. The DEIMA needs less time to conduct execution as compared to other methods. Although the algorithms ALO_LW and ImSMA_LW offered promising results in many evaluation criteria, they need long execution time to candidate the TDM optimal parameters of the PV module.

Figure 9 shows the

R M S E

deviation of each operation condition (

d_{m}

). The DEIMA offers the lowest

d_{m}

values in G1, G2, G4, and G7 operation conditions. The EMA shares the proposed DEIMA in G3, G5, and G6 weather conditions by offering the best

d_{m}

values. The small values of

d_{m}

prove the capability of the proposed method to candidate effective estimation for PV-module parameters. The

S T D

value can be computed for various methods by using

d_{m}

over seven operation conditions. The DEIMA presents 0.0426 as the lowest

S T D

value as compared to IADEA, ALO_LW, EMA, and PDEA with 0.04416, 0.0446, 0.04684, and 0.04937, respectively.

The last criterion used to compare the results of DEIMA with other algorithms is the average absolute error (

A A E

). Figure 10 shows the

A A E

of the proposed DEIMA and other methods. Based on Figure 10, DEIMA presents the lowest

A A E

over seven operation conditions. It is worth mentioning that the

A A E

is significantly increased when the operation conditions are changed from G1 to G7, because the number of I-V points in data set is increased as it was stated in Table 2.

Based on the aforementioned discussions, the radar diagram in Figure 11 can be drawn by scoring each algorithm according to its performance in each criterion. It is noticed that the proposed DEIMA is claiming the first score among other methods over most of criteria. In the meanwhile, PDEA obtained the last score (6) in most of criteria, except for the CPU-execution time.

6. Conclusion

A hybrid optimization algorithm-based PV modeling technique is presented in this paper. The modeling method is utilized to assess the unknown parameters of triple-diode PV module. The introduced algorithm hybridized the conventional DEA and EMA to obtain DEIMA. The mutation stage of DEA is boosted by the attraction-repulsion concept of EMA. A novel formula is proposed for adapting the mutation factor and crossover rate control parameters for each iteration. The formula is using the sigmoid function and the evolution of fitness function. The fitness function is formulated by using the root mean square error between the experimental and computed PV output currents over

n

-points of I-V characteristic under seven operation conditions. The operation conditions are chosen with different solar irradiance and ambient temperature in order to prove the superiority of the proposed PV modeling method. The outcomes of DEIMA are validated with conventional DEA, EMA, and IADE algorithms by evaluating seven statistical criteria. According to results, DEIMA offered a significant superiority than other compared methods. As a future work, the authors are focusing on using DEIMA-based multiobjective functions to estimate nine parameters of triple-diode PV module and integrated with multicriteria decision making method.

Author Contributions

Conceptualization, D.H.M., H.T.H., and Y.A.; data curation, D.H.M. and H.T.H.; formal analysis, D.H.M., Y.A., and H.T.H.; investigation, D.H.M., and H.T.H.; methodology, D.H.M. and H.T.H.; validation, H.T.H. and Y.A.; writing—original draft preparation, D.H.M., H.T.H., and Y.A.; writing—review and editing, D.H.M., H.T.H., and Y. A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no funding

Data Availability Statement

The data presented in this study are available on request from the corresponding authors due to copyright issues.

Acknowledgments

The authors would like to thank Mustansiriyah University (www.uomustansiriyah.edu.iq) Baghdad-Iraq for its support in the present work.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

Mustafa Ibrahim Mansoor, and Haider Tarish Haider, "A multi-objective residential load management based on self-adapting differential evolution", Renewable Energy Focus, Volume 38, (2021). 44-56. [CrossRef]
Kharchouf, Youssef, Rachid Herbazi, and Adil Chahboun. "Parameter’s extraction of solar photovoltaic models using an improved differential evolution algorithm." Energy Conversion and Management 251 (2022): 114972. [CrossRef]
Fan, Yi, Pengjun Wang, Ali Asghar Heidari, Huiling Chen, and Majdi Mafarja. "Random reselection particle swarm optimization for optimal design of solar photovoltaic modules." Energy 239 (2022): 121865. [CrossRef]
Rigo, Paula D., Julio Cezar M. Siluk, Daniel P. Lacerda, and Júlia P. Spellmeier. "Competitive business model of photovoltaic solar energy installers in Brazil." Renewable Energy 181 (2022): 39-50. [CrossRef]
Ridha, Hussein Mohammed, Hashim Hizam, Chandima Gomes, Ali Asghar Heidari, Huiling Chen, Masoud Ahmadipour, Dhiaa Halboot Muhsen, and Mokhalad Alghrairi. "Parameters extraction of three diode photovoltaic models using boosted LSHADE algorithm and Newton Raphson method." Energy 224 (2021): 120136. [CrossRef]
Farah, Anouar, Akram Belazi, Feres Benabdallah, Abdulaziz Almalaq, Mohamed Chtourou, and M. A. Abido. "Parameter extraction of photovoltaic models using a comprehensive learning Rao-1 algorithm." Energy Conversion and Management 252 (2022): 115057. [CrossRef]
Lappalainen, Kari, Michel Piliougine, and Giovanni Spagnuolo. "Experimental comparison between various fitting approaches based on RMSE minimization for photovoltaic module parametric identification." Energy Conversion and Management 258 (2022): 115526. [CrossRef]
Kalliojärvi-Viljakainen, Heidi, Kari Lappalainen, and Seppo Valkealahti. "A novel procedure for identifying the parameters of the single-diode model and the operating conditions of a photovoltaic module from measured current–voltage curves." Energy Reports 8 (2022): 4633-4640. [CrossRef]
Gude, Srihari, Kartick Chandra Jana, Antonino Laudani, and Sudhakar Babu Thanikanti. "Parameter extraction of photovoltaic cell based on a multi-objective approach using nondominated sorting cuckoo search optimization." Solar Energy 239 (2022): 359-374. [CrossRef]
E. E. Kalu, Numerical Methods with Applications: Abridged: Lulu. com, 2008.
R. Navabi, S. Abedi, S. H. Hosseinian, and R. Pal, "On the fast convergence modeling and accurate calculation of PV output energy for operation and planning studies," Energy Conversion and Management, vol. 89, pp. 497-506, 1/1/ 2015. [CrossRef]
S. Lineykin, M. Averbukh, and A. Kuperman, "An improved approach to extract the single-diode equivalent circuit parameters of a photovoltaic cell/panel," Renewable and Sustainable Energy Reviews, vol. 30, pp. 282-289, 2// 2014. [CrossRef]
M. Hejri, H. Mokhtari, M. R. Azizian, M. Ghandhari, and L. Soder, "On the Parameter Extraction of a Five-Parameter Double-Diode Model of Photovoltaic Cells and Modules," Photovoltaics, IEEE Journal of, vol. 4, pp. 915-923, 2014. [CrossRef]
M. Karamirad, M. Omid, R. Alimardani, H. Mousazadeh, and S. N. Heidari, "ANN based simulation and experimental verification of analytical four- and five-parameters models of PV modules," Simulation Modelling Practice and Theory, vol. 34, pp. 86-98, 5// 2013. [CrossRef]
Ram, J. Prasanth, Dhanup S. Pillai, Derick Mathew, Jihun Ha, and Young-Jin Kim. "A simple, reliable and adaptive approach to estimate photovoltaic parameters using spotted hyena optimization: A framework intelligent to predict photovoltaic parameters for any meteorological change." Solar Energy 236 (2022): 480-498. [CrossRef]
Khanna, Vandana, B. K. Das, Dinesh Bisht, and P. K. Singh. "A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm." Renewable Energy 78 (2015): 105-113. [CrossRef]
Qais, Mohammed H., Hany M. Hasanien, Saad Alghuwainem, and Adnan S. Nouh. "Coyote optimization algorithm for parameters extraction of three-diode photovoltaic models of photovoltaic modules." Energy 187 (2019): 116001. [CrossRef]
Shankar, N., and N. Saravanakumar. "Solar photovoltaic module parameter estimation with an enhanced differential evolutionary algorithm using the manufacturer’s datasheet information." Optik 224 (2020): 165700. [CrossRef]
Kumar, C., T. Dharma Raj, M. Premkumar, and T. Dhanesh Raj. "A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters." Optik 223 (2020): 165277. [CrossRef]
Qais, Mohammed H., Hany M. Hasanien, and Saad Alghuwainem. "Transient search optimization for electrical parameters estimation of photovoltaic module based on datasheet values." Energy Conversion and Management 214 (2020): 112904. [CrossRef]
Yousri, Dalia, Mohamed Abd Elaziz, Diego Oliva, Laith Abualigah, Mohammed AA Al-Qaness, and Ahmed A. Ewees. "Reliable applied objective for identifying simple and detailed photovoltaic models using modern metaheuristics: Comparative study." Energy Conversion and Management 223 (2020): 113279. [CrossRef]
Qais, Mohammed H., Hany M. Hasanien, and Saad Alghuwainem. "Parameters extraction of three-diode photovoltaic model using computation and Harris Hawks optimization." Energy 195 (2020): 117040. [CrossRef]
Chenouard, Raphael, and Ragab A. El-Sehiemy. "An interval branch and bound global optimization algorithm for parameter estimation of three photovoltaic models." Energy Conversion and Management 205 (2020): 112400. [CrossRef]
Ibrahim, Ibrahim Anwar, M. J. Hossain, Benjamin C. Duck, and Mithulananthan Nadarajah. "An improved wind driven optimization algorithm for parameters identification of a triple-diode photovoltaic cell model." Energy Conversion and Management 213 (2020): 112872. [CrossRef]
Houssein, Essam H., Gamela Nageh Zaki, Ahmed A. Zaki Diab, and Eman MG Younis. "An efficient Manta Ray Foraging Optimization algorithm for parameter extraction of three-diode photovoltaic model." Computers & Electrical Engineering 94 (2021): 107304. [CrossRef]
Ćalasan, Martin, Shady HE Abdel Aleem, and Ahmed F. Zobaa. "A new approach for parameters estimation of double and triple diode models of photovoltaic cells based on iterative Lambert W function." Solar Energy 218 (2021): 392-412. [CrossRef]
Zhou, Wei, Pengjun Wang, Ali Asghar Heidari, Xuehua Zhao, Hamza Turabieh, Majdi Mafarja, and Huiling Chen. "Metaphor-free dynamic spherical evolution for parameter estimation of photovoltaic modules." Energy Reports 7 (2021): 5175-5202. [CrossRef]
Wang, Da, Xingping Sun, Hongwei Kang, Yong Shen, and Qingyi Chen. "Heterogeneous differential evolution algorithm for parameter estimation of solar photovoltaic models." Energy Reports 8 (2022): 4724-4746. [CrossRef]
El-Fergany, Attia A. "Parameters identification of PV model using improved slime mould optimizer and Lambert W-function." Energy Reports 7 (2021): 875-887. [CrossRef]
D. H. Muhsen, A. B. Ghazali, T. Khatib, and I. A. Abed, “Parameters extraction of double diode photovoltaic module’s model based on hybrid evolutionary algorithm,” Energy Convers. Manag., vol. 105, pp. 552–561, 2015, doi: 10.1016/j.enconman.2015.08.023. [CrossRef]
L. L. Jiang, D. L. Maskell, and J. C. Patra, “Parameter estimation of solar cells and modules using an improved adaptive differential evolution algorithm,” Appl. Energy, vol. 112, pp. 185–193, 2013, doi: 10.1016/j.apenergy.2013.06.004. [CrossRef]
D. H. Muhsen, A. B. Ghazali, T. Khatib, and I. A. Abed, “Extraction of photovoltaic module model’s parameters using an improved hybrid differential evolution/electromagnetism-like algorithm,” Sol. Energy, vol. 119, pp. 286–297, Sep. 2015, doi: 10.1016/j.solener.2015.07.008. [CrossRef]
K. Ishaque, Z. Salam, H. Taheri, and A. Shamsudin, "A critical evaluation of EA computational methods for Photovoltaic cell parameter extraction based on two diode model," Solar Energy, vol. 85, pp. 1768-1779, 9// 2011. [CrossRef]
F. Vitaliy, "Differential evolution–in search of solutions," ed: Springer, New York, 2006.
R. Benkercha, S. Moulahoum, and B. Taghezouit, “Extraction of the PV modules parameters with MPP estimation using the modified flower algorithm,” Renew. Energy, vol. 143, pp. 1698–1709, Dec. 2019, doi: 10.1016/j.renene.2019.05.107. [CrossRef]
K. Ishaque, Z. Salam, S. Mekhilef, and A. Shamsudin, “Parameter extraction of solar photovoltaic modules using penalty-based differential evolution,” Appl. Energy, vol. 99, pp. 297–308, 2012, doi: 10.1016/j.apenergy.2012.05.017. [CrossRef]
L. L. Jiang, D. L. Maskell, and J. C. Patra, “Parameter estimation of solar cells and modules using an improved adaptive differential evolution algorithm,” Appl. Energy, vol. 112, pp. 185–193, 2013, doi: 10.1016/j.apenergy.2013.06.004. [CrossRef]
Ş. I. Birbil and S. C. Fang, “An electromagnetism-like mechanism for global optimization,” J. Glob. Optim., vol. 25, no. 3, pp. 263–282, 2003, doi: 10.1023/A:1022452626305. [CrossRef]
Kanimozhi, G., and Harish Kumar. "Modeling of solar cell under different conditions by Ant Lion Optimizer with Lambert W function." Applied Soft Computing 71 (2018): 141-151. [CrossRef]

Figure 1. Electrical equivalent circuit of Triple-diode PV module model.

Figure 2. DEIMA-based PV modeling method.

Figure 3. I-V characteristics of TDM of PV module under seven distinct operation conditions.

Figure 4. P-V characteristics of TDM of PV module under seven distinct operation conditions.

Figure 5. Fitness function evolution of TDM of PV module parameter estimation using DEIMA under seven operation conditions.