Prerpints.org logo
Preprint
Article

Development of Air Pollution Forecasting Models Applying Artificial Neural Networks in the Greater Area of Beijing City, China

Altmetrics

Downloads

70

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 August 2024

Posted:

26 August 2024

You are already at the latest version

Alerts
Abstract
The ever-increasing industrialization of certain areas of the planet combined with the simultaneous degradation of the natural environment are alarming phenomena, especially in the field of human health. The concentration of Particulate Matter with an aerodynamic diameter of 2.5μm (PM2.5) and 10μm (PM10), nitrogen oxides (NOx), carbon monoxide (CO), sulfur dioxide (SO2), and ozone (O3) needs constant monitoring, as they consist the main cause for many diseases. Based on the existence of statutory limits, by the World Health Organization (WHO), for the concentration of each of the aforementioned air pollutants, it is considered necessary to develop forecasting systems that will have the ability to correlate the current meteorological data with the concentrations of the above pollutants. In this work, the attempt to predict the air pollutants concentrations in the wider area of Beijing, China, is successfully carried out using artificial neural networks (ANNs) models. In the frame of the specific work, a significant number of ANNs was developed. For this purpose, an open-access meteorological and air pollution database was used. Finally, a statistical evaluation of the developed prognostic models was carried out. Results showed that ANNs present a re-markable prognostic ability in order to forecast the air pollution levels in an urban environment.
Keywords: 
Subject: Environmental and Earth Sciences  -   Pollution

1. Introduction

Today's way of life, as it has been shaped by the existing social and economic conditions, requires the continuous exposure of man to an atmosphere with adverse effects on his health. Research findings from all over the world converge in terms of the destructive consequences, that the burdened atmospheric air has on humans, agriculture and infra-structure. The continuous degradation of the climate makes the need of finding a means of predicting the quality of the atmosphere, as well as dealing with the production of atmospheric pollutants, imperative.
Air pollution is defined as the "contamination of the indoor or outdoor environment by any chemical, physical or biological agent that modifies the natural characteristics of the atmosphere."[1]. The effects of air pollution have been studied in many countries, both within and out-side the EU, with each research confirming its catalytic role in the degradation of the quality of life. Exposure to PM10 was found to increase the likelihood of hospitalization for bronchitis symptoms, both for adults and children [2], while exposure to excess concentrations of PM2.5 was found to be a cause of hospitalization for cardiovascular and respiratory causes, as well as cause of death [3,4]. Also, exposure to this type of particles can negatively affect infants, even in the prenatal stage, increase the probability of birth defects, obesity, type I diabetes, neurological and behavioral dysfunctions, premature birth and even neonatal death [5,6,7,8]. Equally important are the excessive concentrations of sulfur dioxide (SO2), as an excess of 10 ppb can increase the number of hospitalizations by 1.7% [8]. Prenatal and postnatal exposure to nitrogen dioxide (NO2) leads to increased chances of bronchopulmonary infections, pneumonia as well as obesity [6,9]. Research that was done in areas of Athens (Thrakomakedones and Athens center) for the period 2001-2018, showed that 6% and 7.5% of deaths in these areas respectively, are due to increased concentrations of ozone (O3) [10].
However, the effects of air pollution are not limited to human health. Extensive research carried in the city of Beijing, China showed a direct correlation between the concentration of ozone (O3) as well as nitrogen oxides (NOx) and the reduction of the amount of grain yielded. The percentages reach up to 15%, while it is predicted that they will reach the height of 23% in the coming years [11]. Correspondingly harmful are the effects on infrastructure due to acid rain as well as the transportation sector. In particular, after research carried out by Hernández et al [12] regarding the effect of this on car paint, it was found that between the two aging methods, Xenon and a mixture of acid rain, the latter had the most destructive consequences. Finally, Ibrahim et al. [13] in their research on the surface treatment of concrete, after exposure to an acidic environment, report the phenomenon of gypsum formation and its destructive properties on building materials, gradually weakening the ability of cement to withstand compression.
The need to design a means of forecasting pollutant concentrations is imperative. Over time, many researchers have tried to design such predictive models. In 2015 Xiao Feng et al. [14] created a model that combined an MLP neural network with a geographical model based on the air trajectory and the use of the wavelet transformation method to forecast the average daily PM2.5 concentration for the next two days in Beijing, China. Similar efforts were made by Madhavi Anushka Elangasinghe et al. [15], in 2014, to forecast the hourly concentration of nitrogen dioxide (NO2), using an MLP neural network with one hidden layer, trained with the Levenburg Marquardt algorithm, for the Auckland, New Zealand region. In 2016 Yun Bai et al.[16] using the static wavelet transform method and the training of an ANN with a back-propagation algorithm, tried to predict the daily concentrations of PM10 particles and the concentrations of sulfur dioxide (SO2) and nitrogen dioxide (NO2). In 2017 Fabio Biancofiore et al. [17] also tried to predict the average daily concentrations of PM2.5 and PM10 particles for the next one to three days, while in 2018 Fabiana Franceschi et al. [18] tried through a statistical study and AΝΝ integration to predict the concentrations of PM2.5 and PM10 particles in Bogotá, Colombia. According to further research published in 2024, Quanchao Chen et al. [19] designed an innovative model for the prediction of hourly concentrations for PM2.5 and PM10 as well as ozone (O3), in the city of Beijing, by creating an AAMGCRN (Adaptive Adjacency Matrix Graph Convolutional Recurrent Network). Accordingly, Sarmad Dashti Latif et al. [20] applied multiple machine learning methods to predict the ozone (O3) concentration for the next 1, 3, 5 and 7 hours in the Klang Valley, Malaysia.
This research was conducted in an attempt to design a universal air pollution forecasting model. It is also mentioned that over the course of a decade, no corresponding studies have been found which use strictly meteorological variables and no other pollutants as training data. The latest reference is in 2014, in the forecasting model created by Madhavi Anushka Elangasinghe et al. [15], who argued that models in which the inputs consist, among other things, of pollutant concentrations, have limited practical use.

2. Materials and Methods

The present study addresses a wide range of atmospheric pollutants, specifically the concentrations of suspended particulate matter with an aerodynamic diameter of 2.5μm (PM2.5) and 10μm (PM10), as well as the concentration of sulfur dioxide (SO2), nitrogen dioxide (NO2), carbon monoxide (CO) and ozone (O3).
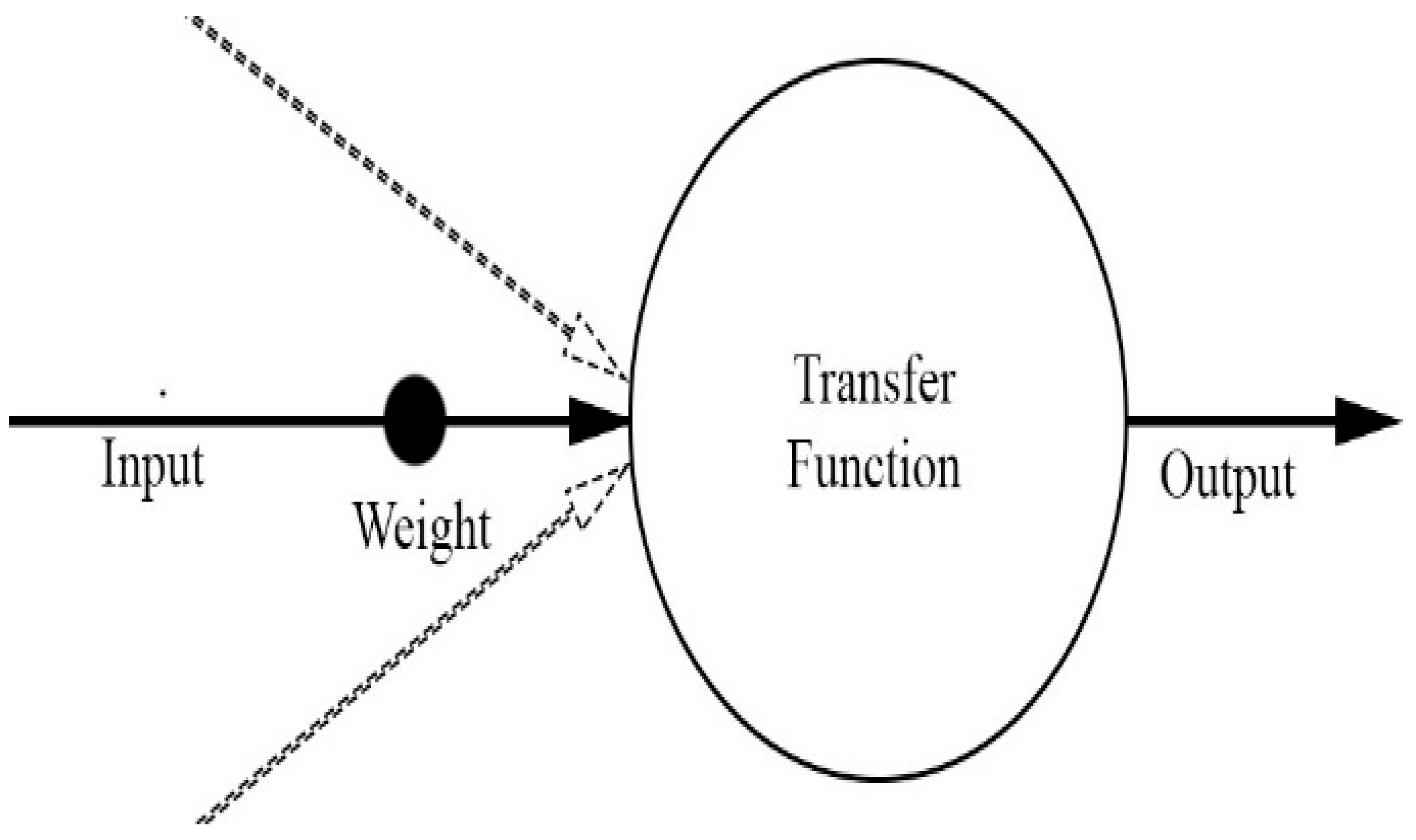
The area of interest is the city of Beijing, China and specifically 12 sub-districts within it. ANNs were developed and used to achieve the requested results. ANNs are a sub-field of Machine Learning (ML) and what sets them apart from other ML techniques is the special way in which they create their systems. ANNs, as their name suggests, try to imitate both the structure and the way of operation of the human brain [21]. Specifically, they consist of artificial neurons, with “nerves” providing them with the required information (input data). The inputs when entering the neuron are multiplied by some "weights" (factors that reduce or enhance the effect that each input has on the final outcome) and after passing through a transfer function, they exit from it (output data) [22]. The schematic representation of the above process is presented in Figure 1.
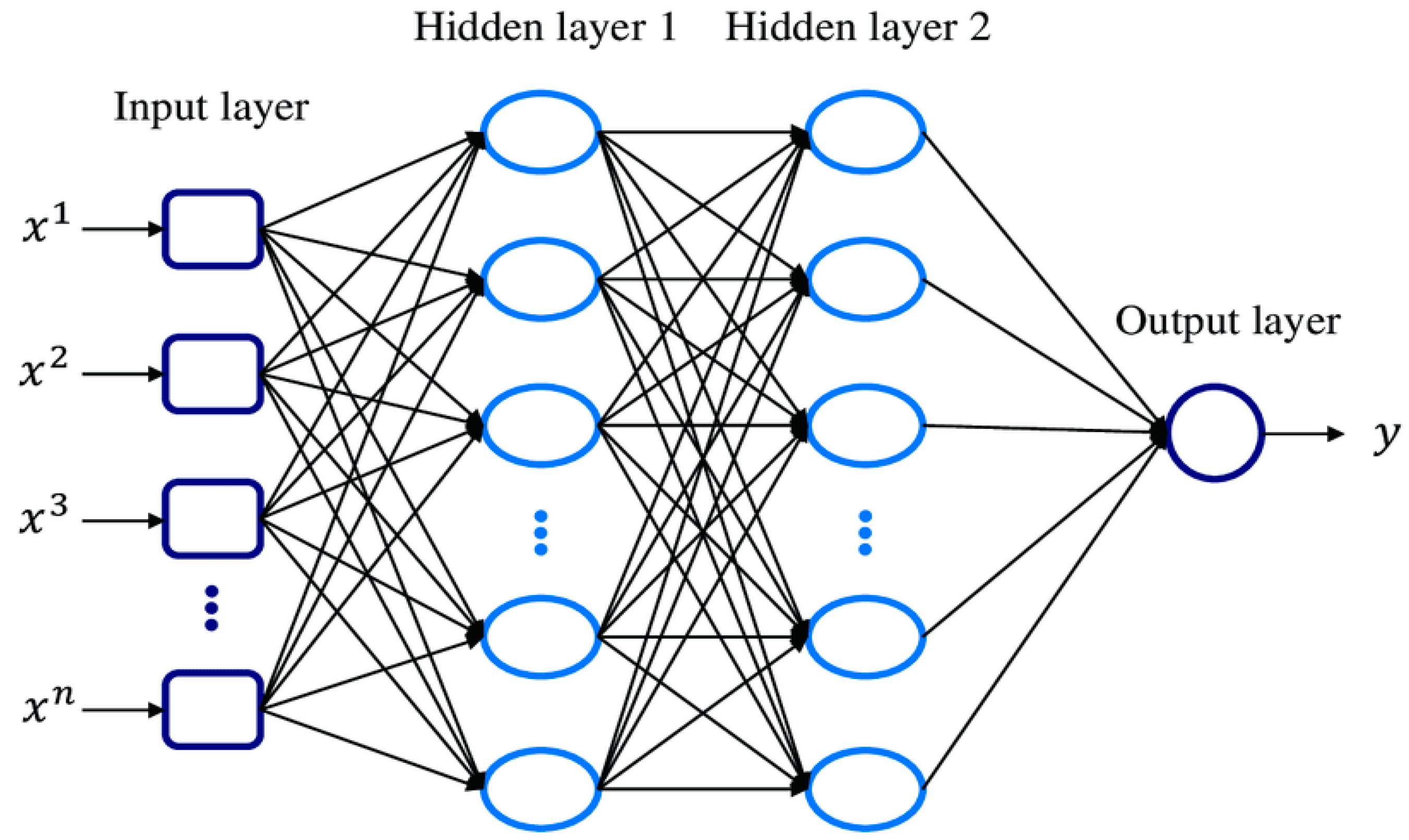
The ANNs that were developed in this work are Multi-Layer Perceptron (MLP) and they stand out for the existence of hidden layers (Figure 2). Simple “perceptrons” use no hidden layers making their use limited due to a lack of credibility. MLP however by using multiple hidden layers can process data much faster and efficient than their predecessors. Their topology and training parameters play a vital role, where if they are not adjusted properly, they can make the training process unsuccessful. If the number of hidden layers is lacking then the training process will be incomplete and the credibility of the final ANN low. However, if the number of hidden layers exceeds the required amount, then the ANN may produce results of high credibility for the current dataset, but will not work properly on different datasets. That’s because of a phenomenon called overfitting or overtraining, where the ANN training process failed making the ANN to replicate, not predict, the exact values of the testing and validation dataset [21].
The way in which the processing of the input data is carried out and their correlation with the output data, make this particular processing method ideal for cases of creating forecasting models. In particular, the present work is called upon to create and evaluate a sufficient number of forecasting ANNs models, in order to select those that present the best predictive ability.

2.1. Study Area and Data Availability

The study area is the city of Beijing, China (39° 54′ 13″ N, 116° 23′ 17″ E) for which hourly measurements of the concentrations of the pollutants of interest as well as meteorological conditions were collected for the time period 1/3/2013 to 28/2/2017. The corresponding values were obtained from a free dataset by Chen Song [24] and were obtained through the link below “https://archive.ics.uci.edu/dataset/501/beijing+multi+site+air+ quality+data”. The following data were given:
  • Concentration of particulate matter with an aerodynamic diameter of up to 2.5 micrometers, PM2.5.
  • Concentration of particulate matter with an aerodynamic diameter of up to 10 micrometers, PM10.
    • Concentration of sulfur dioxide, SO2.
    • Concentration of nitrogen dioxide, NO2.
    • Concentration of carbon monoxide, CO.
    • Ozone concentration, O3.
    • Ambient air temperature, TEMP.
    • Dew temperature, DEWP.
    • Atmospheric pressure, PRES.
    • Height of rain, RAIN.
    • Wind speed, WSPM.
    • Wind Direction, Wd.
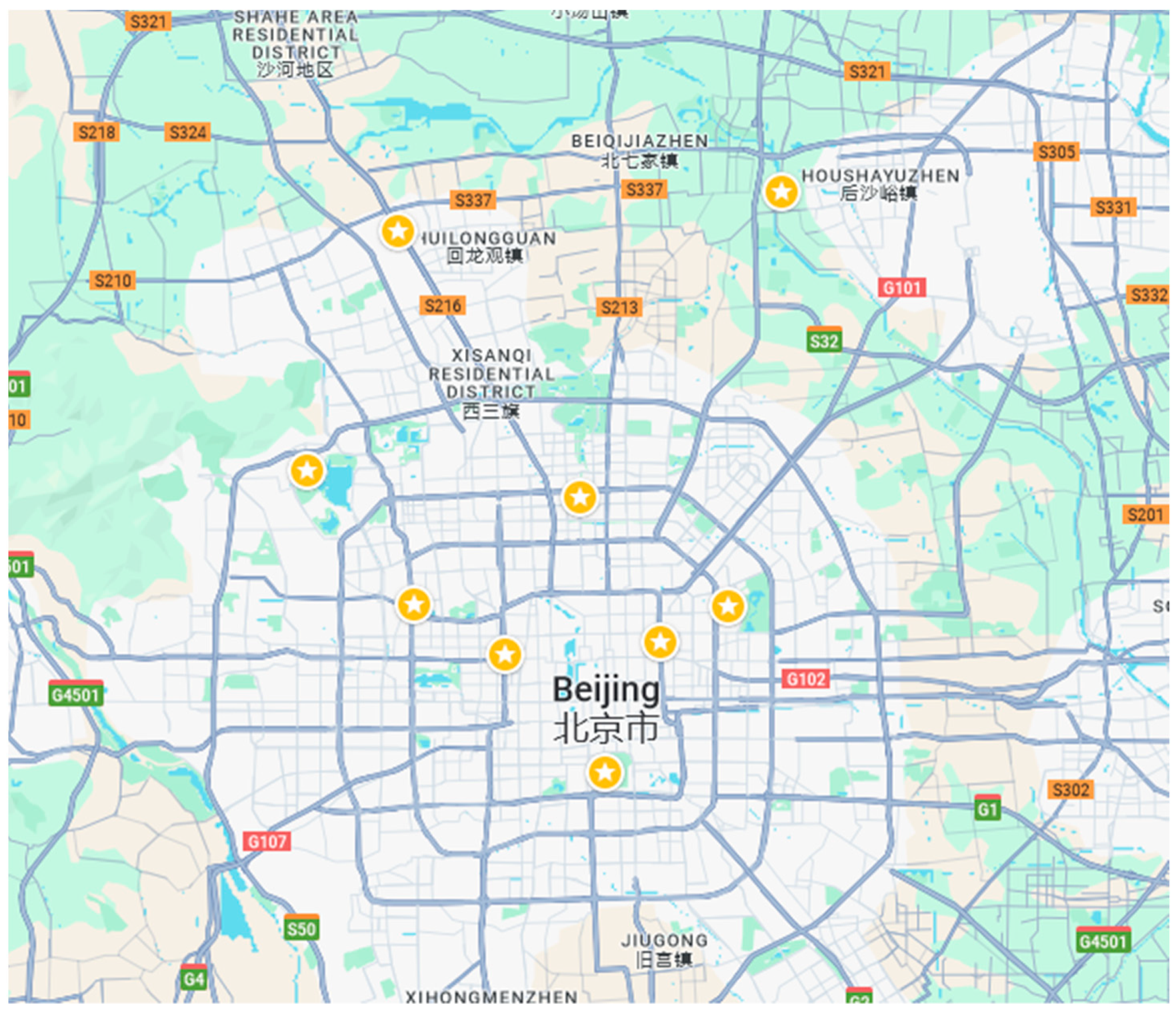
The above values were available for nine (9) total locations of Beijing, namely:
  • Location 1 : Aotizhongxin
  • Location 2 : Changping
  • Location 3 : Dongsi
  • Location 4 : Guanyuan
  • Location 5 : Gucheng
  • Location 6 : Nongzhanguan
  • Location 7 : Tiantan
  • Location 8 : Wanliu
  • Location 9 : Wanshouxigong
The above locations are also shown in Figure 3 (locations with an asterisk). Then, it was decided to be chosen the distance between the examined locations to be no more than 20 kilometers (km). This decision was based on the assumption that within the distance of 20km the influence of the examined locations to each other will be significant as well as the selected locations to be closer to the city’s center. Before any data processing it was necessary to be checked the available data sets for non-available/missing values.
All preliminary screening was done using Microsoft Excel 2021. For example, in Table 1 the data completeness for location 3 is presented. In total, in all nine (9) areas, more than 7000 missing values were found out of a total of 420780 items in each area. Standard methodology dictates that when checking the data for missing values, the researcher is advised to delete the entire row in which they were located. However, such a treatment is possible when there is a large number of available data and/or a small number of missing values. In cases such as in the specific data set, which is not of sufficient size, if the specific methodology was applied, it would lead to a data reduction of 20%. Therefore, it was decided not to follow the specific directive and to make an attempt to cover the missing data through a combination of various methods which are analyzed below.

2.1.1. Method 1: Using Existing Values & Microsoft Excel Commands

In order to apply this method, a basic assumption is made, that the consecutive values within 5 hours do not differ greatly from each other. Having made this assumption renders what must be done quite simple. Initially a check is made for the existence of values within the previous 5 hours and within the next 4 hours. From this check, four (4) individual scenarios emerge as follows:
1. Existence of both values, within the given time limits. In this case the missing value is the average of the two existing values.
2. Existence of only the previous value, within the time limits. In this case the missing value is equal to the previous value plus/minus a certain number, which is listed in Table 2 below.
3. Existence of only the next value, within the time limits. In this case the missing value is equal to the next value plus/minus a specific number, which is listed in Table 2 below.
4. Simultaneous absence of the two values, within the time limits. In this case the element receives the value "NA", so that it can be processed later.
Although the above method is quite effective, it is not able to cover 100% of the missing values, however, it presents an average efficiency of more than 60%. The number of missing values covered are presented in detail in Table 3.

2.1.2. Method 2: Development of a Code within the MATLAB Programming Environment

This method also requires an assumption that the concentrations of pollutants and the values of meteorological factors do not change significantly in an area of about ten (10) kilometers, or less. Initially, the distance between the nine (9) study areas is calculated and for each one the closest areas are selected. Let's take location 3 (Dongsi) as an example. If the distances of the other locations are calculated in relation to location 3, it is found that locations 6,4,8 and 1 (in order of proximity) are within a range of 10 km or less. It is logical that the values of the areas closest to location 3, have a greater influence on the values of interest. In the next step, the relative position of locations 1,4,6 and 8 with respect to location 3 (North, East, North-East, etc.) needs to be determined. Finally, the appropriate code was written within the MATLAB environment, version R2022a, based on which the wind direction is taken into account and the appropriate location is selected based on this. In each case, the missing value in location 3 gets exactly the same value as the corresponding value of the selected area. This method, though much more complicated and detailed than the first one, does not cover a large number of missing values, with a success rate of less than 20%. The remaining values are once again set to “NA” so as to be processed at a later time.
Table 2. Addition and subtraction numbers for each pollutant and meteorological factor.
Table 2. Addition and subtraction numbers for each pollutant and meteorological factor.
Variable Additions/Subtractions Number
PM2.5 1
PM10 1
SO2 0.5
NO2 0.5
CO 50
O3 0.5
TEMP No additions or subtractions were needed.
PRES No additions or subtractions were needed.
DEWP No additions or subtractions were needed.
RAIN No additions or subtractions were needed.
wd No additions or subtractions were needed.
WSPM No additions or subtractions were needed.

2.1.3. Method 3: Applying the Linear Regression Methodology

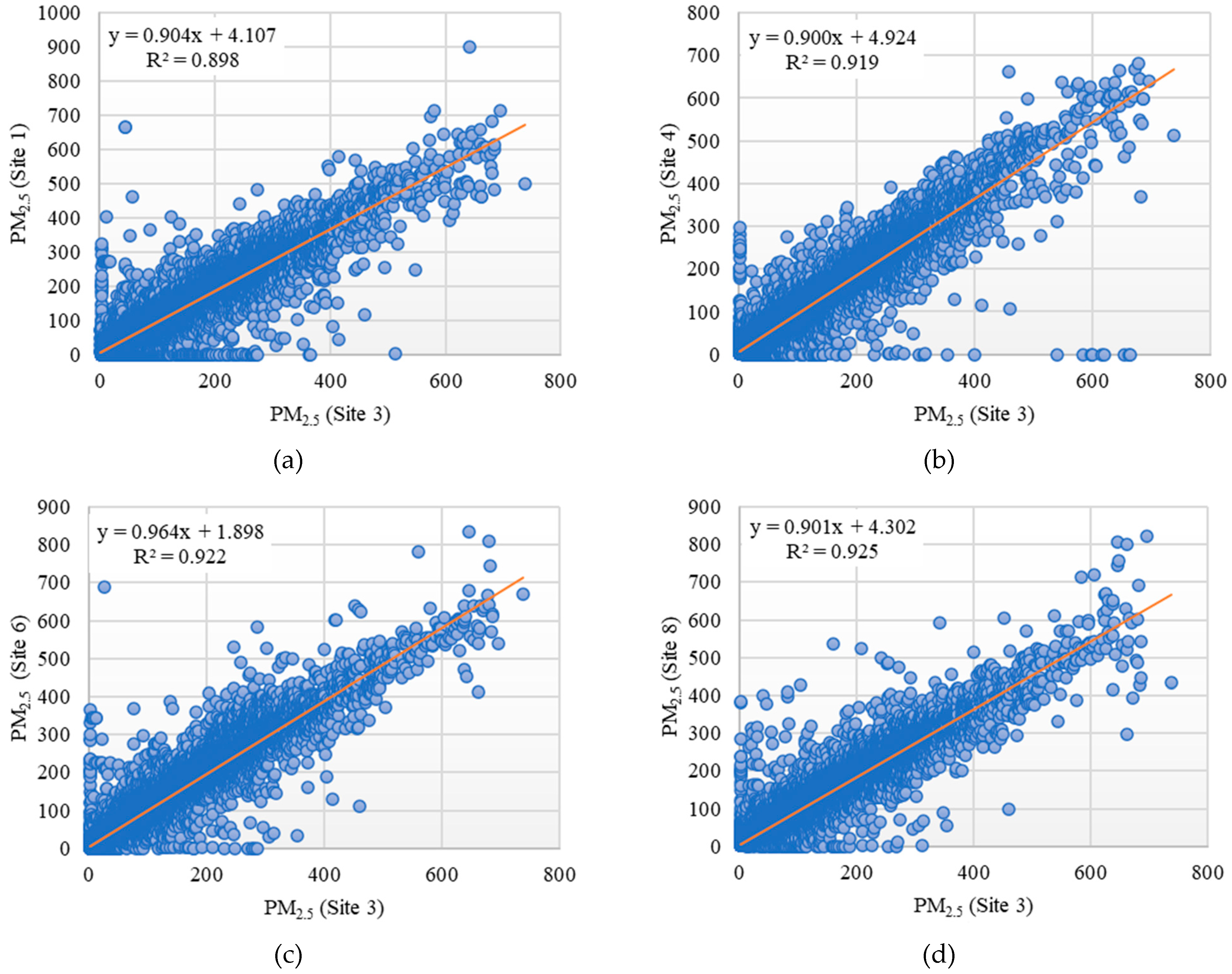
The ideology of this method is directly related to the basic idea behind Method 2. Same as before, the basic assumption here is that the meteorological and atmospheric conditions prevailing in nearby areas, describe with relative accuracy the conditions in the study area. First, the areas are categorized in order of proximity. Then their graphical representation is carried and is followed by the extraction of graphs, structured so that the linear correlation between the values is evident. Finally, these linear equations are extracted and used in order of proximity in the missing values of each region. This method offers 100% coverage of the remaining “NAs”. Figure 4 shows indicatively the graphs concerning the linear correlation between PM2.5 concentrations for location 3 in relation to locations 1,4,6, and 8 respectively.

2.2. Data Preparation

Before the training process of the ANNs can begin, the appropriate processing of the input data was necessary. Initially, it was necessary to be checked the correlation of the variables-data, in order to reveal any existing relationships amongst them. Therefore, the correlation coefficient between the variables was calculated, for each region and in the end the average of them is taken into account as presented in Table 3. However, despite the attempt to extract these "hidden" relationships through the correlation coefficient, Table 3 does not offer much insight. As an alternative method for determining optimal combinations, the Principal Components Analysis (PCA) technique was used, in combination with the k-means clustering method, which showed that 40% of the information can be described solely with the set of temperatures. In practice, however, such a thing is not valid. Although based on methodology we should be satisfied only with the results of the PCA analysis, in the present paper further scenarios are analyzed, which proved to be better than the proposed one. After all, Fabiana Franceschi et al. [18] found a positive correlation between PM10 concentration and wind direction, while a negative correlation was observed between the concentration of the same pollutant in terms of temperature and wind speed. These findings are further reinforced by Zhang et al. [25] in earlier research, in Beijing city, China. Accordingly, for PM2.5, a positive correlation was observed between them and relative humidity [18], which is also verified by this specific research work.
Table 3. Table of mean correlation coefficients.
Table 3. Table of mean correlation coefficients.
PM2.5 PM10 SO2 NO2 CO O3 TEMP PRES DEWP RAIN wd WSPM RH
PM2.5 1.00 0.88 0.48 0.68 0.79 -0.16 -0.14 0.01 0.11 -0.01 -0.12 -0.27 0.39
PM10 1.00 0.46 0.66 0.70 -0.13 -0.11 -0.02 0.06 -0.02 -0.07 -0.18 0.26
SO2 1.00 0.49 0.54 -0.17 -0.34 0.22 -0.28 -0.03 -0.05 -0.10 -0.08
NO2 1.00 0.71 -0.50 -0.29 0.14 -0.03 -0.03 -0.15 -0.42 0.33
CO 1.00 -0.32 -0.34 0.18 -0.07 -0.01 -0.14 -0.29 0.34
O3 1.00 0.60 -0.45 0.32 0.02 0.14 0.29 -0.27
TEMP 1.00 -0.83 0.82 0.06 0.02 0.03 0.10
PRES 1.00 -0.77 -0.01 0.00 0.08 -0.24
DEWP 1.00 0.10 -0.11 -0.28 0.63
RAIN 1.00 -0.01 0.12 0.10
Wd 1.00 0.24 -0.22
WSPM 1.00 -0.52
RH 1.00

2.3. Scenarios Creation

The scenarios that were created were the same for each location, however each of them was studied separately. The goal was to train ANNs forecasting models, for each location and merge them into a universal algorithm. Each location “includes” six (6) pollutants (PM2.5, PM10, SO2, NO2, CO and O3), each pollutant consists of eight (8) scenarios, and each scenario includes ten (10) different ANNs models. The total amount of the developed ANNs was 4320 forecasting models. The training data includes a scenario-different combination of meteorological variables of the hourly values, during the three previous days and predicts the next 24-hourly concentrations. More specifically, in this work the developed ANNs models are able to forecast the hourly air pollutant concentration for the next 24-hours, based on the hourly values from the previous three (3) days. To make it more understandable, let's assume that today is Sunday. At any hour on Sunday, the developed ANNs models are able to give the concentration ​​of each pollutant for the next 24-hours (hourly forecasting step) of Monday (next day forecasting horizon). In any case, the hourly values ​​of the necessary parameters (see scenarios- Table 4) of the three previous days, that is Thursday, Friday and Saturday, are taken into account. The specific structure gives to the developed ANNs forecasting models an operational interest since the forecast can be made at any time during the day, for the next day, giving an advantage in making correct, valid and timely decisions by the competent agencies.
For a better study and analysis of the data, it was considered appropriate to add one more variable, relative humidity (RH), as it combines the dew point temperature (DEWP) and dry bulb temperature (TEMP) data. The developed scenarios are described in Table 4. RH was calculated using the Equation (1) [26]:
RH   =   e ( 17.625 - DEWP / 243.04 + DEWP ) e ( 17.625 - TEMP / 243.04 + TEMP )
As mentioned, for each scenario, 10 different ANNs were trained, which were then evaluated and the best one was selected. For reasons of repeatability of the experiment, the architecture of the developed ANNs is listed in Table 5. The training functions were chosen so that a secondary evaluation, of the way in which the training process can be optimized, can be executed. Specifically, the software’s default training function (Levenburg Marquardt) was chosen as the function to create the first ANN, while its individual parameters were adjusted to require "medium" computational power. For the next four (4) ANNs, they were chosen to be trained with the Bayesian Regularization training algorithm, as it is suitable to train ANNs with the aim of pattern recognition. ANNs number 6 to 10 are examples of other train functions, which were chosen in an effort to find possible functions with better performance. Among the ten (10) developed ANNs models, the first 5 proved to be the most "demanding", as they need a lot of computational power. However, as will be presented in the next section, they consistently offered the most valid results. On the contrary, the second half of Table 5, although it was less "demanding", provided very unstable results, with close to zero utilization capability. However, it is worth mentioning that none of the last five (5) training functions are suitable for training ANNs models of this kind. The topologies/architectures of the developed ANNs models were created in such a way that they could be evaluated by the same standards, while allowing the training process to be commenced by a conventional desktop computer.
Furthermore, the initial dataset was split (randomly) in 3 subsets. The first was the training subset containing 70% of the total data volume, the second was the cross-validation subset and the third was the testing subset containing 15% of the total data volume each one, respectively. Finally, for all of the ten developed ANNs of Table 5, the number of training epochs was equal to 200.

2.4. Software and Infrastructure

The following software were used for the preparation of this work:
  • MATLAB R2022a
  • Microsoft Excel 2021
The ANNs training was carried out on a home desktop computer with the following specifications:
  • CPU: AMD Ryzen 7 5700G
  • RAM: G.Skill Ripjaws V 16GB DDR4-3200MHz
  • GPU: N/A
  • SSD Kingston NV1 500GB M.2 NVMe (SNVS/500G).
In order to be able to evaluate the above neural networks, it was deemed necessary to calculate eight (8) statistical indices [27]. These indices and their equations are listed below: The Equations (2) through (5) describe the statistical evaluation indices for the performance of the models in order to predict the next 24-hourly concentrations, whereas Equations (6) through (9) represent the evaluation indices, that determine the predictive ability of each developed ANN model regarding a certain threshold. More specifically, if the developed model is able to predict the exceedances, in other words the cases where the pollutant concentration was over a specific threshold value or not. These threshold concentrations were determined by the reference values for each pollutant according to WHO. [28]
Mean Absolute Error (MAE) M A E = 1 n · ∑ i = 1 n P i - O i (2)
Root Mean Square Error (RMSE) RMSE = ∑ i = 1 n P i - O i 2 n 2 (3)
Pearson’s Correlation Coefficient (R) R = 1 n · ∑ i = 1 n P i - P mean ) · ( O i - O mean ∑ i = 1 n O i - O m e a n 2 · ∑ i = 1 n P i - P m e a n 2 (4)
Index of Agreement (IA) IA = ∑ i = 1 n P i - O i 2 ∑ i = 1 n P i - O mean + O i - O mean 2 (5)
True Prediction Rate (TPR) TPR = True   Positives True   Positives + False   Negatives (6)
False Prediction Rate (FPR) FPR = False   Positives False   Positives + True   Negatives (7)
False Alarm Rate (FAR) FAR = False   Positives False   Positives + True   Positives (8)
Success Index (SI) SI = True   Positives + True   Negatives Total   Predictions (9)
where, (Oi) and (Pi) represent the observed and the predicted values respectively, (Omean) is the mean of the observed values and (n) is the number of observations in each case.

4. Results & Discussion

Table 6 depicts the values of the statistical evaluation indices (MAE, RMSE, R and IA) for the best developed ANN model, for each one of the six air pollutants among the nine examined locations and for all of the eight examined scenarios. According to Table 6, it seems that for particulate matters and NO2, ANN#5 has the best predictive performance. For SO2, O3 and CO, ANN#4 presents the best predictive ability. In all cases, the most suitable scenarios are S2 and S1 (see Table 4). Location 8 seems to have the best forecasting ability, especially for air pollutants NO2, SO2, O3 and CO. This may lead to the conclusion that location 8 could be the base for air pollution forecasting of the other locations. Concerning the general forecasting ability, we can say that the correlation coefficient (R) is lying between 0.911 and 0.954 as well as the index of agreement (IA) is lying between 95.31% and 97.64%. Both of these indicate a very good forecasting ability for the next 24-hours with an hourly forecasting step.
Table 7 shows the values of the exceedance’s statistical evaluation indices (TPR, FPR, FAR and SI) for the best developed ANN model, for each one of the six air pollutants among the nine examined locations and for all of the eight examined scenarios.
Concerning the forecasting of the exceedances, in other words the cases where the concentration of the examined pollutants is greater than a given threshold value based on WHO directives and was forecasted correctly or not, seems that in all cases model ANN#5 gives the best prediction. Also, location 8 seems that can be considered as a reference location in future works. Furthermore, S1 and S2 were found to be again the best training scenarios among the eight examined scenarios. Finally, TPR, which gives the rate of exceedances that observed and correctly forecasted, lying between 88.16% and 97.75% while SI which shows the overall ability of right forecasting of the exceedances is lying between 93.113% and 99.86%. Both, indicate that the developed ANNs models are able to give a very good and sufficient forecasting of the exceedances.
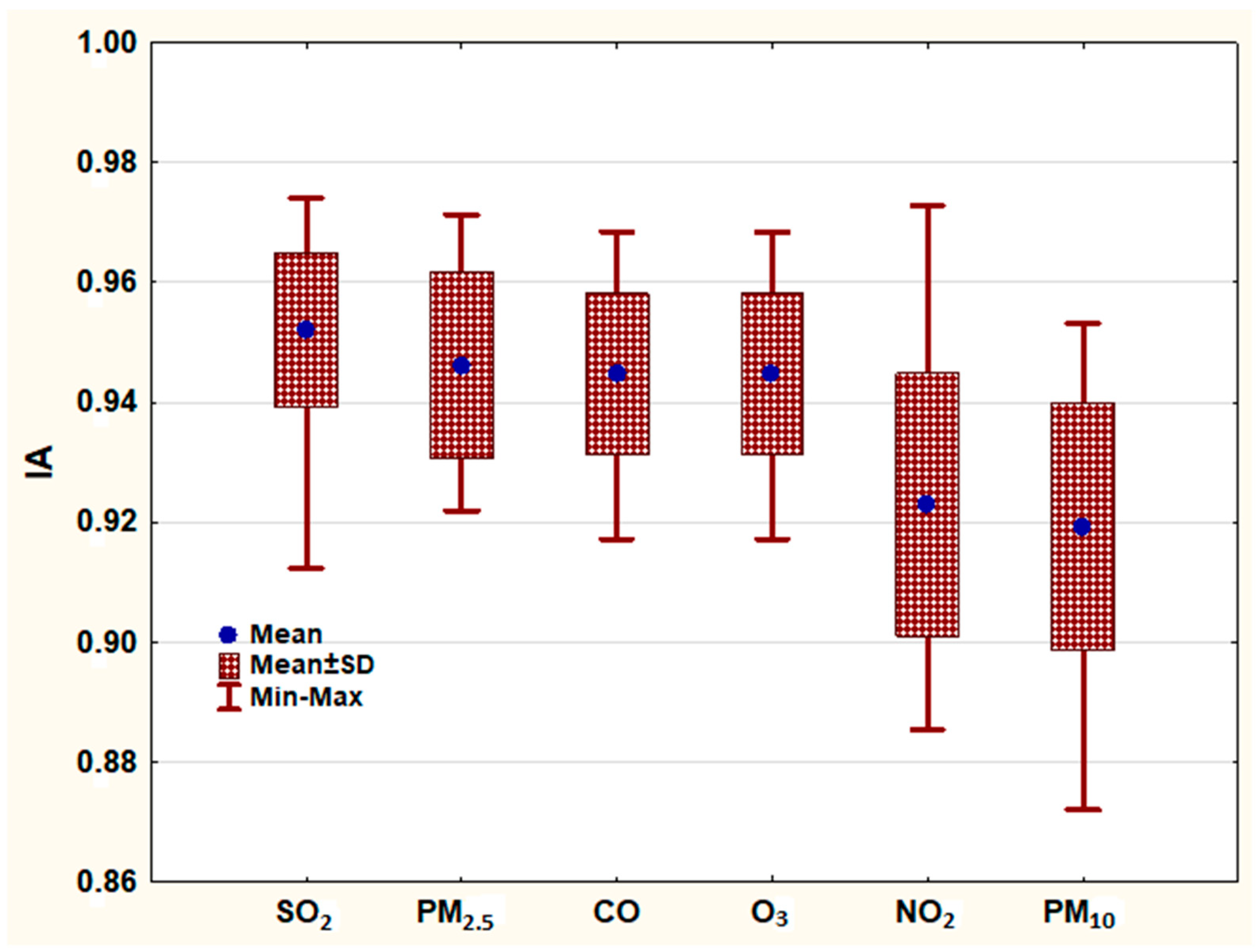
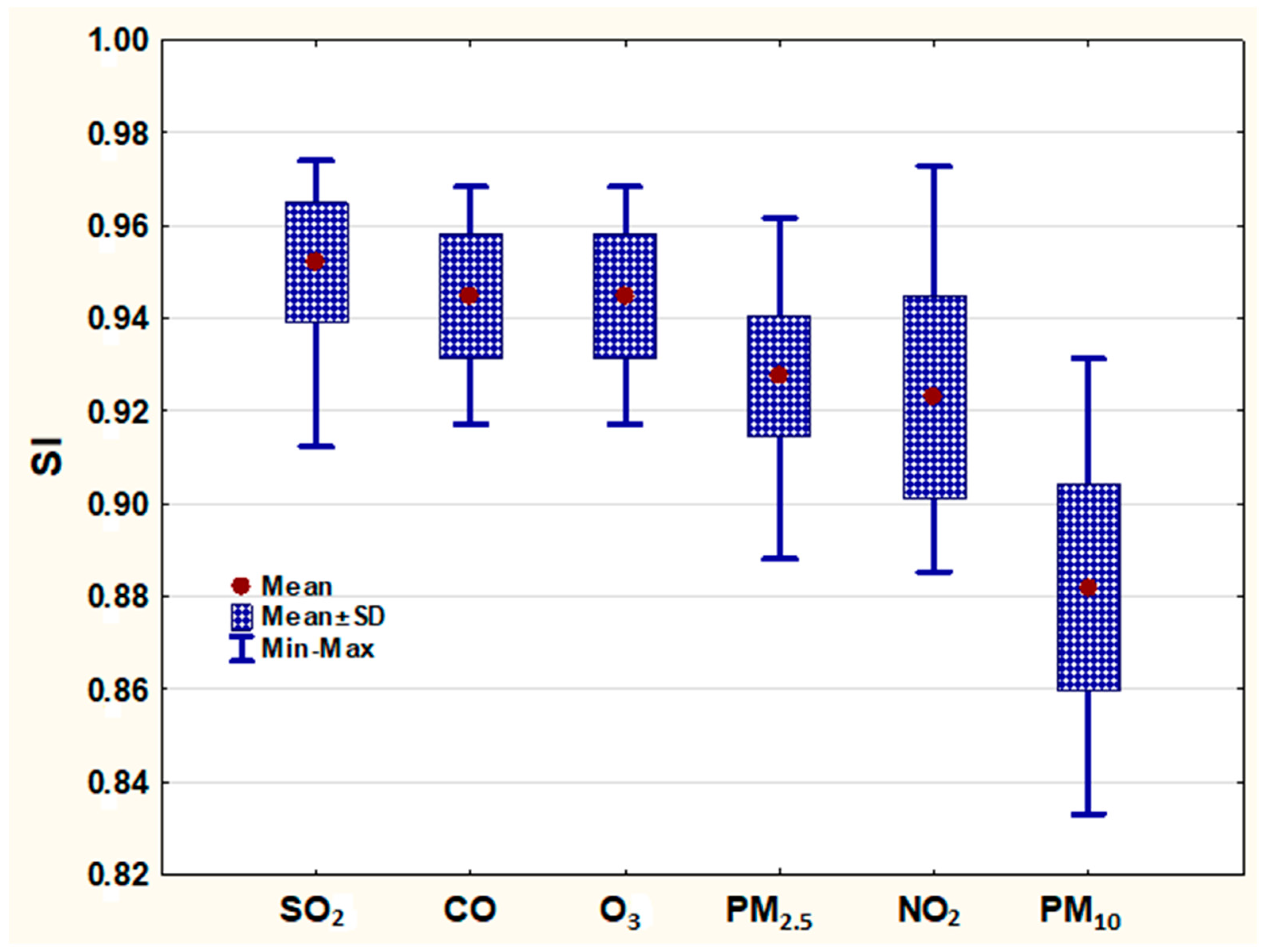
In the effort to be derived the general behavior of the developed ANNs models, in terms of their forecasting ability, appropriate Box & Whisker graphs were created. Necessary data for the design of these graphs are the maximum, average and minimum values of IA (Figure 5) and SI (Figure 6) respectively, concerning all of the developed ANNs, for each air pollutant and for each one of the examined nine locations, within the greater area of Beijing, China. More concretely, data were composed from the best performance values for each pollutant and for the optimal training function, therefore from 72 total values (9 locations X 8 input data training scenarios).
Figure 5 shows that the mean values of IA for all of the developed ANNs models and for all of the forecasted air pollutants is lying between 0.92 and 0.95 indicating an extremely good forecasting performance. In addition, seems that the developed ANNs models are able to forecast next day 24-hours concentrations of SO2, PM2.5, CO and O3 in a more sufficient manner than NO2 and PM10.
In the same fashion as in Figure 5, but in this case concerning the ability of the developed ANNs to forecast the air pollutants concentration exceedances, seems in Figure 6 that the mean values of SI, for all of the developed ANNs models and for all of the examined air pollutants, is lying between 0.88 and 0.95 indicating an extremely good forecasting performance. In addition, seems that the developed ANNs models are able to forecast the exceedances of next day for SO2, PM2.5, CO and O3 in a more sufficient level than NO2 and much more than PM10.

5. Conclusions

The aim of this work was to create a universal forecasting model of air pollutants concentrations, specifically PM2.5 and PM10, as well as SO2, NO2, CO and O3. A basic condition for the training of these models is the appropriate pre-processing of the input data in order to extract any hidden relationships, which will facilitate the subsequent creation of the scenarios. The gap-filling process was an innovation that was not found in any of the forementioned literature and offered satisfactory results. The algorithms created for this process are also universal models, and their application is feasible to any other data set, with minor adjustments. Additionally, the comparison of eight possible input scenarios and the training of each with ten different training functions (ANNs models architecture), was conducted. The results offered valuable insight regarding the optimization of the training of ANNs models having as a constant variable the pollutant of interest. The results were acceptable for the majority of pollutants with average prediction values well above 80.0% accuracy. Through further statistical analysis it was shown that the use of all of the available meteorological variables enhances the training performance of ANNs and does not "confuse" them. It was also observed that the BR4 (ANN#5) structure is the most suitable. It seems that the exported model can be used by both public and private bodies so as to achieve the immediate information of the former and to assist the latter in protecting themselves from the harmful environmental conditions.
Concluding, the developed ANNs forecasting models shows an operational interest since the forecast can be made at any time during the day, for the next day, giving an advantage in making correct, valid and timely decisions by the competent agencies.
Finally, it is suggested that further research is required in order to improve the prediction of air pollution so that the developed models have an optimal design and performance for public and private authorities’ decision making, aiming the protection of public health and also to avoid adverse health effects, as well as adverse effects on constructions and infrastructures, taking into account the climatic crisis in addition.

Author Contributions

Conceptualization; methodology, P.F. and K.M.; software, P.F.; validation, P.F., K.M. and G.S.; formal analysis, P.F., K.M., and G.S.; investigation, P.F., K.M., and G.S.; resources, P.F. and K.M.; data curation, P.F. and K.M.; writing—original draft preparation, P.F. and K.M.; writing—review and editing, P.F., K.M., and G.S.; visualization, P.F., K.M., and G.S.; supervision, K.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available on:
https://archive.ics.uci.edu/dataset/501/beijing+multi+site+air+%20quality+data

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Air Pollution Available online: https://www.who.int/health-topics/air-pollution (accessed on 18 August 2024).
  2. Ntourou, K.; Moustris, K.; Spyropoulos, G.; Fameli, K.-M.; Manousakis, N. Adverse Health Effects (Bronchitis Cases) Due to Particulate Matter Exposure: A Twenty-Year Scenario Analysis for the Greater Athens Area (Greece) Using the AirQ+ Model. Atmosphere 2023, 14, 389. [CrossRef]
  3. Mo, X.; Li, H.; Zhang, L.; Qu, Z. Environmental Impact Estimation of PM2.5 in Representative Regions of China from 2015 to 2019: Policy Validity, Disaster Threat, Health Risk, and Economic Loss. Air Qual Atmos Health 2021, 14, 1571–1585. [CrossRef]
  4. Amoatey, P.; Sicard, P.; De Marco, A.; Khaniabadi, Y.O. Long-Term Exposure to Ambient PM2.5 and Impacts on Health in Rome, Italy. Clinical Epidemiology and Global Health 2020, 8, 531–535. [CrossRef]
  5. Veras, M.M.; Farhat, S.C.L.; Rodrigues, A.C.; Waked, D.; Saldiva, P.H.N. Beyond Respiratory Effects: Air Pollution and the Health of Children and Adolescents. Current Opinion in Environmental Science & Health 2023, 32, 100435. [CrossRef]
  6. Veras, M.; Waked, D.; Saldiva, P. Safe in the Womb? Effects of Air Pollution to the Unborn Child and Neonates. Jornal de Pediatria 2022, 98, S27–S31. [CrossRef]
  7. Elten, M.; Donelle, J.; Lima, I.; Burnett, R.T.; Weichenthal, S.; Stieb, D.M.; Hystad, P.; Van Donkelaar, A.; Chen, H.; Paul, L.A.; et al. Ambient Air Pollution and Incidence of Early-Onset Paediatric Type 1 Diabetes: A Retrospective Population-Based Cohort Study. Environmental Research 2020, 184, 109291. [CrossRef]
  8. Raz, R.; Roberts, A.L.; Lyall, K.; Hart, J.E.; Just, A.C.; Laden, F.; Weisskopf, M.G. Autism Spectrum Disorder and Particulate Matter Air Pollution before, during, and after Pregnancy: A Nested Case–Control Analysis within the Nurses’ Health Study II Cohort. Environ Health Perspect 2015, 123, 264–270. [CrossRef]
  9. Simoncic, V.; Enaux, C.; Deguen, S.; Kihal-Talantikite, W. Adverse Birth Outcomes Related to NO2 and PM Exposure: European Systematic Review and Meta-Analysis. IJERPH 2020, 17, 8116. [CrossRef]
  10. Ntourou, K.; Fameli, K.-M.; Moustris, K.; Augoustinos, A.; Tsitsis, C. The Influence of Ozone Concentrations on Public Health over the Greater Athens Area, Greece. In Proceedings of the 16th International Conference on Meteorology, Climatology and Atmospheric Physics—COMECAP 2023; MDPI, August 28 2023; p. 107.
  11. Feng, Z.; Hu, E.; Wang, X.; Jiang, L.; Liu, X. Ground-Level O3 Pollution and Its Impacts on Food Crops in China: A Review. Environmental Pollution 2015, 199, 42–48. [CrossRef]
  12. Hernández-Peña, A.; Gallardo-Hernández, E.A.; Farfan-Cabrera, L.I.; Vite-Torres, M.; Muñoz-Saldaña, J. Solid Particle Erosion Evaluation of Automotive Paint Coatings under the Influence of Artificial Weathering. Wear 2023, 532–533, 205105. [CrossRef]
  13. Ibrahim, A.M.; Bassuoni, M.T.; Carroll, J.; Ghazy, A. Performance of Concrete Superficially Treated with Nano-Modified Coatings under Sulfuric Acid Exposures. Journal of Building Engineering 2024, 86, 108957. [CrossRef]
  14. Feng, X.; Li, Q.; Zhu, Y.; Hou, J.; Jin, L.; Wang, J. Artificial Neural Networks Forecasting of PM2.5 Pollution Using Air Mass Trajectory Based Geographic Model and Wavelet Transformation. Atmospheric Environment 2015, 107, 118–128. [CrossRef]
  15. Elangasinghe, M.A.; Singhal, N.; Dirks, K.N.; Salmond, J.A. Development of an ANN–Based Air Pollution Forecasting System with Explicit Knowledge through Sensitivity Analysis. Atmospheric Pollution Research 2014, 5, 696–708. [CrossRef]
  16. Bai, Y.; Li, Y.; Wang, X.; Xie, J.; Li, C. Air Pollutants Concentrations Forecasting Using Back Propagation Neural Network Based on Wavelet Decomposition with Meteorological Conditions. Atmospheric Pollution Research 2016, 7, 557–566. [CrossRef]
  17. Biancofiore, F.; Busilacchio, M.; Verdecchia, M.; Tomassetti, B.; Aruffo, E.; Bianco, S.; Di Tommaso, S.; Colangeli, C.; Rosatelli, G.; Di Carlo, P. Recursive Neural Network Model for Analysis and Forecast of PM10 and PM2.5. Atmospheric Pollution Research 2017, 8, 652–659. [CrossRef]
  18. Franceschi, F.; Cobo, M.; Figueredo, M. Discovering Relationships and Forecasting PM10 and PM2.5 Concentrations in Bogotá, Colombia, Using Artificial Neural Networks, Principal Component Analysis, and k-Means Clustering. Atmospheric Pollution Research 2018, 9, 912–922. [CrossRef]
  19. Chen, Q.; Ding, R.; Mo, X.; Li, H.; Xie, L.; Yang, J. An Adaptive Adjacency Matrix-Based Graph Convolutional Recurrent Network for Air Quality Prediction. Sci Rep 2024, 14, 4408. [CrossRef]
  20. Latif, S.D.; Lai, V.; Hahzaman, F.H.; Ahmed, A.N.; Huang, Y.F.; Birima, A.H.; El-Shafie, A. Ozone Concentration Forecasting Utilizing Leveraging of Regression Machine Learnings: A Case Study at Klang Valley, Malaysia. Results in Engineering 2024, 21, 101872. [CrossRef]
  21. Ben Krose; Patrick van der Smagt An Introduction to Neural Networks; 8th ed.; 1996;
  22. Ι. Βλαχάβας; Π. Κεφαλάς; Ν. Βασιλειάδης; Φ. Κόκκορας; H. Σακελλαρίου Τεχνητή Νοημοσύνη; 4th ed.; 2020; ISBN 978-618-5196-44-8.
  23. Sarraf Shirazi, A.; Frigaard, I. SlurryNet: Predicting Critical Velocities and Frictional Pressure Drops in Oilfield Suspension Flows. Energies 2021, 14, 1263. [CrossRef]
  24. Chen, S. Beijing Multi-Site Air Quality 2017.
  25. Zhang, Z.; Zhang, X.; Gong, D.; Quan, W.; Zhao, X.; Ma, Z.; Kim, S.-J. Evolution of Surface O3 and PM2.5 Concentrations and Their Relationships with Meteorological Conditions over the Last Decade in Beijing. Atmospheric Environment 2015, 108, 67–75. [CrossRef]
  26. Relative Humidity Calculator Available online: https://www.omnicalculator.com/physics/relative-humidity (accessed on 27 April 2024).
  27. Moustris, K.P.; Ziomas, I.C.; Paliatsos, A.G. 3-Day-Ahead Forecasting of Regional Pollution Index for the Pollutants NO2, CO, SO2, and O3 Using Artificial Neural Networks in Athens, Greece. Water Air Soil Pollut 2010, 209, 29–43. [CrossRef]
  28. World Health Organization WHO Global Air Quality Guidelines. Particulate Matter (PM2.5 and PM10), Ozone, Nitrogen Dioxide, Sulfur Dioxide and Carbon Monoxide.; World Health Organization; ISBN 978-92-4-003422-8.
Preprints 116222 g001
Figure 1. Schematic representation of an ANN neuron.
Figure 1. Schematic representation of an ANN neuron.
Preprints 116222 g001
Preprints 116222 g002
Figure 2. MLP architecture-topology [23].
Figure 2. MLP architecture-topology [23].
Preprints 116222 g002
Preprints 116222 g003
Figure 3. Map with the positions of the nine (9) examined locations, Beijing, China.
Figure 3. Map with the positions of the nine (9) examined locations, Beijing, China.
Preprints 116222 g003
Preprints 116222 g004
Figure 4. Indicative illustration of the linear correlation of PM2.5 concentrations between sites 3 & 1 (a), sites 3 & 4 (b), sites 3 & 6 (c) and sites 3 & 8 (d).
Figure 4. Indicative illustration of the linear correlation of PM2.5 concentrations between sites 3 & 1 (a), sites 3 & 4 (b), sites 3 & 6 (c) and sites 3 & 8 (d).
Preprints 116222 g004
Preprints 116222 g005
Figure 5. Box and Whisker plot of Index of Agreement (IA) for all of the training scenarios and for each examined pollutant.
Figure 5. Box and Whisker plot of Index of Agreement (IA) for all of the training scenarios and for each examined pollutant.
Preprints 116222 g005
Preprints 116222 g006
Figure 6. Box and Whisker plot of Success Index (SI) for all of the training scenarios for each examined pollutant.
Figure 6. Box and Whisker plot of Success Index (SI) for all of the training scenarios for each examined pollutant.
Preprints 116222 g006
Table 1. Indicative number of data completeness for location 3.
Table 1. Indicative number of data completeness for location 3.
Variable Missing Values Variable Missing Values
PM2.5 750 TEMP 20
PM10 553 PRES 20
SO2 663 DEWP 20
NO2 1601 RAIN 20
CO 3197 wd 78
O3 664 WSPM 14
TOTAL 7428 TOTAL 172
Table 4. Table of scenarios.
Table 4. Table of scenarios.
A/A Variables-Inputs
S1 Pollutant - Temperature - Pressure - Dew Point - Rain - Wind Direction -Wind Speed
S2 Pollutant - Temperature - Pressure - Dew Point - Rain - Wind Direction - Wind Speed - Relative Humidity
S3 Pollutant - Temperature - Pressure - Wind Direction - Wind Speed - Relative Humidity
S4 Pollutant - Temperature - Pressure - Wind Direction - Wind Speed
S5 Pollutant - Temperature - Wind Direction - Wind Speed
S6 Pollutant - Wind Direction - Wind Speed
S7 Pollutant - Temperature - Pressure
S8 Pollutant - Temperature
Table 5. Table of ANNs training parameters.
Table 5. Table of ANNs training parameters.
A/A Training Function Abbreviation Hidden Layers Input Layer Neurons Hidden Layer Neurons
AΝΝ#1 Levenberg-Marquardt LM 2 10 30-15
AΝΝ#2 Bayesian Regularization BR1 2 10 30-15
AΝΝ#3 Bayesian Regularization BR2 2 25 30-15
AΝΝ#4 Bayesian Regularization BR3 3 10 30-15-10
AΝΝ#5 Bayesian Regularization BR4 3 25 30-15-10
AΝΝ#6 Conjugate gradient backpropagation with Powell-Beale restarts CGB 3 30 30-15-10
AΝΝ#7 Fletcher-Powell Conjugate Gradient CGF 3 30 30-15-10
AΝΝ#8 Polak-Ribiére Conjugate Gradient CGP 3 30 30-15-10
AΝΝ#9 One-step secant backpropagation OSS 3 30 30-15-10
AΝΝ#10 Scaled conjugate gradient
backpropagation		 SCG 3 30 30-15-10
Table 6. Statistical evaluation indices for the best ANNs performance and for each air pollutant.
Table 6. Statistical evaluation indices for the best ANNs performance and for each air pollutant.
Air Pollutant/ANN# Location Scenario MAE (μg/m3) RMSE (μg/m3) R IA (%)
PM2.5/AΝΝ#5 4 S2 0.28 26.7 0.945 97.13
PM10/AΝΝ#5 3 S1 0.48 40.61 0.911 95.31
NO2/AΝΝ#5 8 S2 0.12 18.26 0.948 97.28
SO2/AΝΝ#4 8 S2 0.01 7.13 0.950 97.40
O3/AΝΝ#4 8 S2 0.01 16.26 0.954 97.64
CO/AΝΝ#4 8 S1 0.00* 0.44* 0.939 96.84
*For CO the units are mg/m3.
Table 7. Evaluation of exceedances statistical indices for the best ANNs models performance for each air pollutant.
Table 7. Evaluation of exceedances statistical indices for the best ANNs models performance for each air pollutant.
Air Pollutant/ANN# Location Scenario TPR (%) FPR (%) FAR (%) SI (%)
PM2.5/AΝΝ#5 1 S1 97.35 78.26 1.27 96.16
PM10/AΝΝ#5 8 S1 97.75 24.67 6.15 93.13
NO2/AΝΝ#5 9 S2 88.16 1.02 7.46 97.62
SO2/AΝΝ#5 8 S2 96.91 0.23 1.88 99.45
O3/AΝΝ#5 8 S2 89.88 0.89 8.39 98.22
CO/AΝΝ#5 6 S2 97.44 0.07 2.56 99.86
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated