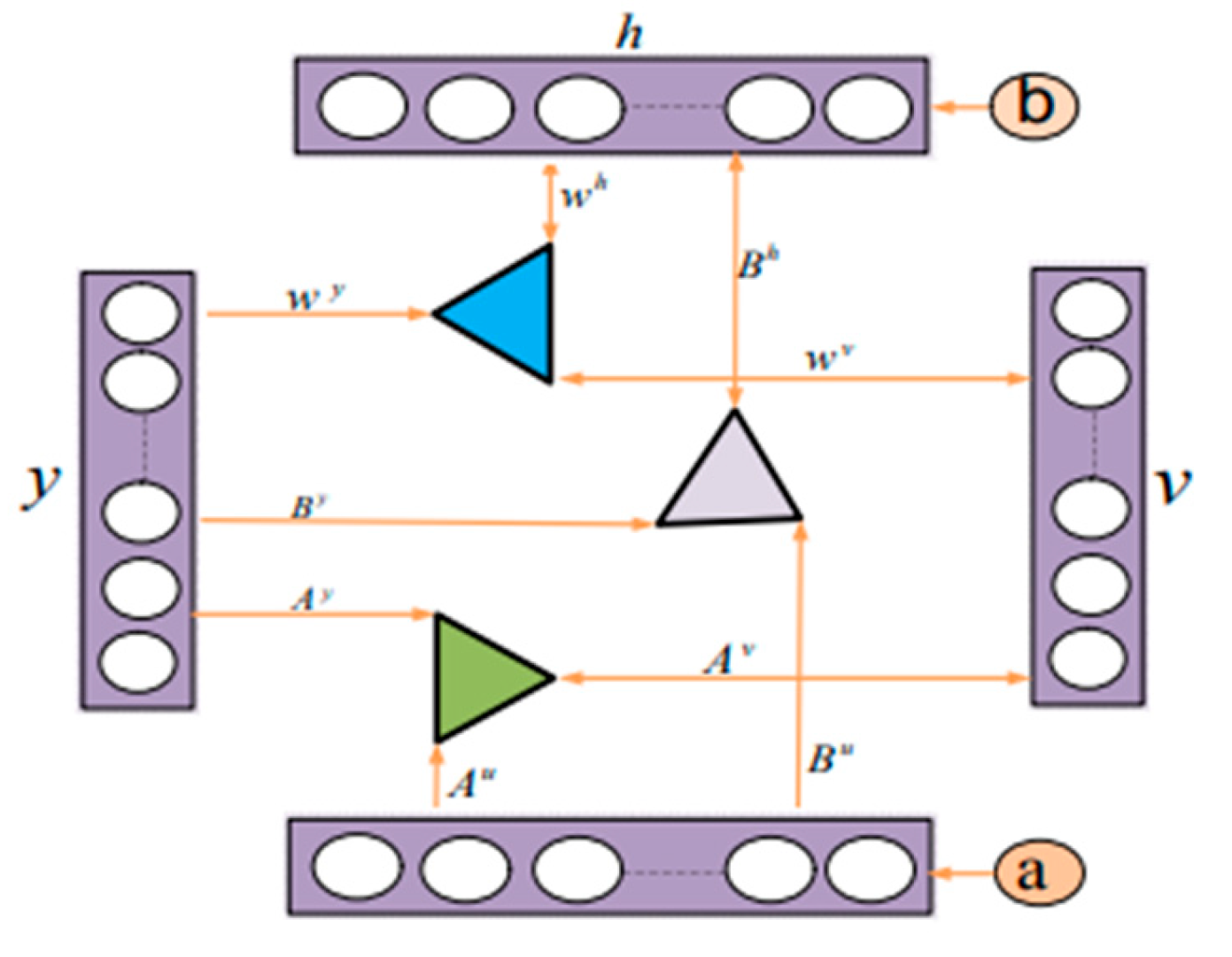
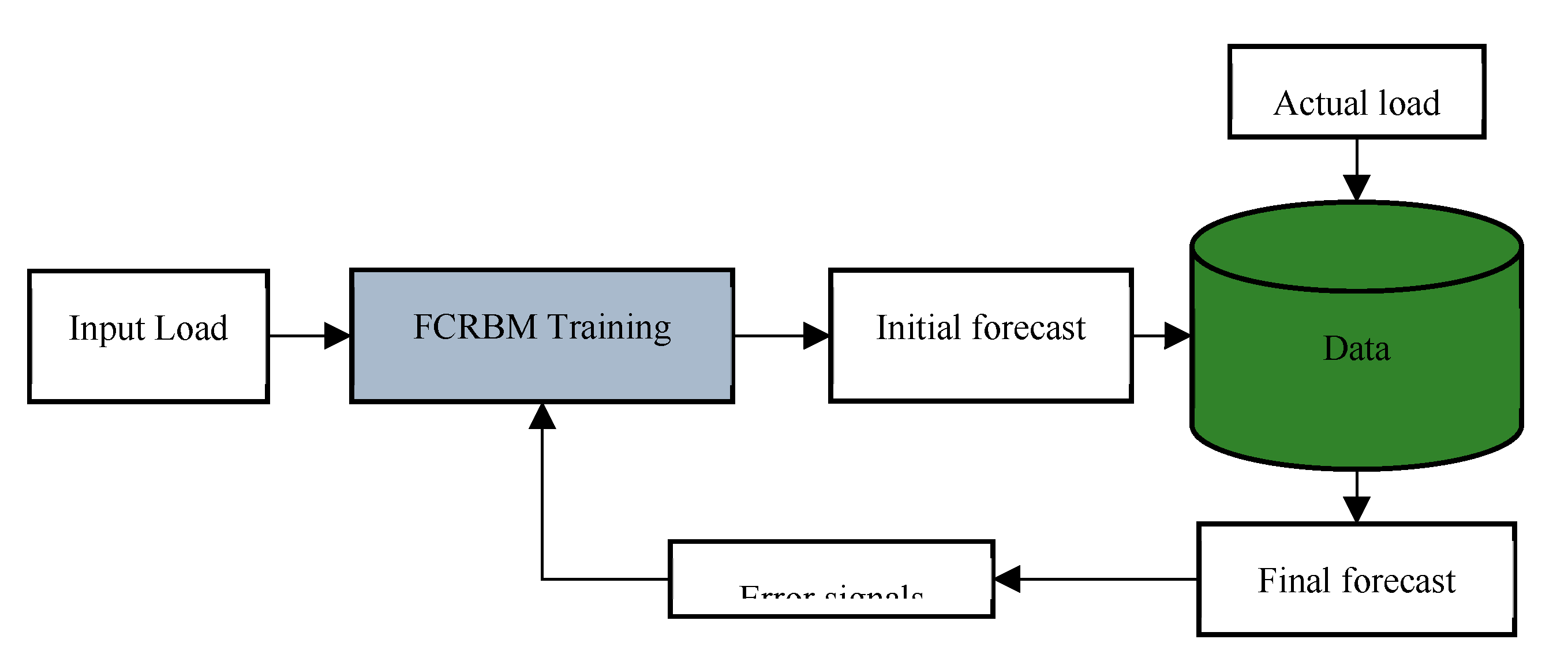
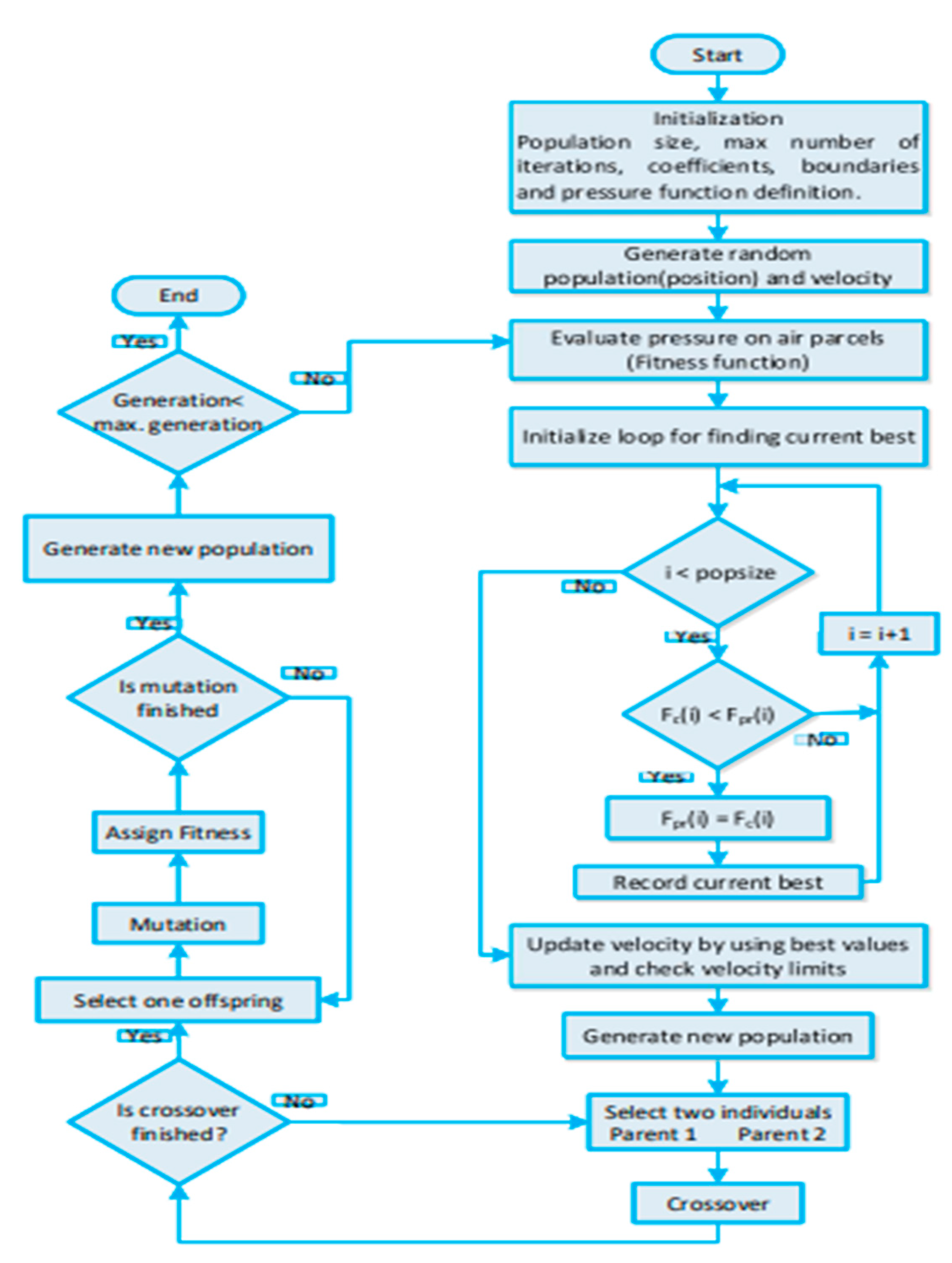
4.1. Stage One: Electrical Load Forecasting
In this stage, the effectiveness of the FS-FCRBM-GWDO framework, along with benchmark frameworks such as AFC-STLF, Bi-level, MI-mEDE-ANN, and FS-ANN, is evaluated. These benchmarks were selected due to their architectural similarities with the proposed framework. However, the FS-FCRBM-GWDO and the benchmark models have distinct computational challenges, focusing on accuracy, convergence rate, or stability. The FS-FCRBM-GWDO model is tested using real-time hourly energy usage data from the Rwandan power system, covering four years from 2018 to 2021. 80% of the data is used for training the FCRBM model, while the remaining 20% is for testing. The control parameters used in the simulations are consistent across both the proposed and benchmark models, ensuring a fair comparison. The FS-FCRBM-GWDO framework is assessed using two performance metrics: (i) accuracy, measured by mean absolute percentage error (MAPE), variance (σ
2), and Pearson correlation coefficient; and (ii) convergence speed, measured by execution time and convergence rate. The variance (
) is mathematically represented as follows in equation 16.
The symbol
indicates the number of timeslots,
identifies the actual load,
represents the predicted load at time
, and
represents the variance. The accuracy of the performance metrics is computed using the following formula.
The convergence speed is determined by both the execution time and the convergence rate. The following is a comprehensive description.
1. Execution Time: This metric refers to the duration required for the forecasting model to predict future electrical energy consumption patterns. It is measured in seconds, with faster models having shorter execution times.
2. Convergence Rate: This aspect measures the speed at which the model reaches a specific epoch where performance stabilizes, and the error ceases to decrease significantly with additional epochs. Models with a high convergence rate reach this stabilization point quickly, often at early epochs. Forecasting models are classified as fast if they exhibit minimal execution time and achieve early convergence, indicating efficient performance.
Table 2.
GWDO’s Simulation parameters.
Table 2.
GWDO’s Simulation parameters.
| Control parameters |
Value |
| Number of hidden layers |
1 |
| Number of neurons in hidden layer |
10 |
| Output layer |
1 |
| Number of output neurons |
1 |
| Number of epochs |
100 |
| Number of iterations |
100 |
| Learning rate |
0.0019 |
| Momentum |
0.6 |
| Initial weight |
0.1 |
| Initial bias |
0 |
| Max |
0.9 |
| Min |
0.1 |
| Decision variables |
2 |
| Population size |
24 |
| Delay of weight |
0.0002 |
| Historical load data |
4 years |
| Exogenous parameters |
4 years |
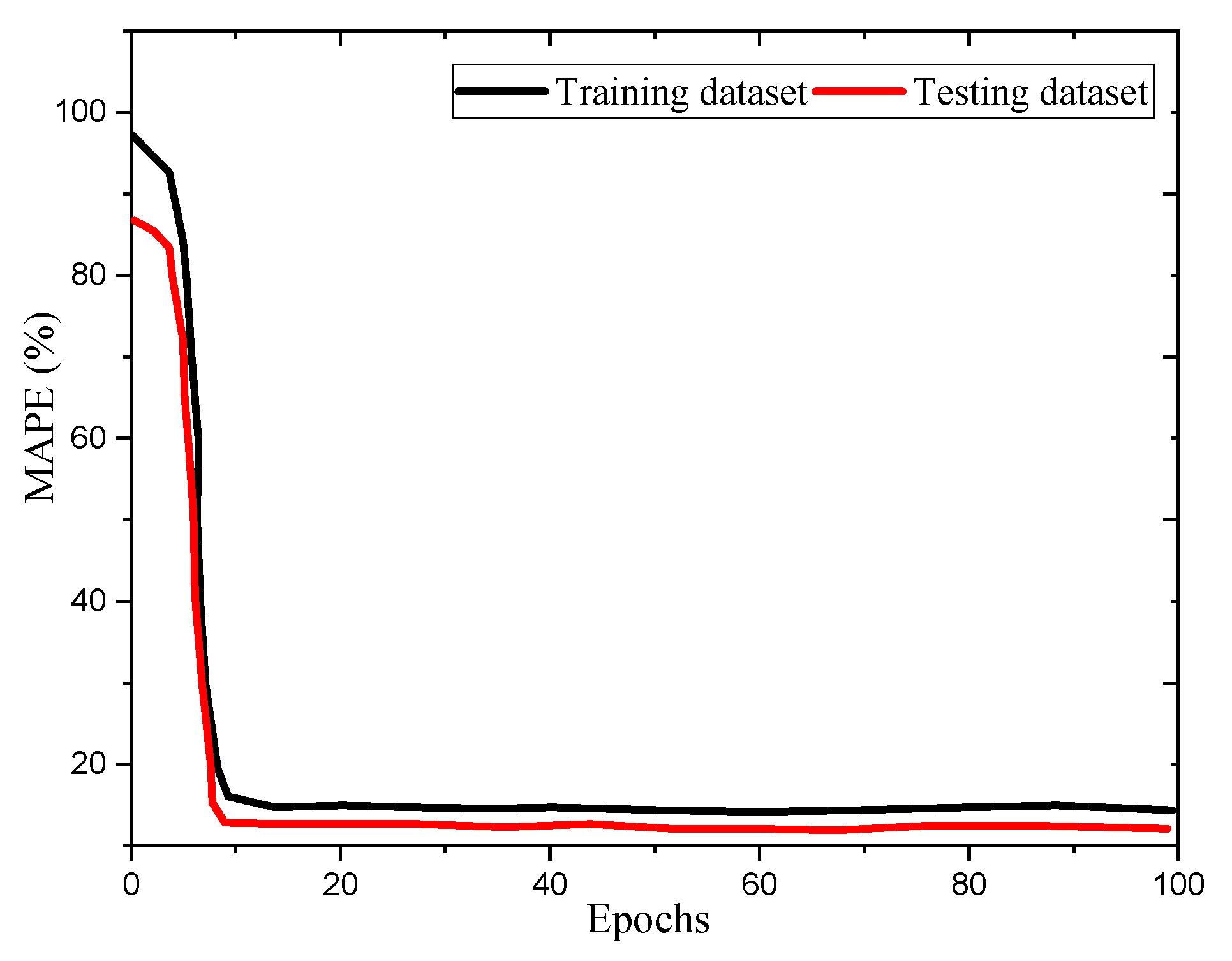
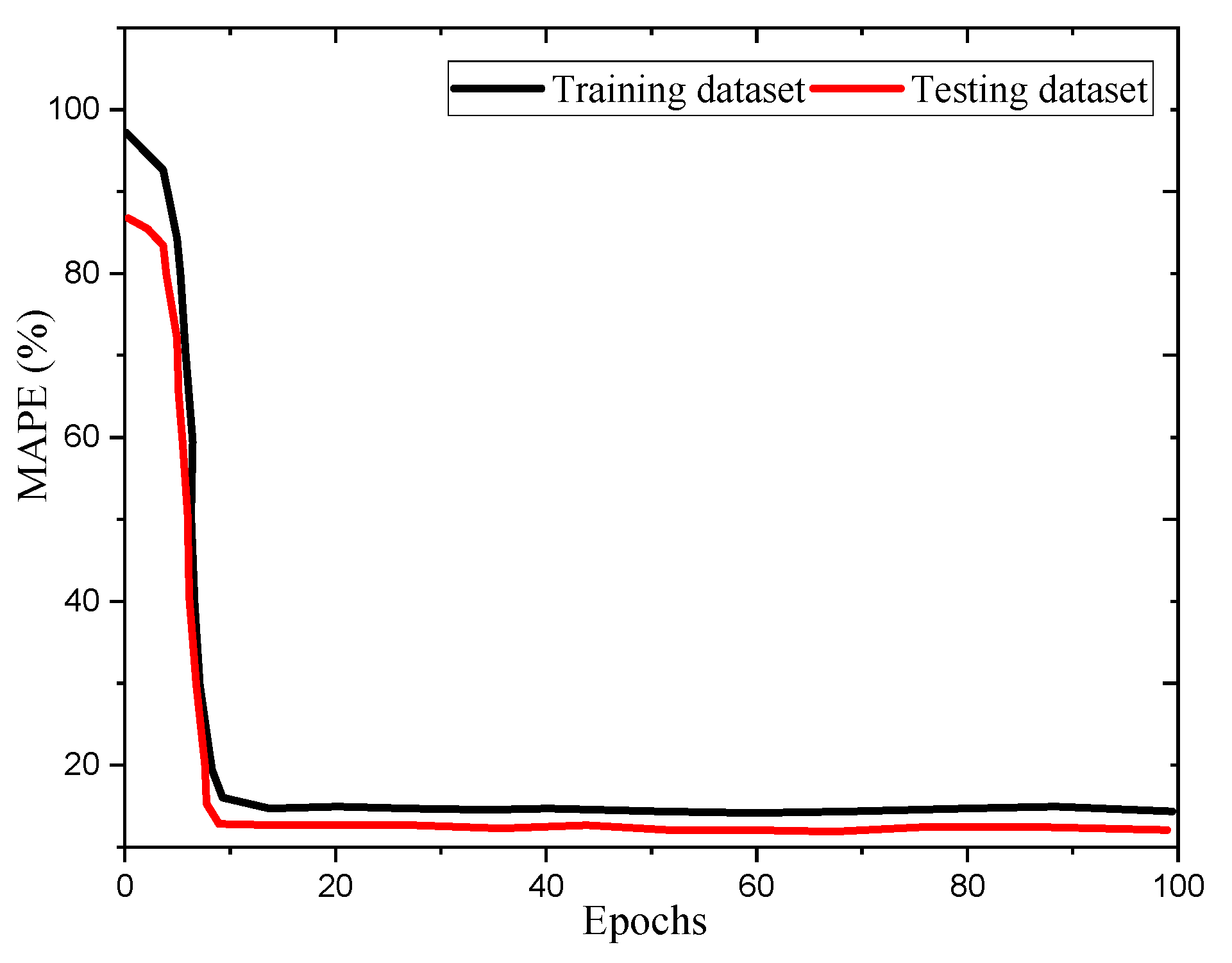
The learning evaluation process compares a model’s performance on training and testing data over multiple epochs to determine if it is genuinely learning. A poor learning curve, with high variance and bias, indicates overfitting, while a good curve, like that of the FCRBM model, shows low variance and bias with decreasing errors. Initially, the model has a high error rate (MAPE), which decreases with more training, reaching a minimal value, indicating effective learning.
Figure 5 illustrates these results.
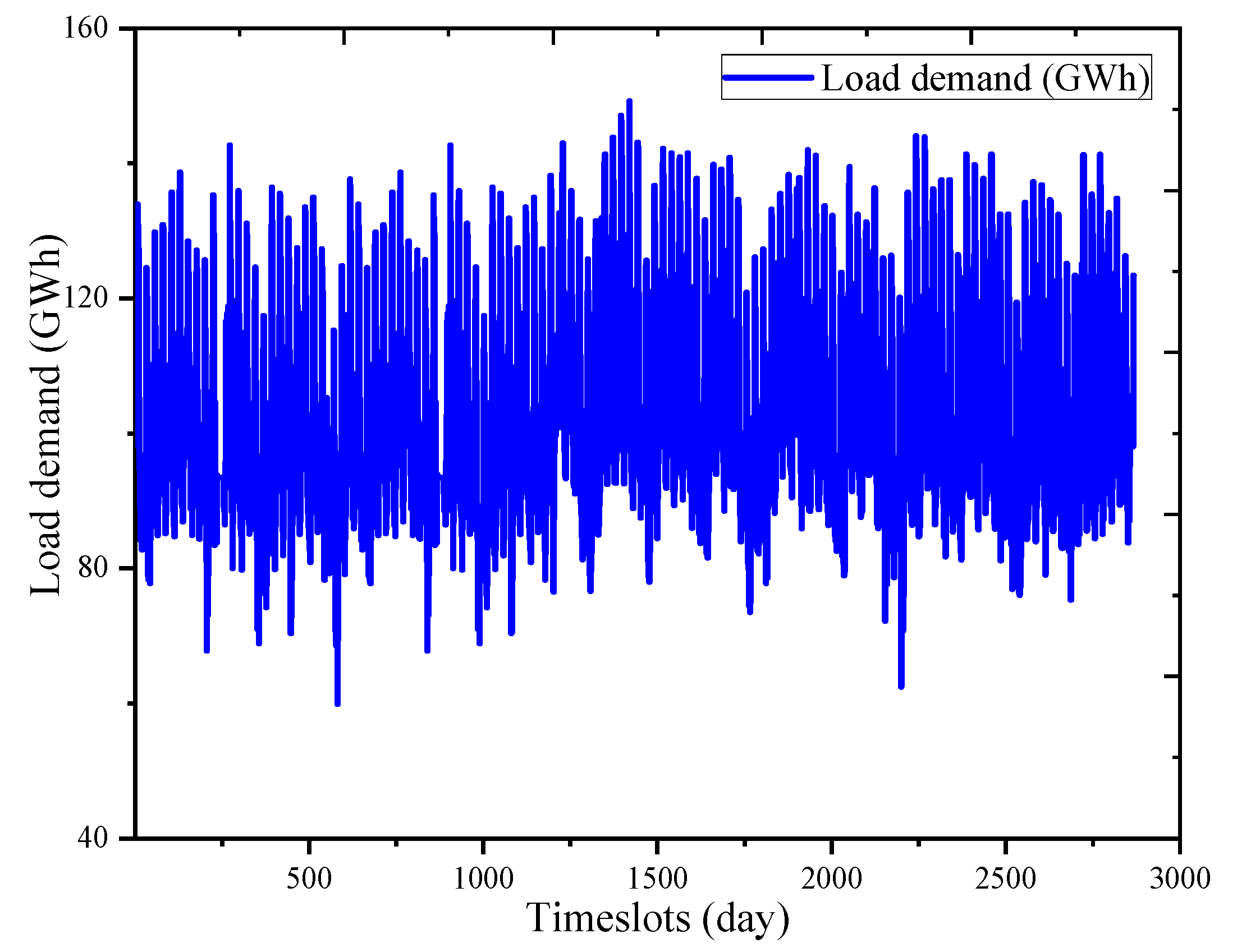
Figure 4.
REG’s dataset with month and year indexes.
Figure 4.
REG’s dataset with month and year indexes.
Figure 6 provides a comparative analysis of the FS-FCRBM-GWDO framework against benchmark models like FS-ANN, AFC-STLF, Bi-level, and MI-mEDE-ANN in predicting day-ahead electrical energy consumption for the REG load data center.
Table 3 further details the accuracy of these models, comparing metrics such as mean absolute percentage error (MAPE), variance, and correlation coefficient. The findings clearly indicate that the FS-FCRBM-GWDO architecture offers superior accuracy in forecasting the next day’s electrical energy consumption for Rwanda’s power system. Both the proposed and benchmark models are adept at capturing and adapting to the non-linear patterns present in historical energy consumption time series data.
The proposed hybrid FS-FCRBM-GWDO model uses nonlinear activation functions like tangent hyperbolic (tanh), sigmoidal, and ReLU to predict energy consumption patterns. Unlike benchmark frameworks like FS-ANN, AFC-STLF, Bi-level, and MI-mEDE-ANN, which use sigmoid activation functions, the proposed model uses ReLU and multivariate autoregressive algorithms for rapid convergence and addressing vanishing gradient and overfitting issues. The model’s energy consumption pattern closely aligns with actual data, with a MAPE of 1.10%, outperforming the standard frameworks with values of 2.2%, 2.1%, 3.4%, and 2.6%, respectively. Hence, the results presented in
Figure 6 and
Table 3 suggested hybrid FS-FCRBM-GWDO model outperforms the standard frameworks in terms of accuracy.
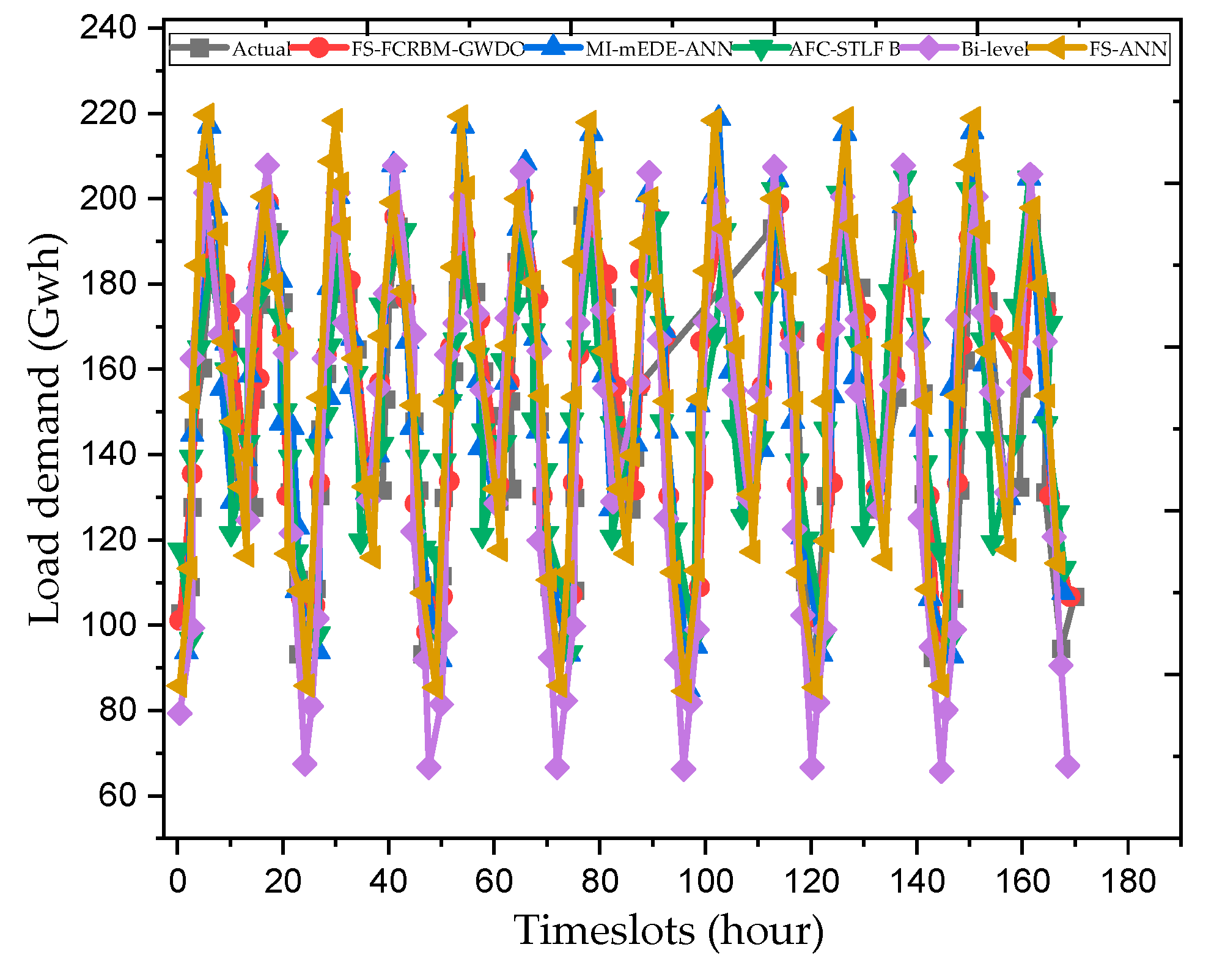
Figure 7 shows a week-long prediction of hourly electrical energy consumption, demonstrating the superior performance of the FS-FCRBM-GWDO model compared to existing models like FS-ANN, AFC-STLF, Bi-level, and MI-mEDE-ANN. The FS-FCRBM-GWDO model achieved a MAPE of 1.18%, significantly outperforming the benchmark models. The model’s accuracy is attributed to the use of a deep learning-based FCRBM with ReLU, a multivariate autoregressive algorithm, and GWDO optimization.
Figure 8 and
Table 3 show that the FS-FCRBM-GWDO model closely tracks the actual energy consumption curve, ensuring better performance in monthly predictions.
Table 4 presents a performance evaluation for the leap year 2018, using MAPE, variance, and correlation coefficient metrics.
FS-FCRBM-GWDO module’s performance in terms of MAPE and convergence speed.
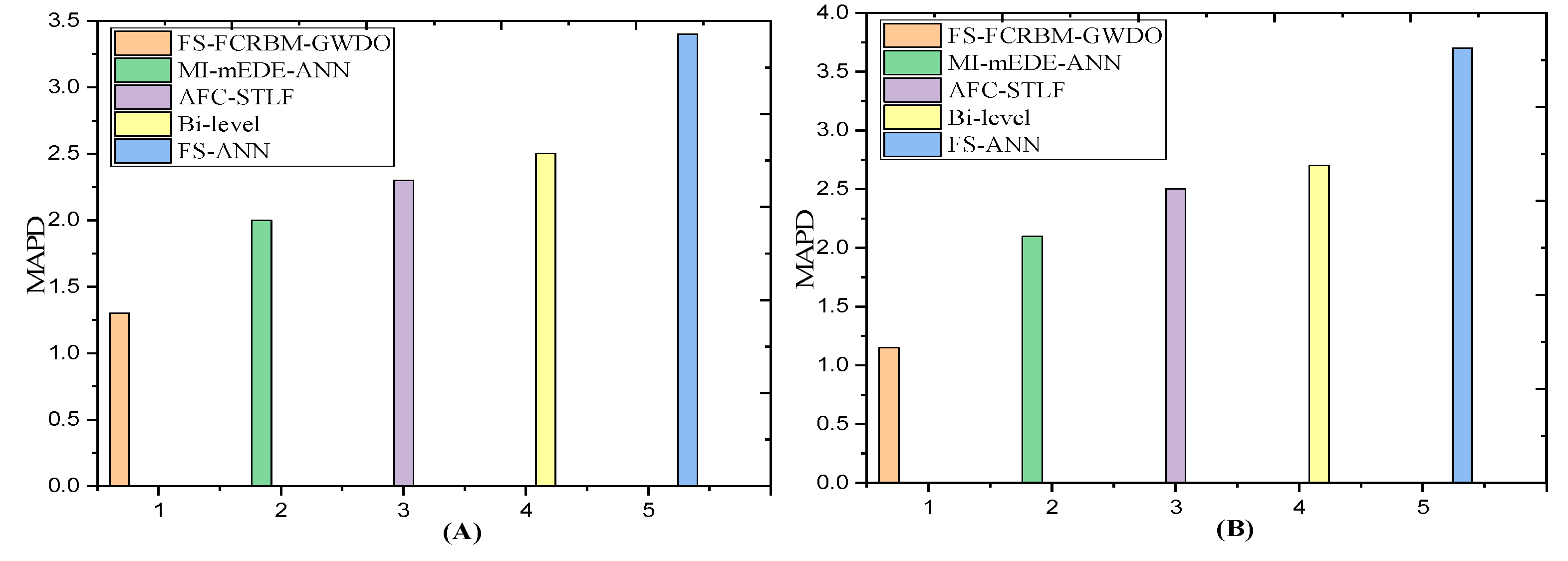
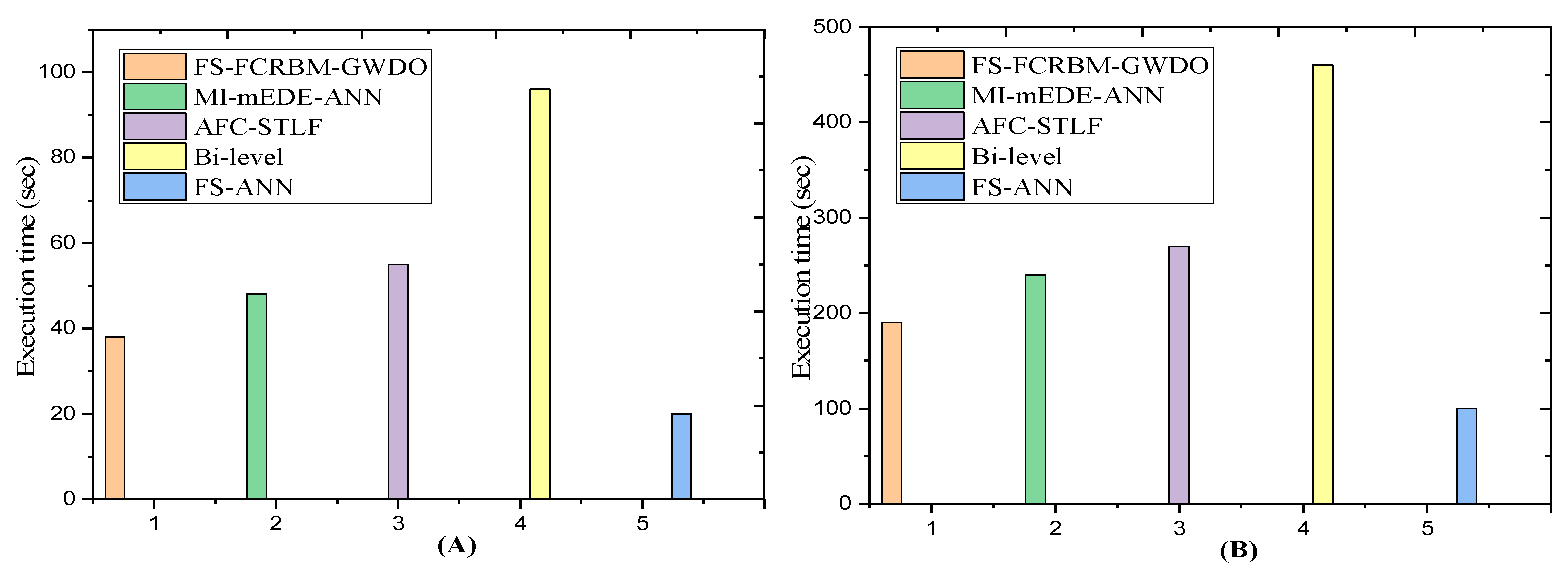
Figure 9,
Figure 10, and
Figure 11 present a statistical assessment of MAPE, execution time, and convergence speed for the proposed FS-FCRBM-GWDO model and benchmark models (FS-ANN, AFC-STLF, MI-mEDE-ANN, and Bi-level). The FS-FCRBM-GWDO model achieves the lowest MAPE of 1.18%, indicating high accuracy, compared to higher MAPE values in the benchmark models of 3.45%, 2.17%, 2.12%, and 2.65%, respectively. However, integrating the optimization module increases execution time from 25 to 95 seconds. The FS-FCRBM-GWDO model balances accuracy and speed by using GWDO for optimization, ReLU activation, a multivariate autoregressive algorithm, deep learning FCRBM, and advanced data preprocessing. Despite longer execution times compared to FS-ANN, the FS-FCRBM-GWDO model offers superior accuracy and efficiency.
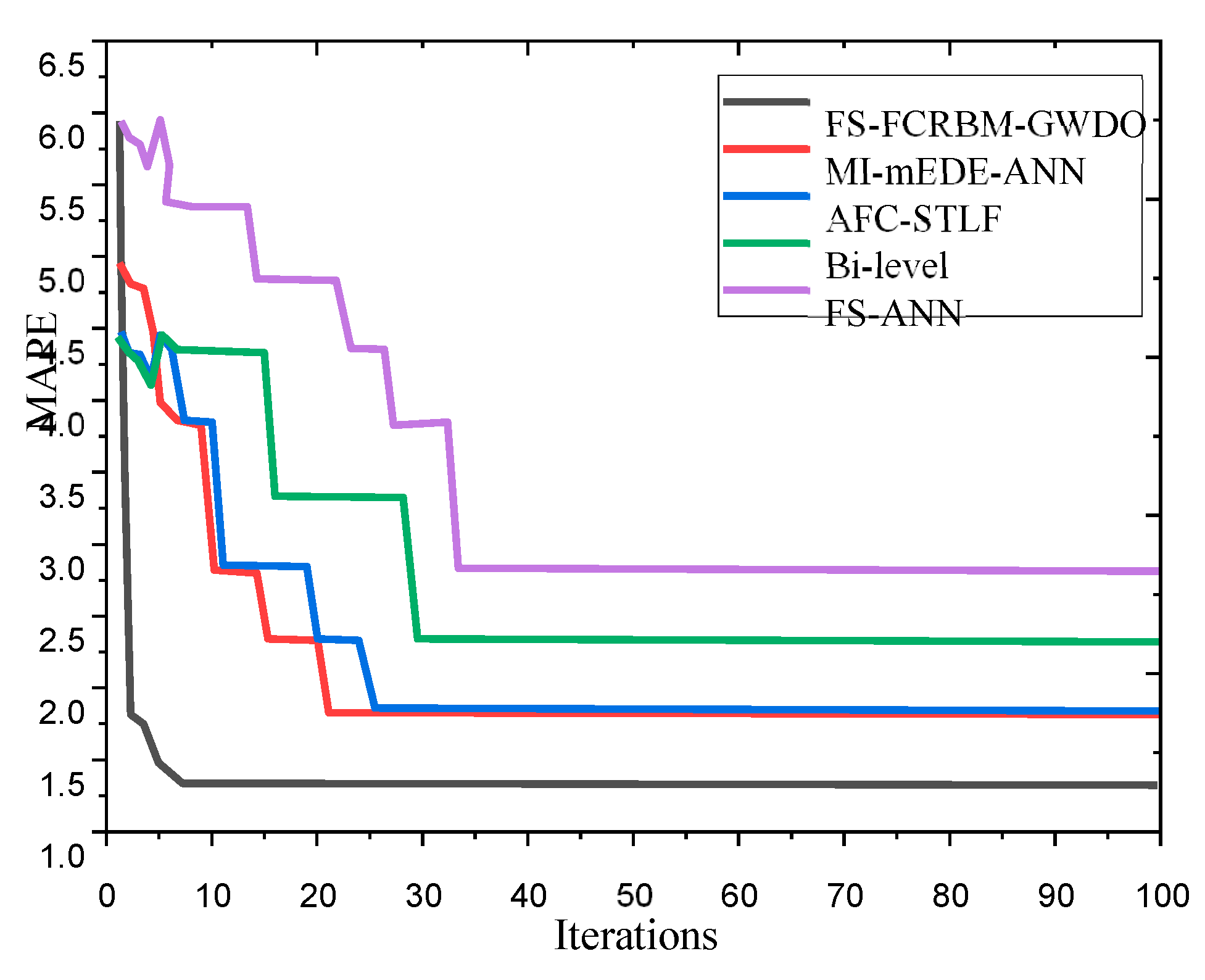
Figure 11 illustrates the convergence speed of the proposed hybrid FS-FCRBM-GWDO model compared to benchmark models including FS-ANN, Bi-level, AFC-STLF, and MI-mEDE-ANN, based on 100 iterations. As the number of iterations increases, MAPE decreases for all models. Notably, the proposed model demonstrates rapid convergence, reaching stability around the 10th iteration, indicating its efficient search ability. In contrast, benchmark models such as FS-ANN, Bi-level, AFC-STLF, and MI-mEDE-ANN, converge later, around the 33rd, 29th, 25th, and 21st iterations respectively, showcasing slower convergence rates. This analysis suggests that the proposed GWDO algorithm offers superior performance for optimization in integrated frameworks due to its faster convergence compared to existing benchmark models. The depicted convergence analysis focuses solely on the MAPE performance metric for both proposed and existing models.
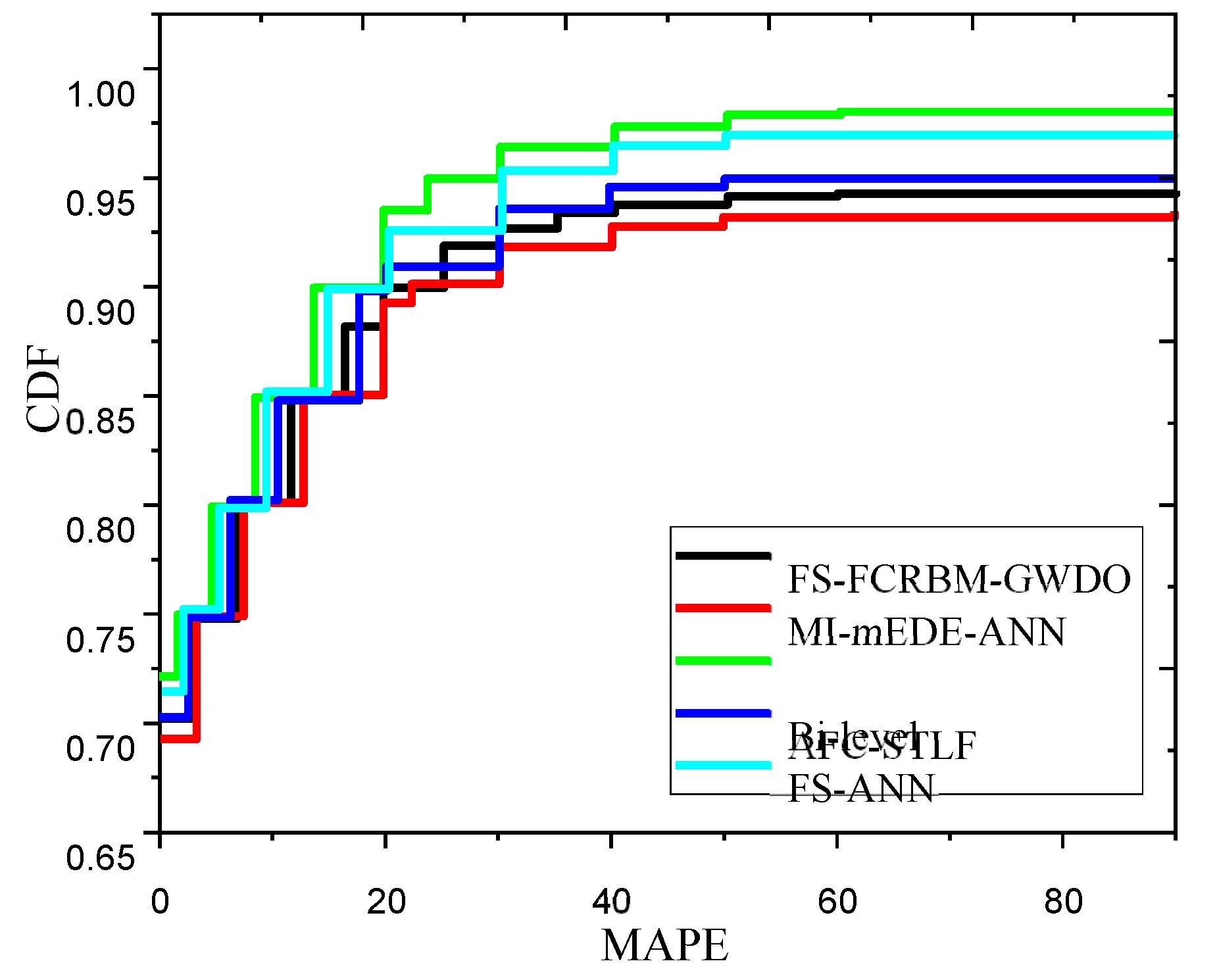
Figure 12 compares the proposed hybrid FS-FCRBM-GWDO model to benchmark models, including FS-ANN, Bi-level, AFC-STLF, and MI-mEDE-ANN, regarding the cumulative distribution function (CDF) of error. The FS-FCRBM-GWDO model outperforms the current models in terms of CDF. The FCRBM model, which utilizes deep learning, is capable of providing accurate predictions even in situations characterized by high levels of uncertainty. This is due to the deep layers of the model being able to effectively capture the essential characteristics. Therefore, our suggested FS-FCRBM-GWDO framework is a superior option for distribution system operators to achieve efficient and effective energy management of the smart grid. The FS-FCRBM-GWDO framework, along with other current frameworks like FS-ANN, Bi-level, AFC-ANN, and MI-mEDE-ANN, has been evaluated in terms of computational complexity, execution time, convergence rate, and accuracy.
Further evaluation of the FS-FCRBM-GWDO framework and existing frameworks, such as FS-ANN, Bi-level, AFC-ANN, and MI-mEDE-ANN is presented in
Table 5. This evaluation encompasses computational complexity, execution time, convergence rate, and accuracy metrics. Based on simulation results, performance analysis, and discussions, it is concluded that the proposed hybrid FS-FCRBM-GWDO model surpasses benchmark models in terms of convergence rate, accuracy, computational complexity, and execution time aspects.
3.2. Energy Management Based on the DA-GmEDE Framework
The study presents the results of a DA-GmEDE-based energy management strategy for residential buildings with three types of appliances: time-shiftable, power-shiftable, and critical appliances. The system module and GmEDE-based solution are used to validate the performance of the strategy, which uses a day ahead demand response price signal and energy consumption forecast generated using ANN. The scheduling time horizon spans 24 hours, and the ANN is trained to forecast DR prices, which the Energy Management Controller (EMC) uses to optimize appliance scheduling. Parameters of the algorithms employed in the simulations, as well as descriptions of all residential appliances, are detailed in
Table 6 and
Table 7 respectively.
The proposed method, based on EMC, is compared to current techniques like DA-GA and DA-game-theoretic. The proposed scheduling approach, DA-GmEDE, is compared to W/O, DA-GA, and DA-game-theoretic strategies. The efficacy of the proposed method is evaluated using electricity cost, PAR, and user discomfort balance.
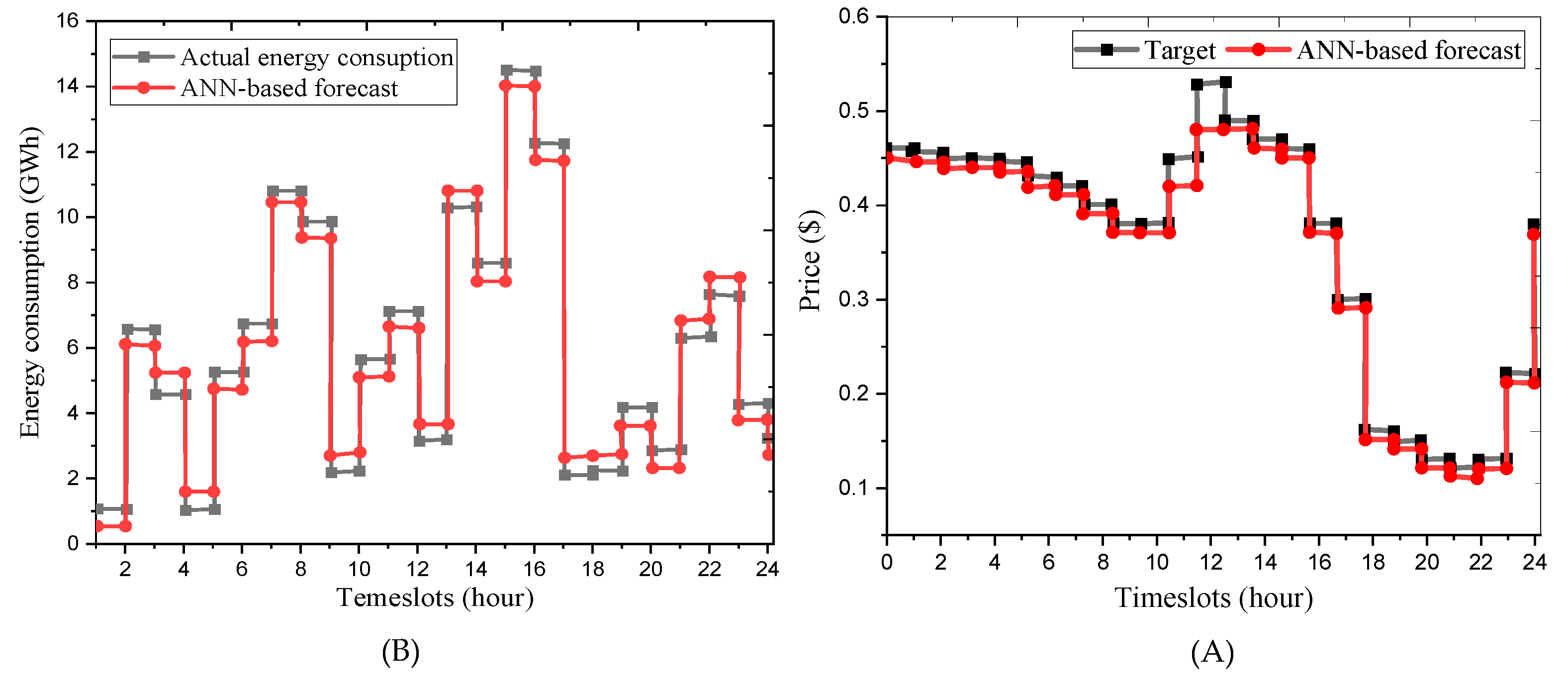
In
Figure 13, A and B illustrate the predicted pricing signal and energy use patterns for the upcoming day.
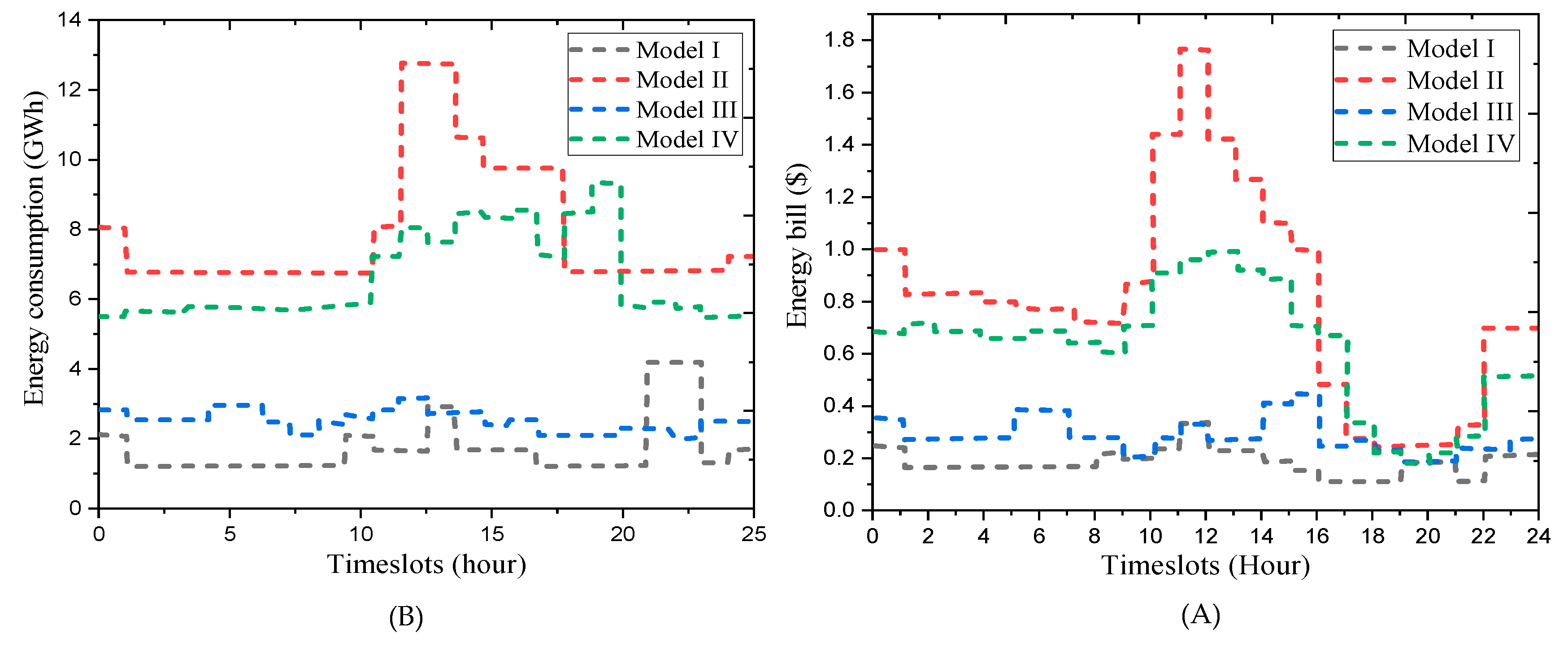
1. Energy Consumption and Corresponding Electricity Bills across Four Different Modes of Operation
The DA-GmEDE method calculates energy consumption and electricity cost profiles for four operational modes. It shows that residential structures’ energy consumption is higher under mode IV compared to modes I and III but lower than mode II within the scheduling time horizon. The peak energy consumption is significantly lower in mode II, attributed to customers prioritizing comfort and continuing activities despite higher costs. These profiles are represented in
Figure 14(A-B), respectively.
Consumers in operation mode III consume more energy but lower than in mode II and IV due to prioritizing PAR. Mode I customers have lower energy usage but prioritize reducing electricity expenses. The EMC, based on DA-GmEDE, allows customers to meet their needs in various operational modes, resulting in lower electricity bills.
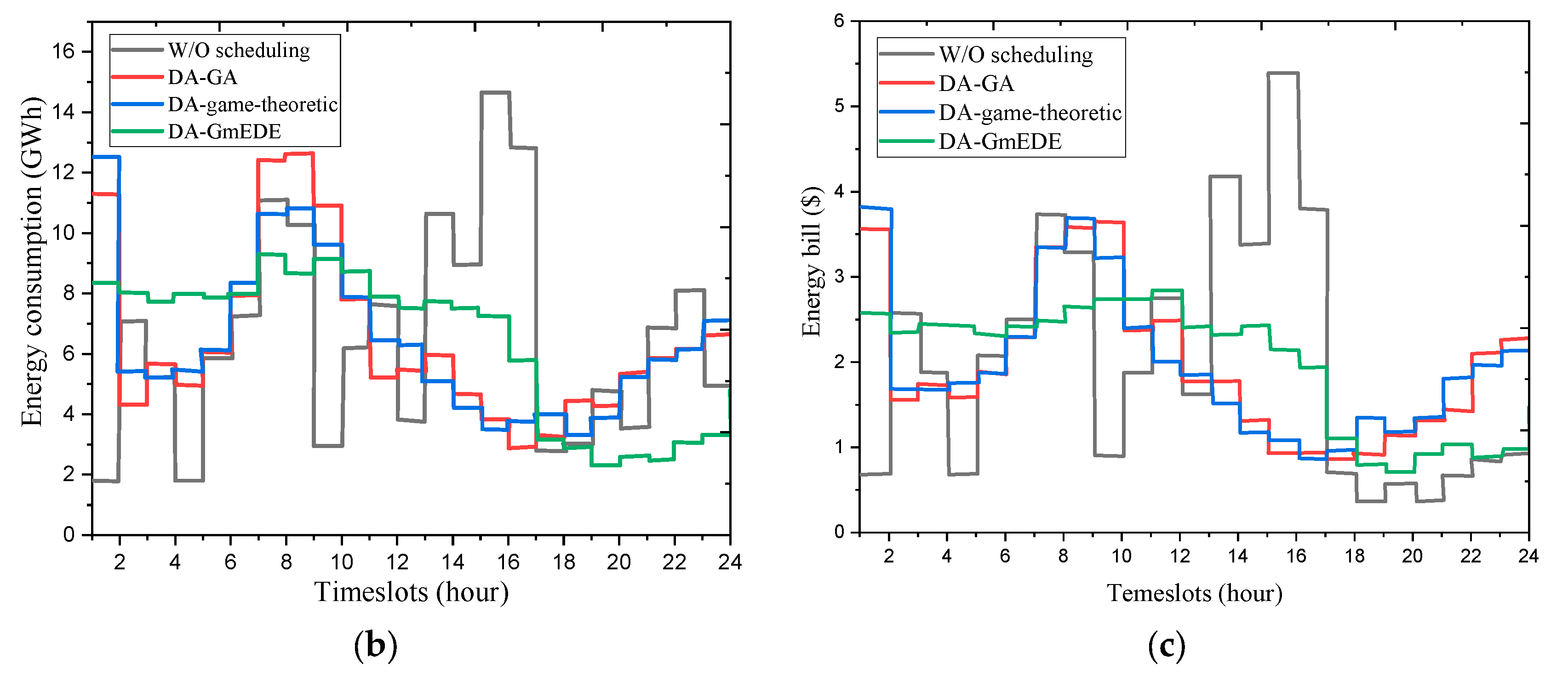
2. Energy consumption of residential buildings within the scheduling time horizon
Figure 15-A and B shows energy consumption patterns in a home without and after scheduling with DA-GA, DA-game-theoretic, and proposed DA-GmEDE strategies. In the absence of scheduling, energy consumption peaks during peak demand hours, leading to high electricity bills and a Peak-to-Average Ratio. After scheduling with these strategies, energy consumption was significantly reduced. The proposed DA-GmEDE strategy achieves a 36.4% improvement over the W/O scheduling case and a 33.3% improvement over both strategies, demonstrating its ability to generate the most suitable load profile for residential buildings.
3. Electricity bill per hour of a home in residential buildings within the scheduling time horizon
Figure 15-B demonstrates the effectiveness of scheduling methods like DA-GmEDE, DA-GA, DA-game-theoretic, and W/O scheduling in reducing electricity bills. Prior to scheduling, peak periods led to increased costs, resulting in a surge of up to
$5.5. By implementing these methods, electricity costs per timeslot decrease by
$0.7,
$1.2, and
$0.9, respectively. The DA-GmEDE-based approach outperforms other strategies by 41.6% and 22.2%.
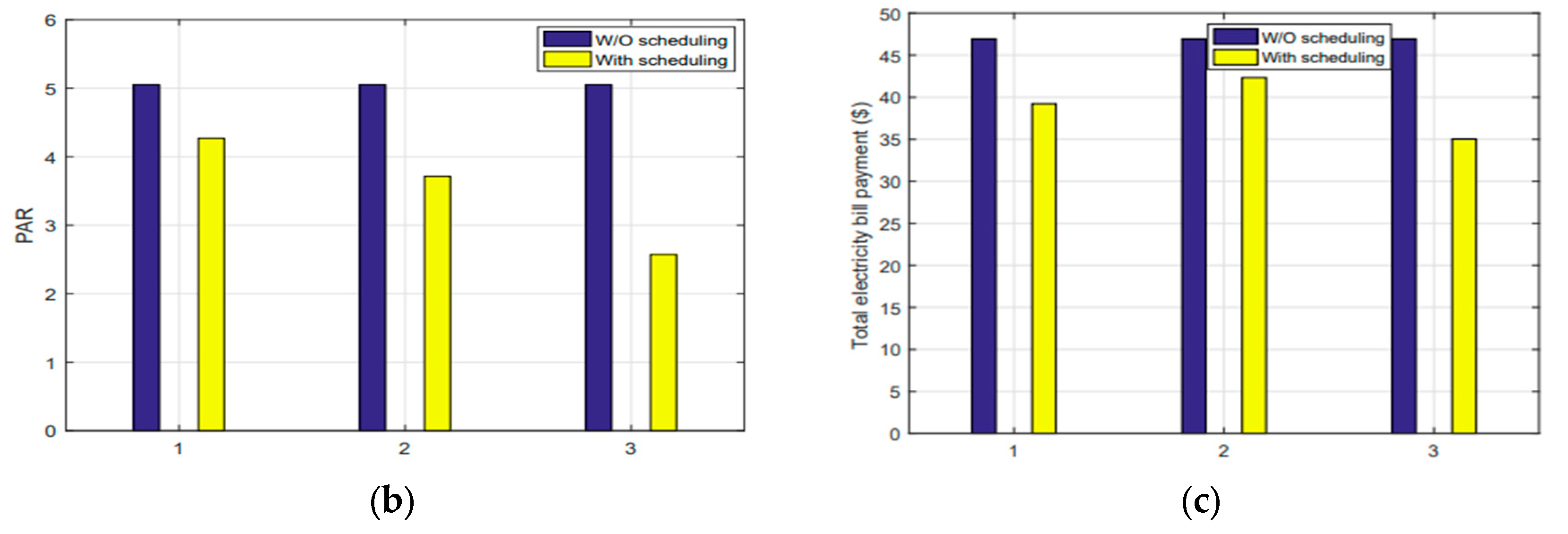
The evaluation of Peak-to-Average Ratio (PAR) is presented, comparing W/O scheduling and scheduling using DA-GA, DA-game-theoretic, and DA-GmEDE strategies. The proposed DA-GmEDE-based strategy outperforms other strategies in terms of PAR.
Figure 16-A demonstrates its effectiveness in maintaining balanced energy consumption and improving power system stability. The EMCs effectively shift load under day-ahead pricing signals, reducing PAR by 17.64%, 25.49%, and 47.05%, respectively.
Figure 16-B evaluates total electricity bill payments using DA-GA, DA-game-theoretic, and DA-GmEDE strategies. The proposed DA-GmEDE strategy achieves the highest reduction in bills, outperforming existing strategies and demonstrating its effectiveness in reducing overall electricity expenses at 15.2%, 8.7%, and 23.9% respectively.
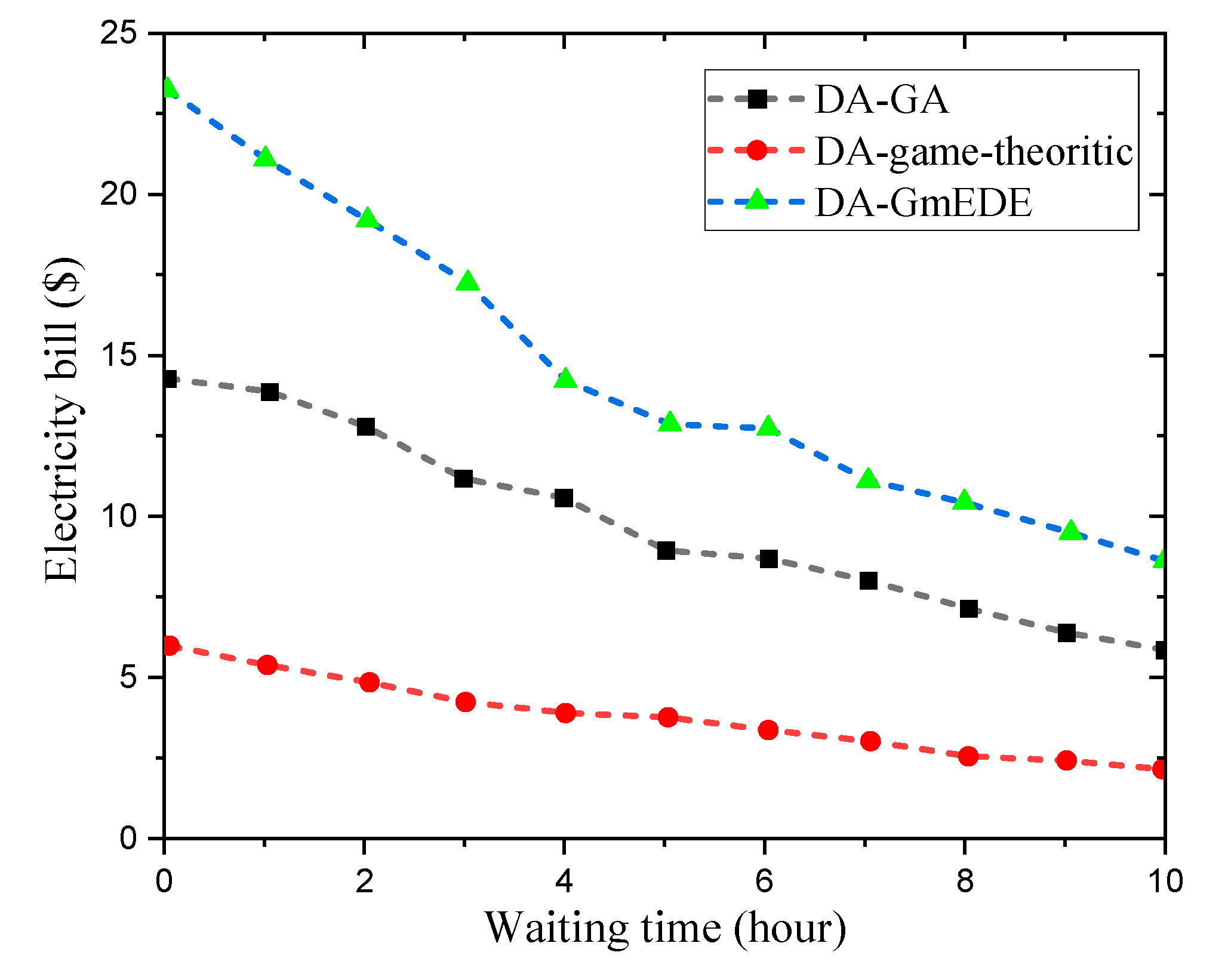
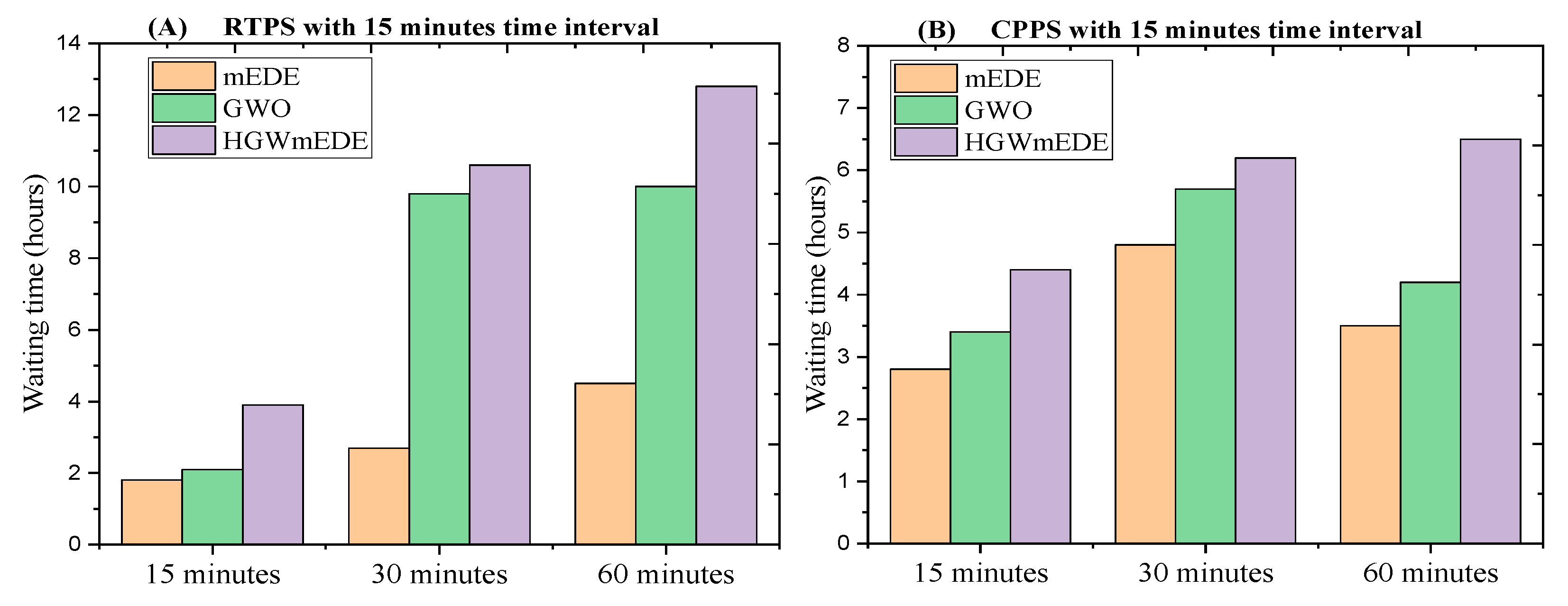
5. Performance Tradeoff Analysis
Figure 17 shows the performance tradeoff between the proposed DA-GmEDE strategy and existing strategies (DA-GA and DA-game-theoretic) in terms of electricity bill and waiting time. The proposed DA-GmEDE strategy minimizes the tradeoff between electricity bill and waiting time, making it a favorable choice for energy management tasks. This balance between electricity bill and user discomfort is more pronounced for DA-GA and DA-game-theoretic based strategies.
3.2. Electricity Cost Evaluation Using RTPS and CPPS under OTI
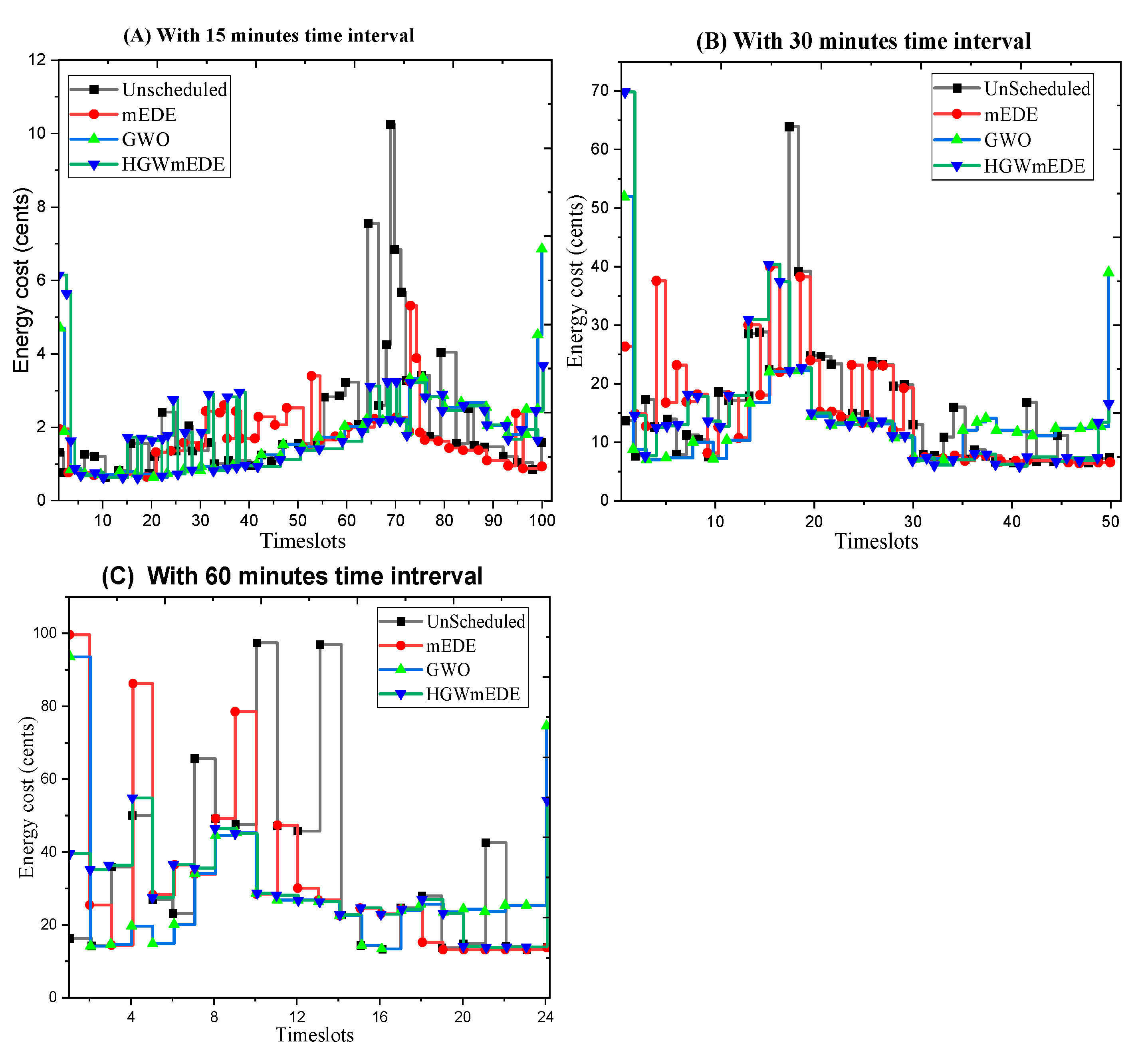
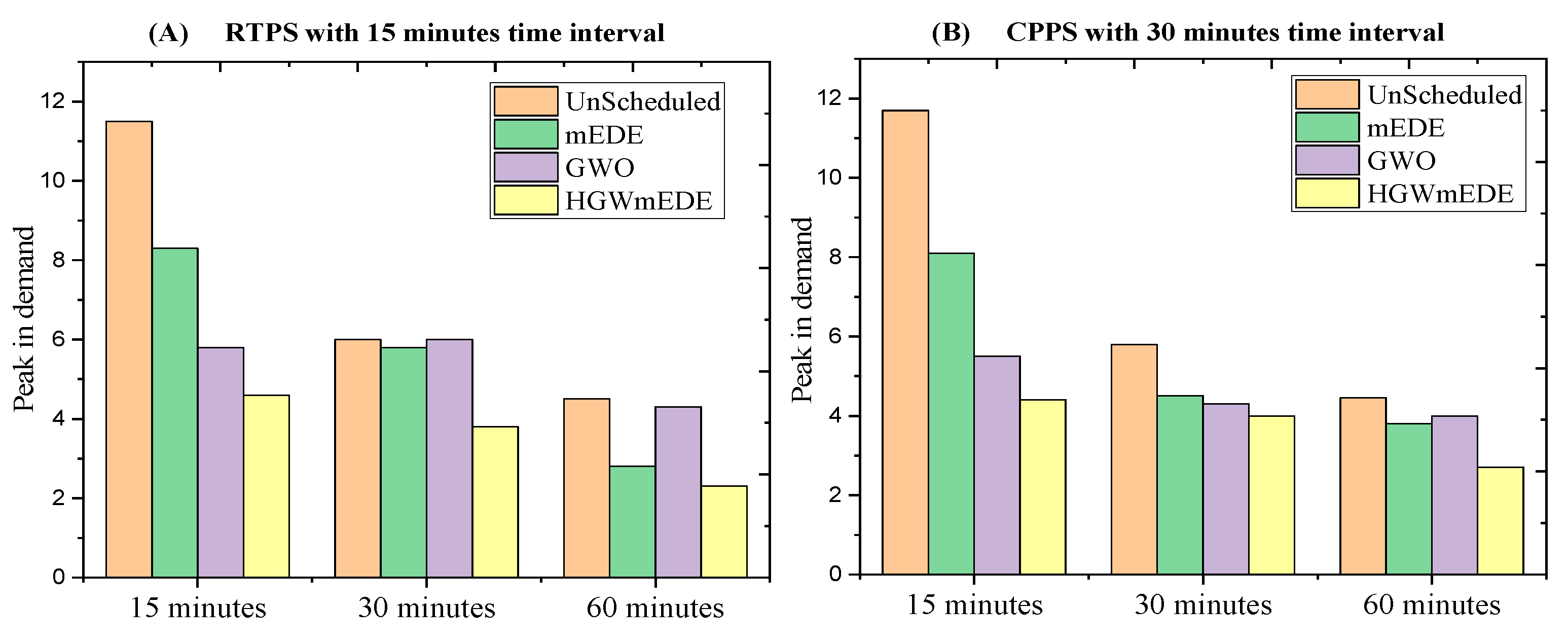
By scheduling smart home appliances using anticipated RTPS, the proposed GmEDE algorithm efficiently reduces electricity cost when compared to modified Evolutionary Differential Evolution (mEDE) and Grey Wolf Optimization (GWO). The program optimizes the transition of appliances from on-peak to off-peak timeslots by coordinating pricing schemes with patterns of energy use. The suggested GmEDE-based expenses reduce demand peaks and energy prices compared to both GWO and mEDE. Simulations demonstrate that by arranging smart home equipment in the best possible way, the suggested GmEDE algorithm continuously lowers power bills.
The proposed GmEDE-based framework outperforms both GWO and mEDE in terms of reducing peaks in demand and electricity costs.
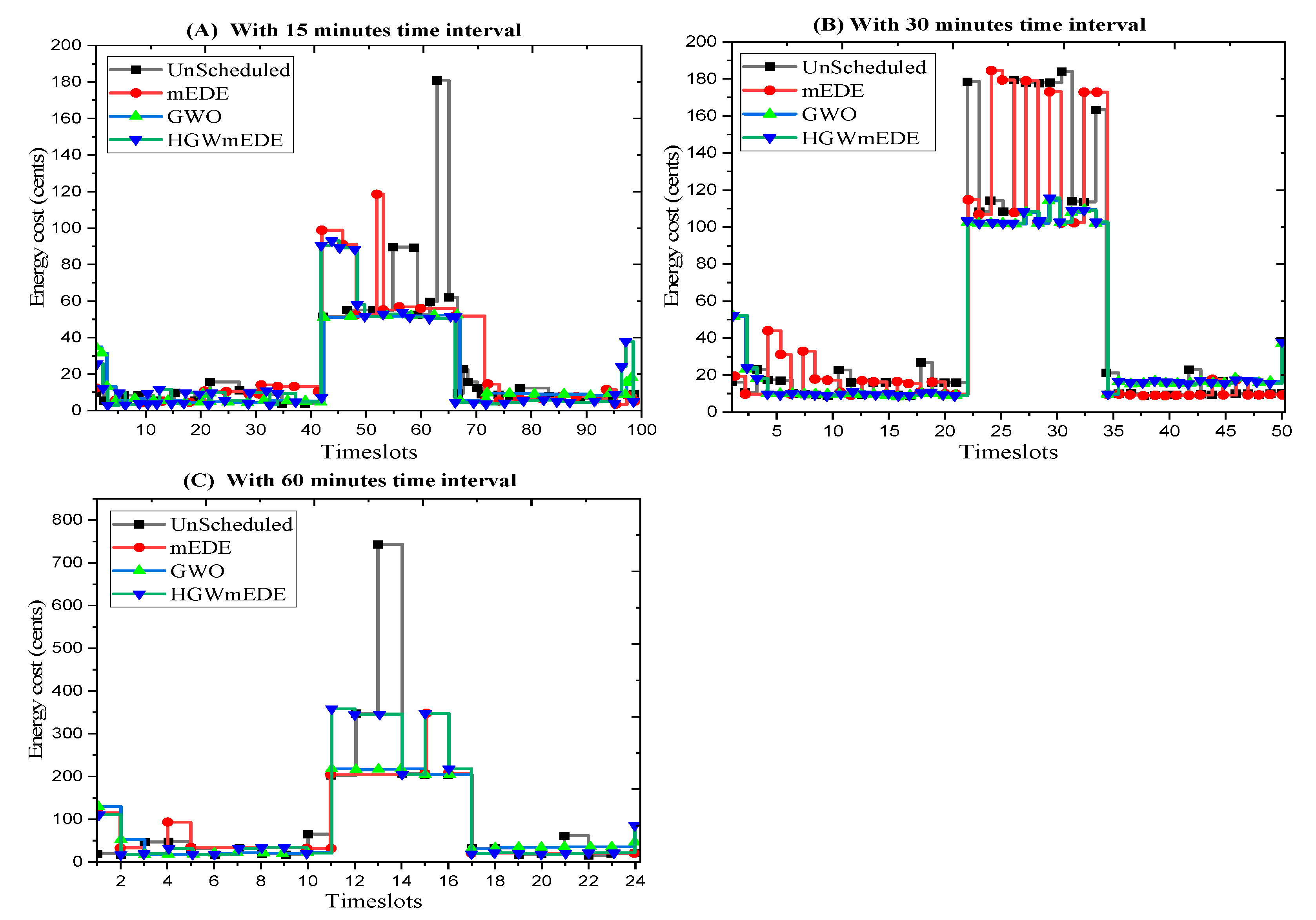
Figure 18-A shows that unscheduled loads result in high demand peaks, resulting in high prices during specific hours.
Figure 18-B shows that GWO shows higher costs at the beginning timeslots, while GmEDE maintains minimum costs throughout the 24 hours.
Figure 18-C shows that the proposed GmEDE algorithm consistently reduces electricity costs by optimally scheduling smart home appliances.
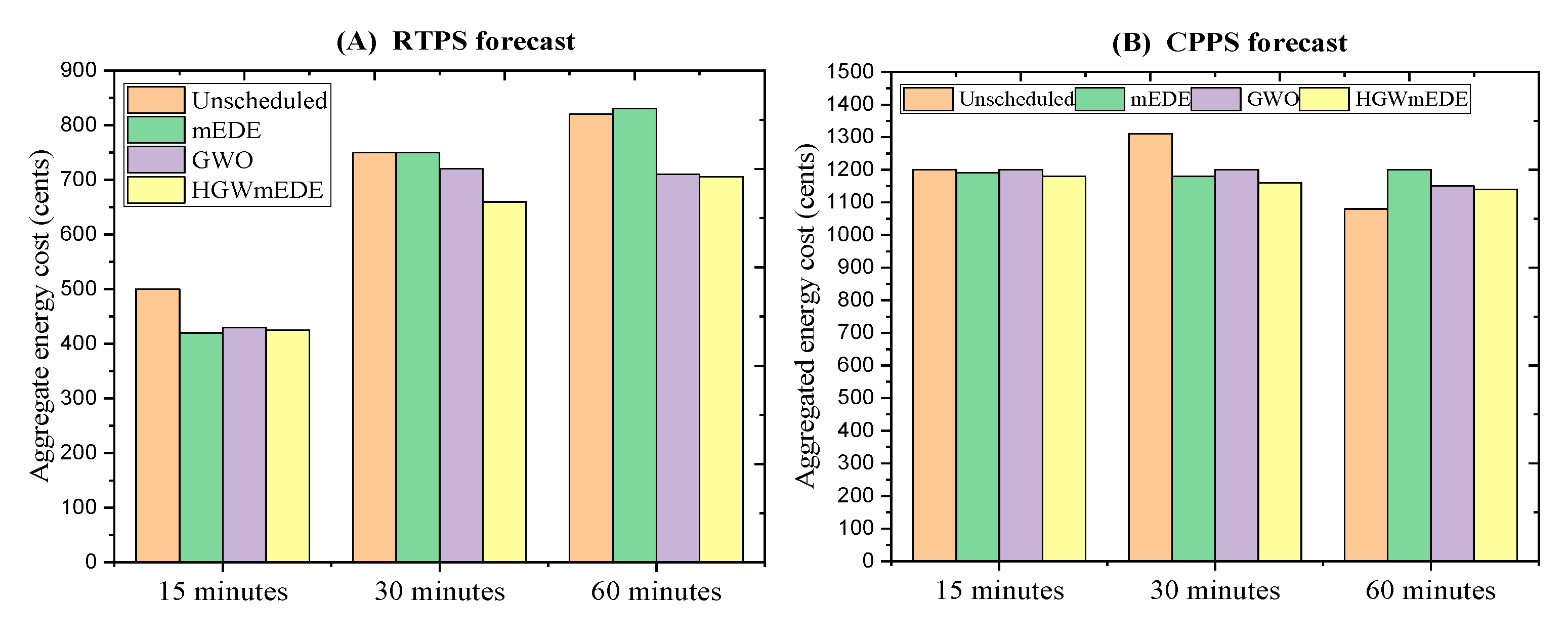
The electricity cost profile for a 15-minute OTI shows that the forecast CPPS remains constant except during critical peak hours. The maximum peak in an unscheduled load scenario is 181.55 cents, but when smart home appliances are scheduled, it reduces to 83.07 cents. The 30-minute OTI has similar costs, but no peaks emerge except at the starting time of the day. The proposed GmEDE algorithm significantly reduces the unscheduled appliance electricity cost from 766.8 cents to 203.46 cents for the 60-minute OTI. The overall unscheduled cost is reduced from 1300.891 cents to 1085.91 cents when smart home appliances are scheduled using the GmEDE algorithm.
Additionally, the overall electricity cost reduction for 30 and 60 minutes OTI is depicted in
Figure 22. A brief comparison of electricity cost under forecasted RTPS and CPPS for 15, 30, and 60 minutes OTI is provided in
Table 8. In summary, the proposed framework optimally schedules smart home appliances, leading to reduced overall aggregated electricity costs for residents compared to mEDE and GWO under forecasted RTPS and CPPS.
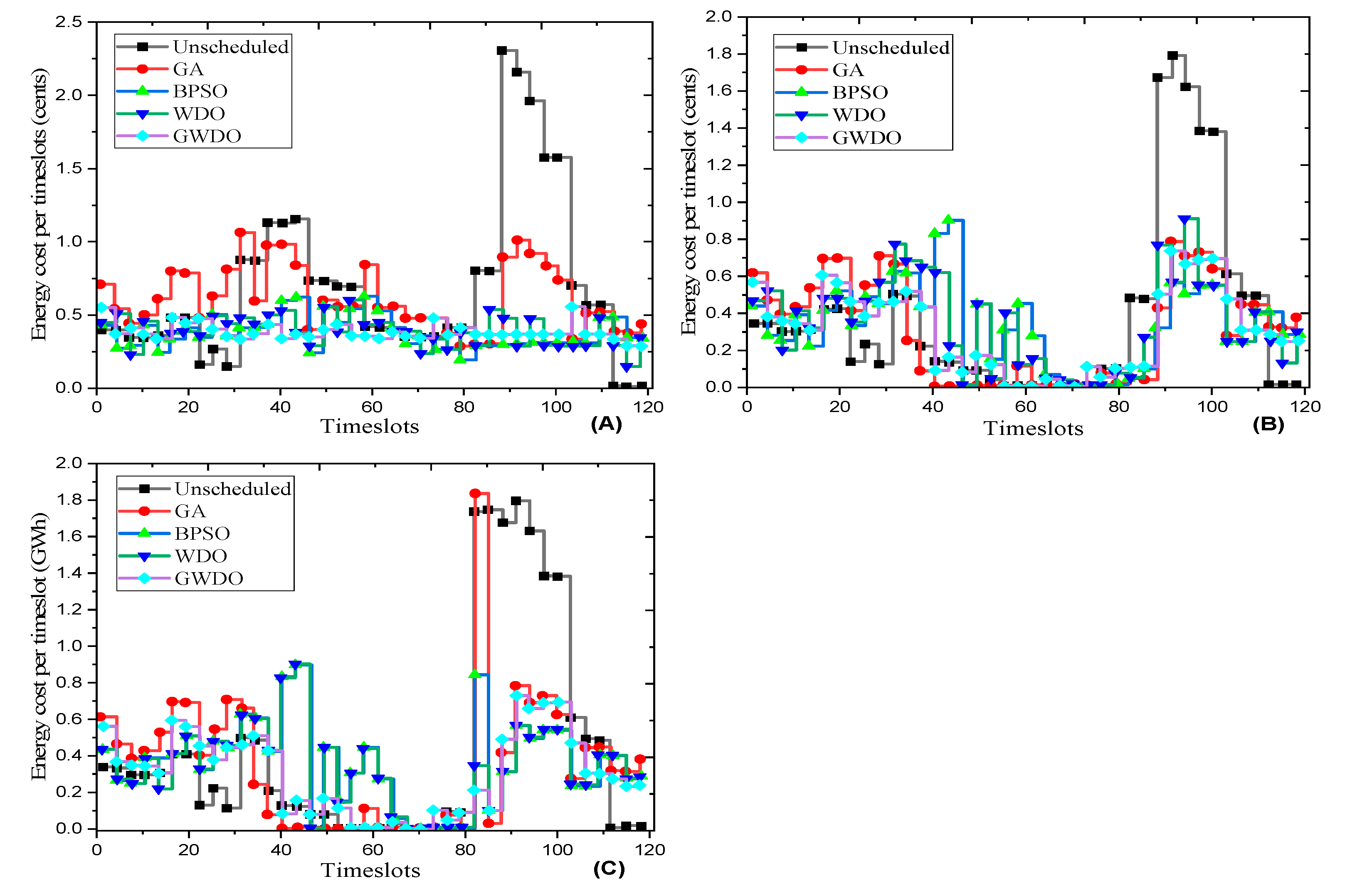
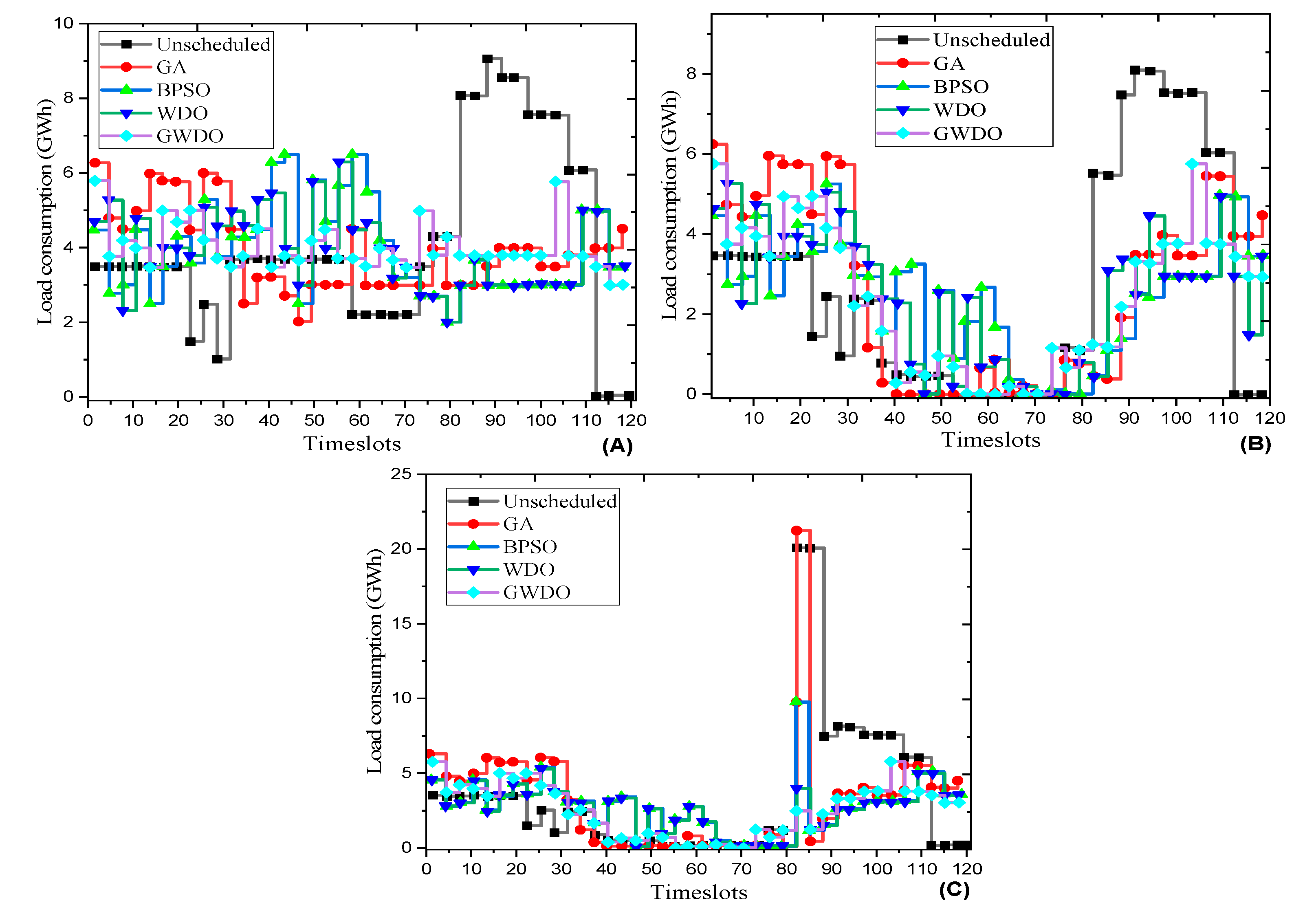
In
Figure 20 and
Figure 21, the results analysis shows that the proposed GWDO algorithm outperforms other heuristic techniques (GA, BPSO, WDO) and unscheduled load in optimizing energy consumption and reducing electricity costs. Without RESs and ESS, GWDO reduces peak power consumption by 35.16% compared to 32.96% for GA, 31.86% for BPSO, and 33.51% for WDO. With RESs, GWDO achieves a 28.39% reduction in peak power consumption, outperforming GA (24.69%), BPSO (30.86%), and WDO (32%). Additionally, GWDO provides the lowest electricity costs, peaking at 0.49 cents/kWh compared to GA (0.9 cents/kWh), BPSO (0.6 cents/kWh), and WDO (0.55 cents/kWh), demonstrating the most stable and optimal profiles across scenarios.
Figure 20.
Energy consumption profile of users: (a) Without RESs and ESS; (b) With RESs; (c) With RESs and ESS.
Figure 20.
Energy consumption profile of users: (a) Without RESs and ESS; (b) With RESs; (c) With RESs and ESS.
Figure 21.
Electricity cost profile: (a) Without RESs and ESS; (b) With RESs; (c) With RESs and ESS.
Figure 21.
Electricity cost profile: (a) Without RESs and ESS; (b) With RESs; (c) With RESs and ESS.
Figure 22.
Aggregated electricity cost evaluation under forecast RTPS and CPPS.
Figure 22.
Aggregated electricity cost evaluation under forecast RTPS and CPPS.