Prerpints.org logo
Preprint
Article

Computing Unified Atomic Mass Unit and Avogadro Number with Various Nuclear Binding Energy Formulae Coded in Python

Altmetrics

Downloads

82

Views

43

Comments

0

This version is not peer-reviewed

Submitted:

25 August 2024

Posted:

27 August 2024

You are already at the latest version

Alerts
Abstract
In this paper, we make an attempt to estimate the famous Avogadro number with programming logics written in Python associated with advanced nuclear binding energy formulae. Average rest mass of nucleon, nuclear binding energy per nucleon and electron rest mass seem to play a vital role in estimating the unified atomic mass unit and Avogadro number. Interesting point to be noted is that, Avogadro number seems to be the inverse of the Unified atomic mass unit. With further study, it seems possible to estimate the unified atomic mass unit and Avogadro number accurately. Our interesting observation is that, short range strong nuclear force seems to have a vital role in deciding the accuracy of Avogadro number. For that purpose one may consider AI techniques along with newly observed atomic nuclides and their nuclear binding energies. For Z=6 to 118 and Alow=2Z and Aupper=3.5Z, estimated average value of Avogadro number is $N_{Average} \cong 6.01938 \times 10 ^{26}$. Considering the saturation of nuclear binding energy, at Z=26, $N_{Z=26} \cong \left(6.02229 \textrm{to} 6.02285\right) \times 10 ^{26}$. At academic level, our proposal can be given a chance as a case study. It is planned to develop a web application for this purpose.
Keywords: 
Subject: Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

Avogadro number and Unified atomic mass unit [1,2,3,4,5,6] play a vital role in every day various branches of physics and chemistry. Scientists are seriously working on estimating them with various methods with advanced engineering techniques. Recently, authors [7,8,9,10,11,12,13,14,15] have developed a very simple method for estimating the unified atomic mass and Avogadro number by means of nuclear binding energy and mean binding energy per nucleons. In this paper, by considering Python programming language, authors are working on developing simple code for estimating the unified atomic mass unit and Avogadro number with various possible nuclear data inputs like selected proton numbers, their selected lower and upper mass numbers and different nuclear mass formulae. This proposal can be considered as a case study at academic level. It needs a vigorous research at fundamental level.

2. Key Physical Logic for Understanding the Unified Atomic Mass Unit

It seems to be a 4 step procedure. First step is to consider the average of neutron and proton rest energies. It can be called as ‘Average nucleon rest energy (ANRE)’. Second step is to estimate the average of nuclear binding energy per nucleon associated with various atomic nuclides starting from Z=2 to 118 and Alow=2Z and Aup=3.5Z. It can be called as ‘average binding energy per nucleon (ABEPN)’. Third step is to deduct the estimated average binding energy per nucleon from the average rest energy of neutron and proton. It can be called as ‘Average nuclear energy unit (ANEU)’. Fourth step is to add the electron rest energy (ERE) to the average nuclear energy unit. It can be called as the ‘unified atomic energy unit (UAEU)’. Dividing the unified atomic energy unit by squared speed of light, one can get the ‘unified atomic mass unit (UAMU)’. In a very simplified approach,
U A E U ≅ ( m n c 2 + m p c 2 2 ) − 〈 A B E P N 〉 + ( m e c 2 ) U A M U ≅ ( m n + m p 2 ) − 〈 A B E P N c 2 〉 + ( m e ) }
where m n , m p and m e represent neutron, proton and electron rest masses respectively.

3. Key Physical Logic for Understanding the Avogadro Number

It is a one step procedure. Inverse of the unified atomic mass unit can be called the Avogadro number. If unified atomic mass is expressed in grams, Avogadro number can be represented in ‘no. of atoms per gram’. If unified atomic mass is expressed in kg, Avogadro number can be represented in ‘no. of atoms per kg’. It may be noted that, ‘no. of atoms per gram’ can be called as ‘gram mole’ and ‘no. of atoms per kg’ can be called as ‘kg mole’. We would like to emphasize the point that Avogadro number is not a pure number and it is having dimensions.
N A ≅ ( 1 U A M U )   No .   of   atoms   kg   or   No .   of   atoms   gram

4. Reference Nuclear Binding Energy Formula

In nuclear physics, at present one can find different semi empirical mass formulae (SEMF) with different energy coefficients with different accuracies [16,17,18,19,20].
Let, Z = Proton number, N = Neutron number, A=Mass number or nucleon number
One of the advanced formula is [20],
B E ≅ { [ 1 + ( 4 k v A 2 ) | T z | ( | T z | + 1 ) ] a v * A } + { [ 1 + ( 4 k s A 2 ) | T z | ( | T z | + 1 ) ] a s * A 2 3 } + { a c * ( Z 2 A 1 / 3 ) } + { f p * Z 2 A } + E p }
where, T z ≅ 3 rd   component   of   isospin   = 1 2 ( Z − N )
{ a v = − 15.4963   MeV ,   a s = 17.7937   MeV k v = − 1.8232 ; k s = − 2.2593 a c = 0.7093   MeV   f p = − 1.2739   MeV d n = 4.6919   MeV ,   d p = 4.7230   MeV d n p = − 6.4920   MeV } and { for   ( Z ,   N   )   Odd ,   E p ≅ d n N 1 / 3 + d p Z 1 / 3 + d n p A 2 / 3 for   ( Odd   Z ,   Even   N   ) ,   E p ≅ d p Z 1 / 3 for   ( Even   Z ,   Odd   N   ) ,   E p ≅ d n N 1 / 3 for   ( Even   Z ,   Even   N   ) ,   E p ≅ 0 }
Based on relation (3), as explained in section -2, we have presented the data in Table 1 for each atomic number with 2Z and 3.5Z as lower and upper mass numbers respectively.

5. Strong and Electroweak Mass Formula

According to the authors [7,8,9,10,11,12], Strong and Electroweak Mass Formula (SEWMF) constitutes 4 simple terms and only one energy coefficient of magnitude 10.1 MeV. First term is a volume term, second term seems to be a representation of free nucleons associated with electroweak interaction, third term is a radial term and fourth one is an asymmetry term about the mean stable mass number. It can be expressed as,
B E ≅ { A − A f r e e − A r a d − A a s y } 10.1   MeV
where, A f r e e ≅ No .   of   free   nucleons   associated   with   Electroweak   interaction . ≅ ( 1 2 ) + 0.0016 [ ( Z 2 + N 2 + ( Z 2 N ) 2 ) − N 2 ( N − Z N + Z ) 2 ]
A r a d ≅ Radial   term ≅ A 1 / 3 A a s y ≅ Asymmetey   about   the   mean   stable   mass   number   ≅ ( A s − A ) 2 A s A s ≅ Light   house   like   stable   mass   number ≅ [ RoundOff { ( Z + 2.9464 ) 1.2 − 1.7165 } + [ 0 , 1 ] ]
where,
1)
If Z is even and obtained A s is odd, then, A s ≅ A s + 1 .
2)
If Z is even and obtained A s is even, then, A s ≅ A s .
3)
If Z is odd and obtained A s is odd, then, A s ≅ A s .
4)
If Z is odd and obtained A s is even, then, A s ≅ A s + 1 .
Using this relation (5), super heavy atomic nuclides can be estimated very easily [21,22,23,24,25]. Based on relations (4) and (5), as explained in section-2, we have presented the data in Table. 1 for each atomic number with 2Z and 3.5Z as lower (AL) and upper mass numbers (AU) respectively.

6. Comparative Results and Discussion

Based on the above two formulae, Navya Sree and Divya Sree, daughters of author Seshavatharam are working on developing a simple web application. It takes the beginning and ending proton numbers and their corresponding lower and upper mass numbers. Following a background written python program, it estimates the Unified atomic mass unit and Avogadro number. With further study and considering the available binding energy formulae, above procedures can be repeated for each atomic number and its isotopes. By considering observed stable and unstable atomic nuclides and their experimental binding energies as default inputs and considering AI techniques [26,27,28], various energy coefficients of the available Semi Empirical Mass Formulae (SEMF) can be refined further and thus accuracy of Unified atomic mass unit and Avogadro number can be improved. One very important point to be noted is that, Avogadro number seems to be the inverse of the unified atomic mass unit. This proposal seems to play a crucial role in defining the fundamental units and building blocks of physics and chemistry in a unified approach. ‘Gram mole’ and ‘kg mole’ concepts can be understood without any ambiguity. Difficulties involved in this procedure are:
1)
At present there is no clear physics for understanding unstable lower and higher mass numbers associated with any proton number. Scientists are working in terms of proton drip lines and neutron drip lines [29,30,31].
2)
Life time of super heavy proton numbers greater than 99 and mass numbers greater than 300 is too small to understand and estimate their ground state binding energies.
We appeal the scientists to look into these issues for better understanding and best possible accuracy. See the following Table. 1 for the reference formula and see Table 2 for the Strong and Electroweak Mass Formula. In the Silicon-28 experiment [4], formula for estimating the Avogadro number is,
N A ≅ Molar   volume   of   Si - 28 Volume   of   unit   cell / 8 ≅ 8 × Molar   mass   of   Si - 28 Density   of   Si - 28   × Volume   of   unit   cell where   No .   of   Si   atoms   in   unit   cell = 8
It may be noted that, considering Silicon-28, recommended value of Avogadro number is 6.022140588 × 10 23   mol - 1 . Following our procedure and by considering so many atomic nuclides and their binding energies, it seems possible to understand and estimate the Average Avogadro number with a marginal error. Interested research scholars can work in this direction. Using AI techniques, accuracy can be improved further. Our approach is completely different from Si-28 experiential concepts. See the following two figures obtained from relation (3). From these two figures, it is very clear that, at Z=26 to 28, as they seem to have high binding energy per nucleon, estimated Unified Atomic Energy Unit seems to be close to (931.37 to 931.5) MeV and Avogadro number seems to be close to ( 6.022   to   6.023 ) × 10 26 . We would like to emphasize the point that,
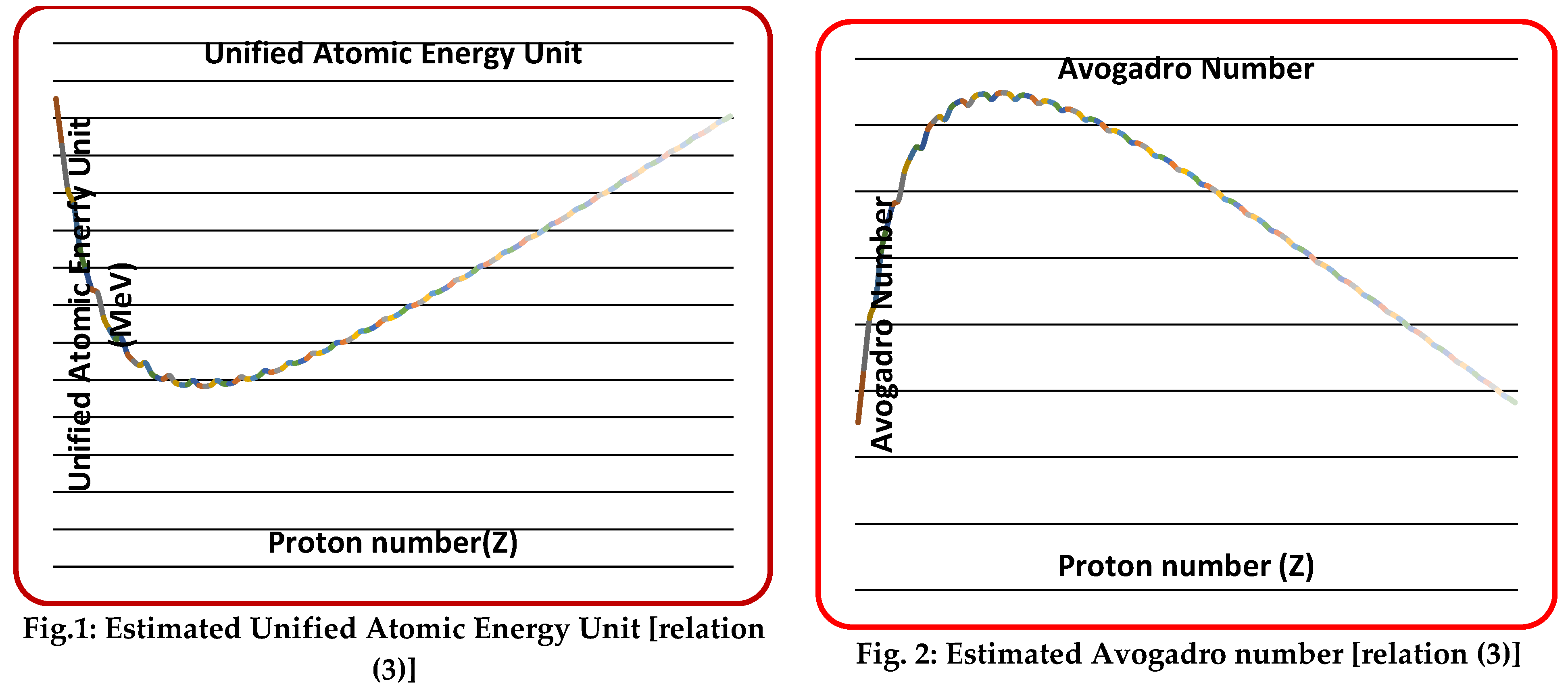
Preprints 116236 i001
Avogadro number is having inherent connection with saturation of nuclear binding energy. In addition to that, there is a chance to consider Avogadro number as a variable within a short range, N r a n g e ≈ ( 6.012   to   6.023 ) × 10 26 . Clearly speaking, short range strong nuclear force seems to have a vital role in deciding the accuracy of Avogadro number. We are working in this direction. Following relations (3) and (5), for Z=5 to 118 and Alow=2Z and Aupper=3.5Z, estimated average value of Avogadro number is N A v e r a g e ≅ 6.01938 × 10 26 .
Proceeding further, currently believed “mole” can be called as ‘gram mole’ and its corresponding SI unit can be called as ‘kg mole’. In CGS system of units, ‘Number of atoms per gram’ can be called as ‘per gram mole’ and in SI system of units, ‘Number of atoms per kg’ can be called as ‘per kg mole’. In this way, ‘mole’ concept can be understood clearly. Considering system of units, currently believed ‘molar mass’ can be called as ‘gram molar mass’ and ‘kg molar mass’. In CGS units, ‘gram molar mass’ of any substance can be assumed to have ≈ 6.022 × 10 23 atoms and in SI units, ‘kg molar mass’ of any substance can be assumed to have ≈ 6.022 × 10 26 atoms. Thinking in this way and by considering proton drip lines and neutron drip lines and by fixing the lower and upper mass numbers of Z=2 to 118, Avogadro number can be estimated with a better understanding and best accuracy
Table 1. Nuclear binding energy based estimation of unified atomic mass unit and Avogadro number.
Z AL AU As Relation (5) Relation (3)
ABEPN
(MeV)		 UAEU
(MeV)		 UAMU
(kg)		 NA
No. of atoms/kg		 ABEPN
(MeV)		 UAEU
(MeV)		 UAMU
(kg)		 NA
No. of atoms/kg
6 12 21 12 6.779 932.651 1.66260E-27 6.01467E+26 6.527 932.903 1.66305E-27 6.01304E+26
7 14 24 15 7.411 932.019 1.66147E-27 6.01875E+26 6.777 932.653 1.66260E-27 6.01466E+26
8 16 28 16 7.097 932.333 1.66203E-27 6.01672E+26 7.014 932.416 1.66218E-27 6.01619E+26
9 18 32 19 7.454 931.975 1.66140E-27 6.01903E+26 7.095 932.335 1.66204E-27 6.01671E+26
10 20 35 20 7.283 932.147 1.66170E-27 6.01792E+26 7.326 932.104 1.66163E-27 6.01820E+26
11 22 38 23 7.656 931.774 1.66104E-27 6.02033E+26 7.442 931.988 1.66142E-27 6.01895E+26
12 24 42 24 7.398 932.032 1.66150E-27 6.01867E+26 7.544 931.886 1.66124E-27 6.01961E+26
13 26 46 27 7.619 931.811 1.66110E-27 6.02009E+26 7.566 931.864 1.66120E-27 6.01975E+26
14 28 49 28 7.471 931.959 1.66137E-27 6.01914E+26 7.698 931.732 1.66096E-27 6.02060E+26
15 30 52 31 7.732 931.698 1.66090E-27 6.02082E+26 7.762 931.668 1.66085E-27 6.02101E+26
16 32 56 32 7.517 931.913 1.66129E-27 6.01944E+26 7.811 931.619 1.66076E-27 6.02133E+26
17 34 60 35 7.672 931.758 1.66101E-27 6.02044E+26 7.809 931.621 1.66076E-27 6.02132E+26
18 36 63 38 7.856 931.574 1.66068E-27 6.02162E+26 7.893 931.537 1.66062E-27 6.02186E+26
19 38 66 39 7.742 931.688 1.66088E-27 6.02089E+26 7.930 931.500 1.66055E-27 6.02210E+26
20 40 70 42 7.842 931.588 1.66071E-27 6.02153E+26 7.953 931.477 1.66051E-27 6.02225E+26
21 42 74 43 7.675 931.755 1.66100E-27 6.02045E+26 7.940 931.490 1.66053E-27 6.02217E+26
22 44 77 46 7.822 931.608 1.66074E-27 6.02141E+26 7.996 931.434 1.66043E-27 6.02253E+26
23 46 80 49 7.942 931.488 1.66053E-27 6.02218E+26 8.018 931.412 1.66039E-27 6.02267E+26
24 48 84 50 7.798 931.632 1.66078E-27 6.02125E+26 8.026 931.404 1.66038E-27 6.02272E+26
25 50 88 53 7.863 931.567 1.66067E-27 6.02167E+26 8.007 931.423 1.66041E-27 6.02260E+26
26 52 91 56 7.958 931.472 1.66050E-27 6.02229E+26 8.045 931.385 1.66034E-27 6.02285E+26
27 54 94 57 7.873 931.557 1.66065E-27 6.02173E+26 8.057 931.373 1.66032E-27 6.02292E+26
28 56 98 60 7.918 931.512 1.66057E-27 6.02203E+26 8.056 931.374 1.66032E-27 6.02292E+26
29 58 102 63 7.956 931.474 1.66050E-27 6.02227E+26 8.034 931.396 1.66036E-27 6.02277E+26
30 60 105 66 8.020 931.410 1.66039E-27 6.02269E+26 8.060 931.370 1.66032E-27 6.02294E+26
31 62 108 67 7.946 931.484 1.66052E-27 6.02221E+26 8.065 931.365 1.66031E-27 6.02297E+26
32 64 112 70 7.972 931.458 1.66047E-27 6.02238E+26 8.058 931.372 1.66032E-27 6.02293E+26
33 66 116 73 7.993 931.437 1.66044E-27 6.02251E+26 8.034 931.396 1.66036E-27 6.02277E+26
34 68 119 74 7.924 931.506 1.66056E-27 6.02207E+26 8.051 931.379 1.66033E-27 6.02289E+26
35 70 122 77 7.973 931.457 1.66047E-27 6.02238E+26 8.051 931.379 1.66033E-27 6.02289E+26
36 72 126 80 7.986 931.444 1.66045E-27 6.02247E+26 8.041 931.389 1.66035E-27 6.02282E+26
37 74 130 83 7.996 931.434 1.66043E-27 6.02253E+26 8.015 931.415 1.66040E-27 6.02265E+26
38 76 133 84 7.935 931.495 1.66054E-27 6.02213E+26 8.026 931.404 1.66038E-27 6.02272E+26
39 78 136 87 7.969 931.461 1.66048E-27 6.02236E+26 8.022 931.408 1.66039E-27 6.02270E+26
40 80 140 90 7.975 931.455 1.66047E-27 6.02239E+26 8.009 931.421 1.66041E-27 6.02261E+26
41 82 144 93 7.977 931.453 1.66047E-27 6.02241E+26 7.982 931.448 1.66046E-27 6.02244E+26
42 84 147 94 7.921 931.509 1.66057E-27 6.02204E+26 7.989 931.441 1.66044E-27 6.02248E+26
43 86 150 97 7.945 931.485 1.66052E-27 6.02220E+26 7.982 931.448 1.66046E-27 6.02244E+26
44 88 154 100 7.945 931.485 1.66052E-27 6.02220E+26 7.966 931.463 1.66048E-27 6.02234E+26
45 90 158 103 7.942 931.488 1.66053E-27 6.02218E+26 7.940 931.490 1.66053E-27 6.02216E+26
46 92 161 106 7.957 931.472 1.66050E-27 6.02228E+26 7.942 931.488 1.66053E-27 6.02218E+26
47 94 164 107 7.907 931.523 1.66059E-27 6.02196E+26 7.933 931.497 1.66054E-27 6.02212E+26
48 96 168 110 7.902 931.528 1.66060E-27 6.02192E+26 7.916 931.514 1.66057E-27 6.02201E+26
49 98 172 113 7.895 931.535 1.66061E-27 6.02188E+26 7.889 931.541 1.66062E-27 6.02184E+26
50 100 175 116 7.906 931.524 1.66059E-27 6.02194E+26 7.889 931.541 1.66062E-27 6.02184E+26
51 102 178 119 7.913 931.517 1.66058E-27 6.02199E+26 7.878 931.552 1.66064E-27 6.02177E+26
52 104 182 122 7.902 931.528 1.66060E-27 6.02192E+26 7.860 931.570 1.66067E-27 6.02165E+26
53 106 186 123 7.840 931.590 1.66071E-27 6.02152E+26 7.833 931.597 1.66072E-27 6.02148E+26
54 108 189 126 7.846 931.584 1.66070E-27 6.02156E+26 7.830 931.600 1.66073E-27 6.02146E+26
55 110 192 129 7.850 931.580 1.66069E-27 6.02159E+26 7.818 931.612 1.66075E-27 6.02138E+26
56 112 196 132 7.837 931.593 1.66072E-27 6.02150E+26 7.799 931.631 1.66078E-27 6.02126E+26
57 114 200 135 7.823 931.607 1.66074E-27 6.02141E+26 7.772 931.658 1.66083E-27 6.02108E+26
58 116 203 138 7.823 931.607 1.66074E-27 6.02141E+26 7.767 931.663 1.66084E-27 6.02105E+26
59 118 206 141 7.821 931.609 1.66074E-27 6.02140E+26 7.754 931.676 1.66086E-27 6.02096E+26
60 120 210 142 7.767 931.663 1.66084E-27 6.02105E+26 7.734 931.696 1.66090E-27 6.02084E+26
61 122 214 145 7.751 931.679 1.66087E-27 6.02095E+26 7.707 931.723 1.66095E-27 6.02066E+26
62 124 217 148 7.749 931.681 1.66087E-27 6.02093E+26 7.701 931.729 1.66096E-27 6.02062E+26
63 126 220 151 7.745 931.685 1.66088E-27 6.02091E+26 7.687 931.743 1.66098E-27 6.02053E+26
64 128 224 154 7.727 931.703 1.66091E-27 6.02079E+26 7.667 931.763 1.66102E-27 6.02040E+26
65 130 228 157 7.709 931.721 1.66094E-27 6.02068E+26 7.640 931.790 1.66107E-27 6.02023E+26
66 132 231 160 7.703 931.727 1.66095E-27 6.02063E+26 7.632 931.798 1.66108E-27 6.02018E+26
67 134 234 163 7.695 931.735 1.66097E-27 6.02059E+26 7.617 931.813 1.66111E-27 6.02008E+26
68 136 238 166 7.676 931.754 1.66100E-27 6.02046E+26 7.597 931.833 1.66114E-27 6.01995E+26
69 138 242 167 7.629 931.801 1.66109E-27 6.02016E+26 7.570 931.860 1.66119E-27 6.01978E+26
70 140 245 170 7.621 931.809 1.66110E-27 6.02011E+26 7.561 931.869 1.66121E-27 6.01972E+26
71 142 248 173 7.612 931.818 1.66112E-27 6.02005E+26 7.545 931.885 1.66124E-27 6.01962E+26
72 144 252 176 7.592 931.838 1.66115E-27 6.01992E+26 7.525 931.905 1.66127E-27 6.01948E+26
73 146 256 179 7.571 931.859 1.66119E-27 6.01979E+26 7.498 931.932 1.66132E-27 6.01931E+26
74 148 259 182 7.561 931.869 1.66121E-27 6.01972E+26 7.488 931.942 1.66134E-27 6.01925E+26
75 150 262 185 7.550 931.880 1.66123E-27 6.01965E+26 7.472 931.958 1.66137E-27 6.01914E+26
76 152 266 188 7.528 931.902 1.66127E-27 6.01951E+26 7.451 931.979 1.66140E-27 6.01901E+26
77 154 270 191 7.506 931.924 1.66130E-27 6.01937E+26 7.425 932.005 1.66145E-27 6.01884E+26
78 156 273 194 7.494 931.936 1.66133E-27 6.01929E+26 7.414 932.016 1.66147E-27 6.01877E+26
79 158 276 197 7.481 931.949 1.66135E-27 6.01920E+26 7.397 932.033 1.66150E-27 6.01866E+26
80 160 280 200 7.458 931.972 1.66139E-27 6.01906E+26 7.376 932.054 1.66154E-27 6.01853E+26
81 162 284 203 7.436 931.994 1.66143E-27 6.01891E+26 7.350 932.079 1.66158E-27 6.01836E+26
82 164 287 206 7.422 932.008 1.66146E-27 6.01882E+26 7.339 932.091 1.66160E-27 6.01828E+26
83 166 290 209 7.407 932.023 1.66148E-27 6.01872E+26 7.322 932.108 1.66163E-27 6.01817E+26
84 168 294 212 7.384 932.046 1.66152E-27 6.01857E+26 7.301 932.129 1.66167E-27 6.01804E+26
85 170 298 215 7.360 932.070 1.66157E-27 6.01842E+26 7.275 932.155 1.66172E-27 6.01787E+26
86 172 301 218 7.345 932.085 1.66159E-27 6.01832E+26 7.263 932.167 1.66174E-27 6.01779E+26
87 174 304 219 7.316 932.114 1.66164E-27 6.01814E+26 7.245 932.185 1.66177E-27 6.01768E+26
88 176 308 222 7.293 932.137 1.66169E-27 6.01798E+26 7.224 932.206 1.66181E-27 6.01754E+26
89 178 312 225 7.269 932.161 1.66173E-27 6.01783E+26 7.199 932.231 1.66185E-27 6.01738E+26
90 180 315 228 7.253 932.177 1.66176E-27 6.01773E+26 7.186 932.244 1.66188E-27 6.01730E+26
91 182 318 231 7.237 932.193 1.66179E-27 6.01763E+26 7.168 932.262 1.66191E-27 6.01718E+26
92 184 322 234 7.213 932.217 1.66183E-27 6.01747E+26 7.147 932.283 1.66195E-27 6.01705E+26
93 186 326 237 7.189 932.241 1.66187E-27 6.01731E+26 7.122 932.308 1.66199E-27 6.01688E+26
94 188 329 240 7.172 932.258 1.66190E-27 6.01721E+26 7.108 932.322 1.66201E-27 6.01680E+26
95 190 332 243 7.155 932.275 1.66193E-27 6.01710E+26 7.091 932.339 1.66205E-27 6.01668E+26
96 192 336 246 7.130 932.300 1.66198E-27 6.01694E+26 7.070 932.360 1.66208E-27 6.01655E+26
97 194 340 249 7.106 932.324 1.66202E-27 6.01678E+26 7.045 932.385 1.66213E-27 6.01638E+26
98 196 343 252 7.088 932.342 1.66205E-27 6.01667E+26 7.031 932.399 1.66215E-27 6.01629E+26
99 198 346 255 7.070 932.360 1.66208E-27 6.01655E+26 7.013 932.417 1.66218E-27 6.01618E+26
100 200 350 258 7.045 932.385 1.66213E-27 6.01639E+26 6.992 932.438 1.66222E-27 6.01604E+26
101 202 354 261 7.021 932.409 1.66217E-27 6.01623E+26 6.967 932.463 1.66227E-27 6.01588E+26
102 204 357 264 7.002 932.428 1.66220E-27 6.01611E+26 6.953 932.477 1.66229E-27 6.01579E+26
103 206 360 269 6.990 932.440 1.66223E-27 6.01603E+26 6.934 932.496 1.66232E-27 6.01567E+26
104 208 364 272 6.965 932.465 1.66227E-27 6.01587E+26 6.913 932.517 1.66236E-27 6.01554E+26
105 210 368 275 6.939 932.491 1.66232E-27 6.01571E+26 6.889 932.541 1.66241E-27 6.01538E+26
106 212 371 278 6.920 932.510 1.66235E-27 6.01558E+26 6.874 932.556 1.66243E-27 6.01529E+26
107 214 374 281 6.901 932.529 1.66238E-27 6.01546E+26 6.856 932.574 1.66246E-27 6.01517E+26
108 216 378 284 6.875 932.555 1.66243E-27 6.01529E+26 6.835 932.595 1.66250E-27 6.01503E+26
109 218 382 287 6.850 932.580 1.66248E-27 6.01513E+26 6.811 932.619 1.66254E-27 6.01488E+26
110 220 385 290 6.830 932.600 1.66251E-27 6.01500E+26 6.796 932.634 1.66257E-27 6.01478E+26
111 222 388 293 6.810 932.620 1.66255E-27 6.01487E+26 6.777 932.653 1.66260E-27 6.01466E+26
112 224 392 296 6.784 932.646 1.66259E-27 6.01471E+26 6.756 932.674 1.66264E-27 6.01453E+26
113 226 396 299 6.759 932.671 1.66264E-27 6.01454E+26 6.732 932.698 1.66268E-27 6.01437E+26
114 228 399 302 6.739 932.691 1.66267E-27 6.01441E+26 6.717 932.713 1.66271E-27 6.01427E+26
115 230 402 305 6.718 932.712 1.66271E-27 6.01428E+26 6.698 932.731 1.66274E-27 6.01415E+26
116 232 406 308 6.692 932.738 1.66276E-27 6.01411E+26 6.678 932.752 1.66278E-27 6.01402E+26
117 234 410 311 6.667 932.763 1.66280E-27 6.01395E+26 6.654 932.776 1.66282E-27 6.01387E+26
118 236 413 314 6.646 932.784 1.66284E-27 6.01381E+26 6.638 932.791 1.66285E-27 6.01377E+26

7. Conclusions

Our proposed method of estimating unified atomic mass unit and Avogadro number seems to be quite different from existing methods and there is a possibility for increasing the accuracy with newly observed atomic nuclides and their binding energy per nucleons. Thus, by fitting them with the available semi empirical mass formulae, binding energy coefficients can be refined. Repeating this process with AI logics, further refinement can be achieved in all aspects. For the time being, our proposal can be given a chance at academic level.

Acknowledgments

Authors are very much thankful to professors shri M. Nagaphani Sarma, Chairman, shri K.V. Krishna Murthy, founder Chairman, Institute of Scientific Research in Vedas (I-SERVE), Hyderabad, India and Shri K.V.R.S. Murthy, former scientist IICT (CSIR), Govt. of India, Director, Research and Development, I-SERVE, for their valuable guidance and great support in developing this subject.

References

  1. Tiesinga, E., Mohr, P. J., Newell, D. B. & Taylor, B. N. “CODATA recommended values of the fundamental physical constants: 2018”. Rev. Mod. Phys. 93, 025010, 2021. [CrossRef]
  2. Workman R.L. et al. (Particle Data Group), Prog. Theor. Exp. Phys. 2022, 083C01, 2022.
  3. Becker Peter and Bettin Horst. “The Avogadro constant: Determining the number of atoms in a single-crystal 28Si sphere”. Phil. Trans. R. Soc. A.3693925–3935, 2011. [CrossRef]
  4. K. Fujii, E. Massa, H. Bettin, N. Kuramoto and G. Mana. “Avogadro constant measurements using enriched 28Si monocrystals”. Bureau International des Poids et Mesures. Metrologia, 55, L1–L4, 2018. [CrossRef]
  5. Bengt Nordén. “The Mole, Avogadro’s Number and Albert Einstein”. Molecular Frontiers Journal. 5, 66-78, 2021. [CrossRef]
  6. Michalis Siafarikas, Georgios Stylos, Theodoros Chatzimitakos, Konstantinos Georgopoulos, Constantine Kosmidis and Konstantinos T Kotsis. “Experimental teaching of the Avogadro constant”. Phys. Educ. 58 (2023) 065026 (12pp). [CrossRef]
  7. Seshavatharam U.V.S and Lakshminarayana S. “A very brief review on strong and electroweak mass formula pertaining to 4G model of final unification”. Proceedings of the DAE Symp. on Nucl. Phys. 67,1173,2023.
  8. Seshavatharam U.V.S and Lakshminarayana S. “Exploring condensed matter physics with refined electroweak term of the strong and electroweak mass formula”. World Scientific News .193(2) 105-13, 2024.
  9. Seshavatharam U.V.S and Lakshminarayana S. “Inferring and confirming the rest mass of electron neutrino with neutron life time and strong coupling constant via 4G model of final unification”. World Scientific News 191, 127-156, 2024.
  10. Seshavatharam U.V.S and Lakshminarayana. “Understanding nuclear stability range with 4G model of nuclear charge”. World Scientific News. 177, 118-136, 2023.
  11. Seshavatharam U.V.S, S. Lakshminarayana, H. K. Cherop and K. M. Khanna, “Three Unified Nuclear Binding Energy Formulae. World Scientific News”. 163, 30-77, 2022.
  12. Seshavatharam U.V.S, Lakshminarayana, S., On the Combined Role of Strong and Electroweak Interactions in Understanding Nuclear Binding Energy Scheme. Mapana Journal of Sciences, 20(1), 1-18, 2021. [CrossRef]
  13. Seshavatharam U.V.S and Lakshminarayana S., “Strong and Weak Interactions in Ghahramany’s Integrated Nuclear Binding Energy Formula”. World Scientific News, 161, 111-129, 2021.
  14. Seshavatharam U. V. S., Gunavardhana Naidu T and Lakshminarayana S. “To confirm the existence of heavy weak fermion of rest energy 585 GeV”. AIP Conf. Proc. 2451 p 020003, 2022.
  15. Seshavatharam U.V.S and Lakshminarayana S. “4G model of final unification – A brief report”. Journal of Physics: Conference Series 2197 p 012029, 2022. [CrossRef]
  16. Myers W. D. and Swiatecki W. J. “Nuclear Properties According to the Thomas-Fermi Model”. LBL-36557 Rev. UC-413, 1995. [CrossRef]
  17. Myers W. D. and Swiatecki W. J. “Table of nuclear masses according to the 1994 Thomas-Fermi model”. United States: N. p., 1994. Web.
  18. X.W. Xia, Y. Lim, P.W. Zhao et al. “The limits of the nuclear landscape explored by the relativistic continuum Hartree–Bogoliubov theory”. Atomic Data and Nuclear Data Tables. 121–122, 1-215, 2018. [CrossRef]
  19. Djelloul Benzaid, Salaheddine Bentridi, Abdelkader Kerraci, Naima Amrani. “Bethe–Weizsa¨cker semiempirical mass formula coefficients 2019 update based on AME2016”. NUCL. SCI. TECH. 31:9, 2020. [CrossRef]
  20. Gao, Z.P., Wang, YJ., Lü, HL. et al., “Machine learning the nuclear mass”. NUCL. SCI. TECH. 32, 109, 2021. [CrossRef]
  21. J.M. Gates et al. “Towards the Discovery of New Elements: Production of Livermorium (Z=116) with 50Ti”. arXiv:2407.16079v1 [nucl-ex], 2024.
  22. Ghiorso Albert. “Einsteinium and Fermium. Chemical and Engineering News”. 81 (36): 174–175, 2003. [CrossRef]
  23. Kondev, F. G.; Wang, M.; Huang, W. J.; Naimi, S.; Audi, G. “The NUBASE2020 evaluation of nuclear properties (PDF)”. Chinese Physics C. 45 (3): 030001, 2021. [CrossRef]
  24. Peter Möller. “The limits of the nuclear chart set by fission and alpha decay”. EPJ Web Conf. 131, 03002, 2016. [CrossRef]
  25. Oganessian, Yu & Rykaczewski, Krzysztof. “A beachhead on the island of stability”. Physics Today. 68. 32-38, 2015.
  26. Hermann, J., Spencer, J., Choo, K. et al. “Ab initio quantum chemistry with neural-network wave functions”. Nat. Rev. Chem. 7, 692–709. 2023. [CrossRef]
  27. Kirkpatrick, J. et al. “Pushing the frontiers of density functionals by solving the fractional electron problem”. Science, 374(6573), 2021. [CrossRef]
  28. Unke, O. T. et al. “Machine learning force fields”. Chemical Reviews, 121(16), 10142–10186,2021. [CrossRef]
  29. Erler, J., Birge, N., Kortelainen, M. et al. “The limits of the nuclear landscape”. Nature 486, 509–512, 2012. [CrossRef]
  30. Tsunoda, N., Otsuka, T., Takayanagi, K. et al. “The impact of nuclear shape on the emergence of the neutron dripline”. Nature 587, 66–71, 2020. [CrossRef]
  31. Léo Neufcourt, Yuchen Cao, Samuel Giuliani, Witold Nazarewicz, Erik Olsen, Oleg B. Tarasov. “Beyond the proton drip line: Bayesian analysis of proton emitting nuclei”. Phys. Rev. C 101, 014319, 2020. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated