Reliability-based Design Optimization for Polymer Electrolyte Membrane Fuel Cells: Tackling Dimensional Uncertainties in Manufacturing and Their Effects on Costs of Cathode Gas Diffusion Layer and Bipolar Plates

Preprint

Article

Reliability-based Design Optimization for Polymer Electrolyte Membrane Fuel Cells: Tackling Dimensional Uncertainties in Manufacturing and Their Effects on Costs of Cathode Gas Diffusion Layer and Bipolar Plates

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Neil Vaz,Kisung Lim,Jaeyoo Choi,

Hyunchul Ju^*

Neil Vaz,Kisung Lim,Jaeyoo Choi,

Hyunchul Ju^*

This version is not peer-reviewed

Submitted:

27 August 2024

Posted:

27 August 2024

You are already at the latest version

Alerts

Abstract

Polymer Electrolyte Membrane Fuel Cells (PEMFCs) have emerged as a pivotal technology in the automotive industry, significantly contributing to the reduction of greenhouse gas emissions. The high material costs of the gas diffusion layer(GDL) and bipolar plate(BP) creates a barrier for large scale commercial application. This study aims towards addressing this challenge by optimizing the material and design of the cathode, GDL and BP. While Deterministic design optimization(DDO) methods have been extensively studied, they often fall short when manufacturing uncertainties are introduced. This issue is addressed by introducing Reliability based design optimization(RBDO) to optimize four key PEMFC design variables i.e., δ_gdl, d_ch, w_ch, and w_land. The objective is to maximize cell voltage(V_cell) considering material cost of cathode gas diffusion layer(Cost_cGDL), and cathode bipolar plate(Cost_cBP) as reliability constraints. Results of the DDO show an increment in V_cell of 31mV, with reliability of around 50% for Cost_cGDL and Cost_cBP. In contrast RBDO method provides a reliability of 95% for both Cost_cGDL and Cost_cBP.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Fuel cells (FCs) are considered as a key enabling technology for emerging hydrogen economy [1]. These devices electrochemically convert fuels such as hydrogen and oxygen to generate electricity. FCs are silent in operation with zero emission of harmful pollutants and can generate electricity if the source of fuel is supplied. FCs are generally classified based on the conducting electrolyte used, operating temperature and the feasible performance region [2]. PEMFCs are considered as one of the most promising sources of energy conversion devices that would perhaps replace the internal combustion engines [3]. PEMFCs are particularly well suited for stationary and mobile applications. In PEMFCs, the electrochemical reaction of hydrogen along with oxygen to form water is divided into the partial reactions of oxidation and reduction by incorporating a proton-conducting membrane between the anode and cathode electrodes. PEMFCs are typically operated at temperatures ranging between 50°C and 80°C and have high power density and low degradation rates [4].

PEMFCs has received immense attention due to its wide range of application. Their application in real world ranges from industrial scale systems for power backup to mobile power for trains, buses, heavy duty trucks and material handling systems [5]. However, in recent years the widespread implementation of PEMFCs have been restricted due to a rise in manufacturing costs and issues pertaining to durability in fuel cell designs [6,7]. Therefore, it is imperative to work over the design aspects of fuel cells. The modern fuel cell market is highly competitive and requires engineers to come up with designs that are inexpensive and highly reliable. The design process is quite intricate and is largely focused on producing products that are characterized by being inexpensive, of excellent quality, and of great durability. The modern design process is based on complex simulation models that can support complexity and fidelity to accomplish the aforementioned objectives and are often termed as simulation-based design approach [8].

Over the past few decades, the computational speed of computers has increased exponentially leading to development and application of large-scale simulation models. Simulation tools like computational fluid dynamics (CFD) and finite element analysis (FEA) have seen large growth and are able to represent an actual physical system. This has lead design engineers with a wide range of opportunity to come up with improved and optimal design strategies. To create high quality design models, the engineering community of today has been using optimization to a greater extent. These design models demonstrate to be cost effective and have acceptable performance abilities. In most cases, engineers consider the design variables to be deterministic during engineering design optimization, and the process of attaining an optimal design on this basis is referred to as DDO.

PEMFCs have been optimized using numerical analysis to improve cell

V_{c e l l}

by considering the design variables to be deterministic. Song et al. [9] optimized the cathode catalyst layer considering the one-dimensional macro homogenous model where the four design parameters such as Nafion content, void volume fraction, thickness, and the amount of platinum (Pt) loading. Grigoriev et al. [10] optimized the geometry of the BP and GDL of a high temperature fuel cell and provided an insight onto the effects of these parameters on

V_{c e l l}

. Kim et al. [11] conducted a comprehensive study considering metallic BPs and evaluated the effects of channel to rib width ratio, draft angle, inner fillet radius and clamping pressure. The study reveals that the GDL intrusion is highly influenced by the channel to rib ratio and draft angle which in turn affects pressure drop within the channels. However, a typical engineering process consists of various uncertainties. Products manufactured based on DDO approach will have varying performance characteristics and a high risk of failure as they do not consider uncertainties in them. In real world scenarios, uncertainties may often arise due to external operating conditions, variations in parameters such as dimensions or material properties, model uncertainties and errors associated with the simulation tools used for simulation-based designs and many more. When the uncertainties are taken into consideration some types of constraints such as initial condition and

V_{c e l l}

maybe violated. Therefore, to avoid the risk of any given product to fail, these uncertainties must be considered during the optimization process.

Optimization methods that consider the uncertainties in design variables and solve an optimization problem with reliability constraints are termed as RBDO [12,13]. With RBDO the designers are able to determine optimal designs that would meet target reliability measures that would achieve satisfactory levels of performance measures and constraints. RBDO has been widely used in the field of structural designs and fluid-structure interactions problems, magnetic energy storage systems and multi body dynamic systems. However, till date there has no research been presented where RBDO has been used to optimize the design variables for a PEMFC.

PEMFCs are highly complex systems that consists of several components. These components have varying material properties and manufacturing tolerances. Any minor changes in the component properties and dimensions along with PEMFC operating conditions such as temperature, humidity and pressure will affect the PEMFC performance. Hence, variability must be considered during design stage itself. RBDO engineers consider the input design variables of a probability distribution and carry out optimization to determine an optimal design solution [14]. The design thus obtained are reliable and have a very less chance of failure. Dimensional tolerances which refer to the allowable deviation from the specified dimension are a critical part of manufacturing of PEMFC components [15,16,17]. Intricate components are expensive to manufacture and must meet strict dimensional tolerance levels. Small deviations in dimensions can cause significant reduction in performance and costs. For example, the membrane electrode assembly (MEA) thickness has to be precisely controlled so that the flow of reactant gases reaches the CL layer. Likewise,

δ_{g d l}

and

d_{c h}

must be controlled to make sure that the reactant gases and flow of liquid water is managed well within the cell.

The dimensional tolerance considered during manufacturing plays a pivotal role in increasing costs of PEMFCs [18]. The process of manufacturing PEMFC components are highly complex and require high precision. In addition, the use of expensive and high-quality materials to meet high dimensional tolerance levels leads to an increase in the overall cost of PEMFCs. A fuel cell stack consists of hundreds of single cells that are arranged in series and generate the required power and voltage for operation. Highly precise manufacturing accuracy in BPs and GDLs are required to obtain uniform contact pressure and electrochemical reactions in the stacks [19,20,21]. However due to the manufacturing process, errors arise in shape, dimensions and assembly that are inevitable. Stamping process is the most preferred choice for manufacturing BPs [22,23]. During the stamping process highly localized stamping forces are induce while channels are formed leading to errors in dimensions of channel height and width [24,25]. In addition, dimensional variation in GDL and BPs would also lead to assembly errors and causes failure of the systems [26]. Thus, there is a need to consider these errors during the optimization stage.

The GDLs serve as a medium for distributing the reactant gases and are generally made of carbon fibers. On the other side, BPs are employed within the fuel cell stack to conduct electricity and separate individual cells. The amount spent on materials is significantly impacted by the dimensional tolerance needed throughout the production process. It will take high-quality materials with reliable properties to achieve tighter tolerance. Also, the material wastage for manufacturing GDLs and BPs with tighter tolerance levels will be high. This is due to the fact that parts must be scrapped or reworked when they do not meet the required dimensional tolerance. Likewise, for looser tolerance there is a possibility of using low-cost material with wide variations in thickness. This may result in lower material cost with additional processing steps required and a compromise in

V_{c e l l}

. Overall, the effect of dimensional tolerance on material cost will be influenced by the manufacturing process and the materials employed. To ensure manufacturing high-quality products at an affordable price, manufacturers must carefully balance the necessary level of precision with the associated material costs.

Based on a comprehensive review of existing literature, it is evident that currently there is a significant gap in research on PEMFCs. Specifically, studies that address how dimensional uncertainties in design variables affect

V_{c e l l}

, while concurrently aiming to reduce material costs during manufacturing. In this study, four key PEMFC design variables i.e.,

δ_{g d l}

d_{c h}

w_{c h},

and

w_{l a n d}

, have been considered for optimization with various optimization methods. At first, under suitable constraint condition, initial data samples for the optimization study are generated using Latin hypercube sampling(LHS) technique. These data samples are then considered as inputs for building a database of

V_{c e l l}

through CFD simulations of a comprehensive, multi-scale, two-phase, 3D numerical PEMFC model. The 3D PEMFC numerical model have been extensively developed and experimentally validated in our previous studies [27,28,29,30]. Further, the database of design variables and their corresponding

V_{c e l l}

values are divided into training and test sample sets. Considering the training samples, a multi-layer perceptron(MLP) surrogate model is constructed using MATLAB R2024a, and then tested on distinct unseen test samples. Next, the MLP is linked to particle swarm optimization (PSO) algorithm and a constrained DDO is performed focusing on maximizing

V_{c e l l}

. We particularly introduce the RBDO technique to account for manufacturing uncertainties, which differs from the current DDO method and centers our study to meet practical engineering reliability norms. Furthermore, to evaluate the effects of uncertainty and present an unfailing design, the reliability of the two constraints

C o s t_{c G D L}

and

C o s t_{c B P}

of a 100kW road vehicle stack has been assessed and presented. This strategy has significant implications that encourage the deployment of PEMFC technology in automobiles.

2. Numerical PEMFC Model

In this optimization study, a 3D, multiscale, two phase PEMFC model has been used. The model is based on the multiphase mixture (M²) model proposed by Wang and Cheng [31] and considers various components of a PEMFC cell which includes the BPs, GDLs, CLs and the membrane. The model has been validated against the experimental polarization curves measured under different cell designs and operating condition [32,33]. For a realistic model, the effects of clamping on the GDL structure and the variation in properties have been considered. Since the model employed in this study is identical to that described in our previous studies [33,34,35], the model assumptions and governing equations are presented in brief in Section 2.1 and Section 2.2. Finally, in Section 2.3 an outline of the boundary conditions and numerical implementation of the PEMFC model using ANSYS fluent (ANSYS Inc., USA) has been presented.

2.1. Model Assumptions

The following are the specific assumption used in this numerical study

The operating pressure is low and hence ideal gas mixtures are assumed in the gas phase.
The velocity of flow is low and laminar.
The effect of gravity is neglected.
In the porous region, immobile liquid saturation is neglected.

2.2. Governing Equations and Source Terms

In this study, the PEMFC model under consideration is governed by the five conservation equations: mass, momentum, species, charge, and thermal energy. The equations stated above are linked to source terms that are related to the hydrogen oxidation reaction (HOR) in the anode and oxygen reduction reaction (ORR) in the cathode. For further reference regarding the governing equations and source terms, readers can refer Table 1 and Table 2.

In Table 3, the kinetic, transport and physiochemical properties of the PEMFC components have been listed. Table 4 lists all the pertaining equations that relate to the M² mixture model suggested my Wang and Cheng [42]. Additionally, Table 5 lists a set of species transport properties which are correlated to the water content

λ

which in turn is a function of the water activity a [43].

2.3. Boundary Conditions and Numerical Implementation

Figure 1 illustrates the micro and macro scale computational domains of the PEMFC along with the various switching variables exchanged during the 3-D multi-scale simulations. The figure includes the structure of an individual unit cell and boundary conditions considered in the present study. Apart from the inlet and outlet regions of the anode and cathode gas channels, all the external surfaces have been considered for mass flow under the no slip and impermeability boundary conditions. In terms of thermal boundary conditions in the computational domain, an isothermal boundary condition is considered for the side walls of the anode and cathode, whereas an adiabatic boundary condition is considered to the top and bottom surfaces. The PEMFC can be operated either in the galvanostatic or potentiostatic mode and this can be achieved by applying a constant voltage or current density at the outer side wall of the cathode, while the electric potential Φ_sis fixed to zero. Figure 1b, presents the results of the grid-independent study and the number of meshes required to achieve good analysis accuracy is determined to be about 240,000. The PEMFC model consider in the study is numerically implemented by employing user-defined functions in the commercially available CFD program ANSYS Fluent ver. 23 (ANSYS, Inc., US) and the convergence criteria is set to 10^-8 for the equation residuals.

3. Overview of Design Optimization Strategies for Engineering Application

In engineering design, the two fundamental strategies typically employed to optimize a design is the DDO and RBDO approach. The DDO method is centered around maximizing or minimizing a single/multi objective function while adhering to a specific set of constraints. This strategy is widely followed in industries and is computationally efficient and provides a well-defined single design solution. However, the RBDO approach considers the uncertainties in design variables and aims to achieve a set level of reliability. This method involves estimating the probability of failure under different uncertain conditions and using this information the design variables are estimated to minimize the probability of failure. When compared to DDO approach, RBDO is a more sophisticated design strategy as it considers the inherent variability and uncertainties associated with the design variables.

A typical DDO problem for a single objective optimization problem with the objective of minimizing the cost function

f (X)

is formulated as

Minimize f (X)

(34)

subjected to

G_{j} (X) \geq 0 f o r j = 1, \dots ., J

X_{i}^{L} \leq X \leq X_{i}^{U}, f o r i = 1, \dots ., N

(35)

where,

X = {\{X_{1}, X_{2}, \dots, X_{N}\}}^{T}

is the vector of

N

input design variables, and

J

is the number of constraints.

G_{j} (X) \geq 0

represents the inequality constraint where all the constraints

J

are satisfied. The constraints are violated if

G_{j} (X) < 0

. The terms

X_{i}^{U}

and

X_{i}^{L}

represent the lower and upper bounds of the design variables

N

design variables.

Figure 2 shows the solution for a deterministic single objective optimization problem with two design variables (

X_{1}, X_{2}

), and two constraints

G_{1} (X)

and

G_{2} (X),

obtained through DDO approach such that Eq. 34 is satisfied. As seen, the deterministic optimum point denoted by

X_{1} = d_{1}, X_{2} = d_{2}

lies at the intersection of the two constraint curves denoted by

G_{1} (X) = 0

and

G_{2} (X) = 0

. The region below the constraint boundaries is known as the infeasible region. The solution for Eqs. (34-35) is said to be violated when the constraint solution is

G_{j} (X_{1}, X_{2}) \leq 0

and is said to be acceptable when

G_{j} (X_{1}, X_{2}) \geq 0

. The region dividing the feasible and infeasible regions denoted are denoted by the constraint boundaries,

G_{1} (X) = 0

and

G_{2} (X) = 0

. When optimization is performed using the DDO approach without accounting for uncertainties in the design variables, there is a significant risk that the optimal design will exceed the constraint limits, potentially resulting in the failure of the DDO design.

The basic idea underlying RBDO is to apply a numerical optimization technique to ensure that the optimal design meets the reliability criteria under uncertainty. The RBDO problem is formulated to balance performance and reliability, incorporating probabilistic constraints to account for uncertainties in design parameters. A general RBDO problem is further formulated as follows,

M i n i m i z e f (d)

(36)

subjected to

P_{F j} (d) = P [G_{j} (X) > 0] \leq P_{F j}^{t a r} for j = 1, …, J

d_{i}^{L} \leq d \leq d_{i}^{U} f o r i = 1, \dots ., N

(37)

where,

d = {\{d_{1}, d_{2}, \dots, d_{N}\}}^{T}

is the vector of

N

random input design variables which is made up of mean values of each of the

N

random design variables.

d

can be further represented as,

d = μ (X)

, where

μ (\cdot)

is the mean value operator and

X = {\{X_{1}, X_{2}, \dots, X_{N}\}}^{T}

is the random design variable vector.

P_{F j} (d)

represents the probability of failure at the

j^{t h}

constraint of the design vector

d

G_{j}

represents the

j^{t h}

constraint,

P [\cdot]

is the probability that the

j^{t h}

constraint is violated,

J

is the number of constraints,

P_{F j}^{t a r}

is the target probability of failure for the

j^{t h}

constraint and,

d_{i}^{L}

and

d_{i}^{U}

are the lower and upper bounds of the random input design variables in the design space.

The RBDO solution to Eqs. (36–37) is shown in Figure 2, where it can be compared to the DDO problem’s solution. The reliable solution, as indicated by the blue star is in the feasible region and has a slightly higher objective functional value than the deterministic design ensuring compliance with reliability constraints. The deterministic optimal point, initially in the failure region (red circle), is adjusted in RBDO to meet a target probability of failure, ensuring the design remains within the feasible region. For instance, at the DDO optimal, 50% of the joint probability contours exceed the constraint boundary, reflecting a 50% reliability. Conversely, the RBDO method achieves a reliable optimal with 95% reliability, as only 5% of the total violate the constraint condition.

Figure 3 demonstrates the process flow for estimating a reliable optimal design solution using RAMDO’s sampling based RBDO software. As seen, the RBDO process starts with a deterministic optimal design. In this study, we attain the deterministic optimal point using the PSO algorithm in conjunction with the MLP surrogate model, as detailed in our previous research. For a comprehensive description of the model and optimization algorithm, interested readers can refer to our earlier studies [27,44]. Further, at the deterministic optimal point the input design variables i.e.,

δ_{g d l}

d_{c h}

w_{c h},

and

w_{l a n d}

are assumed to follow a marginal normal input distribution. These input distributions are further used to construct the DKG surrogate model which is basically an approximation of the true PEMFC numerical model. The construction of the DKG surrogate is based on Design of Experiments (DoE) where a combination of input parameters from the respective normal distributions, and 3D PEMFC simulation model is used to generate the performance of the PEMFC. Once the surrogate is constructed the accuracy of the surrogate must be verified. The mean square error (MSE) is used as a metric for checking the accuracy of the constructed surrogate and is set to 0.001. The surrogates developed are then utilized to direct reliability estimation via MCS. Given that MCS requires very large sample points, evaluations of true samples make it practically impossible. As a result, the use of the DKG surrogate makes the task easier. The entire optimization scheme is based on a single loop optimization structure and has a significant reduction in computational time when compared to reliability-based index approach and the performance measure approach.

4. Estimating the Material Costs of the Cathode GDL and BP in PEMFCs

The fuel cell system’s acquisition cost needs to be reduced to a level comparable with that of an internal combustion engine for PEMFCs to be a viable choice for commercial application. A study by Simon et al. [45] reveals that the fuel cell stack accounts to approximately 45% of the total system cost, while majority of the cost is contributed by the MEAs (includes catalysts, membrane, GDLs and the MEA assembly) and the BPs. At high production volumes of above 500,000 stacks/year the material used in the GDL and BP dominates most of the manufacturing expenses, accounting for 89% and 57% of the total production cost incurred [46]. Thus, estimating the material cost of the GDL and BP in PEMFs is crucial to ensure economic viability of this clean energy technology. In addition, an accurate estimation of material costs enables manufactures to plan budgets effectively and help optimize the production process, thereby reducing the overall costs.

In this study, we base our cathode GDL material cost estimation model on Ballard material products, which are comparable to those from other GDL manufacturers [47]. The production of a GDL involves two main steps: carbon fiber papermaking and hydrophobic treatment. First, carbon fibers are chopped and mixed with water and polyvinyl alcohol. This mixture is then laid onto a web using a wet-laid papermaking technique, dried, and re-spooled. To control the porosity, the carbon and resin content is carefully regulated, followed by heat treatment under oxidation conditions. Finally, fluorinated ethylene propylene (FEP) is added to the surface to enhance hydrophobicity. As reported by Brian et al. [47], the

C o s t_{c G D L}

of a GDL with thickness of 105 microns is 1.58

$ / m^{2}

. This reference material cost includes various components such as paper making, impregnation coating for porosity, oxidation/carbonization/graphitization, and impregnation coating for hydrophobicity. By summing up the individual material cost at each step involved we derive a single equation for the total material cost of GDL as is given as follow,

C o s t_{c G D L} = A_{c e l l} \times N_{c e l l} \times \frac{δ_{g d l}}{δ_{r e f}} \times C o s t_{G D L}^{r e f}

(38)

where,

A_{c e l l}

represents the active area of the cell, set at 0.03

m^{2}

N_{c e l l}

is the number of cells needed to produce a stack of 100kW, set at 550,

δ_{r e f}

is the thickness of the reference GDL, set at 105 micron, and

C o s t_{G D L}^{r e f}

is the material cost of the reference GDL, set at 1.58

$ / m^{2}

Further, to estimate the material cost of the cathode BP the material cost equation reported by Battelle Memorial Institute [48] has been used and is given as follows,

m_{c B P} = ρ_{B P} \times A_{c e l l} \times (2 d_{c h} + d_{B P}) \times O_{a l l w}

(39)

C o s t_{c B P} = m_{B P} \times N_{c e l l} \times C o s t_{B P}^{m a t}

(40)

where,

m_{c B P}

is the mass of the cathode BP,

ρ_{B P}

is the density of the bipolar plate material used and is considered as 1900

kg / m^{3}

, the term

d_{B P}

represents the thickness of the base material in the BP, set at 1mm,

O_{a l l w}

is the overage allowance and is considered as 5%,

C o s t_{B P}^{m a t}

represents the cost of the bipolar material used and is given as 2.066

$ / kg

5. Formulation of the Optimization Problem

The modern engineering community is increasingly using optimization as a design tool to achieve optimal designs that minimize costs while meeting performance constraints. Optimization is used to find optimal designs characterized by lower cost while satisfying performance constraints. In the present study, two design optimization strategies for PEMFCs: DDO and RBDO have been used. In DDO, the primary objective is to maximize the performance of the objective function

(V_{c e l l})

, while adhering to specific deterministic constraints and design variable bounds. This approach ensures that the design variables are optimized within predefined bounds, leading to a solution that meets the set criteria without considering uncertainties. Considering the aforementioned criteria for DDO the optimization problem is formulated as follows:

Maximize V_{c e l l} (X)

(41)

s u b j e c t t o \{\begin{matrix} C o s t_{c G D L} (X) \geq 0 \\ C o s t_{c B P} (X) \geq 0 \end{matrix} for X^{L} \leq X \leq X^{U}

X^{L} = [0.05, 0.3, 0.3, 0.3]

X^{U} = [0.4, 2, 2, 1]

(42)

where,

X

is the vector of the four design variables represented as

X = {\{δ_{g d l}, d_{c h}, w_{c h}, w_{l a n d}\}}^{T}

X^{L}

and

X^{U}

represent the lower and upper bounds of the design variables. The deterministic optimization described in Eqs. 41 and 42 does not account for uncertainties in the design variables. As a result, the optimized designs obtained through DDO have a high probability of failure due to violations of the constraints which would lead to potential design failures.

In a fuel cell system, the material employed has a significant impact on its performance, reliability, and cost. As previously discussed, the material costs on the cathode side, particularly for the GDL and BP are significant throughout the manufacturing process. The permissible variation in the dimensions of the GDLs and BP, known as tolerance, is critical during production. Therefore, it is essential to study the consequences of tolerance variations to mitigate their impact on material costs. To address these challenges, RBDO is employed. In RBDO, material costs for BP and GDL are considered as reliability constraints, ensuring that the design remains robust under uncertainty. The problem can be formulated as follows:

Maximize V_{c e l l} (d)

(43)

s u b j e c t t o \{\begin{matrix} P_{F 1} (d) = P [C o s t_{c G D L} (X) \leq C o s t_{c G D L}^{D D O}] \leq P_{F 1}^{t a r} \\ P_{F 2} (d) = P [C o s t_{c B P} (X) \geq C o s t_{c B P}^{D D O}] \leq P_{F 2}^{t a r} \end{matrix}

(44)

d

represents the design vector and

d = {\{μ (X_{δ_{g d l}}), μ (X_{d_{c h}}), μ (X_{w_{c h}}), μ (X_{w_{l a n d}})\}}^{T}

, which is the mean value of the four design variables,

δ_{g d l}, d_{c h}, w_{c h}

and

w_{l a n d}

. The terms

P_{F 1} (d)

and

P_{F 2} (d)

are defined as the probability of failure of the two constraint function vector at the design vector

d

and,

X

is the random design variable vector represented as

X = \{X_{δ_{g d l}}, X_{d_{c h}}, X_{w_{c h}}, X_{w_{l a n d}}\}

. The two constraints,

C o s t_{c G D L}^{D D O}

and

C o s t_{c B P}^{D D O}

represent the material cost of the cathode GDL and BP at the deterministic optimal as a result of the DDO. The target probability of failure

P_{F 1}^{t a r}

and

P_{F 2}^{t a r}

for the two constraints,

C o s t_{c G D L}

and

C o s t_{c B P}

is considered as

5 %

, where the target reliability is 95%.

6. Results and Discussion

In this study, the results of an optimization framework aimed towards optimizing fuel cell stack performance while taking in account of the cathode, GDL and BP material cost as constraints has been presented. The analysis is carried out with the

V_{c e l l}

as the objective function that is being maximized, while the dimensional uncertainties of the four key PEMFC design variables i.e.,

δ_{g d l},

d_{c h}, w_{c h}

, and

w_{l a n d},

has been considered. In addition, the cost of the materials for the cathode, GDL and BP is also considered as a criterion that must be met. In Section 6.1, we evaluate the predictive capability of the MLP surrogate. In Section 6.2, results of the DDO approach are presented. Furthermore, in Section 6.3, a comprehensive discussion of the RBDO approach wherein the uncertainties in design variables have been considered has been presented.

As seen in Figure 4, to ensure that the 3D numerical PEMFC model considered in the present study can predict the performance of the fuel cell, a 3D PEMFC numerical model that was previously developed and validated against experimental polarization curves under various cell designs and operating conditions has been taken into consideration [31]. This validated model has been considered as the baseline for the present optimization study and has incorporated a

δ_{g d l} = 0.215 mm, d_{c h} = 0.54 mm

w_{c h} = 1 mm

, and

w_{l a n d} = 1 mm

, under 20% GDL compression (the thickness of GDL is reduced by 20% from its initial value). These values are consistent and well defined within the range of the design variable space specified in Eqs. (41) and (42).

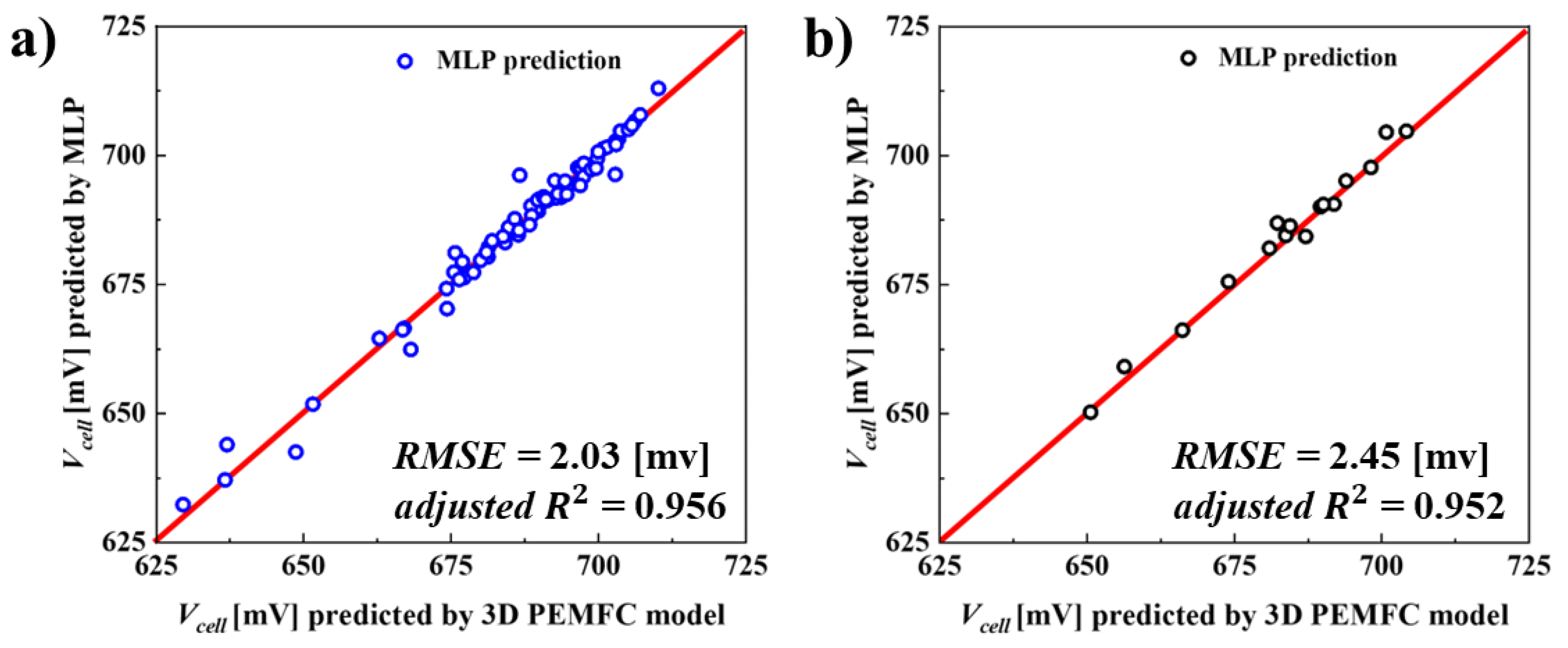
6.1. Evaluation of Predictive Capability of the MLP Surrogate

To estimate maximum

V_{c e l l}

via surrogate-based design optimization under suitable constraint condition as described in Section 5, at first a MLP surrogate model that was developed using MATLAB, with detailed construction and implementation described in our previous work [27,44] has been utilized. The model was trained with a dataset of 75 samples. To effectively evaluate the predictive performance of the trained MLP model, a separate test set comprising of 15 samples, distinct from the trained set was employed. An error analysis was conducted to measure the predictive capability of the trained surrogate, using RMSE and

{adjucted R}^{2}

error metrices which are described in Eqs. (45) and (46), respectively.

R M S E = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} {({\hat{v}}_{i} - v_{i})}^{2}}

(45)

a d j u s t e d R^{2} = 1 - \frac{N - 1}{N - d - 1} (1 - (1 - \frac{\sum_{i = 1}^{N} {(v_{i} - {\hat{v}}_{i})}^{2}}{\sum_{i = 1}^{N} {(v_{i} - {\bar{v}}_{i})}^{2}}))

(46)

where,

v_{i}

and

{\hat{v}}_{i}

denote the responses of the 3D PEMFC simulations and the predicted values of the MLP model, respectively;

{\bar{v}}_{i}

denotes the mean value of the observed data at the

N

test points, and d is the number of design variables. RMSE measures the average magnitude of the errors between predicted and actual values. Lower RMSE values indicate better model performance, with values approaching 0 indicating the best accuracy. The

{adjusted R}^{2}

value ranges from 0 to 1, while a value of 0 indicates that the model does not explain any of the variability in the response data around its mean, and a value of 1 indicates that the model is capable of considering the variability in the response data around its mean.

Figure 5 illustrates a scatter plot comparing the prediction capability of MLP surrogate on both the training and test datasets. As shown in Figure 5a, the MLP model’s predictions on the training data are relatively high and are closer to line of perfect prediction indicated in red. In addition, results of the error analysis indicate a RMSE of 2.03 mV and adjusted

R^{2}

value of 0.956. These values imply that the MLP model is capable of nearly capturing the effects of changes in the training samples. In contrast, Figure 5b illustrates the MLP models performance on the test dataset. The MLP model exhibits a very minor decline in prediction capability, with RMSE of 2.45 mV and adjusted

R^{2}

value of 0.952, when compared to the training dataset. Nevertheless, the resulting scatter plot reveals that the trained MLP is capable to predict near the line of perfect prediction, highlighting the model’s capability to predict unseen data.

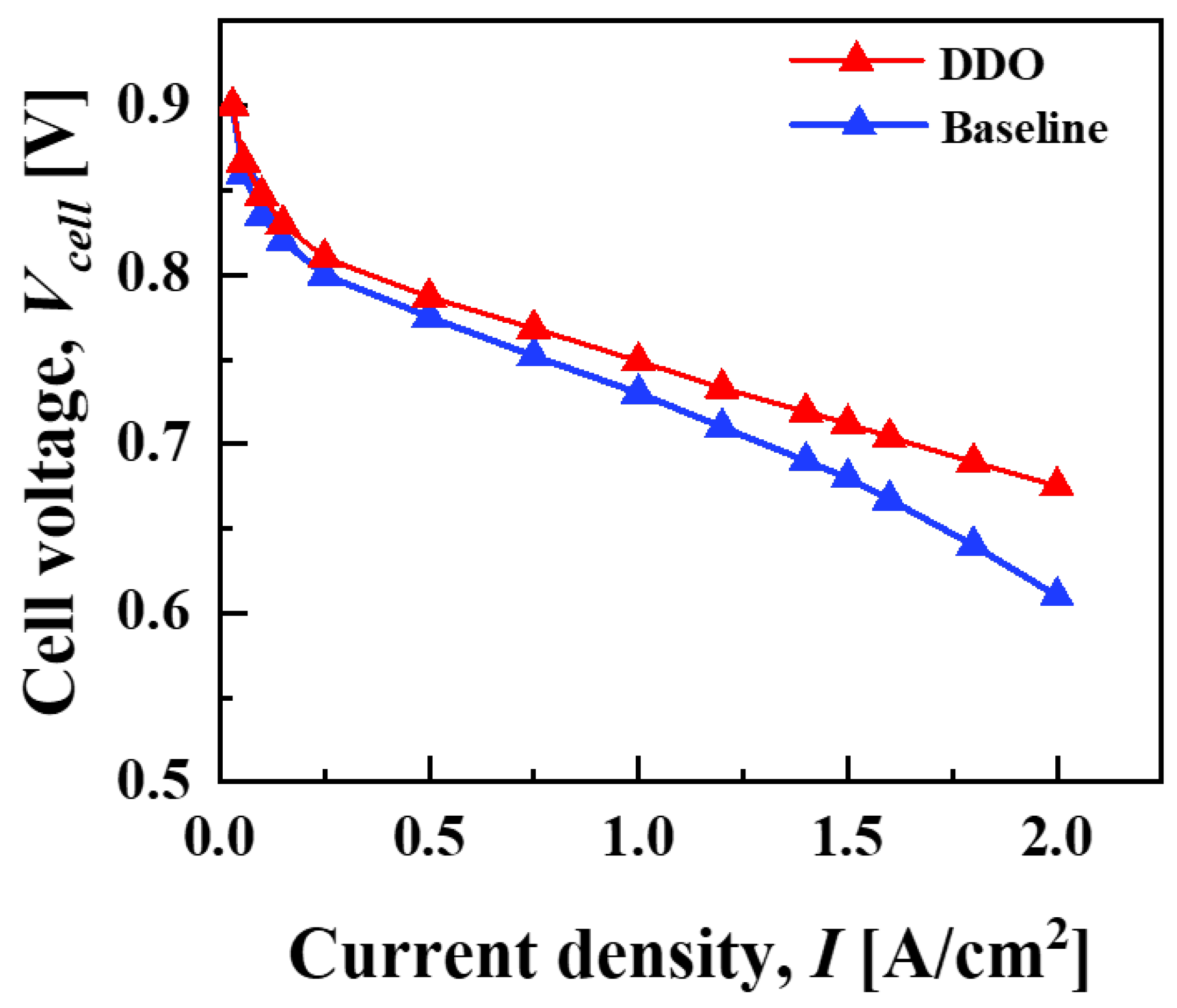
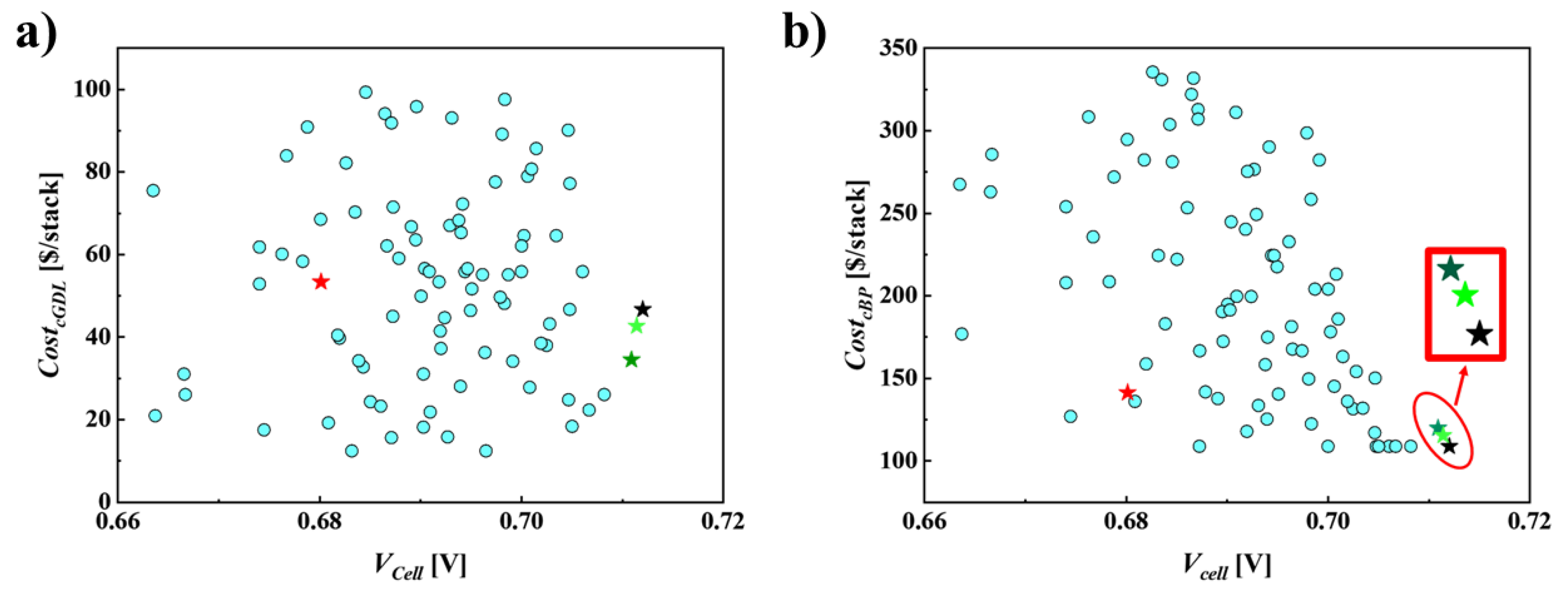
6.2. DDO to Access Superior PEMFC Performance

After evaluating the prediction capability of the MLP model to predict

V_{c e l l}

for a given set of unseen data across a wide range of design variables within the confined design bounds, it was further linked to the PSO algorithm to address a DDO problem, which primarily focuses on predicting maximum

V_{c e l l}

Figure 6, illustrates a scatter plot for the relationship between

V_{c e l l}

and cathode side material cost parameters:

C o s t_{c G D L}

and

C o s t_{c B P}

, across various PEMFC designs, including the baseline, DDO,

{RBDO}_{1}

and

{RBDO}_{2}

. As seen in Figure 6, the optimized PEMFC design via MLP-PSO(DDO) method shows maximum

V_{c e l l}

performance. Table 6 lists the design variables and corresponding

V_{c e l l}

for various PEMFC designs and cathode side material cost parameters i.e.,

C o s t_{c G D L}

and

C o s t_{c B P}

. Particularly, as compared with the baseline design, DDO design shows a rise of 31mV in

V_{c e l l}

. A drop in

V_{c e l l}

performance is seen in the baseline design which is due to

w_{c h} / w_{l a n d}

= 1:1, and a larger

d_{c h}

corresponds to lower overall air velocity in the gas channel; these factors weaken oxygen transport and the removal of water that is accumulated inside the cathode GDL, while a thicker GDL limits oxygen transport along the through-plane direction (x). Interestingly, the increase in

V_{c e l l}

of the DDO design also leads to a drop in

C o s t_{c G D L}

by 6.71 $/stack and

C o s t_{c B P}

by 32.64 $/stack. The resulting difference in cost parameters can be primarily attributed to the fact that the dimensions of the cathode side GDL and BP for the baseline design are significantly larger than the optimal values obtained through the DDO method. However, as noted in Table 6, the resulting DDO design predicted via MLP-PSO predicts design variables with

δ_{g d l} = 0.188 mm

d_{c h} = 0.3 mm

w_{c h} = 0.614 mm

w_{l a n d} = 0.31 mm

with

C o s t_{c G D L} = 46.68 $ / stack

and

C o s t_{c B P} = 108.81 $ / stack

, where the

d_{c h}

is predicted at the extreme end of the design space, in particular the lower bound which corresponds to the least possible cathode BP material cost. Take note, for further discussions, material cost parameters of the cathode side GDL and BP, predicted by DDO will be denoted as

C o s t_{c G D L}^{D D O}

and

C o s t_{c B P}^{D D O}

, respectively.

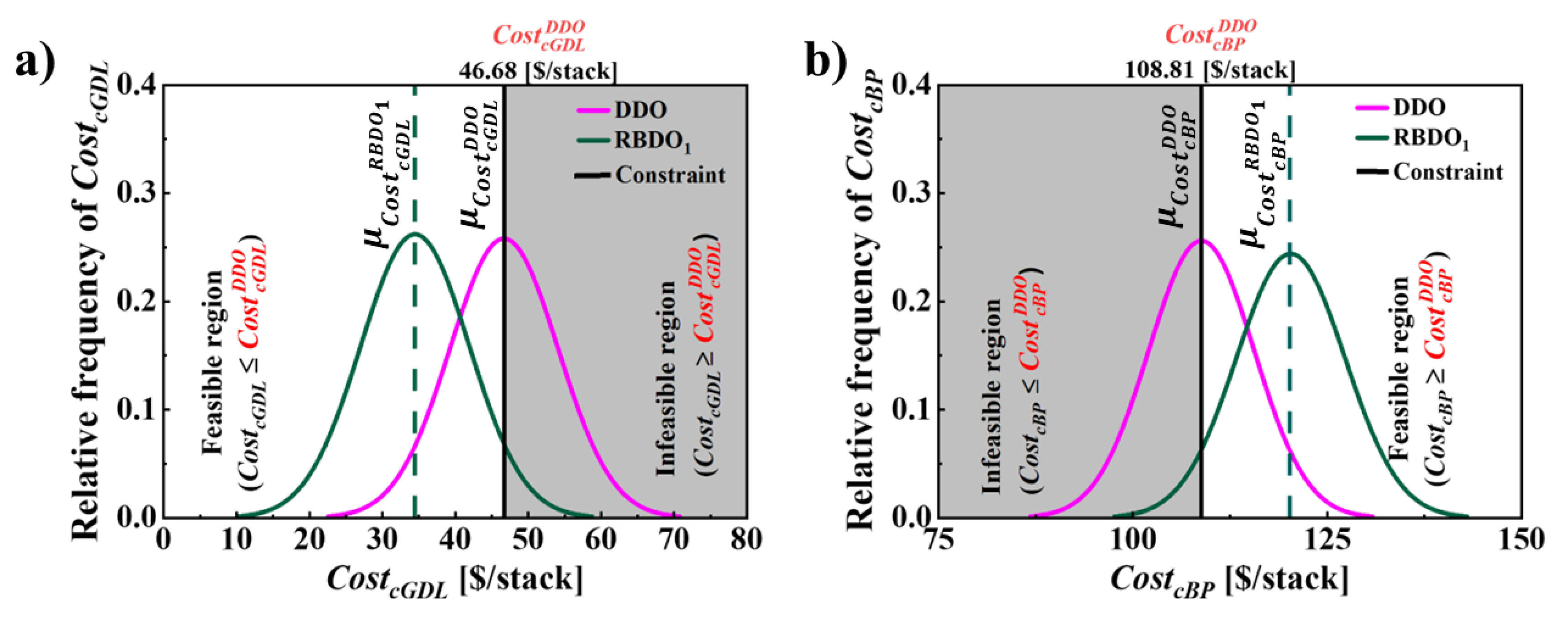
6.3. RBDO for Cathode, GDL and BP Material Costs

In engineering design, DDO models have widely been used to maximize/minimize the cost function in consideration of constraints. Over the past decade, significant efforts have been dedicated to optimizing PEMFC designs and their components using DDO models. However, due to uncertainties in the production process, there is a need to transition to RBDO to ensure robust and reliable designs. As discussed in Section 6.2, DDO offers superior

V_{c e l l}

, with reduction in

C o s t_{c G D L}

and

C o s t_{c B P}

. When manufacturing uncertainties are incorporated into the design variables, the optimal solution often tends to deviate from desired outcome, resulting in unreliable design. To address the limitations of DDO, an RBDO problem is developed, as detailed in Section 5, specifically Eqs. (43-44). In Table 7, the uncertainties that may arise during manufacturing of GDL, and BPs have been considered for RBDO. These uncertainties are analyzed in two cases: Case 1 represents a high level of uncertainty, with standard deviations of

σ_{δ_{g d l}} = 0.03 mm

σ_{d_{c h}} = 0.05 mm

σ_{w_{c h}} = 0.05

mm, and

σ_{wland} = 0.05 mm

. Case 2 represents a lower level of uncertainty, with standard deviations of

σ_{δ_{g d l}} = 0.01 mm

σ_{d_{c h}} = 0.03 mm

σ_{w_{c h}} = 0.03

mm, and

σ_{wland} = 0.03 mm

This distinction helps in understanding the impact of varying uncertainty levels on the reliability of the PEMFC design. Additionally, as seen in the table, the standard deviation of the GDL is typically lower than that of the BP. This is because the GDLs play a critical role in the transport of reactant gases and the removal of product water formed during fuel cell operation. Small variations in thickness and porosity can lead to deviations in the flow of reactants and products, thereby altering the overall performance of the fuel cell. In contrast, BPs primarily provide mechanical support and electrical connectivity in the fuel cell. While dimensional accuracy is necessary, slight changes in dimensional variations do not significantly alter

V_{c e l l}

, compared to the GDL. Additionally, the materials used in BPs provide high structural stability and are less sensitive to dimensional variations compared to porous GDLs. Therefore, the robustness of BPs offers a slightly relaxed edge in terms of manufacturing uncertainties compared to the GDL. Figs. 7a to 7d show the probability distribution(PDF) with 95% probability intervals for the four design variables:

δ_{g d l}

d_{c h}

w_{c h},

and

w_{l a n d}

at DDO optimal. These figures correspond to Case 1, where the design variables are subjected to uncertainties with standard deviations of

σ_{δ_{g d l}} = 0.03 mm

σ_{d_{c h}} = 0.05 mm

σ_{w_{c h}} = 0.05

mm, and

σ_{wland} = 0.05 mm

, respectively.

The objective of RBDO in present study is to maximize the objective function

(V_{c e l l})

considering uncertainties in manufacturing, as defined in Case 1 and Case 2, while ensuring that the constraints i.e.,

C o s t_{c G D L}

and

C o s t_{c B P}

do not violate the boundaries of significant performance metrices. Moreover, these cost parameters are accessed for reliability ensuring that the PEMFC design remains robust under uncertainty. Therefore, setting the limits of these constraints is an important part of RBDO. As seen in Figure 3, the DDO design predicted via MLP-PSO is an optimal starting point for RBDO due to its significant advantages in both cost and performance compared to the baseline design. Specifically,

C o s t_{c G D L}

at the DDO is

46.68 $ / stack

, which is notably lower than 53.38$/stack for the baseline design. Similarly,

C o s t_{c B P}

is at

108.81 $ / stack

, compared to 141.45$/stack for the baseline design. These improvements demonstrate that the DDO not only reduces costs significantly but also enhances

V_{c e l l}

, making it a more optimal starting point for further RBDO.

In Figure 7b and Figure 9b, at the DDO optimal, considering the uncertainties in design variables as defined in

{Case}_{1}

and

{Case}_{2}

, variation in values for

d_{c h}

is observed. Specifically,

d_{c h}

falls significantly below the lower bound of the design space, set at

d_{c h}^{L} = 0.3 mm

. This deviation violates the design bounds. According to Eq. (40),

C o s t_{c B P}

is directly proportional to

d_{c h}

. Therefore,

C o s t_{c B P}

will also fail to meet the design bounds for

d_{c h}

values below

d_{c h}^{L} = 0.3 m

. This necessitates to fix the constraint value to

C o s t_{c B P} \geq 108.81

$/stack, i.e.,

C o s t_{c B P} \geq C o s t_{c B P}^{D D O}

. The

C o s t_{c G D L}

is estimated based on Eq. (38) and is directly proportional to

δ_{g d l}

. As seen in Figure 7a and 7b, when uncertainties in

δ_{g d l}

as defined in

{Case}_{1}

and

{Case}_{2}

are considered, the variation in

δ_{g d l}

set at

δ_{g d l} = 0.188 mm

, is well above the lower bound

δ_{g d l}^{L} = 0.03 mm

. Therefore, the constraint for

C o s t_{c G D L}

is set as

C o s t_{c G D L} \leq C o s t_{c G D L}^{D D O}

As shown in Figure 3, after defining the performance constraints, RBDO is initiated from the DDO considering uncertainties in design variables as defined in Case 1. The aim of the optimization process is to find a reliable optimal solution, referred as

{RBDO}_{1}

. Figure 8a and 8b compares the results of DDO and

{RBDO}_{1}

. As seen, the PDF plots at DDO indicate a clear violation of the constraints

C o s t_{c G D L} \leq C o s t_{c G D L}^{D D O}

and

C o s t_{c B P} \geq C o s t_{c B P}^{D D O}

with the distribution plots extending into the infeasible region depicted by gray shaded area. In contrast,

{RBDO}_{1}

distribution plots are more spread out, reflecting a design strategy that accommodates the uncertainties while staying within the feasible cost region. Comparing and analyzing the detailed result listed in Table 8 reveals that the

C o s t_{c G D L}

at DDO achieves a reliability of 49.87%, indicating that 50.13% of the designs are unreliable and fail to meet

C o s t_{c G D L} \leq C o s t_{c G D L}^{D D O}

. Conversely, the RBDO approach shows that the reliability for achieving

C o s t_{c G D L} \leq C o s t_{c G D L}^{D D O}

{RBDO}_{1}

is 95.0%. Regarding,

C o s t_{c B P}

, at DDO the reliability is 50.0%, which indicates that 50.0% of the designs are unreliable and fall below the

C o s t_{c G D L}^{D D O} = 46.68

$/stack. Furthermore, comparing the nominal values of

C o s t_{c G D L}

indicate that a reduction of 12.25$/stack is achieved, attributed to the RBDO strategy in reducing the material cost of the cathode GDL. Consequently, the material cost for the cathode BP,

C o s t_{c B P}

, inevitably increases by 11.18$/stack, causing the reliability of meeting

C o s t_{c B P} \geq C o s t_{c B P}^{D D O}

to increase from 50.0% to 94.99%.

{RBDO}_{1}

has successfully navigated manufacturing uncertainties while consistently achieving target reliability of 95% for both

C o s t_{c G D L}

and

C o s t_{c B P}

and these are well illustrated in Figure 8. As outlined in Table 6, comparing the results of design variables at DDO and

{RBDO}_{1}

reveal that the DDO design variables, optimize the

V_{c e l l}

by enhancing reactant distribution and water management, resulting in superior

V_{c e l l}

of 0.712V. In contrast, the

{RBDO}_{1}

design achieve a comparable

V_{c e l l}

of 0.710V by balancing efficiency and reliability thereby aiming for a robust and reliable operation.

Accessing the effects of variability in uncertainty on PEMFC performance is of high interest. By analyzing multiple cases

{Case}_{1}

and

{Case}_{2}

ensures that the PEMFC design is robust and reliable under different conditions. Figure 9 illustrates the PDF plots with a 95% probability interval that corresponds to

{Case}_{2}

for four design variables: a)

δ_{g d l}

, b)

d_{c h}

, c)

w_{c h}

, and d)

w_{l a n d}

. These plots account for uncertainties in design variables with standard deviations

σ_{δ_{g d l}} = 0.01 mm

σ_{d_{c h}} = 0.03 mm

σ_{w_{c h}} = 0.03

mm, and

σ_{wland} = 0.03 mm .

The RBDO approach aligns with previous descriptions, so our discussions are focused on how

{RBDO}_{2}

affects PEMFC designs. Figure 10a and 10b display the distributions of

C o s t_{c G D L}

and

C o s t_{c B P}

, where more than half of the distribution curve violate the constraints set at

C o s t_{c G D L} \leq C o s t_{c G D L}^{D D O}

and

C o s t_{c B P} \geq C o s t_{c B P}^{D D O}

. Comparing the values of DDO and

{RBDO}_{2}

shows that the RBDO method predicts a

C o s t_{c G D L}

much lower that DDO and the reduction in cost is 4.09$ with a reliability of 95.02%. Regarding

C o s t_{c B P}

the

RBDO

method shows and inevitable cost rise of 6.71$/stack while achieving a reliability target of 95%. Comparing and analyzing the effects of varying uncertainty as defined in

{Case}_{1}

and

{Case}_{2}

reveals that RBDO method tries to achieve the target reliability of 95% in both the cases. In addition,

{RBDO}_{1}

and

{RBDO}_{2}

show how different levels of uncertainty effect on the design variables and performance.

{RBDO}_{1}

, with higher variability, results in a more conservative design with lower costs but slightly and slightly lower

V_{c e l l}

. In contrast,

{RBDO}_{2}

, with lower variability, achieves a more optimized design with slightly higher costs but similar

V_{c e l l}

. Both approaches maintain comparable cell voltages, demonstrating robust performance despite the differences in design strategies.

7. Conclusions

This study presents a methodology for optimizing the four key PEMFC design variables i.e.,

δ_{g d l}

d_{c h}

w_{c h},

and

w_{l a n d}

. We employed two optimization strategies namely DDO and RBDO, to evaluate and compare effectiveness. At first, an MLP model was developed based on the results from a comprehensive multi-scale, two-phase, 3D numerical PEMFC model. The predictive accuracy of the MLP was evaluated on the test set of 15 design samples using the RMSE and adjusted

R^{2}

, with values of RMSE = 2.45 mV and adjusted

R^{2}

= 0.952. The MLP was integrated with a PSO to perform DDO, which identified a design that improved

V_{c e l l}

by 31 mV at a current density of 1.5 A/cm². This superior

V_{c e l l}

is primarily due to its optimized design parameters by reducing the design variables as compared to the baseline case. These optimized dimensions enhance the flow distribution, leading to higher

V_{c e l l}

of 0.712V. Given the manufacturing variability cathode GDL and BP, these uncertainties were modeled using statistical distributions, and RBDO was conducted. The RBDO results indicated that designs deemed optimal in DDO contexts failed to meet the cost constraint,

C o s t_{c G D L} \leq C o s t_{c G D L}^{D D O}

and

C o s t_{c B P} \geq C o s t_{c B P}^{D D O}

, illustrating the need for RBDO to enhance robustness in the manufacturing process by optimizing design variable to achieve over 95% reliability in

C o s t_{c G D L}

and

C o s t_{C B P}

. The RBDO approach effectively balances efficiency and reliability, achieving a target reliability of 95% for both

C o s t_{c G D L}

and

C o s t_{C B P}

{RBDO}_{1}

, with higher variability, results in a more conservative design with lower costs, while

{RBDO}_{2}

, with lower variability, achieves a more optimized design with slightly higher costs. Both designs maintain comparable

V_{c e l l}

, demonstrating robust performance despite different design strategies.

Acknowledgments

This research was supported by the BK21 Four Program (Education and Research Team for Overcoming Mechanical Challenges in Carbon Neutrality, 4120240314990) funded by the Ministry of Education (MOE, Korea) and the National Research Foundation of Korea (NRF). We would like to sincerely thank Dr. Kyung K. Choi, Roy J. Carver Professor of Mechanical Engineering at the University of Iowa (UI), and Dr. Nicholas Gaul, Lead Developer & Chief Operations Officer, RAMDO Solutions for their unwavering support and services provided throughout this study. We would also like to extend our appreciation to TAESUNG S&E, Inc., Seoul, Republic of Korea, for providing technical support for ANSYS Fluent software.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Nomenclature

a	Ratio of active surface area per unit electrode volume, m²/m³ or water activity
A	Area, m²
C	Molar concentration of species, mol/m³
d	Vector of design variables or solution of a deterministic optimization problem
D	Species diffusivity, m²/s
E	Activation energy, kJ/mol
EW	Equivalent weight of a dry membrane, kg/mol
f	Objective function that needs to be minimized or maximized in the optimization problem
F	Faraday’s constant, 96,487 C/mol
G	Constraint condition for the $j$ -th constraint
i₀	Exchange current density, A/cm²
i_d	Density estimation parameter
I	Operating current density, A/cm²
j	Transfer current density, A/cm³,
$J$	Total number of constraint functions in the optimization problem
k	Thermal conductivity, W/m·K, or Relative permeability, or index representing the specific objective function in the optimization problem
K	Hydraulic permeability, m²
L	Amount of loading, $mg / {cm}^{2}$
n	Number of electrons transferred in the electrode reaction
N	Number of design varaibles
MW	Molecular weight, kg/mol
MSE	Mean squared error
P	Pressure, Pa,
P	Probability
RMSE	Root mean squared error
s	Liquid saturation
S	Source term in the transport equation
t	time
T	Temperature, K
$u →$	Fluid velocity and superficial velocity in a porous medium, m/s
V	Voltage, V or Volume, $m^{3}$
X	Vector of the design variables in the optimization problem
$X_{i}$	Lower or upper bound of the i-th design variable
$x$	Input variable
$v$	Observed response
$\hat{v}$	Predicted response
$\bar{v}$	Mean value of the observed data
Z	Transport resistance coefficient
Greek symbols
α	Transfer coefficient
$β$	Weight coefficient
γ	Reaction order
δ	Thickness, m
ε	Volume fraction or error
η	Surface overpotential, V
$θ$	Contact angle of the gas diffusion layer
$λ$	Water content
$μ$	Mean value of random design variables
κ	Proton conductivity, S/m
	Phase potential, V
Ρ	Density, kg/m
σ	Electronic conductivity, S/m
τ	Viscous shear stress, N/m²
ξ	Stoichiometry flow ratio
Ω	Oxygen transport resistance
Superscripts
c	Catalyst coverage coefficient
eff	Effective
g	Gas
l	Liquid
L	Lower bound of a design variable
max	Maximum
mem	Membrane
min	Minimum
op	Operating
ref	Reference value
tar	Target
T	Transpose operation of a matrix
U	Upper bound of a design variable
Subscripts
A	Anode
aCL	Anode catalyst layer
allw	Allowance
c	Cathode
C	Carbon
CL	Catalyst layer
cCL	Cathode catalyst layer
ch	Gas channel
e	Electrolyte
ECSA	Electro chemical active surface area
Gdl	Gas diffusion layer
$F j$	Index representing the failure of the $j$ -th constraint
I/C	Ionomer to carbon weight ratio
i	Species or index representing the lower or upper bound of the N-th design variable
in	Channel inlet
int	Interface
j	Index representing the specific constraint function in a problem with multiple constraints
k	Index representing the specific objective function in the optimization problem
MEA	Membrane electrode assembly
Mem	Membrane
min	Minimum
N	Number of design varaibles
nd	n-th random design variable
Pt/C	Weight ratio of Platinum to carbon
Pt	Platinum
s	Solid, surface
T	Temperature
U	Momentum equation
w	Water
0	Initial conditions or standard conditions, i.e., 298.15 K and 101.3 kPa (1 atm)

References

D. Parra, L. Valverde, F.J. Pino, M.K. Patel, A review on the role, cost and value of hydrogen energy systems for deep decarbonisation, Renew. Sustain. Energy Rev. 101 (2019) 279–294. [CrossRef]
B. Sundén, Fuel cell types - overview, Hydrog. Batter. Fuel Cells. (2019) 123–144. [CrossRef]
Y. Wang, H. Yuan, A. Martinez, P. Hong, H. Xu, F.R. Bockmiller, Polymer electrolyte membrane fuel cell and hydrogen station networks for automobiles: Status, technology, and perspectives, Adv. Appl. Energy. 2 (2021) 100011. [CrossRef]
S. Chugh, C. Chaudhari, K. Sonkar, A. Sharma, G.S. Kapur, S.S.V. Ramakumar, Experimental and modelling studies of low temperature PEMFC performance, Int. J. Hydrogen Energy. 45 (2020) 8866–8874. [CrossRef]
J.H. Wee, Applications of proton exchange membrane fuel cell systems, Renew. Sustain. Energy Rev. 11 (2007) 1720–1738. [CrossRef]
P. Ponnusamy, B. Pullithadathil, M.K. Panthalingal, Technological risks and durability issues for the Proton Exchange Membrane Fuel Cell technology, PEM Fuel Cells Fundam. Adv. Technol. Pract. Appl. (2022) 279–314. [CrossRef]
W.E. Mustain, M. Chatenet, M. Page, Y.S. Kim, Durability challenges of anion exchange membrane fuel cells, Energy Environ. Sci. 13 (2020) 2805–2838. [CrossRef]
P. Müller, Simulation Based Optimal Design, Handb. Stat. 25 (2005) 509–518. [CrossRef]
D. Song, Q. Wang, Z. Liu, T. Navessin, M. Eikerling, S. Holdcroft, Numerical optimization study of the catalyst layer of PEM fuel cell cathode, J. Power Sources. 126 (2004) 104–111. [CrossRef]
S.A. Grigoriev, A.A. Kalinnikov, N. V. Kuleshov, P. Millet, Numerical optimization of bipolar plates and gas diffusion electrodes for PBI-based PEM fuel cells, Int. J. Hydrogen Energy. 38 (2013) 8557–8567. [CrossRef]
A.R. Kim, H.M. Jung, S. Um, An engineering approach to optimal metallic bipolar plate designs reflecting gas diffusion layer compression effects, Energy. 66 (2014) 50–55. [CrossRef]
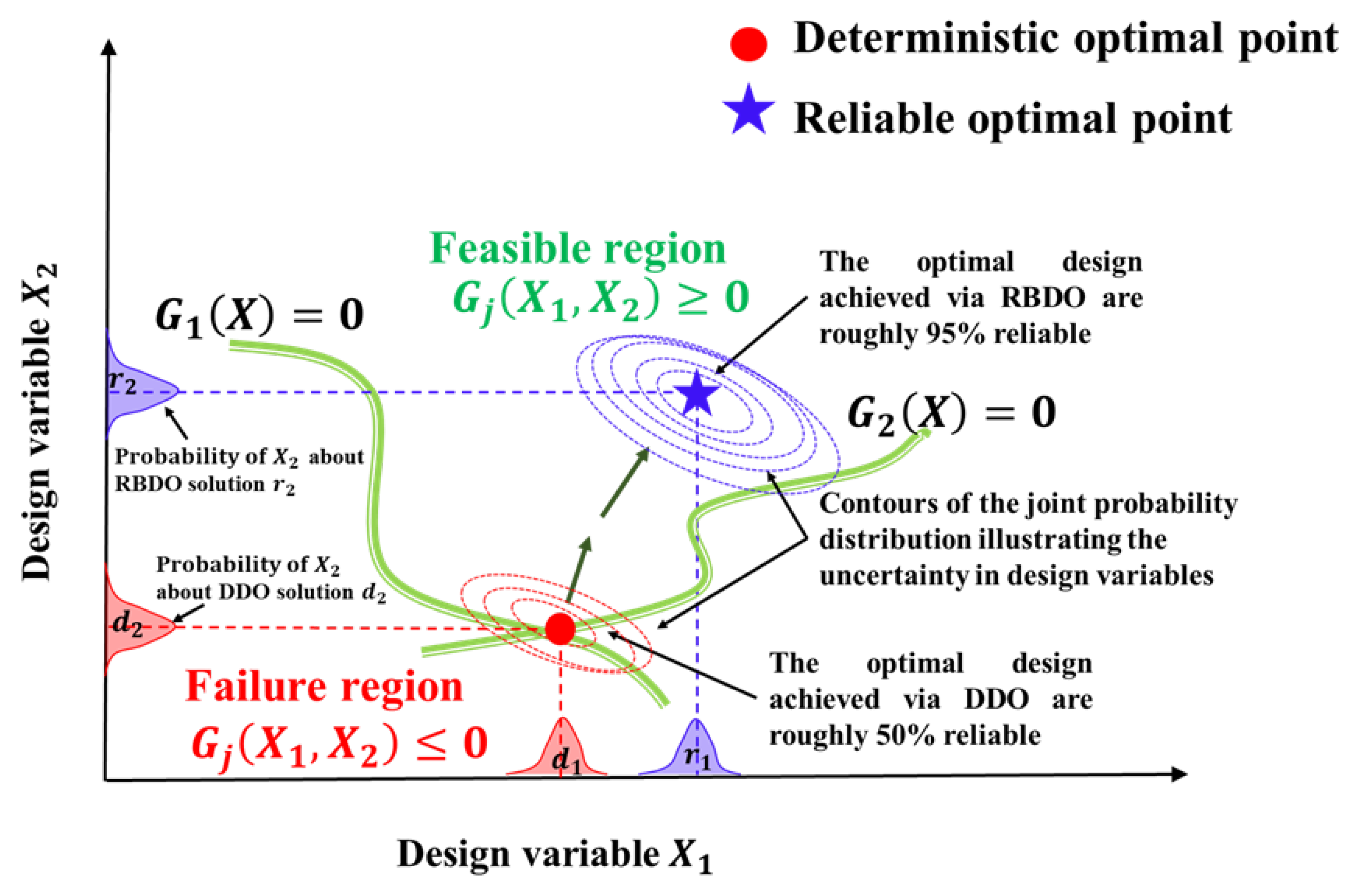
J. Tu, K.K. Choi, Y.H. Park, A new study on reliability- based design optimization, J. Mech. Des. Trans. ASME. 121 (1999) 557–564. [CrossRef]
C. Ling, W. Kuo, M. Xie, An Overview of Adaptive-Surrogate-Model-Assisted Methods for Reliability-Based Design Optimization, IEEE Trans. Reliab. (2022) 1–22. [CrossRef]
H. Cho, K.K. Choi, I. Lee, D. Lamb, Design Sensitivity Method for Sampling-Based RBDO with Varying Standard Deviation, J. Mech. Des. Trans. ASME. 138 (2016) 1–10. [CrossRef]
D.O.E. Managers, N. Garland, J. Adams, Final Technical Report: Metrology for Fuel Cell Manufacturing, (n.d.).
E. Morse, J.Y. Dantan, N. Anwer, R. Söderberg, G. Moroni, A. Qureshi, X. Jiang, L. Mathieu, Tolerancing: Managing uncertainty from conceptual design to final product, CIRP Ann. 67 (2018) 695–717. [CrossRef]
S. Hoffenson, R. Söderberg, Systems thinking in tolerance and quality-related design decision-making, Procedia CIRP. 27 (2015) 59–64. [CrossRef]
L. Peng, Y. Wan, D. Qiu, P. Yi, X. Lai, Dimensional tolerance analysis of proton exchange membrane fuel cells with metallic bipolar plates, J. Power Sources. 481 (2021) 228927. [CrossRef]
Mukherjee, S. Hwang, S.C. Lee, O. Kwon, G.H. Choi, S. Park, Simulation and experimental analysis of the clamping pressure distribution in a PEM fuel cell stack, Int. J. Hydrogen Energy. 38 (2013) 6481–6493. [CrossRef]
D. Qiu, L. Peng, X. Lai, M. Ni, W. Lehnert, Mechanical failure and mitigation strategies for the membrane in a proton exchange membrane fuel cell, Renew. Sustain. Energy Rev. 113 (2019) 109289. [CrossRef]
P. Irmscher, D. Qui, H. Janßen, W. Lehnert, D. Stolten, Impact of gas diffusion layer mechanics on PEM fuel cell performance, Int. J. Hydrogen Energy. 44 (2019) 23406–23415. [CrossRef]
Tang, L. Crisci, L. Bonville, J. Jankovic, An overview of bipolar plates in proton exchange membrane fuel cells, J. Renew. Sustain. Energy. 13 (2021). [CrossRef]
S. Porstmann, T. Wannemacher, W.G. Drossel, A comprehensive comparison of state-of-the-art manufacturing methods for fuel cell bipolar plates including anticipated future industry trends, J. Manuf. Process. 60 (2020) 366–383. [CrossRef]
C. Turan, Ö.N. Cora, M. Koç, Effect of manufacturing processes on contact resistance characteristics of metallic bipolar plates in PEM fuel cells, Int. J. Hydrogen Energy. 36 (2011) 12370–12380. [CrossRef]
M.M. Barzegari, F.A. Khatir, Study of thickness distribution and dimensional accuracy of stamped metallic bipolar plates, Int. J. Hydrogen Energy. 44 (2019) 31360–31371. [CrossRef]
D. Liu, L. Peng, X. Lai, Effect of assembly error of bipolar plate on the contact pressure distribution and stress failure of membrane electrode assembly in proton exchange membrane fuel cell, J. Power Sources. 195 (2010) 4213–4221. [CrossRef]
M.F. Chinannai, J. Lee, H. Ju, Numerical study for diagnosing various malfunctioning modes in PEM fuel cell systems, Int. J. Hydrogen Energy. (2019). [CrossRef]
Jo, H. Ju, Numerical study on applicability of metal foam as flow distributor in polymer electrolyte fuel cells (PEFCs), Int. J. Hydrogen Energy. 43 (2018) 14012–14026. [CrossRef]
Jo, S. Ahn, K. Oh, W. Kim, H. Ju, Effects of metal foam properties on flow and water distribution in polymer electrolyte fuel cells (PEFCs), Int. J. Hydrogen Energy. 43 (2018) 14034–14046. [CrossRef]
C.Y. Wang, P. Cheng, Multiphase Flow and Heat Transfer in Porous Media, Adv. Heat Transf. 30 (1997) 93–196. [CrossRef]
Jo, H. Ju, Numerical study on applicability of metal foam as flow distributor in polymer electrolyte fuel cells (PEFCs), Int. J. Hydrogen Energy. 43 (2018) 14012–14026. [CrossRef]
K. Lim, N. Vaz, J. Lee, H. Ju, Advantages and disadvantages of various cathode flow field designs for a polymer electrolyte membrane fuel cell, Int. J. Heat Mass Transf. 163 (2020) 120497. [CrossRef]
P. Chippar, K. Oh, D. Kim, T.W. Hong, W. Kim, H. Ju, Coupled mechanical stress and multi-dimensional CFD analysis for high temperature proton exchange membrane fuel cells (HT-PEMFCs), Int. J. Hydrogen Energy. 38 (2013) 7715–7724. [CrossRef]
C.Y. Wang, P. Cheng, A multiphase mixture model for multiphase, multicomponent transport in capillary porous media - I. Model development, Int. J. Heat Mass Transf. 39 (1996) 3607–3618. [CrossRef]
T.E. Springer, Polymer Electrolyte Fuel Cell Model, J. Electrochem. Soc. 138 (1991) 2334. [CrossRef]
K. Kang, H. Ju, Numerical modeling and analysis of micro-porous layer effects in polymer electrolyte fuel cells, J. Power Sources. (2009). [CrossRef]
S. Basu, C.Y. Wang, K.S. Chen, Analytical model of flow maldistribution in polymer electrolyte fuel cell channels, Chem. Eng. Sci. 65 (2010) 6145–6154. [CrossRef]
H. Ju, H. Meng, C.Y. Wang, A single-phase, non-isothermal model for PEM fuel cells, Int. J. Heat Mass Transf. 48 (2005) 1303–1315. [CrossRef]
Jo, S. Ahn, K. Oh, W. Kim, H. Ju, Effects of metal foam properties on flow and water distribution in polymer electrolyte fuel cells (PEFCs), Int. J. Hydrogen Energy. 43 (2018) 14034–14046. [CrossRef]
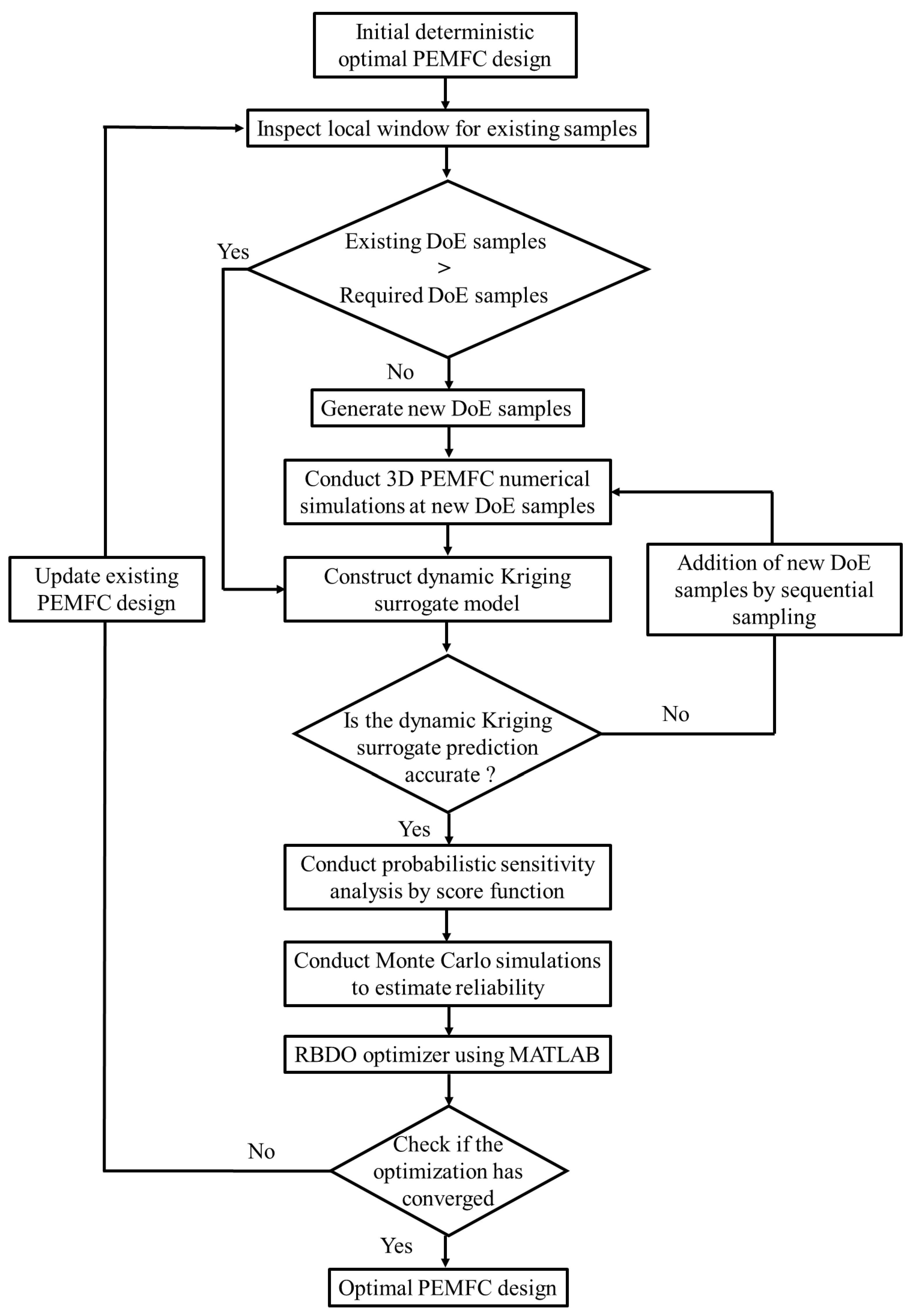
L. Zhao, K.K. Choi, I. Lee, Metamodeling method using dynamic kriging for design optimization, AIAA J. 49 (2011) 2034–2046. [CrossRef]
Lee, K.K. Choi, L. Zhao, Sampling-based RBDO using the stochastic sensitivity analysis and Dynamic Kriging method, Struct. Multidiscip. Optim. 44 (2011) 299–317. [CrossRef]
J. Marcinkoski, J. Spendelow, A. Wilson, D. Papageorgopoulos, DOE Hydrogen and Fuel Cells Program Record - Fuel Cell System Cost - 2017, J. Mech. Robot. 9 (2017) 1–9. Available online: http://mechanismsrobotics.asmedigitalcollection.asme.org/article.aspx?doi=10.1115/1.4036738.
S.T. Thompson, B.D. James, J.M. Huya-Kouadio, C. Houchins, D.A. DeSantis, R. Ahluwalia, A.R. Wilson, G. Kleen, D. Papageorgopoulos, Direct hydrogen fuel cell electric vehicle cost analysis: System and high-volume manufacturing description, validation, and outlook, J. Power Sources. 399 (2018) 304–313. [CrossRef]
B.D. James, D.A. DeSantis, Manufacturing Cost and Installed Price Analysis of Stationary Fuel Cell Systems, Strateg. Anal. (2015) 1–143. Available online: https://www.sainc.com/assets/site_18/files/publications/sa-2015-manufacturing-cost-and-installed-price-of-stationary-fuel-cell-systems_rev3.pdf.
J. Sinha, S. Lasher, Y. Yang, P. Kopf, Direct Hydrogen PEMFC Manufacturing Cost Estimation for Automotive Applications Fuel Cell Tech Team Review Acknowledgement and Disclaimer, (2008). Available online: www.TIAXLLC.com.
B.D. James, J.M. Moton, W.G. Colella, Mass Production Cost Estimation of Direct H2 PEM Fuel Cell Systems for Transportation Applications: 2013 Update, ASME 2014 12th Int. Conf. Fuel Cell Sci. Eng. Technol. Collocated with ASME 2014 8th Int. Conf. Energy Sustain. (2014) V001T07A002–V001T07A002.

Figure 1. (a) Illustration of the micro and macro-scale computational domains in PEMFC, emphasizing the variables exchanged during 3D multi-scale simulations; (b) Grid independence test results, demonstrating the stability and accuracy of the computational model across various grid resolutions.

Figure 2. Illustrations depicting the outcomes of RBDO and DDO on the solution of a hypothetical optimization problem, highlighting the impact of uncertainty in the design variables

X_{1}

and

X_{2}

Figure 2. Illustrations depicting the outcomes of RBDO and DDO on the solution of a hypothetical optimization problem, highlighting the impact of uncertainty in the design variables

X_{1}

and

X_{2}

Figure 3. Flowchart of the RBDO process beginning with the initial deterministic PEMFC design that sequentially follows through scanning for Design of Experiments (DoE) samples, generating additional samples if needed, executing 3D PEMFC simulations, constructing and verifying the dynamic Kriging surrogate model, and performing Monte Carlo simulations for reliability assessment. The process concludes with the RBDO optimizer determining if an optimal design convergence has been achieved.

Figure 4. Comparison of simulated polarization curves for the baseline and deterministic optimal design predicted with DDO optimization strategy via MLP-PSO surrogate. The simulations are conducted under controlled operating conditions for the anode and cathode: both set at pressures of 2 bar and stoichiometries of 1.2 and 2.0 respectively, with inlet relative humidity maintained at 100% for each. The baseline design is with

δ_{g d l} = 0.215 mm, d_{c h} = 0.54 mm, w_{c h} = 1 mm

and

w_{l a n d} = 1 mm

and the deterministic optimal design is with

δ_{g d l} = 0.188 mm, d_{c h} = 0.3 mm, w_{c h} = 0.614 mm

and

w_{l a n d} = 0.310 mm

δ_{g d l} = 0.215 mm, d_{c h} = 0.54 mm, w_{c h} = 1 mm

and

w_{l a n d} = 1 mm

and the deterministic optimal design is with

δ_{g d l} = 0.188 mm, d_{c h} = 0.3 mm, w_{c h} = 0.614 mm

and

w_{l a n d} = 0.310 mm

Figure 5. Scatter plots illustrating the prediction accuracy of the MLP surrogate for (a) training data and (b) test data. The plots highlight the correlation between predicted and actual values, with performance metrics RMSE and adjusted R² indicated for each dataset.

Figure 6. Evaluation of a)

C o s t_{c G D L}

and

V_{c e l l}

C o s t_{c B P}

and

V_{c e l l}

, across various PEMFC designs at

I = 1.5

A / c m^{2}

. This figure illustrates: sample data(●), baseline model(★), the optimal design solutions obtained through, DDO(★) and RBDO:

{RBDO}_{1}

(★) and

{RBDO}_{2}

(★).

Figure 6. Evaluation of a)

C o s t_{c G D L}

and

V_{c e l l}

C o s t_{c B P}

and

V_{c e l l}

, across various PEMFC designs at

I = 1.5

A / c m^{2}

. This figure illustrates: sample data(●), baseline model(★), the optimal design solutions obtained through, DDO(★) and RBDO:

{RBDO}_{1}

(★) and

{RBDO}_{2}

(★).

Figure 7. PDF plots with a 95% probability interval that corresponds to

{Case}_{1}

for four design variables: a)

δ_{g d l}

, b)

d_{c h}

, c)

w_{c h}

, and d)

w_{l a n d}

. These plots account for uncertainties in design variables with standard deviations

σ_{δ_{g d l}} = 0.03 mm

σ_{d_{c h}} = 0.05 mm

σ_{w_{c h}} = 0.05

mm, and

σ_{wland} = 0.05 mm

Figure 7. PDF plots with a 95% probability interval that corresponds to

{Case}_{1}

for four design variables: a)

δ_{g d l}

, b)

d_{c h}

, c)

w_{c h}

, and d)

w_{l a n d}

. These plots account for uncertainties in design variables with standard deviations

σ_{δ_{g d l}} = 0.03 mm

σ_{d_{c h}} = 0.05 mm

σ_{w_{c h}} = 0.05

mm, and

σ_{wland} = 0.05 mm

Figure 8. Comparison of PDF plots that corresponds to

{Case}_{1}

for a)

C o s t_{c G D L}

and b)

C o s t_{c B P}

DDO

(

δ_{g d l} = 0.188 mm

d_{c h} = 0.3 mm

w_{c h} = 0.614 mm

w_{l a n d} = 0.31 mm

) and

{RBDO}_{1}

(

δ_{g d l} = 0.139 mm

d_{c h} = 0.382 mm

w_{c h} = 0.855 mm

w_{l a n d} = 0.3 mm

), incorporating uncertainties in design variables with standard deviations

σ_{δ_{g d l}} = 0.03 mm

σ_{d_{c h}} = 0.05 mm

σ_{w_{c h}} = 0.05

mm, and

σ_{wland} = 0.05 mm

. The operating current density at which

C o s t_{c G D L}

and

C o s t_{c B P}

is estimated is

I = 1.5

A / {cm}^{2}

Figure 8. Comparison of PDF plots that corresponds to

{Case}_{1}

for a)

C o s t_{c G D L}

and b)

C o s t_{c B P}

DDO

(

δ_{g d l} = 0.188 mm

d_{c h} = 0.3 mm

w_{c h} = 0.614 mm

w_{l a n d} = 0.31 mm

) and

{RBDO}_{1}

(

δ_{g d l} = 0.139 mm

d_{c h} = 0.382 mm

w_{c h} = 0.855 mm

w_{l a n d} = 0.3 mm

), incorporating uncertainties in design variables with standard deviations

σ_{δ_{g d l}} = 0.03 mm

σ_{d_{c h}} = 0.05 mm

σ_{w_{c h}} = 0.05

mm, and

σ_{wland} = 0.05 mm

. The operating current density at which

C o s t_{c G D L}

and

C o s t_{c B P}

is estimated is

I = 1.5

A / {cm}^{2}

Figure 9. PDF plots with a 95% probability interval that corresponds to

{Case}_{2}

for four design variables: a)

δ_{g d l}

, b)

d_{c h}

, c)

w_{c h}

, and d)

w_{l a n d}

. These plots account for uncertainties in design variables with standard deviations

σ_{δ_{g d l}} = 0.01 mm

σ_{d_{c h}} = 0.03 mm

σ_{w_{c h}} = 0.03

mm, and

σ_{wland} = 0.03 mm

Figure 9. PDF plots with a 95% probability interval that corresponds to

{Case}_{2}

for four design variables: a)

δ_{g d l}

, b)

d_{c h}

, c)

w_{c h}

, and d)

w_{l a n d}

. These plots account for uncertainties in design variables with standard deviations

σ_{δ_{g d l}} = 0.01 mm

σ_{d_{c h}} = 0.03 mm

σ_{w_{c h}} = 0.03

mm, and

σ_{wland} = 0.03 mm

Figure 10. Comparison of PDF plots that corresponds to

{Case}_{2}

for a)

C o s t_{c G D L}

and b)

C o s t_{c B P}

DDO

(

δ_{g d l} = 0.188 mm

d_{c h} = 0.3 mm

w_{c h} = 0.614 mm

w_{l a n d} = 0.31 mm

) with standard deviation and

{RBDO}_{2}

(

δ_{g d l} = 0.172 mm

d_{c h} = 0.349 mm

w_{c h} = 0.687 mm

w_{l a n d} = 0.3 mm

), incorporating uncertainties in design variables with standard deviations

σ_{δ_{g d l}} = 0.01 mm

σ_{d_{c h}} = 0.03 mm

σ_{w_{c h}} = 0.03

mm, and

σ_{wland} = 0.03 mm

. The operating current density at which

C o s t_{c G D L}

and

C o s t_{c B P}

is estimated is

I = 1.5

A / {cm}^{2}

Figure 10. Comparison of PDF plots that corresponds to

{Case}_{2}

for a)

C o s t_{c G D L}

and b)

C o s t_{c B P}

DDO

(

δ_{g d l} = 0.188 mm

d_{c h} = 0.3 mm

w_{c h} = 0.614 mm

w_{l a n d} = 0.31 mm

) with standard deviation and

{RBDO}_{2}

(

δ_{g d l} = 0.172 mm

d_{c h} = 0.349 mm

w_{c h} = 0.687 mm

w_{l a n d} = 0.3 mm

), incorporating uncertainties in design variables with standard deviations

σ_{δ_{g d l}} = 0.01 mm

σ_{d_{c h}} = 0.03 mm

σ_{w_{c h}} = 0.03

mm, and

σ_{wland} = 0.03 mm

. The operating current density at which

C o s t_{c G D L}

and

C o s t_{c B P}

is estimated is

I = 1.5

A / {cm}^{2}

Table 1. Governing equations for the PEMFC model.

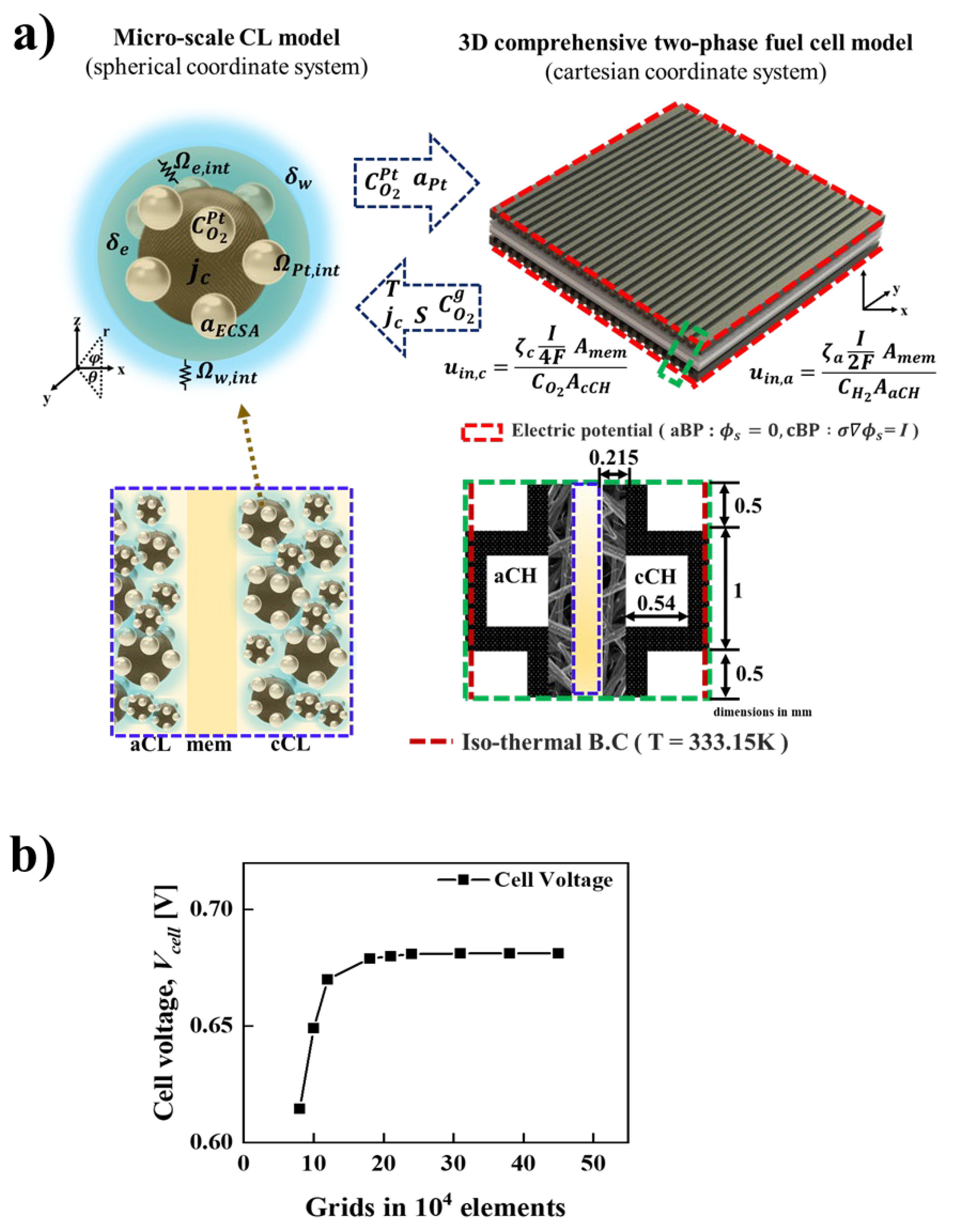
Governing equations
Mass	$\nabla ∙ (ρ \vec{u}) = 0$	(1)
Momentum	$(\frac{1}{ε^{2}}) \nabla ∙ (ρ \vec{u} \vec{u}) = - \nabla P + \nabla ∙ τ + S_{u}$	(2)
Species	Flow channels and porous media: $\nabla ∙ (γ_{i} ρ m_{i} \vec{u}) = \nabla ∙ [ρ^{g} D_{i}^{g, e f f} \nabla (m_{i}^{g})] + \nabla ∙ [(m_{i}^{g} - m_{i}^{l}) {\vec{j}}^{l}] + S_{i}$	(3)
	Water transport in membrane: $\nabla ∙ ((\frac{ρ^{mem}}{E W}) D_{w}^{mem} \nabla λ) M_{w} - \nabla ∙ (n_{d} (\frac{I}{F})) M_{w} + \nabla ∙ ((\frac{κ^{m e m}}{ν^{l}}) \nabla P^{l} = 0$	(4)
Charge	Proton transport: $\nabla ∙ (κ^{eff} \nabla ϕ_{e}) + S_{ϕ} = 0$	(5)
	Electron transport: $\nabla ∙ (σ^{eff} \nabla ϕ_{s}) - S_{ϕ} = 0$	(6)
Energy	$\nabla ∙ (ρ \vec{u} C_{p}^{g} T) = \nabla ∙ (k^{e f f} \nabla T) + S_{T}$	(7)

Table 2. Source/sink terms used in the PEMFC model.

Description			Expressions
Momentum		Porous media	$S_{u} = - \frac{μ}{K} \vec{u}$
Species		H₂ in anode CL	$S_{H_{2}, a} = [- \frac{j}{2 F}] M_{H_{2}}$
		O₂ in cathode CL	$S_{O_{2}, c} = [\frac{j}{4 F}] M_{O_{2}}$
		Water in anode CL	$S_{w, a} = [- \nabla ∙ (\frac{n_{d}}{F} \vec{I}) + \frac{j}{4 F}] M_{w}$
		Water in cathode CL	$S_{w, c} = [- \nabla ∙ (\frac{n_{d}}{F} \vec{I}) - \frac{j}{2 F}] M_{w}$
Energy		In anode CL	$S_{T, a} = j ∙ η + \frac{I^{2}}{k^{e f f}}$
		In cathode CL	$S_{T, c} = j (η + T \frac{d U_{0}}{d T}) + \frac{I^{2}}{k^{e f f}}$
		In membrane	$S_{T} = \frac{I^{2}}{k^{e f f}}$
Charge		In CLs:	$S_{ϕ} = j$
Electrochemical reactions $\sum_{k} s_{i} M_{i}^{z} = n e^{-}, where \{\begin{matrix} M_{i} = c h e m i c a l f o r m u l a o f s p e c i e s i \\ s_{i} = s t o i c h i o m e t r i c c o e f f i c i e n t \\ n = n u m b e r o f e l e c t r o n s t r a n s f e r r e d \end{matrix}$ HOR on the anode side: $H_{2} - 2 H^{+} = 2 e^{-}$ ORR on the cathode side: $2 H_{2} O - O_{2} - 4 H^{+} = 4 e^{-}$
Transfer current density, $[A / m^{3}]$	HOR in anode CL: $j = (1 - s) a i_{0, a}^{r e f} {(\frac{C_{H_{2}}}{C_{H_{2}, r e f}})}^{\frac{1}{2}} \exp [- \frac{E_{a}}{R} (\frac{1}{T} - \frac{1}{353.15})] (\exp (\frac{α_{a} F}{R T} η) - \exp (- \frac{α_{c} F}{R T} η))$			(8)
Transfer current density, $[A / m^{3}]$	ORR in cathode CL: $j = - \frac{3 L_{P t}}{r_{P t} ∙ ρ_{P t} ∙ δ_{C L}} i_{0, c}^{r e f} {(\frac{C_{O_{2}}^{P t}}{C_{O_{2}, r e f}})}^{3 / 4} e x p (- \frac{E_{c}}{R} (\frac{1}{T} - \frac{1}{353.15})) \exp (- \frac{α_{c}}{R_{u} T} F η)$			(9)
Overpotential	$η = ϕ_{s} - ϕ_{e} - U$ where $U = U_{0} - \frac{R T}{n F} \ln \frac{C_{O_{2}}}{C_{O_{2 r e f}}}$			(10)

Table 3. Kinetic, transport, and physiochemical properties.

Description	Value/ Expression
Exchange current density of HOR × ECSA per unit CL volume, $a I_{0, a}^{r e f}$	1.2 × 10¹⁰ A/m³	[36]
Exchange current density for ORR, $I_{0, c}^{r e f}$	2.0 × 10⁻⁴ A/cm²-Pt
Activation energy of anode, $E_{a}$	10.0 kJ/mol	[36]
Activation energy of cathode, $E_{c}$	70.0 kJ/mol	[36]
Transfer coefficient of HOR, $α_{a} = α_{c}$	1	[37]
Transfer coefficient of ORR, $α_{c}$	1	[37]
Reference H₂/O₂ molar concentration, $C^{r e f}$	40.88 mol/m³	[36]
Permeability of GDL/CL, $K_{G D L} / K_{C L}$	1.0 × 10⁻¹²/1.0 × 10⁻¹³ m²	[38]
Equivalent weight of electrolyte in the membrane, $E W$	1.1 kg/mol	[39]
Youngs modulus of GDL	6.16MPa	[40]
Poisson ratio of GDL	0.09	[35]
Faraday’s constant, $F$	96,485 C/mol
Universal gas constant, $R_{u}$	8.314 $J / (m o l ∙ K)$
H₂ diffusivity in the anode gas channel, $D_{0, H_{2}, a}^{g}$	1.1028 × 10⁻⁴ m²/s	[41]
H₂O diffusivity in the anode gas channel, $D_{0 H_{2} O, a}^{g}$	1.1028 × 10⁻⁴ m²/s	[41]
O₂ diffusivity in the cathode gas channel, $D_{0, O_{2}, c}^{g}$	3.2348 × 10⁻⁴ m²/s	[41]
H₂O diffusivity in the cathode gas channel, $D_{0, H_{2} O, c}^{g}$	7.35 × 10⁻⁵ m²/s	[41]
Binary gas diffusivity ( $D_{i}^{g})$	For nonporous regions $D_{i}^{g} = D_{o}^{g} {(\frac{T}{T_{0}})}^{3 / 2} (\frac{P_{0}}{P})$	(11)
Effective diffusivity ( $D_{i}^{g, e f f})$	For porous regions $D_{i}^{g, e f f} = ε^{τ} ∙ D_{i}^{g}$	(12)

Table 4. Expressions used in the two-phase mixture model.

Description	Expression
Mixture density ( $ρ)$	$ρ = ρ^{l} s + ρ^{g} (1 - s)$	(13)
Gas mixture density $(ρ^{g})$	$ρ^{g} = (\frac{P}{R_{u} T}) \frac{1}{\sum_{i} \frac{m_{i}^{g}}{M_{i}}}$	(14)
Mixture velocity ( $ρ \vec{u})$	$ρ \vec{u} = ρ^{l} {\vec{u}}^{l} + ρ^{g} {\vec{u}}^{g}$	(15)
Mixture mass fraction	$m_{i} = \frac{ρ^{l} s m_{i}^{l} + ρ^{g} (1 - s) m_{i}^{g}}{ρ}$	(16)
Relative permeability	$k_{r}^{l} = s^{3} k_{r}^{g} = {(1 - s)}^{3}$	(17) (18)
Kinematic viscosity of the two-phase mixture	$v = {(\frac{k_{r}^{l}}{v^{l}} + \frac{k_{r}^{g}}{v^{g}})}^{- 1}$	(19)
Kinematic viscosity of the gas mixture	$v^{g} = \frac{μ^{g}}{ρ^{g}} = \frac{1}{ρ^{g}} \sum_{i = 1}^{n} \frac{x_{i} μ_{i}}{\sum_{j = 1}^{n} x_{j} ϕ_{i j}}$ where $ϕ_{i j} = \frac{1}{\sqrt{8}} {(1 + \frac{M_{i}}{M_{j}})}^{- 1 / 2} {[1 + {(\frac{μ_{i}}{μ_{j}})}^{1 / 2} {(\frac{M_{j}}{M_{i}})}^{1 / 4}]}^{2}$ and $μ_{i} [N . s . m^{- 2}] = \{\begin{matrix} μ_{H_{2}} = 0.21 \times 10^{- 6} T^{0.66} \\ μ_{w} = 0.00584 \times 10^{- 6} T^{1.29} \\ μ_{N_{2}} = 0.237 \times 10^{- 6} T^{0.76} \\ μ_{O_{2}} = 0.246 \times 10^{- 6} T^{0.78} \end{matrix}$ , T in kelvin	(20) (21) (22)
Relative mobility	$λ^{l} = \frac{k_{r}^{l}}{v^{l}} v λ^{g} = 1 - λ^{l}$	(23) (24)
Diffusive mass flux	$\vec{j^{l}} = ρ^{l} {\vec{u}}^{l} - λ^{l} ρ \vec{u} = \frac{K}{v} λ^{l} λ^{g} \nabla P_{c}$	(25)
Capillary pressure Pc	$P_{c} = P^{g} - P^{l} = σ \cos θ {(\frac{ε}{K})}^{1 / 2} J (s)$	(26)
Leverett function J(s)	$J = \{\begin{matrix} 1.417 (1 - s) - 2.120 {(1 - s)}^{2} + 1.263 {(1 - s)}^{3} \\ 1.417 s - 2.120 s^{2} + 1.263 s^{3} \end{matrix} \begin{matrix} if θ_{c} < 90^{\circ} \\ if θ_{c} > 90^{\circ} \end{matrix}$	(27)

Table 5. Transport properties in the electrolyte.

Description	Expression
Membrane water content (λ)	$λ = \{\begin{matrix} λ_{g} = 0.043 + 17.81 a - 39.85 a^{2} + 36.0 a^{3} f o r 0 < a \leq 1 \\ λ_{l} = 22 \end{matrix}$ Water activity, $a = \frac{C_{w}^{g} R_{u} T}{P_{s a t}}$ [00]	(28) (29)
Electro-osmotic drag (EOD) coefficient of water $(n_{d})$	$n_{d} = \frac{2.5 λ}{22}$	(30)
Proton conductivity ( $κ$ )	$κ = (0.5139 λ - 0.326) \exp [1268 (\frac{1}{303} - \frac{1}{T})]$	(31)
Water diffusion coefficient ( $D_{w}^{m e m}$ )	$D_{w}^{m e m} = \{\begin{matrix} 2.692661843 ∙ 10^{- 10} f o r λ \leq 2 \\ \{0.87 (3 - λ) + 2.95 (λ - 2)} ∙ 10^{- 10} ∙ e^{(7.9728 - 2416 / T)} f o r 2 < λ \leq 3 \\ \{2.95 (4 - λ) + 1.642454 (λ - 3)\} ∙ 10^{- 10} ∙ e^{(7.9728 - 2416 / T)} f o r 3 < λ \leq 4 \\ (2.563 - 0.33 λ + 0.0264 λ^{2} - 0.000671 λ^{3}) ∙ 10^{- 10} ∙ e^{(79728 - 2416 / T)} f o r 4 < λ \leq λ_{a = 1}^{g} \end{matrix}$	(32)
Interfacial resistance of the water film	$Ω_{w, i n t} = z_{w} \frac{δ_{w}}{D_{O_{2}, w}}$	(33)

Table 6. Comparison of design variables and corresponding cell voltage

(V_{c e l l})

and nominal material costs of the cathode GDL and BP across various PEMFC designs: baseline, DDO,

{RBDO}_{1}

and

{RBDO}_{2}

Table 6. Comparison of design variables and corresponding cell voltage

(V_{c e l l})

and nominal material costs of the cathode GDL and BP across various PEMFC designs: baseline, DDO,

{RBDO}_{1}

and

{RBDO}_{2}

Parameters	Baseline design	Optimization approach
Parameters	Baseline design	DDO	${RBDO}_{1}$	${RBDO}_{2}$
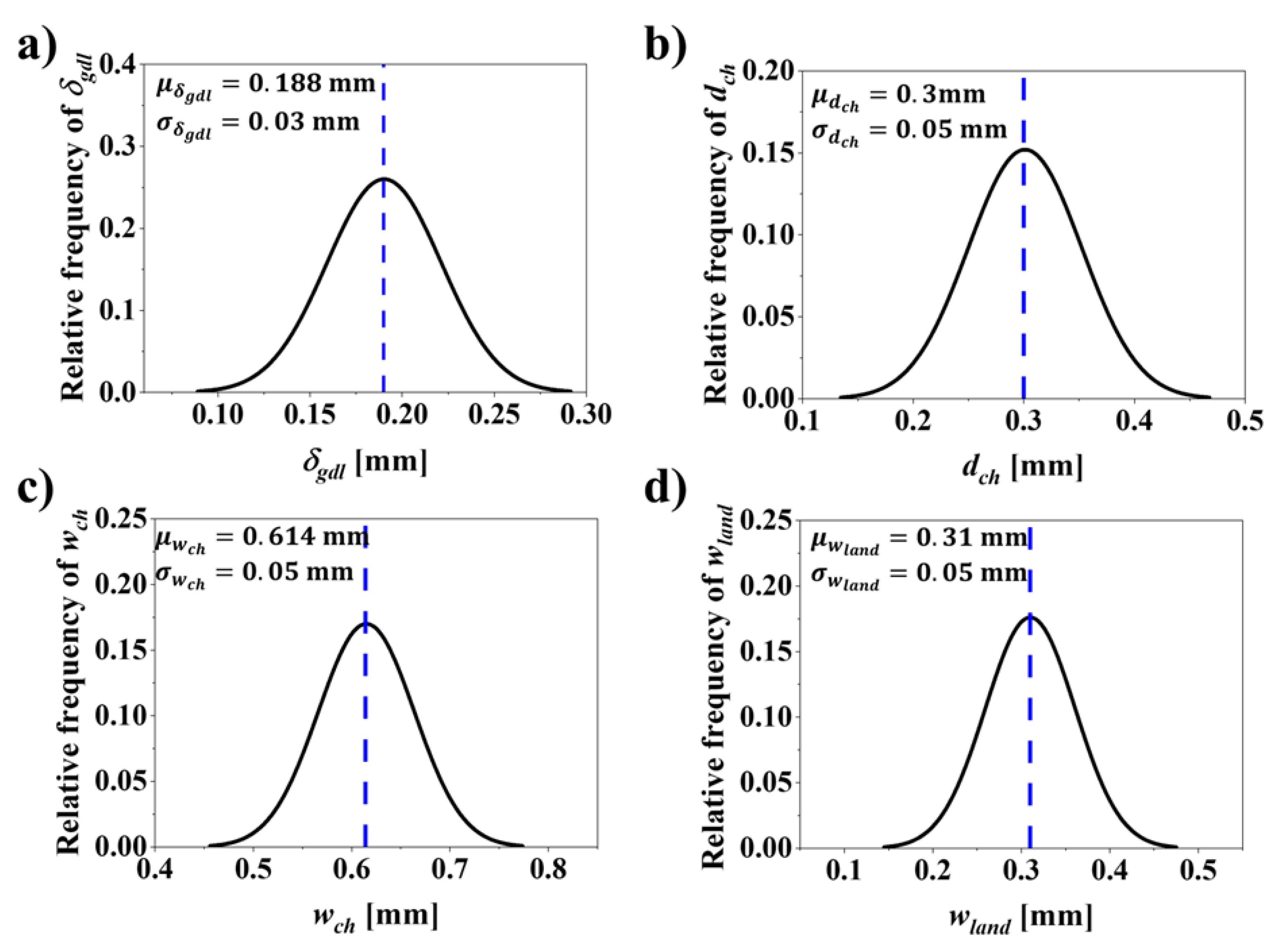
$δ_{g d l}$ , [mm]	0.215	0.188	0.139	0.172
$d_{c h}$ , [mm]	0.54	0.300	0.382	0.349
$w_{c h}$ , [mm]	1	0.614	0.855	0.687
$w_{l a n d}$ , [mm]	1	0.310	0.300	0.300
$V_{c e l l}, [V]$	0.681	0.712	0.710	0.711
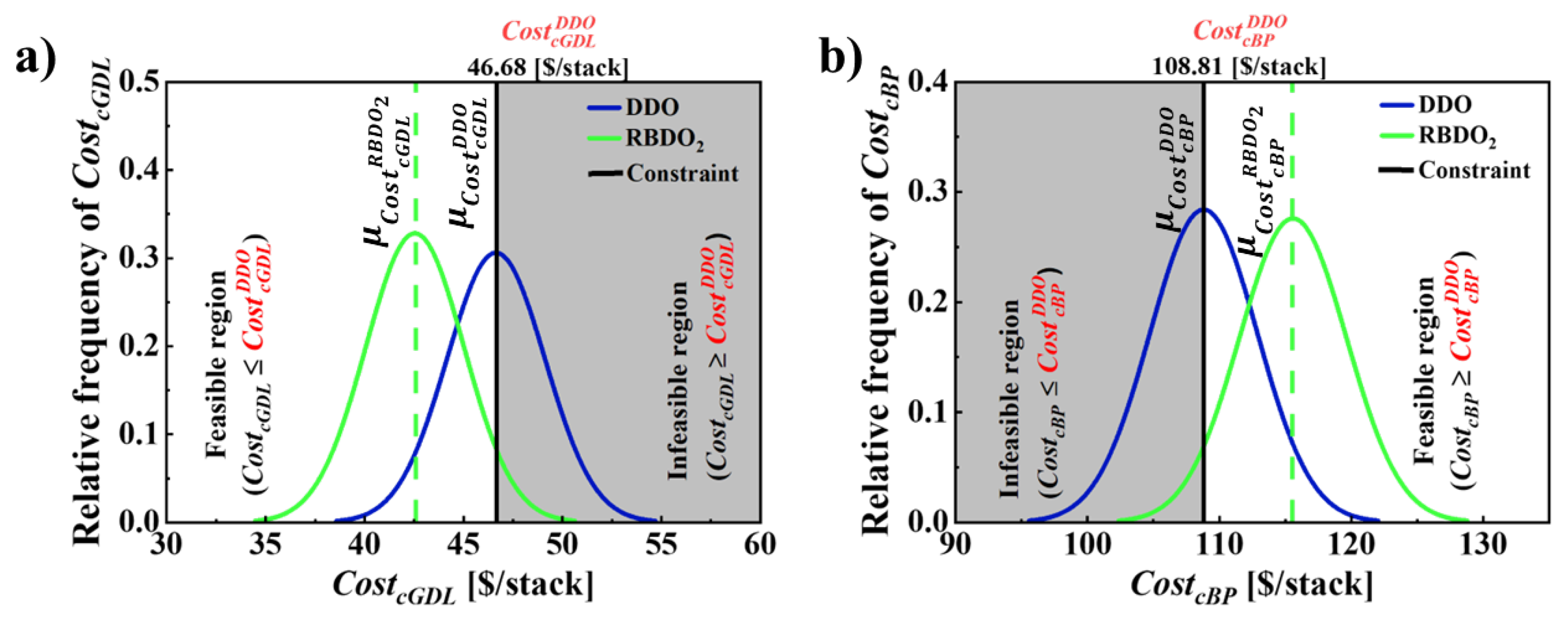
$C o s t_{c G D L}$ [$/stack]	53.38	46.68	34.43	42.59
$C o s t_{c B P}$ [$/stack]	141.45	108.81	119.99	115.52

Table 7. Distribution of design variables with mean

(μ)

and standard deviations

(σ)

for different cases.

Table 7. Distribution of design variables with mean

(μ)

and standard deviations

(σ)

for different cases.

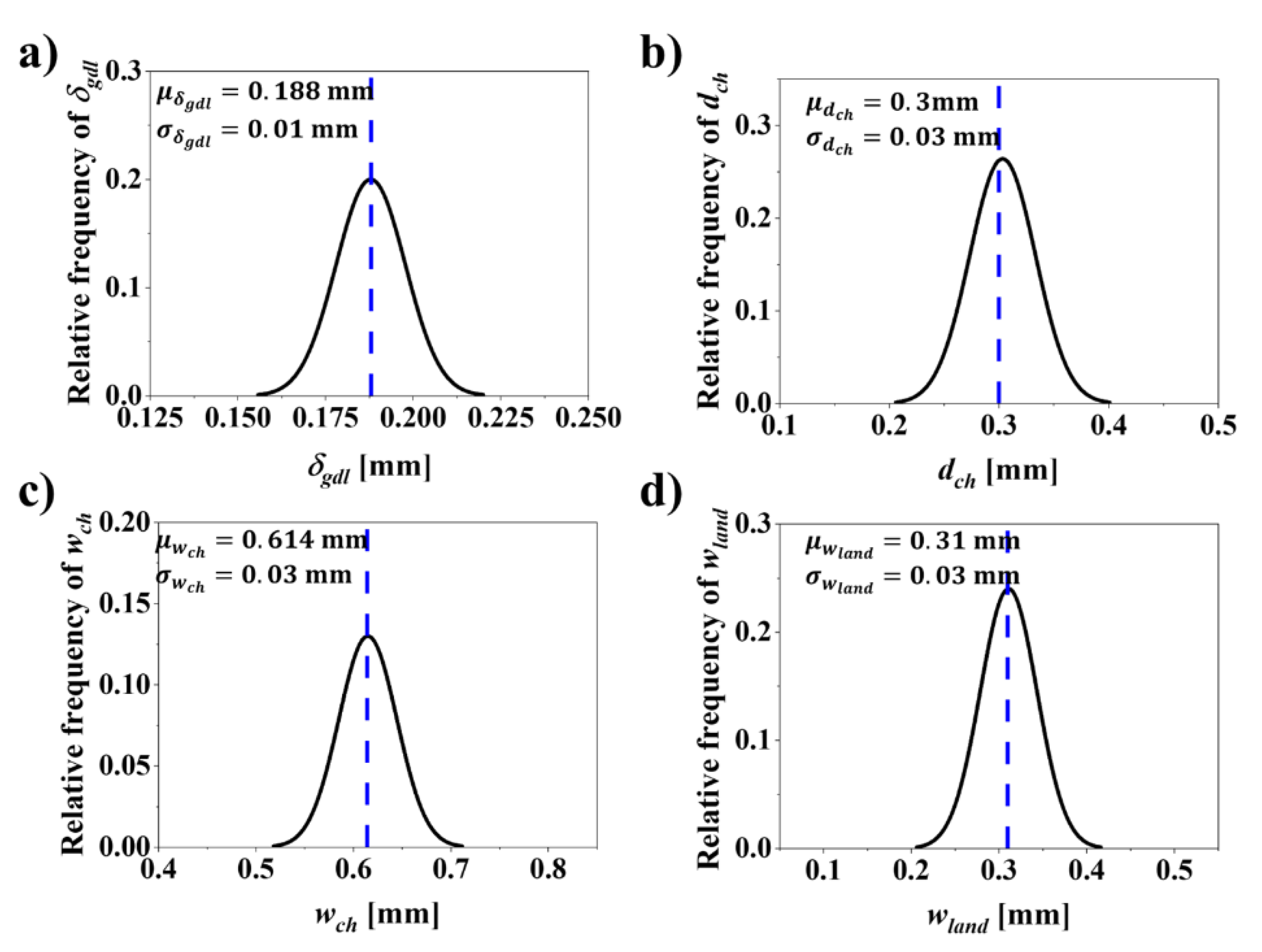
Design variables	Distribution	Mean (μ) [mm]	Standard deviation $σ$ ), [mm]
Design variables	Distribution	DDO	${Case}_{1}$	${Case}_{2}$
GDL thickness ( $δ_{gdl}$ ), [mm]	Normal	0.188	0.03	0.01
Channel depth ( $d_{ch}$ ), [mm]	Normal	0.3	0.05	0.03
Channel width ( $w_{ch}$ ), [mm]	Normal	0.614	0.05	0.03
Land width ( $w_{land}$ ), [mm]	Normal	0.310	0.05	0.03

Table 8. A summary of various performance metrices for the cost parameters:

C o s t_{c G D L}

and

C o s t_{c B P}

, including the nominal and mean

(μ)

value, standard deviation(

σ

) and the reliability assessments for the two cases: case 1 and case 2, predicted through DDO and RBDO approach.

Table 8. A summary of various performance metrices for the cost parameters:

C o s t_{c G D L}

and

C o s t_{c B P}

, including the nominal and mean

(μ)

value, standard deviation(

σ

) and the reliability assessments for the two cases: case 1 and case 2, predicted through DDO and RBDO approach.

Case	Parameter	Optimization approach
		$DDO$				RBDO
		Reliability [%]	Nominal value [$/stack]	Mean value ( $μ$ ) [$/stack]	Standard deviation ( $σ$ ) [$/stack]	Reliability [%]	Nominal value [$/stack]	Mean value ( $μ$ ) [$/stack]	Standard deviation ( $σ$ ) [$/stack]
1	$C o s t_{c G D L}$ [$/stack]	49.87	46.68	46.68	7.45	95.00	34.43	34.42	7.44
1	$C o s t_{c B P}$ [$/stack]	50.00	108.81	108.81	6.78	94.99	119.99	120.0	6.80
2	$C o s t_{c G D L}$ [$/stack]	49.87	46.68	46.68	2.48	95.02	42.59	42.58	2.48
2	$C o s t_{c B P}$ [$/stack]	50.00	108.81	108.81	4.07	94.99	115.52	115.51	4.08

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Reliability-based Design Optimization for Polymer Electrolyte Membrane Fuel Cells: Tackling Dimensional Uncertainties in Manufacturing and Their Effects on Costs of Cathode Gas Diffusion Layer and Bipolar Plates

Abstract

1. Introduction

2. Numerical PEMFC Model

2.1. Model Assumptions

2.2. Governing Equations and Source Terms

2.3. Boundary Conditions and Numerical Implementation

3. Overview of Design Optimization Strategies for Engineering Application

4. Estimating the Material Costs of the Cathode GDL and BP in PEMFCs

5. Formulation of the Optimization Problem

6. Results and Discussion

6.1. Evaluation of Predictive Capability of the MLP Surrogate

6.2. DDO to Access Superior PEMFC Performance

6.3. RBDO for Cathode, GDL and BP Material Costs

7. Conclusions

Acknowledgments

Conflicts of Interest

Nomenclature

References

MDPI Initiatives

Important Links

Subscribe