1. Introduction
The grinding process is typically the final stage of machining, and the condition of the grinding wheel directly impacts the quality of a workpiece’s surface [
1]. In recent years, there has been a significant increase in demand for titanium alloy in the aerospace industry. However, due to its inherent characteristics, titanium alloy is prone to adhere to the grinding wheel, making it difficult to control the quality of grinding processing. This has led to continuous advancements in technology for monitoring grinding wheel wear.
With the widespread adoption of sensor technology in recent years, signals such as acoustic emission signals, grinding force signals, vibration signals, and temperature signals can be used to monitor the grinding process in real time. By comparing these signals with those from normal grinding processing, it becomes possible to predict the wear state of the grinding wheel. This technology offers advantages because of its strong real-time capabilities and ease of operation. It enables the timely detection of abnormal wear on the grinding wheel and facilitates appropriate measures [
2,
3]. Alexandre et al. utilized acoustic emission digital signal processing and a fuzzy mathematical model to assess surface conditions and dressing requirements for grinding wheels during operation. Their results demonstrated that fuzzy modeling is highly effective for diagnosing the state of a grinding wheel’s surface [
4]. In 2013, Ding Ning et al., in a study from Changchun University, employed a Kistler 9275B three-way dynamometer to observe variations in grinding force throughout a wear experiment on a grindstone [
5]. Akpudo and Hur suggested that vibration signals reflect different stages within a grindstone’s lifespan and that they can be utilized for the intelligent monitoring of grindstone status [
6]. Pivkin et al. used accelerometers to track various aspects within a given grindstone’s operational processes; their findings indicated that parameters derived from vibration signals effectively mirrored changes occurring within said grindstones over time [
7]. The research conducted by these scholars demonstrates that single-sensor signals are useful means through which one may effectively monitor grindstone wear. Nevertheless, there are non-linearities and complexities inherent within this particular aspect of grindstone degradation that must be considered, along with potential interferences.
The technology available for monitoring grinding wheel wear state is no longer limited to the monitoring of a single sensor signal. Recently, numerous scholars have conducted extensive research on intelligent algorithms for multi-sensor fusion. In the field of grinding processing, models for predicting grinding wheel wear state are primarily based on neural networks. However, neural network control still has some inherent limitations regarding both theory and design methods [
8]. In practical applications, due to the varying characteristics and performances of different sensor signals, optimizing the network structure becomes challenging. This leads to issues such as local extreme value problems and potential local convergence, ultimately impacting system performance. As a result, it becomes difficult to establish an effective grinding wheel wear monitoring system [
9].
In this paper, a comprehensive monitoring system for precision grinding wheel wear monitoring is established. This system overcomes the limitations of traditional single-sensor on-line monitoring systems, which have low accuracy. A multi-eigenvalue fusion algorithm based on an improved support vector machine (SVM) is proposed, and an intelligent recognition model is developed. The eigenvalues of acoustic emission, grinding force, and vibration signals are extracted separately and then normalized. The normalized characteristic information serves as the input for the model, and the recognition strategy is adjusted using entropy weight evaluation to output different states of the grinding wheel. The results demonstrate that the monitoring system established in this paper can effectively identify the state of grinding wheel wear with an accuracy exceeding 92%.
2. Evaluating Grinding Wheel Wear State
In the grinding process, due to mechanical, physical, and chemical effects caused by grinding wheel wear and because of the random distribution of abrasive particles on the surface of the grinding wheel, grinding wheel wear occurs, and it comes in a variety of forms, including wear, crushing wear, and adhesion plugging. The processing material focused on in this paper is a typical difficult-to-process material: titanium alloy. In the process of precision grinding, the main causes of grinding wheel wear are adhesive wear and crushing wear caused by adhesive wear, accompanied by diffusion wear. Grinding wheel diffusion wear refers to the wear induced by the mutual diffusion of elements, causing the weakening of the surface layer of abrasive particles when the abrasive particles are in contact with the material to be ground under the action of high-temperature grinding. During the grinding process, titanium alloy interacts with atmospheric oxygen to form titanium oxides
and
. As a result, the hardness and strength of the titanium alloy surface increase, while the plasticity decreases, the grinding force increases, and the grinding wheel wear is exacerbated [
10,
11,
12].
During the grinding process, the wear of the grinding wheel gradually increases with the increase in grinding time. The process of grinding wheel wear can be divided into three stages: initial wear, middle wear, and late wear. In the early stage of grinding wheel wear, during titanium alloy grinding, the newly repaired grinding wheel experiences a decline in the strength of its grains and bonds due to the presence of small and more broken grinding grains. This results in a change in the number of effective grinding grains. As for middle wear, there is a gradual expansion from point adhesion to plane adhesion on the surface of the grinding wheel, reaching its maximum value. Finally, at later stages of wear, the force caused by adhesion exceeds that required to break or dislodge individual particles from their bonds due to the adhesion being greater than the ultimate stress levels [
13,
14].
In this study, changes in the state of a green silicon carbide grinding wheel during titanium alloy grinding were observed with a Leica DVM2500 ultra-depth-of-field microscope. Specifically, changes in grinding wheel state during the whole wear process were observed by adopting the time observation method. The experimental device we used is shown in
Figure 1.
Using the Leica DVM2500 ultra-depth-of-field microscope, a constant grinding depth and feed speed were selected for the titanium alloy grinding process, with the surface morphology of the grinding wheel being observed every 10 minutes over a total time of 3 hours. The objectives were to observe the wear characteristics of the grinding wheel and to identify any significant changes indicating entry into the next stage of wear.
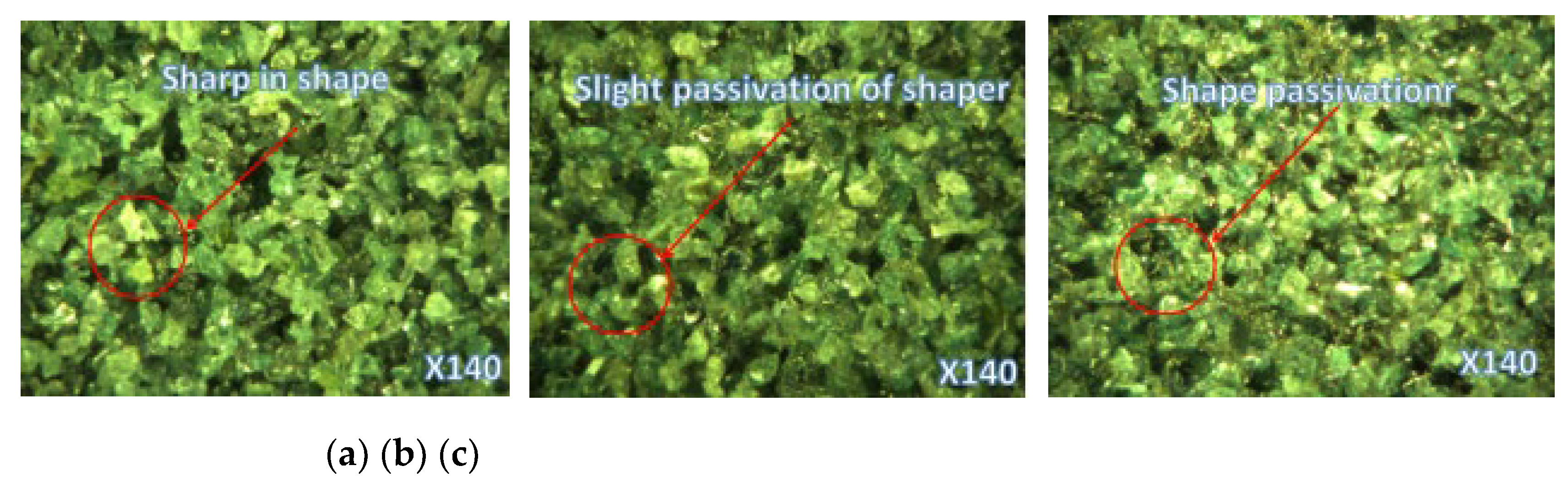
As shown in
Figure 2, the surface morphology of the grinding wheel at different stages of wear was extracted. In the early stage of wheel wear, the abrasive grains are sharp; in the middle stage, abrasive adhesion and abrasive expansion occur on the surface, and in the late stage, severe dulling and extensive adhesion of abrasives are observed. The three micrographs below clearly distinguish the wear status of the grinding wheel at different stages, serving as an important basis for determining wheel wear in this study.
3. Evaluation of Grinding Wheel Wear State
3.1. Acoustic Emission Signal Characteristic Value Extraction
Acoustic emission refers to the phenomenon whereby a material or structure is deformed or broken by the action of external or internal forces, releasing strain energy in the form of elastic waves [
15,
16,
17,
18,
19]. The wavelet energy coefficient method is commonly used in the extraction of acoustic signal eigenvalues in grinding. However, the wavelet energy coefficient method has disadvantages in that the eigenvalue is not obvious and is affected by the singular wavelet coefficient [
20].In this paper, the wavelet packet decomposition coefficient mean square method is used to extract the eigenvalues of the acoustic emission signal.
- (1)
The low-frequency coefficient and high-frequency coefficient of wavelet packet decomposition are determined usings the wavelet packet energy coefficient
method. The low-frequency coefficient Aj and high-frequency coefficient Dj of wavelet packet decomposition are determined by the wavelet packet energy coefficient method.
- (2)
We set the threshold value of the product of the mean square value of the wavelet packet coefficients and the weighting coefficient to be less than 1 in the energy-intensive frequency band, denoted by T.
- (3)
After extracting wavelet coefficients greater than the threshold T to describe the characteristics of the signal,
and
are used to
represent the wavelet packet coefficients after threshold processing of the high-frequency and low-frequency parts of the signal, namely
Among them, j is the
corresponding characteristic frequency band, and T is adjusted according to the
actual situation. When the wavelet packet decomposition coefficient is greater
than T, the number of wavelet packet decomposition coefficients greater than
the wavelet packet decomposition coefficient T is counted, represented by N.
The number of wavelet sub-packet solution coefficients can intuitively reflect
the characteristics of the signal.
3.2. Acoustic Characteristic Value Extraction of Grinding Force and Vibration Signals
Grinding force is an important characteristic of the grinding process. The interaction between the grinding wheel and the workpiece generates the grinding force. As the wear of the grinding wheel increases, the grinding force will increase. The change in the grinding force ratio
can indirectly reflect the grinding wheel wear state [
21,
22,
23,
24,
25].
Vibration is caused by the dynamic component of the grinding force, which is closely related to the wear state of the grinding wheel and the dynamic characteristics of the process system. As the degree of grinding wheel wear increases, the state of interaction between the grinding wheel and the workpiece changes, causing an increase in vibration frequency and amplitude. The RMS value of the vibration signal can best reflect the grinding wheel wear change trend [
26,
27].
This article adopts the commonly used grinding force ratio and the vibration signal RMS value as the characteristic values of the two above-mentioned signals.
3.3. Feature Value Selection
Although the eigenvalues of acoustic emission, grinding force, and vibration signals can each reflect the wear state of the grinding wheel, due to the external environment and various factors, there are singular eigenvalues, and the characteristics of the three signals are not the same, which can easily lead to the weakening or distortion of features. Therefore, this article screens the extracted feature values, namely
where
is the extracted feature value, and
n is
the number of feature values in each group.
Let
S be the eigenvalue screening threshold. If
, it means that the eigenvalue
yi is less disturbed by the outside world and can better
reflect the grinding wheel wear characteristics. If
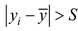
, it means
that the external interference is greater. The feature values obtained after
threshold filtering are used as input feature values for the monitoring model
proposed in this paper.
4. Construction of Intelligent Monitoring System for Grinding Wheel Wear Monitoring
4.1. Support Vector Machine
SVM is a brand-new machine learning algorithm. Compared with traditional machine learning methods, SVM has a simple structure and is easy to converge. It uses a fixed three-layer structure, and the number of hidden layer nodes is determined by the support vector [
28,
29,
30,
31,
32,
33,
34,
35]. The SVM algorithm is essentially an optimization problem of convex quadratic programming; it will eventually obtain the global optimal solution, solving the problem regarding the limit of the neural network. The support vector prediction steps are as follows:
- (1)
Establish the classification hyperplane of the sample data and calculate the distance to the classification hyperplane as follows: .
- (2)
Maximize the interval classification of the samples and ensure that the training samples n meet the following:
- (3)
Solve the inner product of the high-dimensional vector into the inner product of the low-dimensional vector by applying kernel function .
- (4)
Solve the established convex quadratic programming problem, as this will lead to the realization of target sample classification selection.
4.2. Multi-Eigenvalue Fusion Algorithm
Multi-eigenvalue fusion refers to optimizing the eigenvalues of various grinding wheel wear signals according to certain evaluation criteria, thereby reliably reflecting the grinding wheel wear characteristics [
36,
37]. There is a clear distinction between the different stages of grinding wheel wear in the grinding process, and the signals affected by the different wear stages of the grinding wheel are also different. This requires the adjustment of the fusion strategy and an intelligent recognition model. This paper proposes a multi-eigenvalue fusion algorithm based on an improved support vector machine (SVM). The main steps are as follows:
The filtered feature value data
are normalized to obtain a standardized matrix
and to obtain the following:
The entropy of item
is calculated as follows:
The weight of the
indicator is determined as follows:
The comprehensive evaluation value is as follows:
In this way, we obtain the weights of the signals at different stages of grinding wheel wear and bring them into Formula (6):
In the above equation, is the penalty coefficient, which indicates the degree of trust in the classified samples. The higher the degree of trust, the greater the sample weight of the classifier. Therefore, the weight of the signals of different grinding wheel wear stages has an influence on the SVM model, and the intelligent recognition model established by the SVM will be more accurate.
4.2. Support Vector Machine
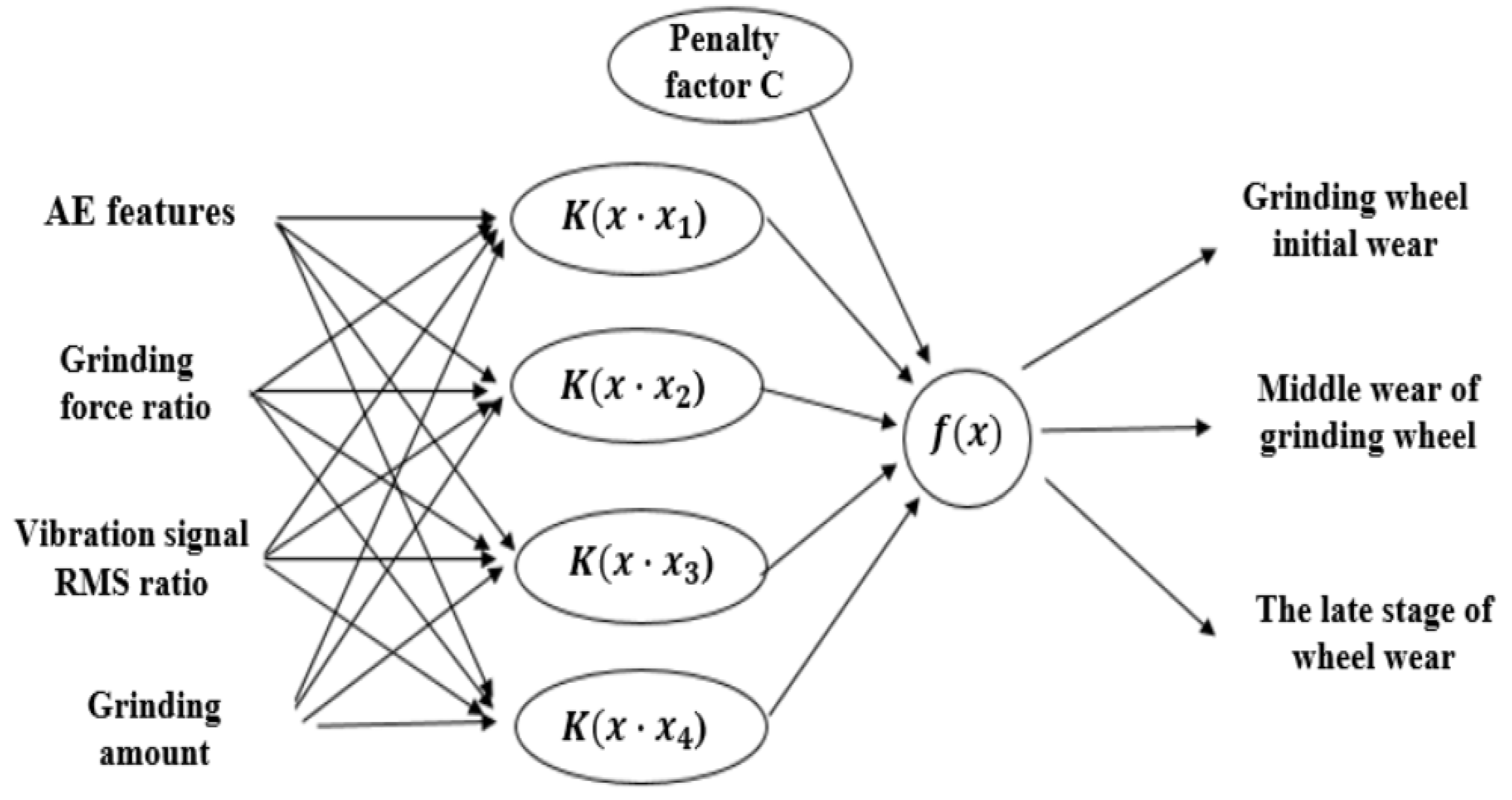
The structure of the SVM network model for precision grinding wheel wear state monitoring based on multi-sensor fusion is shown in
Figure 3. The threshold-valued acoustic emission, grinding force, and vibration signal feature values, including the grinding amount, are used as the feature inputs of the SVM. According to the change in the disciplinary coefficient, the characteristic frequency bands with greater influence are weighted and fused [
38,
39]. Finally, the classifier chooses three different wear states of the final output grinding wheel. The initial code of the grinding wheel is [
1], the intermediate code is [
2], and the later code is [
3].
5. Experimental Study
5.1. The Purpose and Conditions of the Experiment
Through experiments, we verified whether the intelligent monitoring system for precision grinding wheel wear identification established in this paper can realize on-line intelligent monitoring and verify the reliability and accuracy of the system.
The main experimental devices we used were the SL500 ultra-precision surface grinder, a kistler load cell, a vibration sensor, and an AE sensor, as shown in
Figure 4. The experimental conditions are shown in
Table 1.
In order to reduce external interference and improve the reliability of our results, we set up three groups of different grinding amount comparison experiments, as shown in
Table 2.
5.2. Experimental Results
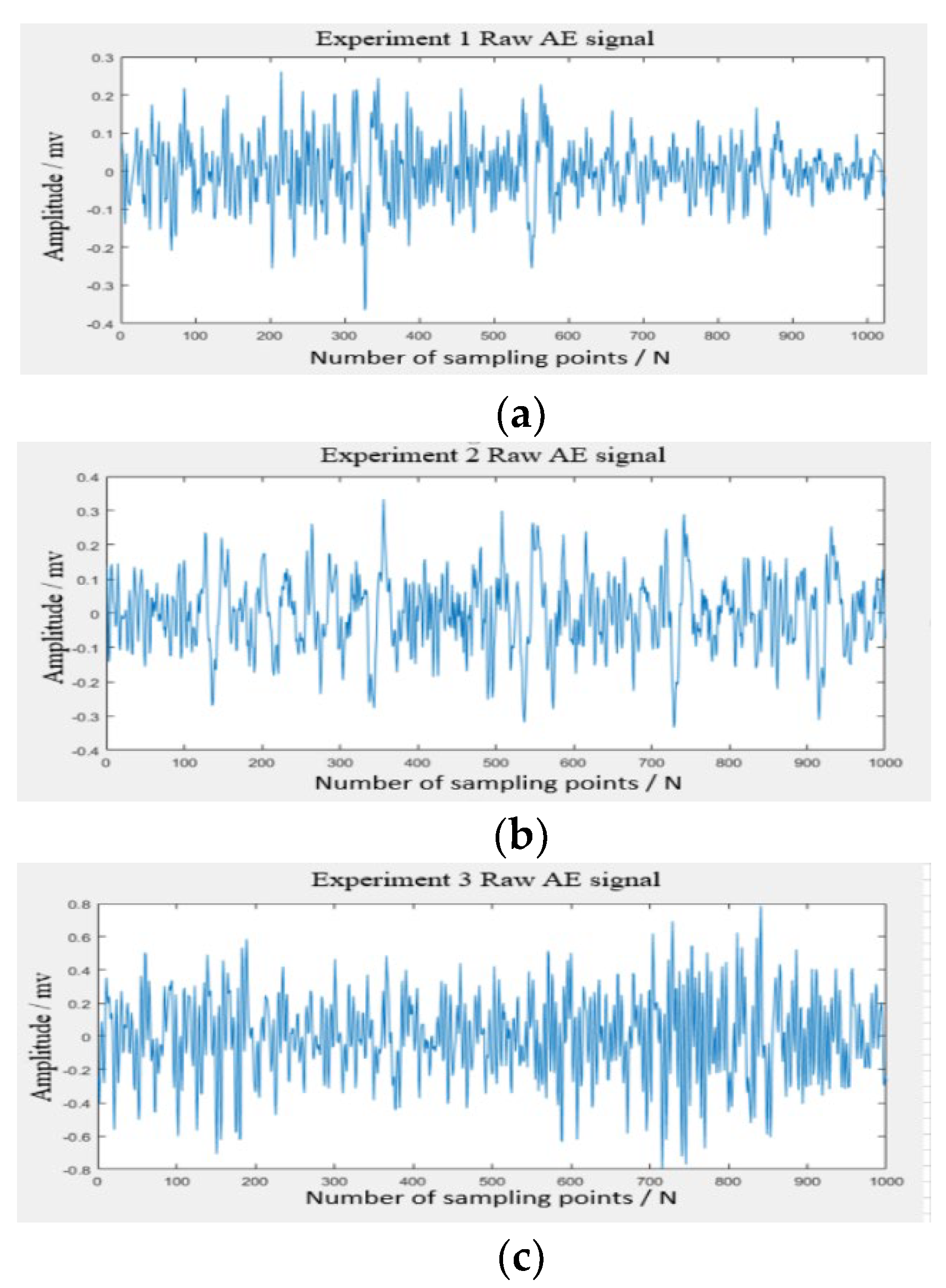
For the processing of the original acoustic emission signals collected in different stages of Experiment 1, Experiment 2, and Experiment 3, the acoustic emission signal processing method proposed in this paper was used. The raw acoustic emission signal data of the grinding wheel are shown in
Figure 5.
The acoustic emission signal processing method proposed in this paper was applied to the raw acoustic emission signal data collected in Experiment 1, Experiment 2, and Experiment 3 at different grinding wheel wear stages. Signal denoising was carried out, and the energy coefficient of wavelet packet was extracted in MATLAB.
Figure 6 comprises diagrams showing the distribution of the energy coefficient of the wavelet packet.
Upon observation, it was noted that the energy signals are predominantly concentrated within the first three signal bands. This paper proposes the application of the mean square method to the wavelet packet decomposition coefficient. To determine grinding wheel wear state, one should statistically analyze the mean square value of the wavelet packet decomposition coefficient and utilize the number N of wavelet decomposition coefficient thresholds processed as input feature vector data. To ensure accuracy and minimize errors, three sets of feature data are extracted from each frequency band, as illustrated in
Table 3.
Grinding force ratio was extracted as characteristic data from the grinding force signals collected in Experiment 1, Experiment 2, and Experiment 3. In order to ensure the accuracy of experimental data and reduce errors, nine groups of grinding force ratio
data were extracted using DynoWare software when the maximum contact area between the grinding wheel and workpiece was realized in each experiment.
Table 4 details the extracted characteristic experimental grinding force ratio data.
For the vibration signals of grinding wheels collected in different stages of Experiments 1, 2 and 3, the RMS value of the vibration signal was extracted as the characteristic data. In order to ensure the accuracy of the experimental data and reduce errors, nine groups of RMS vibration signal data were extracted from each group of experiments, as shown in
Table 5.
The grinding force signal is also collected, and the vibration signal is extracted using the feature value extraction method proposed in this paper. The eigenvalues of the three extracted signals are threshold-filtered and normalized, and the multi-eigenvalue fusion algorithm proposed in this paper is used to determine the penalty coefficient C. The acoustic emission signal feature data, grinding force signal feature data, and vibration signal feature data extracted from the three experiments, as well as the grinding conditions, were used as inputs for the SVM network model for precision grinding wheel wear state monitoring. The results are compared with the real wear state to verify the accuracy of the on-line system for precision grinding wheel wear state monitoring established in this paper.
Table 3.
Results of grinding wheel wear state experiment.
Table 3.
Results of grinding wheel wear state experiment.
| Experiment |
AE feature |
Force feature σ |
Vibration RMS |
Output |
Real |
Right or not |
| 1 |
0.347 |
1.01 |
0.71284 |
Mid-term |
Mid-term |
Right |
| 1 |
0.369 |
1.05 |
0.78429 |
Mid-term |
Mid-term |
Right |
| 2 |
0.387 |
1.1 |
0.70351 |
Mid-term |
Mid-term |
Right |
| |
|
········· |
|
|
|
| 3 |
0.392 |
1.23 |
1.10758 |
Late-term |
Mid-term |
Not |
| 3 |
0.306 |
1.17 |
1.09075 |
Late-term |
Late-term |
Right |
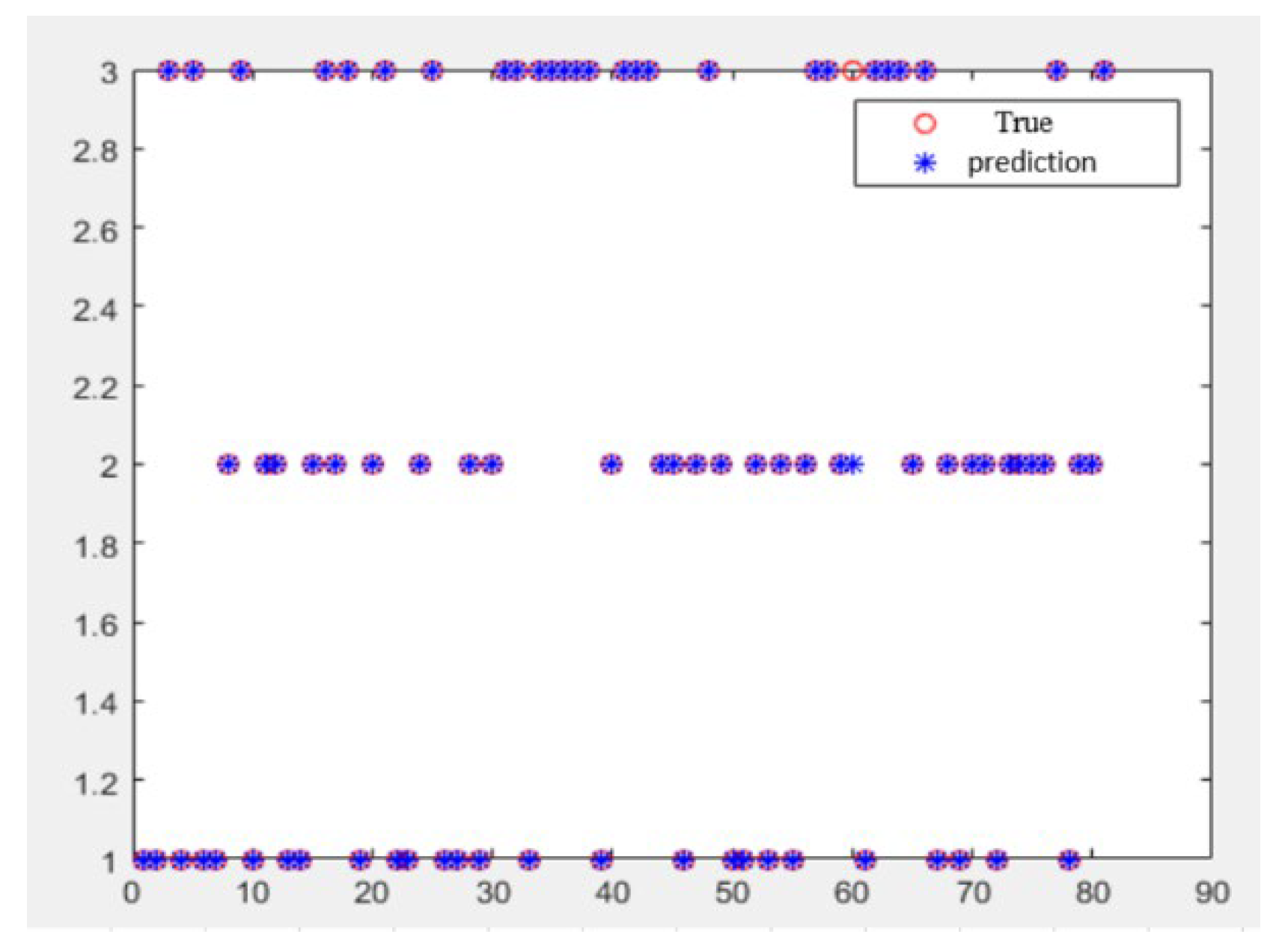
Figure 6.
Results of wheel wear status monitoring simulation.
Figure 6.
Results of wheel wear status monitoring simulation.
Table 3 shows the results of grinding wheel wear state monitoring in the experiments, and FIG. 6 shows the results of the wear state monitoring simulation. The results show that the precision grinding wheel wear state monitoring system proposed in this paper can effectively identify the grinding wheel wear state. The monitoring accuracy is more than 92.5%, meaning the monitoring accuracy is high. The proposed system can be used to monitor grinding wheel wear in precision grinding.
5. Conclusion
This paper introduces an intelligent model for precision grinding wheel wear monitoring based on an improved SVM. We compared the simulated monitoring results with actual wear results. The results show that the proposed method can serve as an effective tool for monitoring the condition of grinding wheels during grinding. Our main conclusions are as follows:
- (1)
This paper presents a multi-eigenvalue fusion algorithm based on an improved support vector machine. This algorithm overcomes the challenges of multi-sensor eigenvalue fusion, as compared to traditional BP neural networks, and significantly enhances the stability and reliability of on-line grinding wheel wear monitoring.
- (2)
We introduced eigenvalue threshold processing and the entropy weight evaluation method to adjust the fusion strategy in order to provide a theoretical basis for the on-line monitoring of grinding wheel wear status.
- (3)
An improved SVM was used to establish an intelligent model for grinding wheel wear monitoring, and the grinding wheel wear state was predicted through the use of this network. The experimental results show that the monitored wear state of the grinding wheel is basically consistent with the actual wear state of the grinding wheel, and the recognition rate can reach more than 92%.
- (4)
At present, the multi-sensor fusion strategy proposed in this paper is limited to the on-line monitoring of grinding wheels in the field of precision grinding. In order to extend the application of this technology to other forms of tool wear diagnosis, its limitations will need to be addressed. However, this strategy of multi-sensor fusion can be used for equipment-based fault diagnosis.
Author Contributions
J.D. and G.C. were responsible for the writing of this article; G.M. was responsible for signal processing; and Z.Y. and C.S. were responsible for conducting experiments. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the China Postdoctoral Science Foundation (2021M692457); the Jilin Province Science and Technology Development Plan Project (YDZJ202301ZYTS263, YDZJ202301ZYTS423); and the Chongqing Natural Science Foundation (CSTC2021jcyj-msxmX0989, CSTC2022NSCQ-MSX1120).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
The data presented in this study are available from the
corresponding author upon request.
Acknowledgments
The authors are grateful for the support they received from the China Postdoctoral Science Foundation, the Jilin Province Science and Technology Development Program, and the Chongqing Natural Science Foundation.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- P. Sabarinathan, V.E. Annamalai, K. Rajkumar. Sustainable application of grinding wheel waste as abrasive for abrasive water jet machining process[J]. J. Clean. Prod. 2020, 261. [Google Scholar] [CrossRef]
- Business - Manufacturing; New Findings on Manufacturing Described by Investigators at Northeastern University (Investigation on the grinding properties of high thermal conductivity vitrified bond CBN grinding wheel for titanium alloy)[J]. J. Technol. 2020.
- Chen Ao, Wu Chaoqun, Tian Liang, Hu Shijing. Research on surface roughness of TC4 titanium alloy grinding with thin grinding wheel [J]. Comb. Mach. Tool Autom. Process. Technol.
- Alexandre F A, Lopes W N, Dotto F L, et al. Tool condition monitoring of aluminum oxide grinding wheel using AE and fuzzy model. Int. J. Adv. Manuf. Technol. 2018, 96, 67–79. [Google Scholar] [CrossRef]
- Ding Ning, Duan Jingsong, Shi Jian, et al. Research on grinding wheel wear Monitoring System based on Acoustic emission [J]. J. Nanjing Univ. Aeronaut. Astronaut. 2019, 52, 48–52. [Google Scholar] [CrossRef]
- Akpudo U E, Hur J W. Exploring the efficiencies of spectral isolation for intelligent wear monitoring of micro drill bit automatic regrinding inline systems. Algorithms 2022, 15, 194. [Google Scholar] [CrossRef]
- Pivkin P M, Kozochkin M P, Minin I V, et al. A new method for monitoring grinding processes using accelerometers. In: Signal Processing, Sensor/Information Fusion, and Target Recognition Xxxi. 2022, 12122, 1212217. [CrossRef]
- Saman Maroufpoor,Omid Bozorg-Haddad,Eisa Maroufpoor. Reference evapotranspiration estimating based on optimal input combination and hybrid artificial intelligent model: Hybridization of artificial neural network with grey wolf optimizer algorithm[J]. J. Hydrol. 2020, 288. [CrossRef]
- HyunWook Lee. The effect of water lubricant on reducing the generation of airborne wear particles from wheel–rail contacts under various train velocities[J]. Tribol. Int. 2020, 150. [CrossRef]
- Michael Behr, Saba Saiel, Valerie Evans, et al. Machine Learning Diagnostic Modeling for Classifying Fibromyalgia Using B-mode. Ultrasound Images 2020, 42, 135–147. [CrossRef]
- Nie Peng, Jia Tong, Zhang Kaifeng, Li Zhengqiang, Wang Huanqi. Tool wear state recognition based on HPSO optimized BP neural network [J]. Comb. Mach. Tool Autom. Process. Technol. 2020, 152–155.
- Jeong Mok Oh,Jae-Keun Hong,Jong-Taek Yeom,Sang Won Lee,Eun-Young Kim,Namhyun Kang,Chan Hee Park. Accelerated formation of an ultrafine-grained structure in a two-phase Ti alloy during compression with decreasing temperatures[J]. Philos. Mag. 2020, 100, 1569–1584. [Google Scholar] [CrossRef]
- S. D. Luo,T. Song,S.L. Lu,B. Liu,J. Tian,M. Qian. High oxygen-content titanium and titanium alloys made from powder[J]. J. Alloys Compd. 2020, 836, 155526. [Google Scholar] [CrossRef]
- Li Guangya, Zou Guofeng, Fu Guixia. Research on visual detection method of ceramic tile surface defects based on Gabor transform and region growth [J]. Mod. Comput. 2019, 24, 37–42. [Google Scholar]
- Guo Li, Huo Coco, Guo Juntao. Acoustic emission monitoring of wear state of diamond grinding wheel based on EMD [J]. J. Hunan Univ. (Nat. Sci. Ed. ) 2019, 46, 58. [Google Scholar]
- J. H. Zhou, C.K. Pang, Z.W. Zhong, F.L. Lewis, Tool wear monitoring using acoustic emissions by dominant-feature identification. IEEE Trans. Instrum.Meas. 2011, 60, 547–559. [Google Scholar] [CrossRef]
- X. Li, Real-time detection of the breakage of small diameter drills with wavelet transform. Int. J. Adv. Manuf. Technol. 1998, 1, 539–543. [Google Scholar]
- Bi Guo, Guo Yinbiao, Han Wei. Research on-line Identification method of Wear State of Precision grinding Wheel based on Information Fusion [J]. Mech. Strength 2013, 35, 737–742. [Google Scholar]
- Pan Yongcheng. Research on Precision dressing and Acoustic Emission on-line Monitoring Technology of Diamond Wheel [D]. 2014.
- Shi Jian. Research on-line Measurement of Surface Roughness based on Acoustic Emission Technology [D]. 2014.
- Mu Deqiang, Cui Bo, Xie Xinwang, Chen Yi. Study on-line monitoring system for grinding wheel wear and passivation [J]. Sci. Technol. Eng. 2014, 14, 91–95. [Google Scholar]
- Ding Ning, Duan Jingsong, Shi Jian, Liu Chao, Jiang shuna. Research on wear monitoring system of grinding wheel based on acoustic emission [J]. J. Nanjing Univ. Aeronaut. Astronaut. 2020, 52, 48–52. [Google Scholar]
- Xin HUANG,Haonan LI,Zhiwen RAO,Wenfeng DING. Fracture behavior and self-sharpening mechanisms of polycrystalline cubic boron nitride in grinding based on cohesive element method[J]. Chin. J. Aeronaut. 2019, 32, 2727–2742. [Google Scholar] [CrossRef]
- Xiaohu XU, Dahu ZHU, Haiyang ZHANG, Sijie YAN,Han DING. Application of novel force control strategies to enhance robotic abrasive belt grinding quality of aero-engine blades[J]. Chin. J. Aeronaut. 2019, 32, 2368–2382. [Google Scholar] [CrossRef]
- Huang Zhi, Dong Huazhang, Zhou Zhenwu, Wu Xiang, Zhao Liao. Digital modeling and prediction of TC4 grinding force for abrasive belt grinding [J]. Surf. Technol. 2018, 47, 250–258. [Google Scholar]
- Ding Wenfeng, Miao Qing, Li Benkai, Xu Jiuhua. Research progress of aeroengine-oriented nickel-based alloy grinding technology [J]. J. Mech. Eng. 2019, 55, 189–215. [Google Scholar] [CrossRef]
- Jing Li,Hui Qian,Biao Li,Nan-Yan Shen. Research on the influences of torsional deformation on contour precision of the crank pin[J]. Adv. Manuf. 2015, 3, 123–129. [Google Scholar] [CrossRef]
- Faramarzi Farhad, Ebrahimi Farsangi Mohammad Ali,Mansouri Hamid. Simultaneous investigation of blast induced ground vibration and airblast effects on safety level of structures and human in surface blasting[J]. Int. J. Min. Sci. Technol. 2014, 24, 663–669. [Google Scholar] [CrossRef]
- Xu Yanwei, Chen Lihai, Yuan Zihao, Jie Tancheng. Intelligent recognition of tool wear status based on information fusion [J]. Vib. Shock 2017, 36, 257–264. [Google Scholar] [CrossRef]
- Guo Weicheng, Li Beizhi, Yang Jianguo, Zhou Qinzhi. Signal Monitoring of grinding process and modeling of GRINDING WHEEL WEAR PREDICTION J. J. Shanghai Jiao Tong Univ. 2019, 5312, 1475–1481. [Google Scholar]
- Bi Guo, Wang Huixue, Zhou Lian, Shao Shengyang. Evaluation of grinding performance degradation of diamond grinding wheels J. Opt. Precis. Eng. 2019, 2707, 1508–1515. [Google Scholar]
- LAI Jizhou,BAI Shiyu,XU Xiaowei,Lü Pin. A Generic Plug-and-Play Navigation Fusion Strategy for Land Vehicles in GNSS-Denied Environment[J]. Trans. Nanjing Univ. Aeronaut. Astronaut. 2019, 36, 197–204. [Google Scholar] [CrossRef]
- Ding Yijie,Yao Xiaofei,Wang Sheliang,Zhao Xindong. Structural damage assessment using improved Dempster-Shafer data fusion algorithm[J]. Earthq. Eng. Eng. Vib. 2019, 18, 395–408. [Google Scholar] [CrossRef]
- Ma Shujun, Yang Lei, Bai Xinhui, Li Zhongming. Improvement of map fusion algorithm for multi-robot simultaneous positioning and map construction [J]. Control Theory Appl. 2019, 36, 1345–1350. [Google Scholar]
- Faquan Yang,Ling Yang,Dong Wang,Peihan Qi,Haiyan Wang. Method of Modulation Recognition Based on Combination Algorithm of K-Means Clustering and Grading Training SVM[J]. China Commun. 2018, 15, 55–63. [Google Scholar]
- V. E. Rubtsov,E. A. Kolubaev,A. V. Kolubaev,V. L. Popov. Using acoustic emission for the analysis of wear processes during sliding friction[J]. Tech. Phys. Lett. 2013, 39, 223–225. [Google Scholar] [CrossRef]
- Zhehe Yao,Deqing Mei,Zichen Chen. On-line chatter detection and identification based on wavelet and support vector machine[J]. J. Mater. Process. Technol. 2010, 210, 713–719. [Google Scholar] [CrossRef]
- Zhang Shuyue, Zhou Kun, Wang Wenjian, Guo Jun, Liu Qiyue. Study on the effect of grinding parameters on the wear and material removal of the grinding stone of the rail [J]. J. Tribol. 2018, 38, 327–333. [Google Scholar] [CrossRef]
- Machine Learning - Support Vector Machines; Reports on Support Vector Machines from King Saud University Provide New Insights (SVM ensembles for named entity disambiguation)[J]. J. Robot. Amp; Mach. Learn.
- Engineering; Studies from China Agricultural University Update Current Data on Engineering (Evaluation On Frozen Shellfish Quality By Blockchain Based Multi-sensors Monitoring and Svm Algorithm During Cold Storage)[J]. News Sci. 2020.
- Mahyar Ghazvini,Mohammad Dehghani Madvar,Mohammad Hossein Ahmadi,Mohammad Hossein Rezaei,Mamdouh El Haj Assad,Narjes Nabipour,Ravinder Kumar. Technological assessment and modeling of energy-related CO2 emissions for the G8 countries by using hybrid IWO algorithm based on SVM[J]. Energy Sci. Eng. 2020, 8.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
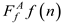 and
and 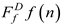 are used to
represent the wavelet packet coefficients after threshold processing of the high-frequency and low-frequency parts of the signal, namely
are used to
represent the wavelet packet coefficients after threshold processing of the high-frequency and low-frequency parts of the signal, namely
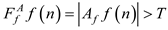
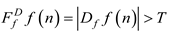
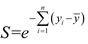
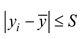
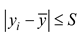 , it means that the eigenvalue yi is less disturbed by the outside world and can better
reflect the grinding wheel wear characteristics. If
, it means that the eigenvalue yi is less disturbed by the outside world and can better
reflect the grinding wheel wear characteristics. If 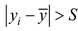 , it means
that the external interference is greater. The feature values obtained after
threshold filtering are used as input feature values for the monitoring model
proposed in this paper.
, it means
that the external interference is greater. The feature values obtained after
threshold filtering are used as input feature values for the monitoring model
proposed in this paper.