Prerpints.org logo
Preprint
Article

Thermomechanical and Viscoelastic Characterization of Continuous GF/PETG Tape for Extreme Environment Applications

Altmetrics

Downloads

63

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 August 2024

Posted:

28 August 2024

You are already at the latest version

Alerts
Abstract
The thermomechanical and viscoelastic properties of a glass fiber polyethylene terephthalate glycol (GF/PETG) continuous unidirectional (UD) tape were investigated using differential scanning calorimetry (DSC), thermo-mechanical analysis (TMA), and dynamic mechanical analysis (DMA). The study identified five operational conditions based on Army Regulation 70-38 Standard. The DSC results revealed a glass transition temperature of 78.0 ± 0.3°C, guiding the selection of temperatures for TMA and DMA tests. TMA provided the coefficient of thermal expansion in three principal directions, consistent with known values for PETG and GF materials. DMA tests, including strain sweep, temperature ramp, frequency sweep, creep, and stress relaxation, defined the linear viscoelastic region and temperature-dependent properties of the material. The frequency sweep indicated an increase in modulus with rising frequency, identifying several natural frequency modes. Creep and stress relaxation tests showed time-dependent behavior, with strain increasing under higher loads and stress decreasing over time for all tested input values. Viscoelastic models fitted to the data yielded R² values of 0.99, demonstrating good agreement. The study successfully measured thermo-mechanical and viscoelastic properties across various conditions, providing insights into how temperature influences the material's mechanical response under extreme conditions.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Polymer composite materials are commonly used in the automotive and aerospace industries due to their strength-to-weight ratio. The extreme environment application of polymer composite materials is drawing attention to new developments in space, superconducting magnets, and electronic technologies [1]. Applications include liquid propellant tanks, satellites, spacecraft, aircraft structures, support elements, electrical insulation for superconducting magnets, and Arctic exploration structures [2]. Due to the viscoelastic nature of polymer material, their properties are dependent on multiple factors like temperature, frequency, deformation, and time [3] which can affect the mechanical and structural performance of the composite part. Understanding material behavior at extreme temperatures is of interest for predicting mechanical failure under extreme conditions [4]. Requirements for polymer materials in these extreme applications are complicated as the material must withstand loading under multiple conditions. The thermo-mechanical properties at low temperatures are critical. At low temperatures, polymers are below their glass transition temperature, showing little viscoelastic behavior [5]. The coefficient of thermal expansion (CTE) is required for predicting thermally induced stresses when different materials are combined and exposed to a range of temperatures [1]. For continuous composite materials, both the fiber and matrix material influence the deformation. For the fiber material, there is a difference in CTE in the longitudinal and transverse directions [6]. For glass fibers, the material contracts in both directions as its cool-down [7]. Differences in CTE values create complex stress states when there is a combination of material expansion and contraction within the composite system, which can increase the interface strength between the components [2]. For other fiber materials at low temperatures, it develops cracks in the interface, which also increases the surface roughness of the fiber [8]. The increase in surface roughness also contributes to the interfacial strength between the fiber and matrix through mechanical interlocking [2].
It has been shown that the temperature-dependent properties of polymer materials depend on material structure. At low temperatures, the strength and modulus of most polymers increase while the elongation to failure decreases to extremely low values [2,9,10]. At these low temperatures, a reduction in polymer chain mobility increases the binding forces between the polymer molecules and increases the material strength. Moreover, the lower the temperature, the longer it takes stress to relax [11]. This behavior limits the use of polymers at extreme temperatures when flexibility and elasticity are required [2]. For polymer systems, the rate-dependent behavior [13] and the frequency-dependent behavior [14] have been demonstrated using various methods. For a polyethylene terephthalate glycol (PETG) material, the increase in frequency input shifts the glass transition temperature to a higher value [12]. For other polymer systems, the increase in modulus has been shown with an increase in frequency input [13]. High-frequency input can cause vibrational characteristics (natural frequencies, damping ratio, and mode shapes) in the polymer material, which induces inherent material nonlinearities [3]. Thermal lag through multiple heating ramps has been measured for other material systems, which can influence the temperature-dependent properties of the polymer material [14]. As polymers are also time-dependent, long-term behavior in the extreme environment is of interest for predicting part performance, as dimensional stability and strength can be affected [15]. Long-term input of fixed deformation (stress relaxation) and load (creep) can cause the material to relax and deform and can be significantly influenced by environmental conditions. The mechanisms by which the polymers can flow are affected at low temperatures [4]. For continuous composite systems, the fiber material can alter the creep behavior of the matrix, affecting the creep rate and the creep magnitude [15]. Creep behavior has three stages: elastic deformation (instantaneous) and primary and secondary creep. For creep, increasing temperature and input load increases material deformation [16,17,18].
The work presented in this study is part of a larger research focus to understand polymer material behavior under extreme environment. Several research objectives have been identified for this work. These are 1) introduce an existing material for extreme environment applications, 2) investigate the thermomechanical properties of a continuous GF/PETG tape material under extreme environments, 3) evaluate the storage modulus under a range of environmental conditions, 4) evaluate the viscoelastic behavior via creep and stress relaxation to predict long-term performance in variable environmental and loading conditions, 5) identify the effect of input frequency on part performance, and 6) identify models to predict the material viscoelastic behavior. Five operational conditions have been identified using the Army Regulation 70-38 Standard [19]. Various tests were performed to measure the material response within the temperature range. The coefficient of thermal expansion, elastic properties, and the viscoelastic properties were measured. Moreover, viscoelastic models have been identified to fit the experimental data showing the need for complex models for the prediction of properties.

2. Materials and Methods

2.1. Materials

A glass fiber reinforced polyethylene terephthalate glycol (GF/PETG) continuous unidirectional (UD) tape (PolystrandTM IE 5843.1) from AVIENT was used in this work. The matrix material, PETG, is widely used in additive manufacturing due to its stiffness, strength, and chemical and UV resistance [20]. The GF/PETG UD tape material has a glass fiber mass content of 58 % and a thickness of 0.203 mm, based on the supplier material data sheet.

2.2. Operational Conditions

Using composite materials to design shelter structures in extreme environments is of interest. Table 1 shows the temperatures selected with the design type and daily cycle designation following the Army Regulation 70-38 Standard [19]. A temperature range covering all five daily cycles was selected to measure the thermomechanical properties of the GF/PETG material.

2.3. Differential Scanning Calorimetry (DSC)

A TA Differential Scanning Calorimeter DSC2500 (TA Instruments, New Castle, DE, USA) was used for the thermal characterization of the materials. TA’s Tzero pans and lids were utilized for testing. Between 3 mg to 10 mg of material was used per specimen. A total of four specimens were tested. Following ASTM E793—06, D3418—21, and E1269 − 11, a 10 K/min ramp was used. The testing procedure consists of a heating-cooling-heating process. The first heating provides the properties resulting from the manufacturing process. The cooling serves as an annealing process. This allows the material to reach a thermodynamic equilibrium. The second heating provides the properties of the polymer material without processing effects. The Tg value was measured using the specific heat capacity versus the temperature curve of the second heating ramp. The measured Tg is 78.0 +- 0.3 °C. The magnitude of the measured Tg value of the PETG matrix material is according to that found in the literature [21,22,23,24]. The measured Tg value allows determining the upper limit for the TMA and DMA testing.

2.4. Thermo-Mechanical Analysis (TMA)

A TA Thermomechanical Analyzer TMA Q400 (TA Instruments, New Castle, DE, USA) was used for the thermo-mechanical characterization of the materials. The TMA measures the change in deformation as a function of temperature. The coefficient of thermal expansion (CTE) was calculated using the initial length of the material. Based on the ASTM E831-19 standard, the sample length was under 10 mm. The CTE was measured in all three principal directions. The CTE was computed between -50 °C and 50 °C. A minimum of three repetitions was performed for all directions. A heating ramp of 5 °C/min was used for the tests.

2.5. Dynamic Mechanical Analysis (DMA)

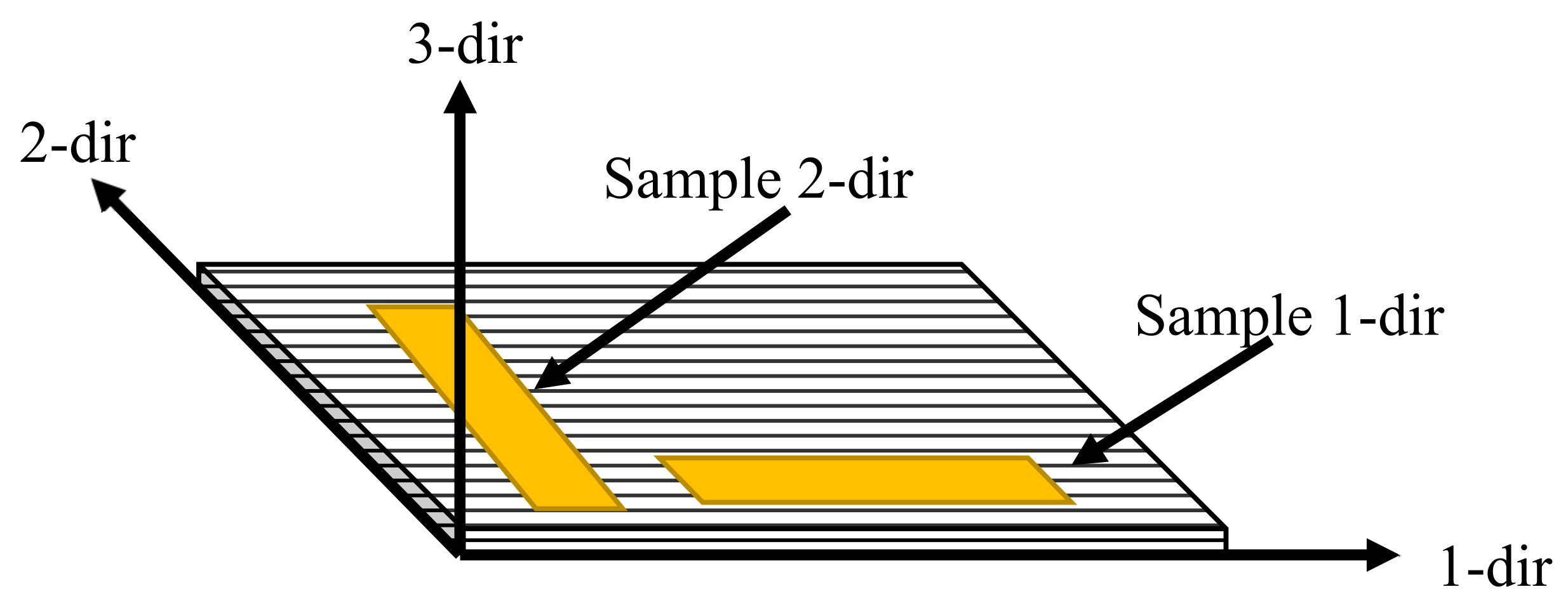
A TA Dynamic Mechanical Analyzer DMA850 (TA Instruments, New Castle, DE, USA) was used to characterize the materials. Strain sweep, temperature ramp, frequency sweep, creep test, and stress relaxation test were performed on the GF/PETG material. ASTM D5023, D7028, E1640, and D2990-17 were referenced when selecting the input parameters. A three-point bending clamp with a span of 50 mm was used for the material characterization to avoid clamping effects on the material’s mechanical response. Samples were machined along the fiber direction (1-dir) and transverse to the fiber direction (2-dir), as schematically depicted in Figure 1.

2.5.1. Strain Sweep Test

A strain sweep test was performed on samples in the 1-dir and 2-dir. The test was performed using a frequency of 1 Hz. The strain percentage used was between 0.001 and 0.1. The strain sweep was performed at -50°C, 30°C, and 60°C. The strain sweep test was performed at multiple temperature values to determine a strain percentage value that falls within the linear viscoelastic region (LVR) for all three temperature values.

2.5.2. Temperature Ramp Test

A temperature ramp test was performed on samples in the 1-dir and 2-dir. The test was performed using a frequency of 1 Hz. A 5°C/min temperature ramp was used following the ASTM standard. A strain percentage of 0.005% and 0.01% was used for samples in the 1-dir and 2-dir, respectively, determined by the strain sweep test. The temperature ramp was performed from -70°C to 100°C. The temperature range was selected to include the five operational conditions in Table 1. A 15-minute soak time was provided for homogenizing samples before the start of the test.

2.5.3. Frequency Sweep Test

A frequency sweep test was performed on samples in the 1-dir and 2-dir. The test used a frequency range of 0.1 Hz to 150 Hz. A soak time of 15 min was provided for homogenizing samples before the start of the test. A strain percentage of 0.005% and 0.01% was used for samples in the 1-dir and 2-dir, respectively. The strain sweep test determined these values. The frequency sweep test was performed at -70°C, -25°C, 0°C, 30°C, and 60°C.

2.5.4. Creep and Stress Relaxation Test

Creep test and stress relaxation test were performed on samples in the 2-dir. A 15-minute soak time was provided for homogenizing samples before the test. Each test was performed for 30 minutes. Table 2 shows the temperature, load, and strain % values used for the creep and stress relaxation test.
A master curve was created by applying the time-temperature-superposition (TTS) principle to predict long-term material performance. An Arrhenius fit was used to predict the shift factor. The concepts are described in detail in the following subsection.

2.6. Manufacturing of Samples

Two-inch-wide tapes were laid by hand to produce plates measuring 14 inches by 14 inches. A layup of [015] was used for DMA testing, while a layup of [025] was used for TMA testing. These layups were selected based on the respective ASTM standards. A Monarch compression molding press (model: CMG30H-15-CPX) (Carver Inc., Wabash, IN, USA) was then used to consolidate and bond the materials into plates. Table 3 shows the processing parameters used to manufacture the GF/PETG material. These parameters were selected based on the results from previous work [25].

2.7. Conditioning of Samples

Before testing, specimens were conditioned for at least 40 hours at 23.0 ± 2°C and 50 ± 10% relative humidity according to Procedure A of the ASTM D618-21 standard.

3. Modeling of Viscoelastic Behavior

Polymer materials, at a specific temperature and molecular weight, may behave as a liquid or as a solid, depending on the time scale (speed) at which the molecules are deformed [26]. This material behavior is generally referred to as the viscoelastic behavior. This work focused on linear viscoelasticity, which is valid for material systems that undergo small deformations. In linear viscoelasticity, the stress relaxation test, creep test, the time-temperature-superposition (TTS) principle, and the Boltzmann superposition principle are often used to explain the behavior of polymer materials during deformation.

3.1. Time-Temperature-Superposition (TTS)

The TTS principle describes the relationship between time scale and temperature. The time-temperature equivalency of the creep test and stress relaxation test can be used to reduce data at various temperatures into one master curve for a reference temperature (curve), Tref. A master curve is generated by fixing the reference curve and shifting the remaining curves horizontally until the ends of all curves become superimposed. The density changes are usually small and negligible, eliminating the need for tedious corrections. The magnitude of each curve’s shift can be plotted as a function of the temperature difference from the reference temperature using a shift factor. Several shift factors are available. As the temperatures for frequency sweep, stress relaxation test, and creep tests are below the Tg of the material, this work used the Arrhenius shift factor defined by Equation (1).
l n a T = − E a R 1 T − 1 T r e f
where Ea is the apparent activation energy, R is the universal gas constant, T is the temperature in Kelvins, and Tref is the reference temperature in Kelvins. For the TTS to apply, the material must be homogeneous, isotropic, and amorphous. The material must also be linear viscoelastic under the deformation of interest. This work applied the TTS principle to the samples oriented in the 2-dir to predict the material performance at long time scales. This is because the material response in the 2-dir is assumed to be predominantly of the matrix material.

3.2. Boltzmann Superposition Principle

The Boltzmann superposition principle states that the deformation of a polymer component is the sum or superposition of all strains that result from the various loads acting on the part at different times. The material response to a specific load is independent of already existing loads. By adding all strain responses, the deformation upon which several loads act at different points in time can be computed [26]. The Boltzmann superposition principle holds if the polymer follows a linear viscoelastic behavior.

3.3. Stress Relaxation and Creep Test

In a stress relaxation test, a material is deformed by a fixed amount (input), while the stress required to hold the input deformation is recorded over time (response). The stress relaxation modulus can be defined by Equation (2).
E r t = σ t ε o
where Er is the relaxation modulus, εo is the input strain, and σ(t) is the measured stress. The stress relaxation of a polymer material is time and temperature dependent. Relaxation time refers to the time applied stresses take to relax within the material. Low temperatures lead to significant relaxation times, while high temperatures lead to small relaxation times.
A creep test measures the material deformation (response) under a fixed load or stress (input). The creep test is performed at a constant temperature using a range of applied stress. There are three phases of creep in polymer materials. These are primary, secondary, and tertiary creep. An initial elastic strain is caused upon the application of the fixed load. The initial strain is followed by the primary and secondary creep phases, also called the steady state. The fixed load causes the polymer chains to untangle and rearrange, resulting in greater chain alignment [27]. During tertiary creep, the strain rate increases, leading to eventual failure [28]. The creep modulus is defined by Equation (3).
E c = σ o ε t
where Ec(t) is the creep modulus, σo is the input stress, and ε(t) is the measured strain.

3.4. Stress Relaxation Modeling

Several viscoelastic models exist to predict the material response under constant stress or strain. A Prony series is a model used to predict the viscoelastic response of a material. In this work, the stress relaxation is modeled using the Prony series [29]. The Prony series has a form as defined by Equation (4).
σ t = ∑ i = 1 N σ i e − t λ i
where σ is the material stress response, λi is the relaxation time (viscosity divided by the storage modulus, μ E ), and σi is the stress coefficient. The Prony series is fitted to the data and compared using 3 (Prony3), 4 (Prony4), and 5 (Prony5) terms.

3.5. Creep Modeling

Several physical models for creep behavior exist for polymer composite materials. Among them, the four-element Burgers model [30] and the Findley empirical power law model has been used for composite materials [27,31]. The Burgers model connects a Maxwell and Kelvin unit in series. The Burgers model divides the creep strain into three parts: 1) the instantaneous deformation, 2) viscoelastic deformation, and viscous deformation. The Burgers model is represented by Equation (5).
ε t = ε 1 + ε 2   1 − e x p − t λ 2 + ε 1 λ 1 t
where ε 1 = σ o E 1 , ε 2 = σ o E 2 , λ 1 = η 1 E 1 , λ 2 = η 2 E 2 , σo is the input stress, E1 and E2 are the elastic modulus of the Maxwell and Kelvin springs, and η1 and η2 are the viscosities of the Maxwell and Kelvin dashpots. The Findley model is represented by Equation (6).
ε t = a t b + ε o
where εo is the instantaneous strain, and a and b are material constants.

4. Results and Discussion

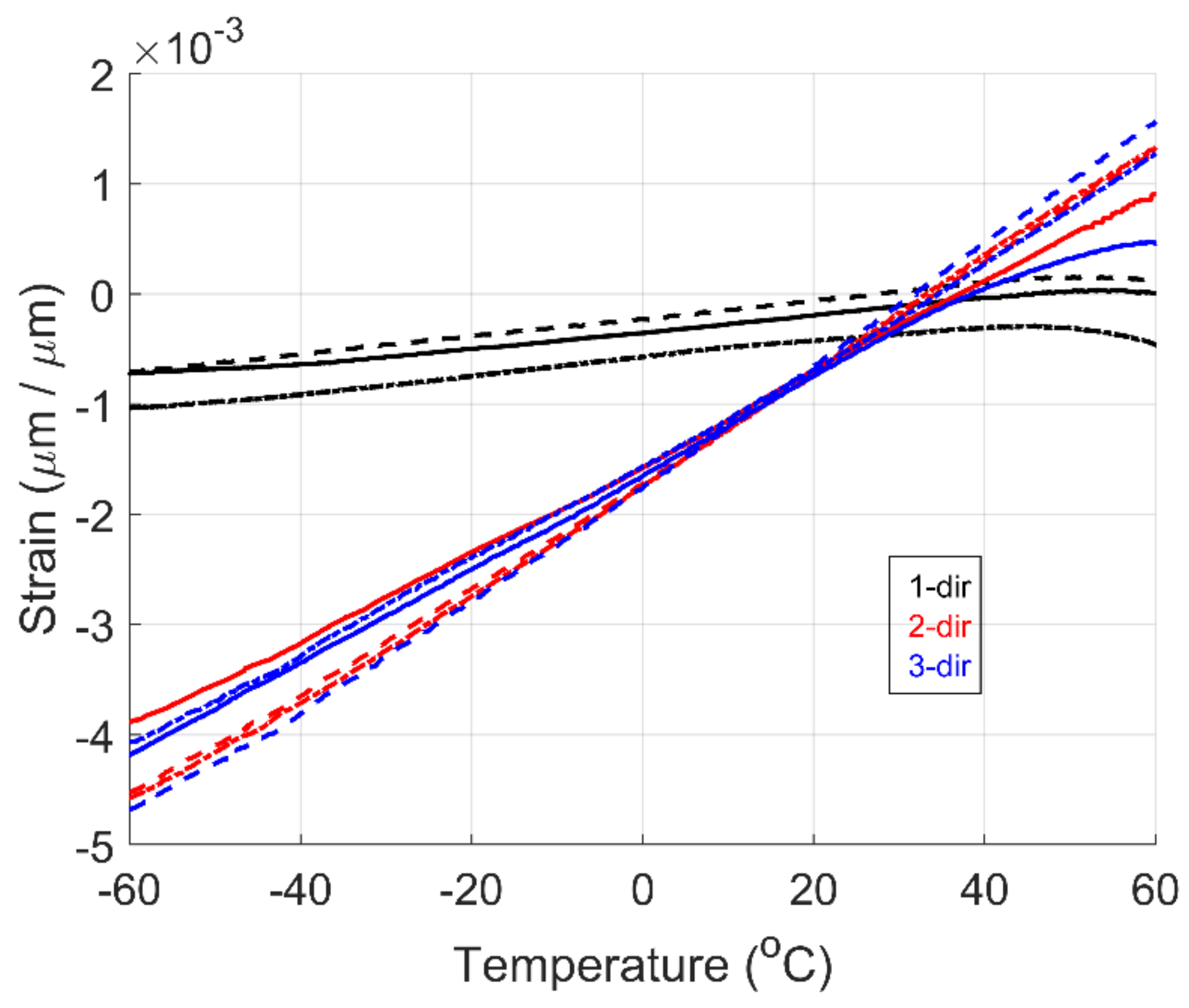
4.1. TMA Results

A temperature ramp was performed in all principal directions to calculate the dimension change as a function of temperature. The coefficient of thermal expansion (CTE) was computed from -50 °C to 50 °C (below Tg). Figure 2 shows the TMA data for the GF/PETG material. Above 75 °C, a shift in deformation is observed. This change in deformation is attributed to the material changing phases from solid elastic to viscoelastic. Residual stresses due to thermal gradients during cooling can affect the material behavior when reaching Tg.
Table 4 shows the average CTE and standard deviation for all principal directions. In practice, all fibers should be oriented in the 1-dir. However, due to processing, the fibers can shift, inducing the orientation of fibers within the plate/material. The average CTE in the 2-dir and 3-dir are within the same magnitude. Visual inspection of the samples showed that some plates have minor fiber orientation in the 2-dir. The CTE value in the 1-dir is that of the glass fiber material [32]. For the 2-dir and 3-dir, the values are similar to that of neat PETG material [33]. The difference between the 2-dir and 3-dir can be attributed to the minor fiber orientation resulting from the manufacturing process. The CTE is linear within the temperature range of interest, as shown in Figure 2.

4.2. DMA Results

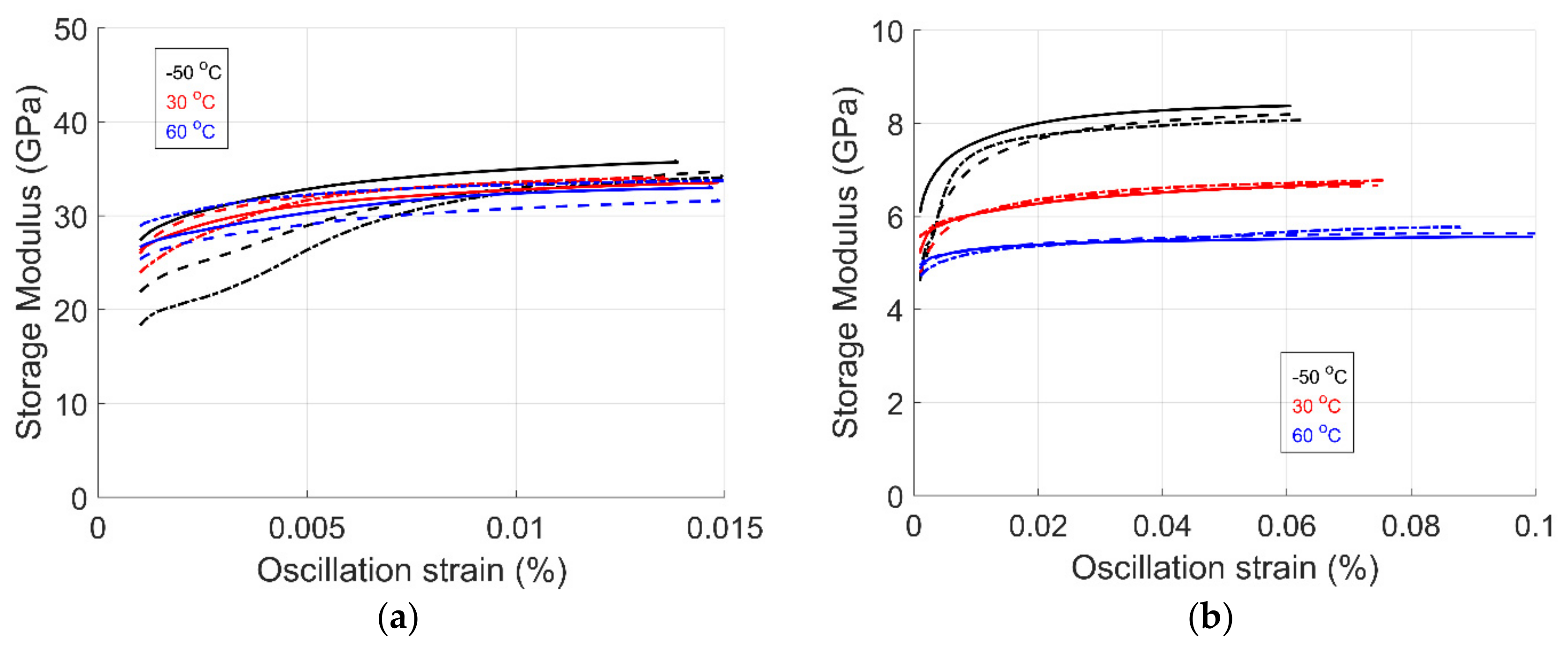
4.2.1. Strain Sweep Test Results

To identify the LVR, a three-point bending strain sweep test was performed. Due to the equipment limitations and stiffness of the samples in the 1-dir, they did not deform above 10-2 strain %. The storage modulus was used as a reference for selecting the LVR. Figure 3 shows the strain sweep results for samples in the 1-dir and 2-dir. The storage modulus of the samples in the 1-dir is significantly higher than that of the 2-dir. The storage modulus of the samples in the 2-dir corresponds primarily to the matrix material, while for samples in the 1-dir, it is represented by the fiber material.
Figure 3a show that for all three temperatures, the modulus increases with strain. There is no significant difference in modulus when comparing the temperature. Figure 3b show that the storage modulus behaves mostly linear over the strain range. The storage modulus increases as temperature decreases, becoming stiffer. As temperature increases, the modulus decreases. This behavior is expected and goes according to what is found in the literature. To help determine the strain percentage within the LVR, the strain limit was calculated using the tensile and flexural strength and modulus based on the material datasheet (MDS). The tensile strain limit was 3.1% and 0.4% for the 1-dir and 2-dir, respectively. For the flexural strain limit, a value of 2.4% was calculated for the 1-dir. Using the storage modulus as the reference property and the reference strain limits, the strain percentage selected is 0.005% for samples in the 1-dir and 0.01% for samples in the 2-dir, which are situated at the beginning of the LVR (as shown in Figure 3), which are below the critical strain. These values were used for the temperature ramp and frequency sweep test, and the strain percentage was used as a reference for selecting the input values for the stress relaxation test.

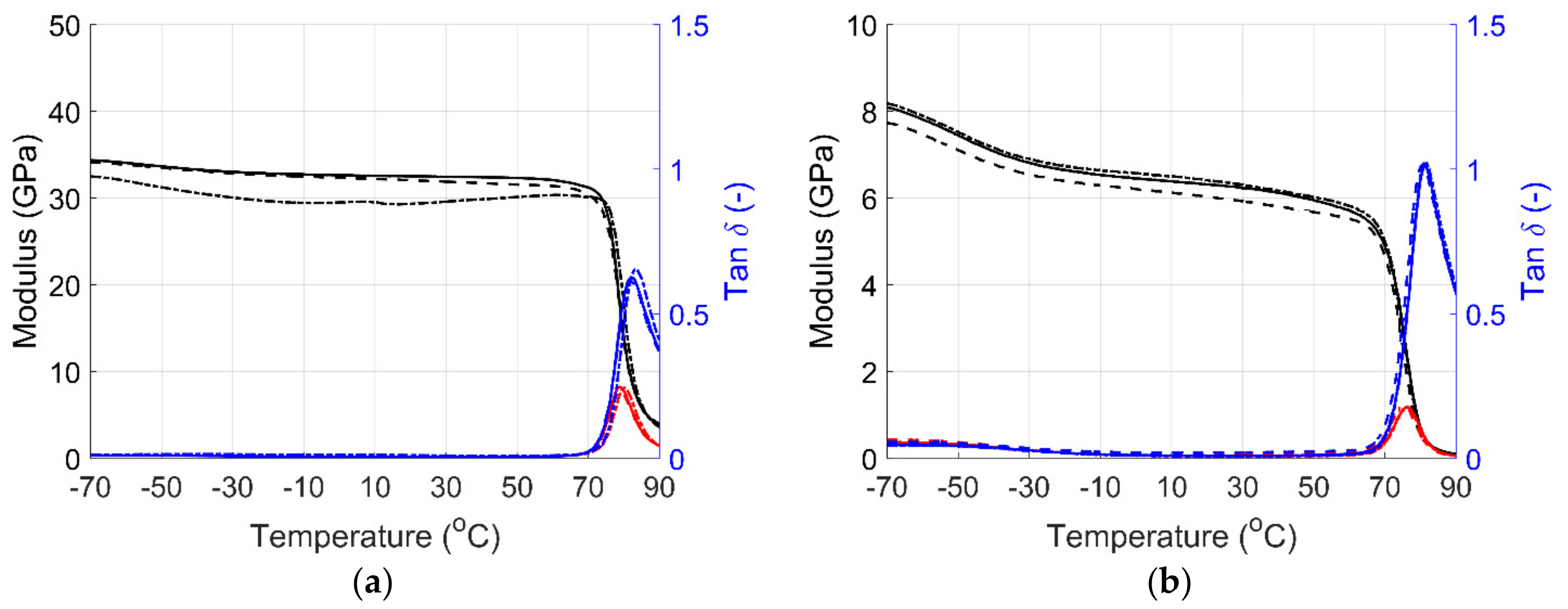
4.2.2. Temperature Ramp Test

A three-point bending temperature ramp test measured the temperature-dependent flexural modulus. The flexural modulus is used as a proxy to compare material properties to tensile properties [34]. Figure 4 shows the temperature ramp test result for GF/PETG. The temperature ramp was performed from -70 °C to 110 °C. The temperature range was selected to include the five operational conditions shown in Table 1 and DSC results. The maximum temperature was chosen according to the Tg measured via DSC. Both the storage and loss modulus decrease with temperature. The increase in stiffness and brittleness is attributed to the extremely low temperatures. The modulus steadily decreased from the lowest temperature up to the Tg. After Tg, the modulus decreases significantly as a result of the phase change of the matrix material. Regarding the magnitude of the values at ambient temperature (15-25°C) for both the strain sweep and temperature ramp, these are within the same magnitude for both the 1-dir and 2-dir when compared to the material datasheet and values found in the literature [25].

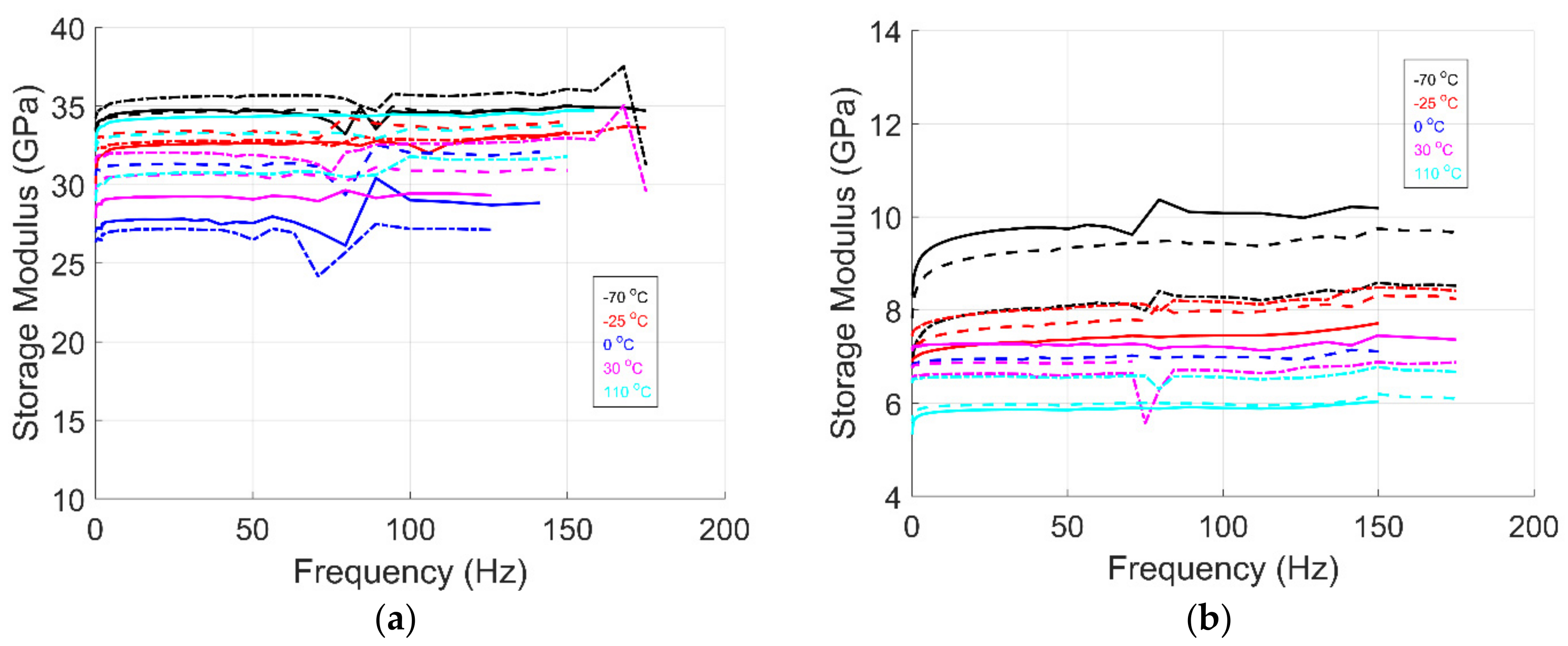
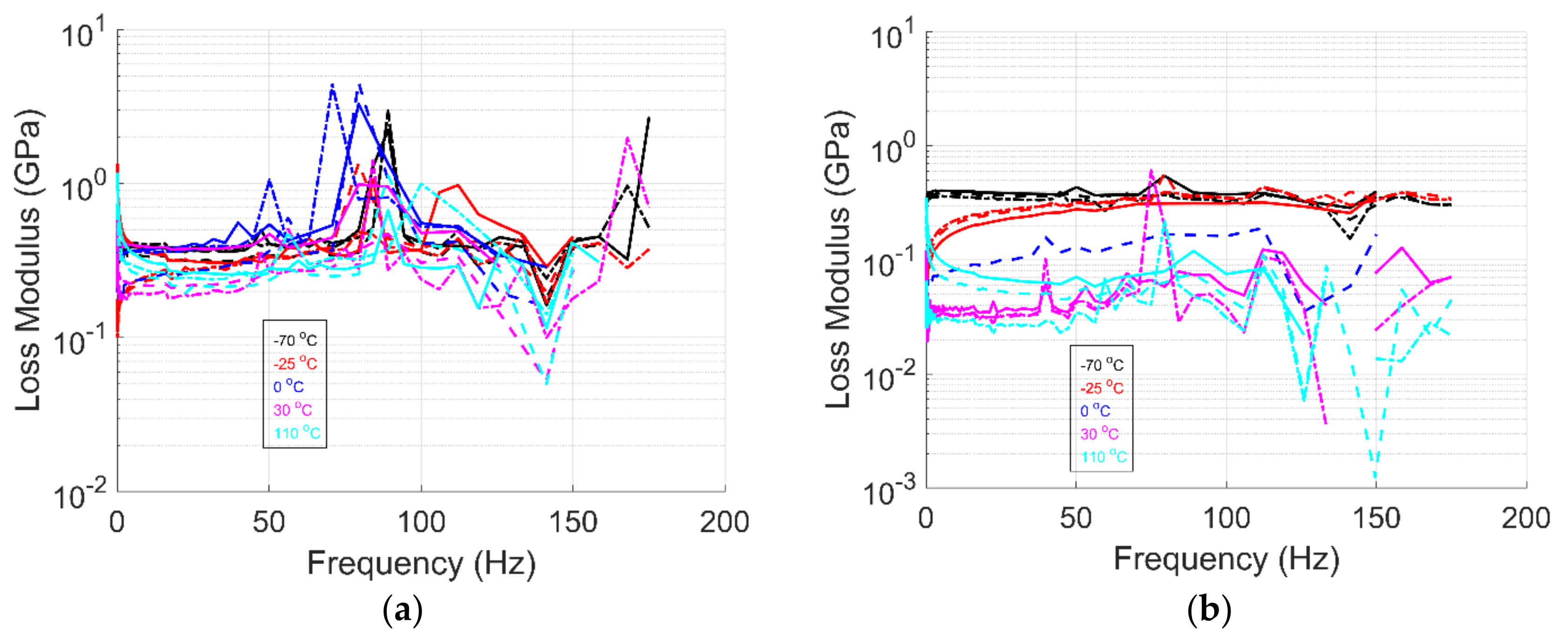
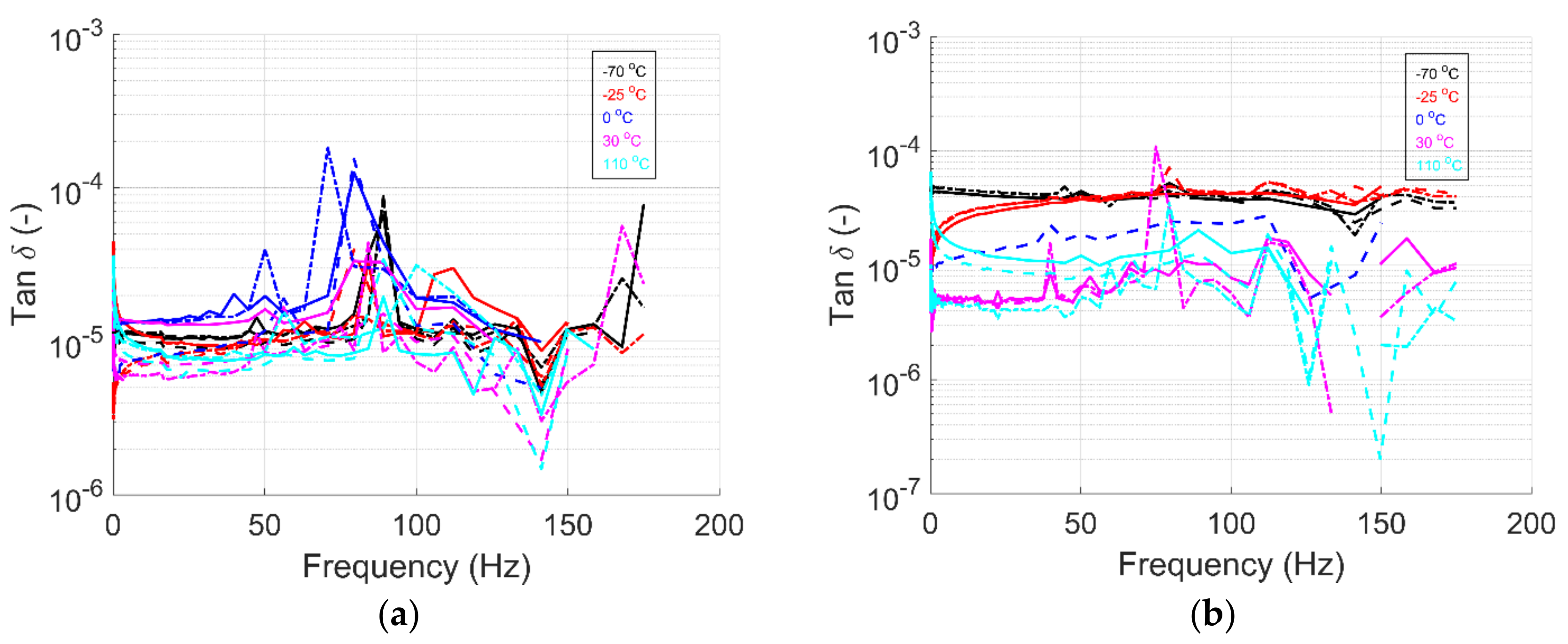
4.2.3. Frequency Sweep Test

A three-point-bending frequency sweep was performed to measure the frequency and temperature dependency on properties. For samples in the 1-dir and 2-dir, a strain percentage of 0.005% and 0.01%, respectively, was used. Figure 5, Figure 6 and Figure 7 show the storage modulus, loss modulus, and tanδ values as a function of frequency for multiple temperature values, respectively. The lower the temperature, the higher the storage modulus is. This is due in part to the increase in stiffness resulting from the temperature change. As frequency increases, the storage modulus also increases [13,35] for both sample orientations. These results were expected. Increasing the frequency input does not allow the material to relax to its initial stage. The frequency increase diminished the loss modulus’s response as it cannot respond to the input loading. As a result, the storage modulus takes control of the material behavior, becoming stiffer with increased frequency loading. When comparing the storage modulus to the other test (strain sweep and temperature ramp), these are within the same order of magnitude and are comparable to the material datasheet [25].
Figure 6a shows the effect of temperature on the loss modulus for samples in the 1-dir. The difference in magnitude due to the impact of temperature is not apparent in the results. The stiffness of the glass fibers may influence the material response. In comparison, the material response for samples in the 2-dir (Figure 6b) is dominated by the PETG matrix, showing the effect of temperature on stiffness.
Figure 7 shows distinct peaks at multiple frequency values. These peaks can be attributed to the natural frequency of the PETG material. These are frequency values at which the material system tends to vibrate in the absence of an input-damping force. A summary of ranges where frequency peak values are present is shown in Table 5. Bradley [3] measured the vibrational behavior of simple supported PETG plates at 30°C and 70°C. Frequency values for the first three modes are within the range of peak values shown in Table 5. Kannan [36] and Mansour [37] performed a vibrational analysis of 3D-printed PETG material. Natural frequency modes are also within the same order of magnitude compared to the measured results for clamp-free end conditions. These results reassure us that the values gathered are, in fact, the natural frequency of the PETG material.
The frequency sweep DMA testing results provide valuable insights into material behavior across a wide range of frequencies. By evaluating the elastic and viscous responses, we can better predict how materials will perform under different conditions. As the input frequency increases, the material properties, such as stiffness and damping, also tend to increase. Excessive vibrations in the system (like walking, equipment vibration, and the vibration due to high winds) can lead to structural and functional issues. Developing a protocol for material characterization is essential to predict material behavior under working conditions and external environmental factors.

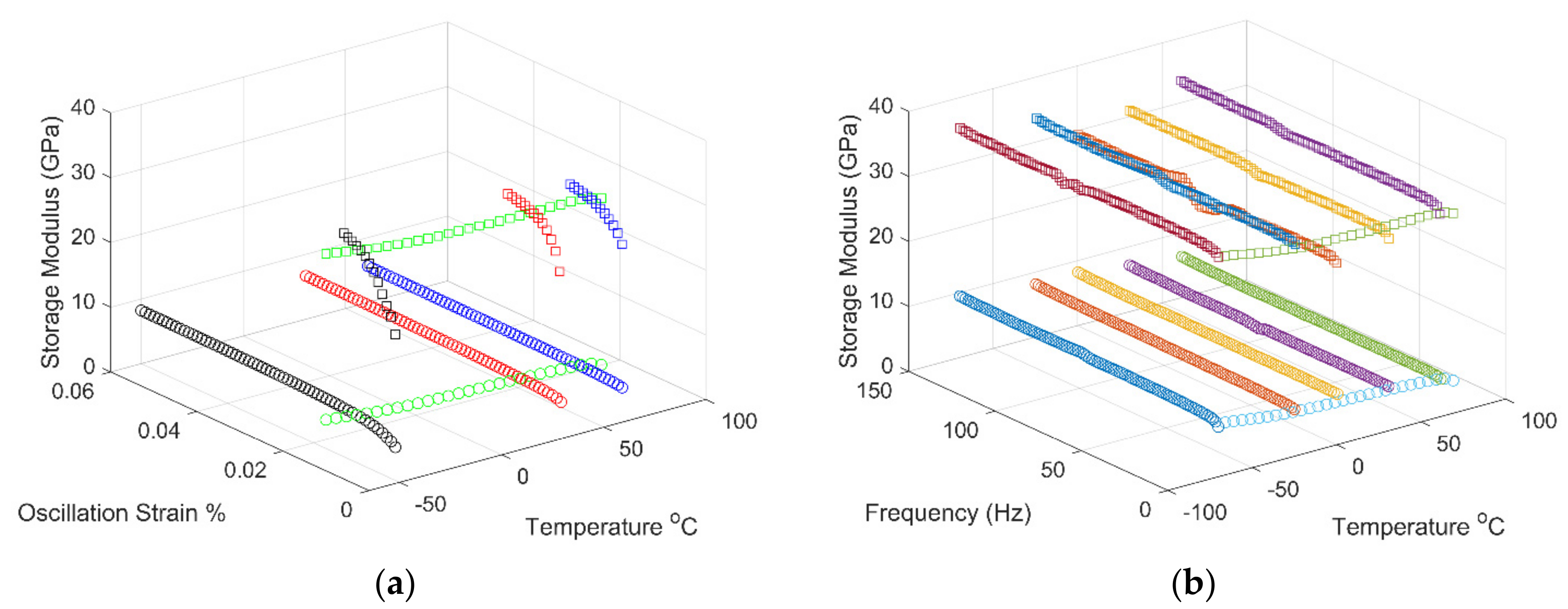
4.2.4. Strain-Temperature-Frequency Dependency

The strain sweep, temperature ramp, and strain sweep test results were combined into two plots. Figure 8 shows the strain-temperature and frequency-temperature dependence on storage modulus. Each data point is the average of three specimens.
When combining the test data, the impact of deformation, temperature, and frequency on the material properties can be observed. An increase in strain % showed a slight increase in the storage modulus. Subsequently, an increase in temperature results in a decrease in storage modulus. An increase in frequency input increased the storage modulus as the response is predominantly elastic. Here, the high-frequency values do not allow the damping effect of the material to interact and respond to the deformation. As the temperature increases, the storage modulus decreases. Multiple frequency modes can be observed, which seem dependent on temperature. The frequency-dependency on storage modulus is higher for samples in the 2-dir. In the 2-dir, the response is predominantly of the matrix material. In the 1-dir, the response is predominantly of the fiber material. The results shown here provide a better visualization and understanding of part performance under different environmental conditions and inputs. Part performance of a polymer material is complex and depends on multiple factors. Understanding the application of the composite part allows for the determination of material characterization techniques required to obtain reliable data for predicting material behavior.

4.2.5. Stress Relaxation Test

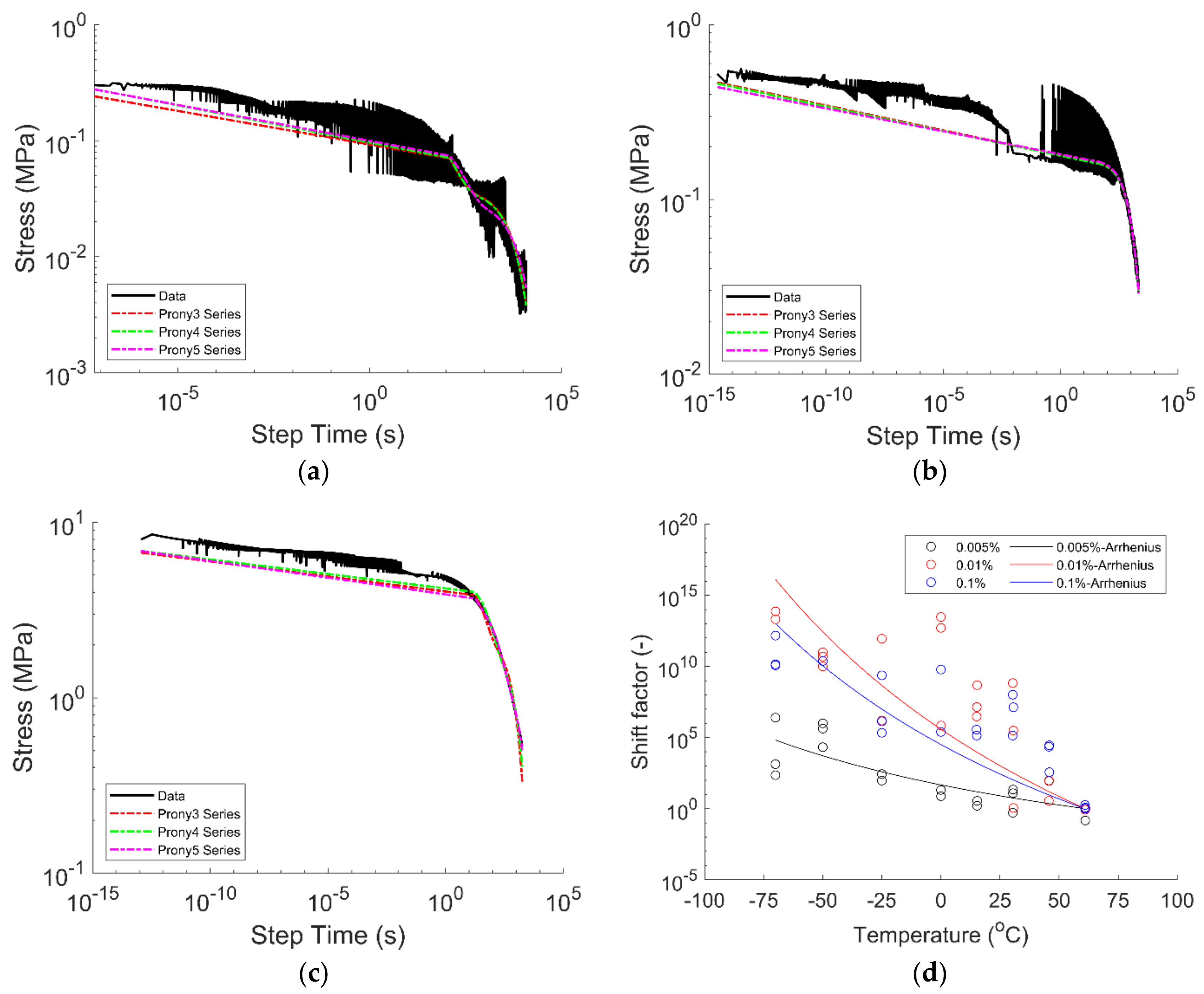
A three-point-bending stress relaxation test was performed at strain % values of 0.005, 0.01, and 0.1. Temperatures used for the stress relaxation test are shown in Table 2. Figure 9 shows the stress as a function of time and the shift factor as a function of temperature for GF/PETG UD tape. These results are for samples oriented in the 2-dir only. Three repetitions were performed for each temperature value. Outliers were removed from the master curve dataset.
The results for the 0.005 and 0.01 strain percentages appear noisy. This may be due in part to the low strain values selected for the test. The master curve was created using the TTS principle at a nominal reference temperature of 60°C. The shift factor was predicted using an Arrhenius model. Table 6 shows the activation energy, Tref, and R2 value for all three strain values.
The strain % values selected are within the LVR, as shown in Figure 3. Figure 9 shows that the stress value also increases as input strain increases. This is expected, as higher deformation results in higher stress values. When looking at the stress development over time, it decreases with increasing time as stress relaxes. This is expected as the polymer molecules relax due to an input deformation. The molecules slip and displace each other to reach an equilibrium state. High temperatures lead to small relaxation times, whereas low temperatures cause the material to have larger relaxation times. This behavior results from the free volume between the polymer molecules, which are reduced at low temperatures, restricting their movement [26]. When looking at the data and master curve plot, it is essential to mention that multiple plates were manufactured for testing. The samples were selected randomly throughout the plates. Variability was observed in the test results during the shifting of the curves and the creation of the master curve. The activation energy is different for all strain values. Higher activation energy lowers the reaction as more energy is needed for this reaction to occur. The R2 values decrease with increased strain value, suggesting that the Arrhenius regression model fits poorly as the strain % input value increases. This can be due to a variety of factors like 1) material properties are affected by variability of processing parameters, 2) range of fiber orientation resulting from fiber wash, 3) experimental error during the sample setup, and 4) variability of properties due to sample location within the manufactured plate. Although these factors can be present in any material processing, it is essential to consider the repeatability of properties. Moreover, due to the fiber wash and resulting fiber orientation, the material may be non-homogeneous and may have a small degree of anisotropy. The CTE values can also corroborate this, which suggests some fiber orientation along the 2-dir.
Prony series were used to predict the material’s stress relaxation response. Table 7 show the R2 values for the Prony series using multiple numbers of terms. The Prony series parameters are shown in Appendix A. The Prony series can predict up to 99% of the material response, depending on the number of terms used. The more terms used, the better the prediction.
The results obtained from stress relaxation testing can significantly aid in predicting residual stresses due to fixed strains, such as those found in bolted joints and connections. Higher torque on a bolt result in higher input strain and, consequently, higher stress values. This may cause the material to take longer to relax at these elevated stress levels. The models used with the experimental data can assist designers and modelers in predicting material performance during the manufacturing and deployment of shelters. For example, designers can predict and mitigate potential issues like warping by understanding how a material relaxes in response to strains caused by thermal events. The predictive capabilities can help ensure that the final product maintains structural integrity and functionality over the intended lifespan.

4.2.6. Creep Test

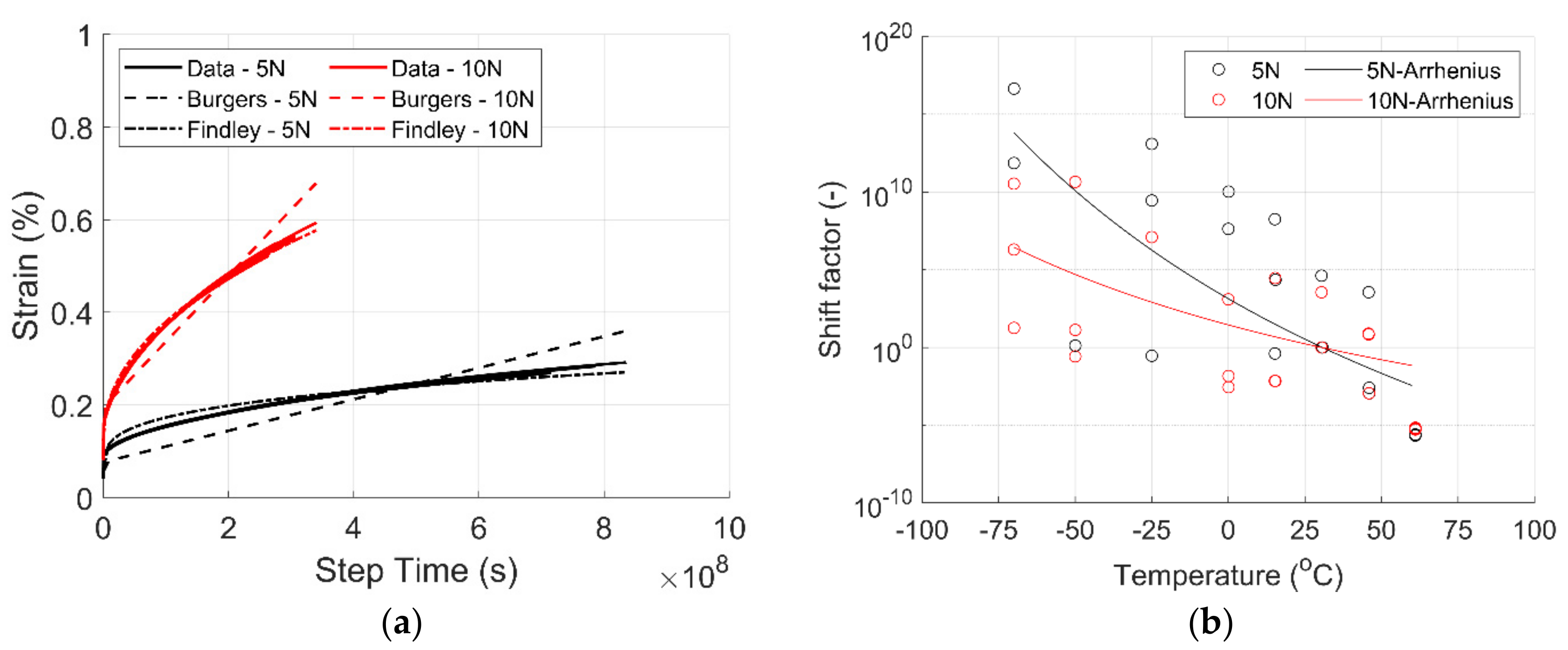
A three-point bending creep test was performed using an input load of 5N and 10N. Temperatures used for the creep test are shown in Table 2. Figure 10 shows the master curve, Burger’s model, Findley’s model, and shift factor for each loading condition. These results are for samples oriented in the 2-dir only. Three repetitions were performed for each temperature value, and outliers were removed from the master curve dataset.
The master curve was created using the TTS principle at a nominal reference temperature of 30 °C. The shift factor was predicted using an Arrhenius model. Table 8 show the activation energy, Tref, and R2 values of all input loads. The fitting parameters for Burger’s and Findley’s models are shown in Table 9 and Table 10, respectively.
Figure 10 shows that the higher the initial input force, the higher the initial deformation will be. As time progresses, the strain increases, showing the material’s viscoelastic response. Like stress relaxation, multiple plates were manufactured for testing, and samples were selected randomly throughout the plates. Variability was observed in the test results during the shifting of the curves and the creation of the master curve. The data shows the first and second stages of creep as the strain increases in the first few hours after the sustained loading. No tertiary creep occurred in either loading condition. The activation energy decreases with an increase in input load. Higher activation energy lowers the reaction speed as more energy is needed for this reaction to occur. The R2 values suggest that the Arrhenius model can predict 50% and 41% of the material response under the input load.
Both Burger’s model and Findley’s model fit the experimental data well, with R2 values above 0.97. Burger’s model seems to produce lower strain values during the first half of the data, while the empirical Findley’s model fits better throughout the data. This was expected as both models have been shown to perform well for other composite systems [27,30,31].
The results found here can aid in predicting the resulting deformation due to a constant input load. The higher the input load, the higher the deformation the material or structure will experience. As a result, the structural integrity will be compromised, and the safety of the operator will be affected. Understanding the material behavior under extreme environments is key to the safety of operations and the completion of the mission.

5. Conclusions

The thermomechanical and viscoelastic properties of continuous GF/PETG tape material were successfully characterized under extreme temperatures. The coefficient of thermal expansion was measured in all principal directions, confirming the transversely isotropic nature of the specimens. The linear viscoelastic region was identified across multiple operational temperatures, and the modulus as a function of temperature and frequency was determined. Master curves for material response under fixed strain (stress relaxation) and load (creep) were developed for various input values. Predictive models, including the Prony series and the Findley model, were employed to forecast long-term material behavior, achieving high accuracy with R² values up to 0.99 for both stress relaxation and creep tests. The shift factor analysis indicated potential heterogeneity or anisotropy in the material’s 2-direction, likely due to fiber distribution and orientation influenced by the material system and manufacturing process. The obtained results align well with existing literature, enhancing our ability to predict material performance under extreme environments and diverse working conditions. Additionally, these findings will help establish protocols for material characterization under such conditions.

Author Contributions

Conceptualization, J.L. Colón Quintana; methodology, J.L. Colón Quintana.; validation, J.L. Colón Quintana, S. Tomlinson and R.A. Lopez-Anido; formal analysis, J.L. Colón Quintana; investigation, J.L. Colón Quintana, S. Tomlinson and R.A. Lopez-Anido; data curation, J.L. Colón Quintana; writing—original draft preparation, J.L. Colón Quintana; writing—review and editing, S. Tomlinson and R.A. Lopez-Anido; supervision, S. Tomlinson and R.A. Lopez-Anido. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by the US Army Combat Capability Development Command (DEVCOM Soldier Center) Expeditionary Maneuver Support Directorate (Contract: W911QY-20-C-0053 P00005). The information has been approved for public release (Approval Number: PR2024-1207).

Acknowledgments

The authors want to thank Danny Pham for helping to manufacture the compression-molded plates, Wesley Bisson, Richard Lafreniere Jr., and Michael McCarty for helping to cut and machine the specimens, Ethan Wasylyna and Benjamin Cobb for performing the testing, and Jeff Hallman for reviewing the manuscript.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this article.

Appendix A: Prony Series Parameters for Stress Relaxation Test

Table A1. Prony series parameters using three terms.
Table A1. Prony series parameters using three terms.
Parameters Strain
0.005 % 0.01 % 0.1
σ 1 0.03801 0.099106 1.788746
σ 2 0.100856 0.202297 2.774809
σ 3 0.103025 0.167182 2.167271
λ 1 5290.396 1.43E-06 0.010216
λ 2 0.003839 0.003383 37.8912
λ 3 108.835 1226.914 960.9927
Table A2. Prony series parameters using four terms.
Table A2. Prony series parameters using four terms.
Parameters Strain
0.005 % 0.01 % 0.1
σ 1 0.101886 0.125352 0.694744
σ 2 0.060999 0.085857 1.864071
σ 3 0.037347 0.166124 2.815188
σ 4 0.077876 0.084475 1.505348
λ 1 114.3204 0.001308 7.59E-05
λ 2 0.022057 0.037773 1178.226
λ 3 5269.863 1242.212 70.45295
λ 4 0.000467 1.22E-06 0.033225
Table A3. Prony series parameters using five terms.
Table A3. Prony series parameters using five terms.
Parameters Strain
0.005 % 0.01 % 0.1 %
σ 1 0.033491 0.138026 0.675695
σ 2 0.077004 0.066438 1.409995
σ 3 0.079044 0.170439 2.051698
σ 4 0.029857 2.93E-10 1.403527
σ 5 0.058365 0.06572 1.33106
λ 1 30.99619 0.001569 7.59E-05
λ 2 0.00046 0.154432 1734.579
λ 3 212.8447 1205.104 165.4361
λ 4 7061.858 0.459256 0.028764
λ 5 0.019483 1.70E-06 16.63023

References

  1. Yano and H. Yamaoka, “Cryogenic properties of polymers,” Prog. Polym. Sci., vol. 20, pp. 585-613, 1995.
  2. Z. Sapi and R. Butler, “Properties of cryogenic and low temperature composite materials—A review,” Cryogenics, vol. 111, p. 103190, 2020.
  3. J. Bradley Carter, “VIBRATION AND AEROELASTIC PREDICTION OF MULTI-MATERIAL STRUCTURES BASED ON 3D-PRINTED VISCOELASTIC POLYMERS,” Miami, 2021.
  4. B. Bonning, C. J. Blackburn, H. A. Stretz, C. D. Wilson and W. R. Johnson, “Superposition-based predictions of creep for polymer films at cryogenic temperatures,” Cryogenics, vol. 104, p. 102979, 2019.
  5. S. Kalia and S.-Y. Fu, Polymers at Cryogenic Temperatures, Springer, 2013.
  6. J. Slifka and D. R. Smith, “Thermal expansion of an E-glass/vinyl ester composite from 4 to 293 K,” Int J Thermophys, vol. 18, pp. 1249-1256, 1997.
  7. Z. Pan, B. Sun and B. Gu, “Thermo-mechanical numerical modeling on impact com- pressive damage of 3-D braided composite materials under room and low tem- peratures,” Aerosp Sci Technol, vol. 54, pp. 23-40, 2016.
  8. Y. Shao, F. Xu, W. Liu, M. Zhou, W. Li, D. Hiu and Y. Qiu, “Influence of cryogenic treatment on mechanical and interfacial properties of carbon nanotube fiber/bisphenol-F epoxy composite,” Composites Part B: Engineering, vol. 125, pp. 195-202, 2017.
  9. L. E. Nielsen and R. F. Landel, Mechanical Properties of Polymers and Composites, New York: Marcel Dekker, 1975.
  10. Y. Kim, M. S. Kim, H. J. Jeon, J. H. Kim and K. W. Chun, “Mechanical Performance of Polymer Materials for Low-Temperature Applications,” Applied Sciences, vol. 12, p. 12251, 2022.
  11. Y. He, S. Yang, H. Liu, Q. Shao, Chen Q., C. Lu,. Y. Jiang, C. Liu and Z. Guo, “Reinforced carbon fiber laminates with oriented carbon nanotube epoxy nanocomposites: Magnetic field assisted alignment and cryogenic temperature mechanical properties,” J. Colloid Interf Sci, vol. 517, pp. 40-51, 2018.
  12. C. V. Subbarao, Y. S. Reddy, V. Inturi and M. I. Reddy, “Dynamic Mechanical Analysis of 3D Printed PETG Material,” in IOP Conf. Series: Materials Science and Engineering, 2021.
  13. J. L. Colon Quintana, A. Redmann, G. A. Mazzei Capote, A. Perez-Irizarry, A. Bechara, T. A. Osswald and R. Lakes, “Viscoelastic properties of fused filament fabrication parts,” Additive Manufacturing, vol. 28, pp. 704-710, 2019.
  14. W. Sun, A. P. Vassilopoulos and T. Keller, “Effect of thermal lag on glass transition temperature of polymers measured by DMA,” International Journal of Adhesion & Adhesives, vol. 52, pp. 31-39, 2014.
  15. J. Raghavan and M. Meshii, “CREEP OF POLYMER COMPOSITES,” Composites Science and Technology, vol. 57, pp. 1673-1688, 1997.
  16. X. Wang, L. X. Gong, L. C. Tang, K. Peng, Y. B. Pei, L. Zhao and L. B. Wu, “Temperature dependence of creep and recovery behaviors of polymer composites filled with chemically reduced graphene oxide,” Composites: Part A, vol. 69, pp. 288-298, 2015.
  17. Kouadri-Boudjelthia, A. Imad, A. Bouabdallah and M. Elmeguenni, “Analysis of the effect of temperature on the creep parameters of composite material,” Materials and Design, vol. 30, pp. 1569-1574, 2009.
  18. Z. Yang, H. Wang, X. Ma, F. Shang, Y. Ma, Z. Shao and D. Hou, “Flexural creep tests and long-term mechanical behavior of fiber-reinforced polymeric composite tubes,” Composite Structures, vol. 193, pp. 154-164, 2018.
  19. J. C. McConville and K. S. Miller, “Research, Development, Test and Evaluation of Material for Worldwide Use,” Department of the Army, Washington, DC, 2020.
  20. V. B. Mohan, B. J. Krebs and D. B. Bhattacharyya, “Development of novel highly conductive 3D printable hybrid polymer-graphene composites,” Mater. Today Commun., vol. 17, pp. 554-561, 2018.
  21. J. L. Colon Quintana, L. Slattery, J. Pinkham, J. Keaton, R. Lopez-Anido and K. Sharp, “Effects of Fiber Orientation on the Coefficient of Thermal Expansion of Fiber-filled Polymer Systems in Large Format Polymer Extrusion-based Additive Manufacturing,” Materials, vol. 15, p. 2764, 2022.
  22. P. Latko-Duralex, K. Dydex and A. Boczkowska, “Thermal, Rheological and Mechanical Properties of PETG/rPETG Blends,” J. Polym. Environ., vol. 27, pp. 2600-2606, 2019.
  23. Q. Shi, R. Xiao, H. Yang and D. Lei, “Effects of physical aging on thermomechanical behaviors of poly(ethylene terephthalate)-glycol (PETG),” Polymer Plastics Technology and Materials, vol. 59, no. 8, pp. 835-846, 2020.
  24. K. Martin, G. A. Riveros, T. Thornel, Z. McClelland, E. Freeman and J. Stinson, “Thermomechanical Material Characterization of Polyethylene Terephthalate Glycol with 30% Carbon Fiber for Large-Format Additive Manufacturing of Polymer Structures,” Polymer, vol. 16, no. 13, p. 1913, 2024.
  25. L. Haviland, “Mechanical Characterization of Automated Fiber Placement and Additive Manufacturing Hybrid Composites,” Orono, 2023.
  26. T. A. Osswald and G. Menges, Material Science of Polymers for Engineers, Munich: Hanser, 2012.
  27. H. G. M. Doan and P. Mertiny, “Creep Testing of Thermoplastic Fiber-Reinforced,” Materials, vol. 13, p. 4637, 2020.
  28. R. Lakes, “Viscoelastic Composite Materials,” in Viscoelastic Materials, Cambridge, UK, Cambridge University Press, 2009, pp. 341-376.
  29. T. Chen, “Determining a Prony Series for a Viscoelastic material From Time Varying Strain Data,” 2000.
  30. Rashid and M. Koc, “Creep and Recovery Behavior of Continuous Fiber-Reinforced 3DP Composites,” Polymers, vol. 13, p. 1644, 2021.
  31. Y. Xu, Q. Wu, Y. Lei and F. Yao, “Creep behavior of bagasse fiber reinforced polymer composites,” Bioresource Technology, vol. 101, pp. 3280-3286, 2010.
  32. X. Chu, Z. Wu, R. Huang, Y. Zhou and L. Li, “Mechanical and thermal expansion properties of glass fibers reinforced PEEK composites at cryogenic temperatures,” Cryogenics, vol. 50, no. 2, pp. 84-88, 2010.
  33. M. Kovacova, J. Kozakovicova, M. Prochazka, I. Janigova, M. Vysopal, I. Cernickova, J. Krajcovic and Z. Spitalsky, “Novel Hybrid PETG Composites for 3D Printing,” Applied Science, vol. 10, p. 3062, 2020.
  34. S. Deng, M. Hou and L. Ye, “Temperature-dependent elastic moduli of epoxies measured by DMA and their correlations to mechanical testing data,” Polymer Testing, vol. 26, pp. 803-813, 2007.
  35. R. B. Dupaix and M. C. Boyce, “Finite strain behavior of poly(ethylene terephthalate) (PET) and poly(ethylene terephthalate)-glycol (PETG),” Polymer, vol. 46, p. 4827–4838, 2005.
  36. S. Kannan, M. Ramamoorthy, E. Sudhagar and B. Gunji, “Mechanical characterization and vibrational analysis of 3D printed PETG and PETG reinforced with short carbon fiber,” in AIP Conference, 2020.
  37. M. Mansour, K. Tsongas, D. Tzetzis and A. Antoniadis, “Mechanical and Dynamic Behavior of Fused Filament Fabrication 3D Printed Polyethylene Terephthalate Glycol Reinforced with Carbon Fibers,” Polymer-Plastics Technology and Engineering, vol. 57, no. 16, pp. 1715-1725, 2018.
Preprints 116466 g001
Figure 1. Schematic of sample orientation. The lines correspond to the fiber direction.
Figure 1. Schematic of sample orientation. The lines correspond to the fiber direction.
Preprints 116466 g001
Preprints 116466 g002
Figure 2. Dimension change as a function of temperature for GF/PETG material. Black lines represent along the fiber direction (1-dir), Red lines transverse to the fiber direction (2-dir), and Blue lines through thickness (3-dir).
Figure 2. Dimension change as a function of temperature for GF/PETG material. Black lines represent along the fiber direction (1-dir), Red lines transverse to the fiber direction (2-dir), and Blue lines through thickness (3-dir).
Preprints 116466 g002
Preprints 116466 g003
Figure 3. Strain sweep results of GF/PETG UD in the (a) 1-dir and (b) 2-dir.
Figure 3. Strain sweep results of GF/PETG UD in the (a) 1-dir and (b) 2-dir.
Preprints 116466 g003
Preprints 116466 g004
Figure 4. Storage modulus (black), loss modulus (red), and tanδ (blue) as a function of temperature for (a) 1-dir and (b) 2-dir.
Figure 4. Storage modulus (black), loss modulus (red), and tanδ (blue) as a function of temperature for (a) 1-dir and (b) 2-dir.
Preprints 116466 g004
Preprints 116466 g005
Figure 5. Storage modulus as a function of frequency for (a) 1-dir and (b) 2-dir.
Figure 5. Storage modulus as a function of frequency for (a) 1-dir and (b) 2-dir.
Preprints 116466 g005
Preprints 116466 g006
Figure 6. Loss modulus as a function of frequency for (a) 1-dir and (b) 2-dir.
Figure 6. Loss modulus as a function of frequency for (a) 1-dir and (b) 2-dir.
Preprints 116466 g006
Preprints 116466 g007
Figure 7. Tand modulus as a function of frequency for (a) 1-dir and (b) 2-dir.
Figure 7. Tand modulus as a function of frequency for (a) 1-dir and (b) 2-dir.
Preprints 116466 g007
Preprints 116466 g008
Figure 8. Storage modulus as a function of (a) strain percentage and temperature and (b) frequency and temperature.
Figure 8. Storage modulus as a function of (a) strain percentage and temperature and (b) frequency and temperature.
Preprints 116466 g008
Preprints 116466 g009
Figure 9. Stress relaxation master curve at (a) 0.005%, (b) 0.01%, (c) 0.1%, and (d) shift factor for GF/PETG UD tape created at a reference temperature of 60 °C.
Figure 9. Stress relaxation master curve at (a) 0.005%, (b) 0.01%, (c) 0.1%, and (d) shift factor for GF/PETG UD tape created at a reference temperature of 60 °C.
Preprints 116466 g009
Preprints 116466 g010
Figure 10. Creep test (a) master curve and (b) shift factor for GF/PETG UD tape created at a reference temperature of 60 °C.
Figure 10. Creep test (a) master curve and (b) shift factor for GF/PETG UD tape created at a reference temperature of 60 °C.
Preprints 116466 g010
Table 1. Temperatures selected based on operational conditions using the Army Regulation 70-38 Standard.
Table 1. Temperatures selected based on operational conditions using the Army Regulation 70-38 Standard.
Temperature
Daily High (°C)		 Design Type Daily Cycle Ambient Relative
Humidity (%RH)
-57 Extreme Cold Extreme Cold (C4) Tending toward saturation
-37 Cold Cold (C2) Tending toward saturation
-6 Basic Mild Cold (C0) Tending toward saturation
24 Basic Constant High Humidity (B1) 95-100
49 Hot Hot Dry (A1) 3-8
Table 2. Temperature, load, and strain % values for creep and stress relaxation tests.
Table 2. Temperature, load, and strain % values for creep and stress relaxation tests.
Test Temperature (°C) Load (N) Strain %
Creep -70 -50 -25 0 15 30 45 60 5, 10 -
Stress Relaxation -70 -50 -25 0 15 30 45 60 - 0.005, 0.01, 0.1
Table 3. GF/PETG UD tape compression molding processing parameters.
Table 3. GF/PETG UD tape compression molding processing parameters.
Parameters Value
Pressure (psi) 100
Processing temperature, °C (°F) 168.3 (335)
Heating rate, °C/min (°F /min) 8 (14.4)
Dwell time (min) 10
Cooling rate, °C/min (°F /min) 25.6 (46)
Run time per part (min) 50
Table 4. Average LCTE for GF/PETG in all principal directions.
Table 4. Average LCTE for GF/PETG in all principal directions.
Direction Average CTE (με/C) Standard deviation (με/C)
1-dir 7.7 0.3
2-dir 47.8 5.2
3-dir 46.5 5.8
Table 5. Tanδ peak values for samples in the 1-dir and 2-dir.
Table 5. Tanδ peak values for samples in the 1-dir and 2-dir.
Orientation Frequency (Hz)—Zone 1 Frequency (Hz)—Zone 2 Frequency (Hz)—Zone 3
1-dir 39-56 70-90 112
2-dir 39-50 74-90 150
Table 6. Summary of the Arrhenius fitting parameters for the stress relaxation test.
Table 6. Summary of the Arrhenius fitting parameters for the stress relaxation test.
Strain % Activation Energy, Ea
(kJ/mol)		 Reference Temperature, Tref
(°C)		 R2
0.005 47.81 61.16 0.66
0.01 159.86 61.11 0.44
0.1 129.25 60.99 0.32
Table 7. Prony series R2 values for stress relaxation test.
Table 7. Prony series R2 values for stress relaxation test.
Prony series terms Strain Percentages
0.005 % 0.01 % 0.1 %
3 0.97 0.99 0.98
4 0.98 0.99 0.99
5 0.98 0.99 0.99
Table 8. Summary of the Arrhenius fitting parameters for the creep test.
Table 8. Summary of the Arrhenius fitting parameters for the creep test.
Load (N) Activation Energy, Ea
(kJ/mol)		 Reference Temperature, Tref
(°C)		 R2
5 162.23 30.73 0.50
10 75.76 30.44 0.41
Table 9. Burgers model fitting parameters.
Table 9. Burgers model fitting parameters.
Load (N) ε1 ε1 λ1 λ2 R2
5 0.05627 0.02038 1.659E8 0.1982 0.99
10 0.1221 0.07217 8.569E7 3.231E5 0.97
Table 10. Findley model fitting parameters.
Table 10. Findley model fitting parameters.
Load (N) a (strain %) b (-) εo (strain %) R2
5 4.77E-4 0.2962 0.0614 0.98
10 4.668E-5 0.4672 0.1249 0.99
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated