Diatomic: An Open-Source Excel Application to Calculate Ther-Modynamic Properties for Diatomic Molecule

Preprint

Article

Diatomic: An Open-Source Excel Application to Calculate Ther-Modynamic Properties for Diatomic Molecule

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.zip (15.52MB )

André Melo^*

This version is not peer-reviewed

Submitted:

30 August 2024

Posted:

02 September 2024

You are already at the latest version

Alerts

Abstract

I present in this paper Diatomic, an open-source Excel application that calculates molar ther-modynamic properties for diatomic ideal gases. This application is very easy to use and requires only a limited number of molecular constants, which are freely available online. Despite its sim-plicity, Diatomic provides methodologies and results that are usually unavailable in general quantum chemistry packages. This application uses the general formalism of statistical mechanics, enabling two models to describe the rotational structure and two models to describe the vibra-tional structure. In this work, Diatomic was used to calculate standard molar thermodynamic properties for a set of fifteen diatomic ideal gases. Special emphasis was placed on the analysis of four properties (standard molar enthalpy of formation, molar heat capacity at constant pressure, average molar thermal enthalpy and standard molar entropy), which were compared with ex-perimental values. The results obtained lead to the following main conclusions: (i) the theoretical model used to describe rotational structure has a small effect on the accuracy of the results, (ii) at moderate and high temperatures, the Morse model gives better results than the harmonic model, and (iii) at the lowest temperatures both models give similar results.

Keywords:

Subject: Chemistry and Materials Science - Theoretical Chemistry

1. Introduction

Diatomic molecules are important in many areas of modern science, such as atmospheric chemistry [1,2], astrobiology [3] and ultracold physics [4]. Despite their simplicity, diatomic molecules are valuable models for understanding the relationship between structure and thermodynamic properties in more complex systems. For this purpose, it is important to develop high-quality theoretical methods to calculate these properties. Two main strategies have usually been adopted to improve the accuracy of these methods: (i) improving the description of the electronic structure [5,6,7,8] and (ii) implementing better models to describe the (rotational and vibrational) nuclear motions [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24].

The electronic structure refinements include [5,6]: (i) a high-level quantum method, (ii) a robust basis set, (iii) the extrapolation to the complete basis set (CBS) limit, (iv) the inclusion of relativistic and spin-orbit effects and (v) a very good description of the electronic correlation.

The rotational structure is usually described by a classical approach, since the temperatures of interest are normally much higher than the characteristic rotational temperatures. However, at low temperatures it is important to adopt a quantum description of this structure to obtain accurate values [9].

At low and moderate temperatures, the vibrational structure can be reasonably described by the harmonic oscillator model [10]. However, this approach is known to overestimate the vibrational frequencies [10], leading to significant errors at high temperatures. To overcome this limitation, several correction methods have been applied [11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Most of them can be classified into two groups: (i) methods that use empirical scaling factors to correct the harmonic frequencies [13,14] and (ii) methods that use anharmonic potentials [15,16,17,18,19,20,21,22,23,24].

The thermodynamic properties of a molecular system can be calculated using general quantum chemistry packages [25,26,27]. However, the required computational resources and level of expertise are considerable.

In this work, I have developed an open-source Excel application to calculate thermodynamic properties for diatomic ideal gases. This application, called Diatomic, is very easy to use and requires only some basic knowledge of theoretical chemistry. In fact, an user of Diatomic only has to input a limited number of molecular constants (the electronic ground state energy and the corresponding spin multiplicity, the atomic masses, the rotational symmetry number, the equilibrium bond length, the harmonic vibrational wave number, and the well depth of the Morse potential) to perform a calculation of this type. This information is freely available from online resources. The pressure and a set of fourteen temperatures must also to be inputted.

Diatomic provides many features, often not available in general quantum chemistry packages, to perform and interpret this type of calculations. These include: (i) two models (classical and quantum) describing the rotational structure, (ii) two models (harmonic and Morse) describing the vibrational structure, (iii) energies and Boltzmann populations for the quantum rotational model, (iv) energies and Boltzmann populations for both vibrational models implemented in the application, (v) molar thermodynamic properties as a function of temperature available in very easy to interpret and process tables, (vi) availability of these tables organized by different criteria.

Most of the refinements to the electronic structure mentioned above can be easily incorporated into Diatomic because they only affect the electronic energy. For this purpose it is necessary to search the literature for these corrected values. However, my goal in this work is not to obtain very accurate values for the molar thermodynamic properties. I try to show here that users can get good results for these properties using Diatomic and molecular data freely available online. Since Diatomic is an open-source collaborative project, anyone can add new vibrational potentials to this application.

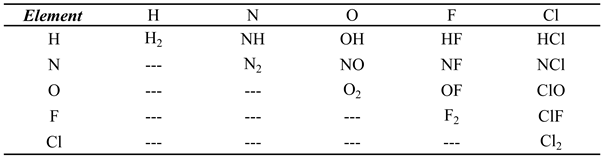
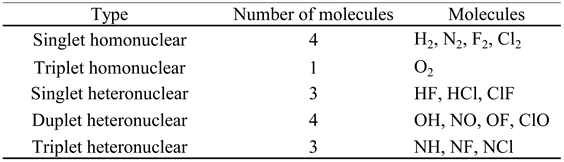
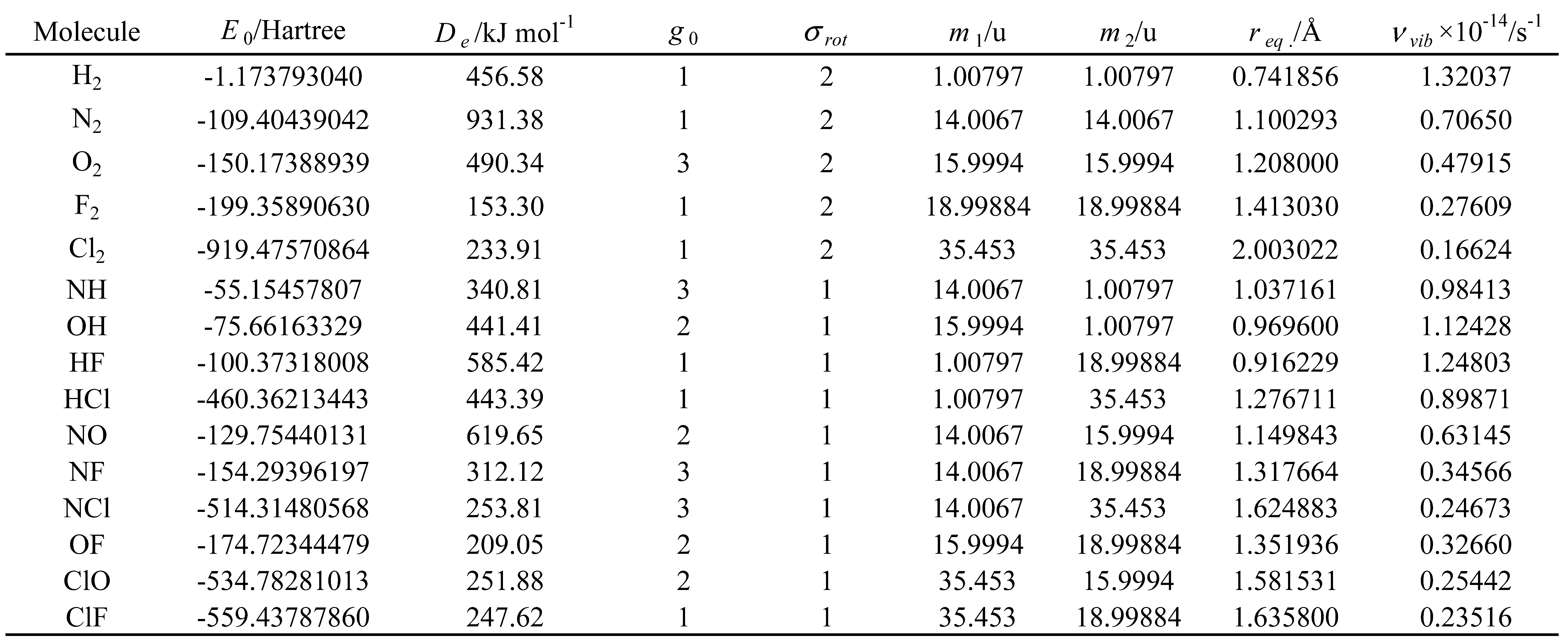
Diatomic was used here to calculate these properties for fifteen ideal gases as a function of temperature and constant pressure. The chemical species studied correspond to all diatomic molecules that can be obtained by combining the five elements: H, N, O, F and Cl (see Table 1).

These molecules are classified according to their symmetry (homonuclear or heteronuclear) and spin multiplicity (singlet, duplet or triplet) (see Table 2).

2. Materials and Methods

2.1. General formalism

According to the well-established formalism of statistical mechanics [28,29,30], all the most relevant thermodynamic properties of an ideal gas can be calculated from its partition function. For a molar canonical ensemble1 and within the Born-Oppenheimer approach, this partition function (Q(N_A, V, T)) can be calculated from its molecular components:

Q (N_{A}, V, T) = \frac{Z^{N_{A}}}{N_{A}!} = {(Z_{e l})}^{N_{A}} \times \frac{{(Z_{t r a n s l})}^{N_{A}}}{N_{A}!} \times {(Z_{r o t})}^{N_{A}} \times {(Z_{v i b})}^{N_{A}}

(1)

In Equation (1), N_A is the Avogadro number and Z is the molecular partition function. In the same equation, Z_el, Z_transl, Z_rot and Z_vib are the (electronic, translational, rotational and vibrational) components of the partition function. Within this formalism, the molar thermodynamic properties can be decomposed in a similar way:

A_{m} = A_{m}^{e l} + A_{m}^{t r a n s l} + A_{m}^{r o t} + A_{m}^{v i b} (molar Helmholtz energy)

(2)

G_{m} = A_{m} + R T \Leftrightarrow G_{m} = A_{m}^{e l} + A_{m}^{t r a n s l} + A_{m}^{r o t} + A_{m}^{v i b} + R T (molar Gibbs energy)

(3)

{〈E〉}_{m} = {〈E^{e l}〉}_{m} + {〈E^{t r a n s l}〉}_{m} + {〈E^{r o t}〉}_{m} + {〈E^{v i b}〉}_{m} (average value of molar energy)

(4)

{〈H〉}_{m} = {〈H〉}_{m} + R T \Leftrightarrow {〈H〉}_{m} = {〈E^{e l}〉}_{m} + {〈E^{t r a n s l}〉}_{m} + {〈E^{r o t}〉}_{m} + {〈E^{v i b}〉}_{m} + R T (average value of molar enthalpy)

(5)

S_{m} = S_{m}^{e l} + S_{m}^{t r a n s l} + S_{m}^{r o t} + S_{m}^{v i b} (molar entropy)

(6)

C_{v, m} = C_{v, m}^{e l} + C_{v, m}^{t r a n s l} + C_{v, m}^{r o t} + C_{v, m}^{v i b} (molar heat capacity at constant volume)

(7)

C_{p, m} = C_{v, m} + R \Leftrightarrow C_{p, m} = C_{v, m}^{e l} + C_{v, m}^{t r a n s l} + C_{v, m}^{r o t} + C_{v, m}^{v i b} + R (molar heat capacity at constant pressure)

(8)

In some of the previous equations ((3), (5) and (8)) an additional non-specific component (RT or R) must also be included. The components of the molar thermodynamic properties can be calculated as

A_{m}^{c o m p} = - R T \ln Z_{c o m p}, c o m p = e l, r o t and v i b; A_{m}^{t r a n s l} = - R T \ln \frac{Z_{t r a n s l}}{N_{A}} - R T

(9)

{〈E^{c o m p}〉}_{m} = R T^{2} {(\frac{\partial \ln Z_{c o m p})}{\partial T})}_{V}, c o m p = e l, t r a n s l, r o t and v i b \Leftrightarrow

(10)

{〈E^{c o m p}〉}_{m} = N_{A} \sum_{i} P_{i} E_{i}^{c o m p}; c o m p = e l, t r a n s l, r o t and v i b

(11)

Equation (10) should be used for partition functions (Z_comp) calculated analytically and Equation (11) for partition functions calculated numerically. In the last equation,

E_{i}^{c o m p}

is the energy of the quantum state i and P_i is the corresponding Boltzmann population given by the following formula,

P_{i} = \frac{\exp (- β E_{i}^{c o m p})}{Z_{c o m p}}; with β = k_{B} T

(12)

In which k_b is the Boltzmann constant.

S_{m}^{c o m p} = R \ln Z_{c o m p} + R T {(\frac{\partial (\ln Z_{c o m p})}{\partial T})}_{V}; c o m p = e l, t r a n s l, r o t and v i b

(13)

S_{m}^{t r a n s l} = R \ln \frac{Z_{t r a n s l}}{N_{A}} + R + R T {(\frac{\partial (\ln Z_{t r a n s l})}{\partial T})}_{V}

(14)

C_{v, m}^{c o m p} = {(\frac{\partial {〈E^{c o m p}〉}_{m}}{\partial T})}_{V} = N_{A} \frac{σ_{E^{c o m p}}^{2}}{k_{B} T^{2}}; c o m p = e l, t r a n s l, r o t and v i b

(15)

In Equation (15),

σ_{E^{c o m p}}^{2}

is the variance associated with the energy component (E^comp) calculated as:

σ_{E^{c o m p}}^{2} = 〈E^{c o m p^{2}}〉 - {〈E^{c o m p}〉}^{2}; c o m p = e l, t r a n s l, r o t and v i b

(16)

In Equation (16),

〈E^{c o m p}〉

and

〈E^{c o m p^{2}}〉

are respectively the average values of the energy component (

E^{c o m p}

) and of its square (

{E^{c o m p}}^{2}

) given by:

〈E^{c o m p}〉 = \sum_{i} P_{i} E_{i}^{c o m p}; c o m p = e l, t r a n s l, r o t and v i b

(17)

{〈{E^{c o m p}}^{2}〉}_{m} = \sum_{i} P_{i} E_{i}^{c o m p^{2}}; c o m p = e l, t r a n s l, r o t and v i b

(18)

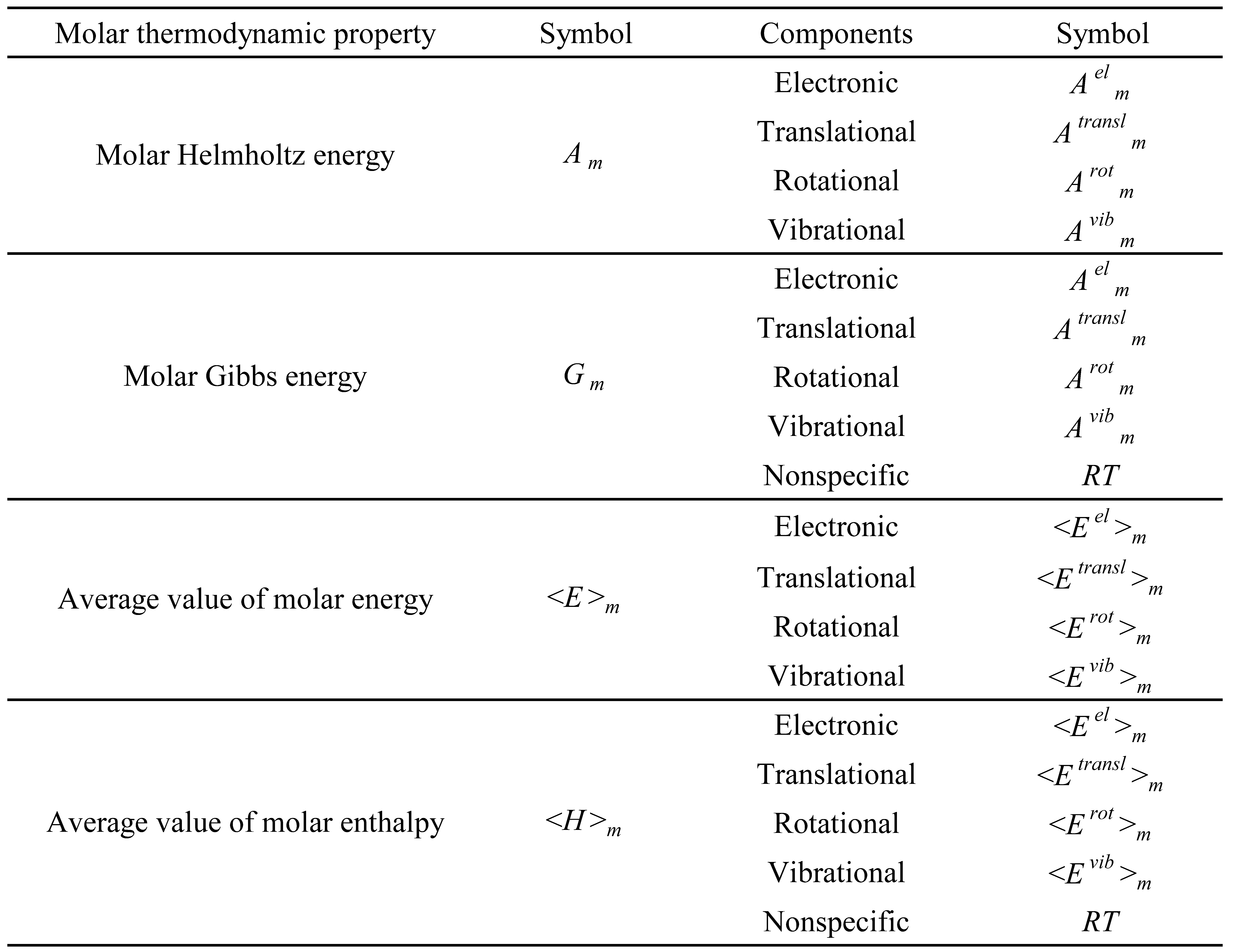
2.2. Classification of the molar thermodynamic properties

The molar thermodynamic properties are classified according to the criteria presented in Table 3.

Some properties of this type depend on the zero point energy (ZPE), which corresponds to the molar energy at 0 K. This quantity can be calculated as the sum of two components: the zero point electronic energy (ZPEE) and the zero point vibrational energy (ZPVE):

Z P E = Z P E E + Z P V E

(19)

Z P E E = N_{A} E_{0}

(20)

Z P V E = N_{A} E_{0}^{v i b}

(21)

In the last two equations,

E_{0}

and

E_{0}^{v i b}

are the energies of the electronic and vibrational ground states, respectively.

The Type 1 molar thermodynamic properties correspond to the absolute values of the thermodynamic properties that depend on the zero-point energy. A list of these properties is given in Table 4.

These properties are functions of temperature (T) and a limited number of molecular constants, which will be presented in section 2.10. The molar entropy (S_m) also depends on the pressure (P) due to its translational component (

S_{m}^{t r a n s l}

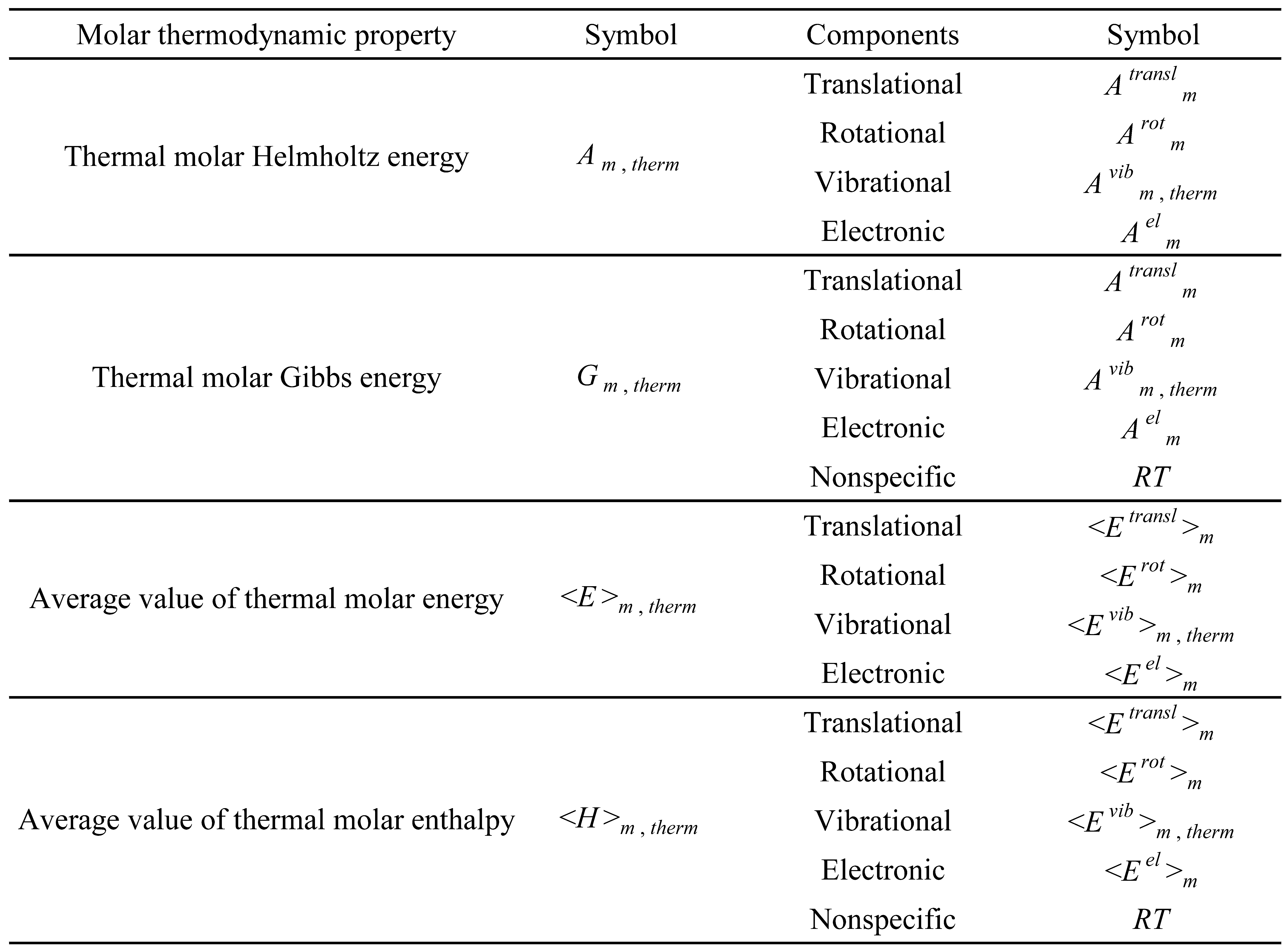
The type 2 molar thermodynamic properties correspond to the thermal values of the thermodynamic properties that depend on zero-point energy. A list of these properties is presented in Table 5.

A generic type 2 molar thermodynamic property (

X_{m, t h e r m}

) can be calculated as,

X_{m, t h e r m} = X_{m} - X_{m, r e f}; X = A, G, 〈E〉 or 〈H〉

(22)

in which

X_{m}

is the molar value of the thermodynamic property (X) at a generic temperature (T) and

X_{m, r ef}

is the corresponding molar value at a reference temperature (T_ref). In this work, two different reference temperatures were used. The original molar thermal values, calculated from the Diatomic application, use the reference temperature of 0 K. Some thermal values, presented in section 3, use the reference temperature of 298.15 K for consistency with the corresponding experimental values.

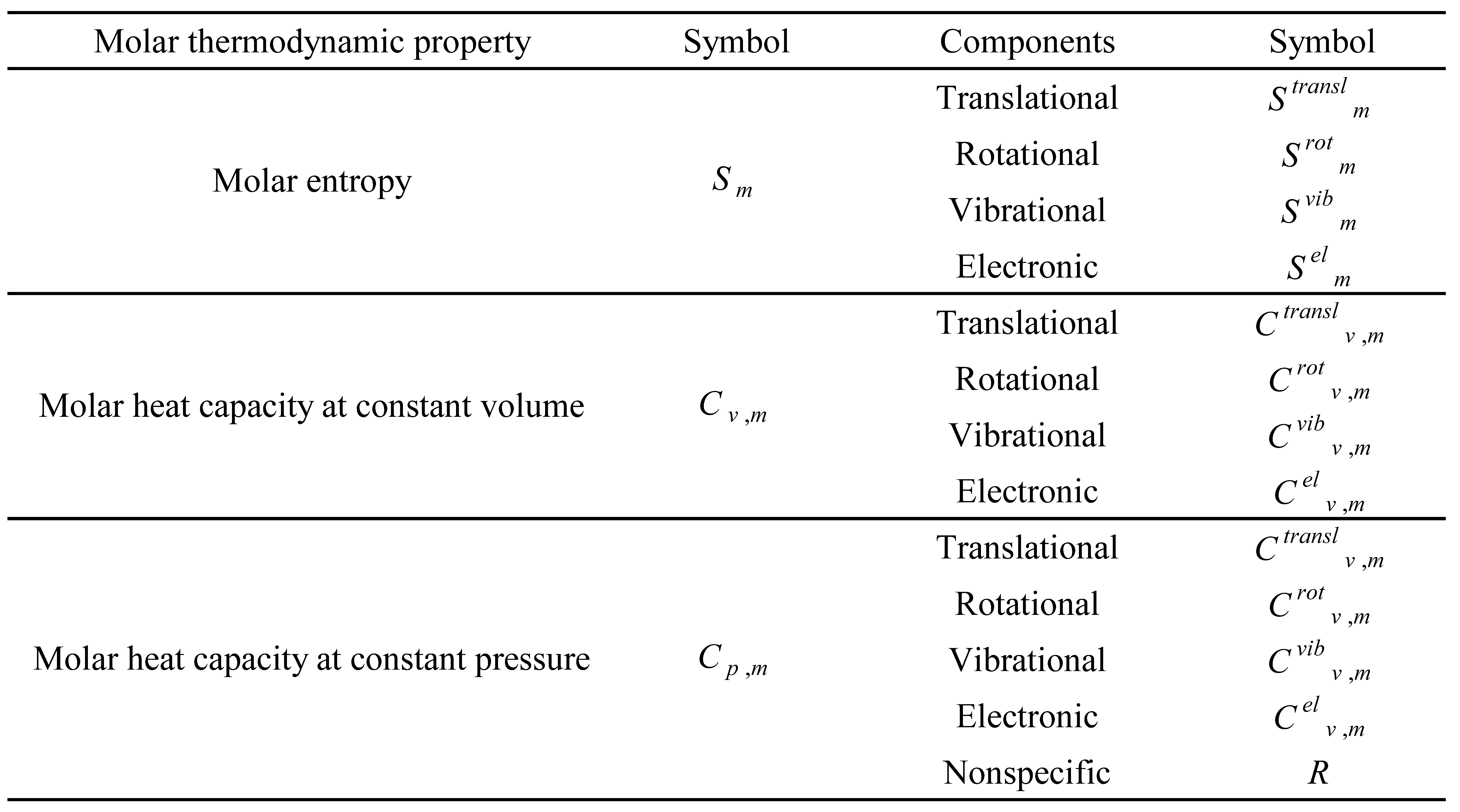
The type 3 molar thermodynamic properties are those that are independent of zero-point energy. A list of these properties is presented in Table 6.

2.3. Classical limit

The general formalism, presented in section 2.1, is based in a quantum formulation. In this case, the partition function associated with a component comp is calculated as a summation over the respective quantum levels (i),

Z_{c o m p} = \sum_{i} g_{i} E_{i}^{c o m p}; c o m p = e l, t r a n s l, r o t and v i b,

(23)

In which g_i is the degeneracy of the quantum level i and

E_{i}^{c o m p}

is the corresponding energy.

However, when the temperature is high enough that the energy difference between two successive levels is much smaller than k_BT, the summation (23) can be replaced by an appropriate integral (classical limit). In this case, it is valid the so-called equipartition theorem, according to which each classical quadratic energy term contributes with: R/2 for the molar heat capacity at constant volume (C_v_,m) and RT/2 for the average value of the molar energy (<E>_m).

Each energy component is associated with a characteristic temperature (Θ_comp), which determines the applicability of the classical limit and the equipartition (T >> Θ_comp). These characteristic temperatures vary considerably depending on the nature of the component. Typically, the electronic temperatures (Θ_el) are very high, the vibrational temperatures (Θ_vib) are moderate or high, the rotational temperatures (Θ_rot) are low and translational temperatures (Θ_transl) are very low.

This theorem is rarely applicable to the electronic component, because the energy differences between two successive electronic levels are usually too large. For diatomic molecules, when this theorem is fully applied to the nuclear motion components (translational, rotational, and vibrational), these molar thermodynamic properties can be estimated as:

The translational component, associated with three normal modes, contributes with 3R/2 to C_v_,m and with 3RT/2 to <E>_m.
The rotational component, associated with two normal modes, contributes with R to C_v_,m and with RT to <E>_m.
The vibrational component2, associated with one normal mode, contributes with R to C_v_,m and with RT to <E>_m.

A translational or rotational normal mode contributes with a single value to the referred molar thermodynamic properties (R/2 to C_v_,m and RT/2 to <E>_m), because it is associated with a single quadratic kinetic energy term in classical mechanics. The vibrational normal mode gives double contributions to the mentioned molar thermodynamic properties (R to C_v_,m and with RT to <E>_m), due to its association with two quadratic energy terms (one kinetic and one potential) in classical mechanics.

For a temperature interval [T_ref, T], where the classical limit and the equipartition are valid for the nuclear motion components but not for the electronic component, the following approximate equations are valid:

{〈E〉}_{m, t h e r m} \approx \frac{7}{2} R (T - T_{r e f})

(24)

{〈H〉}_{m, t h e r m} \approx \frac{9}{2} R (T - T_{r e f})

(25)

C_{v, m} \approx \frac{7}{2} R

(26)

C_{p, m} \approx \frac{9}{2} R

(27)

S_{m} = S_{m, r e f} + \int_{T_{r e f}}^{T} \frac{C_{p, m}}{T} d T \Leftrightarrow S_{m} \approx S_{m, r e f} + \frac{9}{2} R \ln (\frac{T}{T_{r e f}})

(28)

In equation (28),

S_{m, r e f}

is the molar entropy at a reference temperature T_ref.

2.4. Theoretical models

In the Diatomic application, the translational structure is always treated with the classical approach (see section 2.6), whereas the electronic structure is treated in a distinctive manner (see section 2.5). Two models (classical and quantum) have been implemented for the rotational structure (see section 2.7). For the vibrational structure, two models (harmonic oscillator and Morse oscillator) were also available (see section 2.8). In addition, an almost fully classical model (classical rotation, classical vibration) (see section 2.3) is also used in this work. These theoretical models are summarized in Table 7.

2.5. Electronic structure

For the molecules studied, it was assumed that the energy differences between the electronic ground state and the electronic excited states are very large. Under these circumstances, only the first state is occupied for the temperatures studied. Furthermore, in the calculation of the electronic partition function (Z_el), it is usually assumed that the energy of the electronic ground state (E₀) is the zero of the energy scale,

Z_{e l} = g_{0}

(29)

in which g₀ is the spin multiplicity of the electronic ground state.

This implies that some corrections have to be introduced to the general formalism presented in sections 2.1 and 2.3:

A_{m}^{e l} = - R T \ln g_{0} + N_{A} E_{0}

(30)

{〈E^{e l}〉}_{m} = N_{A} E_{0} = Z P E E

(31)

C_{v, m}^{e l} = {(\frac{\partial {〈E^{e l}〉}_{m}}{\partial T})}_{V} = N_{A} \frac{σ_{E^{e l}}^{2}}{k_{B} T^{2}} = 0

(32)

S_{m}^{e l} = R \ln g_{0}

(33)

2.6. Translational structure

The translational structure is fully treated by the classical approach. Thus, the translational partition constant and the translational components of some relevant molar thermodynamic properties can be calculated, respectively, as follows:

Z_{t r a n s l} = \frac{V}{Λ^{3}}

(34)

A_{m}^{t r a n s l} = - R T \ln \frac{k_{B} T}{P Λ^{3}} - R T

(35)

{〈E^{t r a n s l}〉}_{m} = \frac{3}{2} R T

(36)

C_{v, m}^{t r a n s l} = \frac{3}{2} R

(37)

S_{m}^{t r a n s l} = R \ln \frac{k_{B} T}{P Λ^{3}} + \frac{5}{2} R

(38)

In equations (34), (35) and (38), Λ is the thermal de Broglie wavelength given by,

Λ = {(\frac{h^{2}}{2 π m k_{B} T})}^{1 / 2},

(39)

in which m is the molecular mass and h is the Planck constant.

2.7. Rotational structure

The rotational structure is treated using two alternative approaches (quantum and classical). Within the quantum formalism, the rotational partition constant can be calculated as:

\begin{array}{l} Z_{r o t} = \frac{1}{σ_{r o t}} \sum_{J = 0}^{\infty} g_{J} \exp (- \frac{E_{J}^{r o t}}{k_{B} T}), with g_{J} = 2 J + 1 \Leftrightarrow Z_{r o t} = \frac{1}{σ_{r o t}} \sum_{J = 0}^{\infty} g_{J} \exp (\frac{- B J (J + 1)}{k_{B} T}) \Leftrightarrow \\ Z_{r o t} = \frac{1}{σ_{r o t}} \sum_{J = 0}^{\infty} (2 J + 1) \exp (\frac{- Θ_{r o t} J (J + 1)}{T}) \end{array}

(40)

In the Diatomic application, a finite number of terms (J_max = 2000) are used in the summations included in equation (40). However, this was enough to obtain convergence in the rotational partition for all the calculations performed here.

In this equation, σ_rot is the rotational symmetry number (σ_rot = 2 for diatomic homonuclear molecules and σ_rot = 1 for diatomic heteronuclear molecules),

E_{J}^{r o t}

is the energy of the rotational quantum level J,

g_{J}

is the respective degeneracy, B is the rotational constant and

Θ_{r o t}

is the rotational temperature. The last two quantities can be calculated using the following equations:

B = \frac{ℏ^{2}}{2 I}, with ℏ = \frac{h}{2 π}

(41)

Θ_{r o t} = \frac{B}{k_{B}}

(42)

In equation (41), I is the moment of inertia given by,

I = μ r_{e q}^{2}, μ = \frac{m_{1} \times m_{2}}{m},

(43)

in which μ is the reduced mass of the diatomic molecule, m₁ the mass of its first atom, m₂ the mass of its second atom and r_eq its equilibrium bond length.

Within this formalism, the rotational components of some relevant molar thermodynamic properties can be calculated as:

A_{m}^{r o t} = - R T \ln Z_{r o t} \Leftrightarrow A_{m}^{r o t} = - R T \ln [\frac{1}{σ_{r o t}} \sum_{J = 0}^{J_{\max}} (2 J + 1) \exp (\frac{- Θ_{r o t} J (J + 1)}{T})]; with J_{\max} = 2000

(44)

{〈E^{rot}〉}_{m, T} = N_{A} \sum_{J = 0}^{J_{\max}} P_{J} E_{J}^{r o t}; with P_{J} = (2 J + 1) \frac{\exp (- β E_{J}^{r o t})}{σ_{r o t} Z_{r o t}}

(45)

C_{v, m}^{r o t} = N_{A} \frac{σ_{E^{r o t}}^{2}}{k_{B} T^{2}} = N_{A} \frac{(〈E^{r o t^{2}}〉 - {〈E^{r o t}〉}^{2})}{k_{B} T^{2}}

(46)

In Equation (46),

〈E^{r o t}〉

and

〈E^{r o t^{2}}〉

are the average values of the rotational energy (

E^{r o t}

) and of its square (

{E^{r o t}}^{2}

), respectively, given by:

〈E^{r o t}〉 = \sum_{J = 0}^{J_{\max}} P_{J} E_{J}^{r o t}

(47)

〈{E^{r o t}}^{2}〉 = \sum_{J = 0}^{J_{\max}} P_{J} E_{J}^{r o t^{2}}

(48)

S_{m}^{r o t} = \frac{{〈E^{r o t}〉}_{m} - A_{m}^{r o t}}{T}

(49)

Within the classical formalism, equations (40) to (49) must be reformulated as:

Z_{r o t} = \frac{T}{σ_{r o t} Θ_{r o t}}

(50)

A_{m}^{r o t} = - R T \ln Z_{r o t} \Leftrightarrow A_{m}^{r o t} = - R T \ln (\frac{T}{σ_{r o t} Θ_{r o t}})

(51)

{〈E^{r o t}〉}_{m} = R T

(52)

C_{v, m}^{r o t} = R

(53)

S_{m}^{r o t} = R (\ln (\frac{T}{σ_{r o t} Θ_{r o t}}) + 1)

(54)

2.8. Vibrational structure

The vibrational structure is treated using two alternative approaches (harmonic oscillator and Morse oscillator). Within the harmonic oscillator formalism, the vibrational partition constant can be calculated as,

Z_{v i b} = \frac{\exp [- β h ν_{v i b} / 2]}{1 - \exp [- β h ν_{v i b}]} \Leftrightarrow Z_{v i b} = \frac{\exp [- h ν_{v i b} / (2 k_{B} T)]}{1 - \exp [- h ν_{v i b} / (k_{B} T)]} \Leftrightarrow Z_{v i b} = \frac{\exp [- Θ_{v i b} / (2 T)]}{1 - \exp [- Θ_{v i b} / T]},

(55)

where ν_vib is the vibrational frequency and Θ_vib the vibrational temperature, given respectively by,

ν_{v i b} = \frac{1}{2 π} {(\frac{K}{μ})}^{1 / 2}

(56)

in which Κ is the force constant of the diatomic molecule,

Θ_{v i b} = \frac{h ν_{v i b}}{k_{B}}

(57)

Within this formalism, the vibrational components of some relevant molar thermodynamic properties can be calculated as:

A_{m}^{v i b} = - R T \ln Z_{v i b} \Leftrightarrow A_{m}^{v i b} = - R T \ln (\frac{\exp [- Θ_{v i b} / (2 T)]}{1 - \exp [- Θ_{v i b} / T]})

(58)

{〈E^{v i b}〉}_{m} = R \frac{Θ_{v i b}}{2} + R \frac{Θ_{v i b}}{\exp (Θ_{v i b} / T) - 1} \Leftrightarrow {〈E^{v i b}〉}_{m} = \frac{N_{A}}{2} h ν_{v i b} + \frac{N_{A} h ν_{v i b}}{\exp [h ν_{v i b} / (k_{B} T)] - 1}

(59)

C_{v, m}^{v i b} = N_{A} \frac{σ_{E^{v i b}}^{2}}{k_{B} T^{2}} = R [\exp (Θ_{v i b} / T) {(\frac{Θ_{v i b} / T}{\exp (Θ_{v i b} / T) - 1})}^{2}]

(60)

S_{m}^{v i b} = R (\frac{Θ_{v i b} / T}{\exp (Θ_{v i b} / T) - 1} - \ln [1 - \exp (- Θ_{v i b} / T)])

(61)

Within the Morse oscillator formalism, equations (55) to (61) must be reformulated as,

Z_{v i b} = \sum_{v = 0}^{v_{\max}} \exp (- β E_{v}^{v i b}),

(62)

where

E_{v}^{v i b}

is the vibrational energy of a diatomic molecule according to this formalism given by the equation (63):

E_{v}^{v i b} = (v + \frac{1}{2}) h ν_{v i b} - {(v + \frac{1}{2})}^{2} χ_{e} h ν_{v i b}; v = 0, 1, 2, 3, \dots, {v_{\max}}^{3}

(63)

In Equation (63), v is the vibrational quantum number, v_max+1 is the number of bound states associated with the Morse potential and χ_e is the anharmonicity constant. The last two quantities can be calculated by equations (64) and (65), respectively:

v_{\max} = \frac{1 - χ_{e}}{2 χ_{e}}

(65)

χ_{e} = \frac{h ν_{v i b}}{4 D_{e}}

(66)

In Equation (66), D_e is the well depth of the Morse potential.

A_{m}^{v i b} = - R T \ln Z_{v i b} \Leftrightarrow A_{m}^{v i b} = - R T \ln [\sum_{v = 0}^{v_{\max}} \exp (- β E_{v}^{vib})]

(67)

{〈E^{v i b}〉}_{m} = N_{A} \sum_{v = 0}^{v_{\max}} P_{v} E_{v}^{v i b}; with P_{v} = \frac{\exp (- β E_{v}^{v i b})}{Z_{v i b}}

(68)

C_{v, m}^{v i b} = N_{A} \frac{(〈E^{v {ib}^{2}}〉 - {〈E^{v i b}〉}^{2})}{k_{B} T^{2}}

(69)

In Equation (69),

〈E^{v i b}〉

and

〈E^{v i b^{2}}〉

are the average values of the vibrational energy (

E^{v i b}

) and of its square (

{E^{v i b}}^{2}

), respectively, given by:

〈E^{v i b}〉 = \sum_{v = 0}^{v_{\max}} P_{v} E_{v}^{v i b}

(70)

〈{E^{v i b}}^{2}〉 = \sum_{v = 0}^{v_{\max}} P_{v} E_{v}^{v i b^{2}}

(71)

S_{m}^{v i b} = \frac{{〈E^{v i b}〉}_{m} - A_{m}^{v i b}}{T}

(72)

2.9. Standard molar enthalpy of formation

The standard molar enthalpy of formation of a diatomic heteronuclear gas AB (Δ_fH^o(AB, g)) is defined as the enthalpy variation, under standard conditions, associated with the following chemical equation:

½ A₂(g) + ½ B₂(g) ⇌ AB(g)

(73)

Δ_{f} H^{o} (AB, g) = {〈H^{o} (AB, g)〉}_{m} - \frac{1}{2} ({〈H^{o} (A_{2}, g)〉}_{m} + 〈H^{o} (B_{2}, g)〉)

(74)

In equation (74), the standard molar enthalpy of a diatomic gas X (<H^o (X, g)>_m; X= AB, A₂ or B₂) is the average value of the standard molar enthalpy of this chemical species at a pressure 1 bar and a specific temperature (usually 298.15 K).

2.10. Molecular constants

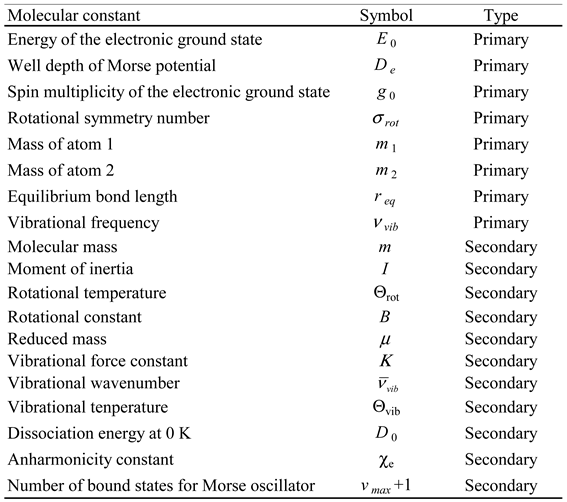
In the theoretical models considered, the molar thermodynamic properties depend only on a limited number of molecular constants (primary molecular constants). However, in many cases, the formalism previously presented in this section was expressed using other molecular constants (secondary molecular constants) that can be obtained from the primary ones. A list of molecular constants, used in this work, is presented in Table 8.

2.11. Diatomic application

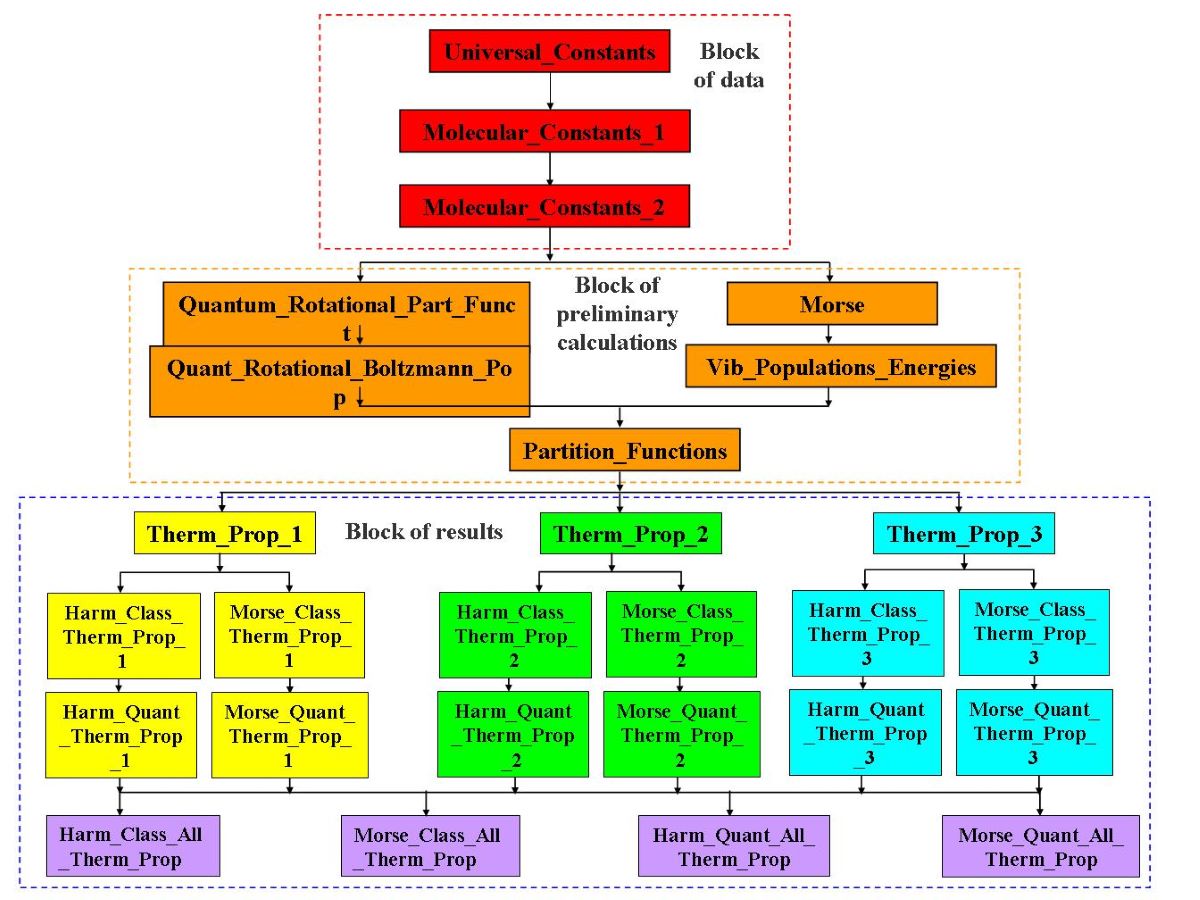
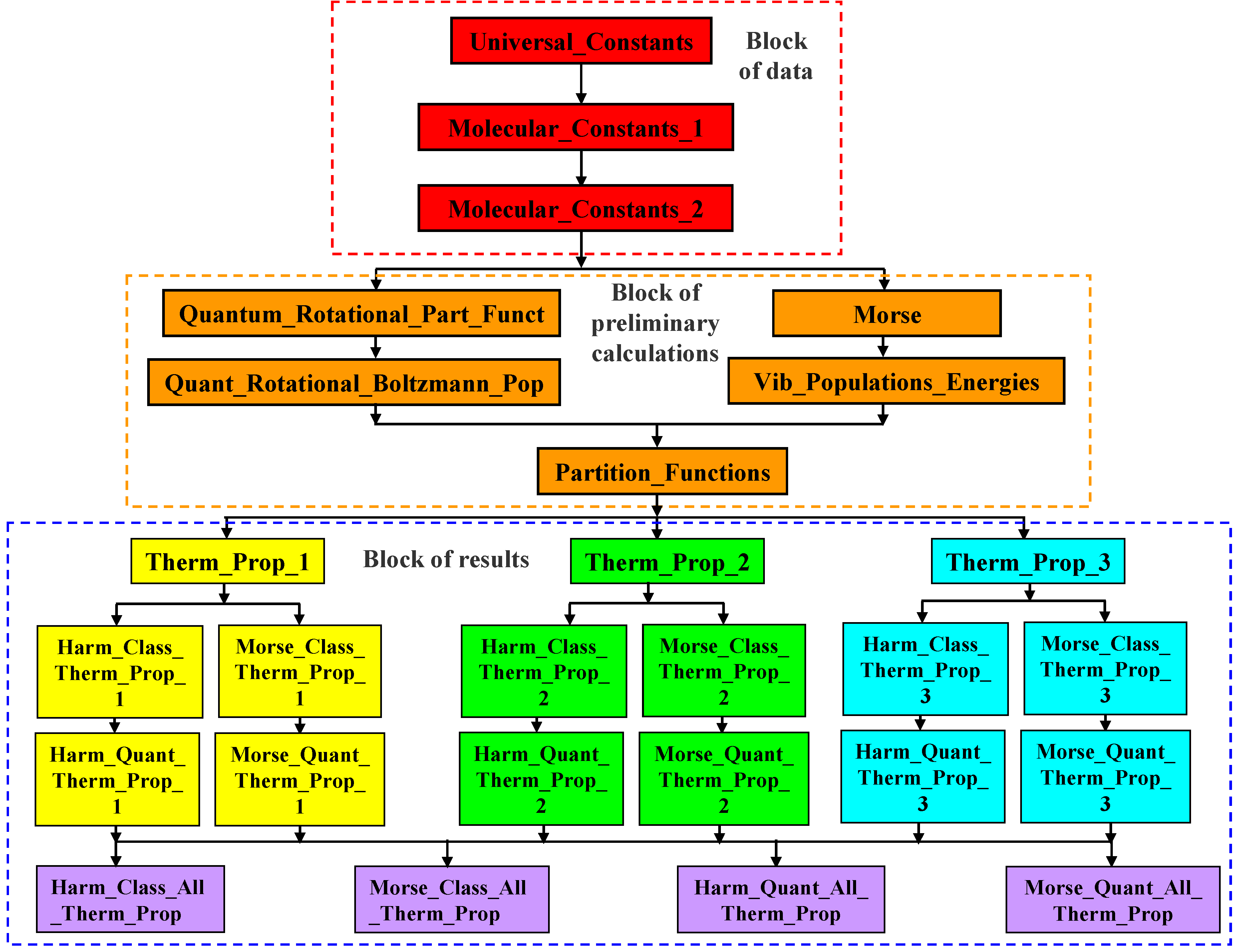
A flowchart of the Diatomic application is shown in Figure 1.

This application is organized in three blocks of spreadsheets: block of data, block of preliminary calculations and block of results.

Yhe block of data contains the following information:

Universal constants and conversion factors (provided by the application in the Universal_Constants spreadsheet);
Pressure value used in the calculations (inputted by the user in the Universal_Constants spreadsheet);
Primary molecular constants and 14 temperature values used in calculations (inputted by the user in the Molecular_Constants_1 spreadsheet4);
Secondary molecular constants (calculated by the application in the Molecular_Constants_2 spreadsheet).

The block of preliminary calculations performs the following calculations:

Rotational partition function using the quantum formulation (performed by the Quantum_Rotational_Part_Funct spreadsheet);
Boltzmann populations and energies, for the rotational levels, using the quantum formulation (performed by the Quant_Rotational_Boltzmann_Pop spreadsheet);
Vibrational partition function using the Morse oscillator formulation (calculated by the Morse spreadsheet);
Vibrational partition function using the harmonic oscillator formulation (calculated by the Vib_Populations_Energies spreadsheet);
Boltzmann populations and energies, for the vibrational states, using both the harmonic and Morse oscillators formulations (calculated by the Vib_Populations_Energies spreadsheet);
Average vibrational molar energy using the Morse oscillator formulation (performed by the Vib_Populations_Energies spreadsheet);
Vibrational molar heat capacity at constant volume using the Morse oscillator formulation (performed by the Vib_Populations_Energies spreadsheet);
Canonical ensemble total partition function and its components, using the various theoretical models available (calculated by the Partition_Functions spreadsheet).

In the block of results, the results are presented/calculated using different criteria:

In a first level, the results are presented/calculated by type as defined in Table 3 (Therm_Prop_1, Therm_Prop_2 and Therm_Prop_3 spreadsheets);
At a second level, the results are presented/calculated by type as defined in Table 3 and by theoretical model as defined in Table 7 (type 1 molar thermodynamic properties with different theoretical models: Harm_Class_Therm_Prop_1, Morse_Class_Therm_Prop_1, Harm_Quantum_Therm_Prop_1 and Morse_Quantum_Therm_Prop_1 spreadsheets; type 2 molar thermodynamic properties with different theoretical models: Harm_Class_Therm_Prop_2, Morse_Class_Therm_Prop_2, Harm_Quantum_Therm_Prop_2 and Morse_Quantum_Therm_Prop_2 spreadsheets; type 3 molar thermodynamic properties with different theoretical models: Harm_Class_Therm_Prop_3, Morse_Class_Therm_Prop_3, Harm_Quantum_Therm_Prop_3 and Morse_Quantum_Therm_Prop_3 spreadsheets);
In a third level, the results are presented/calculated by theoretical model as defined in Table 7 (harm, class: Harm_Class_All_Therm_Prop spreadsheet, Morse, class: Morse_Class_All_Therm_Prop spreadsheet, harm, quant: Harm_Quant_All_Therm_Prop spreadsheet, Morse, quant: Morse_Quant_All_Therm_Prop spreadsheet.

3. Results

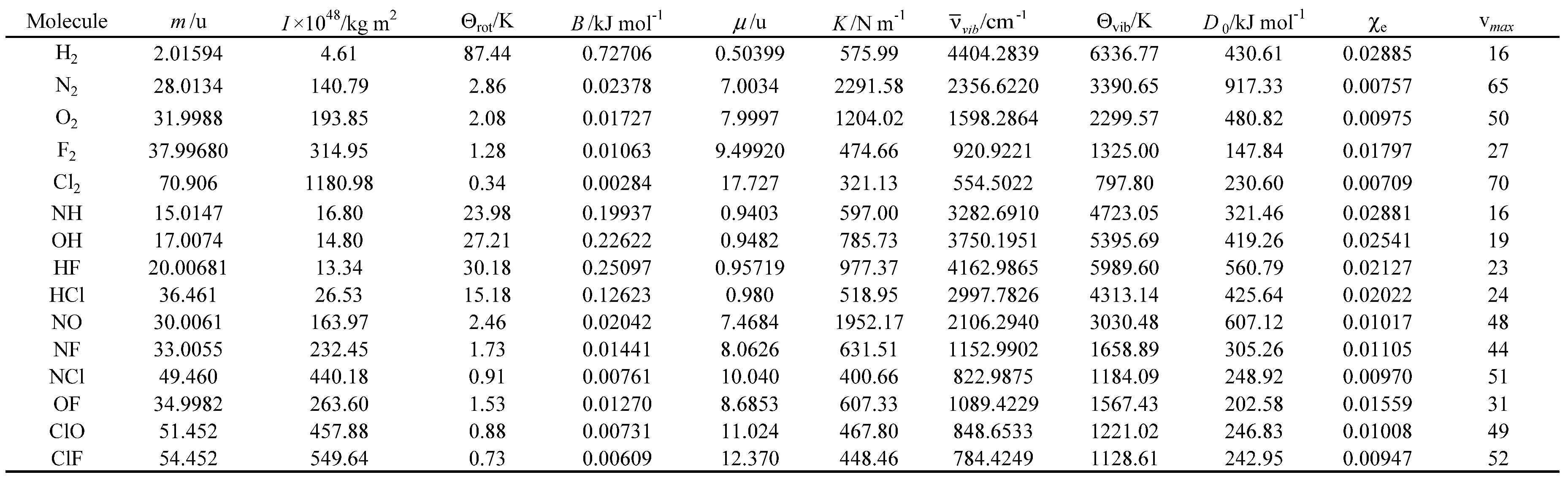
In this study, the Diatomic application was used to calculate the molar thermodynamic properties presented in Table 3, Table 4, Table 5 and Table 6 for the molecules listed in Table 1 and Table 2. The first four models presented in Table 7 (harm, class; Morse, class; harm, quant and Morse, quant) were employed in these calculations. The molecular constants, calculated at a CCSD(T)/cc-pVQZ quantum level, were obtained from the Computational Chemistry Comparison and Benchmark DataBase [31]. These constants are presented in Table 9 and Table 10. These properties were calculated for 14 different temperatures (298.15 K, 373.15 K, 473.15 K, 573.15 K, 673.15 K, 773.15 K, 873.15 K, 973.15 K, 1073.15 K, 1173.15 K, 1273.15 K, 1373.15 K, 1473.15 K and 1573.15 K) and at a constant pressure of 1 bar. Thus, these are standard molar thermodynamic properties at different temperatures. These results are available as supplementary material (see Table S1 and files referred therein).

For comparison, these properties were also calculated using Gaussian 09 [25]. For each molecule studied, a geometry optimization with harmonic frequency calculation was performed. The maximum deviations between the results obtained by these two applications are 0.01, which is in the order of the precision of the thermal results provided by Gaussian 09 (two decimal places).

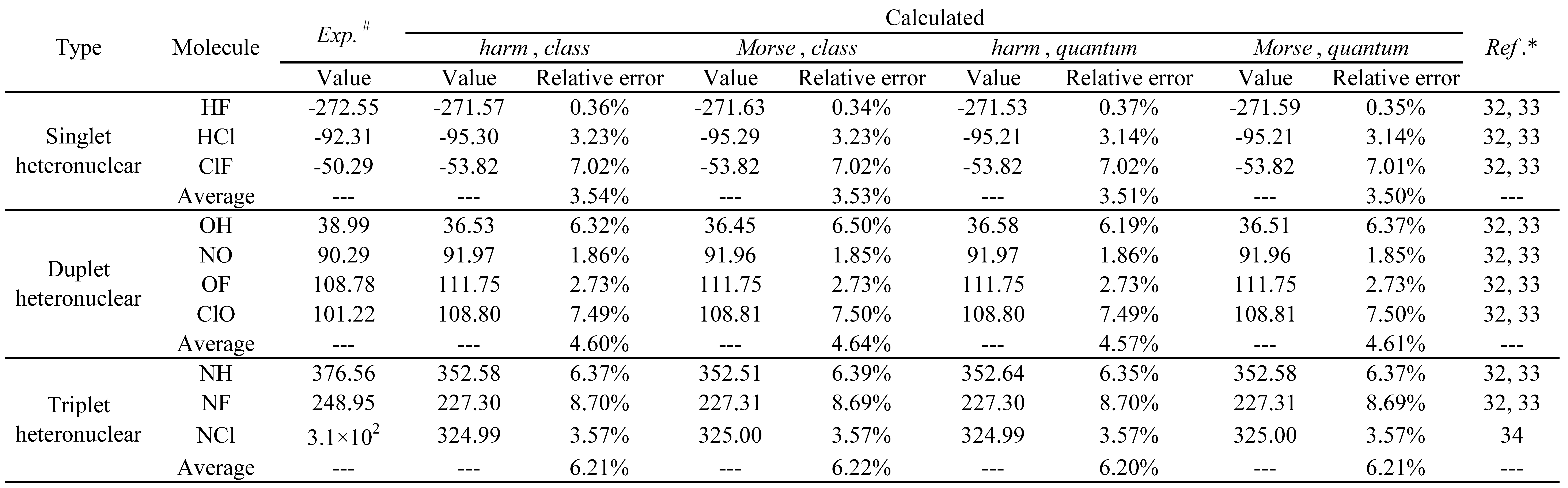
The standard molar enthalpies of formation at 298.15 K, for the diatomic heteronuclear gases studied, were further calculated using the Diatomic application and compared with the corresponding experimental values. The results obtained are presented in Table 11.

Subsequently, three additional molar thermodynamic properties (molar heat capacity at constant pressure (C_p_,m), average value of the standard molar thermal enthalpy (<H^o>_{m, therm}) and standard molar entropy (S^o_m)) were calculated using the Diatomic application for all the molecules studied and compared with corresponding experimental values [32,33]. A reference temperature of 298.15 K was chosen for both the experimental and calculated results. 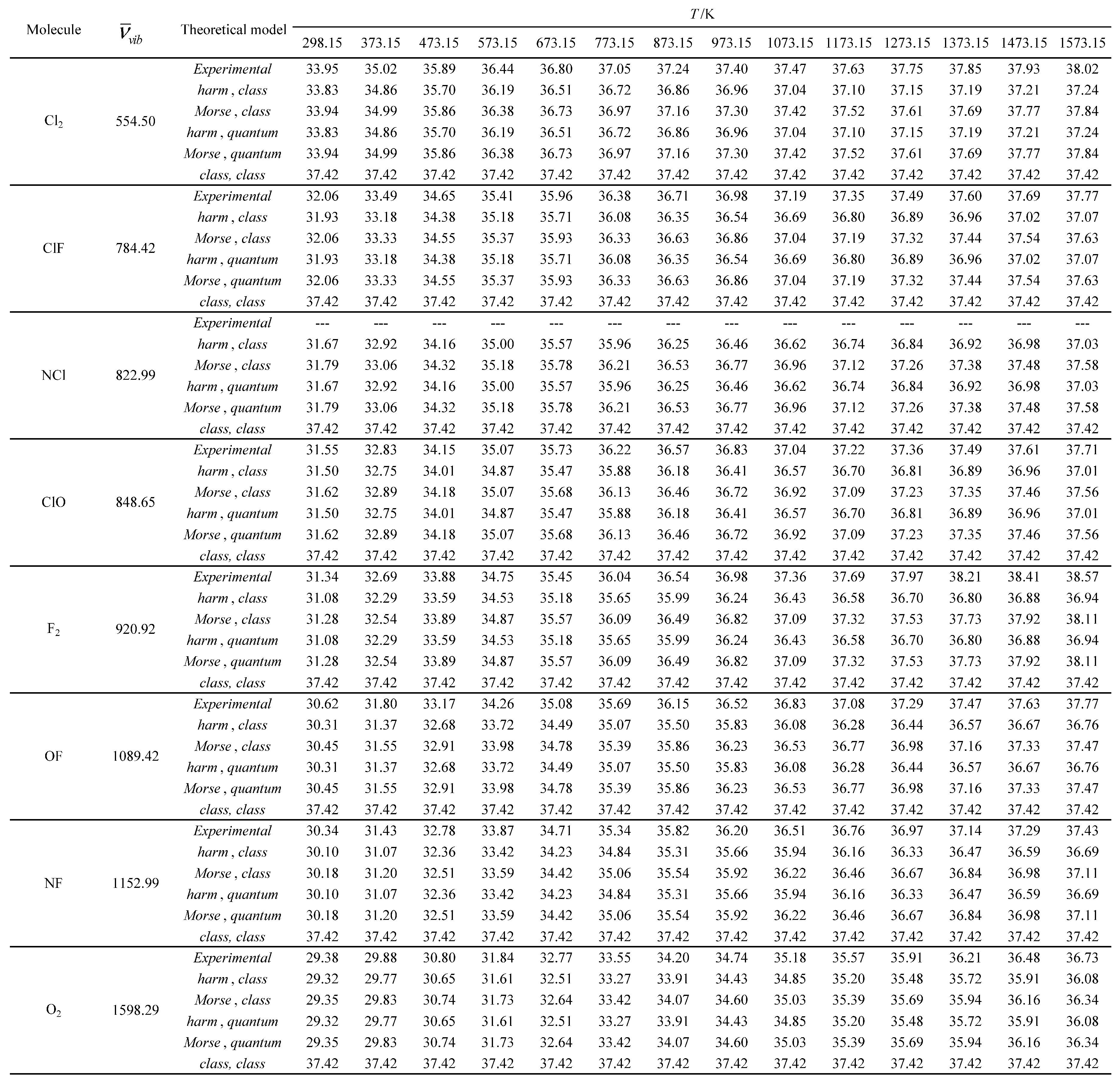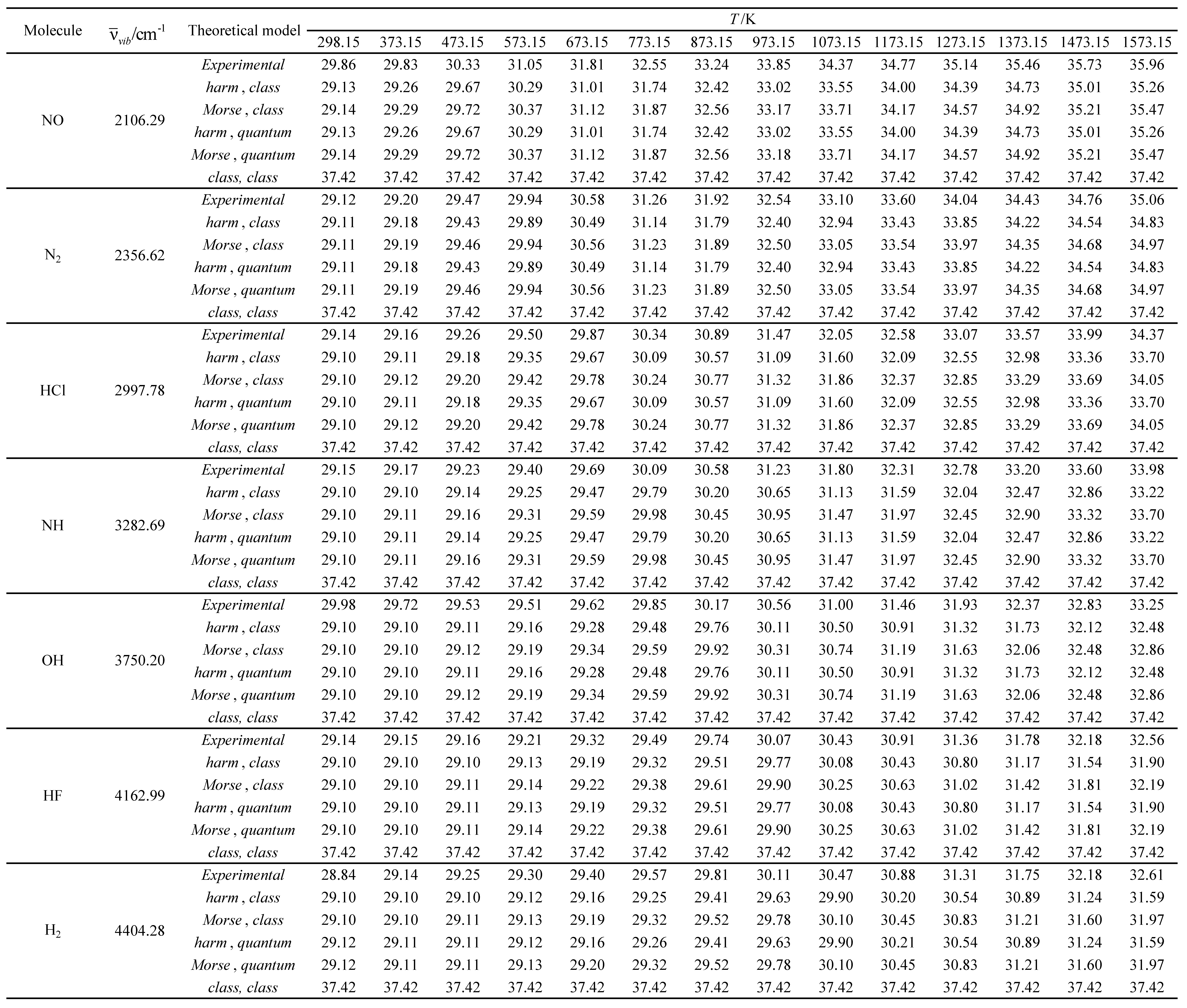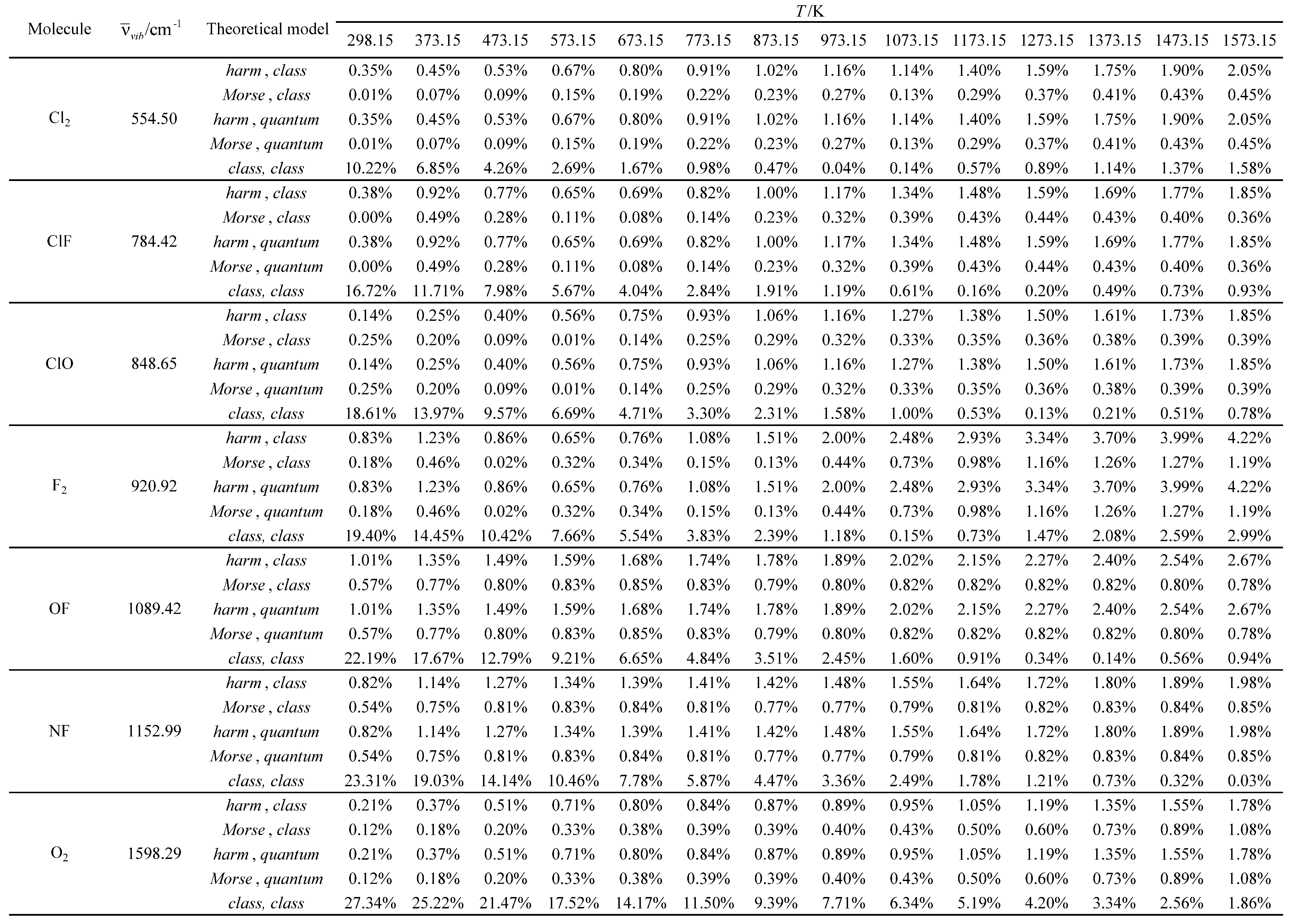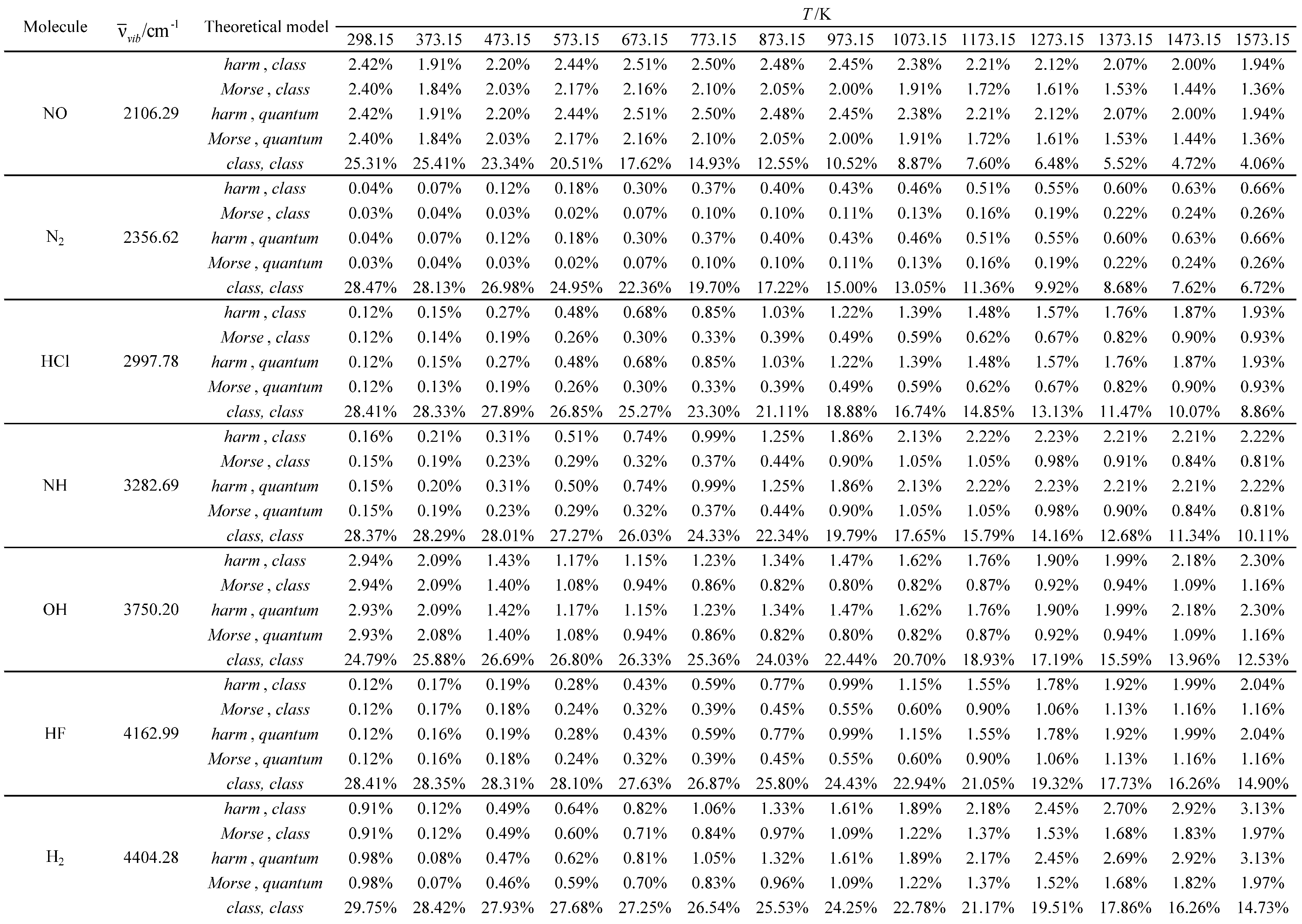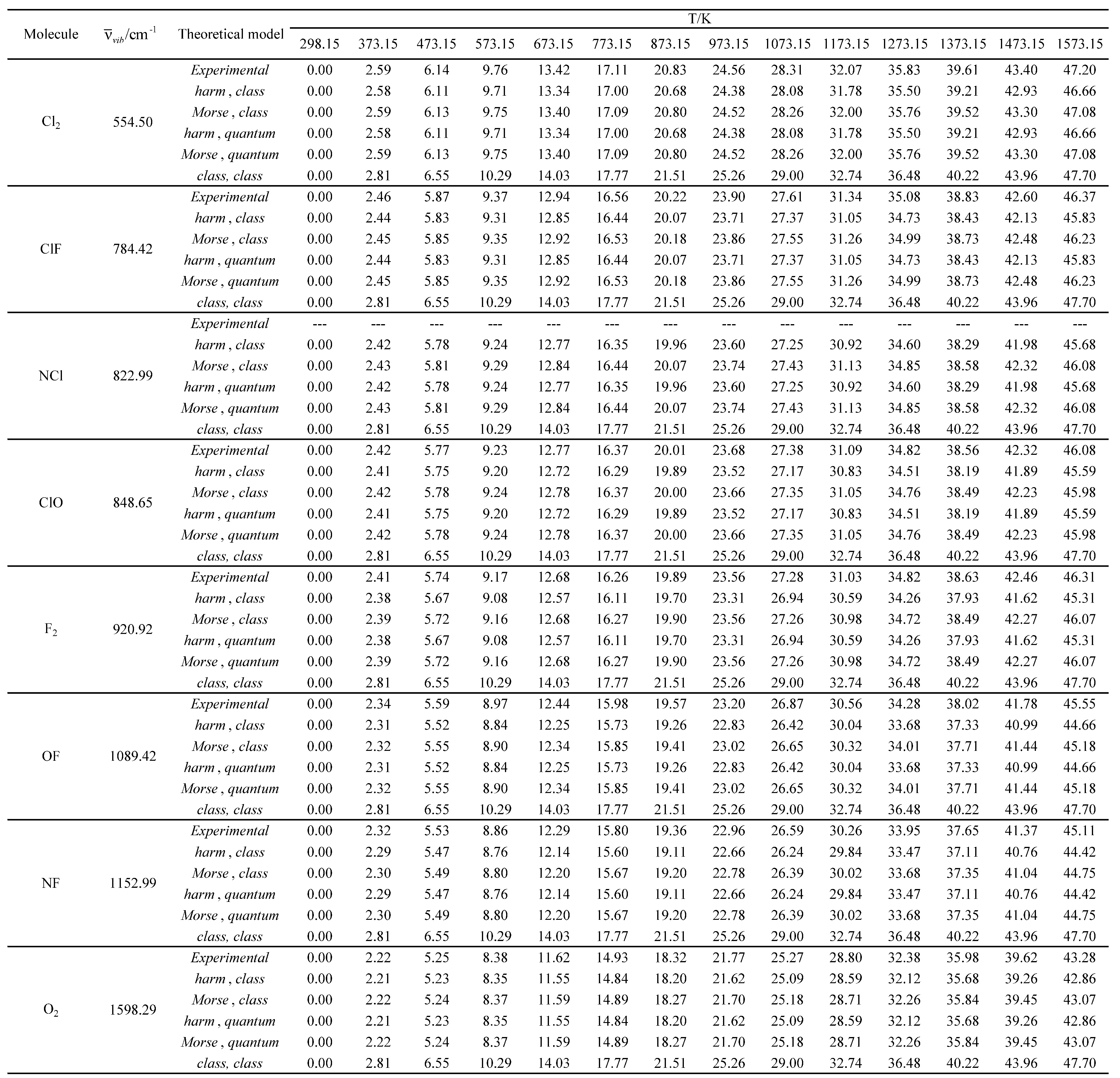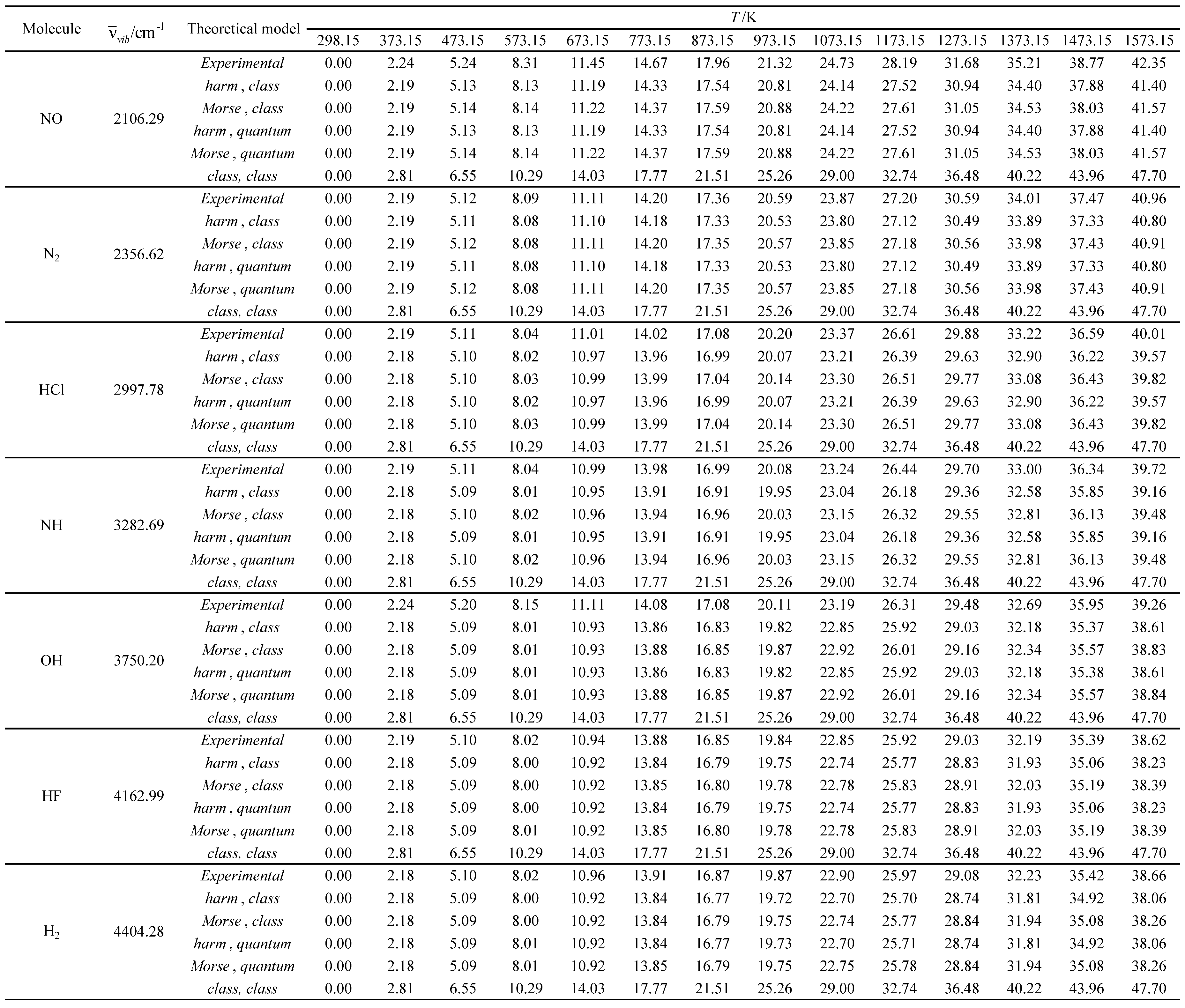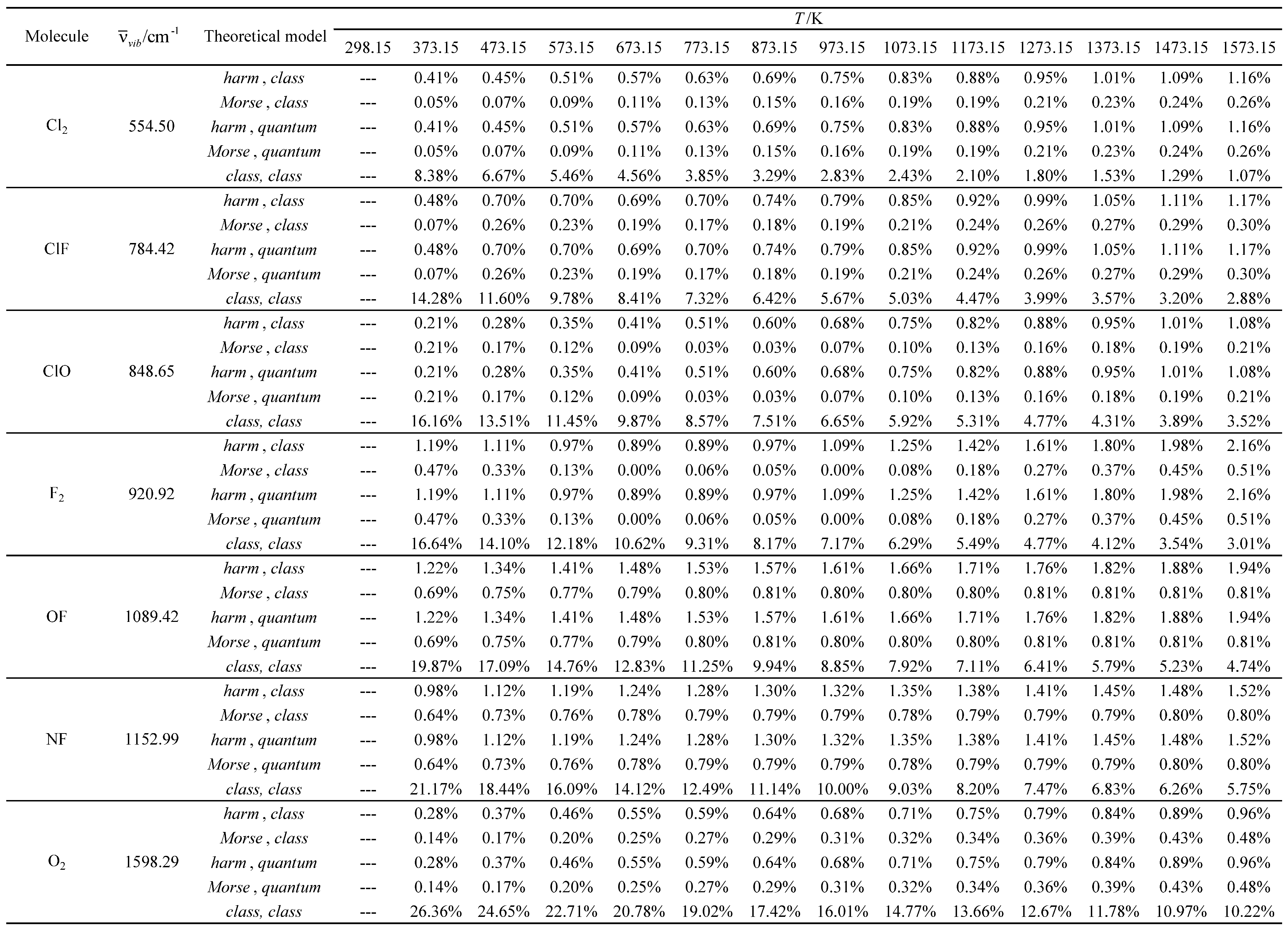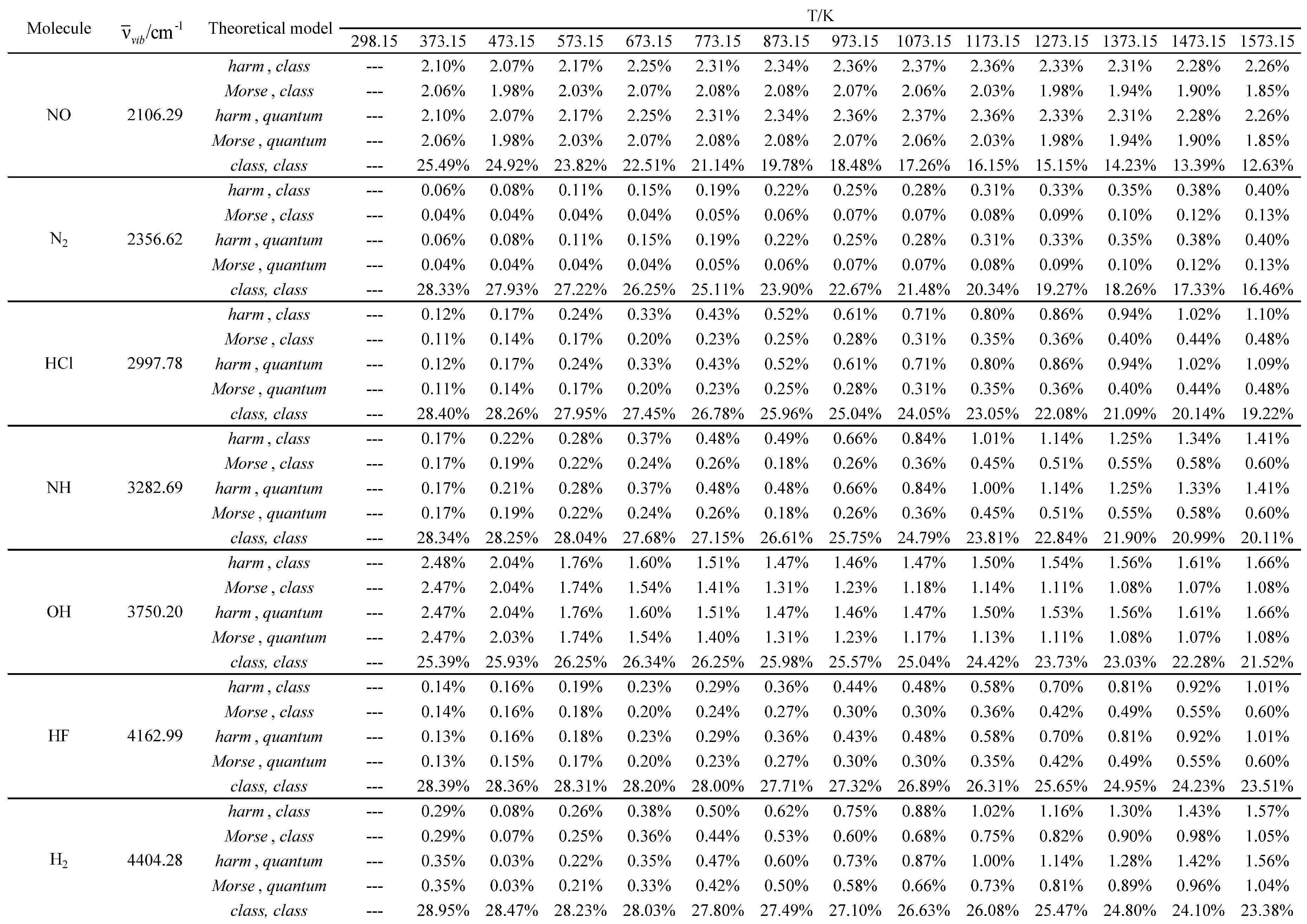The five theoretical models, presented in Table 7, were tested in these calculations. The temperature and pressure constraints were the same as those used in the global calculations. A reference temperature of 298.15 K was selected for both experimental and calculated results. The relative errors for the calculated values were determined, using the experimental values as reference. No experimental values are available for the nitrogen monochloride (NCl) molecule. The results obtained are presented in Tables 12 through 23.

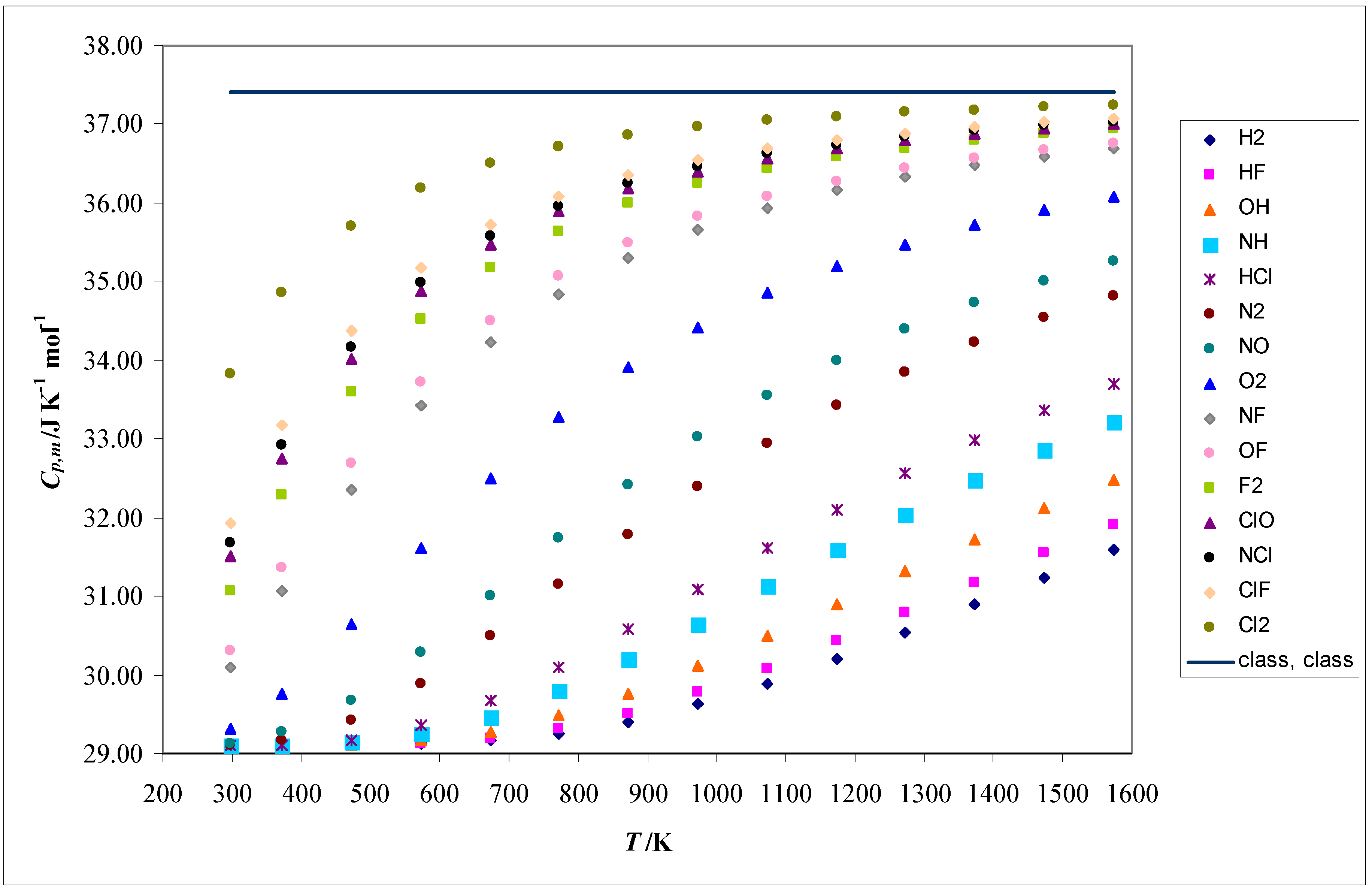
The convergence of the molar heat capacity at constant pressure (C_p,m), calculated using the (harm, class) theoretical model, to the classical limit as a function of temperature is presented in Figure 2 for further analysis.

4. Discussion

The calculated and experimental values of standard molar enthalpy of formation, for the diatomic heteronuclear gas under study, are in reasonable agreement (see table 11). In addition, the following general tendencies can be deduced from the results:

There is no significant difference in the performance of the 4 theoretical models used in these calculations.
The relative errors obtained increase with the spin multiplicity of the molecular systems studied.

For the other three molar thermodynamic properties studied (molar heat capacity at pressure (C_p,m), average value of the standard molar thermal enthalpy (<H^o>_{m, therm}) and standard molar entropy (S^o_m)), the agreement between the experimental and calculated results is generally much better (see Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22 and Table 23). Furthermore, the following general tendencies can be deduced from the results:

The theoretical model, utilized to describe the rotational structure (class or quant), has an almost negligible effect on the results obtained. Only for hydrogen (which exhibits the highest rotational temperature in the investigated series) some residual effects occur at the lowest temperatures.
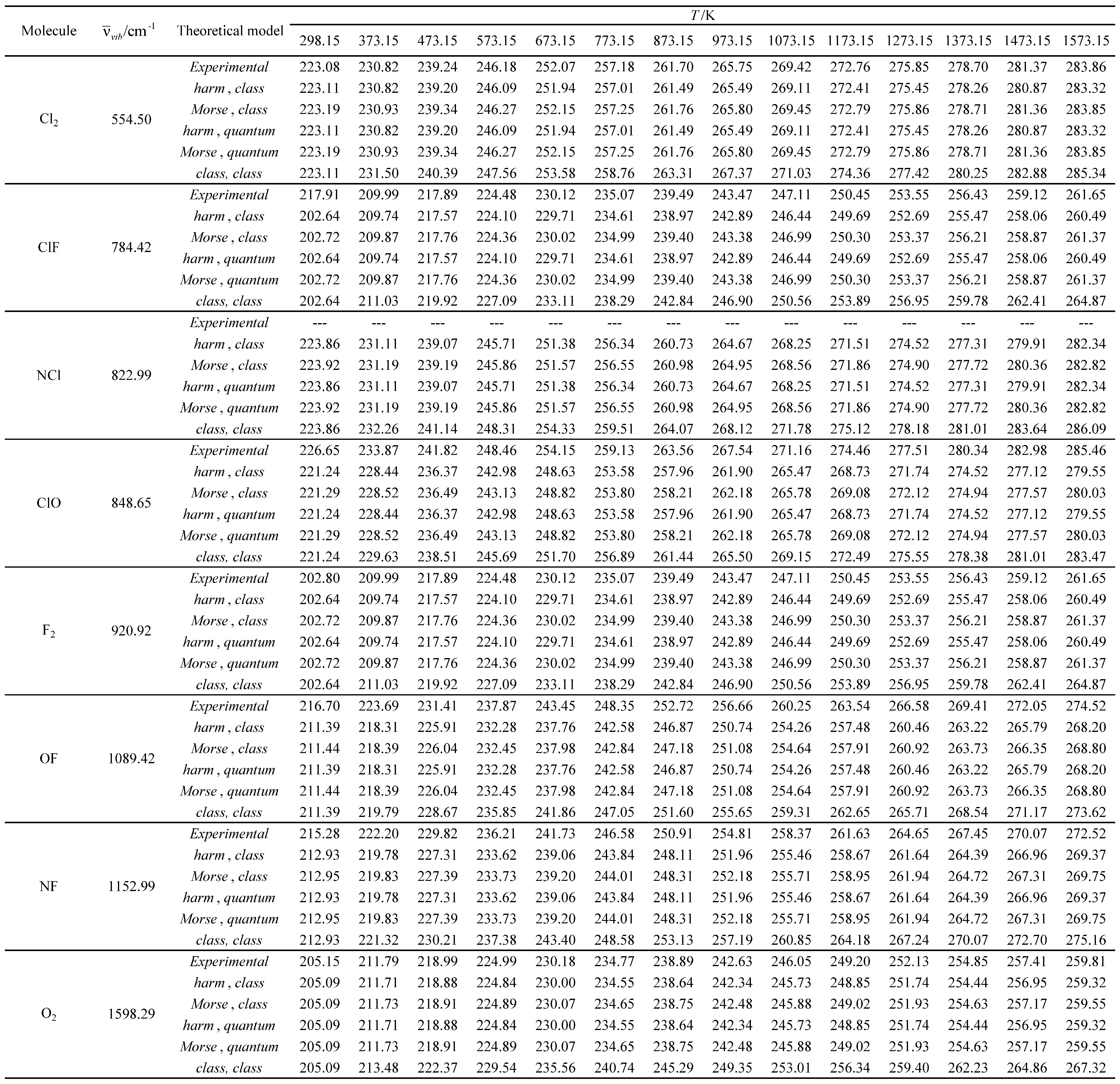
For the lowest temperatures, the Morse oscillator and harmonic oscillator vibrational models have similar performances (similar relative errors).
For moderate and high temperatures, the Morse oscillator model generally gives better results (smaller relative errors) than the harmonic oscillator model. This performance difference usually increases with temperature.
The almost fully classical (class, class) model, which is based on the equipartition principle, usually gives the worst results (largest relative errors) in the calculation of the molar heat capacity at pressure and the average value of the standard molar thermal enthalpy.
However, for the calculation of the standard molar entropy, this model gives similar results to the others. In fact, even for some open-shell systems (ClO, OF, NF, NO, and NH), it is usually associated with the best results (smallest relative errors).

The variations of the molar heat capacity at constant pressure (C_p,m), with temperature and the molecular structure, can be rationalized as follows:

The general tendencies can be deduced from the (harm, class) model, with some anharmonic corrections at high temperatures.
The quantum rotational effects are negligible, because the temperatures under study (T ≥ 298.15 K) are much higher than the typical rotational temperatures. The highest one of these is 87.44 K, associated with the hydrogen molecule.
The equipartition principle is fully applied to the translational and rotational components of C_p,m. For all the molecules studied, the “classical” (translational + rotational + nonspecific) component is (3R/2 + R + R = 7R/2).
Within the model adopted for the electronic structure, the electronic component ( $C_{p, m}^{e l}$ ) of this molar thermodynamic property is null (see equation 32).
The corresponding vibrational component ( $C_{p, m}^{v i b}$ ) increases with temperature, because the variance of the vibrational energy ( $σ_{E^{v i b}}^{2}$ ) follows the same tendency. In fact, the Boltzmann population of the vibrational ground state decreases and the Boltzmann populations of the vibrational excited states increase with temperature.
These tendencies are favored by the decrease of the vibrational frequency (ν_vib), because this decreases the energy difference between two successive vibrational states.
According to the harmonic model, the equipartition principle is also valid for the vibrational components of C_p,m at high or very high temperatures. Thus, this molar thermodynamic property tends to (3R/2 + R + R + R = 9R/2).
This convergence to the classical limit is accelerated by the decrease of the vibrational frequency (ν_vib).
These tendencies are illustrated by results presented Figure 2.
At high temperatures, however, the anharmonic effects cannot be neglected. Therefore, the (Morse, class) model is important to understand the deviations from the harmonic behavior inherent in this situation.

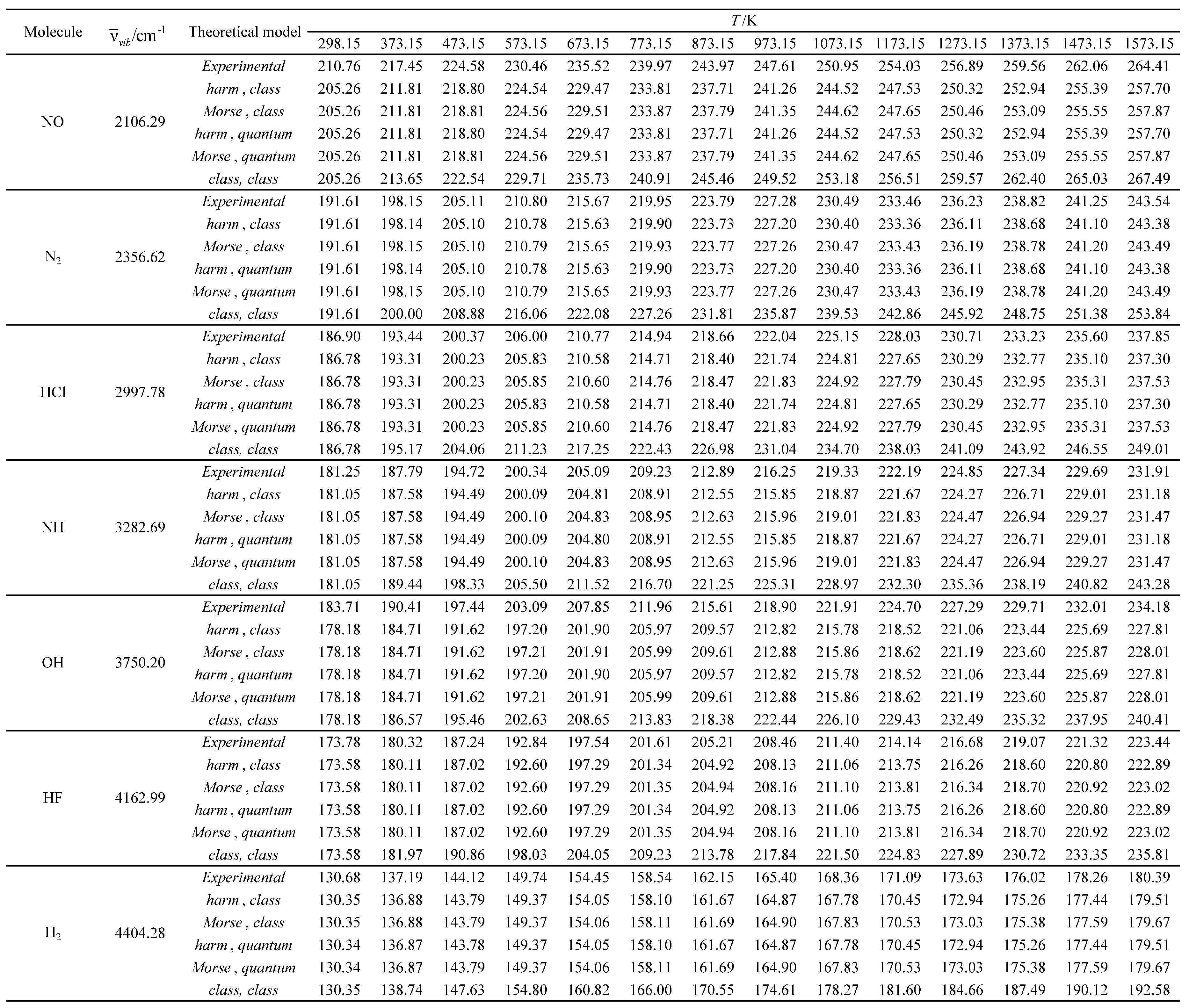
The variations on the average value of the standard molar thermal enthalpy (<H^o>_{m, therm}), with temperature and the molecular structure, follow similar tendencies already described for the molar heat capacity at constant pressure. The main reasons for this behavior are:

The two properties are closely correlated.
The equipartition principle also applies here, despite the classical limit of <H^o>_{m, therm} is a function (9R (T-T_ref)/2) and not a constant (9R/2).

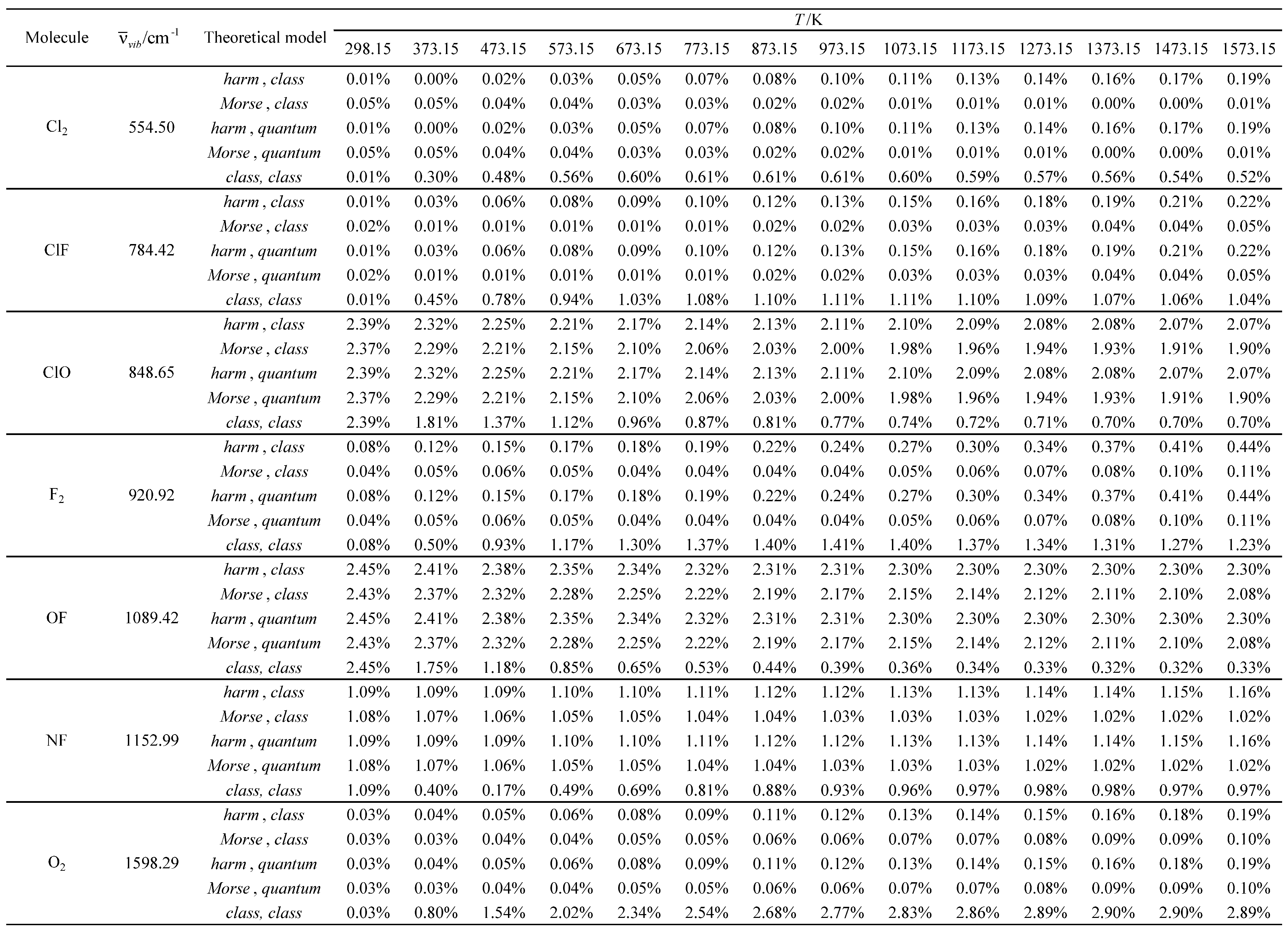
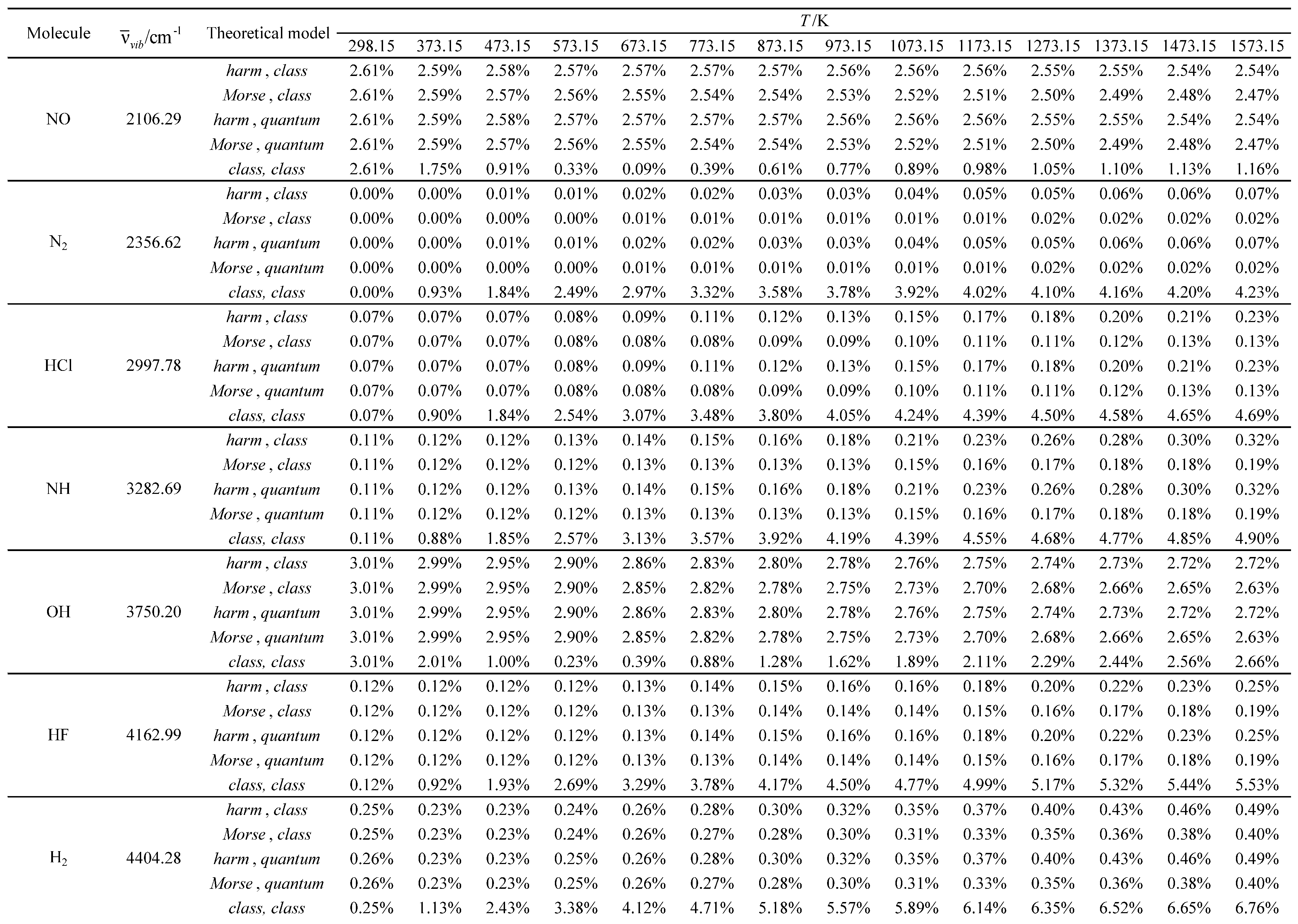
The factors, influencing the variations on C_p,m and <H^o>_m with temperature and the molecular structure, are also crucial to rationalize the corresponding variations on the standard molar entropy (S^o_m). However, this thermodynamic property is much more complex and new factors have to be included in the analysis for a full understanding of its behavior. For this purpose, the following issues must be considered:

The equipartition principle is not directly applied to molar entropy. Even the approximate equation (28), derived for an interval [T_ref, T] where this principle is fully applied to the molar heat capacity at constant pressure and to the average value of molar thermal enthalpy, is not universal. In fact the reference molar entropy ( $S_{m, r e f}$ ) is a specific parameter of each molecule.
The translational molar entropy increases with molecular mass m (see equations 38 and 39).
The rotational molar entropy increases with the reduced mass μ, the equilibrium bond length r_eq and decreases with the rotational symmetry number σ_rot (see equations 41, 42, 43 and 54).
The electronic molar entropy increases with the spin multiplicity of the electronic ground state g₀ (see equation 33).
Consequently, the three components of the molar entropy above mentioned are also specific to each molecule.

5. Conclusions

In this paper, I presented Diatomic as an alternative to quantum chemistry packages for calculating thermodynamic properties of diatomic molecules. Diatomic is an open-source Excel application that requires only a limited number of molecular constants to perform these calculations. In addition, these constants can be easily obtained from freely available online databases.

In this new application, two theoretical models (Morse and harmonic) are available to describe the vibrational structure, and two theoretical models (classical and quantum) are available to describe the rotational structure. By combining the rotational and vibrational structures, four theoretical models can be used within Diatomic (harm-class, Morse-class, harm-quant, and Morse-quant). A fifth model (class-class), based on the equipartition principle, is also used here.

Diatomic was used to calculate four standard molar thermodynamic properties (standard molar enthalpy of formation, molar heat capacity at constant pressure, average value of the standard molar thermal enthalpy, and standard molar entropy) for a set of fifteen diatomic molecules. The results obtained with this application were compared with experimental data.

The theoretical model (classical or quantum) used to describe the rotational structure has a very limited effect on the accuracy of the calculated results. For moderate and high temperatures, the Morse model has better performance (smaller relative errors) than the harmonic model. At low temperatures, both models give similar results.

The results obtained with the molar heat capacity at constant pressure and the average value of the standard molar thermal enthalpy can be rationalized from a harmonic point of view (emphasizing the relevance of the vibrational frequency and the temperature parameters in the analysis), with some anharmonic corrections to the highest temperatures. However, to interpret the standard molar entropy results, some additional factors have to be included in the analysis. These include molecular constants (spin multiplicity of the electronic ground state, molecular mass, reduced mass, equilibrium bond length and rotational symmetry number) that affect the electronic, translational and rotational components of this molar thermodynamic property.

Supplementary Materials

The following supporting information can be downloaded at: Preprints.org; Table S1: List of files used in the calculations performed by the Diatomic application. Files generated with the Diatomic application: h2.xls, n2.xls, o2.xls, f2.xls, cl2.xls, nh.xls, oh.xls, hf.xls, hcl.xls, no.xls, nf.xls, ncl.xls, of.xls, clo.xls and clf.xls.

Funding

This research was funded by FCT/MCTES (LA/P/0008/2020 DOI 10.54499/LA/P/0008/2020, and UIDB/50006/2020 DOI 10.54499/UIDB/50006/2020), through national Portuguese funds.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All the files used in the calculations, performed with the Diatomic application, are available as supplementary information.

Acknowledgments

Not applicable.

Conflicts of Interest

The author declares no conflicts of interest.

Notes

1	The canonical and isothermal-isobaric ensembles are equivalent for an ideal gas.
2	The equipartition theorem can only be applied to the vibrational component for the harmonic oscillator model (see section 2.8). This theorem does not apply to the Morse oscillator model.
3	A harmonic vibrational frequency is used here.
4	In this spreadsheet, the user must input the vibrational wavenumber (secondary molecular constant) and not the vibrational frequency (primary molecular constant). This is because the former is much easier to obtain from freely available online databases than the latter.

References

Abramowitz, S.; Chase, M.W. Thermodynamic properties of gas phase species of importance to ozone depletion. Pure Appl. Chem. 1991, 63, 1449–1454. [CrossRef]
Grein, F. Ab initio studies on complexes of ozone with diatomic molecules. Struct. Chem. 2023, 34, 317–325. [CrossRef]
Ehrenfreund, P.; Charnley, S.B. Organic molecules in the interstellar medium, comets, and meteorites: a voyage from dark clouds to the early Earth. Annu. Rev. Astron. Astrophys. 2000, 38, 427–483. [CrossRef]
Ladjimi, H.; Tomza, M. Diatomic molecules of alkali-metal and alkaline-earth-metal atoms: interaction potentials, dipole moments, and polarizabilities. Phys. Rev. A 2024, 109, 052814. [CrossRef]
Harding, M.E.; Vázquez, J.; Ruscic, B.; Wilson, A.K.; Gauss, J.; Stanton, J.F. High-accuracy extrapolated ab initio thermochemistry. III. Additional improvements and overview. J. Chem. Phys. 2008, 128, 114111. [CrossRef]
Thorpe, J.H.; Kilburn, J.L.; Feller, D.; Changala, P.B.; Bross, D.H.; Ruscic, B.; Stanton, J.F. Elaborated thermochemical treatment of HF, CO, N₂, and H₂O: Insight into HEAT and its extensions. J. Chem. Phys. 2021, 155, 184109. [CrossRef]
Chan, B. DAPD Set of Pd-Containing Diatomic Molecules: Accurate Molecular Properties and the Great Lengths to Obtain Them. J. Chem. Theor. Comput. 2023, 19, 9260−9268. [CrossRef]
Permatahati, L.K.; Cari, C.; Suparmi, A.; Harjana, H. Topological Effects on Relativistic Energy Spectra of Diatomic Molecules Under the Magnetic Field with Kratzer Potential and Thermodynamic-Optical Properties. Int. J. Theor. Phys. 2023, 62, 246. [CrossRef]
Djefoulna, V.H.H.; Fifen, J.J.; Malloum, A.; Jaidane, N-E. Rotational thermodynamic parameters for symmetric-top, linear-top and spherical-top molecules: classical versus quantum approach and New analytical partition functions. Theor. Chem. Acc. 2020, 139, 163.
Hehre, W.J.; Radom, L.; Schleyer, P.v.R.; Pople, J.A. Ab Initio Molecular Orbital Theory; John Wiley: New York, USA, 1986.
Katzer, G.; Sax, A.F. Beyond the Harmonic Approximation: Impact of Anharmonic Molecular Vibrations on the Thermochemistry of Silicon Hydrides. J. Phys. Chem. A 2002, 106, 7204-7215. [CrossRef]
Reinisch, G.; Leyssale, J.-M.; Vignoles, G.L. Hindered rotor models with variable kinetic functions for accurate. J. Chem. Phys. 2010, 133, 154112. [CrossRef]
Irikura, K.K.; Johnson, R.D.; Kacker, R.N. Uncertainties in scaling factors for ab initio vibrational frequencies. J Phys Chem A 2005, 109, 8430-8437. [CrossRef]
Teixeira, F.; Melo, A.; Cordeiro, M.N.D.S. Calibration sets and the accuracy of vibrational scaling. J. Chem. Phys. 2010, 133, 114109. [CrossRef]
Barone, V. Anharmonic vibrational properties by a fully automated second-order. J. Chem. Phys. 2005, 122, 014108. [CrossRef]
Barone, V. Vibrational zero-point energies and thermodynamic functions beyond the harmonic approximation. J. Chem. Phys. 2004, 120, 3059–3065. [CrossRef]
Habibinejad, M.; Ghanbari, A. Enthalpy, Gibbs free energy and specific heat in constant pressure for diatomic molecules using improved deformed exponential-type potential (IDEP). Eur. Phys. J. Plus 2021, 136, 400. [CrossRef]
Reggab, K. Energy spectrum of selected diatomic molecules (H₂ , CO, I₂ , NO) by the resolution of Schrodinger equation for combined potentials via NUFA method. J. Mol. Model. 2024, 30, 53. [CrossRef]
Ayaash, A.N.; Araak, M.A.; Ismaeel, F.R. Potential energy curves and dissociation energies for some diatomic molecules by using two different functions. J. Adv. Res. Appl. Sci. 2016, 3, 43-46. [CrossRef]
Al-Othman, A.B.; Sandouqa, A.S. Comparison study of bound states for diatomic molecules using Kratzer, Morse, and modified Morse potentials. Phys. Scr. 2022, 97, 035401. [CrossRef]
Amila, I.; Fedoul, A.; Idrissi, M.J.; Chatwiti, A.; Sayouri, S. An innovative treatment of anharmonic and Morse potentials to determine the spectroscopic constants of diatomic molecules. Phys. Scr. 2024, 99, 075413. [CrossRef]
Desai, A.M.; Mesquita, N.; Fernandes, V. A new modified Morse potential energy function for diatomic molecules. Phys. Scr. 2020, 95, 085401. [CrossRef]
Pingak, R.K.; Johannes, A.Z.; Ngara, Z.S.; Bukit, M.; Nitti, F.; Tambaru, D.; Ndii, M.Z. Accuracy of Morse and Morse-like oscillators for diatomic molecular interaction: A comparative study. Results Chem. 2021, 3, 100204. [CrossRef]
Denisov, G.S.; Denisov, I.G. More about properties of Morse oscillator. Spectrochim Acta A Mol. Biomol. Spectrosc. 2021, 262, 120111. [CrossRef]
Gaussian 09, Revision A.02, Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; Li, X.; Caricato, M.; Marenich, A.; Bloino, J.; Janesko, B.G.; Gomperts, R.; Mennucci, B.; Hratchian, H.P.; Ortiz, J.V.; Izmaylov, A.F.; Sonnenberg, J.L.; Williams-Young, D.; Ding, F.; Lipparini, F.; Egidi, F.; Goings, J.; Peng, B.; Petrone, A.; Henderson, T.; Ranasinghe, D.; Zakrzewski, V.G.; Gao, J.; Rega, N.; Zheng, G.; Liang, W.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Throssell, K.; Montgomery Jr., J.A.; Peralta, J.E.; Ogliaro, F.; Bearpark, M.; Heyd, J.J.; Brothers, E.; Kudin, K.N.; Staroverov, V.N.; Keith, T.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J.C.; Iyengar, S.S.; Tomasi, J.; Cossi, M.; Millam, J.M.; Klene, M.; Adamo, C.; Cammi, R.; Ochterski, J.W.; Martin, R.L.; Morokuma, K.; Farkas, O.; Foresman, J.B.; Fox, D.J. Gaussian, Inc., Wallingford CT, 2016.
Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [CrossRef]
Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.J.; Windus, T.L.; Dupuis, M.; Montgomery, J.A. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347-1363. [CrossRef]
McQuarrie, D.A. Statistical Mechanics. Harper & Row: New York, USA, 1976.
McQuarrie, D.A.; Simon, J.D. Molecular Thermodynamics. University Science Books: Sausalito, USA, 1999.
Thermochemistry in Gaussian. Ochterski, J.W. Available online: https://gaussian.com/wp-content/uploads/dl/thermo.pdf (accessed on 19 July 2024).
Computational Chemistry Comparison and Benchmark DataBase. Available online: https://cccbdb.nist.gov (accessed on 19 July 2024).
Chase Jr., M.W. NIST-JANAF Thermochemical Tables, Fourth Edition. J. Phys. Chem. Ref. Data 1998, Monograph 9, 1-1951.
NIST Chemistry WebBook Available online: https://webbook.nist.gov/chemistry (accessed on 19 July 2024).
Shamasundar, K.R.; Arunan, E. Chlorofluoroamines: Ab Initio and DFT Studies on Their Structure, Enthalpies of Formation, and Unimolecular Reaction Pathways. J. Phys. Chem. A 2001, 105, 8533-8540. [CrossRef]

Figure 1. Flowchart of the Diatomic application.

Figure 2. Molar heat capacity at constant pressure (C_p,m), calculated using the (harm, class) and the (class, class) theoretical models, as a function of temperature for the molecules under study.

Table 1. Generation of the diatomic molecules under study.

Table 2. Classification of the diatomic molecules under study.

Table 3. Classification of the molar thermodynamic properties under study.

Table 4. List of the type 1 molar thermodynamic properties and respective components.

Table 5. List of the type 2 molar thermodynamic properties and respective components.

Table 6. List of the type 3 molar thermodynamic properties and respective components.

Table 7. Theoretical models used in this work.

Table 8. Classification of the molecular constants used in this work.

Table 9. Values of the primary molecular constants* for the molecules under study.

* Calculated at a CCSD(T)/cc-pVQZ quantum level and obtained from the Computational Chemistry Comparison and Benchmark DataBase [31].

Table 10. Values of the secondary molecular constants* for the molecules under study.

* Calculated at a CCSD(T)/cc-pVQZ quantum level and obtained from the Computational Chemistry Comparison and Benchmark DataBase [31].

Table 11. Experimental and calculated standard molar enthalpy of formation (Δ_fH^o) in kJ mol^-1 and corresponding relative errors.

^# Experimental value. * Reference for the experimental values.

Table 12. Experimental and calculated molar heat capacity at constant pressure (C_p,m) in J K^-1 mol^-1 as a function of temperature for the molecules with the smallest vibrational wavelengths.

Table 13. Experimental and calculated molar heat capacity at constant pressure (C_p,m) in J K^-1 mol^-1 as a function of temperature for the molecules with the largest vibrational wavelengths.

Table 14. Relative errors associated with the calculated molar heat capacity at constant pressure as a function of temperature for the molecules with the smallest vibrational wavelengths.

Table 15. Relative errors associated with the calculated molar heat capacity at constant pressure as a function of temperature for the molecules with the largest vibrational wavelengths.

Table 16. Experimental and calculated average values of the standard molar thermal enthalpy (<H^o>_{m, therm}) in kJ mol^-1 as a function of temperature for the molecules with the smallest vibrational wavelengths.

Table 17. Experimental and calculated average values of the standard molar thermal enthalpy (<H^o>_{m, therm}) in kJ mol^-1 as a function of temperature for the molecules with the largest vibrational wavelengths.

Table 18. Relative errors associated with the calculated average value of the standard molar thermal enthalpy as a function of temperature for the molecules with the smallest vibrational wavelengths.

Table 19. Relative errors associated with the calculated average value of the standard molar thermal enthalpy as a function of temperature for the molecules with the largest vibrational wavelengths.

Table 20. Experimental and calculated standard molar entropies (S^o_m) in J K^-1 mol^-1 as a function of temperature for the molecules with the smallest vibrational wavelengths.

Table 21. Experimental and calculated standard molar entropies (S^o_m) in J K^-1 mol^-1 as a function of temperature for the molecules with the largest vibrational wavelengths.

Table 22. Relative errors associated with the calculated standard molar thermal entropy as a function of temperature for the molecules with the smallest vibrational wavelengths.

Table 23. Relative errors associated with the calculated standard molar thermal entropy as a function of temperature for the molecules with the largest vibrational wavelengths.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Diatomic: An Open-Source Excel Application to Calculate Ther-Modynamic Properties for Diatomic Molecule

Abstract

1. Introduction

2. Materials and Methods

2.1. General formalism

2.2. Classification of the molar thermodynamic properties

2.3. Classical limit

2.4. Theoretical models

2.5. Electronic structure

2.6. Translational structure

2.7. Rotational structure

2.8. Vibrational structure

2.9. Standard molar enthalpy of formation

2.10. Molecular constants

2.11. Diatomic application

3. Results

4. Discussion

5. Conclusions

Supplementary Materials

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Notes

References

MDPI Initiatives

Important Links

Subscribe