Prerpints.org logo
Preprint
Article

Identifying High-Risk Patterns in Single-Vehicle, Single-Occupant Road Traffic Accidents: A Novel Pattern Recognition Approach

Altmetrics

Downloads

70

Views

93

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

02 September 2024

Posted:

03 September 2024

You are already at the latest version

Alerts
Abstract
Despite various interventions in road safety work, fatal and severe road traffic accidents (RTAs) remain a significant challenge leading to human suffering and economic costs. Understanding the multicausal nature of RTAs, where multiple conditions and factors interact, is crucial for developing effective prevention measures in road safety work. This study investigates the multivariate statistical analysis of co-occurring conditions in RTAs, focusing on single-vehicle accidents with single occupancy and personal injury on Austrian roads outside built-up areas from 2012 to 2019. The aim is to detect recurring combinations of accident-related variables, referred to as blackpatterns (BPs), using the Austrian RTA database. The study proposes Fisher’s exact test to estimate the relationship between an accident-related variable and fatal and severe RTAs (severe casualties). In terms of pattern recognition, the study develops the maximum combination value (MCV) of accident-related variables, a procedure to search through all possible combinations of variables to find the one that has the highest frequency. The accident investigation proceeds with the application of pattern recognition methods, including binomial logistic regression and a newly developed method, the PATTERMAX-method, created to accurately detect and analyse variable-specific BPs in RTA data. Findings indicate significant BPs contributing to severe accidents. The combination of binomial logistic regression and the PATTERMAX-method appears to be a promising approach to investigate severe accidents, providing both insights into detailed variable combinations and their impact on accident severity.
Keywords: 
Subject: Engineering  -   Transportation Science and Technology

1. Introduction

1.1. Relevance and Problem Statement

Road traffic accidents ( R T A ) with personal injuries result in substantial material and immaterial costs. According to the Austrian Accident Cost Accounting from 2022, the economic costs of a single fatal R T A are estimated at 4.801.407 Euros, with accidents resulting in severe injuries costing 593.479 Euros each [1]. Despite various interventions, fatal R T A s remain a significant challenge worldwide. Austria experienced a peak in fatal R T A s in 1972, with 2.948 fatalities. Since then, numerous safety interventions, such as speed limits and mandatory seatbelt use, have significantly reduced the number of fatal accidents [2]. However, Austria still ranks 11th in the EU with 47 traffic fatalities per million inhabitants in 2019 [3]. The Austrian Ministry of the Interior [4] identifies several major accident causes, including speeding, distraction, and priority violations. These causes are determined subjectively by police officers at the scene, leading to potential biases. Besides the definition of accident causes, road safety work also focuses on the identification of accident blackspots. Blackspots are road sections where accidents frequently occur. Identifying these points is crucial for implementing targeted safety measures. However, going beyond the definition of a major accident cause and the identification of blackspots, this study aims to identify blackpatterns ( B P s ), which we define as recurring combinations of accident-related variables [5]. We conduct a detailed examination of recorded accident conditions, regardless of the officially designated accident cause. Understanding the multicausal nature of R T A s , where multiple conditions and factors interact, is crucial for developing effective prevention measures. This study addresses the gap in multivariate statistical investigation and pattern analysis approaches of R T A s , proposing that accidents are influenced by a complex interplay of driver, vehicle, roadway, and situational variables.

1.2. Literature Review

R T A s are a significant public health concern, influenced by a complex interplay of factors. Various studies emphasize the need for a multidimensional approach to understand and prevent R T A s. [6] reviewed various data sources and techniques for accident analysis, emphasizing the benefits of combining multiple analytical methods. [7] employed system dynamics to model the complexity of R T A s , highlighting the importance of considering non-linear interactions between variables. [8] proposed a multidimensional and multi-period analysis of road safety, incorporating various criteria such as human factors, accident causes, and road characteristics. [9] reviewed R T A s , emphasizing the multifactorial nature of accidents involving human, vehicular, and environmental elements. [10] reviewed black spot identification methods, emphasizing the coupling of statistical and accident severity index methods for more reliable road safety assessments. [11] used generalized logistic regression and classification trees to identify combinations of factors leading to fatal accidents. [12] applied association rule mining to reveal complex interactions between human, vehicle, road, and environmental factors in multi-fatality crashes. [13] introduced a novel matched crash vs. non-crash approach for analysing severe crash patterns on multilane highways, identifying significant factors for different crash types. [14] developed logistic regression models to estimate fatality and major injury probabilities in single-vehicle accidents, finding that the major injury model had better explanatory power. These studies collectively demonstrate the value of advanced statistical methods in understanding accident circumstances and identifying potential areas for targeted interventions.
When analysing R T A data, one of the major targets is to quantify the influence of an accident-related variable on the degree of injury. Research has identified various factors influencing accident severity and frequency. For example, [15,16] identified collision mode, road configuration, vehicle type, driver characteristics, and environmental conditions. [16] declare motorcycles, male drivers, elderly drivers, nighttime driving, high-speed roads, and darkness without lighting as specific risk factors associated with higher accident severity.
[17] revealed that that safety devices, narrow impact, ejection, airbag deployment, and higher speed are associated with more severe injuries. Other research identified airbag deployment, extrication, ejection, travel speed, and alcohol involvement as the most critical factors affecting injury severity [18,19]. [20] demonstrated that multiple driver mistakes tend to result in more severe crashes. According to [21,22], factors affecting accident severity include environmental conditions, vehicle type, protective devices, and time of day. Understanding these variables is crucial for conducting exploratory data analysis and developing effective road safety measures [23].
Further studies highlight the importance of comprehensive data analysis in developing effective road safety strategies [10,24,25,26]. [27] advocates for a system approach that focuses on the entire road transport system rather than just individual behaviour. [28] highlight the effectiveness of various interventions, including educational, engineering, and multifaceted approaches, in improving pedestrian safety. [29] found that legislation combined with strong enforcement or as part of a multifaceted approach was most effective in low- and middle-income countries. [30] stresses the importance of awareness creation, strict implementation of traffic rules, and scientific engineering measures to prevent R T A s . The dynamic interactions between various factors to analyse R T A s and develop more effective safety measures underscore the necessity of comprehensive, multidimensional approaches to R T A prevention.

1.3. Research Question and Scope

R T A s remain a significant challenge, with single-vehicle accidents accounting for a substantial portion of fatalities in Europe [14]. Within the scope of a multidimensional approach to R T A analysis, this study investigates how multivariate and recurrent B P s   in single-vehicle accidents can be identified, as well as their significance for severe and fatal accidents (referred to as severe casualties). The study aims to represent driver, vehicle, roadway, and situational variables and their correlations with accident severity using advanced statistical methods. Additionally, it identifies significant B P s among these variables. These patterns provide a deeper understanding of accident circumstances and highlight potential areas for targeted safety interventions. By combining descriptive statistics, binomial logistic regression, and innovative methods like the PATTERMAX-method, the study seeks to detect recurring patterns that contribute to severe accidents and evaluate their frequency and impact. The research is intended not only to improve road safety measures but also to facilitate the development of more precise prevention strategies that target the most hazardous accident B P s . Therefore, this paper addresses the following research question: How can multivariate and recurrent variable-specific blackpatterns ( B P s ) in single-vehicle, single-occupant road traffic accidents with personal injury be accurately identified and analysed, and what is their significance in mitigating severe and fatal accidents?

2. Methods

2.1. Data Preparation for Pattern Recognition

Between 2012 and 2019, 303.700 R T A s   occurred on the Austrian road network. 110.666 road accidents occurred outside built-up areas, while 193.034 accidents occurred within built-up areas. The study focuses on single-vehicle accidents with single occupancy that occurred outside built-up areas between 2012 and 2019 ( n = 20.293). The chosen sample amounts to 7 % of all R T A s with a personal injury in Austria between 2012-2019 ( n = 303.700). Within the period under review, 110.666 accidents with personal injury occurred outside the built-up area, of which the extracted sample comprises 18 %. The selection of these specific accidents allows for an analysis that is not confounded by the presence of multiple vehicles or individuals, which could otherwise complicate the already complex nature of road traffic accidents. By isolating these accidents, the study can more effectively identify and examine the underlying B P s and factors contributing to severe outcomes, making this sample particularly valuable for targeted analysis. The data preparation involves creating a binary R T A database with over 150 accident-related variables. Figure 1 illustrates the extracted R T A data sample in relation to all recorded R T A s between 2012-2019 in Austria.

2.2. Accident-Related Variables

After recoding all accident-related characteristics and setting up a binary accident database, the next step in data preparation foresees the assignment of each binary variable to one of the following categories: driver-related variables (54 variables), vehicle-related variables (32 variables), roadway-related variables (50 variables), and situation-related variables (22 variables). Table 1 illustrates the categorisation scheme for the 158 analysed accident-related variables.
We aim to quantify each accident-related variable's impact on the degree of injury. Therefore, the dependent variable shall combine severe injury and fatalities within the category severe casualties. Regarding the Austrian Road Safety Strategy 2021-2030 [31], it is equally important to reduce fatalities and the number of severe injuries. Also, both categories (severe and fatal accidents) entail high economic costs and human suffering. These premises lead to the following classification of the degree of injury:
  • Casualties: minor injury, severe injury, death at accident site, death within 30 days,
  • Severe casualties: severe injury, death at accident site, death within 30 days.
Thus, the degree of injury comprises two categories within this study. The resulting dependent variable is severe casualties. This classification corresponds to the definition within the Handbook Of Transportation System Planning [32, p.73].

2.3. Descriptive Analyses

Initial analyses include calculating conditional and joint probabilities, applying Fisher's exact test, and estimating the Phi coefficient for each accident-related variable in relation to severe casualties, treating severe casualties as the dependent variable. A bootstrap resampling method is used for robust parameter estimation, and a maximum combination value ( M C V ) is calculated as a key indicator for B P   detection. This value indicates how often a specific variable co-occurs with one or more accident-related variables. Each accident-related variable is broken down into a contingency table, where the rows represent the accident variable, and the columns represent the outcomes: casualty and severe casualty. The frequency n i j in the table represents the number of occurrences where the accident variable takes the value x i   and the outcome is either casualty or severe casualty, with severe casualty being treated as the dependent variable. The conditional probability P of an event A given another event B is denoted as P = A B :
P =   P   ( A ∩ B ) P ( B )
Here, P = ( A ∩ B ) is the joint probability of A and B , and P ( B ) is the probability of B . In the context of this analysis, A represents a specific accident variable, and B represents the outcome severe casualties. Fisher's Exact Test calculates the exact probability of observing the distribution in the contingency table. This is particularly useful for small sample sizes or when examining the relationship between an accident variable and severe casualties. The Phi coefficient is a measure of association between each accident-related variable and the outcome severe casualties. The probability P of observing this particular table is calculated using the hypergeometric distribution:
P =   a + b a c + d c n a + c
where:
a + b a is the binomial coefficient, calculated as a + b ! a ! × b ! ,
c + d c is the binomial coefficient for the second row,
n a + c is the binomial coefficient for the total table, where n = a + c + b + d .
As a next step, we apply Bootstrap resampling to estimate robust confidence intervals for the parameters. The 95 % confidence intervals indicate that certain variables consistently contribute to severe accidents, reinforcing the findings from the Fisher's test. As a first step towards pattern recognition, we want to identify the M C V , which tells us how often a specific variable co-occurs with one or more accident-related variables. Let D =   D 1 ,   D 2 , … , D n be a dataset with n entries. Each entry D i consists of a set of binary variables x 1 ,   x 2 ,   … ,   x m where each x j can be either 0 or 1. The goal is to find the combination of variables that maximizes the occurrence of a specific outcome, Y , which could be severe accidents, for instance. To define the combination of variables that includes x j , let C = x j 1 ,   x j 2 , … , x j k be a combination of x j with k other variables, where x j 1 ,   x j 2 , … , x j k are selected from the full set x 1 ,   x 2 ,   … ,   x m . The frequency F ( C ) of each combination C is defined as the number of entries D i , where all variables in C take the value 1.
F C = ∑ i = 1 n I ( C ,   D i )
where the indicator I C ,   D i is defined as:
I C ,   D i = 1     i f x j 1 = 1 ,   x j 2 = 1 ,   … , x j k = 1   i n   D i ,   0     o t h e r w i s e                                                                                            
The M C V   is the combination C * that includes x j and maximises the frequency F ( C ) in relation to a specific outcome Y = 1 :
M C V =   max C ⊆ x 1 ,   x 2 ,   … , x m ,   x j ∈ C ⁡ F ( C | Y = 1 )
The M C V approach involves searching through all possible combinations that include the specific variable x j , calculating the frequency with which these combinations occur when a specific outcome Y = 1 is observed, and identifying the combination with the highest frequency. The M C V method analyses how frequently a particular variable occurs in combination with one or more other variables, identifying the most common combination in which the variable appears.

2.4. Binomial Logistic Regression

The study employs several pattern recognition methods. To investigate to what extent accident-related variable affects the probability of severe casualties, we apply binomial logistic regression, with severe casualties as the dependent variable. The logistic regression model is crucial for understanding how different accident-related variables, such as speeding, alcohol use, or road conditions, contribute to the probability of severe casualties. By examining these relationships, the model helps identify key factors that increase the risk of severe accidents.
log ⁡ P ( Y = 1 ) P ( Y = 0 ) = β 0 + β 1 X 1 + β 2 X 2 + … + β k X k
where:
P ( Y = 1 ) is the probability of the outcome being severe casualty,
P ( Y = 0 ) is the probability of the outcome being a non-severe casualty,
log ⁡ P Y = 1 P Y = 0 is the log-odds of the outcome occurring (severe casualties),
β 0 is the intercept term, representing the log-odds of severe casualties when all predictors X 1 , X 2 , … , X k are zero,
β 1 , β 2 , … , β k are coefficients associated with each accident-related predictor variable, X 1 , X 2 , … , X k . These coefficients indicate the strength and direction of the relationship between each variable and the likelihood of severe casualties.

2.5. PATTERMAX-Method

The developed PATTERMAX-method analyses the frequencies of variable combinations ( B P s ) and examines their association strength with severe casualties. The R T A dataset D consists of n entries, where each entry is a sequence of x binary variables (0s and 1s). We aim to calculate the frequency of each B P , i.e., each identical sequence of 0s and 1s of length m in the dataset D . We define the B P of length m as a string of m binary variables, where B P   =   ( p 1 ,   p 2 ,   . . . ,   p m ) , with p i being either 0 or 1. To calculate the frequency F ( B P ,   D ) of B P in the dataset D , we use the PATTERMAX-method, which proceeds as follows:
F B P , D = ∑ i = 1 n ∑ j = 1 x − m + 1 I ( B P ,   D i j : j + m )
where:
n is the number of entries in the dataset D ,
x is the number of binary variables in each entry,
D i represents the i-th entry in the dataset D ,
j is the position in the entry D i where the B P is checked,
I ( B P , D i j : j + m is an indicator function that returns 1 if the substring B P exactly matches D i from position j to j + m − 1 , and 0 otherwise.
This formula describes the PATTERMAX-method for calculating the frequency of the   B P in the dataset D . To verify if the B P matches at a specific position, we iterate over each entry in the dataset, over all positions in the entry, and use the indicator function. The sum over all entries and positions returns the total frequency of B P in D . After identifying B P s using the PATTERMAX-method, each generated B P is further examined using Fisher's Exact Test to determine the p -value that quantifies the strength of the association between the B P and severe casualties. p F i s h e r ( B P ) represents the p -value obtained from Fisher's Exact Test for B P . This step ensures that the B P s identified are not only frequent but also statistically significant in their relationship to severe accidents.

2.6. Blackpattern Impact Analysis

To calculate a blackpattern impact score ( B I S ), we combine four components: frequency of the B P   F B P , D , the statistical association between the B P and severe causalities (measured by ( p F i s h e r B P ) , the strength of this association (measured by the Phi coefficient ϕ B P ), and the logistic regression coefficients β i corresponding to the variables in B P . These components are integrated into a comprehensive B I S to prioritize the identified B P s . This approach enables a precise assessment of the B P s concerning severe accidents by considering both their frequency and the strength of their association with severe casualties, thereby identifying B P s that are both frequent and impactful.
B I S B P = F ( B P ,   D ) × ϵ ϕ B P × − l o g p F i s h e r B P × ∏ i = 1 k ϵ β i
where:
β i represents the logistic regression coefficient for each variable V i in the B P ,
F B P , D is the frequency of the B P ,
ϕ B P is the Phi coefficient, which measures the strength of the association between the B P and the outcome,
p F i s h e r B P is the p -value from Fisher’s Exact Test, indicating the statistical significance of the association between the B P and the outcome.
To amplify the influence of highly significant B P s (with very small p -values), the negative logarithm of p F i s h e r B P is used. The transformation − l o g p F i s h e r B P converts very small p -values into larger positive numbers. This ensures that B P s with strong statistical significance have a greater impact on the   B I S . Both the logistic regression coefficients β i and the Phi coefficient ϕ B P   represent the strength of association. Small coefficients or ϕ -values might otherwise have a minimal effect on the B I S . The exponential transformation ϵ β i and ϵ ϕ P magnifies these values, particularly when they are small. This emphasizes the contribution of B P s where the variables have a stronger association with the outcome.
The blackpattern impact analysis allows to identify B P s that are not only common and impactful but also statistically significant in their relationship with severe casualties. This approach provides a comprehensive and nuanced prioritization of B P s , ensuring that our analysis highlights the most relevant and meaningful B P s for further investigation or intervention. Table 2 illustrates the features of the blackpattern impact analysis that must be considered when interpreting the retrieved B I S .

3. Results

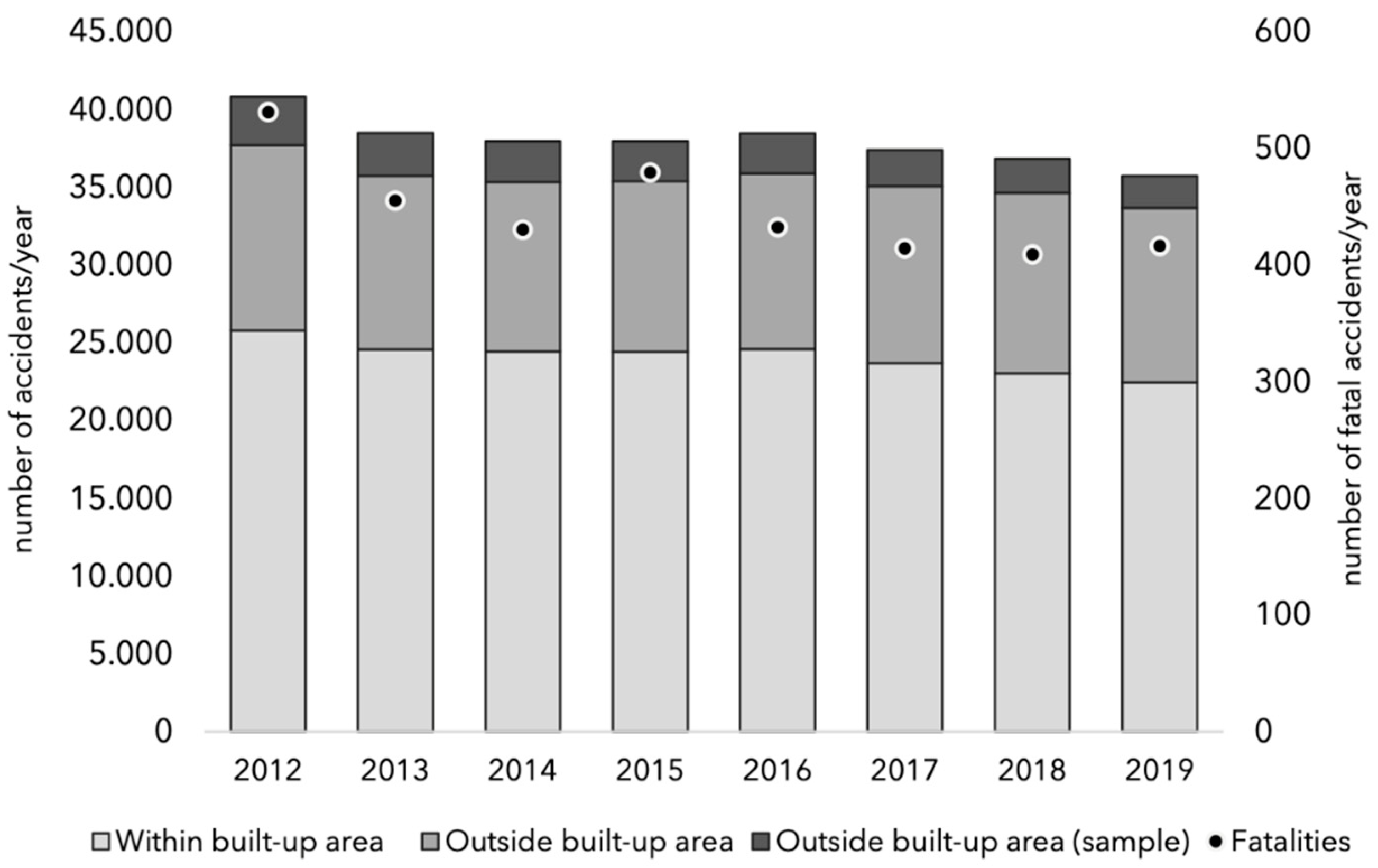
3.1. Descriptive Analyses

Descriptive statistics reveal the frequency and probability of each variable in severe and fatal accidents. Significant relationships between variables and accident severity are identified using Fisher's exact test and the Phi coefficient. Also, we generate the presented M C V . We conduct descriptive analyses for each variable within our defined categories (driver, vehicle, roadway, and situation). Table 3 illustrates the results for driver-related accident variables in Austria.
The driver-related outcomes reveal that male drivers are significantly more likely to be involved in severe accidents compared to female drivers, with a probability of 12,11 % versus 4,79 %, respectively. Age also plays a crucial role, with younger drivers aged 19 to 24 and older drivers aged 64 and above showing a higher likelihood of being involved in severe accidents. The analysis indicates that the absence of a driving license and probationary driving licenses are associated with increased accident severity, although their impact is relatively lower compared to other factors. Impairment due to alcohol, distraction, and fatigue are highlighted as significant contributors to severe accidents, but among these, fatigue shows a particularly strong correlation. The table also underscores the critical impact of not wearing a seatbelt, which is strongly associated with severe casualties, as evidenced by the highest Phi coefficient in the analysis. Various driving manoeuvres, such as skidding, hitting a tree, and sudden braking, also exhibit significant relationships with accident severity, with some manoeuvres like hitting a tree being particularly indicative of severe outcomes. The M C V suggests that certain variables, like the absence of a seatbelt, tend to co-occur with other risk factors more frequently in severe accidents, further emphasizing their role in contributing to accident severity.
Table 4 presents a comprehensive analysis of vehicle-related variables and their association with the severity of accidents. Engine power is a notable factor, with vehicles having higher engine power (over 110 kW) showing a higher probability of severe casualties, as indicated by the Phi coefficient of 0,053 and a significant p -value of 0,000. This suggests that vehicles with greater engine power are more likely to be involved in severe accidents. In contrast, vehicles with lower engine power (24-90 kW) demonstrate a negative correlation with accident severity, as reflected by a negative Phi coefficient (-0,066). Vehicle colours appear to play a neglectable role as the correlations are weak and not statistically significant. The table also highlights the impact of vehicle safety features on accident outcomes. Cases where the airbag did not deploy are strongly associated with severe casualties, as evidenced by a Phi coefficient of -0,149, making it one of the most critical factors in the analysis. Other variables, such as technical defects and insufficient vehicle security, are less prevalent but still present some level of risk, particularly vehicle fires, which have a Phi coefficient of 0,035.
Table 5 provides a detailed analysis of roadway-related variables and their impact on the severity of single-vehicle accidents that took place outside built-up areas in Austria between 2012 and 2019.
One of the most significant findings is the relationship between speed limits and accident severity. Accidents occurring in areas with a 100 km/h speed limit show a higher probability of severe casualties, with a Phi coefficient of 0,019 and a significant   p -value of 0,008, indicating a moderate positive correlation. Similarly, roads with a 130 km/h speed limit also show a notable frequency of severe accidents, although the correlation is slightly weaker. The type of road is another critical factor, with accidents on country roads being particularly severe, as these roads account for the highest number of severe casualties, although the Phi coefficient suggests only a weak correlation. Additionally, certain road characteristics, such as curves and straight roads, are strongly associated with severe accidents. Curves, in particular, have a significant negative Phi coefficient (-0,042), indicating a strong correlation with accident severity. In contrast, straight roads, despite their higher overall accident frequency, show a positive Phi coefficient (0,040), suggesting that while they are common sites for accidents, the severity is more strongly associated with other variables like speed or road conditions. The analysis also reveals that road conditions significantly impact accident severity, with dry roads being the most common setting for severe accidents, supported by a high Phi coefficient (0,095). However, wet and wintry conditions also play a significant role, as indicated by negative Phi coefficients, showing that these conditions are associated with less severe outcomes compared to dry conditions.
Table 6 provides an analysis of situation-related variables and their impact on the severity of single-vehicle accidents. The analysis highlights several critical situation-related factors that influence the severity of single-vehicle accidents. Time of day emerges as a significant variable, with accidents occurring between 12 a.m. and 6 a.m. showing a higher probability of severe casualties, indicated by a Phi coefficient of 0,051 and a significant p -value of 0,000. This suggests that early morning hours are particularly dangerous, likely due to factors such as reduced visibility, fatigue, or lower traffic volumes leading to higher speeds. In contrast, the period from 12 p.m. to 6 p.m., although still significant, shows a negative correlation with accident severity, indicating fewer severe outcomes during daylight hours. The day of the week also plays a role, with accidents from Monday to Thursday slightly more likely to result in severe casualties compared to those occurring from Friday to Sunday. However, the correlation is weak, as reflected by the small Phi coefficient (-0,025). Seasonal variation is evident, with summer showing a slightly higher likelihood of severe accidents, as suggested by a Phi coefficient of 0,025. This could be attributed to increased travel and higher speeds during warmer weather. Winter, on the other hand, despite the challenging driving conditions, shows a negative correlation with severe outcomes, which may be due to more cautious driving during adverse weather conditions. Weather conditions have a notable impact, with clear or overcast weather being strongly associated with severe casualties, as indicated by a Phi coefficient of 0,053. This finding may be counterintuitive, but it suggests that drivers might be less cautious during clear conditions, leading to higher speeds and more severe accidents. Snowy conditions, however, show a significant negative correlation with severe casualties, likely reflecting more careful driving in such conditions. Light conditions further influence accident severity, with darkness being associated with a higher likelihood of severe accidents, as shown by a Phi coefficient of 0,044. This is consistent with the increased risks associated with driving at night, such as reduced visibility and driver fatigue.

3.2. Logistic Regression Analysis

Binomial logistic regression shows the strength of relationships between accident-related variables and severe accidents, identifying high-risk variables with significant odds ratios. The logistic regression analysis in Table 7 reveals several key variables that significantly increase the likelihood of severe R T A s . One of the most influential factors is the non-use of a safety belt, which has the highest odds ratio ( e x p ( β ) = 5,015) among the variables analysed, indicating that drivers not wearing a seatbelt are over five times more likely to be involved in a severe accident. Other critical factors include young drivers, particularly those aged 16 to 18, who have an odds ratio of 2,317, and those aged 19 to 24, with an odds ratio of 2,101, reflecting a significantly higher risk for these age groups.
Environmental and situational factors also play a substantial role. Driving during early morning hours (12 a.m. to 6 a.m.) increases the likelihood of severe accidents by 35,9 % ( e x p ( β ) = 1,359), likely due to factors such as fatigue and reduced visibility. Road conditions, such as driving on a wet road or under wintry conditions, also contribute to higher accident severity, with odds ratios of 1,261 and 1,462, respectively. The presence of specific road features like curves, intersections, and tunnels significantly increases the risk, with tunnels showing an odds ratio of 1,674 and curves 1,198, indicating these features are critical risk factors.
Vehicle-related factors also influence the severity of accidents. Vehicles with engine power between 24-90 kW show a 19,2 % higher likelihood of severe accidents, while certain actions like sudden braking or hitting an obstacle on the road increase the risk significantly, with odds ratios of 2,0 and 3,394, respectively. Interestingly, hitting a guard rail is associated with a lower likelihood of severe accidents, with an odds ratio of 0,731, suggesting that this might serve as a mitigating factor under certain conditions.
The analysis also highlights the significant impact of alcohol, which nearly doubles the likelihood of severe accidents ( e x p ( β ) = 1,916), underscoring the critical danger posed by impaired driving. Additionally, vehicle-related variables like the colour green and the absence of airbag deployment are associated with higher risks, with odds ratios of 1,317 and 2,233, respectively.
When performing multiple logistic regression, some variables may be excluded from the final model, resulting in no regression coefficient being assigned to them. This exclusion occurs because the statistical model deems these variables to have an insignificant or non-contributory effect on the outcome, often due to multicollinearity, lack of variability, or because their contribution is already captured by other variables in the model.

3.3. PATTERMAX-Method

The PATTERMAX-method reveals critical B P s in the data, indicating combinations of factors that significantly contribute to severe accidents (Table 8). One of the most prominent B P s identified is the combination of a 130 km/h speed limit, driving on a highway, drifting to the right, and being a male driver. This B P is statistically significant with a p -value of 0,001 and a Phi coefficient of 0,027, occurring 44 times in the dataset. This suggests that this specific combination of factors is strongly associated with severe accidents. Another significant B P   involves a 100 km/h speed limit on a country road, with left drift and male drivers, showing an even stronger correlation with severe casualties ( p = 0,000, ϕ = 0,032) and a frequency of 41 occurrences. This B P underscores the heightened risk associated with country roads, particularly when combined with drifting and male drivers. Additional B P s include scenarios where male drivers on country roads, particularly under conditions of fatigue or without wearing a safety belt, show a strong association with severe accidents. For example, the combination of a 100 km/h speed limit, left drift, male driver, and no safety belt applied is highly significant ( p = 0,000, ϕ = 0,031), though it occurs less frequently, with 10 recorded instances. This indicates that although less common, this particular combination of factors leads to particularly severe outcomes. Other B P s highlight the risk posed by wet roads and darkness. A B P involving a 100 km/h speed limit on a country road, a wet road surface, a male driver aged 25-34, and a right drift shows a strong association with severe accidents ( p   = 0,001 ,   ϕ   = 0,027). Similarly, driving in darkness on country roads with right drift and male drivers also presents a significant risk ( p = 0,003, ϕ = 0,026).

3.4. Blackpattern Impact Analysis

The blackpattern impact analysis results in Table 9 highlight the varying influence of different combinations of variables on the likelihood of severe R T A s , with the B I S providing a quantitative measure of their overall effect. In cases where a B P generated by the PATTERMAX-method includes variables without a regression coefficient, we assign a value of zero ( β = 0 )   to these variables. By setting the coefficient to zero, we ensure that the variable neither positively nor negatively influences the B I S , reflecting the fact that the variable does not significantly impact the likelihood of severe outcomes according to our logistic regression model.
The B P with the highest B I S   involves a 100 km/h speed limit on a country road, left drift, male driver, and the absence of a safety belt, which has a significant B I S of 982,9. This high B I S reflects the strong influence of not wearing a seatbelt, which substantially increases the likelihood of severe accidents, as indicated by the high regression coefficient ( β = 1,612).
The combination of a 100 km/h speed limit, country road, and male driver, whether drifting left or right, consistently yields high B I S (e.g., 804,7 and 167,6), indicating that these factors together significantly elevate the risk of severe accidents.
A speed limit of 130 km/h on a highway with right drift and male driver results in a relatively high B I S of 628,4 which still presents a notable risk. This B P highlights that while speed and road type are important, the absence of additional high-risk behaviours like seatbelt non-use somewhat mitigates the overall risk.
B P s involving female drivers or those with a speed limit of 80 km/h on a country road with right drift show even lower B I S (e.g., 50,1 and 38,3), reflecting the reduced likelihood of severe outcomes compared to more dangerous combinations. This suggests that gender and lower speed limits contribute to safer outcomes, although they are not completely devoid of risk. The B I S also underscores the combined risk posed by fatigue and specific road conditions (e.g., 167,6 and 37,1).

4. Discussion

The findings from this study underscore the complex and multivariate nature of R T A s , particularly single-vehicle, single-occupant accidents outside built-up areas in Austria. By applying statistical methods, such as binomial logistic regression and the PATTERMAX-method, we have identified significant B P s that consistently correlate with severe casualties. These B P s reveal critical insights into how specific combinations of driver-related, vehicle-related, roadway-related, and situational factors contribute to the severity of accidents.
One of the key observations from the logistic regression analysis is the substantial impact of not wearing a safety belt, which emerged as the most influential variable, increasing the likelihood of severe accidents by over five times. This finding aligns with existing literature that highlights the protective benefits of seatbelt usage, particularly in preventing severe injuries and fatalities. Similarly, the significant influence of young drivers, especially those aged 16 to 24, on accident severity suggests that targeted interventions, such as stricter licensing regulations and enhanced driver education programs, could be crucial in mitigating risks within this demographic.
The PATTERMAX-method further refines our understanding by identifying specific combinations of variables that, when occurring together, significantly increase the likelihood of severe outcomes. For example, B P s involving high-speed limits, rural roadways, and male drivers frequently result in severe accidents, especially when compounded by factors like driver fatigue or adverse weather conditions. These B P s provide valuable guidance for policymakers and road safety experts, emphasizing the need for comprehensive approaches that address multiple risk factors simultaneously.
The blackpattern impact analysis introduces a novel way of quantifying the combined effect of these variables, offering a clear prioritization of the most dangerous combinations. This approach is particularly useful for designing targeted interventions that can address the most critical risks. For instance, the combination of a 100 km/h speed limit, a country road, left drift, and a male driver not wearing a safety belt was identified as having the highest B I S , making it a prime target for road safety campaigns and enforcement measures.

5. Conclusions

This study successfully identifies and quantifies the most significant B P s associated with severe R T A s , providing a deeper understanding of the multicausal interactions that lead to these outcomes. The combination of pattern recognition methods, such as binomial logistic regression and the PATTERMAX-method, with a robust statistical evaluation framework, offers a comprehensive toolset for analysing R T A data. These findings highlight the importance of addressing specific high-risk combinations of variables through targeted road safety interventions.
Future research should expand the scope of this analysis to include other types of accidents and integrate additional data sources, such as behavioural and environmental data, to develop more comprehensive accident prediction models. By doing so, we can further refine our understanding of the factors contributing to severe accidents and enhance the effectiveness of prevention strategies. The insights gained from this study provide a solid foundation for improving road safety and reducing the human and economic costs associated with severe R T A s .

Author Contributions

Conceptualization, T.F.; methodology, T.F.; validation, T.F. and G.H.; formal analysis, T.F.; investigation, T.F.; data curation, T.F.; writing—original draft preparation, T.F.; writing—review and editing, T.F. and G.H.; visualization, T.F.; supervision, G.H. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Herry Conuslt, & KFV. (2022). Unfallkostenrechnung Straße 2022 (UKR 2022). Forschungsarbeiten des österreichischen Verkehrssicherheitsfonds, Wien: Bundesministerium für Klimaschutz, Umwelt, Energie, Mobilität, Innovation und Technologie (BMK).
  2. European Commission. (2020). Handbook on the external costs of transport. Version 2019 – 1.1, CE Delft, Directorate-General for Mobility and Transport.
  3. European Commission. (2019, December 18). Archive: Road safety statistics - characteristics at national and regional level. Retrieved August 8, 2021, from https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Road_safety_statistics__characteristics_at_national_and_regional_level&oldid=463733.
  4. Bundesministerium für Inneres (BMI) I. (2020). Straßenverkehrstote in Österreich. Retrieved July 7, 2021, from bmi.gv.at: https://www.bmi.gv.at/202/Verkehrsangelegenheiten/files/Jahresvergleich_1983_2020.pdf.
  5. Fian, T. (2021). From Blackspots to Blackpatterns: Pattern recognition with road traffic accident data. Dissertation. [CrossRef]
  6. Gutierrez-Osorio, C., & Pedraza, C.A. (2020). Modern data sources and techniques for analysis and forecast of road accidents: A review. Journal of Traffic and Transportation Engineering, 7, 432-446. [CrossRef]
  7. Kizito, A., & Semwanga, A.R. (2020). Modeling the Complexity of Road Accidents Prevention: A System Dynamics Approach. International Journal of System Dynamics Applications, 9, 24-41. [CrossRef]
  8. Martins, M.A., & Garcez, T.V. (2021). A multidimensional and multi-period analysis of safety on roads. Accident analysis and prevention, 162, 106401. [CrossRef]
  9. Khalsa, A. (2019). Study on Road Traffic Accidents and Prevention in India. A Review. International Journal for Research in Applied Science and Engineering Technology. [CrossRef]
  10. Karamanlis, I., Nikiforiadis, A., Botzoris, G.N., Kokkalis, A., & Basbas, S. (2023). Towards Sustainable Transportation: The Role of Black Spot Analysis in Improving Road Safety. Sustainability. [CrossRef]
  11. Reeves, K., Chandan, J.S., & Bandyopadhyay, S. (2019). Using statistical modelling to analyze risk factors for severe and fatal road traffic accidents. International Journal of Injury Control and Safety Promotion, 26, 364 - 371. [CrossRef]
  12. Gu, C., Xu, J., Gao, C., Mu, M., E., G., & Ma, Y. (2022). Multivariate analysis of roadway multi-fatality crashes using association rules mining and rules graph structures: A case study in China. PLOS ONE, 17. [CrossRef]
  13. Pande, A., & Abdel-Aty, M.A. (2009). A novel approach for analyzing severe crash patterns on multilane highways. Accident analysis and prevention, 41 5, 985-94. [CrossRef]
  14. Alin, D., Cofarue, C., & Popesku, M.V. (2023). Investigation of Single Vehicle Accidents Severity by Using a Probabilistic Approach. Mobility and Vehicle Mechanics. [CrossRef]
  15. Cioca, L., & Ivașcu, L. (2017). Risk Indicators and Road Accident Analysis for the Period 2012–2016. Sustainability, 9, 1530. [CrossRef]
  16. Shibani, A., & Pervin, M.S. (2016). Analysis of traffic accident severity on Great Britain roadways and junctions. Engineering, Environmental Science, Geography. [CrossRef]
  17. Ju, Y.H., & Sohn, S.Y. (2011). Quantification method analysis of the relationship between occupant injury and environmental factors in traffic accidents. Accident analysis and prevention, 43 1, 342-51. [CrossRef]
  18. Yaman, T.T., Bilgiç, E., & Esen, M.F. (2020). Analysis of Traffic Accidents to Identify Factors Affecting Injury Severity with Fuzzy and Crisp Techniques. [CrossRef]
  19. Yaman, T.T., Bilgiç, E., & Esen, M.F. (2021). Analysis of traffic accidents with fuzzy and crisp data mining techniques to identify factors affecting injury severity. J. Intell. Fuzzy Syst., 42, 575-592. [CrossRef]
  20. Shaon, M.R., & Qin, X. (2020). Crash Data-Based Investigation into How Injury Severity Is Affected by Driver Errors. Transportation Research Record, 2674, 452 - 464. [CrossRef]
  21. Gilani, V., Hosseinian, S.M., Ghasedi, M., & Nikookar, M. (2021). Data-Driven Urban Traffic Accident Analysis and Prediction Using Logit and Machine Learning-Based Pattern Recognition Models. Mathematical Problems in Engineering, 2021, 1-11. [CrossRef]
  22. Sohn, S.Y., & Shin, H. (2001). Pattern recognition for road traffic accident severity in Korea. Ergonomics, 44, 107 - 117. [CrossRef]
  23. Khyara, H., Amine, A., & Nassih, B. (2023). Dependent and Independent Variables for Exploratory Analysis of Road Traffic Accidents. Proceedings of the International Conference on Industrial Engineering and Operations Management. [CrossRef]
  24. Athiappan, K., Karthik, C., Rajalaskshmi, M., Subrata, C., Rabiei-Dastjerdi, H., Liu, Y., Fernández-Campusano, C., & Gheisari, M. (2022). Identifying Influencing Factors of Road Accidents in Emerging Road Accident Blackspots. Advances in Civil Engineering. [CrossRef]
  25. Theofilatos, A., & Yannis, G. (2014). A review of the effect of traffic and weather characteristics on road safety. Accident analysis and prevention, 72, 244-56. [CrossRef]
  26. Aziz, S., & Ram, S. (2022). A Meta-analysis of the methodologies practiced worldwide for the identification of Road Accident Black Spots. Transportation Research Procedia. [CrossRef]
  27. Khorasani-Zavareh, D. (2011). System versus traditional approach in road traffic injury prevention: a call for action. Journal of Injury and Violence Research, 3, 61 - 61. [CrossRef]
  28. Rezapur-Shahkolai, F., Afshari, M., Doosti-Irani, A., Bashirian, S., & Maleki, S. (2022). Interventions to prevent road traffic injuries among pedestrians: a systematic review. International Journal of Injury Control and Safety Promotion, 29, 533 - 549. [CrossRef]
  29. Staton, C.A., Vissoci, J.R., Gong, E., Toomey, N., Wafula, R.B., Abdelgadir, J., Zhou, Y., Liu, C., Pei, F., Zick, B., Ratliff, C.D., Rotich, C., Jadue, N., de Andrade, L., von Isenburg, M., & Hocker, M.B. (2016). Road Traffic Injury Prevention Initiatives: A Systematic Review and Metasummary of Effectiveness in Low and Middle Income Countries. PLoS ONE, 11. [CrossRef]
  30. Gopalakrishnan, S. (2012). A Public Health Perspective of Road Traffic Accidents. Journal of Family Medicine and Primary Care, 1, 144 - 150. [CrossRef]
  31. KFV, & FGM. (2021). Österreichische Verkehrssicherheitsstrategie 2021–2030. Wien: Bundesministerium für Klimaschutz.
  32. Cerwenka, P., Hauger, G., Hörl, B., & Klamer, M. (2007). Handbuch der Verkehrssystemplanung. Österreichischer Kunst- und Kulturverlag, Wien.
Preprints 117014 g001
Figure 1. Development of road traffic accidents (RTAs) in Austria from 2012-2019. Own compilation based on RTA data from Statistics Austria.
Figure 1. Development of road traffic accidents (RTAs) in Austria from 2012-2019. Own compilation based on RTA data from Statistics Austria.
Preprints 117014 g001
Table 1. Categorisation scheme for accident-related variables.
Table 1. Categorisation scheme for accident-related variables.
Driver Vehicle Roadway Situation
  • Sex
  • Age Class
  • Driving licence
  • Impairment
  • Driving manoeuvres
  • Safety settings
  • Engine power
  • Kilometrage
  • Vehicle colour
  • Vehicle safety settings
  • Speed limits
  • Road characteristics
  • Traffic light
  • Road types
  • Road surface conditions
  • Daytime
  • Weekday
  • Meteorological seasons
  • Weather conditions
  • Light conditions
Table 2. Features of the blackpattern impact score (BIS).
Table 2. Features of the blackpattern impact score (BIS).
BIS Features Description
High Frequency Blackpatterns that occur frequently in the dataset are prioritized.
High Impact Blackpatterns with variables that have a strong influence on severe casualties are emphasized.
Strong Association Blackpatterns that are statistically significant in their association with severe casualties are given higher priority.
Table 3. Single-vehicle accidents with single occupation and personal injury that occurred outside built-up areas between 2012 and 2019 in Austria broken down by driver-related variables. n=20.293 (3.431 are severe casualties).
Table 3. Single-vehicle accidents with single occupation and personal injury that occurred outside built-up areas between 2012 and 2019 in Austria broken down by driver-related variables. n=20.293 (3.431 are severe casualties).
Variable Casualties
n		 Severe
casualties
n		 P (X ∩ SC)
%		 Fisher's
exact test
p		 Phi
Coefficient
ϕ 		MCV
n
Sex Male 11.576 2.458 12,11% ,000 ,133 817
Female 8.706 972 4,79% ,000 -,133 1.132
Unknown sex 11 1 - - - -
Age class 16 to 18 1.465 162 0,80% ,000 -,044 171
19 to 24 6.547 806 3,97% ,000 -,085 1.132
25 to 34 4.323 697 3,43% ,120 -,011 830
35 to 44 2.488 468 2,31% ,008 ,019 432
45 to 54 2.180 476 2,35% ,000 ,046 382
55 to 64 1.404 323 1,59% ,000 ,044 212
64 and higher 1.878 499 2,46% ,000 ,082 303
unknown age class 8 - - - - -
*DL No driving licence 356 94 0,46% ,020 ,034 15
Probationary driving licence 2.805 303 1,49% ,000 -,065 391
Impairment Alcohol 2.858 481 2,37% ,934 -,001 246
Distraction 2.369 431 2,12% ,079 ,012 93
Fatigue 1.518 317 1,56% ,000 ,030 134
Health 432 91 0,45% ,021 ,016 38
Drugs 66 15 0,07% ,247 ,009 3
Medicines 50 10 0,05% ,570 ,004 2
Excitation 7 2 0,01% ,337 ,006 1
Driving manoeuvres Speeding 3.608 579 2,85% ,136 -,011 131
Skidding 1.823 239 1,18% ,000 -.032 80
Hitting an obstacle next to road 1.512 280 1,38% ,086 ,012 35
Hitting the guard rail 1.378 181 0,89% ,000 -,027 37
Hitting a tree 1.217 318 1,57% ,000 ,062 23
Misconduct by pedestrians 503 79 0,39% ,505 -,005 12
Hit and run 371 53 0,26% ,186 -,010 22
Sudden braking 149 11 0,05% ,002 -.022 9
Overtaking 147 26 0,13% ,834 ,002 8
Cutting curves 128 27 0,13% ,194 ,009 4
Hitting an obstacle on the road 117 6 0,03% ,001 -,024 7
Changing lanes 58 9 0,04% 1,000 -,002 3
Inadequate safety distance 38 7 0,03% ,828 ,002 1
Reverse driving 26 6 0,03% ,429 ,006 2
Phoning 25 7 0,03% ,175 ,010 1
Turning around 22 4 0,02% ,780 ,001 3
Fall from the vehicle 22 11 0,05% ,000 ,029 2
Getting in lane 18 4 0,02% ,529 ,004 1
Disregarding driving direction 16 2 0,01% 1,000 -,003 1
Priority violation 15 4 0,02% ,302 ,007 1
Driving towards left-hand side of road 9 3 0,01% ,184 ,009 1
Forbidden overtaking 8 2 0,01% ,630 ,004 1
Hitting a moving vehicle 8 0 0,00% ,367 -,009 2
Disregarding driving ban 5 2 0,01% ,201 ,010 1
Driving in parallel 5 1 0,00% 1,000 ,604 1
Opening the vehicle door 5 2 0,01% ,201 ,010 1
Hitting a stationary vehicle 3 0 0,00% 1,000 -,005 1
Wrong-way driver 1 0 0,00% 1,000 -,003 1
Disregarding red light 1 0 0,00% 1,000 -,003 1
Dangerous stopping and parking 0 0 - - - -
Disregarding turning ban 0 0 - - - -
Missing indication of direction change 0 0 - - - -
Driving against one-way 0 0 - - - -
**ST Driving without mandatory light 0 0 - - - -
No safety belt applied 1.401 699 3,44% ,000 ,240 60
*DL: Driving licence; **ST: Safety Settings.
Table 4. Single-vehicle accidents with single occupation and personal injury that occurred outside built-up areas between 2012 and 2019 in Austria broken down by vehicle-related variables. n=20.293 (3.431 are severe casualties).
Table 4. Single-vehicle accidents with single occupation and personal injury that occurred outside built-up areas between 2012 and 2019 in Austria broken down by vehicle-related variables. n=20.293 (3.431 are severe casualties).
Variable Casualties
n		 Severe
casualties
n		 P (X ∩ SC)
%		 Fisher's
exact test
p		 Phi
Coefficient
ϕ 		MCV
n
Engine power (kW) 0-24 kW 11 3 0,01% ,411 ,006 2
24-90 kW 15.412 2.393 11,79% ,000 -,066 975
90-110 1.928 413 2,04% ,000 ,039 201
110+ 1.947 448 2,21% ,000 ,053 256
Kilometrage
(km)		 0 to 15.000 156 24 0,12% ,662 -,004 13
15.000 to 75.000 605 89 0,44% ,154 -,010 51
75.000 to 100.000 387 70 0,34% ,541 ,004 33
100.000 to 150.000 663 104 0,51% ,428 -,006 44
150.000 to 200.000 942 176 0,87% ,141 ,010 56
Vehicle
colour		 Beige 18 3 0,01% 1,000 ,000 5
Blue 3.166 478 2,36% ,003 -,021 868
Brown 193 35 0,17% ,637 ,003 52
Bronze 1 0 0,00% 1,000 -,003 1
Dark 30 6 0,03% ,626 ,003 6
Yellow 129 18 0,09% ,408 -,006 37
Gold 18 3 0,01% 1,000 ,000 5
Grey 2.702 462 2,28% ,784 ,002 770
Green 1.219 262 1,29% ,000 ,031 281
Bright 8 2 0,01% ,630 ,004 2
Orange 130 24 0,12% ,647 ,003 41
Red 2.272 381 1,88% ,857 -,001 602
Black 3.981 652 3,21% ,334 -,007 958
Silver 716 136 0,67% ,127 ,011 146
Purple 49 8 0,04% 1,000 -,001 11
White 1.907 323 1,59% ,977 ,000 497
Others 1 1 0,00% ,169 ,016 1
Vehicle
safety		 Insufficient vehicle security 16 6 0,03% ,040 ,015 2
Insufficient load securing 6 0 0,00% ,598 -,008 1
Technical defects 102 15 0,07% ,682 -,004 6
Vehicle fire 18 11 0,05% ,000 ,035 1
Airbag not deployed 8.138 819 4,04% ,000 -,149 975
Table 5. Single-vehicle accidents with single occupation and personal injury that occurred outside built-up areas between 2012 and 2019 in Austria broken down by roadway-related variables. n=20.293 (3.431 are severe casualties).
Table 5. Single-vehicle accidents with single occupation and personal injury that occurred outside built-up areas between 2012 and 2019 in Austria broken down by roadway-related variables. n=20.293 (3.431 are severe casualties).

 Variable Casualties
n		 Severe
casualties
n		 P (X ∩ SC)
%		 Fisher's
exact test
p		 Phi
Coefficient
ϕ 		MCV
n
Speed limit
(km/h)		 Driving ban 2.270 380 1,87% ,833 -,002 350
5 1 1 0,00% ,169 ,016 1
10 1 0 0,00% 1,000 -,003 1
20 2 0 0,00% 1,000 -,004 1
30 173 33 0,16% ,479 ,005 13
40 40 8 0,04% ,533 ,004 6
50 505 71 0,35% ,095 -,012 56
60 334 55 0,27% ,877 -,002 43
70 1.421 218 1,07% ,108 -,011 321
80 1.231 192 0,95% ,225 -,009 222
90 3 0 0,00% 1,000 -,005 1
100 12.292 2.148 10,58% ,008 ,019 2.232
110 35 4 0,02% ,502 -,006 10
120 2 0 0,00% 1,000 -,004 1
130 1.983 321 1,58% ,377 -,006 488
Road
type		 Highway 2.593 417 2,05% ,239 -,008 488
Expressway 595 80 0,39% ,024 -,016 82
Country road 14.457 2.416 11,91% ,247 -,008 2.232
Other roads 2.220 463 2,28% ,000 ,037 248
Intersection 439 62 0,31% ,125 -,011 62
Roundabout 68 16 0,08% ,146 ,010 11
Road
characteristics		 Deceleration lane 10 2 0,01% ,681 ,002 1
Acceleration lane 3 1 0,00% ,426 ,005 1
One-way 144 33 0,16% ,054 ,014 26
Construction site 157 21 0,10% ,286 -,008 10
Cycle path 4 0 0,00% 1,000 -,006 1
Crosswalk 3 0 0,00% 1,000 -,006 1
Pedestrian and cycle path 10 2 0,01% ,681 ,002 3
Parking lane 7 0 0,00% ,610 -,008 1
Secondary lane 5 1 0,00% 1,000 ,001 1
Hard shoulder 45 9 0,04% ,551 ,004 7
Banquet 123 22 0,11% ,729 ,002 22
Straight road 11.507 2.095 10,32% ,000 ,040 2.232
Tunnel 89 26 0,13% ,004 ,022 8
Gallery 15 8 0,04% ,001 ,026 1
Rest area 26 6 0,03% ,429 ,006 2
Traffic island 81 18 0,09% ,233 ,009 4
Underpass 32 7 0,03% ,476 ,005 3
Middle separation 777 104 0,51% ,008 -,019 137
Bridge 157 41 0,20% ,003 ,022 7
Curve 8.399 1.264 6,23% ,000 -,042 1.437
Narrow lane 30 8 0,04% ,149 ,010 3
Entry or exit 57 17 0,08% ,019 ,018 5
Tram or bus station 8 2 0,01% ,630 ,004 1
Road
condition		 Dry road 10.441 2.126 10,48% ,000 ,095 2.232
Wet road 5.705 872 4,30% ,000 -0,27 1.225
Sand or grit on the road 297 48 0,24% ,809 -,002 56
Wintry conditions 3.771 370 1,82% ,000 -,090 938
Other conditions (oil, soil) 95 17 0,08% ,796 ,002 16
TL* Traffic light in full operation 29 2 0,01% ,213 -,010 4
*TL: Traffic lights.
Table 6. Single-vehicle accidents with single occupation and personal injury that occurred outside built-up areas between 2012 and 2019 in Austria broken down by situation-related variables. n=20.293 (3.431 are severe casualties).
Table 6. Single-vehicle accidents with single occupation and personal injury that occurred outside built-up areas between 2012 and 2019 in Austria broken down by situation-related variables. n=20.293 (3.431 are severe casualties).
Variable
Casualties
n		 Severe
casualties
n
P (X ∩ SC)
%		 Fisher's
exact test
p		 Phi
Coefficient
ϕ 		MCV
n
Time 12 a.m. to 6 a.m. 3.367 713 3,51% ,000 ,051 245
6 a.m. to 12 p.m. 6.283 889 4,38% ,000 -,049 586
12 p.m. to 6 p.m. 5.915 956 4,71% ,070 -,013 578
6 p.m. to 12 a.m. 4.728 873 4,30% ,001 ,023 368
WD* Mon to Thu 11.131 1.788 8,81% ,000 -,025 586
Fri to Sun 9.162 1.643 8,10% ,000 ,025 430
Season Spring 4.279 774 3,81% ,021 ,016 435
Summer 4.821 896 4,42% ,000 ,025 578
Autumn 4.802 885 4,36% ,001 ,023 394
Winter 6.391 876 4,32% ,000 -0,58 586
Weather
condition		 Clear or overcast weather 15.541 2.797 13,78% ,000 ,053 586
Rain 3.013 458 2,26% ,007 -,019 110
Hail, freezing rain 124 17 0,08% ,398 -,007 12
Snow 1.913 175 0,86% ,000 -,067 147
Fog 636 102 0,50% ,588 -,004 37
High wind 377 52 0,26% ,113 -,011 17
Light
condition		 Daylight 11.546 1.790 8,82% ,000 -,043 586
Dusk or dawn 1.604 266 1,31% ,753 -,003 111
Darkness 6.828 1.311 6,46% ,000 ,044 368
Artificial light 571 93 0,46% ,730 -,003 15
Limited visibility 7 0 0,00% ,610 -,008 1
Glare from the sun 109 24 0,12% ,156 ,010 8
*WD: Weekday.
Table 7. Logistic regression analysis results.
Table 7. Logistic regression analysis results.
Variable Regression coefficient β Standard error SEM p exp(β)
no safety belt applied 1,612 0,062 0,000 5,015
gallery 1,522 0,589 0,010 4,583
vehicle fire 1,394 0,541 0,010 4,029
hitting an obstacle on the road 1,222 0,426 0,004 3,394
age class 16 to 18 0,840 0,104 0,000 2,317
airbag not deployed 0,803 0,046 0,000 2,233
bridge 0,773 0,197 0,000 2,166
age class 19 to 24 0,743 0,057 0,000 2,101
sudden braking 0,693 0,324 0,032 2,000
alcohol 0,650 0,062 0,000 1,916
hit and run 0,552 0,161 0,001 1,737
tunnel 0,515 0,258 0,046 1,674
one-way 0,507 0,219 0,020 1,660
age class 25 to 34 0,492 0,057 0,000 1,635
male driver 0,491 0,045 0,000 1,634
intersection 0,450 0,148 0,002 1,569
other road 0,397 0,082 0,000 1,487
wintry conditions 0,380 0,070 0,000 1,462
hitting a tree 0,365 0,075 0,000 1,441
age class 35 to 44 0,308 0,065 0,000 1,361
0 a.m. to 6 a.m. 0,307 0,058 0,000 1,359
vehicle colour: green 0,275 0,078 0,000 1,317
county road 0,247 0,062 0,000 1,280
dry road 0,232 0,047 0,000 1,261
curve 0,180 0,043 0,000 1,198
engine power 24-90 kW 0,175 0,046 0,000 1,192
probationary driving licence 0,166 0,078 0,033 1,181
darkness 0,165 0,049 0,001 1,180
drifting left 0,147 0,041 0,000 1,158
speed limit 100km/h 0,114 0,046 0,013 1,120
hitting a guard rail -0,313 0,091 0,001 0,731
speed limit 50km/h -0,329 0,144 0,022 0,719
constant -9,285 0,611 0,000
Table 8. Blackpatterns showing a significant relationship with the target variable severe casualties, and a positive Phi coefficient. n=20.293 single-vehicle accidents with single occupation and personal injury occurring outside the built-up area on the Austrian road network (3.431 are severe casualties).
Table 8. Blackpatterns showing a significant relationship with the target variable severe casualties, and a positive Phi coefficient. n=20.293 single-vehicle accidents with single occupation and personal injury occurring outside the built-up area on the Austrian road network (3.431 are severe casualties).
BP ID BP variables Fisher’s
exact test p		 Phi
Coefficient ϕ 		Frequency
n
BP1 speed limit 130km/h, highway, right drift, male driver 0,001 0,027 44
BP2 speed limit 100km/h, country road, left drift, male driver 0,000 0,032 41
BP3 speed limit 100km/h, country road, curve, left drift, male driver 0,011 0,020 30
BP4 country road, right drift, female driver 0,042 0,015 28
BP5 speed limit 100km/h, country road, left drift, male driver, fatigue 0,001 0,028 20
BP6 speed limit 130km/h, highway, drifting right, male driver, fatigue 0,040 0,015 16
BP7 speed limit 100km/h, country road, wet road, age 25-34, right drift, male driver 0,001 0,027 12
BP8 speed limit 100km/h, country road, left drift, male driver, no safety belt applied 0,000 0,031 10
BP9 speed limit 100km/h, country road, darkness, right drift, male driver 0,003 0,026 10
B10 speed limit 80km/h, country road, right drift, male driver 0,016 0,020 10
Table 9. Blackpattern impact analysis results.
Table 9. Blackpattern impact analysis results.
BP ID BP
Frequency
n 		BP Fisher’s exact test
p 		BP Phi
coefficient
ϕ 		BP variables and their regression coefficients β BIS
BP1 44 0,001 0,027 Speed limit 130km/h Highway Right drift Male driver 628,4
0 0 0 0,491
BP2 41 0,001 0,032 Speed limit 100km/h Country road Left drift Male driver 804,7
0,114 0,247 0,147 0,491
BP3 30 0,011 0,020 Speed limit 100km/h Country road curve Left drift Male driver 194,9
0,114 0,247 0,180 0,147 0,491
BP4 28 0,042 0,015 Country road Right drift Female driver 50,1
0,247 0 0
BP5 20 0,001 0,028 Speed limit 100km/h Country road Left drift Male driver Fatigue 167,6
0,114 0,247 0,147 0,491 0
BP6 16 0,040 0,015 Speed limit 130km/h Highway Right drift Male driver Fatigue 37,1
0 0 0 0,491 0
BP7 12 0,001 0,027 Speed limit 100km/h Country road Wet road Age 25-34 Right drift Male driver 141,8
0,114 0,247 0 0,492 0 0,491
BP8 10 0,000 0,031 Speed limit 100km/h Country road Left drift Male driver No safety belt 982,9
0,114 0,247 0,147 0,491 1,612
BP9 10 0,003 0,026 Speed limit 100km/h Country road Darkness Right drift Male driver 71,6
0,114 0,247 0,165 0 0,491
BP10 10 0,016 0,020 Speed limit 80km/h Country road Right drift Male driver 38,3
0 0,247 0 0,491
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated