Prerpints.org logo
Preprint
Article

Prediction Models for the Milling of Heat-Treated Beech Wood Based on the Consumption of Energy

Altmetrics

Downloads

41

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

02 September 2024

Posted:

04 September 2024

You are already at the latest version

Alerts
Abstract
The article is focused mainly on verifying the suitability of data from experimental milling heat-treated beech wood and on investigation of the effect of technical and technological parameters of milling on the energy consumption of this process. The independent parameters of machining process are cutting speed, feed speed, rake angle, and hydrothermal modification of experimental wood material. Based on analysis of variance it can be argued that the greatest statistically significant effect on energy consumption have cutting speed and rake angle of the tool while the feed speed had the least influence. The measured data of cutting power during milling were used to build a regression model and validate it, while the most suitable type of model with correlation of 87 % is Classification and Regression Tree followed by model created by Random Forests method.
Keywords: 
Subject: Engineering  -   Industrial and Manufacturing Engineering

1. Introduction

Wood as a material and its uses as interior and exterior is one of the greatest importance to humanity. Mechanical and aesthetic properties of wood could be reduced by outer influences [1,2]. By using surface inactivation, oil extraction substances can be expulsed onto the surface of the wood, preventing the access of hydroxyl groups to the wood cell wall. Some extracts from wood (namely fatty acids, terpenes, phenols, and so on) may be displaced to outside layer of wood, becoming a resinous layer. Inactivating surface layer for many wood applications shows improvements in smaller roughness, reducing losses in planning machine and higher quality wood surfaces.
In order to achieve better physical and mechanical properties or a color change usage of treatment process is important, which is why usage Heat-treatment is one of the most common methods of material treatment [3]. Depending on medium and material used in treatment process there are several types of heat-treatment [4]. Thermaly modified wood can be found almost everywhere nowadays most common are for example: ThermoWood in Finland, Plato Wood in the Netherlands, oilheat treatment (OHT) in Germany, and Les Bois Perdure and retification process (Retiwood) in France [5,6]. There are also lesser-known treatment processes which use superheated steam, such as Wood Treatment Technology (WTT) in Denmark and Firmolin technology in the Netherlands, or a partial vacuum, like Termovuoto in Italy [7]. Overall process of heat treatment could be defined as treatment in which wood is processed in high temperature in ranges between 100 and 260 °C and is in environment without chemical substance but is in type of medium (steam, nitrogen, oil, etc.) [6,8].
In the furniture industry woodworking processes such as milling are widespread, milling is done by tools—cutters with a rotating motion, trajectory could be described as movement of cutting teeth in cycloid. Depending on requirements and quality milling process has to achieve certain accuracy and roughness of the surfaces [9]. With selection of certain milling parameters one can achieve increased surface quality of woodworking [10,11,12] and better optimization of energy consumption [13,14]. The results of actual research show that heat-treated wood can be used for milling because it does not affect the grain size of chips formed in sawing and milling [15].
Not only in manufacturing sphere, the using models created by machine learning algorithm of artificial intelligence is more common. Based on data acquired by experiments it is possible to create prediction model, that predict factors that influence technical parameters of manufacturing [16]. Machine learning consists of computation of huge amount of acquired data for creation a prediction model which uses three basic types of machine learning for purpose of learning under supervision, unsupervised learning and feedback learning [17]. For predicting process parameters, tools for analysing measured data and subsequent model creation are used. These tools include machine learning as a subfield in artificial intelligence, regression models, artificial neural networks, deep learning [18,19], decision trees and support vector machines [20]. Common algorithms used in unsupervised learning include hidden Markov models, k-means, hierarchical clustering and models of the Gaussian mixture [20].
Currently there exist several types of approaches to machine learning for purpose of prediction of important parameters in machining process [21] such as cutting force, surface roughness [22], cutting performance [23]. However, very few works are dedicated to the creation of models and the analysis of signals in the processing of wood-based materials. New approaches to processing and analysis of measurable signals can also bring new insights in this field. Authors in [24] demonstrated the dependence of vibration amplitude on selected parameters during milling on a CNC machining centre. Furthermore, the currently ongoing digital revolution (Industry 4.0) provides a powerful tool for monitoring and data collection of the production process and their remote online processing by using interconnected cybernetic-physical systems by creating digital twins [25].
In the phase of data training from input database, there is an attempt to teach the algorithm to predict the output as close as is possible. During the training phase, iterations are implemented to improve the success of the algorithm, while the parameters are random or have initialization values, where the results are predicted based on the given parameters. The actual values are subsequently compared with these values and the parameters are adjusted. The data comparison process is repeated cyclically until the model is reached, where it is no longer possible to improve it, i.e., the accuracy of the prediction no longer shows improvement. There are two types of problems in the training process: underfitting and overfitting [17].
In practice, based on experiments and research, there are several machine learning algorithms. In general, there is no algorithm that would be the best or the worst, and each has its advantages and disadvantages, so it is not even possible to compare them. According to [20] among the most well-known machine learning algorithms are:
  • Linear Regression,
  • Support Vector Machine,
  • Decision Trees and Boosted Trees,
  • Random Forest,
  • K-Nearest Neighbours,
  • Neural Network.
The article deals with the use of cutting power data obtained during the milling of hydrothermally modified beech wood for purpose of creation a mathematical models of machine learning. First, the measured data are processed and evaluated statistically to determine the statistical significance of the effects of individual technical-technological milling parameters.
Subsequently, machine learning models are parameterized and created in order to evaluate their suitability for a given type of data. The evaluation is carried out using the correlation coefficient of measured and predicted data. At the end there are recommendations and comparisons with other authors.

2. Materials and Methods

2.1. Experimental Wood Material

European beech wood (Fagus sylvatica L.) was used as a material for the experimental samples. First, the boards of the radial medial timber with a thickness of 25 mm were manipulated from the logs on a band saw. The moisture of boards was higher than 45 %, so they were dried to moisture of 12 % in a wood drying kiln KAD 1x6 (KATRES s.r.o.) in the corporation Sundermann spol. s.r.o (Banská Štiavnica, Slovakia). Experimental samples were machined by circular saw DMMA 35 (Rema s.a., Reszel, Poland) and wood thickness planer machine F2T80 (TOS Svitavy, Czech Republic). Twenty experimental samples were prepared for each steaming mode, their final dimensions were 600 × 100 × 20 mm (h × w × t). Part of the wood cuts were not heat-treated and remained in the native state. Other wood cuts were heat-treated in the APDZ 240 autoclave at a higher saturated water steam pressure. The process of heat-treatment was carried out in the company Sundermann spol. s.r.o (Banská Štiavnica Slovak republic) what is described in more detail in [3]. The course of samples heat treatment is shown in Figure 1 with parameters in Table 1. In this table tmax is maximal temperature of steaming process, tmin is minimal temperature, t4 is temperature of finished controlled cooling.
The density measurement of the prepared samples was carried out in accordance with STN 49 0108. The density is shown in Table 2.

2.2. Milling Blades and Milling Head

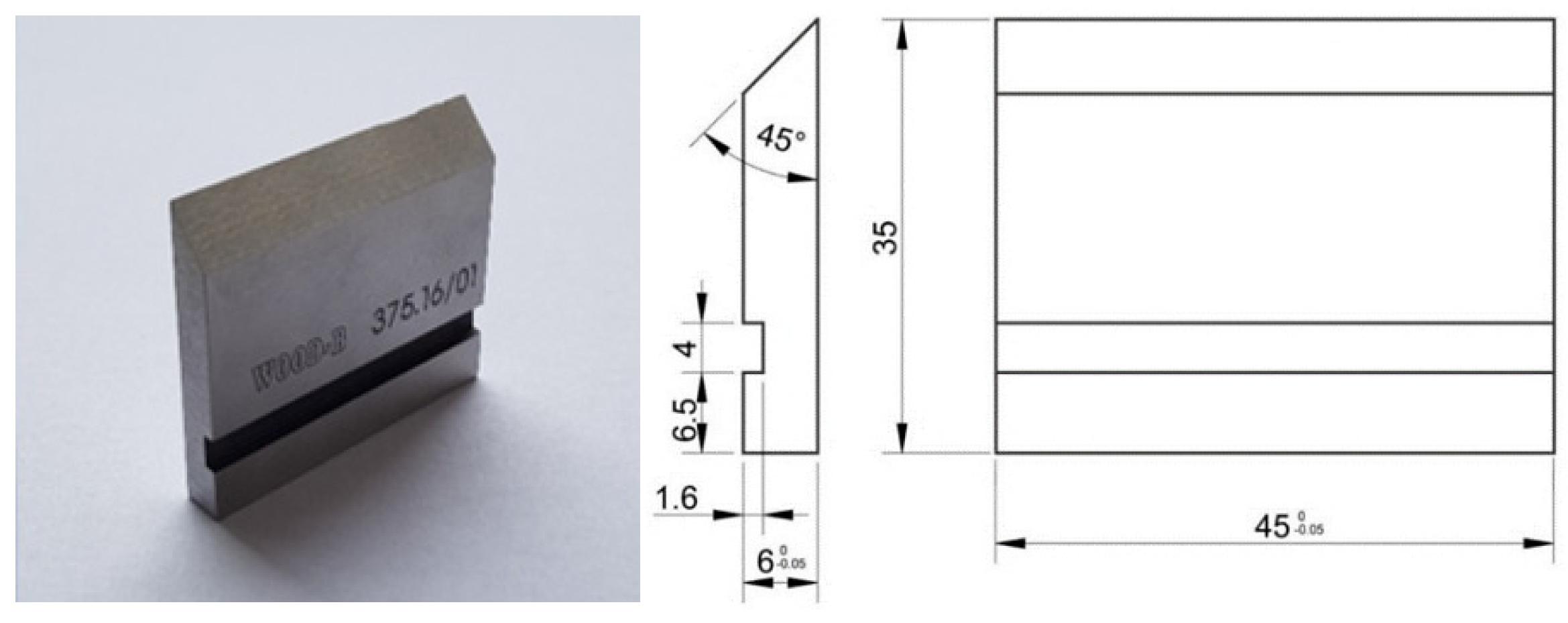
In the experimental milling the milling blades had dimensions of 45 x 35 x 6 mm (h × w × t) (Figure 2). They were manufactured from tool steel 19 573 (STN 41 9573) and induction hardened on the surface. The milling blades were coated by the Physical Vapor Deposition (PVD) method. The coating of the blades was carried out in the corporation WOOD—B s.r.o (Nové Zámky, Slovakia). The milling blades chemical composition is stated in Table 3.
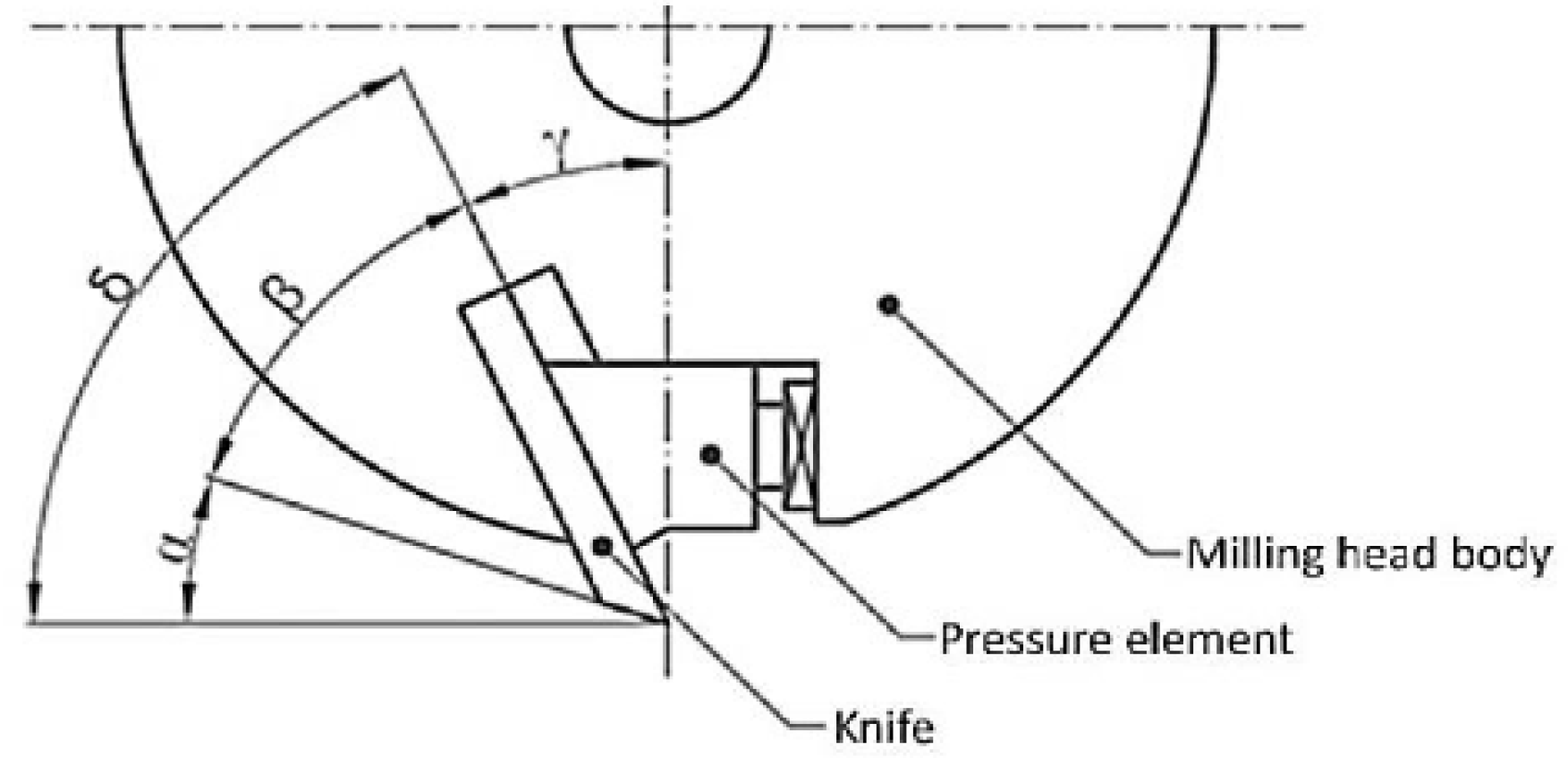
The milling blades were clamped in the milling heads FH 45 STATON manufactured in SZT—machines (Turany, Slovakia) (Figure 3). Parameters of Milling heads were: diameter of cutter body: 125 mm, cutter body thickness: 45 mm, number of blades: 2, maximum speed: 8000 rpm.

2.3. Milling, Feeding and Measuring Devices

The milling process was performed by the lower spindle milling machine ZDS-2 (Liptovské strojárne, Slovakia) (Figure 4) with feeding device Frommia ZMD 252/137 (Maschinenfabrik Ferdinand Fromm, Fellbach, Germany). Main parameters of machinery used are in Table 4. The cutting conditions were as follow: direction of cut: down-cut, depth of cut: 1 mm, cutting speed: 20, 40 a 60 m.s-1, feed rate: 6, 10 a 15 m.min-1, rake angle: 20°, 25° a 30°. Milling was carried out in the direction of the wood fibers 6 times at specific technological conditions.
The bottom spindle milling machine has as electric engine a three-phase induction motor and it was controlled via a frequency converter UNIFREM 400 007M (Vonsch s.r.o., Brezno, Slovak Republic) with technical parameters in Table 5. The frequency of the three-phase supply voltage was then set based on the required spindle revolutions calculated from the values of the selected cutting speeds according to:
n = v c · 1000 π · D ,
where n are revolutions (min-1), vc is cutting speed (m.min-1), D is milling head diameter.
The required revolutions were adjusted by measuring with a non-contact digital tachometer DT-2234BL (Lutron Instruments, Taiwan).
Frequency converter was connected to computer by USB serial converter (Figure 5). The program LPM—View was used to record the values of electrical power (9 values per second) and then these values were saved into a table to another processing in STATISTICA version 12. Cutting power was computed as mathematical difference between the mean power consumption during cutting and idling:
P = PC − PI,
where P is calculated cutting power (W), PC is power during milling (W), PI is power during idling (W).
Processed data of the experiment were tested if they are normally distributed. The results of the effects of factors were generated via one-factorial analysis and multi-factorial analysis. The F-test was used for study the hypothesis if the means of measured data set, having the same standard deviation, are equal. The confidence level was 95 %. Furthermore, measured values were used for analysing their suitability for generating prediction models also using software STATISTICA.

3. Results and Discussion

Results of descriptive statistics of cutting power are presented in Table 6. The cutting power values were calculated according to Equation (2), i.e., as the difference between the recorded power when the milling machine was running and idling.
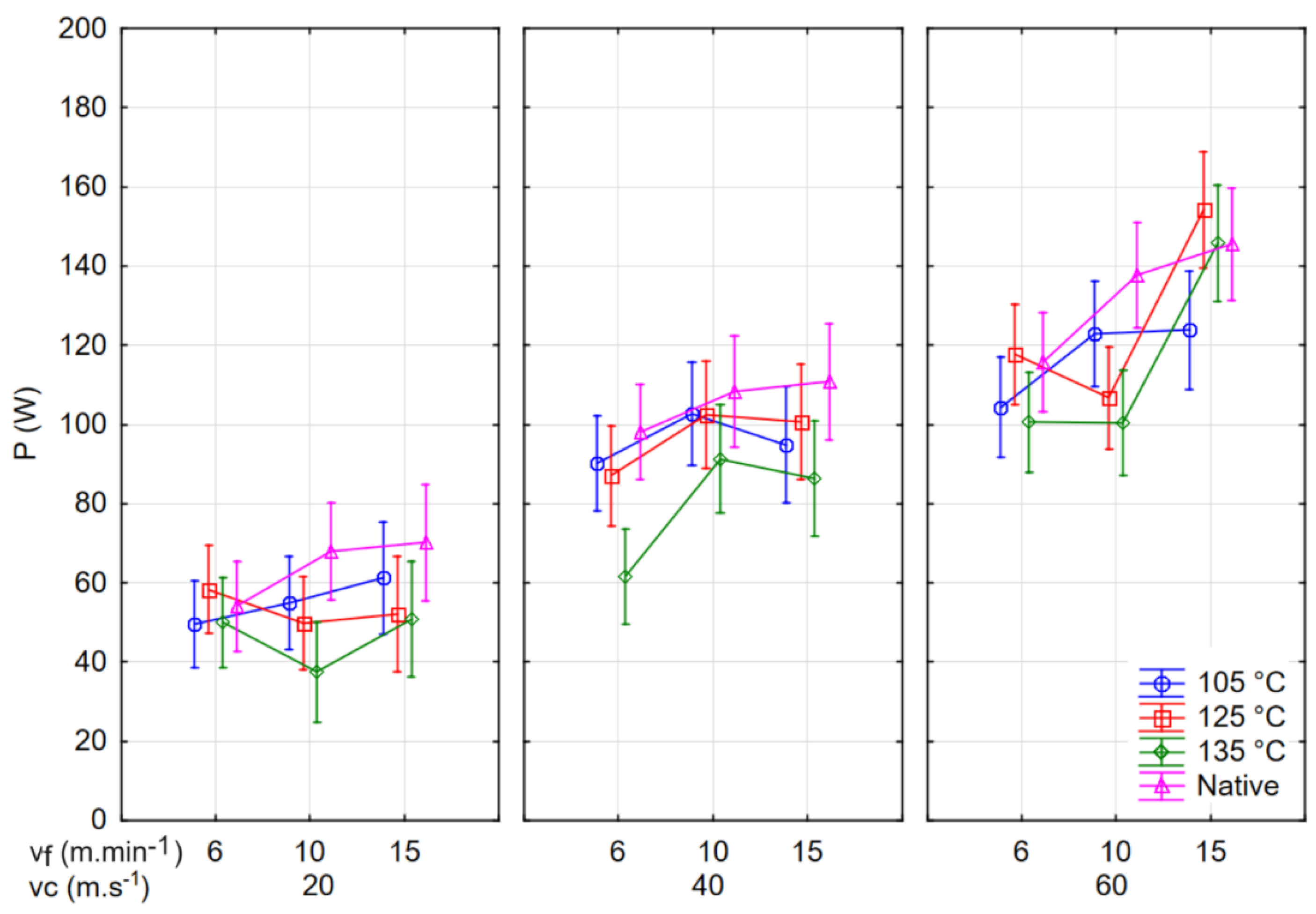
Aspects of statistical significance of the effects of technical-technological parameters on cutting power were evaluated by ANOVA. Whereas the values of cutting power were calculated as difference between milling and idling power consumption at every single milling. The results are shown in Figure 6. The greatest impact on cutting power determined by F-test had cutting speed (F-test: 127.04) followed by rake angle (69.59) and material (F-test: 6.97). Feed speed had smallest impact on cutting input (F-test: 2.32). Similar corelations also found authors in [26].
From the curves in Figure 6, the fact was confirmed that increasing the cutting speed increases the power required to remove the material with the cutting tool, because cutting power is a product of elementary cutting force and cutting speed [27]. The same conclusions are confirmed by both older and more recent results of milling wood and wood-based materials, e.g., in [28,29,30] From the point of view of the material, the highest values of the cutting power are when milling natural wood and the lowest when milling wood treated at the highest temperature. This dependence is related to the density of wood and chemical processes that change it by hydrothermal treatment, which is also confirmed for example in [31,32], although a slight decrease in density was detected at a temperature of 105 °C.
Measured data were tested for probability of similarity by Duncan’s post-hoc test. Here, the effect of changing cutting speed, feed speed and rake angle came out as statistically significant. That means, that the probability of similarity of data sets in individual groups of variables was less than 5 %. At the heat-treatment temperature, the similarity probabilities of the data sets were also below 5 %, except for the data at temperatures of 105 and 125, where this was 33.2 %.
The creation and testing of mathematical models were realized using STATISTICA 12 software with the Data mining tool. Before testing the data itself, it was necessary to define the dependent (target) and independent variables (input) for the most suitable mathematical model. The independent variable was the feed speed vf, the angular geometry of the tool γ, the cutting speed vc and the hydrothermal modification of the material T. The dependent variable was the cutting power P. After definition, the type of variables was chosen, either categorical or continuous, what is displayed in Table 7. In the next step, data training and calculation of the basic statistics of the model were performed, where all the data were inputted to the training. The data were evaluated as suitable for creating a mathematical model. The last step was the selection of methods, where the model methods were: Decision Tree C&RT (Classification and Regression Tree), Random Forests, Neural Networks, Support Trees and Support Vectors Machine (SVM).
In Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 the linear regression of individual methods of the model are shown with regression lines (solid line) and 95 % confidence interval (dotted line). On the x-axis there are the cutting power values calculated according to equation (1), which entered the model as output values; on the y-axis are the values predicted by the model. Regression equation is displayed above each graph. 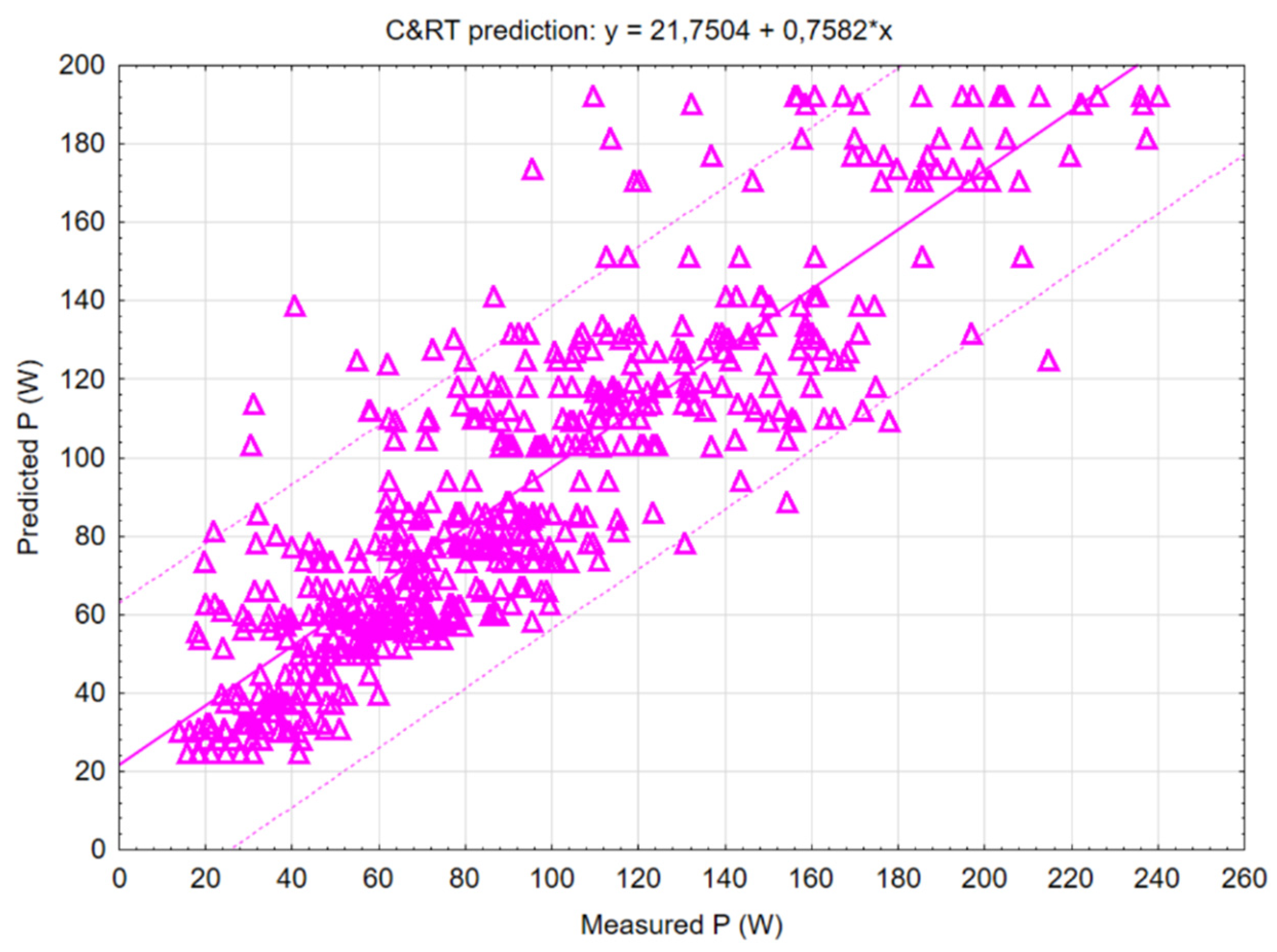Figure 7 shows the C&RT (Classification and regression tree) that determines how the target values of variable can be predicted according to predictor variable. 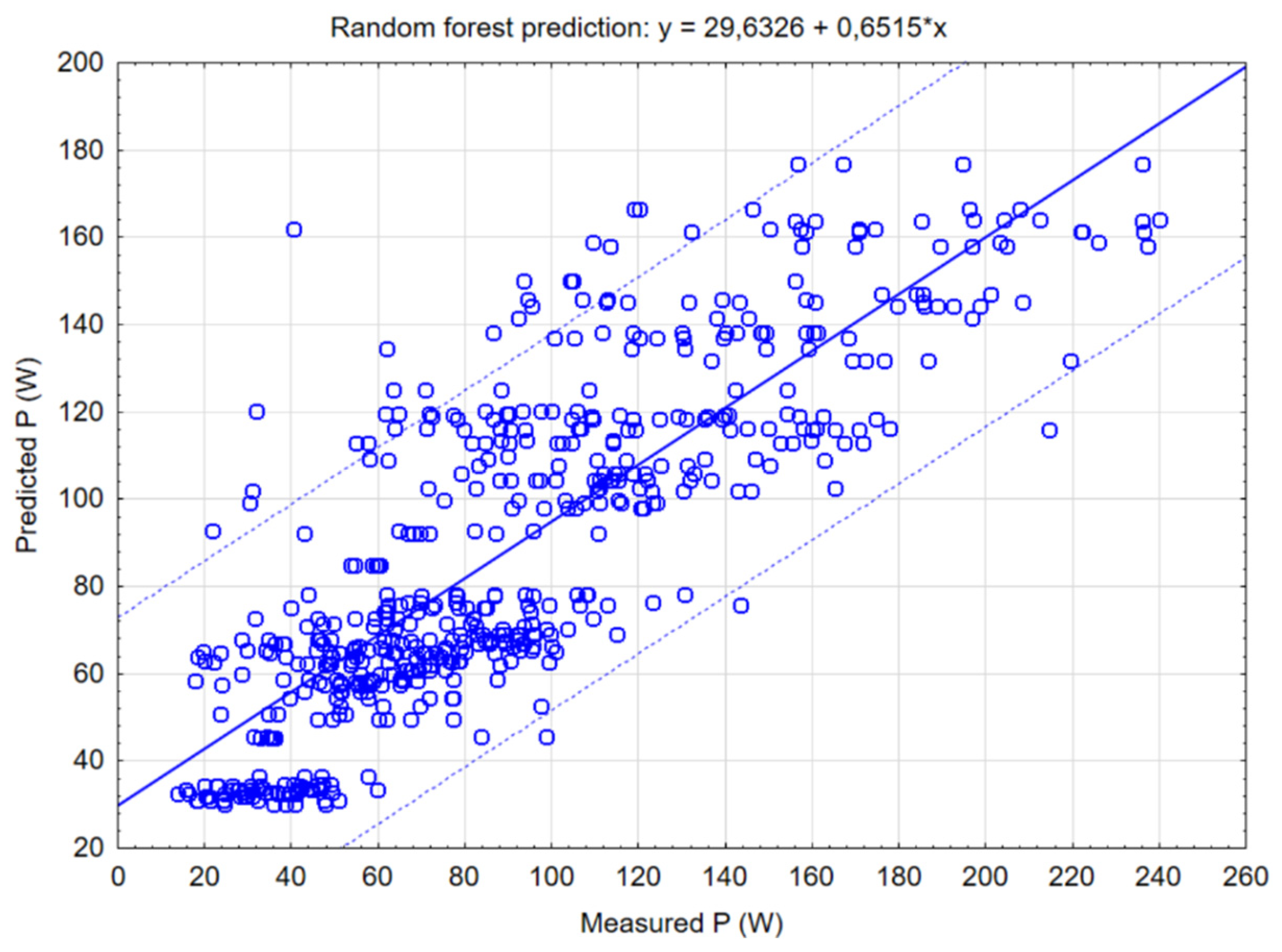Figure 8 shows random forest model that constructs a multitude of decision trees at training time. 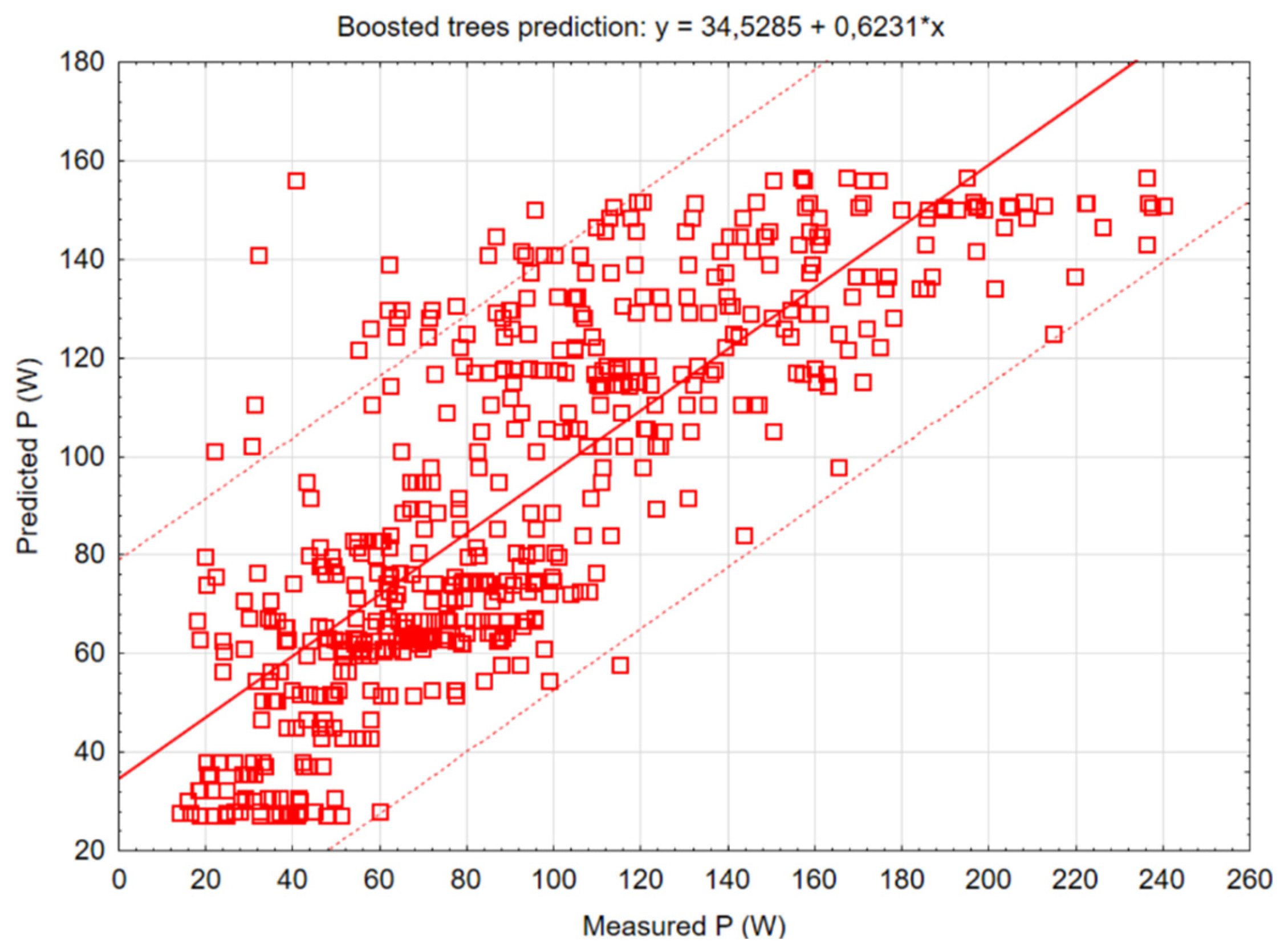Figure 9 shows boosted trees model that creates new trees according to errors of trees in previous training rounds. 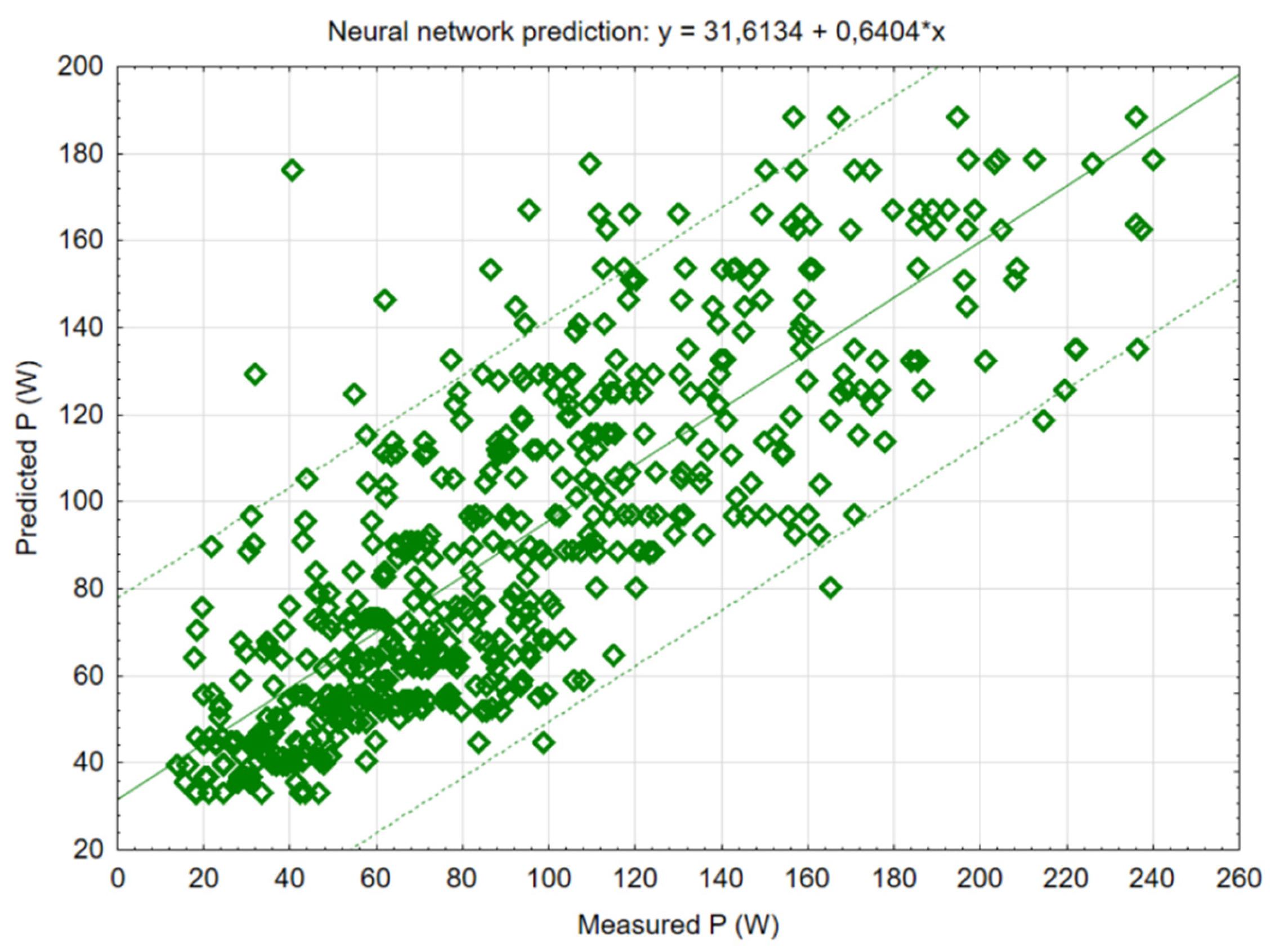Figure 10 shows neural network model based on artificial neural network algorithms. 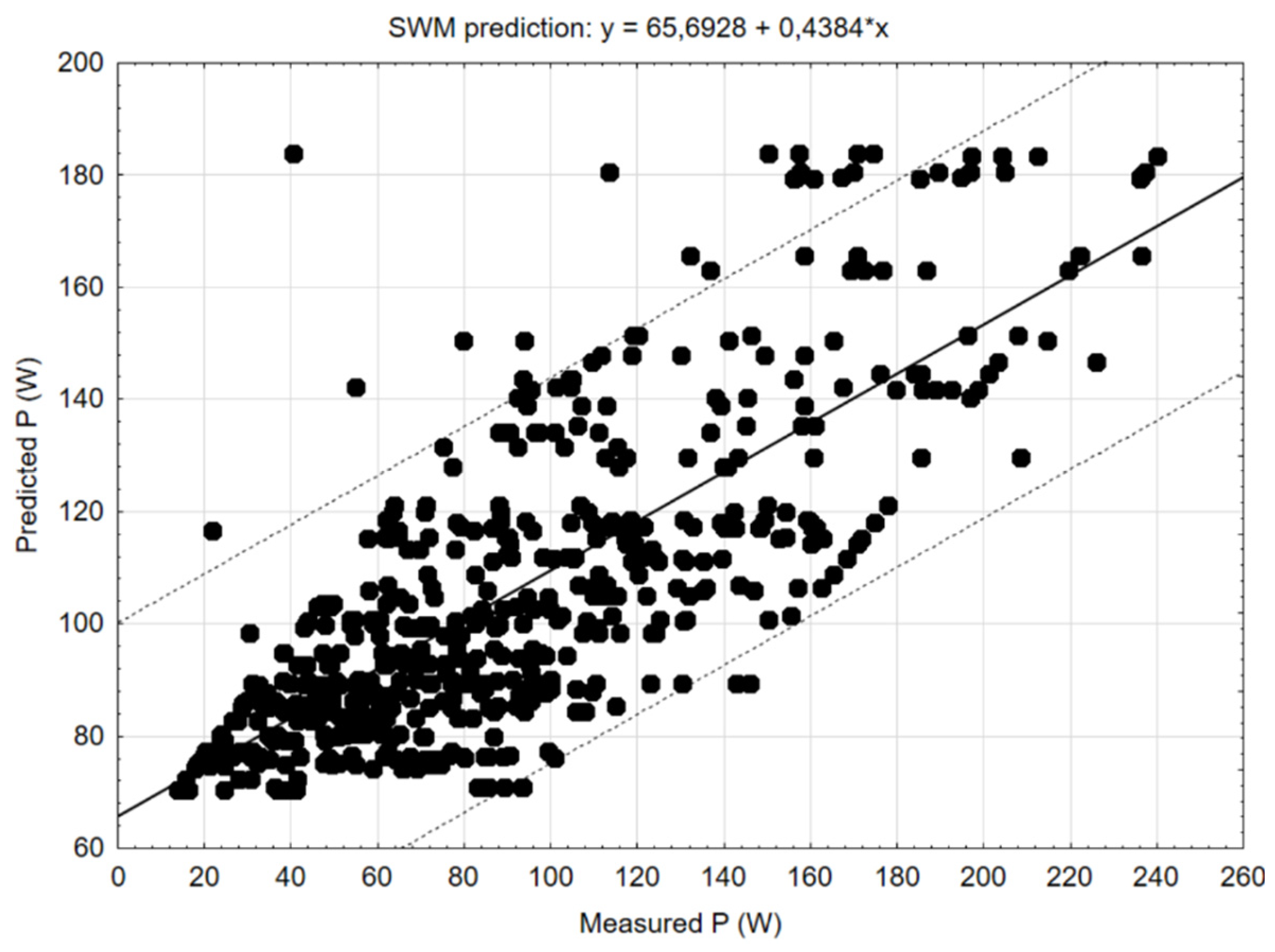Figure 11 shows support vector machine model for classification and regression that tries to find optimal hyperplane in an N-dimensional space separating the data points in different classes.
Based on the results of the linear regression of the correlation matrix and training residuals (Table 8), it was possible to determine the most appropriate mathematical method for modelling a process of woodworking for this type of data.
From the Table 8, the highest correlation coefficient r2 was achieved with the C&RT decision tree method, where the value was 0.87. The correlation coefficient of the worst model changed by 12 % compared to the best. However, it is still possible to claim that all models can be characterized as models with high interpretation (correlation from 0.7 to 0.9). Therefore, based on the value of the correlation coefficient, it can be argued that the most appropriate method of the mathematical model is the C&RT method. Authors in [33] used a quadratic model for modelling a process of medium density fibreboard helical up-milling. Authors in [34] used response surface methodology for prediction of cutting force during gypsum fiber composite milling. They achieved minimal relative errors between predicting results and confirmatory test, which meant that also their models had high predicting accuracy. Authors in [35] stated that power consumption can be used for predictive modelling of wood milling with correlation from 0.92 to 0.99.
The results of the correlation matrix can also be derived from the results of the linear regression graph of the C&RT decision tree method, which is shown in Figure 7. The values of cutting power P obtained by research are placed on the horizontal axis of the graph and the predicted values by the model are placed on the vertical axis. It can be seen in the figure that the lowest deviation of the error rate was at lower values of the cutting power, that is at lower values of the cutting speed, where the values were closest to the regression line, which represents the values predicted by the model. It is also clear from the graph that increasing the cutting power directly increases the error rate, i.e., the deviation from the values generated by the mathematical model.
The last step to create a mathematical model was the generation of the decision tree of the material processing due to the consumption of electricity, which is the cutting power P with the appropriate table of the tree structure. A part of the tree structure table is shown to explain individual abbreviations in the table (Table 9).
In the table of the decision tree, it is possible to see the ID, which is the designation of the node in the tree structure and at the same time the position of the node in the table. The number of nodes on the given subgroup is displayed for the identifiers of individual nodes. For example, the first level of the decision tree has two nodes. The size of the node N defines the number of records, so in this case for the first level it is equal to 556 measurements, which remain for all subgroups of nodes of the decision tree. The value of the size of the node decreases with individual branches and with the nodes in the lowest subgroups. The average of a node is the average value of predicted cutting power at the given level of the decision tree. The variables defined in the next column are the cutting speed vc, the face angle γ, the hydrothermal modification of the material T and the feed speed vf. The criteria of subgroups 1 and 2 are the values calculated and generated by the program during the creation of a mathematical model for achieving optimal values of cutting power in the context of machining parameters. The number in parentheses is the number of the next node when a particular criterion is valid. The structure of the model assembled in this way calculates predicted value of cutting power according to input parameter of milling.

4. Conclusions

The first goal of this article was to determine the influence of technical and technological parameters on the cutting power when milling heat-treated beech wood. Evaluation of analysis of variance showed that the highest impact on cutting power determined by F-test had cutting speed (F-test: 127.04) followed by rake angle (F-test: 69.59) and material (F-test: 6.97). Feed speed had smallest impact on cutting input (F-test: 2.32).
The second goal was to determine the appropriateness of creating a regressive model of the dependence of cutting power on independent technical and technological parameters during milling of heat-treated beech wood.
During the creation of the mathematical model in the STATISTICA 12 software, graphs of the basic methods of mathematical modelling were created, as well as the determination of the most suitable method, which was the C&RT decision tree method, where the value of the correlation coefficient r2 was at the level of 0.87. However, the correlation coefficient of other models was also high: Random Forests (0.82), Boosted trees (0.80), Neural network (0.8), SVM (0.77).
For a better understanding of the creation of the mathematical model, the overall table of the tree structure was explained with the meaning of individual nodes. The creation of a mathematical model in the STATISTICA 12 program demonstrated the appropriateness of using the obtained research data for the mathematical modelling at the level of 87 %, which represents a 13 % difference between the values obtained from the research and the prediction values of the mathematical model. Based on the interpretation of the correlation coefficient r2, the result of all models can be classified as a high interpretation of the model’s prediction, as the suitability ranged from 0.70 to 0.90, which is presented as a high interpretation.
The comprehensive conclusion of this research is that consumption measurement is suitable for creating prediction models for machining not only homogeneous but also non-homogeneous materials such as wood. However, these require a larger amount of experimentally obtained data for adequate training of prediction models. The research results will be further developed for the creation of dynamic models suitable for adaptive control of the machining process.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, Pe.K.; methodology, Pe.K. and Ľ.R.; software, Pe.K and Ľ.R.; validation, Pa.K., Ľ.R. and T.Č.; formal analysis, Ľ.R.; investigation, Pe.K. and Ľ.R.; writing—original draft preparation, Pe.K., Pa.K. and Ľ.R.; writing—review and editing, Pe.K. and T.Č.; project administration, Pe.K.; funding acquisition, Pe.K. All authors have read and agreed to the published version of the manuscript.”

Funding

This research was funded by Slovak Research and Development Agency, grant number APVV-20-0403 and Operational Programme Integrated Infrastructure (OPII), grant number ITMS 313011T720.

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kokutse, A. D.; Stokes, A.; Baillères, H.; Kokou, K.; Baudasse, C. Decay resistance of Togolese teak (Tectona grandis L.f) heartwood and relationship with colour. Trees 2006, 20, 219–223. [Google Scholar] [CrossRef]
  2. Kaplan, L.; Kvietková, M.; Sikora, A.; Sedlecký, M. Evaluation of the effect of individual parameters of oak wood machining and their impact on the values of waviness measured by a laser profilometer. WoodRessearch 2018, 63, 127–140. [Google Scholar]
  3. Dzurenda, L.; Dudiak, M. The Effect of the Temperature of Saturated Water Steam on the Colour Change of Wood Acer Pseudoplatanus L. Acta Facultatis Xylologiae Zvolen 2020, 62. [Google Scholar] [CrossRef]
  4. Navi, P.; Sandberg, D. Thermo-Hydro-Mechanical Processing of Wood, CRC Press, Boca Raton, FL., 2012.
  5. Esteves, B.; Videira, R.; Pereira, H. Chemistry and ecotoxicity of heattreated pine wood extrac-tives. Wood Science and Technology 2011, 45, 661–676. [Google Scholar] [CrossRef]
  6. Sandberg, D.; Kutnar, A. Thermal modified timber (TMT): Recent development in Europe and North America. Wood Fiber Sci. 2016, 48, 28–39. [Google Scholar]
  7. Ferrari, S.; Allegretti, O.; Cuccui, I.; Moretti, N.; Marra, M.; Todaro, L. A revaluation of Turkey oak wood (Quercus cerris L.) through combined steaming and thermo-vacuum treatments. BioResources 2013, 8, 5051–5066. [Google Scholar] [CrossRef]
  8. Reinprecht, L.; Vidholdová, Z. Termodrevo—príprava, vlastnosti a aplikácie. Zvolen, Technical University in Zvolen, 2008, ISBN 978-80-228-1920-6.
  9. Gochev, Z.; Vukov, G. Factors influencing the cutting power in longitudinal milling of solid wood. Ann Warsaw Univ Life Sci-SGGW, for Wood Technol 2018, 102, 103–111. [Google Scholar]
  10. Prokeš, S. Obrábění dřeva a nových hmot ze dřeva. SNZI, Prag, Czech Republic, 1982.
  11. Kačíková, D.; Kačík, F. Chemické a mechanické zmeny dreva pri termickej úprave. Zvolen: Technical university in Zvolen 2011.
  12. Budakçi, M.; İlçe, A. C.; Gürleyen, T.; Utar. M. Determination of the surface roughness of heat-treated wood materials planed by the cutters of a horizontal milling machine, 2013.
  13. Kubš, J.; Gaff, M.; Barcík, Š. Factors affecting the consumption of energy during the milling of thermally modified and unmodified beech wood. BioResources 2016, 11, 736–747. [Google Scholar] [CrossRef]
  14. Koleda, P.; Barcík, Š.; Korčok, M.; Jamberová, Z. Effect of temperature of heat treatment of oak wood and technological parameters of milling on energetic efficiency when planer milling. Acta FaculTatis Technicae 2020, 25, 9–20, ISSN: 1336-4472. [Google Scholar]
  15. Kminiak, R.; Orlowski, K.A.; Dzurenda, L.; Chuchala, D.; Banski, A. Effect of Thermal Treatment of Birch Wood by Saturated Water Vapor on Granulometric Composition of Chips from Sawing and Milling Pro-cesses from the Point of View of Its Processing to Composites. Applied Sciences 2020, 10, 7545. [Google Scholar] [CrossRef]
  16. Bender, E. A. An Introduction to Mathematical Modeling. Dover Books on Computer Science. 1st Edition. United States of America, 2000, 272 p. ISBN 978-0486411804.
  17. Mitchell. T.M. Machine Learning. McGraw-Hill Education. New York, United States of America, 1997, 420 p. ISBN 978-0-07-042807-2.
  18. Okokpujie, I. P.; Tartibu, L. K. Modern Optimization Techniques for Advanced Machining: Heuristic and Metaheuristic Techniques. Springer, 2023, ISBN 978-3-031-35454-0.
  19. Zhang, Y.; Xu, X. Yttrium barium copper oxide superconducting transition temperature modeling through Gaussian process regression. Comput Mater Sci 2020, 179, 109583. [Google Scholar] [CrossRef]
  20. Brownlee. J. Master machine learning algorithms. Jason Brownlee, Melbourne, Australia, 2016, 163 p. ISBN 10 27387468567.
  21. Laouissi, A.; Yallese, M.A.; Belbah, A.; Belhadi, S.; Haddad, A. Investigation, modeling, and optimization of cutting parameters in turning of gray cast iron using coated and uncoated silicon nitride ceramic tools. Based on ANN, RSM, and GA optimization. Int J Adv Manuf Technol 2019, 101, 523–48. [Google Scholar] [CrossRef]
  22. Kumar, K.; Verma, R.K. Nature-inspired grasshopper optimization algorithm (GOA) for predictive modeling and machinability evaluation of laminated polymer nanocomposites. Multiscale Multi. Model 2023, 61–79. [Google Scholar] [CrossRef]
  23. Han, F.; Li, L.; Cai, W.; Li, C.; Deng, X.; Sutherland, J.W. Parameters optimization considering the trade-off between cutting power and MRR based on linear decreasing particle swarm algorithm in milling. J. Clean. Prod. 2020, 262, 121388. [Google Scholar] [CrossRef]
  24. Hortobágyi, Á.; Koleda, P.; Koleda, P.; Kminiak, R. Effect of Milling Parameters on Amplitude Spectrum of Vibrations during Milling Materials Based on Wood. Applied Sciences 2023, 13, 5061. [Google Scholar] [CrossRef]
  25. Sujová, E.; Bambura, R.; Vysloužilová, D.; Koleda, P. Use of the digital twin concept to optimize the production process of engine blocks manufacturing. Production Engi-neering Archives 2023, 29, 168–174. [Google Scholar] [CrossRef]
  26. Zhu, Z.L.; Buck, D.; Guo, X.L.; Xiong, X.Q.; Xu, W.; Cao, P.X. Energy Efficiency Optimization for Machining of Wood Plastic Composite. Machines 2022, 10, 104. [Google Scholar] [CrossRef]
  27. Vasilko, K. Analytic Theory of Chip Manufacturing. Technical University of Košice: Košice, 2007, 338p. ISBN 97-80-8073-759-7.
  28. Piernik, M.; Pinkowski, G.; and Krauss, A. Effect of chip thickness, wood cross-sections, and cutting speed on surface roughness and cutting power during up-milling of beech wood. BioResources 2023, 18, 18–6801. [Google Scholar] [CrossRef]
  29. Li, R.; Yao, Q.; Xu, W.; Li, J.; Wang, X. Study of Cutting Power and Power Efficiency during Straight-Tooth Cylindrical Milling Process of Particle Boards. Materials 2022, 15, 879. [Google Scholar] [CrossRef]
  30. Yu, Y.; Buck, D.; Yang, H.; Du, X.; Song, M.; Wang, J.; Zhu, Z. Cutting Power, Temperature, and Surface Roughness: A Multiple Target Assessment of Beech during Diamond Milling. Forests 2023, 14, 1163. [Google Scholar] [CrossRef]
  31. Percin, O.; Peker, H.; Atilgan, A. The Effect of Heat Treatment on the Some Physical and Mechanical Properties of Beech (Fagus orientalis Lipsky) Wood. Wood Research 2016, 61, 443–456. [Google Scholar]
  32. Esteves, B.; Ferreira, H.; Viana, H.; Ferreira, J.; Domingos, I.; Cruz-Lopes, L.; Jones, D.; Nunes, L. Termite Resistance, Chemical and Mechanical Characterization of Paulownia tomentosa Wood before and after Heat Treatment. Forests 2021, 12, 1114. [Google Scholar] [CrossRef]
  33. Li, R.R.; He, C.J.; Xu, W.; Wang, X.D. Modeling and optimizing the specific cutting energy of medium density fiberboard during the helical up-milling process. Wood Mater. Sci. Eng. 2022, 1–8. [Google Scholar] [CrossRef]
  34. Li, R.; Cao, P.; Zhang, S.; Xu, W.; Ekevad, M.; Guo, X. Prediction of Cutting Force during Gypsum Fiber Composite Milling Process using Response Surface Methodology. Wood and Fiber Science 2017, 49, 453–460. [Google Scholar]
  35. Derbas, M.; Jaquemod, A.; Frömel-Frybort, S.; Güzel, K.; Moehring, HCH.; Riegler, M. Multisensor Data Fusion and Machine Learning to Classify Wood Products and Predict Workpiece Characteristics during Milling. CIRP Journal of Manufacturing Science and Technology 2023, 47, 103–115. [Google Scholar] [CrossRef]
Preprints 116968 g001
Figure 1. Time course of heat-treatment.
Figure 1. Time course of heat-treatment.
Preprints 116968 g001
Preprints 116968 g002
Figure 2. Changeable milling blade.
Figure 2. Changeable milling blade.
Preprints 116968 g002
Preprints 116968 g003
Figure 3. Milling heads used.
Figure 3. Milling heads used.
Preprints 116968 g003
Preprints 116968 g004
Figure 4. Lower spindle milling machine FVS and feeder mechanism Frommia ZMD 252/137.
Figure 4. Lower spindle milling machine FVS and feeder mechanism Frommia ZMD 252/137.
Preprints 116968 g004
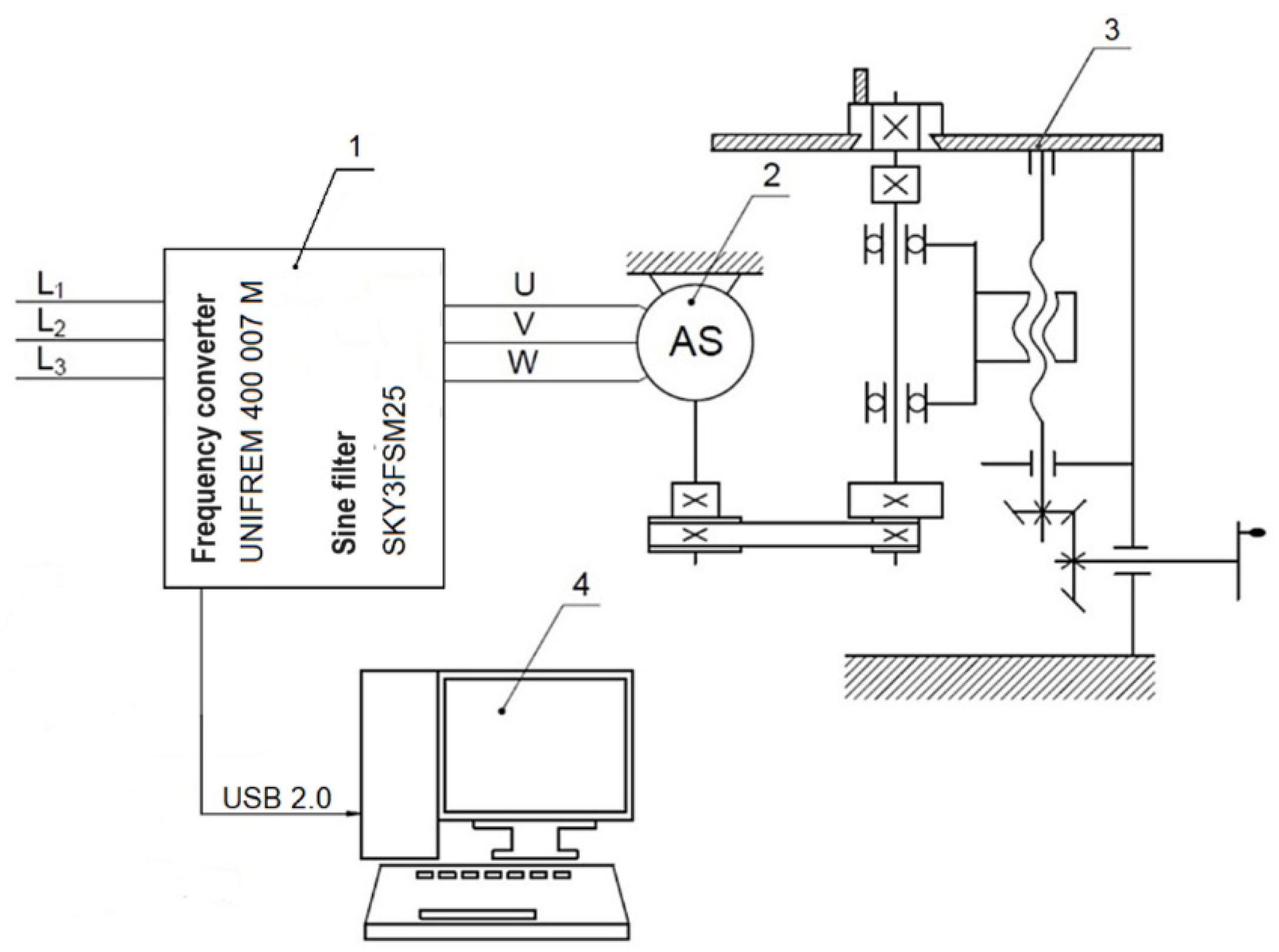
Preprints 116968 g005
Figure 5. Connection of measuring apparatus: 1—frequency converter and sine filter, 2—asynchronous motor, 3—milling machine, 4—computer (laptop), L1, L2, L3—phase wires, U, V, W—motor wires.
Figure 5. Connection of measuring apparatus: 1—frequency converter and sine filter, 2—asynchronous motor, 3—milling machine, 4—computer (laptop), L1, L2, L3—phase wires, U, V, W—motor wires.
Preprints 116968 g005
Preprints 116968 g006
Figure 6. analysis of variance of selected independent variables.
Figure 6. analysis of variance of selected independent variables.
Preprints 116968 g006
Preprints 116968 g007
Figure 7. Decision trees C&RT model.
Figure 7. Decision trees C&RT model.
Preprints 116968 g007
Preprints 116968 g008
Figure 8. Random forests model.
Figure 8. Random forests model.
Preprints 116968 g008
Preprints 116968 g009
Figure 9. Boosted trees model.
Figure 9. Boosted trees model.
Preprints 116968 g009
Preprints 116968 g010
Figure 10. Neural network model.
Figure 10. Neural network model.
Preprints 116968 g010
Preprints 116968 g011
Figure 11. Support vectors machine model.
Figure 11. Support vectors machine model.
Preprints 116968 g011
Table 1. Modes of hydrothermal treatment of beech wood with saturated steam.
Table 1. Modes of hydrothermal treatment of beech wood with saturated steam.
Modes Temperature of saturated steam (°C) Steaming time in hours (hours)
tmax tmin t4 τ0—heating τ1—phase I τ2 —phase II Total time
Steaming mode I. 107.5 102.5 100 ≈1.5 3.5 1.0 ≈ 6.0
Steaming mode II. 130.0 125.0 100 4.0 1.0 ≈ 6.5
Steaming mode III. 140.0 135.0 100 4.5 1.0 ≈ 7.0
Table 2. Density of experimental samples.
Table 2. Density of experimental samples.
Treatment Density[kg.m-3] Change to native [%]
Native 683.5 -
105 °C 671.8 -1.74%
125 °C 691.9 1.21%
135 °C 705.1 3.05%
Table 3. Chemical Composition of Used Milling Blades.
Table 3. Chemical Composition of Used Milling Blades.
Blade from the tool steel 19 573
Co Mn Si P S Cr Mo V
1.4 ÷ 1.65 0.2 ÷ 0.45 0.2 ÷ 0.45 0.03 0.035 11 ÷ 12.5 0.6 ÷ 0.95 0.8 ÷ 1.20
Table 4. Technical Parameters of the milling machine FVS and feeding device Frommia.
Table 4. Technical Parameters of the milling machine FVS and feeding device Frommia.
Lower spindle miller FVS Feeder Frommia ZMD 252/137
Input power (kW) 4 Feed Range (m.min-1) 2,5;10;15;20;30
Voltage System (V) 360/220 Engine (m.min-1) 2800
Year of Production 1976 Year of Production 1972
Table 5. Technical Parameters of the Frequency Converter.
Table 5. Technical Parameters of the Frequency Converter.
Type of Frequency Converter M—Quadratic Load M—Constant Load Nominal Output Current of Converter InIN (A)
Engine Power Pnom (kW) Nominal Output Current INQ (A) Engine Power Pnom (kW) Nominal Output Current INK (A) Max. Output Current INK60 (A) Max. Output Current INK2 (A)
UNIFREM 400 007M 7.5 18.1 5.5 13.2 19.8 26.4 18.1
Table 6. Descriptive statistics of cutting power.
Table 6. Descriptive statistics of cutting power.
Parameter Value Average
P (W)		 Standard
deviation		 Standard
error		 -95 % +95 %
vf (m.min-1) 6 83.57 42.68 2.87 77.91 89.23
10 89.98 50.48 3.68 82.72 97.24
15 99.59 53.90 4.46 90.78 108.41
γ (°) 20 54.93 25.95 2.00 50.98 58.89
25 100.22 45.90 3.31 93.68 106.75
30 110.03 50.84 3.64 102.85 117.21
vc (m.s-1) 20 54.07 23.69 1.66 50.79 57.36
40 95.24 36.27 2.74 89.83 100.65
60 125.48 52.61 3.94 117.70 133.26
T (°C) 105 88.14 46.30 3.88 80.46 95.82
125 91.14 49.77 4.20 82.83 99.46
135 79.29 45.61 3.91 71.56 87.03
N 101.21 51.47 4.39 92.52 109.91
Table 7. Role and type of model variables.
Table 7. Role and type of model variables.
Variable name Role Type Observed min. Observed max.
vf (m.min-1) Input Continuous 6 15
γ (°) Input Continuous 20 30
vc (m.s-1) Input Continuous 20 60
T (°C) Input Categorical
P (W) Target Continuous 13.85 239.94
Table 8. Correlation matrix of regression models.
Table 8. Correlation matrix of regression models.
Method Training residual Correlation coefficient (r2)
C&RT 574.6 0.87076
Random Forests 771.6 0.82316
Boosted trees 843.45 0.80379
Neural network 857.57 0.79962
SVM 1284.69 0.77435
Table 9. Example of model tree structure.
Table 9. Example of model tree structure.
ID Number of nodes Size of node Average of node (W) Variable Criteria of subgroup 1 (next node) Criteria of subgroup 2 (next node)
1 2 556 90 vc (m.s-1) ≤ 29.56 (2) > 29.56 (3)
2 2 202 54 γ (°) ≤ 22.5 (4) > 22.5 (5)
4 2 68 34 T (°C) 135, 125, 105 °C (6) N (7)
6 2 52 33 vf (m.min-1) ≤ 8 (8) > 8 (9)
8 2 21 36 T (°C) 135 °C (10) 105, 125 °C (11)
10 7 31
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated