Importance of a Solid, Neutral Object as a Measuring Device for the Unification of Quantum Theory and General Relativity via Polynomials P(2π)

Preprint

Article

Importance of a Solid, Neutral Object as a Measuring Device for the Unification of Quantum Theory and General Relativity via Polynomials P(2π)

Altmetrics

Downloads

Views

Comments

Helmut C. Schmidt^*

This version is not peer-reviewed

Submitted:

02 September 2024

Posted:

04 September 2024

You are already at the latest version

Alerts

Abstract

For each measurement, at least three objects are needed: a solid, neutral object as a measuring instrument and two objects for comparison. This system of three spatial dimensions per object has a common time. All measurements are based on orbits relative to the firmament and coincidences of the spatial coordinates of the objects after rotations with π and provide the energy of the system. These results in the most suitable coordinate system with dimensions of powers of π in which the radius is curved, as are the longitude and latitude. Polynomials P(2π) correspond to neutral objects, in addition to P(π) for charge, spin, isospin. In addition, it is assumed that the cosmos consists of a single type of particle with a speed of light c. Normalizing to the rest mass of the electron, the neutrinos are ντ=π, νμ=1, and νe=1/π. The energy of an electron is: Ee=gfreq(π)+1−1/π. An algorithm is derived from a Christoffel symbol and similar to a lattice gauge calculation. It provides exact residual masses for neutrons, protons, muons, tauons, quarks u, d, and pions. The theory can be applied to the inner planetary system and the cosmos and explains the hierarchy problem.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

Since Newton, physics has been based on forces and the center of gravity. An alternative is to consider a system of 3 objects, each with 3 spatial coordinates and the time of an observer. This corresponds to Einstein’s idea of explaining matter from the metric of space-time. The 10 independent equations of the general theory of relativity (GR) are the parameters of the system [1,2]. Bohr postulated angular momentum through quanta with

L = n h / (2 π)

[3]. Since then, wave‒particle duality has been a fundamental problem in elementary particle physics. This problem does not exist in astronomy. This leads to the concept of a universe with ur-particles with speed c. Point-like leptons are composed of several ur-particles. The quantum theory of ur-objects or ur-alternatives proposed by C. F. von Weizsäcker was based on a two-dimensional Hilbert space with the universal symmetry group SU(2) or bits [4,5] and led to quantum information. In the following, a distinction is made between ur-particles, dimensions, objects and energy (Figure 1). The number of ur-particles adds up to s according to the objects i and the different dimensions (

t, φ, r, θ

) to E. E contains all possible formulas of physics with energies and objects from the set of natural numbers with past to future. The no-go theorem, all possible symmetries of the S matrix [6], is satisfied.

The task of theoretical physics is to predict the final result of a measuring device in meters and a common point in time from the initial conditions of the meter and day. Forces with the units kg or coulombs are only intermediate steps. c indicates the spatial‒temporal relationship. Measurements are always relative to the firmament and result from coincidences of revolutions, i.e. rational numbers of

π

or epicycles.

Q

contains the ur-particles of all visible and invisible objects with a past and a future. Only the past without zero (

Q^{+}

) is computable and leads to a positive geometry. The energies are polynomials

P (π)

, where each dimension corresponds to a power of

π

The Schrödinger equation can be reformulated without additional normalization to polynomials

P (2 π)

, which results in an energy

E / c^{2}

. With the constancy of the ur-particles

g_{d}

for each of the spatial dimensions d, the conservation of the angular momentum

L_{d}

(as a dimensionless unit) follows.

g_{d}

are the prefactors in the polynomials. The number of ur-particles in the 3 objects i of a system results in ratios

Q

between the spatial coordinates of the objects

g_{d, i}

A central point is therefore the introduction of the most efficient coordinate system for the metric of the cosmos from polynomials

P (2 π)

for neutral objects and

P (π)

for charged objects [7,8].

2. Physics of ur-Particles

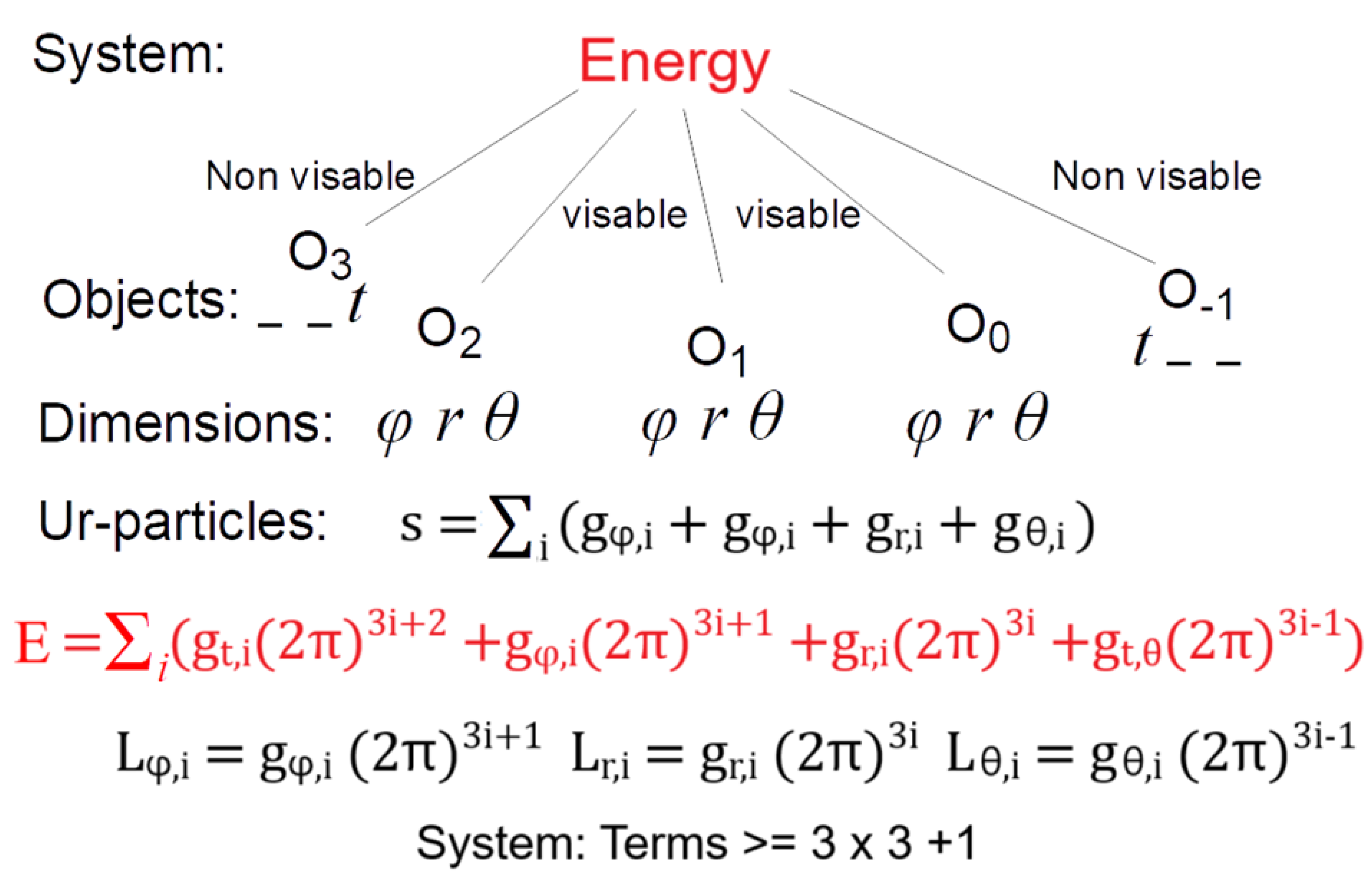
2.1. Ur-Alternatives: ur-Particles - Dimensions - Objects - System

A system consists of at least 3 visible or invisible objects

O_{i}

, each with 3 spatial coordinates. Standardization is performed on the Earth’s surface with a meter and a second (object

O_{0})

O_{i} i \in \{. . ., 0, 1, 2, . . .\}

(2.1)

The number of ur-particles with dimension d

q_{d, i} \in Z

refers to the local spatial coordinates and time:

q_{t, i} q_{φ, i} q_{r, i} q_{θ, i}

(2)

The number s of ur-particles starts in the center of the system.

s_{i} = q_{t, i} + q_{φ, i} + q_{r, i} + q_{θ, i} s = \sum_{d, i} q_{d, i}

(2.2)

At the end of

q_{φ, i}

the object is complete and corresponds to its surface and rest mass.

The distributions of

q_{φ, i}

q_{r, i}

and

q_{θ, i}

lead to different states (elementary particles, atoms and molecules) with different densities and orbits (planets, lunar resonances and eccentric orbits). For example, in the interior of the sun, due to nuclear fusion, neutrino production is

q_{φ, i} \neq q_{r, i} \neq q_{θ, i}

(see 2.7. Muon). For objects at rest or within elementary particles the time $q_{t, i} = 0$ is allowed.

Coincidences can be measured after revolutions of

π

. In the following, the coordinate system for

O r b i t_{i} (s)

is referred to as epicyclic coordinates. The dimensions

t = 2

φ = 1

r = 0

and

θ = - 1

are used in the exponent.

The coordinates q_{k, i} in epicycles π constitute the metric . O r b i t_{i} (s) = E_{i} = q_{t, i} π^{t + 3 i} + q_{φ, i} π^{φ + 3 i} + q_{r, i} π^{r + 3 i} + q_{θ, i} π^{θ + 3 i}

(2.3)

A differentiation between angular momentum L, energy E and action S is not necessary. The meaning of E is indicated by the indices of the object and the dimensions. The difference between the moving and stationary location coordinates of objects is insignificant for the energy ratios

E_{i}

. The radius itself is curved, which allows a simple formulation of general relativity, i.e.

E_{r, i} = q_{r, i} π^{r + 3 i}

is no different from the circular arcs

E_{φ, i}

and

E_{θ, i}

. In a system, the spatial coordinates of objects move in a spiral in the direction of time, analogous to geodesic lines.

Neutral objects (Neutron, Photon or Earth) consist of complete revolutions of

2 π

O r b i t_{i} (s) = E_{i} = q_{t, i} {(2 π)}^{t + 3 i} + q_{φ, i} {(2 π)}^{φ + 3 i} + q_{r, i} {(2 π)}^{r + 3 i} + q_{θ, i} {(2 π)}^{θ + 3 i}

(2.4)

A measuring device is a neutral, solid object with a surface as a sensor to vacuum. A vacuum can consist of invisible objects (e.g. photons/gluons) or, for comparison, two immediately adjacent objects

O_{2}

and

O_{1}

Since the angular momentum is conserved for each of the dimensions, there can be no algebraic function between the dimensions. Thus,

π

, 1 and

π^{- 1}

are the epicyclic coordinates of the ur-particles and correspond to the neutrinos

ν_{τ}

ν_{μ}

and

ν_{e}

respectively. The electron is the first object with 3 spatial coordinates:

Elektron : O r b i t_{e} (s) = E_{e} = g_{φ, e} π + 1 - π^{- 1} + E_{0} Positron : O r b i t_{p} (s) = E_{p} = g_{φ, e} π - 1 - π^{- 1} + E_{0}

(2.5)

The term

E_{θ} = - π^{- 1}

is negative and causes attraction in the gravitational field to a neighboring object. In quantum theory,

- 1 / π

corresponds to spin 1/2 and explains the interaction between objects. According to the theory, an electron consists of 2 ur-particles, or neutrinos, which move orthograde with c, with the combined energy

c^{2}

. Orthograde to this is

g_{φ, e}

g \in Q

, which is the relative speed in the electric field and leads to the Lorenz gauge. Further decimal places are summarized with

E_{0}

and only result together with another object or the measurement (see 2.4. Muon). A free electron moves in spacetime 4D with time

g_{t, e} {(2 π)}^{2}

free electron : O r b i t_{e} (s) = E_{e} = g_{t, e} {(2 π)}^{2} + g_{φ, e} π + 1 - π^{- 1} + E_{0}

(2.6)

A basic principle of the theory is that the number of ur-particles is countable. The energies are always transcendental powers of

π

{(2 π)}^{d}

are orthogonal and unique for the dimensions d. If the rest mass of the electron is normalized to 1, the spin is always a rational number of

1 / π

g_{f} (π)

is a frequency, e.g. for the electron

E_{e} = g_{f} (π) + 1 - 1 / π

. All calculations for neutrons, protons or atoms involve at least

{(2 π)}^{4}

. The question of dimensions in space is secondary in this theory. The rest mass of a neutron

P (2 π)

can be formulated in 10 dimensions (see 2.5 Neutron) or, in our imagination in 4 dimensions (

t, φ, r, θ

, Poincare group

R^{3 + 1}

) or one dimension in our brain network. The increase of dimensions i by

P (π)

for the binding energy is consistent with the no-go theorem "all possible symmetries of the S matrix" [6].

2.2. Photon - Speed of Light

2.2.1. Normalization of c with the Earth’s Surface and Day - Thought Experiment

The system Sun, Earth with the bound Moon is unique in the planetary system. Imagine a laboratory table at the North Pole. On the laboratory table is an interference experiment (Michelson) set up with a laser and a mirror. A foucault pendulum describes an epicycloid and rotates once a day. The light beam from the laser to the mirror and back is also bent and results in a very narrow area. After one day, a circle with

2 π

is full. For a single photon this corresponds to spin 1. The light beam is attracted to the earth and can be described mit der syndischen Periode with the formula c m day for the area A. c is the only required parameter as substitute for the number of unknown particles

N_{E a r t h}

. The area A

\vec{Δ_{a r e a}} = \vec{Δ_{q +}} \times \vec{Δ_{q -}}

rotates

\propto h ν

with rotation time in 4-dimensional space (see Quarks u and d 2.42), where the angular momentum between Earth and photon is conserved. The opposite pole to the photon is the earth with an area

D_{E a r t h}^{2}

. The ratio is

1 / (2 π)

, similar to the lever law.

c m 86400 s / D_{e q u a t o r i a l}^{2} = 1 / (2 π)

(2.7)

This formula could be exact when the contour line is above zero 489 (e.g. the 1000 km wide Congo Basin is just under 500 m opposite the Pacific).

It allows a simple, new interpretation of forces, which is based solely on the number of ur-particles in 4D space-time. The Foucault pendulum, orthograde to the Earth’s axis, rotates with the minimum energy. General relativity explains the difference to the syndic period of the entire system of sun, moon, ecliptic, precession and nutation. The photon can be explained by a superposition of two electrons, or an even number of particles. Even if the epicycloid of a photon

P (2 p i)

intersects the center, the trajectory of its particles

P (π)

from the laser to the mirror is half a wave. It never intersects the center! When c and m are standardized, the light beam is bent in the laboratory and this also applies to an electron around an atomic nucleus. This makes the wave-particle discussion obsolete.

All observation is based on orthograde spatial coordinates, whether

x, y, z

φ, r, θ

. The marking is usually done with a beam of light and is correct according to the theory of relativity and is done with the quadratic equations

{(m c^{2})}^{2} + {\vec{p}}^{2} c^{2} = E^{2}

. Spin and Coriolis force have the same cause, namely the rotation of the laboratory table. Spin points in the direction of the gravity of a neighboring object.

For the connection between

h G_{N} c^{5}

see 2.11 Gravitational constant – Planck constant, (2.50)

h G_{N} c^{5} s^{8} / m^{10} \sqrt{π^{4} - π^{2} - π^{- 1} - π^{- 3}} = 0.999991

(2.50)

2.3. Photon - Composed of Neutrinos

A photon are world lines of superimposed and entangled neutrinos (

ν_{τ}

ν_{μ}

ν_{e}

and also corresponds to superimposed electrons

e^{-}

and

e^{+}

with a minimum energy

E_{γ} > 0

. A photon can be calculated only as a system of emission (object

O_{2}

) and absorption

O_{1}

. For the spatial part of

O r b i t_{1, 2}

E_{γ}

can be used together with the prefactors

g_{2} - g_{1} \in Q

and

φ = 1

r = 0

and

θ = - 1

. For simplification, a prefactor

g_{2} - g_{1} = g

is used in the photon.

E_{γ} = p c = E_{φ} + E_{r} + E_{θ} = g_{φ} {(2 π)}^{φ} + g_{r} {(2 π)}^{r} + g_{θ} {(2 π)}^{θ}

(2.8)

The term

g_{φ} {(2 π)}^{φ} > 0

determines the frequency. The dimensionless formula is adjusted to

c / f / m

c / f / m = g_{φ} E_{φ} = g_{φ} {(2 π)}^{φ} > 0

(2.9)

The radial component

g_{r} = (g_{r, 1} - g_{r, 2}) {(2 π)}^{0}

is the length of the wave train and, depending on the polarization

ψ

, leads to two opposite components

g_{r, 1}

and

g_{r, 2}

, which can be summarized as

g_{r} e^{- i 2 π c / f / m + ψ}

. For a wave,

g_{r}

and

g_{φ}

are reciprocal.

g_{r} = 1 / g_{φ}

. For a complete wave train, the following applies:

n λ / m = n / g_{φ} e^{2 π c / f / m + ψ} n \in N

(2.10)

the mean of the energy component

E_{r} = 0

of the photon is independent of the length of the wave train

n λ

The

θ

component has a negative energy and leads to an attraction in the gravitational field relative to a measuring device, with the smallest possible prefactor for a neutral object

g_{θ} = - 1

E_{θ} = g_{θ} / (2 π) = - 1 / (2 π) s p i n 1 = - 1 / (2 π)

(2.11)

2.3.1. Interpretation of the Compton Effect via Polynomials $P (π)$

For the Compton effect between photon, electron, and measuring device (

O_{0}

), the common momentum is zero. The increase

λ_{C, t h e o r y} = 1 / λ^{'} - 1 / λ

does not depend on the original photon energy, but on the absorption of the energy

E_{0}

. With the Compton wavelength

Δ λ = λ_{C} = h / (m_{e} c) (1 - cos ϕ)

there is a connection between

h / (m_{e} c)

in quantum theory and the macro world with

m^{2} / (c d a y)

. The approach of the polynomials for the Compton effect between the electron, photon and recoil

O_{0}

is as follows:

E_{e} = g_{φ, e} π + 1 - π^{- 1} E_{p h o t o n} = g_{φ, 2} {(2 π)}^{1} + g_{r, 2} - {(2 π)}^{- 1} E_{0} = g_{φ, 2} {(2 π)}^{4} + g_{r, 2} {(2 π)}^{3} + {(2 π)}^{2} - E_{0, - 1}

(14)

For a resting electron,

g_{φ, e} = 0

with

g_{r, e} = 1

. For the dimension r, the absorption is caused by the excitations of the term

g_{r, 2} {(2 π)}^{3}

. The minimum energy from this term is

π^{3}

and results in the total energy term of

2 π^{3}

Estimate for

λ_{C}

with the 3 required terms for a photon:

λ_{C, t h e o r y} = m^{2} / (c 86400 s) (1 - cos ϕ) (2 π^{3} + 1 - {(2 π)}^{- 1}) = 2.4265784 10^{- 12} m m e a s u r e m e n t λ_{C} = 2.42631023538 (76) 10^{- 12} m

(2.12)

This value is accurate to 4 decimal places. h cannot be replaced by this. The calculation is again dependent on the Planetary System. (see Chapter 3 Planetary System). Further research is needed for this purpose.

2.3.2. Fine structure constant $α$

Using the simple concept of the Bohr atomic model,

c α

is the speed of the electron in orbit. In the ground state,

g_{φ, e} = 0

. For the binding of the electron,

g_{r, e} = - 1

. Approximation for

1 / α

1 / α = π^{4} + π^{3} + π^{2} - 1 - π^{- 1} + E_{0} = 136.96 Measurementt 1 / α = 137.035999177 (21)

(2.13)

The calculation is accurate to ‰. It remains to be seen whether a further series expansion will produce a more accurate result or whether it is limited by the gravitational constant.

2.3.3. Neutrino Oscillation

The rotations of the neutrino world lines correspond to the energies.

O r b i t_{ν_{τ}} = E_{ν_{τ}} = q_{t} π^{t} + g_{φ} π^{φ} = q_{t} π^{t} + g_{φ} π ν_{τ} O r b i t_{ν_{μ}} = E_{ν_{μ}} = q_{t} π^{t} + g_{r} π^{r} = q_{t} π^{t} + g_{r} ν_{μ} O r b i t_{ν_{e}} = E_{ν_{e}} = q_{t} π^{t} + g_{θ} π^{θ} = q_{t} π^{t} + g_{θ} / π ν_{e}

(2.14)

Accordingly, in quantum theory, neutrino mass eigenstates

ν_{j}

are plane waves [9].

ℏ |ν_{j} (t)〉 = |ν_{j} (0)〉 e^{- i (E t - p_{j} x) / ℏ}

Neutrino oscillations are caused by the shift of the phase

O r b i t_{ν}

compared with the measuring device with base

2 π

and, in other words, a consequence of the gravitational field.

The measurements of the neutrion energies are only possible in a system of emission/decay and absorption in the detector:

μ \to e + ν_{μ} + {\bar{ν}}_{e}

. The calculation of the muon mass from

P (2 π)

and

P (π)

via the algorithm (see 2.7 Muon) leads to

ν_{μ}

with mass

p i^{0}

, where normalization is related to the electron mass

{(2 π)}^{0} = 0.510998 M e V

. For the spatial dimensions r, the following would be assumed for

ν_{μ}

m_{ν_{μ}} \approx 0.510998 / π = 0.162 < 0.17 M e V / c^{2} Measurement < 0.17 M e V / c^{2}

(2.15)

An important decay of the Tau into leptons is

τ \to e + ν_{τ} + {\bar{ν}}_{e}

. Other decay channels lead to hadrons, such as pions and kaons. The largest term of the tau mass is

2 {(2 π)}^{4} + 2 {(2 π)}^{3} - 3 {(2 π)}^{2} - {(2 π)}^{1} - 2 + {(2 π)}^{- 1} - π - π^{- 3} m_{e} = 3477.34 m_{e}

(see 2.8 Tau). The term

{(2 π)}^{4}

is crucial for neutrino

ν_{τ}

. For a single

ν_{τ}

with

p i^{4}

, the relationship to the electron

{(2 π)}^{0}

is analogous to

ν_{μ}

m_{ν_{τ}} \approx 0.510998 π^{4} / π = 15.8 Measurement < 18.2 M e V / c^{2}

(2.16)

When muons and Taus decay, an antineutrino

{\bar{ν}}_{e}

is created.

ν_{e}

is the

s p i n 1 / 2 = - 1 / p i

and causes gravity. The rest mass of

ν_{e}

is theoretically negative, but contradicts the principle that the longitudinal velocity

v < = c

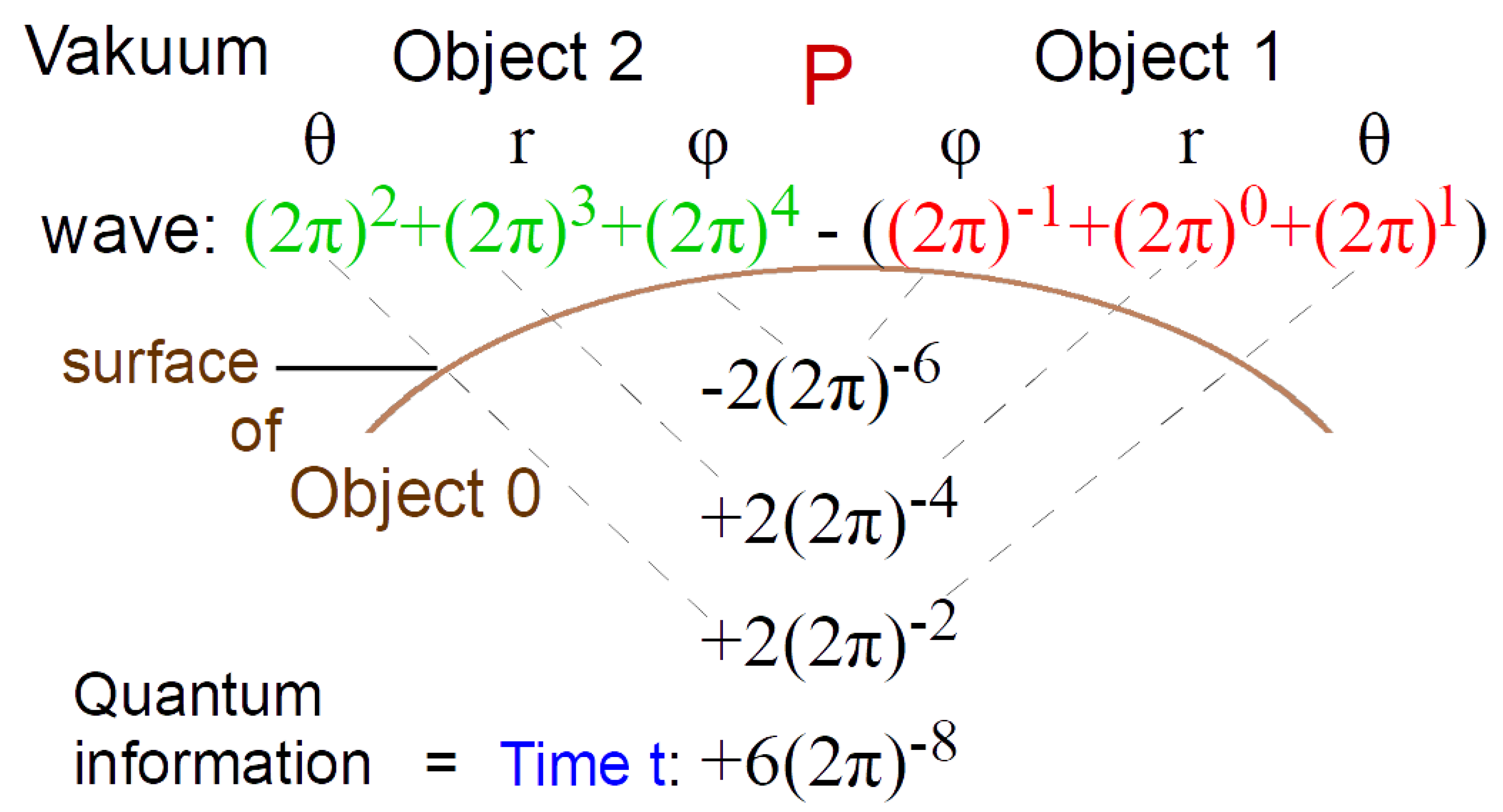
2.4. Neutral Objects

The surface of every object rotates with a frequency

f_{i}

. Only a system of at least 3 objects provides conclusions about frequencies

f_{i}

and radii

q_{r, i}

O r b i t_{i} (s) = E_{i} = q_{φ, i} {(2 π)}^{φ + 3 i} + q_{r, i} {(2 π)}^{r + 3 i} + q_{θ, i} {(2 π)}^{θ + 3 i} E_{φ, i} = c / m t_{i} = c / m / f_{i} = q_{φ, i} {(2 π)}^{φ + 3 i}

(2.17)

1 / f_{1, 2} = 1 / f_{1} - 1 / f_{2} E_{r, i} = q_{r, i} {(2 π)}^{r + 3 i}

(2.18)

The frequency

1 / f_{1, 2}

and the phase are unique relative to object

O_{0}

. In a measuring device

O_{0}

the common time

q_{t, 0} > 0

is determined and can also be given as a measured value in spatial coordinates. The curved surface of

O_{0}

can be considered a sensor (see Figure 2). For each of the three spatial dimensions there are three focal points of

O_{1}

and

O_{2}

below the curved surface of

O_{0}

r_{f, 1, 2}, φ_{f, 1, 2}, θ_{f, 1, 2} with energies E_{f, φ} E_{f, r} E_{f, θ}

(2.19)

The energies of the spatial coordinates are summarized as

E_{f, s p a c e}

E_{f, s p a c e} = E_{f, φ} + E_{f, r} - E_{f, θ}

(2.20)

E_{f, s p a c e}

leads to the common time

E_{f, t i m e}

and gives the total energy in the measuring device.

E_{f} = E_{f, s p a c e} + E_{f, t i m e}

(2.21)

This gives an algorithm to calculate

E_{f}

step by step from high to low energies, with two loops for

O_{1}

and

O_{2}

. In detail, the dimensions

φ, r, θ

for objects

O_{2}

and

O_{1}

are marked with the parameters

λ \in

{4,3,2} and

ν \in

{1,0,-1}. According to the law of gravitation

F = (m_{1} m_{2}) r^{- 2}

, F decreases with the second power of r. Similarly,

E_{f, s p a c e}

decreases for neutral objects with

{(2 π)}^{- λ - ν}

f o r λ = φ_{2} t o θ_{2} s t e p - 1 f o r ν = φ_{1} t o θ_{1} s t e p - 1 i f g_{2, λ} > 0 t h e n E_{f, - λ - ν - 1} = - s g n (ν) g_{2, λ} g_{1, ν} (2 π)^{- λ - ν} / π i f g_{2, λ} < 0 t h e n E_{f, - λ - ν} = - s g n (ν) g_{2, λ} g_{1, ν} (2 π)^{- λ - ν} 2 E_{f, t} = | g_{2, λ} g_{1, ν} | (2 π)^{- 2 φ_{2}} n e x t n e x t

(2.22)

The starting values are those of objects 1 and 2 and are calculated for object 0 with the reciprocal of the corresponding dimension, the exponent

- λ - ν

. This geometric mean also contains the factor

1 / π

or 2. If this factor was 1, there would be straight lines in the cosmos. For a curved space, the factor

1 / π

is minimal.

The equation

E_{f, - λ - ν - 1} = - s g n (ν) g_{2, λ} g_{1, ν} {(2 π)}^{- λ - ν} / π

is the core of the algorithm. The structure corresponds to a Christoffel symbol from GR:

Γ_{λ ν}^{μ} = g^{μ ρ} (\partial_{λ} g_{ν ρ} + \partial_{ν} g_{λ ρ} - \partial_{ρ} g_{λ ν})

(2.23)

The essential point is to replace the partial derivatives with respect to the dimensions by the quanta

\partial_{d} = 1 / π

and apply this to matter. The equation

E_{f, - λ - ν} = - s g n (ν) g_{2, λ} g_{1, ν} {(2 π)}^{- λ - ν}

includes negative energies of

E_{2}

, i.e. antimatter. This also allows other elementary particles such as muons, Taus and pions to be calculated. If

g_{2, λ} {(2 π)}^{λ} = 0

, a pair of neutrino and antineutrino can be created (see 2.7. Muon). Another interpretation of a system by

P (2 π)

is the reflection / inversion of the external worlds of

O_{2}

and

O_{1}

into the internal world

O_{0}

of the observer at the unit circle

e^{i 2 π + Ψ}

(see 2.9. Quarks u and d).

The algorithm is similar to a lattice gauge calculation and is based on the specifications of two objects that are compared in the measuring device. This comparison is carried out step by step with 2 loops to speak into the depth of the measuring device until the result is processed at the common point in time (see Figure 2 and Figure 3 for neutrons and protons). In lattice gauge theory, this common point in time corresponds to the minimum distance with a cut-off in momentum space, i.e., the point at which no more divergence occurs. In lattice gauge theory, the effect S is also summed via loops (Wilson loops). The normalization for the lattice gauge theory is based on the coupling constants, whereas the algorithm is based on powers of

π

2.5. Neutron

The starting point for calculating the rest mass of the neutron is a comparison of the simplest polynomials

P (2 π)

E_{2}

and

E_{1}

with the parity operator - for an attraction. For a visible object, the energy

E = E_{2} - E_{1} > 0

. For a resting object,

g_{t, 2} = g_{t, 1} = 0

E_{2} = {(2 π)}^{4} + {(2 π)}^{3} + {(2 π)}^{2} E_{1} = - ({(2 π)}^{1} + {(2 π)}^{0} + {(2 π)}^{- 1})

(2.24)

From the energies

E_{2, 1}

it follows that with 2.11 to 2.15

E_{0} = E_{f, s p a c e} + E_{f, t i m e}

E_{f, s p a c e} = 2 {(2 π)}^{- 2} + 2 {(2 π)}^{- 4} - 2 {(2 π)}^{- 6} E_{f, t i m e} = 6 {(2 π)}^{- 8}

(2.25)

m_{N e u t r o n} / m_{e} = {(2 π)}^{4} + {(2 π)}^{3} + {(2 π)}^{2} - {(2 π)}^{1} - {(2 π)}^{0} - {(2 π)}^{- 1} + 2 {(2 π)}^{- 2} + 2 {(2 π)}^{- 4} - 2 {(2 π)}^{- 6} + 6 {(2 π)}^{- 8} = 1838.6836611 Theory : 1838.6836611 m_{e} Measurement : 1838.68366173 (89) m_{e} [10]

(2.26)

The decimal places of

m_{n e u t r o n} / m_{e}

extend to

{(2 π)}^{- 8} = 4 10^{- 7}

and are within a standard deviation of

1838.68366173 (89)

The calculation requires only 10 terms and is therefore the most efficient method for determing

m_{neutron} / m_{e} . This result is unique because of to the transcendental numbers π^{d} .

In Figure 2,

φ

, r and

θ

are arranged in a half wave. The algorithm is a Fourier transformation from the outer wave (6 terms) into the quantum information of the inner world (6 prefactors).

Figure 2.

m_{N e u t r o n} / m_{e}

as a polynomial

P (2 π)

Figure 2.

m_{N e u t r o n} / m_{e}

as a polynomial

P (2 π)

2.6. Proton

The electric charge should correspond to three neutrions, with a mass difference between neutrons and protons. The approach for the energy of the charge

E_{C +}

is itself a system of 3 objects (

E_{C, 2}, E_{C, 1}, E_{C, 0}

π^{φ}

and

π^{θ}

rotate around the center

π^{r} = 1

, with the minimum energy

E_{C, 2, 1}

similar to the Coriolis force:

E_{C, 2, 1} = - π^{1} + 2 π^{- 1} < 0 .

(2.26)

The decimal places

E_{C, 0} = E_{C, 0, s p a c e} + E_{C, 0, t i m e}

result from a series expansion of

π^{d}

. The decimal places of the neutron

E_{f} = 2 {(2 π)}^{- 2} + 2 {(2 π)}^{- 4} - 2 {(2 π)}^{- 6} + 6 {(2 π)}^{- 8}

contain only even powers.

E_{C, 0}

fills the odd powers. A further explanation for this is speculative. It is assumed that after 4 spatial dimensions the type of neutrinos remains the same with

{ν_{φ}}^{- 4}

and

{ν_{θ}}^{- 4}

E_{C, 0, s p a c e} = - π^{- 3} + 2 π^{- 5}

(2.27)

Similarly, in

E_{C, 0, t i m e}

the phase of the third neutrino

π^{θ}

changes to

{ν_{μ}}^{- 12}

in the gravitational field with a neutrino oscillation.

E_{C, 0, t i m e} = - π^{- 7} + π^{- 9} - π^{- 12}

(2.28)

Together with the neutron mass, this gives the proton mass:

E_{C +} = - π^{1} + 2 π^{- 1} - π^{- 3} + 2 π^{- 5} - π^{- 7} + π^{- 9} - π^{- 12} m_{P r o t o n} = m_{N e u t r o n} + E_{c} m_{e} = 1836.15267363 m_{e}

(2.29)

Figure 3.

m_{P r o t o n} / m_{e}

as a polynomial

P (2 π)

Figure 3.

m_{P r o t o n} / m_{e}

as a polynomial

P (2 π)

m_{P r o t o n} / m_{e} = {(2 π)}^{4} + {(2 π)}^{3} + {(2 π)}^{2} - {(2 π)}^{1} - {(2 π)}^{0} - {(2 π)}^{- 1} + 2 {(2 π)}^{- 2} + 2 {(2 π)}^{- 4} - 2 {(2 π)}^{- 6} + 6 {(2 π)}^{- 8} + (- π + 2 π^{- 1} - π^{- 3} + 2 π^{- 5} - π^{- 7} + π^{- 9} - π^{- 12}) = 1836.15267363 Theory : 1836.15267363 m_{e} Measurement : 1836.15267343 (11) m_{e} [10]

(2.30)

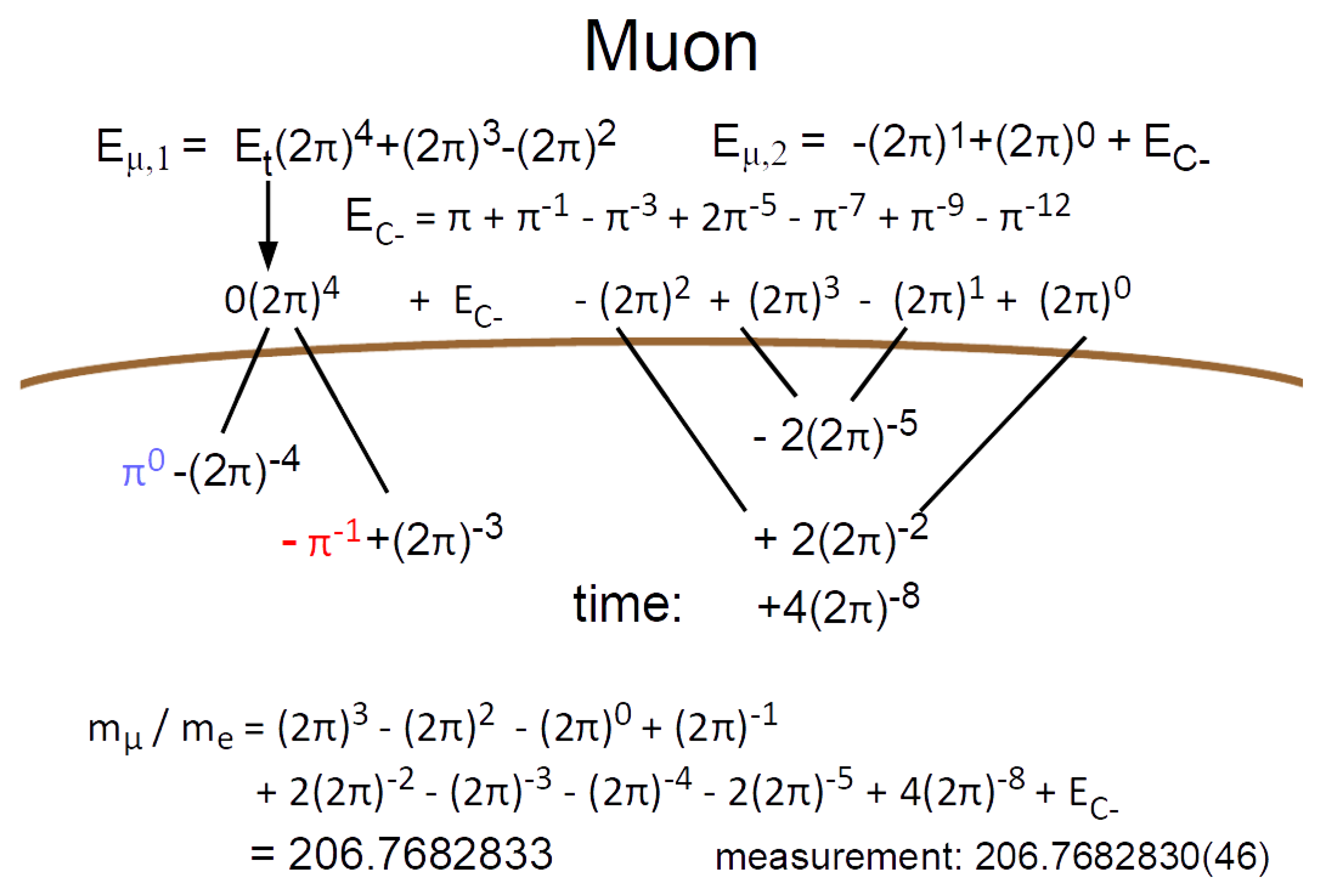
2.7. Muon

First estimate for the rest mass:

E_{μ, 1, 2} = {(2 π)}^{3} - {(2 π)}^{2} - π + {(2 π)}^{0} + 1 / π = 206.748 measurement : 206.7682830 (46) m_{e}

(2.31)

This follows from a minimum energy with a frequency

{(2 π)}^{3} > 0

and a radial component

{(2 π)}^{r} = 1 > 0

. It is assumed that the negative and positive charges are related:

E_{C -} = {(2 π)}^{1} - π^{- 1} + E_{C +} E_{C +} = - π^{1} + 2 π^{- 1} - π^{- 3} + 2 π^{- 5} - π^{- 7} + π^{- 9} - π^{- 12} E_{C -} = π^{1} + π^{- 1} - π^{- 3} + 2 π^{- 5} - π^{- 7} + π^{- 9} - π^{- 12}

(2.32)

The neutral part can be separated from

E_{C -}

E_{μ, 1, 2} - E_{C -} = {(2 π)}^{3} - {(2 π)}^{2} - {(2 π)}^{1} + {(2 π)}^{0}

(2.33)

The calculation of the energy

E_{0, f}

O_{0}

is carried out step by step according to algorithm (2.22). Depending on the signs in

E_{2}

and

E_{1}

, multiplication is carried out by

1 / π

for matter or by 2 for antimatter:

\begin{matrix} E_{1, 2} = {(2 π)}^{3} - {(2 π)}^{2} - {(2 π)}^{1} + {(2 π)}^{0} (2.34) \\ Matter + E_{θ} > > {(2 π)}^{3} (- {(2 π)}^{1}) > > E_{0, f, 1} = - {(2 π)}^{- 4} / π = - 2 {(2 π)}^{- 5} \\ E_{0, f, t} = | 2 {(2 π)}^{- 8} | \end{matrix}

\begin{matrix} E_{1, 2, - 1} = - {(2 π)}^{2} + {(2 π)}^{0} (2.35) \\ Antimatter - E_{r} > > (- {(2 π)}^{2}) {(2 π)}^{0} > > E_{0, f, 2} = 2 {(2 π)}^{- 2} \\ E_{0, f, t} + = | 2 {(2 π)}^{- 8} | E_{0, f, t} = 4 {(2 π)}^{- 8} \end{matrix}

To fully calculate

E_{0}

, the placeholder

0 {(2 π)}^{4}

must be included. According to the Heisenberg uncertainty principle, the decay of muon

μ \to e + ν_{μ} + {\bar{ν}}_{e}

is possible with an energy of

0 {(2 π)}^{4} = {(2 π)}^{4} - {(2 π)}^{4}

Production from

ν_{μ} = π^{0}

\begin{matrix} - {(2 π)}^{4} > > E_{n u, f, 3} = - {(2 π)}^{- 4} + π^{0} (2.36) \end{matrix}

Production of

{\bar{ν}}_{e} = - π^{- 1}

\begin{matrix} + {(2 π)}^{4} > > E_{n u, f, 3} = - {(2 π)}^{- 3} - π^{- 1} (2.37) \end{matrix}

In summary, the rest mass of the muon is:

m_{μ} / m_{e} = {(2 π)}^{3} - {(2 π)}^{2} - {(2 π)}^{1} + {(2 π)}^{0} + + 2 {(2 π)}^{- 2} - {(2 π)}^{- 3} - {(2 π)}^{- 4} - 2 {(2 π)}^{- 5} + 4 {(2 π)}^{- 8} + E_{C -} = 206.7682833

(2.38)

Theory: 206.7682833 $m_{e}$ Measurement: 206.7682830(46) $m_{e}$ [10]

The decay results from the division of the energies

m_{μ} / m_{e}

into 3 new objects with kinetic energy

E_{φ}

E_{φ} = {(2 π)}^{3} - {(2 π)}^{2} = E_{φ, ν_{μ}} + E_{φ, {\bar{ν}}_{e}} + E_{φ, e}

(2.39)

Figure 4 corresponds to a Feynman diagram. The probabilities for the energies and momenta are given by the QT.

Figure 4.

m_{m u o n} / m_{e}

as a polynomial

P (2 π)

with the decays in

ν_{μ}

and

{\bar{ν}}_{e}

Figure 4.

m_{m u o n} / m_{e}

as a polynomial

P (2 π)

with the decays in

ν_{μ}

and

{\bar{ν}}_{e}

2.8. Tau

The first particle with a factor of

{(2 π)}^{4}

is the proton. Tau has a factor of

2 {(2 π)}^{4}

and can be explained by the superposition of 3 elementary particles:

E_{τ, 3} = 2 {(2 π)}^{4} + 2 {(2 π)}^{3} - 2 {(2 π)}^{2} E_{τ, 2} = - {(2 π)}^{2} - {(2 π)}^{1} - 1 E_{τ, 1} = - 2 π - 1 - {(2 π)}^{- 1}

(2.40)

The requirements are

E_{φ} = 2 {(2 π)}^{4} > 0

and

E_{r} = 2 {(2 π)}^{3} > 0

E_{θ} = - 3 {(2 π)}^{2} - 2 {(2 π)}^{1} - 2 - {(2 π)}^{- 1}

with negative energy explaining gravity.

Together with

E_{C -} = π^{1} + π^{- 1} - π^{- 3} + . . .

the first estimate is:

m_{τ} = 2 {(2 π)}^{4} + 2 {(2 π)}^{3} - 3 {(2 π)}^{2} - 2 {(2 π)}^{1} - 2 - {(2 π)}^{- 1} + (π^{1} + π^{- 1} - π^{- 3} + . . .) m_{e} = = 2 {(2 π)}^{4} + 2 {(2 π)}^{3} - 3 {(2 π)}^{2} - {(2 π)}^{1} - 2 + {(2 π)}^{- 1} - π - π^{- 3} m_{e} = 3477.34 m_{e}

(2.41)

Theory: 3477.34 $m_{e}$ measurement: 3477.23(23)

m_{e}

[10]

2.9. Quarks u and d

Table 1 lists the quarks [11] with rest masses from the mean

\bar{m_{q}}

and standard deviation in MeV [10]. The first estimate of

E_{q}

m_{e}

is the highest power d

{(2 π)}^{d}

with

E_{q} / m_{e}

(Table 1). The standard deviations in powers of

π

are estimated as

\bar{m_{q}} / (Δ_{q -} + Δ_{q +})

Table 1. quarks with rest masses from the mean

m_{q}

and standard deviation in MeV.

Table 1. quarks with rest masses from the mean

m_{q}

and standard deviation in MeV.

Quark	$\bar{m_{q}}$ in MeV	$Δ_{q -}$	$Δ_{q +}$	estimate $E_{q}$ in $m_{e}$	$E_{q} / m_{e}$	$\bar{m_{q}} / (Δ_{q -} + Δ_{q +})$
u	2.16	-0.26	0.49	$2 / 3 (2 π)$	1.0091	$1 / 4 π^{2} = 1.167$
d	4.67	-0.17	0.48	$3 / 2 (2 π)$	0.9696	$1 / 4 π^{3} = 0.926$
s	93.4	-3.4	8.6	$2 / 3 {(2 π)}^{3}$	1.1052	$1 / 4 π^{3} = 1.004$
c	1270	-20	20	$3 / 2 {(2 π)}^{4}$	1.0630	$π^{3} = 1.023$
b	4180	-20	30	$3 / 4 {(2 π)}^{5}$	1.1137	$2^{3} / 3 π^{3} = 1.011$
t	172760	-300	300	$3 / 4 {(2 π)}^{7}$	0.9947	$2^{4} π^{3} = 1.160$
Higgs	125110	-110	110	$4 {(2 π)}^{6}$ boson	1.1660	$2^{3} π^{3} = 1.146$
Atom				$> 2 {(2 π)}^{4}$

The charges of quarks u, s and b are -1/3, and those of quarks d, c and t are +2/3 and can be measured only relative to the environment. Only the energies of the quarks whose measurement ranges are within one standard deviation are relevant.

In first order, the energy difference between neutrons (udd) and protons (uud) results from the three ur-particles

π - 2 / π

. By swapping

π, 1 / π, 2 / π

between

O_{2}

O_{1}

and

O_{0}

, the third charges

\pm 1 / 3

and

\pm 2 / 3

of the quarks result. Quarks u and d have frequencies

f_{u} = 2 / 3 (2 π)

and

f_{d} = 3 / 2 (2 π)

Assuming that the prefactors

g_{r} \in

-1, -1/2, 0, 1/2, 1 and

g_{θ} \in

- 1, 0, 1

, the energies are

E_{q} = f_{q} + g_{r} + g_{θ} / π

. For various combinations of

g_{r}

and

g_{θ}

, the mean

\bar{E_{q}}

and standard deviation of

Δ_{d -}

and

Δ_{d +}

follow (Table 2):

Table 2. Quarks and d. Comparison between theory

g_{f} + g_{r} + g_{θ}

and the measurement.

Table 2. Quarks and d. Comparison between theory

g_{f} + g_{r} + g_{θ}

and the measurement.

u	$f_{u}$	$+ g_{r}$	$+ g_{θ}$	=	Theory $1 / m_{e}$	Measurement
$\bar{E_{u}}$	$2 / 3 (2 π)$	+ 0	$+ 0 / π$	4.19	2.14	2.16 MeV
$\bar{E_{u}} + Δ_{u +}$	$2 / 3 (2 π)$	+ 1	$+ 0 / π$	5.19	2.66	2.65 MeV
$\bar{E_{u}} + Δ_{u -}$	$2 / 3 (2 π)$	- 1/2	$+ 0 / π$	3.69	1.89	1.90 MeV

d	$f_{u}$	$+ g_{r}$	$+ g_{θ}$	=	Theory $1 / m_{e}$	Measurement
$\bar{E_{d}}$	$3 / 2 (2 π)$	+ 0	$- 1 / π$	9.106	4.65	4.67 MeV
$\bar{E_{d}} + Δ_{d +}$	$3 / 2 (2 π)$	+ 1	$- 1 / π$	10.11	5.16	5.15 MeV
$\bar{E_{d}} + Δ_{d -}$	$3 / 2 (2 π)$	- 1	$+ 1 / π$	8.74	4.47	4.50 MeV

The energy results from the 3-dimensional components of the particles on the orbit. From the maximum range of energies

Δ_{+} - Δ_{-}

, a common constant

Δ_{a r e a}

can be derived, which corresponds to an area. The area

\vec{Δ_{a r e a}} = \vec{Δ_{q +}} \times \vec{Δ_{q -}}

around the center

\bar{E_{d}}

results in the area

\vec{Δ_{a r e a}} = \vec{Δ_{q +}} \times \vec{Δ_{q -}}

and rotates

\propto h ν

with the rotation time in 4-dimensional space, i.e. taking gravity into account.

Δ_{q +} + i Δ_{q -} = e^{- i 2 π c t + g_{r}} + 1 / π e^{- i 2 π c t + g_{θ}}

(2.42)

The ranges of

E_{u}

and

E_{d}

with limits

g_{r}

and

g_{θ}

depend not only on

O_{2}

and

O_{1}

in the interior, but also on the environment and thus on the measurements. The limits change with the distance a of the quarks with the required time

c t = 2 a

. The closer the quarks are, the more common angular momentum is determined by the prefactors

g_{r}

and

g_{θ}

with quanta and the minimum energy. The inversion at the unit circle

e^{- i 2 π c t + g_{r}}

and

1 / π e^{- i 2 π c t + g_{θ}}

reflects the objects

O_{2}

and

O_{1}

in the measuring device

O_{0}

. The number of ur-particles remains constant. The theory requires c as the only parameter and is standardized with units of meters (m). The circumference

c m t / Δ_{a r e a} = 1 / (2 π)

is the smallest possible string for a complete rotation from the multitude of strings according to string theory.

The charge, iso, spin, mean and standard deviation result from the symmetry in the unit circle with multiples z of 30° with

z \in Z

\begin{matrix} Prefactor & charge in π & g_{r} & g_{θ} in 1 / π for the spin \\ z / 3 = s i n (60^{\circ} z) = e^{i π z / 3} & 1 / 3 z \\ z / 2 = s i n (90^{\circ} z) = e^{i π z / 2} & 1 / 2 z \\ z = c o s (180^{\circ} z) = e^{i π z} & z \end{matrix}

Quarks u:

E_{u} = 2 / 3 (2 π) + e^{- i 2 π c t + g_{u, r}} + 1 / π e^{- i 2 π c t + g_{u, θ}} \bar{E_{u}} = 2 / 3 (2 π) + e^{- i 2 π c t - g_{u, r}} + 1 / π e^{- i 2 π c t - g_{u, θ}}

(2.43)

Quarks d:

E_{d} = 3 / 2 (2 π) + e^{- i 2 π c t + g_{d, r}} + 1 / π e^{- i 2 π c t + g_{d, θ}} \bar{E_{d}} = 3 / 2 (2 π) + e^{- i 2 π c t - g_{d, r}} + 1 / π e^{- i 2 π c t - g_{d, θ}}

(2.44)

2.10. Pion

The approach for the rest mass of the pions requires bosons/gluons in

O_{2}

with

{(2 π)}^{3}

for the frequency

f > 0

and

{(2 π)}^{2}

for the majority of the rest mass

m > 0

E_{2} = {(2 π)}^{3} + {(2 π)}^{2}

Pions: $π^{+}$ $u \bar{d}$ and $π^{-}$ $\bar{u} d$ :

E_{1}

results from the addition of the energies of the quarks:

E_{1} = - 2 / 3 {(2 π)}^{1} + g_{u, r} + g_{u, θ} / π - 3 / 2 {(2 π)}^{1} + g_{\bar{d}, r} + g_{\bar{d}, θ} / π =

- (2 / 3 + 3 / 2) {(2 π)}^{1} + g_{u, r} - g_{d, r} + g_{u, θ} / π - g_{d, θ} / π =

Minimum of the energy of

g_{r}

and

g_{θ}

(see table for u and d):

g_{u, r} - g_{d, r} = - 1 / 2 g_{u, θ} / π - g_{d, θ} / π = - 1 / π

E_{1} = - (2 / 3 + 3 / 2) {(2 π)}^{1} - 1 / 2 - 1 / π E_{2} + E_{1} = {(2 π)}^{3} + {(2 π)}^{2} - (2 / 3 + 3 / 2) {(2 π)}^{1} - 1 / 2 - 1 / π = = {(2 π)}^{3} + {(2 π)}^{2} - 2 {(2 π)}^{1} - 1 / 2 - 1 / 3 π - 1 / π

(2.45)

First estimate from

E_{2} + E_{1}

273.096 m_{e} = 139.552 M e V

Measurement: 139.57039(18)

For a more precise calculation of the decimal places, the powers

P (2 π)

are separated from

P (π)

E_{2, 1, 2 π} = {(2 π)}^{3} + {(2 π)}^{2} - 2 {(2 π)}^{1} - 1 / 2

E_{1, 2, π} = π / 3 - π^{- 1} - . . .

With algorithm (2.15) and the symmetry point

r = 1 / 2

, it follows that:

E_{0, 2 π} = {(2 π)}^{- 2} - 1 / 2 {(2 π)}^{- 3} - 1 / 2 {(2 π)}^{- 4}

It can be assumed that the term

π / 3

is crucial for the symmetry of the charges. The entire term for charged pions is currently speculative:

E_{π} = π / 3 - π^{- 1} - π^{- 2} - π^{- 3}

E_{2, 1, 2 π} + E_{0, 2 π} + E_{0, 2 π} = {(2 π)}^{3} + {(2 π)}^{2} - 2 {(2 π)}^{1} - 1 / 2 + {(2 π)}^{- 1}

+ 2 {(2 π)}^{- 2} - 1 / 2 {(2 π)}^{- 3} - 1 / 2 {(2 π)}^{- 4} + π / 3 - π^{- 1} - π^{- 2} - π^{- 3}

(2.46)

$E_{π^{\pm}}$ = 139.5705 MeV measurement: 139.57039(18) [10]

Pion $π^{0}$ $1 / \sqrt{2} (u \bar{u} - d \bar{d})$ :

E_{1} = - 2^{2} {(2 π)}^{1} + g_{u, r} + g_{\bar{u}, r} + g_{d, θ} / π + g_{\bar{u}, θ} / π =

Extremum of the energy of

g_{r}

and

g_{θ}

(see table for u and d):

g_{u, r} + g_{u, θ} / π = 1 + 0 / π

g_{d, r} + g_{d, θ} / π = 1 - 1 / π

E_{1} = - 4 {(2 π)}^{1} + 2 - π^{- 1}

E_{2} + E_{1} = {(2 π)}^{3} + {(2 π)}^{2} - 4 {(2 π)}^{1} + 2 - π^{- 1}

(2.47)

First estimate from

E_{2} + E_{1}

: 134.94336 MeV Measurement: 134.9768(5)

The decay of the neutral pion occurs with stronger and faster electromagnetic interaction:

π^{0} \to 2 γ

(probability of

98.823 (32) %

) or

π^{0} \to e^{+} + e^{-} + γ

(probability of

1.174 (35) %

- π^{- 1}

is the only term in

E_{2} + E_{1}

that holds the pion

π^{0}

together before decay. It is the spin for the 2 entangled photons after decay.

E_{0}

is thus a neutral polynomial

P (2 π)

. According to the symmetry at r = 2,

E_{2, 1} = {(2 π)}^{3} + {(2 π)}^{2} - 4 {(2 π)}^{1} + 2

follows with an extension of the algorithm (2.15):

E_{0} = 2 {(2 π)}^{- 2} + (4 - 1) {(2 π)}^{- 3} + 2 {(2 π)}^{- 4}

E_{2} + E_{1} + E_{0} = {(2 π)}^{3} + {(2 π)}^{2} - 4 {(2 π)}^{1} + 2 - π^{- 1} +

+ 2 {(2 π)}^{- 2} + (4 - 1) {(2 π)}^{- 3} + 2 {(2 π)}^{- 4}

(2.48)

$E_{π^{0}}$ = 134.9761 MeV Measurement : 134.9768(5) [10]

Further research into the algorithm and calculations for quarks s, c, b and t and the Higgs-boson are needed.

2.11. Gravitational Constant – Planck constant

The unit kg is not needed in this theory and

G_{N} h

becomes a common constant. The Planck time

t_{p} = \sqrt{G_{N} ℏ / c^{5}}

describes the smallest possible time interval according to quantum theory. The observation of the cosmos is the reference for the normalization of m, day and c and is based on atoms with powers of

π^{4}

. At the zenith the energy

g_{2, r} = 0

. The minimum rotation is

g_{2, φ} = 1

and

g_{2, θ} = - 1

E_{G, 2} = π^{4} + 0 π^{3} - π^{2}

Using algorithm (2.22) we obtain

E_{G, 0}

and

E_{G}

E_{G, 0} = - π^{- 1} - π^{- 3} E_{G} = π^{4} - π^{2} - π^{- 1} - π^{- 3}

(2.49)

E_{G}

corresponds to a surface in the firmament. For the comparison with

G_{N} ℏ / c^{5}

, the root of

E_{G}

is as follows:

h G_{N} c^{5} s^{8} / m^{10} \sqrt{π^{4} - π^{2} - π^{- 1} - π^{- 3}} = 0.999991

(2.50)

The units meter and second must appear in this formula. The value of

G_{N}

is only known up to the fifth decimal place [10]. In this respect, the result can be assumed to be 1. h and c are already precisely defined. The only parameter that still has to be determined by measurement is

G_{N}

. The only force that holds the world together is the natural number of ur-particles with c.

3. Planetary System

3.1. Sun – Earth – Moon

The system of the Sun, Earth and Moon is unique in the planetary system. The bound moon has, relative to the Earth, largely the minimum energy in angular velocities (

\dot{φ}

\dot{θ}

). The radial component of a photon is on average = 0:

E_{p h o t o n, r} = n g_{r} e^{2 π c / f / m + ψ} = 0

(see 2.10). Seen from the Earth, the angle of view is on average the same and gives an extremum for the energy. In this sense, the system is in a ground state. Sun, Earth

R_{E a r t h} = 6356.75 k m

, and the bound Moon has a stable ratio of radii and orbits. For the three spatial dimensions,

2^{3} = 8

is the ratio between the rotations/orbital periods of the celestial bodies.

R_{M o o n} / (R_{E a r t h} + R_{M o o n}) = 8 / (2 π) = 4 / π R_{E a r t h} (4 / π - 1) = 1736.9 k m

(3.2)

In terms of to the polar diameter, the deviation is only 0.00011.

The distance between the moon and the Earth

D_{M o o n - E a r t h}

increases by 38.2 mm per year:

d / d t D_{M o o n - E a r t h} = 38.2 m m / 384400 k m / y e a r = 3 . 1510^{- 18} / s

(3.3)

H 0 [12] : H 0 = (67.8 \pm 0.9) k m s^{- 1} {M p c}^{- 1} = 2 . 21810^{18} / s d / d t D_{M o o n - E a r t h} (1 - 1 / p i) = 2 . 14710^{- 18} / s \approx H 0

(3.4)

It is assumed that the distances between celestial bodies are also a consequence of the expansion H0 of the universe.

3.2. Orbits in the inner planetary system

The advantage of the solar system is that apoapsis and periapsis are directly observable, whereas in the atom some energy levels are degenerate. The observation of a celestial body is based on powers of

{(2 π)}^{4}

. Between the celestial bodies,

G_{N} c^{5} s^{8} / m^{10} \sqrt{π^{4} - π^{2} - π^{- 1} - π^{- 3}} = 0.999991

applies.

c^{5}

describes the invisible dimensions between the orbits. As with ladder operators, orbits can be constructed iteratively. It can therefore be assumed that the polynomials of the orbits begin with

{(2 π)}^{5}

. Normalizing to

R_{s u n} = 696342 k m

gives the orbits and energies:

r_{a p o a p s i s}^{2} + r_{p e r i a s i s}^{2} = R_{s u n}^{2} E_{n} r_{a p o / p e r i a s i s} = R_{s u n} \sqrt{g_{φ} {(2 π)}^{5} + g_{r} {(2 π)}^{4} + g_{θ} {(2 π)}^{3}}

(3.5)

The first three terms for

φ

, r and

θ

represent apoasis and periasis respectively with an accuracy of approximately 1‰ (Table 3):

Table 3. Apoapsis and periapsis of Mercuryand Venus. (3.6)

Mercury

The minimum energy with the half-integer quantum number

for the frequency gives the apoapsis

r_{a p o a p s i s} = 696342 k m \sqrt{1 / 2 {(2 π)}^{5} - 1 / 2 {(2 π)}^{4} + {(2 π)}^{3}} = 46006512 k m

M e a s u r e m e n t : 46.002 10^{6} k m r e l . D e v i a t i o n = 0.0001

r_{p e r i a p s i s} = 696342 k m \sqrt{{(2 π)}^{5} - 0 {(2 π)}^{4} + {(2 π)}^{3}} = 69775692 k m

M e a s u r e m e n t : 69.81 10^{6} k m r e l . D e v i a t i o n = 0.0005

Venus

r_{a p o a p s i s} = 696342 k m \sqrt{2 {(2 π)}^{5} + 3 {(2 π)}^{4} - {(2 π)}^{3}} = 107905705 k m

M e a s u r e m e n t : 107.4128 10^{6} k m r e l . D e v i a t i o n = 0.004

r_{p e r i a p s i s} = 696342 k m \sqrt{2 {(2 π)}^{5} + 3 {(2 π)}^{4} + {(2 π)}^{3}} = 109014662 k m

M e a s u r e m e n t : 108.9088 10^{6} k m r e l . D e v i a t i o n = 0.001

r_{V e n u s} / r_{M e r c u r y} = 6123.80 / 2448.57 = 2.50094

(3.7)

The ratios of the radii of Mercury and Venus can be viewed as quantum numbers. These calculations constitutes only the first approach to transferring

P (2 π)

to the planetary system. An improvement in calculations for the Titus Bode series [12], resonances in the asteroid belt and lunar orbits [13], and exoplanets [14] would be possible.

3.3. H0 and Cosmic Microwave Background Radiation (CMBR)

The number of ur-particles

Q

determines the future expansion of the universe with

Q^{+}

and positive geometry. With the number of ur-particles

Q

, for the past and future, the expansion of the universe is given with

Q^{+}

and a positive geometry. In 5-dimensional space with

c^{5}

, the number of ur-particles is constant on average.

In the equation of the gravitational constant (2.50), the term of mass (

h G_{N} s^{3} / m^{5}

) can be separated from the photons

(c^{5} s^{5} / m^{5})

h G_{N} s^{3} / m^{5} c^{5} s^{5} / m^{5} \sqrt{π^{4} - π^{2} - π^{- 1} - π^{- 3}} = 1

(3.8)

The number of ur-particles in masses

N = 1 / (h G_{N}) s^{3} / m^{5}

can be equated with the photons

c^{5} s^{5} / m^{5}

and the curvature over time

ρ / d t

ρ / d t = \sqrt{π^{4} - π^{2} - π^{- 1} - π^{- 3}} / s = 9.337501 / s . N = 1 / (h G_{N}) m^{5} / s^{3} / s = 2.2611962 10^{43} / s = c^{5} s^{5} / m^{5} ρ / d t

(3.9)

For the expansion H0, the observation at the boundaries of the universe is two-dimensional, with photons

c^{2} m^{2} / s^{2}

and a curvature

ρ / s

. The factor

\sqrt{π}

is given by the ratio to the radius

1 / M p c

H 0_{T h e o r y} = \sqrt{π} / c^{2} m^{2} / s^{2} / ρ / s = 2.11 10^{- 18} / s = 65.1 k m / s / M p c Measurement : H 0 = 67.8 \pm 0.9 k m / s / M p c [12]

(3.10)

One possible interpretation is that over time, visible and invisible particles are added to each object. For isotropic photons in the background radiation and a space curvature of

1 / ρ^{3} m

, the wavelength is

λ

λ_{t h e o r y} = \sqrt{π} / 2 / ρ^{3} m = 1.0885 m m Measurement : λ = 1.063 m m (peak  value of the spectral radiance d E λ / d λ)

(3.11)

The factor 1/2 results from the visible photons with energy

E_{γ} > 0

. The theory could thus explain a significant part of the CMBR monopole term [15].

4. Summary and Conclusions

Ur-particles, dimensions (

t, φ, r, θ

), objects and systems are the necessary categories for the calculation of energies. It is crucial to introduce the most efficient coordinate system to describe the cosmos, using the polynomials

P (2 π)

for neutral objects and

P (π)

for charged objects. The basics of general relativity are already contained in

P (2 π)

, with a constancy of c and the assumption that the radius r of an object is curved in the same way as longitude and latitude. An algorithm is derived from a Christoffel symbol. The partial differential equations of general relativity are replaced by a differential quotient

1 / π

, resulting in quanta. Calculating the

m_{n e u t r o n} / m_{e l e c t r o n}

ratio with the required accuracy of 10 digits is the key to the ratio of the rest masses of all the elementary particles.

A basic principle of the theory is that the number of primary particles is countable; thus the wave‒particle problem is obsolete. The energies are transcendental powers of

π

{(2 π)}^{d}

are orthogonal and unique for the dimensions d. If the rest mass of the electron is normalized to 1, the spin is always a rational number of

1 / π

g π

is a frequency. Every calculation for the neutron or proton begins with

{(2 π)}^{4}

. The question of dimensions in space is secondary in this theory. The rest mass of a neutron

P {(2 π)}^{4}

can be formulated in 10 dimensions, or as we imagine, in 3 dimensions.

QT describes elementary particle physics with probabilities. This aspect is also adopted for the calculation of quarks, u, d and pions with the inversion on the unit circle. This means that the most efficient theory should be a combination of

P (2 π)

and QT. Neutrinos are ur- particles. The electron, positron and photon are the simplest, assembled elementary particles. From this, the rest masses of protons, neutrons, muons, taus, pions, and quarks u and d can be calculated exactly with the shortest possible polynomials.

P (2 π)

contains more information than the time-symmetric, squared equations from QT and GR with constants. The calculations surpass the results of various variants of axiomatic quantum field theory [16-26] in terms of accuracy and brevity. Preons (subquarks) were discussed as hypothetical, point-like particles as an extension of quarks, but did not lead to a provable theory [27]. New approaches to emergence [28-35] through chance, selection and self-organization are emerging.

The system of the sun, earth and moon is unique to the planetary system. According to the polynomials

P (2 π)

, the equatorial diameter of the Earth (489 m above sea level) is as follows:

c m d a y / {D_{E a r t h}}^{2} = 1 / (2 π)

(3.1)

Here,

h G_{N} c^{5}

is a common constant:

h G_{N} c^{5} s^{8} / m^{10} \sqrt{π^{4} - π^{2} - π^{- 1} - π^{- 3}} = 0.999991

(2.45)

Apoasis and periasis of Mercury and Venus can be calculated with an accuracy of 1‰.

The first estimates of HO and background radiation are as follows:

curvature of space-time : ρ / d t = \sqrt{π^{4} - π^{2} - π^{- 1} - π^{- 3}} / s . H 0_{t h e o r y} = \sqrt{π} / c^{2} m^{2} / s^{2} / ρ / s = 65.1 k m / s / M p c λ_{t h e o r y} = \sqrt{π} / 2 / ρ^{3} m = 1.0885 m m Measurement : λ = 1.063 m m

The object to be measured is always located between the measuring device and the firmament or background radiation. The power of the ur-particles is countable, but without beginning and without end. Given the constancy of the speed of light c, it can be assumed that every observer is the center of his own universe. Emergence is only possible with a random increase in the number of ur-particles through the expansion of the universe. The outside world of the object is reflected into the interior at the surface of the measuring device. A neutral, solid measuring device is necessary for physics but is not sufficient. Observers also need interpretation through a highly complex network that can arise only in a stable Sun-Earth-Moon system. In 2005, it was shown that string theory dominates with the expansion of the universe, with 3-branes and 7-branes [35]. This is similar to the theory of polynomials

P (2 π)

. Emergence is crucial for our conception of the world. We choose a 3D world with gravity and normalize it with m, day and c. The view of the world is the surface of a three-dimensional space, at the edge of the vacuum with the highest anisotropy and complexity.

This article provides a summary of many important results from

P (2 π)

, some of which are still speculative. The theory

P (2 π)

is not yet complete. However, it has the potential to be a theory of everything.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No new data were created.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Einstein A. The Foundation of the General Theory of Relativity. Annalen Phys. 1916, 49, 7, 769-822.
Charles W. Misner, Kip S. Thorne, John A. Wheeler: Gravitation. Princeton University Press, Princeton 2017, ISBN 978-0-691-17779-3.
Haken H.; Wolf H.C. Atomic and Quantum Physics ISBN: 978-3-540-17702-9 1987, pp. 105-108.
von Weizsäcker C.F; Scheibe E.; Süssmann G. Komplementarität und Logik,III. Mehrfache Quantelung. Z. Naturforschung, 1958, 13a:705.
Holger L. Quantum Theory of Ur-Objects as a Theory of Information 1996,arXiv:quant-ph/9611048. [CrossRef]
Coleman S.; Mandula J. All Possible Symmetries of the S Matrix. Phys. Rev. 1967,159, 1251. [CrossRef]
Schmidt H. Berechnung der Ruhemassen von Elementarteilchen durch Polynome mit der Basis π. Frühlingstagung der Deutschen Physikalischen Gesellschaft 2023www.dpg-verhandlungen.de/year/2023/conference/samop/part/a.
Schmidt C. H. The significance of rational numbers Q⁺ and the coordinate system with epicycles P(2π) for the energy relationships in physics 2024. [CrossRef]
Grossman Y; Lipkin H.J. Flavor oscillations from a spatially localized source — A simple general treatment. Physical Review D. 1997, 55 (5): 2760. doi:10.1103/PhysRevD.55.2760.
CODATA Task Group on Fundamental Constants: CODATA Recommended Values. National Institute of Standards and Technology, accessed November 22, 2022 (English).
Pich A. Quantum Chromodynamics (1984). [CrossRef]
Nieto M. The Titius–Bode Law of Planetary Distances. Pergamon Press. 1972.
Dermott S. F. On the origin of commensurabilities in the solar system Monthly Notices Roy. Astron. Soc. 1968 Band 141, S. 349, 363.
Bovaird T.; Lineweaver C. Exoplanet predictions based on the generalized Titius–Bode relation, Monthly Notices Royal Astron. Soc., Band 435, (2013), pp. 1126–1139.
Fixsen D.J. The Temperature of the Cosmic Microwave Background. The Astrophysical Journal 2009,707 (2) 916–920: arXiv:0911.1955. [CrossRef]
Araki H. Mathematical Theory of Quantum Fields. Oxford University Press. 1999 ISBN 0-19-851773-4.
Witten E. APS Medal for Exceptional Achievement in Research: Invited article on entanglement properties of quantum field theory Rev. Mod. Phys. 2018, 90, 045003.
Penrose R. Twistor geometry of light rays. Classical and Quantum Gravity 1987 Volume 14, Number 1Adx. [CrossRef]
Jacobson T. Thermodynamics of Spacetime: The Einstein Equation of State. Phys. Rev. Lett. 1995, 75 (7): 1260–1263. [CrossRef]
Guido D.; Longo R.; Roberts J.E.; Verch R. Charged Sectors, Spin and Statistics in Quantum Field Theory on Curved Spacetimes Rev. Math. Phys. 2001, 13, 125 . [CrossRef]
Freidel L. Group Field Theory: An Overview. International Journal of Theoretical Physics 2005, 44, (10): 1769–1783 . arXiv:hep-th/0505016. [CrossRef]
Rovelli C. Loop Quantum Gravity. Living Rev. Relativ. 2008, 11, 5 . [CrossRef]
Connes A.; Marcolli M. Noncommutative geometry, quantum fields and motives, American Mathematical Society Colloquium Publications 2008 vol. 55, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-4210-2, MR 2371808.
Pfeifer C., Siemssen D. Electromagnetic potential in pre-metric electrodynamics: Causal structure, propagators and quantization Phys. Rev. D 2016, 93, 105046. [CrossRef]
Loll R. Quantum gravity from causal dynamical triangulations: a review. Classical and Quantum Gravity 2019, 37 (1): 013002 arXiv:1905.08669. [CrossRef]
Quiros I. Nonmetricity theories and aspects of gauge symmetry Phys. Rev. D 2022, 105 104060. [CrossRef]
Basu B.; Lynden-Bell D. A survey of entropy in the universe. Q. J. R. Astron. Soc. 1990, 31, 359 [20].
Zeh, H.D. Open Questions Regarding the Arrow of Time. In The Arrows of Time Mersini-Houghton, L., Vaas, R. (eds) Fundamental Theories of Physics, 2012 vol 172. Springer, Berlin, Heidelberg. [CrossRef]
Stöltzner, M. Where to Put It? The Direction of Time Between Axioms and Supplementary Conditions. In Direction of Time Albeverio, S., Blanchard, P. (eds). Springer, Cham. 2014 . [CrossRef]
Csáki C.; Ma T.; Shu J.; Yu J.-H. Emergence of Maximal Symmetry Phys. Rev. Lett. 2020, 124, 241801. [CrossRef]
Gemsheim S.; Jan M.; Rost J.M. Emergence of Time from Quantum Interaction with the Environment Phys. Rev. Lett. 2023, 131, 140202 . [CrossRef]
Buchholz, D., Fredenhagen, K. Arrow of Time and Quantum Physics. Found Phys 2023, 53, 85. [CrossRef]
Karch A., Randall L. Relaxing to Three Dimensions. Phys. Rev. Lett 2005, 95, 161601.

Figure 1. Cosmos of ur-alternatives with energy

E / c^{2}

Figure 1. Cosmos of ur-alternatives with energy

E / c^{2}

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Importance of a Solid, Neutral Object as a Measuring Device for the Unification of Quantum Theory and General Relativity via Polynomials P(2π)

Abstract

1. Introduction

2. Physics of ur-Particles

2.1. Ur-Alternatives: ur-Particles - Dimensions - Objects - System

2.2. Photon - Speed of Light

2.2.1. Normalization of c with the Earth’s Surface and Day - Thought Experiment

2.3. Photon - Composed of Neutrinos

2.3.1. Interpretation of the Compton Effect via Polynomials P ( π )

2.3.2. Fine structure constant α

2.3.3. Neutrino Oscillation

2.4. Neutral Objects

2.5. Neutron

2.6. Proton

2.7. Muon

2.8. Tau

2.9. Quarks u and d

2.10. Pion

2.11. Gravitational Constant – Planck constant

3. Planetary System

3.1. Sun – Earth – Moon

3.2. Orbits in the inner planetary system

3.3. H0 and Cosmic Microwave Background Radiation (CMBR)

4. Summary and Conclusions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

2.3.1. Interpretation of the Compton Effect via Polynomials $P (π)$

2.3.2. Fine structure constant $α$