Submitted:
04 September 2024
Posted:
05 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
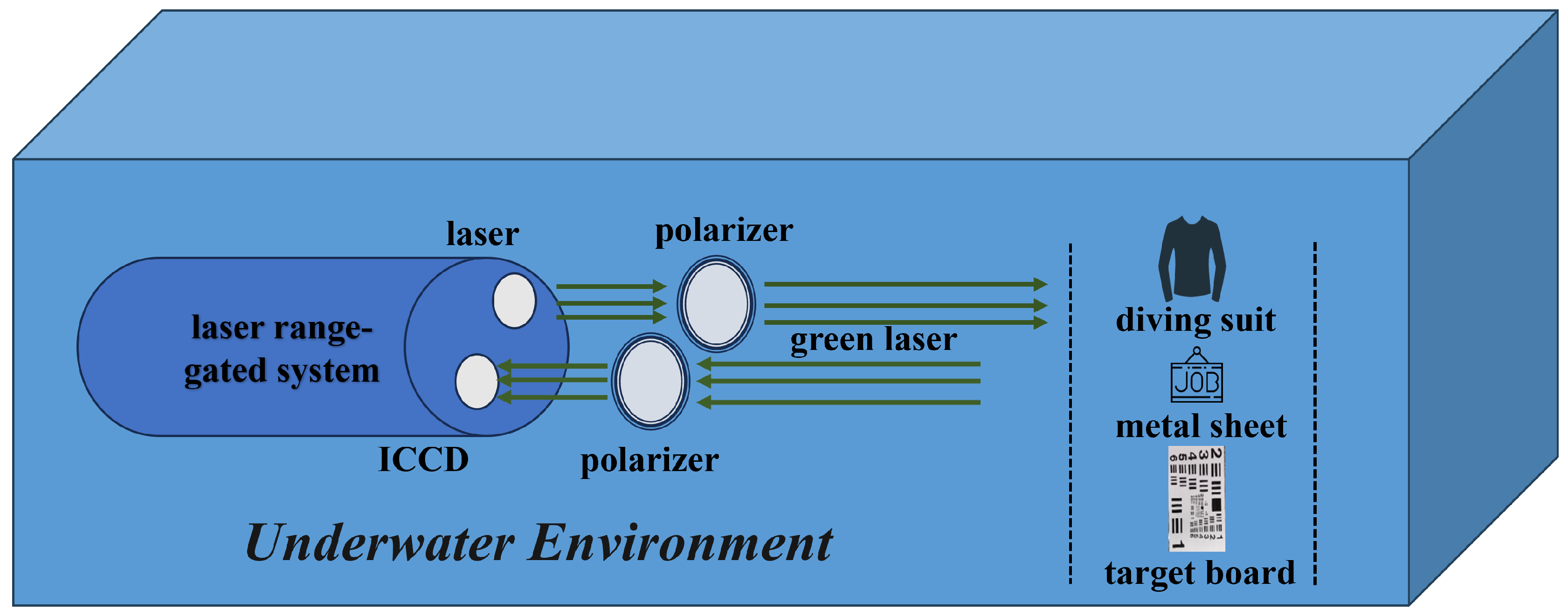
2.1. Principles of Polarization-Enhanced Range-Gated Imaging Technology
2.1.1. Polarization Enhancement
2.1.2. Range-Gated Imaging
2.2. Principle Verification Experiment
2.2.1. Image Evaluation Indicators
2.2.2. Practical Parameters Acquisition in Polarization-Enhanced Range-Gated Imaging Experiment
2.2.3. Verification of the Polarization State Received in the Range-Gated System
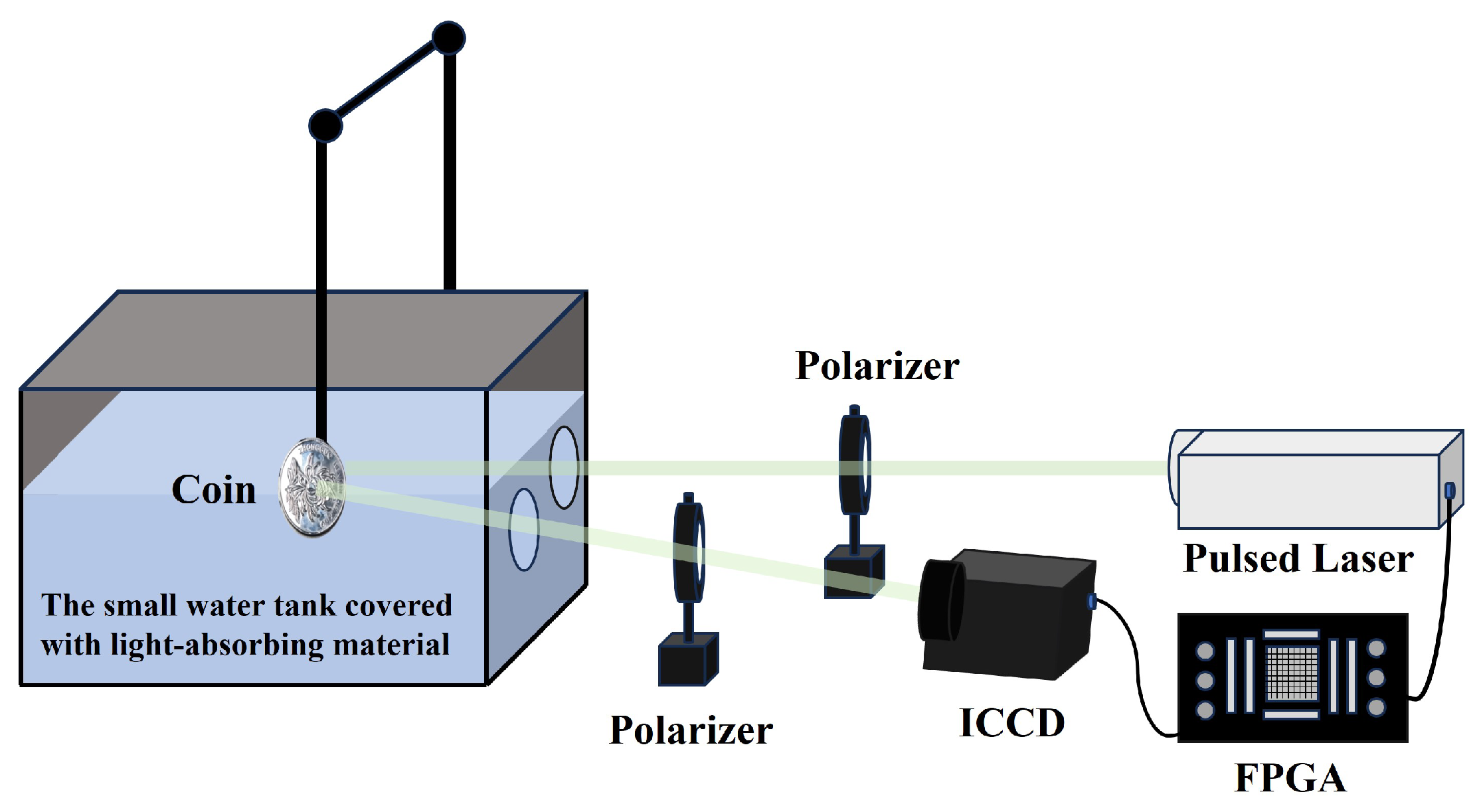
2.2.4. Validation Experiment in a Small Water Tank
3. Polarization-Enhanced Range-Gated Imaging Experiment Results
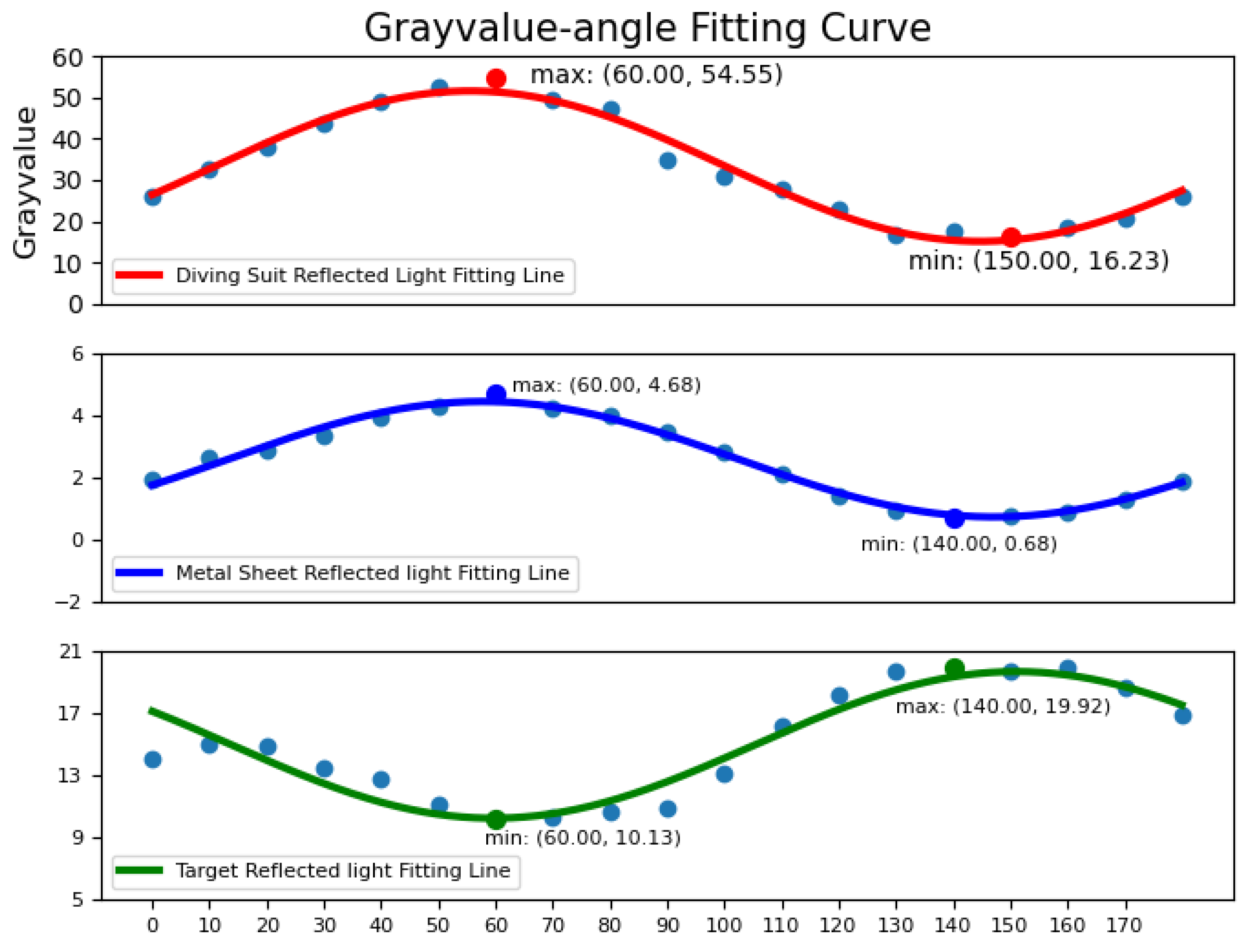
3.1. Polarization Enhancement Effect under Different Materials Conditions
3.2. Polarization Enhancement Effect under Different Turbidity Conditions
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, Z.; Yu, L.; Cao, D.; Wu, Q.; Yu, X.; Lin, G. Airborne ultraviolet imaging system for oil slick surveillance: oil–seawater contrast, imaging concept, signal-to-noise ratio, optical design, and optomechanical model. Applied Optics 2015, 54, 7648–7655. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Zhao, C.; Liu, Y.; Wang, S.; Huang, F. Underwater optical imaging: Key technologies and applications review. IEEE Access 2021, 9, 85500–85514. [Google Scholar] [CrossRef]
- Wolff, L.B. Polarization vision: a new sensory approach to image understanding. Image and Vision computing 1997, 15, 81–93. [Google Scholar] [CrossRef]
- Huo, G.; Wu, Z.; Li, J.; Li, S. Underwater target detection and 3D reconstruction system based on binocular vision. Sensors 2018, 18, 3570. [Google Scholar] [CrossRef]
- He, D.M.; Seet, G.G. Underwater LIDAR imaging in highly turbid waters. Ocean Optics: Remote Sensing and Underwater Imaging. SPIE 2002, 4488, 71–81. [Google Scholar]
- Shashar, N.; Cronin, T.W. Polarization contrast vision in Octopus. Journal of experimental biology 1996, 199, 999–1004. [Google Scholar] [CrossRef] [PubMed]
- Schechner, Y.Y.; Karpel, N. Recovery of underwater visibility and structure by polarization analysis. IEEE Journal of oceanic engineering 2005, 30, 570–587. [Google Scholar] [CrossRef]
- Treibitz, T.; Schechner, Y.Y. Active polarization descattering. IEEE transactions on pattern analysis and machine intelligence 2008, 31, 385–399. [Google Scholar] [CrossRef]
- Dubreuil, M.; Delrot, P.; Leonard, I.; Alfalou, A.; Brosseau, C.; Dogariu, A. Exploring underwater target detection by imaging polarimetry and correlation techniques. Applied optics 2013, 52, 997–1005. [Google Scholar] [CrossRef]
- Liu, F.; Han, P.; Wei, Y.; Yang, K.; Huang, S.; Li, X.; Zhang, G.; Bai, L.; Shao, X. Deeply seeing through highly turbid water by active polarization imaging. Optics letters 2018, 43, 4903–4906. [Google Scholar] [CrossRef]
- Huang, B.; Liu, T.; Hu, H.; Han, J.; Yu, M. Underwater image recovery considering polarization effects of objects. Optics express 2016, 24, 9826–9838. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Zhao, L.; Li, X.; Wang, H.; Liu, T. Underwater image recovery under the nonuniform optical field based on polarimetric imaging. IEEE Photonics Journal 2018, 10, 1–9. [Google Scholar] [CrossRef]
- Li, H.; Zhu, J.; Deng, J.; Guo, F.; Yue, L.; Sun, J.; Zhang, Y.; Hou, X. Visibility enhancement of underwater images based on polarization common-mode rejection of a highly polarized target signal. Optics Express 2022, 30, 43973–43986. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Cao, L.; Shao, X.; Han, P.; Bin, X. Polarimetric dehazing utilizing spatial frequency segregation of images. Applied Optics 2015, 54, 8116–8122. [Google Scholar] [CrossRef] [PubMed]
- Feng, F.; Wu, G.; Wu, Y.; Miao, Y.; Liu, B. Algorithm for underwater polarization imaging based on global estimation. Acta Opt. Sin 2020, 40, 75–83. [Google Scholar]
- Wang, H.; Hu, H.; Jiang, J.; Li, X.; Zhang, W.; Cheng, Z.; Liu, T. Automatic underwater polarization imaging without background region or any prior. Optics express 2021, 29, 31283–31295. [Google Scholar] [CrossRef]
- Liang, J.; Ren, L.; Liang, R. Low-pass filtering based polarimetric dehazing method for dense haze removal. Optics Express 2021, 29, 28178–28189. [Google Scholar] [CrossRef]
- Yu, T.; Wang, X.; Xi, S.; Mu, Q.; Zhu, Z. Underwater polarization imaging for visibility enhancement of moving targets in turbid environments. Optics Express 2023, 31, 459–468. [Google Scholar] [CrossRef]
- Heckman, P.; Hodgson, R. 2.7-Underwater optical range gating. IEEE Journal of Quantum Electronics 1967, 3, 445–448. [Google Scholar] [CrossRef]
- Fournier, G.R.; Bonnier, D.; Forand, J.L.; Pace, P.W. Range-gated underwater laser imaging system. Optical Engineering 1993, 32, 2185–2190. [Google Scholar] [CrossRef]
- Wang, X.; Sun, L.; Lei, P.; Chen, J.; He, J.; Zhou, Y. High-resolution 3D range gated laser imaging for unmanned underwater vehicles. Real-time Photonic Measurements, Data Management, and Processing VI. SPIE 2021, 11902, 24–41. [Google Scholar]
- Hou, W.; Gray, D.J.; Weidemann, A.D.; Fournier, G.R.; Forand, J. Automated underwater image restoration and retrieval of related optical properties. 2007 IEEE international geoscience and remote sensing symposium. IEEE 2007, 1889–1892. [Google Scholar]
- Driewer, A.; Abrosimov, I.; Alexander, J.; Benger, M.; O’Farrell, M.; Haugholt, K.H.; Softley, C.; Thielemann, J.T.; Thorstensen, J.; Yates, C. UTOFIA: an underwater time-of-flight image acquisition system. Electro-Optical Remote Sensing XI. SPIE 2017, 10434, 9–18. [Google Scholar]
- XINWEI, W.; YAN, Z.; SONGTAO, F.; YULIANG, L.; HONGJUN, L. Echo broadening effect in range-gated active imaging technique. Proceedings of SPIE, the International Society for Optical Engineering. Society of Photo-Optical Instrumentation Engineers; 2009. [Google Scholar]
- Wang, M.; Wang, X.; Sun, L.; Yang, Y.; Zhou, Y. Underwater 3D deblurring-gated range-intensity correlation imaging. Optics Letters 2020, 45, 1455–1458. [Google Scholar] [CrossRef] [PubMed]
- Xi, L.; Guosui, L.; Ni, J. Autofocusing of ISAR images based on entropy minimization. IEEE Transactions on Aerospace and Electronic Systems 1999, 35, 1240–1252. [Google Scholar] [CrossRef]
- Agaian, S.S.; Panetta, K.; Grigoryan, A.M. Transform-based image enhancement algorithms with performance measure. IEEE Transactions on image processing 2001, 10, 367–382. [Google Scholar] [CrossRef]
- Zuiderveld, K. Contrast limited adaptive histogram equalization. Graphics gems 1994, 474–485. [Google Scholar]








| Reconstruction method | EME | Contrast | Entropy |
| Original image | 6.745 | 2.334 | 2.934 |
| Schechner’s method | 20.078 | 49.416 | 5.609 |
| CLAHE | 9.030 | 55.521 | 5.147 |
| Polynomial fitting | 1.590 | 14.651 | 5.618 |
| Butterworth filter | 1.509 | 36.140 | 4.713 |
| Method in the paper | 3.855 | 115.405 | 6.829 |
| turbidity/NTU | 41.8 | 52 | 61.8 | 69.3 |
| Pictures from conventional range-gated imaging |  |
 |
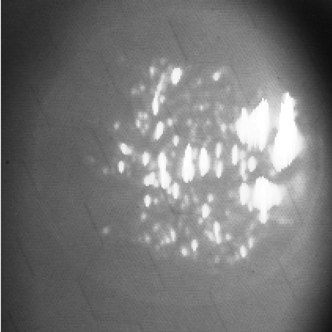 |
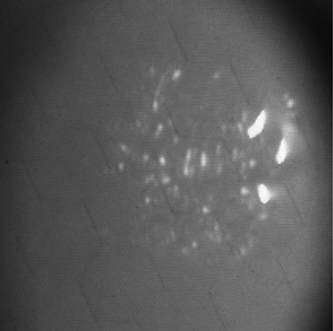 |
| Pictures from polarization-enhanced range-gated imaging | 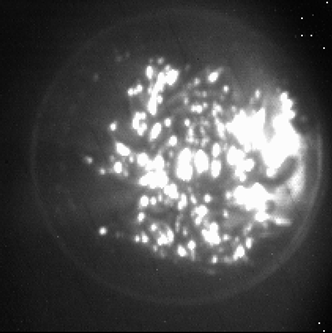 |
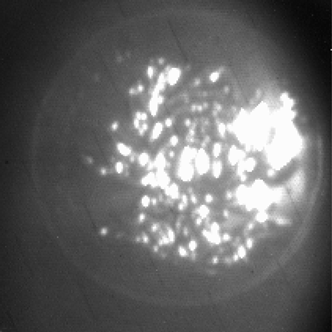 |
 |
 |
| polarization imaging optimization | Turbidity (NTU) | EME | Contrast | Entropy |
| NO | 41.8 | 10.575 | 143.894 | 6.985 |
| YES | 41.8 | 11.758 | 157.358 | 7.180 |
| NO | 52.0 | 5.861 | 75.569 | 7.498 |
| YES | 52.0 | 7.276 | 90.700 | 7.396 |
| NO | 61.8 | 5.073 | 59.639 | 7.492 |
| YES | 61.8 | 24.898 | 107.390 | 7.547 |
| NO | 69.3 | 4.533 | 27.877 | 6.750 |
| YES | 69.3 | 42.124 | 125.698 | 7.335 |
| target | polarization enhancement | EME | Contrast | Entropy |
| target board | NO | 10.919 | 4.959 | 6.365 |
| YES | 16.077 | 310.995 | 7.782 | |
| metal sheet | NO | 62.194 | 1.297 | 3.825 |
| YES | 82.792 | 402.347 | 5.260 | |
| diving suit | NO | 8.251 | 22.171 | 7.260 |
| YES | 9.541 | 124.775 | 7.431 |
| polarization enhancement | Turbidity/NTU | EME | Contrast | Entropy |
| NO | 1.70 | 8.026 | 5.978 | 6.084 |
| YES | 1.70 | 135.374 | 571.302 | 7.032 |
| NO | 3.89 | 6.913 | 3.250 | 4.771 |
| YES | 3.89 | 28.690 | 28.901 | 5.094 |
| NO | 5.41 | 1.517 | 0.172 | 4.511 |
| YES | 5.41 | 4.421 | 140.437 | 6.204 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





