Submitted:
05 September 2024
Posted:
05 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
- 1.
- The quality of the input graph significantly determines the performance of downstream tasks [21]. For parking graphs, a high-quality parking graph is not only an abstraction of spatial topology but also a adequate representation of parking behavior and decision-making. Neglecting either aspect will limit the understanding of parking scenarios, thereby negatively affecting the effectiveness of subsequent coarsening tasks as well as the accuracy and robustness of prediction tasks.
- 2.
- Most of the existing coarsening methods only consider reducing the size of the graph structure [22], and the node features of the coarsened graph still being obtained by concatenating the original data. This means that the amount of data has not changed. If the model is trained directly based on the coarsened parking graph, the training overhead is not significantly reduced. Moreover, since the coarsened parking graph loses the original topology, the merged data corresponding to the hypernodes also lose their spatial features, leading to a decrease in prediction accuracy.
- We have proposed a method for constructing parking graphs that leverages a ParkingRank graph attention mechanism. This method intricately integrates the real-time service capacity assessment of parking lots into a graph attention network, creating a parking graph that accurately mirrors real-world parking behavior preferences. This graph is adept at capturing the complexity of parking scenarios, while also remaining flexible enough to adapt to its dynamic shifts, laying the foundation for downstream coarsening as well as prediction tasks.
- We introduce a novel framework for parking prediction that employs a graph coarsening techniques and temporal convolutional autoencoder [30], designed to diminish the resource and time expenditures associated with urban parking prediction models. The scheme can make up for the shortcomings of traditional coarsening methods that neglect the dimensionality reduction of node features, and realize the unified dimensionality reduction of urban parking graph structure and features. Moreover, by incorporating temporal convolutional networks in the encoding-decoding phase, our approach not only significantly enhances the dimensionality reduction and reconstruction capabilities for parking time series data but also ensures the accuracy of the parking prediction task. Additionally, the compact data volume within each hypernode allows for the parallel processing of encoding-decoding operations across different sets of parking time series data, further boosting the overall training efficiency of the parking prediction task.
2. Related WORK
2.1. Spatio-Temporal Graph Convolutional Models
2.2. Techniques for Dimensionality Reduction in Large-Scale Graphs
2.3. Applications of Autoencoders
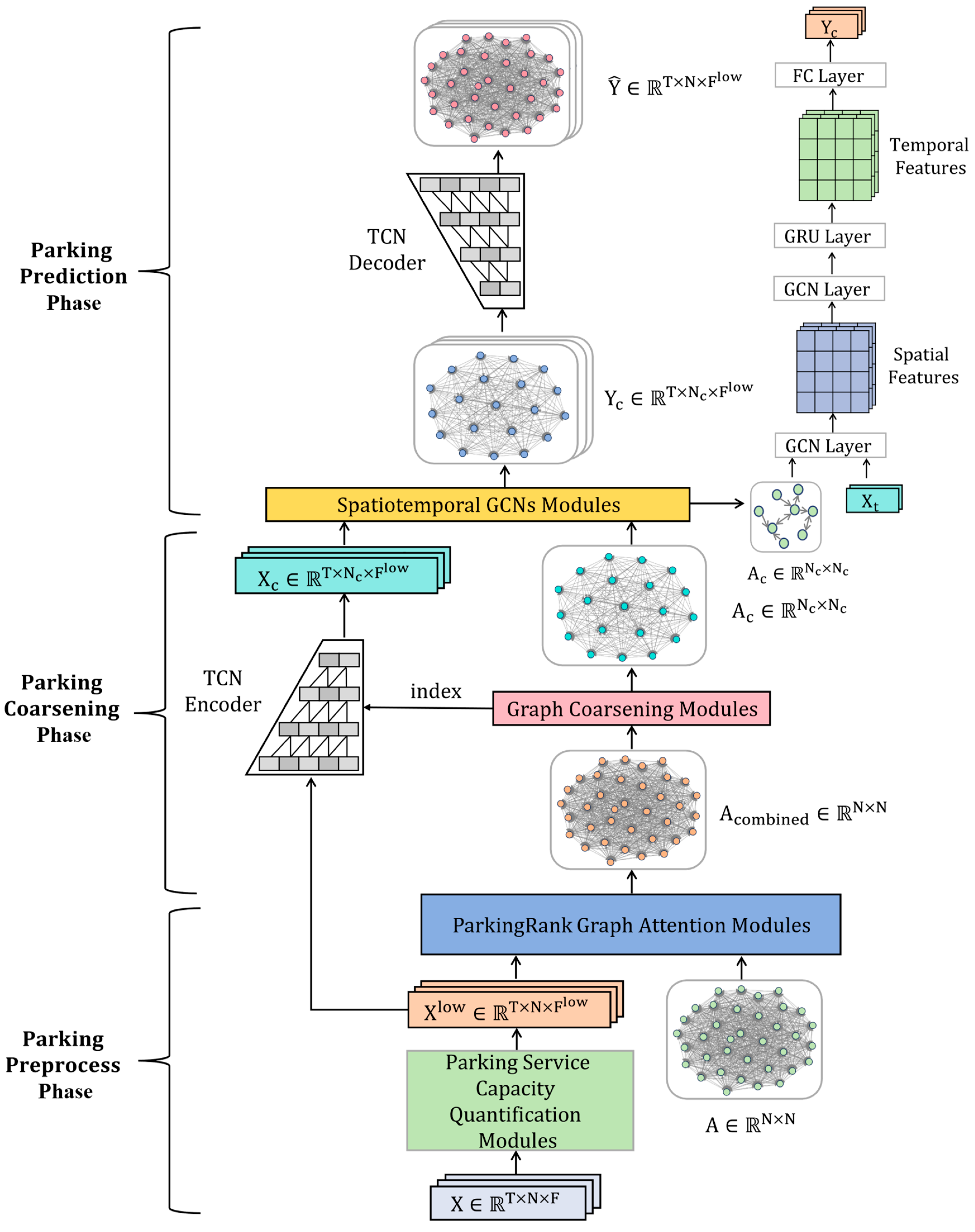
3. Methodology
3.1. Problem Definition
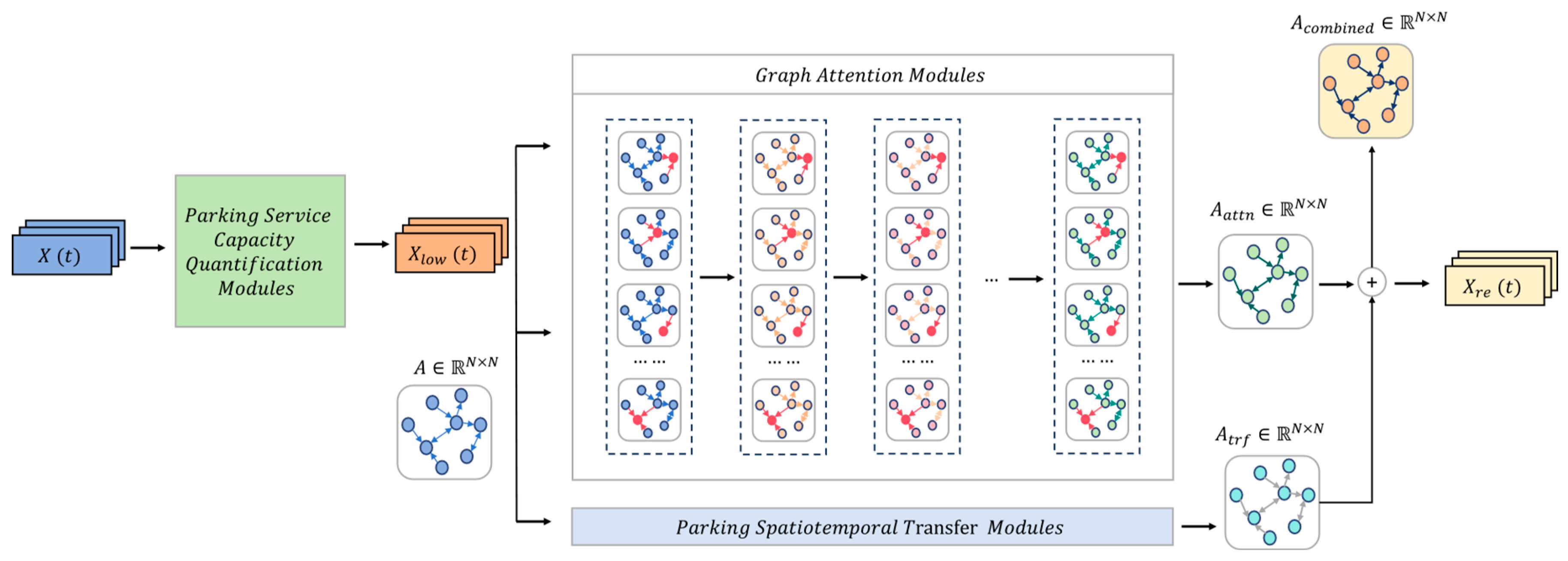
3.2. ParkingRank Graph Attention
- Parking lot service range: This aspect considers which types of vehicles are allowed to park in the parking lot. For example, parking lots at shopping centers may be open to all vehicles, while those in residential areas may only serve residents. Therefore, parking lots with a broader service scope generally have stronger service capabilities.
- Total number of parking spaces: The more internal parking spaces a parking lot has, the stronger its service capacity usually is.
- Price of parking: Higher parking prices may reduce the number of vehicles able to afford parking fees. Thus, expensive prices may lower the service capacity of the parking lot.
| Algorithm 1: ParkingRank Graph Attention (PRGAT) |
|
3.3. Parking Graph Coarsening
| Algorithm 2: Parking graph Coarsening |
|
3.4. Prediction Framework Based on Coarsened Parking Graphs
- TCN is able to mine the intrinsic laws behind the parking time-series data itself [44], such as the tidal characteristics, which helps in the compression and reconstruction of the parking data.
- The encoder is able to embed the high-dimensional sparse parking data into the low-dimensional dense tensor form, which reduces the computational overhead of the training model.
- The decoder is able to achieve an approximate lossless reduction and can reconstruct the spatial structure of the original parking graph.
4. Experiments
4.1. Experiment Setup
- T-GCN [33]: A classical model for traffic prediction that combines Graph Convolutional Networks (GCNs) and Gated Recurrent Units (GRU) to establish spatio-temporal correlations among traffic data.
- STGCN [46]: Utilizes multiple ST-Conv blocks to model multi-scale traffic graphs, proven to effectively capture comprehensive spatio-temporal correlations.
- STSGCN [47]: By stacking multiple STSGCL blocks for synchronous spatio-temporal modeling, it can effectively capture complex local spatio-temporal traffic correlations.
- SparRL [37]: A universal and effective graph sparsification framework implemented through deep reinforcement learning, capable of flexibly adapting to various sparsification objectives.
4.2. Modeling Real Scenes
4.3. Selection of Coarsening Ratio

4.4. Quantitative Results
4.5. Scalability Results
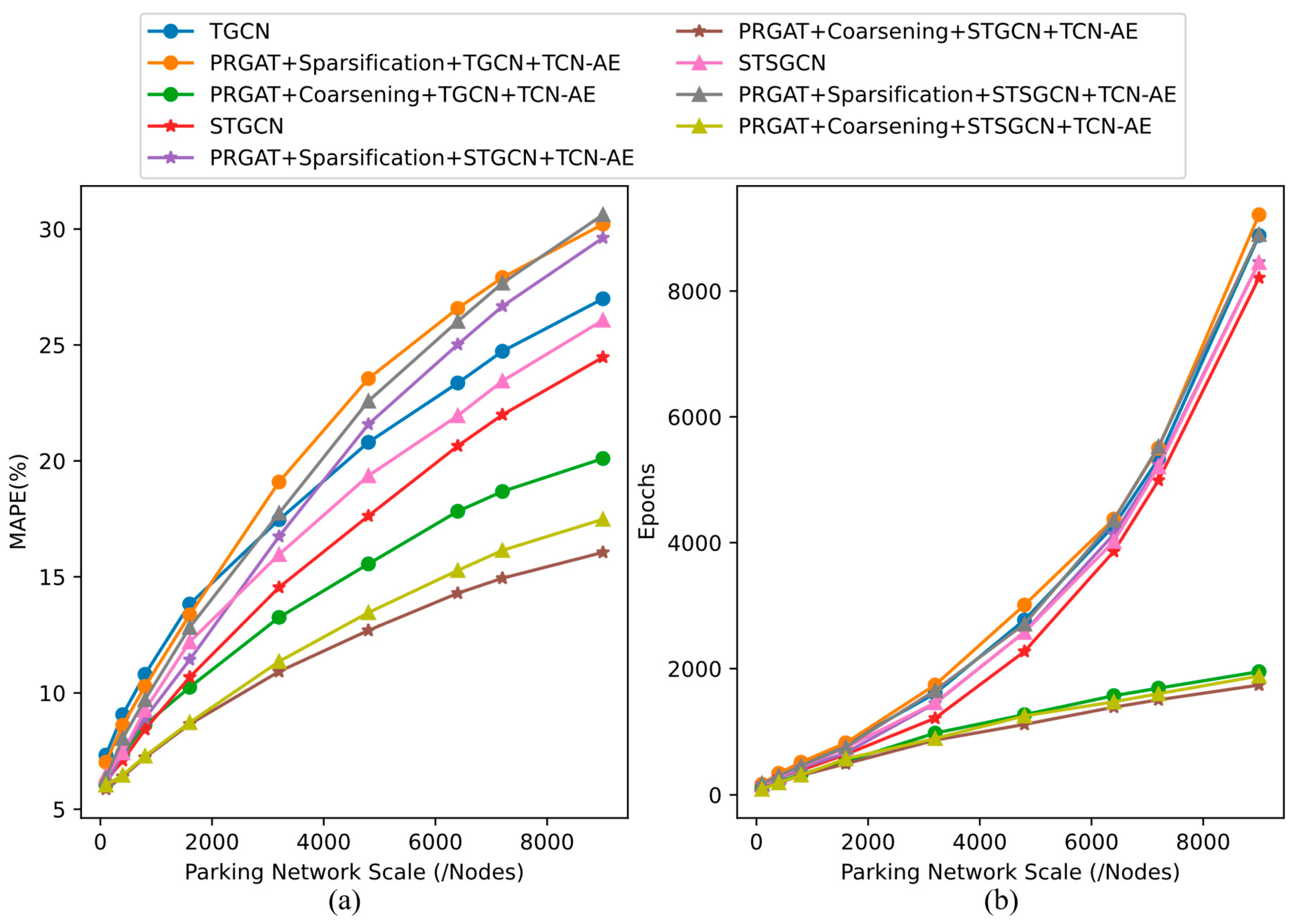
4.6. Ablation Results
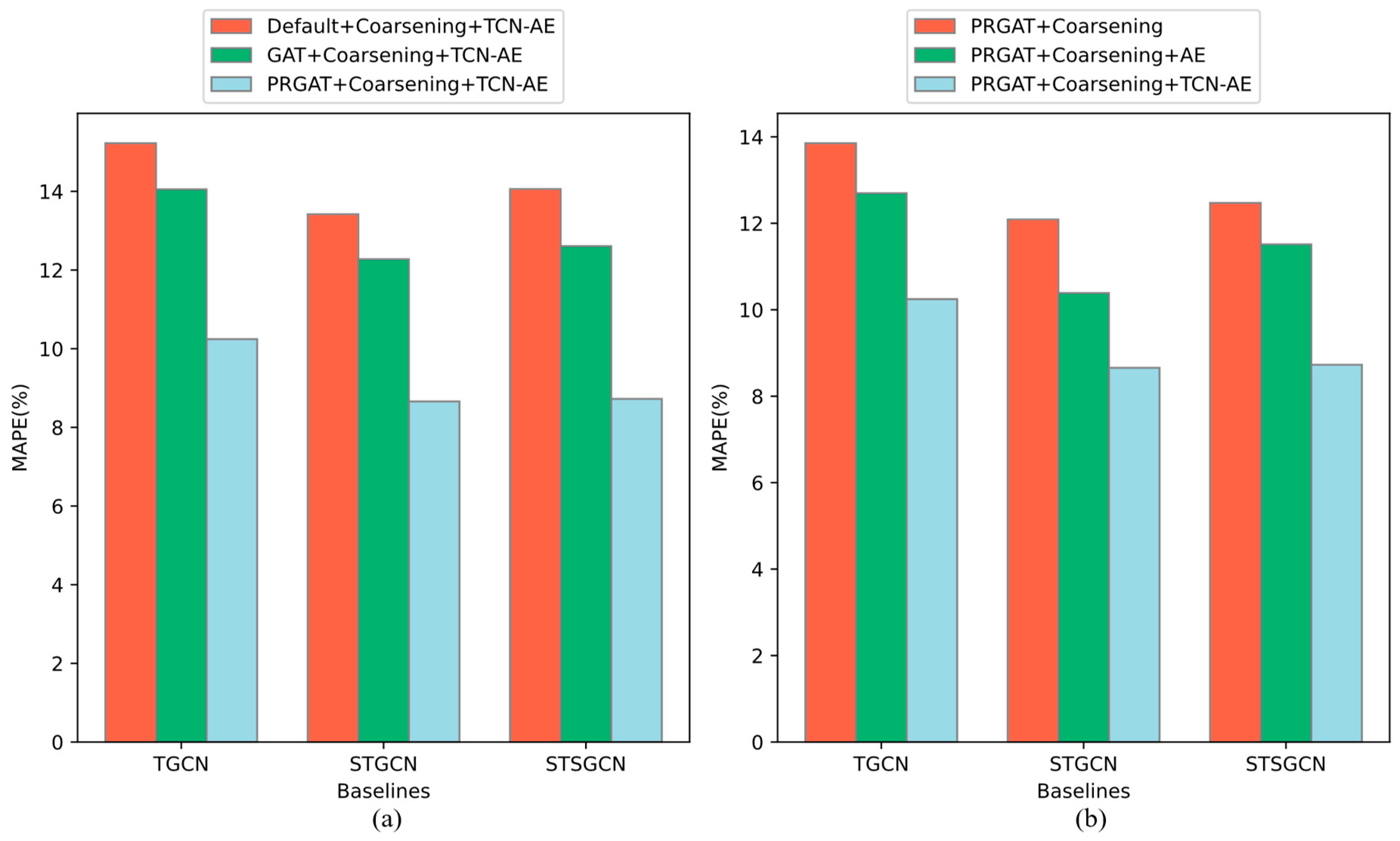
5. Conclusion
- Selection of Coarsening Ratio: The coarsening dimension utilized in this study was determined through experimentation with a grid search strategy, yielding a general range that may limit its applicability to the specific dataset used and not be accurate enough for others. Therefore, in our subsequent efforts, we aim to employ deep learning methods to automatically learn and ascertain the optimal coarsening dimension.
- Integration of Multi-source Data: Given that parking demand is influenced by a wide array of factors, including nearby traffic flow, weather conditions, and more, we intend to incorporate multiple data sources for feature fusion in the future. This approach will enhance the model’s comprehension of parking scenarios, providing a richer understanding of the complex dynamics at play.
- Global Information Aggregation: The PRGAT algorithm proposed in this paper aggregates node feature information considering only the 2nd-order neighborhood, thus overlooking the influence of distant global nodes. In our future research, we plan to incorporate higher-order global information by employing concepts from fractal theory.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xin, H. China registers 415 million motor vehicles, 500 million drivers. Website, 2024. https://english.www.gov.cn/archive/statistics/202212/08/content_WS6391cafcc6d0a757729e41bc.html.
- Zou, W.; Sun, Y.; Zhou, Y.; Lu, Q.; Nie, Y.; Sun, T.; Peng, L. Limited sensing and deep data mining: A new exploration of developing city-wide parking guidance systems. IEEE Intelligent Transportation Systems Magazine 2020, 14, 198–215. [Google Scholar] [CrossRef]
- Ke, R.; Zhuang, Y.; Pu, Z.; Wang, Y. A smart, efficient, and reliable parking surveillance system with edge artificial intelligence on IoT devices. IEEE Transactions on Intelligent Transportation Systems 2020, 22, 4962–4974. [Google Scholar] [CrossRef]
- Research.; ltd, M. China Smart Parking Industry Report, 2022; Research In China, 2022.
- Rizvi, S.R.; Zehra, S.; Olariu, S. Aspire: An agent-oriented smart parking recommendation system for smart cities. IEEE Intelligent Transportation Systems Magazine 2018, 11, 48–61. [Google Scholar] [CrossRef]
- Kotb, A.O.; Shen, Y.c.; Huang, Y. Smart parking guidance, monitoring and reservations: a review. IEEE Intelligent Transportation Systems Magazine 2017, 9, 6–16. [Google Scholar] [CrossRef]
- Yang, K.; Tang, X.; Qin, Y.; Huang, Y.; Wang, H.; Pu, H. Comparative study of trajectory tracking control for automated vehicles via model predictive control and robust H-infinity state feedback control. Chinese Journal of Mechanical Engineering 2021, 34, 1–14. [Google Scholar] [CrossRef]
- Tang, X.; Yang, Y.; Liu, T.; Lin, X.; Yang, K.; Li, S. Path planning and tracking control for parking via soft actor-critic under non-ideal scenarios. IEEE/CAA Journal of Automatica Sinica, 2023. [Google Scholar]
- Fan, J.; Hu, Q.; Xu, Y.; Tang, Z. Predicting vacant parking space availability: a long short-term memory approach. IEEE Intelligent Transportation Systems Magazine 2020, 14, 129–143. [Google Scholar] [CrossRef]
- Lin, T.; Rivano, H.; Le Mouël, F. A survey of smart parking solutions. IEEE Transactions on Intelligent Transportation Systems 2017, 18, 3229–3253. [Google Scholar] [CrossRef]
- Anand, D.; Singh, A.; Alsubhi, K.; Goyal, N.; Abdrabou, A.; Vidyarthi, A.; Rodrigues, J.J. A smart cloud and IoVT-based kernel adaptive filtering framework for parking prediction. IEEE Transactions on Intelligent Transportation Systems 2022, 24, 2737–2745. [Google Scholar] [CrossRef]
- Ku, Y.; Guo, C.; Zhang, K.; Cui, Y.; Shu, H.; Yang, Y.; Peng, L. Toward Directed Spatiotemporal Graph: A New Idea for Heterogeneous Traffic Prediction. IEEE Intelligent Transportation Systems Magazine 2024, 16, 70–87. [Google Scholar] [CrossRef]
- Li, J.; Qu, H.; You, L. An integrated approach for the near real-time parking occupancy prediction. IEEE Transactions on Intelligent Transportation Systems 2022, 24, 3769–3778. [Google Scholar] [CrossRef]
- Shuai, C.; Zhang, X.; Wang, Y.; He, M.; Yang, F.; Xu, G. Online car-hailing origin-destination forecast based on a temporal graph convolutional network. IEEE Intelligent Transportation Systems Magazine 2023. [Google Scholar] [CrossRef]
- Li, D.; Wang, J. A Fusion Deep Learning Model via Sequence-to-Sequence Structure for Multiple-Road-Segment Spot Speed Prediction. IEEE Intelligent Transportation Systems Magazine 2022, 15, 230–243. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Z.; Xu, Z.; Du, M.; Yang, W.; Guo, L. A distributed collaborative urban traffic big data system based on cloud computing. IEEE Intelligent Transportation Systems Magazine 2018, 11, 37–47. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, Y.; Li, Z.; Wang, X.; Zhao, J.; Zhang, Z. Large-scale cellular traffic prediction based on graph convolutional networks with transfer learning. Neural Computing and Applications 2022, 1–11. [Google Scholar] [CrossRef]
- Fahrbach, M.; Goranci, G.; Peng, R.; Sachdeva, S.; Wang, C. Faster graph embeddings via coarsening. In Proceedings of the international conference on machine learning. PMLR; 2020; pp. 2953–2963. [Google Scholar]
- Cai, C.; Wang, D.; Wang, Y. Graph coarsening with neural networks. arXiv 2021, arXiv:2102.01350. [Google Scholar]
- Loukas, A. Graph reduction with spectral and cut guarantees. Journal of Machine Learning Research 2019, 20, 1–42. [Google Scholar]
- Kumar, M.; Sharma, A.; Kumar, S. A unified framework for optimization-based graph coarsening. Journal of Machine Learning Research 2023, 24, 1–50. [Google Scholar]
- Jin, Y.; Loukas, A.; JaJa, J. Graph coarsening with preserved spectral properties. In Proceedings of the International Conference on Artificial Intelligence and Statistics. PMLR, 2020, pp. 4452–4462.
- Chen, Y.; Shu, T.; Zhou, X.; Zheng, X.; Kawai, A.; Fueda, K.; Yan, Z.; Liang, W.; Kevin, I.; Wang, K. Graph attention network with spatial-temporal clustering for traffic flow forecasting in intelligent transportation system. IEEE Transactions on Intelligent Transportation Systems 2022. [Google Scholar] [CrossRef]
- Lu, Z.; Lv, W.; Xie, Z.; Du, B.; Xiong, G.; Sun, L.; Wang, H. Graph sequence neural network with an attention mechanism for traffic speed prediction. ACM Transactions on Intelligent Systems and Technology (TIST) 2022, 13, 1–24. [Google Scholar] [CrossRef]
- Lu, Q.; Tang, Z.; Nie, Y.; Peng, L. ParkingRank-D: A Spatial-temporal Ranking Model of Urban Parking Lots in City-wide Parking Guidance System. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (iTSC). IEEE; 2019; pp. 388–393. [Google Scholar]
- Dong, S.; Chen, M.; Peng, L.; Li, H. Parking rank: A novel method of parking lots sorting and recommendation based on public information. In Proceedings of the 2018 IEEE International Conference on Industrial Technology (ICIT). IEEE; 2018; pp. 1381–1386. [Google Scholar]
- Huang, C.J.; Ma, H.; Yin, Q.; Tang, J.F.; Dong, D.; Chen, C.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Realization of a quantum autoencoder for lossless compression of quantum data. Physical Review A 2020, 102, 032412. [Google Scholar] [CrossRef]
- Liu, M.; Zhu, T.; Ye, J.; Meng, Q.; Sun, L.; Du, B. Spatio-temporal autoencoder for traffic flow prediction. IEEE Transactions on Intelligent Transportation Systems 2023. [Google Scholar] [CrossRef]
- Fainstein, F.; Catoni, J.; Elemans, C.P.; Mindlin, G.B. The reconstruction of flows from spatiotemporal data by autoencoders. Chaos, Solitons & Fractals 2023, 176, 114115. [Google Scholar]
- Guo, G.; Yuan, W.; Liu, J.; Lv, Y.; Liu, W. Traffic forecasting via dilated temporal convolution with peak-sensitive loss. IEEE Intelligent Transportation Systems Magazine 2021, 15, 48–57. [Google Scholar] [CrossRef]
- Du, W.; Li, B.; Chen, J.; Lv, Y.; Li, Y. A spatiotemporal hybrid model for airspace complexity prediction. IEEE Intelligent Transportation Systems Magazine 2022, 15, 217–224. [Google Scholar] [CrossRef]
- Yao, Z.; Xia, S.; Li, Y.; Wu, G.; Zuo, L. Transfer learning with spatial–temporal graph convolutional network for traffic prediction. IEEE Transactions on Intelligent Transportation Systems 2023. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-gcn: A temporal graph convolutional network for traffic prediction. IEEE transactions on intelligent transportation systems 2019, 21, 3848–3858. [Google Scholar] [CrossRef]
- Sun, Y.; Jiang, X.; Hu, Y.; Duan, F.; Guo, K.; Wang, B.; Gao, J.; Yin, B. Dual dynamic spatial-temporal graph convolution network for traffic prediction. IEEE Transactions on Intelligent Transportation Systems 2022, 23, 23680–23693. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, W.; Zheng, W.; Dong, C.; Wang, S.; Chen, Q. Lane-level heterogeneous traffic flow prediction: A spatiotemporal attention-based encoder–decoder model. IEEE Intelligent Transportation Systems Magazine 2022. [Google Scholar] [CrossRef]
- Li, D.; Lasenby, J. Spatiotemporal attention-based graph convolution network for segment-level traffic prediction. IEEE Transactions on Intelligent Transportation Systems 2021, 23, 8337–8345. [Google Scholar] [CrossRef]
- Wickman, R.; Zhang, X.; Li, W. A Generic Graph Sparsification Framework using Deep Reinforcement Learning. arXiv preprint arXiv:2112.01565, arXiv:2112.01565 2021.
- Sadhanala, V.; Wang, Y.X.; Tibshirani, R. Graph sparsification approaches for laplacian smoothing. In Proceedings of the Artificial Intelligence and Statistics. PMLR; 2016; pp. 1250–1259. [Google Scholar]
- Wu, H.Y.; Chen, Y.L. Graph sparsification with generative adversarial network. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM). IEEE; 2020; pp. 1328–1333. [Google Scholar]
- Chen, J.; Saad, Y.; Zhang, Z. Graph coarsening: from scientific computing to machine learning. SeMA Journal 2022, 79, 187–223. [Google Scholar] [CrossRef]
- Dhillon, I.S.; Guan, Y.; Kulis, B. Weighted graph cuts without eigenvectors a multilevel approach. IEEE transactions on pattern analysis and machine intelligence 2007, 29, 1944–1957. [Google Scholar] [CrossRef] [PubMed]
- Rhouma, D.; Ben Romdhane, L. An efficient multilevel scheme for coarsening large scale social networks. Applied Intelligence 2018, 48, 3557–3576. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, H.; Qiu, M.; Liu, Y.; Ye, D. Tgae: Temporal graph autoencoder for travel forecasting. IEEE Transactions on Intelligent Transportation Systems 2022. [Google Scholar] [CrossRef]
- Mo, R.; Pei, Y.; Venkatarayalu, N.V.; Joseph, P.N.; Premkumar, A.B.; Sun, S.; Foo, S.K.K. Unsupervised TCN-AE-based outlier detection for time series with seasonality and trend for cellular networks. IEEE Transactions on Wireless Communications 2022, 22, 3114–3127. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting. arXiv 2017, arXiv:1709.04875. [Google Scholar]
- Song, C.; Lin, Y.; Guo, S.; Wan, H. Spatial-temporal synchronous graph convolutional networks: A new framework for spatial-temporal network data forecasting. In Proceedings of the Proceedings of the AAAI conference on artificial intelligence, 2020, Vol.; 2020; Volume 34, pp. 914–921. [Google Scholar]
- Wang, Y.; Ku, Y.; Liu, Q.; Yang, Y.; Peng, L. Large-Scale Parking Data Prediction: From A Graph Coarsening Perspective. In Proceedings of the 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC). IEEE; 2023; pp. 1410–1415. [Google Scholar]
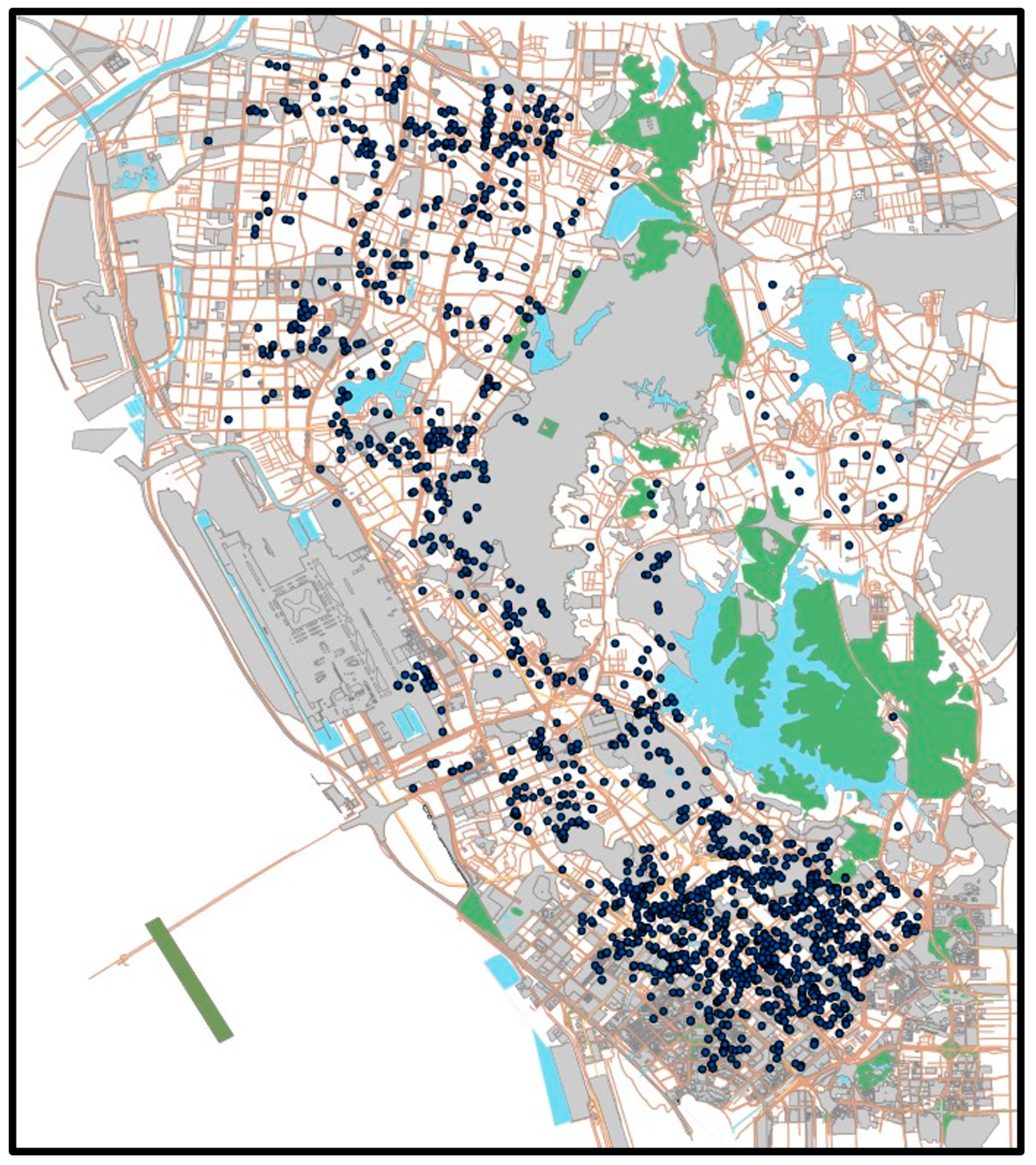
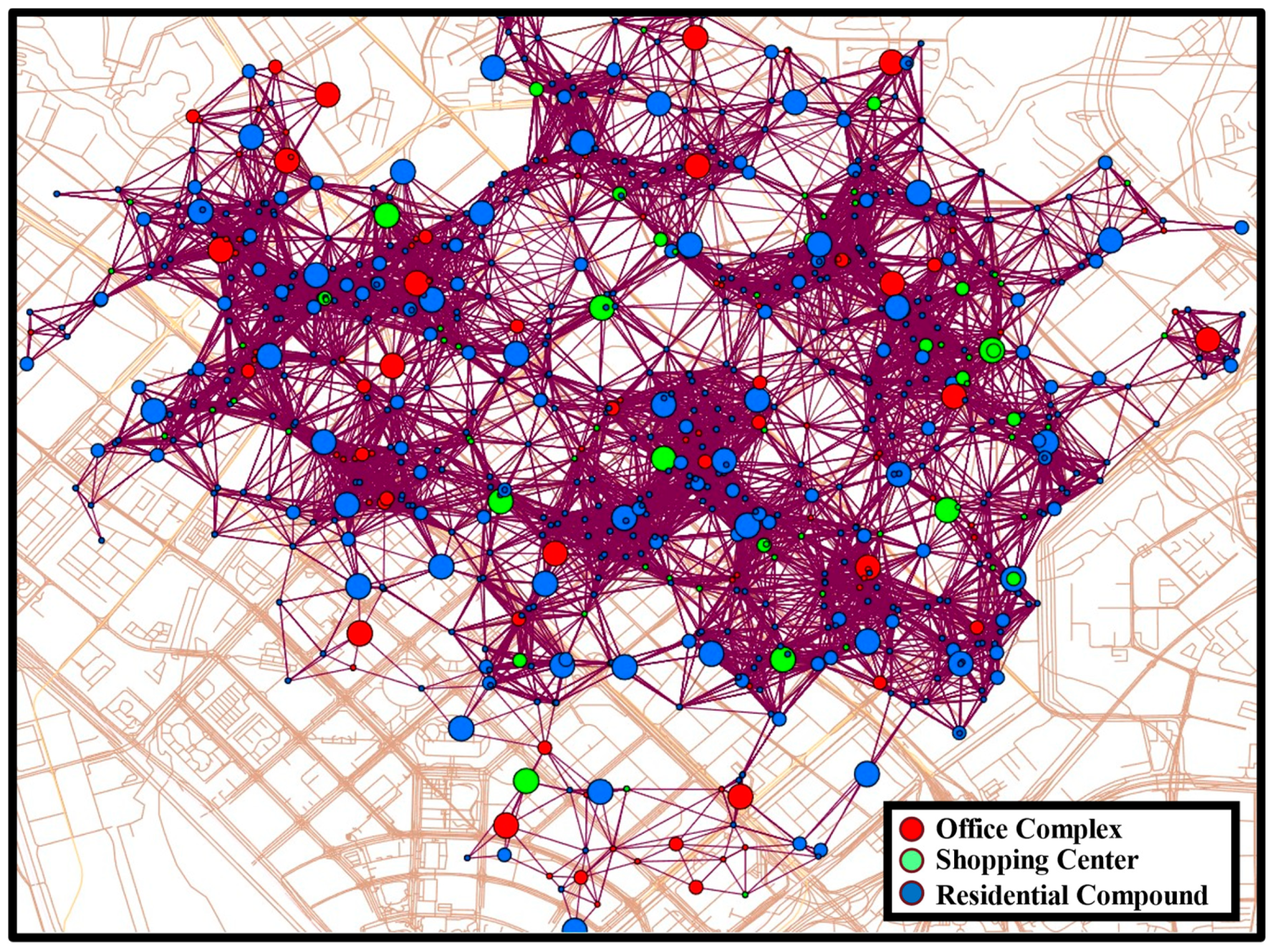
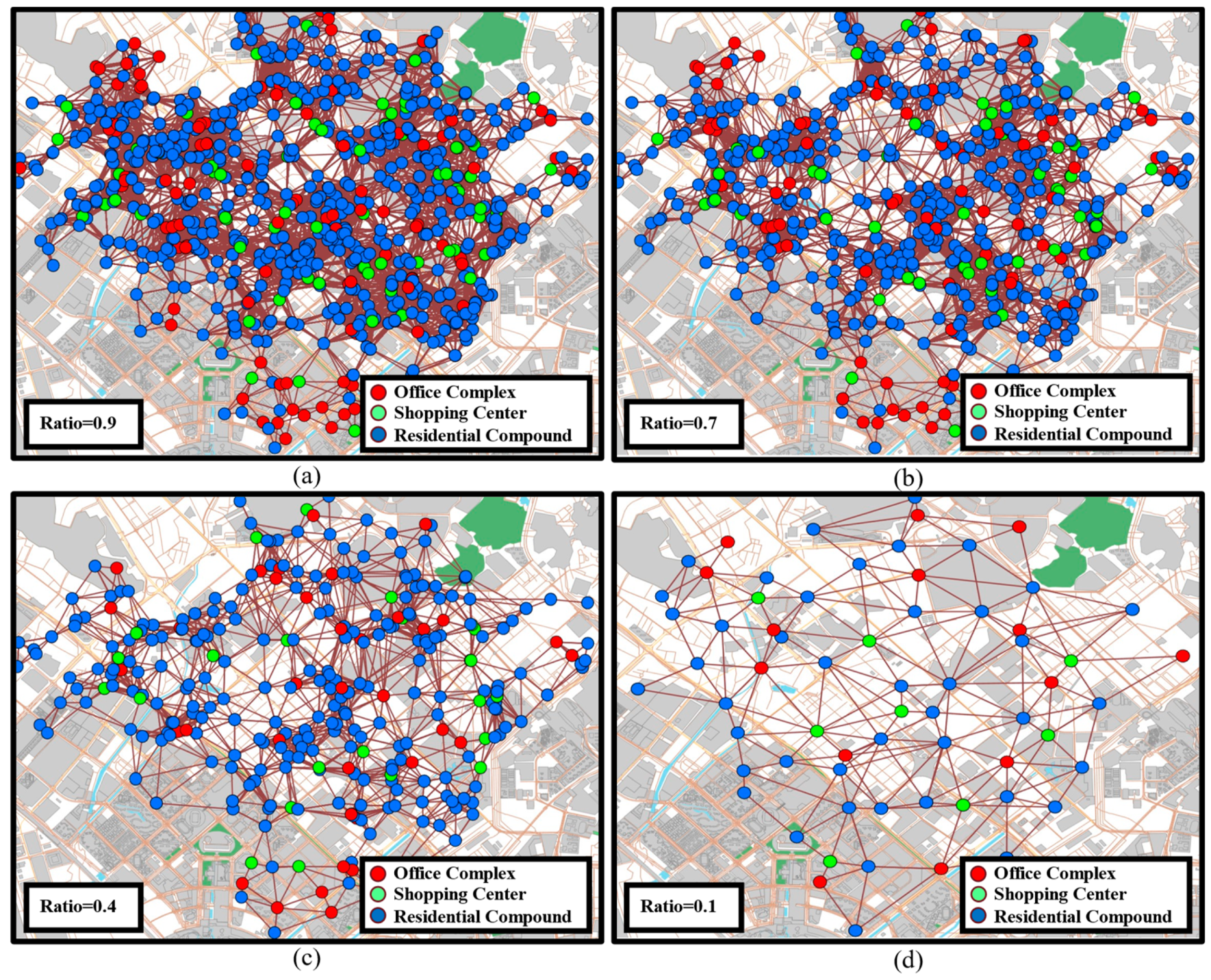
| District | #Nodes | Start Time | Granularity | Time Steps |
| Bao’an | 1660 | 2016/6/1 | 15min | 17,280 |
| Luohu | 1730 | 2016/6/1 | 15min | 17,280 |
| Futian | 1806 | 2016/6/1 | 15min | 17,280 |
| Longgang | 1473 | 2016/6/1 | 15min | 17,280 |
| Longhua | 2531 | 2016/6/1 | 15min | 17,280 |
| Method | Configuration | Batch Size | Learning Rate | Optimizer | Loss Function | Weight Decay | Patience (/Epoch) | |
| PRGAT | Number of Attention Heads | Feature Dimension per Head | 64 | 1e-4 | Adam | MSE | 1e-4 | 100 |
| 8 | 128 | |||||||
| SGC | Threshhold | - | - | - | - | - | - | |
| 1e-8 | ||||||||
| SparRL | Maximum number of neighbors to pay attention to | 64 | 1e-4 | Adam | Huber Loss | 1e-4 | 500 | |
| 64 | ||||||||
| TGCN | GRU Hidden Units | 64 | 1e-5 | Adam | Huber Loss | 1e-4 | 200 | |
| 100 | ||||||||
| STGCN | Graph Convolution Dimension | Temporal Convolution Dimension | 64 | 1e-5 | Adam | Huber Loss | 1e-4 | 200 |
| 16 | 64 | |||||||
| STSGCN | GCNs per Module | Spatio-temporal GCNs Layers(STSGCL) | 64 | 1e-5 | Adam | Huber Loss | 1e-4 | 200 |
| 3 | 4 | |||||||
| TCN-AE | TCN Dilation Rates | Filter Count and Kernel Size | 64 | 1e-4 | Adam | MSE | 1e-4 | 100 |
| (1,2,4,8,16) | 20 | |||||||
| Method | MAE | RMSE | MAPE(%) | Epoch | ||||||
| 15min | 30min | 60min | 15min | 30min | 60min | 15min | 30min | 60min | ||
| Default+TGCN | 7.933 | 8.7224 | 11.3431 | 11.2128 | 12.3413 | 15.1087 | 13.82 | 16.23 | 20.59 | 834 |
| GAT+TGCN | 7.7224 | 8.3431 | 10.2926 | 10.0689 | 11.4238 | 12.3675 | 12.74 | 14.41 | 19.82 | 839 |
| PRGAT+TGCN | 4.2631 | 4.719 | 5.8398 | 7.4103 | 8.7885 | 10.7526 | 9.89 | 10.38 | 13.09 | 844 |
| Default+Coarsening+TGCN+AE | 8.0153 | 8.9607 | 11.8285 | 11.4731 | 13.455 | 16.0598 | 14.31 | 17.25 | 20.77 | 655 |
| Default+Sparsification+TGCN+AE | 9.9726 | 11.1673 | 13.6201 | 13.4071 | 14.757 | 18.6382 | 14.22 | 17.54 | 22.96 | 827 |
| PRGAT+Sparsification+TGCN+TCN-AE | 7.851 | 9.0267 | 11.5006 | 12.4467 | 12.6782 | 15.483 | 13.36 | 15.28 | 18.64 | 846 |
| PRGAT+Coarsening+TGCN+TCN-AE | 4.6552 | 5.209 | 7.3209 | 7.8395 | 9.4337 | 10.9448 | 10.24 | 10.53 | 13.49 | 558 |
| Default+STGCN | 4.728 | 5.5534 | 9.598 | 10.7798 | 11.7946 | 14.9729 | 10.68 | 16.47 | 19.12 | 673 |
| GAT+STGCN | 3.7947 | 4.3721 | 7.6845 | 7.44 | 10.9601 | 12.4731 | 9.42 | 14.2 | 16.93 | 645 |
| PRGAT+STGCN | 2.159 | 2.7601 | 4.328 | 4.893 | 6.4853 | 10.4475 | 7.63 | 10.65 | 11.74 | 639 |
| Default+Coarsening+STGCN+AE | 5.4295 | 7.6965 | 10.2398 | 11.4307 | 12.9623 | 16.0431 | 11.74 | 17.83 | 20.01 | 568 |
| Default+Sparsification+STGCN+AE | 6.5246 | 7.9378 | 11.0445 | 12.6193 | 14.7207 | 17.8087 | 13.47 | 18.55 | 20.79 | 651 |
| PRGAT+Sparsification+STGCN+TCN-AE | 5.0214 | 6.5779 | 9.538 | 10.6814 | 12.5294 | 15.7111 | 11.43 | 14.84 | 17.17 | 662 |
| PRGAT+Coarsening+STGCN+TCN-AE | 2.1977 | 3.3915 | 5.3604 | 4.9548 | 7.8741 | 10.9849 | 8.65 | 11.6 | 12.31 | 476 |
| Default+STSGCN | 6.5194 | 6.5358 | 9.5476 | 10.8984 | 14.4152 | 17.1354 | 12.19 | 14.37 | 16.33 | 788 |
| GAT+STSGCN | 5.6569 | 6.1912 | 8.1355 | 9.8521 | 13.534 | 16.7885 | 10.71 | 11.75 | 12.49 | 752 |
| PRGAT+STSGCN | 4.1645 | 4.6743 | 7.6569 | 7.1038 | 9.4388 | 11.8712 | 7.85 | 8.22 | 8.89 | 769 |
| Default+Coarsening+STSGCN+AE | 7.3511 | 7.8178 | 11.0491 | 11.4534 | 14.6645 | 18.5779 | 12.67 | 15.03 | 16.82 | 661 |
| Default+Sparsification+STSGCN+AE | 8.1708 | 10.319 | 12.4703 | 13.3065 | 15.2423 | 19.1752 | 14.11 | 17.33 | 19.8 | 776 |
| PRGAT+Sparsification+STSGCN+TCN-AE | 6.6163 | 7.656 | 9.7815 | 11.8712 | 13.9123 | 18.7807 | 12.82 | 13.94 | 17.25 | 740 |
| PRGAT+Coarsening+STSGCN+TCN-AE | 4.6079 | 4.9813 | 8.093 | 7.9218 | 10.0797 | 12.9521 | 8.72 | 9.31 | 10.09 | 556 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





