Prerpints.org logo
Preprint
Article

Neural Network Models Synchronization and Stability through Calculated Incommensurate Fractional-Orders

Altmetrics

Downloads

54

Views

29

Comments

0

This version is not peer-reviewed

Submitted:

06 September 2024

Posted:

09 September 2024

You are already at the latest version

Alerts
Abstract
Artificial neural networks are highly efficient tools for numerous kinds of tasks, which include forecasting, regression, and recognizing patterns in classification and pattern recognition. An artificial neural network is a model for processing information using essential components called artificial neurons that are inspired by the human brain. Two significant aspects of delayed neural networks dynamic activity are their stability and the synchronization phenomenon. This work presents a bidirectional associative memory (BAM) incommensurate fractional-order delay neural network model. The incommensurate fractional orders are calculated within the stability region through the corresponding eigenvalues and their points of equilibrium. The involved neuron states are synchronized with each other for the calculated incommensurate stable fractional orders. The reduction of the time delay will give more relaxation time for the state variable $w_4(t)$ to be stable as compared to the state variable $w_3(t)$ due to the induction of extra activation functions. The theoretical findings of this research have significance for providing guidance and controlling the dynamic behavior of artificial neural networks.
Keywords: 
Subject: Computer Science and Mathematics  -   Computational Mathematics

1. Introduction

The previous work examined a neural network model featuring six and seven neurons with multiple time delays. It is well known that many scholars are becoming more involved in analysing neural networks because of their broad range of usage in many areas of science, ranging from biological mechanisms, auto-control, brain modelling, sensor technology, computer vision, etc. [1,2,3]. The dynamical features of various kinds of neural networks have been demonstrated to provide vast applications in a number of regions, such as recognizing patterns, control processes, artificial intelligence, the processing of images, medical sciences, and so on, since Hopfield provided a class of simpler neural networks in 1984 [4,5,6,7]. Time delay frequently arises from the lag in signal propagation between distinct neurons in artificial neural networks. Accordingly, it is acknowledged that delayed neural networks are much better models than classical neural networks with no time delays in order to provide insight into the real world of artificial neural networks. Time delays frequently lead neural networks to become unstable, provide periodic phenomena, indicate chaotic distinctive features, and more [8,9,10]. In current times, there is a lot of interest in understanding how time delay affects several delayed neural network dynamics. Many neural networks containing time delays have already been built and studied these days, and many interesting studies have been published. As an example, we established a new necessary condition that ensures the existence and global exponential stability of pseudo-approximately periodic solutions for delayed fuzzy cell-based neural network models with quaternion values. The stability of moving wave results for a class that consists of distributed delay cell-based neural network models was examined by Hsu and Lin [11]. The fuzzy cell-based neural network finite-time cluster synchronization problem has been addressed by Tang et al. [12]. For a greater understanding, study [13].
Many scholars in the areas of mathematics, neurology, and control technology have focused strongly on the study of the numerous dynamical features of various neural network structures in order to optimize neural networks for the benefit of humans. Time delay usually results from the delay in the feedback of transmitted signals over multiple neurons in a number of models of neural networks. As a result, research on delayed neural networks has developed interest nowadays. Many significant results on delayed neural structures have been achieved in the current time. A paper by Wang et al. [14] explored the use of adapted pin control and pin management for attaining fixed-time synchronization of a type of complex-valued BAM neural network structures with delays; time-delayed impulsive behavior was used by Zhao et al. [15] to study the global stabilization in quaternion-valued inertial BAM artificial neural networks with delays. A sufficiently strong criterion for guaranteeing the existence and global exponential nature of the stability of periodic solutions to quaternion-valued cell-based neural networks with delays was found by Li and Qin [16]. The stability analysis of virtually periodic results of a certain type of inconsistency-delayed BAM neural network model with regard to the D-operator has been conducted by Kong et al. [17], the anti-periodic results of the Cohen-Grossberg shift restricting artificial neural networks, including time-varying impulses and delays, were examined by Xu and Zhang [18]. Stochastic stability in Markovian-jumping BAM neural network models with time delay was studied by Syed Ali et al. [19]. For more thoroughly comprehensive research on this area of study [20,21].
Although many dynamic problems in delayed neural networks have been resolved by the aforementioned works, they focus on the integer-order aspect. Many academics have suggested in recent times that fractional-order differential equations, which readily explain long-term mechanisms of change and memory, are a more appropriate tool for revealing the practical relationships of dynamical systems in daily life [22]. Fractional calculus is currently used extensively in a wide variety of fields, including finance engineering, the field of neuroscience, electromagnetic radiation, light and electrical engineering, and biology [23,24,25]. Recent times have included the receipt of several significant papers on fractional dynamical systems. Most recently, there has been suitable work on fractional-order neural networks that deal with delays. For instance, fractional impulsive delayed BAM artificial neural networks’ global stability was investigated by Wang et al. [26]. Global Mittag-Leffler synchronization in fractional-order octonion-valued BAM artificial neural networks was examined by Xiao et al. [27]. The impact of leakage delay on the Hopf bifurcation of fractional-order quaternion-valued artificial neural networks was discovered by Xu et al. [28]. For more information, visit [29,30,31].
In delayed systems with dynamics, Hopf bifurcation manners are a vital dynamical characteristic. More specifically, delay-driven Hopf bifurcation plays a key role in neural network system optimization and control. Therefore, many researchers are extremely interested in delay-driven Hopf bifurcation. Researchers might successfully improve the stability region and the time of launch of Hopf bifurcation in delayed neural systems by analysing delay-driven Hopf bifurcation. Valuable results on delay-driven Hopf bifurcation of integer-order neural network structures have been generated over the last few decades. But there are not a lot of studies on fractional-order neural systems and delay-driven Hopf bifurcation. Additionally, there are currently a few works on this topic. The delay-driven Hopf bifurcation in fractional-order double-ring structured neural networks was studied by Li et al. [32]. The effect of the total of the various delays on the bifurcation of fractional-order BAM neural networks was investigated by Xu et al. [33], and Yuan et al. [34] discovered several fresh insights on the bifurcation of fractional-order delayed complex-valued neural systems. Wang et al. [35] performed a comprehensive investigation of the Hopf bifurcation of fractional-order BAM neural networks in mixed delays and n + 2 neurons. It suggests the readers go to [36,37,38] for further details. Although the research on the Hopf bifurcation of the fractional delayed model of neural networks has been implemented, many issues remain that require further discussion. Motivated by such a viewpoint, we are going to tackle the following major areas of the work: (i) Examine if a particular type of fractional BAM neural network model solution is bounded, exists, and is unique with regard to delays: (ii) Determine a delay-independent criteria for the stability of the stability of the fractional BAM neural network models and the formation of the bifurcation phenomenon: (iii) Look for the most effective controllers for managing the fractional BAM neural network model stability section and the resulting development of the bifurcation phenomenon through the use of delays.
Nowadays, fractional calculus is commonly utilized in many different domains, such as biology, finance engineering, neuroscience, electromagnetic radiation, light engineering, and electrical engineering. A number of important publications on fractional dynamical systems have been received recently.
In the above review of the literature, it seems that so many researchers have worked with and addressed integer as well as fractional-order problems in delayed neural networks. All these neural network models are examined for fractional orders by taking arbitrary values of the orders. The present article gives a detailed procedure for calculating the incommensurate fractional orders by using points of equilibrium and their corresponding eigenvalues. On the basis of these incommensurate fractional orders, the neural network models are examined and analysed numerically within the calculated stability region. The calculated incommensurate fractional orders will help to converge the numerical solution rapidly and accurately. The present research work will open a new area of research for time delay involving neural network models for incommensurate fractional orders. The simulated neural network weights are synchronized and stabilized with each other for the calculated incommensurate fractional values. The graphical presentation of the synchronized different neural network weights depicts stable and converged images with each other.

2. Mathematical Formulation

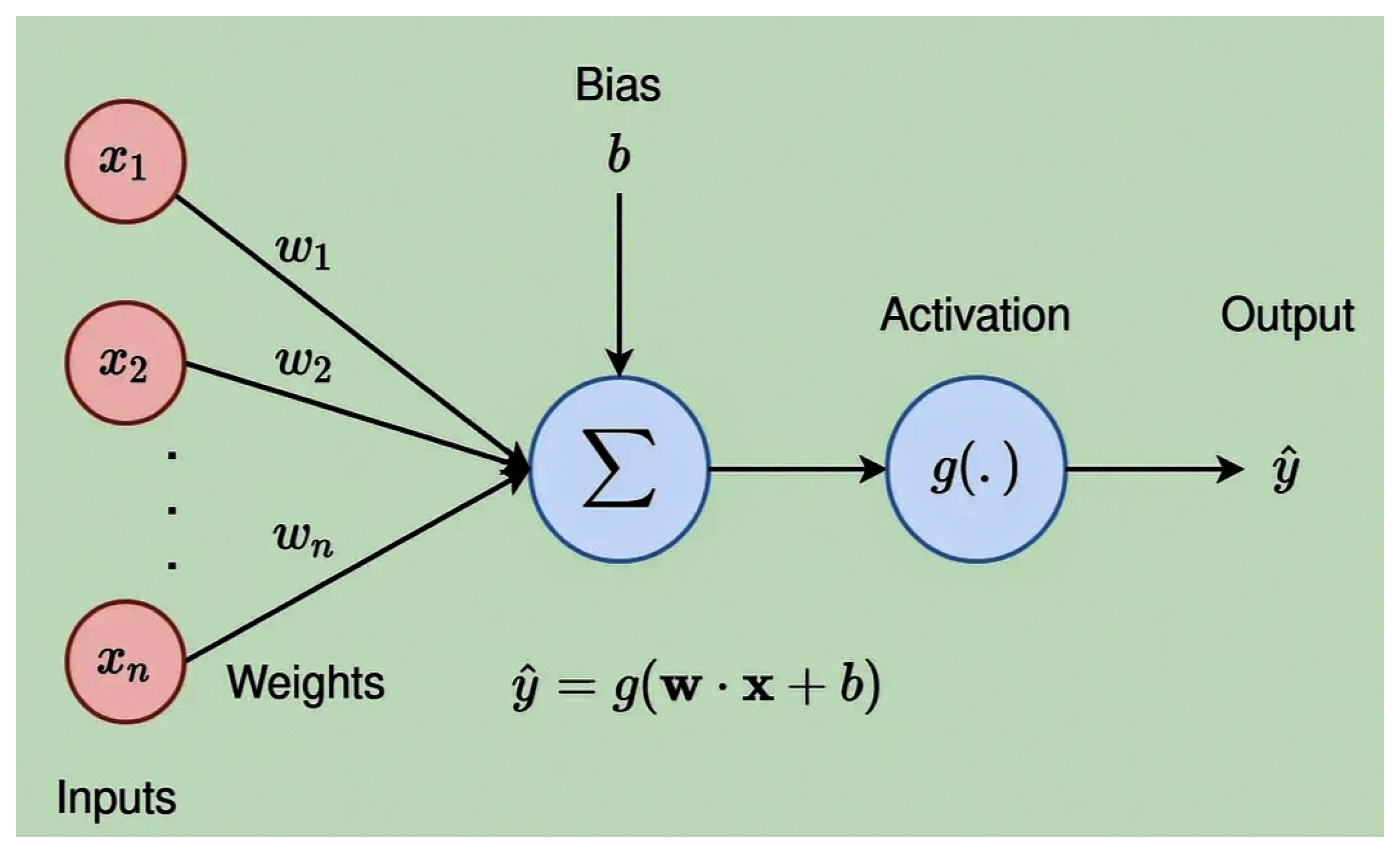
The extended bidirectional associative memory neural network is described as follows:
x i ˙ ( t ) = − μ i x i ( t ) + ∑ j = 1 m c j i f i ( y j ( t − τ j i ) + I i , i = 1 , 2 , 3 , . . . , n .
y i ˙ ( t ) = − μ i y i ( t ) + ∑ j = 1 m d i j g i ( x j ( t − ν i j ) + J j , j = 1 , 2 , 3 , . . . , m .
Where μ i and ν j represent the stability of internal neuron activities on the I-layer and J-layer, respectively, and c j i , d i j ( i = 1 , 2 , … , n ; j = 1 , 2 , … , m ) indicate connecting weights through neurons in two layers: the I-layer and J-layer. The neurons on the I-layer whose states have been designated by x i ( t ) receive the inputs I i and the inputs that those neurons in the J-layer output through activation functions f i , while the neurons on the J-layer whose associated states are revealed by y j ( t ) obtain the inputs J j and the inputs that those neurons in the I-layer output via activation functions g j [39]. The majority of writers only take into consideration small delayed neural networks that consist of two, three, four, five, or six neurons in order to understand the rule of extensive structures [40], as neural networks are large-scale, complicated, non-linear dynamical systems.
Preprints 117482 g001
Figure 1. Schematic diagram
Figure 1. Schematic diagram
Preprints 117482 g001
In 2009, Zhang et al. [41] considered the following delayed BAM neural networks:
d w 1 d t = − α w 1 ( t ) + g [ w 4 ( t − σ ) ] + h [ w 5 ( t − σ ) ] + h [ w 6 ( t − σ ) ] d w 2 d t = − α w 2 ( t ) + g [ w 5 ( t − σ ) ] + h [ w 6 ( t − σ ) ] + h [ w 4 ( t − σ ) ] d w 3 d t = − α w 3 ( t ) + g [ w 6 ( t − σ ) ] + h [ w 4 ( t − σ ) ] + h [ w 5 ( t − σ ) ] d w 4 d t = − α w 4 ( t ) + g [ w 1 ( t − σ ) ] + h [ w 2 ( t − σ ) ] + h [ w 3 ( t − σ ) ] d w 5 d t = − α w 5 ( t ) + g [ w 2 ( t − σ ) ] + h [ w 3 ( t − σ ) ] + h [ w 1 ( t − σ ) ] d w 6 d t = − α w 6 ( t ) + g [ w 3 ( t − σ ) ] + h [ w 1 ( t − σ ) ] + h [ w 2 ( t − σ ) ]
Where w i , i = 1 , 2 , 3 , . . . , 6 denotes the state of neurons or state variables, by α > 0 is the stability of the internal neuron process, while activation functions are indicated by g and h. Considering a , a 1 , b , and b 1 are all real constants, they can assume that g ( u ) = a u + a 1 u 3 and h ( u ) = b u + b 1 u 3 in many situations. Zhang et al. [41] created the condition on the stability and appearance of the Hopf bifurcation of the system (3) by referencing the characteristic equation of the system. Multi-periodic solutions to the system (3) were found to exist by Zhang et al. [41], utilizing the symmetric bifurcation of Hopf’s theory of Wu [42].
d w 1 d t = − α w 1 ( t ) + a w 4 ( t − σ ) + b w 5 ( t − σ ) + b w 6 ( t − σ ) d w 2 d t = − α w 2 ( t ) + a w 5 ( t − σ ) + b w 6 ( t − σ ) + b w 4 ( t − σ ) d w 3 d t = − α w 3 ( t ) + a w 6 ( t − σ ) + b w 4 ( t − σ ) + b w 5 ( t − σ ) d w 4 d t = − α w 4 ( t ) + a w 1 ( t − σ ) + b w 2 ( t − σ ) + b w 3 ( t − σ ) d w 5 d t = − α w 5 ( t ) + a w 2 ( t − σ ) + b w 3 ( t − σ ) + b w 1 ( t − σ ) d w 6 d t = − α w 6 ( t ) + a w 3 ( t − σ ) + b w 1 ( t − σ ) + b w 2 ( t − σ )
Based on the preceding description, the modified system (3) is the fractional-order example in order to more accurately define the long-term modifications to the process and memory among distinct neurons and also the global connection of neurons. The proposed system (4) can be modified for incommensurate fractional orders as follows:
d q 1 w 1 d t q 1 = − α w 1 ( t ) + a w 4 ( t − σ ) + b w 5 ( t − σ ) + b w 6 ( t − σ ) d q 2 w 2 d t q 2 = − α w 2 ( t ) + a w 5 ( t − σ ) + b w 6 ( t − σ ) + b w 4 ( t − σ ) d q 3 w 3 d t q 3 = − α w 3 ( t ) + a w 6 ( t − σ ) + b w 4 ( t − σ ) + b w 5 ( t − σ ) d q 4 w 4 d t q 4 = − α w 4 ( t ) + a w 1 ( t − σ ) + b w 2 ( t − σ ) + b w 3 ( t − σ ) d q 5 w 5 d t q 5 = − α w 5 ( t ) + a w 2 ( t − σ ) + b w 3 ( t − σ ) + b w 1 ( t − σ ) d q 6 w 6 d t q 6 = − α w 6 ( t ) + a w 3 ( t − σ ) + b w 1 ( t − σ ) + b w 2 ( t − σ )
Where q i , i = 1 , 2 , 3 , . . . , 6 are the incommensurate fractional-orders to be calculated.
The appropriate initial condition of system (5) is stated as follows:
w 1 ( ϕ ) = w 1 ϕ , ϕ ∈ [ − σ , t 0 ] w 2 ( ϕ ) = w 2 ϕ , ϕ ∈ [ − σ , t 0 ] w 3 ( ϕ ) = w 1 ϕ , ϕ ∈ [ − σ , t 0 ] w 4 ( ϕ ) = w 4 ϕ , ϕ ∈ [ − σ , t 0 ] w 5 ( ϕ ) = w 5 ϕ , ϕ ∈ [ − σ , t 0 ] w 6 ( ϕ ) = w 6 ϕ , ϕ ∈ [ − σ , t 0 ]
Where σ is a time delay and t 0 > 0 denotes a constant.

3. Stability Analysis

Before discussing the reliability of the neural network model, it is impossible to calculate the fractional incommensurate orders q i ≠ q j , where i ≠ j . For fixed values of the included parameters, Equation (5) for the neural network model leads to a fractional-order system with the following form:
D q 1 0 w 1 ( t ) = − 12.2 w 1 ( t ) + 0.21 w 4 ( t − 0.001 ) + 2.6 w 5 ( t − 0.001 ) + 2.6 w 6 ( t − 0.001 ) D q 2 0 w 2 ( t ) = − 12.2 w 2 ( t ) + 0.21 w 5 ( t − 0.001 ) + 2.6 w 6 ( t − 0.001 ) + 2.6 w 4 ( t − 0.001 ) D q 3 0 w 3 ( t ) = − 12.2 w 3 ( t ) + 0.21 w 6 ( t − 0.001 ) + 2.6 w 4 ( t − 0.001 ) + 2.6 w 5 ( t − 0.001 ) D q 4 0 w 4 ( t ) = − 12.2 w 4 ( t ) + 0.21 w 1 ( t − 0.001 ) + 2.6 w 2 ( t − 0.001 ) + 2.6 w 3 ( t − 0.001 ) D q 5 0 w 5 ( t ) = − 12.2 w 5 ( t ) + 0.21 w 2 ( t − 0.001 ) + 2.6 w 3 ( t − 0.001 ) + 2.6 w 1 ( t − 0.001 ) D q 6 0 w 6 ( t ) = − 12.2 w 6 ( t ) + 0.21 w 3 ( t − 0.001 ) + 2.6 w 1 ( t − 0.001 ) + 2.6 w 2 ( t − 0.001 ) .
By choosing the random values of the involved parameters as α = 12.2 , σ = 0.001 , a = 0.21 and b = 2.6 , the different points of equilibra are founded for the Jacobian matrix of the model (5) (omitted for the sack of brevity). On the basis of these equilibrium points, the upper bounds of incommensurate fractional orders are calculated as q 1 = 0.965 , q 2 = 0.780 , q 3 = 0.800 , q 4 = 0.785 , q 5 = 0.789 and q 6 = 1.58 , using the necessary condition for system A to be stable [43], if the following condition is satisfied:
| a r g ( λ i ) | > q i π 2 , for all i ,
where q i is the incommensurate fractional-orders and λ i is the i t h eigenvalue of the system.
The corresponding incommensurate fractional orders are determined as q 1 = 0.965 , q 2 = 0.780 , q 3 = 0.800 , q 4 = 0.785 , q 5 = 0.789 and q 6 = 1.58 , respectively. The incommensurate fractional orders from q 1 to q 5 are physically stable because they lie in the first Riemann sheet region. On the other hand, q 6 does not lie in the stable region, which is not physical. It is possible to improve the reliability and stability of neural networks for a variety of practical purposes. The stability of a neural network to generate reliable and consistent outputs in response to changing inputs or conditions is often referred to as stability in neural network models. For neural networks to be successfully implemented and used in many kinds of applications, stability must be exceeded. The points that follow a few essential details about neural network stability are: When trained on a certain data set, a stable neural network needs to consistently converge to its solution. The network can possibly be determined to be unstable if it is unable to converge or converge to an alternative solution for identical inputs. Reliability to changes in input information, noisy environments, or perturbations is another component of stability in neural networks. Additionally, in the event that the input data is slightly modified or transferred, a stable network should still provide trustworthy results. Whenever applied to new data, a stable neural network replicates very well. It is not appropriate to be too sensitive to slight changes in the input feature or over-fit the training set. Artificial neural networks are able to become more stable by using weight initialization techniques that prevent gradients from inflating or disappearing during training. Stable neural network training requires selecting the most appropriate learning rate. Clearly, high learning rates can cause instability, which in turn can result in oscillations or divergence while training. Neural networks can be made more stable and more capable of over-fitting by applying regularization methods.
Artificial neural networks represent a novel form of dynamical system. The ability to clarify the solutions of dynamical systems that are not linear makes the theory of dynamical systems extremely potent. When neural network models reliably and accurately forecast unknown data, they can identify a meaningful pattern from a training set of data, and this is when the models are considered stable. The model’s architectural design, training process, and data quantity and quality are only a few examples of those factors that can affect its stability.

4. Convergence and Accuracy

The concept of fractional calculus is derived from integral calculus, as has already been discussed earlier. The precision, convergence, consistency, stability, and other aspects of the fractional order techniques are discussed by the fundamental results of integral calculus, which are also relevant to fractional solutions. The requirements that must be met in order for the applied fractional simulation’s solution to be roughly accurate are mentioned in the discussion that follows.
Definition 1. 
Consistency: Let F * ( s ) = 0 is the approximate solution of a partial differential equation F ( r ) in time and space, with the exact solution as r. Then the truncation error Υ i , j ( y ) at the point ( i m , j n ) is defined as [44]:
Υ i , j ( y ) = F * ( y ) − F ( y i , j ) ,
 where y be a continuous function of time and space with infinite numbers of continuous derivatives. Then the numerical method is said to be consistent with partial differential equation F ( r ) = 0 , if Υ i , j ( y ) ⟶ 0 as m ⟶ 0 and n ⟶ 0 .
Definition 2. 
Lax’s equivalence theorem: Lax’s equivalence theorem can be stated that the stability is the necessary and sufficient condition for convergence for a numerical scheme if it satisfies the condition of consistency [44].
Based on the results mentioned above, it can be concluded that the accuracy, consistency, and convergence of the solutions are granted by the stability of the current numerical scheme.

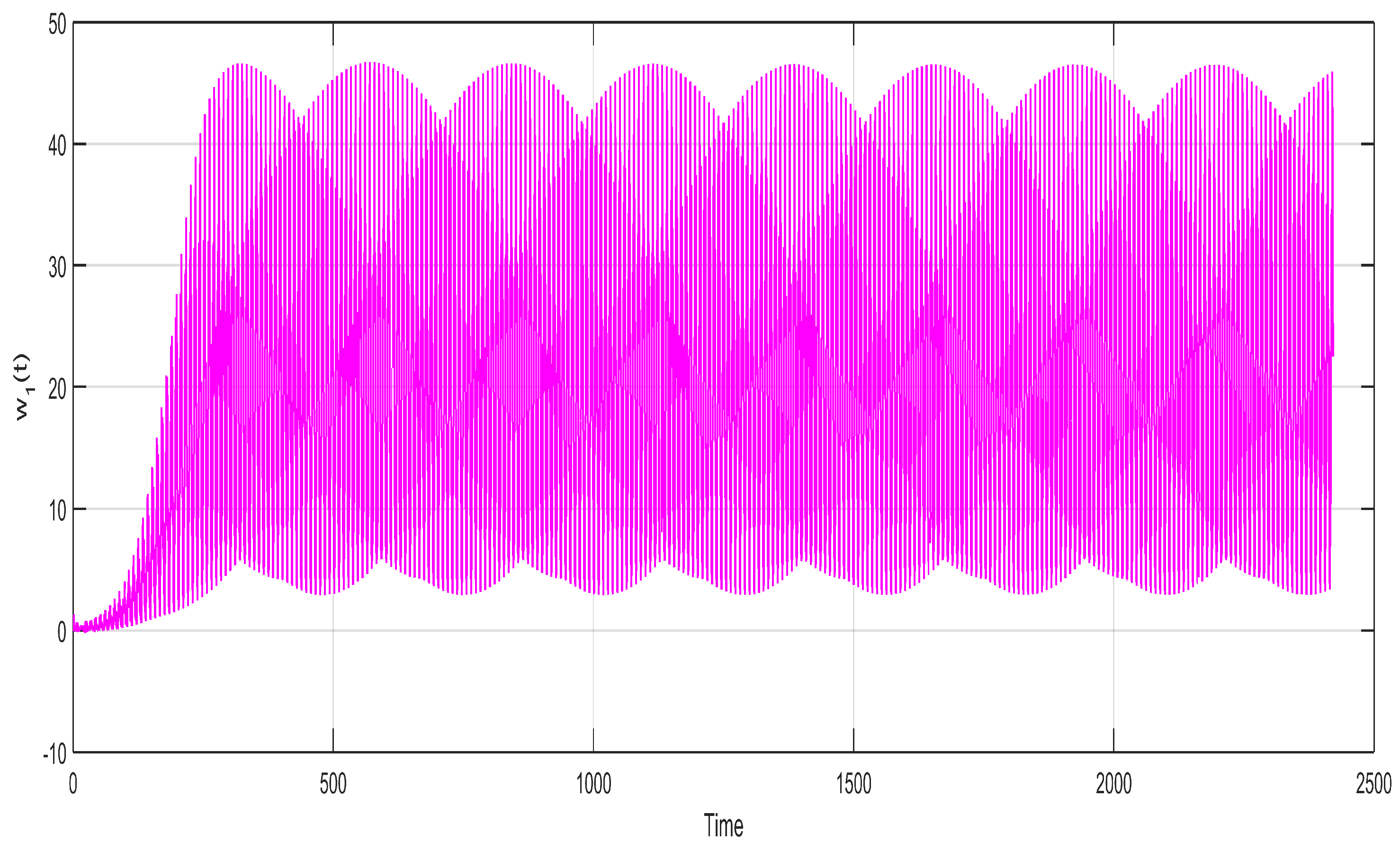
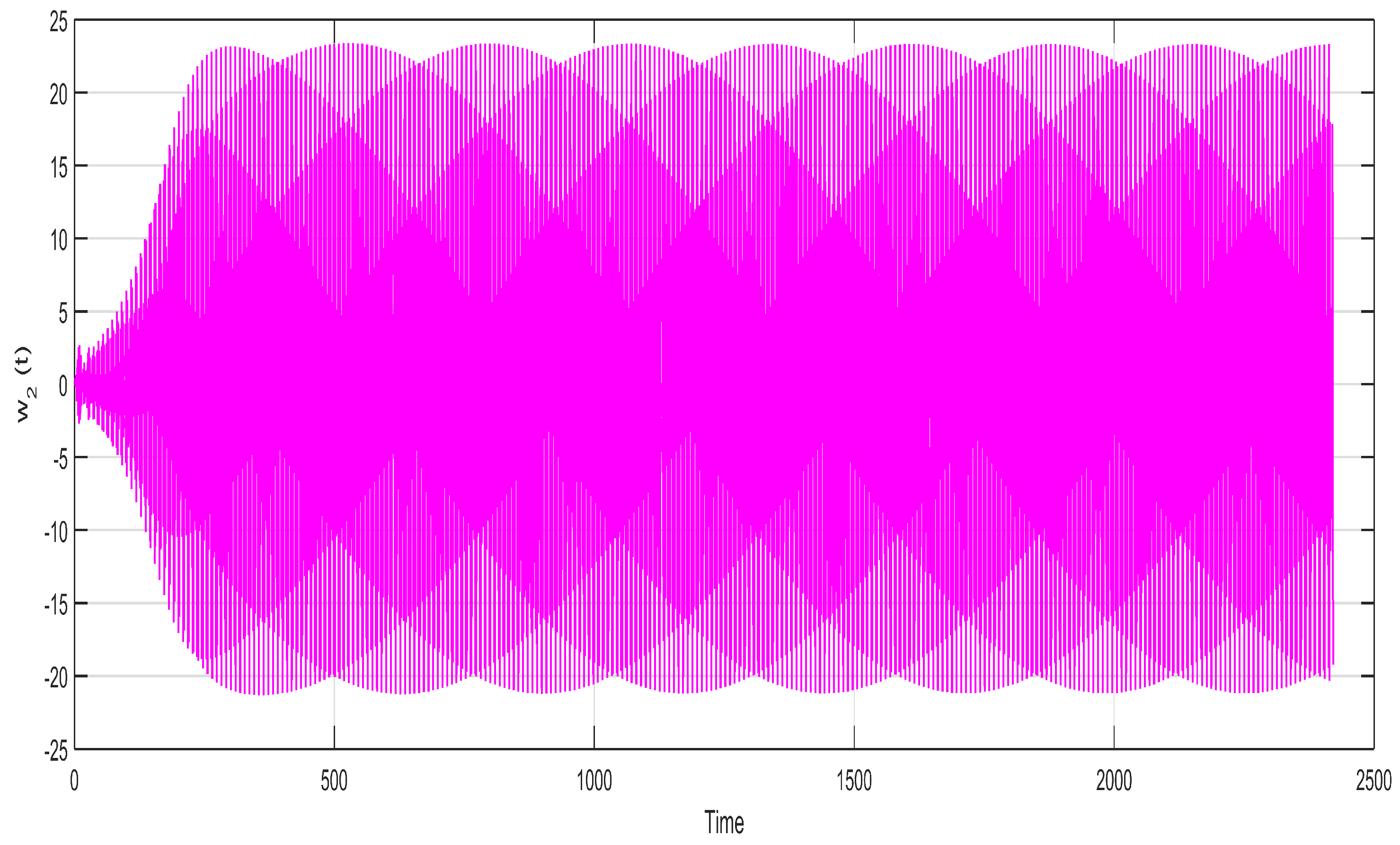
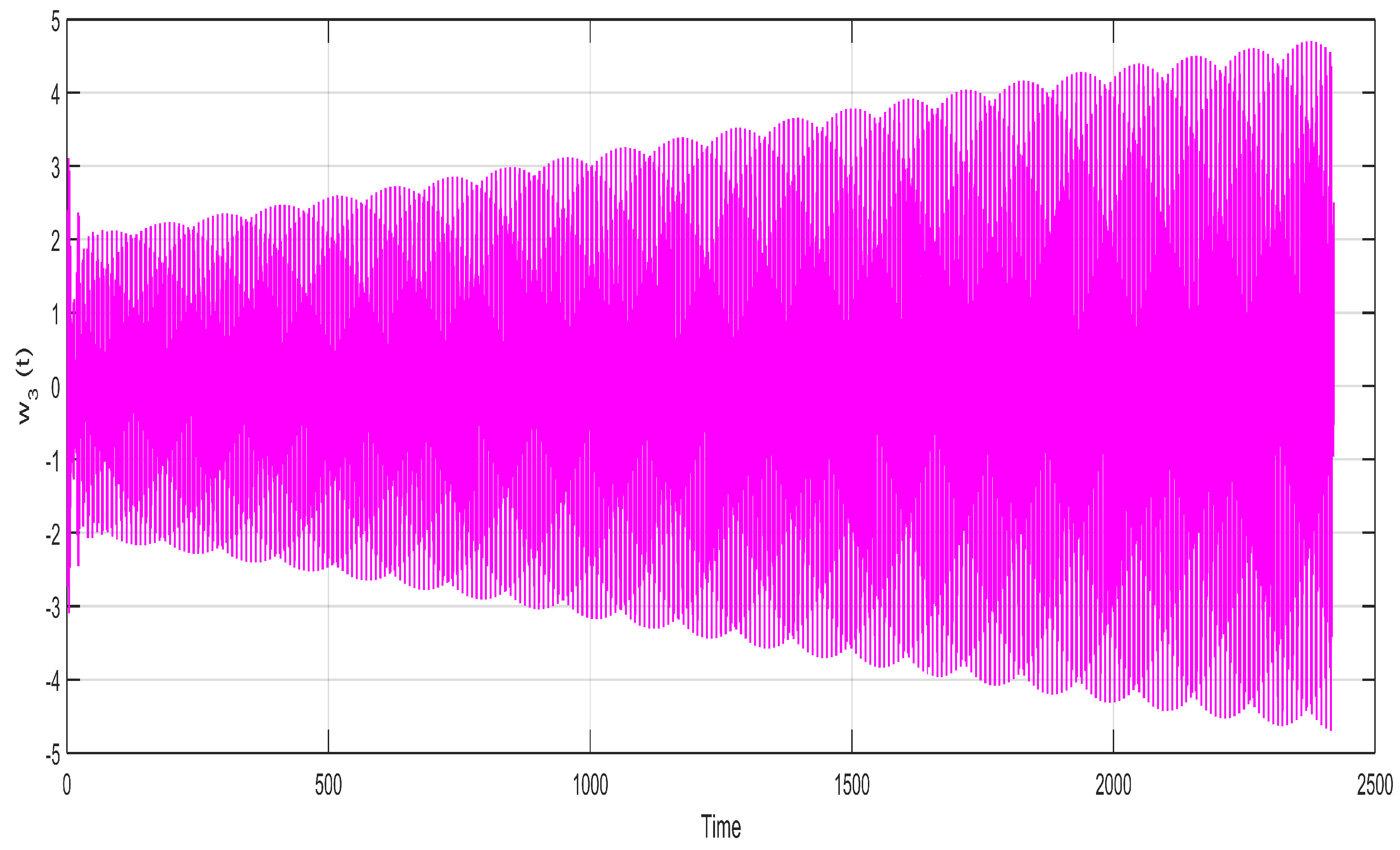
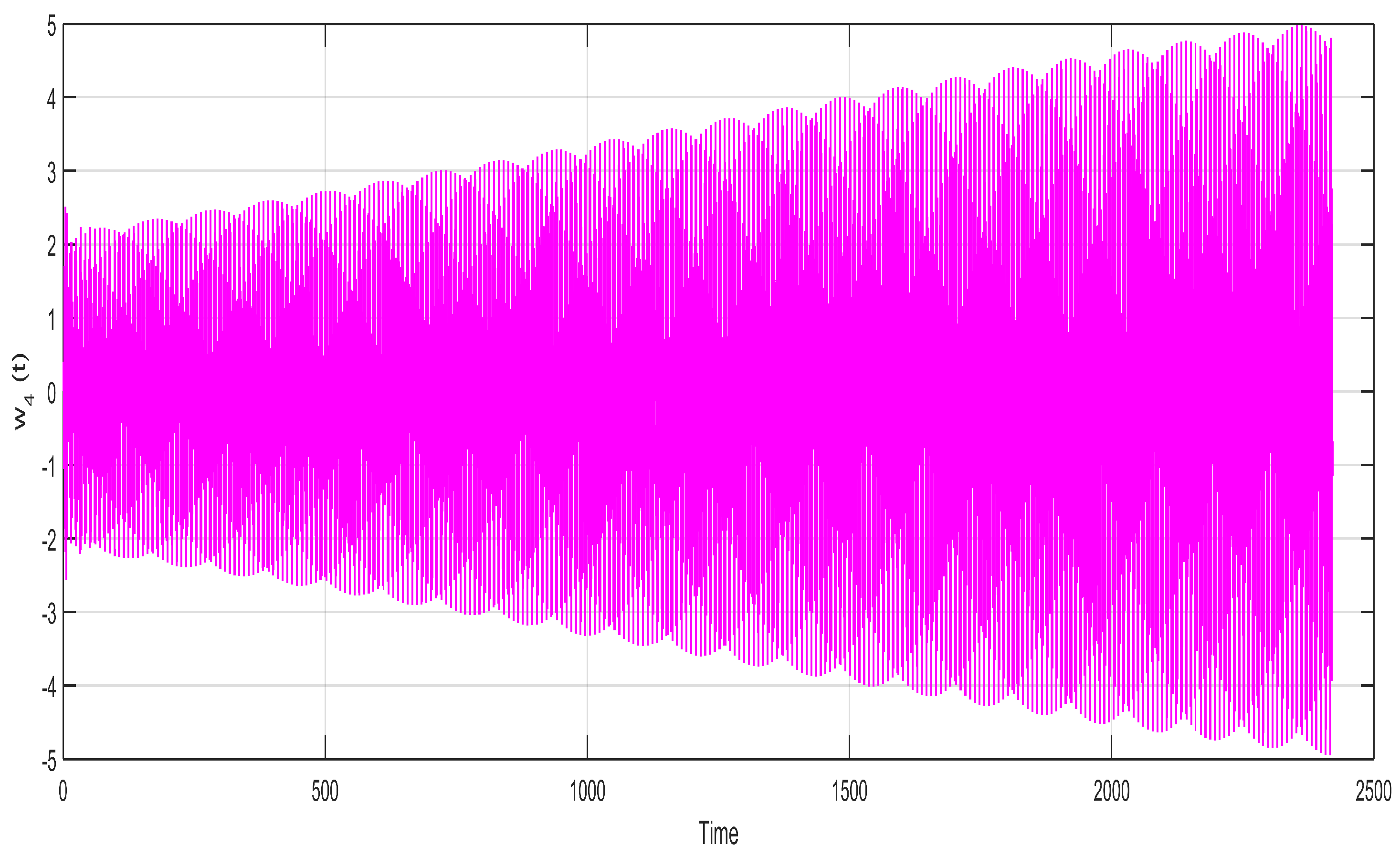
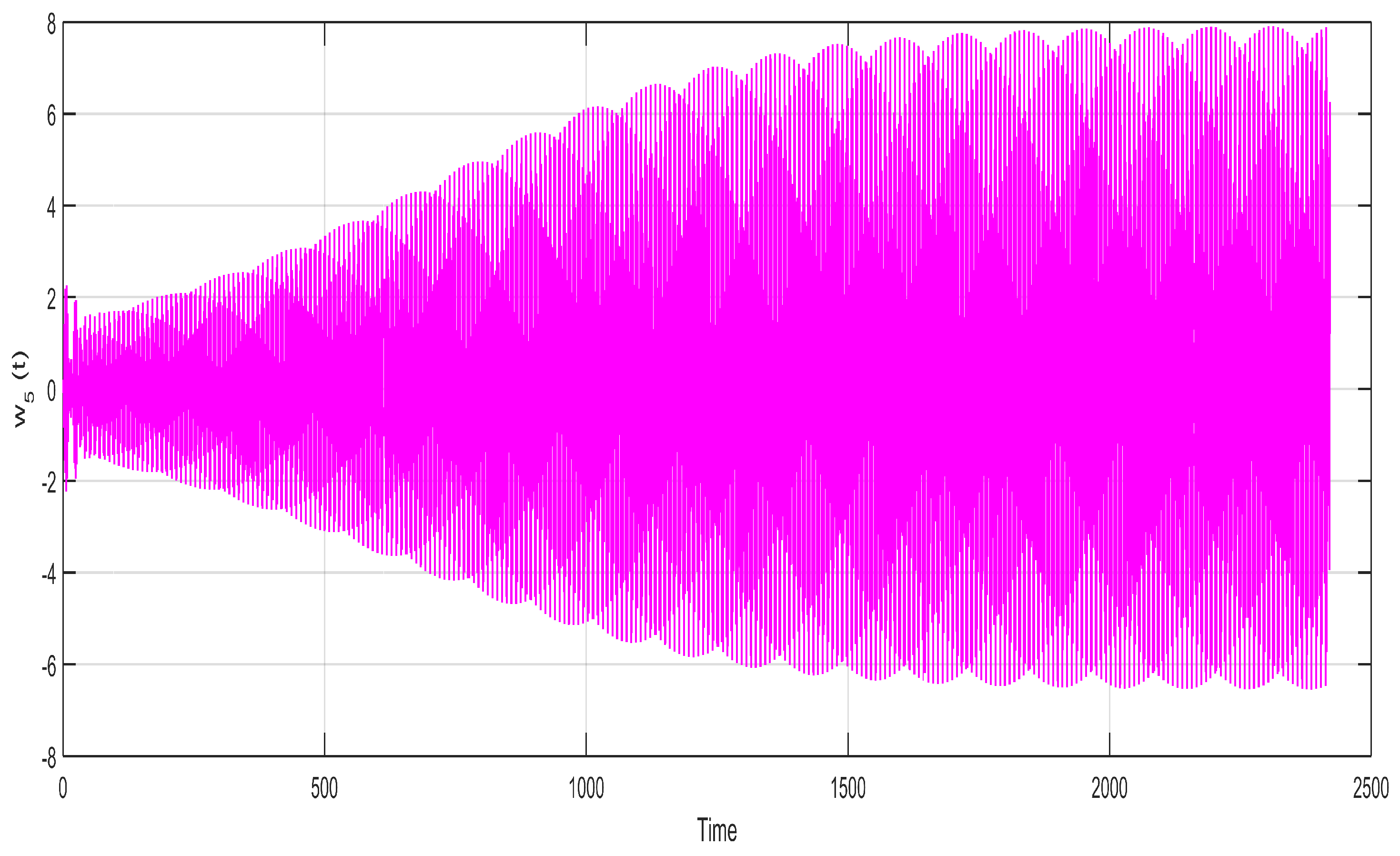
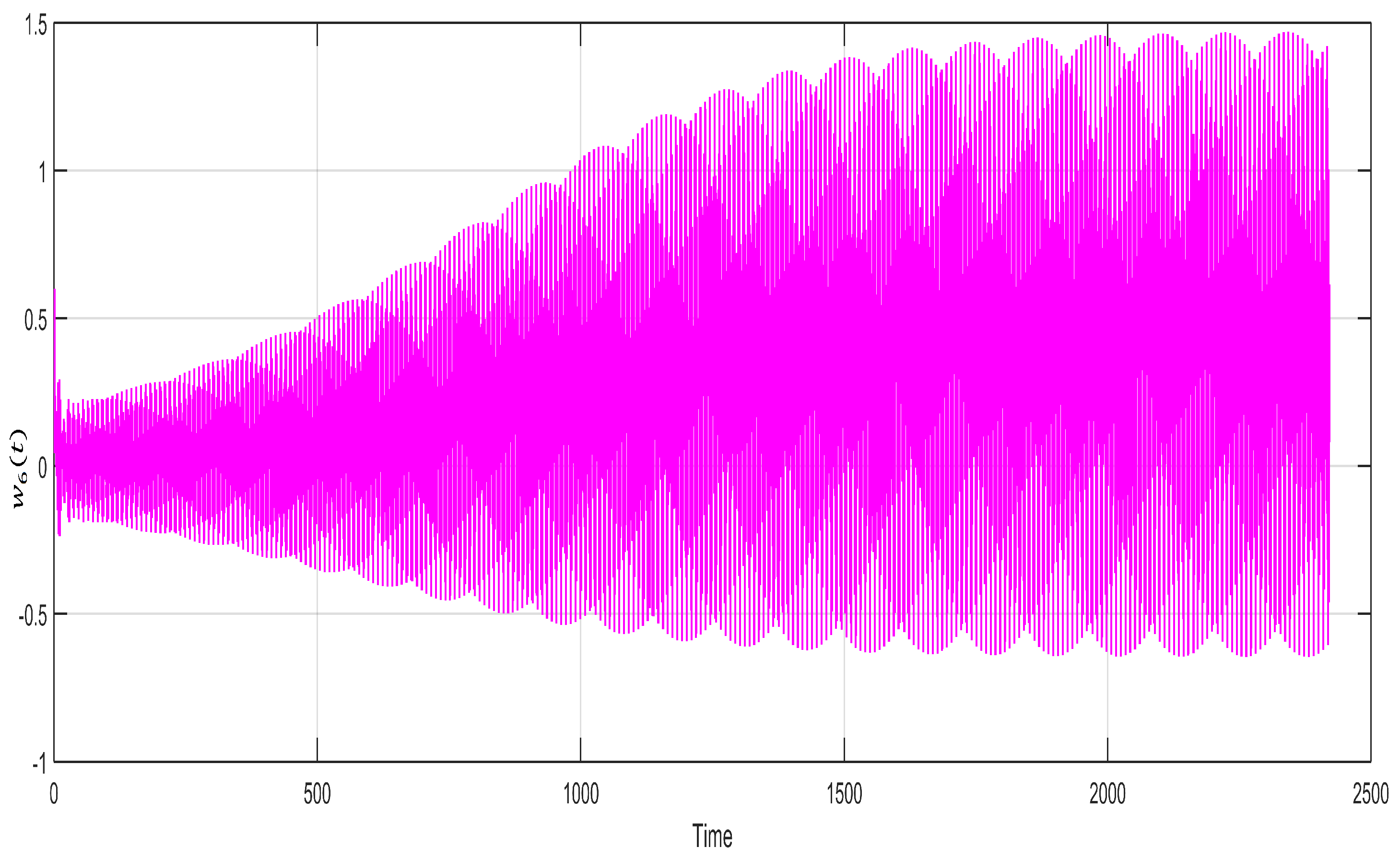
5. Results and Discussion

Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 indicate the relationship between the state variables w i with time t and show a very uniform and stable two-layer sketch of the neuron stable w i with passage of time. This uniform and stable sketch is the result of the calculated incommensurate fractional orders within the region of stability q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.650 , q 5 = 0.670 and q 6 = 0.910 and the state variable w i ( t ) of the neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 . They are drawn for the purpose of showing the variation of neuron states with the passage of time. The neural network fractional model system’s (5) stability are simulated under the neuron process state. It is possible to determine that each of the variables q i becomes closer to zero with the help of the system (5). This suggests that the fractional orders system’s null equilibrium point E ( 0 , 0 , 0 , 0 , 0 , 0 ) is locally asymptotically stable which satisfies system (8). All these graphs are sketched for the calculated incommensurate fractional orders as q 1 = 0.932 , q 2 = 0.670 , q 3 = 0.600 , q 4 = 0.650 , q 5 = 0.668 and q 6 = 0.980 , with a little bit of variation and keeping it within the stable region. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 depict very stable and converged images of different neuron states over time. The different states of the neuron will behave unstable whenever the incommensurate fractional orders exceed their upper bounds, as calculated in Section 3.
Preprints 117482 g002
Figure 2. State variable w 1 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.650 , q 5 = 0.670 , and q 6 = 0.910 .
Figure 2. State variable w 1 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.650 , q 5 = 0.670 , and q 6 = 0.910 .
Preprints 117482 g002
Preprints 117482 g003
Figure 3. State variable w 2 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.650 , q 5 = 0.670 , and q 6 = 0.910 .
Figure 3. State variable w 2 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.650 , q 5 = 0.670 , and q 6 = 0.910 .
Preprints 117482 g003
Preprints 117482 g004
Figure 4. State variable w 3 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.670 , and q 6 = 0.910 .
Figure 4. State variable w 3 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.670 , and q 6 = 0.910 .
Preprints 117482 g004
Preprints 117482 g005
Figure 5. State variable w 4 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.670 , and q 6 = 0.910 .
Figure 5. State variable w 4 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.670 , and q 6 = 0.910 .
Preprints 117482 g005
Preprints 117482 g006
Figure 6. State variable w 5 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.669 , and q 6 = 0.910 .
Figure 6. State variable w 5 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.669 , and q 6 = 0.910 .
Preprints 117482 g006
Preprints 117482 g007
Figure 7. State variable w 6 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.669 , and q 6 = 0.910 .
Figure 7. State variable w 6 ( t ) of neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 and for incommensurate fractional orders q 1 = 0.800 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.669 , and q 6 = 0.910 .
Preprints 117482 g007
Neurons play an important role in the human brain as well as in other parts of the human body’s processing, such as receiving and transmitting signals from the affected body part. Artificial neural networks process information just like a human brain. It functions similarly to the human brain in the way that it processes information. The human brain is a very complex and complicated portion of the body and performs different tasks simultaneously. While ANNs have the deficiency to perform different functions accurately and precisely at the same time, when a neuron receives information from another neuron in a confined area, the activity level is able to transfer the impulses to another neuron. Only one signal can be fired by a neuron at a time, and that signal can reach multiple other neurons. However, artificial neural networks aim to perform the majority of tasks performed by the human brain.
The variables that indicate state during training are referred to as state variables in neural network models. These parameters are vary as the network gains experience, include things like weights, biases, and activations. During training, they are modified iteratively in order to reduce the loss function and boost efficiency. When state variables do not vary much over time, they are considered stable. Weight is the term for the value-carrying (signal-carrying) connection between neurons. Similar to weight, bias also has a value. Every neuron that is not in the input layer is biased. Activation is a standard test in which a function from the test-function set is applied to run the neural network in order to evaluate its performance.
The region of stability, synchronization, and chaos are be classified on the basis of calculated incommensurate fractional-orders within the stability region through the corresponding eigenvalues and their equilibrium points. The eigenvalue lies outside the Riemann sheet region, which leads to the detection of chaos. The physical root of incommensurate fractional-orders q i situated in the Riemann sheet region, maintains stability for the system. The collaboration of different tasks to ensure data consistency and avoid conflicts when gaining access to common resources is referred to as synchronization, which enables the smooth and effective operation of diverse elements.
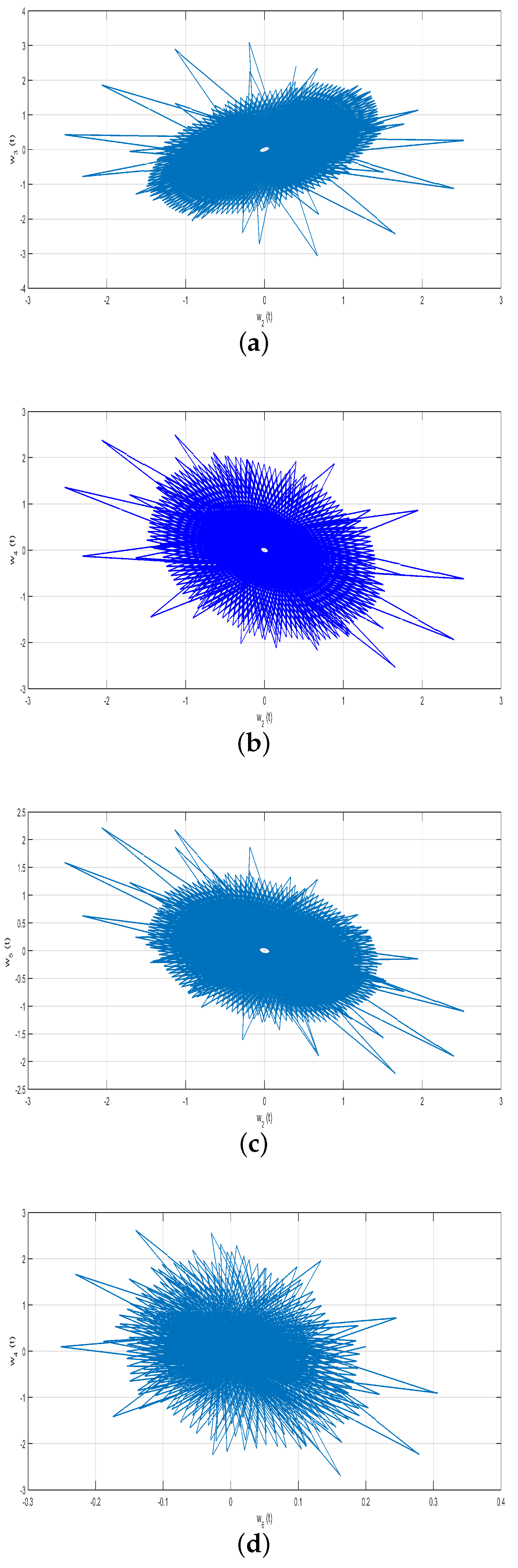
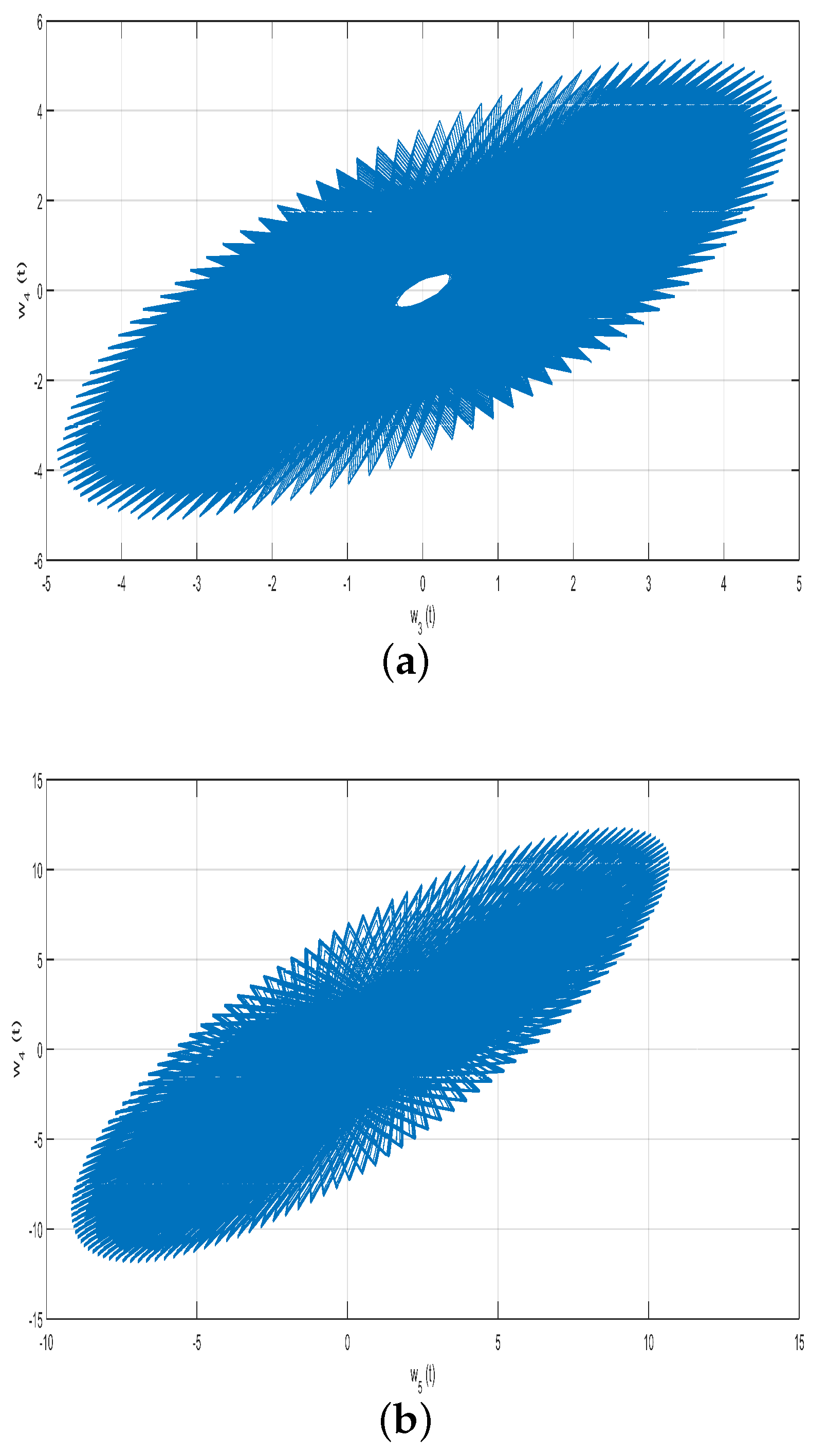
Algorithms used in machine learning or optimization issues where the objective is to modify the weights assigned to various neuron states in a model may be related to weight synchronization. Through this procedure, the relative importance of each neuron state is adjusted in an attempt to maximize accuracy and performance. On the other hand, two significant dynamical behaviors of delayed neural networks are stability and synchronization phenomena. In particular, the neural network element relies on synchronization brought forth by delay. Under the neuron process state, synchronization and stability of the neural network fractional model (7) are simulated and depicted in Figure 8 and Figure 9. These simulations are performed on the basis of the incommensurate fractional-orders q i for their calculated values. The different state variables synchronization, stability, and their chaotic effects are shown in Figure 8(a–d). Figure 8(a) shows a congested stability within the interval ( − 1.5 , 1.5 ) and a chaotic effect beyond this interval of neuron state w 2 ( t ) synchronized against w 3 ( t ) . On the other hand, the stability is a little bit uncongested and uniformly distributed within the same interval ( − 1.5 , 1.5 ) for the synchronized values of w 2 ( t ) with w 4 ( t ) , while the chaotic effect is reduced all around, as shown in Figure 8(b). The enhancement of stability in Figure 8(b) is due to the exclusion of two neuron states w 5 ( t ) and w 6 ( t ) from the fourth equation of the system (7). The exclusion of these neuron states w 5 ( t ) and w 6 ( t ) will reduce the time delay effect as compared to the third equation of the system (7). The reduction of the time delay will give more relaxation time for the state variable w 4 ( t ) to be stable as compared to the state variable w 3 ( t ) (Figure 8(a)). Figure 8(c) shows a stable within the interval ( − 2.5 , 2.5 ) and a chaotic effect beyond this interval of neuron state w 2 ( t ) versus w 5 ( t ) . Figure 8(d) loses stability compared to Figure 8(a-c). All the state variables w i remain to show a chaotic influence around zero in Figure 8 and Figure 9, implying that system (7) instability exists around the null equilibrium point E ( 0 , 0 , 0 , 0 , 0 , 0 ) . Figure 9(a) indicates the synchronization between the state variables w 3 ( t ) and w 4 ( t ) , which seem very stable in nature. It is relaxed and uniformly distributed with the passage of time. On the other hand, Figure 9(b) is quite a little bit losing its stability for the synchronization of w 4 ( t ) and w 5 ( t ) and chaotic behavior is increased in Figure 9(b). The enhancement of stability in Figure 9(a) is reasoned out by the addition of the extra parameter b with the neuron state w 4 ( t ) in the dynamical equation of w 3 ( t ) in system (5).

6. Conclusions

  • The neuron states w i become unstable whenever the incommensurate fractional orders q i exceeds their upper bounds.
  • A congested stability within the interval ( − 1.5 , 1.5 ) and a chaotic effect beyond this interval of neuron state w 2 ( t ) synchronized against w 3 ( t ) are reported.
  • The reduction of the time delay will give more relaxation time for the state variable w 4 ( t ) to be stable as compared to the state variable w 3 ( t ) .
  • The exclusion of two neuron states w 5 ( t ) and w 6 ( t ) , enhances the stability of the system.
  • The enhancement of stability in Figure 9(a) is reasoned out by the addition of the extra parameter b.

Nomenclature

The following abbreviations are used in this manuscript:
D q i 0 Fractional-order derivative
q i Incommensurate fractional-orders
a and b Real numbers
t 0 Constant
t Time
σ Time delay
w i States variables or Neuron states
α Training parameter or Stability of neuron state
g and h Activation functions
c j i and d i j Connecting weights through neurons
μ i and ν i Stability of internal neuron activities

References

  1. Li, Y., & Shen, S. (2020). Almost automorphic solutions for Clifford-valued neutral-type fuzzy cellular neural networks with leakage delays on time scales. Neurocomputing, 417, 23-35. [CrossRef]
  2. Xiu, C., Zhou, R., & Liu, Y. (2020). New chaotic memristive cellular neural network and its application in secure communication system. Chaos, Solitons & Fractals, 141, 110316.
  3. Ji, L., Chang, M., Shen, Y., & Zhang, Q. (2020). Recurrent convolutions of binary-constraint cellular neural network for texture recognition. Neurocomputing, 387, 161-171.
  4. Kumar, R., & Das, S. (2020). Exponential stability of inertial BAM neural network with time-varying impulses and mixed time-varying delays via matrix measure approach. Communications in Nonlinear Science and Numerical Simulation, 81, 105016.
  5. Xu, C., Liao, M., Li, P., Liu, Z., & Yuan, S. (2021). New results on pseudo almost periodic solutions of quaternion-valued fuzzy cellular neural networks with delays. Fuzzy Sets and Systems, 411, 25-47.
  6. Kobayashi, M. (2021). Complex-valued Hopfield neural networks with real weights in synchronous mode. Neurocomputing, 423, 535-540.
  7. Cui, W., Wang, Z., & Jin, W. (2021). Fixed-time synchronization of Markovian jump fuzzy cellular neural networks with stochastic disturbance and time-varying delays. Fuzzy Sets and Systems, 411, 68-84.
  8. Huang, C., Su, R., Cao, J., & Xiao, S. (2020). Asymptotically stable high-order neutral cellular neural networks with proportional delays and D operators. Mathematics and Computers in Simulation, 171, 127-135.
  9. Meng, B., Wang, X., Zhang, Z., & Wang, Z. (2020). Necessary and sufficient conditions for normalization and sliding mode control of singular fractional-order systems with uncertainties. Science China Information Sciences, 63, 1-10.
  10. Hsu, C. H., & Lin, J. J. (2019). Stability of traveling wave solutions for nonlinear cellular neural networks with distributed delays. Journal of Mathematical Analysis and Applications, 470(1), 388-400. [CrossRef]
  11. Li, Y., & Qin, J. (2018). Existence and global exponential stability of periodic solutions for quaternion-valued cellular neural networks with time-varying delays. Neurocomputing, 292, 91-103.
  12. Tang, R., Yang, X., & Wan, X. (2019). Finite-time cluster synchronization for a class of fuzzy cellular neural networks via non-chattering quantized controllers. Neural Networks, 113, 79-90.
  13. Wang, W. (2018). Finite-time synchronization for a class of fuzzy cellular neural networks with time-varying coefficients and proportional delays. Fuzzy Sets and Systems, 338, 40-49.
  14. Wang, S., Zhang, Z., Lin, C., & Chen, J. (2021). Fixed-time synchronization for complex-valued BAM neural networks with time-varying delays via pinning control and adaptive pinning control. Chaos, Solitons & Fractals, 153, 111583.
  15. Zhao, R., Wang, B., & Jian, J. (2022). Global μ-stabilization of quaternion-valued inertial BAM neural networks with time-varying delays via time-delayed impulsive control. Mathematics and Computers in Simulation, 202, 223-245.
  16. Li, Y., & Qin, J. (2018). Existence and global exponential stability of periodic solutions for quaternion-valued cellular neural networks with time-varying delays. Neurocomputing, 292, 91-103.
  17. Kong, F., Zhu, Q., Wang, K., & Nieto, J. J. (2019). Stability analysis of almost periodic solutions of discontinuous BAM neural networks with hybrid time-varying delays and D operator. Journal of the Franklin Institute, 356(18), 11605-11637.
  18. Xu, C., & Zhang, Q. (2014). On antiperiodic solutions for Cohen-Grossberg shunting inhibitory neural networks with time-varying delays and impulses. Neural Computation, 26(10), 2328-2349.
  19. Ali, M. S., Yogambigai, J., Saravanan, S., & Elakkia, S. (2019). Stochastic stability of neutral-type Markovian-jumping BAM neural networks with time varying delays. Journal of Computational and Applied Mathematics, 349, 142-156.
  20. Cong, E. Y., Han, X., & Zhang, X. (2020). Global exponential stability analysis of discrete-time BAM neural networks with delays: A mathematical induction approach. Neurocomputing, 379, 227-235. [CrossRef]
  21. Ayachi, M. (2022). Measure-pseudo almost periodic dynamical behaviors for BAM neural networks with D operator and hybrid time-varying delays. Neurocomputing, 486, 160-173.
  22. Shi, J., He, K., & Fang, H. (2022). Chaos, Hopf bifurcation and control of a fractional-order delay financial system. Mathematics and Computers in Simulation, 194, 348-364.
  23. Xiao, J., Wen, S., Yang, X., & Zhong, S. (2020). New approach to global Mittag-Leffler synchronization problem of fractional-order quaternion-valued BAM neural networks based on a new inequality. Neural Networks, 122, 320-337.
  24. Xu, C., Mu, D., Pan, Y., Aouiti, C., Pang, Y., & Yao, L. (2022). Probing into bifurcation for fractional-order BAM neural networks concerning multiple time delays. Journal of Computational Science, 62, 101701.
  25. Xu, C., Liao, M., Li, P., Guo, Y., & Liu, Z. (2021). Bifurcation properties for fractional order delayed BAM neural networks. Cognitive Computation, 13, 322-356.
  26. Wang, F., Yang, Y., Xu, X., & Li, L. (2017). Global asymptotic stability of impulsive fractional-order BAM neural networks with time delay. Neural Computing and Applications, 28, 345-352.
  27. Ye, R., Liu, X., Zhang, H., & Cao, J. (2019). Global Mittag-Leffler synchronization for fractional-order BAM neural networks with impulses and multiple variable delays via delayed-feedback control strategy. Neural Processing Letters, 49, 1-18.
  28. Xu, C., Liu, Z., Aouiti, C., Li, P., Yao, L., & Yan, J. (2022). New exploration on bifurcation for fractional-order quaternion-valued neural networks involving leakage delays. Cognitive Neurodynamics, 16(5), 1233-1248.
  29. Xiao, J., Guo, X., Li, Y., Wen, S., Shi, K., & Tang, Y. (2022). Extended analysis on the global Mittag-Leffler synchronization problem for fractional-order octonion-valued BAM neural networks. Neural Networks, 154, 491-507.
  30. Popa, C. A. (2023). Mittag–Leffler stability and synchronization of neutral-type fractional-order neural networks with leakage delay and mixed delays. Journal of the Franklin Institute, 360(1), 327-355.
  31. Ci, J., Guo, Z., Long, H., Wen, S., & Huang, T. (2023). Multiple asymptotical ω-periodicity of fractional-order delayed neural networks under state-dependent switching. Neural Networks, 157, 11-25.
  32. Li, S., Huang, C., & Yuan, S. (2022). Hopf bifurcation of a fractional-order double-ring structured neural network model with multiple communication delays. Nonlinear Dynamics, 108(1), 379-396.
  33. Xu, C., Aouiti, C., & Liu, Z. (2020). A further study on bifurcation for fractional order BAM neural networks with multiple delays. Neurocomputing, 417, 501-515.
  34. Yuan, J., Zhao, L., Huang, C., & Xiao, M. (2019). Novel results on bifurcation for a fractional-order complex-valued neural network with leakage delay. Physica A: Statistical Mechanics and its Applications, 514, 868-883. [CrossRef]
  35. Wang, Y., Cao, J., & Huang, C. (2022). Exploration of bifurcation for a fractional-order BAM neural network with n+2 neurons and mixed time delays. Chaos, Solitons & Fractals, 159, 112117.
  36. Si, X., Wang, Z., & Fan, Y. (2023). Quantized control for finite-time synchronization of delayed fractional-order memristive neural networks: The Gronwall inequality approach. Expert Systems with Applications, 215, 119310.
  37. Xu, C., Zhang, W., Liu, Z., & Yao, L. (2022). Delay-induced periodic oscillation for fractional-order neural networks with mixed delays. Neurocomputing, 488, 681-693.
  38. Xu, C., Mu, D., Liu, Z., Pang, Y., Liao, M., Li, P., ... & Qin, Q. (2022). Comparative exploration on bifurcation behavior for integer-order and fractional-order delayed BAM neural networks. Nonlinear Analysis: Modelling and Control, 27, 1-24.
  39. Gopalsamy, K., & He, X. Z. (1994). Delay-independent stability in bidirectional associative memory networks. IEEE Transactions on Neural Networks, 5(6), 998-1002.
  40. Yu, W., & Cao, J. (2006). Stability and Hopf bifurcation analysis on a four-neuron BAM neural network with time delays. Physics Letters A, 351(1-2), 64-78.
  41. Zhang, C., Zheng, B., & Wang, L. (2009). Multiple Hopf bifurcations of symmetric BAM neural network model with delay. Applied Mathematics Letters, 22(4), 616-622.
  42. Wu JH. (1998). Symmetric functional diferential equations and neural networks with memory. Trans Amer Meth Soc. 350(12), 4799–838.
  43. Tavazoei M. S. and Haeri M., 2007, Unreliability of frequency-domain approximation in recognizing chaos in fractional-order systems, IET Signal Proc., 1, 171-181.
  44. Smith, G. D. (1985). Numerical solution of partial differential equations: finite difference methods. Oxford university press.
Preprints 117482 g008
Figure 8. Synchronization of state variables of the neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 , and for incommensurate fractional orders q 1 = 0.78 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.669 , and q 6 = 0.910 .
Figure 8. Synchronization of state variables of the neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 , and for incommensurate fractional orders q 1 = 0.78 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.655 , q 5 = 0.669 , and q 6 = 0.910 .
Preprints 117482 g008
Preprints 117482 g009
Figure 9. Synchronization of state variables of the neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 , and for incommensurate fractional orders q 1 = 0.8 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.65 , q 5 = 0.67 , and q 6 = 0.910 .
Figure 9. Synchronization of state variables of the neuron for the fixed values of α = 12.2 , a = 0.5 , b = 2.0 , and for incommensurate fractional orders q 1 = 0.8 , q 2 = 0.673 , q 3 = 0.600 , q 4 = 0.65 , q 5 = 0.67 , and q 6 = 0.910 .
Preprints 117482 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated