Evaluating Changes in the Local Protein Physicochemical Environment induced by Molecular Dynamics Simulation

Chuyi Wang; Khalid Mahmood; Daniel Park

doi:10.20944/preprints202409.0689.v1

Submitted:

07 September 2024

Posted:

09 September 2024

You are already at the latest version

Abstract

Mutation of a single amino acid residue may significantly affect the structure and function of an entire protein. The effect of single amino acid substitutions can be assessed by examining the physicochemical environment surrounding the amino acid of interest, an emerging form of quantification of which is multidimensional tensors. However, the effect with respect to a protein variant’s inherent dynamics in tensor space is rarely assessed despite the potential importance of this form of analysis in revealing local physicochemical properties of the protein and response to mutation. Using the wild-type and 936 mutant structures of the protein domain 1pga, the present research evaluated the effects of local protein context and single amino acid substitutions on molecular dynamics simulation-derived structural distributions via the use of tensors capturing a range of biochemical properties. It was observed that the extent of simulated physicochemical variation local to a substituted amino acid is positively associated with local mechanical stiffness, loss of protein thermostability and decreased local hydrophobicity. In addition, it was observed that the largest tensor variation occurs in densely-packed, hydrophobic core-associated regions of protein structures. In summary, the pattern of tensor change aligns with prior knowledge about protein stability and physicochemical properties.

Keywords:

molecular dynamics simulation

;

protein

;

single amino acid substitution

;

protein local physicochemical environment

;

tensors

;

variant effect prediction

;

FireProtDB

Subject:

Biology and Life Sciences - Biochemistry and Molecular Biology

1. Introduction

A protein’s properties, including its three-dimensional structure, stability, mechanical stiffness and affinity to ligand molecules, are determined to a large extent by the identity of and interactions between its amino acid residues [1,2,3,4,5,6]. A single amino acid substitution, i.e., mutation of a single amino acid residue, may induce significant change in protein structure and function [2,3]. Thus, the evaluation and prediction of the changes in protein physicochemistry due to single-point amino acid substitutions deserve in-depth study.

An important way of assessing the effect of single amino acid substitutions is to examine the difference in the physicochemical environment surrounding the mutant and wild-type residues (‘local variation’), which has been represented in multiple applications with tensors - multidimensional matrices that can serve as quantifications of a protein’s three-dimensional structure and biochemical properties (wherein, separate “channels” can capture different specific properties) [7,8,9,10]. Indeed, tensors have become a contemporary form of input for emerging variant effect prediction programs that are capable of extracting informative high-dimensional patterns [9,10,11].

However, a protein’s three-dimensional structure is inherently mobile, and the ‘native’ state of the protein (as determined via x-ray crystallography for example) is only a single representation of the vast number of conformations a protein can assume. As such, upon protein mutation, evaluating the environment around the residue of interest in a static protein structure may be insufficient [12,13]. More informative, offering new perspectives, would be to assess the changes in a protein’s local physicochemistry in the context of a range of the protein’s inherent dynamic states.

The present research assessed the profiles of tensor changes relating to single amino acid substitutions via molecular dynamics simulation. New structures were sampled from molecular dynamics simulation trajectories in a range of mutant settings, and the relative profiles of tensors were examined with regard to a range of physicochemical parameters, i.e., the mechanical stiffness of the residue of interest, the change in whole-protein thermostability as a result of mutation and the change in the residue’s hydrophobicity upon single amino acid substitution. The protein structure 1pga (B1 immunoglobulin-binding domain of Streptococcal protein G) was selected as the model system due to the availability of thermostability change data for a large number of single amino acid substitutions.

2. Methods

2.1 Preliminary Dataset and Selection of Targets for Analysis

Raw protein thermostability change data were imported from FireProtDB, a manually-curated database established by Stourac et al. that records changes in thermostability as a result of single-point mutation [14]. FireProtDB is relatively current and manual curation (validation against original publications) has removed erroneous entries and annotations prevalent in earlier protein thermostability databases such as ProTherm and ProtaBank [14].

The present research used ΔΔG (as defined in FireProtDB, where ΔG refers to the Gibbs free energy of protein unfolding;

Δ Δ G = {Δ G}_{w i l d - t y p e} - {Δ G}_{m u t a n t}

) [14,15] as the quantification of protein thermostability change.

Data from FireProtDB were accessed and bulk-exported on Dec 11, 2023. The present research selected 1pga, a small protein domain containing both beta sheet and alpha helix structures, for focused molecular dynamic simulation and tensor sampling (local structural analysis), as it had 936 curated and ΔΔG-labelled mutant entries recorded in FireProtDB and at least 17 amino acid substitutions recorded for every residue (except residue 239). Furthermore, as a non-ligand-bound protein structure it was amenable to full automation of a molecular dynamics simulation pipeline.

Of the 936 mutant entries of 1pga, 105 entries had recorded ΔΔG value of 4 kcal/mol. In the original research by Nisthal et al. [15], the main source of 1pga thermostability data in FireProtDB, 4 kcal/mol was used to represent 'unspecified ΔΔG greater than or equal to 4 kcal/mol'. Therefore, the 105 1pga mutants with recorded ΔΔG value of 4 kcal/mol were removed in ΔΔG-related analyses. However, they were still taken into account in all other analyses, since all other parameters analysed were produced in the current research. In addition, the distribution of data points corresponding to ΔΔG greater than or equal to 4 kcal/mol can also be indicative of the relationship between ΔΔG, local structural variation and other variables.

Some unique 1pga mutations in FireProtDB were found to have multiple curated ΔΔG values recorded. In these cases, the arithmetic mean was used to represent the empirical ΔΔG.

2.2. Molecular Dynamics Simulation

Mutant protein structure PDBs were derived from wild-type PDBs with MODELLER, a homology-based biological macromolecular building programme [16,17], using a 'Mutate model' script written by Webb [18].

The protein dynamics of the wild-type structure and the 936 mutant structures of 1pga in aqueous solution were simulated via OpenMM [19,20]. A ‘protein in water’ simulation protocol was followed similar to that described in the paper by Eastman et al. that first described OpenMM 7 [19]. The current research used the AMBER-14 force field and the TIP3P-FB water model to simulate the solvent box surrounding the protein domain [19,21]. With the aim of sampling a variety of representational structures to reflect the dynamic nature of a protein structure in solution, the total runtime of molecular dynamics simulation was set as 80000 steps (320 ps), and snapshots were taken every 800 steps (3.2 ps). 1000 distinct frames of dynamic protein structures were yielded for each starting structure.

2.3. Local Physicochemical Variation Analysis

Tensors were generated around the residue of interest according to the protocol outlined in Li et al.’s research on predicting protein thermostability change with a 3D Convolutional Neural Network [9]. Given that their full tensor of dimensionality (1, 14, 16, 16, 16) actually represented the concatenation of two (1, 7, 16, 16, 16) component tensors (one describing the mutant residue and one describing the corresponding wild-type residue), the current research only generated and compared the (1, 7, 16, 16, 16) tensors. Of these numbers, ‘7’ refers to the seven physicochemical properties (‘channels’): hydrophobicity, aromaticity, H-bond acceptor, H-bond donor, positive ionisability, negative ionisability and occupancy [9]. Each number in the tensor space has a real value on a scale ranging from 0 to 1 [9].

A tensor is produced for each of the 1000 frames of a multi-frame PDB. For the set of 1000 tensors derived from each starting structure, the mean and standard deviation for both the Euclidean distance between every two whole unique tensors (‘whole-tensor Euclidean distance’) and the Euclidean distance between each channel of every two unique tensors (‘intra-channel Euclidean distance’) were calculated. For the purpose of the current research, ‘inter-tensor Euclidean distance’ serves as a general term that encompasses both whole-tensor Euclidean distance and intra-channel Euclidean distance. The Euclidean distances were calculated by subtracting one tensor from another, squaring all items in the matrix, taking the matrix sum and performing a square root operation.

Relationships between three physicochemical parameters, i.e., residual mechanical stiffness, ΔΔG (as recorded in FireProtDB) and change in residual hydrophobicity, and the distribution of whole-tensor and intra-channel Euclidean distances were assessed respectively. The mechanical stiffness of a residue, a constant with arbitrary unit, is calculated by building an anisotropic network model based on the inter-residue contacts of a protein and measuring the magnitude required to produce a certain degree of deformation of the forces applied along the direction of any two residues [22]. The Python-based protein dynamics analysis package ProDy (version 2.4.0) provides functions including ‘calcModes’ and ‘calcMechStiff’ that were used to build anisotropic network models and calculate mechanical stiffness [23]. The present research used Eisenberg et al.’s normalised consensus hydrophobicity scale as a quantification of residual hydrophobicity [24]. The original ‘consensus hydrophobicity scale’ was derived in 1982 when Eisenberg et al. unified five pre-existing experimentally determined hydrophobicity scales by using the hydrophobicity values of Serine as mean and measuring the distance of the hydrophobicity of each amino acid type from the mean in terms of number of standard deviations [25]; the normalised consensus hydrophobicity scale was established by further normalising the ‘consensus hydrophobicity scale’ to fit a normal distribution of mean 0 and standard deviation 1 [24]. In the current research, the change in residual hydrophobicity is calculated by subtracting the normalized consensus hydrophobicity value of the mutant residue from the normalized consensus hydrophobicity value of the wild-type residue (decrease in hydrophobicity will lead to positive ‘change of residual hydrophobicity’ and vice versa).

2.4. Physicochemical Property Correlation Analysis

To further interpret the outcomes of local physicochemical variation analysis, associations between residual mechanical stiffness, ΔΔG and change in residual hydrophobicity in the context of the wild-type structure and the 936 mutant structures of 1pga were assessed by calculating the Pearson’s correlation coefficient between the parameters.

3. Results

3.1. Local Physicochemical Variation Analysis

3.1.1. Magnitude and Spread of Variation in Tensor Space

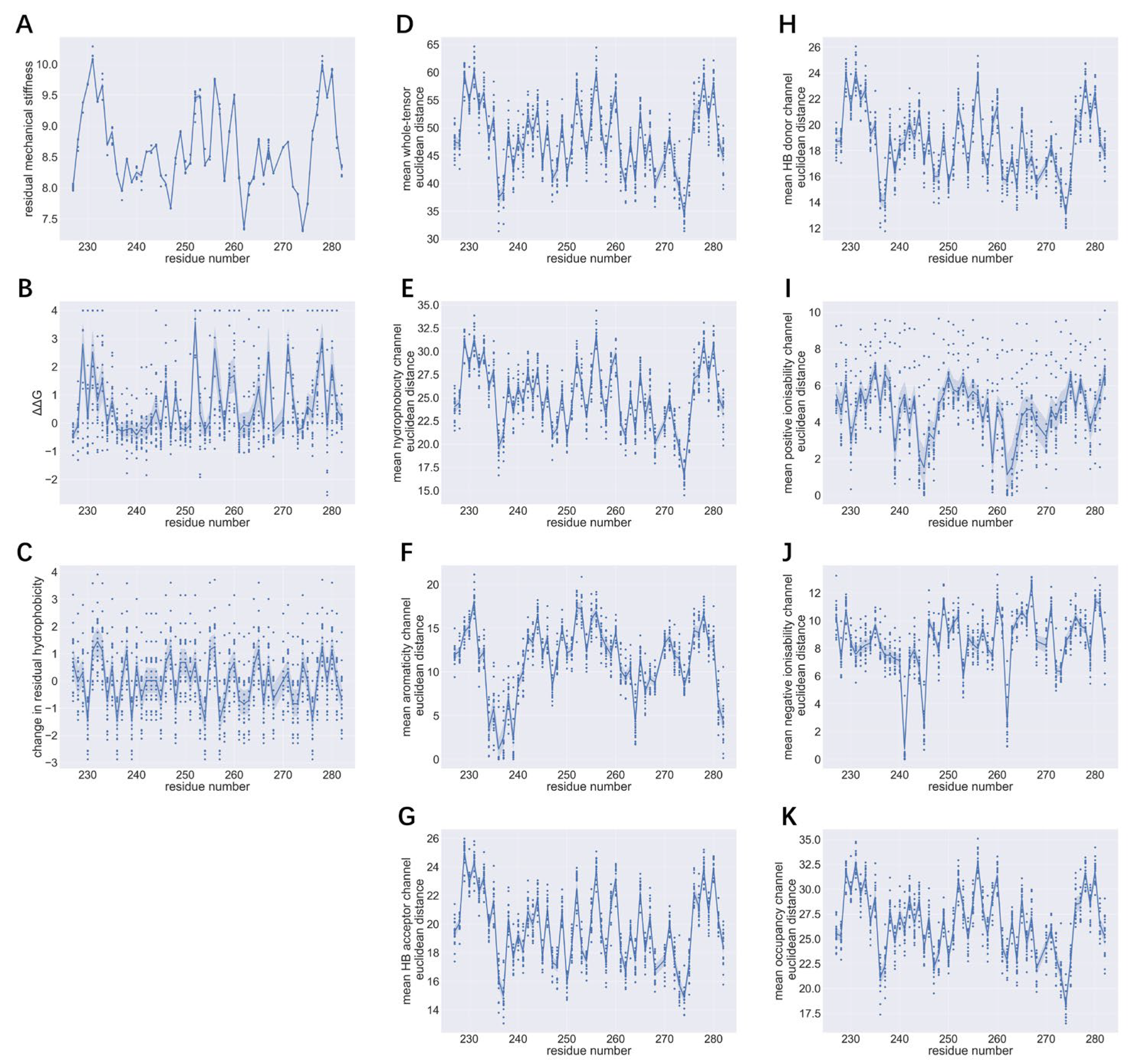
As shown in Figure 1 and Figure 2, residue substitution does not significantly change the mechanical stiffness at a given position. Figure 1A indicates that mechanical stiffness values of different amino acid variants of the same residue are closely clustered around a mean value.

As shown in Figure 1D, the mean Euclidean distance between whole tensors describing variants of 1pga can vary between 30 and 65 (arbitrary units). Of the seven channels (Figure 1E-K), the greatest contributors to inter-tensor differences were the hydrophobicity and occupancy channels, with both having mean intra-channel Euclidean distance ranging from 15 to 35; moderate orders of intra-channel variation were observed for the H-bond acceptor and H-bond donor channels (around 10-26); zero mean Euclidean distances were apparent for aromaticity, positive ionisability and negative ionisability channels, and the mean intra-channel Euclidean distances of these three channels were relatively small. As aromaticity and ionisability are physicochemical properties that are intrinsically linked with the type of amino acid around which the tensor is established, small variation in channels representing such properties is as expected in the absence of amino acid residues with such properties.

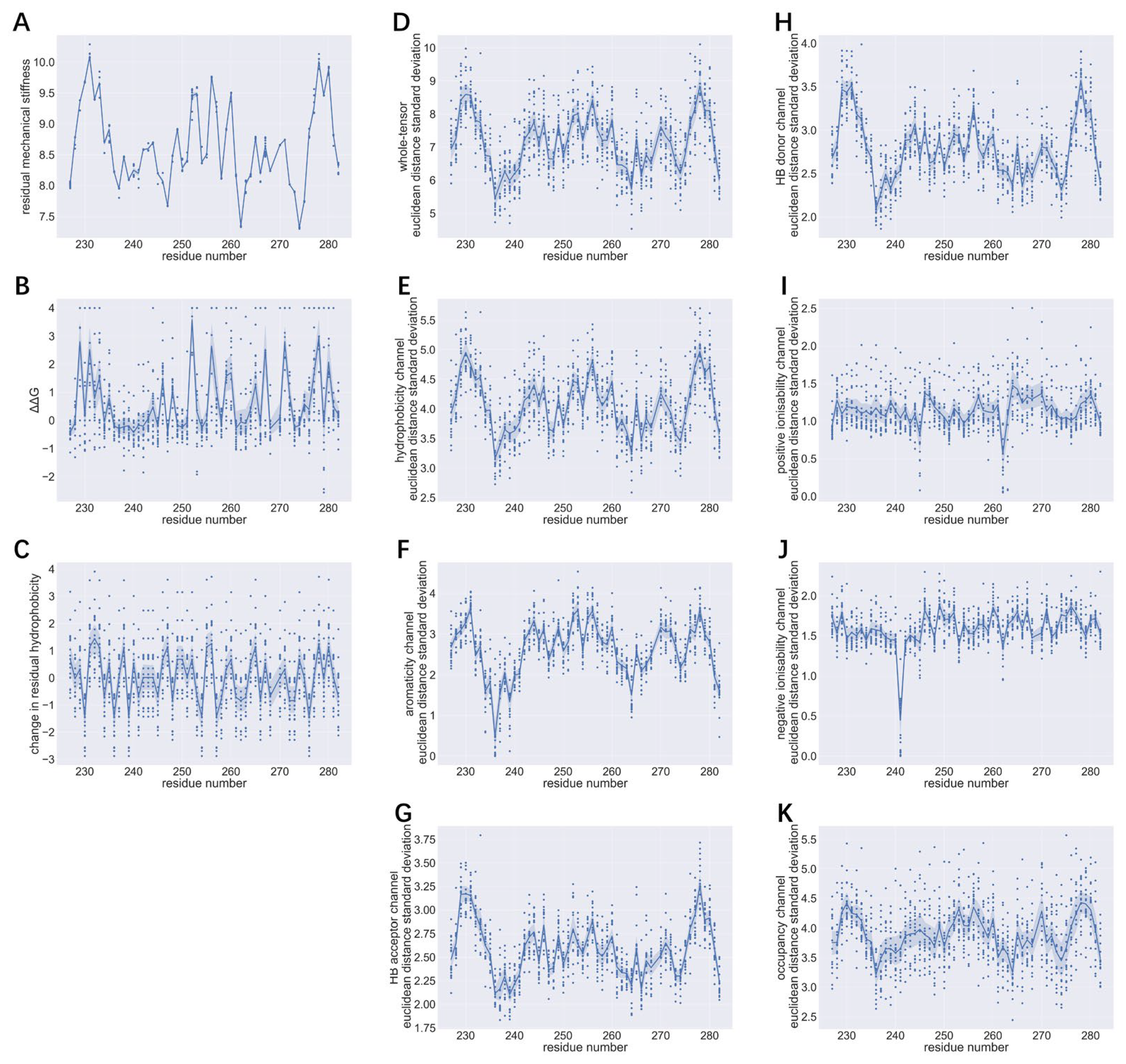
As shown in Figure 2D, standard deviation of whole-tensor Euclidean distances ranges from 5 to 10. The smallest mean whole-tensor Euclidean distance being over 30 indicates that even for a residue with minimal whole-tensor Euclidean distance and maximum whole-tensor Euclidean distance standard deviation, 95% of Euclidean distance values will fall between 10 and 50 (mean ± 2 standard deviations). This means that for each PDB model, the 1000 tensors generated are mostly substantially distinct from each other. Regarding each channel, the largest intra-channel Euclidean distance standard deviation is seen in hydrophobicity and occupancy channels (both 2.5-5.5, Figure 2E, 2K). This suggests that the amount of intra-channel change induced by protein dynamics simulation is also the most variable for these two channels. Similar levels of intra-channel Euclidean distance standard deviations are seen for the H-bond acceptor and H-bond donor channels (1.75-4, Figure 2G-H). As assessed by mean intra-channel Euclidean distance, channels highly-dependent on residual physicochemical properties (aromaticity and ionisability channels) are the smallest contributors to inter-tensor Euclidean distance standard deviation and can have zero intra-channel standard deviation (Figure 2F, 2I, 2J).

The shapes of the profiles of mean whole-tensor Euclidean distance and whole-tensor Euclidean distance standard deviation share similarities with profiles of mechanical stiffness, ΔΔG and hydrophobicity change, and particularly resemble the profile of mechanical stiffness (Figure 1A). Peaks in the profile of mean whole-tensor Euclidean distances are associated with large values of whole-tensor Euclidean distance standard deviation (Figure 2D), high residual mechanical stiffness (Figure 1A), high ΔΔG (Figure 1B) and significant decrease in hydrophobicity at mutant residue (Figure 1C).

Of the seven channels, the shapes of the mean intra-channel Euclidean distance profiles of channels representing hydrophobicity, H-bond donor, H-bond acceptor and occupancy bear the strongest resemblance to the shape of the profile for mean whole-tensor Euclidean distance (Figure 1E, G, H, K), while the shapes of the intra-channel Euclidean distance standard deviation profiles for hydrophobicity, H-bond donor and H-bond acceptor channels are most similar to the shape of the profile of whole-tensor Euclidean distance standard deviation (Figure 2E, G, H). Notably, the intra-channel Euclidean distance standard deviations for the ionisability channels (Figure 2I-J) approach uniformity across the entire protein structure.

Peaks in distribution profiles for whole-tensor and intra-channel Euclidean distance standard deviations correlate with large residual mechanical stiffness and high ΔΔG, but the association between tensor Euclidean distance standard deviations and change of hydrophobicity at the site of interest appears to be more ambiguous, for the peak positions do not show a clear correspondence.

3.1.2. Relationship between Mean Inter-Tensor Euclidean Distance, Residual Mechanical Stiffness, ΔΔG and Decrease in Residual Hydrophobicity

As shown in Figure S1-S3, all subplots can be fitted with linear regression.

Table 1 indicates that mean whole-tensor Euclidean distance has strong and positive association with residual mechanical stiffness. Mean whole-tensor Euclidean distance’s respective associations with ΔΔG and decrease of hydrophobicity are positive and visible, but are less significant than the relationship between mean whole tensor Euclidean distance and residual mechanical stiffness.

As shown in Table 1, regarding separate channels, strong positive associations are identified between residual mechanical stiffness and mean Euclidean distance of channels describing hydrophobicity, H-bond acceptor, H-bond donor and occupancy respectively. Weaker associations are found between residual mechanical stiffness and mean Euclidean distance of aromaticity, positive ionisability and negative ionisability channels respectively.

The relationships between mean intra-channel Euclidean distances and ΔΔG follow similar patterns to those between mean inter-tensor Euclidean distances and residual mechanical stiffness (Table 1), though relatively weakly.

The relationships between mean intra-channel Euclidean distances and decrease of residual hydrophobicity are similar to those between mean intra-channel Euclidean distances and ΔΔG in terms of magnitude, but exhibit patterns different from those between intra-channel Euclidean distances and other parameters (Table 1). The strongest positive associations with decrease of hydrophobicity are identified in channels describing positive ionisability, H-bond acceptor and H-bond donor. Channels describing hydrophobicity and occupancy show less significant associations with decrease of residual hydrophobicity, the magnitudes of which are closer to the association between negative ionisability channel and decrease of hydrophobicity. The least association with decrease of residual hydrophobicity is identified for the aromaticity channel.

3.1.3. Relationships between Inter-Tensor Euclidean Distance Standard Deviations, Residual Mechanical Stiffness, ΔΔG and Decrease in Residual Hydrophobicity

As shown in Figure S4-S6, all subplots can be fitted with linear regression.

As indicated by Table 2, the relationships between intra-channel Euclidean distance standard deviations, mechanical stiffness, ΔΔG and change in residual hydrophobicity follow similar patterns to those between mean intra-channel Euclidean distances, residual mechanical stiffness, ΔΔG and decrease of residual hydrophobicity shown in Table 1. Notably, though comparable to the Euclidean distance standard deviation of hydrophobicity channel in terms of magnitude (Figure 2K), the Euclidean distance standard deviation of occupancy channel has much less significant correlation with residual mechanical stiffness, ΔΔG and change in residual hydrophobicity.

3.2. Physicochemical Property Correlation Analysis

As shown in Table 3, there is positive correlation between residual mechanical stiffness, ΔΔG and change in residual hydrophobicity. Since the 936 mutations of 1pga cover almost all possible mutants of the protein domain except those with substituted residue 269, the results from Table 4 have a low possibility of being a result of confounding.

4. Discussion

The present research shows that, regarding variants of the protein domain 1pga, for a tensor describing the environment around a residue of interest, the magnitude of tensor change induced by molecular dynamics simulation is positively associated with the mechanical stiffness of the residue, the ΔΔG of the protein structure variant and the decrease in the residue’s hydrophobicity due to single-amino-acid substitution.

Of the seven channels examined, the hydrophobicity and occupancy channels contribute most to the change of the tensor (having the largest mean inter-tensor Euclidean distance values). Changes in hydrophobicity, H-bond acceptor, H-bond donor and occupancy channels exhibit the strongest positive association with residual mechanical stiffness and ΔΔG, while changes in positive ionisability, H-bond acceptor and H-bond donor channels exhibit the strongest positive association with decrease in residual hydrophobicity. Changes in the aromaticity channel and negative ionisability channels show less association with residual mechanical stiffness, ΔΔG and decrease of residual hydrophobicity compared to those of the other channels, since they depend on the presence or absence of aromatic or ionisable amino acid residues in the vicinity of the residue of interest.

The analysis conducted by Eyal et al. on green fluorescent protein, human ubiquitin and E2lip3 domain of pyruvate dehydrogenase revealed possible correlation between protein regions with relatively-high mechanical stiffness values and protein secondary structure elements [22]. As higher mechanical stiffness is significantly associated with greater mean and spread of inter-tensor Euclidean distance (Table 1 and Table 2), residues that belong to secondary structures are more likely to experience notable local physicochemical environment change as a result of molecular dynamics simulation. However, a more rigorous statistical analysis performed on a larger number of residues from a more diverse range of proteins is required to conclusively prove this association.

Peaks of mean whole-tensor Euclidean distance are found at residue numbers 229, 231, 233, 252, 256, 260, 278 and 280 (Figure 1 and Figure 2). These regions correspond to large values of whole-tensor Euclidean distance standard deviation and largely coincide with peaks of residual mechanical stiffness, ΔΔG and decrease of residual hydrophobicity.

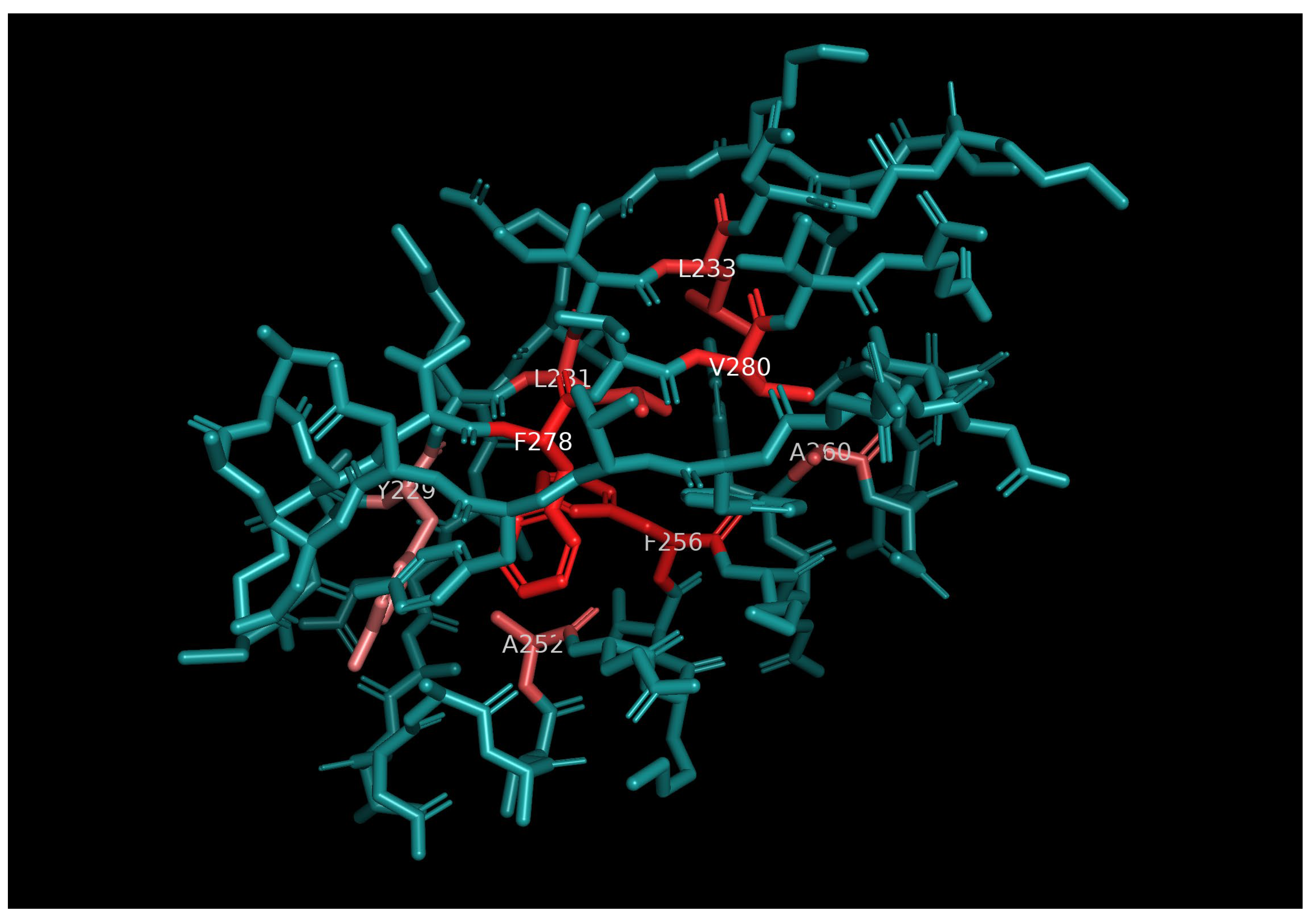
As shown in Figure 3, the residues corresponding to large mean whole-tensor Euclidean distance and whole-tensor standard deviation values are to a large extent the residues that form the hydrophobic core of the protein domain 1pga, which is the region within 1pga with the highest hydrophobicity, occupancy and stiffness.

The current knowledge of factors influencing protein thermostability indicates that hydrophobicity and Van Der Waals forces are regarded as the dominant driving forces of thermostability and stable folding [3,26], while H-bonding and ionic interactions contribute less to protein thermostability [3,27]. The combined effect of numerous hydrophobic interactions and inter-residual Van Der Waals forces within the hydrophobic core stabilises the protein at its native, folded state, and mutations that occur at rigid, high-occupancy (high Van Der Waals force concentration) regions of a protein structure, especially hydrophobic core regions, are most likely to result in the structure’s thermal destabilisation [3].

The aforementioned knowledge aligns with the observations from Figure 1, Figure 2 and Figure 3 and Table 1 and Table 2, i.e., regions that are more densely packed, more hydrophobic and more crucial to the overall structural integrity of the protein domain tend to undergo greater alteration to tensor space, and regions that are loosely-packed, disordered, less important to protein structural integrity and further away from the hydrophobic core tend to experience less tensor alteration. This shows that the new tensors generated through molecular dynamics simulation are composed in accordance with the established determinants for protein thermostability, conferring confidence in their validity in representing a range of protein dynamic states.

In view of the associations between the distribution of inter-tensor Euclidean distance and various physicochemical parameters, it may be possible to use the mean and spread of both whole-tensor Euclidean distance and intra-channel Euclidean distances as predictor variables in machine learning models describing a protein’s change in physicochemical properties upon single amino acid substitution.

Tensors have been applied as inputs for variant effect predictors such as the protein thermostability change predictor ThermoNet (the tensor generation programme of which is used in the current research) [9]. As prediction accuracy of variant effect predictors is limited by the amount and quality of data fed into the program for training [9,28], another application of the findings of the current research may be the expansion of pre-existing protein local physicochemical data with the aid of molecular dynamics simulation in order to provide variant effector predictors with a larger training set for the derivation of more accurate predictions, i.e. ‘molecular dynamics simulation-based data augmentation’ [29]. However, as the scope of the current research is limited to the evaluation of the change in tensor space induced by molecular dynamics simulation, further experiments involving the comparison of variant effector predictor instances trained on original and expanded datasets are needed to confirm the validity of this approach.

In fact, a major issue with ‘molecular dynamics simulation-based data augmentation’ might be that for the residues situated at unstructured and flexible regions distal to the hydrophobic core, the diversity of data generated may be limited. When they are involved in an expanded training dataset, the results produced by a variant effect predictor may be biased. However, the problem may be circumvented by using molecular dynamics simulation-based data augmentation in conjunction with other data augmentation techniques such as protein model rotation. Thus, more research is necessary to fully understand the properties and applicability of molecular dynamics simulation-based data augmentation, as well as the ways to mitigate its potential issues.

In conclusion, the current research can be further expanded in multiple directions, and may eventually prove important for the prediction of protein physicochemical property change upon mutation.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure S1: Association between residual mechanical stiffness and mean Euclidean distance between pairs of tensors for: (A) whole-tensor (all channels); (B) hydrophobicity channel; (C) aromaticity channel; (D) H-bond acceptor channel; (E) H-bond donor channel; (F) positive ionisability channel; (G) negative ionisability channel; (H) occupancy channel. For Figure 1A-H: BLUE LINES: linear regression line; BLUE SHADE: 95% confidence interval of regression line; Figure S2: Association between ΔΔG and mean Euclidean distance between pairs of tensors for: (A) whole-tensor (all channels); (B) hydrophobicity channel; (C) aromaticity channel; (D) H-bond acceptor channel; (E) H-bond donor channel; (F) positive ionisability channel; (G) negative ionisability channel; (H) occupancy channel. For Figure 1A-H: BLUE LINES: linear regression line; BLUE SHADE: 95% confidence interval of regression line; Figure S3: Association between change in hydrophobicity and mean Euclidean distance between pairs of tensors for: (A) whole-tensor (all channels); (B) hydrophobicity channel; (C) aromaticity channel; (D) H-bond acceptor channel; (E) H-bond donor channel; (F) positive ionisability channel; (G) negative ionisability channel; (H) occupancy channel. For Figure 1A-H: BLUE LINES: linear regression line; BLUE SHADE: 95% confidence interval of regression line; Figure S4: Association between residual mechanical stiffness and Euclidean distance standard deviation between pairs of tensors for: (A) whole-tensor (all channels); (B) hydrophobicity channel; (C) aromaticity channel; (D) H-bond acceptor channel; (E) H-bond donor channel; (F) positive ionisability channel; (G) negative ionisability channel; (H) occupancy channel. For Figure 1A-H: BLUE LINES: linear regression line; BLUE SHADE: 95% confidence interval of regression line; Figure S5: Association between ΔΔG and Euclidean distance standard deviation between pairs of tensors for: (A) whole-tensor (all channels); (B) hydrophobicity channel; (C) aromaticity channel; (D) H-bond acceptor channel; (E) H-bond donor channel; (F) positive ionisability channel; (G) negative ionisability channel; (H) occupancy channel. For Figure 1A-H: BLUE LINES: linear regression line; BLUE SHADE: 95% confidence interval of regression line; Figure S6: Association between change in hydrophobicity and Euclidean distance standard deviation between pairs of tensors for: (A) whole-tensor (all channels); (B) hydrophobicity channel; (C) aromaticity channel; (D) H-bond acceptor channel; (E) H-bond donor channel; (F) positive ionisability channel; (G) negative ionisability channel; (H) occupancy channel. For Figure 1A-H: BLUE LINES: linear regression line; BLUE SHADE: 95% confidence interval of regression line.

Author Contributions

The manuscript was written through the contributions of all authors. Conceptualization: Chuyi Wang, Daniel Park, Khalid Mahmood; data curation: Chuyi Wang, Daniel Park, Khalid Mahmood; formal analysis: Chuyi Wang, Daniel Park, Khalid Mahmood; methodology: Chuyi Wang, Daniel Park, Khalid Mahmood; software: Chuyi Wang, Daniel Park, Khalid Mahmood; supervision: Daniel Park, Khalid Mahmood; visualisation: Chuyi Wang, Daniel Park, Khalid Mahmood; writing – original draft: Chuyi Wang; writing – review and editing: Chuyi Wang, Daniel Park, Khalid Mahmood.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

PDB files of all 1pga variants and scripts used for the research can be found at https://github.com/cywangbio/IJMS-tensor-MDS. Further inquiries can be directed to the corresponding authors.

Acknowledgments

The authors would like to acknowledge the Research Computing Services at The University of Melbourne whose high-performance computing system SPARTAN significantly enhanced the efficiency of the current research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Anfinsen C. B. (1973). Principles that govern the folding of protein chains. Science (New York, N.Y.), 181(4096), 223–230. [CrossRef]
Choudhury, A., Mohammad, T., Anjum, F., Shafie, A., Singh, I. K., Abdullaev, B., Pasupuleti, V. R., Adnan, M., Yadav, D. K., & Hassan, M. I. (2022). Comparative analysis of web-based programs for single amino acid substitutions in proteins. PloS one, 17(5), e0267084. [CrossRef]
Goldenzweig, A., & Fleishman, S. J. (2018). Principles of Protein Stability and Their Application in Computational Design. Annual review of biochemistry, 87, 105–129. [CrossRef]
Jankovic, B., & Polovic, N. (2017). The protein folding problem. 39, 105–111. [CrossRef]
Thusberg, J., & Vihinen, M. (2009). Pathogenic or not? And if so, then how? Studying the effects of missense mutations using bioinformatics methods. Human mutation, 30(5), 703–714. [CrossRef]
Torrisi, M., Pollastri, G., & Le, Q. (2020). Deep learning methods in protein structure prediction. Computational and structural biotechnology journal, 18, 1301–1310. [CrossRef]
Bakkers, M. J. G., Ritschel, T., Tiemessen, M., Dijkman, J., Zuffianò, A. A., Yu, X., van Overveld, D., Le, L., Voorzaat, R., van Haaren, M. M., de Man, M., Tamara, S., van der Fits, L., Zahn, R., Juraszek, J., & Langedijk, J. P. M. (2024). Efficacious human metapneumovirus vaccine based on AI-guided engineering of a closed prefusion trimer. Nature communications, 15(1), 6270. [CrossRef]
Diaz, D. J., Kulikova, A. V., Ellington, A. D., & Wilke, C. O. (2023). Using machine learning to predict the effects and consequences of mutations in proteins. Current opinion in structural biology, 78, 102518. [CrossRef]
Li, B., Yang, Y. T., Capra, J. A., & Gerstein, M. B. (2020). Predicting changes in protein thermodynamic stability upon point mutation with deep 3D convolutional neural networks. PLoS computational biology, 16(11), e1008291. [CrossRef]
Wen, T., & Altman, R. B. (2017). 3D deep convolutional neural networks for amino acid environment similarity analysis. BMC bioinformatics, 18(1), 302. [CrossRef]
Betts, M. J., Lu, Q., Jiang, Y., Drusko, A., Wichmann, O., Utz, M., Valtierra-Gutiérrez, I. A., Schlesner, M., Jaeger, N., Jones, D. T., Pfister, S., Lichter, P., Eils, R., Siebert, R., Bork, P., Apic, G., Gavin, A. C., & Russell, R. B. (2015). Mechismo: predicting the mechanistic impact of mutations and modifications on molecular interactions. Nucleic acids research, 43(2), e10. [CrossRef]
Nam, K., & Wolf-Watz, M. (2023). Protein dynamics: The future is bright and complicated!. Structural dynamics (Melville, N.Y.), 10(1), 014301. [CrossRef]
Rueda, M., Ferrer-Costa, C., Meyer, T., Pérez, A., Camps, J., Hospital, A., Gelpí, J. L., & Orozco, M. (2007). A consensus view of protein dynamics. Proceedings of the National Academy of Sciences of the United States of America, 104(3), 796–801. [CrossRef]
Stourac, J., Dubrava, J., Musil, M., Horackova, J., Damborsky, J., Mazurenko, S., & Bednar, D. (2021). FireProtDB: database of manually curated protein stability data. Nucleic acids research, 49(D1), D319–D324. [CrossRef]
Nisthal, A., Wang, C. Y., Ary, M. L., & Mayo, S. L. (2019). Protein stability engineering insights revealed by domain-wide comprehensive mutagenesis. Proceedings of the National Academy of Sciences of the United States of America, 116(33), 16367–16377. [CrossRef]
Eswar, N., Webb, B., Marti-Renom, M. A., Madhusudhan, M. S., Eramian, D., Shen, M. Y., Pieper, U., & Sali, A. (2006). Comparative protein structure modeling using Modeller. Current protocols in bioinformatics, Chapter 5, Unit–5.6. [CrossRef]
Webb, B., & Sali, A. (2014). Protein structure modeling with MODELLER. Methods in molecular biology (Clifton, N.J.), 1137, 1–15. [CrossRef]
Webb, B. (2022). Mutate model. Modeller Wiki. https://salilab.org/modeller/wiki/Mutate_model.
Eastman, P., Swails, J., Chodera, J. D., McGibbon, R. T., Zhao, Y., Beauchamp, K. A., Wang, L. P., Simmonett, A. C., Harrigan, M. P., Stern, C. D., Wiewiora, R. P., Brooks, B. R., & Pande, V. S. (2017). OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLoS computational biology, 13(7), e1005659.
Eastman, P., Galvelis, R., Peláez, R. P., Abreu, C. R. A., Farr, S. E., Gallicchio, E., Gorenko, A., Henry, M. M., Hu, F., Huang, J., Krämer, A., Michel, J., Mitchell, J. A., Pande, V. S., Rodrigues, J. P., Rodriguez-Guerra, J., Simmonett, A. C., Singh, S., Swails, J., Turner, P., … Markland, T. E. (2024). OpenMM 8: Molecular Dynamics Simulation with Machine Learning Potentials. The journal of physical chemistry. B, 128(1), 109–116. [CrossRef]
Orozco M. (2014). A theoretical view of protein dynamics. Chemical Society reviews, 43(14), 5051–5066. [CrossRef]
Eyal, E., & Bahar, I. (2008). Toward a molecular understanding of the anisotropic response of proteins to external forces: insights from elastic network models. Biophysical journal, 94(9), 3424–3435. [CrossRef]
Bakan, A., Meireles, L. M., & Bahar, I. (2011). ProDy: protein dynamics inferred from theory and experiments. Bioinformatics (Oxford, England), 27(11), 1575–1577. [CrossRef]
Eisenberg, D., Schwarz, E., Komaromy, M., & Wall, R. (1984). Analysis of membrane and surface protein sequences with the hydrophobic moment plot. Journal of molecular biology, 179(1), 125–142. [CrossRef]
Eisenberg, D.S., Weiss, R.M., Terwilliger, T.C., & Wilcox, W.R. (1982). Hydrophobic moments and protein structure. Faraday Symposia of The Chemical Society, 17, 109-120.
Dill K. A. (1990). Dominant forces in protein folding. Biochemistry, 29(31), 7133–7155. [CrossRef]
Pace, C. N., Scholtz, J. M., & Grimsley, G. R. (2014). Forces stabilizing proteins. FEBS letters, 588(14), 2177–2184. [CrossRef]
Fang J. (2020). A critical review of five machine learning-based algorithms for predicting protein stability changes upon mutation. Briefings in bioinformatics, 21(4), 1285–1292. [CrossRef]
Mumuni, A., & Mumuni, F. (2022). Data augmentation: A comprehensive survey of modern approaches. Array, 16, 100258. [CrossRef]

Figure 1. Profiles across 1pga residue positions (dots represent individual amino acid variants) with respect to: (A) mechanical stiffness; (B) ΔΔG; (C) change in hydrophobicity; and mean Euclidean distance between pairs of tensors for: (D) whole-tensor (all channels); (E) hydrophobicity channel; (F) aromaticity channel; (G) H-bond acceptor channel; (H) H-bond donor channel; (I) positive ionisability channel; (J) negative ionisability channel; (K) occupancy channel. For Figure 1A-K: BLUE LINES: mean of parameter/mean inter-tensor Euclidean distance at each residue position. BLUE SHADE: 95% confidence interval of the mean values at each residue position.

Figure 2. Profiles across 1pga residue positions (dots represent individual amino acid variants) with respect to: (A) mechanical stiffness; (B) ΔΔG; (C) change in hydrophobicity; and Euclidean distance standard deviation between pairs of tensors for: (D) whole-tensor (all channels); (E) hydrophobicity channel; (F) aromaticity channel; (G) H-bond acceptor channel; (H) H-bond donor channel; (I) positive ionisability channel; (J) negative ionisability channel; (K) occupancy channel. For Figure 1A-K: BLUE LINES: mean of parameter/inter-tensor Euclidean distance standard deviation at each residual position. BLUE SHADE: 95% confidence interval of the mean values at each residual position.

Figure 3. Positions of the residues that are associated with high mean inter-tensor Euclidean distances. Key residues were coloured red, with the intensity of red hue reflecting magnitude of hydrophobicity. PINK RESIDUES (MODERATE HYDROPHOBICITY): Y229, A252, A260; RED RESIDUES (STRONG HYDROPHOBICITY): L231, L233, F256, F278, V280.

Table 1. Relationships between mean inter-tensor Euclidean distances, residual mechanical stiffness, ΔΔG and change in residual hydrophobicity as quantified with Pearson’s correlation coefficients. For determination of Pearson’s correlation coefficients with ΔΔG, data with ΔΔG labelled in FireProtDB as 4 kcal/mol are excluded.

Mean Intra-channel Euclidean distance	Residual mechanical stiffness	ΔΔG (kcal/mol)	Change in residual hydrophobicity
Whole-tensor (all channels)	0.823 (p-value 6.729×10-245)	0.324 (p-value 3.359×10-23)	0.300 (p-value 4.009×10-22)
Hydrophobicity	0.807 (p-value 5.300×10-228)	0.318 (p-value 2.73 × 10-22)	0.269 (p-value 7.058×10-18)
Aromaticity	0.530 (p-value 1.026×10-72)	0.167 (p-value 5.39 × 10-7)	0.114 (p-value 3.312×10-4)
H-bond acceptor	0.786 (p-value 8.047×10-209)	0.353 (p-value 2.00 × 10-27)	0.288 (p-value 2.232×10-20)
H-bond donor	0.809 (p-value 1.387×10-230)	0.301 (p-value 5.38 × 10-20)	0.347 (p-value 2.319×10-29)
Positive ionisability	0.125 (p-value 8.139×10-5)	0.0131 (p-value 0.696)	0.431 (p-value 4.290×10-46)
Negative ionisability	0.251 (p-value 9.299×10-16)	0.201 (p-value 1.53 × 10-9)	0.224 (p-value 1.044×10-12)
Occupancy	0.806 (p-value 2.365×10-227)	0.301 (p-value 4.63 × 10-20)	0.266 (p-value 1.738×10-17)

Table 2. Relationship between intra-channel Euclidean distance standard deviations, residual mechanical stiffness, ΔΔG and change in residual hydrophobicity as quantified with Pearson’s correlation coefficients. For determination of Pearson’s correlation coefficients with ΔΔG, data with ΔΔG labelled in FireProtDB as 4 kcal/mol are excluded.

Intra-channel Euclidean distance standard deviation	Residual mechanical stiffness	ΔΔG (kcal/mol)	Change in residual hydrophobicity
Whole-tensor (all channels)	0.624 (p-value 5.438×10^-108)	0.216 (p-value 7.265×10^-11)	0.196 (p-value 4.756×10^-10)
Hydrophobicity	0.642 (p-value 3.95 × 10^-116)	0.228 (p-value 5.97 × 10^-12)	0.198 (p-value 3.473×10^-10)
Aromaticity	0.479 (p-value 5.92 × 10^-58)	0.151 (p-value 5.99× 10^-6)	0.102 (p-value 0.00126)
H-bond acceptor	0.670 (p-value 6.14 × 10^-130)	0.262 (p-value 1.88 × 10^-15)	0.240 (p-value 1.798×10^-14)
H-bond donor	0.701 (p-value 2.41 × 10^-147)	0.245 (p-value 1.21 × 10^-13)	0.244 (p-value 6.780×10^-15)
Positive ionisability	0.129 (p-value 4.43 × 10^-5)	0.0588 (p-value 0.0797)	0.282 (p-value 1.428×10^-19)
Negative ionisability	0.081 (p-value 0.0109)	0.163 (p-value 1.10× 10^-6)	0.193 (p-value 8.300×10^-10)
Occupancy	0.436 (p-value 2.37 × 10^-47)	0.115 (p-value 0.000588)	0.114 (p-value 0.000321)

Table 3. Pearson’s correlation coefficients between residual mechanical stiffness, ΔΔG and change in residual hydrophobicity. During the derivation of the table, data with ΔΔG labelled in FireProtDB as 4 kcal/mol are excluded.

	Residual mechanical stiffness	ΔΔG (kcal/mol)
Residual mechanical stiffness
ΔΔG (kcal/mol)	0.461 (p-value 3.57 × 10^-53)
Change in residual hydrophobicity	0.204 (p-value 8.52 × 10^-11)	0.277 (p-value 5.62 × 10^-19)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.