Submitted:
09 September 2024
Posted:
09 September 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
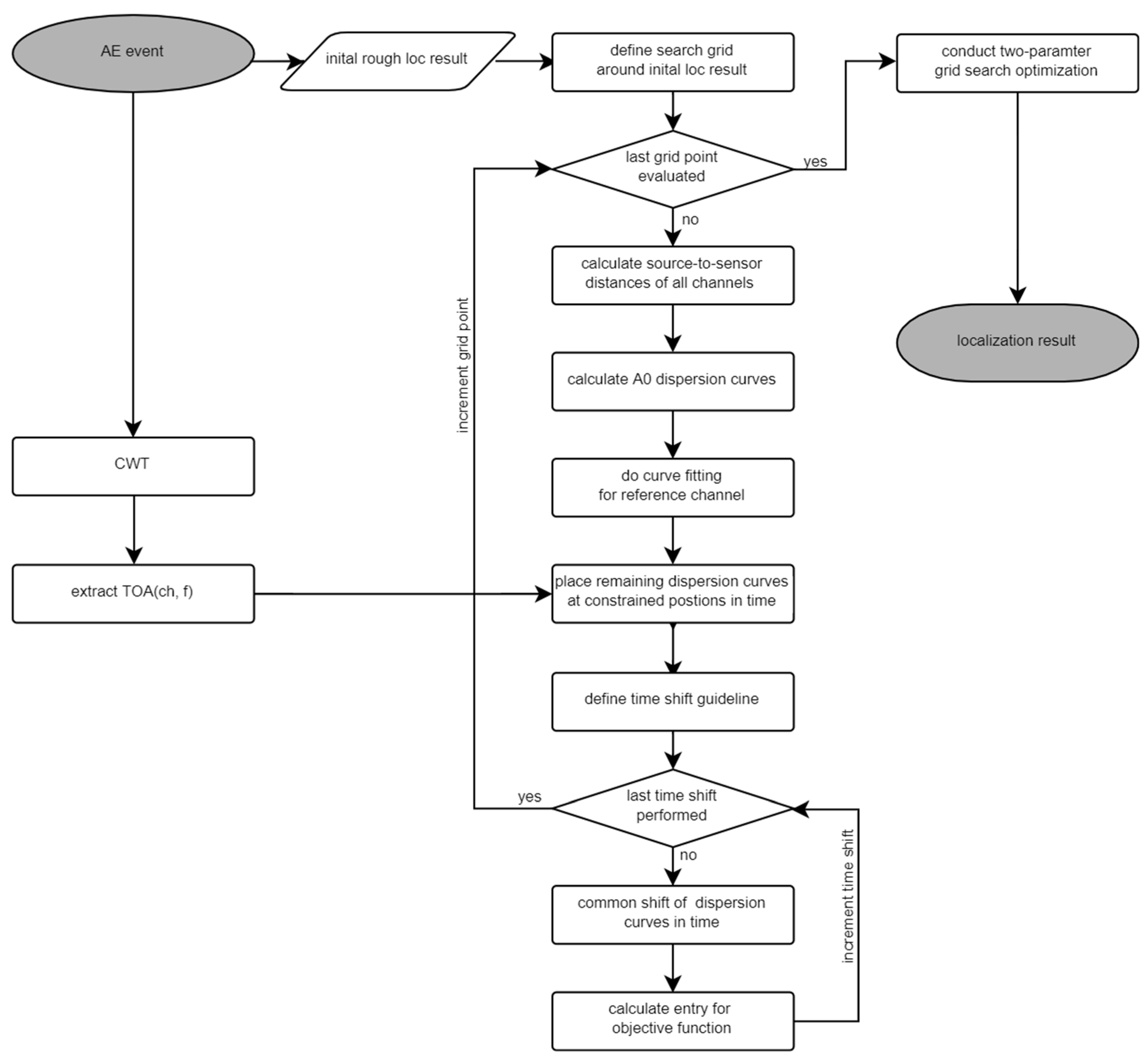
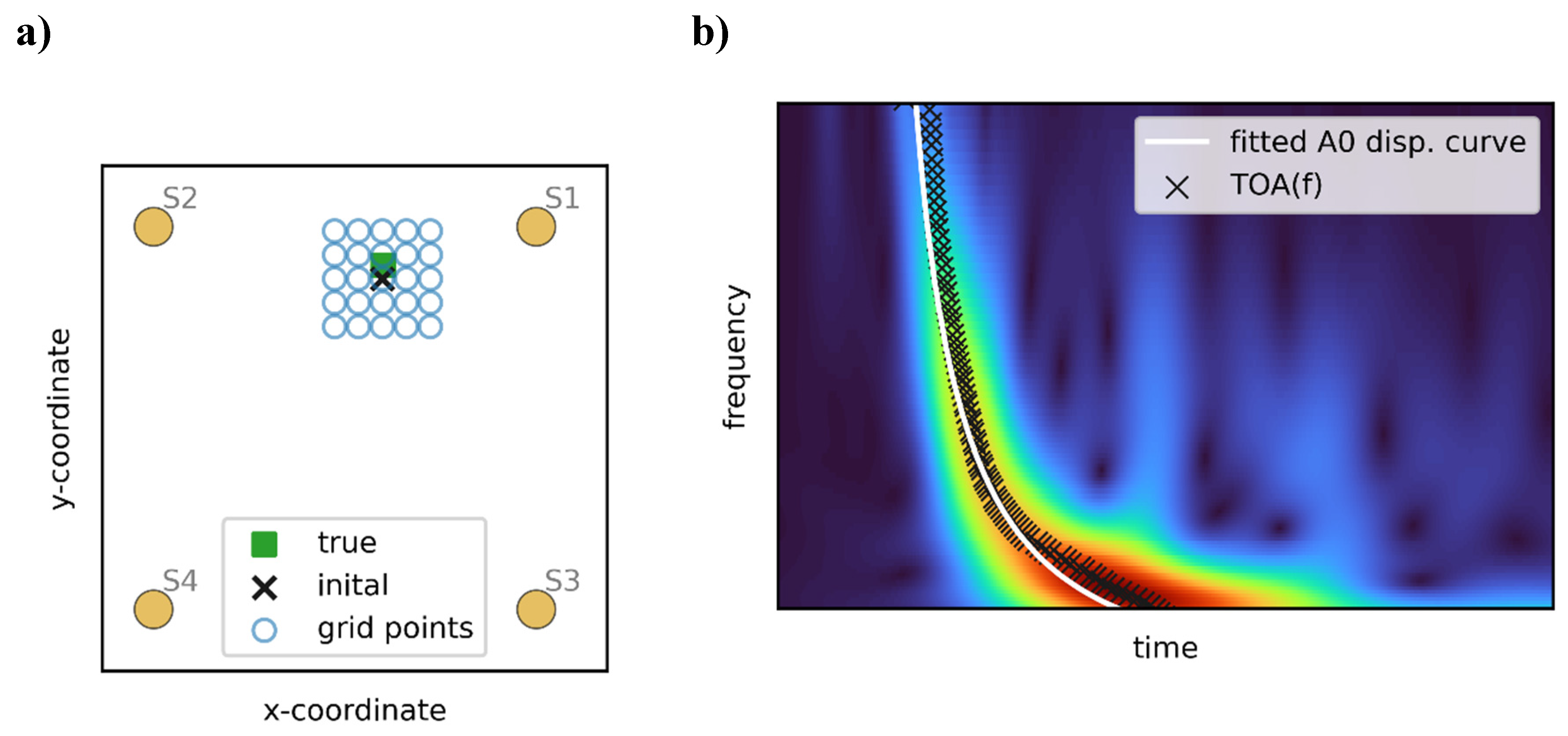
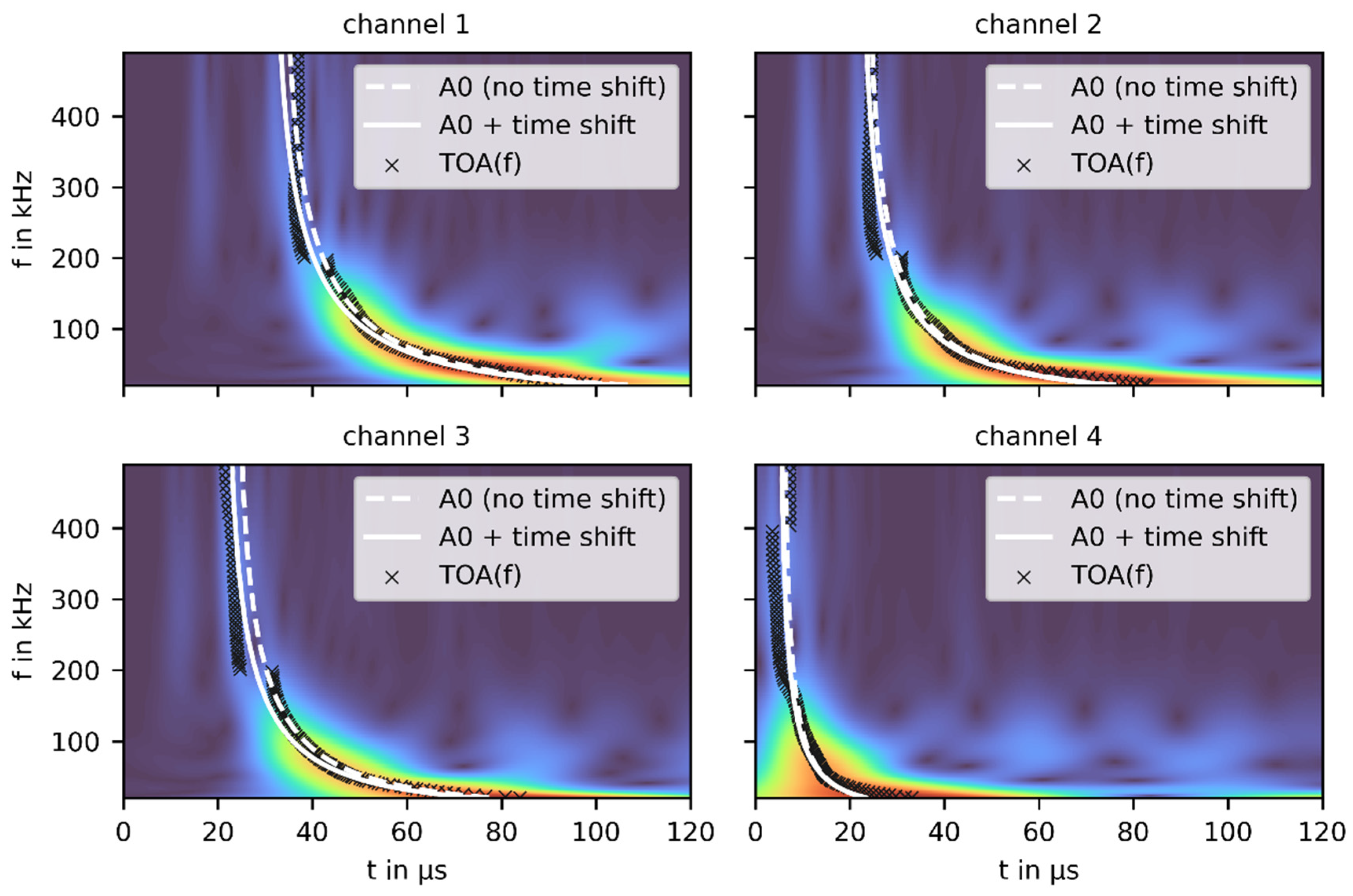
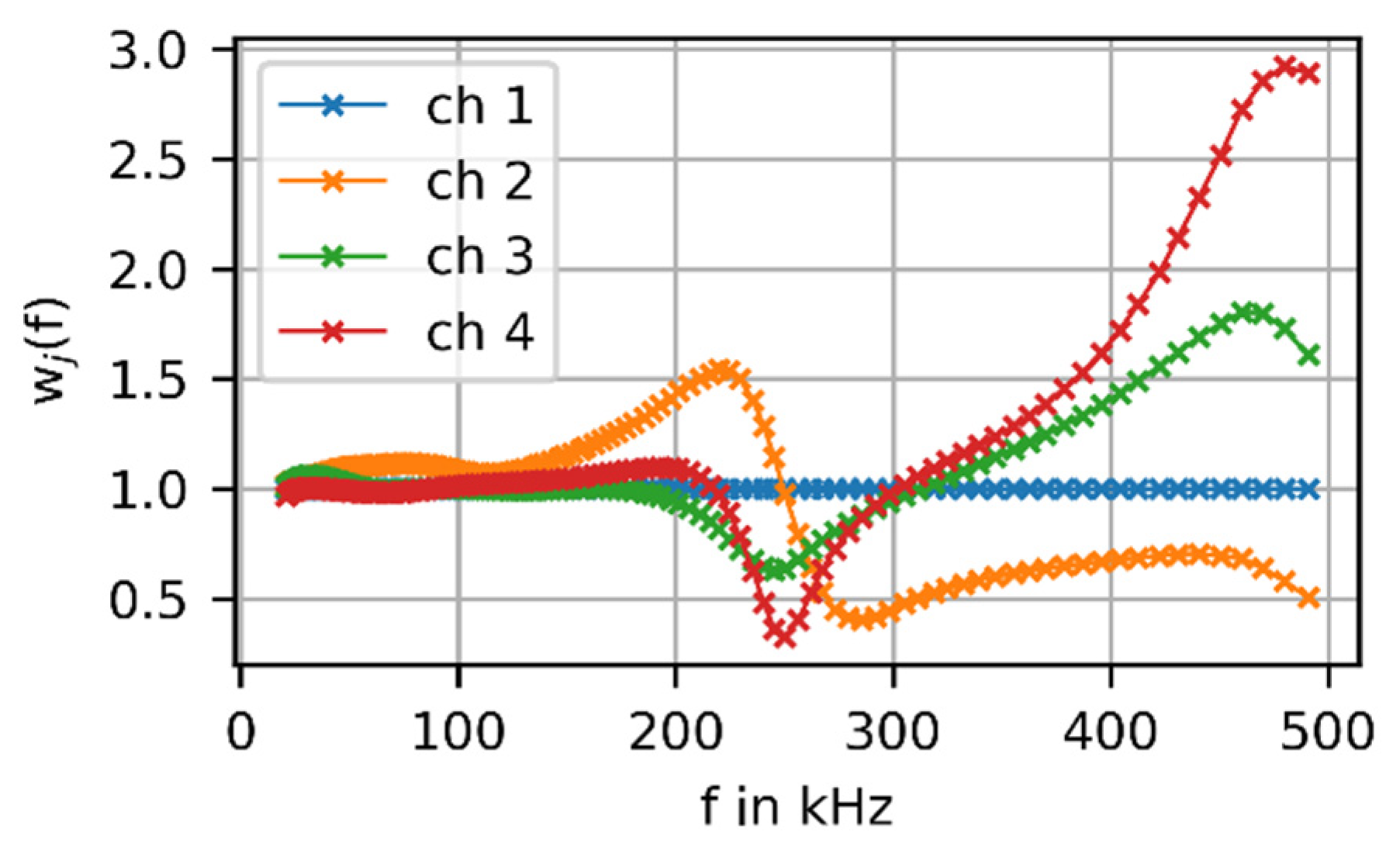
2. Model-Based AE Source Localization Algorithm
3. Experimental Investigation
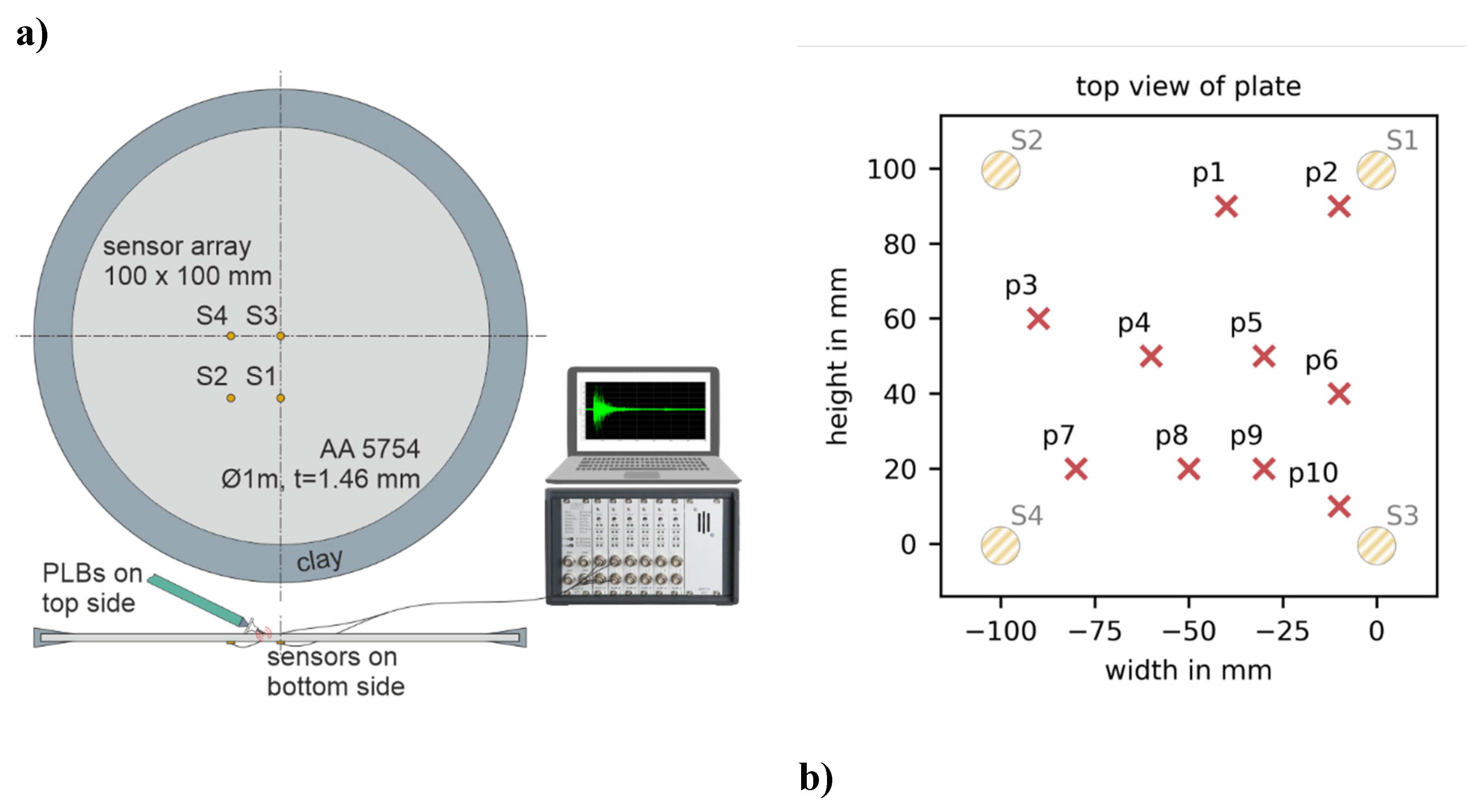
3.1. Setup and Procedure
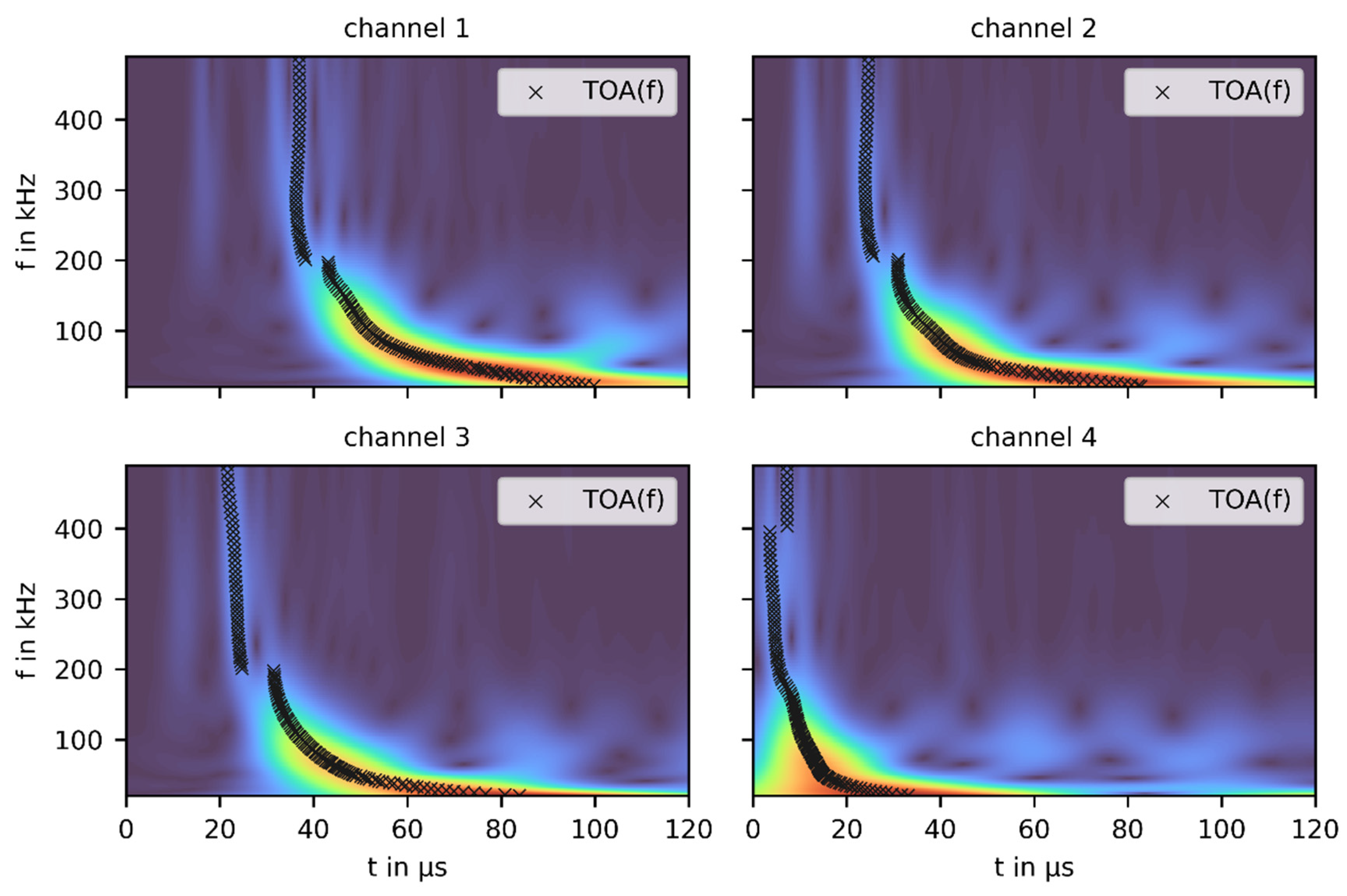
3.2. Results
3.3. Discussion
4. Conclusions
Acknowledgements
References
- Giurgiutiu, V., “Structural Health Monitoring with Piezoelectric Wafer Active Sensors,” Academic Press, Amsterdam, 2014.
- Kralovec, C., and Schagerl, M., “Review of Structural Health Monitoring Methods Regarding a Multi-Sensor Approach for Damage Assessment of Metal and Composite Structures,” Sensors, Vol. 20, No. 3, 2020, p. 826. [CrossRef]
- Giurgiutiu, V., “Structural Health Monitoring of Aerospace Composites,” Academic Press, Oxford, 2016.
- Ono, K., “Review on Structural Health Evaluation with Acoustic Emission,” Applied Sciences, Vol. 8, No. 6, 2018, p. 958. [CrossRef]
- Kundu, T., “Acoustic Source Localization,” Ultrasonics, Vol. 54, No. 1, 2014, pp. 25–38. [CrossRef]
- Hassan, F., Mahmood, A. K. B., Yahya, N., Saboor, A., Abbas, M. Z., Khan, Z., and Rimsan, M., “State-of-the-Art Review on the Acoustic Emission Source Localization Techniques,” IEEE Access, Vol. 9, 2021, pp. 101246–101266. [CrossRef]
- McLaskey, G. C., Glaser, S. D., and Grosse, C. U., “Beamforming Array Techniques for Acoustic Emission Monitoring of Large Concrete Structures,” Journal of Sound and Vibration, Vol. 329, No. 12, 2010, pp. 2384–2394. [CrossRef]
- Erlinger, T., Kralovec, C., and Schagerl, M., “Monitoring of Atmospheric Corrosion of Aircraft Aluminum Alloy AA2024 by Acoustic Emission Measurements,” Applied Sciences, Vol. 13, No. 1, 2023, p. 370. [CrossRef]
- Suzuki, H., Kinjo, T., Hayashi, Y., and Takemoto, M., “Wavelet Transform of Acoustic Emission Signals,” Journal of acoustic emission, Vol. 14, 1996, pp. 69–84.
- Jiao, J., He, C., Wu, B., Fei, R., and Wang, X., “Application of Wavelet Transform on Modal Acoustic Emission Source Location in Thin Plates with One Sensor,” International Journal of Pressure Vessels and Piping, Vol. 81, No. 5, 2004, pp. 427–431. [CrossRef]
- Rotea, F., “Lambwaves,” GitHub, 2020. Retrieved 18 March 2024. https://github.com/franciscorotea/Lamb-Wave-Dispersion.
- Muradeli, J., “Ssqueezepy,” GitHub, 2020. Retrieved 5 March 2024. https://github.com/OverLordGoldDragon/ssqueezepy.
| PLB | (x / y) localization results in mm | ||||
| label | (x / y) in mm | triangulation (AIC) | TOA(f) | constrained | sensor sensitivities |
| p1 | (-40 / 90) | (-40.2 / 86.4) | (-39.6 / 92.4) | (-39.4 / 91.4) | (-40,2 / 91,4) |
| p2 | (-10 / 90) | (-9.8 / 88.2) | (-9.3 / 91.2) | (-9.8 / 91.1) | (-10,6 / 91,1) |
| p3 | (-90 / 60) | (-88.2 / 59.6) | (-91.7 / 60.0) | (-92.0 / 60.0) | (-92,4 / 59,6) |
| p4 | (-60 / 50) | (-62.2 / 53.8) | (-60.4 / 50.4) | (-59.3 / 49.6) | (-60,5 / 49,6) |
| p5 | (-30 / 50) | (-29.2 / 52.2) | (-29.2 / 50.4) | (-28.8 / 49.7) | (-29,6 / 49,3) |
| p6 | (-10 / 40) | (-15.0 / 39.4) | (-6.7 / 40.0) | (-10.0 / 39.8) | (-10,0 / 39,8) |
| p7 | (-80 / 20) | (-80.4 / 21.8) | (-79.6 / 19.0) | (-79.2 / 19.3) | (-80,0 / 18,9) |
| p8 | (-50 / 20) | (-50.6 / 22.4) | (-49.8 / 18.4) | (-49.4 / 18.2) | (-49,4 / 18,2) |
| p9 | (-30 / 20) | (-28.2 / 23.6) | (-29.6 / 19.4) | -(29.0 / 18.6) | (-29,5 / 19,0) |
| p10 | (-10 / 10) | (-10.4 / 12.0) | (-9.1 / 8.5) | (-8.7 / 9.1) | -(9,6 / 8,7) |
| mean abs. error | 2.94 mm | 1.54 mm | 1.31 mm | 1.23 mm | |
| improv. vs. triangulation | - | 48 % | 55 % | 58 % | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





