RANS Simulation of Minimum Ignition Energy of Stoichiometric and Leaner CH4/Air Mixtures at Higher Pressures in Quiescent Conditions

Preprint

Article

RANS Simulation of Minimum Ignition Energy of Stoichiometric and Leaner CH4/Air Mixtures at Higher Pressures in Quiescent Conditions

Altmetrics

Downloads

Views

Comments

Sooraj Paleli Vasudevan,

Siva Muppala^*

Sooraj Paleli Vasudevan,

Siva Muppala^*

This version is not peer-reviewed

This preprints belongs to the Topic

Theoretical, Numerical and Experimental Studies on Clean Energy and Combustion

Submitted:

09 September 2024

Posted:

10 September 2024

You are already at the latest version

Alerts

Abstract

The minimum ignition energy (MIE) has been extensively studied via experiments and simulations. However, our literature review reveals little quantitative consistency, with results varying for f=1.0 from 0.324 to 1.349 mJ, and for f=0.9 from 0.22 to 0.944 mJ. Therefore, there is a need to resolve these discrepancies. This RANS study aims to partially address this knowledge gap. Additionally, it presents other flame evolution parameters essential for robust combustion design. Using the reactingFOAM solver we predict the threshold energy required to ignite the fuel mixture. For this, the single step using the Arrhenius law is selected to model ignition in the flame kernel of stochiometric and lean CH₄/air mixtures, allowing it to develop into a self-sustained flame. The ignition power density, an energy quantity normalised with volume is incrementally varied keeping the kernel critical radius r_s constant 0.5 mm in the quiescent mixture of two equivalence ratios fs 0.9, and 1.0, for varied operating pressures 1, 5 and 10 bar at constant initial temperature 300 K. The minimum ignition energy is validated with twelve independent 1 bar data sets both numerical and experiments. Finally, a mathematical formulation of MIE is devised, a function of pressure and equivalence ratio shows a slightly curved relationship.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Climate changes in recent years have profoundly impacted the environment. This impact necessitates a transition towards carbon-neutral fuels. Such a transition aims to meet global energy needs while mitigating climate change. Whilst the understanding of hydrocarbons and their combustion is well-established, the significant increase in global temperatures demands further validation across a wide range of temperatures and higher pressures for their safe storage and infrastructure of combustion systems [1]. Among all hydrocarbons, methane stands out as highly diffusive and flammable, yet it offers the advantage of being the least carbon-intensive fuel, as one mole of CH₄ releases one mole of CO₂. Methane's structure as a single-carbon hydrocarbon underscores its potential as a significant and sustainable energy source [2]. Therefore, methane, a simple single-carbon hydrocarbon abundant on Earth, emerges as a promising fuel for a cleaner energy future when coupled with Carbon Capture, Utilization, and Storage (CCUS) technology to manage its CO₂ emissions [3-4]. Hahn [5] in §A.1.3 cites World Bank data that indicates that CO₂ emissions have tripled since 1990, placing immense strain on ecosystems, with CCUS emerging as a potential solution to mitigate climate change while allowing continued fossil fuel use during the transition to cleaner energy sources. Bio-methane and methanation processes remain economically challenging and have not yet achieved the scale required to substantially displace fossil natural gas utilization. Recent studies, such as those by Zhao et al. [6] have illuminated the complexities of methane ignition and combustion kinetics at elevated temperatures and pressures, highlighting the importance of considering pressure-dependent reaction pathways and accurately capturing low-temperature chemistry for reliable predictions. Bjørgen, K.O.P. et al. [7] used advanced computational techniques to study non-conventional pathways in methane ignition and combustion, highlighting their significance at elevated temperatures and improving kinetic parameters for better modelling. These advancements in understanding methane ignition mechanisms, alongside developments in CCUS technology and sustainable bio-methane production, are crucial for a reliable and environmentally responsible transition to a carbon-neutral energy future. Studying minimum ignition energy (MIE) contributes to sustainability by enhancing our understanding of fuel combustion processes, leading to the development of more efficient and cleaner burning technologies.

The minimum amount of energy or heat required to initiate combustion in a gas mixture. Specifically, it's the threshold energy that, when applied instantaneously to a small volume of the gas, will trigger a self-sustaining flame that can propagate through the rest of the mixture [8]. To ignite a flammable mixture of hydrocarbons and air, the minimum ignition energy serves as a crucial parameter for evaluating safety risks. When the energy level of ignition is insufficient, it causes heat dissipation from the reaction zone, resulting in flame extinction. Knowing the MIE is crucial for creating safety measures to protect people and property from the dangers of handling flammable gases. According to ignition engine combustion plays an important in the overall engine performance. Kundu et al. [3] observes highly ignitable mixture of methane–air is 9.5%. by vol.%). Additionally, Jia et al. [9] ignition limits, lower LEL 5.05 ± 0.3% and the upper 14.95 ± 0.4% of CH₄/air mixtures at ambient temperature and pressure. According to Zeldovich, Y [10], MIE is the definite ignition temperature T_s exists such that the reaction rate ʘ is zero below this temperature of the premixed mixture i.e., ʘ (T_u< T_s) = 0, where T_u is the varying temperature of the unburned mixture, and ʘ is constant inside the T_s<T<T_b reaction zone, where b represents the burned temperature. For more comprehensive information, refer to the original article. In a combustion system, the formation of a flame kernel is a crucial onset of flame which is affected by equivalence ratio and pressure, collectively determines the influence of energy density [11]. Improving the comprehension of flame initiation and propagation mechanisms offers potential for expanding practical applications in this field [12-13]. This enables the development of more efficient and safe engine designs with enhanced fuel economy and reduced emissions.

This study determines the MIE and flame evolution of CH₄/air mixtures at three pressures 1, 5 and 10 bar for equivalence ratios 0.9 and 1.0, at initial temperature 300 K. Precise modelling of mixture properties and ignition power density was crucial for accurately predicting early flame kernel development [14]. The progression of the flame is tracked in both space and time until the temperature reached adiabatic levels and subsequently plateaued. In accordance with the conservation of energy, T_adia is primarily determined by the energy released during combustion, which is largely independent of pressure. Notably, this study did not account for any heat losses during the analysis process. A complete chemical kinetic model for methane oxidation requires 50 species and hundreds of reactions, which is unnecessarily complex for evaluating temperature and minimum ignition energy. The Arrhenius reaction step is considered appropriate, as this study primarily focuses on energy evaluation derived from temperature and pressure variations. The present numerical results' validation confirms this simplification's adequacy. Therefore, we choose to use the single-step reaction rate using Arrhenius law and rigorously validate with the existing literature.

A single-step overall methane chemical reaction, which includes inert gas N₂

CH₄ + 2 (O₂ + 3.76N₂) → CO₂ + 2 H₂O +7.52 N₂

The volume and mass %s of equivalence ratios is calculated, for illustration using (Warnatz et al. [15]. p4-6) x_fuel, vol% = 1/(1+4.762n/ φ). For CH₄ oxidation, CH₄ + 2O₂ → CO₂ + 2H₂O, for φ =1 where n is the number of moles of O₂ for one mole of CH₄ gives x_fuel =0.095; x_{O2 =} x_air/4.762 = 0.19; x_N2 = x_O2 * 3.762 = 0.715, and equivalently, 0.056, 0.219, and 0.725 in mass fraction. We input six-digit accuracy values.

2. Formulation and Numerical Method

The assessment of ignition success criterion holds significant importance in determining the MIE, an important characteristic of a developing flame. For practical reasons, it is considered an essential safety criterion for combustible gases. The ignition power density q is adjusted to three decimal places for each scenario. This adjustment initiates successful flame evolution. In all three pressure cases, the initial phase is slower at lower pressure. It decreases proportionally as pressure increases.

The moment at which a flame kernel initiates at a specific location, and continues to propagate consistently, is considered the point of successful ignition. The analysis examines temperature and species profiles to understand flame progression. The results from the initial transient phase are influenced by both the properties of the lean mixtures, in the flammability limits and operating pressures, which significantly influence the rate at which the flame evolves and achieves stability [16-17]. Theoretical prediction model for minimum ignition energy of combustible gas mixtures.

The reactingFOAM solver of open-source code OpenFOAM is used to carry out this research. The computational configuration is a frozen premixed methane/air distributed homogenously in the domain. The computational domain is a cubic shape with dimensions of 75 mm on each side. It is discretised into a grid with hexahedral mesh with 200 cells with mesh resolution 0.375 mm along the x, y, and z directions. The spherical flame mixture at the centre of the domain is ignited in a quiescent initial condition in a pocket of radius r of 0.5 mm, with a volumetric heat source q, for equivalence ratio 1.0, and a leaner mixture 0.9 at atmospheric pressure, and for higher pressures 5 and 10 bar. In this context, three simulations for φs 0.9 and 1.0 at initial pressures 1, 5, and 10 bar are performed. The power density, q is varied by keeping T_i =300 K, r = 0.5 mm constant across all cases.

3. Governing Equations

Spherical laminar flames propagating from a volumetric heat source at the centre of the domain, filled with homogeneous combustion products are characterized by the following set of balance equations:

Mass Conservation Equation

\frac{\partial ρ}{\partial t} + \nabla \cdot (ρ U) = 0

\frac{\partial ρ}{\partial t}

(partial derivative of density with respect to time): This term represents the rate of change of density with time at a fixed point in space. It accounts for the accumulation or depletion of mass due to transient effects.

\nabla . (ρ U)

: (divergence of the product of density and velocity): This term represents the net flow of mass into or out of an infinitesimal control volume. It describes the mass transfer due to convective transport.

This equation ensures that the total mass of the fluid remains constant throughout the simulation domain.

Momentum Equation

\frac{\partial}{\partial t} (ρ U) + \nabla \cdot (ρ U U) - \nabla \cdot (τ) = - \nabla \cdot (p)

τ = μ [(\nabla U + \nabla U^{T}) - \frac{2}{3} \nabla U \cdot I]

where

\frac{\partial}{\partial t} (ρ U)

: This term represents the rate of change of momentum with respect to time.

\nabla \cdot (ρ U U)

: This term is related to the convective acceleration of the fluid. It represents the rate of change of momentum due to the fluid's motion.

\nabla \cdot (p)

: Pressure gradient force.

\nabla \cdot (τ)

: This term accounts for the effects of viscous forces and pressure gradients on the fluid momentum.

Species Concentration Equations

\frac{\partial}{\partial t} (ρ Y_{i}) + \nabla \cdot (ρ U Y_{i}) = \nabla (μ \nabla Y_{i}) + {\dot{ω}}_{i}

where

\frac{\partial}{\partial t} (ρ Y_{i})

, the rate of change of the mass of species i per unit volume with respect to time.

\nabla \cdot (ρ U Y_{i})

, the net rate of mass flow of species i into a volume element due to convection.

\nabla (μ \nabla Y_{i})

, the net rate of mass flow of species i into a volume element due to diffusion.

{\dot{ω}}_{i}

, represents the source term for i^th species.

Energy Equation

\frac{\partial}{\partial t} (ρ h) + \nabla \cdot (ρ U h) + \frac{d}{d t} (ρ K) + \nabla \cdot (ρ U K) + \{\begin{matrix} \nabla \cdot (|ϕ \cdot ρ \cdot U| \cdot \frac{p}{ρ}) \dots \dots . i f h = e \\ - \frac{d P}{d t} \dots \dots \dots . O t h e r w i s e \end{matrix} + \nabla \cdot (α \cdot \nabla h) + \dot{q}

\frac{\partial}{\partial t} (ρ h)

: This term represents the rate of change of enthalpy per unit volume with time.

\nabla \cdot (ρ \vec{U} h)

: This term accounts for the transport of enthalpy due to fluid motion.

\nabla \cdot (ρ \vec{U} K)

: This term accounts for the transport of kinetic energy due to fluid motion.

\{\begin{matrix} \nabla \cdot (|ϕ \cdot ρ \cdot U| \cdot \frac{p}{ρ}) \dots \dots . i f h = e \\ - \frac{d P}{d t} \dots \dots \dots . O t h e r w i s e \end{matrix}

). This term is conditional and represents different forms of energy transfer (like pressure work, heat conduction, etc.), depending on whether the specific enthalpy h is equal to internal energy (e) otherwise the time rate of change of pressure (

- \frac{d P}{d t}

\nabla \cdot (α \cdot \nabla h)

: This term represents the transport of enthalpy due to heat conduction or diffusion.

\dot{q}

: This term represents rate of heat addition per unit volume.

For an elementary reaction such as

ϑ_{A} A

ϑ_{B} B \to ϑ_{P} P + ϑ_{Q} Q

, the reaction rate,

ω

depends on the concentration as

{\dot{ω}}_{i} = {k [A]}^{ϑ_{A}} {[B]}^{ϑ_{B}}

according to the law of mass action, where [A] and [B] are the mole concentrations of species A and B, respectively (mole per unit volume), and

ϑ_{A}, ϑ_{B}

are stoichiometric coefficients for species A and B, respectively. The reaction rate constant at an initial temperature 300 K is given as

k = A \exp (- \frac{E_{a}}{R T})

= 5.2

\cdot

10¹⁶

\cdot

exp [–(14906 / (8.314

\cdot

300)] where A is the pre-exponential factor is 5.2

\cdot

10¹⁶, E_a is the activation energy is 14906 K, a default value in reactingFoam solver, and R is the universal gas constant, 8.314 J/mol · K [18].

The blockMeshDict utility is to define the vertices, number of grid points, and boundaries for the cubic geometry. Five boundaries were specified: top, left, right, bottom, and frontAndBack as patches. In this case, a volumetric heat source is input at the centre of the cubical domain, with the expectation that the flame would develop symmetrically towards the walls. This ignition is designed and coded in heatSource.C and values given in fvOptions as :

const scalar t = mesh().time().value();

const scalar heatSourceValue = 1e⁸ ; // 1

\cdot

10⁸ W/m³

const scalar heatSourceDuration = 0.01; // 10 ms

const scalar heatSource = (t<=heatSourceDuration)? heatSourceValue: 0.0;

const scalar t = mesh(). time().value(): retrieves the current simulation time from the mesh object.

const scalar heatSourceValue = 1e⁸: sets the desired heat source value of 1 ·10⁸ W/m³.

const scalar heatSourceDuration = 0.01: sets the duration for which the heat source should be active (10 ms).

const scalar heatSource = (t <= heatSourceDuration)? heatSourceValue : 0.0 uses a conditional expression to set the heat source value. If the current time t is less than or equal to heatSourceDuration (10 ms), the heat source is set to heatSourceValue (1 · 10⁸ W/m³). Otherwise, the heat source is set to zero.

The spherical ignition source is implemented by employing the 'topoSetDict' utility in conjunction with the 'SphereToCell' command; the coding is given below. The location and dimensions of the ignition source are specified by defining the centre and radius parameters within the utility.

actions

(

{

name hs1;

type cellSet;

action new;

source sphereToCell;

sourceInfo

{

centre (0.0375 0.0375 0.0375);

radius 0.0005;

}

// create cellZone from cellSet

{

name heater;

type cellZoneSet;

action new;

source setToCellZone;

sourceInfo

{

set hs1; //name of cellset

}}

);

The controlDict dictionary specifies the numerical control of the whole simulation that commands the start time, end time, and the deltaT (time step) of the simulation. A constant volumetric heat source term was applied at the centre of the domain from computational time t = 0 to t = 10 ms, (

τ_{i} = 10 m s),

representing the ignition duration of 10 ms, for all three pressure cases. The computational start time and end time, respectively, are 0 and 10 s. We enter species-specific data for molecular weight, density, enthalpy/internal energy, and transport parameters. For the chemical properties of CH₄/air mixtures, Euler implicit solver is used, as a first order transient solver to solve the transport equations governing the behaviour of scalar quantities (e.g., temperature, species concentrations). It is an implicit time integration scheme, meaning that the solution at the next time step depends on the solution at the current time step and the solution itself at the next time step. The significance of using the Euler implicit solver in this case (stagnant mixture) lies in its stability and accuracy for solving stiff ODEs, involving chemical reactions or other processes with widely varying time scales. To analyse the simulation results to determine whether a spherical flame develops, or quenches involves visualising the temperature, species concentrations, and other relevant variables to identify the presence and characteristics of the flame.

4. Model Geometry, Initial and Boundary Conditions

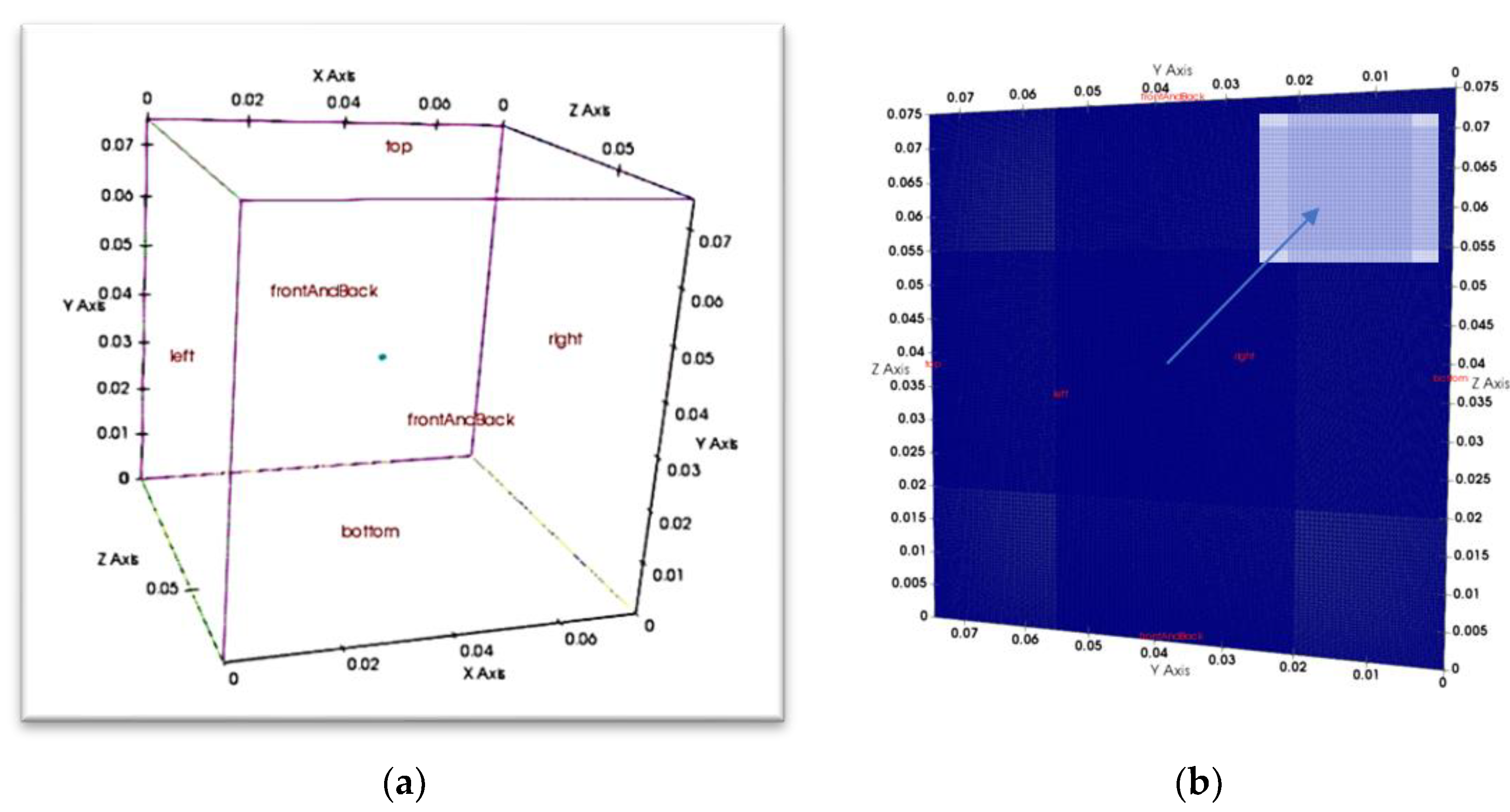
Initial and boundary conditions are defined for the walls, the Top, Left, Right, Bottom and patches frontAndBack, on two faces. The computational domain is filled with CH₄ and air (comprising 21% O₂ and 79% N₂) at initial pressure (p_i) and temperature (T_i). Gravitational force acts along the y-direction. There is no internal flow within the domain, and the domain size is 150 times the flame kernel radius 0.5 mm, to ensure the flame expansion remained unaffected by the domain boundary.

The simulation commences at t=0 s, with the initial field data stored in a sub-directory labelled "0", with initial conditions at 1 bar and 300 K. fixedValue boundary conditions specifies a constant value of pressure boundaries where the pressure is specified. The inletOutlet boundary condition in OpenFOAM is a versatile option employed in situations where the flow direction at a boundary is not predetermined. This condition allows the boundary to dynamically adapt its behaviour based on the local flow conditions, providing flexibility and robustness. In this context of a quiescent mixture, the inletOutlet boundary condition is utilized to specify the boundary conditions for various fields, such as pressure and velocity. For the pressure field, the inletOutlet boundary condition is set to a fixed value, acting as a reference value within the computational domain. Conversely, for velocity fields, the inletOutlet boundary condition is often set to a zeroGradient condition, implying that the normal derivative of the field at the boundary is set to zero (see Figure 1a,b).

4.1. Evaluation of Minimum Ignition Energy

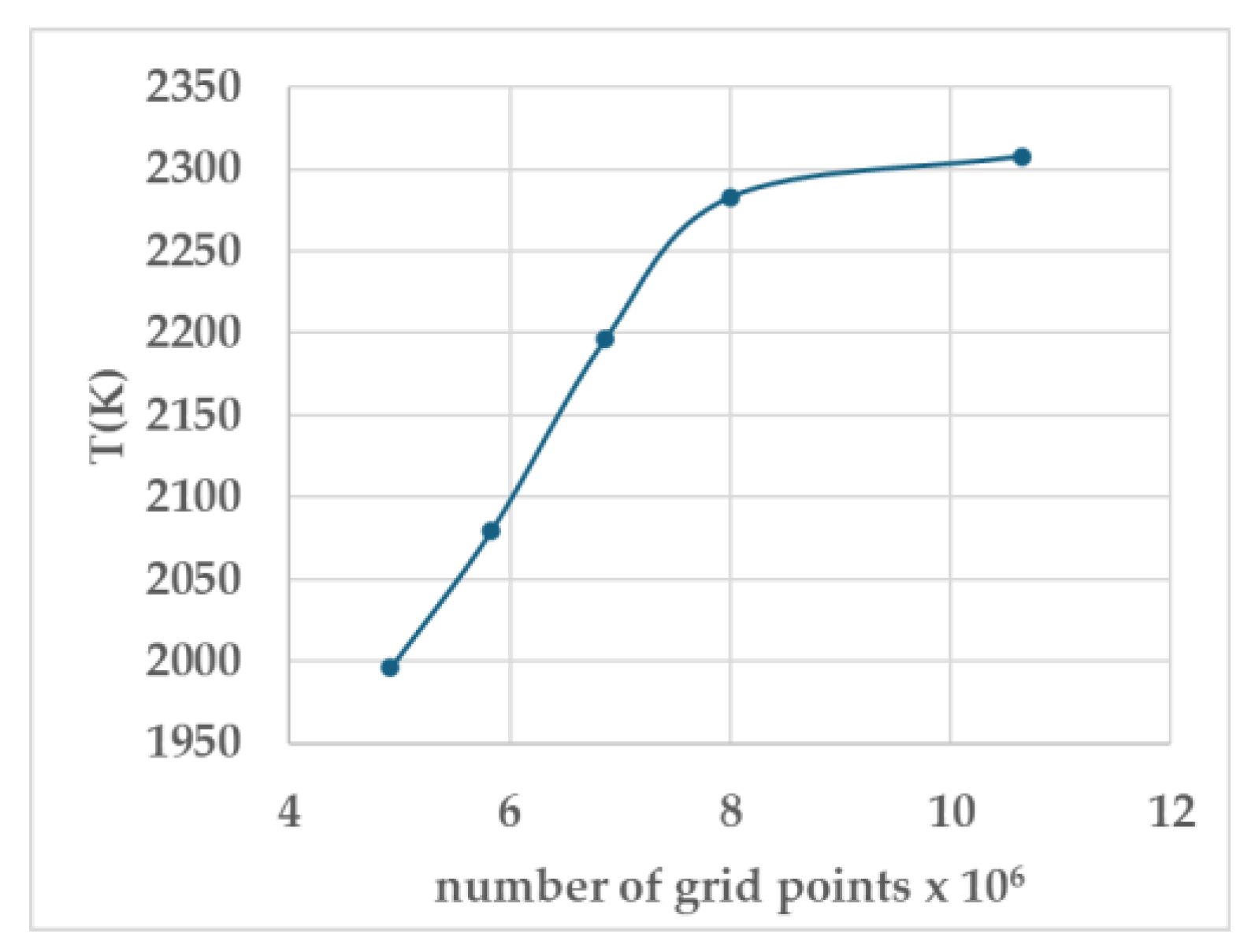
An optimal grid mesh size of 200 x 200 x 200 mm was identified, which significantly reduced computational resource requirements while maintaining accuracy. Consequently, an 8 million element mesh was selected, resulting in a temperature difference ranging from 1.08% to 3.8% compared to other grid sizes, as depicted in Table 2 and Figure 2. The kernel diameter 1 mm, with 32 cells. For all simulations, the kernel space point is at the centre of the computational domain. The space independency is not studied in this work.

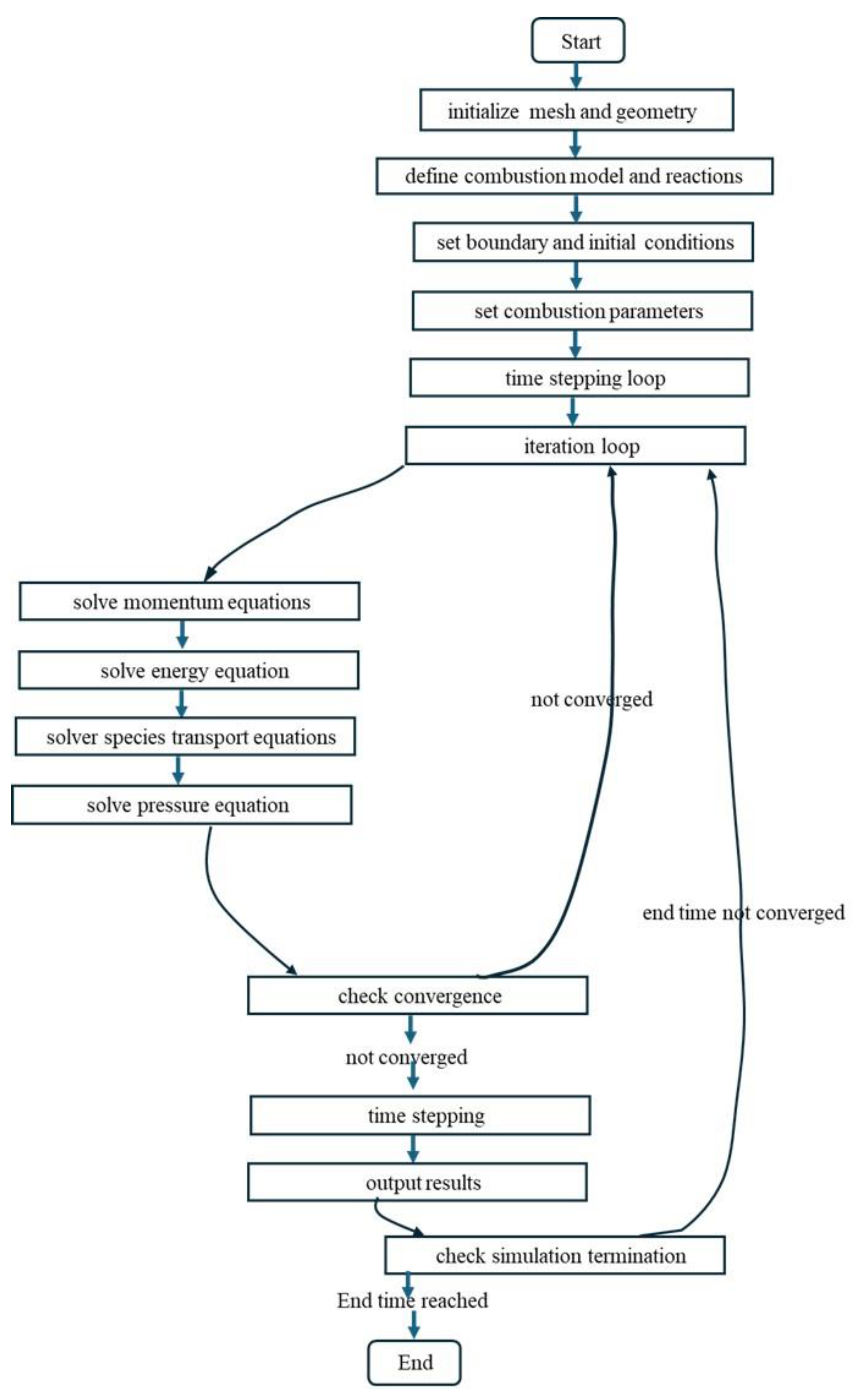
5. Numerical Methodology

The numerical solution in a reactingFOAM solver of the open-source code OpenFOAM is outlined in a series of steps in Table 3 and also in Figure 3.

6. Results and Discussion

Successful ignition occurs when a flame kernel forms at a specific point and subsequently maintains consistent propagation throughout the combustible mixture. The spherical ignition in a cubical computational domain. Temperature and species profiles are analysed to understand the flame's progression. In this context, three simulations were conducted at varying initial pressures 1, 5, and 10 bar.

6.1. Evaluation of Minimum Ignition Energy

Using the input parameter, the power density, denoted ‘q’, the necessary ignition energy is calculated,

Q = q· t_i· V

where

Q

, the ignition source in mJ,

V

the ignition kernel volume in m³,

τ_{i}

the ignition duration in seconds. q is numerically evaluated by iterative testing. For MIE, the Equation (6) is re-written as

Q_MIE = q_MIE· t_i· V

The ignition is set at the centre of the gas mixture for a possible ignition power density q. The minimum ignition power density q_MIE for the flame kernel is rewritten in Equation (8).

q_{MIE} = / (\frac{4}{3} π \cdot {r_{s}}^{3} \cdot t_{i})

A sample calculation, for phi = 1 at 1 bar, given

r_{s}

=0.5 mm and for set value of

τ_{i} = 10 m s

Q_{MIE} = q_{MIE} \cdot t_{i} \cdot V = (1 \cdot 10^{8}) \cdot 0.010 \cdot [\frac{4}{3} 3.1416 \cdot (0.0005)^{3}] = 0.524 mJ

The heat source was confined to a cubic volume determined by the ignition kernel radius

r_{s}

, ensuring sufficient space for uninterrupted ignition and initial flame propagation.

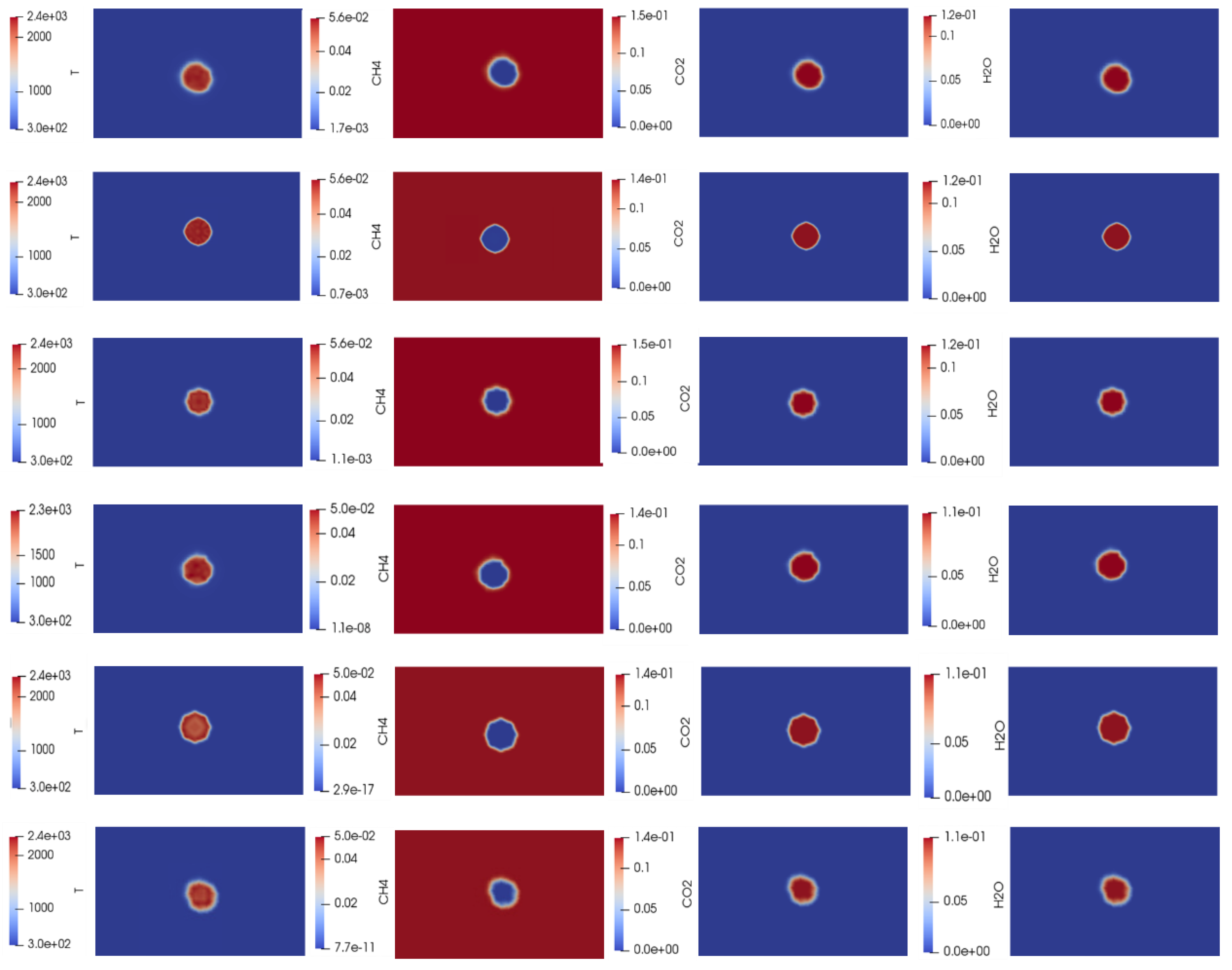
Figure 4 displays contours of temperature and species concentration evolution during combustion. It shows the process from initiation at 300 K to the adiabatic flame temperature T_adia, assuming no heat losses occur. The red contours show CH₄ consumption, while the blue contours indicate CO₂ and H₂O formation, respectively.

6.2. Comparsion of MIE with literature

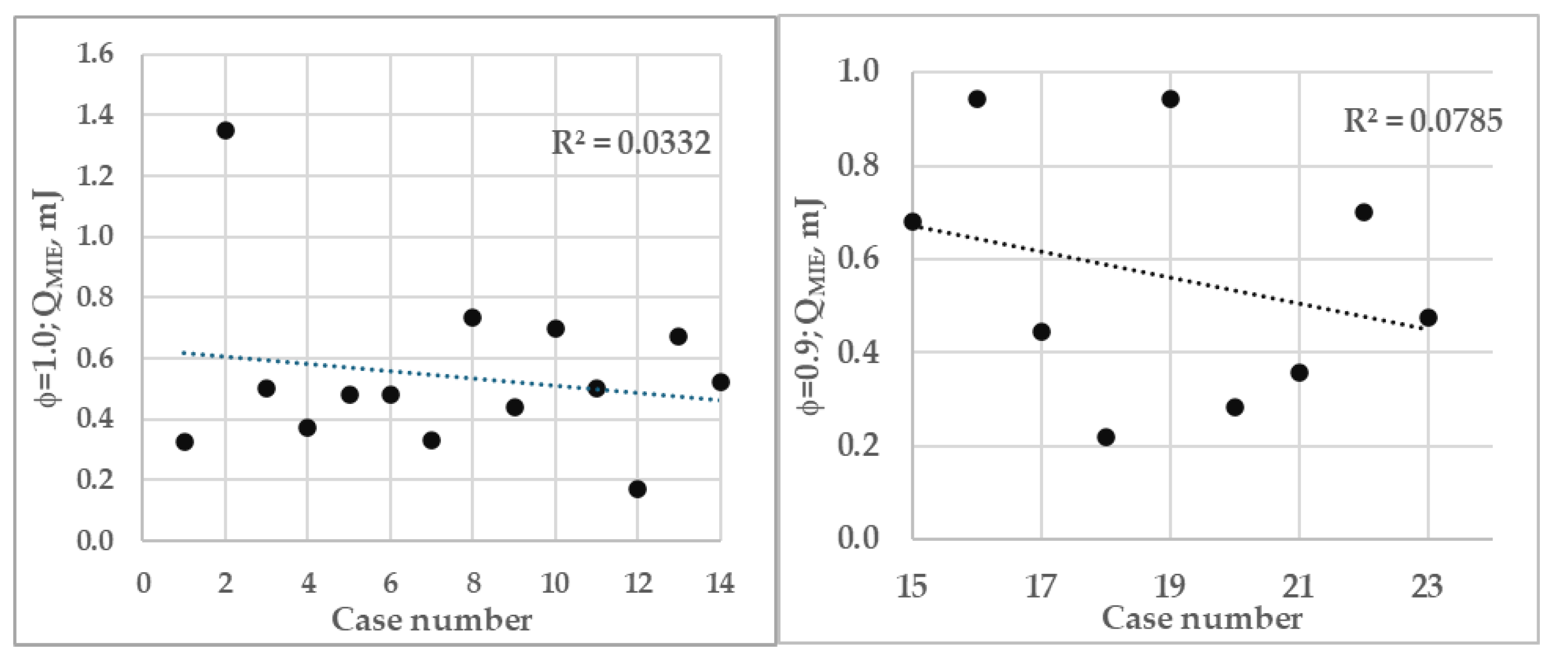
Compared to stoichiometric mixtures (φ=1.0), leaner mixtures (φ=0.9) show a steeper negative slope. This is attributed to two factors: 1) significant dependence on molecular parameters, and 2) pressure's dominant influence in fuel-lean conditions, particularly when the fuel is lighter than the oxidant mixtures, which mitigates the fuel scarcity effect. The two studies [19-20] show the effect of preferential diffusion of lighter fuels is more predominant in achieving higher reaction rate. The opposite phenomenon is expected in richer mixtures, though not examined in this study.

MIEs are compared with eleven distinct flame measurements at 1 bar, given in Table 4. The present simulation outcomes are shown in the third column from the left in both figure rows (see Figure 7). Han et al. [15] noted a significant gap between empirical data and computational models. Their simulations yielded results about four times higher than observed measurements. Disregarding a few model predictions, this investigation's outcomes correspond well with other cited data, given in Table 4. This table (Table 4) with Q_MIE data are presented in correlation plots as shown in Figure 7 for φs 0.9 and 1.0 against case numbers and should be viewed as indicative. The very low coefficient of determination(R) suggests no significant correlation exists between experimental values, including those from simulations. However, a few data points show some correlation.

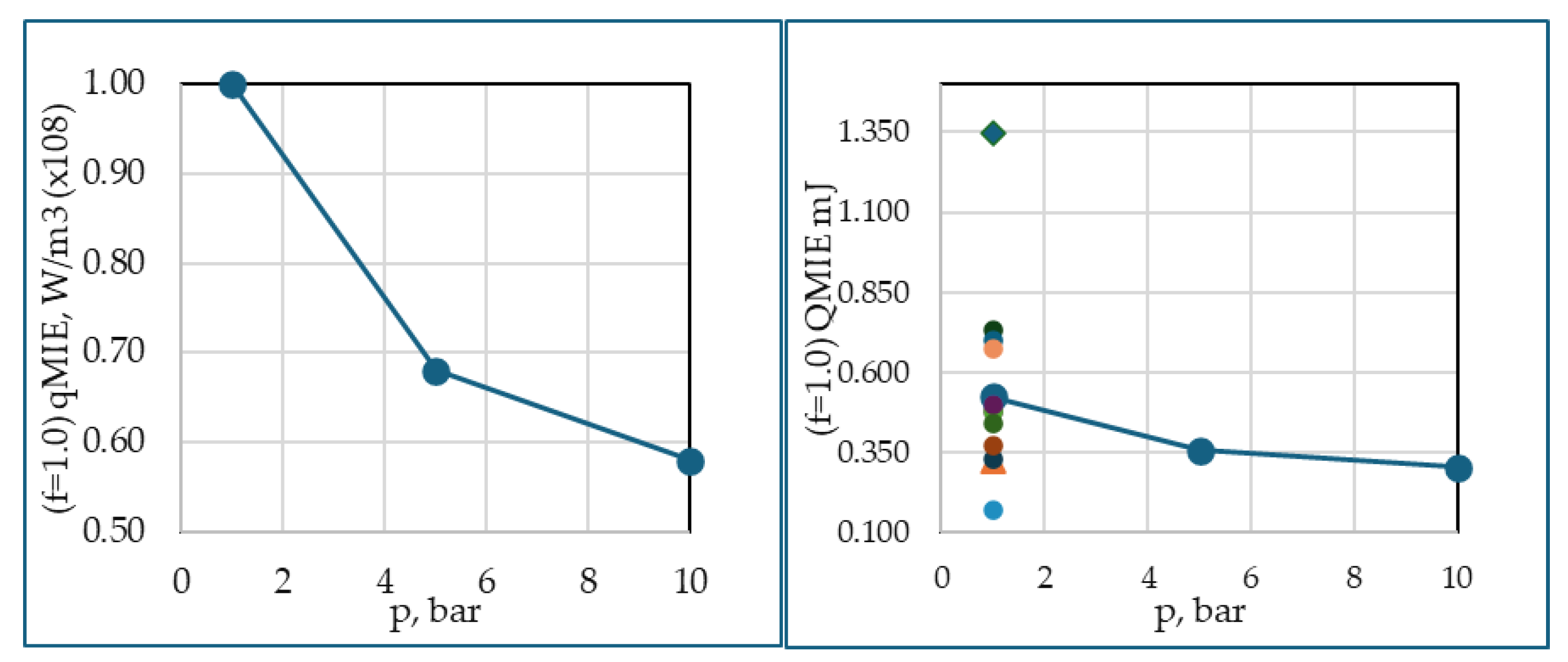
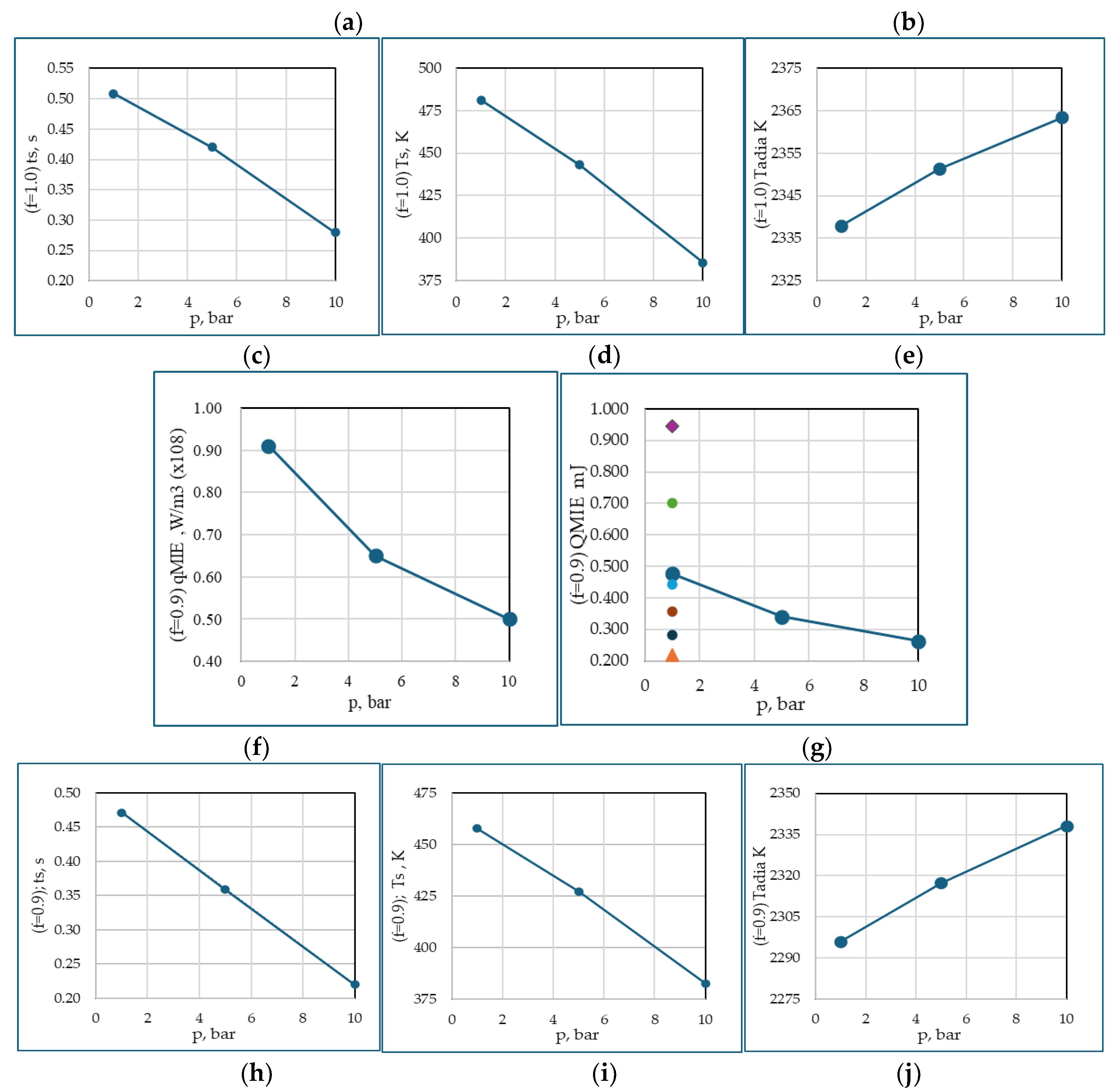
Figure 8 shows a consistent trend of variation of MIE with equivalence ratio and operating pressures. These results validate very closer to four experiments and several other simulations. This shows the use of single step reaction for estimation of MIE is suffices, if the intermediary chemical species concentrations are of no interest, which is not the aim of the present study. The figure also a distant qualitative similar trend for all the five quantities.

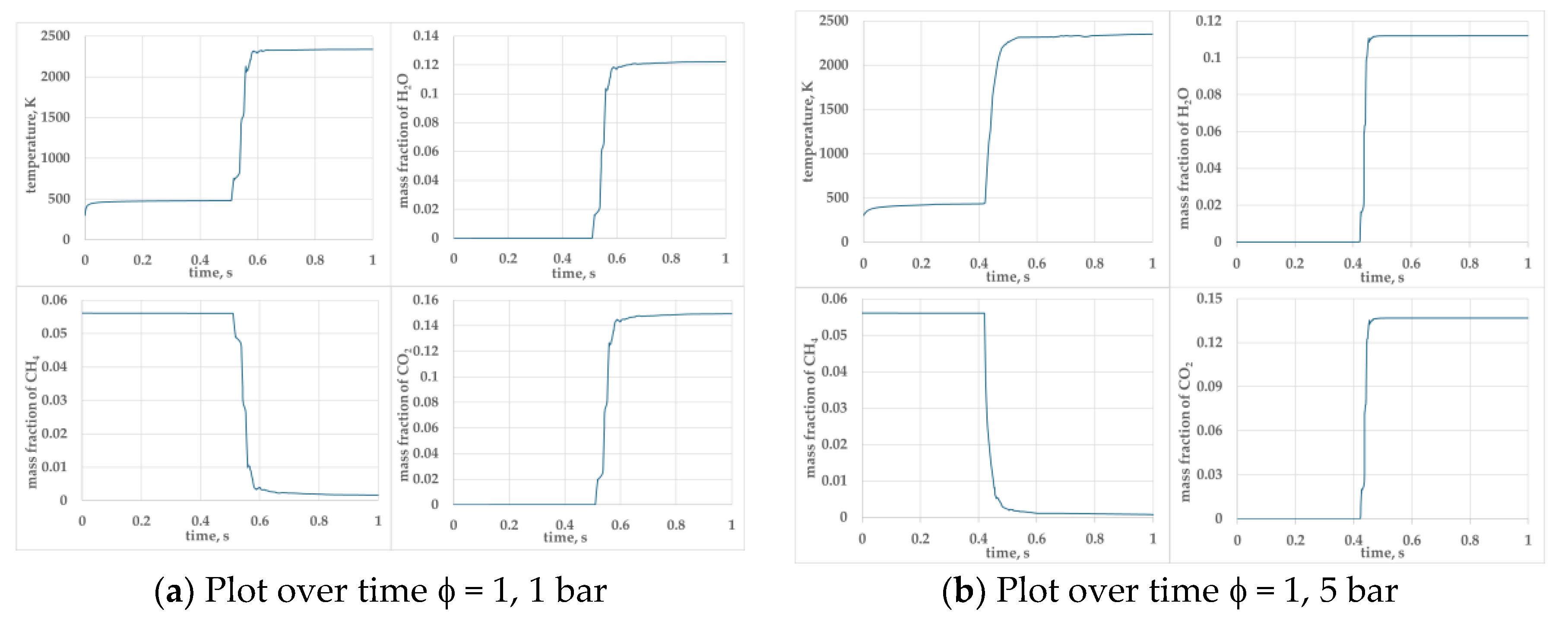
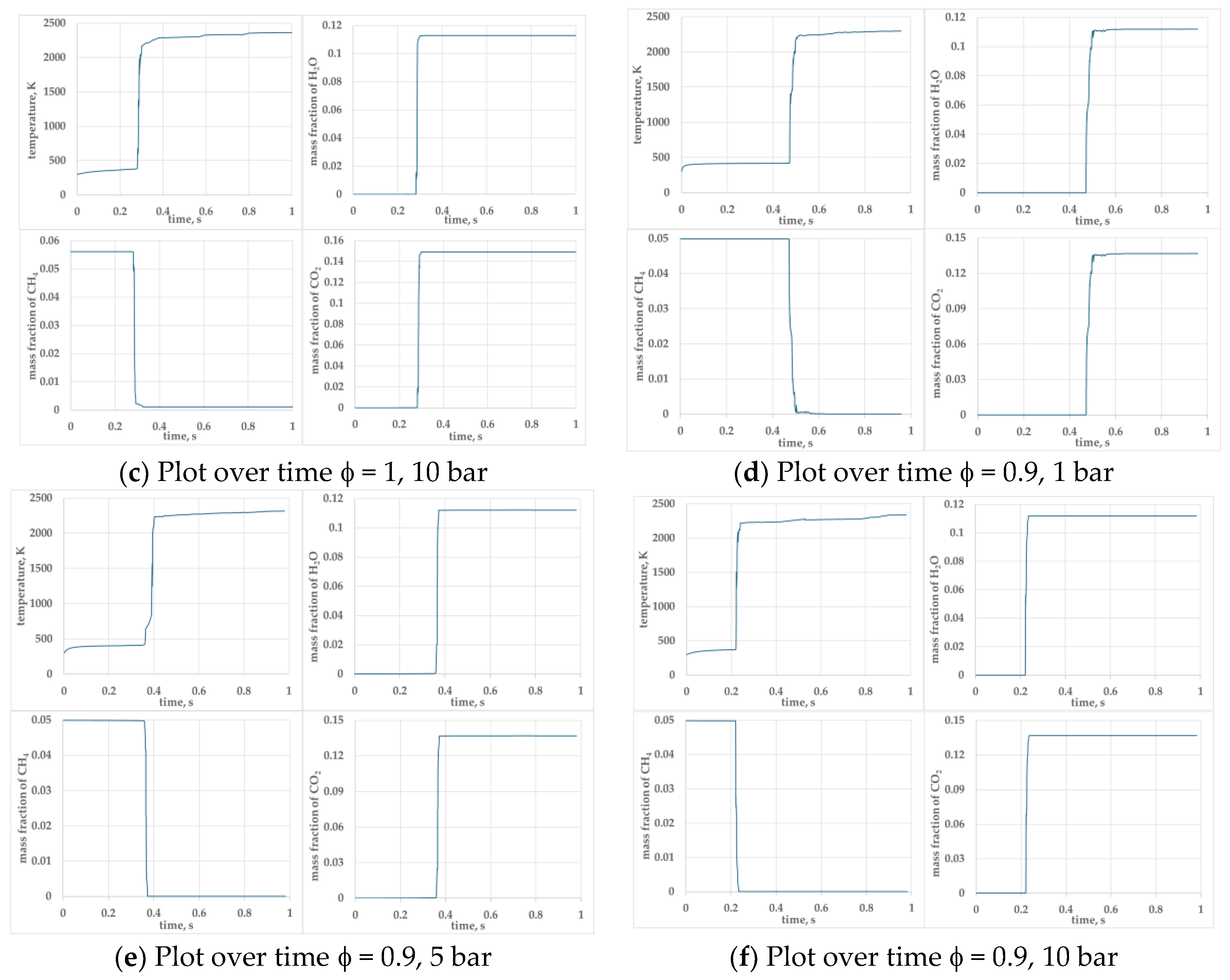
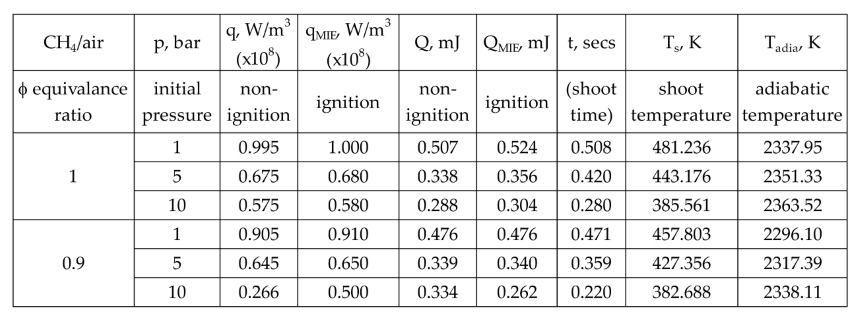
For φ=0.9, the decrease in MIE from 1 to 5 bar is more pronounced than from 5 to 10 bar, indicating a nonlinear trend. In the former, the relative change in density is greater. Therefore, flame ignition occurs much quicker between 0.359 s and 0.220 s than between 0.471 s and 0.359 s. Similarly, for φ=1.0, the range is 0.420 s and 0.280 s, and 0.508 s and 0.420 s. The faster ignition at higher pressures could be attributed to more intensive molecular activity and thus a higher reaction rate, leading to near-instantaneous combustion compared to the conditions at 1 to 5 bar compared to 5 to 10 bar, showing a non-linear relationship between pressure and flammability. The time between the initial temperature of reactant mixture and the onset of rapid combustion, i.e., the initial stages of flame development is analogous to auto-ignition. However, the time at which temperature shoots up shows an inverse trend because higher pressures also increase heat capacity and thermal conductivity of the gas mixture. This means that while ignition becomes easier at higher pressures, the evolution of the flame may be slightly delayed due to enhanced heat dissipation, especially in the 5 to 10 bar range where the pressure effects on ignition sensitivity start to level off.

For φ of 1 at 1 bar and 300 K, the current simulation of MIEs is compared with twelve different models, both experiments and simulations. In a numerical study, Kim et al. [22] found that the MIE of the stoichiometric CH₄/air mixture is 0.500 mJ. This was observed with an ignition source radius of 2.5 mm and a supply duration of 60 μs. Ghosh et al. [17] conducted a comprehensive study of MIE for various equivalence ratios: 0.7, 0.8, 0.9, 1.0, and 1.2, respectively, 0.98 mJ, 0.59 mJ, 0.42 mJ, 0.48 mJ, and 0.93 mJ using a spark duration of 100μs. In contrast to these results, Han et al. [15] numerical study predicts MIE of 1.349 mJ for φ = 1, and for φ = 0.9, the MIE of 1.100 mJ. The present simulations, the MIE was determined to be 0.524 mJ. Lewis and von Elbe [24].p357 predict 0.944 mJ, and Lewis and von Elbe [18], gave 0.330 mJ. The current simulation result of 0.524 mL demonstrates good agreement with various experimental findings but shows significant discrepancies when compared to other computational studies.

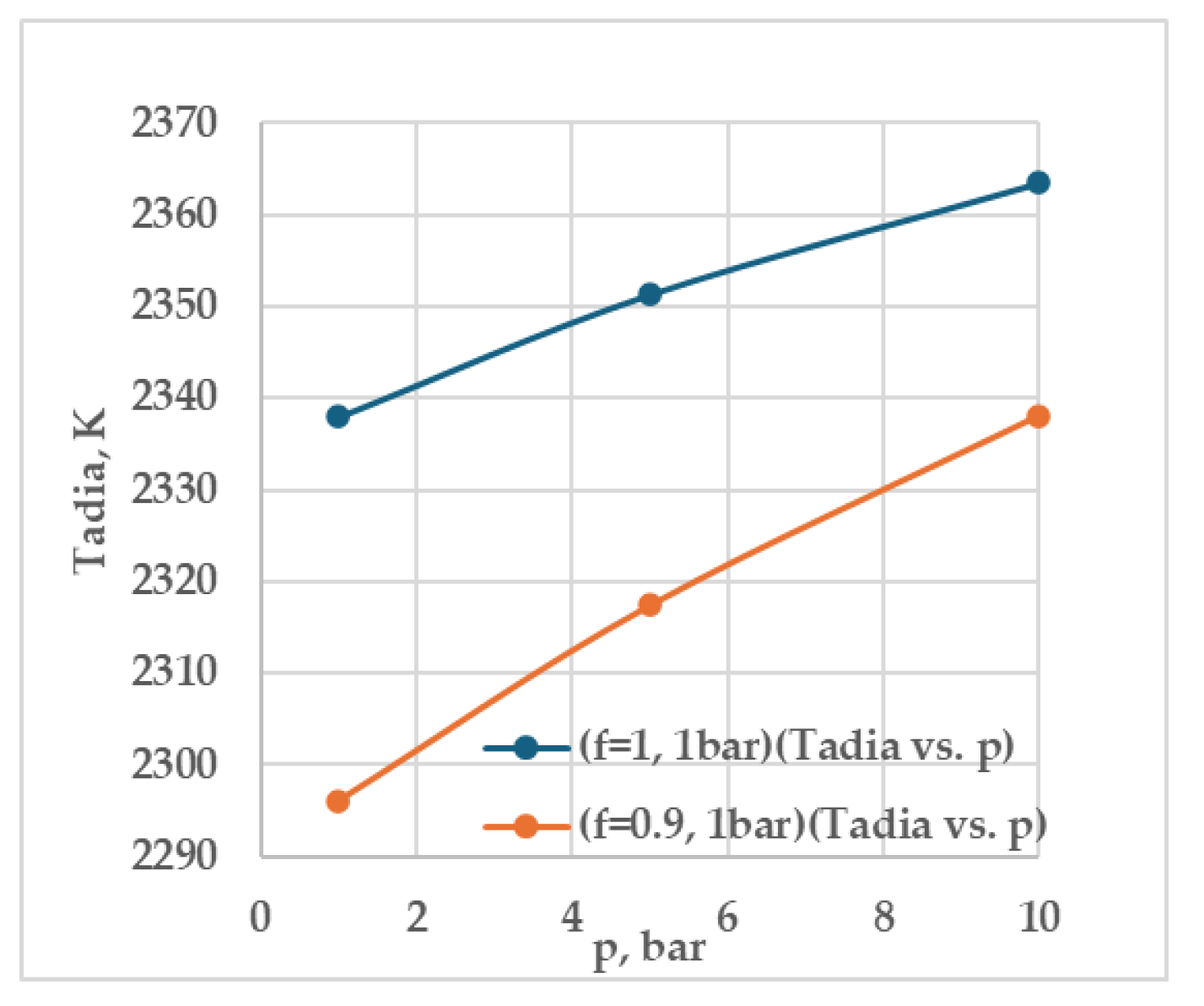
Table 5 results complement with that of numerical data by Wu et al. [32], which indicate that within the flammability range, the MIE remains nearly constant for both mixtures and increases rapidly near the limits. The leaner CH₄/air mixture produces a lower T_adia compared to stoichiometric conditions (φ = 1.0), while T_adia increases with pressure, most notably from 1 to 5 bar and less significantly from 5 to 10 bar (Figure 9). This temperature elevation at higher pressures is due to increased molecular collisions and enhanced reaction rates. As pressure rises, the difference between T_adia values for lean and stoichiometric mixtures gradually decreases, indicating a convergence in flame temperatures under high-pressure conditions. This convergence can be attributed to the increased density and reactivity of the mixture at higher pressures, which partially compensates for the reduced fuel concentration in lean mixtures.

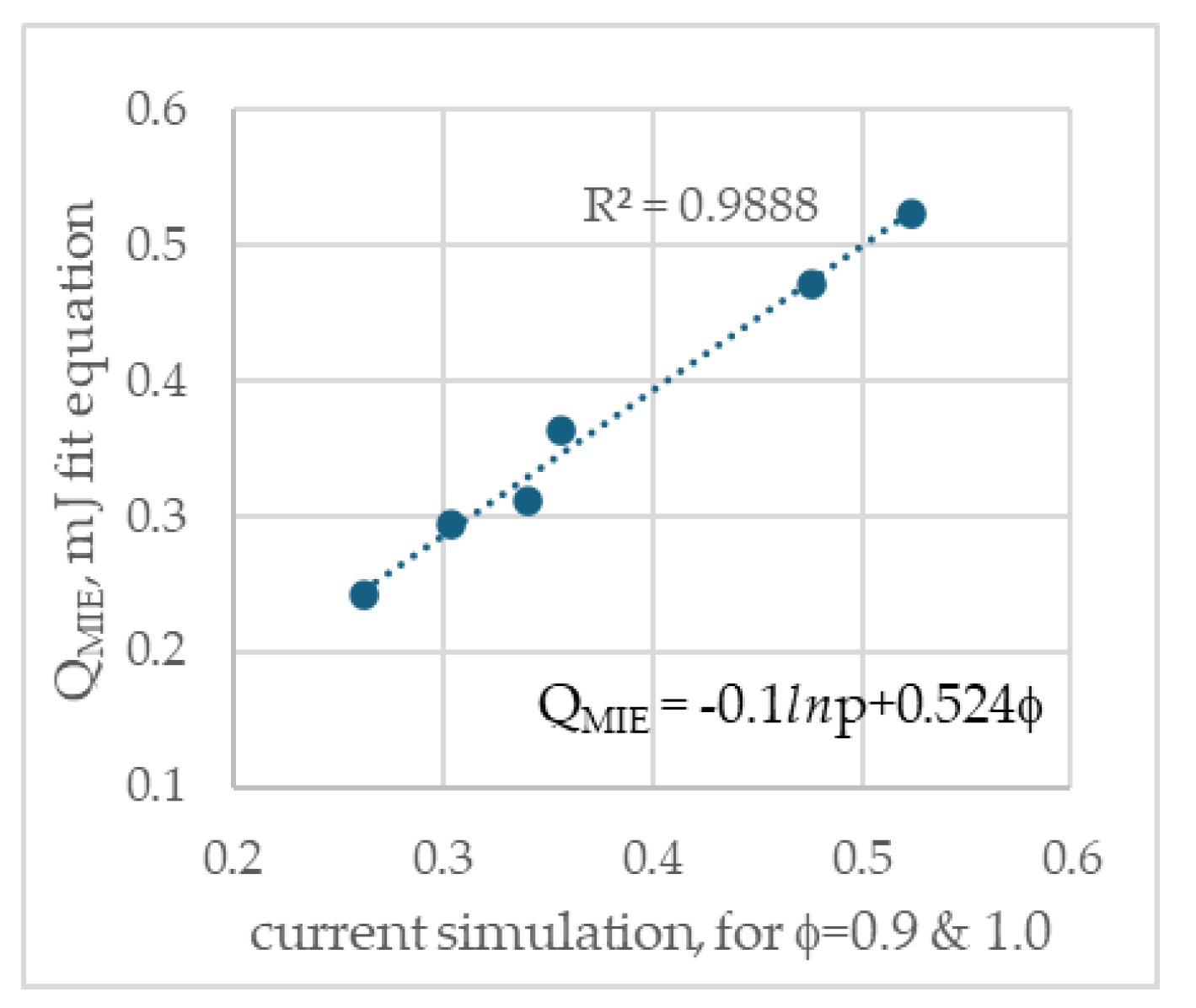
The analytical fit equation that satisfies all six Q_MIE data values (is shown in Figure 10).

Q_MIE = -0.1 lnp + 0.524f

where –0.1 is a fit constant, and 0.524 is taken as the reference value of φ=1.0, 1 bar, which is the MIE for φ =1, at 1 bar. It yields an excellent fit, with coefficient of determination 0.99.

7. Conclusions

This numerical study using reactingFOAM solver examines 1) the prediction of the minimum ignition energy (MIE) of CH₄/air mixtures and 2) estimation of the transient flame evolution until reaches the adiabatic flame temperature at higher pressures which is crucial in understanding in the safety design of the combustions systems. In this RANS study, the flame regime between non-ignition and ignition regime is identified, ignition power density to accuracy up to 3 d.p. The flame evolution is estimated as a function of both time and distance for two equivalence ratios 1.0 and 0.9. The leaner mixture trough curve of MIE occurs at equivalence ratio is at φ =0.9 that requires the lowest minimum ignition energy, which is found to be consistency with many experiments. We found that the difference between MIE of both mixtures is less predominant for pressures between 1 and 5 bar than from 5 and 10 bar. The time required for the flame-fuel mixture to reach the shoot temperature (and subsequently to adiabatic flame temperature) is longer at 1 bar and it substantially decreases from 1 to 5, and to a lesser degree from 5 to 10 bar. The intermediary temperature (from initial mixture 300 K to 481 K) is observed as a crucial parameter, previously unreported in literature, which characterises the process of ignition: successful evolution of flame and transition to self-sustaining combustion. The minimum ignition energy is validated against numerous independent data sets from both numerical simulations and experiments, showing very good consistency with most data. Mathematical formulations of MIE as a function of pressure and equivalence ratio revealed a mildly nonlinear relationship.

Nomenclature

e	Internal energy, J
h	Specific enthalpy, J/kg
K	Kinetic Energy, J
p	Operating pressure, bar
p_i	Initial pressure, bar.
$Q$	Ignition source [(E_min/V_s³)/(r)³], mJ
q	Minimum ignition power density, W/m³
$Q_{M I E}$	Ignition source [(E_min/V_s³)/(r)³], mJ
$q_{M I E}$	Minimum ignition power density, W/m³
r_s	Flame kernel radius, m
t	time, s
T_adia	Adiabatic flame temperature, K
T_i	Initial temperature, K
U	Velocity, m/s
$V$	The ignition kernel volume, m³
Y_i	Mass fraction of i^th species
Greek
$ρ$	Average density of fuel/air mixture, kg/m³
$τ$	Viscous stress tensor, Pa
$τ_{i}$	Ignition duration, ms
$\nabla$	Gradient operator, 1/m
$α_{e f f}$	Effective thermal diffusivity, m²/s
$μ$	Dynamic viscosity of the fluid, kg-m/s
${\dot{ω}}_{i}$	Reaction rate of the i^th species, kg/(m³s)
f	Equivalence ratio (or in instances used as f)
Subscripts
i	initial time
Abbreviations
MIE	Minimum ignition energy
LEL	Lower energy limits
UEL	Upper energy limits

References

Cui, G.; Li, Z.; Yang, C.; Zhou, Z.; and Li, J. Experimental Study of Minimum Ignition Energy of Methane–Air Mixtures at Low Temperatures and Elevated Pressures. Energy & Fuels. 2016, 30, 6738–6744. [Google Scholar]
Sevillano, C.A.; Pesantes, A.A.; Carpio, E.P.; Martinez, E.J.; Gomez, X. Anaerobic Digestion for Producing Renewable Energy—The Evolution of This Technology in a New Uncertain Scenario. Entropy. 2021, 23, 145. [Google Scholar] [CrossRef] [PubMed]
Kundu, S.K.; Zanganeh, J.; Eschebach, D.; Mahinpey, N.; Moghtaderi, B. Explosion characteristics of methane–air mixtures in a spherical vessel connected with a duct. Process Safety and Environmental Protection. 2017, 111, 85–93. [Google Scholar] [CrossRef]
Kundu, S.; Zanganeh, J.; Moghtaderi, B. A review on understanding explosions from methane–air mixture. J. Loss Prev. Process Ind. 2016, 40, 507–523. [Google Scholar] [CrossRef]
Hahn, R. Sustainability Management: Global Perspectives on Concepts, Instruments, and Stakeholders. 2022 [Print Replica] Kindle Edition.
Zhao, Y.; Wang, X.; Cheng, Y.; Mei, Z.; Chen, X.; Tang, S. Ignition and combustion mechanism of alcohol/aluminium suspension nano-fluid droplets. Fuel. 2024, 358A, 130047. [Google Scholar] [CrossRef]
Bjørgen, K.O.P.; Emberson, D.R.; Løvås, T. Combustion of liquid ammonia and diesel in a compression ignition engine operated in high-pressure dual fuel mode. Fuel. 2024, 360, 130269. [Google Scholar] [CrossRef]
Calcote, H. F.; Gregory, C. A.; Barnett, C. M. ; Gilmer, Ruth B. Spark Ignition. Effect of Molecular Structure. Industrial & Engineering Chemistry. 1952, 44, 2656–2662. [Google Scholar]
Jia, J.; Zhu, J.; Niu, W.; & Zhang, J. Influence of acetylene on methane–air explosion characteristics in a confined chamber. Sci. Rep. 2021, 11, 13895. [Google Scholar] [CrossRef]
Zeldovich, Y. Flame propagation in a substance reacting at initial temperature. Combustion and Flame. 1980, 39, 219–224. [Google Scholar] [CrossRef]
Bianco, Y.; Cheng, W.; and Heywood, J. “The Effects of Initial Flame Kernel Conditions on Flame Development in SI Engine,”. SAE Technical Paper. 1991, 100, 1852–1862. [Google Scholar]
Huang, C.C.; Shy, S.; Liu, C.; Yan, Y. A transition on minimum ignition energy for lean turbulent methane combustion in flame let and distributed regimes. Proc Combust Inst. 2007, 31, 1401–1409. [Google Scholar] [CrossRef]
Wang, Q.; Yan, Y.; Yang, S.; Shu, C.; Jiang, J.; Wang, Q.; Yu, C.; Zhu, L. Comparative study of the effects of ignition location on the flame propagation characteristics and spectral properties of a methane–air premixed gas in a vertical pipeline. Journal of the Energy Institute. 2024, 113, 101508. [Google Scholar] [CrossRef]
Kravchik, T.; Sher, E. Numerical modeling of spark ignition and flame initiation in a quiescent methane-air mixture. Combust. Flame. 1994, 99, 635–643. [Google Scholar] [CrossRef]
Warnatz, J.; Maas, U.; Dibble, R.W. Combustion: Physical and Chemical Fundamentals, Modeling and Simulation, Experiments, Pollutant Formation. 2006 , Textbook (pages 4-6). 4/e.
Scott, F.; Van Dolah, R.; Zabetakis, M. Flammability characteristics of the system H₂-NO-N₂O-air. Proc. Combust. Inst. 1957, 6, 540–545. [Google Scholar] [CrossRef]
Rabl, S.; Davies, T.J.; McDougall, A.P.; Cracknell, R.F. Understanding the relationship between ignition delay and burn duration in a constant volume vessel at diesel engine conditions. Proc. Combust. Ins 2015, 35, 2967–2974. [Google Scholar] [CrossRef]
The open source CFD toolbox, Standard boundary conditions, available from https://www.openfoam.com/documentation/user-guide/standard boundary conditions. (accessed 22 April 2024). Version v2012.
Muppala, S.P.R.; & Papalexandris, M.V. "A Modelling Approach for Hydrogen-Doped Lean Premixed Turbulent Combustion." Proceedings of the ASME International Mechanical Engineering Congress and Exposition. Heat Transfer. 2006, 2. Chicago, Illinois, USA. November 5–10, 21-30.
Muppala, S.P.R.; Nakahara, M.; Aluri, N.K.; Kido, H.; Wen, J.X.; Papalexandris, M.V. Experimental and analytical investigation of the turbulent burning velocity of two-component fuel mixtures of hydrogen, methane, and propane. International Journal of Hydrogen Energy. 2009, 34, 9258–9265. [Google Scholar] [CrossRef]
Han, J.; Yamashita, H.; Hayashi, N. Numerical study on the spark ignition characteristics of a methane–air mixture using detailed chemical kinetics: Effect of equivalence ratio, electrode gap distance, and electrode radius on MIE, quenching distance, and ignition delay. Combustion and Flame 2010, 157, 101–113. [Google Scholar] [CrossRef]
Yuasa, T.; Kadota, S.; Tsue, M.; Kono, M.; Nomura, H.; Ujiie, Y. Effects of energy deposition schedule on minimum ignition energy in spark ignition of methane/air mixtures. Proc. of Combust Inst. 2002, 29, 743–750. [Google Scholar] [CrossRef]
Ghosh, A.; Munoz-Munoz, N.M.; Lactose, D.A. Minimum ignition energy of hydrogen-air and methane-air mixtures at temperatures as low as 200 K. Inter. J. of H2 energy. 2022, 47, 53–59. [Google Scholar] [CrossRef]
Lewis, B.; Von Elbe, G. Combustion, flames, and explosions of gases, Elsevier 2012.Hankinson, G.; Mathurkar, H.; Lowensmith, B.J. Ignition energy and ignition probability of methane-hydrogen-air mixtures. 3rd International Conference on Hydrogen Safety. 2009, Ajaccio, France.
Wu, C.; Schibi, R.; Mass, U. Numerical studies on minimum ignition energies in CH₄/air and iso-octane/air mixtures. J. of loss prevention in the process industries. 2021, 72, 1–11. [Google Scholar] [CrossRef]
Lu, H.; Liu, F.; Wang, K.; Xu, G.; Curran, H.J. Numerical study on the minimum ignition energy of a methane-air mixture. Fuel 2021, 285, 119230. [Google Scholar] [CrossRef]
Kim, H.J.; Chung, S.H.; Sohn, C.H. Numerical Calculation of Minimum Ignition Energy for hydrogen and Methane Fuels. KSME International Journal 2004, 18, 838–846. [Google Scholar] [CrossRef]
Wang, B.; Zhou, L.; Xu, K.; Wang, Q. Fast prediction of minimum ignition energy from molecular structure using simple QSPR model. Journal of Loss Prevention in the Process Industries. 2017, 50A, 290–294. [Google Scholar] [CrossRef]
Lewis, B.; and von Elbe, G. Combustion, flames, and explosions of gases. third ed. Orlando: Academic Press; 1987. p357.
Su, Z.; Liu, L.; Li, K.; Chen, X.; Chen, T.; Huang, C. Theoretical prediction model for minimum ignition energy of combustible gas mixtures. International Journal of Hydrogen Energy. 2024, 69, 103–112. [Google Scholar] [CrossRef]
Wu, C.; Chen, Y.; Schießl, R.; Shy, S.S.; Maas, U. Numerical and experimental studies on minimum ignition energies in primary reference fuel/air mixtures. Proceedings of the Combustion Institute 2023, 39, 1987–1996. [Google Scholar] [CrossRef]

Figure 1. a): Cubical computational domain, 75 mm cubical domain is a constant volume filled with frozen premixed methane/air mixtures. It shows different patch faces such representing the top, left, right, bottom, front and back boundaries. (to note: in the solver, a ‘patch’ is a general term for any boundary surface in the computational domain, while a ‘wall’ is a specific type of patch that represents a solid boundary where the no-slip condition is usually enforced for fluid flow simulations). (b) Mesh configuration: R) slice in the positive x-direction, with 200 grid points per side, contains a centred spherical flame kernel of 0.5 mm radius on a hexahedral mesh. The inset image displays the grid resolution within the kernel's domain.

Figure 2. The grid sensitivity test (also see Table 2).

Figure 3. The numerical methodology of reactingFOAM solver.

Figure 4. (R1: f =1.0, 1 bar; for a successful ignition of a premixed CH₄/air mixture at q =1 · 10⁸ W/m³; T_adia=2337.95 K); R1 should be seen along with Figure 5a and Figure 6a. (R2: f =1, 5 bar; q =0.68 · 10⁸ W/m^3; T_adia= 2351.33 K); see Figure 5b and Figure 6b. (R3: f =1, 10 bar; q=0.58 · 10⁸ W/m³; T_adia=2363.52 K); see Figure 5c and Figure 6c. (R4: f =0.9, 1 bar; at q =0.91 · 10⁸ W/m³; T_adia= 2296.10 K); see Figure 5d and Figure 6d. (R5: f =0.9, 5 bar; at q =0.65 · 10⁸ W/m³; T_adia= 2317.39 K); see Figure 5e and Figure 6e. (R6: f =0.9, 10 bar; at q = 0.50 · 10⁸ W/m³; T_adia= 2338.11 K); see Figure 5f and Figure 6f. with the contours of temperature (K), CH₄, CO₂ & H₂O (in mass fraction). R represents row, and number 1 is top row. Note: the computational time 0.51 s, for example, for f=1 at 1 bar, [computational time 0 to 1 s ≡ 10000 iterations].

Figure 5. presents the temporal evolution of key parameters temperature, mass fraction of H₂O, CH₄ and CO₂ for φ =1.0 and φ=0.9 mixtures at pressures 1, 5, and 10 bar.

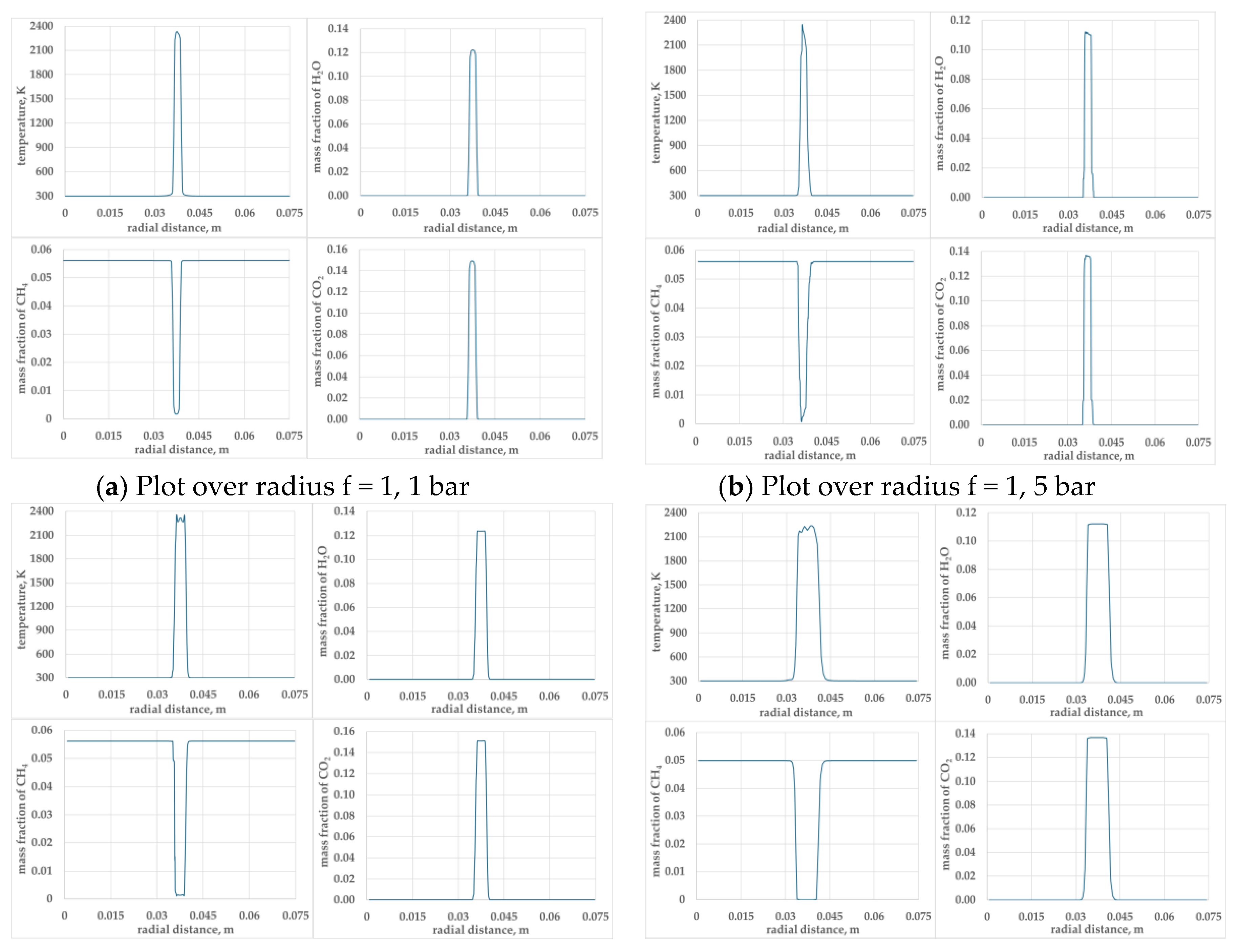
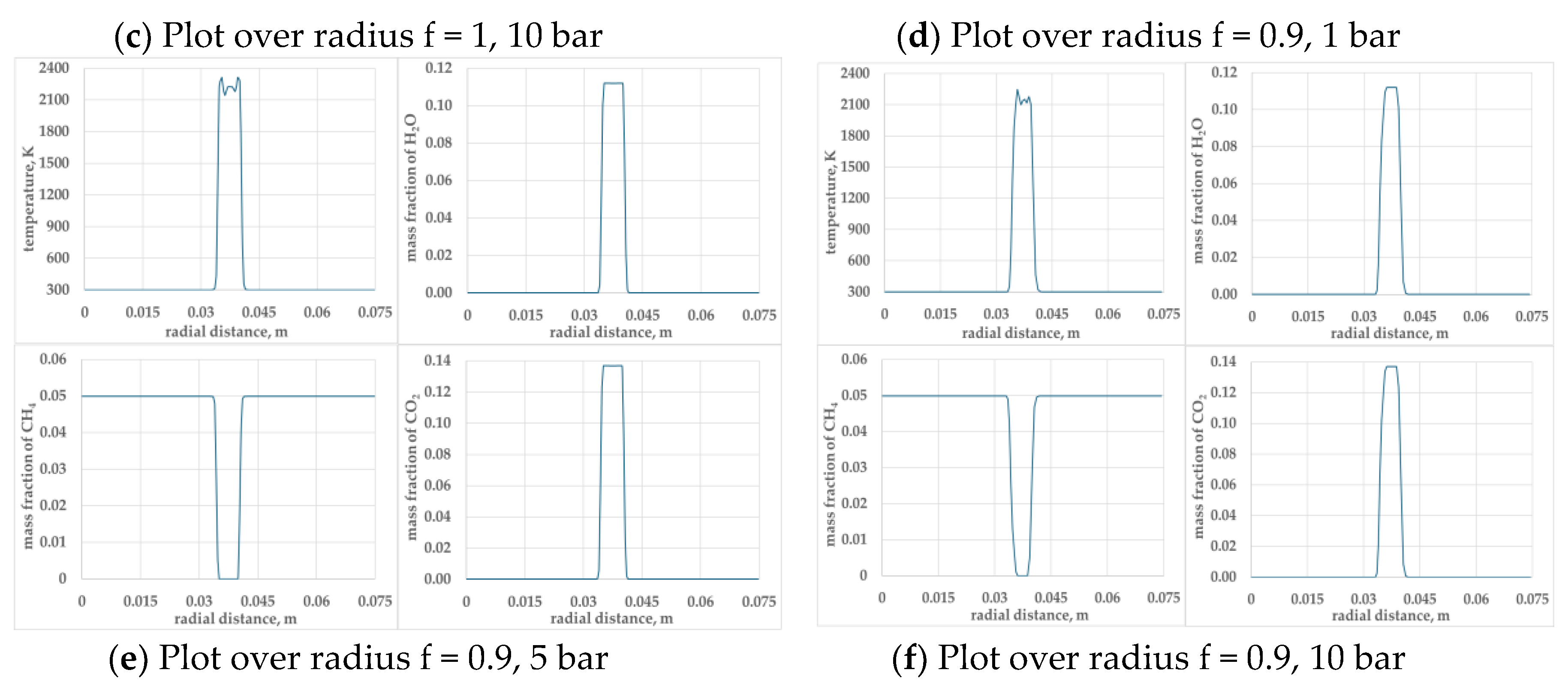
Figure 6. Presents profiles of temperature, mass fraction of CO₂, CH₄ and H₂O along the radius, passing through the centre of the kernel for φ =1.0 and φ = 0.9 mixtures at pressures 1, 5 and 10 bar.

Figure 7. Correlation plots of Q_MIE against case numbers from Table 4, left: φ = 1.0 and p = 1 bar, and right: φ = 0.9 and p = 1 bar. Both figures show the MIE values spanning over a period of sixty years. The MIE data is selected based on chronology from 1952, but this is in no way complete.

Figure 8. Lists: a summary of all simulation results for the CH₄/air mixtures, φs 1.0 and 0.9. Read for φ =1.0 from (a) to (e); and φ =0.9 from (f) to (j). The five quantities q_MIE, Q_MIE, t_s, T_s, and T_adia plotted verses operating pressures 1, 5, and 10 bar. t_s represents the computational time at which the temperature rises from 300 K to T_s (refer to the figure first row, second from left). When examining Q_MIE plots, refer to Table 4 for additional context.

Figure 9. Demonstrates the effect of pressure on adiabatic flame temperature, where φ represents the equivalence ratio (f could not be changed to the symbol φ), given in Table 5.

Figure 10. Shows the correlation between the current simulations with that obtained from a fit equation.

Table 2. Grid sensitivity test for φ =1 at 1 bar. conducted for stoichiometric methane/air mixture. The flame temperature converged to an optimal value as mesh resolution increased.

Number of grid points	Number of grids over 75 mm	Grid size ratio	T (K)	Ignition
4,913,000	170·170·170	0.85	1996	Yes
5,832,000	180·180·180	0.90	2080	Yes
6,859,000	190·190·190	0.95	2196	Yes
*8,000,000	200·200·200	1.00	2283	Yes
10,648,000	220·220·220	1.10	2308	Yes

Table 3. shows the computational methodology of the reactingFOAM solver.

Start
1. Initialize Mesh and Geometry
Define the cubical domain geometry.
Generate a mesh suitable for the simulation.
2. Define Combustion Model and Reactions
Choose appropriate combustion
model.
Specify single step using Arrhenius law for
Premixed combustion.
3. Set Boundary and Initial Conditions
Set boundary conditions for temperature, pressure, and velocity
Initialize T, p, and U fields
4. Set Combustion Parameters
Define parameters in ‘fvOptions’.
Initialize the term minimum ignition power density ’q’ with the ignition duration.
5. Time Stepping Loop
Set initial time
Specify time step size and total simulation time
6. Iteration Loop
Initialize iteration counter
7. Solve Momentum Equations (Navier-Stokes)
Calculate velocity field considering combustion effects.
Account for pressure-velocity coupling (e.g.,
pressure correction)
Update velocity field.

8. Solve Energy Equation (Temperature)
Calculate temperature field considering
combustion heat release
Account for energy transport (conduction,
convection)
Incorporate volumetric heat source term for
combustion
9. Solve Species Transport Equations
Calculate transport of chemical species (e.g.,
fuel, oxidizer, products)
10. Solve Pressure Equation
Formulate and solve pressure equation (e.g.,
SIMPLE algorithm)
Update pressure field
11. Check Convergence
Evaluate convergence criteria for solution
fields (e.g., T and species concentrations)
If converged, exit iteration loop; otherwise, g
to step.
12. Time Stepping
Update time
if the simulation reaches the desired end time.
13. take the Output results
Write simulation results (e.g., temperature,
pressure, species distributions)
Visualization of results
14. Check Simulation Termination
If the end time is reached, exit the time.
stepping loop; otherwise, go to step 6
End

Table 4. presents ten literature sources spanning sixty years for comparison with the current computational data, validating MIE in mJ, with φs of 0.9 and 1.0 at 1 bar. The abbreviations are: Expt (Experiment) and Sim (Simulation).

Case number	Author(s), year & Equivalence ratio, pressure	MIE, mJ		Case number	Author(s), year & Equivalence ratio, pressure		MIE, mJ
1	Han et al. [21]/ f=1.0, 1bar	Expt.	0.324	12	Wang, B. et al. [29] f=1.0, 1 bar	Sim	0.169
2	Han et al. [21]/ f=1.0, 1bar	Sim.	1.349	13	Wang, B. et al. [29] f =1.0, 1bar	Expt.	0.672
3	Yuasa, T. et al. [22]/ f =1.0, 1 bar	Expt.	0.500	14	Current data f =1.0, 1 bar	Sim	0.524
4	Yuasa, T. et al. [22]/ f =1.0, 1 bar	Sim.	0.370	15	Hankinson et al. [25] f =0.9, 1 bar	Exp	0.679
5	Ghosh et al., [23]/ f =1.0, 1 bar	Sim.	0.480	16	Lewis, B. & von Elbe, G. [30]. p357 f =0.9, 1 bar	Exp	0.944
6	Calcote et al.[8] / f =1.0, 1 bar	Expt.	0.480	17	Wu et al. [26] / f =0.9, 1bar	Sim.	0.444
7	Lewis, B. and von Elbe, G. [24] f =1.0, 1 atm.	Expt.	0.330	18	Han et al. [21]/ f =0.9, 1 bar	Expt.	0.220
7	Lewis, B. and von Elbe, G. [24] f =1.0, 1 atm.	Expt.	0.330	19	Han et al. [21]/ f =0.9, 1 bar	Sim.	0.944
8	Hankinson et al. [25] f =1.0, 1 bar	Exp	0.732	20	Su et al. et al. [31]/ f =0.9, 1 bar	Expt.	0.282
8	Hankinson et al. [25] f =1.0, 1 bar	Exp	0.732	21	Su et al. et al. [31]/ f =0.9, 1 bar	Sim.	0.356
9	Wu et al. [26]/ f=1.0, 1 bar	Sim.	0.441	22	Lu, H. [27]/ f =0.9, 1 bar	Sim.	0.700
10	Lu, H. [27]/ f =1.0, 1 bar	Sim.	0.700	23	Current data f =0.9, 1 bar	Sim	0.476
11	Kim [28] f =1.0, 1bar	Sim.	0.500	23	Current data f =0.9, 1 bar	Sim	0.476

Table 5. Simulation results of MIE and power density for two equivalence ratios at three different pressures. It also shows the non-ignition and ignition energy values.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

RANS Simulation of Minimum Ignition Energy of Stoichiometric and Leaner CH4/Air Mixtures at Higher Pressures in Quiescent Conditions

Abstract

1. Introduction

2. Formulation and Numerical Method

3. Governing Equations

4. Model Geometry, Initial and Boundary Conditions

4.1. Evaluation of Minimum Ignition Energy

5. Numerical Methodology

6. Results and Discussion

6.1. Evaluation of Minimum Ignition Energy

6.2. Comparsion of MIE with literature

7. Conclusions

Nomenclature

References

MDPI Initiatives

Important Links

Subscribe