Alternative Slope-Deflection Equations for Static Analysis of Indeterminate Structures

Preprint

Article

Alternative Slope-Deflection Equations for Static Analysis of Indeterminate Structures

Altmetrics

Downloads

Views

Comments

Dayakar Naik Lavadiya^*,

Eric Vincent Garcia,Clare M Pankratz,Kristine M Kalthoff

Dayakar Naik Lavadiya^*,

Eric Vincent Garcia,Clare M Pankratz,Kristine M Kalthoff

This version is not peer-reviewed

Submitted:

16 September 2024

Posted:

17 September 2024

You are already at the latest version

Alerts

Abstract

This paper provides an alternative Slope-Deflection equation for performing the static analysis of the indeterminate structures. While the conventional Slope-Deflection method introduced in undergraduate structural analysis course involves the use of fixed end moments in the Slope-Deflection equations, the proposed method employs the slope of a simply supported beam to obtain the unknown moments at the joints. Three numerical examples of continuous beams with different load configurations are chosen and the efficacy of the proposed equations is demonstrated. From the perspective of undergraduate structural analysis course in Civil Engineering education, the approach proposed in this paper offers two advantages: (1) prior knowledge of fixed beams is not required and (2) the concepts gained from determinate structural analysis are directly applicable.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

The slope deflection method is a displacement method introduced by George Maney in 1915 [1]. It is employed to perform the analysis of statically indeterminate beams and rigid joint frames [2]. This method is often taught in undergraduate structural analysis courses across universities worldwide. In this traditional method the end moments of each member of the structure are first expressed in terms of the unknown slope (

θ

) and deflection (

δ

) at the joints referred to as ‘Slope-Deflection’ equations (see Equation (1)).

M_{A B} = M_{F A B} + \frac{2 E I}{L} (2 θ_{A} + θ_{B} - \frac{3 δ}{L})

(1a)

M_{B A} = M_{F B A} + \frac{2 E I}{L} (2 θ_{B} + θ_{A} - \frac{3 δ}{L})

(1b)

where

M_{A B}

M_{B A}

are the moments (unknown) at support A and B respectively (see Figure 1,

M_{F A B}

M_{F B A}

(known) are the fixed end moments at support A and B respectively,

θ_{A}

and

θ_{B}

are the slopes at support A and B respectively,

δ

is the relative vertical deflection between two ends and

E

I

and

L

are the Young’s modulus, moment of inertia and length of the structural member respectively.

The moment equilibrium at each joint is then applied and simultaneous set of equations are obtained. These simultaneous equations are then solved to determine the slopes and deflections at the joints. Consequently, the moments in the structural members are then evaluated. When compared to methods like moment distribution, the main advantage possessed by slope – deflection method is the ease of programing and the wide range applicability for the indeterminate structures [3].

Since the slope-deflection equations consists of fixed end moments (see Equation (1)), it becomes essential to learn how fixed end moments are obtained for various loading conditions prior to the introduction of the method. Furthermore, the original derivation of the slope-deflection assumes that the ends of the structural member are fixed, and the moment is acting clockwise at both ends. This often leads to two questions, (1) what happens if the structural members are assumed to be simply supported instead of fixed and (2) what if the moment at the left support is considered to be counterclockwise in the derivation.

In this paper, an alternative method of deriving slope-deflection equations is proposed which addresses the above-mentioned questions. The resulting slope-deflection equations are expressed in terms of slopes of the simply supported beam instead of fixed end moments. Numerical examples are provided, and the results are compared to that of the traditional slope-deflection method. Unlike the traditional method, no prior knowledge of fixed end moments is required for the proposed equations.

2. Derivation of Slope-Deflection Equation

In this section the alternative slope-deflection equation is derived. For this purpose, the same assumptions employed in conventional slope-deflection method are considered i.e., only flexural deformations are taken into account and axial and shear deformations are ignored [4].

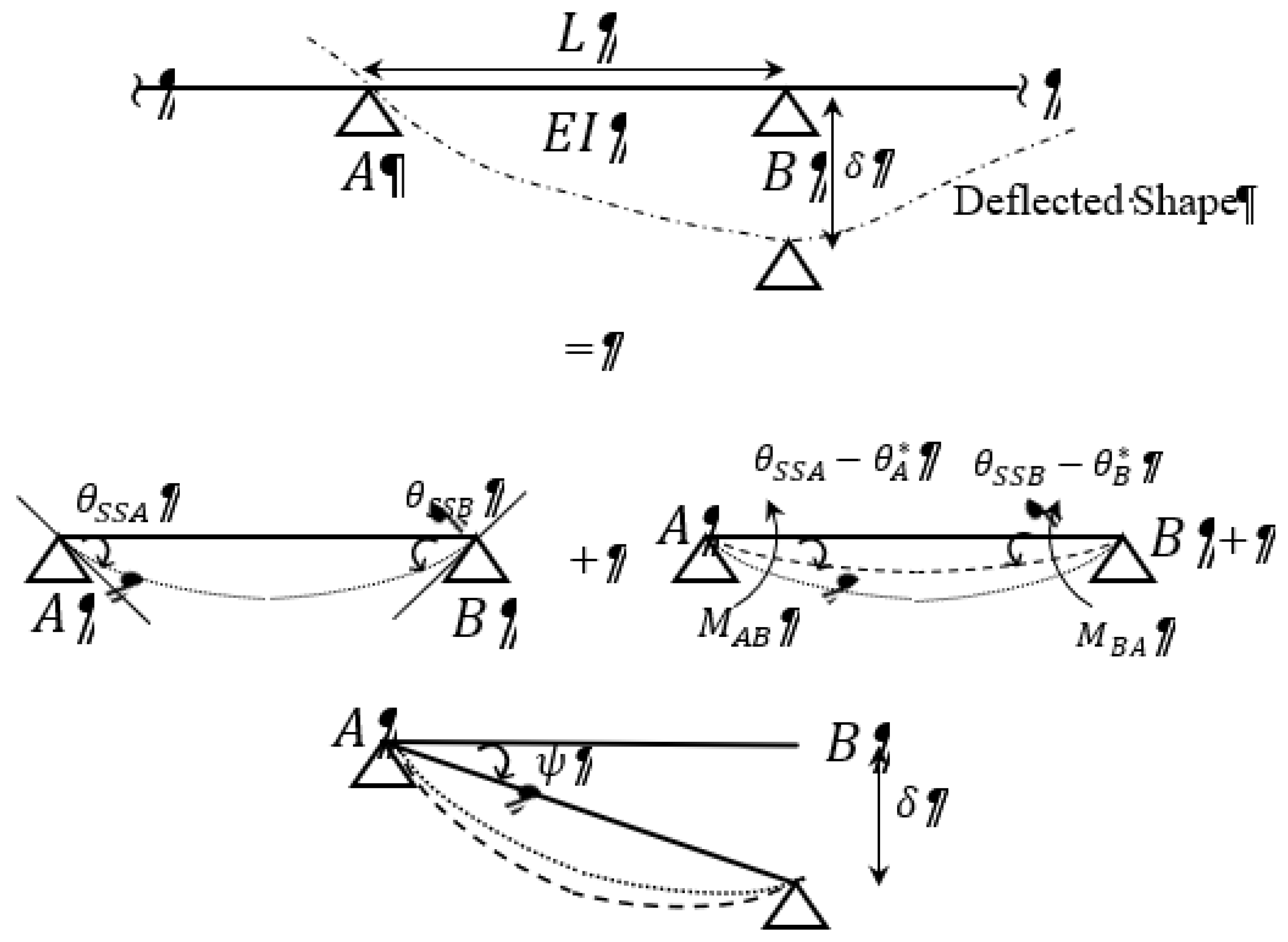
Let

A B

represent any intermediate span of a continuous prismatic beam with length

L

(see Figure 1). Unlike conventional Slope-Deflection method, wherein joints A and B are considered fixed, in this alternative approach, beam

A B

is first considered to be simply supported. Let

θ_{S S A}

and

θ_{S S B}

represent the absolute slopes at A and B respectively for the associated loading (see Figure 1). Since, the moment at joint A and B in a continuous beam are non-zero, two unknown moments

M_{A B}

(counterclockwise) and

M_{B A}

(clockwise) are applied at joint A and B respectively for a simply supported beam (see Figure 2).

The resulting slope at A (denoted by

θ_{A}^{*}

) and B (denoted by

θ_{B}^{*}

) due to applied moments can then be evaluated using conjugate beam method and principle of superposition [2].

θ_{A}^{*} = \frac{2}{3} (\frac{1}{2} \frac{M_{A B}}{E I} L) + \frac{1}{3} (\frac{1}{2} \frac{M_{B A}}{E I} L)

(2)

θ_{B}^{*} = \frac{1}{3} (\frac{1}{2} \frac{M_{A B}}{E I} L) + \frac{2}{3} (\frac{1}{2} \frac{M_{B A}}{E I} L)

(3)

Let

δ

represent the settlement of support B (see Figure 1). Consequently, beam

A B

undergoes clockwise rotation

ψ

at joint A. The relationship between

δ

and

ψ

for small rotation can then be expressed as

ψ = \frac{δ}{L}

(4)

The net slope at A (

θ_{A}

) and B (

θ_{B}

) due to applied moments and settlement of support can then be expressed as

θ_{A} = θ_{S S A} - θ_{A}^{*} + ψ

(5)

θ_{B} = - θ_{S S B} + θ_{B}^{*} + ψ

(6)

At this juncture it is important to note that overall

θ_{A}

is positive and overall

θ_{B}

is negative based on the sign convention that clockwise rotation about a joint is positive and counterclockwise rotation about a joint is negative. In other words,

θ_{A}

and

θ_{B}

are not absolute quantities.

Substituting Equation (2) and 3 in Equation (5) and 6,

θ_{A} = θ_{S S A} - (\frac{1}{3} \frac{M_{A B}}{E I} L) + (\frac{1}{6} \frac{M_{B A}}{E I} L) + ψ

(7)

θ_{B} = - θ_{S S B} + (\frac{1}{6} \frac{M_{A B}}{E I} L) + (\frac{1}{3} \frac{M_{B A}}{E I} L) + ψ

(8)

Solving Equations (7) and (8), the unknown moments

M_{A B}

and

M_{B A}

can then be expressed as

M_{A B} = \frac{2 E I}{L} (2 θ_{S S A} - θ_{S S B} - 2 θ_{A} - θ_{B} + 3 δ / L)

(9)

M_{B A} = \frac{2 E I}{L} (2 θ_{S S B} - θ_{S S A} + 2 θ_{B} + θ_{A} - 3 δ / L)

(10)

For the settlement of joint A, the equation Equations (9) and (10) can be modified as

M_{A B} = \frac{2 E I}{L} (2 θ_{S S A} - θ_{S S B} - 2 θ_{A} - θ_{B} - 3 δ / L)

(11)

M_{B A} = \frac{2 E I}{L} (2 θ_{S S B} - θ_{S S A} + 2 θ_{B} + θ_{A} + 3 δ / L)

(12)

Equations (9)-(12) represents the alternative slope-deflection equations. This equation appears to be same as that of conventional slope-deflection equation except the fixed end moments are replaced by the slopes of simply supported beam (see Table 1).

3. Numerical Example

In this section numerical examples are provided to demonstrate the efficacy of the alternative slope-deflection equations. The exactness of the results is compared with the conventional slope-deflection equations (see Figure 3).

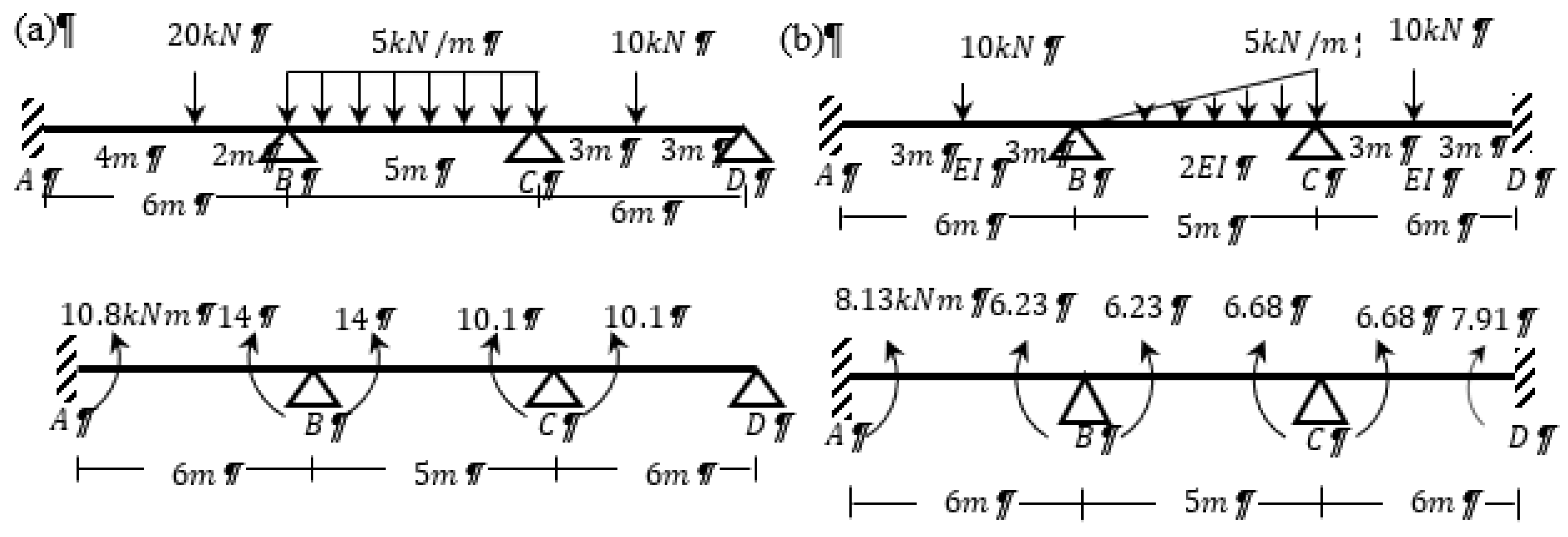
Example 1: Continuous beam with no settlement: Determine the moments at the joints for the continuous beam shown in Figure 3(a).

Segment	$2 θ_{S S A} - θ_{S S B}$	$2 θ_{S S B} - θ_{S S A}$	Slope-Deflection Equations
AB	$\frac{80}{3 E I}$	$\frac{160}{3 E I}$	$M_{A B} = \frac{2 E I}{6} (\frac{80}{3 E I} - 2 θ_{A} - θ_{B})$ $M_{B A} = \frac{2 E I}{6} (\frac{160}{3 E I} + 2 θ_{B} + θ_{A})$	(13a) (13b)
BC	$\frac{625}{24 E I}$	$\frac{625}{24 E I}$	$M_{B C} = \frac{2 E I}{5} (\frac{625}{24 E I} - 2 θ_{B} - θ_{C})$ $M_{C B} = \frac{2 E I}{5} (\frac{625}{24 E I} + 2 θ_{C} + θ_{B})$	(14a) (14b)
CD	$\frac{45}{2 E I}$	$\frac{45}{2 E I}$	$M_{C D} = \frac{2 E I}{6} (\frac{45}{2 E I} - 2 θ_{C} - θ_{D})$ $M_{D C} = \frac{2 E I}{6} (\frac{45}{2 E I} + 2 θ_{D} + θ_{C})$	(15a) (15b)

Since A is a fixed end and D is a roller,

θ_{A} = 0

and

M_{D C} = 0

. Applying equilibrium equation (

\sum M = 0

) at the joint B (see Equations (13b) and (14a)) and joint C (see Equations (14b) and (15a)),

M_{B A} = M_{B C} ⟹ 1.467 E I θ_{B} + 0.4 E I θ_{C} = - 7.36

(16a)

M_{C B} = M_{C D} ⟹ 0.4 E I θ_{B} + 1.467 E I θ_{C} + 0.333 E I θ_{D} = - 2.92

(16b)

M_{D C} = 0 ⟹ θ_{C} + 2 E I θ_{D} = - 22.5

(16c)

Solving Eq. 16a, 16b and 16c

E I θ_{B} = - 5.657; E I θ_{C} = 2.347; E I θ_{D} = - 12.423

(17)

Therefore, the moments at each joint (see Figure 3(a)) are determined to be

M_{A B} = 10.8 k N m; M_{B C} = 14 k N m; M_{C D} = 10.1 k N m

(18)

Example 2: Continuous beam with sinking of support: Determine the moments at the joints for the continuous beam shown in Figure 3(a) if joint B sinks downward by 15mm and

E = 200 \times 10^{5} \frac{k N}{m^{2}}, I = 120 \times 10^{- 6} m^{4}

Segment	$2 θ_{S S A} - θ_{S S B}$	$2 θ_{S S B} - θ_{S S A}$	Slope-Deflection Equations
AB	$\frac{80}{3 E I}$	$\frac{160}{3 E I}$	$M_{A B} = \frac{2 E I}{6} (\frac{80}{3 E I} - 2 θ_{A} - θ_{B} + 3 (\frac{0.015}{6}))$ $M_{B A} = \frac{2 E I}{6} (\frac{160}{3 E I} + 2 θ_{B} + θ_{A} - 3 (\frac{0.015}{6}))$	(19a) (19b)
BC	$\frac{625}{24 E I}$	$\frac{625}{24 E I}$	$M_{B C} = \frac{2 E I}{5} (\frac{625}{24 E I} - 2 θ_{B} - θ_{C} - 3 (\frac{0.015}{5}))$ $M_{C B} = \frac{2 E I}{5} (\frac{625}{24 E I} + 2 θ_{C} + θ_{B} + 3 (\frac{0.015}{5}))$	(20a) (20b)
CD	$\frac{45}{2 E I}$	$\frac{45}{2 E I}$	$M_{C D} = \frac{2 E I}{6} (\frac{45}{2 E I} - 2 θ_{C} - θ_{D})$ $M_{D C} = \frac{2 E I}{6} (\frac{45}{2 E I} + 2 θ_{D} + θ_{C})$	(21a) (21b)

Applying equilibrium equation (

\sum M = 0

) at the joint B (see Eq. 19b and 20a) and joint C (see Equations (20b) and (21a)),

M_{B A} = M_{B C} ⟹ 1.467 E I θ_{B} + 0.4 E I θ_{C} = - 10

(22a)

M_{C B} = M_{C D} ⟹ 0.4 E I θ_{B} + 1.467 E I θ_{C} + 0.333 E I θ_{D} = - 11.56

(22b)

M_{D C} = 0 ⟹ θ_{C} + 2 E I θ_{D} = - 22.5

(22c)

Solving the equations 22a, 22b and 22c

E I θ_{B} = - 5.646; E I θ_{C} = - 4.2926; E I θ_{D} = - 9.104

(23)

Therefore, the moments at each joint (see Figure 3(a)) are determined to be

M_{A B} = 16.77 k N m; M_{B C} = 8.01 k N m; M_{C D} = 13.36 k N m

(24)

Example 3: Continuous beam with varying moment of inertia for each span Determine the moments at the joints for the continuous beam shown in Figure 3(b).

Segment	$2 θ_{S S A} - θ_{S S B}$	$2 θ_{S S B} - θ_{S S A}$	Slope-Deflection Equations
AB	$\frac{45}{2 E I}$	$\frac{45}{2 E I}$	$M_{A B} = \frac{2 E I}{6} (\frac{45}{2 E I} - 2 θ_{A} - θ_{B})$ $M_{B A} = \frac{2 E I}{6} (\frac{45}{2 E I} + 2 θ_{B} + θ_{A})$	(25a) (25b)
BC	$\frac{625}{120 E I}$	$\frac{625}{80 E I}$	$M_{B C} = \frac{2 (2 E I)}{5} (\frac{625}{120 E I} - 2 θ_{B} - θ_{C})$ $M_{C B} = \frac{2 (2 E I)}{5} (\frac{625}{80 E I} + 2 θ_{C} + θ_{B})$	(26a) (26b)
CD	$\frac{45}{2 E I}$	$\frac{45}{2 E I}$	$M_{C D} = \frac{2 E I}{6} (\frac{45}{2 E I} - 2 θ_{C} - θ_{D})$ $M_{D C} = \frac{2 E I}{6} (\frac{45}{2 E I} + 2 θ_{D} + θ_{C})$	(27a) (27b)

Applying equilibrium equation (

\sum M = 0

) at the joint B (see Equations (25b) and (26a)) and joint C (see Equations (26b) and (27a)),

M_{B A} = M_{B C} ⟹ 2.267 E I θ_{B} + 0.8 E I θ_{C} = - 3.33

(28a)

M_{C B} = M_{C D} ⟹ 0.8 E I θ_{B} + 2.267 E I θ_{C} = 1.25

(28b)

Solving the equations Eq. 28a and 28b

E I θ_{B} = - 1.9; E I θ_{C} = 1.22

(29)

Therefore, the moments at each joint (see Figure 3(b)) are determined to be

M_{A B} = 8.13 k N m; M_{B C} = 6.23 k N m; M_{C D} = 6.68 k N m; M_{D C} = 7.91 k N m

(30)

4. Conclusions

Alternative Slope-Deflection equations for indeterminate structures are proposed and the efficacy of the equations for evaluating unknown moments is compared. From this study the following conclusions are drawn.

The results obtained from the proposed approach are exactly same as that of conventional slope-deflection equation.
The proposed approach does not require prior knowledge of fixed end moments. The principle of superposition, conjugate beam method, and slopes of simply supported beam for desired load configuration obtained in the determinate structures are sufficient.
This approach will serve as an alternative explanation for slope-deflection method in the structural analysis class for civil engineering undergraduates.

Funding

This research received no funding.

Data Availability Statement

All data, models, and code generated or used during the study appear in the submitted article.

Conflicts of Interest

All authors declare that they have no conflicts of interest.

References

Maney G. Studies in Engineering. Minneapolis: 1915.
Hibbeler RC, Yap KB, Abed F. Structural Analysis. vol. 10th Edition. 2020.
Abbas M. New Modification for Slope-Deflection Equation in Structural Analysis. International Journal of Engineering and Technical Research 2015:387.
Kotrasova K, Kormanikova E, Loukili M. Using Software Applications in Teaching of Slope-deflection Method in Subject Static Analysis of Constructions. International Journal of Education and Information Technologies 2021;15:353–63. [CrossRef]

Figure 1. (a) Schematic of a continuous beam with a deflected shape and application of principle of superposition to obtain the slopes at joint A and B, (b) considering AB as a simply supported beam, (c) Moments applied at joint A and B for reduction in slope, (d) change in slope of beam AB due to settlement of support B.

Figure 2. Application of conjugate beam method to evaluate the slope at A and B due to concentrated moments

M_{A B}

and

M_{B A}

at joint A and B respectively.

Figure 2. Application of conjugate beam method to evaluate the slope at A and B due to concentrated moments

M_{A B}

and

M_{B A}

at joint A and B respectively.

Figure 3. Numerical examples (a) continuous beam with no sinking of support (b) continuous beam with varying

E I

Figure 3. Numerical examples (a) continuous beam with no sinking of support (b) continuous beam with varying

E I

Table 1. Absolute slopes of simply supported beam for typical loading conditions.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Alternative Slope-Deflection Equations for Static Analysis of Indeterminate Structures

Abstract

1. Introduction

2. Derivation of Slope-Deflection Equation

3. Numerical Example

4. Conclusions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe