Prerpints.org logo
Preprint
Article

Elucidating the z-dependence of the MOND acceleration (a0) within the Scale Invariant Vacuum (SIV) paradigm

Altmetrics

Downloads

30

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 September 2024

Posted:

19 September 2024

You are already at the latest version

Alerts
Abstract
In a recent paper: “On the time dependency of a0” the authors claim that they have tested “one of the predictions of the Scale Invariant Vacuum (SIV) theory on MOND” by studying the dependence of the Modified Newtonian Dynamics (MOND) accelera- tion at two data sets, low-z (3.2 × 10−4 ≤ z ≤ 3.2 × 10−2) and high-z (0.5 ≤ z ≤ 2.5). They claim “both samples show a dependency of a0 from z”. Here, the work men- tioned above is revisited. The explicit analytic expression for the z-dependence of the a0 within the SIV theory is given. Furthermore, the first estimates of the Ωm within SIV theory give Ωm = 0.28 ± 0.04 using the low-z data only, while a value of Ωm = 0.055 is obtained using both data sets. This much lower Ωm leaves no room for non-baryonic matter! Unlike in the mentioned paper above, the slope in the z- dependence of A0 = log10(a0) is estimated to be consistent with zero Z-slope for the two data sets. Finally, the statistics of the data are consistent with the SIV predic- tions; in particular, the possibility of change in the sign of the slopes for the two data sets is explainable within the SIV paradigm; however, the uncertainty in the data is too big for the clear demonstration of a z-dependence yet.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

Modern physics is well understood based on two main contemporary pillars: Einstein’s General Relativity (EGR) and the Relativistic Quantum Field Theory. However, there are some perplexing observations about the motion of stars within galaxies and clusters. Within the popular current model of Cosmology and Astrophysics, the resolution of these perplexing phenomena is often associated with concepts such as Dark Matter and Dark Energy [1]. However, for over 30 years, there has not been a definite detection of any new particles or fields. An alternative to the Dark Matter approach to resolving the observational discrepancies in galaxies and clusters of galaxies is the idea of the Modified Newtonian Dynamics (MOND, [2]) that has steadily gained support in the Astrophysics communities. While the concept of Dark Matter is a natural continuation of the matter paradigm into a non-luminous matter to explain the observational fact of the flat rotational curves, the MOND idea does not need extra matter1; instead, it modifies the dynamics once the observed acceleration g = v 2 / r falls below the certain cut-off value a 0 ≫ g . In this deep MOND regime, one expects scale invariance to be present in the system under study [7].
Scale invariance is an old idea introduced by Weyl as early as 1918 [8,9] as a gauge invariant gravity, where along with the metric tensor g μ ν there is a connexion vector κ μ controlling the length change d l = l κ μ d x μ , and a scalar field λ that describes the gauge freedom g μ ν → λ 2 g μ ν . The shortcomings of the original Weyl geometry pointed out by [10] were addressed by the introduction of the Weyl Integrable Geometry (WIG) [11], where the connexion vector satisfies κ μ = − ∂ μ ln λ . Consequently, [12,13] have applied the idea to formulate scale invariant cosmology and tried to fix λ based on Dirac’s Large Numbers Hypothesis [14]. The recent reincarnation of the notion of scale invariance was introduced by Maeder [15], Maeder [16], where the scalar field λ was fixed to be only time-dependent by the requirement of homogeneity and isotropy of space. In doing so, the specific functional form of λ ( t ) is determined by the requirement that the macroscopic vacuum must be scale invariant and thus introducing the Scale Invariant Vacuum (SIV) paradigm [17]. This new approach has been explored only in the past few years by [18] as a potential alternative to the standard cosmological model of dark energy plus cold dark matter paradigm ( Λ CDM) [19]. This new alternative approach suggests a possible connection to dark matter and dark energy [20]. It has been shown recently by Maeder [21] that the MOND fundamental acceleration a 0 could be derived within the SIV-paradigm, and the result depends on the cosmological parameters such as Hubble constant H 0 and the total current mass fraction Ω m = ρ m / ρ c , where ρ c = 3 H 0 2 / ( 8 π G ) is the critical density.
By taking this result at face value along with the epoch-dependent scale factor λ ( t ) , it is natural to expect that the SIV-derived MOND acceleration a 0 may have an epoch-dependent value, just as it is the case for the mass content of the Universe ρ m , and the Hubble parameter as well ( H = a ˙ / a , where a ( t ) is the usual FLRW expansion factor).
In this respect, the recent papers by Del Popolo and Chan [22], Del Popolo and Chan [23] have initiated interesting research about testing the connection between MOND by [2] and its possible justification within the SIV paradigm by [21]. In doing so, they studied the z-dependence of a 0 using observational data but didn’t derive the explicit z-dependence, nor did they discuss the relevant SIV model parameters for Ω m . As a new model different from Λ CDM, one should expect that some of the standard cosmological parameters may have different values within the SIV model. In this case, Ω m is a model parameter to be determined, while the Hubble constant H 0 is a model-constraining observational parameter.
In what follows, I will present my analyses of the z-dependency of the MOND acceleration a 0 along with the specific z-dependent expression of a 0 within SIV. Furthermore, the results of the statistical analyses will be utilized to perform one of the first determinations of the SIV parameter Ω m representing the fraction of the total matter-energy content of the Universe. The results will illustrate a puzzling situation that needs a better understanding of the data or the model utilized.

2. Results from Statistics

Before going into more detail about the SIV theory, it is important to note that a simple statistical analysis of the two main variables A 0 = log 10 ( a 0 ) with a 0 in km/s2 and Z = log 10 ( z ) based on data reported by Del Popolo and Chan [23] gives averaged values A 0 ¯ = − 13.07 ± 0.06 and Z ¯ = − 2.49 ± 0.04 (see Table 1) for the low-z data set from [24].
For notational and pragmatic reasons, I maintain the choice of the main variables to be the dimensionless A 0 and Z. Using, the log 10 on a 0 in km/s2 keeps the corresponding range of A 0 between − 15 and − 10 , while the log 10 on z is in the range − 4 to 1. Since a 0 should be in km/s2 for evaluating log 10 ( a 0 ) to compute A 0 , that is, A 0 = log 10 ( a 0 / ( km / s 2 ) ) for a 0 in arbitrary units, then the units of A 0 are dimensionless, and so are the corresponding average values A 0 ¯ .
The high-z data shown in Del Popolo and Chan [23] is based on the work done by Nestor Shachar et al. [25]. It contains only 17 high-z Galaxies for which the inferred a 0 is less than 1.2 × 10 − 13 km/s2; that is, A 0 < − 12.92 . Such selection criteria cut a large data segment from the high-z data, while it has not been applied to the low-z data, thus introducing a bias. In my opinion, a fair, unbiased, and appropriate data selection procedure, if any, should be applied to both sets. Here, I disagree with such a selection criteria applied to high-z data and not to the low-z data, so I use all 100 data points in Nestor Shachar et al. 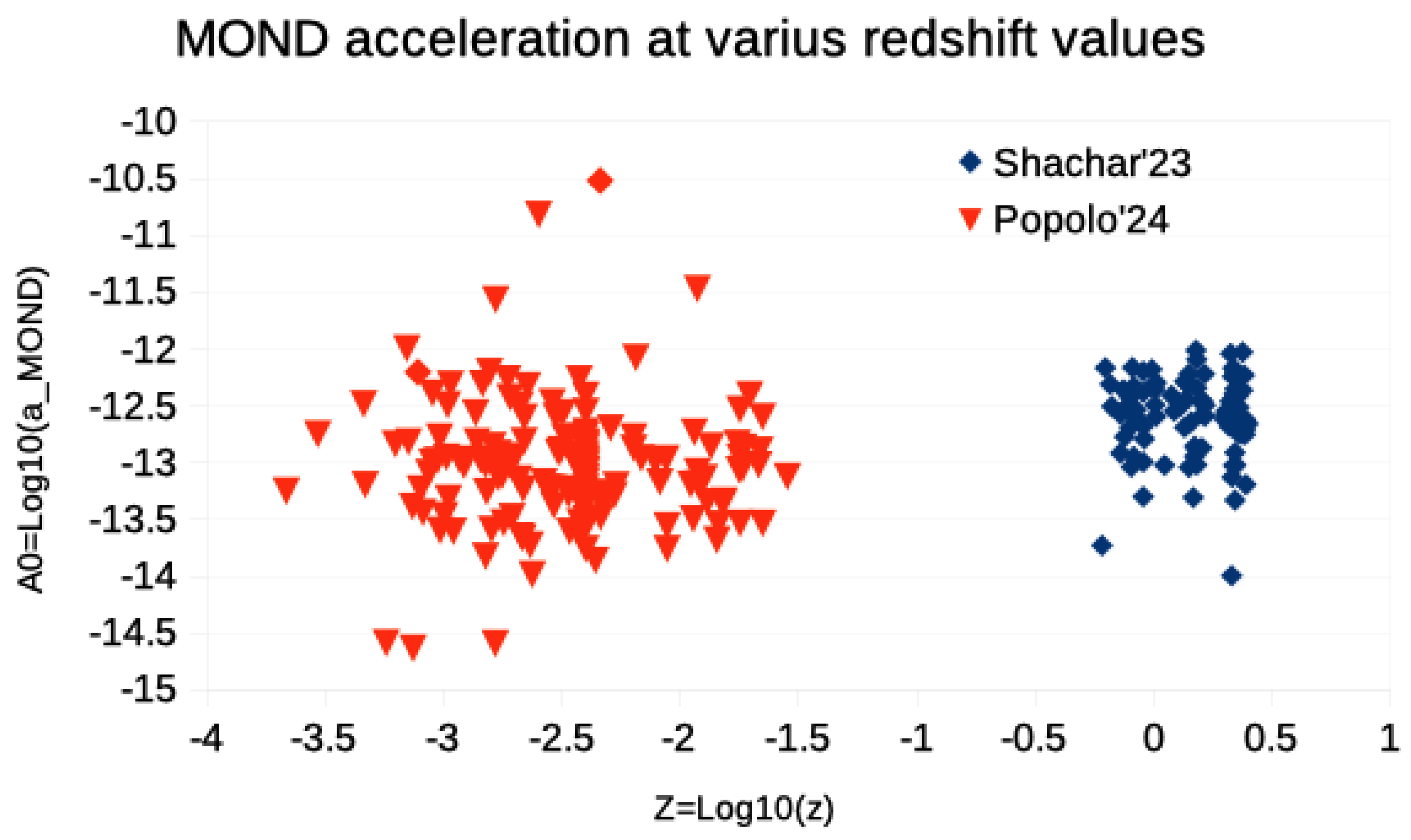[25] as seen in Fig. Figure 1, both data sets have a compatible spread of A 0 -values. The relevant values follow the calculation of a 0 using Eq. (5) in Del Popolo and Chan [23] based on the data from Nestor Shachar et al. [25]. In doing the calculations, an error was noticed in the initial evaluations by Del Popolo and Chan [22] due to units conversion; upon communicating with the authors, this was later recognized by Del Popolo and Chan [26] and corrected in the subsequent version of their paper Del Popolo and Chan [23]; the proper conversion is necessary to obtain a 0 in km/s2 for the correct evaluation of the corresponding A 0 . It is worth noticing that the corresponding simple statistical analysis gives A 0 ¯ = − 12.60 ± 0.03 and Z ¯ = 0.17 ± 0.02 for all of the 100 high-z data points (see Table 1). Thus, the Z-slope based on these two aggregated data sets is Δ A 0 ¯ / Δ Z ¯ = ( − 12.6 + 13.07 ) / ( 0.17 + 2.49 ) ≈ 0.18 ± 0.03 indicating a change in the MOND acceleration as seen from Table 1. This is an overly simplified estimate of the Z-slop based on both sets, marked in Table 2 with an asterisk.
The statistical analyses can be taken further, as done in the paper by Del Popolo and Chan [23], where they do a linear fit to the two sets and derive a Z-slope of 0.6 ± 0.2 with an intercept of A 0 = − 11.6 ± 0.5 for the low-z data. Simple linear regression on the same data gives agreement with the zero slope since the result is a Z-slope of 0.12 ± 0.13 with a different intercept of A 0 = − 12.8 ± 0.3 . Such intercept should be regarded as related to Z = 0 ; thus, to the value of a 0 at z=1 and not at z = 0 . Therefore, this corresponds to about 11 % or only 2 % change of A 0 from A 0 ¯ = − 13.07 near z ≈ 0 to A 0 = − 11.6 or A 0 = − 12.8 near z ≈ 1 .
Regarding the high-z data, the Z-slope of − 0.2 ± 0.4 is consistent with zero while the intercept of A 0 = − 9.61 ± 0.08 for the high-z data is questionable due to the applied data selection criteria and the possible error of their analyses mentioned earlier. The simple linear regression on the full data set derived from Nestor Shachar et al. [25] gives again agreement with the zero Z-slope since the result is Z-slope is 0.01 ± 0.2 with an intercept of A 0 = − 12.603 ± 0.05 . Notice that for the current analysis, the low-z and high-z data sets have intercepts that agree with each other unlike those in Del Popolo and Chan [23]. There must be an agreement between these two intercepts since they should reflect the value of the MOND acceleration at z = 1 .

3. SIV Framework

Within SIV the fundamental MOND acceleration a 0 can be related to the Hubble constant H 0 and the current matter content of the Universe Ω m Maeder [21], Maeder and Gueorguiev [27]. For the derivations and formulas to be used in this section, I will denote the MOND fundamental acceleration a 0 by a M whenever appropriate to avoid confusion with the expansion scale factor a but will use a 0 in the absence of such a problem. This is done to avoid confusion with the FLRW expansion scale factor a, which by convention should be denoted by a 0 at the current epoch; and to also avoid awkward notation a 00 for the current value of the MOND acceleration.
Within SIV, there is an extra velocity-dependent term, denoted as dynamical acceleration [20]:
d 2 r → d t 2 = − G t M ( t ) r 2 r → r + κ ( t ) d r → d t ,
where κ = − λ ˙ / λ is the time component of the SIV connexion vector, with a simple functional form κ = 1 / t within the SIV gauge, where the SIV cosmic time t is a dimensionless parameter such that t ∈ [ t i n , t 0 = 1 ] . Here, t i n is the moment of the Bing Bang when the FLRW scale factor satisfies a ( t i n ) = 0 , happening near t i n = Ω 1 / 3 , while at the current epoch a ( t 0 ) = 1 and time is set so that t 0 = 1 . Within SIV the conformal-scale factor is λ = 1 / t and is used to perform Weyl transformation g μ ν ′ = λ 2 g μ ν that relates EGR metric g μ ν ′ to the metric g μ ν within the WIG framework [20].
To arrive at an expression for the MOND acceleration a 0 , one considers the ratio of the magnitudes of the Newtonian acceleration g N = G M / r 2 to the additional acceleration κ ( t ) v in (1), where v denotes the magnitude of the velocity v → = d r → / d t :
x = κ v r 2 G M .
Now, one can use the relation given by the instantaneous radial acceleration v 2 / r = G M / r 2 to eliminate the speed v from the expression of x given by (2); then using g N = G M / r 2 to remove G M , one arrives at:
x = κ v r 2 G M = κ r 3 G M = κ r g N .
When the dynamic acceleration dominates over the Newtonian acceleration ( x ≫ 1 ), one has:
g = g N + x g N ≈ x g N = κ r g N .
Therefore, one arrives at the MOND type relation g ∼ a 0 g N from which one can deduce an expression for a 0 :
a 0 ≈ κ 2 r .
The above expression indicates a possible r dependence of a 0 , thus demoting a 0 of its fundamental parameter status within MOND, which may be testable with future high-precision data. Such dependence may explain the variance of a 0 . To restore the fundamental character of the above expression (5) as in MOND, one could consider the limit r → r H , where the Hubble radius reflects the influence of the Universe causally connected to the object studied. Thus, the time-dependent MOND acceleration within SIV is the upper bound of (5) given by the expression:
κ 2 r → κ 2 r H = κ 2 c / H = a M ( t ) ,
During the matter-dominated epoch, SIV has an analytic form for expansion scale-factor a ( t ) [20,28]:
a ( t ) = t 3 − Ω m 1 − Ω m 2 / 3 ⇒ H = 2 t 2 t 3 − Ω m .
Thus, from (6) with SIV time in units t ∈ [ t i n , t 0 = 1 ] , one obtains for the MOND fundamental acceleration:
a M ( t ) = c ( t 3 − Ω m ) 2 t 4 .
To express a M in the usual time units, where τ i n = 0 at the Big Bang when the scale factor a = 0 while the age of the Universe now is τ 0 = 13.8 billion years, one has to use the chain rule for differentiation, that is:
a M ( τ ) = c λ ˙ λ 2 a a ˙ = c κ ( τ ) κ ( t ) H ( t ) = d t d τ a M ( t ) .
The value of d t / d τ is assessed based on the assumption that the following relation provides a connection between the two time-scales ( t − t i n ) / ( t 0 − t i n ) = ( τ − τ i n ) / ( τ 0 − τ i n ) where t i n = Ω m 1 / 3 , t 0 = 1 , τ i n = 0 , and τ 0 = 13.8 billion years [20]. Thus, one has:
d t / d τ = ( 1 − t i n ) / τ 0 ,
and therefore:
a M ( τ ) = c 1 − Ω m 1 / 3 τ 0 t 3 − Ω m 2 t 4 =
= c 2 b 1 − b τ 0 x 3 − 1 x 4 ,
where x = t / b , Ω m = t i n 3 = b 3 . Set a ˜ = a 1 − b 3 b 3 2 / 3 and revisit (7) to get:
a = b 3 1 − b 3 2 / 3 x 3 − 1 2 / 3 ⇒ a ˜ = x 3 − 1 2 / 3 .
Thus, upon utilization of (11) and the above substitution, the MOND acceleration (9), as a function of the scale factor, becomes:
a M ( τ ) = c 2 b 1 − b τ 0 a ˜ 3 / 2 a ˜ 3 / 2 + 1 4 / 3 .
Next, look at the z-dependence, and use a = 1 / ( z + 1 ) ; thus, when z is 0, or 1, and even 2, then a is 1, or 1 / 2 , and correspondingly 1 / 3 . Therefore, one has:
a M ( z ) = a M ( z = 0 ) × 1 z + 1 3 / 2 a ˜ 0 3 / 2 + 1 4 / 3 1 z + 1 3 / 2 a ˜ 0 3 / 2 + 1 4 / 3
= a M 0 × z + 1 − 3 / 2 1 − Ω m z + 1 3 / 2 + Ω m − 4 / 3
where a ˜ 0 = 1 − Ω m Ω m 2 / 3 was utilized. The above expression (15) provides the formula for the explicit z-dependence of the MOND fundamental acceleration within the SIV framework. It can be used to test this SIV prediction against the observational data. When evaluated at z = 1 and 2, one finds that a M ( z ) is about 79 % and 58 % of the current value a M 0 = a M ( z = 0 ) for Ω m = 0.3 . Thus, the z-dependence of the MOND acceleration is weak, and it is likely buried within the scatter of the current observational data and its uncertainty (see Del Popolo and Chan [23]); as one can see later, the value of a M 0 , at best, is accurate within 13% while the 1 σ error of the data on A 0 reported by Del Popolo and Chan [23] usually translates in more than 29 % uncertainty for observationally deduced MOND acceleration data points.
The value of a M 0 could be used to assess the parameter Ω m within the SIV theory. That is, by using (11) one has:
a M 0 = c ( 1 − b ) ( 1 − b 3 ) 2 τ 0 = c ( 1 − Ω m 1 / 3 ) ( 1 − Ω m ) 2 τ 0 .
One can solve for Ω m by taking log 10 of (17):
A 0 − log 10 ( c 2 τ 0 ) = log 10 1 − Ω m 1 / 3 1 − Ω m ,
for low-z data with A 0 ¯ = − 13.07 this gives Ω m = 0.28 . Such a value of Ω m aligns with the comparative study of the SIV and Λ CDM cosmologies that demonstrated only light adjustments in Ω m if the expansion factors a ( t ) of these models are to be very similar [15]. However, it contrasts with the MOND idea of dark matter redundancy. Notably, the range of values of A 0 based on (18) for Ω m given by 0.01 , 0.1 , 0.3 , 0.6 , 0.8 are − 12.57 , − 12.78 , − 13.098 , − 13.67 , − 14.31 .
Based on (17), the corresponding fractional uncertainties are related in the following way:
Δ a M 0 a M 0 = Δ Ω m Ω m Ω m 1 − Ω m + 1 3 Ω m 1 / 3 1 − Ω m 1 / 3 .
The slope of the z − dependence, m = d log 10 a M ( z ) d z when taking log 10 of (15), is then:
m = 1 − ( 1 + 3 ( 1 + z ) 3 / 2 ) Ω m ( 1 + z ) ( 1 + ( ( 1 + z ) 3 / 2 − 1 ) Ω m ) ln ( 100 ) .
giving m 0 = ( 1 − 4 Ω m ) / ln ( 100 ) at z = 0 , which is positive only for Ω m < 0.25 . While for the Z-slope one has:
d A 0 d Z = d A 0 d z d z d Z = m ln ( 10 ) z = m ln ( 10 ) 10 Z ,
where d z / d Z = ( exp ( Z ln ( 10 ) ) ) ′ is utilized. Based on the data provided: A 0 = log 10 a M 0 = − 13.067 ± 0.056 for a M 0 in km/s2. The fractional uncertainty is Δ A 0 / | A 0 | = 0.0043 = Δ ( a M 0 ) / ( | A 0 | a M 0 ln ( 10 ) ) . That is, Δ ( a M 0 ) / a M 0 = 0.13 ; therefore, using (19) one has Ω m = 0.28 ± 0.04 . The z-slope is then m 0 = − 0.01 ± 0.3 , while the Z-slope is − 0.0001 using Z ¯ = − 2.49 . This results practically in a horizontal line that changes very little from being − 13.0667 at Z = − 4 to − 13.0671 at Z = 2 . This change is well within the current error ( ± 0.06 ) for the low-z. For the high-z data, one can now evaluate m 1 to be − 0.11 ; therefore, the Z-slope is − 0.25 in agreement with the Z-slope of − 0.2 ± 0.4 reported by [23].

4. Discussion and Conclusion

It is still inconclusive about the z-dependence of the MOND fundamental acceleration, but such dependence is present within the SIV theory (16); furthermore, the SIV expression (20) does suggest that there is a change in the sign of the slope when going through z = 1 / 3 × ( 1 − Ω m ) / Ω m 2 / 3 − 1 with m 0 positive for Ω m < 0.25 and negative otherwise; this could explain the change in the sign of the slope of the two data sets as noticed by Del Popolo and Chan [23]. However, the corresponding value of A 0 at z = 1 , which is the intercept, is about the same as A 0 ¯ based on low-z with A 0 ¯ = − 13.07 , but Del Popolo & Chan’s high-z intercept differs significantly from the corresponding A 0 ¯ values around A 0 = − 12.6 . However, if one is to embrace the matching values of A 0 at z = 1 , that is, to use A 0 = − 12.6 ± 0.05 along with (17) in (16), Then, the value of Ω m is significantly lower; that is, one gets Ω m = 0.055 . In this case, the sign change of the slopes will be happening around z = 2.7 . For Ω m = 0.055 , equation (18) gives A 0 = − 12.69 , which is lower than A 0 = − 12.6 but is bigger than A 0 = − 13.07 . Note that such a low value for Ω m does not leave much room for any dark matter. Such a result is better aligned with the MOND view about dark matter but seems to be a drastic departure from the need for dark matter and dark energy as required by Λ CDM. This approach may be favorable as a method of determining Ω m since it relies on the two data sets and their consistent Z-intercepts, which is in contrast to the first method presented that utilized only the low-z data and assumed that A 0 ¯ = − 13.07 at Z ¯ = − 2.49 is sufficiently close to z = 0 even though z → 0 would imply Z → − ∞ . Therefore, further studies are needed to determine the correct Ω m values within the SIV framework. Thus, more precise data analyses are needed along with improved uncertainties of the observational data points (for the currently used data see Fig. Figure 1) to confirm the z-dependence of the MOND fundamental acceleration and to potentially test the SIV theory via its model prediction for a 0 ( z ) as well as to deduce the relevant SIV model parameters.
In conclusion, the long-standing mystery of galactic rotation curves has fueled the development of Modified Newtonian Dynamics (MOND). This work presents a significant contribution by providing the first explicit analytic expressions for the z-dependence of the fundamental MOND acceleration ( a 0 ) within the framework of the Scale Invariant Vacuum (SIV) theory (16). This novel approach goes beyond previous studies Del Popolo and Chan [22], Del Popolo and Chan [23]. Furthermore, we leverage existing observational data to perform the first-ever estimation of the cosmological matter density parameter ( Ω m ) within the SIV framework. The current analysis yields a value of Ω m = 0.28 ± 0.04 based on low-z data and Ω m = 0.055 based on the consistency of both data sets at z = 1 , potentially removing the need for dark matter entirely. The above is a puzzling result as to why the two methods presented to determine the value of Ω m within SIV result in relevant values within the Λ CDM model.
On the one hand, the SIV value 28 % for Ω m deduced by using only the dataset with z ≈ 0 is close to the Λ CDM model of about 30 % [19], while on the other hand, the value 5.5 % deduced by using both datasets (via the A 0 intercept at z = 1 ) is close to the baryon matter value within the Λ CDM model of about 5 % . This could be just a numerical coincidence, or there may be some deeper reason for why the values are like that. For example, it may be related to the transition from a matter-dominated epoch to a cosmological constant (dark-energy) dominated epoch within the Λ CDM model. However, within the SIV paradigm, one does not expect dark-matter and dark-energy components. For example, the energy density Ω Λ E due to the Einstein Cosmological Constant Λ E , which within the Λ CDM model is estimated to be 70 % , does not exist within SIV but is replaced by Ω λ = − 2 H λ ˙ λ that also compliments Ω m to 1 (assuming flat Universe Ω k = 0 ) within the SIV paradigm [20].
Interestingly, the data suggests an almost flat z-dependence of A 0 = log 10 ( a 0 ) , contrasting with previous claims by Del Popolo and Chan [22], Del Popolo and Chan [23]. While the current data limitations prevent the definitive confirmation of the z-dependence (15), the observed trends are consistent with SIV predictions. SIV offers a unique explanation for the potential sign change in the slopes previously indicated across different redshift ranges. Future higher precision data will be crucial for definitively resolving the presence or absence of z-dependence in a 0 .

Data Availability Statement

No new data was generated or analyzed in support of this research.

Acknowledgments

The author is grateful for the moral and financial support by particularly close private parties during the various stages of the research presented and to Prof. A. Maeder for the long and fruitful scientific collaboration over the years. This research does not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. However, the publishing charges were waived graciously by the Author Support, Oxford Journals, at Oxford University Press - for which the author is very grateful!

References

  1. Bertone, G.; Hooper, D. History of dark matter. Reviews of Modern Physics 2018, 90, 045002. [Google Scholar] [CrossRef]
  2. Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. ApJ 1983, 270, 365–370. [CrossRef]
  3. Pazy, E. Quantum statistical modified entropic gravity as a theoretical basis for MOND. 87, 0840; 63. [Google Scholar] [CrossRef]
  4. Verlinde, E.P. Emergent Gravity and the Dark Universe. SciPost Physics 2017, 2, 016. [Google Scholar] [CrossRef]
  5. Lelli, F.; McGaugh, S.S.; Schombert, J.M. Testing Verlinde’s emergent gravity with the radial acceleration relation. 2017, 468, L68–L71. [CrossRef]
  6. Bekenstein, J.D.; Sagi, E. Do Newton’s G and Milgrom’s a0 vary with cosmological epoch? 2008, 77, 103512. 1035; 12. [Google Scholar] [CrossRef]
  7. Milgrom, M. The Mond Limit from Spacetime Scale Invariance. ApJ 2009, 698, 1630–1638. [CrossRef]
  8. Weyl, H. Space - Time - Matter; Dutton, 1922.
  9. Weyl, H. Raum, Zeit, Materie. Vorlesungen über allgemeine Relativitätstheorie.; Berlin: Springer, 1970. [Google Scholar]
  10. Einstein, A. Kommentar zu “Hermann Weyl: Gravitation und Elektrizität”. Sitzungsberichte der Königlich, Preussischen Akademie der Wissenschaften zu Berlin 1918, p. 478.
  11. Eddington, A.S. The mathematical theory of relativity, 2nd edition ed.; Cambridge University Press, 1923; p. 284.
  12. Dirac, P.A.M. Long Range Forces and Broken Symmetries. Proceedings of the Royal Society of London Series A 1973, 333, 403–418. [Google Scholar] [CrossRef]
  13. Canuto, V.; Adams, P.J.; Hsieh, S.H.; Tsiang, E. Scale-covariant theory of gravitation and astrophysical applications. 1977, 16, 1643–1663. [CrossRef]
  14. Dirac, P.A.M. Cosmological Models and the Large Numbers Hypothesis. Proceedings of the Royal Society of London Series A 1974, 338, 439–446. [Google Scholar] [CrossRef]
  15. Maeder, A. An Alternative to the ΛCDM Model: The Case of Scale Invariance. ApJ 2017, 834, 194. [CrossRef]
  16. Maeder, A. Dynamical Effects of the Scale Invariance of the Empty Space: The Fall of Dark Matter? ApJ 2017, 849, 158. [CrossRef]
  17. Maeder, A.; Gueorguiev, V.G. Action Principle for Scale Invariance and Applications (Part I). Symmetry 2023, 15, 1966. [Google Scholar] [CrossRef]
  18. Gueorguiev, V.G.; Maeder, A. The Scale Invariant Vacuum Paradigm: Main Results and Current Progress Review (Part II). Symmetry 2024, 16, 657. [Google Scholar] [CrossRef]
  19. Planck Collaboration:, Ade; et al. Planck 2015 results. XIII. Cosmological parameters. 2016, 594, A13. [CrossRef]
  20. Maeder, A.; Gueorguiev, V.G. The Scale-Invariant Vacuum (SIV) Theory: A Possible Origin of Dark Matter and Dark Energy. Universe 2020, 6, 46. [Google Scholar] [CrossRef]
  21. Maeder, A. MOND as a peculiar case of the SIV theory. 2023, 520, 1447–1455. [CrossRef]
  22. Del Popolo, A.; Chan, M.H. On the time dependency of a0. Physics of the Dark Universe 2024, 43, 101393. [Google Scholar] [CrossRef]
  23. Del Popolo, A.; Chan, M.H. On the time dependency of a0. Physics of the Dark Universe 2024, 43, 101415. [Google Scholar] [CrossRef]
  24. Marra, V.; Rodrigues, D.C.; de Almeida, Á.O.F. A fundamental test for MOND. 2020, 494, 2875–2885. [CrossRef]
  25. Nestor Shachar, A.; Price, S.H.; Förster Schreiber, N.M.; Genzel, R.; Shimizu, T.T.; Tacconi, L.J.; Übler, H.; Burkert, A.; Davies, R.I.; Dekel, A.; et al. RC100: Rotation Curves of 100 Massive Star-forming Galaxies at z = 0.6-2.5 Reveal Little Dark Matter on Galactic Scales. ApJ 2023, 944, 78. 2023, 944, 78. [Google Scholar] [CrossRef]
  26. Del Popolo, A.; Chan, M.H. Corrigendum to “On the time dependency of a0” [Phys. Dark Univ. (2024) DARK 101393]. Physics of the Dark Universe 2024, 43, 101414. [Google Scholar] [CrossRef]
  27. Maeder, A.; Gueorguiev, V.G. Scale-invariant dynamics of galaxies, MOND, dark matter, and the dwarf spheroidals. 2020, 492, 2698–2708. [CrossRef]
  28. Jesus, J.F. Exact Solution for Flat Scale-Invariant Cosmology. arXiv e-prints 2017. [CrossRef]
1
Some fashionable models of gravity are trying to explain MOND and its fundamental acceleration a 0 [3,4], but these models have failed the observational tests by [5], while the relativistic implementation of MOND suggests imperceptible variation of a 0 “to redshift unity or even beyond it” [6].
Preprints 118506 g001
Figure 1. Low-z and high-z data sets are discussed in the text. For this figure only, I have dropped the outlier related to the NGC2976 Galaxy data in the low-z data set since its value A 0 = − 18.32 is too low compared to the other values shown; however, the data point has been used in the various data analyses presented. Unlike in Del Popolo and Chan [23], where only 17 high-z data points have been used, here I have shown all 100 data points related to the data in Nestor Shachar et al. [25]. For the relevant error bars, the reader is referred to the paper by Del Popolo and Chan [23].
Figure 1. Low-z and high-z data sets are discussed in the text. For this figure only, I have dropped the outlier related to the NGC2976 Galaxy data in the low-z data set since its value A 0 = − 18.32 is too low compared to the other values shown; however, the data point has been used in the various data analyses presented. Unlike in Del Popolo and Chan [23], where only 17 high-z data points have been used, here I have shown all 100 data points related to the data in Nestor Shachar et al. [25]. For the relevant error bars, the reader is referred to the paper by Del Popolo and Chan [23].
Preprints 118506 g001
Table 1. Results from simple statistical analysis for the two sets of redshifts; the first set of low-z data with 0.00032 ≤ z ≤ 0.032 [24] and the second high-z data with 0.5 ≤ z ≤ 2.5 [23].
Table 1. Results from simple statistical analysis for the two sets of redshifts; the first set of low-z data with 0.00032 ≤ z ≤ 0.032 [24] and the second high-z data with 0.5 ≤ z ≤ 2.5 [23].
data Z ¯ A 0 ¯
low-z − 2.49 ± 0.04 − 13.07 ± 0.06
high-z + 0.17 ± 0.02 − 12.60 ± 0.03
Table 2. Values of the Z-slopes and intercepts for the current work and the values deduced in ref. [23].
Table 2. Values of the Z-slopes and intercepts for the current work and the values deduced in ref. [23].
Current work Del Popolo & Chan
data intercept Z-slope intercept Z-slope
low-z − 12.8 ± 0.3 0.12 ± 0.13 − 11.6 ± 0.5 + 0.6 ± 0.2
high-z − 12.60 ± 0.05 0.01 ± 0.2 − 9.6 ± 0.1 − 0.2 ± 0.4
both − 12.6 ± 0.1 0.18 ± 0 . 03 * − 8.6 ± 0.5 + 0.6 ± 0.2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated