Decision Analysis Approaches on the Collection Methods of Polyethylene Terephthalate Waste

Preprint

Article

Decision Analysis Approaches on the Collection Methods of Polyethylene Terephthalate Waste

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Johnson A. Oyewale^*,

Lagouge K. Tartibu

and Imhade P. Okokpujie

Johnson A. Oyewale^*,

Lagouge K. Tartibu

and Imhade P. Okokpujie

This version is not peer-reviewed

Submitted:

18 September 2024

Posted:

19 September 2024

You are already at the latest version

Alerts

Abstract

The rising challenge of polyethylene terephthalate (PET) waste necessitates efficient collection methods to mitigate environmental impacts. The Analytic Hierarchy Process (AHP) is one of the Multi-Criteria Decision Analysis (MCDA) approaches utilized in this study. The Technique for Order of Preference by Similarity to the Ideal Solution (TOPSIS) was used to rank each alternative according to the objective weight that AHP had produced. Also, sensitivity analysis was performed to determine how robust the findings were when considering equal weights and entropy weights to maximize PET waste collection techniques. The alternative achieved the objective of obtaining the best collection method, Threshold Plastic Bottle Waste Collection (Tpbw), out of all the three alternatives considered. Another MCDA approach, VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR), was used to compare the results and validate the ranking result achieved by the TOPSIS method. The VIKOR technique's validation of the TOPSIS approach showed that the outcomes were highly consistent. Data for the study were gathered from the archives of waste management companies on possible practices of plastic waste collection addressing costs, environmental impacts, social acceptance, feasibility, and efficiency. The findings provide a prioritized framework for enhancing PET waste collection strategies, contributing to sustainable waste management. Many criteria are considered when deciding the best collecting method for PET waste recycling, making it challenging. By using criteria importance, multi-criteria decision analysis (MCDA) was applied in this study, and the objective weight of the criteria was determined using the analytic hierarchy process (AHP). The five criteria considered in this study are Initial investment cost, Operational cost, Transportation cost, Environmental risk, Employment potential, and the objective weights allocated to them. AHP results 0.4952, 0.1997, 0.1565, 0.0870, and 0.0616 are respectively determined.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The current state of the issue of plastic use and production is very alarming. Yet, it is one of the most vital components of human activities as it consists of various features, such as strength, durability, mechanical properties, thermal properties, etc. without any doubt [1]. According to Alex Olanrewaju Adekanmbi, et al. (2024), the manufacturing, distribution, and extraction processes of plastic from virgin materials influence the environment greatly. Also, aside from the physical characteristics of plastics itself, the use of plastics has health effects due to additives, pollutants, and degradation products [2]. Plastic can accomplish an easy extermination of both humans and the environment. Plastic is capable of replacing mainly wood, metal, and glass in the first stage of development [3]. Plastics became ubiquitous as it started finding use in everyone’s household and office. The study by [4], established the significance of households as an integral part of plastic pollution lacking the information, attitude, and awareness necessary to separate plastic waste before disposing of it, the community nevertheless exhibited the behaviors associated with it because they understood that they were responsible for managing the waste in their respective households [4], as we are enjoying the convenience of plastics [5].

The most widely recycled plastic is polyethylene terephthalate (PET), used in many products, such as food packaging and beverage bottles [6]. Unlike the other thermoplastic polymers, polyethylene terephthalate is a widely used polyester class [7]. This substance is mainly used to make clothes and food containers, such as plastic water bottles [8]. PET is a solid material that does not absorb water; hence, it is suitable for food containers. The manufacture of PET and its consumption resulted in unintended consequences for the environment and human health due to the large amount of PET disposal in natural ecosystems. With the growth of the income level, the volume of waste becomes bigger, which is also in proportion to the income [9]. Over the past few years, top scientists have researched how plastics and chemicals used in production might affect human health. The use of polyethylene terephthalate (PET) bottles has been a cause of insulin resistance [10], as affirmed by [11] that exposing PET to the sunlight temperature of (30°–60°) agitates the chemical substance contained in PET bottled water, reduced anogenital distance in male infants, and low levels of sex hormones in addition to adverse effects on the immune systems, particularly on the young people [12]. The damage caused by littered plastics to ecological systems is more visible and disastrous. In a study by [13] plastic waste has many different sizes and forms. Nevertheless, the breakdown of plastic into smaller pieces, known as microplastics (MPs), is the most significant and recent harm posed by plastic pollution. Figure 1 shows improper plastic waste treatment has caused great pollution in enormous water bodies such as lakes, rivers, and oceans.

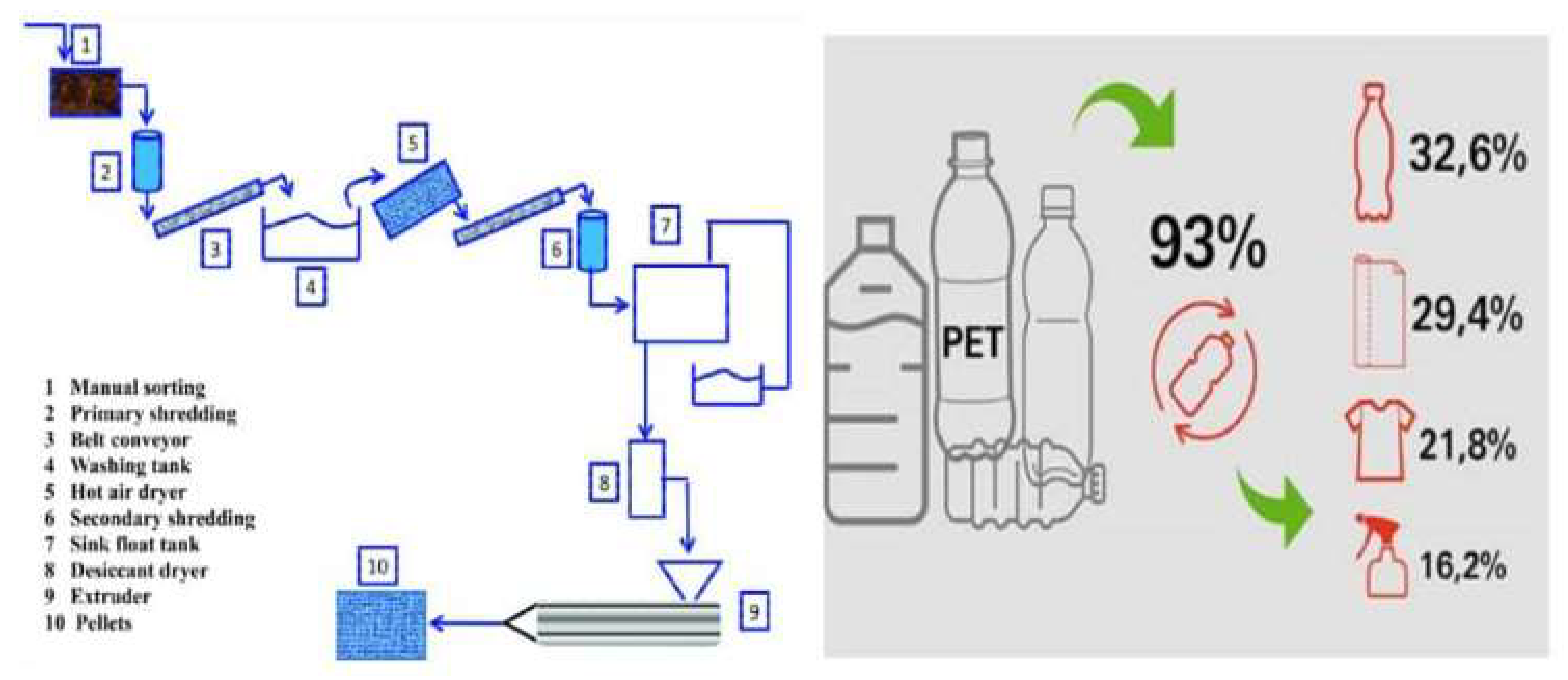
The rapid increase in plastic production and consumption, particularly PET products, has led to a corresponding rise in plastic waste generation, posing significant environmental and health risks [14]. Plastic waste from PET can last for centuries, making it difficult for animals and plants in the environment to live. Suitable collection methods are vital in lowering the environmental impact of PET waste and encouraging recycling. Recycling of collected PET waste follows a schematic process layout represented in Figure 2. In recent years, emphasis on sustainability and PET recycling has grown significantly relevant to companies and customers. Recycling PET bottles has drawn consumer attention. The percentage of PET single-use bottles keeps rising more and more as beverages in PET packaging materials are drank "on the go [15]. The multi-criteria decision method (MCDM) is the primary strategy used in this study, and there are other approaches to collecting plastic waste. MCDA is widely used to analyze and prioritize alternatives with multiple conflicting criteria. MCDM methods aim to equip decision-makers with knowledge and structure for complex problems, intangible factors, and better choices [16].

Different MCDA methodologies exist as tools for decision-makers in this process. A few commonly used approaches are AHP, a pair-wise comparison method that models complex problems as a hierarchy of criteria, sub-criteria, and alternatives and allows for ranking decision priorities [17]. AHP is widely used in strategic planning, resource allocation, engineering and manufacturing, healthcare, business, supply chain, and project selection [17,18]. In TOPSIS, the ideal solution is closest to the positive ideal and farthest from the negative ideal. The decision matrix is normalized, and criteria weights are calculated. Then, the Euclidean distance is calculated for each alternative from the ideal and negative-ideal solutions [19]. A wide range of problems, such as supplier selection, facility location, and portfolio management, have benefited from applying TOPSIS, designed explicitly for quantitative data analysis [20]. PROMETHEE groups alternatives by comparing their preferences pair-wise. Then, a preference function is assigned to each criterion, and positive and negative outranking flows are computed, resulting in the final ranking [21]. PROMETHEE is well-suited explicitly for problems involving qualitative data. It is commonly used in environmental, transportation, pollution control, and water management [22]. The use of MCDA in sustainable energy planning demonstrates its ability to incorporate both qualitative and quantitative criteria and involve stakeholders in decision-making [23].

Figure 2. Schematic process flow of PET waste recycling and applications of recycled PET [24].

This paper aims to identify the best methods for collecting PET waste using Multi-Criteria Decision Analysis (MCDA) methods. This study aims to address this issue by examining different collection strategies from an efficiency and sustainability perspective while considering stakeholders' preferences.

2. Materials and Methods

Secondary data collected includes collecting statistics and feedback from all stakeholders involved in the PBW business chain, such as manufacturers, distributors, retailers, policymakers, and researchers. Issues concerning PET waste generation, collection methods, environmental problems, industry practices, and government rules were explored.

Information was also gathered on preferences for plastic bottle products and how plastic bottle waste can be recycled. Findings revealed that plastic bottle waste pollution poses health or environmental risks, with them naming certain risks associated with pollution. The data provided gave insight into the level of plastic bottle waste pollution in the study.

The information also covered the nature of the plastic products the post-consumers used the most and the volume of disposable plastic bottle waste produced by their households each month. Experts revealed their approaches to handling plastic bottle waste, such as whether they segregate biodegradable and non-degradable waste and whether they work with waste recyclers. This information helped to get practical insights about waste disposal behaviors from the post-consumers regarding what usually occurs and what may need to change.

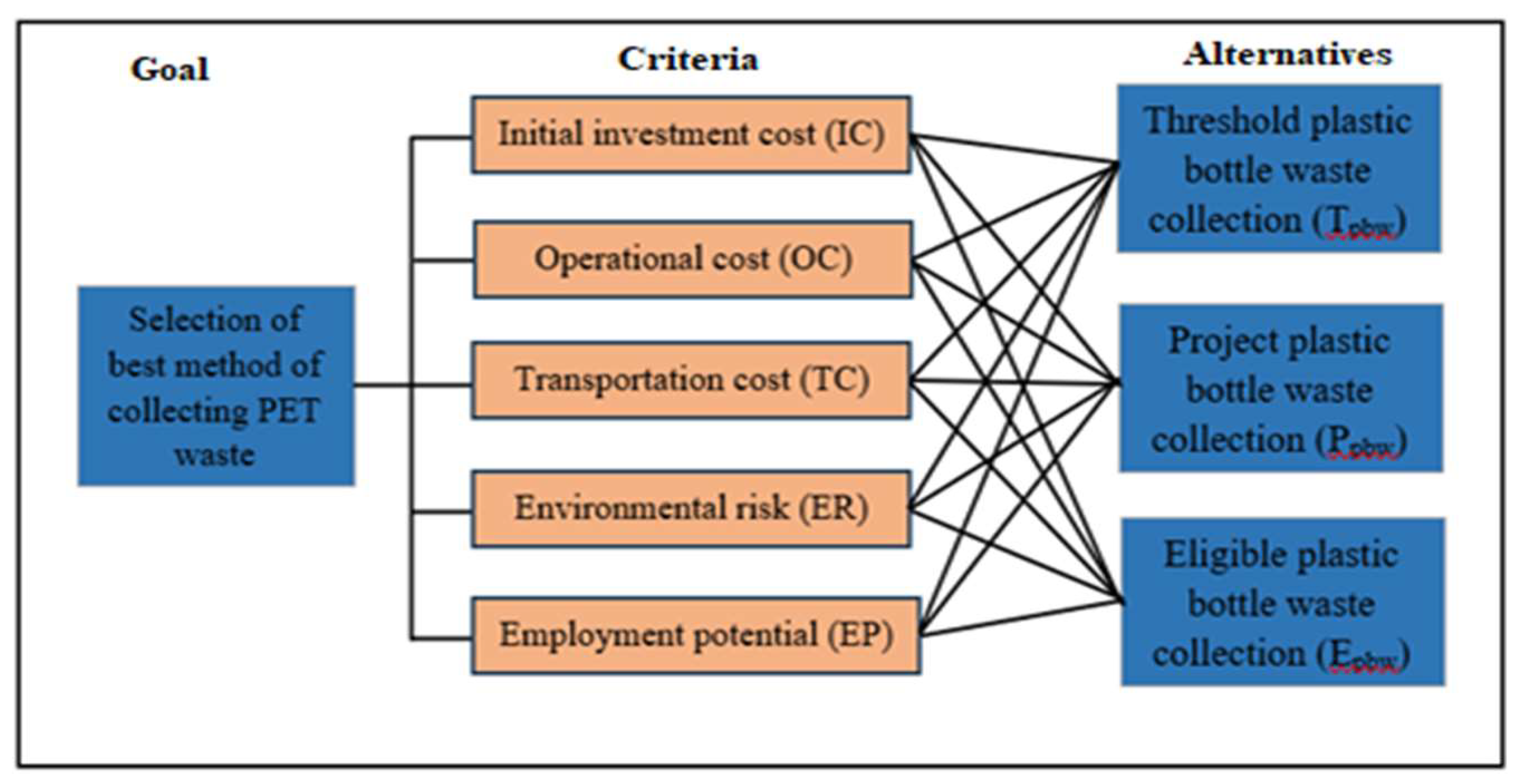
Experts gave their awareness to government or non-government campaigns about reducing the use of plastic bottles in their city or area and asked to name any that they were aware of. This section analyzed levels of public post consumers and the success of the current campaigns in advocating for waste reduction methods. Figure 3 illustrates the decision framework of AHP, while Table 1 clearly describes the assessment of the criteria under consideration.

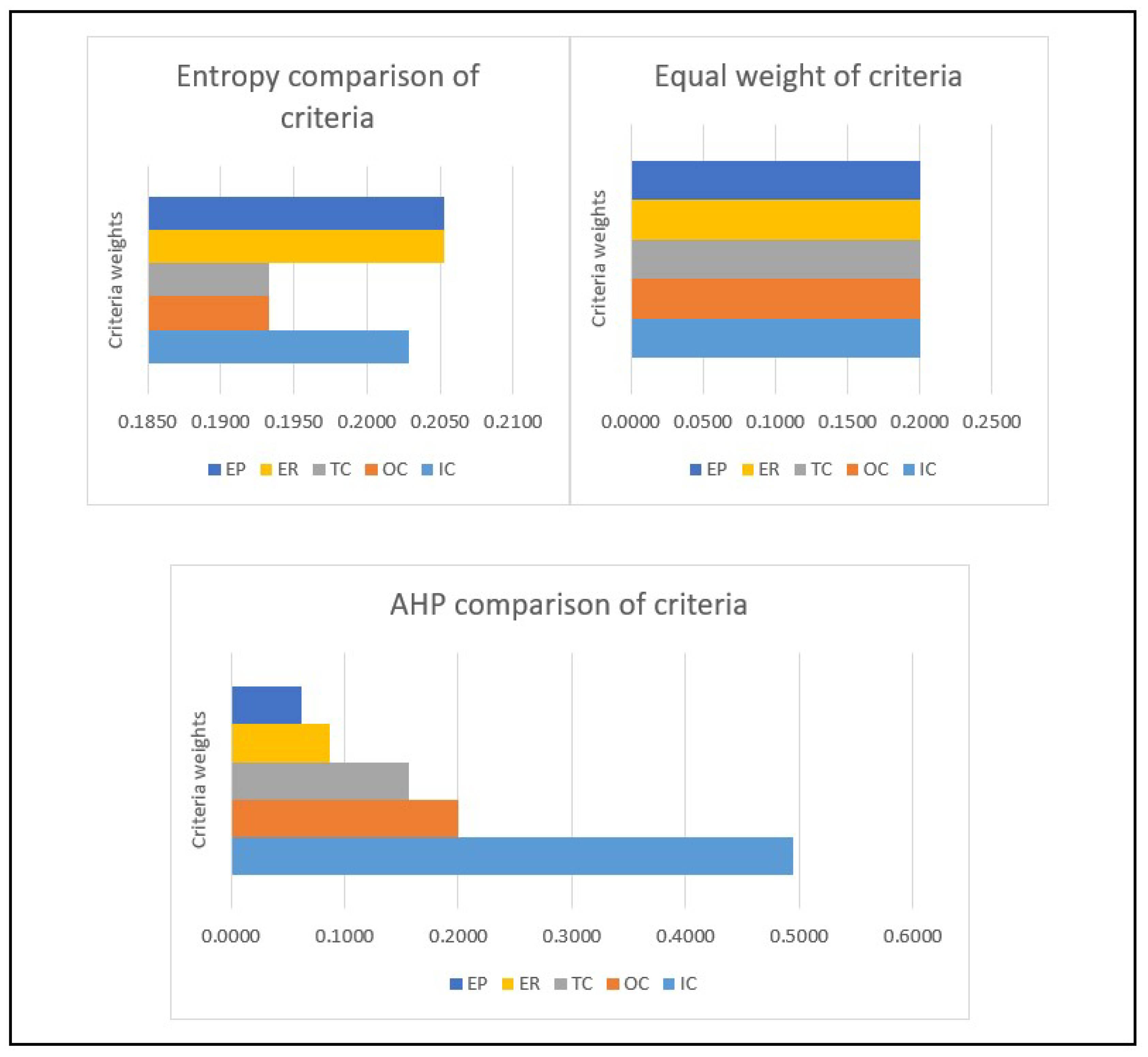
The secondary data also established how the post-consumers access information on plastic bottle waste pollution and what alternatives to plastic they use. Finally, the post-consumers identified the main reasons for the continued use of plastics and their opinions on the most effective ways to reduce plastic bottle waste pollution in the city. The methodology employed the utilization of various MCDA methods, including the Analytic Hierarchy Process (AHP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), VlseKrierijumska Optimizacija I Kompromisno Resenje (VIKOR), entropy weights, and equal weights. Three criteria weights were estimated using AHP, entropy weights, and equal weights methods, as shown in Figure 4.

Three alternatives for PET waste collection methods are identified: Tpbw – Threshold Plastic Bottle Waste Collection; Ppbw – Project Plastic Bottle Waste Collection; and Epbw – Eligible Plastic Bottle Waste Collection in a Region. Criteria are categorized into two main groups: Costs (Initial investment cost, Operational cost, Transportation cost) and Benefits (Environmental risk, Employment potential). These three (3) criteria were used in estimating the alternatives and were determined from the standardized Equations 1 and 2.

I n i t i a l i n v e s t m e n t c o s t ($) = \frac{F C}{(1 - \frac{P C 1}{100})}

(1)

O p e r a t i o n c o s t ($) = J C + P C 2

(2)

where

F C

is the final cost ($),

P C 1

is the percentage change in cost (%),

J C

is the job cost,

P C 2

is the process cost. The transportation cost

T C

, depends on other costs in operation such as the estimated fuel consumption, the mileage for each shipment and multiplying it with the fuel cost, expenses on vehicle maintenance, and considering wages of the drivers involved in the transportation process with some other fees that may be added.

3. Analytic Hierarchy Process (AHP)

The objective weights were determined using the AHP approach by adopting these six steps [25].

(a): The problem and goal are defined by prioritizing the criteria (Table 2). Constructing a pair-wise comparison matrix.
(b): Normalizing the constructed pair-wise comparison matrix (Table 3). Normalize the pair-wise comparison matrix by dividing each element by the sum of its column as given in Equation 3.

${\tilde{a}}_{i j} = \frac{a_{i j}}{\sum_{k = 1}^{n} a_{k j}}$

(3)
(c): Sum the values in each row to obtain a set of values called weighted sum, as shown in Table 3.
(d): Calculate the mean of the values from the preceding stage; this value is known as $λ_{m a x}$ :

$λ_{m a x} = \frac{6.9857 + 4.9082 + 5.2015 + 4.8194 + 4.8020}{5} = 5.343$
(e): The consistency index (CI) is calculated as follows:

$C o n s i s t e n c y I n d e x (C . I) = \frac{λ_{m a x} - n}{n - 1}$

(4)

$= \frac{5.343 - 5}{5 - 1} = 0.085$

where $n$ is the number of compared elements (in this case $n = 5$ )
(f): Now we can calculate the consistency ratio, given as:

$C o n s i s t e n c y R a t i o = \frac{C o n s i s t e n c y I n d e x (C . I .)}{R a t i o I n d e x (R I)}$

(5)

$= \frac{0.085}{1.12} = 0.076$

Table 4 contains a randomly generated comparison matrix's ratio index (RI), which is available and given as shown in Table 4. For n = 5, RI = 1.12. It is possible to compute that using these CI and RI values. The authors presume that our judgment matrix is reasonably consistent because the proportion of inconsistency (CR) value of 0.076 is less than 0.10, allowing us to proceed with the AHP decision-making process.

4. Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)

Determining the best alternatives with the shortest distance from the positive ideal solution and farthest distance from the negative ideal solution with these nine (9) steps [26,27].

(a): Determining the objective, alternatives, and criteria.
(b): The objective is to optimize the three (3) alternatives (T_pbw – Threshold Plastic Bottle Waste Collection; P_pbw – Project Plastic Bottle Waste Collection; and E_pbw – Eligible Plastic Bottle Waste Collection in a Region) based on the criteria (initial investment cost, operational cost, transportation cost environmental risk, and employment potentials).
(c): The decision matrix X is defined by equation (6), with values given.
(d): $X = [X_{I J}] = |\begin{matrix} X_{11} & X_{12} & X_{1 n} \\ X_{21} & X_{22} & X_{2 n} \\ X_{m 1} & X_{m 2} & X_{m n} \end{matrix}|$

(6)

The Normalization of the decision matrix is done using Equation 7.

$r_{i j} = \frac{X_{i j}}{\sqrt{\sum_{n = 1}^{m} X_{i j}^{2}}}$

(7)
(e): Calculate the values of the objective weight coefficients with Equation 8.

$\sum_{j}^{n} w_{j} = 1$

(8)
(f): Determine the weighted decision-making matrix using Equation (9), this represents the multiplication of elements of a column of the normalized matrix with appropriate objective weight coefficients obtained from Equation (3).

$V_{i j} = r_{i j} . w_{i j}$

(9)

f. Identify the positive and negative ideal solution based on Equations (10) and (11).

$V^{+} = \{m a x (v_{i j}), j ϵ J, m i n (v_{i j}), j ϵ J, i = 1\} = \{V_{1}^{+}, V_{2}^{+}, \dots V_{n}^{+}\}$

(10)

$V^{-} = \{m i n (v_{i j}), j ϵ J, m a x (v_{i j}), j ϵ J, i = 1\} = \{V_{1}^{+}, V_{2}^{+}, \dots V_{n}^{+}\}$

(11)
(g): Calculate the Euclidean separation distance of each competitive alternative from the positive and negative solution using Equations (12) and (13)

$S_{i}^{+} = \sqrt{\sum_{j = 1}^{n} {(v_{i j} - v_{j}^{+})}^{2}}$

(12)

$S_{i}^{-} = \sqrt{\sum_{n}^{j = 1} {(v_{i j} - v_{j}^{-})}^{2}}$

(13)
(h): Calculate the distance between each location of the ideal solution. $P_{i}$ . To determine how close a potential location is to the ideal solution for each competitive alternative using (14).

$P_{i} = \frac{S_{i}^{-}}{S_{i}^{+} + S_{i}^{-}}$

(14)
(i): The alternatives are arranged in order based on the value of $P_{i}$ Found in Equation (14)

5. VlseKrierijumska Optimizacija I Kompromisno Resenje (VIKOR)

VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje) is a Serbian language that means Multi-criteria Optimization and Compromise Solution, which was practically applied in 1998 [28]. The following steps comprise the traditional VIKOR's compromise-ranking algorithm in Equation (15-19).

(a): Setting up the decision matrix according to Equation.

$I = [I_{I J}] = |\begin{matrix} I_{11} & I_{12} & I_{1 n} \\ I_{21} & I_{22} & I_{2 n} \\ I_{m 1} & I_{m 2} & I_{m n} \end{matrix}|$

(15)
(b): Normalization of the decision matrix is done using Equation 16.

$f_{i j} = \frac{I_{i}^{j}}{\sqrt{\sum_{i = 1}^{m} {(I_{i}^{j})}^{2}}}$

(16)
(c): Calculate utility measure $S_{i}$ and Regret measure $R_{i}$ using Equations (17a, b), (18a, b)

$S_{i} = \sum_{i = 1}^{n} w_{i} [\frac{{(f_{i j})}_{m a x} - (f_{i j})}{{(f_{i j})}_{m a x} - {(f_{i j})}_{m i n}}] B e n e f i c i a l c r i t e r i a$

(17a)

$S_{i} = \sum_{i = 1}^{n} w_{i} [\frac{(f_{i j}) - {(f_{i j})}_{m i n}}{{(f_{i j})}_{m a x} - {(f_{i j})}_{m i n}}] N o n b e n e f i c i a l c r i t e r i a$

(17b)

$R_{i} = m a x i m u m \{w_{i} [\frac{{(f_{i j})}_{m a x} - (f_{i j})}{{(f_{i j})}_{m a x} - {(f_{i j})}_{m i n}}]\} B e n e f i c i a l$

(18a)

$R_{i} = m a x i m u m \{w_{i} [\frac{(f_{i j}) - {(f_{i j})}_{m i n}}{{(f_{i j})}_{m a x} - {(f_{i j})}_{m i n}}]\} N o n b e n e f i c i a l$

(18b)
(d): Rank the alternatives by $Q_{i}$ The less the value of $Q_{i}$ is the better decision of the alternatives using Equation 19.

$Q_{i} = v [\frac{(S_{i}) - {(S_{i})}_{m i n}}{{(S_{i})}_{m a x} - {(S_{i})}_{m i n}}] + (1 - v) [\frac{(R_{i}) - {(R_{i})}_{m i n}}{{(R_{i})}_{m a x} - {(R_{i})}_{m i n}}]$

(19)

In this context,

f_{i j}

represents the decision matrix that has been normalized;

S_{i}

denotes the utility measure associated with each option while

R_{i}

signifies the regret measure.

w_{i}

represents the objective weight assigned to each criterion, as determined through the Analytic Hierarchy Process (AHP). The value of

v

(the strategy that is compromised) is set to 0.5, and

Q_{i}

is the index that indicates the ranking of the options.

6. Results and Discussion

Table 1 presents the datasets collected from plastic waste stakeholders, suggesting the cost implications for plastic waste collection based on the selected alternatives of the study. Based on a three-point scale (1 – Equal importance, 3 – Moderate importance, 5 – Strong importance), the two considered beneficial criteria are measured in relative relationships with alternatives. The pair-wise comparison matrix was created with the help of a scale of relative importance, as listed and defined in Table 5.

Table 5. Relative ranking scale.

The scale of relative importance	Definition
1	Equal importance
3	Moderate importance
5	Strong importance
7	Very strong importance
9	Extreme importance
2,4,6,8	Intermediate values

Table 6. Pair-wise comparison matrix.

Criteria	IC	OC	TC	ER	EP
IC	1	9	5	3	9
OC	1/9	1	1	3	5
TC	1/5	1	1	2	3
ER	1/3	1/3	¼	1	1
EP	1/9	1/5	1/3	1	1

Table 3 also displays the components of the normalized decision matrix for the criteria: the coefficient of objective weight and the amount of information related to each criterion, respectively. The initial investment cost ($) has the highest coefficient of the objective weight of 0.495, among other criteria, while the employment potential has the lowest coefficient of 0.062, as presented in Table 3. The implication is that the initial investment cost ($) contributes more to the overall objective weight, while the employment potential has the least contribution.

After each criterion's objective weight coefficient was determined, each alternative's ranking was created using TOPSIS.

Table 7. Calculating the consistency.

	IC	OC	TC	ER	EP
IC	0.50	1.80	0.78	0.26	0.12
OC	0.06	0.20	0.16	0.26	0.31
TC	0.10	0.20	0.16	0.17	0.18
ER	0.17	0.07	0.04	0.09	0.06
EP	0.06	0.04	0.05	0.09	0.06

7. TOPSIS

Table 8 displays the outcome of normalizing Table 2 using TOPSIS. The weightage normalized decision matrix, also shown in Table 9, is then created by multiplying Table 8 by the objective weight coefficient of each criterion.

Table 10 displays the results of ranking each competing alternative by Euclidean distance from the positive.

S_{i}^{+}

and negative

S_{i}^{-}

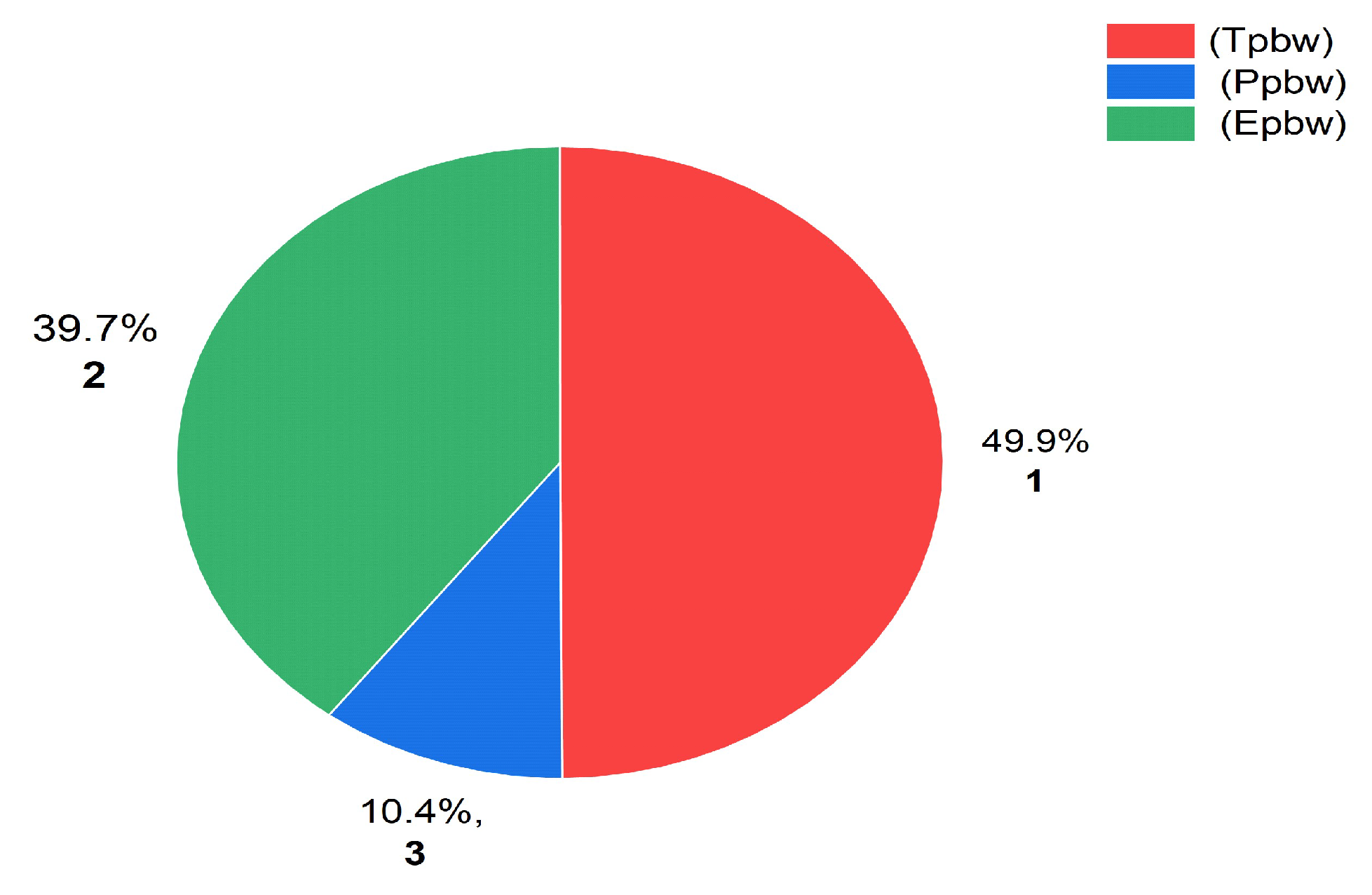
solutions based on the ideal best and ideal worst values. Figure 5 shows the alternatives and their ranking position via Euclidean distances.

8. VIKOR

The VIKOR method was used to normalize Table 3; the result is shown in Table 11. Table 9 is then multiplied by the coefficient of the criteria objective weights, determined by AHP, to produce the weightage normalized decision matrix shown in Table 12.

Subsequent computations from Table 12 are provided in Table 13, displaying the Measure of Utility Si, the Measure of Regret Ri, and the final Ranking index Qi.

Both methods have different normalization processes. The TOPSIS method employs vector normalization, whereas the VIKOR method uses linear normalization. The normalized value in linear normalization is independent of the criteria's unit. The normalized value in the TOPSIS method may vary depending on the evaluation unit used for a given criterion. The ranking index with distances from the ideal and negative-ideal points is introduced by the TOPSIS method. In TOPSIS, these distances are summed without considering their relative significance [29].

While the TOPSIS approach employs n-dimensional Euclidean distance, which might suggest a balance between overall and individual satisfaction, it does so in a different manner than VIKOR, which introduces weight. Both techniques produce listings. The option that scores the highest on VIKOR is the one that comes closest to the perfect answer. Although the option with the highest ranking by TOPSIS is the best according to the ranking index, this does not always imply that it is the best option overall. The VIKOR method ranks and suggests an acceptable solution with an improved rating [29].

However, it is interesting that the normalization processes of TOPSIS and VIKOR resulted in similar results, as presented in Table 8 and Table 11.

The alternative T_pbw was considered the ideal alternative, having the highest ranking among the two MCDA methods used in the analysis. However, the alternative P_pbw was considered the worst alternative of the two analysis methods.

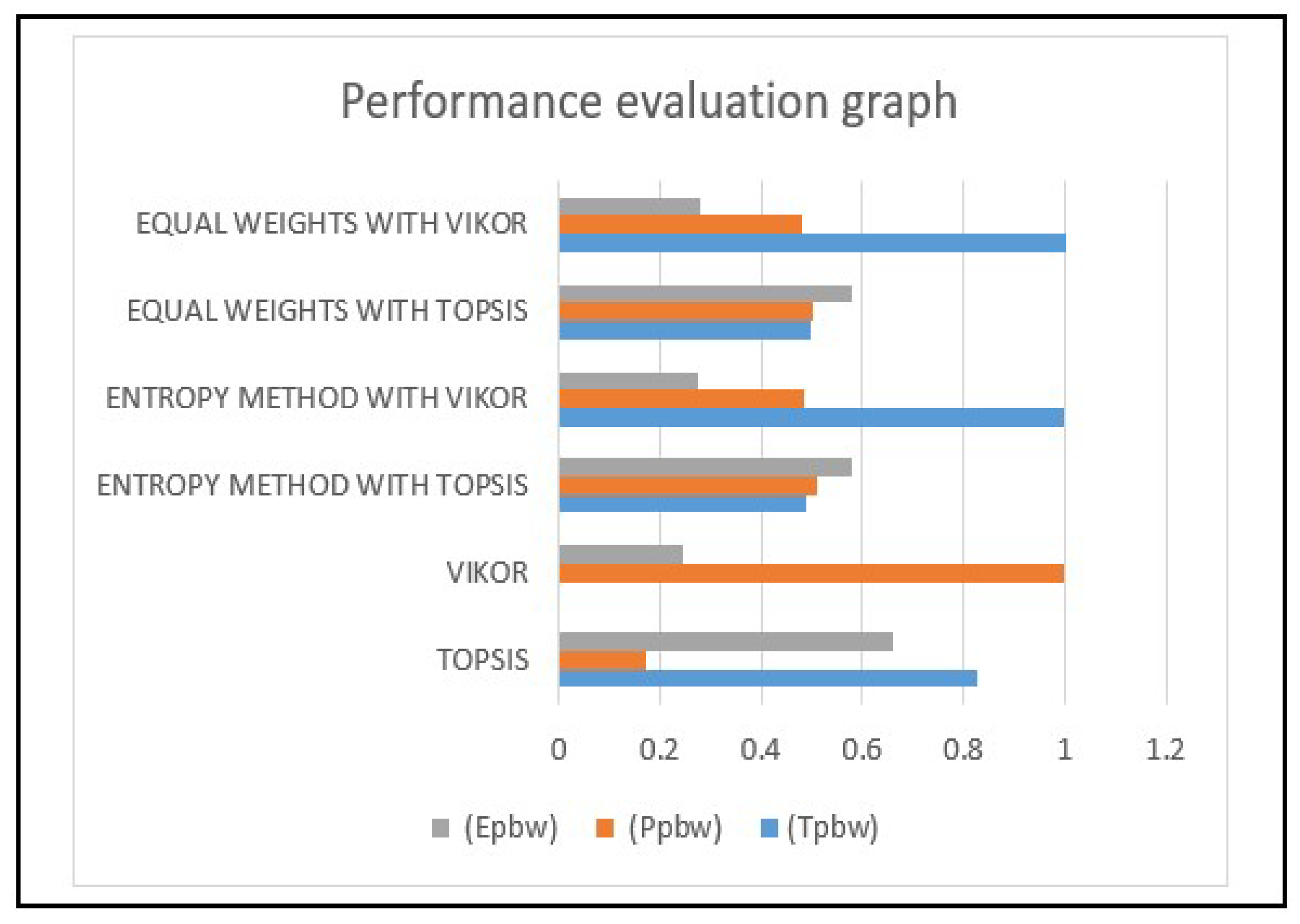
The graph provides a comparative analysis of three PBW (Plastic Bottle Waste) collection alternatives (T_pbw, P_pbw, and E_pbw) using six different Multi-Criteria Decision Analysis (MCDA) approaches TOPSIS, VIKOR, Entropy Method with TOPSIS, Entropy Method with VIKOR, equal weights with TOPSIS and equal weights with VIKOR. The performance results of each alternative against each method are presented in Table 14 and represented in a histogram graph in Figure 6 to reflect the performance of each alternative under multiple criteria.

The TOPSIS method indicates that T_pbw has the highest performance value, approximately 0.8. This shows that T_pbw is the most preferred alternative under TOPSIS, which relies on the geometric distance from the ideal solution. On the other hand, P_pbw is the lowest performer with a performance value of 0.2, thus making it the least favorable alternative. E_pbw has a performance value of about 0.65, is moderately preferred, and can be chosen as an alternative to T_pbw.

The VIKOR method shows a different strength of preference. T_pbw has the lowest performance value of 0; thus, it is the least preferred alternative for the VIKOR approach, as it favors compromise solutions. However, P_pbw has the highest performance at 1 and is the best alternative under VIKOR. E_pbw has an estimated performance value of approximately 0.25, which is therefore not too high compared to the total source size and thus not too low, implying moderate suitability.

With the entropy method with TOPSIS, the performance values for all three alternatives are similar, varying between 0.48 and 0.58. E_pbw is slightly higher than the other alternatives, with a value of about 0.58, while Tpbw and Ppbw have almost similar performance values, slightly lower than E_pbw. This minute change implies that when criteria weights are balanced through entropy, the performance gap between alternatives decreases so that all alternatives become equally desirable.

The entropy method with VIKOR presented the performance value of Tpbw, the most preferred alternative, with a value of 1. P_pbw scores around 0.48, and E_pbw has the lowest value at about 0.28. This method recommends T_pbw as the best alternative, so the results of adjusting the weights according to entropy and employing VIKOR confirm the preference for T_pbw.

The equal weights with the TOPSIS method showed that the performance values of all the alternatives were similar at about 0.5, with E_pbw slightly higher at about 0.58. This implies that if all concerns are treated equally, E_pbw takes a slightly higher position. The close performance indicators mean no significant difference between the alternatives when considering equal weights.

The performance values using equal weights with VIKOR indicated that Tpbw and Ppbw performance values are comparable at around 0.48, while Epbw has the lowest value at approximately 0.28. This method shows a significant preference for T_pbw and P_pbw instead of E_pbw, and it is in line with the Entropy Method with VIKOR results. It is apparent from the graph that the preference of alternatives is significantly influenced by the MCDA method used. T_pbw has consistently scored high in all methods, especially TOPSIS and entropy, with VIKOR showing that it is the best PET waste collection method. P_pbw has its strength mainly in VIKOR and demonstrates its use when group utility and compromise matter the most. However, E_pbw is the most consistent moderately performing method and is preferred in equal weight or entropy with TOPSIS methods.

9. Sensitivity Analysis

Sensitivity analysis is performed to determine the impact of altering the objective weights of criteria on evaluating alternatives. This is done by identifying the various alternative ranking changes that arise for each method if the weight of each sub-criteria value is altered [30,31]. When the original ranking is altered by altering the objective weights of the criteria, the results are considered sensitive; otherwise, the results are referred to as robust. These modifications produce various scenarios that could change the ranking of alternatives [32].

Through the utilization of four (4) scenarios, sensitivity analysis was performed. Instead of using the original AHP approach, the objective weights were redistributed using the entropy method. The second possibility involved giving each criterion the same weight. Table 12 presents each of the four situations. This indicates that alterations in the criteria' objective weights can impact the ranking outcomes determined by the two techniques. Alternative E_pbw is confirmed to be the best choice in all four scenarios, and it was considered for the sensitivity analysis of the TOPSIS and VIKOR procedures since it was ranked first in all four scenarios.

The MCDA tools AHP, TOPSIS, and VIKOR have been effectively utilized to choose the most effective techniques for collecting plastic bottle waste. The weight of each criterion's objective costs associated with initial investment, operations, transportation, environmental risk, and employment potential are determined using the AHP method. TOPSIS and VIKOR were used to rank and ultimately choose among the alternatives for the PET waste collection methods: Threshold Plastic Bottle Waste Collection, Project Plastic Bottle Waste Collection, and Eligible Plastic Bottle Waste Collection in a Region. The results were the same when the ranking results from TOPSIS were compared as a further investigation with the VIKOR method. T_pbw was ranked as the best alternative by TOPSIS and VIKOR methods.

According to sensitivity analysis, changes in the objective weight of the criteria impact both TOPSIS and VIKOR, which were used to rank the alternatives. The selection of additional criteria to strengthen the process can be further explored in future research to examine the robustness of the outcomes. This can include the following: social impact, environmental impact, ease of sorting plastic waste [33], energy consumption, sustainability, processing cost [34], and other waste management factors.

10. Conclusions

The best PET waste collection method has been chosen with the help of MCDA tools like AHP and TOPSIS. The AHP approach was used to calculate the objective weight of the consideration criteria, which included employment potential, environmental risk, operational costs ($), transportation costs ($), and initial investment costs ($). TOPSIS was used to rank and decide the alternative (collection method). To confirm this, the ranking findings from TOPSIS were compared with those from the VIKOR approach. T_pbw was ranked as the top alternative by the VIKOR technique as well. This study reveals the best alternatives to achieve the optimal collection method to enhance PET waste recycling further. According to the sensitivity analysis conducted, changes in the objective weight of the criteria impacted both TOPSIS and VIKOR, which were used to rank the alternatives. The study can be strengthened by adding more criteria and conducting research to incorporate other PET waste disposal techniques.

Author Contributions

Conceptualization, J.O. and I.O.; methodology, J.O. and I.O.; formal analysis, J.O.; investigation, J.O.; resources, J.O.; data curation, J.O. and I.O.; writing—original draft preparation, J.O.; writing—review and editing, J.O., I.O. and LT.; supervision, I.O. and LT. All authors have read and agreed to the published version of the manuscript.

Funding

Please add: No funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Acknowledgments

This work was carried out as a part of a PhD thesis by Johnson Adekanmi Oyewale, completed under the supervision of Lagouge Tartibu, Imhade Okokpujie. The authors also acknowledge the valuable insights of the reviewers and academic editor who contributed extensively to improving the article’s quality.

Conflicts of Interest

The authors declare that they have no competing interests.

References

O. Oladele, T. F. Omotosho, and A. A. Adediran, “Polymer-Based Composites: An Indispensable Material for Present and Future Applications,” Int. J. Polym. Sci., vol. 2020, 2020. [CrossRef]
Alex Olanrewaju Adekanmbi, Emmanuel Chigozie Ani, Ayodeji Abatan, Uchenna Izuka, Nwakamma Ninduwezuor-Ehiobu, and Alexander Obaigbena, “Assessing the environmental and health impacts of plastic production and recycling,” World J. Biol. Pharm. Heal. Sci., vol. 17, no. 2, pp. 232–241, 2024. [CrossRef]
N. Singh, D. Hui, R. Singh, I. P. S. Ahuja, L. Feo, and F. Fraternali, “Recycling of plastic solid waste: A state of art review and future applications,” Compos. Part B Eng., vol. 115, pp. 409–422, 2017. [CrossRef]
N. Nasir, H. A. Malek, S. S. Januri, I. A. Malek, and J. N. Jamidin, “Plastic waste knowledge of households towards a sustainable environment,” IOP Conf. Ser. Earth Environ. Sci., vol. 1151, no. 1, 2023. [CrossRef]
F. Puluhulawa and M. R. Puluhulawa, “Plastic Waste: Environmental Legal Issues and Policy Law Enforcement for Environmental Sustainability,” E3S Web Conf., vol. 259, 2021. [CrossRef]
C. Ayukawa and L. Frankel, An Interdisciplinary Approach to Accessible Museum Exhibitions, vol. 1202 AISC. 2020. [CrossRef]
S. Senthilkannan, M. Miguel, and A. Gardetti, Sustainable Textiles: Production, Processing, Manufacturing & Chemistry Sustainability in the Textile and Apparel Industries Sourcing Synthetic and Novel Alternative Raw Materials. 2020. [Online]. Available: http://www.springer.com/series/16490.
R. Ajaj, W. Abu Jadayil, H. Anver, and E. Aqil, “A Revision for the Different Reuses of Polyethylene Terephthalate (PET) Water Bottles,” Sustain., vol. 14, no. 8, pp. 1–14, 2022. [CrossRef]
N. A. Al-Thani, T. Al-Ansari, and M. Haouari, “Integrated TOPSIS-COV approach for selecting a sustainable PET waste management technology: A case study in Qatar,” Heliyon, vol. 8, no. 8, p. e10274, 2022. [CrossRef]
M. Pjanic, “The role of polycarbonate monomer bisphenol-A in insulin resistance,” PeerJ, vol. 2017, no. 9, 2017. [CrossRef]
M. S. Molonia et al., “The p-Phthalates Terephthalic Acid and Dimethyl Terephthalate Used in the Manufacture of PET Induce In Vitro Adipocytes Dysfunction by Altering Adipogenesis and Thermogenesis Mechanisms,” Molecules, vol. 27, no. 21, 2022. [CrossRef]
N. Rustagi, S. K. Pradhan, and R. Singh, “Public health impact of plastics: An overview,” Indian J. Occup. Environ. Med., vol. 15, no. 3, pp. 100–103, 2011. [CrossRef]
S. D’Angelo and R. Meccariello, “Microplastics: A threat for male fertility,” Int. J. Environ. Res. Public Health, vol. 18, no. 5, pp. 1–11, 2021. [CrossRef]
J. A. Oyewale, L. K. Tartibu, and I. P. Okokpujie, “A Review and Bibliometric Analysis of Sorting and Recycling of Plastic Wastes,” Int. J. Des. Nat. Ecodynamics, vol. 18, no. 1, pp. 63–74, 2023. [CrossRef]
Y. Xu and P. S. Ward, “ENVIRONMENTAL ATTITUDES AND CONSUMER PREFERENCE FOR ENVIRONMENTALLY-FRIENDLY BEVERAGE PACKAGING : THE ROLE OF INFORMATION PROVISION AND IDENTITY LABELING IN INFLUENCING CONSUMER BEHAVIOR,” vol. 10, no. 1, pp. 95–108, 2023.
P. Hansen and N. Devlin, “Multi-Criteria Decision Analysis ( MCDA ) in Healthcare Decision- Healthcare Decision-Making and Multi-Criteria Decision Analysis,” no. August, pp. 1–26, 2024.
S. AChaube, “An Overview of Multi-Criteria Decision Analysis and the Applications of AHP and TOPSIS Methods,” vol. 9, no. 3, pp. 581–615, 2024.
A. C. Mondragon, E. Mastrocinque, and P. Hogg, “An AHP and Fuzzy AHP Multifactor Decision Making Approach for Technology and Supplier Selection in the High-Functionality Textile Industry,” 2019.
S. Chakraborty, “TOPSIS and Modified TOPSIS: A comparative analysis,” Decis. Anal. J., vol. 2, no. December 2021, p. 100021, 2022. [CrossRef]
R. R. Menon and V. Ravi, “Using AHP-TOPSIS methodologies in the selection of sustainable suppliers in an electronics supply chain,” Clean. Mater., vol. 5, no. September 2021, p. 100130, 2022. [CrossRef]
“PREFERENCE RANKING ORGANIZATION METHOD FOR ENRICHMENT EVALUATION,” 2024.
Journal, H. Taherdoost, and M. Madanchian, “Using PROMETHEE Method for Multi-Criteria Decision Making : Applications and Procedures,” pp. 1–7, 2023. [CrossRef]
F. Ezbakhe and A. Pérez-foguet, “Decision analysis for sustainable development : The case of renewable energy planning under uncertainty,” vol. 291, pp. 601–613, 2021. [CrossRef]
P. Rajan, A. Gopanna, and S. P. Thomas, “A project based learning (PBL) approach involving PET recycling in chemical engineering education,” Recycling, vol. 4, no. 1, 2019. [CrossRef]
E. Mu and P. D. Making, “Understanding the Analytic Hierarchy Process,” no. 2012, 2015. [CrossRef]
P. Okokpujie, U. C. Okonkwo, C. A. Bolu, O. S. Ohunakin, M. G. Agboola, and A. A. Atayero, “Implementation of multi-criteria decision method for selection of suitable material for development of horizontal wind turbine blade for sustainable energy generation,” Heliyon, vol. 6, no. 1, 2020. [CrossRef]
O. O. Agboola, B. O. Akinnuli, B. Kareem, and M. A. Akintunde, “Decision on the selection of the best height-diameter ratio for the optimal design of 13,000 m3 oil storage tank,” Cogent Eng., vol. 7, no. 1, pp. 0–17, 2020. [CrossRef]
C. L. Chang, “A modified VIKOR method for multiple criteria analysis,” Environ. Monit. Assess., vol. 168, no. 1–4, pp. 339–344, 2010. [CrossRef]
F. SARI, “Comparison of Topsis and Vikor Multi Criteria Decision Analysis Techniques,” Selcuk Univ. J. Eng. ,Science Technol., vol. 6, no. Özel (Special), pp. 825–831, 2018. [CrossRef]
Więckowski and W. Sałabun, “Sensitivity analysis approaches in multi-criteria decision analysis : A systematic review,” vol. 148, no. June, 2023.
V. Maliene, R. Dixon-Gough, and N. Malys, “Dispersion of relative importance values contributes to the ranking uncertainty: Sensitivity analysis of Multiple Criteria Decision-Making methods,” Appl. Soft Comput. J., vol. 67, pp. 286–298, 2018. [CrossRef]
M. Jiří, “The robustness of TOPSIS results using sensitivity analysis based on weight tuning,” IFMBE Proc., vol. 68, no. 2, pp. 83–86, 2018. [CrossRef]
Balwada, S. Samaiya, and R. P. Mishra, “ScienceDirect Packaging Plastic Waste Management for a Circular Economy and Identifying a better Waste Collection System using Analytical Hierarchy Process ( AHP ),” Procedia CIRP, vol. 98, no. March, pp. 270–275, 2023. [CrossRef]
Sindhwani, P. Gupta, A. Kumar, and R. Srivastava, “Evaluation of Plastic Waste Management Methods Using Multi Criteria Decision Making Tool – AHP,” vol. 0, 2022. [CrossRef]

Figure 1. Plastic waste pollution in water bodies.

Figure 3. The hierarchal framework of PET waste collection for maximum recycling.

Figure 4. Criteria weights of AHP, entropy, and equal weights methods.

Figure 5. The Euclidean ranking positions the three alternatives.

Figure 6. Performance evaluation graph of decision-making matrices.

Table 1. Appraising criteria and accompanying the descriptions.

Criteria	Acronym	Description of criteria
Initial investment cost	IC	The initial investment cost is the necessary financial amount to begin a project, business, or investment.
Operational cost	OC	The operational cost is the continuous expenses needed for the daily operation of a business or project.
Transportation cost		Transportation costs are the expenses of moving goods or people between locations.
Environmental risk	ER	Environmental risk is the possibility of environmental harm from human actions or natural occurrences.
Employment potential	EP	Employment potential signifies generating and maintaining job opportunities within a business, industry, or region.

Table 2. Secondary data on plastic bottle waste collection methods.

	Criteria/Alternatives	(T_pbw) ($)	(P_pbw) ($)	(E_pbw) ($)
Cost criteria	Initial investment cost (IC)	9,352	37,407	18,703
	Operational cost (OC)	25	63	38
	Transportation cost (TC)	11	28	17
Benefit criteria	Environmental risk (ER)	1	5	3
Benefit criteria	Employment potential (EP)	1	5	3

Table 3. Normalized pair-wise comparison matrix.

Criteria	IC	OC	TC	ER	EP	Criteria weights	Weighted Sum value	Ratio
IC	0.5696	0.7803	0.6593	0.3000	0.1667	0.4952	3.46	6.9857
OC	0.0633	0.0867	0.1319	0.3000	0.4167	0.1997	0.98	4.9082
TC	0.1139	0.0867	0.1319	0.2000	0.2500	0.1565	0.81	5.2015
ER	0.1899	0.0289	0.0330	0.1000	0.0833	0.0870	0.42	4.8194
EP	0.0633	0.0173	0.0440	0.1000	0.0833	0.0616	0.30	4.8020

Table 4. Consistency indices for a randomly generated matrix.

N	1	2	3	4	5	6	7	8	9	10
RI	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

Table 8. Normalized decision matrix using TOPSIS.

Weightage	0.495	0.200	0.156	0.087	0.062
Alternative/Criteria	IC ($)	OC ($)	TC ($)	ER	EP
(T_pbw)	0.218	0.324	0.324	0.169	0.169
(P_pbwx)	0.873	0.811	0.811	0.845	0.845
(E_pbw)	0.436	0.487	0.487	0.507	0.507

Table 9. Weighted normalized decision matrix using TOPSIS.

Weightage	0.495	0.200	0.156	0.087	0.062
	IC ($)	OC ($)	TC ($)	ER	EP
(T_pbw)	0.108	0.065	0.051	0.015	0.010
(P_pbwx)	0.432	0.162	0.127	0.074	0.052
(E_pbw)	0.216	0.097	0.076	0.044	0.031

Table 10. Euclidean distances and ranking.

Alternatives	$S_{i}^{+}$	$S_{i}^{-}$	$S_{i}^{+} + S_{i}^{-}$	$P_{i}$	Rank position
(T_pbw)	0.072	0.347	0.419	0.8280	1
(P_pbwx)	0.347	0.072	0.419	0.1720	3
(E_pbw)	0.121	0.234	0.355	0.6590	2

Table 11. Normalized decision matrix using VIKOR.

Weightage	0.495	0.200	0.156	0.087	0.062
Alternative/Criteria	IC ($)	OC ($)	TC ($)	ER	EP
(T_pbw)	0.218	0.324	0.324	0.169	0.169
(P_pbwx)	0.873	0.811	0.811	0.845	0.845
(E_pbw)	0.436	0.487	0.487	0.507	0.507

Table 12. Weighted normalized decision matrix using TOPSIS.

Weightage	0.495	0.200	0.156	0.087	0.062
	IC ($)	OC ($)	TC ($)	ER	EP
(T_pbw)	0.108	0.065	0.051	0.015	0.010
(P_pbwx)	0.432	0.162	0.127	0.074	0.052
(E_pbw)	0.216	0.097	0.076	0.044	0.031

Table 13. Values of measure of unity, measure of individual regret, and ranking index.

0.5
	$S_{i}$	$R_{i}$	$Q_{i}$	$Rank based on Q_{i}$
(T_pbw)	0.1486	0.0870	0.0000	1
(P_pbwx)	0.8514	0.4952	1.0000	3
(E_pbw)	0.3581	0.1651	0.2447	2
$S^{}, R^{}$	0.1486	0.0870
$S^{-}, R^{-}$	0.8514	0.4952

Table 14. Performance results.

	TOPSIS	VIKOR	ENTROPY METHOD WITH TOPSIS	ENTROPY METHOD WITH VIKOR	EQUAL WEIGHTS WITH TOPSIS	EQUAL WEIGHTS WITH VIKOR
(T_pbw)	0.828	0.000	0.489	1.000	0.498	1.002
(P_pbw)	0.172	1.000	0.511	0.484	0.502	0.482
(E_pbw)	0.659	0.245	0.578	0.276	0.580	0.278

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Decision Analysis Approaches on the Collection Methods of Polyethylene Terephthalate Waste

Abstract

1. Introduction

2. Materials and Methods

3. Analytic Hierarchy Process (AHP)

4. Technique for Order Preference by Similarity to Ideal Solution (TOPSIS)

5. VlseKrierijumska Optimizacija I Kompromisno Resenje (VIKOR)

6. Results and Discussion

7. TOPSIS

8. VIKOR

9. Sensitivity Analysis

10. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe