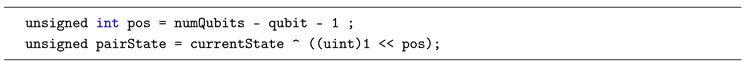1. Introduction
One of the primary reasons to develop quantum computing is that, theoretically, it has been demonstrated that it allows efficient solutions to some complex problems whose best-known solution has an exponential cost for the input size. Quantum superposition, quantum uncertainty, and quantum entanglement are powerful resources that we can use to encode, decode, transmit, and process information in a highly efficient way that is impossible in the classical world.
Recent technological advances have enabled the development of real quantum devices accessed through the cloud. However, these devices are expected to be limited in the short term in terms of the number and quality of their fundamental component, the qubit. Most current quantum devices have a limited number of qubits. In the quantum circuit model, Atom Computing has 1180 qubits, and IBM Osprey has 433 qubits. In the adiabatic model, the D-Wave 2000Q has 2000 qubits. These quantum computers represent prototypes that are not scalable and sufficient to test complex quantum algorithms. Constructing a full-scale quantum computer comprising millions of qubits is a longer-term prospect.
The growing interest in Quantum Computing and the limitations of real quantum devices have caused many organizations to focus on developing software quantum simulators that run on classical computers. These simulators are trendy tools suitable for testing quantum computing concepts on ideal conditions, avoiding hardware challenges like the limited number and quality of physical qubits and quantum error correction. A list of the very recent initiatives is maintained on several websites [
1,
2,
3,
4]. This large number of projects reflects the area’s growth and makes it difficult for researchers to decide which tool to use in their research.
Quantum computing simulators, which operate on classical computers, have emerged as valuable and widely used tools in the field of quantum computing. These simulators play a crucial role in the development, testing, and validation of quantum algorithms before they are implemented on actual quantum hardware. One of the primary advantages of quantum simulators is their accessibility. Unlike quantum computers, which are still relatively scarce and often require significant resources and expertise to operate, simulators can be run on conventional computers. This accessibility allows a broader range of researchers and developers to explore quantum algorithms and concepts without the need for physical quantum computing resources.
Quantum simulators offer a controlled environment for designing and refining quantum algorithms. They can simulate ideal quantum systems without the noise and error rates present in current quantum hardware, providing clearer insights into the theoretical performance of an algorithm. This is particularly useful for educational purposes and theoretical research, where understanding the principles of quantum computation and algorithm design is the main focus.
However, the simulation of quantum computing models in classical computers requires exponential time and involves highly complex memory management. The problem is that using conventional techniques to simulate an arbitrary quantum process significantly more prominent than any of the existing quantum prototypes would soon require considerable memory on a classical computer. For instance, to simulate a 60-qubit quantum state, the process would take 18.000 petabytes (18 Exabytes) of classical computer memory. Therefore, researchers try to reduce such challenges by proposing efficient simulators.
This work explores the fundamental principles of developing a software-based quantum simulator capable of performing simulations on classical computers.
2. Fundamental Concepts of Quantum Computing
To better understand the quantum computing model, it is necessary to know the key aspects of the inheritance of quantum mechanics. This section describes the fundamental concepts on which quantum computing is based.
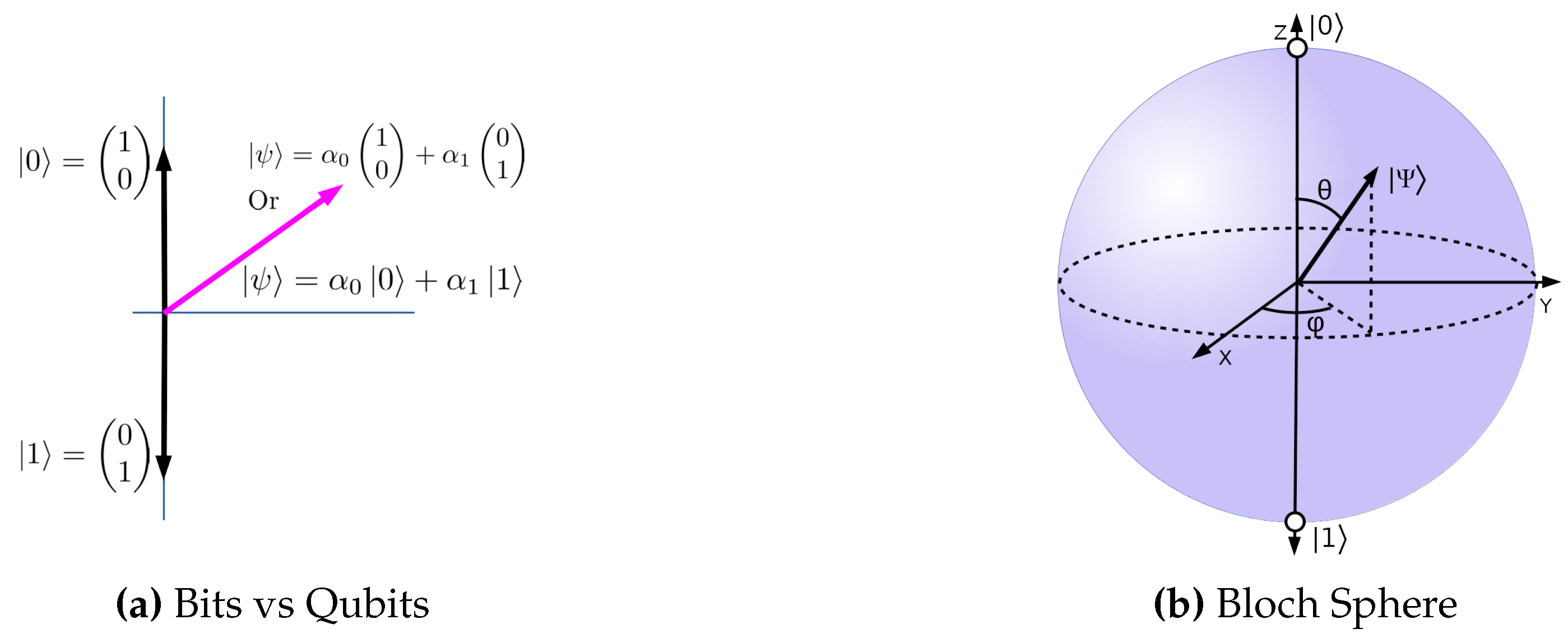
A
Logical Qubit is a unitary vector in a two-dimensional Hilbert space. The Boolean states 0 and 1 are represented by a prescribed pair of normalized and mutually orthogonal quantum states denoted using Dirac’s notation |0〉 and |1〉 [
5]. The two states form a “computational basis,” and any other (pure) state of the qubit can be written as a superposition
[
6]. Formally, a
Quantum State is a vector
representing a superposition of basis elements
if it is a nontrivial linear combination of
and
, if
where
and
are non-zero. The state of a bit is a particular case of a two-dimensional vector; that is to say, there are only two vectors in the whole two-dimensional vector space with real meaning; these are the two orthogonal vectors |0〉 and |1〉, this is depicted in the
Figure 1a. Conversely, qubits do not suffer from this limitation. The general state of a qubit is
where
and
are two complex numbers constrained only by the requirement that
, like 0 and 1, should be a unit vector in the complex vector space, in other words, only by the normalization.
The Bloch sphere is commonly used to depict a qubit,
Figure 1b. Two angles represent the state,
and
. Thus, the state
can be rewrited as
The vector from the origin to the point representing the state makes an angle of
with the z-axis and its component in the x-y plane make an angle of
with the x-axis. The state |0〉 is the North Pole of the sphere, and the state |1〉 is the South Pole.
The general equation of a n-qubit state is
Or, in its expanded form
Where | As we can see, a single complex number can specify a single-qubit state, so n complex numbers can specify any tensor product of n individual single-qubit states.
The special characteristic of quantum states is that they allow the system to be in a few states simultaneously, this is called
superposition [
7].
Quantum bits are not constrained to be wholly 0 or wholly 1 at a given instant. In quantum physics if a quantum system can be found to be in one of a discrete set of states, which we’ll write as |0〉 or |1〉, then, whenever it is not being observed it may also exist in a superposition, or blend of those states simultaneously [
8].
Because a qubit can take on any one of infinitely many states, one can think that a single qubit could store lots of classical information. However, the properties of
quantum measurement severely restrict the amount of information that can be extracted from a qubit. Information about a quantum bit can be obtained only by measurement, and any measurement results in one of only two states, the two basis states associated with the measuring device; thus, a single measurement yields, at most, a single classical bit of information [
9].
The
quantum entanglement describes a correlation between different parts of a quantum system that surpasses anything classically possible. It happens when the subsystems interact so that the resulting state of the whole system can not be expressed as the direct product of the states of its parts [
5]. States that cannot be written as the tensor product of
n single-qubit states are called
entangled states. Thus, most quantum states are entangled [
9]. If we can write the tensor product of those states, they are said to be
separate states.
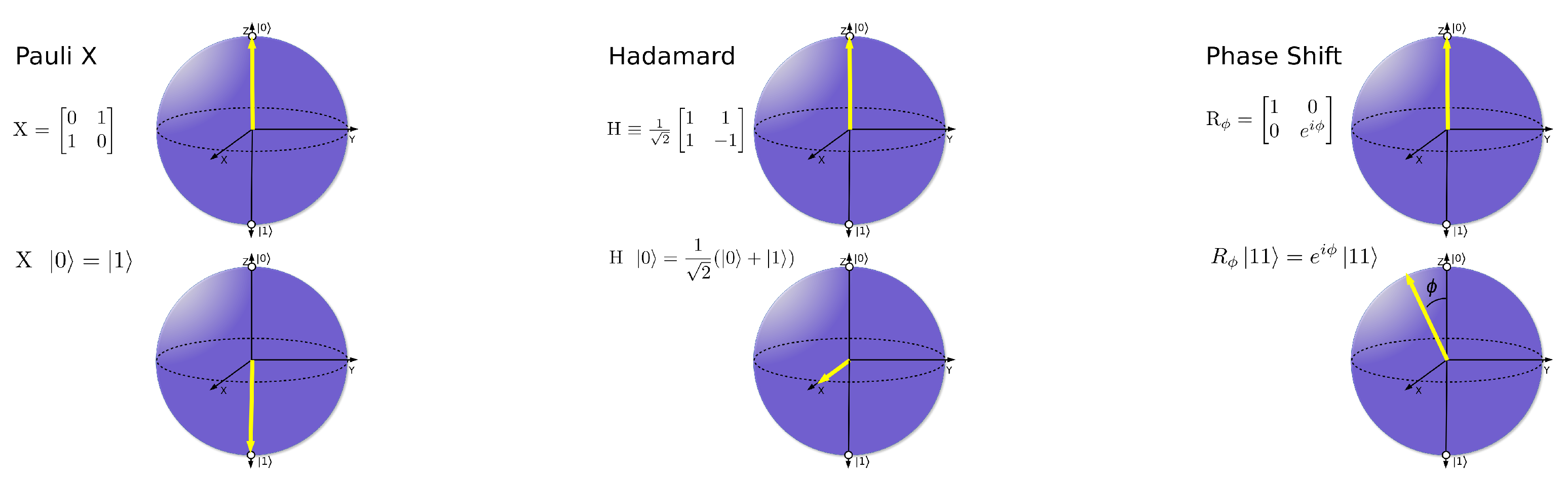
In the Quantum Circuits model, the fundamental transformation of a quantum state is carried out using Quantum Gates, which are the basic components of quantum circuits. Quantum gates are analogous to classical logic gates but operate on qubits instead of classical bits.
To transform the state of the Equation (
1), we need
unitary matrices. Applying a single-qubit gate
G to the
i-th qubit of an
n-qubit quantum state amounts to multiplying the state vector of coefficients
by the matrix.
Figure 2 depicts some popular quantum gates.
A classical (or non-quantum) algorithm is a finite sequence of instructions or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer. Similarly, a Quantum Algorithm is a step-by-step procedure for performing each step on a quantum computer. Although all classical algorithms can also be performed on a quantum computer, the term quantum algorithm is generally used for those algorithms that incorporate some essential feature of quantum computing, such as superposition or entanglement. There are three classes of quantum algorithms with clear advantages over known classical algorithms: algorithms based upon quantum versions of the Fourier transform, quantum search algorithms and quantum simulations.
3. Leading Open-Source Simulators for Quantum Computing
From a recent review, we take some quantum simulators that currently lead the field to characterize their main properties, performance, execution mode, and simulation results to provide comparison and analysis. To facilitate this task, we work with open-source simulators. These simulators are considered state-of-the-art due to several factors [
10]:
Innovative Features: Each simulator offers unique capabilities that set them apart, such as optimized algorithms, integration with widely-used programming frameworks, or novel approaches to handling quantum state representations. For example, qsim’s integration with Cirq and its ability to simulate up to 40 qubits on a high-performance workstation make it a significant tool for developers and researchers.
Adoption and Partnerships: Some of these simulators are backed by major tech companies and have extensive partnerships within the industry, increasing their influence and credibility.
Academic and Commercial Use: These tools are not only used in academic research but are also increasingly adopted by industries for practical applications, which demonstrates their effectiveness and robustness.
Recent Updates and Community Support: The continual updates, community support, and documentation available for these tools contribute to their status as leaders in the field. This ongoing development ensures they remain relevant and useful as quantum computing technology evolves.
Open Collaboration: Open-source projects encourage open collaboration among developers, researchers, and users. Ensuring the source code is available for modification and redistribution fosters a community-driven development approach. This can lead to rapid improvements and innovations, as a diverse group of contributors can work on the software.
The combination of these factors makes these simulators outstanding in the current world of quantum computing, pointing towards their innovativeness and leadership in technological advancement.
To evaluate the performance of the selected simulators, the following platforms were used:
Platform 1: One of the nodes of the cluster Guane of Supercomputing Center of Universidad Industrial de Santander with the following configuration: two AMD EPYC 9554 64-Core Processors and 375 GB of RAM memory.
Platform 2: A workstation with One Intel(R) Xeon(R) E-2136 CPU @ 3.30GHz processor with 32 GiB of RAM and a NVIDIA Corporation GP106GL Quadro P2000.
3.1. Intel-QS
It is an open-source quantum circuit simulator implemented in C++. It uses multiprocessing and has an intuitive Python interface. It is a full-state vector simulator using arbitrary single-qubit gates and gates controlled by two qubits. [
10]. The Intel Quantum Simulator leverages the full capabilities of an HPC system through its shared and distributed memory implementation. The implementation on a single node incorporates enhancements such as vectorization, threading, and cache optimization through the process of gate fusion. The primary object in the Intel Quantum Simulator (IQS) is the QubitRegister, representing the quantum state of the qubits in the system of interest. When declaring a QubitRegister, the number of qubits must be specified to allocate enough memory to describe their state. The state can then be initialized to any computational basis state, uniquely identified by its index.
3.2. Quantum++
Is a general-purpose multi-threaded quantum simulator with high performance. The library is not restricted to qubit systems or specific quantum information processing tasks, being capable of simulating arbitrary quantum processes [
11]. Quantum++ is developed using standard C++17 and has minimal external dependencies. It primarily utilizes the Eigen 3 linear algebra template library, which is header-only. Additionally, when available, it employs the OpenMP library to facilitate multi-processing. The primary data types are complex vectors and complex matrices, such as complex dynamic matrices, double dynamic matrices, complex dynamic column vectors, complex dynamic row vectors, etc.
3.3. qsim
Developed by Google, qsim is an optimized quantum circuit simulator that uses gate fusion and vectorized instructions to simulate up to 40 qubits on a powerful workstation [
12]. Integrated with Cirq, it provides a robust environment for developing and testing quantum algorithms. To achieve cutting-edge simulations of quantum circuits, it uses gate fusion, AVX/FMA vectorized instructions, and openMP multi-threading. This relies on cuQuantum to integrate GPU support.
3.4. cuQuantum
NVIDIA’s cuQuantum SDK is another leading tool, designed to accelerate quantum circuit simulations on GPUs. This toolkit is essential for developers looking to leverage the power of GPUs to enhance simulation performance and scalability. It provides an integrated programming model tailored for a hybrid environment, enabling the combined operation of CPUs, GPUs, and QPUs.
3.5. QuEST
QuEST, or the Quantum Exact Simulation Toolkit, is a high-performance open-source quantum computing simulator designed for simulating quantum circuits, state-vectors, and density matrices. Developed by the Quantum Technology Theory Group at the University of Oxford, QuEST is distinguished by its ability to utilize multithreading, GPU acceleration, and distribution, making it highly effective across various computing environments, from laptops to networked supercomputers. The toolkit is capable of simulating both pure quantum states and mixed states with precision, and supports a wide array of quantum operations. It allows for simulations that are extensible and adaptable, thanks to its open-source nature and support for various back-end hardware via its simple and flexible interface [
13]. QuEST represents a pure state for a system of
n qubits using
complex floating-point numbers, with each real and imaginary component having double precision by default. However, QuEST can be configured to use single or quad precision if desired. The simulator stores the state using C/C++ primitives, which means that by default, the state vector alone consumes
bytes of memory.
3.6. Qrack
Qrack is a high-performance quantum computer simulator that is written in C++ and supports OpenCL and CUDA [
14] [
16]. It is particularly notable for its ability to simulate arbitrary numbers of entangled qubits, limited only by system resources. Qrack is designed to be embedded in other projects and includes a comprehensive suite of standard quantum gates, along with variations suitable for register operations and arbitrary rotations. The simulator is integrated with other quantum computing frameworks like ProjectQ and Qiskit, enhancing its versatility and application. Qrack also features optimizations for noiseless pure state simulations and includes tools that aid in the control, extension, and visualization of data from quantum circuits. Qrack maintains the state representation in a factorized form to enhance simulation efficiency. A general ket state
of
n qubits is described by
complex amplitudes.
3.7. Simulators Comparison
Regarding academic, community and industry support for these simulators, the continual updates, active support, and documentation for these tools contribute to their status as leaders in the field. This ongoing development ensures they remain relevant and valuable as quantum computing technology evolves. Each of these simulators offers unique features and optimizations, making them suitable for various aspects of quantum computing research and development. Their continual evolution is critical as the quantum computing field strives to solve more complex problems and improve algorithm efficiency.
Table 1 shows a comparison of the evaluated simulators of their design properties and optimization mechanisms.
Other projects, like XACC and Qiskit, provide a full-stack approach to quantum computing, including a simulator and compilers and the possibility to run the program on real quantum processors.
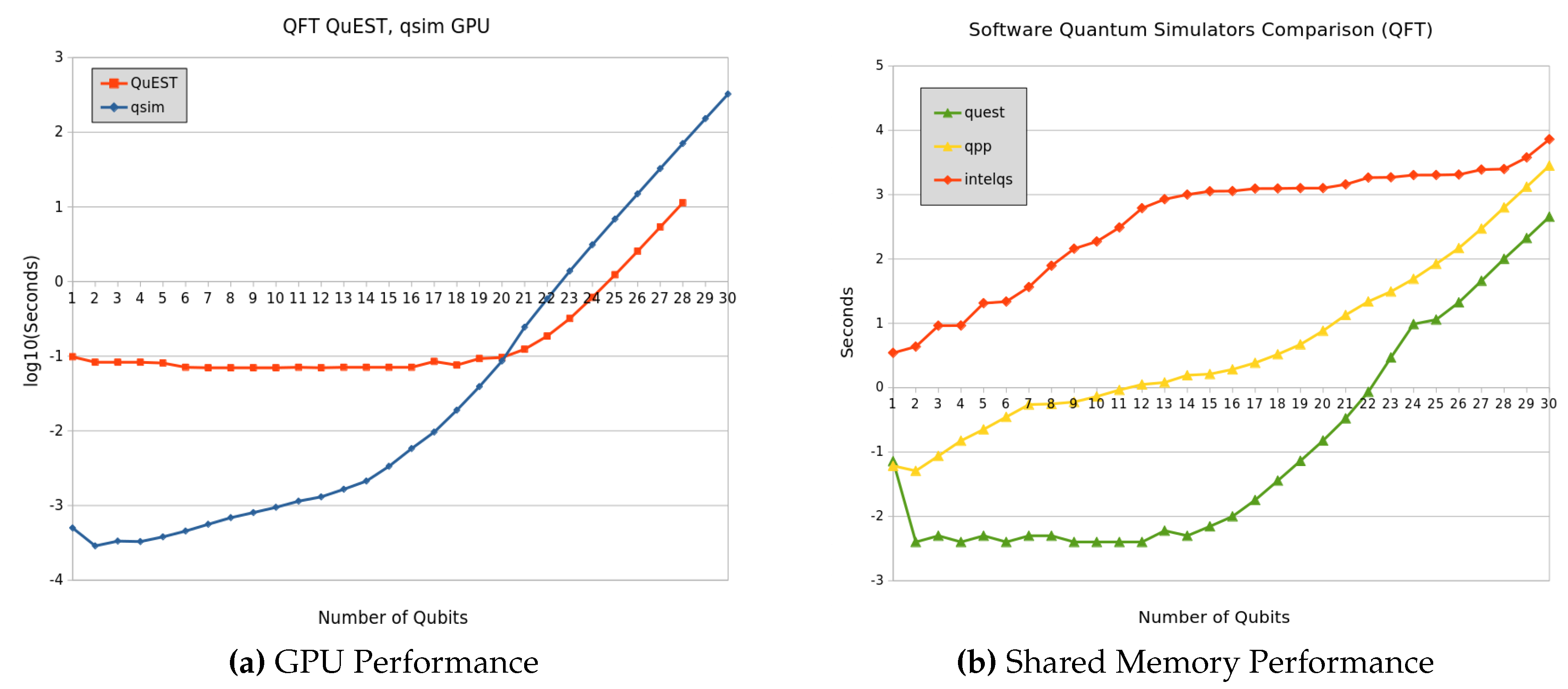
The following graphs are shown to compare some of these simulators under equal conditions. First, GPU capable simulators are depicted in
Figure 3a. Second, OpenMP capable simulators are shown in
Figure 3b.
4. Implementing a Simulator
To gain a deeper understanding of the fundamental operations of quantum computing and to test the various memory management approaches, a software quantum simulator prototype was developed in C++. (The Memory eFficient Quantum Simulator, TMFQS) [
15]. This prototype was designed in such a way that it allows us to change strategies easily through minimal modifications. It allows us to easily adjust the data structures to represent the fundamental concepts of quantum computing and the use of compression libraries.
It has to be pointed out that this prototype does not implement all the concepts of quantum computing, such as quantum error correction, entanglement, measurement and an extended set of quantum gates. This prototype’s primary purpose is to provide a minimal platform for understanding the principles of building a software quantum simulator. Several scenarios were implemented to carry out the tests.
Dynamic memory management. The primary purpose is to test the strategy of removing less probable states.
Full State: The objective is to accelerate the simulations, avoiding the overhead introduced by the search of the states.
Full State with OpenMP: The intention is to accelerate the simulations of the previous version.
Full State with data compression: The purpose is to test a lossy compression library like ZFP.
Full State with MPI: The main objective of this scenario is to distribute the amplitude vector among different computing nodes, allowing for a greater number of qubits.
Full State with MPI and data compression: Here, data compression was incorporated into the previous scenario.
4.1. Representation of Fundamental Concepts
As we saw in previous section, the basic simulation concepts include the following elements.
Quantum Register: comprised of states vector and amplitudes vector.
Quantum Gates: matrix representation of quantum gates. Only one-qubit and two-qubit gates were considered.
Applying quantum gates to a quantum register.
We have used an array of double-precision floating point numbers to store the amplitudes. No data structure has been used to represent the states, since the vector indices are used to refer to them. To implement the method to apply a quantum gate to a quantum register (
QuantumRegister::applyGate), we use the technique represented in Equation (
6) proposed by [
16]. In the
Figure 4, we can observe the main classes of the prototype.
4.2. Single Processor Case
4.2.1. State Vector
The state vector is a linear combination of states represented by the following expression.
Where are the amplitudes. As we said previously, these amplitudes are complex numbers, so we need two float or two double numbers to represent them in the code. Of course, the state vector must fit in the local memory.
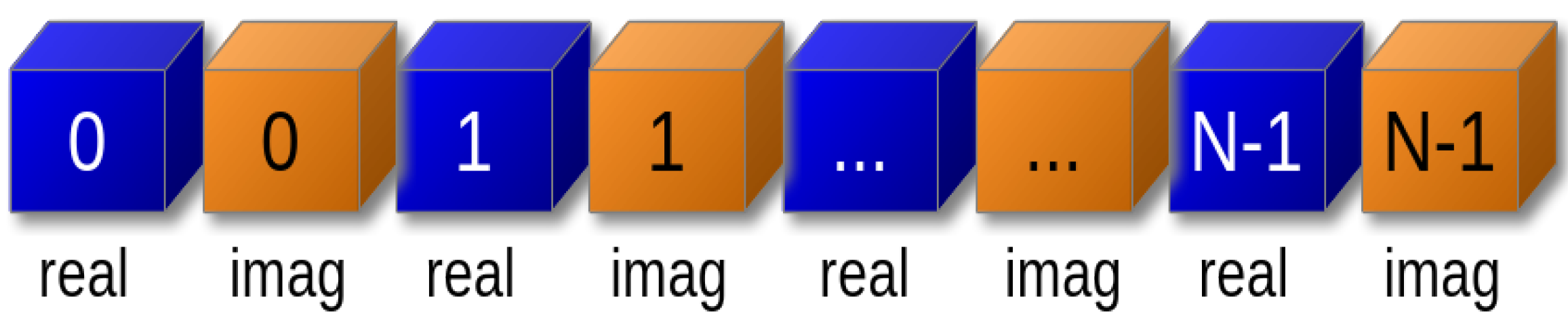
The amplitudes of the states are implemented using a single-dimension double-precision array stored in a continuous memory space. To increase performance, a single array was used to store both the real and the imaginary parts of each amplitude; that is, the state vector was linearized. The real parts are placed in the odd positions of this arrangement, and the imaginary parts are placed in the even positions. This strategy avoids jumping between two arrays, one for the real part and one for the imaginary part.
Figure 5 depicts this data structure.
4.2.2. Quantum Gates
Like other simulators such as Intel-QS, this prototype only implements single-qubit gates and controlled two-qubit gates. The minimum list of quantum gates developed to implement the Quantum Fourier Transform algorithm are: Identity, Hadamard, ControlledPhaseShift, ControlledNot, Swap. All these quantum gates are implemented as two-dimensional double-precision arrays. This reduced set of quantum gates limits the simulation of algorithms that require additional gates. However, adding new single-qubit and controlled two-qubit gates is very easy. Just insert the corresponding matrix into the quantumGate.cpp source file.
4.2.3. Applying a Quantum Gate to a Quantum Register
To apply a quantum gate
to the
qubit of a state vector
we have the following result.
4.2.3.1. Applying Single-Qubit Gates
The first traditional approach to face this problem is using sparse matrix management methods. However, [
16,
17] states that applying a single-qubit gate
To the k-th qubit of a quantum register of N qubits is equivalent to applying the gate to pairs of amplitudes whose indices differ by k-th bits from their binary index.
This implies that all state vector elements must be processed in pairs. Let’s see how to apply the Hadamard gate to the first qubit of the state 00. For the values:
,
,
,
,
and Hadamard gate.
Replacing these values in Equation (
6), we obtain the following results.
4.2.3.2. Applying Two-Qubits Gates
Similarly, to apply a controlled two-qubit quantum gate to a quantum register, using a control qubit
c on a target qubit
t, authors of [
17] state that the new amplitudes can be obtained by performing the following operations:
Let’s see how to apply the CPS gate to the second qubit of the state 11 controlled by the first qubit. All amplitudes are equal to 0 except
which is equal to 1. Replacing these values in the Equation (
9) we have:
Thus, we obtain the amplitude values for the states |10〉 and |11〉
4.2.3.3. Qubits Order
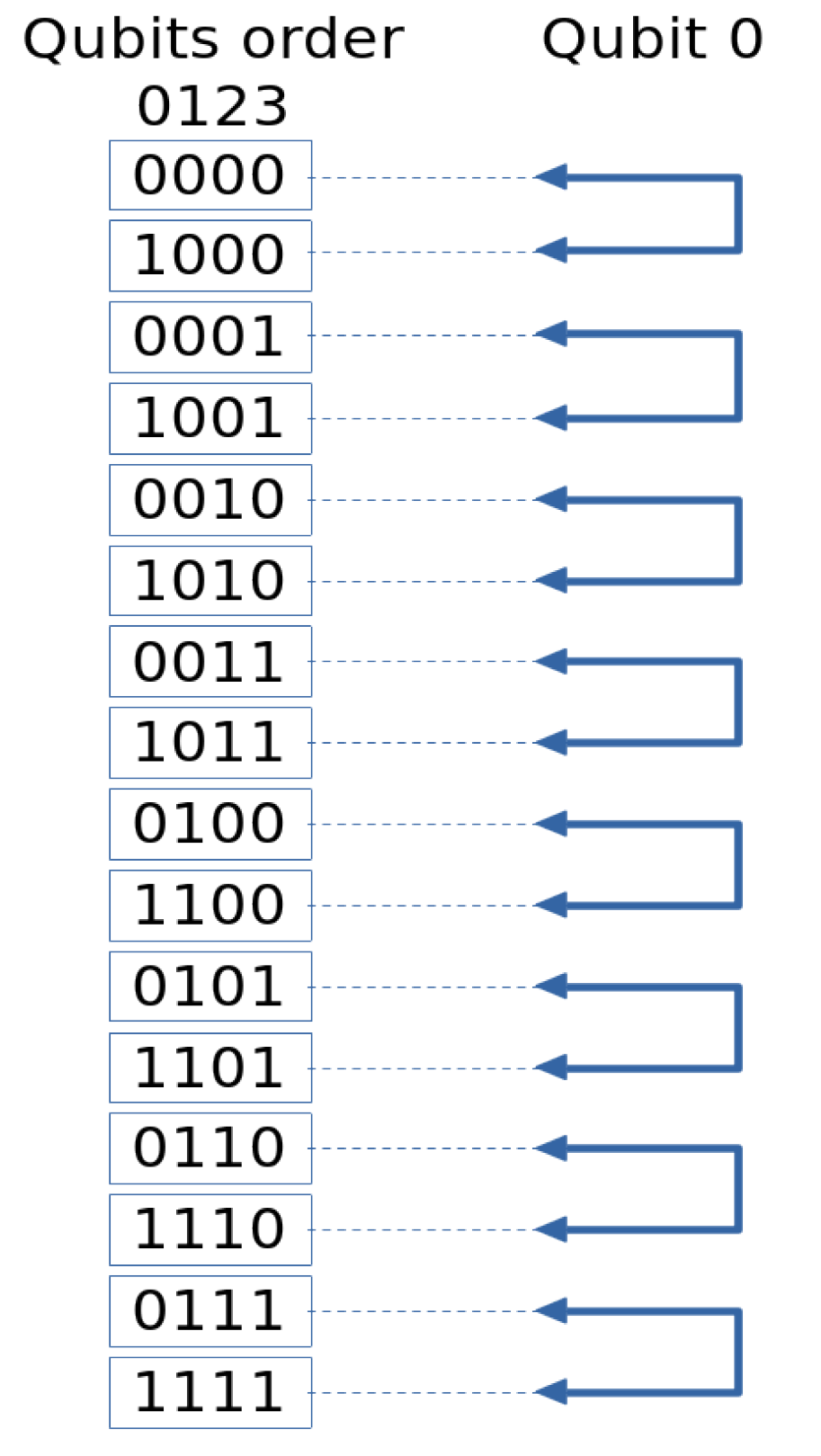
Some simulators, like qiskit, reverse the order of the qubits such that qubit 0 corresponds to the least significant bit of the binary representation of the state. In this case, the distance between and is equal to .
In this work, we maintain the natural order of the qubits. For example, in state 011, qubit 0 is the leftmost, qubit 1 is in the middle, and qubit 2 is the rightmost. Therefore, the distance between
and
is equal to
. To illustrate this,
Figure 6 shows the distance between the states of a 4-qubit state vector.
Generally, a single-qubit gate can be applied to a quantum register performing the following pseudo-code.
In summary, calculating the amplitudes for the current state and the new affected state is done as follows: Determine the value of the current state’s amplitude using Equation (
6). Then, find the pair corresponding to the current state, and finally, calculate the value of the latter using that same equation.
To find the pair corresponding to the current state, we can use two methods: the first calculates the distance using the relation
, as we explained before. The second method applies an XOR operation between the binary representation of the current state and a sequence of 0s with a 1 placed in the k-th position corresponding to the qubit we are working on. For example, applying a quantum gate on the 0th qubit on a for 4-qubits state 0101 we can find the corresponding pair using the following operation.
This result can be corroborated in
Figure 6. C++ offers binary operations to execute this operation efficiently and effortlessly.
4.2.4. State Prunning
In the version of the simulator where the least probable states are pruned, we use a dynamic memory management because the states are stored non-sequentially in memory. This arrangement results from their computation via Equation (
6). Consequently, a state search method was developed to facilitate access to a specific state for calculations in subsequent iterations. However, performance is negatively impacted because a lot of time has to be spent searching for a state’s values before they are used in a calculation.
Figure 7 depicts the order of a 3-qubits state vector after applying a single-qubit gate (Hadamard) on the qubit 0.
Because of this, the less probable states elimination approach was discarded early, therefore, we focus on pure states, which imply that the state vector contains the complete information about the quantum state; and this approach was adopted for the rest of this simulator’s design.
4.2.5. Shared Memory Case
In order to improve performance, parallelizing the code is necessary. The first method is to apply a shared memory programming model. This was done using OpenMP.
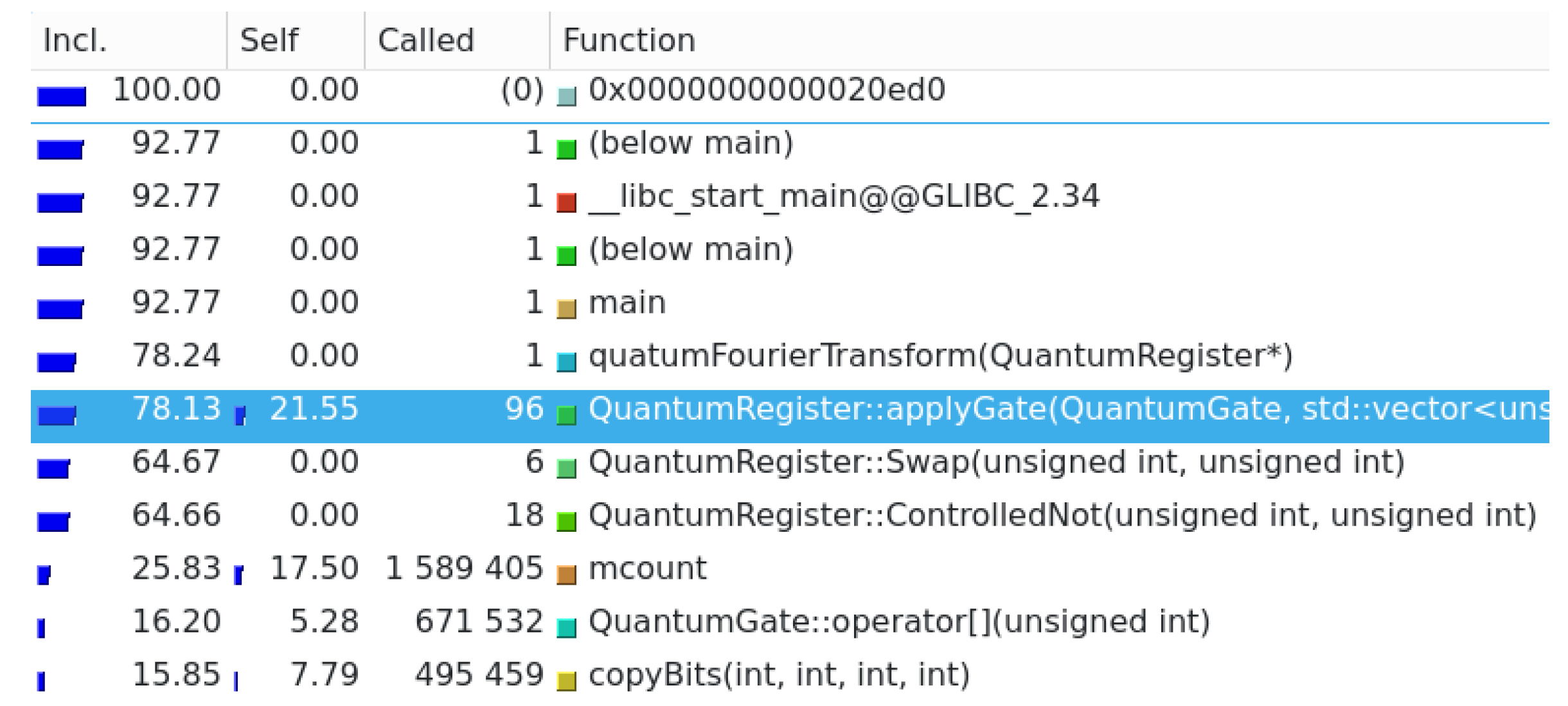
We use
valgrind to run program profiling and determine the sections of code that consume the most resources. Afterward, it was determined that the
QuantumRegister::applyGate method is the component of the simulator where we had to focus on increasing performance.
Figure 8 shows the profiling results.
The
QuantumRegister::applyGate method iterates through the state vector, implementing Equation (
6). To enhance performance, we partition the data and execute instructions on segments of the state vector, thereby speeding up the simulation. It is crucial to carefully manage the method’s internal variables to prevent race conditions.
4.3. Distributed Memory Case
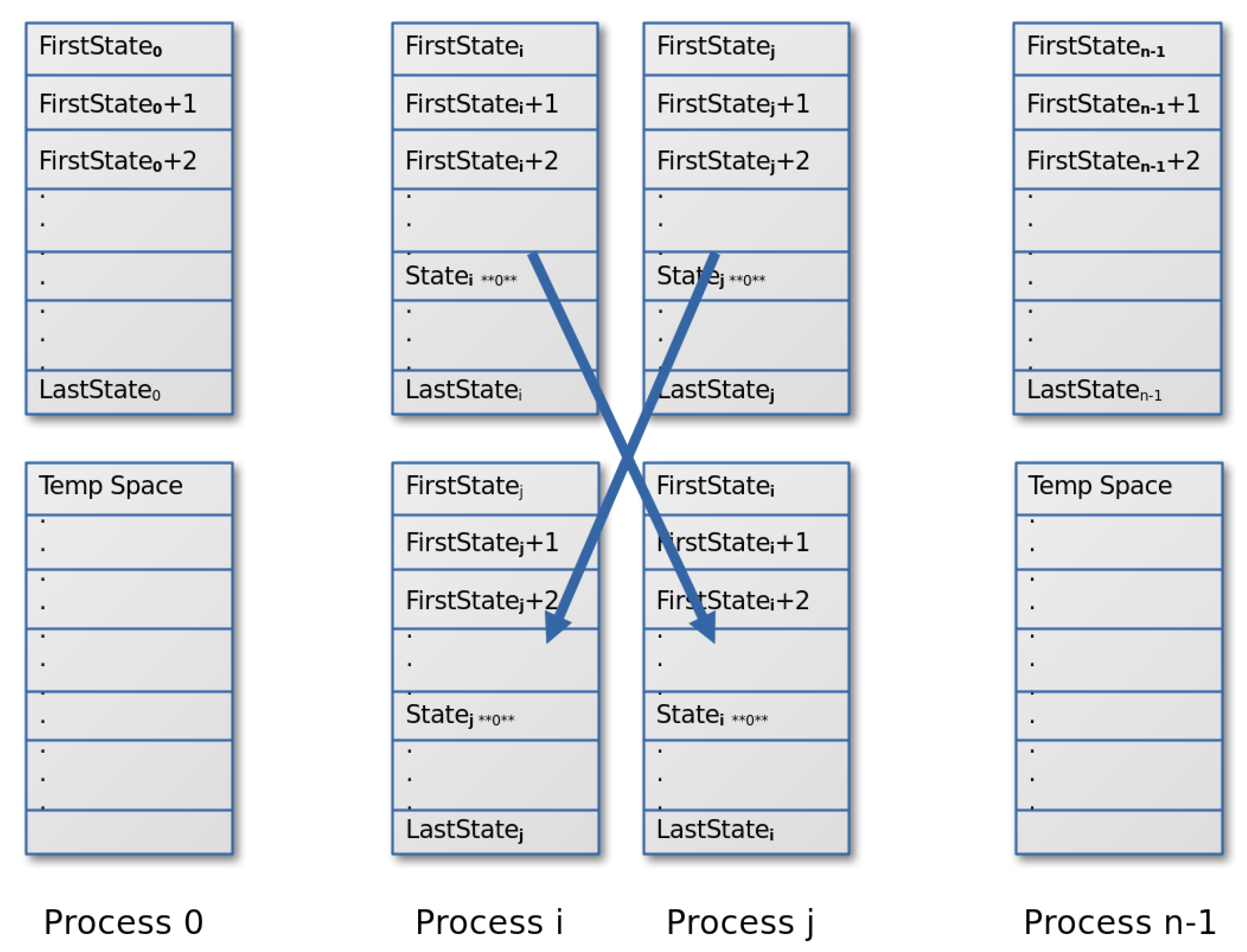
In the distributed memory model, the state vector needs to be divided among
processes. On the other hand, the Equation (
6), proposed in [
16], indicates that the calculation of the amplitudes of the states must be done in pairs, therefore, we must guarantee that the number of amplitudes per process is even. To achieve this, we use the relationship
Where is the number of states per process. In this case we can face two cases:
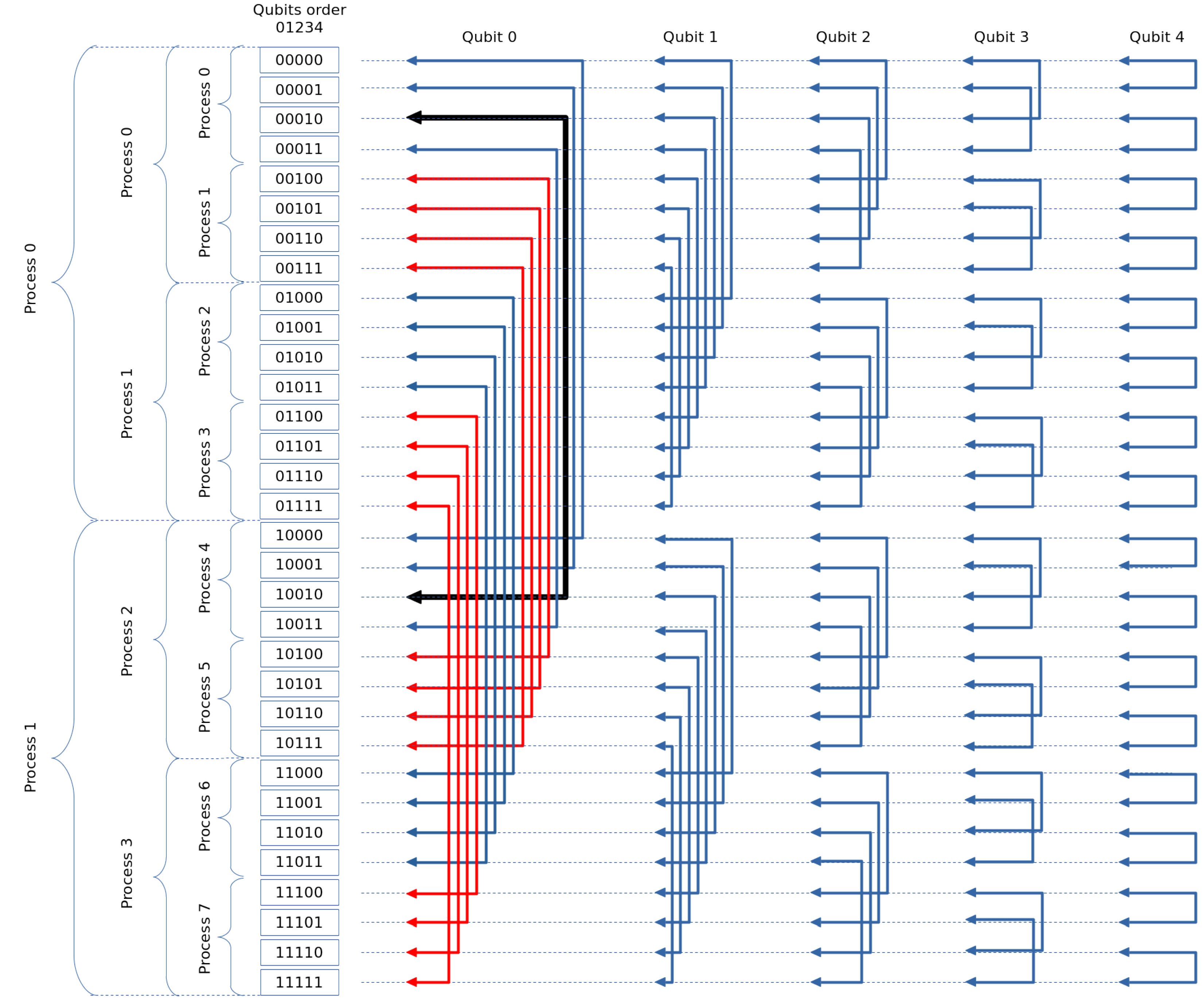
Figure 9 shows the pairwise calculation scheme for a 5-qubit state vector, applying each qubit. Partitioning with 2, 4, and 8 processes is also shown to visualize the communication process easily when we use the distributed programming model.
For instance, consider performing a calculation on qubit 0 of the state 00010; the corresponding pair would be 10010. If two processes are used, communication should be established with process 1. If four processes are utilized, the remote process is process 2. Lastly, if eight processes are employed, the remote process will be process 4.
We use the following expression to calculate the process’s identifier where the corresponding pair is located.
In
Figure 9, it is evident that for 2 processes, specifically regarding qubit 0, the number of communications required is
. This substantially degrades performance. To mitigate the overhead caused by the extensive number of communications, the entire segment of the state vector is exchanged between the peer processes involved, as outlined in Equation (
6). The calculations are then made locally, and the results are communicated back to the original process.
For this reason, we are unable to use the the total sum of local memory of each node to augment the number of qubits, and can only utilize half of the combined memory from all nodes.
Figure 10 depicts this idea.
4.3.1. Compressing The State Vector
To compress the amplitude vector, we use the ZFP library [
18] as it provides significant performance in accuracy and data size reduction. ZFP supports both lossy and lossless compression. For the development of this prototype, the lossy compression method was selected to achieve a higher level of data size reduction. To go from a vector of amplitudes using traditional data types to a compressed vector, change the corresponding line in the
types.h source file from
typedef std::vector<double> AmplitudesVector; to
typedef zfp::array1<double> AmplitudesVector; Of course, the corresponding header file from the ZFP library must be included.
Combining amplitude vector compression with amplitude vector distribution across multiple processes is an approach that can be effective both in terms of efficient memory usage and overall simulation performance. The version where a compressed vector is used to store the amplitudes was parallelized to achieve this. To obtain effective performance, the state vector portions are transmitted in a compressed manner. This makes communications faster because the message size is reduced.
To achieve compressed messaging, the compressed portions of the state vector must be serialized, and a custom MPI data type must be used in send and receive functions.
4.4. Simulator Verification
In order to validate the accuracy of our quantum simulator, we have excecuted different tests and compare the outputs with intel-qs and quantum++.
4.4.1. Quantum Gates Tests
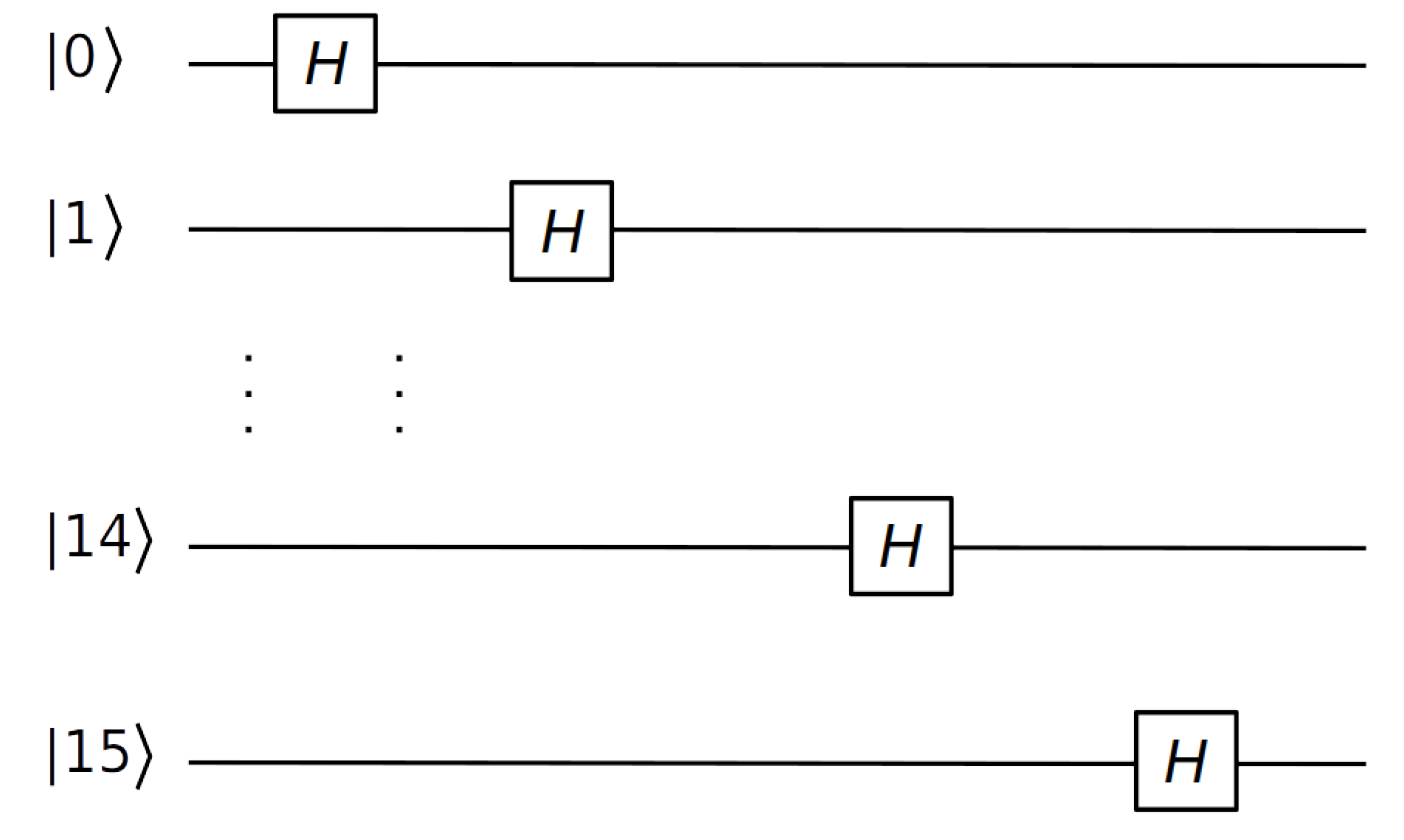
To test the superposition principle we apply Hadamard gate to a quantum register of 4-qubits. The following quantum circuit was used:
The test was executed by initializing the first state with a probability equal to one, that is to say, . Then, we repeat the experience with and so on until executing the test with the last state . The results of excecuting this quantum circuit with intel-qs, quantum++ and TMFQS were the same.
5. Results
This section presents the results of several quantum simulation tests performed using the prototype software quantum simulator developed in C++. By simulating fundamental quantum operations, we can assess how well these strategies reduce memory consumption and improve the efficiency of quantum computing simulations on classical hardware. Throughout the section, we compare the simulator’s performance with and without the proposed memory management techniques, highlighting the improvements achieved. By providing a comprehensive evaluation of these memory management strategies, this section aims to contribute to ongoing efforts to make quantum computing simulations more efficient and scalable, ultimately advancing the field of quantum computing.
5.1. Algorithm Selected for Testing
The quantum Fourier transform was selected to carry out the simulations because it offers the advantages listed below. It is a well-studied quantum algorithm with known properties, making it a reliable benchmark for validating the accuracy and efficiency of quantum simulators on classical hardware. QFT’s performance scales predictably with the number of qubits, allowing researchers to analyze how the simulator handles increasing complexity. Performing QFT simulations helps estimate the computational resources (memory, processing power) required for larger, more complex quantum algorithms. Finally, QFT is a crucial component in many quantum algorithms, such as Shor’s algorithm for factoring large integers. Simulating QFT provides a foundation for testing and understanding these more complex algorithms. These advantages make the Quantum Fourier Transform a valuable tool for advancing the field of quantum computing, even when simulations are executed on classical computers.
5.2. Test Platform
To run the simulations, we use two high-performance nodes from the scientific computing center of the Universidad Industrial de Santander (SC3-UIS) with the following characteristics: Two AMD EPYC 9554 64-Core Processors and 384GiB of RAM.
5.2.1. States Pruning
We can free up memory that is not needed by eliminating the quantum states that have the smallest chance of occurring, that is, eliminating those states whose amplitude is close to zero. However, in addition to all the points against this approach like: loss of fidelity, impact on algorithm accuracy, error accumulation, threshold sensitivity and impact on quantum entanglement, this requires dynamic memory management, which introduces a lot of extra work because before applying a quantum gate to a state, we need to search for it in the array due the states are not ordered. That is to say, to apply every quantum gate, we need to execute search operations. This approach was tested using the Quantum Fourier Transform algorithm. The quantum register contains all the states at the end of executing the Quantum Fourier transform algorithm. Due to the initial superposition process, the quantum register also has all the states in the first stage of Grover’s algorithm. Therefore, this approach does not work well for these algorithms.
For these reasons, along with the risks outlined previously, we have decided to discard this approach because its numerous disadvantages outweigh its benefits.
5.2.2. Full-State Quantum Register
A quantum register with all the states arranged in a sequence can reduce the overhead of searching for quantum states. This also eliminates the need for an extra data structure to store the states and uses the indices of the amplitude vector to handle the quantum states. The total amount needed using this strategy Bytes for double precision floating point numbers. However, we save bytes, avoiding the state vector array.
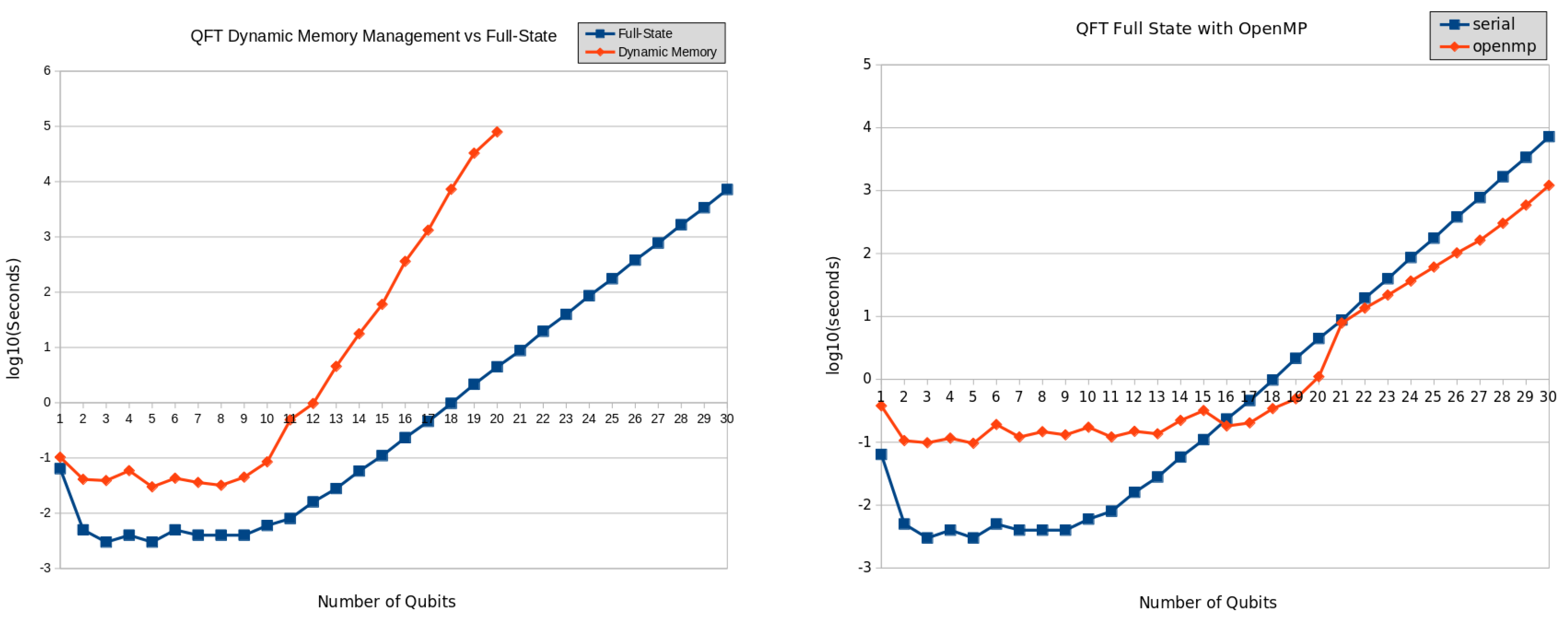
The graph of
Figure 12a shows the performance of QFT applying state pruning (dynamic memory) vs full-state strategies. Simulations using dynamic memory involving more than 20 qubits were discarded due to their execution time exceeding one day.
Exponential growth is observed from an 18-qubit state vector in dynamic memory approach. This is a consequence of a substantial increase in the memory needed to represent the state in question and, therefore, the processing time required. As can be seen by comparing these strategies, the workload overhead using dynamic memory is significant. We have parallelized the full-state version to increase performance using the shared memory model with OpenMP. In the graph of the
Figure 12b we can see the results.
We observe a significant decrease in the processing time between the serial and parallel execution of the full-state version as the number of qubits increases. That is, a considerable acceleration is obtained by parallelizing the simulation. However, for clearer interpretation of the results, we show the results calculating the base 10 logarithm of the simulation time. In the graph shown in
Figure 12b, it is evident that for smaller numbers of qubits, there is an overhead caused by the setup of the parallel environment.
5.2.3. Data Compression
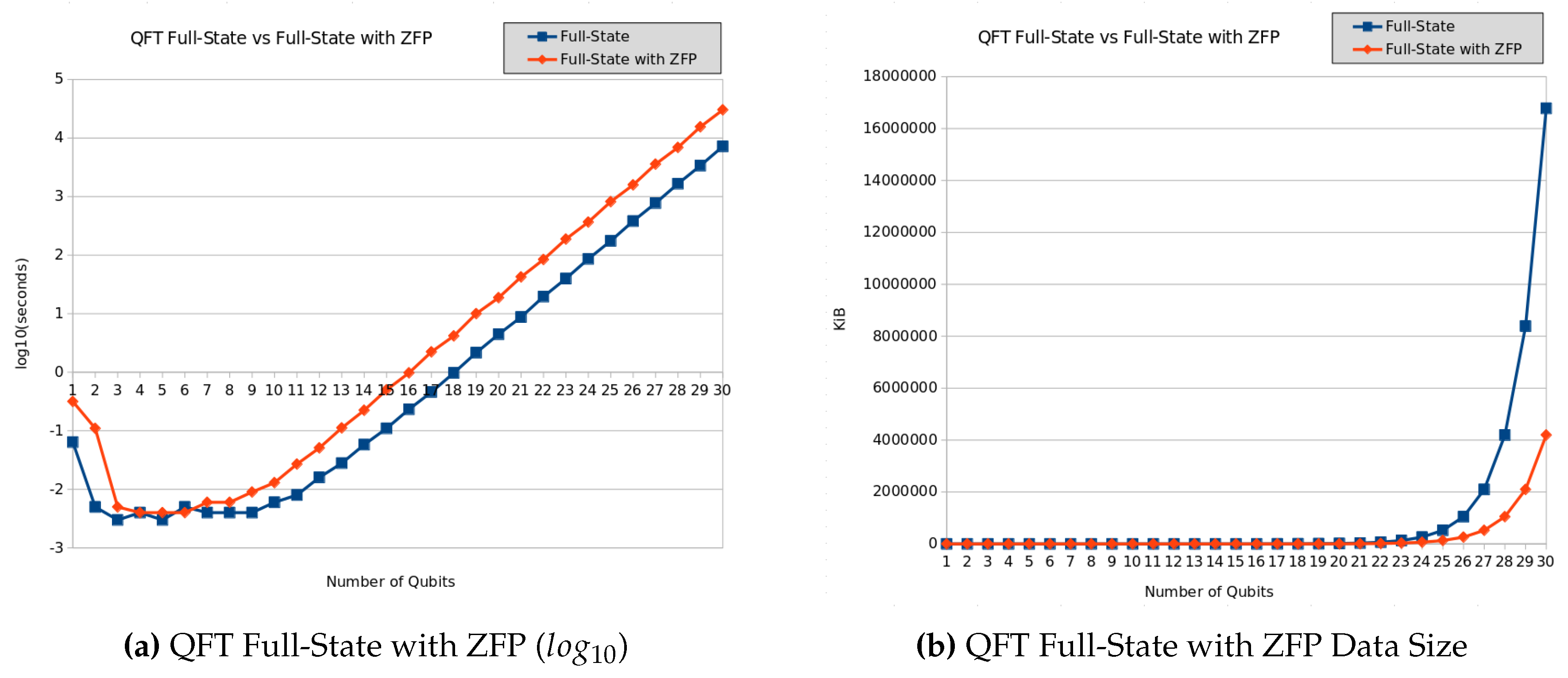
We have selected one of the most widely used C++ libraries for data compression, ZFP, to test this approach. We modified the full-state version of the simulator to compress the amplitude vector. The graph of
Figure 13a shows the performance comparison between full-state vs full-state using ZFP.
We can observe that the overhead introduced by the compression and decompression procedure is significant.
The graph of
Figure 13b shows the amount of memory used by both simulator versions. We can observe that the compression approach is highly efficient. This enables the possibility of increasing the number of qubits in simulations.
5.2.4. Distribute the Quantum Register across Multiple Nodes
We have developed a simulation version employing MPI to increase memory capacity by leveraging the RAM of additional computer nodes. To uphold computational efficiency, it is essential to underscore the necessity of maintaining an optimal ratio between the number of processes and the allocation of qubits per process. The graph shown in
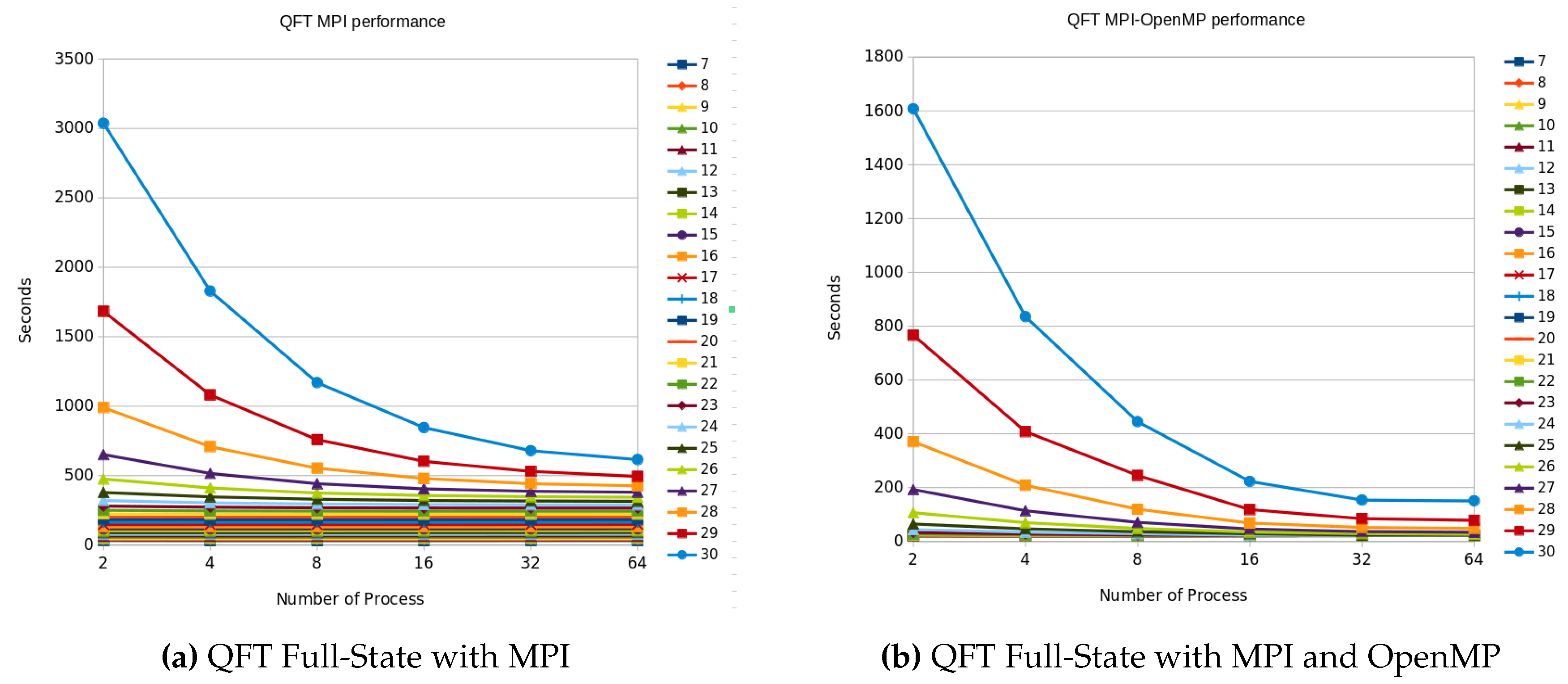
Figure 14a demonstrates the performance of the Quantum Fourier Transform across a range of qubit counts from 7 to 30, using 2, 4, 8, 16, 32, and 64 processes. The reason for starting at seven qubits is to preserve the relation mentioned previously. In addition to achieving better performance, we can see that by increasing the number of processes, we can increase the number of qubits and reduce the size of messages required to exchange partial results between processes. We can see also that parallelism is helpful for a number greater than 26 qubits.
5.2.5. Combination of Distributed Memory and Shared Memory Approaches
We have developed a simulator version that combines MPI with OpenMP to achieve better performance. The graph in
Figure 14b illustrates the performance of Quantum Fourier Transform using this hybrid approach.
Comparing the results of the graphs in
Figure 14a,b, we see that the combination of MPI and OpenMP increases the performance, especially for cases where the size of the state vector portion at each node is large.
5.2.6. Combination of Distributed Memory and Data Compression Approaches
Taking advantage of distributed resources to have more memory available, combined with data compression, makes it possible to perform simulations with a larger number of qubits. We have already seen that there is a processing overhead introduced by the compression process, however, the transmission of compressed data contributes positively to overall performance. We have modified the prototype to test this approach.
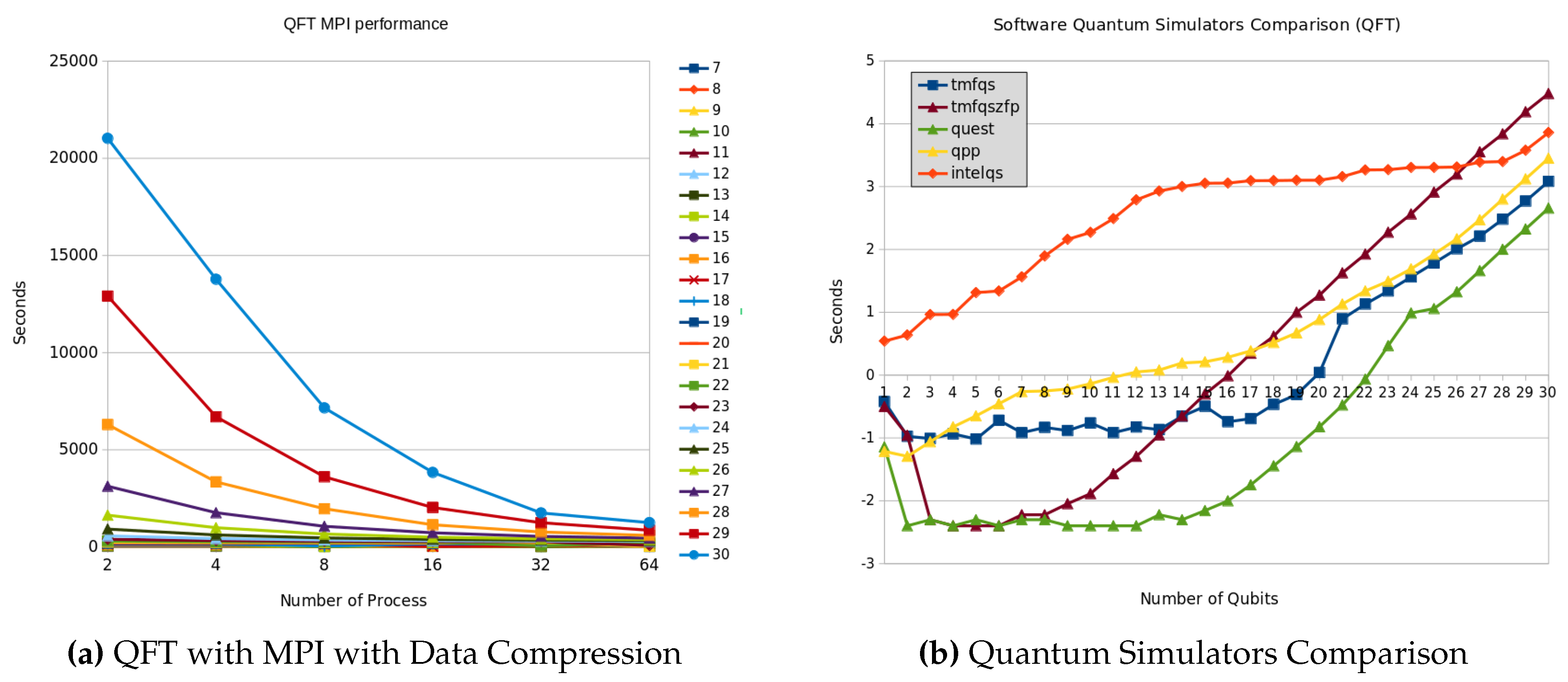
Figure 15a shows the execution for a range of 7 to 30 qubits with a variation in the number of processes equal to 2, 4, 8, 16, 32, 64. It shows the performance of the distributed memory approach with data compression.
In this graph, we can see that performance has decreased; however, the reduction of the required memory is significant because the same strategy used in the section on data compression is adopted here. It has to be pointed out that this strategy is valid only if portions of the quantum register are transmitted in a compressed form.
5.2.7. Quantum Simulators Comparison
To validate the results obtained with our prototype, a comparison is made with other simulators. First, specific conditions must be established to allow a fair comparison of the simulators studied. The common conditions were using a single computing node with a shared memory model. Simulators that use GPUs are excluded because their performance is much higher than the others, but their scaling is limited. The case of using distributed memory is also excluded because only some include this capability. The graph in
Figure 15b shows the performance of the quantum Fourier transform for intel-qs, quantum++, QuEST, and TMFQS. The selected simulators use the C++ complex numbers data type for memory management. They use a full-state vector scheme, which allows better performance but does not reduce memory consumption.
As can be seen in the graph in
Figure 15b, the Intel-QS simulator performs lower than the other simulators. QuEST exhibited the best performance. Our prototype TMFQS performs acceptably compared to these mature tools that have been optimized, for example, by using libraries such as MKL in the case of Intel-QS.
In conclusion, building a software quantum simulator requires a delicate balance between theoretical understanding and practical implementation strategies. The limitations of current quantum hardware, including qubit count and quality, drive the need for quantum simulators that allow researchers to explore quantum algorithms on classical computers. This work has shown that memory management techniques, such as dynamic pruning, full-state representation, and data compression, are essential for optimizing the simulation of quantum systems. While pruning techniques introduce certain challenges, such as fidelity loss and increased computational complexity, full-state representation with parallelization (via OpenMP or MPI) provides a robust framework for simulating larger quantum states. The use of data compression, such as ZFP, further extends the capacity to simulate a greater number of qubits without exceeding memory limits, though it introduces some overhead in processing time.
The comparative performance of the prototype simulator against established simulators like Intel-QS, QuEST, and qsim demonstrates the viability of these memory management techniques. By combining distributed and shared memory models, along with data compression, the simulator can handle increasingly complex simulations. Ultimately, this work contributes valuable insights into making quantum computing simulations more scalable and efficient, supporting the broader field of quantum computing as it continues to evolve.
References
- Report, Q.C. Qbit Count. https://quantumcomputingreport.com/scorecards/qubit-count/, 2019.
- Quantiki. List of QC simulators. https://www.quantiki.org/wiki/list-qc-simulators, 2019.
- Fingerhuth, M. Open-Source Quantum Software Projects. https://github.com/qosf/os_quantum_software, 2019.
- Team, Q.O.S.F. Quantum Open Source Foundation. https://qosf.org/, 2019.
- Bergou, J.A.; Hillery, M. Introduction to the Theory of Quantum Information Processing; Springer Publishing Company, Incorporated, 2013.
- Artur Ekert, P.H.; Inamori, H. Basic concepts in quantum computation. Coherent atomic matter waves 2001, pp. 661–701.
- Shoshany, B. In layman’s term, what is a quantum state? https://www.quora.com/In-laymans-term-what-is-a-quantum-state, 2018.
- Williams, C.P. Explorations in Quantum Computing, Second Edition; Texts in Computer Science, Springer, 2011. doi:10.1007/978-1-84628-887-6. [CrossRef]
- Eleanor, R.; Wolfgang, P. Quantum Computing, A Gentle Introduction; The MIT Press, 2011.
- Guerreschi, G.G.; Hogaboam, J.; Baruffa, F.; Sawaya, N. Intel Quantum Simulator: A cloud-ready high-performance simulator of quantum circuits, 2020, [arXiv:quant-ph/2001.10554].
- Gheorghiu, V. Quantum++: A modern C++ quantum computing library 2014. [arXiv:1412.4704]. doi:10.1371/journal.pone.0208073. [CrossRef]
- team, Q.A.; collaborators. qsim, 2020. doi:10.5281/zenodo.4023103. [CrossRef]
- Jones, T.; Brown, A.; Bush, I.; Benjamin, S.C. QuEST and High Performance Simulation of Quantum Computers. Scientific Reports 2019, 9, 10736. doi:10.1038/s41598-019-47174-9. [CrossRef]
- Strano, D. Qrack. https://vm6502q.readthedocs.io/en/latest/, 2019.
- Díaz, G. Prototype Quantum Computing Simulator. https://github.com/diaztoro/TMFQSfullstate.git, 2024.
- Trieu, D.B. Large-Scale Simulations of Error-Prone Quantum Computation Devices. Dr. (univ.), Universität Wuppertal, Jülich, 2009. Record converted from VDB: 12.11.2012; Universität Wuppertal, Diss., 2009.
- Smelyanskiy, M.; Sawaya, N.P.D.; Aspuru-Guzik, A. qHiPSTER: The Quantum High Performance Software Testing Environment. CoRR 2016, abs/1601.07195. [CrossRef]
- Lindstrom, P. Fixed-Rate Compressed Floating-Point Arrays. IEEE Transactions on Visualization and Computer Graphics 2014, 20, 2674–2683. doi:10.1109/TVCG.2014.2346458. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).