Ramsey Approach to Vector Fields

Preprint

Article

Ramsey Approach to Vector Fields

Altmetrics

Downloads

Views

Comments

Edward Bormashenko^*

This version is not peer-reviewed

Submitted:

18 September 2024

Posted:

19 September 2024

You are already at the latest version

Alerts

Abstract

Ramsey approach to the vectors fields is introduced. Set of vectors defined on R^3, taken as the generators of the bi-colored complete graph, is introduced. Vectors are considered as the vertices of the graph. Following coloring procedure is suggested: vertices numbered i and j are linked with the red edge if their scalar product is non-negative; and they are linked with the green edge if their scalar product is negative. This procedure gives rise to the complete, bi-color graph. Graph generated by six vectors inevitably contains the monochromatic triangle: the Ramsey number Ring-like systems of generating vectors are addressed. Applications of the graphs emerging from the vector fields are discussed.

Keywords:

Subject: Computer Science and Mathematics - Discrete Mathematics and Combinatorics

1. Introduction

In this paper we consider Ramsey graphs emerging from vector fields. In its general meaning Ramsey theory refers to any mathematical problem which states that a structure of a given kind is guaranteed to contain a well-defined substructure. The classical problem in Ramsey theory is the so-called “party problem”, which asks the minimum number of guests denoted R(m,n) that must be invited so that at least m will know each other, or at least n will not know each other (i.e., there exists an independent set of order n [1,2,3,4,5]). When Ramsey theory is re-shaped in the notions of the graph theory, it states that any structure will necessarily contain an interconnected substructure [4,5,6,7]. The Ramsey theorem, in its graph-theoretic forms, states that one will find monochromatic cliques in any edge color labelling of a sufficiently large complete graph [4,5,6,7]. In our paper we address the Ramsey graphs emerging from vector fields.

2. Ramsey Graphs Generated by Vector Fields

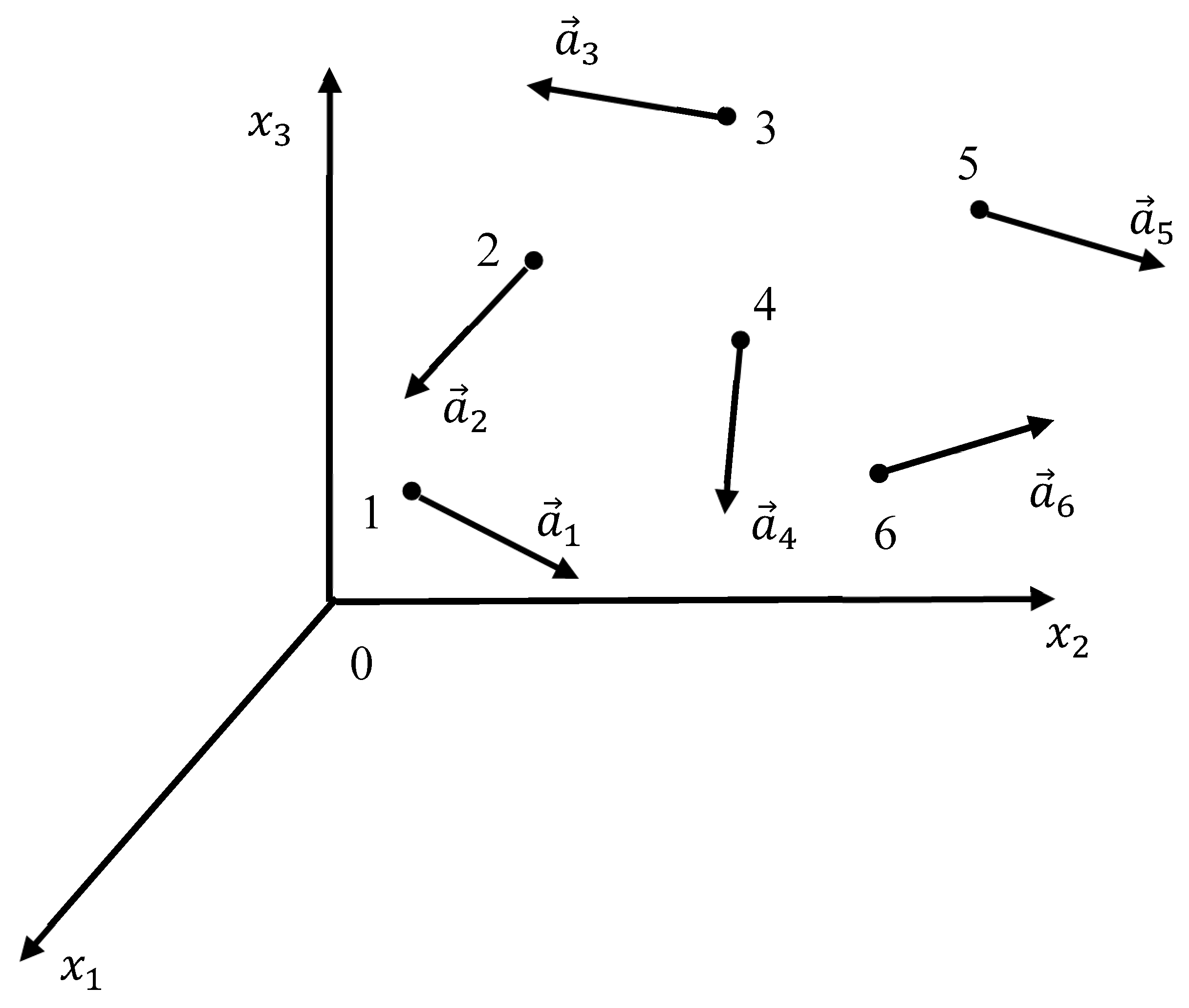
Consider vector field defined on

R^{3}

. Consider sets of six points

{(X}_{k i}, X_{l i}, X_{m i}; k, l, m = 1 . . 3; i = 1 \dots 6)

and six vectors related to these points

{\vec{a}}_{i}, i = (1 \dots 6)

depicted in Figure 1. Uppercase letters denote the coordinates of the points in

R^{3} .

Origin of the vectors

{\vec{a}}_{i}, i = (1 \dots 6)

is related to the points

{(X}_{k i}, X_{l i}, X_{m i}; k, l, m = 1 . . 3; i = 1 \dots 6

) (actually, the vectors are seen as sliding ones, and the location of their origin is not important);

{\vec{a}}_{i} = (x_{1 i}, x_{2 i,} x_{3 i}, i = 1 \dots 6)

; lowercase letters denote the coordinates of the vectors (again, seen as sliding vectors). We define the set

{\vec{a}}_{i}, i = (1 \dots 6)

as the set of vectors generating the complete bi-colored graph. Vectors

{\vec{a}}_{i}, i = (1 \dots 6)

we denote as the “generators” of the Ramsey graph. The graph is built according to the following procedure. Points

{(X}_{k i}, X_{l i}, X_{m i}; k, l, m = 1 . . 3; i = 1 \dots 6)

serve as the vertices of the graph.

Vertices numbered i and j are connected with the red link, when Eq. 1 takes place:

{(\vec{a}}_{i} \cdot {\vec{a}}_{j}) = x_{1 i} x_{1 j} + x_{2 i} x_{2 j} + x_{3 i} x_{3 j} = e_{i j} \geq 0

(1)

And, correspondingly, the vertices numbered i and j are connected with the green link, when Eq. 2 occurs:

{(\vec{a}}_{i} \cdot {\vec{a}}_{j}) = e_{i j} < 0

(2)

It is easily seen, that the exact location of the vectors/generators is not important, when the coloring procedure defined by Eqs. 1-2 is adopted. Vectors/generators

{\vec{a}}_{i} = (x_{1 i}, x_{2 i,} x_{3 i}, i = 1 \dots 6)

themselves may be considered as the vertices of the graph. Vectors are “acquainted” each with another and they are connected with the red link, when Eq. 1 takes place, and vectors are “not acquainted” each with another, and they are connected with the green link, when Eq. 2 is true. The aforementioned procedure gives rise to the complete, bi-colored, Ramsey graph. Consider that the scalar product of vectors is independent of the system of coordinates; thus, the suggested coloring procedure defined by Eqs. 1-2 is invariant relatively to rotation of frames.

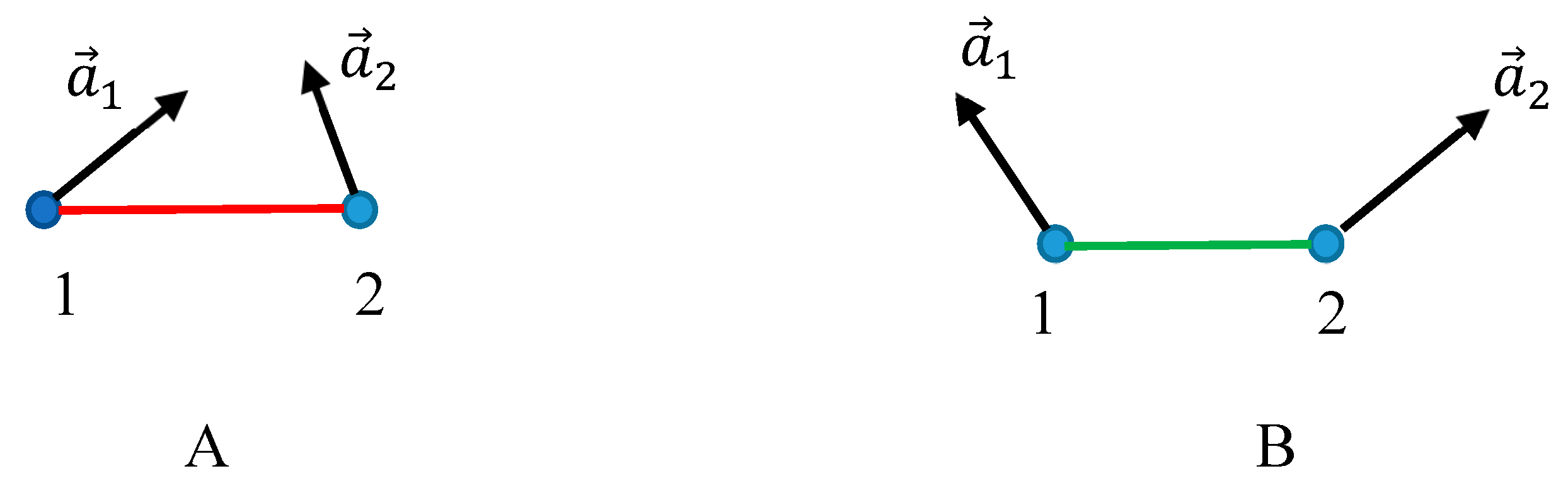
Let us illustrate the introduced procedure with Figure 2, demonstrating two vectors

{\vec{a}}_{1}

and

{\vec{a}}_{2}

, belonging to the same plane. Sketch A depicts the situation, where points “1” and “2” are connected with the red link, i.e.,

{(\vec{a}}_{i} \cdot {\vec{a}}_{j}) = e_{i j} \geq 0

takes place; whereas, sketch B depicts the situation, where points “1” and “2” are connected with the green link, i.e.,

{(\vec{a}}_{i} \cdot {\vec{a}}_{j}) = e_{i j} < 0

takes place

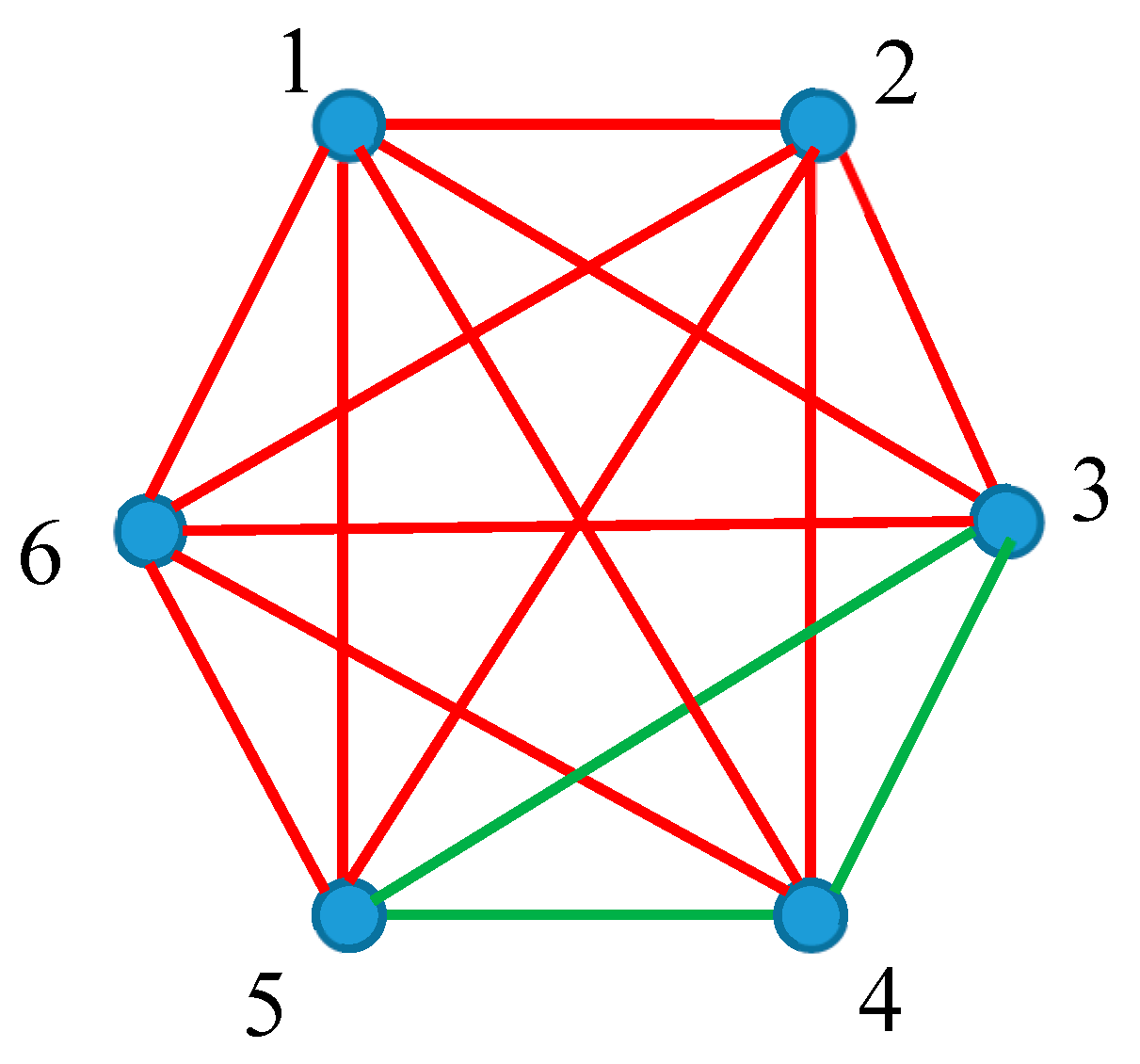
The aforementioned mathematical procedure gives rise to the bi-colored, complete, Ramsey graph, such as that depicted in Figure 3, supplied as an example.

According to the Ramsey theorem, this graph should necessarily contain at least one monochromatic (mono-colored triangle); due to the:

R (3,3) = 6

. Indeed, we recognize in Figure 3 the green subgraph, labeled “345”; whereas, the triangles “123”, “124”,”125”, “126”, ”136”, “146”, ”156”, “236”, “246” and “256” are monochromatic red ones.

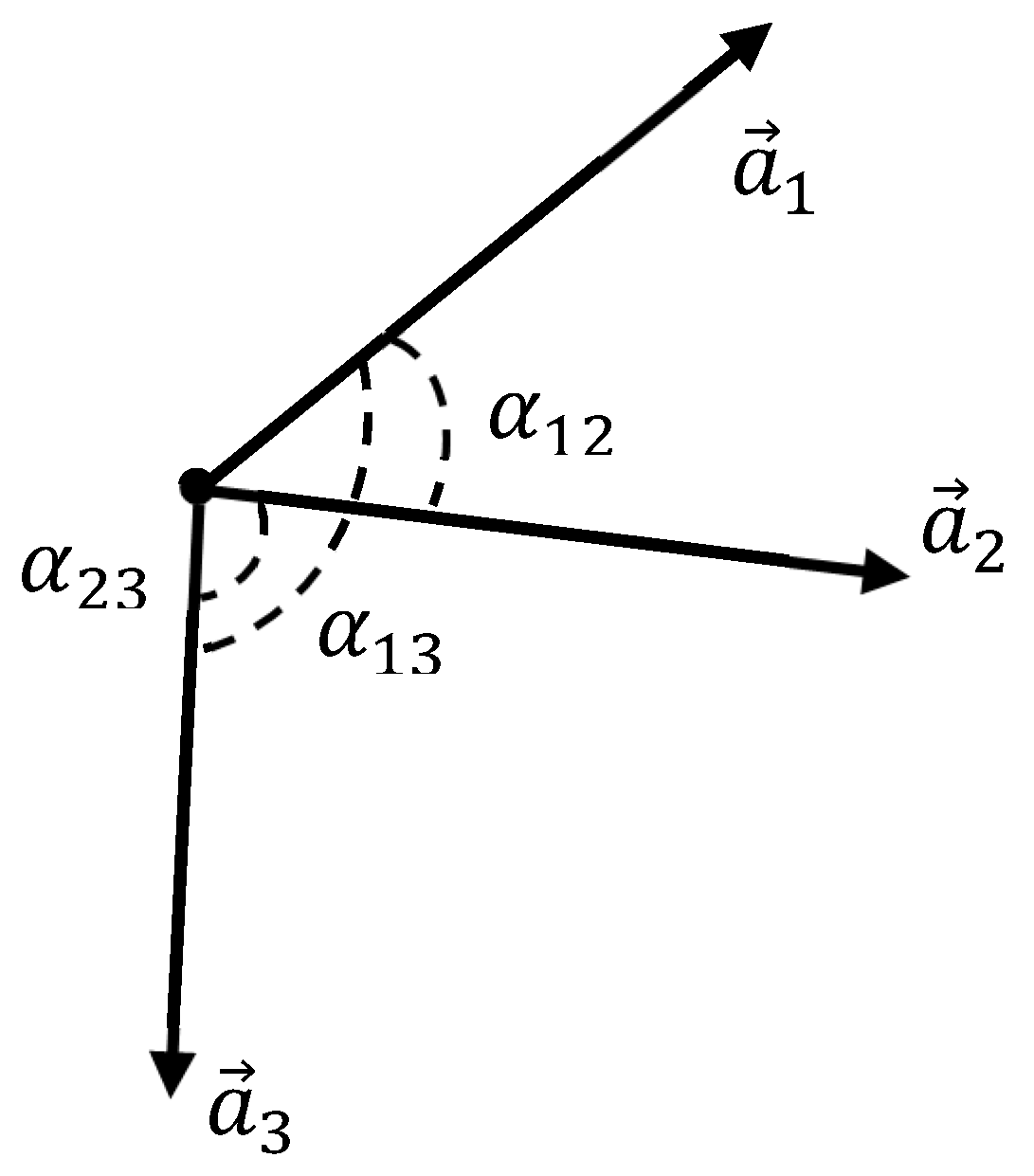
It should be emphasized that the introduced procedures of coloring, defined by Eqs. 1-2 are not transitive. In other words, if:

{(\vec{a}}_{i} \cdot {\vec{a}}_{j}) \geq 0

and

{(\vec{a}}_{j} \cdot {\vec{a}}_{k}) \geq 0

is assumed, it is not necessarily that:

{(\vec{a}}_{i} \cdot {\vec{a}}_{k}) \geq 0

. Let us illustrate this. Consider the planar system of vectors

{\vec{a}}_{1}, {\vec{a}}_{2}, {\vec{a}}_{3}

, depicted in Figure 4. Angles

α_{12}, α_{23} a n d α_{13}

are shown in Figure 4. We adopt

α_{12} < \frac{π}{2}, α_{23} < \frac{π}{2}

, however

α_{12} + α_{23} = α_{13} > \frac{π}{2}

. Thus,

{(\vec{a}}_{1} \cdot {\vec{a}}_{2}) > 0

and

{(\vec{a}}_{2} \cdot {\vec{a}}_{3}) > 0

takes place. However,

{(\vec{a}}_{1} \cdot {\vec{a}}_{3}) < 0

is true (see Figure 4). Thus, the introduced procedure of coloring of the graph edges is not transitive. The green-colored relation between the vectors/generators is also non-transitive; namely, if:

{(\vec{a}}_{i} \cdot {\vec{a}}_{j}) < 0

and

{(\vec{a}}_{j} \cdot {\vec{a}}_{k}) < 0

is assumed, it is not necessarily that:

{(\vec{a}}_{i} \cdot {\vec{a}}_{k}) < 0 .

This is important, due to the fact that the transitive Ramsey numbers are different from the non-transitive ones [8,9].

It is also should be stressed, that only directions of the generating vectors are important; the generating vectors may be considered as the unit ones. We finally come to following theorem.

Theorem: Consider set of the six vectors

{\vec{a}}_{i} = (x_{1 i}, x_{2 i,} x_{3 i}, i = 1 \dots 6)

defined on

R^{3} .

Vectors are taken as the vertices of the graph. Vertices are connected with the red link, if:

{(\vec{a}}_{i} \cdot {\vec{a}}_{j}) = x_{1 i} x_{1 j} + x_{2 i} x_{2 j} + x_{3 i} x_{3 j} \geq 0

takes place, and they are connected with the green link if:

{(\vec{a}}_{i} \cdot {\vec{a}}_{j}) < 0 .

The graph contains at least one monochromatic triangle.

3. Ramsey Graph Generated by the Ring-Like Systems of Generating Vectors

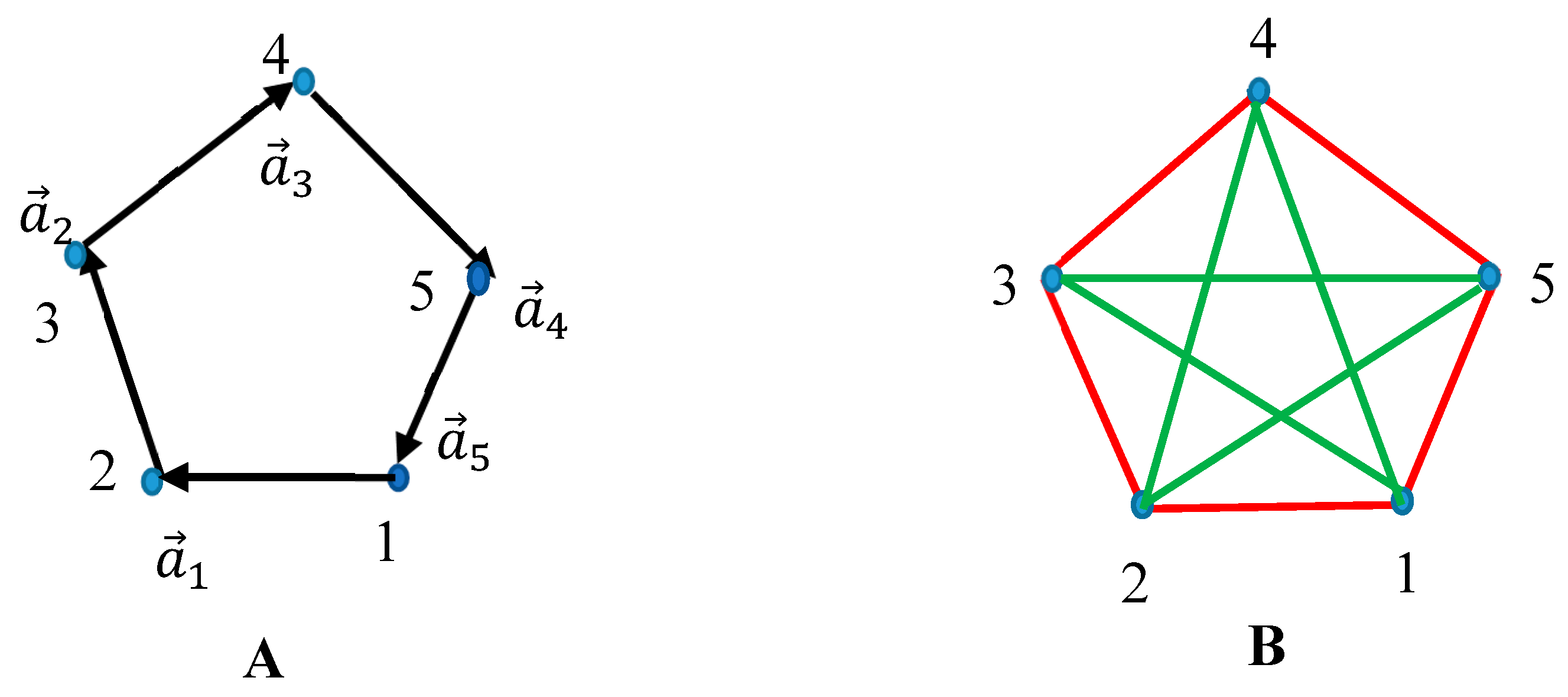
It will be instructive to demonstrate the introduced procedure of formation of bi-colored graphs with the ring-like system of generating vectors depicted in Figure 5A. Five generating vectors

{\vec{a}}_{i}, i = 1 \dots 5

form pentagon. In this specific case, Eq. 5 is true:

\sum_{i = 1}^{5} {\vec{a}}_{i} = 0

(5)

The bi-colored graph generated by the vectors

{\vec{a}}_{i}, i = 1 \dots 5

according to Eqs. 1-2 is shown in Figure 5B. The coloring of the graph follows Eqs. 1-2. Five generating vectors

{\vec{a}}_{i}, i = 1 \dots 5

serve as the vertices of the Ramsey graph.

Complete bi-colored graph shown in Figure 5B does not contain any mono-colored triangle. Indeed, the Ramsey number

R (3,3) = 6 .

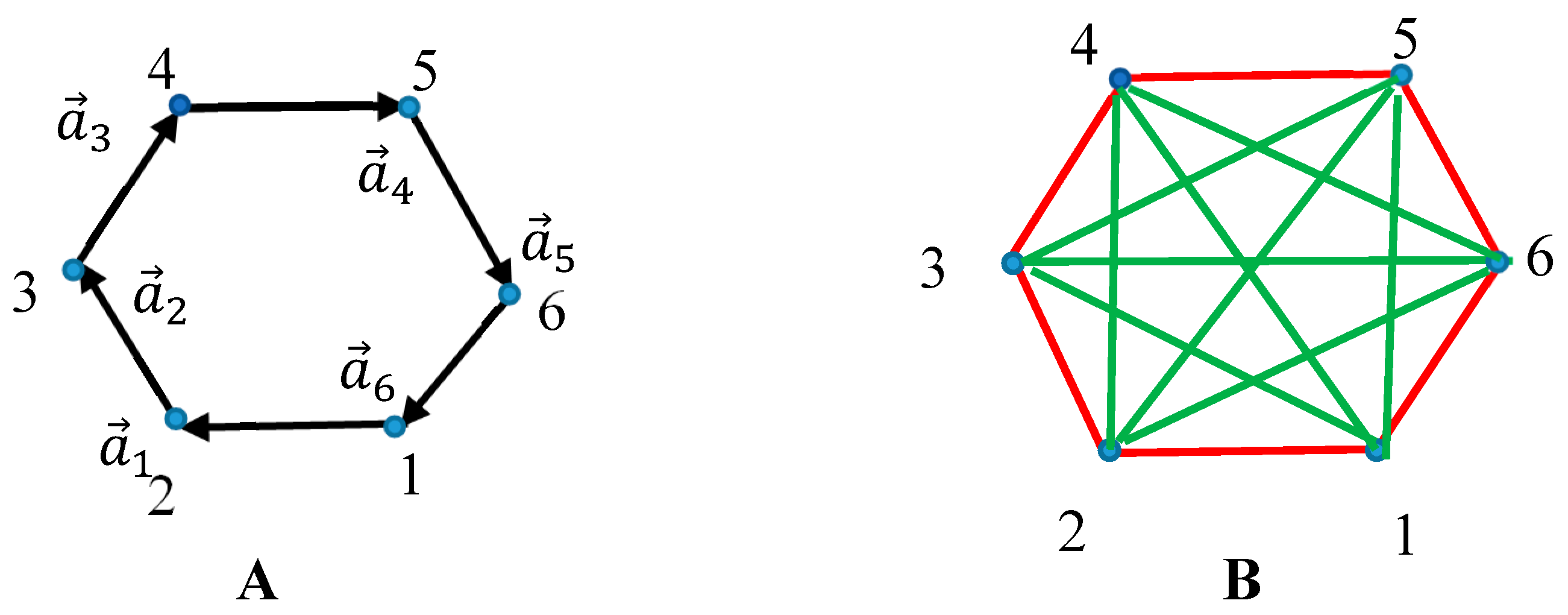
Now, consider the complete bi-colored graph generated by the ring-like system of six vectors

{\vec{a}}_{i}, i = 1 \dots 6

forming hexagon, shown in Figure 6A. The bi-colored, complete Ramsey graph generated by the vectors

{\vec{a}}_{i}, i = 1 \dots 6

according to Eqs. 1-2, is shown in Figure 6B. Again,

\sum_{i = 1}^{6} {\vec{a}}_{i} = 0

is true.

According to the Ramsey Theorem

R (3,3) = 6;

this guarantees presence of at least one mono-colored triangle in the graph, presented in Figure 6B. Indeed, triangles “135” and “246” appearing in Figure 6B are green ones.

The suggested procedure is easily generalized for an arbitrary number of generating vectors. However, calculation of the large Ramsey numbers remains an unsolved problem.

4. Discussion and Applications

The procedure enabling converting of the system of vectors into the bi-colored, complete graph is suggested. The vectors serve as the vertices of the graph. The dual relations between vectors are prescribed by the sign of their scalar product. The suggested coloring procedure defined by Eqs. 1-2 is invariant relatively to rotation of frames. The suggested procedure is applicable for a broad diversity of vector fields. The vectors may represent, for example, velocities or accelerations of the moving particles. Thus, the Ramsey theory imposes non-obvious restrictions on the orientation of these vectors, demanding appearance of mono-colored structures within the graphs generated by the vectors.

Data Availability

No data was used for the research described in the article.

Acknowledgements

The author is thankful to Dr. Nir Shvalb for useful discussions.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

F. P. Ramsey, On a Problem of Formal Logic. In: Gessel, I., Rota, GC. (eds) Classic Papers in Combinatorics. Modern Birkhäuser Classics. Birkhäuser Boston, 2009, pp. 264-286.
R. L. Graham, B. L. Rothschild, J. H. Spencer, Ramsey theory, 2nd ed., Wiley-Interscience Series in Discrete Mathematics and Optimization, John Wiley & Sons, Inc., New York, A Wiley-Interscience Publication, 1990, pp. 10-110.
M. Di Nasso, I. Goldbring, M. Lupini, Nonstandard Methods in Combinatorial Number Theory, Lecture Notes in Mathematics, vol. 2239, Springer-Verlag, Berlin, 2019.
M. Katz, J. Reimann, Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathemati-cal Library Volume: 87; 2018; pp. 1-34.
D. Conlon, J. Fox, B. Sudakov, Recent developments in graph Ramsey theory, Surveys in Combinatorics, 424 (2015) 49-118.
F. D. Dubo, Stein M. On the Ramsey number of the double star, Discrete Mathematics, 348 (1) (2025) 114227. [CrossRef]
X. Hu, Q. Li, Ramsey numbers and a general Erdős-Rogers function, Discrete Mathematics, 347 (12) (2024) 114203.
S. A. Choudum, B Ponnusamy, Ramsey numbers for transitive tournaments, Discrete Mathematics 206 (1999) 119–129. [CrossRef]
N. Shvalb, M. Frenkel, S. Shoval, Ed. Bormashenko, A Note on the Geometry of Closed Loops, Mathematics 11(8) (2023) 1960. [CrossRef]

Figure 1. Six vectors

{\vec{a}}_{i}, i = (1 \dots 6)

defined on

R^{3}

Figure 1. Six vectors

{\vec{a}}_{i}, i = (1 \dots 6)

defined on

R^{3}

Figure 2. The coloring procedure is illustrated. Vectors

{\vec{a}}_{1}

and

{\vec{a}}_{2}

, belong to the same plane. A.

{(\vec{a}}_{1} \cdot {\vec{a}}_{2}) = e_{12} > 0

. Points “1” and “2” are connected with the red link. B.

{(\vec{a}}_{1} \cdot {\vec{a}}_{2}) = e_{12} < 0

. Points “1” and “2” are connected with the green link.

Figure 2. The coloring procedure is illustrated. Vectors

{\vec{a}}_{1}

and

{\vec{a}}_{2}

, belong to the same plane. A.

{(\vec{a}}_{1} \cdot {\vec{a}}_{2}) = e_{12} > 0

. Points “1” and “2” are connected with the red link. B.

{(\vec{a}}_{1} \cdot {\vec{a}}_{2}) = e_{12} < 0

. Points “1” and “2” are connected with the green link.

Figure 3. Bi-colored, complete graph generated by the vectors

{\vec{a}}_{i}, i = (1 \dots 6)

, and colored according to the Eqs. 1-2 is depicted. Vectors

{\vec{a}}_{i}, i = (1 \dots 6)

are the vertices of the graph. The coloring of the edges is carried out as follows:

e_{56}

e_{16}

e_{12}, e_{23}

e_{26}

e_{13}

e_{36}

e_{25},

e_{26}, e_{13}, e_{14}, e_{15} \geq 0

is true (see Eq. 1).

e_{34}, e_{35}, e_{45} < 0

is true (see Eq. 2).

Figure 3. Bi-colored, complete graph generated by the vectors

{\vec{a}}_{i}, i = (1 \dots 6)

, and colored according to the Eqs. 1-2 is depicted. Vectors

{\vec{a}}_{i}, i = (1 \dots 6)

are the vertices of the graph. The coloring of the edges is carried out as follows:

e_{56}

e_{16}

e_{12}, e_{23}

e_{26}

e_{13}

e_{36}

e_{25},

e_{26}, e_{13}, e_{14}, e_{15} \geq 0

is true (see Eq. 1).

e_{34}, e_{35}, e_{45} < 0

is true (see Eq. 2).

Figure 4. Triad of planar vectors

{\vec{a}}_{1}, {\vec{a}}_{2}, {\vec{a}}_{3}

is depicted. It is adopted:

α_{12} < \frac{π}{2}, α_{23} < \frac{π}{2}

, however

α_{12} + α_{23} = α_{13} > \frac{π}{2}

. Thus,

{(\vec{a}}_{1} \cdot {\vec{a}}_{2}) > 0

and

{(\vec{a}}_{2} \cdot {\vec{a}}_{3}) > 0

takes place. However,

{(\vec{a}}_{1} \cdot {\vec{a}}_{3}) < 0

is true. The procedure of coloring of links defined by Eq. 1 is non-transitive.

Figure 4. Triad of planar vectors

{\vec{a}}_{1}, {\vec{a}}_{2}, {\vec{a}}_{3}

is depicted. It is adopted:

α_{12} < \frac{π}{2}, α_{23} < \frac{π}{2}

, however

α_{12} + α_{23} = α_{13} > \frac{π}{2}

. Thus,

{(\vec{a}}_{1} \cdot {\vec{a}}_{2}) > 0

and

{(\vec{a}}_{2} \cdot {\vec{a}}_{3}) > 0

takes place. However,

{(\vec{a}}_{1} \cdot {\vec{a}}_{3}) < 0

is true. The procedure of coloring of links defined by Eq. 1 is non-transitive.

Figure 5. Ramsey complete bi-colored graph emerging from the system of five generating vectors forming pentagon. A.

{\vec{a}}_{1} \dots {\vec{a}}_{5}

generating vectors are depicted. B. Complete bi-colored graph emerging from the system of generating vectors

{\vec{a}}_{1} \dots {\vec{a}}_{5} .

Eqs. 1-2 establish the green-red coloring of the graph. No monochromatic triangle is recognized.

Figure 5. Ramsey complete bi-colored graph emerging from the system of five generating vectors forming pentagon. A.

{\vec{a}}_{1} \dots {\vec{a}}_{5}

generating vectors are depicted. B. Complete bi-colored graph emerging from the system of generating vectors

{\vec{a}}_{1} \dots {\vec{a}}_{5} .

Eqs. 1-2 establish the green-red coloring of the graph. No monochromatic triangle is recognized.

Figure 6. Ramsey complete bi-colored graph emerging from the system of six generating vectors forming hexagon. A.

{\vec{a}}_{1} \dots {\vec{a}}_{5}

generating vectors, forming a ring are depicted. B. Complete bi-colored graph emerging from the system of generating vectors

{\vec{a}}_{1} \dots {\vec{a}}_{6} .

Eqs. 1-2 establish the green-red coloring of the graph. Triangles “135” and “246” are monochromatic.

Figure 6. Ramsey complete bi-colored graph emerging from the system of six generating vectors forming hexagon. A.

{\vec{a}}_{1} \dots {\vec{a}}_{5}

generating vectors, forming a ring are depicted. B. Complete bi-colored graph emerging from the system of generating vectors

{\vec{a}}_{1} \dots {\vec{a}}_{6} .

Eqs. 1-2 establish the green-red coloring of the graph. Triangles “135” and “246” are monochromatic.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Ramsey Approach to Vector Fields

Abstract

1. Introduction

2. Ramsey Graphs Generated by Vector Fields

3. Ramsey Graph Generated by the Ring-Like Systems of Generating Vectors

4. Discussion and Applications

Data Availability

Acknowledgements

Declaration of Competing Interest

References

MDPI Initiatives

Important Links

Subscribe