Prerpints.org logo
Preprint
Article

Multi-Timescale Reactive Power Optimization and Regulation Method for Distribution Networks Under Multisource Interaction Environment

Altmetrics

Downloads

30

Views

14

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 September 2024

Posted:

19 September 2024

You are already at the latest version

Alerts
Abstract
In the context of constructing new power systems, distribution networks are increasingly incorporating distributed resources such as distributed photovoltaic (PV) systems, decentralized wind turbines (WT), and new types of energy storage system (ESS), which may lead to prominent issues such as voltage overruns and reverse heavy overloads in the distribution network. While distributed resources are valuable for voltage regulation, their regulation characteristics vary with their operation means, and the randomness and volatility of renewable power generation will also influence the optimization and regulation of voltage in the distribution network. This paper proposes a multi-time scale reactive power optimization and regulation method for distribution networks in a multi-source interactive environment. Firstly, the voltage regulation characteristics of distributed PV systems, decentralized ES, and distributed WT are analyzed. Based on this analysis, then a multi-time scale voltage optimization scheme for distribution networks using MPC method is proposed, which optimizes the voltage regulation strategies for each distributed resource in a rolling manner. Furthermore, an event-triggered real-time voltage zoning control strategy based on voltage sensitivity is proposed to address the real-time sudden voltage overlimit problems. The modified IEEE 33-node system is used to verify the performance of proposed method, simulation results indicate that the issue of voltage overruns at distribution network nodes has been improved, and the intraday rolling optimization yields results that are more realistic compared to the day-ahead optimization method.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

With the growing problem of climate change, energy transition on a global scale has become a common goal for governments and energy companies. The rapid development of renewable energy generation technologies such as PV and WT, and the continuous expansion of their installed capacity have provided new development opportunities for power systems [1,2,3]. However, the stochastic and fluctuating nature of PV power generation has brought significant impacts on the voltage stability of distribution networks, which has become an important challenge in the current grid operation management [4,5,6,7].
The output power of PV and wind turbine power generation is greatly affected by weather conditions, for example, the intensity of sunlight, cloud cover, and weather changes can lead to drastic fluctuations in PV power generation [8,9]. This volatility not only affects the stability of power supply, but also directly affects the voltage level of the distribution network, leading to voltage fluctuations, overruns, and other distribution network voltage problems [10,11]. For distribution system with a high proportion of distributed resources, a sudden increase or decrease in power generation can lead to dramatic fluctuations in system voltage level. If the power generation increases, it may lead to grid voltage overruns; conversely, a decrease in power may lead to a voltage drop, which in turn affects the normal operation of power equipment and the performance of power-using equipment. Traditional voltage regulation methods such as adjusting transformer taps and using capacitor banks [12,13] have limited effect in coping with the volatility of renewable energy power generation, the stochastic nature of PV and wind turbine power generation makes the voltage regulation more complex and difficult, especially in the case of drastic changes in renewable energy power generation, the traditional regulation equipment may not be able to respond in time, which affects the stability of the voltage of the power grid [14,15].
In recent years, the use of distributed resources such as PV, WT, and ES systems to effectively regulate the voltage of the distribution network has received extensive attention and research, through the active and reactive regulation of distributed PV power, WT, ES and other flexible resources, to achieve dynamic adjustment of the voltage and improve the flexibility and adaptability of the distribution network. Ref. [16] assesses various reactive control modes and ranks them according to the Voltage Regulation Index, instances of over-voltage, maximum and average voltage levels, as well as their effects on the PV hosting capacity of the distribution system. Ref. [17] introduced a novel voltage regulation approach for a distributed energy resource (DER) inverter that utilizes a parabolic droop curve. This method optimizes the speed and flexibility of DER inverters by restoring grid voltage more slowly when the voltage deviation is minor and more quickly when the voltage deviation is significant. Ref. [18] develops an iterative quadratic constrained quadratic programming model aimed at minimizing voltage deviations while maximizing the active power output of DERs in a three-phase unbalanced distribution system. Ref. [19] proposes a coordination control strategy that integrates the use of on-load tap changer (OLTC) transformers and PV inverters (PVI) within a microgrid to regulate the voltage of the examined distribution feeder. Ref. [20] presents a bi-level mixed-scale strategy designed to utilize multiple resources for enhancing voltage stability in the presence of uncertainties.
Considering the stochastic and fluctuating nature of renewable energy generation such as distributed PV and WT, some literatures have used model predictive control (MPC) methods to establish a multi-time scale voltage optimization and regulation model, which is used to accommodate short-term forecast errors in renewable energy generation For example, Ref. [21] introduces a reactive power control strategy that leverages power predictions from WT applicable to the distribution network. Ref. [22] presents an effective coordinated control strategy that integrates controllable devices with varying time response scales within low-voltage distribution networks. Ref. [23] proposes a strategy aimed at optimizing the economy and security of daily operations in the distribution network by incorporating the active support of distributed PV systems and ES systems for day-ahead intra-day co-optimization. However, most of these literatures only consider reactive regulation of PV inverters or active regulation of ES, and less research is carried out from the perspective of integrated active-reactive joint regulation of multiple distributed resources, in addition to paying less attention to short-term fluctuations of voltage and emergencies in real-time time-scale grids. For example, in Germany, where the installed capacity of PV systems is huge, a PV-induced voltage fluctuation event occurred in Bavaria in April 2018, when the PV generation system in the region experienced a sharp drop in PV power from 80% of full power to 20% in less than 10 minutes due to fast-moving overcast clouds [24]. This sharp fluctuation caused the voltage in the distribution network to instantly decrease beyond the safety range of the lower voltage limit, causing the voltage in some areas to fall below the standard range. Therefore, how to analyze the voltage regulation characteristics of different resources such as decentralized WT, distributed PV, ES, etc., and comprehensively utilize multi-source interaction and synergy in order to adapt to short-term fluctuations in voltage and sudden overruns in the grid is still a difficult point that requires further research.
Based on the above research challenges, this paper proposes a day-ahead, intraday and real-time multi-timescale reactive voltage optimization and regulation method for distribution networks based on the friendly interaction and synergy of multiple distributed resources, with the following specific innovations:
  • The active-reactive joint voltage regulation mechanism of distributed photovoltaic inverters, doubly-fed wind turbines and distributed energy storage units is analyzed, based on which a day ahead, intraday and real-time multi-timescale distribution network reactive voltage optimization and regulation method is proposed. Firstly, for the day-ahead stage, the objective is to minimize the total system network loss and node voltage deviation based on short-term prediction of renewable outputs and loads, and the active-reactive resources of PV, WT and ES units are comprehensively utilized to regulate the voltage; and then for the intraday stage, considering the short-term prediction uncertainty, the results of the ultrashort-term power prediction are used to realize the rolling optimization of active and reactive compensation for each distributed resource, and dynamically adjusting active and reactive outputs of distributed resources in response to the dynamic adjustment of active and reactive power output of distributed resources to cope with power changes.
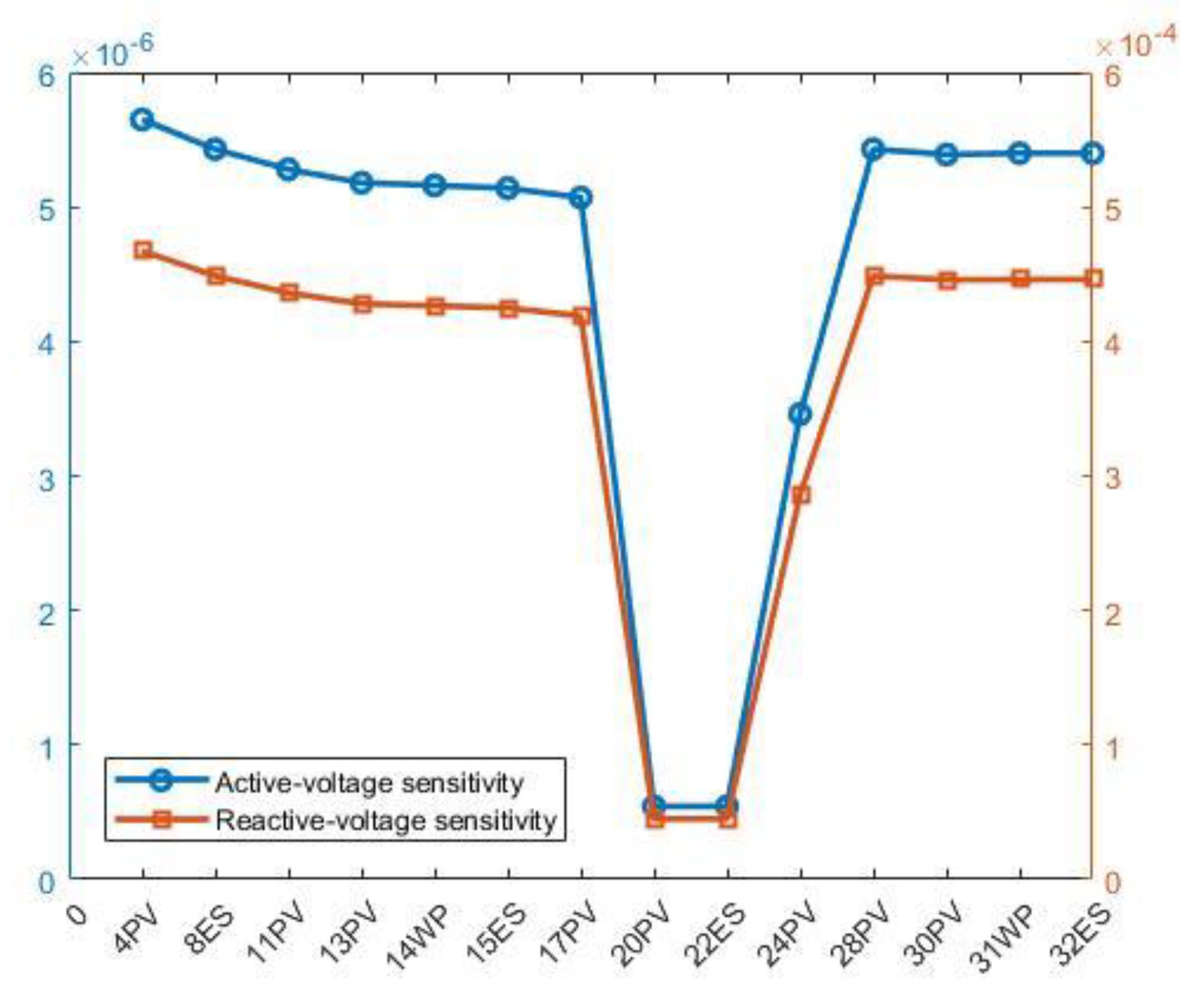
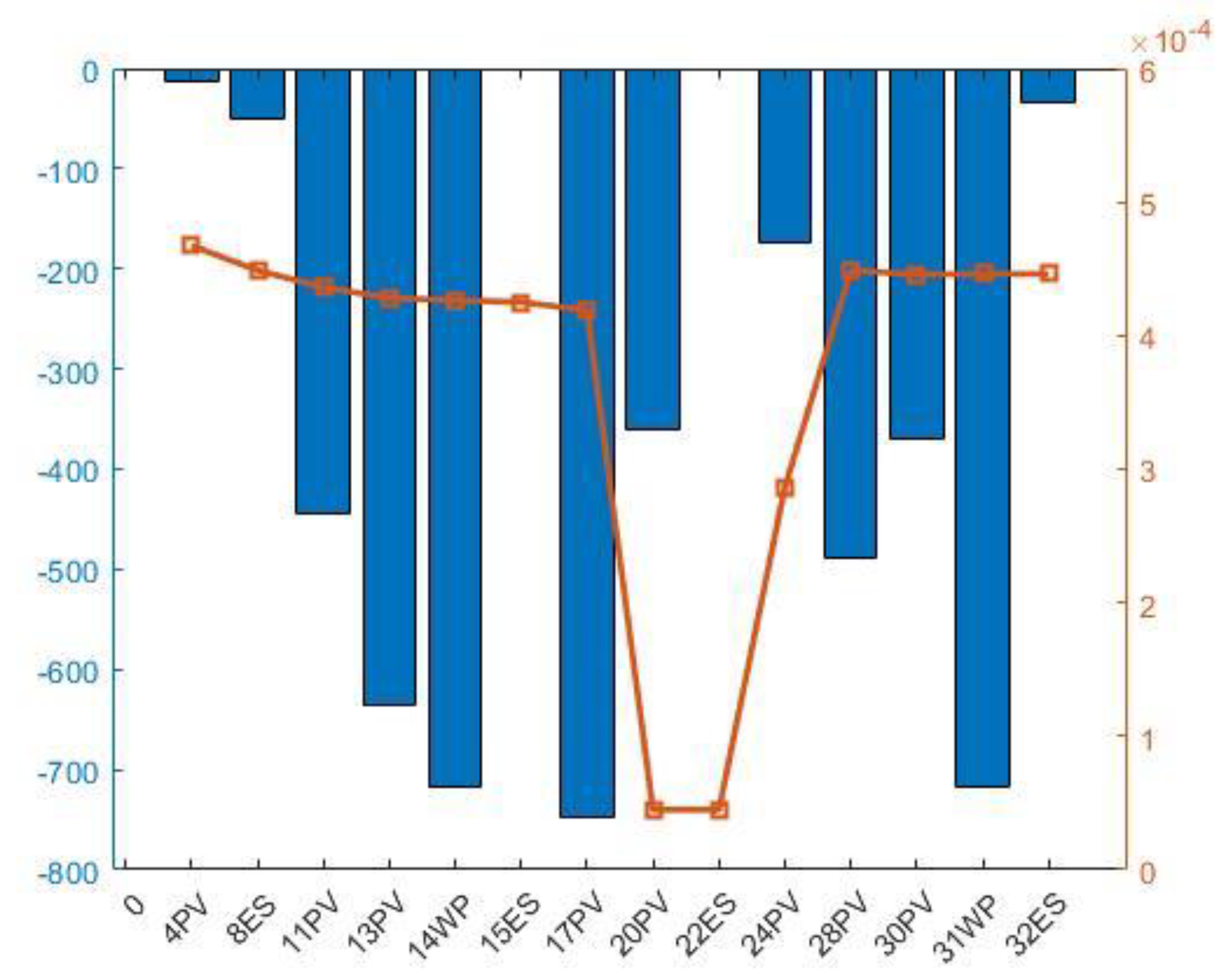
  • In order to solve the short-term fluctuation and sudden overrun of voltage in the grid, an event-triggered real-time voltage zoning control strategy based on voltage sensitivity is proposed, which calculates the reactive-voltage sensitivity and active-voltage sensitivity between distributed resources and overrun nodes, and establishes the “active first, reactive later” distributed voltage zoning control strategy, and establishes the “active first, reactive later” distributed voltage zoning control strategy. The distributed resource partitioning control model of “active first - reactive second” is established, and the nodes with high sensitivity are prioritized to call the regulating resources to realize real-time fast voltage regulation.

2. Background: Distributed Resource Regulation Mechanism

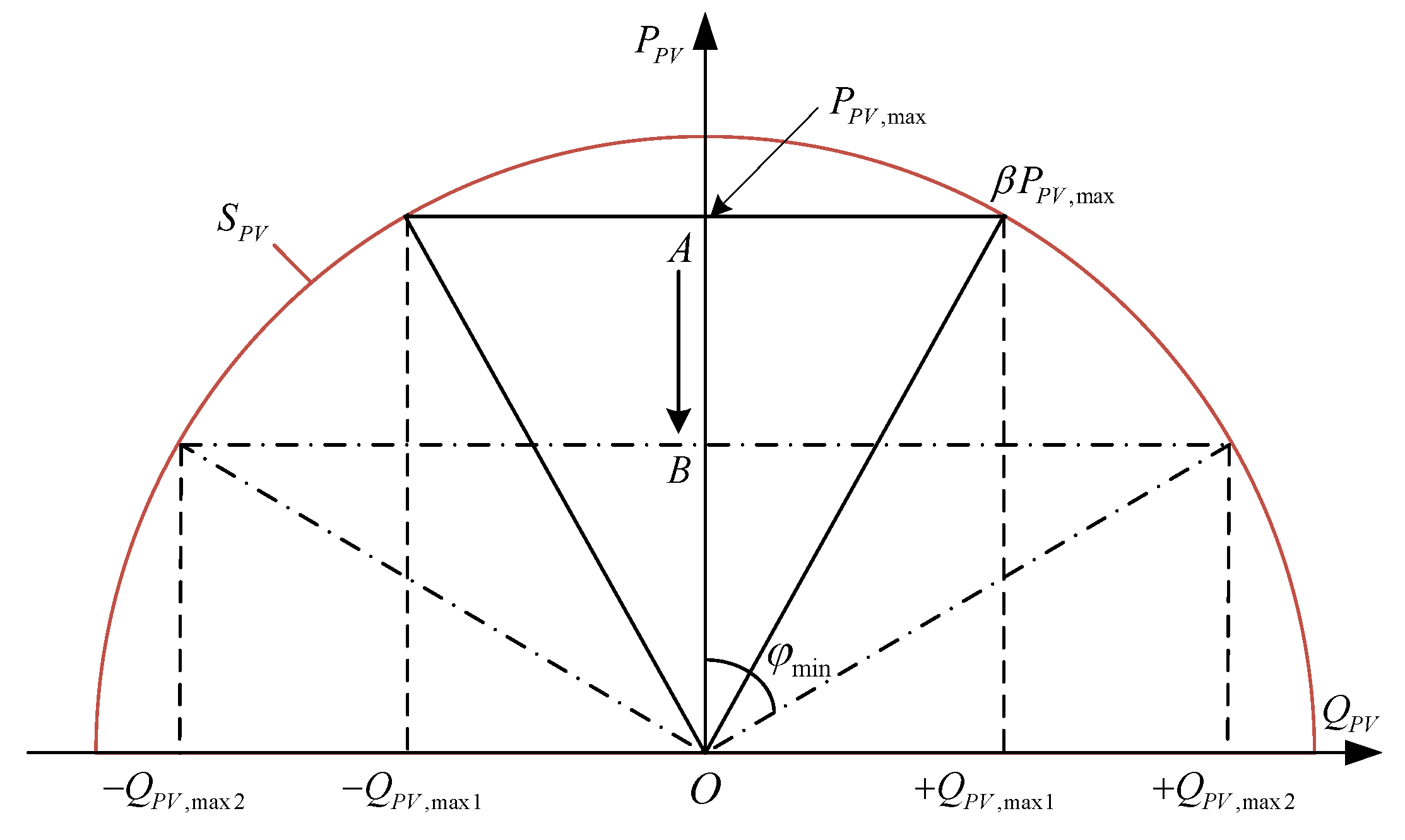
2.1. PV Inverter Based Voltage Regulation Mechanism

In medium and low voltage distribution networks, due to the large number of distributed PV systems, voltage overruns may occur at certain nodes close to the PV systems during peak PV output times [25,26]. When the voltage exceeds the upper limit, the PV system can help regulate the grid voltage by either reducing the active power supplied by the PV systems or by adjusting the reactive power through the PV inverters (assuming no curtailment of PV generation). The voltage regulation mechanism of the PV inverter is specifically shown in Figure 1: where the upper half-circle arc indicates the available capacity of the PV inverter S P V , and the point A indicates the maximum active power that can be generated when the PV is running, and its corresponding inverter reactive capacity is [ − Q P V , max 1 , + Q P V , max 1 ] ; when the PV active output is cut down to the point B , i.e., P P V = β P P V , max , the corresponding inverter reactive capacity changes to [ − Q P V , max 2 , + Q P V , max 2 ] . Considering that the PV inverter power factor should not be too low, in Figure 1, φ min is the power factor angle corresponding to the minimum power factor.
The formula for the adjustable reactive power capacity of the PV inverter can be obtained by combining Figure 1:
P P V = P P V , max − Δ P P V Q P V = S P V 2 − P P V 2
where P P V , max is the maximum active power of PV, Δ P P V is the power curtailment of PV, P P V is the active power of PV after regulation, S P V is the capacity of PV inverter, which is generally set as 1 ~ 1.1 times of the rated active power of PV, and Q P V is the maximum adjustable reactive power of PV after regulation of active power.

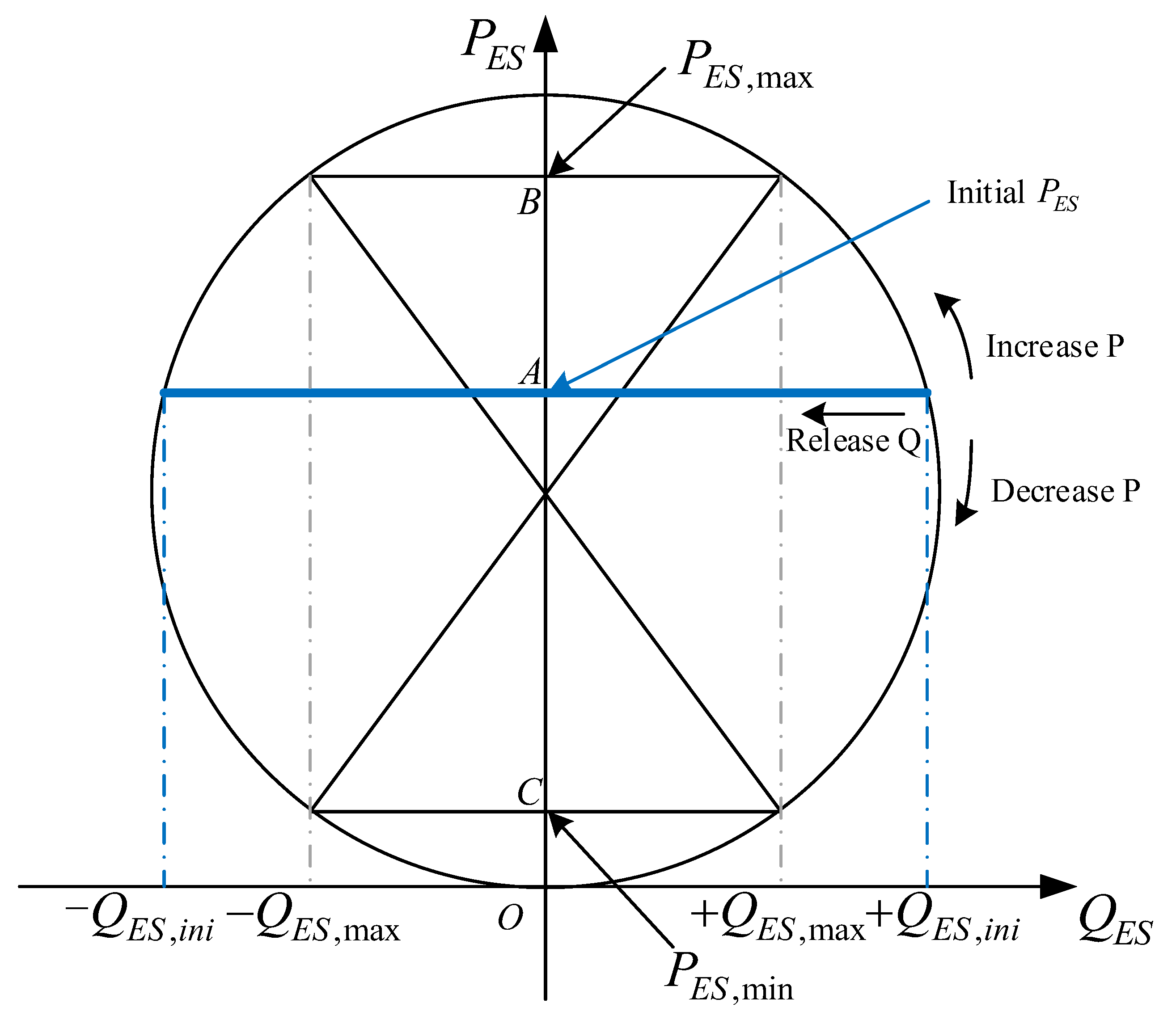
2.2. Regulation Mechanism of ES

ES batteries can both store and release electrical energy, so in voltage regulation, ES has more regulation options compared to PV [27,28]. The voltage regulation mechanism of ES is shown in Figure 2, and the difference with PV is that the variation curve of the ES inverter is a whole circle, which can be used for reasonable charging and discharging of ES within the range of [ P P V , min , P P V , max ] . When the initial active power is at A, the corresponding reactive power regulation range of the ES is [ − Q P V , i n i , + Q P V , i n i ] ; when the ES is charging, the active curve of the ES moves from A to B, and the reactive power of the ES changes along with the active power, and when it reaches the maximum value of the charging capacity of the ES at P P V , max , the corresponding reactive power regulation range of the ES is [ − Q P V , max , + Q P V , max ] ; when the ES is discharging, it is similar to charging, and the active curve of the ES moves from A to C, and the adjustable range of the reactive power changes accordingly, and the calculation formula is the same as that of the PV. The calculation formula is also similar to that of PV:
Q E S = S E S 2 − P E S 2
where P E S is the active power stored after charging and discharging the ES, S E S is the capacity of the PV inverter, and Q E S is the adjustable reactive power range of the ES inverter under the current active power.

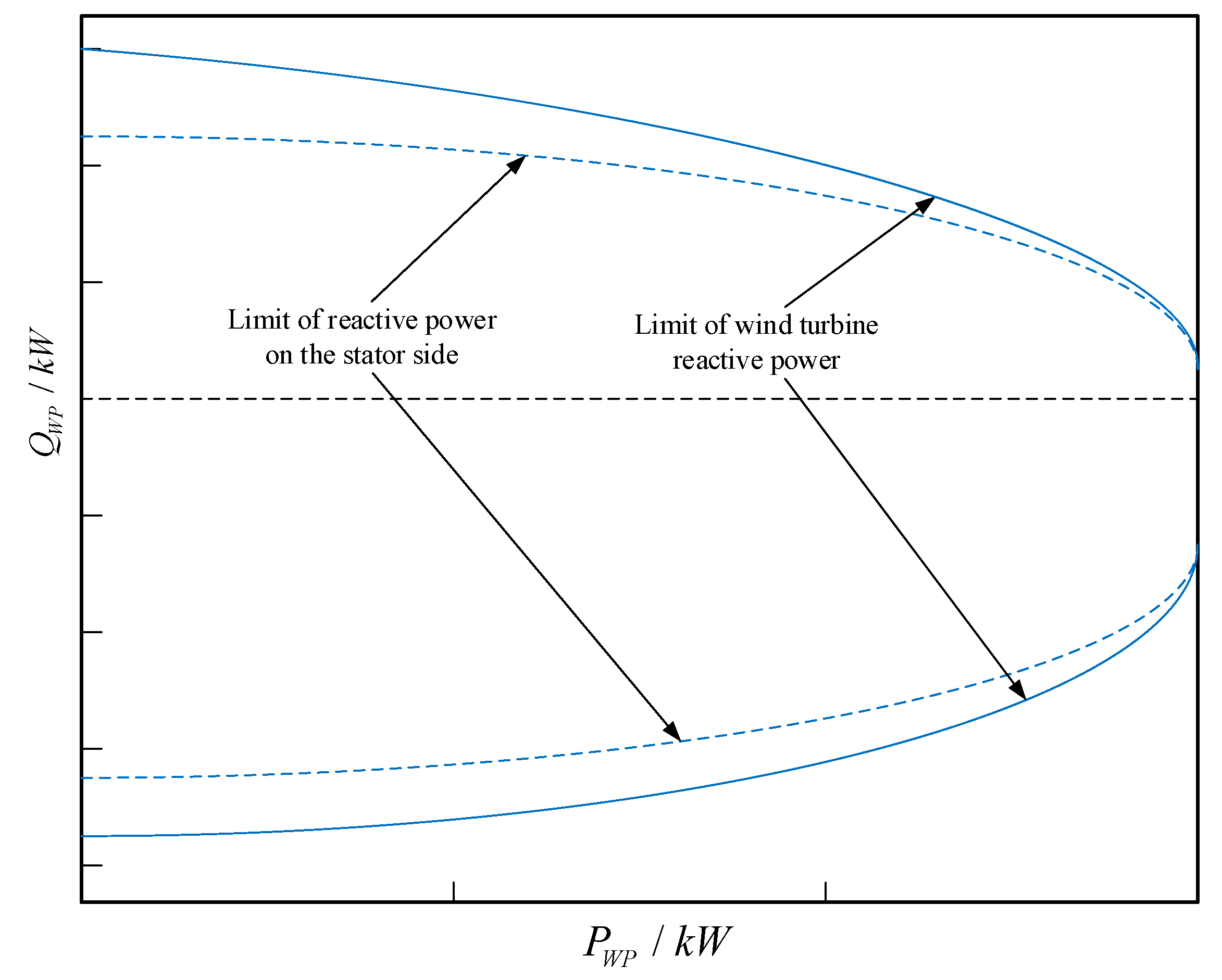
2.3. Voltage Regulation Mechanism of Doubly-Fed Wind Turbine

The voltage regulation mechanism of a Doubly-Fed Induction Generator (DFIG) is illustrated in Figure 3. As shown, the greater the active power output of the DFIG, the smaller the range of adjustable reactive power. Moreover, for a given active power, the DFIG's ability to release reactive power is less than its ability to absorb reactive power. The DFIG does not always operate at its rated state. If Maximum Power Point Tracking (MPPT) is not considered in certain situations, i.e., if the principle of active power priority is not adopted, the reactive power regulation capability can be improved by reducing the active power output. The dashed line in the figure represents the reactive power limit range on the stator side of the DFIG, while the solid line represents the total reactive power limit range of the Wind Turbine Generator (WTG). It is evident that most of the reactive power comes from the stator side, with the rotor side having a very limited adjustable reactive power range [29,30].
Considering that the reactive power on the stator side is constrained by the currents on both the stator and rotor sides, its adjustable range of reactive power can be expressed as follows:
Q s , min = − 3 U s 2 2 ω 1 L s − 3 L m U s I r , max 2 L s 2 − P m 1 − s 2
Q s , max = − 3 U s 2 2 ω 1 L s + 3 L m U s I r , max 2 L s 2 − P m 1 − s 2
where L s and L m are the stator inductance and excitation inductance respectively; I r , max is the maximum value of rotor side current, s is the slew rate, ω 1 is the synchronous rotational angular velocity; U s is the effective value of stator voltage. And the two equations can be seen from the DFIG stator side in the absorption of reactive power and the release of reactive power when the adjustable range of different.
Assume that the maximum active power for which the grid-side converter is designed is S c , max , and the reactive power range of the grid-side converter is:
Q c , min = − S c , max 2 − s P m 1 − s 2
Q c , max = S c , max 2 − s P m 1 − s 2
The adjustable reactive power range of the DFIG can be determined by considering both the stator side reactive power limit and the grid-side converter reactive power limit:
Q g , max = Q s , max + Q c , max
Q g , min = Q s , min + Q c , min

3. Proposed Scheme: Multi-Timescale Voltage Control Strategies for Distribution Networks

In this section, we firstly introduce the proposed multi-timescale reactive power control framework for distribution system, then formulate the optimization model of day-ahead and intraday timescale, and lastly we propose the event-triggered real-time voltage zoning control strategy based on voltage sensitivity to solve the short-term fluctuation and sudden overrun of voltage.

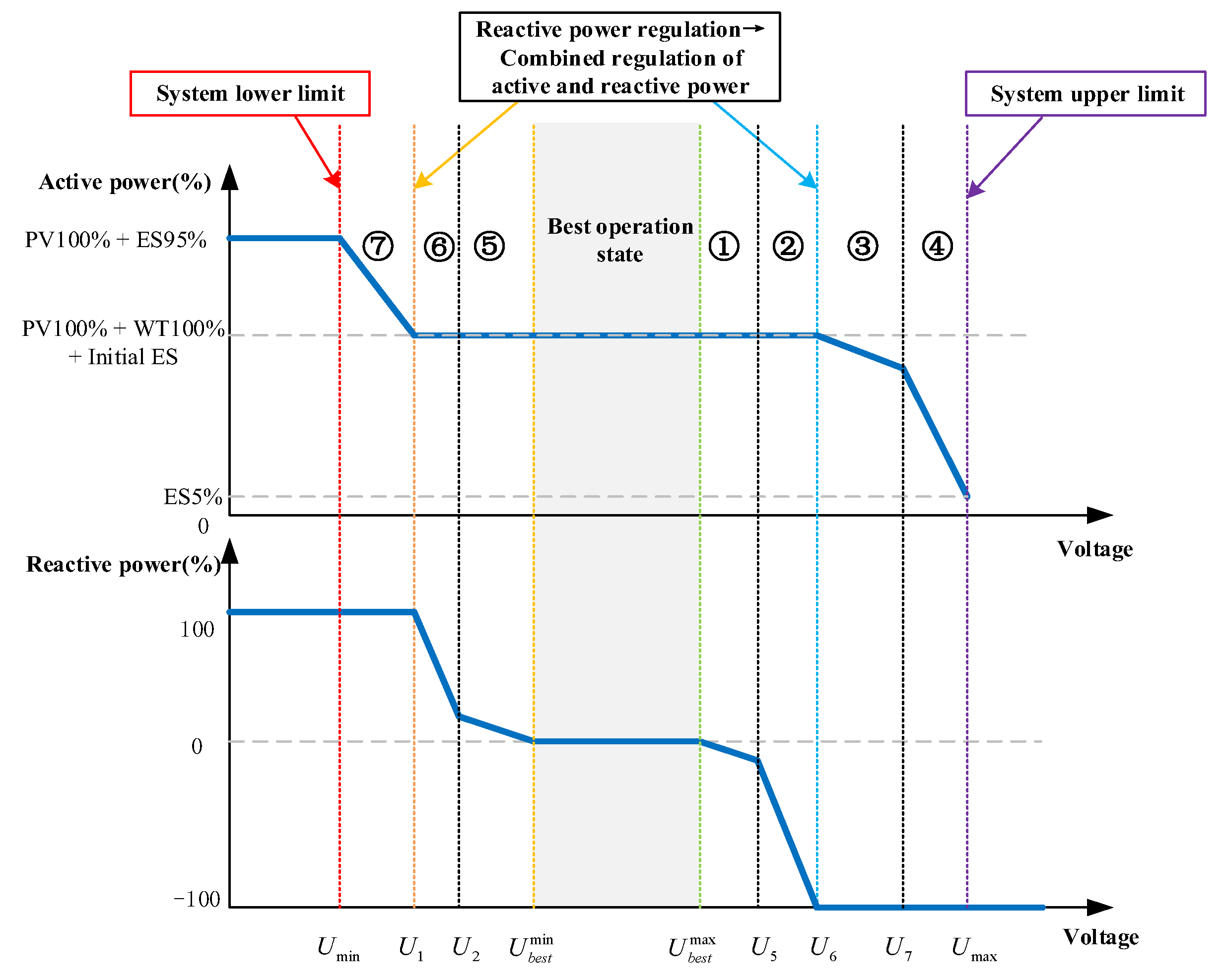
3.1. Multi-Timescale Reactive Power Control Scheme for Distribution Networks

MPC is a fuzzy predictive control theory used in the optimization and regulation of dynamic systems [31,32]. The basic idea is to predict the future behavior of the system by combining the measured data at the current moment in order to optimize the control action in a future period of time. Considering the uncertainties that may exist in the input data, this control method optimizes its own prediction results by rolling iterations and feedback of the prediction results over multiple single time intervals. At each time interval the MPC builds a new optimization model based on the current operating parameters, so the set iteration length affects the MPC output results, and if the iteration length is shortened, the data sampling rate needs to be increased at the same time as the MPC accuracy is improved. MPC acts on the stochastic system by means of unfixed feedback control values. Through intra-day rolling optimization, the system is able to automatically generate an optimization model that gradually approaches the optimal control strategy by continuously reducing the error.
In the operation and control of distribution networks, the uncertainty of renewable energy power outputs means that the day-ahead optimal model may not achieve system optimization during intra-day operation. Therefore, the MPC method can be adopted to develop more effective strategies for multi-source interactive distribution networks. Considering the uncertainty of distributed new energy resources, this approach calculates the active and reactive regulation strategies of these resources in the distribution network and compares the roles of different distributed resources in the voltage regulation process. By utilizing the principles of model predictive control to coordinate the varying voltage regulation capabilities of each distributed resource, the method effectively addresses voltage overrun issues in the distribution network. With its multi-step optimization and prediction capabilities, MPC can determine a multi-scale voltage optimization model for distribution networks in a multi-source interactive environment.
The multi-timescale reactive power control framework based on MPC method for distribution system is shown in Figure 4, which includes day-ahead prediction optimization, intra-day rolling optimization, and real-time voltage control. Intra-day rolling optimization uses the active and reactive power data of distributed resources obtained from day-ahead predictions to continuously perform feedback iterations. The day-ahead optimization layer aims to reduce network losses and maintain voltage stability, with a time scale of 1 hour, coordinated by the distributed resource voltage regulation model in Section 2.2. The intra-day rolling optimization layer operates on a 15-minute time scale, focusing more on voltage stability control and the uncertainty of distributed resource output. Real-time voltage control, building on the previous layers, operates on a 5-minute time scale to keep voltage limits within the optimal operating range.
(1) Objective function
In order to maintain the stable operation of the distribution network, the day-ahead optimization model takes the optimal operation of the system as the objective, therefore the optimization objective function is modeled as minimizing the branch loss and voltage deviation of the distribution network, which is formulated as follows
min F 1 = ∑ t = 1 T W 1 ⋅ ∑ j ∈ Π P l o s s , t + ∑ i ∈ Ω W 2 ⋅ U i , t − U r e f
where P l o s s , t denotes the line loss, U i , t denotes the voltage of node i at time slot t, U r e f denotes the reference voltage, which is generally set to 1, Ω  and  Π denote the node set and branch set, respectively, and W 1  and  W 2 are the weight coefficients.
(2) Constraints
There are the following constraints that need to be satisfied during the optimization:
1) Power flow constraints
For each node i, P i , t and Q i , t denote the active and reactive power injected into the node at the time slot t ; for each line l i − j , G i - j and B i − j denote the conductance and conductance of the line respectively, P i − j , t denotes the active power flowing through the line at time slot t, and θ i − j , t d enotes the difference in the phase between the end and the beginning of the line. Є i is the set of all nodes connected with node i. In this paper, the polar coordinate form of the power flow model is used:
P i , t = U i , t ∑ j ∈ Є i U j , t ( G i − j cos θ i − j , t + B i − j sin θ i − j , t )
Q i , t = U i , t ∑ j ∈ Є i U j , t ( G i − j sin θ i − j , t − B i − j cos θ i − j , t )
P i − j , t = ( U i , t 2 − U i , t U j , t cos θ i − j , t ) G i − j − U i , t U j , t sin θ i − j , t B i j
P i , t = P PV , i , t + P W T , i , t + P E S , i , t c h a − P E S , i , t d i s − P l o a d , i , t
U i , min < U i , t < U i , max
I i j , t 2 ≤ I i j , t max 2
where P P V , i , t and P W T , i , t denote the PV and WT output of node i at time slot t, P E S , i , t c h a and P E S , i , t d i s denote the charging and discharging power of node i at time slot t, P l o a d , i , t denotes the user load of node i at time slot t, U i , min and U i , max denote the upper and lower voltage limits of the distribution node i, I i j , t and I i j , t max denote the current on the branch i − j and the maximum value allowed.
3) PV operation constraints
0 ≤ P PV , m , t ≤ P PV , m , t max , ∀ m ∈ Ω P V
P P V , m , t 2 + Q P V , m , t 2 ≤ S P V , m , ∀ m ∈ Ω P V
where P P V , m , t is the predicted active power of PV node m, S P V , m is the capacity of the grid-connected PV converter, and Q P V , m , t is the reactive power regulation strategy, with upper and lower bounds Δ Q max , m , t and Δ Q min , m , t , respectively:
Δ Q max , m , t = S P V , m 2 − P P V , m , t 2
Δ Q min , m , t = − S P V , m 2 − P P V , m , t 2
4) WT operation constraints
0 ≤ P W T , n , t ≤ P W T , n , t max , ∀ n ∈ Ω W T
P W T , n , t 2 + Q W T , n , t 2 ≤ S W T , n , ∀ n ∈ Ω W T
where P W T , m , t is the active power generation at the WT node n; S W T , m is the capacity of the grid-connected converter for WT, and Q W T , n , t is the reactive power regulation strategy, and according to models given by Eqs. (3)-(8), the reactive power of WT is constrained by:
Q W T , n , t s , min + Q W T , n , t c , min ≤ Q W T , n , t ≤ Q W T , n , t s , max + Q W T , n , t c , max
5) ESS operation constraints
ε k , t c h a + ε k , t d i s ≤ 1 , ∀ t
P E S , k , t = P E S , k , t c h a ε k , t c h a + P E S , k , t d i s ε k , t d i s
0 ≤ P E S , k , t ≤ P E S , k d i s , max ε k , t d i s + P E S , k c h a , max ε k , t c h a , ∀ t , ∀ k ∈ Ω E S
E E S , k , t = E E S , k , t − 1 + P E S , k , t c h a η c h a − P E S , k , t d i s / η d i s , ∀ t
E C , k ⋅ S O C k min ≤ E E S , k , t ≤ E C , k ⋅ S O C k max
( P E S , k , t ) 2 + ( Q E S , k , t ) 2 ≤ S E S , k 2
where ε k , t c h a and ε k , t d i s are binary variables representing the charging and discharging state of the k-th ES unit respectively, P E S , k , t c h a and P E S , k , t d i s are the charging and discharging power of the ES unit k at the time slot t, P E S , k c h a , max P c , m a x , t and P f , m a x , t   P E S , k d i s , max are the upper limits of the charging and discharging power, P E S , k , t and Q E S , k , t are the active and reactive power issued or absorbed by the k-th ES at time slot t, S E S , k is the inverter capacity, and E C , k denotes the maximum capacity of the ES battery, S O C k min and S O C k max denote the minimum and maximum state of charge, respectively.

3.3. Intra-Day Rolling Optimization Model

Based on the day-ahead optimization results, the intraday rolling optimization model shortens the forecast time scale to cope with the fluctuation of renewable energy output. Therefore, the renewable energy outputs are forecasted and updated with a time resolution of 15 minutes, and the day-ahead optimization dispatch value is used as a reference value to calculate the regulation strategy of DERs in the control time horizon (4 hours) in a rolling manner.
When performing the intraday rolling optimization, the day-ahead operation plan of distributed resources must be followed, so the intraday objective function is to minimize the voltage deviation value and the penalty of distributed resource output regulation, which is formulated by:
min F 2 = Z 1 ⋅ ∑ i ∈ Ω U i , t i n − U r e f + Z 2 ⋅ ∑ i ∈ Ω P V ∪ Ω W T ∪ Ω E S Δ P i , t i n μ i , t a c t i v e + Δ Q i , t i n μ i , t r e a c t i v e
where U i , t i n denotes the voltage of node i at time slot t of intraday stage, Δ P i , t i n and Δ Q i , t i n denote the active and reactive output correction compared with day-ahead optimization results of DERs, μ i , t a c t i v e and μ i , t r e a c t i v e are the corresponding penalty coefficients, and Z 1 and Z 2 are the weight coefficients.
(2) Constraints
In addition to power flow constraints, the following operation constraints of DERs also need to be satisfied:
0 ≤ P PV , m , t + Δ P PV , m , t i n ≤ P PV , m , t max , ∀ m ∈ Ω P V
P P V , m , t + Δ P PV , m , t i n 2 + Q P V , m , t + Δ Q PV , m , t i n 2 ≤ S P V , m , ∀ m ∈ Ω P V
0 ≤ P W T , n , t + Δ P WT , m , t i n ≤ P W T , n , t max , ∀ n ∈ Ω W T
P W T , n , t + Δ P WT , n , t i n 2 + Q W T , n , t + Δ Q WT , n , t i n 2 ≤ S W T , n , ∀ n ∈ Ω W T
P E S , k , t i n = P E S , k , t c h a + Δ P E S , k , t i n , c h a ε k , t c h a η c h a − P E S , k , t d i s + Δ P E S , k , t i n , d i s ε k , t d i s / η d i s
0 ≤ P E S , k , t i n ≤ P E S , k d i s , max ε k , t d i s + P E S , k c h a , max ε k , t c h a , ∀ t , ∀ k ∈ Ω E S
E E S , k , t i n = E E S , k , t − 1 i n + P E S , k , t i n , ∀ t
E C , k ⋅ S O C k min ≤ E E S , k , t i n ≤ E C , k ⋅ S O C k max
( P E S , k , t i n ) 2 + ( Q E S , k , t + Δ Q E S , k , t i n ) 2 ≤ S E S , k 2
where Δ P P V , m , t i n and Δ Q P V , m , t i n are the active and reactive output correction compared with day-ahead optimization results of PV, similarly, Δ P W T , n , t i n and Δ Q W T , n , t i n are the active and reactive output correction of WT, and Δ P E S , k , t i n , c h a , Δ P E S , k , t i n , d i s and Δ Q E S , k , t i n are the active and reactive output correction of ES.

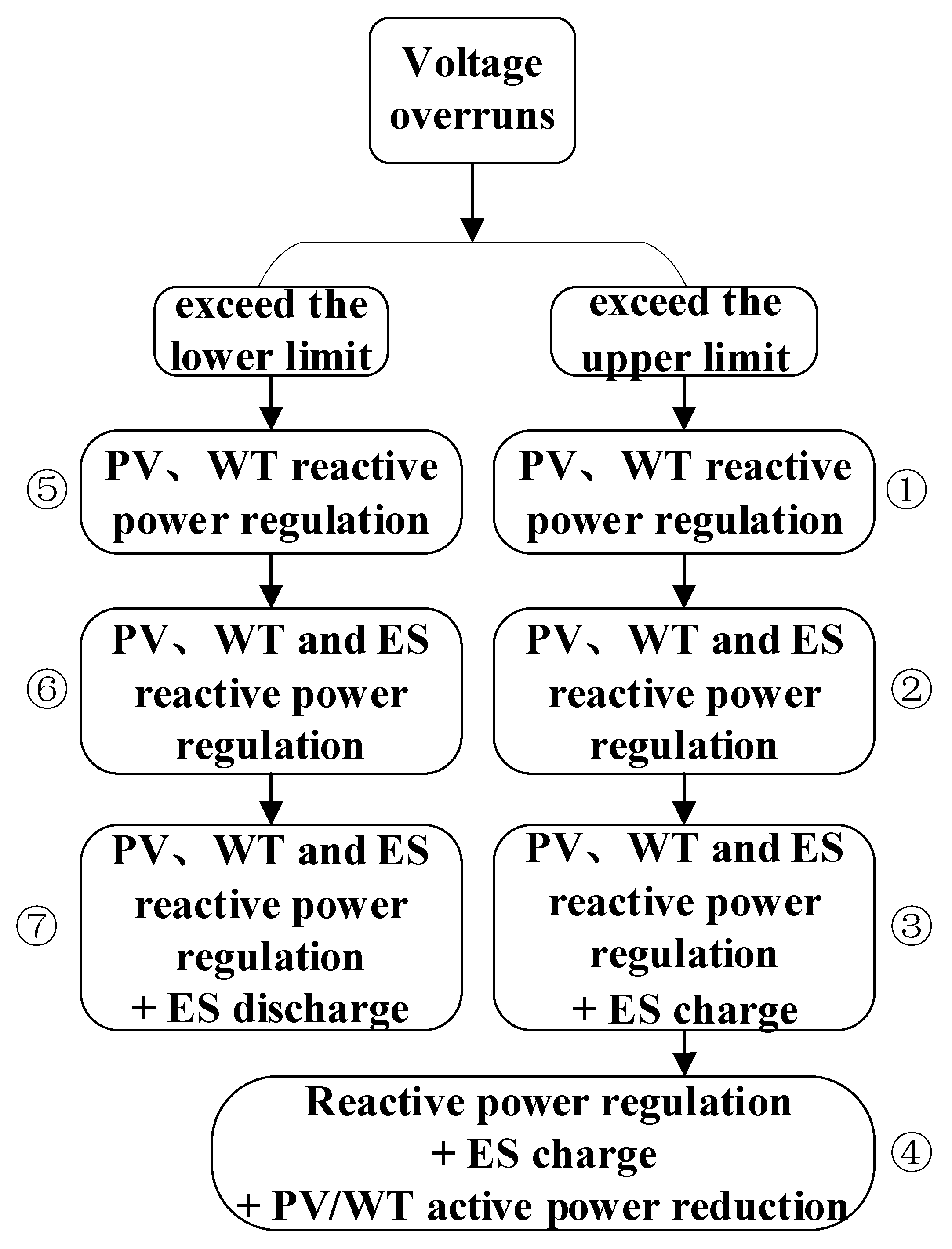
3.4. Real Time Control Model

For voltage fluctuations and over-limits in a short period of time in the real-time stage, the optimization method is not used to solve the regulation instructions of each distributed resource, in this paper the ‘event-triggered’ voltage partition control strategy is directly used to obtain the control signal. And in order to further improve the rapidity and effectiveness of the distributed resource response to the voltage over-limit node, the distributed resource regulation priority is determined based on the active power-voltage sensitivity and reactive power-voltage sensitivity.
For each node in the system, the power-voltage sensitivity is used to measure the effect that a power change at one node has on the voltage at another node, as shown in equation (27):
S P , i , j , t = Δ U i , t Δ P j , t , S Q , i , j , t = Δ U i , t Δ Q j , t
where S P , i , j , t , S Q , i , j , t are the active-voltage sensitivity and reactive-voltage sensitivity between nodes i and j respectively, representing the change in voltage of node i when node j changes unit active power and reactive power, Δ U i , t is the voltage change amount of the node i, Δ P j , t and Δ Q j , t are the active and reactive power change amount of the node j at time slot t. S P , i , j , t and S Q , i , j , t can be calculated from the modified equation of power flow calculation.
The distribution system can allocate the amount of active and reactive power to be regulated based on the power-voltage sensitivity between different distributed resource nodes to nodes of voltage violations. Nodes with higher sensitivity are better at voltage regulation. During the regulation process, nodes with voltage violations are adjusted according to the descending order of power-voltage sensitivity, which means DER nodes with high sensitivity being regulated first. Once the capacity of high sensitivity nodes is exhausted, regulation proceeds to lower sensitivity nodes. In addition, the regulation process also follows the voltage regulation strategy of “reactive power followed by active power, renewable power followed by energy storage system”, the specific strategy is shown in the figure below:
In the figure, the horizontal coordinate represents the current node voltage value, U min and U max represents the upper and lower limits of system voltage, U b e s t min and U b e s t max represent the upper and lower limits of the optimal voltage interval. The vertical coordinate represents the amount of active and reactive power that needs to be regulated by the system under the current voltage level. When the node voltage is not in the optimal voltage range, a “node with voltage violations” event is triggered, and the vertical coordinate corresponding to the current voltage level is the amount of active and reactive power to be regulated by multiple DERs. From Figure 5, we can observe that the control area is divided into several different zones according to voltage intervals, and each zone corresponds to a corresponding distributed resource adjustment strategy, which is shown in Figure 6:
For each voltage interval in the voltage partitioning control strategy of Figure 5 and Figure 6, the order of regulation of distributed resources is determined based on the active-voltage sensitivity or reactive-voltage sensitivity calculated in Eq. (39), and when the regulation capacity of all distributed resources is utilized, then it is transferred to the next interval, and so on.

4. Case Study

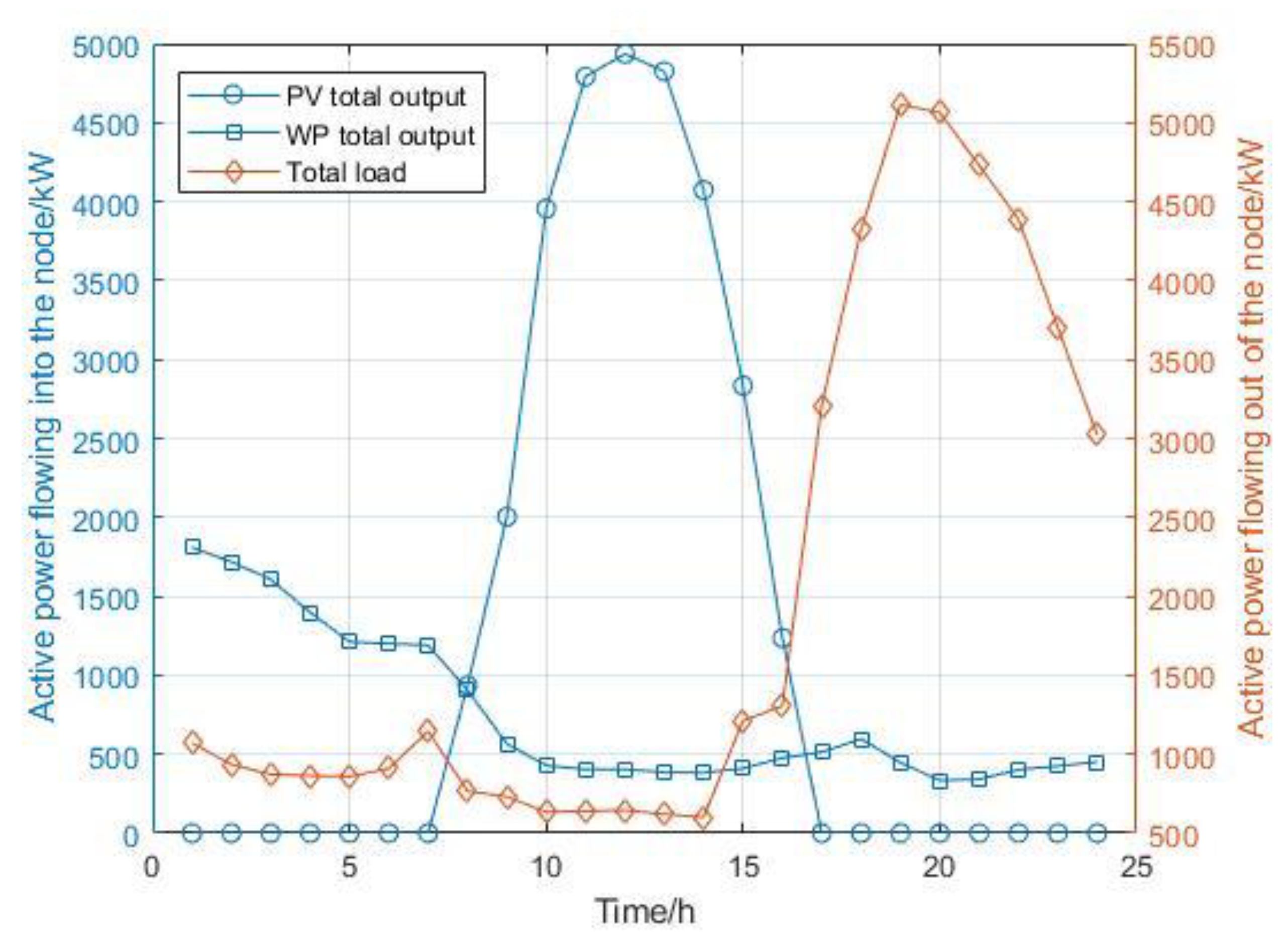
4.1. Basic Data

As shown in Figure 7, a modified IEEE 33-node distribution system is used here with the distribution of distributed resources. The PV output, wind power output, and load for a typical day are used as the base data for the analysis, as illustrated in Figure 8. The PV power moment is from 8:00 to 16:00, and the wind power is out all day, based on this parameter the distribution network is optimized.
The voltage specification of reference node 1 is set to 1, and a 5% prediction error is considered between short-term power prediction and ultrashort-term power prediction, and the relevant parameters for the PV, energy storage, and wind power systems are presented in Table 1 below.

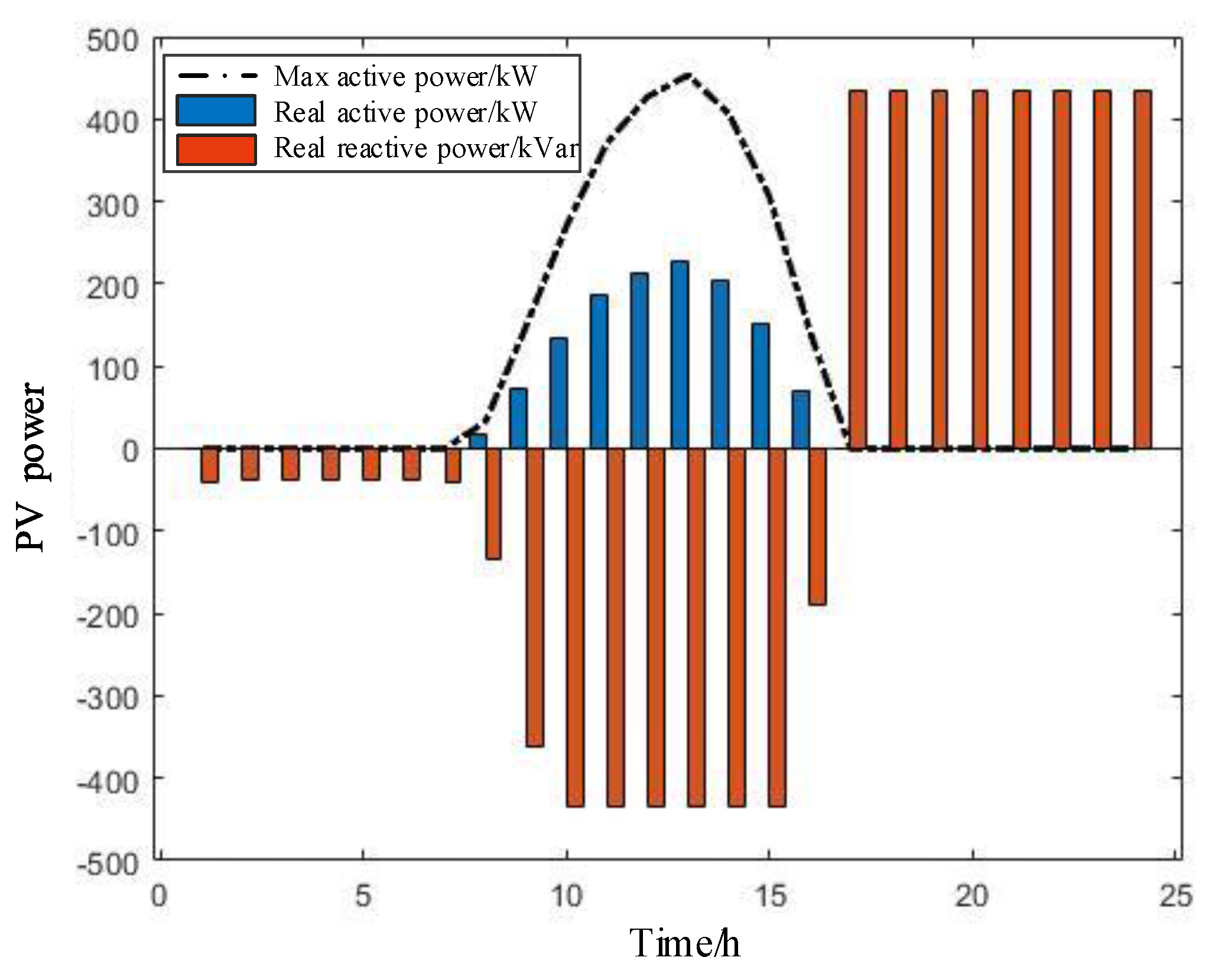
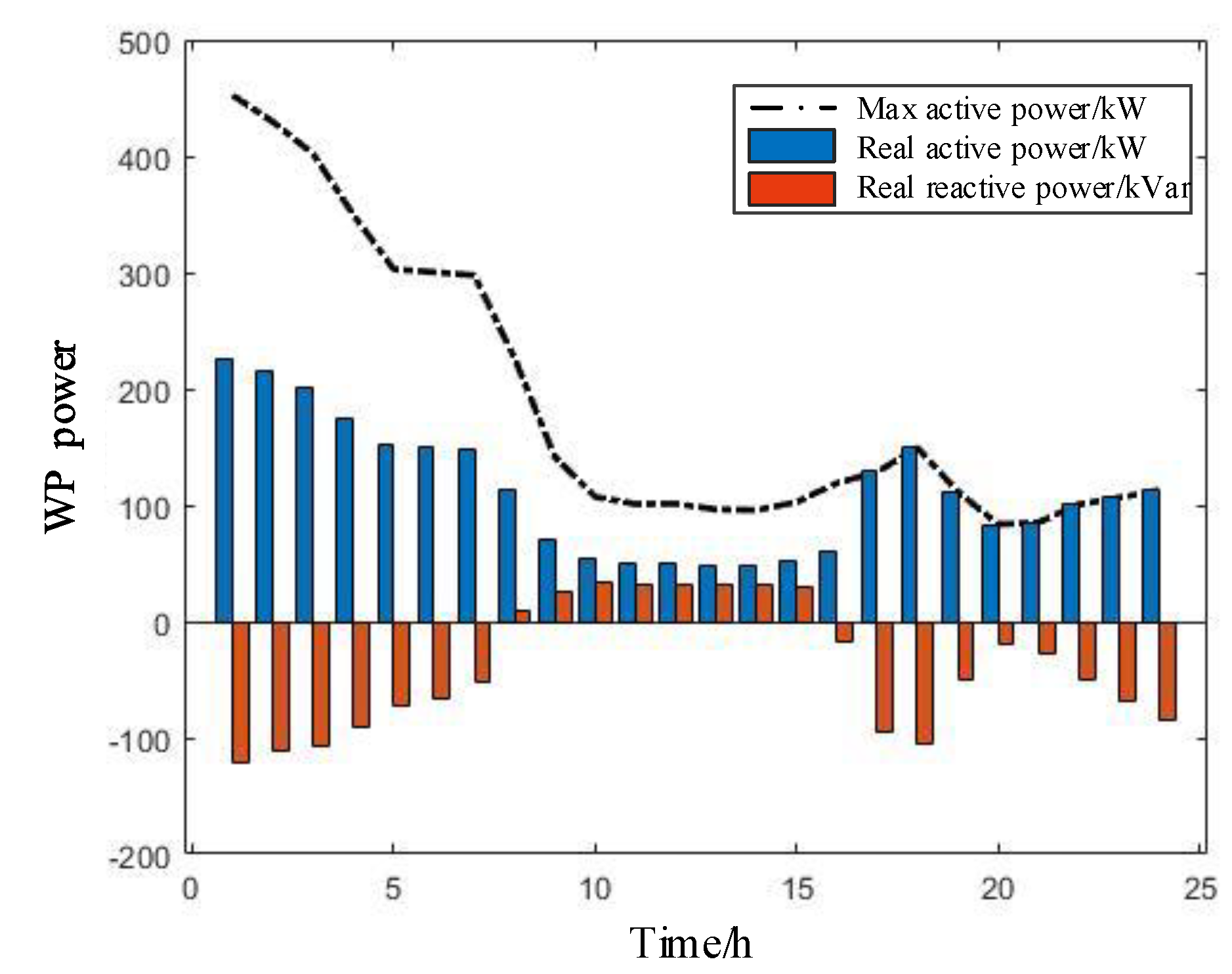
4.2. Day-Ahead Optimization Results Analysis

Figure 9, Figure 10 and Figure 11 show the typical regulation curves for PV, energy storage, and wind power over one day, and from these figures, we can obtain the following information: (1) From 0:00 to 7:00 time slots, higher wind power output results in higher node voltages, but these do not exceed the upper voltage limit. To keep voltage stability, WT reduces active power and releases reactive power to lower the voltage; (2) From 8:00 to 15:00 time slots, as PV output significantly increases (see Figure 8), the voltage at PV nodes and adjacent nodes exceeds limits. To address this problem, PV nodes reduce voltage by decreasing active power and releasing reactive power, while energy storage discharges to lower the voltage and absorbs reactive power to balance it in the grid; (3) From 16:00 to 24:00 time slots, reduced PV and wind power output combined with increased load leads to voltage dropping below the lower limit. During this period, PV and storage absorb reactive power, and ESS charging and other actions help increase grid voltage.
To evaluate the effectiveness of the proposed MV optimization control methods proposed in this paper, the following control schemes are compared:
(1) No optimization or control is applied, serving as a baseline for comparison with other control strategies.
(2) Based on the day-ahead optimization objective, the MV distribution grid is optimized at the day-ahead scale using 24-hour PV, wind, and load data for a typical day predicted from historical data. The resulting regulation scenarios and voltage regulation effects for each distributed resource are shown in Figure 9, Figure 10, Figure 11 and Figure 12.
Figure 12 shows the results of the distribution network node voltage distribution with and without MPC, where the average voltage of the 33 nodes is displayed. Simulation results indicate that, before applying optimization control, during periods of high PV output, the power injected by nodes exceeded the load power, causing many nodes—especially PV nodes—to exceed voltage limits, resulting in poor voltage quality. After applying the voltage control strategy described in this paper, the voltage at each node remains within the set range of 0.95–1.05 p.u., achieving effective voltage regulation.

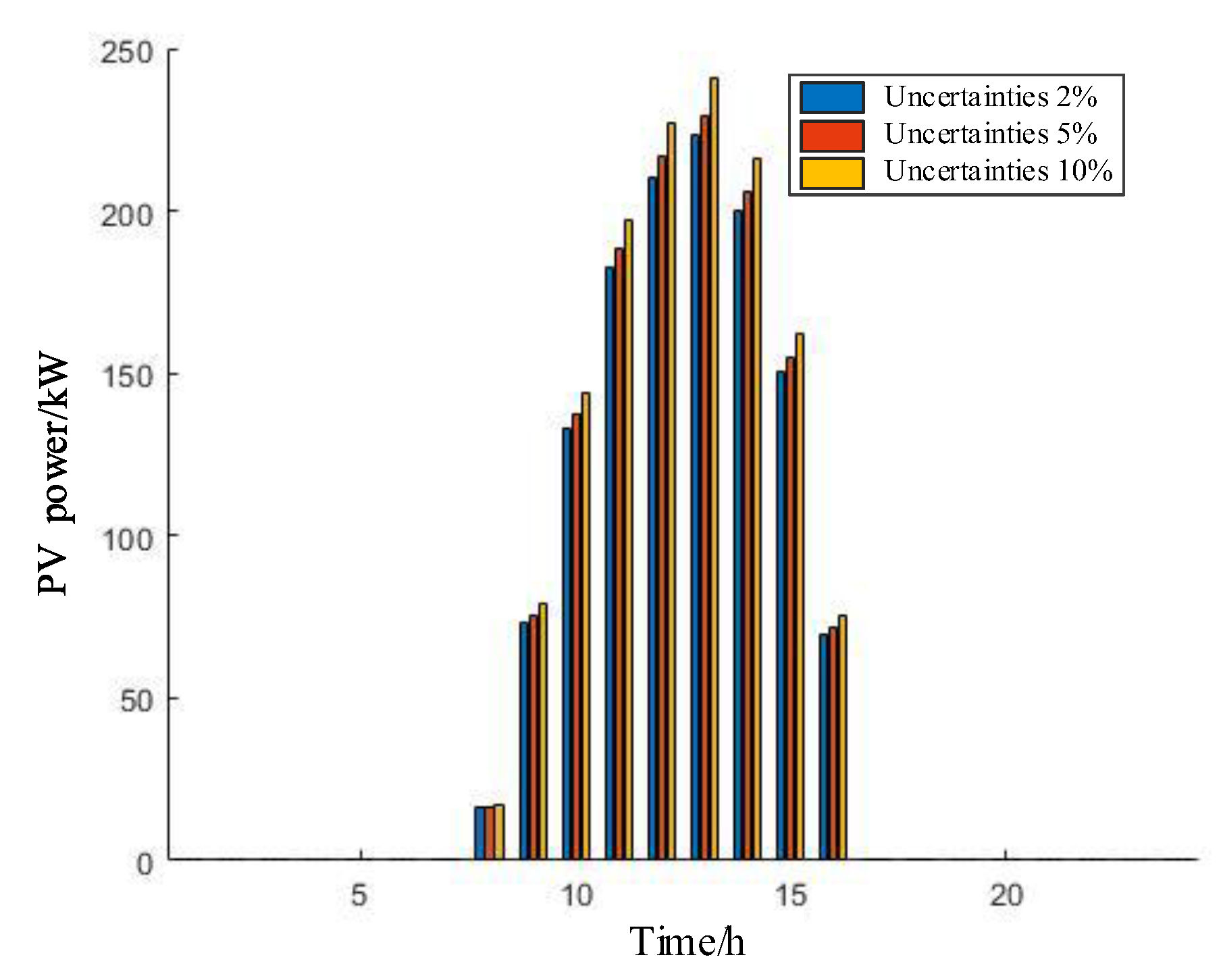
4.3. Intraday Optimization Results Analysis

In this paper, a 5% prediction error is considered between short-term power prediction and ultrashort-term power prediction, then based on the optimization of day-ahead optimization results, the active and reactive power regulation amounts of distributed resources are adjusted based on ultrashort-term power prediction data, the comparison of day-ahead and intraday active and reactive power outputs for each distributed resource at 12:00 is shown in Table 2.
Furthermore, in order to verify the proposed intraday optimization model is applicable for scenarios under different prediction errors, the comparison results under different prediction errors are analyzed, Figure 13, Figure 14 and Figure 15 show the changes of the regulation amount of typical distributed resource nodes under prediction errors of 2%, 5% and 10%.
Form Figure 13, Figure 14 and Figure 15, we can obtain that the amount of PV nodes’ active regulation increases with the increases of uncertainty when performing active regulation, leading to fluctuations in the corresponding reactive regulation based on day-ahead predictions. And for energy storage nodes, due to uncertainties, the voltage at each node may experience some fluctuations from the day-ahead prediction. To maintain voltage stability, energy storage needs to be adjusted accordingly. As shown in the figure, the energy storage regulation curve within the day does not exhibit significant fluctuations compared to the day-ahead. For wind power nodes, with increasing uncertainty, the active power regulated by wind power first increases and then decreases, displaying a trend different from that of PV.

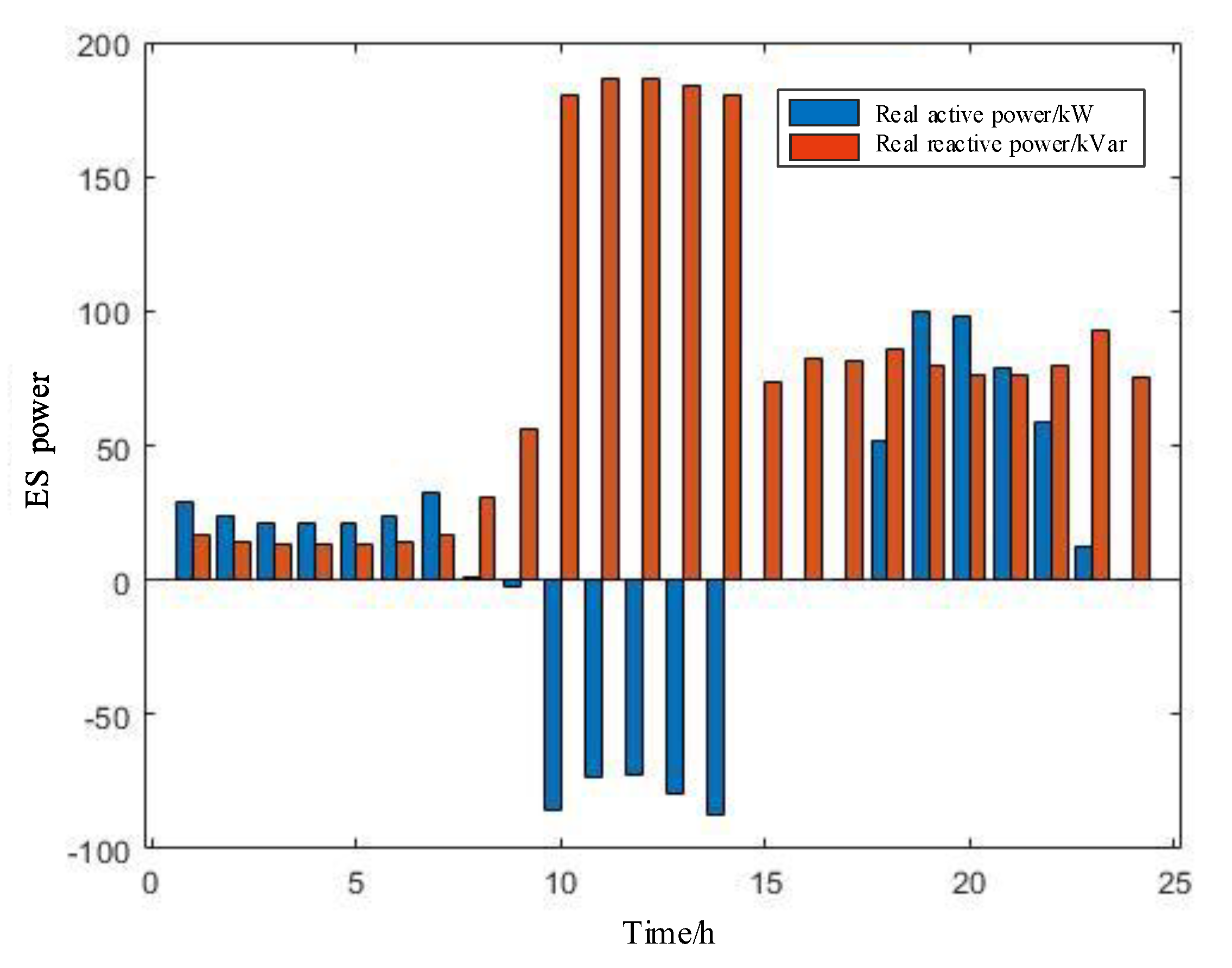
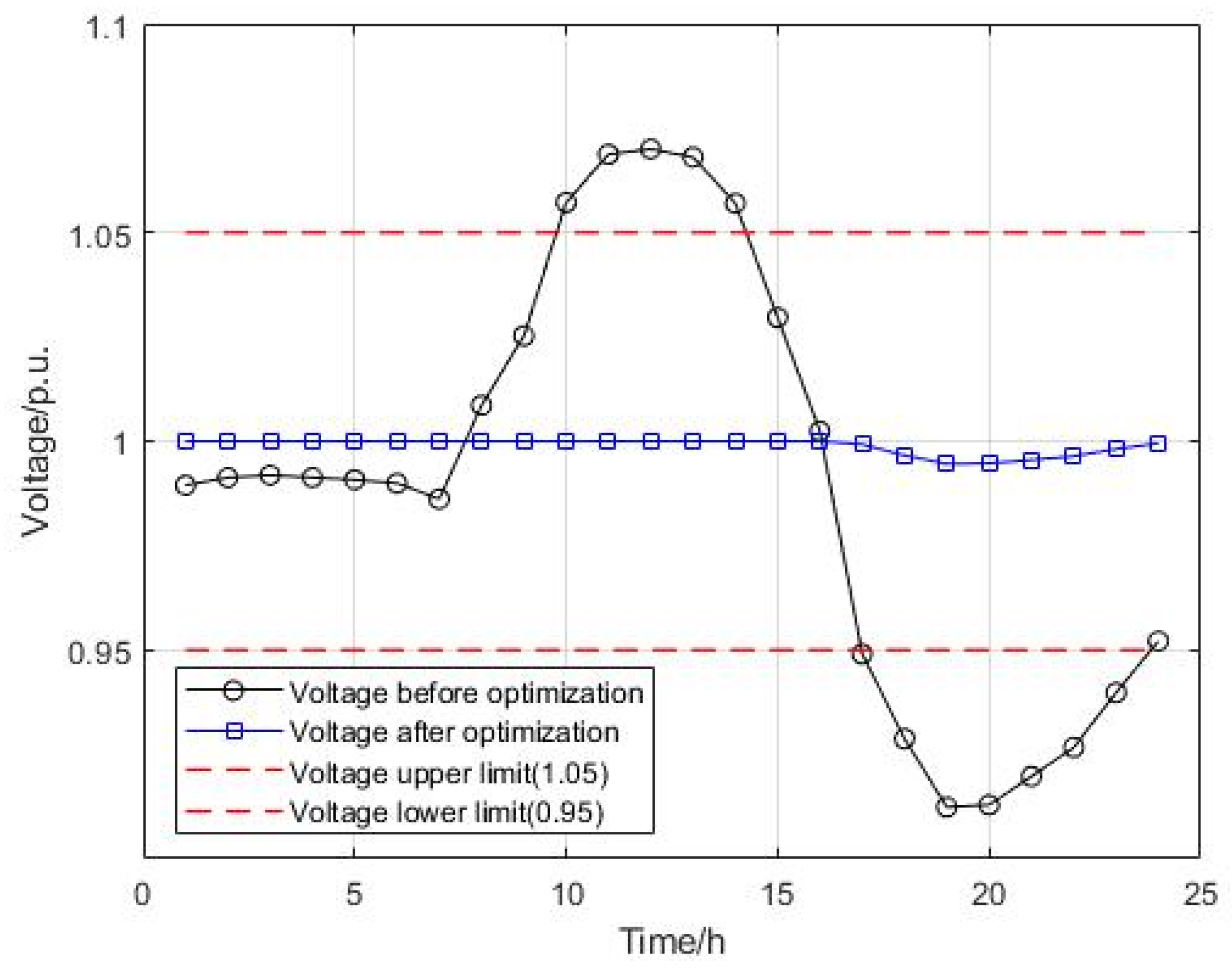
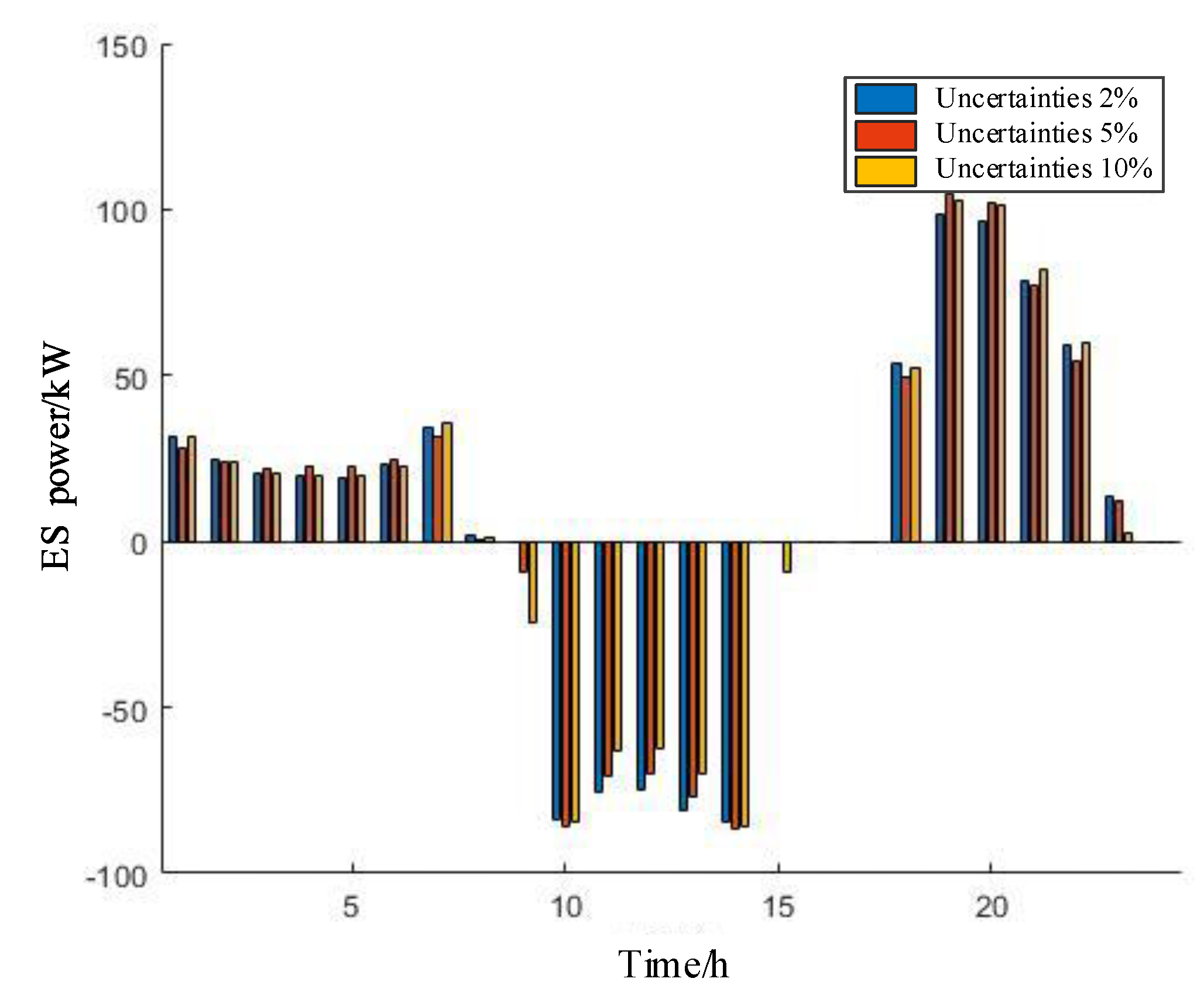
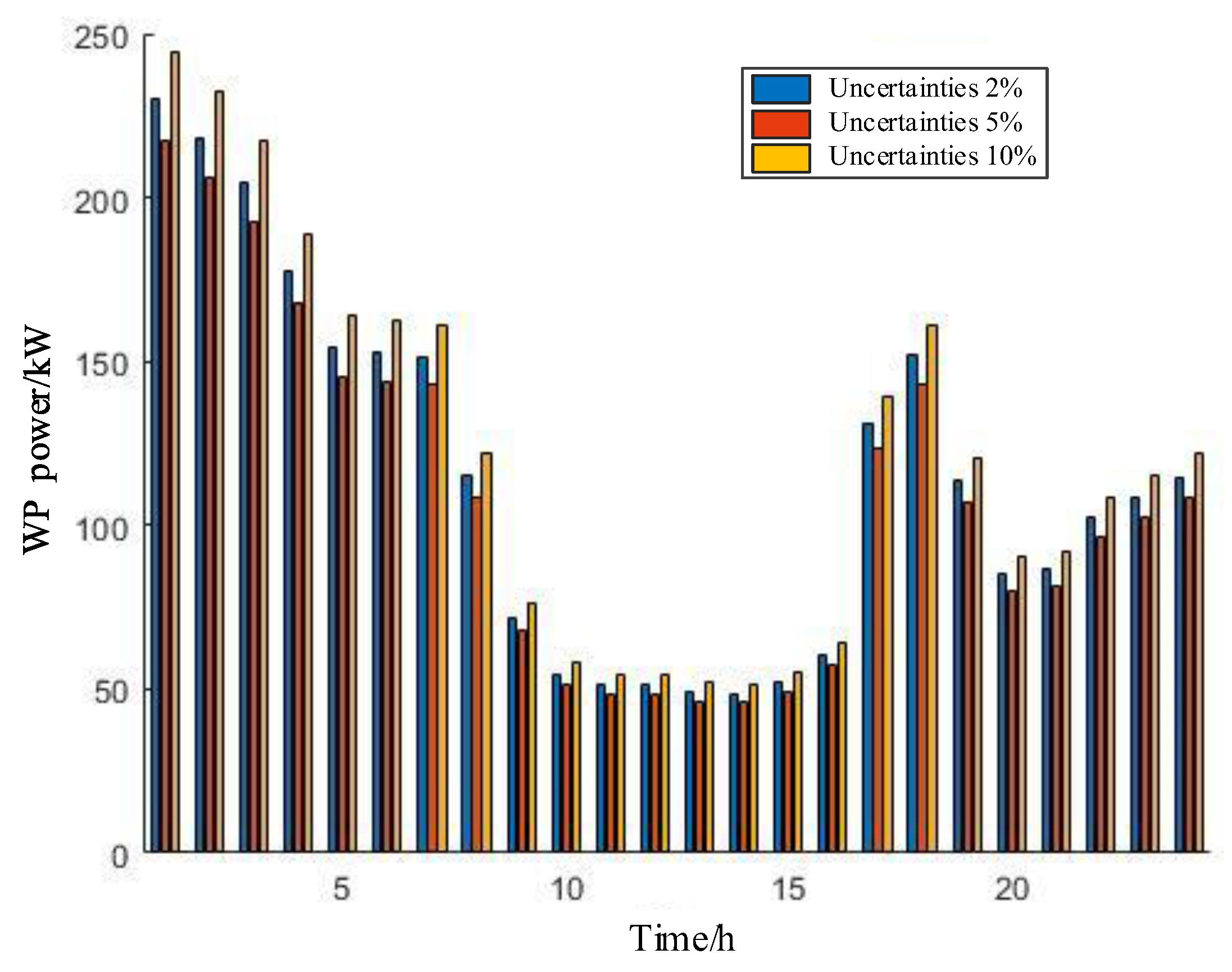
4.4. Real-Time Control Results and Strategy Analysis

In order to verify the performance of proposed event-triggered real-time voltage zoning control strategy, assuming that at 12:00, the PV output at node 4 increases suddenly, causing the voltage to exceed the safe operation range. This subsection analyzes how the voltage regulation strategies for each distributed resource change under different voltage conditions at node 4.
Figure 16 shows the active-voltage sensitivity and reactive-voltage sensitivity of the remaining distributed resource nodes in the 33-node distribution system with respect to node 4. Nodes closer to node 4 in the topology exhibit higher sensitivity and provide better regulation for node 4. Therefore, priority is given to these nodes for voltage regulation. Based on the corrected active-reactive strategy in Table 2, the remaining adjustable active and reactive power for each distributed resource is calculated, and the results are shown in Table 3.
The optimal voltage interval is set to [0.99,1.01], assuming that the voltage at node 4 is U = 1.03 , and the regulated power at each node is obtained as shown below:
As shown in Figure 17, the voltage at node 4 exceeds the optimal voltage limit, but only the reactive power of each distributed resource is used for voltage regulation. After the reactive power from PV and WT is adjusted, ES nodes participate in regulation based on their sensitivity. In the figure, only ES at nodes 32 and 8 are involved in voltage regulation, while nodes 15 and 22 do not participate since they have lower sensitivity.

5. Conclusions

In this paper, we propose a day-ahead, intraday and real-time multi-time scales reactive power optimization and regulation method for distribution networks in a multi-source interactive environment, aiming to address problems of voltage violations and renewable energy output uncertainty via considering the regulation strategies of PV, WT and ESS. Through the numerical results, we can demonstrate that: the proposed voltage optimization and control scheme has a good performance in improving voltage level and reducing line losses by integrately optimizing the active and reactive power output strategies. Besides, the proposed intraday optimization model is applicable for scenarios under different prediction errors, and the power-voltage sensitivity based real-time voltage control has a good performance in fast response to the real-time sudden voltage overlimit problems. In the future, we will continue to work on the following two challenges: first, deciding the best voltage intervals of the real-time voltage zoning control strategy through optimization model; second, utilizing the DERs of low-voltage area to achieve a wider range of resource complementarity and collaborative optimization.

References

  1. X. Yang, C. Xu, Y. Zhang, W. Yao, J. Wen and S. Cheng, "Real-Time Coordinated Scheduling for ADNs With Soft Open Points and Charging Stations," in IEEE Transactions on Power Systems, vol. 36, no. 6, pp. 5486-5499, Nov. 2021. [CrossRef]
  2. Z. Tang, D. J. Hill and T. Liu, "Fast Distributed Reactive Power Control for Voltage Regulation in Distribution Networks," in IEEE Transactions on Power Systems, vol. 34, no. 1, pp. 802-805, Jan. 2019. [CrossRef]
  3. T. Stetz, F. Marten and M. Braun, "Improved Low Voltage Grid-Integration of Photovoltaic Systems in Germany", IEEE Trans. Sustainable Energy, vol. 4, no. 2, pp. 534-542, 2013.
  4. R. A. Shayani and M. A. G. d. Oliveira, "Photovoltaic Generation Penetration Limits in Radial Distribution Systems", IEEE Trans. Power Syst., vol. 26, no. 3, pp. 1625-1631, 2011.
  5. R. Tonkoski, L. A. C. Lopes and T. H. M. El-Fouly, "Coordinated Active Power Curtailment of Grid Connected PV Inverters for Overvoltage Prevention", IEEE Trans. Sustainable Energy, vol. 2, no. 2, pp. 139-147, 2011.
  6. X. Lu, K. W. Chan, S. Xia, X. Zhang, G. Wang and F. Li, "A model to mitigate forecast uncertainties in distribution systems using the temporal flexibility of EVAs", IEEE Trans. Power Syst., vol. 35, no. 3, pp. 2212-2221, May 2020.
  7. A. Ali, D. Raisz, K. Mahmoud and M. Lehtonen, "Optimal placement and sizing of uncertain PVs considering stochastic nature of PEVs", IEEE Trans. Sustain. Energy, vol. 11, no. 3, pp. 1647-1656, Jul. 2020.
  8. D. C. Jordan, K. Perry, R. White and C. Deline, "Extreme Weather and PV Performance," in IEEE Journal of Photovoltaics, vol. 13, no. 6, pp. 830-835, Nov. 2023. [CrossRef]
  9. A.M. A. Acuzar, I. P. E. Arguelles, J. C. S. Elisan, J. K. D. Gobenciong, A. M. Soriano and J. M. B. Rocamora, "Effects of weather and climate on renewable energy resources in a distributed generation system simulated in Visayas, Philippines," 2017IEEE 9th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management (HNICEM), Manila, Philippines, 2017, pp. 1-6. [CrossRef]
  10. S. Shivashankar, S. Mekhilef, H. Mokhlis and M. Karimi, "Mitigating methods of power fluctuation of photovoltaic (PV) sources – A review", Renewable Sustain. Energy Rev., vol. 59, pp. 1170-1184, 2016.
  11. A. Dubey, S. Santoso and M. P. Cloud, "Understanding the effects of electric vehicle charging on the distribution voltages", Proc. IEEE Power Energy Soc. General Meeting, pp. 1-5, 2013.
  12. C. Gao and M. A. Redfern, "Automatic Compensation Voltage Control strategy for on-load tap changer transformers with distributed generations," 2011 International Conference on Advanced Power System Automation and Protection, Beijing, China, 2011, pp. 737-741. [CrossRef]
  13. P. Penkey, H. Samkari, B. K. Johnson and H. L. Hess, "Voltage control by using capacitor banks and tap changing transformers in a renewable microgrid," 2017 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 2017, pp. 1-5. [CrossRef]
  14. S. Liemann, L. Robitzky and C. Rehtanz, "Impact of Varying Shares of Distributed Energy Resources on Voltage Stability in Electric PowerSystems," 2019 IEEE Milan PowerTech, Milan, Italy, 2019, pp. 1-6. [CrossRef]
  15. T. Van Cutsem and T. Weckesser, "Searching for plausible N-k contingencies endangering voltage stability", 2017 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), pp. 1-6, Sept. 2017.
  16. A. M. Amuna, R. Karandeh and V. Cecchi, "Voltage Regulation in Distribution Systems using Distributed Energy Resources," SoutheastCon 2021, Atlanta, GA, USA, 2021, pp. 1-7. [CrossRef]
  17. S. Xu, B. Cao, H. Hassan, G. Song and L. Chang, "Parabolic Droop Voltage Regulation by DER Inverter for Power System Support Functions," 2021 IEEE 12th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Chicago, IL, USA, 2021, pp. 1-5.
  18. G. Liu, O. Ceylan, Y. Xu and K. Tomsovic, "Optimal voltage regulation for unbalanced distribution networks considering distributed energy resources," 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 2015, pp. 1-5. [CrossRef]
  19. Y. -J. Liu, S. -C. Yang, W. -M. Liu, Y. -D. Lee and C. -C. Cheng, "Voltage Regulation of Distribution Feeders by Distributed Energy Resources Coordination Control in Microgrid," 2021 IEEE International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 2021, pp. 1-6. [CrossRef]
  20. Chaoxian Lv, Kaiping Qu, Rui Liang, Guanyu Song,Multi-resource spatio-temporal coordinated voltage regulation for active distribution network with multiple integrated energy stations under uncertainties,Sustainable Energy, Grids and Networks,Volume 37,2024,101253,ISSN 2352-4677. [CrossRef]
  21. W. Huang and W. Zhang, "Research on Distributed WT Reactive Voltage Coordinated Control Strategy Connected to Distribution Network," 2021 4th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 2021, pp. 529-534. [CrossRef]
  22. B. Li et al., "Voltage Coordinated Control Strategy for Distribution Network With Controllable Devices Based on Different Time Response Scales," 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 2024, pp. 4245-4252. [CrossRef]
  23. Q. Zhang, J. Shang, J. Wang and H. Liu, "Coordinated Day-ahead and Intra-day Operation of Distribution Networks Considering the Active Support of Distributed PV and ES System," 2023 IEEE 4th China International Youth Conference On Electrical Engineering (CIYCEE), Chengdu, China, 2023, pp. 1-6. [CrossRef]
  24. https://german.cri.cn/.
  25. Y. Shang, A. Tang, L. Ma and Z. Tong, "Hybrid Power Transformer Voltage Control Strategy for Grid-connected Photovoltaics," 2024 7th International Conference on Energy, Electrical and Power Engineering (CEEPE), Yangzhou, China, 2024, pp. 1432-1437. [CrossRef]
  26. H. Zhang, C. Xia, P. Peng, N. Chen and B. Gao, "Research on the Voltage Regulation Strategy of Photovoltaic Power Plant," 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 2018, pp. 1620-1624. [CrossRef]
  27. M. He, K. Ji, J. Hou, T. Zhang and F. Xiao, "Study on the Participation Strategy of Multi-Energy Storage System Based on Battery Energy Storage in Grid Voltage Regulation," 2023 7th International Conference on Power and Energy Engineering (ICPEE), Chengdu, China, 2023, pp. 153-157. [CrossRef]
  28. X. Li, L. Wang, N. Yan and R. Ma, "Cooperative Dispatch of Distributed Energy Storage in Distribution Network With PV Generation Systems," in IEEE Transactions on Applied Superconductivity, vol. 31, no. 8, pp. 1-4, Nov. 2021, Art no. 0604304. [CrossRef]
  29. J. Kim, E. Muljadi, J. -W. Park and Y. C. Kang, "Flexible IQ–V Scheme of a DFIG for Rapid Voltage Regulation of a Wind Power Plant," in IEEE Transactions on Industrial Electronics, vol. 64, no. 11, pp. 8832-8842, Nov. 2017. [CrossRef]
  30. D. Mascarella, S. Li, G. Joos and P. Venne, "Reactive power coordination in DFIG based wind farms for voltage regulation & flicker mitigation," 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 2015, pp. 1-5. [CrossRef]
  31. H. Zhao, J. Yang, T. Li and X. Mei, "Coordinated Optimal Dispatching Method for Distributed Energy Storage and Distribution Network Under Multi-time Scale," 2023 3rd International Conference on Electrical Engineering and Mechatronics Technology (ICEEMT), Nanjing, China, 2023, pp. 403-406. [CrossRef]
  32. P. Li et al., "MPC-Based Local Voltage Control Strategy of DGs in Active Distribution Networks," in IEEE Transactions on Sustainable Energy, vol. 11, no. 4, pp. 2911-2921, Oct. 2020. [CrossRef]
Preprints 118695 g001
Figure 1. Voltage regulation mechanism of PV inverter.
Figure 1. Voltage regulation mechanism of PV inverter.
Preprints 118695 g001
Preprints 118695 g002
Figure 2. Voltage regulation mechanism of ES.
Figure 2. Voltage regulation mechanism of ES.
Preprints 118695 g002
Preprints 118695 g003
Figure 3. Voltage regulation mechanism of WT.
Figure 3. Voltage regulation mechanism of WT.
Preprints 118695 g003
Preprints 118695 g004
Figure 4. Multi-timescale reactive power control framework for distribution system.
Figure 4. Multi-timescale reactive power control framework for distribution system.
Preprints 118695 g004
Preprints 118695 g005
Figure 5. Event-triggered real-time voltage zoning control strategy.
Figure 5. Event-triggered real-time voltage zoning control strategy.
Preprints 118695 g005
Preprints 118695 g006
Figure 6. Control process under multi-source interaction environment.
Figure 6. Control process under multi-source interaction environment.
Preprints 118695 g006
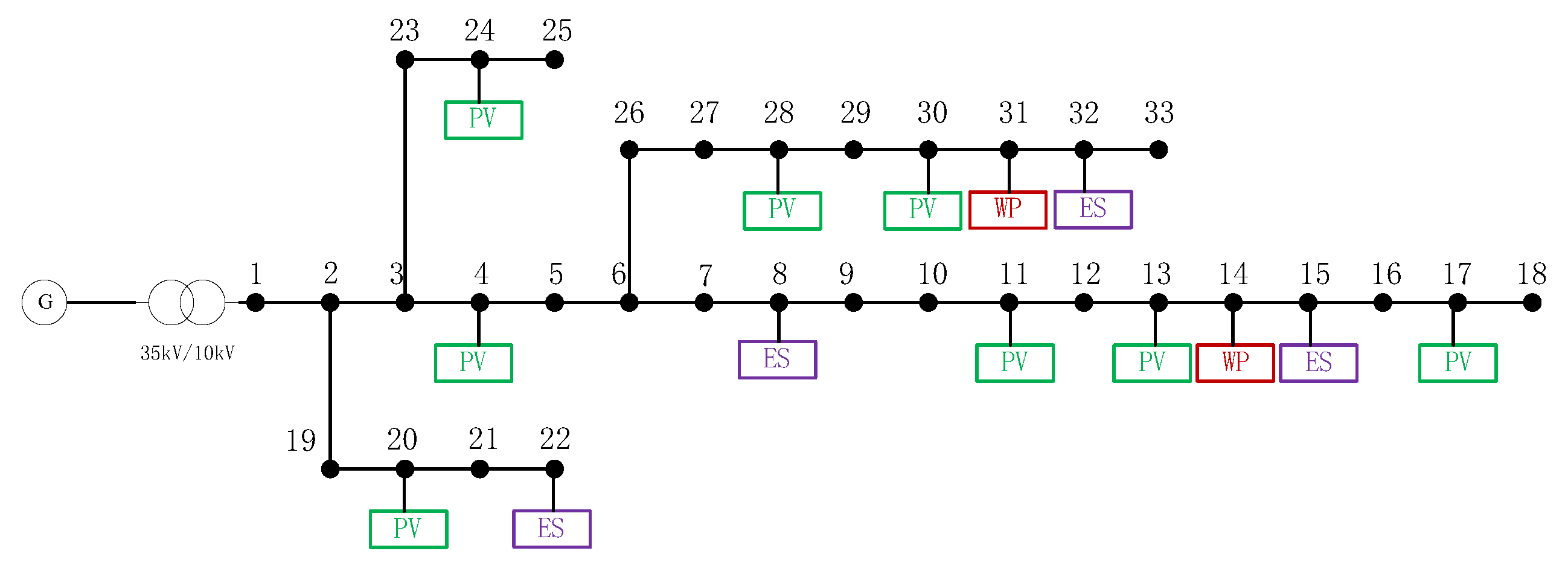
Preprints 118695 g007
Figure 7. Schematic diagram of IEEE33 nodes.
Figure 7. Schematic diagram of IEEE33 nodes.
Preprints 118695 g007
Preprints 118695 g008
Figure 8. PV total output, WP total output, and total load curve in typical day.
Figure 8. PV total output, WP total output, and total load curve in typical day.
Preprints 118695 g008
Preprints 118695 g009
Figure 9. PV power on node 4.
Figure 9. PV power on node 4.
Preprints 118695 g009
Preprints 118695 g010
Figure 10. ES power on node 8.
Figure 10. ES power on node 8.
Preprints 118695 g010
Preprints 118695 g011
Figure 11. WP power on node 14.
Figure 11. WP power on node 14.
Preprints 118695 g011
Preprints 118695 g012
Figure 12. Comparison chart of voltage of the distribution network before and after adjustment based on day-ahead strategy.
Figure 12. Comparison chart of voltage of the distribution network before and after adjustment based on day-ahead strategy.
Preprints 118695 g012
Preprints 118695 g013
Figure 13. Changes in the amount of PV regulation on node 4.
Figure 13. Changes in the amount of PV regulation on node 4.
Preprints 118695 g013
Preprints 118695 g014
Figure 14. Changes in the amount of ES regulation on node 8.
Figure 14. Changes in the amount of ES regulation on node 8.
Preprints 118695 g014
Preprints 118695 g015
Figure 15. Changes in the amount of ES regulation on node 14.
Figure 15. Changes in the amount of ES regulation on node 14.
Preprints 118695 g015
Preprints 118695 g016
Figure 16. Sensitivity of the remaining nodes to the 4-node.
Figure 16. Sensitivity of the remaining nodes to the 4-node.
Preprints 118695 g016
Preprints 118695 g017
Figure 17. Real-time reactive power regulation.
Figure 17. Real-time reactive power regulation.
Preprints 118695 g017
Table 1. Parameters related to distributed resources.
Table 1. Parameters related to distributed resources.
Distributed resource Access node Capacity/kVA
PV 4, 11, 24 500
13, 20, 30 800
17, 28 1000
ES 8, 15, 22, 32 200
WT 14, 31 750
Table 2. Active and reactive power regulation strategies before and after correction.
Table 2. Active and reactive power regulation strategies before and after correction.
node Predicted output/kW Pre-calibration reactive power strategy/kVar Pre-correction meritorious strategy/kW Actual
output/kW		 Post-calibration reactive power strategy
/kVar		 Post-correction credit strategy
/kW		 Inverter Configuration Capacity
/kVA
4 427.44 -433 213.72 454.35 -433.01 227.17 500
11 427.44 433 213.72 454.35 433.01 227.17 500
13 664.26 -72.1 332.13 706.07 -81.24 353.04 800
17 830.32 -141.5 415.16 882.59 -150.9 441.29 1000
20 664.26 -332.85 332.13 706.07 -356.7 353.04 800
24 427.44 -254.4 213.72 454.35 -271.43 227.17 500
28 830.32 -392.88 415.16 882.59 -408.91 441.29 1000
30 664.26 -320.21 332.13 706.07 -348.7 353.04 800
14 279.7 32.3895 50.6 299.4 29.9738 54.71 750
31 160 32.3874 50.6 156.9 29.9724 54.71 750
8 - 186.39 -72.51 - -62.66 189.93 200
15 - 176.35 -94.34 - -91.87 177.65 200
22 - 83.6 -95.16 - -95.04 83.5 200
32 - 140.37 -138.85 - -138.78 140.31 200
Table 3. Real-time adjustable active and reactive power.
Table 3. Real-time adjustable active and reactive power.
Node Post-calibration reactive
power strategy /kVar		 Post-correction
credit strategy /kW		 Inverter Configuration Capacity /kVA Adjustable reactive
power capacity/kVar		 Adjustable active capacity /kW
4 -433.01 227.17 500 [-12.4,878.42] 227.17
11 433.01 227.17 500 [-878.42,12.4] 227.17
13 -81.24 353.04 800 [-636.65,799.13] 353.04
17 -150.9 441.29 1000 [-746.46,1048.26] 441.29
20 -356.7 353.04 800 [-361.19,1074.59] 353.04
24 -271.43 227.17 500 [-173.98,716.84] 227.17
28 -408.91 441.29 1000 [-488.45,1306.27] 441.29
30 -348.7 353.04 800 [-369.19,1066.59] 353.04
14 29.9738 54.71 750 [-778,718] 54.71
31 29.9724 54.71 750 [-778,718] 54.71
8 -62.66 189.93 200 [-110.54,235.86] 100
15 -91.87 177.65 200 [-81.34,265.07] 100
22 -95.04 83.5 200 [-78.16,268.24] 100
32 -138.78 140.31 200 [-34.42,311.98] 100
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated