Prerpints.org logo
Preprint
Article

New Tests on Lorentz Invariance Violation Using Energy-Resolved Polarimetry of Gamma-Ray Bursts

This version is not peer-reviewed.

Submitted:

19 September 2024

Posted:

20 September 2024

You are already at the latest version

Abstract
One of the manifestations of Lorentz invariance violation (LIV) is vacuum birefringence, which leads to an energy-dependent rotation of the polarization plane of linearly polarized photons arising from an astrophysical source. Here we use the energy-resolved polarization measurements in the prompt $\gamma$-ray emission of five bright gamma-ray bursts (GRBs) to constrain this vacuum birefringent effect. Our results show that at the 95\% confidence level, the birefringent parameter $\eta$ characterizing the broken degree of Lorentz invariance can be constrained to be $|\eta|<\mathcal{O}(10^{-15}-10^{-16})$, which represent an improvement of at least eight orders of magnitude over existing limits from multi-band optical polarization observations. Moreover, our constraints are competitive with previous best bounds from the single $\gamma$-ray polarimetry of other GRBs. We emphasize that, thanks to the adoption of the energy-resolved polarimetric data set, our results on $\eta$ are statistically more robust. Future polarization measurements of GRBs at higher energies and larger distances would further improve LIV limits through the birefringent effect.
Keywords: 
Subject: 
Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

Lorentz invariance is a fundamental postulate of Einstein’s theory of relativity as well as of the Standard Model of particle physics. However, a violation or deformation of Lorentz invariance at around the Planck energy scale E Pl = ℏ c 5 / G ≃ 1.22 × 10 19 GeV are predicted in many quantum gravity theories attempting to unify quantum theory and gravity [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Experimental searches for potential signatures of Lorentz invariance violation (LIV) have been conducted in various systems (see [17] for a continuously updated compilation).
For photons with energy E ≪ E Pl , one of the most discussed LIV-induced modifications to the dispersion relation can be parameterized as [18]
E ± 2 = p 2 c 2 ± 2 η E Pl p 3 c 3 ,
where ± represents opposite helicities, i.e., right- and left-handed circular polarization states of the photon, and η is a dimensionless parameter describing the broken degree of Lorentz invariance. This modified dispersion relation with η ≠ 0 implies that group velocities of photons with different circular polarizations should differ slightly. Consequently, the polarization vector of a linearly polarized light may experience an energy-dependent rotation, also known as vacuum birefringence. Observations of linear polarization can therefore be used to test Lorentz invariance (e.g., [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41]). Although the effects of vacuum birefringence are supposed to be minuscule at attainable energies, they can increase with energy and accumulate over vast propagation distances, leading to a measurable rotation of the plane of linear polarization as a function of energy. The rotation angle during the propagation from the redshift z to the observer is given by [30,32]:
Δ ϕ LIV ( E ) ≃ η E 2 ℏ E Pl ∫ 0 z 1 + z ′ H ( z ′ ) d z ′ ,
where E is the observed photon energy. Also, H ( z ) = H 0 Ω m ( 1 + z ) 3 + Ω Λ is the cosmic expansion rate, assuming a flat Λ CDM model with Hubble constant H 0 = 67.4 km s − 1 Mpc − 1 , matter energy density Ω m = 0.315 , and vacuum energy density Ω Λ = 1 − Ω m [42].
To date, the most stringent limits on the birefringent parameter η have been obtained using the single multi-hundred keV polarimetry of gamma-ray bursts (GRBs), yielding η < O ( 10 − 15 − 10 − 16 ) [32,33,34,35,38]. These upper limits stem from the argument that vacuum birefringence would produce opposite oriented polarization vectors, thereby washing out most of the net polarization of the signal. Hence, the detection of highly polarized sources can place upper bounds on η . Even though such LIV tests have reached an extremely high accuracy [32,33,34,35,38], the outcomes of these upper limits on η are lack of significantly statistical robustness.
Instead of requiring the indirect argument that the net polarization would be severely depleted by the presence of LIV, some studies directly searched for an energy-dependent change of the linear polarization angle, resulting from vacuum birefringence, in the energy-resolved spectro-polarimetric data [28,40,41]. By fitting the energy-resolved polarization data of the optical afterglows of GRB 020813 and GRB 021004, Fan et al. [28] obtained a limit of − 2 × 10 − 7 < η < 1.4 × 10 − 7 at the 3 σ confidence level (see also [40]). Zhou et al. [41] applied the same treatment to multi-band optical polarization measurements of five blazars, and showed that Lorentz invariance passes the strict test with a similar accuracy of O ( 10 − 7 ) . It is obvious from Equation (2) that the greater sensitivity to small values of η can be expected from those astrophysical sources with higher-energy polarimetry and larger cosmological distances. Compared to γ -ray polarization constraints [32,33,34,35,38], observations of optical polarization set less stringent constraints on η as expected [28,40,41].
Recently, Gupta et al. [43] presented a systematic and uniform spectro-polarimetric analysis on five bright GRBs detected by A s t r o S a t CZTI, providing the first energy-resolved polarization measurements in the prompt γ -ray emission of GRBs. In this work, we study Lorentz-violating effects by analyzing the energy-dependent behavior of polarization angle during the prompt phase of these five GRBs.

2. Energy-Resolved Polarization Measurements of Prompt GRB Emission

Gupta et al. [43] performed an energy-resolved polarization analysis on the prompt γ -ray emission of five bright GRBs using archival data from A s t r o S a t CZTI. The linear polarization measurements obtained using the energy sliding binning algorithm are displayed in Figure 8 of Gupta et al. [43], from which we can extract the calculated values of the energy-resolved polarization angles and the corresponding energy segments of all the five bursts.
In order to obtain bounds on LIV with observations of γ -ray linear polarization, we also need to know the source distances. But except for GRB 160623A at z = 0.367 [44], the other four GRBs have no measured redshifts. The well-known luminosity relation with a standard deviation σ sc = 0.30 [45,46], log 10 [ E p ( 1 + z ) / keV ] = ( − 22.98 ± 1.81 ) + ( 0.49 ± 0.03 ) log 10 [ L iso / erg s − 1 ] , is therefore adopted to estimate the redshifts of the four GRBs. Here E p is the spectral peak energy in the observer frame and L iso is the isotropic peak luminosity. We use the observed flux and E p of the four bursts (GRB 160325A: 10–40000 keV flux 5.28 × 10 − 7 erg cm − 2 s − 1 and E p = 228.54 keV ; GRB 160703A: 15–150 keV flux 2.29 × 10 − 7 erg cm − 2 s − 1 and E p = 332.46 keV ; GRB 160802A: 10–40000 keV flux 5.05 × 10 − 6 erg cm − 2 s − 1 and E p = 279.43 keV ; GRB 160821A: 10–40000 keV flux 3.12 × 10 − 5 erg cm − 2 s − 1 and E p = 941.35 keV ) to calculate L iso for different redshifts. Detailed information regarding the time-integrated spectral parameters for these GRBs can be found in Table B1 of Gupta et al. [43]. By requiring that the bursts enter the 3 σ region of the luminosity relation, we derive z ≥ 0.267 for GRB 160325A, z ≥ 0.316 for GRB 160703A, z ≥ 0.102 for GRB 160802A, and z ≥ 0.153 for GRB 160821A. Hereafer, we conservatively take the lower limits of redshifts for robust discussions on LIV.

3. New Precision Limits on LIV

Considering the energy-dependent rotation angle of the linear polarization plane induced by the vacuum birefringent effect ( Δ ϕ LIV ; i.e., Equation 2), the observed linear polarization angle ( ϕ obs ) for photons emitted at a certain energy range from a given astrophysical source should consist of two terms
ϕ obs = ϕ 0 + Δ ϕ LIV E ,
where ϕ 0 denotes the intrinsic polarization angle. In practice, it is hard to distinguish the LIV-induced rotation angle Δ ϕ LIV from an unknown intrinsic polarization angle ϕ 0 caused by the source’s unknown emission mechanism. Following Fan et al. [28], we simply assume that all photons in different energy channels are emitted with the same (unknown) intrinsic polarization angle (see also [40,41]). As ϕ 0 is assumed to be an unknown constant, potential evidence for vacuum birefringence (or robust limits on the birefringent parameter η and ϕ 0 ) could be directly obtained by fitting the energy-dependent behavior of observed polarization angles with Equation (3). Here we explore the implications and limits that can be set from the energy-resolved polarization measurements of the prompt γ -ray emission of five GRBs [43].
The observed polarization angles as a function of energy for all five GRBs are shown in Figure 1. For each GRB, the two free parameters ( η and ϕ 0 ) are optimized via a maximization of the likelihood function:
L = ∏ i 1 2 π σ tot , i exp − ϕ obs , i − ϕ 0 − Δ ϕ LIV η , E i 2 2 σ tot , i 2 ,
where the variance
σ tot , i 2 = σ ϕ obs , i 2 + 2 Δ ϕ LIV E i σ E i 2
is given by the quadratic sum of the measurement error σ ϕ obs , i in ϕ obs , i and the propagated error of σ E i . The Python Markov chain Monte Carlo module, EMCEE [47], is applied to explore the posterior probability distributions of the free parameters. The 1D marginalized probability distributions and 2D contours with 1–2 σ confidence levels for the two parameters, constrained by the energy-resolved polarization data of each GRB, are presented in Figure 2. These contours show that at the 95% confidence level, the inferred values are η = ( 1 . 7 − 3.2 + 4.8 ) × 10 − 16 and ϕ 0 = 0 . 15 − 1.12 + 0.93 rad for GRB 160325A, η = ( 2 . 0 − 2.1 + 3.8 ) × 10 − 16 and ϕ 0 = − 0 . 31 − 1.36 + 0.96 rad for GRB 160623A, η = ( 1 . 9 − 5.1 + 4.6 ) × 10 − 16 and ϕ 0 = − 0 . 29 − 1.39 + 1.33 rad for GRB 160703A, η = ( − 9 . 4 − 15.4 + 15.9 ) × 10 − 16 and ϕ 0 = 1 . 25 − 1.34 + 1.31 rad for GRB 160802A, and η = ( 1 . 2 − 5.2 + 6.7 ) × 10 − 16 and ϕ 0 = 0 . 49 − 1.03 + 0.82 rad for GRB 160821A. The resulting constraints on η and ϕ 0 for each GRB data are summarized in Table 1. We can see that all the inferred values of η are consistent with 0 at the 2 σ confidence level, implying that there is no evidence of LIV. To illustrate the fits, the energy-dependence of polarization angle expected from the LIV model (see Equation 3; with each set of the best-fit parameters) are shown as solid curves in Figure 1. Also, the resulting goodness-of-fit values of reduced χ dof 2 are provided in Figure 1.
Compared with previous results obtained from multi-band optical polarization measurements ( | η | < 2 × 10 − 7 [28,40,41]), our limits on η represent an improvement of at least eight orders of magnitude. While our limits are essentially as good as previous best bounds from γ -ray polarimetry of other GRBs ( η < O ( 10 − 15 − 10 − 16 ) [32,33,34,35,38]), there is merit to the results. Thanks to the adoption of the energy-resolved polarization data, our constraints on η could be statistically more robust compared to previous results, which were based on a single polarization measurement in the 100s keV energy range and the argument that vacuum birefringence would significantly suppress the net polarization over a broad bandwidth.

4. Summary

Violations of Lorentz invariance can lead to vacuum birefringence of light, which results in an energy-dependent rotation of the polarization plane of linearly polarized photons. Lorentz invariance can therefore be tested with astrophysical polarization measurements. Very recently, Gupta et al. [43] reported the energy-resolved polarization measurements in the prompt γ -ray emission of five bright GRBs detected by A s t r o S a t CZTI. In this work, we investigated the implications and limits on LIV that can be set from these unique polarization observations.
Assuming an unknown constant for the intrinsic polarization angle, we searched for the energy-dependent change of the linear polarization angle, resulting from the birefringent effect, in the spectro-polarimetric data of these five GRBs. By fitting the polarization angle and energy measurements of each GRB, we place a statistically robust limit on the birefringent parameter η quantifying the broken degree of Lorentz invariance. For instance, with the data of GRB 160623A, we have − 0.1 × 10 − 16 < η < 5.8 × 10 − 16 at the 2 σ confidence level. Similar η constraints have been obtained from the other four GRBs. Our new results represent sensitivities improved by at least eight orders of magnitude over existing η bounds from multi-band optical polarization measurements. Moreover, our constraints are competitive with previous best bounds from γ -ray polarimetry of other GRBs. Unlike previous analyses that only rely on a single polarization measurement in the 100s keV rang, our constraints derived from energy-resolved polarimetric data set are statistically more robust. Future polarization measurements of astrophysical sources such as GRBs at higher γ -ray energies and larger distances would further enhance sensitivity to LIV tests through the vacuum birefringent effect.
It is well known that magnetized plasma can also produce the energy-dependent rotation of the linear polarization plane (the so-called Faraday rotation). The dependence of the rotation angle on Faraday rotation is Δ ϕ Far ∝ E − 2 , quite different from its dependence on LIV effects as Δ ϕ LIV ∝ E 2 shown in Equation (2). The Faraday rotation angle Δ ϕ Far would be significant at the low-frequency radio band. But for high-energy photons, such as the γ -ray signals considered here, Δ ϕ Far is negligible.

Funding

This research was funded by the Strategic Priority Research Program of the Chinese Academy of Sciences (grant No. XDB0550400), the National Natural Science Foundation of China (grant Nos. 12422307, 12373053, and 12321003), the Key Research Program of Frontier Sciences (grant No. ZDBS-LY-7014) of Chinese Academy of Sciences, and the Natural Science Foundation of Jiangsu Province (grant No. BK20221562).

Data Availability Statement

The data underlying this article are available in Gupta et al. [43].

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kostelecký, V.A.; Samuel, S. Spontaneous breaking of Lorentz symmetry in string theory. Phys. Rev. D 1989, 39, 683–685. [Google Scholar] [CrossRef]
  2. Amelino-Camelia, G.; Ellis, J.; Mavromatos, N.E.; Nanopoulos, D.V. Distance Measurement and Wave Dispersion in a Liouville-String Approach to Quantum Gravity. International Journal of Modern Physics A 1997, 12, 607–623. [arXiv:hep-th/hep-th/9605211]. [CrossRef]
  3. Ellis, J.; Mavromatos, N.E.; Nanopoulos, D.V. Search for Quantum Gravity. General Relativity and Gravitation 1999, 31, 1257. [arXiv:gr-qc/gr-qc/9905048]. [CrossRef]
  4. Amelino-Camelia, G. Relativity: Special treatment. Nature 2002, 418, 34–35. [arXiv:gr-qc/gr-qc/0207049]. [CrossRef] [PubMed]
  5. Magueijo, J.; Smolin, L. Lorentz Invariance with an Invariant Energy Scale. Phys. Rev. Lett. 2002, 88, 190403. [arXiv:hep-th/hep-th/0112090]. [CrossRef]
  6. Alfaro, J.; Morales-Técotl, H.A.; Urrutia, L.F. Loop quantum gravity and light propagation. Phys. Rev. D 2002, 65, 103509. [arXiv:hep-th/hep-th/0108061]. [CrossRef]
  7. Mattingly, D. Modern Tests of Lorentz Invariance. Living Reviews in Relativity 2005, 8, 5. [arXiv:gr-qc/gr-qc/0502097]. [CrossRef]
  8. Li, T.; Mavromatos, N.E.; Nanopoulos, D.V.; Xie, D. Time delays of strings in D-particle backgrounds and vacuum refractive indices. Physics Letters B 2009, 679, 407–413. [arXiv:hep-th/0903.1303]. [CrossRef]
  9. Amelino-Camelia, G. Quantum-Spacetime Phenomenology. Living Reviews in Relativity 2013, 16, 5. [arXiv:gr-qc/0806.0339]. [CrossRef]
  10. Tasson, J.D. What do we know about Lorentz invariance? Reports on Progress in Physics 2014, 77, 062901. [arXiv:hep-ph/1403.7785]. [CrossRef]
  11. Wei, J.J.; Wu, X.F. Testing fundamental physics with astrophysical transients. Frontiers of Physics 2021, 16, 44300. [arXiv:astro-ph.HE/2102.03724]. [CrossRef]
  12. He, P.; Ma, B.Q. Lorentz Symmetry Violation of Cosmic Photons. Universe 2022, 8, 323. [arXiv:astro-ph.HE/2206.08180]. [CrossRef]
  13. Addazi, A.; Alvarez-Muniz, J.; Alves Batista, R.; Amelino-Camelia, G.; Antonelli, V.; Arzano, M.; Asorey, M.; Atteia, J.L.; Bahamonde, S.; Bajardi, F.; Ballesteros, A.; Baret, B.; Barreiros, D.M.; Basilakos, S.; Benisty, D.; Birnholtz, O.; Blanco-Pillado, J.J.; Blas, D.; Bolmont, J.; Boncioli, D.; Bosso, P.; Calcagni, G.; Capozziello, S.; Carmona, J.M.; Cerci, S.; Chernyakova, M.; Clesse, S.; Coelho, J.A.B.; Colak, S.M.; Cortes, J.L.; Das, S.; D’Esposito, V.; Demirci, M.; Di Luca, M.G.; di Matteo, A.; Dimitrijevic, D.; Djordjevic, G.; Prester, D.D.; Eichhorn, A.; Ellis, J.; Escamilla-Rivera, C.; Fabiano, G.; Franchino-Viñas, S.A.; Frassino, A.M.; Frattulillo, D.; Funk, S.; Fuster, A.; Gamboa, J.; Gent, A.; Gergely, L.Á.; Giammarchi, M.; Giesel, K.; Glicenstein, J.F.; Gracia-Bondía, J.; Gracia-Ruiz, R.; Gubitosi, G.; Guendelman, E.I.; Gutierrez-Sagredo, I.; Haegel, L.; Heefer, S.; Held, A.; Herranz, F.J.; Hinderer, T.; Illana, J.I.; Ioannisian, A.; Jetzer, P.; Joaquim, F.R.; Kampert, K.H.; Uysal, A.K.; Katori, T.; Kazarian, N.; Kerszberg, D.; Kowalski-Glikman, J.; Kuroyanagi, S.; Lämmerzahl, C.; Said, J.L.; Liberati, S.; Lim, E.; Lobo, I.P.; López-Moya, M.; Luciano, G.G.; Manganaro, M.; Marcianò, A.; Martín-Moruno, P.; Martinez, M.; Martinez, M.; Martínez-Huerta, H.; Martínez-Miravé, P.; Masip, M.; Mattingly, D.; Mavromatos, N.; Mazumdar, A.; Méndez, F.; Mercati, F.; Micanovic, S.; Mielczarek, J.; Miller, A.L.; Milosevic, M.; Minic, D.; Miramonti, L.; Mitsou, V.A.; Moniz, P.; Mukherjee, S.; Nardini, G.; Navas, S.; Niechciol, M.; Nielsen, A.B.; Obers, N.A.; Oikonomou, F.; Oriti, D.; Paganini, C.F.; Palomares-Ruiz, S.; Pasechnik, R.; Pasic, V.; Pérez de los Heros, C.; Pfeifer, C.; Pieroni, M.; Piran, T.; Platania, A.; Rastgoo, S.; Relancio, J.J.; Reyes, M.A.; Ricciardone, A.; Risse, M.; Frias, M.D.R.; Rosati, G.; Rubiera-Garcia, D.; Sahlmann, H.; Sakellariadou, M.; Salamida, F.; Saridakis, E.N.; Satunin, P.; Schiffer, M.; Schüssler, F.; Sigl, G.; Sitarek, J.; Peracaula, J.S.; Sopuerta, C.F.; Sotiriou, T.P.; Spurio, M.; Staicova, D.; Stergioulas, N.; Stoica, S.; Strišković, J.; Stuttard, T.; Cerci, D.S.; Tavakoli, Y.; Ternes, C.A.; Terzić, T.; Thiemann, T.; Tinyakov, P.; Torri, M.D.C.; Tórtola, M.; Trimarelli, C.; Trześniewski, T.; Tureanu, A.; Urban, F.R.; Vagenas, E.C.; Vernieri, D.; Vitagliano, V.; Wallet, J.C.; Zornoza, J.D. Quantum gravity phenomenology at the dawn of the multi-messenger era-A review. Progress in Particle and Nuclear Physics 2022, 125, 103948. [arXiv:hep-ph/2111.05659]. [CrossRef]
  14. Wei, J.J.;Wu, X.F., Tests of Lorentz Invariance. In Handbook of X-ray and Gamma-ray Astrophysics; Springer Nature Singapore: Singapore, 2022; pp. 1–30. [CrossRef]
  15. Alves Batista, R.; Amelino-Camelia, G.; Boncioli, D.; Carmona, J.M.; di Matteo, A.; Gubitosi, G.; Lobo, I.; Mavromatos, N.E.; Pfeifer, C.; Rubiera-Garcia, D.; Saridakis, E.N.; Terzić, T.; Vagenas, E.C.; Vargas Moniz, P.; Abdalla, H.; Adamo, M.; Addazi, A.; Anagnostopoulos, F.K.; Antonelli, V.; Asorey, M.; Ballesteros, A.; Basilakos, S.; Benisty, D.; Boettcher, M.; Bolmont, J.; Bonilla, A.; Bosso, P.; Bouhmadi-López, M.; Burderi, L.; Campoy-Ordaz, A.; Caroff, S.; Cerci, S.; Cortes, J.L.; D’Esposito, V.; Das, S.; de Cesare, M.; Demirci, M.; Di Lodovico, F.; Di Salvo, T.; Diego, J.M.; Djordjevic, G.; Domi, A.; Ducobu, L.; Escamilla-Rivera, C.; Fabiano, G.; Fernández-Silvestre, D.; Franchino-Viñas, S.A.; Frassino, A.M.; Frattulillo, D.; Garay, L.J.; Gaug, M.; Gergely, L.Á.; Guendelman, E.I.; Guetta, D.; Gutierrez-Sagredo, I.; He, P.; Heefer, S.; Jurić, T.; Katori, T.; Kowalski-Glikman, J.; Lambiase, G.; Levi Said, J.; Li, C.; Li, H.; Luciano, G.G.; Ma, B.Q.; Marciano, A.; Martinez, M.; Mazumdar, A.; Menezes, G.; Mercati, F.; Minic, D.; Miramonti, L.; Mitsou, V.A.; Mustamin, M.F.; Navas, S.; Olmo, G.J.; Oriti, D.; Övgün, A.; Pantig, R.C.; Parvizi, A.; Pasechnik, R.; Pasic, V.; Petruzziello, L.; Platania, A.; Rasouli, S.M.M.; Rastgoo, S.; Relancio, J.J.; Rescic, F.; Reyes, M.A.; Rosati, G.; Sakallı, İ.; Salamida, F.; Sanna, A.; Staicova, D.; Strišković, J.; Sunar Cerci, D.; Torri, M.D.C.; Vigliano, A.; Wagner, F.; Wallet, J.C.; Wojnar, A.; Zarikas, V.; Zhu, J.; Zornoza, J.D. White Paper and Roadmap for Quantum Gravity Phenomenology in the Multi-Messenger Era. arXiv e-prints 2023, p. arXiv:2312.00409. [arXiv:gr-qc/2312.00409]. [CrossRef]
  16. Desai, S. Desai, S., Astrophysical and Cosmological Searches for Lorentz Invariance Violation. In Recent Progress on Gravity Tests: Challenges and Future Perspectives; Springer Nature Singapore: Singapore, 2024; pp. 433–463. [CrossRef]
  17. Kostelecký, V.A.; Russell, N. Data tables for Lorentz and CPT violation. Reviews of Modern Physics 2011, 83, 11–32. [arXiv:hep-ph/0801.0287]. [CrossRef]
  18. Myers, R.C.; Pospelov, M. Ultraviolet Modifications of Dispersion Relations in Effective Field Theory. Phys. Rev. Lett. 2003, 90, 211601. [arXiv:hep-ph/hep-ph/0301124]. [CrossRef]
  19. Carroll, S.M.; Field, G.B.; Jackiw, R. Limits on a Lorentz- and parity-violating modification of electrodynamics. Phys. Rev. D 1990, 41, 1231–1240. [Google Scholar] [CrossRef]
  20. Colladay, D.; Kostelecký, V.A. Lorentz-violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [hep-ph/9809521]. [CrossRef]
  21. Gleiser, R.J.; Kozameh, C.N. Astrophysical limits on quantum gravity motivated birefringence. Phys. Rev. D 2001, 64, 083007. [gr-qc/0102093]. [CrossRef]
  22. Kostelecký, V.A.; Mewes, M. Cosmological Constraints on Lorentz Violation in Electrodynamics. Physical Review Letters 2001, 87, 251304. [hep-ph/0111026]. [CrossRef]
  23. Kostelecký, V.A.; Mewes, M. Sensitive Polarimetric Search for Relativity Violations in Gamma-Ray Bursts. Physical Review Letters 2006, 97, 140401. [hep-ph/0607084]. [CrossRef]
  24. Kostelecký, V.A.; Mewes, M. Lorentz-Violating Electrodynamics and the Cosmic Microwave Background. Physical Review Letters 2007, 99, 011601. [astro-ph/0702379]. [CrossRef] [PubMed]
  25. Kostelecký, V.A.; Mewes, M. Constraints on Relativity Violations from Gamma-Ray Bursts. Physical Review Letters 2013, 110, 201601. [arXiv:astro-ph.HE/1301.5367]. [CrossRef] [PubMed]
  26. Mitrofanov, I.G. Astrophysics (communication arising): A constraint on canonical quantum gravity? Nature 2003, 426, 139. [Google Scholar] [CrossRef] [PubMed]
  27. Jacobson, T.; Liberati, S.; Mattingly, D.; Stecker, F.W. New Limits on Planck Scale Lorentz Violation in QED. Physical Review Letters 2004, 93, 021101. [astro-ph/0309681]. [CrossRef] [PubMed]
  28. Fan, Y.Z.; Wei, D.M.; Xu, D. γ-ray burst ultraviolet/optical afterglow polarimetry as a probe of quantum gravity. Mon. Not. R. Astron. Soc. 2007, 376, 1857–1860. [astro-ph/0702006]. [CrossRef]
  29. Gubitosi, G.; Pagano, L.; Amelino-Camelia, G.; Melchiorri, A.; Cooray, A. A constraint on Planck-scale modifications to electrodynamics with CMB polarization data. J. Cosmol. Astropart. Phys. 2009, 8, 021. [arXiv:astro-ph.CO/0904.3201]. [CrossRef]
  30. Laurent, P.; Götz, D.; Binétruy, P.; Covino, S.; Fernandez-Soto, A. Constraints on Lorentz Invariance Violation using integral/IBIS observations of GRB041219A. Phys. Rev. D 2011, 83, 121301. [arXiv:astro-ph.HE/1106.1068]. [CrossRef]
  31. Stecker, F.W. A new limit on Planck scale Lorentz violation from γ-ray burst polarization. Astroparticle Physics 2011, 35, 95–97. [arXiv:astro-ph.HE/1102.2784]. [CrossRef]
  32. Toma, K.; Mukohyama, S.; Yonetoku, D.; Murakami, T.; Gunji, S.; Mihara, T.; Morihara, Y.; Sakashita, T.; Takahashi, T.; Wakashima, Y.; Yonemochi, H.; Toukairin, N. Strict Limit on CPT Violation from Polarization of γ-Ray Bursts. Phys. Rev. Lett. 2012, 109, 241104. [arXiv:astro-ph.HE/1208.5288]. [CrossRef]
  33. Götz, D.; Covino, S.; Fernández-Soto, A.; Laurent, P.; Bošnjak, Ž. The polarized gamma-ray burst GRB 061122. Mon. Not. R. Astron. Soc. 2013, 431, 3550–3556. [arXiv:astro-ph.HE/1303.4186]. [CrossRef]
  34. Götz, D.; Laurent, P.; Antier, S.; Covino, S.; D’Avanzo, P.; D’Elia, V.; Melandri, A. GRB 140206A: the most distant polarized gamma-ray burst. Mon. Not. R. Astron. Soc. 2014, 444, 2776–2782. [arXiv:astro-ph.HE/1408.4121]. [CrossRef]
  35. Lin, H.N.; Li, X.; Chang, Z. Gamma-ray burst polarization reduction induced by the Lorentz invariance violation. Mon. Not. R. Astron. Soc. 2016, 463, 375–381. [arXiv:hep-ph/1609.00193]. [CrossRef]
  36. Kislat, F.; Krawczynski, H. Planck-scale constraints on anisotropic Lorentz and C P T invariance violations from optical polarization measurements. Phys. Rev. D 2017, 95, 083013. [arXiv:astro-ph.HE/1701.00437]. [CrossRef]
  37. Friedman, A.S.; Leon, D.; Crowley, K.D.; Johnson, D.; Teply, G.; Tytler, D.; Keating, B.G.; Cole, G.M. Constraints on Lorentz invariance and C P T violation using optical photometry and polarimetry of active galaxies BL Lacertae and S5 B 0716 +714. Phys. Rev. D 2019, 99, 035045. [arXiv:astro-ph.HE/1809.08356]. [CrossRef]
  38. Wei, J.J. New constraints on Lorentz invariance violation with polarized gamma-ray bursts. Mon. Not. R. Astron. Soc. 2019, 485, 2401–2406. [arXiv:astro-ph.HE/1905.03413]. [CrossRef]
  39. Friedman, A.S.; Gerasimov, R.; Leon, D.; Stevens, W.; Tytler, D.; Keating, B.G.; Kislat, F. Improved constraints on anisotropic birefringent Lorentz invariance and C P T violation from broadband optical polarimetry of high redshift galaxies. Phys. Rev. D 2020, 102, 043008. [arXiv:astro-ph.HE/2003.00647]. [CrossRef]
  40. Wei, J.J.; Wu, X.F. Testing the weak equivalence principle and Lorentz invariance with multiwavelength polarization observations of GRB optical afterglows. European Physical Journal Plus 2020, 135, 527. [arXiv:astro-ph.HE/2006.11528]. [CrossRef]
  41. Zhou, Q.Q.; Yi, S.X.; Wei, J.J.; Wu, X.F. Constraints on Lorentz Invariance Violation with Multiwavelength Polarized Astrophysical Sources. Galaxies 2021, 9, 44. [arXiv:astro-ph.HE/2106.05733]. [CrossRef]
  42. Planck Collaboration. ; others. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [arXiv:astro-ph.CO/1807.06209]. [CrossRef]
  43. Gupta, R.; Pandey, S.B.; Gupta, S.; Chattopadhayay, T.; Bhattacharya, D.; Bhalerao, V.; Castro-Tirado, A.J.; Valeev, A.; Ror, A.K.; Sharma, V.; Racusin, J.; Aryan, A.; Iyyani, S.; Vadawale, S. A Detailed Time-resolved and Energy-resolved Spectro-polarimetric Study of Bright Gamma-Ray Bursts Detected by AstroSat CZTI in Its First Year of Operation. Astrophys. J. 2024, 972, 166. [Google Scholar] [CrossRef]
  44. Malesani, D.; de Ugarte Postigo, A.; de Pasquale, M.; Kann, D.A.; Cano, Z.; Perley, D.A.; Izzo, L.; Thoene, C.C.; Butler, N.; Watson, A.M.; Kutyrev, A.; Lee, W.H.; Richer, M.G.; Fox, O.; Prochaska, J.X.; Bloom, J.S.; Cucchiara, A.; Troja, E.; Littlejohns, O.; Ramirez-Ruiz, E.; de Diego, J.A.; Georgiev, L.; Gonzalez, J.; Roman-Zuniga, C.; Gehrels, N.; Moseley, H.; Capone, J.; Golkhou, V.Z.; Toy, V. GRB 160623A: optical astrometry, photometry, and redshift. GRB Coordinates Network 2016, 19708, 1. [Google Scholar]
  45. Yonetoku, D.; Murakami, T.; Nakamura, T.; Yamazaki, R.; Inoue, A.K.; Ioka, K. Gamma-Ray Burst Formation Rate Inferred from the Spectral Peak Energy-Peak Luminosity Relation. Astrophys. J. 2004, 609, 935–951. [arXiv:astro-ph/astro-ph/0309217]. [CrossRef]
  46. Nava, L.; Salvaterra, R.; Ghirlanda, G.; Ghisellini, G.; Campana, S.; Covino, S.; Cusumano, G.; D’Avanzo, P.; D’Elia, V.; Fugazza, D.; Melandri, A.; Sbarufatti, B.; Vergani, S.D.; Tagliaferri, G. A complete sample of bright Swift long gamma-ray bursts: testing the spectral-energy correlations. Mon. Not. R. Astron. Soc. 2012, 421, 1256–1264. [arXiv:astro-ph.HE/1112.4470]. [CrossRef]
  47. Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [arXiv:astro-ph.IM/1202.3665]. [CrossRef]
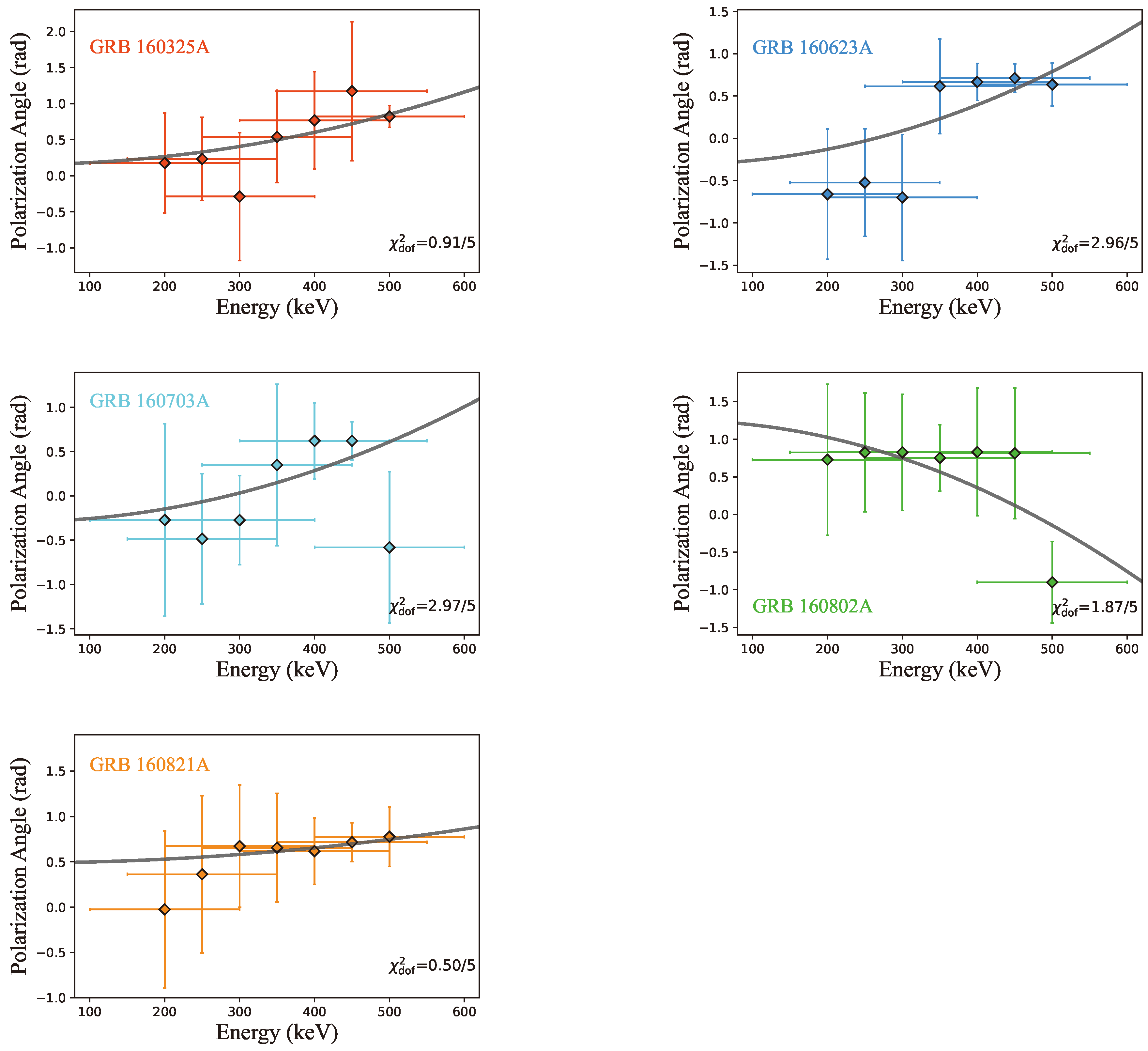
Preprints 118705 g001
Figure 1. The evolution of polarization angle with energy. Data points are the energy-resolved polarization measurements of five GRBs, and the vertical and horizontal error bars, respectively, correspond to the measurement errors of the polarization angles and the ranges of each energy bin. Curves show the optimal predictions of the LIV model (see text and Equation 3). The goodness-of-fit χ dof 2 are also listed.
Figure 1. The evolution of polarization angle with energy. Data points are the energy-resolved polarization measurements of five GRBs, and the vertical and horizontal error bars, respectively, correspond to the measurement errors of the polarization angles and the ranges of each energy bin. Curves show the optimal predictions of the LIV model (see text and Equation 3). The goodness-of-fit χ dof 2 are also listed.
Preprints 118705 g001
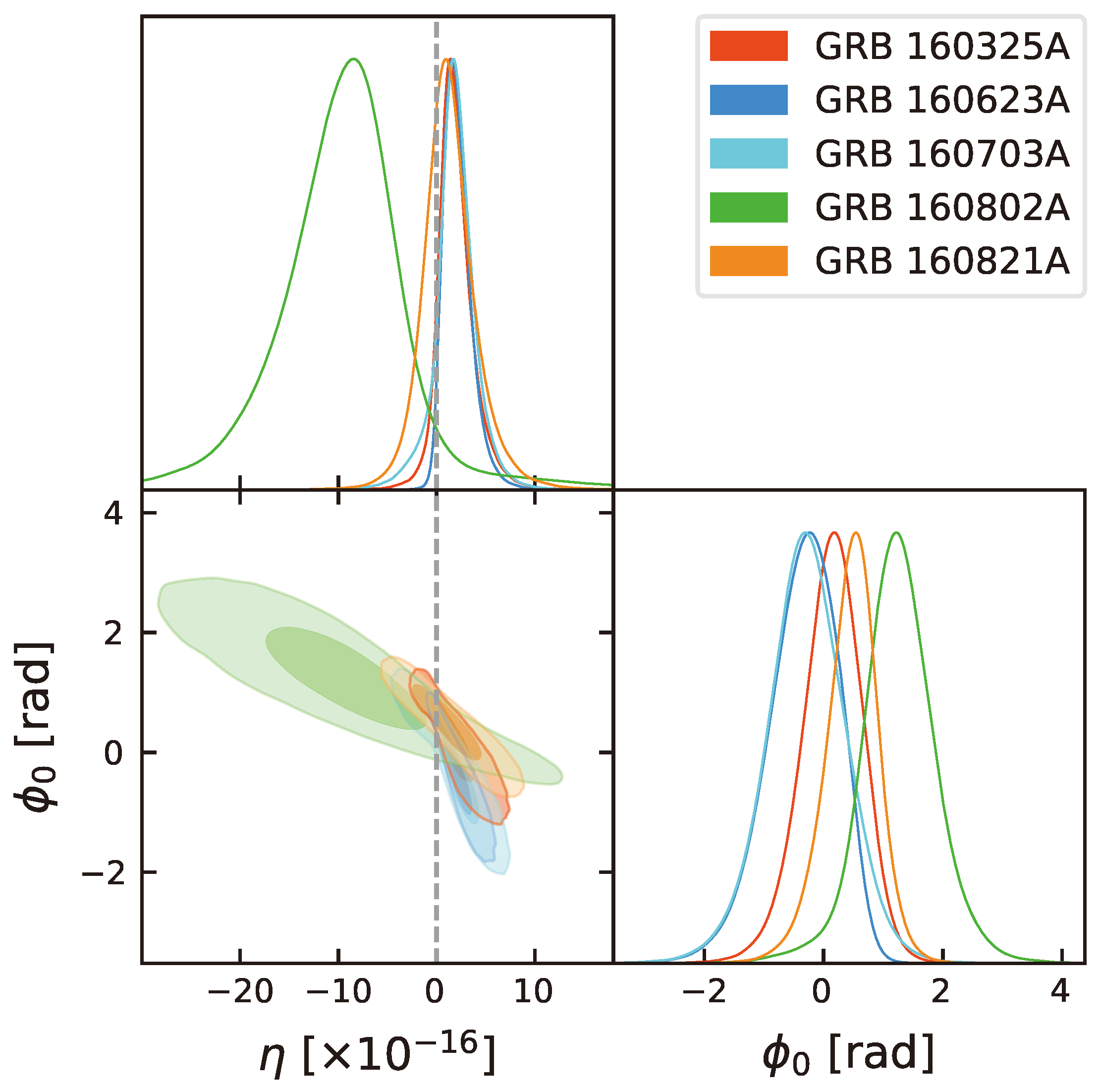
Preprints 118705 g002
Figure 2. 1D and 2D marginalized probability distributions with 1–2 σ confidence contours for the birefringent parameter η and the intrinsic polarization angle ϕ 0 , constrained by the energy-resolved polarization data of the five different GRBs. The vertical dashed line corresponds to the case of no LIV (i.e., η = 0 ).
Figure 2. 1D and 2D marginalized probability distributions with 1–2 σ confidence contours for the birefringent parameter η and the intrinsic polarization angle ϕ 0 , constrained by the energy-resolved polarization data of the five different GRBs. The vertical dashed line corresponds to the case of no LIV (i.e., η = 0 ).
Preprints 118705 g002
Table 1. Best-fit results (with 95% confidence-level uncertainties) on the birefringent parameter η and the intrinsic polarization angle ϕ 0 from energy-resolved polarization measurements of five GRBs.
Table 1. Best-fit results (with 95% confidence-level uncertainties) on the birefringent parameter η and the intrinsic polarization angle ϕ 0 from energy-resolved polarization measurements of five GRBs.
Source z η ( × 10 − 16 ) ϕ 0 ( rad )
GRB 160325A 0.2671 1 . 7 − 3.2 + 4.8 0 . 15 − 1.12 + 0.93
GRB 160623A 0.367 2 . 0 − 2.1 + 3.8 − 0 . 31 − 1.36 + 0.96
GRB 160703A 0.3161 1 . 9 − 5.1 + 4.6 − 0 . 29 − 1.39 + 1.33
GRB 160802A 0.1021 − 9 . 4 − 15.4 + 15.9 1 . 25 − 1.34 + 1.31
GRB 160821A 0.1531 1 . 2 − 5.2 + 6.7 0 . 49 − 1.03 + 0.82
1 The redshifts of the four GRBs are estimated by the luminosity realtion.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated