Covariant Representation of Spin and Entanglement --- A Review and Reformulation

1. Introduction

The phenomenon of entanglement is a distinguishing feature of quantum theory and an increasingly important topic in contemporary physics, from the continuing debate of philosophical questions deriving from the papers of Einstein, Podolsky, and Rosen [1] to new technological applications in computation, communications, and radar [2,3,4]. The representation of entanglement as a superposition of states

$$\left|\psi \right.〉=\sum _{i_1\cdots i_n}{\alpha }_{i_1\cdots i_n}\left|{\psi }_{i_1}\right.〉\cdots \left|{\psi }_{i_n}\right.〉\left|{\psi }_{i_k}\right.〉\in {\mathcal{H}}_k$$

(1)

belonging to the direct product space $\mathcal{H}={\mathcal{H}}_1\otimes \cdots \otimes {\mathcal{H}}_n$ necessarily involves a precise and rigorous characterization of each Hilbert space ${\mathcal{H}}_k$. Moreover, a covariant theory of relativistic entanglement requires detailed attention to the basis eigenstates of the commuting operators formed from the generators of a unitary representation of the Poincaré group.

In particular, the treatment of temporal entanglement must be performed in a fully covariant relativistic framework that places space and time on an equal footing in a consistent manner. This can be seen in the comparative analysis of experiments showing spatial and temporal interference: just as a quantum wavefunction split in space by a pair of slits produces spatial interference fringes, a wavefunction split in time can produce temporal interference fringes.

The demonstration by Davisson and Germer [5] of the wavelike nature of particles in the double-slit experiment was a foundational contribution to quantum theory.

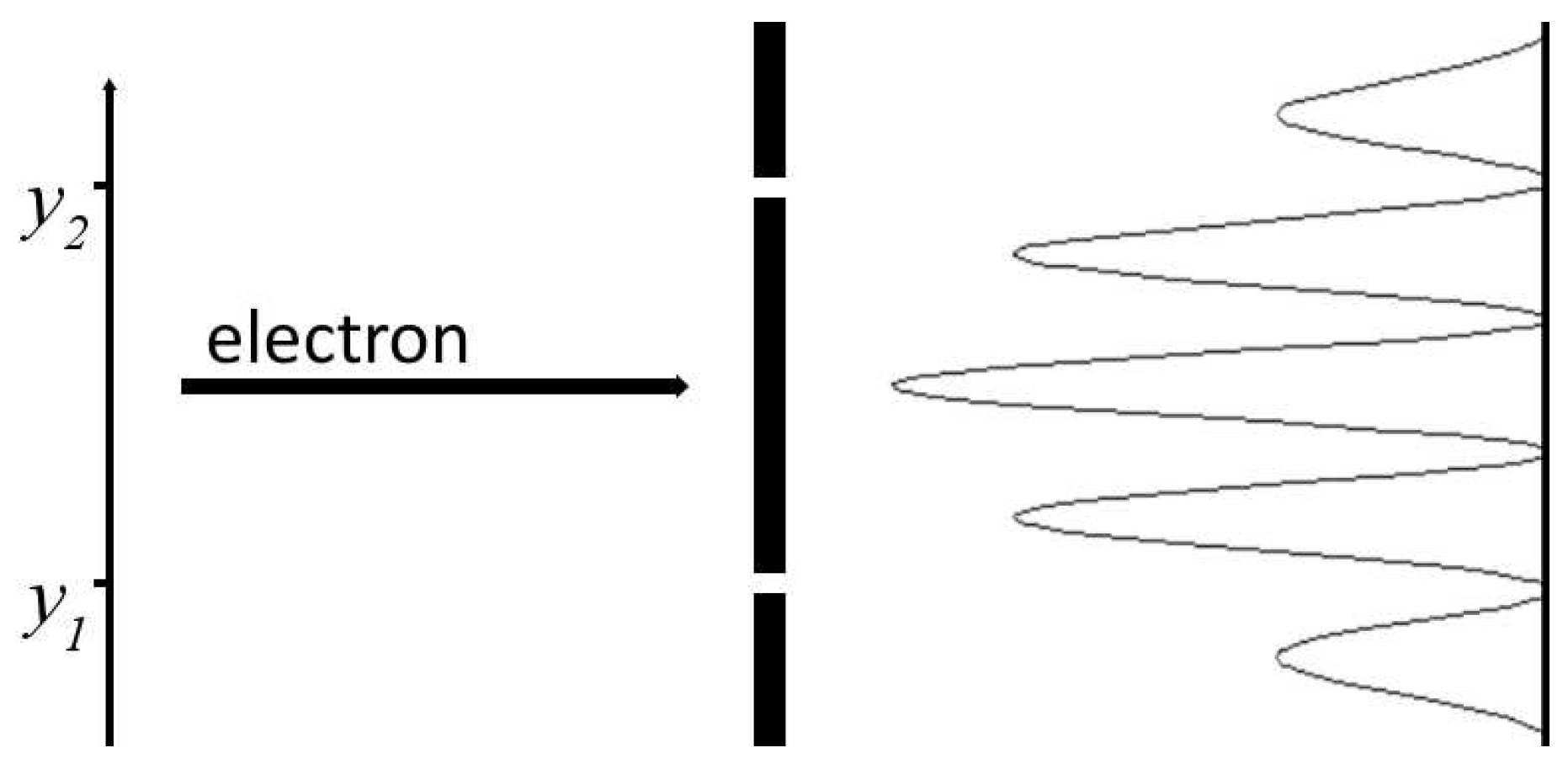
As shown schematically in Figure 1, an electron passes through a slit at either $y=y_1$ or $y=y_2$ leading to a spatial superposition

$$|\psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|y_1\rangle +|y_2\rangle \right)⟶\langle p|\psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(e^{-ip{y}_1}+e^{-ip{y}_2}\right)$$

(2)

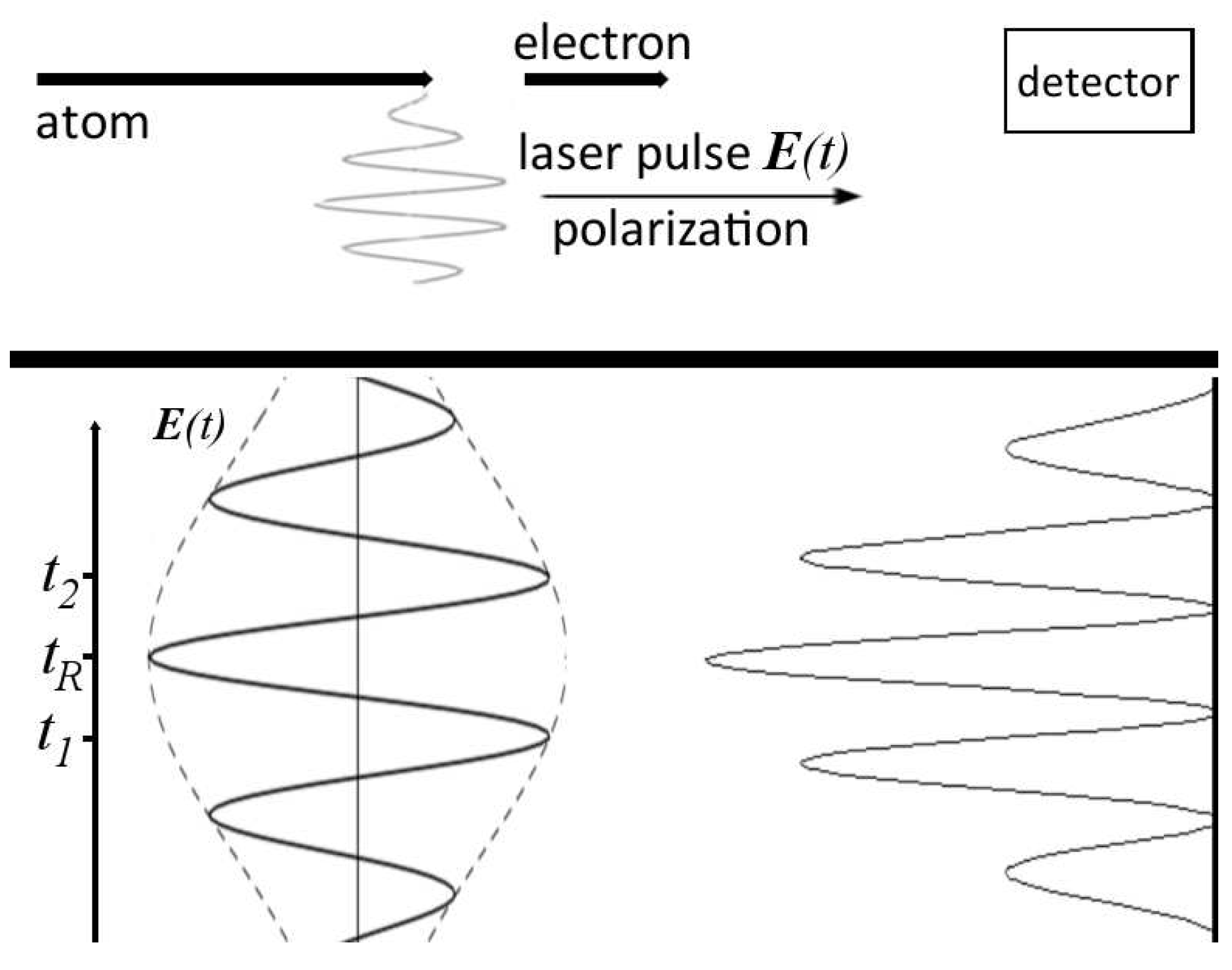
producing interference fringes in space. In the temporal double-slit experiment shown schematically in Figure 2, Lindner [6] et. al. showed that an aperture opened and closed at temporal separation can produce interference in time. An ultra-short laser pulse ionizes an atom when $\mathit{E}\left(t\right)={\mathit{E}}_{max}$ causing an electron to be emitted at either $t=t_1$ or $t=t_2$ and accelerated toward the detector. The resulting wavefunctions were shown to interfere coherently, producing temporal fringes.

In analogy to (2), one might be tempted to describe this emission by a temporal superposition

$$|\psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|t_1\rangle +|t_2\rangle \right)⟶\langle E|\psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(e^{-iE{t}_1}+e^{-iE{t}_2}\right)$$

(3)

showing an energy state producing interference fringes in time. Although wavefunction interference is superficially similar for space and time separations, the nonrelativistic states defined at different times in (3) belong to different Hilbert spaces and cannot be said to form a coherent superposition. To see this, we simply recall that the time evolution of an unperturbed nonrelativistic state is determined by a Hamiltonian-generated unitary transformation

$$|t_2\rangle =U(t_2,t_1)|t_1\rangle {\displaystyle \frac{d}{dt}}|t\rangle ={\left.{\displaystyle \frac{d}{dt}}U(t,t_0)\right|}_{t_0}|t_0\rangle =-{\displaystyle \frac{i}{\hslash }}H|t_0\rangle .$$

(4)

But expressing the proposed temporal superposition in the form

$$|\psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|t_1\rangle +|t_2\rangle \right)={\displaystyle \frac{1}{\sqrt{2}}}\left[1+U(t_2,t_1)[-6pt]0pt6pt\right]|t_1\rangle$$

(5)

there is no obvious way to define the unitary evolution of this state or formulate a nonrelativistic many-body theory. Another temporal interference experiment has been proposed by Palacios et. al. [7] involving a sequential double ionization of helium to produce a pair of entangled electrons in a singlet state. Horwitz and Arshansky [8,9] have discussed the conceptual difficulties associated with these experiments, and presented a rigorous relativistic analysis.

The challenges associated with formulating a consistent relativistic quantum mechanics for a single particle and its application to the description of many-body states are well-known. These difficulties are often reviewed in motivating the transition to quantum field theory (QFT). At minimum, constructing a consistent theory of superposition of states for the experiments of Lindner and Palacios requires a relativistic Hilbert space that treats space and time on the same footing. By definition, this space consists of the coherent eigenstates of a complete set of operators in a given representation defined with respect to a shared continuous parameterization. These operators are formed from the generators of the Poincaré group, with states characterized with respect to an induced representation of spin through the $SU\left(2\right)$ subgroup of the $SL(2,C)$ covering group for $O(3,1)$. As seen above, the time coordinate $x^0$ cannot be used to define the coherent states or parameterize their unitary evolution.

In this paper, we discuss the construction of relativistic Hilbert spaces in a framework developed by Stueckelberg, Horwitz, and Piron (SHP) to overcome the most serious difficulties associated with covariant quantum mechanics. This approach is described at length in a series of books [10,11,12,13] and only more recent references will be given explicitly in the following. Here we provide an updated review of the SHP framework, while introducing a novel representation of spin as a property of extra dimensions, organized as follows. Section 2 presents an short review of the SHP formalism for spinless particles, and briefly introduces a new approach to representation of spin as a characteristic of an extended phase space. The extension of the classical phase space to include extra dimensions is formalized in Section 3 and the electromagnetic interaction in the extended space is explored. Section 4 reviews the construction of unitary representations of the Poincaré group for quantum states, and presents the induced representation of spin in the extra dimensions. Although these developments follow the standard presentation given by Wigner, they are implemented in the extended space, along side usual 4D spacetime, and so lead to new interpretations. Quantum mechanics in the extended phase space is then developed in Section 5. This section generalizes the presentation by Horwitz and Arshansky, leading to an electromagnetic Hamiltonian in the new dimensions, along with solutions. In Section 6 we construct entangled bipartite states and specify the singlet state to a discussion of the Palacios experiment.

2. The Stueckelberg, Horwitz, Piron (SHP) Formalism

The Stueckelberg, Horwitz, Piron (SHP) formalism [10,11,12,13] is a framework for special and general relativity in the classical and quantum realms developed to overcome the difficulties associated with the problem of time. In describing an antiparticle as a particle moving backward in time, Stueckelberg introduced an external parameter $\tau$, similar to the Newtonian time in nonrelativistic physics, so that the spacetime event $x^{\mu }\left(\tau \right)$ can change direction in coordinate time $x^0$ while $\tau$ advances monotonically. In order to permit the event velocity ${\dot{x}}^{\mu }\left(\tau \right)=d{x}^{\mu }/d\tau$ to evolve continuously through the spacelike region between the forward and reverse lightlike regions, the 8D phase space $(x^{\mu },{\dot{x}}^{\mu })$ must be unconstrained, so that the usual constraint ${\dot{x}}^2=1$ is reduced to the status of a conservation law that applies under appropriate interactions. Unlike the convention in SHP theory, we take the flat metric to be ${\eta }_{\mu \nu }=\mathrm{diag}(1,-1,-1,-1)$ for consistency with familiar descriptions of spin. Horwitz and Piron extended the Stueckelberg framework into a fully covariant canonical theory with many-body interactions, whose applications include solutions to relativistic bound state and scattering problems under central forces, a microdynamical theory of electrodynamics, and more recently, motion in curved spacetime and evolution of the gravitational field [14,15,16].

A free classical event in SHP theory is described by the Lagrangian and equivalent Hamiltonian

$$L={\displaystyle \frac{1}{2}}M{\dot{x}}^{\mu }{\dot{x}}_{\mu }K={\displaystyle \frac{1}{2M}}{p}^{\mu }{p}_{\mu }$$

(6)

where $p_{\mu }=\partial L/\partial {\dot{x}}^{\mu }$, with Euler-Lagrange and Hamilton equations

$$0={\displaystyle \frac{d}{d\tau }}{\displaystyle \frac{\partial L}{\partial {\dot{x}}^{\mu }}}-{\displaystyle \frac{\partial L}{\partial x^{\mu }}}{\dot{x}}^{\mu }={\displaystyle \frac{\partial K}{\partial p_{\mu }}}{\dot{p}}_{\mu }=-{\displaystyle \frac{\partial K}{\partial x_{\mu }}}$$

(7)

to which interactions may be added in much the same manner as in nonrelativistic theory. The Stueckelberg-Schrodinger equation

$$i\hslash {\partial }_{\tau }\psi \left(x,\tau \right)=K\psi \left(x,\tau \right)=\left[{\displaystyle \frac{p^2}{2m}}+V\left(x\right)\right]\psi \left(x,\tau \right)$$

(8)

describes a single quantum mechanical event, and may also describe the reduced motion of a pair of interacting events after separation of the free center of mass motion. Solutions to this equation undergo unitary evolution in $\tau$ as

$$|{\tau }_2\rangle =U({\tau }_2,{\tau }_1)|{\tau }_1\rangle {\displaystyle \frac{d}{d\tau }}|\tau \rangle ={\left.{\displaystyle \frac{d}{d\tau }}U(\tau ,{\tau }_0)\right|}_{{\tau }_0}|{\tau }_0\rangle =-{\displaystyle \frac{i}{\hslash }}K|{\tau }_0\rangle .$$

(9)

By generalizing the central force problem for particles of spacelike separation $x^2<0$ as

$$V\left(r\right)⟶V\left(\rho \right)\rho =\sqrt{{\mathbf{r}}^2-c^2{t}^2}$$

(10)

Horwitz and Arshansky found relativistic generalizations of the classical bound state solutions. States with the correct spectrum and multiplicity are obtained by choosing an arbitrary spacelike vector $n^{\mu }$ and solving (8) in a coordinate parameterization that guarantees $x^2\le 0$ and $x_{\perp }^2\le 0$, where $x_{\perp }^{\mu }{n}_{\mu }=0$. These solutions lower the spectrum by breaking the $O(3,1)$ symmetry of the original system to $O(2,1)\subset O(3,1)$. As a result, wavefunctions that transform under the full Lorentz group must be constructed as an induced representation with respect to $n^{\mu }$, leading to generators of $O(3,1)$ in a form that includes $n^{\mu }$ and $\partial /\partial n^{\mu }$. The Lie algebra for these transformations was found and new wavefunctions were then obtained as eigenstates of the commuting operators formed from these generators, providing an induced representation of $O(3,1)$. Although the value of $n^{\mu }$ was chosen arbitrarily, Land and Horwitz showed that it shifts under radiative transitions. By treating $n^{\mu }\left(\tau \right)$ as a dynamical quantity and extending the classical phase space to include $(n^{\mu },{\dot{n}}^{\mu })$, the gauge invariant Hamiltonian acquires an interaction term in which the electromagnetic field is coupled in a natural way to the generators of the induced $O(3,1)$. Thus, the Zeeman and Stark effects were found by Land and Horwitz in manifestly covariant form as a first order perturbation, reproducing the expected lifting of energy degeneracy.

Equations (6) to (8) describe a spinless particle. In standard relativistic quantum theory [17] massive particles may be characterized in their rest frame, where $p=(p^0,\mathbf{0})$. Spin is introduced, following Wigner, by studying the unitary representations of the Poincaré group, involving an induced representation of $O(3,1)$ with respect to the momentum $p^{\mu }$. But in the SHP formalism $p^2$ is unconstrained and may vanish or be negative for real particles, precluding the identification of a rest frame. Therefore, Horwitz, Piron, and Reuse modified Wigner’s method by specifying a position state and inducing a representation of $SL(2,C)$ with respect to an arbitrarily chosen timelike unit vector designated $n^{\mu }$. The resulting spin operators act in the spacelike hypersurface normal to $n^{\mu }$, characterizing the chosen $SU\left(2\right)$ subgroup of $SL(2,C)$. Because a singlet state belongs to an irreducible representation of the direct product of identical spin-1/2 states in the same representation, the entanglement requires that the individual wavefunctions be defined at the same value of $\tau$ and with the same value of $n^{\mu }$.

In this paper, we will treat $n^{\mu }\left(\tau \right)$ as a dynamical quantity, as was done for the induced representation of $O(3,1)$ in the analysis of the Zeeman and Stark effects for relativistic bound states. More specifically, we introduce an auxiliary momentum ${\pi }^{\mu }=M{n}^{\mu }$ conjugate to a position ${\zeta }^{\mu }$ and study the classical and quantum dynamics on the extended phase space $\{\left(x^{\mu },p^{\nu }\right),\left({\zeta }^{\mu },{\pi }^{\nu }\right)\}$. Applying Wigner’s method, we construct a unitary representation of the Poincaré group for quantum states, leading to a representation of spin induced on ${\pi }^{\mu }$ rather than $p^{\mu }$. Since a superposition can only be formed from coherent states in the same Hilbert space, characterized by a representation of spin, a singlet state formed from pair of free particles must have identical values of ${\pi }_i^{\mu }$, even as this extended momentum evolves dynamically. In the following, we explore the implications of this requirement.

3. Classical Extended Phase Space

We write the classical phase space

$$\left\{\left(x^{\mu },{\zeta }^{\mu }\right),\left({\dot{x}}^{\mu },{\dot{\zeta }}^{\mu }\right)\right\}$$

(11)

and introduce the fields $A^{\mu }\left(x,\zeta \right)$ and ${\chi }^{\mu }\left(x,\zeta \right)$ to write the classical Lagrangian

$$L={\displaystyle \frac{1}{2}}M{\dot{x}}^{\mu }{\dot{x}}_{\mu }+{\displaystyle \frac{1}{2}}M{\dot{\zeta }}^{\mu }{\dot{\zeta }}_{\mu }+e{\dot{x}}_{\mu }{A}^{\mu }\left(x,\zeta \right)+e{\dot{\zeta }}_{\mu }{\chi }^{\mu }\left(x,\zeta \right)$$

(12)

for which the action is invariant under the gauge transformations

$$A^{\mu }\left(x,\zeta \right)⟶A^{\mu }\left(x,\zeta \right)+{\displaystyle \frac{\partial \Lambda }{\partial x^{\mu }}}{\chi }^{\mu }\left(x,\zeta \right)⟶{\chi }^{\mu }\left(x,\zeta \right)+{\displaystyle \frac{\partial \Lambda }{\partial {\zeta }^{\mu }}}.$$

(13)

Variation with respect to $x^{\mu }$ and ${\zeta }^{\mu }$ leads to the Lorentz force

$$\begin{array}{ccc}\hfill M{\ddot{x}}^{\mu }\left(\tau \right)=& & e{F}^{\mu \nu }\left(x,\zeta \right){\dot{x}}_{\nu }\left(\tau \right)+e{H}^{\mu \nu }\left(x,\zeta \right){\dot{\zeta }}_{\nu }\left(\tau \right)\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill M{\ddot{\zeta }}^{\mu }\left(\tau \right)=& & e{G}^{\mu \nu }\left(x,\zeta \right){\dot{\zeta }}_{\nu }\left(\tau \right)-e{H}^{\mu \nu }\left(x,\zeta \right){\dot{x}}_{\nu }\left(\tau \right)\hfill \end{array}$$

(15)

where

$$F^{\mu \nu }={\displaystyle \frac{\partial A^{\nu }}{\partial x_{\mu }}}-{\displaystyle \frac{\partial A^{\mu }}{\partial x_{\nu }}}{G}^{\mu \nu }={\displaystyle \frac{\partial {\chi }^{\nu }}{\partial {\zeta }_{\mu }}}-{\displaystyle \frac{\partial {\chi }^{\mu }}{\partial {\zeta }_{\nu }}}{H}^{\mu \nu }={\displaystyle \frac{\partial {\chi }^{\nu }}{\partial x_{\mu }}}-{\displaystyle \frac{\partial A^{\mu }}{\partial {\zeta }_{\nu }}}$$

(16)

are the field strengths.

We may define the canonical momenta

$$\begin{array}{ccc}\hfill p_{\mu }={\displaystyle \frac{\partial L}{\partial {\dot{x}}^{\mu }}}=M{\dot{x}}_{\mu }+e{A}_{\mu }& ⟶& {\dot{x}}_{\mu }={\displaystyle \frac{1}{M}}\left(p_{\mu }-e{A}_{\mu }\right)\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill {\pi }_{\mu }={\displaystyle \frac{\partial L}{\partial {\dot{\zeta }}^{\mu }}}=M{\dot{\zeta }}_{\mu }+e{\chi }^{\mu }& ⟶& {\dot{\zeta }}_{\mu }={\displaystyle \frac{1}{M}}\left({\pi }_{\mu }-e{\chi }_{\mu }\right)\hfill \end{array}$$

(18)

and perform a Legendre transformation on the classical Lagrangian (12) to obtain the classical gauge invariant scalar Hamiltonian

$$K={\displaystyle \frac{1}{2M}}\left[\left(p^{\mu }-e{A}^{\mu }\right)\left(p_{\mu }-e{A}_{\mu }\right)+\left({\pi }^{\mu }-e{\chi }^{\mu }\right)\left({\pi }_{\mu }-e{\chi }_{\mu }\right)\right].$$

(19)

In Section 5 we will see how the quantum Hamiltonian acquires a spin interaction term. As discussed in Section 2, a pair of quantum particles must have the same value of ${\pi }^{\mu }$ in order to enter a singlet state. To get a sense of how this quantity behaves in an external field, we consider two classical particles with initial conditions

$${\zeta }_1^{\mu }\left(0\right)={\zeta }_2^{\mu }\left(0\right){\pi }_1^{\mu }\left(0\right)={\pi }_2^{\mu }\left(0\right)$$

(20)

and write the Hamilton equations

$${\dot{p}}_{\mu }={\displaystyle \frac{e}{M}}\left[\left(p^{\nu }-e{A}^{\nu }\right){\displaystyle \frac{\partial A_{\nu }}{\partial x^{\mu }}}+\left({\pi }^{\nu }-e{\chi }^{\nu }\right){\displaystyle \frac{\partial {\chi }_{\nu }}{\partial x^{\mu }}}\right]$$

(21)

$${\dot{\pi }}_{\mu }={\displaystyle \frac{e}{M}}\left[\left(p^{\nu }-e{A}^{\nu }\right){\displaystyle \frac{\partial A_{\nu }}{\partial {\zeta }^{\mu }}}+\left({\pi }^{\nu }-e{\chi }^{\nu }\right){\displaystyle \frac{\partial {\chi }_{\nu }}{\partial {\zeta }^{\mu }}}\right].$$

(22)

In the case that $A^{\mu }=A^{\mu }\left(x\right)$ and ${\chi }^{\mu }={\chi }^{\mu }\left(\zeta \right)$ we have

$${\dot{\pi }}_1^{\mu }={\displaystyle \frac{e}{M}}\left[{\pi }_1^{\nu }-e{\chi }^{\nu }\left({\zeta }_1\right)\right]{\displaystyle \frac{\partial {\chi }_{\nu }\left({\zeta }_1\right)}{\partial {\zeta }_{\mu }^1}}{\dot{\pi }}_2^{\mu }={\displaystyle \frac{e}{M}}\left[{\pi }_2^{\nu }-e{\chi }^{\nu }\left({\zeta }_2\right)\right]{\displaystyle \frac{\partial {\chi }_{\nu }\left({\zeta }_2\right)}{\partial {\zeta }_{\mu }^2}}$$

(23)

and note that by (16), $H^{\mu \nu }=0$ in this case. Since the forces and initial conditions are the same for each particle, they will evolve without divergence in their values of ${\pi }^{\mu }$. We note that transforming the interaction terms in the Lagrangian (12) as

$$e{\dot{x}}_{\mu }{A}^{\mu }\left(x,\zeta \right)+e{\dot{\zeta }}_{\mu }{\chi }^{\mu }\left(x,\zeta \right)⟶e{J}_{\mu }^x\left(x\right)A^{\mu }\left(x,\zeta \right)+e{J}_{\mu }^{\zeta }\left(\zeta \right){\chi }^{\mu }\left(x,\zeta \right)$$

(24)

and introducing kinetic terms for the fields, we may write a field Lagrangian as

$$\mathcal{L}=e\left[J_{\mu }^x\left(x\right)A^{\mu }\left(x,\zeta \right)+J_{\mu }^{\zeta }\left(\zeta \right){\chi }^{\mu }\left(x,\zeta \right)\right]+{\displaystyle \frac{1}{4\pi }}\left[F^{\mu \nu }{F}_{\mu \nu }+G^{\mu \nu }{G}_{\mu \nu }+H^{\mu \nu }{H}_{\mu \nu }\right].$$

(25)

Variation of this Lagrangian with respect to the potentials $A^{\mu }$ and ${\chi }^{\mu }$ leads to Maxwell-like field equations for which the sources are $J_{\mu }^x\left(x\right)$ and $J_{\mu }^{\zeta }\left(\zeta \right)$, suggesting that the field solutions will be of the type $A^{\mu }=A^{\mu }\left(x\right)$ and ${\chi }^{\mu }={\chi }^{\mu }\left(\zeta \right)$

Nevertheless, if either potential depends on both x and $\zeta$ then we have

$$\begin{array}{c}{\dot{\pi }}_1^{\mu }={\displaystyle \frac{e}{M}}\left[\left[p_1^{\nu }-e{A}^{\nu }\left(x_1,{\zeta }_1\right)\right]{\displaystyle \frac{\partial A_{\nu }\left(x_1,{\zeta }_1\right)}{\partial {\zeta }_{\mu }^1}}+\left[{\pi }_1^{\nu }-e{\chi }^{\nu }\left(x_1,{\zeta }_1\right)\right]{\displaystyle \frac{\partial {\chi }_{\nu }\left(x_1,{\zeta }_1\right)}{\partial {\zeta }_{\mu }^1}}\right]\hfill \\ {\dot{\pi }}_2^{\mu }={\displaystyle \frac{e}{M}}\left[\left[p_2^{\nu }-e{A}^{\nu }\left(x_2,{\zeta }_2\right)\right]{\displaystyle \frac{\partial A_{\nu }\left(x_2,{\zeta }_2\right)}{\partial {\zeta }_{\mu }^2}}+\left[{\pi }_2^{\nu }-e{\chi }^{\nu }\left(x_2,{\zeta }_2\right)\right]{\displaystyle \frac{\partial {\chi }_{\nu }\left(x_2,{\zeta }_2\right)}{\partial {\zeta }_{\mu }^2}}\right]\hfill \end{array}$$

(26)

so that the forces on ${\pi }_1$ and ${\pi }_2$ may differ at spacetime separated locations $x_1$ and $x_2$, leading to a relative change in their values. In the quantum context, divergent evolution in ${\pi }^{\mu }$ may indicate a mechanism of decoherence.

4. Unitary Representation of the Poincaré Group

Basis quantities for quantum states are found as eigenstates of the commuting operators formed from the generators of a unitary representation of the Poincaré group

$$\left|{\psi }^{\prime }\right.〉=U\left(\Lambda ,a\right)\left|\psi \right.〉$$

(27)

for $\Lambda \in O(3,1)$ and translation a. The spacetime Lorentz transformations $x^{\prime \mu }={\Lambda }_{\nu }^{\mu }{x}^{\nu }$ and translations $x^{\mu }⟶x^{\prime \mu }=x^{\mu }+a^{\mu }$ have generators

$$L_{\mu \nu }=\left(X_{\mu }{P}_{\nu }-X_{\nu }{P}_{\mu }\right)P_{\mu }=i{\displaystyle \frac{\partial }{\partial X^{\mu }}}$$

(28)

from which one may write unitary transformations

$$U\left(\Lambda ,a\right)\simeq 1+i{a}^{\mu }{P}_{\mu }+i{\omega }^{\mu \nu }{L}_{\mu \nu }$$

(29)

where $P_{\mu }$ and $L_{\mu \nu }$ satisfy the well-known Lie algebra

$$\left[P_{\mu },P_{\nu }\right]=0\left[L_{\mu \nu },P_{\sigma }\right]=i\left(g_{\nu \sigma }{P}_{\mu }-g_{\mu \sigma }{P}_{\nu }\right)$$

(30)

$$\left[L^{\mu \nu },L^{\rho \sigma }\right]=i\left(g^{\nu \rho }{L}^{\mu \sigma }+g^{\mu \sigma }{L}^{\nu \rho }-g^{\mu \rho }{L}^{\nu \sigma }-g^{\nu \sigma }{L}^{\mu \rho }\right)$$

(31)

leading to spinor representations.

We treat the extra dimensions as an inequivalent representation of the Poincaré group, and so in the extended phase space, the transformations of ${\zeta }^{\mu }$ and ${\pi }^{\mu }$ are generated by

$$N_{\mu \nu }=\left({\zeta }_{\mu }{\pi }_{\nu }-{\zeta }_{\nu }{\pi }_{\mu }\right){\pi }_{\mu }=i{\displaystyle \frac{\partial }{\partial {\zeta }^{\mu }}}$$

(32)

defined in analogy to (28) but independent of $X^{\mu }$ and $P_{\mu }$. With these, we may consider extended unitary transformations of the quantum states of the type

$$U\left(\Lambda ,a\right)\simeq 1+i{a}^{\mu }\left(P_{\mu }+{\pi }_{\mu }\right)+i{\omega }^{\mu \nu }\left(L_{\mu \nu }+N_{\mu \nu }\right)$$

(33)

whose generators satisfy the Poincaré algebra. Although the spacetime 4-momentum is unconstrained and $p^{\mu }{p}_{\mu }$ is not necessarily non-negative definite, we now stipulate that the momentum ${\pi }^{\mu }$ must satisfy the mass-shell constraint ${\pi }^2=M^2$.

4.1. Representations of the Lorentz Group

For later reference, we briefly review the spinor and vector representations of the Lorentz group, obtained from the combined generators $M_{\mu \nu }=L_{\mu \nu }+N_{\mu \nu }$. The operators are partitioned into boost and rotation generators as

$$K_i=M_{0i}{J}_i={\displaystyle \frac{1}{2}}{ϵ}_{ijk}{M}_{jk}i,j,k=1,2,3$$

(34)

with commutation relations

$$\left[J_i,J_j\right]={ϵ}_{ijk}{J}_k\left[J_i,K_j\right]={ϵ}_{ijk}{K}_k\left[K_i,K_j\right]=-{ϵ}_{ijk}{J}_k$$

(35)

decomposing the Lorentz transformation as $\Lambda =exp\left\{i\left(\mathit{\beta }·\mathit{K}+\mathit{\omega }·\mathit{J}\right)\right\}$. Under space reflection P, $K_i⟶-K_i$ and $J_i⟶J_i$ which leads to the left and right handed operators

$${\mathit{N}}^L={\displaystyle \frac{1}{2}}\left(\mathit{J}+i\mathit{K}\right){\mathit{N}}^R={\displaystyle \frac{1}{2}}\left(\mathit{J}-i\mathit{K}\right)P\left[{\mathit{N}}^{L,R}\right]={\mathit{N}}^{R,L}$$

(36)

with commutation relations

$$\left[N_i^L,N_j^L\right]={ϵ}_{ijk}{N}_k^L\left[N_i^R,N_j^R\right]={ϵ}_{ijk}{N}_k^R\left[N_i^L,N_j^R\right]=0.$$

(37)

The $N_i^L$ and $N_i^R$ generate two inequivalent representations of the $SU\left(2\right)$ Lie algebra with Casimir operators

$${\left({\mathit{N}}^L\right)}^2=n\left(n+1\right){\left({\mathit{N}}^R\right)}^2=m\left(m+1\right)$$

(38)

so that representations

$$SO(3,1)=SU{\left(2\right)}_L\otimes SU{\left(2\right)}_R$$

(39)

are characterized as $\left(n,m\right)$. Since $\mathit{J}={\mathit{N}}^R+{\mathit{N}}^L$, the spin of a given representation is given by $n+m$. For the two-component spinor

$${\xi }^{L,R}=\left({\xi }_{1/2}^{L,R},{\xi }_{-1/2}^{L,R}\right)$$

(40)

$J_i$ and $K_i$ are represented by Pauli matrices, and (36) leads to

$$J_3{\xi }_{\alpha }^{L,R}={\displaystyle \frac{1}{2}}{\sigma }_3{\xi }_{\alpha }^{L,R}=\alpha {\xi }_{\alpha }^{L,R}{K}_3{\xi }_{\alpha }^{L,R}=\mp {\displaystyle \frac{i}{2}}{\sigma }_3{\xi }_{\alpha }^{L,R}=\mp i\alpha {\xi }_{\alpha }^{L,R}.$$

(41)

which transform as ${\xi }_{\alpha }^{L,R}⟶A^{L,R}{\xi }_{\alpha }^{L,R}$ where

$$A^L=exp\left(\mathit{\beta }·\mathit{\sigma }/2+i\mathit{\omega }·\mathit{\sigma }/2\right)A^R=exp\left(-\mathit{\beta }·\mathit{\sigma }/2+i\mathit{\omega }·\mathit{\sigma }/2\right)$$

(42)

belong to the group $SL\left(2,C\right)$, and we have ${\left(A^{L,R}\right)}^{†}={\left(A^{L,R}\right)}^{-1}$. In particular, pure rotations and boosts are

$$R=cos{\displaystyle \frac{\omega }{2}}+isin{\displaystyle \frac{\omega }{2}}\widehat{\mathit{\omega }}·\mathit{\sigma }H=cosh{\displaystyle \frac{\beta }{2}}\pm sinh{\displaystyle \frac{\beta }{2}}\widehat{\mathit{\beta }}·\mathit{\sigma }.$$

(43)

For $A\in SL(2,C)$ the anti-Hermitian operator $C=i{\sigma }^2$ acts as

$$C^{-1}{A}^{T}C=A^{-1}$$

(44)

and taking the complex conjugate of a left handed Lorentz transformation

$${\xi }_L^{\prime }=A_L{\xi }_L⟶{\xi }_L^{\prime *}=A_L^{*}{\xi }_L^{*}={\left(A_L^{†}\right)}^T{\xi }_L^{*}={\left(A_R^{-1}\right)}^T{\xi }_L^{*}=C{\Lambda }_R{C}^{-1}{\xi }_L^{*}$$

(45)

we see that $C^{-1}{\xi }_L^{\prime *}={\Lambda }_R\left(C^{-1}{\xi }_L^{*}\right)$. Thus, $C^{-1}{\xi }_L^{*}$ transforms as ${\xi }_R$, implementing the parity transformation ${\xi }_R=P\left[{\xi }_L\right]=C^{-1}{\xi }_L^{*}$. Introducing ${\sigma }^0=I=\mathrm{diag}\left(1,1\right)$, the matrices

$${\sigma }^{\mu }=\left\{{\sigma }^0,\mathit{\sigma }\right\}{\underline{\sigma }}^{\mu }=C{\sigma }_{\mu }^{*}{C}^{†}=\left\{{\sigma }^0,-\mathit{\sigma }\right\}=P\left[{\sigma }^{\mu }\right]$$

(46)

provide two inequivalent bases for $SL\left(2,C\right)$. Deploying the indices of C as

$$C=∥C_{\alpha \beta }∥C^{-1}=∥C^{-1\alpha \beta }∥$$

(47)

the spinor with upper index is defined as

$${\xi }^{\alpha }=C^{-1\alpha \beta }{\xi }_{\beta }{\xi }_{\alpha }=C_{\alpha \beta }{\xi }^{\beta }$$

(48)

with C playing the role of a metric. Under Lorentz transformation

$$\begin{array}{ccc}\hfill {\xi }_{\alpha }^{\prime }=& & A_{\alpha }^{\beta }{\xi }_{\beta }\hfill \end{array}$$

(49)

$$\begin{array}{ccc}\hfill {\xi }^{\prime \alpha }=& & {\left(A^{-1T}\right)}_{\beta }^{\alpha }{\xi }^{\beta }={\left(C^{-1}AC\right)}_{\beta }^{\alpha }{\xi }^{\beta }=C^{-1\alpha \beta }{A}_{\beta }^{\gamma }{C}_{\gamma \delta }{\xi }^{\delta }\hfill \end{array}$$

(50)

where here C plays the role of a similarity transformation between the equivalent representations ${\xi }_{\beta }$ and ${\xi }^{\beta }$.

The vector representation of $O(3,1)$ by $SL(2,C)$ is found by writing

$$X=x^0{\sigma }^0+x^1{\sigma }^1+x^2{\sigma }^2+x^3{\sigma }^3{X}^{\prime }=AX{A}^{†}$$

(51)

which conserves $det{X}^{\prime }=detX=x_0^2-x_1^2-x_2^2-x_3^2=x^{\mu }{x}_{\mu }$ because $detA=1$.

4.2. The Little Group and Wigner Operator

By imposing the mass-shell constraint on the extended momenta ${\pi }^{\mu }$ we may follow Wigner’s method for representation of spin. The little group $\mathcal{L}\left(\pi \right)\subset O\left(3,1\right)$ consists of all Lorentz transformations $\widehat{\Lambda }\left(\pi \right)$ for which

$${\pi }^{\prime }=\widehat{\Lambda }\left(\pi \right)\pi =\pi$$

(52)

preserves the momentum $\pi$. One may construct the little group for $\pi$ by choosing a standard vector $\mathring{\pi }$ with known $\mathcal{L}\left(\mathring{\pi }\right)$ and defining the Wigner operator $\widehat{\Lambda }\left(\pi ,\mathring{\pi }\right)\in O\left(3,1\right)$ generated by $N_{\mu \nu }$ such that

$$\pi =\widehat{\Lambda }\left(\pi ,\mathring{\pi }\right)\mathring{\pi }.$$

(53)

In the $SL(2,C)$ representation this becomes

$$\Pi =\alpha \left(\pi \right)\mathring{\Pi }{\alpha }^{†}\left(\pi \right)\Pi =\sum _{\mu }{\pi }^{\mu }{\sigma }^{\mu }$$

(54)

where we denote by

$$\alpha \left(\pi \right)=\alpha \left(\pi ,\mathring{\pi }\right)$$

(55)

the $SL(2,C)$ matrix associated with the Wigner operator $\widehat{\Lambda }\left(\pi ,\mathring{\pi }\right)$. For any ${\widehat{A}}_{\pi }\in SL(2,C)$ associated with $\widehat{\Lambda }\left(\pi \right)\in \mathcal{L}\left(\pi \right)$ we may find the corresponding element of $\mathcal{L}\left(\mathring{\pi }\right)$

$${\widehat{A}}_{\mathring{\pi }}={\alpha }^{-1}\left(\pi \right){\widehat{A}}_{\pi }\alpha \left(\pi \right)⟶{\widehat{A}}_{\mathring{\pi }}\mathring{\Pi }{\widehat{A}}_{\mathring{\pi }}^{†}=\mathring{\Pi }$$

(56)

and by inversion we may find the little group $\mathcal{L}\left(\pi \right)$ from a known little group $\mathcal{L}\left(\mathring{\pi }\right)$ as

$$\mathcal{L}\left(\pi \right)=\alpha \left(\pi \right)\mathcal{L}\left(\mathring{\pi }\right){\alpha }^{-1}\left(\pi \right).$$

(57)

It follows that every Lorentz transformation $A\in SL(2,C)$ can be expressed as a combination of a little group element ${\widehat{A}}_{\mathring{\pi }}\in \mathcal{L}\left(\mathring{\pi }\right)$ and the Wigner operator $\alpha \left(\pi \right)$ in the form

$$A=\alpha \left({\pi }^{\prime }\right){\widehat{A}}_{\mathring{\pi }}{\alpha }^{†}\left(\pi \right)$$

(58)

establishing the isomorphism $SL(2,C)\approx \mathcal{L}\left(\mathring{\pi }\right)$.

For the discussion of spin, it is convenient to choose the standard timelike $\mathring{\pi }$ vector as pure time

$$\mathring{\pi }=M\left(1,0,0,0\right)\mathring{\Pi }=M{\sigma }^0=MI$$

(59)

and so we write

$$n^{\mu }={\displaystyle \frac{1}{M}}{\pi }^{\mu }\mathring{n}=\left(1,0,0,0\right)N={\displaystyle \frac{1}{M}}\Pi =\sum _{\mu }{n}^{\mu }{\sigma }^{\mu }$$

(60)

making explicit the connection with the arbitrary timelike unit vector in the work of Horwitz et. al. This leads to the requirement

$$I={\widehat{A}}_{\mathring{n}}I{\widehat{A}}_{\mathring{\pi }}^{†}={\widehat{A}}_{\mathring{\pi }}{\widehat{A}}_{\mathring{\pi }}^{†}⟶{\widehat{A}}_{\mathring{\pi }}^{†}={\widehat{A}}_{\mathring{\pi }}^{-1}$$

(61)

so that $\mathcal{L}\left(\mathring{\pi }\right)$ is the group of spatial rotations represented by

$$\mathcal{L}\left(\mathring{\pi }\right)=SU\left(2\right)\subset SL\left(2,C\right)$$

(62)

and a general $\mathcal{L}\left(\pi \right)$ is the $SU\left(2\right)$ rotation group in the spacelike hypersurface normal to $\pi$. An explicit form of the standard transformation $\alpha \left(\pi \right)$ is the pure boost

$$\alpha \left(\pi \right)=exp\left(\beta \widehat{\mathit{\beta }}·\mathit{\sigma }/2\right)=cosh{\displaystyle \frac{\beta }{2}}+\widehat{\mathit{\beta }}·\mathit{\sigma }sinh{\displaystyle \frac{\beta }{2}}$$

(63)

so that

$${\displaystyle \frac{1}{M}}\Pi ={\alpha }^{†}\left(\pi \right)I\alpha \left(\pi \right)={\left[\alpha \left(\pi \right)\right]}^2=exp\left(\beta \widehat{\mathit{\beta }}·\mathit{\sigma }\right)=cosh\beta +\widehat{\mathit{\beta }}·\mathit{\sigma }sinh\beta =\left({\pi }^0,\mathit{\pi }\right)$$

(64)

where

$$\beta ={tanh}^{-1}{\displaystyle \frac{\left|\mathit{\pi }\right|}{{\pi }^0}}$$

(65)

is the velocity parameter.

4.3. Basis Quantities for States with Spin

Horwitz et. al. defined quantum states in the position representation as eigenstates of $X_{\mu }$, but here we work in the extended momentum representation and define eigenstates of the operators $P_{\mu }$ and ${\pi }_{\mu }$. With the notation

$$N_{\mu }={\displaystyle \frac{1}{M}}{\pi }_{\mu }$$

(66)

we introduce the Pauli–Lubanski pseudovector in the extended sector

$$W_{\mu }=-{\displaystyle \frac{1}{2}}{ϵ}_{\mu \nu \lambda \sigma }{N}^{\nu \lambda }{N}^{\sigma }$$

(67)

where

$$W_{\mu }{N}^{\mu }=-{\displaystyle \frac{1}{2}}{ϵ}_{\mu \nu \lambda \sigma }{N}^{\nu \lambda }{N}^{\sigma }{N}^{\mu }=0$$

(68)

$$\left[W_{\mu },N_{\rho }\right]=-{\displaystyle \frac{1}{2}}{ϵ}_{\mu \nu \lambda \sigma }\left[N^{\nu \lambda }{N}^{\sigma },N_{\rho }\right]=-{\displaystyle \frac{1}{2}}{ϵ}_{\mu \nu \lambda \sigma }i\left(g_{\rho }^{\nu }{N}^{\lambda }-g_{\rho }^{\lambda }{N}^{\nu }\right)N^{\sigma }=0$$

(69)

indicate the orthogonality of $W_{\mu }$ to $n^{\mu }$. The scalar

$$W^{\mu }{W}_{\mu }={\displaystyle \frac{1}{2}}{N}^{\mu \nu }{N}_{\mu \nu }{N}^{\lambda }{N}_{\lambda }-N^{\nu \sigma }{N}_{\mu \sigma }{N}^{\mu }{N}_{\nu }={\displaystyle \frac{1}{2}}{N}^{\mu \nu }{N}_{\mu \nu }-N^{\nu \sigma }{N}_{\mu \sigma }{N}^{\mu }{N}_{\nu }$$

(70)

commutes with the other operators and in the special frame $\mathring{n}=\left(1,0,0,0\right)$ takes the form

$$W^{\mu }{W}_{\mu }={\displaystyle \frac{1}{2}}\left(N^{0i}{N}_{0i}+N^{i0}{N}_{i0}+N^{ij}{N}_{ij}\right)-N^{0i}{N}_{0i}={\displaystyle \frac{1}{2}}{N}^{ij}{N}_{ij}$$

(71)

which represents the total spin as the Casimir invariant of the rotation subgroup in the hypersurface normal to $\mathring{\pi }=M\mathring{n}$.

Writing $\sigma$ for the diagonal spin component, while suppressing the total spin J and any additional eigenvalues associated with internal symmetries, we expect a Lorentz transformation to act on the momentum eigenvalue as

$$p^{\prime \mu }={\Lambda }_{\nu }^{\mu }{p}^{\nu }⟶P^{\mu }U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉=p^{\prime \mu }U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉$$

(72)

where $U(\Lambda )$ is a unitary representation of $\Lambda$. This is demonstrated by expressing the transformed operator $P^{\prime }$ as

$$P^{\prime \mu }={\Lambda }_{\nu }^{\mu }{P}^{\nu }=U^{-1}\left(\Lambda \right)P^{\mu }U\left(\Lambda \right)$$

(73)

so that

$$P^{\mu }U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉=\left[U\left(\Lambda \right)U^{-1}\left(\Lambda \right)\right]P^{\mu }U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉=U\left(\Lambda \right)P^{\prime \mu }\left|\pi ,p,\sigma \right.〉.$$

(74)

The wavefunction for a spinless momentum state is

$$\psi \left(\pi ,p\right)=〈\pi ,p|\psi 〉$$

(75)

so that frame covariance requires

$${\psi }^{\prime }({\pi }^{\prime },p^{\prime })=\psi (\pi ,p)⟶{\psi }^{\prime }(\pi ,p)=\psi ({\Lambda }^{-1}n,{\Lambda }^{-1}p).$$

(76)

The Lorentz transformed momentum state is

$${\psi }^{\prime }(\pi ,p)=〈\pi ,p|{\psi }^{\prime }〉=\langle \pi ,p|\left[U(\Lambda )|\psi \rangle \right]=\left[\langle \pi ,p|U(\Lambda )\right]|\psi \rangle$$

(77)

and so

$$\langle \pi ,p|U(\Lambda )={\left[U^{†}(\Lambda )|\pi ,p\rangle \right]}^{†}={\left[U\left({\Lambda }^{-1}\right)|\pi ,p\rangle \right]}^{†}=\left.〈{\Lambda }^{-1}\pi ,{\Lambda }^{-1}p\right|$$

(78)

confirming that

$${\psi }^{\prime }(\pi ,p)=\langle {\Lambda }^{-1}n,{\Lambda }^{-1}p|\psi \rangle .$$

(79)

The matrix element of $U(\Lambda )$ for the spinless state is thus

$$\begin{array}{ccc}\hfill \left.〈{\pi }^{\prime },p^{\prime }\right|U(\Lambda )|\pi ,p\rangle & =& {\delta }^4\left(p-{\Lambda }^{-1}{p}^{\prime }\right){\delta }^4\left(\pi -{\Lambda }^{-1}{\pi }^{\prime }\right)\hfill \end{array}$$

(80)

$$\begin{array}{ccc}& =& {\delta }^4\left(p^{\prime }-\Lambda p\right){\delta }^4\left({\pi }^{\prime }-\Lambda \pi \right)\hfill \end{array}$$

(81)

where the delta functions represent the action of $U\left(\Lambda \right)$ on the left, taking $p^{\prime }$ to ${\Lambda }^{-1}{p}^{\prime }$ and ${\pi }^{\prime }$ to ${\Lambda }^{-1}{\pi }^{\prime }$, while the last equality follows from $det\Lambda =1$.

For states with spin the identity operator is

$$I={\displaystyle \sum }_{{\sigma }^{\prime }}\int d\mu \left(p^{\prime }\right)d\mu \left({\pi }^{\prime }\right)\left|{\pi }^{\prime },p^{\prime },{\sigma }^{\prime }\right.〉\left.〈\pi {,}^{\prime }{p}^{\prime }{\sigma }^{\prime }\right|$$

(82)

and so the transformation acts as

$$U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉={\displaystyle \sum }_{{\sigma }^{\prime }}\int d\mu \left(p^{\prime }\right)d\mu \left({\pi }^{\prime }\right)\left|{\pi }^{\prime },p^{\prime },{\sigma }^{\prime }\right.〉\left.〈{\pi }^{\prime },p^{\prime }{\sigma }^{\prime }\right|U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉$$

(83)

with the matrix element

$$\left.〈{\pi }^{\prime },p^{\prime }{\sigma }^{\prime }\right|U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉={\delta }^4\left(p^{\prime }-\Lambda p\right){\delta }^4\left({\pi }^{\prime }-\Lambda \pi \right)V_{{\sigma }^{\prime }\sigma }\left(\pi ,p,\Lambda \right)$$

(84)

where $V_{{\sigma }^{\prime }\sigma }\left(\pi ,p,\Lambda \right)$ is a discrete matrix representation of the action of the Lorentz transformation on the spin state. Thus

$$U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉={\displaystyle \sum }_{{\sigma }^{\prime }}{V}_{{\sigma }^{\prime }\sigma }\left(\pi ,p,\Lambda \right)\left|\Lambda \pi ,\Lambda p,{\sigma }^{\prime }\right.〉$$

(85)

expresses the action of the unitary Lorentz transformation. Unitarity requires

$$1=U\left(\Lambda \right)U{\left(\Lambda \right)}^{†}={\displaystyle \sum }_{\sigma }\int d\mu \left(p\right)d\mu \left(\pi \right)U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉\left.〈\pi ,p,\sigma \right|U{\left(\Lambda \right)}^{†}$$

(86)

and using the matrix element this becomes

$${\displaystyle \sum }_{{\sigma }^{\prime }}{V}_{\sigma {\sigma }^{\prime }}{V}_{{\sigma }^{\prime \prime }{\sigma }^{\prime }}^{*}={\displaystyle \sum }_{{\sigma }^{\prime }}{V}_{\sigma {\sigma }^{\prime }}{\left(V_{{\sigma }^{\prime }{\sigma }^{\prime \prime }}\right)}^{†}={\delta }_{\sigma {\sigma }^{\prime \prime }}$$

(87)

showing that $V_{\sigma {\sigma }^{\prime }}\left(\Lambda \right)$ is a unitary matrix.

The Wigner operator $\alpha \left(\pi \right)$ is a pure boost constructed from the operators $N^{0i}$ and so does not act on p or $\sigma$. The unitary representation $U\left(\alpha \left(\pi \right)\right)$ is defined such that

$$U\left(\alpha \left(\pi \right)\right)\left|\mathring{\pi },p,\sigma \right.〉=\left|\pi ,p,\sigma \right.〉.$$

(88)

Inserting this definition into (85) and multiplying both sides by $U^{†}\left(\alpha \left({\pi }^{\prime }\right)\right)$ leads to

$$U^{†}\left(\alpha \left({\pi }^{\prime }\right)\right)U\left(\Lambda \right)U\left(\alpha \left(\pi \right)\right)\left|\mathring{\pi },p,\sigma \right.〉={\displaystyle \sum }_{{\sigma }^{\prime }}{V}_{{\sigma }^{\prime }\sigma }\left(\pi ,p,\Lambda \right)\left|\mathring{\pi },p^{\prime },{\sigma }^{\prime }\right.〉$$

(89)

so that writing $U^{†}\left(\alpha \left({\pi }^{\prime }\right)\right)=U\left({\alpha }^{-1}\left({\pi }^{\prime }\right)\right)$, combining unitary matrices on the LHS, and using (56) this becomes

$$U\left({\widehat{\Lambda }}_{\mathring{\pi }}\right)\left|\mathring{\pi },p,\sigma \right.〉={\displaystyle \sum }_{{\sigma }^{\prime }}{V}_{{\sigma }^{\prime }\sigma }\left(\pi ,p,\Lambda \right)\left|\mathring{\pi },p,\sigma \right.〉.$$

(90)

The matrix element for $U\left({\tilde{\Lambda }}_{\mathring{\pi }}\right)$ is thus

$$\left.〈\pi ,p^{\prime },{\sigma }^{\prime }\right|U\left({\tilde{\Lambda }}_{\mathring{\pi }}\right)\left|\mathring{\pi },p,\sigma \right.〉=V_{{\sigma }^{\prime \prime }\sigma }\left(\pi ,p,\Lambda \right){\delta }^4\left(p-p^{\prime }\right){\delta }^4\left(n-\mathring{\pi }\right)$$

(91)

showing that $V_{{\sigma }^{\prime }\sigma }\left(\pi ,p,\Lambda \right)$ belongs to the little group $\mathcal{L}\left(\mathring{\pi }\right)$. This can be written as

$$V_{{\sigma }^{\prime }\sigma }\left(\pi ,p,\Lambda \right)=V_{{\sigma }^{\prime }\sigma }\left(\mathring{\pi },{\widehat{\Lambda }}_{\mathring{\pi }}\right)=V_{{\sigma }^{\prime }\sigma }\left(\mathring{\pi },{\alpha }^{-1}\left({\pi }^{\prime }\right)A\alpha \left(\pi \right)\right)=D_{{\sigma }^{\prime }\sigma }^J\left(\Lambda ,\pi \right)$$

(92)

where A is the $SL(2,C)$ representation of $\Lambda$ and $D_{{\sigma }^{\prime }\sigma }^J\left(\Lambda ,\pi \right)$ is the Wigner matrix representation of the rotation

$$R={\alpha }^{-1}\left({\pi }^{\prime }\right)A\alpha \left(\pi \right).$$

(93)

Since this combination is an element of $SL\left(2,C\right)$ and a rotation, it belongs to the subgroup $SU\left(2\right)$ and is therefore unitary, and we have simply

$$U\left({\widehat{\Lambda }}_{\mathring{\pi }}\right)=U\left({\alpha }^{-1}\left({\pi }^{\prime }\right)A\alpha \left(\pi \right)\right)={\alpha }^{-1}\left({\pi }^{\prime }\right)A\alpha \left(\pi \right).$$

(94)

Together, the matrix element $\left.〈{\pi }^{\prime },p^{\prime }{\sigma }^{\prime }\right|U\left(\Lambda \right)\left|\pi ,p,\sigma \right.〉$ in (84) is a combination of a pure boost with a rotation of the spin indices in the hypersurface normal to ${\pi }^{\mu }$.

In wavefunction notation with $D_{{\sigma }^{\prime }\sigma }^J(\Lambda ,\pi )$ as defined in (92) the transformation can be written

$${\psi }_{\sigma }^{\prime }(\pi ,p)={\displaystyle \sum }_{{\sigma }^{\prime }}{\left[{\alpha }^{-1}\left(\pi \right)A\right]}_{{\sigma }^{\prime }\sigma }{\left[\alpha \left({\Lambda }^{-1}\pi \right)\psi \left({\Lambda }^{-1}\pi ,{\Lambda }^{-1}p\right)\right]}_{{\sigma }^{\prime }}$$

(95)

and multiplying both sides by $\alpha \left(\pi \right)$ this becomes

$${\left[\alpha \left(\pi \right)\psi (\pi ,p)\right]}_{\sigma }^{\prime }={\displaystyle \sum }_{{\sigma }^{\prime }}{A}_{{\sigma }^{\prime },\sigma }{\left[\alpha \left({\Lambda }^{-1}\pi \right)\psi \left({\Lambda }^{-1}\pi ,{\Lambda }^{-1}p\right)\right]}_{{\sigma }^{\prime }}$$

(96)

showing that $\alpha \psi$ undergoes Lorentz transform as ${\left(\alpha \psi \right)}^{\prime }=A\left(\alpha \psi \right)$. As we saw in Section 4.1 there is an inequivalent representation that transforms under the complex conjugate representation as ${\left(\underline{\alpha }\varphi \right)}^{\prime }=\underline{A}\left(\underline{\alpha }\varphi \right)$, so together

$$\alpha \psi \in (1/2,0)\underline{\alpha }\varphi \in (0,1/2)$$

(97)

are the fundamental spinorial bases for the $SL\left(2,C\right)$ representation of the Lorentz group.

5. Quantum Mechanics in the Extended Phase Space

5.1. Bispinors

Using the basis states defined in (97) we construct a bispinor in the Weyl basis as

$$\xi =\left({\xi }_L,{\xi }_R\right)=\left(\alpha \psi ,\underline{\alpha }\varphi \right)$$

(98)

leading to the Dirac spinor

$$\Psi (n,x)={\displaystyle \frac{1}{\sqrt{2}}}\left[\begin{array}{c}\alpha \psi (n,x)+\underline{\alpha }\varphi (n,x)[-10pt]0pt10pt\\ -\alpha \psi (n,x)+\underline{\alpha }\varphi (n,x)\end{array}\right]$$

(99)

in which the upper and lower sectors have even and odd parity, respectively. This field must transform as

$${\Psi }^{\prime }(n,x)=S(\Lambda )\Psi ({\Lambda }^{-1}n,{\Lambda }^{-1}x)$$

(100)

where $S(\Lambda )$ mixes components of the bispinor and acts on the standard gamma matrices as

$$S\left(\Lambda \right){\gamma }^{\mu }{S}^{-1}\left(\Lambda \right)={\left({\Lambda }^{-1}\right)}_{\nu }^{\mu }{\gamma }^{\nu }$$

(101)

in analogy to the $SL\left(2,C\right)$ transformation. Comparing the forms of the transformation

$${\Lambda }_{\beta }^{\alpha }={\eta }_{\beta }^{\alpha }+{\displaystyle \frac{1}{2}}{\left(M^{\mu \nu }\right)}_{\beta }^{\alpha }{\omega }_{\mu \nu }S\left(\Lambda \right)=1-{\displaystyle \frac{i}{2}}{\Sigma }^{\mu \nu }{\omega }_{\mu \nu }$$

(102)

leads to the condition

$$\left[{\gamma }^{\mu },{\Sigma }^{\alpha \beta }\right]=i\left({\eta }^{\mu \alpha }{\gamma }^{\beta }-{\eta }^{\mu \beta }{\gamma }^{\alpha }\right)$$

(103)

which is satisfied by

$${\Sigma }^{\alpha \beta }={\displaystyle \frac{i}{4}}\left[{\gamma }^{\alpha },{\gamma }^{\beta }\right].$$

(104)

It is convenient here to adopt the Hestenes approach to Clifford algebra [18] and treat ${\gamma }^{\mu }$ as the 4D basis vectors. Thus, we write vectors and bivectors as

$$a=a_{\mu }{\gamma }^{\mu }a\wedge b=a_{\mu }{b}_{\nu }{\gamma }^{\mu }\wedge {\gamma }^{\nu }$$

(105)

with the products

$$ab=a·b+a\wedge b={\displaystyle \frac{1}{2}}\{a,b\}+{\displaystyle \frac{1}{2}}[a,b]a·(b\wedge c)=(a·b)c-(a·c)b$$

(106)

and so

$${\gamma }^{\mu }·{\gamma }^{\nu }={\displaystyle \frac{1}{2}}\left\{{\gamma }^{\mu },{\gamma }^{\nu }\right\}={\eta }^{\mu \nu }{\Sigma }^{\mu \nu }={\displaystyle \frac{i}{2}}{\gamma }^{\mu }\wedge {\gamma }^{\nu }.$$

(107)

The explicit matrix form of ${\Sigma }^{\mu \nu }$ is

$${\Sigma }^{0i}={\displaystyle \frac{i}{4}}\left[{\gamma }^0,{\gamma }^i\right]={\displaystyle \frac{i}{2}}\left[\begin{array}{cc}0& {\sigma }^i\\ {\sigma }^i& 0\end{array}\right]{\Sigma }^{ij}={\displaystyle \frac{i}{4}}\left[{\gamma }^i,{\gamma }^j\right]={\displaystyle \frac{1}{2}}{ϵ}_k^{ij}\left[\begin{array}{cc}{\sigma }^k& 0\\ 0& {\sigma }^k\end{array}\right]$$

(108)

so that only ${\Sigma }^{12}$ is diagonal. The four bivectors $K^{\mu }$ are defined as

$$K^{\mu }={\Sigma }^{\mu \nu }{n}_{\nu }={\displaystyle \frac{i}{2}}{\gamma }^{\mu }\wedge {\gamma }^{\nu }{n}_{\nu }={\displaystyle \frac{i}{2}}{\gamma }^{\mu }\wedge n⟶K^{\mu }{n}_{\mu }={\displaystyle \frac{i}{2}}n\wedge n=0$$

(109)

and take the explicit form

$$K^0=-{\displaystyle \frac{i}{2}}\left[\begin{array}{cc}0& \mathit{n}·\mathit{\sigma }\\ \mathit{n}·\mathit{\sigma }& 0\end{array}\right]K^i={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}{ϵ}_k^{ij}{n}_j{\sigma }^k& -i{n}_{\left(0\right)}{\sigma }^i\\ -i{n}_{\left(0\right)}{\sigma }^i& {ϵ}_k^{ij}{n}_j{\sigma }^k\end{array}\right].$$

(110)

Writing the transverse projection of the basis vectors as

$${\gamma }_{\perp }^{\mu }={\gamma }^{\mu }-n(n·{\gamma }^{\mu })$$

(111)

Horwitz et. al. define

$${\Sigma }_{\perp }^{\mu \nu }={\displaystyle \frac{i}{4}}\left[{\gamma }_{\perp }^{\mu },{\gamma }_{\perp }^{\nu }\right]={\Sigma }^{\mu \nu }+K^{\nu }{n}^{\mu }-K^{\mu }{n}^{\nu }⟶{\Sigma }_{\perp }^{\mu \nu }{n}_{\nu }=0.$$

(112)

Thus, $K^{\mu }$ and ${\Sigma }_{\perp }^{\mu \nu }$ each have 3 independent components, satisfying the $O(3,1)$ Lie algebra and generating boosts and rotations in the spacelike hypersurface transverse to ${\pi }^{\mu }=M{n}^{\mu }$.

5.2. Quantum Hamiltonian

Using $n^2={\pi }^2/M^2=1$, the projections of spacetime momentum can be expressed as

$$p=n^{2}p=n\left(n·p\right)+n·\left(n\wedge p\right)=n\left(n·p\right)+\left[p-n\left(n·p\right)\right]=p_{\Vert }+p_{\perp }$$

(113)

and the parity transformation is given by

$$npn=n\left(p·n\right)+n·\left(p\wedge n\right)=n\left(p·n\right)-n·\left(n\wedge p\right)=p_{\Vert }-p_{\perp }.$$

(114)

Generalizing the work of Horwitz and Arshansky to the extended phase space, we write the longitudinal and transverse parts of the momenta in the form

$$p_{\Vert }={\displaystyle \frac{1}{2}}\left(p+npn\right)p_{\perp }={\displaystyle \frac{1}{2}}\left(p-npn\right)$$

(115)

$${\pi }_{\Vert }={\displaystyle \frac{1}{2}}\left(\pi +n\pi n\right){\pi }_{\perp }={\displaystyle \frac{1}{2}}\left(\pi -n\pi n\right).$$

(116)

Using

$$\mathring{n}={\mathring{n}}_{\mu }{\gamma }^{\mu }={\gamma }^0={\left({\gamma }^0\right)}^{†}$$

(117)

we define

$$K_L^p=p_{\Vert }=p_0{\gamma }^0=p_{\Vert }^{†}{K}_T^p={\gamma }^5{p}_{\perp }={\gamma }^5\left(p_k{\gamma }^k\right)={\left({\gamma }^5{p}_{\perp }\right)}^{†}$$

(118)

$$K_L^{\pi }={\pi }_{\Vert }={\pi }_0{\gamma }^0={\pi }_{\Vert }^{†}{K}_T^{\pi }={\gamma }^5{\pi }_{\perp }={\gamma }^5\left({\pi }_k{\gamma }^k\right)={\left({\gamma }^5{\pi }_{\perp }\right)}^{†}$$

(119)

so that the four operators $K_{\left\{L,T\right\}}^{\left\{p,\pi \right\}}$ may be treated as Hermitian with respect to the standard ${\gamma }^{\mu }$ matrices. Using $\left\{{\gamma }^5,{\gamma }^{\mu }\right\}=0$ we have

$${\left(K_L^p\right)}^2={\left(p_{\Vert }\right)}^2={\left(p·n\right)}^2{\left(K_T^p\right)}^2=-{\left({\gamma }^5\right)}^2{\left(p_{\perp }\right)}^2=-p_{\perp }^2$$

(120)

$${\left(K_L^{\pi }\right)}^2={\left({\pi }_{\Vert }\right)}^2={\left(\pi ·n\right)}^2{\left(K_T^{\pi }\right)}^2=-{\left({\gamma }^5\right)}^2{\left({\pi }_{\perp }\right)}^2=-{\pi }_{\perp }^2$$

(121)

so that

$${\left(K_L^p\right)}^2-{\left(K_T^p\right)}^2=p_{\Vert }^2+p_{\perp }^2=p^2{\left(K_L^{\pi }\right)}^2-{\left(K_T^{\pi }\right)}^2={\pi }_{\Vert }^2+{\pi }_{\perp }^2={\pi }^2$$

(122)

leading to the expression

$$K_0={\displaystyle \frac{p^2+{\pi }^2}{2M}}={\displaystyle \frac{1}{2M}}\left[{\left(K_L^p\right)}^2-{\left(K_T^p\right)}^2\right]+{\displaystyle \frac{1}{2M}}\left[{\left(K_L^{\pi }\right)}^2-{\left(K_T^{\pi }\right)}^2\right]$$

(123)

as the free particle quantum Hamiltonian. With the minimal gauge substitution

$$\begin{array}{ccc}\hfill K_L^p=p_{\Vert }-e{A}_{\Vert }& & K_T^p={\gamma }^5\left(p_{\perp }-e{A}_{\perp }\right)\hfill \end{array}$$

(124)

$$\begin{array}{ccc}\hfill K_L^{\pi }={\pi }_{\Vert }-e{\chi }_{\Vert }& & K_T^{\pi }={\gamma }^5\left({\pi }_{\perp }-e{\chi }_{\perp }\right)\hfill \end{array}$$

(125)

we expand the longitudinal components of the Hamiltonian as

$$\begin{array}{ccc}\hfill {\left(K_L^p\right)}^2=& & \left(p_{\Vert }-e{A}_{\Vert }\right)·\left(p_{\Vert }-e{A}_{\Vert }\right)+\left(p_{\Vert }-e{A}_{\Vert }\right)\wedge \left(p_{\Vert }-e{A}_{\Vert }\right)\hfill \end{array}$$

(126)

$$\begin{array}{ccc}\hfill =& & {\left(p_{\Vert }-e{A}_{\Vert }\right)}^2-e\left(p_{\Vert }\wedge A_{\Vert }+A_{\Vert }\wedge p_{\Vert }\right)\hfill \end{array}$$

(127)

and

$${\left(K_L^{\pi }\right)}^2={\left({\pi }_{\Vert }-e{\chi }_{\Vert }\right)}^2-e\left({\pi }_{\Vert }\wedge {\chi }_{\Vert }+{\chi }_{\Vert }\wedge {\pi }_{\Vert }\right)$$

(128)

where the wedge products all vanish because the longitudinal components are colinear and so these terms are proportional to $n\wedge n=0$. The transverse components are

$$\begin{array}{ccc}\hfill {\left(K_T^p\right)}^2=& & {\gamma }^5\left(p_{\perp }-e{A}_{\perp }\right){\gamma }^5\left(p_{\perp }-e{A}_{\perp }\right)\hfill \end{array}$$

(129)

$$\begin{array}{ccc}\hfill =& & -\left(p_{\perp }-e{A}_{\perp }\right)·\left(p_{\perp }-e{A}_{\perp }\right)-\left(p_{\perp }-e{A}_{\perp }\right)\wedge \left(p_{\perp }-e{A}_{\perp }\right)\hfill \end{array}$$

(130)

$$\begin{array}{ccc}\hfill =& & -{\left(p_{\perp }-e{A}_{\perp }\right)}^2+e\left(p_{\perp }\wedge A_{\perp }+A_{\perp }\wedge p_{\perp }\right)\hfill \end{array}$$

(131)

$$\begin{array}{ccc}\hfill {\left(K_T^{\pi }\right)}^2=& & -{\left({\pi }_{\perp }-e{\chi }_{\perp }\right)}^2+e\left({\pi }_{\perp }\wedge {\chi }_{\perp }+{\chi }_{\perp }\wedge {\pi }_{\perp }\right)\hfill \end{array}$$

(132)

where the interaction terms act on a state as

$$\left(p_{\perp }\wedge A_{\perp }+A_{\perp }\wedge p_{\perp }\right)\psi =\psi \left(p_{\perp }\wedge A_{\perp }\right)+\left(p_{\perp }\psi \right)\wedge A_{\perp }+A_{\perp }\wedge \left(p_{\perp }\psi \right).$$

(133)

Using $A_{\perp }\wedge \left(p_{\perp }\psi \right)=-\left(p_{\perp }\psi \right)\wedge A_{\perp }$ and the commutation relations

$$\left[p_{\mu },Q_{\nu }(x,\xi )\right]=i{\displaystyle \frac{\partial }{\partial x^{\mu }}}{Q}_{\nu }(x,\xi )\left[{\pi }_{\mu },Q_{\nu }(x,\xi )\right]=i{\displaystyle \frac{\partial }{\partial n^{\mu }}}{Q}_{\nu }(x,\xi )$$

(134)

we are left with

$$p_{\perp }\wedge A_{\perp }+A_{\perp }\wedge p_{\perp }=\left(p_{\mu }{A}_{\nu }\right){\gamma }_{\perp }^{\mu }\wedge {\gamma }_{\perp }^{\nu }=2i\left(p_{\mu }{A}_{\nu }\right){\Sigma }_{\perp }^{\mu \nu }=-F_{\mu \nu }{\Sigma }_{\perp }^{\mu \nu }$$

(135)

and similarly

$${\pi }_{\perp }\wedge {\chi }_{\perp }+{\chi }_{\perp }\wedge {\pi }_{\perp }=-G_{\mu \nu }{\Sigma }_{\perp }^{\mu \nu }$$

(136)

where again

$$F^{\mu \nu }={\displaystyle \frac{\partial }{\partial x_{\mu }}}{A}^{\nu }-{\displaystyle \frac{\partial }{\partial x_{\nu }}}{A}^{\mu }{G}^{\mu \nu }={\displaystyle \frac{\partial }{\partial n_{\mu }}}{\chi }^{\nu }-{\displaystyle \frac{\partial }{\partial n_{\nu }}}{\chi }^{\mu }.$$

(137)

Putting together the longitudinal and transverse components we find the electromagnetic Hamiltonian as

$$\begin{array}{ccc}\hfill K=& & {\displaystyle \frac{1}{2M}}\left[{\left(K_L^p\right)}^2-{\left(K_T^p\right)}^2\right]+{\displaystyle \frac{1}{2M}}\left[{\left(K_L^{\pi }\right)}^2-{\left(K_T^{\pi }\right)}^2\right]\hfill \end{array}$$

(138)

$$\begin{array}{ccc}\hfill =& & {\displaystyle \frac{1}{2M}}\left[{\left(p_{\Vert }-e{A}_{\Vert }\right)}^2+{\left(p_{\perp }-e{A}_{\perp }\right)}^2+e{F}_{\mu \nu }{\Sigma }_{\perp }^{\mu \nu }\right]\hfill \end{array}$$

(139)

$$\begin{array}{ccc}& & +{\displaystyle \frac{1}{2M}}\left[{\left({\pi }_{\Vert }-e{\chi }_{\Vert }\right)}^2+{\left({\pi }_{\perp }-e{\chi }_{\perp }\right)}^2+e{G}_{\mu \nu }{\Sigma }_{\perp }^{\mu \nu }\right]\hfill \end{array}$$

(140)

$$\begin{array}{ccc}\hfill =& & {\displaystyle \frac{1}{2M}}\left[{\left(p-eA\right)}^2+{\left(\pi -e\chi \right)}^2\right]+{\displaystyle \frac{e}{2M}}\left(F_{\mu \nu }+G_{\mu \nu }\right){\Sigma }_{\perp }^{\mu \nu }\hfill \end{array}$$

(141)

which is equivalent to the classical spinless Hamiltonian (19) with the addition of the spin interaction terms. As in Section 3, terms containing $H_{\mu \nu }$ do not directly appear in the Hamiltonian or couple to the spin operator ${\Sigma }_{\perp }^{\mu \nu }$.

5.3. Plane wave Solutions

Taking $A=\chi =0$ in the Hamiltonian (138), the free particle Stueckelberg-Schrodinger equation

$$i{\partial }_{\tau }\Psi \left(\zeta ,x,\tau \right)=\left({\displaystyle \frac{p^2}{2M}}+{\displaystyle \frac{{\pi }^2}{2M}}\right)\Psi \left(\zeta ,x,\tau \right)$$

(142)

admits the plane wave solution

$$\Psi \left(\zeta ,x,\tau \right)=\left[\begin{array}{c}{\chi }^{\left(1\right)}\left(\pi \right)\\ {\chi }^{\left(2\right)}\left(\pi \right)\\ {\chi }^{\left(3\right)}\left(\pi \right)\\ {\chi }^{\left(4\right)}\left(\pi \right)\end{array}\right]exp\left[i\left(p·x+\pi ·\zeta -{\displaystyle \frac{p^2+{\pi }^2}{2M}}\tau \right)\right]$$

(143)

where ${\chi }^{\left(\sigma \right)}\left(\pi \right)$ is a constant amplitude. In the special frame $\pi =\mathring{\pi }=M\left(1,0,0,0\right)$ we can write the four independent amplitudes as

$${\chi }^{\left(\sigma \right)}\left(\pi \right)=\mathcal{N}{\psi }^{\left(\sigma \right)}$$

(144)

where $\mathcal{N}$ is some normalization and

$${\psi }^{\left(1\right)}=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]{\psi }^{\left(2\right)}=\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]{\psi }^{\left(3\right)}=\left[\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right]{\psi }^{\left(4\right)}=\left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right].$$

(145)

The general plane wave solution (143) is found by boosting ${\mathring{\pi }}^{\mu }$ to

$$\pi =\Lambda \mathring{\pi }=exp\left(i{\beta }^k{M}_{0k}\right)\mathring{\pi }=M\left(cosh\beta ,sinh\beta \widehat{\mathit{\beta }}\right)$$

(146)

and transforming the state as

$${\Psi }^{\left(\sigma \right)}(\zeta ,x,\tau )=S(\Lambda ){\Psi }^{\left(\sigma \right)}({\Lambda }^{-1}\mathring{\zeta },{\Lambda }^{-1}x)=S(\Lambda ){\Psi }^{\left(\sigma \right)}(\mathring{\zeta },x,\tau )$$

(147)

where the phase of the plane wave is a Lorentz invariant and

$$S\left(\Lambda \right)=exp\left(-i{\Sigma }^{0k}{\beta }_k\right)=\left[\begin{array}{cc}cosh{\displaystyle \frac{\beta }{2}}{\sigma }^0& sinh{\displaystyle \frac{\beta }{2}}\widehat{\mathit{\beta }}·\mathit{\sigma }[-16pt]0pt16pt\\ sinh{\displaystyle \frac{\beta }{2}}\widehat{\mathit{\beta }}·\mathit{\sigma }& cosh{\displaystyle \frac{\beta }{2}}{\sigma }^0\end{array}\right].$$

(148)

We can now write the four independent solutions as

$${\Psi }^{\left(\sigma \right)}(\zeta ,x,\tau )=\mathcal{N}{u}^{\left(\sigma \right)}exp\left[i\left(p·x+\pi ·\zeta -{\displaystyle \frac{p^2+{\pi }^2}{2M}}\tau \right)\right]$$

(149)

where

$$u^{\left(\sigma \right)}=S\left(\Lambda \right){\psi }^{\left(\sigma \right)}$$

(150)

so that using

$$\widehat{\mathit{\beta }}·\mathit{\sigma }=\left(\begin{array}{cc}{\widehat{\beta }}^3& {\widehat{\beta }}^1-i{\widehat{\beta }}^2\\ {\widehat{\beta }}^1+i{\widehat{\beta }}^2& -{\widehat{\beta }}^3\end{array}\right)$$

(151)

we find the transformed amplitudes as

$$u^{\left(1\right)}=\left[\begin{array}{c}cosh{\displaystyle \frac{\beta }{2}}\\ 0\\ sinh{\displaystyle \frac{\beta }{2}}{\widehat{\beta }}^3\\ sinh{\displaystyle \frac{\beta }{2}}\left({\widehat{\beta }}^1+i{\widehat{\beta }}^2\right)\end{array}\right]u^{\left(2\right)}=\left[\begin{array}{c}0\\ cosh{\displaystyle \frac{\beta }{2}}\\ sinh{\displaystyle \frac{\beta }{2}}\left({\widehat{\beta }}^1-i{\widehat{\beta }}^2\right)\\ -sinh{\displaystyle \frac{\beta }{2}}{\widehat{\beta }}^3\end{array}\right]$$

(152)

$$u^{\left(3\right)}=\left[\begin{array}{c}sinh{\displaystyle \frac{\beta }{2}}{\widehat{\beta }}^3\\ sinh{\displaystyle \frac{\beta }{2}}\left({\widehat{\beta }}^1+i{\widehat{\beta }}^2\right)\\ cosh{\displaystyle \frac{\beta }{2}}\\ 0\end{array}\right]u^{\left(4\right)}=\left[\begin{array}{c}sinh{\displaystyle \frac{\beta }{2}}\left({\widehat{\beta }}^1-i{\widehat{\beta }}^2\right)\\ -sinh{\displaystyle \frac{\beta }{2}}{\widehat{\beta }}^3\\ 0\\ cosh{\displaystyle \frac{\beta }{2}}\end{array}\right].$$

(153)

Using (49) the conjugate bispinor is

$${\overline{\Psi }}^{\left(\sigma \right)}(\zeta ,x,\tau )=\mathcal{N}{\overline{u}}^{\left(\sigma \right)}exp\left[-i\left(p·x+\pi ·\zeta -{\displaystyle \frac{p^2+{\pi }^2}{2M}}\tau \right)\right]$$

(154)

where

$${\overline{u}}^{\left(\sigma \right)}=\overline{\left[S\left(\Lambda \right){\psi }^{\left(\sigma \right)}\right]}={\left[\left(C^{-1}S\left(\Lambda \right)C\right){\psi }^{\left(\sigma \right)}\right]}^{†}={\left[S^{-1}\left(\Lambda \right){\psi }^{\left(\sigma \right)}\right]}^{†}$$

(155)

so that

$$\begin{array}{ccc}\hfill {\overline{u}}^{\left(1\right)}=& & \left[cosh{\displaystyle \frac{\beta }{2}}0-sinh{\displaystyle \frac{\beta }{2}}{\widehat{\beta }}^3-sinh{\displaystyle \frac{\beta }{2}}\left({\widehat{\beta }}^1-i{\widehat{\beta }}^2\right)\right]\hfill \end{array}$$

(156)

$$\begin{array}{ccc}\hfill {\overline{u}}^{\left(2\right)}=& & \left[0cosh{\displaystyle \frac{\beta }{2}}-sinh{\displaystyle \frac{\beta }{2}}\left({\widehat{\beta }}^1+i{\widehat{\beta }}^2\right)sinh{\displaystyle \frac{\beta }{2}}{\widehat{\beta }}^3\right]\hfill \end{array}$$

(157)

$$\begin{array}{ccc}\hfill {\overline{u}}^{\left(3\right)}=& & \left[-sinh{\displaystyle \frac{\beta }{2}}{\widehat{\beta }}^3-sinh{\displaystyle \frac{\beta }{2}}\left({\widehat{\beta }}^1-i{\widehat{\beta }}^2\right)cosh{\displaystyle \frac{\beta }{2}}0\right]\hfill \end{array}$$

(158)

$$\begin{array}{ccc}\hfill {\overline{u}}^{\left(4\right)}=& & \left[-sinh{\displaystyle \frac{\beta }{2}}\left({\widehat{\beta }}^1+i{\widehat{\beta }}^2\right)sinh{\displaystyle \frac{\beta }{2}}{\widehat{\beta }}^{3}0cosh{\displaystyle \frac{\beta }{2}}\right]\hfill \end{array}$$

(159)

leading to

$${\overline{\Psi }}^{\left(\sigma \right)}(\zeta ,x,\tau ){\Psi }^{\left({\sigma }^{\prime }\right)}(\zeta ,x,\tau )={\mathcal{N}}^2{\overline{u}}^{\left(\sigma \right)}{u}^{\left({\sigma }^{\prime }\right)}={\mathcal{N}}^2{\delta }^{\sigma {\sigma }^{\prime }}.$$

(160)

5.4. The Spin Operator

For the bispinor representation, the Pauli–Lubanski pseudovector (67) takes the form of the four matrices

$$W_{\mu }=-{\displaystyle \frac{1}{2}}{ϵ}_{\mu \nu \lambda \sigma }{\Sigma }_{\perp }^{\nu \lambda }{N}^{\sigma }=-{\displaystyle \frac{1}{2}}{ϵ}_{\mu \nu \lambda \sigma }{\Sigma }^{\nu \lambda }{N}^{\sigma }$$

(161)

where the second equality follows from (112). The scalar product

$$W^{\mu }{W}_{\mu }={\displaystyle \frac{1}{2}}{\Sigma }^{\nu \lambda }{\Sigma }_{\nu \lambda }{n}^{\sigma }{N}_{\sigma }-{\Sigma }_{\mu \sigma }{\Sigma }^{\nu \sigma }{N}^{\mu }{N}_{\nu }={\displaystyle \frac{1}{2}}{\Sigma }^{\nu \lambda }{\Sigma }_{\nu \lambda }$$

(162)

is independent of $N^{\mu }$ and commutes with all the other generators. By direct calculation we find the explicit forms

$$W_0=-{\displaystyle \frac{1}{2}}\left[\begin{array}{cc}\mathit{\sigma }·\mathit{n}& 0\\ 0& \mathit{\sigma }·\mathit{n}\end{array}\right]W_i={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}{n}^{\left(0\right)}{\delta }_{ik}{\sigma }^k& i{\left(\mathit{\sigma }\times \mathit{n}\right)}_i[-6pt]0pt6pt\\ i{\left(\mathit{\sigma }\times \mathit{n}\right)}_i& n^{\left(0\right)}{\delta }_{ik}{\sigma }^k\end{array}\right]$$

(163)

with the 3D inner product $\mathit{\sigma }·\mathit{n}={\delta }_{ij}{n}^i{\sigma }^j$ and cross product ${\left(\mathit{\sigma }\times \mathit{n}\right)}_i={ϵ}_{ijk}{\sigma }^j{n}^k$, from which we obtain

$$-W^{\mu }{W}_{\mu }=-W_0^2-{\eta }^{i{i}^{\prime }}{W}_i{W}_{i^{\prime }}={\displaystyle \frac{3}{4}}\left[\begin{array}{cc}{\sigma }^0& 0\\ 0& {\sigma }^0\end{array}\right]={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{2}}+1\right)I$$

(164)

describing the bispinor as a spin-1/2 state. In the special frame $n=\mathring{n}=\left(1,0,0,0\right)$ we have

$$W_0=0W_i={\displaystyle \frac{1}{2}}{\delta }_{ik}\left[\begin{array}{cc}{\sigma }^k& 0\\ 0& {\sigma }^k\end{array}\right]$$

(165)

so that acting on the plane wave solutions, $W^3$ has eigenvalue $+1$ on ${\Psi }^{\left(1\right)}$ and ${\Psi }^{\left(3\right)}$, and eigenvalue $-1$ on ${\Psi }^{\left(2\right)}$ and ${\Psi }^{\left(4\right)}$.

Since $W_{\mu }$ is orthogonal to $n^{\mu }$ it has three independent components in the spacelike hypersurface, for which we may find an orthonormal basis ${\mathit{e}}^i$ for $i=1,2,3$. Expanding

$$W=W_{\mu }{\gamma }^{\mu }=J_k{\mathit{e}}^k⟶W^{\mu }=W·{\gamma }^{\mu }=J_k{\left({\mathit{e}}^k\right)}^{\mu }$$

(166)

where ${\left({\mathit{e}}^k\right)}^{\mu }$ is the $\mu$ component of ${\mathit{e}}^k$ in the ${\gamma }^{\mu }$ basis. From (164) we see that the components $J_k$ satisfy

$$-{\eta }_{\mu \nu }{W}^{\mu }{W}^{\nu }=-{\eta }^{k{k}^{\prime }}{J}_k{J}_{k^{\prime }}={\mathit{J}}^2={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1}{2}}+1\right)I$$

(167)

as expected for the 3-vector spin operator $\mathit{J}$.

For simplicity we may consider a boost along one of the three space axes a so that

$$n=n_{\left(0\right)}{\gamma }^0+n_{\left(a\right)}{\gamma }^a=n^{\left(0\right)}{\gamma }^0-n^{\left(a\right)}{\gamma }^a=\sqrt{1+n_{\left(a\right)}^2}{\gamma }^0-n^{\left(a\right)}{\gamma }^a$$

(168)

leading to

$$W_0=-{\displaystyle \frac{1}{2}}\left[\begin{array}{cc}{n}^{\left(a\right)}{\sigma }^{\left(a\right)}& 0\\ 0& n^{\left(a\right)}{\sigma }^{\left(a\right)}\end{array}\right]W_j={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}{n}^{\left(0\right)}{\delta }_{jk}{\sigma }^k& i{ϵ}_{jik}{\sigma }^i{n}^{\left(a\right)}{\delta }^{ak}\\ i{ϵ}_{jik}{\sigma }^i{n}^{\left(a\right)}{\delta }^{ak}& n^{\left(0\right)}{\delta }_{jk}{\sigma }^k\end{array}\right].$$

(169)

Taking the boost along the 3-axis this becomes

$$W_0=-{\displaystyle \frac{1}{2}}\left[\begin{array}{cc}{n}^{\left(3\right)}{\sigma }^{\left(3\right)}& 0\\ 0& n^{\left(3\right)}{\sigma }^{\left(3\right)}\end{array}\right]W_j={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}{n}^{\left(0\right)}{\delta }_{jk}{\sigma }^k& i{n}^{\left(3\right)}{ϵ}_{ji3}{\sigma }^i\\ i{n}^{\left(3\right)}{ϵ}_{ji3}{\sigma }^i& n^{\left(0\right)}{\delta }_{jk}{\sigma }^k\end{array}\right]$$

(170)

so that $W_0$ and $W_3$ are diagonal while $W_1$ and $W_2$ are off-diagonal.

Using the Gram-Schmidt method we can define the orthonormal basis ${\mathit{e}}^{\mu }$ starting with ${\mathit{e}}^0=n$ and leading to

$$\begin{array}{c}{\mathit{e}}^0=n=n^{\left(0\right)}{\gamma }^0-n^{\left(3\right)}{\gamma }^3=\sqrt{1+n_{\left(3\right)}^2}{\gamma }^0-n^{\left(3\right)}{\gamma }^3\hfill \\ {\mathit{e}}^{\left(1\right)}={\gamma }^1\hfill \\ {\mathit{e}}^{\left(2\right)}={\gamma }^2\hfill \\ {\mathit{e}}^{\left(3\right)}=n^{\left(0\right)}{\gamma }^3-n^{\left(3\right)}{\gamma }^0=-n^{\left(3\right)}{\gamma }^0+\sqrt{1+n_{\left(3\right)}^2}{\gamma }^3\hfill \end{array}$$

(171)

so that although ${\mathit{e}}^{\left(3\right)}$ has a 0-component, it is spacelike in the 4D spacetime and normal to n. Using

$$J^k=W·{\mathit{e}}^k=\left(W_0{\gamma }^0+W_i{\gamma }^i\right)·{\mathit{e}}^k$$

(172)

we find

$$\begin{array}{ccc}\hfill J^1=& & \left(W_0{\gamma }^0+W_i{\gamma }^i\right)·{\gamma }^1=W_i{\eta }^{i1}\hfill \end{array}$$

(173)

$$\begin{array}{ccc}\hfill J^2=& & \left(W_0{\gamma }^0+W_i{\gamma }^i\right)·{\gamma }^2=W_i{\eta }^{i2}\hfill \end{array}$$

(174)

$$\begin{array}{ccc}\hfill J^3=& & \left(W_0{\gamma }^0+W_i{\gamma }^i\right)·\left({\gamma }^3{n}^{\left(0\right)}-n^{\left(3\right)}{\gamma }^0\right)=n^{\left(0\right)}{W}_i{\eta }^{i3}-n^{\left(3\right)}{W}_0\hfill \end{array}$$

(175)

so that

$$J_1={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}{n}^{\left(0\right)}{\sigma }^1& i{n}^3{\sigma }^2\\ i{n}^3{\sigma }^2& n^{\left(0\right)}{\sigma }^1\end{array}\right]J_2={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}{n}^{\left(0\right)}{\sigma }^2& -i{n}^3{\sigma }^1\\ -i{n}^3{\sigma }^1& n^{\left(0\right)}{\sigma }^2\end{array}\right]$$

(176)

and

$$J_3={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}{\sigma }^3& 0\\ 0& {\sigma }^3\end{array}\right]$$

(177)

which is diagonal and independent of n. Using the n-dependent bispinors (152) and (153) we see

$$J_3{\Psi }^{\left(1\right)}={\displaystyle \frac{1}{2}}{\Psi }^{\left(1\right)}{J}_3{\Psi }^{\left(3\right)}={\displaystyle \frac{1}{2}}{\Psi }^{\left(3\right)}$$

(178)

$$J_3{\Psi }^{\left(2\right)}=-{\displaystyle \frac{1}{2}}{\Psi }^{\left(2\right)}{J}_3{\Psi }^{\left(4\right)}=-{\displaystyle \frac{1}{2}}{\Psi }^{\left(4\right)}$$

(179)

as expected.

6. Entanglement

6.1. A Singlet State

We write the plane wave state (149) as

$${\Psi }^{\left(\sigma \right)}(\zeta ,x,\tau )=\phi \left(\zeta ,x,\tau \right)u^{\left(\sigma \right)}\left(\pi \right)$$

(180)

where

$$\phi \left(\zeta ,x,\tau \right)=\mathcal{N}exp\left[i\left(p·x+\pi ·\zeta -{\displaystyle \frac{p^2+{\pi }^2}{2M}}\tau \right)\right]$$

(181)

describes a spinless plane wave on the extended spacetime. A two-body plane wave state is the direct product

$${\Psi }^{({\sigma }_1,{\sigma }_2)}\left({\zeta }_1,{\zeta }_2,x_1,x_2,\tau \right)={\phi }_1\left({\zeta }_1,x_1,\tau \right){\phi }_2\left({\zeta }_2,x_2,\tau \right)u_1^{\left({\sigma }_1\right)}\left(\pi \right)u_2^{\left({\sigma }_2\right)}\left(\pi \right)$$

(182)

and so the singlet state is

$${\Psi }^{\left(0\right)}\left({\zeta }_1,{\zeta }_2,x_1,x_2,\tau \right)=\phi \left({\zeta }_1,{\zeta }_2,x_1,x_2,\tau \right)u^{\left(0\right)}\left(\pi \right)$$

(183)

where the spacetime part

$$\phi \left({\zeta }_1,{\zeta }_2,x_1,x_2,\tau \right)={\displaystyle \frac{1}{\sqrt{2}}}\left[{\phi }_1\left({\zeta }_1,x_1,\tau \right){\phi }_2\left({\zeta }_2,x_2,\tau \right)+{\phi }_2\left({\zeta }_1,x_1,\tau \right){\phi }_1\left({\zeta }_2,x_2,\tau \right)\right]$$

(184)

is symmetric under $\left({\zeta }_1,x_1\right)\leftrightarrow \left({\zeta }_2,x_2\right)$ while the spin part

$$u^{\left(0\right)}\left(\pi \right)={\displaystyle \frac{1}{\sqrt{2}}}\left[u_1^{\left({\sigma }_1\right)}\left(\pi \right)u_2^{\left({\sigma }_2\right)}\left(\pi \right)-u_1^{\left({\sigma }_2\right)}\left(\pi \right)u_2^{\left({\sigma }_1\right)}\left(\pi \right)\right]$$

(185)

requires

$$J_3{u}^{\left({\sigma }_1\right)}+J_3{u}^{\left({\sigma }_2\right)}=0$$

(186)

and is antisymmetric under ${\sigma }_1\leftrightarrow {\sigma }_2$. Since the one-particle states must transform under the same representation of $SL(2,C)$, we may form singlets from the pairs $\{u^1,u^2\}$ and $\{u^3,u^4\}$.

6.2. The Palacios Experiment

The experiment proposed by Palacios et. al. involves the sequential double ionization of helium, producing a pair of entangled electrons with a small time separation. The electrons are emitted with energies $10.4eV$ and $14.6eV$ separated in time by $\Delta t\simeq .75fs$ (femtoseconds) and each with an emission pulse width of $\simeq 0.5fs$. Since the SHP formalism treats time/space and energy/momentum on an equal footing, the uncertainly relation $\Delta E\Delta t\ge \hslash /2$ holds rigorously, and in this case leads to $\Delta E\ge 4eV$ which is seen to apply for this process. The electrons may thus be considered identical particles and may form a singlet state.

Describing the singlet using (183) — (185) the spin part describes the anti-symmetric combination of spin up and spin down states, where the states must be chosen with the same parity. In the special frame $\pi =\mathring{\pi }=M\left(1,\mathbf{0}\right)$ the spin factor is either

$$u^{\left(0\right)}\left(\pi \right)={\displaystyle \frac{1}{\sqrt{2}}}\left(\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]\otimes \left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]-\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]\otimes \left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right]\right)$$

(187)

or

$$u^{\left(0\right)}\left(\pi \right)={\displaystyle \frac{1}{\sqrt{2}}}\left(\left[\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right]\otimes \left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right]-\left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right]\otimes \left[\begin{array}{c}0\\ 0\\ 1\\ 0\end{array}\right]\right)$$

(188)

and the spacetime part in the extended phase space is the symmetric combination

$$\phi \left({\zeta }_1,{\zeta }_2,x_1,x_2,\tau \right)={\displaystyle \frac{1}{\sqrt{2}}}\left[{\phi }_1\left({\zeta }_1,x_1,\tau \right){\phi }_2\left({\zeta }_2,x_2,\tau \right)+{\phi }_2\left({\zeta }_1,x_1,\tau \right){\phi }_1\left({\zeta }_2,x_2,\tau \right)\right]$$

(189)

where taking $p^2={\pi }^2=M^2$ on-shell for the free particles, (181) reduces to

$$\phi \left(\zeta ,x,\tau \right)=\mathcal{N}exp\left[i\left(-\mathit{p}·\mathit{x}+Et+M{\zeta }^0-M\tau \right)\right].$$

(190)

Now (189) is just

$$\begin{array}{ccc}\hfill \phi \left({\zeta }_1,{\zeta }_2,x_1,x_2,\tau \right)=& & {\displaystyle \frac{1}{\sqrt{2}}}{e}^{i\left[{\mathit{p}}_1·{\mathit{x}}_1+{\mathit{p}}_2·{\mathit{x}}_2-M\left({\zeta }_1^0+{\zeta }_2^0\right)\right]}{e}^{-i\left(E_1{t}_1+E_2{t}_2\right)}\hfill \\ & & +{\displaystyle \frac{1}{\sqrt{2}}}{e}^{i\left[{\mathit{p}}_1·{\mathit{x}}_2+{\mathit{p}}_2·{\mathit{x}}_1-M\left({\zeta }_1^0+{\zeta }_2^0\right)\right]}{e}^{-i\left(E_1{t}_2+E_2{t}_1\right)}\hfill \end{array}$$

(191)

and defining

$$T={\displaystyle \frac{1}{2}}\left(t_1+t_2\right)\Delta t=t_2-t_{1}E=E_1+E_2\Delta E=E_1-E_2\zeta ={\zeta }_1^0+{\zeta }_2^0$$

(192)

this simplifies to

$$\phi \left({\zeta }_1,{\zeta }_2,x_1,x_2,\tau \right)={\displaystyle \frac{1}{\sqrt{2}}}{e}^{-i\left(ET+M{\zeta }^0\right)}\left[e^{i\left({\mathit{p}}_1·{\mathit{x}}_1+{\mathit{p}}_2·{\mathit{x}}_2+{\displaystyle \frac{1}{2}}\Delta E\Delta t\right)}+e^{i\left({\mathit{p}}_1·{\mathit{x}}_2+{\mathit{p}}_2·{\mathit{x}}_1-{\displaystyle \frac{1}{2}}\Delta E\Delta t\right)}\right]$$

(193)

which is compatible with the expression obtained by Palacios et. al. and indicates interference fringes over time $\Delta t$.

7. Summary

The phenomenon of quantum entanglement is an increasingly important topic in contemporary physics, and new developments in this area will depend on determining appropriate frameworks for its representation. The description of entanglement as a superposition of distinguishable states necessarily involves a precise and rigorous characterization of the Hilbert space of each constituent particle. Although nonrelativistic methods are adequate in many applications, relativistic considerations become relevant at high energy, short distance, and as we have seen here, for describing temporal interference. Therefore, a proper treatment of relativistic states requires a fully covariant framework that places space and time on an equal footing in a natural and consistent manner. Moreover, the covariant Hilbert space must include the coherent eigenstates of the commuting operators found from the Poincaré algebra, and be defined with respect to a shared continuous parameterization left invariant by these operators.

As we have seen, the Stueckelberg-Horwitz-Piron (SHP) formalism satisfies these requirements by introducing a Poincaré invariant evolution parameter and relaxing the mass-shell constraint on spacetime momenta. But since $p^2$ is unconstrained and has no definitive rest-frame value, Wigner’s construction of $SU\left(2\right)$ spin states in the spacelike hypersurface normal to $\mathring{p}=M(1,0,0,0)$ cannot be carried out. Horwitz et. al. circumvented this problem by introducing an arbitrary timelike unit vector $n^{\mu }$, defining spin states in the spacelike hypersurface normal to $n^{\mu }$, and inducing the $SL(2,C)$ representation on the orbit of these arbitrarily defined states. Because the possible spin states are defined with respect to a representation of $SU\left(2\right)$ determined by the chosen value of $n^{\mu }$, coherent states and their superpositions must share this choice.

In this paper, we have attempted to provide a dynamical interpretation to $n^{\mu }$ by associating it with the momentum ${\pi }^{\mu }$ in an extended phase space. By constructing a classical Lagrangian and Hamiltonian gauge theory on the extended phase space and considering the classical equations of motion in the extended electromagnetic field, we identified the conditions under which the values of ${\pi }^{\mu }$ can diverge for a particle pair, indicating a possible mode of disruption of a quantum singlet. Defining the generators of Poincaré transformation on the extended phase space, we developed the spinor representations of the Lorentz group. To introduce spin states, we constructed the little group and Wigner operator acting on the momenta ${\pi }^{\mu }$ in the extended sector, leading to a Pauli-Lubanski operator and pure spin operator in this sector. The matrix elements for a Lorentz transformation on these states consists of a pure boost in the spacetime and extended sectors and a rotation of the spin indices in the spacelike hypersurface of the extended sector orthogonal to ${\pi }^{\mu }$. Projecting onto the longitudinal and transverse components of the momentum $\{p^{\mu },{\pi }^{\mu }\}$ we found the electromagnetic quantum Hamiltonian, and wrote plane wave solutions on the extended phase space. In the absence of an external field, these free particle states evolve with constant $\{p^{\mu },{\pi }^{\mu }\}$ and permit the construction of singlet states defined in the same representation of $SU\left(2\right)$. Such states contain a spacetime part symmetric under exchange of particles, and an antisymmetric spin part. We finally presented an analysis of the proposed Palacios experiment, showing the appearance of interference fringe from a temporal superposition.

As discussed in Section 2, the Zeeman and Stark effects were found by treating an arbitrary vector quantity required for the induced representation of $SL(2,C)$ as a dynamical quantity. In a subsequent paper, we will discuss the transitions of singlet states discussed in Section (Section 6) under perturbations induced by an external electromagnetic field. We anticipate that under certain conditions, such transitions may shift the respective values of ${\pi }^{\mu }$ differentially, and thus place the constituent particles into different representations of spin. Such a process would imply perturbative decoherence and breaking of the singlet state.