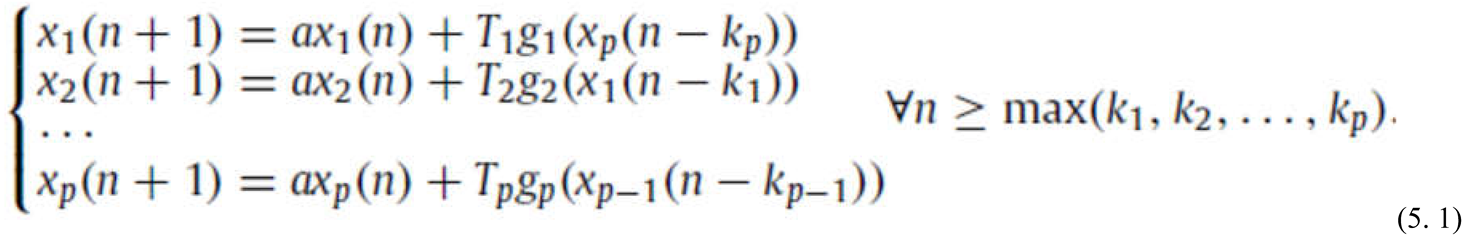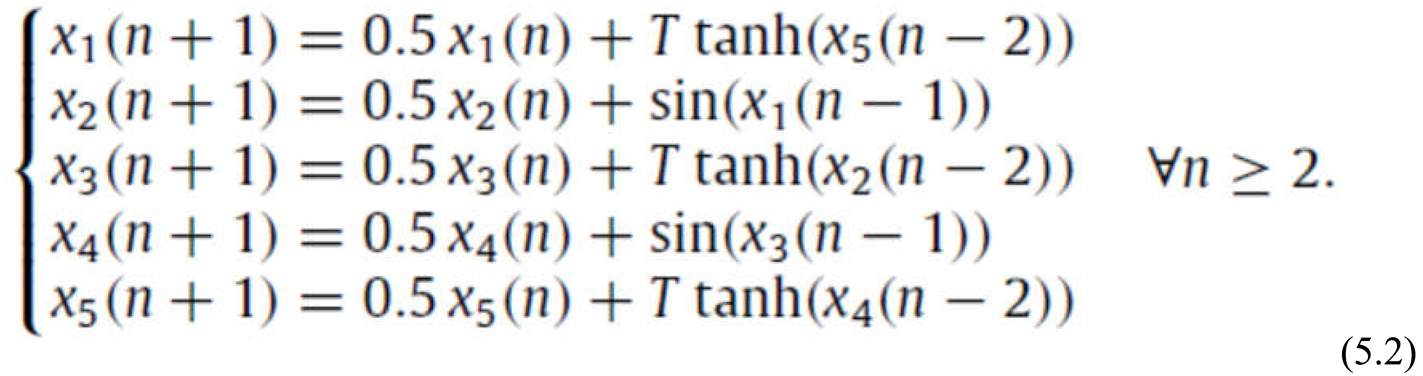1. Introduction
There is some disagreement among mathematician about how the concept of fractal should be formally defined. Mandelbrot himself summarized it is as “beautiful damn hard increasingly useful. That’s fractals’. [
1] More formally, in 1982Mandelbrot defined fractal as follows: "A fractal is by definition a set for which the Hausdorff–Besicovitch dimension strictly exceeds the topological dimension."[
2]
Later, seeing this as too restrictive, he simplified and expanded the definition to this: "A fractal is a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole."[
1] Still later, Mandelbrot proposed, "to use fractal without a pedantic definition, to use fractal dimension as a generic term applicable to all the variants". [
3] The consensus among mathematicians is that theoretical fractals are infinitely self-similar iterated and detailed mathematical constructs, of which many examples have been formulated and studied [
1,
2,
3]. Fractals are not limited to geometric patterns, but can also describe processes in time [
4,
5,
6,
7,
8,
9]. Fractal patterns with various degrees of self-similarity have been rendered or studied in visual physical, and aural media and found in nature, [
10,
11,
12,
13] technology, [
14,
15,
16,
17] art, [
18,
19] and architecture. [
20] In this context fractal geometry lies within the mathematical branch of measure theory [
3] presenting different measures and algorithms for the computation of different types of fractal dimensions of geometrical patterns; box counting dimension, correlation dimension ,generalized or Renyi dimensions, Higuchi dimension, Lyapunov dimension, Multifractal dimensions, Hausdorff dimension, Packing dimension, Assouad dimension, Local connected dimension, Degree dimension, Parabolic Hausdorff dimension. These fractal dimensions strictly exceed the topological dimension and although for compact sets with exact affine self-similarity all these dimensions coincide; in general, they are not equivalent. When fractal describe processes in time, then for the analysis of statistical data, fractal analysis use also tools for: investigate statistical self-similarity, find probability density function (PDF), fractal scaling in time, time series analysis, fractal kinetic description ,power law and fractal statistics. [4–9,16,21–33]
Beside the mathematical description of the voltage dynamics of neural cells and systems using fractals, there exist a large amounts of papers, which use classical theory of electrical circuits or fractional order derivative circuits for describe the neural cells dynamics.
Papers [
34,
35,
36,
37,
38,
39,
40,
41] use classical theory of electricity (integer order differential equations) for the description of the ion transport through the nervous cell membrane. Papers [
42,
43] use time fractional order circuits [
44] for the description of the ion transport through the nervous cell membrane. In the papers [
45,
46] it was shown that: Mathematical descriptions of the ion transport, across passive or active biological neuron membrane, voltage propagation along neuron axons and dendrites having passive or active membrane and ion transport in biological neuron networks, using classic Caputo or Riemann-Liouville fractional order derivatives, is nonobjective. The no objectivity is originated in the incompatibility of the classic Caputo and Riemann- Liouville fractional order derivatives with the understanding of the time evolution, used in case of the mathematical description of real word phenomena.
Hopfield paper [
47] claims to be mathematical descriptions of electrical phenomena appearing in nervous system.Later in [
48,
49,
50] this model was extended to optimization and cryptography. In papers [
51,
52,
53,
54,
55,
56,
57,
58,
59,
60,
61,
62,
63,
64,
65,
66,
67,
68,
69,
70,
71], theoretical studies of the Hopfield neural system are carried out in the continuous time and discrete time versions.Papers reveal configuration of steady states , local exponential stability of steady states in Lyapunov sense,regions of attraction of exponentia stable steady states, bifurcation properties etc.Several example of low dimensional (two, fife neurons) neural network are presented which exhibit extremely interesting orbits and bifurcation diagrams.
Although for some values of the bifurcation parameter the orbits completely disintegrate and no longer resemble what we call orbit in classical sense, their fractal quality is not analyzed and highlighted. Also, no reference is made to the question: whether or not these completely dismembered orbits have a real counterpart? In the case of strange bifurcation diagrams, their approach with fractals, as far as we know, is not done.
In this paper, we will present in case of four neural networks, examples of strange orbits and bifurcation diagrams, and try to bring arguments to support that they are fractals. We also hypothesize that they do not have a real counterpart. They exists just in theory.
2. Case of a Discrete-Time Hopfield Neural Network of Two Neurons with Two Delays and No Self- Connections
In [
67] an extended analysis of the chaotic dynamics of the neural network defined by
was undertaken. The external inputs are equal to zero and the system parameters are regarded as numerical expresion of the state of network..The network state can change due to a disease for example. Therefore the network voltage dynamics change too. In [
67] this kind of change is analyzed with respect to the product of the interconnection coefficients as aggregated characteristic parameter for the system. The main result obtained in [
67], is that, if the magnitudes of the interconnection coefficients are large enough, then the neural network exhibits Marotto’s chaotic behavior.
For illustrate what this means the following numerical example was considered:
For different values of b, trajectory of the neurons voltages were computed and represented. We will present some of these trajectories.
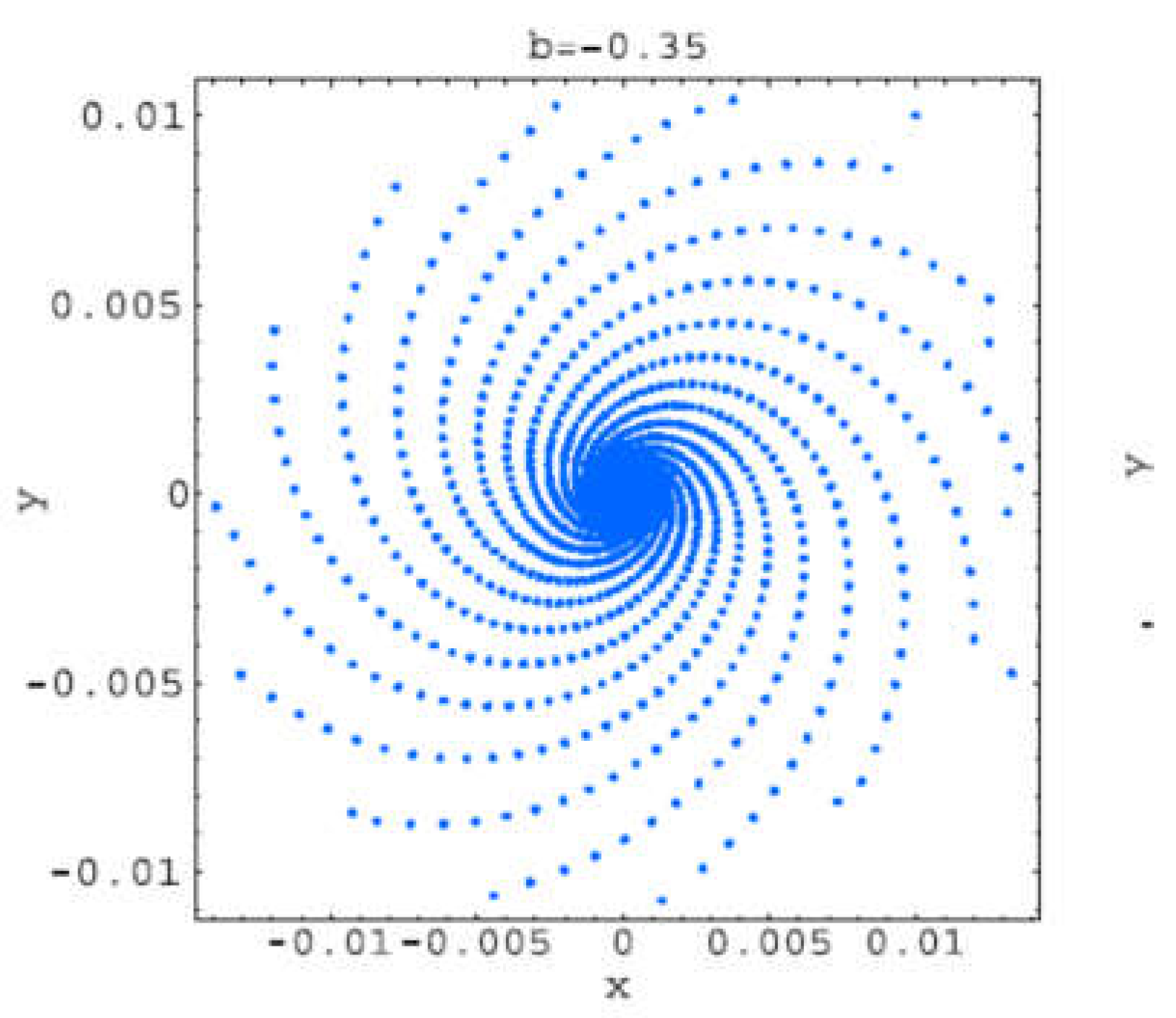
For b=−0.35, the null solution is asymptotically stable, and the trajectories converges to the origin.
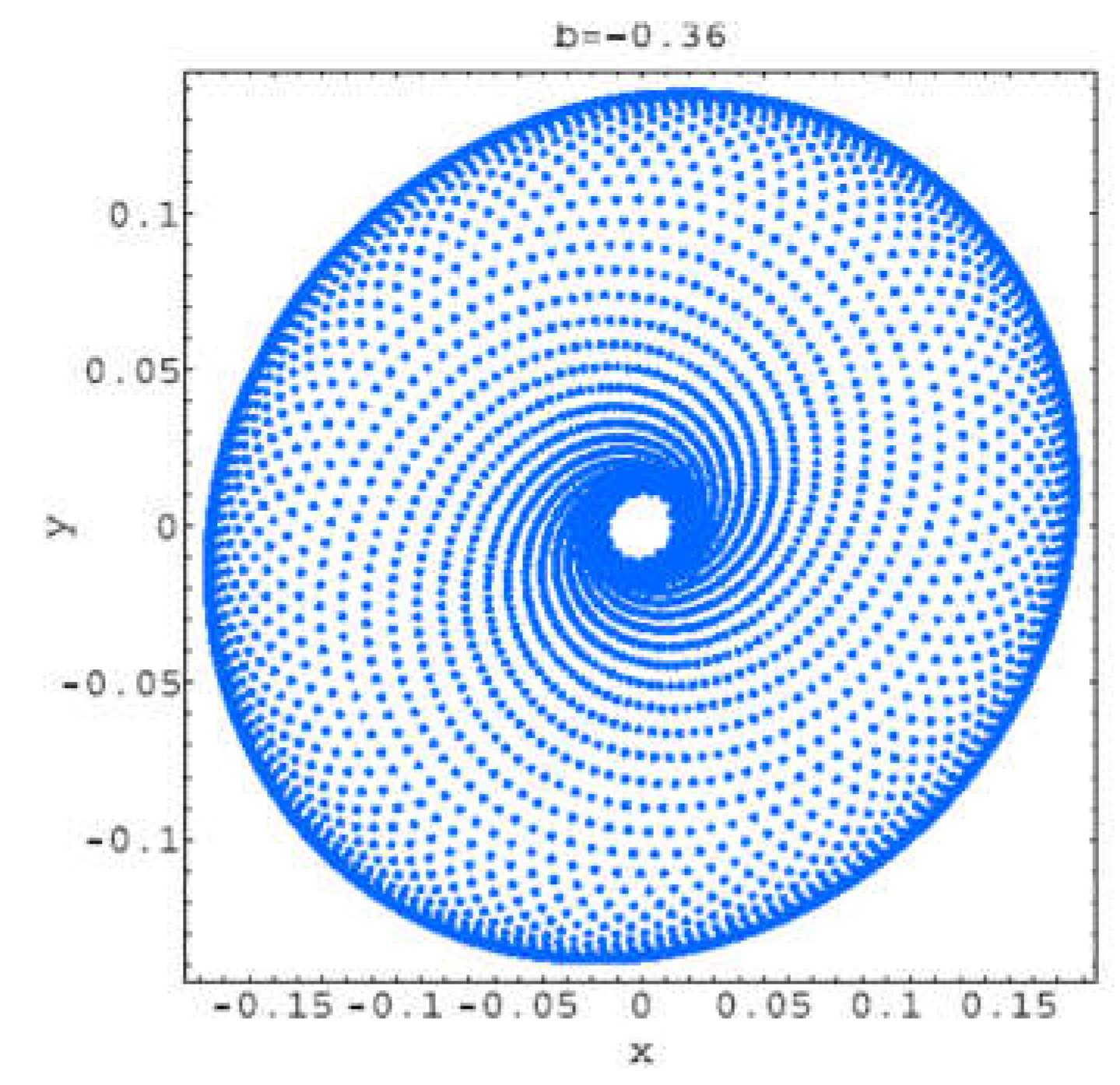
For b=−0.36, an asymptotically stable cycle (1-torus, drift ring) is present, and the trajectories converges to this cycle. At b = b1 =−0.35635 a supercritical Neimark–Sacker bifurcation takes place.
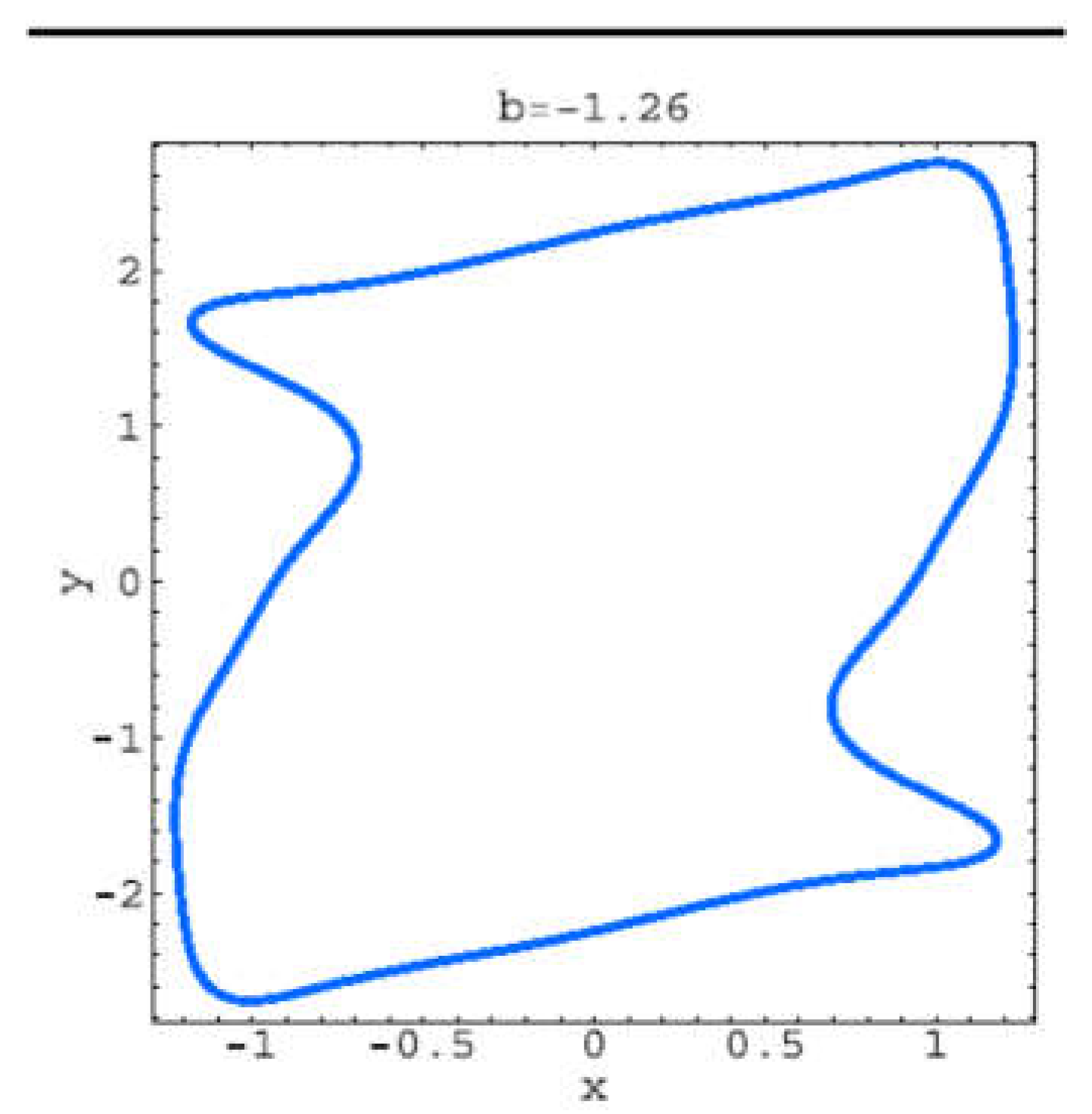
For b = −1.26, there is only one asymptotically stable limit cycle (1-torus), symmetrical to the origin.
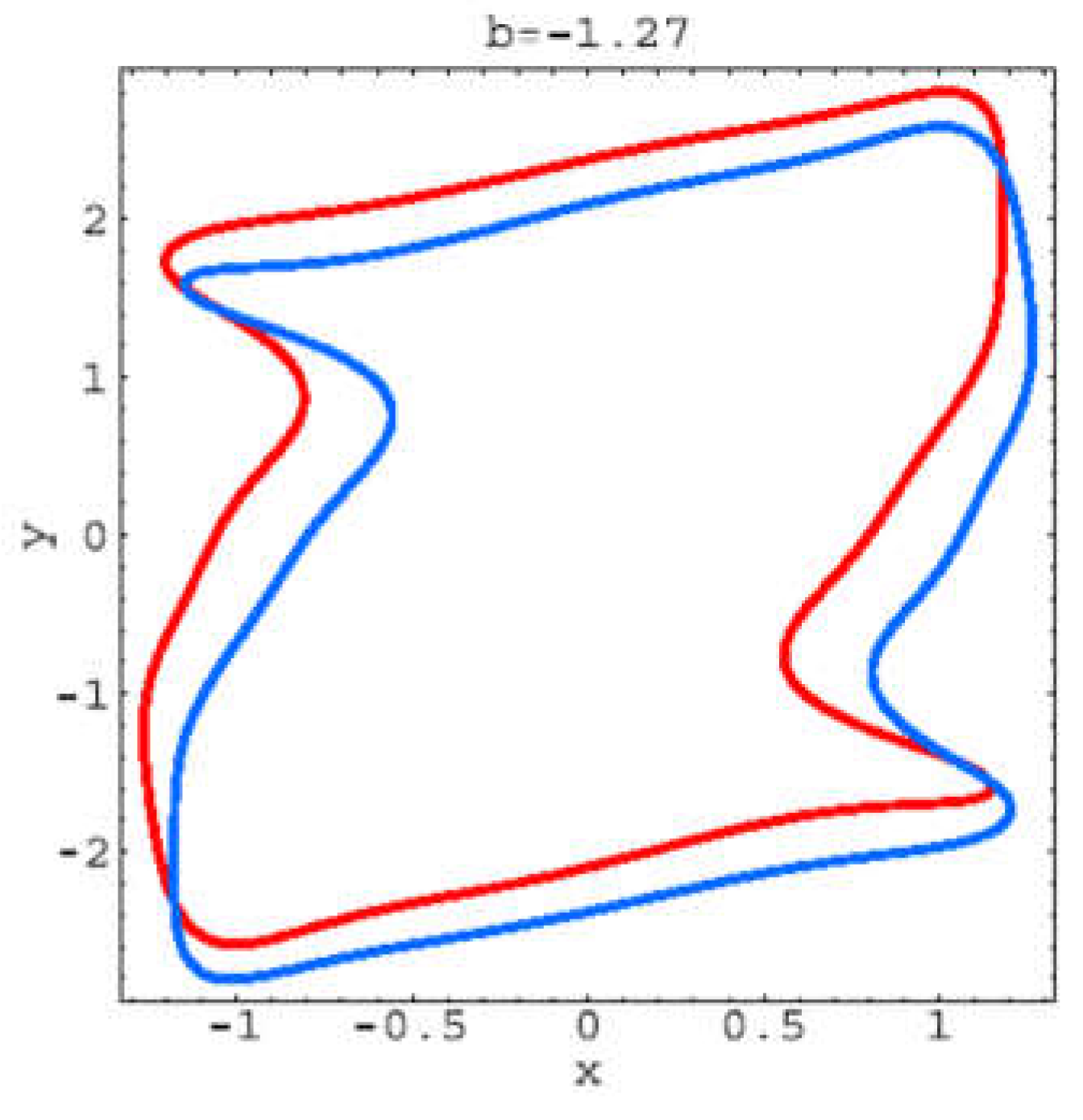
For b =−1.27, there are two stable limit cycles, not symmetrical to the origin. For each plot, the first 106 iterations have been dropped, and the next 104 iterations have been plotted. At around b =−1.265, a bifurcation phenomenon takes place, which determines the appearance of two stable limit cycles (1-tori) close to the origin.
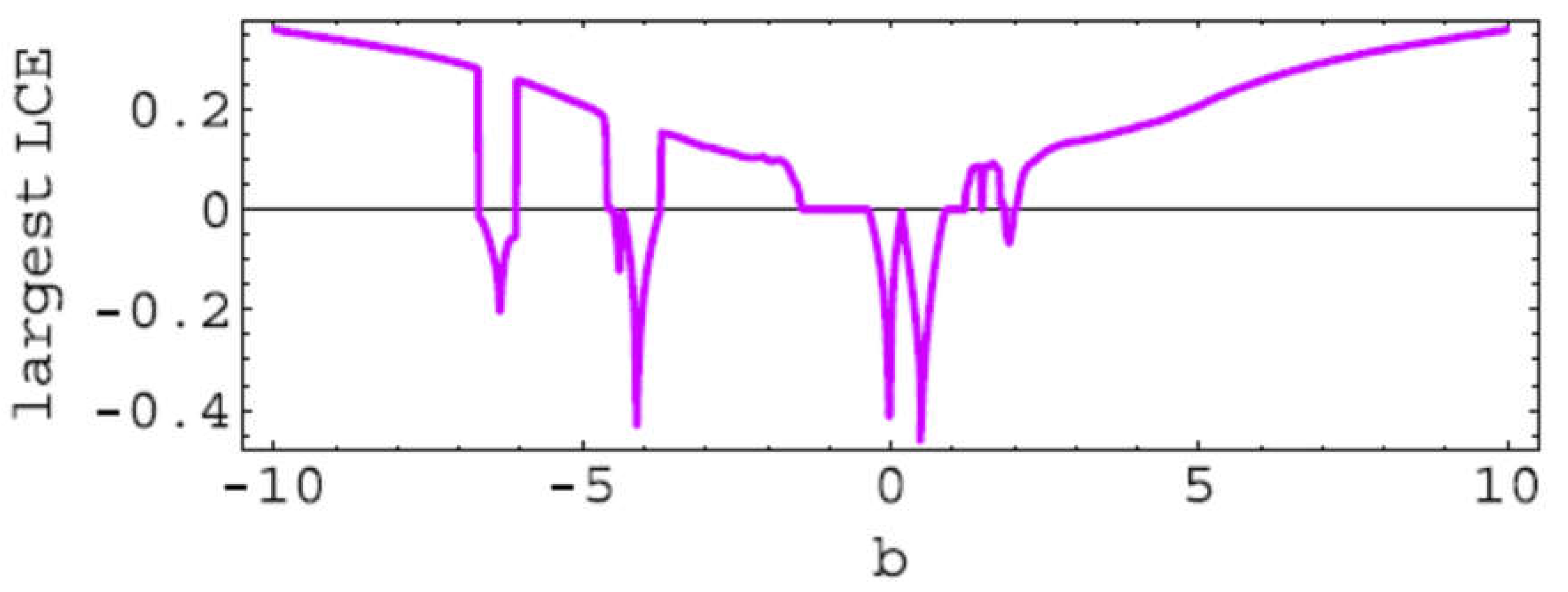
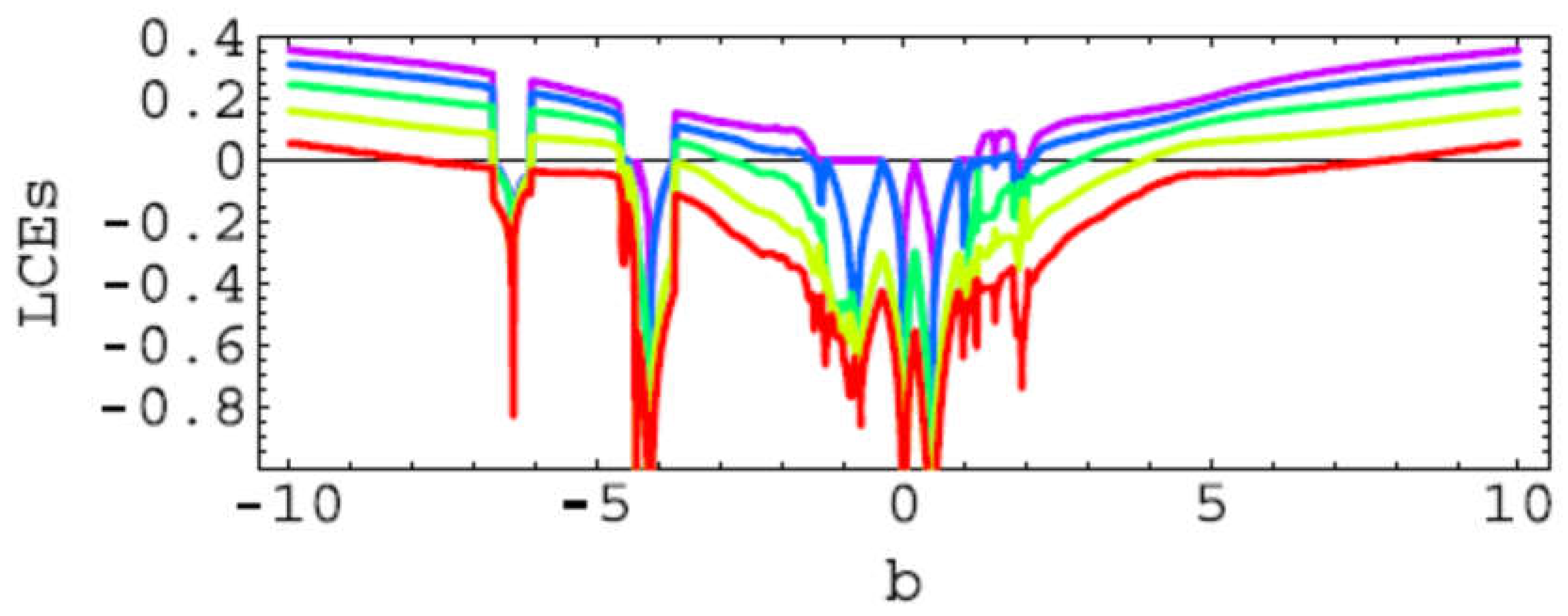
For the localization of bifurcations values the Largest Lyapunov Characteristic Exponent (LCE) and the Lyapunov spectrum (LCEs) for system (2.1) was used. For the computation of the Lyapunov spectrum, for each
b value (step size 0.01 for
b), the initial conditions were reset and 10
5 time-steps were iterated before calculating the LCEs (which were computed over the next 10
5 time steps). The Lyapunov spectrum was computed using the Householder QR based (HQRB) method.The obtained LCE and LCEs are represented in
Figure 2.5 and
Figure 2.6. respectively.
The trajectories presented in
Figure 2.1,
Figure 2.2,
Figure 2.3 and
Figure 2.4 are what we call orbits in classical sense. However, they become more and more complex for various values of
b ∈
(−1.5
, −1.4
). This can be seen on the following figures.
Figure 2.1.
Trajectory for b=-0.35.
Figure 2.1.
Trajectory for b=-0.35.
Figure 2.2.
Trajectory for b=-0.36.
Figure 2.2.
Trajectory for b=-0.36.
Figure 2.3.
Trajectory for b=-1.26.
Figure 2.3.
Trajectory for b=-1.26.
Figure 2.4.
Trajectory for b=-1.27.
Figure 2.4.
Trajectory for b=-1.27.
Figure 2.5.
Largest Lyapunov Characteristic Exponent.
Figure 2.5.
Largest Lyapunov Characteristic Exponent.
Figure 2.6.
Largest Lyapunov Characteristic Spectrum.
Figure 2.6.
Largest Lyapunov Characteristic Spectrum.
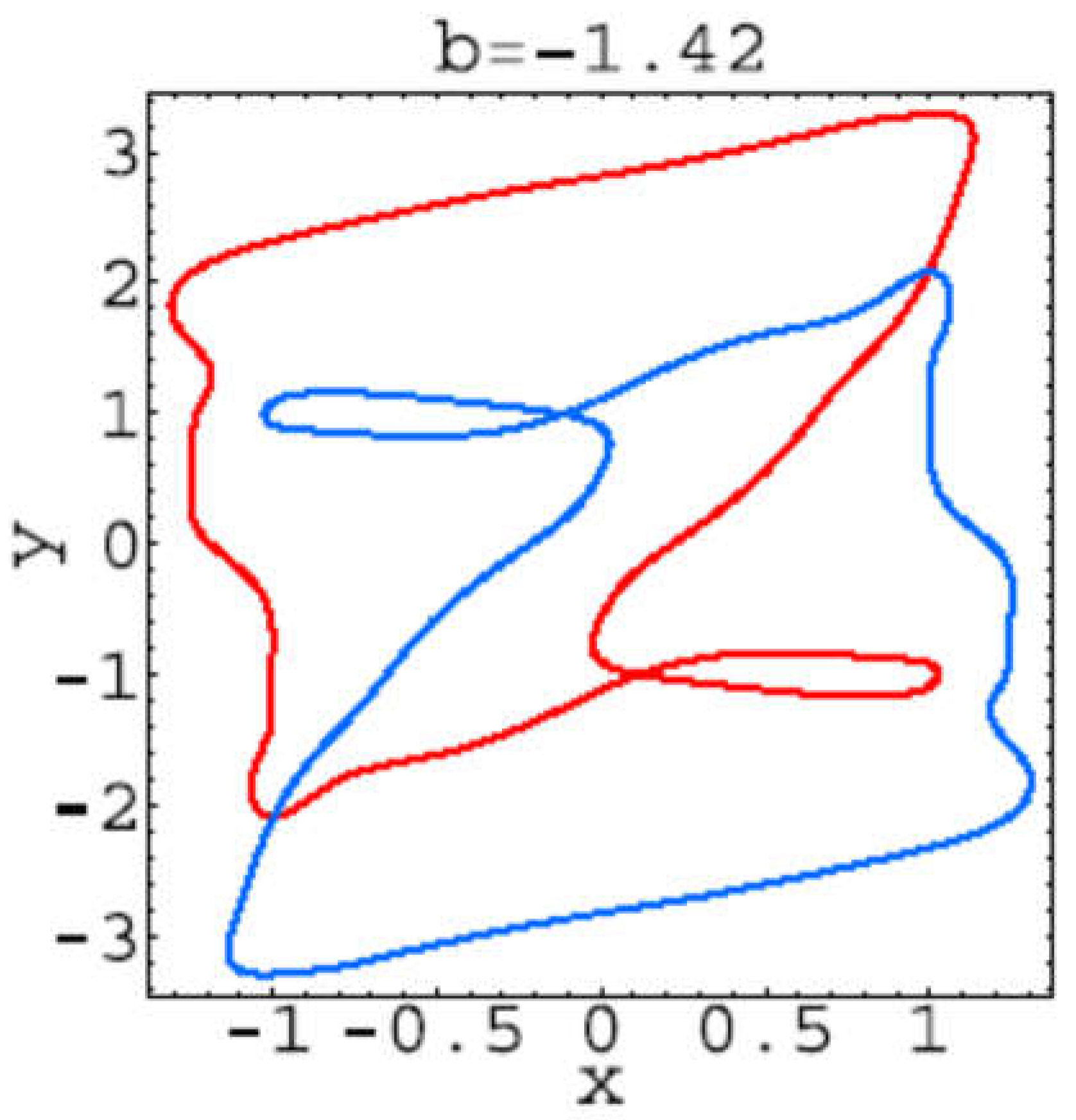
Figure 2.7.
Trajectory for b=-1.42.
Figure 2.7.
Trajectory for b=-1.42.
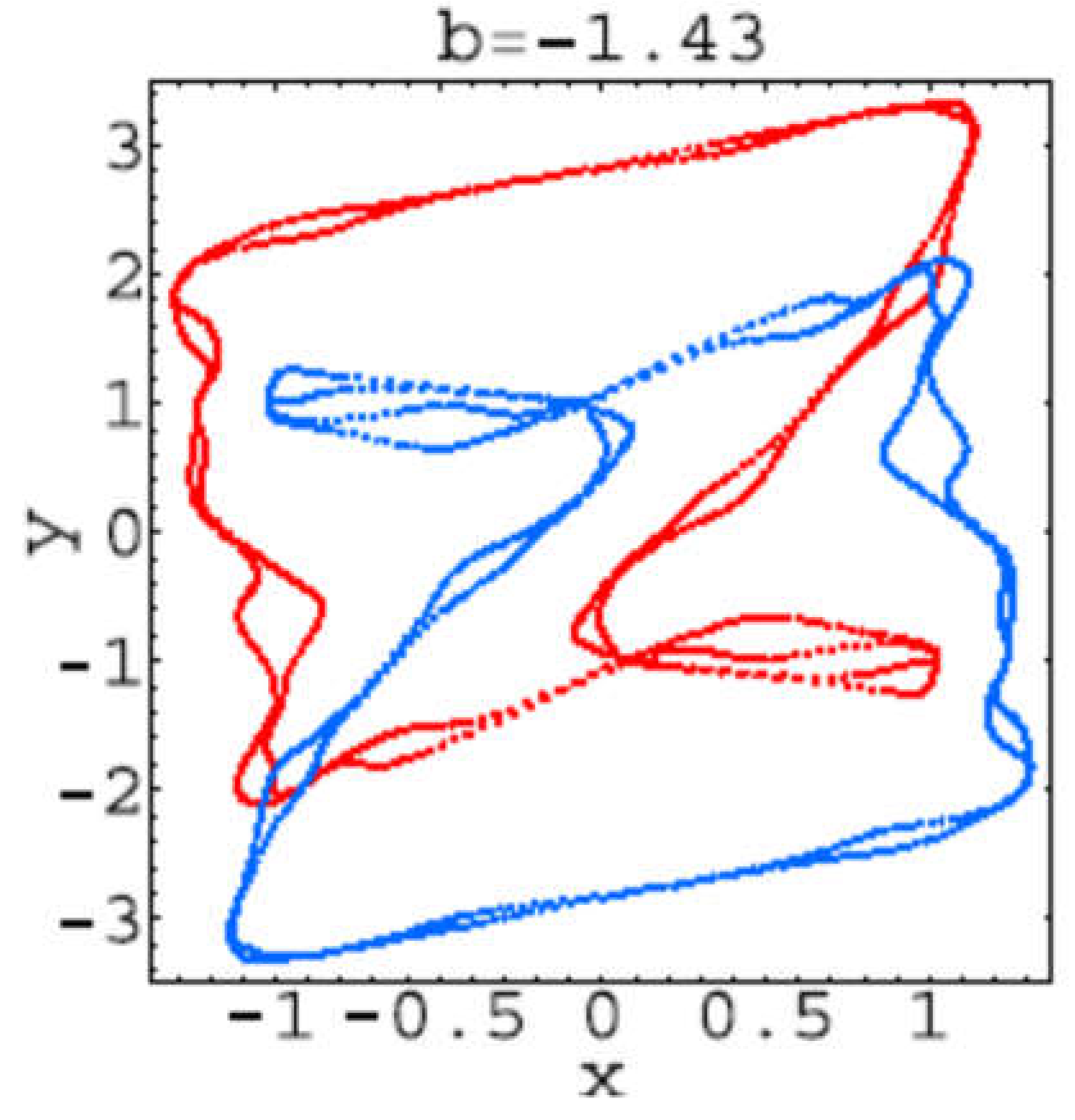
Figure 2.8.
Trajectory for b=-1.43.
Figure 2.8.
Trajectory for b=-1.43.
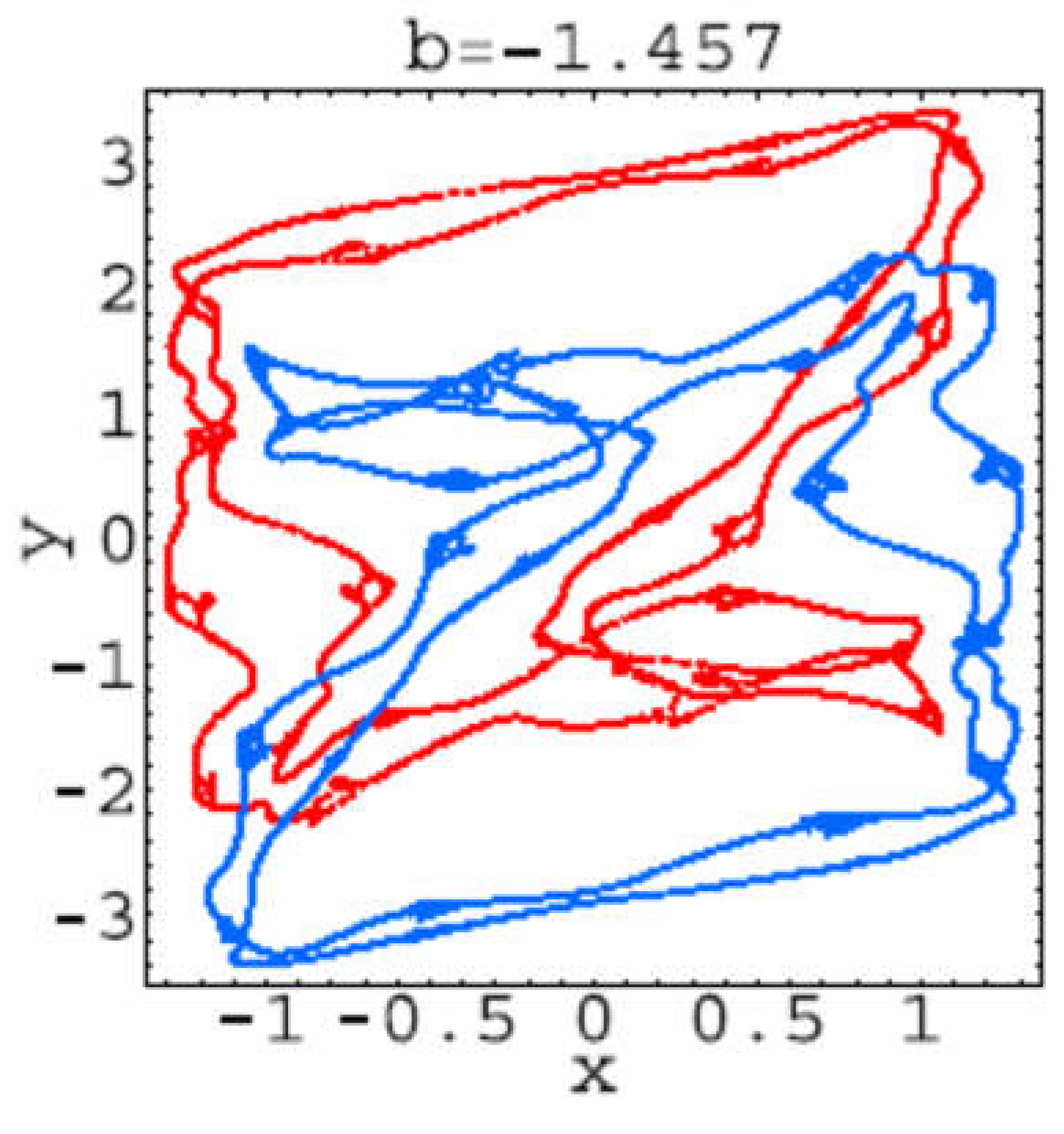
Figure 2.9.
Trajectory for b=-1.457.
Figure 2.9.
Trajectory for b=-1.457.
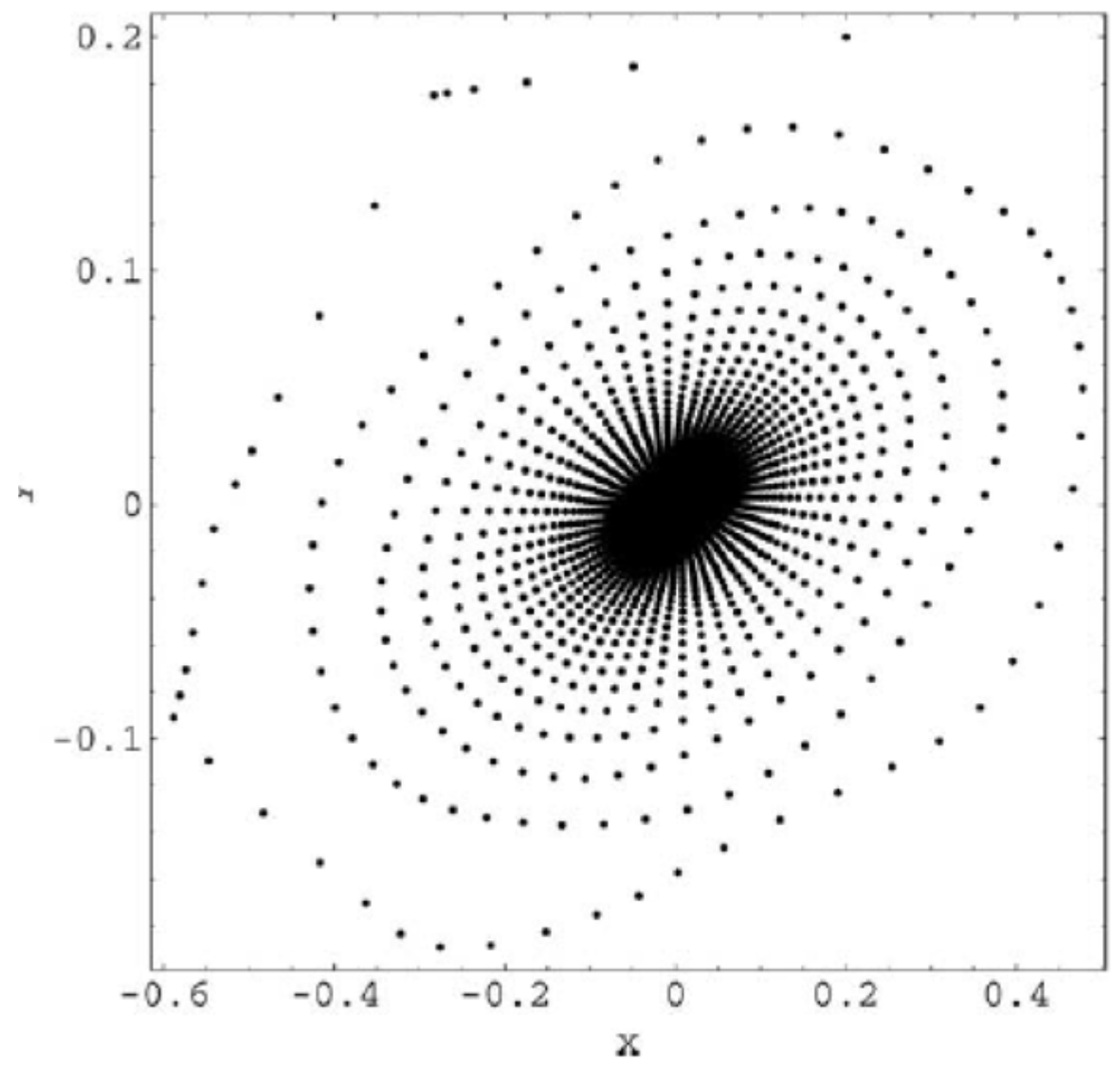
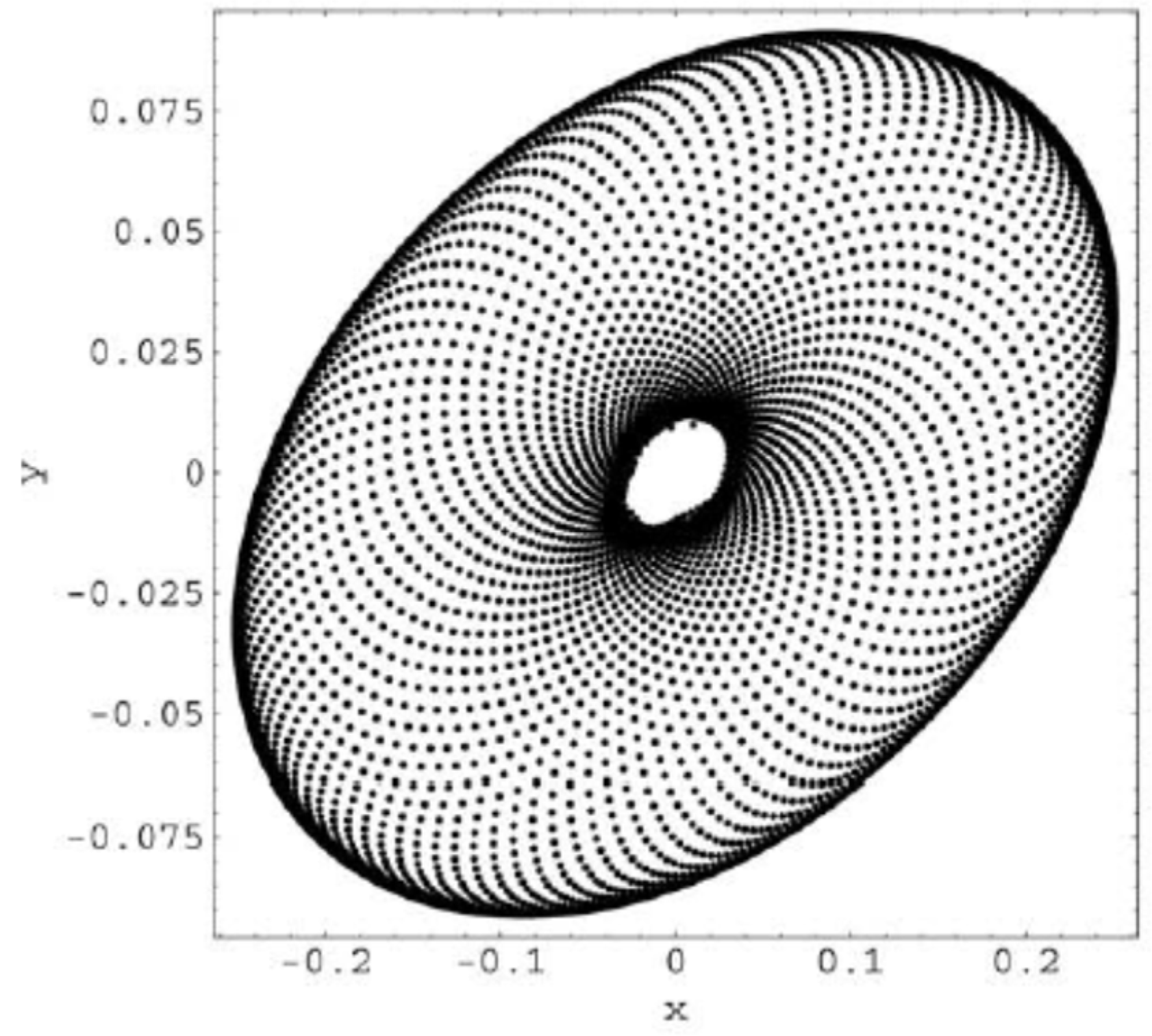
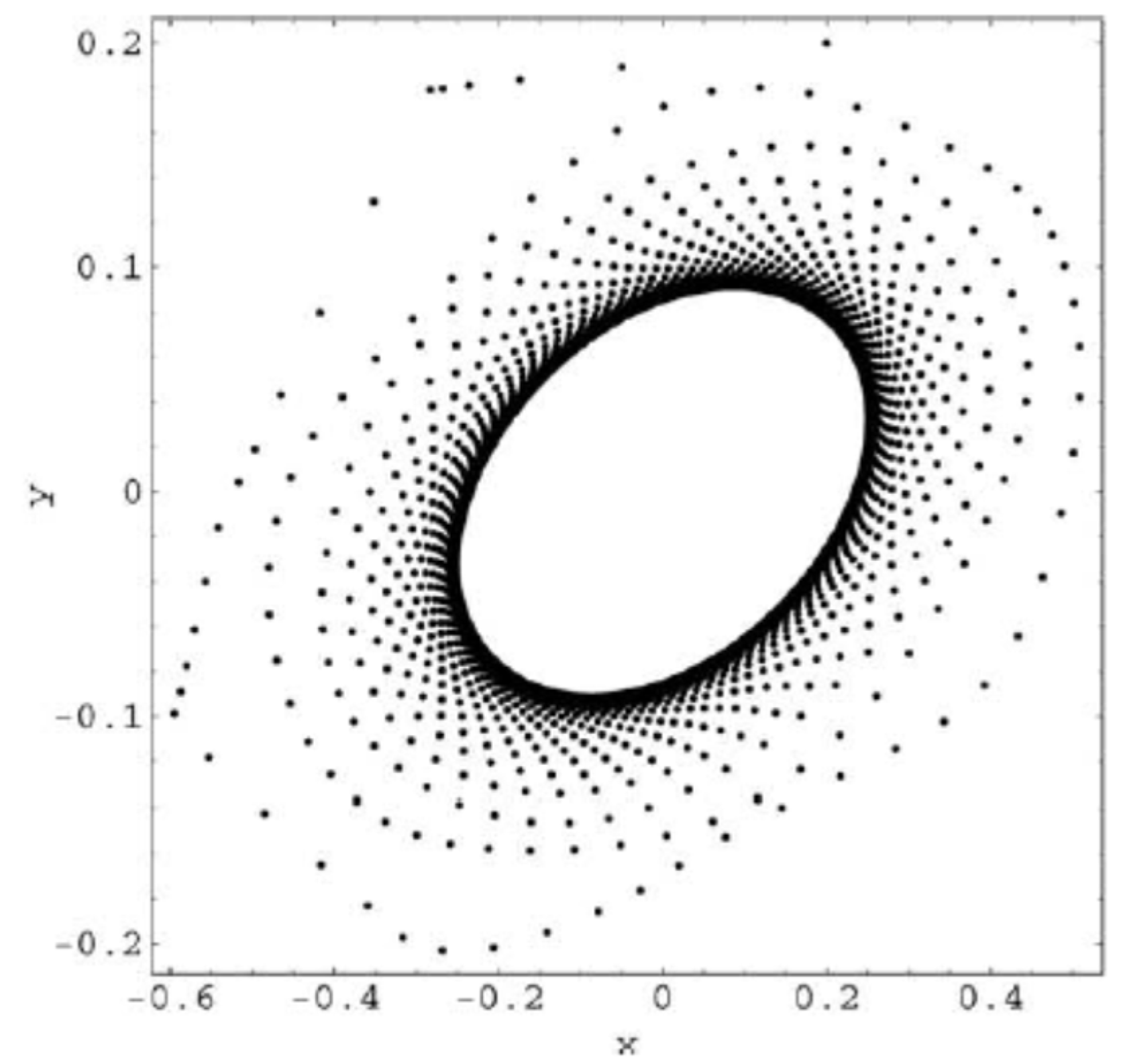
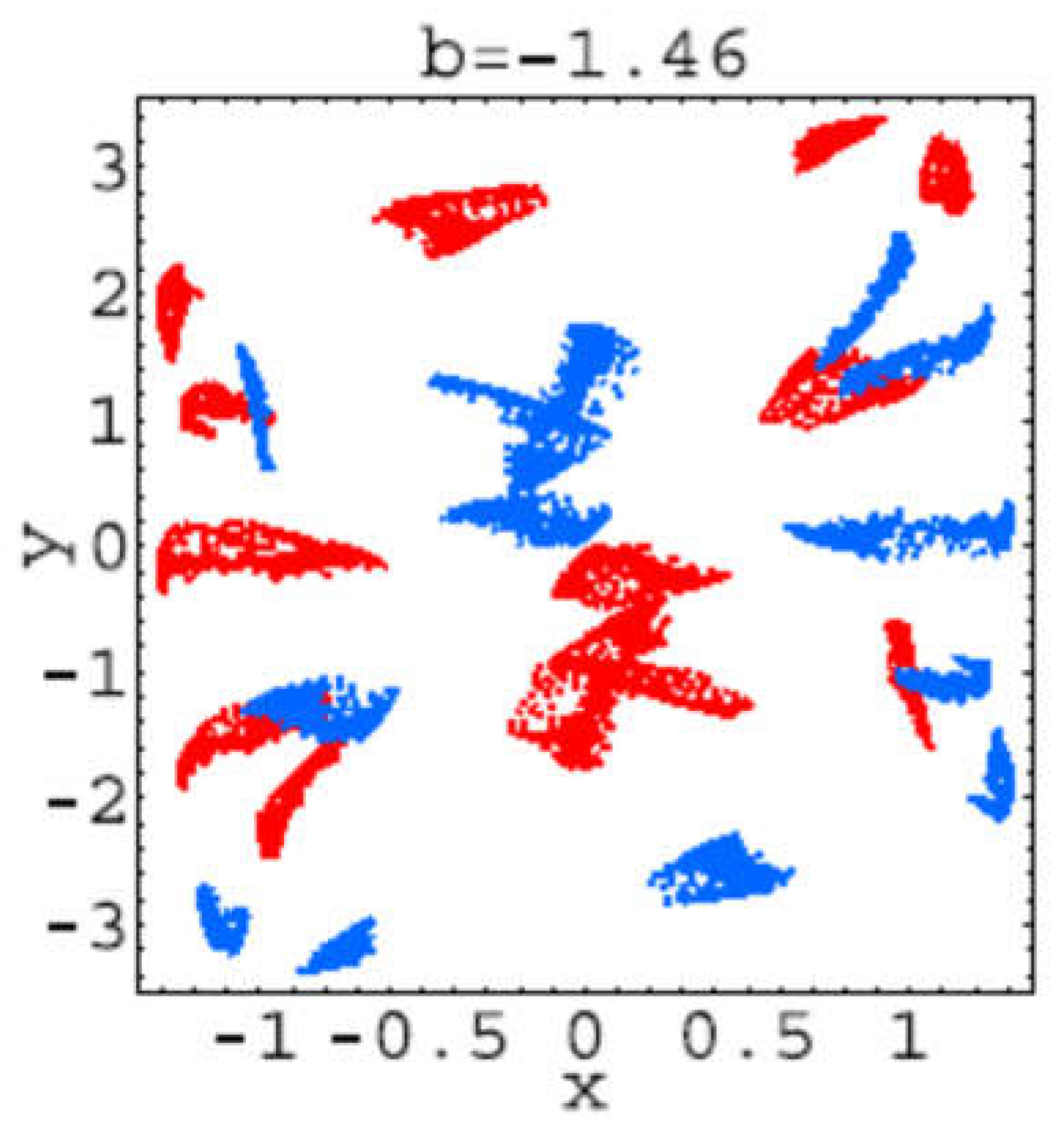
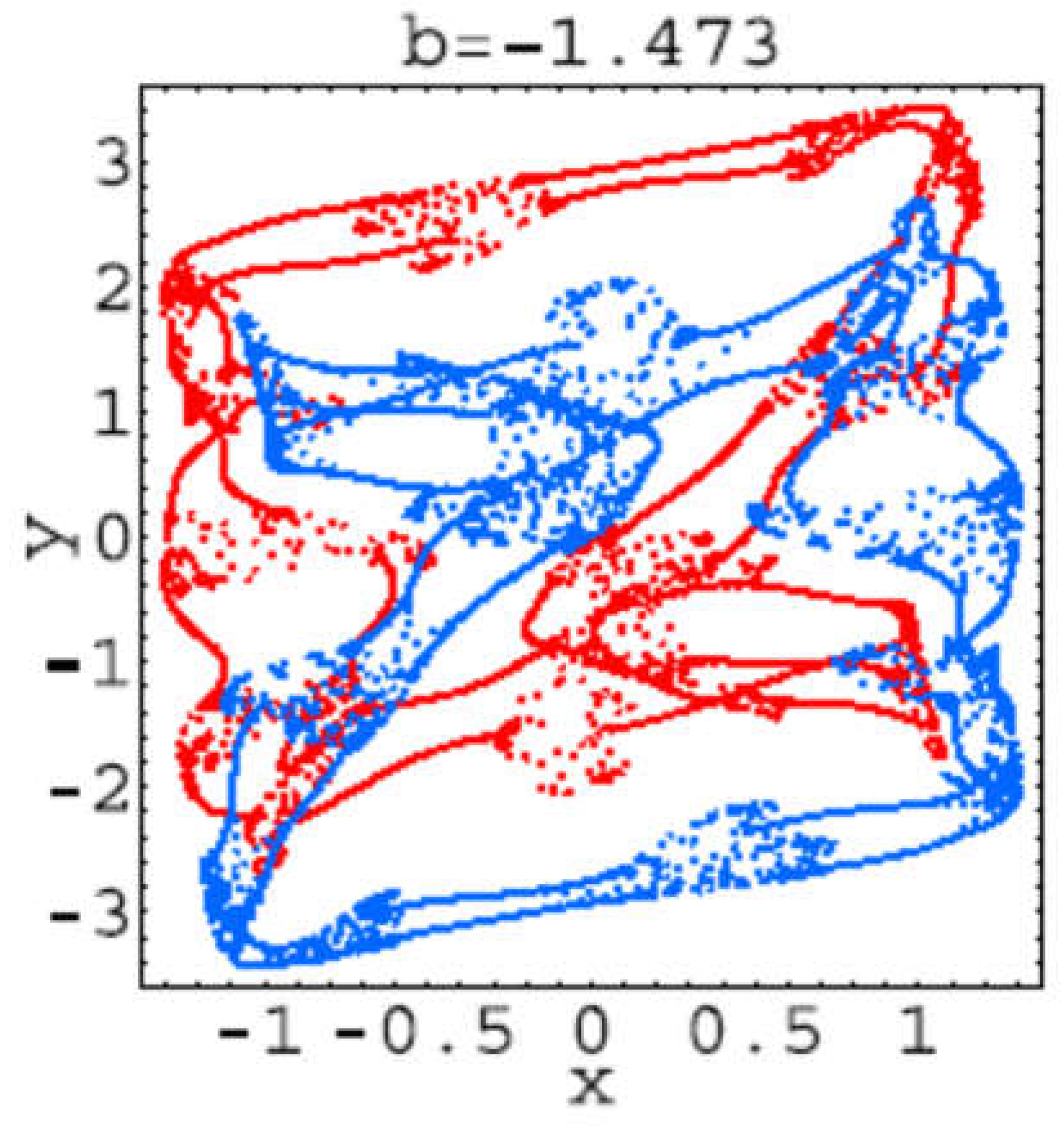
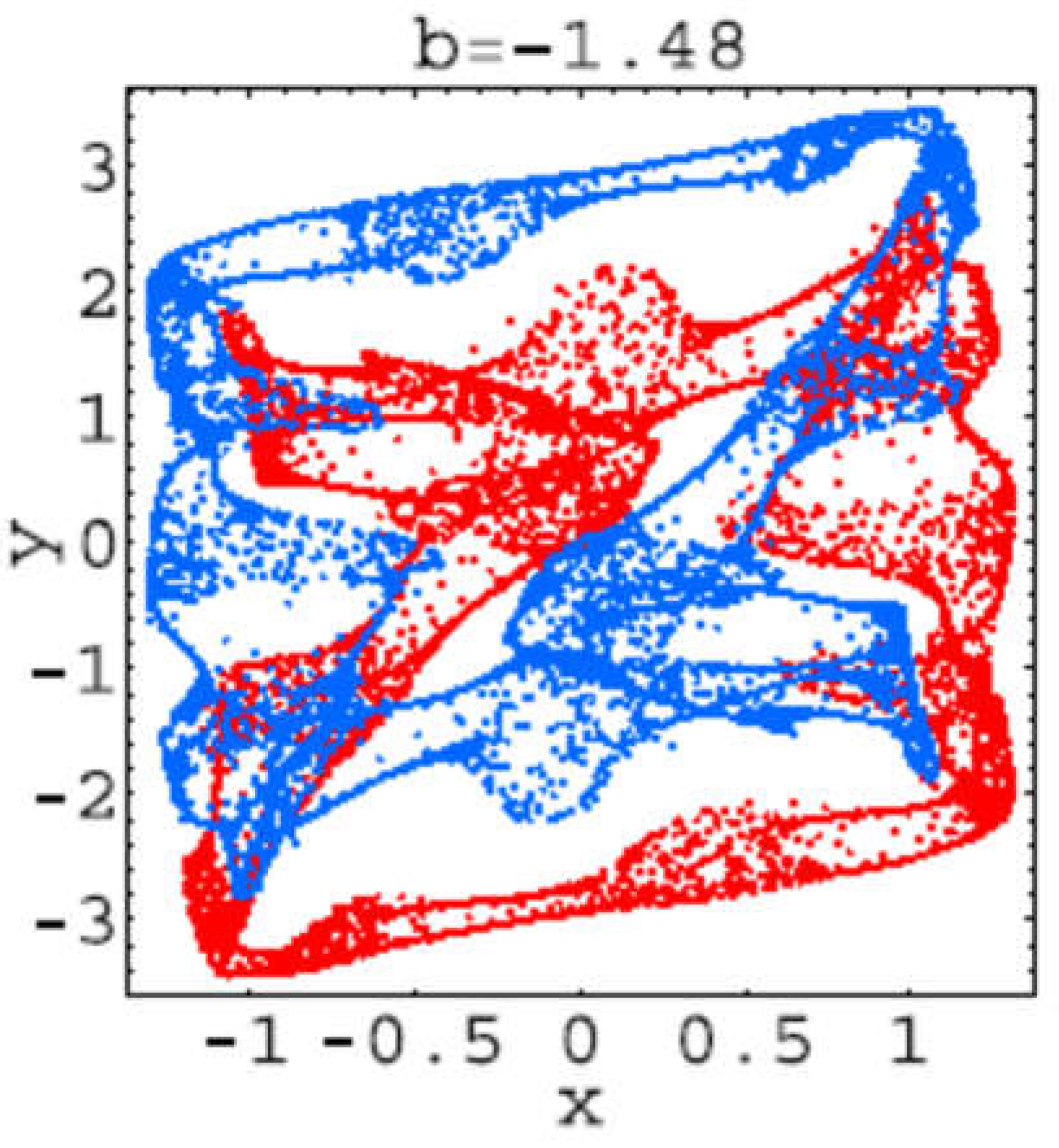
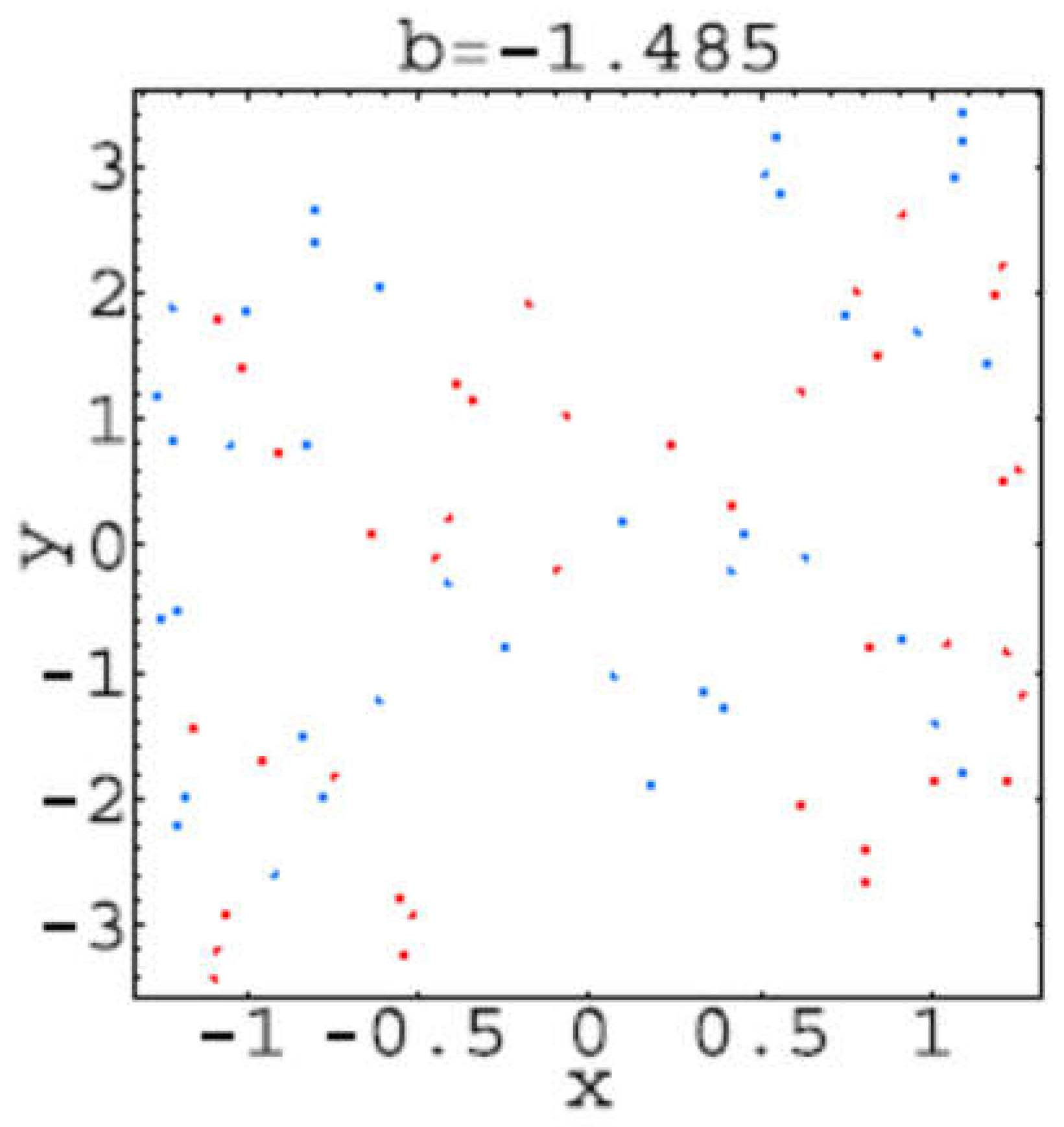
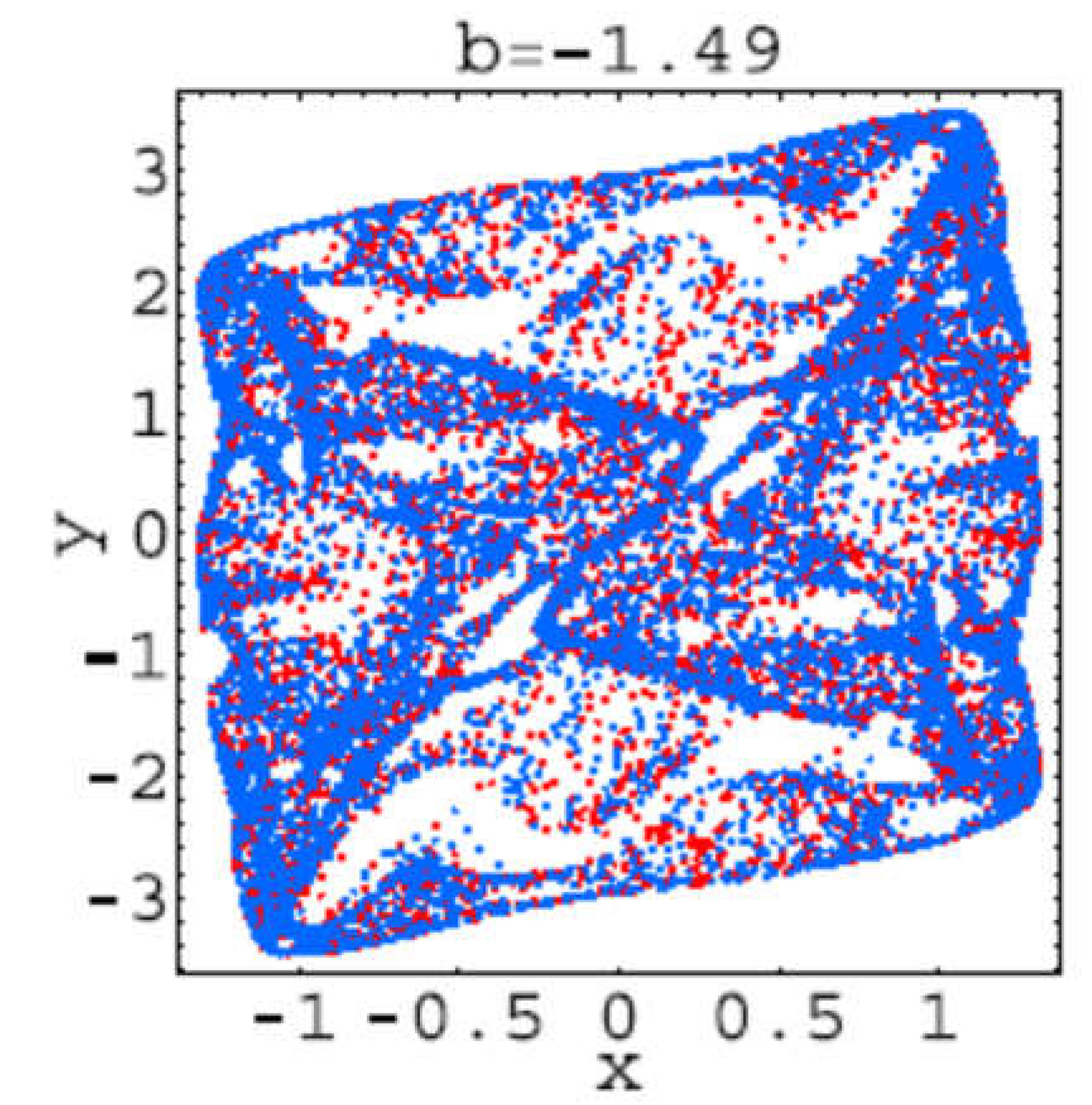
Hear for each plot, the first 106 iterations of system (2.1) have been dropped, and the next 104 iterations have been plotted. These trajectories corresponds to the bifurcations values: b=−1.42: 1-tori; b=−1.43: 2-tori; b=−1.457: 2-tori declining into strange attractors; b =−1.46: strange attractors; b =−1.47: two stable period-52 orbits; b =−1.473: strange attractors; b =−1.48: strange attractors; b =−1.485: two stable period-39 orbits; b=−1.49: strange attractors.
It seems that from bifurcation point of view everything is clear but from the point of view of the trajectory geometry is not at all clear. That is because it can be seen that “Trajectories” presented in
Figure 2.10,
Figure 2.11,
Figure 2.12,
Figure 2.13,
Figure 2.14 and
Figure 2.15. are not at all what we call orbits in classic sense. Their geometry moreover is fractal . Are “Trajectories” presented in
Figure 2.10,
Figure 2.11,
Figure 2.12,
Figure 2.13,
Figure 2.14 and
Figure 2.15 objects of Fractal Geometry? Have they real counterpart or they exist just in theory? There are similar behavior mentioned in [
10,
11,
12,
16,
21,
22,
23,
24,
25,
27,
28,
29,
30,
31,
32,
33] or elsewhere in specialized literature? These are our main questions.
Figure 2.10.
Trajectory for b=-1.46.
Figure 2.10.
Trajectory for b=-1.46.
Figure 2.11.
Trajectory for b=-1.47.
Figure 2.11.
Trajectory for b=-1.47.
Figure 2.12.
Trajectory for b=-1.473.
Figure 2.12.
Trajectory for b=-1.473.
Figure 2.13.
Trajectory for b=-1.48.
Figure 2.13.
Trajectory for b=-1.48.
Figure 2.14.
Trajectory for b=-1.485.
Figure 2.14.
Trajectory for b=-1.485.
Figure 2.15.
Trajectory for b=-1.49.
Figure 2.15.
Trajectory for b=-1.49.
For various values of b ∈ (−10,−2) the trajectories were also computed using the same procedure i.e. the first 106 Iterations of system (2.1) have been dropped, and the next 104 iterations have been plotted.
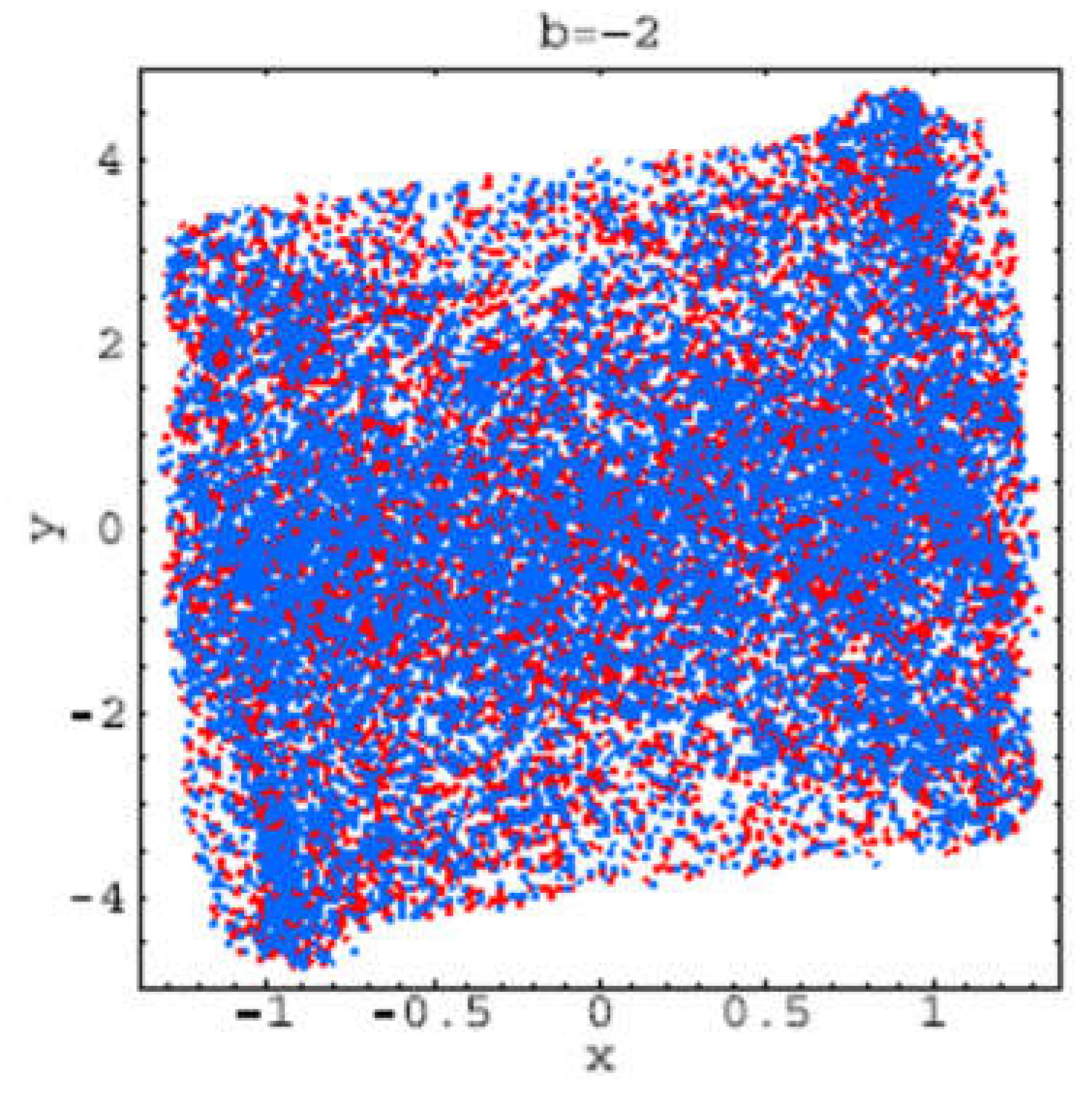
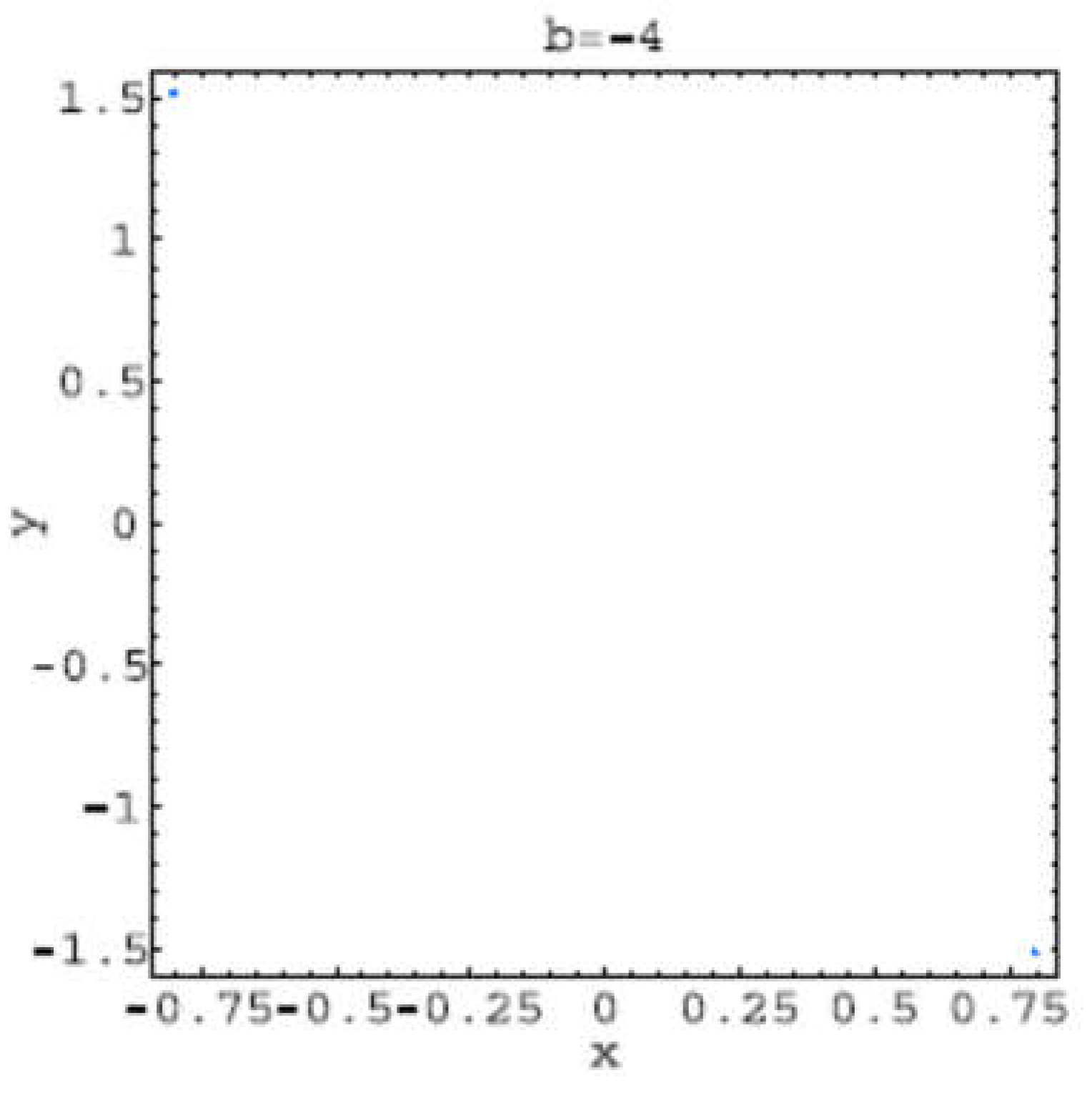
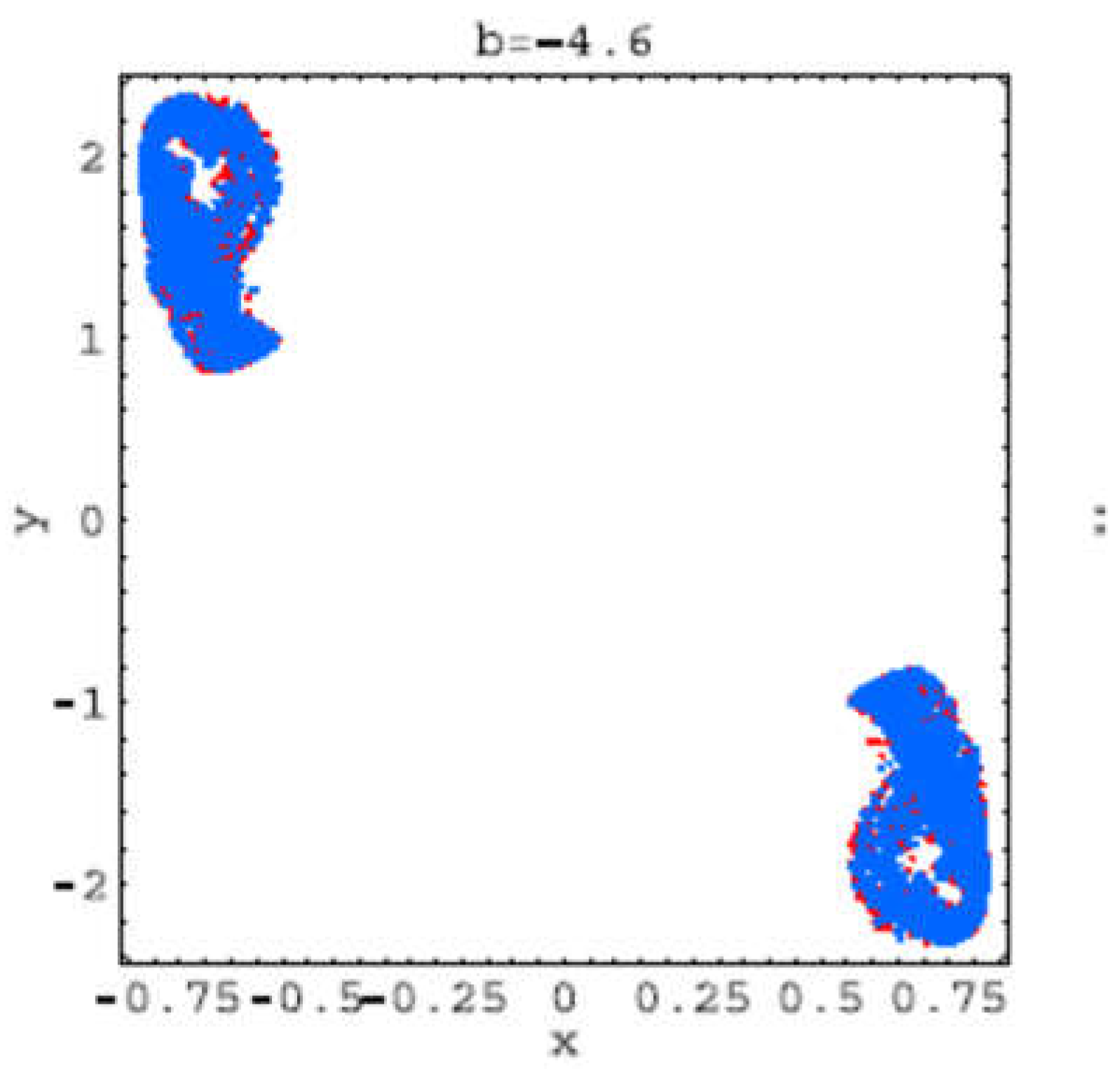
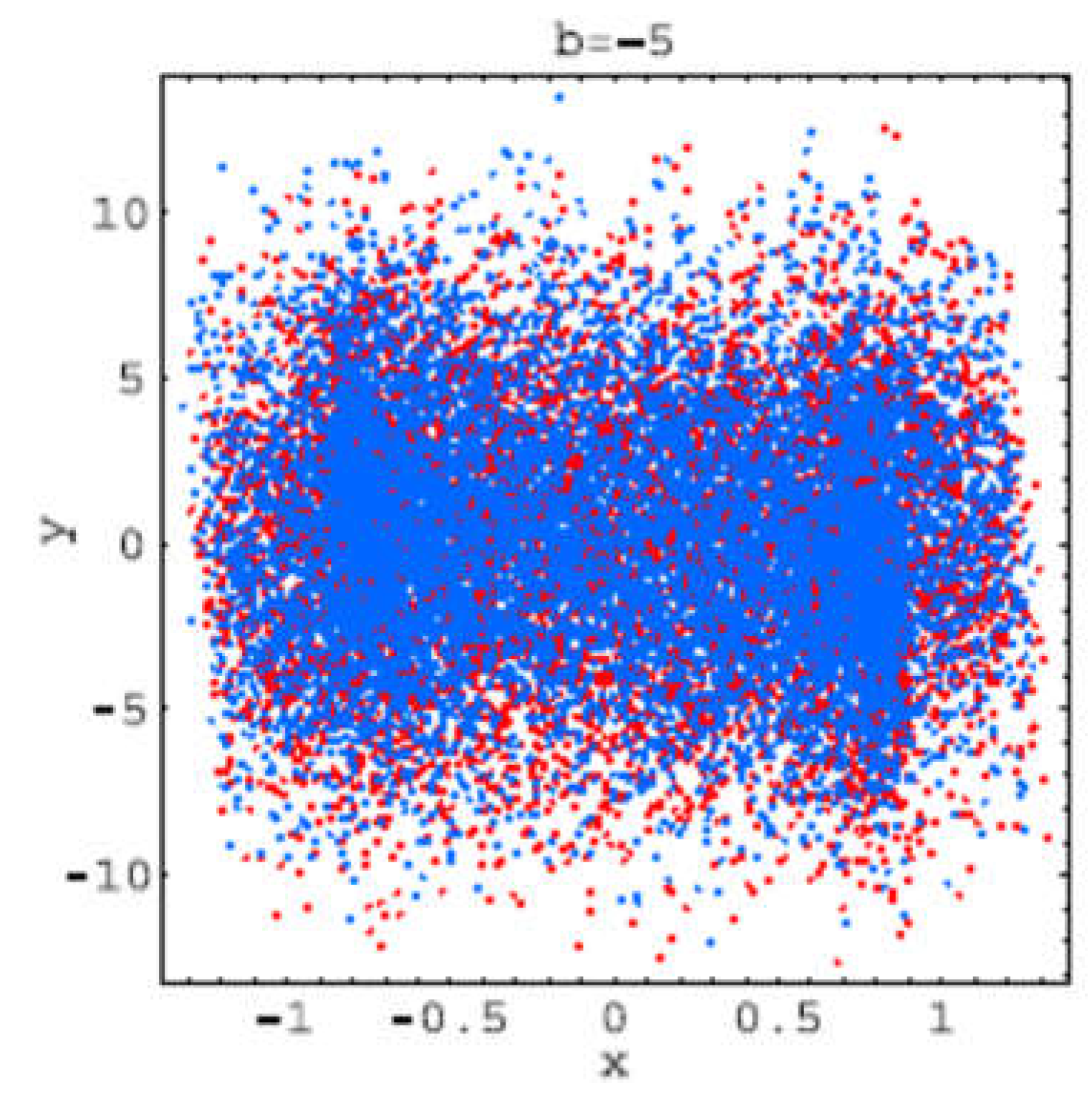
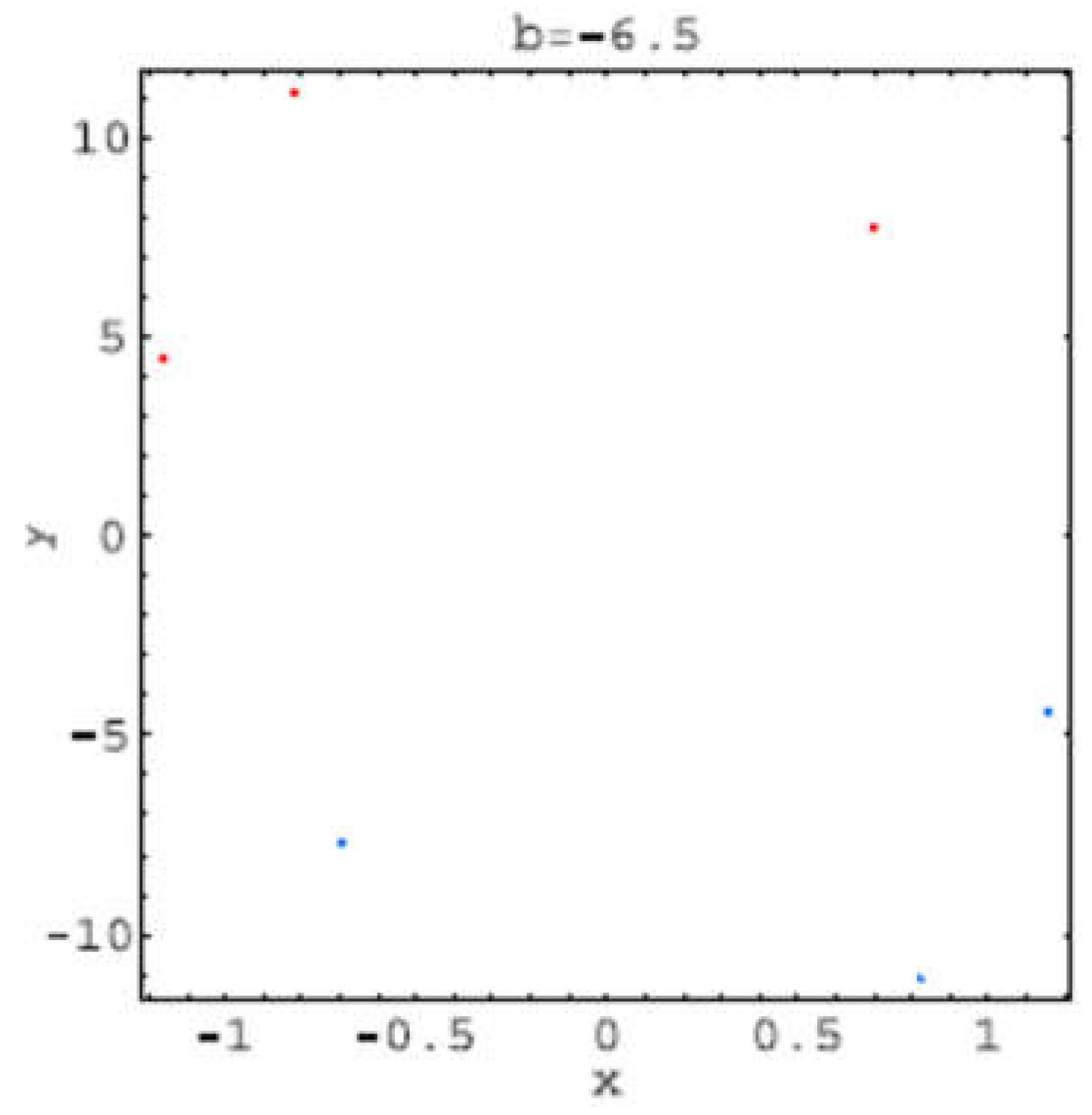
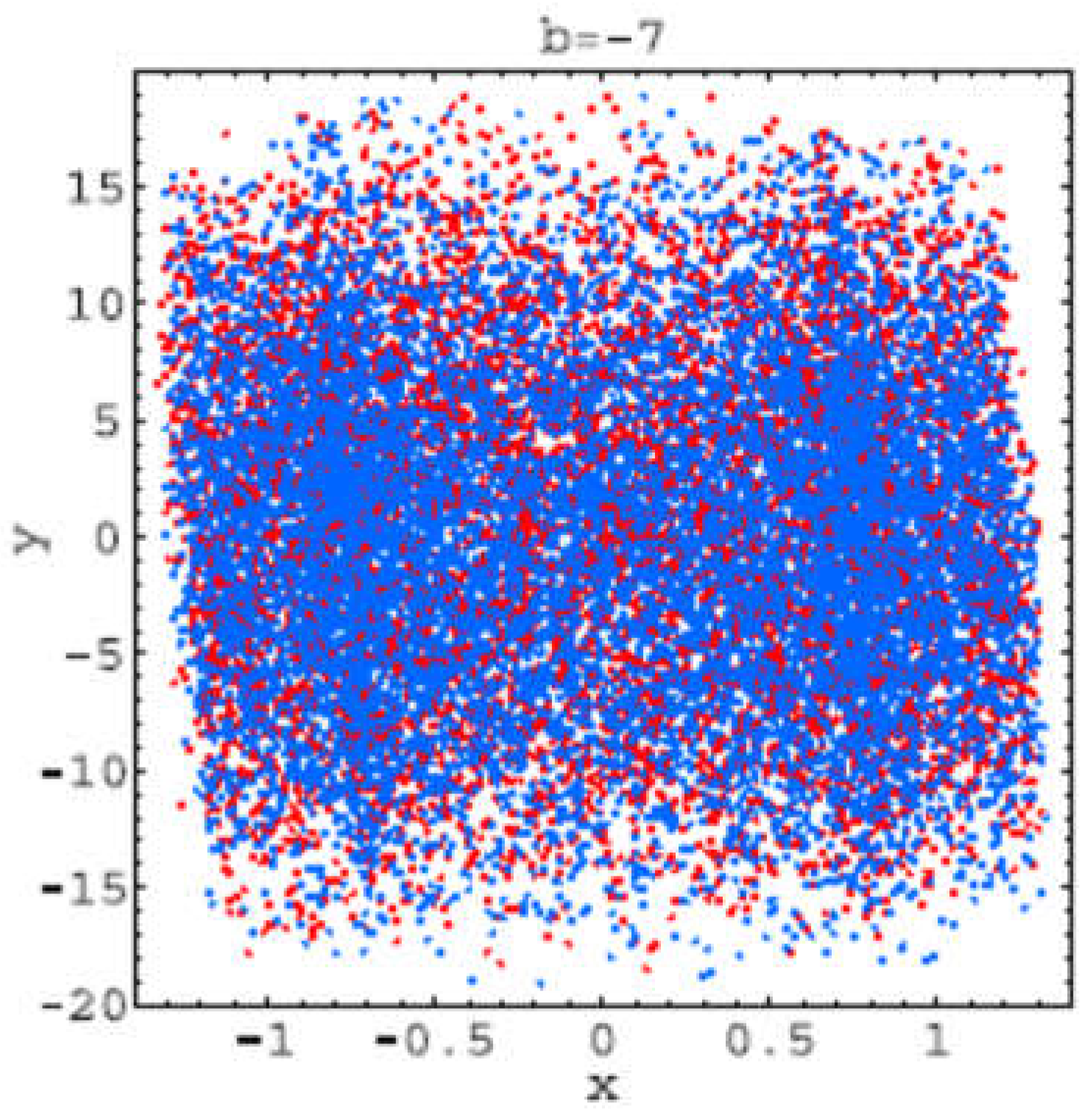
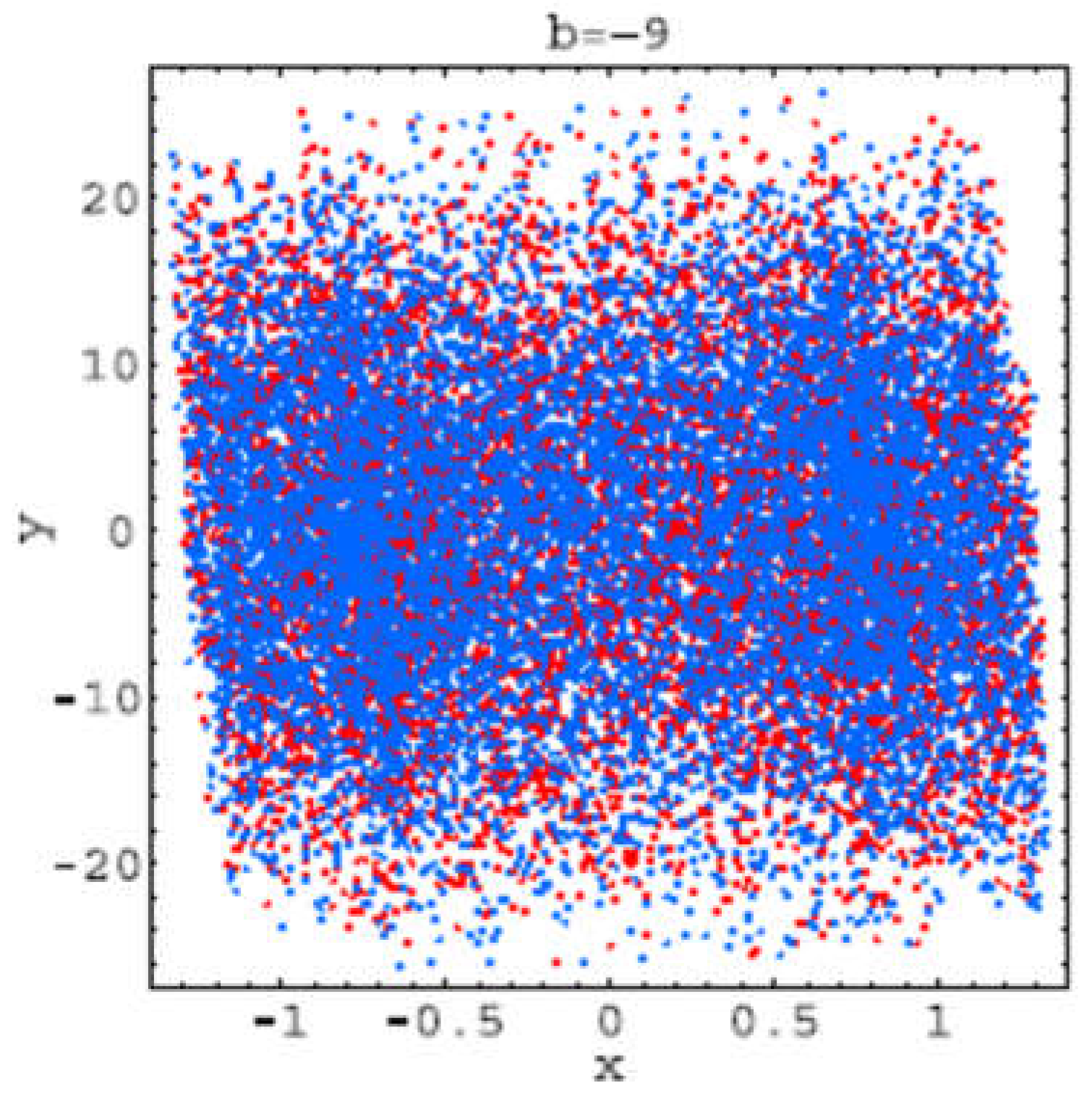
These trajectories corresponds to the bifurcations values: b =−2: hyperchaos (LE2 > 0, LE3 < 0); b=−3: hyperchaos (LE3 > 0, LE4 < 0); b=−4: one stable period-2 orbit (LE1 < 0); b=−4.6: strange attractor developing from the period-2 solution; b = −5: hyperchaos (LE4 > 0, LE5 < 0); b = −6.5: two stable period-3 orbits (LE1 < 0); b = −7: hyperchaos (LE4 > 0, LE5 < 0); b = −9: hyperchaos (LE5 > 0).
Our main questions arethe same: are “Trajectories” presented in
Figure 2.16,
Figure 2.17,
Figure 2.18,
Figure 2.19,
Figure 2.20 ,
Figure 2.21,
Figure 2.22 and
Figure 2.23 objects of Fractal Geometry? Have they real counterpart or they exist just in theory? If not, what are these geometrical figures? There are similar behavior mentioned in [
10,
11,
12,
16,
21,
22,
23,
24,
25,
27,
28,
29,
30,
31,
32,
33] or elsewhere in specialized literature? Our conjecture is that ‘Trajectories” presented in
Figure 2.10,
Figure 2.11,
Figure 2.12,
Figure 2.13,
Figure 2.14,
Figure 2.15,
Figure 2.16,
Figure 2.17,
Figure 2.18,
Figure 2.19,
Figure 2.20 ,
Figure 2.21,
Figure 2.22 and
Figure 2.23. are fractals and has real counterpart.
Figure 2.16.
Trajectory for b=-2.
Figure 2.16.
Trajectory for b=-2.
Figure 2.17.
Trajectory for b=-3.
Figure 2.17.
Trajectory for b=-3.
Figure 2.18.
Trajectory for b=-4.
Figure 2.18.
Trajectory for b=-4.
Figure 2.19.
Trajectory for b=-4.6.
Figure 2.19.
Trajectory for b=-4.6.
Figure 2.20.
Trajectory for b=-5.
Figure 2.20.
Trajectory for b=-5.
Figure 2.21.
Trajectory for b=-6.5.
Figure 2.21.
Trajectory for b=-6.5.
Figure 2.22.
Trajectory for b=-7.
Figure 2.22.
Trajectory for b=-7.
Figure 2.23.
Trajectory for b=-9.
Figure 2.23.
Trajectory for b=-9.
3. Case of a Discrete-Time Hopfield Neural Network of Two Neurons with a Single Delay and Self- Connections
In [
68] an analysis of the dynamics of the neural network defined by
was undertaken. The external inputs are equal to zero and the system parameters are regarded as numerical expresion of the state of network..The network state can change due to a disease for example.
Therefore the network voltage dynamics change too. In [
68] this kind of change is analyzed .The conclusion in [
68], is: The bifurcation analysis of two-dimensional discrete-time Hopfield neural networks with a single delay reveals the existence of Neimark–Sacker, fold and some codimension 2bifurcations for certain values of the bifurcation parameters that have been chosen
. For illustrate what this means the following numerical example was considered:
The origin is asymptotically stable if and only if
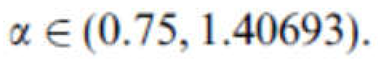
. At 1.40693 a supercritical Neimark–Sacker bifurcation occurs.
For α = 1.4, the null solution of (3.2) is asymptotically stable.
Figure 3.1 illustrate that the trajectories of (3.2) converges to the null solution. These trajectories are what we call orbits in classic sense.
For α = 1.5. the null solution is unstable and an asymptotically stable closed invariant curve is present.
The trajectory of (3.2) converges to the asymptotically stable invariant curve as is shown in
Figure 3.2.Figure 3.3.
Figure 3.1.
Trajectory for α = 1.4,.
Figure 3.1.
Trajectory for α = 1.4,.
Figure 3.2.
Trajectory for α = 1.5..
Figure 3.2.
Trajectory for α = 1.5..
Figure 3.3.
Trajectory for α = 1.5..
Figure 3.3.
Trajectory for α = 1.5..
This summary analysis does not reveal trajectories that are no longer classic curves. Even the asymptotically stable closed invariant curve, corresponding to the bifurcation value is α = 1.5. a classical curve.
4. Case of a Discrete-Time Hopfield Neural Network of Two Neurons with a Two Delays and Self- Connections
In [
69] an analysis of the dynamics of the neural network defined by
is undertaken. The external inputs are equal to zero and the system parameters are regarded as numerical expresion of the state of network..The network state can change due to a disease for example.
Therefore the network voltage dynamics change too. In [
69] this kind of change is analyzed .The conclusion in [
69], is: “The results presented in this paper complete the bifurcation results obtained for discrete-time Hopfield neural networks with a single delay and self-connections presented in [
68] and for networks with two delays and no self-connections presented in [
66], with new results concerning the case of neural networks with two different delays and self-connections, revealing some resemblances (the existence of Neimark-Sacker, Fold, resonance 1:1, double Neimark-Sacker bifurcations) and some differences (the possible existence of Flip and Flip–Neimark-Sacker bifurcations), as well”.
For illustrate what this means the following numerical example was considered:
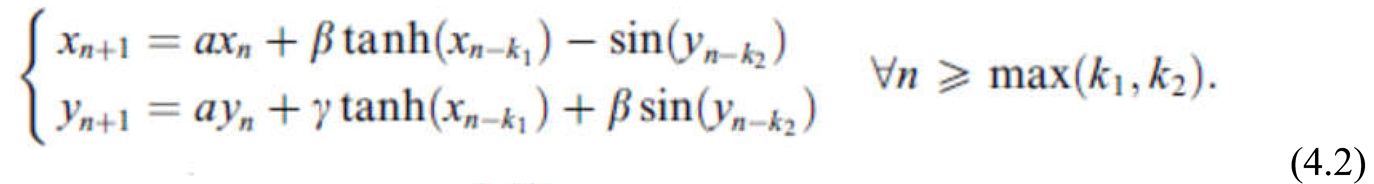
with; a = 0.5, k1 = 4, k2 = 10, For γ = 0.19 the null solution of (4.2) is asymptotically stable and trajectories converges to the null solution.
Figure 4.1 illustrate that the trajectories of
(4.2) converges to the null solution and the fact that these trajectories are what we call orbits in classic sense.
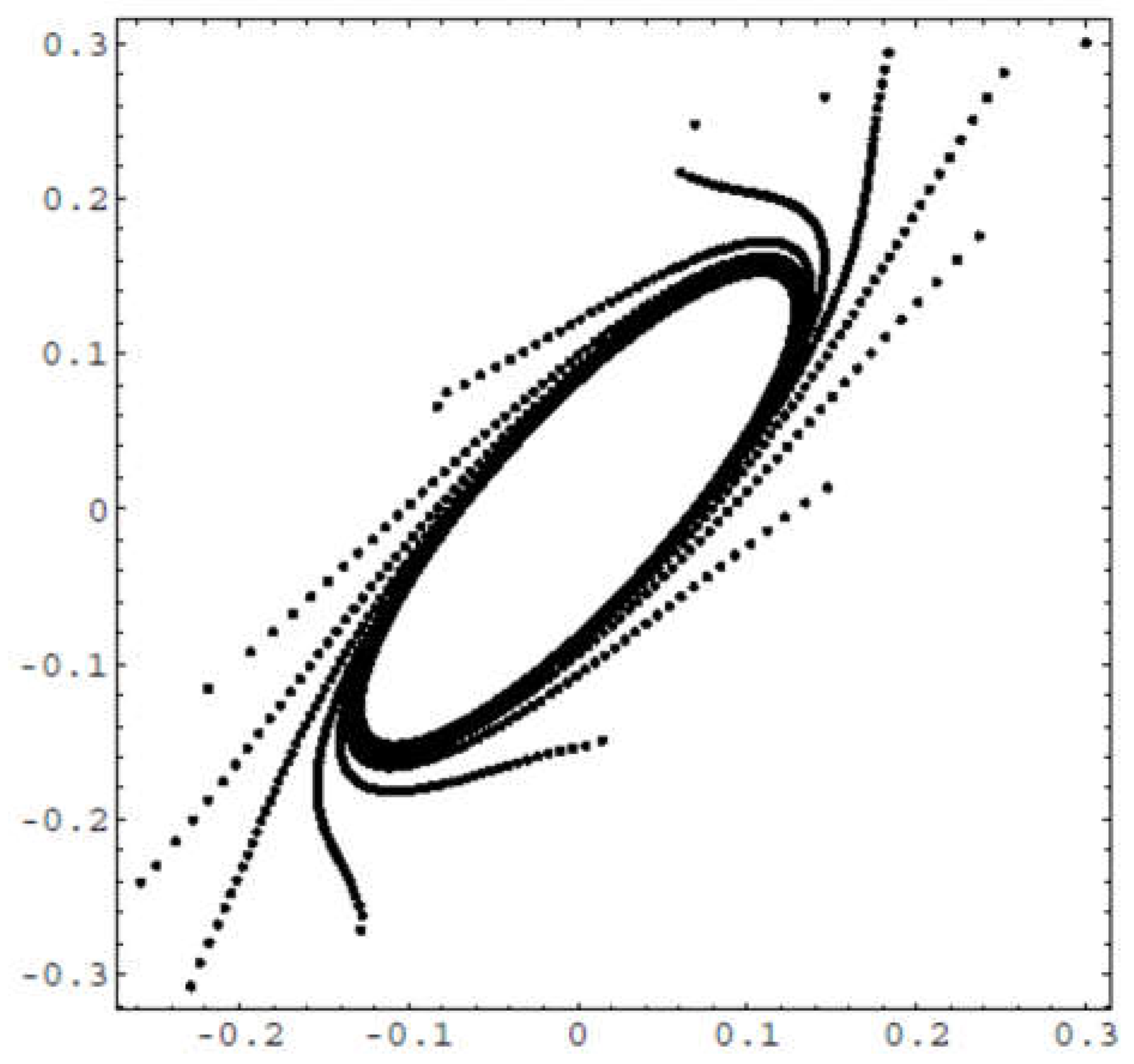
For γ = 0.2 the null solution is unstable and an asymptotically stable closed invariant curve is present.
The trajectories of (4.2) converges to the asymptotically stable invariant curve as is shown in
Figure 4.2.,
Figure 4.3.
For β = −0.82 and γ = −0.47 the null solution of
(4.2) is unstable and an asymptotically stable cycle of period 2 is present. The trajectory of
(4.2) converges to the asymptotically stable cycle i.e. Flip (period-doubling) bifurcation occurs as is shown in
Figure 4.4.. The trajectory presented in
Figure 4.4, are what we call orbit in classical sense.
This summary analysis does not reveal trajectories that are no longer classic curves.
Figure 4.1.
Trajectory for γ = 0.19,.
Figure 4.1.
Trajectory for γ = 0.19,.
Figure 4.2.
Trajectory for γ = 0.2.
Figure 4.2.
Trajectory for γ = 0.2.
Figure 4.3.
Trajectory for γ = 0.2.
Figure 4.3.
Trajectory for γ = 0.2.
Figure 4.4.
Trajectory for β = −0.82, γ = −0.47.
Figure 4.4.
Trajectory for β = −0.82, γ = −0.47.
5. Case of a Discrete-Time Hopfield Neural Network with Delay and Ring Architecture
In [
70] an extended analysis of the chaotic dynamics of the neural network with delay and ring architecture defined by
was undertaken. The external inputs are equal to zero and the system parameters are regarded as numerical expresion of the state of network..The network state can change due to a disease for example.
Therefore the network voltage dynamics change too. In [
70] this kind of change is analyzed with respect to the network parameters. The stability domain of the null solution is found, the values of the characteristic parameter for which bifurcations occur at the origin are identified and the existence of Fold/Cusp,
Neimark-Sacker and Flip bifurcations is proved. These bifurcations were analyzed by applying the center manifold theorem and the normal form theory. It is proved that resonant 1:3 and 1:4 bifurcations may also be present. It is shown that the dynamics in a neighborhood of the null solution become more and more complex as the characteristic parameter grows in magnitude and passes through the bifurcation values. A theoretical proof is given for the occurrence of Marotto's chaotic behavior, if the magnitudes of the interconnection coefficients are large enough and at least one of the activation functions has two simple real roots. For illustrate what this means the following numerical example was considered:
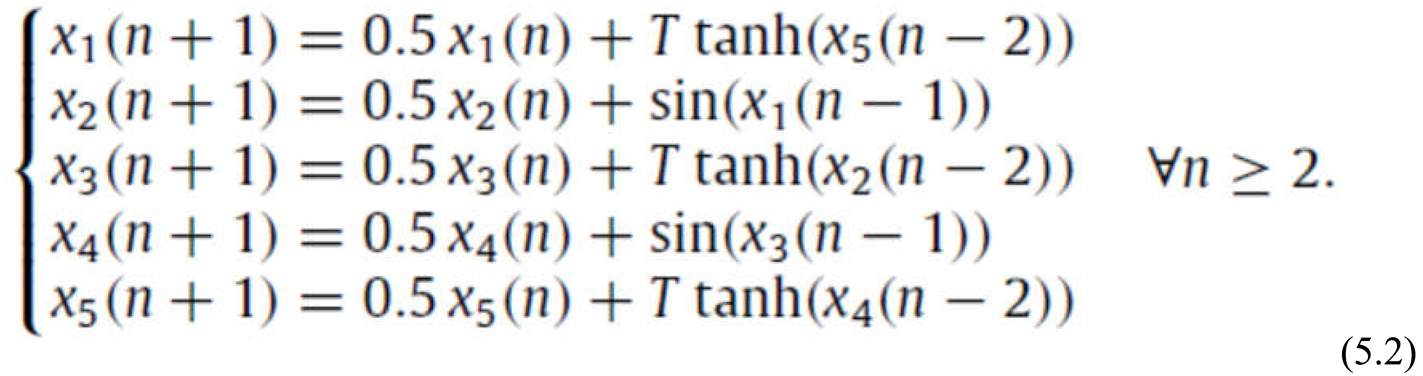
All numerical computations have been done using Mathematica. Denoting b=T3, based on the theoretical result presented, we find that the critical values of b are{-7.593;-6.396;-3.784; -1.538; -0.433; -0.102; -0.036; 0.031; 0.055; 0.209; 0.851; 2.531; 5.148; 7.276}. The stability domain of the null solution, with respect to T is DS= (-0.331116; 0.31498).
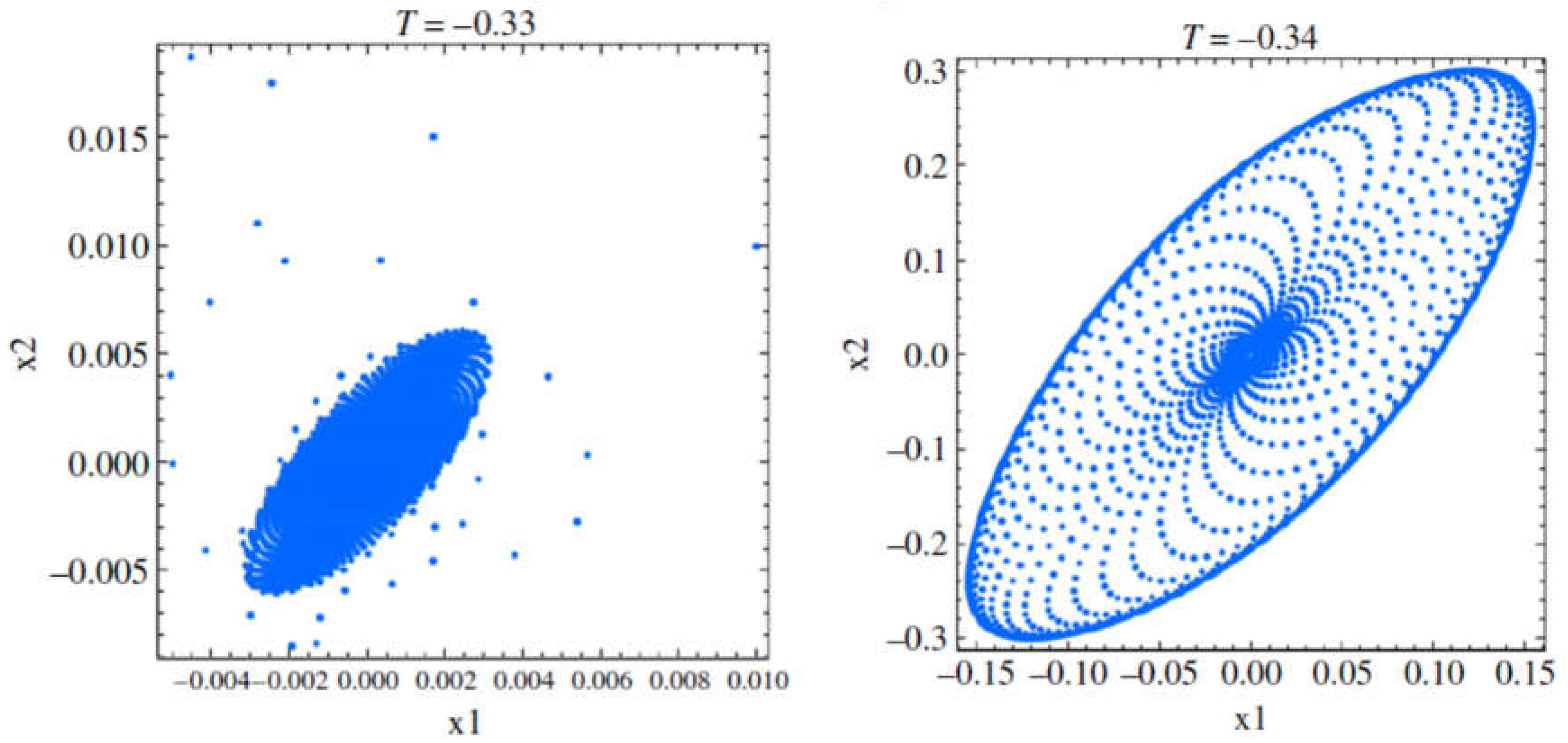
At T= 0.31498, a Cusp bifurcation occurs at the origin, while at T=-0.331116 a supercritical Neimark-Sacker bifurcation takes place (as shown in
Figure 5.1)
Figure 5.1.
Supercritical Neimark-Sacker bifurcation at T=-0.331116.
Figure 5.1.
Supercritical Neimark-Sacker bifurcation at T=-0.331116.
For T=-0.33, the null solution is asymptotically stable, and the trajectory converges to the origin.
For T=-0-34, an asymptotically stable cycle (1-torus, drift ring) is present, and the trajectory converges to this cycle.
If modulus T is sufficiently large, chaotic behavior may be expected.
Figure 5.1,
Figure 5.2,
Figure 5.3 and
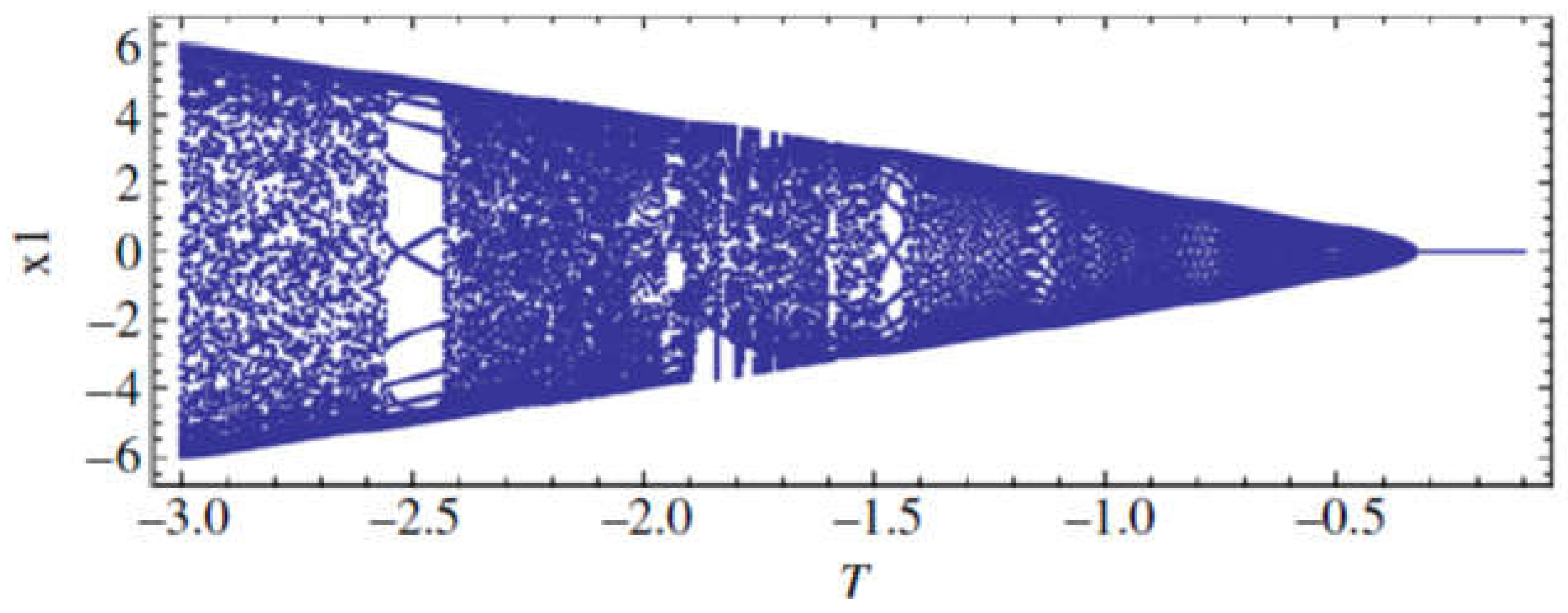
Figure 5.4 describe the route towards chaos occurring in system (5.2) in a neighborhood of the origin, as T decreases from 0 to -3. The bifurcation diagram (
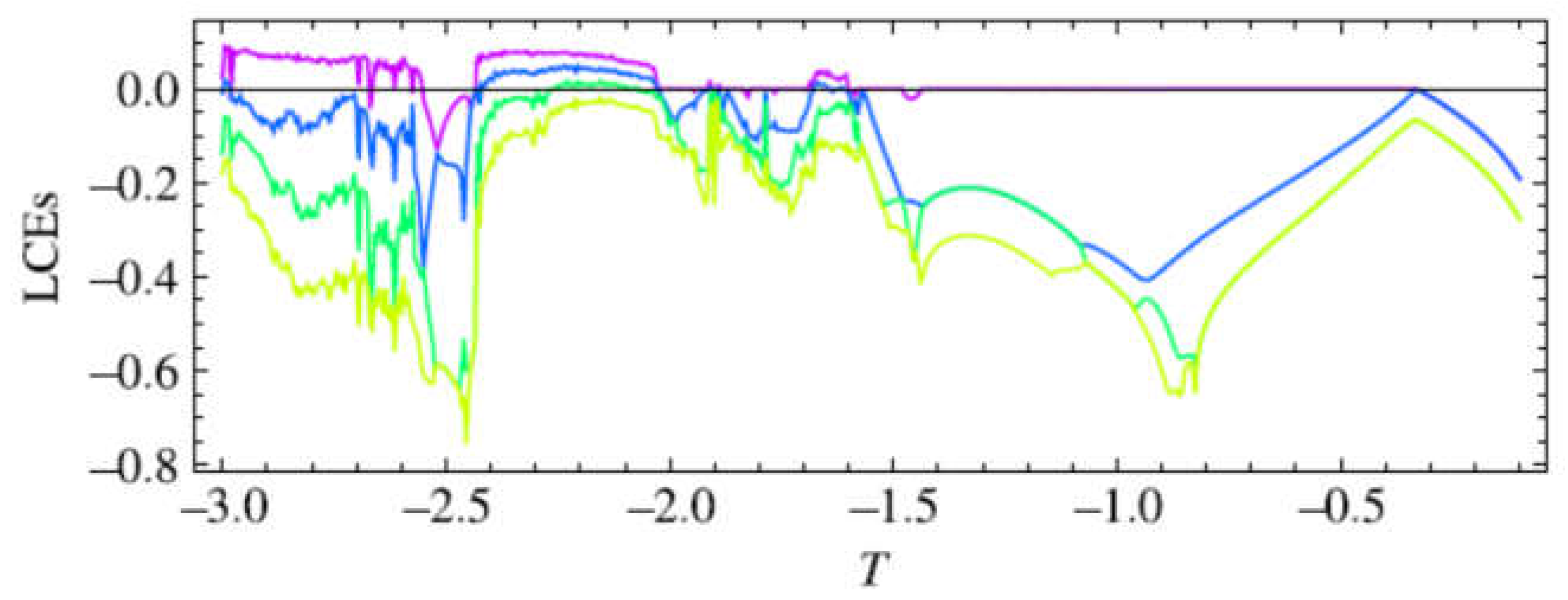
Figure 5.2) and the computed four largest Lyapunov Characteristic Exponents shown in
Figure 5.3, (computed using the Householder QR based method developed by Bremen, Udwadia, and Proskurowski (1997)), clearly describe this route, being consistent with the theoretical results presented.
Figure 5.2.
Bifurcation diagram for system (5.2), in the (T, x1) -plane, for -3< T<0, with the step size of 0:005 for T.
Figure 5.2.
Bifurcation diagram for system (5.2), in the (T, x1) -plane, for -3< T<0, with the step size of 0:005 for T.
Figure 5.3.
Four largest Lyapunov Characteristic Exponents for system (5.2).
Figure 5.3.
Four largest Lyapunov Characteristic Exponents for system (5.2).
For the computation of the Lyapunov spectrum, for each T value (step size 0:005 for T) the initial conditions were reset and 105 time steps were iterated before calculating the LCEs (which were computed over the next 105 time steps).
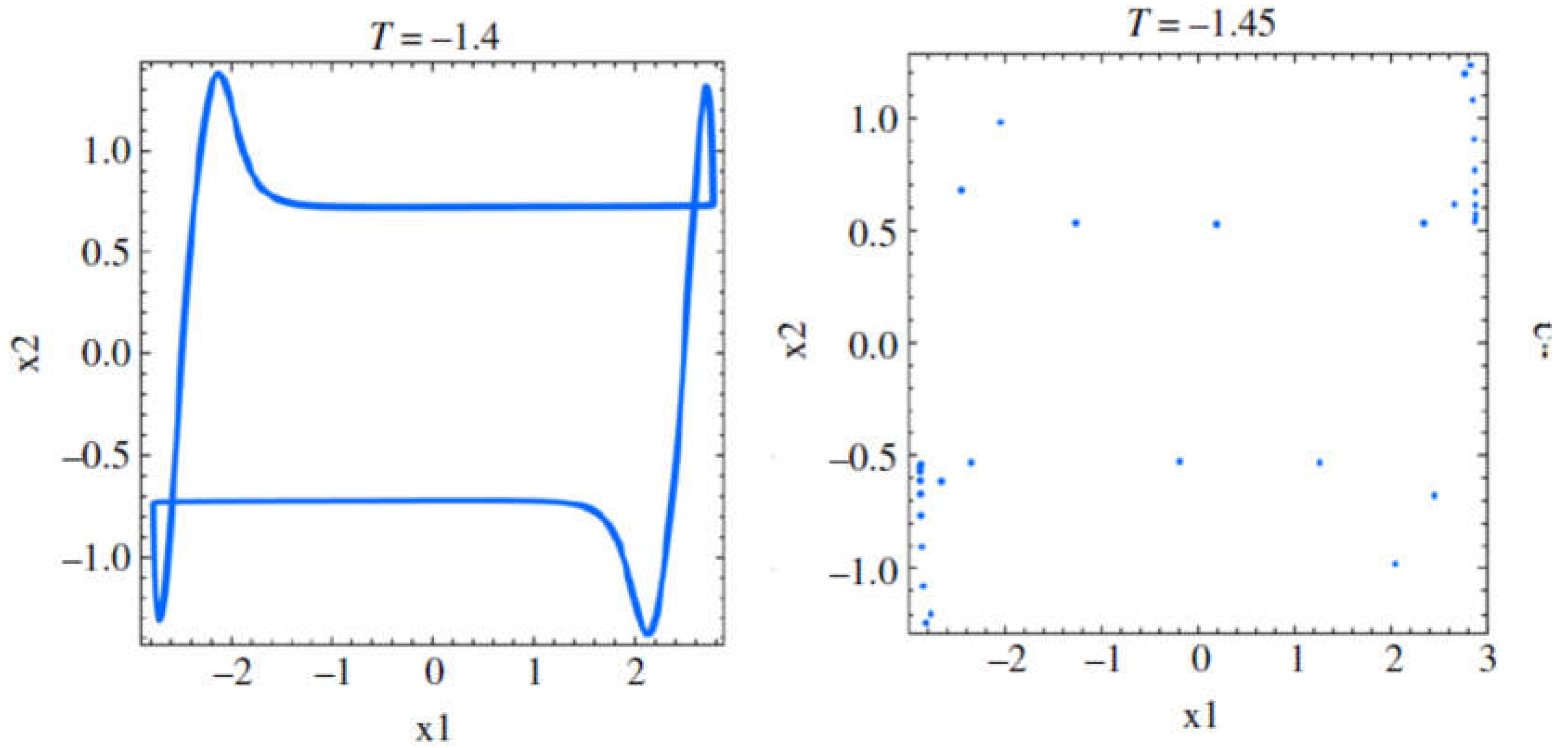
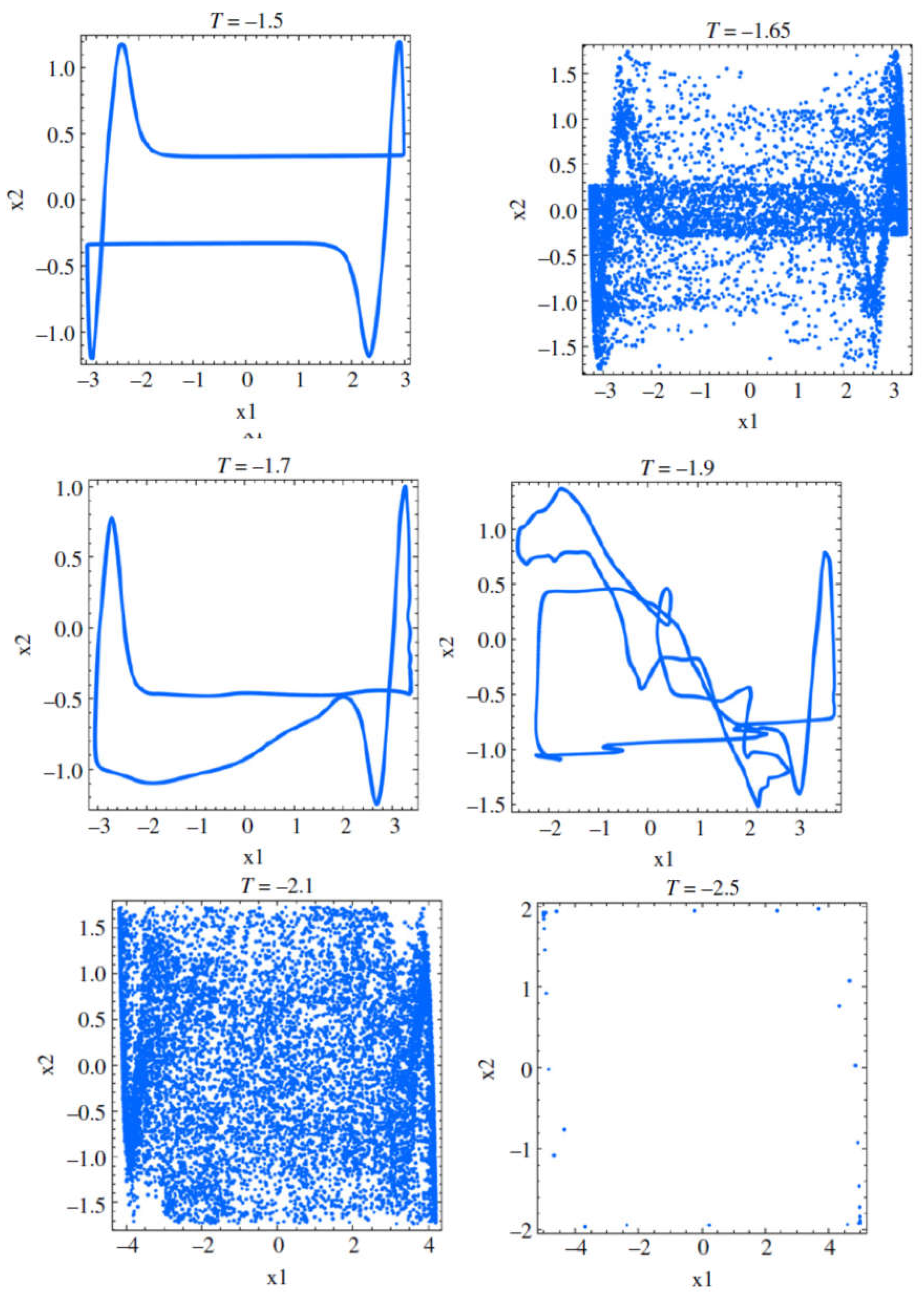
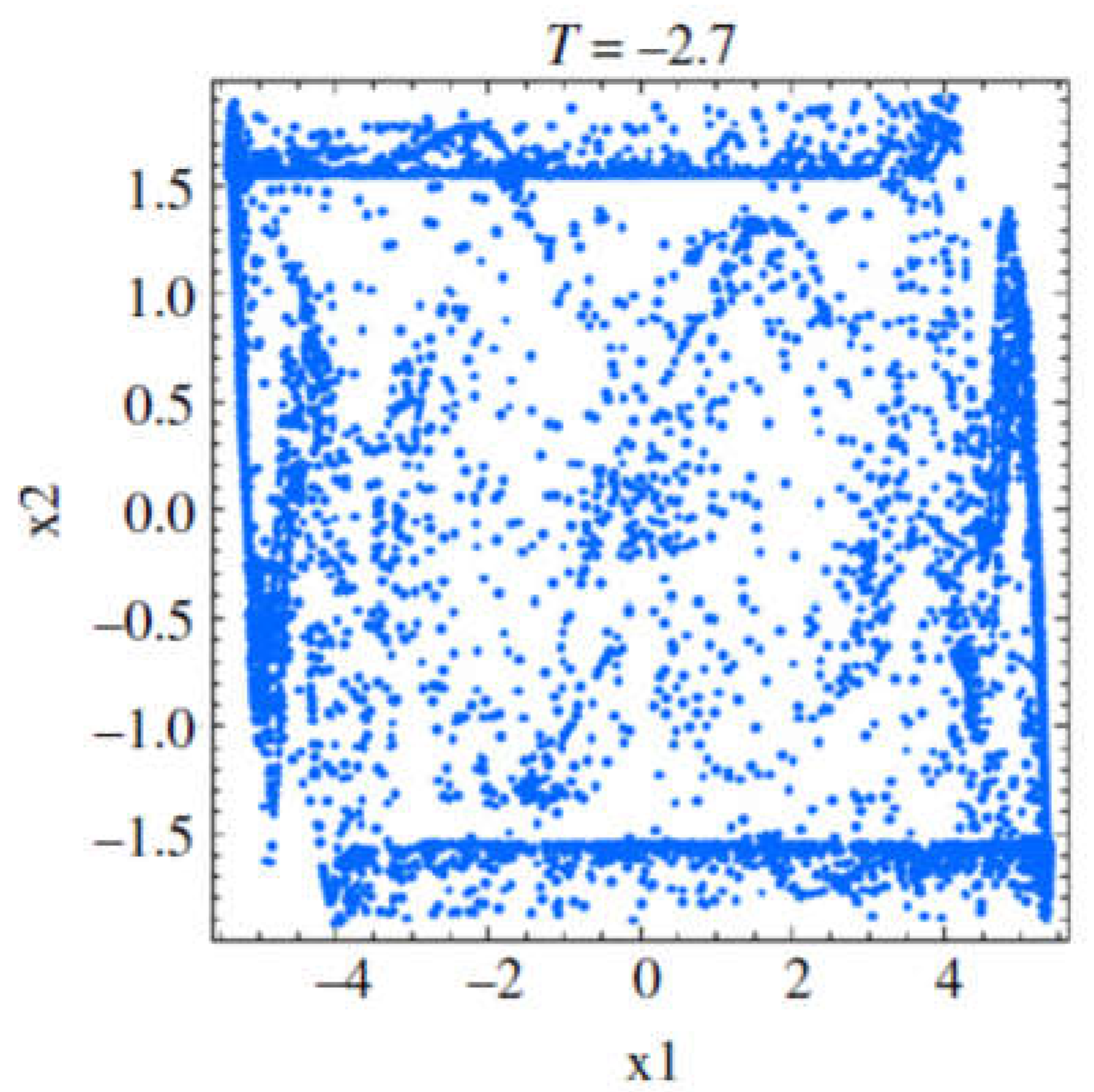
In
Figure 5.4. Phase portraits for various values of T, -3<T<-1/4 can be seen:
Figure 5.4.
Phase portraits for: T=-1.4; T=-1.45; T=-1.5; T=-1.65; T=-1.7; T=-1.9; T=-2.1; T=-2.5; T=-2.7.
Figure 5.4.
Phase portraits for: T=-1.4; T=-1.45; T=-1.5; T=-1.65; T=-1.7; T=-1.9; T=-2.1; T=-2.5; T=-2.7.
From the bifurcation point of view, the meaning of these figures is clear: T=-1.4, stable torus (LE1= 0); T=-1.45, stable period-32 orbit (LE1 < 0); T=-1.5, stable torus (LE1= 0); T=1.65, chaos (LE1 > 0); T=-1.7; T =-1.9, stable tori (LE1= 0);T =-2.1, hyperchaos (LE3 > 0); T=-2.5, stable period-38 orbit (LE1 < 0); T=-2.7, chaos (LE1 > 0).
The question is: are the phase portrait corresponding to T=-1.45, T=-1.65, T=-2.1, T=_2.5, T=--2.7 objects of Fractal Geometry? Have they real corresponding or they exist just in theory?
Our conjecture, based on the geometrical aspect, is that the phase portraits for T=-1.45, T=-1.65, T=-2.1, T=_2.5, T=--2.7 are fractals and they have real counterpart.
6. Results
6.1. In Case of a Discrete-Time Hopfield Neural Network of Two Neurons with Two Delays and No Self- Connections 23 Voltage trajectories are computed at bifurcation points. Among the 23 voltage trajectories we find 14 voltage trajectory which are not what we can call orbits in classic sense.The geometrical aspect of these trajectories suggest that they are fractals. Our conjecture is that the 14 trajectories in discussion are fractals and has real couterpart.
6.2. In case of a discrete-time Hopfield neural network of five neuron with delay and ring architecture 9 voltage trajectories appear at bifurcation points. Among the 9 voltage trajectories we find 5 voltage trajectory which are not what we can call orbits in classic sense.The geometrical aspect of these trajectories suggest that they are fractals. Our conjecture is that the 5 trajectories in discussion are fractals having real couterpart..
7. Discussion
The scientific literature concerning fractals in the description of nervous system is extensive.
In [
21] for example it is shown that, Currents through Ion Channels has fractal properties in time, Electrical Activity of Auditory Nerve Cells is described in terms of fractal.
In [
22] authors sustain that “fractal and conventional morphometry may represent complementary analytical/ quantitative tools to elucidate the diversity of morphological patterns and functional parameters which characterize neural cells and brain structures”.
In [
23] the author writ: “the present survey provides experimental data confirming that biological processes including growth, proliferation, apoptosis, epigenetic and genetic mechanism, morphologic/ultrastructural and functional organization occurring in living shaped elements and complex structured tissues may follow fractal rules. The large agreement with the fractal nature of the brain and nervous cell system sustained by theoretical, experimental and heuristic foundations is nowadays consolidated and intervenes more than thirty years after the publication of the Fractal Geometry of Nature, in which Mandelbrot recognized that “the notion that neurons are fractals remains conjectural” Its relevance and contribution to the cultural development of mankind (as comprehensive of humanistic and scientific thinking) is keen underlined by the observation of some years ago arguing that the fractal geometry could be considered as a biological design principle for living organisms.
Paper [
24] use fractal time series analysis (detrended fluctuation analysis; DFA) to examine the spontaneous activity of single neurons in an anesthetized animal model, specifically, the mitral cells in the rat main olfactory bulb. DFA bolstered previous research in suggesting two subclasses of mitral cells. Although there was no difference in the fractal scaling of the interspike interval series at the shorter timescales, there was a significant difference at longer timescales.
Neurons in Group B exhibited fractal, power-law scaled interspike intervals, whereas neurons in Group A exhibited random variation. These results raise questions about the role of these different cells within the olfactory bulb and potential explanations of their dynamics. Specifically, self-organized criticality has been proposed as an explanation of fractal scaling in many natural systems, including neural systems. However, this theory is based on certain assumptions that do not clearly hold in the case of spontaneous neural activity, which likely reflects intrinsic cell dynamics rather than activity driven by external stimulation. Moreover, it is unclear how self-organized criticality might account for the random dynamics observed in Group A, and how these random dynamics might serve some functional role when embedded in the typical activity of the olfactory bulb.
In the paper [
25] the authors conclude:” Given the central role of brain’s “wiring”, our previous research focused on the importance of fractal scaling in establishing connectivity between neurons. Diagnostic Analysis (DA} was show to relate to the optimization of competing functional constraints—the ability of dendrites to reach out and connect to other neurons versus the costs associated with doing so. Within this model, different neuron types were predicted to different DA values depending on the relative importance of connectivity and material cost with higher DA values indicating a greater emphasis on connectivity. In the current investigation, we hypothesize that pathological state of neurons might also affect this fractal optimization and consider whether changes in DA might therefore, be used as a diagnostic tool. This analysis represents an appealing development because it relates form to function rather than relying purely on pattern characterization.”
Our approach in this paper is different from those presented in the above refered literature.We start considering the discrete-time Hopfield neural network model which claim to describe the electrical activity of a neural system. The bifurcation analysis of some low dimensional networks show that for certain values of the bifurcation parameter the geometry of the voltage orbits of neurons are what we call classic orbits and there exists other bifurcation values for which the geometrical aspect of trajectories are not at all what we call classic orbits.Their geometrical aspects suggest that they are moreover fractals. In the present paper present to the reader both type of trajectories putting the natural question: Are some of the presented voltage state orbits,fractals? Exists these orbits in reality or they exists just in theory i.e.has these orbits a real couterpart?
Our conjecture is that some of the voltage trajectories presented here are fractals and have real counterpart.
Author Contributions
The two authors contributed equally to the realization of this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from founding agencies in the public,comercial or not-for-profit sectors.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mandelbrot, Benoit (July 8, 2013). 24/7 Lecture on Fractals (https://www.youtube.com/watch?v=5e7HB5Oze4g#t=70). 2006 Ig Nobel Awards. Improbable Research. Archived (https://ghostarchive.org/varchive/youtube/20211211/5e7HB5Oze4g) from the original on December 11, 2021.
- Mandelbrot, B. B.: The Fractal Geometry of Nature. W. H. Freeman and Company, New York (1982); p. 15.
- Edgar, Gerald (2007). Measure, Topology, and Fractal Geometry (https://books.google.com/books?id=dk2vruTv0_gC&pg=PR7). Springer Science & Business Media. p. 7. ISBN 978-0-387-74749-1.
- Vicsek, Tamás (1992). Fractal growth phenomena. Singapore/New Jersey: World Scientific. pp. 31, 139–146. ISBN 978-981-02-0668-0.
- Gouyet, Jean-François (1996). Physics and fractal structures. Paris/New York: Masson Springer. ISBN 978-0-387-94153-0.
- Peters, Edgar (1996). Chaos and order in the capital markets: a new view of cycles, prices, and market volatility. New York: Wiley. ISBN 978-0-471-13938-6.
- Krapivsky, P. L.; Ben-Naim, E. (1994). Multiscaling in Stochastic Fractals. Physics Letters A. 1994, 196, 168. Bibcode:1994PhLA..196..168K (https://ui.adsabs.harvard.edu/abs/1994Ph LA..196..168K). [CrossRef]
- Hassan, M. K.; Rodgers, G. J. (1995). Models of fragmentation and stochastic fractals. Physics Letters A. 1995, 208, 95. Bibcode:1995PhLA..208...95H (https://ui.adsabs.harvard.edu/abs/1995PhLA..208...95H). [CrossRef]
- Hassan, M. K.; Pavel, N. I.; Pandit, R. K.; Kurths, J. Dyadic Cantor set and its kinetic and stochastic counterpart. Chaos, Solitons & Fractals. 2014, 60, 31–39. arXiv:1401.0249 . [CrossRef]
- Tan, Can Ozan; Cohen, Michael A.; Eckberg, Dwain L.; Taylor, J. Andrew Fractal properties of human heart period variability: Physiological and methodological implications(https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2746620). The Journal of Physiology. 2009, 587, 3929–3941. [CrossRef] [PubMed]
- Liu, Jing Z. ; Zhang, Lu D.; Yue, Guang H. Fractal Dimension in Human Cerebellum Measured by Magnetic Resonance Imaging (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1303704). Biophysical Journal. 2003, 85, 4041–4046. [Google Scholar] [CrossRef] [PubMed]
- Karperien, Audrey L. ; Jelinek, Herbert F.; Buchan, Alastair M. Box-Counting Analysis of Microglia Form in Schizophrenia, Alzheimer's Disease and Affective Disorder. Fractals 2008, 16, 103. [Google Scholar] [CrossRef]
- Jelinek, Herbert F.; Karperien, Audrey; Cornforth, David; Cesar, Roberto; Leandro, Jorge de Jesus Gomes (2002). MicroMod-an L-systems approach to neural modelling. In Sarker, Ruhul (ed.). Workshop proceedings: the Sixth Australia-Japan Joint Workshop on Intelligent and Evolutionary Systems, University House, ANU (https://books.google.com/books?id=FFSUGQAACAAJ). University of New South Wales. ISBN 978-0-7317-0505-4. OCLC 224846454 (https://search.worldcat.org/oclc/224846454). Retrieved February 3, 2012.Event location: Canberra, Australia.
- Hu, Shougeng; Cheng, Qiuming; Wang, Le; Xie, Shuyun Multifractal characterization of urban residential land price in space and time. Applied Geography. 2012, 34, 161–170. [CrossRef]
- Karperien, Audrey; Jelinek, Herbert F.; Leandro, Jorge de Jesus Gomes; Soares, João V. B.;Cesar Jr, Roberto M.; Luckie, Alan (2008). Automated detection of proliferative retinopathy in clinical practice (https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2698675). Clinical Ophthalmology. [CrossRef] [PubMed]
- Losa, Gabriele A.; Nonnenmacher, Theo F. (2005). Fractals in biology and medicine (https://books.google.com/books?id=t9l9GdAt95gC). Springer. ISBN 978-3-7643-7172-2.
- Vannucchi, Paola; Leoni, Lorenzo (2007). Structural characterization of the Costa Rica décollement: Evidence for seismically-induced fluid pulsing. Earth and Planetary Science Letters 2007, 262, 413–Bibcode:2007E. [Google Scholar] [CrossRef]
- Wallace, David Foster (August 4, 2006). Bookworm on KCRW (https://web.archive.org/web/20101111033857/http://www.kcrw.com/etc/programs/bw/bw960411david_foster_wallace). Kcrw.com. Archived from the original (http://www.kcrw.com/etc/programs/bw/bw960411david_foster_wallace) on November 11, 2010. Retrieved October 17, 2010.
- Eglash, Ron (1999). African Fractals: Modern Computing and Indigenous Design (https://web.archive.org/web/20180103005701/http://homepages.rpi.edu/~eglash/eglash.dir/afractal/afbook.htm). New Brunswick: Rutgers University Press. Archived from the original (http://www.rpi.edu/~eglash/eglash.dir/afractal/afractal.htm) on January 3, 2018. Retrieved October 17, 2010.
- Ostwald, Michael J., and Vaughan, Josephine (2016) The Fractal Dimension of Architecture Birhauser, Basel. [CrossRef]
- Larry, S. Liebovitch, Fractals and Chaos Simplified for the Life Sciences; Oxford Univ. Press, 1998.
- Gabriele Angelo Losa; Antonio Di Ieva; Fabio Grizzi; and Gionata De Vico; On the fractal nature of nervous cell system, NEUROANATOMY, 21 July 2011. [CrossRef]
- Gabriele A. Losa, On the Fractal Design in Human Brain and Nervous Tissue; Applied Mathematics, 2014, 5,1725-1732 Published Online June 2014 in Sci.Res. http://www.scirp.org/journal/am.
- Luis H. Favela, Charles A. Coey, Edwin R. Griff, Michael J. Richardson; Fractal analysis reveals subclasses of neurons and suggests an explanation of their spontaneous activity, Neuroscience Letters (2016) 54–58.
- Conor Rowland, Bruce Harland, Julian H. Smith, Saba Moslehi, John Dalrymple-Alford and Richard P. Taylor; Investigating Fractal Analysis as a Diagnostic Tool That Probes the Connectivity of Hippocampal Neurons; Front. Physiol. 13, 932598. [CrossRef]
- Ian Pilgrim and Richard P. Taylor, Fractal Analysis of Time-Series Data Sets: Methods and Challenges. [CrossRef]
- Zaletel, I. Fractal analysis in neuroanatomy and neurohistology. MedPodml 2016, 67, 1–7. [Google Scholar] [CrossRef]
- Wonsang You, Sophie Achardy, J¨org Stadler, Bernd Bruckner, and Udo Seiffert, Fractal analysis of resting state functional connectivity of the brain, WCCI 2012 IEEE World Congress on Computational Intelligence, June, 10-15, 2012 - Brisbane, Australia.
- Malvin C. Teich, Conor Heneghan, Steven B. Lowen, Tsuyoshi Ozaki and Ehud Kaplan, Fractal character of the neural spike train in the visual system of the cat. J. Opt. Soc. Am. A 1997, 14.
- Antonio Di Ieva, Fabio Grizzi, Herbert Jelinek, Andras J. Pellionisz, and Gabriele Angelo Losa, Fractals in the Neurosciences, Part I: General Principles and Basic Neurosciences. The Neuroscientist 2014, 20, 403–417. [Google Scholar] [CrossRef] [PubMed]
- Antonio Di Ieva, Francisco J. Esteban, Fabio Grizzi,Wlodzimierz Klonowski, and Miguel Martín-Landrove, Fractals in the Neurosciences, PartII: Clinical Applications and Future Perspectives. The Neuroscientist 2015, 21, 30–43. [Google Scholar] [CrossRef]
- Gerhard Werner, Fractals in the nervous system: conceptual implications for theoretical neuroscience, Frontiers in Physiology. Fractal Physiology 2010, 1, 15.
- Erhard Bieberich, Recurrent fractal neural networks: a strategy for the exchange of local and global information processing in the brain, BioSystems 2002, 66, 145_/164.
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Lond) 1952, 117, 500–544. [Google Scholar] [CrossRef]
- S. Hagiwara, S. Nakajimao. Effects of the intracellular Ca ion concentration upon excitability of the muscle fiber membrane of a barnacle. J. Gen. Physiol. 1966, 49, 807–818. [CrossRef] [PubMed]
- S. S. Hagiwara, H. Hayashi, K. Takahashi. Calcium and potassium currents of the membrane of a barnacle muscle fiber in relation to the calcium spike. J. Physiol. 1969, 205, 115–129. [Google Scholar] [CrossRef] [PubMed]
- R. Keynes, D. Rojas, T. Eduardo, E. Robert, J.R. Vergara. Calcium and potassium systems of a giant barnacle muscle fiber under membrane potential control. J. Physiol. (Lond.) 1973, 229, 409–455. [CrossRef] [PubMed]
- S. Hagiwara, J. Fukuda, D.C. Eaton. Membrane currents carried by Ca, Sr, and Ba in barnacle muscle fiber during voltage clamp. J. Gen. Physiol. 1974, 63, 564–578. [CrossRef] [PubMed]
- K. Murayama, N. Lakshminarayanaiah. Some electrical properties of the membrane of the barnacle muscle fibers under internal perfusion. J. Membr. Biol. 1977, 35, 257–283. [CrossRef]
- P. P.S. Beirao, N. Lakshminarayanaiah. Calcium carrying system in the giant muscle fibre of the barnacle species Balanus Nubilus. J. Physiol. 1979, 293, 319–327. [Google Scholar] [CrossRef]
- C. Morris, & Lecar, Harold. Voltage oscillations in the barnacle giant muscle fiber. Biophysical J. 1981, 35, 193–213.
- S.H.Weinberg, Membrane Capacitive Memory Alters Spiking in Neurons Described by the Fractional Order Hodgkin-Huxley Model. PloS ONE, 2015; 10, e0126629.
- Brandibur O , Kaslik E . Stability properties of a two dimensional system involv- ing one Caputo derivative and applications to the investigation of a fractional order Morris-Lecar neuronal model. Nonlinear Dyn 2017, 90, 2371–2386. [CrossRef]
- M. A. Moreles, & Lainez, Rafael. Mathematical Modelling of Fractional Order Circuits. ArXiv 2016, arXiv:1602.03541.
- Agneta M. Balint , Stefan Balint , Robert Szabo , Mathematical description of the ion transport across biological neuron membrane and in biological neuron networks, voltage propagation along neuron axons and dendrites, which uses temporal classic Caputo or Riemann-Liouville fractional partial derivatives, is non-objective, MATHEMATICS IN ENGINEERING, SCIENCE AND AEROSPACE MESA - www.journalmesa.com Vol. 12, No. 4, pp. 1057–1079, 2021 c CSP - Cambridge, UK; I&S - Florida, USA, 2021.
- Agneta, M. Agneta M. Balint , Stefan Balint , Adrian Neculae , On the objectivity of mathematical description of ion transport processes using general temporal Caputo and Riemann-Liouville fractional partial Derivatives. Chaos, Solitons and Fractals 2022, 156, 111802. [Google Scholar]
- J. Hopfield, Neural networks and physical systems with emergent collective computational abilities, Proc. Nat. Acad. Sci. 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Tank, D.W.; Hopfield, J.J. Simple neural optimization networks: an A/D converter, signal decision circuit and a linear programming circuit. IEEE Transactions on Circuits and Systems 1986, 33, 533–541. [Google Scholar] [CrossRef]
- Yu, W.; Cao, J. Cryptography based on delayed chaotic neural networks. Physics Letters A, 2006; 356, 333–338. [Google Scholar]
- Mirela Darau, Eva Kaslik, Stefan Balint; Cryptography using chaotic discrete-time delayed Hopfield neural networks; MATHEMATICS IN ENGINEERING, SCIENCE AND AEROSPACE MESA - www.journalmesa.com Vol. 3, No. 1, pp. 31–40, 2012 CSP - Cambridge, UK; I&S - Florida, USA, 2012.
- Adachi, M.; Aihara, K. Associative dynamics in a chaotic neural network. Neural Networks 1997, 10, 83–98. [Google Scholar] [CrossRef]
- Bremen, H. F.; Udwadia, F.E.; Proskurowski, W. An efficient QR based method for the computation of Lyapunov exponents. Physica D: Nonlinear Phenomena 1997, 101, 1–16. [Google Scholar] [CrossRef]
- Chen, L.; Aihara, K. Chaotic simulated annealing by a neural network model with transient chaos. Neural Networks 1995, 8, 915–930. [Google Scholar] [CrossRef]
- Chen, L.; Aihara, K. Chaos and asymptotical stability in discrete-time neural networks. Physica D: Nonlinear Phenomena 1997, 104, 286–325. [Google Scholar] [CrossRef]
- Chen, L.; Aihara, K. Chaotic dynamics of neural networks and its application to combinatorial optimization. Journal of Dynamical Systems and Differential Equations 2001, 9, 139–168. [Google Scholar]
- Chen, S.S.; Shih, C.W. Transversal homoclinic orbits in a transiently chaotic neural network. Chaos 2002, 12, 654–671. [Google Scholar] [CrossRef]
- Guo, S.; Huang, L. Periodic oscillation for discrete-time Hopfield neural networks. Physics Letters A 2004, 329, 199–206. [Google Scholar] [CrossRef]
- Guo, S.; Huang, L.; Wang, L. Exponential stability of discrete-time Hopfield neural networks. Computers and Mathematics with Applications 2004, 47, 1249–1256. [Google Scholar] [CrossRef]
- Guo, S.; Tang, X.; Huang, L. (2007). Stability and bifurcation in a discrete system of two neurons with delays. Nonlinear Analysis: Real World Applications, in press. [CrossRef]
- He, W.; Cao, J. Stability and bifurcation of a class of discrete-time neural networks. Applied Mathematical Modelling 2007, 31, 2111–2122. [Google Scholar] [CrossRef]
- E. Kaslik, St. Balint; Configurations of steady states for Hopfield-type neural networks. Applied Mathematics and Computation 2006, 182, 934–946. [Google Scholar] [CrossRef]
- St. Balint, L. Braescu and E. Kaslik, Regions of attraction and applications to control theory; Cambridge Scientific Publishers Ltd. 2008. Edited by S. Sivasundaram.
- Yuan, Z.; Hu, D.; Huang, L. Stability and bifurcation analysis on a discrete-time system of two neurons. Applied Mathematical Letters 2004, 17, 1239–1245. [Google Scholar] [CrossRef]
- Yuan, Z.; Hu, D.; Huang, L. Stability and bifurcation analysis on a discrete-time neural network. Journal of Computational and Applied Mathematics 2005, 177, 89–100. [Google Scholar] [CrossRef]
- Zhang, C.; Zheng, B. Hopf bifurcation in numerical approximation of a n dimension neural network model with multi-delays. Chaos, Solitons & Fractals 2005, 25, 129–146. [Google Scholar]
- Zhang, C.; Zheng, B. Stability and bifurcation of a two-dimension discrete neural network model with multi-delays. Chaos, Solitons & Fractals 2007, 31, 1232–1242. [Google Scholar]
- E. Kaslik, S. E. Kaslik, S. Balint.Chaotic Dynamics of a Delayed Discrete-Time Hopfield Network of Two No identical Neurons with no Self-Connections. J Nonlinear Sci. [CrossRef]
- E. Kaslik, St. Balint. Bifurcation analysis for a two-dimensional delayed discrete-time Hopfield neural network. Chaos, Solitons and Fractals 2007, 34, 1245–1253. [CrossRef]
- E. Kaslik, St. Balint. Bifurcation analysis for a discrete-time Hopfield neural network of two neurons with two delays and self-connections. Chaos, Solitons and Fractals 2009, 39, 83–91. [CrossRef]
- Eva Kaslik, Stefan Balint. Complex and chaotic dynamics in a discrete-time-delayed Hopfield neural network with ring architecture. Neural Networks 2009, 22, 1411_1418. [Google Scholar]
- Feifei Yang, Jun Ma, Fuqiang Wu; Review on memristor application in neural circuit and network. Chaos, Solitons&Fractals 2024, 187, 115361.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).


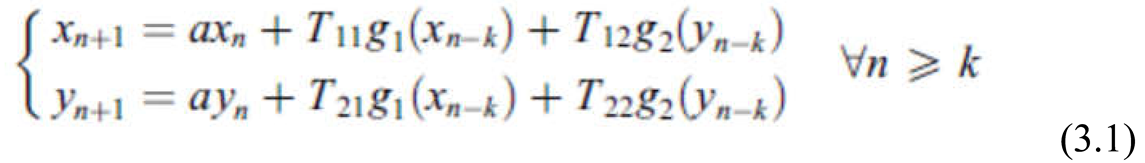
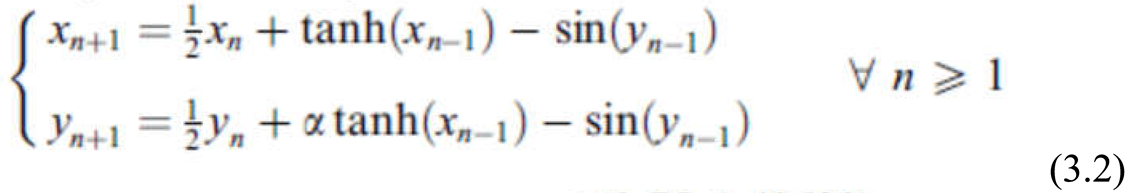
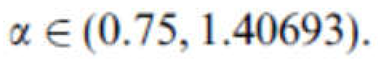 . At 1.40693 a supercritical Neimark–Sacker bifurcation occurs.
. At 1.40693 a supercritical Neimark–Sacker bifurcation occurs.
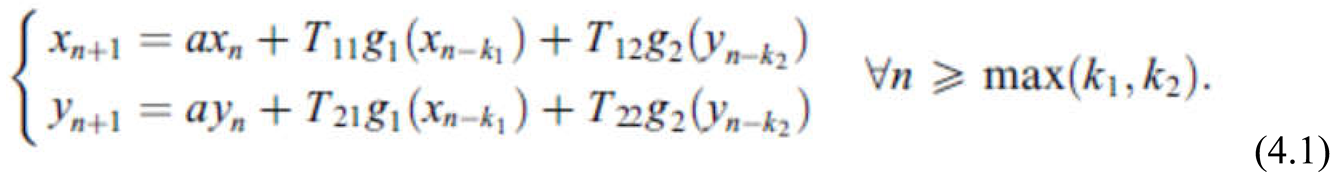
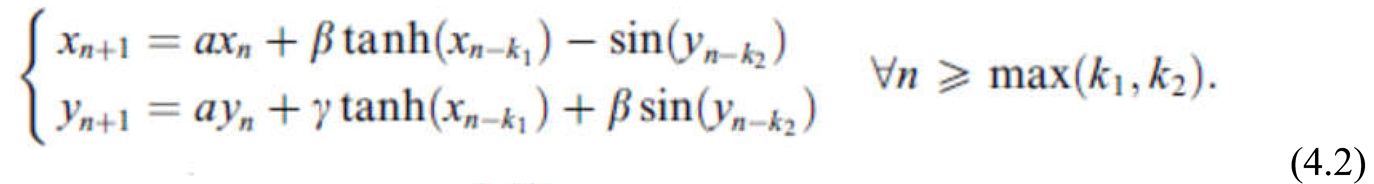 with; a = 0.5, k1 = 4, k2 = 10, For γ = 0.19 the null solution of (4.2) is asymptotically stable and trajectories converges to the null solution.
with; a = 0.5, k1 = 4, k2 = 10, For γ = 0.19 the null solution of (4.2) is asymptotically stable and trajectories converges to the null solution.