Submitted:
21 September 2024
Posted:
23 September 2024
You are already at the latest version
Abstract
Keywords:
1. Distances and Intervals in General Relativity
1.1. Time Intervals
1.2. Spatial Distance
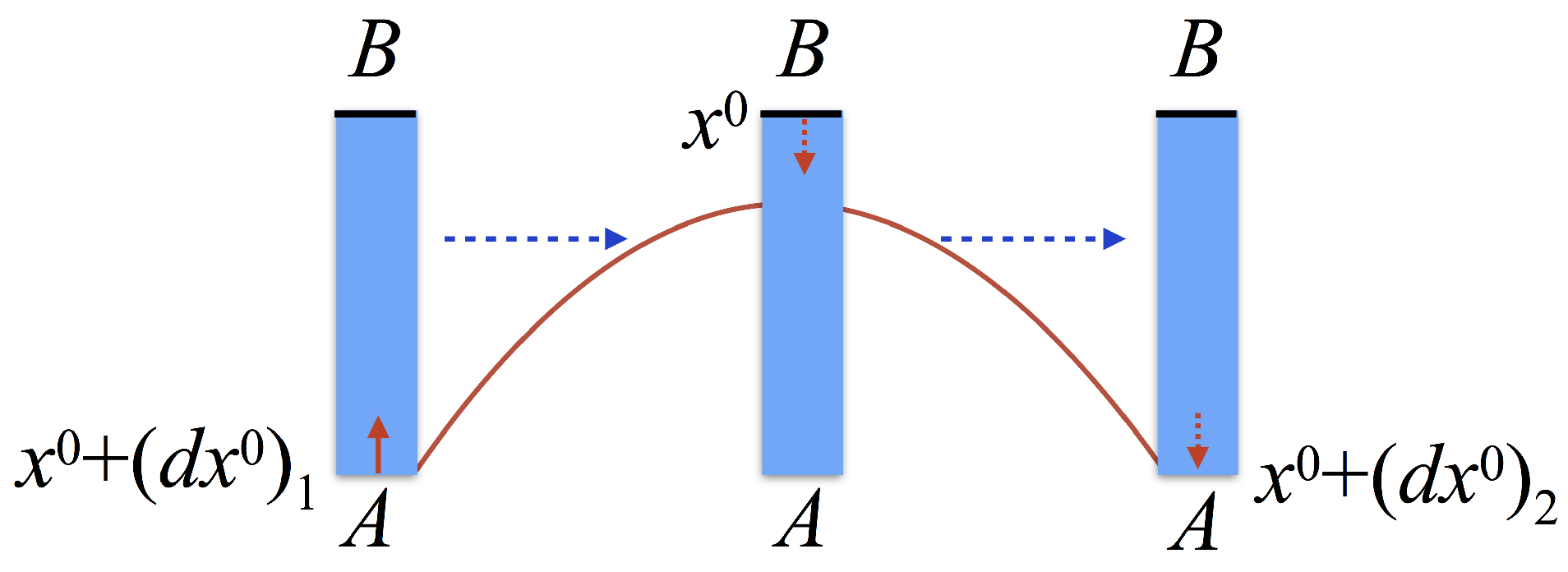
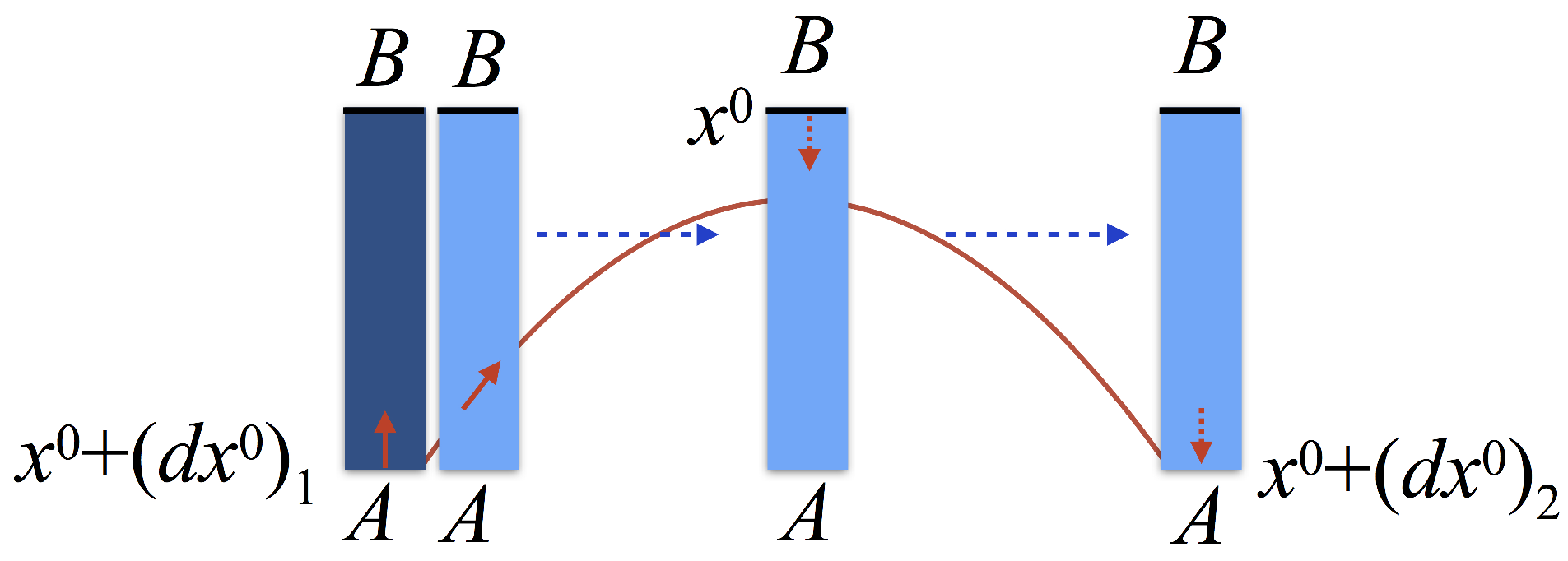
1.3. Synchronisation in General Relativity
2. Energy-Momentum Density Tensor of the Matter
2.1. Generalised Energy-Momentum Density Tensor
2.2. Action Function of Gravitational Field
2.3. System of Discrete Point-like Particles
2.4. Macroscopic Masses
3. Conservation Laws in General Relativity
3.1. Conservation Law of Total Energy in General Relativity
3.2. Other Conservation Laws in General Relativity
4. Conclusions
Acknowledgments
References
- Edited by M. J. Klein, A. J. Kox, and R. Schulman. The Collected Papers of Albert Einstein: The Berlin Years: Writings, 1914-1917, Vol 6. Princeton University Press, (2016).
- R. M. Wald. General Relativity. The University of Chicago Press, (1984).
- L. D. Landau and E. M. Lifshitz. The Classical Theory of Fields. Pergamon Press, (1971).
- S. B. Rüster. The fundamental conservation law in the theory of general relativity: an unconventional approach is feasible and correct. Parana Journal of Science and Education, 6(9), 1-11, (2020).
- S. B. Rüster. Why in general relativity the energy density of the gravitational field must be localizable?. Parana Journal of Science and Education, 7(1), 1-9, (2021).
- S. B. Rüster. Energy is Conserved in General Relativity. Parana Journal of Science and Education, 8(6), 13-22, (2022).
- S. B. Rüster. Energy Conservation in General Relativity and Flat Rotation Curves of Spiral Galaxies. Parana Journal of Science and Education, 9(6), 20-27, (2023). [CrossRef]
- R. P. Feynman. Feynman Lectures on Gravity. Addison Wesley, (1995).
- G. Hooft. Introduction to general relativity. Utrecht University, Utrecht, 2010.
- D. Giulini. The Rich Structure of Minkowski Space. Part of the Fundamental Theories of Physics. FTPH, Vol. 165, (2009).
- S. Barak. Electric Charge and its Field as Deformed Space. Applied Physics Research, 11(4), 29-40, (2019). [CrossRef]
- F. Cabral and F. S. N. Lobo. Electrodynamics and Space-time Geometry: Foundations. Foundations of Physics, 47, 208-228, (2017).
- M. Born and L. Infeld. Foundations of the New Field Theory. In: Proc. Royal Soc. A 144, 852, (1934).
- E. Bergshoeff et al. The Born-Infeld Action from Conformal Invariance of the Open Superstring. In: Phys. Lett. B 188, 1, (1987).
- A. A. Chernitskii. On unification of gravitation and electromagnetism in the framework of a general-relativistic approach. Gravitation and Cosmology. 15, 151-153, (2009).
- G. Boillat. Nonlinear Electrodynamics: Lagrangians and Equations of Motion. In: J. Math. Phys. 11, 941, (1970).
- M. Nakahara. Geometry, Topology, and Physics. Institute of Physics Publishing, (1996).
- B. P. Schmidt and N. B. Suntzeff and M. M. Phillips and R. A. Schommer and A. Clocchiatti and R. P. Kirshner and P. Garnavich and P. Challis and B. Leibundgut and J. Spyromilio and A. G. Riess and A. V. Filippenko and M. Hamuy and R. C. Smith and C. Hogan and C. Stubbs and A. Diercks and D. Reiss and R. Gilliland and J. Tonry and J. Maza and A. Dressler and J. Walsh and R. Ciardullo. The High-Z Supernova Search: Measuring Cosmic Deceleration and Global Curvature of the Universe Using Type Ia Supernovae The Astrophysical Journal, 507(1), 46, (1998). [CrossRef]
- H. Sykja. Bazat e Elektrodinamikës. SHBUT, (2006).
- D. J. Griffiths. Introduction to Electrodynamics. Prentice Hall, 3rd Edition, (1999).
- H. Kamberaj. Electromagnetism. With Solved Problems. Springer Nature, (2022).
- J. D. Jackson. Classical Electrodynamics. John Wiley & Sons, 3rd Edition, (1999).
- H. Goldstein, C. Poole, and J. Safko. Classical Mechanics. Third Edition. Addison Wesley, (2002).
- U. J. Nöckel. Maxwell’s equations as mechanical law. Eur. J. Phys., 43(4), 045202, (2022).
- M. A. Jaswon. Mechanical Interpretation of Maxwell’s Equations. Nature, 224, 1303-1304, (1969).
- S. B. Rüster. The Importance of the Cosmological Constant for Understanding Dark Matter and Dark Energy. Parana Journal of Science and Education, 6(5), 1-8, (2020).
- D. Holliday, R. Resnick, and J. Walker. Fundamentals of Physics. John Wiley & Sons, (2011).
- D. Clery. Event Horizon Telescope Images Second Black Hole’s Jets. Science, 373, 6553, (2021).
- M. Modugno and D. Saller and J. Tolksdorf. Classification of infinitesimal symmetries in covariant classical mechanics. J. Math. Phys., (2006).
- A. Einstein. Die Feldgleichungen der Gravitation. Preuss. Akad. Wiss. Berlin Sitzungsber, 47, 844-847, (1915).
- B. P. Abbott et al. LIGO Scientific Collaboration and Virgo Collaboration, Observation of Gravitation Waves from a Binary Black Hole Merger. Phys. Rev. Lett., 116, 061102, 2016; B. P. Abbott et al., LIGO Scientific Collaboration and Virgo Collaboration, GW170817: Observation of Gravitation Waves from a Binary Neutron Star Inspiral, Phys. Rev. Lett., 119, 161101, (2017). [CrossRef]
- A. Einstein. The Collected Papers of Albert Einstein: The Berlin Years: Writings, 1914-1917, Vol 6, Edited by M. J. Klein, A. J. Kox, and R. Schulman.
- L. C. Loveridge. Physical and Geometrical Interpretations of the Riemann Tensor, Ricci Tensor, and Scalar Curvature. 2016, http://arxiv.org/abs/gr-qc/0401099v1.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




