1. Introduction
Let
X be a compact Riemann surface of genus
and
G be a semisimple complex Lie group with Lie algebra
. A
G-Higgs bundle over
X is defined to be a pair
where
E is a holomorphic principal
G-bundle over
X and
is a holomorphic global section of the adjoint bundle of
E,
, twisted by the canonical bundle,
K. The section
is called Higgs field of the Higgs bundle. Suitable notions of stability and polystability can be given for
G-Higgs bundles that extend that given by Ramanathan [
1,
2] for principal
G-bundles and in [
3] for stable principal
G-bundles, obtaining that the moduli space of polystable
G-Higgs bundles,
, is a complex algebraic variety of dimension
.
Higgs bundles were introduced by Hitchin in his groundbreaking 1987 paper [
4] and posses a remarkable wealth of geometric structures, so they are of interest in many different areas and have been intensively studied. Indeed,
G-Higgs bundles provide the framework for the extension of the theorem of Narasimhan and Seshadri [
5], whose analogue states that the moduli space of polystable
G-Higgs bundles is isomorphic to the moduli space of reductive representations of the fundamental group
in
G[
6,
7,
8,
9,
10]. In other directions,
G-Higgs bundles are of interest in different areas of mathematics and physics, including gauge theory, mirror symmetry, Langlands duality, or symplectic, Kähler and hyperkähler geometry [
11,
12,
13].
Hitchin proved the existence of an integrable system in the moduli space of polystable
G-Higgs bundles over an algebraic curve for any reductive complex Lie group
G[
14]. A relevant and classical theorem by Chevalley [
15] states that, for any complex reductive Lie group
G with adjoint representation
, the algebra of all Ad-invariant polynomials is finitely generated and the degrees
, where
, of the elements of a basis of homogeneous polynomials are well-defined. Given any principal
G-bundle
E over
X, an Ad-invariant (or
G-invariant, or simply invariant) homogeneous polynomial
p of degree
d defines a map
by the evaluation of
p on the corresponding Higgs field
, where ⊗ denotes the tensor product of bundles (and also a spectral curve
S is induced by each
G-Higgs bundle
by taking the characteristic polynomial of the Higgs field through the adjoint representation, which is a cover of
X whose fibers correspond to the eigenvalues of
). This can be computed for a basis of invariant polynomials to finally obtain a map
This map, called
Hitchin map, is indeed proper. The space
is an affine space called the
base of the Hitchin map. For each stable and simple principal
G-bundle
E (i.e. a stable principal
G-bundle whose only automorphisms are those induced by the action of the center of the structure group
G, which is a smooth point in the moduli space of principal
G-bundles), the space
is isomorphic, by Serre duality, to
, the cotangent bundle to the moduli space of stable and simple principal
G-bundles at
E. This cotangent bundle is naturally embedded in the moduli space
of polystable
G-Higgs bundles. Hitchin defined a global symplectic structure in
that extends the natural symplectic structure of that cotangent space in a way that the Hitchin map defines an integrable system. The Hitchin fibration has proven to be an essential tool for understanding the Geometric Langlands program, as Kapustin and Witten [
13] pointed out.
A fruitful way of studying the geometry of the moduli spaces
of
G-Higgs bundles is by describing the subvarieties and maps between these moduli spaces [
16,
17,
18]. Specifically, given an automorphism of
, a subvariety is naturally defined by taking the of fixed points of that automorphism. It is then useful to study automorphisms of finite order of
. The case of involutions of the moduli space of
-Higgs bundles was developed by García-Prada in [
17], where he related Higgs bundles with representations of the fundamental group of the surface in the real forms of the group. A larger family of finite-order automorphisms is studied in [
19], but in the context of orthogonal bundles over a curve. Also, the case of involutions of
induced by the action of outer automorphisms of order 2 of
G have been studied in [
18] and, with different techniques for simple classical complex Lie groups in [
20].
This paper is interested in Higgs bundles whose structure group is
. This group is the only simple complex Lie group that admits an outer automorphism of order 3, called triality automorphism. This unique fact makes the geometric structures related to this group (including
-Higgs bundles) have both interesting and very specific geometric features, which usually require specific studies [
21,
22,
23]. In particular, in the previous literature it has been proved that the triality automorphism acts on the moduli space
and its fixed points can be described as reductions of structure group to the subgroups
or
of
. This leads the existence of two maps of algebraic varieties
and
. In this work, the study of the first map
is deepened. The way to carry out this deepening is through the study of the Hitchin integrable system associated to the two moduli spaces involved. Specifically, if
B is the basis of the Hitchin map of
and
is the basis of the Hitchin map of
, it is proved that the triality automorphism acts on
B, that there exists a homomorphism
compatible with the map between moduli spaces, and that the image of
j is formed by fixed points of the action of the triality automorphism on
B (Lemma 2). This allows to state that the map between moduli spaces is restricted to maps between Prym varieties
, where
and
and
are the associated spectral curves. Following this, in this paper the geometry of the Prym varieties involved is studied to the extent of providing necessary and sufficient conditions for these Prym varieties to be disjoint (Proposition 5).
Prym varieties play a key role in the study of the geometry of moduli spaces of Higgs bundles and
G-Higgs bundles. In particular, the connection or disconnection of Prym varieties, understood as branched coverings, allows to identify irreducible components of the fibers of the moduli space. Not only this, but several authors have shown that the knowledge of the topology of Prym varieties helps to deepen the knowledge of the topology of moduli spaces of
G-Higgs bundles [
14,
24] and to study automorphisms of moduli spaces of principal bundles [
25].
As a consequence of the above results, sufficient conditions are provided for the two Prym varieties involved to be disjoint. Thus, the paper provides innovative results on the geometry of the map
and also provides novel techniques for the mentioned geometryc study (consisting specifically in studying the Hitchin integrable system). In particular, it is intended to provide tools to advance the knowledge about the map
and to be able in the future to prove properties such as, for example, whether it is injective, in the spirit of Serman [
26].
In addition, the map
has been considered because the preceding literature provides sufficient results on the Hitchin integrable system of
[
22] and on the relationship between
-invariant polynomials and
-invariant polynomials [
27] to be able to carry out the analysis intended here. Indeed, Hitchin [
22] deepened the study of the integralble system of the moduli space of
-Higgs bundles, because the special characteristics of the group
make it of great interest in differential equations [
28], or geometry and physics [
16,
29]. Thus, Hitchin [
22] described the spectral curves
S associated to the Hitchin fibration for the group
and the associated Prym varieties. In particular, he proved the existence of an intermediate curve
C such that the covering
factors through
C, and an involution
of
S so that
is given by those
satisfying
. He also proved that the
-Higgs bundle can be reconstructed form the associated spectral curve. It has also been proved that every
-invariant polynomial is also a
-invariant polynomial fixed by the action of the triality automorphism [
27].
In summary, the main results of this work are as follows. First, it is proved the existence of a map between the bases of the Hitchin map of and which commutes with the forgetful map and whose image is composed of fixed points of the -action on the base of the Hitchin map of (Proposition 1). Secondly, necessary and sufficient conditions are provided so that the characteristic polynomial of the Higgs field of a -Higgs bundle (Proposition 2) or of a -Higgs bundle (Proposition 3) admits irreducible factors of all possible degrees. Finally, the above results are used to give necessary and sufficient conditions for the Prym varieties of and to be disjoint (Proposition 5).
The article is organized in the following way. In
Section 2 some foundations on the geometry of the Lie group
and the triality automorphism are recalled. The action of the group
of outer automorphisms of any semisimple complex Lie group
G on the moduli space
of
G-Higgs bundles over
X, introduced in [
16], is described and studied in
Section 3. It is also explained in a more detailed way the particular case of
and the specific characteristics of the triality automorphism. In
Section 4, the action of the triality automorphism on the base and on the fibers of the Hitchin integrable system is constructed.
Section 5 is devoted to providing the main geometric features on the Prym varieties coming from the Hitchin integrable system associated to
. Finally, the main conclusions of the paper are drawn.
2. The group and the Triality Automorphism
In this section, some basics on the Lie group
, its subgroups, and the triality automorphism are provided. Suitable references for this topic are [
16,
21,
30]. The group
is the only simple and simply connected complex Lie group of type
. Its Lie algebra is
, its center is isomorphic to
. It is indeed the double cover of the special orthogonal Lie group
and then it can be described as an extension of
by
:
Of course, the action of the group of automorphisms of leaves the center invariant, hence there is a homomorphism of into the group of permutations of the set of central elements of order 2. The subgroup of inner automorphisms clearly acts trivially on Z, thus this induces a homomorphism of the group of outer automorphisms of into , which is actually an isomorphism. Recall that is the quotient of the group of automorphisms of by the normal subgroup of inner automorphisms. The triality automorphism is then a choice of an order 3 outer automorphism (the other outer automorphism of order 3 is ).
Since
is the simply connected complex Lie group with Lie algebra
, there is an isomorphism of short exact sequences of the form
Given any complex Lie algebra
, if
, it is stated that
if there exists
such that
[
18]. Thus defined,
is an equivalence relation such that the obvious map
is well-defined [
18,
21].
Notice that the order of an automorphism of
clearly coincides with the order of its class modulo
. Then, if
denotes the subset of automorphisms of order 3 of
and an analogous definition is given for
and for
, it is satisfied that
It is also clear that the automorphisms of order 3 are sent to elements of
of order 3 or to the identity through the map defined in (
4). This implies that
is sent onto
through the natural map, that is,
There are exactly two pre-images of the triality automorphism
by the map defined in (
6) [
18,
21]. Then there are two possibilities for the subalgebra of fixed points of an automorphism of order 3 of
representing
. Wolf and Gray [
31] (Theorem 5.5) proved that these two different representatives of
by the map (
6) have
and
as subalgebras of fixed points (with simply connected subgroups
and
), respectively.
3. The Action of the Triality Automorphism on the Moduli Space of -Higgs Bundles
Let
X be a compact Riemann surface of genus
. A principal
-bundle over
X is a complex rank-8 and trivial determinant vector bundle equipped with a globally-defined holomorphic non-degenerate symmetric bilinear form. The set of isomorphism classes of principal
-bundles is parametrized by the cohomology set
. A map
is defined which assigns to each principal
-bundle
E its second Stiefel-Whitney class
. The bundle
E lifts to a principal
-bundle over
X if and only if
, two of such lifts differing in a line bundle of order 2. However, every principal
-bundle admits an associated
-bundle through the covering map
defined in (
2).
In the next definitions, the notions of Higgs bundles are specified for the structure groups
and
following the original notion of
G-Higgs bundle introduced by Hitchin [
4]. Recall that, given a semisimple complex Lie group
G, a
G-Higgs bundle over
X is a pair
where
E is a principal
G-bundle over
X (i.e., a bundle over
X whose fiber is
G, so a right action of
G on it is given) and
is a holomorphic global section of
, where
is the vector bundle whose fiber is the Lie algebra
of
G induced by the adjoint action
, ⊗ denotes the tensor product, and
K is the canonical line bundle over
X. Depending on the specific form of the structure group,
G-Higgs bundles may have particular interpretations, such as the given below for
and
.
Definition 1. An -Higgs bundle over X is a pair where E is a principal -bundle over X with associated bilinear form q and is a complex vector bundle homomorphism preserving the bilinear form q, where K denotes the canonical bundle over X.
Definition 2. A -Higgs bundle over X is a pair where E is a principal -bundle over X and . Here, K is the canonical bundle over X, is the adjoint vector bundle of E and is a vector bundle morphism preserving the bilinear form with which the special orthogonal bundle associated to E is equipped.
For both principal -Higgs bundles and -Higgs bundles, the element is called Higgs field and it can be understood on each fiber of the orthogonal bundle E as an 8-dimensional complex matrix of the Lie algebra .
There are suitable notions of stability and polystability that allows to construct the moduli space of
G-Higgs bundles for any complex reductive Lie group
G[
32], which will be denoted by
. These notions extend to Higgs pairs the notions given by Ramanathan [
1,
2] for principal bundles and by Ramanan [
33] for orthogonal and Spin bundles. The moduli space of
-Higgs bundles over
X is then the algebraic variety which parameterizes isomorphism classes of polystable
-bundles over
X.
Given any
-Higgs bundle
, an automorphism of
is an automorphism
of the principal
-bundle
E such that the following diagram commutes:
that is,
.
Consider now any semisimple complex Lie group
G with Lie algebra
. In [
16,
18] it is proved that the following defines an action of the group
on the moduli space
of
G-Higgs bundles: if
and
, then
is defined to be the
G-Higgs bundle
where
is an automorphism of
G representing
and
is the principal
G-bundle whose total space is that of
E but it is equipped with the right action of
G given by
, for
and
. It can be proved that this action preserves the stability and polystability of the
G-Higgs bundles and that it does not depend on the choice of the representative
A of
, since inner automorphisms act trivially on
G-Higgs bundles [
16,
18].
Let
be the triality automorphism and let
be a
-Higgs bundle over
X fixed by the action of
. If
is an automorphism of
representing
, then
. A way to understand the action of the triality automorphism on the moduli space of
-Higgs bundles is by attending to the action of triality on vector representations of the group. Bijective correspondence exists between the nodes of the Dynkin diagram of
(
Figure 1), its irreducible representations, which are 8-dimensional, and the non-trivial elements of its center [
30]. The triality automorphism acts by permuting the three fundamental representations and also the three non-trivial central elements of
. At the level of vectorial forms of the principal
-bundles, it should be recalled that the underlying vector bundle of every stable
-bundle
E through the homomorphism of groups
admits a vector decomposition of the form
for some rank 2 vector subbundles
,
,
, and
[
21] (Proposition 2.3). The action of the triality automorphism is by fixing one of these vector subbundles and permuting the other three mentioned subbundles, so that in a fixed point of the action of the triality automorphism three of these vector subbundles are isomorphic. Thus a
-bundle whose underlying vector bundle is of the form
for certain rank 2 stable vector bundles
F and
V over
X is an example of a
-bundle on which the triality acts trivially.
Recall that there are only two possibilities for the group
of fixed points of
A depending on the lifting of the triality automorphism by the relation
. These two possibilities are
or
[
31] (Theorem 5.5). In [
16,
18] it is proved that the fixed points of the action of the triality automorphism on the moduli space of
-Higgs bundles are those which admit a reduction of structure group to
or
. Then there are maps
and
such that their images complete the subvariety of fixed points of the action of the triality automorphism. In this work, the study of map
is deepened, taking advantage of the existence of results relating the invariant polynomials of
and
, which will be key in the study.
4. The Triality Automorphism and the Hitchin Integrable System
In the context of the moduli space
of
G-Higgs bundles over
X for a semisimple complex Lie group
G, the Hitchin map projects
over an affine space
B called base which parametrizes certain invariant polynomials (for the adjoint action of
G) associated to the Higgs fields of the Higgs bundles [
14]. Specifically, these invariant polynomials, when evaluated on a Higgs field
, lead to global sections of the canonical line bundle
K tensored with Casimir polynomials of the Lie algebra of
G. This defines the Hitchin map
. This map not only projects
, but transforms it in the integrable system of the induced fibration, thus it is called Hitchin integrable system. There are some remarkable properties of this system. Between them, the generic fiber of this fibration is an abelian variety, called Prym variety. This Hitchin system admits a natural symplectic structure from that of the cotangent bundle in a way that the Poisson bracket of the functions defined by the Hitchin map is zero. This is key for the system to be integrable in the sense of Liouville [
14]. The study of this integrable system, particularly the geometry and topology of the Prym varieties, is key to address and study problems concerning the topology of
.
Given a finite covering
of
X, the Prym variety
(or simply
) is the subgroup of the Jacobian of
that parametrizes divisors on
of zero norm, which is an abelian variety, the norm being the map that moves divisors on
to divisors on
X. In the contexto of the moduli space of
G-Higgs bundles over
X,
G being a semisimple complex Lie group acting as structure group of the Higgs bundles, the Higgs field
of each
G-Higgs bundle
induces a spectral covering of
X, which is essentially the zero locus of the characteristic polynomial of the Higgs field, taken through the adjoint representation of
G on its Lie algebra
. Then the associated Prym variety is given by the Prym variety of this spectral covering, which can be proved to be isomorphic to the fiber of the Hitchin map [
14].
Specifically, let
G be a semisimple complex Lie group with Lie algebra
and
be a basis of the ring of invariant homogeneous polynomials of
, where
r is the rank of
. The action of each polynomial on the Higgs field defines a map
where
for
. This map allows to define the so-called
Hitchin map,
where
is the moduli space of
G-Higgs bundles. The vector space
is called the
base of the Hitchin map. In [
14] it is proved that
. If
n is the dimension of
, the Hitchin map induces
n complex valued functions
defined on
, where by
it is denoted the moduli space of stable and simple principal
G-bundles, which is a dense open subset of the moduli space
of principal
G-bundles. The tangent space to
at an element
is isomorphic to
, which coincides with
by Serre duality. Hitchin also proved that the
n functions
Poisson-commute with the canonical symplectic structure of the cotangent bundle [
14] (Proposition 4.5). This then defines a completely integrable system on
[
34].
As will be proved below, the group of outer automorphisms of G acts on the base of the Hitchin map so that this action is compatible qith the action of on when G is simply connected (which is the case of ).
Lemma 1. Let G be a semisimple and simply connected complex Lie group. Let f be an automorphism of the Lie algebra of G and p be an invariant homogeneous polynomial of G. Then is also an invariant homogeneous polynomial of G.
Proof. Since f is a linear map, it is clear that is a homogeneous polynomial. Therefore, it suffices to show that it is invariant.
Let
be an automorphism of
G such that
(such automorphism exists because
G is simply connected) and let
. Then for any
,
(where
is defined as the inner automorphism induced by
g,
), so
is invariant, as desired. □
From this, the announced action of
on the base
B of the Hitchin map can be defined for a semisimple and simply-connected complex Lie group
G. Hitchin [
14] proved that the Hitchin map
is surjective. Then, for each
, there exists
such that
. If
, it is defined
where
is an automorphism of
G representing
.
Lemma 2. If G is a semisimple and simply connected complex Lie group, then the action of on the base of the Hitchin map defined in (13) is well-defined and it is compatible with the action of on defined in (8).
Proof. To check that the action given in (
13) is well-defined, notice the following:
It is clear from Lemma 1 that are invariant homogeneous polynomials of G.
If f is an inner automorphism of G, then, since are invariant under this kind of automorphisms, the action is trivial, so the above action descends to an action of .
If
and
are polystable
G-Higgs bundles over
X such that
then, since
is a basis of invariant polynomials of
G,
for every invariant polynomial
p of
G, so, in particular,
The above three points lead to the conclusion that the action under consideration is well-defined.
Let now
. To check that the action of
on the base of the Hitchin map is compatible with the action on
it suffices to show that
for all
. Notice that
as it was intended to prove. □
Remark. Since, by Lemma 2, the action of an outer automorphism
on the base of the Hitchin map does not depend on the representative of
chosen in
, if
is an element if the base of the Hitchin map for some
G-Higgs bundle
, it can be denoted
The above study will now be particularized to the case of
and
-Higgs bundles. The algebra of invariant polynomials of
is generated by four invariant homogeneous polynomials
where
for each
i and
is the Pfaffian, so
[
14]. Indeed, as it can be found in [
35],
Then the base of the Hitchin map is
Given a quadruple
, it induces the polynomial
in the sense that the characteristic polynomial of the Higgs field of any
in the fiber of the Hitchin map at
a is
, where each
or
is a holomorphic global section of
over
X and
defines the Hitchin map
.
The mentioned characteristic polynomial defines the spectral curve in the total space of the canonical bundle . Then, given any , it defines the equation of the corresponding spectral curve, which will be called as the divisor of a section of defined by the induced polynomial where x is the tautological section of and it is a single-valued eigenvalue of the Higgs field .
Consider now the Lie group
, seen as a subgroup of
. The algebra of invariant polynomials of
is generated by two polynomials,
, of degrees 2 and 6, respectively
Then the base of the Hitchin map of the moduli space of
-Higgs bundles is
and, given a pair
, the induced invariant polynomial is
, so by taking a common factor
it follows that the polynomial
is also
-invariant [
22,
35].
Roughly speaking, the triality automorphism of
acts in each fiber of the Hitchin map
by permuting the orbits corresponding to the three 8-dimensional irreducible representations of
above mentioned (the vectorial one and the two spinor ones, positive and negative, corresponding to the Weyl spinors [
30]). In
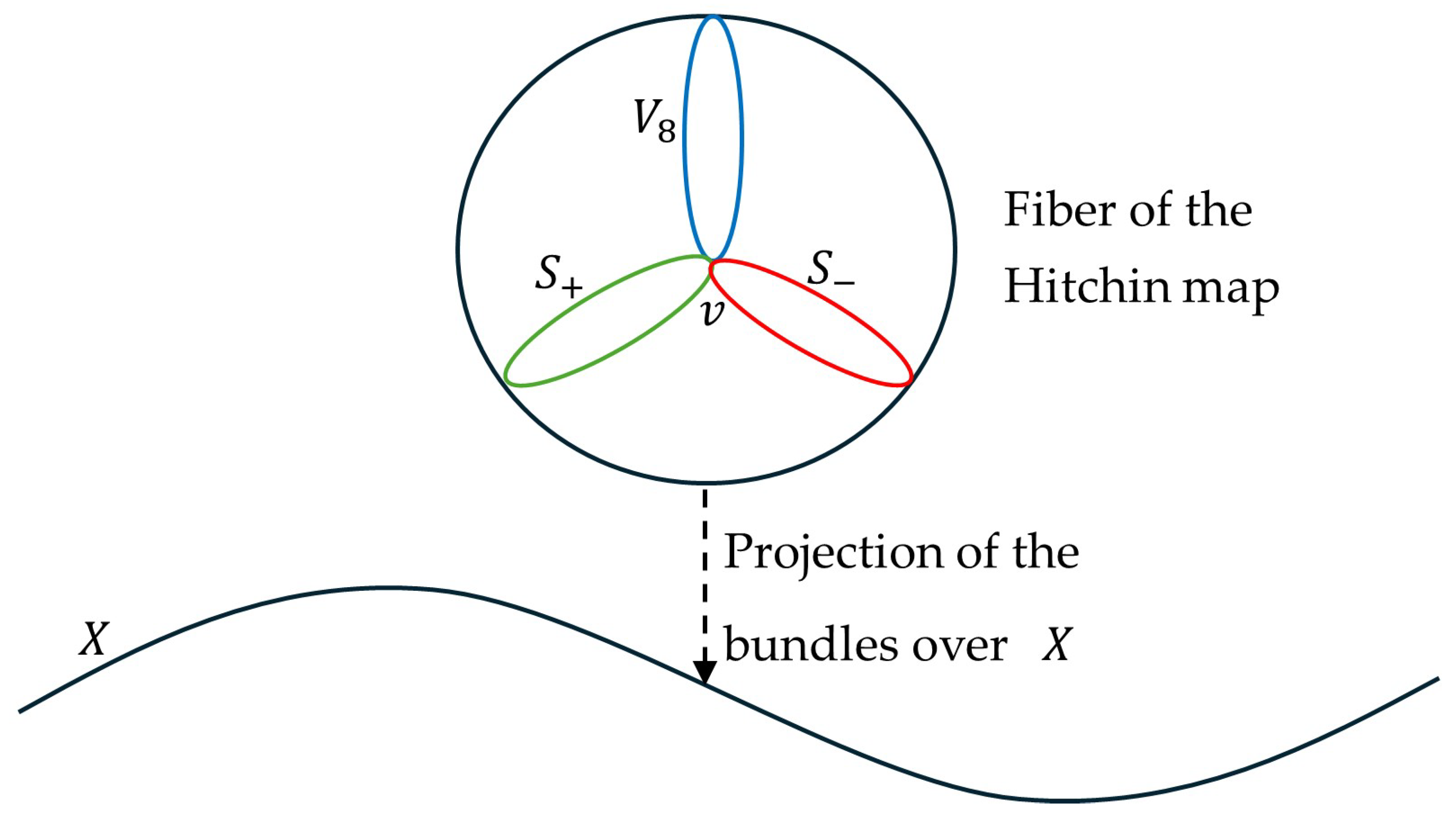
Figure 2, a generic fiber of the mentioned Hitchin map of the moduli space of
-Higgs bundles over the compact Riemann surface
X is represented and also three orbits interchanged by the triality automorphisms are shown in a very simple and schematic way. The point called
v in the intersection of the orbits represents a fixed point of the action of triality on the fiber.
Some facts on spectral curves and Prym varieties associated to the moduli spaces
and
will be now recalled. Given a
-Higgs bundle
over
X, the characteristic polynomial of the Higgs field
defines an element
, so a spectral cover
and an 8-sheeted covering map
are defined, whose fibers are identified with the eigenvalues of
. A detailed construction of this curve can be found in [
22,
36,
37]. There exists an exact sequence on the spectral curve
where
E denotes both the principal
-bundle and the orthogonal bundle that it induces ([
22,
36]). By dualizing the sequence (
26) and tensoring with
the following is obtained:
Here,
L is a line bundle which satisfies that
(as a vector bundle). It is constructed as the coker of
, where
x denotes the tautological global section of
, and
can be identified with the support of
L. The covering map
gives a norm map Nm defined by
on divisor classes. The norm defines a map at the level of Jacobian varieties
. Then the Prym variety of the spectral curve
is defined to be the connected component of the kernel of
. This Prym variety is then an abelian subvariety of the jacobian of the sectral curve
. Observe that, since
takes values in
, the opposite of an eigenvalue of
is also an eigenvalue of
, so an involution
of
is defined by change of sign and the eigenspace
V of eigenvalue
of
is moved to
for eigenvalue
. Then
by (
26) and (
27), so
. This means that
satisfies that
is trivial (the choice of a square root of
K is required here). Then the Prym variety is the collection of those elements
M of the Jacobian of
such that
is trivial. This is equivalent to stating that the desired Prym variety coincides with
, the last Prym variety being defined from the covering map
. Notice that, given any
, one has that
, where
and, since
, then
as a consequence of (
26) and (
27), so the special orthogonal bundle is obtained from the element of the Prym variety. Then the fiber
is a
-sheeted covering of the Prym variety of
(details on this construction can be found in [
22]).
Consider now the Lie group
. The fundamental complex representation of
has rank 7 and defines, in addition, an inclusion
. A holomorphic antisymmetric 3-form can be defined in
in a way that
is the group of elements of
which preserves this 3-form [
29]. For any
-Higgs bundle
over
X, Hitchin [
22] considered the spectral curve
assocated to it and constructed an intermediate curve
C such that the covering map
admits a factorization
and proved the existence of an involution
of
such that
and
is the subspace of those
for which
is trivial. From this description, Hitchin [
22] proved that the globally-defined holomorphic antisymmetric 2-form defined in
E by its
-structure can be reconstructed from the corresponding point of the Prym variety
. In this way, it was proved that the fiber of the Hitchin map of
is isomorphic to
[
22].
Notice that if
is a
-Higgs bundle, then, seen as a
-Higgs bundle through the contention of groups
, it satisfies that the Pfaffian
is 0. Then, if
a is the
-invariant polynomial
and
is the associated spectral curve,
b is the
-invariant polynomial and
is the associated spectral curve, the map
restricts to a map
Proposition 1.
Let B and be the base of the Hitchin maps of and defined in (21) and (24), respectively. Then there exists a map such that the diagram
is commutative and is given by fixed points for the action of the triality automorphism of on B. Moreover, the generating homogeneous -invariant polynomials and can be described as
where are the generating homogeneous -invariant polynomials given in (21).
Proof. The algebra of homogeneous
-invariant polynomials is naturally embedded in the algebra of homogeneous polynomials of
which are invariant for the action of the subgroup
, and there is also a surjective map of this subalgebra on the algebra of homogeneous
-invariant polynomials [
27] (Corollary 2.2.3). From this, the map
j making the diagram above commutative is defined by the composition of the two maps described. It has been also proved that the image by
j of the algebra of homogeneous
-invariant polynomials are exactly the fixed points of the action of the triality automorphism on the algebra of homogeneous
-invariant polynomials [
35] (Propositions 4.2 and 4.3). Moreover, Hitchin proved that a matrix of the Lie algebra
, when considered as a matrix of
, has eigenvalues
such that
and that the homogeneous invariant polynomials
and
which generate the algebra of invariant polynomials of
take values
and
, respectively [
22,
35]. From this, in [
35] (Proposition 4.3) the explicit expressions for
and
of the statement are computed. □
Remark. Notice that, if , is the spectral curve of the -invariant polynomial induced by a and is the spectral curve associated to , where j is defined in Proposition 1, then the map restricts to a map . The image of are fixed points of the action of the triality automorphism on .
5. Connectedness Criteria for the Prym Varieties
In this section the geometry of the Prym varieties
and
of
and
, respectively, will be studied, where
defined in (
24). In particular, necessary and sufficient conditions for the above Prym varieties to be disconnected will be established.
Lemma 3. Let G be the complex simple Lie group or . Let be the moduli space of G-Higgs bundles over X and be the Hitchin map defined in (10), where B denotes the base of the Hitchin map. Let and let be the associated spectral curve. Then admits a copy of X in it if and only if the polynomial defined in (22) or (25), respectively, induced by a admits a global linear factor.
Proof. Consider the polynomial on
t induced by
a defined in (
22) or (
25), which will also be called
a for simplicity. Let
d be the degree of
a. Suppose that
a admits a linear factor, say
, where
and
. Then
on a dense open subset
U of
X. The element
defines an isomorphism
By taking the dual, it is induced an isomorphism
Then there exists a unique element
such that
. Since
, this implies that
for all
. This then defines a morphism
such that
, where
is the spectral covering. Therefore,
is injective. Since
X and
are projective curves,
extends to the desired morphism.
Reciprocally, suppose that is an inclusion of curves. It is then clear that is a linear factor of a. □
Proposition 2. Let be the moduli space of -Higgs bundles over X and B be the base of the Hitchin map defined in (21). Let and let be the associated spectral curve. Let be the invariant polynomial defined by a, where and for all i. This polynomial will also be denoted by a. Then
Proof. The first part is a consequence of Lemma 3. For the second part notice that the polynomial induced by
a admits a factor of degree 2 if and only if there exist elements
for
and
for
such that
This gives the following system of equations:
Since, by hypothesis, the factor is irreducible, it follws that . Therefore, from the first seven equations it is obtained that the ’s are determined by the ’s, so the other two equations give the necessary and sufficient conditions which the ’s should satisfy for the existence of a solution. Straightforward computations show that these two conditions are those announced in the statement.
The third part is analogous to the case above by considering the system in
for
induced by the expression
where
for
. That is,
The ’s are determined by the ’s from the first six equations since it must be . Then the necessary and sufficient conditions on the ’s for the existence of a solution are given by the last three equations. These conditions are those of the statement.
Finally, the fourth par is similar. It follows from the expression
which induces a system on the
’s with coefficients in
’s of the form
From the first five equations, the ’s can be expressed in terms of the ’s (notice that, in this case, it must be ), so the four conditions of the statement follow from the four last equations of the system. □
Consider now the moduli space of -Higgs bundles over X. From Lemma 3, similar computations as made in Proposition 2 allow to prove the following analogous result.
Proposition 3. Let the moduli space of -Higgs bundles over X and be the base of the Hitchin map of defined in (24). Let and be the induced spectral curve. Suppose that the invariant polynomial induced by a, which will be also called a, is , where for all . Then
Proof. The first part is an immediate consequence of Lemma 3. For the second, note that the polynomial induced by
a admits a factor of degree two if and only if there exist elements
for
and
for
such that
This gives the following system of equations.
It must be , since, by hypothesis, the factor is irreducible. It is then clear that the ’s are determined by the ’s from the first five equations of this system, so the other two equations give the necessary and sufficient conditions which the ’s should verify for the existence of a solution. Straightforward computations then readily show that these two conditions are those of the statement.
For the third part, notice that the condition for the polynomial induced by
a to admit a degree three factor is the existence of elements
for
and
for
such that
from which a similar system of equations follows, thus an analogous computation as the above leads to the expressions of the statement since it must be
by irreducibility of
. Specifically, the induced system is of the form
Here, it also must be
, so the first four equations allow to express the
’s in terms of the
’s. The rest three equations give the conditions announced. □
A result of Hausel and Pauly [
38] (Corollary 1.3) is recalled here, as it will be useful in the to study the geometry of Prym varieties associated to the Hitchin system in the moduli spaces
and
. Although [
38] works with the
-case, the results that will be used here are directly applicable to the cases of interest in the present work, since the representations that considered allow to interpret the curves as spectral curves associated to some
-Higgs bundle which admits an additional structure.
Proposition 4. [
38] (Corollary 1.3)
Let be an n-sheeted spectral cover of the complex irreducible projective curve X. The Prym variety is not connected if and only if there exists a prime number d with such that the spectral cover comes from a degree spectral cover over the étale Galois cover of degree d over X.
Consider the moduli space
of
-Higgs bundles over
X. Let
B be the base of the Hitchin map of
defined in (
21). In Proposition 4, Hausel and Pauly prove that the Prym variety of a given spectral curve
with
is connected if and only if the polynomial
does not divide the polynomial defined by
a in (
22) whatever
,
, and
d is a prime number which divides the degree of the cover
.
Similarly, if the moduli space
of
-Higgs bundles over
X is considered and
deonotes the base of its Hitchin map defined in (
24), Proposition 4 states that, for any
with associated spectral curve
, the Prym variety
is connected if and only if for every
,
and every prime number
d such that
d divides the degree of the cover
, the polynomial
does not divide the polynomial defined by
a in (
25).
From Proposition 4 and the discussion above, one can prove the following result, which determines the condition of a Prym variety given by the groups or to be connected.
Proposition 5. Let G be the complex simple Lie group or and let be the moduli space of G-Higgs bundles over X. Let a be an element of the base of the associated Hitchin map. Then the following is satisfied:
-
If and the invariant polynomial associated to a is with for and , then the Prym variety is not connected if and only if one of the following conditions holds:
- (a)
contains a copy of X.
- (b)
There exists a global section such that β is a solution of the polynomial
which takes values in .
-
If and the invariant polynomial associated to a is with for , then the Prym variety is not connected if and only if one of the following conditions holds:
- (a)
contains a copy of X.
- (b)
There exists a global section such that β is a solution of the polynomial
which takes values in .
- (c)
and there exists a global section such that β is a solution of the polynomial
which takes values in .
Proof. As a consequence of Proposition 4, in both cases is disconnected if and only if there exists a polynomial of the form , with and , which divides the polynomial associated to a and such that d is a prime number which divides the degree of the polynomial associated to a. Consequently:
If , the only possibility for d is , since the degree of the polynomial associated to a is 8. There are two possibilities for the polynomial to have a factor of the form : first, the polynomial is reducible if and only if contains a copy of X, by the first part of Proposition 2; secondly, the polynomial is irreducible if and only if satisfy the conditions of the second part of Proposition 2. Notice that, since is supposed to be irreducible, both sections, and , should be non-zero. By taking in that expressions it follows that is a solution of the polynomial , which takes values in .
-
If , since the polynomial associated to a has degree 6, there are two possibilities for de degree d:
- (a)
If , the polynomial may be reducible or irreducible. It is reducible if and only if contains a copy of X, by the first part of Proposition 3; it is irreducible if and only if satisfy the two conditions given in the second part of Proposition 3. Since is supposed to be irreducible, and are nonzero sections and by taking in that expressions it is deduced that is a solution of the polynomial , which takes values in .
- (b)
If then, as in the previous item, the polynomial may be reducible or irreducible. It is easily seen that the reducible case falls in the preceding case. It is irreducible if and only if satisfy the conditions given in the third part of Proposition 3. Since it should be and , taking and to that expressions, it follows that and is a solution of in .
□
Remark. Proposition 5 gives necessary and sufficient conditions on the elements of the base of the Hitchin map of for the Prym varieties and to be connected or disconnected, where j is the map defined in Proposition 1. Recall that these two Prym varieties are related to each other through the map defined in the Remark after Proposition 1. At the present moment, it is not easy, in the light of what has been proved, to give a simple criterion for deriving, for example, the connection of from the connection of . To illustrate this difficulty, consider criterion 2(c) of Proposition 5. In the case illustrated in that item, , so by Proposition 1, the polynomial associated to is . Even if criterion 2(c) of disconnection of (existence of such that ) is satisfied, it is not possible to ensure that is disjoint, because this would require the existence of such that . However, taking the intersection of both criteria, it is possible to give a sufficient condition for the two Prym varieties to be disjoint, as it is stated in the following result, which is an immediate consequence of Proposition 5.
Corollary 1. Let be an element of the base of the Hitchin map of defined in (24) whose associated polynomial is (that is ). Then, if there exists such that , then the Prym varieties and are both disconnected, where j is defined in Proposition 1.
6. Conclusions
Let X be a compact Riemann surface of genus and let and be the moduli spaces of and -Higgs bundles over X, respectively. It is known that there is a map of algebraic varieties whose image is composed by fixed points of the action of the triality automorphism on . In this paper it has been proved that acts on the base B of the Hitchin map given by the Hitchin integrable system associated to , that there exists a homomorphism , where is the base of the Hitchin map of and that the image of j is composed by fixed points of the action of . This led the definition of maps between Prym varieties , where , given by restriction of the map . As a way of studying the geometry of the maps (which, in turn, deepens the study of the grometry of the map ), results on the geometry of the Prym varieties involved have been provided. In particular, it has been characterized when the Prym varieties are disjoint. As a consequence, a sufficient condition is provided for both Prym varieties, and , to be disjoint. All this contributes to a better understanding and deepening of the map and, therefore, of the geometry of the moduli spaces of Higgs bundles involved. Specifically, the main implication of the present work is to provide criteria for deciding the connection or disconnection of Prym varieties of the two moduli spaces above which, moreover, are related, because there is an obvious homomorphism of one in the other. These findings allow to deepen the knowledge of the topology of moduli spaces with structure groups and , which is key in the identification of irreducible components, computation of Betti numbers and characteristic classes. Specifically, the disconnection of the Prym varieties implies the existence of a stratification in the corresponding fiber of the moduli space. This leads, not only to the existence of different irreducible components, but to the existence of non-isomorphic Higgs bundles with different geometric properties. In addition, when the Prym varieties are connected, the cohomology of the moduli space can be simplified and also it should be easier to compute Betti numbers and other topological invariants. In mathematical physics, the connection or disconnection of the Prym varieties affects the way in which certain dualities, such as Langlands duality, act. Thus the results provided here provide to mathematical physicists a suitable framework to study the mentioned dualities in the context of string theory.
Consequently, it is proposed as a future line of research the analysis of the topological invariants of both moduli spaces and, definitely, the discussion about whether the forgetful map
is or is not injective and, in any case, the behavior of its image concerning the irreducible components of
. Specifically, it is proposed to explicitly compute the number of connected components of the considered Prym varieties, which is an open problem that may help to identify irreducible components in the fibers of the Hitchin map of the moduli spaces of
and
-Higgs bundles over a curve
X. It is also proposed to prove whether the map above is injective and to explicitly identify the image of the homomorphism
, where
is the base of the Hitchin map of
and
B is the base of the Hitchin map of
. It may make use of the results on connectedness of the Prym varieties provided here and would also be interesting to analyze the effect of the action of triality automorphism on certain subvarieties of
, such as the Lagrangian subspaces that are defined as reductions to real forms of the structure group coming from the action of involutions of
, which are identified in [
11]. All these are open problems related to the one addressed here that would strengthen the applications of the study to mirror symmetry and Langlands duality.