Prerpints.org logo
Preprint
Article

Remote Sensing Analysis of Wood Volume and Volume Increments in Pine Forest Ecosystems: Insights from Vegetation Indices

Altmetrics

Downloads

51

Views

28

Comments

0

This version is not peer-reviewed

Remote Sensing and Visualization Methods: Monitoring, Modeling, Simulations and Interaction of Forest Resource

Submitted:

20 September 2024

Posted:

23 September 2024

You are already at the latest version

Alerts
Abstract

This article explores the use of vegetation indices (VIs) in remote sensing for estimating standing wood volume and volume increments in forest ecosystems. The study investigates the correlations between various VIs and wood volume across different forest stand age classes, focusing on the effectiveness of commonly used indices such as Squared Ratio Simple Red Edge (SQSR) and Red-Edge Ratio Vegetation Index (RERVI), as well as other typical indicators including Enhanced Vegetation Index (EVI), Red-Edge EVI (RE-EVI), and Green Normalized Difference Vegetation Index (GNDVI). Additionally, the analysis considers a pair of indicators based on blue and near-infrared channels, resembling the Blue-normalized Difference Vegetation Index (BNDVI). The research reveals that quadratic and power-law models of SQSR and RERVI demonstrate higher correlations (>0.40) with wood volume, especially in younger forest stands (>0.80). Furthermore, the study highlights the potential of NDII and NDWI indices for estimating volume increments in certain classes of forest stands (0.70). However, correlations vary across different forest stand classes, suggesting the need for further investigation into the reliability of VIs for monitoring wood volume and volume increments in forest ecosystems. Overall, this research contributes to the understanding of the applicability of VIs in remote sensing for forest management and ecosystem monitoring.

Keywords: 
Subject: Biology and Life Sciences  -   Forestry

1. Introduction

Amidst the progression of climate change, forest young nursery crops are highly vulnerable components within forest ecosystems, susceptible to adverse climatic alterations such as rising temperatures, shifts in precipitation patterns, increased drought frequency, and extreme weather events. These factors can significantly impact the growth dynamics and survival rates of young plants, potentially destabilizing entire forest ecosystems [1,2,3] Monitoring these crops is crucial for maintaining high-quality planting material, as it directly affects the health, growth rate, and overall condition of future forest stands [4]. Precise control of growth parameters, including biomass accumulation, leaf condition, resistance to abiotic stress (e.g., drought), and root system health, is essential since seedlings with well-developed traits are less susceptible to diseases and damage during early growth stages after transplantation [5]. This is critical for ensuring uniform and rapid tree growth, which correlates with higher wood productivity in mature stands [6].
The integration of modern monitoring techniques, such as remote sensing, mathematical modeling and vegetation index analysis, allows for the real-time detection of growth-related issues in seedlings, including nutrient deficiencies, water stress, and pathogen infections [7]. These technologies enable rapid identification of problems and corrective actions, minimizing losses in seedling production and ensuring a continuous supply of high-quality planting material. Remote sensing also aids in the early detection of environmental stresses, such as water shortages or pest infestations, enabling faster and more precise interventions [8]. As a result, remote sensing techniques have become indispensable in modern forest management, supporting dynamic and effective monitoring of young forest crops under changing climatic conditions. These models effectively utilize economic theory to analyze supply and demand interactions with endogenous commodity prices, and we review their recent developments, applications to forest policy, and future research directions [9].
In Poland, forest management organizations like the State Forests National Forest Holding utilize systems such as SILP and BDL to store information about timber availability for logging. However, data acquisition is time-consuming due to extensive data collection across diverse forest areas. Recently, remote sensing methods using satellite data have been explored to estimate timber growth, offering real-time modeling during the vegetation season and enhancing predictions of timber increments. Various models like TAMM, IIASA-GTM, and FASOM have been developed since the 1990s to incorporate timber growth models, but integrating satellite data into these models could improve predictions of harvestable timber and market equilibrium in sectors like construction and renewable energy.
Mura et al. (2018) evaluated Sentinel-2 multispectral imagery for estimating forest growth volume in Italian study areas, with S2 outperforming Landsat and RapidEye in predicting growth volume [10] . Ma et al. (2023) used the NDVIRE vegetation index and the random forest algorithm with Sentinel-2 data to assess forest stock volume in the Helan Mountains, China, achieving >80% accuracy [11]. Khan et al. (2020) explored correlations between 25 vegetation indices and biomass using LANDSAT data in Pakistan, finding RERVI to have the highest correlation with biomass (r2 = 0.68), surpassing other indices in sensitivity to biomass variations. RE-EVI and RE-NDVI also showed notable correlations (R2 = 0.67), with reduced saturation effects [12]. Yu et al. (2023) estimated forest stock volume in China by integrating multispectral satellite imagery and LiDAR data, using a random forest model to assess larch forest stock volume based on training samples from Airborne Laser Scanning (ALS) and Sentinel-2 imagery [13].
This study aims to apply earlier methods for assessing growing stock volume in the Toruń Forestry District, located in north-central Poland. The area was chosen for its uniformity, allowing statistical calculations based on Sentinel data (14,599.46 ha). The forests in this district exhibit a relatively low level of habitat fertility and tree species richness, with Scots pine covering 84.8% of the area, and other species like oak, birch, alder, beech, and poplar along the Vistula River.

2. Materials and Methods

In this article, the validation of individual algorithms was conducted using a) in-situ data from Forest Data Bank (BDL) and b) SENTINEL data from the 2023 vegetation season, focusing on the territory of the Toruń Forestry District.

2.1. Reference Data

The information used in this study originated from the Forest Data Bank, which undergoes regular updates on an annual basis through on-site forest inventories conducted by forestry authorities [14]. Each entry in the dataset provides details about an individual forest stand, defined in forestry as a uniform forest area distinguished by economically significant characteristics that necessitate consistent management practices. These individual forest stands typically cover areas ranging from one to several hectares. The database for the year 2023 for the Toruń Forest District encompassed a total of 8 860 records. For the subsequent analysis, specific forest stand parameters were considered, including (1) species, (2) age, (3) density, (4) height, (5) timber volume vyear for vegetation seasons 2022 and 2023.
For further analyses, only those forest stands were selected in which the percentage contribution of Scots pine was not less than 80%.
The timber growth (T) was calculated by taking the difference in timber volume between the years 2023 and 2022: T = v2023 - v2022. It was assumed that this growth must be positive. Additionally, if the difference is negative for a particular forest stand, it was inferred that timber extraction occurred in the year 2023 or natural events such as windbreaks, etc. took place. Consequently, such forest stands were excluded from further analysis.

2.2. Satellite Data

Image selections were made, specifically opting for those with cloud coverage below 20%, ensuring high data quality. For each chosen time point, two vectors: I and VI, were defined based on the imagery. Vector I represents the intensity of reflected light across all SENTINEL channels, while Vector VI is derived from I and consists of calculated values of vegetation indices. The vegetation indices are detailed in the Table 1.
Data were acquired using Sentinel Hub and Python software (v3.0). Forest stand shapefiles were obtained from the Forest Data Bank. Mean light reflectance (R) and standard deviation (dR) were computed monthly for the 2023 growing season, and vegetation indices (VI) were derived accordingly (Table 1).

2.3. Statistical Analysis

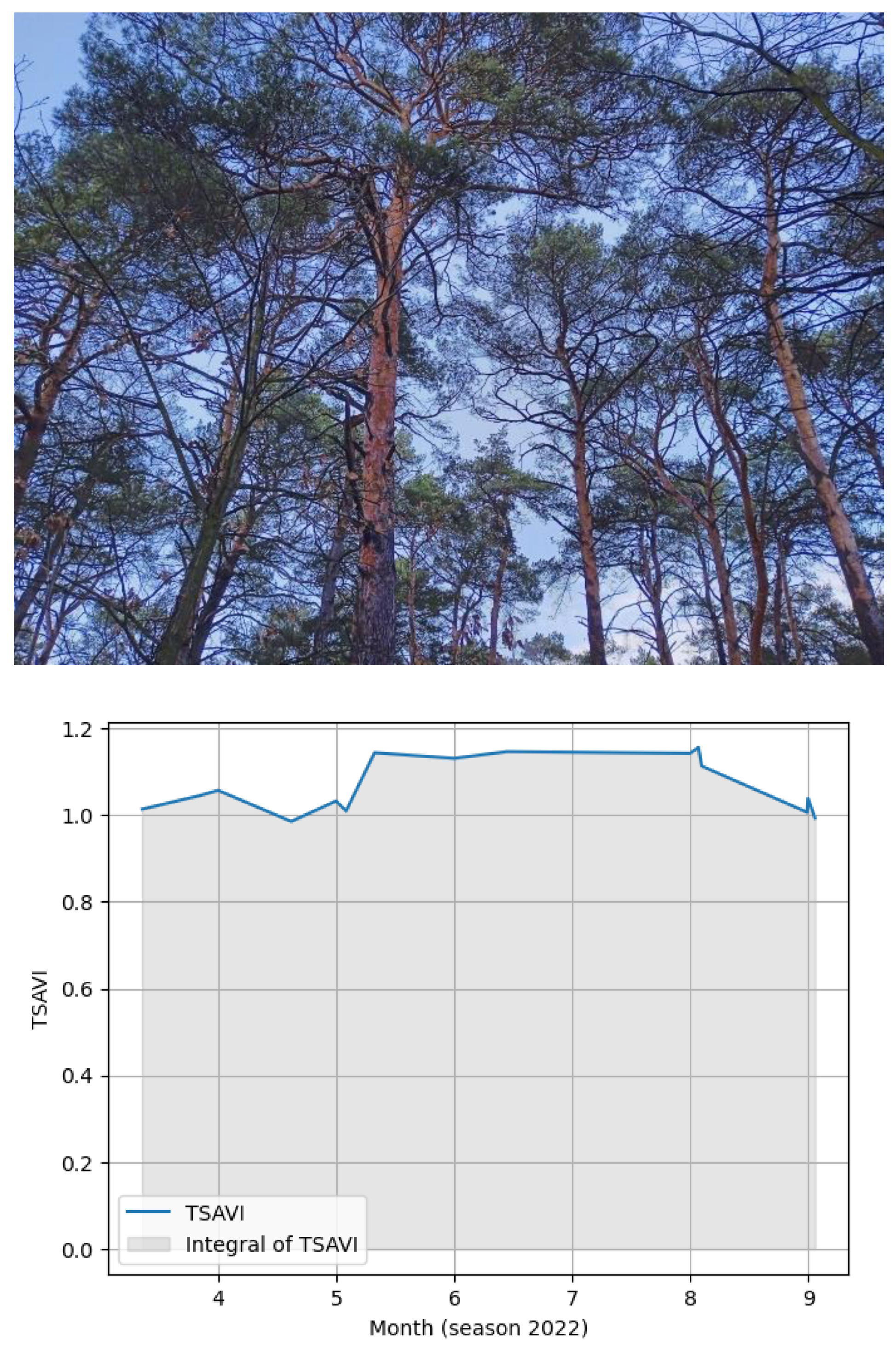
For each forest stand and for each month between April and September, the Cloud Index was computed based on channels 3 and 11. Records where the Cloud Index exceeded 0.3 were excluded from further analysis. For each forest stand and for each month, the Vegetation Index (VI) described in Table 1 was calculated. For the months of the growing season from April to Spetember, the time integral of VI was computed for each forest stand and for each VI indicator (refer to Figure 1). As a second approach - apart from calculating the indices from Table 1 - for each pair of optical channels, a normalized difference index was computed (66 pairs). For each of them, a procedure similar to that for the indices from the literature was performed.
Two hypotheses were proposed.
H1: The time integral of VI indicators corresponds to the biomass quantity and should therefore be correlated with the volume of wood per hectare (stand biomass).
H2: The time integral of VI indicators corresponds to the amount of green biomass (chlorophyll) and should therefore be correlated with the volume increment of wood per hectare (biomass increment) during the growing season.
For each indicator, the following fitting models were computed for a) v22 and b) dv:
  • linear: v 22 = a V I + b ,
  • quadratic: v 22 = a V I 2 + b V I + c ,
  • logarithmic: v 22 = a + b ln ⁡ ( c V I ) , and
  • power-law v 22 = a + b c d V I
  • where a, b, c and d are optimal fitting coefficients. The same procedure was applied to dv. For each model of each indicator, the correlation with v22 and dv was calculated accordingly.

3. Results

According to the forest database in the Toruń Forestry District in 2022, there were 4908 forest stands covering an area of 13,311 hectares. Further analysis included 1619 forest stands where Scots pine constituted 100% of the uppermost layer, regardless of age and other environmental parameters. These stands covered an area of 5451 hectares.
In the research sample, over 91% of forest stands consisted of pine forests or mixed pine forests, with 88% categorized as fresh and 3% as dry. Moisture type was predominantly fresh habitats at 95% and dry habitats at 3%. A significant division was observed between natural habitats (59%) and those degraded by economic activity (41%). Habitats were situated mainly on rusty soils, arenosols (6%), and peaty soils (4%). Approximately 94% of habitats were subject to at least one form of protection, with 79% of them showing damages primarily caused by insect factors (69%), fungal factors (5%), and animal-related factors (4%).
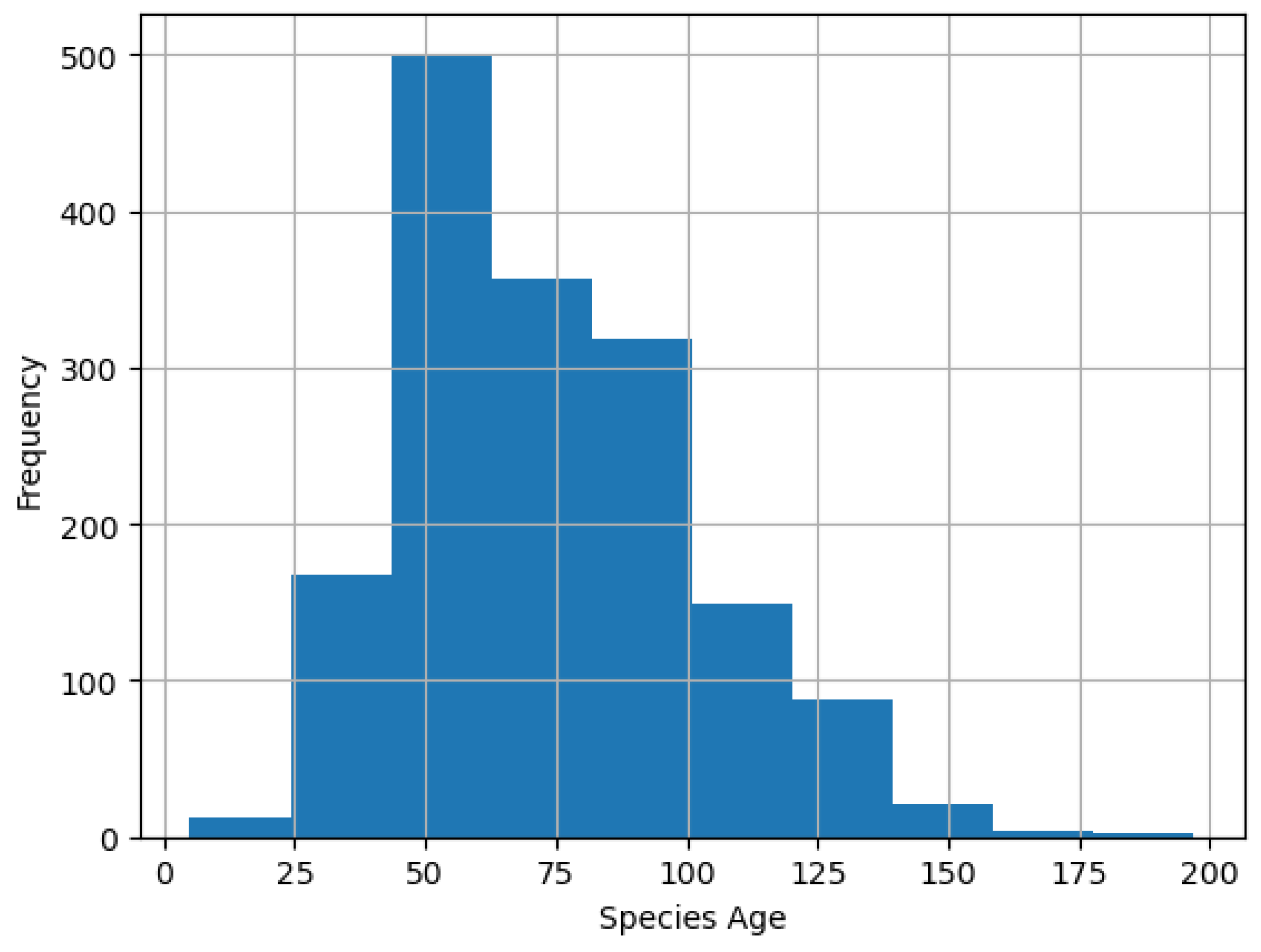
The productivity index of forest habitat and stands, which assesses the potential production capabilities of forest habitats for Scots pine, indicated that 74% of stands were in the two highest classes (referred to as I and II bonitation classes), 23% were in the medium class (III bonitation class), and only 3% were in the lowest bonitation classes. The age distribution of Scots pines in all forest stands (73.4 years +/- 27.5 years) is presented in Figure 2.
The considered forest stands mainly differ due to two parameters: the first one is the age of trees, and the second one is the degradation or absence of habitat degradation. Correlations of indices with wood volume or wood volume increment are calculated first for all forest stands and then separately for the following categories: young stands (< 40 years old), middle-sized stands (40-80 years old), older stands (> 80 years old), natural stands, and degraded stands.

3.1. Correlations between Forest Stand Volume and Its Growth with Typical Vegetation Indices.

For all forest stands the r2 values between literature VI models (linear, quadratic, logarithmic, and power-law) and wood volume in 2022 did not exceed 0.21 (0.208 for quadratic forms for RERVI, 0.170 for SQSR, 0.133 for EVI and GNDVI. For the wood volume increase between 2022 and 2023 r2 values did not exceed 0,01 (Table 2-
The correlation between forest stand volumes in 2022 and any vegetation index did not exceed 0.5. Correlations above 0.4 were observed only for the SQSR and RERVI indices, specifically for their quadratic and power-law models. Additionally, the correlation of quadratic models for the EVI, GNDVI, and REEVI indices exceeded 0.35. For wood volume increases, the correlation of VI models ranged up to 0.1 (Table 2).
For the youngest forest stand class (< 40 years), the quadratic form of all indices was the most correlated with wood volume in 2022. The average correlation between the quadratic form of indices and wood volume exceeded 0.78. The highest correlations were observed for the quadratic form of RERVI (0.84), SQSR, and GNDVI (>0.8), as well as EVI, NDVI, SAVI, TSAVI, REEVI, and RENDVI (>0.75). The correlation for other forms of indices ranged from 0.3 to 0.5. Similarly, for forest stands up to 40 years old, the quadratic form was also the most correlated with annual growth, with an average VI correlation of 0.76. A similar result was obtained for the logarithmic form, with an average correlation of 0.71. Regarding volume increases, the most highly correlated indices were NDWI and NDII, as well as RENVI and RERVI (on average > 0.7) (Table 3)
For middle-aged forest stands (40-80 years), only two indices (RERVI and SQSR) show an average correlation with wood volume in 2022 above 0.4. Among these, the power-law and quadratic forms of RERVI exhibit the highest correlations (0.51 and 0.50 respectively). Similarly to all forest stands, quadratic and power-law forms of indices are the most highly correlated, with all indices except TSAVI correlating with volume above 0.33. The weakest correlations are observed for logarithmic forms of indices. Regarding wood volume increases, the NDII index shows the highest correlation, ranging from 0.17 to 0.18 depending on its form. The other indices do not exceed a correlation of 0.10 (Table 4).
For the oldest trees aged above 80 years, once again, the indices RERVI and SQSR exhibit the highest relationships with wood volume in 2022, but their average correlation does not exceed 0.50 (the highest correlation occurs for the quadratic form of RERVI). In the case of this class, the form of the index is not as significant as in the other tree classes: the average correlation for quadratic forms is 0.40, while for other forms it is 0.38. Regarding wood volume increases, correlations do not exceed 10% except for NDWI. Once again, the quadratic form of the index shows clearer correlations (0.08 – 0.17), while for other forms, it is below 0.10 (Table 5).
For degraded forest stands, the correlation with wood volume in 2022 pertains to RERVI indices (power-law, quadratic, and linear forms – 0.54-0.61) and SQSR (the same 3 forms – 0.51-0.57). Slightly lower correlations are observed for EVI and GNDVI in power-law and quadratic forms (0.52). Regarding annual wood volume increments, the highest correlation does not exceed 0.2 - this is observed with the quadratic form of the RERVI index (Table 6).
For natural forest stands, the correlation with wood volume in 2022 pertains to RERVI indices (all forms – 0.30-0.38) and SQSR (quadratic, linear and power-law forms – 0,32-0,34). Slightly lower correlations are observed for EVI, REEVI and GNDVI in quadratic form (0.30). Regarding annual wood volume increments, the highest correlation does not exceed 0.14 - this is observed with the quadratic form of the TSAVI index (Table 7).

3.2. The Correlations between Forest Stand Volume and Its Growth, and Normalized Difference Indices for Sentinel Optical Channels.

In the case of all records, correlations with wood volume in 2022 exceeding 30% were achieved by the following difference indices, apart from the standard GNDVI, NDVI, NDWI, and RENDVI (see Table 2):
  • • • based on channels C1 and C7 (r2 = 0.11 for quadratic and power forms),
  • • • based on channels C1 and C8 (r2 = 0.13 for quadratic and 0.12 for power forms),
  • • • based on channels C2 and C8 (r2 = 0.10 for quadratic and 0.10 for power forms).
All other combinations yielded correlations below 30%.
In the case of all records, the correlation with wood volume increase in 2022 was highest for the combination of channels C2 and C8, with r2 = 0.04.
For young stands (<40 years), the highest correlations with wood volume in 2022, apart from the standard GNDVI, NDVI, NDWI, and RENDVI (see Table 3), were achieved by the following difference indices:
  • • • based on channels C1 and C7-C9 (r2 = 0.56 – 0.60 for quadratic forms),
  • • • based on channels C3 and C5 (r2 = 0.59 for quadratic forms).
The highest correlations with wood volume increase, apart from the aforementioned standard indices, were obtained for the index based on channels C2 and C6-C7, with r2 = 0.82-0.89. It is worth noting that for the NDVI, NDWI, and RENDVI indices, all versions based on NIR channels in Sentinel (C6 – C8) had correlations with wood volume increase as high as the originally formulated indices.
For middle-aged stands (40-80 years), correlations with wood volume in 2022 exceeding 30% were achieved by the difference index based on channels C1 and C6-C8, apart from the standard GNDVI, NDVI, NDII, NDWI, and RENDVI (see Table 4) (r2 = 0.09 – 0.16 for forms other than logarithmic). The highest correlation with wood volume increase was obtained for the index based on channels C7 and C8, with r2 = 0.10 for all forms other than logarithmic. It is better correlated with wood volume increase than any standard index in this age class of pines.
For older stands (>80 years), correlations with wood volume in 2022 exceeding 30% were achieved by the difference index based on channels C2 and C6-C8, apart from the standard GNDVI, NDVI, NDII, NDWI, and RENDVI (see Table 5) (r2 = 0.14 – 0.21 for forms other than logarithmic). No correlations with wood volume increase above 20% were recorded.
For degraded stands, correlations with wood volume in 2022 exceeding 30% were achieved by the index based on channels C1 and C7 or C8 in quadratic and power forms (r2 = 0.32-0.38). This combination also had a 30-40% correlation with wood volume increase in this class (r2 = 0.08-0.15). In the case of natural stands, no additional correlations were observed beyond those listed in Table 7.

4. Discussion

The application of vegetation indices for estimating wood volume and volume increments differs significantly. For wood volume estimation, indices such as SQSR and RERVI, particularly their quadratic and power-law models, demonstrate higher correlations. On the other hand, for volume increments, indices like NDII and NDWI show stronger correlations in some classes of forest stands.

4.1. Standing Wood Volume

The correlations between various vegetation indices and wood volume, as indicated by the coefficient of determination (r2), vary across different forest stand classes and indices. Generally, the quadratic and power-law models of indices like SQSR and RERVI exhibit higher r2 values compared to standard vegetation indices like GNDVI, NDVI, NDWI, and RENDVI. For example, in younger forest stands (<40 years), the quadratic forms of these indices show strong correlations with wood volume, with average r2 values exceeding 0.78. However, the effectiveness of these indices diminishes for middle-aged and older stands, with r2 values typically ranging from 0.4 to 0.5. In contrast, standard vegetation indices like GNDVI, NDVI, and NDWI tend to have lower r2 values, ranging from 0.3 to 0.5 across different forest stand classes. Further investigation is needed to better understand the variability in r2 values and to assess the reliability of different vegetation indices for monitoring wood volume in forest ecosystems, but the SQSR and RERVI indices demonstrate promising potential for monitoring wood volume in forest ecosystems, particularly when considering their quadratic and power-law models.

4.2. SQSR and RERVI Correlations with Standing Wood Volume and Wood Increament

Comparing the results obtained for the SQSR index with the findings presented in Khan et al. (2020), it is evident that SQSR exhibits notable correlations with wood volume across various forest stand age classes. In my study, correlations above 0.4 were observed specifically for the quadratic and power-law models of SQSR, indicating its effectiveness in estimating wood volume. This aligns with the observations made by Khan et al. (2020), where narrowband red-edge vegetation indices, including SQSR, demonstrated better performance in biomass estimation compared to broadband vegetation indices. Particularly, the quadratic form of SQSR exhibited correlations exceeding 0.8 for the youngest forest stands, indicating its strong association with wood volume. Additionally, in middle-aged stands and old stands, SQSR, along with RERVI, showed average correlations above 0.4 with wood volume.
Comparing findings regarding RERVI with the results presented in Ahmad et al. (2023), it is evident that there are notable differences in the performance of RERVI in estimating biomass [26]. In my study, RERVI demonstrated an average correlation of 0.50 for all forest stand age classes, indicating its effectiveness in estimating wood volume. However, Ahmad et al. (2023) reported a lower correlation of 0.11 for RERVI in their study, suggesting a poor performance of RERVI in biomass estimation [26]. Additionally, while RERVI exhibited the highest correlations with wood volume for young stands (~0.8) in my study, the correlation decreased to 0.4 - 0.5 for middle-aged and older stands. Interestingly, the correlation was higher for degraded stands (~0.6) compared to natural stands (~0.3). This discrepancy suggests that the performance of RERVI may vary depending on forest stand characteristics, indicating the need for further investigation into this matter.
It is worth noting that correlations with wood volume increment occur only for RERVI for the youngest forest stands, however, its magnitude is comparable to other typical indices such as NDWI, NDII, RENDVI.

4.3. VI Correlations with Standing Wood Volume

Apart from these two commonly used indicators in individual classes, other typical indicators can also be applied. In particular, this includes a pair of enhanced indicators: EVI and RE-EVI. In the all and young forest stand classes, they have correlations lower than the SQSR-RERVI pair by 0.05, namely 0.35 and 0.75, respectively. Unfortunately, they cannot be used in older tree classes. EVI, like the SQSR-RERVI pair, can also be useful in degraded forest stand classes. These data confirm the results of Ogaya et al. 2015, where it was found that, among other factors, aboveground biomass growth correlated with certain MODIS products, such as NDVI and EVI specifically [27]. EVI, similar to NDVI, proved to be effective indicators of forest productivity and tree mortality. In the case of pine forests in the Toruń Forest District, NDVI can be used like EVI and RE-EVI only for pines under 40 years old. Similarly to this case, Olofsson et al. 2008 observed a correlation between ground biomass and EVI (0.85-0.67 for coniferous tree data), but did not find linear relationships with NDVI [28].
Another indicator to consider is GNDVI, whose correlation in the tree class under 40 years old is 0.35. However, when considering degraded and natural forests separately, the quadratic model of GNDVI correlates with wood volume by 0.50 and 0.30, respectively, regardless of the age class. Nevertheless, based on the study by Pertille et al. 2019, it can be assumed that GNDVI may be considered only for Sentinel data, where this indicator was one of the three most correlated with biomass per plot for Pinus taeda L. species. On the other hand, for Landsat data, this indicator was not as useful [29].
The statistical analysis among indicators outside the list in Table 1 also identified a pair of indicators based on blue and near-infrared channels. The first indicator is a normalized difference index based on channels 1 and 8 or 9 (in some cases also 1 and 7). This indicator has an overall correlation with wood volume comparable to EVI and GNDVI (~0.35). Its correlation in the youngest tree class increases to >0.7. In the middle-aged tree class, its correlation again is 0.3. Interestingly, in degraded forest stands, it correlates with wood volume at the level of the best indicator in this class, namely RERVI (~0.6). The second indicator differs from the first by using the blue channel (channel 2). It is useful for estimating wood volume in older stands where, depending on the NIR channel used, its correlation ranges from 0.3 to 0.4. These indicators can be considered equivalent to the BNDVI (Blue-normalized difference vegetation index, [30]):
B N D V I = N I R − B L U E N I R + B L U E

4.4. VI Correlations with Wood Increment

For all pine forest stands, none of the single indicators proposed in the table were correlated with wood volume increment. The strongest correlation was observed with the indicator based on blue and near-infrared channels, BNDVI (~0.2). Therefore, the use of other vegetation indices for assessing wood volume increment was unsuccessful.
For middle-aged, older, natural, and degraded forest stand classes, correlations in the range of 0.1 - 0.2 were also exhibited by NDII, NDWI, TSAVI, and RERVI, respectively. Additionally, the BNDVI indicator correlated with wood volume increments for middle-aged and degraded stands at the level of 0.3.
The situation is different for the youngest forest stands up to forty years old. Here, as many as five vegetation indices collaborated with increments at a level of 0.7. These were: NDWI, NDII, RENDVI, REEVI, and BNDVI.

5. Conclusions

The application of vegetation indices for estimating wood volume and volume increments varies significantly across different forest stand classes and indices. For wood volume estimation, indices such as SQSR and RERVI, particularly their quadratic and power-law models, demonstrate higher correlations, indicating their effectiveness, especially in younger forest stands. On the other hand, for volume increments, indices like NDII and NDWI show stronger correlations in some classes of forest stands.
The correlations between various vegetation indices and wood volume vary across different forest stand classes and indices. Quadratic and power-law models of indices like SQSR and RERVI exhibit higher correlations compared to standard vegetation indices like GNDVI, NDVI, NDWI, and RENDVI. However, the effectiveness of these indices diminishes for middle-aged and older stands. Standard vegetation indices tend to have lower correlations across different forest stand classes. Further investigation is needed to assess the reliability of different vegetation indices for monitoring wood volume in forest ecosystems.
Comparing the results obtained for the SQSR index with the findings presented in Khan et al. (2020), SQSR exhibits notable correlations with wood volume across various forest stand age classes, especially when considering its quadratic and power-law models. Similarly, RERVI demonstrates effectiveness in estimating wood volume across different forest stand age classes. However, the correlation with wood volume increment occurs only for RERVI for the youngest forest stands, with comparable magnitude to other typical indices such as NDWI, NDII, RENDVI.
Apart from commonly used indicators like SQSR and RERVI, other typical indicators such as EVI, RE-EVI, and GNDVI can also be applied in certain scenarios. EVI and RE-EVI show correlations lower than the SQSR-RERVI pair but can be useful, especially in degraded forest stand classes. GNDVI shows potential, particularly when considering Sentinel data. Additionally, a pair of indicators based on blue and near-infrared channels, resembling BNDVI, demonstrate promising correlations with wood volume, especially in younger forest stands.
For all pine forest stands, none of the single indicators proposed in the table were correlated with wood volume increment. However, correlations in the range of 0.1 - 0.2 were exhibited by NDII, NDWI, TSAVI, and RERVI in middle-aged, older, natural, and degraded forest stand classes. The BNDVI indicator correlated with wood volume increments for middle-aged and degraded stands at the level of 0.3. In contrast, for the youngest forest stands up to forty years old, as many as five vegetation indices collaborated with increments at a level of 0.7, including NDWI, NDII, RENDVI, REEVI, and BNDVI.

References

  1. Kubiak, K.; Żółciak, A.; Damszel, M.; Lech, P.; Sierota, Z. Armillaria pathogenesis under climate changes. Forests 2017, 8, 100. [CrossRef]
  2. Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Cobb, N. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [CrossRef]
  3. Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Marchetti, M. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [CrossRef]
  4. Grossnickle, S.C. Importance of root growth in overcoming planting stress. New For. 2005, 30, 273–294. [CrossRef]
  5. Landis, T.D.; Dumroese, R.K.; Haase, D.L. The Container Tree Nursery Manual: Seedling Processing, Storage, and Outplanting; US Department of Agriculture, Forest Service, 2010.
  6. Irland, L.C.; Adams, D.; Alig, R.; Betz, C.J.; Chen, C.C.; Hutchins, M.; Sohngen, B.L. Assessing socioeconomic impacts of climate change on US forests, wood-product markets, and forest recreation: : The effects of climate change on forests will trigger market adaptations in forest management and in wood-products industries and may well have significant effects on forest-based outdoor recreation. BioScience 2001, 51 (9), 753–764. [CrossRef]
  7. Jacobs, D.F.; Salifu, K.F.; Seifert, J.R. Relative contribution of initial root and shoot morphology in predicting field performance of hardwood seedlings. New For. 2004, 28, 283–294. [CrossRef]
  8. Anderson, M.; Daughtry, C.; Johnson, D. Assessing the variability of corn and soybean yields in Central Iowa using high spatiotemporal resolution multi-satellite imagery. Remote Sens. 2018, 10, 1489. [CrossRef]
  9. Latta, G.S.; Sjølie, H.K.; Solberg, B. A review of recent developments and applications of partial equilibrium models of the forest sector. J. For. Econ. 2013, 19, 350–360. [CrossRef]
  10. Mura, M.; Bottalico, F.; Giannetti, F.; Bertani, R.; Giannini, R.; Mancini, M.; Chirici, G. Exploiting the capabilities of the Sentinel-2 multi-spectral instrument for predicting growing stock volume in forest ecosystems. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 126–134. [CrossRef]
  11. Ma, T.; Hu, Y.; Wang, J.; Beckline, M.; Pang, D.; Chen, L.; Li, X. A novel vegetation index approach using Sentinel-2 data and random forest algorithm for estimating forest stock volume in the Helan Mountains, Ningxia, China. Remote Sens. 2023, 15, 1853. [CrossRef]
  12. Khan, K.; Iqbal, J.; Ali, A.; Khan, S.N. Assessment of Sentinel-2-derived vegetation indices for the estimation of above-ground biomass/carbon stock, temporal deforestation, and carbon emissions estimation in the moist temperate forests of Pakistan. Appl. Ecol. Environ. Res. 2020, 18, 45–65. [CrossRef]
  13. Yu, T.; Pang, Y.; Liang, X.; Jia, W.; Bai, Y.; Fan, Y.; Wang, X. China’s larch stock volume estimation using Sentinel-2 and LiDAR data. Geo-spat. Inf. Sci. 2023, 26, 392–405. 28. [CrossRef]
  14. Talarczyk, A. Bank danych o lasach w Polsce na tle baz danych i systemów udostępniania informacji z zakresu leśnictwa w innych krajach. Probl. World Agric. 2015, 15, 150–158. [CrossRef]
  15. Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [CrossRef]
  16. Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [CrossRef]
  17. Rouse, J.W. Jr.; Haas, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the vernal advancement and retrogradation (green wave effect) of natural vegetation. NASA Tech. Rep. 1974, No. E75-10354. 15.
  18. Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [CrossRef]
  19. Itkonen, P. Estimating leaf area index and aboveground biomass by empirical modeling using Spot HRVIR satellite imagery in the Taita Hills, SE Kenya. Master’s Thesis, University of Helsinki, Finland, 2012.
  20. Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [CrossRef]
  21. Hunt, E.R. Jr.; Wang, L.; Qu, J.J.; Hao, X. Remote sensing of fuel moisture content from the ratios of canopy water indices with a foliar dry matter index. In Proceedings of the Remote Sensing and Modeling of Ecosystems for Sustainability IX, Kyoto, Japan, 29 October 2012; SPIE: Bellingham, WA, USA, 2012; Vol. 8513, pp. 9–16. [CrossRef]
  22. Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [CrossRef]
  23. Abdel-Rahman, E.M.; Landmann, T.; Kyalo, R.; Ong’amo, G.; Mwalusepo, S.; Sulieman, S.; Le Ru, B. Predicting stem borer density in maize using RapidEye data and generalized linear models. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 61–74. [CrossRef]
  24. Chen, J.C.; Yang, C.M.; Wu, S.T.; Chung, Y.L.; Charles, A.L.; Chen, C.T. Leaf chlorophyll content and surface spectral reflectance of tree species along a terrain gradient in Taiwan’s Kenting National Park. Stud. Taiwan Acad. Sci. 2007, 48, 71–77.
  25. Cao, Q.; Miao, Y.; Shen, J.; Yu, W.; Yuan, F.; Cheng, S.; Liu, F. Improving in-season estimation of rice yield potential and responsiveness to topdressing nitrogen application with Crop Circle active crop canopy sensor. Precis. Agric. 2016, 17, 136–154. [CrossRef]
  26. Ahmad, N.; Ullah, S.; Zhao, N.; Mumtaz, F.; Ali, A.; Ali, A.; Shakir, M. Comparative analysis of remote sensing and geo-statistical techniques to quantify forest biomass. Forests 2023, 14, 379. [CrossRef]
  27. Ogaya, R.; Barbeta, A.; Başnou, C.; Peñuelas, J. Satellite data as indicators of tree biomass growth and forest dieback in a Mediterranean holm oak forest. Ann. For. Sci. 2015, 72, 135–144. [CrossRef]
  28. Olofsson, P.; Lagergren, F.; Lindroth, A.; Lindström, J.; Klemedtsson, L.; Kutsch, W.; Eklundh, L. Towards operational remote sensing of forest carbon balance across Northern Europe. Biogeosciences 2008, 5, 817–832. [CrossRef]
  29. Pertille, C.T.; Nicoletti, M.F.; Topanotti, L.R.; Stepka, T.F. Biomass quantification of Pinus taeda L. from remote optical sensor data. Adv. For. Sci. 2019, 6, 603–610. [CrossRef]
  30. Yang, C.; Everitt, J.H.; Bradford, J.M.; Murden, D. Airborne hyperspectral imagery and yield monitor data for mapping cotton yield variability. Precis. Agric. 2004, 5, 445–461. [CrossRef]
Preprints 118837 g001
Figure 1. Forest stand: id= 1224008699, degradation: natural, pine cover = 100%, pine age 87 years, dv = 7,20 m3ha−1. Left: Tree crowns in January 2024. Right: Temporal evolution of TSAVI index in 2022 and its integral between April and September.
Figure 1. Forest stand: id= 1224008699, degradation: natural, pine cover = 100%, pine age 87 years, dv = 7,20 m3ha−1. Left: Tree crowns in January 2024. Right: Temporal evolution of TSAVI index in 2022 and its integral between April and September.
Preprints 118837 g001
Preprints 118837 g002
Figure 2. The age distribution of Scots pine trees in 1619 forest stands where this species constituted a monoculture in the uppermost layer of the stand. Mean age: 73,4 +/- 27.5 years.
Figure 2. The age distribution of Scots pine trees in 1619 forest stands where this species constituted a monoculture in the uppermost layer of the stand. Mean age: 73,4 +/- 27.5 years.
Preprints 118837 g002
Table 1. Vegetation Indices used for timber volume estimation. VIs are mainly sourced from the Table A1 from Khan et al. (2020).
Table 1. Vegetation Indices used for timber volume estimation. VIs are mainly sourced from the Table A1 from Khan et al. (2020).
Vegetation Index Formula Reference
EVI – Enhanced VI E V I 2 = 2.5 N I R − R E D N I R + 2.4   R E D + 1 [15]
GNDVI – Green Normalized Difference VI G N D V I = N I R − G R E E N N I R + G R E E N [16])
NDVI – Normalized Difference VI N D V I = N I R − R E D N I R + R E D [17]
SAVI – Soil Adjusted VI S A V I = N I R − R E D N I R + R E D + L ( 1 + L ) [18]
SQSR – Square Root Simple Ratio S Q S R = N I R R E D [19]
TSAVI – Transformed Soil Adjusted VI T S A V I = a ( N I R − a R E D − b ) a N I R − b + 0.08 ( 1 + a 2 ) [20]
NDII – Normalized Difference Infrared Index N D I I = N I R − S W I R N I R + S W I R [21]
NDWI – Normalized Difference Water Index N D W I = N I R − S W I R ' N I R + S W I R ' [22]
RE-EVI – Re-Edge Enhanced VI R E E V I = 2.5 N I R − R E N I R + 2.4   R E + 1 [23]
RENDVI – Red-Edge Normalized Difference VI R E N D V I = N I R − R E N I R + R E [24]
RERVI – Red Edge Ratio Vegetation Index R E R V I = N I R R E [25]
Table 2. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023.
Table 2. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023.
VI r2 between wood volume in 2022 and the model based on VI r2 between wood volume increase between 2022 an 2023 and the model based on VI
Linear Quadratic Logarithmic Power-law Linear Quadratic Logarithmic Power-law
NDVI 0.0875 0.1081 0.0618 0.1003 0.0005 0.0041 0.0009 0.0005
EVI 0.1074 0.1329 0.0762 0.1234 0.0005 0.0019 0.0005 0.0005
GNDVI 0.1049 0.1334 0.0744 0.124 0.0001 0.0046 0.0019 0.0001
SAVI 0.0876 0.1083 0.0619 0.1005 0.0005 0.0041 0.0009 0.0005
SQSR 0.1353 0.1701 0.0957 0.1578 0.0003 0.0007 0.0004 0.0003
TSAVI 0.071 0.0892 0.0497 0.0711 0.0004 0.0098 0.0019 0.0004
NDII 0.0864 0.088 0.0707 0.0873 0.0072 0.0079 0.0044 0.0072
NDWI 0.0966 0.0971 0.0825 0.0969 0.0051 0.0074 0.0027 0.0051
REEVI 0.103 0.1312 0.0721 0.1211 0.0 0.0042 0.0016 0.0
RENDVI 0.0899 0.1108 0.0645 0.1036 0.0 0.0051 0.0033 0.0
RERVI 0.1631 0.2081 0.1151 0.1929 0.0001 0.0001 0.0003 0.0001
Table 3. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for pine forests with age below 40 years.
Table 3. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for pine forests with age below 40 years.
VI r2 between wood volume in 2022 and the model based on VI r2 between wood volume increase between 2022 an 2023 and the model based on VI
Linear Quadratic Logarithmic Power-law Linear Quadratic Logarithmic Power-law
NDVI 0.1162 0.5883 0.05 0.1159 0.3865 0.5623 0.4626 0.386
EVI 0.133 0.6245 0.0608 0.1327 0.4103 0.5661 0.4853 0.4098
GNDVI 0.1886 0.6631 0.1013 0.1883 0.3821 0.5291 0.4544 0.602
SAVI 0.1165 0.5901 0.0501 0.1162 0.3864 0.5619 0.4625 0.386
SQSR 0.1616 0.6719 0.0803 0.3758 0.4402 0.5662 0.5119 0.4398
TSAVI 0.1102 0.5888 0.0455 0.2679 0.379 0.571 0.4575 0.3788
NDII 0.1798 0.4779 0.1105 0.1795 0.538 0.6249 0.6057 0.5377
NDWI 0.2741 0.549 0.1908 0.2738 0.5301 0.5813 0.585 0.5299
REEVI 0.16 0.5862 0.0824 0.1596 0.4319 0.609 0.513 0.4315
RENDVI 0.189 0.5978 0.1051 0.1887 0.394 0.5472 0.4659 0.5914
RERVI 0.1936 0.7123 0.1041 0.4369 0.4617 0.5547 0.5272 0.4613
Table 4. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for middle-age pine forests (40 – 80 years).
Table 4. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for middle-age pine forests (40 – 80 years).
VI r2 between wood volume in 2022 and the model based on VI r2 between wood volume increase between 2022 an 2023 and the model based on VI
Linear Quadratic Logarithmic Power-law Linear Quadratic Logarithmic Power-law
NDVI 0.0984 0.1207 0.0849 0.1303 0.0026 0.0219 0.0001 0.0026
EVI 0.1241 0.1507 0.1068 0.159 0.0039 0.0174 0.0006 0.0038
GNDVI 0.1181 0.1496 0.1006 0.16 0.0017 0.0262 0.0001 0.0017
SAVI 0.0985 0.1208 0.085 0.1305 0.0026 0.0221 0.0001 0.0026
SQSR 0.1637 0.2016 0.1391 0.2096 0.0054 0.0157 0.0015 0.0054
TSAVI 0.0799 0.1014 0.0686 0.0799 0.0021 0.0353 0.0001 0.0021
NDII 0.1255 0.1301 0.1165 0.1317 0.031 0.0311 0.0295 0.031
NDWI 0.1166 0.1171 0.1127 0.1172 0.0108 0.0117 0.0107 0.0108
REEVI 0.1288 0.1695 0.1075 0.1841 0.0031 0.024 0.0002 0.0031
RENDVI 0.0939 0.1173 0.0806 0.1284 0.0 0.0221 0.0026 0.0
RERVI 0.2041 0.2547 0.1717 0.262 0.007 0.0144 0.0026 0.007
Table 5. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for old pine forests (over 80 years).
Table 5. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for old pine forests (over 80 years).
VI r2 between wood volume in 2022 and the model based on VI r2 between wood volume increase between 2022 an 2023 and the model based on VI
Linear Quadratic Logarithmic Power-law Linear Quadratic Logarithmic Power-law
NDVI 0.1372 0.1428 0.1367 0.1371 0.0025 0.0082 0.0003 0.0025
EVI 0.1627 0.1676 0.1614 0.1626 0.0014 0.0114 0.0003 0.0014
GNDVI 0.1627 0.1634 0.1572 0.1626 0.0005 0.0078 0.0009 0.0005
SAVI 0.1374 0.1429 0.1368 0.1373 0.0024 0.0082 0.0003 0.0024
SQSR 0.1946 0.1979 0.1917 0.1945 0.0002 0.0147 0.0006 0.0002
TSAVI 0.1117 0.1159 0.1107 0.1117 0.0024 0.0042 0.0009 0.0024
NDII 0.0853 0.1237 0.0946 0.0852 0.0028 0.0129 0.001 0.0028
NDWI 0.1088 0.1384 0.1168 0.1087 0.0124 0.0279 0.004 0.0124
REEVI 0.1508 0.1567 0.1507 0.1507 0.0002 0.0065 0.0014 0.0002
RENDVI 0.1493 0.1533 0.1477 0.1493 0.0037 0.0089 0.0004 0.0037
RERVI 0.2249 0.2268 0.22 0.2248 0.0001 0.0198 0.0011 0.0001
Table 6. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for degraded pine forests.
Table 6. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for degraded pine forests.
VI r2 between wood volume in 2022 and the model based on VI r2 between wood volume increase between 2022 an 2023 and the model based on VI
Linear Quadratic Logarithmic Power-law Linear Quadratic Logarithmic Power-law
NDVI 0.2021 0.2363 0.1627 0.2019 0.003 0.0035 0.0005 0.003
EVI 0.2251 0.2703 0.1786 0.2692 0.0062 0.0097 0.0001 0.0067
GNDVI 0.2174 0.2655 0.172 0.2671 0.0028 0.0059 0.0009 0.0028
SAVI 0.2026 0.2367 0.1632 0.2023 0.003 0.0035 0.0005 0.003
SQSR 0.2583 0.3217 0.201 0.3213 0.0113 0.0206 0.0001 0.0113
TSAVI 0.1866 0.2113 0.1533 0.1866 0.0003 0.0009 0.0019 0.0003
NDII 0.1611 0.1643 0.1427 0.1611 0.0066 0.0166 0.0 0.0066
NDWI 0.1746 0.1753 0.1605 0.1746 0.0044 0.0187 0.0007 0.0044
REEVI 0.2187 0.2631 0.1727 0.2184 0.0065 0.0091 0.0 0.0065
RENDVI 0.1946 0.2264 0.1574 0.2258 0.0022 0.0025 0.0009 0.0022
RERVI 0.2891 0.373 0.2212 0.3739 0.018 0.0361 0.0007 0.0228
Table 7. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for non-degraded, natural pine forests.
Table 7. The correlation between vegetation index-based models and a) pine wood volume in 2022, b) wood volume increment between 2022 and 2023 for non-degraded, natural pine forests.
VI r2 between wood volume in 2022 and the model based on VI r2 between wood volume increase between 2022 an 2023 and the model based on VI
Linear Quadratic Logarithmic Power-law Linear Quadratic Logarithmic Power-law
NDVI 0.0572 0.0655 0.0404 0.0572 0.0 0.0123 0.0099 0.0
EVI 0.0755 0.0861 0.054 0.0753 0.0001 0.0098 0.0079 0.0001
GNDVI 0.0742 0.0877 0.0529 0.0741 0.0004 0.0175 0.0142 0.0004
SAVI 0.0572 0.0657 0.0404 0.0572 0.0 0.0124 0.01 0.0
SQSR 0.1015 0.1177 0.0726 0.1014 0.0002 0.0088 0.0067 0.0002
TSAVI 0.042 0.0502 0.0287 0.042 0.0001 0.0185 0.0139 0.0001
NDII 0.0663 0.0663 0.0561 0.0663 0.0082 0.0095 0.0004 0.0082
NDWI 0.0778 0.0778 0.0681 0.0778 0.0048 0.0048 0.0 0.0048
REEVI 0.0707 0.0839 0.0495 0.0706 0.0001 0.0181 0.0122 0.0001
RENDVI 0.0618 0.0715 0.0445 0.0617 0.0007 0.0141 0.0158 0.0007
RERVI 0.1285 0.151 0.092 0.1409 0.0003 0.0077 0.0054 0.0003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated